理学院数学系博士入学考试Word版
武汉理工考博离散数学

武汉理工大学博士入学考试《离散数学》考试大纲
一、考试要求共济
要求考生系统地掌握离散数学的基本概念、基本定理和方法,具有较强的逻辑思维和抽象思维能力,能够灵活运用所学的内容和方法解决实际问题。
考
二、考试内容济
1、数理逻辑济
1)命题和联结词,谓词与量词,合适公式,赋值,解释与指派,范式共
2) 命题形式化,等价式与对偶式,蕴含式,推理与证明
3) 证明方法3
4)数学归纳法
2、集合论院
1)集合代数,笛卡尔乘积,关系与函数,关系的性质与运算
2)等价关系,划分共济
3)偏序关系与偏序集,格辅导
3、计数336260 37
1) 排列与组合,容斥原理,鸽巢原理共
2) 离散概率正门
3) 函数的增长与递推关系院
4、图论共济网
1) 欧拉图与哈密顿图,平面图与对偶图,二部图与匹配,图的着色021-
2) 树,树的遍历,最小生成树正门
3) 最短路经,最大流量
5、形式语言与自动机院
1) 语言与文法,正则表达式与正则集
2) 有限状态自动机,自动机与正则语言
6、代数系统
1) 二元运算,群与半群,积群与商群,同态与同构
2) 群与编码
3) 格与布尔代数,环与域
三、试卷结构
1、考试时间为3小时,满分100分。
2、题目类型:计算题、简答题和证明题。
参考书
1.离散数学,胡新启,武汉大学出版社,2007年。
2.离散数学,尹宝林、何自强、许光汉、檀凤琴等,高等教育出版社,1998年。
3.离散数学及其应用,Kenneth H. Rosen,机械工业出版社,2002年。
数学博士考试科目

数学博士考试科目摘要:数学博士考试科目及备考建议一、数学博士考试科目概述1.数学基础课程2.专业课程3.英语课程4.计算机课程二、数学基础课程备考建议1.高等数学2.线性代数3.概率论与数理统计4.数学分析三、专业课程备考建议1.解析几何2.拓扑学3.微分几何4.偏微分方程四、英语课程备考建议1.词汇积累2.阅读训练3.写作练习4.口语提高五、计算机课程备考建议1.编程语言2.数据结构与算法3.计算机网络4.操作系统六、总结与建议1.制定合理的学习计划2.注重基础知识的学习和巩固3.勤做练习题,参加模拟考试4.保持良好的心态,调整作息时间正文:数学博士考试是对考生在数学领域的专业知识和研究能力的全面考察。
考试科目主要包括数学基础课程、专业课程、英语课程和计算机课程。
下面我们将分别对这些科目的备考建议进行详细阐述。
一、数学基础课程概述数学基础课程主要包括高等数学、线性代数、概率论与数理统计、数学分析等。
这些课程是数学专业的基石,对于后续专业课程的学习具有重要意义。
1.高等数学:高等数学是数学专业的基础课程之一,主要包括微积分、线性代数、概率论与数理统计等内容。
备考时要注意概念的理解、方法的掌握和运算能力的提高。
2.线性代数:线性代数主要研究向量空间、线性方程组、矩阵论等。
备考时要注重基本概念的理解,熟悉矩阵运算和线性变换。
3.概率论与数理统计:概率论与数理统计是研究随机现象和数据规律的课程。
备考时要掌握基本概率分布、假设检验、回归分析等方法。
4.数学分析:数学分析主要研究实数、复数及其函数、极限、连续性等概念。
备考时要注重理论的严密性和方法的灵活性。
二、专业课程备考建议数学博士专业课程主要包括解析几何、拓扑学、微分几何、偏微分方程等。
备考时要注重课程的内在联系,形成知识体系。
1.解析几何:研究曲线和曲面的性质,以及它们与方程的关系。
备考时要熟练掌握曲线和曲面的方程、性质及分类。
2.拓扑学:研究空间的同构、同伦、维数等概念。
博士入学数学(高等数学、数值分析)课考试大纲

博士入学数学(高等数学、数值分析)课考试大纲
高等数学部分(50分)
1. 极限与连续
数列的极限,函数及函数的极限,极限的性质及运算法则,无穷小的比较,函数的连续性。
2. 导数与微分
导数的概念,导数的基本公式,导数的四则运算及求导法则,高阶导数,微分,函数的极值。
3. 微分中值定理
微分中值定理,洛必达法则,泰勒公式。
4. 积分
原函数与不定积分,定积分的概念与性质,换元积分法,分部积分法,微积分学基本定理,定积分的应用。
5. 微分方程
微分方程的基本概念,一阶微分方程,几种可积的高阶微分方程,线性微分方程及其通解的结构,常系数齐次(非齐次)线性微分方程。
6. 多元函数微积分
多元函数,偏导数与高阶偏导数,全微分,复合函数及隐函数的求导法,多元函数的极值,二重积分。
7. 无穷级数
无穷级数的敛散性,正项级数敛散性的判别,任意项级数,绝对收敛,幂级数及幂级数的收敛半径和收敛域,函数的幂级数展开。
数值分析部分(50分)
1.非线性方程求根
简单迭代法、牛顿法、割线法及其计算效率。
2.线性代数方程组的数值解法
向量与矩阵范数,高斯列主元消去法,误差分析;雅可比迭代法、高斯—赛德尔迭代法、超松弛迭代法及其收敛性讨论。
3.插值与拟合逼近
函数的拉格朗日插值、牛顿插值、埃尔米特插值、样条插值;曲线拟合的最小二乘逼近方法;误差分析。
4.数值积分
代数精度,低阶牛顿—柯特斯求积公式及其复化,龙贝格算法;高斯积分公式;数值积分公式的稳定性。
5.常微分方程初值问题的数值解法
常用单步法和多步法及其稳定性讨论;预测—校正格式。
博士研究生入学考试《数值分析(机电院)》考试大纲

博士研究生入学考试《数值分析(机电院)》考试大纲第一部分考试形式和试卷结构一、考试方式:考试采用闭卷笔试方式,试卷满分为100分。
二、考试时间:180分钟。
三、试卷内容结构:约占 60%,主观题约占 40%。
四、试卷题型结构:试卷由三部分组成:选择/判断、填空、分析/计算。
其中:1、选择/判断题,约占20%。
测试考生对本课程基本概念、基本知识和数值计算常用算法设计与分析方法的掌握程度。
2、填空题,约占40%。
测试考生运用数值计算相关基础知识和基本方法,开展计算、简要分析以及求解实际问题的能力。
3、分析、计算题,约占40%。
测试考生综合运用数值计算理论、典型方法解决综合问题,并开展相关计算方法收敛性以及误差分析等能力。
第二部分考察的知识及范围1.误差度量与数值算法设计误差基本概念:误差来源与分类,截断误差、舍入误差、绝对误差、相对误差,有效数字以及数值稳定性。
函数计算误差分析:一元函数误差估计,四则运算误差估计。
数值算法设计原则:简化计算步骤以节省计算量(秦九韶算法)、减少有效数字损失,选择数值稳定的算法。
2.函数的插值方法以及误差估计插值问题的基本概念:插值问题的描述,插值多项式的存在和唯一性,差商、差分的概念以及性质。
拉格朗日插值:线性插值与抛物插值,n次拉格朗日插值,插值余项公式。
牛顿插值:均差的概念与性质,牛顿插值公式及其余项,差分的概念与性质。
埃尔米特插值:两点三次埃尔米特插值及其余项,n点埃尔米特插值,非标准埃尔米特插值及其余项。
分段低次插值:分段线性插值,分段三次埃尔米特插值。
三次样条插值:三次样条函数建立,三次样条插值方法。
3.函数逼近与曲线拟合正交多项式:函数内积、欧几里德范数,正交函数序列,正交多项式,勒德让多项式,切比雪夫多项式。
最佳平方逼近:最佳平方逼近问题及解法,基于正交函数、勒德让多项式、切比雪夫多项式的最佳平方逼近。
最小二乘法:最小二乘曲线拟合问题的提出和解法,最小二乘计算,最小二乘法的应用(算术平均、超定方程组)。
[金牌原创]博士生综合考试(口试)参考题.doc
![[金牌原创]博士生综合考试(口试)参考题.doc](https://img.taocdn.com/s3/m/52d75241998fcc22bdd10da5.png)
博士生综合考试(口试)参考题(2014. 12)1、基础部分分类参考题现代数学1.请你谈谈数学与其他学科发展的关系,并列举一些你的研究领域中所常用的数学方法和技巧。
2.按照数学的历史发展,它可以分为初等数学、高等数学和现代数学。
请你描述现代数学的特征。
3.矩阵理论被称为高等数学屮的算术(R. Bellman语)。
请举例说明矩阵理论的一些运用。
近代物理、光学1.简述牛顿时空观和爱因斯坦时空观之特点。
2.简述相对论中同时的相对性和运动的时钟变慢的物理意义。
3.物体运动时的质量m和静止时的质量m()有何区别。
4.说明相对论质能关系E=mc2的物理意义和E=mc2-m()c2的意义。
5.简述光电效应的物理意义。
6.在量子物理学中微观粒子具有哪二重性?7.不确定关系说明了微观粒子的什么性质。
高等化学1.碳的同素异形体有哪些?并简述碳纳米管研究的新进展。
2.阐述键价理论的基本概念?请举例说明。
3.矿物表面荷电的原因是什么?4.简述纳米材料(粒子)的待征。
5.举例说明亲水性大分子在矿物加工中的应用。
6.DLVO理论的本质是什么?举例说明DLVO理论的应用。
7.化学电源的种类有哪些?8.消除NOx和SO2带來的环境污染一直是一个热门研究课题,请简要叙述消除NOx和煤及石油加工、使用中脱硫的方法。
思想政治1.试述中国特色社会主义的一条道路和一个理论体系的内容,以及坚持这条道路和这个理论体系的重大意义。
2.试述构建社会主义和谐社会的指导思想、目标任务和原则。
3.联系当前实际,谈谈怎样增强社会主义意识形态的吸引力和凝聚力。
4.着眼改革创新,谈谈怎样在思想政治工作中注重人文关怀和心理疏导。
5.谈谈你对唯物辩证法与科学发展观的关系的看法。
2、扩充知识部分分类参考题知识经济与技术创新1.什么是技术创新扩散?2.什么是知识创新?高技术创新有哪些风险?现代信息技术3.请给岀信息的定义?信息可以计量吗?信息量与事物发生的概率有什么关系?4.请说明什么是现代信息技术?它涉及到哪些技术?5.请说明现代信息技术的核心技术是什么?知识经济与技术创新6.人类经济发展可分为哪几个阶段,各阶段发展起决定作用的关键因素是什么?7.知识经济的主要特点是什么?8.为什么说知识经济是可持续发展的经济?9.什么是高科技,知识经济的支柱产业有哪些?10.发展知识经济需要哪些必要条件?什么叫技术创新?煤炭加工利用11.试从我国能源资源结构说明煤炭在廿一世纪上半叶仍应为第一能源?12.一次能源一般有那些,我国主要的一次能源是什么,和发达国家相比,我国一次能源的结构有什么特点?13.什么叫水煤浆,使用它的优点是什么?煤炭是否是一种洁净燃料,为什么?14.在一次能源屮现称为洁净能源的有哪几种?环境学、环境生态学15.为什么说,我国的大气污染是煤烟型污染16.何谓可持续发展,在可持续发展战略中环境保护的地位和作用是什么?17.什么是清洁生产,它对环境保护工作的作用是什么?1&白色污染指的是什么,对它的控制途径主要有那些?19.为什么要保护大气臭氧层,破坏因素是什么?20.什么是环境意识?今天的主要世界环境问题有那些?21.什么是温室效应,对资源与环境保护有何不利影响?22.对三峡工程可能带来的环境影响你能说出多少?23.生态意识有那些主要观点?24.什么是绿色消费?在大学校园中倡导“绿色文化”你认为应发展的主要方面有哪些?25.煤炭开采过程中对环境产生那些影响?SK方程族的代数几何解(2014. 6.4)26.己知谱问题怎样从该谱问题得到该族方程?27.刘维尔定理在弯曲的Riemann面上是否依然成立?2&矩阵W —是否满足驻定的?W⑵29.3是全纯的吗?30.是否可以用相同的方法求解kk方程的代数几何解?生物遗迹学理论与应用研究(2014. 5.9)31.遗迹化石与实体化石的区别?32.遗迹化石的研究方法有哪些?33.遗迹化石有哪些种类?34.遗迹化石具备哪些性质?35.遗迹化石的描述方法?选煤工程设计思路与进展(2014. 4. 29)36.简述我国煤炭资源分布有何特点?37.简要说明我国选煤现状?3&简要说明我国选煤设备发展现状39.选煤厂工程设计主要有哪几个阶段?40.选煤厂车间设备布置遵循原则是什么?煤岩剪切变形及其结构演化(2014. 4. 20)41.当煤层围岩为沉积岩时,煤层为什么却发生了变质和变形作用?42.与构造岩的分类相比,构造煤的分类有什么不同?43.煤岩为有机岩,能否向无机岩转化?其转化的条件是什么?44.煤岩为什么易发生剪切变形,其剪切变形特征有哪些?45.煤岩构造变形是否影响到微-纳米结构的变化?改进的Anderson断层模式及在裂陷盆地中的应用(2014. 4. 7)46.Anderson断层模式的假设前提是什么?47.Anderson断层模式在应用屮发现存在哪些问题?48.什么是“摩尔空间” ?49.用改进的Anderson断层模式如何解释裂陷盆地复杂断裂系统的成因机制?50.改进的Anderson断层模式对经典断层模式的改进表现在哪几个方面?SVC和STATC0M应用于提髙交直流混联电网稳定性和抑制次同步振荡(2014. 3. 29)51.HVDC引起次同步振荡的可能來源主要有哪些?52.电网的静态电压稳定性和暂态电压稳定性分别指什么?53.按照传统方式两套直接并联运行的独立控制的SVC之间出现无功振荡的原因?54.SVC抑制次同步谐振是通过什么原理实现的?55.为什么电网需要动态无功电压支撑?低渗透油气储层裂缝的分布规律与预测评价方法(2014. 3. 27)56.储层裂缝有哪些成因类型?57.储层裂缝有哪些控制因素?5&拉张裂缝和扩张裂缝形成的地质条件哟哟什么差异?59.裂缝在致密低渗透储层中的作用有哪些?60.储层裂缝的预测方法有哪几类?根据气候条件设计一如何建造适合当地气候坏境的绿色建筑(2014. 3. 17)61.绿色建筑的特征是什么?62.为什么要做轻质建筑呢?63.绿色建筑为什么要大量使用钢材?64.中国政府对待绿色建筑的态度是什么?65.如何看待清华的节能楼?当代中国文化软实力构建与大学的文化担当(2013. 12.3)66.建构当代中国文化软实力的重要意义?67.如何理解文化软实力是综合国力的重要组成部分?6&如何理解道德是文化软实力的制高点?69.大学在中国文化软实力建构过程中的地位?70.大学生在当代中国文化软实力建构中的责任?中国共产党与中国梦(2013. 11. 19)71.中国梦的基本概念是什么?72.孔子的大同世界思想的内容是什么?73.陈独秀的新社会理想是什么样子的?74.中国共产党靠什么实现了救国救民的梦想?75.如何理解党中央的富民强国战略?Novel Tailings Management Technologies (2013. 11. 15)76.传统的尾矿处理方式是什么?77.使用尾矿库处理尾矿会对坏境产生哪些危害?78.新型的尾矿处理方法有哪些?79.尾矿根据其颗粒粒径的组成分为儿类?80.固结尾矿的技术有哪些?岩石力学若干进展与面临挑战(2013. 11. 13)81.我国目前试验技术的发展如何?82.我国关于岩石力学的数值分析方法有哪些?83.岩石力学发展面临的挑战有哪些?84.我国学者过去30年对岩石力学的研究情况是怎样的?85.中国岩石力学的研究现状是怎样的?注:本参考题适用于2014年12月综合考试(口试);口试时专家将根据研究牛的选题情况、所学专业等参考此有关的参考题进行提问。
理工大学博士研究生入学考试数学考试大纲

招收攻读博士学位研究生入学考试数学考试大纲解放军理工大学研究生招生办公室编理工大学招收攻读博士学位研究生入学考试数学考试大纲第一部分考试说明一、考试性质《数学》是理工大学为招收我校各学科专业博士研究生而设置的数学水平考试,由我校自行命题,它的评价标准是高等学校优秀硕士毕业生应达到的基本数学水准,以保证录取者具有基本的数学素养和数学能力。
二、学科范围考试分必考与选考两部分,必考部分为下列两门课程的内容:1.微积分与常微分方程2.线性代数选考部分为下列课程之一:3.概率论与数理统计4.随机过程5. 数值分析6.数学物理方法7.泛函分析8. 大气科学中的数学物理问题(报考大气科学必选)三、考核重点重点考察考生对数学基本知识、基本理论及基本方法的把握,同时考查考生的数学思维能力和分析问题、解决问题的能力,对纯理论证明不作要求。
第二部分考试形式与试卷结构一、答卷方式闭卷、笔试二、答卷时间180分钟三、试卷结构试卷题型分为选择题、填空题、解答题。
满分100分,各学科分值比例如下:1.微积分与常微分方程,20分2.线性代数,20分3.概率论与数理统计,随机过程,数值分析,数学物理方法,泛函分析,大气科学中的数学物理问题(报考大气科学必选)(任选一门),每门60分第三部分考试范围一、微积分与常微分方程1.函数与极限:映射与函数;数列的极限;函数的极限;无穷小与无穷大;极限运算法则;极限存在准则;两个重要极限;无穷小的比较;函数的连续性与间断点;连续函数的运算与初等函数的连续性;闭区间上连续函数的性质;一致连续性2.一元函数微分学:导数概念;函数的求导法则;高阶导数;隐函数及由参数方程所确定的函数的导数;相关变化率;函数的微分;罗尔定理;拉格朗日中值定理;洛必达法则;函数的单调性与曲线的凹凸性;函数的极值与最大值最小值3.一元函数积分学:不定积分的概念与性质;定积分的概念与性质;换元积分法;分部积分法;有理函数的积分;微积分基本公式;反常积分;反常积分的审敛法;定积分在几何学上的应用4.多元函数微分学:多元函数的基本概念;偏导数;全微分的定义;多元复合函数的求导法则;隐函数的求导公式;多元函数微分学的几何应用;方向导数与梯度;多元函数的极值及其求法5.多元函数积分学:二重积分的概念与性质;二重积分的计算法;三重积分;重积分的几何应用;对弧长的曲线积分;对坐标的曲线积分;格林公式及其应用;对面积的曲面积分;对坐标的曲面积分;高斯公式;斯托克斯公式6.无穷级数:常数项级数的概念;收敛级数的基本性质;正项级数及其审敛法;交错级数及其审敛法;绝对收敛与条件收敛;绝对收敛级数的性质;幂级数;函数展开成幂级数;函数项级数的一致收敛性及一致收敛级数的基本性质;傅里叶级数;周期为2l的周期函数的傅里叶级数7.常微分方程:微分方程的基本概念;可分离变量的微分方程;齐次方程和可化为齐次的方程;一阶线性微分方程;伯努利方程;可降阶的高阶微分方程;线性微分方程解的结构;常系数齐次线性微分方程;常系数非齐次线性微分方程;欧拉方程二、线性代数1.行列式:二阶与三阶行列式;全排列及其逆序数;n阶行列式的定义;对换;行列式的性质;行列式按行(列)展开;克拉默法则2.矩阵及其运算:矩阵;矩阵的运算;逆矩阵;矩阵分块法3.矩阵的初等变换与线性方程组:矩阵的初等变换;矩阵的秩;线性方程组的解4.向量组的线性相关性:向量组及其线性组合;向量组的线性相关性;向量组的秩;线性方程组的解的结构;向量空间5.相似矩阵及二次型:向量的内积、长度及正交性;方阵的特征值与特征向量;相似矩阵;对称矩阵的对角化;二次型及其标准形;用配方法化二次型成标准形;正定二次型6.线性空间与线性变换:线性空间的定义与性质;维数、基与坐标;基变换与坐标变换;线性变换;线性变换的矩阵表示式三、概率论与数理统计1.概率论的基本概念:随机试验;样本空间、随机事件;频率与概率;等可能概型;条件概率;独立性2.随机变量及其分布:随机变量;离散型随机变量及其分布律;随机变量的分布函数;连续型随机变量及其概率密度;随机变量的函数的分布;二维随机变量;边缘分布;相互独立的随机变量;两个随机变量的函数的分布3.随机变量的数字特征:数学期望;方差;协方差及相关系数;矩、协方差矩阵4.大数定律及中心极限定理:大数定律;中心极限定理5.数理统计的基本概念:随机样本;抽样分布6.参数估计与假设检验:点估计;估计量的评选标准;区间估计;正态总体均值与方差的区间估计;(0-1)分布参数的区间估计;单侧置信区间;7.假设检验:假设检验;正态总体均值的假设检验;正态总体方差的假设检验;置信区间与假设检验之间的关系四、随机过程1.预备知识:概率空间;特征函数、母函数;n维正态分布;条件期望2.随机过程的概念与基本类型:随机过程的基本概念;随机过程的分布律和数字特征;几种重要的随机过程3.泊松过程:泊松过程的定义和例子;泊松过程的基本性质;非齐次泊松过程;复合泊松过程4.马尔可夫链:马尔可夫链的概念及转移概率;马尔可夫链的状态分p n的渐近性质与平稳分布类;状态空间的分解;()ij5.连续时间的马尔可夫链:连续时间的马尔可夫链;柯尔莫哥洛夫微分方程;生灭过程。
中科院武汉物理与数学研究所博士生入学考试
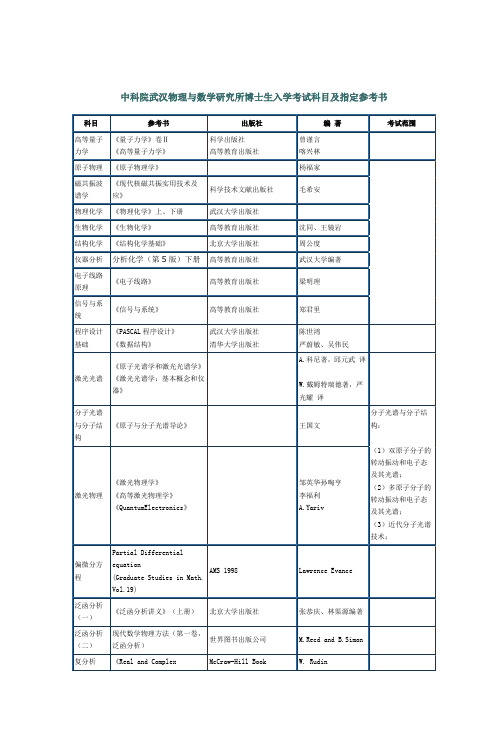
北京大学出版社
张恭庆、林渠源编著
泛函分析(二)
现代数学物理方法(第一卷,泛函分析)
世界图书出版公司
M.Recd and B.Simon
复分析
《Real and Complex Analysis》
McCraw-Hill Book Company,1987(有中译本)
W. Rudin
实分析与概率论
《Real and Complex Analysis》
《概率论教程》
McCraw-Hill Book Company,1987(有中译本);
上海科技出版社,(1989年第一版)
W. Rudin
钟开莱著刘文、吴让泉译
量子概率
量子随机分析引论
K.P.Parthasarathy, Birkhauser Verlag, 1992
算子代数
Banach代数在算子理论中的应用(第二版)
R.G.Douglas, Springer-Verlag, 1998.
天然药物化学
《天然药物化学》
人民卫生出版社
姚新生
统计物理
《热力学与统计物理学》
高等教育出版社2003
马本昆,高尚惠,孙煜
统计物理学部分(热力学不考)
量子化学
《量子化学》
科学出版社
《固体物理学》
上海科学技术出版社2003
Springer-Verlag, 1995
人民教育出版社1979
陆栋,蒋平,徐至中编著
Harald Ibach, Hans Luth.
黄昆著
陈世鸿
严蔚敏、吴伟民
激光光谱
《原子光谱学和激光光谱学》
《激光光谱学:基本概念和仪器》
XX大学攻读博士学位研究生入学考试《离散数学》

XX 大学攻读博士学位研究生入学考试《离散数学》样题一、填空题(共20分,每小题2分)1. 已知集合A是由6个元素组成的集合,那么集合A上可以产生个不同的划分。
2. 已知集合A={Ф,{Ф}},则A的幂集ρ(A) = 。
3. 已知集合A={a,b,c,d },A上的二元关系R={<a,a>,<a,c>,<b,d>,<d,a>},则R-1 =_______ __。
4.设f(x)=2-x,g(x)=2x2+1,那么复合函数:f g x=_____ __。
()()5. 已知命题公式(p↑q)→(r↓T),则它的对偶式为。
6. 设F(x): x是人,H(x,y):x与y一样高,则命题“不是所有的人都一样高”的符号化形式为。
7.设A={3,6,9},集合A上的二元运算◎定义为:a◎b = min{a,b},则集合A 上◎运算的零元是__ __。
8.整数集Z中的运算*定义如下:a*b=a+b+3ab,设a有逆元,则其逆元a-1为__ __。
9.无向图G的结点数n和边数m相等,2度和3度结点各2个,其余结点均为悬挂点,则G的边数m=__ __。
10.设T是各边带权均为a的带权图G=<n,m>的一棵最小生成树,则其树权W(T)= _ __。
二、计算与证明题(共80分)1.求下面公式的主析取范式和主合取范式:(10分)(p→(q∧r))∧(~p→(~q∧~r))2.设T是无向树,它有40个1度结点,20个2度结点,31个3度结点,且没有6度或6度以上结点,问T中有多少个4度结点,多少个5度结点?说明理由。
(10分)3.把2n个人分成n组,每组2人,求不同的分法数。
(5分)4.求1~500之间能被3,5,7中任一数整除的整数个数。
(5分)5.如图所示为邮递员负责的街区图(长度单位为百米),邮局位于V1处,试设计一条邮递员的最短投递路线。
(5分)6.已知函数f : X →Y ,g :Y →X ,且复合关系g ︒f 为X 上的恒等函数。
[考研类试卷]2009年攻读理学博士学位研究生入学考试(数值分析)真题试卷.doc
![[考研类试卷]2009年攻读理学博士学位研究生入学考试(数值分析)真题试卷.doc](https://img.taocdn.com/s3/m/8bf1fd72eefdc8d377ee321e.png)
[考研类试卷]2009年攻读理学博士学位研究生入学考试(数值分析)真题试卷1 设n次代数方程x n+a1x n-1+a2x n-2+…+a n-1x+a n=0有n个实根,其最大实根为x*.任取x0,用Newton迭代法可得迭代序列{x k}k=0∞证明:如果x0>x*,则有2 给定线性方程组Ax=b,其中1)写出Gauss-Seidel迭代格式.2)设A是按行严格对角占有矩阵,即A满足|a ij|<|a ii|,i=1,2,…n,证明:Gauss-Seidel迭代法收敛.3 求a和b,使得|x4-(a+bx)|取最小值,并求该最小值.4 给定积分I(f)=∫a b f(x)sinnxdx,其中n为较大的正整数.取正整数M,将区间[a,b]作M等分,并记x i=a+ih,i=0,1,…,M.1)利用函数值f(x0),f(x1),…,f(x M)作f(x)的分段一次插值多项式S(x),给出S(x)的表达式;2)利用S(x)构造计算I(f)的数值求积公式I N(f)=∫a b S(x)sinnxdx,并写成的形式,给出A i的表达式;3)设f(x)∈C2[a,b],试估计截断误差I(f)-I N(f).5 考虑常微分方程初值问题取正整数n,记h=(b-a)/n,x i=a+ih,0≤i≤n.试分析下列求解公式的局部截断误差,并指出其阶数.6 设两点边值问题(A)具有光滑解u(x),取正整数M,并记h=1/M.将区间[0,1]作步长为h的网格剖分.试对问题(A)建立一个4阶精度的差分格式.1)给出差分格式截断误差的表达式;2)证明差分格式的收敛性;3)给出求解差分格式的思路.7 设二阶抛物方程初边值问题(B)有光滑解u(x,t),其中a(x,t)>0.取正整数M和N,并记h=1/M,τ=T/N,x i=ih,0≤i≤M,t k=kτ,0≤k≤N.对(B)建立一个无条件稳定且是收敛的差分格式.1)给出差分格式截断误差的表达式;2)分析差分格式的解对右端函数和初值的稳定性;3)证明差分格式的收敛性.。
大连理工大学博士生入学考试

七、大连理工大学博士生入学考试(rù xué kǎo shì)用课程参考书、考试(kǎoshì)大纲一览1.矩阵(jǔ zhèn)分析(101) (6)2.计算方法(102) (6)3.数理方程(fāngchéng)(103) (7)4.数理统计(shù lǐ tǒnɡ jì)(104) (8)5.优化方法(105) (8)6.数值代数(106) (9)7.现代数值分析(107) (9)8.凸分析(108) (9)9.优化算法(109) (10)10.上图分析与计算(110) (11)11.近世代数(111) (11)12.泛函分析(112) (12)13.高等代数(113) (12)14.随机过程与规划(114) (13)15.高等微积分(115) (13)16.数值逼近(116) (14)17.高等组合学(117) (15)18.微分几何(118) (16)19.应用光学(201) (16)20.傅立叶光学导论(202) (17)21.光纤传感理论(203) (18)22.激光物理、原子与分子光谱(204) (19)23.光的量子理论(205) (19)-1-24.近场光学与纳米技术(206) (20)25.固体物理(二)(207) (20)26.高等(gāoděng)量子力学(208) (21)27.固体量子(liàngzǐ)理论(209) (21)28.等离子体(děnglízǐtǐ)实验与诊断(210) (22)29.等离子体(děnglízǐtǐ)物理(211) (22)30.计算(jì suàn)物理(212) (22)31.广义相对论(213) (23)32.半导体器件物理(214) (23)33.半导体理论(215) (24)34.弹性力学与有限元(301) (24)35.有限元分析方法(302) (26)36.实验应力分析(303) (26)37.结构力学(含动力学)(304) (27)38.复合材料力学(305) (27)39.数学规划(306) (28)40.金属切削原理(401) (28)41.金属工艺学(402) (29)42.机制工艺(含特种加工)(403) (30)43.机械制造工艺学(404) (30)44.现代控制工程(405) (31)45.计算机图形学(406) (31)46.数控技术(407) (32)47.微机原理与应用(408) (32)48.数理综合基础(409) (33)49.机械设计(410) (33)50.液压系统动力学(411) (34)51.机械动力学(412) (34)52.时间序列分析(413) (35)53.CAD/CAM及CIMS(414) (36)-2-54.可靠性设计(415) (36)55.机械制造技术基础(416) (37)56.传感器原理(yuánlǐ)(417) (37)57.半导体物理(wùlǐ)(418) (38)58.测试(cèshì)技术(419) (38)59.机器人机构(jīgòu)学(420) (39)60.电子显微学(501) (39)61.材料(cáiliào)强度学(502) (40)62.材料热力学(503) (40)63.金属凝固原理(504) (41)64.材料表面与界面(505) (42)65.高等建筑材料(506) (42)66.弹性力学及有限元(601) (43)67.水电站建筑物及机组振动(602) (43)68.钢筋混凝土结构(603) (45)69.高等土力学(604) (46)70.土动力学(605) (46)71.环境水力学(606) (47)72.工程模糊数学(607) (48)73.水资源系统分析(608) (48)74.结构动力学(609) (49)75.计算流体力学(610) (49)76.水文水资源系统模糊集分析(611) (50)77.暖通空调热质交换与系统过程分析(612) (51)78.桥梁设计理论(613) (52)79.水电系统决策方法论(614) (53)80.岩石力学(615) (54)81.化工容器及设备的设计与分析方法(701) (55)82.金属有机化学(703) (57)83.等离子体化学(704) (57)-3-84.量子化学(705) (58)85.化工热力学(706) (59)86.现代(xiàndài)环境工程(707) (60)87.高等(gāoděng)无机化学(708) (61)88.高等(gāoděng)有机合成(709) (61)89.化工(huàgōng)数学(710) (62)90.煤化学(huàxué)及煤化学工程(711) (63)91.化学反应工程(712) (64)92.高等有机化学(713) (66)93.两相流与传热、传质(714) (66)94.腐蚀工程原理(715) (67)95.化工系统工程(716) (67)96.遗传工程原理(717) (68)97.基因工程原理与技术(718) (69)98.生物化学(719) (69)99.生化工程原理(720) (70)100.染料化学(721) (70)101.表面活性剂(722) (71)102.分子光谱学(723) (72)103.化工传递过程(724) (72)104.催化化学(725) (73)105.物理有机化学(726) (74)106.生物有机化学(727) (75)107.细胞工程(728) (75)108.理论电化学(729) (76)109.船舶设计理论与计算机实现方法(801) (76)110.船舶高等流体力学(802) (77)111.船舶高等结构力学(803) (78)112.随机过程(901) (78)113.数字信号处理(902) (79)-4-114.图像处理与模式识别(903) (79)115.人工智能原理(904) (80)116.算法设计(shèjì)与分析(905) (80)117.形式语言(906) (80)118.数据库系统(907) (81)119.高等(gāoděng)传热学(1001) (82)120.高等(gāoděng)工程热力学(1002) (83)121.振动(zhèndòng)学(1003) (84)122.流体力学(liú tǐ lì xué)(1004) (85)123.系统工程(1101) (85)124.运筹学(1102) (86)125.专家系统(1103) (86)126.软件工程(1104) (87)127.经济学(1105) (87)128.管理信息与决策支持系统(1106) (87)129.线性代数(1107) (87)130.概率与统计(1108) (88)131.离散数学(1109) (88)132.模糊数学(1110) (88)133.技术经济学(1111) (88)134.财务管理学(1113) (89)135.产业组织学(1114) (89)136.环境经济学(1115) (89)137.环境管理学(1116) (89)138.项目管理(1117) (89)139.信息系统分析与设计(1118) (90)140.市场营销学(1119) (90)141.科学学基础(1202) (90)142.技术论原理(1203) (91)143.静电物理(1301) (91)-5-144.高压电器(1302) (92)145.电网络理论(1303) (92)矩阵(jǔ zhèn)分析(101)课程(kèchéng)考试大纲一、适用(shìyòng)报考的专业:理、工科(gōngkē)各专业二、题目(tímù)类型:概念题20~25%;证明题15~20%;计算题60~70%三、参考教材:1.《矩阵理论基础》姜家辉编著大工出版社(主要参考)2.《矩阵理论基础习题解答》陈桂芝大工研教材3.《矩阵分析》杨克绍等著哈工大出版4.《矩阵分析》王朝闻等著北工出版四、基本内容及要求:1.熟练掌握矩阵的基础知识,包括矩阵的基本概念、基本运算;了解线性空间、内积空间及线性变换等概念。
数学博士考试科目

数学博士考试科目摘要:一、数学博士考试科目概述二、数学博士考试的主要科目三、数学博士考试科目对考生的要求四、备考数学博士考试的建议正文:一、数学博士考试科目概述数学博士考试是选拔具有一定数学研究能力和创新精神的高级人才的重要环节。
数学博士考试科目旨在全面考察考生的数学基础知识、理论素养和应用能力,为国家培养高素质的数学人才。
二、数学博士考试的主要科目数学博士考试主要包括以下几个科目:1.数学分析:主要考察考生对实分析、复分析、泛函分析等方面的基本概念、原理和方法的理解和运用能力。
2.高等代数:主要考察考生对线性代数、抽象代数、同调代数等方面的基本概念、定理和方法的理解和运用能力。
3.数学建模:主要考察考生运用数学方法和技术解决实际问题的能力,包括微分方程建模、概率论与数理统计、最优化方法等方面的内容。
4.偏微分方程:主要考察考生对偏微分方程的基本概念、定理和解法等方面的理解和运用能力。
5.实变函数论:主要考察考生对实变函数的基本概念、性质和方法的理解和运用能力。
三、数学博士考试科目对考生的要求数学博士考试科目对考生的要求较高,需要考生具备扎实的数学基础知识和较强的逻辑思维能力。
此外,考生还需要具备良好的数学素养,如创新意识、独立思考能力和团队协作精神等。
四、备考数学博士考试的建议1.系统学习:考生需要系统学习各个科目的基本概念、原理和方法,形成完整的数学知识体系。
2.勤做习题:通过大量的练习,提高自己的解题能力和技巧,培养解题思路和方法。
3.查漏补缺:针对自己的薄弱环节进行有针对性的学习和训练,提高自己的整体水平。
4.模拟考试:参加模拟考试,熟悉考试环境和要求,提高应试能力。
博士研究生入学考试《概率论与数理统计》考试大纲.doc

博士研究生入学考试《概率论与数理统计》考试大纲第一部分考试说明一、考试性质全国博士研究生入学考试是为高等学校招收博士研究生而设置的。
其中概率论与数理统计是为管理学科各类考生设置的专业基础课程考试科目,属招生学校自行命题性质。
它的评价标准是高等学校优秀硕士研究生能达到的及格或及格以上水平,以保证被录取者具有坚实的概率论与数理统计基本理论知识和较好的分析实际概率论与数理统计问题的能力,有利于招生学校在专业上录取。
考试对象为参加2010年全国博士研究生入学考试的应届硕士毕业生或具有同等学历的在职人员。
二、考式的学科范围应考范围包括:随机事件及其概率、随机变量及其分布、随机变量的数字特征、样本及抽样分布、参数估计、假设检验和线性回归分析等七部分。
具体考查要点详见本纲第二部分。
三、评价目标概率论与数理统计考试的目标在于考查考生对概率论与数理统计的基本概念、基本理论和方法的掌握以及分析和求解较为复杂的概率论与数理统计问题的能力。
考生应能:1.正确理解概率论中的基本概念和基本理论。
2.掌握求解概率论中较为复杂的实际问题的方法。
3.掌握数理统计中的基本原理和方法及计算公式,并能正确地解释计算结果。
4.正确应用数理统计的基本理论知识分析和解决较为复杂的实际问题。
四、考试形式与试卷结构答卷方式:闭卷,笔试;试卷中的所有题目全部为必答题;答题时间:180分钟;试卷分数:满分为100分;试卷结构及考查比例:试卷主要分为三部分,即:基本理论和方法题40%,分析与应用题60%。
第二部分考查要点1 随机事件及其概率随机事件的概念,事件间的关系及运算。
概率的定义及性质,古典概型,几何概型。
条件概率,乘法公式,全概率公式,逆概率公式。
事件的相互独立性,独立重复试验。
2 随机变量及其分布随机变量及其分布的概念,离散型随机变量及其分布律的定义和性质,连续型随机变量及其概率密度的定义和性质,分布函数的定义和性质,常用的随机变量的分布及其在工程与管理中的应用,随机变量的函数及其分布律; 二维随机变量及其分布.3 随机变量的数字特征随机变量的期望与方差的定义和性质,随机变量及其函数的期望与方差的计算,几种常用分布的期望与方差。
数学系直博考试题及答案

数学系直博考试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项是函数f(x) = x^2 + 3x + 2的根?A. -1B. -2C. 1D. 2答案:B2. 计算极限lim(x→0) (sin(x)/x)的值。
A. 0B. 1C. -1D. 不存在答案:B3. 判断以下哪个序列是发散的。
A. 1/nB. n/n^2C. n^2/n^3D. 1/n^2答案:A4. 给定矩阵A = [[1, 2], [3, 4]],求矩阵A的行列式。
A. -2B. 2C. -5D. 5答案:B二、填空题(每题5分,共20分)5. 计算定积分∫(0 to 1) x^2 dx的结果为______。
答案:1/36. 函数f(x) = e^x的导数为______。
答案:e^x7. 给定复数z = 3 + 4i,其共轭复数为______。
答案:3 - 4i8. 计算二项式(1 + x)^n的展开式中x^2的系数,当n=4时,系数为______。
答案:6三、解答题(每题15分,共40分)9. 证明:对于任意实数x,不等式x^2 + 2x + 2 ≥ 2成立。
证明:要证明x^2 + 2x + 2 ≥ 2,只需证明x^2 + 2x ≥ 0。
观察到x^2 + 2x = x(x + 2),由于x和x + 2同号或至少有一个为0,所以它们的乘积非负,即x^2 + 2x ≥ 0。
因此,x^2 + 2x + 2 ≥ 2成立。
10. 求解微分方程dy/dx = 2x,且y(0) = 1。
解:对两边积分,得到∫dy = ∫2x dx,即y = x^2 + C。
根据初始条件y(0) = 1,代入得1 = 0^2 + C,解得C = 1。
因此,微分方程的解为y = x^2 + 1。
数学所博士资格考试

数学所博士资格考试是评估候选人在数学领域深度研究能力和学术素养的重要考试。
该考试旨在选拔具备独立思考、创新能力和扎实数学基础的优秀人才,为他们提供进一步深造和从事高水平科研工作的机会。
数学所博士资格考试要求候选人具备扎实的数学基础,包括对高等数学、线性代数、概率论与数理统计等基础课程的全面掌握。
只有在这些基础知识的基础上,候选人才能更好地理解和应用数学知识。
此外,数学所博士资格考试还注重候选人的研究能力和学术素养。
候选人需要具备独立思考和解决问题的能力,能够独立完成研究工作并发表高质量的学术论文。
同时,候选人还需要具备良好的学术道德和科研诚信,遵守学术规范和职业道德。
在考试过程中,候选人需要展示自己的研究能力和学术素养。
他们需要提交一份研究计划书,介绍自己的研究方向和目标,以及拟采取的研究方法和步骤。
同时,候选人还需要参加面试,与评委进行交流和讨论,展示自己的研究能力和学术素养。
总之,数学所博士资格考试是评估候选人在数学领域深度研究能力和学术素养的重要考试。
候选人需要具备扎实的数学基础、独立思考和解决问题的能力、良好的学术道德和科研诚信等素质。
通过考试
后,候选人将有机会进一步深造和从事高水平科研工作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理学院数学系博士入学考试
——导师考核及专家小组考核大纲
一、导师考核部分
导师考核内容自定,可以采用笔试或面试方式,满分100分。
二、专家小组考核部分
数学系专家小组考核采用笔试、面试相结合的考试方式。
面试考试部分满分为50分,全面考评考生的基本专业知识掌握、基本原理掌握及分析问题和解决问题的能力。
主要考评考生的表达能力、逻辑思维能力、外语能力,以及所从事的工作或研究经历等内容。
笔试考试满分为50分,考试大纲如下:
(一)考试要求
1.在以下6个科目中选择二个科目(专业基础与专业综合不能选同名的科目),每科25分,共50分:
泛函分析、抽象代数、现代数值分析、概率论、常微分方程、偏微分方程。
2.各科目要求:要求考生全面系统地掌握所选科目的基本知识,具备较强的分析问题与解决问题的能力。
(二)考试内容
1.泛函分析:
1) 度量空间、赋(准)范线性空间、内积空间的基本定义,基本定理,基本性质及这些空间的具体例子;凸集与Minkowski泛函的定义及基本性质。
2) 算子和泛函的线性性、有界性、连续性的定义、关系、基本性质;Riesz定理及应用。
3) 纲,开映像定理与闭图像定理及推论(含Banach逆算子定理等),共鸣定理及应用。
4) 线性泛函的延拓定理及其几何形式。
5) 共轭空间(含例子)与共轭算子,以及二次共轭空间与空间的自反性,弱收敛及弱* 收敛,弱列紧性及弱*列紧性。
6) 线性算子的譜的定义和例;紧算子的定义和基本性质。
2.抽象代数:
1) 群论:在掌握群、子群、正规子群、商群等概念和有关性质及群同态基本定理的基础上,要求应试者进一步了解与掌握:作用在集上的群;p群•Sylow子群;可解群与Jordan-Holder定理;有限生成Abel群的结构。
2) 环论:在掌握环、子环、理想、商环等概念和有关性质及环同态基本定理的基础上,要求应试者进一步了解与掌握:交换环中的素理想、极大理想的基本性质,交换环中的可逆元,幂等元,零因子等的基本性质;交换环的大根与小根;有关交换环的局部化理论;链条件;分式理想与类群。
3) 模论:模与模同态;Hom与⊗;直积与直和;自由模、投射模、入射模;正合列与交换图;一些特殊环上的模。
4) 域论:单纯扩张与有限扩张;分裂域,正规扩张;可离扩张;有限域;有限扩张的单纯性。
5) Galois 理论:Galois群;域与群的结对关系;多项式的Galois群。
3.现代数值分析:
1) 数值逼近:多项式插值、样条插值、有理插值;正交多项式的性质及构造方法;最佳一致逼近、最佳平方逼近、曲线拟合的最小二乘法。
2) 数值积分与微分:高斯型求积公式的一般理论;奇异积分与振荡函数积分数值计算;数值微分公式的构造方法。
3) 线性代数方程组数值解法:直接解法;矩阵的条件数与扰动方程组的误差界估计;迭代解法的方法构造及收敛性判定;共轭梯度法。
4) 非线性方程组数值解法:牛顿法及其变形方法、拟牛顿法。
5) 常微分方程数值解法:初值问题数值解法(单步法的收敛性与稳定性、线性多步法);边值问题数值解法(打靶法、差分法)。
4.概率论:
1) 集类与单调类定理,测度与概率,测度的扩张定理及测度的完备化,独立事件类。
2) 随机变量与可测函数,分布函数,独立随机变量,随机变量序列的收敛性。
3) 积分的定义和性质,收敛定理,数学期望,不定积分与σ-可加集函数的分解。
4) 有限维乘积测度,Fubini定理。
5) 条件概率与条件数学期望,正则条件概率。
5.常微分方程:
1) 常微分方程的基本理论:线性稳定性理论, Liapunov 稳定性的基本理论,Poincare-Bendixson 定理及应用。
2) 中心流形理论和规范型方法:关于常微分方程的中心流形定理,向量场的规范型。
3) 常微分方程的局部分支:不动点分支,Hopf分支。
能够用中心流形理论和规范型方法结合常微分方程的基本理论讨论某些常微分方程的动力学性质。
6.偏微分方程:
1) 线性椭圆型偏微分方程的2L理论。
主要包括: Lax-Milgram定理, 散度型线性椭圆型偏微分方程的弱解, Fredholm二择一定理, 弱解的极值原理和弱解的正则性。
2) 线性椭圆型偏微分方程古典解的Schauder理论。
主要包括: Holder空间, 磨光核, 位势方程解的2,
C 估计, Schauder估计, 古典解的极值原理和Dirichlet问题的可解性。
3) 线性椭圆型偏微分方程的p L理论。
主要包括: Sobolev空间, Marcinkiewicz内插定理, Calderon-Zygmund 分解, 位势方程解的p L估计, 强解的2,p
W估计和强解的存在性。
4) De Giorgi-Nash估计。
主要包括: 弱解的局部性质, 内部Holder连续性, 全局Holder连续性。
(三)试卷结构
1.考试时间180分钟,满分50分。
2.各科目试题结构:每个科目出5个题目,每个题目5分,其中有些考查基本概念、基本理论的掌握情况,有些考查基本理论的应用和理论推导的能力。
(四)参考书目
1.“泛函分析”科目:
张恭庆等,《泛函分析》上册,北京大学出版社
2.“抽象代数”科目:
1)T. W. Hungerford,《Algebra》,Springer-Verbag
2)张海权、游宏,《抽象代数》,东北师大出版社
3.“现代数值分析”科目:
李庆扬、关治、白峰杉,《数值计算原理》,清华大学出版社,2000
4.“概率论”科目:
严士健等,《概率论基础》,科学出版社
5.“常微分方程”科目:
1)S. Wingins,《Intr oduction to Applied Nonlinear Dynamics and Chaos》, Springer-Verlag, New
York, 1990.
2)张芷芬、李承治、郑志明、李伟固,《向量场的分岔理论基础》,高等教育出版社,1997. 6.“偏微分方程”科目:
陈亚浙、吴兰成,《二阶椭圆型方程和椭圆型方程组》,科学出版社
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
