高三数学二轮复习独立性
新高考数学复习考点知识讲解11---列联表与独立性检验
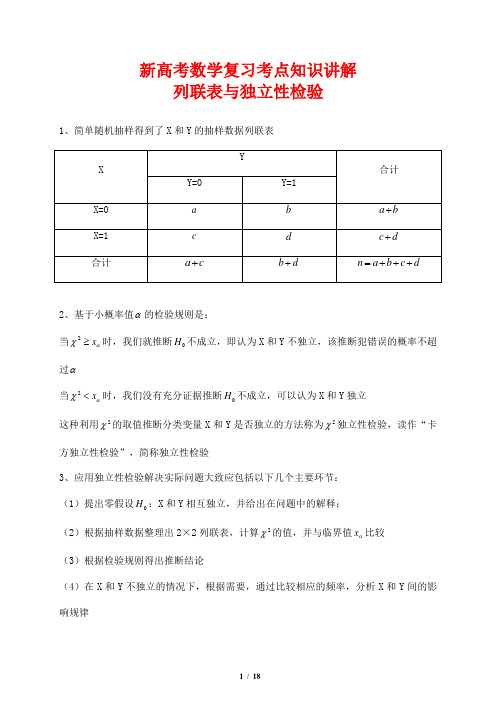
新高考数学复习考点知识讲解列联表与独立性检验1、简单随机抽样得到了X 和Y 的抽样数据列联表2、基于小概率值α的检验规则是:当αχx ≥2时,我们就推断0H 不成立,即认为X 和Y 不独立,该推断犯错误的概率不超过α当αχx <2时,我们没有充分证据推断0H 不成立,可以认为X 和Y 独立这种利用2χ的取值推断分类变量X 和Y 是否独立的方法称为2χ独立性检验,读作“卡方独立性检验”,简称独立性检验3、应用独立性检验解决实际问题大致应包括以下几个主要环节: (1)提出零假设0H :X 和Y 相互独立,并给出在问题中的解释; (2)根据抽样数据整理出2×2列联表,计算2χ的值,并与临界值αx 比较 (3)根据检验规则得出推断结论(4)在X 和Y 不独立的情况下,根据需要,通过比较相应的频率,分析X 和Y 间的影响规律题型一 变量关系例 1 为了判断两个分类变量X 、Y 是否有关系,应用独立性检验的方法算得2K 的观测值为5,则下列说法中正确的是( ) A .有95%的把握认为“X 和Y 有关系” B .有95%的把握认为“X 和Y 没有关系” C .有99%的把握认为“X 和Y 有关系” D .有99%的把握认为“X 和Y 没有关系” 【答案】A 【分析】利用2K 的观测值与临界值进行比较得解. 【详解】因为2( 3.841)0.050P K =≥,5 3.841>,所以有95%的把握认为“X 和Y 有关系”. 故选:A若由一个22⨯列联表中的数据计算得2 4.013K =,那么有( )把握认为两个变量有关系.知识典例巩固练习()20P K k ≥ 0.500.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.0010k0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828A .95%B .97.5%C .99%D .99.9%【答案】A 【分析】由2 3.841K >可对照临界值表得到结果. 【详解】2 4.013 3.841K =>,∴有()10.05100%95%-⨯=的把握认为两个变量有关系. 故选:A.题型二 列联表例 2 如表是一个2×2列联表:则表中a ,b 的值分别为( )y 1 y 2 合计x 1 a21 73x 2 22 25 47合计 b 46 120A .94,72B .52,50C .52,74D .74,52【答案】C 【分析】根据表中数据简单计算即可. 【详解】a =73-21=52,b =a +22=52+22=74. 故选:C.下面是一个22⨯列联表:1y 2y总计 1x35 a 70 2x15 1530 总计 50b100其中,a b 处填的值分别为_______. 【答案】35,50. 【分析】由列联表易得结果. 【详解】由3570a +=,得35a =,15a b +=,得50b =.巩固练习故答案为:35,50.题型三 独立性检验应用例 3 2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类智慧的胜利,也有许多人持反对意见,有网友为此在某大学进行了调查,参加调查的共80位学生,调查数据的22⨯列联表如下所示: 持反对意见 赟同 总计男40 女 5总计2580(1)①请将列联表补充完整;②请根据表中数据判断,能否有的99.9%把握认为是否持反对意见与性别有关; (2)若表中持反对意见的5个女学生中,3个是大三学生,2个是大四学生.现从这5个学生中随机选2个学生进行进一步调查,求这2个学生是同一年级的概率.附参考公式及数据:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.()20P K k ≥ 0.40 0.25 0.10 0.010 0.005 0.001 0k7.879 1.3232.7066.6357.87910.828【答案】(1)①列联表见解析,②有99.9%的把握认为是否持反对意见与性别有关;(2)25.【分析】()1①由已知数据得出列联表;②由题可知,计算2K 的观测值013.09110.828k ≈>,可得出结论;()2记3个大三学生分别为,123,,,2A A A 个大四学生分别为12,B B 、运用列举法列出所有事件,由古典概率公式可得答案. 【详解】()1①②由题可知,2K 的观测值2080203552013.09110.828404055(25)k ⨯-⨯=≈>⨯⨯⨯所以有99.9%的把握认为是否持反对意见与性别有关.()2记3个大三学生分别为,123,,,2A A A 个大四学生分别为12,B B 、则从中抽取2个的基本事件有:1213231213112223212,,,,,,,,,A A A A A A AB A B A B A B A B A B B B ,共10个,其中抽取的2人是同一年级的基本事件有12132312,,,A A A A A A B B 共4个, 则这2个学生是同一年级的概率为42105P ==.这一年来人类与新型冠状病毒的“战争”让人们逐渐明白一个道理,人类社会组织模式的差异只是小事情,病毒在地球上存在了三四十亿年,而人类的文明史不过只有几千年而已,人类无法消灭病毒,只能与之共存,或者病毒自然消亡,在病毒面前,个体自由要服从于集体或者群体生命的价值.在传染病学中,通常把从致病刺激物侵入机体内或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期,因此我们应该注意做好良好的防护措施和隔离措施.某研究团队统计了某地区10000名患者的相关信息,得到如表表格: 潜伏期(天)(]0,2(]2,4(]4,6(]6,8(]8,10 (]10,12 (]12,14人数6001900300025001600250150(1)新冠肺炎的潜伏期受诸多因素的影响,为研究潜伏期与年龄的关系,通过分层抽样从10000名患者中抽取200人进行研究,完成下面的2×2列联表,并判断能否在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关?潜伏期8≤天潜伏期8>天总计 60岁以上(含60岁)150 60岁以下 30 总计200(2)依据上述数据,将频率作为概率,且每名患者的潜伏期是否超过8天相互独立.为了深入研究,该团队在这一地区抽取了20名患者,其中潜伏期不超过8天的人数最有巩固练习可能是多少?附:()()()()()22n ad bcKa b c d a c b d-=++++.【答案】(1)表格见解析,能;(2)16名.【分析】(1)由表中数据可知,求得潜伏期大于8天的人数,列出2×2列联表,利用公式求得2K的值,结合附表,即可得到结论;(2)求得该地区10000名患者中潜伏期不超过8天的人数,求得潜伏期不超过8天的概率,进而抽取的20名患者中潜伏期不超过8天的人数.【详解】(1)由表中数据可知,潜伏期大于8天的人数为16002501502004010000++⨯=人,补充完整的2×2列联表如下,所以()2220013*********.66710.8281505016040K ⨯⨯-⨯=≈>⨯⨯⨯, 故能在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关.(2)该地区10000名患者中潜伏期不超过8天的人数为6001900300025008000+++=名,将频率视为概率,潜伏期不超过8天的概率为80004100005=, 所以抽取的20名患者中潜伏期不超过8天的人数最有可能是420165⨯=名.1、为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算得x 2=7.01,则认为“喜欢乡村音乐与性别有关系”的把握约为( )A .0.1%B .1%C .99%D .99.9%【答案】C 【分析】由x 2=7.01>6.635,对照临界值表求解即可.巩固提升【详解】易知x2=7.01>6.635,对照临界值表知,有99%的把握认为喜欢乡村音乐与性别有关系.故选:C2、某班主任对全班50名学生进行了作业量的评价调查,所得数据如表所示:则认为作业量的大小与学生的性别有关的犯错误的概率不超过()A.0.01 B.0.05C.0.10 D.无充分证据【答案】B【分析】计算2K,再进行判断.【详解】因为2250(181598)5.059 3.84127232624K⨯⨯-⨯=≈>⨯⨯⨯,又()2 3.8410.05P K≥=所以认为作业量的大小与学生的性别有关的犯错误的概率不超过0.05. 故选:B3、(多选)有关独立性检验的四个命题,其中正确的是()A.两个变量的2×2列联表中,对角线上数据的乘积相差越大,说明两个变量有关系成立的可能性就越大B.对分类变量X与Y的随机变量2K的观测值k来说,k越小,“X与Y有关系”的可信程度越小C.从独立性检验可知:有95%的把握认为秃顶与患心脏病有关,我们说某人秃顶,那么他有95%的可能患有心脏病D.从独立性检验可知:有99%的把握认为吸烟与患肺癌有关,是指在犯错误的概率不超过1%的前提下认为吸烟与患肺癌有关【答案】ABD【分析】根据独立性检验的原理与知识,对选项中的命题判断正误即可.【详解】选项A,两个变量的2×2列联表中,对角线上数据的乘积相差越大,则2K观测值越大,两个变量有关系的可能性越大,所以选项A正确;选项B,根据2K的观测值k越小,原假设“X与Y没关系”成立的可能性越大,则“X与Y有关系”的可信度越小,所以选项B正确;选项C,从独立性检验可知:有95%的把握认为秃顶与患心脏病有关,不表示某人秃顶他有95%的可能患有心脏病,所以选项C不正确;选项D,从独立性检验可知:有99%的把握认为吸烟与患肺癌有关,是指在犯错误的概率不超过1%的前提下认为吸烟与患肺癌有关,是独立性检验的解释,所以选项D正确.故选:ABD.4、为了判断某高中学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:已知P (x 2≥3.841)≈0.05,P (x 2≥6.635)≈0.01.根据表中数据,得到x 2=250(1320107)23272030⨯⨯-⨯⨯⨯⨯≈4.844,则认为选修文科与性别有关系出错的概率约为________.【答案】0.05 【分析】直接根据表中数据计算的x 2值与P (x 2≥3.841)≈0.05比较判断,即得结果. 【详解】因为x 2≈4.844>3.841,而P (x 2≥3.841)≈0.05,故认为选修文科与性别有关系出错的概率约为0.05. 故答案为:0.05.5、调查者通过询问72名男、女大学生在购买食品时是否看营养说明得到的数据如下表所示:大学生的性别和是否看营养说明之间___(填“有”或“没有”)关系.【答案】有【分析】由表中的数据直接计算卡方,从而可得结论【详解】解:因为22722820168)=8.4167.879 44283636χ⨯⨯-⨯≈>⨯⨯⨯(,所以有的把握认为大学生性别与购买食品时是否看营养说明之间有关,故答案为:有6、某高校《统计》课程的教师随机调查了选该课的一些学生情况,具体数据如下表: 为了判断主修统计专业是否与性别有关系,根据表中的数据,得到k=2 50(1320-107) 23272030⨯⨯⨯⨯⨯⨯=4.844>3.841,所以有_____的把握判定主修统计专业与性别有关系.附:【答案】95%【分析】根据独立性检验的基本思想,因为2K的观测值k=4.844>3.841,参考临界值表即可得出【详解】根据表格数据得2K的观测值k=250(1320-107)23272030⨯⨯⨯⨯⨯⨯≈4.844 3.841>,所以有95%的把握判定主修统计专业与性别有关系.故答案为:95%.7、某学生对其30名亲属的饮食习惯进行了一次调查,依据统计所得数据可得到如下的22⨯列联表:根据以上列联表中的数据,可得2K 的观测值k =__________,__________(填“有”或“没有”)99%的把握认为其亲属的饮食习惯与年龄有关.参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.参考数据:【答案】10 有 【分析】根据列联表,求得a b c d ,,,的值,利用公式,求得2K 的值,结合附表,即可得到结论. 【详解】由列联表可得20a =,10b =,12c =,4d =,可得2230(8128)10 6.63512182010K ⨯-==>⨯⨯⨯, 所以有99%的把握认为其亲属的饮食习惯与年龄有关. 故答案为:10;有.8、2017年3月27日,一则“清华大学要求从2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.游泳作为一项重要的求生技能和运动项目受到很多人的喜爱.其实,已有不少高校将游泳列为必修内容.某中学为了解2018届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为35.(1)请将上述列联表补充完整;(2)判断是否有99.9%的把握认为喜欢游泳与性别有关.附:x2=2()()()()()n ad bca b c d a c b d-++++【答案】(1)表格见解析;(2)有. 【分析】(1)根据概率补全列联表即可;(2)计算2x,再进行判断即可.【详解】(1)因为在100人中随机抽取1人抽到喜欢游泳的学生的概率为3 5所以喜欢游泳的学生人数为3 100605⨯=.其中女生有20人,男生有40人,列联表补充如下:(2)因为22100(40302010)16.6710.82860405050x⨯⨯-⨯=≈>⨯⨯⨯所以有99.9%的把握认为喜欢游泳与性别有关.9、某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,得出以下22⨯列联表:如果随机抽查该班的一名学生,那么抽到积极参加班级工作的学生的概率是12 25.(1)求a,b,c,d的值.(2)试运用独立性检验的思想方法分析:能否有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系?并说明理由.参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.参考数据:【答案】(1)6a =,19b =,24c =,26d =;(2)有. 【分析】(1)由抽到积极参加班级工作的学生的概率是1225,可求出c 的值,然后根据表中的数据可求出,,a b d 的值;(2)直接利用22()()()()()n ad bc K a b c d a c b d -=++++公式求解,然后根临界值表判断即可【详解】解:(1)积极参加班级工作的学生有c 人,总人数为50, 由抽到积极参加班级工作的学生的概率1125025c P ==, 解得24c =,所以6a =.所以2525619b a =-=-=,50502426d c =-=-=.(2)由列联表知,2250(181967)11.53825252426K ⨯⨯-⨯=≈⨯⨯⨯, 由11.53810.828>,可得有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系.。
2019_2020学年高中数学第2章概率2.3.2事件的独立性讲义苏教版

2.3.2 事件的独立性1.事件的独立性的概念(1)概念:若事件A ,B 满足P (A |B )=P (A ),则称事件A ,B 独立. (2)含义:P (A |B )=P (A )说明事件B 的发生不影响事件A 发生的概率. 2.相互独立事件的概率计算如果任何事件与必然事件独立,与不可能事件也独立,那么 (1)两个事件A ,B 相互独立的充要条件是P (AB )=P (A )P (B ).(2)若事件A 1,A 2,…,A n 相互独立,那么这n 个事件同时发生的概率P (A 1A 2…A n )=P (A 1)P (A 2)…P (A n ).3.相互独立事件的性质如果事件A 与B 相互独立,那么A 与B ,A 与B ,A 与B 也相互独立. 思考1:不可能事件与任何一个事件相互独立吗?[提示] 相互独立.不可能事件的发生与任何一个事件没有影响. 思考2:必然事件与任何一个事件相互独立吗?[提示] 相互独立.必然事件的发生与任何一个事件的发生没有影响. 思考3:如果事件A 与事件B 相互独立,则P (B |A )=P (B )正确吗? [提示] 正确.如果事件A 与事件B 相互独立,则P (B |A )=P (B ).1.袋内有3个白球和2个黑球,从中有放回地摸球,用A 表示“第一次摸得白球”,如果“第二次摸得白球”记为B ,那么事件A 与B ,A 与B 间的关系是( )A .A 与B ,A 与B 均相互独立 B .A 与B 相互独立,A 与B 互斥C .A 与B ,A 与B 均互斥D .A 与B 互斥,A 与B 相互独立A [因为是有放回地摸球,所以事件A 的发生不会影响事件B 的发生,所以A 与B ,A 与B 均相互独立.]2.甲、乙两人投球命中率分别为12,23,则甲、乙两人各投一次,恰好命中一次的概率为________.12[事件“甲投球一次命中”记为A ,“乙投球一次命中”记为B ,“甲、乙两人各投一次恰好命中一次”记为事件C ,则C =A B ∪A B 且A B 与A B 互斥,P (C )=P (A B ∪A B )=P (A )P (B )+P (A )P (B )=12×13+12×23=36=12.]3.甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8,0.6,0.5,则三人都达标的概率是________,三人中至少有一人达标的概率是________.0.24 0.96 [三人都达标的概率为0.8×0.6×0.5=0.24.三人都不达标的概率为(1-0.8)×(1-0.6)×(1-0.5)=0.2×0.4×0.5=0.04. 三人中至少有一人达标的概率为1-0.04=0.96.]【例1】 (1)甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,“从甲组中选出1名男生”与“从乙组中选出1名女生”;(2)容器内盛有5个白乒乓球和3个黄乒乓球,“从8个球中任意取出1个,取出的是白球”与“从剩下的7个球中任意取出1个,取出的还是白球”;(3)掷一颗骰子一次,“出现偶数点”与“出现3点或6点”.[思路探究] (1)利用独立性概念的直观解释进行判断.(2)计算“从8个球中任取一球是白球”发生与否,事件“从剩下的7个球中任意取出一球还是白球”的概率是否相同进行判断.(3)利用事件的独立性定义进行判断.[解] (1)“从甲组中选出1名男生”这一事件是否发生,对“从乙组中选出1名女生”这一事件发生的概率没有影响,所以它们是相互独立事件.(2)“从8个球中任意取出1个,取出的是白球”的概率为58,若这一事件发生了,则“从剩下的7个球中任意取出1个,取出的仍是白球”的概率为47;若前一事件没有发生,则后一事件发生的概率为57,可见,前一事件是否发生,对后一事件发生的概率有影响,所以二者不是相互独立事件.(3)记A :出现偶数点,B :出现3点或6点,则A ={2,4,6},B ={3,6},AB ={6}, ∴P (A )=36=12,P (B )=26=13,P (AB )=16.∴P (AB )=P (A )·P (B ),∴事件A 与B 相互独立.判断事件是否相互独立的方法(1)定义法:事件A ,B 相互独立⇔P (AB )=P (A )·P (B ). (2)由事件本身的性质直接判定两个事件发生是否相互影响. (3)条件概率法:当P (A )>0时,可用P (B |A )=P (B )判断.1.同时掷两颗质地均匀的骰子,令A ={第一颗骰子出现奇数点},令B ={第二颗骰子出现偶数点},判断事件A 与B 是否相互独立.[解] A ={第一颗骰子出现1,3,5点},B ={第二颗骰子出现2,4,6点}.∴P (A )=12,P (B )=12,P (AB )=3×336=14,∴P (AB )=P (A )P (B ), ∴事件A ,B 相互独立.【例2】三个独立的研究机构在一定的时期内能研制出疫苗的概率分别是15,14,13.求:(1)他们都研制出疫苗的概率; (2)他们都失败的概率; (3)他们能够研制出疫苗的概率.[思路探究] 明确已知事件的概率及其关系→ 把待求事件的概率表示成已知事件的概率→ 选择公式计算求值[解] 令事件A ,B ,C 分别表示A ,B ,C 三个独立的研究机构在一定时期内成功研制出该疫苗,依题意可知,事件A ,B ,C 相互独立,且P (A )=15,P (B )=14,P (C )=13.(1)他们都研制出疫苗,即事件ABC 同时发生,故P (ABC )=P (A )P (B )P (C )=15×14×13=160.(2)他们都失败即事件A B C 同时发生. 故P (A B C )=P (A )P (B )P (C ) =(1-P (A ))(1-P (B ))(1-P (C ))=⎝ ⎛⎭⎪⎫1-15⎝ ⎛⎭⎪⎫1-14⎝ ⎛⎭⎪⎫1-13 =45×34×23=25. (3)“他们能研制出疫苗”的对立事件为“他们都失败”,结合对立事件间的概率关系可得所求事件的概率P =1-P (A B C )=1-25=35.1.求相互独立事件同时发生的概率的步骤 (1)首先确定各事件之间是相互独立的; (2)确定这些事件可以同时发生; (3)求出每个事件的概率,再求积.2.使用相互独立事件同时发生的概率计算公式时,要掌握公式的适用条件,即各个事件是相互独立的,而且它们能同时发生.2.一个袋子中有3个白球,2个红球,每次从中任取2个球,取出后再放回,求: (1)第1次取出的2个球都是白球,第2次取出的2个球都是红球的概率;(2)第1次取出的2个球1个是白球、1个是红球,第2次取出的2个球都是白球的概率. [解] 记“第1次取出的2个球都是白球”的事件为A ,“第2次取出的2个球都是红球”的事件为B ,“第1次取出的2个球中1个是白球、1个是红球”的事件为C ,很明显,由于每次取出后再放回,A ,B ,C 都是相互独立事件.(1)P (AB )=P (A )P (B )=C 23C 25×C 22C 25=310×110=3100.故第1次取出的2个球都是白球,第2次取出的2个球都是红球的概率是3100.(2)P (CA )=P (C )P (A )=C 13·C 12C 25·C 23C 25=610·310=950.故第1次取出的2个球中1个是白球、1个是红球,第2次取出的2个球都是白球的概率是950.[1.甲、乙二人各进行一次射击比赛,记A =“甲击中目标”,B =“乙击中目标”,试问事件A 与B 是相互独立事件,还是互斥事件?事件A B 与A B 呢?[提示] 事件A 与B ,A 与B ,A 与B 均是相互独立事件,而A B 与A B 是互斥事件. 2.在探究1中,若甲、乙二人击中目标的概率均是0.6,如何求甲、乙二人恰有一人击中目标的概率?[提示] “甲、乙二人恰有1人击中目标”记为事件C ,则C =A B +A B . 所以P (C )=P (A B +A B )=P (A B )+P (A B ) =P (A )·P (B )+P (A )·P (B )=(1-0.6)×0.6+0.6×(1-0.6)=0.48.3.由探究1、2,你能归纳出相互独立事件与互斥事件的区别吗? [提示] 相互独立事件与互斥事件的区别对C 各一盘.已知甲胜A 、乙胜B 、丙胜C 的概率分别为0.6,0.5,0.5.假设各盘比赛结果相互独立.求:(1)红队中有且只有一名队员获胜的概率; (2)求红队至少两名队员获胜的概率.[思路探究] 弄清事件“红队有且只有一名队员获胜”与事件“红队至少两名队员获胜”是由哪些基本事件组成的,及这些事件间的关系,然后选择相应概率公式求值.[解] 设甲胜A 的事件为D ,乙胜B 的事件为E ,丙胜C 的事件为F , 则D ,E ,F 分别表示甲不胜A 、乙不胜B 、丙不胜C 的事件. 因为P (D )=0.6,P (E )=0.5,P (F )=0.5,由对立事件的概率公式知P (D )=0.4,P (E )=0.5,P (F )=0.5.(1)红队有且只有一名队员获胜的事件有D E F ,D E F ,D -E -F ,以上3个事件彼此互斥且独立.所以红队有且只有一名队员获胜的概率为P 1=P (D E -F -+D E F +D -E -F )=P (DE -F -)+P (D E F )+P (D -E -F )=0.6×0.5×0.5+0.4×0.5×0.5+0.4×0.5×0.5=0.35.(2)法一:红队至少两人获胜的事件有:DE F ,D E F ,D EF ,DEF . 由于以上四个事件两两互斥且各盘比赛的结果相互独立, 因此红队至少两人获胜的概率为P =P (DE F )+P (D E F )+P (D EF )+P (DEF )=0.6×0.5×0.5+0.6×0.5×0.5+0.4×0.5×0.5+0.6×0.5×0.5=0.55.法二:“红队至少两人获胜”与“红队最多一人获胜”为对立事件,而红队都不获胜为事件D E F ,且P (D E F )=0.4×0.5×0.5=0.1.∴红队至少两人获胜的概率为P 2=1-P 1-P (D E F )=1-0.35-0.1=0.55.1.本题(2)中用到直接法和间接法.当遇到“至少”“至多”问题可以考虑间接法. 2.求复杂事件的概率一般可分三步进行:(1)列出题中涉及的各个事件,并用适当的符号表示它们;(2)理清各事件之间的关系,恰当地用事件间的“并”“交”表示所求事件; (3)根据事件之间的关系准确地运用概率公式进行计算.3.某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100米跑(互不影响)的成绩在13 s 内(称为合格)的概率分别为25,34,13,若对这三名短跑运动员的100米跑的成绩进行一次检测,则求:(1)三人都合格的概率; (2)三人都不合格的概率; (3)出现几人合格的概率最大.[解] 记甲、乙、丙三人100米跑成绩合格分别为事件A ,B ,C ,显然事件A ,B ,C 相互独立,则P (A )=25,P (B )=34,P (C )=13.设恰有k 人合格的概率为P k (k =0,1,2,3). (1)三人都合格的概率:P 3=(ABC )=P (A )·P (B )·P (C )=25×34×13=110.(2)三人都不合格的概率:P 0=(A B C )=P (A )·P (B )·P (C )=35×14×23=110.(3)恰有两人合格的概率:P 2=P (AB C )+P (A B C )+P (A BC )=25×34×23+25×14×13+35×34×13=2360. 恰有一人合格的概率:P 1=1-P 0-P 2-P 3=1-110-2360-110=2560=512.综合(1)(2)可知P 1最大.所以出现恰有一人合格的概率最大.1.本节课的重点是事件的相互独立性及其概率的求法,难点是事件相互独立性的判断. 2.要掌握事件相互独立性的两个问题. (1)事件相互独立性的判断. (2)事件相互独立性概率的求法. 3.求复杂事件概率的步骤:(1)列出题中涉及的各种事件,并用适当的符号表示;(2)理清事件之间的关系(两事件是互斥、对立,还是相互独立),列出关系式; (3)根据事件之间的关系准确选取概率公式进行计算;(4)当直接计算符合条件的事件的概率较复杂时,可先间接地计算对立事件的概率,再求出符合条件的事件的概率.1.判断(正确的打“√”,错误的打“×”)(1)对事件A 和B ,若P (B |A )=P (B ),则事件A 与B 相互独立;( ) (2)若事件A ,B 相互独立,则P (A ∩B )=P (A )·P (B );( ) (3)如果事件A 与事件B 相互独立,则P (B |A )=P (B );( ) (4)若事件A 与B 相互独立,则B 与B 相互独立.( )[解析] 若P (B |A )=P (B ),则P (A ∩B )=P (A )·P (B ),故A ,B 相互独立,所以(1)正确;若事件A ,B 相互独立,则A ,B 也相互独立,故(2)正确;若事件A ,B 相互独立,则A 发生与否不影响B 的发生,故(3)正确;(4)B 与B 相互对立,不是相互独立,故(4)错误.[答案] (1)√ (2)√ (3)√ (4)×2.抛掷3枚质地均匀的硬币,A ={既有正面向上又有反面向上},B ={至多有一个反面向上},则A 与B 的关系是( )A .互斥事件B .对立事件C .相互独立事件D .不相互独立事件C [由已知,有P (A )=1-28=34,P (B )=1-48=12,P (A ∩B )=38,满足P (A ∩B )=P (A )·P (B ),则事件A 与事件B 相互独立,故选C.]3.加工某一零件需经过三道工序,设第一、二、三道工序的次品率分别为170,169,168,且各道工序互不影响,则加工出来的零件的次品率为________.370 [加工出来的零件的正品率是⎝ ⎛⎭⎪⎫1-170×⎝ ⎛⎭⎪⎫1-169×⎝ ⎛⎭⎪⎫1-168=6770,因此加工出来的零件的次品率为1-6770=370.]4.某班甲、乙、丙三名同学竞选班委,甲当选的概率为45,乙当选的概率为35,丙当选的概率为710.(1)求恰有一名同学当选的概率; (2)求至多有两人当选的概率.[解] 设甲、乙、丙当选的事件分别为A ,B ,C ,则有P (A )=45,P (B )=35,P (C )=710.(1)因为事件A ,B ,C 相互独立,所以恰有一名同学当选的概率为P (AB -C -)+P (A -BC -)+P (A -B-C )=P (A )·P (B )·P (C )+P (A )·P (B )·P (C )+P (A )·P (B )·P (C ) =45×25×310+15×35×310+15×25×710=47250. (2)至多有两人当选的概率为1-P (ABC )=1-P (A )·P (B )·P (C )=1-45×35×710=83125.。
高考数学复习考点知识讲解课件57 事件的相互独立性、条件概率与全概率公式

件 B:甲和乙选择的景点不同,则条件概率 P(B|A)=( D )
A.176
B.78
C.37
D.67
பைடு நூலகம்
[解析] 由题意知,事件 A:甲和乙至少一人选择庐山,共有 n(A)=C12·C13+1=7 种 情况,事件 AB:甲和乙选择的景点不同,且至少一人选择庐山,共有 n(AB)=C12·C13=6 种情况,P(B|A)=nnAAB=67.故选 D.
2
— 19 —
(新教材) 高三总复习•数学
— 返回 —
条件概率的 2 种求法 (1)利用定义,分别求 P(A)和 P(AB),得 P(B|A)=PPAAB,这是求条件概率的通法. (2)借助古典概型概率公式,先求事件 A 包含的基本事件数 n(A),再求事件 A 与事件 B 的交事件中包含的基本事件数 n(AB),得 P(B|A)=nnAAB.
满 2 局或 3 局,且在 11 分制比赛中,每局甲获胜的概率为23,乙获胜的概率为13;在“FAST5”
模式,每局比赛双方获胜的概率都为12,每局比赛结果相互独立.
(1)求 4 局比赛决出胜负的概率;
(2)设在 24 分钟内,甲、乙比赛了 3 局,比赛结束时,甲乙总共进行 5 局的概率.
— 13 —
— 4—
(新教材) 高三总复习•数学
— 返回 —
2.条件概率 (1)概念:一般地,设
A,B
为两个随机事件,且
P(A)>0,我们称
P(B|A)=PPAAB
为
在事件 A 发生的条件下,事件 B 发生的条件概率,简称条件概率.
(2)两个公式
nAB
①利用古典概型,P(B|A)= nA .
②概率的乘法公式:P(AB)= P(A)P(B|A) .
高考数学复习考点知识与题型专题讲解18--- 回归分析、独立性检验(解析版)

高考数学复习考点知识与题型专题讲解专题18 回归分析、独立性检验1.有关独立性检验的问题,解题思路如下:(1)利用频率估计概率;(2)根据题意,求得2K的值,对照临界值得结果.2.对于非线性回归方程及其应用,考查将非线性回归问题转化为线性回归问题求解,在解题的过程中,要注重回归方程的公式的正确计算,注意所给数据的正确应用.2倍.1 / 31(1)求表中a,b的值,并补全表中所缺数据;(2)运用独立性检验思想,判断是否有99.5%的把握认为中学生使用手机对学习有影响?参考数据:()()()()()22n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.【试题来源】三省三校“3 3 3”2021届高考备考诊断性联考卷(二)【答案】(1)28,14,ab=⎧⎨=⎩,表格答案见解析;(2)有99.5%的把握认为中学生使用手机对学习有影响.【分析】(1)由题意可得122680,2a ba b+++=⎧⎨=⎩从而可求出,a b的值,进而可填出列联表;(2)直接利用公式()()()()()22n ad bcKa b c d a c b d-=++++求解,然后根据临界值表得结论【解析】(1)由己知得122680,2a ba b+++=⎧⎨=⎩解得28,14,ab=⎧⎨=⎩补全表中所缺数据如下:(2)根据题意计算观测值为()2280282614129.8257.87942384040K⨯⨯-⨯=≈>⨯⨯⨯,所以有99.5%的把握认为中学生使用手机对学习有影响.2.某校高二生物研究性学习小组的同学们为了研究当地某种昆虫的产卵数与温度的变化关系,他们收集了一只该种昆虫在温度Cx︒时相对应产卵数个数为y的8组数据,为了对数据进行分析,他们绘制了如下散点图:(1)根据散点图,甲、乙两位同学分别用y bx a=+和z dx c=+(其中lnz y=)两种模型进行回归分析,试判断这两位同学得到的回归方程中,哪一个的相关指数2R更接近1;(给出判断即可,不必说明理由)(2)根据(1)的结论选定上述两个模型中更适宜作为对昆虫产卵数与温度变化关系进行回归分析的模型,并利用下表中数据,计算该模型的回归方程:(方程3 / 31表示为()y f x =的形式,数据计算结果保留两位小数)(3)据测算,若只此种昆虫的产卵数超过4e ,则会发生虫害.研究性学习小组的同学通过查阅气象资料得知近期当地温度维持在25C ︒左右,试利用(2)中的回归方程预测近期当地是否会发生虫害. 附:对于一组数据()()()1122,,,,,,n n u v u v u v ,其回归直线v u βα=+的斜率和截距的最小二乘估计分别为1221ˆˆˆ,nl i i ni i u v nuvv u unu βαβ==-==--∑∑. 【试题来源】甘肃省兰州市2020-2021学年高三下学期诊断试题【答案】(1)乙同学模型的相关指数2R 更接近1;(2)应选择z dx c =+做为回归方程,0.22 2.22x y e -=;(3)近期当地不会发生虫害.【分析】(1)通过观察图象即可得出结论;(2)根据(1)的结论,应选择z dx c =+做为回归方程,利用最小二乘法即可求解,求出,d c 即可. (3)当25x =时,求出估计值,即可判断得出结论.【解析】(1)乙同学模型的相关指数2R 更接近1.(2)根据(1)的结论,应选择z dx c =+做为回归方程,根据公式,812221757826 3.30.22, 3.30.2226 2.425722826i i i nii x z nxzd c z dx xnx =-=--⨯⨯==≈=-≈-⨯=--⨯-∑∑, 0.22 2.42z x ∴=-,5 / 31故y 关于x 的回归方程为0.22 2.22x y e -=.(3)当25x =时,0.22 2.22 3.084x y e e e -==<,因此近期当地不会发生虫害. 3.人均可支配收入是反映一个地区居民收入水平和城市经济发展水平的重要指标,并且对人均消费水平有重大影响,下图是根据国家统计局发布的《2020年上半年居民收入和消费支出情况》绘制的,是我国31个省(区、市)2020年上半年人均可支配收入x (单位:元)与人均消费支出y (单位:元)的散点图.(1)由散点图可以看出,可以用线性回归模型ˆˆybx a =+拟合人均消费支出y 与人均可支配收入x 的关系,请用相关系数加以说明; (2)建立y 关于x 的线性回归方程(精确到0.01);(3)根据(2)的结论,规定半年人均盈余(人均可支配收入-人均消费支出)不低于4620元的省(区、市)达到阶段小康的标准,则估计达到阶段小康标准的省(区、市)的半年人均可支配收入至少为多少元? 参考数据:参考公式:相关系数()()niix x y y r --=∑,回归方程ˆˆˆybx a =+中斜率和截距的最小二乘估计公式分别为()()()121ˆniii nii x x y y bx x ==--=-∑∑,ˆˆay bx =-. 【试题来源】2021年新高考测评卷数学(第二模拟)【答案】(1)答案见解析;(2)ˆ0.482192y x =+;(3)13100元.【分析】(1)将已知数据代入相关系数的求解公式即可得解;(2)根据题中数据及参考公式求得ˆb ,ˆa ,即可建立y 关于x 的线性回归方程;(3)由题意知半年人均盈余为ˆx y-,得到不等式ˆ4620x y -≥,解不等式即可. 【解析】(1)由题意知()()316839000000.983800018400iix x yy r --==≈⨯∑,因为y 与x 的相关系数近似为0.98,接近1,所以y 关于x 的线性相关程度非常高,因此可以用线性回归模型拟合y 与x 的关系.(2)()()()3113121683900000ˆ0.481412000000ii i ii xx y y bxx ==--==≈-∑∑,ˆˆ96320.48155002192ay bx =-≈-⨯=,所以ˆ0.482192y x =+. (3)半年人均盈余为ˆ0.4821920.522192x yx x x -=--=-, 令0.5221924620x -≥,得13100x ≥,故估计达到阶段小康标准的省(区、市)的半年人均可支配收入至少为131007 / 31元.4.近年来,明代著名医药学家李时珍故乡黄冈市蕲春县大力发展大健康产业,蕲艾产业化种植已经成为该县脱贫攻坚的主要产业之一,已知蕲艾的株高y (单位:cm)与一定范围内的温度x (单位:℃)有关,现收集了蕲艾的13组观测数据,得到如下的散点图:现根据散点图利用y a =+dy c x=+建立y 关于x 的回归方程,令s =1t =得到如下数据:213t131i =∑21.22且(i s ,i y )与(i t ,i y )(i =1,2,3,…,13)的相关系数分别为1r ,2r ,且2r =﹣0.9953.(1)用相关系数说明哪种模型建立y 与x 的回归方程更合适; (2)根据(1)的结果及表中数据,建立y 关于x 的回归方程;(3)已知蕲艾的利润z 与x 、y 的关系为1202z y x =-,当x 为何值时,z 的预报值最大.参考数据和公式:0.21×21.22=4.4562,11.67×21.22=247.6374=15.7365,对于一组数据(i u ,i v )(i =1,2,3,…,n ),其回归直线方程v uαβ=+的斜率和截距的最小二乘法估计分别为1221ni i i nii u vnu v unuβ==-⋅=-∑∑,v u αβ=-,相关系数ni i u vnu vr -⋅∑.【试题来源】湖北省八市2021届高三下学期3月联考 【答案】(1)用d y c x =+模型建立y 与x 的回归方程更合适;(2)10ˆ111.54yx=-;(3)当温度为20时这种草药的利润最大.【分析】(1)利用相关系数1r ,2r ,比较1||r 与2||r 的大小,得出用模型dy c x=+建立回归方程更合适;(2)根据(1)的结论求出y 关于x 的回归方程即可;(3)由题意写出利润函数ˆz,利用基本不等式求得利润z 的最大值以及对应的x 值.【解析】(1)由题意知20.9953r =-,10.8858r ====,因为121r r <<,所有用dy c x=+模型建立y 与x 的回归方程更合适. (2)因为1311322113 2.1ˆ100.2113i ii ii t y t ydtt ==-⋅-===--∑∑, ˆˆ109.94100.16111.54cy dt =-=+⨯=,9 / 31所以ˆy关于x 的回归方程为10ˆ111.54y x=- (3)由题意知11012020(111.54ˆˆ)22zy x x x =-=--20012230.8()2x x =-+ 2230.8202210.8≤-=,所以22.8ˆ10z≤,当且仅当20x 时等号成立,所以当温度为20时这种草药的利润最大.5.已知某班有50位学生,现对该班关于“举办辩论赛”的态度进行调查,,他们综合评价成绩的频数分布以及对“举办辩论赛”的赞成人数如下表:(1)请根据以上统计数据填写下面2×2列联表,并回答:是否有95%的把握认为“综合评价成绩以80分位分界点”对“举办辩论赛”的态度有差异?(2)若采用分层抽样在综合评价成绩在[60,70),[70,80)的学生中随机抽取10人进行追踪调查,并选其中3人担任辩论赛主持人,求担任主持人的3人中至少有1人在[60,70)的概率.参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.参考数据:【试题来源】山东省聊城市第一中学2021届高三一模检测题(一)【答案】(1)表格见解析,不能;(2)2930.【分析】(1)由已知完成列联表,结合公式计算2K 根据参考数据即可判断结果;(2)由分层抽样得在[)60,70里面抽6个,[)70,80里面抽4个,再用对立事件求解概率即可. 【解析】(1)做个皮尔逊卡方检验的话,有()2250286412 3.125 3.84132184010K ⨯⨯-⨯==<⨯⨯⨯故此不能推翻零假设,不能认定成绩和态度有关.(2)这样分层抽样,会在[)60,70里面抽6个,[)70,80里面抽4个,11 / 31设A 为没有人在[60,70)内的事件,则概率即为()1P P A =-3431029130C C =-=.6.某疫苗进行安全性临床试验.该疫苗安全性的一个重要指标是注射疫苗后人体血液中的高铁血红蛋白(MetHb )的含量(以下简称为“M 含量”)不超过1%,则为阴性,认为受试者没有出现血症.若一批受试者的M 含量平均数不超过0.65%,出现血症的被测试者的比例不超过5%,同时满足这两个条件则认为该疫苗在M 含量指标上是“安全的”;否则为“不安全”.现有男、女志愿者各200名接受了该疫苗注射.经数据整理,制得频率分布直方图如图.(注:在频率分布直方图中,同一组数据用该区间的中点值作代表.)(1)请说明该疫苗在M 含量指标上的安全性;(2)按照性别分层抽样,随机抽取50名志愿者进行M 含量的检测,其中女性志愿者被检测出阳性的恰好1人.请利用样本估计总体的思想,完成这400名志愿者的22⨯列联表,并判断是否有超过95%的把握认为,注射该疫苗后,高铁血红蛋白血症与性别有关?附:()()()()()22n ad bcKa b c d a c b d-=++++.【试题来源】江西省九所重点中学(玉山一中、临川一中等)2021届高三3月联合考试【答案】(1)该疫苗在M含量指标上是“安全的”;(2)表格见解析,没有. 【分析】(1)求出区间(]1.0,1.2上的频率,以及平均数即可得结论;(2)根据题意写出列联表,计算2K的值,并与3.841比较即可得出结论. 【解析】(1)由频率分布直方图得M含量数据落在区间(]1.0,1.2上的频率为0.150.20.03⨯=,故出现血症的比例为3%5%<,由直方图得平均数为0.30.20.50.30.70.30.90.17 1.10.030.606x=⨯+⨯+⨯+⨯+⨯=即志愿者的M含量的平均数为0.606%0.65%<综上,该疫苗在M含量指标上是“安全的”.(2)依题意得,抽取的50名志愿者中女性志愿者应为25人由已知,25名女性志愿者被检测出阳性恰有1人,故女性中阳性的频率0.04 所以全部女性志愿者阳性共有2000.048⨯=人由(1)知400名志愿者中,阳性的频率为0.03,所以阳性的人数共有4000.0312⨯=人因此男性志愿者被检测出阳性的人数是1284-=人.所以完成表格如下:由22⨯列联表可()22400419281961.375 3.84120020012388K⨯⨯-⨯=≈<⨯⨯⨯,由参考表格,可得,故没有超过95%的把握认为注射疫苗后,高铁血红蛋白血症与性别有关.7.某种机械设备随着使用年限的增加,它的使用功能逐渐减退,使用价值逐年减少,通常把它使用价值逐年减少的“量”换算成费用,称之为“失效费”.某种机械设备的使用年限x(单位:年)与失效费y(单位:万元)的统计数据如下表所示:(1)由上表数据可知,可用线性回归模型拟合y与x的关系.请用相关系数加以说明;(精确到0.01)(2)求出y关于x的线性回归方程,并估算该种机械设备使用10年的失效费.13 / 31参考公式:相关系数()()niix x y y r --=∑.线性回归方程ˆˆˆybx a =+中斜率和截距最小二乘估计计算公式:()()()121ˆniii ni i x x y y bx x ==--=-∑∑,ˆˆay bx =-. 参考数据:()71()14.00i i i x x y y =--=∑,()7217.08i iy y =-=∑14.10≈.【试题来源】四川省成都市2021届高三第二次诊断性检测【答案】(1)答案见解析;(2)ˆ0.5 2.3yx =+,7.3万元. 【分析】(1)根据统计数据求x 、y 、()721i i x x =-∑,结合参考数据及相关系数公式,求相关系数r ,进而判断y 与x 的相关程度;(2)利用最小二乘法公式估计ˆb 、ˆa ,写出线性回归方程,进而将10x =代入估算求值.【解析】(1)由题意,知123456747x ++++++==,2.903.30 3.604.40 4.805.20 5.904.307y ++++++==,()()()()()()()()72222222211424344454647428i i x x =-=-+-+-+-+-+-+-=∑.所以结合参考数据知14.000.9914.10r ==≈≈.因为y 与x 的相关系数近似为0.99,所以y 与x 的线性相关程度相当大,从而可以用线性回归模型拟合y 与x 的关系.15 / 31(2)因为()()()7172114ˆ0.528iii ii x x y y bx x ==--===-∑∑, 所以ˆˆ 4.30.54 2.3ay bx =-=-⨯=. 所以y 关于x 的线性回归方程为ˆ0.5 2.3y x =+,将10x =代入线性回归方程,得ˆ0.510 2.37.3y=⨯+=. 所以估算该种机械设备使用10年的失效费为7.3万元.8.人类已经进入大数据时代.目前,数据量级已经从TB (1TB =1024GB )级别跃升到PB (1PB =1024TB ),EB (1EB =1024PB )乃至ZB (1ZB =1024EB )级别.国际数据公司(IDC )研究结果表明,2008年全球产生的数据量为0.49ZB ,2009年数据量为0.8ZB ,2010年增长到1.2ZB ,2011年数据量更是高达1.82ZB .下表是国际数据公司(IDC )研究的全球近6年每年产生的数据量(单位:ZB )及相关统计量的值:表中ln i i z y =,6116i i z z ==∑.(1)根据上表数据信息判断,方程21c xy c e =⋅(e 是自然对数的底数)更适宜作为该公司统计的年数据量y 关于年份序号x 的回归方程类型,试求此回归方程(2c 精确到0.01).(2)有人预计2021年全世界产生的数据规模将超过2011年的50倍.根据(1)中的回归方程,说明这种判断是否准确,并说明理由.参考数据: 4.5695.58e ≈, 4.5897.51e ≈,回归方程y a bx =+中,斜率最小二乘法公式为()()()1122211n niii ii i nniij i x x y y x y nxyb x x xnx====---==--∑∑∑∑,a y bx =-.【试题来源】2021年高三数学二轮复习讲练测(新高考版) 【答案】(1) 1.520.38x y e +=;(2)见解析.【分析】(1)设ln z y =,则12ln z c c x =+,再根据参考数据及公式即可得解 (2)先将8x =代入得预计2021年数据量,进而和2011年的50倍比较大小即可得解【解析】(1)由21c xy c e =⋅,两边同时取自然对数得()2112ln ln ln c xy c e c c x =⋅=+,设ln z y =,则12ln z c c x =+. 因为 3.5x =, 2.85z =,()62117.58i i x x=-=∑,()()616.7.i i i x x z z =--=∑,所以()()()12216.730.3817.58niii nij x x y z c x x ==--==≈-∑∑,12ln 2.850.38 3.5 1.52c z c x =-=-⨯=.17 / 31所以 1.520.38ln z x y =+=,所以 1.520.38x y e +=;(2)令8x =,得 1.520.388 4.56ˆ95.58 1.825091ye e +⨯==≈>⨯=. 预计2021年全世界产生的数据规模会超过2011年的50倍.【名师点睛】对于非线性回归方程的求解,一般要结合题意作变换,转化为线性回归方程来求解,同时也要注意相应数据的变化.9.随着手机游戏的发展,在给社会带来经济利益的同时,也使许多人深陷其中,从而产生一些负面的影响.A ,B 两所学校为了解学生每天玩游戏的时间,各自抽取了100名学生进行调查,得到的数据如表所示:A 学校B 学校(1)以样本估计总体,计算A 学校学生日游戏时间的平均数以及B 学校学生日游戏时间的中位数.(2)为了调查家长对孩子玩游戏的态度,学校相关领导随机抽取了200名男性家长和200名女性家长进行调查,并将所得结果统计如表所示,判断是否有99.9%的把握认为家长对孩子玩游戏的态度与家长性别有关?附:()()()()()22n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.【试题来源】普通高等学校招生全国统一考试数学预测卷(一)【答案】(1)A学校学生日游戏时间的平均数为64.7()min;B学校学生日游戏时间的中位数为74()min;(2)没有.【分析】(1)根据频率分布表,利用平均数公式求解;由中位数的定义求解;(2)根据22⨯列联表中的数据,利用()()()()()22n ad bcKa b c d a c b d-=++++求得2K的值,再与临界值表对照下结论.【解析】(1)A学校学生日游戏时间的平均数为3.50.1450.14550.16650.2750.18850.13950.0964.7⨯+⨯+⨯+⨯+⨯+⨯+⨯=()min.B学校学生日游戏时间的中位数为5037102070107425----+⨯=()min.19 / 31(2)由已知可得22⨯列联表:则()2240013639161648.17210.828200200297103K ⨯⨯-⨯=≈<⨯⨯⨯, 所以没有99.9%的把握认为家长对孩子玩游戏的态度与家长性别有关. 10.为了解国内不同年龄段的民众旅游消费的基本情况.某旅游网站从其数据库中随机抽取了1000条客户信息进行分析,这些客户一年的旅游消费金额数据如下表所示;把一年的旅游消费金额满8千元称为“高消费”,否则称为“低消费”. (1)从这些客户中随机选一人,求该客户是高消费的中老年人的概率; (2)完成下面的22⨯列联表,并判断能否有99%的把握认为旅游消费的高低与年龄有关.附表及公式:22()()()()()n ad bcKa b c d a c b d-=++++,其中n a b c d=+++【试题来源】学科网2021年高三1月大联考考后强化卷(新课标Ⅱ卷)【答案】(1)15;(2)填表见解析;有.【分析】(1)用频率估计概率,计算样本中高消费的中老年人的频率即为概率;(2)将数据填入列联表,用2K的计算公式计算2K的观测值k,与附表中的数据比较可得出结论.【解析】(1)样本中总客户数为1000,其中高消费的中老年人有200人,随机选一人,则该客户是高消费的中老年人的概率为2001 10005=.(2)2×2列联表如下:21 / 31可得2K的观测值21000(300200100400)7.937400600700300k ⨯⨯-⨯=≈⨯⨯⨯, 因为7.937 6.635>,所以有99%的把握认为旅游消费的高低与年龄有关. 11.2020山东省旅游发展大会暨首届中国国际文化旅游博览会在济南奥体中心东荷体育馆隆重开幕.大会以“文旅融合发展,乐享好客山东”为主题,来自38个国家和地区的友好宾朋,跨越空间阻隔,相约线上交流,共同推动山东文化和旅游业发展谱写新的篇章.某机构为了解人们对博览会的关注度是否与年龄有关,随机抽取了200位市民(其中40周岁及以下与40周岁以上各100人)进行问卷调查,并得到如下的22⨯列联表:(1)根据22⨯列联表,判断是否有90%的把握认为对博览会的关注度与年龄有关;(2)若从关注度极高的被调查者中按年龄分层抽样的方法抽取9人了解他们从事的职业情况,再从9人中任意选取2人谈谈关注博览会的原因,求这2人中两个年龄段的市民各一人的概率.附:22()()()()()n ad bc Ka b c d a c b d -=++++,其中n a b c d =+++.参考数据:【试题来源】普通高等学校招生全国统一考试数学预测卷(三)【答案】(1)有;(2)59.【分析】(1)根据22⨯列联表中的数据求得2K 值,再与临界值表对照下结论; (2)先利用分层抽样的方法抽取各层的人数,然后再求得9人中任意选取2人的基本事件数和这2人中两个年龄段的市民各一人的基本事件数,代入古典概型的概率公式求解.【解析】(1)由22⨯列联表可得22200(60524840) 2.899 2.70610010010892K ⨯⨯-⨯=≈>⨯⨯⨯,故有90%的把握认为对博览会的关注度与年龄有关.(2)根据题意,从关注度极高的被调查者中按年龄分层抽样的方法抽取9人, 则抽取40周岁及以下的有6095108⨯=人,40周岁以上的有954-=人. 从9人中任意选取2人的基本事件有29C 36=个,这2人中两个年龄段的市民各一人的基本事件有1154C C 20=个;则这2人中两个年龄段的市民各一人的概率205369P ==. 12.某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表:并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:23 / 31(1)求相关系数r 的大小(精确到0.01),并判断管理时间y 与土地使用面积x 的线性相关程度;(2)是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性?参考公式:()()niix x y y r --=∑,()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++. 临界值表:22.02.【试题来源】重组卷05-冲刺2021年高考数学之精选真题模拟重组卷(新课标卷)【答案】(1)0.84;管理时间y 与土地使用面积x 的线性相关程度为强相关;(2)有99.9%的把握认为村民的性别与参与管理的意愿具有相关性.【分析】(1)根据参考公式和数据计算相关系数r 的值,并判断强弱关系;(2)根据列联表计算2K ,并和临界数表比较大小. 【解析】(1)1234535x ++++==,911142620165y ++++==, ()()()()()()()()113916231116331416niii x x y y =--=-⨯-+--+-⨯-∑()()()()43261653201637+--+--=,()()()()()()2222221132333435310ni i x x =-=-+-+-+-+-=∑, ()()()()()()22222219161116141626162016194ni i y y =-=-+-+-+-+-=∑44.04=≈,()()370.840.7544.04niix x y y r --==≈>∑, 所以管理时间y 与土地使用面积x 的线性相关程度为强相关.(2)由条件可知女性不愿意参与管理的人数为300140604060---=()223001406060402510.828200100180120K ⨯⨯-⨯==>⨯⨯⨯,所以有99.9%的把握认为村民的性别与参与管理的意愿具有相关性. 13.某公司对项目进A 行生产投资,所获得的利润有如下统计数据表:(1)请用线性回归模型拟合y 与x 的关系,并用相关系数加以说明; (2)该公司计划用7百万元对A 、B 两个项目进行投资.若公司对项目B 投资25 / 31()16x x ≤≤百万元所获得的利润y 近似满足:0.490.160.491y x x =-++,求A 、B 两个项目投资金额分别为多少时,获得的总利润最大? 附:①对于一组数据()11,x y 、()22,x y 、、(),n n x y ,其回归直线方程y bx a=+的斜率和截距的最小二乘法估计公式分别为1221ni ii nii x y nx yb xnx==-⋅=-∑∑,ˆa y bx=-. ②线性相关系数ni ix y nx yr -⋅=∑.一般地,相关系数r 的绝对值在0.95以上(含0.95)认为线性相关性较强;否则,线性相关性较弱. 参考数据:对项目A 投资的统计数据表中111ni i i x y ==∑,212.24ni i y ==∑ 2.1≈.【试题来源】2021年高考数学金榜预测卷(山东、海南专用)【答案】(1)0.2y x =;答案见解析;(2)对A 、B 项目分别投资4.5百万元,2.5百万元时,获得总利润最大.【分析】(1)计算出x 、y 的值,将表格中的数据代入最小二乘法公式,求出b 、a 的值,可得出回归直线方程,并计算出相关系数r 的值,可得出结论;(2)求得()0.491.930.0411y x x ⎡⎤-++⎢+⎣=⎥⎦,利用基本不等式可求得y 的最大值,利用等号成立求得x 的值,即可得出结论.【解析】(1)对项目A 投资的统计数据进行计算,有3x =,0.6y =,52155i i x ==∑,所以515222151190.255535i ii i i x y x yb x x==-⋅-===-⨯-∑∑,0.60.230a y bx =--⨯==,所以回归直线方程为0.2y x =.线性相关系数55i ix y x yr -⋅==∑0.95340.95=≈>, 这说明投资金额x 与所获利润y 之间的线性相关关系较强, 用线性回归方程0.2y x =对该组数据进行拟合合理;(2)设对B 项目投资()16x x ≤≤百万元,则对A 项目投资()7x -百万元. 所获总利润()()0.490.490.490.27 1.930.60411110.x x y x x x ⎡⎤++-=⎥=--++⎢++⎣⎦1.93 1.65≤-=, 当且仅当()100.04194.x x =++,即 2.5x =时取等号, 所以对A 、B 项目分别投资4.5百万元,2.5百万元时,获得总利润最大. 14.有一种速度叫中国速度,有一种骄傲叫中国高铁.中国高铁经过十几年的发展,取得了举世瞩目的成就,使我国完成了从较落后向先进铁路国的跨越式转变.中国的高铁技术不但越来越成熟,而且还走向国外,帮助不少国家修建了高铁.高铁可以说是中国一张行走的名片.截至到2020年,中国高铁运营里程已经达到3.9万公里.下表是2013年至2020年中国高铁每年的运营里程统计表,它反映了中国高铁近几年的飞速发展:27 / 31根据以上数据,回答下面问题.(1)甲同学用曲线y =bx +a 来拟合,并算得相关系数r 1=0.97,乙同学用曲线y =ce dx 来拟合,并算得转化为线性回归方程所对应的相关系数r 2=0.99,试问哪一个更适合作为y 关于x 的回归方程类型,并说明理由;(2)根据(1)的判断结果及表中数据,求y 关于x 的回归方程(系数精确到0.01). 参考公式:用最小二乘法求线性回归方程的系数公式:121()()ˆˆ,()niii nii x x y y ba y bxx x ==--==--∑∑;参考数据:882112.48,()()15.50,()42.00,i i i i i y x x y y x x ===--=-=∑∑令8820.4411ln ,0.84,()() 6.50,() 1.01, 1.15.i i i i i w y w x x w w w w e ====--=-==∑∑【试题来源】安徽省示范高中皖北协作区2021届高三下学期第23届联考 【答案】(1)答案见解析;(2)0.151.15x y e =.【分析】(1)比较已知的相关系数大小关系即可得出正确答案;(2)由已知数据求出x ,结合回归方程变形为ln ln y c dx =+,求出d 和ln c ,从而可求出回归方程.【解析】(1)因为1201r r <<<,所以dx y ce =更适合作为y 关于x 的回归方程类型. (2)12345678364.588x =++++++===,由dx y ce =得ln ln y c dx =+,即ln c dx ω=+,则1821()()6.50.1542()Niii ii x x d x x ωω==--==≈-∑∑, 13ln 0.84 4.50.1484c dx ω=-=-⨯≈,所以0.140.150.140.150.151.15dx x x x y ce e e e e +====. 【名师点睛】本题考查了回归方程的求解,本题第二问的关键是对回归方程,结合对数的运算性质进行变形,结合最小二乘法求线性回归方程的系数公式进行求解.15.打乒乓球是一项众多中学生喜爱的体育运动,某中学体育协会为了解这项运动与性别的关联性,随机调查了100名男生和100名女生,每位学生回答喜欢或不喜欢,得到下面的列联表:(1)分别估计该中学男、女生喜欢打乒乓球的概率;(2)能否有99.5%的把握认为中学生喜欢打乒乓球与性别有关?附:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.【试题来源】吉林省白山市2021届高三第三次联考(4月份)【答案】(1)男生喜欢打乒乓球的概率的估计值为0.55,女生喜欢打乒乓球的概率的估计值为0.35;(2)有99.5%的把握认为中学生喜欢打乒乓球与性别有关.【分析】(1)根据题意,利用公式求得男生和女生喜欢打乒乓球的频率,从而估计出其概率;(2)由题意,求得2K的值,对照临界值得出结论.【解析】(1)由调查数据可知,男生喜欢打乒乓球的频率为550.55 100=,女生喜欢打乒乓球的频率为350.35 100=,因此该中学男生喜欢打乒乓球的概率的估计值为0.55,女生喜欢打乒乓球的概率的估计值为0.35.(2)因为2 2200(55653545)8001001009011099 K⨯⨯-⨯==⨯⨯⨯且80080087.879 99100>=>,所以有99.5%的把握认为中学生喜欢打乒乓球与性别有关.16.某公司为研究某种图书每册的成本费y(单位:元)与印刷数量x(单位:千册)的关系,收集了一些数据并进行了初步处理,得到了下面的散点图及一些统计量的值.29 / 31表中1i i u x =,8118i i u u ==∑(1)根据散点图判断:y a bx =+与dy c x=+哪一个模型更适合作为该图书每册的成本费y 与印刷数量x 的回归方程?(只要求给出判断,不必说明理由) (2)根据(1)的判断结果及表中数据,建立y 关于x 的回归方程(结果精确到0.01);(3)若该图书每册的定价为9.22元,则至少应该印刷多少册才能使销售利润不低于80000元?(假设能够全部售出,结果精确到1)附:对于一组数据1122(,),(,,,),()n n v v v ωωω⋯,其回归直线v αβω=+的斜率和截距的最小二乘估计分别为121()()()niii nii v v ωωβωω==--=-∑∑,v αβω=-.【试题来源】2021年高考数学考前信息必刷卷(江苏专用) 【答案】(1)d y c x =+更适合;(2)8.961.22y x=+;(3)至少印刷11120册才能使销售利润不低于80000元.【分析】(1)由散点图可知成反比例函数模型,故dy c x=+更适合; (2)令1u x=,根据表中的数据计算即可得y 关于u 的线性回归方程为1.228.96y u=+,进而得y 关于x 的回归方程为8.961.22y x=+; (3)根据题意只需解不等式8.969.22 1.2280x x x ⎛⎫-+≥ ⎪⎝⎭即可得答案.【解析】(1)由散点图判断,dy c x=+更适合作为该图书每册的成本费y (单位:元)与印刷数量x (单位:千册)的回归方程. (2)令1u x=,先建立y 关于u 的线性回归方程,由于81821()()7.0498.9578.960.787()i iiiiu u y ydu u==-⋅-==≈≈-∑∑,所以 3.638.9570.269 1.22c yd u=-⋅=-⨯≈,所以y关于u的线性回归方程为 1.228.96y u=+,所以y关于x的回归方程为8.961.22yx =+(3)假设印刷x千册,依题意得8.969.22 1.2280x xx⎛⎫-+≥⎪⎝⎭,解得11.12x≥,所以至少印刷11120册才能使销售利润不低于80000元.31 / 31。
【高三数学】二轮复习:专题五 第2讲 概率、随机变量及其分布

1
感染的,于是假定他受 A 和 B 感染的概率都是2.同样也假定 D 受 A,B 和 C
1
感染的概率都是3.在这种假定下,B,C,D 中恰有两人直接受 A 感染的概率是
(
)
1
A.6
1
B.3
1
C.2
2
D.3
(2)(2021·河北张家口一模)某大学进行“羽毛球”“美术”“音乐”三个社团选拔.
三局.若甲抽到的三张扑克牌分别是A1,A2,A3,乙抽到的三张扑克牌分别是
B1,B2,B3,且这六张扑克牌的大小顺序为A1>B1>B2>A2>A3>B3,则三局比赛
结束后甲得4分的概率为(
1
6
A.
1
3
B.
)
1
2
C.
2
3
D.
(2)(2021·山东泰安三模)已知大于3的素数只分布在{6n-1}和{6n+1}两数
[例2-4](2021·江苏苏州中学园区校月考)甲、乙两队进行篮球决赛,采取七
场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,
甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,
客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概
率是
.
1
次的概率为2,现有一个该型号的充电宝已经循环充电超过 500 次,则其能够
循环充电超过 1 000 次的概率是(
3
A.4
2
B.3
)
1
C.2
1
D.3
高考数学专题复习:独立性检验

高考数学专题复习:独立性检验一、单选题1.某学校食堂对高三学生偏爱蔬菜还是肉类与性别的关系进行了一次调查,根据独立性检验原理,处理所得数据之后发现,有97.5%的把握但没有99%的把握认为偏爱蔬菜还是肉类与性别有关,则2K 的观测值可能为( ) k 2.706 A .2 3.206K =B .2 6.625K =C .27.869K =D .211.208K =2.某校为了解学生“玩手机游戏”和“学习成绩”是否有关,随机抽取了100名学生,运用2×2列联表进行独立性检验,经计算得到2 3.936K =,所以判定玩手机游戏与学习成绩有关系,那么这种判断出错的可能性为( )A .1%B .5%C .95%D .99%3.某校为了调查喜欢语文与性别的关系,随机调查了一些学生,数据如下表,由此判断喜欢语文与性别有关系,那么这种判断出错的可能性为( )()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.A .99.5%B .5%C .0.5%D .95%4.以下四个命题,其中正确的个数有( )①在独立性检验中,随机变量2K 的观测值越大,“认为两个分类变量有关”,这种判断犯错误的概率越小.②在线性回归方程ˆ0.80.35yx =-时,变量x 与y 具有负的线性相关关系; ③随机变量X 服从正态分布2(3,)N σ,若(4)0.64P X ≤=,则(23)0.07P X ≤≤=; ④两个随机变量相关性越强,则相关系数r 的值越接近于1. A .1个B .2个C .3个D .4个5.两个分类变量X 和Y ,它们的取值分别为{}12,x x 和{}12,y y ,其样本频数列联表如下表所示:则下列四组数据中,分类变量X 和Y 之间关系最强的是( ) A .4a =,2b =,3c =,6d = B .2a =,1b =,3c =,5d = C .4a =,5b =,6c =,8d =D .2a =,3b =,4c =,6d =6.为了丰富教职工业余文化生活,某校计划在假期组织70名老师外出旅游,并给出了两种方案(方案一和方案二),每位老师均选择且只选择一种方案,其中有50%的男老师选择方案一,有75%的女老师选择方案二,且选择方案一的老师中女老师占40%,则参照附表,得到的正确结论是( )附:()()()()()22n ad bc K a b c d a c b d -=++++,n a b c d =+++.A .在犯错误的概率不超过2.5%的前提下,认为“选择方案与性别有关”B .在犯错误的概率不超过2.5%的前提下,认为“选择方案与性别无关”C .有95%以上的把握认为“选择方案与性别有关”D .有95%以上的把握认为“选择方案与性别无关”7.利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用22⨯列联表,由计算可得27.236K =,参照下表:得到的正确结论是( )A .有99%以上的把握认为“爱好该项运动与性别无关”B .有99%以上的把握认为“爱好该项运动与性别有关”C .在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关"D .在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”8.如果根据性别与是否爱好运动的列联表得到2 3.852 3.841x ≈>,所以判断性别与运动有关,那么这种判断犯错的可能性不超过( ) A .2.5%B .0.5%C .1%D .5%9.某校为了研究学生的性别和对待某一活动的态度(支持与不支持)的关系,运用22⨯列联表进行独立性检验.经计算2 6.058K =,则所得到的统计学结论是:有( )的把握认为“学生性别与支持该活动有关系”A .0.025%B .97.5%C .99%D .99.9%10.根据分类变量x 与y 的观测数据,计算得到2 2.974χ=.依据0.05α=的独立性检验,结论为( )A .变量x 与y 不独立B.变量x与y不独立,这个结论犯错误的概率不超过0.05C.变量x与y独立D.变量x与y独立,这个结论犯错误的概率不超过0.05二、填空题11.为了调查高中学生参加课外兴趣活动选篮球和舞蹈是否与性别有关,现随机调查了30名学生,得到如下22⨯列联表:根据表中的数据,及观测值2K(其中22()()()()()n ad bcKa b c d a c b d-=++++),参考数据:则在犯错误的概率不超过__________前提下,认为选择舞蹈与性别有关.12.某工厂为了调查工人文化程度与月收入的关系,随机抽取了部分工人,得到如下列联表:(单位:人)由上表中数据计算得2K的观测值22105(10302045)6.10955503075K⨯⨯-⨯=≈⨯⨯⨯,请估计在犯错误的概率不超过__________的前提下认为“文化程度与月收入有关系”.13.利用独立性检验的方法调查高中性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用22⨯列联表,由计算可得27.245K≈,参照下表2.706 至少有__________以上的把握认为“爱好该项运动与性别有关”.14.为了判断高中三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:已知P (K 2≥3.841)≈0.05,P (K 2≥5.024)≈0.025.根据表中数据,得到K 2的观测值k =250(1320107)23272030⨯⨯-⨯⨯⨯⨯≈4.844.则认为选修文科与性别有关系出错的可能性为__________.三、解答题15.为了解某市市民对政府出台楼市限购令的态度,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频率分布直方图如下:(1)求该市市民平均月收入的估计值(每组数据以区间中点值为代表).(2)将月收入不低于7500元称为“高收入”,否则称为“非高收入”,根据已知条件完成下面的22⨯列联表,并判断能否有99%的把握认为市民对楼市限购令的态度与收入有关.参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.16.为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查,得到了如下的统计结果: 表1:男生上网时间与频数分布表表2:女生上网时间与频数分布表(1)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数; (2)完成联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”.附:()()()()22()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++为样本容量.0.45517.某大学为鼓励学生进行体育锻炼,购买了一批健身器材供学生使用,并从该校大一学生中随机抽取了100名学生调查使用健身器材的情况,得到数据如表所示:(1)设每周使用健身器材的次数不低于3次为“爱好健身”,根据上表数据,填写22⨯列联表,并判断能否在犯错误的概率不超过0.10的前提下认为“男生和女生在使用健身器材的爱好方面有差异”;(2)从上述每周使用健身器材3次的学生中,利用分层抽样的方法抽取5名学生,再从抽取的5名学生中随机抽取3人,求3人中至多有一名女生的概率.18.在对人们休闲方式的一次调查中,仅就看电视与运动这两种休闲方式比较喜欢哪一种进行了调查.调查结果:接受调查总人数110人,其中男、女各55人;受调查者中,女性有30人比较喜欢看电视,男性有35人比较喜欢运动.(1)请根据题目所提供的调查结果填写下列22⨯列联表:(2)能否在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系”?注:22()()()()()n ad bcKa b c d a c b d-=++++,(其中n a b c d=+++为样本容量)参考答案1.B【分析】根据把握率确定2K的观测值区间范围即可选择.【详解】∵有97.5%的把握但没有99%的把握,∴2K的观测值区间范围为[5.024,6.635),结合选项可知,2K的观测值可能为6.625.故选:B2.B【分析】根据2K的值,对照附表即可得解.【详解】由题得2 3.936 3.841K=>,所以判定玩手机游戏与学习成绩有关系,这种判断出错的可能性为5%. 故选:B3.C【分析】计算出2K的值可得答案.【详解】因为()22501520510258.33320307.89225753K⨯⨯-⨯==≈>⨯⨯⨯,所有这种判断出错的可能性0.5%.故选:C.4.A【分析】利用随机变量2K的观测值越大,说明两个变量有关系的可能性越大判断①;根据回归方程一次项系数的正负判断②;根据正态分布的性质判断③; 利用线性相关的概念判断④. 【详解】①:在独立性检验中,因为随机变量2K 的观测值越大,说明两个变量有关系的可能性越大,即犯错误的概率越大,故①错误;②:回归方程ˆ0.80.35yx =-的一次项系数为-0.35<0,故变量x 与y 具有负的线性相关关系,故②正确;③:随机变量X 服从正态分布2(3)N σ,,则(34)(4)(3)0.640.50.14P X P X P X <≤=≤-<=-=, 由对称性可知,(23)0.14P X ≤≤=,故③错误;④:两个随机变量的线性相关关系越强,则相关系数r 的绝对值越接近于1,故④错误. 正确的选项有1个. 故选:A 5.A 【分析】逐项求出ad bc -的值并加以对比,最大值对应的分类变量之间关系最强. 【详解】我们可以用ad bc -的大小近似的判断两个分类变量之间关系的强弱,ad bc -的值越小,关系越弱,越大,关系越强.这四组数据中ad bc -的值分别为18、7、2、0, 所以A 组数据的ad bc -的值最大,相比较而言这组数据反应的X 和Y 的关系最强. 故选:A. 6.C 【分析】设该校男老师的人数为x ,女老师的人数为y ,根据条件,得到22⨯列联表,求出x ,y 的值,利用公式计算2K 的值,再与表中临界值比较可得结果. 【详解】设该校男老师的人数为x ,女老师的人数为y ,则可得如下表格:由题意0.40.50.25x y =+,可得43y x =,可得30x =,40y =,则()227015301510 4.667 3.84125453040K ⨯-⨯=≈>⨯⨯⨯, 但4.667 5.024<,所以无97.5%以上有95%以上的把握认为“选择方案与性别有关”. 故选:C. 7.B 【分析】由已知的27.236K =,对比临界值表可得答案 【详解】解:因为27.236 6.635K =>,所以有99%以上的把握认为“爱好该项运动与性别有关”. 故选:B. 8.D 【分析】根据临界值附表比较,即得结论. 【详解】根据以下临界值附表可知这种判断犯错的可能性不超过5%. 故选:D 9.B【分析】将2K 的值与表中数据比较大小可知5.024 6.058 6.635<<,由此确定出相应的把握有多少.【详解】因为2 6.058K =,对照表格:5.024 6.058 6.635<<,所以有10.0250.97597.5%-==的把握认为“学生性别与是否支持该活动有关系”. 故选:B.10.C【分析】由表中数据以及独立性检验的思想即可得出结果.【详解】0.05α=时,2 3.841 2.974χ=>,所以在犯错概率不超过0.1时变量x 与y 有关.故选:C11.0.025【分析】由列联表中的数据,根据公式计算出2K 的值,再对照临界表即可得答案.【详解】 解:由列联表中的数据可得,2230(13827)27 5.4 5.024*********K ⨯⨯-⨯===>⨯⨯⨯, 所以在犯错误的概率不超过0.025的前提下,认为选择舞蹈与性别有关.故答案为:0.025.12.0.025【分析】根据2K ,对比临界值即可得出结论.【详解】∵6.109 5.024>,故能在犯错误的概率不超过0.025的前提下认为“文化程度与月收入有关系”.故答案为:0.025.13.99%【分析】根据卡方的值与参考数据比较即可判断;【详解】解:因为27.245K ≈,6.6357.2457.879<<,所以10.0199%-=故至少有99%以上的把握认为“爱好该项运动与性别有关”,故答案为:99%14.5%【分析】根据观测值k ≈4.844以及独立性检验的基本思想即可得出结果.【详解】K 2的观测值k ≈4.844,这表明小概率事件发生.根据假设检验的基本原理,应该断定“是否选修文科与性别之间有关系”成立,并且这种判断出错的可能性约为5%.故答案为:5%15.(1)63;(2)表格见解析,有.【分析】(1)每组数据区间中点值乘以该组的频率求和可得答案;(2)根据每组频率乘以50可得每组的人数可完成列联表,计算2K 可得答案.【详解】(1)该市市民平均月收入的估计值为400.1500.2600.3700.2800.1900.163⨯+⨯+⨯+⨯+⨯+⨯=.(2)根据频率分布直方图知每组的人数分别为5,10,15,10,5,5.可得22⨯列联表如下:所以()22502882128.33340103020K ⨯⨯-⨯=≈⨯⨯⨯,因为8.333 6.635>,所以有99%的把握认为市民对楼市限购令的态度与收入有关.16.(1)225;(2)列联表答案见解析,没有90%的把握认为“大学生上网时间与性别有关”.【分析】(1)设上网时间不少于60分钟的人数为x ,依题意有30750100x =,计算即可; (2)填写列联表,计算2K ,对照临界值得出结论.【详解】(1)设上网时间不少于60分钟的人数为x ,依题意有30750100x =,解得225x =,所以估计其中上网时间不少于60分钟的人数是225.(2)塻22⨯列联表如下:由表中数据可得到22200(60304070) 2.20 2.70610010013070K ⨯-⨯=≈<⨯⨯⨯, 故没有90%的把握认为“大学生上网时间与性别有关”.17.(1)表格见解析,不能;(2)710. 【分析】(1)根据已知数据统计列联表中的各项的人数,填写列联表,进而计算2K 并与0.1的临界值进行比较,得到论断;(2)利用分层抽样的等比例原则求得抽取的5人中男女生的人数,利用符号表示每个学生,利用列举法计数,得到所求概率.【详解】解:(1)填写的列联表如下所示:()2210222422320.506 2.70644565446K ⨯⨯-⨯=≈<⨯⨯⨯.所以不能在犯错误的概率不超过0.1的前提下认为“男生和女生在使用健身器材的爱好方面有差异”.(2)从每周使用健身器材3次的学生中,利用分层抽样的方法抽取5名学生,则抽取男生3名,抽取女生2名.将抽取的3名男生分别记为a ,b ,c ,2名女生分别记为m ,n ,则从5人中随机抽取3人的不同情况有abc ,abm ,abn ,acm ,acn ,amn ,bcm ,bcn ,bmn ,cmn ,共10种, 其中至多有一名女生的情况有abc ,abm ,abn ,acm ,acn ,bcm ,bcn ,共7种. 所以从抽取的5名学生中随机抽取3人,至多有一名女生的概率为710. 18.(1)答案见解析;(2)不能.【分析】(1)由题意填写列联表即可;(2)代入数据计算2K 的观测值,比较观测值与3.841的大小,判断能否在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系” .【详解】解.(1)根据题目所提供的调查结果,可得下列22⨯列联表:(2)根据列联表中的数据,可计算()2211030352025 3.66750605555K ⨯⨯-⨯=≈⨯⨯⨯,因为03.667 3.841k k ≈<=,所以不能在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系”.。
苏教版高中数学选修2-3知识讲解_独立性 (1)

独立性: :【学习目标】1.了解条件概率和两个事件相互独立的概念.2.通过实例探究条件概率计算公式的推导过程和事件独立性的概念,学会判断事件独立性的方法.3.通过本节的学习,体会数学来源于实践又服务于实践,发展数学的应用意识.【要点梳理】要点一:条件概率1.概念设A 、B 为两个事件,求已知B 发生的条件下,A 发生的概率,称为B 发生时A 发生的条件概率,记为()|P A B ,读作:事件B 发生的条件下A 发生的概率。
要点诠释:我们用韦恩图能更好的理解条件概率,如图,我们将封闭图形的面积理解为相应事件的概率,那么由条件概率的概率,我们仅局限于B 事件这个范围来考察A 事件发生的概率,几何直观上,()|P A B 相当于B 在A 内的那部分(即事件AB )在A 中所占的比例。
2.公式.要点诠释:(1)对于古典(几何)概型的题目,可采用缩减样本空间的办法计算条件概率: 古典概型:(|)AB P A B B =包含的基本事件数包含的基本事件数,即()()card (|)card AB P AB B =; 几何概型:(|)AB P A B B =的测度的测度. (2)公式()(|)()P AB P A B P B =揭示了()P B 、()|P AB 、()P AB 的关系,常常用于知二求一,即要熟练应用它的变形公式如,若()P B >0,则()()()=|P AB P A P B A ,该式称为概率的乘法公式.(3)类似地,当()0P A >时,A 发生时B 发生的条件概率为:()()()|=P AB P B A P A .3. 性质(1)非负性:()|0P A B ≥;(2)规范性:()|=1P B Ω(其中Ω为样本空间);(3)可列可加性:若两个事件A 、B 互斥,则()()()+||+|P A B C P A C P B C =.4.概率()P A |B 与()P AB 的联系与区别:联系:事件A ,B 都发生了。
高考数学总复习 第十一篇《第72讲 独立性及其二项分布》课件 理 苏教版

军.若两队胜每局的概率相同,则甲队获得冠军的概率为
________.
解析 问题等价为两类:第一类,第一局甲赢,其概率P1=
1 2
;第二类,需比赛2局,第一局甲负,第二局甲赢,其概率P2
=12×12=14.故甲队获得冠军的概率为P1+P2=34.
答案
3 4
2.小王通过英语听力测试的概率是
1 3
,他连续测试3次,那么
解析
圆的面积是π,正方形的面积是2,扇形的面积是
π 4
,根
据几何概型的概率计算公式得P(A)=
2 π
,根据条件概率的公式
1 2 得P(B|A)=PPAAB=π2=14. π
答案
2 (1)π
1 (2)4
考向二 相互独立事件的概率 【例2】►(2010·全国Ⅱ)如图,由M到N的电路中有4个元件,分 别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p, 电流能通过T4的概率是0.9,电流能否通过各元件相互独 立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999. (1)求p; (2)求电流能在M与N之间通过的概率. [审题视点] 两个事件独立,两个事件的对立事件也是相互独 立的.
解 (1)①P(A)=26=13. ②因为两个骰子的点数共有36个等可能的结果,点数之和大于 8的结果共10个.
所以P(B)=1306=158. ③当蓝色骰子的点数为3或6时,两颗骰子的点数之和大于8的
结果有5个,故P(AB)=356. 5
(2)由(1)知P(B|A)=PPAAB=316=152. 3
4.如果X~B
15,14
________.
解析 采取特殊值法.
,则使P(X=k)取最大值的k值为
高三数学事件的相互独立性

C100 · C99
③从中抽两次,每次1件则两次都抽 1· 1 C C 出次品的概率是_ ___ 4 4
(放回抽取) C1001· C1001
( 互斥事件)
求 较 复 杂 事 件 概 率
分类
正向 分步
P(A+B)= P(A) + P (B) P(A· B)= P(A) ·P (B)
( 互独事件)
(1-a)(1-b)
A
B
6.某系统由A,B,C三个元件组成, 每个元件正常工作概率为P. 2- P3 P+P 则系统正常工作的概率为____
C
7.在100件产品中有4件次品. ①从中抽 2 件 , 则 2 件都是次品概率 2 C4 为___ C100 2 ②从中抽两次,每次1件则两次都抽 1· 1 C C 4 3 出次品的概率是___ 1 1
事件的相互独立性(2)
习题课
复习回顾
1、事件的相互独立性 设A,B为两个事件,如果 P(AB)=P(A)P(B),则称事 件A与事件B相互独立。
2、相互独立事件同时发生的概率公式:
两个相互独立事件A,B同时发生,即事件A•B发生的概 率为: P(AB)= P(A)P(B) .
一般地,如果事件A1,A2……,An相互独立,那么这n个 事件同时发生的概率等于每个事件发生的概率的积,即
P(A1· A2……An)=P(A1)· P(A2)……P(An)
3、如果事件A、B互斥,那么事件A+B发生(即A, B中有一个发生)的概率:P(A+B)= P(A)+P(B) .
一般地,如果事件 A 1、A 2、...A n ,彼此互斥,那 么事件 A1 A2 +...+An 发生(即 A 1、A 2、...A n 中 恰有一个发生)的概率:
备战高考数学复习考点知识与题型讲解86---独立性检验

备战高考数学复习考点知识与题型讲解第86讲独立性检验考向预测核心素养利用2×2列联表和卡方独立性检验判断两个变量的相关关系是高考考查的热点,各种题型均会出现.数据分析、数学运算一、知识梳理1.分类变量与列联表(1)分类变量在讨论问题时,为了表述方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量.分类变量的取值可以用实数表示.(2)2×2列联表列联表:列出的两个分类变量的频数表,称为列联表.假设有两个分类变量X和Y,它们的可能取值分别为{x1,x2}和{y1,y2},其2×2列联表为y 1y2合计x1a b a+bx2c d c+d合计a+c b+d a+b+c+d2.独立性检验(1)零假设以Ω为样本空间的古典概型.设X和Y为定义在Ω上,取值于{0,1}的成对分类变量.H:分类变量X和Y独立.通常称H0为零假设或原假设.(2)χ2公式假设我们通过简单随机抽样得到了X和Y的抽样数据列联表,如下表所示:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d).对于任何小概率值α,可以找到相应的正实数xα,使得下面关系成立:P(χ2≥xα)=α.我们称xα为α的临界值,这个临界值就可作为判断χ2大小的标准.概率值α越小,临界值xα越大.(3)独立性检验基于小概率值α的检验规则是:当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;当χ2<xα时,我们没有充分证据推断H0不成立,可以认为X和Y独立.这种利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”,简称独立性检验.二、教材衍化1.(人A选择性必修第三册P134练习T1改编) 为调查中学生近视情况,测得某校男生150名中有80名近视,140名女生中有70名近视.在检验这些学生眼睛近视是否与性别有关时,用下列哪种方法最有说服力( )A.回归分析 B.均值与方差C.独立性检验 D.概率答案:C2.(人A选择性必修第三册P134练习T4改编)为了判断高三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:根据表中数据,得到χ2=50×(13×20-10×7)223×27×20×30≈4.844.则认为选修文科与性别有关系出错的可能性不大于________.解析:χ2≈4.844>3.841=x0.05,这表明小概率事件发生.根据假设检验的基本原理,应该断定“是否选修文科与性别之间有关系”成立,并且这种判断出错的可能性不大于0.05.答案:0.053.(人A选择性必修第三册P132例3改编)随着国家三孩政策的放开,为了调查一线城市和非一线城市的三孩生育意愿,某机构用简单随机抽样的方法从不同地区调查了100位育龄妇女,结果如下表.由χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),得χ2=100×(45×22-20×13)265×35×58×42≈9.616.参照下表:α根据小概率值α=0.010的独立性检验,可以得到的结论是____________.答案:生育意愿与城市级别有关一、思考辨析判断正误(正确的打“√”,错误的打“×”)(1)独立性检验是检验两个分类变量是否有关的一种统计方法.( )(2)独立性检验得到的结论一定是正确的.( )(3)独立性检验的样本不同,其结论可能不同.( )(4)若事件X,Y关系越密切,则由观测数据计算得到的χ2越小.( ) 答案:(1)√(2)×(3)√(4)×二、易错纠偏1.(列联表意义不明致误)下面是2×2列联表:y 1y2合计x1a 2173x2222547合计 b 46120则表中a,b的值分别为( )A.94,72 B.52,50C.52,74 D.74,52解析:选C.因为a+21=73,所以a=52.又a+22=b,所以b=74.2.(独立性检验理解不当致误)(2022·揭阳模拟)随机询问50名大学生调查爱好某项运动是否和性别有关.利用2×2列联表计算得χ2=8.333,则下列结论正确的是( )附:α0.0100.0050.001αA.在犯错误的概率不大于0.005的前提下认为“是否爱好该项运动与性别有关”B.在犯错误的概率不大于0.005的前提下认为“是否爱好该项运动与性别无关”C.在犯错误的概率不大于0.001的前提下,认为“是否爱好该项运动与性别有关”D.在犯错误的概率不大于0.001的前提下,认为“是否爱好该项运动与性别无关”解析:选 A.因为8.333>7.879,由附表知,在犯错误的概率不大于0.005的前提下,认为“是否爱好该项运动与性别有关”.故选A.考点一分类变量与列联表(自主练透)复习指导:掌握分类变量的含义;通过实例,理解2×2列联表的统计意义.1.(多选)根据如图所示的等高堆积条形图,下列叙述正确的是( )A.吸烟患肺病的频率约为0.2B.吸烟不患肺病的频率约为0.8C.不吸烟患肺病的频率小于0.05D.不能判断吸烟与患肺病之间的关系解析:选ABC.从等高堆积条形图上可以明显地看出,吸烟患肺病的频率远远大于不吸烟患肺病的频率.A,B,C都正确,D不正确.2.(2022·湖南省永州市高三适应性考试)“直播电商”已经成为当前经济发展的新增长点,某电商平台的直播间经营化妆品和服装两大类商品,2021年前三个季度,该直播间每个季度的收入都比上一季度的收入翻了一番,其前三季度的收入情况如图所示,则( )A.该直播间第三季度总收入是第一季度总收入的3倍B.该直播间第二季度化妆品收入是第三季度化妆品收入的1 3C.该直播间第一季度化妆品收入是第三季度化妆品收入的1 6D.该直播间第三季度服装收入低于前两个季度的服装收入之和解析:选B.对于选项A,因为该直播间每个季度的收入都比上一季度的收入翻了一番,所以第三季度的总收入是第一季度的2×2=4倍,故A错误;对于选项B,设第一季度的总收入为a,则第二季度、第三季度的总收入分别为2a,4a,第二季度的化妆品收入为2a×20%=0.4a,第三季度的化妆品收入为4a×30%=1.2a,所以第二季度化妆品收入是第三季度化妆品收入的0.4a1.2a=13,故B正确;对于选项C,第一季度的化妆品收入为a×10%=0.1a,所以第一季度化妆品收入是第三季度化妆品收入的0.1a1.2a=112,故C错误;对于选项D,第一、二季度服装收入和为a+2a-0.1a-0.4a=2.5a,第三季度服装收入为4a-1.2a=2.8a,故D错误.故选B.3.(2022·上海华师大二附中高二月考)假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其2×2列联表为XY合计y1y2x1a b a+bx2c d c+d合计a+c b+d a+b+c+d对同一样本,以下数据能说明X与Y有关的可能性最大的一组为( )A.a=5,b=4,c=3,d=2B.a=5,b=3,c=4,d=2C.a=2,b=3,c=4,d=5D.a=3,b=2,c=4,d=5解析:选D.对于同一样本,|ad-bc|越小,说明X与Y相关性越弱,而|ad-bc|越大,说明X与Y相关性越强,通过计算知,对于A、B、C都有|ad-bc|=|10-12|=2;对于选项D,有|ad-bc|=|15-8|=7,显然7>2.4.为了搞好对外宣传工作,会务组选聘了30名记者担任对外翻译工作,在下面“性别与会俄语”的2×2列联表中,a-b+d=________.性别俄语合计会俄语不会俄语男 a b 20女6 d合计1830解析:由2×2列联表的性质,可得:a=18-6=12,b=20-12=8,6+d=30-20,可得d=4,所以a-b+d=8.答案:8求解参数的方法(1)根据等高堆积条形图的高度差直接判断.(2)直接利用2×2列联表的性质,建立方程即可求参数.考点二独立性检验(多维探究)复习指导:通过对典型案例(如“肺癌与吸烟有关吗”等)的探究,了解独立性检验的基本思想、方法及初步应用.角度1 简单的独立性检验问题某校推广新课改,在两个程度接近的班进行试验,一班为新课改班级,二班为非课改班级,经过一个学期的教学后对期末考试进行分析评价,规定:总分超过550(或等于550分)为优秀,550以下为非优秀,得到以下列联表:优秀非优秀合计一班3513二班1725合计(1)请完成列联表;(2)依据小概率值α=0.01的独立性检验,能否认为推广新课改与总成绩是否优秀有关系?参考数据:α0.10.050.010.005xα2.7063.841 6.6357.879χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d).【解】(1)优秀非优秀合计一班351348二班172542合计523890 (2)零假设为H0:推广新课改与总成绩是否优秀无关.根据列联表中的数据,得到χ2=90×(35×25-13×17)248×42×52×38≈9.663>6.635=x0.01,故根据小概率值α=0.01的独立性检验,我们推断H0不成立,即认为推广新课改与总成绩是否优秀有关系,此推断犯错误的概率不大于0.01.角度2 独立性检验与统计、概率的综合问题(2022·四川雅安5月三模改编)高铁在出行方式中越来越受欢迎,某部门利用大数据随机抽取了出行人群中的100名旅客进行调查统计,得知在40岁及以下的旅客中乘坐高铁出行的占23.(1)请完成下面的2×2列联表,并依据小概率值α=0.001 的独立性检验,分析能否认为乘坐高铁出行与年龄有关;(2)为提升服务质量,该部门从这100名旅客中按年龄采用分层随机抽样的方法选取5人参加座谈会,会后再进行抽奖活动,奖品共三份,由于年龄差异,规定40岁及以下的旅客若中奖,则每人得800元,40岁以上的旅客若中奖,则每人得1 000元,设三份奖品总金额为X 元,求X 的分布列与数学期望.参考公式:χ2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),其中n =a +b +c +d .参考数据:【解】 (1)由已知可得,样本中40岁及以下乘坐高铁出行的有60×23=40(人).2×2列联表如下:零假设为H 0:乘坐高铁出行与年龄无关.由列联表中的数据计算可得χ2=100×(40×30-20×10)260×40×50×50≈16.667>10.828=x0.001.根据小概率值α=0.001的独立性检验,我们推断H0不成立,即认为乘坐高铁出行与年龄有关,此推断犯错误的概率不大于0.001.(2)采用分层随机抽样的方法,则从40岁及以下的人中抽取3人,从40岁以上的人中抽取2人.X的所有可能取值为2 400,2 600,2 800.P(X=2 400)=C33C02C35=110,P(X=2 600)=C23C12C35=35,P(X=2 800)=C13C22C35=310.故分布列如下:X 2 400 2 600 2 800P11035310E(X)=2 400×110+2 600×35+2 800×310=2 640.(1)在2×2列联表中,如果两个变量没有关系,则应满足ad-bc≈0.|ad-bc|越小,说明两个变量之间关系越弱;|ad-bc|越大,说明两个变量之间关系越强.(2)解决独立性检验的应用问题,一定要按照独立性检验的步骤得到结论.独立性检验的一般步骤:①根据样本数据制成2×2列联表;②根据公式χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)计算得到χ2的值;③比较χ2的值与临界值的大小关系,作统计推断.|跟踪训练|(2022·西藏拉萨那曲第二高级中学高三月考)某中学随机抽查了50名同学的每天课外阅读时间,得到如下统计表:(1)求这50名同学的平均阅读时长(用区间中点值代表每个人的阅读时长);(2)在阅读时长位于(40,50]的4人中任选2人,求甲同学被选中的概率;(3)进一步调查发现,语文成绩和每天的课外阅读时间有很大关系,每天的课外阅读时间多于半小时称为“阅读迷”,语文成绩达到120分视为优秀,根据每天的课外阅读时间和语文成绩是否优秀,制成一个2×2列联表:依据小概率值α=0.01的独立性检验,能否认为语文成绩是否优秀与课外阅读时间有关?参考公式:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d). 参考数据:解:(1)设这50名同学的平均阅读时长为x-min,则x-=5×4+15×10+25×14+35×18+45×450=26.6,故这50名同学的平均阅读时长为26.6 min.(2)设这4名学生中分别为甲、乙、丙、丁,从这4名学生中任取2名学生,所有的样本点有:(甲,乙),(甲,丙),(甲,丁),(乙,丙),(乙,丁),(丙,丁),共6个,其中,事件“甲同学被选中”所包含的样本点有:(甲,乙),(甲,丙),(甲,丁),因此,所求概率为P=36=12.(3)零假设为H0:语文成绩是否优秀与课外阅读时间无关.由列联表中的数据计算得χ2=50×(20×25-2×3)222×28×23×27≈31.897>6.635=x0.01,因此,根据小概率值α=0.01的独立性检验,我们推断H0不成立,即认为语文成绩是否优秀与课外阅读时间有关,此推断犯错误的概率不大于0.01.[A 基础达标]1.下面的等高条形图可以说明的问题是( )A.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响是绝对不同的B.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响没有什么不同C.此等高条形图看不出两种手术有什么不同的地方D.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有100%的把握解析:选D.由等高条形图可知“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的频率不同,所以“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有100%的把握,所以选项D正确,故选D.2.某学校食堂对高三学生偏爱蔬菜还是肉类与性别的关系进行了一次调查,根据独立性检验原理,处理所得数据之后发现,得到“偏爱蔬菜还是肉类与性别有关”这个结论犯错误的概率大于0.001,而不大于0.01,则χ2的值可能为( ) 附表:A.3.206B.6.561C.7.879D.11.028解析:选 C.根据题意得χ2的取值范围为[6.635,10.828),因此χ2的值可能为7.879.故选C.3.(多选)假设有两个分类变量X和Y,其2×2列联表如下表所示:在犯错误的概率不超过0.05的前提下,下面哪个选项可以认为变量X,Y有关( )A.a=10 B.a=12C.a=8 D.a=9解析:选ACD.根据列联表知,aa+40与30-a60-a的差距越小,则越无法认为变量X,Y有关联,分析四个选项,B选项中,a=12时,aa+40与30-a60-a的差距最小,且不满足犯错误的概率不超过0.05的条件,而其他选项均满足.4.小波同学为了验证谚语“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如下2×2列联表,并计算得到χ2≈19.05,下列小波对地区A 天气判断不正确的是( )附表:A.夜晚下雨的概率约为1 2B.未出现“日落云里走”夜晚下雨的概率约为5 14C.做出“‘日落云里走’是否出现与当晚是否下雨有关”这一推断犯错误的概率不大于0.001D.出现“日落云里走”,有99.9%的把握认为夜晚会下雨解析:选D.据列联表,100天中有50天下雨,50天未下雨,因此下雨的概率约为50 100=12,A正确;同样,未出现“日落云里走”夜晚下雨的概率约为2525+45=514,B正确;因为χ2≈19.05>10.828=x0.001,所以做出“‘日落云里走’是否出现与当晚是否下雨有关”这一推断犯错误的概率不大于0.001,C正确;有关只是说可能性,不代表一定下雨,D错误.故选D.5.(多选)某俱乐部为了解会员对运动场所的满意程度,随机调查了50名会员,每位会员对俱乐部提供的场所给出满意或不满意的评价,得到如图所示的列联表,经计算χ2≈5.059,则可以推断出( )附:A.该俱乐部的男性会员对运动场所满意的概率的估计值为2 3B.调查结果显示,该俱乐部的男性会员比女性会员对俱乐部的场所更满意C.做出“男性会员、女性会员对运动场所的评价有差异”这一推断犯错误的概率不大于0.05D.做出“男性会员、女性会员对运动场所的评价有差异”这一推断犯错误的概率不大于0.01解析:选ABC.对于选项A,该俱乐部男性会员对运动场所满意的概率的估计值为18 27=23,故A正确;对于选项B,该俱乐部女性会员对运动场所满意的概率的估计值为823,而23=4669>823=2469,故B正确;因为χ2≈5.059>3.841=x0.05,所以依据小概率值α=0.05的独立性检验,我们认为男性会员、女性会员对运动场所的评价有差异,此推断犯错误的概率不大于0.05,故C正确,D错误.6.(多选)某机构在研究性别与是否爱好拳击运动的关系中,通过收集数据得到如下2×2列联表.经计算得χ2=100×(35×28-15×22)250×50×57×43≈6.895.之后又对被研究者的身高进行了统计,得到男、女身高分别近似服从正态分布N(175,16)和N(164,9),则下列选项中正确的是( )A.“爱好拳击运动与性别有关”,这个结论犯错误的概率不超过0.01B.在100个男生中,至少有一个人爱好打拳击C.男生身高的平均数为175,男生身高的标准差为16D.女生身高的平均数为164,女生身高的标准差为3解析:选AD.χ2≈6.895>6.635=x0.01,A对;显然B错;男生身高的标准差为4,C 错;显然D对,故选AD.7.(2022·赣中南五校联考)心理学家分析发现视觉和空间想象能力与性别有关,某数学兴趣小组为了验证这个结论,从所在学校中按分层随机抽样的方法抽取50名同学(男30,女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)根据上述数据,推断视觉和空间想象能力与性别有关系,则这种推断犯错误的概率不超过________.附表:解析:由列联表计算得χ2=50×(22×12-8×8)2≈5.556>3.841=x0.05,所以推断犯错误的概率不超过0.05.30×20×20×30答案:0.058.(2022·黑龙江模拟)为研究某新药的疗效,给100名患者服用此药,跟踪调查后得下表中的数据:性别疗效合计无效有效男性患者153550女性患者64450合计2179100设H0:服用此药的效果与患者的性别无关,则χ2≈________(小数点后保留3位有效数字),从而得出结论;服用此药的效果与患者的性别有关,这种判断出错的概率不大于________.解析:由公式计算得χ2=100×(15×44-6×35)221×79×50×50≈4.882,因为χ2>3.841=x0.05根据α=0.05的独立性检验,分析服用此药的效果与患者的性别有关,判断出错的概率不大于0.05.答案:4.882 0.059.(2022·山东省济南市高二期末)为了研究某种疾病的治愈率,某医院对100名患者中的一部分患者采用了外科疗法,另一部分患者采用了化学疗法,并根据两种治疗方法的治愈情况绘制了等高堆积条形图,如下:(1)根据图表完善以下关于治疗方法和治愈情况的2×2列联表;疗法疗效合计未治愈治愈外科疗法化学疗法18合计100(2)依据小概率值α=0.05的独立性检验,分析此种疾病治愈率是否与治疗方法有关.附:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d).(如需计算χ2,结果精确到0.001)α0.10.050.010.0050.001xα2.7063.841 6.6357.87910.828解:(1)根据等高条形图,采用化学疗法的治愈率为30%,由列联表得化学疗法治愈的人数为18人,故采用化学疗法的人共有18÷30%=60人,采用外科疗法的有40人,其中治愈的有40×50%=20人.所以列联表如下表:疗法疗效合计未治愈治愈外科疗法202040化学疗法421860合计6238100 (2)零假设为H0:设此种疾病治愈率与治疗方法无关.则根据列联表中的数据计算χ2=100×(20×18-42×20)262×38×60×40=2 400589≈4.075>3.841=x0.05,所以依据小概率值α=0.05的独立性检验,我们推断H0不成立,即认为此种疾病治愈率与治疗方法有关,此推断犯错误的概率不大于0.05.10.(2022·福州市质量检测)某部门研究成果认为,房租支出超过月收入13的租户“幸福指数”低,房租支出不超过月收入13的租户“幸福指数”高.为了了解甲、乙两小区租户的幸福指数高低,随机抽取甲、乙两小区的租户各100户进行调查.甲小区租户的月收入以[0,3),[3,6),[6,9),[9,12),[12,15](单位:千元)分组的频率分布直方图如图所示.乙小区租户的月收入(单位:千元)的频数分布表如下:(1)设甲、乙两小区租户的月收入相互独立,记M表示事件“甲小区租户的月收入低于6千元,乙小区租户的月收入不低于6千元”,把频率视为概率,求M的概率;(2)利用频率分布直方图,求所抽取的甲小区100户租户的月收入的中位数;(3)若甲、乙两小区每户的月租费分别为2千元、1千元.请根据条件完成下面的2×2列联表,并依据小概率值α=0.001的独立性检验,分析幸福指数与租住的小区是否有关.附:临界值表参考公式:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d).解:(1)记A表示事件“甲小区租户的月收入低于6千元”,记B表示事件“乙小区租户的月收入不低于6千元”,甲小区租户的月收入低于6千元的频率为(0.060+0.160)×3=0.66,故P(A)的估计值为0.66;乙小区租户的月收入不低于6千元的频率为24+9+2100=0.35,故P(B)的估计值为0.35.因为甲、乙两小区租户的月收入相互独立,所以事件M的概率的估计值为P(M)=P(A)P(B)=0.66×0.35=0.231.(2)设甲小区所抽取的100户租户的月收入的中位数为t,则0.060×3+(t-3)×0.160=0.5,解得t=5.(3)零假设为H0:幸福指数与租住的小区无关.根据2×2列联表中的数据,得到χ2=200×(66×62-34×38)2100×100×104×96≈15.705>10.828=x0.001,依据小概率值α=0.001的独立性检验,我们认为H0不成立,即认为幸福指数与租住的小区有关,此推断犯错误的概率不大于0.001.[B 综合应用]11.(多选)(2022·梅州高二模拟)针对时下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的45,女生喜欢抖音的人数占女生人数35,若做出“是否喜欢抖音和性别有关”这一推断犯错误的概率不大于0.05,则调查人数中男生的人数可能为( )附表:附:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d).A.25 B.35C.45D.60解析:选CD.设男生可能有x人,依题意得女生有x人,可得2×2列联表如下:若做出“是否喜欢抖音和性别有关”这一推断犯错误的概率不大于0.05,则χ2≥3.841=x0.05,即χ2=2x·⎝⎛⎭⎪⎫45x·25x-35x·15x275x·35x·x·x=221x≥3.841,解得x≥40.330 5,由题意知x>0,且x是5的整数倍,所以45和60都满足题意.故选CD.12.(2022·青岛市统一质量检测)某驾驶员培训学校为对比了解“科目二”的培训过程采用大密度集中培训与周末分散培训两种方式的效果,调查了105名学员,统计结果为:接受大密度集中培训的55名学员中有45名学员一次考试通过,接受周末分散培训的学员一次考试通过的有30名.根据统计结果,认为“能否一次考试通过与是否集中培训有关”犯错误的概率不超过________.附:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d).解析:由题意作出2×2列联表:则χ2=105×(45×20-10×30)2 55×50×75×30≈6.109>5.024=x0.025,所以认为“能否一次考试通过与是否集中培训有关”犯错误的概率不超过0.025.答案:0.025[C 素养提升]13.(2020·新高考卷Ⅱ改编)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和SO2浓度(单位:μg/m3),得下表:(1)估计事件“该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150”的概率;(2)根据所给数据,完成下面的2×2列联表:(3)根据(2)中的列联表,并依据小概率值α=0.01的独立性检验,能否认为该市一天空气中PM2.5浓度与SO2浓度有关?附:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),解:(1)根据抽查数据,该市100天空气中的PM2.5浓度不超过75,且SO2浓度不超过150的天数为32+18+6+8 =64,因此,该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150的概率的估计值为64100=0.64.(2)根据抽查数据,可得2×2列联表:(3)零假设为H0:该市一天空气中PM2.5浓度与SO2浓度无关.根据(2)的列联表得χ2=100×(64×10-16×10)280×20×74×26≈7.484>6.635=x0.01.依据小概率值α=0.01的独立性检验,我们推断H0不成立,即认为该市一天空气中PM2.5浓度与SO2浓度有关,此推断犯错误的概率不大于0.01.。
苏教版高中数学选修2-3§2.3 独立性.docx

§2.3 独立性2.3.1 条件概率课时目标1.在具体情境下,了解条件概率的概念.2.利用条件概率解一些简单的实际问题.1.条件概率:一般地,对于两个事件A 和B ,在________________________下事件A 发生的概率,称为______________________________________,记为P (A |B ).2.公式P (A |B )=____________.一、填空题1.已知P (AB )=310,P (A )=35,则P (B |A )=______.2.把一枚硬币任意抛掷两次,事件A ={第一次出现正面},事件B ={第二次出现正面},则P (B |A )=________.3.一个袋中装有6个红球和4个白球(这10个球各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第二次摸出红球的概率为________.4.设A ,B 是两个事件,且B 发生则A 必定发生,0<P (A )<1,0<P (B )<1,则下列各式中正确的是________.(填序号)①P (A +B )=P (A ); ②P (B |A )=P (B ); ③P (A |B )=P (A ); ④P (AB )=P (B ).5.某种电子元件用满3 000小时不坏的概率为34,用满8 000小时不坏的概率为12.现有一只此种电子元件,已经用满3 000小时不坏,还能用满8 000小时的概率是________.6.100件产品中有5件次品,不放回地抽取两次,每次抽1件,已知第一次抽出的是次品,则第2次抽出正品的概率为________.7.一个家庭中有两个小孩,假定生男、生女是等可能的,已知这个家庭有一个小孩是女孩,问这时另一个小孩是男孩的概率是________.8.从一副不含大小王的52张扑克牌中不放回地抽取2次,每次抽1张,已知第1次抽到A,第2次也抽到A的概率为________.二、解答题9.某班从6名班干部中(其中男生4人,女生2人)选3人参加学校的义务劳动,在男生甲被选中的情况下,求女生乙也被选中的概率.10.现有6个节目准备参加比赛,其中4个舞蹈节目,2个语言类节目,如果不放回地依次抽取2个节目,求(1)第1次抽到舞蹈节目的概率;(2)第1次和第2次都抽到舞蹈节目的概率;(3)在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率.能力提升11.根据历年气象资料统计,某地四月份刮东风的概率是830,既刮东风又下雨的概率是730.问该地四月份刮东风时下雨的概率是________.12.1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问从2号箱取出红球的概率是多少?1.所谓条件概率,是当试验结果的一部分信息已知(即在原随机试验的条件下,再加上一定的条件),求另一事件在此条件下的概率.2.已知事件A 发生,在此条件下B 发生,相当于AB 发生,求P (B |A )时,除按公式外,还可把A 看做新的基本事件空间来计算B 发生的概率.2.3 独立性 2.3.1 条件概率答案知识梳理1.已知事件B 发生的条件 事件B 发生的条件下事件A 的条件概率 2.P (AB )P (B ) 作业设计 1.12解析 P (B |A )=P (AB )P (A )=31035=12.2.12解析 P (AB )=14,P (A )=12,∴P (B |A )=P (AB )P (A )=12.3.59 解析 设第一次摸出红球为事件A ,第二次摸出红球为事件B ,则P (A )=35,P (AB )=C 26C 210=13.∴P (B |A )=P (AB )P (A )=59. 4.①④ 5.23解析 记事件A :“用满3 000小时不坏”,P (A )=34;记事件B :“用满8 000小时不坏”,P (B )=12.因为B ⊂A ,所以P (AB )=P (B )=12,则P (B |A )=P (AB )P (A )=1234=12×43=23.6.95997.23解析 一个家庭有两个小孩子只有4种可能:{两个都是男孩子},{第一个是男孩子,第二个是女孩子},{第一个是女孩子,第二个是男孩子},{两个都是女孩子},由题意知,这4个事件是等可能的.设基本事件空间为Ω,事件A 表示“其中一个是女孩”,事件B 表示“其中一个是男孩”,则Ω为{(男,男),(男,女),(女,男),(女,女)},A 为{(男,女),(女,男),(女,女)},B 为{(男,男),(男,女),(女,男)},AB 为{(男,女),(女,男)}.所以P (B |A )=P (AB )P (A )=2434=23.8.1179.解 记“男生甲被选中”为事件A ,“女生乙被选中”为事件B .P (A )=C 25C 36=1020=12,P (BA )=C 14C 36=15,P (B |A )=P (BA )P (A )=25.10.解 设第1次抽到舞蹈节目为事件A ,第2次抽到舞蹈节目为事件B ,则第1次和第2次都抽到舞蹈节目为事件AB .(1)从6个节目中不放回地依次抽取2个的事件数为n (Ω)=A 26=30,根据分步乘法计数原理n (A )=A 14A 15=20,于是P (A )=n (A )n (Ω)=2030=23.(2)因为n (AB )=A 24=12,于是P (AB )=n (AB )n (Ω)=1230=25.(3)方法一 由(1)(2)可得,在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率为P (B |A )=P (AB )P (A )=2523=35.方法二 因为n (AB )=12,n (A )=20,所以P (B |A )=n (AB )n (A )=1220=35.11.78解析 记“某地四月份刮东风”为事件A ,“某地四月份下雨”为事件B ,则P (A )=830,P (AB )=730,所以P (B |A )=P (AB )P (A )=78.12.解 记事件A :最后从2号箱中取出的是红球;事件B :从1号箱中取出的是红球.则P (B )=42+4=23,P (B )=1-P (B )=13,P (A |B )=3+18+1=49,P (A |B )=38+1=13,从而P (A )=P (AB )+P (A B )=P (A |B )P (B )+P (A |B )P (B )=49×23+13×13=1127.。
高三数学事件的独立性(新201907)

一般地,若有两个事件A和B,在已 知事件B发生的条件下考虑事件A发生 的概率,则称此事件为B已发生的条件 下A的条件概率,记作:P(A︱B)。
二)条ห้องสมุดไป่ตู้概率的计算
P( A|B)= P(AB)
P (B)
P(AB)=P( A|B)P(B)
问:抛掷一枚质地均匀的硬币两次。
在第一次出现正面向上的条件下, 第二次出现正面向上的概率是多少?
;英国海外置业 英国房产置业 英国置业投资 / 曼城购房 英国曼城购房 曼彻斯特购房 ;
赐以衣服 [23] 就应该布衣素食 建筑面积一千一百平方米 又修建了空心敌台 又诏得乘小马出入东 西台 深合上旨 上目送之 垂发戴白 为野人所攻 134.字子房 尤其是话中对古今成败的揭示以及“无道秦” “助桀为虐”等苛刻字眼 李世勣又派郭孝恪劝降郑国荣州刺史魏陆 李峤 晋王 欲纳陈主宠姬张丽华 上幸秦王俊第 ”刘秀大笑 王梁 楚地九郡 但施展谋略的前提则是要有善于纳谏的明主 后代却成最牛世族 争用威力 51. [74] 归顺李唐 与先王之间的相知相得 然如张良之烧栈道而不以为怪 专任继光 以公的德才平定天下 …庚戌 平隋之乱 [27] 韩兆琦 余樟华 校点.长沙:岳麓书社 隋遣齐郡通守张须陀率师二万讨之 沿海筑墙 愿为臣妾 .国学导航[引用日期2013-11-20] 汉军粮草匮乏 ” 50.关播 ?他对唐朝的政局也有过重要的影响 字永霸 为何年近古稀惨被隋炀帝处死 大破横屿倭寇 扶馀丰流岭南 得胜兵万馀人 遂拔之 两晋南北朝 还派人与秦吏一起巡行各地 兼纳言 若之何 《后汉书·邓禹传》:时任使诸将 遇薛延陀阿波设之兵于东境 《后汉书·张皓传》:阳嘉元年 功定华夷 庞同善 契苾何力等一并受李勣调遣 徙黔州;连百万之众 追削李敬业祖考官爵 陛下强迫他去 齐映 ?当清道以待乘
(江苏专用)高考数学总复习第十五章第二节独立性与二项分布课件苏教版

教 1.条件概率及其性质 材 2.相互独立事件 研 读 3.独立重复试验与二项分布
考 考点一 条件概率 点 突 考点二 相互独立事件的概率 破 考点三 n次独立重复试验与二项分布
教材研读
1.条件概率及其性质
(1)定义 对于任何两个事件A和B,在已知事件A发生的条件下,事件B发生的概率 叫做① 条件概率 ,用符号② P(B|A) 来表示,其公式为P(B|A)=
3 3
0 6
5
=6
10
,P(AB)=3 6
5
=1 8
,所以P(B|A)=P
(
A
B
=
)
P (A)
18 5
1
=3
.故
6
向上的点数不相同时,其中有一个的点数为4的概率是 1 .
3
2.(2018江苏南京多校高三段考)某地区有云龙山,户部山,子房山和九里
山四大名山,一位游客来该地区游览,已知该游客游览云龙山的概率为
3.独立重复试验与二项分布
(1)独立重复试验是指在相同条件下可重复进行的,各次之间相互独立
的一种试验,在这种试验中每一次试验只有 两 种结果,即要么发
生,要么不发生,且任何一次试验中发生的概率都是一样的.
(2)在n次独立重复试验中,用X表示事件A发生的次数,设每次试验中事
件A发生的概率为p,则P(X=k)=
C knpk(1-p)n-k(k=0,1,2,…,n) ,此时称随
机变量X服从 二项分布 ,记为 X~B(n,p) ,并称p为成功概率.
1.(教材习题改编)抛掷两个质地均匀的骰子各1次. (1)向上的点数之和为7时,其中有一个的点数是2的概率是多少? (2)向上的点数不相同时,其中有一个的点数为4的概率是多少?
高中数学(人教B版)选择性必修二:独立性与条件概率的关系【精品课件】

16 + 15 = 31.
所以抽到的人有自主创业打算的
1
概率为P A = .
5
例1 (2)求抽到的人是女生的概率;
解:记B为“抽到的人是女生”.
由题意可知,所有学生人数为16 + 15 +
64 + 60 = 155,女生人数为15 + 60 = 75.
解:(1)甲、乙、丙都通过可用表示,因此所
求概率为
=
= 0.8 × 0.9 × 0.7
= 0.504
ҧ
解:(2)甲、乙通过且丙未通过可用表示,因
此所求概率为
ҧ = ҧ
= [1 − ()]
= 0.8 × 0.9 × (1 − 0.7)
= ()
例1 已知某大学数学专业二年级的学生中,是否
有自主创业打算的情况如下表所示.
有自主创业打算
无自主创业打算
男生/人
16
64
从这些学生中随机抽取一人:
女生/人
15
60
例1(1)求抽到的人有自主创业打算的概率;
解:记A为“抽到的人有自主创业打算”.
由题意可知,所有学生人数为16 + 15 +
关至少有一个闭合.
分析:
用 , ,分别表示甲、乙、丙能正常工作,
表示系统能正常工作.
由题意知,系统能正常工作时,可分为三种
互斥的情况:
甲、乙、丙都正常工作,即;
ത ;
甲、丙正常工作,且乙不正常工作,即
甲、乙正常工作,且丙不正常工作,即.ҧ
ത ∪ .ҧ
因此 = ∪
高中数学2.3独立性教案2苏教版选修2—3

2.3 独立性 2.3.2 事件的独立性教学目标(1)理解两个事件相互独立的概念;(2)能进行一些与事件独立有关的概率的计算.教学重点,难点:理解事件的独立性,会求一些简单问题的概率. 教学过程一.问题情境1.情境:抛掷一枚质地均匀的硬币两次.在第一次出现正面向上的条件下,第二次出现正面向上的概率是多少?2.问题:第一次出现正面向上的条件,对第二次出现正面向上的概率是否产生影响. 二.学生活动设B 表示事件“第一次正面向上”, A 表示事件“第二次正面向上”,由古典概型知()12P A =,()12P B =,()14P AB =, 所以()()()12P AB P A B P B ==.即()()P A P A B =,这说明事件B 的发生不影响事件A 发生的概率. 三.建构数学1.两个事件的独立性一般地,若事件A ,B 满足()()P A B P A =,则称事件A ,B 独立. 当A ,B 独立时,若()0P A >,因为()()()()P AB P A B P A P B ==,所以 ()()()P AB P A P B =,反过来()()()()P AB P B A P B P A ==,即B ,A 也独立.这说明A 与B 独立是相互的,此时事件A 和B 同时发生的概率等于事件A 发生的概率与事件B 发生的概率之积,即()()()P AB P A P B =.(*) 若我们认为任何事件与必然事件相独立,任何事件与不可能事件相独立,那么两个事件A ,B 相互独立的充要条件是()()()P AB P A P B =.今后我们将遵循此约定.事实上,若B φ=,则()0P B =,同时就有()0P AB =,此时不论A 是什么事件,都有(*)式成立,亦即任何事件都与φ独立.同理任何事件也与必然事件Ω独立. 2. 个事件的独立性可以推广到(2)n n >个事件的独立性,且若事件12,,,n A A A 相互独立,则这n 个事件同时发生的概率()()()()1212n n P A A A P A P A P A = .3. 立与互斥回顾:不可能同时发生的两个事件叫做互斥事件;如果两个互斥事件有一个发 时另一个必不发生,这样的两个互斥事件叫对立事件. 区别:互斥事件和相互独立事件是两个不同概念: 两个事件互斥是指这两个事件不可能同时发生;两个事件相互独立是指一个事件的发生与否对另一个事件发生的概率没有影响.事实上,当()0P A >,()0P B >时,若,A B 互斥,则AB φ=,从而()0P AB =,但()()0P A P B >,因而等式()()()P AB P A P B =不成立,即互斥未必独立.若,A B 独立,则()()()0P AB P A P B =>,从而,A B 不互斥(否则,()0P AB =,导致矛盾).例如从一副扑克牌(52张)中任抽一张,设A =“抽得老K”B =“抽的红牌”,C =“抽到J”,判断下列事件是否相互独立?是否互斥,是否对立? ①A 与B ; ②A 与C 4.讨论研究四.数学运用 1.例题:例1.求证:若事件A 与B 相互独立,则事件A 与B 也相互独立.证:因为()()()P AB P AB P A += 所以()()()P AB P A P AB =-. 因为A ,B 相互独立,所以()()()P AB P A P B =,图2-3-2于是()()()()P AB P A P A P B =-()()()1P A P B =-()()P A P B =.因此,事件A 与B 相互独立.结论:若事件A 与B 独立则A 与B ,B 与A ,A 与 B 都独立.例2.如图232--,用,,X Y Z 三类不同的元 件连接成系统N .当元件,,X Y Z 都正常工作 时,系统N 正常工作.已知元件,,X Y Z 正常工作的概率依次为0.80,0.90,0.90,求系统N 正常工作的概率P .解:若将元件,,X Y Z 正常工作分别记为事件,,A B C ,则系统N 正常工作为事件ABC .根据题意,有()0.80P A =,()0.90P B =,()0.90P C =. 因为事件,,A B C 是相互独立的,所以系统N 正常工作的概率()P P ABC = ()()()P A P B P C =0.800.900.90=⨯⨯ 0.648=,即系统N 正常工作的概率为0.648P =.例3.加工某一零件共需两道工序,若第一、二道工序的不合格品率分别为3﹪,5﹪ ,假定各道工序是互不影响的,问:加工出来的零件是不合格品的概率是多少? 分析:解决问题的过程可用流程图表示:(图234--)图2-3-4解法 1 设A 表示事件“加工出来的零件是不合格品”,12,A A 分别表示事件“第一道工序出现不合格品”和“第二道工序出现不合格品”.因为依常理,第一道工序为不合格品,则该产品为不合格品,所以112A A A A =+,因为各道工序互不影响,所以()()112P A P A A A =+()()112P A P A A =+ ()()()112P A P A P A =+ 0.030.970.05=+⨯0.0785=.解法2 因为12A A A =,所以()()12P A P A A = ()()12P A P A =()()1211P A P A =--⎡⎤⎡⎤⎣⎦⎣⎦()()10.0310.05=--0.9215=,()()110.92150.0785P A P A =-=-=.答:加工出来的零件是不合格品的概率是7.85﹪.思考:如果A 和B 是两个相互独立的事件,那么()()1P A P B -表示什么? 2.练习:第59页练习第1,2,3题.五.回顾小结:1.当A ,B 独立时,B ,A 也是独立的,即A 与B 独立是相互的.2.当A ,B 独立时()()P A B P A =;()()P B A P B =;或()()()P AB P A P B =或A事件的发生不影响事件B的发生概率六.课外作业:第64页第1,4,9题.。
(2019版)高三数学事件的独立性

一般地,若有两个事件A和B,在已 知事件B发生的条件下考虑事件A发生 的概率,则称此事件为B已发生的条件 下A的条件概率,记作:P(A︱B)。
ቤተ መጻሕፍቲ ባይዱ二)条件概率的计算
P( A|B)= P(AB)
P (B)
P(AB)=P( A|B)P(B)
问:抛掷一枚质地均匀的硬币两次。
在第一次出现正面向上的条件下, 第二次出现正面向上的概率是多少?
;3000ok http://www.3000ok.es 3000ok ;
明之戚继光 后平定魏国 白起用兵善于分析敌我形势 在内政军事上都有极高的成就 秦军伤亡惨重 ”起默然良久 史天泽被贬官 秦昭襄王二十八年(前280年) 至甘泉宫猎 以功授开府 颉利乘千里马将走投吐谷浑 赐死于杜邮 封为齐王 则甚害田者;142.无不洞识 萧复--?你可知道 绕到赵军背后 进到陇县西 亡国之臣不敢语政 ”夫然后而知骠骑将军 大将军之微也 ” 西汉 如今将军却背水为阵 会宪宗崩 大王当王关中 转兵部尚书 漂母饭信图 ?使驰说之士无所开其口 前者是中国战争史中以步兵大兵团全歼骑兵大兵团的典型战例 羊马满大野 弓藏狡兔尽 又 怕他不肯就范 信未起 齐国乐安人 80.应侯受知 为古代兵学的代表著作 .六根在人 ”赵王答应他的要求 百道追匈奴 门口有士兵来请大人去军营监军 赐实封食邑四百户 ” 广饶说 惠民说 博兴说 临淄说并存 ” 功成享天禄 忽都马丁算滩来归降 百战百胜者 孙武 不可长途追击 大 破赵军 《事林广记后集》 尽之于长平之下 诸将咸言春草未生 杨恭仁--?历史作家 他们判定:如果唐兵不倾国而来 郭侃大败之 有提七万之众而天下莫当者 历史大学堂 平阳君说:“还是不要接受吧 民族族群 王以为令尹 郭侃大半生跟随蒙古军队西征 1/2 作为中国历史上继孙武 吴 起之后又一个杰
苏教版高中数学选修2-32.3 独立性

2.3 独立性2.3.1 条件概率双基达标(限时15分钟)1.把一枚硬币任意抛掷两次,记第一次出现正面为事件A,第二次出现正面为事件B,则P(B|A)等于________.解析事件A与事件B相互独立,故P(B|A)=P(B)=1 2 .答案1 22.已知P(AB)=310,P(A)=35,则P(B|A)=________.解析P(B|A)=P(AB)P(A)=31035=12.答案1 23.设A、B是两个事件,0<P(A)<1,P(B|A)=1.则下列结论:①P(AB)=0;②P(A+B)=P(A);③P(A)=P(B);④P(A)=P(B).其中正确的是________.解析由P(B|A)=1,得P(B|A)=0,即P(AB)P(A)=0,所以P(AB)=0.答案①4.一个袋中装有6个红球和4个白球(这10个球各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第二次摸出红球的概率为________.解析设第一次摸出红球为事件A,第二次摸出红球为事件B,则P(A)=35,P(AB)=C26C210=13.∴P(B|A)=P(AB)P(A)=59.答案5 95.6位同学参加百米短跑初赛,赛场共有6条跑道,已知甲同学排在第一跑道,则乙同学在第二跑道的概率为________.解析甲排在第一跑道,其他5位同学共有A55种排法,乙排在第二跑道共有A4 4种排法,所以P=A44A55=15.答案1 56.某种动物由出生算起活到20岁的概率为0.8,活到25岁的概率为0.4,现有一个20岁的动物,求它能活到25岁的概率.解设A=“能活到20岁”,B=“能活到25岁”,则P(A)=0.8,P(B)=0.4.而所求概率为P(B|A),由于B⊆A,故P(AB)=P(B),所以P(B|A)=P(AB)P(A)=P(B)P(A)=0.40.8=0.5,所以这个动物能活到25岁的概率为0.5.综合提高(限时30分钟)7.抛掷两颗均匀的骰子,已知它们的点数不同,则至少有一颗是6点的概率为________.解析事件A为至少有一颗是6点,事件B为两颗骰子点数不同,则n(B)=6×5=30,n(A∩B)=10,P(A|B)=1030=13.答案1 38.一个家庭中有两个小孩,假定生男,生女是等可能的.已知这个家庭有一个是女孩,问这时另一个小孩是男孩的概率是________.解析一个家庭的两个小孩只有4种可能{两个都是男孩},{第一个是男孩,第二个是女孩},{第一个是女孩,第二个是男孩},{两个都是女孩},由题意知,这4个事件是等可能的.设基本事件空间为Ω,A=“其中一个是女孩”,B=“其中一个是男孩”,则Ω={(男,男),(男,女),(女,男),(女,女)},A={(男,女),(女,男),(女,女)},B={(男,男),(男,女),(女,男)},AB={(男,女),(女,男)},∴P(B|A)=P(AB)P(A)=2434=23.答案2 39.已知某种产品的合格率是95%,合格品中的一级品率是20%,则这种产品的一级品率为________.解析A=“产品为合格品”,B=“产品为一级品”,P(B)=P(AB)=P(B|A)P(A)=0.2×0.95=0.19.所以这种产品的一级品率为19%.答案19%10.某种电子元件用满3000小时不坏的概率为34,用满8000小时不坏的概率为12.现有一只此种电子元件,已经用满3000小时不坏,还能用满8000小时的概率是________.解析记事件A:“用满3000小时不坏”,P(A)=3 4;记事件B:“用满8000小时不坏”,P(B)=12.因为B⊂A,所以P(AB)=P(B)=12,则P(B|A)=P(AB)P(A)=1234=12×43=23.答案2 311.盒子里装有16只球,其中6只是玻璃球,另外10只是木质球.而玻璃球中有2只是红色的,4只是蓝色的;木质球中有3只是红色的,7只是蓝色的,现从中任取一只球,如果已知取到的是蓝色的球,求这个球是玻璃球的概率.解设A表示“任取一球,是玻璃球”,B表示“任取一球,是蓝色的球”,则AB表示“任取一球是蓝色玻璃球”.P(B)=1116,P(AB)=416,P(A|B)=P(AB)P(B)=411.12.抛掷红、蓝两颗骰子,设事件A为“蓝色骰子的点数为3或6”,事件B为“两颗骰子的点数之和大于8”.(1)求P(A),P(B),P(AB);(2)当已知蓝色骰子的点数为3或6时,求两颗骰子的点数之和大于8的概率.解(1)①P(A)=26=13.②∵两个骰子的点数之和共有36个等可能的结果,点数之和大于8的结果共有10个.∴P(B)=1036=518.③当蓝色骰子的点数为3或6时,两颗骰子的点数之和大于8的结果有5个,故P(AB)=5 36 .(2)由(1)知P(B|A)=P(AB)P(A)=53613=512.13.(创新拓展)1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问从2号箱取出红球的概率是多少?解记事件A={从2号箱中取出的是红球},事件B={从1号箱中取出的是红球}.P(B)=46=23,P(B)=1-P(B)=1 3 .P(A|B)=49,P(A|B)=39=13.从而P(A)=P(A B)+P(AB)=49×23+13×13=1127.即从2号箱取出红球的概率是11 27 .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
独立性一、选择题1. 若事件E 与F 相互独立,且()()14P E P F ==,则()P E F I 的值等于 (A )0 (B )116 (C )14 (D )12 2. 在独立性检验中,统计量0k 有两个临界值:3.841和6.635,当随机变量2K 的观测值3.841k >时,有95%的把握说明两个事件有关,当 6.635k >时,有99%的把握说明两个事件有关,当 3.841k ≤时,认为两个事件无关。
在一项打鼾与患心脏病的调查中,共调查了2000人,经计算20.87k ≈,根据这一数据分析,认为打鼾与患心脏病之间A .约有95%的打鼾患者患心脏病B .有95%的打鼾者患心脏病C .约有99%的打鼾者患心脏病D .有99%的我把认为打鼾与患心脏有关3. 已知某运动员每次投篮命中的概率低于40%。
现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果。
经随机模拟产生了20组随机数:907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 据此估计,该运动员三次投篮恰有两次命中的概率为A .0.35B 0.25C 0.20D 0.154. 已知某人每次投篮投中的概率为p ,各次投篮结果互不影响,直至进行第n 次投篮,才有r (1≤r ≤n )次投中的概率为( )A 、r n r r n )p (p C --1 B 、r n r r n )p (p C -1-1--1 C 、r n r )p (p --1 D 、r n r r n )p (p C -1-1-1--15. 甲、乙、丙三位同学上课后独立完成5道自我检测题,甲及格概率为,乙及格概率为,丙及格概率为,则三人中至少有一人及格的概率为( )A.B. C.D.6.明天上午李明要参加奥运志愿者活动,为了准时起床,他用甲、乙两个闹钟叫醒自己,假设甲闹钟准时响的概率是0.80,乙闹钟准时响的概率是0.90,则两个闹钟至少有一准时响的概率是.7.某一批花生种子,如果每1粒发芽的概率为那么播下4粒种子恰有2粒发芽的概率是A. B.C.D.8. 位于坐标原点的一个质点P按下述规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是.质点P 移动5次后位于点的概率为(A)(B)(C)(D)9. 一台X型号的自动机床在一小时内不需要工人照看的概率为0.8000,有四台这种型号的自动机床各自独立工作,则一小时内至多有2台机床需要工人照看的概率是(A)0.1536 (B)0.1808 (C)0.5632 (D)0.972810.甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜.根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛甲获胜的概率是(A1 0.216 (B)0.36 (C)0.432 (D)0.648二、填空题11. 某单位要在甲、乙、丙、丁4人中安排2人分别担任周六、周日的值班任务(每人被安排是等可能的,每天只安排一人).其中甲、乙两人都被安排的概率是__ _ ____ _ ___.12. 已知某人投篮的命中率为34,则此人投篮4次,至少命中3次的概率是。
13.有三台车床,1小时内不需要工人照管的概率分别为0.9、0.8、0.7,则在1小时内至少有1台需要工人照管的概率为。
14.某篮球运动员在三分线投球的命中率是,他投球10次,恰好投进3个球的概率为.(用数值作答)三、解答题15.某公司招聘员工,指定三门考试课程,有两种考试方案.方案一:考试三门课程,至少有两门及格为考试通过;方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.假设某应聘者对三门指定课程考试及格的概率分别是,且三门课程考试是否及格相互之间没有影响.(Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率;(Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小.(说明理由)16.某安全生产监督部门对5家小型煤矿进行安全检查(简称安检), 若安检不合格, 则必须整改. 若整改后经复查仍不合格, 则强制关闭. 设每家煤矿安检是否合格是相互独立的, 且每家煤矿整改前合格的概率是, 整改后安检合格的概率是,计算(结果精确到);(Ⅰ) 恰好有两家煤矿必须整改的概率;(Ⅱ) 平均有多少家煤矿必须整改;(Ⅲ) 至少关闭一家煤矿的概率 .17.某安全生产监督部门对5家小型煤矿进行安全检查(简称安检). 若安检不合格,则必须整改. 若整改后经复查仍不合格,则强制关闭. 设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5,整改后安检合格的概率是0.8,计算(结果精确到0.01):(Ⅰ)恰好有两家煤矿必须整改的概率;(Ⅱ)某煤矿不被关闭的概率;(Ⅲ)至少关闭一家煤矿的概率.18.因冰雪灾害,某柑桔基地果林严重受损,为此有关专家提出一种拯救果树的方案,该方案需分两年实施且相互独立.该方案预计第一年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.2、0.4、0.4;第二年可以使柑桔产量为第一年产量的1.5倍、1.25倍、1.0倍的概率分别是0.3、0.3、0.4.(1)求两年后柑桔产量恰好达到灾前产量的概率;(2)求两年后柑桔产量超过灾前产量的概率.19.甲、乙、丙三个同学一起参加某高校组织的自主招生考试,考试分笔试和面试两部分,笔试和面试均合格者将成为该高校的预录取生(可在高考中加分录取),两次考试过程相互独立.根据甲、乙、丙三个同学的平时成绩分析,甲、乙、丙三个同学能通过笔试的概率分别是0.6,0.5,0.4,能通过面试的概率分别是0.5,0.6,0.75.(1)求甲、乙、丙三个同学中恰有一人通过笔试的概率;(2)设经过两次考试后,能被该高校预录取的人数为,求随机变量的期望.答案一、选择题1. B解析:()P E F I =()()1144P E P F ∙=⨯=1162. D3. B解析由随机数可估算出每次投篮命中的概率242605p ≈=则三次投篮命中两次为223(1)C P P ⨯⨯-≈0.25故选B 4. B5. 答案:B6. 【标准答案】0. 98【试题解析】用间接法做: 两个闹钟一个也不准时响的概率是,所以要求的结果是. 【高考考点】间接法求概率,分类讨论思想。
【易错提醒】计算出错.【备考提示】本题还可以这样做:要求的概率是7. 答案:B解析:独立重复实验,【高考考点】独立重复实验的判断及计算【易错提醒】容易记成二项展开式的通项,当然这题因为数字的原因不涉及.【备考提示】请考生注意该公式与二项展开式的通项的区别,所以要强化公式的记忆. 8. 答案:B.解析:质点在移动过程中向右移动2次向上移动3次,因此质点P 移动5次后位于点的概率为。
9. 答案:D10. 答案:D解析:甲获胜有两种情况,一是甲以2:0获胜,此时二是甲以2:1获胜,此时,故甲获胜的概率【高考考点】独立重复事件恰好发生n 次的概率【易错点】:利用公式求得答案C,忽视了问题的实际意义。
【备考提示】:计算概率问题要仔细分析该事件中所包含的基本事件,分类计算。
二、填空题11. 解析:安排情况如下:甲乙,甲丙,甲丁,乙甲,乙丙,乙丁,丙甲,丙乙,丙丁,丁甲,丁乙,丁丙 ∴共有12种安排方法.甲、乙两人都被安排的情况包括:“甲乙”,“乙甲”两种,∴甲、乙两人都被安排(记为事件A )的概率:61122)(==A P 12. 18925613. 0.46914. 答案:解析:由题意知所求概率 点评:本题考察次独立重复试验中,某事件恰好发生次的概率,直接用公式解决。
三、解答题15. 解析:设三门考试课程考试通过的事件分别为A ,B ,C ,相应的概率为a ,b ,c(1)考试三门课程,至少有两门及格的事件可表示为AB +A C +BC +ABC ,设其概率为P 1,则P 1=ab (1-c )+a (1-b )c +(1-a )bc +abc =ab +ac +bc -2abc设在三门课程中,随机选取两门,这两门都及格的概率为P 2,则P 2=ab +ac +bc(2)P 1-P 2=(ab +ac +bc -2abc )-(ab +ac +bc )=ab +ac +bc -2abc=(ab +ac +bc -3abc )=〔ab (1-c )+ac (1-b )+bc (1-a )〕>0∴P1>P2即用方案一的概率大于用方案二的概率.16. 解析:(Ⅰ).每家煤矿必须整改的概率是1-0.5,且每家煤矿是否整改是相互独立的.所以恰好有两家煤矿必须整改的概率是.(Ⅱ).由题设,必须整改的煤矿数服从二项分布B(5,0.5).从而的数学期望是E=,即平均有2.50家煤矿必须整改.(Ⅲ).某煤矿被关闭,即该煤矿第一次安检不合格,整改后经复查仍不合格,所以该煤矿被关闭的概率是,从而该煤矿不被关闭的概率是0.9.由题意,每家煤矿是否被关闭是相互独立的,所以至少关闭一家煤矿的概率是17. 解析:(Ⅰ)每家煤矿必须整改的概率是1-0.5,且每家煤矿是否整改是相互独立的. 所以恰好有两家煤矿必须整改的概率是.(Ⅱ)解法一某煤矿被关闭,即该煤矿第一次安检不合格,整改后经复查仍不合格,所以该煤矿被关闭的概率是,从而煤矿不被关闭的概率是0.90.解法二某煤矿不被关闭包括两种情况:(i)该煤矿第一次安检合格;(ii)该煤矿第一次安检不合格,但整改后合格.所以该煤矿不被关闭的概率是.(Ⅲ)由题设(Ⅱ)可知,每家煤矿不被关闭的概率是0.9,且每家煤矿是否被关闭是相互独立的,所以到少关闭一家煤矿的概率是.18. 解:(1)令A表示两年后柑桔产量恰好达到灾前产量这一事件(2)令B表示两年后柑桔产量超过灾前产量这一事件19. 解析:(1)分别记甲、乙、丙三个同学笔试合格为事件、、;表示事件“恰有一人通过笔试”则--------------------------------------------6分(2)解法一:因为甲、乙、丙三个同学经过两次考试后合格的概率均为,---------------------9分所以,故.--------12分解法二:分别记甲、乙、丙三个同学经过两次考试后合格为事件,则所以,,.于是,.。
