对数与对数运算知识点

合集下载

高中数学对数的运算

对数函数专题对数及对数运算【要点梳理】要点一、对数概念 1．对数的概念如果()01b a N a a =>≠，且，那么数b 叫做以a 为底N 的对数，记作:log a N=b ．其中a 叫做对数的底数，N 叫做真数．要点诠释：对数式log a N=b 中各字母的取值范围是：a>0 且a ≠1， N>0， b ∈R ． 2．对数()log 0a N a >≠，且a 1具有下列性质：（1）0和负数没有对数，即0N >；（2）1的对数为0，即log 10a =；（3）底的对数等于1，即log 1a a =．3．两种特殊的对数通常将以10为底的对数叫做常用对数，N N lg log 10简记作．以e （e 是一个无理数， 2.7182e =⋅⋅⋅）为底的对数叫做自然对数， log ln e N N 简记作． 4．对数式与指数式的关系由定义可知:对数就是指数变换而来的，因此对数式与指数式联系密切，且可以互相转化．它们的关系可由下图表示．由此可见a ，b ，N 三个字母在不同的式子中名称可能发生变化．要点二、对数的运算法则已知()log log 010a a M N a a M N >≠>，且，、（1）正因数的积的对数等于同一底数各个因数的对数的和； ()log log log a a a MN M N =+ 推广：()()121212log log log log 0a k a a a k k N N N N N N N N N =+++>、、、（2）两个正数的商的对数等于被除数的对数减去除数的对数；log log log a a a M M N N=-（3）正数的幂的对数等于幂的底数的对数乘以幂指数； log log a a M M αα=要点诠释：（1）利用对数的运算法则时，要注意各个字母的取值范围，即等式左右两边的对数都存在时等式才能成立．如：log 2（-3）（-5）=log 2（-3）+log 2（-5）是不成立的，因为虽然log 2（-3）（-5）是存在的，但log 2（-3）与log 2（-5）是不存在的．（2）不能将和、差、积、商、幂的对数与对数的和、差、积、商、幂混淆起来，即下面的等式是错误的：log a （M ±N ）=log a M ±log a N ， log a （M ·N ）=log a M ·log a N ，log a N M N M a a log log =．要点三、对数公式 1．对数恒等式：log log a b Na a N a N Nb ⎫=⇒=⎬=⎭2．换底公式同底对数才能运算，底数不同时可考虑进行换底，在a>0， a ≠1， M>0的前提下有:（1）)(log log R n M M n a a n ∈=令 log a M=b ，则有a b =M ，（a b ）n =M n ，即n b n M a =)(，即n a M b n log =，即:n a a M M n log log =．（2）)1,0(log log log ≠>=c c aMM c c a ，令log a M=b ，则有a b =M ，则有)1,0(log log ≠>=c c M a c b c即M a b c c log log =⋅，即a M b c c log log =，即)1,0(log log log ≠>=c c aMM c c a 当然，细心一些的同学会发现（1）可由（2）推出，但在解决某些问题（1）又有它的灵活性．而且由（2）还可以得到一个重要的结论:)1,0,1,0(log 1log ≠>≠>=b b a a ab b a ．【典型例题】类型一、对数的概念例1．求下列各式中x 的取值范围：（1）2log (5)x -；（2）(1)log (2)x x -+；（3）2(1)log (1)x x +-．【答案】（1）5x >；（2）1,2x x >≠且；（3）1x >-且0,1x x ≠≠ 【解析】（1）由题意50x ->，5x ∴>，即为所求．（2）由题意20,10,11,x x x +>⎧⎨->-≠⎩且即2,1,2,x x x >-⎧⎨>≠⎩且1,2x x ∴>≠且．（3）由题意2(1)0,10,11,x x x ⎧->⎨+>+≠⎩且解得1x >-且0,1x x ≠≠．【总结升华】在解决与对数有关的问题时，一定要注意：对数真数大于零，对数的底数大于零且不等于1．举一反三：【变式1】函数21log (2)x y x -=+的定义域为．【答案】1|12x x x ⎧⎫>≠⎨⎬⎩⎭且类型二、指数式与对数式互化及其应用例2．将下列指数式与对数式互化：（1）2log 164=；（2）13log 273=-；（3）3x =；（4）35125=；（5）1122-=；（6）2193-⎛⎫= ⎪⎝⎭．【解析】运用对数的定义进行互化．（1）4216=；（2）31273-⎛⎫= ⎪⎝⎭；（33x =；（4）5log 1253=；（5）21log 12=-；（6）13log 92=-．【总结升华】对数的定义是对数形式和指数形式互化的依据，而对数形式和指数形式的互化又是解决问题的重要手段．举一反三：【变式1】求下列各式中x 的值：（1）161log 2x =- （2）log 86x = （3）lg1000=x （4）2-2ln e x =【答案】（1）14；（2；（3）3；（4）-4．【解析】将对数式化为指数式，再利用指数幂的运算性质求出x ．（1）1112()212221(16)(4)444x --⋅--=====；（2）111166366628()(8)(2)2x x x ======，所以（3）10x =1000=103，于是x=3；（4）由22222ln ln 42x x e x e e e x --=-===-，得，即所以．例3．（2014 广东湛江期中）不用计算器计算：7log 203log lg25lg47(9.8)+++- 【答案】132【解析】原式323log 3lg(254)21=+⨯++23lg1032=++3132322=++=【总结升华】对数恒等式log a N a N =中要注意格式：①它们是同底的；②指数中含有对数形式；③其值为真数．举一反三：【变式1】求log log log a b c b c N a ⋅⋅的值（a ，b ，c ∈R +，且不等于1，N>0）【答案】N【解析】将幂指数中的乘积关系转化为幂的幂，再进行运算．log log log log log log log log log ()()c a b c a b b c c Nb c N b cc N N a a b c N ⋅⋅⎡⎤====⎣⎦类型四、积、商、幂的对数例4． z y x a a a log ,log ,log 用表示下列各式35(1)log ;(2)log ();(3)log a a a a xy x y z 【解析】（1）log log log log aa a a xyx y z z=+-；（2）3535log ()log log 3log 5log a a a a a x y x y x y =+=+；（3）1log log log ()log log log 2a a a a a a yz x y z yz ==--；（4）log a211log ()log 2log log log 23a a a a a x y x y z -=+-．(有错误）【总结升华】利用对数恒等式、对数性质及其运算性质进行化简是化简对数式的重要途径，因此我们必须准确地把握它们．在运用对数的运算性质时，一要注意真数必须大于零；二要注意积、商、幂的对数运算对应着对数的和、差、积得运算．举一反三：【变式1】求值（1）1log 864log 325log 21025-+ （2）lg2·lg50+（lg5）2 （3）lg25+lg2·lg50+（lg2）2【答案】（1）22；（2）1；（3）2．【解析】（1）1log 864log 325log 21025-+.220184082log 35log 26225=-+=⨯-+⋅=（2）原式=lg2（1+lg5）+（lg5）2=lg2+lg2lg5+（lg5）2=lg2+lg5（lg2+lg5）=lg2+lg5=1（3）原式=2lg5+lg2（1+lg5）+（lg2）2=2lg5+lg2+lg2lg5+（lg2）2=1+lg5+lg2（lg5+lg2）=1+lg5+lg2=2．类型五、换底公式的运用例5．已知18log 9,185b a ==，求36log 45．【答案】2a ba+- 【解析】解法一：18log 9,185b a ==，18log 5b ∴=，于是181818183618181818log 45log (95)log 9log 5log 4518log 36log (182)1log 221log 9a b a ba ⨯+++=====⨯+-+．【总结升华】（1）利用换底公式可以把题目中不同底的对数化成同底的对数，进一步应用对数运算的性质．（2）题目中有指数式和对数式时，要注意指数式与对数式的互化，将它们统一成一种形式．（3）解决这类问题要注意隐含条件“log 1a a =”的灵活运用．【变式1】求值：（1）)2log 2)(log 3log 3(log 9384++；【解析】（1）)2log 2)(log 3log 3(log 9384++452log 233log 65)22log 2)(log 33log 23log ()9log 2log 2)(log 8log 3log 4log 3log (3233223332222=⋅⋅=++=++=类型六、对数运算法则的应用例6．求值（1）91log 81log 251log 32log 53264⋅⋅⋅（2）7lg142lg lg 7lg183-+-【解析】（1）原式=103log 2log 5log 2log 253322526-=---（2）原式=2lg(27)2(lg 7lg 3)lg 7lg(32)⨯--+-⨯ =lg 2lg72lg72lg3lg72lg3lg 20+-++--=举一反三：【变式1】计算下列各式的值（1）()222lg5lg8lg5lg 20lg 23+++【解析】（1）原式=()22lg52lg 2lg5(2lg 2lg5)lg 2++++=22lg10(lg 5lg 2)++=2+1=3；【巩固练习】一、选择题1. 有以下四个结论：①lg （lg10）=0；②ln （lne ）=0；③若10=lg x ，则x =10；④若e =ln x ，则x =e 2，其中正确的是（）A ．①③B ．②④C ．①②D ．③④ 【答案】C【解析】由log 1,log 10a a a ==知①②正确．2. 下列等式成立的有（）①1lg 2100=-；②33log 2=；③2log 525=；④ln 1e e =；⑤lg 333=；A ．①②B ．①②③C ．②③④D ．①②③④⑤ 【答案】B【解析】21lg lg102100-==-；3. 对数式2log (5)a a b --=中，实数a 的取值范围是（）A ．(),5-∞B ． ()2,5C ．()()2,33,5D ．()2,+∞【答案】C【解析】由对数的定义可知50,20,21,a a a ->⎧⎪->⎨⎪-≠⎩所以25a <<且3a ≠，故选C ．4. 若0,1a a >≠，则下列说法正确的是（）①若M N =，则log log a a M N =；②log log a a M N =，则M N =； ③22log log a a M N =，则M N =；④若M N =，则22log log a a M N =． A ．①③ B ．②④ C ．② D ．①②③④ 【答案】C【解析】注意使log log a a M N =成立的条件是M 、N 必须为正数，所以①③④不正确，而②是正确的，故选C ．5. 若56789log 6log 7log 8log 9log 10y =⋅⋅⋅⋅，则（）A ．(0,1)y ∈B ．(1,2)y ∈C ．(2,3)y ∈D ．(3,4)y ∈ 【答案】B 【解析】55lg 6lg 7lg8lg9lg10log 101log 2lg5lg 6lg 7lg8lg9y =⨯⨯⨯⨯==+，因为50log 21<<，所以12y <<，故选B ．6. （2014江西三县月考）计算662log 3log 4+的结果是（）A ．6log 2B ． 2C ． 6log 3D ． 3【答案】B【解析】666662log 3log 4log 9log 4log 362+=+==．故选：B ．二、填空题1. 若312log 19x-=，则x = ．【答案】-13【解析】由指数式与对数式互化，可得1239x-=，解得13x =-． 2. 若2log 2,log 3,m n a a m n a +=== ；【答案】12【解析】 2log 2log 3log 4log 34312a a a a a a a +=⋅=⨯=．3. 若2510a b ==，则11a b+= ．【答案】1【解析】因为210,a =所以21log 10lg 2a ==，又因为510,b =所以51log 10lg 5b ==，所以原式=lg 2lg51+=．。

对数与对数函数

对数与对数函数知识梳理1、对数式log a N 可看作一记号，表示底为a （a ＞0，且a ≠1），幂为N 的指数工表示方程xa N =（a ＞0，且a ≠1）的解. 也可以看作一种运算，即已知底为a （a ＞0，且a ≠1）幂为N ，求幂指数的运算. 因此，对数式log a N 又可看幂运算的逆运算.为a ＞0，a ≠1时，log x N a a N x =⇔= 【扩展】两类对数① 以10为底的对数称为常用对数，10log N 常记为lg N .② 以无理数e=2.71828…为底的对数称为自然对数，log e N 常记为ln N .以后解题时，在没有指出对数的底的情况下，都是指常用对数，如100的对数等于2，即lg1002=.说明：在例1中，10log 0.010.01,log 10ln10e 应改为lg 应改为. 2、对数的运算法则如果a ＞0且a ≠1，M ＞0，N ＞0，那么：（1）log log log a a a MN M N =+ （2）log log log aa a MM N N=- （3）log log ()n a a M n Mn R =∈3、画出函数2log xy =的图象, 再利用电脑软件画出0.5log .x y =的图象42-2-4-55探究：选取底数(a a ＞0，且a ≠1）的若干不同的值，在同一平面直角坐标系内作出相应的对数函数的图象．观察图象，你能发现它们有哪些特征吗？画出4log y x =，3log y x =，13log y x =和14log y x =提问：通过函数的图象，你能说出底数与函数图象的关系吗？函数的图象有何特征，性质又如何？先由学生讨论、交流，教师引导总结出函数的性质. (投影) 图象的特征函数的性质（1）图象都在y 轴的右边（1）定义域是（0，+∞）（2）函数图象都经过（1，0）点（2）1的对数是0（3）从左往右看，当a ＞1时，图象逐渐上升，当0＜a ＜1时，图象逐渐下降 .（3）当a ＞1时，log xa y =是增函数，当0＜a ＜1时，log a y x =是减函数. （4）当a ＞1时，函数图象在（1，0）点右边的纵坐标都大于0，在（1，0）点左边的纵坐标都小于0. 当0＜a ＜1时，图象正好相反，在（1，0）点右边的纵坐标都小于0，在（1，0）点左边的纵坐标都大于0 .（4）当a ＞1时x ＞1，则log a x ＞00＜x ＜1，log a x ＜0 当0＜a ＜1时x ＞1，则log a x ＜00＜x ＜1，log a x ＜0由上述表格可知，对数函数的性质如下（先由学生仿造指数函数性质完成，教师适当启发、引导）：a ＞10＜a ＜1图象性质（1）定义域（0，+∞）；（2）值域R ；（3）过点（1，0），即当x =1，y =0；（4）在（0，+∞）上是增函数在（0，+∞）是上减函数精讲精练（1）对数运算的例题【例1】将下列指数式化为对数式，对数式化为指数式：（1）712128-=；（2）327a =；（3）1100.1-=；（4）12log 325=-；（5）lg0.0013=-；（6）ln100=4.606.【例2】求证：（1）log n a a n =；（2）log log log a a a MM N N-=.【例3】试推导出换底公式：log log log c a c bb a= （0a >，且1a ≠；0c >，且1c ≠；0b >）.【例4】化简与求值：（1）221(lg 2)lg2lg5(lg 2)lg212++-+ ；（2）2log (4747)++-.【例5】若2510a b ==，则11a b+= . （教材P 83 B 组2题）【例6】（1）方程lg lg(3)1x x ++=的解x =________；（2）设12,x x 是方程2lg lg 0x a x b ++=的两个根，则12x x 的值是 .【例7】（1）化简：532111log 7log 7log 7++；（2）设23420052006log 3log 4log 5log 2006log 4m ⋅⋅⋅= ，求实数m 的值.（2）对数函数图象和性质的例题【例1】比较大小：（1）0.9log 0.8，0.9log 0.7，0.8log 0.9；（2）3log 2，2log 3，41log 3.【例2】求下列函数的定义域：（1）2log (35)y x =-；（2）0.5log (4)3y x =-.【例3】已知函数()log (3)a f x x =+的区间[2,1]--上总有|()|2f x <，求实数a 的取值范围.【例4】求不等式log (27)log (41)(0,1)a a x x a a +>->≠且中x 的取值范围.【例5】讨论函数0.3log (32)y x =-的单调性.【例6】（05年山东卷.文2）下列大小关系正确的是（）. A. 30.440.43log 0.3<< B. 30.440.4log 0.33<< C. 30.44log 0.30.43<< D. 0.434log 0.330.4<<【例7】指数函数(0,1)x y a a a =>≠的图象与对数函数log (0,1)a y x a a =>≠的图象有何关系？课堂作业（1）对数幂的运算1. 将下列指数式与对数式互化，有x 的求出x 的值 .（1）12155-=（2）42log x = （3）1327x =（4）1()644x= （5）lg0.0001x = （6）5ln e x =2．求log log log ,a b c b c Na⋅⋅∈+的值(a,b,c R 且不等于1，N ＞0）.3．计算331log log 5533+的值.4、判断下列式子是否正确，a ＞0且a ≠1，x ＞0且a ≠1，x ＞0，x ＞y ，则有（1）log log log ()a a a x y x y ⋅=+ （2）log log log ()a a a x y x y -=-（3）log log log aa a xx y y=÷ （4）log log log a a a xy x y =- （5）(log )log n a a x n x = （6）1log log a a x x=- （7）1log log n a a x x n=5. 用log a x ，log a y ，log a z 表示出（1）（2）小题，并求出（3）、（4）小题的值.（1）log a xyz =____________; （2）23log 8a x y =______________________;（3）75log (42)z ⨯=______________; （4）5lg 100=_____________________; 6. 已知32a=，那么33log 82log 6-用a 表示是（）A 、2a -B 、52a -C 、23(1)a a -+D 、 23a a - 7、2log (2)log log a a a M N M N -=+，则NM的值为（） A 、41B 、4C 、1D 、4或1 8、已知221,0,0x y x y +=>>，且1log (1),log ,log 1y a a a x m n x+==-则等于（）A 、m n +B 、m n -C 、()12m n +D 、()12m n -9、如果方程2lg (lg5lg7)lg lg5lg70x x +++= 的两根是,αβ，则αβ 的值是（）A 、lg5lg 7B 、lg 35C 、35D 、351 10、已知732log [log (log )]0x =，那么12x -等于（）A 、13 B 、123 C 、122 D 、13311. 若2log 2,log 3,m n a a m n a +=== 。

知识讲解_对数及对数运算_基础

(2)
log a
M

logc M logc a
(c 0, c 1) ，
令
logaM=b，
则有 ab=M，
则有
logc ab logc M (c 0, c 1)
即 b logc
a

log c
M
，
即b

logc M logc a
，即 log a
M

logc M logc a
(c
(1)0 和负数没有对数，即 N 0 ； (2)1 的对数为 0，即 loga 1 0 ； (3)底的对数等于 1，即 loga a 1.
3．两种特殊的对数
通常将以 10 为底的对数叫做常用对数， log10 N作作作为底的对数叫做自然对数， loge N简记作 ln N .
4．对数式与指数式的关系
质．
（2）题目中有指数式和对数式时，要注意指数式与对数式的互化，将它们统一成一种形式．
（3）解决这类问题要注意隐含条件“ loga a 1”的灵活运用．
举一反三：
【变式
1】求值：(1)
(log 4
3

log8
3)(log3
2

log 9
27
32
；(3)
91 2
log3
2

log 3 2
2 )

5 6

log 2
3
3 2
log 3
2

5 4
；
(2) log8
loga
M N
loga M
loga
N
(3) 正数的幂的对数等于幂的底数的对数乘以幂指数；

对数与对数运算学习讲解

对数与对数运算学习讲解1.对数的定义一般地，如果a x ＝N (a ＞0，且a ≠1)，那么x 叫做以a 为底N 的对数，记做x ＝log a N ，其中a 叫做对数的底数，N 叫做真数.解读：(1)由对数定义可以知道，当a ＞0，且a ≠1时，a x ＝N ⇔x ＝log a N ，也就是说指数式与对数式实际上是表示a 、N 之间的同一种关系的两种形式，因此可以互相转化；(2)根据对数定义可以知道，a log a N ＝N ，即a 的log a N 次方等于N ，对数恒等式也是化简或计算的重要公式.2.对数的性质(1)零和负数没有对数，由于在实数范围内，正数的任何次幂都是正数，所以a x ＝N (a ＞0，且a ≠1)中N 总是正数；(2)1的对数为0，由于任何非零实数的零次幂都等于1，所以log a 1＝0；(3)底数的对数等于1，由于a 1＝a 对于任何非零实数都成立，所以log a a ＝1.3.对数的运算性质若a ＞0，且a ≠1，M ＞0，N ＞0，那么：(1)log a (MN )＝log a M ＋log a N ，即正数积的对数，等于同一底数的各个数的对数和；(2)log a M N＝log a M －log a N ，即两个正数商的对数，等于被除数的对数减去除数的对数；(3)log a M n ＝n log a M ，正数的幂的对数等于幂的底数的对数乘以幂指数.这些性质一般运用于对数的计算、化简或证明中.例1 将下列对数式化成指数式、指数式化成对数式：(1)log3127＝－3；(2)log232＝5；(3)63＝216；(4)10－3＝0.001.解(1)3－3＝127；(2)25＝32；(3)log6216＝3；(4)log100.001＝－3，也可写成lg 0.001＝－3.评注本题考查了对数式与指数式的互化.解题所用知识都是依据对数的定义，要注意对数的真数是指数的幂，对数的值是指数式中的指数.例2 求下列各式的值：(1)3log72－log79＋2log7322；(2)lg 25＋23lg 8＋lg 5·lg 20＋(lg 2)2.解(1)原式＝log723－log79＋log7(322)2＝log723×32229＝log71＝0；(2)原式＝2lg 5＋2lg 2＋lg 5·(lg 5＋2lg 2)＋(lg 2)2＝2(lg 5＋lg 2)＋(lg 5)2＋2lg 5·lg 2＋(lg 2)2＝2＋(lg 5＋lg 2)2＝3.评注利用对数的运算性质求值和化简，是对数运算常见的题型，对数运算性质的正向运用可以把真数的乘、除、乘方、开方运算转化为对数的加、减、乘、除运算，这样就简化了计算，体现了利用对数运算的优越性.。

对数及其运算性质

x
loga1=0 logaa=1 logaa =b a 3.对数的运算性质:
b
loga N
=N
log a(MN)=log a M+log a N
loga(M N )=loga M-loga N n loga(M )=nloga M(n ∈R)
-1
换底公式及推论:
1.换公 : 底式 2.推论:
log c b loga b= log c a
思考：
在复习提问3：log264=6,log24=2的基础上增加log464=3，你还有何猜想？你能证明它吗？由它还能得出什么结论？
2
2
对数与对数运算(三对数与对数运算三)
复习提问: 1.对数式与指数式的互化:
a = N ⇔ x = loga N(a > 0, a ≠ 1, N > 0) 2.对数的基本性质:
例6：科学研究表明，宇宙射线在大气中能够产生：科学研究表明，放射性碳14。的衰变极有规律，放射性碳。碳14的衰变极有规律，其精确性可以的衰变极有规律称为自然界的“标准时钟” 称为自然界的“标准时钟”。动植物在生长过程中衰变的碳14，可以通过与大气的相互作用得到补充，变的碳，可以通过与大气的相互作用得到补充，所以活着的动植物每无组织中的碳14含量不变含量不变。所以活着的动植物每无组织中的碳含量不变。死亡后的动植物，停止了与外界环境的相互作用，亡后的动植物，停止了与外界环境的相互作用，机体中原有的碳１４按确定的规律衰减，１４按确定的规律衰减体中原有的碳１４按确定的规律衰减，我们已经知道其“半衰期” ５７３０年道其“半衰期”为５７３０年。湖南长沙马王堆汉墓女尸出土时碳１４１４的残余湖南长沙马王堆汉墓女尸出土时碳１４的残余量约占原始含量的７６％，试推算马王堆古墓的７６.７量约占原始含量的７６７％，试推算马王堆古墓的年代。年代。

对数的运算与对数函数

1.对数的概念如果 ,那么数b 叫做以a 为底N 的对数，记作，其中a 叫做对数的，N 叫做对数的。

即指数式与对数式的互化：log ba aN b N =⇔=2.常用对数：通常将以10为底的对数10log N 叫做常用对数，记作lg N 。

自然对数：通常将以无理数 2.71828e =⋅⋅⋅为底的对数叫做自然对数，记作ln N 。

3．对数的运算性质：如果0a >，且1,0,0a M N ≠>>，那么：⑴log ()log log a a a M N M N ⋅=+；（积的对数等于对数的和）推广1212log (...)log log ...log a k a a a k N N N N N N ⋅=+++ ⑵log log log aa a MM N N=-；（商的对数等于对数的差） ⑶log log (R)a a M M ααα=∈，则log a = 。

⑷log a N a N =2．换底公式：log log log a b a NN b=（,0,,1,0a b a b N >≠>）换底公式的意义：把以一个数为底的对数换成以另一个大于0且不等于1的数为底的对数，以达到计算、化简或证明的目的．推广：⑴1log log a b b a=⑵log log log log a b c a b c d d =， ⑶1log log n a a M M n =，则log na m M = 。

特别地：log log 1a b b a =知识要点对数运算与对数函数【例1】求下列各式中x 的取值范围。

（1）2log (5)x +（2）1log (10)x x --【例2】将下列指数式化为对数式，对数式化为指数式。

（1） 1642= （2） 9132=- （3） 481log 3=（4） 6125log -=a （5）lg0.0013=-；（6）ln100=4.606【例3】计算（1）lg 4lg 25+ （2）22log 24log 6-（3）531log ()3（4） 001.0lg （5）e1ln （6）1lg【巩固1】3log =2log =(2log (2= 21log 52+=【巩固2】）. A. 1 B. －1 C. 2 D. －2【巩固3】计算2(lg5)lg 2lg50+⋅＝ .知识要点【例4】（1）（2 。

高一对数与对数函数知识点+例题+练习含答案

1．对数的概念一般地，如果a (a >0，a ≠1)的b 次幂等于N ，即a b ＝N ，那么就称b 是以a 为底N 的对数，记作log a N ＝b ，N 叫做真数． 2．对数的性质与运算法则 (1)对数的运算法则如果a >0且a ≠1，M >0，N >0，那么 ①log a (MN )＝log a M ＋log a N ； ②log a MN ＝log a M －log a N ；③log a M n ＝n log a M (n ∈R )；④log am M n ＝nm log a M (m ，n ∈R ，且m ≠0)．(2)对数的性质①a log a N ＝__N __；②log a a N ＝__N __(a >0且a ≠1)． (3)对数的重要公式①换底公式：log b N ＝log a Nlog a b (a ，b 均大于零且不等于1)；②log a b ＝1log b a，推广log a b ·log b c ·log c d ＝log a d . 3．对数函数的图象与性质a >10<a <1图象性质(1)定义域：(0，＋∞)(2)值域：R(3)过定点(1,0)，即x ＝1时，y ＝0当0<x <1时，y <0 (4)当x >1时，y >0 当0<x <1时，y >0 (6)在(0，＋∞)上是增函数(7)在(0，＋∞)上是减函数4.反函数指数函数y ＝a x 与对数函数y ＝log a x 互为反函数，它们的图象关于直线__y ＝x __对称．【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”) (1)若MN >0，则log a (MN )＝log a M ＋log a N .( × ) (2)log a x ·log a y ＝log a (x ＋y )．( × )(3)函数y ＝log 2x 及y ＝log 133x 都是对数函数．( × )(4)对数函数y ＝log a x (a >0，且a ≠1)在(0，＋∞)上是增函数．( × ) (5)函数y ＝ln 1＋x 1－x与y ＝ln(1＋x )－ln(1－x )的定义域相同．( √ )(6)对数函数y ＝log a x (a >0且a ≠1)的图象过定点(1,0)，且过点(a,1)，⎝⎛⎭⎫1a ，－1，函数图象只在第一、四象限．( √ )1．(2015·湖南改编)设函数f (x )＝ln(1＋x )－ln(1－x )，则有关f (x )的性质判断正确的是________(填序号)．①奇函数，且在(0,1)上是增函数； ②奇函数，且在(0,1)上是减函数； ③偶函数，且在(0,1)上是增函数； ④偶函数，且在(0,1)上是减函数．答案 ①解析易知函数定义域为(－1，1)，f (－x )＝ln(1－x )－ln(1＋x )＝－f (x )，故函数f (x )为奇函数，又f (x )＝ln 1＋x 1－x＝ln ⎝ ⎛⎭⎪⎫－1－2x －1，由复合函数单调性判断方法知，f (x )在(0,1)上是增函数．2．设a ＝log 1312，b ＝log 1323，c ＝log 343，则a ，b ，c 的大小关系是________．答案 c 32>43，∴c 1时，函数单调递增，所以只有②正确．4．(2015·浙江)若a ＝log 43，则2a ＋2－a ＝________. 答案4 33解析 2a＋2－a ＝4log 32＋4log 32－＝3log log 322＋＝3＋33＝4 33. 5．(教材改编)若log a 34<1(a >0，且a ≠1)，则实数a 的取值范围是________________．答案 ⎝⎛⎭⎫0，34∪(1，＋∞) 解析当0<a <1时，log a 34<log a a ＝1，∴0<a <34；当a >1时，log a 34<log a a ＝1，∴a >1.∴实数a 的取值范围是⎝⎛⎭⎫0，34∪(1，＋∞).题型一对数式的运算例1 (1)设2a ＝5b ＝m ，且1a ＋1b ＝2，则m ＝________.(2)lg 5＋lg 20的值是________．答案 (1)10 (2)1解析 (1)∵2a ＝5b ＝m ，∴a ＝log 2m ，b ＝log 5m ， ∴1a ＋1b ＝1log 2m ＋1log 5m ＝log m 2＋log m 5＝log m 10＝2. ∴m ＝10.(2)原式＝lg 100＝lg 10＝1.思维升华在对数运算中，要熟练掌握对数的定义，灵活使用对数的运算性质、换底公式和对数恒等式对式子进行恒等变形，多个对数式要尽量先化成同底的形式再进行运算．(1)计算：(1－log 63)2＋log 62·log 618log 64＝________.(2)已知log a 2＝m ，log a 3＝n ，则a 2m ＋n ＝________. 答案 (1)1 (2)12 解析 (1)原式＝1－2log 63＋(log 63)2＋log 663·log 6(6×3)log 64＝1－2log 63＋(log 63)2＋(1－log 63)(1＋log 63)log 64＝1－2log 63＋(log 63)2＋1－(log 63)2log 64＝2(1－log 63)2log 62＝log 66－log 63log 62＝log 62log 62＝1.(2)∵log a 2＝m ，log a 3＝n ，∴a m ＝2，a n ＝3， ∴a 2m ＋n ＝(a m )2·a n ＝22×3＝12.题型二对数函数的图象及应用例2 (1)函数y ＝2log 4(1－x )的图象大致是________．(填序号)(2)当0<x ≤12时，4x <log a x ，则a 的取值范围是____________．答案 (1)③ (2)(22，1) 解析 (1)函数y ＝2log 4(1－x )的定义域为(－∞，1)，排除①、②；又函数y ＝2log 4(1－x )在定义域内单调递减，排除④.故③正确．(2)构造函数f (x )＝4x 和g (x )＝log a x ，当a >1时不满足条件，当0<a <1时，画出两个函数在⎝⎛⎦⎤0，12上的图象，可知f ⎝⎛⎭⎫12<g ⎝⎛⎭⎫12，即2<log a 12，则a >22，所以a 的取值范围为⎝⎛⎭⎫22，1. 思维升华应用对数型函数的图象可求解的问题(1)对一些可通过平移、对称变换作出其图象的对数型函数，在求解其单调性(单调区间)、值域(最值)、零点时，常利用数形结合思想．(2)一些对数型方程、不等式问题常转化为相应的函数图象问题，利用数形结合法求解．(1)已知lg a ＋lg b ＝0，则函数f (x )＝a x 与函数g (x )＝－log b x 的图象可能是________．(2)已知函数f (x )＝⎩⎪⎨⎪⎧|lg x |，0<x ≤10，－12x ＋6，x >10，若a ，b ，c 互不相等，且f (a )＝f (b )＝f (c )，则abc 的取值范围是____________．答案 (1)② (2)(10,12)解析 (1)∵lg a ＋lg b ＝0，∴ab ＝1，∵g (x )＝－log b x 的定义域是(0，＋∞)，故排除①. 若a >1，则01，g (x )＝－log b x 是减函数，排除③，故填②.(2)作出f (x )的大致图象(图略)．由图象知，要使f (a )＝f (b )＝f (c )，不妨设a b >c解析由对数运算法则得a ＝log 36＝1＋log 32，b ＝1＋log 52，c ＝1＋log 72，由对数函数图象得log 32>log 52>log 72，所以a >b >c . 命题点2 解对数不等式例4 若log a (a 2＋1)<log a 2a <0，则a 的取值范围是__________．答案 (12，1)解析由题意得a >0，故必有a 2＋1>2a ，又log a (a 2＋1)<log a 2a <0，所以0<a <1，同时2a >1，所以a >12.综上，a ∈(12，1)．命题点3 和对数函数有关的复合函数例5 已知函数f (x )＝log a (3－ax )．(1)当x ∈[0,2]时，函数f (x )恒有意义，求实数a 的取值范围；(2)是否存在这样的实数a ，使得函数f (x )在区间[1,2]上为减函数，并且最大值为1？如果存在，试求出a 的值；如果不存在，请说明理由．解 (1)∵a >0且a ≠1，设t (x )＝3－ax ，则t (x )＝3－ax 为减函数，x ∈[0,2]时，t (x )的最小值为3－2a ，当x ∈[0,2]时，f (x )恒有意义，即x ∈[0,2]时，3－ax >0恒成立． ∴3－2a >0.∴a <32.又a >0且a ≠1，∴a ∈(0,1)∪⎝⎛⎭⎫1，32. (2)t (x )＝3－ax ，∵a >0，∴函数t (x )为减函数． ∵f (x )在区间[1,2]上为减函数，∴y ＝log a t 为增函数，∴a >1，x ∈[1,2]时，t (x )最小值为3－2a ，f (x )最大值为f (1)＝log a (3－a )，∴⎩⎪⎨⎪⎧3－2a >0，log a (3－a )＝1，即⎩⎨⎧a <32，a ＝32.故不存在这样的实数a ，使得函数f (x )在区间[1,2]上为减函数，并且最大值为1.思维升华在解决与对数函数相关的比较大小或解不等式问题时，要优先考虑利用对数函数的单调性来求解．在利用单调性时，一定要明确底数a 的取值对函数增减性的影响，及真数必须为正的限制条件．(1)设a ＝log 32，b ＝log 52，c ＝log 23，则a ，b ，c 的大小关系为____________．(2)若f (x )＝lg(x 2－2ax ＋1＋a )在区间(－∞，1]上递减，则a 的取值范围为__________． (3)设函数f (x )＝⎩⎪⎨⎪⎧log 2x ，x >0，log 12(－x )，x <0，若f (a )>f (－a )，则实数a 的取值范围是__________________．答案 (1)c >a >b (2)[1,2) (3)(－1,0)∪(1，＋∞) 解析 (1)∵3<2<3,1<2<5，3>2，∴log 33<log 32<log 33，log 51<log 52<log 55，log 23>log 22， ∴12<a <1,01，∴c >a >b . (2)令函数g (x )＝x 2－2ax ＋1＋a ＝(x －a )2＋1＋a －a 2，对称轴为x ＝a ，要使函数在(－∞，1]上递减，则有⎩⎪⎨⎪⎧ g (1)>0，a ≥1，即⎩⎪⎨⎪⎧2－a >0，a ≥1，解得1≤a <2，即a ∈[1,2)．(3)由题意可得⎩⎪⎨⎪⎧a >0，log 2a >log 12a或⎩⎪⎨⎪⎧a <0，log 12(－a )>log 2(－a )，解得a >1或－1<a <0.2．比较指数式、对数式的大小典例 (1)设a ＝0.50.5，b ＝0.30.5，c ＝log 0.30.2，则a ，b ，c 的大小关系是__________． (2)设a ＝log 2π，b ＝log 12π，c ＝π－2，则a ，b ，c 的大小关系为____________．(3)已知324log 0.3log 3.4log 3.6155()5，＝，＝，＝a b c 则a ，b ，c 大小关系为__________．思维点拨 (1)可根据幂函数y ＝x 0.5的单调性或比商法确定a ，b 的大小关系，然后利用中间值比较a ，c 大小．(2)a ，b 均为对数式，可化为同底，再利用中间变量和c 比较．(3)化为同底的指数式．解析 (1)根据幂函数y ＝x 0.5的单调性，可得0.30.5<0.50.5<10.5＝1，即b <a <1；根据对数函数y ＝log 0.3x 的单调性，可得log 0.30.2>log 0.30.3＝1，即c >1.所以b <a <c . (2)∵a ＝log 2π>log 22＝1，b ＝log 12π＝log 21π<log 21＝0,0<c ＝1π2<1，∴b <c <a .(3)c ＝(15)3log 0.3＝53log 0.3－＝5310log 3.方法一在同一坐标系中分别作出函数y ＝log 2x ，y ＝log 3x ，y ＝log 4x 的图象，如图所示．由图象知：log 23.4>log 3103>log 43.6.方法二 ∵log 3103>log 33＝1，且103<3.4，∴log 3103<log 33.4<log 23.4.∵log 43.6<log 44＝1，log 3103>1，∴log 43.6<log 3103.∴log 23.4>log 3103>log 43.6.由于y ＝5x 为增函数， ∴52log 3.4>5310log 3>54log 3.6.即52log 3.4>(15)3log 0.3 >54log 3.6，故a >c >b . 答案 (1)b <a <c (2)a >c >b (3)a >c >b温馨提醒 (1)比较指数式和对数式的大小，可以利用函数的单调性，引入中间量；有时也可用数形结合的方法．(2)解题时要根据实际情况来构造相应的函数，利用函数单调性进行比较，如果指数相同，而底数不同则构造幂函数，若底数相同而指数不同则构造指数函数，若引入中间量，一般选0或1.[方法与技巧]1．对数值取正、负值的规律当a >1且b >1或0<a <1且00；当a >1且01时，log a b <0. 2．对数函数的定义域及单调性在对数式中，真数必须是大于0的，所以对数函数y ＝log a x 的定义域应为(0，＋∞)．对数函数的单调性和a 的值有关，因而，在研究对数函数的单调性时，要按0<a <1和a >1进行分类讨论．3．比较幂、对数大小有两种常用方法：(1)数形结合；(2)找中间量结合函数单调性． 4．多个对数函数图象比较底数大小的问题，可通过比较图象与直线y ＝1交点的横坐标进行判定． [失误与防范]1．在运算性质log a M α＝αlog a M 中，要特别注意条件，在无M ＞0的条件下应为log a M α＝αlog a |M |(α∈N *，且α为偶数)．2．解决与对数函数有关的问题时需注意两点：(1)务必先研究函数的定义域；(2)注意对数底数的取值范围．A 组专项基础训练 (时间：40分钟)1．已知log 7[log 3(log 2x )]＝0，那么x 12-＝________.答案24解析由条件知，log 3(log 2x )＝1，∴log 2x ＝3， ∴x ＝8，∴x12-＝24. 2．已知x ＝ln π，y ＝log 52，z ＝e 12-，则x ，y ，z 的大小关系为____________．答案 y <z <x解析 ∵x ＝ln π>ln e ，∴x >1. ∵y ＝log 52<log 55，∴0<y <12.∵z ＝e12-＝1e >14＝12，∴12<z <1.综上可得，y <z <x .3．已知函数f (x )＝⎩⎪⎨⎪⎧3x ＋1， x ≤0，log 2x ， x >0，则使函数f (x )的图象位于直线y ＝1上方的x 的取值范围是__________．答案 (－1,0]∪(2，＋∞)解析当x ≤0时，3x ＋1>1⇒x ＋1>0，∴－1<x ≤0；当x >0时，log 2x >1⇒x >2，综上所述：－1<x ≤0或x >2.4．设f (x )＝lg ⎝⎛⎭⎫21－x ＋a 是奇函数，则使f (x )<0的x 的取值范围是__________．答案 (－1,0)解析由f (x )是奇函数可得a ＝－1，∴f (x )＝lg 1＋x 1－x，定义域为(－1,1)．由f (x )<0，可得0<1＋x 1－x<1，∴－1<x <0. 5．定义在R 上的函数f (x )满足f (－x )＝－f (x )，f (x －2)＝f (x ＋2)，且x ∈(－1,0)时，f (x )＝2x ＋15，则f (log 220)＝________.答案－1解析由f (x －2)＝f (x ＋2)，得f (x )＝f (x ＋4)，因为4＜log 220＜5，所以f (log 220)＝f (log 220－4)＝－f (4－log 220)＝－f (log 245)＝－(224log 5＋15)＝－1. 6．(2015·安徽)lg 52＋2lg 2－⎝⎛⎭⎫12－1＝________. 答案－1解析 lg 52＋2lg 2－⎝⎛⎭⎫12－1＝lg 52＋lg 22－2 ＝lg ⎝⎛⎭⎫52×4－2＝1－2＝－1.7．设函数f (x )满足f (x )＝1＋f (12)log 2x ，则f (2)＝_____________________. 答案 32解析由已知得f (12)＝1－f (12)·log 22，则f (12)＝12，则f (x )＝1＋12·log 2x ，故f (2)＝1＋12·log 22＝32.8．(2015·福建)若函数f (x )＝⎩⎪⎨⎪⎧ －x ＋6，x ≤2，3＋log a x ，x ＞2(a ＞0，且a ≠1)的值域是[4，＋∞)，则实数a 的取值范围是_____________________________________．答案 (1,2]解析由题意f (x )的图象如右图，则⎩⎪⎨⎪⎧a ＞1，3＋log a 2≥4，∴1＜a ≤2. 9．已知函数y ＝log 12(x 2－ax ＋a )在区间(－∞，2)上是增函数，求a 的取值范围．解函数y ＝log 12(x 2－ax ＋a )是由函数y ＝log 12t 和t ＝x 2－ax ＋a 复合而成．因为函数y ＝log 12t 在区间(0，＋∞)上单调递减，而函数t ＝x 2－ax ＋a 在区间(－∞，a 2)上单调递减，又因为函数y ＝log 12(x 2－ax ＋a )在区间(－∞，2)上是增函数，所以⎩⎪⎨⎪⎧ 2≤a 2，(2)2－2a ＋a ≥0，解得⎩⎪⎨⎪⎧ a ≥22，a ≤2(2＋1)，即22≤a ≤2(2＋1)．10．设f (x )＝log a (1＋x )＋log a (3－x )(a >0，a ≠1)，且f (1)＝2.(1)求a 的值及f (x )的定义域；(2)求f (x )在区间[0，32]上的最大值．解 (1)∵f (1)＝2，∴log a 4＝2(a >0，a ≠1)，∴a ＝2.由⎩⎪⎨⎪⎧ 1＋x >0，3－x >0，得x ∈(－1,3)， ∴函数f (x )的定义域为(－1,3)．(2)f (x )＝log 2(1＋x )＋log 2(3－x )＝log 2(1＋x )(3－x )＝log 2[－(x －1)2＋4]，∴当x ∈(－1,1]时，f (x )是增函数；当x ∈(1,3)时，f (x )是减函数，故函数f (x )在[0，32]上的最大值是f (1)＝log 24＝2. B 组专项能力提升(时间：20分钟)11．(2015·陕西改编)设f (x )＝ln x,0＜a ＜b ，若p ＝f (ab )，q ＝f ⎝⎛⎭⎫a ＋b 2，r ＝12(f (a )＋f (b ))，则p 、q 、r 的大小关系是____________．答案 p ＝r <q解析 ∵0＜a ＜b ，∴a ＋b 2＞ab ，又∵f (x )＝ln x 在(0，＋∞)上为增函数，∴f ⎝ ⎛⎭⎪⎫a ＋b 2＞f (ab )，即q ＞p . 又r ＝12(f (a )＋f (b ))＝12(ln a ＋ln b )＝ln ab ＝p ，故p ＝r ＜q .12．设函数f (x )定义在实数集上，f (2－x )＝f (x )，且当x ≥1时，f (x )＝ln x ，则f ⎝⎛⎭⎫13，f ⎝⎛⎭⎫12，f (2)的大小关系是______________．答案 f (12)<f (13)<f (2) 解析由f (2－x )＝f (x )知f (x )的图象关于直线x ＝2－x ＋x 2＝1对称，又当x ≥1时，f (x )＝ln x ，所以离对称轴x ＝1距离大的x 的函数值大，∵|2－1|>|13－1|>|12－1|， ∴f (12)<f (13)<f (2)． 13．若函数f (x )＝lg(－x 2＋8x －7)在区间(m ，m ＋1)上是增函数，则m 的取值范围是__________．答案 [1,3]解析由题意得⎩⎪⎨⎪⎧m ＋1≤4，－m 2＋8m －7≥0，解得1≤m ≤3，所以答案应填[1,3]．14．已知函数f (x )＝ln x 1－x，若f (a )＋f (b )＝0，且0<a <b <1，则ab 的取值范围是________．答案 ⎝⎛⎭⎫0，14 解析由题意可知ln a 1－a ＋ln b 1－b ＝0，即ln ⎝ ⎛⎭⎪⎫a 1－a ×b 1－b ＝0，从而a 1－a ×b 1－b＝1，化简得a ＋b ＝1，故ab ＝a (1－a )＝－a 2＋a ＝－⎝⎛⎭⎫a －122＋14，又0<a 0，且a ≠1)的最大值是1，最小值是－18，求a 的值．解由题意知f (x )＝12(log a x ＋1)(log a x ＋2) ＝12(log 2a x ＋3log a x ＋2)＝12(log a x ＋32)2－18. 当f (x )取最小值－18时，log a x ＝－32. 又∵x ∈[2,8]，∴a ∈(0,1)．∵f (x )是关于log a x 的二次函数，∴函数f (x )的最大值必在x ＝2或x ＝8时取得．若12(log a 2＋32)2－18＝1，则a ＝2－13，此时f (x )取得最小值时，x ＝1332(2)＝--2∉[2,8]，舍去．若12(log a 8＋32)2－18＝1，则a ＝12，此时f(x)取得最小值时，x＝(12)32＝22∈[2,8]，符合题意，∴a＝12.。

对数与对数函数知识点及例题讲解

对数与对数函数1.对数（1）对数的定义：）对数的定义：如果a b =N （a ＞0，a ≠1），那么b 叫做以a 为底N 的对数，记作log a N =b . （2）指数式与对数式的关系：a b =N Ûlog a N =b （a ＞0，a ≠1，N ＞0）.两个式子表示的a 、b 、N 三个数之间的关系是一样的，并且可以互化. （3）对数运算性质: ①log a （MN ）=log a M +log a N . ②log a NM =log a M －log a N . ③log a M n =n log a M .（M ＞0，N ＞0，a ＞0，a ≠1）④对数换底公式：log b N =bNN a a log log log （a ＞0，a ≠1，b ＞0，b ≠1，N ＞0）. 2.对数函数（1）对数函数的定义）对数函数的定义函数y =log a x （a ＞0，a ≠1）叫做对数函数，其中x 是自变量，函数的定义域是（0，+∞）. 注意：真数式子没根号那就只要求真数式大于零,如果有根号,要求真数大于零还要保证根号里的式子大于零，底数则要大于0且不为1 对数函数的底数为什么要大于0且不为1呢？在一个普通对数式里在一个普通对数式里 a<0,或=1 的时候是会有相应b 的值的。

但是，根据对数定义: : loglog a a=1；如果a=1或=0那么log a a 就可以等于一切实数（比如log 1 1也可以等于2，3，4，5，等等）第二，根据定义运算公式：log a M^n = nlog a M 如果a<0,那么这个等式两边就不会成立（比如，log (-2) 4^(-2) 就不等于(-2)*log (-2) 4；一个等于1/16，另一个等于-1/16）（2）对数函数的图象）对数函数的图象O xyy = l o g x a > Oxy<a <a y = l o g x a 1111( ())底数互为倒数的两个对数函数的图象关于x 轴对称. （3）对数函数的性质: ①定义域：（0，+∞）. ②值域：R . ③过点（1，0），即当x =1时，y =0. ④当a ＞1时，在（0，+∞）上是增函数；当0＜a ＜1时，在（0，+∞）上是减函数. 基础例题1.函数f （x ）=|log 2x |的图象是的图象是1 1 1-1 1111 1 xxxxy y y y O OOOA BC D解析：f （x ）=îíì<<-³.10,log ,1,log 22x x x x答案：A 2.若f －－1（x ）为函数f （x ）=lg （x +1）的反函数，则f －－1（x ）的值域为___________________. 解析：f －1（x ）的值域为f （x ）=lg （x +1）的定义域.由f （x ）=lg （x +1）的定义域为（－1，+∞），∴f －－1（x ）的值域为（－1，+∞）. 答案：（－1，+∞）∞）3.已知f （x ）的定义域为［0，1］，则函数y =f ［log 21（3－x ）］的定义域是__________. 解析：由0≤log 21（3－x ）≤1Þlog 211≤log 21（3－x ）≤log 2121Þ21≤3－x ≤1Þ2≤x ≤25. 答案：［2，25］4.若log x7y=z ，则x 、y 、z 之间满足之间满足A.y 7=x zB.y =x 7zC.y =7x zD.y =z x解析：由logx 7y=z Þx z=7y Þx 7z=y ，即y =x 7z. 答案：B 5.已知1＜m ＜n ，令a =（log n m ）2，b =log n m 2，c =log n （log n m ），则，则A.a ＜b ＜cB.a ＜c ＜bC.b ＜a ＜cD.c ＜a ＜b解析：∵1＜m ＜n ，∴0＜log n m ＜1. ∴log n （log n m ）＜0. 答案：D 6.若函数f （x ）=log a x （0＜a ＜1）在区间［a ，2a ］上的最大值是最小值的3倍，则a 等于等于 A.42 B.22 C.41 D.21解析：∵0＜a ＜1，∴f （x ）=log a x 是减函数.∴log a a =3·log a 2a . ∴log a 2a =31.∴1+log a 2=31.∴log a 2=－32.∴a =42. 答案：A 7.函数y ＝log 2｜ax －1｜（a ≠0）的对称轴方程是x ＝－2，那么a 等于A. 21 B.－21 C.2 D.－2 解析：y =log 2|ax －1|=log 2|a （x －a1）|，对称轴为x =a1，由a1=－2 得a =－21. 答案：B 注意：此题还可用特殊值法解决，如利用f （0）=f （－4），可得0=log 2|－4a －1|.∴|4a +1|=1.∴4a +1=1或4a +1=－1. ∵a ≠0，∴a =－21. 8.函数f （x ）=log 2|x |，g （x ）=－x 2+2，则f （x ）·g （x ）的图象只可能是能是OxyOxyOxyOxyABC D解析：∵f （x ）与g （x ）都是偶函数，∴f （x ）·g （x ）也是偶函数，)111-1O xy注意：研究函数的性质时，利用图象会更直观. 【例3】已知f （x ）=log 31［3－（x －1）2］，求f （x ）的值域及单调区间. 解：∵真数3－（x －1）2≤3，∴log 31［3－（x －1）2］≥log 313=－1，即f （x ）的值域是［－1，+∞）.又3－（x －1）2＞0，得1－3＜x ＜1+3，∴x ∈（1－3，1］时，］时，3－（x －1）2单调递增，从而f （x ）单调递减；x ∈［1，1+3）时，f （x ）单调递增. 注意：讨论复合函数的单调性要注意定义域. 【例4】已知y =log a （3－ax ）在［0，2］上是x 的减函数，求a 的取值范围. 解：∵a ＞0且a ≠1，∴t =3－ax 为减函数.依题意a ＞1，又t =3－ax 在［0，2］上应有t ＞0，∴3－2a ＞0.∴a ＜23.故1＜a ＜23. 【例5】设函数f （x ）=lg （1－x ），g （x ）=lg （1+x ），在f （x ）和）和 g （x ）的公共定义域内比较|f （x ）|与|g （x ）|的大小. 解：f （x ）、g （x ）的公共定义域为（－1，1）. |f （x ）|－|g （x ）|=|lg （1－x ）|－|lg （1+x ）|. （1）当0＜x ＜1时，|lg （1－x ）|－|lg （1+x ）|=－lg （1－x 2）＞0；（2）当x =0时，|lg （1－x ）|－|lg （1+x ）|=0；（3）当－1＜x ＜0时，|lg （1－x ）|－|lg （1+x ）|=lg （1－x 2）＜0. 综上所述，当0＜x ＜1时，|f （x ）|＞|g （x ）|；当x =0时，|f （x ）|=|g （x ）|；当－1＜x ＜0时，|f （x ）|＜|g （x ）|. 【例6】求函数y =2lg （x －2）－lg （x －3）的最小值. 解：定义域为x ＞3，原函数为y ＝lg 3)2(2--x x . 又∵3)2(2--x x x ＝3442-+-x x x ＝31)3(2)3(2-+-+-x x x ＝（x －3）＋31-x ＋2≥4， ∴当x ＝4时，y min ＝lg4. 【例7】（2003年北京宣武第二次模拟考试）在f 1（x ）=x 21，f 2（x ）=x 2，f 3（x ）=2x ，f 4（x ）=log 21x 四个函数中，x 1＞x 2＞1时，能使21［f（x 1）+f （x 2）］＜f （221x xx x +）成立的函数是）成立的函数是A.f 1（x ）=x 21B.f 2（x ）=x 2C.f 3（x ）=2xD.f 4（x ）=log 21x解析：由图形可直观得到：只有f 1（x ）=x 21为“上凸”的函数. 答案：A 探究创新1.若f （x ）=x 2－x +b ，且f （log 2a ）=b ，log 2［f （a ）］=2（a ≠1）. （1）求f （log 2x ）的最小值及对应的x 值；值；（2）x 取何值时，f （log 2x ）＞f （1）且log 2［f （x ）］＜f （1）？）？解：（1）∵f （x ）=x 2－x +b ，∴f （log 2a ）=log 22a －log 2a +b . 由已知有log 22a －log 2a +b =b ，∴（log 2a －1）log 2a =0. ∵a ≠1，∴log 2a =1.∴a =2.又log 2［f （a ）］=2，∴f （a ）=4. ∴a 2－a +b =4，b =4－a 2+a =2.故f （x ）=x 2－x +2，127m +m －+m ）－+m+2m ≥+xm+2m ）+x m ≥2m （当且仅当=xm ，即=m 时等号成立）+x m +2m ）=4m ，即4m ≥≥169. 可以首先将它们与零比较，分出正负；正数通常都再与1比较分出大于1还是小于1，然后在各类中间两两相比较. 3.在给定条件下，求字母的取值范围是常见题型，要重视不等式知识及函数单调性在这类问题上的应用. 。

对数及对数函数知识点总结及题型分析

对数及对数函数1、对数的基本概念（1）一般地，如果a （1,0≠>a a ）的b 次幂等于N ，就是N a b =，那么数b 叫做以a 为底N 的对数，记作b N a=log ，其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式（2）常用对数：N 10log ，记作N lg ；自然对数N e log （e =2.71828…），记作N ln .（3）指数式与对数式的关系：log xa a N x N =⇔=（0>a ，且1≠a ，0N >）（4）对数恒等式：2、对数的性质（1）负数和零没有对数，即0>N ；（2）1的对数是零，即01log =a ；（3）底的对数等于1，即1log =a a3、对数的运算性质（1）如果a ＞0，a ≠1，M ＞0，N ＞0，那么①N M MN a a a log log )(log +=； ②N M NMa a alog log log -=； ③M n M a n alog log =（2）换底公式：推论：① b N N b log 1log =； ② ； ③ 1log log =⋅a b b a4、对数函数的定义：函数叫做对数函数，其中x 是自变量（1）研究对数函数的图象与性质：由于对数函数与指数函数互为反函数，所以的图像和的图像关于直线对称。

（2）复习)10(≠>=a a a y x且的图象和性质()010log >≠>=N a a N aNa ，且bNN a a b log log log =b mn b a na m log log =a y log x =(a 0a 1)>≠且a y log x =x y a =a y log x=xy a =y x =2．对数函数的图像：3．对数函数的性质：【回顾一下】① 定义：函数称为对数函数，1) 函数的定义域为；2) 函数的值域为； 3) 当____ __时，函数为减函数，当_________时为增函数； 4) 函数与函数 ______ 互为反函数.① 1) 图象经过点( )，图象在；2) 对数函数以为渐近线(当时，图象向上无限接近y 轴；当时，图象向下无限接近y 轴)； 4) 函数y ＝log a x 与的图象关于x 轴对称． ① 函数值的变化特征：题型一、对数式的运算例题1：填空（1）[])81(log loglog 346＝_____ ___；（2）19lg 3lg 2+-＝；（3）04.0log 10log 222+＝_____ ___；（4）3log 28log 316161+＝_____ ___；（5）=⋅⋅⋅4log 5log 7log 3log 7352例题2：若a y x =-lg lg ，则=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛332lg 2lg y x （）.A a 3 .Ba 23 .C a .D 2a 题型二变式、对数运算性质运用变式1：计算变式2：3128x y ==，则11x y-= .xy a log =)1,0(≠>=a a a y x 且10<<a 1>a 2(lg 2)lg 2lg 50lg 25+⋅+题型三、解对数式方程例题1：已知216log =x ，则=x （）.A 2 .B 4 .C 8 .D 32例题2：已知 ① 3log 1log 266-=x ，求x 的值； ② 2)25(log 22=--x x ，求x 的值。

对数与对数的运算

对数与对数运算基础知识扫描：1、概念：一般地，如果ba N =)1,0(≠>a a ，那么数b 叫做以a 为底 N 的对数. 记作，其中a 叫做对数的底数，N 叫做真数.2、重要公式：⑴负数与零没有对数； ⑵log 1________a =，log a a =⑶对数恒等式log __________________.a N a =n a na =log 3、对数的运算法则：如果 a ＞0，a ≠ 1，M ＞0， N ＞0 有：=)(log MN a ，=NMalog ，=n a M log ．log a N n=nlog a N (n ∈R)知识点一对数的概念 1、如果a 的b 次幂等于N ：，其中隐藏条件为a ＞0, a ≠1 N ＞0 2、常用对数：通常把常用对数10log N 简记为lg N 例如：5log 10简记作lg5；3、自然对数: 以e=2.71828……e 为底的对数叫自然对数，并把自然对数N e log 简记作N ln 例1、求使对数)5(log 2a b a -=-有意义的a 取值范围.例2、将下列指数式写成对数式，对数式写成指数式．（1）62554=；（2）73.531=m）（；（3）416log 21-= ；（4）303.210ln =知识点二对数的化简、求值例3、求下列各式中的x 的值．（1）32log 64-=x ；（2）68log =x ；（3）x =100lg ；（4）x e =-2ln例4、计算．（1）27log 9；（2）81log 3；（3）125log 5；（4）()()32log 32-+例5、计算.(1) 18lg 7lg 37lg 214lg -+-； (2) 5lg 2lg )5(lg 2⋅+.例6、已知3010.02lg =，4771.03lg =，求108lg ．_____(01)a b c =>≠换底公式：log 且c log log 1a b b a ∙=log log m na a nN N m=⇔=N a b例7、计算. （1）;25log 20lg 100+ (2) 3log 12.05+；（3）4log 16log 327.例8、已知 2log 3 = a ， 3log 7 = b ，用b a ，表示42log 56.巩固练习一：一、选择题 1、25)(log 5a -（a ≠0）化简得结果是（） A 、－aB 、a 2C 、｜a ｜D 、a2、log 7［log 3（log 2x ）］＝0，则21-x 等于（）A 、31B 、321 C 、221 D 、3313、nn ++1log（n n －＋1）等于（）A 、1B 、－1C 、2D 、－24、已知32a=，那么33log 82log 6-用表示是（）A 、2a -B 、52a -C 、23(1)a a -+D 、 23a a - 5、2log (2)log log a a a M N M N -=+，则NM的值为（） A 、41B 、4C 、1D 、4或1 6、若log m 9<log n 9<0,那么m,n 满足的条件是（）A 、m>n>1B 、n>m>1C 、0<n<m<1D 、0<m<n<17、若1<x<b,a=log ２b x,c=log a x,则a,b,c 的关系是（） A 、a<b<c B 、 a<c<b C 、c<b<a D 、c<a<b 二、填空题8、若log a x ＝log b y ＝－21log c 2，a ，b ，c 均为不等于1的正数，且x ＞0，y ＞0，c ＝ab ，则xy ＝________ 9、若lg2＝a ，lg3＝b ，则log 512＝________ 11、若2log 2,log 3,m na a m n a+===___________________12、lg25+lg2lg50+(lg2)2= 三、解答题13、222522122(lg )lg lg (lg )lg +⋅+-+14、若lga 、lgb 是方程01422=+-x x 的两个实根，求2)(lg )lg(ba ab ⋅的值。

对数与对数运算知识点

对数与对数运算1.对数：如果a x=N(a>0,且a ≠1)，那么数x 叫做以a 为底N 的对数,记作x=log a N，其中a 叫做对数的底数，N 叫做真数.2.对数的性质:(1)1的对数等于0 ;(2)底数的对数等于1;(3)零和负数没有对数3.以10为底的对数叫做常用对数,log 10N 记作lg N.4.以无理数e=2.718 28…为底的对数称为自然对数，logeN 记作ln N5.对数的运算性质：如果a>0，且a ≠1，M>0;N>0，那么：（1）log a (MN)=log a M +log a N ；log a (N1N2…Nk )=log a N1+log a N2+…log a N3；（2）log a (M ／N)=log a M -log a N ；（3）log a M n =nlog a M6.对数换底公式：log aN=abN bloglog ；7.对数运算中的三个常用结论：N aNa =log ,log aa =1,log a 1=08.两个常用的推论：a ，b ＞0且均不为1,m,n,为正整数（1）logab ×log b a=1；log ab ×log bc ×log c a=1；（2） b a b a m n nm log log =；ba b anm n m log log =；9.指数和对数的关系：a x =N ⇔log a N=x比较指数式、根式、对数式：几个对数运算公式的证明证明下列公式：（1）对数的运算性质:log a (M ／N)=log a M -log a N（2）对数的运算性质:log a M n =nlog a M（3）对数的换底公式：log ab=ab c c log log（4）对数运算中的常用结论：N a Na log（5）a ，b ＞0且均不为1,log a b×log b a=1 （6）a ，b ＞0且均不为1,m 为正整数,mmb alog =log a b（7）a ，b ＞0且均不为1,m,n 为正整数, n mb a log =m n log a b证明：（1）设a x =M ，a y=N ，则N M =y x aa =a x-y ．∴x-y=log a NM，∵x=log a M ，y=log a N，∴x-y= log a M - log a N ，∴log a N M = log a M - log a N（2）设a x=M ，则x=log a M，∴nx=nlog a M．∵（a x ）n=M n ，∴a xn =M n，∴xn=log a M n ，∴log a M n = nlog a M（3）设log a b =x ，则a x =b ．∴log c a x =log c b x ，∴xlog c a =log c b ，∴x=log c b÷log ca ，∴logab =ab c c log log（4）设log a N =x ，则a x=N ．∵log a a x=x ，∴xaa alog =a x，∴xaa a log =N（5）∵log a b =ab lg lg ，log b a =ba lg lg ，∴log ab ×log b a=a b lg lg ×ba lg lg =1（6）设mabm log =x ，则（a m）x=b m，∴a mx=b m，∴ mxa alog =log a b m ，∴mxlog a a=mlog ab，∴x=log ab ，∴mmb a log =log a b（7）设n a b mlog =x ，则（am）x=b n ，∴mxa alog =log a b n ，∴mxlog a a=nlogab，∴x=mnlog ab ，∴nmb alog =mn log a b。

03-4.2 对数与对数函数-4.2.1 对数运算 4.2.2 对数运算法则高中必修第二册人教B版

. .
（2）［多选题］(2024·山东省淄博市期末)若,,都是正数，且 ,则( )
BCD
A. B. C. D.
【解析】设,则，，，，，，所以 ,A错误，B正确.,因为，所以，则等号不成立，所以，则，C正确.因为，所以 ,D正确.
（3）已知,,,则的值为___.
（2）(全国Ⅰ卷)设,则 ( )
B
A. B. C. D.
【解析】因为，所以，
则有，所以 .
因为，所以，所以，所以 .
因为，所以，所以，两边同时平方得，所以 .
（1）；
【解析】 .
（2） ;
【解析】 .
（3） .
【解析】 .
例1-3 将下列对数式改写成指数式：
（1） ;
【解析】 .
（2） ;
【解析】 .
（3） .
【解析】 .
例1-4 ［多选题］(2024·辽宁省大连八中期中)下列式子中正确的是( )
AB
A. B. C.若,则 D.若,则
知识点3 换底公式
例3-6 ［教材改编P24 T1］的值为__.
【解析】 .（【巧解】利用推论三求解：）
例3-7 (2024·河北省唐山市期中)计算： ( )
B
A. B. C.1 D.2
【解析】原式 .
方法帮丨关键能力构建
题型1 对数的简单运算
例8 化简下列各式：
（1） ;
【解析】原式 .
B
A. B. C. D.
【解析】由对数运算法则可得 .
3.(2024·浙江省杭州市期中)若,则 ( )
C
A. B. C.1 D.
【解析】因为,所以,,所以, ,则 .

对数与对数运算专题

对数与对数运算第一部分：知识清单 1.几个对数恒等式：(1)负数和零没有对数；(2)log a 1＝0(a ＞0，且a ≠1)； (3)log a a ＝1(a ＞0，且a ≠1)． (4)对数恒等式a log a N ＝N 2．对数的运算性质如果a >0，且a ≠1，M >0，N >0那么： (1)log a (M ·N )＝log a M ＋log a N ． (2)log a M N＝log a M －log a N ． (3)log a M n ＝n log a M (n ∈R)． 3．换底公式log a b ＝log c blog c a(a >0，且a ≠1；c >0，且c ≠1；b >0)．牢记换底公式的三个常用推论(1)推论一：log a c ·log c a ＝1.此公式表示真数与底数互换，所得的对数值与原对数值互为倒数．(2)推论二：log a b ·log b c ·log c a ＝1.(3)推论三：log a m b n ＝n mlog a b .此公式表示底数变为原来的m 次方，真数变为原来的n 次第二部分：微题快测一、对数的定义域（注：学生在解对数不等式、方程的时候常常忽略定义域） 1.若b ＝log a (5－a )，则（）A.⎩⎨⎧a >0，5－a >0， B.⎩⎨⎧a ≠1，5－a >0，C.⎩⎨⎧a >0，5-a ≠1，5－a >0，D.⎩⎨⎧a >0，a ≠1，5－a >0，答案：D2.若b ＝log a (1+a )，则（）A.⎩⎨⎧a >0，1+a >0，B.⎩⎨⎧a >0，a ≠1，1+a >0，C.⎩⎨⎧a >0，1+a >0，D.⎩⎨⎧a >0，1+a ≠1，1+a >0，答案：B3.若b ＝log (a -1)a ，则（）A.⎩⎪⎨⎪⎧a >0，a-1>0，a ≠1 B.⎩⎨⎧a >0，a-1≠1，a-1>0， C.⎩⎨⎧a >0，a-1>0， D.⎩⎨⎧a ≠1，1+a >0，答案：B4.若b ＝log (a -2)a ，则（）A.⎩⎪⎨⎪⎧a >0，a-2>0，a ≠1B.⎩⎪⎨⎪⎧a ≠1，a-2>0，C.⎩⎪⎨⎪⎧a >0，a-2≠1，D.⎩⎪⎨⎪⎧a >0，a-2>0，a-2≠1答案：D5.若b =log (a -2)（6－a ），则（）A.⎩⎪⎨⎪⎧a-2>0，6-a >0，a-2≠1B.⎩⎪⎨⎪⎧a-2≠1，6-a >0，C.⎩⎪⎨⎪⎧a-2>0，6-a >0，6-a ≠1D.⎩⎪⎨⎪⎧a-2>0，6-a ≠1，答案：A6.若a =log (b+8)b ，则（）A.⎩⎪⎨⎪⎧b+8>0，b >0，b+8≠1B.⎩⎪⎨⎪⎧b+8≠1，b >0，C.⎩⎪⎨⎪⎧b+8>0，b ≠1，D.⎩⎪⎨⎪⎧b+8>0，b >0，b ≠1答案：A 7.若b =log1x-1（6－x ），则（）A.⎩⎨⎧1x-1>0，6-x >0，6-x ≠1B.⎩⎨⎧1x-1≠1，6-x >0，C.⎩⎨⎧6-x >0，1x-1≠1，D.⎩⎪⎨⎪⎧1x-1>0，6-x >0，1x-1≠1答案：D8.若m =log(n +1)n ，则（）A.⎩⎪⎨⎪⎧n +1>0，n >0，n ≠1B.⎩⎪⎨⎪⎧n +1>0，n >0，n +1≠1C.⎩⎪⎨⎪⎧n >0，n +1≠1D.⎩⎪⎨⎪⎧n +1>0，n ≠1，答案：B9.若m =log(a 2-1)a ，则（）A.⎩⎪⎨⎪⎧a 2-1>0，a >0，a ≠1B.⎩⎪⎨⎪⎧a 2-1>0，a >0，a 2-1≠1C.⎩⎪⎨⎪⎧a >0，a 2-1>0D.⎩⎪⎨⎪⎧a 2-1>0，a ≠1，B.答案：B10.若a=log ⎝ ⎛⎭⎪⎫2x x-2(6-x )3，则（） A.⎩⎨⎧2xx-1>0，(6-x )3>0，(6-x )3≠1B.⎩⎨⎧2x x-1≠1，(6-x )3>0，C.⎩⎪⎨⎪⎧2xx-1>0，(6-x )3>0，2x x-1≠1 D.⎩⎨⎧(6-x )3>0，2x x-1≠1，答案：C二、同底法解对数方程（注：同底法解对数方程算是一个必拿分的知识点，然而学生对此遗忘频率非常高，失分非常严重） 1.若log 2x ＝1，则x =（）A. 1B. 2C. 4D.－1 答案：B2.若log 3x ＝－1，则x =（）A. 3B. 13 C.4 D. 9答案：B3.若lg x＝1，则x=（）A. 10B.1100C.110D.1e答案：A4.若ln x＝0，则x=（）A. 1B.1100C.110D.1e答案：A4.若ln x＝1，则x=（）A. eB. 0C. －eD. 1e答案：A5.若log2x＝1024，则x=（）A. 2B. 1024C. 21024D. 10 答案：C7.若log2x＝3，则x=（）A. 5B. 9C. 6D. 8答案：D8.若log2x＝3，则x=（）A. 5B. 9C. 6D. 8答案：D9.若log2x+1 ＝2，则x=（）A. 15B. 8C. 3D. 0答案：A10.若lg x=2，则x=（）A. 10B. 100C.110 D.1100答案：B11.若log2(x－1)=2，则x=（）A. 3B. 5C. 7D. 9 答案：B12.若log3||x=2，则x=（）A. 3B. ±3C.9D. ±9 答案：D13.若log2||x－1=2，则x=（）A.－3或5B.3或－1C.±5D.2或0 答案：A14.若log2错误!=1，则x=（）A. 2B.± 2C.22D.±22答案：B三、对数的加减运算（注：对数的运算法则是一个必拿分的知识点，然而学生对此遗忘频率非常高，失分非常严重）1.计算log510－log52等于( )A．log58 B．lg 5 C．1 D．2 答案：C2.计算log52+log53等于( )A．log56 B．log55 C．lg6 D．ln6答案：A3.计算log x2+log x3等于( )A．log x6 B．log x 5 C．lg6 D．ln6 答案：A4.计算log22+log28等于( )A．log210 B. 6 C．4 D．2 答案：C5.计算lg100+lg10等于( )A.1000B.10C.3D.1答案：C6.计算lg100－lg10等于( )A.1000B.10C.3D.1 答案：D7.计算lg2+lg5等于( )A.10B.lg7C.lg ⎝ ⎛⎭⎪⎫25 D.1答案：D8.计算ln e+ln(2e )等于( )A.1+ln2B.1－ln2C.2+ln2D.ln(2e ·e ) 答案：C9.计算log 23+log 25+log 21等于( )A.log 215B.log 29C.4D.log 28 答案：A10.计算log 2(2x +2)－log 2(x +1)等于( )A.log 2(x +1)B.log 2(3x +3)C.log 23D.1 答案：D11.下列各式计算结果为log 2⎝ ⎛⎭⎪⎫57的是( )A.log 25－log 27B.log 25+log 27C.log 52－log 72D.log 52+log 72 答案：A12.计算lg e +lg2等于( )A.lg(2e )B.log 2 e C .lg ()e 2 D.lg ⎝ ⎛⎭⎪⎫e 2答案：A13.计算lg6－lg2+lg 13等于( )A.1B.0C.lg 133D.lg 43答案：B14.计算log 2()x 2－1－log 2()x －1－log 2()x+1等于( ) A.log 2()x －1 B.log 2()x+1 C.1 D.0 答案：D15.计算log 4(x+1)－log 4(x －1)等于( )A.log 42B.log 4⎝ ⎛⎭⎪⎫x+1x －1C.log 4()2xD.log 4()x 2－1答案：B16.下列各式计算结果为log 2错误!的是( ) A.log 2()x －1+log 2(x +1)+log 2(x 2+1)B.log 2()x －1+log 2(x +1)－log 2(x 2+1)C.log 2()x －1－log 2(x +1)－log 2(x 2+1)D.－log 2()x －1－log 2(x +1)－log 2(x 2+1)答案：A四、对数的乘法运算（注：用换底公式计算对数的乘法运算是一个必拿分的知识点，然而学生对此遗忘频率非常高，失分非常严重） 1.log 35·log 59等于( )A ．log 1545B ．log 814C ．1D ．2 答案：D2.log 95·log 253等于( )A ．2B ．4C ．12D ．14答案：D3.log 29·log 38等于( )A ．2B ．4C ．6D ．8 答案：C4.log 38·log 227等于( )A ．1B ．3C ．6D ．9 答案：D5.log 98·log 23等于( )A ．32B ．23C ．34D ．43答案：A6.log 38·log 83等于( )A ．0B ．1C ．－1D ．4 答案：B7.log 38·log 89·log 93等于( )A ．0B ．1C ．－1D ．±1 答案：B8.log 23·log 34·log 45·log 52等于( ) A ．0 B ．1 C ．－1 D ．4 答案：B9.log 34·log 1627等于( )A ．32B ．23C ．94D ．49答案：A 10.log 4127·log 32等于( ) A ．32 B ．23 C ．－32 D ．－23答案：C11.log 23·log 38·log 416等于( ) A ．2 B ．4 C ．6 D ．8 答案：C12.log (x －1)2·log 8(x 2－2x +1)等于( ) A ．23 B ．32 C ．－23 D ．－32答案：A13.log (x +1)16·log 4(x 3+3x 2+3x +1)等于( ) A ．23 B ．32 C ．－6 D ．6答案：D五、推论三：log a m b n＝nmlog a b 的应用（注：考查用推论化简底数、真数中的幂和根式，是大多数学生失分的重灾区） 1.lg1000等于（）A ．1B ．2C ．3D ．13答案：C2.log 832等于（）A ．1B ．2C ．53D ．35答案：C3.lg0.01等于（）A ．0.1B ．100C ．-2D ．-e 答案：C4.log 5325等于（）A ．1B ．23C ．53D ．35答案：B4.log 21024等于（）A ．4B ．6C ．8D ．10 答案：D5.lne 5等于（）A ．3B ．4C ．5D ．6 答案：C6.log 10248等于（）A ．310B ．103C ．1128 D ．128答案：A7.log 279等于（）A ．32B ．23C ．13D ．3答案：B8..log 644等于（）A ．3B ．23C ．13D ．－13答案：C9.log 1614等于（）A ．13B ．－23C ．12D ．－12答案：D10.log a b +log a 1b等于（）A ．1B ．－1C ．12 D ．0答案：D11.log 279－log 1664等于（）A ．－23B ．23C ．－56D ．56答案：C12.log 279·log 1664等于（）A ．－1B ．0C ．1D ．2 答案：C13.已知(log a b+log b a )2=4，且a >b ，则log a b 等于（） A ．－1 B ．0 C ．1 D ．1或－1 答案：A14.((2log 2-等于（）A ．－1B ．0C ．1D ．2 答案：A 15.lg110·lg 1100+lg 11000+lg 110000A．－1 B．0 C．－5 D．1答案：C组题说明：1.针对性：每一组题针对一个知识点，比如上面的第一组题针对的是对数的定义域，第二组针对的是同底法解对数方程，第三组针对的是对数的加减运算，第四组针对的是对数的乘法运算，第五组针对的是推论三：log a m b n＝nmlog a b的应用；2.最小阻力原则：要最大限度简化运算，降低阻力，使学生以最小的阻力、最快的速度体验公式的结构、性质和用法；3.有效重复原则：每个知识点尽量组织20个左右的微题，让学生有充分亲身体验的机会，也避免了学生死记答案或互相抄袭4.原创性：尽量原创，避免学生上网搜答案，从而保证学生课外使用的效度与可信度.。

对数及对数函数知识点总结及典例

对数及对数函数一．知识梳理（一）．对数的概念①定义：如果)1,0(≠>a a a 且的b 次幂等于N ，就是ba ＝ N ，那么数b 称以a 为底N 的对数，记作log a N ＝ b 其中a 称对数的底，N 称真数。

1）以10为底的对数称常用对数，N 10log 记作N lg ；2）以无理数)71828.2( =e e 为底的对数称自然对数，log e N ，记作N ln ；3）指数式与对数式的互化 ba ＝ N ⇔log a N ＝b ②基本性质：1）真数N 为正数（负数和零无对数）；2）log 10a =；3）1log =a a ；4）对数恒等式：N a Na =log 。

③运算性质：如果,0,0,0,0>>≠>N M a a 则 1）N M MN a a a log log )(log +=； 2）N M N M a a a log log log -=；3）∈=n M n M a na (log log R ）。

④换底公式：),0,1,0,0,0(log log log >≠>≠>=N m m a a aNN m m a1）1log log =⋅a b b a ；2）b mnb a na m log log =。

（二）对数函数1、对数函数的概念：函数0(log >=a x y a ，且)1≠a 叫做对数函数，其中x 是自变量，函数的定义域是（0，+∞）．2三．【例1】比较下列各组数的大小：（1）3log 2与()23log 3x x -+（2） 1.1log 0.7与 1.2log 0.7（3）32log 3与56log 5【变式训练1】比较大小：4.0lg 4.0log 4.0log 4.0log 3211.0【变式训练2】已知01a <<，log log 0a a m n <<，则（）.A 1n m << .B 1m n << .C 1m n << .D 1n m <<【例2】下列指数式与对数式互化不正确的一组是（） A 、0lg11100==与 B 、3131log 31272731-==-与 C 、39921log 213==与 D 、5515log 15==与【变式训练1】.若()125log -=-x，则x 的值为（）A 、25-B 、25+C 、2525+-或D 、52- 【变式训练2】.若()log lg ,x ______x ==20则【变式训练3】=-+7log 3log 49log 212121 。

知识讲解_对数及对数运算_基础(学生)

对数及对数运算【要点梳理】要点一、对数概念1．对数的概念如果()01b a N a a =>≠，且，那么数b 叫做以a 为底N 的对数，记作:log a N=b ．其中a 叫做对数的底数，N 叫做真数．要点诠释：对数式log a N=b 中各字母的取值范围是：a>0 且a ≠1， N>0， b ∈R ．2．对数()log 0a N a >≠，且a 1具有下列性质：（1）0和负数没有对数，即0N >；（2）1的对数为0，即log 10a =；（3）底的对数等于1，即log 1a a =．3．两种特殊的对数通常将以10为底的对数叫做常用对数，N N lg log 10简记作．以e （e 是一个无理数， 2.7182e =⋅⋅⋅）为底的对数叫做自然对数， log ln e N N 简记作．4．对数式与指数式的关系由定义可知:对数就是指数变换而来的，因此对数式与指数式联系密切，且可以互相转化．它们的关系可由下图表示．由此可见a ，b ，N 三个字母在不同的式子中名称可能发生变化．要点二、对数的运算法则已知()log log 010a a M N a a M N >≠>，且，、（1）正因数的积的对数等于同一底数各个因数的对数的和；()log log log a a a MN M N =+推广：()()121212log log log log 0a k a a a k k N N N N N N N N N =+++>、、、（2）两个正数的商的对数等于被除数的对数减去除数的对数；log log log a a a M M N N=- （3）正数的幂的对数等于幂的底数的对数乘以幂指数；log log a a M M αα=要点诠释：（1）利用对数的运算法则时，要注意各个字母的取值范围，即等式左右两边的对数都存在时等式才能成立．如：log 2（-3）（-5）=log 2（-3）+log 2（-5）是不成立的，因为虽然log 2（-3）（-5）是存在的，但log 2（-3）与log 2（-5）是不存在的．（2）不能将和、差、积、商、幂的对数与对数的和、差、积、商、幂混淆起来，即下面的等式是错误的：log a （M ±N ）=log a M ±log a N ，log a （M·N ）=log a M·log a N ，log aNM N M a a log log =．要点三、对数公式1．对数恒等式： log log a b N a a Na N Nb ⎫=⇒=⎬=⎭2．换底公式同底对数才能运算，底数不同时可考虑进行换底，在a>0， a≠1， M>0的前提下有:（1）)(log log R n M M n a a n ∈=令 log a M=b ，则有a b =M ，（a b ）n =M n ，即n b n M a =)(，即n a M b n log =，即:n aa M M n log log =．（2）)1,0(log log log ≠>=c c aM M c c a ，令log a M=b ，则有a b =M ，则有)1,0(log log ≠>=c c M a c b c 即M a b c c log log =⋅，即a M b c c log log =，即)1,0(log log log ≠>=c c a M M c c a 当然，细心一些的同学会发现（1）可由（2）推出，但在解决某些问题（1）又有它的灵活性．而且由（2）还可以得到一个重要的结论:)1,0,1,0(log 1log ≠>≠>=b b a a ab b a ．【典型例题】类型一、对数的概念例1．求下列各式中x 的取值范围：（1）2log (5)x -；（2）(1)log (2)x x -+；（3）2(1)log (1)x x +-．举一反三：【变式1】函数21log (2)x y x -=+的定义域为．类型二、指数式与对数式互化及其应用例2．将下列指数式与对数式互化：（1）2log 164=；（2）13log 273=-；（3）3x =；（4）35125=；（5）1122-=；（6）2193-⎛⎫= ⎪⎝⎭．举一反三：【变式1】求下列各式中x 的值：（1）161log 2x =- （2）log 86x = （3）lg1000=x（4）2-2ln e x = 【变式2】计算：222log 4;log 8;log 32并比较．类型三、利用对数恒等式化简求值例3．不用计算器计算：7log 203log lg25lg47(9.8)+++-举一反三：【变式1】求log log log a b c b c N a ⋅⋅的值（a ，b ，c ∈R +，且不等于1，N>0）．类型四、积、商、幂的对数例4． z y x a a a log ,log ,log 用表示下列各式举一反三：【变式1】求值（1）1log 864log 325log 21025-+ （2）lg2·lg50+（lg5）2 （3）lg25+lg2·lg50+（lg2）2类型五、换底公式的运用例5．已知18log 9,185ba ==，求36log 45．35(1)log ;(2)log ();(3)log a a a a xy x y z yz举一反三：【变式1】求值：（1）)2log 2)(log 3log 3(log 9384++；（2）32log 9log 278⋅；（3）31log 529-．类型六、对数运算法则的应用例6．计算（1）34331654()log log 8145-++ （2）7lg142lg lg 7lg183-+-（3）)36log 43log 32(log log 42122++ （4）353log 21log 235++-举一反三：【变式1】计算下列各式的值（1）()222lg5lg8lg5lg 20lg 23+++；（2）33(lg 2)3lg 2lg5(lg5)++．【变式2】已知1,(1,0)()44,(0,1)x x x f x x ⎧∈-⎪=⎨⎪∈⎩，则4(log 3)f = ．。

高中数学对数和对数函数知识点与例题讲解

对数与对数函数1.对数（1）对数的定义：如果a b=N（a＞0，a≠1），那么b叫做以a为底N的对数，记作logaN=b.（2）指数式与对数式的关系：a b=NlogaN=b（a＞0，a≠1，N＞0）.两个式子表示的a、b、N三个数之间的关系是一样的，并且可以互化.（3）对数运算性质:①log a（MN）=log a M+log a N.②log aMN=log a M－log a N.③logaM n=nlogaM.（M＞0，N＞0，a＞0，a≠1）④对数换底公式：logbN= l oglogaaNb（a＞0，a≠1，b＞0，b≠1，N＞0）.2.对数函数（1）对数函数的定义函数y=log a x（a＞0，a≠1）叫做对数函数，其中x是自变量，函数的定义域是（0，+∞）.注意：真数式子没根号那就只要求真数式大于零,如果有根号,要求真数大于零还要保证根号里的式子大于零，底数则要大于0且不为1对数函数的底数为什么要大于0且不为1呢？在一个普通对数式里a<0,或=1的时候是会有相应b的值的。

但是，根据对数定义:log a a=1；如果a=1或=0那么log a a就可以等于一切实数（比如log11也可以等于2，3，4，5，等等）第二，根据定义运算公式：log a M^n=nlogaM如果a<0,那么这个等式两边就不会成立（比如，log(-2)4^(-2)就不等于(-2)*log(-2)4；一个等于1/16，另一个等于-1/16）（2）对数函数的图象yyy =l ogxa>(1)a1O1xOxy =l o g a x (<a <1) 0底数互为倒数的两个对数函数的图象关于x 轴对称. （3）对数函数的性质: ①定义域：（0，+∞）. ②值域：R.③过点（1，0），即当x=1时，y=0.④当a ＞1时，在（0，+∞）上是增函数；当0＜a ＜1时，在（0，+∞）上是减函数.基础例题题型1（对数的计算） 1．求下列各式的值．（1）35 log ＋25log2－1 21 50log － 514 log ；（2）log5 2 1 25 ×lo g 3 1 8 ×lo g 5 1 9. 练习题1．计算：lg 1 2 －lg5 8 ＋lg12.5－log 89·log 278；3.log535＋21log2－log51502 －log514；3.log2125×log318×log519.1loglog4log3 4.399222．5.lg5lg2lg41(6).log24lglog27lg2log33222 7.2lg2lg3111lg0.36lg823例2．已知实数x、y、z满足3x＝4y＝6z＞1.(1)求证：2x＋1y＝2z；(2)试比较3x、4y、6z的大小．练习题．已知log189＝a，18b＝5，用a、b表示log3645.题型二：（对数函数定义域值域问题）例1．已知函数fxlog22xx1aax的定义域为集合A，关于x的不等式22 的解集为B，若AB，求实数a的取值范围．2．设函数2ylog(ax2x2)定义域为A．2（1）若AR，求实数a的取值范围；（2）若2log(ax2x2)2在x[1,2]上恒成立，求实数a的取值范围．2练习题1．已知函数2 fxlgax2x1（1）若fx的定义域是R,求实数a的取值范围及fx的值域；（2）若fx的值域是R，求实数a的取值范围及fx的定义域2求函数y=2lg （x －2）－lg （x －3）的最小值.题型三（奇偶性及性）例题1．已知定义域为R 的函数f (x )为奇函数足f(x ＋2)＝－f(x)，当x ∈[0,1]时，f(x)＝2x －1.(1)求f(x)在[－1,0)上的解析式； (2)求f(1 log24)的值． 2 4.已知f （x ）=l o g 1［3－（x －1）2］，求f （x ）的值域.3 5.已知y =l o g a （3－a x ）在［0，2］上是x 的减函数，求a 的围.4．已知函数f(x)lg(2x)lg(2x).（Ⅰ）求函数yf(x)的定义域；（Ⅱ）判断函数yf(x)的奇偶性；（Ⅲ）若f(m2)f(m)，求m的取值范围.练习题1．已知函数f(x)＝loga(x＋1)－loga(1－x)(a＞0，a≠1)(1)求f(x)的定义域；(2)判断f(x)的奇偶性，并给出证明；(3)当a＞1时，求使f(x)＞0的x的取值范围2．函数f(x)是定义在R上的偶函数，f(0)0，当x0时，1f(x)logx.2 （1）求函数f(x)的解析式；（2）解不等式2f(x1)2；3．已知f(x)是定义在R上的偶函数，且x0时，1f(x)log(x1)．2 （Ⅰ）求f(0)，f(1)；（Ⅱ）求函数f(x)的表达式；（Ⅲ）若f(a1)1，求a的取值范围．题型4（函数图像问题）例题1.函数f（x）=|log2x|的图象是yy111x-11xOOAByy111x1xOOCD6.求函数y＝log2｜x｜的定义域，并画出它的图象，指出它的单调区间.f(x)＝|lgx|，a，b为实数，且0＜a＜b.(1)求方程f(x)＝1的解；(2)若a，b满足f(a)＝f(b)＝2fa b2，求证：a·b＝1，a b2 ＞1.练习题：1．已知a0且a1，函数f(x)log(x1)a，1g(x)log a，记F(x)2f(x)g(x)1x（1）求函数F(x)的定义域及其零点；（2）若关于x的方程2 F2．已知函数f(x)＝log4(4x＋1)＋kx(k∈R)是偶函数．(1)求k的值；(2)设g(x)＝log44xa?237.函数y＝log2｜ax－1｜（a≠0）的对称轴方程是x＝－2，那么a等于题型五：函数方程1方程lgx+lg（x+3）=1的解x=___________________.5.已知函数f（x）= 1()2x,x4,则f（2+log23）的值为f(x1),x4,4．已知函数f(x)log a(axx)(a0,a1为常数）. （Ⅰ）求函数f(x)的定义域；（Ⅱ）若a2，x1,9,求函数f(x)的值域；（Ⅲ）若函数f(x)ya的图像恒在直线y2x1的上方，求实数a的取值范围.1xxyloglog(2x8).5．已知函数22242（Ⅰ）令tlog2x，求y关于t的函数关系式及t的取值范围；（Ⅱ）求函数的值域，并求函数取得最小值时的x的值.8.设函数f（x）=lg（1－x），g（x）=lg（1+x），在f（x）和g（x）的公共定义域内比较|f（x）|与|g（x）|的大小.您好，欢迎您阅读我的文章，本WORD文档可编辑修改，也可以直接打印。

对数与对数知识点

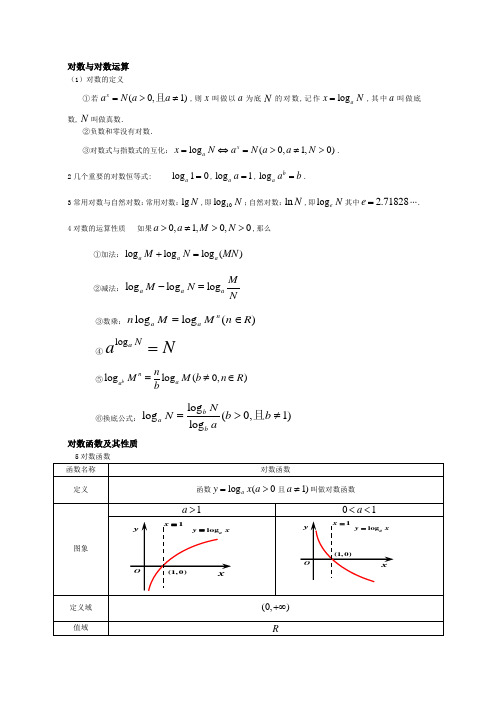
对数与对数运算（1）对数的定义①若(0,1)x a N a a =>≠且,则x 叫做以a 为底N的对数,记作log a x N=,其中a 叫做底数,N 叫做真数．②负数和零没有对数． ③对数式与指数式的互化：log (0,1,0)x a xN a N a a N =⇔=>≠>．2几个重要的对数恒等式: log 10a =,log 1a a =,log b a a b =．3常用对数与自然对数：常用对数：lg N ,即10log N ；自然对数：ln N ,即log e N 其中 2.71828e =…．4对数的运算性质如果0,1,0,0aa M N >≠>>,那么①加法：log log log ()aa a M N MN +=②减法：log log log a a a MM N N-=③数乘：log log ()n aa n M M n R =∈④log a N a N = ⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式：log log (0,1)log b a b NN b b a=>≠且对数函数及其性质5对数函数过定点图象过定点(1,0),即当1x =时,0y =．奇偶性非奇非偶单调性在(0,)+∞上是增函数在(0,)+∞上是减函数函数值的变化情况log 0(1)log 0(1)log 0(01)a a a x x x x x x >>==<<<log 0(1)log 0(1)log 0(01)a a a x x x x x x <>==><<a 变化对图象的影响在第一象限内,a 越大图象越靠低,越靠近x 轴在第四象限内,a 越大图象越靠高,越靠近y 轴在第一象限内,a 越小图象越靠低,越靠近x 轴在第四象限内,a 越小图象越靠高,越靠近y 轴基础练习：1.将下列指数式与对数式互化：12－2＝错误!； 2102＝100； 3e a ＝16； 464－错误!＝错误!； 2. 若log 3x ＝3,则x ＝_________ 3.计算：2lg 25lg 2lg 50(lg 2)++= ;4.1 错误!＝________．5. 设a ＝log 310,b ＝log 37,则3a －b ＝_________.6.若某对数函数的图象过点4,2,则该对数函数的解析式为______________.7.1如图2－2－1是对数函数y ＝log a x 的图象,已知a 值取错误!,错误!,错误!,错误!,则图象C 1,C 2,C 3,C 4相应的a 值依次是______________2函数y ＝lg x ＋1的图象大致是4. 求下列各式中的x 的值：1log 8x ＝－错误!；2log x 27＝错误!；8.已知函数fx ＝1＋log 2x ,则f 错误!的值为__________. 9. 在同一坐标系中,函数y ＝log 3x 与y ＝lg 错误!x 的图象之间的关系是_______________ 10. 已知函数fx ＝错误!那么ff 错误!的值为___________. 例题精析：例1.求下列各式中的x 值：1log 3x ＝3； 2log x 4＝2； 3log 28＝x ； 4lgln x ＝0.变式突破：求下列各式中的x的值：1log8x＝－错误!；2log x27＝错误!；3log2log5x＝0；4log3lg x＝1.例2.计算下列各式的值：12log510＋log50.25; 2错误!lg 错误!－错误!lg 错误!＋lg 错误!3lg 25＋错误!lg 8＋lg 5×lg 20＋lg 22.变式突破：计算下列各式的值：13错误!log错误!4；232＋log35；371－log75；44错误! log29－log25．例3.求下列函数的定义域：1y＝错误!；2y＝错误!；3y＝log2x－1－4x＋8．变式突破：求下列函数的定义域：1y＝错误!;例4.比较下列各组中两个值的大小：1ln 0.3,ln 2；2log a3.1,log a5.2a>0,且a≠1；3log30.2,log40.2；4log3π,logπ3.变式突破：若a＝log0.20.3,b＝log26,c＝log0.24,则a,b,c的大小关系为________．2设y1＝40.9,y2＝80.48,y3＝错误!－1.5,则A．y3>y1>y2 B．y2>y1>y3 C．y1>y2>y3D．y1>y3>y23．已知0<a<1,x＝log a错误!＋log a错误!,y＝错误!log a5,z＝log a错误!－log a错误!,则A．x>y>z B．z>y>x C．y>x>z D．z>x>y4．下列四个数ln22,lnln2,ln错误!,ln2中最大的为________．5．已知log m7<log n7<0,则m,n,0,1之间的大小关系是________．6．函数y＝log错误!－x2＋4x＋12的单调递减区间是________．7．若log a2<1,则实数a的取值范围是A．1,2B．0,1∪2,＋∞ C．0,1∪1,2 D．0,错误!8．下列不等式成立的是A．log32<log23<log25 B．log32<log25<log23C．log23<log32<log25 D．log23<log25<log32例5.解对数不等式1解不等式log2x＋1＞log21－x；2若log a错误!＜1,求实数a的取值范围．变式突破：解不等式：1log32x＋1>log33－x．2若log a2>1,求实数a的取值范围．课后作业：1. 已知log x16＝2,则x等于___________.2. 方程2log3x＝错误!的解是__________.3. 有以下四个结论：①lglg 10＝0；②lnln e＝0；③若10＝lg x,则x＝10；④若e＝ln x,则x＝e2.其中正确的是_____________.4.函数y＝log a x＋2＋1的图象过定点___________.5. 设a＝log310,b＝log37,则3a－b＝6. 若log错误!a＝－2,log b9＝2,c＝log327,则a＋b＋c等于___________.7.. 设3x＝4y＝36,则错误!＋错误!=___________.。

高中数学对数与对数函数知识点及经典例题讲解

对数与对数函数1.对数（1）对数的定义：如果a b =N （a ＞0，a ≠1），那么b 叫做以a 为底N 的对数，记作log a N =b .（2）指数式与对数式的关系：a b =N log a N =b （a ＞0，a ≠1，N ＞0）.两个式子表示的a 、b 、N 三个数之间的关系是一样的，并且可以互化.（3）对数运算性质:①log a （MN ）=log a M +log a N .②log a =log a M －log a N .NM ③log a M n =n log a M .（M ＞0，N ＞0，a ＞0，a ≠1）④对数换底公式：log b N =（a ＞0，a ≠1，b ＞0，b ≠1，N ＞0）.bN a a log log 2.对数函数（1）对数函数的定义函数y =log a x （a ＞0，a ≠1）叫做对数函数，其中x 是自变量，函数的定义域是（0，+∞）.注意：真数式子没根号那就只要求真数式大于零,如果有根号,要求真数大于零还要保证根号里的式子大于零，底数则要大于0且不为1在一个普通对数式里 a<0,或=1 的时候是会有相应b 的值的。

但是，根据对数定义: log a a=1；如果a=1或=0那么log a a 就可以等于一切实数（比如log 1 1也可以等于2，3，4，5，等等）第二，根据定义运算公式：log a M^n = nlog a M 如果a<0,那么这个等式两边就不会成立（比如，log (-2) 4^(-2) 就不等于(-2)*log (-2) 4；一个等于1/16，另一个等于-1/16）（2）对数函数的图象11))底数互为倒数的两个对数函数的图象关于x 轴对称.（3）对数函数的性质:①定义域：（0，+∞）.②值域：R .③过点（1，0），即当x =1时，y =0.④当a ＞1时，在（0，+∞）上是增函数；当0＜a ＜1时，在（0，+∞）上是减函数.基础例题1.函数f （x ）=|log 2x |的图象是?2.若f－1（x ）为函数f （x ）=lg （x +1）的反函数，则f－1（x ）的值域为___________________.3.已知f （x ）的定义域为［0，1］，则函数y =f ［log（3－x ）］的定21义域是__________.4.若log x =z ，则x 、y 、z 之间满足7y A.y 7=x z B.y =x 7z C.y =7x zD.y =z x5.已知1＜m ＜n ，令a =（log n m ）2，b =log n m 2，c =log n （log n m ），则A.a ＜b ＜cB.a ＜c ＜bC.b ＜a ＜cD.c ＜a ＜b6.若函数f （x ）=log a x （0＜a ＜1）在区间［a ，2a ］上的最大值是最小值的3倍，则a 等于A.B.C. D.422241217.函数y ＝log 2｜ax －1｜（a ≠0）的对称轴方程是x ＝－2，那么a 等于 (x=-2非解)A.B.－C.2D.－221218.函数f （x ）=log 2|x |，g （x ）=－x 2+2，则f （x ）·g （x ）的图象只可能是AB9.设f－1（x ）是f （x ）=log 2（x +1）的反函数，若［1+ f－1（a ）］［1+ f －1（b ）］=8，则f （a +b ）的值为A.1B.2C.3D.log 2310.方程lg x +lg （x +3）=1的解x =___________________.典型例题【例1】已知函数f （x ）=则f （2+log 23）的值为⎪⎩⎪⎨⎧<+≥,4),1(,4,21(x x f x xA.B.C.D.3161121241【例2】求函数y ＝log 2｜x ｜的定义域，并画出它的图象，指出它的单调区间.【例3】已知f （x ）=log ［3－（x －1）2］，求f （x ）的值域及单31调区间.【例4】已知y =log a （3－ax ）在［0，2］上是x 的减函数，求a 的取值范围.【例5】设函数f （x ）=lg （1－x ），g （x ）=lg （1+x ），在f （x ）和g （x ）的公共定义域内比较|f （x ）|与|g （x ）|的大小.【例6】求函数y =2lg （x －2）－lg （x －3）的最小值.【例7】在f 1（x ）=x ，f 2（x ）=x 2，f 3（x ）=2x ，f 4（x ）=log x 四2121个函数中，x 1＞x 2＞1时，能使［f （x 1）+f （x 2）］＜f （）成21221x x 立的函数是A.f 1（x ）=x(平方作差比较)B.f 2（x ）21=x 2C.f3（x）=2xD.f4（x）=log x12探究创新1.若f（x）=x2－x+b，且f（log2a）=b，log2［f（a）］=2（a≠1）.（1）求f（log2x）的最小值及对应的x值；（2）x取何值时，f（log2x）＞f（1）且log2［f（x）］＜f（1）？2.已知函数f（x）=3x+k（k为常数），A（－2k，2）是函数y=f －1（x）图象上的点.（1）求实数k的值及函数f－1（x）的解析式；（2）将y= f－1（x）的图象按向量a=（3，0）平移，得到函数y=g（x）的图象，若2f－1（x+－3）－g（x）≥1恒成立，试求m实数m的取值范围.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

对数与对数运算
1. 对数：如果a x
=N(a>0,且az 1)，那么数 x=log a N
,其中a 叫做对数的底数， 2. 对数的性质:(1)1的对数等于有对数 3. 以10为底的对数叫做常用对数
x 叫做以a 为底N 的对数，记作
N 叫做真数. 0 ；(2)底数的对数等于1;(3)零和负数没 ,log io N
记作 lg
N . 4. 以无理数e=2.718 28…为底的对数称为自然对数， logeN 记作ln N
5. 对数的运算性质：如果 a>0,且a 工1 , M>0;N>0,那么：
(MN) .
M .
N
N1N …Nk
N1 .
N2
.
N3
(1) log a =log a +log a ； log a ( )=log a +log a + …log a ；
(M / N)
M
N
(2) log a =log a -log a ；
(3) log a M i =nlog a M
N I N 6.对数换底公式：log - =log
N a ； log
7. 对数运算中的三个常用结论： a logaN N ,log a a =1,log a 1=0 8. 两个常用的推论：a , b >0且均不为1,m,n,为正整数
(1)
log a b
x log b a
=1; log a b
x log b C
x log c a
=1;
b
n
n
b
(2)
log a m m"og a ； log m a 9. 指数和对数的关系：a x
=N
a ‘
b lo g a N
n b m
log a b
;
1 =1
n
log a N
=x
比较指数式、根式、对数式:
几个对数运算公式的证明
证明下列公式:
(1)
(2) (3) 对数的运算性质对数的运算性质对数的换底公式:
(4) (5) (6) 对数运算中的常用结论: a , (M / N)
M
:log a =log a -log
:log a M=nlog a M
log
a b =晋
logc
a logaN N
1,log a b X log b a =1 1,m 为正整数,log 1,m,n 为正整数，log 则 M =M=a x-y N M a y
• x-y= log a ： log a N ,. log a~N
(2)设 a x
=M 贝» x=log a M
,
M n , • log a M n = nlog a b =x ,贝廿 a x
=b . b =logc b
a = a logc I a N =x ，贝廿 a x
=N.v log a a x =x ,. a a b =3 , log b a
=必,• log a b
X log lg a lg b b m
=x ，则(a °) x =b m , • a mx =b m ,. log b m
b ，…log
a m
=log a
mx
贝廿(a 。

x =b n , •• log/
=log nlog a b , • x= n log a b , •- log a m
b =-log a b
m m
(7) a ,
a ,
b > 0且均不为 b > 0且均不为 b > 0且均不为 b m
a m
证明：(1)设 a x =M a y
=N, M . N a - log a
• xn=log (3)设 log -log c a ,. log (4) 设 log (5) v log (6)设 log mlog a b ,.•. x=log (7)设 log a m
b n =x , =log a
=-log m
IM
a~N , b n
m
a M N -x=log a , y=log a , x-y=log M . N log a - log a • • nx=nlog a .- M a
xx a b b
• • log c a =log c b ，…xlog c =log c ，…x=log c (a x ) x
l0
9a a
a b n=M ,「・ a xn =M , =a x ,A a log
a ax
=N =lgb x lga =1 lgb = log a b m , mxlog a a
= lg a mx a a b n ,「. mxlog a a
=。

对数与对数运算知识点

高中数学对数的运算

对数与对数函数

知识讲解_对数及对数运算_基础

对数与对数运算学习讲解

对数及其运算性质

对数的运算与对数函数

高一 对数与对数函数知识点+例题+练习 含答案

对数与对数函数知识点及例题讲解

对数及对数函数知识点总结及题型分析

对数与对数的运算

对数与对数运算知识点

03-4.2 对数与对数函数-4.2.1 对数运算 4.2.2 对数运算法则高中必修第二册人教B版

对数与对数运算专题

对数及对数函数 知识点总结及典例

知识讲解_对数及对数运算_基础(学生)

高中数学对数和对数函数知识点与例题讲解

对数与对数知识点

高中数学对数与对数函数知识点及经典例题讲解

高一对数与对数函数知识点+例题+练习含答案

对数及对数函数知识点总结及典例