二次函数专题训练1——图像特征与a、b、c、△符号的关系

合集下载

中考——二次函数图像特征与a、b、c、△符号的关系

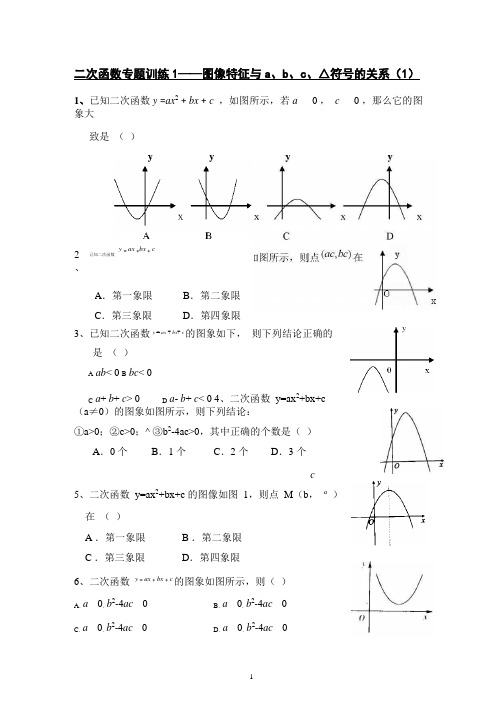
二次函数专题训练1——图像特征与a、b、c、△符号的关系（1）1、已知二次函数y =ax2+ bx + c，如图所示，若a0 ，c0 ，那么它的图象大致是（）C．第三象限D．第四象限3、已知二次函数y = ax + bx+ c的图象如下，则下列结论正确的是（）Aab< 0 B bc< 0Ca+ b+ c> 0 D a- b+ c< 0 4、二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①a>0；②c>0；^ ③b2-4ac>0，其中正确的个数是（）A．0 个B．1 个C．2 个D．3 个c5、二次函数y=ax2+bx+c 的图像如图1，则点M（b，a）在（）A ．第一象限B ．第二象限C ．第三象限D．第四象限6、二次函数y = ax + bx + c的图象如图所示，则（）A、a0，b 2-4ac0 B、a0，b2-4ac0C、a0，b2-4ac0 D、a 0，b2-4ac02、已知二次函数y = ax +bx + cA．第一象限B．第二象限7、已知函数y=ax+b 的图象经过第一、二、三象限，那么y=ax2+bx+1 的图象大致为（）9、二次函数y = ax +bx+c（a 0）的图象如图所示，则下列说法不正确的是（）A．b2-4ac 0 B．a 0-b 012、如图是二次函数y＝ax2＋bx＋c图象的一部分，图象过点A（－3，0），对称轴为x＝－1．给出四个结论：①b2>4ac；② 2a＋b=0；③ a－b＋c=0；④5a<b．其中正确结论是（）．A ②④B ①④C ②③D ①③28、已知函数y = ax正确的是（A．a>0，c>0C．a<0，c>0C．c0D．2aA. 2 个B. 3 个C. 4 个D. 5 个13、二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①c<0，②b>^ 0，^ ③4a+2b+c>0，④（a+c）2<b2．其中正确的有（）A．1 个B．2 个C．3 个D．4 个14、如图，抛物线y =ax2+bx+c（a0）的对称轴是直线x =1，且经过点P（3，0），则a -b+c的值为（）A. 0B. －1C. 1D. 219、已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，^ 则下列结论：①a、b 同号；②当x=1 和x=3 时，函数值相等；③4a+b=0；④当y=-2时，x 的值只能取0.其中正确的个数是( )))23、函数y=ax+b 与y=ax2+bx+c 的图象如图所示, 则下列选项中正确的是( )A. ab>0,c>0B. ab<0,c>0A．B．C．D．二次函数专题训练1——图像特征与a 、b 、c 、△符号的关系（2）5、在同一直角坐标系中，函数y=mx+ m 和y = -mx 2 +2x +2（m 是常数，且m 0）的图象可．能．是（））1、，则它们在同一坐标系中的大致图象是（）2、已知函数 y=ax 2+ax 与函数Ａ．Ｂ．Ｃ．Ｄ．a6、次函数y＝ax2＋bx＋c的图象如图所示，反比例函数y＝a与正比例函数y＝（b＋c）x9、如图为二次函数y=ax2＋b x＋c 的图象，在下列说法中：①ac<0；②方程ax2＋b x＋c=0 的根是x1= －1, x2= 3③a＋b＋c>0 ④当x>1 时，y 随x 的增大而增大。

二次函数图像性质专题复习——二次函数图象与a,b,c的关系

直线x=-1
0
x
团结协作以形助数
若二次函数y=ax2＋bx＋ c(a≠0) 的图象与x轴交于点A，对称轴为直线x=1，下列结论： ①abc＜0；②2a+b=0; ③ 3a+c>0；④方程ax2＋bx＋ c=0(a≠0)必有一个根大于-1且小于0.正确的是______
---中考பைடு நூலகம்线
y
直线x=1
团结协作以形助数---慧眼识图见本真
活动要求：
直线x=1 y
1、观察二次函数图象，把你
能从图中得出哪些a，b，c的
信息？写到学案上
2、组长编序号汇总到卡纸上 3、组内代表展示
0
x
团结协作以形助数---慧眼识图见本真
直线x=-1y
0
x
团结协作以形助数 ---中考在线
团结协作以形助数
y
---中考在线
-1 0 1 2 3 x
团结协作以形助数---慧眼识图见本真
直线x=1 y
0
x
y
直线x=1 y=ax2+bx+c
-1 0 1 2 3 x
直线x=1 y=ax2+bx+c
3 -1
变式：给出以下5个结论：
①2a+b=0；②a-b+c>0; ③ 8a+c<0；④若点P（，12 y1）、Q 特殊点，要发现
二次函数专题复习
——二次函数图象与a，b，c的关系
聚焦中考扬帆起航
齐心协力以数定形
---匠心巧手绘“蓝”图
若二次函数y=ax2＋bx＋c(a≠0) a＞0，b＞0，c＜0，在下列的
平面直角坐标系中画出二次函数的简图

中考数学专题复习及练习：二次函数图像与系数a、b、c的关系

2020中考数学复习专题：二次函数图像与a、b、c的关系专题能力提升专练一．规律探究问题1：a，b，c符号与图象的关系：a的符号决定了抛物线的________，当_______时，开口________；当________时，开口________；c是抛物线与________交点的________；b的符号与a________，根据________可推导．问题2：a，b，c组合的符号判断的解题思路：①确定________符号及________的信息；②找特殊点的___________，获取等式或不等式；③________代入不等式，组合判断残缺式符号．（残缺型式子是指不同时含有a，b，c三个系数的式子，例如有时式子中只含有a，b时，我们就称之为残缺式或残缺型）二.练习反馈1.如图所示的抛物线是二次函数y=ax2+bx+c（a≠0）的图象，则下列结论：①；②b+2a=0；③抛物线与x轴的另一个交点为(4，0)；④；⑤．其中正确的结论有( )A.5个B.4个C.3个D.2个2.如图，二次函数y=ax2+bx+c（a≠0）的图象的顶点在第一象限，且过点(0，1)和(-1，0)．下列结论：①；②；③；④当时，．其中正确结论的个数是( )A.1个B.4个C.3个D.2个3.小轩从如图所示的二次函数的图象中，观察得到如下四个结论：①；②；③；④．其中正确的结论是( )A.①②③B.②③④C.①②④D.①②③④4.从如图所示的二次函数的图象中，得到下列几个结论：①；②；③；④；⑤；⑥；⑦．则正确的结论有( )个．A.2B.3C.4D.55.已知二次函数的图象如图所示，有下列5个结论：①；②；③；④；⑤（）．其中正确的结论有( )A.2个B.3个C.4个D.5个6.二次函数图象的一部分如图所示，其对称轴为直线，且过点．下列说法：①；②；③；④若是抛物线上的两点，则．其中正确的是( )A.①②B.②③C.①②④D.②③④7.已知二次函数的图象如图所示，它与x轴的两个交点分别为(-1，0)，(3，0)．下列结论：①；②b-2a=0；③；④；⑤（）．其中正确的是( )A.③⑤B.②③C.③④⑤D.①②8.已知二次函数的图象如图所示，有下列结论：①；②2a+b=0；③；④．其中正确的有( )A.1个B.2个C.3个D.4个9.抛物线的顶点为D(-1，2)，与x轴的一个交点A在点(-3，0)和(-2，0)之间，其部分图象如图，则以下结论：①；②；③c-a=2；④方程有两个相等的实数根．其中正确的有( )A.1个B.2个C.3个D.4个10.已知二次函数的图象经过()，(2，0)两点，且，图象与y轴正半轴的交点在(0，2)的下方，则下列结论：①；②；③；④．其中正确的是( )A.①②B.②③C.①②④D.①②③④11.如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(-1,0);⑤当1<x<4时,有y2<y1,其中正确的是 ( )A.①②③B.①③④C.①③⑤D.②④⑤12.已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是 ( )A.1B.2C.3D.413.二次函数y=ax2+bx+c的图象如图所示，则下列结论：①a<0 ②b<0 ③c>0④4a+2b+c=0, ⑤b+2a=0⑥ b2-4ac>0其中正确的是________．（写出所有正确结论的序号）14.已知二次函数的图象与轴交于点、，且，与轴的正半轴的交点在的下方．下列结论：①；②；③；④．其中正确结论的个数是个．15.已知二次函数y＝ax2+bx+c（a≠0）的图象如图，有下列6个结论：①abc＜0；②b＜a﹣c；③4a+2b+c＞0；④2c＜3b；⑤a+b＜m（am+b），（m≠1的实数）⑥2a+b+c＞0，其中正确的结论的有．16.如图，已知二次函数y＝ax2+bx+c的图象与x轴分别交于A、B两点，与y 轴交于C点，OA＝OC，则由抛物线的特征写出如下结论：①abc＞0；②4ac-b2＞0；③a﹣b+c＞0；④ac+b+1＝0．其中正确的个数是.17.已知抛物线2(0)y ax bx c a=++≠的对称轴是直线1x=，其部分图象如图所示，下列说法中：①0y>，正x-<<时，0+=；④当13-+<；③30abc<；②0a b ca c确的是（填写序号）．18.二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：①b＞0；②a ﹣b+c＝0；③一元二次方程ax2+bx+c+1＝0（a≠0）有两个不相等的实数根；④当x＜﹣1或x＞3时，y＞0．上述结论中正确的是．（填上所有正确结论的序号）19.如图，若二次函数y=ax2+bx+c（a≠0）图象的对称轴为x=1，与y轴交于点C，与x轴交于点A、点B（﹣1，0），则①二次函数的最大值为a+b+c；②a﹣b+c＜0；③b2﹣4ac＜0；④当y＞0时，﹣1＜x＜3，其中正确的．（填上所有正确结论的序号）20.如图是二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的一部分，与x 轴的交点A在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab ＜0；②2a+b=0；③3a+c＞0；④a+b≥m（am+b）（m为实数）；⑤当﹣1＜x＜3时，y＞0，其中正确的是．（填上所有正确结论的序号）21.如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，2）与（0，3）之间（不包括这两点），对称轴为直线x=2．下列结论：①abc＜0；②9a+3b+c＞0；③若点M（，y1），点N（，y2）是函数图象上的两点，则y1＜y2；④﹣＜a＜﹣．其中正确结论．（填上所有正确结论的序号）22.抛物线y=ax2+bx+c的对称轴为直线x=﹣1，部分图象如图所示，下列判断中：①abc＞0；②b2﹣4ac＞0；③9a﹣3b+c=0；④若点（﹣0.5，y1），（﹣2，y2）均在抛物线上，则y1＞y2；⑤5a﹣2b+c＜0．其中正确的．（填上所有正确结论的序号）23.如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标（1，n）与y轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：①3a+b＜0；②﹣1≤a≤﹣；③对于任意实数m，a+b≥am2+bm总成立；④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根．其中结论正确的．（填上所有正确结论的序号）24.二次函数y=ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①4a+2b+c＞0；②5a﹣b+c=0；③若方程a（x+5）（x﹣1）=﹣1有两个根x1和x2，且x1＜x2，则﹣5＜x1＜x2＜1；④若方程|ax2+bx+c|=1有四个根，则这四个根的和为﹣4．其中正确的结论有．（填上所有正确结论的序号）。

二次函数系数a、b、c与图像的关系专项练习

二次函数系数a 、b 、c 与图像的关系专项练习知识要点二次函数y=ax 2+bx+c 系数符号的确定：（1）a 由抛物线开口方向确定：开口方向向上，则a ＞0；否则a ＜0．（2）b 由对称轴和a 的符号确定：由对称轴公式x=判断符号．（3）c 由抛物线与y 轴的交点确定：交点在y 轴正半轴，则c ＞0；否则c ＜0．（4）b 2-4ac 的符号由抛物线与x 轴交点的个数确定：2个交点，b 2-4ac ＞0；1个交点，b2-4ac=0；没有交点，b 2-4ac ＜0．（5）当x=1时，可确定a+b+c 的符号，当x=-1时，可确定a-b+c 的符号．（6）由对称轴公式x=，可确定2a+b 的符号．一．选择题（共9小题）1．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a ；④am 2+bm+a ＞0（m ≠﹣1）．其中正确的个数是（）A ．1B ．2C ．3D ．42．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，给出以下结论：①a+b+c ＜0；②a ﹣b+c ＜0；③b+2a ＜0；④abc ＞0．其中所有正确结论的序号是（）A ．③④B ．②③C ．①④D ．①②③3．二次函数y=ax 2+bx+c 的图象如图所示，那么关于此二次函数的下列四个结论：①a ＜0；②c ＞0；③b 2﹣4ac ＞0；④＜0中，正确的结论有（）A ．1个B ．2个C ．3个D ．4个4．函数y=x 2+bx+c 与y=x 的图象如图，有以下结论：①b 2﹣4c ＜0；②c ﹣b+1=0；③3b+c+6=0；④当1＜x ＜3时，x 2+（b ﹣1）x+c ＜0．其中正确结论的个数为（）A ．1B ．2C ．3D ．45．如图是二次函数y=ax 2+bx+c 图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc ＜0；②2a ﹣b=0；③4a+2b+c ＜0；④若（﹣5，y 1），（2，y 2）是抛物线上的两点，则y 1＞y 2．其中说法正确的是（）A ．①②B ．②③C ．②③④D ．①②④6．如图，二次函数y=x 2+（2﹣m ）x+m ﹣3的图象交y 轴于负半轴，对称轴在y 轴的右侧，则m 的取值范围是（）A ．m ＞2B ．m ＜3C ．m ＞3D ．2＜m ＜37．如图是二次函数y=ax 2+bx+c 图象的一部分，图象过点A （﹣3，0），对称轴为x=﹣1．给出四个结论：①b 2＞4ac ；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A ．1个B ．2个C ．3个D ．4个8．如图，抛物线y=ax 2+bx+c 与x 轴交于点A （﹣1，0），顶点坐标为（1，n ），与y 轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x ＞3时，y ＜0；②3a+b ＞0；③﹣1≤a ≤﹣；④≤n ≤4．其中正确的是（）A ．①②B ．③④C ．①③D ．①③④9．已知二次函数y=ax 2+bx+c （a ＞0）的图象与x 轴交于点（﹣1，0），（x 1，0），且1＜x 1＜2，下列结论正确的个数为（）①b ＜0；②c ＜0；③a+c ＜0；④4a ﹣2b+c ＞0．A ．1个B ．2个C ．3个D ．4个10、已知抛物线y=ax 2+bx+c （a ≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A 、a ＞0 B 、b ＜0 C 、c ＜0 D 、a+b+c ＞011、已知二次函数y=ax 2+bx+c 的图象如图，其对称轴x=-1，给出下列结果①b 2＞4ac ；②abc ＞0；③2a+b=0；④a+b+c ＞0；⑤a-b+c ＜0，则正确的结论是（）A 、①②③④B 、②④⑤C 、②③④D 、①④⑤12、如图，二次函数y=ax 2+bx+c 的图象与y 轴正半轴相交，其顶点坐标为（12，1），下列结论：①ac ＜0；②a+b=0；③4ac-b 2=4a ；④a+b+c ＜0．其中正确结论的个数是（）A 、1B 、2C 、3D 、4答案一．选择题（共9小题）1．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a ；④am 2+bm+a＞0（m ≠﹣1）．其中正确的个数是（）A ．1B ．2C ．3D ．4考点：二次函数图象与系数的关系．分析：由抛物线与y 轴的交点判断c 与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：抛物线与y 轴交于原点，c=0，（故①正确）；该抛物线的对称轴是：，直线x=﹣1，（故②正确）；当x=1时，y=a+b+c∵对称轴是直线x=﹣1，∴﹣b/2a=﹣1，b=2a ，又∵c=0，∴y=3a ，（故③错误）；x=m 对应的函数值为y=am 2+bm+c ，x=﹣1对应的函数值为y=a ﹣b+c ，又∵x=﹣1时函数取得最小值，∴a ﹣b+c ＜am 2+bm+c ，即a ﹣b ＜am 2+bm ，∵b=2a ，∴am 2+bm+a ＞0（m ≠﹣1）．（故④正确）．故选：C ．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax 2+bx+c （a ≠0）系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点、抛物线与x轴交点的个数确定．2．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，给出以下结论：①a+b+c ＜0；②a ﹣b+c ＜0；③b+2a ＜0；④abc ＞0．其中所有正确结论的序号是（）A ．③④B ．②③C ．①④D ．①②③考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a 的符号，由抛物线与y 轴的交点判断c 的符号，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．解答：解：①当x=1时，y=a+b+c=0，故①错误；②当x=﹣1时，图象与x 轴交点负半轴明显大于﹣1，∴y=a ﹣b+c ＜0，故②正确；③由抛物线的开口向下知a ＜0，∵对称轴为0＜x=﹣＜1，∴2a+b ＜0，故③正确；④对称轴为x=﹣＞0，a＜0∴a、b异号，即b＞0，由图知抛物线与y轴交于正半轴，∴c＞0 ∴abc＜0，故④错误；∴正确结论的序号为②③．故选：B．点评：二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0；（2）b由对称轴和a的符号确定：由对称轴公式x=﹣判断符号；（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0；（4）当x=1时，可以确定y=a+b+c的值；当x=﹣1时，可以确定y=a﹣b+c的值．3．二次函数y=ax 2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c 与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解解：①∵图象开口向下，∴a＜0；故本选项正确；答：②∵该二次函数的图象与y轴交于正半轴，∴c＞0；故本选项正确；③∵二次函数y=ax2+bx+c的图象与x轴有两个不相同交点，∴根的判别式△=b2﹣4ac＞0；故本选项正确；④∵对称轴x=﹣＞0，∴＜0；故本选项正确；综上所述，正确的结论有4个．故选D．点评：本题主要考查了二次函数的图象和性质，解答本题关键是掌握二次函数y=ax2+bx+c系数符号的确定，做题时要注意数形结合思想的运用，同学们加强训练即可掌握，属于基础题．4．函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由函数y=x2+bx+c与x轴无交点，可得b2﹣4c＜0；当x=﹣1时，y=1﹣b+c＞0；当x=3时，y=9+3b+c=3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．解答：解：∵函数y=x2+bx+c与x轴无交点，∴b2﹣4ac＜0；故①正确；当x=﹣1时，y=1﹣b+c＞0，故②错误；∵当x=3时，y=9+3b+c=3，∴3b+c+6=0；。

二次函数的图像与系数a,b,c之间的关系(解析版)

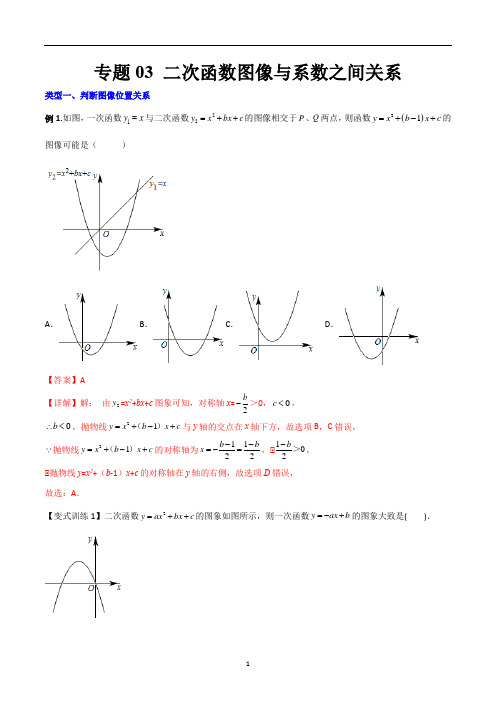
专题03 二次函数图像与系数之间关系类型一、判断图像位置关系例1.如图，一次函数1y x =与二次函数22y x bx c =++的图像相交于P 、Q 两点，则函数()21y x b x c =+-+的图像可能是（）A ．B ．C ．D ．【答案】A【详解】解：由2y =x 2+bx +c 图象可知，对称轴x =2b -＞0，0c <， 0b ∴<，抛物线21y x b x c =+-+（）与y 轴的交点在x 轴下方，故选项B ，C 错误，抛物线21y x b x c =+-+（）的对称轴为1122b b x --=-=，∴102b -＞， ∴抛物线y =x 2+（b -1）x +c 的对称轴在y 轴的右侧，故选项D 错误，故选：A ．【变式训练1】二次函数2y ax bx c =++的图象如图所示，则一次函数y ax b =-+的图象大致是( )．A ．B ．C ．D ．【答案】C【详解】解：观察二次函数2y ax bx c =++的图象得：0,02b a a<-<， ∴0b <，0a ->，∴一次函数y ax b =-+的图象经过第一、三、四象限．故选：C【变式训练2】在同一平面直角坐标系中，函数()20y ax bx a =+≠与y ax b =+的图象可能是（） A ．B ．C ．D ．【答案】A【详解】解：函数()20y ax bx a =+≠经过原点（0，0），则B 错误；当a <0时，y ax b =+经过二、四象限，则D 错误；当02b a->时，b >0， y ax b =+经过一、二、四象限，则C 错误；当a >0，02b a ->时，b <0， y ax b =+经过一、三、四象限，则A 符合题意．故选：A ．【变式训练3】在同一平面直角坐标系中，函数2y ax bx =+与y ＝ax ＋b 的图象不可能是( )A ．B ．C ．D ．【答案】D【详解】解：当a >0，b >0时，y =ax 2+bx 的开口上，与x 轴的一个交点在x 轴的负半轴，y =ax +b 经过第一、二、三象限，且两函数图象交于x 的负半轴，无选项符合；当a >0，b <0时，y =ax 2+bx 的开口向上，与x 轴的一个交点在x 轴的正半轴，y =ax +b 经过第一、三、四象限，且两函数图象交于x 的正半轴，故选项A 正确，不符合题意题意；当a <0，b >0时，y =ax 2+bx 的开口向下，与x 轴的一个交点在x 轴的正半轴，y =ax +b经过第一、二、四象限，且两函数图象交于x 的正半轴，C 选项正确，不符合题意；当a <0，b <0时，y =ax 2+bx 的开口向下，与x 轴的一个交点在x 轴的负半轴，y =ax +b 经过第二、三、四象限，B 选项正确，不符合题意；只有选项D 的两图象的交点不经过x 轴，故选D.【变式训练4】如图，一次函数1y x =与二次函数22y ax bx c =++的图像相交于P ，Q 两点，则函数()21y ax b x c =+-+的图像可能是（）A ．B ．C ．D ．【答案】D【详解】∴一次函数1y x =与二次函数22y ax bx c =++的图像相交于P ，Q 两点， ∴一元二次方程()210ax b x c +-+=有两个不相等的实数根，∴函数()21y ax b x c =+-+与x 轴有两个交点，由题意可知：02b a ->，0a >，∴110222b b a a a --=-+>， ∴函数()21y ax b x c =+-+的对称轴102b x a -=->，∴选项D 符合条件．故选D ．类型二、根据图像判断a ，b ，c 之间关系例1．二次函数()20y ax bx c a =-+≠的图象如图所示，下列选项错误的是（）A ．0ac <B ．1x >时，y 随x 的增大而增大C ．0a b c ++>D ．方程20ax bx c ++=的根是11x =-，23x =【答案】C 【详解】A.由二次函数的图象开口向上可得a >0，由抛物线与y 轴交于x 轴下方可得c <0，所以ac <0，正确；B.由a >0，对称轴为x =1，可知x >1时，y 随x 的增大而增大，正确；C.把x =1代入()20y ax bx c a =-+≠得，y =a +b +c ，由函数图象可以看出x =1时二次函数的值为负，错误；D.由二次函数的图象与x 轴交点的横坐标是-1或3，可知方程20ax bx c ++=的根是121,3x x =-=，正确．故选：C ．例2．如图，已知抛物线2y ax bx c =++（a ，b ，c 为常数，0a ≠）经过点()2,0，且对称轴为直线12x =，有下列结论：①0abc >；②0a b +>；③4330a b c ++<；④无论a ，b ，c 取何值，抛物线一定经过,02c a ⎛⎫ ⎪⎝⎭；⑤2440am bm b +-≥；⑥一元二次方程21ax bx c ++=有两个不相等的实数根，其中正确结论有（）A ．2个B ．3个C ．4个D ．5个【答案】D 【详解】解：①∴抛物线图象开口朝上，0a > ，∴抛物线对称轴为直线12x =，∴122b a -=， ∴0b a =-<，即0a b +=，故②错误；∴抛物线图象与y 轴交点位于x 轴下方，∴c <0，0abc ∴>，故①正确；③2y ax bx c =++经过()2,0，420a b c ∴++=又由①得c <0，0b <，4330a b c ∴++<，故③正确；④根据抛物线的对称性，得到2x =与1x =-时的函数值相等，∴当1x =-时0y =，即0a b c -+= a b =-，20a c ∴+=即12c a =-，∴2y ax bx c =++经过,02c a ⎛⎫ ⎪⎝⎭，即经过(1,0)-，故④正确； ⑤当12x =时，1142y a b c =++，当x m =时，2y am bm c =++， 0a >，∴函数有最小值1142a b c ++，∴21142am bm c a b c ++≥++， ∴2442am bm a b +≥+，∴2440am bm b +-≥，故⑤正确；⑥方程21ax bx c ++=的解即为抛物线2y ax bx c =++与直线1y =的交点的横坐标，结合函数图象可知，抛物线2y ax bx c =++与直线1y =有两个不同的交点，即方程21ax bx c ++=有两个不相等的实数根，故⑥正确；综上所述：①③④⑤⑥正确．故选D ．【变式训练1】如图，二次函数2(0)y ax bx c a =++≠图象的一部分与x 轴的一个交点坐标为()1,0，对称轴为1x =-，结合图象给出下列结论：①0a b c ++=；②20a b c -+<；③关于x 的一元二次方程20(a 0)++=≠ax bx c 的两根分别为-3和1；④若点()14,y -，()22,y -，()33,y 均在二次函数图象上，则123y y y <<；⑤()a b m am b -<+（m 为任意实数）．其中正确的结论有（）A ．1个B ．2个C ．3个D ．4个【答案】C【解析】∴二次函数2(0)y ax bx c a =++≠图象的一部分与x 轴的一个交点坐标为()1,0， ∴当x =1时，0a b c ++=，故结论①正确；根据函数图像可知，当10x y =-<，，即0a b c -+<，对称轴为1x =-，即12b a-=-，根据抛物线开口向上，得0a ＞，∴20b a =＞，∴0a b c b -+-<，即20a b c -+<，故结论②正确；根据抛物线与x 轴的一个交点为()1,0，对称轴为1x =-可知：抛物线与x 轴的另一个交点为(-3，0)， ∴关于x 的一元二次方程20(a 0)++=≠ax bx c 的两根分别为-3和1，故结论③正确；根据函数图像可知：213y y y <<，故结论④错误；当x m =时，2()y am bm c m am b c =++=++，∴当1m =-时，()a b c m am b c -+=++，即()a b m am b -=+，故结论⑤错误，综上：①②③正确，故选：C ．【变式训练2】二次函数2y ax bx c =++的部分图象如图所示，有以下结论：①3a －b ＝0；②240b ac ->；③520a b c -+>；④430b c +>，其中正确结论的个数是（）A ．1B ．2C ．3D ．4【答案】C 【详解】解：由图象可知a ＜0，c ＞0，对称轴为32x =-，∴322b x a=-=-，∴3b a =，①正确； ∴函数图象与x 轴有两个不同的交点，∴240b ac ∆=-＞，②正确；当1x =-时，0a b c -+＞，当3x =-时，930a b c -+＞，∴10420a b c -+＞，∴520a b c -+＞，③正确；由对称性可知1x =时对应的y 值与4x =-时对应的y 值相等，∴当1x =时，0a b c ++＜，∴3b a =，∴433333330b c b b c b a c a b c +=++=++=++（）＜，∴430b c +＜，④错误；故选：C ．【变式训练3】抛物线2y ax bx c =++（0a ≠）如图所示，下列结论中：①20a b +=；②0a b c -+>；③当1x ≠时，2a b ax bx +>+；④24ac b <．正确的个数是（）A ．1个B ．2个C ．3个D ．4个【答案】C 【详解】解：从图象上可以看出二次函数的对称轴是直线x =1．∴12b a -=．∴2a b =-．∴20a b +=．故①符合题意．从图象上可以看出当x =-1时，二次函数的图象在x 轴下方．∴当x =-1时，y <0即()()2110a b c a b c ⨯-+⨯-+=-+<．故②不符合题意．从图象上可以看出当x =1时，二次函数取得最大值．∴当1x ≠时，2211ax bx c a b c a b c ++<⨯+⨯+=++．∴2ax bx a b +<+．故③符合题意．从图象上可以看出二次函数图象与x 轴有两个交点．∴240b ac ->．∴24b ac >．故④符合题意．故①③④共3个符合题意．故选：C ．【变式训练4】已知二次函数y =ax 2−4ax −5a +1(a >0)下列结论正确的是（）①已知点M (4，y 1)，点N (−2，y 2)在二次函数的图象上，则y 1>y 2；②该图象一定过定点（5，1）和（－1，1）；③直线y =x −1与抛物线y =ax 2−4ax −5a +1一定存在两个交点；④当−3≤x ≤1时，y 的最小值是a ，则a =110 A ．①④B ．②③C ．②④D ．①②③④ 【答案】B【详解】解：二次函数y =ax 2−4ax −5a +1(a >0)，开口向上，且对称轴为x =-42a a-=2， ①点N (−2，y 2)关于对称轴对称的点为(6，y 2) ，∴a >0，∴y 随x 的增加而增加，∴4<6，∴y 1<y 2；故①错误；②当y =1时，ax 2−4ax −5a +1=1，即x 2−4x −5=0，解得：x =5或x =-1，该图象一定过定点（5，1）和（-1，1）；故②正确；③由题意得方程：ax 2−4ax −5a +1= x −1，整理得：ax 2−(4a +1)x −5a +2=0，()()241452a a a =+--+=16a 2+8a +1+20a 2-8a =36a 2+1>0，直线y =x −1与抛物线y =ax 2−4ax −5a +1一定存在两个交点；故③正确；④当−3≤x ≤1时，y 随x 的增加而减少，∴当x =1时，y 有最小值为a ，即a −4a −5a +1=a ，解得：a =19，故④错误；综上，正确的有②③，故选：B ．【变式训练5】抛物线2y ax bx c =++的对称轴是直线2x =-．抛物线与x 轴的一个交点在点()4,0-和点(3,0)-之间，其部分图象如图所示，下列结论：①40a b -=；②3c a ≤；③关于x 的方程22ax bx c ++=有两个不相等实数根；④若()15,y -，()22,y 是抛物线上的两点，则12y y <；⑤224b b ac +>．正确的个数有（）A ．1个B ．2个C ．3个D ．4个【答案】C【详解】解：∴抛物线的对称轴为直线x =-2b a =-2， ∴4a -b =0，所以①正确；∴与x 轴的一个交点在（-3，0）和（-4，0）之间，∴由抛物线的对称性知，另一个交点在（-1，0）和（0，0）之间，∴x =-1时，y ＞0，且b =4a ，即a -b +c =a -4a +c =-3a +c ＞0，∴c ＞3a ，所以②错误；∴抛物线与x 轴有两个交点，且顶点为（-2，3），∴抛物线与直线y =2有两个交点，∴关于x 的方程ax 2+bx +c =2有两个不相等实数根，所以③正确；∴抛物线的对称轴为直线x =-2b a =-2，∴22(5)2-----＜， ∴a ＜0，∴12y y ＞所以④错误；∴抛物线的顶点坐标为（-2，3），∴2434ac b a-=，∴b 2+12a =4ac ， ∴4a -b =0，∴b =4a ，∴b 2+3b =4ac ，∴a ＜0，∴b =4a ＜0，∴b 2+2b ＞4ac ，所以⑤正确；∴正确的为①③⑤．故选：C【变式训练6】如图，抛物线()20y ax bx c a =++≠的对称轴为直线1x =，与x 轴的一个交点坐标为()1,0-，其部分图象如图所示，下列结论：①24ac b <，②30a c ->，③方程20ax bx c ++=的两个根是11x =-，23x =，④当0y >时，x 的取值范围是13x ，其中正确的有（）A ．①②B ．①②③C ．①③④D ．①②④【答案】C 【详解】解：∴抛物线的对称轴为直线1x =，，与x 轴的一个交点坐标为()1,0-，∴抛物线与x 轴的另一个交点坐标为()3,0，12b a-=， ∴2b a =-，2=40b ac ∆->，即24ac b <，故①正确；∴抛物线开口向下，与y 轴交于y 轴正半轴，∴00a c <>，，∴30a <，∴30a c -<，故②错误；∴抛物线与x 轴的交点坐标为（-1，0），（3，0），∴方程20ax bx c ++=的两个根是11x =-，23x =，故③正确；由函数图象可知当0y >时，x 的取值范围是13x ，故④正确；故选C ．11。

二次函数图形练习

二次函数专题训练——图像特征与a 、b 、c 、△符号的关系1、已知二次函数2y ax bx c =++，如图所示，若0a <，0c >，那么它的图象大致是（） y y y yxx x x A B C D2、已知二次函数2y ax bx c =++的图象如图所示，则点(,)ac bc 在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3、已知二次函数2y ax bx c =++的图象如下，则下列结论正确的是（） A 0ab < B 0bc < C 0a b c ++> D 0a b c -+<4、二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，则下列结论： ①a>0；②c>0；•③b 2-4ac>0，其中正确的个数是（）A ．0个B ．1个C ．2个D ．3个5、二次函数y=ax 2+bx+c 的图像如图1，则点M （b ，ca ）在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限6、二次函数2y ax bx c =++的图象如图所示，则（） A 、0a >，240b ac -< B 、0a >，240b ac -> C 、0a <，240b ac -< D 、0a <，240b ac ->y x一、二次函数图象的平移变换（1）具体步骤：先利用配方法把二次函数化成2()y a x h k =-+的形式，确定其顶点(,)h k ，然后做出二次函数2y ax =的图像，将抛物线2y ax =平移，使其顶点平移到(,)h k .具体平移方法如图所示：（2）平移规律：在原有函数的基础上“左加右减”.二、二次函数图象的对称变换二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称 2y a x b x c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---； 2. 关于y 轴对称2y a x b x c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++； 3. 关于原点对称 2y a x b x c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4. 关于顶点对称2y a x b x c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．5. 关于点()m n ，对称()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-二次函数图象的几何变换一、二次函数图象的平移变换【例1】函数23(2)1y x =+-的图象可由函数23y x =的图象平移得到，那么平移的步骤是：（）A. 右移两个单位，下移一个单位B. 右移两个单位，上移一个单位C. 左移两个单位，下移一个单位D. 左移两个单位，上移一个单位【例2】函数22(1)1y x =---的图象可由函数22(2)3y x =-++的图象平移得到，那么平移的步骤是（）A. 右移三个单位，下移四个单位B. 右移三个单位，上移四个单位C. 左移三个单位，下移四个单位D. 左移四个单位，上移四个单位【例3】二次函数2241y x x =-++的图象如何移动就得到22y x =-的图象（）A. 向左移动1个单位，向上移动3个单位.B. 向右移动1个单位，向上移动3个单位.C. 向左移动1个单位，向下移动3个单位.D. 向右移动1个单位，向下移动3个单位.【例4】将函数2y x x =+的图象向右平移()0a a >个单位，得到函数232y x x =-+的图象，则a 的值为（）A ．1B ．2C ．3D ．4【例5】把抛物线2y ax bx c =++的图象先向右平移3个单位，再向下平移2个单位，所得的图象的解析式是235y x x =-+，则a b c ++=________________．【例6】对于每个非零自然数n ，抛物线()()221111n y x x n n n n +=-+++与x 轴交于n n A B 、两点，以n n A B 表示这两点间的距离，则112220092009A B A B A B +++…的值是（）A ． 20092008B ．20082009C ．20102009D ．20092010【例7】把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为A ．()213y x =---B ．()213y x =-+-C ．()213y x =--+D ．()213y x =-++【例8】将抛物线22y x =向下平移1个单位，得到的抛物线是（）A ．()221y x =+B ．()221y x =-C ．221y x =+D ．221y x =-【例9】将抛物线23y x =向上平移2个单位，得到抛物线的解析式是（）A. 232y x =-B. 23y x =C. 23(2)y x =+D. 232y x =+【例10】一抛物线向右平移3个单位，再向下平移2个单位后得抛物线224y x x =-+，则平移前抛物线的解析式为________________．【例11】已知二次函数5632+-=x x y ，求满足下列条件的二次函数的解析式：例题精讲（1）图象关于x 轴对称；（2）图象关于y 轴对称；（3）图象关于经过其顶点且平行于x 轴的直线对称【例12】如图，ABCD 中，4AB =，点D 的坐标是(0，8)，以点C 为顶点的抛物线2y ax bx c =++经过x 轴上的点A ，B ．⑴ 求点A ，B ，C 的坐标． ⑵ 若抛物线向上平移后恰好经过点D ，求平移后抛物线的解析式．DCBAO【例13】抛物线254y ax x a =-+与x 轴相交于点A B 、，且过点()54C ，． ⑴ 求a 的值和该抛物线顶点P 的坐标．⑵ 请你设计一种平移的方法，使平移后抛物线的顶点落要第二象限，并写出平移后抛物线的解析式．二、二次函数图象的对称变换【例14】函数2y x =与2y x =-的图象关于______________对称，也可以认为2y x =是函数2y x =-的图象绕__________旋转得到．【例15】已知二次函数221y x x =--，求：⑴关于x 轴对称的二次函数解析式；⑵关于y 轴对称的二次函数解析式；⑶关于原点对称的二次函数解析式．【例16】在平面直角坐标系中，先将抛物线22y x x =+-关于x 轴作轴对称变换，再将所得的抛物线关于y 轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为A ．22y x x =--+B ．22y x x =-+-C ．22y x x =-++D ．22y x x =++【例17】已知二次函数2441y ax ax a =++-的图象是1c ．⑴ 求1c 关于()10R ，成中心对称的图象2c 的函数解析式；⑵ 设曲线12c c 、与y 轴的交点分别为A B ，，当18AB =时，求a 的值．【例18】已知抛物线265y x x =-+，求⑴ 关于y 轴对称的抛物线的表达式； ⑵ 关于x 轴对称的抛物线的表达式； ⑶ 关于原点对称的抛物线的表达式．【例19】设曲线C 为函数()20y ax bx c a =++≠的图象，C 关于y 轴对称的曲线为1C ，1C关于x 轴对称的曲线为2C ，则曲线2C 的函数解析式为________________．【例20】对于任意两个二次函数：()2211112222120y a x b x c y a x b x c a a =++=++≠，，当12a a =时，我们称这两个二次函数的图象为全等抛物线，现有ABM ∆，()()1010A B -，，，，记过三点的二次函数抛物线为“C”（“□□□”中填写相应三个点的字母）．图3图2图1yxOABMy xOABMMNBAO xy⑴ 若已知()01M ，，ABM ABN ∆∆≌（图1），请通过计算判断ABM C 与ABN C 是否为全等抛物线；⑵ 在图2中，以A B M 、、三点为顶点，画出平行四边形． ① 若已知()0M n ，，求抛物线ABM C 的解析式，并直接写出所有过平行四边形中三个顶点且能与ABM C 全等的抛物线解析式．② 若已知()M m n ，，当m n 、满足什么条件时，存在抛物线ABM C ？根据以上的探究结果，判断是否存在过平行四边形中三个顶点且能与ABM C 全等的抛物线．若存在，请写出所有满足条件的抛物线“C ”；若不存在，请说明理由．【例21】已知：抛物线2:(2)5f y x =--+．试写出把抛物线f 向左平行移动2个单位后，所得的新抛物线1f 的解析式；以及f 关于x 轴对称的曲线2f 的解析式．画出1f 和2f 的略图，并求： ⑴ x 的值什么范围，抛物线1f 和2f 都是下降的；⑵ x 的值在什么范围，曲线1f 和2f 围成一个封闭图形； ⑶ 求在1f 和2f 围成封闭图形上，平行于y 轴的线段的长度的最大值．Oyxg(x)=-x 2+5h(x)=(x -2)2-5。

二次函数图像与a、b、c的关系

● ④关于 x 的方程ax2 + bx + c = n -1有两个不相等的实数
● 其中结论正确的个数为
（D ）
● A .1个 B．2 个 C．3 个 D．4 个
巩固练习
2.
抛物线与a,b,c的关系
A
巩固练习
抛物线与a,b,c的关系
3.如图是抛物线y=ax2+bx+c(a≠0)的一部分,下列结论：①abc＜0；②b2-
A．1
B．2
C．3
D．4
解析：由图象开口向下可得 a＜0，由对称轴在 y 轴左侧可得 b＜0，由图象与 y 轴交于正半轴可得 c＞0，则 abc＞0，故①正确；由对称轴 x＞－1可得2a－b＜0，故②正确；由图象上横坐标为 x＝－2的点在第三象限可得4a－2b＋c＜0，故 ③正确；
由图象上横坐标为 1 的点在第四象限得出a＋b＋c＜0，由图象上横坐标为－1 的点在第二象限得出
二次函数重点要关注四点一线。
考点聚焦
抛物线与a,b,c的关系
判断常见式子的符号
判断方法
a
a的符号决定抛物线的开口方向及大小
b
a,b决定抛物线对称轴的位置,“左同右异”
c
c决定抛物线与y轴交点的位置
b2-4ac
b2-4ac决定抛物线与x轴的交点个数
a+b+c
当x= 1时，y=a+b+c
a-b+c
当x=-1时，y=a-b+c
4ac＞0；③9a-3b+c＜0；④b-4a=0；⑤方程ax2+bx=0的两根为x1=0,x2=-4.
其中正确的结论有( B )
y
A.①③④ B.②④⑤ C.①②⑤ D.②③⑤

芝罘区数学二次函数题型-函数的图象特征与a、b、c的关系

二次函数题型-函数的图象特征与a 、b 、c 的关系教学目标: 二次函数的函数的图象特征与a 、b 、c 的关系1.已知抛物线y=ax 2+bx+c 的图象如右图所示，则a 、b 、c 的符号为（）A.a>0,b>0,c>0B.a>0,b>0,c=0C.a>0,b<0,c=0D.a>0,b<0,c<02.已知抛物线y=ax 2+bx+c 的图象2如图所示，则下列结论正确的是（）A ．a+b+c> 0B ．b> -2aC ．a-b+c> 0D ．c< 03.抛物线y=ax 2+bx+c 中，b ＝4a ，它的图象如图3，有以下结论：①c>0； ②a+b+c> 0 ③a-b+c> 0 ④b 2-4ac<0 ⑤abc< 0 ；其中正确的为（）A ．①②B ．①④C ．①②③D ．①③⑤ 4.当b<0是一次函数y=ax+b 与二次函数y=ax 2+bx+c 在同一坐标系内的图象可能是（）5.已知二次函数y ＝ax 2＋bx ＋c ，如果a>b>c ，且a ＋b ＋c ＝0，则它的图象可能是图所示的( )6．二次函数y ＝ax 2＋bx ＋c 的图象如图5所示，那么abc ，b 2－4ac ， 2a ＋b ，a ＋b ＋c四个代数式中，值为正数的有( )A.4个B.3个C.2个D.1个7.在同一坐标系中，函数y= ax 2+c 与y= c x (a<c)图象可能是图所示的( ) 1x Ay O 1x B y O 1x C y O 1x D y OA B C D8.反比例函数y= k x 的图象在一、三象限，则二次函数y ＝kx 2-k 2x-1c 的图象大致为图中的（）A B C D9.反比例函数y= k x中，当x> 0时，y 随x 的增大而增大，则二次函数y ＝kx 2+2kx 的图象大致为图中的（）A B C D10.已知抛物线y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，则下列结论：①a ，b 同号； ②当x ＝1和x ＝3时，函数值相同；③4a ＋b ＝0; ④当y ＝－2时，x 的值只能取0；其中正确的个数是（）A ．1B ．2C ．3D ．411.已知二次函数y ＝ax 2＋bx ＋c 经过一、三、四象限（不经过原点和第二象限）则直线y ＝ax ＋bc 不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限。

中考数学专题复习及练习：二次函数图像与系数a、b、c的关系

二次函数系数abc与图像的关系专项训练

二次函数系数a、b、c与图像的关系知识要点二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0．（2）b由对称轴和a 的符号确定：由对称轴公式x=判断符号．（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0．（4）b2-4ac的符号由抛物线与x轴交点的个数确定：2个交点，b2-4ac＞0；1个交点，b2-4ac=0；没有交点，b2-4ac＜0．（5）当x=1时，可确定a+b+c的符号，当x=-1时，可确定a-b+c的符号．（6）由对称轴公式x=，可确定2a+b的符号．一．选择题（共9小题）1．已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）B．2C．3D．4A．|12．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）B．②③C．①④D．①②③A．）③④3．二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac ＞0；④＜0中，正确的结论有（）1个B．2个C．3个D．4个，A．4．函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）、A．1B．2C．3D．45．如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：—①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．]①②④6．如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2B．m＜3C．m＞3D．{2＜m＜37．如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．'D．4个3个8．如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）C．①③D．①③④A．①②B．\③④9．已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．`C．3个D．4个2个10、已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A、a＞0B、b＜0C、c＜0D、a+b+c＞0\11、已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结果①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，则正确的结论是（）A、①②③④B、②④⑤C、②③④D、①④⑤12、如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为（ 12，1），下列结论：①ac＜0；②a+b=0；③4ac-b2=4a；④a+b+c＜0．其中正确结论的个数是（）A、1B、2C、3D、4。

专题训练二次函数图象与abcbac等符号问题

专题训练(二)二次函数图象与a，b，c，b2－4a c等符号问题二次函数y＝ax2＋bx＋c(a≠0)的图象特征与a，b，c及判别式b2－4ac的符号之间的关系：一、选择题1．2016·宁波已知函数y＝ax2－2ax－1(a是常数，a≠0)，下列结论正确的是()A．当a＝1时，函数图象过点(－1，1)B．当a＝－2时，函数图象与x轴没有交点C．若a＞0，则当x≥1时，y随x的增大而减小D．若a＜0，则当x≤1时，y随x的增大而增大2．二次函数y＝ax2＋bx＋c的图象如图2－ZT－1所示，则下列关系式错误的是()图2－ZT－1A．a＜0B．b＞0C．b2－4ac＞0D．a＋b＋c＜03．以x为自变量的二次函数y＝x2－2(b－2)x＋b2－1的图象不经过第三象限，则实数b的取值范围是()A．b≥B．b≥1或b≤－1C．b≥2D．1≤b≤24．2017·威海已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图2－ZT－2所示，则正比例函数y＝(b＋c)x与反比例函数y＝在同一坐标系中的大致图象是()图2－ZT－2图2－ZT－35．2017·安徽已知抛物线y＝ax2＋bx＋c与反比例函数y＝的图象在第一象限有一个公共点，其横坐标为1，则一次函数y＝bx＋ac的图象可能是()图2－ZT－46．2017·烟台二次函数y＝ax2＋bx＋c(a≠0)的图象如图2－ZT－5所示，对称轴是直线x＝1.下列结论：①ab＜0；②b2＞4ac；③a＋b＋2c＜0；④3a＋c＜0.其中正确的是()图2－ZT－5A．①④B．②④C．①②③D．①②③④7．2017·鄂州如图2－ZT－6，抛物线y＝ax2＋bx＋c的图象交x轴于点A(－2，0)和点B，交y轴负半轴于点C，且OB＝OC.下列结论：①2b－c＝2；②a＝；③ac＝b－1；④＞0，其中正确的结论有()图2－ZT－6A．1个B．2个C．3个D．4个8．2017·齐齐哈尔抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝－2，与x轴的一个交点在(－3，0)和(－4，0)之间，其部分图象如图2－ZT－7所示，则下列结论：①4a－b＝0；②c＜0；③－3a＋c＞0；④4a－2b＞at2＋bt(t为实数)；⑤点，，是该抛物线上的点，则y1＜y2＜y3.正确的结论有()图2－ZT－7A．4个B．3个C．2个D．1个二、填空题9．二次函数y＝ax2＋bx＋c的图象的一部分如图2－ZT－8所示，则a的取值范围是________．图2－ZT－810．2017·天水如图2－ZT－9是抛物线y1＝ax2＋bx＋c(a≠0)的图象的一部分，抛物线的顶点坐标是A(1，3)，与x轴的一个交点是B(4，0)，直线y2＝mx＋n(m≠0)与抛物线交于A，B两点，下列结论：①abc＞0；②方程ax2＋bx＋c＝3有两个相等的实数根；③抛物线与x轴的另一个交点是(－1，0)；④当1＜x＜4时，有y2＞y1；⑤x(ax＋b)≤a＋b.其中正确的结论是________．(只填写序号)图2－ZT－911．2017·株洲如图2－ZT－10，二次函数y＝ax2＋bx＋c的图象的对称轴在y轴的右侧，其图象与x轴交于点A(－1，0)，C(x2，0)，且与y轴交于点B(0，－2)，小强得到以下结论：①0＜a＜2；②－1＜b＜0；③c＝－1；④当|a|＝|b|时，x2＞－1.以上结论中，正确的结论序号是________．图2－ZT－1012．如图2－ZT－11，二次函数y＝ax2＋bx＋c(a>0)的图象的顶点为D，其图象与x轴的交点A，B的横坐标分别为－1，3，与y轴负半轴交于点C.在下面五个结论中：①2a－b＝0；②a＋b＋c>0；③c＝－3a；④当a＝时，△ABD是等腰直角三角形；⑤使△ACB为等腰三角形的a的值可以有四个．其中正确的结论是________(只填序号)．图2－ZT－11三、解答题13．如图2－ZT－12，二次函数y＝ax2＋bx＋c的图象与x轴交于B，C两点，交y轴于点A.(1)根据图象确定a，b，c的符号；(2)如果OC＝OA＝OB，BC＝4，求这个二次函数的表达式．图2－ZT－1214．已知函数y＝ax2＋bx＋c，若a＞0，b＜0，c＜0，则这个函数的图象与x轴交点的情况是怎样的？若无交点，请说明理由；若有交点，请说明有几个交点及交点分别在x轴的哪个半轴上．详解详析专题训练(二)二次函数图象与a，b，c，b2－4ac等符号问题1．[答案]D2．[解析]D抛物线开口向下，则a＜0，所以A选项的关系式正确；抛物线的对称轴在y轴的右侧，a，b异号，则b＞0，所以B选项的关系式正确；抛物线与x轴有2个交点，则b2－4ac＞0，所以C选项的关系式正确；当x＝1时，y＞0，即a＋b＋c＞0，所以D选项的关系式错误．3．[答案]A4．[答案]C5．[解析]B由公共点的横坐标为1，且在反比例函数y＝的图象上，当x＝1时，y＝b，即公共点的坐标为(1，b)．又点(1，b)在抛物线上，得a＋b＋c＝b，即a＋c＝0.由a≠0知ac＜0，一次函数y＝bx＋ac的图象与y轴的交点在负半轴上，而反比例函数y＝的图象的一支在第一象限，故b＞0，一次函数的图象满足y随x的增大而增大，选项B符合条件．故选B.6．[解析]C①抛物线的开口向上，所以a>0.抛物线的对称轴为直线x＝－＝1，所以b<0，所以ab＜0.所以①正确；②抛物线与x轴有两个交点，所以b2－4ac>0，所以b2＞4ac.所以②正确；③由图象知，当x＝1时，y＝a＋b＋c<0.又抛物线与y轴交于负半轴，所以c<0，所以a＋b ＋2c＜0.所以③正确；④由抛物线的对称性知当x＝3时，y＝9a＋3b＋c>0.又－＝1，所以b＝－2a，所以3a＋c>0.所以④错误．综上可知，正确的是①②③.故选C.7．[解析]C在y＝ax2＋bx＋c中，当x＝0时y＝c，∴C(0，c)，∴OC＝－c.∵OB＝OC，∴B(－c，0)．∵A(－2，0)，∴－c，－2是一元二次方程ax2＋bx＋c＝0的两个不相等的实数根，∴－c·(－2)＝.∵c≠0，∴a＝，②正确；∵－c，－2是一元二次方程x2＋bx＋c＝0的两个不相等的实数根，∴－c＋(－2)＝－，即2b－c＝2，①正确；把B(－c，0)代入y＝ax2＋bx＋c，得0＝a(－c)2＋b·(－c)＋c，即ac2－bc＋c＝0.∵c≠0，∴ac－b＋1＝0，∴ac＝b－1，③正确；∵抛物线开口向上，∴a＞0.∵抛物线的对称轴在x轴左侧，∴－＜0，∴b＞0，∴a＋b＞0.∵抛物线与y轴负半轴交于点C，∴c＜0.∴＜0，④错误．8．[解析]B∵抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝－2，∴－＝－2，∴4a－b＝0，故①正确；∵抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝－2，与x轴的一个交点在(－3，0)和(－4，0)之间，∴另一个交点位于(－1，0)和(0，0)之间，∴抛物线与y轴的交点在原点的下方，∴c＜0.故②正确；∵4a－b＝0，∴b＝4a.∵当x＝－3时，y＝9a－3b＋c＝9a－12a＋c＝－3a＋c>0，故③正确；∵4a－b＝0，∴b＝4a，∴at2＋bt－(4a－2b)＝at2＋4at－(4a－2×4a)＝at2＋4at＋4a＝a(t2＋4t ＋4)＝a(t＋2)2.∵t为实数，a＜0，∴a(t＋2)2≤0，∴at2＋bt－(4a－2b)≤0，∴at2＋bt≤4a－2b，即4a－2b≥at2＋bt，∴④错误；∵点，，是该抛物线上的点，∴将它们描在图象上可得由图象可知：y1<y3<y2，故⑤错误．综上所述，正确的有3个．故选B.9．[答案]－1＜a＜0[解析]∵抛物线开口向下，∴a＜0.∵函数图象过点(0，1)，∴c＝1.∵函数图象过点(1，0)，∴a＋b＋c＝0，∴b＝－(a＋c)＝－(a＋1)．由题意知，当x＝－1时，应有y＞0，∴a－b＋c＞0，∴a＋(a＋1)＋1＞0，∴a＞－1，∴a的取值范围是－1＜a＜0.10．[答案]②⑤[解析]①根据函数图象的开口方向、对称轴、与y轴交点可知，a＜0，b＞0，c＞0，故abc＜0；②根据函数图象的顶点坐标可知，方程ax2＋bx＋c＝3有两个相等的实数根，即x1＝x2＝1；③根据抛物线的对称性可知，抛物线与x轴的另一个交点是(－2，0)；④根据函数图象，当1＜x＜4时，有y2＜y1；⑤当x＝1时，y＝a＋b＋c＝3≥x(ax＋b)＋c，∴x(ax＋b)≤a＋b.故正确的结论有②⑤.11．[答案]①④[解析]由抛物线的开口向上可知，a＞0，且抛物线经过点A(－1，0)，B(0，－2)，对称轴在y轴的右侧可得即a－b＝2，b＜0，故a＝2＋b＜2.综合可知0＜a＜2；由a－b＝2可得a＝b＋2，将其代入0＜a＜2中，得0＜b＋2＜2，即－2＜b＜0；当|a|＝|b|时，因为a＞0，b＜0，故有a＝－b.又a－b＝2，可得a＝1，b＝－1.故原函数为y＝x2－x－2，当y＝0时，即有x2－x－2＝0，解得x1＝－1，x2＝2，此时x2＝2＞－1.故答案为：①④.12．[答案]③④[解析]∵抛物线与x轴的交点A，B的横坐标分别为－1，3，∴AB＝4，对称轴为直线x＝－＝1，∴b＝－2a，即2a＋b＝0.故①错误；根据图象知，当x＝1时，y＜0，即a＋b＋c＜0.故②错误；∵点A的坐标为(－1，0)，∴a－b＋c＝0，而b＝－2a，∴a＋2a＋c＝0，即c＝－3a.故③正确；当a＝时，b＝－1，c＝－，抛物线的函数表达式为y＝x2－x－.设对称轴直线x＝1与x轴的交点为E，∴把x＝1代入y＝x2－x－，得y＝－1－＝－2，∴点D的坐标为(1，－2)，∴AE＝2，BE＝2，DE＝2，∴△ADE和△BDE都为等腰直角三角形，∴△ABD为等腰直角三角形．故④正确；要使△ACB为等腰三角形，则必须保证AB＝BC＝4或AB＝AC＝4或AC＝BC，当AB＝BC＝4时，∵BO＝3，△BOC为直角三角形，OC的长为|c|，∴c2＝16－9＝7.∵抛物线与y轴的交点在y轴的负半轴上，∴c＝－，与2a＋b＝0，a－b＋c＝0联立组成方程组，解得a＝；当AB＝AC＝4时，∵AO＝1，△AOC为直角三角形，OC的长为|c|，∴c2＝16－1＝15.∵抛物线与y轴的交点在y轴的负半轴上，∴c＝－，与2a＋b＝0，a－b＋c＝0联立组成方程组，解得a＝；当AC＝BC时，在△AOC中，AC2＝1＋c2，在△BOC中，BC2＝c2＋9.∵AC＝BC，∴1＋c2＝c2＋9，此方程无解．∴只有两个a值满足条件．故⑤错误．综上所述，正确的结论是③④.13．解：(1)∵抛物线开口向上，∴a>0.又∵对称轴x＝－<0，∴a，b同号，即b>0.∵抛物线与y轴交于负半轴，∴c<0.综上所述，a>0，b>0，c<0.(2)∵OC＝OA＝OB，BC＝4，∴点A的坐标为(0，－1)，点B的坐标为(－3，0)，点C的坐标为(1，0)．把A，B，C三点的坐标分别代入y＝ax2＋bx＋c中，可得解得∴该二次函数的表达式是y＝x2＋x－1.14．解：∵a＞0，b＜0，c＜0，∴b2－4ac＞0，∴这个函数图象与x轴有两个交点．设这个函数图象与x轴的交点坐标为(x1，0)，(x2，0)．∵x1·x2＝，a＞0，c＜0，∴x1·x2＜0，∴这个函数图象与x轴有两个交点，一个交点在x轴的正半轴上，另一个交点在x轴的负半轴上．。