七年级数学几何证明入门专项练习
七年级数学典型几何证明50题
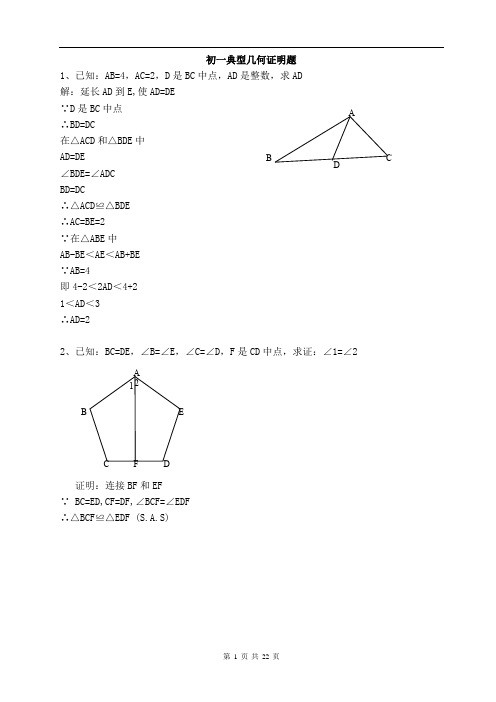
初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
初中数学几何证明经典试题(含答案)
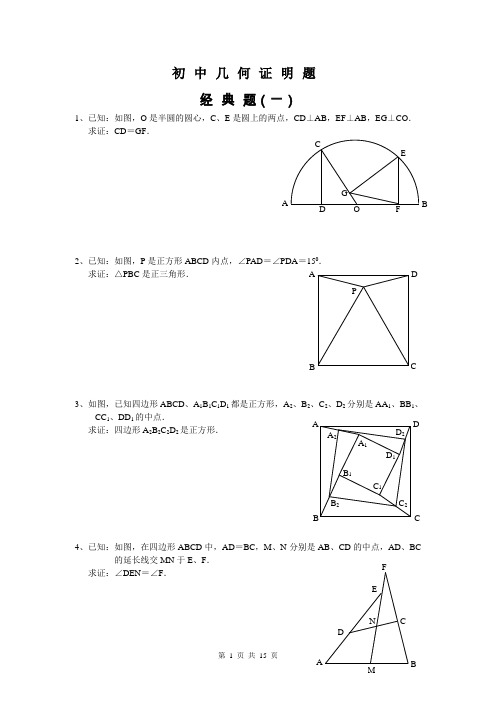
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .3、设P 是正方形ABCD 一边求证:PA =PF .4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF B、D .求证:AB =DC ,BC =AD .经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.2、设P是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC·4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线APCDB AFGCEBODD 2C 2B 2A 2D 1C 1B1CBDAA 1交MN 于E 、F . 求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 求证:AP =AQ .(初二)F4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA=∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
七年级数学几何证明题(典型)

七年级数学几何证明题1.如图,在ABC中,D在AB上,且ΔCAD和ΔCBE都是等边三角形,求证:(1)DE=AB,(2)∠EDB=60°2.如图,在ΔABC中,AD平分∠BAC,DE||AC,EF⊥AD交BC延长线于F。
求证:∠FAC=∠B3.已知,如图,在△ ABC中,AD,AE分别是△ ABC的高和角平分线,若∠B=30∠C=50°求:(1),求∠DAE的度数。
(2)试写出∠DAE与∠C - ∠B有何关系?(不必证明)B AC D4、一个零件的形状如图,按规定∠A=90º ,∠ C=25º,∠B=25º,检验已量得∠BDC=150º,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
CDA B5、如图,已知DF ∥AC,∠C=∠D,你能否判断CE ∥BD?试说明你的理由6、如图,△ABC 中,D 在BC 的延长线上,过D 作DE ⊥AB 于E,交AC 于F. 已知∠A=30°,∠FCD=80°,求∠D 。
7、如图,BE 平分∠ABD ,CF 平分∠ACD ,BE 、CF 交于G , 若∠BDC = 140°,∠BGC = 110°,则∠A ?G FEDCB A8、如图,AD ⊥BC 于D ,EG ⊥BC 于G ,∠E =∠1,求证AD 平分∠BAC 。
EDC BA G 3219、如图,直线DE 交△ABC 的边AB 、AC 于D 、E ,交BC 延长线于F , 若∠B =67°,∠ACB =74°,∠AED =48°,求∠BDF 的度数.10、如图,将一副三角板叠放在一起,使直角的顶点重合于O , 则∠AOC+∠DOBEDCBAE O DCBA11、如图,将两块直角三角尺的直角顶点C 叠放在一起. (1)若∠DCE=350,求∠ACB 的度数; (2)若∠ACB=1400,求∠DCE 的度数;(3)猜想:∠ACB 与∠DCE 有怎样的数量关系,并说明理由12、已知:直线AB 与直线CD 相交于点O ,∠BOC=45,(1)如图1,若EO ⊥AB ,求∠DOE 的度数; (2)如图2,若EO 平分∠AOC ,求∠DOE 的度数.13、已知AOB ∠,P 为OA 上一点.(1)过点P 画一条直线PQ ,使PQ ∥OB ;(2)过点P 画一条直线PM ,使PM ⊥OA 交OB 于点M ; (3)若︒=∠40AOB ,则=∠PMO ?14、如图。
七年级数学典型几何证明50题

初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
初一几何证明题及答案

初一几何证明题及答案【篇一:七年级数学几何证明题(典型)】3.已知,如图,在△ abc中,ad,ae分别是△ abc的高和角平分线,若∠b=30dc4、一个零件的形状如图,按规定∠a=90o ,∠c=25o,∠b=25o,检验已量得∠bdc=150o,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
db5、如图,已知df∥ac,∠c=∠d,你能否判断ce∥bd?试说明你的理由 aebc8、如图,ad⊥bc于d,eg⊥bc于g,∠e =∠1,求证ad平分∠bac。
e3gdc10、如图,将一副三角板叠放在一起,使直角的顶点重合于o,则∠aoc+∠dob11、如图,将两块直角三角尺的直角顶点c叠放在一起. (1)若∠dce=35,求∠acb的度数;(2)若∠acb=140,求∠dce的度数;(3)猜想:∠acb与∠dce有怎样的数量关系,并说明理由12、已知:直线ab与直线cd相交于点o,∠boc=45,(1)如图1,若eo⊥ab,求∠doe的度数;(2)如图2,若eo平分∠aoc,求∠doe的度数.13、已知?aob,p为oa上一点.(1)过点p画一条直线pq,使pq∥ob;(2)过点p画一条直线pm,使pm⊥oa交ob于点m;(3)若?aob?40?,则?pmo? ?adecodbad cob16、已知:线段ab=5cm,延长ab到c,使ac=7cm,在ab的反向延长线上取点d,使bd=4bc,设线段cd的中点为e,问线段ae 是线段cd的几分之一?【篇二:初中数学几何证明经典试题(含答案)】题(一)1、已知:如图,o是半圆的圆心,c、e是圆上的两点,cd⊥ab,ef⊥ab,eg⊥co.求证:cd=gf.(初二).如下图做gh⊥ab,连接eo。
由于gofe四点共圆,所以∠gfh=∠oeg, 即△ghf∽△oge,可得eogf=gogh=cocd,又co=eo,所以cd=gf得证。
eadofb2、已知:如图,p是正方形abcd内点,∠pad=∠pda=150.求证:△pbc是正三角形.(初二) a.如下图做gh⊥ab,连接eo。
七年级几何证明题训练含答案

七年级下几何证明题训练
1. 已知:如图11所示,∆ABC 中,∠=︒C 90,D 是AB 上一点,DE ⊥CD 于D ,交BC 于E ,且有AC AD CE ==。
求证:DE CD =12
2. 已知:如图12所示,在∆ABC 中,∠=∠A B 2,
CD 是∠C 的平分线。
求证:BC =AC +AD
3. 已知:如图13所示,过∆ABC 的顶点A ,在∠A 内任引一射线,过B 、C 作此射线的垂线BP 和CQ 。
设M 为BC 的中点。
求证:MP =MQ
4. ∆ABC 中,∠=︒⊥BAC AD BC 90,于D ,求证:()AD AB AC BC <++14
【试题答案】
1. 证明:取CD的中点F,连结AF
又∠+∠=︒∠+∠=︒
,
14901390
2. 分析:本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法。
“截长”即将长的线段截成两部分,证明这两部分分别和两条短线段相等;“补短”即将一条短线段延长出另一条短线段之长,证明其和等于长的线段。
证明:延长CA至E,使CE=CB,连结ED
在∆CBD和∆CED中,
又∠=∠+∠
BAC ADE E
3. 证明:延长PM交CQ于R
又BM CM BMP CMR
,
=∠=∠
∴QM是Rt QPR
∆斜边上的中线
4. 取BC中点E,连结AE。
初一数学几何图形的性质与证明练习题及答案

初一数学几何图形的性质与证明练习题及答案几何图形是数学中的一个重要概念,它们具有独特的性质和特征。
在初一的数学学习中,学生需要了解不同几何图形的性质,并且能够通过证明来验证这些性质。
本文将提供一些初一数学几何图形的性质与证明练习题及答案,帮助学生深入理解几何图形。
一、直线和线段的性质及证明性质1:两点确定一条直线。
证明:设有两点A和B,我们可以通过连接这两个点的直线来得到一条直线。
性质2:直线上的任意一点都在直线的同一侧。
证明:设直线上有一点C,在直线上我们可以找到一点D,并通过连接点C和D得到一条直线。
点C和点D的连接线与原始直线重合,因此点C和原始直线上的点A、B都在直线的同一侧。
性质3:线段的中点即为线段上到两个端点距离相等的点。
证明:设线段AB上有一点E,若点E到点A和点B的距离相等,则点E为线段AB的中点。
二、三角形的性质及证明性质4:三角形的内角和等于180度。
证明:设三角形ABC,我们可以通过在点B处做一条平行于边AC的直线,连接点A和点C,构成直线ABCD。
由于直线ABCD是一条直线,所以角ABC + 角BCD = 180度。
因此,三角形ABC的内角和等于180度。
性质5:等腰三角形的底边上的高线也是中位线。
证明:设等腰三角形ABC中,AB = AC,点D为底边BC上的中点,我们需要证明AD是三角形ABC的高线。
通过连接点A和点D,我们可以得到线段AD。
由于AB=AC,所以角BAD =角CAD,即角B = 角C。
又因为线段AD是BC的中点,所以BD = CD。
根据三角形的SAS相等性质,我们可以得知三角形ABD与三角形ACD全等。
根据全等三角形的性质,我们可以得出AD是三角形ABC的高线。
性质6:直角三角形的斜边平方等于两直角边平方和。
证明:设直角三角形ABC ,其中∠C为直角。
我们需要证明AB² = AC² + BC²。
通过在边AC上做一条垂直于AC的高线AD,我们可以将直角三角形ABC分为两个矩形,分别为ABCD和ABDE。
初中几何基础证明题(初一)

初中几何基础证明题(初一)第一篇:初中几何基础证明题(初一)几何证明题(1)1.如图,AD∥BC,∠B=∠D,求证:AB∥CD。
ADC2.如图CD⊥AB,EF⊥AB,∠1=∠2,求证:∠AGD=∠ACB。
AD/F2BG BE3.已知∠1=∠2,∠1=∠3,求证:CD∥OB。
APC 3D /2 BO4.如图,已知∠1=∠2,∠C=∠CDO,求证:CD∥OP。
D P/2CBO3C5.已知∠1=∠2,∠2=∠3,求证:CD∥EB。
C3D / BOE6.如图∠1=∠2,求证:∠3=∠4。
/3BADC427.已知∠A=∠E,FG∥DE,求证:∠CFG=∠B。
ABCG F ED8.已知,如图,∠1=∠2,∠2+∠3=1800,求证:a∥b,c∥d。
cd ab329.如图,AC∥DE,DC∥EF,CD平分∠BCA,求证:EF平分∠BED。
ADFEBC10、已知,如图,∠1=450,∠2=1450,∠3=450,∠4=1350,求证:l1∥l2,l3∥l5,l3l2∥l4。
l11l22344 l511、如图,∠1=∠2,∠3=∠4,∠E=900,求证:AB∥CD。
BA 12E CD12、如图,∠A=2∠B,∠D=2∠C,求证:AB∥CD。
CDOAB13、如图,EF∥GH,AB、AD、CB、CD是∠EAC、∠FAC、∠GCA、∠HCA的平分线,求证:∠BAD=∠B=∠C=∠D。
AFEBDGHC14、已知,如图,B、E、C在同一直线上,∠A=∠DEC,∠D=∠BEA,∠A+∠D=900,求证:AE⊥DE,AB∥CD。
ADCEB15、如图,已知,BE平分∠ABC,∠CBF=∠CFB=650,∠EDF=500,求证:BC∥AE。
ECDBA16、已知,∠D=900,∠1=∠2,EF⊥CD,求证:∠3=∠B。
AD1E3FBC17、如图,AB∥CD,∠1=∠2,∠B=∠3,AC∥DE,求证:AD∥BC。
DA 312BCE第二篇:初一几何证明题三角形1、已知ΔABC,AD是BC边上的中线。
七年级上册几何证明题

七年级上册几何证明题
好的,以下是一道七年级上册几何证明题:
题目:已知△ABC和直线l,过△ABC的顶点A,B分别作AB和AB的垂线
与直线l交于点P,Q。
求证:点P,Q在同一直线上。
为了证明点P,Q在同一直线上,我们可以按照以下步骤逐步推导:
第一步,由于过一点A有且只有一条直线与已知直线l垂直,所以点A、P、Q三点共线。
第二步,同理,由于过一点B有且只有一条直线与已知直线l垂直,所以点B、P、Q三点共线。
第三步,根据两点确定一条直线,我们知道A、B两点确定一条直线,而点P、Q都在该直线上,所以点P、Q在同一直线上。
综上,我们证明了过三角形的顶点作垂线与直线的交点在同一直线上。
(完整word版)七年级数学几何证明入门专项练习

几何证明题专项训练1 1、(1 )•.•/ 仁/A (已知),•- _________ 〃__________ ,((2 ) •/ Z 3= / 4 (已知),••• ____________ // _____________ ( )(3) •/ Z 2= / 5 (已知),• _________________ // _____________ ( );(4 )•••/ ADC+/ C=180o (已知),• _________ // __________ ( ).2,如图,(1 )•••/ ABD=/ BDC(已知),• — //—,( );(2)vZ DBC M ADB(已知),•- _________ // _________ ,( );(3)vZ CBE=/ DCB (已知),•- _________ // _________ ,( );(4)vZ CBE=/ A,(已知),• _______________ // __________ ,((5)______________________________________ vZ A+ZADC=180 (已知),•__________________________ // _________ ,( (6)______________________________________ vZ A+ZABC=18(0 (已知),•__________________________ // _________ ,( 3、如图,Z 1 = Z 2, AC平分Z DAB 试说明:DC// AB.4,如图,Z ABC=/ ADC BF和DE分别平分Z ABC和Z ADC Z 1 = Z 2,试说明:DE// FB.);r r);5、作图题(用直尺和圆规作图,保留作图痕迹,要求写出作法)已知Z 1,求作ZACB,使Z ACB= Z 1。
-1 -106 .如图2-67,已知/ 1 = / 2,求/ 3+ / 4的度数.7、如图2-56①••• AB//CD (已知),•••/ ABC=( )=(两直线平行,内错角相等)•••/ BCD+ ____________ = 180 ()② •••/ 3= / 4 (已知),•- ____________ 〃 _______________ ( ) ③ •••/ FAD= / FBC (已知),•- ____________ 〃 _______________ ( )8、如图 2-57,直线 AB , CD , EF 被直线 GH 所截,/ 仁 70,/ 2=110,/ 3=70 .求 证:AB//CD .证明:•••/ 仁 70,/ 3= 70 (已知),•••/ 仁/ 3 ()•- ________ // __________ ( )•••/ 2=110,/ 3= 70(),•- ___________ + __________ = _____________ , •- ___________ // ______________ ,• AB//CD ().9•如图2-58,①直线DE , AC 被第三条直线 BA 所截, 则/ 1和/ 2是 __________________________ ,如果/ 1= / 2 ,则// , 其理由是( ).BC图 2-56E£H iM2 57②/ 3和/ 4是直线 ______________ 、 ___________ ,/ 3 ________ /4,其理由是().10. 如图2-59,已知AB//CD , BE 平分/ ABC , CE 平分/ BCD,求证/ 1+ / 2=90 .证明:••• BE 平分/ ABC (已知),•••/ 2= _______ ()同理/ 1= ______________ ,1• / 1 + Z 2= ()2_又••• AB//CD (已知),•••/ ABC+ / BCD= __________________ ():丄 1 + Z 2=90 ()11、如图2-60 , E、F、G 分别是AB、AC、BC 上一点.①如果/ B= / FGC,则// ,其理由是()②/ BEG= / EGF,贝U _______ // _______ ,其理由是()③如果/ AEG+ / EAF= 180,则___________ // _____ ,其理由是(12.如图2-61,已知AB//CD , AB//DE,求证:/ B+ / D= / BCF+ / DCF . 证明:•/ AB//CF (已知),_____ = / ________ (两直线平行,内错角相等).•/ AB//CF , AB//DE (已知),• CF//DE ()••/ _________ = / _________ ()•••/ B+ / D= / BCF+ / DCF (等式性质).几何证明题专项训练21 如图,/ B= / C, AB // EF,试说明:/ BGF= / C。
七年级数学几何证明入门专项练习

几何证明题专项训练11、(1) V Z1=ZA (己知), /。
〃,( (2) V Z 3= Z 4 (己知),//( )(3) V Z2=Z5 (己知),/。
//( ):(4)V ZADC+ZC=180° (),,//( )。
2,如图,(1) V ZABD=ZBDC (), ,—〃—,( (2) V ZDBC=ZADB (), '•〃,( (3) V ZCBE=ZDCB (),'•〃,( ):(4) V ZCBE=ZA ,(己知),,〃,( (5) V ZA+ZADC=180° (己知),,// (6)V ZA+ZABC=180° (己知),,〃3、如图,N1=N2, AC 平分NDAB ,试说明:DC/7AB 。
4,如图,NABC 二NADC , BF 和 DE 分别平分NABC 和NADC ,5、作图题〔用直尺和圆规作图,保存作图痕迹,要求写出作法〕。
N1,求作NACB ,使NACB=N1。
Z1=Z2,试说明:DE/7FB 。
〕:7、如图2-56©VAB//CD (), /。
ZABC= ()=(两直线平行,错角相等), /。
ZBCD+= 180° ( )@V Z3=Z4 (己知), ,// ( )@VZFAD=ZFBC (), 〃 ( )8、如图 2-57,直线 AB , CD , EF 被直线 GH 所截,Zl = 70°, Z2=110°, Z3=7(T 。
求 证:AB//CD 。
9 。
如图2-58,①直线DE , AC 被第三条直线BA 所截, 那么N1和N2是,如果N1=N2,那么 // 。
其理由是〔〕。
②N3和N4是直线、,6。
如图 2-67,N1=N2,3D求N3+N4的度数。
AC图 2-56图 2-58被直线 所截,因此 ________________________ // N3 N4,其理由是〔〕。
七年级几何证明题训练(含答案)之欧阳术创编

七年级下几何证明题训练
时间:2021.02.02 创作:欧阳术
1. 已知:如图11所示,中,,D是AB上一点,DE⊥CD于D,交BC于E,且有。
求证:
2. 已知:如图12所示,在中,,CD是∠C的平分线。
求证:BC=AC+AD
3. 已知:如图13所示,过的顶点A,在∠A内任引一射线,过B、C作此射线的垂线BP和CQ。
设M为BC的中点。
求证:MP=MQ
4. 中,于D,求证:
【试题答案】
1. 证明:取CD的中点F,连结AF
又
2. 分析:本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法。
“截长”即将长的线段截成两部分,证明这两部分分别和两条短线段相等;“补短”即将一条短线段
延长出另一条短线段之长,证明其和等于长的线段。
证明:延长CA至E,使CE=CB,连结ED
在和中,
又
3. 证明:延长PM交CQ于R
又
是斜边上的中线
4. 取BC中点E,连结AE
时间:2021.02.02 创作:欧阳术。
七年级几何证明和计算题入门.doc

七年级几何证明和计算题入门几何证明和计算题是七年级数学的一个重点,因为刚接触这门学科,很多学生反映不知道如何着手分析解题,为了帮助学生们快速掌握学会这类题型,本文就几个典型例题详细讲解解题思路和解题全过程。
例题1如图,已知:点A在射线BG上,∠1=∠2,∠1+∠3=180°,∠EAB=∠BCD.求证:EF∥CD.1、根据需要证明的结论添加辅助线证明:EF∥CD,需要构造同位角、内错角或同旁内角,因此考虑添加辅助线,延长AE交CD于M。
2、根据需要证明的结论反推需要先证明的结论证明:EF∥CD,需要先证明∠3=∠EMD;根据题目中的条件:∠1+∠3=180°,需要先证明∠EMD +∠3=180°;根据平行线的性质:两直线平行,同旁内角互补,需要先证明BG∥CD。
3、根据题目中的条件推断可以得到的结论由题目中的条件:∠1=∠2,根据平行线的判定:同位角相等,两直线平行,则AE∥BC;根据平行线的性质:两直线平行,同旁内角互补,则∠EAB+∠2=180°;根据题目中的条件:∠EAB=∠BCD,则∠BCD+∠2=180°;根据平行线的判定:同旁内角互补,两直线平行,则BG ∥CD。
4、具体证明过程延长AE交CD于M∵∠1=∠2∴AE∥BC∴∠EAB+∠2=180°∵∠EAB=∠BCD∴∠BCD+∠2=180°∴BG∥CD∴∠1+∠EMD=180°∵∠1+∠3=180°∴∠EMD=∠3∴EF∥CD例题2如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,求∠F1、根据题目需要求解的值反推需要先求解的值需要求解∠F,由题目中的条件:∠AGF为△EFG的外角,根据三角形外角的性质:三角形的外角等于不相邻两个内角的和,则∠AGF=∠AEF+∠F,即∠F=∠AGF-∠AEF,因此,需要先求解∠AEF;根据题目中的条件:∠AEF=∠AED+∠DEF,需要先求解∠AED,∠DEF;由题目中的条件EF为∠DEB的平分线,根据角平分线的性质:角平分线可以得到两个相等的角,则∠DEF=1/2∠DEB,因此需要先求解∠DEB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明题专项训练11、(1)∵∠1=∠A(已知),∴∥,();(2)∵∠3=∠4(已知),∴∥,()(3)∵∠2=∠5(已知),∴∥,();(4)∵∠ADC+∠C=180º(已知),∴∥,().2,如图,(1)∵∠ABD=∠BDC(已知),∴∥,();(2)∵∠DBC=∠ADB(已知),∴∥,();(3)∵∠CBE=∠DCB(已知),∴∥,();(4)∵∠CBE=∠A,(已知),∴∥,();(5)∵∠A+∠ADC=180º(已知),∴∥,();(6)∵∠A+∠ABC=180º(已知),∴∥,().3、如图,∠1=∠2,AC平分∠DAB,试说明:DC∥AB.4,如图,∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,∠1=∠2,试说明:DE∥FB.5、作图题(用直尺和圆规作图,保留作图痕迹,要求写出作法)。
已知∠1,求作∠ACB,使∠ACB=∠1。
6.如图2-67,已知∠1=∠2,求∠3+∠4的度数.7、如图2-56①∵AB//CD (已知),∴∠ABC=__________( ) ____________=______________(两直线平行,错角相等), ∴∠BCD+____________=︒180( ) ②∵∠3=∠4(已知),∴____________∥____________( ) ③∵∠FAD=∠FBC (已知),∴_____________∥____________( )8、如图2-57,直线AB ,CD ,EF 被直线GH 所截,∠1=︒70,∠2=︒110,∠3=︒70.求证:AB//CD .证明:∵∠1=︒70,∠3=︒70(已知), ∴∠1=∠3( )∴ ________∥_________( ) ∵∠2=︒110,∠3=︒70( ), ∴_____________+__________=______________, ∴_____________//______________, ∴AB//CD ( ).9.如图2-58,①直线DE ,AC 被第三条直线BA 所截,则∠1和∠2是________,如果∠1=∠2,则_____________//_____________, 其理由是( ).②∠3和∠4是直线__________、__________,被直线____________所截,因此____________//____________. ∠3_________∠4,其理由是( ).10.如图2-59,已知AB//CD ,BE 平分∠ABC ,CE 平分∠BCD ,求证∠1+∠2=︒90.证明:∵ BE 平分∠ABC (已知),∴∠2=_________( ) 同理∠1=_______________,∴∠1+∠2=21____________( ) 又∵AB//CD (已知),∴∠ABC+∠BCD=__________________( ) ∴∠1+∠2=︒90( )11、如图2-60,E 、F 、G 分别是AB 、AC 、BC 上一点.①如果∠B=∠FGC ,则_______//______,其理由是( ) ②∠BEG=∠EGF ,则__________//_______,其理由是( ) ③如果∠AEG+∠EAF=︒180,则________//_______,其理由是( )12.如图2-61,已知AB//CD ,AB//DE ,求证:∠B+∠D=∠BCF+∠DCF .证明: ∵AB//CF (已知),∴∠______=∠________(两直线平行,错角相等). ∵AB//CF ,AB//DE (已知),∴CF//DE ( ) ∴∠_________=∠_________( ) ∴∠B+∠D=∠BCF+∠DCF (等式性质).几何证明题专项训练21、如图,∠B=∠C ,AB ∥EF ,试说明:∠BGF=∠C 。
(6分) 解:∵ ∠B=∠C∴ AB ∥CD ( ) 又∵ AB ∥EF ( )∴ ∥ ( ) ∴ ∠BGF=∠C ( )2、如图,在△ABC 中,CD ⊥AB 于D ,FG ⊥AB 于G ,ED//BC ,试说明 ∠1=∠2,以下是证明过程,请填空:(8分) 解:∵CD ⊥AB ,FG ⊥AB∴∠CDB=∠ =90°( 垂直定义)∴_____//_____ (∴∠2=∠3 ( ) 又∵DE//BC∴∠ =∠3 ( ) ∴∠1=∠2 ( )3、已知:如图,∠1+∠2=180°,试判断AB 、CD 有何位置关系?并说明理由。
(8分)4、如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B = 30°,你能算出∠EAD 、∠DAC 、∠C 的度数吗?(7分)D CBAED5、如图,已知EF∥AD,∠1=∠2,∠BAC=70 o,求∠AGD。
解:∵EF∥AD(已知)∴∠2= ()又∵∠1=∠2(已知)∴∠1=∠3(等量替换)∴AB∥()∴∠BAC+ =180 o()∵∠BAC=70 o(已知)∴∠AGD= °6、如图,已知∠BED=∠B+∠D,试说明AB与CD的位置关系。
解:AB∥CD,理由如下:过点E作∠BEF=∠B∴AB∥EF()∵∠BED=∠B+∠D(已知)且∠BED=∠BEF+∠FED∴∠FED=∠D∴CD∥EF()∴AB∥CD()7、如图,AD是∠EAC的平分线,AD∥BC,∠B=30 o,求∠EAD、∠DAC、∠C的度数。
(6分)8、如图,EB∥DC,∠C=∠E,请你说出∠A=∠ADE的理由。
(6分)9、已知,如图,∠1=∠ABC=∠ADC ,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°.将下列推理过程补充完整:(1)∵∠1=∠ABC (已知), ∴AD ∥______(2)∵∠3=∠5(已知), ∴AB ∥______,(_______________________________) (3)∵∠ABC+∠BCD=180°(已知), ∴_______∥________,(________________________________)10、已知,如图14,∠1=∠ABC=∠ADC ,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°。
(1)∵∠1=∠ABC(已知)∴AD ∥ ( ) (2)∵∠3=∠5(已知)∴AB ∥ ( ) (3)∵∠2=∠4(已知)∴∥( ) (4)∵∠1=∠ADC(已知)∴ ∥ ( ) (5)∵∠ABC+∠BCD=180°(已知)∴∥( )11、如图15,(1)∵∠A= (已知)∴AC ∥ED( ) (2)∵∠2= (已知)∴AC ∥ED ( ) (3)∵∠A+ =180°(已知)∴AB ∥FD ( )(4)∵AB ∥ (已知) ∴∠2+∠AED=180°( ) (5)∵AC ∥ (已知) ∴∠C=∠1 ( )A12 34 5 B CD图14AEFD BC1 2 3图1512、(4分)已知:如图15,AB⊥BC于B,CD⊥BC于C,∠1=∠2。
求证:BE∥CF。
证明:∵AB⊥BC,CD⊥BC(已知)∴∠1+∠3=90º,∠2+∠4=90º()∴∠1与∠3互余,∠2与∠4互余又∵∠1=∠2()∵∠3=∠4()∴BE∥CF()13、(9分)已知:如图16,AB∥CD,∠1=∠2,求证:∠B=∠D。
证明:∵∠1=∠2(已知)∴∥()∴∠BAD+∠B=()又∵AB∥CD(已知)∴+=180º()∴∠B=∠D()14、在空格填上推理的理由(1)如图,已知AB//DE,∠B=∠E,求证:BC//EF。
证明: AB//DE ()∴∠B= ()又 ∠B=∠E()∴= (等量代换)BEADOFC∴ // ( )(2)已知,如图,∠1=120°,∠2=120°,求证:AB//CD 。
证明: ∠1=120°,∠2=120°( ) ∴∠1=∠2( )又 = ( )∴∠1=∠3( )∴AB//CD ( ) (3)已知,如图,AB//CD ,BC//AD ,∠3=∠4。
求证:∠1=∠2证明: AB//CD ( )∴ = ( )又 BC//AD ( )∴ = ( ) 又 ∠3=∠4( )∴∠1=∠2( )15、(1)如图12,根据图形填空:直线a 、b 被直线c 所截(即直线c 与直线a 、b 都相交),已知a ∥b ,若∠1=120°,则∠2的度数=__________,若∠1=3∠2,则∠1的度数=___________;如图13中,已知a ∥b ,且∠1+2∠2=1500,则∠1+∠2=_________0 (2)如图14,根据图形填空:∵∠B =∠______;∴AB ∥CD (________________________); ∵∠DGF =______;∴CD ∥EF (________________________); ∵AB ∥EF ;∴∠B +______=180°(________________________); (3)已知:如图15,AB ⊥BC ,BC ⊥CD 且∠1=∠2,求证:BE ∥CF 。
证明:∵AB ⊥BC ,BC ⊥CD (已知) ∴ = =90°( )132ABC DBCD1 2 3 4 A A B CDG EF 图14abc 12 图13a bc 1 2图12C A BE 1∵∠1=∠2(已知) ∴ = (等式性质) ∴BE ∥CF ( )(4)已知:如图16,AC ⊥BC ,垂足为C ,∠BCD 是∠B 的余角。
求证:∠ACD=∠B 。
证明:∵AC ⊥BC (已知) ∴∠ACB=90°( ) ∴∠BCD 是∠DCA 的余角 ∵∠BCD 是∠B 的余角(已知)∴∠ACD=∠B ( )(5)已知,如图17,BCE 、AFE 是直线,AB ∥CD ,∠1=∠2,∠3=∠4。
求证:AD ∥BE 。
证明:∵AB ∥CD (已知)∴∠4=∠ ( ) ∵∠3=∠4(已知) ∴∠3=∠ ( ) ∵∠1=∠2(已知)∴∠1+∠CAF=∠2+∠CAF ( )即∠ =∠ ∴∠3=∠ ( ) ∴AD ∥BE ( )16、已知,如图,∠1=∠2,∠A =∠F 。
求证:∠C =∠D 。
证明:∵∠1=∠2(已知)∠1=∠3( )∴∠2=∠ ( ) ∴BD ∥ ( ) ∴∠4=∠C ( ) 又∵∠A = (已知)∴AC ∥ ( ) ∴ =∠D ( ) ∴∠C =∠D ( )17、已知,如图,∠1=∠2,CF ⊥AB ,DE ⊥AB ,求证:FG ∥BC 。
