第二章 行列式
第二章行列式Cramer法则

2 x1 4 x 2 1 例1 求解二元线性方程组 x1 3 x 2 2 2 4 解 因为 D 6420, 1 3 2 1 1 4 413, D 38 5, D 2 1 1 2 2 3
所以
D1 x1 D x2 D 2 D 5 2 . 3 2
a a 1 1 2 2 a 1 2a 2 1
可按下图所示的对角线法则确定其值:
a 11
a 12
a
21
a 22
a 1 1 a 2 2 a12 a 21
2
方阵与矩阵的区别:二阶方阵是 2 个数按确定 的方式排成的一个数表,而二阶行列式是这些 数(也就是二阶矩阵 A )按一定的运算法则所 确定的一个数.
方阵 A 所确定的二阶行列式,记为
a1 1 D a 21
a1 2 . a 22
矩阵 A 的行列式还记作 A
或 det A ,即
a a 11 12 aa aa det A A 1 12 2 1 2 2 1 a21 a22
一般地,二阶行列式
a a 1 1 1 2 a a 2 1 2 2
a12 a 22
用消元法求解线性方程组(1),得
( aa aa ) x b a b a 1 12 2 1 22 1 1 1 2 2 2 1 2 ( aa aa ) x b a b a 1 12 2 1 22 1 2 2 1 1 1 2 1
该式中 x 1 ,
x 2 的系数 a a a a 1 1 2 2 1 2 2 1 称为由二阶
T
3. n 阶行列式 采用递归的方法给出其定义:
a (1)设 A a 1 1 1 1是一阶方阵,则它所 确定的一阶行列式 det A a11 定义成 数 a 11.
考研数学第二章---行列式

第二章 行列式知识点考点精要一、排列1、基本概念 定义1:由1,2,,n 组成的一个有序数组称为一个n 级排列。
定义2:排列中,若一对数前后位置与大小顺序相反,则称为一个逆序,一个排列中逆序总数称为该排列的逆序数。
定义3:逆序数为偶(奇)数的排列称为偶(奇)排列。
2、性质性质1 对换改变排列的奇偶性。
性质2 任一n 级排列与排列1,2,,n 都可经过一系列对换而互变,并且所作对换个数与该排列有相同奇偶性。
性质3 n 级排列共有!n 个,其中奇排列、偶排列的个数各有!2n 个。
二、n 级行列式1、定义1212121112121222()12()12(1)n n n n n j j j j j nj j j j n n nna a a a a a a a a a a a τ=-∑这里12()n j j j ∑是对所有的n 级排列12nj j j 求和。
要点:(1)n 级行列式是!n 项的代数和;(2)每一项是取自不同行、不同列的n 个元素的乘积;(3)在行下表按自然顺序排列的前提下,每项的符号由列指标排列的逆序数的奇偶性确定;(4)行列式的值是一个数。
2、行列式的性质性质1 行列式的行列互换,行列式的值不变; 性质2 数k 乘行列式某行(列)等于数k 乘此行列式;性质3 如果行列式中某行(列)是两组数的和,那么行列式等于两个行列式的和; 性质4 如果行列式中有两行(列)相同,行列式等于零;性质5 如果行列式中有两行(列)对应分量成比例,行列式等于零; 性质6 把一行(列)的倍数加到另一行(列),行列是不变; 性质7 对换行列式中两行(列)的位置,行列式反号。
3、行列式按行(列)展开 设111212122212n n n n nna a a a a a d a a a =则下列公式成立:10nik jk k d i ja A i j ==⎧=⎨≠⎩∑当当; 10nsk sls d k la A k l ==⎧=⎨≠⎩∑当当。
线性代数第二章方阵的行列式

2 n阶行列式的性质
本节教学内容
行列式按一行(列)展开定理
Laplace定理
3 展开定理与行列式的计算
3 展开定理与行列式的计算
行列式按一行(列)展开定理 三阶行列式的一个计算公式 Mij称为aij的余子式 Aij称为aij的代数余子式
3 展开定理与行列式的计算
线性代数 第二章
本章教学内容
1 n阶行列式的定义
2 方阵行列式的性质
3 展开定理与行列式的计算
第二章 方阵的行列式
1 n阶行列式的定义
1.排列与逆序数 定义 由1,2,…,n按任何一种次序排成的有序数 组i1 i2… in称为一个n级排列,简称排列. 例 3级排列:123,132,213,231,312,321,共6个 性质 不同的n级排列共n!个. 排列123,从小到大排,全顺; 排列132,3>2,但3排在2之前,即32是一个逆序 定义 在一个排列i1 i2… in中,若it> is中,但it排在 is之前,则称it与is组成一个逆序.i1 i2… in中所有逆 序的总数称为此排列的逆序数, 记为(i1 i2… in).
2 n阶行列式的性质
例 =0 2r1+r2
2 n阶行列式的性质
性质2.5 即
2 n阶行列式的性质
或 证 由性质2.1及推论2.3得到.
2 n阶行列式的性质
例1
2 n阶行列式的性质
例2
2 n阶行列式的性质
例3 计算行列式 解
2 n阶行列式的性质
2.方阵行列式的性质 定理2.1 设A,B为n阶方阵,为常数,m为正整 数,则 ⑴ A=nA ; ⑵ AB=AB ; ⑶ Am=Am . 注① 一般的A+B≠A+B ; ② 虽然AB≠BA,但AB=BA ; ⑶由⑵推得,下证⑴ ⑵
第二章 行列式

pi 这个元素的逆序数是 τi,即:
τ ( p1 p2 …pn)= τ 1 + τ 2 +…+ τ n
就是这个排列的逆序数 逆序数。 逆序数 例1 求排列13…(2n − 1)24…(2n)的逆序数。 解:在该排列中,1 ~(2n−1)中每个奇数的逆 序数全为0,2的逆序数为(n − 1),4的逆序数为 (n − 2),…,(2n − 2)的逆境序数为1,2n的逆序数 为0,于是该排列的逆序数为 τ=(n-1)+(n-2)+…+1+0=n(n-1)/2
τ1 =τ (l1l2 Lln )
2011-9-1
τ2 = τ (s1s2 L sn )
19
这就表明,对换乘积项中两元素的位置, 这就表明,对换乘积项中两元素的位置, 从而行标排列与列标排列同时做了相应的对 换,但行标排列与列标排列的逆序数之和的 奇偶性并不改变。 奇偶性并不改变。
2011-9-1
2011-9-1
... ... ... ... ... ... ... ...
0 0 = a11a22...ann ... ann a1n a2n = a11a22...ann ... ann
17
3)次上三角行列式 次上三角行列式
4)次下三角行列式 次下三角行列式
2011-9-1
18
定理2: 阶行列式 阶行列式D= 定理 :n阶行列式 aij的一般项可以记为
λn
0 0 = λλ2...λn 1 ...
=1+ 2 + ... + (n − 2) + (n −1) n (n −1) = 2
λ1
0 = (−1) ... 0
高等代数第2章行列式

同理可得
2 2 1
1 2 1
D1 1 1 3 5, D2 2 1 3 10,
0 1 1
1 0 1
1 2 2
D3 2 1 1 5, 1 1 0
故方程组的解为:
x1
D1 D
1,
x2
D2 D
2,
x3
D3 D
1.
三、小结
m 次相邻对换
a1 al abb b1 bmc1 cn
m 1 次相邻对换 a1 al bb b1 bm aa c1 cn
a1 alab1 bmbc1 cn ,
2m 1次相邻对换 a1 al bb1 bmac1 cn ,
所以一个排列中的任意两个元素对换,排列改变 奇偶性.
说明: (1)项数:2阶行列式含2项, 3阶行列式含6项,
这恰好就是2!,3!. (2)每项构成:2阶和3阶行列式的每项分别是位于
不同行不同列的2个和3个元素的乘积 (.3)各项符号:2阶行列式含2项,其中1正1负, 3阶
行列式6项,3正3负.
对角线法则只适用于二阶与三阶行列式. 为此,我们用排列与逆序来定义n阶行列式.
第2章 行列式
§2.1 2阶、3阶行列式 §2.2 n 元排列 §2.3 n 阶行列式 §2.4 n 阶行列式的性质 §2.5 行列式按一行(列)展开 §2.6 Cramer 法则 §2.7 Laplace 定理
2.1.2 二阶行列式
用消元法解二元线性方程组
aa1211
x1 x1
2 14,
1
3 D2 2
12 1
21,
x1
第二章行列式

第二章 行列式 基本内容及考点综述一、基本概念 1.逆序、逆序数在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序,一个排列中逆序的总数称为这个排列的逆序数.2.n 级行列式. n 级行列式n n nnj j j j j j j j j nnn n nna a a a a a a a a a a a ,,,)1(21212121)(212222111211τ-∑=.二、基本性质1. 行列式与其转置列式相等即T D D =.2. 用一个数乘行列式等于用这个数乘行列式某一行(列)的所有元素,或行列式中某一行(列)的所有元素的公因子可以提到行列式记号的外面.3. 如果行列式中有两行相同,那么行列式为零.4. 如果行列式中两行成比例,那么行列式为零.5. 对换行列式中两行的位置,行列式反号.6. 把一行的倍数加到另一行,行列式不变.7.11112111121111211211221221212n n n n n n n n n nnn n nnn n nna a a a a a a a ab b b bc b c b c c c c a a a a a a a a a +++=+11221122||,8.0,||,0,k i k i kn in k j k j nk nj A i k a A a A a A i kA j ka A A A a A j k=⎧+++=⎨≠⎩=⎧+++=⎨≠⎩当当当当其中ij A 是元素ij a 的代数余子式.9. (拉普拉斯定理)设在行列式D 中任意取定了)11(-≤≤n k k 个行,由这k 行元素所组成的一切k 级子式与它们的代数余子式的乘积的和等于行列式D .三、基本方法本章的重点是行列式的计算,关键是观察、分析行列式的特点,探索、寻找最佳的解题思路.下面介绍几种常见的行列式计算方法.1.化三角形法.利用行列式的性质,将行列式化成上(下)三角行列式.2.降价法,将行列式D 按某一行展开或将D 按某k 行展开,将较高阶的行列式化成较低阶的行列式计算.3.升阶法.将n 阶行列式D 增加一行一列变成1+n 阶行列式,使它更容易计算.4.递推法.利用行列式的性质将n 阶行列式n D 用较低阶的形状与n D 完全一样的行列式1-n D 、2-n D 来表示.如果n 阶行列式n D 满足021=++--n n n cD bD aD .作特征方程02=++c bx ax如果,0≠∆则特征方程有两个不相等的复根21,x x ,令.1211--+=n n n Bx Ax D 其中B A ,为待定常数,令2,1=n 可求出B A ,.如果,0=∆则特征方程有重根21x x =,令11)(-+=n n x nB A D ,其中B A ,为待定常数,令2,1=n ,可求出B A ,.值得注意的是,三对角行列式经常在试题中出现,一般都可用递推法来解.5.拆项法.将行列式D 的某一行都写成两个元素和的形式,将D 表成两个行列式的和.6.数学归纳法.先观察 ,,,321D D D ,得出猜想,然后用数学归纳法证明.试题精选1.(华东师大,1996) 计算n 阶行列式.xzy x x z y x z y x D n +++++=10100000100010001其中yz x =. 解法1:数学归纳法.22211)1(,1x x yz x D x D ++=-+=+=. .1323x x x D +++=猜想 n n x x x D ++++= 21.用数学归纳法证明.当1=n 时,x D +=11,结论成立. 假定小于n 时结论成立,将n D 按第1行展开.++=+++-+++++=-+=----x x x x x x x x x yzD D x D n n n n n 1)1()1)(1()1(221221 .2n x x ++ 所以结论成立.解法2:递推法..)1()1(2121-----+=-+=n n n n n xD D x yzD D x D 于是2211)(x D D x D D n n n n =-=---- n n n n n n x D D x D D x D D =-==-=------)()()(12243332 .以上等式对所有1>n 都成立.那么有2123231211x D D x D D x D D x D D n n n n n n =-=-=-=-----将以上1-n 个等式相加,有1321.n n n D D x x x x --=++++所以n n x x x D ++++= 21.解法3:拆项法.将n D 的第1列都写成两个数的和的形试,1,0,,00.x z +++ 那么110100000100010001-+++++=n n xD xzy x x z y x z y D将以上行列式的第1列的)(y -倍加到第2列,第2列的)(y -倍加到第3列,…,第1-n 列的)(y -倍加到第n 列,那么21222233212111(1)11(1)111n n n n n n n nD xD x xD x x D x x xD x x x D x x x D x x x ------=+=++=++=+++=+++==++++=++++32.(华东师大,1995) 计算n 阶行列式1100110110=n D解:将n D 先按第1行展开,然后按第1列展开,有2--=n n D D 所以24462()(1)k n n n n n n k D D D D D D -----=-=--==-==-当n 为奇数时,令12+=m n ,则0)1()1(1212=-=-=-+D D D m m n m m . 当n为偶数时,令m n 2=,则21122(2)2(1)(1)(1)(1)(1)n m m m m n n D D D -----=-=-=--=-= ⎩⎨⎧+=-=.12,1.2,1t m t m3.(华东师大,1991)计算n 阶行列式123111111111111111111111n n n n n D n n---=--解:将第2列,第3列,…,第n 列都加到第1列上.(1,2,,(1)23111112011111111(1)0111121111011111111011111111000111100(1)(1)22111100011111111(1)(1)2n n n n n n n n n n n n n D n n n n n nn n n n n n n n n n τ--+----+-===----------++=-----+=-(1)(2)2,1)2122(1)12(1)(1)()(1)(1)2(1)(1)2n n n n n n n n n n n n n n -------+-⋅-=--⋅+=-⋅注:对n 阶行列式的计算结果,一般情况下都应当检验,用3,2=n 代入,即可检验结果是否正确,例如本题2=n 时,2123,11D ==--用2=n 代入,结果也等于-3,因此可以初步断定结果是正确的.4.(华东师大,1991)计算n 阶行列式.011011110n D --=-解:将n D 按第1行展开,再按第1列展开.===--42n n n D D D当n 为偶数时,121====-D D D n n .当n 为奇数时,令,12+=m n 0122=====--D D D D m n n n 5.(华东师大,1994)计算n 阶行列式1123112221000000n n n n na x a a a a x x D x xx x --+-=--,其中01≠∏=i ni x .解:将n D 第1列都写成两个数和的形式,,00,,00,0,111++-+ x x a 那么2312123123123412312314322312321231311000000000110000100001000010001000000000000n n n n n n n n n nn n n nn na a a a x D a x x x x x x x x a a a a a x x a x x x x x x a a a a a a a x x x x a x x x x x x -----=+----=+--++++=+321231223121212(1)(1).nn n nnn na a a a x x x x x x x x x a a a x x x x x x =+++++=++++6.(华东师大,2002)计算n 阶行列式xx x x x D n22212221222122214444=解:将第1列的-2倍依次加到以下各列.)2)](1(2[2000100201000210000)1(2200010020100021242424241---+=----+=-------=n n x n x x x x n x x x x x x x x x D 7.(大连理工,2004)计算n 阶行列式111121112121111n n n D n--=-解 将第2行,第3行,,第n 行都加到第1行上(1)1(1,2,,2,1)12111111111111121000102111110(1)(1)(1)(1).n n n n n n n n n D nnn n τ-------==--=--=--8.(浙江大学,2004)计算n 阶行列式123123413451211321221n n n n D n n n n nn n -=-----解:将第1-n 行的(-1)倍加到第n 行,第2-n 行的(-1)倍加到第1-n 行,…,第1行的(-1)倍加到第2行.1(1,2,,1)12311122111111100011111100011111101111111211122100000000000012(1)(1)()(1)(1)n n n n n n n n n n n n n D n n n n n n n n nnn n n n n n nτ----------==-----++++----=--+++-=+--=-(1)121.2n n n n --+⋅⋅9.(江苏大学,2004)计算n 阶行列式.xx x x D n αααααααααααααααα-------=解:111()0000000000()2000222()()n n n n x xD x xx xDx xx D x ααααααααααααααααααααααααααααααααα----++-+=-+--+------=++----+----=+--由行列与其转置行列式相等,于是有1111()()()()n n n n n n D x D x D x D x αααααα----⎧=+--⎪⎨=-++⎪⎩解关于1,-n n D D 的方程组得()()2n nn x x D αα++-=10.(武汉大学,1998)设)(,),(),(,221x f x f x f n n ≥是关于x 的次数2-≤n 的多项式,n a a a ,,,21 为任意数,证明:行列式0)()()()()()()()()(212222111211=n n n n n n a f a f a f a f a f a f a f a f a f并举例说明条件“次数2-≤n ”是不可缺少的.证明1:121112(),(),,()[],dim []1,(),(),,()n n n n f x f x f x P x P x n f x f x f x --∈=-于是线性相关,不妨假定.).()()()(112211x f k x f k x f k x f n n n --+++= 显然有112211()()()(),1,,n i i i n n i f a k f a k f a k f a i n --=+++=将以上行列式第1列的1)k -(倍,第2列的2k -()倍,…,第1-n 列的1n k --()倍加到第n 列,那么它的第n 列全变成零,因此行列式为零.证明2:当n a a a ,,,21 中有两个数相等时,等式显然成立. 当n a a a ,,,21 是n 个互不相等的数时,令)()()()()()()()()()(212222121n n n n n n a f a f a f a f a f a f x f x f x f x F=假定)(x F 不是零多项式,则(())2F x n ∂≤-,令n a a a x ,,,32 =,则0)()()(32====n a F a F a F .)(x F 有1-n 个根,矛盾,所以)(x F 是零多项式,当然0)(1=a F ,因此结论成立.当3=n 时,令.1)(,1)(,1)(2321+=-==x x f x x f x f 取1230,2,1,a a a ===-那么.06110420111221511111)1()1()1()2()2()2()0()0()0(321321321≠=--=--=---f f f f f f f f f 因此条件“次数2-≤n ”是不可缺少的。
高等代数课件PPT之第2章行列式

例5 证明上三角行列式
a11 0 D 0 a12 a1n a22 a2 n a11a22 ann 0
( j1 j2 jn ) ( 1 ) a1 j1 a2 j2 anjn
ann
证: 由定义 D 和式中,只有当
jn n, jn1 n 1,, j2 2, j1 1时,
ai1 1ai2 2 ain n
记
上三角行列式的值
a11 a12 a1n
i1i 2 i n
(1)
( i1i 2 i n )
0 D 0
a22 a2 n a11a22 ann 0 ann
§2.4 ∼2.5 n级行列式的性质与计算
考虑
a11 a 21 D a n1 a12 a1n a 22 a 2 n a n 2 a nn
( 1)
( i1i2 in ) ( j1 j2 jn )
ai1 j1 ai2 j2 ain jn
另一定义形式
其中i1i2…in和j1 j2 …jn都是n级排列 .
推论:n级行列式D=det (aij) 的值为
D (1) ( i1i2 in ) ( j1 j2 jn ) ai1 j1 ai2 j2 ain jn
是所有取自不同行、不同列n个元素的乘积 a1 j1 a2 j2 anjn ( j1 j2 jn ) ( 1 ) 并冠以符号 的项的和. (i) a1 j1 a2 j2 anjn 是取自不同行、不同列的n个元素的乘积 (ii)行标按自然顺序排列,列标排列的奇偶性 决定每一项的符号;
于是方程组的解为
D3 15 D1 55 D2 20 x1 11,x2 4, x3 3. D 5 D 5 D 5
高等代数2

和
a11 a12 La1n
a21 a22 La2n LLLLL an1 an2 Lann
= ∑ (−1) a a La τ (i1i2Lin )+τ ( j1 j2L jn )
i1 j1 i2 j2
in jn
i1j1i2jL2 Lin jn
第 4 页 共 11 页
高等代数第二章 行列式
§2.4 行列式的性质与计算
一般用 i ↔ j 写在等号上面表示交换第 i 行与第 j 行; 写在等号下面表示交换第 i 列与 第 j 列。
方法提示:计算行列式的基本方法——化行列式为三角形行列式。
0 1 1 −1 例 1 计算四阶行列式 1 0 2 1 。
−1 1 2 0 −2 0 1 1
(答案:1)
例 2 计算 n 阶行列式
高等代数第二章 行列式
第二章 行列式
§2.1 引言
高等代数的另一个重要概念是行列式。 它是一个形式化运算或表示数字运算结果的符 号形式。下面我们从简单的解方程组问题引进二阶和三阶行列式概念,再通过其定义中所涉
及的排列性质,找出规律,用来定义一般的 n 阶行列式。
设有一个二元线性方程组
⎧⎨⎩ aa1211xx11
(答案: a1a2a3 Lan−1an ⎜⎜⎝⎛1 +
1 a1
+
1 a2
+
1 a3
+L+
1 an−1
+
1 an
⎟⎟⎠⎞ )
第 6 页 共 11 页
高等代数第二章 行列式
二、 行列式按某行(列)展开
一般来说,低阶行列式的计算较高阶行列式要简单。 因此,我们自然要考虑能否用较 低阶行列式来表示高阶行列式的问题。为了研究这个问题,先引进行列式元素的余子式和代 数余子式的概念。
第二章知识点总结(高等代数)

第二章行列式知识点总结一行列式定义1、n 级行列式111212122212n n ijnn n nna a a a a a a a a a =L LM M M L(1)等于所有取自不同行不同列的n 个元素的乘积1212n j j nj a a a L (2)的代数和,这里12n j j j L 是一个n 级排列。
当12n j j j L 是偶排列时,该项前面带正号;当12n j j j L 是奇排列时,该项前面带负号,即:1212121112121222()1212(1)n n nn n j j j ij j j nj nj j j n n nna a a a a a a a a a a a a τ==-∑LL L L L M M M L。
2、等价定义121212()12(1)n n ni i i ij i i i n ni i i a a a a τ=-∑L L L 和121211221212()()(1)n n n n n ni i i j j j ij i j i j i j ni i i j j j a a a a ττ+=-∑L LL L L 和3、由n 级排列的性质可知,n 级行列式共有!n 项,其中冠以正号的项和冠以负号的项(不算元素本身所带的负号)各占一半。
4、常见的行列式1)上三角、下三角、对角行列式111111222222112200nn nn nnnna a a a a a a a a a a a *===*L LLL2)副对角方向的行列式111(1)212,12,1212,111110(1)nnnn n n n n n n n n n n a a a a a a a a a a a a -----*===-*L L LL3)范德蒙行列式:1222212111112111()(2)n n i j j i nn n n na a a a a a a a a a a n ≤<≤---=-≥∏L L L L L L L L二、行列式性质1、行列式与它的转置行列式相等。
第二章 行列式

2 0 例如:矩阵A = 1 4 −2 3 4 0 a11的余子式 = = 4, 3 1
4 0 1
4 0 a11的余子矩阵A11 = 3 1
1+1
a11的代数余子式 A11 = (−1)
4 0 =4 3 1
1 0 a12的余子矩阵A12 = −2 1 1 0 0 1+ 2 1 a12的余子式 = = 1, a12的代数余子式 A12 = (−1) = −1 −2 1 −2 1 ⋯⋯
1+ n
⋮ ⋱ 0 + (−1)1+ n b ⋮
= a×a
n −1
+ (−1)
b×b
n −1
= a + (−1)
n
1+ n
b
n
定 2.3 理
(1) 用 个 乘 列 的 一 ( ) 一 数 行 式 任 列 行 ,
等 用 个 乘 行 式 即 于 这 数 此 列 , det(A ,⋯, kAj ,⋯, A ) = k ⋅ det(A ,⋯, Aj ,⋯, A ) 1 n 1 n 这 , 1,⋯, Aj ,⋯, A 都 n ×1列 量 里 A 是 向 。 n 上 就 式 是 a11 ⋯ ka1 j ⋯ a1n a11 ⋯ a1 j ⋯ a1n ⋮ ⋯ ⋮ ⋯ ⋮ =k ⋮ ⋯ ⋮ ⋯ ⋮ an1 ⋯ kanj ⋯ ann an1 ⋯ anj ⋯ ann
2 × 0 − 3 ×1 3 = = −13 13
a11 a12 一般地,矩阵A = , a21 a22 a11 a12 其对应的行列式 是一个数, a21 a22 其值为a11 a22 − a21 a12
6
2.1.2 n阶行列式的定义
第2章 行列式

行列式的定义 行列式的性质▲ 行列式的应用
第1页 共84页
§2.1 行列式的定义
二阶行列式 三阶行列式 n 阶行列式
第2页 共84页
一、二阶行列式
用消元法解二元线性方程组
a11 x1 a12 x2 b1 , a21 x1 a22 x2 b2 .
a 21 a 22 0 a n1 a n 2 a nn
第18页 共84页
课堂练习
用行列式的定义计算
0 0 0 1 0 0 0 2 0 0 Dn n1 0 0 0 0 0 0 0 0 n
Dn 1
n1 n 2
如:
ka11 la21
ka12 a11 a12 lk la22 a21 a22
矩阵提取公因子是提取矩阵中所有元素的公因子
ka11 ka 21
ka12 a11 a12 k ka22 a21 a22
第25页 共84页
推论2
行列式中如果有两行(列)元素成比例,
a11 b1 D2 . a21 b2 b1 a12
a11
a22 a21 D1 b2 D 2 x2 , 则当 D 0时,方程组的解为 x1 a a D a11 第D 12 7页 共84页 11
考虑
n元线性方程组(n个方程)的解
Di xi ? D
第8页 共84页
二、三阶行列式
n
aij Aij
i 1
行列式等于它的任一 行(列)的各元素与其 对应的代数余子式乘 积之和 第13页 共84页
3 例1:求行列式D= 5 2 并求行列式D的值.
第二章行列式

说明
1. 对角线法则只适用于二阶与三阶行列式.
2.三阶行列式包括3!项,每项都是位于不同行, 不同列的三个元素的乘积,其中三项为正,三项为 负.
利用三阶行列式求解三元线性方程组
如果三元线性方程组
⎪⎨⎧aa2111xx11
+ +
a12 x2 a22 x2
+ +
a13 x3 a23 x3
= =
b1 , b2 ,
n个不同的元素的所有排列的种数为n!
排列的逆序数
我们规定各元素之间有一个标准次序, n 个不同 的自然数,规定由小到大为标准次序.
( ) 定义 在一个排列 i1i2 Lit is Lin 中,若数
it > is 则称这两个数组成一个逆序. 例如 排列32514 中,
逆序
32514
逆序 逆序
定义 一个排列中所有逆序的总数称为此排列的逆序数.
x2
=
a11b2 − b1a21 . a11a22 − a12a21
(3)
由方程组的四个系数确定.
定义 由四个数排成二行二列(横排称行、竖排
称列)的数表
a11 a12
a21 a22
(4)
表达式 a11a22 − a12a21称为数表( 4)所确定的二阶
行列式,并记作 a11 a12
(5)
a21 a22
对
D
的前
k
行作运算
ri
+
kr
,再对后
j
n
列作运
算 ci + kc j ,把 D 化为下三角形行列式
p11
MO
0
D=
pk1 c11
L L
线性代数 第二章 行列式

例 1 2 3 4
A
5 9
6 10
7 11
8
12
13 14 15 16
1 2 3
B 95
6 10
171
余子矩阵:在n 阶方阵 A [aij ]中,把元素aij 所在
的第i行和第j列划去,余下来的n-1阶方阵叫做 aij的
余子矩阵,记作M ij .
1 0 3 4
例
A
0 3 1
1 2 6
i 1,2, ,n
j 1,2, , n
性质2 行列式与它的转置行列式相等。
314
按第1列展开 2 5
14
1 2 5
3
(1) ( )
30
30
130
1 1
4 3 15 12 13 20
2 5
314
1 2 5按第3行展开 1 1
4
3 3(
4 )
2 5
1 5
130
13 3 11 20
当 n 2 时,假设对 n 1 阶行列式已有定义,则
n
A a11 A11 a12 A12 a1n A1n a1 j A1 j j 1
其中Aij (1)i j M ij 称为代数余子式。
a11 a21
a12 a22
a11a22 a12a21
a11 a21 a31
a12 a22 a32
ab
LLLLL
O
1 b bL a
ab
a (n 1)b(a b)n1.
思考
0 1 0 0 0 0 2 0 0 0 0 n1 n 0 0 0
和的性质 若行列式 某一行(列)的所有元素都是两
个数的和,则此行列式等于两个行列式的和. 这两个 行列式的这一行(列)的元素分别为对应的两个加数 之一,其余各行(列)的元素与原行列式相同 .
第二章第二节 行列式性质
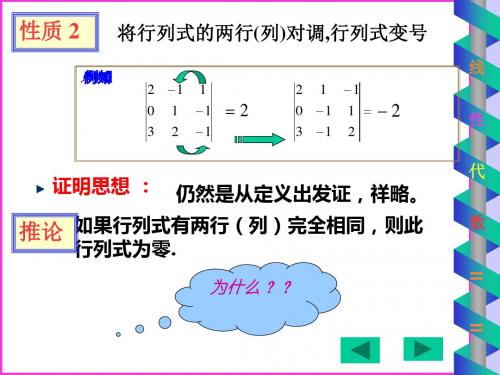
a a c
0 b d
b
D2 n 0
0
线
0 a b c d b
解 按第一行展开,有
a 0 a b c d 0 b
c
d
0
0 a
性 代 数
D2 n a
0
0
b(1) 0 d
2 n 1
0
0
c 0
d 0
0 c c 0
d 0
再对两个(2n-1)阶行列式各按最后一行展开,得
= =
D2n adD2(n1) bc(1)(2n1)1 D2( n1) (ad bc)D2( n1)
a12 ai 2
a1n ain a jn ann
a11 a j1 ai1 an1
a12 a j2 ai 2 an 2
a1n
线
a jn
性
a j2 an
ain
代
ann
数
性质 3(展开法则)
n
行列式等于它的任意一行(列)中所
有元素与它们对应的代数余子式乘积之和.即
Dn aik Aik , 或 Dn akj Akj
线
性 代
1 x 1 0 1 x
1 x 1 0 1 x n 1 0 0 0 0
0 x
0 x
0 x 0 0 x 1 x 0
1 x 1
(1)
x 0 1 x x 0 1 x n 1 0 0 0 0
数
(1) n 1 x n 2
= =
1 x 1
例
计算行列式
1 2 2 2 2 2 D 2 2 3 2 2 2
行列式中任一行(列)中元素与另一行(列)对应元素的 代数余子式乘积之和等于零,即
第二章(行列式)

代
数
( 2)求排列中每一个 数前面有多少个比其大 的数的个数,再将所有 的个数相加即得。
如:求“3874251”的逆序数。
§2.2
行列式的定义
线 性
先来看一个二元一次线性方程组: a11 x1 a12 x2 b1 (1) a21 x1 a22 x2 b2
其中 a
, b(i, ij i
( 1) ( j1 j2 ... jn ) (1 1 ... 1) ( 1) ( j1 j2 ... jn )
代
数
j1 j2 ... jn
显然,根据行列式的
性质,有An=0
显然,上式中包括有n!项,要 An=0,则只有-1的奇、偶次方 的个数相等,即奇、偶排列各 占一半。命题得证!
a11 a12 a13 D a21 a22 a23 a33
③
看看D1与D有 何关系。
代
数
则
a31
a32
a11a22 a33 a12 a23a31 a13a21a32 a13a22 a31 a12 a21a33 a11a23 a32
b1 b3
a12 a22 a23
a13 a23 a33
(1)项的形式: 1 j1 a2 j2 a3 j3( j1 j2 j3 是1, 2, 3的排列 ) a (2)项的个数:3! = 6 (1, 2, 3的全部排列的数目 )
( 1) ( j1 j2 j3 ) (3)项的符号:
于是,三阶行列式的展开式可表示为
a11 a21 a12 a22 a32
a11 a21 a31 a11 a21 a31 a12 a22 a32 a12 a22 a32
线 性
[理学]第二章、行列式_OK
![[理学]第二章、行列式_OK](https://img.taocdn.com/s3/m/0e4e65b2be1e650e53ea993b.png)
x1 1 2
f x 1 x 1 1 求 x3 的系数.
32 x 1 1 1 2x 1
30
思考题解答解 含 Biblioteka 3 的项有两项,即x1 1 2
f x 1 x 1 1
32 x 1
对应于
1 1 2x 1
1 a a a a 1 a a a a (1234) 11 22 33 44
1243
2
2
数 in1 后面比 in1 小的数的个数
或者
12
(i1i2 in ) = 数 in 前面比 in 大的数的个数
数 in1 前面比 in1 大的数的个数
数 i 前面比i 大的数的个数
2
2
例1 求排列 32514 的逆序数.
例2 求排列 453162 的逆序数.
例3 求排列 423165 的逆序数.
53214
注:n个数的不同排列有 n ! 个
定义2.2 按照由小到大的顺序排成的排列称为
自然排列.
10
定义2.3
在一个排列中,若某个较大的数排在某 个较小的数前面,就称这个排列有一个 逆序. 一个排列中出现的逆序的总数
称为这个排列的逆序数,排列 k1k2 kn
的逆序数通常记为 (k1k2 kn )
次相邻 对换
a1 al bb1 bmac1 cn
所以一个排列中的任意两个元素对换,排列都改变
奇偶性.
16
推论1 推论2
偶数次对换不改变排列的奇偶性;奇数次 对换改变排列的奇偶性。
任意一个n 级排列都可以经过一系列对换
变成自然排列,并且所作对换的次数与该 排列有相同的奇偶性.
定理2.2 n 时2,n 个数的所有排列中,奇偶排列各
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d , 当 l j , a1l A1j a2l A2 j L anl Anj 0 , 当 l j .
4.拉普拉斯定理 设在行列式中任意取定了k( 1 k n 1 ) 个行.由
这k行元素所组成的一切k级子式与它们的代数余子式
的乘积之和等于行列式的值。
5. 范德蒙德行列式
1 1 1 1
从而,它本身表示 n!个行列式的和。
1
1
例15.求n阶行列式 D L 1
1
1 L 1L LL 1L 1L
1 1
L 展开后的正项总数。
1 1
解:易知D=2n1 设D的展开式中有P个正项,N个负项.
由于D的每一项不是1就是-1,故
P N n! P N 2n1
从而 P 1 (2n1 n!) 2n2 1 n!
a11 a12 a1n a11 a21 an1
a21 a22 a2n a12 a22 an2
an1 an2 ann a1n a2n ann
性质2 有公因数,可以提取.
a11 a12
a1n
a11 a12
kai1 kai2
kain k ai1 ai2
an1 an2 ann
2.逆序(数)
定义2 在一个排列中,如果一对数的前后位置与大
小顺序相反,即前面的数大于后面的数,那么它们就称 为一个逆序,一个排列中逆序的总数就称为这个排列的 逆序数.
排列 j1 j2 jn 的逆序数记为 ( j1 j2 jn ) 3.奇偶排列
定义3 逆序数为偶数的排列称为偶排列;逆序数为 奇数的排列称为奇排列. 4.对换
二、行列式的计算 n级行列式的计算或证明一般比较麻烦,有一
定的难度。但在计算或证明时有一个中心指导思想: 就是化行列式使其元素中出现较多的零,并向下面 两种形式的行列式化简:
(1)上(下)三角形行列式(特殊的是对角行列式) (2)某一行(列)除少数元素不为零其余全为零,
然后按行列展开(降阶)
行列式的计算方法一般有以下几种。 1.上(下)三角形方法 2.降阶法 3.加边法(升阶法)
a11 a12 a1n
的系数矩阵
A
a21 an1
a22 an2
a2n ann
的行列式 d | A | 0
(2)
那么线性方程组(2)有解,并且解是唯一的,解可
以通过系数表示为公式:
x1
d1 d
,
x2
d2 d
,
,
xn
dn d
(2)
其中 d j 是把矩阵中第j列换成常数项所成的矩阵的行列
a0 a1 a2 x
证明:x b, f (x) 1.
分析:x b 为一次多项式,它和 f (x) 的关系不整除就互素,
故只需证明不整除即可。
性质3可以推广到某一行为多组数的和的情形.
性质4 两行相同,其值为零. 性质5 两行比例成,其值必为零.
性质6 把一行的倍数加到另一行,行列式不变.
性质7 两行互换,符号改变.
3. 行列式按行(列) 展开 定理3:按行展开:
d , 当 k i, ak1Ai1 ak2 Ai2 L akn Ain 0 , 当 k i .
4.拆项法 5.全一法(归一法) 6.逐行(列)相加减
7.递推法 8.数学归纳法 9.利用(构造)范德蒙德行列式 10.利用拉普拉斯定理 说明:这些方法并不是相互独立,可以交错使用,只 是侧重面不同而已。
三、典型例题
例1.数字行列式的计算。例 P73的计算题.
1 2 3 L n1 n
2 3 4L
例2.计算 D 3 4 5 L
这一定义可写成如下表达式
a11 a12 a21 a22 an1 an2
a1n
a2n
( j1 j2 jn )
(1) a a a 1 j1 2 j2
njn
j1 j2 jn
ann
表示对所有n级排列求和.
j1 j2 jn
类似的还有定义
a11 a12 a1n
a21 a22
a2n
例6.计算 Dn a2a1 x a22 a2a3
ana1 ana2 ana3
a1an a2an
x an2
注:此行列式的特征比较明显,可以采用拆项法
(递推法)和加边法来做。
0 L 0 0 1 L 0 0
例7.计算 Dn 0 1 L 0 0
L L L LL L 0 0 0 L 1
式,即
a11
dj
a21
an1
a1, j1 b1 a1, j1 a2, j1 b2 a2, j1
an, j1 bn an, j1
a1n a2n , j 1,2, ,n. ann
7. 定理5 如果齐次线性方程组
a11 x1 a12 x2 a1n xn 0 ,
a
21
(i1i2 in )
(1) a a a i11 i2 2
inn
i1i2 in
和
an1 an2 ann
a11 a12 a21 a22 an1 an2
a1n
a2n
(i1i2 in ) ( j1 j2 jn )
(1) a a a i1 j1 i2 j2
in jn
ann
2.性质 性质1 行列互换,其值不变.
2
2
例16. 证明:若三阶行列式的所有元素均等于1或者-1,则
D 4
证明:因D的展开式中只含6项,且每一项的值为 1 ,
所以 D 6
另外若将D的第二行加到第一行,
则变后的第一行元素全为偶数,
从而D的值是偶数。下面证明 D 6
,
假设 D 6, 则D的6项 a11a22 a33 ,a12 a23a31 ,a13a21a32
故有 D 4。
例17. 若 n(n 3)阶行列式 D 的元素为 1
那么 D (n 1)(n 1)!
分析:此题是上一题目的推广,可以用数学归纳法证明。
例18. 设 b, a0 , a1, an 是 n 2个互不相同的数,a0 0 .
a0 a1 a2 an a0 x a2 an f (x) a0 a1 x an
第二章 行列式
本章的主要内容是行列式的定义与计算,因此要 理解掌握行列式的定义,熟练掌握行列式的计算方法 和技巧,其次是会应用克兰姆规则。
一、内容提要 (一)n级排列
1. n级排列 定义1. 由数字1,2,3…n组成的一个有序数组称 为一个n级排列。n级排列的总数是n!,其中1,
2,3…n称为自然排列。
(P101第18题3)
此题按照第一行(列)或者第n行(列)展开均可,
然后递推.
1
例8.计算 D
x12 L
x n 1 1 x1n
1L
x22 L
LL
x n 1 2
L
x2n L
1 xn2 L x n 1
n
xnn
(P103补充题4-5比较)
注:此题特征也很明显,添加一行可以构造成为n
阶范德蒙德行列式.
(2n 1)n (2n 2)n L
相同的奇偶性.
(二)n级行列式 1.定义4 n级行列式
a11 a12 a1n
a21 a22 a2n
an1 an2 ann
等于所有取自不同行不同列的n个元素的乘积
a a 1 j1 2 j2 anjn
(1)
的代数和,这里 j1 j2 jn 是1,2,…,n的一个排列,每
一项(1)都按下面规则带有符号;j1 j2 jn 是偶排列时, (1)带有正号,j1 j2 jn 是奇排列时,(1)带有负号.
把一个排列中某两个数的位置互换,而其余的数不 动,就得到另一个排列.这样一个变换称为一个对换.
5.两个定理 定理1 对换改变排列的奇偶性。
推论 在全部n级排列排列中,奇、偶排列的个数相等,
各有
1 2
n! 个.
定理2 任意一个 n 级排列与排列12 …n 都可经过
一系列对换互变,并且所作对换的个数与这个排列有
Sn1
Sn
L
(xi xj )2 (P200第13题)
1 jin
SHale Waihona Puke n2分析:从等式的右端看恰是两个范德蒙行列式的乘积, 因此,可以考虑利用范德蒙德行列式的结果来证明.
1
3
O
N
例11.计算 D2n
k k2 k 1 k 3
N
O
2
4
a
b
O
N
例12.计算 D2n
ab ba
N
O
b
a
分析:以上两个题结构相同,都可以利用拉普拉斯定理。
an1 an2
a1n ain ann
推论 一行为零,其值也同.
性质3 一行为和,拆成两个.
a11
a12 a1n
a11 a12 a1n
a11 a12 a1n
b1 c1 b2 c2 bn cn b1 b2 bn c1 c2 cn
an1
an2 ann
an1 an2 ann an1 an2 ann
x1
a22 x2
a2n xn
0
,
an1 x1 an2 x2 ann xn 0
(3)
的系数矩阵的行列式 | A | 0 ,那么它只有零解.
换句话说,如果方程组(3)有非零解,那么必有
| A | 0
8.几个重要概念 矩阵的初等行(列)变换、行列式中元素的余子
式、代数余子式 k级子式、k级子式的代数余子式
a1
a2 a3 an
a12
a22
a32
an2
(ai a j )
1 jin
