《线性代数(修订版)》教学课件 1.4 分块矩阵
合集下载
线性代数 矩阵 第4节 分块矩阵
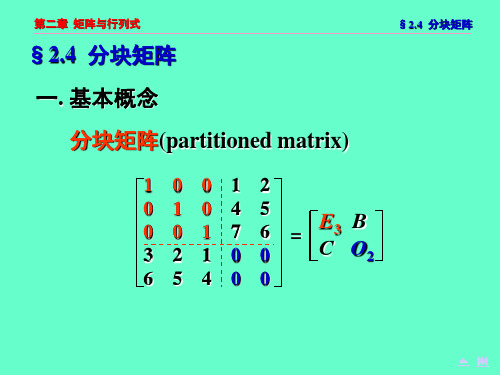
…
…
…
qn2 q 1T q 2T q nT
qnn
QT =
, QT Q =
[q1, q2, …, qn]
…
第二章 矩阵与行列式
§2.4 分块矩阵
QTQ =
q1T q2T q nT … …
[q1, q2, …, qn]
=
q1Tq1 q1Tq2 … q1Tqn q2Tq1 q2Tq2 … q2Tqn
.
q nT q 1 q nT q 2 … q nT q n
则 A =
A11 A12 … A1r A21 A22 … A2r
… … … … As1 As2 … Asr
.
第二章 矩阵与行列式
§2.4 分块矩阵
3. 分块乘法
设A为ml矩阵, B为l n矩阵, 将它们分块如下 A11 A12 … A1t B11 B12 … B1r A21 A22 … A2t B21 B22 … B2r A= … … … … , B= , … … … … As1 As2 … Ast Bt1 Bt2 … Btr 其中Ai1, Ai2, …, Ait的列数分别与B1j, B2j, …, Btj的 行数相等. C11 C12 … C1r t C21 C22 … C2r 则AB = … … … … , 其中Cij = AikBkj , k=1 Cs1 Cs2 … Csr (i = 1, 2, …, s; j = 1, 2, …, r.)
2 0 例如 0 0 0 1 2 0 0 0 0 1 2 0 0 0 0 0 1 3 0 0 0 . 2 4
第二章 矩阵与行列式
§2.4 分块矩阵
三. 基本运算 1.分块加法
A11 A21 A= … As1 A12 … A1r B11 A22 … A2r B21 … … … ,B= … As2 … Asr Bs1 B12 … B1r B22 … B2r … … … , Bs2 … Bsr
线性代数—矩阵的分块、子矩阵

数,
那
么
As1 Asr
A
A11
A1r
.
As1 Asr
3 设A为m l矩阵, B为l n矩阵,分块成
A
A11
A1t
,
B
B11
B1r
,
As1 Ast
Bt1 Btr
其中Ai1 , Ai2 ,, Ait的列数分别等于B1 j , B2 j ,, Bij
的
行
数,
上有非零子块,其余子块都为零矩阵,且非零子块都
是方阵.即
A1
A
A2
O
O
,
As
A1
A
A2
O
O
,
As
其中 Ai i 1,2,s 都是方阵,那末称 A为分块
对角矩阵.
若每一块 Ai 均可逆, 则A可逆,并有
A11
o
A1
A21
o
. As 1
A1 0
0 A2
0 B1 0 0
那么
AB
C11
C1r
t
Cs1 Csr
其中Cij Aik Bkj i 1,, s; j 1,, r .
k 1
4
设
A
A11
A1r
, 则则
AATT
AA1T1T11
AAsTsT11 ..
As1 Asr
AA1Tr1Tr
AAsTsTrr
5 设A为n阶矩阵,若A的分块矩阵只有在主对角线
0
0 1 0 0 0 1 3 1
0
0
2
1
0
21
4
ቤተ መጻሕፍቲ ባይዱ
线性代数课件:2-4分块矩阵

其中子块和Bi(i=1,2,…,s)为同阶方阵,则 有下述性质:
(1)
A1 B1
A
B
(2)
A1 B1
AB
A2 B2
; As Bs
A2 B2
; As Bs
(3) |A|=|A1||A2|…|As|;
(4) 若|Ai|0(i =1,2,…,s),则
A1
1
A1 1
A2
As
2. 分块矩阵的乘法
设矩阵A=(aij)m×s,B=(bij)s×n,用分块矩 阵计算A,B的乘积AB时, 一定要使A的列 的分法与B的行的分法一致,这样不仅可以
, 保证A,B作为分块矩阵可乘,而且它们相 应的各子块间的乘法也有意义,即
,
s1
s2
s
p
n1
n2 nq
A11
A
A21
A12
, 矩阵的每一子块.
设分块矩阵
,
A11
A
A21
A12
A22
A1q
A2q
,
Ap1 Ap2 Apq
则
,
AT 11
AT
AT 12
AT 1q
AT 21
AT p1
AT 22
AT p2
,
AT 1q
AT pq
, 即对分块矩阵做转置时,要将其行、列位 置互换,而且还要将每一子块进行转置.
,
k 1
j=1,2,…,q).
这说明,如果把分块矩阵的子块象数 一样看待,它们的乘法与通常的矩阵乘法 规则在形式上是完全相同的.
例2.4.1 设
1 0 0 0
A
0 1 1
1 2 1
线性代数第-章1.4PPT课件

向量空间的性质
总结词
向量空间具有一些重要的性质,如加法的结合律、交换律和分配律,数乘的结合律和分配律等。
详细描述
向量空间的加法满足结合律和交换律,即对任意向量u、v、w∈V,有u+(v+w)=(u+v)+w和u+v=v+u;数乘也 满足结合律和分配律,即对任意标量k、l∈F和任意向量u∈V,有k(l(u))=(kl)(u)和k(u+v)=ku+kv。
线性组合的应用
向量表示
线性组合可以用来表示向量,使得向量的运算更加简洁明了。
线性方程组
线性组合可以用来求解线性方程组,通过将方程组中的未知数表示 为已知向量的线性组合,简化方程组的求解过程。
向量空间
线性组合是向量空间中向量运算的基本形式之一,可以用来研究向 量空间的性质和结构。
04
向量的线性相关性
中任意向量可以由这组基线性表示。
基的个数
02 一个向量空间的一组基的个数是有限的,且等于该向
量空间的维数。
基的特性
03
基中的向量是线性无关的,且可以作为该向量空间的
坐标系。
基的性质
唯一性
一个向量空间的一组基是唯一的,即如果存在另一组基也可 以表示向量空间中的任意向量,则这两组基之间存在一一对 应的关系。
05
向量组的秩
秩的定义
01
秩的定义
向量组的秩是指该向量组构成的 矩阵的秩,即该矩阵的最高阶非 零子式的阶数。
02
03
秩的符号表示
秩的性质
用符号“秩”表示,常用大写英 文字母表示,如A的秩记作r(A) 。
向量组的秩是该向量组线性无关 的向量的个数,与向量组的维数 有关。
线性代数第一章、矩阵PPT课件

矩阵的秩的计算方法
可以通过初等行变换或初等列变换将矩阵转化为行阶梯形或列阶梯形,然后数非零行的个数即为矩阵的秩。
矩阵的秩的定义
矩阵的秩是其行向量组或列向量组的一个极大线性无关组中向量的个数。
矩阵的秩
通过初等行变换将增广矩阵化为行阶梯形,然后回代求解。
高斯消元法
克拉默法则
迭代法
适用于线性方程组系数行列式不为0的情况,通过解方程组求出方程的解。
n阶方阵A的行列式记为det(A),是一个n阶的方阵,其值是一个实数。
行列式与转置矩阵的行列式相等,即det(A^T) = det(A);行列式的乘法性质,即det(kA) = k^n * det(A);行列式的初等变换性质,即行列式在初等变换下保持不变。
行列式的定义与性质
行列式的性质
行列式的定义
线性代数第一章、矩阵ppt课件
目录
CONTENTS
矩阵的定义与性质 矩阵的逆与行列式 矩阵的秩与线性方程组 矩阵的特征值与特征向量 矩阵的分解与正交矩阵 矩阵在实际问题中的应用
01
矩阵的定义与性质
CHAPTER
矩阵的定义与性质
about the subject matter here refers to the subject matter here.
相似法
如果存在可逆矩阵P,使得P^(-1)AP=B,则矩阵A的特征值和特征向量可以通过矩阵B的特征值和特征向量来求解。
特征值与特征向量的计算方法
如果矩阵A的所有特征值都是实数且没有重复,则矩阵A可以对角化。
判断矩阵是否可对角化
求解线性方程组
判断矩阵是否相似
优化问题
通过将线性方程组Ax=b转化为特征值问题,可以求解线性方程组。
可以通过初等行变换或初等列变换将矩阵转化为行阶梯形或列阶梯形,然后数非零行的个数即为矩阵的秩。
矩阵的秩的定义
矩阵的秩是其行向量组或列向量组的一个极大线性无关组中向量的个数。
矩阵的秩
通过初等行变换将增广矩阵化为行阶梯形,然后回代求解。
高斯消元法
克拉默法则
迭代法
适用于线性方程组系数行列式不为0的情况,通过解方程组求出方程的解。
n阶方阵A的行列式记为det(A),是一个n阶的方阵,其值是一个实数。
行列式与转置矩阵的行列式相等,即det(A^T) = det(A);行列式的乘法性质,即det(kA) = k^n * det(A);行列式的初等变换性质,即行列式在初等变换下保持不变。
行列式的定义与性质
行列式的性质
行列式的定义
线性代数第一章、矩阵ppt课件
目录
CONTENTS
矩阵的定义与性质 矩阵的逆与行列式 矩阵的秩与线性方程组 矩阵的特征值与特征向量 矩阵的分解与正交矩阵 矩阵在实际问题中的应用
01
矩阵的定义与性质
CHAPTER
矩阵的定义与性质
about the subject matter here refers to the subject matter here.
相似法
如果存在可逆矩阵P,使得P^(-1)AP=B,则矩阵A的特征值和特征向量可以通过矩阵B的特征值和特征向量来求解。
特征值与特征向量的计算方法
如果矩阵A的所有特征值都是实数且没有重复,则矩阵A可以对角化。
判断矩阵是否可对角化
求解线性方程组
判断矩阵是否相似
优化问题
通过将线性方程组Ax=b转化为特征值问题,可以求解线性方程组。
大学线性代数课件矩阵第三章 矩 阵4

设A为m×k矩阵,B为k×n矩阵,对A,B作分块,使得A的列 分法与B的行分法一致,即
k1
k2
A
A11 A21
A12 A22
Ar1 Ar 2
ks
A1s A2 s
m1 m2 ,
Ars
mr
n1
n2
B11
B12
B B21 B22
Br1 Br 2
np
B1s
B2s
k1 k2
A
A21
A22
Ar 1
Ar 2
则
AT
A1T1 A1T2
A2T1 A2T2
ArT1 ArT2
.
A1Ts
A2Ts
ArTs
A1s
A2 s
,
Ars
如矩阵
1 0 2 1 1
A
0 1
1 4
4 3
5 5
2 6
A11 A21
A12 A22
A13
A23
其中 则
1 0
2 1
1
A11
A11
1 5
;
A2
3 2
1 1
,
A21
1 2
31;
0 1 1
A1
O A11
A21 O
0
1
2
3
5 0 0
§5 矩阵的秩
一、矩阵的秩
定义定12义一:一、矩、矩阵矩阵A阵的的的秩k阶秩子式
设 A 是 mn 的矩阵,任取 A 的 k 个行和 k 个列 (1≤k≤min{m, n}),位于这些行列交叉点处的 kk 个元 素,按照原来的顺序组成一个 k 阶方阵,该方阵对应 的行列式称为矩阵 A 的 k阶子式.
k1
k2
A
A11 A21
A12 A22
Ar1 Ar 2
ks
A1s A2 s
m1 m2 ,
Ars
mr
n1
n2
B11
B12
B B21 B22
Br1 Br 2
np
B1s
B2s
k1 k2
A
A21
A22
Ar 1
Ar 2
则
AT
A1T1 A1T2
A2T1 A2T2
ArT1 ArT2
.
A1Ts
A2Ts
ArTs
A1s
A2 s
,
Ars
如矩阵
1 0 2 1 1
A
0 1
1 4
4 3
5 5
2 6
A11 A21
A12 A22
A13
A23
其中 则
1 0
2 1
1
A11
A11
1 5
;
A2
3 2
1 1
,
A21
1 2
31;
0 1 1
A1
O A11
A21 O
0
1
2
3
5 0 0
§5 矩阵的秩
一、矩阵的秩
定义定12义一:一、矩、矩阵矩阵A阵的的的秩k阶秩子式
设 A 是 mn 的矩阵,任取 A 的 k 个行和 k 个列 (1≤k≤min{m, n}),位于这些行列交叉点处的 kk 个元 素,按照原来的顺序组成一个 k 阶方阵,该方阵对应 的行列式称为矩阵 A 的 k阶子式.
华东理工大学线性代数课件LA 1-4

由于要求Ai 1 , Ai 2 ,, Ait的列数分别等于B1 j , B2 j ,, Bij 的行数, 那末常见的应用一般出现在A, B为4 × 4阶方阵中。
1 例: 0 A= 1 0 0 0 0 1 0 0 , 0 1 2 1 3 4
5 7 B = 0 0 6 8 0 0 1 0 0 0 0 1 , 0 0
其中Ai1 , Ai 2 ,, Ait的列数分别等于 1 j , B2 j ,, Btj B 的行数, 那末
C 11 AB = C s1 t 其中 C ij = ∑ A ik B kj
k =1
C 1r C sr (i = 1 , , s ; j = 1 , , r ).
0 , 3 0 3 0 0
O A = A2
1
例
设n阶方阵 A的逆矩阵为B , 即满足AB = I ,
可以将 B 和 I都按列分成 1 × n 的分块矩阵,
可得: A[b1 , b2 , bn ] = [e1 , e 2 , , e n ] 即: Abi = e i ( i = 1,2, , n ) 其中 e i 是n阶单位矩阵的第 i列, 即e i = [0, ,,] 1, 0
A1 O A2 A= O As
A1 O A2 A= O As
A可逆 Ai 可逆i = 1,2,, s且
A1 = diag ( A11 , A2 1 ,, As1 ).
思考题
B 设 A= O D , 其中 B和 C都是可逆方阵 , C
证明 A可逆 , 并求 A1 .
A2
o
, As
o
O A2 B= As
A1 O
若 每个子块 Ai (i = 1,2,, s )都可逆, 则 A、B均可逆, 并有
《线性代数》矩阵的秩与分块矩阵课件

T A s1 . T A sr
(5) 分块对角阵及其运算(重点) 分块对角阵___设A为阶方阵,若A的分块矩阵的主对角线元素为 非零子块,其余子块均为零子块,且非零子块为方阵,即
A A1 O O O A2 O O O 或 As A1 A As
其中 C ij A i1 B1 j A i 2 B 2 j A it B tj
k 1
t
A ik B kj ( i 1, 2 , , s , j 1, 2 , , r )
(4) 分块矩阵的转置
A11 设A A s1 A T A1 r 11 T ,则 A A1 r T A sr
下面举出两种分块形式分成子块的方法很多矩阵34333231242322211413121122211211343332312423222114131211333231232221131211343332312423222114131211rsrsijijrs1111其中的方式分块即为同型矩阵且以相同kjiktjijsr其中的行的分法一致则的列的分法与矩阵既矩阵的行数的列数分别等于子块其中子块阵分别为矩阵若它们的分块矩分块对角阵及其运算重点分块对角阵设a为阶方阵若a的分块矩阵的主对角线元素为非零子块其余子块均为零子块且非零子块为方阵即分块对角阵的运算一般地设有两个分块对角矩阵则有
( i 1, 2 , , m ),则有:
A mBm
1
A 2B2
2
A
n
An 1
A2
n
; n Am
(5) 分块对角阵及其运算(重点) 分块对角阵___设A为阶方阵,若A的分块矩阵的主对角线元素为 非零子块,其余子块均为零子块,且非零子块为方阵,即
A A1 O O O A2 O O O 或 As A1 A As
其中 C ij A i1 B1 j A i 2 B 2 j A it B tj
k 1
t
A ik B kj ( i 1, 2 , , s , j 1, 2 , , r )
(4) 分块矩阵的转置
A11 设A A s1 A T A1 r 11 T ,则 A A1 r T A sr
下面举出两种分块形式分成子块的方法很多矩阵34333231242322211413121122211211343332312423222114131211333231232221131211343332312423222114131211rsrsijijrs1111其中的方式分块即为同型矩阵且以相同kjiktjijsr其中的行的分法一致则的列的分法与矩阵既矩阵的行数的列数分别等于子块其中子块阵分别为矩阵若它们的分块矩分块对角阵及其运算重点分块对角阵设a为阶方阵若a的分块矩阵的主对角线元素为非零子块其余子块均为零子块且非零子块为方阵即分块对角阵的运算一般地设有两个分块对角矩阵则有
( i 1, 2 , , m ),则有:
A mBm
1
A 2B2
2
A
n
An 1
A2
n
; n Am
线性代数1.4分块矩阵(崔丽鸿)
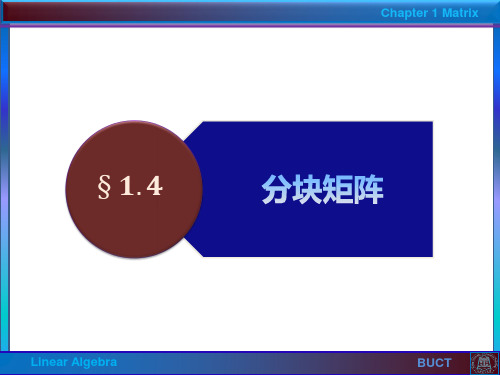
Ak diag A1k , A2k ,L , Ask , k为任意整数
Linear Algebra
BUCT
Chapter 1 Matrix
a 1 0 0
【例1.17】
设
A
0
0
a 0
0 b
0
,
0
ab 0.
0
0
1
b
(1)按照分块矩阵, 求 A1. (2)对正整数n, 求 An .
j A j , j 1,2,L , n. 即得(1).同理说明(2).
Linear Algebra
BUCT
1. 分块对角阵的概念: 2.分块矩阵的运算规则. 3.分块对角阵及其性质.
Chapter 1 Matrix
Linear Algebra
BUCT
§ ������. ������
Linear Algebra
Chapter 1 Matrix BUCT
CONTENTS
Chapter 1 Matrix
在实际问题中经常碰到行数和列数都很大的矩阵.当 人们碰到一张很大的表格时,自然是分部分来看.这 就引出来把矩阵“分块”的概念.
在这一讲,我们重点介绍 分块矩阵
B1 B2 B3
,
即
a
A
0 00
1 a
1 1
0 0
1 1
0 0
bb
B1 BB32
Linear Algebra
Chapter 1 Matrix BUCT
Chapter 1 Matrix
a 1 0 0
A
Linear Algebra
BUCT
Chapter 1 Matrix
a 1 0 0
【例1.17】
设
A
0
0
a 0
0 b
0
,
0
ab 0.
0
0
1
b
(1)按照分块矩阵, 求 A1. (2)对正整数n, 求 An .
j A j , j 1,2,L , n. 即得(1).同理说明(2).
Linear Algebra
BUCT
1. 分块对角阵的概念: 2.分块矩阵的运算规则. 3.分块对角阵及其性质.
Chapter 1 Matrix
Linear Algebra
BUCT
§ ������. ������
Linear Algebra
Chapter 1 Matrix BUCT
CONTENTS
Chapter 1 Matrix
在实际问题中经常碰到行数和列数都很大的矩阵.当 人们碰到一张很大的表格时,自然是分部分来看.这 就引出来把矩阵“分块”的概念.
在这一讲,我们重点介绍 分块矩阵
B1 B2 B3
,
即
a
A
0 00
1 a
1 1
0 0
1 1
0 0
bb
B1 BB32
Linear Algebra
Chapter 1 Matrix BUCT
Chapter 1 Matrix
a 1 0 0
A
线性代数PPT课件:矩阵 第4节 分块矩阵
(2)
(3)
x1a1 + x2a2 + … + xnan = b .
( 4)
A11 A1t B11 B1r A ,B , A A B B st tr s1 t1
其中 Ai1 , Ai2 , …, Ait 的列数分别等于 B1j , B2j ,
…, Btj 的行数,那么
其中 A 称为系数矩阵,x 称为未知向量,b 称为常
数项向量,B 称为增广矩阵. 按分块矩阵的记法,
可记
B=(A b),
或 B = ( A , b ) = ( a1 , a2 , … , an , b ) .
利用矩阵的乘法,此方程组可记作 Ax = b . (1) 的解向量. (2) 方程(2)以向量 x 为未知量,它的解称为方程组
a11 a12 a13 a14 A a21 a22 a23 a24 a a a a 31 32 33 34
分成子块的分法很多, 下面举出三种分块形式:
a11 a12 a13 a14 (1) a21 a22 a23 a24 , a a a a 31 32 33 34
即 A11, A12, A21, A22 为 A 的子块,而 A 形式上成为
以这些子块为元素的分块矩阵. 分法 (2) 及 (3) 的
分块矩阵可类似写出, 这里略.
2.4.2 分块矩阵的运算
分块矩阵的运算规则与普通矩阵的运算规则 相类似, 分别说明如下:
1.加法运算
设矩阵 A 与 B 的行数相同、列数相同, 采用 相同的分块法, 有
如果把系数矩阵 A 按行分成 m 块,则线性方
程组 Ax = b 可记作
线性代数课件_第二章_矩阵及其运算——4

求AB, AB . A
2019/7/23
课件
20
解 将A, B分块
a
A
0 0
0
1 a 0 0
0 0 b 1
0
0 1 b
A1 0
0 , A2
其中
A1
a 0
A2
b 1
1, a 1; b
a
B
1 0
A
.
As1 Asr
2019/7/23
课件
9
例
2,
1 A3
2 2
3 1
4 5 6
1 2 2 2 3 2 2A3 2 2 2 1 2
4 2 5 2 6 2 4 4 6 6 4 2 . 8 10 12
2019/7/23
课件
33
A1B1A1 0 0 A2B2A2
a3 a 2a2 1 0
0
a2 0 0
a3 a 0 0
0 b3 2b
3b2
b23b2021b.
2019/7/23
课件
25
5 0 0
例3 设 A 0 3 1 , 求A1.
0 2 1
课件
5
a 1 0 0
A
0 1
0
a 0 1
0 b 1
0 1 b
C1 C3
C2 , C4
a 1 0 0
即
A
0 1 0
a 0 1
0 b
0 1
线性代数第07讲 矩阵的分块

T m
T 2
T 1
T i
T m
向量组 , , …, 称为矩阵A的行向量组.
反之,由有限个向量所组成的向量组可以构 成一个矩阵.
m个n维列向量所组成的向量组 1 , 2 ,, m , 构成一个m n矩阵
A ( 1 , 2 ,, m )
m个n维行向量所组成 的向量组 1 , 2 , m ,
1 0 0 1 4 1 2 0
B11 B21
E B22
E 则 AB A1
O B11 E B21
E B22 . A1 B22 E
9
B11 A1 B11 B21
B11 AB A1 B11 B21
A11 B11 A B A B s1 s1
A1r B1r . Asr Bsr
5
A11 A1r 2 设 A , 为数, 那末 A A s1 sr
A11 A1r A . A Asr s1
4
1 设矩阵A与B的行数相同, 列数相同, 采用
相同的分块法, 有
同型 同分法
A11 A A s1
A1r B11 , B B Asr s1
B1r Bsr
其中Aij与Bij的行数相同, 列数相同, 那末
a1 , a2 , , an 称为向量 的负向量
向量减法:
( )
注意:两个向量只有维数相同时,才能进行加法和减法运算!
T 数乘向量:设k是一个数,向量 ( ka1 , ka2 , , kan )
T 2
T 1
T i
T m
向量组 , , …, 称为矩阵A的行向量组.
反之,由有限个向量所组成的向量组可以构 成一个矩阵.
m个n维列向量所组成的向量组 1 , 2 ,, m , 构成一个m n矩阵
A ( 1 , 2 ,, m )
m个n维行向量所组成 的向量组 1 , 2 , m ,
1 0 0 1 4 1 2 0
B11 B21
E B22
E 则 AB A1
O B11 E B21
E B22 . A1 B22 E
9
B11 A1 B11 B21
B11 AB A1 B11 B21
A11 B11 A B A B s1 s1
A1r B1r . Asr Bsr
5
A11 A1r 2 设 A , 为数, 那末 A A s1 sr
A11 A1r A . A Asr s1
4
1 设矩阵A与B的行数相同, 列数相同, 采用
相同的分块法, 有
同型 同分法
A11 A A s1
A1r B11 , B B Asr s1
B1r Bsr
其中Aij与Bij的行数相同, 列数相同, 那末
a1 , a2 , , an 称为向量 的负向量
向量减法:
( )
注意:两个向量只有维数相同时,才能进行加法和减法运算!
T 数乘向量:设k是一个数,向量 ( ka1 , ka2 , , kan )
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
γmT β1
γ1T β2
γ
T 2
β2
γmT β2
γ1T
γ
T 2
βn βn
cij
mn
γ
T m
βn
b1 j
中
cij γiT β j ai1 , ai2 ,
, ais
b2
j
s
aik bkj
k1
bsj
与矩阵乘法的定义是一致的
对于n 个未知数,m 个方程的线性方程组
a11 a12
0 1
0
0
0 0 0 1
验证,上面的运算结果与直接用原矩阵运算结果是相同的。 矩阵按行、按列分块的应用(1)中的有关内容,可以作为乘 特殊情况的证明。
§1.4.3 矩阵按行分块与按列
行与按列分块,是矩阵最为常用的两种分块方法。
a11 a12
于矩阵
A
a21
a22
a1n
a2n
,若按行分块,且记
数矩阵
A
a21
a22
am1 am2
a11 x1 a12 x2
a21 x1 a22 x2
a1n xn b1 a2n xn b2
am1 x1 am2 x2 amn xn bm
a1n
a2n
,未知数向量
x1
x
x2
,
amn
xn
b1
项向量
b
b2
amj
a11 a12
矩阵 A 可表示为
A
a21
a22
am1 am2
a1n
a2n
α1 , α2 ,
amn
, αn
论矩阵按行、按列分块在矩阵乘法及线性方程组中的应用。
于矩阵 A (aij )ms , B (bij )sn 的乘积矩阵 AB C (cij )mn ,将
0,
0,
0
,
O2
0 11
;
1 0 0 2
1 0 0 2
0
0
1 0
0 1
5
(F
,
b),其中
3
F
0
0
1 0
0 1
,
b
5 3
;
0
0
0
0
0 0 0 0
:
1 0 0 2
1 0 0
A
0 0
1 0
0 1
5
3
(a1 , a2 , a3 , b),其中a1
0 0
,
a2
1 0
bm
a11 a12
,增广矩阵
A
a21
a22
am1 am2
a1n b1
a2n
b2
amn bm
块矩阵的记发,有 A A,b α1, α2, , αn, b ,且线性方程
)可以写成如下三种形式: Ax b
γ1T γ2T
x
b1 b2
γ
T m
bm
1, α2,
am1 am2
amn
γiT ai1,ai2, ,aim , i 1, 2, , m ,
a11 a12
则矩阵
A 可表示为
A
a21
a22
a1n a2n
γ1T
γ
T 2
;
am1 am2
amn
γmT
a1 j
若按列分块,且记
αj
a2 j
( j 1, 2,
, n)
0
0
0
,
0
2 2
B
E O
O E
B1 B2
O E
E
B1 B2
O
O
2 1
0
2 3 2
1 2 0 0
AB
E O
O B1
E
B2
O
E
B1 B2
O
E
2 1
0
1 3 2
0
0
1 0
0
1
1 0 0 0
A1
E 1
O
O E 1
0 0
1 0
A
As1
A1r
Asr
设 A 为 m l 矩阵,B 为 l n 矩阵,若 A , B 分块成
A11
A
As1
A1t
Ast
B11
,B
Bt1
B1r
Btr
Ai1 , Ai2 , , Ait 的列数分别等于 B1 j , B2 j , , Btj 的行数,那
A
A11
As1
A1t
,
B
B11
Ast
Bt1
B1r
Btr
t
Cij Aik Bkj (i 1, 2, , s; j 1, 2, , r) 。 k 1
A11
设
A
As1
A1r
Asr
,则
AT
A1T1
A1Tr
A1
O
形如
A
A2
O
As
AsT1
。
AsTr
分块矩阵,其中 Ai (i 1, 2, , s)都是方阵,称为分块对角
§1.4
分块矩阵
§1.4.1
分块矩阵
分析:将矩阵适当分块,便于计算.
引例
试写出矩阵
1 0 0 2
A
0 0
1 0
0 1
5
3
的三种分块形式。
0 0 0 0
1 0 0 2
0
0
0
1 0 0
0 1 0
5 3 0
=
E O1
1
D O2
,其中
E
0
0
0 1 0
0 2
0
,
d
5
1 3
若Ai (i 1, 2, , s),可逆,则 A 可逆,
A11
且
A1
A21
O
A1 还是分块对角阵。
O ,
As1
还能注意到,同结构的分块对角阵的和、差、数乘仍为分 块对角阵,且运算表现为对应的子块的运算
1 0 0 0 1 2 0 0
例
设
A
0
1
0
0
,
B
2
1
0
0
0 0 1 0 1 3 1 0
,
a3
0 1
,
b
0
0
0
0
0 0 0
:一个 m n 阶矩阵也可以看作以每个 aij 元素为一
子块的分块矩阵。
§1.4.2
分块矩阵的运算
析: 经过分块后,矩阵在形式上成为以它的子块为元素的 块矩阵.分块矩阵与普通矩阵有着类似的运算规律,运算 把子块当作元素来处理.这样处理时,运算的两矩阵要可 运算,参与运算的子块之间也要能运算.
行分成 m 块,第 i 行记为 γiT ai1,ai2, ,ais , i 1, 2, , m; B 按
n 块,第 j 列记为 βTj b1 j ,b2 j , , bsj j 1, 2, , n ,
可表示为
AB
γ1T
γ
T 2
β1 , β2 ,
γ
T m
, βn
γ1T γ2T
β1 β1
0
0
0
1
0
2
0
1
A , A B,AB 及 A1 。
把 A, B 分块成
1 0 0 0
1 2 0 0
0
0
0
1 0 0
0 1 0
0 0 1
E O
O
E
B
2 1
1 3
0 1
0 0
B1 B2
O
E0 2 0 1源自 0 0 0 AE
O
O
E
0 0
0
0 0
A11
设A
As1
A1r
B11
,
B
Asr
Bs1
B1r 为同型矩阵,且分块结
Bsr
中对应的子块 Aij 与 Bij 的行数、列数相同,则有
A11 B11
B
As1 Bs1
A1r B1r
Asr Bsr
A11
(2)
设
A
As1
A1r
,
为数,则有
Asr
A11
