数学人教版八年级上册课后练习.3.1.1等腰三角形同步练习

合集下载

人教版八年级上册数学《等腰三角形》同步训练含答案

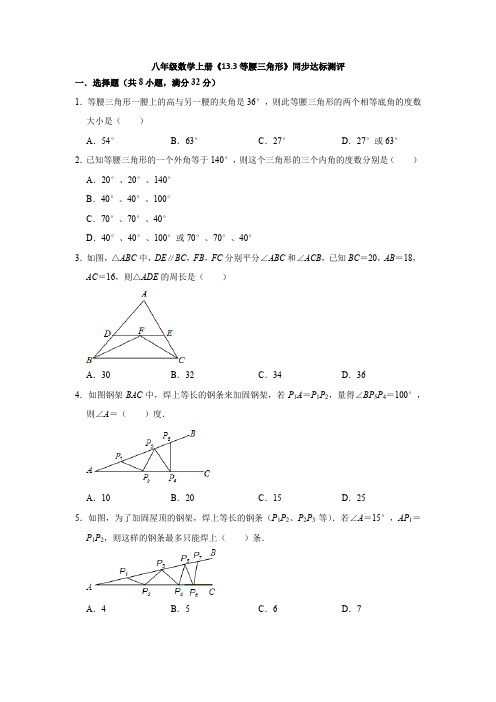
八年级数学上册《13.3等腰三角形》同步达标测评一．选择题（共8小题，满分32分）1．等腰三角形一腰上的高与另一腰的夹角是36°，则此等腰三角形的两个相等底角的度数大小是（）A．54°B．63°C．27°D．27°或63°2．已知等腰三角形的一个外角等于140°，则这个三角形的三个内角的度数分别是（）A．20°、20°、140°B．40°、40°、100°C．70°、70°、40°D．40°、40°、100°或70°、70°、40°3．如图，△ABC中，DE∥BC，FB，FC分别平分∠ABC和∠ACB，已知BC＝20，AB＝18，AC＝16，则△ADE的周长是（）A．30B．32C．34D．364．如图钢架BAC中，焊上等长的钢条来加固钢架，若P1A＝P1P2，量得∠BP5P4＝100°，则∠A＝（）度．A．10B．20C．15D．255．如图，为了加固屋顶的钢架，焊上等长的钢条（P1P2、P2P3等）．若∠A＝15°，AP1＝P1P2，则这样的钢条最多只能焊上（）条．A．4B．5C．6D．76．如图，AB＝BC＝CD＝DE＝EF＝FG，则∠A的范围是（）A．0°＜∠A＜15°B．0°＜∠A＜18°C．0°＜∠A＜20°D．0°＜∠A＜22.5°7．如图，已知∠MON＝30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM 上；△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形．若OA1＝1，则△A2021B2021A2022的边长为（）A．4044B．4046C．22020D．220218．如图，直线AB⊥CD，垂足为O，点P在∠BOC的平分线上，点E在直线AB上，且△EOP是等腰三角形，则这样的点P有（）A．1个B．2个C．3个D．4个二．填空题（共7小题，满分28分）9．如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．则下列结论：①AD＝BE；②PQ∥AE；③AP＝BQ；④DE＝DP．其中正确的是．10．如图，△ABC是等边三角形，BD平分∠ABC，点E在BC的延长线上，且CE＝1，∠E＝30°，则BC＝．11．如图，在第1个△A1BC中，∠B＝30°，A1B＝CB；在边A1B上任取一点D，延长CA1到A2，使A1A2＝A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第3个△A2A3E，…按此做法继续下去，则第n个三角形中以A n为顶点的底角度数是．12．如图，在△ABC中，AB＝AC，∠BAD＝30°，AE＝AD，则∠EDC的度数是．13．已知等腰三角形一腰上的高与另一腰的夹角为30°，则这个等腰三角形顶角为°．14．如图，线段OP的一个端点O在直线a上，以OP为一边画等腰三角形，并且使另一个顶点在直线a上，这样的等腰三角形能有个．15．如果△ABM和△ACN分别是以△ABC的边AB、AC为边的形外等边三角形，MC交BN 于P，连P A，则∠APN＝．三．解答题（共9小题，满分60分）16．如图，在△ABC中，已知AD平分∠BAC，过AD上一点P作EF⊥AD，交AB于E、交AC于F，交BC延长线于M，则有正确结论：∠M＝（∠ACB﹣∠B）．请说明理由．17．如图，在△ABC中，∠B＝60°，延长BC到D，延长BA到E，使AE＝BD，连接CE、DE，使EC＝DE，求证：△ABC是等边三角形．18．如图，已知△ABC中，AB＝AC，DE⊥AB，DF⊥AC，BG⊥AC．求证：DE+DF＝BG．19．如图，已知∠EAC是△ABC的外角，AD平分∠EAC，AD∥BC，点F为BC中点．求证：AF⊥BC．20．如图，在等腰△ABC中，AB＝AC，BD为∠ABC平分线，延长BC到点E，使CE＝CD，作DH⊥BE于H，求证：H为BE的中点．21．已知：如图，在等边三角形ABC的三边上，分别取点D，E，F，使AD＝BE＝CF．求证：△DEF是等边三角形．22．如图，已知△ABC是等边三角形，E是AC延长线上一点，选择一点D，使得△CDE是等边三角形，如果M是线段AD的中点，N是线段BE的中点，求证：△CMN是等边三角形．23．如图，等边△ABC的边长为12cm，D为AC边上一动点，E为AB延长线上一动点，DE 交CB于点P，点P为DE中点（1）求证：CD＝BE；（2）若DE⊥AC，求BP的长．24．如图，过等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，且P A＝CQ，连PQ交AC边于D．（1）求证：PD＝DQ；（2）若△ABC的边长为1，求DE的长．参考答案一．选择题（共8小题，满分32分）1．解：在三角形ABC中，设AB＝AC，BD⊥AC于D．①若是锐角三角形，∠A＝90°﹣36°＝54°，底角＝（180°﹣54°）÷2＝63°；②若三角形是钝角三角形，∠BAC＝36°+90°＝126°，此时底角＝（180°﹣126°）÷2＝27°．所以等腰三角形底角的度数是63°或27°．故选：D．2．解：（1）当40°角是顶角时，另两个底角度数为70°，70°；（2）当40°角是底角时，另两个角度数为40°，100°．故选：D．3．解：∵DE∥BC，∴∠BFD＝∠FBC，∠EFC＝∠BCF，∵FC分别平分∠ABC和∠ACB，∴∠DBF＝∠FBC，∠ECF＝∠BCF，∴∠BFD＝∠DBF，∠EFC＝∠ECF，∴DF＝DB，EF＝EC，∵△ADE的周长＝AD+AE+DE，DE＝DF+EF，∴△ADE的周长＝AD+BD+AE+EC＝AB+AC，∵AB＝18，AC＝16，∴△ADE的周长＝34．故选：C．4．解：∵AP1＝P1P2，P1P2＝P2P3，P3P4＝P2P3，P3P4＝P4P5，∴∠A＝∠P1P2A，∠P2P1P3＝∠P2P3P1，∠P3P2P4＝∠P3P4P2，∠P4P3P5＝∠P4P5P3，∴∠P3P5P4＝4∠A，∵∠P3P5P4+∠BP5P4＝180°，∠BP5P4＝100°，∴∠P3P5P4＝80°，∴∠A＝20°．故选：B．5．解：∵∠A＝∠P1P2A＝15°∴∠P2P1P3＝30°，∠P1P3P2＝30°∴∠P1P2P3＝120°∴∠P3P2P4＝45°∴∠P3P2P4＝45°∴∠P2P3P4＝90°∴∠P4P3P5＝60°∴∠P3P5P4＝60°∴∠P3P4P5＝60°∴∠P5P4P6＝75°∴∠P4P6P5＝75°∴∠P4P5P6＝30°∴∠P6P5P7＝90°，此时就不能在往上焊接了，综上所述总共可焊上5条．故选：B．6．解：采用排除法：①∵AB＝BC＝CD＝DE＝EF＝FG，当∠A＝15°，∴∠BCA＝∠A＝15°，∴∠CBD＝∠BDC＝∠BCA+∠A＝15°+15°＝30°，∴∠BCD＝180°﹣（∠CBD+∠BDC）＝180°﹣60°＝120°，∴∠ECD＝∠CED＝180°﹣∠BCD﹣∠BCA＝180°﹣120°﹣15°＝45°，∴∠CDE＝180°﹣（∠ECD+∠CED）＝180°﹣90°＝90°，∴∠EDF＝∠EFD＝180°﹣∠CDE﹣∠BDC＝180°﹣90°﹣30°＝60°，∴∠FGE＝∠GEF＝∠EFD+∠A＝60°+15°＝75°，即此时符合；①当∠A＝18°时，同法求出∠FEG＝∠FGE＝90°，此时△FEG不存在，此时不符合，同样，当∠A取大于18°的角都不符合，当∠A＝小于18°的数时，△FEG存在，即选项A、C、D错误，只有选项B正确；故选：B．7．解：∵△A1B1A2是等边三角形，∴A1B1＝A2B1，∵∠MON＝30°，∴OA1＝A1B1＝1，∴A2B1＝1，∵△A2B2A3、△A3B3A4是等边三角形，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴A2B2＝2B1A2，B3A3＝2B2A3，∴A3B3＝4B1A2＝4，A4B4＝8B1A2＝8，A5B5＝16B1A2＝16，以此类推：△A2021B2021A2022的边长为22020．故选：C．8．解：如图，①当OP＝OE时，这样的点E由2个，②当PE＝OE时，这样的点E由1个，③当OP＝PE时，这样的点E由1个，∴这样的点P有4个，故选：D．二．填空题（共7小题，满分28分）9．解：∵等边△ABC和等边△CDE，∴AC＝BC，CD＝CE，∠ACB＝∠ECD＝60°，∴180°﹣∠ECD＝180°﹣∠ACB，即∠ACD＝∠BCE，在△ACD与△BCE中，，∴△ACD≌△BCE（SAS），∴AD＝BE，故①小题正确；∵△ACD≌△BCE（已证），∴∠CAD＝∠CBE，∵∠ACB＝∠ECD＝60°（已证），∴∠BCQ＝180°﹣60°×2＝60°，∴∠ACB＝∠BCQ＝60°，在△ACP与△BCQ中，，∴△ACP≌△BCQ（ASA），∴AP＝BQ，故③小题正确；PC＝QC，∴△PCQ是等边三角形，∴∠CPQ＝60°，∴∠ACB＝∠CPQ，∴PQ∥AE，故②小题正确；∵AD＝BE，AP＝BQ，∴AD﹣AP＝BE﹣BQ，即DP＝QE，∠DQE＝∠ECQ+∠CEQ＝60°+∠CEQ，∠CDE＝60°，∴∠DQE≠∠CDE，故④小题错误．综上所述，正确的是①②③．故答案为：①②③．10．解：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，BA＝BC，∵BD平分∠ABC，∴∠DBC＝∠E＝30°，BD⊥AC，∴∠BDC＝90°，∴BC＝2DC，∵∠ACB＝∠E+∠CDE，∴∠CDE＝∠E＝30°，∴CD＝CE＝1，∴BC＝2CD＝2，故答案为211．解：∵在△CBA1中，∠B＝30°，A1B＝CB，∴∠BA1C＝＝75°，∵A1A2＝A1D，∠BA1C是△A1A2D的外角，∴∠DA2A1＝∠BA1C＝×75°；同理可得∠EA3A2＝（）2×75°，∠F A4A3＝（）3×75°，∴第n个三角形中以A n为顶点的内角度数是（）n﹣1×75°．故答案为：（）n﹣1×75°．12．解：设∠EDC＝x，∠B＝∠C＝y，∠AED＝∠EDC+∠C＝x+y，又因为AD＝AE，所以∠ADE＝∠AED＝x+y，则∠ADC＝∠ADE+∠EDC＝2x+y，又因为∠ADC＝∠B+∠BAD，所以2x+y＝y+30，解得x＝15，所以∠EDC的度数是15°．故答案是：15°．13．解：当高在三角形内部时（如图1），顶角是60°；当高在三角形外部时（如图2），顶角是120°．故答案为：60或120．14．解：△AOP，△BOP，△COP，△DOP就是所求的三角形．15．解：∵△ABM和△ACN都是等边三角形，∴AB＝AM，AN＝AC，∠BAM＝∠CAN＝60°，∴∠BAM+∠BAC＝∠CAN+∠BAC，即∠CAM＝∠BAN，在△ABN与△AMC中，，∴△ABN≌△AMC（SAS），∴∠ANP＝∠ACP，又∵∠AEN＝∠PEC（对顶角相等），∵∠AEP＝∠NEC（对顶角相等），∴∠APN＝∠ACN＝60°．故答案为：60°．三．解答题（共9小题，满分60分）16．证明：∵EF⊥AD，AD平分∠BAC，∴∠1＝∠2，∠APE＝∠APF＝90°，又∵∠AEF＝180°﹣∠1﹣∠APE，∠AFE＝180°﹣∠2﹣∠APF，∴∠AEF＝∠AFE，∵∠CFM＝∠AFE，∴∠AEF＝∠AFE＝∠CFM，∵∠AEF＝∠B+∠M，∠MFC＝∠ACB﹣∠M，∴∠B+∠M＝∠ACB﹣∠M，即：∠M＝（∠ACB﹣∠B）．17．证明：延长BD至F，使DF＝BC，连接EF，∵EC＝ED，∴∠ECD＝∠EDC，∴∠ECB＝∠EDF，∴△ECB≌△EDF（SAS），∴BE＝EF，∠B＝60°，∴△BEF为等边三角形，∴BE＝BF，∵AE＝BD，∴DF＝AB，BC＝DF，∴AB＝BC，∴△ABC是等边三角形．18．证明：连接AD．则△ABC的面积＝△ABD的面积+△ACD的面积，AB•DE+AC•DF＝AC•BG，∵AB＝AC，∴DE+DF＝BG．19．证明：∵AD∥BC，∴∠EAD＝∠B，∠DAC＝∠C，∵AD平分∠EAC，∴∠EAD＝∠DAC，∴∠B＝∠C，∴AB＝AC，∵点F为BC中点，∴AF⊥BC．20．证明：∵AB＝AC，∴∠ABC＝∠SCB，∵BD平分∠ABC，∴∠ABD＝∠CBD，∵CE＝CD，∴∠CDE＝∠E，∵∠ACB＝∠E+∠CDE＝2∠DBC，∴∠DBC＝∠E，∴△BDE为等腰三角形，BD＝ED，∵DH垂直于BE，∴H为BE中点（三线合一）．21．证明：∵△ABC是等边三角形，∴AB＝BC＝AC，∵AD＝BE＝CF，∴AF＝BD，在△ADF和△BED中，，∴△ADF≌△BED（SAS），∴DF＝DE，同理DE＝EF，∴DE＝DF＝EF．∴△DEF是等边三角形．22．证明：∵△ABC是等边三角形，△CDE是等边三角形，M是线段AD的中点，N是线段BE的中点，∴∠ACB＝∠ECD＝60°，∴∠ACB+∠BCD＝∠ECD+∠BCD，即∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE，∴AD＝BE，AM＝BN；∴AC＝BC，∠CAD＝∠CBE，AM＝BN，∴△AMC≌△BNC（SAS），∴CM＝CN，∠ACM＝∠BCN；又∵∠NCM＝∠BCN﹣∠BCM，∠ACB＝∠ACM﹣∠BCM，∴∠NCM＝∠ACB＝60°，∴△CMN是等边三角形．23．（1）证明：作DF∥AB交BC于F，如图所示：∵△ABC是等边三角形，∴∠A＝∠ABC＝∠C＝60°，∵DF∥AB，∴∠CDF＝∠A＝60°，∠DFC＝∠ABC＝60°，∠DFP＝∠EBP，∴△CDF是等边三角形，∴CD＝DF，∵点P为DE中点，∴PD＝PE，在△PDF和△PEB中，，∴△PDF≌△PEB（AAS），∴DF＝BE，∴CD＝BE；（2）解：∵DE⊥AC，∴∠ADE＝90°，∴∠E＝90°﹣∠A＝30°，∴AD＝AE，∠BPE＝∠ACB﹣∠E＝30°＝∠E，∴BP＝BE，由（1）得：CD＝BE，∴BP＝BE＝CD，设BP＝x，则BE＝CD＝x，AD＝12﹣x，∵AE＝2AD，∴12+x＝2（12﹣x），解得：x＝4，即BP的长为4．24．（1）证明：如图，过P做PF∥BC交AC于点F，∴∠AFP＝∠ACB，∠FPD＝∠Q，∠PFD＝∠QCD ∵△ABC为等边三角形，∴∠A＝∠ACB＝60°，∴∠A＝∠AFP＝60°，∴△APF是等边三角形；∵AP＝PF，AP＝CQ，∴PF＝CQ∴△PFD≌△QCD，∴PD＝DQ．（2）△APF是等边三角形，∵PE⊥AC，∴AE＝EF，△PFD≌△QCD，∴CD＝DF，DE＝EF+DF＝AC，∵AC＝1，DE＝．。

人教版八年级数学上册 13.3 等腰三角形同步练习

人教版八年级数学上册13.3 等腰三角形同步练习（含答案）一、选择题（本大题共7道小题）1. 如图，等腰三角形的对称轴是()A．直线l1B．直线l2C．直线l3D．直线l42. 如图，已知P A＝PB，在证明∠A＝∠B时，需要添加辅助线，下面有甲、乙两种辅助线的作法：甲：作底边AB的中线PC；乙：作PC平分∠APB交AB于点C.则()A．甲、乙两种作法都正确B．甲的作法正确，乙的作法不正确C．甲的作法不正确，乙的作法正确D．甲、乙两种作法都不正确3. 如图，在等边三角形ABC中，AD⊥BC于点D，则∠BAD的度数为()A．60° B．50° C．40° D．30°4. 已知：如图，直线PO与AB交于点O，P A＝PB，则下列结论中正确的是()A．AO＝BOB．PO⊥ABC．PO是线段AB的垂直平分线D．点P在线段AB的垂直平分线上5. 已知实数x、y满足|x－4|＋y－8＝0，则以x、y的值为两边长的等腰三角形的周长是()A. 20或16B. 20C. 16D. 以上答案均不对6. 如图，在△ABC中，∠ABC的平分线交AC于点D，AD＝6，过点D作DE∥BC交AB于点E.若△AED的周长为16，则边AB的长为()A．6 B．8 C．10 D．127. 如图，△ABC中，AB＝AC，AD是△BAC的平分线，已知AB＝5，AD＝3，则BC的长为()A. 5B. 6C. 8D. 10二、填空题（本大题共7道小题）8. 如图，∠AOB＝30°，点P在OA上，且OP＝2，点P关于直线OB的对称点是Q，则PQ＝________．9. 若等腰三角形的一个内角为50°，则它的顶角的度数为____________．10. 如图，在△ABC中，AB＝AC，D是AC上一点，且BC＝BD.若∠CBD＝46°，则∠A＝________°.11. 如图，在等边三角形ABC中，点D在边AB上，点E在边AC上，将△ADE 折叠，使点A落在BC边上的点F处，则∠BDF＋∠CEF＝________°.12. 如图，AD是△ABC的边BC上的高，由下列条件中的某一个就能推出△ABC 是等腰三角形的是________．(把所有正确答案的序号都填写在横线上)①∠BAD＝∠ACD ②∠BAD＝∠CAD③AB＋BD＝AC＋CD ④AB－BD＝AC－CD13. 如图，六边形ABCDEF的六个内角都相等．若AB＝1，BC＝CD＝3，DE＝2，则这个六边形的周长为________．14. 规律探究如图，∠BOC＝9°，点A在OB上，且OA＝1，按下列要求画图：以A为圆心，1为半径向右画弧交OC于点A1，得第1条线段AA1；再以A1为圆心，1为半径向右画弧交OB于点A2，得第2条线段A1A2；再以A2为圆心，1为半径向右画弧交OC于点A3，得第3条线段A2A3……这样画下去，直到得第n条线段，之后就不能再画出符合要求的线段了，则n＝________．三、解答题（本大题共3道小题）15. 如图，在△ABC中，AB＝AC，∠A＝36°，以B为圆心，BC长为半径作弧，交AC于点D，连接BD，求∠ABD的度数.16. 如图，已知△ABC中，D为BC边上一点，且AB＝AC＝BD，AD＝CD，求∠BAC的度数.17. 如图，在△ABC中，∠ABC，∠ACB的平分线相交于点O，过点O作OE∥AB，OF∥AC，分别交BC于点E，F.(1)若BC＝8 cm，求△OEF的周长；(2)若∠BOC＝130°，求∠EOF的度数．人教版八年级数学上册13.3 等腰三角形同步练习-答案一、选择题（本大题共7道小题）1. 【答案】A2. 【答案】A3. 【答案】D[解析] ∵△ABC是等边三角形，∴∠BAC＝60°.∵AB＝AC，AD⊥BC，∴∠BAD＝12∠BAC＝30°.4. 【答案】D5. 【答案】B【解析】∵|x－4|＋y－8＝0，∴x－4＝0，y－8＝0，解得x＝4，y＝8.分两种情况讨论：①当4为腰时，根据三角形三边关系知4＋4＝8，∴这样的等腰三角形不存在；②当8为腰时，则有4＋8>8，这样能够组成等腰三角形，∴此三角形的周长是8＋8＋4＝20.6. 【答案】C[解析] ∵BD平分∠ABC，∴∠EBD＝∠CBD.∵DE∥BC，∴∠EDB＝∠CBD.∴∠EBD＝∠EDB.∴BE＝DE.∵△AED的周长为16，∴AE＋DE＋AD＝AE＋BE＋AD＝AB＋AD＝16.∵AD＝6，∴AB＝10.7. 【答案】C【解析】∵AB＝AC，AD平分∠BAC，∴根据等腰三角形三线合一性质可知AD⊥BC，BD＝CD，在Rt△ABD中，AB＝5，AD＝3，由勾股定理得BD＝4，∴BC＝2BD＝8.二、填空题（本大题共7道小题）8. 【答案】2[解析] 如图，连接OQ.∵点P关于直线OB的对称点是Q，∴OB垂直平分PQ.∴∠POB＝∠QOB＝30°，OP＝OQ.∴∠POQ＝60°.∴△POQ为等边三角形．∴PQ＝OP＝2.9. 【答案】50°或80°10. 【答案】46[解析] ∵BC＝BD，∠CBD＝46°，∴∠C＝∠BDC＝12(180°－46°)＝67°.∵AB＝AC，∴∠ABC＝∠C＝67°.∴∠A＝46°.11. 【答案】120[解析] 由于△ABC是等边三角形，所以∠A＝60°.所以∠ADE＋∠AED＝120°.因为将△ADE折叠，使点A落在BC边上的点F处，所以∠ADE＝∠EDF，∠AED＝∠DEF.所以∠ADF＋∠AEF＝2(∠ADE＋∠AED)＝240°.所以∠BDF＋∠CEF＝360°－(∠ADF＋∠AEF)＝120°.13. 【答案】15[解析] 由多边形的内角和定理可知，这个六边形的每个内角都是120°，因此直线AB，CD，EF围成一个等边三角形，且这个等边三角形的边长为7.因此AF＝4，EF＝2.所以这个六边形的周长＝1＋3＋3＋2＋2＋4＝15.14. 【答案】9三、解答题（本大题共3道小题）15. 【答案】解：∵AB＝AC，∠A＝36°，∴∠ABC＝∠ACB＝72°.∵BC＝BD，∴∠BDC＝∠BCD＝72°.∴∠DBC＝36°.∴∠ABD＝∠ABC－∠DBC＝36°.16. 【答案】解：∵AD＝CD，∴设∠DAC＝∠C＝x°.∵AB＝AC＝BD，∴∠BAD＝∠BDA＝∠DAC＋∠C＝2x°，∠B＝∠C＝x°.∴∠BAC＝3x°.∵∠B＋∠BAC＋∠C＝180°，∴5x＝180，解得x＝36.∴∠BAC＝3x°＝108°.17. 【答案】解：(1)∵BO，CO分别是∠ABC，∠ACB的平分线，∴∠ABO＝∠EBO，∠ACO＝∠FCO.∵OE∥AB，OF∥AC，∴∠ABO＝∠BOE，∠ACO＝∠COF.∴∠EBO＝∠BOE，∠FCO＝∠COF.∴BE＝OE，OF＝FC.∴BC＝BE＋EF＋FC＝OE＋EF＋OF.∵BC＝8 cm，∴△OEF的周长＝OE＋EF＋OF＝8 cm.(2)∵∠BOC＝130°，∴∠OBC＋∠OCB＝50°.由(1)得∠OBC＝∠BOE，∠COF＝∠OCB，∴∠BOE＋∠COF＝50°.∴∠EOF＝∠BOC－(∠BOE＋∠COF)＝80°.。

等腰三角形同步练习题人教版八年级数学上册

13.3.1等腰三角形同步练习题 2021-2022学年人教版八年级数学上册一、选择题1．已知一个等腰三角形的顶角为30°，则它的一个底角等于( )A．30°B．75°C．150° D．125°2．如图，在△ABC中，AB＝AC，点D在CA的延长线上，DE⊥BC于点E，∠BAC＝100°，则∠D＝( )A．40°B．50° C．60°D．80°3．如图，下列条件不能推出△ABC是等腰三角形的是( )A．∠B＝∠C B．AD⊥BC，∠BAD＝∠CADC．AD⊥BC，∠BAD＝∠ACD D．AD⊥BC，BD＝CD4．如图，在Rt△ABC中，∠ACB＝90°，∠A＝50°，以点B为圆心，BC长为半径画弧，交AB于点D，连接CD，则∠ACD的度数是( )A．50°B．40° C．30°D．20°5．如图，AD是等腰△ABC的顶角平分线，BD＝5，则CD等于( )A．10 B．5 C．4 D．36．等腰三角形的一个内角为70°，则另外两个内角的度数分别是( )A．55°，55°B．70°，40°或70°，55°C．70°，40°D．55°，55°或70°，40°7．如图，在△ABC中，DE垂直平分AB，垂足为D，交BC于点E.若∠B＝32°，AC＝CE，则∠C的度数是( )A．52°B．55°C．60°D．65°8．如图是钢架的一部分，为使钢架更加坚固，在其内部添加了一些钢管DE，EF，FG，…，添加的这些钢管的长度都与BD的长度相等．如果∠ABC＝10°，那么添加这样的钢管的根数最多是( )A．7 B．8 C．9 D．10二、填空题9．如图，在△ABC中，AB＝AC，AD⊥BC，垂足为D.若∠BAC＝70°，则∠BAD＝_____．10．定义：等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的特征值．若在等腰△ABC中，∠A＝70°，则它的特征值k＝_____．11．如图，△ABC的周长为18，且AB＝AC，AD⊥BC于点D，△ACD的周长为12，那么AD的长为_____．12．如图，已知点P是射线ON上一动点(即P可在射线ON上运动)，∠AON＝45°，当∠A＝__________时，△AOP为等腰三角形．13．如图，一艘海轮位于灯塔P的南偏东70°方向的M处，它以40海里/时的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°方向的N处，则N处与灯塔P的距离为_____．14.如图，∠ABC的平分线BF与△ABC中的外角∠ACM的平分线CF相交于点F，过点F作DF∥BC，,交AB于点D，交AC于点E，则BD，CE，DE之间存在的数量关系是_____三、解答题15．如图，在△ABC中，AB＝AC，AD是BC边上的中线，BE⊥AC于点E.求证：∠CBE＝∠BAD.16．如图，在△ABC中，点D，E分别在边AC，AB上，BD与CE相交于点O，给出下列三个条件：①∠EBO＝∠DCO；②BE＝CD；③OB＝OC.(1)上述三个条件中，由哪两个条件可以判定△ABC是等腰三角形？(将所有成立的情形用序号写出来)(2)请选择(1)中的一种情形，写出证明过程．17．如图，AB＝AC，点E在AB上，DE⊥BC于点D，交CA的延长线于点F.求证：△AEF是等腰三角形．18．已知：如图，△ABC是等腰三角形，AB＝AC，且∠ABO＝∠ACO.求证：(1)∠1＝∠2；(2)OA⊥BC.19．如图，在△ABC中，AB＝AC，AD⊥BC，CE⊥AB，EF＝BE.(1)△AEF与△CEB全等吗？请说明理由；(2)说明AF＝2BD的理由．20．如图，在△ABC中，AB＝AC＝2，∠B＝40°，点D在线段BC上运动(点D不与B，C两点重合)，连接AD，作∠ADE＝40°，DE交线段AC于点E.(1)当∠BDA＝115°时，∠BAD＝_____；点D从B向C运动时，∠BDA逐渐变_____(填“大”或“小”)；(2)当△ABD≌△DCE时，求CD的长；(3)在点D的运动过程中，△ADE的形状也在改变，当∠BDA＝110°时，请判断△ADE的形状，并证明．21．如图1，在△ABC中，AB＝AC，∠BAC＝60°，D，E分别是AB，AC上的点，AD＝AE，不难发现BD 与CE的关系．(1)将△ADE绕A点旋转到图2的位置时，直接写出BD与CE的关系；(2)当∠BAC＝90°时，将△ADE绕A点旋转到图3的位置．①猜想BD与CE有什么关系？请就图3的情形进行证明；②当点C，D，E在同一直线上时，直接写出∠ADB的度数．参考答案13.3.1等腰三角形同步练习题 2021-2022学年人教版八年级数学上册一、选择题1．已知一个等腰三角形的顶角为30°，则它的一个底角等于(B)A．30°B．75°C．150° D．125°2．如图，在△ABC中，AB＝AC，点D在CA的延长线上，DE⊥BC于点E，∠BAC＝100°，则∠D＝(B)A．40°B．50° C．60°D．80°3．如图，下列条件不能推出△ABC是等腰三角形的是(C)A．∠B＝∠C B．AD⊥BC，∠BAD＝∠CADC．AD⊥BC，∠BAD＝∠ACD D．AD⊥BC，BD＝CD4．如图，在Rt△ABC中，∠ACB＝90°，∠A＝50°，以点B为圆心，BC长为半径画弧，交AB于点D，连接CD，则∠ACD的度数是(D)A．50°B．40° C．30°D．20°5．如图，AD是等腰△ABC的顶角平分线，BD＝5，则CD等于(B)A．10 B．5 C．4 D．36．等腰三角形的一个内角为70°，则另外两个内角的度数分别是(D) A ．55°，55° B ．70°，40°或70°，55° C ．70°，40°D ．55°，55°或70°，40°7．如图，在△ABC 中，DE 垂直平分AB ，垂足为D ，交BC 于点E.若∠B ＝32°，AC ＝CE ，则∠C 的度数是(A)A ．52°B ．55°C ．60°D ．65°8．如图是钢架的一部分，为使钢架更加坚固，在其内部添加了一些钢管DE ，EF ，FG ，…，添加的这些钢管的长度都与BD 的长度相等．如果∠ABC ＝10°，那么添加这样的钢管的根数最多是(B)A ．7B ．8C ．9D ．10二、填空题9．如图，在△ABC 中，AB ＝AC ，AD ⊥BC ，垂足为D.若∠BAC ＝70°，则∠BAD ＝35°．10．定义：等腰三角形的顶角与其一个底角的度数的比值k 称为这个等腰三角形的特征值．若在等腰△ABC 中，∠A ＝70°，则它的特征值k ＝1411或47．11．如图，△ABC 的周长为18，且AB ＝AC ，AD ⊥BC 于点D ，△ACD 的周长为12，那么AD 的长为3．12．如图，已知点P 是射线ON 上一动点(即P 可在射线ON 上运动)，∠AON ＝45°，当∠A ＝45°或67.5°或90°时，△AOP 为等腰三角形．13．如图，一艘海轮位于灯塔P的南偏东70°方向的M处，它以40海里/时的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°方向的N处，则N处与灯塔P的距离为80海里．14.如图，∠ABC的平分线BF与△ABC中的外角∠ACM的平分线CF相交于点F，过点F作DF∥BC，,交AB于点D，交AC于点E，则BD，CE，DE之间存在的数量关系是BD＝CE＋DE．)三、解答题15．如图，在△ABC中，AB＝AC，AD是BC边上的中线，BE⊥AC于点E.求证：∠CBE＝∠BAD.证明：∵AB＝AC，AD是BC边上的中线，∴∠ABD＝∠C，AD⊥BC.∵BE⊥AC，∴∠BEC＝∠ADB＝90°.∴∠C＋∠CBE＝∠ABD＋∠BAD＝90°.∴∠CBE＝∠BAD.16．如图，在△ABC中，点D，E分别在边AC，AB上，BD与CE相交于点O，给出下列三个条件：①∠EBO＝∠DCO；②BE＝CD；③OB＝OC.(1)上述三个条件中，由哪两个条件可以判定△ABC是等腰三角形？(将所有成立的情形用序号写出来)(2)请选择(1)中的一种情形，写出证明过程．解：(1)①②；①③.(2)选①③，证明如下：∵OB＝OC，∴∠OBC＝∠OCB.∵∠EBO＝∠DCO，且∠ABC＝∠EBO＋∠OBC，∠ACB＝∠DCO＋∠OCB，∴∠ABC＝∠ACB.∴AB＝AC.∴△ABC是等腰三角形．17．如图，AB＝AC，点E在AB上，DE⊥BC于点D，交CA的延长线于点F.求证：△AEF是等腰三角形．证明：∵AB＝AC，∴∠B＝∠C.∵DE⊥BC，∴∠BDE＝∠CDF＝90°.∴∠C＋∠F＝90°，∠B＋∠BED＝90°.∴∠BED＝∠F.又∵∠AEF＝∠BED，∴∠F＝∠AEF.∴AF＝AE.∴△AEF是等腰三角形．18．已知：如图，△ABC是等腰三角形，AB＝AC，且∠ABO＝∠ACO.求证：(1)∠1＝∠2；(2)OA⊥BC.证明：(1)∵AB ＝AC ， ∴∠ABC ＝∠ACB.∵∠ABO ＝∠ACO ，∴∠1＝∠2. (2)∵∠1＝∠2， ∴OB ＝OC.在△ABO 和△ACO 中，⎩⎪⎨⎪⎧AB ＝AC ，∠ABO ＝∠ACO ，OB ＝OC ，∴△ABO ≌△ACO(SAS)． ∴∠BAO ＝∠CAO. ∴AO 平分∠BAC. ∵△ABC 是等腰三角形， ∴OA ⊥BC.19．如图，在△ABC 中，AB ＝AC ，AD ⊥BC ，CE ⊥AB ，EF ＝BE. (1)△AEF 与△CEB 全等吗？请说明理由； (2)说明AF ＝2BD 的理由．解：(1)全等．理由：∵AD ⊥BC ， ∴∠B ＋∠EAF ＝90°. ∵CE ⊥AB ，∴∠B ＋∠BCE ＝90°，∠AEF ＝∠CEB ＝90°. ∴∠EAF ＝∠ECB. 又∵EF ＝BE ，∴△AEF≌△CEB(AAS)．(2)∵△AEF≌△CEB，∴AF＝BC.∵AB＝AC，AD⊥BC，∴BC＝2BD.∴AF＝2CD.20．如图，在△ABC中，AB＝AC＝2，∠B＝40°，点D在线段BC上运动(点D不与B，C两点重合)，连接AD，作∠ADE＝40°，DE交线段AC于点E.(1)当∠BDA＝115°时，∠BAD＝25°；点D从B向C运动时，∠BDA逐渐变小(填“大”或“小”)；(2)当△ABD≌△DCE时，求CD的长；(3)在点D的运动过程中，△ADE的形状也在改变，当∠BDA＝110°时，请判断△ADE的形状，并证明．解：(2)∵△ABD≌△DCE，∴CD＝AB＝2.(3)当∠BDA＝110°时，△ADE是等腰三角形．证明：∵∠BDA＝110°，∴∠ADC＝70°.∵AB＝AC，∴∠C＝∠B＝40°.∴∠DAC＝70°.在△ADE中，∠ADE＝40°，∠DAE＝70°，∴∠AED＝180°－40°－70°＝70°.∴∠AED＝∠DAE.∴DA＝DE，即△ADE是等腰三角形．21．如图1，在△ABC中，AB＝AC，∠BAC＝60°，D，E分别是AB，AC上的点，AD＝AE，不难发现BD 与CE的关系．(1)将△ADE绕A点旋转到图2的位置时，直接写出BD与CE的关系；(2)当∠BAC＝90°时，将△ADE绕A点旋转到图3的位置．①猜想BD与CE有什么关系？请就图3的情形进行证明；②当点C，D，E在同一直线上时，直接写出∠ADB的度数．解：(1)BD ＝CE.(2)①BD ＝CE ，BD ⊥CE ，证明：记BD 与AC 的交点为F ，与CE 的交点为M ，∵∠BAC ＝∠DAE ＝90°，∴∠BAD ＝∠CAE.在△BAD 和△CAE 中，⎩⎪⎨⎪⎧AB ＝AC ，∠BAD ＝∠CAE ，AD ＝AE ，∴△BAD ≌△CAE(SAS)．∴BD ＝CE ，∠ABD ＝∠ACE.∵∠BAC ＝90°，∠AFB ＝∠MFC ，∴∠FMC ＝∠BAC ＝90°.∴BD ⊥CE.②∠ADB 的度数为45°或135°15．如图，在△ABC 中，AD ⊥BC ，EF 垂直平分AC ，交AC 于点F ，交BC 于点E ，且BD ＝DE ，连接AE.(1)若∠BAE ＝30°，求∠C 的度数；(2)若AC ＝6 cm ，DC ＝5 cm ，求△ABC 的周长．解：(1)∵AD ⊥BC ，BD ＝DE ，∴AB ＝AE.∵EF 垂直平分AC ，∴AE ＝EC.∴∠C ＝∠CAE.∵∠BAE ＝30°，∴∠AED ＝12×(180°－30°)＝75°.∴∠C ＝12∠AED ＝37.5°. (2)由(1)知：AE ＝EC ＝AB ，∵BD ＝DE ，∴AB ＋BD ＝EC ＋DE ＝DC.∴△ABC 的周长为AB ＋BC ＋AC ＝AB ＋BD ＋DC ＋AC ＝2DC ＋AC ＝2×5＋6＝16(cm)．。

人教版数学八年级上册13.3 等腰三角形同步练习(解析版)

人教版数学八年级上册13.3：等腰三角形同步练习一．选择题（共15小题）1．在Rt△ABC中，∠C＝90°，∠B＝30°，斜边AB的长为2cm，则AC长为（）A．4 cm B．2 cm C．1 cm D．cm2．一个等腰三角形但不是等边三角形，它的角平分线、高线、中线总数共（）条．A．9B．7C．6D．33．如图，△ABC是等边三角形，AE⊥BC于E，AD⊥CD于D，AB∥CD，则图中60°的角有（）A．3个B．4个C．5个D．6个4．下列判断不正确的是（）A．等腰三角形的两底角相等B．等腰三角形的两腰相等C．等边三角形的三个内角都是60°D．两个内角分别为120°、40°的三角形是等腰三角形5．在△ABC中，∠ACB＝90°，∠B＝30°，CD⊥AB于D，若AC＝6，则BD等于（）A．6B．3C．9D．126．等腰三角形的对称轴，最多可以有（）A．1条B．3条C．6条D．无数条7．等腰三角形两边的长分别为2cm和5cm，则这个三角形的周长是（）A．9cm B．12cmC．9cm或12cm D．在9cm或12cm之间8．如图，在△ABC中，AB＝AC，D为BC的中点，E为AC边上一点，且AE＝AD，∠BAC ＝40°，则∠EDC的度数是（）A．10°B．20°C．30°D．40°9．一个三角形有两条边相等，这个三角形一边等于5cm，一边等于10cm，则另一边等于（）A．5cm B．10cm C．15cm D．12cm10．如图，△ABC是等腰三角形，AD是底边BC上的高线，DE⊥AB于E，DF⊥AC于F，图中除AB＝AC外，相等的线段共有（）A．1对B．2对C．3对D．4对11．等腰三角形一腰上的高与底边所夹的角为a，则这个等腰三角形的顶角为（）A．a B．90°﹣a C．12a D．2a12．等腰三角形的底角为a，则a的取值范围是（）A．a≤45°B．0°＜a＜90°C．45°＜a＜90°D．0°≤a＜90°13．如图，在等边三角形ABC中，三条中线AE，BD，CF相交于点O，则等边三角形ABC 中，从△BOF到△COD需要经过的变换是（）A．轴对称变换B．旋转变换C．平移变换D．相似变换14．如果以4cm长的线段为底组成一个等腰三角形，腰长x的取值范围是（）A．x＞4cm B．x＞2cm C．x≥4cm D．x≥2cm15．等腰三角形周长是32cm，一边长为10cm，则其他两边的长分别为（）A．10cm，12cm B．11cm，11cmC．11cm，11cm或10cm，12cm D．不能确定二．填空题（共6小题）16．若等腰三角形的一腰上的高与另一腰的夹角等于50°，则其顶角的度数为．若等腰三角形的一腰上的高与底边的夹角等于50°，则其顶角的度数为．17．一个等腰三角形的腰长为3cm，则底边长的取值范围是．18．如图，AB＝AC，∠A＝100°，AB∥CD，则∠BCD＝度．19．等腰三角形的顶角与底角的度数之比为4：1，则它的各内角度数为．20．△ABC中，∠A：∠B：∠C＝1：2：3，AB＝10，则BC＝．21．（1）等腰三角形的一个角为100°，那么另外两个角分别为．（2）等腰三角形的一个角为50°，则底角是．三．解答题（共9小题）22．已知等腰三角形的周长为28cm，其中的一边长是另一边长的倍，求这个等腰三角形各边的长．23．如图，已知AB＝AC，D为BC边中点，你能说出AD与BC的位置关系吗？请说明理由．24．如图，△ABC是等腰三角形，且AB＝AC，试作出BC边上的中线和高以及∠A的平分线，从中你发现了什么？与其他同学进行交流．25．如图，在△ABC中，AB＝AC，∠C＝2∠A，BD平分∠ABC．请找出图中其他的等腰三角形，并选择其中的一个说明理由．26．已知D是等腰△ABC底边BC上的一个点，DE⊥AB于E，DF⊥AC于F，当D点在什么位置时，DE＝DF，并加以证明．27．如图，AD是等腰△ABC顶角的外角的平分线，那么AD与BC平行吗？为什么？28．如图，在△ABC中，AD平分∠BAC，G是CA延长线上一点，GE∥AD交AB于F．交BC于E，试判断△AGF的形状并加以证明．29．如图，在等腰△ABC中，AB＝AC，AD是BC边上的高，点E、F分别是边AB、AC上的点，且EF∥BC．（1）试说明△AEF是等腰三角形；（2）试比较DE与DF的大小关系，并说明理由．30．已知：如图，△ABC中，AB＝AC，D是BC延长线上一点，E是AC延长线上一点，且DE∥AB，求证：ED＝EC．人教版数学八年级上册13.3：等腰三角形同步练习参考答案一．选择题（共15小题）1．在Rt△ABC中，∠C＝90°，∠B＝30°，斜边AB的长为2cm，则AC长为（）A．4 cm B．2 cm C．1 cm D．cm【解答】解：∵∠C＝90°，∠B＝30°，∴AB＝2AC，∵AB＝2cm，∴AC＝AB＝1cm，故选：C．2．一个等腰三角形但不是等边三角形，它的角平分线、高线、中线总数共（）条．A．9B．7C．6D．3【解答】解：由于任意一个三角形都有三条角平分线、三条高线、三条中线，而等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合，所以一个等腰三角形但不是等边三角形，它的角平分线、高线、中线总数共7条．故选：B．3．如图，△ABC是等边三角形，AE⊥BC于E，AD⊥CD于D，AB∥CD，则图中60°的角有（）A．3个B．4个C．5个D．6个【解答】解：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝∠CAB＝60°∵AB∥CD，∴∠ACD＝∠CAB＝60°，∵AD⊥CD，∴∠DAB＝90°，∵AE⊥BC，∴∠BAE＝∠CAE＝30°，∴∠DAE＝60°∴图中60°的角有5个，故选：C．4．下列判断不正确的是（）A．等腰三角形的两底角相等B．等腰三角形的两腰相等C．等边三角形的三个内角都是60°D．两个内角分别为120°、40°的三角形是等腰三角形【解答】解：A、等腰三角形的两底角相等，正确，故本选项错误；B、等腰三角形的两腰相等，正确，故本选项错误；C、等边三角形的三个内角都是60°，正确，故本选项错误；D、两个内角分别为120°、40°的三角形的第三个内角为20°，不是等腰三角形，故本选项正确．故选：D．5．在△ABC中，∠ACB＝90°，∠B＝30°，CD⊥AB于D，若AC＝6，则BD等于（）A．6B．3C．9D．12【解答】解：∵∠ACB＝90°，CD⊥AB，∴∠ACD＝∠B＝30°，∵AC＝6，∴AD＝AC＝×6＝3，AB＝2AC＝2×6＝12，∴BD＝AB﹣AD＝12﹣3＝9．故选：C．6．等腰三角形的对称轴，最多可以有（）A．1条B．3条C．6条D．无数条【解答】解：等腰三角形为等边三角形时对称轴最多，可以有3条．故选：B．7．等腰三角形两边的长分别为2cm和5cm，则这个三角形的周长是（）A．9cm B．12cmC．9cm或12cm D．在9cm或12cm之间【解答】解：当腰长是2cm时，因为2+2＜5，不符合三角形的三边关系，应排除；当腰长是5cm时，因为5+5＞2，符合三角形三边关系，此时周长是12cm．故选：B．8．如图，在△ABC中，AB＝AC，D为BC的中点，E为AC边上一点，且AE＝AD，∠BAC ＝40°，则∠EDC的度数是（）A．10°B．20°C．30°D．40°【解答】解：∵在△ABC中，D为BC中点，AB＝AC，∴AD⊥BC，AD是∠BAC的角平分线，又∵AD＝AE，∠BAC＝40°，∴∠ADE＝80°∴∠EDC＝∠ADC﹣∠ADE＝90°﹣80°＝10°．故选：A．9．一个三角形有两条边相等，这个三角形一边等于5cm，一边等于10cm，则另一边等于（）A．5cm B．10cm C．15cm D．12cm【解答】解：当第三边是5cm时，则5+5＝10，不能构成三角形，当另一边长是10cm时，能构成三角形．故选：B．10．如图，△ABC是等腰三角形，AD是底边BC上的高线，DE⊥AB于E，DF⊥AC于F，图中除AB＝AC外，相等的线段共有（）A．1对B．2对C．3对D．4对【解答】解：∵△ABC是等腰三角形，AD是底边BC上的高线，∴BD＝CD，∠BAD＝∠CAD，∵DE⊥AB，DF⊥AC，∴DE＝DF，∠BED＝∠DFC＝90°，在Rt△BED和Rt△CFD中，，∴Rt△BED≌Rt△CFD（HL），∴BE＝CF，∵AB＝AC，∴AE＝AF．故图中除AB＝AC外，相等的线段共有4对．故选：D．11．等腰三角形一腰上的高与底边所夹的角为a，则这个等腰三角形的顶角为（）A．a B．90°﹣a C．12a D．2a【解答】解：如图，AB＝AC，BD是腰AC的高，则∠DBC＝α∴∠C＝90°﹣α∴∠A＝180°﹣2（90°﹣α）＝2α故选：D．12．等腰三角形的底角为a，则a的取值范围是（）A．a≤45°B．0°＜a＜90°C．45°＜a＜90°D．0°≤a＜90°【解答】解：∵等腰三角形的底角为a，且三角形的内角和等于180°，∴0°＜2a＜180°，∴0°＜a＜90°．故选：B．13．如图，在等边三角形ABC中，三条中线AE，BD，CF相交于点O，则等边三角形ABC 中，从△BOF到△COD需要经过的变换是（）A．轴对称变换B．旋转变换C．平移变换D．相似变换【解答】解：∵△BOF与△COD是关于OE的轴对称图形，∴从△BOF到△COD需要经过轴对称变换．故选A14．如果以4cm长的线段为底组成一个等腰三角形，腰长x的取值范围是（）A．x＞4cm B．x＞2cm C．x≥4cm D．x≥2cm【解答】解：此等腰三角形的底为4cm，则有2x＞4，解得x＞2，故选：B．15．等腰三角形周长是32cm，一边长为10cm，则其他两边的长分别为（）A．10cm，12cm B．11cm，11cmC．11cm，11cm或10cm，12cm D．不能确定【解答】解：当该边是腰时，底边是32﹣20＝12cm，则另外两边是10cm，12cm；当该边是底时，则腰的长为：（32﹣10）÷2＝11cm，则另外两边是11cm，11cm；经检验，两种情况都符合三角形的三边关系．故选：C．二．填空题（共6小题）16．若等腰三角形的一腰上的高与另一腰的夹角等于50°，则其顶角的度数为40°或140°．若等腰三角形的一腰上的高与底边的夹角等于50°，则其顶角的度数为100°．【解答】解：（1）①当为锐角三角形时可以画图，高与右边腰成50°夹角，由三角形内角和为180°可得，顶角为40°；②当为钝角三角形时可画图，此时垂足落到三角形外面，因为三角形内角和为180°，由图可以看出等腰三角形的顶角的补角为40°，三角形的顶角为140°．（2）如图，①顶角是钝角时，∠B＝90°﹣50°＝40°，则顶角＝180°﹣2×40°＝100°，是钝角，符合；②顶角是锐角时，∠B＝90°﹣50°＝40°，∠A＝180°﹣2×40°＝100°，是钝角，不符合．故答案为：40°或140°；100°．17．一个等腰三角形的腰长为3cm，则底边长的取值范围是0＜底边＜6cm．【解答】解：∵3﹣3＝0，3+3＝6cm，∴底边的取值范围是0＜底边＜6cm．故答案为：0＜底边＜6cm．18．如图，AB＝AC，∠A＝100°，AB∥CD，则∠BCD＝40度．【解答】解：∵AB＝AC∴∠B＝∠ACB＝（180﹣∠A）＝40°∵AB∥CD∴∠BCD＝∠B＝40°．故填40．19．等腰三角形的顶角与底角的度数之比为4：1，则它的各内角度数为120°，30°，30°．【解答】解：设等腰三角形的各角为4x，x，x∵4x+x+x＝180°∴x＝30°∴三个内角分别是120°，30°，30°．故填120°，30°，30°．20．△ABC中，∠A：∠B：∠C＝1：2：3，AB＝10，则BC＝5．【解答】解：由∠A：∠B：∠C＝1：2：3，可设∠A＝x°，则∠B＝2x°，∠C＝3x°．∵∠A+∠B+∠C＝180°，∴x+2x+3x＝180，∴x＝30，∴∠A＝30°，∠B＝60°，∠C＝90°，∴BC＝AB＝×10＝5．故答案为5．21．（1）等腰三角形的一个角为100°，那么另外两个角分别为40°，40°．（2）等腰三角形的一个角为50°，则底角是50°，65°．【解答】解：（1）∵等腰三角形的一个角为100°∴两底角的和＝180°﹣100°＝80°又∵等腰三角形的两底角相等∴两底角都为40°．（2）当50°的角是底角，则底角就为50°；当50°的角是顶角，则两底角的和等于130°，所以底角等于65°．故填40°，40°；50°，65°．三．解答题（共9小题）22．已知等腰三角形的周长为28cm，其中的一边长是另一边长的倍，求这个等腰三角形各边的长．【解答】解：设等腰三角形的一边长为xcm，则另一边长为xcm，则等腰三角形的三边有两种情况：xcm，xcm，xcm或xcm，xcm，xcm，则有：①x+x+x＝28，得x＝8cm，所以三边为：8cm、8cm、12cm；②x+x+x＝28，得x＝7cm，所以三边为7cm、10.5cm、10.5cm．因此等腰三角形的三边的长为：8cm，8cm，12cm或7cm，10.5cm，10.5cm．23．如图，已知AB＝AC，D为BC边中点，你能说出AD与BC的位置关系吗？请说明理由．【解答】解：AD⊥BC．理由如下：∵AB＝AC，D为BC边中点，∴AD⊥BC．24．如图，△ABC是等腰三角形，且AB＝AC，试作出BC边上的中线和高以及∠A的平分线，从中你发现了什么？与其他同学进行交流．【解答】解：如图，过点A作AD⊥BC于点D，在Rt△ABD和Rt△ACD中，∵AB＝AC，AD＝AD，∴Rt△ABD≌Rt△ACD（HL）∴BD＝CD，即AD也是中线，∴∠BAD＝∠CAD，即AD又是高线，所以等腰三角形底边上的中线、高以及顶角的角平分线重合．25．如图，在△ABC中，AB＝AC，∠C＝2∠A，BD平分∠ABC．请找出图中其他的等腰三角形，并选择其中的一个说明理由．【解答】解：△ABD、△BCD．理由：∵在△ABC中，AB＝AC，∠C＝2∠A，∴∠ABC＝∠C＝2∠A，∵∠A+∠ABC+∠C＝180°，∴∠A+2∠A+2∠A＝180°，解得：∠A＝36°，∴∠ABC＝∠C＝72°，∵BD平分∠ABC，∴∠ABD＝∠DBC＝36°，∴∠A＝∠ABD＝36°，∠BDC＝∠C＝72°，∴△ABD与△BCD是等腰三角形．26．已知D是等腰△ABC底边BC上的一个点，DE⊥AB于E，DF⊥AC于F，当D点在什么位置时，DE＝DF，并加以证明．【解答】解：当D是BC中点时DE＝DF，理由：∵AB＝AC，∴∠B＝∠C；∵∠BED＝∠CFD＝90°，BD＝CD；∴△BDE≌△CDF；∴DE＝DF．27．如图，AD是等腰△ABC顶角的外角的平分线，那么AD与BC平行吗？为什么？【解答】解：AD∥BC．∵△ABC是等腰三角形，∴∠B＝∠C，又∵∠EAC是△ABC的一个外角，∴∠EAC＝∠B+∠C＝2∠B，∵AD是等腰△ABC顶角的外角的平分线，∴2∠DAC＝∠EAC，∴∠C＝∠DAC，∴AD∥BC（内错角相等，两直线平行）．28．如图，在△ABC中，AD平分∠BAC，G是CA延长线上一点，GE∥AD交AB于F．交BC于E，试判断△AGF的形状并加以证明．【解答】解：△AGF是等腰三角形；理由：∵GE∥AD，∴∠G＝∠CAD，∠BAD＝∠GF A，∵AD平分∠BAC，∴∠CAD＝∠BAD，∴∠G＝∠GF A，∴AG＝AF，∴△AGF是等腰三角形．29．如图，在等腰△ABC中，AB＝AC，AD是BC边上的高，点E、F分别是边AB、AC上的点，且EF∥BC．（1）试说明△AEF是等腰三角形；（2）试比较DE与DF的大小关系，并说明理由．【解答】解：（1）∵EF∥BC，∴∠AEF＝∠B，∠AFE＝∠C．又∵AB＝AC，∴∠B＝∠C，∴∠AEF＝∠AFE，∴AE＝AF，即△AEF是等腰三角形；（2）DE＝DF．理由如下：∵AD是等腰三角形ABC的底边上的高，∴AD也是∠BAC的平分线．又∵△AEF是等腰三角形，∴AG是底边EF上的高和中线，∴AD⊥EF，GE＝GF，∴AD是线段EF的垂直平分线，∴DE＝DF．30．已知：如图，△ABC中，AB＝AC，D是BC延长线上一点，E是AC延长线上一点，且DE∥AB，求证：ED＝EC．【解答】证明：∵AB＝AC，∴∠B＝∠ACB，∵AB∥ED，∴∠B＝∠D，∴∠ACB＝∠D，又∵∠ACB＝∠ECD，∴∠ECD＝∠D，∴ED＝EC．。

人教版八年级上册数学《等腰三角形》同步训练附答案

人教版八年级数学上册《13.3等腰三角形》同步训练1．如图，△ABC是等边三角形，△BCD是等腰三角形，且BD＝CD，过点D作AB的平行线交AC于点E，若AB＝8，DE＝6，则BD的长为（）A．6B．C．D．2．求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．已知：如图，∠CAE是△ABC的外角，∠1＝∠2，AD∥BC．求证AB＝AC．以下是排乱的证明过程：①又∠1＝∠2，②∴∠B＝∠C，③∵AD∥BC，④∴∠1＝∠B，∠2＝∠C，⑤∴AB＝AC．证明步骤正确的顺序是（）A．③→②→①→④→⑤B．③→④→①→②→⑤C．．①→②→④→③→⑤D．①→④→③→②→⑤3．如图，△ABC是等边三角形，AD是BC边上的中线，点E在AD上，且DE＝BC，则∠AFE＝（）A．100°B．105°C．110°D．115°4．如图，已知△ABC是等边三角形，D是BC边上的一个动点（异于点B、C），过点D作DE⊥AB，垂足为E，DE的垂直平分线分别交AC、BC于点F、G，连接FD，FE．当点D在BC边上移动时，有下列三个结论：①△DEF一定为等腰三角形；②△CFG一定为等边三角形；③△FDC可能为等腰三角形．其中正确的有（）A．0个B．1个C．2个D．3个5．如图，在Rt△ABC中，∠A＝90°，CM平分∠ACB交AB于点M，过点M作MN∥BC 交AC于点N，且MN平分∠AMC，若AN＝2，则BC的长为（）A．12B．16C．20D．86．如图，AB∥CD，CB平分∠ACD，点E在AB上，DE⊥CB，垂足为F，连接AF则下列结论中错误的是（）A．AB＝AC B．∠AFC＝∠DC．∠AEF+∠D＝180°D．∠AFC＞∠FCD7．如果一个等腰三角形的两边长为2和5，那么这个三角形的周长是（）A．9B．12C．9或12D．不确定8．若等腰三角形的一个内角比另一个内角大30°，则这个等腰三角形的底角度数是（）A．50°B．80°C．50°或70°D．80°或40°9．若等腰三角形一边长9cm，另一边长4cm，则它的周长为（）A．22cm B．17cm C．22cm或17cm D．22cm或19cm 10．等腰三角形一边长9cm，另一边长4cm，它的第三边是（）cm．A．4 B．9 C．4或9 D．大于5且小于1311．下列对△ABC的判断，错误的是（）A．若∠A：∠B：∠C＝1：2：3，则△ABC是直角三角形B．若AB＝BC，∠C＝50°，则∠B＝50°C．若AB＝BC，∠A＝60°，则△ABC是等边三角形D．若∠A＝20°，∠C＝80°，则△ABC是等腰三角形12．已知等腰三角形的周长为19，一边长为8，则此等腰三角形的底边长为（）A．3B．8C．3或8D．8或5.513．若等腰三角形的顶角是大于60°的锐角，则底角度数的取值范围是（）A．x＜60°B．x≤60°C．45°＜x＜60°D．45°≤x＜60°14．△ABC中，∠BAC＝∠BCA，AD平分∠BAC，DE∥AC，下列说法正确的是（）A．∠B＝36°B．∠ADB＝108°C．∠ADB＝3∠EDA D．∠AED＝3∠B 15．等腰三角形的两边长为3和8，则这个等腰三角形的周长是（）A．14B．19C．14或19D．2016．如图，在△ABC中，AB＝AC，尺规作图：（1）分别以B，C为圆心，BC长为半径作弧，两弧交于点D；（2）作射线AD，连接BD，CD．则下列结论中错误的是（）A．∠BAD＝∠CAD B．△BCD是等边三角形C．AD垂直平分BC D．S四边形ABDC＝AD⋅BC17．如图，在△ABC中，AB＝AC，AC的垂直平分线l交BC于点D．若∠BAD＝78°，则∠B的度数是（）A．34°B．30°C．28°D．26°18．如图，在△ABC中，AB＝AC，以点C为圆心，CB长为半径画弧，交AB于点B和点D，再分别以点B，D为圆心，大于BD长为半径画弧，两弧相交于点M，作射线CM 交AB于点E．若AE＝5，BE＝1，则EC的长度是（）A．B．C．9D．19．如图，在等腰△ABD中，∠A＝32°，取大于AB的长为半径，分别以点A，B为圆心作弧相交于两点，过此两点的直线交AD边于点E（作图痕迹如图所示），连接BE，BD，则∠EBD的度数为．20．如图，在△ABC中，AB＝AC，以点B为圆心，BC长为半径画弧交AC于点C和点D，再分别以点C和点D为圆心，大于DC长为半径画弧，两弧相交于点F，作射线BF交AC于点E．若∠A＝40°，则∠EBC＝度．21．如图，在边长为2的等边三角形ABC中，D，E分别为AB，BC的中点，EF⊥AC于点F，G为EF的中点，连接DG，则DG的长为．22．如图，在△ABC中，AB＝AC，∠B＝35°，D是BC边上的动点，连接AD，若△ABD 为直角三角形，则∠DAC的度数为．23．已知等腰三角形的一个内角为110°，则等腰三角形的底角的度数为．24．用三根木棒首尾相连围成一个等腰三角形，其中两根木棒的长度分别为3cm和6cm，则第三根木棒长为cm．25．如图，在△ABC中，AB＝AC，AD平分∠BAC交BC于点D，BC＝16cm，则BD＝cm．26．如图，在平面直角坐标系中，点A的坐标为（0，2），点B的坐标为（4，0），在y轴上取一点C使△ABC为等腰三角形，符合条件的C点有个．27．如图，在△ABC中，AB＝AC，∠BAC＝108°，AC的中垂线交BC于点D，交AC于点E，连接AD，则图中等腰三角形有个．28．如图，在△ABC中，以点B为圆心，BA长为半径画弧，交BC边于点D，连接AD．若∠B＝40°，∠C＝32°，求∠DAC的度数．29．如图，已知△ABC中，AB＝AC，∠ABC、∠ACB的平分线交于点E，直线AE交BC于点D，说明AD⊥BC的理由．30．若关于x，y的二元一次方程组的解都是正数．（1）求a的取值范围；（2）若此方程组的解是一个等腰三角形的一条腰和底边的长，且这个等腰三角形的周长为12，求a的值．31．如图，在△ABC中，D是三角形内一点，连接DA、DB、DC，且∠1＝∠2，∠3＝∠4，求证：AB＝AC．参考答案1．解：连接AD交BC于点O，取AC中点N，连接ON，如图，∵△ABC是等边三角形，∴AB＝AC＝BC＝8，∠ABC＝60°，∵△BCD是等腰三角形，∴BD＝DC，∴AD垂直平分BC，∴BO＝CO＝4，∵AN＝CN，∴ON＝AB＝4，ON∥AB，∵AB∥DE，∴ON∥DE，∴OD＝AO，∴AO＝4，∴OD＝2，在Rt△BOD中，BD＝＝2．故选：B．2．解：∵③AD∥BC，∴④∠1＝∠B，∠2＝∠C，∵①∠1＝∠2，∴②∠B＝∠C，∴⑤AB＝AC，故证明步骤正确的顺序是③→④→①→②→⑤，3．解：∵△ABC是等边三角形，∴∠BAC＝60°，∵AD是BC边上的中线，∴∠BAD＝BAC＝30°，AD⊥BC，BD＝CD＝BC，∴∠CDE＝90°，∵DE＝BC，∴DE＝DC，∴∠DEC＝∠DCE＝45°，∴∠AEF＝∠DEC＝45°，∴∠AFE＝180°﹣∠BAD﹣∠AEF＝180°﹣30°﹣45°＝105°，故选：B．4．解：∵DE的垂直平分线分别交AC、BC于点F、G，∴FE＝FD，∴△DEF一定为等腰三角形，故①正确；∵DE⊥AB，DE⊥FG，∴AB∥FG，∴∠FGC＝∠B＝60°，又∵△ABC是等边三角形，∴∠C＝60°，∴△CFG中，∠C＝∠CFG＝∠CGF，∴△CFG一定为等边三角形；故②正确；∵∠FDC＞∠FGC＝60°，∠C＝60°，∠CFD＜∠CFG＝60°，∴△FDC不可能为等腰三角形．故③错误；5．解：∵CM平分∠ACB交AB于点M，∴∠NCM＝∠BCM，∵MN∥BC∴∠NCM＝∠BCM＝∠NMC，∵MN平分∠AMC，∴∠AMN＝∠NMC＝∠B，∴∠ACB＝2∠B，NM＝NC，∴∠B＝30°；∵AN＝2，∠AMN＝∠B＝30°，∴MN＝2AN＝4，∴NM＝NC＝4，∴AC＝AN+NC＝6，∴BC＝2AC＝12，故选：A．6．解：∵AB∥CD，∴∠B＝∠BCD，∠AEF+∠D＝180°，故C选项正确；∵CB平分∠ACD，∴∠ACB＝∠BCD，∴∠ACB＝∠B，∴AC＝AB，故A选项正确；∵DE⊥CB，∴∠CFD＝90°，∴∠D+∠BCD＝90°，假如∠AFC＝∠D，则∠CAF＝∠CFD＝90°，而∠CAF不一定是90°，∴∠AFC与∠D不一定相等，故B选项错误；∵∠AFC是△ABF的外角，∴∠AFC＞∠B，∵∠B＝∠FCD，∴∠AFC＞∠FCD，故D选项正确，故选：B．7．解：∵2+2＝4＜5，∴腰的长不能为2，只能为5，∴等腰三角形的周长＝2×5+2＝12，故选：B．8．解：在△ABC中，设∠A＝x，∠B＝x+30°，分情况讨论：当∠A＝∠C为底角时，2x+（x+30°）＝180°，解得x＝50°，底角∠A＝50°；当∠B＝∠C为底角时，2（x+30°）+x＝180°，解得x＝40°，底角∠B＝70°．故这个等腰三角形的底角的度数为50°或70°．故选：C．9．解：①当腰为4cm时，三边为4cm，4cm，9cm，∵4+4＜9，∴不符合三角形的三边关系定理，此种情况舍去；②当腰为9cm时，三边为4cm，9cm，9cm，此时符合三角形的三边关系定理，此时等腰三角形的周长是4cm+9cm+9cm＝22cm，故选：A．10．解：①当腰为4cm时，三边为4cm，4cm，9cm，∵4+4＜9，∴不符合三角形的三边关系定理，此种情况舍去；②当腰为9cm时，三边为4cm，9cm，9cm，此时符合三角形的三边关系定理，所以三角形的第三边为9cm，故选：B．11．解：A．若∠A：∠B：∠C＝1：2：3，则∠A＝30°，∠B＝60°，∠C＝90°，所以△ABC是直角三角形，故此选项正确，不符合题意；B．若AB＝BC，∠C＝50°，则∠A＝∠C＝50°，∠B＝100°，故此选项错误，符合题意；C．若AB＝BC，∠A＝60°，则∠A＝∠C＝60°，∠B＝60°，所以△ABC是等边三角形，故此选项正确，不符合题意；D．若∠A＝20°，∠C＝80°，则∠B＝80°，∠C＝∠B＝80°，所以△ABC是等腰三角形，故此选项正确，不符合题意．故选：B．12．解：本题可分两种情况：①当腰长为8时，底边长＝19﹣2×8＝3；经检验，符合三角形三边关系；②底边长为8，此时腰长＝（19﹣8）÷2＝5.5，经检验，符合三角形三边关系；因此该等腰三角形的底边长为3或8．故选：C．13．解：设等腰三角形的底角为x°，则顶角为（180°﹣2x），由题意可得：60°＜180°﹣2x＜90°，∴45°＜x＜60°，∴底角度数的取值范围是45°＜x＜60°，故选：C．14．解：设∠CAD＝x°，∵AD平分∠BAC，∠BAC＝∠BCA，∴∠BCA＝∠BAC＝2x°，∵DE∥AC，∴∠BDE＝∠BCA＝2x°，∠ADE＝∠CAD＝x°，∴∠ADB＝∠BDE+∠ADE＝2x°+x°＝3x°，即∠ADB＝3∠EDA，故选：C．15．解：①若3是腰，则另一腰也是3，底是8，但是3+3＜8，故不构成三角形，舍去．②若3是底，则腰是8，8．3+8＞8，符合条件．成立．故周长为：3+8+8＝19．故选：B．16．解：根据作图方法可得BC＝BD＝CD，∵BD＝CD，∴点D在BC的垂直平分线上，∵AB＝AC，∴点A在BC的垂直平分线上，∴AD是BC的垂直平分线，故C结论正确；∴O为BC中点，∴AO是△BAC的中线，∵AB＝AC，∴∠BAD＝∠CAD，故A结论正确；∵BC＝BD＝CD，∴△BCD是等边三角形，故B结论正确；∵四边形ABDC的面积＝S△BCD+S△ABC＝BC•DO+BC•AO＝BC•AD，故D选项错误，故选：D．17．解：∵AB＝AC，∴∠B＝∠C，∵AC的垂直平分线l交BC于点D，∴AD＝DC，∴∠DAC＝∠C，∵∠ADB＝∠DAC+∠C＝2∠C，∴∠ADB＝2∠B，∵∠BAD＝78°，∴∠B+∠ADB+∠BAD＝∠B+2∠B+78°＝180°，∴∠B＝34°，故选：A．18．解：由作法得CE⊥AB，则∠AEC＝90°，AC＝AB＝BE+AE＝5+1＝6，在Rt△ACE中，CE＝＝，故选：A．19．解：∵AD＝AB，∠A＝32°，∴∠ABD＝∠ADB＝（180°﹣∠A）＝74°，由作图可知，EA＝EB，∴∠ABE＝∠A＝32°，∴∠EBD＝∠ABD﹣∠ABE＝74°﹣32°＝42°，故答案为：42°．20．解：∵AB＝AC，∠A＝40°，∴∠ACB＝（180°﹣40°）÷2＝70°，由题意可知，BC＝BD，∴∠BDC＝∠ACB＝70°，∴∠CBD＝180°﹣70°×2＝40°，由题意可知，BF平分∠DBC，∴∠EBC＝∠CBD＝20°．故答案为：20．21．解：连接DE，∵在边长为2的等边△ABC中，D，E分别为AB，BC的中点，∴DE是△ABC的中位线，∴DE＝1，且DE∥AC，BD＝BE＝EC＝1，∵EF⊥AC于点F，∠C＝60°，∴∠FEC＝30°，∠DEF＝∠EFC＝90°，∴FC＝EC＝，故EF＝＝＝，∵G为EF的中点，∴EG＝，∴DG＝＝，故答案为：．22．解：如图，∵AB＝AC，∠B＝35°，∴∠B＝∠C＝35°，∴∠BAC＝110°，当∠BAD＝90°时，∠DAC＝110°﹣90°＝20°；当∠ADB＝90°时，∵AB＝AC，AD⊥BC，∴∠DAC＝∠BAD＝55°．故答案为：20°或55°．23．解：∵等腰三角形的一个内角是110°，∴等腰三角形的顶角为110°，∴等腰三角形的底角为35°，故答案为：35°．24．解：组成等腰三角形的两根木棒的长度分别为3cm和6cm，根据三角形三边关系可得，组成等腰三角形的第三根木棒长为6cm，故答案为：6．25．解：∵AB＝AC，AD平分∠BAC交BC于点D，∴BD＝DC＝BC，∵BC＝16cm，故答案为：8．26．解：观察图形可知，若以点A为圆心，以AB为半径画弧，与y轴有2个交点，但其中一个与B点重合，故此时符合条件的点由1个；若以点B为圆心，以AB为半径画弧，与y轴有2个交点；线段AB的垂直平分线与y轴有1个交点；∴符合条件的C点有：1+2+1＝4（个），故答案为：4．27．解：∵AB＝AC，∠BAC＝108°，∴△ABC是等腰三角形，∠B＝∠C＝（180°﹣∠BAC）÷2＝36°，∵AC的中垂线交BC于点D，交AC于点E，∴AD＝CD，∴△ADC是等腰三角形，∠DAC＝∠C＝36°，∴∠BAD＝∠BAC﹣∠DAC＝72°，∠ADB＝∠DAC+∠C＝72°，∴∠BAD＝∠ADB，∴△BAD是等腰三角形．故图中等腰三角形有3个．故答案为：3．28．解：∵∠B＝40°，∠C＝32°，∴∠BAC＝180°﹣∠B﹣∠C＝108°，由作图可知：BA＝BD，∴∠BAD＝∠BDA＝（180°﹣∠B）÷2＝70°，∴∠DAC＝∠BAC﹣∠BAD＝38°．29．证明：∵AB＝AC，∴∠ABC＝∠ACB，∵BE平分∠ABC，CE平分∠ACB，∴∠EBC＝，，∴∠EBC＝∠ECB，∴EB＝EC，∴AE垂直平分BC，∴AD⊥BC．30．解：（1）解得，∵若关于x、y的二元一次方程组的解都为正数，∴，解得：a＞1；（2）∵二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长，这个等腰三角形的周长为12，∴2（a﹣1）+a+2＝12，解得：a＝4，∴x＝3，y＝6，故3，3，6不能组成三角形，∴2（a+2）+a﹣1＝12，解得：a＝3，∴x＝2，y＝5，故2，5，5能组成等腰三角形，∴a的值是3．31．证明：∵∠1＝∠2，∴DB＝CD，在△ABD和△ACD中，，∴△ABD≌△ACD（SAS），∴AB＝AC．。

人教版八年级数学上册《13.3.1等腰三角形的性质》同步测试题及答案

人教版八年级数学上册《13.3.1等腰三角形的性质》同步测试题及答案一、单项选择题。

1．已知一个等腰三角形的一个底角为30°，则它的顶角等于( )A．130° B．120° C．115° D．110°2．如图，在△ABC中，AB＝AC，∠A＝40°，CD∥AB，则∠BCD等于( )A．50° B．60° C．70° D．75°3．如图，等腰三角形ABC中，AB＝AC，∠A＝46°，CD⊥AB于点D，则∠DCB等于( )A．20° B．23° C．25° D．30°4．如图，在△ABC中，AB＝AC，点D是BC边的中点．下列结论中不正确的是( )A．∠B＝∠C B．AD平分∠BAC C．AD⊥BC D．AB＝2BD5．如图，AD，CE分别是△ABC的中线和角平分线．若AB＝AC，∠CAD＝20°，则∠ACE 的度数是( )A．20° B．35° C．40° D．70°6．若等腰三角形ABC中有一个内角为40°，则这个等腰三角形的一个底角的度数为( )A．40° B．100° C．40°或100° D．40°或70°7．如图，在△ABC中，AB＝AC，AD⊥BC于点D，DE⊥AB于点E，BF⊥AC于点F，BF＝10cm，则DE等于( )A．5cm B．7cm C．9cm D．12cm8．如图，已知∠AOB＝10°，且OC＝CD＝DE＝EF＝FG＝GH，则∠BGH＝( )A．50° B．60° C．70° D．80°二、填空题。

9．已知：如图，在△ABC中，点D在边BC上，AB＝AD＝DC，∠C＝35°，则∠BAD＝_____．10．如图，AB∥CD，AD＝CD，∠1＝65°，则∠2＝_____．11．如图，以△ABC的顶点B为圆心，BA长为半径画弧，交BC边于点D，连接AD.若∠B ＝40°，∠C＝36°，则∠DAC的大小为_____．12．如图，在△ABC中，AB＝AC，AD⊥BC于点D，若AB＝6，CD＝4，则△ABC的周长是____．13．如图，在△ABC中，AB＝AC，∠A＝40°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D＝____．14．如图，在△ABC中，AD＝BD＝BC，若∠ABD＝36°，则∠DBC＝________．15．如图，在△ABC中，AB＝AC，AD平分∠BAC且BD＝4，AB＝6，则CD＝____，△ABC 的周长为____．16．如图，在△ABC中，AB＝AC，AB的垂直平分线MN交AC于点D，连接BD.若∠DBC＝30°，则∠A＝____．17．如图，在△ABC中，DE垂直平分AB，垂足为D，交BC于点E，若∠B＝32°，AC＝CE，则∠C的度数是________．18．等腰三角形的一个内角为70°，则另外两个内角的度数分别为______________．三、解答题。

人教版数学八年级上册第十三章 13.3.1 等腰三角形同步练习2 (答案版)

人教版数学八年级上册第十三章13.3.1 等腰三角形同步练习2一、选择题1. 已知一个等腰三角形的顶角为30°，则它的一个底角等于( )A．30°B．75°C．150°D．125°【答案】B2. 如图的正方形网格中，网格线的交点称为格点．已知A，B是两格点，若点C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数有( )A．6个B．7个C．8个D．9个【答案】C3. 在如图所示的三角形中，若AB＝AC，则能被一条直线分成两个小等腰三角形的是( )A．(1)(2)(3) B．(1)(2)(4)C．(2)(3)(4)D．(1)(3)(4)【答案】D4. △ABC中，△A△△B△△C＝1△2△3，则BC△AB等于( )A．2△1 B．1△2C．1△3 D．2△3【答案】B5. 如图，在△ABC中，AB＝AC，BD是AC边上的高，CE是AB边上的高，它们相交于点O，则图中除△ABC外一定是等腰三角形的是( )A．△ABD B．△ACE C．△OBC D．△OCD 【答案】C6. 如图，△ABC是等边三角形，AD是角平分线，△ADE是等边三角形，下列结论：△AD△BC；△EF＝FD；△BE＝BD，其中正确结论的个数为( )A．3 B．2 C．1 D．0【答案】A7. 如图，点A，B，C在一条直线上，△ABD和△BCE是等边三角形，连接AE，交BD于P，连接CD，分别交BE，AE于Q，M，连接BM，PQ，则△AMD的度数为( )A．45° B．60° C．75° D．90°【答案】B8. (呼伦贝尔中考)如图，在△ABC中，AB＝AC，过点A作AD△BC，若△1＝70°，则△BAC的大小为( )A．40° B．30° C．70° D．50°【答案】A二、填空题1. 在△ABC中，如果△A△△B△△C＝3△2△3，那么△ABC是三角形．【答案】等腰2．如图，在△ABC中，AB＝AC，AD△BC，垂足为点D，若△BAC＝70°，则△BAD＝________．【答案】35°3. 如图，在△ABC中，AD△BC于D，请你再添加一个条件，就可以确定△ABC是等腰三角形，你添加的条件是．【答案】BD＝CD或△BAD＝△CAD4. 如图所示，射线BA、CA交于点A，连接BC，已知AB＝AC，△B＝40°，那么x的值是________．【答案】.805.如图，在△ABC中，BD△AC，△A＝50°，△CBD＝25°，若AC＝5 cm，则AB＝_ cm．【答案】56.如图，在△ABC中，BP平分△CBA，AP平分△CAB，且DE△AB，若CB＝12，AC＝18，则△CDE的周长是．【答案】307. 如图，在△ABC中，AB＝AC，D是BC中点，DE△AC，垂足为E，△BAC ＝50°，则△ADE= ．【答案】65°。

人教版数学八年级上册：13.3 等腰三角形同步练习(附答案)

13．3等腰三角形13．3.1等腰三角形第1课时等腰三角形的性质知识点1等边对等角1．若等腰三角形的顶角为40°，则它的底角度数为()A．40° B．50° C．60° D．70°2．如图，AB∥CD，点E在线段BC上，CD＝CE.若∠ABC＝30°，则∠D为() A．85°B．75°C．60°D．30°3．如图1是一把园林剪刀，把它抽象为图2，其中OA＝OB.若剪刀张开的角为30°，则∠A ＝．4．如图，在△ABC中，∠B＝90°，AB＝BD，AD＝CD，求∠CAD的度数．5．如图，在△ABC中，AB＝AC，D是△ABC内一点，且BD＝DC.求证：∠ABD＝∠ACD.知识点2等腰三角形“三线合一”6．如图，△ABC中，AB＝AC，D是BC中点，下列结论中不正确的是() A．∠B＝∠CB．AD⊥BCC．AD平分∠BACD．AB＝2BD7．如图，在△ABC中，AB＝AC，AD⊥BC，垂足为D.若BD＝2 cm，则CD＝cm.第7题图第8题图8．如图，在△ABC中，AB＝AC，D为BC中点，∠BAD＝35°，则∠C的度数为．9．如图，在△ABC中，AB＝AC，AD是BC边上的中线，BE⊥AC于点E.求证：∠CBE ＝∠BAD.10．已知等腰三角形的一个外角为130°，则它的顶角的度数为．11．如图，在△ABC中，AB＝AC，BD⊥AC于点D，∠A＝50°，则∠DBC的度数为．12．如图，在△ABC中，AB＝AC，∠A＝30°，AB的垂直平分线l交AC于点D，则∠CBD 的度数为()A．30° B．45°C．50°D．75°第12题图第13题图13．如图，在△ABC中，AB＝AC，点E在BC边上，在线段AC的延长线上取点D，使得CD＝CE，连接DE，CF是△CDE的中线．若∠FCE＝52°，则∠A的度数为() A．38° B．34°C．32° D．28°14．如图，在△ABC中，AB＝BC，∠ABC＝110°，AB的垂直平分线DE交AC于点D，连接BD，则∠ABD＝．第14题图第15题图15．如图，在△ABC中，点D在BC边上，BD＝AD＝AC，E为CD的中点．若∠CAE＝16°，则∠B＝．16．如图，点D，E在△ABC的边BC上，AB＝AC，BD＝CE.求证：AD＝AE.17．如图，在△ABC中，AC＝BC，∠ACB＝90°，点D是AB的中点，点E是AB边上一点，直线BF垂直于直线CE于点F，交CD于点G.求证：AE＝CG.第2课时等腰三角形的判定知识点1等角对等边1．如图，在△ABC中，∠B＝∠C，AB＝5，则AC的长为()A．2B．3C．4D．52．在△ABC中，∠A和∠B的度数如下，能判定△ABC是等腰三角形的是() A．∠A＝50°，∠B＝70°B．∠A＝70°，∠B＝40°C．∠A＝30°，∠B＝90°D．∠A＝80°，∠B＝60°3．如图，已知OC平分∠AOB，CD∥OB，则△COD 等腰三角形．(填“是”或“不是”)第3题图第4题图4．如图，在△ABC中，BD⊥AC，∠A＝50°，∠CBD＝25°，若AC＝5 cm，则AB＝．5．如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF⊥AC 于点F.求证：△ABC是等腰三角形．6．如图，△ABC的边AB的延长线上有一个点D，过点D作DF⊥AC于F，交BC于E，且BD＝BE，求证：△ABC为等腰三角形．知识点2用尺规作等腰三角形7．已知等腰三角形的底边长为a，顶角的平分线长为b，求作这个等腰三角形．8．如图，已知点P是射线ON上一动点(即P可在射线ON上运动)，∠AON＝45°，当∠A ＝时，△AOP为等腰三角形．9．如图，在△ABC中，∠B＝∠C＝40°，D，E是BC上的两点，且∠ADE＝∠AED＝80°，则图中共有等腰三角形()A．6个B．5个C．4个D．3个第9题图第10题图10．如图，在△ABC中，BP平分∠CBA，AP平分∠CAB，且DE∥AB，若CB＝12，AC ＝18，则△CDE的周长是．11．如图，AD平分∠BAC，AD⊥BD，垂足为D，DE∥AC.求证：△BDE是等腰三角形．12．如图，在△ABC中，AB＝AC，∠BAC＝36°，CD是∠ACD的平分线，交AB于点D，过点A作AE∥BC，交CD的延长线于点E.(1)求∠ADC的度数；(2)求证：AE＝AC；(3)试问△ADE是等腰三角形吗？请说明理由．13．如图，OA平分∠BAC，∠1＝∠2.求证：△ABC是等腰三角形．参考答案第1课时等腰三角形的性质1．D 2．B 3．75°．4．解：∵△ABC 中，∠B ＝90°，AB ＝BD ，AD ＝CD ，∴∠BAD ＝∠ADB ＝45°，∠DCA ＝∠CAD. ∴∠BDA ＝2∠CAD ＝45°. ∴∠CAD ＝22.5°. 5．证明：∵AB ＝AC ，∴∠ABC ＝∠ACB. ∵BD ＝CD ，∴∠DBC ＝∠DCB.∴∠ABC －∠DBC ＝∠ACB －∠DCB ，即∠ABD ＝∠ACD. 6．D 7．2 8．55°．9．证明：∵AB ＝AC ，∴∠ABD ＝∠C.又∵AD 是BC 边上的中线， ∴AD ⊥BC.∵BE ⊥AC ，∴∠BEC ＝∠ADB ＝90°. ∴∠C ＋∠CBE ＝∠ABD ＋∠BAD ＝90°. ∴∠CBE ＝∠BAD. 10．50°或80°． 11．25°． 12．B 13．D 14．35°． 15．37°．16．证明：∵AB ＝AC ，∴∠B ＝∠C.在△ABD 和△ACE 中，⎩⎪⎨⎪⎧AB ＝AC ，∠B ＝∠C ，BD ＝CE ，∴△ABD ≌△ACE(SAS )． ∴AD ＝AE.17．证明：∵点D 是AB 中点，AC ＝BC ，∠ACB ＝90°，∴CD ⊥AB ，∠ACD ＝∠BCD ＝45°，∠CAD ＝∠CBD ＝45°. ∴∠CAE ＝∠BCG. 又∵BF ⊥CE ，∴∠CBG ＋∠BCF ＝90°. 又∵∠ACE ＋∠BCF ＝90°， ∴∠ACE ＝∠CBG.在△AEC 和△CGB 中， ⎩⎪⎨⎪⎧∠CAE ＝∠BCG ，AC ＝CB ，∠ACE ＝∠CBG ， ∴△AEC ≌△CGB(ASA )． ∴AE ＝CG.第2课时等腰三角形的判定1．D 2．B 3．是4．5__cm ．5．证明：∵AD 平分∠BAC ，DE ⊥AB 于点E ，DF ⊥AC 于点F ，∴DE ＝DF.∵点D 是BC 的中点， ∴BD ＝CD.在Rt △BDE 和Rt △CDF 中，⎩⎪⎨⎪⎧BD ＝CD ，DE ＝DF ， ∴Rt △BDE ≌Rt △CDF(HL )． ∴∠B ＝∠C.∴AB ＝AC ，即△ABC 为等腰三角形． 6．证明：∵DF ⊥AC ，∴∠DFA ＝∠EFC ＝90°. ∴∠A ＝∠EFC －∠D ， ∠C ＝∠DFA －∠CEF. ∵BD ＝BE ， ∴∠BED ＝∠D. ∵∠BED ＝∠CEF ， ∴∠D ＝∠CEF. ∴∠A ＝∠C.∴△ABC 为等腰三角形． 7．解：①作线段AB ＝a ；②作线段AB 的垂直平分线MN ，与AB 交于点D ； ③以点D 为圆心，b 为半径画弧，交MN 于点C ； ④连接AC ，BC ，则△ABC 就是所求作的三角形． 8．45°或67.5°或90° 9．C 10．30．11．证明：∵DE ∥AC ，∴∠CAD ＝∠ADE.∵AD 平分∠BAC ， ∴∠CAD ＝∠DAE. ∴∠ADE ＝∠DAE. ∵AD ⊥BD ，∴∠DAE ＋∠B ＝90°， ∠ADE ＋∠BDE ＝90°. ∴∠B ＝∠BDE.∴BE ＝DE ，即△BDE 是等腰三角形． 12．解：(1)∵AB ＝AC ，∠BAC ＝36°，∴∠B ＝∠ACB ＝12(180°－∠BAC )＝72°.∵CD 是∠ACB 的平分线， ∴∠DCB ＝12∠ACB ＝36°.∴∠ADC ＝∠B ＋∠DCB ＝72°＋36°＝108°. (2)证明：∵CD 是∠ACB 的平分线， ∴∠BCE ＝∠ACE. ∵AE ∥BC ， ∴∠BCE ＝∠E. ∴∠ACE ＝∠E. ∴AE ＝AC.(3)△ADE 是等腰三角形．理由：∵AE ∥BC ， ∴∠EAB ＝∠B ＝72°.∵∠B ＝72°，∠DCB ＝36°，∴∠ADE ＝∠BDC ＝180°－72°－36°＝72°. ∴∠EAD ＝∠ADE. ∴AE ＝DE.∴△ADE 是等腰三角形． 13．证明：过点O 作OD ⊥AB 于点D ，OE ⊥AC 于点E ，则△BOD 和△COE 都是直角三角形．∵OA 平分∠BAC ，OD ⊥AB ，OE ⊥AC ， ∴OD ＝OE. ∵∠1＝∠2， ∴OB ＝OC.∴Rt △BOD ≌Rt △COE(HL )． ∴∠ABO ＝∠ACO.又∵∠1＝∠2，∴∠ABC＝∠ACB.∴AB＝AC.∴△ABC是等腰三角形．。

人教八年级数学上册第13章《等腰三角形》同步练习及(含答案)4

人教八年级数学上册第13章《等腰三角形》同步练习及（含答案）4一．选择题（共8小题）1．如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是（）A． 3.5 B． 4.2 C． 5.8 D． 7第1题第2题第3题2．如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于E，垂足为D．若ED=5，则CE的长为（）A． 10 B． 8 C． 5 D． 2.53．如图，Rt△ABC中，∠C=90°，以点B为圆心，适当长为半径画弧，与∠ABC的两边相交于点E，F，分别以点E和点F为圆心，大于的长为半径画弧，两弧相交于点M，作射线BM，交AC于点D．若△BDC的面积为10，∠ABC=2∠A，则△ABC的面积为（）A． 25 B． 30 C． 35 D． 404．在Rt△ABC中，∠C=90°，∠B=30°，斜边AB的长为2cm，则AC长为（）A．4cm B． 2cm C． 1cm D．m5．如图，△ABC中，∠ACB=90°，CD是高，∠A=30°，则BD与AB的关系是（）A． BD=AB B． BD=AB C． BD=AB D． BD=AB第5题第6题第7题第8题6．如图是屋架设计图的一部分，立柱BC垂直于横梁AC，AB=10m，∠A=30°，则立柱BC 的长度是（）A． 5m B． 8m C． 10m D． 20m7．如图，一棵树在一次强台风中于离地面3米处折断倒下，倒下部分与地面成30°角，这棵树在折断前的高度为（）A． 6米B． 9米 C． 12米D． 15米8．如图，已知∠ABC=60°，DA是BC的垂直平分线，BE平分∠ABD交AD于点E，连接CE．则下列结论：①BE=AE；②BD=AE；③AE=2D E；④S△ABE=S△CBE，其中正确的结论是（）A．①②③B．①②④C．①③④D．②③④二．填空题（共10小题）9．如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，DE=1，则BE的长是_________．10．如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB，若EC=1，则EF=_________．11．如图，在△ABC中，∠C=90°，∠B=60°，AB=10，则BC的长为_________．12．如图，在等腰三角形ABC中，AB=AC=12cm，∠ABC=30°，底边上的高AD=_______cm．第9题第10题第11题第12题13．如图，在△ABC中，AB=BC，∠B=120°，AB的垂直平分线交AC于点D．若AC=6cm，则AD=_________cm．第13题第14题第15题第16题14．如图，在△ABC中．∠B=90°，∠BAC=30°．AB=9cm，D是BC延长线上一点．且AC=DC．则AD=_________cm．15．如图是某超市一层到二层滚梯示意图．其中AB﹨CD分别表示超市一层﹨二层滚梯口处地面的水平线，∠ABC=150°，BC的长约为12米，则乘滚梯从点B到点C上升的高度h 约为_________米．16．在△ABC中，已知A B=4，BC=10，∠B=30°，那么S△ABC=_________．17．如图，△ABC是等边三角形，AD⊥BC，DE⊥AC，若AB=12c m，则CE=______cm．18．有一轮船由东向西航行，在A处测得西偏北15°有一灯塔P．继续航行20海里后到B 处，又测得灯塔P在西偏北30°．如果轮船航向不变，则灯塔与船之间的最近距离是_________海里．三．解答题（共5小题）19．如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．（1）求证：△ACD≌△AED；（2）若∠B=30°，CD=1，求BD的长．20．如图，在△ABC中，BA=BC，∠B=120°，AB的垂直平分线MN交AC于D，求证：AD=DC．21．如图，△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，若AD=6，求AC的长．22．如图，△ABC中，∠ACB=90°，CD是△ABC的高，∠A=30°，AB=4，求BD长．23．如图，已知∠MAN=120°，AC平分∠MAN．B﹨D分别在射线AN﹨AM上．（1）在图（1）中，当∠ABC=∠ADC=90°时，求证：AD+AB=AC．（2）若把（1）中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°，其他条件不变，如图（2）所示．则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．等边三角形（2）：一﹨DABCCABC二﹨9﹨2；10﹨2；11﹨5；12﹨6；13﹨2；14﹨18；15﹨6；16﹨10；17﹨3；18﹨10三﹨19﹨（1）证明：∵AD平分∠CAB，DE⊥AB，∠C=90°，∴CD=ED，∠DEA=∠C=90°，∵在Rt△ACD和Rt△AED中∴Rt△ACD≌Rt△AED（HL）；（2）解：∵DC=DE=1，DE⊥AB，∴∠DEB=90°，∵∠B=30°，∴BD=2DE=2．20﹨解：如图，连接DB．∵MN是AB的垂直平分线，∴AD=DB，∴∠A=∠ABD，∵BA=BC，∠B=120°，∴∠A=∠C=（180°﹣120°）=30°，∴∠ABD=30°，又∵∠ABC=120°，∴∠DBC=120°﹣30°=90°，∴BD=DC，∴AD=DC．21﹨解：∵△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，∴∠2=∠3=30°；在Rt△BCD中，CD= BD，∠4=90°﹣30°=60°（直角三角形的两个锐角互余）；∴∠1+∠2=60°（外角定理），∴∠1=∠2=30°，∴AD=BD（等角对等边）；∴AC=AD+CD=AD；又∵AD=6，∴AC=9．22﹨解：∵△ABC中，∠ACB=90°，∠A=30°，AB=4，∴BC=AB=×4=2，∵CD是△A BC的高，∴∠CDA=∠ACB=90°，∠B=∠B，故∠BCD=∠A=30°，∴在Rt△BCD中，BD=BC=×2=1，∴BD=1．23﹨（1）证明：∵∠MAN=120°，AC平分∠MAN，∴∠DAC=∠BAC=60°∵∠AB C=∠ADC=90°，∴∠DCA=∠BCA=30°，在Rt△ACD中，∠DCA=30°，Rt△ACB中，∠BCA=30°∴AC=2AD，AC=2AB，∴AD+AB=AC；（2）解：结论AD+AB=AC成立．理由如下：在AN上截取AE=AC，连接C E，∵∠BAC=60°，∴△CAE为等边三角形，∴AC=CE，∠AEC=60°，∵∠DAC=60°，∴∠DAC=∠AEC，∵∠ABC+∠ADC=180°，∠ABC+∠EBC=180°，∴∠ADC=∠EBC，∴△ADC≌△EBC，∴DC=BC，DA=BE，∴AD+AB=AB+BE=AE，∴AD+AB=AC．。

人教版八年级数学上册 13.3 等腰三角形同步训练(含答案)

人教版八年级数学上册13.3 等腰三角形同步训练一、选择题1. 如图，等腰三角形的对称轴是()A．直线l1B．直线l2C．直线l3D．直线l42. 如图，AC＝AD，BC＝BD，则有()A．CD垂直平分ABB．AB垂直平分CDC．AB与CD互相垂直平分D．CD平分∠ACB3. 已知等腰三角形的一个角等于42°，则它的底角为()A．42°B．69°C．69°或84°D．42°或69°4. 已知实数x、y满足|x－4|＋y－8＝0，则以x、y的值为两边长的等腰三角形的周长是()A. 20或16B. 20C. 16D. 以上答案均不对5. 如图，AD是△ABC的中线，下列条件中不能推出△ABC是等腰三角形的是()A．∠BAD＋∠B＝∠CAD＋∠C B．AB－BD＝AC－CDC．AB＋BD＝AC＋CD D．AD＝BC6. 如图，∠AOB＝50°，OM平分∠AOB，MA⊥OA于点A，MB⊥OB于点B，则∠MAB等于()A．50°B．40°C．25°7. 如图，△ABC是等边三角形，DE∥BC.若AB＝10，BD＝6，则△ADE的周长为()A．4 B．12 C．18 D．308. 如图，在五边形ABCDE中，AB＝AC＝AD＝AE，且AB∥ED，∠EAB＝120°，则∠BCD的度数为()A．150°B．160°C．130°D．60°9. 如图所示的正方形网格中，网格线的交点称为格点. 已知A，B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形．．．．．，那么符合题意的点C的个数是()A. 6B. 7C. 8D. 910. “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在点O相连并可绕点O转动，点C固定，OC＝CD＝DE，点D，E可在槽中滑动．若∠BDE＝75°，则∠CDE的度数是()A．60°B．65°C．75°D．80°二、填空题11. 如图，在△ABC中，AB＝AC，D是AC上一点，且BC＝BD.若∠CBD＝46°，则∠A＝________°.12. 如图，直线a∥b，△ABC的顶点C在直线b上，边AB与直线b相交于点D.若△BCD是等边三角形，∠A＝20°，则∠1＝________．13. 一个等腰三角形的一边长是2，一个外角是120°，则它的周长是________．14. 如图所示，在△ABC中，DE是AC的垂直平分线，AE=5 cm，△ABD的周长为18 cm，则△ABC的周长为.15. 如图，BO平分∠CBA，CO平分∠ACB，MN过点O且MN∥BC，设AB＝12，AC＝18，则△AMN的周长为________．16. 如图，在△ABC中，若AB＝AC＝8，∠A＝30°，则S△ABC＝________．三、解答题17. 如图，在△ABC中，AB＝BD，根据图中的数据，求∠BAC的度数．18. 如图，在△ABC中，O是边AC上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交△ABC的外角平分线于点F.探究线段OE与OF的数量关系，并说明理由．19. 如图，已知Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，∠BAC的平分线分别交BC，CD于点E，F.求证：△CEF是等腰三角形．人教版八年级数学上册13.3 等腰三角形同步训练-答案一、选择题1. 【答案】A2. 【答案】B3. 【答案】D[解析] 在等腰三角形中，当一个锐角在未指明为顶角还是底角时，一定要分类讨论．①42°的角为等腰三角形的底角；②42°的角为等腰三角形的顶角，则底角为(180°－42°)÷2＝69°.所以底角为42°或69°.4. 【答案】B【解析】∵|x－4|＋y－8＝0，∴x－4＝0，y－8＝0，解得x＝4，y＝8.分两种情况讨论：①当4为腰时，根据三角形三边关系知4＋4＝8，∴这样的等腰三角形不存在；②当8为腰时，则有4＋8>8，这样能够组成等腰三角形，∴此三角形的周长是8＋8＋4＝20.5. 【答案】D[解析] 由∠BAD＋∠B＝∠CAD＋∠C可得∠ADB＝∠ADC，又∠ADB＋∠ADC＝180°，所以∠ADB＝∠ADC＝90°，又BD＝DC，由垂直平分线的性质可得AB ＝AC.由等式的性质，根据AB －BD ＝AC －CD ，AB ＋BD ＝AC ＋CD ，又BD ＝CD ，均可得AB ＝AC.选项D 不能得到AB ＝AC.6. 【答案】C[解析] ∵OM 平分∠AOB ，MA ⊥OA 于点A ，MB ⊥OB 于点B ，∴∠AOM ＝∠BOM ＝25°，MA ＝MB.∴∠OMA ＝∠OMB ＝65°.∴∠AMB ＝130°.∴∠MAB ＝12×(180°－130°)＝25°.故选C.7. 【答案】B[解析] ∵△ABC 为等边三角形，∴∠A ＝∠B ＝∠C ＝60°.∵DE ∥BC ，∴∠ADE ＝∠B ＝60°，∠AED ＝∠C ＝60°.∴△ADE 为等边三角形．∵AB ＝10，BD ＝6，∴AD ＝AB －BD ＝10－6＝4.∴△ADE 的周长为4×3＝12.8. 【答案】A[解析] ∵AB ∥ED ，∴∠E ＝180°－∠EAB ＝180°－120°＝60°. 又∵AD ＝AE ，∴△ADE 是等边三角形．∴∠EAD ＝60°.∴∠BAD ＝∠EAB －∠EAD ＝120°－60°＝60°.∵AB ＝AC ＝AD ，∴∠B ＝∠ACB ，∠ACD ＝∠ADC.在四边形ABCD 中，∠BCD ＝∠B ＋∠ADC ＝12(360°－∠BAD)＝12×(360°－60°)＝150°. 故选A. 9. 【答案】C10. 【答案】D[解析] ∵OC ＝CD ＝DE ，∴∠O ＝∠ODC ，∠DCE ＝∠DEC. ∴∠DCE ＝∠O ＋∠ODC ＝2∠ODC. ∵∠O ＋∠OED ＝3∠ODC ＝∠BDE ＝75°， ∴∠ODC ＝25°.∵∠CDE ＋∠ODC ＝180°－∠BDE ＝105°， ∴∠CDE ＝105°－∠ODC ＝80°.二、填空题11. 【答案】46[解析] ∵BC＝BD，∠CBD＝46°，∴∠C＝∠BDC＝12(180°－46°)＝67°.∵AB＝AC，∴∠ABC＝∠C＝67°.∴∠A＝46°.12. 【答案】40°[解析] 如图．∵△BCD是等边三角形，∴∠BDC＝60°.∵a∥b，∴∠2＝∠BDC＝60°.由三角形的外角性质和对顶角的性质可知，∠1＝∠2－∠A＝40°.13. 【答案】6[解析] 已知三角形的一外角为120°，则相邻内角度数为60°，那么含有60°角的等腰三角形是等边三角形．已知等边三角形的一边长为2，则其周长为6.14. 【答案】28 cm15. 【答案】30[解析] ∵MN∥BC，∴∠MOB＝∠OBC.∵∠OBM＝∠OBC，∴∠MOB＝∠OBM.∴MO＝MB.同理NO＝NC.∴△AMN的周长＝AM＋MO＋AN＋NO＝AM＋MB＋AN＋NC＝AB＋AC＝30.16. 【答案】16[解析] 如图，过点C作CD⊥AB，垂足为D，则△ADC是含30°角的直角三角形，那么DC＝12AC＝4，∴S△ABC＝12AB·DC＝12×8×4＝16.三、解答题17. 【答案】解：∵∠ADB＝30°＋40°＝70°，AB＝BD，∴∠BAD＝∠ADB＝70°.∴∠BAC＝∠BAD＋∠CAD＝100°.18. 【答案】解：OE＝OF.理由：∵MN∥BC，∴∠OEC＝∠BCE，∠OFC＝∠DCF.∵CE平分∠ACB，CF平分∠ACD，∴∠OCE＝∠BCE，∠OCF＝∠DCF.∴∠OEC＝∠OCE，∠OFC＝∠OCF.∴OE＝OC，OC＝OF.∴OE＝OF.19. 【答案】证明：∵∠ACB＝90°，∴∠B＋∠BAC＝90°.∵CD⊥AB，∴∠CAD＋∠ACD＝90°.∴∠ACD＝∠B.∵AE是∠BAC的平分线，∴∠CAE＝∠EAB.∵∠EAB＋∠B＝∠CEF，∠CAE＋∠ACD＝∠CFE，∴∠CFE＝∠CEF. ∴CF＝CE.∴△CEF是等腰三角形．。

12.3.1等腰三角形同步练习(人教版八年级上册)

ED CAF 12.3.1等腰三角形同步练习一、选择题1．等腰三角形的对称轴是（）A ．顶角的平分线B ．底边上的高C ．底边上的中线D ．底边上的高所在的直线2．等腰三角形有两条边长为4cm 和9cm ，则该三角形的周长是（） A ．17cm B ．22cm C ．17cm 或22cm D ．18cm 3．等腰三角形的顶角是80°，则一腰上的高与底边的夹角是（） A ．40° B ．50° C ．60° D ．30° 4．等腰三角形的一个外角是80°，则其底角是（） A ．100° B ．100°或40° C ．40° D ．80°5．如图1，C 、E 和B 、D 、F 分别在∠GAH 的两边上，且AB=BC=CD=DE=EF ，若∠A=18°，则∠GEF 的度数是（）A ．80°B ．90°C ．100°D ．108°如图1二、填空题6．等腰△ABC 的底角是60°，则顶角是________度． 7．等腰三角形“三线合一”是指___________．8．等腰三角形的顶角是n °，则两个底角的角平分线所夹的钝角是_________． 9．如图2，△ABC 中AB=AC ，EB=BD=DC=CF ，∠A=40°，则∠EDF•的度数是_____．如图2E CAHFG10．△ABC 中，AB=AC ．点D 在BC 边上（1）∵AD 平分∠BAC ，∴_______=________；________⊥_________；（2）∵AD 是中线，∴∠________=∠________；________⊥________；（3）∵AD ⊥BC ，∴∠________=∠_______；_______=_______． 11．△ABC 中，∠A=65°，∠B=50°，则AB ：BC=_________．12．已知AD 是△ABC 的外角∠EAC 的平分线，要使AD•∥BC ，•则△ABC•的边一定满足________． 13．△ABC 中，∠C=∠B ，D 、E 分别是AB 、AC 上的点，•AE=•2cm ，•且DE•∥BC ，•则AD=________．三、解答题15．如图，CD 是△ABC 的中线，且CD=12AB ，你知道∠ACB 的度数是多少吗？由此你能得到一个什么结论？请叙述出来与你的同伴交流．16．如图，在四边形ABCD 中，AB=AD ，CB=CD ，求证：∠ABC=∠ADC.17．如图，△ABC 中BA=BC ，点D 是AB 延长线上一点，DF ⊥AC 于F 交BC 于E ，• 求证：△DBE 是等腰三角形．DCABDCAB答案:一、1．D 2．B 3．A 4．C 5．B二、6．60 7．等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合 8．（90+ 12n ）° 9．70° 10．略 11．1 12．AB=AC 13．2cm 14．30海里三、15．∠ACB=90°．结论：若一个三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形16．连接BD ，∵AB=AD ，∴∠ABD=∠ADB ．∵CB=CD ，∴∠CBD=∠CDB ． ∴∠ABC=∠ADC 17．证明∠D=∠BEDED CABF。

人教八年级数学上册13.3.1等腰三角形一课一练(含答案)

13. 3.1 等腰三角形同步练习一．单项选择。

1.等腰三角形一腰上的高与另一腰的夹角是50°，则这个等腰三角形的底角为( )A．70°B．20° C.70°或20°D．40°或140°2.如图13 -3 -1-13，在△ABC中．AB=AC，∠BAC= 108°，∠ADB= 72°．DE：平分∠ADB，则图中等腰三角形的个数是( )A.3B.4C.5D.63.如图13 -3 -1-17，AB∥CD,AD= CD，11= 65°，则∠2的度数是( ) A．50°B．60°C．65° D.70°4.如图13 -3 -1-18，AD，CE分别是△ABC的中线和角平分线．若AB=AC，二CAD=20°，则∠ACE的度数是( )A.20°B.35°C.40°D.70°二、填空题5.在△ABC中，AB=AC，∠BAC=40°，点D在直线BC上，CD= CA，则∠BDA为度．6.如图13 -3 -1-14，△ABC中，AB= AC，D是AC上一点且BC= BD，若∠CBD= 46°．则∠A= °7.如图13 -3 -1-19，在△ABC中．AB=AC.点C为圆心，以CB长为半径作圆弧．交AC的延长线于点D，连接BD.若∠A= 32°，则∠CDB的大小为度．8.我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=21，则该等腰三角形的顶角为度．9.已知等腰三角形的一个外角为130°，则它的顶角的度数为.10.如图13 -3 -1- 20，△ABC中，点D在BC边上，BD=AD=AC，E为CD的中点．若∠CAE= 16°，则∠B为度．三．解答题1.如图13 -3 -1-16，在△ABC中，AB=AC，∠BAC= 36°，BD是∠ABC的平分线，交AC于点D，E是AB的中点，连接ED并延长，交BC的延长线于点F，连接AF，求证：(1) EF ⊥AB；(2)△ACF为等腰三角形．2.如图13 -3 -1- 21，AD平分∠BAC，AD⊥BD，垂是为点D，DE∥AC.求证：△BDE是等腰三角形．3.如图13-3-1-22，已知在△ABC中，AD⊥BC于点D，E是AB的中点．(1)E点一定在的垂直平分线上；(2)如果AD=16 cm，AC= 20 cm，F点在AC边上，且从A点向C点运动，速度是2 cm/s，求当运动几秒钟时，△ADF是等腰三角形．4.数学课上，张老师举了下面的例题：例1：等腰三角形ABC中，∠A=110°，求∠B的度数．（答案：35°）例2：等腰三角形ABC中，∠A= 40°，求∠B的度数．（答案：40°或70°或100°）张老师启发同学们进行变式，小敏编了如下一题：变式：等腰三角形ABC中，∠A= 80°，求∠B的度数．(1)请你解答以上的变式题；(2)解(1)后，小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同，如果在等腰三角形ABC中，设∠A=x°，当∠B有三个不同的度数时，请你探索x的取值范围．答案：一．1.C ①如图1．当该等腰三角形为钝角三角形时，∵一腰上的高与另一腰的夹角是50°．∴底角=21×（90°-50°）= 20°，②如图2，当该等腰三角形为锐角三角形时，∵一腰上的高与男一腰的夹角是50°，∴底角=21×[180°-（90°-50°）]=70°，故选c．2.C∵AB=AC，∴△ABC是等腰三角形，又∠BAC=108°,∴∠C=∠B=2108180︒-︒=36°，∴∠BAD=180°-∠B-∠ADB=180°-36°-72°=72°=∠ADB．∴AB=BD，∴△ADB是等腰三角形，∴∠DAC=∠BAC-∠BAD=108°-72°=36°=∠C．∴CD=AD，∴△ACD是等腰三角形，∵DE平分∠ADB，∴∠BDE=∠ADE=36°=∠B，∴BE=ED，∴△EBD是等腰三角形，∵∠AED=180°-72°-36°=72°=∠EAD，∴ED=AD，∴△AED是等腰三角形.∴共有5个等腰三角形．故选C．3.A∵AB∥CD,∴∠1= ∠ACD=65°,∵AD=CD．∴∠DCA=∠CAD= 65°．∴∠2的度数是180°-65°-65°= 50°.故选A．4.B ∵AD是△ABC的中线，AB=AC,∠CAD=20°,∴∠CAB=2∠CAD= 40°，∠B=∠ACB=21(180°-∠CAB)= 70°.∵CE是△ABC的角平分线，∴∠ACE = 1.ACB= 35°．故选B．二．1.答案55或35解析①如图①，当点D在CB的延长线上时，∵AB=AC．∠BAC= 40°．∴∠ABC= ∠C=70°,∵CA= CD，∠C= 70°．∴∠D= ∠CAD= 55°．②如图2，当点D在BC的延长线上时，∵AB =AC, ∠BAC = 40°,∴∠ABC= ∠ACB= 70°,∵CA= CD, ∠ACB=70°, ∠ACB= ∠D+∠CAD,∴∠D=21×70°=35°,故答案为55或35.2.答案46解析∵BC=BD．∠C8D=46°，∴∠c=∠BDC=21×（180°-46°）=67°，∵AB=AC．∴∠ABC= ∠C=67°,∴∠A= 46°,故答案为46.3.答案37解析∵AB=AC,∠A=32°,∴∠ABC= ∠ACB=74°,又∵BC=DC,∴∠CDB=∠CBD=21∠ACB=37°，故答案为37.4.答案36解析∵△ABC中,AB =AC,∴∠B=∠C．∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角的“特征值”，记作k，若k=21，则∠A：∠B=1:2，所以5∠A= 180°,∴∠A= 36°，故答案为36.5.答案50°或80°解析由等腰三角形的一个外角为130°知一个内角为50°当50°为顶角时，其他两角都为65°、65°，当50°为底角时，他两角为50°、80°，所以等腰三角形的顶角力50°或80°．故案为50°或80°.6.答案37解析∵AD=AC，点E是CD的中点，∴AE⊥CD,∴∠AEC= 90°,∴∠C=90°-∠CAE=74°,∵AD=AC．∴∠ADC= ∠C=74°,∵AD=BD,∴2∠B-∠ADC=74°,∴∠B=37°．故答案为37.三．1.证明(1)∵AB=AC,∠BAC=36°,∴∠ABC=72°,又∵BD是∠ABC的平分线'∴∠ABD= 36°，∴∠BAD= ∠ABD,∴AD=BD．又∵E是AB的中点，∴DE⊥AB,即EF⊥AB.(2)∵EF⊥AB,AE=BE,∴FE垂直平分AB,∴AF=BF,∴∠BAF= ∠ABF,又∵∠ABD=∠BAD,∴∠FAD= ∠FBD=36°,又∵∠ACB=72°,∴∠AFC= ∠ACB-∠CAF=36°,∴∠_CAF= ∠AFC=36°,∴AC=CF．即△ACF为等腰三角形．2.证明如图，∵DE∥AC，∴∠1= ∠3.∵AD平分∠BAC,∴∠1= ∠2，∴∠2= ∠3.∵AD⊥BD，∴∠2+∠B= 90°, ∠3+∠BDE= 90°,∴∠B= ∠BDE，∴BE=DE，∴△BDE是等腰三角形．3.解析(1)∵AD⊥BC，∴∠ADB= 90°,∵E是AB的中点，∴AE=DE=BE，鹳AE=DE，BE =DE，AE =BE，∴E点一定在AD或BD或AB的垂直平分线上，故填AD或BD或AB.(2)当FA=AD=16 cm时，t=2FA=8 s，当FA= FD时，∠FAD= ∠ADF，又∵∠FAD+∠C= ∠ADF+∠FDC=90°,∴∠C= ∠FDC．∴FD =FC，∴FA=FC=21AC=10cm,∴t=2FA=5 s,当DF=AD时，点F不存在．综上所述，当点F运动5s或8s时，△ADF是等腰三角形．4.解析(1)若∠A为顶角，则∠B=（180°-∠A）÷2=50°；若∠A为底角，∠B为顶角，则∠B=180°-2×80°= 20°；若∠A为底角，∠B为底角，则∠B= 80°，故∠B= 50°或20°或80°．(2)分两种情况：①当90≤x<180时，∠A只能为顶角，∴∠B的度数只有一个：②当0<x<90时，若∠A为顶角，则∠B=）（2x180-︒；若∠A为底角，∠B为顶角，则∠B=( 180-2x)°；若∠A为底角，∠B为底角，则∠B=x°，当2180x-≠180- 2x且180- 2x≠x且2180x-≠x，即x≠60时，∠B有三个不同的度数．综上所述，当O<x<90且x≠60时，∠B有三个不同的度数．。

人教版八年级上册数学13.3.1 等腰三角形同步练习

13.3.1等腰三角形同步习题一、单选题1．如图，在△ABC中，∠ABC=45°，AC=5，F是高AD和BE的交点，则BF的长( )A．7 B．6 C．5 D．42.一个等腰三角形的两边长分别是 3 和 7，则它的周长为（）A．17 B．15 C．13 D．13 或 173.如图，在等腰三角形ABC 中，AB＝AC，AB 的垂直平分线MN 交AC 于点D，连接BD，∠A＝45°，则∠DBC 的度数为（）A．22.5° B．25° C．27.5° D．30°4．如图，在△ABC中， AB=AC，∠A=36° ，BD、CE分别是∠ABC、∠BCD 的角平分线，则图中的等腰三角形有（）A．5个B．1个C．3个D．2个5．如果三角形二条边的中垂线的交点在第三条边上，那么，这个三角形是（）A．直角三角形B．锐角三角形C．钝角三角形D．等边三角形6．等边△ABC，在平面内找一点P，使△PBC、△PAB、△PAC均为等腰三角形，具备这样条件的P点有多少个？（）A．1个B．4个C．7个D．10个7.等腰三角形的一个顶角为 150°，则它的底角为（）A ．30°B ．15°C ．30° 或 15°D ．50°8.如图，在△ABC 中，AB ＝AC ，AD 是△ABC 的中线．若∠CAD ＝25°，则∠B的度数是（）A ．25°B ．55°C ．65°D ．75°二、填空题1．在ABC ∆中，AB AC =，AC 的垂直平分线交AC 于D ，交BC 于E ，若ABE ∆的周长为10，6BC =，则=AC ______.2．如图，△ABC 中，AD 平分∠BAC，CD⊥AD，若∠ABC 与∠ACD 互补，CD=8，则BC 的长为_____________．3．如图，上午8时，一条船从A 处出发，以15海里／时的速度向正北航行，10时到达B 处，从A 、B 望灯塔C ，测得∠NAC＝42°，∠NBC=84°，则从B 处到灯塔C 的距离_______．4．一个等腰三角形的周长是44厘米，三边长度之比是3:5:3，这个等腰三角形的底边长是_______厘米．5.小明有两根长度分别为4cm 和9cm 的木棒，他想再取一根木棒，组成等腰三角形，那么等腰三角形的周长为 cm6．如图，在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，过点O 作EF ∥BC 交AB 于E ，交AC 于F ，过点O 作OD ⊥AC 于D ，下列四个结论：①EF ＝BE +CF ；②∠BOC ＝90°+∠A ；③点O 到△ABC 各边的距离相等；④设OD ＝m ，AE +AF ＝n ，则S △AEF ＝mn ．其中正确的结论是．（填序号）三、解答题1．如图，在ABC 中，AB AC =，D 为BC 的中点，DE AB ⊥，DF AC ⊥，垂足为E 、F ，求证：DE DF =．2．如图，△ABC 中，∠BAC=90度，AB=AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD=2CE ．3．在△ABC中，AB=AC，AC上的中线BD把三角形的周长分为24㎝和30㎝的两个部分，求三角形的三边长．4.如图，在△ABC 中，AB＝AC，∠A＝36°，DE 是AC 的垂直平分线，求证：△BCD 是等腰三角形.5.如图，在△ABC 中，∠ABC 和∠ACB 的平分线交于点E，过点E 作MN∥BC 交AB 于M，光AC 于N，若△ABC、△AMN 周长分别为 13cm 和 8cm．（1）求证：MN＝BM+CN；（2）线段BC 的长6．如图，直线l1，l2交于点B，A是直线l1上的点，在直线l2上寻找一点C，使△ABC是等腰三角形，请画出所有的等腰三角形．7．等腰△ABC中，AB＝AC，∠ACB＝72°，（1）如图1，若BD⊥AC于D，求∠ABD的度数；（2）如图2，若CE平分∠ACB，求证：AE＝BC．。

《等腰三角形》同步练习题2021-2022学年八年级数学人教版上册

2021-2022学年人教新版八年级上学期《13.3 等腰三角形》同步练习一．选择题（共6小题）1．如图，已知等腰△ABC ，AB ＝AC ，若以点B 为圆心，BC 长为半径画弧，交腰AC 于点D ，则下列结论一定正确的是（）A.AD ＝CDB.AD ＝BDC.∠DBC ＝∠BACD.∠DBC ＝∠ABD2．如图，△ABC 是等边三角形，D 是AC 边的中点，延长BC 到点E ，使CE ＝CD ，连接DE ，则下列结论错误是（）A ．CE ＝AB B ．BD ＝EDC ．∠BDE ＝∠DCED ．∠ADE ＝120° 3．在△ABC 中，AB ＝BC ，两个完全一样的三角尺按如图所示摆放，BC 上，另一组较长的对应边的顶点重合于点P ，则下列结论错误的是（）A ．AB ＝2ADB ．BP 平分∠ABC C ．BD 垂直平分AC D ．AD ＝DC4．如图,在Rt ABC 中,90,A CM ∠=︒平分ACB ∠交AB 于点M ,过点M 作MN BC 交AC 于点N ,且MN 平分AMC ∠.若1AN =,则BC 的长为( )A.4B.6C.D.85．如图，在△ABC 中，BC 的垂直平分线分别交BC ，AB 于点D 、E ，BE ＝7，则CE 的长是（） A ．5 B ．6 C ．7 D ．86．如图，△ABC 是等边三角形，AD 是角平分线，下列结论不正确的是（）A ．AD ⊥BCB ．EF ＝FDC ．BE ＝BD D ．AE ＝AC 二．填空题（共5小题）7．等腰三角形的两边长分别为10和5，则这个等腰三角形的周长为．8．△ABC 是等腰三角形，若有一个角等于100°，则另两个角度数分别为．9．如图，线段AB 、BC 的垂直平分线l 1、l 2相交于点O ，若∠1＝39°，则∠AOC ＝．10．如图,在ABC 中,,ED BC ABC ∠和ACB ∠的平分线分别交ED 于点,G F .若2,4FG ED ==,则EB DC +的值为______________.11．如图，AC=BC=6cm，∠B=15∘，AD⊥BC于点D，则AD的长为________．三．解答题（共5小题）12．已知等腰三角形的腰长为8cm，一腰上的中线把等腰三角形分成周长之差为2cm的两个三角形，求等腰三角形的周长．13．如图，已知AD平分∠EAC，且AD∥BC，求证AB＝AC．14．如图，是屋架设计图的一部分，点D时斜梁AB的中点，立柱BC、DE垂直于横架AC，AB=7.4m，∠A=30∘，立柱BC、DE需要多长？问题分析：Rt△ABC中，∠A=30∘，那么BC与AB有何关系？同样DE与AD有何关系？15．如图，在△ABC中，∠C＝90°，∠B＝30°，AB的垂直平分线ED交AB于点E，交BC于点D，若CD＝3，求BD的长．16．如图，四边形ABCD中，AB∥CD，点E为CD上一点，连接BE，AE，且BE、AE分别平分∠ABC、∠BAD．求证：CD＝AD+BC．。

数学人教版八年级上册等腰三角形课后练习

等腰三角形课后练习题班级姓名一.填空题等腰三角形的底角是35°,顶角为________°.等腰三角形的一个内角为100°,那么它的其余各角的度数分别为_______3.等腰三角形的顶角等于一个底角的4倍时,那么顶角为_________度等腰三角形中,AC长是BC长的2倍,三角形的周长是40,那么AB的长为.5.如图，A、D、C在一条直线上AB＝BD＝CD,∠C＝40°,那么∠ABD＝°第6题P为等边△ABC所在平面上一点,且△PAB,△PBC,△PCA都是等腰三角形,这样的点P有______个.二.单项选择题1.不满足△ABC是等腰三角形的条件是()A.∠A:∠B:∠C=2:2:1B.∠A:∠B:∠C=1:2:5C.∠A:∠B:∠C=1:1:2D.∠A:∠B:∠C=1:2:2等腰三角形的一个角等于20°,那么它的另外两个角等于()°,140°°,140°或80°,80°°,80°°,80°3.以下命题正确的选项是()A.等腰三角形的对称轴是高B.等腰三角形的对称轴是底边上的中线C.直角三角形都不是轴对称图形D.任何一个角都是轴对称图形4.如图,在△ABC中,AB＝AC,CD⊥AB于D,那么以下判断正确的选项是()A.∠A＝2∠BCDB.∠A＝∠BC.∠A＝∠DCBD.∠A＝∠ACD5.等腰三角形一底角为30°,底边上的高为第4题9cm,那么腰长为___cm．[]36.等腰三角形两边分别为30厘米和20厘米,那么它的第三边长为或20cm()三.证明题1.如图,：点D,E在△ABC的边BC上,AB=AC,AD=AE求.证：BD=CE第1题2.如图：△ABC中,AB=AC,PB=PC．求证：AD⊥BC第2题等腰三角形课后练习题参考答案一.填空题°2.40°和40°或20二.选择题三．证明题证明：过点A作AM⊥BC于点M∵AD=AE,∴DM=EM∵AB=AC,∴BM=CM∴BM－DM=CM－EM∴BD=CE第1题.证明：在△ABP和△ACP中∵AB=AC,BP=PC,AP=AP∴△ABP≌△ACP(SSS)∴∠BAP=∠CAP∴AD⊥BC(等腰三角形顶角平分线又是底边的垂线)第2题。

数学：《等腰三角形》同步练习1(人教版八年级上)

数学：《等腰三角形》同步练习1（人教版八年级上）1. 如图，点P 是∠BAC 的平分线AD 上一点，PE ⊥AC 于点E ．已知PE=3，则点P 到AB 的距离是（）A ．3B ．4C ．5D ．6＆2. 在△ABC 中，∠ACB =90°,BE 平分∠ABC ，DE ⊥AB 于D ，如果AC =3 cm ，那么AE +DE 等于（） A.2 cmB.3 cmC.4 cmD.5 cm＆3. 如图所示，在△ABC 中，AC 的垂直平分线交AC 于E ，交BC 于D ，△ABD 的周长是12 cm ，AC =5cm ，△ABC 的周长是__________cm4. 如图所示是一个风筝骨架.为使风筝平衡，须使∠AOP =∠BOP .我们已知PC ⊥OA ，PD ⊥OB ，那么PC 和PD满足条件，才能保证OP 为∠AOB 角平分线＆5. 如图所示，已知BE ⊥AC 于E ，CF ⊥AB 于F ，BE 、CF 相交于点D ，若BD =CD . 求证：AD 平分∠BAC .第1题图第2题图第4题图第5题图第3题图6.已知：如图，AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC＝DC.你能说明BE与DF相等吗？※7. 已知：如图，AB=AC=12 cm，AB的垂直平分线分别交AC、AB于D、E，△ABD的周长等于29 cm，求DC的长.＃8. 如图所示，一辆汽车在笔直的公路AB上由A向B行驶，M，N分别是位于公路AB两侧的村庄，当汽车行驶到哪个位置时，与村庄M，N的距离相等第二课时＃1.下列图形中，不一定是轴对称图形的是（）A．等腰三角形 B．等腰直角三角形C．等边三角形 D．直角三角形＆2. 若等腰三角形的顶角的外角是80°，那么它的底角是____________．A BCDEF12第6题图第8题图第7题图※3. 如图，B 、D 、F 在AN 上，C 、E 在AM 上，且AB=BC=CD ，EC=ED=EF ，∠A=20°，则∠FEM 度数是．＆4. 在△ABC 中，AB=AC ，∠A=36°，角平分线BE 与CD 相交于点F ，那么图中等腰三角形有（） A ．6个 B ．7个 C ．8个 D ．9个＃5. 如图，已知AC=CD=DA=CB=DE ，则此图中共有 ______ 个等腰三角形．※6..如图所示，在△ABC 中，BO 平分∠ABC ，CO 平分∠ACB ，MN ∥BC ，MN 经过点O ，若AB=12,AC=18,那么△AMN 的周长是＆7. 已知：∠CAE 是△ABC 的外角，∠1=∠2，AD ∥BC （如图）．求证：AB=AC ．8. 在△ABD 中，C 是BD 上的一点，且AC ⊥BD ，AC=BC=CD ．（1）求证：△ABD 是等腰三角形．（2）求∠BAD 的度数．＃9. 已知，如图，点B 、F 、C 、E 在同一直线上，AC 、DF 相交于点G ，AB ⊥BE ，垂足为B ，DE ⊥BE ，垂足为E ，且AC ＝DF ，BF ＝CE 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

13.3.1 等腰三角形（1）
一、选择题：
1、等腰三角形的对称轴是（）
A．顶角的平分线 B．底边上的高
C．底边上的中线 D．底边上的高所在的直线
2、等腰三角形有两条边长为4cm和9cm，则该三角形的周长是（）
A．17cm B．22cm C．17cm或22cm D．18cm
3、等腰三角形的一个外角是80°，则其底角是（）
A．100° B．100°或40° C．40° D．80°
4、如图，在△ABC中，AB=AC，点D、E在BC上，连接AD、AE，如果只添加一个条件使∠DAB=∠EAC，则添加的条件不能为（）
A． BD=CE B． AD=AE C． DA=DE D． BE=CD
5、等腰三角形的一个角是80°，则它顶角的度数是（）
A．80° B．80°或20°C．80°或50°D．20°
6、已知实数x，y满足，则以x，y的值为两边长的等腰三角形的周长是（）
A． 20或16 B． 20 C． 16 D．以上答案均不对
二、填空题：
1、在△ABC中，AB=AC,BD是角平分线，如果∠A=40 o，那么∠BDC= .
2、在△ABC中，点D在CB上，且AB=AD=CD,∠C=25 o,那么∠BAC= .
3、如图，在△ABC中，AB=AD=DC，∠BAD=32°，则∠BAC=_________．
第3题第4题第5题第6题
4、如图，等腰△ABC中，AB=AC，AD平分∠BAC，点E是线段BC延长线上一点，连接AE，点C在AE的垂直平分线上，若DE=10cm，则AB+BD= _________ cm．
5、如图，在△ABC中，AB=AC，CD平分∠ACB，∠A=36°，则∠BDC的度数为_________．
6、如图，在△ABC中，AB=AC，点D为BC边的中点，∠BAD=20°，则∠C=_________ ．
三、解答题：
1、已知△ABC中AB=AC，AD⊥BC于D，若△ABC、△ABD的周长分别是20cm和16cm，•求AD的长．
2、已知：如图，在等腰△ABC中，AB=AC，O是底边BC上的中点，OD⊥AB于D，OE⊥AC 于E．
求证：AD=AE．
3、如图，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．
求证：（1）△ABD≌△ACD；（2）BE=CE．
参考答案
一、选择题：
１、D 2、B 3、C 4、C 5、B 6、B
二、填空题：
1、75°
2、105°
3、69°
4、10
5、72°
6、70°
三、解答题：
１、6cm
2、证明：∵AB=AC，
∴∠B=∠C．
∵OD⊥AB，OE⊥AC，
∴∠ODB=∠OEC=90°．
∵O是底边BC上的中点，
∴OB=OC，
在△OBD与△OCE中，
∴△OBD≌△OCE（AAS）．
∴BD=CE．
∵AB=AC，
∴AB﹣BD=AC﹣CE．
即AD=AE．
3、证明：（1）∵D是BC的中点，
∴BD=CD，
在△ABD和△ACD中，，
∴△ABD≌△ACD（SSS）；…（4分）
（2）由（1）知△ABD≌△ACD，
∴∠BAD=∠CAD，即∠BAE=∠CAE，
在△ABE和△ACE中，
∴△ABE≌△ACE （SAS），
∴BE=CE（全等三角形的对应边相等）．。