矩阵与变换练习题
矩阵与变换二阶矩阵平面逆变换等二轮复习专题练习(一)含答案新教材高中数学

高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关
检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.若22
11
x x x y y y =--,则______x y +=(汇编年高考上海卷(理)) 2.已知线性方程组的增广矩阵为116 12a ⎛⎫ ⎪⎝⎭,若该线性方程组解为42⎛⎫ ⎪⎝⎭
,则实数a =_1-__. 评卷人
得分 二、解答题
3.选修4—2:矩阵与变换
已知二阶矩阵M 有特征值1λ=及对应的一个特征向量111⎡⎤=⎢⎥-⎣⎦e ,且M 11⎡⎤⎢⎥⎣⎦
=
31⎡⎤⎢⎥⎣⎦
.求矩阵M .
4.二阶矩阵M 对应的变换将点(1,1)-与(2,1)-分别变换成点(1,1)--与(0,2)-.
(1)求矩阵M 的逆矩阵1-M ;
(2)设直线l 在变换M 作用下得到了直线:24m x y -=,求l 的方程.。
矩阵与变换练习题

矩阵与变换编写:陈爱兵 审核:黄爱华1.由曲线22221x y 变换为曲线221812x y ,变换矩阵为____________; 2.已知矩阵31 cos60 sin 6022,31sin60 cos60 22A B ,则先A 后B 的变换所对应的矩阵是______________;3.若81 1 10 10 1x ,则12log x =__________; 4.若点22,A 在矩阵cos sin sin cos αααα对应的变换作用下得到的点为(1,0),则α=________; 5.若矩阵 a b A c d 有两个不等的特征值,m n ,则22m n =___________;6.在密码学中,常用二阶矩阵对信息进行加密。
现在我们先将英文字母数字化1,2,,26a b z ,发送方要传递的信息是:come on 。
双方约定的矩阵是5 17 3,则发送的密码应该是_______________;7.已知在矩阵M 的作用下点(1,2)A 变成了点(11,5)A ,点(3,1)B 变成了点(5,1)B ,点(,0)C x 变成了(,2)C y ,求矩阵M 并求,x y 的值。
8.若cos sin (R)sin cos xθθθθθ,试求2()23f x x x 的最值。
9.已知矩阵(), 1,2x A f x B x x C a ,若A BC ,求函数()f x 在1,2上最小值。
10.已知矩阵A 对应的变换是先将某平面图形上的点的横坐标保持不变,纵坐标变为原来的2倍,再将所得图形绕原点按顺时针方向旋转90°。
⑴求矩阵A 及A 的逆矩阵B ;⑵已知矩阵 3 32 4M,求M 的特征值和特征向量; ⑶若81α在矩阵B 的作用下变换为β,求50M β(运算结果用指数式表示)。
11.在直角坐标系中,已知△ABC 的顶点坐标为A(0,0),B(1,1),C(0,2),求△ABC 在矩阵MN 作用下变换所得到的图形的面积,这里矩阵0 10 1N=1 0 1 0M ,-⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦。
矩阵与变换二阶矩阵平面逆变换等二轮复习专题练习(一)带答案人教版高中数学新高考指导

高中数学专题复习《矩阵与变换二阶矩阵平面逆变换等》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上 评卷人得分 一、填空题1.若矩阵A 有特征值122,1λλ=-=,它们所对应的特征向量分别为10i ⎡⎤=⎢⎥⎣⎦和01j ⎡⎤=⎢⎥⎣⎦,则矩阵A =______________. 2.有下列四种变换方式:①向左平移4π,再将横坐标变为原来的21; ②横坐标变为原来的21,再向左平移8π; ③横坐标变为原来的21,再向左平移4π; ④向左平移8π,再将横坐标变为原来的21; 其中能将正弦曲线x y sin =的图像变为)42s i n (π+=x y 的图像的是______________ 评卷人得分 二、解答题3.选修4—2:矩阵与变换已知点M (3,-1)绕原点按逆时针旋转90°后,且在矩阵02a b ⎡⎤=⎢⎥⎣⎦A 对应的变换作用下,得到点N (3,5), 求a ,b 的值.4.选修4-2:矩阵与变换在平面直角坐标系xOy 中,直线:210l x y ++=在矩阵23a M b -⎡⎤=⎢⎥⎣⎦对应的变换作用下得到直线:m x 20y --=,求实数a 、b 的值.将上述结果代入直线l 的方程得()2321066x ay bx y ab ab ''-+''+++=++,5.已知矩阵M 221a ⎡⎤=⎢⎥⎣⎦,其中R a ∈,若点(1,2)P -在矩阵M 的变换下得到点(4,0)P '-(1)求实数a 的值;(2)求矩阵M 的特征值及其对应的特征向量.6. 若点A (2,2)在矩阵M= ⎢⎣⎡ααsin cos ⎥⎦⎤-ααc oss in 对应变换的作用下得到的点为B (-2,2),求矩阵M 的逆矩阵。
(本小题满分10分)7.已知二阶矩阵A 有特征值31=λ及其对应的一个特征向量111轾犏=犏臌α,特征值12-=λ及其对应的一个特征向量211轾犏=犏-臌α,求矩阵A 的逆矩阵1A -.8.变换1T 是逆时针旋转2π的旋转变换,对应的变换矩阵是1M ;变换2T 对应用的变换矩阵是21101M ⎡⎤=⎢⎥⎣⎦。
矩阵与变换二阶矩阵平面逆变换等强化训练专题练习(三)带答案人教版高中数学

高中数学专题复习《矩阵与变换二阶矩阵平面逆变换等》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上 评卷人得分 一、填空题1.已知矩阵27b A a -⎡⎤=⎢⎥-⎣⎦的逆矩阵是273a B ⎡⎤=⎢⎥⎣⎦,则=+b a . 2.已知2和3是矩阵25m A n ⎡⎤=⎢⎥⎣⎦的特征值,则A =_____; 1A -=_____。
2()(2)25f n n m λλλ=-++-30n m =⎧⎨=⎩ 20,53A ⎡⎤=⎢⎥⎣⎦ ,11025163A -⎡⎤⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦ 评卷人得分 二、解答题3. (本小题14分)设矩阵0 0ab ⎡⎤=⎢⎥⎣⎦M (其中0,0a b ><). (1)若2,3a b ==,求矩阵M 的逆矩阵-1M ;(2)若曲线22:1C x y +=在矩阵M 所对应的线性变换作用下得到曲线2/2:14x C y +=,求,a b 的值.4.已知矩阵⎥⎦⎤⎢⎣⎡-=1001A ,1201B -⎡⎤=⎢⎥⎣⎦. (1)若点P 在矩阵B 的变换下得到点)1,3('-P ,求点P 的坐标;(2)把直线02:=++y x l 先进行矩阵A 所对应的变换,再进行矩阵B 所对应的变换得到直线'l ,求直线'l 的方程.5.已知曲线22:1C x y +=,对它先作矩阵A =⎣⎢⎡⎦⎥⎤1 00 2对应的变换,再作矩阵B=⎣⎢⎡⎦⎥⎤0 b 1 0对应的变换,得到曲线22:14x C y +=.求实数b 的值。
6.求曲线C :xy=1在矩阵⎥⎦⎤⎢⎣⎡-=1111M 对应的变换作用下得到的曲线C 1的方程。
7.已知矩阵11A ⎡=⎢-⎣ a b ⎤⎥⎦,A 的一个特征值2λ=,其对应的特征向是是121α⎡⎤=⎢⎥⎣⎦. (1)求矩阵A ; (2)若向量74β⎡⎤=⎢⎥⎣⎦,计算5A β的值.8.在平面直角坐标系xOy 中,直线20x y ++=在矩阵14a M b ⎡⎤=⎢⎥⎣⎦对应的变换作用下得到直线:40m x y --=,求实数,a b 的值.【参考答案】***试卷处理标记,请不要删除评卷人得分 一、填空题1.82. 评卷人得分 二、解答题3. (1)01 2103-⎤⎡⎥⎢=⎥⎢⎣⎦1M ; ………………………7分 (2)2,1a b ==. ………………………14分4.(1))1,1(-P ; (2)02:'=++y x l .5.6.7.8.。
矩阵与变换二阶矩阵平面逆变换等考前冲刺专题练习(三)带答案新教材高中数学

高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关
检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.圆221x y +=在矩阵1300⎡⎤⎢⎥⎣⎦
对应的变换作用下的曲线方程为___________. 2.已知 1 04 31 2 4 1-⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦
B , 则矩阵B= . 评卷人
得分 二、解答题
3.已知矩阵213122A -⎡⎤⎢⎥=⎢⎥-⎣⎦
(Ⅰ)求矩阵A 的逆矩阵B ;
(Ⅱ)若直线l 经过矩阵B 变换后的直线方程为730x y -=,求直线l 的方程.
4.设M 是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变。
矩阵与变换二阶矩阵平面逆变换等考前冲刺专题练习(二)含答案人教版高中数学考点大全

依题意可得 , 或 而由 可得 .………6分
故 , .…………………………………………10分
5.解:由题意得 ,…………………………………………………5分
, …………………………10分
6.
7.
8.解:设 为曲线 上的任意一点,在矩阵A变换下得到另一点 ,
则有 ,…………………………………4分
8.求曲线 : 在矩阵 对应的变换下得到的曲线 的方程。
【参考答案】***试卷处理标记,请不要删除
评卷人
得分
一、填空题
1.A.解析:设直线上任一点经变换后,变为,则,又P′在直线上,∴,从而即与是同一条直线∴,从而.
解析:A.解析:设直线 上任一点 经变换后,变为 ,则 ,又P′在直线 上,
∴ ,从而
即 所以 ……………………………………………………8分
又因为点P在曲线 上,所以 ,
故有 即所得曲线方程 .…………………………………………………10分
评卷人
得分
二、解答题
3.选修4—2:矩阵与变换
已知矩阵 .
(1)求矩阵A的特征值和特征向量;(2)若 ,求 .
4.设曲线 在矩阵 对应的变换作用下得到的曲线为 ,求矩阵M的逆矩阵 .
5.已知矩阵 , ,求满足 的二阶矩阵 .
6.试用逆矩阵解二元一次方程组
[来源:学科网]
7.已知 为矩阵 属于λ的一个特征向量,求实数a,λ的值及A2。
即 与 是同一条直线
∴ ,从而 .
2.易得……3分,在直线上任取一点,经矩阵变换为点,则,∴,即……8分代入中得,∴直线的方程为……………10分
解析:易得 ……3分,在直线 上任取一点 ,经矩阵 变换为
矩阵与变换二阶矩阵平面逆变换等强化训练专题练习(四)带答案人教版高中数学考点大全

高中数学专题复习《矩阵与变换二阶矩阵平面逆变换等》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 评卷人得分一、填空题1.已知A(0,0),B (1,3),C(0,2),△ABC 在矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-21232321对应的变换作用下得到的图形的面积为 .2.在直角坐标系中,已知椭圆2241x y +=,矩阵阵⎥⎦⎤⎢⎣⎡=0110M ,0210N ⎡⎤=⎢⎥⎣⎦,求在矩阵MN 作用下变换所得到的图形的面积.评卷人得分二、解答题3.选修4—2:矩阵与变换若矩阵012a ⎡⎤=⎢⎥-⎣⎦M 把直线:20l x y +-=变换为另一条直线:40l x y '+-=,试求实数a 值.4.已知121217⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,M β,计算5M β.5.已知曲线22:1C x y +=,对它先作矩阵A =⎣⎢⎡⎦⎥⎤1 00 2对应的变换,再作矩阵B=⎣⎢⎡⎦⎥⎤0 b 1 0对应的变换,得到曲线22:14x C y +=.求实数b 的值。
6.给定矩阵⎢⎣⎡=32A ⎥⎦⎤01,.22⎥⎦⎤⎢⎣⎡-=B(1)求A 的特征值21,λλ及对应的特征向量21,αα; (2)求.4B A7.已知矩阵 1 22 x ⎡⎤=⎢⎥⎣⎦M 的一个特征值为3,求另一个特征值及其对应的一个特征向量.[来8.已知2143M -⎛⎫= ⎪-⎝⎭,4131N -⎛⎫= ⎪-⎝⎭,求二阶方阵X ,使MX N =.【参考答案】***试卷处理标记,请不要删除评卷人得分一、填空题1.2.,..................4分设为椭圆上任一点,它在的作用下所对应的点为,则,..................6分∴,即, (10)分代入得, (12)分∴.………………14分解析: 010*********MN ⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦, ………………4分设00(,)x y 为椭圆2241x y +=上任一点,它在MN 的作用下所对应的点为(,)x y ,则000010202x x x y y y ⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦, ………………6分 ∴ 002x x y y =⎧⎨=⎩,即002x xy y =⎧⎪⎨=⎪⎩, ………………10分代入220041x y +=得221x y +=, ………………12分∴ S π=. ………………14分 评卷人得分二、解答题3.设直线l 上任意一点(,)P x y 在矩阵M 作用下的点P '的坐标为(,)x y '', 则'012'x a x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦,所以,2.x ax y x y '=⎧⎨'=-+⎩……………………………4分将点(,)P x y '''代入直线:40l x y '+-=, 得(1)240a x y -+-=.即直线l 的方程为1202a x y -+-=.所以3a =. ……………………………10分 4.矩阵M的特征多项式为212()2321f λλλλλ--==----.………………………………3分 令12()031f λλλ===-,解得,,从而求得对应的一个特征向量分别为121111⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦,αα. ………………………………………………………………………5分令m n =+12,βαα所以求得4m =, 3n =-.………………………………………………7分55551212(43)4()3()=-=-M M ααM αM αβ5511224()3()λλ=-αα5511975433(1)11969⎡⎤⎡⎤⎡⎤=⋅--=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦.…………………………………………………………10分 5. 6. 7.8.解:设x y X z w ⎛⎫=⎪⎝⎭,按题意有21414331x y z w --⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪--⎝⎭⎝⎭⎝⎭……2分根据矩阵乘法法则有2421433431x z y w x z y w -=⎧⎪-=-⎪⎨-+=-⎪⎪-+=⎩ ……6分解之得92151xyzw⎧=⎪⎪⎪=-⎨⎪=⎪=-⎪⎩ (8)分∴91251X⎛⎫-⎪=⎪-⎝⎭……10分。
矩阵与变换二阶矩阵平面逆变换等二轮复习专题练习(一)含答案高中数学

高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关
检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.函数221log ()2y x =+的值域为_______________. 关键字:复合函数;求值域;对数
2.方程组21320x y x y +=⎧⎨-=⎩
对应的增广矩阵为 . 评卷人
得分 二、解答题
3.(本小题满分12分)
二阶矩阵M 对应的变换将点(1,1)-变换成点(1,1)--,点(2,1)-变换成点(0,2)-.
(1)求矩阵M ;
(2)设直线l 在变换M 作用下得到了直线m :24x y -=,求l 的方程. (12,13班做)设不等式|2x -1|<1的解集为M .
(1)求集合M ;。
矩阵与变换二阶矩阵平面逆变换等考前冲刺专题练习(六)含答案人教版高中数学考点大全

另 =1 , .
另 ,看作绕原点O逆时针旋转90°旋转变换矩阵,于是 .
7.解(1)由题意知: ,……………………2分
= ,
即: = ,
……………………6分
∴解得: . ……………………8分
(2) 时,矩阵 的特征多项式为
,
令 , ……………………12分
得到 的特征值为 1=5, 2=-4.……………………14分
高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、填空题
1.已知点 , , , 在矩阵 对应的变换作用下变成 ,
则 的面积为8.
2.设曲线 在 对应的变换下变成另一条曲线 ,则曲线 的方程为______
8.设 则 ,…………………………5分
故 ………………………10分
评卷人
得分
二、解答题
3.已知矩阵A= ,B= ,
求满足AX=B的矩阵B把直线 的方程。
5.试用行列式解二元一次方程组
6.若点A(2,2)在矩阵 对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵.
7.已知矩阵 ,
(1)若矩阵 的逆矩阵 ,求 ;
(2)若 ,求矩阵 的特征值.
8.已知 ,求矩阵B.
【参考答案】***试卷处理标记,请不要删除
评卷人
得分
一、填空题
1.
2.
评卷人
得分
二、解答题
3.解:由题意得 ,…………………………5′
矩阵与变换二阶矩阵平面逆变换等强化训练专题练习(一)附答案人教版高中数学考点大全

即 所以 ……………………………………………………8分
又因为点P在曲线 上,所以 ,
故有 即所得曲线方程 .…………………………………………………10分
7.设直线 在 对应变换下变成另一个图形 ,(1)求变换矩阵 ;(2)求图形 的方程。
8.求曲线 : 在矩阵 对应的变换下得到的曲线 的方程。
【参考答案】***试卷处理标记,请不要删除
评卷人
得分
一、填空题
1.
2.考查行列式运算法则=
评卷人
得分
二、解答题
3. ; ;
4.解:MN= = ,…………………………………4分
高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号人
得分
一、填空题
1.已知 ,则矩阵B=.
2.行列式 的值是0。
评卷人
得分
二、解答题
3.二阶矩阵 对应的变换将点 与 分别变换成点 与 .
(1)求矩阵 的逆矩阵 ;
(2)设直线 在变换 作用下得到了直线 ,求 的方程.
4.求曲线 在矩阵MN对应的变换作用下得到的曲线方程,其中 , 。
5.试求曲线 在先经过矩阵M= 的变换,再经过矩阵N= 的变换后所得的新曲线方程.
6.求矩阵 的逆矩阵.
【解析】本小题主要考查逆矩阵的求法,考查运算求解能力。满分10分。
设 是曲线 上任意一点,点 在矩阵MN对应的变换下变为点 ,
则有 ,于是 , .…………………8分
代入 得 ,
所以曲线 在MN对应的变换作用下得到的曲线方程为 ………………………10分
矩阵与变换二阶矩阵平面逆变换等早练专题练习(三)含答案高中数学

高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关
检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 评卷人
得分
一、填空题
1.现代社会对破译密码的难度要求越来越高,有一处密码把英文的明文(真实名)按字母分解,其中英文a ,b ,c …,z 这26个字母(不论大小写)依次对应1,2,3…,26这26个正整数。
(见下表)
a b c d e f g h i J k l m 1 2 3 4 5 6 7 8 9 10 11 12 13 n o p q r s t u v w x y z 14
15
16
17
18
19
20
21
22
23
24
25
26
用如下变换公式:⎪⎪⎩⎪⎪⎨
⎧≤≤∈+≤≤∈+=')
2,261,(132
)
2,261,(2
1整除能被整除不能被x x N x x x x N x x x 将明文转换
成密码。
如:132
12525::,1713288=+→=+→
再如变成即q h ,即y 变成m ; 上述变换规则,若将明文译成的密码是live ,那么原来的明文是
2.若).,,(1)1(2
是虚数单位i R b a bi ai ∈+-=+则bi a += .。
矩阵与变换练习题

4.假设点A (2,2)在矩阵M =⎣⎡⎦⎤cos αsin α -sin αcos α对应变换的作用下得到的点为B (-2,2),求矩阵M 的逆矩阵. 解 由题意,知M ⎣⎡⎦⎤22=⎣⎡⎦⎤-22, 即⎣⎡⎦⎤2cos α-2sin α2sin α+2cos α=⎣⎡⎦⎤-22,∴⎩⎨⎧ cos α-sin α=-1,sin α+cos α=1,解得⎩⎨⎧cos α=0,sin α=1. ∴M =⎣⎡⎦⎤01 -10.由M -1M =⎣⎡⎦⎤10 01,解得M -1=⎣⎡⎦⎤0-1 10. 5.二阶矩阵A =⎣⎢⎡⎦⎥⎤a b cd ,矩阵A 属于特征值λ1=-1的一个特征向量为a 1=⎣⎢⎡⎦⎥⎤ 1-1,属于特征值λ2=4的一个特征向量为a 2=⎣⎢⎡⎦⎥⎤32,求矩阵A .解 由特征值、特征向量定义可知,Aa 1=λ1a 1, 即⎣⎢⎡⎦⎥⎤a b cd ⎣⎢⎡⎦⎥⎤ 1-1=-1×⎣⎢⎡⎦⎥⎤1-1,得⎩⎨⎧a -b =-1,c -d =1.同理可得⎩⎨⎧3a +2b =12,3c +2d =8.解得a =2,b =3,c =2,d =1.因此矩阵A =⎣⎢⎡⎦⎥⎤2 32 1.6.矩阵M =⎣⎡⎦⎤3-1 -13,求M 的特征值及属于各特征值的一个特征向量.解 由矩阵M 的特征多项式f (λ)=⎪⎪⎪⎪λ-31 1λ-3=(λ-3)2-1=0,解得λ1=2,λ2=4,即为矩阵M 的特征值. 设矩阵M 的特征向量为⎣⎢⎡⎦⎥⎤x y ,当λ1=2时,由M ⎣⎢⎡⎦⎥⎤x y =2⎣⎢⎡⎦⎥⎤x y ,可得⎩⎨⎧-x +y =0,x -y =0.x =1,得y =1,∴α1=⎣⎢⎡⎦⎥⎤11是M 的属于λ1=2的特征向量.当λ2=4时,由M ⎣⎢⎡⎦⎥⎤x y =4⎣⎢⎡⎦⎥⎤x y ,可得⎩⎨⎧x +y =0,x +y =0,取x =1,得y =-1,∴α2=⎣⎢⎡⎦⎥⎤1-1是M 的属于λ2=4的特征向量.7.求曲线C :xy =1在矩阵M =⎣⎢⎡⎦⎥⎤1 1-1 1 对应的变换作用下得到的曲线C 1的方程. 解 设P (x 0,y 0)为曲线C :xy =1上的任意一点, 它在矩阵M =⎣⎢⎡⎦⎥⎤1 1-1 1对应的变换作用下得到点Q (x ,y ) 由⎣⎢⎡⎦⎥⎤ 1 1-11 ⎣⎢⎡⎦⎥⎤x 0y 0=⎣⎢⎡⎦⎥⎤x y ,得⎩⎨⎧x 0+y 0=x ,-x 0+y 0=y .解得⎩⎪⎨⎪⎧x 0=x -y 2,y 0=x +y2.因为P (x 0,y 0)在曲线C :xy =1上,所以x 0y 0=1. 所以x -y 2×x +y2=1,即x 2-y 2=4. 所以所求曲线C 1的方程为x 2-y 2=4.8.矩阵A =⎣⎢⎡⎦⎥⎤1002,B =⎣⎢⎡⎦⎥⎤0 -11 0,求(AB )-1. 解 AB =⎣⎢⎡⎦⎥⎤1 00 2 ⎣⎢⎡⎦⎥⎤0 -11 0=⎣⎢⎡⎦⎥⎤0 -12 0. 设(AB )-1=⎣⎢⎡⎦⎥⎤ab cd ,那么由(AB )·(AB )-1=⎣⎢⎡⎦⎥⎤1 00 1, 得⎣⎢⎡⎦⎥⎤0 -12 0 ⎣⎢⎡⎦⎥⎤ab cd =⎣⎢⎡⎦⎥⎤1 001,即⎣⎢⎡⎦⎥⎤-c -d 2a 2b =⎣⎢⎡⎦⎥⎤1 00 1, 所以⎩⎨⎧-c =1,-d =0,2a =0,2b =1,解得⎩⎪⎨⎪⎧a =0,b =12,c =-1,d =0.故(AB )-1=⎣⎢⎢⎡⎦⎥⎥⎤012-1 0. 9.设矩阵M =⎣⎢⎡⎦⎥⎤a00b (其中a >0,b >0). (1)假设a =2,b =3,求矩阵M 的逆矩阵M -1;(2)假设曲线C :x 2+y 2=1在矩阵M 所对应的线性变换作用下得到曲线C ′:x 24+y 2=1,求a 、b 的值.解 (1)设矩阵M 的逆矩阵M -1=⎣⎢⎡⎦⎥⎤x 1 y 1x 2 y 2, 那么MM -1=⎣⎢⎡⎦⎥⎤1001. 又M =⎣⎢⎡⎦⎥⎤2 00 3.∴⎣⎢⎡⎦⎥⎤2 00 3 ⎣⎢⎡⎦⎥⎤x 1 y 1x 2 y 2=⎣⎢⎡⎦⎥⎤1 00 1. ∴2x 1=1,2y 1=0,3x 2=0,3y 2=1, 即x 1=12,y 1=0,x 2=0,y 2=13,故所求的逆矩阵M -1=⎣⎢⎢⎡⎦⎥⎥⎤12 00 13.(2)设曲线C 上任意一点P (x ,y ),它在矩阵M 所对应的线性变换作用下得到点P ′(x ′,y ′),那么⎣⎢⎡⎦⎥⎤a00 b ⎣⎢⎡⎦⎥⎤x y =⎣⎢⎡⎦⎥⎤x ′y ′,即⎩⎨⎧ax =x ′,by =y ′,又点P ′(x ′,y ′)在曲线C ′上,∴x ′24+y ′2=1.那么a 2x 24+b 2y 2=1为曲线C 的方程. 又曲线C 的方程为x 2+y 2=1,故⎩⎨⎧a 2=4,b 2=1.又a >0,b >0,∴⎩⎨⎧a =2,b =1.10. 矩阵M =⎣⎢⎡⎦⎥⎤2a 21,其中a ∈R ,假设点P (1,-2)在矩阵M 的变换下得到点P ′(-4,0),求: (1)实数a 的值;(2)矩阵M 的特征值及其对应的特征向量. 解 (1)由⎣⎢⎡⎦⎥⎤2a 21 ⎣⎢⎡⎦⎥⎤ 1-2=⎣⎢⎡⎦⎥⎤-4 0, 所以2-2a =-4.所以a =3. (2)由(1)知M =⎣⎢⎡⎦⎥⎤2321,那么矩阵M 的特征多项式为 f (λ)=⎪⎪⎪⎪⎪⎪λ-2 -3-2 λ-1=(λ-2)(λ-1)-6=λ2-3λ-4. f (λ)=0,得矩阵M 的特征值为-1与4. 当λ=-1时,⎩⎨⎧(λ-2)x -3y =0,-2x +(λ-1)y =0⇒x +y =0.所以矩阵M 的属于特征值-1的一个特征向量为⎣⎢⎡⎦⎥⎤1-1.当λ=4时,⎩⎨⎧(λ-2)x -3y =0,-2x +(λ-1)y =0⇒2x -3y =0.所以矩阵M 的属于特征值4的一个特征向量为⎣⎢⎡⎦⎥⎤32.11.二阶矩阵M 有特征值λ=8及对应的一个特征向量e 1=⎣⎢⎡⎦⎥⎤11,并且矩阵M 对应的变换将点(-1,2)变换成(-2,4). (1)求矩阵M ;(2)求矩阵M 的另一个特征值,及对应的一个特征向量e 2的坐标之间的关系; (3)求直线l :x -y +1=0在矩阵M 的作用下的直线l ′的方程. 解 (1)设M =⎣⎢⎡⎦⎥⎤a b cd ,那么⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤11=8⎣⎢⎡⎦⎥⎤11=⎣⎢⎡⎦⎥⎤88,故⎩⎨⎧a +b =8,c +d =8.因⎣⎢⎡⎦⎥⎤ab c d ⎣⎢⎡⎦⎥⎤-1 2=⎣⎢⎡⎦⎥⎤-2 4,故⎩⎨⎧-a +2b =-2,-c +2d =4. 联立以上两方程组解得a =6,b =2,c =4,d =4, 故M =⎣⎢⎡⎦⎥⎤6244. (2)由(1)知,矩阵M 的特征多项式为 f (λ)=(λ-6)(λ-4)-8=λ2-10λ+16, 故其另一个特征值为λ=2.设矩阵M 的另一个特征向量是e 2=⎣⎢⎡⎦⎥⎤x y ,那么Me 2=⎣⎢⎡⎦⎥⎤6x +2y 4x +4y =2⎣⎢⎡⎦⎥⎤x y ,解得2x +y =0. (3)设点(x ,y )是直线l 上的任一点,其在矩阵M 的变换下对应的点的坐标为(x ′,y ′),那么⎣⎢⎡⎦⎥⎤6244⎣⎢⎡⎦⎥⎤x y =⎣⎢⎡⎦⎥⎤x ′y ′, 即x =14x ′-18y ′,y =-14x ′+38y ′,代入直线l 的方程后并化简得x ′-y ′+2=0,即x -y +2=0.12.矩阵A =⎣⎢⎡⎦⎥⎤ 1 a -1 b ,A 的一个特征值λ=2,其对应的特征向量是α1=⎣⎢⎡⎦⎥⎤21.(1)求矩阵A ;(2)假设向量β=⎣⎢⎡⎦⎥⎤74,计算A 5β的值.解 (1)A =⎣⎢⎡⎦⎥⎤ 12-14. (2)矩阵A 的特征多项式为f (λ)=⎪⎪⎪⎪⎪⎪λ-1 -2 1 λ-4=λ2-5λ+6=0,得λ1=2,λ2=3,当λ1=2时,α1=⎣⎢⎡⎦⎥⎤21,当λ2=3时,得α2=⎣⎢⎡⎦⎥⎤11.由β=m α1+n α2,得⎩⎨⎧2m +n =7,m +n =4,解得m =3,n =1.∴A 5β=A 5(3α1+α2)=3(A 5α1)+A 5α2=3(λ51α1)+λ52α2=3×25⎣⎢⎡⎦⎥⎤21+35⎣⎢⎡⎦⎥⎤11=⎣⎢⎡⎦⎥⎤435339.。
矩阵变换练习题

矩阵变换练习题考虑以下矩阵变换练习题,通过解题的过程,加深对矩阵变换的理解。
题目一:已知矩阵A = [[2, 3], [1, 4]],矩阵B = [[5, 1], [2, 3]],求矩阵A与矩阵B的乘积。
解答一:首先,我们需要了解矩阵的乘法运算法则。
矩阵A与矩阵B的乘积C = A × B,其结果矩阵C的行数等于矩阵A的行数,列数等于矩阵B 的列数。
而C的第i行第j列元素等于A的第i行与B的第j列元素逐个相乘之后再求和。
根据上述规则,我们可以进行矩阵A与矩阵B的乘积计算。
首先,计算矩阵C的第1行第1列元素:C[1][1] = A[1][1] × B[1][1] + A[1][2] × B[2][1] = 2 × 5 + 3 × 2 = 4 + 6 = 10。
接着,计算矩阵C的第1行第2列元素:C[1][2] = A[1][1] × B[1][2] + A[1][2] × B[2][2] = 2 × 1 + 3 × 3 = 2 + 9 = 11。
然后,计算矩阵C的第2行第1列元素:C[2][1] = A[2][1] × B[1][1] + A[2][2] × B[2][1] = 1 × 5 + 4 × 2 = 5 + 8 = 13。
最后,计算矩阵C的第2行第2列元素:C[2][2] = A[2][1] × B[1][2] + A[2][2] ×B[2][2] = 1 × 1 + 4 × 3 = 1 + 12 = 13。
综上所述,矩阵A与矩阵B的乘积为矩阵C = [[10, 11], [13, 13]]。
已知矩阵D = [[2, 4, 1], [3, 0, 2]],矩阵E = [[-1, 3], [2, -2], [5, 1]],求矩阵D与矩阵E的乘积。
矩阵与变换二阶矩阵平面逆变换等章节综合检测专题练习(二)附答案高中数学
高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
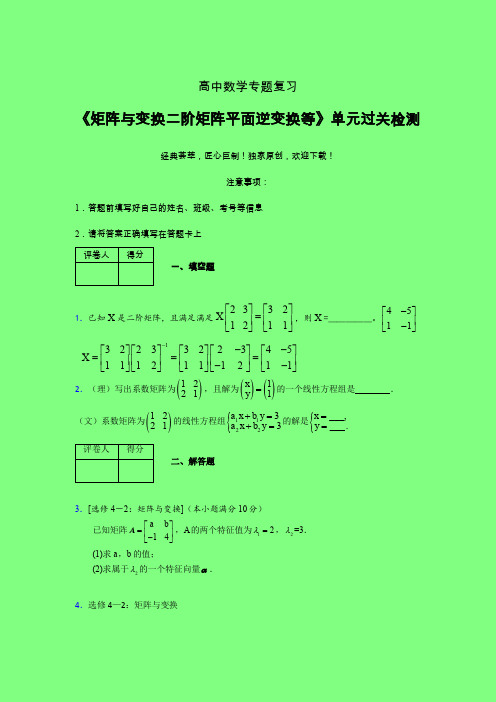
1.已知X 是二阶矩阵,且满足满足23321211X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,则X =_____。
4511-⎡⎤⎢⎥-⎣⎦
132233223451112111211X ---⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦
2.(理)写出系数矩阵为()1221,且解为()()11x y =的一个线性方程组是 . (文)系数矩阵为
()1221的线性方程组{112233a x b y a x b y +=+=的解是{___,___.x y == 评卷人
得分
二、解答题
3.[选修4-2:矩阵与变换](本小题满分10分)
已知矩阵14a b ⎡⎤=⎢⎥-⎣⎦A ,A 的两个特征值为12λ=,2λ=3.
(1)求a ,b 的值;
(2)求属于2λ的一个特征向量α.
4.选修4—2:矩阵与变换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩阵与变换
1. 定义运算bc ad d b c a
-=,则符合条件1
21211-+--x y y x = 0的点P (x , y )的轨迹方程为( ) A .(x – 1)2 + 4y 2 = 1 B .(x –1)2 – 4y 2 = 1
C .(x –1)2 + y 2 = 1
D .(x –1)2 – y 2 = 1
2. 定义运算:4321
a a a a =a 1a 4-a 2a 3,则函数f(x)=1
sin 1cos x x -的最大值是 . 3、已知矩阵M =⎣⎢⎡⎦
⎥⎤1 -23 -7,若矩阵X 满足MX =⎣⎡⎦⎤1-1,求矩阵X .
4、设A =⎣⎢⎡⎦⎥⎤1 23 4,B =⎣⎢⎡⎦
⎥⎤4 2k 7,若AB =BA ,则实数k =________. 5. 若点A (2,2)在矩阵M= ⎢⎣⎡ααsin cos ⎥⎦
⎤-ααcos sin 对应变换的作用下得到的点为B (-2,2),求矩阵M 的逆矩阵。
6.求矩阵3221A ⎡⎤=⎢⎥⎣⎦
的逆矩阵.
7. 已知二阶矩阵M 满足:M=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡0110,M ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡1221=,求M
100⎥⎦
⎤⎢⎣⎡-22
8.已知角α的顶点在原点,始边与x
轴的正半轴重合,终边经过点(P -. (1)定义行列式a b a d b c c d =∙-∙ 解关于x 的方程:cos sin 10sin cos x x αα+=;
(2)若函数()sin()cos()f x x x αα=+++(x ∈R )的图像关于直线
0x x =对称,求0tan x 的值.
9. 已知矩阵M 221a ⎡⎤=⎢⎥⎣⎦
,其中R a ∈,若点(1,2)P -在矩阵M 的变换下得到点
(4,0)P '-,(1)求实数a 的值; (2)求矩阵M 的特征值及其对应的特征向量.
10. 曲线22421x xy y ++=在二阶矩阵11a M b ⎡⎤=⎢⎥⎣⎦
的作用下变换为曲线2221x y -=, (1)求实数,a b 的值;(2)求M 的逆矩阵1M -.
11已知曲线C :xy=1,将曲线C 绕坐标原点逆时针旋转45度后,得到的曲线c ’的方程?
12设a,b 都是实数,若矩阵⎢⎣
⎡⎥⎦⎤-=b a A 10把直线l:2x+y-7=0变换为另一直线l ’:9x+y-91=0,求a,b 的值。
13已知在一个二阶矩阵M 的变换作用下,点A (1,2)变成了A ’(4,5),点B (3,-1)变成了点B ’(5,1),求矩阵M
14.(2011年高考江苏卷21)
已知矩阵1121A ⎡⎤=⎢⎥⎣⎦,向量12β⎡⎤=⎢⎥⎣⎦
,求向量α,使得2A αβ=.
15在平面直角坐标系xOy 中,A (0,0),B (-3,),C (-2,1),设k ≠0,k ∈R ,M=⎥⎦⎤⎢⎣⎡100k ,N=⎥⎦⎤⎢⎣⎡0110,点A 、B 、C 在矩阵MN 对应的变换下得到点A 1,B 1,C 1,△A 1B 1C 1的面积是△ABC 面积的2倍,求实数k 的值。
