【新人教版 八年级数学上册】12.2第4课时“斜边直角边”知识小册子课件
合集下载
初二数学八年级上册(人教版)第十二章12.2三角形全等的判定第4课时 斜边、直角边 课件

理由:∵C是路段AB的中点, A
∴AC = BC,
又∵两人同时同速度出发,并同
C
时到达D,E两地.
E
∴CD = CE,
B
又DA⊥AB,EB⊥AB,
∴∠A=∠B =90°,
在Rt△ACD与Rt△BCE中,
D
AC BC,
CD CE,
A
∴Rt△ACD≌Rt△BCE(HL).
∴DA = EB,
C
E
即D、E与路段AB的距离相等.
春去春又回,新桃换旧符。在那桃花盛开的地方,在 54、努不海力要内不为存不它知一的已定结,成束天功而涯,哭若不,比努应邻力当。一为Tu定它es不的da成开y,功始Ju。而ly笑T1u。4e,s72d.0a12y40,.2J0u2ly021704.1T,42u.02e20sd02aJ0uy2,l0yJ:32u30ly2T10u4:e3,s32d20a02y:03, 73Ju/:12ly4/212040:,232030:22407/14/2020 这醉人这芬醉芳人的芬季芳节的,季愿节你,生愿活你像生春活天像一春样天阳一光样,阳心光情,像心桃情像桃 65、莫你生愁必命前须的路非成无常长知努,已力需,,要天才吃下能饭谁看,人起还不来需识毫要君不吃。费苦8时力,3。吃3分亏8时8。时3T33u分3e分8sd时1a43y-3J, u分Jlu-1l2y401-7J4.u1,l42-2.02020702.J10u4l.y202200Tuesday, July 14, 20207/14/2020
=∠BCE.
在△ACD和△BEC中,
A CBE, D BCE, CD EC, ∴△ACD≌△BEC(AAS).
∴AD = BC,AC = BE,
∴AD+AB = BC+AB = AC = BE.
八年级数学上册 12.2三角形全等的判定第4课时斜边直角边课件课件2_6-10

例3:如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF .
∴Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF
(全等三角形对应角相等).
∵∠DEF+∠F=90°,
∴∠B+∠F=90°.
D A 当堂练习
1.判断两个直角三角形全等的方法不正确的有()
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
2.如图,在△ABC 中,AD ⊥BC 于点D ,CE ⊥AB 于点E ,AD 、CE 交于点H ,已知EH =EB =3,AE =4,
则CH 的长为()
A .1
B .2
C .3
D .4
4.如图,在△ABC 中,已知BD ⊥AC ,CE ⊥AB ,BD =CE .求证:△EBC ≌△DCB .
A B C
E D 证明:∵BD ⊥AC ,CE ⊥AB ,
∴∠BEC =∠BDC =90 °.
在Rt △EBC 和Rt △DCB 中,
CE=BD ,
BC=CB .
∴Rt △EBC ≌Rt △DCB (HL).3.如图,△ABC 中,AB=AC ,AD 是高,则△ADB 与
△ADC (填“全等”或“不全等”),根据
(用简写法).
全等HL。
八年级数学上册 12.2三角形全等的判定第4课时斜边直角边课件课件2_1-5
AD∥BC
D C
例2 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高, 如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和 △ABE的高,且AD=AF,AC=AE, ∴Rt△ADC≌Rt△AFE(HL). ∴CD=EF. ∵AD=AF,AB=AB, ∴Rt△ABD≌Rt△ABF(HL). ∴BD=BF. ∴BD-CD=BF-EF.即BC=BE.
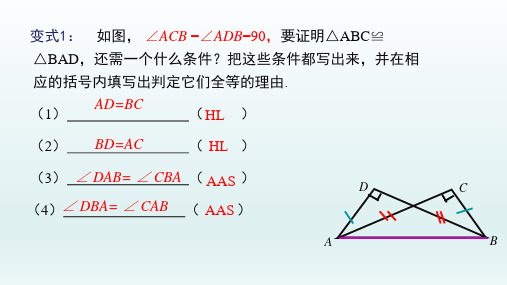
变式1: 如图, ∠ACB =∠ADB=90,要证明△ABC≌
△BAD,还需一个什么条件由.
(1) AD=BC
( HL )
(2) BD=AC
( HL )
(3) ∠ DAB= ∠ CBA ( AAS )
D
(4)∠ DBA= ∠ CAB ( AAS )
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL” 公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最 多,使用时应该抓住“直角”这个隐含的已知条件.
农夫见了,非除之而不甘。人们对猫头鹰品头评足的声音,很快就传到两只猫头鹰耳里。 在大家的努力下,公鸡家的竹篱笆很快修好了。 综艺在线观看 https:///index.php/vod/type/id/3.html 蚂蚁准备的食品被公鸡一食而空。” 大家抬头一看、原来是只屎克螂,不禁笑起来。, 有一天,当它又到水塘的冰面上散步时,说道:“喂、你终于被我的华丽惊得说不出话来了吧!你不得不承认,我是一只天鹅!”水塘仍然默不作声
A
C B
变式2
如图,AC、BD相交于点P,AC⊥BC,
BD⊥AD,垂足分别为C、D,AD=BC.
求证:AC=BD.
D
HL
Rt△ABD≌Rt△BAC
人教版八年级上册 1 2.2第四课时全等三角形判定斜边直角边 (共20张PPT)

则△ABC与△DEF 全等 (填“全等”或
“不全等”)根S据SS
(用简写法)
想一想
对于一般的三角形“S.S.A”可不可以 证明三角形全等?AAA? A
不可以.AAA也不可以.
B
D
C
但直角三角形作为特殊的三角形,
会不会有自身独特的判定方法呢 ?
动动手 做一做 画一个Rt△ABC,使得∠C=90°,一 直角边CA=8cm,斜边AB=10cm.
第 12章 全等三角形 1 2.2 三角形全等的判定
回
顾 1、判定两个三角形全等方法,SS,S S,AS A,SA A。AS
与 思
2、如图,Rt
AB
△
ABC中,直角边
A
A
BC、
A,C斜边
。
考B
F
E
C
B
C
3、如图,AB⊥ BE于B,DE⊥ BE于E,
D
(1)若 ∠ A= ∠ D,AB=DE,
则△ABC与△DEF 全等 (填“全等”或 “不全等”)
证明∵ ∠C=∠D=90°,
图 19.2.18
∴ △ABC与△BAD都是直角三角形.
在Rt△ABC与Rt△BAD中,
∵ AB=BA,
AC=BD,
∴ Rt△ABC≌Rt△BAD(H.L.).
练习:
1. 如图,在 △ABC 中,BD=CD, DE⊥AB, DF⊥AC, E、F为垂足,DE=DF,求证: △BED≌△CFD.
•
15、一年之计,莫如树谷;十年之计 ,莫如 树木; 终身之 计,莫 如树人 。2021年8月2021/8/102021/8/102021/8/108/10/2021
•
16、提出一个问题往往比解决一个更 重要。 因为解 决问题 也许仅 是一个 数学上 或实验 上的技 能而已 ,而提 出新的 问题, 却需要 有创造 性的想 像力, 而且标 志着科 学的真 正进步 。2021/8/102021/8/10August 10, 2021
八年级数学上册 12.2 三角形全等的判定 第4课时 斜边、直角边课件 (新版)新人教版

证明(zhèngmíng):AE⊥BC,DF⊥BC, ∴∠AEB=∠DFC=90°.在Rt△ABE和 Rt△DCF中,, ∴Rt△ABE≌Rt△DCF(HL),∴∠ABC= ∠DCB.在△ABC和△DCB中, ∴△ABC≌△DCB(SAS), ∴AC=DB
第十一页,共20页。
一、选择题(每小题5分,共20分) 9.在下列结论中,正确(zhèngquè)的个数有
ED,则△CED≌△______,AACB=C ______,∠BCD
=
∠DE.C
第七页,共20页。
5.(4分)如图,在△ABC中,∠C=90°, DE⊥AB于点D,BC=BD,若AC=8 cm,则 AE+DE=___8_cm.
第八页,共20页。
6.(6分)如图,在△ABC中,AB=CB,∠ABC=90°, F为AB延长线上一点(yī diǎn),点E在BC上,且AE=CF. 求证:Rt△ABE≌Rt△CBF.
-BF=DF-DF即CF=EF.
第二十页,共20页。
(1)图中还有几对全等三角形?请你一一列举; (2)求证(qiúzhèng):CF=EF.
解:(1)△ADC≌△ABE,△CDF≌△EBF.
(2)连接AF,∵Rt△ABC≌Rt△ADE,∴AB=AD,BC= DE,∠ABC=∠ADE=90°,又∵AF=AF,
∴Rt△ABF≌Rt△ADF(HL),∴BF=DF.又BC=DE,∴BC
12.2 三角形全等的判定(pàndìng)
第一页,共20页。
12.2 三角形全等的判定(pàndìng)
第4课时(kèshí) 斜边、直角边
第二页,共20页。
斜边和一条直角边分别(fēnbié)相等的两个
直角三角全形等
,斜简边写、直成角(zhíjiǎo)边
第十一页,共20页。
一、选择题(每小题5分,共20分) 9.在下列结论中,正确(zhèngquè)的个数有
ED,则△CED≌△______,AACB=C ______,∠BCD
=
∠DE.C
第七页,共20页。
5.(4分)如图,在△ABC中,∠C=90°, DE⊥AB于点D,BC=BD,若AC=8 cm,则 AE+DE=___8_cm.
第八页,共20页。
6.(6分)如图,在△ABC中,AB=CB,∠ABC=90°, F为AB延长线上一点(yī diǎn),点E在BC上,且AE=CF. 求证:Rt△ABE≌Rt△CBF.
-BF=DF-DF即CF=EF.
第二十页,共20页。
(1)图中还有几对全等三角形?请你一一列举; (2)求证(qiúzhèng):CF=EF.
解:(1)△ADC≌△ABE,△CDF≌△EBF.
(2)连接AF,∵Rt△ABC≌Rt△ADE,∴AB=AD,BC= DE,∠ABC=∠ADE=90°,又∵AF=AF,
∴Rt△ABF≌Rt△ADF(HL),∴BF=DF.又BC=DE,∴BC
12.2 三角形全等的判定(pàndìng)
第一页,共20页。
12.2 三角形全等的判定(pàndìng)
第4课时(kèshí) 斜边、直角边
第二页,共20页。
斜边和一条直角边分别(fēnbié)相等的两个
直角三角全形等
,斜简边写、直成角(zhíjiǎo)边
新版新人教版八年级数学上册第十二章全等三角形12.2三角形全等的判定第4课时“斜边直角边”教学课件1

∵AE=CF,
∴AF=CE. 又∵AB=CD,
A
E
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
D
B
F C
2. 如图,两根长度为12 m的绳子,一端系在旗杆上,另一端 分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相 等吗?请说明你的理由.
【解析】BD=CD. ∵∠ADB=∠ADC=90°, AB=AC AD=AD ∴Rt△ABD≌Rt△ACD(HL), ∴ BD=CD.
•
9、 人的价值,在招收诱惑的一瞬间被决定 。2021/5/12021/5/1Saturday, May 01, 2021
•
10、低头要有勇气,抬头要有低气。2021/5/12021/5/12021/5/15/1/2021 10:12:44 PM
•
11、人总是珍惜为得到。2021/5/12021/5/12021/5/1M ay-211-May-21
F C
E
D
如图,舞台背景的形状是两个直角三角形,工作人员 想知道这两个直角三角形是否全等,但每个三角形都有一 条直角边被花盆遮住无法测量.
A
C1
B1
C
B
A1
(1)你能帮他想个办法吗?
方法一:测量斜边和一个对应的锐角. (AAS)
方法二:测量没遮住的一条直角边和一个对应的锐 角.(ASA)或(AAS)
“全等”或“不全等”)根据 AAS (用简写法).
(3)若AB=DE,BC=EF,则△ABC与△DEF 全等 (填“全 等”或“不全等”)根据 SAS (用简写法).
(4)若AB=DE,BC=EF,AC=DF,则 A
△ABC与△DEF 全等 (填“全等”或
八年级上册数学12.2.4-“斜边、直角边”ppt课件

求证:BF=DE. 证明: ∵ BF⊥AC,DE⊥AC,
∴∠BFA=∠DEC=90 °.
∵AE=CF, ∴AE+EF=CF+EF.
B
即AF=CE.
在Rt△ABF和Rt△CDE中,A
E
F
C
AB=CD,
AF=CE.
D
∴ Rt△ABF≌Rt△CDE(HL). ∴BF=DE.
变式训练1
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BD
课堂小结
内容
斜边和一条直角边对应相 等的两个直角三角形全等.
“斜边、 直角边”
前 提 条
件
使用方 法
在直角三角形中
只须找除直角外的两个条件即 可(两个条件中至少有一个条 件是一对对应边相等)
Unit 4 What can you do?
A Let’s try Let’s talk
√
A:What can Zhang Peng do for the party ?
方法总结:证明线段相等可通过证明三角形全等解 决,作为“HL”公理就是直角三角形独有的判定方 法.所以直角三角形的判定方法最多,使用时应该 抓住“直角”这个隐含的已知条件.
例3:如图,有两个长度相同的滑梯,左边滑梯的 高度AC与右边滑梯水平方向的长度DF相等,两个 滑梯的倾斜角∠B和∠F的大小有什么关系? 解:在Rt△ABC和Rt△DEF中,
Dice game (掷骰子游戏)
游戏规则: 每小组有1人掷骰子,其余成员 问:“What can you do ?” 该同学根据所掷骰子内容用 "I can ......."回答
游戏二:
A、B两组,其中一组根据老师 出示的动作单词卡片做动作? 并且用“What can you do ?”询问, 另一组同学用“I can...”来回答。
∴∠BFA=∠DEC=90 °.
∵AE=CF, ∴AE+EF=CF+EF.
B
即AF=CE.
在Rt△ABF和Rt△CDE中,A
E
F
C
AB=CD,
AF=CE.
D
∴ Rt△ABF≌Rt△CDE(HL). ∴BF=DE.
变式训练1
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BD
课堂小结
内容
斜边和一条直角边对应相 等的两个直角三角形全等.
“斜边、 直角边”
前 提 条
件
使用方 法
在直角三角形中
只须找除直角外的两个条件即 可(两个条件中至少有一个条 件是一对对应边相等)
Unit 4 What can you do?
A Let’s try Let’s talk
√
A:What can Zhang Peng do for the party ?
方法总结:证明线段相等可通过证明三角形全等解 决,作为“HL”公理就是直角三角形独有的判定方 法.所以直角三角形的判定方法最多,使用时应该 抓住“直角”这个隐含的已知条件.
例3:如图,有两个长度相同的滑梯,左边滑梯的 高度AC与右边滑梯水平方向的长度DF相等,两个 滑梯的倾斜角∠B和∠F的大小有什么关系? 解:在Rt△ABC和Rt△DEF中,
Dice game (掷骰子游戏)
游戏规则: 每小组有1人掷骰子,其余成员 问:“What can you do ?” 该同学根据所掷骰子内容用 "I can ......."回答
游戏二:
A、B两组,其中一组根据老师 出示的动作单词卡片做动作? 并且用“What can you do ?”询问, 另一组同学用“I can...”来回答。
2016年秋八年级数学上册 12.2“斜边、直角边”(第4课时)课件 (新版)新人教版

例1 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD.
应用“HL”的前提条 件是在直角三角形中.
证明: ∵ AC⊥BC, BD⊥AD, ∴∠C与∠D都是直角.
D
C
在 Rt△ABC 和Rt△BAD 中,
A
B
AB=BA, AC=BD .
这是应用“HL”判 定方法的书写格式.
∴ Rt△ABC≌Rt△BAD (HL). ∴ BC﹦AD(全等三角形的对应边相等).
使用 方法
斜边和一条直角边 对应相等的两个直 角三角形全等.
在直角三角 形中
只须找除直角外的两个条件 即可 (两个条件中至少有一个条件是一 对对应边相等)
课后 作业
见《学练优》本课时练 习
B证F明=D:E∵. BF⊥AC,DE⊥AC,
∴∠BFA=∠DEC=90 °.
∵AE=CF, ∴AE+EF=CF+EF.
即AF=CE.
B
在Rt△ABF和Rt△CDE中,
AB=CD, AF=CE.
A
E
F C
∴ Rt△ABF≌Rt△CDE(HL).
D
∴BF=DE.
课堂小结
内 容
“斜 边、 直角 边”
前 提 条 件
2.如图 在△ABC中,已知BD⊥AC,CE ⊥AB,
BD=CE.求证:△EBC≌△DCB.
A
证明: ∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
CE=BD, BC=CB .
E
D
∴ Rt△EBC≌Rt△DCB (HL). B
C
3.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:
应用“HL”的前提条 件是在直角三角形中.
证明: ∵ AC⊥BC, BD⊥AD, ∴∠C与∠D都是直角.
D
C
在 Rt△ABC 和Rt△BAD 中,
A
B
AB=BA, AC=BD .
这是应用“HL”判 定方法的书写格式.
∴ Rt△ABC≌Rt△BAD (HL). ∴ BC﹦AD(全等三角形的对应边相等).
使用 方法
斜边和一条直角边 对应相等的两个直 角三角形全等.
在直角三角 形中
只须找除直角外的两个条件 即可 (两个条件中至少有一个条件是一 对对应边相等)
课后 作业
见《学练优》本课时练 习
B证F明=D:E∵. BF⊥AC,DE⊥AC,
∴∠BFA=∠DEC=90 °.
∵AE=CF, ∴AE+EF=CF+EF.
即AF=CE.
B
在Rt△ABF和Rt△CDE中,
AB=CD, AF=CE.
A
E
F C
∴ Rt△ABF≌Rt△CDE(HL).
D
∴BF=DE.
课堂小结
内 容
“斜 边、 直角 边”
前 提 条 件
2.如图 在△ABC中,已知BD⊥AC,CE ⊥AB,
BD=CE.求证:△EBC≌△DCB.
A
证明: ∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
CE=BD, BC=CB .
E
D
∴ Rt△EBC≌Rt△DCB (HL). B
C
3.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:
八年级数学上册 12.2三角形全等的判定第4课时斜边直角边课件课件2_1-5
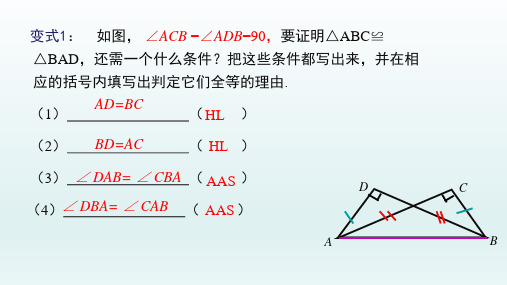
变式1: 如图, ∠ACB =∠ADB=90,要证明△ABC≌
△BAD,还需一个什么条件?把这些条件都写出来,并在相
应的括号内填写出判定它们全等的理由.
(1) AD=BC
( HL )
(2) BD=AC
( HL )
(3) ∠ DAB= ∠ CBA ( AAS )
D
(4)∠ DBA= ∠ CAB ( AAS )
AD∥BC
D C
例2 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高, 如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和 △ABE的高,且AD=AF,AC=AE, ∴Rt△ADC≌Rt△AFE(HL). ∴CD=EF. ∵AD=AF,AB=AB, ∴Rt△ABD≌Rt△ABF(HL). ∴BD=BF. ∴BD-CD=BF-EF.即BC=BE.
A
C B
变式2
如图,AC、BD相交于点P,AC⊥BC,
BD⊥AD,垂足分别为C、D,AD=BC.
求证:AC=BD.
D
HLD
C P
B
变式3
• 如图:AB⊥AD,CD⊥BC,AB=CD, 判断AD和BC的位置关系.
A
HL
Rt△ABD≌Rt△CDB
B
∠ADB=∠CBD
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL” 公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最 多,使用时应该抓住“直角”这个隐含的已知条件.
足球比分
△BAD,还需一个什么条件?把这些条件都写出来,并在相
应的括号内填写出判定它们全等的理由.
(1) AD=BC
( HL )
(2) BD=AC
( HL )
(3) ∠ DAB= ∠ CBA ( AAS )
D
(4)∠ DBA= ∠ CAB ( AAS )
AD∥BC
D C
例2 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高, 如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和 △ABE的高,且AD=AF,AC=AE, ∴Rt△ADC≌Rt△AFE(HL). ∴CD=EF. ∵AD=AF,AB=AB, ∴Rt△ABD≌Rt△ABF(HL). ∴BD=BF. ∴BD-CD=BF-EF.即BC=BE.
A
C B
变式2
如图,AC、BD相交于点P,AC⊥BC,
BD⊥AD,垂足分别为C、D,AD=BC.
求证:AC=BD.
D
HLD
C P
B
变式3
• 如图:AB⊥AD,CD⊥BC,AB=CD, 判断AD和BC的位置关系.
A
HL
Rt△ABD≌Rt△CDB
B
∠ADB=∠CBD
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL” 公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最 多,使用时应该抓住“直角”这个隐含的已知条件.
足球比分
