初中数学找规律题
初一数学找规律练习题

初一数学找规律练习题一、数字规律1. 观察下列数列,找出规律,并写出下一个数:2, 4, 8, 16, 32, ____1, 3, 6, 10, 15, ____1, 4, 9, 16, 25, ____二、图形规律1. 观察下列图形,找出规律,并画出下一个图形:(图形:△ △△ △△△ △△△△)(图形:○□○□○□○□)3. 观察下列图形,找出规律,并画出下一个图形:(图形:□■□■■□■■■)三、数列与图形结合规律1. 观察下列数列与图形的结合,找出规律,并写出下一个数和画出对应的图形:数列:1, 2, 3, 4, 5图形:(△)(△△)(△△△)(△△△△)数列:1, 3, 6, 10, 15图形:(○)(□□)(△△△)(■■■■)四、应用题1. 小明发现一个有趣的现象,从1开始,连续几个自然数的和等于这几个自然数的个数乘以(个数加1)除以2。
请你找出这个规律,并计算1到100的和。
2. 小华在纸上画了一排正方形,每个正方形的边长分别为1cm、2cm、3cm、4cm……,请问这排正方形总面积是多少平方厘米?3. 一个数字三角形,第一行有1个数字,第二行有2个数字,以此类推,第n行有n个数字。
求这个数字三角形前10行的数字总和。
五、数表规律1 2 3 42 3 4 53 4 5 64 5 6 __1 3 6 102 5 9 143 7 12 184 __ __ __六、操作规律A → A + 1B → B + 2C → C + 3D → D + 4(初始值:A=1, B=2, C=3, D=4)A → A × 2B → B × 3C → C × 4D → D × 5(初始值:A=1, B=1, C=1, D=1)七、逻辑推理规律A > B,B > C,C > D那么 A > D 是否成立?如果 P 则 Q,如果 Q 则 R那么如果 P 则 R 是否成立?八、综合应用题1. 一个班级有50名学生,每名学生都有一个唯一的编号,编号从1到50。
初中数学找规律找规律
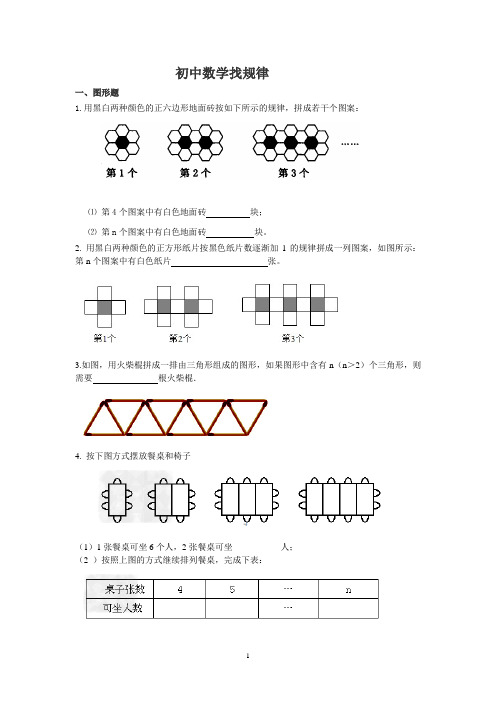
初中数学找规律一、图形题1.用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:⑴第4个图案中有白色地面砖块;⑵第n个图案中有白色地面砖块。
2. 用黑白两种颜色的正方形纸片按黑色纸片数逐渐加1的规律拼成一列图案,如图所示:第n个图案中有白色纸片张。
3.如图,用火柴棍拼成一排由三角形组成的图形,如果图形中含有n(n>2)个三角形,则需要根火柴棍.4. 按下图方式摆放餐桌和椅子(1)1张餐桌可坐6个人,2张餐桌可坐___________人;(2 )按照上图的方式继续排列餐桌,完成下表:5.如图是某同学在沙滩上用石子摆成的小房子:观察图形的变化规律,写出第n 个小房子用了 块石子. 6.如下图是用棋子摆成的“上”字:第一个“上”字 第二个“上”字 第三个“上”字 如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第五个“上” 字需用 枚棋子 (2) 第n 个“上” 字需用 枚棋子 7. 根据下列5个图形及相应点的个数的变化规律:猜想第6个图形有 个点,第n 个图形中有 个点。
8. 用边长为1cm 的小正方形搭成如下的塔状图形,则第n 次所搭图形的周长是_______________cm (用含n 的代数式表示)。
9. 如图,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,……则第⑩个图形中共有_________个平行四边形.第1次 第2次 第3次 第4次 ······10. 下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为( )A .50B .64C .68D .7211. 将一些形状相同的小五角星如下图所示的规律摆放,据此规律,第10个图形有 个五角星.12.观察下列图形:13.它们是按一定规律排列的,依照此规律,第16个图形共有 个★. 14. 观察下列图形(每幅图中最小..的三角形都是全等的),请写出第n 个图中最小..的三角形的个数有 个.二、循环题15.如图,如图所示的图案是按一定规律排列的,照此规律,在第1至第2012个图案中“♣”,第1个图 第2个图第3个图 第4个图16. 观察下列算式,用你所发现的规律得出22018的末位数字是( ) 21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256…… A 、2 B 、4 C 、6 D 、817.观察下列等式:31=3, 32=9, 33=27, 34=81, 35=243, 36=729, 37=2187…18.把编号为1,2,3,4,…的若干盆花按如图所示摆放,花盆中 的花按红、黄、蓝、紫的颜色依次循环排列,则第8行从左边数第6盆花的颜色为______色.19.已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:第1行 1第2行 -2 3第3行 -4 5 -6第4行 7 -8 9 -10第5行 11 -12 13 -14 15 …按照上述规律排下去,那么第10行从左边数第5个数等于 .三、数字规律题20. (1) 3,6,9,12, 15,… , (2) 2,5,8,11, 14, …,(3)3,9,27, 81,… , (4)-2,-4,,-8,-16,…,(4) 1,-1,1,-1,1,..., (5) -1,1,-1,1,1,...,(6)1,4 ,9,16,25,… , (7)3,6,11,18,27,…,(8)1+2+3+4+…+n= (9)有一列数1234251017--,,,,…,那么第7个数是 21.一组按规律排列的式子: 则第n 个式子是22. 一组按规律排列的式子:,,,…(ab ≠0).其中第2018个式子是________,第n 个式子是______ __ (n 为正整数)23. 一组按规律排列的式子:,,916,79,54,34433232⋅⋅⋅+-+-b a b a b a b a 则第n 个式子为24.一组按规律排列的多项式:a b +,23a b -,35a b +,47a b -,……,其中第10个式子是() A .1019a b +B .1019a b -C .1017a b -D .1021a b -四、复杂题25.将自然数按下列三角形规律排列,则第10行的各数之和是 1 2 3 4 5 6 7 8 910 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 …26.观察下面排列的等式: 9×0+1=1; 9×1+2=11; 9×2+3=21;… 猜想第n 个等式(n 为正整数)应为____ __ 27.观察下列等式 1=1 ,2+3+4=9 ,3+4+5+6+7=25,4+5+6+7+8+9+10=49,…照此规律,请你猜测出第n 个等式:28.观察下列等式:,,,……猜想并写出第n 个等式 29. 观察下列式子: 1×3+1=22; 7×9+1=82; 25×27+1=262; 79×81+1=802; …可猜想第2018个式子为 .30.观察下列算式:23451=+⨯ ,24462=+⨯,25473=+⨯,24846⨯+=,请你在察规律之后并用你得到的规律填空:250___________=+⨯, 第n 个式子呢? _______________ ___ _31.如图,在一单位为1的方格纸上,△A 1A 2A 3,△A 3A 4A 5,△A 5A 6A 7,…,都是斜边在x 轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A 1A 2A 3的顶点坐标分别为A 1(2,0),A 2(1,﹣1),A 3(0,0),则依图中所示规律,A 2018的坐标为 .D 132.已知22223322333388+=⨯+=⨯,,244441515+=⨯,……,若288a a b b +=⨯(a 、b 为正整数)则a b += .33. 已知22223322333388+=⨯+=⨯,,244441515+=⨯,……,若288a a b b +=⨯(a 、b 为正整数)则a b += .34.如图,边长为1的菱形ABCD 中,︒=∠60DAB .连结对角线AC ,以AC 为边作第二个菱形11D ACC ,使 ︒=∠601AC D ;连结1AC ,再以1AC 为边作第三个菱形221D C AC ,使 ︒=∠6012AC D ;……,按此规律所作的第n 个菱形的边长为 .35.请看杨辉三角①,并观察下列等式②:根据前面各式的规律,则(a +b )6=______________ __36. 如图所示,直线y =x +1与y 轴相交于点A 1,以OA 1为边作正方形OA 1B 1C 1,记作第一个正方形;然后延长C 1B 1与直线y =x +1相交于点A 2,再以C 1A 2为边作正方形C 1A 2B 2C 2,记作第二个正方形;同样延长C 2B 2与直线y =x +1相交于点A 3,再以C 2A 3为边作正方形C 2A 3B 3C 3,记作第三个正方形;…依此类推,则第n 个正方形的边长为________________.。
初中数学找规律练习题(有答案)

精心整理一、简答题1、已知a、b互为相反数,c、d互为倒数,m的倒数等于它本身,则的值是多少?(4分)2、先阅读,再解题:因为,?,?……所以.参照上述解法计算:3、目前市场上有一种数码照相机,售价为3800元/架,预计今后几年内平均每年比上一年降价4%.3年后这种数码相机的售价估计为每架多少元(精确到1元)?4、已知a、b互为相反数,m、n互为倒数,x绝对值为2,求的值5、如果规定符号“﹡”的意义是﹡=,求2﹡﹡4的值。
6、某商店营业员每月的基本工资为300元,奖金制度是:每月完成规定指标10000元营业额的,发奖金300元;若营业额超过规定指标,另奖超额部分营业额的5%,该商店的一名营业员九月份完成营业额13200元,问他九月份的收入为多少元?7、王叔叔家的装修工程接近尾声,油漆工程结束了,经统计,油漆工共做50工时,用了150升油漆,已知油漆每升128元,共粉刷120平方米,在结算工钱时,有以下几种结算方案:(1)按工时算,每6工时300元。
(2)按油漆费用来算,油漆费用的15%为工钱;(3)按粉刷面积来算,每6平方米132元。
请你帮王叔叔算一下,用哪种方案最省钱?8、定义一种新的运算:观察下列式子1⊙3=1×4+3=7;3⊙(-1)=3×4+(-1)=11;5⊙4=5×4+4=24;4⊙(-3)=4×4+(-3)=13.⑴请你想一想:a⊙b=??????????;⑵请你判断a⊙b??????b⊙a(填入“=”或“≠”)???⑶若a=-2,b=-4,求(2a-b)⊙(a-2b)的值.9、阅读下列材料:1×2=(1×2×3-0×1×2),2×3=(2×3×4-1×2×3),3×4=(3×4×5-2×3×4),由以上三个等式相加,可得1×2+2×3+3×4=×3×4×5=20.读完以上材料,请你计算下列各题:(1)1×2+2×3+3×4+…+10×11(写出过程);(2)1×2+2×3+3×4+…+n×(n+1)=________;(3)1×2×3+2×3×4+3×4×5=________.10、从2004年8月1日起,浙江省城乡居民生活用电执行新的电价政策:安装“一户一表”的居民用户,按所抄见电量(每家用户电表所表示的用电量)实行阶梯式累进加价,收费标准如下:月用电量不超过50千瓦时的部分超过50千瓦时不超过200千瓦时的部分超过200千瓦时的部分收费标准(元/千瓦时)0.53 0.56 0.63 ????例:若某户月用电300千瓦时,需交电费为????(元)(1)若10月份许老师家用电量为130千瓦时,则10月份许老师家应付电费多少元??(2)已知许老师家10月份的用电量为千瓦时,请完成下列填空(用代数式表示):①若千瓦时,则10月份许老师家应付电费为?????????????元;②若千瓦时,则10月份许老师家应付电费为???????元;③若千瓦时,则10月份许老师家应付电费为??????????元。
中考数学复习专题——找规律(含答案)

中考数学试复习专题——找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有8个小圆圈,第100个图中有个小圆圈.(1) (2) (3)2、 找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有 个菱形,第n 幅图中有 个菱形.3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 枚(用含n 的代数式表示).4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为.5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个22⨯的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个33⨯的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个44⨯的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个1010⨯的正方形图案, 则其中完整的圆共有 个.1 2 3n … … 第1个图 第2个图 第3个图 …6、如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子枚(用含有n的代数式表示,并写成最简形式).○○○○○○○○○○○○○●●○○●●●○○●○○●●○○●●●○○○○○○○○○●●●○○○○○○7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9,则表示实数17的有序实数对是.9、如图2,用n表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n的关系是10、观察图4的三角形数阵,则第50行的最后一个数是()1-2 3-4 5 -67 -8 9 -10。
11、下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第n个图案中白色正方形的个数为.12、观察下列各式:3211=332123+=33221236++=33332123410+++=……猜想:333312310++++=.第一个第二个第三个……第n个第一排第二排第三排第四排6┅┅10 9 8 73 2154答案解析:1解析:1时,5.n再每增加一个数时,m就增加3个数.解答:根据所给的具体数据,发现:8=5+3,11=5+3×2,14=5+3×3,….以此类推,第n个圈中,5+3(1)=32.2解析:分析可得:第1幅图中有1×2-1=1个,第2幅图中有2×2-1=3个,第3幅图中有3×2-1=5个,…,故第n幅图中共有21个3解析:在4的基础上,依次多3个,得到第n个图中共有的棋子数.观察图形,发现:在4的基础上,依次多3个.即第n个图中有4+3(1)=31.当6时,即原式=19.故第6个图形需棋子19枚4解析:此题只要找出截取表一的那部分,并找出其规律即可解.解答:解:表二截取的是其中的一列:上下两个数字的差相等,所以15+3=18.表三截取的是两行两列的相邻的四个数字:右边一列数字的差应比左边一列数字的差大1,所24+25-20+1=30.表四中截取的是两行三列中的6个数字:18是3的6倍,则c应是4的7倍,即28.故选D.认真观察表格,熟知各个数字之间的关系:第一列是1,2,3,…;第二列是对应第一列的2倍;等三列是对应第一列的3倍5解析:据给出的四个图形的规律可以知道,组成大正方形的每个小正方形上有一个完整的圆,因此圆的数目是大正方形边长的平方,每四个小正方形组成一个完整的圆,从而可得这样的圆是大正方形边长减1的平方,从而可得若这样铺成一个10×10的正方形图案,则其中完整的圆共有102+(10-1)2=181个.解答:解:分析可得完整的圆是大正方形的边长减1的平方,从而可知铺成一个10×10的正方形图案中,完整的圆共有102+(10-1)2=181个.点评:本题难度中等,考查探究图形的规律.本题也只可以直接根据给出的四个图形中计数出的圆的个数,找出数字之间的规律得出答案.6解析:解:第1个正方形图案有棋子共32=9枚,其中黑色棋子有12=1枚,白色棋子有(32-12)枚;第2个正方形图案有棋子共42=16枚,其中黑色棋子有22=4枚,白色棋子有(42-22)枚;…由此可推出想第n个图案的白色棋子数为(2)22=4(1).故第n个图案的白色棋子数为(2)22=4(1).点评:根据图形提供的信息探索规律,是近几年较流行的一种探索规律型问题.解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论7解析:根据题意分析可得:搭第1个图形需12根火柴;搭第2个图形需12+6×1=18根;搭第3个图形需12+6×2=24根;…搭第n个图形需12+6(1)=66根.解答:解:搭第334个图形需6×334+6=2010根火柴棒8解析:寻找规律,然后解答.每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.解答:解:观察图表可知:每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.实数15=1+2+3+4+5,则17在第6排,第5个位置,即其坐标为(6,5).故答案填:(6,5).对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.9解析:根据题意分析可得:第n行有n个小圆圈.故f(n)和n的关系是ƒ(n)= (n2).10解析:根据题意可得:第n行有n个数;且第n行第一个数的绝对值为+1,最后一个数的绝对值为;奇数为正,偶数为负;故第50行的最后一个数是1275.解答:解:第n行第一个数的绝对值为+1,最后一个数的绝对值为,奇数为正,偶数为负,第50行的最后一个数是1275第一个图中白色正方形的个数为3×3-1;第二个图中白色正方形的个数为3×5-2第三个图中白色正方形的个数为3×7-3;…当其为第n个时,白色正方形的个数为3(21)5312解析:根据所给的等式,可以发现右边的底数是前边的底数的和,指数是平方,则最后的底数是1+2+310=5×11=55,则原式=552.解答:解:根据分析最后的底数是1+2+310=5×11=55,则原式=552.故答案552。
(完整版)七年级找规律经典题汇总带答案

……一、数字排列规律题1、观察下列各算式: 1+3=4=22,1+3+5=9=23,1+3+5+7=16=24… 按此规律 (1)试猜想:1+3+5+7+…+2005+2007的值 ?(2)推广: 1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢? 2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个( )二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球 个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是 (填图形名称).三、数、式计算规律题 1、已知下列等式:① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102 ;由此规律知,第⑤个等式是 . 2、观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,… 根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____.3、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+ =+⨯=+b a aba b 则符合前面式子的规律,,若…21010 规律发现专题训练1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n )个图案中有白色..地砖 块。
初中数学找规律
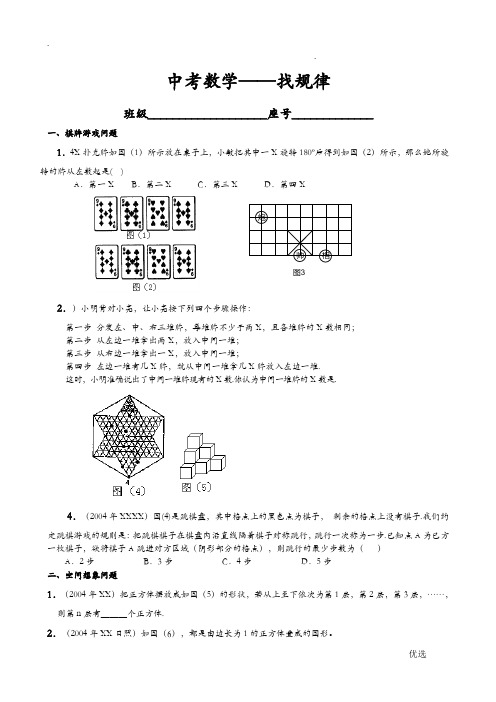
中考数学——找规律班级___________________座号_____________一、棋牌游戏问题1.4X 扑克牌如图(1)所示放在桌子上,小敏把其中一X 旋转180º后得到如图(2)所示,那么她所旋转的牌从左数起是( )A .第一XB .第二XC .第三XD .第四X2.)小明背对小亮,让小亮按下列四个步骤操作:第一步 分发左、中、右三堆牌,每堆牌不少于两X ,且各堆牌的X 数相同; 第二步 从左边一堆拿出两X ,放入中间一堆; 第三步 从右边一堆拿出一X ,放入中间一堆;第四步 左边一堆有几X 牌,就从中间一堆拿几X 牌放入左边一堆. 这时,小明准确说出了中间一堆牌现有的X 数.你认为中间一堆牌的X 数是.4.(2004年XXXX )图(4)是跳棋盘,其中格点上的黑色点为棋子, 剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子在棋盘内沿直线隔着棋子对称跳行,跳行一次称为一步.已知点A 为已方一枚棋子,欲将棋子A 跳进对方区域(阴影部分的格点),则跳行的最少步数为( ) A .2步 B .3步 C .4步 D .5步 二、空间想象问题1.(2004年XX )把正方体摆放成如图(5)的形状,若从上至下依次为第1层,第2层,第3层,……,则第n 层有___个正方体.2.(2004年XX 日照)如图(6),都是由边长为1的正方体叠成的图形。
图3相帅炮例如第①个图形的表面积为6个平方单位,第②个图形的表面积为18个平方单位,第③个图形的表面积是36个平方单位。
依此规律,则第⑤个图形的表面积个平方单位。
3.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图(7),是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面.则“祝”、“你”、“前”分别表示正方体的.4..观察下列由棱长为1的小立方体摆成的图形,寻找规律:如图(8)①中:共有1个小立方体,其中1个看得见,0个看不见;如图(8)②中:共有8个小立方体,其中7个看得见,1个看不见;如图(8)③中:共有27个小立方体,其中19个看得见,8个看不见;……,则第⑥个图中,看不见...的小立方体有个.5.图(1)是一个黑色的正三角形,顺次连结它的三边的中点,得到如图(2)所示的第2个图形(它的中间为一个白色的正三角形);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第3个图形。
(完整word版)七年级数学找规律练习题和答案

找规律练习题1 •用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第X 1=1,第二个数为X 2=3,第三个数开始依次记为 X 3, X 4,…,X n ;从第二个数开始,每个数是它相中有白色地砖 块。
2.我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非。
在一个边长为1的正方形纸版上, 形彩色纸片(n 1 规律,计算丄 2为大于1 1 1 48的整数) 1 班1 1 依次贴上面积为 1 , 1 ,2 4 。
请你用“数形结合”的思想, 8 ”如图, 1 丄的矩 2n 依数形变化的 邻两个数和的一半。
(如: X 2=^l X3 )2 (1)求第三、第四、第五个数,并写出计算过程; (2)根据(1)的结果,推测X 8= (3)探索这一列数的规律,猜想第 k 个数X k = . ( k 是大于2的整数) 4•将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线) .继续对折,对折时每次折痕与上次的折痕保持平行,连 续对折三次后,可以得到 7条折痕,那么对折四次可以得到 ________________ 条折痕.如果对折n 次,可以得到 ______________ 条折 痕• 1 1 1 1 1 1 1 ■ ■ 1 4 1 | 1 1 1 1 1 111 1 1 V 1 1 1 1 1 1 1 hL1 V 1 1 a ii k i 1119 1 l> V i i I I I I l> 1 1 I l> I 1 I I I i 1 >1 1 ■ KPI ■ ・ W P a L h h F 1I 4 1 il >1 I ii ■l >l 4 I A I 第一次对折第二次对折第三友对折5.观察下面一列有规律的数 1 2 _5 _6_ 3,8,15,24,35,48 根据这个规律可知第 n 个数是(n 是正整数) 6.古希腊数学家把数 1, 3, 6, 10, 15, 21 ,……,叫做三角形数,它有一定的规律性,则第 形数的差为 _____________________ 。
七年级数学找规律经典题型

七年级数学找规律经典题型一、数字规律1. 数列规律例1:观察数列1,3,5,7,9,…,求第n个数。
解析:首先观察这个数列,发现相邻两个数的差值都是2。
第1个数是1 = 2×1 1;第2个数是3 = 2×2 1;第3个数是5 = 2×3 1;第4个数是7 = 2×4 1;第5个数是9 = 2×5 1。
所以可以得出第n个数为2n 1。
例2:观察数列2,4,8,16,32,…,求第n个数。
解析:这个数列中,后一个数都是前一个数的2倍。
第1个数是2 = 2^1;第2个数是4 = 2^2;第3个数是8 = 2^3;第4个数是16 = 2^4;第5个数是32 = 2^5。
所以第n个数为2^n。
2. 数字循环规律例:有一组数按照1, 1,1, 1,…的规律排列,求第n个数。
解析:观察这组数字,发现数字是1和 1交替出现。
当n为奇数时,第n个数为1;当n为偶数时,第n个数为 1。
可以用(-1)^(n + 1)来表示,当n = 1时,(-1)^(1+1)=1;当n = 2时,(-1)^(2 + 1)= 1。
二、图形规律1. 图形数量规律例1:用火柴棒搭三角形,搭1个三角形需要3根火柴棒,搭2个三角形需要5根火柴棒,搭3个三角形需要7根火柴棒,…,求搭n个三角形需要多少根火柴棒。
解析:搭1个三角形需要3根火柴棒,即2×1+1;搭2个三角形时,第二个三角形和第一个三角形共用一条边,所以需要3 + 2 = 5根火柴棒,即2×2+1;搭3个三角形时,第三个三角形和前面的三角形共用两条边,所以需要3+2×2 = 7根火柴棒,即2×3 + 1。
所以搭n个三角形需要2n+1根火柴棒。
例2:观察下列图形的点数规律:第1个图形有1个点;第2个图形有1 + 3 = 4个点;第3个图形有1+3 + 5 = 9个点;第4个图形有1+3+5 + 7 = 16个点;求第n个图形的点数。
初中数学找规律专题练习

找规律专题练习1、你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,2、如以下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按 同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去; (1)填表:(2)如果剪n 次,共剪出多少个小正方形?(3)如果剪了 100次,共剪出多少个小正方形? (4)观察图形,你还能得出什么规律?3、小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住局部的整数的和是4、填表并答复以下问题x0.010.11101001000( 100 1 2x(1)根据上表结果,描述所求得的一列数的变化规律 (2)当x 非常大时,学的值接近于什么数? x5、现有黑色三角形“▲和△〞共200个,根据一定规律排列如下:那么黑色三角形有 个,白色三角形有 个7、用火柴棒按如下方式搭三角形:(1)填写下表:反复几次,就把这根很粗的面条拉成了许多细的面条,如下面草图所示.这样捏合到第 64根细面条.次后可拉出第一次捏合第三次捏合剪的次数 1 2 3 4 5正方形个数第二次捏合 6、仔细观察以下图形.当梯形的个数是n 时,图形的周长是12的规律填空: 502, 第n 个式子呢?①张桌子拼在一起可坐 ________ 入.3张桌子拼在一起可坐 _________ 人,n 张桌子拼在一起可坐 __________ 人. ②一家餐厅有40张这样的长方形桌子,根据上图方式每 5张桌子拼成1张大桌子,那么40张桌子可 拼成8张大桌子,共可坐 ____________ 人.③假设在②中,改成每8张桌子拼成1张大桌子,那么共可坐 __________________ 人. 12、用计算器计算以下各式,并将结果填写在横线上.① 1X7X15873= ______________ ② 2X7 X15873= _____________ ③ 3X7 X15873= _____________ ④ 4X7 X15873= _____________你发现了什么规律?把你发现的规律用简练的语言写出来;13、观察以下顺序排列的等式:9 >0+1=19 >1+2=11 9>2+3=21 9>3+4=31 9X4+5=41猜测:第n 个等式(n 为正整数)应为.14、 一个两位数的个位数是a,十位数字是b,请用代数式表示这个两位数是15、观察以下各式:31=3, 32 =9, 33=27, 34=81, 35=243, 36=729…你能从中发现底数为 3的事的9、一列数:1,- -2 , 3,- -4, 5, —6, 7,…将这列数排成第1行 1第2行 一23第3行 —45 一 6第4行 7 一 8 9 -10第5行 11 -1213 —141510、观察以下算式:1 5 4 32 , 2 6 4 42 ,3 74 52 , 4 8 4 62 ,请你在察规律之后并用你得到(2)照这样的规律搭下去,搭n 个这样的三角形需要 _______________ 根火柴棒8、把编号为1, 2, 3, 4,…的假设干盆花按右图所示摆放,花盆中 蓝、紫的颜色依次循环排列,那么第 8行从左边数第6盆花的颜色为 色.根据上述规律排下去,那么第10行从左边数第5个数等于的花按红、黄、卜列形式:个位数有什么规律吗?根据你发现的规律答复:3 2004的个位数字是16、观察以下各式,你会发现什么规律?3X5=15,而 15=42 1 0 5X7=35,而 35= 62 111X13=143,而 143= 122 1将你猜测到的规律用只含一个字母的式子表示出来:.17、问题:你能比拟20052006和20062005的大小吗?为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比拟n n+1和(n+1)n 的大小(n为正整数),我们从n=1,n=2,n=3 ••…这些简单的情况入手,从中发现规律,经过归纳,猜出结论.(1)通过计算,比拟以下各组数字大小① 12 22 ② 23 32 ③ 34 43④ 45 54⑤ 54 65⑥ 67 7(2)把第(1)题的结果经过归纳,你能得出什么结论?你能用只含有一个字母的式子表示吗? (3)根据上面的归纳猜测得到的结论,试比拟两个数的大小(1分) 20052006200召005 (填〞 >〞," <"),“二〞18、为了美化城市,某商场在门前的空地上用花盆按如下图的方式搭正方形,(1)填写下表正方形的层 数12345花盆的个数4(2)按这个规律搭下去,搭第n 层正方形,需要 _______________________________ 盆花?19、下面有三组数,请你填上适宜的运算符号,使每一组数的结果都为 10. (1) 1 5 5 9 =10 ; (2) 3 3 3 3=10 ; (3) 1 1 9 9 =10请你修忙算一算得多少?21、黑蚂蚁和红蚂蚁都认为自己跑得比对方快,刚好它们看到地上的几个半圆(图 1),于是它们决定比 一比.黑蚂蚁沿着大半圆从甲处跑到乙处;红蚂蚁沿着两个小半圆也从甲处跑到乙处.两只蚂蚁同时起 跑,说也奇怪,两只蚂蚁同时到达了乙处.(1)两只蚂蚁请你帮助判断:谁跑得快?20、小红和小花在玩一种计算的游戏,计算的规那么是a b ........................... 1 2=ad- bCo 现在轮到小红计算的值,c d3 4(2)两只蚂蚁对你的判断结果很不满意,决定再到(图 2)的几个半圆处再比赛一次,请你猜一猜,哪 一只蚂蚁先从甲处跑到乙处?,总的比赛场数是多少? 4个球队呢? m23.按一定规律排列的一串数:1 23 1 2 34 51 2Q , Q , G ,匚, 匚,匚,匚,匚,7,73 3 3 5 5 5 5 57714.下面的算式里,符号.、△、和口分别代表三个不同的自然数,这三个数的和是1111 118. △口24. 一群整数朋友根据一定的规律排成一排,可排在口位置的数跑掉了,请帮它们把跑掉的朋友找回来.(1) 5, 8, 11, 14, □ , 20; (2) 1, 3, 7, 15, 31, 63, □;(3) 1, 1, 2, 3, 5,8, □, 21 25.以下两列数:2, 4, 6, 8, 10, 12,……1994;6, 13, 20, 27, 34, (1994)这两列数中,相同的数的个数是( )A 、 142B 、 143C 、 284D 、 28526. 一串数字的排列规律是:第一个数是 20,从第二个数起,每一个数比前一个数小 8(1)第10个数是多少? ( 2)第n 个数是多少? ( 3)第几个数是一6027.某仓库堆放一批圆木,一共 20层,第一层3根,每往下一层多1根,问这堆圆木一共有多少根? 28.在如下图的2003年1月份的日历中,用一个方框圈出任意 3X3个数 星期日星期一星期二 星期三 星期四 星期五 星期六1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920212223242526 27 28 29 30 31(1)从左下角到右上角的三个数字之和为 45,那么这9个数的和是多少?这9个日期中最后一天是 1月几日?(2)用这样的方框能否圈出总和为162的9个数? 37,…中,第98个数是 ______________22. (1) 3个球队进行单循环赛 (参赛的每一个队都与其它所有各队比赛一场) 个球队呢?(代数式表示出来)(2)当m=12时,总共比赛几场?29 .观察以下数据,按某种规律在横线上填上适当的数:♦ 3 5 7 9 1, 一, 一, 一,——, ,…49162530 .如图,△ ABC 中,D 是边BC 上的中点, F 是线段CD 的中点,E 是边AC 的中点,那么图中有 条线段,有 个角,假设4 DEF 的面积是2,那么△ ABC 的面积是31 .平面内两两相交的 6条直线,其交点个数最少为 m 个,最多为n 个,那么m+n 等于〔〕A 、12B 、16C 、20D 、以上都不对32 .如图,可以看成是边长为4的小正方形的巧克力糖,请你用尽可能多的不同方法把它分成形状、大小完全相同的四块,要求不把正方形糖块划破〔至少五种方法〕40、观察公式:公式 1 : (x a)3 x 3 3x 2a 3xa 2 a 333 .在某月日历上一个竖列相邻的五个数之和为 80,这五个数是34 .某月日历有一竖列四个日期,其中第二个日期与第四个日期的和是 36,那么第三个日期是35 .今年暑假,李老师一家三口人外出旅行一周,这一周各天的日期之和是 36 .如果这个月的5号是星期三,那么20号是星期 37 .三个连续偶数中,n 是最小的一个,这三个数的和为 , 38 .以下图形中三角形的个数是〔〕A.4 个B.6 个C. 9 个D.10 个 91,那么李老师是 号回家的39、至少找出以下几何体的 4个共同点4 4 3_22 3 4公式2:(x a) x 4x a 6x a 4xa a(1) 这两个公式有什么特点?(2) 利用公式计算:_ 4 _ 3 1 __2 1 2 _ 1 3 1242()62()42()() 2 2 2 241、下面有三组数,请你填上适宜的运算符号,使每一组数的结果都为10.(1) 1 5 5 9 =10 ; (2) 3 3 3 3 =10 ; (3) 1 1 9 9 =1042 .造一个含有字母p和q的代数式,使得不管p、q取何值,代数式的值永远不是正的.43 .图是2002年6月份的日历,现用一矩形在日历中任意框出4个数| a b] ,请用一个等式表示,a、b、c、d之间的关系. c d日一一三四五六12345678910111213141516171819202122232425262728293044 .右图,是用火柴棒摆成的一个大三角形,它是由九个小三角形组成的,试将1、2、3、4、5、6、7、8、9分别填入这9个小三角形哪(每个小三角形内只填一个数) ,要求靠近大三角形每条边的每五个数相加的和相等,请想一想,怎样填这些数才能使五个数的和尽可能大一些,这五个数的和最大是多少?45.王容许了大臣的一个要求:即在国际象棋棋盘上2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到64格〞.但是不久国王九发现国库里没有这么多米,然而国王的话不能不算数,国王又不好意思向别人借,怎么办呢?请你帮国王想一个好方法来解决这个问题. (方法必须符合情理,有创意者可适当多加分.方法多者亦可多加分)46.如果连结多边形的一边上一点与其余各顶点可将某多边形分割成2004个三角形,求该多边形的边数47 .如图1-26,在ABC中,点D,E,F分别是AB,BC,AC三边中点,图中与BOD面积相等的三角形有几个?48 .观察图1-27中有几个三角形?由此你发现三角形的个数有什么规律呢49.求个数图 1-29(1)将下表填写完整. 图形符号52、以下图形经过折叠能否围成一个正方体?一个三角形3个三角形个三角形个三角形(n 个点)(3)(4)53、某种细胞每过54、有一张厚度是 30分便由1个分裂成2个,经过5小时,这种细胞由1个能分裂成0 .1毫米的纸,将它对折 1次后,厚度为2X0.1毫米.(1)图1-28(1)中有多少个三角形?(2)图1-28(2)中有多少个四边形?50.如图1-29所示,图①是一个三角形别连结图②中间的小三角形三边的中点,分别连结这个三角形三边的中点(将这条边分为相等的两局部的点 ,得到图③,按此方法继续下去,请你根据图中三角形个数的规律)得到图②;再分 ,完成以下问(2)〔1〕、对折2次后,厚度为毫米. 〔2〕对折20次后,厚度为毫米.〔3〕对折n次后,厚度为毫米.55、以下图〔1〕表示1张餐桌和6张椅子〔每个小半圆代表1张椅子〕,假设按这种方式摆放20张餐桌需要的椅子张数是.你认为220的末位数字是〔〕.57、某种细菌在培养过程中,每半小时分裂1次,每次一分为二.假设这种细菌由1个分裂到16个,那么这个过程要经过〔〕A. 1.5小时B , 2小时C , 3小时D , 4小时58、计算:1—2+3—4+……+2001 —2002+2003= . .会在与数字2所在的平面相对的平面上.,4 5 6 _1 2pv2 , 22 4, 23 8, 24 1 6, 25 32, 26 64, 27 1 28, 28 2 56, 根据上述算式中的规律,63、(A)观察以下数据,(B)按某种规律在横线上填上适当的数:4 9一列数7二72,7一,1673…72003 ,其中末位数是3的有个.56、观察以下算式: 2159、当下面这个图案被折起来组成一个正方体,数字61、根据规律填上适宜的数:〔1〕—9, —6, —3, /64、在下面的图形中〔62、〕是正方体的展开图.66、指出以下平面图形是什么几何体的展开图〔 6分〕:67、在下面的图形中,〔 〕是正方体的外表展开图68、探索规律:用棋子按下面的方式摆出正方形①按图本规律填写下表: 图形编号 (1) ⑵ (3) (4) ⑸ (6)棋子个数②根据这种方式才g 下去,摆第 n 个正方形需要多少个棋子? ③根据这种方式才g 下去,第第 20个正方形需要多少个棋子?69、,13 1 - 12 22,4,3 c3 c 1 -2 八21 2 9 — 2 3, 4□ □ □ □ □ □,3 八3 八3 "1 2 3 36 32 42⑴猜测填空:1323 334()(2)假设1323 33 240 2,试求n的值.70、用火柴棒按下面方式搭图形,那么20个图形需要的火柴棒是根. 第1 2。
十道初中数学找规律的题型及解题思路

十道初中数学找规律的题型及解题思路这里有10道初中数学找规律的题目,涵盖了常见的数列、图形等多种类型,希望能帮助学生更好地掌握找规律的技巧:数列找规律1.等差数列:1.1, 4, 7, 10, ... 下一个数是多少?2.100, 97, 94, ... 第10个数是多少?2.等比数列:1.2, 4, 8, 16, ... 第8个数是多少?2.81, 27, 9, ... 第6个数是多少?3.混合数列:1.1, 4, 9, 16, 25, ... 下一个数是多少?(提示:考虑每个数的平方)2.2, 5, 10, 17, ... 下一个数是多少?(提示:观察相邻两数的差)4.周期数列:1.1, 2, 3, 1, 2, 3, ... 第20个数是多少?2.A, B, C, A, B, C, ... 第100个数是多少?图形找规律图形的变化:1.一组图形,每个图形由小方块组成,观察图形的变化规律,画出下一个图形。
图形的旋转:1.一个图形不断旋转,观察旋转的规律,画出旋转后的图形。
图形的翻转:1.一个图形不断翻转,观察翻转的规律,画出翻转后的图形。
数字与图形结合数字与图形对应:1.一组图形,每个图形对应一个数字,找出数字与图形之间的对应关系。
图形中的数字规律:1.一个图形中包含多个数字,找出数字之间的规律。
综合题型1.数字和图形的综合:1.一组图形和数字交替出现,找出数字和图形之间的关系。
解题技巧:•观察:仔细观察数列或图形的变化规律,找出其中的共同点和差异点。
•比较:比较相邻的数或图形,找出它们的递增、递减或其他变化关系。
•联想:将题目与以前学过的知识联系起来,寻找解题思路。
•归纳:根据观察和比较的结果,归纳出一般性的规律。
•验证:将得到的规律代入后面的数或图形中进行验证,确保规律的正确性。
注意事项:•找规律题的答案可能不唯一,只要找到一种合理的规律即可。
•遇到困难时,可以尝试从不同的角度去观察和分析。
七年级数学有理数找规律题型

七年级数学有理数找规律题型一、数字规律。
题1。
观察下列数:1, -2, 3, -4, 5, -6,…,按照这样的规律,第100个数是多少?解析。
可以发现这些数的绝对值是连续的自然数,且奇数项为正,偶数项为负。
第100个数是偶数项,所以为 - 100。
题2。
给出一组数: - 1,2, - 4,8, - 16,32,…,则第7个数是多少?解析。
先看绝对值,后一个数是前一个数绝对值的2倍,再看符号,奇数项为负,偶数项为正。
第7个数是奇数项,绝对值为2^6=64,所以第7个数是 - 64。
题3。
有一列数:(1)/(2),(2)/(3),(3)/(4),(4)/(5),…,那么第n个数是多少?解析。
分子依次是1,2,3,4,…,n;分母依次是2,3,4,5,…,n + 1。
所以第n 个数是(n)/(n + 1)。
题4。
观察数:1,4,9,16,25,…,第10个数是多少?解析。
这组数是1^2,2^2,3^2,4^2,5^2,…,第n个数是n^2,所以第10个数是10^2=100。
题5。
数列:0,3,8,15,24,…,第n个数是多少?解析。
这组数可以写成1^2-1,2^2-1,3^2-1,4^2-1,5^2-1,…,第n个数是n^2-1。
二、算式规律。
题6。
观察下列算式:1 = 1^2;1+3 = 2^2;1 + 3+5=3^2;1+3 + 5+7 = 4^2;…,求1+3+5+·s+99的值。
解析。
从算式可以看出,从1开始连续奇数的和等于数的个数的平方。
1到99的奇数有50个,所以1+3+5+·s+99 = 50^2=2500。
题7。
观察算式:2^1=2,2^2=4,2^3=8,2^4=16,2^5=32,2^6=64,…,求2^20的个位数字是多少?解析。
通过观察2^n的个位数字依次是2、4、8、6循环。
20÷4 = 5,刚好整除,所以2^20的个位数字是6。
题8。
有这样一组算式:(1-(1)/(2))(1+(1)/(2))=(1)/(2)×(3)/(2)=(3)/(4);(1 -(1)/(3))(1+(1)/(3))=(2)/(3)×(4)/(3)=(8)/(9);(1-(1)/(4))(1+(1)/(4))=(3)/(4)×(5)/(4)=(15)/(16);…,求(1-(1)/(10))(1+(1)/(10))的值。
初中找规律练习题

初中找规律练习题一、选择题1. 观察下列数列,找出下一个数:2, 4, 6, 8, 10, ____A. 12B. 11C. 13D. 92. 下列图形序列中,哪一个图形是下一个?圆形,正方形,三角形,圆形,正方形,____ A. 圆形 B. 正方形 C. 三角形 D. 五边形3. 根据以下数字序列找出规律:1, 3, 6, 10, 15, ____A. 21B. 20C. 19D. 224. 观察下列数列,找出规律:1, 1, 2, 3, 5, 8, ____A. 13B. 12C. 11D. 105. 根据以下图形序列找出规律:△, □, ○, △, □, ____A. △B. □C. ○D. △□二、填空题6. 完成下列数列:1, 3, 5, 7, ________, ____, ____。
7. 完成下列图形序列:□, ○, △, □, ○, ____ ____, ____, ____。
8. 根据以下数字序列找出规律并填空:2, 5, 10, 17, 26, __________, ______。
9. 完成下列数列:1, 4, 9, 16, ________, ____, ____。
10. 根据以下图形序列找出规律并填空:△, □, ○, △, □, ○, __________, ______, ______。
三、解答题11. 观察下列数列:2, 5, 10, 17, 26, 37, 50,找出数列的规律,并计算下一个数。
12. 给定图形序列:□, ○, △, □, ○, △, □,○, △, □, 请找出规律,并预测接下来的三个图形。
13. 根据以下数字序列找出规律:1, 2, 4, 7, 11, 16, 22,计算下一个数,并说明规律。
14. 完成下列数列:2, 6, 12, 20, 30, ____并解释数列的规律。
15. 观察下列图形序列:△, □, ○, △, □, ○, △, □, ○, △, □, 请找出规律,并预测接下来的两个图形。
初中数学找规律习题大全

1找规律专项训练一:数式问题223344aa2222,?4??48??8??3?2,,3???2?为正整数)……,若b(1.(湛江)已知a、1515bb3388a?b?则.2.(贵阳)有一列数a,a,a,a,a,…,a,其中a=5×2+1,a=5×3+2,a=5×4+3,a45122n3314=5×5+4,a=5×6+5,…,当a=2009时,n的值等于()n5A.2010 B.2009 C.401 D.334345aaa23.(沈阳)有一组单项式:a,-,,-,….观察它们构成规律,用你发现的规律写出第10个单234项式为.1234,??,,,…,那么第7个数是.4.(牡丹江)有一列数105172 233547a?ba?ba?b b?a,……,其中第10,,,个式子是5.(南充)一组按规律排列的多项式:()1910191017102110b?ba?bbaa?a?B. D .C.A.112233?1?2??2?3??3?1?(安徽)观察下列等式:6.,,……,422343 2)证明你写出的等式的正确性.n个等式;((1)猜想并写出第7.(绵阳)将正整数依次按下表规律排成四列,则根据表中的排列规律,数2009应排的位置是第行第列.第1列第2列3第列4列第?n;▲22,3,…从小到大按下面规律排列.若第4行第列的数为32,则①18.(台州)将正整数,jj ii.表示)▲(用②第,行第列的数为n321第…列列第第列第列n1312…第行22n3??2nn?1n2…第行33n3?2n?22nn2?1…第行………………二:定义运算问题22b?a?a?b???24x? 3,其法则为:),求方程(4(定西)在实数范围内定义运算“1.的解.”aaaa?a21,与它前面那个数的倒数的差,每一个数都等于,,若,2.有一列数从第二个数开始,,,1321n a 为(则)200712007?21D.B.A.C.2三:剪纸问题1.(2004年河南)如图(9),把一个正方形三次对折后沿虚线剪下则得到的图形是()2.(2004年浙江湖州)小强拿了一张正方形的纸如图(10)①,沿虚线对折一次得图②,再对折一次得图③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是()3.(2004年浙江衢州)如图(11),将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,……,根据以上操作方法,请你填写下表:3N 4 5 1 2 3 操作次数N ……7 10 4 正方形的个数……x A、A、AA、A、A?A?OAAA?AA?AA过点,轴的正半轴上依次截取3.(莆田)如图,在??x P、、PP、P、P0?xy?,得直角三角形轴的垂线与反比例函数的图象相交于点分别作53214532314142253124x,PAPA、AAAP、APA、AAOP、并设其面积分别为514224131243352?y x yS,、S、S、S、SS的值为则.551432P1P 2 P3PP4 5O x AAAAA5 3 4 1 2 10题图)(第(长春)用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个4.的代数式n (用含n图案多一个正六边形和两个正三角形,则第个图案中正三角形的个数为. 表示)题)(第4100,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第6(丹东)如图5.4枚.个图案需棋子……32图案图案1图案6图n个图中最小的三角形的个数有 6.(抚顺)观察下列图形(每幅图中最小的三角形都是全等的),请写出第....个.个图第4 第3个图第1个图第2个图题图)(第167.(哈尔滨)观察下列图形:它们是按一定规律排列的,依照此规律,第16个图形共有个★.五:对称问题、1.(伊春)在平面直角坐标系中,已知3个点的坐标分别为、. 一只电子蛙位于,A1)(11) 1,A(0,2)A(132坐标原点处,第1次电子蛙由原点跳到以为对称中心的对称点,第2次电子蛙由点跳到以为对APAP2111称中心的对称点,第3次电子蛙由点跳到以为对称中心的对称点,…,按此规律,电子蛙分别PPAP3223以、、为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是(_______ ,AAAP3122009_______).2.(2004年宁波)仔细观察下列图案,如图(12),并按规律在横线上画出合适的图形。
初一数学找规律练习题

初一数学找规律练习题初一数学找规律的练习题对于培养学生的观察力、分析力和推理能力非常重要。
以下是一些适合初一学生的数学找规律练习题:1. 观察数列,找出规律并填写缺失的数字:2, 4, 6, 8, __, 14, 162. 根据给出的数列,找出规律并完成数列:3, 6, 11, 18, __, 47, 763. 观察下列图形序列,找出规律并画出下一个图形:第一个图形:一个正方形第二个图形:两个正方形第三个图形:三个正方形,排成一行第四个图形:四个正方形,排成两行,每行两个第五个图形:______(请画出)4. 观察下列数列,找出规律并填写下一个数字:2, 5, 10, 17, 26, __5. 根据给出的图形序列,找出规律并完成下一个图形:第一个图形:一个圆形第二个图形:两个圆形,中间有一个正方形第三个图形:三个圆形,中间有一个正方形,正方形周围有四个三角形第四个图形:______(请画出)6. 观察下列数列,找出规律并计算第10个数字:1, 3, 6, 10, 15, ...7. 根据给出的图形序列,找出规律并画出第5个图形:第一个图形:一个三角形第二个图形:两个三角形,一个在另一个上面第三个图形:三个三角形,一个在另一个上面,最上面的三角形是倒立的第四个图形:四个三角形,最上面的三角形是倒立的,下面三个三角形依次排列第五个图形:______(请画出)8. 观察下列数列,找出规律并填写下一个数字:1, 4, 9, 16, 25, __9. 根据给出的图形序列,找出规律并完成下一个图形:第一个图形:一个圆形,里面有一个正方形第二个图形:一个圆形,里面有一个正方形和一个三角形第三个图形:一个圆形,里面有一个正方形,一个三角形和一个五边形第四个图形:______(请画出)10. 观察下列数列,找出规律并填写下一个数字:1, 1, 2, 3, 5, 8, ...答案提示:1. 102. 273. 五个正方形,排成两行,每行三个4. 375. 五个圆形,中间有一个正方形,正方形周围有五个三角形6. 1207. 五个三角形,最上面的三角形是倒立的,下面四个三角形依次排列,最下面的三角形也是倒立的8. 369. 一个圆形,里面有一个正方形,一个三角形,一个五边形和一个六边形10. 13这些练习题旨在帮助学生通过观察和分析来发现数字和图形的规律,从而提高他们的数学思维能力。
(完整word)初中数学找规律

例题:(10西城二模)一组按规律排列的整数 5, 7, 11, 19,…,第6个整数为,根据上述规律,第n 个整数为 _____________ ( n 为正整数)•••第6个整数是26 3 67,第n 个整数是2n 3 (n 为正整数).练习:1 4 9 16 1' (10怀柔二莫)按一定规律排列的一列数依次为:3,产,亍……,按此规 律排列下去,这列数中的第5个数是 ____________ ,第n 个数是 ______________________________________2、(09东城一模)按一定规律排列的一列数依次为: -…,按此规律排列下去,这列数中的第 9个数是 35 答案:12 n1n ( 1)例题:(10通州一模)某些植物发芽有这样一种规律:当年所发新芽第二年不发 芽,老芽在以后每年都发芽.发芽规律见下表(设第一年前的新芽数为 a )照这样下去,第8年老芽数与总芽数的比值为.解:第8年的老芽数是21a ,新芽数是13a ,总芽数是34a ,贝吐匕值为 •34 练习:1、( 08石景山一模)小说《达•芬奇密码》中的一个故事里出现了一串神秘排列 的数,将这串令人费解的数从小到大的顺序排列为:1,1, 2, 3, 5, 8 ,则答案: 25 n 211 , 2n 11 ] 丄 丄 丄2,3,10,15, 26这列数的第8个数是______________ .2答案:212、(09房山二模)填在下面三个田字格内的数有相同的规律,根据此规律,请填 出图4中的数字.答案:7,9,11,176((1)n 与(1)n1)例题:(09通州二模)12.观察并分析下列数据,寻找规律:0,..、36 ,3,- 2、.3,,15,— 3・.2,……那么第10个数据是 _____________ ;第n 个数据 是 ______ .•••第10个数据是3-3,第n 个数据是(1)n1.. 3n 3 . 练习:1、(10房山一模)一组按规律排列的式子: 4,%~|,■16,...(a 0),其中第a a a a 8个式子是 _____ ,第n 个式子是 ________ (n 为正整数). 答案: 64( 1)n 1 n 223 3n 1aa58112、(10门头沟二模)一组按一定规律排列的式子:一a 2,-,—-,—,…,23 4(a ^ 0),则第n 个式子是 ________ (n 为正整数)3n 1答案:(1)0-—n3、(09崇文一模)一组按规律排列的数:2, 0, 4, 0, 6, 0,…,其中第7个数 是 ________ ,第n 个数是 _________ ( n 为正整数). 答案:8,』^(n 1)57 9108例题:(08通州二模)世界上著名的莱布尼茨三角形如图所示:贝U排在第10行从左边数第3个位置上的数是_______ .•••第10行倒数第三个数是———.72 90 360练习:1、(08大兴一模)自然数按一定规律排成下表,那么第200行的第5个数是_____ .12 34 5 67 89 101113 14 1512答案:199052、如图的数字方阵中,方框所缺的数,按照适宜的规律填上(A、100B、128C、129D、130答案:C例题:(11平谷二模)如图,将连续的正整数1,2,3,4……依次标在下列三角形中,那么2011这个数在第 ____ 个三角形的 ________ 顶点处(第二空填:上,左下,右下).• 2011 这个数在第671个三角形的上顶点处.故答案为:671, 上.练习:1、(08 崇文一模)观察下列等式:31 1 2 , 32 1 8 , 33 1 26 , 34 1 80 , 35 1 242 ,…….通过观察,用你所发现的规律确 定32008 1的个位数字是 ______ . ___ 答案:32、右图为手的示意图,在各个手指间标记字母A ,B ,C, D 请你按图中箭头所指 方向(即A — B ^C T C T B ^B^d …的方式)从 A 开始 数连续的正整数1, 2, 3, 4,…,当数到12时,对应的字母是 当字母C 第201次出现时,恰好数到的数是 当字母C 第2n 1次出现时(n 为正整数),恰 好数到的数是 ____ (用含n 的代数式表示). 答案:B, 603, 6n+3例题:(09平谷一模)已知:£2£2232 34 44 4……若b x1 1 '2 2 ‘3 3'10=a +10 (a 、b 都是正整数),则a+b 的最小值是 _________ . 二a+b 的最小值是19 练习:1. ( 10密云一模)下面是按一定规律排列的一列数:第1个数: 1 1 122第2个数: 1 1 11 (1)211 1323 第3个数: 1 1 11 (1)2 1423232n 11 1L 1(“第n 个数:2n(1)3;4 ;4 5 6那么,在第10个数、第11个数、第12个数、第13个数中,最大的数是()A.第10个数B .第11个数 C.第12个数 D.第13个数答案:A例题1: (10昌平一模)观察下列图案:照这样它们是按照一定规律排列的,依照此规律,第5个图案中共有________ 个三角形,第n (n 1,且n为整数)个图案中三角形的个数为_________ (用含有n的式子表示).解答:解:第5个图案中,有6+4X4=22 (个)三角形;第n个图案中,有6+4(n-1 )=4n+2 (个)三角形.例题2. (10西城一模)在平面直角坐标系中,我们称边长为1、且顶点的横、纵坐标均为整数的正方形为单位格点正方形.如图,在菱形ABCD中,四个顶点坐标分别是(一8,0 ),(0,4 ),(8,0 ),(0,点正方形的个数是个;若菱形ABGD n的四个顶点坐标分别为(—2n,0 ),(0, n), (2n,0), (0,—n)(n 为正整数),则菱形ABnG D n能覆盖的单位格点正方形的个数为_______________________ (用含有n的式子表示).答案为:4n2-4n .—4),贝U菱形ABCD能覆盖的单位格练习:.1、(10大兴一模)如图4所示,把同样大小的黑色棋子摆放在正多边形的边上,按的规律摆下去,则第n个图形需要黑色棋子的个数是_______________第1个图形第2个图形第3个图形第4个图形(图4)答案:n(n 2)2、(08顺义二模)如图,图①,图②,图③,图④……是用围棋棋子摆成的一列图①图②图③图④具有一定规律的“山”字•则第n个“山”字中的棋子个数是______________答案:5n+23、(08丰台二模)用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一列图案:请问第n个图案中有白色纸片的张数为A. 4n 3B. 3n 1C. nD. 2n 2答案:B第1个第2个第3个4、(10丰台一模)在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点•请你观察图中正方形ABCD, ABC2D2,AB3C3D3…每个正方形四条边上的整点答案:80个.的个数•按此规律推算出正方形Ao BwC o D。
初中数学中考复习专题:找规律专项练习及答案解析(50道)

初中数学中考复习专题:找规律专项练习及答案解析(50道)一、选择题1、连结多边形不相邻的两个顶点的线段,叫做多边形的对角线.观察上述图形并阅读相关文字,思考回答问题:显然四边形对角线有2条;五边形的对角线有5条;对于六边形的对角线条数,光靠“数”数,也能数出来,但已感到较麻烦!需寻找规律!从一个顶点A 出发,显然有3条,同理从B出发也3条,每个顶点出发都是3条,但从C顶点出发,就有重复线段!用此方法算出六边形的对角线条数为a;且能归纳出n边形的对角线条数的计算方法;若一个n边形有35条对角线,则a和n的值分别为()A.12,20 B.12,15C.9,10 D.9,122、寻找规律计算1 - 2+3 - 4+5 - 6+…+2015 - 2016等于()A.0 B.- 1C.- 1008 D.10083、观察下列各式并找规律,再猜想填空:,则______ .4、观察一列数:,,,,,……根据规律,请你写出第10个数是()A.B.C.D.二、填空题5、观察一下几组勾股数,并寻找规律:① 3, 4, 5;② 5,12,13;③ 7,24,25;④ 9,40,41;……请你写出有以上规律的第⑤组勾股数:6、找规律填空:……7、已知…,观察上面的计算过程,寻找规律并计算:= .8、观察分析下列数据,寻找规律:0,,,3,2,……那么第10个数据应是_________.9、找规律.一张长方形桌子可坐6人,按下图方式讲桌子拼在一起。
① 2张桌子拼在一起可坐______人;(1分)3张桌子拼在一起可坐______人;(1分)n张桌子拼在一起可坐______人。
(3分)②一家餐厅有40张这样的长方形桌子,按照上图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐______人。
(3分)10、观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:_________________.11、找规律填上合适的数:-2,4,-8,16,,64,……………12、用火柴棒按以下方式搭“小鱼”.…………搭1条“小鱼”需用8根火柴棒,搭2条“小鱼”需用14根火柴棒,搭3条“小鱼”需用20根火柴棒……观察并找规律,搭10条“小鱼”需用火柴棒的根数为.13、观察分析下列数据,寻找规律:0,,,3,2,,3,……,那么第10个数据应是.14、填空找规律(结果保留四位有效数字).(1)利用计算器分别求:=________,=________,=________,=________;(2)由(1)的结果,我们发现所得的结果与被开方数间的规律是________;(3)运用(2)中的规律,直接写出结果:=________,=________.15、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a+b+c 的值为.16、找规律填上合适的数:﹣2,4,﹣8,16,,64,…17、观察下列数据:0,,,,,……,寻找规律,第9个数据应是.18、观察烟花燃放图形,找规律:依此规律,第9个图形中共有_________个★.19、观察并分析下列数据,寻找规律: 0,,-,3,-2,,-3,……那么第10个数据是___________ ;第n个数据是_______________ .20、观察一下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;……请你写出有以上规律的第⑤组勾股数:______________________.21、寻找规律,根据规律填空:,,,,,,…,第n个数是.22、找规律,并按规律填上第五个数:.23、阅读下文,寻找规律.计算:(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1﹣x3,(1﹣x)(1+x+x2+x3)=1﹣x4….(1)观察上式,并猜想:(1﹣x)(1+x+x2+…+x n)= .(2)根据你的猜想,计算:1+3+32+33…+3n= .(其中n是正整数)24、找规律,如图有大小不同的平行四边形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第n幅图中有个。
七年级上册找规律数学题

七年级上册找规律数学题一、数字规律题。
1. 观察下列数:1,4,9,16,25,…,按此规律,第n个数是()- 解析:- 第1个数是1 = 1^2;- 第2个数是4=2^2;- 第3个数是9 = 3^2;- 第4个数是16=4^2;- 第5个数是25 = 5^2。
- 所以第n个数是n^2。
2. 有一组数:1, - 2,3,-4,5,-6,·s,按此规律,第n个数是()- 解析:- 当n为奇数时,数为正数,即第n个数为n;- 当n为偶数时,数为负数,即第n个数为-n。
- 所以第n个数是( - 1)^n + 1n。
3. 观察数列:2,5,8,11,·s,则第n个数是()- 解析:- 可以发现每一个数都比前一个数大3。
- 第1个数2 = 3×1 - 1;- 第2个数5=3×2 - 1;- 第3个数8 = 3×3-1;- 所以第n个数是3n - 1。
4. 数列1,(1)/(2),(1)/(3),(1)/(4),(1)/(5),·s,第n个数是()- 解析:- 很明显,第n个数是(1)/(n)。
5. 找规律:0,3,8,15,24,·s,第n个数是()- 解析:- 第1个数0 = 1^2-1;- 第2个数3=2^2-1;- 第3个数8 = 3^2-1;- 第4个数15=4^2-1;- 第5个数24 = 5^2-1;- 所以第n个数是n^2-1。
二、图形规律题。
6. 用火柴棒按下图的方式搭三角形:- 照这样的规律搭下去,搭n个这样的三角形需要多少根火柴棒?- 解析:- 搭1个三角形需要3根火柴棒;- 搭2个三角形需要3 + 2=5根火柴棒;- 搭3个三角形需要3+2×2 = 7根火柴棒;- 搭n个三角形需要3 + 2(n - 1)=2n + 1根火柴棒。
7. 观察下列图形的构成规律,根据此规律,第n个图形中有多少个圆?- 第1个图形有1个圆;- 第2个图形有1 + 2 = 3个圆;- 第3个图形有1+2 + 3=6个圆;- 第4个图形有1+2+3 + 4 = 10个圆;- 解析:- 第n个图形中圆的个数为1 + 2+3+·s+n=(n(n + 1))/(2)。
完整)初中数学找规律专项练习题(有答案)

完整)初中数学找规律专项练习题(有答案)1、观察规律:1=1;1+3=4;1+3+5=9;1+3+5+7=16;…,则2+6+10+14+…+2014的值是多少?2、用四舍五入法对取近似数,并精确到千位,用科学计数法表示为多少?3、观察下面的一列数:-1,2,-3,4,-5,6…请找出其中排列的规律,并按此规律填空。
(1)第10个数是多少?第21个数是多少?(2)-40是第几个数?26是第几个数?4、一组按规律排列的数:1,3,6,10,15…请推断第9个数是多少?5、计算:(-100)+(-101)=多少?(-2)+(-2)=多少?6、若。
则等于多少?7、大肠杆菌每过20分钟便由1个分裂成2个,经过3小时后这种大肠杆菌由1个分裂成多少个?8、猜数字游戏中,XXX写出如下一组数:1,3,5,7,9…n个数是…,XXX猜想出第六个数字是多少?根据此规律,第9、10个数字分别是多少?9、若。
与|b+5|的值互为相反数,则等于多少?10、在计数制中,通常我们使用的是“十进位制”,即“逢十进一”.而计数制方法很多,如60进位制:60秒化为1分,60分化为1小时;24进位制:24小时化为1天;7进位制:7天化为1周等…而二进位制是计算机处理数据的依据.已知二进位制与十进位制的比较如下表:十进位制二进制 1 1 2 10 3 11 4 100 5 101 6 110 …… 请将二进位制xxxxxxxx(二)写成十进位制数为多少?11、为求。
值,可令S=。
则2S=。
因此所以。
仿照以上推理计算出的值是多少?二、选择题13、的值是多少?【】A.-2 B.-1 C.0 D.114、已知8.62=73.96,若x=0.7396,则x的值等于()A.86.2B.862C.±0.862D.±86215、计算:(-2)+(-2)的值是多少?A.2B.-1C.-2D.-416、计算等于多少?A. B. C. D.17、已知a、b互为相反数,c、d互为倒数,m的绝对值为1,p是数轴到原点距离为1的数,那么的值是多少?A.3 B.2 C.1 D.018、若。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
探索题训练—找规律
1、我们平常用的数是十进制数,如2639=2×103+6×102+3×101+9×100,表示十进制的数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9。
在电子数字计算机中用的是二进制,只要两个数码:0和1。
如二进制中101=1×22+0×21+1×20等于十进制的数5,10111=1×24+0×23+1×22+1×21+1×20等于十进制中的数23,那么二进制中的1101等于十进制的数 。
2、从1开始,将连续的奇数相加,和的情况有如下规律:1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52;…按此规律请你猜想从1开始,将前10个奇数(即当最后一个奇数是19时),它们的和是。
3、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:
输入 (1)
2
3
4
5
… 输出
…
21
52 103 174 265
…
那么,当输入数据是8时,输出的数据是( ) A 、
618 B 、638 C 、65
8 D 、678
4、如下左图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,则摆第30个“小屋子”要 枚棋子.
5、如下右图是某同学在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第n 个小房子用了 块石子。
6、如下图是用棋子摆成的“上”字:
(1)
(2)
(3)
第4题
第一个“上”字第二个“上”字第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第四、第五个“上”
字分别需用和
枚棋子;(
2)第
n
个“上”字需用
枚棋子。
7、如图一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分,则这串珠子被盒子遮住的部分有_______颗.
8、根据下列5个图形及相应点的个数的变化规律:猜想第6个图形有
个点,第n个图形中有个点。
9、下面是按照一定规律画出的一列“树型”图:
经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出个“树枝”。
10、观察下面的点阵图和相应的等式,探究其中的规律:
(1)在④和⑤后面的横线上分别写出相应的等式;
(2)通过猜想写出与第n个点阵相对应的等式_____________________。
11、用边长为1cm的小正方形搭成如下的塔状图形,则第n次所搭图形的周长是
_______________cm(用含n 的代数式表示)。
……
……
①1=12;②1+3=22;③1+3+5=32④;⑤;
第1次第2次第3次第4次···
···
第7题图
⑴ ⑵ ⑶
(1) (2) (3)
(4)
12、如图,都是由边长为1的正方体叠成的图形。
例如第(1)个图形的表面积为6个平方单位,第(2)个图形的表面积为18个平方单位,第(3)个图形的表面积是36个平方单位。
依此规律。
则第(5)个图形的表面积 个平方单位。
13、图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是( )
A 25
B 66
C 91
D 120
14、如图是由大小相同的小立方体木块叠入而成的几何体,图⑴中有1个立方体,图⑵中有4个立方体,图⑶中有9个立方体,…… 按这样的规律叠放下去,
第8个图中小立方体个数是 .
(1)
(2)
(3)
14题
15、图1是棱长为a 的小正方体,图2、图3由这样的小正方体摆放而成.按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n 层,第n 层的小正方体的个数为s .解答下列问题:
(
(2)写出当n =10时,s= .
16、如图用火柴摆去系列图案,按这种方式摆下去,当每边摆10根时(即10 n )时,需要的火柴棒总数为 根;
17、用火柴棒按如图的方式搭一行三角形,搭一个三角形需3支火柴棒,搭2个三角形需5支火柴棒,搭3个三角形需7支火柴棒,照这样的规律下去,搭n 个三角形需要S 支火柴棒,那么用n 的式子表示S 的式子是 _______ (n 为正整数).
18、如图所示,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下图:则第n 个图形中需用黑色瓷砖 ____ 块.(用含n 的代数式表示)
第18
题图
19、如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空:
当黑色瓷砖为20块时,白色瓷砖为块;当白色瓷砖为n2(n为正整数)块时,黑色瓷砖为块.
17题图
20、观察下列由棱长为1的小立方体摆成的图形,寻找规律:如图1中:共有1 个小立方
体,其中1个看得见,0个看不见;如图2中:共有8个小立方体,其中7个看得见,1个看不见;如图3中:共有27个小立方体,其中有19个看得见,8个看不见;……,则第6个图中,看不见的小立方体有个。
21、下面的图形是由边长为l的正方形按照某种规律排列而组成的.
(1)观察图形,填写下表:
A
图形①②③
正方形的个数 8
图形的周长 18
(2)推测第n个图形中,正方形的个数为________,周长为______________(都用含n 的代数式表示).
22、观察下图,我们可以发现:图⑴中有1个正方形;图⑵中有5个正方形,图⑶中共有14个正方形,按照这种规律继续下去,图⑹中共有_______个正方形。
23、某正方形园地是由边长为1的四个小正方形组成的,现要在园地上建一个花坛(阴影
部分)使花坛面积是园地面积的一半,以下图中设计不合要求
....的是( )
24、如下图中的四个正方形的边长均相等,其中阴影部分面积最大的图形是( )
25、如图,在方格纸中有四个图形<1>、<2>、<3>、<4>,其中面积相等的图形是()
A. <1>和<2>
B. <2>和<3>
C. <2>和<4>
D. <1>和<4>
A D
C
B
26、某体育馆用大小相同的长方形木块镶嵌地面,第1次铺2块,如图1;第2次把第1次铺的完全围起来,如图2;第3次把第2次铺的完全围起来,如图3;…依此方法,
第n次铺完后,用字母n表示第n
次镶嵌所使用的木块块数为 .
(n为
正整数)
27、用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:
⑴第4个图案中有白色地面砖块;
⑵第n个图案中有白色地面砖块。
28、分析如下图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.。
