2019高一数学必修一上册第二章复习要点语文
必修一数学第二章知识点总结

必修一数学第二章知识点总结必修一数学第二章知识点总结函数简介函数的定义通常分为传统定义和近代定义,函数的两个定义本质是相同的,只是叙述概念的出发点不同,传统定义是从运动变化的观点出发,而近代定义是从集合、映射的观点出发。
函数的近代定义是给定一个数集A,假设其中的元素为x,对A中的元素x施加对应法则f,记作f(x),得到另一数集B,假设B中的元素为y,则y与x之间的等量关系可以用y=f(x)表示。
函数概念含有三个要素:定义域A、值域B和对应法则f。
其中核心是对应法则f,它是函数关系的本质特征。
函数最早由中国清朝数学家李善兰翻译,出于其著作《代数学》。
之所以这么翻译,他给出的原因是“凡此变数中函彼变数者,则此为彼之函数〞,也即函数指一个量随着另一个量的变化而变化,或者说一个量中包含另一个量。
一、一次函数定义与定义式:自变量x和因变量y有如下关系:y=kx+b则此时称y是x的一次函数。
特别地,当b=0时,y是x的正比例函数。
即:y=kx(k为常数,k≠0)二、一次函数的性质:1.y的变化值与对应的x的变化值成正比例,比值为k即:y=kx+b(k为任意不为零的实数b取任何实数)2.当x=0时,b为函数在y轴上的截距。
三、一次函数的图像及性质:1.作法与图形:通过如下3个步骤(1)列表;(2)描点;(3)连线,可以作出一次函数的图像——一条直线。
因此,作一次函数的图像只需知道2点,并连成直线即可。
(通常找函数图像与x轴和y轴的交点)2.性质:(1)在一次函数上的任意一点P(x,y),都满足等式:y=kx+b。
(2)一次函数与y轴交点的坐标总是(0,b),与x轴总是交于(-b/k,0)正比例函数的图像总是过原点。
3.k,b与函数图像所在象限:当k0时,直线必通过一、三象限,y随x的增大而增大;当k0时,直线必通过二、四象限,y随x的增大而减小。
当b0时,直线必通过一、二象限;当b=0时,直线通过原点当b0时,直线必通过三、四象限。
高一必修一数学第二章知识点总结

高一必修一数学第二章知识点总结高一的数学学习是一个新的开始,它需要我们重新理解和掌握一些基础知识,其中第二章是一个很重要的章节。
在这一章中,我们主要学习了一元二次函数、二次函数的图象和性质以及解一元二次方程的方法。
本文将对这些知识点进行总结和归纳。
一、一元二次函数一元二次函数是数学中常见的一类函数,它的一般形式是y=ax²+bx+c。
其中,a、b、c是常数,a不等于0。
主要学习了以下几个内容:1. 解析式:一元二次函数的解析式就是上述的一般形式,它可以描述函数的性质和特点。
2. 坐标系与图像:通过建立直角坐标系,我们可以绘制一元二次函数的图像。
根据a的正负和b的正负,可以得出函数的开口方向和对称轴。
同时,我们还可以通过平移、伸缩等方式来改变函数的图像。
3. 零点:一元二次函数的零点即方程y=0的解。
它们对应了函数图像与x轴的交点。
通过求解一元二次方程,可以求得函数的零点。
二、二次函数的图象和性质在学习了一元二次函数的基本知识后,我们进一步深入了解了二次函数的图象和性质。
主要学习了以下内容:1. 零点和顶点:二次函数的零点和顶点是图象的重要特征。
零点对应函数与x轴的交点,顶点是图像的最低(或最高)点。
通过求解一元二次方程,可以求得函数的零点,而顶点则通过平移、伸缩等变换得到。
2. 对称轴:对称轴是二次函数图像的重要特征之一。
它是图像的中线,可以通过求解一元二次方程得到。
对称轴将图像分为左右对称的两部分。
3. 判别式和函数的性质:通过判别式来分析二次函数的零点情况和图像形状。
当判别式大于0时,函数有两个不同的零点,图像为开口向上的抛物线;当判别式等于0时,函数有一个重根,图像为与x轴相切的抛物线;当判别式小于0时,函数没有实数根,图像位于x轴上方或下方。
三、解一元二次方程的方法在处理实际问题时,我们经常需要解一元二次方程。
学习了一元二次函数后,我们掌握了以下几种解法:1. 因式分解法:当二次方程可以被因式分解时,我们可以利用分解得到的二次因式为0的性质,求得方程的解。
人教A版2019必修第一册第二章不等式知识要点梳理

〈二〉不等式1.比较数(式)的大小依据:a-b>0⇔a>b;a-b<0⇔a<b;a-b=0⇔a=b.适用范围:若数(式)的大小不明显,作差后可化为积或商的形式.步骤:①作差;②变形;③判断差的符号;④下结论.变形技巧:①分解因式;②平方后再作差;③配方法;④分子(分母)有理化.2.利用基本不等式证明不等式(1)充分利用条件是关键,要注意“1”的整体代换及几个“=”必须保证同时成立.(2)利用基本不等式证明不等式是综合法证明不等式的一种情况,其实质就是从已知的不等式入手,借助不等式的性质和基本不等式,经过逐步的逻辑推理,最后推得所证结论,其特征是“由因导果”.(3)证明不等式时要注意灵活变形,可以多次利用基本不等式的变形形式.3.利用基本不等式求最值(1)利用基本不等式求最值,必须同时满足以下三个条件:一正、二定、三相等.即:①x,y都是正数.②积xy(或和x+y)为常数(有时需通过“配凑、分拆”凑出定值).③x与y必须能够相等(等号能够取到).(2)构造定值条件的常用技巧①加项变换;②拆项变换;③统一换元;④平方后利用基本不等式.4.解一元二次不等式的步骤当a>0时,解形如ax2+bx+c>0(≥0)或ax2+bx+c<0(≤0)的一元二次不等式的一般步骤如下:(1)确定对应方程ax2+bx+c=0的解;(2)画出对应函数y=ax2+bx+c的图象的简图;(3)由图象写出不等式的解集.特别提醒:(1)在通过图象获取解集时,注意不等式中的不等号方向、是否为严格不等关系及Δ=0时的特殊情况.(2)当a<0时,解不等式可以从两个方面入手:①画出对应图象进行直接判定(此时图象开口向下);②两边同乘以-1,把a转变为-a再进行求解.5.一元二次不等式的实际应用不等式在解决生活、生产中的一些实际问题中有着广泛的应用,主要有范围问题、最值问题等.解一元二次不等式的应用问题的关键在于构造一元二次不等式模型.解题的一般步骤是:(1)理清题意:弄清问题的实际背景和意义,用数学语言来描述问题.(2)简化假设:精选问题中的关键变量.(3)列出关系式:建立变量间的不等关系式.(4)求解:运用数学知识解相应不等式.(5)检验并作答:将所得不等式的解集放回原题中检验是否符合实际情况,然后给出问题的答案.过关训练一、不等式的性质及应用1(1)若A=a2+3ab,B=4ab-b2,则A,B的大小关系是()A.A≤B B.A≥B C.A<B或A>B D.A>B(2)若a >b ,x >y ,下列不等式正确的是( )A .a +x <b +yB .ax >byC .|a |x ≥|a |yD .(a -b )x <(a -b )y练1 若1≤a ≤5,-1≤b ≤2,则a -b 的取值范围为________.二、利用基本不等式求最值题型一:构造积为定值1.当x >0时,y =12x+4x 的最小值为 变式1、当x <0时,y =12x+4x 的最 值为 变式2、若a <1,则a +1a -1有最____值为________ 变式3、已知x <3,则f (x )=4x -3+x 的最大值为变式4、设x >-1,则函数y =(x +5)(x +2)x +1的最小值是________ 变式5、若对任意x >0,x x 2+3x +1≤a 恒成立,则a 的取值范围是________题型二:构造和为定值2.已知0<x <1,则x (3-3x )取得最大值时x 的值为________变式1、当0<x <13时,则x (1-3x )的最大值为变式2、若x >0,则的最大值为变式3、若x >0,y >0,且x 2+y 2=8,则的最大值为变式4、若x >0,y >0,且2x 2+y 23=8,则x 6+2y 2的最大值为 题型三:“1”的妙用 3.已知正数x ,y 满足x +2y =1,则1x +1y的最小值为________变式1、设x >0,y >0,且821x y +=,则x +y 的最小值为_______变式2、设x >0,y >0,且2x +8y =xy ,则x +y 的最小值为________变式3、已知a >0,b >0,a +b =2,则y =1a +4b的最小值是 变式4、若0<x <1,则y =491x x+-的最小值为________ 变式5、若x >-1,y >0且满足x+2y =1,则121x y ++的最小值为________ 题型四:建立求解目标不等式求最值4.已知x ,y 均为正实数,且xy =x +y +3,则xy 的最小值为__________变式1、若正数x ,y 满足4x 2+9y 2+3xy =30,则xy 的最大值是________变式2、若正实数x ,y 满足2x +y +6=xy ,则2x +y 的最小值是________变式3、若实数x 、y 满足x 2+y 2+xy =1,则x +y 的最大值是________题型五:代换减元求最值5.若实数a ,b 满足ab -4a -b +1=0(a >1),则(a +1)·(b +2)的最小值是__________变式1、设正实数x ,y ,z 满足x 2-3xy +4y 2-z =0,则当z xy取得最小值时,x +2y -z 的最大值为__________变式2、【2020年江苏高考12题】已知22451(,)x y y x y +=∈R ,则22x y +的最小值为__________【2020年天津高考14题】已知a >0,b >0,且ab =1,则11822a b a b +++的最小值为 三、三个二次之间的关系若不等式ax 2+bx+2>0的解集是)31,21(-,则a-b 的值为 练:不等式ax 2 +bx+c>0的解集为(-1,2),则不等式cx 2+bx+a<0的解集为四、解含参-元二次不等式1、能分解因式:比较两根大小2、不能分解:讨论判别式解关于x的不等式x2- 5ax +6a2>0,a≠0. 解关于x的不等式(m2+1)x2-4x+1≥0.3、二次项系数含参:讨论开口方向4、综合讨论解关于x的不等式ax2+(a+2)x+1>0. 解关于x的不等式ax2-(a+1)x+1<0.。
高一数学必修一第二章知识点总结

高一数学必修一第二章知识点总结本文将总结高一数学必修一第二章的知识点,帮助学生们对这一章内容有一个清晰的概述。
2.1 向量的概念与表示- 向量是有大小和方向的量,用于表示平面或空间中的位移、速度等概念。
通常用箭头表示,箭头的长度表示向量的大小,箭头的方向表示向量的方向。
- 向量的表示方式有两种:用坐标表示和用定点与方向向量表示。
坐标表示方式将向量表示为一组有序数的组合,定点与方向向量表示方式则将向量表示为起点和终点之间的位移。
- 向量的相等与数量乘法:两个向量相等表示大小和方向相同,向量的数量乘法是将向量的大小与一个实数相乘。
2.2 向量的加减- 向量的加法:两个向量相加得到一个新的向量,新向量的大小是两个向量大小的和,方向由两个向量的夹角决定。
- 向量的减法:两个向量相减得到一个新的向量,新向量的大小是两个向量大小的差,方向由两个向量的夹角决定。
2.3 平行向量和共线向量- 平行向量:如果两个向量的方向相同或相反,那么这两个向量是平行的。
- 共线向量:如果两个向量在同一直线上,那么这两个向量是共线的。
2.4 向量与数的乘法- 向量与数的乘法:用一个实数乘以一个向量,得到的新向量大小等于原向量大小的绝对值与这个实数的乘积,方向与原向量相同或相反,取决于实数的正负。
- 数的乘法具有分配律、结合律等性质,方便在向量的计算中进行运算。
2.5 平面向量的线性运算- 平面向量的线性运算:指将两个向量进行加法和数量乘法得到一个新的向量。
- 加法满足交换律和结合律,而数量乘法满足分配律。
以上就是高一数学必修一第二章的主要知识点总结。
希望这份总结能够帮助同学们快速回顾并掌握这一章的知识,为接下来的学习打下坚实的基础。
高一数学必修一第二章知识点总结
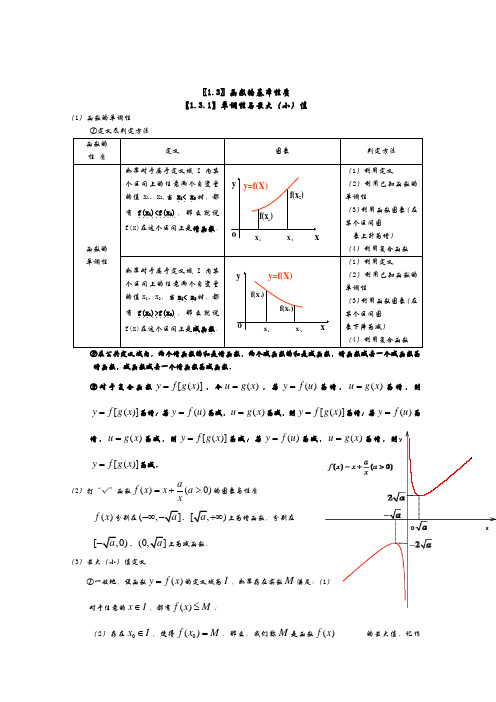
yxo〖1.3〗函数的基本性质 【1.3.1】单调性与最大(小)值(1)函数的单调性①定义及判定方法 函数的 性 质定义图象判定方法 函数的 单调性如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x .1.< x ..2.时,都有f(x ...1.)<f(x .....2.).,那么就说f(x)在这个区间上是增函数.... x 1x 2y=f(X)xy f(x )1f(x )2o(1)利用定义(2)利用已知函数的单调性(3)利用函数图象(在某个区间图象上升为增) (4)利用复合函数 如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x .1.< x ..2.时,都有f(x ...1.)>f(x .....2.).,那么就说f(x)在这个区间上是减函数.... y=f(X)yxox x 2f(x )f(x )211(1)利用定义(2)利用已知函数的单调性(3)利用函数图象(在某个区间图象下降为减) (4)利用复合函数②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数. ③对于复合函数[()]y f g x =,令()u g x =,若()y f u =为增,()u g x =为增,则[()]y f g x =为增;若()y f u =为减,()u g x =为减,则[()]y f g x =为增;若()y f u =为增,()ug x =为减,则[()]y f g x =为减;若()y f u =为减,()u g x =为增,则[()]y f g x =为减.(2)打“√”函数()(0)af x x a x=+>的图象与性质 ()f x 分别在(,]a -∞-、[,)a +∞上为增函数,分别在[,0)a -、]a 上为减函数.(3)最大(小)值定义 ①一般地,设函数()y f x =的定义域为I,如果存在实数M 满足:(1)对于任意的x I ∈,都有()f x M≤;(2)存在0x I ∈,使得0()f x M =.那么,我们称M 是函数()f x 的最大值,记作max ()f x M =.②一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足:(1)对于任意的x I ∈,都有()f x m ≥;(2)存在0x I ∈,使得0()f x m =.那么,我们称m 是函数()f x 的最小值,记作max ()f x m =.【1.3.2】奇偶性(4)函数的奇偶性①定义及判定方法 函数的 性 质定义图象判定方法 函数的 奇偶性如果对于函数f(x)定义域内任意一个x ,都有f(..-.x)=...-.f .(x)...,那么函数f(x)叫做奇函..数..(1)利用定义(要先判断定义域是否关于原点对称)(2)利用图象(图象关于原点对称)如果对于函数f(x)定义域内任意一个x ,都有f(..-.x)=...f(x)....,那么函数f(x)叫做偶函数....(1)利用定义(要先判断定义域是否关于原点对称)(2)利用图象(图象关于y 轴对称) ②若函数()f x 为奇函数,且在0x =处有定义,则(0)0f =.③奇函数在y 轴两侧相对称的区间增减性相同,偶函数在y 轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.〖补充知识〗函数的图象(1)作图利用描点法作图:①确定函数的定义域; ②化解函数解析式; ③讨论函数的性质(奇偶性、单调性); ④画出函数的图象. 利用基本函数图象的变换作图:要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象. ①平移变换0,0,|()()h h h h y f x y f x h ><=−−−−−−−→=+左移个单位右移|个单位0,0,|()()k k k k y f x y f x k ><=−−−−−−−→=+上移个单位下移|个单位②伸缩变换01,1,()()y f x y f x ωωω<<>=−−−−→=伸缩01,1,()()A A y f x y Af x <<>=−−−−→=缩伸③对称变换()()x y f x y f x =−−−→=-轴()()y y f x y f x =−−−→=-轴()()y f x y f x =−−−→=--原点 1()()y x y f x y f x -==−−−−→=直线 ()(||)y y y y f x y f x =−−−−−−−−−−−−−−−→=去掉轴左边图象保留轴右边图象,并作其关于轴对称图象()|()|x x y f x y f x =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折上去(2)识图对于给定函数的图象,要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性,注意图象与函数解析式中参数的关系. (3)用图函数图象形象地显示了函数的性质,为研究数量关系问题提供了“形”的直观性,它是探求解题途径,获得问题结果的重要工具.要重视数形结合解题的思想方法.。
2019新人教版高中数学必修第一册第二章一元二次函数方程和不等式知识点和题型总结

第2章一元二次函数、方程和不等式2.1等式和不等式性质课程标准:1.梳理等式的性质,理解不等式的概念,掌握不等式的性质,能运用不等式的性质比较大小2能运用不等式的性质证明不等式和解决简单的实际问题.教学重点:1.不等式的性质2用不等式的性质证明不等式.教学难点:用作差法比较代数式的大小.【知识导学】知识点一等式的性质(1)如果a=b,那么a+c=b+c.(2妆口果a=b,那么ac = be或学=#(CH0).(3妆口果a=b, b=c,那么a=c.知识点二作差比较法(1)理论依据:因d_/2>OOa>b:^a-b = 0<^a = b; ^g-b<0<^a<b.⑵方法步骤:①叵I作差;②西整理;③西判断符号;④因下结论.知识点三两个实数大小的比较(1)“> 如凹"-b>0:(2)"=bO"-b 図=0:(3)固αvZ?Ua —b<0.知识点四不等式的性质⑴如果a>b,那么b<a;如果b<cb那么回“>/?,即国台Z?V".(2妆口果a>b,且b>c,那么歴輕,即a>b, b>c=叵I ">c.(3)如果a>b,那么d+o画R+c.(4)如果a>b, c>0,那么ac >bc;如果a>b, c<O,那么UC <bc.(5)如果a>b, OcL那么α+c 画 >/?+〃.(6)如果a>b>O, c>d>O,那么ac回如果α>b>O, c<(l<0,那么ac 回G"∙⑺如果a>b>O,那么0 凹R"(n∈N, π≥2).(8)如果回^/>∕x>0,那么,∖[cι>,yfb(n^N, 2).【新知拓展】1.关于不等式性质的理解两个同向不等式可以相加,但不可以相减,如">/?, c>d不能推出“一c>/?—d.2.常用的结论(1 )a>b,(2)bvO<"W>*;(3)a>b>O,o√>0=>^>p... r,I a a+m a a~m b b+m b b~m(4)右Qb>0,加>0,则沪书p丹百卩一心0); £片;茗二需(方_心0).3.比较大小的方法比较数(式)的大小常用作差与0比较.作差法中常用的变形手段是分解因式和配方等恒等变形,前者将“差”化为“积”,后者将“差”化为一个完全平方式或儿个完全平方式的“和”,也可二者并用.4.利用不等式求范围应注意的问题求指定代数式的取值范围,必须依据不等式的性质进行求解,同向不等式具有可加性与可乘性,但是不能相减或相除,解题时必须利用性质,步步有据,避免改变代数式的取值范围.题型一作差法比较大小例1比较下列各组中两数的大小:(1)已知S 〃为正数,且a≠b,比较/+,与局+“2;⑵已知XV1,比较X3-I与2X2-2X:(3)已知X, y均为正数,设加=出,“=古,比较加与〃的大小.[解](1 )(Λ3 ÷b3)—(a2b ÷ ab2)=a3+b3-a1b-ab2=a2{a-b)-b2(a—b)= (a-b)(a2-b2)= {a~b)2(a+b).Vt∕>O, b>0 且a≠b, Λ(a-b)2>Q9 a+b>O9/. (a y÷ /?3) — (a2b ÷ ab2)>O,即cr+b^>a2b+ab2.(2)X3- 1 — (2x2-2x)=x3-2X2÷2X- 1=(√-X2)-(X2-2X÷1)=X2(Λ:- I)-(X-1)2= (X-I)(X2-χ+1) = (X- 1 {(^-∣)2+∣•Txvl, Λχ- l<0.X^x-^2÷j>0,•••(XT)-(x^⅛+fl <0, ΛX3~1<2Λ2~2X.4 x+y 4 (x+y)2_4Xy (χ∙~y)'χ+y Xy x+y Q(X+y) xy(x÷y)* 乂“ y均为正数,Λ.r>0, y>0, xy>0, x÷y>0, (X-y)2≥0.Λ∕n-∕2≥0,即〃总舁(当x=y时,等号成立)・金版点睛作差比较法的四个步骤[结论〕—(根据差的符号,判断两数(式)的大小「题型二 不等式的性质及应用例2下列命题正确的是 ___________②α>b 且 c>d=>ac>bch解析]①戸’ n 知 当XO, b>0时,满足已知条件,但推不出a>b, IoO (・•・①错误.②当a = 3, b=∖, C= —2, Cl=—3时,命题显然不成立∙ ∙°∙②错误•④显然c 2>0t Λ两边同乘以$得a>b.④正确.[答案]③④金版点睛 解决这类问题,主要是根据不等式的性质判定,其实质是看是否满足性质所 需的条件,若要判断一个命题是假命题,可以从条件入手,推出与结论相反的结 论,也可举出一个反例予以否定・题型三 利用不等式的性质证明不等式例 3 (1)已知e>f 9 c>0,求证:f-ac<e~bc;(2)已知CVdV0,求证:土缶;-∖a>h>09‰>o一成立・・:③正确・ ③a>b>O 且 c>√>0=>=>^>p*0=>(3)已知bc-ad20, bd>O.求证:一T —W 〃・[证明](I)Tα>∕?, c>O, .*.ac>hc./. -ac<-hc.'∙f<e,:・f— ac<e—be.(2) T CVdVO, /. —c>—d>0.乂a>b>O, C. ci—c>b—d>0.(3) •: be—adMO, :∙QdWbc,乂T bcl>O,金版点睛利用不等式的性质证明不等式的实质与技巧(1)实质:就是根据不等式的性质把不等式进行变形,要注意不等式的性质成立的条件.(2)技巧:若不能直接由不等式的性质得到,可先分析需要证明的不等式的结构.然后利用不等式的性质进行逆推,寻找使其成立的充分条件.题型四利用不等式的性质求取值范围例4 (1)已知2vαW5,3WbVl0,求a~b,彳的取值范围;(2)已知一∣≤cc<^≤^,求笞迫,生亍©的取值范圉.[解](I)V3≤∕^<10,・•・一10v-bW-3.乂2<t∕≤5τ •:—8<f∕-Z>≤2.⑵T —彳WaV厂W号,・•・-共鈴γ<⅛两式相加得一两式相加得一又*0,・・・三篡0, Λ[变式探究]将本例(1)中,条件不变,求a+b,“b的取值范围.解由2<t∕≤5,3≤^<10 得2 +3 V/+b<5 ÷ 10,2 ×3<ab<5 ×10,即5<a÷b< 15,6<ab<50.金版点睛利用不等式的性质求取值范围应注意的问题本题中不能直接用G的范围去减或除b的范围,应严格利用不等式的性质去求范围;其次在有些题目中,还要注意整体代换的思想,即弄清要求的与已知的"范围”间的联系.如已知20<x+yV30,15Vχ-y<18,要求2x+3y的范围,不能分别求出X, y的范围,再求"+3y的范围,应把已知的"x+y” “x—y” 视为整体,即2x+3y=I(X+>-)—∣(Λ—y),所以需分别求出∣(x+y), —∣(χ-y)的范围,两范围相加可得2r+3y的范围.“范围”必须对应某个字母变量或代数式,一旦变化出其他的范围问题,则不能再间接得出,必须“直来直去”,即直接找到要求的量与已知的量间的数量关系,然后去求.2.2基本不等式课程标准:1•掌握基本不等式的内容2能熟练地运用基本不等式来比较两个实数的大小.3.能初步运用基本不等式来证明简单的不等式.4 •熟练掌握基本不等式及变形的应用∙5.会用基本不等式解决简单的最大(小)值问题.教学重点:1.理解基本不等式的内容及其证明过程2运用基本不等式来比较两个实数的大小及进行简单的证明.3.运用基本不等式解决简单的最大值或最小值问题.教学难点:基本不等式条件的创设.【知识导学】知识点一基本不等式如果。
高一数学必修一第二章知识点

高一数学必修一第二章知识点高一新生要主动地适应环境,而不是环境适应你。
因为你走向社会参加工作也得适应社会。
以下内容是无忧考网为你整理的高一数学必修一第二章知识点,希望你不负时光,努力向前,加油。
高一数学必修一第二章知识点1方程的根与函数的零点1、函数零点的概念:对于函数,把使成立的实数叫做函数的零点。
2、函数零点的意义:函数的零点就是方程实数根,亦即函数的图象与轴交点的横坐标。
即:方程有实数根函数的图象与轴有交点函数有零点.3、函数零点的求法:求函数的零点:1(代数法)求方程的实数根;2(几何法)对于不能用求根公式的方程,可以将它与函数的图象联系起来,并利用函数的性质找出零点.4、二次函数的零点:二次函数.1)△>0,方程有两不等实根,二次函数的图象与轴有两个交点,二次函数有两个零点.2)△=0,方程有两相等实根(二重根),二次函数的图象与轴有一个交点,二次函数有一个二重零点或二阶零点.3)△<0,方程无实根,二次函数的图象与轴无交点,二次函数无零点.高一数学必修一第二章知识点2空间几何体表面积体积公式:1、圆柱体:表面积:2πRr+2πRh体积:πR2h(R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR2+πR[(h2+R2)的]体积:πR2h/3(r为圆锥体低圆半径,h为其高,3、a-边长,S=6a2,V=a34、长方体a-长,b-宽,c-高S=2(ab+ac+bc)V=abc5、棱柱S-h-高V=Sh6、棱锥S-h-高V=Sh/37、S1和S2-上、下h-高V=h[S1+S2+(S1S2)^1/2]/38、S1-上底面积,S2-下底面积,S0-中h-高,V=h(S1+S2+4S0)/69、圆柱r-底半径,h-高,C—底面周长S底—底面积,S侧—,S表—表面积C=2πrS底=πr2,S侧=Ch,S表=Ch+2S底,V=S底h=πr2h10、空心圆柱R-外圆半径,r-内圆半径h-高V=πh(R^2-r^2)11、r-底半径h-高V=πr^2h/312、r-上底半径,R-下底半径,h-高V=πh(R2+Rr+r2)/313、球r-半径d-直径V=4/3πr^3=πd^3/614、球缺h-球缺高,r-球半径,a-球缺底半径V=πh(3a2+h2)/6=πh2(3r-h)/315、球台r1和r2-球台上、下底半径h-高V=πh[3(r12+r22)+h2]/616、圆环体R-环体半径D-环体直径r-环体截面半径d-环体截面直径V=2π2Rr2=π2Dd2/417、桶状体D-桶腹直径d-桶底直径h-桶高V=πh(2D2+d2)/12,(母线是圆弧形,圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15(母线是抛物线形)高一数学必修一第二章知识点3(1)直线的倾斜角定义:x轴正向与直线向上方向之间所成的角叫直线的倾斜角。
高一数学必修一第二章知识点归纳笔记

高一数学必修一第二章知识点归纳笔记第一篇嘿,小伙伴们!今天来跟大家唠唠高一数学必修一第二章的那些知识点哈。
先说说函数的概念,这可是个很重要的家伙呢!简单来说,函数就是两个非空数集之间的一种对应关系。
就好像是一个神秘的魔法,给一个输入,就会有特定的输出。
再讲讲函数的三要素,定义域、值域和对应法则。
定义域就像是函数的“出生地”,得搞清楚哪些数能进来;值域呢,就是函数能产生的“成果”范围;对应法则就是那个神奇的魔法规则啦。
函数的表示方法也有好几种哦,像解析式法,能清楚地写出函数的式子;图像法,一目了然,看着图就能知道函数的走势;还有列表法,简单直接,把数值列出来。
还有函数的单调性,这可有趣啦!增函数就是函数值越来越大,减函数就是越来越小。
判断单调性的时候,可要看清楚区间哦。
复合函数呢,就像是几个函数手拉手一起玩,要弄明白它们之间的关系。
说说函数的奇偶性,奇函数图像关于原点对称,偶函数图像关于y 轴对称。
是不是还挺神奇的?好啦,这些知识点大家可要好好记住哦,加油!第二篇亲耐的小伙伴们,咱们接着来聊聊高一数学必修一第二章的知识点哟!函数的定义域,这可是个关键哟!比如说分式函数,分母不能为零;根式函数,根号下的数得大于等于零。
不然函数就要闹脾气啦!值域的求法也有不少门道呢。
可以通过观察函数的单调性,找到最大值和最小值;还可以通过换元法,把复杂的式子变得简单,再求出值域。
函数的图像可得好好研究。
知道了函数的特点,就能画出大致的图像,反过来,看着图像也能更好地理解函数的性质。
分段函数也很常见哟,不同的区间有不同的表达式,就像人在不同的场合有不同的表现一样。
反函数嘛,就像是原函数的“倒影”,它们的关系可紧密啦。
还有哦,函数的周期性有时候也会出来考考我们。
如果函数每隔一段固定的距离,图像就重复出现,那它就有周期性啦。
怎么样,这些知识点有没有在你的小脑袋里留下印象呀?要多做题多巩固哟,相信咱们都能搞定它们!。
(完整)高一数学必修一第二章基本初等函数知识点总结,推荐文档

n a n;当 为偶数时,⎨-a2.1.1 指数与指数幂的运算(1)根式的概念第二章基本初等函数知识点整理〖2.1〗指数函数①如果 x n = a , a ∈ R , x ∈ R , n > 1,且 n ∈ N + ,那么 x 叫做 a 的 n 次方根.当 n 是奇数时, a 的 n 次方根用符号表示;当 n 是偶数时,正数 a 的正的 n 次方根用符号 0;负数 a 没有 n 次方根.表示,负的 n 次方根用符号- n a 表示;0 的n 次方根是②式子na 叫做根式,这里 n 叫做根指数, a 叫做被开方数.当 n 为奇数时, a 为任意实数;当 n 为偶数时, a ≥ 0 .③根式的性质: ( n a )n = a ;当 n 为奇数时, = a n =| a |= ⎧a⎩(a ≥ 0) .(a < 0)(2) 分数指数幂的概念m①正数的正分数指数幂的意义是: an= (a > 0, m , n ∈ N +, 且 n > 1) .0 的正分数指数幂等于 0.②正数的负分a -m= ( )1 m( ) 1(a > 0, m , n ∈ N , n > 1) 注意口诀:数指数幂的意义是:nn = n m+且 .0 的负分数指数幂没有意义.aa底数取倒数,指数取相反数.(3) 分数指数幂的运算性质① a r ⋅ a s = a r +s (a > 0, r , s ∈ R ) ② (ar )s= a rs (a > 0, r , s ∈ R ) ③ (ab )r = a r b r (a > 0, b > 0, r ∈ R )2.1.2 指数函数及其性质(4) 指数函数函数名称指数函数定义函数 y = a (a > 0且 a ≠ 1) 叫做指数函数a > 1 0 < a < 1图象y 1yOya x(0,1)xya xy 1Oy(0,1)x定义域 R值域 (0,+∞)过定点 图象过定点(0,1),即当 x=0 时,y=1.奇偶性 非奇非偶单调性在 R 上是增函数在 R 上是减函数n a n a nn a m nab〖2.2〗对数函数【2.2.1】对数与对数运算(1) 对数的定义①若 a x = N (a > 0,且a ≠ 1) ,则 x 叫做以 a 为底 N 的对数,记作 x = log a N ,其中 a 叫做底数, N 叫做真数.②负数和零没有对数.③对数式与指数式的互化: x = log a N ⇔ a x = N (a > 0, a ≠ 1, N > 0) .(2) 几个重要的对数恒等式:log a 1 = 0 , log a a = 1, log a a b = b .(3) 常用对数与自然对数:常用对数: lg N , 即log 10 N ;自然对数: ln N , 即log e N (其中 e = 2.71828 …).(4) 对数的运算性质如果 a > 0, a ≠ 1, M > 0, N > 0 ,那么①加法: log M + log N = log (MN )②减法: log M - log N = logMaa aaaaN③数乘: n log a M= log a M n (n ∈ R )log aN = NlogM n =nlog M (b ≠ 0, n ∈ R ) log N =log b N(b > 0,且b ≠ 1)⑤a bba⑥换底公式:alog aa ④【2.2.2】对数函数及其性质(5)对数函数函数名称对数函数定义函数y = log a x(a >0 且a≠ 1) 叫做对数函数图象a > 1 0 <a < 1yOx 1(1, 0)y log a xxyOx 1(1, 0)y logaxx定义域(0, +∞)值域R过定点图象过定点(1, 0) ,即当x = 1 时,y = 0 .奇偶性非奇非偶单调性在(0, +∞) 上是增函数在(0, +∞) 上是减函数函数值的变化情况log a x > 0 (x > 1)log a x = 0 (x = 1)log a x < 0 (0 <x < 1)log a x < 0 (x > 1)log a x = 0 (x = 1)log a x > 0 (0 <x < 1)a 变化对图象的影响在第一象限内,a 越大图象越靠低,越靠近 x轴在第四象限内,a 越大图象越靠高,越靠近 y轴在第一象限内,a 越小图象越靠低,越靠近 x 轴在第四象限内,a 越小图象越靠高,越靠近 y 轴(6)反函数的概念设函数y =f (x) 的定义域为A ,值域为C ,从式子y =f (x) 中解出x ,得式子x =( y) .如果对于y 在C 中的任何一个值,通过式子x =(y) ,x 在A 中都有唯一确定的值和它对应,那么式子x =(y) 表示x 是y 的函数,函数x =(y) 叫做函数y =f (x) 的反函数,记作x =f -1( y) ,习惯上改写成y =f -1(x) .(7)反函数的求法①确定反函数的定义域,即原函数的值域;②从原函数式y =f (x) 中反解出x =f -1( y) ;③将x =f -1( y) 改写成y =f -1(x) ,并注明反函数的定义域.(8)反函数的性质q①原函数 y = f (x ) 与反函数 y = f -1(x ) 的图象关于直线 y = x 对称.②函数 y =f (x ) 的定义域、值域分别是其反函数 y = f -1(x ) 的值域、定义域.③若 P (a , b ) 在原函数 y = f (x ) 的图象上,则 P ' (b , a ) 在反函数 y =f -1(x ) 的图象上.④一般地,函数 y =f (x ) 要有反函数则它必须为单调函数.〖2.3〗幂函数(1) 幂函数的定义一般地,函数 y = x 叫做幂函数,其中 x 为自变量,是常数.(2) 幂函数的图象(3) 幂函数的性质①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于 y 轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.②过定点:所有的幂函数在(0, +∞) 都有定义,并且图象都通过点(1,1) .③单调性:如果> 0 ,则幂函数的图象过原点,并且在[0, +∞) 上为增函数.如果< 0 ,则幂函数的图象在(0, +∞) 上为减函数,在第一象限内,图象无限接近 x 轴与 y 轴.④奇偶性:当为奇数时,幂函数为奇函数,当为偶数时,幂函数为偶函数.当= (其中 p , q 互质, p 和 pqqq ∈ Z ),若 p 为奇数 q 为奇数时,则 y = x p 是奇函数,若 p 为奇数 q 为偶数时,则 y = x p是偶函数,若 p 为偶数∆ qq 为奇数时,则 y = x p 是非奇非偶函数.⑤图象特征:幂函数 y = x , x ∈(0, +∞) ,当> 1 时,若 0 < x < 1,其图象在直线 y = x 下方,若 x > 1 ,其图象在直线 y = x 上方,当< 1时,若 0 < x < 1,其图象在直线 y = x 上方,若 x > 1 ,其图象在直线 y = x 下方.(1) 二次函数解析式的三种形式〖补充知识〗二次函数①一般式: f (x ) = ax 2 + bx + c (a ≠ 0) ②顶点式: f (x ) = a (x - h )2 + k (a ≠ 0)③两根式: f (x ) = a (x - x 1 )(x - x 2 )(a ≠ 0)(2) 求二次函数解析式的方法①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式.③若已知抛物线与 x 轴有两个交点,且横线坐标已知时,选用两根式求 f (x ) 更方便.(3) 二次函数图象的性质2bb 4ac -b 2①二次函数 f (x ) = ax + bx + c (a ≠ 0) 的图象是一条抛物线,对称轴方程为 x = - , 顶点坐标是(- , )②当 a > 0 时,抛物线开口向上,函数在(-∞, -4ac - b 2b ] 上递减,在[- 2a2a b , +∞) 上递增,当 x = - b 时,2a 2a b b2a 4af min (x ) =;当 a < 0 时,抛物线开口向下,函数在(-∞, - ] 上递增,在[- , +∞) 上递减,当 4a 2a 2ax = - b时 , f (x ) = 2amax4ac - b 2.4a③二次函数 f (x ) = ax 2 + bx + c (a ≠ 0) 当∆ = b 2 - 4ac > 0 时,图象与 x 轴有两个交点M (x ,0), M (x ,0),| M M |=| x - x |= . 1 1 2 2 1 2 1 2 | a |(4) 一元二次方程 ax 2 + bx + c = 0(a ≠ 0) 根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整, 且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质, 系统地来分析一元二次方程实根的分布.设一元二次方程 ax 2 + bx + c = 0(a ≠ 0) 的两实根为 x , x ,且 x≤ x .令 f (x ) = ax 2 + bx + c ,从以下四个1212b方面来分析此类问题:①开口方向: a②对称轴位置: x = -③判别式: ∆ ④端点函数值符号.2a(5) 二次函数 f (x ) = ax 2 + bx + c (a ≠ 0) 在闭区间[ p , q ] 上的最值b b设f (x) 在区间[ p, q] 上的最大值为M ,最小值为m ,令x0=1 ( p +q).2(Ⅰ)当a > 0 时(开口向上)b b b b①若-<p ,则m =2af ( p) ②若p ≤-≤q ,则m =2af (-)2a③若->q ,则m =2af (q)①若-2a≤x,则M =f (q) ②- 2a >x0 ,则M =f ( p)(Ⅱ)当a < 0 时(开口向下)b b b b①若-<p ,则M =2af ( p) ②若p ≤-≤q ,则M =2af (-)2a③若->q ,则M =2af (q)①若-2a ≤x0 ,则m = f (q) ②-2a >x0 ,则m =f ( p) .x0f (-b)2ax0f (-b)2a“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
必修一数学第二章知识点总结

必修一数学第二章知识点总结第二章是《函数与导数》,是高中数学必修一中的重要章节之一、本章主要讲述了函数的基本概念和性质,以及导数的概念和计算方法。
下面是本章的知识点总结。
1.函数的概念和表示方法:-函数的定义:函数是一个从一个集合到另一个集合的映射关系。
通常用f(x)表示函数,其中f是函数名,x是自变量。
-自变量和因变量:函数中自变量的值经映射得到相应的因变量的值。
-函数的表示方法:集合表示法、解析表示法、图像表示法。
2.函数的性质:-定义域和值域:函数的定义域是自变量的取值范围,值域是因变量的值的集合。
-奇偶性:函数f在对称中心O处满足f(-x)=f(x)或f(-x)=-f(x)时,称函数f是偶函数或奇函数。
-单调性:函数的单调性可以是递增的、递减的或者常数函数。
-周期性:周期函数的值在一定区间内具有循环性,满足f(x+T)=f(x),其中T是函数的周期长度。
3.导数的概念和性质:-导数的定义:函数在其中一点的导数表示函数在该点的变化率。
导数可以用极限来定义,也可以用差商表示。
-导数的几何意义:导数表示函数在特定点处的切线斜率。
-导数的计算方法:常数的导数为0,幂函数的导数为指数乘以底数的幂次减1-导数的基本性质:导数与函数的线性运算、导数与函数的乘积法则、导数与函数复合的链式法则。
-导数与函数的单调性、奇偶性、最值和极值。
4.导数的应用:-切线和法线:切线的斜率等于函数导数的值,法线的斜率为导数的倒数的负值。
-凸函数与凹函数:函数的导数是单调递增或递减的,可以判断函数的凸凹性。
-极值点和极值:极值点是函数在其中一区间内取得最大值或最小值的点。
-函数图像的绘制:通过求解函数在定义域各点处的导数和极值来绘制函数的图像。
以上是第二章《函数与导数》的主要知识点总结。
掌握这些知识点对于理解函数的基本概念、性质和导数的计算方法非常重要,也是以后学习高级数学的基础。
高一数学必修一第二章知识点总结
o (
i n
t h
e i r
b e
i n g
a r
01,1,()()y f x y f x ωωω<<>=−−−−→=伸
缩01,1,()()A A y f x y Af x <<>=−−−−→=缩
伸
③对称变换
()()x y f x y f x =−−−→=-轴()()
y y f x y f x =−−−→=-轴 ()()y f x y f x =−−−→=--原点1()()
y x y f x y f x -==−−−−→=直线()(||)y
y y
y f x y f x =−−−−−−−−−−−−−−−→=去掉轴左边图象保留轴右边图象,并作其关于轴对称图象()|()|x
x
y f x y f x =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折上去(2)识图
对于给定函数的图象,要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性,注意图象与函数解析式中参数的关系.(3)用图
函数图象形象地显示了函数的性质,为研究数量关系问题提供了“形”的直观性,它是探求解题途径,
获得问题结果的重要工具.要重视数形结合解题的思想方法.。
数学必修一第二章知识点总结

数学必修一第二章知识点总结第二章是数学必修一中的基本几何知识章节,主要包括了点、线、面及其相互关系的基础概念和性质。
下面是对该章节的知识点进行总结。
1. 点、线、面的定义:- 点:几何中最基本的概念,没有实际长度、宽度和高度,仅有位置。
用大写字母表示,如A、B、C。
- 线:两个点之间的直线连接,是没有实际宽度的。
用小写字母表示,如a、b、c。
- 面:由多条线围成的平面图形,具有宽度和高度。
用大写字母表示,如∆ABC、□ABCD。
2. 直线的表示方法:- 两点式:通过两个点来确定一条直线,可以使用直线上的两个点的坐标(x1, y1)、(x2, y2)来表示。
- 斜截式:使用直线的斜率k和截距b来表示,形如y=kx+b。
- 截距式:使用直线在y轴和x轴上的截距a、b来表示,形如y=ax+b。
- 一般式:使用直线一般方程Ax+By+C=0来表示。
3. 直线的性质:- 平行:两条直线的斜率相等且不相交。
- 垂直:两条直线的斜率乘积为-1。
- 相交:两条直线有且仅有一个交点。
- 重合:两条直线完全一致,有无穷多个交点。
4. 角的概念与分类:- 角:由两条射线共享一个端点而成的图形。
- 顶点:两条射线共享的端点。
- 两条射线的初始边:分别是与顶点相交的两条射线。
- 内角:在两条射线之间的角,其度数小于180°。
- 外角:在两条射线的延长线之间的角,其度数大于180°。
- 全周角:两条相互垂直的圆弧与其相应的圆心连线构成的角,度数为360°。
- 直角:角的度数为90°。
- 锐角:角的度数小于90°。
- 钝角:角的度数大于90°。
5. 角的性质:- 互补角:两个角的度数之和为90°。
- 余补角:两个角的度数之和为180°。
- 同位角:两条直线被一条截线交叉形成的对应角。
- 内错角:两条平行线被一条截线交叉形成的对应角。
- 垂直交角:两条直线垂直交叉形成的对应角。
高一上册前两章知识点

高一上册前两章知识点第一章:数学基本概念与初等数论本章主要介绍了数的分类、集合及其运算、数的间的关系以及初等数论的一些基本概念。
一、数的分类1. 自然数:正整数,即1、2、3、4...2. 整数:包括自然数、0和负整数,即...-3、-2、-1、0、1、2、3...3. 有理数:可以表示为两个整数的比值的数,包括整数、分数以及循环小数或有限小数。
4. 无理数:不能表示为两个整数的比值的数,如π、√2等。
二、集合及其运算1. 集合:由各种对象组成的整体,具有互异性和确定性。
2. 元素:集合中的个体。
3. 子集:若一个集合的所有元素都是另一个集合的元素,则前者是后者的子集。
4. 并集:由两个或多个集合中的所有元素组成的集合。
5. 交集:由同时属于两个或多个集合的所有元素组成的集合。
6. 差集:从一个集合中减去另一个集合中的所有元素所得的集合。
三、数的间的关系1. 相等关系:两个数相等。
2. 大于关系:一个数大于另一个数。
3. 小于关系:一个数小于另一个数。
4. 不等关系:两个数不等。
四、初等数论1. 奇数与偶数:一个数能被2整除的称为偶数,否则称为奇数。
2. 因数与倍数:若一个整数a除以另一个整数b余0,则称a是b的倍数,b是a的因数。
3. 素数与合数:大于1的整数,如果只有1和其本身两个因数,则称为素数,否则称为合数。
4. 最大公约数与最小公倍数:两个或多个整数公有的约数中最大的一个称为最大公约数,两个或多个整数公有的倍数中最小的一个称为最小公倍数。
第二章:代数式与方程本章主要介绍了代数式的概念、代数式的运算、一元一次方程、方程的解、解方程的一般步骤以及在实际问题中应用代数式和方程的方法。
一、代数式及其运算1. 代数式:由数字、字母及运算符号组成的表达式。
2. 代数式的加、减、乘、除运算。
3. 同类项的合并。
二、一元一次方程1. 一元一次方程:方程中只有一个未知数,并且未知数的最高次是1。
2. 解方程的基本步骤:移项、合并同类项、消元、求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学必修一上册第二章复习要点
每章都有要掌握的必备知识点,以下是查字典数学网为您提供的高一数学上册第二章复习要点,希望对大家有帮助。
函数的有关概念
1.函数的概念:设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B
中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数.记作: y=f(x),x∈A.其中,x 叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)| x∈A }叫做函数的值域.
注意:1、如果只给出解析式y=f(x),而没有指明它的定义域,则函数的定义域即是指能使这个式子有意义的实数的集合;2、函数的定义域、值域要写成集合或区间的形式.
定义域补充:
能使函数式有意义的实数x的集合称为函数的定义域,求函数的定义域时列不等式组的主要依据是:(1)分式的分母不等于零; (2)偶次方根的被开方数不小于零; (3)对数式的真数必须大于零;(4)指数、对数式的底必须大于零且不等于1.
(5)如果函数是由一些基本函数通过四则运算结合而成的.
那么,它的定义域是使各部分都有意义的x的值组成的集
合.(6)指数为零底不可以等于零 (7)实际问题中的函数的
定义域还要保证实际问题有意义.
(注意:求出不等式组的解集即为函数的定义域。
)
2、构成函数的三要素:定义域、对应关系和值域
注意:(1)构成函数三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域和对应关系完全一致,即称这两个函数相等(或为同一函数)。
(2)两个函数相等当且仅当它们的定义域和对应关系完全一致,而与表示自变量和函数值的字母无关。
相同函数的判断方法:①定义域一致;②表达式相同 (两点必须同时具备) 值域补充
(1)、函数的值域取决于定义域和对应法则,不论采取什么方法求函数的值域都应先考虑其定义域.
(2)、应熟悉掌握一次函数、二次函数、指数、对数函数及各三角函数的值域,它是求解复杂函数值域的基础。
3. 函数图象知识归纳
(1)定义:在平面直角坐标系中,以函数y=f(x) , (x∈A)中的x为横坐标,函数值y为纵坐标的点P(x,y)的集合C,叫做函数y=f(x),(x ∈A)的图象.
C上每一点的坐标(x,y)均满足函数关系y=f(x),反过来,以满足y=f(x)的每一组有序实数对x、y为坐标的点(x,y),
均在C上 . 即记为C={ P(x,y) | y= f(x) , x∈A }
图象C一般的是一条光滑的连续曲线(或直线),也可能是由与任意平行于Y轴的直线最多只有一个交点的若干条曲线或离散点组成。
(2) 画法:
A、描点法:根据函数解析式和定义域,求出x,y的一些对应值并列表,以(x,y)为坐标在坐标系内描出相应的点P(x, y),最后用平滑的曲线将这些点连接起来.
B、图象变换法:
常用变换方法有三种,即平移变换、对称变换和伸缩变换Ⅰ、对称变换:
(1)将y= f(x)在x轴下方的图象向上翻得到y=∣f(x)∣的图象如:书上P21例5
(2) y= f(x)和y= f(-x)的图象关于y轴对称
(3) y= f(x)和y= -f(x)的图象关于x轴对称。
如
Ⅱ、平移变换: 由f(x)得到f(x
a) 左加右减; 由f(x)得到f(x)
a 上加下减
(3)作用:A、直观的看出函数的性质;B、利用数形结合的方法分析解题的思路;C、提高解题的速度;发现解题中的错误。
4.区间的概念
(1)区间的分类:开区间、闭区间、半开半闭区间;(2)无穷
区间;(3)区间的数轴表示.
5.映射
定义:一般地,设A、B是两个非空的集合,如果按某一个确定的对应法则f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称对应f:A
B为从集合A到集合B的一个映射。
记作“f:AB”
给定一个集合A到B的映射,如果a∈A,b∈B.且元素a和元素b对应,那么,我们把元素b叫做元素a的象,元素a叫做元素b的原象
说明:函数是一种特殊的映射,映射是一种特殊的对应,①集合A、B及对应法则f是确定的;②对应法则有“方向性”,即强调从集合A到集合B的对应,它与从B到A的对应关系一般是不同的;
③对于映射f:A→B来说,则应满足:(Ⅰ)集合A中的每一个元素,在集合B中都有象,并且象是唯一的;(Ⅱ)集合A
中不同的元素,在集合B中对应的象可以是同一个;(Ⅲ)不要求集合B中的每一个元素在集合A中都有原象。
6、函数的表示法:
常用的函数表示法及各自的优点:
1 函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等,注意判断一个图形是否是函数图象的依据:作
垂直于x轴的直线与曲线最多有一个交点。
2 解析法:必须注明函数的定义域;
3 图象法:描点法作图要注意:确定函数的定义域;化简函数的解析式;观察函数的特征;
4 列表法:选取的自变量要有代表性,应能反映定义域的特征.
注意:解析法:便于算出函数值。
列表法:便于查出函数值。
图象法:便于量出函数值
高一数学上册第二章复习要点就为大家提供这些,更多内容请关注查字典数学网!。
