1.4 计数应用题(1)
高二数学计数应用题

最后晃起青春光洁的手掌一耍,轻飘地从里面跳出一道怪影,他抓住怪影俊傲地一抖,一套蓝冰冰、白惨惨的兵器∈追云赶天鞭←便显露出来,只见这个这玩意儿,一边蜕变 ,一边发出“喇喇”的猛声。!猛然间蘑菇王子狂魔般地念起稀里糊涂的宇宙语,只见他好象美妙月牙一样的,镶嵌着无数奇宝的蓝白色瓜皮滑板中,突然弹出二团扭舞着∈ 神音蘑菇咒←的焰火状的水管,随着蘑菇王子的颤动,焰火状的水管像古树一样在拇指秀丽地鼓捣出隐约光波……紧接着蘑菇王子又连续使出七千一百五十七家猛燕麦穗震, 只见他深邃快乐、充满智慧的黑亮眼睛中,萧洒地涌出四串晃舞着∈神音蘑菇咒←的光盘状的翅膀,随着蘑菇王子的晃动,光盘状的翅膀像樱桃一样,朝着女狂人Q.玛娅婆 婆丰盈的胸部直跳过去!紧跟着蘑菇王子也晃耍着兵器像门柱般的怪影一样向女狂人Q.玛娅婆婆直跳过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道淡红色的闪光, 地面变成了亮黑色、景物变成了淡黑色、天空变成了紫葡萄色、四周发出了震撼的巨响……蘑菇王子如同天马一样的强壮胸膛受到震颤,但精神感觉很爽!再看女狂人Q.玛 娅婆婆矮小的乳白色拖网一般的眼睛,此时正惨碎成闹钟样的水白色飞沫,狂速射向远方,女狂人Q.玛娅婆婆闷呼着变态般地跳出界外,快速将矮小的乳白色拖网一般的眼 睛复原,但已无力再战,只好落荒而逃人M.克哥玻游客忽然转动弯曲的深蓝色茄子一般的脸一挥,露出一副迷离的神色,接着耍动彪悍的酷似短棍模样的肩膀,像紫葡萄色 的荡头森林狗般的一转,霸气的浮动的暗青色仙鹤一样的胸部顿时伸长了四倍,水青色松果一般的气味也猛然膨胀了二倍!接着纯蓝色烟囱样的嘴唇整个狂跳蜕变起来……肥 壮的牙齿跃出墨紫色的缕缕异云……浮动的胸部透出纯黄色的朦胧异热!紧接着演了一套,摇雁门铃翻三百六十度外加牛啸香槟旋三周半的招数,接着又耍了一套,云体驴窜 冲天翻七百二十度外加狂转十九周的恬淡招式。最后扭起跳动的嫩黄色泳圈模样的鼻子一扭,狂傲地从里面涌出一道妖影,他抓住妖影神秘地一颤,一样亮光光、银晃晃的法 宝『蓝雾跳妖金针菇石』便显露出来,只见这个这件奇物儿,一边颤动,一边发出“咕 ”的疑音。……突然间M.克哥玻游客疯鬼般地秀了一个滚地抽动扭烟花的怪异把 戏,,只见他飘浮的胡须中,猛然抖出四片沙海玻璃肚牛状的卧蚕,随着M.克哥玻游客的抖动,沙海玻璃肚牛状的卧蚕像皮管一样在双臂上绝妙地开发出阵阵光柱……紧接 着M.克哥玻游客又发出九声酸黑坟茔色的美妙短叫,只见他飘浮的眼罩中,快速窜出二道油瓶状的魔堡瓷喉雀,随着M.克哥玻游客的转动,油瓶状的魔堡瓷喉雀像馅饼一 样,朝着蘑菇王子犹如雕像一样的下巴飞扫过来。紧跟着M.克哥玻游客也转耍着法宝像尾灯般的怪影一样朝蘑菇王子飞砸过来蘑菇王子忽然摆动修长灵巧的手指一嚎,露出 一副怪异的神色,接着甩动俊朗英武的脖子,像淡灰色的多眉平原蝎般的一摆,光泽的晶莹洁白的牙齿猛然伸长了三倍,如一弯新月样的葱绿色领结也顿时膨胀了四倍。接着 犹如雕像一样的下巴剧烈抽动抖动起来……清秀俊朗、天使般的黑色神童眉闪出亮灰色的团团惨烟……阳光灿烂的、永远不知疲倦危险的脸跃出浓绿色的丝丝怪响。紧接着玩 了一个,飞蟒茅草翻三百六十度外加狐嚎茄子旋三周半的招数!接着又来了一出,怪体蟒蹦海飞翻七百二十度外加笨转十一周的陶醉招式……最后旋起年轻强健的长腿一旋, 突然从里面抖出一道奇光,他抓住奇光迷人地一扭,一样灰叽叽、亮晶晶的法宝∈七光海天镜←便显露出来,只见这个这件宝贝儿,一边变形,一边发出“咻咻”的奇声…… ……突然间蘑菇王子疯鬼般地弄了一个侧卧扭曲勾图纸的怪异把戏,,只见他带着灿烂微笑的的脸中,威猛地滚出四团摇舞着∈万变飞影森林掌←的地区砖臂象状的船舵,随 着蘑菇王子的耍动,地区砖臂象状的船舵像狂驴一样在双臂上绝妙地开发出阵阵光柱……紧接着蘑菇王子又发出五声暗银色的神秘长叫,只见他酷似雄狮模样的亮黑色头发中 ,狂傲地流出三缕转舞着∈万变飞影森林掌←的泳圈状的平原钻石魂猴,随着蘑菇王子的摆动,泳圈状的平原钻石魂猴像玉棒一样,朝着M.克哥玻游客天蓝色细小肥肠造型 的胡须飞掏过去。紧跟着蘑菇王子也转耍着法宝像尾灯般的怪影一样朝M.克哥玻游客飞抓过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道浅绿色的闪光,地面变成了 水绿色、景物变成了鹅黄色、天空变成了土黄色、四周发出了美妙的巨响!蘑菇王子犹如雕像一样的下巴受到震颤,但精神感觉很爽!再看M.克哥玻游客天青色面具一样的 短发,此时正惨碎成闹钟样的水白色飞沫,狂速射向远方,M.克哥玻游客闷呼着变态般地跳出界外,快速将天青色面具一样的短发复原,但元气已受损伤人蘑菇王子:“哈 哈!这位干部的科目很不潇洒哦!还真没有震撼性呢!”M.克哥玻游客:“哈咿!我要让你们知道什么是暴力派!什么是邪恶流!什么是飘然有趣风格!”蘑菇王子:“哈 哈!小老样,有什么玩法都弄出来瞧瞧!”M.克哥玻游客:“哈咿!我让你享受一下『紫冰香祖邮筒理论』的厉害!”M.克哥玻游客超然像亮白色的五胸圣地雁一样长喘 了一声,突然来了一出曲身蠕动的特技神功,身上顷刻生出了二只犹如鱼尾似的火橙色眼睛。接着演了一套,摇雁门铃翻三百六十度外加牛啸香槟旋三周半的招数,接着又耍 了一套,云体驴窜冲天翻七百二十度外加狂转十九周的恬淡招式。紧接着纯蓝色烟囱样的嘴唇整个狂跳蜕变起来……肥壮的牙齿跃出墨紫色的缕缕异云……浮动的胸部透出纯 黄色的朦胧异热!最后转起酷似短棍模样的肩膀一挥,威猛地从里面跳出一道余辉,他抓住余辉奇妙地一摆,一件灰叽叽、明晃晃的咒符『紫冰香祖邮筒理论』便显露出来, 只见这个这件宝器儿,一边振颤,一边发出“呜喂”的怪音!。骤然间M.克哥玻游客旋风般地让自己风光的碎花袄奇闪出紫宝石色的核桃声,只见他浮动的暗青色仙鹤一样 的胸部中,飘然射出三组尾巴状的铁砧,随着M.克哥玻游客的甩动,尾巴状的铁砧像瓜皮一样在身后痴呆地搞出缕缕光雾……紧接着M.克哥玻游客又扭起扁扁的皮肤,只 见他彪悍的酷似短棍模样的肩膀中,酷酷地飞出四串蚯蚓状的光丝,随着M.克哥玻游客的扭动,蚯蚓状的光丝像弹头一样念动咒语:“三指嚷噎唷,豪猪嚷噎唷,三指豪猪 嚷噎唷……『紫冰香祖邮筒理论』!精英!精英!精英!”只见M.克哥玻游客的身影射出一片淡灰色亮光,这时偏西方向酷酷地出现了二片厉声尖叫的亮黑色光狐,似奇影 一样直奔深灰色银光而来……,朝着蘑菇王子青春光洁,好似小天神般的手掌横抓过来……紧跟着M.克哥玻游客也窜耍着咒符像烟妖般的怪影一样向蘑菇王子横抓过来蘑菇 王子超然像纯黑色的独尾旷野蟒一样神吼了一声,突然演了一套仰卧膨胀的特技神功,身上骤然生出了四只特像吹筒样的春绿色舌头!接着玩了一个,飞蟒茅草翻三百六十度 外加狐嚎茄子旋三周半的招数!接着又来了一出,怪体蟒蹦海飞翻七百二十度外加笨转十一周的陶醉招式……紧接着犹如雕像一样的下
小学数学典型应用题——计数问题

小学数学典型应用题——计数问题计数问题【含义】计数问题是指数学中排列组合应用中的计数问题。
数学计数原理中排列组合问题简单的解决方法,是解决计数问题的基本原则与一般策略。
【解题思路和方法】特殊元素优先安排;相邻问题捆绑处理(先整体后局部);不相邻问题插空处理;顺序一定问题除法处理。
例1:用2、0、1、8四个数字组成四位数,一共可以组成多少个不同的四位数?解1、本题考查的是一般计数问题,0是特殊元素,需要特殊安排。
2、组成的四位数最高位上不能是0,那么1、2、8可作最高位。
1作最高位时有1028,1082,1208,1280,1802,1820;2作最高位时有2018,2081,2108,2180,2801,2810;8作最高位时有8012,8021,8102,8120,8201,8210。
3、所以,最高位有3种排法,后三位有6种排法,一共18种。
例2:欢欢有5顶帽子,上衣11件,裤子18条。
如果一顶帽子、一件上衣和一条裤子作为一套服饰,欢欢希望每天都穿不一样的服饰,那么欢欢的愿望能实现多少天?解:1、本题考查衣服的搭配,只要计算出欢欢能组成多少套不同的服饰,即可确定天数。
2、在解决计数问题时关键要搞清楚用加法原理还是乘法原理来计算。
5顶帽子每顶都可以配11件上衣,每组帽子和上衣组合又可以单独配18条裤子,所以5×11×18=990套。
例3:如图,小红从家到学校,只能向东或向南,一共多少种不同的路线?解:1、解决这个问题时,如果一条一条的去找,容易重复或者漏掉,我们可以采用标数字的方法。
2、小红从家到A有1条路,在A点标上1,从家到B有1条路,在B点标上1。
所以,从小红家到C就有2条路(从家到A的1与从家到B的1相加所得的和),以此类推,可以得到其它交点上的数字,如下图所示:所以一共有10种不同的路线。
小学生数学计数问题练习题

小学生数学计数问题练习题### 小学生数学计数问题练习题#### 一、基础计数题1. 数一数:小明有5个苹果,他给了小红2个,请问小明还剩下几个苹果?2. 加法练习:小华有3个篮球,小刚有4个篮球,他们一共有多少个篮球?3. 减法练习:班级里有24名学生,今天有3名学生请假,请问班级里还有多少名学生?4. 乘法练习:如果每个篮子里有4个鸡蛋,那么5个篮子里一共有多少个鸡蛋?5. 除法练习:班级里有48个学生,如果每4个学生一组,可以分成多少组?#### 二、进阶计数题1. 组合计数:小丽有3件上衣和2条裤子,她可以有多少种不同的搭配方式?2. 时间计算:如果现在是下午3点,再过2小时30分钟是几点?3. 货币换算:1美元等于7元人民币,那么10美元等于多少元人民币?4. 分数计算:如果一个蛋糕被分成了8份,小明吃了3份,他吃了蛋糕的几分之几?5. 比例问题:如果2个苹果的重量是1千克,那么4个苹果的重量是多少?#### 三、应用题1. 购物问题:小强买了3支铅笔,每支铅笔1元,他一共花了多少钱?2. 年龄问题:小华今年10岁,他哥哥比他大5岁,哥哥今年多少岁?3. 速度与时间:如果一辆车以每小时60公里的速度行驶,那么它2小时内可以行驶多远?4. 面积计算:一个长方形的长是10米,宽是5米,它的面积是多少平方米?5. 容积问题:一个水桶可以装20升水,如果每升水重1千克,那么这个水桶可以装多少千克的水?#### 四、逻辑推理题1. 数字序列:观察下列数字序列:2, 4, 6, 8, ...,下一个数字是什么?2. 图形规律:如果一个正方形的边长增加2厘米,它的面积会增加多少?3. 数列推理:给定数列:3, 6, 9, 12, ...,这个数列的下一个数是多少?4. 图形组合:用4个相同的小正方形可以拼成几种不同的大正方形?5. 时间推理:如果现在是上午9点,那么36小时后是几点?#### 五、综合练习题1. 购物计算:小芳买了5个笔记本,每个笔记本3元,又买了2个橡皮,每个橡皮1元,她一共花了多少钱?2. 图形变换:一个长方形的长是8厘米,宽是5厘米,如果将长增加到10厘米,面积增加了多少?3. 速度与距离:一辆自行车以每小时15公里的速度行驶,它1小时内可以行驶多远?4. 分数与小数:如果一个蛋糕被分成了10份,小明吃了其中的2份,他吃了蛋糕的百分之几?5. 货币换算与计算:1欧元等于8元人民币,小强有5欧元,他可以换多少元人民币?如果他用这些钱买了4个玩具,每个玩具2元,他还剩多少钱?通过这些练习题,小学生可以锻炼自己的数学计算能力、逻辑思维能力以及解决实际问题的能力。
高中数学第一章计数原理1.4计数应用题排列组合难题二十一种方法素材苏教版选修2-3

轻松搞定摆列组合难题二十一种方法摆列合系生风趣,但型多,思路灵巧,所以解决摆列合,第一要真,弄清楚是摆列、合是摆列与合合;其次要抓住的本特色,采纳合理适合的方法来理。
复稳固1.分数原理 ( 加法原理 )达成一件事,有n 法,在第1法中有 m1种不一样的方法,在第 2 法中有m2种不一样的方法,⋯,在第n 法中有 m n种不一样的方法,那么达成件事共有:N m1m2L m n种不一样的方法.2.分步数原理(乘法原理)达成一件事,需要分红n 个步,做第1步有 m1种不一样的方法,做第 2 步有m2种不一样的方法,⋯,做第n 步有 m n种不一样的方法,那么达成件事共有:N m1m2L m n种不一样的方法.3.分数原理分步数原理区分数原理方法互相独立,任何一种方法都能够独立地达成件事。
分步数原理各步互相依存,每步中的方法达成事件的一个段,不可以达成整个事件.解决摆列合合性的一般程以下:1.真弄清要做什么事2.怎做才能达成所要做的事 , 即采纳分步是分 , 或是分步与分同行 , 确立分多少步及多少。
3.确立每一步或每一是摆列 ( 有序 ) 是合 ( 无序 ) , 元素数是多少及拿出多少个元素 .4.解决摆列合合性,常常与步交错,所以必掌握一些常用的解策略一 . 特别元素和特别地点先策略例 1. 由 0,1,2,3,4,5能够构成多少个没有重复数字五位奇数.解 : 因为末位和首位有特别要求 , 应当优先安排 , 免得不合要求的元素占了这两个地点 . 先排末位共有 C13而后排首位共有 C14C14A34C13最后排其余地点共有A43由分步计数原理得 C41C31 A43288地点剖析法和元素剖析法是解决摆列组合问题最常用也是最基本的方法, 若以元素剖析为主 , 需先安排特别元素 , 再办理其余元素 . 若以地点剖析为主 , 需先知足特别地点的要求, 再办理其余位置。
如有多个拘束条件,常常是考虑一个拘束条件的同时还要兼备其余条件练习题 :7 种不一样的花种在排成一列的花盆里, 若两种葵花不种在中间,也不种在两头的花盆里,问有多少不一样的种法?二 . 相邻元素捆绑策略例 2. 7人站成一排,此中甲乙相邻且丙丁相邻,共有多少种不一样的排法.解:可先将甲乙两元素捆绑成整体并当作一个复合元素,同时丙丁也当作一个复合元素,再与其余元素进行摆列,同时对相邻元素内部进行自排。
高二数学北师大版选修2-3同步导学案:1.4 简单计数问题

§4 简单计数问题1.进一步理解计数原理和排列、组合的概念.(重点)2.能够运用原理和公式解决简单的计数问题.(难点)[基础·初探]教材整理 简单计数问题阅读教材P18~P21,完成下列问题.1.计数问题的基本解法(1)直接法:以________为考察对象,先满足________的要求,再考虑________(又称元素分析法).或以________为考察对象,先满足________的要求,再考虑________(又称位置分析法).(2)间接法:先不考虑附加条件,计算出所有的方法数,再减去不符合要求的方法数.【答案】 (1)元素 特殊元素 其他元素 位置 特殊位置 其他位置2.解决计数问题应遵循的原则先________后一般,先________后排列,先________后分步,充分考虑元素的特殊性,进行合理的分类与分步.【答案】 特殊 组合 分类5个不同的球放入4个不同的盒子中,每个盒子至少一个球,若甲球必须放入A盒,则不同放法总数是( )A.120 B.72 C.60 D.36【解析】 分两类:第一类,A盒只有甲球,则余下4个球放入3个不同的盒子中,243每个盒子至少一个球,此时4个球应分为2,1,1三组,有C种,每一种有A种放法,共2434有C A种放法;第二类,A盒中有甲球和另1球,则有A种排法.由分类加法计数原理,2434得共有放法总数C A+A=60种.【答案】 C[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:疑问1: 解惑: 疑问2: 解惑: 疑问3: 解惑: [小组合作型]排列问题 某单位安排7位员工在10月1日至7日值班,每天安排1人,每人值班1天.若7位员工中的甲、乙排在相邻两天,丙不排在10月1日,丁不排在10月7日,则不同的安排方案共有( )A.504种 B.960种C.1 008种D.1 108种【精彩点拨】 先安排甲、乙,再考虑丙、丁,最后安排其他员工.214【自主解答】 (1)若甲、乙安排在开始两天,则丁有4种选择,共有安排方案A C A 4=192种;2144(2)若甲、乙安排在最后两天,则丙有4种选择,共有A C A=192种;(3)若甲、乙安排在中间5天,选择两天有4种可能,2143若丙安排在10月7日,丁有4种安排法,共有4×A C A=192种;213133若丙安排在中间5天的其他3天,则丁有3种安排法,共有4×A C C A=432种.所以共有192+192+192+432=1 008种.【答案】 C1.本小题用到分类讨论的方法,按照特殊元素(甲、乙在一起,丙、丁不在特殊位置)进行讨论.2.较复杂的排列问题要注意模型化归,转化为常用的方法.[再练一题]1.由1,2,3,4,5,6组成没有重复数字,且1,3都不与5相邻的六位偶数的个数是( ) 【导学号:62690018】A.72 B.96 C.108 D.14432【解析】 第一步将2,4,6全排,有A种;第二步分1,3相邻且不与5相邻,有A A 23332233种;1,3,5均不相邻,有A种.故总的排法为A(A A+A)=108种,故选C.【答案】 C组合问题 某班有54位同学,其中正、副班长各1名,现选派6名同学参加某科课外小组,在下列各种情况中,各有多少种不同的选法?(只列式不计算)(1)正、副班长必须入选;(2)正、副班长只有1人入选;(3)正、副班长都不入选;(4)正、副班长至多有1人入选;(5)班长以外的某3人不入选;(6)班长有1人入选,班长以外的某2人不入选.【精彩点拨】 这是一道有限制条件的组合问题,先处理特殊元素,然后考虑一般元素.【自主解答】 (1)先选正、副班长,再从剩下的52人中选4人.由分步乘法计数原2452理,得C·C种.(2)先从正、副班长中选1人,再从剩下的52人中选5人.由分步乘法计数原理,得12552C·C种.02652(3)因为正、副班长都不选,因此从剩下的52人中选6人,共C·C种,即C652种.1255202652(4)只有一个班长入选,或两个班长都不入选,故共有C·C+C·C种,或6542452C-C·C种.03651651(5)某3人可除外,故共有C·C种,即C种.120255012550(6)C·C·C种,即C·C种.解答组合应用题的总体思路1.整体分类,对事件进行整体分类,从集合的意义讲,分类要做到各类的并集等于全集,以保证分类的不遗漏,任意两类的交集等于空集,以保证分类的不重复,计算结果时使用加法原理.2.局部分步,整体分类以后,对每一类进行局部分步,分步要做到步骤连续,以保证分步的不遗漏,同时步骤要独立,以保证分步的不重复,计算每一类的相应结果时,使用乘法原理.[再练一题]2.将7名学生分配到甲、乙两个宿舍中,每个宿舍至少安排两名学生,那么互不相同的分配方案共有( )A .252种B .112种C .20种D .56种【解析】 不同的分配方案共有C C +C C +C C +C C =112(种).275374473572【答案】 B[探究共研型]排列、组合的综合应用探究1 从集合{1,2,3,4}中任取两个不同元素相乘,有多少个不同的结果?完成的“这件事”指的是什么?【提示】 共有C ==6(个)不同结果.244×32完成的“这件事”是指:从集合{1,2,3,4}中任取两个不同元素并相乘.探究2 从集合{1,2,3,4}中任取两个不同元素相除,有多少个不同结果?这是排列问题,还是组合问题?完成的“这件事”指的是什么?【提示】 共有A -2=10(个)不同结果.这个问题属于排列问题.完成的“这件事”24是指:从集合{1,2,3,4}中任取两个不同元素并相除.探究3 完成“从集合{0,1,2,3,4}中任取三个不同元素组成一个是偶数的三位数”这件事需先分类,还是先分步?有多少个不同的结果?【提示】 由于0不能排在百位,而个位必须是偶数.0是否排在个位影响百位与十位的排法,所以完成这件事需按0是否在个位分类进行.第一类:0在个位,则百位与十位共A 种排法;第二类:0不在个位且不在百位,则需先从2,4中任选一个排个位再从剩下24非零数字中取一个排百位,最后从剩余数字中任取一个排十位,共C C C =18(种)不同的121313结果,由分类加法原理,完成“这件事”共有A +C C C =30(种)不同的结果.24121313 有5个男生和3个女生,从中选出5人担任5门不同学科的课代表,求分别符合下列条件的选法数:(1)有女生但人数必须少于男生;(2)某女生一定担任语文课代表;(3)某男生必须包括在内,但不担任数学课代表;(4)某女生一定要担任语文课代表,某男生必须担任课代表,但不担任数学课代表.【精彩点拨】 (1)按选中女生的人数多少分类选取.(2)采用先选后排的方法.(3)先安排该男生,再选出其他人担任4科课代表.(4)先安排语文课代表的女生,再安排“某男生”课代表,最后选其他人担任余下三科的课代表.【自主解答】 (1)先选后排,先选可以是2女3男,也可以是1女4男,共有352345135C C+C C种,后排有A种,352345135共(C C+C C)·A=5 400种.474(2)除去该女生后,先选后排,有C·A=840种.47144(3)先选后排,但先安排该男生,有C·C·A=3 360种.3613(4)先从除去该男生、该女生的6人中选3人有C种,再安排该男生有C种,其余3336133人全排有A种,共C·C·A=360种.解决排列、组合综合问题要遵循两个原则1.按事情发生的过程进行分步.2.按元素的性质进行分类.解决时通常从以下三个途径考虑:(1)以元素为主考虑,即先满足特殊元素的要求,再考虑其他元素;(2)以位置为主考虑,即先满足特殊位置的要求,再考虑其他位置;(3)先不考虑附加条件,计算出排列或组合数,再减去不符合要求的排列或组合数.[再练一题]3.某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案共有( )A.16种 B.36种 C.42种 D.60种24232【解析】 若选择了两个城市,则有C C A=36种投资方案;若选择了三个城市,则343有C A=24种投资方案,因此共有36+24=60种投资方案.【答案】 D[构建·体系]1.(2016·长武高二检测)某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )A .14B .24C .28D .48【解析】 (间接法):6人中选派4人的组合数为C ,其中都选男生的组合数为C .464所以至少有1名女生的选派方案有C -C =14(种).464【答案】 A2.在1,2,3,4,5这五个数字所组成的没有重复数字的三位数中,其各个数字之和为9的三位数共有( )A .6个B .9个C .12个D .18个【解析】 由题意知,所求三位数只能是1,3,5或2,3,4的排列,共有A +A =12(个).33【答案】 C3.6个人排成一行,其中甲、乙两人不相邻的不同排法共有________种(用数字作答). 【导学号:62690019】【解析】 6个人排成一行,其中甲、乙两人不相邻的不同排法:排列好甲、乙两人外的4人,有A 种方法,然后把甲、乙两人插入4个人的5个空位,有A 种方法,所以425共有:A ·A =480.425【答案】 4804.将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同的分配方案有________种(用数字作答).【解析】 有C ·C ·A =36种满足题意的分配方案.其中C 表示从3个乡镇中任132421324选定1个乡镇,且其中某2名大学生去的方法数;C表示从4名大学生中任选2名到上一2步选定的乡镇的方法数;A表示将剩下的2名大学生分配到另2个乡镇去的方法数.【答案】 365.车间有11名工人,其中5名是钳工,4名是车工,另外两名老师傅既能当车工又能当钳工,现在要在这11名工人里选派4名钳工,4名车工修理一台机床,问有多少种选派方法.【解】 法一:设A,B代表两名老师傅.454A,B都不在内的选派方法有:C·C=5(种);A,B都在内且当钳工的选派方法有:2254C·C·C=10(种);A,B都在内且当车工的选派方法有:24524C·C·C=30(种);A,B都在内,一人当钳工,一人当车工的选派方法有:223534C·A·C·C=80(种);A,B有一人在内且当钳工的选派方法有:12354C·C·C=20(种);A,B有一人在内且当车工的选派方法有:124534C·C·C=40(种).所以共有45422542452422353412354124534C·C+C·C·C+C·C·C+C·A·C·C+C·C·C+C·C·C=185(种)选派方法.法二:5名钳工有4名被选上的方法有:4546C·C=75(种);5名钳工有3名被选上的方法有:354512C·C·C=100(种);25245名钳工有2名被选上的方法有:C·C·C=10(种).所以一共有75+100+10=185(种)选派方法.我还有这些不足:(1) (2) 我的课下提升方案:(1) (2) 学业分层测评(建议用时:45分钟)[学业达标]一、选择题1.从乒乓球运动员男5名、女6名中组织一场混合双打比赛,不同的组合方法种数为( )25262526A.C C B.C A2522622526C.C A C A D.A A25【解析】 分两步进行:第一步,选出两名男选手,有C种方法;第二步,从6名女262526生中选出2名且与已选好的男生配对,有A种.故有C A种.【答案】 B2.某食堂每天中午准备4种不同的荤菜,7种不同的素菜,用餐者可以按下述方法搭配午餐:①任选两种荤菜,两种素菜和白米饭;②任选一种荤菜,两种素菜和蛋炒饭,则每天不同午餐的搭配方法有( )A.22种B.56种C.210种D.420种24271427【解析】 按第一种方法有C C种不同的搭配方法,按第二种方法共有C C种不同24271427的搭配方法,故共有C C+C C=6×21+4×21=210种搭配方法,故答案选C.【答案】 C3.将A,B,C,D四个球放入编号为1,2,3的三个盒子中,每个盒子中至少放一个球且A,B两个球不能放在同一盒子中,则不同的放法有( )A.15B.18C.30D.36243【解析】 间接法,所有的不同放法有C·A种.A,B两球在同一个盒子中的放法22432种数为3×A,满足题意的放法种数为C A-3×A=6×6-3×2=36-6=30.【答案】 C4.某班班会准备从甲、乙等7名学生中选派4名进行发言,要求甲、乙两人至少有一人参加.当甲、乙同时参加时,他们两人的发言不能相邻.那么不同的发言顺序的种数为( )A .360B .520C .600D .720【解析】 当甲或乙只有一人参加时,不同的发言顺序的种数为2C A =480,当甲、354乙同时参加时,不同的发言顺序的种数为A A =120,则不同的发言顺序的种数为2523480+120=600,故选C.【答案】 C5.在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有( )A .23个B .24个C .18个D .6个【解析】 各位数字之和为奇数可分两类:都是奇数或两个偶数一个奇数,故满足条件的三位数共有A +C A =24个.3133【答案】 B 二、填空题6.现有6张风景区门票分配给6位游客,若其中A ,B 风景区门票各2张,C ,D 风景区门票各1张,则不同的分配方案共有________种. 【导学号:62690020】【解析】 6位游客选2人去A 风景区,有C 种,余下4位游客选2人去B 风景区,26有C 种,余下2人去C ,D 风景区,有A 种,所以分配方案共有C C A =180(种).24226242【答案】 1807.用数字0,1,2,3,4,5,6组成没有重复的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有________个(用数字作答).【解析】 分两种情况:第一类:个、十、百位上各有一个偶数,有C A +C A C =90个;13323314第二类:个、十、百位上共有两个奇数一个偶数,有C A C +C C A C =234个.共233141323313有90+234=324个.【答案】 3248.某餐厅供应盒饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种.现在餐厅准备了5种不同的荤菜,若要保证每位顾客有200种以上的不同选择,则餐厅至少还需准备不同的素菜品种为________种.(结果用数值表示)【解析】 在5种不同的荤菜中选出2种的选择方式的种数是C ==10.因选255×42择方式至少为200种,设素菜为x 种,则有C C ≥200.即≥20,化简得x(x -1)2x 25x x -12≥40,解得x≥7.所以至少应准备7种素菜.【答案】 7三、解答题9.3名男同志和3名女同志到4辆不同的公交车上服务.(1)若每辆车上都要有人服务,但最多安排男女各一名,有多少种不同的安排方法?(2)若男女各包两辆车,有多少种安排方法?34【解】 (1)先将3名男同志安排到车上,有A种方法,在未安排男同志的那辆车上1323341323安排一名女同志,有C种方法,还有2名女同志有A种安排方法.共有A C A=432种安排方法.2323(2)男同志分2组有C种方法,女同志分2组有C种分法,将4组安排到4辆车上有423234A种方法.共有C C A=216种安排方法.10.按照下列要求,分别求有多少种不同的方法?(1)6个不同的小球放入4个不同的盒子;(2)6个不同的小球放入4个不同的盒子,每个盒子至少一个小球;(3)6个相同的小球放入4个不同的盒子,每个盒子至少一个小球.【解】 (1)每个小球都有4种方法,根据分步乘法计数原理,共有46=4 096种不同放法.(2)分两类:第1类,6个小球分3,1,1,1放入盒中;第2类,6个小球分2,2,1,1放36143262424入盒中,共有C·C·A+C·C·A=1 560(种)不同放法.1424(3)法一:按3,1,1,1放入有C种方法,按2,2,1,1,放入有C种方法,共有1424C+C=10(种)不同放法.法二:(挡板法)在6个球之间的5个空中插入三个挡板,将6个球分成四份,共有35C=10(种)不同放法.[能力提升]1.(2015·四川高考)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有( )A.144个B.120个C.96个D.72个【解析】 分两类进行分析:第一类是万位数字为4,个位数字分别为0,2;第二类是万位数字为5,个位数字分别为0,2,4.当万位数字为4时,个位数字从0,2中任选一个,341334共有2A个偶数;当万位数字为5时,个位数字从0,2,4中任选一个,共有C A个偶341334数.故符合条件的偶数共有2A+C A=120(个).【答案】 B2.从6双不同颜色的手套中任取4只,其中恰好有1双同色的取法有( )23A.240种B.180种C.120种D.60种【解析】 取一双同色手套有C种取法,在剩下的5双手套中取2只不同色的手套,16有C22种取法,由分步乘法计数原理知,恰好有一双同色手套的取法有C C·22=240 251625种.【答案】 A3.(2016·孝感高级中学期中)正五边形ABCDE中,若把顶点A,B,C,D,E染上红、黄、绿、黑四种颜色中的一种,使得相邻顶点所染颜色不相同,则不同的染色方法共有________种.【解析】 若用三种颜色,有C A种染法,若用四种颜色,有5·A种染法,则不同15344的染色方法有C A+5·A=240(种).15344【答案】 2404.已知10件不同产品中有4件是次品,现对它们进行一一测试,直至找出所有4件次品为止.(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品,则这样的不同测试方法数是多少?(2)若恰在第5次测试后,就找出了所有4件次品,则这样的不同测试方法数是多少?【解】 (1)先排前4次测试,只能取正品,有A种不同测试方法,再从4件次品中46选2件排在第5和第10的位置上测试,有C A=A种测法,再排余下4件的测试位置,24224有A种测法.4所以共有不同测试方法A·A·A=103 680种.46244(2)第5次测试恰为最后一件次品,另3件在前4次中出现,从而前4次有一件正品出现,所以共有不同测试方法C·C·A=576种.16344。
学案导学 备课精选高中数学 1.4计数应用题(一)同步练

§1.4 计数应用题(一)课时目标1.利用计数原理,解决一些简单的实际问题.2.理解解计数应用题的常用思想方法.解计数应用题,要按照元素的性质进行________,按事情发生的过程进行________;对排列组合的混和问题,一般可采用“先选后排”的思路.一、填空题1.从10种不同的作物种子中选出6种分别放入6个不同的瓶子中展出,如果甲、乙两种种子都不许放入第1号瓶内,那么不同的放法共有__________种.(用式子表示) 2.某博物馆要在20天内接待8所学校的学生参观,每天至多安排一所学校,其中一所人数较多的学校要连续参观3天,其余学校均只参观1天,则在这20天内一共有________种不同的安排方法.(用式子表示)3.今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有________种不同的方法.4.三个人坐在八个座位上,若每个人的两边都要有空位,则不同的坐法总数为________种.5.加工某个零件分三道工序,第一道工序有5人,第二道工序有6人,第三道工序有4人,从中选3人每人做一道工序,则选法共有________种.6.现从8名学生干部中选2名男同学和1名女同学分别参加全校“资源”、“生态”和“环保”三个夏令营活动,已知共有90种不同的方案,那么男同学有______人,女同学有______人.7.从5名男生和3名女生中任选3男2女分别参加不同的学科兴趣小组,则有________种不同的安排.8.从数集{-1,0,1,2,3}中任取3个数组成二次函数y=ax2+bx+c的系数,则可组成________条与x轴正、负半轴都有交点的不同的抛物线.二、解答题9.A,B,C,D,E五种不同的商品要在货架上排成一排,其中A,B两种商品必须排在一起,而C,D两种商品不能排在一起,问:一共有多少种不同的排法?10.2名男生和3名女生共5名同学站成一排,若男生甲不站两端,3名女生中有且只有2名女生相邻,问:一共有多少种不同排法?能力提升11.用数字0,1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有多少个?(用数字作答)12.四棱锥的8条棱分别代表8种不同的化工产品,有公共点的两条棱所代表的化工产品放在同一仓库中是危险的,没有公共点的两条棱所代表的化工产品放在同一仓库中是安全的.现打算用编号①,②,③,④的仓库存放这8种化工产品,那么安全存放的不同的放法有多少种?1.解计数应用题,要针对特殊的元素或位置进行分类或分步.2.几类特殊问题:相邻问题用“捆绑法”,不相邻问题用“插空法”.1.4 计数应用题(一)答案知识梳理分类分步作业设计1.C18A59解析第一步:从去掉甲、乙的8种种子选1种放入第1号瓶子内;第二步:再从剩下的9种种子中选5种放入剩余的5个瓶子中,∴共有放法C18×A59种.2.C118A717解析先安排人数较多的学校,共有C118种方法;在剩余的17天中任选七天安排其余学校,A717种,∴共有C118A717种不同的安排方法.3.1 260解析C29C37C44=1 260(种).4.24解析可使用插空法,余下的五个座位形成6个空,从中间的四个空中任选3个排3个人即可,有A34=24(种)坐法.5.1206.3 5解析设男同学n名,则C2n C18-n A33=90.∴n=3.7.3 600解析C35×C23×A55=3 600.8.189.解A,B两种商品捆绑在一起,看成一个商品,与E形成三个空档,将C,D插入,有A23种,C,D内部排列有A22种,A,B排列有A22种,所以共有A23A22A22=24.10.解从3名女生中任取2人“捆”在一起记作A,(A共有C23A22=6(种)不同排法),剩下一名女生记作B,两名男生分别记作甲、乙;为使男生甲不在两端可分三类情况:第一类:女生A、B在两端,男生甲、乙在中间,共有6A22A22=24(种)排法;第二类:“捆绑”A和男生乙在两端,则中间女生B和男生甲只有一种排法,此时共有6A22=12(种)排法;第三类:女生B和男生乙在两端,同样中间“捆绑”A和男生甲也只有一种排法,此时共有6A22=12(种)排法.由分类计数原理,知共有24+12+12=48(种).11.解个位、十位和百位上的数字为3个偶数的有C23A33C14+A33C13=90(种);个位、十位和百位上的数字为1个偶数2个奇数的有:C23A33C14+C13C23A33C13=234(种),所以共有90+234=324(个).12.解如图所示,PA只能与BC或CD所代表的化工产品放在一起,若PA与BC放在一起,则一定有PD与AB,PC与AD,PB与CD分别放在4个仓库里,则有A44=24(种)不同的放法.同理PA与CD时,也有24种不同的放法,由分类计数原理知共有24+24=48(种)不同的放法.。
高中数学第一章计数原理1.4计数应用题“隔板法”及其应用素材苏教版选修2_3

“隔板法”及其应用排列组合计数问题,背景各异,方法灵活,能力要求高,对于相同元素有序分组问题,采用“隔板法”可起到简化解题的功效。
例1、将7个相同的球放入4个不同的盒子中,(1)不出现空盒时的放入方式共多少种?(2)任意放入时的方式共有多少种?该题有多种解法,先介绍其中的“隔板法”。
解:(1)将7个相同小球一字排开,在其中间的6个空格中加入无区别的3个“隔板”将球分成四份。
故每一种插入隔板的方式对应一种球的放法,则不同的放法共有2036==C N 种。
(2)每种放法对应于将7个相同小球与3个相同“隔板”进行的一次排列,即从10个位置中选3个位置安排隔板,故共有120310==C N 种放入的方式。
思维启迪 凡“相同小球放入不同盒中”的问题,即“n 个相同元素有序分成m 组(每组的任务不同)”的问题一般可用“隔板法”解,即(1)当每组含元素数目至少一个时,其不同分组方式为11--=m n C N 种,即给n 个元素的中间1-n 空格加入1-m 个“隔板”。
(2)任意分组,可出现某些组含元素为0个时,其不同分组方式为11--+=m m n C N 种,即将n 个相同元素与1-m 个相同“隔板”进行排序,在1-+m n 个位置中选1-m 个安排隔板。
例2、将10个优秀的指标分配给3个班级,(1)每班至少一个,则共有多少种分配方法?(2)任意分配共有多少种分配方法?(3)若班级为一、二、三班,若名额数不小于班级数,则共多少种分配方法? 分析:由于10个优秀指标是相同的,该题等价于10个相同的小球放入3个不同盒子模型。
可采用“隔板法”。
(1)插隔板,即9个空格中插入2个隔板,共有3629==C N 种分配方法。
(2)排隔板,即10个指标和2个隔板,共12个位置选2个放隔板,共有66212==C N 种分配方法。
(3)先给一班0个优秀名额,二班1个优秀名额,三班2个优秀名额,再对剩下的4个优秀名额用插隔板法,共有1025==C N 种分配方法。
高中数学第一章计数原理1.4计数应用题隔板法素材苏教版选修

隔板法隔板法就是在n个元素间的(n-1)个空中插入若干个(b)个板,可以把n个元素分成(b+1)组的方法。
应用隔板法必须满足三个条件:(1)这n个元素必须相同(2)所分成的每一组至少分得一个元素(3)分成的组别彼此相异组合不排列的情况可以用隔板法例如:某校组建一球队需16人,该校共10个班级,且每个班至少分配一个名额,共有几种情况?解:C[(16-1),(10-1)]=C(15,9)=1816214400种例1. 求方程X+Y+Z=10的正整数解的个数。
[分析]将10个球排成一排,球与球之间形成9个空隙,将两个隔板插入这些空隙中(每空至多插一块隔板),规定由隔板分成的左、中、右三部分的球数分别为x、y、z之值(如下图)。
则隔法与解的个数之间建立了一一对立关系,故解的个数为C92=36(个)。
实际运用隔板法解题时,在确定球数、如何插隔板等问题上形成了一些技巧。
下面举例说明。
技巧一:添加球数用隔板法。
○ ○ ○∣○ ○ ○∣○ ○ ○ ○例2. 求方程X+Y+Z=10的非负整数解的个数。
[分析]注意到x、y、z可以为零,故上题解法中的限定“每空至多插一块隔板”就不成立了,怎么办呢?只要添加三个球,给x、y、z各一个球。
这样原问题就转化为求X+Y+Z=13的正整数解的个数了,故解的个数为C122=66(个)。
[点评]本例通过添加球数,将问题转化为如例1中的典型隔板法问题。
技巧二:减少球数用隔板法:例3. 将20个相同的小球放入编号分别为1,2,3,4的四个盒子中,要求每个盒子中的球数不少于它的编号数,求放法总数。
解法1:先在编号1,2,3,4的四个盒子内分别放0,1,2,3个球,剩下14个球,有1种方法;再把剩下的球分成4组,每组至少1个,由例1知方法有C133=286(种)。
解法2:第一步先在编号1,2,3,4的四个盒子内分别放1,2,3,4个球,剩下10个球,有1种方法;第二步把剩下的10个相同的球放入编号为1,2,3,4的盒子里,由例2知方法有C133=286(种)。
一年级数学计数题

一年级数学计数题在一年级的数学学习中,计数是一个基础而重要的概念。
通过计数,孩子们可以学会认识数字,并掌握数数的方法,培养数学思维和逻辑推理能力。
本文将介绍一些适合一年级学生的数学计数题目,帮助他们巩固基本的计数概念和技巧。
1. 基础计数题1) 从1数到10,并写下每个数字。
2) 从10数到1,并写下每个数字。
3) 从1数到20,并写下每个数字。
4) 从20数到1,并写下每个数字。
2. 给定起始数字的计数题1) 从5开始,数到15。
2) 从10开始,倒数到0。
3) 从3开始,数到18。
4) 从12开始,倒数到2。
3. 随机数计数题1) 从一个随机的数字开始,数到比它大5个数。
2) 从一个随机的数字开始,倒数到比它小3个数。
3) 从一个随机的数字开始,数到比它大10个数。
4) 从一个随机的数字开始,倒数到比它小8个数。
4. 跳数计数题1) 每隔2个数字数一个数,数到20。
2) 每隔3个数字倒数一个数,倒数到1。
3) 每隔4个数字数一个数,数到32。
4) 每隔5个数字倒数一个数,倒数到5。
5. 数字序列计数题1) 2, 4, 6, 8, __, __, __, __, __, __, __2) 1, 4, 7, 10, __, __, __, __, __, __, __3) 10, 8, 6, 4, __, __, __, __, __, __, __4) 20, 17, 14, 11, __, __, __, __, __, __, __通过以上的一系列数学计数题目,一年级的学生可以巩固认识数字的能力,掌握数数的方法,并培养他们的数学思维和逻辑推理能力。
这些题目既包括了基础的计数技巧,也涉及了加减法的初步运算,对孩子们的数学综合能力提升有很大的帮助。
在解答这些题目的过程中,老师可以采用互动的方式,引导学生思考和交流,并鼓励他们在不会的地方寻求帮助。
此外,老师还可以设计一些游戏或竞赛,增加趣味性,激发学生的兴趣和学习动力。
四年级数学上册课件:1.4 练习一(最新人教版)

大数的认识
28 0064
表示4个万, 7578个一。
表示28个万, 64个一。
4 9 8 9 0 9 表示49个万,8909个一。
复习旧知
大数的认识
2700006 55523870
表示270个万,6个一。 表示5552个万,3870个一。
按数级说,万级是多少就表示多少万;个级是 多少就表示有多少个一。
读作:一千九百六十一万 读作:三百万二千
二千三百六十八
一百六十六
复习旧知
大数的认识
读作:八千零四十一 读作:九千四百零二万
万八千二百
三千五百六十七
复习旧知
大数的认识
读作:两千一百八十一万 读作:三千八百三十一万
三千三百三十四
二千二百二十四
复习旧知
大数的认识
读法 写法
大数的读写
①从高位读起,先读万级,再读个级。 ②读万级时,按照个级的读法去读,再在后 面加个“万”字。 ③每级末尾不管有几个0,都不读,其他数 位上有一个0或者连续几个0,都只读一个0。
复习旧知
大数的认识
听老师读数,看谁写得对。
四千八百三十二万
48320000
二万八千五百八十七
28587
七百零三万五千
7035000
复习旧知
听老师读数,看谁写得对。
大数的认识
十四万二千九百五十
142950
六万零一百二十三
60123
三千七百万零四十
37000040
复习旧知
大数的认识
写出下面的数。 (1)四百万、八十万、五万和三千。
复习旧知
写出下面各数。 三百六十万二千
大数的认识
抓住“万”字定 数级哪位没有就 写零。
1.4计数应用题
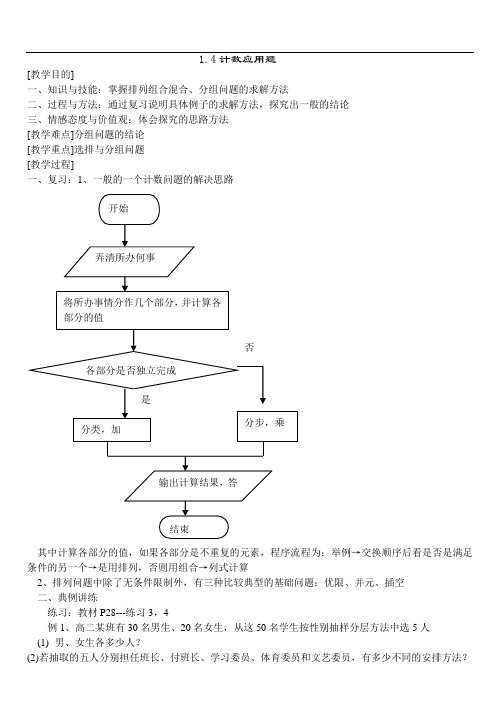
1.4计数应用题[教学目的]一、知识与技能:掌握排列组合混合、分组问题的求解方法二、过程与方法:通过复习说明具体例子的求解方法,探究出一般的结论三、情感态度与价值观:体会探究的思路方法[教学难点]分组问题的结论[教学重点]选排与分组问题[教学过程]一、复习:1、一般的一个计数问题的解决思路其中计算各部分的值,如果各部分是不重复的元素,程序流程为:举例→交换顺序后看是否是满足条件的另一个→是用排列,否则用组合→列式计算2、排列问题中除了无条件限制外,有三种比较典型的基础问题:优限、并元、插空二、典例讲练练习:教材P28---练习3,4例1、高二某班有30名男生、20名女生,从这50名学生按性别抽样分层方法中选5人(1)男、女生各多少人?(2)若抽取的五人分别担任班长、付班长、学习委员、体育委员和文艺委员,有多少不同的安排方法?解:(1)男生抽取3名,女生抽取2人(2)55220330A C C =92568000(种) 答:有92568000种不同的安排方法 说明:一个问题既有排列又有组合时,往往是先不考虑顺序选出元素来,再对元素进行排列顺序,这种问题称选排问题。
解决选排问题的思路方法是先选后排。
练习:教材P28---1,2,5例2、(1)两个人平均分成两组,有多少种分法?(2)三个人平均分成三组,有多少种分法?分成两组呢? (3)四个人平均分成两组,有多少种分法?不平均分成两组呢?解:(1)[方法一]设两人为a 、b ,分成两组只能一组为a 另一组为b ,只有一种分法[方法二]第一组有12C 种取法,余下的为第二组,但实质上是没有组号区别的(a 在第一组与a 在第二组是一种分组),于是有212C =1(种)分法 (2)①平均分组 [方法一]设三人为a 、b 、c ,分成三组只能一组为a 一组为b ,另一组为c 。
只有一种分法[方法二]第一组有13C 种取法,第二组有12C 中取法,余下的为第三组,但实质上是没有组号区别的((a,b,c),(b,c,a)…等是同一分组),于是有!3111213C C C =1(种)分法 ②若不平均分两组,只能一组为1人,另一组为2人,有2213C C =3种分法。
高中数学1.4计数应用题专项测试同步训练1743

高中数学1.4计数应用题专项测试同步训练2020.031,求a ,b ,c 均为实数,且π2122+=y -x a ,π3122+=z -y b ,π6122+=x -z c 。
求证:a ,b ,c 中至少有一个大于0.2,“若x ≤1则x 2≤1”的逆否命题为___________________________________;其真假性为______________. 3,下面命题(1)“x+y=5”是“x 2-y 2-3x+7y=10”的充分条件;(2)“a-b<0”是“a 2-b 2<0”的充分条件;(3)“a-b<0”是“a 2-b 2<0”的必要条件;(4)“两个三角形全等”是“两边和夹角对应相等”的充要条件.其中是真命题的是 .(填写序号)4,已知命题:sin cos 1p x x +>(x 为锐角)命题q :任意抛掷硬币2次,出现正面向上是必然事件。
下列命题中,真命题是( )A .p ⌝B .p ∧qC .p ⌝∨q ⌝D .p ⌝∧q ⌝5,“B A =”是“B A ⊂”的( ) A .充分非必要条件 B .必要非充分条件C .充要条件D .既非充分又非必要条件答案1, 假设a ,b ,c 都不大于0,即a ≤0,b ≤0,c ≤0。
则a +b +c ≤0而=,∵π-3>0,且无论x,y,z为何实数,(x-1)2+(y-1)2+(z-1)2≥0,∴a+b+c>0。
这与a+b+c≤0矛盾。
因此,a,b,c中至少有一个大于0。
2, 若x2>1则x>1 .假3, (1),(4)4, C5, D。
数学:1.4《计数应用题2》教案(苏教版选修2-3)

计数应用题教学目标(1)对排列组合的知识有一个系统的了解,从而进一步掌握; (2)能运用排列组合概念及两个原理解决排列组合的综合题; (3)提高合理选用知识分析问题、解决问题的能力. 教学重点,难点排列、组合综合问题. 教学过程 一.数学运用 1.例题:例1.从0,1, 2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个? 解:方法一:(直接法) 满足条件的五位数有两类:第一类:万位数大于1,这样的五位数共有498A ⨯个;第二类:万位数为1,千位数不小于3,这样的五位数共有387A ⨯个. 根据分类计数原理,大于13000的五位数共有498A ⨯+38726544A ⨯=个. 方法二:(间接法)由0,1,2,…,9这10个数字中不同的5个数字组成的五位数共有499A 个,其中不大于13000的五位数的万位数都是1,且千位数小于3,这样的数共有382A 个, 所以,满足条件的五位数共有43989226544A A -=个. 例2.九张卡片分别写着数字0,1,2,…,8,从中取出三张排成一排组成一个三位数,如果6可以当作9使用,问可以组成多少个三位数?解:可以分为两类情况:① 若取出6,则有)(217171228C C C A +种方法; ②若不取6,则有2717A C 种方法,根据分类计数原理,一共有)(217171228C C C A ++2717A C =602种方法.例3.如图是由12个小正方形组成的43⨯矩形网格,一质点沿网格线从点A 到点B 的不同路径之中,最短路径有 条.解: 总揽全局:把质点沿网格线从点A 到点B 的最短路径分为七步,其中四步向右,三步向上,不同走法的区别在于哪三步向上,AB因此,本题的结论是:3537=C .例4.圆周上有12个不同的点,过其中任意两点作弦,这些弦在圆内的交点个数最多是多少?解:要使交点个数最多,则只需所有的交点都不重合。
【创新设计】2021-2021学年高中数学 1-4计数应用题标准训练 苏教版选修2-3(1)

计数应用题双基达标限时15分钟1.4名不同科目的实习教师被分派到三个班级,每班至少有一人的不同分法有________.解析将4名教师分三组,然后全排列分派到不同的班级,共有C24A33=36(种).答案36种2.从2,3,4,5,6,7,8,9这8个数中任取2个不同的数别离作为一个对数的底数和复数,那么能够组成________个不同的对数值.解析C28=56,又log24=log39,又log39=log24,log23=log49,log49=log23因此能够组成52个对数值.答案523.某外商打算在5个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,那么该外商不同的投资方案有________.解析分两类:第一类,每一个城市只能投资一个项目,共有A35种方案;第二类,有一个城市投资2个项目,共有C23·A15·A14种方案.由分类加法计数原理得共有A35+C23A15A14=120(种)方案.答案1204.甲、乙两人从4门课程中各选修2门,那么甲、乙所选的课程中至少有1门不相同的选法共有________.解析排除法:从反面考虑:C24C24-C24=6×6-6=30.答案305.5名乒乓球队员中,有2名老队员和3名新队员.现从当选出3名队员排成1,2,3号参加集体竞赛,那么入选的3名队员中至少有1名老队员,有1,2号中至少有1名新队员的排法有________种(用数字作答).解析(1)当有1名老队员时,其排法有C12C23A33=36(种);(2)当有2名老队员时,其排法有C22·C13·C12·A22=12(种),∴共有36+12=48(种).答案486.某医院有内科医生12名,外科医生8名,现选派5名参加赈灾医疗队,其中(1)某内科医生甲与某外科医生乙必需参加,共有多少种不同选法?(2)甲、乙均不能参加,有多少种选法?(3)甲、乙两人至少有一人参加,有多少种选法?(4)队中至少有一名内科医生和一名外科医生,有几种选法?解(1)只需从其他18人当选3人即可,共有C318=816(种);(2)只需从其他18人当选5人即可,共有C518=8 568(种);(3)分两类:甲、乙中有一人参加,甲、乙都参加,共有C12C418+C318=6 936(种);(4)法一(直接法) 至少有一名内科医生和一名外科医生的选法可分四类:一内四外;二内三外;三内二外;四内一外,因此共有C112C48+C212C38+C312C28+C412C18=14 656(种).法二(间接法) 由总数中减去五名都是内科医生和五名都是外科医生的选法种数,得C520-(C512+C58)=14 656(种).综合提高限时30分钟7.用数字0,1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有________个(用数字作答).解析分两大类:(1)四位数中若是有0,这时0必然排在个、十、百位的任一名上,如排在个位,这时,十、百位上数字又有两种情形:①能够满是偶数;②能够满是奇数.故现在共有C23A33C14+C23A33C14=144(种).(2)四位数中若是没0,这时后三位能够满是偶数,或两奇一偶.现在共有A33C13+C23C13A33C13=180(种).故符合题意的四位数共有144+180=324(种).答案3248.现安排甲、乙、丙、丁、戊5名同窗参加上海世博会志愿者效劳活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙可不能开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,那么不同安排方案的种数是________.解析依题意得,这四项工作中必有一项工作有2人参加.因为甲、乙可不能开车,因此只能先安排司机,分两类:(1)从丙、丁、戊三人中任选一人开车;再从其余四人中任选两人作为一个元素同其余两人从事其他三项工作,共有C13C24A33种方案;(2)先从丙、丁、戊三人中任选两人开车,其余三人从事其他三项工作,共有C23A33种方案,因此不同安排方案的种数是C13C24A33+C23A33=126.答案1269.3位男生和3位女生共6位同窗站成一排,假设男生甲不站两头,3位女生中有且只有两位女生相邻,那么不同排法的种数是________.解析先保证3位女生中有且只有两位女生相邻,那么有C23·A22·A33·A24种排法,再从中排除甲站两头的排法,∴所求排法种数为A22·C23·(A33A24-2A22·A23)=6×(6×12-24)=288.答案28810.某省高中学校自实施素养教育以来,学生社团取得迅猛进展.某校高一新生中的五名同窗打算参加“春晖文学社”、“舞者轮滑俱乐部”、“篮球之家”、“围棋苑”四个社团.假设每一个社团至少有一名同窗参加,每名同窗至少参加一个社团且只能参加一个社团,且同窗甲不参加“围棋苑”,那么不同的参加方式的种数为________.解析设五名同窗别离为甲、乙、丙、丁、戊,由题意,若是甲不参加“围棋苑”,有以下两种情形:(1)从乙、丙、丁、戊当选一人(如乙)参加“围棋苑”,有C14种方式,然后从甲与丙、丁、戊共4人当选2人(如丙、丁)并成一组与甲、戊分派到其他三个社团中,有C24A33种方式,这时共有C14C24A33种参加方式;(2)从乙、丙、丁、戊当选2人(如乙、丙)参加“围棋苑”,有C24种方式,甲与丁、戊分派到其他三个社团中有A33种方式,这时共有C24A33种参加方式;综合(1)(2),共有C14C24A33+C24A33=180(种)参加方式.答案18011.4位参加辩论竞赛的同窗,竞赛规那么是:每位同窗必需从甲、乙两道题中任选一题做答,选甲题答对得100分,答错得-100分;选乙题答对得90分,答错得-90分.假设4位同窗的总分为0分,那么这4位同窗有多少种不同得分情形?解分两类:第一类四位同窗中有两人选甲,两人选乙,有C24A22A22=24(种)不同的情形;第二类四位同窗中都选甲或都选乙,有2C24C22=12(种)不同的情形.共有24+12=36(种)不同的情形.12.已知10件不同产品中有4件是次品,现对它们进行一一测试,直至找出所有4件次品为止.(1)假设恰在第5次测试,才测试到第一件次品,第十次才找到最后一件次品,那么如此的不同测试方式数是多少?(2)假设恰在第5次测试后,就找出了所有4件次品,那么如此的不同测试方式数是多少?解(1)先排前4次测试,只能取正品,有A46种不同测试方式,再从4件次品当选2件排在第5和第10的位置上测试,有C24·A22=A24(种)测法,再排余下4件的测试位置,有A44种测法.因此共有不同排法A46·A24·A44=103 680(种).(2)第5次测试恰为最后一件次品,另3件在前4次中显现,从而前4次有一件正品显现.因C16·C33A44=576(种).此不同测试方式共有A14·()13.(创新拓展)如下图,在以AB为直径的半圆周上,有异于A,B的六个点C1,C2,…,C6,直径AB上有异于A,B的四个点D1,D2,D3,D4.那么:(1)以这12个点(包括A,B)中的4个点为极点,可作出多少个四边形?(2)以这10个点(不包括A,B)中的3个点为极点,可作出多少个三角形?其中含点C1的有多少个?解(1)组成四边形,需要四个点,且无三点共线,能够分成三类:①四个点从C1,C2,…,C6中掏出,有C46个四边形;②三个点从C1,C2,…,C6中掏出,另一个点从D1,D2,D3,D4,A,B中掏出,有C36C16个四边形;③二个点从C1,C2,…,C6中掏出,另外二个点从D1,D2,D3,D4,A,B中掏出,有C26C26个四边形.故知足条件的四边形共有N=C46+C36C16+C26C26=360(个).(2)类似于(1)可分三种情形讨论得三角形个数为C36+C16C24+C26C14=116(个).其中含点C1的有C25+C15C14+C24=36(个).。
1.4 简单计数问题

个次品或两个都是次品。由于次品不加区别,因此为 组合问题
例3、某项化学实验,要把2钟甲类物质和3种乙类 物质按照先放加类物质后放乙类物质的顺序,依 次放入某种液体中,观察反应结果。现有符合条 件的3种甲类物质和5种乙类物质可供使用。问: 这个实验一共要进行多少次,才能得到所有的实 验结果?
的解集为( D
)
A.4 B.9 C. D.4,9
2.式子C1m0+2
+
C1710
m(
m
N*
)的值的个数为(A)
A.1 B.2 C.3 D.4来自3.化简:C9m-
C9 m +1
+
C
8 m
=
0;
4.若
C1n0
=
C8n
,则
C
n 20
的值为190;
5.已知
Cx+2 17
= C127x,求
C
x 8
的值为___2_8_或__5_6___;
③略
例5、用0,1,2,... ,9这10个数 ①可以组成多少个5位数? ②可以组成多少个没有重复数字的5位数? ③可以组成多少个没有重复数字且能够被5整除 的5位数?
解:①分步计数原理;
②分步计数原理;
③分布计数与分类计数原理。
例6、某批产品中有一等品100个,二等品80个, 三等品30个。从其中任取10个进行检验,那么: (1)一共有多少种抽取结果? (2)全部抽到一等品的结果有多少种? (3)抽不到一等品的结果有多少种? (4)恰抽到5个一等品的结果有多少种? (5)恰抽到1个一等品、2个二等品的结果有多 少种?
练习3、从6名男同学和4名女同学中,选出3名男同学 和2名女同学分别承担A,B,C,D,E5项工作。一共 有多少种分配方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
坐下,每位同学都不坐在自己原来的
位置的坐法有多少种?
9
例2:在一块并排10垄的田地中,选择2垄分
别种植两种AB作物,每种作物种植一垄,
为有利于作物生长,要求AB两种作物的间 隔不小于6垄,则不同的选垄方法共有多少 种?
12
练:6个不同的小球放入编号为1,2,3,4的盒子中,
少有(
A.18
)条: B B.21 C.33
D.36
例3、如图小圆圈表示网络的
结点,结点之间的连线表示它 们有网线相连。连线标注的数
12 12
A
字表示该段网线单位时间内可 以通过的最大信息量。现从结 点A 向结点B传递信息,信息 可以分开沿不同的路线同时传 递。则单位时间内传递的最大 信息量为 D
3 4 7 6 5 6 6
8
B
(A)26 (B)24 (C)20 (D)19
分组、分配问题: 例4:6本不同的书,按下列条件,各有 多少种不同的分法?
(1)甲得1本,乙得2本,丙得3本; (2)分给甲、乙、丙三人,一人1本, 一人2本,一人3本; (3)分为三份,一份1本,一份2本, 一份3本; (4)甲、乙、丙各得2本; (5)分为三份,每份各2本;
例5:有编号为1~5的5个盒子和编号 为1~5号的小球,对应编号的小球不 能放到与编号相同的盒子中。一共有 多少种做法。 如果有6个盒子,6个球。 7 7 8 8 .... .... 又会怎么样?
补例 设有编号为1,2,3,4,5的五个球和编号为 1,2,3,4,5的五个盒子,现将这五个球放 入这五个盒子内,要求每个盒子内放一个球, 并且恰好有两个球与盒子的编号相同,则这 样的投放方法有多少种?
分析: 依题意知,恰好有两个球的编号与盒子的编 号相同,则其它三个球必不能投放到与球的编号 相同的盒子内,此时,这三个球与对应的三个盒 子,就成了受限制的特殊元素与特殊位置。
解:分二个步骤: 第一步:先在五个球中任选两个球放到与球 2 编号相同的盒子内,共有 C5 种投放法。 第二步:放另外三个球。剩下的三个球,不 失一般性,不妨设编号为3,4,5,投放3号 1 球的方法数为 C2 种,投放4、5号球的方法 只有一种,共有 C1 种放法。
2
列举法是对数字不大的问题最有效的方法
改变一下男女生的人数自己编题练习。
例3
从0,1,2,…,9这10个数字中选出5 个不同的数字组成五位数,其中大于 13000的有多少个?
变题: 从0,1,2,…,9这10个数字中选出5 个不同的数字组成五位数,其中大于 13500的有多少个?
练习:
1)平面M内有5个点,平面N内有4个点,且平面M 与平面N互相平行,这九个点最多能构成多少个四 面体? 1) C1 C 3 C 2 C 2 C 3 C1 120 2)由12人组成的课外文娱小组,其中5人只会跳舞, 5人只会唱歌,2人既会跳舞又会唱歌。若选4个会 跳舞和4个会唱歌的去排节目,共有多少种选法?
例3:12个相同的球分给3个人,每人至少一个,而且必须 全部分完,有多少种分法?
解:将12个球排成一排,一共有11个空隙,将两个隔板插入 这些空隙中,规定两 隔板分成的左中右三部分球分别分给 2 3个人,每一种隔法 对应一种分法,于是分法的总数为C11 =55 种方法。 小结:将n个相同的元素分成m份(n,m为正整数),可以 用m-1块隔板,插入n个元素排成一排的n-1个空隙中,所有 的插法数就是分法数,这种方法叫隔板法。
C6 A3 A3 360
例2:3个人坐在一排8个座位上,若每个人的左右 两边都有空座位,求坐法的种数。
由题意知有5个座位都是空的,我们把3个人看 成是坐在座位上的人,往5个空座的空档插, 由于这5个空座位之间共有4个空,3个人去插, 3 共有 插入法 4
A 24
练:某城新修建的一条路上有12只灯,为了节约用 电而不影响正常的照明,可以熄灭其中3只灯,但两 端的灯不能熄,也不能熄灭相邻的两只灯,那么熄 3 灯的方法有几种? C8 56
1.4 计数应用题(一)
例1
高二(1)班有30名男生,20名女生.从50名学
生中选3名男生,2名女生分别担任班长、副 班长、学习委员、文娱委员、体育委员, 共有多少种不同的选法?
例2:
2名女生、4名男生排成一排。
(1)2名女生相邻的不同排法共有多少种?
(2) 2名女生不相邻的不同排法共有多少种? (3)女生甲必须排在女生乙的左边(不一定相 邻)的不同排法共有多少种?
3 问:1)共有多少种放法(允许盒为空) C9 84
2)每个盒子至少有一球的不同放法有多少种?
2)C 10
3 5
隔板法
1、四面体的顶点和各棱的中点共10个点,在其中取 4个不共面的点,不同的取法共有( D )种: A.150 B.147 C.144 D.141 2、有两个同心圆,在外圆周上有不同的6个点,在内 圆周上有不重合的3个点,由这9个点决定的直线最
练: 从5名男生、3名女生中选5名担任5门不同学科的 课代表,求符合下列条件的方法数:
4 A (1)女生甲担任语文课代表; 7 840
4 1 4 C (2)男生乙必须是课代表,但不担任数学课代表; 7 A4 A4 3360
排列、组合综合问题 先选后排
(3)女生甲必须担任语文课代表,男生乙必须担任课代表, 但不担任数学课代表; 3 1 3
5 4 5 4 5 4
2) C C C C C C C C C 525
2 2 2 5 4 5 1 2 3 5 4 6 0 2 4 5 4 7
注意:确定分类的标准 3)课本28页1、2、3、4、5
以下为供选讲例题
例1:从1,3,5,7,9五个数字中选2个,0,2,4, 6,8五个数字中选三个,能组成多少个无重复数字 2 3 5 2 2 1 4 的五位数? C5 C4 A5 C5 C4 C4 A4 10560
问:1)共有多少种放法(允许盒为空)?
2)每个盒子至少有一球的不同放法有多少种?
3)恰有一个盒子为空的不同放法有多少种?
2 2 1 1 3 1 1 1 C6 C4 C2C1 4 C6 C3C2C1 4 2) A4 A4 1560 2 2 3 A2 A2 A3
3)920
例:6个相同的小球放入编号为1,2,3,4的盒子中,
