江苏省淮安市淮阴区棉花中学九年级数学下册 第三章 中心对称图形《3.6梯形的中位线》同步练习(无答案
江苏省淮安市淮阴区棉花中学中考数学 整式方程复习教案 新人教版

江苏省淮安市淮阴区棉花中学中考数学 整式方程复习教案 新人教版一、典型例题:例1、解方程81314112+--=-+x x例2、某条船从A 地顺流而下至B 地,然后逆流而上到C 地,共用4小时,已知水流速度为2.5千米/小时,船在静水中的速度为7.5千米/小时,A 、C 两地之间相距离10千米,求A 、B 两地间的距离。
例3、若关于x 的方程kx 2-6x+9=0有两个不相等的实数根,求k 的取值范围。
例4、m 取何值时,关于x 的方程mx 2+2(m -1)x+ m -3=0有两个实数根?例5、已知a,b,c 是三角形的三边,判别方程b 2x 2+(b 2+c 2-a 2)x+c 2=0根的情况。
例6、正数m 为甚么值时,方程组⎩⎨⎧+-==+2222mx y y x 只需一组实数解?求出这个方程组的实数解。
二、练习题:1、两年期定期储蓄的年利率为2.25%,按国家规定,所得利息要缴纳20%的利息税.王大爷于2002年6月存入银行一笔钱,两年到期时,共得税后利息540元,则王大爷2002年6月存款额为( )元.(A)20000 (B)18000 (C)15000 (D)128002、解以下方程:(1)5134)!(23-=-+x x x (2))1(2)1(2121-=⎥⎦⎤⎢⎣⎡--x x x 3、已知关于x 方程3x+2m=2x+1和方程41347+=-x m 的解相反,求代数式(2m+1)2004的值。
4、能否存在整数k,使关于x 的方程(k+1)x -1=-2x+3在整数范围内有解?为甚么?5、解以下方程:(1)3x 2-4x -2=0 (2)x 2-22x+2=o(3)3(2x+1)2-5(2x+1)+2=06、如果关于x 的方程x 2+b 2-16=0和x 2-3b+12=0有相反的实数根,求b 的7、若一元二次方程022=--m x x 无实数根,则一次函数1)1(-++=m x m y 的图象不经过第 象限( )A .一B .二C .三D .四 8、函数c bx ax y ++=2的图象如图5所示,则a 、b 、ac b 42-的取值范围是 ( )A .04002<->>ac b b a B .04002>-<>ac b b a9、将进货单价为40元的商品按50元出售时,能卖500个,已知该商品每涨价1元时,其销售量就减少10个,为了赚8000元的利润,售价应定为多少,这时分应进货多少个?10、甲、乙二人合干某项工作,合干4天后,乙另有任务调出,甲单独干2天赋能完成,已知单独完成这项工作,甲比乙少用3天,问甲、乙单独干各用几天完成?科学睡眠健康成长——在国旗下的发言各位尊敬的老师、各位亲爱的同学:大家上午好!我是来自预备二班的***。
江苏省淮安市淮阴区棉花中学九年级数学下册 第三章 中心对称图形《图形的旋转》同步练习(无答案) 新人

基础与巩固1、下列现象属于旋转的是 ( )A 、摩托车在急刹车时向前滑动B 、飞机起飞后冲向空中的过程C 、幸运大转盘转动的过程D 、笔直的铁轨上飞驰而过的火车2、在图形旋转中,下列说法不正确的是 ( )A 、图形上各点的旋转角度相同B 、对应点到旋转中心距离相等C 、由旋转得到的图形也一定可以由平移得到D 旋转不改变图形的大小、形状3、如图,是一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数可以是 ( )A 、90°B 、60°C 、45°D 、30°4、如图,△ABC 绕点O 旋转得到△DEF ,以下结论中不正确的是 ( )A 、△ABC ≌△DEFB 、∠ABC=∠COEC 、∠AOD=∠COFD 、∠CAB=∠FDE5、下图中的图案,绕中心旋转多少度后能和原来的图案互相重合?答:_______________________ 答:___________________________6、如图,△ABC 为等边三角形,D 是△ABC 内一点,若将△ABD 经过旋转后到△ACP 位置,则旋转中心是__________,旋转角等于_________度,△ADP 是___________三角形.7、试举出一个日常生活中的旋转现象__________________________________________。
F E D C A A D P 第3题图 第4题图 第6题图8、在如图所示的方格纸中:;(1)将△ABC 向右平移11格,画出平移后得到的△A 1B 1C 1 ;(2)以点O 为旋转中心,将△A 1B 1C 1按逆时针方向旋转90°,画出旋转后得到的△A 2B 2C 2。
9、如图,已知△ABC ,将△ABC 绕点A 顺时针旋转30°得到△A 1B 1C 1,画出△A 1B 1C 1 。
10、如图所示,四边形AOBC ,它绕O 点按顺时针旋转得到四边形DOEF ,在此旋转过程中:(1)旋转中心是点_______; (2)经过旋转,点A 、B 分别移到点____、点____; (3)AO 与DO 的长有什么关系?BO 与EO 呢?(4)∠AOD 与∠BOE 有什么大小关系?拓展与延伸 11、如图,把△ABC 绕点C 顺时针旋转35°, 得到△A ′B ′C ,A ′B ′交AC 于点D ,若∠A ′DC=90°,则∠A 度数为 ( )A 、45°B 、55°C 、65°D 、75°12、已知:如图,在△ABC 中,∠BAC=120°,以BC 为边向形外作等边三角形△BCD ,把△ABD 绕着点D 按顺时针方向旋转60°后得到△ECD ,A 、C 、E 恰好在一条直线上,若AB=3,AC=2,求∠BAD 的度数与AD 的长。
初二数学第三章《中心对称图形》知识梳理
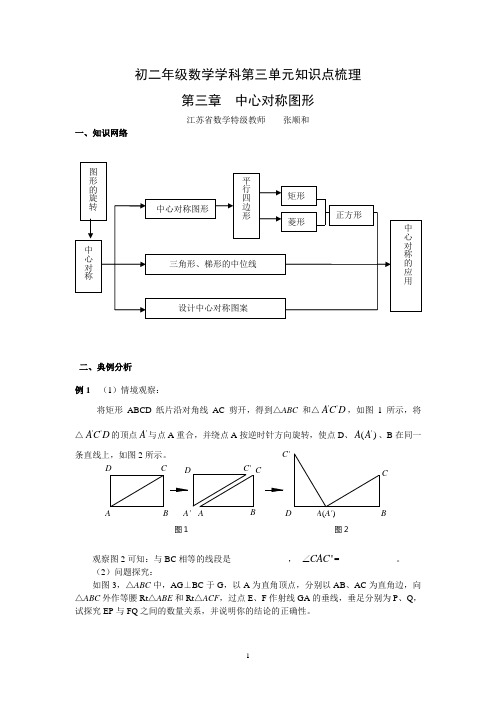
初二年级数学学科第三单元知识点梳理第三章 中心对称图形江苏省数学特级教师 张顺和一、知识网络二、典例分析 例1 (1)情境观察:将矩形ABCD 纸片沿对角线AC 剪开,得到△ABC 和△''A C D ,如图1所示,将△''A C D 的顶点'A 与点A 重合,并绕点A 按逆时针方向旋转,使点D 、'()A A 、B 在同一条直线上,如图2所示。
观察图2可知:与BC 相等的线段是_____________, 'C AC =_____________。
(2)问题探究:如图3,△ABC 中,AG ⊥BC 于G ,以A 为直角顶点,分别以AB 、AC 为直角边,向△ABC 外作等腰Rt △ABE 和Rt △ACF ,过点E 、F 作射线GA 的垂线,垂足分别为P 、Q ,试探究EP 与FQ 之间的数量关系,并说明你的结论的正确性。
图1 图2C'A'BADCABCDBCDA (A')C'解 (1)情境观察: AD (或A′D ),90°(2)问题探究:结论:EP =FQ . 理由如下:∵△ABE 是等腰三角形,∴AB =AE ,∠BAE=90°. ∴∠BAG +∠EAP =90°.∵AG ⊥BC , ∴∠BAG +∠ABG =90°,∴∠ABG =∠EAP . ∵EP ⊥AG ,∴∠AGB =∠EPA =90°, ∴Rt △ABG ≌Rt △EAP . ∴AG =EP .同理AG =FQ . ∴EP =FQ .说明 情境观察所得结论是容易的,但它是为问题探究服务的,图3中以PG 为分界线的左、右两个图形实际上就是图2,你看出来了吗?分析问题时应多注意前后的联系,体会用化归思想解决问题。
例2 如图,AB//CD ,GM 平分AGH ∠,HM 平分CHG ⊥,HN 平分DHG ∠,GN平分BGH ∠。
苏科版数学九年级上册 第五章 中心对称图形(二)(§5.5~§5.6) 淮安市淮阴区开明中学专题复习(含答案)

【回顾与思考】1.直线与圆的位置关系有_____种:____________,___________,____________.2.当直线与圆_________________时,叫直线与圆_______;当直线与圆_________________时,叫直线与圆_______;当直线与圆_________________时,叫直线与圆_______.3.已知圆半径为r,圆心到直线距离为d,则直线与圆_____<=>d___r;直线与圆_____<=>d___r;直线与圆_____<=>d___r;4.圆的切线垂直于经过______的半径.5.与三角形三边都相切的圆叫做三角形的________,圆心叫做三角形的_____,它是三角形三条_________的交点.6.在平面内两个半径不等的圆的位置关系有___种:_______,_______,_______,_______,_______.7.两圆半径为R,r(R>r),圆心距为d,写出两圆在各种位置关系下R,r,d之间的关系.⑴若两圆________,则______________;⑵若两圆________,则______________;⑶若两圆________,则______________;⑷若两圆________,则______________;⑸若两圆________,则______________;【经典试题】一、选择题1.已知⊙O的半径r=3cm,直线和点O的距离为d,如果直线与有公共点,那么( )A.d=3cmB.d≤3cmC.d>3cmD.d<3cm2.如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是 ( )A.0≤x≤ 2B.-2≤x≤ 2C.-1≤x≤1D.x> 23.圆的半径为5cm ,圆心到一条直线的距离是7cm ,则直线与圆 ( )A.有两个交点B.有一个交点C.没有交点D.交点个数不定4.△ABC 中,∠A:∠B:∠C=1:2:3,以B 为圆心,BC 为半径的⊙O 与边AC 的位置关系是()A.外离B.相切C.相交D.不能确定5.如图,⊙O 内切于△ABC ,切点分别为D ,E ,F ,已知∠B=50°,∠C=60°,连结OE ,OF ,DE ,DF ,那么∠EDF 等于 ( )A.40°B.55°C.65°D.70°第5题第8题6.已知⊙O 1的半径r 为3cm ,⊙O 2的半径R 为4cm ,两圆的圆心距O 1O 2为1cm ,则这两圆的位置关系是()A.相交B.内含C.内切D.外切7.已知⊙O 1和⊙O 2相切,两圆的圆心距O 1O 2为9cm ,⊙O 1的半径为4cm ,则⊙O 2的半径()A.5cmB.13cmC.9cm 或13cmD.5cm 或13cm二、填空题8.如图,⊙O 半径为3cm ,B 为⊙O 外一点,OB 交⊙O 于点A ,AB=OA ,动点P 从点A 出发,以πcm/s 的速度在⊙O 上按逆时针方向运动一周回到点A ,立即停止.当点P 运动时间为________s 时,BP 与⊙O 相切.9.若⊙O 1与⊙O 2的半径分别为3cm ,4cm ,圆心距为1cm ,则两圆的位置关系是__ __________.10.两圆半径之比为5:7,两圆外切时,圆心距为6cm,则两圆的半径为分别为___ _____和__________.三、解答题(每题10分,共40分)11.如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,DE⊥AC.求证:DE是⊙O的切线.C 12.如图,△ABC中,AB=AC=5,BC=6,求△ABC内切圆的半径长.C13.已知一个三角形的三边长分别为3cm,4cm,5cm,以各顶点为圆心的三个圆两两相切.求这三个圆的半径分别是多少?14.已知⊙O1与⊙O2外切于点P,AB是⊙O1的直径,AP,BP的延长线分别交⊙O2于点C,D.求证:⑴CD是⊙O2的直径; ⑵CD∥AB.探究学习如图,⊙O1的半径为1cm,⊙O2的半径为2cm,两圆外切.若⊙P的半径为3cm,且与⊙O1,⊙O2都相切,请画出⊙P,符合条件的⊙P有几个.参考答案一、1.B 2.A 3.C4.B5.B6.C7.D二、8.1或3 9.内切 10.2.5cm ,3.5cm三、12.3213.2cm ,3cm ,1cm 14.⑴证∠CPD=∠APB=90°;⑵连结O 1O 2,证∠D=∠B.5个探究学习。
江苏省淮安市淮阴区棉花中学2014届九年级数学模拟测试试题

A.B.C.D.一.选择题(本大题共8小题,每小题3分,共计24分。
在每小题所给出的四个选项中,恰.有一项...是符合题目要求的,请将正确选项的序号填涂在答题卡上) 1. 2009的相反数是( ▲ ) A. 2009 B. -2009 C.12009 D. 12009- 2.下列运算不正确...的是( ▲ ) A.632)(a a = B. 532a a a =⋅ C. a a a =÷23D. 532a a a =+ 3. 两圆的半径及两圆心之间的距离都是5㎝,则这两圆的位置关系是( ▲ ) A. 外离 B.外切 C. 相交 D.内切 4. 反比例函数xm y 1-=在第二象限内的图象如图所示,则m 的值为( ▲ ) A. -1 B. -2 C. 1 D. 2 5.如图,AC 是电杆AB 的一根拉线,测得BC =6米,∠ACB =52°,则拉线AC 的长为 ( ▲ ) A. 6sin 米 B. ︒6米 C. 6·cos 52°米 D. ︒526cos 米第5题图6.在共有道自己是否进入决赛,只需要了解自己的成绩以及全部成绩的( ▲ ) A.平均数 B.众数 C.中位数 D.方差7.图3是韩老师早晨出门散步时,离家的距离..()y 与时间()x 之间的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是( ▲ )8.该机器人所走的总路程为( ▲ )A .6米.B.8米. C .12米. D.二.填空题(本大题共10小题,每小题3分,共计30ABC┐第18题图E D CBA9.化简64的结果是_________________.10. 太阳的半径约是69660千米,用科学记数法表示 (保留3个有效数字)约是_________________千米。
11.不等式组110210x x ⎧+≥⎪⎨⎪->⎩的解集是___________________.12.如图已知等腰△ABC 中,∠C=90°,点D 、E 分别是AC 、AB 的中点且DE=2,则△ABC 的面积是_______________.第12题图 第13题图 第14题图 第15题图13.一个长方体的主视图和左视图如图所示(单位:㎝),则其俯视图的面积是____2cm14.如图,直线443y x =-+与x 轴、y 轴分别交于A 、B 两点,把△AOB 绕点A 顺时针旋转90°后得到△AO B '',则点B '的坐标是__________________.15.直线b kx y l +=:1与直线x y l 3:2-=在同一平面直角坐标系内的图象如图所示,则关于y x ,的方程组⎩⎨⎧-=+=xy bkx y 3的解为_____________________.16.二次函数c bx ax y ++=2的部分对应值如下表所示,则x=4对应的函数值y=___17. 在平面直角坐标系中,规定一个点先向上平移2个单位,再向右平移1个单位为1次运动。
2020-2021学年苏科版数学八年级下册第9章《中心对称图形—平行四边形》常考题专练(二)

八年级下册第9章《中心对称图形—平行四边形》常考题专练(二)1.如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.(1)求证:四边形ABEC是平行四边形;(2)若∠AFC=2∠ADC,求证:四边形ABEC是矩形.2.如图,已知正方形ABCD的边长是2,∠EAF=m°,将∠EAF绕点A顺时针旋转,它的两边分别交BC、CD于点E、F,G是CB延长线上一点,且始终保持BG=DF.(1)求证:△ABG≌△ADF;(2)求证:AG⊥AF;(3)当EF=BE+DF时:①求m的值;②若F是CD的中点,求BE的长.3.已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.4.已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:(1)AE=AB;(2)如果BM平分∠ABC,求证:BM⊥CE.5.在图的正方形网格中有一个三角形OAB,请你在网格中分别按下列要求画出图形①画出△OAB向左平移3个单位后的三角形;②画出△OAB绕点O旋转180°后的三角形;③画出△OAB沿y轴翻折后的图形.6.一块矩形纸片,利用割补的办法可以拼成一块与它面积相等的平行四边形(如图1所示):请你根据图1作法的提示,利用图2画出一个平行四边形,使该平行四边形的面积等于所给的矩形面积.要求:(1)画出的平行四边形有且只有一个顶点与B点重合;(2)写出画图步骤;(3)写出所画的平行四边形的名称.7.如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在A、E的异侧,BD⊥AE于D,CE⊥AE于E(1)试说明:BD=DE+CE.(2)若直线AE绕A点旋转到图(2)位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请直接写出结果;(3)若直线AE绕A点旋转到图(3)位置时(BD>CE),其余条件不变,问BD与DE、CE的关系如何?请直接写出结果,不需说明理由.8.如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°;(1)请说明∠EAB=∠FAC的理由;(2)△ABC可以经过图形的变换得到△AEF,请你描述这个变换;(3)求∠AMB的度数.9.如图1,已知Rt△ABC中,AB=BC,AC=2,把一块含30°角的三角板DEF的直角顶点D 放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),点C在DE上点B在DF上.(1)求重叠部分△BCD的面积;(2)如图2,将直角三角板DEF绕D点按顺时针方向旋转30度,DE交BC于点M,DF交AB于点N,①请说明DM=DN;②在此条件下重叠部分的面积会发生变化吗?若发生变化,请求出重叠部分的面积,若不发生变化,请说明理由;(3)如图3,将直角三角板DEF绕D点按顺时针方向旋转α度(0<α<90),DE交BC于点M,DF交AB于点N,则DM=DN的结论仍成立吗?重叠部分△DMN的面积会变吗?(请直接写出结论不需说明理由)10.如图①,在正方形ABCD中,点E,F分别在AB、BC上,且AE=BF.(1)试探索线段AF、DE的数量关系,写出你的结论并说明理由;(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图②中补全图形,并说明理由.参考答案1.证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵CE=DC,∴AB=EC,AB∥EC,∴四边形ABEC是平行四边形;(2)∵由(1)知,四边形ABEC是平行四边形,∴FA=FE,FB=FC.∵四边形ABCD是平行四边形,∴∠ABC=∠D.又∵∠AFC=2∠ADC,∴∠AFC=2∠ABC.∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB,∴FA=FE=FB=FC,∴AE=BC,∴四边形ABEC是矩形.2.解:(1)证明:在正方形ABCD中,AB=AD=BC=CD=2,∠BAD=∠C=∠D=∠ABC=∠ABG=90°.∵BG=DF,在△ABG和△ADF中,,∴△ABG≌△ADF(SAS);(2)证明:∵△ABG≌△ADF,∴∠GAB=∠FAD,∴∠GAF=∠GAB+∠BAF=∠FAD+∠BAF=∠BAD=90°,∴AG⊥AF;(3)①解:△ABG≌△ADF,∴AG=AF,BG=DF.∵EF=BE+DF,∴EF=BE+BG=EG.∵AE=AE,在△AEG和△AEF中.,∴△AEG≌△AEF(SSS).∴∠EAG=∠EAF,∴∠EAF=∠GAF=45°,即m=45;②若F是CD的中点,则DF=CF=BG=1.设BE=x,则CE=2﹣x,EF=EG=1+x.在Rt△CEF中,CE2+CF2=EF2,即( 2﹣x)2+1 2=( 1+x)2,得x=.∴BE的长为.3.(1)证明:如图,∵D、E分别是AB、AC的中点,F是BC延长线上的一点,∴ED是Rt△ABC的中位线,∴ED∥FC.又EF∥DC,∴四边形CDEF是平行四边形;(2)解:由(1)知,四边形CDEF是平行四边形,则DC=EF=2cm.∵点D是Rt△ABC斜边AB的中点,∴DC=AB,∴AB=2DC=4cm.4.证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠E=∠DCM,在△AEM和△DCM中,,∴△AEM≌△DCM(AAS),∴AE=CD,∴AE=AB;(2)∵BM平分∠ABC,∴∠ABM=∠CBM,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠CBM=∠AMB,∴∠ABM=∠AMB,∴AB=AM,∵AB=AE,AM=DM,∴点M是AD的中点,∴BC=2AM,∴BC=BE,∴△BCE是等腰三角形.∵BM平分∠ABC,∴BM⊥CE.5.解:①如图所示:△A′B′O′即为所求;②如图所示:△A″B″O即为所求;③如图所示:△A″B″′O即为所求.6.解:作图:如图所示(1)过点C作射线CE(不过A、D点);(2)过点B作射线BF∥CE,且交DA的延长线于点F;(3)在CE上任取一点G,连接BG;(4)过点F作FE∥BG,交射线CE于点E,则四边形BGEF为所画的平行四边形.7.解:(1)证明:∵∠BAC=90°,∴∠BAD+∠EAC=90°,又∵BD⊥AE,CE⊥AE,∴∠BDA=∠AEC=90°,∠BAD+∠ABD=90°,∴∠ABD=∠EAC,又∵AB=AC,∴△ABD≌△CAE,∴BD=AE,AD=CE,∵AE=AD+DE=CE+DE,∴BD=DE+CE.(2)同理可得,DE=BD+CE;(3)同理可得,DE=BD+CE.8.解:(1)∵∠B=∠E,AB=AE,BC=EF,∴△ABC≌△AEF,∴∠C=∠F,∠BAC=∠EAF,∴∠BAC﹣∠PAF=∠EAF﹣∠PAF,∴∠BAE=∠CAF=25°;(2)通过观察可知△ABC绕点A顺时针旋转25°,可以得到△AEF;(3)由(1)知∠C=∠F=57°,∠BAE=∠CAF=25°,∴∠AMB=∠C+∠CAF=57°+25°=82°.9.解:(1)连结BD.∵AB=BC,AC=2,∴CD=AD=1,则△BCD的面积是×CD•BD=×1×1=;(2)作DQ⊥BC,DP⊥AB分别于点Q,P,又∵AB=BC,CD=AD,∴∠A=∠C,∴△CDQ≌△ADP,∴DQ=DP,则四边形BQDP是正方形.∵∠EDQ+∠QDN=∠NDP+∠QDN∴∠EDQ=∠NDP又∵∠MQD=∠NPD∴△MDQ≌△NDP,∴DM=DN,∴直角三角板DEF绕D点按顺时针方向旋转30度,此条件下重叠部分的面积等于正方形BQDP的面积是DQ2=()2=.(3)DM=DN的结论仍成立,重叠部分△DMN的面积会变.10.解:(1)AF=DE.∵ABCD是正方形,∴AB=AD,∠DAB=∠ABC=90°,∵AE=BF,∴△DAE≌△ABF,∴AF=DE.(2)四边形HIJK是正方形.如下图,H、I、J、K分别是AE、EF、FD、DA的中点,∴HI=KJ=AF,HK=IJ=ED,∵AF=DE,∴HI=KJ=HK=IJ,∴四边形HIJK是菱形,∵△DAE≌△ABF,∴∠ADE=∠BAF,∵∠ADE+∠AED=90°,∴∠BAF+∠AED=90°,∴∠AOE=90°∴∠KHI=90°,∴四边形HIJK是正方形.。
苏科版数学九年级上册 第五章 中心对称图形(二)(§5.1~§5.3) 淮安市淮阴区开明中学专题复习(含答案)

【回顾与思考】1._______________________________叫圆.2.平面内点与圆的位置关系有____种:__________,__________,__________.3.圆既是________对称图形,也是________对称图形,其对称中心是_______,对称轴是________.4.垂径定理:________________________________________________________.5._________________________________________________________叫圆周角.6.在同圆或等圆中,同弧或等弧所对的圆周角________,都等于该弧所对的_____的一半. 【经典试题】 一、选择题1.下列命题正确的是()A.平分弦的直径必垂直于弦B.不都是直径的两弦不能互相平分C.与直径不垂直的弦,不通被直径平分D.弦所对的两条弧的中点的连线,不一定经过圆心2.如图,AC 是⊙O 直径,BD 是⊙O 的弦,EC ∥AB ,交⊙O 于点E ,则图中与12∠BOC相等的角共有 ( ) A.2个B.3个C.4个D.5个第2题第3题第4题E第5题3.如图,点A,B,C,D在同一个圆上,AC,BD为四边形ABCD的对角线,则图中相等的角有( )A.3对B.4对C.5对D.6对4.如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D=50°,则∠C的度数是( )A.50°B.40°C.30°D.25°5.正三角形ABC内接于⊙O,动点P在圆周的劣弧AB上,且不与A,B重合,则∠BPC等于( )A.30°B.60°C.90°D.45°二、填空题(每题3分,共30分)6.已知⊙O的面积为36π.⑴若PO=6.5,则点P在_________; ⑵若PO=4,则点P在_________;⑶若PO=_________,则点P在⊙O上.7.一个点与定圆上最近点的距离为4cm,与最远点的距离为9cm,则圆的半径是_________.8.半径为10的圆中,垂直平分半径的弦长为_________.9.在半径为5cm的圆中,两条平行弦的长度分别为6cm,8cm,则这两条弦之间的距离为___________.10.已知⊙O的半径为10cm,弦AB=16cm,P为AB上一个动点,则点P到圆心O的最短距离为_____cm.11.已知四边形ABCD内接于⊙O,∠BOD=100°,则∠DAB=______.第11题三、解答题(每题10分,共40分)12.如图,BD,CE分别是△ABC中,AC,AB边上的高.求证:B,C,D,E四点在同一个圆上.13.已知M是⊙O中,弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=43cm.⑴求圆心O到弦MN的距离;⑵求∠ACM的大小.14.用尺规四等分已知弧AB.(不写作法,保留作图痕迹)15.如图,AB是⊙O的直径,以OA为直径的⊙C与⊙O的弦AD相交于点E,线段AE与DE相等吗?为什么?探究学习某居民区一处圆形污水管破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面至管道顶部的距离为10cm,则维修人员应准备内径为多大的管道?参考答案一、1.B 2.C 3.C 4.D 5.B二、6.圆外,圆内,6 7.132cm或52cm 8.10 3 9.1cm或7cm10.6 11.130°三、13.2cm,60°探究学习半径50cm。
江苏省淮安市淮阴区棉花中学九年级数学下册 第三章 中

1 第三章中心对称图形《矩形》同步练习(1) 新人教版基础与巩固1、矩形的相邻两边分别为4㎝和3㎝,则它的对角线长为_________,面积为________.2、矩形的面积为24,一条边为6,则矩形的对角线长为_________.3、如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,AB=2㎝,AC=4㎝(1)根据“矩形的对角线_________”,可以得到BD=_____㎝; (2)根据“矩形的对角线_________”,可以得到 AO=BO=21AC=_____㎝,又因为AB=2㎝,所以 △AOB 是_______三角形,△COB 分别是_______三角形. 4、如图,在矩形ABCD 中,沿AE 折叠,点D 落在BC 边的F 处,若∠BAF=60°,则∠DAE= .5、如图,矩形ABCD 中,DE 平分∠ADC 交BC 于E ,若AB=4,AE=5,则AD=_________.6、如图,四边形ABCD 是矩形,对角线AC 、BD 交于点O ,CE//DB 交AB 的延长线于点E ,则△A CE 是_________三角形.题4 题5 题6 7、矩形具有而平行四边形不一定具有的性质是 ( )A 、两组对角相等B 、对角线相等OD C B AED C B A O ED CB A F E DC B A2 C 、对角线互相平分 D 、两组对边平行且相等8、矩形的一个内角平分线把矩形一边分成3㎝和5㎝两部分,则矩形的周长为( )A 、16㎝B 、22㎝C 、26㎝D 、22㎝或26㎝9、如图,矩形ABCD 中,DE ⊥AC 于点E ,∠ADE :∠EDC=3:2,则∠BDE 的度数为( )A 、18°B 、15°C 、22.5°D 、30°10、如图,用8块相同的长方形地砖拼成一个矩形,则每个长方形地砖的面积是( )A 、2002cmB 、3002cmC 、6002cmD 、 24002cm题9 题10 11、如图,矩形ABCD 的对角线AC 、BD 交于点O ,∠AOD=120°,AB=4㎝,求矩形对角线的长.12、如图,把矩形ABCD 沿对角线AC 折叠,使点B 落在点E 处,试说明EF=DF.13、如图,P 是矩形A BCD 内的一点,PA=PB ,那么PC 与PD 相等吗?为什么?拓展与延伸 14、在矩形ABCD 中,AB=2,BC=3,F 是CD 中点,一束光线从A 点出发,40cmO E D C B A O D C B AF E D C B A FE D C B A P D C B A通过BC边反射,恰好落在F点,那么反射点E与C点距离为_________3。
江苏省淮安市淮阴区棉花中学九年级数学下册 第三章 中

1 第三章中心对称图形《3.6 三角形的中位线新》同步练习 新人教版基础与巩固1、已知三角形的一边长是12cm ,则另两边的中点连线之长是 ( ) A.8cm B.6cm C.4cm D.2cm2、顺次连结等腰梯形的四边中点所得的四边形是 ( )A.平行四边形B. 矩形C.菱形D.正方形3、 直角三角形斜边上的中线与两直角边中点连线的关系是 ( )A.相等B. 相等且互相垂直C. 相等且互相平分D. 相等且互相垂直平分4、等腰三角形中有一条边为4,其三条中位线长度总和为8,则底边长为 ( )A .4B .6C .6或4D .8和45、已知三角形的各边分别为6cm,8cm 和10cm,则连结各边中点所成三角形的周长为cm, 面积为 cm 2 .6、△ABC 中,点D 、E 三等分AB ,AD<AE ,DF ∥BC ,EG ∥BC ,分别交AC 于点F 、G.(1)若AC=9cm ,则FC= cm ;(2)若DF=3cm ,则BC= cm .7、已知,四边形ABCD 的对角线互相垂直且相等,那么顺次连结这个四边形各边中点得到的四边形是 .8、如图, △ABC 的中线AF 与中位线DE 相交于点O 。
AF 与DE 有怎样的关系?为什么?A F E D CB29、如图,四边形ABCD 中,AB=CD ,点E 、F 、G 、H 分别是 BC 、AD 、BD 、AC 的中点,猜想四边形EHFG 的形状并说明理由。
10、如图,E 、F 分别是AB 、AC 的中点,延长EF 交∠ACD 的平分线于点G 。
AG 与CG 有怎样的位置关系?说明你的理由。
拓展与延伸.11、如图, △ABD 中,C 是BD 上一点, ∠BAC =90°,∠CAD=45°,且BC=CD ,试说明AB=2AC 。
AG F E D C BH G F E D CB A DC B A。
九年级数学下册 第三章 中心对称图形(梯形的中位线)同步练习 试题

轧东卡州北占业市传业学校第三章中心对称图形<梯形的中位线>同步练习 教1、梯形的下底长5cm ,中位线长4cm ,那么它的上底长是 〔 〕 A.2.5cm B.3cm C.3.5cm D.4.5cm2、如图,DE 是△ABC 的中位线,FG 是梯形BCED 的中位线.如果DE=4,那么FG= ( ) A.6 B. 8 C.10 D.123、如图,等腰梯形ABCD 的中位线EF 的长为6,腰AD 的长为5,那么该等腰梯形的周长为〔 〕A.11B. 16C. 17D.224、如图, 梯形ABCD 中,AD ∥BC,BD 为对角线,中位线EF 交BD 于O 点,假设FO-EO=3,那么BC-AD 等于 ( )A .4B .6C .8D .102题图 3题图 4题图5、梯形的中位线长为9cm,上、下底之比是4:5,那么两底长分别是 。
6、等腰梯形腰长等于中位线长,周长为12cm ,那么腰长为 。
GFEDC B A7、等腰梯形的一角为45°,高为2cm ,中位线长为6cm ,那么它的上底长 。
8、梯形的中位线将梯形的面积分成1:2两局部,那么上底a ,中位线b 和下第c 之比等于 。
9、如图, 在梯形ABCD 中,AD ∥BC, 中位线EF 分别与BD 、AC 交于点G 、H ,假设AD=6cm ,BC=10cm ,求GH 的长。
10、如图,EF 是梯形ABCD 的中位线,AC 平分∠DAB 交EF 于M ,延长DM 交AB 于N ,试说明△AND 是等腰三角形。
拓展延伸11、,△ABC 中,AB=10。
〔1〕如图甲,假设点D 、E 分别是AC 、BC 边的中点,求DE 的长。
甲 〔2〕如图乙,假设点A 1、A 2把AC 边三等分,点B 1、B 2把BC 边三等分,那么〔3〕假设点A 1、A 2、…、A 10把AC 边十一等分,点B 1、B 2、…、B 10把律,直接写出A 1B 1+A 2B 2+…+ A 10 B 10的结果是 。
江苏省淮安市淮阴区凌桥乡2018届九年级数学下学期复习作业30轴对称与中心对称

复习作业 30 轴对称与中心对称一、选择题1.以下“慢行经过,注意危险,严禁行人通行,严禁非灵活车通行”四个交通标记图( 黑白暗影图片 ) 中,为轴对称图形的是()2.以下图形中既是轴对称图形又是中心对称图形的是()3.以下几何图形中,既是轴对称图形,又是中心对称图形的是()A.等腰三角形B.正三角形C.平行四边形D.正方形4.一张菱形纸片按如图①②挨次对折后,再按图③打出一个圆形小孔,则睁开摊平后的图案是()5.如图,在△ ABC 的中点 E 处,直线中, AB= AC,BC= 24,tan C= 2,假如将△ ABCl 与边 BC交于点 D,那么 BD的长为 ()沿直线l翻折后,点 B 落在边AC 1527A.13B. 2C. 2D.12(第 5题)(第6题)(第7题)(第8题)二、填空题6.如图,∠ AOB= 30°,点 M、 N 分别在边 OA、 OB上,且 OM= 1, ON= 3,点 P、 Q分别在边 OB、OA 上,则 MP+ PQ+ QN的最小值是 ________.7.如图,有一个英语单词,四个字母都对于直线l对称,请在图上补全字母,在横线上写出这个单词所指的物件________.8.如图,在正方形网格中,暗影部分是涂黑7 个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使获得的新图案成为一个轴对称图形的涂法有_______种.9.如图,在Rt△ABC中,∠ ACB= 90°,点 D 在 AB边上,将△ CBD 沿 CD折叠,使点 B 恰巧落在 AC 边上的点 E 处.若∠ A= 26°,则∠ CDE= ________.(第 10题)(第11题)(第12题)11.如图,已知∠ AOB 内一点 P, P1、 P2分别是 P 对于 OA、OB的对称点, P1P2交 OA于点 M,交 OB于点 N,若 P1P2= 5,则△ PMN的周长是 ________.12. 如图,四边形 ABCD是菱形,部分.当菱形的两条对角线的长分别O是两条对角线的交点,过点 O的三条直线将菱形分为 6 和 8 时,则暗影部分的面积为 ________.成暗影和空白三、解答题14.[ 2015·扬州 ]如图,将?ABCD沿过点A的直线l折叠,使点D落到AB 边上的点 D′处,折痕l交 CD边于点 E,连结 BE.(1) 求证:四边形 B CED′是平行四边形;(2) 若 BE均分∠ ABC,求证:222 AB= AE+ BE .B 组:如图 ( a) ,要在燃气管道l上修筑一个泵站,分别向A、 B两镇供气.泵站修在管道的什么地方,可使所用的输气管道最短?你能够在l 上找几个点试一试,能发现什么规律?聪慧的小华经过独立思虑,很快得出认识决这个问题的正确方法.他把管道l当作一条直线( 如图 ( b)) ,问题就转变为,要在直线 l 上找一点 P,使 AP 与 BP 的和最小.他的做法是这样的:①作点 B对于直线 l 的对称点 B′;②连结 AB′交直线 l 于点 P,则点 P 即为所求.请你参照小华的做法解决以下问题.以以下图,在△ ABC 中, D、 E 分别是边AB、 AC 的中点,BCP,使△ PDE 的周长最小.= 6, BC边上的高为4,请你在BC边上确立一点(1) 在图中作出点P( 保存作图痕迹,不写作法);(2)请直接写出△ PDE周长的最小值________.。
苏教科版初中数学八年级下册《第9章+中心对称图形-平行四边形+9.4矩形(1)》PPT课件

探索活动:矩形的性质
平行四边形有哪些性质? 平行四边形的对边平行且相等; 平行四边形的对角相等; 平行四边形的对角线互相平分;
矩形具有上面的性质吗?为什么? 矩形还具有普通平行四边形所不具有的特殊性质吗?
矩形的四个角都是直角; 矩形的对角线相等;
探索活动 矩形的性质:
矩形的对边平行且相等; 矩形的四个角都是直角; 矩形的对角线相等且互相平分;
拓展与提高:
已知:如图,在矩形ABCD中, 对角线相交于点 O,∠AOB=60°,AE平分∠BAC,AE交BC于E, 求∠BOE的度数.
A
D
O
BE
C
课堂反思: 角线相 交于点O,∠AOD=120°, AB=4cm,求BC的长.
课堂练习:
1.矩形ABCD中,AP⊥BD于P,BP:PD=1:3,且AC、 BD相交于点O,则∠OAD的度数是_______.
课堂练习:
2、已知如图,矩形ABCD中,对角线AC、BD 相交于O,CE∥DB,交AB的延长线于E. 求证:AC=CE.
初中数学 八年级(下册)
9.4 矩形(1)
昭阳湖初级中学八年级数学备课组
你能说出下面图形的名称吗?
矩形 ,也叫长方形
矩形是平行四边形吗? 矩形是特殊的平行四边形。
你能说出下面图形的名称吗?
学科网 学科网
矩形 ,也叫长方形
矩形是平行四边形吗? 矩形是特殊的平行四边形。 有一个角是直角 的平行四边形叫做矩形。
普通平行四边形不具有的矩形性质:
矩形的四个角都是直角; 矩形的对角线相等;
探索发现:
△AOD是什么三角形? △AOB呢? 矩形被两条对角线分成四个等腰三角形.
你还能发现什么?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
、已知梯形的下底长5cm ,中位线长4cm ,则它的上底长是 ( )
A.2.5cm
B.3cm
C.3.5cm
D.4.5cm
2、如图,DE 是△ABC 的中位线,FG 是梯形BCED 的中位线.如果DE=4,那么FG= ( ) A.6 B. 8 C.10
D.12
3、如图,已知等腰梯形ABCD 的中位线EF 的长为6,腰AD 的长为5,则该等腰梯形的周长为
( )
A.11
B. 16
C. 17
D.22
4、如图, 梯形ABCD 中,AD ∥BC,BD 为对角线,中位线EF 交BD 于O 点,若FO-EO=3,则BC-AD 等于 ( ) A .4 B .6 C .8 D .10
2题图 3题图 4题图
5、梯形的中位线长为9cm,上、下底之比是4:5,则两底长分别是 。
6、等腰梯形腰长等于中位线长,周长为12cm ,则腰长为 。
7、等腰梯形的一角为45°,高为2cm ,中位线长为6cm ,则它的上底长 。
8、梯形的中位线将梯形的面积分成1:2两部分,则上底a ,中位线b 和下第c 之比等于
G F E D
C
B
A
O
F E D C
B
A F E D C B
A。
9、如图, 在梯形ABCD 中,AD ∥BC, 中位线EF 分别与BD 、AC 交于点G 、H ,若AD=6cm ,BC=10cm ,求GH 的长。
10、如图,EF 是梯形ABCD 的中位线,AC 平分∠DAB 交EF 于M ,延长DM 交AB 于N ,试说明△AND 是等腰三角形。
拓展延伸
11、已知,△ABC 中,AB=10。
(1)如图甲,若点D 、E 分别是AC 、BC 边的中点,求DE 的长。
甲 乙
(2)如图乙,若点A 1、A 2把AC 边三等分,点B 1、B 2把BC 边三等分,则A 1B 1+A 2B 2= 。
(3)若点A 1、A 2、…、A 10把AC 边十一等分,点B 1、B 2、…、B 10把BC 边十一等分,根据你
G F E
H
D C
B A N
M F E D
C B
A
E
D
C B
A
A 1
B 2A 2
B 1
C B
A
所发现的规律,直接写出A1B1+A2B2+…+ A10 B10的结果是。
