本科经济计量学第2章(第4版)
李子奈《计量经济学》(第4版)笔记和课后习题(含考研真题)详解

李子奈《计量经济学》(第4版)笔记和课后习题(含考研真题)详解李子奈《计量经济学》(第4版)笔记和课后习题详解第1章绪论一、计量经济学1计量经济学计量经济学,又称经济计量学,是由经济理论、统计学和数学结合而成的一门经济学的分支学科,其研究内容是分析经济现象中客观存在的数量关系。
2计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。
根据描述和模拟办法的不同,对模型进行分类,如表1-1所示。
表1-1 模型分类(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系,计量经济学模型的研究内容是经济现象各因素之间的定量关系。
②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式,计量经济学模型的描述和模拟办法主要是随机性的数学形式。
③位置和作用不同数理经济模型可用于对研究对象的初步研究,计量经济学模型可用于对研究对象的深入研究。
3计量经济学的内容体系(1)根据所应用的数理统计方法划分广义计量经济学根据所应用的数理统计方法包括回归分析方法、投入产出分析方法、时间序列分析方法等;狭义计量经济学所应用的数理统计方法主要是回归分析方法。
需要注意的是,通常所述的计量经济学指的是狭义计量经济学。
(2)根据内容深度划分初级计量经济学的主要研究内容是计量经济学的数理统计学基础知识和经典的线性单方程计量经济学模型理论与方法;中级计量经济学的主要研究内容是用矩阵描述的经典的线性单方程计量经济学模型理论与方法、经典的线性联立方程计量经济学模型理论与方法,以及传统的应用模型;高级计量经济学的主要研究内容是非经典的、现代的计量经济学模型理论、方法与应用。
(3)根据研究目标和研究重点划分理论计量经济学的主要研究目标是计量经济学的理论与方法的介绍与研究;应用计量经济学的主要研究目标是计量经济学模型的建立与应用。
理论计量经济学的研究重点是理论与方法的数学证明与推导;应用计量经济学的研究重点是建立和应用计量模型处理实际问题。
计量经济学精要习题参考答案(第四版)

计量经济学(第四版)习题参考答案第一章 绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2 NS S x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即此样本不是取自一个均值为120元、标准差为10元的正态总体。
计量经济学(第四版)习题参考答案

第一章 绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据(4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2N SS x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 原假设120:0=μH备择假设120:1≠μH检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即此样本不是取自一个均值为120元、标准差为10元的正态总体。
经济计量学精要(第4版)(美)古扎拉蒂

⭐️经济计量学精要(第4版)/(美)古扎拉蒂大佬点个赞支持一下呗ヽ(´▽`)ノヽ(´▽`)ノヽ(´▽`)ノ经济计量学精要(第4版)/(美)古扎拉蒂•综述1.1 什么是经济计量学1.2 为什么要学习经济计量学1.3 经济计量学方法论经济计量分析步骤:(1)建立一个理论假说(2)收集数据(3)设定数学模型线性回归模型为例线性回归模型中,等式左边的变量称为应变量,等式右边的变量称为自变量或解释变量。
线性回归分析的主要目标就是解释一个变量(应变量)与其他一个或多个变量(解释变量)之间的行为关系。
简单数学模型•(4)设立统计或经济计量模型误差项u•u代表随机误差项,简称误差项。
u包括了X以外其他所有影响Y,但并未在模型中具体体现的因素以及纯随机影响。
(5)估计经济计量模型参数线性回归模型常用最小二乘法估计模型中的参数^读做"帽",表示某的估计值(6)核查模型的适用性:模型设定检验(7)检验源自模型的假设:假设检验(8)利用模型进行预测数据类型时间序列数据:按时间跨度收集得到的截面数据:一个或多个变量在某一时间点上的数据集合合并数据:既包括时间序列数据又包括截面数据面板数据:也称纵向数据、围观面板数据,即同一个横截面单位的跨期调查数据模型因果关系统计关系无论有多强,有多紧密,也决不能建立起因果关系,如果两变量存在因果关系,则一定建立在某个统计学之外的经济理论基础之上。
第一部分线性回归模型2.1回归的含义回归分析的主要目的:根据样本回归函数SRF估计总体回归函数PRF2.2总体回归函数(PRF):假想一例总体回归线给出了对应于自变量的每个取值相应的应变量的均值。
(总体回归线表明了Y的均值与每个X的变动关系)PRL•E(Y|xi)表示与给定x值相对应的Y的均值。
下标i代表第i个子总体。
B1、B2称为参数,也称为回归系数。
B1称为截距,B2称为斜率。
斜率系数度量了X每变动一单位,Y( 条件)均值的变化率。
计量经济学(第四版)习题及参考答案详细版知识讲解

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NSS x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
计量经济学(李子奈第4版)大数据表(全)
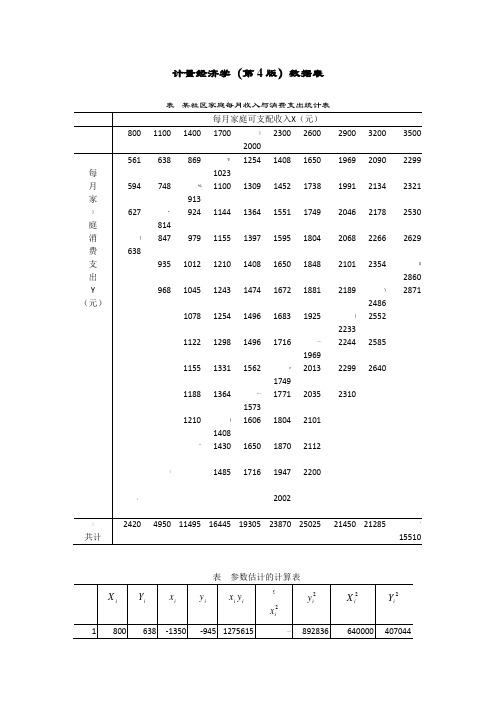
计量经济学(第4版)数据表表某社区家庭每月收入与消费支出统计表表中国各地区居民家庭人均全年可支配收入与人均全年消费性支出(元)资料来源:《中国统计年鉴》(2014)。
第2章练习12中国某年各地区税收Y和国内生产总值GDP的统计资料单位:亿元~表2013年中国各地区城镇居民人均收入与人均消费性支出(元)资料来源:根据《中国统计年鉴》(2014)整理。
,表2010年中国制造业各行业的总产出及要素投入表2013年中国居民人均收入与人均生活消费支出数据(元)资料来源:《中国统计年鉴》(2014)。
表2012年中国农村居民对蛋类食物的消费及相关食物的价格指数蛋类消费量Q¥(千克)各类食品的消费价格指数(上年=100)居民消费价格指数P0(上年=100)人均消费支出X(元)蛋类P肉禽类P1水产类P2粮食P01油脂P02蔬菜P03*北京-天津【河北{山西-内蒙古;辽宁\吉林%黑龙江?上海~江苏:浙江.安徽:福建)江西(山东|河南{湖北\湖南—广东]广西|海南¥重庆)四川、贵州;云南!西藏;陕西@甘肃`青海}宁夏¥新疆#资料来源:《中国统计年鉴》(2013)。
第3章练习17中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资表中国粮食生产与相关投入资料、资料来源:《中国统计年鉴》(2014)。
表中国2001年各地区农村居民家庭人均纯收入与消费支出(单位:元)注:从事农业经营的纯收入由从事第一产业的经营总收入与从事第一产业的经营支出之差计算,其他来源的纯收入由总纯收入减去从事农业经营的纯收入后得到。
资料来源:《中国农村住户调查年鉴(2002)》、《中国统计年鉴(2002)》。
…表1995年美国48个州人均香烟消费、收入与对香烟的课税)某年中国部分省市城镇居民家庭人均年可支配收入(X)与消费性支出(Y)统计数据中国各地区2006、2006年中国城镇居民人均消费、人均可支配收入以及2005年人均政府表中国居民总量消费支出与收入资料单位:亿元\GDP CONS CPI TAX X Y年份1980>1981~ 19821983》1984¥19851986\1987…1988~19891990¥1991~ 19921993…1994。
伍德里奇《计量经济学导论》(第4版)笔记和课后习题详解(2-8章)

使用普通最小二乘法,此时最小化的残差平方和为()211niii y x β=-∑利用一元微积分可以证明,1β必须满足一阶条件()110niiii x y x β=-=∑从而解出1β为:1121ni ii nii x yxβ===∑∑当且仅当0x =时,这两个估计值才是相同的。
2.2 课后习题详解一、习题1.在简单线性回归模型01y x u ββ=++中,假定()0E u ≠。
令()0E u α=,证明:这个模型总可以改写为另一种形式:斜率与原来相同,但截距和误差有所不同,并且新的误差期望值为零。
证明:在方程右边加上()0E u α=,则0010y x u αββα=+++-令新的误差项为0e u α=-,因此()0E e =。
新的截距项为00αβ+,斜率不变为1β。
2(Ⅰ)利用OLS 估计GPA 和ACT 的关系;也就是说,求出如下方程中的截距和斜率估计值01ˆˆGPA ACT ββ=+^评价这个关系的方向。
这里的截距有没有一个有用的解释?请说明。
如果ACT 分数提高5分,预期GPA 会提高多少?(Ⅱ)计算每次观测的拟合值和残差,并验证残差和(近似)为零。
(Ⅲ)当20ACT =时,GPA 的预测值为多少?(Ⅳ)对这8个学生来说,GPA 的变异中,有多少能由ACT 解释?试说明。
答:(Ⅰ)变量的均值为: 3.2125GPA =,25.875ACT =。
()()15.8125niii GPA GPA ACT ACT =--=∑根据公式2.19可得:1ˆ 5.8125/56.8750.1022β==。
根据公式2.17可知:0ˆ 3.21250.102225.8750.5681β=-⨯=。
因此0.56810.1022GPA ACT =+^。
此处截距没有一个很好的解释,因为对样本而言,ACT 并不接近0。
如果ACT 分数提高5分,预期GPA 会提高0.1022×5=0.511。
(Ⅱ)每次观测的拟合值和残差表如表2-3所示:根据表可知,残差和为-0.002,忽略固有的舍入误差,残差和近似为零。
计量经济学复习资料2

n
n
Q (Yi Yˆi )2 (Yi (ˆ0 ˆ1 X i ))2
1
1
xi2
(X i X )2
X
2 i
1 n
Xi 2
xi yi
(X i X )(Yi Y )
X
iYi
1 n
X i Yi
上述参数估计量可以写成:
ˆ1
xi yi
x
2 i
ˆ 0 Y ˆ1 X
在其他条件不变的前提下,我们估计午餐项目对学生成绩有正影响,即其他条件不变,若一 个学生太贫穷而不能保证正常的伙食,就可以有资格享受学校午餐项目的资助,他的成绩应 该会提高。 用 Lnchprg 表示有资格接受午餐计划的学生百分比。那么,一个简单的回归模型就是 Math10=b0+b1Lnchprg+u 其中,u 包含了影响学校整体成绩的学校和学生特征。Meap93.RAW 包含了密歇根的 408 所 高中 1992-1993 学年的数据,利用这些数据,我们得到 Math10hat=32.14-0.319Lnchprg n=408 R2=0.171 解释斜率 若有资格接受午餐项目的学生增加 10 个百分点,则通过数学考试的学生会减少 3.2 个百分 点。 可能吗?哪里错了? 事实上,u 包含着既影响学生成绩又与午餐项目资格高度相关的因素,比如在校贫困学生的 比率。像学校质量和资源这样的变量也被包含在 u 中,它们都可能与 Lnchprg 相关。
Cov(i , j ) E(i j ) 0
假设 3,解释变量与随机项不相关
Cov( X ji , i ) 0 j 1,2, k
假设 4,随机项满足正态分布
i ~ N (0, 2 )
一、
§3.2 多元线性回归模型的估计 普通最小二乘估计
经济计量学精要第四版课后练习题含答案

经济计量学精要第四版课后练习题含答案前言经济计量学是运用数学和统计方法研究经济现象及其规律的一门学科。
经济计量学精要第四版是经济计量学的入门教材,本文将为各位读者提供该教材课后练习题及答案,帮助读者更好地掌握该门学科。
第一章经济计量学基础选择题1.什么是偏差?A.衡量回归直线的直角离散程度B.已知均值估计总体标准差C.样本中的观测值与其相应总体值之差D.对称分布的方差答案:C2.在经济计量分析中,线性关系是基本关系之一。
下列哪个假设是错误的?A.线性关系是基本关系之一B.线性关系是在整个取值区间内成立的C.在一些情况下线性关系只在某一特定范围内成立D.线性方程存在可比较的斜率答案:B填空题1.在经验研究中,一般采用______________式估计总体参数。
答案:样本2.如果增加自变量个数,再加上满足一定条件,使得求出的参数估计仍有标准正态分布的概率较大,这就是多元_____________中的问题。
答案:线性回归第二章单一线性回归模型选择题1.在单一线性回归中,为使OLS估计量无偏,必须假定误差项都等于____。
A.正态分布B.泊松分布C.自变量D.零答案:D2.投资量与利息率之间可能存在一种哪种关系?A.负向线性关系B.正向线性关系C.非线性关系D.都不正确答案:B填空题1.在单一线性回归模型中,因变量和自变量之间需要满足线性关系,使散点图大致呈现出一个______________。
答案:直线趋势2.单一线性回归模型的OLS估计量被定义为将所有预测误差的平方之和最小化得来的样本_______________。
答案:回归方程第三章多元线性回归模型选择题1.当模型自变量与因变量的简单相关系数大于0.7时,发生的问题是什么?A.多重共线性B.异方差性C.自相关D.标准误增大答案:A2.关于多解释变量线性回归模型,下列哪个描述是错误的?A.利用OLS估计法估计各个参数的估计值B.OLS含有多个系数,这些系数代表因变量特定解释变量的影响。
本科经济计量学第2章(第4版)

模型的拟合度与检验
拟合度指标
用于评估模型对数据的拟合程度 ,常用的拟合度指标包括R平方、 调整R平方、残差平方和等。
模型的检验
包括对回归系数的显著性检验、 模型的假设检验(如误差的正态 性、同方差性等)、模型的预测 能力检验等。
变量选择与多重共线性
变量选择
在多元线性回归分析中,选择合适的自变量对于模型的构建至关重要。常用的变量选择方法包括逐步回归法、向 前选择法和向后消除法等。
β2Xi2 + ...))^2 =最小值
模型的拟合度
模型的拟合度是指模型对数据的拟合程度,通常用R平 方值来表示。
R平方值的计算公式为:R^2 = 1 - (SSE/SST)
R平方值越接近于1,说明模型的拟合度越高,预测效果 越好。
其中,SSE是残差平方和,SST是总平方和。
模型的检验
在构建线性回归模型后,需要 进行一系列检验来评估模型的 适用性和可靠性。
05
回归分析的应用
预测与决策
预测
通过建立回归模型,利用历史数据对 未来趋势进行预测,为决策提供依据 。
决策
基于回归分析的结果,制定最优策略 或选择最佳方案,实现资源的最优配 置。
结构分析
揭示变量间关系
通过回归分析,揭示自变量与因变量之间的 数量关系,了解经济现象的内在机制。
检验经济理论
通过实证检验,验证经济理论或假说是否成 立,为理论发展提供依据。
包括但不限于:线性关系检验、 多重共线性检验、异方差性检 验、自相关性检验等。
通过这些检验可以发现模型存 在的问题,并进行相应的修正 和改进。
03
多元线性回归模型
多元线性回归模型的定义
多元线性回归模型
第四讲_(计量经济学第二章)

^ − ^ − ^ − β0 = Y − β1 X1 − β2 X2 ^ ( ∑ yi x1i )∑ x22i −( ∑ yi x2i )∑ x1i x2i 2 2 2 β1 = ∑ x1i ∑ x2 i −( ∑ x1i x2 i ) ^ ( y x ) x2 −( y x ) x x β 2 = ∑ i 2i 2∑ 1i 2 ∑ i 1i ∑2 1i 2i ∑ x1i ∑ x2 i −( ∑ x1i x2 i )
∑x1i x2i )x2i ]Y
= ∑k1iYi
∑ x12i −( ∑ yi x1i )∑ x1i x2i β2 = ∑ x2 x2 −( ∑ x x )2 1i 2 i 1i ∑ 2 i 2 ∑[(∑ x1i ) x2 i yi ]−∑[(∑ x1i x2 i ) x1i yi ] = 2 2 2 ∑ x1i ∑ x2 i −( ∑ x1i x2 i ) 2 [(∑ x1i ) x2 i −( ∑ x1i x2 i ) x1i ] = ∑{ ∑ x2 x2 −( ∑ x x )2 yi } 1i 2 i 1i ∑ 2 i
二元线性回归 模型参数的普 通最小二乘估 计。
1、将解简化: 、将解简化:
β1 =
=
∑[(
^
( ∑ yi x1i )
∑ ∑x1i x2i 2 2 2 ∑ x1i ∑x2i −( ∑ x1i x2i )
2 x2i −( ∑ yi x2i )
∑
2 x2i )x1i yi ]−∑[(
∑
(
x1i x2i )x2i yi ]
α
2
1 − α p{| T1 |< t } = 1 − α
^ ^
^ ^ 2 1 2 1
得置信区间: 得置信区间: ( β 1 − t α × S β , β 1 + t α × S β )
庞皓计量经济学 第二章 练习题及参考解答(第四版)说课讲解

国内生产总值(亿元) 48637.5 61339.9 71813.6 79715 85195.5 90564.4 100280.1 110863.1 121717.4 137422 161840.2 187318.9 219438.5 270232.3 319515.5 349081.4 413030.3 489300.6 540367.4 595244.4 643974 689052.1 743585.5
一般预算总收 入
(亿元)
地区生产总 值(亿元)
收集于网络,如有侵权请联系管理员删除
精品文档
1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991
1992
1993
1994 1995
1996
1997
Y 27.45 25.87 31.13 34.34 36.64 41.79 46.67 58.25 68.61 76.36 85.55 98.21 101.59 108.94
118.36
166.64
209.39 248.50
291.75
340.52
X 123.72 157.75 179.92 204.86 234.01 257.09 323.25 429.16 502.47 606.99 770.25 849.44 904.69 1089.33
1375.70
1925.91
铁路里程(万公里) 5.9 6.24 6.49 6.6 6.64 6.74 6.87 7.01 7.19 7.3 7.44 7.54 7.71 7.8 7.97 8.55 9.12 9.32 9.76 10.31 11.18 12.1 12.4
计量经济学第四版李子奈课后答案

计量经济学第四版李子奈课后答案第一章:简介1.什么是计量经济学?它与其他学科有什么区别?计量经济学是经济学的一个重要分支,主要研究经济现象的数理模型、计量方法以及经济政策的评估方法。
它与其他学科的区别在于,计量经济学着重于将经济理论转化为具体的计量模型,并利用统计分析方法对经济数据进行验证和评估,以获得对经济问题的深入理解和预测能力。
2.请简要介绍计量经济学的基本步骤。
计量经济学的基本步骤包括以下几个方面:•确定经济理论模型:根据研究的经济问题和理论基础,构建适当的经济理论模型。
•收集数据:收集所需的经济数据,包括自变量和因变量的观测值。
•数据处理:对数据进行处理和清洗,包括缺失数据的处理、异常值的检测和处理等。
•模型估计:利用统计方法对经济模型的参数进行估计,获得合适的模型参数估计值。
•模型检验:利用统计检验方法对模型的合理性进行检验,包括参数的显著性检验、模型拟合优度的检验等。
•模型应用和预测:根据模型估计结果,应用模型进行实际问题的分析和预测。
第二章:线性回归模型1.请解释简单线性回归模型的含义。
简单线性回归模型是一种描述两个变量之间线性关系的模型。
它假设因变量(被解释变量)可以通过一个线性函数来解释,该线性函数包含一个自变量(解释变量)。
形式化地表示为:$y_i = \\beta_0 + \\beta_1x_i + u_i$,其中y i表示因变量的观测值,x i表示自变量的观测值,$\\beta_0$和$\\beta_1$表示模型的参数,u i表示误差项。
2.如何进行线性回归模型的估计和检验?线性回归模型的参数可以通过最小二乘法进行估计。
最小二乘法通过最小化观测值和模型估计值之间的差异,来获取最优的模型参数估计。
具体的估计方法可以通过计算样本数据的一阶矩和二阶矩来获得。
线性回归模型的检验可以通过对模型参数的显著性进行检验来进行。
通常使用t检验或F检验来判断模型参数的显著性。
t检验用于检验单个参数的显著性,而F检验用于检验多个参数的显著性。
计量经济学02

4-21
关于 R2 及 SER 的例子
TestScore = 698.9 – 2.28×STR, R2 = 0.051, SER = 18.6
学生/教师之比只解释了测试成绩变化中很小的一部分。这合理么?这 是否意味着学生/教师之比在政策制定中无关紧要?
4-22
Copyright © 2011 Pearson Addison-Wesley. All rights reserved.
Copyright © 2011 Pearson Addison-Wesley. All rights reserved.
4-4
一元线性回归模型
问题:缩小班级规模会对学生的成绩有什么影响?
数据:加州所有K-6和K-8的学区(n=420) 变量: • 5年级考试分数(标准化考试,包括数学和阅 读),学区平均分数 • 学生教师比(STR)=学生数除以全职教师的 数量
残差:
ˆ Antelope u
= 657.8 – 654.8 = 3.0
4-15
Copyright © 2011 Pearson Addison-Wesley. All rights reserved.
OLS 回归: STATA 结果
regress testscr str, robust Regression with robust standard errors Number of obs = 420 F( 1, 418) = 19.26 Prob > F = 0.0000 R-squared = 0.0512 Root MSE = 18.581 ------------------------------------------------------------------------| Robust testscr | Coef. Std. Err. t P>|t| [95% Conf. Interval] --------+---------------------------------------------------------------str | -2.279808 .5194892 -4.39 0.000 -3.300945 -1.258671 _cons | 698.933 10.36436 67.44 0.000 678.5602 719.3057 -------------------------------------------------------------------------
(完整版)伍德里奇计量经济学(第4版)答案

(4)对profmarg的显著性进行T检验:t= 1.087<1.311,因为它在统计上并不显著。
第五章
5.3风险承受能力越强,越愿意投资于股票市场,因此 假设funds 和 risktol正相关,我们使用等式 因此 具有高度不一致(渐进有偏),这表明如果我们在回归方程中省略risktol,并且它和funds高度相关,funds 的估计效应取决于risktol的效应。(省略risktol,回归方程倾向于高估funds的影响)
(4)因为T检验与F检验是建立在同方差假定与其他线性模型假定基础上的,所以如果睡眠方程中含有异方差性,就意味着我们对方程的检验是无效的。
4.11(1)假定profmarg不变,当sales变化10%时, rdinters=(0.321/100)*10=0.0321,j即rdintens变化大约3%。相对于sales的变化,rdintens的变化是个较小的影响。
第六章
6.3(1)当其他要素固定时,我们有
等式两边同除以 得到结果, 是不显著的,尽管 大于0,如果来我们考虑一个孩子多得一年教育,孩子的父母会有更高的学历。
(2)我们选择pareduc的两个具体值来解释交叉项系数,比如父母双方都受过大学教育时pareduc=32或父母都是高中毕业时pareduc=24,educ的估计回报差额是0.00078(32-24)=0.0062,或者说0.62%。
性别差异的证据是相当强烈的。
(2)totwrk的t统计是−0.163/0.018 ≈ −9.06,这是统计性水平是很显著的。这个系数意味着多工作一个小时(60分钟)就会少睡0.163(60) ≈ 9.8分钟。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2-3) (2-4)
(2-1)
(2-2)
(2-6)
(2-7) 总结
16
Yi E (Y | Xi ) ui
线性
OLS
第2章
图2-4
Y 需 求 量
总体回归线与样本回归线
.
u1
Y1
.ˆ .Y
e1
ˆ b b X Y i 1 2 i
A
1
un
. Y . . ˆ Y
n
EY | X B1 B2 X i
31
第2章
32
第2章
例2-4:美国中等房价与贷款利率(1980~2007年)
为了研究贷款利率对房价的影响,表2-7给出了纽约 1980~2007年中等房价和30年固定贷款利率的数据。 (散点图见下页)
ˆ 329.004117.3694X Y i i
回归结果表明,如果贷款利率提高一个百分点,则 中等房价平均降低约17.4个单位,即17400美元。
2 ˆ min{ e } min{ (Yi Yi ) } 2 i
min{ Yi b1 b2 X i }
2
(2-13)
21
第2章
普通最小二乘法就是寻找使RSS达到最小时的参数 作为参数估计值的一种方法。
利用极值原理可以得到: 正规方程
Y nb b X Y X b X b X
随机总体回归方程(stochastic PRF)
Yi B1 B2 X i ui
(2-2)
ui表示随机误差项(random error term),简称误差项。
10
第2章
2.4
随机误差项的性质
(1)在解释变量中被忽略的因素的影响; (2)变量观测值的观测误差的影响;
(3)其它随机因素的影响包括人类行为中的一些 内在随机性;
i 1 2 i i i 1 i 2
i i 2 i i i 2 2
2 i
(2-14) (2-15) (2-16)
求解得到: b1 Y b 2 X
x y X X Y Y b x X X X Y nXY X nX
i i i 2 i 2
回归结果表明,在其他条件不变的情况下,受教育年限 每增加一年,平均小时工资增加72美分。
前面已经提到过,在大多数情况下,截距没有什么明显 的经济含义,本例亦如此。 28
第2章
29
第2章
例2-2:奥肯定律: 布鲁金斯学会主席,前总统经济顾问委员会主席奥肯 (Arthur Okun)根据美国1947-1960年的数据,得到如下回 归方程,称之为奥肯定律: ˆ
问题:降低利率是否对房价有显著的影响?是否应 该考虑中等家庭收入水平的影响?
33
第2章
34
第2章
例2-5:古董钟与拍卖价格
德国Triberg钟表公司每年都举行钟表拍卖会。表214给出了32个钟表的信息数据(钟表的年代、投标人的 个数、中标的价格)。
利用数据得到的散点图和回归结果见Excel文件。
en
n
0
X1
价格
Xn
X
17
第2章
2.6 “线性”回归的特殊含义
解释变量线性与参数线性 1. 解释变量线性 例如:
非线性举例:
E (Y ) B1 B 2 Xi 2 1 E (Y ) B1 B 2 Xi
图2-5 线性和非线性需求曲线
2. 参数线性 例如: 非线性举例:
E(Y ) B1 B2 Xi
第2章 线性回归的基本思想
——双变量模型
第2章
2.1 回归的含义 2.2 总体回归函数 2.3 总体回归函数的统计或随机设定 2.4 随机误差项的性质
2.5 样本回归函数
2.6 “线性”回归的特殊含义 2.7 从双变量回归到多元线性回归 2.8 参数估计:普通最小二乘法 2.9 综合
2.10 一些例子
E(Y) B1 B 2 X 2i B3 X 3i B 4 X 4i E(Y) E(Y | X 2i, X 3i, X 4i)
(2-11)
个体学生分数函数(即随机总体回归函数)为:
Yi B1 B 2 X 2i B3 X 3i B 4 X 3i ui E(Y) ui
(regression coefficients)。
B1又称为截距(intercept),B2又称为斜率(slope)。
斜率度量了X每变动一个单位,Y的条件均值的变化
率。 注意:回归分析是条件回归分析(conditional regression analysis)。
9
第2章
2.3 总体回归函数的统计或随机设定
Yt B1 B ( ut 2 1 / X t)
利用Eviews软件得到如下结果:
ˆ 15.57848 2606 Y .424 ( 1/ X t) t
如果我们拟合线性模型,可以得到:
ˆ 902.1917 69.3493X Y t t
究竟哪一个模型更好?我们应该如何进行模型的选择?
2
18
第2章
图2-5 线性和非线性需求曲线
Y Y
需 求 B2 量
Yi B1 B2 X i
1
B2
B2
1
Yi B1 B2 1 X i
B2
1
1
X X
价 格
价 格
a)线性需求曲线
b) 非线性需求曲线 19
第2章
2.7 从双变量回归到多元线性回归
多元线性回归:
如果数学S.A.T分数是收入(X2)、选修数学课程(X3)和年龄 (X4)的函数,则扩展的数学S.A.T分数的函数如下:
如果已知整个总体的数据,如上例,问题就比较简单, 但在实际中,我们往往不能得到整个总体的数据,只 有来自总体的某一个样本数据,我们该怎么做?
12
第2章
表2-2 、2-3 来自表2-1总体的两个随机样本
做散点图及估计样本回归直线如下:
13
第2章
14
第2章
样本回归直线可用样本回归函数SRF来表示:
例如研究商品的需求量与该商品的价格、消费者 的收入以及其他同类商品的价格之间的关系。 通常我们用Y表示应变量,用X表示自变量。
3
第2章
回归分析是用来处理一个应变量与另一个或多个 自变量的关系,但它并不一定表明因果关系的存在。 两个变量是否存在因果关系,哪一个是应变量,哪一 个是自变量是由正确的经济理论决定的。 需要注意的是具有因果关系的变量之间一定具有 数学上的相关关系,而具有相关关系的变量之间并不 一定具有因果关系。 例如:中国的国内生产总值与印度的人口之间具 有较强的相关性(相关系数较高),因为二者都以较 快的速度增长,但显然二者之间不具有因果关系。
35
第2章
2.11 总结
1. 回归分析的基本思想
2. 总体回归函数PRF、随机总体回归函数、样本 回归函数SRF和随机样本回归函数
3. 普通最小二乘法OLS方法 4. 对估计的样本回归函数的解释 作业:P34: 2.7、 2.9、2.10、2.11、2.12、2.13 2.14、2.15.
36
4
第2章
回归分析的应用
(1)通过已知变量的值来估计应变量的均值 (2)根据经济理论建立适当的假设并对其进行 检验 (3)根据自变量的值对应变量的均值进行预测 (4)上述多个目标的综合
5
第2章
2.2 总体回归函数:假想一例
下面我们通过一个具体例子说明回归分析的用途。
6
第2章
分析步骤:
Yt 0.4( X t 2.5)
其中,Yt表示失业率的变动(百分数),Xt表示实际产 出的增长率(百分率),用实际GNP度量,2.5是对美国历史 的观察得到的长期产出增长率。 在上面方程中,截距为零,斜率为-0.4。奥肯定律是说 实际GNP的增长每超过2.5%一个百分点,失业率将降低0.4个 百分点。 奥肯定律被用来预测失业率减少到一定的百分点而所需 的实际GNP的增长率。当实际GNP增长率为5%时,将使失业 率减少一个百分点,或者说若使增长率达到7.5%,则减少失 业率2个百分点。 30
(1)以家庭年收入X为横轴,学生的数学S.A.T分 数Y为纵轴,对表中数据作散点图。
(2)分析两变量间的关系 (3)做出总体回归直线
7
第2章
图2-1 家庭年收入与数学S.A.T分数
8
第2章Leabharlann 总体回归函数PRFE(Y | X i ) B1 B2 X i
(2-1) Y的条件期望,可简写为E(Y) B1和B2是参数(parameters),也称回归系数
ˆi b1 b2 Xi Y
E(Y | X i ) B1 B2 X i
随机的样本函数:
(2-3) (2-1)
Yi b1 b 2 Xi ei (2-4)
Yi B1 B2 X i ui
(2-2)
15
第2章
ˆi b1 b 2 Xi Y 随机样本回归函数 Yi b1 b 2 Xi ei 总体回归函数 E (Y | Xi ) B1 B 2 Xi 随机总体回归方程 Yi B1 B 2 Xi ui 观察值可表示为 ˆi ei Yi Y
第2章
例 2-3:股票价格与利率 股票价格和利率是重要的经济指标。利用S&P500综合指数 (1941~1943年=10)度量股票价格,三月期国债利率(%)度量利 率。表2-13给出了1980~1999年这些变量的数据。 根据散点图(下页)(见Excel文件和Eviews文件),两变 量间的关系可能不是线性的,我们可以尝试拟合如下模型:
