广东省珠海一中等六校2015届高三11月第二次联考数学理试题 Word版含答案
广东省珠海一中等六校2015届高三第一次联考数学理试题_Word版含答案

AB C D2015届广东六校联盟第一次联考试题数学(理科)(满分150分) 考试时间:120分钟一.选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合M ={x |x 2-3x -4<0},N ={x |0≤x ≤5},则M ∩N =( ) A .(0,4] B .[0,4) C .[-1,0) D .(-1,0]2.设i 是虚数单位,z -表示复数z 的共轭复数.若z =1+i ,则 z i +i ·z -=( )A .-2B .-2iC .2D .2i3. 已知实数x y ,满足1218y y x x y ⎧⎪-⎨⎪+⎩≥≤≤,则目标函数z x y =-的最小值为( )A. 5B. 6C. 7D. -24. 若双曲线221x ky +=的离心率是2,则实数k 的值是 ( )A.3B.13C. 3-D. 13-5. 已知平行四边形ABCD 中,AC 为一条对角线,若()()2,4,1,3,AB AC AD BD ==⋅=u u u r u u u r u u u r u u u r则( )A. 8-B. 6-C.6D.8 6. 已知某企业上半年前5个月产品广告投入与利润额统计如下:由此所得回归方程为y =,若6月份广告投入10(万元)估计所获利润为( )A .95.25万元B .96.5万元C .97万元D .97.25万元7.如图:正方体1111ABCD A B C D -的棱长为1,,E F 分别是棱11,A B CD 的 中点,点M 是EF 的动点,FM x =,过点M 、直线AB 的平面将正方体分 成上下两部分,记下面那部分的体积为()V x ,则函数()V x 的大致图像是( )18.以A 表示值域为R 的函数组成的集合,B 表示具有如下性质的函数φ(x )组成的集合:对于函数φ(x ),存在一个正数M ,使得函数φ(x )的值域包含于区间[-M ,M ].例如,当φ1(x )=x 3,φ2(x )=sin x 时,φ1(x )∈A ,φ2(x )∈B .现有如下命题:①设函数f (x )的定义域为D ,则“f (x )∈A ”的充要条件是“∀b ∈R ,∃a ∈D ,f (a )=b ”; ②函数f (x )∈B 的充要条件是f (x )有最大值和最小值;③若函数f (x ),g (x )的定义域相同,且f (x )∈A ,g (x )∈B ,则f (x )+g (x )∉B ;④若函数f (x )=a ln(x +2)+xx 2+1(x >-2,a ∈R )有最大值,则f (x )∈B ;⑤若函数f (x ))ln(2a x +=A ∈,则0>a .其中的真命题有( )A .①③④⑤B .②③④⑤C .①③⑤D .①③④二 填空题(本大题共6小题,每小题5分,共30分)(一)必做题(9~13题)9. 若不等式4|1||4|x x a a+--≥+,对任意的x R ∈恒成立,则实数a 的取值范围是_ _. 10. 已知函数f (x )=ln(1+x )-ax 的图象在x =1处的切线与直线x +2y -1=0平行,则实数a 的值为___. 11. 已知数组(12345,,,,a a a a a )是1,2,3,4,5五个数的一个排列,如数组(1,4,3,5,2)是符合题意的一个排列。
珠海市2015届高三上学期期末考试数学理答案

2 x0 则 x1 + x 2 = k1 + k 2 - 2 x0 = 2 x0 (2x 0 - 4) - 2 x 0 = - 6 2 x0 - 1 x0 - 1 3 x 3 \x = - 2 0 = …………………………………………………11 分 1 x0 - 1 x0 x0
Q x0 -
1 在 x0 Î [2 , 4] 上为增函数 x0
x1 + x2 2
即 ( x - x0 )[ x - ( k - x0 )] = 0 得 x = x0 (舍)或 x = k - x0
\ x1 + x2 = k1 + k2 - 2 x0 …………………………………………………………………8 分
= 1, 1+ k 2 2 2 2 两边平方得 ( x0 - 1) k 2 + 2 x0 (4 - x0 ) k + ( x0 - 4) 2 - 1 = 0LL “*” …………………9 分
三、解答题:
p p ì w × + j = ìw = 2 ï ï ï 12 2 16.解: (1)由题意可得 í ,即 í p ……………………………2 分 7 p 3 p j = ïw × ï +j = 3 î ï î 12 2 ìA + B = 4 ìA = 3 由题意可得 í ,即 í ……………………………………………4 分 î - A + B = -2 îB =1 p ∴ 函数 f ( x ) 的解析式为: f ( x ) = 3sin(2 x + ) + 1 ………………………………5 分 3 a p 17 a p p 17 p 4 (2)由 f ( - ) = 可得 3sin[2( - ) + ] + 1 = ,化简得 sin(a + ) = …7 分 2 12 5 2 12 3 5 6 5 p p p p Q f (a + ) = 3sin[2(a + ) + ] + 1 = 3sin(2a + p + ) + 1 2 2 3 3 p = -3sin(2a + ) + 1 ………………………………………………………9 分 3 p p = -6sin(a + ) × cos(a + ) + 1 ……………………………………10 分 6 6 p p 2p 7p p 3 又Q a Î ( , p ) ,\ a + Î ( , ) ,\ cos(a + ) = - …………………11 分 2 6 3 6 6 5 p p p 4 3 97 ………………12 分 f (a + ) = -6 sin(a + ) cos(a + ) + 1 = -6 ´ ´ ( - ) + 1 = 6 6 6 5 5 25
2015届广东珠海市一模数学理考试试题
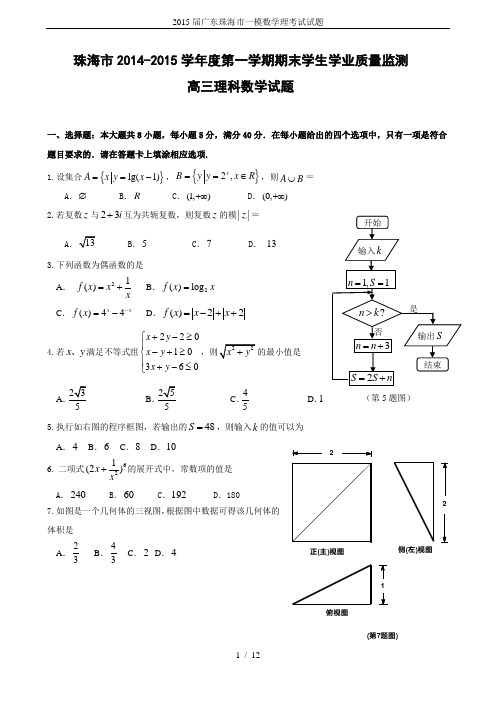
珠海市2014-2015学年度第一学期期末学生学业质量监测高三理科数学试题一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项.1.设集合{}lg(1)A x y x ==-,{}2,xB y y x R ==∈,则A B ⋃=A .∅B .RC .(1,)+∞D .(0,)+∞ 2.若复数z 与23i +互为共轭复数,则复数z 的模||z =A.5 C .7 D . 13 3.下列函数为偶函数的是 A . 21()f x x x=+B .2()log f x x =C .()44x x f x -=-D .()22f x x x =-++4.若x y 、满足不等式组22010360x y x y x y +-≥⎧⎪-+≥⎨⎪+-≤⎩的最小值是ABC .45D .1 5.执行如右图的程序框图,若输出的48S =,则输入k 的值可以为 A .4 B .6 C .8 D .10 6. 二项式621(2)x x+的展开式中,常数项的值是 A .240 B .60 C .192 D .180 7.如图是一个几何体的三视图,根据图中数据可得该几何体的体积是 A .23 B .43C .2D .4(第5题图)俯视图侧(左)视图正(主)视图(第7题图)1228.已知集合123{|(,,),{0,1},1,2,3}i S P P x x x x i ==∈=对于123(,,)A a a a =,123(,,)B b b b S =∈,定义A 与B的差为112233(||,||,||)A B a b a b a b -=---,定义A 与B 之间的距离为31(,)||i i i d A B a b ==-∑.对于,,A B C S ∀∈,则下列结论中一定成立的是( )A. (,)(,)(,)d A C d B C d A B +=B. (,)(,)(,)d A C d B C d A B +>C. (,)(,)d A C B C d A B --=D. (,)(,)d A C B C d A B -->二、填空题:本大题共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.请将答案填在答题卡相应位置. 9.不等式21x x -≥的解集为 .10.三个学生、两位老师、三位家长站成一排,则老师站正中间的概率是 . 11.已知等差数列{}n a 的前n 项和记为n S ,且35a =,36S =,则7a = .12.已知函数()f x 的导函数为()f x ',且满足3()=(2)f x x x f '-⋅,则函数()f x 在点(2,(2)f )处的切线方程为 .13.已知平面向量a b 、满足231a b +=,则a b ⋅的最大值为 . 14.(坐标系与参数方程选做题)在极坐标系中,曲线1:2C ρ=与曲线2:4sin ()2C πρθθπ=<<交点的极坐标是 .15.(几何证明选讲选做题)如图,四边形ABCD 内接于圆O ,DE 与圆O 相切于点D ,AC BD F ⋂=,F 为AC 的中点,O BD ∈,CD =5BC =,则AE = .(第15题图)三、解答题:本题共有6个小题,共80分.请写出解答的步骤与详细过程。
广东省海珠区等四区2015届高三联考数学(理)Word版含答案

-海珠区2014学年高三综合测试(二)数学(理科)2014.11本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将答题卡交回。
参考公式:锥体体积公式Sh V 31=,其中S 为锥体的底面积,h 为锥体的高. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}4),(,2),(=-==+=y x y x B y x y x A ,那么集合A B 为A .(){}1,3-B .()3,1-C .{}3,1-D .(){}3,1-2.若复数z 满足()1i z i -=,则z 在复平面内对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限3.函数cos 2sin 2y x x =-的一条对称轴为 A. 4x p =B. 8x p =C. 8x p =-D. 4x p =-4.已知向量,a b 的夹角为120,2a =,且8a b ⋅=-,则b = A .6B .7C .8D .95.函数ln y x =与y =-在同一平面直角坐标系内的大致图象为6.阅读如图所示的程序框图,输出的结果S 的值为A .0 BCD. 7.已知椭圆2219x y +=与双曲线22221x y a b-=共焦点12,F F ,设它们在第一象限的交点为P , 且120PF PF ⋅=,则双曲线的渐近线方程为 A.y =B.y x =C.y x = D.y x = 8.若实数,,,a b c d 满足222(3ln )(2)0b a a c d +-+-+=,则22()()a c b d -+-的最小值为A .8 B. C .2D.二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.已知{}n a 是等差数列,124a a +=,91028a a +=,则该数列前10项和10S = . 10.一个几何体的正(主)视图和侧(左)视图都是边长为2的等边 三角形,俯视图如图所示,则这个几何体的体积为 . 11.不等式13x x +-≤的解集是 .12.从5种不同的书中买3本送给3名同学,每人各1本,则不同的送法有 种(用数字作答). 13.给出下列四个命题:①已知ξ服从正态分布()2,0σN ,且()4.022=≤≤-ξP ,则()2.02=>ξP ; ②“2450x x --=”的一个必要不充分条件是“5x =”;③函数()3132f x =x x +-在点()()2,2f 处的切线方程为3y =-;④命题:,tan 1p x x ∃∈=R ;命题2:,10q x x x ∀∈-+>R .则命题“()p q ∧⌝”是假命题.其中正确命题的序号是 .(二)选做题(14、15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在极坐标中,圆4sin ρθ=与直线(sin cos )4ρθθ+=相交所得的弦长为 .15.(几何证明选讲选做题)如图,⊙O 是ABC ∆的外接圆,AB AC =,延长BC 到点D ,使得CD AC =,连结AD 交⊙O 于点E ,连结BE ,若035D ∠=,则ABE ∠的大小为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)在ABC ∆中,内角,,A B C 所对的边长分别是,,a b c ,已知4A π=,4cos 5B =. (1)求cos C 的值;(2)若10a =,D 为AB 的中点,求CD 的长.17.(本小题满分12分)甲、乙两种元件的质量按测试指标划分为:指标大于或等于85为正品,小于85为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:(2)生产一件元件甲,若是正品可盈利50元,若是次品则亏损10元;生产一件元件乙,若是正品可盈利100元,若是次品则亏损20元. 在(1)的前提下,记X 为生产1件元件甲和1件元件乙所得的总利润,求随机变量X 的分布列和数学期望.18.(本小题满分14分)如图所示,已知PD 垂直以AB 为直径的圆O 所在平面,点D 在线段AB 上,点C 为圆O 上一点,且3BD PD ==,22AC AD ==, (1)求证:PA ⊥CD ;(2)求二面角C PB A --的余弦值.19.(本小题满分14分)已知数列}{n a 的前n 项和为n S ,满足12()n n nS a n S N *++=?. (1)求123,,S S S ; (2)求n S ;(3)设()221n n b n a =+,求证:对任意正整数n ,有121n b b b +++<L .20.(本小题满分14分)在平面直角坐标系xOy 中,,A B 两点的坐标分别为()0,1、()0,1-,动点P 满足直线AP 与直线BP 的斜率之积为14-,直线AP 、BP 与直线2y =-分别交于点,M N .(1)求动点P 的轨迹方程; (2)求线段MN 的最小值;(3)以MN 为直径的圆是否经过某定点?若经过定点,求出定点的坐标;若不经过定点,请说明理由.21.(本小题满分14分)已知函数1(0)()e (0)x x f x x x ⎧>⎪=⎨⎪≤⎩,()()F x f x kx =+(k ∈R ).(1)当1k =时,求函数()F x 的值域; (2)试讨论函数()F x 的单调性.海珠区2014学高三综合测试(二)理科数学参考答案与评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16. 解:(1)4cos ,5B =且(0,)B π∈,∴3sin 5B ==.………………1分∴3cos cos()cos()4C A B B ππ=--=- ………………2分 33cos cos sin sin 44B B ππ=+ ………………4分4355= ………………5分= ………………6分 (2)由(1)可得sin C ===. ………………7分 由正弦定理得sin sin a cA C==, ………………8分………………12分17.解:(1)在分别抽取的100件产品中,为正品的元件甲有80件,为正品的元件乙有75件. ………………1分 所以元件甲、乙为正品的频率分别为5410080=,4310075=. ………………3分 根据频率可估计元件甲、乙为正品的概率分别为45,34. ………………4分 (2)随机变量X 的所有取值为150,90,30,-30, ………………5分 则433(150)545P X ==⨯=,133(90)5420P X ==⨯=, 411(30)545P X ==⨯=,111(30)5420P X =-=⨯=. ………………9分 所以X 的分布列为:10分X 的数学期望为EX 3311150903030108520520=⨯+⨯+⨯-⨯=.……………12分(3,(3,1,1121n n n ⋅==⨯19.解:(1)当1n =时,11112S S S ++=,∴112S =-, ……………1分 当2n ³时,112n n n n S S S S -++=-,∴112n n S S -=-+, ……………2分∴2323,34S S =-=-. ……………4分 (2)由(1)猜想:1n nS n =-+. ……………5分 下面用数学归纳法证明:当1n =,112S =-显然成立; 假设当n k =时命题成立,即1k kS k =-+,那么当1n k =+时, 11112221k k k S k S k k ++=-=-=-++-+, 即1n k =+时命题也成立, 综上可知,1n nS n =-+. ……………9分 (3)由(2)知()1121n n n a S S n n =++=-+, ……………10分∴()()()()()2222222221211121111n n n n n b n a n n n n n n +-+=+===-+++, ………11分∴()()12222222211111111122311n b b b n n n +++=-+-++-=-++L L ,…13分 ∴121n b b b +++<L . ……………14分 20. 解:(1)已知()()0,1,0,1A B -,设动点P 的坐标(),x y ,∴直线AP 的斜率11y k x -=,直线BP 的斜率21y k x+=(0x ≠), ………2分 又1214k k ⨯=-,∴1114y y x x -+⨯=-, ………………3分 即()22104x y x +=≠. ………………4分(2)设直线AP 的方程为的()110y k x -=-,直线BP 的方程为的()210y k x +=-,………………6分由112y k x y -=⎧⎨=-⎩,得132x k y ⎧=-⎪⎨⎪=-⎩, ∴13,2M k ⎛⎫-- ⎪⎝⎭; ………………7分 由212y k x y +=⎧⎨=-⎩,得212x k y ⎧=-⎪⎨⎪=-⎩,∴21,2N k ⎛⎫-- ⎪⎝⎭, ………………8分 由1214k k ⨯=-,∴11213134MN k k k k =-=+≥9分当且仅当1134k k =,即1k = ∴线段MN长的最小值 ………………10分 (3)设点(),Q x y 是以MN 为直径的圆的任意一点,则0QM QN =,即()()1231220x x y y k k ⎛⎫⎛⎫+++++= ⎪⎪⎝⎭⎝⎭,………………11分 又1214k k ⨯=-, 故以MN 为直径的圆的方程为:()2211342120x k x y k ⎛⎫+-++-= ⎪⎝⎭, ………………12分令0x =,得()2212y +=,解得2y =-± ………………13分 ∴以MN为直径的圆经过定点(0,2-+或(0,2--. ………………14分21.解:(1)当1=k 时,1(0)()e (0)x x x F x x x x ⎧+>⎪=⎨⎪+⎩≤, ………………1分当0>x 时,1()2=+F x x x≥,当且仅当1=x 时,()F x 取最小值2. …………2分 当0x ≤时,()e x F x x =+,()e 10x F x '=+>, ()F x 在()0,∞-上单调递增,所以()(0)1=F x F ≤. ………………3分所以当1=k 时,()F x 的值域为(,1][2,)-∞+∞. ………………4分(2)由1(0)()e (0)x kx x F x x kx x ⎧+>⎪=⎨⎪+⎩≤,得21(0)()e (0)x k x F x x k x ⎧->⎪'=⎨⎪+⎩≤, ………………5分①当0=k 时,21(0)()e (0)x x F x x x ⎧->⎪'=⎨⎪⎩≤,当0>x 时,()0F x '<,()F x 在区间(0,)+∞上单调递减, ………………6分 当0x ≤时,()0F x '>,()F x 在区间(,0]-∞上单调递增. ………………7分②当0>k 时,21(0)()e (0)x k x F x x k x ⎧->⎪'=⎨⎪+⎩≤, 当0x ≤时,()e 0x F x k '=+>,()F x 在区间(,0]-∞上单调递增.………………8分当0>x 时,令21()0F x k x '=-=,解得x =±,舍去负值,得x =当0x <<时,()0F x '<,()F x在区间上单调递减, ………………9分当x >'()0>F x ,()F x在区间)+∞上单调递增. ………………10分 ③当0k <时,21(0)()e (0)x k x F x x k x ⎧->⎪'=⎨⎪+⎩≤, 当0>x 时,21()0F x k x'=-<,()F x 在区间(0,)+∞上单调递减.……………11分 当0x ≤时,令()e 0x F x k '=+=,得ln()=-x k , 下面讨论ln()=-x k 是否落在区间(,0)-∞上,令ln()0k -≥,解得1-k ≤,令ln()0k -<,解得10-<<k ,当1-k ≤时,当0x ≤时,()0F x '<,()F x 在(),0-∞上单调递减.……………12分 当10-<<k 时,在(),0-∞上存在极值点ln()=-x k ,当ln()0-<<k x 时,()0F x '>,()F x 在(ln(),0]-k 上单调递增,当ln()<-x k 时,()0F x '<,()F x 在(,ln())-∞-k 上单调递减.……………13分 综上所述:当0>k 时,()F x 在(,0]-∞和)+∞上单调递增,在上单调递减; 当0=k 时,()F x 在(,0]-∞上单调递增,在(0,)+∞上单调递减;当10-<<k 时,()F x 在(ln(),0]-k 上单调递增,在(,ln())-∞-k 和(0,)+∞上 单调递减;当1-k ≤时,()F x 在(],0-∞和()0,+∞上单调递减. ……………14分。
广东省珠海市2015届高三下学期学业质量监测(二模)数学理试题(PDF版)

7.如下图,为一旋转体沙漏,上部为一倒立圆台,下部为一圆柱,单位时间流出的沙量固定,假定沙的上 表面总能保持平整,则沙漏内剩余沙的高度 h 与时间 t 的函数关系图像最接近的是
理科数学试题 B 第 1 页( 共 10 页)
A
B
C
D
xn 1 yn xn 8.在平面直角坐标系中,定义 ( n N ) 为点 Pn ( xn,yn ) 到点 Pn 1 ( xn 1,yn 1 ) 的一个变换:附中变换. yn 1 yn xn
(2) m n
3 …………………………………………4分 5
m n ac a 2 b 2 c 2 0 …………………………………………5分
(1)求 sin A ; (2)求角 B 与 c . 解:(1) ABC 中, 2sin A cos A sin 2 A
8 sin A ,b 3 , 5
8 sin A …………………………………………2分 5
cos A
4 5
…………………………………………3分
A ( 0, ) sin A
100
被 9 除所得的余数是
.
4 .2/3
11. B(2 , 0) ,C (2 , 0) , A 为动点, ABC 的周长为 10 ,则点 A 的轨迹的离心率为
12.变量 x , y 满足约束条件: x 0 , y 0 , kx y 2k 0 .当 k 2 时,对应的可行域面积为 s ,则
z
ks 的范围是 k2
. [2 , )
13.某代表团有 a 、b 、c 、d 、e 、f 六名男性成员全部住进 A 、B 、C 三个房间,每房间住 2 人,其中 a 没住房间 A ,同时 b 没住房间 B 的概率是 .
2015届广东珠海一中等六校第二次联考理科数学试题附答案

广东珠海一中、中山纪念中学、广州六中、东莞中学、惠州一中深圳实验学校六校联盟2015届高三第二次联考(文科)数学试题命题学校: 深圳实验学校高中部本试题共4页,20小题,满分150分,考试用时120分钟第Ⅰ卷选择题(满分50分)一.选择题:本大题共10小题;每小题5分,共50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的1. 等差数列{}n a 的前n 项和为n S ,若2341,3,a a S ==则=A. 12B. 10 C . 8 D. 62. 下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是A. 3y x =B. |1|y x =+C. 2y x =-D. ||1y x =+ 3.已知向量(1,),(2,2),a k b a b a ==+且与共线,那么k 的值为 A. 1B. 2C. 3D. 44. 设函数⎩⎨⎧>-≤=-1,log 11,2)(21x x x x f x ,则[](4)=f fA. 2B. 4C. 8D. 165. 函数2sin(2)2y x π=+是A. 周期为π的奇函数B. 周期为π的偶函数C. 周期为2π的奇函数D. 周期为2π的偶函数6. 已知,21tan =α则α2cos 的值为 A. 51- B. 35- C. 45D. 537. 设向量,a b 均为单位向量,且||1a b +=,则 a 与 b 夹角为 A.3π B. 2πC.23πD.34π8. 下列各函数中,最小值为2的是A. 1y x x =+B. 1sin sin y x x =+,(0,)2x π∈C. 44(x >2)-2y x x =+-D. 2y =9.设偶函数()f x 对任意x R ∈,都有1(3)()f x f x +=-,且当[3,2]x ∈--时,()4f x x =,则(113.5)f = A. 10 B.110 C. 10- D. 110- 10. 已知等差数列{}n a 的公差0d ≠ ,且1313,,a a a 成等比数列,若11a =, n S 为数列{}n a 的前n 项和,则2163n n S a ++ 的最小值为A. 4B. 3C. 2D. 92第Ⅱ卷非选择题(满分100分)二.填空题:本大题共4小题,每小题5分,满分20分 11.数列{}n a 的前n 项和n S 满足2+1n nS n =,则6=a _________. 12. 实数,x y 满足|-2|13y x y ≥⎧⎨≤≤⎩,则不等式组所表示的平面区域的面积为_________.13.已知21tan (+)=,tan =,53αββ 则 tan (+)4πα的值为____________.14. 下列四种说法:①命题“x R ∃∈,使得213x x +> ”的否定是“x R ∀∈,都有213x x +≤”; ②设p 、q 是简单命题,若“p q ∨”为假命题,则“p q ⌝∧⌝” 为真命题; ③若p 是q 的充分不必要条件,则p q ⌝⌝是的必要不充分条件; ④把函数()sin 2y x =-()R x ∈的图像上所有的点向右平移8π个单位即可得到函数sin 24y x π⎛⎫=-+ ⎪⎝⎭()R x ∈的图像.其中所有正确说法的序号是 .三.解答题:本大题共6小题,满分80分.解答须写出文字说明,证明过程或演算步骤.15. (本小题满分12分)已知集合{}|||2A x x a =-≤,{}2|lg (+6x +9)>0B x x =. (Ⅰ)求集合A 和RB ;(Ⅱ)若A B ⊆,求实数a 的取值范围.16. (本小题满分12分) 在数列{}n a 中,已知*111411,;23log ,()44n n n n a a b a n N a +==+=∈ (Ⅰ)求数列{}n a 、{}n b 的通项公式;(Ⅱ)设数列{}n c 满足n n n b a c ⋅=,求{}n c 的前n 项和n S .17. (本小题满分14分) 已知向量()3sin 2,1m x =,()1,3cos 2n x =+,设函数()f x m n =⋅.(Ⅰ)求)(x f 的单调递增区间;(Ⅱ)在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边, 若22ACBC ab ⋅=,c =()4,f A =求b .18. (本小题满分14分)制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损率分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?19. (本小题满分14分) 已知函数()1=+x f x ex e(Ⅰ)求函数()f x 的最小值; (Ⅱ)若对所有0≤x 都有1)(+≥ax x f ,求实数a 的取值范围.20. (本小题满分14分)已知二次函数2()f x ax x =+(a R ∈).(Ⅰ)当0<a <12时,(sin )f x (x R ∈)的最大值为54,求实数a 的值; (Ⅱ)对于任意的 x R ∈,总有|(sin cos )f x x |1≤.试求a 的取值范围;(III )若当*N n ∈时,记1231ni n i a a a a a ==++++∑,令1a =,求证:312()ni nif i =<<∑成立.2015届高三六校第二次联考(文科)数学试题参考答案及评分标准命题:深圳实验学校 张春丽 审题:高三文科数学备课组(1人)第Ⅰ卷选择题(满分50分)一、选择题:本大题共10小题,每小题5分,共50分. 1.(C ) 2.(D ) 3.(A ) 4.(B ) 5.(B ) 6.(D ) 7.(C ) 8.(C ) 9.(B) 10.(A )第Ⅱ卷非选择题(满分100分)二、填空题:本大题共4小题,每小题5分,共20分. 11. 61=21a ; 12. 8; 13. 98; 14.①②③④ 三、解答题:本大题共6小题,满分80分.解答应写出文字说明、证明过程或演算步骤. 15.解:(Ⅰ)||22222x a x a a x a-≤⇒-≤-≤⇒-≤≤+集合A ={|22}x a x a -+≤≤+ ………………………… 3分222lg (+6x+9)>0,+6x+91+6x+8042x x x x x ∴>∴>⇒<->-或集合B ={|42}x x x <->-或 ……… 6分[]42R C B =--, ……………… 8分(Ⅱ)由A B ⊆得 24a +<-或者 22a -<-+ …….10 分 解得 6a <- 或 0a > ….. 11分 综上所述,a 的取值范围为{|a 6a <- 或 0a >} ………… 12分 16.(1)1111,,44n n a a a +==∴数列{n a }是首项为41,公比为41的等比数列, …………………… 2分 ∴)()41(*N n a n n ∈=. …………………… 4分∵2log 341-=n n a b , ∴1413log ()2324nn b n =-=-. …………………… 6分(2)由(Ⅰ)知,n n a )41(=,23-=n b n (n *N ∈)∴)(,)41()23(*N n n c n n ∈⨯-=.∴n n n n n S )41()23()41()53()41(7)41(4411132⨯-+⨯-+⋯+⨯+⨯+⨯=-, ①……… 7分于是1432)41()23()41()53()41(7)41(4)41(141+⨯-+⨯-+⋯+⨯+⨯+⨯=n n n n n S ②……… 8分两式①-②相减得132)41()23(])41()41()41[(34143+⨯--+⋯+++=n n n n S ……… 9分=1)41()23(21+⨯+-n n . ………11分 ∴ )()41(381232*1N n n S n n ∈⨯+-=+. ……… 12分 17. 解:(1)()3sin 2,1m x =,()1,3cos 2x =+n()3sin 2cos23f x m n x x ∴=⋅++=………………… 1分π2sin 236x ⎛⎫=++ ⎪⎝⎭ ………………… 3分令πππ2π22π262k x k -≤+≤+,故()ππππ,36k x k k -≤≤+∈Z ……………… 5分 )(x f ∴的单调递增区间为()πππ,π36k k k ⎡⎤-+∈⎢⎥⎣⎦Z . …………………… 6分(2)22AC BC ab ⋅=,∴2cos ba C =,cos C =. 0<,4C C ππ<∴=.………………… 9分由4)(=A f 得π()2sin 2346f A A ⎛⎫=++= ⎪⎝⎭,π1sin 262A ⎛⎫∴+= ⎪⎝⎭.又A 为ABC ∆的内角,ππ13π2666A <+< ,π5π266A +=, π3A ∴=. ………………… 11分22c ==4sin (+)sin sin sin()432b c b b B C A C πππ=⇒=⇒--,…… 13分14(2222b =+=… … 14分 18.解:设投资人分别用x 万元、y 万元投资甲、乙两个项目.由题意知⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+.0,0,8.11.03.0,10y x y x y x ,目标函数z =x +0.5y. …………………… 4分上述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域. …………………… 7分作直线05.0:0=+y x l ,并作平行 于直线0l 的一组直线,,5.0R z z y x ∈=+与可行域相交,其中有一条直线经过可行域上的M 点,且与直线05.0=+y x 的距离最大,即z 有最大值 …………………… 10分 M 点是直线10=+y x 和8.11.03.0=+y x 的交点.解方程组⎩⎨⎧=+=+,8.11.03.0,10y x y x 得x =4,y=6 …………………… 12分此时765.041=⨯+⨯=z (万元).07> ∴当x =4,y=6时z 取得最大值.答:投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8万元的前提下,使可能的盈利最大。
广东省珠海一中等六校2015届高三数学上学期第二次联考试卷 文(含解析)

广东省珠海一中等六校2015届高三上学期第二次联考数学试卷(文科)一.选择题:本大题共10小题;每小题5分,共50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的1.(5分)等差数列{a n}的前n项和为S n若a2=1,a3=3,则S4=()A.12 B.10 C.8 D.62.(5分)下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是()A.y=x3B.y=﹣x2+1 C.y=2﹣|x|D.y=|x|+13.(5分)已知向量=(1,k),=(2,2),且+与共线,那么k的值为()A.1 B.2 C.3 D.44.(5分)设函数f(x)=,则f[f(4)]=()A.2 B.4 C.8 D.165.(5分)函数是()A.周期为π的奇函数B.周期为π的偶函数C.周期为2π的奇函数D.周期为2π的偶函数6.(5分)已知tanα=,则cos2α的值为()A.B.C.D.7.(5分)设向量,均为单位向量,且|+|=1,则与夹角为()A.B.C.D.8.(5分)下列各函数中,最小值为2的是()A.y=x+B.y=sinx+,C.y=x+﹣4(x>2)D.y=9.(5分)设偶函数f(x)对任意x∈R,都有f(x+3)=﹣,且当x∈[﹣3,﹣2]时,f(x)=4x,则f(107.5)=()A.10 B.C.﹣10 D.﹣10.(5分)已知等差数列{a n}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,S n是数列{a n}前n项的和,则(n∈N+)的最小值为()A.4 B.3 C.2﹣2 D.二.填空题:本大题共4小题,每小题5分,满分20分11.(5分)数列{a n}的前n项和S n满足S n=,则a6=.12.(5分)实数x,y满足,则不等式组所表示的平面区域的面积为.13.(5分)已知tan(α+β)=,tanβ=,则tan(α+)的值为.14.(5分)下列四种说法:①命题“∃x∈R,使得x2+1>3x”的否定是“∀x∈R,都有x2+1≤3x”;②设p、q是简单命题,若“p∨q”为假命题,则“¬p∧¬q”为真命题;③若p是q的充分不必要条件,则¬p是¬q的必要不充分条件;④把函数y=sin(﹣2x)(x∈R)的图象上所有的点向右平移个单位即可得到函数(x∈R)的图象.其中所有正确说法的序号是.三.解答题:本大题共6小题,满分80分.解答须写出文字说明,证明过程或演算步骤.15.(12分)已知集合A={x||x﹣a|≤2},B={x|lg(x2+6x+9)>0}.(Ⅰ)求集合A和∁R B;(Ⅱ)若A⊆B,求实数a的取值范围.16.(12分)在数列{a n}中,已知a1=,,b n+2=3a n(n∈N*).(1)求数列{a n}、{b n}的通项公式;(2)设数列{c n}满足c n=a n•b n,求{c n}的前n项和S n.17.(14分)已知向量,,设函数f(x)=.(Ⅰ)求f(x)的单调递增区间;(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,若2ab,c=2,f(A)=4,求b.18.(14分)制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?19.(14分)已知函数f(x)=ex+(Ⅰ)求函数f(x)的最小值;(Ⅱ)若对所有x≤0都有f(x)≥ax+1,求实数a的取值范围.20.(14分)已知二次函数f(x)=ax2+x(a∈R).(1)当0<a<时,f(sinx)(x∈R)的最大值为,求f(x)的最小值.(2)对于任意的x∈R,总有|f(sinxcosx)|≤1.试求a的取值范围.(3)若当n∈N*时,记,令a=1,求证:成立.广东省珠海一中等六校2015届高三上学期第二次联考数学试卷(文科)参考答案与试题解析一.选择题:本大题共10小题;每小题5分,共50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的1.(5分)等差数列{a n}的前n项和为S n若a2=1,a3=3,则S4=()A.12 B.10 C.8 D.6考点:等差数列的性质.专题:计算题.分析:由等差数列的前n项和得到,求前四项的和要用第一项和第四项的和,根据等差数列的性质第一项和第四项的和等于第二项与第三项的和,得到结果.解答:解:由等差数列的性质可得:a1+a4=a2+a3,∵a2=1,a3=3,∴s4=2(1+3)=8故选C.点评:若已知等差数列的两项,则等差数列的所有量都可以求出,只要简单数字运算时不出错,问题可解.2.(5分)下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是()A.y=x3B.y=﹣x2+1 C.y=2﹣|x|D.y=|x|+1考点:奇偶性与单调性的综合.专题:函数的性质及应用.分析:根据基本初等函数的单调性奇偶性,逐一分析答案四个函数在(0,+∞)上的单调性和奇偶性,逐一比照后可得答案.解答:解:y=x3在(0,+∞)上单调递增,但为奇函数;y=﹣x2+1为偶函数,但在(0,+∞)上单调递减;y=2﹣|x|为偶函数,但在(0,+∞)上单调递减;y=|x|+1为偶函数,且在(0,+∞)上单调递增;故选D点评:本题考查的知识点是函数的奇偶性与单调性的综合,熟练掌握各种基本初等函数的单调性和奇偶性是解答的关键.3.(5分)已知向量=(1,k),=(2,2),且+与共线,那么k的值为()A.1 B.2 C.3 D.4考点:平面向量共线(平行)的坐标表示.专题:平面向量及应用.分析:由向量的坐标加法运算求得+的坐标,然后直接利用向量共线的坐标表示列式求解k的值.解答:解:∵=(1,k),=(2,2),∴+=(3,k+2),又+与共线,∴1×(k+2)﹣3k=0,解得:k=1.故选:A.点评:平行问题是一个重要的知识点,在2015届高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若=(a1,a2),=(b1,b2),则⊥⇔a1a2+b1b2=0,∥⇔a1b2﹣a2b1=0,是基础题.4.(5分)设函数f(x)=,则f[f(4)]=()A.2 B.4 C.8 D.16考点:对数的运算性质.专题:函数的性质及应用.分析:本题可以根据不同的条件选择不同的解析式进行求值,得到本题结论.解答:解:∵函数f(x)=,∴f(4)=1﹣log24=1﹣2=﹣1,f[f(4)]=f(﹣1)=21﹣(﹣1)=22=4.故选B.点评:本题考查的是分段函数的函数值求法,本题难度不大,属于基础题.5.(5分)函数是()A.周期为π的奇函数B.周期为π的偶函数C.周期为2π的奇函数D.周期为2π的偶函数考点:三角函数的周期性及其求法;正弦函数的奇偶性.专题:计算题.分析:利用诱导公式化简函数,然后直接求出周期,和奇偶性,确定选项.解答:解:因为:=2cos2x,所以函数是偶函数,周期为:π故选B.点评:本题考查三角函数的周期性及其求法,正弦函数的奇偶性,考查计算能力,是基础题.6.(5分)已知tanα=,则cos2α的值为()A.B.C.D.考点:二倍角的余弦;同角三角函数基本关系的运用.专题:三角函数的求值.分析:利用余弦的二倍角公式可求得cos2α=cos2α﹣sin2α,进而利用同角三角基本关系,使其除以sin2α+cos2α,分子分母同时除以cos2a,转化成正切,然后把tanα的值代入即可.解答:解:cos2α=cos2α﹣sin2α====.故选:D.点评:本题主要考查了同角三角函数的基本关系和二倍角的余弦函数的公式.解题的关键是利用同角三角函数中的平方关系,完成了弦切的互化.7.(5分)设向量,均为单位向量,且|+|=1,则与夹角为()A.B.C.D.考点:数量积表示两个向量的夹角;单位向量.专题:计算题.分析:设与的夹角为θ,将已知等式平方,结合向量模的含义和单位向量长度为1,化简整理可得•=﹣,再结合向量数量积的定义和夹角的范围,可得夹角θ的值.解答:解:设与的夹角为θ,∵|+|=1,∴(+)2=2+2•+2=1…(*)∵向量、均为单位向量,可得||=||=1∴代入(*)式,得1+2•+1=1=1,所以•=﹣根据向量数量积的定义,得||•||cosθ=﹣∴cosθ=﹣,结合θ∈[0,π],得θ=故选C点评:本题已知两个单位向量和的长度等于1,求它们的夹角,考查了得数量积的定义、单位向量概念和向量的夹角公式等知识,属于基础题.8.(5分)下列各函数中,最小值为2的是()A.y=x+B.y=sinx+,C.y=x+﹣4(x>2)D.y=考点:基本不等式.专题:函数的性质及应用;不等式的解法及应用.分析:根据函数的单调性可知;y=x+,(0,1)(﹣1,0)单调递减,(1,+∞),(﹣∞,﹣1)单调递增,结合不等式的等号问题判断.解答:解:根据函数的单调性可知;y=x+,(0,1),(﹣1,0)单调递减,(1,+∞),(﹣∞,﹣1)单调递增,f(1)=2,f(﹣1)=﹣2,∴A不正确.因为B.D中的函数式子等号不成了,所以B,D不正确.故选:C点评:本题考查了y=x+的单调性,均值不等式的应用;属于中档题.9.(5分)设偶函数f(x)对任意x∈R,都有f(x+3)=﹣,且当x∈[﹣3,﹣2]时,f(x)=4x,则f(107.5)=()A.10 B.C.﹣10 D.﹣考点:函数的周期性.专题:计算题.分析:先通过有f(x+3)=﹣,且可推断函数f(x)是以6为周期的函数.进而可求得f(107.5)=f(5.5),再利用f(x+3)=﹣以及偶函数f(x)和x∈[﹣3,﹣2]时,f(x)=4x即可求得f(107.5)的值.解答:解:因为f(x+3)=﹣,故有f(x+6)=﹣=﹣=f(x).函数f(x)是以6为周期的函数.f(107.5)=f(6×17+5.5)=f(5.5)=﹣=﹣=﹣=.故选B点评:本题主要考查了函数的周期性.要特别利用好题中有f(x+3)=﹣的关系式.在解题过程中,条件f(x+a)=﹣通常是告诉我们函数的周期为2a.10.(5分)已知等差数列{a n}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,S n是数列{a n}前n项的和,则(n∈N+)的最小值为()A.4 B.3 C.2﹣2 D.考点:等差数列的性质.专题:计算题;等差数列与等比数列.分析:由题意得(1+2d)2=1+12d,求出公差d的值,得到数列{a n}的通项公式,前n项和,从而可得,换元,利用基本不等式,即可求出函数的最小值.解答:解:∵a1=1,a1、a3、a13 成等比数列,∴(1+2d)2=1+12d.得d=2或d=0(舍去),∴a n =2n﹣1,∴S n==n2,∴=.令t=n+1,则=t+﹣2≥6﹣2=4当且仅当t=3,即n=2时,∴的最小值为4.故选:A.点评:本题主要考查等比数列的定义和性质,等比数列的通项公式,考查基本不等式,属于中档题.二.填空题:本大题共4小题,每小题5分,满分20分11.(5分)数列{a n}的前n项和S n满足S n=,则a6=.考点:数列的概念及简单表示法.专题:点列、递归数列与数学归纳法.分析:根据题中给出的数列{a n}的前n项和的公式便可求出数列{a n}的通项公式,将n=6代入通项公式便可得出答案.解答:解:S6﹣S5==,所以;故答案为:.点评:本题考查了数列的基本知识,考查了学生的计算能力,解题时要认真审题,仔细解答,避免错误,属于中档题.12.(5分)实数x,y满足,则不等式组所表示的平面区域的面积为8.考点:二元一次不等式(组)与平面区域.专题:计算题;作图题;不等式的解法及应用.分析:作出其平面区域,可知是上底长2,下底长6,高为2的梯形,从而求面积.解答:解:作出其平面区域如下图:可知是上底长2,下底长6,高为2的梯形,则阴影部分的面积为×(2+6)×2=8;故答案为:8.点评:本题考查了学生的作图能力,属于基础题.13.(5分)已知tan(α+β)=,tanβ=,则tan(α+)的值为.考点:两角和与差的正切函数.专题:计算题;三角函数的求值.分析:利用tanα=tan[(α+β)﹣β],求出tanα,再利用和角的正切公式,求tan(α+)的值解答:解:∵tan(α+β)=,tanβ=,∴tanα=tan[(α+β)﹣β]==,∴tan(α+)==.故答案为:.点评:本题考查两角和与差的正切函数,考查学生的计算能力,利用tanα=tan[(α+β)﹣β],求出tanα是关键.14.(5分)下列四种说法:①命题“∃x∈R,使得x2+1>3x”的否定是“∀x∈R,都有x2+1≤3x”;②设p、q是简单命题,若“p∨q”为假命题,则“¬p∧¬q”为真命题;③若p是q的充分不必要条件,则¬p是¬q的必要不充分条件;④把函数y=sin(﹣2x)(x∈R)的图象上所有的点向右平移个单位即可得到函数(x∈R)的图象.其中所有正确说法的序号是①②③④.考点:命题的真假判断与应用;特称命题.专题:简易逻辑.分析:利用命题的否定判断①的正误;复合命题的真假判断②的正误;充要条件判断③的正误;三角函数图象的平移判断④的正误;解答:解:对于①,命题“∃x∈R,使得x2+1>3x”的否定是“∀x∈R,都有x2+1≤3x”;满足命题的否定形式,所以①正确.对于②,设p、q是简单命题,若“p∨q”为假命题,说明两个命题都是假命题,命题的否定是真命题,则“¬p∧¬q”为真命题;所以②正确.对于③,若p是q的充分不必要条件,则¬p是¬q的必要不充分条件;满足充要条件的关系,所以③正确;对于④,把函数y=sin(﹣2x)(x∈R)的图象上所有的点向右平移个单位即可得到函数(x∈R)的图象.符号平移原则,所以④正确;故答案为:①②③④.点评:本题考查命题的子啊的判断,特称命题与全称命题的否定关系,充要条件以及复合命题的真假,三角函数图象的平移,基本知识的考查.三.解答题:本大题共6小题,满分80分.解答须写出文字说明,证明过程或演算步骤.15.(12分)已知集合A={x||x﹣a|≤2},B={x|lg(x2+6x+9)>0}.(Ⅰ)求集合A和∁R B;(Ⅱ)若A⊆B,求实数a的取值范围.考点:绝对值不等式的解法;对数函数的定义域.专题:不等式的解法及应用.分析:(Ⅰ)利用绝对值不等式可求得集合A={x|﹣2+a≤x≤2+a};解对数不等式lg(x2+6x+9)>0可得B,从而可得∁R B;(Ⅱ)由A⊆B得:2+a<﹣4或者﹣2<﹣2+a,从而可求得实数a的取值范围.解答:解:(Ⅰ)|x﹣a|≤2⇒﹣2≤x﹣a≤2⇒a﹣2≤x≤2+a,集合A={x|﹣2+a≤x≤2+a};…(3分),∴,集合B={x|x<﹣4或x>﹣2},…(6分)∴C R B=[﹣4,﹣2];…(8分)(Ⅱ)由A⊆B得:2+a<﹣4或者﹣2<﹣2+a….10 分解得:a<﹣6或a>0,…..(11分)综上所述,a的取值范围为{a|a<﹣6或 a>0}.…(12分)点评:标题考查绝对值不等式的解法及对数函数的定义域的确定,考查集合的包含关系及应用,属于中档题.16.(12分)在数列{a n}中,已知a1=,,b n+2=3a n(n∈N*).(1)求数列{a n}、{b n}的通项公式;(2)设数列{c n}满足c n=a n•b n,求{c n}的前n项和S n.考点:数列的求和.专题:等差数列与等比数列.分析:(1)由条件建立方程组即可求出数列{a n}、{b n}的通项公式;(2)根据错位相减法即可求{c n}的前n项和S n.解答:解:(1)∵a1=,,∴数列{a n}是公比为的等比数列,∴,又,故 b n=3n﹣2(n∈N*).(2)由(1)知,,∴,∴,于是.两式相减,得=.∴点评:本题主要考查等差数列和等比数列的通项公式的计算,以及利用错位相减法进行求和的内容,考查学生的计算能力.17.(14分)已知向量,,设函数f(x)=.(Ⅰ)求f(x)的单调递增区间;(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,若2ab,c=2,f(A)=4,求b.考点:正弦定理的应用;平面向量的综合题.专题:计算题;三角函数的图像与性质;平面向量及应用.分析:(Ⅰ)运用平面向量的数量积的坐标公式,及两角和的正弦公式,以及正弦函数的增区间,即可得到所求;(Ⅱ)由向量的数量积的定义,求得C,再由f(A)=4,求得A,再由正弦定理,即可得到b.解答:解:(Ⅰ)∵,∴=,令2kπ≤2x≤2k,故,则f(x)的单调递增区间为.(Ⅱ)∵,∴,,∵0<C<π,∴,由f(A)=4得,∴,又A为△ABC的内角,,,∴A=,由于,由正弦定理,得,则.点评:本题考查平面向量的数量积的坐标公式和三角函数的恒等变换公式的运用,同时考查正弦函数的单调性,以及正弦定理的运用,考查两角和差公式,以及运算能力,属于中档题.18.(14分)制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?考点:基本不等式在最值问题中的应用.专题:应用题;数形结合.分析:设投资人对甲、乙两个项目各投资x和y万元,列出x和y的不等关系及目标函数z=x+0.5y.利用线性规划或不等式的性质求最值即可.解答:解:设投资人对甲、乙两个项目各投资x和y万元,则,设z=x+0.5y=0.25(x+y)+0.25(3x+y)≤0.25×10+0.25×18=7,当即时,z取最大值7万元答:投资人对甲、乙两个项目分别投资4万元和6万元时,才能使可能的盈利最大.点评:本题考查线性规划的应用问题,利用不等式的性质求最值问题,考查对信息的提炼和处理能力.19.(14分)已知函数f(x)=ex+(Ⅰ)求函数f(x)的最小值;(Ⅱ)若对所有x≤0都有f(x)≥ax+1,求实数a的取值范围.考点:导数在最大值、最小值问题中的应用.专题:导数的综合应用.分析:(Ⅰ)利用导数判断函数的单调性,进而可求出函数的最小值;(Ⅱ)令g(x)=f(x)﹣ax﹣1=e﹣x+(e﹣a)x﹣1,即g(x)≥g(0)=0成立,分类讨论并利用导数判断函数的单调性,即可得出结论.解答:解:(Ⅰ)由已知得f'(x)=﹣e﹣x+e,…(1分)令f'(x)>0得x>﹣1;令f'(x)<0得x<﹣1.因此,函数f (x)在(﹣∞,﹣1]上单调减函数,在[﹣1,+∞)上是单调增函数,…(5分)当x=﹣1时,f(x)的有极小值也是最小值,f(x)min=0…(6分)(Ⅱ)令g(x)=f(x)﹣ax﹣1=e﹣x+(e﹣a)x﹣1,则g'(x)=﹣e﹣x+(e﹣a),g(0)=0.…(8分)(1)当e﹣a≤0,即a≥e时,g'(x)=﹣e﹣x+(e﹣a)<0,g(x)在(﹣∞,0]是减函数,因此当x≤0时,都有g(x)≥g(0)=0,即f(x)﹣ax﹣1≥0,f(x)≥ax+1;…(10分)(2)当a<e时,令g'(x)<0得x<﹣ln(e﹣a);令g'(x)>0得x>﹣ln(e﹣a),因此函数g(x)在(﹣∞,﹣ln(e﹣a)]上是减函数,在[﹣ln(e﹣a),+∞)上是增函数.由于对所有x≤0都有f(x)≥ax+1,即g(x)≥g(0)=0成立,因此﹣ln(e﹣a)≥0,e﹣a≤1,a≥e﹣1,又a<e,所以e﹣1≤a≤e.…(13分)综上所述,a的取值范围是[e﹣1,+∞).…(14分)点评:本题主要考查利用导数研究函数的单调性、极值、最值等知识,考查学生恒成立问题的等价转化思想及分类讨论思想的运用能力,属于难题.20.(14分)已知二次函数f(x)=ax2+x(a∈R).(1)当0<a<时,f(sinx)(x∈R)的最大值为,求f(x)的最小值.(2)对于任意的x∈R,总有|f(sinxcosx)|≤1.试求a的取值范围.(3)若当n∈N*时,记,令a=1,求证:成立.考点:数列与不等式的综合;二次函数的性质;数列的求和;正弦函数的定义域和值域.专题:综合题.分析:(1)由知,故当sinx=1时f(x)取得最大值为,由此得到,从而能够得到f(x)的最小值.(2)对于任意的x∈R,总有|f(sinxcosx)|≤1.令,则命题转化为,不等式|f(t)|≤1恒成立.由此入手,能够求出实数a的 a的取值范围.(3)由题意,,由此入手,能够证明成立.解答:解:(1)由,知,故当sinx=1时,f(x)取得最大值为,即,∴∴,所以f(x)的最小值为﹣1;(5分)(2)∵对于任意的x∈R,总有|f(sinxcosx)|≤1,令,则命题转化为,不等式|f(t)|≤1恒成立当t=0时,f(t)=0使|f(t)|≤1成立;(7分)当t≠0时,有,对于任意的恒成立;∵,则,故要使①式成立,则有a≤2,又,故要使②式成立,则有a≥﹣2,由题a≠0.综上,a∈[﹣2,0)∪(0,2]为所求.(10分)证明:(3)由题意,令则,∴g(n)在n∈N*时单调递增,∴(13分)又,∴综上,原结论成立.(16分)点评:本题考查数列与不等式的综合,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,是2015届高考的重点,易错点是知识体系不牢固.。
广东省珠海一中等六校2015届高三第二次联考英语试题含答案

2015届“六校联盟”第二次联合考试英语试题命题学校:珠海市第一中学本试卷共10页,三大题,满分135分。
考试用时120分钟。
注意事项:1. 答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型填涂在答题卡相应位置上。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3. 非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
Ⅰ语言知识及应用(共两节,满分45分)第一节完形填空(共15小题;每小题2分,满分30分)阅读下面短文,掌握其大意,然后从1~15各题所给的A、B、C和D项中,选出最佳选项,并在答题卡上将该项涂黑。
Though giant pandas may appear perfectly happy chewing bamboos, scientists recently discovered that they would rather have something sweeter. Scientists chose 1because the animals are herbivores (食草动物), which would mean that they would love sweets. However, the plant they choose, the bamboos, has a very 2 sugar content and is therefore not considered sweet. Could this mean that pandas have 3 their hobby for sweet things?The pandas were given six kinds of sweet liquids that are 4 found in fruits and vegetables. They were also given 5 at the same time. In each of the taste tests, the animals 6 the natural sweeter liquids and ignored the water 7 . They ate up all the sweet liquids and the water was left untouched.What was even more interesting is that when the scientists 8 the water with five different man-made sweeteners, ones that humans find delicious, the pandas were not as 9 . In these tests, they picked the water instead. The scientists believe that it could be either because pandas found them to be too 10 or not sweet enough and that the mixture could not 11 the pandas.The scientists were not too 12 by the results, since pandas in zoos have always shown a preference for treats like apples, sweet potatoes and even mooncakes. Scientists believe that the pandas may have once 13 sweeter foods that were available in the lowland areas that they used to live in. But when human settlement in the lowland areas 14 them to the bamboo forests in the mountains, they had no 15 but to settle for the almost sugarless plants.1. A. horses B. bears C. monkeys D. pandas2. A. high B. simple C. low D. different3. A. lost B. followed C. started D. kept4. A. specially B. hardly C. naturally D. rarely5. A. fruits B. water C. bamboos D. oxygen6. A. picked B. hid C. rejected D. shared7. A. largely B. gradually C. occasionally D. completely8. A. mixed B. covered C. exchanged D. replaced9. A. funny B. picky C. perfect D. interested10. A. salty B. sweet C. sour D. hot11. A. harm B. save C. attract D. change12. A. delighted B. surprised C. disappointed D. concerned13. A. enjoyed B. disliked C. controlled D. ignored14. A. encouraged B. forced C. introduced D. guided15. A. desire B. chance C. wonder D. choice第二节语法填空(共10小题;每小题1.5分,满分15分)阅读下面短文,按照句子结构的语法性和上下文连贯的要求,在空格处填入一个适当的词或使用括号中词语的正确形式填空,并将答案填写在答题卡标号为16-25的相应位置上。
广东省珠海一中等六校2015届高三第二次联考语文试题 Word版含答案

珠海一中等六校2015届高三第二次联考语文试题本试卷共8页,24小题,满分150分。
考试用时l50分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、考场号、座位号填写在答题卡上。
用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B铅笔填涂选做题的题组号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、本大题4小题,每小题3分,共12分。
1.下列词语中加点的字,每对读音都不相同的一组是A.款识./咫尺.楔.子/歇.息揆情度.理/度.德量力B.靓妆./菁.华感喟./惭愧.济.世安民/光风霁.月C.内疚./针灸.隐蔽./幽僻.拾.人牙慧/拾.级而上D.拮.据/诘.难悱.恻/蜚.声钻.木取火/拍马钻.营2.下面语段中画线的词语,使用不恰当的一项是没有思想的支撑,散文充其量只是一具徒有其表的空壳;但是,在呼吁散文精神的同时,也出现了一些矫枉过正的情况。
《时代的稻草人》因敏锐地把握了时代的问题,并用犀利的文笔批判剖析当下社会的种种乱象而受到专家的激赏。
但平心而论,它缺少了优秀散文应具备的情调、意蕴与美感。
它之所以获得“在场主义”散文奖头奖,惟其说是得益于审美,毋宁说是思想性与批判性的胜利。
A.矫枉过正 B.激赏 C.平心而论 D.惟其3.下列句子中,没有语病的一项是A.今年下半年,广州登革热疫情高发,为防止疫情扩散,保证地铁工地和车站,广州地铁已启动了多项措施,开展以灭蚊为重点的防治工作。
广东省珠海市2015-2016学年第一学期高三摸底考试数学理试卷 Word版含答案

珠海市2015-2016学年度第一学期高三摸底考试理科数学参考答案一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合2{|log 3}M x x =<,{|21,}N x x n n N ==+∈,则M N ⋂=( ) A. (0,8) B. {3,5,7} C. {0,1,3,5,7} D. {1,3,5,7} 2. 已知复数11z i =+,232z i =-,则复数21z z 在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限3. 若x ,y 满足不等式组240300x y x y y +-≥⎧⎪+-≤⎨⎪≥⎩,则32x y +的最大值是( )A. 6B. 7C. 9D. 10 4a 与b 的夹角为( )A. 30oB.45o C. 60o D. 120o 5. 当2x ππ-≤≤时,函数()sinf x x x =的( )A .最大值是1,最小值是.最大值是2,最小值是 C .最大值是1,最小值是1- D .最大值是2,最小值是1- 6. 函数2cos y x =的单调增区间是( )A. (2,2),k k k Z πππ-∈B. (2,2),2k k k Z πππ-∈C. (,),k k k Z πππ-∈D. (,),2k k k Z πππ-∈7.已知函数2()(1)xf x e x ax =++在点(0,(0))f 的切线与直线260x y -+=垂直,则a =( )A .3-B .2-C .2D .38. 已知cos()(0,[0,2))y x ωϕωϕπ=+>∈的部分图象如图所示,则ϕ=( )A.32π B. 74π C. 4πD. 09.执行如右下图的程序框图,若输入2015n =,则输出T 的值为( ) A .12- B .23 C .3 D .3410.正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体,该几何体的三视图如左上图所示,则该几何体的表面积为( )A.3π B.3π C.2π D.2π11.若0a >,且1a ≠,设函数2,1()2,1x a x f x x x x ⎧<⎪=⎨-≥⎪⎩,若不等式()3f x ≤的解集是(,3]-∞,则a 的取值范围是( )A. (1,)+∞B. (1,3)C. (0,1)D. [3,)+∞12.若偶函数()f x 的图像关于1x =对称,且当[0,1]x ∈时,()f x x =,则函数()y f x =的图象与函数lg y x =的图象的交点个数为( )A. 14B. 16C. 18D. 20二、填空题:本大题共4小题,每小题5分,共20分.(第10题图)俯视图左视图正视图2222213.已知数列{}n b 的前n 项和为n S ,且231n n S b =-,则n b = .13n -14.由数字0,1,2,3,4,5组成无重复数字的五位数,则该五位数是奇数的概率为 .122515.已知双曲线22221(0,0)x y a b a b-=>>的半焦距为c ,直线l 过(,0)c ,(0,)b 两点,若直线l与双曲线的一条渐近线垂直,则双曲线的离心率为.16.(3)nx y +展开式中,所有项的系数和比二项式系数和多240,则展开式中的中间项是 .2254x y选择题答案:DDCCB DABBA CC三、解答题: 解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知等差数列{}n a 的前n 项和为n S ,公差2d =,10120S =. (1)求n a ; (2)若n b =求数列{}n b 的前n 项和为n T .解(1)1(1)2n n n S na d -=+Q ,2d =,10120S =……………………………………………………2分11091021202a ⨯∴+⨯=,即13a =………………………………………………………………………3分所以1(1)21n a a n d n =+-=+……………………………………………………………………………4分(2)12n b ===Q ………………………………7分11112222n T ∴=++++L ……………10分即11)2n T =-……………………………………………………………………………………12分 18.(本小题满分12分)某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动),该校合唱团共有100名学生,他们参加活动的次数统计如图所示; (1)求合唱团学生参加活动的人均次数; (2)从合唱团中任选两名学生,用ξ表示这两人参加活动次数的和,求ξ的分布列.(结果用最简分数) 解:(1)由题意得:1102603302.2100⨯+⨯+⨯=………………………………………………………… 2分 ∴ 合唱团学生参加活动的人均次数为2.2………………………………………………………………… 3分 (2)由题意得ξ的所有可能取值为2,3,4,5,6…………………………………………………………… 5分1091(2)10099110P ξ⨯===⨯, 210604(3)1009933P ξ⨯⨯===⨯,21030605923(4)100991009955P ξ⨯⨯⨯==+=⨯⨯, 230604(5)1009911P ξ⨯⨯===⨯,302987(6)10099990P ξ⨯===⨯,………………………………………………………………………………10分 ∴ξ的分布列为:…………………………………………………………………………………………………………………12分 19.(本小题满分12分) 已知如图:四边形ABCD 是矩形,BC ⊥平面ABE ,且2AE EB BC ===,点F 为CE 上一点,且BF ⊥平面ACE . (1)求证://AE 平面BFD ;(2)求二面角C DE A --的余弦值.解:(1)证明:连接AC 交BD 于G ,连结GF , ABCD 是矩形∴G 为AC 的中点…………………………………… 1分 由BF ⊥平面ACE 得:BF CE ⊥由EB BC =知:点F 为CE 中点…………………………………………………………… 2分 ∴FG 为ACE ∆的中位线∴FG //AE …………………………………………………………………………………… 3分 ∵ AE ⊄平面BFD ;FG ⊂平面BFD ;∴ //AE 平面BFD ;…………………………………………………………………………4分 (2)由BF ⊥平面ACE 得:BF AE ⊥;由BC ⊥平面ABE 得: BC AE ⊥,BCBE ⊥;∴AE ⊥平面BCE ,则BE AE ⊥ (6)分 在BCE Rt ∆中,CE ===同理可得:DE AB CD ===,AC =;……………………………………… 8分 ∵ 2AD BC AE ===∴ 取DE 中点H ,连结AH ,CH ,则AH DE ⊥,CH DE ⊥且12AH DE ==,CH DE ==………………………………………………… 10分 ∴CHA ∠即为二面角C DE A --的平面角;在CHA ∆中,222cos 2CH AH AC CHA CH AH +-∠===⋅; ∴二面角C DE A--的余弦值为………………………………………………………………… 12分 F E DC BA20.(本小题满分12分)已知动圆过定点1(0,)4F ,且与定直线1:4l y =-相切. (1)求动圆圆心的轨迹曲线C 的方程;(2)若点00(,)A x y 是直线10x y --=上的动点,过点A 作曲线C 的切线,切点记为,M N ,求证:直线MN 恒过定点,并求AMN ∆面积S 的最小值.解:(1)根据抛物线的定义,由题意可得:动圆圆心的轨迹C 是以点1(0,)4F 为焦点,以定直线1:4l y =-为准线的抛物线;………………………………………………………………………………………………2分 设2:2(0)C x py p => ∵ 点1(0,)4F 到准线1:4l y =-的距离为12,∴12p = ∴圆心的轨迹C 的方程为2x y =………………………………………………………………………… 4分(2) ∵2x y =,∴2y x '=设切点,M N 的坐标分别为11(,)M x y ,22(,)N x y ,则211x y =,222x y =则过点11(,)M x y 的切线方程为1112()y y x x x -=-,即2112y x x x =-,即112y x x y =- 过点22(,)N x y 的切线方程为2222()y y x x x -=-,即2222y x x x =-,即222y x x y =- ∵过点,M N 的切线都过点00(,)A x y ∴01012y x x y =-,02022y x x y =-∴点11(,)M x y ,22(,)N x y 都在直线002y xx y =-上 ∴直线MN的方程为002y xx y=-,即0020x x y y --=…………………………………………………6分又因为点00(,)A x y 是直线10x y --=上的动点,所以0010x y --= ∴直线MN 的方程为002(1)0x x y x ---=,即0(21)(1)0x x y -+-= ∴直线MN恒过定点1(,1)2…………………………………………………………………………………8分 联立00220x x y y y x--=⎧⎨=⎩得到20020x x x y -+= 又因为点00(,)A x y 是直线10x y --=上的动点,所以0010x y --=,即200210x x x x -+-=…①则12x x 、是①的二根∴20012012044(1)021x x x x x x x x ⎧∆=-->⎪+=⎨⎪⋅=-⎩,==………………………………………………………………………………10分点00(,)A x y 到直线0020x x y y --=的距离是:d ………11分∴0112S MN d x ∆=⋅=-+即14AMN S ∆==≥=∴面积的最小值是14…………………………………………12分 21.(本小题满分12分) 已知函数21()(2)2ln ()2f x ax a x x a R =-++∈. (1)若0a =,证明:()0f x <; (2)讨论函数()f x 零点的个数.解(1) 证明:当0a =时, ()22ln (0)f x x x x =-+>22(1)()2x f x x x-'=-+=列表:max ()(1)20f x f ∴==-< max ()()0f x f x ≤<,即()0f x <………………………………………………………………………………2分(2)2()(2)(0)f x ax a x x'=-++>…………………………………………………………………………3分2(2)2(1)(2)()(0)ax a x x ax f x x x x-++--'==>讨论: 01当0a =时,由第(1)问可得函数()f x 没有零点; ……………………………………………4分02 当21a>,即02a <<时, 令(1)(2)()0x ax f x x --'=>得01x <<,或2x a >,即函数()f x 的增区间为(0,1),2(,)a +∞令(1)(2)()0x ax f x x --'=<得21x a <<,即函数()f x 的减区间为2(1,)a而11(1)(2)2ln12022f a a a =-++=--<,因为函数()f x 的减区间为2(1,)a ,所以2()(1)0f f a <<又函数()f x 的增区间为(0,1),2(,)a+∞所以当(0,1)x ∈时,()(1)0f x f <<所以当2(,)x a∈+∞时, 2()()f x f a >,x →+∞时,()f x →+∞ 所以函数()f x 在区间2(0,)a 没有零点,在区间2(,)a+∞有一个零点………………………………………6分03 当21a=,即2a =时, 2(1)(2)(1)(22)2(1)()0x ax x x x f x x x x-----'===≥恒成立即函数()f x 在(0,)+∞上递增 而11(1)222022f a =--=-⨯-<,x →+∞时,()f x →+∞ 所以函数()f x 在区间(0,)+∞有一个零点……………………………………………………………………8分04 当201a<<,即2a >时, 令(1)(2)()0x ax f x x --'=>得20x a <<,或1x >,即函数()f x 的增区间为2(0,)a ,(1,)+∞令(1)(2)()0x ax f x x --'=<得21x a <<,即函数()f x 的减区间为2(,1)a因为2a >,所以2222()22ln 22ln10f a a a a=--+<--+<,又x →+∞时,()f x →+∞根据函数单调性可得函数()f x 在区间(0,1)没有零点,在区间(1,)+∞有一个零点……………………10分05 当20a<,即0a <时, 令(1)(2)()0x ax f x x--'=>得01x <<,即函数()f x 的增区间为(0,1)令(1)(2)()0x ax f x x --'=<得1x >,即函数()f x 的减区间为(1,)+∞0x →时,()f x →-∞ x →+∞时,()f x →-∞而114(1)(2)2ln12222a f a a a --=-++=--=当4(1)02a f --=>即4a <-时, 函数()f x 有两个零点;当4(1)02a f --==即4a =-时, 函数()f x 有一个零点;当4(1)02a f --=<即40a -<<时, 函数()f x 没有零点. ………………………………………11分 综上,4a <-时, 函数()f x 有两个零点;4a =-时, 函数()f x 有一个零点; 40a -<≤时, 函数()f x 没有零点;0a >时, 函数()f x 有一个零点;………………………………………12分请考生在22、23、24三题中任选一题作答,如果多做,则按所做第一个题目计分,做答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑.22.(本小题满分10分)选修4—1:几何证明选讲如图,过圆O 外一点M 作它的一条切线,切点为A ,过A 作直线AP OM ⊥于P(1)证明:2OA OM OP =⋅;(2)N 为线段AP 上一点,直线NB ON ⊥且交圆O 于B 点,过B 点的切线交直线ON 于K .证明:090OKM ∠=.证明:(1)由MA是圆O 的切线知:AM OA ⊥ …………………………………………………………2分 又∵AP OM ⊥;∴ 在Rt OAM 中,由射影定理知:2OA OM OP =⋅……………………………………………………4分(2)证明:由BK是圆O 的切线知:BN OK ⊥.同(1)2OB ON OK =⋅……………………………6分由OB OA=得:O M O P O N O K ⋅=⋅………………………………………………………………………7分即:OP OKON OM=.又NOP MOK∠=∠,则NOP MOK V :V …………………………………………9分∴090OKM OPN ∠=∠=.………………………………………………………………………………10分(用M P N K 、、、四点共圆来证明也得分) 23.(本小题满分10分)选修4-4:坐标系与参数方程在极坐标系中,已知射线1C :()03πθρ=≥,动圆2C :220002cos 40()x x x R ρρθ-+-=∈.(1)求1C ,2C 的直角坐标方程;(2)若射线1C 与动圆2C 相交于M 与N 两点,求0x 的取值范围.解(1) ()tan ,03y x πθθρ==≥Q(0)y x x ∴=≥, 所以1C 的直角坐标方程为(0)y x x =≥…………………………………………………………2分cos sin x y ρθρθ=⎧⎨=⎩Q ,所以2C 的直角坐标方程22200240x y x x x +-+-=.…………………………2分(2) 联立()22000032cos 40()x x x R πθρρρθ⎧=≥⎪⎨⎪-+-=∈⎩ 关于ρ的一元二次方程2200040()x x x R ρρ-+-=∈在[0,)+∞内有两个实根…………………………6分即220012021204(4)0040x x x x x x x x ⎧∆=-->⎪+=>⎨⎪⋅=->⎩,……………………………………………………………………………………8分得000002,2x x x x ⎧<<⎪⎪⎪>⎨⎪><-⎪⎪⎩或,即02x <<10分 (用数形结合法解出也给分)24.(本小题满分10分)选修4—5:不等式选讲 已知不等式221x x a +-->.(1)当0a =时,求不等式的解集;(2)若不等式在区间[4,2]-内无解,求实数a 的取值范围.解: (1)由题意得:2210x x +-->,即:221x x +>-……………………………………………1分∴22(22)(1)x x +>-,即:231030x x ++>……………………………………………………………3分解得:3x <-或13x >-; ∴不等式的解集为1(,3)(,)3-∞-⋃-+∞……………………………………………………………………5分 (2)设()221([4,2])f x x x x =+--∈-,则:3,(41)()31,(11)3,(12)x x f x x x x x ---≤<-⎧⎪=+-≤<⎨⎪+≤≤⎩, ……………………………7分其图像如图示:则()f x 的最大值为(2)5f =……………………8分∵ 不等式221x x a +-->在区间[4,2]-无解,∴实数a 的取值范围为[5,)+∞…………………………………………10分。
广东省2015届六校高三毕业班第二次联考

广东省2015届六校高三毕业班第二次联考历史试题(2014.11.8)六校分别为:广州二中、中山纪中、东莞中学、珠海一中、深圳实验、惠州一中一.选择题(24小题,每题2分,共48分。
在每小题列出的四个选项中,只有一项符合题目要求,请将答案涂在答题卡相应位置)1. 汉武帝设置十三州刺史以监察地方,并将豪强大族“田宅逾制”作为重要的监察内容,各地财产达300万钱的豪族被迁到长安附近集中居住。
这表明A.政权的政治与经济支柱是豪强大族B.政治权力与经济势力出现严重分离C.经济手段是巩固专制集权的主要方式D.抑制豪强是缓解土地兼并的重要措施2.《论衡》中记载“深耕细锄,厚加粪壤,勉致人工,以助地力”,“地力盛者,草木畅茂,一亩之收,当中田五亩之分”。
这体现出我国古代农业生产中A.“重农”的思想B.“靠天吃饭”的观念C.“不误农时”的思想 D.“精耕细作”的特点3.唐太宗太和六年(832年)宰相王涯上奏:“商人乘马,前代所禁。
近日得以恣其乘骑,雕鞍银鉴,装饰焕烂,从以童骑,骋以康庄。
最为僭越,伏请切令禁断。
”这表明A.商人的经济地位优越 B.商人的行为违反社会良俗C.抑商观念仍未得到改观 D.商人仍未获得自由民的政治地位4. 唐诗“慢束罗裙半露胸”、“绮罗纤缕见肌肤”,描写了唐朝服饰的艳丽奢华和开放。
但宋朝时的服饰却简洁质朴,女装拘谨、保守,色彩淡雅恬静。
唐宋服饰的演变,反映了人们审美观的变化,此种审美观的转变主要是由于A.封建经济的衰退B.专制集权的巩固C.理学思想的影响D.审美意识的觉醒5.据考证,从公元994年起,成都的铁钱监铸钱就停止了,一直到公元1005年,成都没有再铸过钱,但成都市场上并没有出现钱荒。
造成这种现象的原因最有可能是A.白银成为主流货币B.铜钱取代铁钱C.民间发行交子,对铁钱的依赖降低D.经济萧条,对铁钱的需求减少6. 有人这样评论当时的政治制度:如果宰相制尚未废除,宰相就会用古代圣人贤君的德行来劝谏君主,君主就不会肆无忌惮。
广东省珠海市第一中学2015届高三9月阶段考数学理试题Word版含答案

珠海一中2015届高三阶段考试数学(理)试题 2014.9一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项. 1.已知集合{{,A x R y B y R y =∈==∈=,则AB =A. ∅B.{}1 C. []0,1 D.(){}1,02. 若命题p :2,210x R x ∀∈+>,则⌝p 是A .2,210x R x ∀∈+≤B .2,210x R x ∃∈+>C .2,210x R x ∀∈+<D .2,210x R x ∃∈+≤ 3.函数()ln 26f x x x =+-的零点位于A .[1,2]B .[2,3]C .[3,4]D .[4,5] 4.“1cos 22α=”是“1sin 2α=”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件5. 设a b <,函数23()()ya x xb =--的图像可能是6. 已知函数f (x )=sin(ωx +π6)(ω>0)的最小正周期为4π,则 A .函数f (x )的图像关于点(),03π对称;B .函数f (x )的图像关于直线x =π3对称;C .函数f (x )的图像向右平移π3个单位后,图像关于原点对称; D .函数f (x )在区间()0,π上单调递增.7. 设函数()y f x =的反函数是()y g x =.如果()()()f ab f a f b =+,则有A .()()()g ab g a g b =⋅ B .()()()g a b g a g b +=+ C .()()()g a b g a g b +=⋅ D .()()()g ab g a g b =+8.当[]2,1x ∈-时,不等式32430ax x x -++≥恒成立,则实数a 的取值范围是A .[-5,-3] B.⎣⎡⎦⎤-6,-98 C .[-6,-2] D .[-4,-3]二、填空题:本大题共6小题,每小题5分,满分30分.请将答案填在答题卡相应位置.9.已知函数()sin,6f x x π=则(2014)f = .10. 如图是函数()sin(),(0,0,||)2f x A x A πωϕωϕ=+>><在一个周期内的的图象,则函数()f x 的解析式是 . (第10题图)11. 已知函数2log ()3xx f x ⎧=⎨⎩(0)(0)x x >≤,则方程()1f x =解的个数为 .12. 如图,由0,,0.,ln ,x xx e y y e y x y e ======六条曲线共同围成的面积为 . (第12题图)13.如果函数y =sin 2x +a cos 2x 的图像关于直线x =-π8对称,则实数a 的值为 . 14.设函数f (x )=⎩⎪⎨⎪⎧x 2+x ,x <0,-x 2, x ≥0.则不等式[]()2f f x≤的解集为 .三、解答题:本题共有6个小题,满分80分.解答须写出文字说明、证明过程和演算步骤,格式要规范.15.(本小题满分12分)完成下列各题:(Ⅰ)求函数()f x =(Ⅱ)求函数sin 1()cos 3x f x x +=+的值域;16. (本小题满分12分)求y =(sin x -2)(cos x -2)的最大值和最小值.17. (本小题满分14分)已知函数2()22cos f x x x =+.(Ⅰ) 求函数()f x 的最小正周期和单调递增区间.(Ⅱ)将()f x 的图像向右平移π12个单位长度,得到函数()g x 的图像;再将得到函数()g x 的图像向下平移1个单位,同时将周期扩大1倍,得到函数()h x 的图像,分别写出函数()g x 与()h x 解析式;18. (本小题满分14分)已知函数()f x 的定义域为R,对任意实数,m n 都有()()()f m n f m f n +=∙,且当0x >时,0()1f x <<.(Ⅰ)证明:(0)1,f =且0x <时()1f x >; (Ⅱ)证明: ()f x 在R 上单调递减;(Ⅲ)设A=22{(,)()()(1)}x y f x f y f ∙>,B={(,)(2)1,x y f ax y a R -+=∈},若A B =∅,试确定a 的取值范围.19. (本小题满分14分)已知xxx g e x x ax x f ln )(],,0(,ln )(=∈-=,其中e 是自然常数,.a R ∈ (Ⅰ)讨论1=a 时, ()f x 的单调性、极值; (Ⅱ)当1=a 时,求证:1()()2f xg x >+; (Ⅲ)是否存在实数a ,使()f x 的最小值是3,若存在,求出a 的值;若不存在,说明理由.20. (本小题满分14分)已知函数).(12ln)(R ∈-+=m mx x x f(I )求函数)(12ln )(R ∈-+=m mx x x f 的单调区间;(II )若函数m m x f 求恒成立,1)(2+≤的取值范围; (III )当.2)()(34:,10,1<--<≤<≤-=ba b f a f a b m 证明时且珠海一中2015届高三阶段考试数学(理)试题参考答案一、选择题:1-8 C D B B C C C C二、填空题:本大题共6小题,每小题5分,满分30分.请将答案填在答题卡相应位置.9.2-. 10.()=3sin(2)3f x x π+. 11. 2. 12.22e -.13.-1.14.(-∞.三、解答题:本题共有6个小题,满分80分.解答须写出文字说明、证明过程和演算步骤,格式要规范.15.解:(Ⅰ)由3-tan x ≥0,得tan x ≤3, ……………………………………3分.∴k π-π2<x ≤k π+π3(k ∈Z),∴()f x 的定义域为⎝ ⎛⎦⎥⎤k π-π2,k π+π3(k ∈Z).……………………………6分.(Ⅱ)由y =1+sin x3+cos x得sin x -y cos x =3y -1,∴y 2+1sin(x +φ)=3y -1,这里cos φ=11+y 2, sin φ=-y1+y 2.…………………………………8分. ∵|sin(x +φ)|≤1,∴|3y -1|≤y 2+1, ………………………………………10分.解得0≤y ≤34,∴原函数的值域为30,4⎡⎤⎢⎥⎣⎦. ………………………………………12分. 16.解:原函数可化为y =sin x cos x -2(sin x +cos x )+4. ……………………………2分. 令sin x +cos x =t (|t |≤2),则sin x cos x =t 2-12,……………………………………4分. ∴y =t 2-12-2t +4 ……………………………………………………………6分. =12(t -2)2+32 ………………………………………………………………7分. ∵t =2∉[-2,2],且函数在[-2,2]上为减函数, ……………………………8分. ∴当t =2,即x =2k π+π4(k ∈Z)时,y min =92-22; ……………………………10分. 当t =-2,即x =2k π-3π4(k ∈Z)时,y max =92+2 2. …………………………12分.17.解:(Ⅰ)1)62sin(21)2cos 212sin 23(212cos 2sin 3)(++=++=++=πx x x x x x f ……3分 ()f x 的最小正周期为π。
广东省各市2015年高考二模数学理试题分类汇编.三角函数

广东省各市2015年高考二模数学理试题分类汇编三角函数1.(2015届广州市)函数()sin y A x ωϕ=+()0,0,0A ωϕ>><<π的图象的一部分如图1所示,则此函数的解析式为A .3sin y x ππ⎛⎫=+⎪44⎝⎭ B .3sin y x π3π⎛⎫=+ ⎪44⎝⎭C .3sin y x ππ⎛⎫=+⎪24⎝⎭ D .3sin y x π3π⎛⎫=+ ⎪24⎝⎭2(2015届揭阳市)已知1sin()3πα+=,则cos 2α= A.429B.89C.79-D.793.(2015届茂名市) 在△ABC 中,54sin =A ,6=∙AC AB ,则△ABC 的面积为( ). A .3B .125C .6D .44(2015届肇庆市)在∆ABC 中,AB =5,AC =3,BC =7,则∠BAC = A .65π B .32π C .3π D .6π 答案:A D D B二.填空题5(2015届广州市)已知()s i n 6fx x π⎛⎫=+⎪⎝⎭,若3c o s 5α=02απ⎛⎫<< ⎪⎝⎭,则12f απ⎛⎫+= ⎪⎝⎭ .6(2015届揭阳市)在△ABC 中,已知角C B A ,,所对的边分别为c b a ,,, 且2(cos cos )c a B b A b -=,则sin sin AB= . 答案:72102y xO 1 5 3 -3图1NMPoyx7(2015届潮州市)(本小题满分12分)已知向量⎪⎭⎫⎝⎛-=1,3sin x m ,)0(,3cos 21,23>⎪⎪⎭⎫ ⎝⎛=A x A A n ,函数()f x n m =⋅ 的最大值为2.(1)求()f x 的最小正周期和解析式; (2)设,[0,]2παβ∈,10(3)213f πα+=,6(32)5f βπ+=,求sin()αβ-的值.8(2015届广州市)(本小题满分12分)已知△ABC 的三边a ,b ,c 所对的角分别为A ,B ,C ,且::7:5:3a b c =. (1)求cos A 的值;(2)若△ABC 的面积为453,求△ABC 外接圆半径的大小.9(2015届惠州市)(本小题满分12分)已知函数()sin()6f x A x πω=+(0,0)A ω>>的最小正周期为6T π=,且(2)2f π=.(1)求()f x 的表达式; (2)设,[0,]2παβ∈,16(3)5f απ+=,520(3)213f πβ+=-,求cos()αβ-的值.10(2015届揭阳市)(本小题满分12分)已知函数()sin()6f x A x πω=+(00)A ω>>,的部分图象如图4示,其中M 1(,0)6-为图象与x 轴的交点,1(,2)3P 为图象的最高点.(1)求A 、ω的值;(2)若2()3f απ=,(,0)3πα∈-,求cos()3πα+的值.11(2015届茂名市) (本小题满分12分)已知函数)0,0)(6sin()(>>+=ωπωA x A x f 图象的一部分如图所示.(1)求函数)(x f 的解析式; (2)设]0,2[,πβα-∈,1310)3(=+παf , 56)253(=+πβf ,求sin()αβ-的值.12(2015届深圳市)(本小题满分12分)设函数)2cos()(ϕ+=x x f (其中π0<<ϕ,R ∈x ).已知21)0(-=f . (1)求函数)(x f 的解析式;(2)若角θ满足)()3πsin(θθf =+,且π0<≤θ,求角θ的值.13(2015届肇庆市)(本小题满分12分)已知函数x x x x f 2cos )23sin()sin(3)(-++=ππ. (1)求函数)(x f 的最小正周期; (2)若]0,2[πθ-∈,103)32(=+πθf ,求)42sin(πθ-的值.7解:(1)⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=-=63(sin 3cos 213sin 233cos 213sin 23)(πx A x x A x A x A x f …3分 ()f x 的最小正周期2613T ππ== ……………………………………………4分因为 0A >,由题意知A=2, ……………………………5分 所以 1()2sin(),36f x x x R π=-∈ (6)分 (2)10132sin 32sin ,132326f πππααα⎛⎫⎛⎫⎛⎫=+=⨯+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭61(32)2sin (32)2sin 2cos ,5362f ππβπβπββ⎛⎫⎛⎫=+=⨯+-=+= ⎪ ⎪⎝⎭⎝⎭ ………8分53sin ,cos ,135αβ∴==,[0,]2παβ∈22512cos 1sin 1,1313αα⎛⎫∴=-=-= ⎪⎝⎭2234sin 1cos 1,55ββ⎛⎫=-=-= ⎪⎝⎭……………………………10分 5312433sin()=sin cos cos sin 13513565αβαβαβ--=⨯-⨯=- (12)分8(1)因为::7:5:3a b c =,所以可设7a k=,5b k=,3c k =()0k >,…………………………………………………………2分由余弦定理得,222cos 2b c a A bc +-=()()()222537253k k k k k+-=⨯⨯…………………………………………………………3分12=-.………………………………………………………………………………………………4分(2)由(1)知,1cos 2A =-, 因为A 是△ABC 的内角, 所以2s i A A =-32=.………………………………………………………………………6分由(1)知5b k =,3c k =, 因为△ABC的面积为453,所以1s i n 4532b c A =,……………………………………………8分即135345322k k ⨯⨯⨯=,解得23k =.…………………………………………………………………………………………10分由正弦定理2s ina R A=,即71432s i n32k R A ==,…………………………………………………11分 解得14R =.所以△ABC 外接圆半径的大小为14.…………………………………………………………………12分 9(本小题满分12分)解:(1)依题意得2π2π1==T 6π3ω=,∴x πf(x)=Asin(+)36, ……2分 由f(2π)=2,得2ππAsin(+)=236,即5πAsin =26,∴A=4, ……4分 ∴x πf(x)=4sin(+)36. ……5分(2)由16f(3α+π)=5,得1π164sin[(3α+π)+)]=365,即π164sin(α+)=25,∴4cos 5α=, ……6分又∵πα[0]2∈,,∴3sin 5α=, ……7分由5π20f(3+)=213β-,得15ππ204sin[(3+)+)]=32613β-, 即5sin(+π)=13β-,∴5sin β13=, ……9分又∵πβ[0]2∈,,∴12cos β13=, ……10分cos(α-β)= cosαcosβ+ sinαsinβ412356351351365=⨯+⨯=. ……12分 10解:(1)由1(,2)3P 为图象的最高点知2A =,---------------------1分又点M 1(,0)6-知函数()f x 的最小正周期114()236T =+=,-----------------------3分∵2T πω= ∴ωπ=,-------------------------------------------------5分(2)由(1)知,()2sin()6f x x ππ=+由2()3f απ=得1sin()63πα+=,----------------------------------------6分∵(,0)3πα∈- ∴666πππα-<+<----------------------------------------7分∴2122cos()1sin ()16693ππαα+=-+=-=-------------------------9分 ∵cos()cos()366πππαα+=++cos()cos sin()sin 6666ππππαα=+-+-------------11分∴cos()3πα+2231126132326-=⨯-⨯=------------12分 11解:(1)由图象可知2=A , …………………………………………………………1分,2921143πππ=-=Tωππ26==∴T 31=∴ω. ………………………3分 )631sin(2)(π+=∴x x f . ………………………4分(2)∵10(3)2sin()2cos ,213f παπαα+=+==∴5cos 13α=,………………6分 又∵56sin 2)sin(2)253(=-=+=+βπβπβf ∴53sin -=β,……………8分 ∵]0,2[,πβα-∈,,1312)135(1cos 1sin 22-=--=--=∴αα54)53(1sin 1cos 22=--=-=ββ. ………………………………………10分∴sin()sin cos cos sin αβαβαβ-=-.6533)53(13554)1312(-=-⨯-⨯-=………………………………12分 12(本小题满分12分)设函数()cos(2)f x A x =+ϕ(其中0A >,0π<<ϕ,R ∈x ).已知π6x =时,()f x 取得最小值2-.(1)求函数)(x f 的解析式; (2)若角θ满足π2sin()()3f +=θθ,且π0<≤θ,求πsin()3θ+的值.解:(1)由()f x 最小值2-且0A >,所以2A =. …………………………………………1分因为π()26f =-,所以πcos()13ϕ+=-, ……………………………………………………2分由0π<<ϕ可得ππ4π333ϕ<+<,所以ππ3ϕ+=, ………………………………………3分 所以2π3ϕ=. ……………………………………………………………………………………4分 故)(x f 的解析式为2π()2cos(2)3f x x =+. …………………………………………………5分 (2)(法1)由(1),得)3π22cos()3πsin(+=+θθ,即)3π(sin 21)3πsin(2+-=+θθ,01)3πsin()3π(sin 22=-+++θθ, ……………………8分所以1)3πs in-=+θ或21)3πsin(=+θ. ………………………………………………10分又0πθ≤<,所以ππ4π333θ≤+<. …………………………………………………11分所以21)3πsi =+θ. ………………………………………………………………………12分(法2)由(1),得)3π22cos()3πsin(+=+θθ, 即)3π22cos()6πcos(+=-θθ.………………………………………………………8分所以θθ-+=+6ππ23π22k 或θθ+-=+6ππ23π22k ,Z ∈k . …………………………10分即6π3π2-=k θ或65ππ2-=k θ,Z ∈k .又0πθ≤<,所以2π=θ. …………………………………………………………11分 所以21)3πsi =+θ. ………………………………………………………………………12分13(本小题满分12分)解:(1)x x x x f 2cos cos sin 3)(-= (2分)212cos 2sin 23+-=x x (4分) 21)62sin(--=πx (5分) 所以函数)(x f 的最小正周期ππ==22T . (6分) (2)由(1)得21cos 21)2sin(21]6)32(2sin[)32(-=-+=--+=+θπθππθπθf ,(7分)由10321cos =-θ,得54cos =θ. (8分) 因为]0,2[πθ-∈,所以53sin -=θ. (9分)所以2524cos sin 22sin -==θθθ,2571cos 22cos 2=-=θθ, (11分)所以502314sin2cos 4cos2sin )42sin(-=-=-πθπθπθ. (12分)。
广东省珠海市2015届高三上学期期末数学试卷(理科)Word版含解析

广东省珠海市2015届高三上学期期末数学试卷(理科)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项.1.(5分)设集合A={x|y=lg(x﹣1)},B={y|y=2x,x∈R},则A∪B=()A.∅B.R C.(1,+∞)D.(0,+∞)2.(5分)若复数z与2+3i互为共轭复数,则复数z的模|z|=()A.B.5C.7D.133.(5分)下列函数为偶函数的是()A.f(x)=x2+B.f(x)=log2x C.f(x)=4x﹣4﹣x D.f(x)=|x﹣2|+|x+2| 4.(5分)若x、y满足不等式组,则的最小值是()A.B.C.D.15.(5分)执行如图的程序框图,若输出的S=48,则输入k的值可以为()A.4B.6C.8D.106.(5分)二项式(2x+)6的展开式中,常数项的值是()A.240 B.60 C.192 D.1807.(5分)如图是一个几何体的三视图,根据图中数据可得该几何体的体积是()A.B.C.2D.48.(5分)已知集合S={P|P=(x1,x2,x3),x i∈{0,1},i=1,2,3}对于A=(a1,a2,a3),B=(b1,b2,b3)∈S,定义A与B的差为A﹣B=(|a1﹣b1|,|a2﹣b2|,|a3﹣b3|),定义A与B之间的距离为d(A,B)=|a i﹣b i|.对于∀A,B,C∈S,则下列结论中一定成立的是()A.d(A,C)+d(B,C)=d(A,B)B.d(A,C)+d(B,C)>d(A,B)C.d(A﹣C,B﹣C)=d(A,B)D.d(A﹣C,B﹣C)>d(A,B)二、填空题:本大题共5小题,每小题5分,满分25分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.请将答案填在答题卡相应位置.9.(5分)不等式|2x﹣1|≥x的解集为.10.(5分)三个学生两位老师三位家长站成一排,则老师站正中间的概率是.11.(5分)已知等差数列{a n}的前n项和记为S n,且a3=5,S3=6,则a7=.12.(5分)已知函数f(x)的导函数为f′(x),且满足f(x)=x3﹣x•f′(2),则函数f(x)在点(2,f(2))处的切线方程为.13.(5分)已知平面向量满足|2+3|=1,则•的最大值为.(坐标系与参数方程选做题)14.(5分)在极坐标系中,曲线C1:ρ=2与曲线C2:ρ=4sinθ(<θ<π)交点的极坐标是.(几何证明选讲选做题)15.如图,四边形ABCD内接于圆O,DE与圆O相切于点D,AC∩BD=F,F为AC的中点,O∈BD,CD=,BC=5,则AE=.三、解答题:本题共有6个小题,共80分.请写出解答的步骤与详细过程.16.(12分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<)在某一个周期内的图象时,列表并填入的部分数据如下表:x x1x2x3ωx+φ0 π2πAsin(ωx+φ)+B 1 4 1 ﹣2 1(1)求函数f(x)的解析式;(2)若<α<π,f(﹣)=,求f(α+)的值.17.(12分)某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:x i(月) 1 2 3 4 5y i(千克)0.5 0.9 1.7 2.1 2.8(1)在给出的坐标系中,画出关于x,y两个相关变量的散点图.(2)请根据上表提供的数据,用最小二乘法求出变量y关于变量x的线性回归直线方程.(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克)(参考公式:=,=﹣)18.(14分)已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2).(1)求证:BF∥面A1DE;(2)求证:面A1DE⊥面DEBC;(3)求二面角A1﹣DC﹣E的正切值.19.(14分)已知数列{a n}的前n项和为S n,且S n=n•a n+1,n∈N*,其中a1=1(1)求数列{a n}的通项公式;(2)若b n=,数列{b n}的前n项和为T n,求证:T n<.20.(14分)已知抛物线C1:x2=y,圆C2:x2+(y﹣4)2=1.(1)在抛物线C1上取点M,C2的圆周取一点N,求|MN|的最小值;(2)设P(x0,y0)(2≤x0≤4)为抛物线C1上的动点,过P作圆C2的两条切线,交抛物线C1于A,B两点.求AB的中点D的横坐标的取值范围.21.(14分)已知函数f(x)=alnx+x2﹣(1+a)x.(1)求函数f(x)的单调区间;(2)证明:m、n∈N+时,m(m+n)[+++…+]>n.广东省珠海市2015届高三上学期期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项.1.(5分)设集合A={x|y=lg(x﹣1)},B={y|y=2x,x∈R},则A∪B=()A.∅B.R C.(1,+∞)D.(0,+∞)考点:并集及其运算.专题:集合.分析:求出集合A,B,根据并集运算进行求解.解答:解:A={x|y=lg(x﹣1)}={x|x>1},B={y|y=2x,x∈R}={y|y>0},则A∪B={x|x>0},故选:D点评:本题主要考查集合的基本运算,比较基础.2.(5分)若复数z与2+3i互为共轭复数,则复数z的模|z|=()A.B.5C.7D.13考点:复数求模.专题:数系的扩充和复数.分析:利用共轭复数的定义、模的计算公式即可得出.解答:解:∵复数z与2+3i互为共轭复数,∴z=2﹣3i,∴|z|==.故选:A.点评:本题考查了共轭复数的定义、模的计算公式,属于基础题.3.(5分)下列函数为偶函数的是()A.f(x)=x2+B.f(x)=log2x C.f(x)=4x﹣4﹣x D.f(x)=|x﹣2|+|x+2|考点:函数奇偶性的判断.专题:函数的性质及应用.分析:根据函数奇偶性的定义进行判断即可.解答:解:A.f(1)=1+1=2,f(﹣1)=1﹣1=0,则f(﹣1)≠f(1),故f(x)不是偶函数,B.函数的定义域为(0,+∞),定义域关于原点不对称,故函数f(x)是非奇非偶函数.C.f(﹣x)=4﹣x﹣4x=﹣(4x﹣4﹣x)=﹣f(x),则f(x)是奇函数,D.f(﹣x)=|﹣x﹣2|+|﹣x+2|=|x+2|+|x﹣2|=f(x),故函数f(x)是偶函数,故选:D点评:本题主要考查函数奇偶性的判断,根据函数奇偶性的定义是解决本题的关键.4.(5分)若x、y满足不等式组,则的最小值是()A.B.C.D.1考点:简单线性规划.专题:数形结合.分析:由约束条件作出可行域,根据的几何意义可知,的最小值为原点O 到直线x+2y﹣2=0的距离,由点到直线的距离公式得答案.解答:解:由约束条件作出可行域如图,的几何意义为可行域内的动点到原点的距离,由图可知,的最小值为原点O到直线x+2y﹣2=0的距离,等于.故选:B.点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.5.(5分)执行如图的程序框图,若输出的S=48,则输入k的值可以为()A.4B.6C.8D.10考点:程序框图.专题:算法和程序框图.分析:模拟执行程序框图,依次写出每次循环得到的n,S的值,当S=48时,由题意,此时应该满足条件n=10>k,退出循环,输出S的值为48,故应有:7<k<10.解答:解:模拟执行程序框图,可得n=1,S=1不满足条件n>k,n=4,S=6不满足条件n>k,n=7,S=19不满足条件n>k,n=10,S=48由题意,此时应该满足条件n=10>k,退出循环,输出S的值为48,故应有:7<k<10故选:C.点评:本题主要考查了程序框图和算法,根据退出循环的条件分析k的取值范围是解题的关键,属于基础题.6.(5分)二项式(2x+)6的展开式中,常数项的值是()A.240 B.60 C.192 D.180考点:二项式系数的性质.专题:概率与统计.分析:利用通项公式T r+1==x6﹣3r,令6﹣3r=0,解得r=2.即可得出.解答:解:T r+1==x6﹣3r,令6﹣3r=0,解得r=2.∴常数项的值是==240.故选:A.点评:本题考查了二项式定理的通项公式、常数项,属于基础题.7.(5分)如图是一个几何体的三视图,根据图中数据可得该几何体的体积是()A.B.C.2D.4考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:由三视图复原几何体是四棱锥,它的底面是主视图,棱锥的高为1,根据公式可求体积.解答:解:由三视图复原几何体是四棱锥,它的底面是主视图,棱锥的高为1,这个几何体的体积:V==故选B.点评:本题考查三视图、棱锥的体积;考查简单几何体的三视图的运用;考查空间想象能力和基本的运算能力.8.(5分)已知集合S={P|P=(x1,x2,x3),x i∈{0,1},i=1,2,3}对于A=(a1,a2,a3),B=(b1,b2,b3)∈S,定义A与B的差为A﹣B=(|a1﹣b1|,|a2﹣b2|,|a3﹣b3|),定义A与B之间的距离为d(A,B)=|a i﹣b i|.对于∀A,B,C∈S,则下列结论中一定成立的是()A.d(A,C)+d(B,C)=d(A,B)B.d(A,C)+d(B,C)>d(A,B)C.d(A﹣C,B﹣C)=d(A,B)D.d(A﹣C,B﹣C)>d(A,B)考点:进行简单的合情推理.专题:推理和证明.分析:因为每个数位上都是0或者1,取差的绝对值仍然是0或者1,符合S n的要求.然后是减去C的数位,不管减去的是0还是1,每一个a和每一个b都是同时减去的,因此不影响他们原先的差.解答:解:设A=(a1,a2,a3),B=(b1,b2,b3),C=(c1,c2,c3)∈S因a i,b i∈0,1,故|a i﹣b i|∈0,1,(i=1,2,3)a1b1∈0,1,即A﹣B=(|a1﹣b1|,|a2﹣b2|,|a3﹣b3|)∈S又a i,b i,c i∈(0,1),i=1,2,3当c i=0时,有||a i﹣c i|﹣|b i﹣c i||=|a i﹣b i|;当c i=1时,有||a i﹣c i|﹣|b i﹣c i||=|(1﹣a i)﹣(1﹣b i)=|a i﹣b i|,故d(A﹣C,B﹣C)=d(A,B)成立.点评:本题是综合考查集合、数列与推理综合的应用,这道题目的难点主要出现在读题上,需要仔细分析,以找出解题的突破点.题目所给的条件其实包含两个定义,第一个是关于S n 的,其实S n中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1,第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了.二、填空题:本大题共5小题,每小题5分,满分25分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.请将答案填在答题卡相应位置.9.(5分)不等式|2x﹣1|≥x的解集为{x|x≥1或x≤}.考点:绝对值不等式的解法.专题:计算题;不等式的解法及应用.分析:由绝对值的定义可得,或,分别解出它们,再求并集即可.解答:解:不等式|2x﹣1|≥x即为或,即有或,则有x≥1或x≤.则解集为{x|x≥1或x≤}.故答案为:{x|x≥1或x≤}.点评:本题考查绝对值不等式的解法,考查定义法解不等式,考查运算能力,属于基础题.10.(5分)三个学生两位老师三位家长站成一排,则老师站正中间的概率是.考点:计数原理的应用.专题:概率与统计.分析:先求出没有任何要求的站法,再求出老师站正中间站法,根据古典概型的概率公式可得.解答:解:没有要求的站队方法共有,老师站正中间的站队方法共有,根据古典概型的概率公式可得,三个学生两位老师三位家长站成一排,则老师站正中间的概率P==,故答案为:点评:本题主要考查了古典概型的概率问题,关键是利用排列组合求出基本事件,属于基础题.11.(5分)已知等差数列{a n}的前n项和记为S n,且a3=5,S3=6,则a7=17.考点:等差数列的前n项和.专题:计算题;等差数列与等比数列.分析:运用等差数列的求和公式,由a3=5,S3=6,可得a1=﹣1,再由通项公式可得d=3,再由通项公式即可得到所求.解答:解:∵S3==6,∴a1+a3=4,而a3=5,∴a1=﹣1,∴d==3.则a7=a1+6d=﹣1+6×3=17.故答案为:17.点评:本题主要考查等差数列的通项公式,等差数列的前n项和公式的应用,属于基础题.12.(5分)已知函数f(x)的导函数为f′(x),且满足f(x)=x3﹣x•f′(2),则函数f(x)在点(2,f(2))处的切线方程为6x﹣y﹣16=0.考点:导数的运算;利用导数研究曲线上某点切线方程.专题:导数的综合应用.分析:f(x)=x3﹣x•f′(2),可得f′(x)=3x2﹣f′(2),令x=2,可得f′(2)=6.可得f(x),利用点斜式即可得出切线方程.解答:解:∵f(x)=x3﹣x•f′(2),∴f′(x)=3x2﹣f′(2),令x=2,可得f′(2)=6.∴f(x)=x3﹣6x,∴f(2)=23﹣6×2=﹣4.∴函数f(x)在点(2,f(2))处的切线方程为y﹣(﹣4)=6(x﹣2),化为6x﹣y﹣16=0,故答案为:6x﹣y﹣16=0.点评:本题考查了导数的几何意义、切线方程、点斜式,属于基础题.13.(5分)已知平面向量满足|2+3|=1,则•的最大值为.考点:平面向量数量积的运算.专题:计算题;不等式的解法及应用;平面向量及应用.分析:利用•=﹣,结合条件和不等式的性质即可得出最大值.解答:解:由|2+3|=1,则•=﹣=﹣≤,当且仅当2=3,即||=时,上式等号成立.∴•最大值为.故答案为:.点评:本题考查平面向量的数量积的运算,考查不等式的性质,属于中档题.(坐标系与参数方程选做题)14.(5分)在极坐标系中,曲线C1:ρ=2与曲线C2:ρ=4sinθ(<θ<π)交点的极坐标是.考点:简单曲线的极坐标方程.专题:坐标系和参数方程.分析:曲线C1:ρ=2化为x2+y2=4,曲线C2:ρ=4sinθ(<θ<π)化为x2+y2=4y,(x<0,y∈(0,4)).联立解得,利用,即可得出.解答:解:曲线C1:ρ=2化为x2+y2=4,曲线C2:ρ=4sinθ(<θ<π)化为ρ2=4ρsinθ,即x2+y2=4y,(x<0,y∈(0,4)).联立,解得,∴=2,,解得.∴交点的极坐标是.点评:本题考查了极坐标与直角坐标的互化,考查了计算能力,属于基础题.(几何证明选讲选做题)15.如图,四边形ABCD内接于圆O,DE与圆O相切于点D,AC∩BD=F,F为AC的中点,O∈BD,CD=,BC=5,则AE=2.考点:与圆有关的比例线段.专题:直线与圆;推理和证明.分析:由已知条件,利用切割线定理、垂径定理、勾股定理,推导出(EA+5)2=EA(EA+AB)+35,由此能求出EA.解答:解:∵DE与圆O相切于点D,∴DE2=EA(EA+AB),(EA+AB)2=DE2+BD2∵AC∩BD=F,F为AC的中点,O∈BD,CD=,BC=5,∴BD2=CD2+BC2=10+25=35,AB=BC=5,∴(EA+5)2=EA(EA+AB)+35,解得EA=2.故答案为:2.点评:本题考查圆中线段长的求法,是中档题,解题时要认真审题,注意切割线定理、垂径定理、勾股定理的合理运用.三、解答题:本题共有6个小题,共80分.请写出解答的步骤与详细过程.16.(12分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<)在某一个周期内的图象时,列表并填入的部分数据如下表:x x1x2x3ωx+φ0 π2πAsin(ωx+φ)+B 1 4 1 ﹣2 1(1)求函数f(x)的解析式;(2)若<α<π,f(﹣)=,求f(α+)的值.考点:由y=Asin(ωx+φ)的部分图象确定其解析式;正弦函数的图象.专题:计算题;三角函数的求值.分析:解:(1)由题意可得,即解得ω,φ的值,由,即解得A,B的值,即可求得函数f(x)的解析式.(2)由f()=可化简得sin()=;由f()=﹣6sin()+1,又∈(,),可求得cos()=﹣,从而由f()=﹣6sin()cos()+1即可求值.解答:解:(1)由题意可得,即,…(2分)由题意可得,即,…(4分)∴函数f(x)的解析式为:f(x)=3sin(2x+)+1,…(5分)(2)由f()=,可得3sin[2()+]+1=,化简得sin()=,…(7分)∵f()=3sin[2()+]+1=3sin(2)+1=﹣3sin(2)+1=﹣6sin()+1,…(10分)又∵,∴∈(,),∴cos()=﹣,…(11分)∴f()=﹣6sin()cos()+1=﹣6×=.…(12分)点评:本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质,考查了计算能力,属于中档题.17.(12分)某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:x i(月) 1 2 3 4 5y i(千克)0.5 0.9 1.7 2.1 2.8(1)在给出的坐标系中,画出关于x,y两个相关变量的散点图.(2)请根据上表提供的数据,用最小二乘法求出变量y关于变量x的线性回归直线方程.(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克)(参考公式:=,=﹣)考点:线性回归方程.专题:计算题;概率与统计.分析:(1)利用所给数据,可得散点图;(2)利用公式,计算回归系数,即可得到回归方程;(3)x=12代入回归方程,即可得到结论.解答:解:(1)散点图如图所示…(3分)(2)由题设=3,=1.6,…(4分)∴===0.58,a=﹣=﹣0.14…(9分)故回归直线方程为y=0.58x﹣0.14…(10分)(3)当x=12时,y=0.58×12﹣0.14=6.82…(11分)饲养满12个月时,这种鱼的平均体重约为6.82千克.…(12分)点评:本题考查回归分析的初步运用,考查学生的计算能力,属于中档题.18.(14分)已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2).(1)求证:BF∥面A1DE;(2)求证:面A1DE⊥面DEBC;(3)求二面角A1﹣DC﹣E的正切值.考点:二面角的平面角及求法;直线与平面平行的判定;平面与平面垂直的判定.专题:空间位置关系与距离;空间角.分析:(1)取A1D中点G,并连接FG,EG,能够说明四边形BFGE为平行四边形,从而根据线面平行的判定定理即可得出BF∥面A1DE;(2)先根据已知的边、角值说明△A1DE为等边三角形,然后取DE中点H,连接CH,从而得到A1H⊥DE,根据已知的边角值求出A1H,CH,得出,从而得到A1H⊥CH,从而根据线面垂直及面面垂直的判定定理即可证出面A1DE⊥面DEBC;(3)过H作HO⊥DC,垂足为O,并连接A1O,容易说明DC⊥面A1HO,从而得出∠A1OH 为二面角A1﹣DC﹣E的平面角,能够求出HO,从而求出tan∠A1OH,即求出了二面角A1﹣DC﹣E的正切值.解答:解:(1)证明:如图,取DA1的中点G,连FG,GE;F为A1C中点;∴GF∥DC,且;∴四边形BFGE是平行四边形;∴BF∥EG,EG⊂平面A1DE,BF⊄平面A1DE;∴BF∥平面A1DE;(2)证明:如图,取DE的中点H,连接A1H,CH;AB=4,AD=2,∠DAB=60°,E为AB的中点;∴△DAE为等边三角形,即折叠后△DA1E也为等边三角形;∴A 1H⊥DE,且;在△DHC中,DH=1,DC=4,∠HDC=60°;根据余弦定理,可得:HC2=1+16﹣4=13,在△A 1HC中,,,A1C=4;∴,即A1H⊥HC,DE∩HC=H;∴A1H⊥面DEBC;又A1H⊂面A1DE;∴面A1DE⊥面DEBC;(3)如上图,过H作HO⊥DC于O,连接A1O;A1H⊥面DEBC;∴A1H⊥DC,A1H∩HO=H;∴DC⊥面A1HO;∴DC⊥A1O,DC⊥HO;∴∠A1OH是二面角A1﹣DC﹣E的平面角;在Rt△A 1HO中,,;故tan;所以二面角A1﹣DC﹣E的正切值为2.点评:考查中位线的性质,平行四边形的概念,线面平行的判定定理,能根据折叠前图形的边角值得到折叠后对应的边角值,直角三角形边的关系,线面垂直、面面垂直的判定定理,二面角的平面角的定义及求法.19.(14分)已知数列{a n}的前n项和为S n,且S n=n•a n+1,n∈N*,其中a1=1(1)求数列{a n}的通项公式;(2)若b n=,数列{b n}的前n项和为T n,求证:T n<.考点:数列的求和;数列递推式;数列与不等式的综合.专题:等差数列与等比数列.分析:(1)令n=1,得,由a1=1,得a2=2.当n≥2时,推导出,由此利用累乘法能求出a n=n.(2)由b n====<,利用放缩法和不等式的性质能证明T n<.解答:(1)解:∵S n=n•a n+1,n∈N*,∴令n=1,得,由已知a1=1,得a2=2.…(1分)当n≥2时,a n=S n﹣S n﹣1=,即,即得:,n≥2,…(4分)∴,n≥3,即,n≥3,…(6分)又∵a2=2,∴a n=n,又∵a1=1,∴a n=n,n∈N*.…(7分)(2)证明:∵a n=n,∴b n====<,…(11分)∴T n=b1+b2+…+b n<=()==,∴T n<.…(14分)点评:本题考查数列的通项公式和不等式的证明,解题时要认真审题,注意累乘法和放缩法的合理运用.20.(14分)已知抛物线C1:x2=y,圆C2:x2+(y﹣4)2=1.(1)在抛物线C1上取点M,C2的圆周取一点N,求|MN|的最小值;(2)设P(x0,y0)(2≤x0≤4)为抛物线C1上的动点,过P作圆C2的两条切线,交抛物线C1于A,B两点.求AB的中点D的横坐标的取值范围.考点:圆与圆锥曲线的综合.专题:圆锥曲线的定义、性质与方程.分析:(1)设出M的坐标,由圆C2:x2+(y﹣4)2=1可知圆心C2(0,4),写出|MC2|,利用配方法求其最小值,则|MN|的最小值为|MC2|的最小值减去圆的半径;(2)设出P,A,B的坐标,再设过点P的圆C2的切线方程为y﹣x02=k(x﹣x0),由点到直线的距离公式得到方程,则其两根为PA,PB的斜率,利用根与系数关系得到其两根和,再把y﹣x02=k(x﹣x0)代入y=x2得,,结合x0是此方程的根得到x1=k1﹣x0,x2=k2﹣x0,然后把AB的中点D的横坐标x用含有x0的代数式表示,再利用单调性结合x0的范围求得AB的中点D 的横坐标的取值范围.解答:解:(1)设M(x,y),由圆C2:x2+(y﹣4)2=1可知圆心C2(0,4),则|MC2|===.当且仅当M()时取“=”,∴|MN|的最小值为;(2)设P(x0,),,再设过点P的圆C2的切线方程为y﹣x02=k(x﹣x0),①则,即,设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2是上述方程的两根,∴,,将①代入y=x2得,,由于x0是此方程的根,故x1=k1﹣x0,x2=k2﹣x0,∴AB的中点D的横坐标x===.∵y=是[2,4]上的减函数,且2≤x0≤4,∴y∈,则x.点评:本题主要考查圆与圆锥曲线的综合问题,其中涉及到直线与圆相切的问题,考查了学生的逻辑思维能力和运算能力,是压轴题.21.(14分)已知函数f(x)=alnx+x2﹣(1+a)x.(1)求函数f(x)的单调区间;(2)证明:m、n∈N+时,m(m+n)[+++…+]>n.考点:利用导数研究函数的单调性;利用导数求闭区间上函数的最值.专题:导数的综合应用.分析:(1)由题意先求函数的定义域,再求导f′(x)=+x﹣(1+a)=,从而讨论导数的正负以确定函数的单调性;(2)由(2)知,当a=﹣时,f(x)=﹣lnx+x2﹣x≥0;当且仅当x=1时,等号成立;从而可化出当>1时,>﹣;从而证明.解答:解:(1)f(x)=alnx+x2﹣(1+a)x的定义域为{x|x>0},f′(x)=+x﹣(1+a)=;①当a=1时,f′(x)≥0,f(x)在定义域上是增函数;②当a>1时,1<x<a时,f′(x)<0,0<x<1或x>a时,f′(x)>0;故f(x)的单调减区间为(1,a);单调增区间为(0,1),(a,+∞);③当0<a<1时,a<x<1,f′(x)<0,0<x<a或x>1时,f′(x)>0;故f(x)的单调减区间为(a,1);单调增区间为(0,a),(1,+∞);④当a<0时,0<x<1,f′(x)<0,x>1时,f′(x)>0;故f(x)的单调减区间为(0,1);单调增区间为(1,+∞);(2)证明:由(1)知,当a=﹣时,f(x)=﹣lnx+x2﹣x≥0;当且仅当x=1时,等号成立;即lnx≤x2﹣x,当>1时,>﹣;故+++…+>﹣+﹣+…+﹣=﹣=;故m(m+n)[+++…+]>n.点评:本题考查了导数的综合应用及构造函数证明不等式的方法应用,属于中档题.。
广东省珠海一中等六校高三物理第二次联考试卷

广东省珠海一中等六校2015届高三物理第二次联考试卷一. 单选题(本大题共6小题,每小题3分,共18分.在每小题给出的四个选项中,只有一个选项是正确的)1.伽利略用两个对接的斜面,一个斜面固定,让小球从固定斜面上滚下,又滚上另一个倾角可以改变的斜面,斜面倾角逐渐改变至零,如图所示.伽利略设计这个实验的目的是为了说明A.如果没有摩擦,小球将运动到与释放时相同的高度B.如果没有摩擦,物体运动时机械能守恒C.维持物体做匀速直线运动并不需要力D.如果物体不受到力,就不会运动2.体操运动员静止悬挂在单杠上,当两只手掌握点之间的距离减小时,运动员手臂受到的拉力,下列判断正确的是A.不变 B.变小 C.变大 D.无法确定3.水平足够长运动的皮带,取向右为速度的正方向。
将一物块P轻轻放上皮带,之后P最初一段时间的速度时间图像如图乙,关于皮带的运动情况描述正确的是A.可能是向右的匀加速B.可能是向右的匀速C.一定是向左的匀加速D.可能是向左的匀速4.如图示,竖直悬挂于C点的小球,另两根细绳BC、AC与竖直方向的夹角分别是30、60,静止时三根绳子的拉力分别为F1、F2、F3(如图标示),关于三个拉力的大小关系,下列判断正确的是A.F1>F2>F3 B.F1< F2<F3C.F2>F3>F1 D. F2<F1<F35.下列实例属于超重现象的是A.拱形桥顶端汽车驶过时B.汽车驶过凹形桥最低位置时C.跳水运动员被跳板弹起离开跳板向上运动D.蹦床运动员在空中下落过程6.目前我国已发射北斗导航地球同步卫星十六颗,大大提高了导航服务质量,这些卫星A.环绕地球运行可以不在同一条轨道上B.运行角速度和周期不一定都相同C.运行速度大小可以不相等,但都小于7.9km/sD.向心加速度大于放在地球赤道上静止物体的向心加速度二.双选题(本大题共6小题,每小题4分,共24分.在每小题给出的四个选项中,只有两个选项正确,只选一项且正确得2分)7.如图,质量为m的滑块从倾角为30°的固定斜面上无初速地释放后匀加速下滑,加速度,取出发位置水平面为参考平面,能正确描述滑块的速率、动能、势能、机械能、时间t、位移关系的是8.如图,两个完全相同的小球A、B,在同一高度处以相同大小的初速度v分别水平抛出和竖直向上抛出,下列说法正确的是A.两小球落地时的速度相同B.两小球落地时,A球重力的瞬时功率较小C.从开始运动至落地,A球速度的变化率较大D.从开始运动至落地,重力对两球做功的平均功率A的大于B的9.宇宙飞船在返回地球的过程中,有一段时间由于受到稀薄大气的阻力作用,飞船的轨道半径会越来越小,在此进程中,以下说法中正确的是A.飞船绕地球运行的周期将增大B.飞船所受到的向心力将减小C.飞船的向心加速度将增大D.飞船绕地球运行的速率将增大10.如图为建筑材料被吊车竖直向上提升过程的简化运动图象,下列判断正确的是A.前5s的平均速度是0.5m/sB.0~10s的平均速度等于30s~36s的平均速度C.30s~36s材料处于超重状态D.前10s钢索最容易发生断裂11.在光滑的水平面上,有质量相同的甲、乙两物体,甲原来静止,乙以速度v做匀速直线运动,俯视图如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
启用前:绝密2015届广东六校联盟第二次联考试题数学(理科)(满分150分) 考试时间:120分钟一、选择题:(本大题共8小题,每小题5分,共计40分.每小题只有一个正确答案,请把正确答案填涂在答题卡相应位置)1.已知集合1{|()1}2x A x =<,{|1}B x x =<,则AB =A. ΦB. RC. (0,1)D. (-∞,1) 2. 命题:“x ∃∈R ,0x ≤”的否定是A. x ∃∈R ,||0x >B. x ∀∈R ,||0x >C. x ∃∈R ,0x <D. x ∀∈R ,||0x <3.设n S 是等差数列{}n a 的前n 项和,已知7S =49,则26,a a 的等差中项是 A.492 B. 7 C. 7± D. 724.函数2()x f x e =在点(0,1)处的切线的斜率是A. 2eB. eC. 2D. 1 5. 已知等边ABC ∆的边长为1,则=⋅BC ABA .21-B .23-C .21D .236. 已知角α终边上一点P 的坐标是)3cos 2,3sin 2(--,则=αsinA. cos3-B. cos3C. sin 3-D. sin 37.数列}{n a 中,d qa a p a n n +==+11,(n ∈N *,d q p ,,是常数),则0=d 是数列}{n a 成等比数列的A.必要不充分条件B.充分不必要条件C.充要条件D.不充分也不必要条件8. 已知向量,OA OB 不共线,向量=OC xOA yOB +,则下列命题正确的是 A. 若y x +为定值,则C B A 、、三点共线. B. 若y x =,则点C 在AOB ∠的平分线所在直线上. C. 若点C 为AOB ∆的重心,则1=3x y +.D. 若点C 在AOB ∆的内部(不含边界),则01011x y x y <<⎧⎪<<⎨⎪+<⎩.二、填空题:(本大题共6小题,每小题5分,共计30分.)9.已知函数()=2ln sin f x x x +,则()2f π'= .10. 已知函数3()=2f x x m +-是定义在[,4]n n +上的奇函数,则m n += .11. 右图是函数()sin()(0,0,||)2f x A x A πωϕωϕ=+>><的部分图象,则=ϕ .12.0214x dx --=⎰.13. 已知1a b c >>>,且a b c ,,依次成等比数列,设=log log log a b c m b n c p a ==,,,则m n p ,,这三个数的大小关系为 .14.给出下列命题:(1)设21e e 、是两个单位向量,它们的夹角是60,则=+-⋅-)23()2(2121e e e e 29-; (2)已知函数22log (1)()+1 (1)x x f x x x >⎧=⎨-≤⎩,若函数()y f x m =-有3个零点,则0<m <1;(3)已知函数()12-=x x f 的定义域和值域都是[]()a b b a >,,则a b +=1;(4)定义在R 上的函数()f x 满足(2)[1()]1()(1)23f x f x f x f +⋅-=+-=+,,则(2015)=32f -. 其中,正确命题的序号为 .参考答案1、C ;2、B ;3、B ;4、C ;5、A ;6、A ;7、D ;8、D9、4π;10、0;11、6π;12、3+23π;13、p m n >>;14、(1)(2)(3)三、解答题(本大题共六个小题,共80分.解答应写出文字说明、证明过程和演算步骤)15.(本小题满分12分)在ABC ∆中,设角C B A ,,的对边分别为c b a ,,,且2cos 2a C b c =-. (1)求角A 的大小;(2)若21a =,4b =,求边c 的大小.解:(1)因为2cos 2a C b c =-,所以C B C A s i n s i n 2c o s s i n2-= ()C C A sin sin 2-+=C C A C A sin )sin cos cos (sin 2-+= ………………………………4分即C A C sin cos 2sin =,x3-y O 31356又因为π<<C 0,所以0sin ≠C , 所以21cos =A , 又因为π<<A 0 所以3π=A . ………………………………8分(2) 因为A bc c b a cos 2222-+=,即221164c c =+-所以2450c c --=,解得1c =-(舍),5c =. ………………………………12分16.(本小题满分12分)已知正项等比数列}{n a 中,11=a ,且2313,,2a a a 成等差数列. (1)求数列}{n a 的通项公式;(2)设n n a n b ⋅-=)12(,求数列}{n b 的前n 项和n T . 解:设等比数列{}n a 的公比为q ,由2313,,2a a a 成等差数列知,321232a a a =+,∴02322=--q q ∵0>n a ∴2=q ………………………………4分 (1)∵11=a ∴*)(21N n a n n ∈=- ………………………………6分(2)∵n n a n b ⋅-=)12(,*)(21N n a n n ∈=-∴.2)12(2523112-⨯-++⨯+⨯+=n n n T∴.2)12(2)32(2523212132n n n n n T ⨯-+⨯-++⨯+⨯+⨯=- ……………8分 ∴.2)12()2222(21132n n n n T ⨯--+++++=--.32)32(2)12(322)12(21)21(22111-⨯--=⨯---=⨯----⋅+=+-n n n nn n n n∴*).(32)32(N n n T n n ∈+⨯-= ………………………………12分17.(本小题满分14分) 已知函数1sin 2)62sin()62sin()(2-+-++=x x x x f ππ.(1)求()3f π的值;(2)求函数()f x 的最小正周期和单调增区间;(3)说明()y f x =的图像是如何由函数sin y x =的图像变换所得. 17.解: ∵1sin 2)62sin()62sin()(2-+-++=x x x x f ππx x x 2cos )62sin()62sin(--++=ππx x 2cos 2sin 3-= )62sin(2π-=x ………………………4分(1) ()=2sin232f ππ= ………………………6分(2) ()f x 的最小正周期为22ππ= ………………………8分 当222262k x k πππππ-≤-≤+(k ∈Z ),即63k x k ππππ-≤≤+(k ∈Z )时,函数()f x 单调递增,故所求单调增区间为每一个[,]63k k ππππ-+(k ∈Z ). ………………………11分 (3)解法1:把函数sin y x =的图像上每一点的向右平移6π个单位, 再把所得图像上的每一点的横坐标缩短到原来的12(纵坐标不变),再把所得图像上的每一点的纵坐标伸长到原来的2倍(横坐标不变),就得到函数()y f x =的图像. .………………………14分 解法2:把函数sin y x =的图像上每一点的横坐标缩短到原来的12(纵坐标不变), 再把所得图像上的每一点的向右平移12π个单位, 再把所得图像上的每一点的纵坐标伸长到原来的2倍(横坐标不变),就得到函数()y f x =的图像. .………………………14分18.(本小题满分14分)已知数列{}n a 的首项1a a =,其前n 和为n S ,且满足21)1(3+=++n S S n n (n ∈N *).(1)用a 表示2a 的值; (2)求数列{}n a 的通项公式;(3)对任意的n ∈N *,1n n a a +>,求实数a 的取值范围.解析:(1)由条件1=n 得12121=++a a a , a a 2122-=. ………………………2分(2)由条件21)1(3+=++n S S n n 得,213(2)n n S S n n -+=≥ ………………………3分两式相减得361+=++n a a n n (2)n ≥, 解法1:故9612+=+++n a a n n ,两式再相减得62=-+n n a a (2)n ≥,,,,642a a a ∴构成以2a 为首项,公差为6的等差数列;,,,753a a a 构成以3a 为首项,公差为6的等差数列;………………………………5分 由(1)得a n a n 2662-+=;由条件2=n 得2721321=++++a a a a a ,得a a 233+=, 从而a n a n 23612+-=+,∴,13(62)(1)2n na n a n a n =⎧=⎨+--≥⎩, ………………………………9分 解法2:设1(1)()n n a x n y a xn y ++++=-++,即122n n a a xn y x +=----则263230x x y x y -==-⎧⎧⇒⎨⎨--==⎩⎩∴有13(1)(3)n n a n a n +-+=--∴2n ≥时,223(6)(1)n n a n a --=-⋅-,即23(62)(1)n n a n a -=+-⋅- ∴2,13(62)(1)2n n a n a n a n -=⎧=⎨+--≥⎩, ………………………………9分 (3)对任意的n ∈N*,1n n a a +>,当1n =时,由21a a >,有32(62)a a ⨯+->得4a <………①; 当2n ≥时,由1n n a a +>,有123(1)(62)(1)3(62)(1)n n n a n a --++-⋅->+-⋅-,即123(62)(1)(62)(1)n n a a --+-⋅->-⋅-若n 为偶数,则3(62)62a a -->-得94a >………②;若n 为奇数,则3(62)(62)a a +->--得154a <………③.由①、②、③得 41549<<a . …………………………………………14分19.(本小题满分14分)已知函数d cx bx x x f ++-=2331)(,设曲线)(x f y =过点(30),,且在点(30),处的切线的斜率等于4,)(x f y '=为)(x f 的导函数,满足)()2(x f x f '=-'.(1)求)(x f ; (2)设)()(x f xx g '=,0m >,求函数)(x g 在]0[m ,上的最大值;(3)设t x x f x h )12()()(++'=,若4)(<x h 对[0,1]t ∈恒成立,求实数x 的取值范围. 解:(1)求导可得c bx x x f +-='2)(2 ………………………………………1分 ∵)()2(x f x f '=-', ∴)(x f '的图像关于直线1=x 对称,∴1=b ……………2分 又由已知有:4)3('0)3(==f f ,∴31-==d c , ………………………………4分 ∴331)(23-+-=x x x x f ………………………………………5分(2)22()21(1)f x x x x '=-+=-,222,1,()(1)1, 1.x x x g x x x x x x x x ⎧-≥⎪=-=-=⎨-<⎪⎩ ………………………………………7分 其图像如图所示.当214x x -=时,122x ±=,根据图像得: (ⅰ)当102m <≤时,()g x 最大值为2m m -;(ⅱ)当11222m +<≤时,()g x 最大值为14;(ⅲ)当122m +>时,()g x 最大值为2m m -. …………………………………10分(3)t x x t x x f x h )12()1()12()()(2++-=++'=,记4)1()12()(2--++=x t x t g ,有 …………………………………………11分 当[0,1]t ∈时,4)(<x h ⇔04)1()12()(2<--++=x t x t g ,∴只要21223104)1(1204)1(0)1(0)0(22<<-⇔⎩⎨⎧<<-<<-⇔⎪⎩⎪⎨⎧<--++<--⇔⎩⎨⎧<<x x x x x x g g , ∴实数x 的取值范围为12x -<<, …………………………………………14分20.(本小题满分14分)设函数2()ln (,f x a x x bx a b =++∈R ,0)a ≠,且1x =为()f x 的极值点. (1)当1a =时,求()f x 的单调递减区间; (2)若()0f x =恰有两解,试求实数a 的取值范围;(3)在(1)的条件下,设2()(1)2g x f x x x =+-++,证明:2*1135(N )()(1)(2)nk n nn g k n n =+>∈++∑. 解:由已知求导得:()2af x x b x '=++,1x =为()f x 的极值点,(1)0f '∴=, 20a b ++=. ………………2分 (1)当1a =时,3b =-,进而21231(21)(1)()23x x x x f x x x x x-+--'=+-==,函数()f x 的定义域为(0,)+∞,()f x ∴的单调减区间为1(,1)2. ………………………………4分(2)由20a b ++=,得2b a =--,则2()ln (2)f x a x x a x =+-+ ,(0)x >,(2)(1)()2(2)a x a x f x x a x x--'=+-+=,(0)x >, (ⅰ)当0a <时,()f x 在(0,1)递减,在(1,)+∞递增,则()f x 的极小值为(1)f ,ln 1x x ≤-,22()(1)(2)2f x a x x a x x x a ∴≥-+-+=--,O x y 12122+11-2则当x →+∞时,()f x →+∞,又当0x +→时,()f x →+∞, ∴要使()0f x =恰有两解,须(1)0f <,即1a >-. 因此,当10a -<<时,()0f x =恰有两解.(ⅱ)当02a <<时,()f x 在(0,)2a、(1,)+∞递增,在(,1)2a 递减, 则()f x 的极大值为()2a f ,()f x 的极小值为(1)f .2222()ln ()(1)()(8)22422424a a a a a a a a f a a a a a =+-+≤-+-+=-, ∴当02a <<时,()02af <,此时()0f x =不可能恰有两解.(ⅲ)当2a >时,()f x 在(0,1)、(,)2a+∞递增,在(1,)2a 递减,则()f x 的极大值为(1)f ,()f x 的极小值为()2af .(1)10f a =--<,∴当2a >时,()0f x =不可能恰有两解.(ⅳ)当2a =时,()f x 在(0,)+∞单调递增,()0f x =不可能恰有两解.综合可得,若()0f x =恰有两解,则实数a 的取值范围是10a -<<. ………………9分 (3)当1a =时,2()(1)2ln(1)g x f x x x x =+-++=+,即证:21135ln(1)(1)(2)nk n nk n n =+>+++∑.(方法一)先证明:当2x ≥时,21ln (1)4x x <-.设21()ln (1)4h x x x =--, 212()22x x h x x x-'=-=,当2x ≥时,()0h x '<,则()h x 在(2,)+∞递减,()(2)h x h ≤,316e >,3ln164ln2∴>=,即3ln 24<,3(2)ln 204h ∴=-<,()0h x ∴<,即21ln (1)4x x <-.14112()ln (1)(1)11x x x x x ∴>=--+-+. 令1x k =+,得1112()ln(1)2k k k >-++, 则211111111352()2(1)ln(1)2212(1)(2)nnk k n nk k k n n n n ==+>-=+--=++++++∑∑. …………14分(方法二)数学归纳法:1.当1n =时,左边=1ln 2,右边=43,316e >,3ln164ln2∴>=, 14ln 23∴>,即1n =时,命题成立.2.设n k =时,命题成立,即211135ln 2ln3ln(1)(1)(2)k k k k k ++++>+++.当1n k =+时,左边=21111351ln 2ln3ln(1)ln(2)(1)(2)ln(2)k k k k k k k +++++>++++++ 右边=223(1)5(1)3118(2)(3)(2)(3)k k k k k k k k +++++=++++, 要证223513118(1)(2)ln(2)(2)(3)k k k k k k k k k ++++>+++++,即证221311835ln(2)(2)(3)(1)(2)k k k kk k k k k +++>-+++++, 即证14ln(2)(1)(3)k k k >+++,也即证1ln(2)(1)(3)4k k k +<++.令2k x +=,即证:21ln (1)4x x <-,(证法见方法一)因此,由数学归纳法可得命题成立. …………………………………………14分。
