2015年全国高中数学联赛江苏赛区初赛试卷(含答案)

合集下载

全国高中数学联赛江苏赛区初赛试题001

全国高中数学联赛江苏赛区初赛试题（时间：4月20日上午8：00—10：00）一、选择题（本题满分30分，每小题6分）1. 如果实数m ，n ，x ，y 满足a n m =+22，b y x =+22，其中a ，b 为常数，那么mx+ny 的最大值为 []A. 2b a +B. abC. 222ba + D. 222b a +2. 设)(x f y =为指数函数xa y =. 在P(1,1)，Q(1,2)，M(2,3)，⎪⎭⎫ ⎝⎛41,21N 四点中，函数)(x f y =与其反函数)(1x f y -=的图像的公共点只可能是点 []A. PB. QC. MD. N3. 在如图的表格中，如果每格填上一个数后，每一横行成等差数列，每一纵列成等比数列，那么z y x ++的值为答：[] A. 1 B. 2C. 3D. 44. 如果111C B A ∆的三个内角的余弦值分别是222C B A ∆的三个内角的正弦值，那么 []A. 111C B A ∆与222C B A ∆都是锐角三角形B. 111C B A ∆是锐角三角形，222C B A ∆是钝角三角形C. 111C B A ∆是钝角三角形，222C B A ∆是锐角三角形D. 111C B A ∆与222C B A ∆都是钝角三角形5. 设a ，b 是夹角为30°的异面直线，则满足条件“α⊆a ，β⊆b ，且βα⊥”的平面α，β[] A. 不存在 B. 有且只有一对 C. 有且只有两对 D. 有无数对二、填空题（本题满分50分，每小题10分）6. 设集合[]{}{}222<==-=x x B x x x A 和，其中符号[]x 表示不大于x 的最大整数，则A B =___________________.7. 同时投掷三颗骰子，于少有一颗骰子掷出6点的概率是P =__________(结果要求写成既约分数）.8. 已知点O 在ABC ∆内部，022=++OC OB OA .OCB ABC ∆∆与的面积之比为____________. 9. 与圆0422=-+x y x 外切，且与y 轴相切的动圆圆心的轨迹方程为________________________.10. 在ABC ∆中，若tanAtanB=tanAtanC+tanctanB ，则 222c b a +=______________.三、解答题（本题满分70分，各小题分别为15分、15分、20分、20分）11. 已知函数c bx x x f ++-=22)(在1=x 时有最大值1，n m <<0，并且[]n m x ,∈时，)(x f 的取值范围为⎥⎦⎤⎢⎣⎡m n 1,1. 试求m ，n 的值.1 2 0.5 1 xyz12. A 、B 为双曲线19422=-y x 上的两个动点，满足0=⋅OB OA 。

2009_2015年江苏省数学竞赛初赛试题(原题+详细讲解)

2009年全国高中数学联赛赛区初赛一、填空题(每题7分，共70分) 1．sin αcos β＝1，那么cos(α＋β)＝．2．等差数列{a n }的前11项的和为55，去掉一项a k 后，余下10项的算术平均值为4．假设a 1＝－5，那么k ＝． 3．设一个椭圆的焦距、短轴长、长轴长成等比数列，那么此椭圆的离心率e ＝． 4．＝，那么实数x ＝．5．如图，在四面体ABCD 中，P 、Q 分别为棱BC 与CD 上的点，且BP ＝2PC ，CQ ＝2QD ．R 为棱AD 的中点，那么点A 、B 到平面PQR 的距离的比值为．6．设f (x )＝log 3x －4－x ，那么满足f (x )≥0的x 的取值围是．7．右图是某种净水水箱结构的设计草图，其中净水器是一个宽10cm 、体积为3000cm 3的长方体，长和高未定．净水水箱的长、宽、高比净水器的长、宽、高分别长20cm 、20cm 、60cm ．假设不计净水器中的存水，那么净水水箱中最少可以存水cm 3．8．设点O 是△ABC 的外心，AB ＝13，AC ＝12，那么→BC ·→AO ＝．9．设数列{a n }满足：a n ＋1a n ＝2a n ＋1－2(n ＝1，2，…)，a 2009＝2，那么此数列的前2009项的和为． 10．设a 是整数，0≤b ＜1．假设a 2＝2b (a ＋b )，那么b ＝．二、解答题(本大题共4小题，每题20分，共80分)11．在直角坐标系xOy 中，直线x －2y ＋4＝0与椭圆＋＝1交于A ，B 两点，F 是椭圆的左焦点．求以O ，F ，A ，B 为顶点的四边形的面积．12．如图，设D 、E 是△ABC 的边AB 上的两点，∠ACD ＝∠BCE ，AC ＝14，AD ＝7，AB ＝28，CE ＝12．求BC ．13．假设不等式x ＋y ≤k 2x ＋y 对于任意正实数x ，y 成立，求k 的取值围．14．⑴ 写出三个不同的自然数，使得其中任意两个数的乘积与10的和都是完全平方数，请予以验证；⑵ 是否存在四个不同的自然数，使得其中任意两个数的乘积与10的和都是完全平方数？请证明你的结论．2009年全国高中数学联赛赛区初赛(2009年5月3日8∶00－10∶00)一、填空题(每题7分，共70分)1．sin αcos β＝1，那么cos(α＋β)＝．填0．解：由于|sin α|≤1，|cos β|≤1，现sin αcos β＝1，故sin α＝1，cos β＝1或sin α＝－1，cos β＝－1，∴α＝2kπ＋，β＝2lπ或α＝2kπ－，β＝2lπ＋πα＋β＝2(k ＋l )π＋(k ，l ∈Z)． ∴cos(α＋β)＝0．2．等差数列{a n }的前11项的和为55，去掉一项a k 后，余下10项的算术平均值为4．假设a 1＝－5，那么k ＝．填11．解：设公差为d ，那么得 55＝－5×11＋×11×10d55d ＝110d ＝2．a k ＝55－4×10＝15＝－5＋2(k －1)k ＝11．3．设一个椭圆的焦距、短轴长、长轴长成等比数列，那么此椭圆的离心率e ＝．填－1＋52．解：由(2b )2＝2c ×2aa 2－c 2＝ac e 2＋e －1＝0e ＝－1＋52． 4．＝，那么实数x ＝．填1．解：即＝32x－4×3x＋3＝03x ＝1(舍去)，3x＝3x ＝1．5．如图，在四面体ABCD 中，P 、Q 分别为棱BC 与CD 上的点，且BP ＝2PC ，CQ ＝2QD ．R 为棱AD 的中点，那么点A 、B 到平面PQR 的距离的比值为．填14．解：A 、B 到平面PQR 的距离分别为三棱锥APQR 与BPQR 的以三角形PQR 为底的高．故其比值等于这两个三棱锥的体积比．V APQR ＝V APQD ＝×13V APCD ＝×13×13V ABCD ＝V ABCD ；又，S BPQ ＝S BCD －S BDQ －S CPQ ＝(1－13－23×13)S BCD ＝49S BCD ，V RBPQ ＝49V RBCD ＝×49V ABCD ＝418V ABCD ．∴A 、B 到平面PQR 的距离的比＝1∶4．又，可以求出平面PQR 与AB 的交点来求此比值：在面BCD ，延长PQ 、BD 交于点M ，那么M 为面PQR 与棱BD 的交点．由Menelaus 定理知，··＝1，而＝，＝，故＝4．在面ABD ，作射线MR 交AB 于点N ，那么N 为面PQR 与AB 的交点．由Menelaus 定理知，··＝1，而＝4，＝1，故＝14．∴A 、B 到平面PQR 的距离的比＝1∶4．6．设f (x )＝log 3x －4－x ，那么满足f (x )≥0的x 的取值围是．填[3，4]．解：定义域(0，4]．在定义域f (x )单调增，且f (3)＝0．故f (x )≥0的x 的取值围为[3，4]．7．右图是某种净水水箱结构的设计草图，其中净水器是一个宽10cm 、体积为3000cm 3的长方体，长和高未定．净水水箱的长、宽、高比净水器的长、宽、高分别长20cm 、20cm 、60cm ．假设不计净水器中的存水，那么净水水箱中最少可以存水cm 3．填78000．解：设净水器的长、高分别为x ，y cm ，那么xy ＝300，V ＝30(20＋x )(60＋y )＝30(1200＋60x ＋20y ＋xy )≥30(1200＋260x ×20y ＋300)＝30(1500＋1200)＝30×2700．∴ 至少可以存水78000cm 3．8．设点O 是△ABC 的外心，AB ＝13，AC ＝12，那么→BC ·→AO ＝．填－．解：设|→AO |＝|→BO |＝|→OC |＝R ．那么→BC ·→AO ＝(→BO ＋→OC )·→AO ＝→BO ·→AO ＋→OC ·→AO ＝R 2cos(π－2C )＋R 2cos2B＝R 2(2sin 2C －2sin 2B )＝(2R sin B )2－(2R sin C )2＝(122－132)＝－．9．设数列{a n }满足：a n ＋1a n ＝2a n ＋1－2(n ＝1，2，…)，a 2009＝2，那么此数列的前2009项的和为．填2008＋2．解：假设a n ＋1≠0，那么a n ＝2－，故a 2008＝2－2，a 2007＝2－＝－2，a 2006＝2＋2，a 2005＝2．一般的，假设a n ≠0，1，2，那么a n ＝2－，那么a n －1＝a n ＋1－2a n ＋1－1，a n －2＝，a n －3＝a n ＋1，故a n －4＝a n ．于是，a n ＝502(a 1＋a 2＋a 3＋a 4)＋a 2009＝502(a 2005＋a 2006＋a 2007＋a 2008)＋a 2009＝2008＋2． 10．设a 是整数，0≤b ＜1．假设a 2＝2b (a ＋b )，那么b ＝．填0，3－12，3－1．解：假设a 为负整数，那么a 2＞0，2b (a ＋b )＜0，不可能，故a ≥0．于是a 2＝2b (a ＋b )＜2(a ＋1)a 2－2a －2＜00≤a ＜1＋3a ＝0，1，2．a ＝0时，b ＝0；a ＝1时，2b 2＋2b －1＝0b ＝3－12； a ＝2时，b 2＋2b －2＝0b ＝3－1．说明：此题也可以这样说：数x ，使[x ]2＝2{x }x ．二、解答题(本大题共4小题，每题20分，共80分)11．在直角坐标系xOy 中，直线x －2y ＋4＝0与椭圆＋＝1交于A ，B 两点，F 是椭圆的左焦点．求以O ，F ，A ，B 为顶点的四边形的面积．解：取方程组代入得，25y 2－64y ＋28＝0．此方程的解为y ＝2，y ＝．即得B (0，2)，A (－，)，又左焦点F 1(－5，0)．连OA 把四边形AFOB 分成两个三角形．CFyxOBA得，S ＝×2×＋×5×＝(72＋75)．也可以这样计算面积：直线与x 轴交于点C (－4，0)．所求面积＝×4×2－×(4－5)×＝(72＋75)．也可以这样计算面积：所求面积＝(0×2－0×0＋0×－(－)×2＋(－)×0－(－5)×＋(－5)×0－0×0)＝(＋5)＝(72＋75)．12．如图，设D 、E 是△ABC 的边AB 上的两点，∠ACD ＝∠BCE ，AC ＝14，AD ＝7，AB ＝28，CE ＝12．求BC ．解：＝△ACD ∽△ABC ∠ABC ＝∠ACD ＝∠BCE ． ∴CE ＝BE ＝12．AE ＝AB －BE ＝16． ∴cos A ＝＝＝＝．∴BC 2＝AC 2＋AB 2－2AC ·AB cos A ＝142＋282－2·14·28·＝72·9BC ＝21． 13．假设不等式x ＋y ≤k 2x ＋y 对于任意正实数x ，y 成立，求k 的取值围．解法一：显然k ＞0．(x ＋y )2≤k 2(2x ＋y )(2k 2－1)x －2xy ＋(k 2－1)y ≥0对于x ，y ＞0恒成立．令t ＝x y＞0，那么得f (t )＝(2k 2－1)t 2－2t ＋(k 2－1)≥0对一切t ＞0恒成立．当2k 2－1≤0时，不等式不能恒成立，故2k 2－1＞0．此时当t ＝时，f (t )取得最小值－＋k 2－1＝＝(k 2(2k 2－3),2k 2－1)．当2k 2－1＞0且2k 2－3≥0，即k ≥62时，不等式恒成立，且当x ＝4y ＞0时等号成立． ∴k ∈[62，＋∞)．解法二：显然k ＞0，故k 2≥＝．令t ＝x y＞0，那么k 2≥＝(1＋)．令u ＝4t ＋1＞1，那么t ＝u －14．只要求s (u )＝的最大值．s (u )＝≤＝2，于是，(1＋)≤(1＋2)＝32．∴k 2≥32，即k ≥62时，不等式恒成立(当x ＝4y ＞0时等号成立)．又：令s (t )＝，那么s (t )＝＝，t ＞0时有驻点t ＝．且在0＜t ＜时，s (t )＞0，在t ＞时，s (t )＜0，即s (t )在t ＝时取得最大值2，此时有k 2≥(1＋s ())＝32．解法三：由Cauchy 不等式，(x ＋y )2≤(＋1)(2x ＋y )．即(x ＋y )≤622x ＋y 对一切正实数x ，y 成立．当k ＜62时，取x ＝14，y ＝1，有x ＋y ＝32，而k 2x ＋y ＝k 62＜62×62＝32．即不等式不能恒成立．而当k ≥62时，由于对一切正实数x ，y ，都有x ＋y ≤622x ＋y ≤k 2x ＋y ，故不等式恒成立．∴k ∈[62，＋∞)． 14．⑴ 写出三个不同的自然数，使得其中任意两个数的乘积与10的和都是完全平方数，请予以验证； ⑵ 是否存在四个不同的自然数，使得其中任意两个数的乘积与10的和都是完全平方数？请证明你的结论．解：对于任意n ∈N*，n 2≡0，1(mod 4)．设a ，b 是两个不同的自然数，①假设a ≡0(mod 4)或b ≡0(mod 4)，或a ≡b ≡2(mod 4)，均有ab ≡0(mod 4)，此时，ab ＋10≡2(mod 4)，故ab ＋10不是完全平方数；② 假设a ≡b ≡1(mod 4)，或a ≡b ≡3(mod 4)，那么ab ≡1(mod 4)，此时ab ＋10≡3(mod 4)，故ab ＋10不是完全平方数．由此知，ab ＋10是完全平方数的必要不充分条件是ab (mod 4)且a 与b 均不能被4整除．⑴ 由上可知，满足要求的三个自然数是可以存在的，例如取a ＝2，b ＝3，c ＝13，那么2×3＋10＝42，2×13＋10＝62，3×13＋10＝72．即2，3，13是满足题意的一组自然数．⑵ 由上证可知不存在满足要求的四个不同自然数．这是因为，任取4个不同自然数，假设其中有4的倍数，那么它与其余任一个数的积加10后不是完全平方数，如果这4个数都不是4的倍数，那么它们必有两个数mod 4同余，这两个数的积加10后不是完全平方数．故证．2010年全国高中数学联赛赛区·初赛一、填空题〔此题总分值70分，每题7分〕1．方程9135x x+-=的实数解为．2．函数sin cos y x x =+(x ∈R )的单调减区间是 .3．在△ABC 中，4AB AC ⋅=，12AB BC ⋅=-，那么AB ＝. 4．函数()()()221f x x x =-+在区间[]0,2上的最大值是，最小值是．5．在直角坐标系xOy 中，圆心在原点O 、半径为R 的圆与△ABC 的边有公共点，其中()4,0A =、()6,8B =、()2,4C =，那么R 的取值围为．6．设函数()f x 的定义域为R ，假设()1f x +与()1f x -都是关于x 的奇函数，那么函数()y f x =在区间[]0,100上至少有个零点.7．从正方体的12条棱和12条面对角线中选出n 条，使得其中任意两条线段所在的直线都是异面直线，那么n 的最大值为．8．圆环形手镯上等距地镶嵌着4颗小珍珠，每颗珍珠镀金、银两色中的一种．其中镀2金2银的概率是．9．在三棱锥A BCD -中，ACB CBD ∠=∠，ACD ADC BCD BDC ∠=∠=∠=∠θ=，且cos θ=．棱AB的长为． 10．设复数列{}n x 满足1n x a ≠-，0，且11n n n a x x x +=+．假设对任意n ∈N *都有3n n x x +=，那么a 的值是．二、解答题〔此题总分值80分，每题20分〕11．直角坐标系xOy 中，设A 、B 、M 是椭圆22:14x C y +=上的三点．假设3455OM OA OB =+，证明：AB 的中点在椭圆22212x y +=上．12．整数列{}n a 满足31a =-，74a =，前6项依次成等差数列，从第5项起依次成等比数列．(1) 求数列{}n a 的通项公式；(2) 求出所有的正整数m ，使得1212m m m m m m a a a a a a ++++++=．13．如图，圆接五边形ABCDE 中，AD 是外接圆的直径，BE AD ⊥，垂足H .过点H 作平行于CE 的直线，与直线AC 、DC 分别交于点F 、G ．证明： (1) 点A 、B 、F 、H 共圆； (2) 四边形BFCG 是矩形．14．求所有正整数x ，y ，使得23x y +与23y x +都是完全平方数．参考答案1、x ＜0无解; 当0x ≥时，原方程变形为32x+3x －6=0，解得3x=2，x =log 32． 2、与f (x )=y 2=1+|sin2x |的单调减区间一样，[,],2422k k k ππππ++∈Z ． 3、216AB AC AB BC AB ⋅-⋅==，得4AB =．4、极小值－4，端点函数值f (2)=0，f (0)=－2，最小值－4，最大值0．5、画图观察，R 最小时圆与直线段AC 相切，R 最大时圆过点B ．[855，10]．6、f (2k -1)=0，k ∈Z. 又可作一个函数()f x 满足问题中的条件，且()f x 的一个零点恰为21x k =-，k ∈Z. 所以至少有50个零点. 7、不能有公共端点，最多4条，图上知4条可以．8、穷举法，注意可翻转，有6种情况，2金2银有两种，概率为 13 ．9、4面为全等的等腰三角形，由体积公式可求得三棱锥的体积为 144 ．10、由11n n n a x x x +=+，2321n n n a x x x +++==+()21111n n a x a x ++=++()3211n n n a x x a a x =+++恒成立，即()()2110n n a a x x a +++-=. 因为1n x a ≠-或0，故210a a ++=，所以122a i =-±． 11、解：设A (x 1，y 1)，B (x 2，y 2)，那么＋y 12＝1，＋y 22＝1．由3455OM OA OB =+，得 M (35x 1＋45x 2，35y 1＋45y 2)．因为M 是椭圆C 上一点，所以35x 1＋45x 2)2,4)＋(35y 1＋45y 2)2＝1， …………………6分即 (＋y 12)(35)2＋(＋y 22)(45)2+2(35)(45)(＋y 1y 2)=1，得 (35)2＋(45)2+2(35)(45)(＋y 1y 2)＝1，故＋y 1y 2＝0． …………………14分又线段AB 的中点的坐标为 (，)，所以＋2()2＝12(＋y 12)+12(＋y 22)+＋y 1y 2＝1，从而线段AB 的中点(，)在椭圆＋2y 2＝1上． ………………20分12、解：(1) 设数列前6项的公差为d ，那么a 5=－1+2d ，a 6=－1+3d ，d 为整数. 又a 5，a 6，a 7成等比数列，所以(3d －1)2=4(2d －1)，即 9d 2－14d +5=0，得d =1. …………………6分当n ≤6时，a n =n －4，由此a 5=1，a 6=2，数列从第5项起构成的等比数列的公比为2，所以，当n ≥5时，a n =2n -5.故 a n =⎩⎪⎨⎪⎧n －4，n ≤4，2n -5， n ≥5．…………………10分(2) 由〔1〕知，数列{}n a 为：－3，－2，－1，0，1，2，4，8，16，… 当m =1时等式成立，即－3－2－1=―6=(－3)(－2)(－1)；当m =3时等式成立，即－1+0+1=0；当m =2、4时等式不成立；…………………15分当m ≥5时，a m a m +1a m +2=23m -12， a m +a m +1+a m +2=2m -5(23－1)=7×2m -5，7×2m -5≠23m -12，所以 a m +a m +1+a m +2≠a m a m +1a m +2.故所求 m = 1，或m =3． …………………20分13、证明：(1) 由HG ∥CE ，得∠BHF =∠BEC ，又同弧的圆周角 ∠BAF =∠BEC ， ∴∠BAF =∠BHF ，ABC DEFH∴ 点 A 、B 、F 、H 共圆； …………………8分(2) 由(1)的结论，得 ∠BHA =∠BFA ，∵BE ⊥AD ， ∴BF ⊥AC ，又AD 是圆的直径，∴CG ⊥AC ， …………………14分由A 、B 、C 、D 共圆及A 、B 、F 、H 共圆，∴∠BFG =∠DAB =∠BCG ， ∴B 、G 、C 、F 共圆. ∴∠BGC =∠AFB=900, ∴BG ⊥GC ， ∴ 所以四边形BFCG 是矩形． …………………20分14、解：假设x =y ，那么x 2+3x 是完全平方数. ∵x 2＜x 2+3x ＜x 2+4x +4= (x +2)2， ∴x 2+3x = (x +1)2，∴x =y =1. ………………5分假设x ＞y ，那么x 2＜x 2+3y ＜x 2+3x ＜x 2+4x +4= (x +2)2. ∵x 2+3y 是完全平方数， ∴x 2+3y = (x +1)2，得3y =2x +1，由此可知y 是奇数，设y =2k +1，那么x =3k +1，k 是正整数. 又 y 2+3x = 4k 2+4k +1+9k +3=4k 2+13k +4是完全平方数，且 (2k +2)2=4k 2+8k +4＜4k 2+13k +4＜4k 2+16k +16= (2k +4)2， ∴y 2+3x =4k 2+13k +4=(2k +3)2，得 k =5，从而求得x =16，y =11. …………………15分假设x ＜y ，同x ＞y 情形可求得 x =11，y =16.综上所述，(x ，y )= (1，1), (11，16), (16，11)． …………………20分2011年全国高中数学联赛赛区初赛题一、填空题〔此题共10小题，总分值70分，每题7分．要求直接将答案写在横线上〕 1．复数44(1i)(1i)++-= ．2．直线10x my -+=是圆22:4450C x y x y +-+-=的一条对称轴，那么实数m =.3．某班共有30名学生，假设随机抽查两位学生的作业，那么班长或团支书的作业被抽中的概率是〔结果用最简分数表示〕．4． 1cos45θ=，那么44sin cos θθ+=．5．向量a ，b 满足π2,,3==<>=a b a b ，那么以向量2+a b 与3-a b 表示的有向线段为邻边的平行四边形的面积为．6．设数列{a n }的前n 项和为S n ．假设{S n }是首项及公比都为2的等比数列，那么数列{a n 3}的前n 项和等于． 7．设函数2()2f x x =-．假设f (a )＝f (b )，且0＜a ＜b ，那么ab 的取值围是． 8．设f (m )为数列{a n }中小于m 的项的个数，其中2,n a n n =∈N*，那么[(2011)]f f =． 9．一个等腰直角三角形的顶点分别在底边长为4的正三棱柱的三条侧棱上，那么此直角三角形的斜边长是．10．m 是正整数，且方程2100x m -+=有整数解，那么m 所有可能的值是．二、解答题〔本大题共4小题，每题20分，共80分〕AB CP11．圆221x y +=与抛物线2y x h =+有公共点，数h 的取值围．12．设2()(,)f x x bx c b c =++∈R ．假设2x ≥时，()0f x ≥，且()f x 在区间(]2,3上的最大值为1，求22b c +的最大值和最小值．13．如图，P 是ABC 一点．〔1〕假设P 是ABC 的心，证明：1902BPC BAC ∠=+∠；〔2〕假设1902BPC BAC ∠=+∠且1902APC ABC ∠=+∠，证明：P 是ABC 的心．14．α是实数，且存在正整数n 0证明：存在无穷多个正整数n2011年全国高中数学联赛赛区初赛题答案及点评一、填空题〔此题共10小题，总分值70分，每题7分．要求直接将答案写在横线上〕 1．复数44(1i)(1i)++-= ．答案：－8 根底题，送分题，高考难度2．直线10x my -+=是圆22:4450C x y x y +-+-=的一条对称轴，那么实数m =.答案：32-根底题，送分题，高考难度3．某班共有30名学生，假设随机抽查两位学生的作业，那么班长或团支书的作业被抽中的概率是〔结果用最简分数表示〕．答案：19145根底题，送分题，高考难度，但需要认真审题，否那么很容易有错 4． 1cos45θ=，那么44sin cos θθ+=．答案：45计算量挺大的，要注重计算的方法，对于打酱油的同学有一定难度5．向量a ，b 满足π2,,3==<>=a b a b ，那么以向量2+a b 与3-a b 表示的有向线段为邻边的平行四边形的面积为．答案：可以用特殊法，把向量放在直角坐标系中，很容易可以得出答案6．设数列{a n }的前n 项和为S n ．假设{S n }是首项及公比都为2的等比数列，那么数列{a n 3}的前n 项和等于．答案：1(848)7n +高考难度级别，根底好的同学可以做出来7．设函数2()2f x x =-．假设f (a )＝f (b )，且0＜a ＜b ，那么ab 的取值围是．答案：(0,2) 这是一道高考题8．设f (m )为数列{a n }中小于m 的项的个数，其中2,n a n n =∈N*，那么[(2011)]f f =．答案：6 这也是一道高考题9．一个等腰直角三角形的顶点分别在底边长为4的正三棱柱的三条侧棱上，那么此直角三角形的斜边长是．答案：43还是一道高考题 10．m是正整数，且方程2100x m -+=有整数解，那么m 所有可能的值是．答案：3,14,30 这是2011年市一模的第十四题。

2015年高中数学竞赛试题精选及答案

已知1111ABCD A BC D -是一个棱长为1的正方体，1O 是底面1111A B C D 的中心，M 是棱1BB 上的点，且:2:3S S =11△DBM△O B M ，则四面体1O ADM 的体积为748（江苏2007夏令营）在正方体1111D C B A ABCD -中，P 是侧面C C BB 11内一动点，若P 到直线BC 与直线C 1D 1的距离相等，则动点P 的轨迹所在的曲线是抛物线已知x 为锐角，则22cos sin33=+x x 是4π=x 的（充要条件）同信一寝室的四名女生，她们当中有一人在修指甲，一人在看书，一人在梳头发，另一人在听音乐。

①A 既不在修指甲，也不在看书；②B 既不在听音乐，也不在修指甲；③如果A 不在听音乐，那么C 不在修指甲；④D 既不在看书，也不在修指甲；⑤C 既不在看书，也不在听音乐。

若上面的命题都是真命题，问她们各在干什么？答：ABCD 分别在听音乐；看书；修指甲；梳头发已知)1(3tan m +=α，且βαββα,,0t a n )t a n (t a n 3=++⋅m 为锐角，则βα+的值为3π=︒-︒︒-︒︒+)5tan 5(cot 10sin 20sin 220cos 12330cos =︒=函数d cx bx ax x x f ++++=234)(，若3)3(,2)2(,1)1(===f f f ，那么)4()0(f f +的值为（28 ）在ABC ∆中，角A 、B 、C 所对的边分别为c b a ,,，且31cos =A 。

（1）求A CB 2cos 2sin2++的值；（2）若3=a ，求bc 的最大值。

（-1/9； 9/4）若m 、{}22101010n x x aa a ∈=⨯+⨯+，其中{}1234567i a ∈，，，，，，，012i =，，，并且 636m n +=，则实数对(,)m n 表示平面上不同点的个数为（ 90 ）圆锥曲线0|3|102622=+--+-++y x y x y x 的离心率是 2.斜三棱柱111ABC A B C -中，面11AAC C 是菱形，160ACC ∠=︒，侧面11ABB A ⊥11AAC C ，11A B AB AC ===.求证：（1）1AA ⊥1BC ；（2）求点1A 到平面ABC 的距离. 515满足20073+++=x x y 的正整数数对（x ，y ）恰有两对设集合M={-2，0，1}，N={1，2，3，4，5}，映射f ：M →N 使对任意的x ∈M ，都有)()(x xf x f x ++是奇数，则这样的映射f 的个数是（45）将一个三位数的三个数字顺序颠倒，将所得到的数与原数相加，若和中没有一个数字是偶数，则称这个数为“奇和数”。

2015年全国高中数学联赛江苏赛区初赛参考答案与评分细则 (1)

=2‰ ,求 g的值岛刀
解:若
若
,
g=1,则 ‰=%=2,蜣 =4,则岛ヵ =4刀 ,马 =4刀 ,s9″ ≠2‰
g=-1,则
‰
.
=2×
(—
1)刀
,蜣
=4,则
岛刀=0,‰
=4刀 ,岛
刀≠
2‰
.
・ … … … … …… …… … … … ¨ 5分
若 g≠ ±1,则 ‰=勿
刀2,
柙峤狎艹岬
11=55个
.
・ … …… … … …… … 5分
.
=2时 ,设其中 /″ ,/刀染成红色 ,其余染成蓝色当斤
以
'励
为顶角顶点的等腰三角形有 5个 ,以
'仞
为底角顶点的等腰三角形有 10个 ;同
,/刀为顶点的等腰三角形有 3个 ,这些等腰三角形的顶点不同色 ,且共有 6+10) 时以彳泖
⒈
3.
)⒍ 滋 +狞 ⒋ 且夕由题意知 ,b酞 4均 =⒈ 即夕
L份
解
解 :有两类情况 :同为自球的概率是 ,同为红球的概率是磊矮埕←亻头岩搌臁醮・
解
解
: :
⒐ 从而扔 ≤ 叩
=⒋
=3=2时 ,汕的最大值是 4. 当曰
⒉ 函数炯
=币顿
⒉
F篑均在
处的值是
一 ⒉ =辔 =岢 =2犷￠ =雨 ⒍ 以灭繁碍畀所爹宀谔=钅 =畏 ℃
若不等式 |锚 +1}≤ 3的解集为姒 |-2≤ y≤ 1),则实数 ε的值是
.

2015年全国高中数学联赛参考答案(A卷word版本)

2015 年全国高中数学联合竞赛（A 卷）参考答案及评分标准一试说明：1.评阅试卷时，请依据本评分标冶填空题只设。

分和香分两档；其他各题的评阅，请严格按照本评分标准的评分档次给分，不要增加其他中间档次.2.如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，解答题中第9小题4分为一个档次，第10、11小题该分为一个档次，不要增加其他中间档次．一、填空题：本大题共8小题，每小题份分，满分64分．1．设b a ,为不相等的实数，若二次函数b ax x x f ++=2)(满足)()(b f a f =，则=)2(f 答案：4.解：由己知条件及二次函数图像的轴对称性，可得22a b a+=-，即20a b +=，所以(2)424f a b =++=．2．若实数α满足ααtan cos =，则αα4cos sin 1+的值为．答案：2. 解：由条件知，ααsin cos 2=，反复利用此结论，并注意到1sin cos 22=+αα，得)cos 1)(sin 1(sin sin sin cos cos sin 122224αααααααα-+=++=+ 2cos sin 22=-+=αα．3．已知复数数列{}n z 满足),2,1(1,111⋅⋅⋅=++==+n ni z z z n n ，则=2015z ．答案：2015 + 1007i ．解：由己知得，对一切正整数n ，有211(1)11(1)2n n n n z z n i z ni n i z i ++=+++=+++++=++, 于是201511007(2)20151007z z i i =+⨯+=+．4．在矩形ABCD 中，1,2==AD AB ，线段DC 上的动点P 与CB 延长线上的动点Q 满=，则PQ PA ⋅的最小值为．答案34．解：不妨设 A ( 0 , 0 ) , B ( 2 , 0 ) , D ( 0 , l ) ．设 P 的坐标为（t , l) （其中02t ≤≤），则由||||DP BQ =得Q 的坐标为（2，-t )，故(,1),(2,1)PA t PQ t t =--=---,因此，22133()(2)(1)(1)1()244PA PQ t t t t t t ⋅=-⋅-+-⋅--=-+=-+≥．当12t =时，min 3()4PA PQ ⋅=．5．在正方体中随机取三条棱，它们两两异面的概率为．答案：255．解：设正方体为ABCD-EFGH ，它共有12条棱，从中任意取出3条棱的方法共有312C =220种．下面考虑使3条棱两两异面的取法数．由于正方体的棱共确定3个互不平行的方向（即 AB 、AD 、AE 的方向），具有相同方向的4条棱两两共面，因此取出的3条棱必属于3个不同的方向．可先取定AB 方向的棱，这有4种取法．不妨设取的棱就是AB ，则AD 方向只能取棱EH 或棱FG ，共2种可能．当AD 方向取棱是EH 或FG 时，AE 方向取棱分别只能是CG 或DH ．由上可知，3条棱两两异面的取法数为4×2=8，故所求概率为8222055=．6．在平面直角坐标系中，点集{}0)63)(63(),(≤-+-+y x y x y x 所对应的平面区域的面积为．答案：24．解：设1{(,)||||3|60}K x y x y =+-≤．先考虑1K 在第一象限中的部分，此时有36x y +≤,故这些点对应于图中的△OCD 及其内部．由对称性知，1K 对应的区域是图中以原点O为中心的菱形ABCD 及其内部．同理，设2{(,)||3|||60}K x y x y =+-≤，则2K 对应的区域是图中以O 为中心的菱形EFGH 及其内部．由点集K 的定义知，K 所对应的平面区域是被1K 、2K 中恰好一个所覆盖的部分，因此本题所要求的即为图中阴影区域的面积S ．由于直线CD 的方程为36x y +=，直线GH 的方程为36x y +=，故它们的交点P 的坐标为33(,)22．由对称性知，138842422CPG S S ∆==⨯⨯⨯=．7．设ω为正实数，若存在实数)2(,ππ≤<≤b a b a ，使得2sin sin =+b a ωω，则ω的取值范围为．答案：9513[,)[,)424w ∈+∞．解：2sin sin =+b a ωω知，1sin sin ==b a ωω，而]2,[,ππωωw w b a si ∈，故题目条件等价于：存在整数,()k l k l <，使得 ππππππw l k w 22222≤+≤+≤． ①当4w ≥时，区间]2,[ππw w 的长度不小于π4，故必存在,k l 满足①式．当04w <<时，注意到)8,0(]2,[πππ⊆w w ，故仅需考虑如下几种情况：(i) ππππw w 2252≤<≤，此时21≤w 且45>w 无解；(ii) ππππw w 22925≤<≤，此时2549≤≤w ;(iii) ππππw w 221329≤<≤，此时29413≤≤w ,得4413<≤w ．综合(i)、(ii)、(iii)，并注意到4≥w 亦满足条件，可知9513[,)[,)424w ∈+∞．8．对四位数abcd ，若,,,d c c b b a ><>则称abcd 为P 类数，若d c c b b a <><,,，则称abcd 为Q 类数，则P 类数总量与Q 类数总量之差等于．答案：285．解：分别记P 类数、Q 类数的全体为A 、B ，再将个位数为零的P 类数全体记为0A ，个位数不等于零的尸类数全体记为1A ．对任一四位数1A abcd ∈，将其对应到四位数dcba ，注意到1,,≥><>d c c b b a ，故B dcba ∈．反之，每个B dcba ∈唯一对应于从中的元素abcd ．这建立了1A 与B 之间的一一对应，因此有011()()||||||||||||N P N Q A B A A B A -=-=+-=．下面计算0||A 对任一四位数00A abc ∈, b 可取0, 1，…，9，对其中每个b ，由9≤<a b 及9≤<c b 知，a 和c 分别有b -9种取法，从而992200191019||(9)2856b k A b k ==⨯⨯=-===∑∑．因此，()()285N P N Q -=．三、解答题9．（本题满分16分）若实数c b a ,,满足cb ac b a 424,242=+=+，求c 的最小值．解：将2,2,2abc分别记为,,x y z ，则,,0x y z >．由条件知，222,x y z x y z +=+=，故2222224()2z y x z y z y z y -==-=-+．8分因此，结合平均值不等式可得，4221111(2)244y y z y y y y +==++≥⋅=12分当212y y =，即y =时，zx求）．由于2log c z =，故c的最小值225log log 33=-．16分 10．（本题满分20分）设4321,,,a a a a 为四个有理数，使得：{}⎭⎬⎫⎩⎨⎧----=≤<≤3,1,81,23,2,2441j i aa ji，求4321a a a a +++的值．解：由条件可知，(14)i j a a i j ≤<≤是6个互不相同的数，且其中没有两个为相反数，由此知，4321,,,a a a a 的绝对值互不相等，不妨设||||||||4321a a a a <<<，则||||(14)i j a a i j ≤<≤中最小的与次小的两个数分别是12||||a a 及13||||a a ，最大与次大的两个数分别是34||||a a 及24||||a a ，从而必须有121324341,81,3,24,a a a a a a a a ⎧=-⎪⎪⎪=⎨⎪=⎪=-⎪⎩ 10 分于是2341112113,,248a a a a a a a =-===-．故2231412113{,}{,24}{2,}82a a a a a a =--=--，15分结合1a Q ∈，只可能114a =±．由此易知，123411,,4,642a a a a ==-==-或者123411,,4,642a a a a =-==-=．检验知这两组解均满足问题的条件．故123494a a a a +++=±． 20 分 11．（本题满分20分）设21,F F 分别为椭圆1222=+y x 的左右焦点，设不经过焦点1F 的直线l 与椭圆交于两个不同的点B A ,，焦点2F 到直线l 的距离为d ，如果11,,BF l AF 的斜率依次成等差数列，求d 的取值范围．解：由条件知，点1F 、2F 的坐标分别为（-1, 0）和（l, 0) ．设直线l 的方程为y kx m =+，点A 、B 的坐标分别为11(,)x y 和22(,)x y ，则12,x x 满足方程22()12x kx m ++=，即 222(21)4(22)0k x kmx m +++-=．由于点A 、B 不重合，且直线l 的斜率存在，故12,x x 是方程①的两个不同实根，因此有①的判别式22222(4)4(21)(22)8(21)0km k m k m ∆=-⋅+⋅-=+->，即2221k m +>．②由直线11,,BF l AF 的斜率1212,,11y y k x x ++依次成等差数列知，1212211y yk x x +=++，又1122,y kx m y kx m =+=+，所以122112()(1)()(1)2(1)(1)kx m x kx m x k x x +++++=++，化简并整理得，12()(2)0m k x x -++=．假如m k =，则直线l 的方程为y kx k =+，即 z 经过点1F （-1, 0)，不符合条件．因此必有1220x x ++=，故由方程①及韦达定理知，1224()221kmx x k =-+=+，即12m k k=+．③ 由②、③知，222121()2k m k k +>=+，化简得2214k k>，这等价于||2k >．反之，当,m k满足③及||2k >l 必不经过点1F （否则将导致m k =，与③矛盾）, 而此时,m k 满足②，故l 与椭圆有两个不同的交点A 、B ，同时也保证了1AF 、1BF 的斜率存在（否则12,x x 中的某一个为- l ，结合1220x x ++=知121x x ==-，与方程①有两个不同的实根矛盾）．10分点2F （l , 0）到直线l: y kx m =+的距离为211|2|(2)22d k kk ==+=+．注意到||2k >t =t ∈，上式可改写为 21313()()222t d t t t=⋅+=⋅+．考虑到函数13()()2f t t t=⋅+在上上单调递减，故由④得，(1)f d f <<，即2)d ∈．20 分加试1．（本题满分40分）设)2(,,,21≥⋅⋅⋅n a a a n 是实数，证明：可以选取{}1,1,,,21-∈⋅⋅⋅n εεε，使得))(1()()(122121∑∑∑===+≤+ni i i n i i ni i a n a a ε．证法一：我们证明：2[]222111[]2()(1)()n n n n i i j i n i i i j a a a n a ====⎛⎫ ⎪+-≤+ ⎪ ⎪⎝⎭∑∑∑∑，① 即对1,2,,[]2n i =，取1i ε=，对[]1,,2ni n =+，取1i ε=-符合要求．（这里，[]x 表示实数x 的整数部分．） 10分事实上，①的左边为2222[][][]222111[]1[]1[]122222n n n n n n i j i j i j n n n i i i j j j a a a a a a ====+=+=+⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪++-=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∑∑∑∑∑∑ []2221[]122222n n i j n i j n n a n a ==+⎛⎫⎛⎫⎛⎫⎡⎤⎡⎤ ⎪ ⎪≤+- ⎪⎢⎥⎢⎥ ⎪ ⎪⎣⎦⎣⎦⎝⎭ ⎪ ⎪⎝⎭⎝⎭∑∑（柯西不等式）30分 []2221[]1212222n n i j n i j n n a a ==+⎛⎫⎛⎫⎛+⎫⎡⎤⎡⎤ ⎪ ⎪=+ ⎪⎢⎥⎢⎥ ⎪ ⎪⎣⎦⎣⎦⎝⎭ ⎪⎪⎝⎭⎝⎭∑∑（利用122n n n +⎡⎤⎡⎤-=⎢⎥⎢⎥⎣⎦⎣⎦） []2221[]12(1)n n i j n i j n a n a ==+⎛⎫⎛⎫ ⎪ ⎪≤++ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭∑∑（利用[]x x ≤） 21(1)()ni i n a =≤+∑．所以 ① 得证，从而本题得证．证法二：首先，由于问题中12,,,n a a a 的对称性，可设12n a a a ≥≥≥．此外，若将12,,,n a a a 中的负数均改变符号，则问题中的不等式左边的21)(∑=n i i a 不减，而右边的21ni i a=∑不变，并且这一手续不影响1i ε=±的选取，因此我们可进一步设120n a a a ≥≥≥≥． 10分引理：设120n a a a ≥≥≥≥，则1110(1)ni i i a a -=≤-≤∑．事实上，由于1(1,2,,1)i i a a i n +≥=-，故当n 是偶数时，1123411(1)()()()0ni i n n i a a a a a a a --=-=-+-++-≥∑，11232111(1)()()ni i n n n i a a a a a a a a ---=-=------≤∑．当n 是奇数时，11234211(1)()()()0ni i n n n i a a a a a a a a ---=-=-+-++-+≥∑，1123111(1)()()ni i n n i a a a a a a a --=-=-----≤∑．引理得证． 30 分回到原题，由柯西不等式及上面引理可知22122211111(1)(1)n n n ni i i i i i i i i a a n a a n a -====⎛⎫⎛⎫⎛⎫+-≤+≤+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∑∑∑，这就证明了结论． 40分证法三：加强命题：设12,,,n a a a ⋅⋅⋅（2n ≥）是实数，证明：可以选取12,,,{1,1}n εεε⋅⋅⋅∈-，使得 2221111()()()()n nn i i i i i i i a a n a n ε===+≤+∑∑∑.证明不妨设22212n a a a ≥≥⋅⋅⋅≥，以下分n 为奇数和n 为偶数两种情况证明.当n 为奇数时，取12121n εεε-==⋅⋅⋅==，13221n n n εεε++==⋅⋅⋅==-，于是有12221112()[()()]n nni i jn i i j a a a -+===+-∑∑∑12221122[()+()]n ni jn i j a a -+===∑∑1222112112()+2()()22n n i j n i j n n a n a -+==--≤⋅⋅-∑∑（应用柯西不等式）.1222112(1)()+(1)()n ni jn i j n a n a -+===-+∑∑ ①另外，由于22212n a a a≥≥⋅⋅⋅≥，易证有122211211(1)(1)n n i j n i j a a n n -+==+≥-∑∑，因此，由式①即得到1222112(1)()+(1)()n nijn i j n a n a -+==-+∑∑211()()n i i n a n =≤+∑，故n 为奇数时，原命题成立，而且由证明过程可知，当且仅当12121n εεε-==⋅⋅⋅==，13221n n n εεε++==⋅⋅⋅==-，且12n a a a ==⋅⋅⋅=时取等号.当n 为偶数时，取1221n εεε==⋅⋅⋅==，24221n n n εεε++==⋅⋅⋅==-，于是有2222112()[()()]n nni i j n i i j a a a +===+-∑∑∑22222122[()+()]n ni j n i j a a +===∑∑2222122()+2()()22nn i j n i j n n a n a +==≤⋅⋅-∑∑（应用柯西不等式）.222212[()+()]n nijn i j n a a +===∑∑22111()()()nn ii i i n a n a n ===≤+∑∑，故n 为偶数时，原命题也成立，而且由证明过程可知，当且仅当120n a a a ==⋅⋅⋅==时取等号，若12,,,n a a a ⋅⋅⋅不全为零，则取不到等号.综上，联赛加试题一的加强命题获证. 2．（本题满分40分）设{},,,,21n A A A S ⋅⋅⋅=其中n A A A ,,,21⋅⋅⋅是n 个互不相同的有限集合)2(≥n ，满足对任意的S A A j i ∈,，均有S A A j i ∈ ，若2min 1≥=≤≤i ni A k ，证明：存在i ni A x 1=∈ ，使得x 属于n A A A ,,,21⋅⋅⋅中的至少kn个集合．证明：不妨设1||A k =．设在12,,,n A A A 中与1A 不相交的集合有s 个，重新记为12,,,s B B B ，设包含1A 的集合有t 个，重新记为12,,,t C C C ．由已知条件，1()i B A S ∈，即112(){,,,}i t B A C C C ∈，这样我们得到一个映射12121:{,,,}{,,,},()s t i i f B B B C C C f B B A →=．显然f 是单映射，于是，s t ≤． 10 分设112{,,,}k A a a a =．在n A A A ,,,21⋅⋅⋅中除去12,,,s B B B ，12,,,t C C C 后，在剩下的n s t --个集合中，设包含i a 的集合有i x 个（1i k ≤≤），由于剩下的n s t --个集合中每个集合与从的交非空，即包含某个i a ，从而12k x x x n s t +++≥--． 20 分不妨设11max i i k x x ≤≤=，则由上式知i n s tx k --≥，即在剩下的n s t --个集合中，包含1a的集合至少有n s tk--个．又由于),,2,1(1t i C A i ⋅⋅⋅=⊆，故12,,,t C C C 都包含1a ，因此包含1a 的集合个数至少为(1)n s t n s k t n s tt k k k---+---+=≥（利用2k ≥） nk ≥（利用s t ≤)． 40 分 3．（本题满分50分）如图，ABC ∆内接于圆O ，P 为BC 弧上一点，点K 在AP 上，使得BK 平分ABC ∠，过C P K ,,三点的圆Ω与边AC 交于D ，连接BD 交圆Ω于E ，连接PE ，延长交AB 于F ，证明：FCB ABC ∠=∠2．证法一：设CF 与圆Q 交于点L （异于C)，连接PB 、PC 、 BL 、KL ．注意此时C 、D 、L 、K 、E 、P 六点均在圆Ω上，结合A 、 B 、P 、C 四点共圆，可知∠FEB=∠DEP=180°-∠DCP=∠ABP=∠FBP ，因此△FB E ∽△FPB ，故FB 2=FE ·FP ．10分又由圆幂定理知，FE ·FP= FL ·FC ，所以FB 2=FL ·FC ．从而△FBL ∽△FCB ．因此, ∠FLB=∠FBC=∠APC=∠KPC=∠FLK, 即B 、K 、L 三点共线． 30 分再根据△FBL ∽△FCB 得，∠FCB=∠FBL=12∠ABC, 即∠ABC=2∠FCB ．证法二：设CF 与圆Ω交于点L （异于C)．对圆内接广义六边形DCLKPE 应用帕斯卡定理可知， DC 与KP 的交点A 、CL 与PE 的交点F 、LK 与ED 的交点了共线，因此B ’是AF 与ED 的交点，即B ’=B ．所以B 、K 、L 共线．10分根据A 、B 、P 、C 四点共圆及L 、K 、P 、C 四点共圆，得 ∠ABC=∠APC=∠FLK=∠FCB+∠LBC,又由BK 平分∠ABC 知，∠FBL=12∠ABC ，从而 ∠ABC=2∠FCB ．4．（本题满分50分）求具有下述性质的所有正整数k ：对任意正整数n 都有1)1(2+-n k 不整除!)!(n kn ．解：对正整数m ，设2()v m 表示正整数m 的标准分解中素因子2的方幂，则熟知2(!)()v m m S m =-，①这里()S m 表示正整数m 在二进制表示下的数码之和．由于1)1(2+-n k 不整除()!!kn n ，等价于2()!()(1)!kn v k n n ≤-，即22(()!)(!)kn v kn n v n -≥-，进而由①知，本题等价于求所有正整数k ，使得()()S kn S n ≥对任意正整数n 成立． 10分我们证明，所有符合条件的k 为2(0,1,2,)aa =．一方面，由于(2)()aS n S n =对任意正整数n 成立，故2ak =符合条件． 20 分另一方面，若k 不是2的方幂，设2,0,ak q a q =⋅≥是大于1的奇数．下面构造一个正整数n ，使得()()S kn S n <．因为()(2)()aS kn S q S qn <⋅=, 因此问题等价于我们选取q 的一个倍数m ，使得()()m S m S q <．由（2，q ）=l ，熟知存在正整数u ，使得21(mod )uq ≡．（事实上，由欧拉定理知，u 可以取()q ϕ的．)设奇数q 的二进制表示为1212222,0,2t a a at a a a t +++=<<<≥．取1122222t t a a tu aa-+++++，则()S m t =，且2(21)0(mod )t a tu m q q =+-≡．我们有1(1)02121211212(122)12t t ttu uu t a a lu a u t ul m q q q q q -+-=---=++⋅=+⋅+++=+⋅∑由于2102u uq -<<，故正整数21u q -的二进制表示中的最高次幂小于u ，由此易知，对任意整数,(01)i j i j t ≤<≤-，数212t u iu a q +-⋅与212tu ju a q+-⋅的二进制表示中没有相同的项．又因为0i a >，故212(0,1,,1)tu lu a l t q +-⋅=-的二进制表示中均不包含1，故由②可知21()1()()u m S S t t S m q q-=+⋅>=, 因此上述选取的m 满足要求．综合上述的两个方面可知，所求的k 为2(0,1,2,)aa =．50分。

2015年高考真题高中数学江苏卷(1)和答案

2015年普通高等学校招生全国统一考试（江苏卷）数学I一、填空题：本大题共14小题，每小题5分，共计70分.请把答案填写在答题卡相应的位置1.已知集合{}123A =，，，{}245B =，，，则集合A B 中元素的个数为_______.解析：{}5,4,3,2,1=⋃B A ，故答案5 2.已知一组数据4，6，5，8，7，6，那么这组数据的平均数为________. 解析：66678564=+++++，故答案63.设复数z 满足234z i =+（i 是虚数单位），则z 的模为_______.解析：设z=a+bi,，则()i bi a 432+=+化为i abi b a 43222+=+-，所以⎩⎨⎧==-42322ab b a解得⎪⎩⎪⎨⎧==1422b a ，所以z 的模为522=+b a ，故答案54.根据如图所示的伪代码，可知输出的结果S 为________.解析：第一次：S=1+2=3，I=1+3=4；第二次：S=3+2=5，I=4+3=7；第三次：S=5+2=7，I=7+3=10；因为10>8，所以程序结束，故S=75.袋中有形状、大小都相同的4只球，其中1只白球，1只红球，2只黄球，从中一次随机摸出2只球，则这2只球颜色不同的概率为________.6.已知向量()21a =，，()2-1，=b ，若()()R n m b n a m ∈-=+,89，，则m-n 的值为______. 解析：因为()()R n m b n a m ∈-=+,89，，所以⎩⎨⎧-=-=+8292n m n m ，所以352-=-⎩⎨⎧==n m n m ， S ←1 I ←1While I<8 S ←S+2 I ←I+3 End While Print S7.不等式224x x-<的解集为________.解析：因为224x x-<，所以()()2102102222<<-<-+<--<-x x x x x x x ，，，，故解析为()21，-8.已知tan 2α=-，()1tan 7αβ+=，则tan β的值为_______. 解析：()[]()()3757152711271tan tan 1tan tan tan tan ==⨯-+=++-+=-+=αβααβααβαβ，故答案3 9.现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2、高为8的圆柱各一个。

2015年全国高中数学联赛试题及答案详解(A卷)

(i ) 5 2 ，此时 1 且 5 ，无解；
22
2
4
(ii) 5 9 2 ，此时有 9 5 ；
件等价于：存在整数 k, l (k l) ，使得
2k 2l 2 ．
①
2
2
当 4 时，区间[, 2]的长度不小于 4 ，故必存在 k, l 满足①式．
当 0 4 时，注意到[, 2] (0, 8) ，故仅需考虑如下几种情况：
．

答案： 2015 1007i ．
解：由已知得，对一切正整数 n ，有
zn2 zn1 1n 1i zn 1 ni 1n 1i zn 2 i ，于是 z2015 z1 10072 i 2015 1007i ．
4. 在矩形 ABCD 中， AB 2, AD 1 ，边 DC 上（包含点 D 、 C ）的动点 P 与 CB 延长线上（包含点 B ）的动点 Q 满足 DP BQ ，则向量 PA 与向量 PQ 的数量积 PA PQ 的
6. 在平面直角坐标系 xOy 中，点集 K (x, y) x 3y 6 3x y 6 0所对
应的平面区域的面积为
．
答案：24．
解：设 K1 (x, y) x 3y 6 0 ．先考虑 K1
在第一象限中的部分，此时有 x 3y 6 ，故这些点对
应于图中的 OCD 及其内部．由对称性知， K1 对应的区域是图中以原点 O 为中心的菱形 ABCD 及其内部．
同理，设 K2 (x, y) 3x y 6 0 ，则 K2 对
应的区域是图中以 O 为中心的菱形 EFGH 及其内部．
由点集 K 的定义知， K 所对应的平面区域是被

2015年全国高中数学联赛试题及答案解析

5. 已知点 P (1, 2, 5) 是空间直角坐标系 O xyz 内一定点，过 P 作一平面与三坐标轴的正半轴分别交于 A, B, C 三点，则所有这样的四面体 OABC 的体积的最小值为． x y z 解：设此平面的方程为 1 ， a, b, c 0 分别是该平面在 x, y, z 轴上的截距，又点 P 在平面 ABC 内， a b c 3 1 2 5 1 10 1 1 2 5 1 1 2 5 1 2 5 ，即，得 VOABC abc 45 ．当，故 1 ，由于 1 3 a b c a b c 27 abc a b c 3 a b c 6 即 (a, b, c) (3, 6,15) 时， VOABC 的最小值为 45．
2015 年全国高中数学联赛模拟试题 04 第一试参考解答一、填空题：本大题共 8 小题，每小题 8 分，共 64 分. 1. 集合 A = {x, y} 与 B = {1, log 3 ( x + 2)} 恰有一个公共元为正数 1 + x ，则 A B = 解：由于 1 + x ¹ x ，故 1 + x = y ．由 log 3 ( x + 2) ¹ 1 知 x ¹ 1 ，又因为 1 + x > 0 ，所以 3

2
，
1 tan tan
tan tan
tan .
2 tan 1 3tan 2
2 1 3tan tan

3 ， u 的最大值为 . 6 3
4.在单调递增数列 an 中，已知 a1 2 ， a2 4 ，且 a2 n 1 ， a2 n ， a2 n 1 成等差数列， a2 n ， a2 n 1 ， a2 n 2 成解：因为 an 单调递增， a1 0 ，所以 an 0 .因为 a2 n 1 ， a2 n ， a2 n 1 成等差数列， a2 n ， a2 n 1 ， a2 n 2 成等比数列，所以所以 a2 n 所以 a2 n 等比数列， n 1, 2,3, .那么， a100 _________.

2015年全国高中数学联合竞赛试题及解答.(A卷)

2k 2 1 m2 ．②
由直线
AF1, l, BF1
的斜率
y1 , k, y2 x1 1 x2 1
依次成等差数列知，
y1 x1 1
y2 2k x2 1
，又
y1 kx1 m, y2 kx2 m ，所以 (kx1 m)(x2 1) (kx2 m)(x1 1) 2k(x1 1)(x2 1) ，化简并
棱两两异面的取法数为 4×2=8，故所求概率为 8 2 ． 220 55
2015A6、在平面直角坐标系 xOy 中，点集 K (x, y) | ( x 3 y 6)( 3x y 6) 0 所对应的平
面区域（如图所示）的面积为
◆答案： 24 ★解析：设 K1 {(x, y) || x | | 3y | 6 0} ．先考虑 K1 在第一象限中的部分，此时有 x 3y 6 ,故这些点
对应于图中的△OCD 及其内部．由对称性知， K1 对应的区
域是图中以原点 O 为中心的菱形 ABCD 及其内部．
同理，设 K2 {(x, y) || 3x | | y | 6 0} ，则 K2 对应
的区域是图中以 O 为中心的菱形 EFGH 及其内部．
由点集 K 的定义知，K 所对应的平面区域是被 K1 、K2
1 sin
cos4

cos 2 sin 2 sin
sin 2

(1 sin )(1 cos2 )

2 sin
cos2

2．
2015A 3、已知复数数列 zn 满足 z1 1，zn1 zn 1 ni (n 1,2,) ，其中 i 为虚数单位，zn 表

全国高中数学联赛江苏赛区初赛试卷001

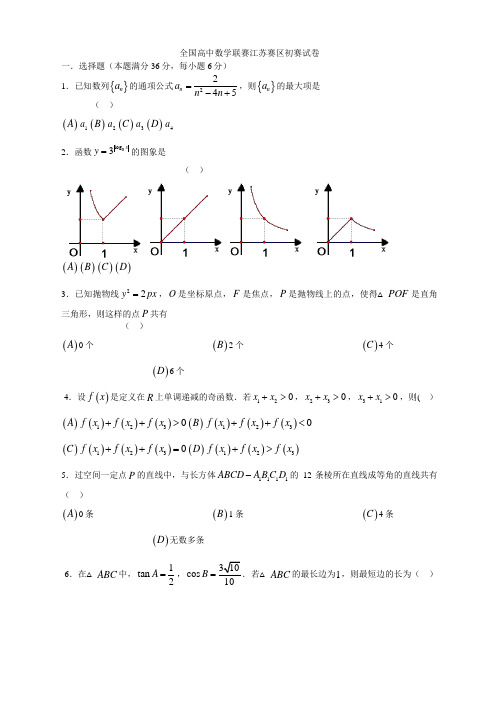
全国高中数学联赛江苏赛区初赛试卷一．选择题（本题满分36分，每小题6分） 1．已知数列{}n a 的通项公式2245n a n n =-+，则{}n a 的最大项是（）()A 1a ()B 2a ()C 3a ()D 4a2．函数3log 3xy =的图象是（）()A ()B ()C ()D3．已知抛物线22y px =，O 是坐标原点，F 是焦点，P 是抛物线上的点，使得△POF 是直角三角形，则这样的点P 共有（）()A 0个()B 2个()C 4个()D 6个4．设()f x 是定义在R 上单调递减的奇函数．若120x x +>，230x x +>，310x x +>，则( ）()A ()()()1230f x f x f x ++>()B ()()()1230f x f x f x ++< ()C ()()()1230f x f x f x ++=()D ()()()123f x f x f x +>5．过空间一定点P 的直线中，与长方体1111ABCD A B C D -的12条棱所在直线成等角的直线共有（）()A 0条()B 1条()C 4条()D 无数多条6．在△ABC 中，1tan 2A =，310cos B =．若△ABC 的最长边为1，则最短边的长为（）()A ()B ()C ()D 二．填空题（本题满分54分，每小题9分）7．集合{}3,,010A x x n n N n ==∈<<，{}5,,06B y y m m N m ==∈≤≤，则集合A B 的所有元素之和为． 8．设cos 2ϑ=，则44cos sin ϑϑ+的值是． 9．()323x x-的展开式中，5x 的系数为．10．已知030330y x y x y ≥⎧⎪-≥⎨⎪+-≤⎩，则22x y +的最大值是．11．等比数列{}n a 的首项为12020a =，公比12q =-．设()f n 表示这个数列的前n 项的积，则当n =时，()f n 有最大值．12．长方体1111ABCD A B C D -中，已知14AB =，13AD =，则对角线1AC 的取值范围是．三．解答题（本题满分60分，第13题、第14题各12分，第15题16分，第16题20分） 13．设集合()12log 32A x x ⎧⎫⎪⎪=-≥-⎨⎬⎪⎪⎩⎭，21a B xx a ⎧⎫=>⎨⎬-⎩⎭．若A B ≠∅，求实数a 的取值范围．14．椭圆22194x y +=的右焦点为F ，1224,,,P P P 为24个依逆时针顺序排列在椭圆上的点，其中1P 是椭圆的右顶点，并且122334241PFP P FP P FP P FP ∠=∠=∠==∠．若这24个点到右准线的距离的倒数和为S ，求2S 的值．15．△ABC 中，AB AC <，AD 、AE 分别是BC 边上的高和中线，且BAD EAC ∠=∠．证明BAC ∠是直角．16．设p 是质数，且271p +的不同正因数的个数不超过10个．求p ．全国高中数学联赛江苏赛区初赛试卷【参考答案】1．B 2．A 3．B 4．B 5．C 6．D7．2258．11189．27 10．9 11．1212．()4,513．解：{}13A x x =-≤<，()(){}30B x x a x a =--<．当0a >时，{}03B x a x a =<<<，由A B ≠∅得03a <<；当0a <时，{}30B x a x a =<<<，由A B ≠∅得1a >-；当0a =时，{}20B x x =<=∅，与A B ≠∅不符．综上所说，()()1,00,3a ∈-．B14．解：椭圆中，3a =，2b =，故c =)F，e =设i FP 与x 轴正向的夹角为i ϑ，i d 为点i P 到右准线的距离．则()2cos 1i i a d e c cϑ+=-．即()21cos 1i i c e d b ϑ=+．同理()()1222121cos 1cos 1i i i c c e d b bϑϑ++=+=-+．所以2121122i i c d d b ++==．从而2411i id ==∑ 2180S =． 15．如图，取AB 中点I ，连ID 、IE ．则IE 为中位线，所以//IE AC ，且IEA EAC ∠=∠．而BAD EAC ∠=∠，所以IEA BAD ∠=∠．…………①在直角△ADB 中，I 为斜边中点，所以ID IA =，从而BAD IDA ∠=∠．…………②联合①、②得A 、I 、D 、E 四点共圆．所以BAD IEB C ∠=∠=∠，∴90B C ∠+∠=︒，即90BAC ∠=︒．16．解：当2p =时，22717535p +==⨯，有()()11216++=个正因数；当3p =时，24718025p +==⨯，有()()411110++=个正因数．所以2p =、3p =满足条件．当3p >时，()()2711172p p p +=-++．其中p 为奇质数，所以()1p -与()1p +是相邻的两个偶数，从而必然有一个2的倍数和4个倍数，还必然有一个3的倍数，从而()()11p p -+是24的倍数．设23712423p m m +=⨯=⨯⨯，其中4m ≥．若m 中有不同于2、3的质因数，则271p +的正因数个数()()()31111110≥+++>；若m 中含有质因数3，则则271p +的正因数个数()()312110≥++>；BC若m 中仅有质因数2，则271p +的正因数个数()()511110≥++>．所以3p >不满足条件．综上所说，所求得的质数p 是2或3．高考数学（文）一轮：一课双测A+B精练(四十八) 直线与圆、圆与圆的位置关系1．(·人大附中月考)设m＞0，则直线2(x＋y)＋1＋m＝0与圆x2＋y2＝m的位置关系为( )A．相切B．相交C．相切或相离D．相交或相切2．(·福建高考)直线x＋3y－2＝0与圆x2＋y2＝4相交于A，B两点，则弦AB的长度等于( )A．25B．23C.3D．13．(·安徽高考)若直线x－y＋1＝0与圆(x－a)2＋y2＝2有公共点，则实数a的取值范围是( )A．[－3，－1]B．[－1,3]C．[－3,1]D．(－∞，－3]∪[1，＋∞)4．过圆x2＋y2＝1上一点作圆的切线与x轴，y轴的正半轴交于A，B两点，则|AB|的最小值为( )A.2B.3C．2D．35．(·兰州模拟)若圆x2＋y2＝r2(r＞0)上仅有4个点到直线x－y－2＝0的距离为1，则实数r的取值范围为( )A．(2＋1，＋∞) B．(2－1, 2＋1)C．(0, 2－1) D．(0, 2＋1)6．(·临沂模拟)已知点P(x，y)是直线kx＋y＋4＝0(k＞0)上一动点，PA，PB是圆C：x2＋y2－2y＝0的两条切线，A，B是切点，若四边形PACB的最小面积是2，则k的值为( )A.2B.21 2C．22D．27．(·朝阳高三期末)设直线x－my－1＝0与圆(x－1)2＋(y－2)2＝4相交于A、B两点，且弦AB的长为23，则实数m的值是________．8．(·东北三校联考)若a，b，c是直角三角形ABC三边的长(c为斜边)，则圆C：x2＋y2＝4被直线l：ax＋by＋c＝0所截得的弦长为________．9．(·江西高考)过直线x ＋y －22＝0上点P 作圆x2＋y2＝1的两条切线，若两条切线的夹角是60°，则点P 的坐标是________．10．(·福州调研)已知⊙M ：x2＋(y －2)2＝1，Q 是x 轴上的动点，QA ，QB 分别切⊙M 于A ，B 两点．(1)若|AB|＝423，求|MQ|及直线MQ 的方程；(2)求证：直线AB 恒过定点．11．已知以点C ⎝ ⎛⎭⎪⎫t ，2t (t ∈R ，t ≠0)为圆心的圆与x 轴交于点O 、A ，与y 轴交于点O 、B ，其中O 为原点．(1)求证：△AOB 的面积为定值；(2)设直线2x ＋y －4＝0与圆C 交于点M 、N ，若|OM|＝|ON|，求圆C 的方程． 12．在平面直角坐标系xOy 中，已知圆x2＋y2－12x ＋32＝0的圆心为Q ，过点P(0,2)，且斜率为k 的直线与圆Q 相交于不同的两点A 、B.(1)求k 的取值范围；(2)是否存在常数k ，使得向量OA ＋OB 与PQ ―→共线？如果存在，求k 值；如果不存在，请说明理由．1．已知两圆x2＋y2－10x －10y ＝0，x2＋y2＋6x －2y －40＝0，则它们的公共弦所在直线的方程为________________；公共弦长为________．2．(·上海模拟)已知圆的方程为x2＋y2－6x －8y ＝0，a1，a2，…，a11是该圆过点(3,5)的11条弦的长，若数列a1，a2，…，a11成等差数列，则该等差数列公差的最大值是________．3.(·江西六校联考)已知抛物线C ：y2＝2px(p ＞0)的准线为l ，焦点为F ，圆M 的圆心在x 轴的正半轴上，圆M 与y 轴相切，过原点O 作倾斜角为π3的直线n ，交直线l 于点A ，交圆M 于不同的两点O 、B ，且|AO|＝|BO|＝2.(1)求圆M 和抛物线C 的方程；(2)若P 为抛物线C 上的动点，求PM ―→,·PF ―→,的最小值；(3)过直线l 上的动点Q 向圆M 作切线，切点分别为S 、T ，求证：直线ST 恒过一个定点，并求该定点的坐标．[答题栏] A 级1._________2._________3._________4._________5B 级1.______2.______.__________6._________7.__________8.__________9.__________答案高考数学（文）一轮：一课双测A+B 精练(四十八)A 级1．C2.B3.C4.C5．选A 计算得圆心到直线l 的距离为22＝ 2＞1，如图．直线l ：x －y －2＝0与圆相交，l1，l2与l 平行，且与直线l 的距离为1，故可以看出，圆的半径应该大于圆心到直线l2的距离2＋1.6．选D 圆心C(0,1)到l 的距离 d ＝5k2＋1，所以四边形面积的最小值为2×⎝ ⎛⎭⎪⎫12×1×d2－1＝2，解得k2＝4，即k ＝±2. 又k ＞0，即k ＝2.7．解析：由题意得，圆心(1,2)到直线x －my －1＝0的距离d ＝4－3＝1，即|1－2m －1|1＋m2＝1，解得m ＝±33.答案：±338．解析：由题意可知圆C ：x2＋y2＝4被直线l ：ax ＋by ＋c ＝0所截得的弦长为24－⎝⎛⎭⎪⎫c a2＋b22，由于a2＋b2＝c2，所以所求弦长为2 3.答案：239．解析：∵点P 在直线x ＋y －22＝0上，∴可设点P(x0，－x0＋22)，且其中一个切点为M.∵两条切线的夹角为60°， ∴∠OPM ＝30°.故在Rt △OPM 中，有OP ＝2OM ＝2.由两点间的距离公式得OP ＝x20＋－x0＋222＝2，解得x0＝ 2.故点P 的坐标是( 2，2)．答案：( 2， 2)10．解：(1)设直线MQ 交AB 于点P ，则|AP|＝223，又|AM|＝1，AP ⊥MQ ，AM ⊥AQ ，得|MP|＝12－89＝13，又∵|MQ|＝|MA|2|MP|，∴|MQ|＝3.设Q(x,0)，而点M(0,2)，由x2＋22＝3，得x ＝±5，则Q 点的坐标为(5，0)或(－5，0)．从而直线MQ 的方程为2x ＋5y －25＝0或2x －5y ＋25＝0.(2)证明：设点Q(q,0)，由几何性质，可知A ，B 两点在以Q M 为直径的圆上，此圆的方程为x(x －q)＋y(y －2)＝0，而线段AB 是此圆与已知圆的公共弦，相减可得AB 的方程为qx －2y ＋3＝0，所以直线AB 恒过定点⎝ ⎛⎭⎪⎫0，32. 11．解：(1)证明：由题设知，圆C 的方程为 (x －t)2＋⎝ ⎛⎭⎪⎫y －2t 2＝t2＋4t2，化简得x2－2tx ＋y2－4t y ＝0，当y ＝0时，x ＝0或2t ，则A(2t,0)；当x ＝0时，y ＝0或4t ，则B ⎝ ⎛⎭⎪⎫0，4t ，所以S △AOB ＝12|OA|·|OB|＝12|2t|·⎪⎪⎪⎪⎪⎪4t ＝4为定值．(2)∵|OM|＝|ON|，则原点O 在MN 的中垂线上，设MN 的中点为H ，则CH ⊥MN ， ∴C 、H 、O 三点共线，则直线OC 的斜率 k ＝2t t ＝2t2＝12，∴t ＝2或t ＝－2. ∴圆心为C(2,1)或C(－2，－1)，∴圆C 的方程为(x －2)2＋(y －1)2＝5或(x ＋2)2＋(y ＋1)2＝5，由于当圆方程为(x ＋2)2＋(y ＋1)2＝5时，直线2x ＋y －4＝0到圆心的距离d ＞r ，此时不满足直线与圆相交，故舍去，∴圆C 的方程为(x －2)2＋(y －1)2＝5.12．解：(1)圆的方程可写成(x －6)2＋y2＝4，所以圆心为Q(6,0)．过P(0,2)且斜率为k 的直线方程为y ＝kx ＋2，代入圆的方程得x2＋(kx ＋2)2－12x ＋32＝0，整理得(1＋k2)x2＋4(k －3)x ＋36＝0.①直线与圆交于两个不同的点A 、B 等价于Δ＝[4(k －3)]2－4×36(1＋k2)＝42(－8k2－6k)>0，解得－34<k<0，即k 的取值范围为⎝ ⎛⎭⎪⎫－34，0. (2)设A(x1，y1)、B(x2，y2) 则OA ＋OB ＝(x1＋x2，y1＋y2)，由方程①得x1＋x2＝－4k －31＋k2.②又y1＋y2＝k(x1＋x2)＋4.③因P(0,2)、Q(6,0)，PQ ＝(6，－2)，所以OA ＋OB 与PQ 共线等价于－2(x1＋x2)＝6(y1＋y2)，将②③代入上式，解得k ＝－34.而由(1)知k ∈⎝ ⎛⎭⎪⎫－34，0，故没有符合题意的常数k. B 级1．解析：由两圆的方程x2＋y2－10x －10y ＝0，x2＋y2＋6x －2y －40＝0，相减并整理得公共弦所在直线的方程为2x ＋y －5＝0.圆心(5,5)到直线2x ＋y －5＝0的距离为105＝25，弦长的一半为50－20＝30，得公共弦长为230.答案：2x ＋y －5＝02302．解析：容易判断，点(3,5)在圆内部，过圆内一点最长的弦是直径，过该点与直径垂直的弦最短，因此，过(3,5)的弦中，最长为10，最短为46，故公差最大为10－4610＝5－265. 答案：5－2653．解：(1)易得B(1，3)，A(－1，－3)，设圆M 的方程为(x －a)2＋y2＝a2(a ＞0)，将点B(1，3)代入圆M 的方程得a ＝2，所以圆M 的方程为(x －2)2＋y2＝4，因为点A(－1，－3)在准线l 上，所以p2＝1，p ＝2，所以抛物线C 的方程为y2＝4x.(2)由(1)得，M(2,0)，F(1,0)，设点P(x ，y)，则PM ,＝(2－x ，－y)，PF ,＝(1－x ，－y)，又点P 在抛物线y2＝4x 上，所以PM ,·PF ,＝(2－x)(1－x)＋y2＝x2－3x ＋2＋4x ＝x2＋x ＋2，因为x ≥0，所以PM ,·PF ,≥2，即PM ,·PF ,的最小值为2.(3)证明：设点Q(－1，m)，则|QS|＝|QT|＝m2＋5，以Q 为圆心，m2＋5为半径的圆的方程为(x ＋1)2＋(y －m)2＝m2＋5，即x2＋y2＋2x －2my －4＝0，①又圆M 的方程为(x －2)2＋y2＝4，即x2＋y2－4x ＝0，② 由①②两式相减即得直线ST 的方程3x －my －2＝0，显然直线ST 恒过定点⎝ ⎛⎭⎪⎫23，0.高考数学（文）一轮：一课双测A+B精练(四十)空间几何体的结构特征及三视图和直观图1．(·青岛摸底)如图，在下列四个几何体中，其三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是( )A．②③④B．①②③C．①③④D．①②④2．有下列四个命题：①底面是矩形的平行六面体是长方体；②棱长相等的直四棱柱是正方体；③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体；④对角线相等的平行六面体是直平行六面体．其中真命题的个数是( )A．1B．2C．3D．43．一个锥体的正视图和侧视图如图所示，下面选项中，不可能是该锥体的俯视图的是( )4．如图是一几何体的直观图、正视图和俯视图．在正视图右侧，按照画三视图的要求画出的该几何体的侧视图是( )5.如图△A′B′C′是△ABC的直观图，那么△ABC是( )A．等腰三角形B．直角三角形C．等腰直角三角形D．钝角三角形6．(·东北三校一模)一个几何体的三视图如图所示，则侧视图的面积为( )A．2＋3B．1＋3C．2＋23D．4＋37．(·昆明一中二模)一个几何体的正视图和侧视图都是边长为1的正方形，且体积为1，则这个几何体的俯视图可能是下列图形中的________．(填入所有可能的图形前的编号) 2①锐角三角形；②直角三角形；③四边形；④扇形；⑤圆8．(·安徽名校模拟)一个几何体的三视图如图所示，则该几何体的体积为________．9．正四棱锥的底面边长为2，侧棱长均为3，其正视图(主视图)和侧视图(左视图)是全等的等腰三角形，则正视图的周长为________．10．已知：图1是截去一个角的长方体，试按图示的方向画出其三视图；图2是某几何体的三视图，试说明该几何体的构成．11．(·银川调研)正四棱锥的高为3，侧棱长为7，求侧面上斜高(棱锥侧面三角形的高)为多少？12．(·四平模拟)已知正三棱锥V－ABC的正视图、侧视图和俯视图如图所示．(1)画出该三棱锥的直观图；(2)求出侧视图的面积．1．(·江西八所重点高中模拟)底面水平放置的正三棱柱的所有棱长均为2，当其正视图有最大面积时，其侧视图的面积为( )A．23B．3C.3D．42．(·深圳模拟)如图所示的几何体中，四边形ABCD是矩形，平面ABCD⊥平面ABE，已知AB＝2，AE＝BE＝3，且当规定正视方向垂直平面ABCD时，该几何体的侧视图的面积为22.若M，N分别是线段DE，CE上的动点，则AM＋MN＋NB的最小值为________．3．一个多面体的直观图、正视图、侧视图如图1和2所示，其中正视图、侧视图均为边长为a的正方形．(1)请在图2指定的框内画出多面体的俯视图；(2)若多面体底面对角线AC，BD交于点O，E为线段AA1的中点，求证：OE∥平面A1C1C；(3)求该多面体的表面积．[答题栏]A级1._________2._________3._________4._________5._________6._________B级 1.______2.______ 7.__________8.__________9.__________答案高考数学（文）一轮：一课双测A+B精练(四十)A级1．A2.A3.C4.B5．选B由斜二测画法知B正确．6．选D依题意得，该几何体的侧视图的面积等于22＋12×2×3＝4＋ 3.7．解析：如图1所示，直三棱柱ABE－A1B1E1符合题设要求，此时俯视图△A BE是锐角三角形；如图2所示，直三棱柱ABC－A1B1C1符合题设要求，此时俯视图△ABC是直角三角形；如图3所示，当直四棱柱的八个顶点分别是正方体上、下各边的中点时，所得直四棱柱ABCD－A1B1C1D1符合题设要求，此时俯视图(四边形ABCD)是正方形；若俯视图是扇形或圆，体积中会含有π，故排除④⑤.答案：①②③8．解析：结合三视图可知，该几何体为底面边长为2、高为2的正三棱柱除去上面的一个高为1的三棱锥后剩下的部分，其直观图如图所示，故该几何体的体积为12×2×2sin60°×2－13×12×2×2sin60°×1＝533.答案：5339.解析：由题意知，正视图就是如图所示的截面PEF ，其中E 、F 分别是AD 、BC 的中点，连接AO ，易得AO ＝2，而PA ＝3，于是解得PO ＝1，所以PE ＝2，故其正视图的周长为2＋2 2.答案：2＋2210．解：图1几何体的三视图为：图2所示的几何体是上面为正六棱柱，下面为倒立的正六棱锥的组合体． 11．解：如图所示，正四棱锥S －ABCD 中，高OS ＝3，侧棱SA ＝SB ＝SC ＝SD ＝7，在Rt △SOA 中，OA ＝SA2－OS2＝2，∴AC ＝4. ∴AB ＝BC ＝CD ＝DA ＝2 2. 作OE ⊥AB 于E ，则E 为AB 中点．连接SE ，则SE 即为斜高，在Rt △SOE 中，∵OE ＝12BC ＝2，SO ＝3，∴SE ＝5，即侧面上的斜高为 5.12．解：(1)三棱锥的直观图如图所示． (2)根据三视图间的关系可得BC ＝23， ∴侧视图中VA ＝42－⎝ ⎛⎭⎪⎫23×32×232＝12＝23，∴S △VBC ＝12×23×23＝6.B 级1．选A 当正视图的面积达最大时可知其为正三棱柱某个侧面的面积，可以按如图所示位置放置，此时侧视图的面积为2 3.2．解析：依题意得，点E 到直线AB 的距离等于32－⎝ ⎛⎭⎪⎫222＝2，因为该几何体的左(侧)视图的面积为12·BC ×2＝22，所以BC ＝1，DE ＝EC ＝DC ＝2.所以△DEC 是正三角形，∠DEC ＝60°，tan ∠DEA ＝AD AE ＝33，∠DEA ＝∠CEB ＝30°.把△DAE ，△DEC 与△CEB 展在同一平面上，此时连接AB ，AE ＝BE ＝3，∠AEB ＝∠DEA ＋∠DEC ＋∠CEB ＝120°，AB2＝AE2＋BE2－2AE ·BEcos120°＝9，即AB ＝3，即AM ＋MN ＋NB 的最小值为3.答案：33．解：(1)根据多面体的直观图、正视图、侧视图，得到俯视图如下：(2)证明：如图，连接AC ，BD ，交于O 点，连接OE. ∵E 为AA1的中点，O 为AC 的中点， ∴在△AA1C 中，OE 为△AA1C 的中位线． ∴OE ∥A1C.∵OE ⊄平面A1C1C ，A1C ⊂平面A1C1C ， ∴OE ∥平面A1C1C.(3)多面体表面共包括10个面，SABCD ＝a2， SA1B1C1D1＝a22，S △ABA1＝S △B1BC ＝S △C 1DC ＝S △ADD1＝a22，S △AA1D1＝S △B1A1B ＝S △C1B1C ＝S △DC1D1 ＝12×2a 2×32a 4＝3a28， ∴该多面体的表面积S ＝a2＋a22＋4×a22＋4×3a28＝5a2.。

2015年全国高中数学联赛江苏赛区复赛参考答案与评分标准(加试)(定稿).pdf

C
F
K
D
B
E
R
C
F
K
D
ER．同理， CD ＝ FK ，所以 BC＝ CD ．
AC AD CD 由 AB＝ AC＝ BC＝ 1，得△ ABC≌△ ADC ，于是 AB＝ AC＝ AD ，
即 A 为△ BCD 外接圆的外心． .....................................
40 分
若 b＝pt， 1≤ t≤ α－ 1，则 a＝ pα－t， (c， p)＝ 1，1≤ c≤ b；若 b＝ pα，则
因此， f(pα)＝ 1 α－1 t ＋ pα＝ pα－1＋ pα． (这里 φ(x)为 Euler 函数 )．＋ φ(p )
t=1
a＝ 1， 1≤c≤ b．
……………………………… 20 分
所以 ER∥AC．
A
同理 FK ∥AC，
于是 ER∥FK ．又因为 RK∥ EF ，
………………………… 20 分
所以四边形 EFKR 为平行四边形，从而 ER＝
FK ．因为 ER∥AC，所以∠ REC＝∠ ECA＝ ∠ ECB．又因为∠ EBC＝∠ ERC， EC＝ EC，
所以△ BEC≌△ ECR，从而 BC＝
……………………………… 40 分
显然 (a1， b1， c)＝ (a1， b1， c1)＝ 1， (a2， b2， c)＝ (a2， b2， c2)＝ 1，从而 (a， b， c)＝ (( a，b)， c)＝ (( a1， b1)(a2， b2)， c)＝ (a1， b1， c) ( a2，b2 ，c) ＝
的外心．
B
E
R
A
证明：如图，连接 ER， FK ．因为∠ BAC＝∠ CAD， AC2＝ AB· AD ，

2015年全国高中数学联赛试卷解析

2015 年全国高中数学联合竞赛（A 卷）参考答案及评分标准一试说明：1.评阅试卷时，请依据本评分标冶填空题只设。

2015全国高中数学联赛江苏预赛试题及答案

2015年全国高中数学联赛江苏赛区初赛参考答案与评分细则一、填空题（本题共10小题，满分70分，每小题7分．要求直接将答案写在横线上．） 1．已知点P (4，1)在函数f (x )＝log a (x －b ) (b ＞0)的图象上，则ab 的最大值是．解：由题意知，log a (4－b )＝1，即a ＋b ＝4，且a ＞0，a ≠1，b ＞0，从而ab ≤(a ＋b )24＝4，当a ＝b ＝2时，ab 的最大值是4．2．函数f (x )＝3sin(2x －π4)在x ＝43π24处的值是．解：2x －π4＝43π12－π4＝40π12＝10π3＝2π＋4π3，所以f (43π24)＝3sin 4π3＝－32．3．若不等式|ax ＋1|≤3的解集为{x |－2≤x ≤1}，则实数a 的值是．解：设函数f (x )＝|ax ＋1|，则f (－2)＝ f (1)＝3，故a ＝2．4．第一只口袋里有3个白球、7个红球、15个黄球，第二只口袋里有10个白球、6个红球、9个黑球，从两个口袋里各取出一球，取出的球颜色相同的概率是．解：有两类情况：同为白球的概率是3×1025×25＝30625，同为红球的概率是7×625×25＝42625，所求的概率是72625．5．在平面直角坐标系xOy 中，设焦距为2c 的椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)与椭圆x 2b 2＋y 2c 2＝1有相同的离心率e ，则e 的值是．解：若c ＞b ，则c 2a 2＝c 2－b 2c 2，得a ＝b ，矛盾，因此c ＜b ，且有c 2a 2＝b 2－c 2b 2，解得e ＝－1＋52．6．如图，在长方体ABCD －A 1B 1C 1D 1中，对角线B 1D 与平面A 1BC 1交于E 点．记四棱锥E －ABCD 的体积为V 1，长方体ABCD －A 1B 1C 1D 1的体积为V 2，则V 1V 2的值是．（第6题图） A 1解：记四棱锥B 1－ABCD 的体积为V ．如图，DE ＝23DB 1，从而V 1＝23V ．又V ＝13V 2，所以V 1V 2＝29．7．若实数集合A ＝{31x ，65y }与B ＝{5xy ，403}仅有一个公共元素，则集合A ∪B 中所有元素之积的值是．解：因为31x ×65y ＝5xy ×403＝2015xy ．若xy ≠0，则集合A 和集合B 中有一组相等，则另一组也必然相等，这不合题意．所以xy ＝0，从而A ∪B 中所有元素之积的值为0． 8．设向量a ＝(cos α，sin α)，b ＝(－sin α，cos α)．向量x 1，x 2，…，x 7中有3个为a ，其余为b ；向量y 1，y 2，…，y 7中有2个为a ，其余为b ．则7∑i =1x i y i 的可能取值中最小的为．解：因为a ·a ＝b ·b ＝1，a ·b ＝0，所以7∑i =1x i y i 的最小值为2．9．在3×3的幻方中填数，使每行、每列及两条对角线上的三个数之和都相等．如图，三个方格中的数分别为1，2，2015，则幻方中其余6个数之和为．解：如图，设幻方正中间的数为x ，则由题意知a ＝－2012，从而对角线上三个数的和为x －2011．因此b ＝x －2014，c ＝－4026，d ＝－2013，e ＝x ＋2014．由b ＋e ＋x ＝x －2011，解得x ＝－20112．这9个数的和为3×(－20112－2011)＝－180992，所以幻方中其余6个数之和为－180992－2018＝－221352．10．在平面直角坐标系xOy 中，设D 是满足x ≥0，y ≥0，x ＋y ＋[x ]＋[y ]≤19的点(x ，y )形成的区域（其中[x ]是不超过x 的最大整数）．则区域D 中整点的个数为．解：区域D 中整点的个数为1＋2＋3＋…＋10＝55．（第9题图） 12 2015（第9题图）e c d ab1 2 2015x （第6题图）A 1二、解答题（本大题共4小题，每小题20分，共80分）11．在等比数列{a n }中，a 2＝2，q 是公比．记S n 为{a n }的前n 项和，T n 为数列{a 2n }的前n 项和．若S 2n ＝2T n ，求q 的值．解：若q ＝1，则a n ＝a 2＝2，a 2n ＝4，则S 2n ＝4n ，T n ＝4n ，S 2n ≠2T n ．若q ＝－1，则a n ＝2×(－1)n ，a 2n ＝4，则S 2n ＝0，T n ＝4n ，S 2n ≠2T n ．……………………………… 5分若q ≠±1，则a n ＝2q n －2，a 2n ＝4q 2n －4，从而S 2n ＝2q ×(1－q 2n )1－q ，T n ＝4q 2×(1－q 2n )1－q 2． ……………………………… 15分由S 2n ＝2T n ，则4q (1＋q )＝1，q 2＋q －4＝0，解得q ＝－1±172．综上，q 的值为－1＋172和－1－172． ……………………………… 20分12．如图，△ABC 中，AB ＞AC ，点D 、E 分别在边AB 、AC 上，且BD ＝CE ．∠BAC 的外角平分线与△ADE 的外接圆交于A 、P 两点．求证：A 、P 、B 、C 四点共圆．证明：如图，连结PD ，PE ，PC ．因为四边形APDE 是圆内接四边形, 所以∠P AD ＝∠PED ，∠P AF ＝∠PDE ．又因为AP 是∠BAC 的外角平分线，所以∠P AD ＝∠P AF ，从而∠PED ＝∠PDE ，故PD ＝PE ． ……………………………… 10分又∠ADP ＝∠AEP ，所以∠BDP ＝∠CEP ．又因为BD ＝CE ，所以△BDP ≌△CEP ，从而∠PBD ＝∠PCE ，即∠PBA ＝∠PCA ，ABCDP(第12题图)EA BC DP (第12题图)EF所以A 、P 、B 、C 四点共圆． ……………………………… 10分13．如图，在平面直角坐标系xOy 中，圆O 1、圆O 2都与直线l ：y ＝kx 及x 轴正半轴相切．若两圆的半径之积为2，两圆的一个交点为P (2，2)，求直线l 的方程．解：由题意，圆心O 1，O 2都在x 轴与直线l若直线l 的斜率k ＝tanα，设t ＝tan α2，则k ＝2t1－t 2．圆心O 1，O 2在直线y ＝tx 上，可设O 1(m ，mt )，O 2(n ，nt )．交点P (2，2)在第一象限，m ，n ，t ＞0． ……………………………… 4分所以⊙O 1：(x －m )2+(y －mt )2=(mt )2，⊙O 1：(x －n )2+(y －nt )2=(nt )2，所以⎩⎨⎧(2－m )2＋(2－mt )2＝(mt )2，(2－n )2＋(2－nt )2＝(nt )2，即⎩⎨⎧m 2－(4＋4t )m ＋8＝0，n 2－(4＋4t )n ＋8＝0，……………… 8分所以 m ，n 是方程X 2－(4+4t )X ＋8=0的两根，mn ＝8．由半径的积(mt )(nt )＝2，得t 2＝14，故t ＝12．……………………………… 16分所以 k ＝2t 1－t 2＝11－14＝43，直线l ：y ＝43x ． ……………………………… 20分14．将正十一边形的k 个顶点染红色，其余顶点染蓝色．（1）当k ＝2时，求顶点均为蓝色的等腰三角形的个数；（2）k 取何值时，三个顶点同色(同红色或同蓝色)的等腰三角形个数最少？并说明理由．解：（1）设正十一边形的顶点A 1，A 2，A 3，…，A 11，则易知其中任意三点为顶点的三角形都不是正三角形．以这些点为顶点的等腰三角形个数可以如此计算：以A i (i ＝1，2，3，…，11)为顶角顶点的等腰三角形有11－12＝5个，这些三角形均不是等边三角形，即当j ≠i 时，以A j 为顶角顶点的等腰三角形都不是上述等腰三角形．故所有的等腰三角形共有5×11＝55个． …………………… 5分当k ＝2时，设其中A m ，A n 染成红色，其余染成蓝色．以A m 为顶角顶点的等腰三角形有5个，以A m 为底角顶点的等腰三角形有10个；同时以A m ，A n 为顶点的等腰三角形有3个，这些等腰三角形的顶点不同色，且共有(5＋10)×2－3＝27个．注意到仅有这些等腰三角形的三个顶点不同蓝色，故所求三个顶点同为蓝色的等腰三角形有55－27＝28个． ………………………… 10分（2）若11个顶点中k 个染红色，其余11－k 个染蓝色．则这些顶点间连线段(边或对角线)中，两端点染红色的有k (k －1)2条，两端点染蓝色的有(11－k )(10－k )2条，两端点染一红一蓝的有k (11－k )条．并且每条连线段必属于且仅属于3个等腰三角形．把等腰三角形分4类：设其中三个顶点均为红色的等腰三角形有x 1个，三个顶点均为蓝色的等腰三角形有x 2个，两个顶点为红色一个顶点为蓝色的等腰三角形有x 3个，两个顶点为蓝色一个顶点为红色的等腰三角形有x 4个，则按顶点颜色计算连线段，3x 1＋x 3＝3×k (k －1)2， ①3x 2＋x 4＝3×(11－k )(10－k )2， ②2x 3＋2x 4＝3×k (11－k )， ③由①＋②得 3(x 1＋x 2)＋x 3＋x 4＝32[k (k －1)＋(11－k )(10－k )]，用③代入得 x 1＋x 2＝12[ k (k －1)＋(11－k )(10－k )－k (11－k )]＝12(3k 2－33k ＋110)．当k ＝5或6时，(x 1＋x 2)min ＝12(5×4＋6×5－5×6)＝10．即顶点同色的等腰三角形最少有10个，此时k ＝5或6．………… 20分。

全国高中数学联赛江苏赛区初赛试卷

全国高中数学联赛江苏赛区初赛试卷一、选择题(本题满分36分，每小题6分)本题共有6小题，每题均给出A 、B 、C 、D 四个结论，其中有且仅有一个是正确的．请将正确答案的代表字母填在题的括号内，每小题选对得6分；不选、选错或选出的字母超过一个（不论是否写在括号内），一律得0分．1．已知数列{an}的通项公式an ＝，则{an}的最大项是（） A ．a1 B ．a2 C ．a3 D ．a42．函数y ＝3 |log 3x|的图象是（） A ．B ．C ．D ．3．已知抛物线y2＝2px ，O 是坐标原点，F 是焦点，P 是抛物线上的点，使得△POF 是直角三角形，则这样的P 点共有（） A ．0个 B ．2个 C ．4个 D ．6个4．设f(x)是定义在R 上单调递减的奇函数，若x1＋x2＞0，x2＋x3＞0，x3＋x1＞0，则（） A ．f(x1)＋f(x2)＋f(x3)＞0 B ．f(x1)＋f(x2)＋f(x3)＜0 C ．f(x1)＋f(x2)＋f(x3)＝0 D ．f(x1)＋f(x2)＞f(x3)5．过空间一定点P 的直线中，与长方体ABCD －A1B1C1D1的12条棱所在直线所成等角的直线共有（） A ．0条 B ．1条 C ．4条 D ．无数多条6．在△ABC 中，tanA ＝，cosB ＝,10)．若的最长边为1，则最短边的长为（） A ．,5)B ．,5)C ．,5)D ．,5)二、填空题（本题满分54分，每小题9分）本小题共有6小题，要求直接将答案写在横线上．7．集合A ＝｛x|x ＝3n ，n ∈N ，0＜n ＜10｝，B ＝｛y|y ＝5m ，m ∈N ，0≤n≤6｝则集合A ∪B 的所有元素之和为__________________．8．设cos2θ＝,3)，则cos4θ＋sin4θ的值是__________________． 9．(x －3x2)3的展开式中，x5的系数为__________________．10．已知⎩⎪⎨⎪⎧y≥0，3x －y≥0，x ＋3y －3≤0，则x2＋y2的最大值是__________________．11．等比数列{an}的首项为a1=，公比q ＝－，设f(n)表示这个数列的前n 项的积，则当n ＝_________________时，f(n)有最大值．12．长方体ABCD －A1B1C1D1中，已知AB1＝4，AD1＝3，则对角线AC1的取值范围是______________________________．三、解答题（本题满分60分，第13题，第14题各12分，第15题16分，第16题20分）13．设集合A ＝｛x|log 12(3－x)≥－2｝，B ＝｛x|≥1｝，若A∩B ＝，求实数a 的取值范围．14．椭圆＋＝1的有焦点为F ，P1，P2，…，P24为24个依逆时针顺序排列在椭圆上的点，其中P1是椭圆的右顶点，并且∠P1FP2＝∠P2FP3＝∠P3FP4＝…＝∠P24FP1，x O yx O yx O yx O y若这24个点到右准线的距离的倒数和为S ，求S 的值．15．△ABC 中，AB ＜AC ，AD 、AE 分别是BC 边上的高和中线，且∠BAD ＝∠EAC ．证明是直角．16．设p 是质数，且p2＋71的不同正因数的个数不超过10个，求p ．全国高中数学联赛江苏赛区初赛试卷一、选择题(本题满分36分，每小题6分)本题共有6小题，每题均给出A 、B 、C 、D 四个结论，其中有且仅有一个是正确的．请将正确答案的代表字母填在题的括号内，每小题选对得6分；不选、选错或选出的字母超过一个（不论是否写在括号内），一律得0分．1．已知数列{an}的通项公式an ＝，则{an}的最大项是（） A ．a1 B ．a2 C ．a3 D ．a4解：an ＝1(n －2)2＋1，当n ＝2时，an 取最大值，故选B ．2．函数y ＝3的图象是（） A ．B ．C ．D ．解：由于|log3x|≥0，故y≥1，只有A 满足此条件，故选A ．3．已知抛物线y2＝2px ，O 是坐标原点，F 是焦点，P 是抛物线上的点，使得△POF 是直角三角形，则这样的P 点共有（） A ．0个 B ．2个 C ．4个 D ．6个解：作垂直于x 轴的焦点弦交抛物线于点P1、P2，则△P1OF 、△P2OF是直角三角形．对于抛物线上异于O 、P1、P2的点Q ，显然∠QFO≠90˚，∠QOF≠90˚，从而若△QOF 为直角三角形，则只能是∠FQO ＝90˚．设点Q 坐标为(y22p，y)(y≠0，±p)，则有y22p (y22p －p2)＋y2＝0，由y≠0得，y22p ＋3p2＝0，此方程无实解，从而这样的点P 只能2个，选B ．4．设f(x)是定义在R 上单调递减的奇函数，若x1＋x2＞0，x2＋x3＞0，x3＋x1＞0，则（）A ．f(x1)＋f(x2)＋f(x3)＞0B ．f(x1)＋f(x2)＋f(x3)＜0C ．f(x1)＋f(x2)＋f(x3)＝0D ．f(x1)＋f(x2)＞f(x3)解：则x1＞－x2，知f(x1)＜f(－x2)＝－f(x2)f(x1)＋f(x2)＜0；同理，f(x2)＋f(x3)＜0，f(x3)＋f(x1)＜0；所以，f(x1)＋f(x2)＋f(x3)＜0．选B ．5．过空间一定点P 的直线中，与长方体ABCD －A1B1C1D1的12条棱所在直线所成等角的直线共有（） A ．0条 B ．1条 C ．4条 D ．无数多条解：首先，过角的顶点与角的两边成等角的直线在角所在平面的射影是角(或其外角)的平分线．故若以长方体的过一个顶点的三个平面为坐标平面建立空间坐标系，则方程|x|＝|y|＝|z|共有8解，此8解共组成4条直线，故选C ．6．在△ABC 中，tanA ＝，cosB ＝,10)．若的最长边为1，则最短边的长为（） A ．,5)B ．,5)C ．,5)D ．,5)解：作辅助图如右：取高CD ＝a ，则AD ＝2a ，BD ＝ A B C D Ex O y x O y x O y x O yABDC3a2aa3a ，最短边AC ＝5a ；由5a ＝1，得a ＝，故选D ．二、填空题（本题满分54分，每小题9分）本小题共有6小题，要求直接将答案写在横线上．7．集合A ＝｛x|x ＝3n ，n ∈N ，0＜n ＜10｝，B ＝｛y|y ＝5m ，m ∈N ，0≤n≤6｝则集合A ∪B 的所有元素之和为__________________．解：A∩B ＝{15}；故所求和＝(3＋6＋…＋27)＋(0＋5＋…＋30)－15＝225． 8．设cos2θ＝,3)，则cos4θ＋sin4θ的值是__________________．解：已知即cos2θ－sin2θ＝,3)cos4θ＋sin4θ－2cos2θsin2θ＝； ① 又，cos2θ＋sin2θ＝1cos4θ＋sin 4θ＋2cos2θsin2θ＝1． ② (①＋②)÷2： cos4θ＋sin4θ＝．9．(x －3x2)3的展开式中，x5的系数为__________________．解：(x －3x2)3＝x3－3x2×3x2＋3x×9x4－27x6．x5 的系数＝27．10．已知⎩⎪⎨⎪⎧y≥0，3x －y≥0，x ＋3y －3≤0，则x2＋y2的最大值是__________________．解：满足条件的点集组成的图形为图中阴影部分及其边界．其中点(3，0)与原点距离最大，故(x2＋y2)max ＝9．11．等比数列{an}的首项为a1=，公比q ＝－，设f(n)表示这个数列的前n 项的积，则当n ＝_________________时，f(n)有最大值．解：由于f(4k)＞0，f(4k ＋1)＞0，(k ∈N*)．f(4k)＝a 4k 1 q2k(4k －1)；f(4k ＋1)＝a 4k ＋11q2k(4k ＋1)．故＝a1q4k ．于是f(12)＞f(13)，且当k≥3时，f(4k ＋1)＜f(4k)；又＝a 31q30，有f(9)＜f(12)；＝a 41q2(8k ＋3)，故f(8)＜f(12)，且k≥3时，f(4k ＋4)＜f(4k)，从而f(12)最大．12．长方体ABCD －A1B1C1D1中，已知AB1＝4，AD1＝3，则对角线AC1的取值范围是______________________________．解：设长方体的三度分别为x ，y ，z ，对角线AC ＝d ．则可得x2＋z2＝16，y2＋z2＝9．d2＝x2＋y2＋z2＝25－z2，但0＜z ＜3，从而16＜d2＜254＜d ＜5所求取值范围为(4，5)．三、解答题（本题满分60分，第13题，第14题各12分，第15题16分，第16题20分）13．设集合A ＝｛x|log 12(3－x)≥－2｝，B ＝｛x|≥1｝，若A∩B ＝，求实数a 的取值范围．解：由log 12(3－x)≥－20＜3－x≤4－1≤x ＜3．由≥1(x －a)(x －3a)≤0．1321Oyx① 当a ＞0时，解为a ＜x ＜3a ； ② 当a ＝0时，解为；③ 当a ＜0时，解为3a ＜x ＜a ．若A∩B≠，则当a ＜0时，有a ＞－1－1＜a ＜0；当a ＞0时，有3a ＜30＜a ＜1．所以，a 的取值范围为(－1，0)∪(0，1)．14．椭圆＋＝1的有焦点为F ，P1，P2，…，P24为24个依逆时针顺序排列在椭圆上的点，其中P1是椭圆的右顶点，并且∠P1FP2＝∠P2FP3＝∠P3FP4＝…＝∠P24FP1，若这24个点到右准线的距离的倒数和为S ，求S 的值．解法一：已知椭圆的a ＝3，b ＝2，c ＝5，e ＝53，p ＝b2c ＝45．对于椭圆上任一点P ，|FP|＝r ，P 到准线的距离|PH|＝d ，FP 与Ox 正向夹角为θ，则有 rcosθ＋d ＝p ，rd＝e ．于是， d(1＋ecosθ)＝p ，1d ＝1p(1＋ecosθ)．所以， S ＝i ＝1∑241di ＝1p i ＝1∑24(1＋ecosθ)＝24p ＋e p i ＝1∑24co sθ＝24p ．故 S2＝242p2＝180．解法二：设过焦点且斜率为k 的直线交椭圆于A 、B 两点．则有⎩⎨⎧y ＝k(x －c)， ①4x2＋9y2＝36． ②①代入②： 4x2＋9k2(x －5)2－36＝0．即， (4＋9k2)x2－185xk2＋45k2－36＝0．所以， x1＋x2＝185k24＋9k2，x1x2＝45k2－364＋9k2．而点P 到准线距离d ＝a2c －x ＝9－5x 51d ＝59－5x ，故直线①与椭圆的两个交点到准线距离的倒数和为59－5x1＋59－5x2＝5[18－5(x1＋x2)]81－95(x1＋x2)＋5x1x2＝5[18－5·185k24＋9k2]81－95·185k24＋9k2＋545k2－364＋9k2＝185(4＋9k2)－905k281(4＋9k2)－810k2＋225k2－180＝725＋725k2144＋144k2＝52．而过焦点且倾斜角θ＝90˚时，两交点到准线的距离＝a2c －c ＝45，故θ＝90˚及270˚的pθF P OxyH rd两个点到准线距离倒数和也＝52．所以，S ＝12×52＝65；S2＝180．解法三：令⎩⎨⎧x ＝5＋tcosθ，y ＝tsinθ．代入椭圆方程得，t2(4cos 2θ＋9sin2θ)＋85tcosθ－16＝0．同上．15．△ABC 中，AB ＜AC ，AD 、AE 分别是BC 边上的高和中线，且∠BAD ＝∠EAC ．证明是直角．证明一：延长AE 到F ，使EF ＝AE ，延长AD 到K ，使DK ＝AD ．连FK ，FB ．因FB ∥AC ∠AFB ＝∠EAC ．又BD 垂直平分AK ，故∠AKB ＝∠BAD ，因∠BAD ＝∠EAC ，所以∠AKB ＝∠AFB ．所以A 、F 、K 、B 四点共圆． FK ∥BC ∠FKA ＝90˚．故AF 为该圆直径．E 为此圆圆心．故EA ＝EB ＝EC ，即点C 在此圆上．此圆为△ABC 的外接圆，BC 为圆的直径．所以∠BAC 为直角．证明二：取△ABC 的外接圆，延长AE 交圆于点F ，连FB ，则∠CBF ＝∠CAF ＝∠BAD ，但∠BAD ＋∠ABD ＝90˚，从而∠FBC ＋∠ABC ＝90˚，即∠ABF ＝90˚．从而AF 为圆的直径．若E 不是圆心，则AF ⊥BC ，AB ＝AC ．与已知矛盾．故E 为外心．从而∠BAC ＝90˚．证明三：作△ABC 的外接圆，作EF ⊥BC ，交外接圆于点F ，连AF ．则EF 是BC 的垂直平分线，故F 为⌒BC 的中点，于是AF 是∠BAC的平分线．由∠BAD ＝∠EAC ，得∠DAF ＝∠EAF ．又，EF ∥AD ，故∠DAF ＝∠EFA ∠EAF ＝∠EFA ．EA ＝EF ．故AF 的垂直平分线经过点E ．由于△ABC 的外接圆圆心应是弦AF 、BC 的垂直平分线的交点，故E 为△ABC 的外心．从而△ABC 为直角三角形，得，∠BAC 为直角．证明四：取AC 中点F ，连DF 、EF ，由EF ∥AB ∠AEF ＝∠EAB ＝∠BAD ＋∠DAE ＝∠EAC＋∠DAE ＝∠DAC ，由AD 为高，故∠DAC ＝∠ADF ，所以，∠ADF ＝∠AEF A 、D 、E 、F 四点共圆．于是有∠EFA ＝90˚，从而∠BAC ＝90˚，故证．证明五：以D 为原点，BC 所在直线为x 轴建立坐标系．设点A 、B 、C 的坐标分别为A(0，a)，B(b ，0)，C(0，c)．FE D CB AA B C D E FK FD E C B A设AB 到AD 的角为α，则tanα＝－ba ．kAC ＝－a c ，kAE ＝－2ab ＋c ，tan ∠EAC ＝－a c ＋2a b ＋c 1＋2a2c(b ＋c)＝a(c －b)2a2＋bc ＋c2．由tan ∠EAC ＝tanα－ba ＝a(c －b)2a2＋bc ＋c2．化简得a2＝－bc ．即|AD|2＝|DB|·|DC|．故△ABC 为直角三角形．证明六：设BC ＝a ，BD ＝p ，AD ＝h ，则tanB ＝hp ，tan ∠AEB ＝h 12a －p ＝2ha －2p ．∠BAE ＝∠DACtan ∠BAE ＝tan ∠DAC ＝a －ph．在△ABE 中，有h p ＋2ha －2p ＋a －p h ＝h p ·2h a －2p ·a －p h ＝2h(a －p)p(a －2p)．即h2(a －2p)＋2ph2＋p(a －p)(a －2p)＝2h2(a －2p)．h2＝p(a －p)．从而|AD|2＝|DB|·|DC|．故△ABC 为直角三角形．得证．证明七：设∠BAD ＝∠EAC ＝α，则AD ＝ABcosα＝ACsinC ， ①∠BAE ＝∠DAC ＝90˚－C ．而S △BAE ＝S △CAE AB·AEsin(90˚－C)＝AC·AEsinαABcosC ＝ACsinα．②①×②：sin2α＝sin2C α＋C ＝90˚或α＝C ．若α＋C ＝90˚，则D 、E 重合，与AC ＞AB 矛盾，α＝C ．则有∠BAC ＝90˚，得证． 16．设p 是质数，且p2＋71的不同正因数的个数不超过10个，求p ．解 p ＝2时，p2＋71＝75＝3×52，d(75)＝2×3＝6＜10，故p ＝2是本题的解； p ＝3时，p2＋71＝80＝24×5，d(80)＝5×2＝10≤10，故p ＝3是本题的解；若质数p ＞3，则p2≡1(mod 8)p2＋71≡0(mod 8)，故23|p2＋71； p2≡1(mod 3)p2＋71≡0(mod 3)，故3|p2＋71．所以，p2＋71＝2α×3β×t ．其中α、β∈N*，且α≥3．当α＝3，β＝1，t 若有大于3的质因子，则d(p2＋71)≥4×2×2，故t ＝1．此时无质数p 满足题意；当α＝4，β＝1，必有t ＝1，此时有d(p2＋71)≥5×2＝10．此时无质数p 满足题意；当α≥4，β≥1，且等号不同时成立时，d(p2＋71)＞10．综上可知，解为p ＝2，3．xyA (0,a )B (b ,0)C (c ,0)D EahpABCED高考理科数学试卷普通高等学校招生全国统一考试注意事项： 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页，第Ⅱ卷3至5页. 2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成，答在本试题上无效. 4.考试结束后，将本试题和答题卡一并交回.第Ⅰ卷一. 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.（1）已知集合{1,}A =2,3，{|(1)(2)0,}B x x x x =+-<∈Z ，则AB =（A ）{1}（B ）{12}，（C ）{0123}，，，（D ）{10123}-，，，，（2）已知(3)(1)i z m m =++-在复平面内对应的点在第四象限，则实数m 的取值范围是（A ）(31)-，（B ）(13)-，（C ）(1,)∞+（D ）(3)∞--，（3）已知向量(1,)(3,2)m =-，=a b ，且()⊥a +b b ，则m= （A ）－8（B ）－6 （C ）6 （D ）8（4）圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1，则a= （A ）43-（B ）34-（C ）3（D ）2（5）如图，小明从街道的E 处出发，先到F 处与小红会合，再一起到位于G 处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为（A ）24 （B ）18 （C ）12 （D ）9（6）右图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（A ）20π（B ）24π（C ）28π（D ）32π（7）若将函数y=2sin 2x 的图像向左平移π12个单位长度，则评议后图象的对称轴为（A ）x=kπ2–π6 (k ∈Z) （B ）x=kπ2+π6 (k ∈Z) （C ）x=kπ2–π12 (k ∈Z) （D ）x=kπ2+π12 (k ∈Z)（8）中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图.执行该程序框图，若输入的x=2，n=2，依次输入的a 为2，2，5，则输出的s= （A ）7 （B ）12 （C ）17 （D ）34 （9）若cos(π4–α)=35，则sin 2α=（A ）725（B ）15（C ）–15（D ）–725（10）从区间[]0,1随机抽取2n 个数1x ,2x ，…，nx ，1y ，2y ，…，ny ，构成n 个数对()11,x y ，()22,x y ，…，(),n n x y ，其中两数的平方和小于1的数对共有m 个，则用随机模拟的方法得到的圆周率π的近似值为（A ）4n m （B ）2n m （C ）4m n （D ）2m n（11）已知F1，F2是双曲线E 22221x y a b-=的左，右焦点，点M 在E 上，M F1与x 轴垂直，sin 2113MF F ∠=,则E 的离心率为（AB ）32（CD ）2（12）已知函数学.科网()()f x x ∈R 满足()2()f x f x -=-，若函数1x y x+=与()y f x =图像的交点为1122(,),(,),,(,),m m x y x y x y ⋅⋅⋅则1()mi i i x y =+=∑（A ）0 （B ）m （C ）2m （D ）4m第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题，每个试题考生都必须作答.第(22)题~第(24)题为选考题，考生根据要求作答.二、填空题：本大题共3小题，每小题5分(13)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，若cos A=45，cos C=513，a=1，则b=. (14)α、β是两个平面，m 、n 是两条直线，有下列四个命题：（1）如果m ⊥n ，m ⊥α，n ∥β，那么α⊥β. （2）如果m ⊥α，n ∥α，那么m ⊥n.（3）如果α∥β，m ⊂α，那么m ∥β. （4）如果m ∥n ，α∥β，那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号）（15）有三张卡片，分别写有1和2，1和3，2和3。

2015年全国高中数学联赛江苏赛区初赛试卷(含答案)

2015年全国高中数学联赛江苏赛区初赛参考答案与评分细则一、填空题（本题共10小题，满分70分，每小题7分．要求直接将答案写在横线上．） 1．已知点P (4，1)在函数f (x )＝log a (x －b ) (b ＞0)的图象上，则ab 的最大值是．解：由题意知，log a (4－b )＝1，即a ＋b ＝4，且a ＞0，a ≠1，b ＞0，从而ab ≤(a ＋b)24＝4，当a ＝b ＝2时，ab 的最大值是4．2．函数f (x )＝3sin(2x －π4)在x ＝43π24处的值是．解：2x －π4＝43π12－π4＝40π12＝10π3＝2π＋4π3，所以f (43π24)＝3sin 4π3＝－32．3．若不等式|ax ＋1|≤3的解集为{x |－2≤x ≤1}，则实数a 的值是．解：设函数f (x )＝|ax ＋1|，则f (－2)＝ f (1)＝3，故a ＝2．4．第一只口袋里有3个白球、7个红球、15个黄球，第二只口袋里有10个白球、6个红球、9个黑球，从两个口袋里各取出一球，取出的球颜色相同的概率是．解：有两类情况：同为白球的概率是3×1025×25＝30625，同为红球的概率是7×625×25＝42625，所求的概率是72625．5．在平面直角坐标系xOy 中，设焦距为2c 的椭圆x2a2＋y2b2＝1(a ＞b ＞0)与椭圆x2b2＋y2c2＝1有相同的离心率e ，则e 的值是．解：若c ＞b ，则c2a2＝c2－b2c2，得a ＝b ，矛盾，因此c ＜b ，且有c2a2＝b2－c2b2，解得e ＝－1＋52．6．如图，在长方体ABCD －A 1B 1C 1D 1中，对角线B 1D 与平面A 1BC 1交于E 点．记四棱锥E －ABCD 的体积为V 1，长方体ABCD －A 1B 1C 1D 1的体积为V 2，则V1V2的值是．（第6题图） A 1解：记四棱锥B 1－ABCD 的体积为V ．如图，DE ＝23DB 1，从而V 1＝23V ．又V ＝13V 2，所以V1V2＝29．7．若实数集合A ＝{31x ，65y }与B ＝{5xy ，403}仅有一个公共元素，则集合A ∪B 中所有元素之积的值是．解：因为31x ×65y ＝5xy ×403＝2015xy ．若xy ≠0，则集合A 和集合B 中有一组相等，则另一组也必然相等，这不合题意．所以xy ＝0，从而A ∪B 中所有元素之积的值为0． 8．设向量a ＝(cos α，sin α)，b ＝(－sin α，cos α)．向量x 1，x 2，…，x 7中有3个为a ，其余为b ；向量y 1，y 2，…，y 7中有2个为a ，其余为b ．则错误!x i y i 的可能取值中最小的为．解：因为a ·a ＝b ·b ＝1，a ·b ＝0，所以错误!x i y i 的最小值为2．9．在3×3的幻方中填数，使每行、每列及两条对角线上的三个数之和都相等．如图，三个方格中的数分别为1，2，2015，则幻方中其余6个数之和为．解：如图，设幻方正中间的数为x ，则由题意知a ＝－2012，从而对角线上三个数的和为x －2011．因此b ＝x －2014，c ＝－4026，d ＝－2013，e ＝x ＋2014．由b ＋e ＋x ＝x －2011，解得x ＝－20112．这9个数的和为3×(－20112－2011)＝－180992，所以幻方中其余6个数之和为－180992－2018＝－221352．10．在平面直角坐标系xOy 中，设D 是满足x ≥0，y ≥0，x ＋y ＋[x ]＋[y ]≤19的点(x ，y )形成的区域（其中[x ]是不超过x 的最大整数）．则区域D 中整点的个数为．解：区域D 中整点的个数为1＋2＋3＋…＋10＝55．（第9题图） 12 2015（第9题图）e c d ab1 2 2015x （第6题图）A 1二、解答题（本大题共4小题，每小题20分，共80分）11．在等比数列{a n }中，a 2＝2，q 是公比．记S n 为{a n }的前n 项和，T n 为数列{a 2n }的前n 项和．若S 2n ＝2T n ，求q 的值．解：若q ＝1，则a n ＝a 2＝2，a 2n ＝4，则S 2n ＝4n ，T n ＝4n ，S 2n ≠2T n ．若q ＝－1，则a n ＝2×(－1)n ，a 2n ＝4，则S 2n ＝0，T n ＝4n ，S 2n ≠2T n ．……………………………… 5分若q ≠±1，则a n ＝2q n －2，a 2n ＝4q 2n －4，从而S 2n ＝2q ×(1－q 2n )1－q ，T n ＝4q2×(1－q 2n )1－q 2． ……………………………… 15分由S 2n ＝2T n ，则4q(1＋q)＝1，q 2＋q －4＝0，解得q ＝－1±172．综上，q 的值为－1＋172和－1－172． ……………………………… 20分12．如图，△ABC 中，AB ＞AC ，点D 、E 分别在边AB 、AC 上，且BD ＝CE ．∠BAC 的外角平分线与△ADE 的外接圆交于A 、P 两点．求证：A 、P 、B 、C 四点共圆．证明：如图，连结PD ，PE ，PC ．因为四边形APDE 是圆内接四边形, 所以∠P AD ＝∠PED ，∠P AF ＝∠PDE ．又因为AP 是∠BAC 的外角平分线，所以∠P AD ＝∠P AF ，从而∠PED ＝∠PDE ，故PD ＝PE ． ……………………………… 10分又∠ADP ＝∠AEP ，所以∠BDP ＝∠CEP ．又因为BD ＝CE ，所以△BDP ≌△CEP ，从而∠PBD ＝∠PCE ，即∠PBA ＝∠PCA ，ABCDP(第12题图)EA BC DP (第12题图)EF所以A 、P 、B 、C 四点共圆． ……………………………… 10分13．如图，在平面直角坐标系xOy 中，圆O 1、圆O 2都与直线l ：y ＝kx 及x 轴正半轴相切．若两圆的半径之积为2，两圆的一个交点为P (2，2)，求直线l 的方程．解：由题意，圆心O 1，O 2都在x 轴与直线l若直线l 的斜率k ＝tanα，设t ＝tan α2，则k ＝2t1－t2．圆心O 1，O 2在直线y ＝tx 上，可设O 1(m ，mt )，O 2(n ，nt )．交点P (2，2)在第一象限，m ，n ，t ＞0． ……………………………… 4分所以⊙O 1：(x －m )2+(y －mt )2=(mt )2，⊙O 1：(x －n )2+(y －nt )2=(nt )2，所以⎩⎨⎧(2－m)2＋(2－mt)2＝(mt)2，(2－n)2＋(2－nt)2＝(nt)2，即⎩⎨⎧m2－(4＋4t)m ＋8＝0，n2－(4＋4t)n ＋8＝0，……………… 8分所以 m ，n 是方程X 2－(4+4t )X ＋8=0的两根，mn ＝8．由半径的积(mt )(nt )＝2，得t 2＝14，故t ＝12．……………………………… 16分所以 k ＝2t 1－t2＝11－14＝43，直线l ：y ＝43x ． ……………………………… 20分14．将正十一边形的k 个顶点染红色，其余顶点染蓝色．（1）当k ＝2时，求顶点均为蓝色的等腰三角形的个数；（2）k 取何值时，三个顶点同色(同红色或同蓝色)的等腰三角形个数最少？并说明理由．解：（1）设正十一边形的顶点A 1，A 2，A 3，…，A 11，则易知其中任意三点为顶点的三角形都不是正三角形．以这些点为顶点的等腰三角形个数可以如此计算：以A i (i ＝1，2，3，…，11)为顶角顶点的等腰三角形有11－12＝5个，这些三角形均不是等边三角形，即当j ≠i 时，以A j 为顶角顶点的等腰三角形都不是上述等腰三角形．故所有的等腰三角形共有5×11＝55个． …………………… 5分当k ＝2时，设其中A m ，A n 染成红色，其余染成蓝色．以A m 为顶角顶点的等腰三角形有5个，以A m 为底角顶点的等腰三角形有10个；同时以A m ，A n 为顶点的等腰三角形有3个，这些等腰三角形的顶点不同色，且共有(5＋10)×2－3＝27个．注意到仅有这些等腰三角形的三个顶点不同蓝色，故所求三个顶点同为蓝色的等腰三角形有55－27＝28个． ………………………… 10分（2）若11个顶点中k 个染红色，其余11－k 个染蓝色．则这些顶点间连线段(边或对角线)中，两端点染红色的有k(k －1)2条，两端点染蓝色的有(11－k)(10－k)2条，两端点染一红一蓝的有k (11－k )条．并且每条连线段必属于且仅属于3个等腰三角形．把等腰三角形分4类：设其中三个顶点均为红色的等腰三角形有x 1个，三个顶点均为蓝色的等腰三角形有x 2个，两个顶点为红色一个顶点为蓝色的等腰三角形有x 3个，两个顶点为蓝色一个顶点为红色的等腰三角形有x 4个，则按顶点颜色计算连线段，3x 1＋x 3＝3×k(k －1)2， ①3x 2＋x 4＝3×(11－k)(10－k)2， ②2x 3＋2x 4＝3×k (11－k )， ③由①＋②得 3(x 1＋x 2)＋x 3＋x 4＝32[k (k －1)＋(11－k )(10－k )]，用③代入得 x 1＋x 2＝12[ k (k －1)＋(11－k )(10－k )－k (11－k )]＝12(3k 2－33k ＋110)．当k ＝5或6时，(x 1＋x 2)min ＝12(5×4＋6×5－5×6)＝10．即顶点同色的等腰三角形最少有10个，此时k ＝5或6．………… 20分。