二次函数单元检测试卷(含答案)

合集下载

二次函数单元检测试卷(含答案)

二次函数单元检测试卷(含答案)二次函数复套卷时间：120分钟满分：150分班级：__________ 姓名：__________ 得分：__________一、选择题（本题共12小题，每小题3分，共36分）1.下列各式中，y是x的二次函数的是（）A。

y = 1/2xB。

y = 2x + 1C。

y = x^2 + x - 2D。

y^2 = x^2 + 3x / x2.抛物线y = 2x^2 + 1的顶点坐标是（）A。

(2.1)B。

(0.1)C。

(1.0)D。

(1.2)3.二次函数y = ax^2 + bx - 1 (a ≠ 0)的图像经过点(1.1)，则a +b + 1的值是（）A。

-3B。

-1C。

2D。

34.抛物线y = x^2 - 2x - 3与x轴的交点个数是（）A。

0个B。

1个C。

2个D。

3个5.下列函数中，当x。

0时，y随x值的增大而先增大后减小的是（）A。

y = x^2 + 1B。

y = x^2 - 1C。

y = (x + 1)^2D。

y = -(x - 1)^26.二次函数y = ax^2 + bx + c的部分对应值如下表：x。

y2.51.-31.-42.-33.…二次函数图像的对称轴是（）A。

直线x = 1B。

y轴C。

直线x = -1D。

直线x = -27.如图，二次函数y = ax^2 + bx + c的图像与x轴相交于(-2.0)和(4.0)两点，当函数值y。

0时，自变量x的取值范围是（）A。

x < -2B。

-2 < x < 4C。

x。

0D。

x。

48.二次函数y = ax^2 + bx + c的图像如图所示，那么一次函数y = ax + b的图像大致是（）9.某种品牌的服装进价为每件150元，当售价为每件210元时，每天可卖出20件，现需降价处理，且经市场调查：每件服装每降价2元，每天可多卖出1件。

在确保盈利的前提下，若设每件服装降价x元，每天售出服装的利润为y元，则y与x的函数关系式为（）A。

人教版九年级数学上册《二次函数》试卷(含答案)

二次函数单元检测题一、选择题（每题3分，共30分） 1、下列函数是二次函数的是（）A 、12+=x yB 、12+-=x yC 、22+=x y D 、221-=x y 2、二次函数221x y =的图象的顶点坐标是（） A 、（1，0） B （0，0） C （1-，0） D 、（0，21） 3、二次函数132+-=x y 的图象是将（）A 、抛物线23x y -=向左平移3个单位得到B 、抛物线23x y -=向左平移1个单位得到 C 、抛物线23x y -=向上平移1个单位得到 D 、抛物线23x y -=向下平移1个单位得到 4、要得到抛物线2)4(31-=x y ，可将抛物线231x y =（）A 、向上平移4个单位B 、向下平移4个单位C 、向右平移4个单位D 、向左平移4个单位 5、抛物线1)2(32+-=x y 的对称轴是（） A 、2-=x B 、1-=x C 、1=x D 、2=x6、二次函数)0(2≠++=a c bx ax y 的大致图象如图所示，则关于该二次函数的说法错误的是（）A 、函数有最小值B 、对称轴是直线21=x C 、当21<x 时，y 随x 的增大而减小 D 、当21<<-x 时，0>y7、如图，小兰画了一个函数b ax x y ++=2的图象，则间于x 的一元二次方程ax x +20=+b 的解是（）A 、无解B 、1=xC 、4-=xD 、1-=x 或4=x8、已知二次函数的图象经过点（1，10），顶点坐标为（1-，2-），则此二次函数的解析式为（）A 、1632++=x x y B 、1632-+=x x y C 、1632+-=x x y D 、1632+-=x x y 9、如图，二次函数c bx ax y ++=2的图象与x 轴相交于（2-，0）和（4，0）两点，当函数值0>y 时，自变量x 的取值范围是（）A 、2-<xB 、42<<-xC 、0>xD 、4>x 10、如图，假设篱笆（虚线部分）的长度为16cm ，则所围成矩形ABCD 的最大面积是（） A 、602m B 、632m C 、642m D 、662m 二、填空题（每题4分，共24分）11、若二次函数2)1(x m y -=的图象开口向下，则m 的取值范围是 . 12、二次函数c x y +=2的图象经过点（2，0），则当2-=x 时，=y . 13、已知点A （1x ，1y ），B （2x ，2y ）为函数3)1(22+--=x y 的图象上的两点，若121>>x x ，则1y 2y .14、二次函数362+-=x kx y 的图象与x 轴有交点，则k 的取值范围是 . 15、如图，已知抛物线c bx ax y ++=2与x 轴的一个交点为A （1，0），对称轴是直线1-=x ，则02=++c bx ax 的解是 .16、将抛物线122+-=x y 向右平移1个单位，再向上平移2个单位后所得到的抛物线为 .三、解答题一（每题6分，共18分） 17、已知72)2(--=a x a y 是二次函数，且当0>x 时，y 随x 的增大而增大，求a 的值.18、已知抛物线12-=ax y 的图象经过点（3-，2），求该抛物线的解析式.19、已知二次函数222m m x y -+=的最小值是3-，求m 的值.四、解答题二（每题7分，共21分）20、已知一个二次函数的图象的对称轴是y 轴，顶点是（0，1），且经过点（1-，2-）. （1）求这个函数的解析式；（2）在对称轴的左侧，y 随x 的增大怎样变化？21、已知二次函数4)1(2--=x a y 的图象经过点（3，0）（1）求a 的值；（2）若A （m ，1y ），B （n m +，2y ）（0>n ）是该函数图象上的两点，当21y y =时，求m ，n 之间的数量关系.22、已知抛物线81232-+-=x x y .（1）用配方法求它的顶点坐标；（2）求它与y 轴的交点坐标.五、解答题三（每题9分，共27分）23、如图，抛物线c bx ax y ++=2经过A （2-，4-），O （0，0），B （2，0）三点，（1）求抛物线的解析式；（2）若点M 是抛物线的对称轴上一点，求AOM ∆周长的最小值.24、某种商品每天的销售利润y （元）与销售单价x （元）之间满足函数关系752-+=bx ax y ，其函数图象如图所示.（1）销售单价为多少元时，该种商品每天的销售利润最大？最大利润为多少元？（2）销售单价在什么范围时，该种商品每天的销售利润不低于16元？25、如图，在平面直角坐标系中，抛物线经过点A （0，4），B （1，0），C （5，0），其对称轴与x 轴相交于点M.（1）求抛物线的解析式和对称轴；（2）在抛物线的对称轴上是否存在一点P ，使PAB ∆的周长最小？若存在，请求出点P 的坐标；若不存在，请说明理由；（3）边结AC ，在直线AC 下方的抛物线上，是否存在一点N ，使NAC ∆的面积最大？若存在，请求出点N 的坐标；若不存在，请说明理由.二次函数单元检测题参考答案一、CBCCD DDABC 二、11、1<m 12、0 13、< 14、3≤k 且0≠k 15、31-=x ，12=x 16、3)1(22+--=x y 三、17、解：由已知，得272=-a ，且02≠-a ，解得3±=a .又当0>x 时，y 随x 的增大而增大，∴02>-a ，即.2<a .3-=∴a18、解：抛物线12-=ax y 的图象经过点（3-，2）1)3(22--⨯=∴a ，解得31=a ，所求的解析式为：1312-=x y19、解：函数的最小值为3-，所以抛物线222m m x y -+=的顶点坐标是（0，3-），把此点坐标代入222m m x y -+=得223m m -=-，解得31=m ，.12-=m四、20、解：（1）设函数的解析式为c ax y +=2，由函数的图象过（0，1）和（1-，-2）两点，得⎩⎨⎧-=+=21c a c ，⎩⎨⎧-==∴31a c ，故函数解析式为132+-=x y . （2）在对称轴的左侧，y 随x 的增大而增大.21、解：（1）将（3，0）代入4)1(2--=x a y ，得440-=a ，解得.1=a （2）函数4)1(2--=x y 的图象的对称轴是直线1=x ，m n m -=-+∴11，化简，得.22=+n m22、解：（1）4)2(3812)44(38123222+--=-++--=-+-=x x x x x y ，∴它的顶点坐标是（2，4）（2）令0=x ，则8=y ，∴它与y 轴的交点坐标为（0，8-）. 五、23、解：（1）x x y +-=221 （2）抛物线的对称轴为1=x ，当OM+AM 最小时，AOM ∆的周长最小，又点O 、B 关于直线1=x 对称，∴AB 与直线1=x 的交点就是点M ，∴OM+AM=AB=.244422=+又 OA=25，AOM ∆∴周长的最小值是.5224+24、解：（1）二次函数752-+=bx ax y 的图象经过点（5，0），（7，6），,1675749075525⎩⎨⎧=-+=-+∴b a b a 解得⎩⎨⎧=-=201b a ， 25)10(752022+--=-+-=∴x x x y ，2510==∴最大时当，yx ，故销售单价为10元时，该种商品每天的销售利润最大，最大利润为25元.（2）函数75202-+-=x x y 图象的对称轴为10=x ，∴点（7，16）关于对称轴的对称点是（13，16），又函数75202-+-=x x y 图象开口向下，∴当713≤≤x 时，16≥y ，故销售单价不低于7元且不超过13元时，该种商品每天的销售利润不低于16元. 25、解：（1）设抛物线的解析式为)5)(1(--=x x a y ，把（0，4）代入上式，得54=a ， ,516)3(54452454)5)(1(5422--=+-=--=∴x x x x x y.3:=∴x 抛物线的对称轴是（2）存在，点 A （0，4），抛物线的对称轴是3=x ，∴点A 关于对称轴的对称点A '的坐标为（6，4），如图1，连接B A '交对称轴于点P ，连接AP ，此时PAB ∆的周长最小.设直线B A '的解析式为b kx y +=，把（6，4），（1，0）代入，得⎩⎨⎧=+=+,0,46b k b k解得⎪⎩⎪⎨⎧-==5454b k ，,5454-=∴x y 当3=x 时，∴=-⨯=,5854354y P （3，58）. （3）存在，设N （t ，4524542+-t t ）（50<<t ），如图2，过点N 作y NG //轴交AC于点G 、交BC 于点F ，作NG AD ⊥于点D,由点A （0，4）和点C （5，0）可求出直线AC 的解析式为454+-=x y ，则G （t ，454+-t ），此时NG=.454)452454(45422t t t t t +-=+--+-AD+CF=CO=5，OC NG CF NG NG AD S S S CGN ANG ACN ⨯=⨯+⨯=+=∴∆∆∆212121,225)25(21025)454(21222+--=+-=⨯+-⨯=t t t t t 25=∴t 时，ACN ∆的面积最大，为.225由25=t ，得34524542-=+-=t t y ，∴N （25，3-）.。

二次函数单元测试卷含答案

二次函数单元测试卷一、选择题每小题3分,共30分1. 当-2≤ x ≦1,二次函数y=-x-m 2 + m 2 +1有最大值4,则实数m 值为47B. 3或-3 或-3 D. 2或3或-47 2. 函数22y mx x m =+-m 是常数的图像与x 轴的交点个数为A. 0个 B ．1个 C ．2个 D ．1个或2个3. 关于二次函数2y ax bx c =++的图像有下列命题：①当0c =时,函数的图像经过原点；②当0c >,且函数的图像开口向下时,方程20ax bx c ++=必有两个不相等的实根；③函数图像最高点的纵坐标是244ac b a -；④当0b =时,函数的图像关于y 轴对称．其中正确命题的个数是A. 1个 B ．2个 C ．3个 D ．4个4. 关于x 的二次函数22(81)8y mx m x m =+++的图像与x 轴有交点,则m 的范围是A ．116m <-B ．116m -≥且0m ≠C ．116m =-D ．116m >-且0m ≠5. 下列二次函数中有一个函数的图像与x 轴有两个不同的交点,这个函数是A ．2y x =B ．24y x =+C ．2325y x x =-+D ．2351y x x =+-6. 若二次函数2y ax c =+,当x 取1x 、2x 12x x ≠时,函数值相等,则当x 取12x x +时,函数值为A ．a c +B ．a c -C ．c -D ．c7. 下列二次函数中有一个函数的图像与坐标轴有一个交点,这个函数是A ．1x y 2—=B ．24y x =+C ．1x 2x y 2+=—D ．2351y x x =+-8. 抛物线2321y x x =-+-的图象与坐标轴交点的个数是A ．没有交点B ．只有一个交点C ．有且只有两个交点D ．有且只有三个交点9. 函数2y ax bx c =++的图象如图所示,那么关于x 的一元二次方程230ax bx c ++-=的根的情况是A ．有两个不相等的实数根B ．有两个异号的实数根C ．有两个相等的实数根D ．没有实数根10..若把函数y=x 的图象用Ex,x 记,函数y=2x+1的图象用Ex,2x+1记,……则Ex,122+-x x 可以由Ex,2x 怎样平移得到A ．向上平移１个单位B ．向下平移１个单位C ．向左平移１个单位D ．向右平移１个单位二、填空题每小题3分,共24分11. 抛物线2283y x x =--与x 轴有个交点,因为其判别式24b ac -= 0,相应二次方程23280x x -+=的根的个数为． 12. 关于x 的方程25mx mx m ++=有两个相等的实数根,则相应二次函数25y mx mx m =++-与x 轴必然相交于点,此时m = ．13. 抛物线2(21)6y x m x m =---与x 轴交于两点1(0)x ，和2(0)x ，,若121249x x x x =++,要使抛物线经过原点,应将它向右平移个单位．14. 如图所示,函数2(2)(5)y k x k =-+-的图像与x 轴只有一个交点,则交点的横坐标0x = ．15. 已知二次函数212y x bx c =-++,关于x 的一元二次方程212x -根是1-和5-,则这个二次函数的解析式为16. 若函数y=m ﹣1x 2﹣4x+2m 的图象与x 轴有且只有一个交点,则m 的值为17. 若根式有意义,则双曲线y =x2-k 2与抛物线y =x 2+2x +2－2k 的交点在第象限. 18. 将二次三项式x 2+16x+100化成x+p 2+q 的形式应为三、解答题本大题共7小题,共66分19..7分已知一个二次函数的图象经过点0,0,1,﹣3,2,﹣8,求函数解析式;20. 8分已知抛物线21()3y x h k =--+的顶点在抛物线2y x =上,且抛物线在x 轴上截得的线段长是求h 和k 的值．21. 8分已知函数22y x mx m =-+-．1求证：不论m 为何实数,此二次函数的图像与x 轴都有两个不同交点；2若函数y 有最小值54-,求函数表达式． 22.9分已知二次函数2224y x mx m =-+．1求证：当0m ≠时,二次函数的图像与x 轴有两个不同交点；2若这个函数的图像与x 轴交点为A ,B ,顶点为C ,且△ABC 的面积为求此二次函数的函数表达式23. 10分下图是二次函数2y ax bx c =++的图像,与x 轴交于B ,C 两点,与y 轴交于A 点． 1根据图像确定a ,b ,c 的符号,并说明理由；2如果A 点的坐标为(03)-，,45ABC ∠=,60ACB ∠=,求这个二次函数的函数表达式．24.12分已知抛物线222m y x mx =-+与抛物线2234m y x mx =+-图所示,其中一条与x 轴交于A ,B 两点．1试判断哪条抛物线经过A ,B 两点,并说明理由；2若A ,B 两点到原点的距离AO ,OB 满足条件1123OB OA -=,求经过A ,B 两点的这条抛物线的函数式．25. 12分已知抛物线2y ax bx c =++与y 轴交于C 点,与x 轴交于1(0)A x ，,212(0)()B x x x <，两点,顶点M 的纵坐标为4-,若1x ,2x 是方程222(1)70x m x m --+-=的两根,且221210x x +=． 1求A ,B 两点坐标；2求抛物线表达式及点C 坐标；3在抛物线上是否存在着点P ,使△PAB 面积等于四边形ACMB 面积的2倍,若存在,求出P 点坐标；若不存在,请说明理由．参考答案一、选择题每选对一题得3分,共30分1．C 2．C 3．D 4．B 5．D 6．D 7．B 8．B 9．C 10．D二、填空题每填对一题得3分,共24分11．0 < 0 12.一625 或9 7 15．25-x 3-x 21-y 2= 16．-1或1或2 17．2 18．()368x 2++ 三、解答题 7小题,共66分19．7分解：x 2--x y 2=20．1略 213x -x y 1-x -x y 22+==或21．1略 248x x 2y 48x -x 2y 22++=+=或 22．1a>0,b>0,c<0(2)A0,-3, B-3, 0 C0 , -323．14m 3-mx x y 22+= (2)设Ax 1 ,0,Bx 2 ,0, 则有32x 1x 121=+ 解得3-x 2x y 2+=25. 1A-1,0, B3, 0（2）3-x 2-x y 2=,C0,-3（3）存在;P1()()9,131P29,131-+，.。

二次函数测试题及答案

二次函数测试题及答案一、选择题（每题3分，共30分）1. 以下哪个选项是二次函数的一般形式？A. y = 2x + 1B. y = x^2 + 3x + 2C. y = 3x^3 - 5D. y = 4/x答案：B2. 二次函数y = ax^2 + bx + c的顶点坐标为（h, k），那么h的值为：A. -b/2aB. -b/aC. b/2aD. b/a答案：C3. 二次函数y = 2x^2 - 4x + 3的对称轴方程是：A. x = 1B. x = -1C. x = 2D. x = -2答案：A4. 如果二次函数y = ax^2 + bx + c的图象开口向上，那么a的值：A. 大于0B. 小于0C. 等于0D. 可以是任意实数答案：A5. 二次函数y = -x^2 + 4x - 3的顶点坐标是：A. (1, 2)B. (2, 1)C. (3, 0)D. (3, 4)答案：C6. 二次函数y = 3x^2 - 6x + 5的图象与x轴的交点个数是：A. 0个B. 1个C. 2个D. 3个答案：C7. 二次函数y = x^2 - 4x + 4的最小值是：A. 0B. 4C. -4D. 1答案：A8. 二次函数y = 2x^2 - 4x + 3的图象开口方向是：A. 向上B. 向下C. 向左D. 向右答案：A9. 二次函数y = -x^2 + 2x + 3的图象与y轴的交点坐标是：A. (0, 3)B. (0, -3)C. (0, 5)D. (0, -5)答案：A10. 二次函数y = 5x^2 - 10x + 8的图象与x轴的交点坐标是：A. (2, 0)B. (-2, 0)C. (1, 0)D. (-1, 0)答案：A二、填空题（每题4分，共20分）1. 二次函数y = ax^2 + bx + c的图象开口向上，且经过点（2, 0），则a的值至少为______。

答案：02. 二次函数y = 2x^2 - 4x + 3的顶点坐标是（______, ______）。

二次函数单元测试题及答案

二次函数单元测试题及答案1. 选择题（每题2分）1. 下列函数中，属于二次函数的是：A. y = 3x + 2B. y = x^2 + 3x - 2C. y = √xD. y = |x|答案：B2. 二次函数y = 2x^2 + 3x - 4的图像开口方向是：A. 向上开口B. 向下开口答案：A3. 函数y = -x^2 + 5x + 3的顶点坐标是：A. (3, 8)B. (-3, 2)C. (5, 8)D. (-5, 3)答案：A4. 函数y = x^2 - 4x + 4的轴对称线方程为：A. x = 2B. x = 4C. x = -2D. x = -4答案：A5. 函数y = x^2 + 6x + 9的值域是：A. (-∞, 9)B. [9, +∞)C. (-∞, 0)D. [0, +∞)答案：B2. 填空题（每题3分）1. 二次函数y = -2x^2 + 4x - 1的判别式为_______。

答案：402. 函数y = x^2 + bx + c的顶点坐标是（-2, 1），则b和c的值分别为_______。

答案：b = 4，c = -33. 函数y = 3x^2 - 6x + k的图像与x轴有两个交点，则k的值为_______。

答案：k > 04. 函数y = -x^2 - 4x + m的轴对称线方程为x = 2，则m的值为_______。

答案：m = 35. 函数y = ax^2 + bx + 2的值域是(-∞, 1]，则a和b的关系是_______。

答案：a < 0，b > 03. 计算题（每题5分）1. 求二次函数y = -3x^2 + 6x + 9的顶点坐标和对称轴方程。

解答：首先，二次函数的顶点坐标可以通过公式 h = -b/2a 和 k = f(h) 来求得。

其中，h 表示对称轴的横坐标，k 表示顶点的纵坐标。

对于给定的函数 y = -3x^2 + 6x + 9，我们可以得到 a = -3，b = 6，c = 9。

二次函数测试题及答案

二次函数测试题及答案一、选择题1. 下列哪个选项是二次函数的一般形式？A. y = x + 2B. y = x^2 + 3x + 1C. y = 2x^3D. y = 1/x答案：B2. 二次函数y = ax^2 + bx + c（a ≠ 0）的顶点坐标是：A. (-b, a)B. (-b/a, c)C. (-b/2a, 4ac - b^2/4a)D. (-b/2a, 4ac + b^2/4a)答案：C3. 如果二次函数y = ax^2 + bx + c的图像与x轴有两个交点，那么a、b、c之间的关系是：A. b^2 - 4ac > 0B. b^2 - 4ac < 0C. b^2 - 4ac = 0D. b^2 - 4ac ≠ 0答案：A二、填空题4. 二次函数y = -3x^2 + 6x - 5的顶点坐标是______。

答案：(1, -2)5. 如果二次函数y = ax^2 + bx + c的图像开口向上，那么a的值是______。

答案：> 0三、解答题6. 已知二次函数y = 2x^2 - 4x + 3，求其图像与x轴的交点。

解：令y = 0，得到方程2x^2 - 4x + 3 = 0。

通过求解这个方程，我们可以得到x的值。

首先计算判别式Δ = b^2 - 4ac = (-4)^2 - 4 * 2 * 3 = 16 - 24 = -8。

因为Δ < 0，所以这个二次方程没有实数解，即二次函数的图像与x轴没有交点。

7. 已知二次函数y = 3x^2 + 6x - 5，求其图像的对称轴。

解：二次函数y = ax^2 + bx + c的对称轴是x = -b/(2a)。

将a= 3, b = 6代入公式，得到对称轴为x = -6 / (2 * 3) = -1。

四、应用题8. 某工厂生产一种产品，其成本函数为C(x) = 0.5x^2 - 100x + 1000，其中x表示产品的数量。

2024年九年级数学上册《二次函数》单元测试及答案解析

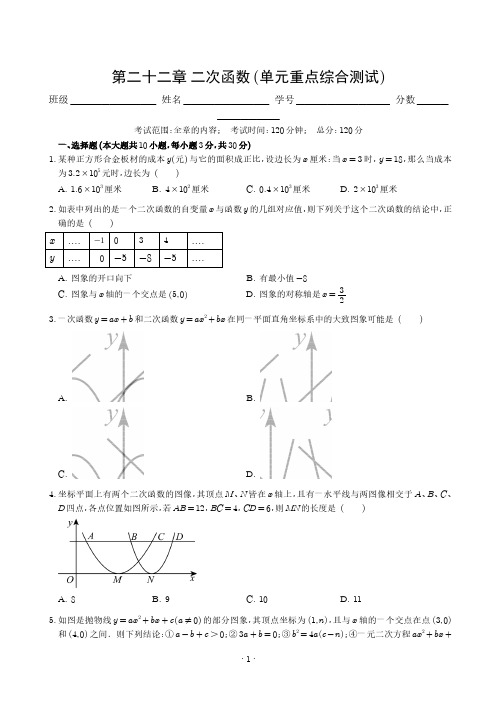
第二十二章二次函数(单元重点综合测试)班级___________姓名___________学号____________分数____________考试范围：全章的内容；考试时间：120分钟；总分：120分一、选择题(本大题共10小题，每小题3分，共30分)1.某种正方形合金板材的成本y(元)与它的面积成正比，设边长为x厘米：当x=3时，y=18，那么当成本为3.2×105元时，边长为()A.1.6×103厘米B.4×102厘米C.0.4×103厘米D.2×103厘米2.如表中列出的是一个二次函数的自变量x与函数y的几组对应值，则下列关于这个二次函数的结论中，正确的是()x....-1034....y....0-5-8-5....A.图象的开口向下B.有最小值-8C.图象与x轴的一个交点是5,0D.图象的对称轴是x=3 23.一次函数y=ax+b和二次函数y=ax2+bx在同一平面直角坐标系中的大致图象可能是()A. B.C. D.4.坐标平面上有两个二次函数的图像，其顶点M、N皆在x轴上，且有一水平线与两图像相交于A、B、C、D四点，各点位置如图所示，若AB=12，BC=4，CD=6，则MN的长度是()A.8B.9C.10D.115.如图是抛物线y=ax2+bx+c(a≠0)的部分图象，其顶点坐标为1,n，且与x轴的一个交点在点3,0和4,0之间．则下列结论：①a-b+c>0；②3a+b=0；③b2=4a c-n；④一元二次方程ax2+bx+c =n -1有两个不相等的实数根；⑤若方程ax 2+bx +c =0的两根分别为x 1，x 2，则x 1+x 2=2．其中正确结论的个数有()A.5个B.4个C.3个D.2个6.如图，在正方形ABCD 中，点B ，C 的坐标分别是(-2,1)，(2,0)，点D 在抛物线y =13x 2+bx 的图像上，则b 的值是()A.23B.13C.73D.437.如图，排球运动员站在点O 处练习发球，球从点O 正上方2m 的A 处发出，其运行的高度y (m )与水平距离x (m )满足关系式y =-160x -6 2+2.6．已知球网与点O 的水平距离为9m ，高度为2.43m ，球场的边界距点O 的水平距离为18m ．下列判断正确的是()A.球运行的最大高度是2.43mB.球不会过球网C.球会过球网且不会出界D.球会过球网且会出界8.如图，抛物线G :y 1=a (x +1)2+2与抛物线H :y 2=-(x -2)2-1交于点B (1,-2)，且分别与y 轴交于点D ，E ．过点B 作x 轴的平行线，交抛物线于点A ，C ．则以下结论：①抛物线H可由抛物线G向右平移3个单位，再向下平移3个单位得到；②无论x取何值，y2总是负数；③当-3<x<1时，随着x的增大，y1-y2的值先增大后减小；④四边形AECD为正方形．其中正确的个数是()A.1B.2C.3D.49.设二次函数y=a x+mx+m-k(a<0，m，k是实数)，则()A.当k=2时，函数y的最大值为-4aB.当k=2时，函数y的最大值为-2aC.当k=4时，函数y的最大值为-4aD.当k=4时，函数y的最大值为-2a10.如图，已知点A-1,0，点B2,3．若抛物线y=ax2-x+2(a为常数，a≠0)与线段AB有两个不同的公共点，则a的取值范围是()A.a≥3B.a≤-3或34≤a<1C.-3<a<1或a≥3D.34≤a<1二、填空题(本大题共6小题，每小题3分，共18分)11.标准大气压下，质量一定的水的体积V cm3与温度t°C之间的关系满足二次函数V=18t2+104t>0，则当温度为4°C时，水的体积为cm3．12.已知二次函数y=x2-2x+1的图象向左平移两个单位得到抛物线C，点P2,y1，Q3,y2在抛物线C 上，则y1y2(填“>”或“<”)；13.在单位为1的正方形网格中，存在一平面直角坐标系．二次函数y1=a1x2+b1x+c1，y2=a2x2+b2x+c2的图象位于如图位置上，若它们的图象位置关系具有对称性，请描述它们的对称关系：，求出y2与直线y=32x+7的交点坐标为．14.如图，将抛物线y =x 2-2x -3在x 轴下方部分沿x 轴翻折，其余部分保持不变，得到图像C 1,当直线y =x +b 与图像C 1恰有两个公共点时，b 的取值范围是．15.九(1)班劳动实践基地内有一块面积足够大的平整空地．地上两段围墙AB ⊥CD 于点O (如图)，其中AB 上的EO 段围墙空缺．同学们测得AE =6.6m ，OE =1.4m ，OB =6m ，OC =5m ，OD =3m ．班长买来可切断的围栏16m ，准备利用已有围墙，围出一块封闭的矩形菜地，则该菜地最大面积是cm 2．16.如图，二次函数y =33x 2-433x +3的图象交x 轴于点A ,B (点A 在点B 的左侧)，交y 轴于点C ．现有一长为3的线段DE 在直线y =32上移动，且在移动过程中，线段DE 上始终存在点P ，使得三条线段P A ,PB ,PC 能与某个等腰三角形的三条边对应相等．若线段DE 左端点D 的橫坐标为t ，则t 的取值范围是．三、(本大题共4小题，每小题6分，共24分)17.已知二次函数的图像以A-1,4．为顶点，且过点B2,-5(1)求该函数图像与坐标轴的交点坐标；(2)将函数图像向左平移几个单位，该函数图像恰好经过原点．18.飞机降落后滑行的距离S(单位：m)关于滑行时间t(单位：s)的函数解析式是S=at²+bt，当t=5时，S=262.5；当t=10时，S=450．(1)求该函数的解析式；(2)请结合平面直角坐标系中给出的点，画出符合题意的函数图象，并写出飞机降落后滑行到停下来前进了多远？19.已知一次函数y=ax+b的图像上有两点A、B，它们的横坐标分别是2、-1，若二次函数y=x 2的图像经过A、B两点．(1)求一次函数解析式并在平面直角坐标系内画出两个函数的图像；(2)若P m,y1两点都在二次函数y=x 2的图像上，试比较y1与y2的大小．，Q m+1,y220.在平面直角坐标系中，抛物线y=x2+bx+c交x轴于A-1,0两点，交y轴于点C，点P m,n，B3,0在抛物线上．(1)求抛物线的表达式及顶点坐标；(2)若此抛物线点P右侧的部分(不含点P)上恰好有三个点到x轴的距离均为2，请直接写出m的取值范围．四、(本大题共3小题，每小题8分，共24分)21.如图，在平面直角坐标系xOy中，已知抛物线的解析式是y1=x2，直线l的解析式是y2=-14，点F0,1 4，点P是在该抛物线上的动点，连接PF，过P作PN⊥l．(1)求证：PF=PN；(2)设点E-2,6，求PE+PF的最小值及此时点P的坐标．22.甲、乙两汽车出租公司均有50辆汽车对外出租，下面是两公司经理的一段对话：甲公司经理：如果我公司每辆汽车月租费3000元，那么50辆汽车可以全部租出，如果每辆汽车的月租费每增加50元，那么将少租出1辆汽车，另外，公司为每辆租出的汽车支付月维护费200元．乙公司经理：我公司每辆汽车月租费3500元，无论是否租出汽车，公司均需一次性支付月维护费共计1850元．说明：①汽车数量为整数；②月利润=月租车费-月维护费；在两公司租出的汽车数量相等且都为x(单位：辆，0<x≤50)的条件下，甲的利润用y1表示(单位：元)，乙的利润用y2(单位：元)表示，根据上述信息，解决下列问题：(1)分别表示出甲、乙的利润，什么情况下甲、乙的利润相同？(2)甲公司最多比乙公司利润多多少元？(3)甲公司热心公益事业，每租出1辆汽车捐出a元(a>0)给慈善机构，如果捐款后甲公司剩余的月利润仍高于乙公司月利润，且仅当两公司租出的汽车均为16辆时，甲公司剩余的月利润与乙公司月利润之差最大，求a的取值范围．23.为了测量抛物线的开口大小，某数学兴趣小组将两把含有刻度的直尺垂直放置，并分别以水平放置的直尺和竖直放置的直尺为x，y轴建立如图所示平面直角坐标系，该数学小组选择不同位置测量数据如下表所示，设BD的读数为x，CD读数为y，抛物线的顶点为C．(1)(Ⅰ)列表：①②③④⑤⑥x023456y01 2.254 6.259(Ⅱ)描点：请将表格中的x,y描在图2中；(Ⅲ)连线：请用平滑的曲线在图2将上述点连接，并求出y与x的关系式；(2)如图3所示，在平面直角坐标系中，抛物线y=a x-h2+k的顶点为C，该数学兴趣小组用水平和竖直直尺测量其水平跨度为AB，竖直跨度为CD，且AB=m，CD=n，为了求出该抛物线的开口大小，该数学兴趣小组有如下两种方案，请选择其中一种方案，并完善过程：方案一：将二次函数y=a x-h2+k平移，使得顶点C与原点O重合，此时抛物线解析式为y=ax2．①此时点B 的坐标为；②将点B 坐标代入y=ax2中，解得a=；(用含m，n的式子表示)方案二：设C点坐标为h,k①此时点B的坐标为；②将点B坐标代入y=a x-h2+k中解得a=；(用含m，n的式子表示)(3)【应用】如图4，已知平面直角坐标系xOy中有A，B两点，AB=4，且AB∥x轴，二次函数C1:y1=2x+h2+k和C2:y2=a x+h2+b都经过A，B两点，且C1和C2的顶点P，Q距线段AB的距离之和为10，求a的值．五、(本大题共2小题，每小题12分，共24分)24.中新社上海3月21日电(记者缪璐)21日在上海举行的2023年全国跳水冠军赛女子单人10米跳台决赛中，陈芋汐以416.25分的总分夺得冠军，全红婵位列第二，掌敏洁获得铜牌．在精彩的比赛过程中，全红婵选择了一个极具难度的270C(向后翻腾三周半抱膝)．如图2所示，建立平面直角坐标系xOy．如果她从点A3,10起跳后的运动路线可以看作抛物线的一部分，从起跳到入水的过程中，她的竖直高度y(单位：米)与水平距离x(单位：米)近似满足函数关系式y=a x-h．2+k a<0(1)在平时训练完成一次跳水动作时，全红蝉的水平距离x与竖直高度y的几组数据如下：水平距离x/m03 3.54 4.5竖直高度y/m1010k10 6.25根据上述数据，直接写出k的值为，直接写出满足的函数关系式：；(2)比赛当天的某一次跳水中，全红婵的竖直高度y与水平距离x近似满足函数关系y=-5x2+40x-68，记她训练的入水点的水平距离为d1，比赛当天入水点的水平距离为d2，请通过计算比较d1与d2的大小；(3)在(2)的情况下，全红婵起跳后到达最高点B开始计时，若点B到水平面的距离为c，则她到水面的距离y与时间t之间近似满足y=-5t2+c，如果全红婵在达到最高点后需要1.6秒的时间才能完成极具难度的270C动作，请通过计算说明，她当天的比赛能否成功完成此动作？25.综合与实践问题提出某兴趣小组开展综合实践活动，如图1，在正方形ABCD中，E,F分别是AB,AD上一点，且AF=2AE．点M从点E出发，沿正方形ABCD的边顺时针运动；点N同时从点F出发，沿正方形ABCD的边逆时针运动．若两动点的运动速度相同，都为每秒1个单位长度，相遇时M,N两点都停止运动，设点M运动的时间为t秒，△AMN的面积为S，探究S与t的关系．初步感知根据运动的变化，绘制了如图2所示的图象，按不同的函数解析式，图象可分为四段，还有最后一段未画出．(1)AE的长为，AB的长为．(2)a的值为，S的最大值为．延伸探究(3)请求出图2中未画出的最后一段图象对应的函数解析式，并将图象补充完整．(4)求b的值，并求出当S>3时，t的取值范围．第二十二章二次函数(单元重点综合测试)班级___________姓名___________学号____________分数____________考试范围：全章的内容；考试时间：120分钟；总分：120分一、选择题(本大题共10小题，每小题3分，共30分)1.某种正方形合金板材的成本y(元)与它的面积成正比，设边长为x厘米：当x=3时，y=18，那么当成本为3.2×105元时，边长为()A.1.6×103厘米B.4×102厘米C.0.4×103厘米D.2×103厘米【答案】B【分析】本题考查了待定系数法求函数解析式的运用，求出函数的解析式是解答本题的关键．设y=kx2，由待定系数法就可以求出解析式，把y=3.2×105代入函数解析式就可以求出结论．【详解】解：设y=kx2，∵当x=3时，y=18，∴9k=18，k=2，∴y=2x2，当成本为3.2×105元时，有2x2=3.2×105，x2=1.6×105，x=4×102．故选：B．2.如表中列出的是一个二次函数的自变量x与函数y的几组对应值，则下列关于这个二次函数的结论中，正确的是()x....-1034....y....0-5-8-5....A.图象的开口向下B.有最小值-8C.图象与x轴的一个交点是5,0D.图象的对称轴是x=3 2【答案】C【分析】本题考查了待定系数法求二次函数解析式，二次函数的图象和性质等知识点，学会根据表格中的信息求得函数的解析式是解题的关键．由表格中的几组数求得二次函数的解析式，然后通过函数的性质即可得出结果．【详解】解：设二次函数的解析式为y=ax2+bx+c(a、b、c为常数，a≠0)，由题意可知a-b+c=0c=-59a+3b+c=-8 ，解得a=1b=-4 c=-5 ，∴二次函数的解析式为y=x2-4x-5 =x-5x+1=x -2 2-9，∴函数的图象开口向上，顶点为2,-9 ，图象与x 轴的交点分别为-1,0 和5,0 ，∴图象的对称轴是x =2，函数有最小值-9，∴选项A 、B 、D 不符合题意，选项C 符合题意．故选：C ．3.一次函数y =ax +b 和二次函数y =ax 2+bx 在同一平面直角坐标系中的大致图象可能是()A. B.C. D.【答案】B 【分析】本题考查抛物线和直线的性质，本题可先由一次函数y =ax +b 图象得到字母系数的正负，再与二次函数y =ax 2+bx 的图象相比是否一致．【详解】解：A 、由抛物线可知，a <0，x =-b 2a<0，得b <0，由直线可知，a >0，b >0，故本选项不符合题意；B 、由抛物线可知，a >0，x =-b 2a <0，得b >0，由直线可知，a >0，b >0，故本选项符合题意；C 、由抛物线可知，a <0，x =-b 2a <0，得b <0，由直线可知，a <0，b >0，故本选项不符合题意；D 、由抛物线可知，a >0，x =-b 2a>0，得b <0，由直线可知，a <0，b >0，故本选项不符合题意．故选：B4.坐标平面上有两个二次函数的图像，其顶点M 、N 皆在x 轴上，且有一水平线与两图像相交于A 、B 、C 、D 四点，各点位置如图所示，若AB =12，BC =4，CD =6，则MN 的长度是()A.8B.9C.10D.11【答案】B 【分析】本题考查了二次函数的图像与性质，线段长度的相关计算，熟练掌握以上知识点是解题的关键．由AB ，BC ，CD 的长度以及根据二次函数的对称性可以知道，M 和C ，N 和B ，C 和B 横坐标的差，从而推出M 和N 的横坐标之差，得到MN 的长度．【详解】由A、B、C、D四点在同一水平线，可以知道四点纵坐标相同∵AB=12，BC=4，CD=6，∴AC=AB+BC=16,BD=4+6=10∴x C-x M=AC2=8，x N-x B=BD2=5又∵x C-x B=BC=4∴MN=x N-x M=(x N-x B)+(x C-x M)-(x C-x B)=5+8-4=9．故选：B．5.如图是抛物线y=ax2+bx+c(a≠0)的部分图象，其顶点坐标为1,n，且与x轴的一个交点在点3,0和4,0之间．则下列结论：①a-b+c>0；②3a+b=0；③b2=4a c-n；④一元二次方程ax2+bx+ c=n-1有两个不相等的实数根；⑤若方程ax2+bx+c=0的两根分别为x1，x2，则x1+x2=2．其中正确结论的个数有()A.5个B.4个C.3个D.2个【答案】B【分析】本题主要考查了二次函数图象与其系数的关系，二次函数的性质等等，根据开口向下得到a<0，再根据顶点坐标结合对称轴公式得到b=-2a>0，即b+2a=0，则可判断②；由对称性可得当x=-1时，y=a-b+c>0，则可判断②；根据函数图象可知抛物线与直线y=n-1有两个交点，则可判断④；根据二次函数与一元二次方程之间的关系可判断④．【详解】解：∵抛物线开口向下，∴a<0，∵顶点坐标为1,n，∴抛物线对称轴为直线x=-b2a=1，∴b=-2a>0，即b+2a=0，∴3a+b=2a+b+a=a<0，②错误；∵当x=3时y>0，抛物线对称轴为直线x=1，∴当x=-1时，y=a-b+c>0，①正确；∵抛物线顶点纵坐标为n，∴4ac-b24a=n，∴b2=4ac-4an=4a c-n，③正确；由图象可得抛物线与直线y=n-1有两个交点，∴ax2+bx+c=n-1有两个不相等的实数根，④正确；∵抛物线对称轴为直线x=1，方程ax2+bx+c=0的两根分别为x1，x2，，∴x1+x22=1，∴x1+x2=2，⑤正确．故选：B ．6.如图，在正方形ABCD 中，点B ，C 的坐标分别是(-2,1)，(2,0)，点D 在抛物线y =13x 2+bx 的图像上，则b 的值是()A.23B.13C.73D.43【答案】B【分析】本题考查二次函数与几何的综合应用，作BE ⊥x 轴，DF ⊥x 轴，证明△BEC ≌△CFD ，进而求出D 点坐标，代入解析式进行求解即可．【详解】解：如图所示，作BE ⊥x 轴，DF ⊥x 轴，则：∠BEO =∠CFD =90°，∵四边形ABCD 是正方形，∴BC =CD ，∠BCD =90°，∴∠BCE =∠CDF =90°-∠DCF ，∴△BEC ≌△CFD ，∴CF =BE ,DF =CE ，∵点B ，C 的坐标分别是(-2,1)，(2,0)，∴BE =CF =1,OC =2,DF =CE =2+2=4，∴OF =3，∴D 3,4 ，∵点D 在抛物线y =13x 2+bx 的图像上，∴4=13×32+3b ，∴b =13；故选B ．7.如图，排球运动员站在点O 处练习发球，球从点O 正上方2m 的A 处发出，其运行的高度y (m )与水平距离x (m )满足关系式y =-160x -6 2+2.6．已知球网与点O 的水平距离为9m ，高度为2.43m ，球场的边界距点O 的水平距离为18m ．下列判断正确的是()A.球运行的最大高度是2.43mB.球不会过球网C.球会过球网且不会出界D.球会过球网且会出界【答案】D【分析】本题主要考查了二次函数的实际应用．根据顶点式的特点可知球运行的最大高度为2.6m，由此即可判断A；求出当x=9时，y的值，再与2.43m进行比较即可判断B；求出当x=18时，y的值，再与0比较即可判断C、D．【详解】解：∵抛物线解析式为y=-160x-62+2.6，∴球运行的最大高度为2.6m，故A说法错误，不符合题意；在y=-160x-62+2.6中，当x=9时，y=-1609-62+2.6=2.45>2.43，∴球会过球网，故B说法错误，不符合题意；在y=-160x-62+2.6中，当x=18时，则y=-16018-62+2.6=0.2>0，∴球会过球网且会出界，故C说法错误，不符合题意，D说法正确，符合题意；故选D．8.如图，抛物线G:y1=a(x+1)2+2与抛物线H:y2=-(x-2)2-1交于点B(1,-2)，且分别与y轴交于点D，E．过点B作x轴的平行线，交抛物线于点A，C．则以下结论：①抛物线H可由抛物线G向右平移3个单位，再向下平移3个单位得到；②无论x取何值，y2总是负数；③当-3<x<1时，随着x的增大，y1-y2的值先增大后减小；④四边形AECD为正方形．其中正确的个数是()A.1B.2C.3D.4【答案】C【分析】①先求抛物线G的解析式，再根据抛物线G,H的顶点坐标，判断平移方向和平移距离即可判断②；②根据非负数的相反数或者直接由图像判断即可；③先根据题意得出-3<x<1时，观察图像可知y1 >y2，然后计算y1-y2，进而根据一次函数的性质即可判断；④分别计算出A,E,C,D的坐标，根据正方形的判定定理进行判断即可．【详解】①∵抛物线G:y1=a(x+1)2+2与抛物线H:y2=-(x-2)2-1交于点B1,-2，∴x=1,y=-2，即-2=a(1+1)2+2，解得a=-1，∴抛物线G:y1=-x+12+2，∴抛物线G的顶点(-1,2)，抛物线H的顶点为(2,-1)，将(-1,2)向右平移3个单位，再向下平移3个单位即为(2,-1)，即抛物线H可由抛物线G向右平移3个单位，再向下平移3个单位得到，故①正确；②∵(x-2)2≥0，∴-(x-2)2≤0，∴y2=-x-22-1≤-1，∴无论x取何值，y2总是负数，故②正确；③∵B1,-2，∵将y=-2代入抛物线G:y1=-x+12+2，解得x1=-3,x2=1，∴A(-3,-2)，将y=-2代入抛物线H:y2=-x-22-1，解得x1=3,x2=1，∴C(3,-2)，∵-3<x<1，从图像可知抛物线G的图像在抛物线H图像的上方，∴y1>y2∵y1-y2=-(x+1)2+2-[-(x-2)2-1]=-6x+6∴当-3<x<1，随着x的增大，y1-y2的值减小，故③不正确；④设AC与y轴交于点F，∵B1,-2，∴F(0,-2)，由③可知∴A(-3,-2)，C(3,-2)，∴AF=CF，AC=6，当x=0时，y1=1,y2=-5，即D(0,1),E(0,-5)，∴DE=6，DF=EF=3，∴四边形AECD是平行四边形，∵AC=DE,AC⊥DE，∴四边形AECD是正方形，故④正确，综上所述，正确的有①②④，故选：C ．【点睛】本题考查了二次函数图像与性质，一次函数的性质，平移，正方形的判定定理，解题的关键是综合运用以上知识．9.设二次函数y =a x +m x +m -k (a <0，m ，k 是实数)，则()A.当k =2时，函数y 的最大值为-4aB.当k =2时，函数y 的最大值为-2aC.当k =4时，函数y 的最大值为-4aD.当k =4时，函数y 的最大值为-2a【答案】C【分析】此题考查了二次函数的图象和性质、求二次函数的最值，求出二次函数y =a x +m (x +m -k )与x 轴的交点坐标是-m ，0 ,-m +k ，0 ．得到二次函数的对称轴是直线x =-m -m +k 2=-2m +k 2．根据开口方向进一步求出最值即可．【详解】解：由题意，令y =0，∴a x +m (x +m -k )=0，∴x 1=-m ，x 2=-m +k ．∴二次函数y =a x +m (x +m -k )与x 轴的交点坐标是-m ，0 ,-m +k ，0 ．∴二次函数的对称轴是：直线x =-m -m +k 2=-2m +k 2．∵a <0，∴y 有最大值．当x =-2m +k 2，y 最大，即y =a -2m +k 2+m -2m +k 2+m -k =-k 24a 当k =4时，函数y 的最大值为-4a ；当k =2时，函数y 的最大值为-a ．综上，C 选项正确．故选：C ．10.如图，已知点A -1,0 ，点B 2,3 ．若抛物线y =ax 2-x +2(a 为常数，a ≠0)与线段AB 有两个不同的公共点，则a 的取值范围是()A.a ≥3B.a ≤-3或34≤a <1C.-3<a <1或a ≥3D.34≤a <1【答案】B【分析】本题考查了二次函数和一次函数的综合问题，先求出直线AB 的解析式，令x +1=ax 2-x +2，根据有两个交点求出a 的取值范围，再分a >0和a <0两种情况讨论即可得到答案；【详解】解：设AB 所在直线为y =kx +b ，∵A -1,0 ，B 2,3 ，∴-k +b =02k +b =3，解得：k =1b =1 ，∴y =x +1，当x +1=ax 2-x +2时，∵二次函数与线段AB 有两个不同的公共点，∴(-2)2-4a ×1>0，解得：a <1，①当0<a <1时，此时函数的开口向上，∴a ×(-1)2-(-1)+2≥0，a ×22-2+2≥3，解得：34≤a <1，②当a <0时此时函数的开口向下，∴a ×(-1)2-(-1)+2≤0，a ×22-2+2≤3，解得：a ≤-3，综上所述得：34≤a <1，a ≤-3，故选：B ．二、填空题(本大题共6小题，每小题3分，共18分)11.标准大气压下，质量一定的水的体积V cm 3 与温度t °C 之间的关系满足二次函数V =18t 2+104t >0 ，则当温度为4°C 时，水的体积为cm 3．【答案】106【分析】本题考查二次函数的应用，细心计算是解题的关键．将t =4代入解析式求值即可．【详解】解：∵V =18t 2+104t >0 ，当t =4°C 时，V =18×42+104=106cm 3 ，∴水的体积为106cm 3．故答案为：106．12.已知二次函数y =x 2-2x +1的图象向左平移两个单位得到抛物线C ，点P 2,y 1 ，Q 3,y 2 在抛物线C 上，则y 1y 2(填“>”或“<”)；【答案】<【分析】本题主要考查了二次函数图象的平移以及二次函数的性质，由平移的规律可得出抛物线C 的解析式为y =x +1 2，再利用二次函数图象的性质可得出答案．【详解】解：y =x 2-2x +1=x -1 2，∵二次函数y =x 2-2x +1的图象向左平移两个单位得到抛物线C ，∴抛物线C 的解析式为y =x +1 2，∴抛物线开口向上，对称轴为x =-1，∴当x >-1时，y 随x 的增大而增大，∵2<3，∴y 1<y 2，故答案为：<．13.在单位为1的正方形网格中，存在一平面直角坐标系．二次函数y 1=a 1x 2+b 1x +c 1，y 2=a 2x 2+b 2x +c 2的图象位于如图位置上，若它们的图象位置关系具有对称性，请描述它们的对称关系：，求出y 2与直线y =32x +7的交点坐标为．【答案】关于点-32,0 成中心对称-1,112 ，8,19 【分析】本题主要考查了二次函数的图像和性质，以及二次函数与一次函数的交点等知识．(1)根据抛物线图像可求出y 1顶点坐标为-5,-1 ，开口向下；抛物线y 2顶点坐标为2，1 ，开口向上，根据点坐标与二次函数的图像可得出答案．(2)用待定系数法求出抛物线y 2的函数解析式，再令32x +7=12x -2 2+1，进一步求解即可求出y 2与直线y =32x +7的交点坐标．【详解】解：由图象可得抛物线y 1顶点坐标为-5,-1 ，开口向下；抛物线y 2顶点坐标为2，1 ，开口向上，∵点-5,-1 与点2，1 关于点-32，0对称，∴抛物线y 1与抛物线y 2关于点-32，0成中心对称．设抛物线y 2解析式为y 2=a x -2 2+1，由图象可得抛物线经过(4，3)，将(4，3)代入y 2=a x -2 2+1得3=4a +1，解得a =12，∴y 2=12x -2 2+1，令32x +7=12x -2 2+1，解得x 1=-1，x 2=8，将x 1=-1代入y =32x +7得y =112，把x 2=8代入y =32x +7得y =19，∴y 2与直线y =32x +7的交点坐标为-1,112 ，8，19 ，故答案为：-1,112 ，8，19 ．14.如图，将抛物线y =x 2-2x -3在x 轴下方部分沿x 轴翻折，其余部分保持不变，得到图像C 1,当直线y =x +b 与图像C 1恰有两个公共点时，b 的取值范围是．【答案】b >134或-3<b <1【分析】本题考查了抛物线与x 轴的交点：把求二次函数y =ax 2+bx +c (a ,b ,c 是常数，a ≠0)与x 轴的交点坐标问题转化为解关于x 的一元二次方程，也考查了抛物线与直线的交点问题．解决本题的关键是利用数形结合的思想的运用．通过解方程x 2-2x -3=0得到A 、B 的坐标，利用二次函数的性质得到顶点的坐标，可写出图象y =x -1 2-4-1<x <3 沿x 轴翻折所得图象的解析式为y =-x -1 2+4=-x 2+2x +3-1<x <3 ，然后求出直线y =x +b 与y =-x 2+2x +3-1<x <3 相切b 的值，直线y =x +b 过A 和过B 点所对应的b 的值，再利用图象可判断直线y =x +b 与此图象有且只有两个公共点时b 的取值范围．【详解】解：当y =0时，x 2-2x -3=0，解得x 1=-1，x 2=3，则A -1,0 ，B 3,0 ，y =x 2-2x -3=x -1 2-4，则顶点坐标为1,-4 ，把图象y =x -1 2-4-1<x <3 沿x 轴翻折所得图象的解析式为y =-x -1 2+4=-x 2+2x +3-1<x <3 ，如图，当直线y =x +b 与y =-x 2+2x +3-1<x <3 相切时，直线与新函数图象有三个交点，此时x +b =-x 2+2x +3有两个相等的实数解，方程整理得x 2-x +b -3=0，Δ=(-1)2-4(b -3)=0，解得b =134，∴当b >134时，直线y =x +b 与图像C 1恰有两个公共点，当直线y =x +b 过A -1,0 时，-1+b =0，解得b =1，当直线y =x +b 过B 3,0 时，3+b =0，解得b =-3，所以，当-3<b <1时，直线y =x +b 与此图象有且只有两个公共点．综上可知，当直线y =x +b 与图像C 1恰有两个公共点时，b 的取值范围是b >134或-3<b <1．故答案为：b >134或-3<b <1．15.九(1)班劳动实践基地内有一块面积足够大的平整空地．地上两段围墙AB ⊥CD 于点O (如图)，其中AB 上的EO 段围墙空缺．同学们测得AE =6.6m ，OE =1.4m ，OB =6m ，OC =5m ，OD =3m ．班长买来可切断的围栏16m ，准备利用已有围墙，围出一块封闭的矩形菜地，则该菜地最大面积是cm 2．【答案】46.4【分析】本题考查了二次函数的应用．要利用围墙和围栏围成一个面积最大的封闭的矩形菜地，那就必须尽量使用原来的围墙，观察图形，利用AO 和OC 才能使该矩形菜地面积最大，分情况，利用矩形的面积公式列出二次函数，利用二次函数的性质求解即可．【详解】解：要使该矩形菜地面积最大，则要利用AO 和OC 构成矩形，设矩形在射线OA 上的一段长为xm ，矩形菜地面积为S ，当x ≤8时，如图，则在射线OC 上的长为16-x -1.4+52=19.6-x 2则S =x ⋅19.6-x 2=-12x 2+9.8x =-12x -9.8 2+48.02，∵-12<0，∴当x ≤9.8时，S 随x 的增大而增大，∴当x =8时，S 的最大值为46.4；当x >8时，如图，则矩形菜园的总长为16+6.6+5 =27.6m ，则在射线OC 上的长为27.6-2x 2则S =x ⋅13.8-x =-x 2+13.8x =-x -6.9 2+47.61，∵-1<0，∴当x <6.9时，S 随x 的增大而减少，∴当x >8时，S 的值均小于46.4；综上，矩形菜地的最大面积是46.4cm 2；故答案为：46.4．16.如图，二次函数y =33x 2-433x +3的图象交x 轴于点A ,B (点A 在点B 的左侧)，交y 轴于点C ．现有一长为3的线段DE 在直线y =32上移动，且在移动过程中，线段DE 上始终存在点P ，使得三条线段P A ,PB ,PC 能与某个等腰三角形的三条边对应相等．若线段DE 左端点D 的橫坐标为t ，则t 的取值范围是．【答案】-32≤t ≤2【分析】本题考查了二次函数的性质，两点距离公式，轴对称的性质，三角形三边关系，先求出点A ，点B ，点C 坐标，分三种情况讨论，由两点间距离公式和三角形三边关系可求解．【详解】解：∵二次函数y =33x 2-433x +3的图象交x 轴于点A ,B (点A 在点B 的左侧)，交y 轴于点C 当x =0时，y =3，当y =0时，33x 2-433x +3=0，解得：x 1=1,x 2=3∴A 1,0 ,B 3,0 ,C 0,3 ，对称轴为直线x =2如图所示，∵线段DE 上始终存在点P ，使得三条线段P A ,PB ,PC 能与某个等腰三角形的三条边对应相等∴P A =PB 或PB =PC 或PC =P A ，∵段DE 在直线y =32上移动，∴点P 的纵坐标为32,设P x ,32①若PC =P A ，∴x 2+3-322=x -1 2+32 2解得：x =12∴P 12,32∴P A =PC =1,PC =7∵P A +PB =2<7∴不能构成三角形，舍去；②若PB =PC ，∴x 2+3-322=x -3 2+32 2解得：x =32∴P 32,32∵PB =PC =3,P A =1∴能构成三角形，③若P A =PB∴x-12+322=x-32+322解得：x=2∴P A=PB=72,PC=194∵P A+PB>PC，∴P A，PB，PC能组成三角形；∵点P在长为3的线段DE上，∴线段DE左端点D的横坐标为t的取值范围为32-3≤t≤2，即-32≤t≤2故答案为：-32≤t≤2．三、(本大题共4小题，每小题6分，共24分)17.已知二次函数的图像以A-1,4为顶点，且过点B2,-5．(1)求该函数图像与坐标轴的交点坐标；(2)将函数图像向左平移几个单位，该函数图像恰好经过原点．【答案】(1)与y轴的交点坐标为(0,3)；与x轴的交点坐标为(-3,0),(1,0)(2)向左平移1个单位，该函数图象恰好经过原点【分析】本题考查了二次函数的图象和性质，待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．(1)设顶点式y=a(x+1)2+4，然后把(2,-5)代入求出a的值即可得出二次函数解析式；通过解方程-(x+1)2+4=0可得抛物线与x轴的交点坐标，通过计算自变量为0时的函数值可得到抛物线与y轴的交点坐标；(2)由于抛物线与x轴的交点坐标为(-3,0),(1,0)，把点(1,0)向左平移1个单位到原点，所以把抛物线解析式y=-(x+1)2+4向左平移1个单位，该函数图象恰好经过原点．【详解】(1)解：设抛物线解析式为y=a(x+1)2+4，把(2,-5)代入得9a+4=-5，解得a=-1，所以抛物线解析式为y=-(x+1)2+4；当x=0时，y=-(x+1)2+4=-1+4=3，则抛物线与y轴的交点坐标为(0,3)；当y=0时，-(x+1)2+4=0，解得x1=1,x2=-3，则抛物线与x轴的交点坐标为(-3,0),(1,0)；(2)解：因为抛物线与x轴的交点坐标为(-3,0),(1,0)，所以把抛物线解析式y=-(x+1)2+4向左平移1个单位，该函数图象恰好经过原点．18.飞机降落后滑行的距离S(单位：m)关于滑行时间t(单位：s)的函数解析式是S=at²+bt，当t=5时，S=262.5；当t=10时，S=450．。

二次函数单元测试卷(含答案)

二次函数单元测试卷(含答案) 二次函数单元测试卷一、选择题（每小题3分，共30分）1.当-2≤x≦1，二次函数y=-(x-m)²+ m+1有最大值4，则实数m值为（）A。

-7/4 B。

3或-3 C。

2或-3 D。

2或3或-742.二次函数y=ax²+bx+c（a≠0）的图像与x轴的交点个数为（）A。

0个 B。

1个 C。

2个 D。

1个或2个3.关于二次函数y=ax²+bx+c，下列命题中正确的个数是（）①当c=0时，函数的图像经过原点；②当c>0，且函数图像开口向下时，方程ax²+bx+c=0必有两个不相等的实根；③函数图像最高点的纵坐标是4ac-b²/4a；④当b=0时，函数的图像关于y轴对称。

A。

1个 B。

2个 C。

3个 D。

4个4.二次函数y=2mx+(8m+1)x+8m的图像与x轴有交点，则m的范围是（）A。

m-1/16 D。

m≥1/16且m≠-1/165.下列二次函数中有一个函数的图像与x轴有两个不同的交点，这个函数是（）A。

y=x² B。

y=x+4 C。

y=3x²-2x+5 D。

y=3x+5x²-16.若二次函数y=ax+c，当x取x1、x2（x1≠x2）时，函数值相等，则当x取x1+x2时，函数值为（）A。

a+c B。

a-c C。

-c D。

c7.下列二次函数中有一个函数的图像与坐标轴有一个交点，这个函数是（）A。

y=x²-2x+1 B。

y=x²+4 C。

y=x²-2x+1 D。

y=3x+5x²-18.抛物线y=-3x²+2x-1的图像与坐标轴交点的个数是（）A。

没有交点B。

只有一个交点C。

有且只有两个交点D。

有且只有三个交点9.函数y=ax²+bx+c的图像如图所示，关于x的一元二次方程ax²+bx+c-3=0的根的情况是（）A。

九年级数学二次函数测试题含答案(精选5套)

九年级数学二次函数单元试卷（一）时间90分钟满分：100分一、选择题（本大题共10小题，每小题３分，共30分） 1．下列函数不属于二次函数的是（）A.y=(x －1)(x+2)B.y=21(x+1)2C. y=1－3x 2D. y=2(x+3)2－2x 22. 函数y=-x 2-4x+3图象顶点坐标是（）A.（2，-1）B.（-2，1）C.（-2，-1）D.（2， 1）3. 抛物线()12212++=x y 的顶点坐标是（）A ．（2，1）B ．（-2，1）C ．（2，-1）D ．（-2，-1）4. y=(x －1)2＋2的对称轴是直线（）A ．x=－1B ．x=1C ．y=－1D ．y=1 5．已知二次函数)2(2-++=m m x mx y 的图象经过原点，则m 的值为（） A ． 0或2 B ． 0 C ． 2 D ．无法确定6. 二次函数y ＝x 2的图象向右平移3个单位，得到新的图象的函数表达式是（）A. y ＝x 2＋3B. y ＝x 2－3C. y ＝(x ＋3)2D. y ＝(x －3)27．函数y=2x 2-3x+4经过的象限是（）A.一、二、三象限B.一、二象限C.三、四象限D.一、二、四象限 8．下列说法错误的是（）A ．二次函数y=3x 2中，当x>0时，y 随x 的增大而增大B ．二次函数y=－6x 2中，当x=0时，y 有最大值0 C ．a 越大图象开口越小，a 越小图象开口越大D ．不论a 是正数还是负数，抛物线y=ax 2(a ≠0)的顶点一定是坐标原点9．如图，小芳在某次投篮中，球的运动路线是抛物线y ＝－15x 2＋3.5的一部分，若命中篮圈中心，则他与篮底的距离l 是（）A ．3.5mB ．4mC ．4.5mD ．4.6m10．二次函数y=ax 2＋bx ＋c 的图象如图所示，下列结论错误的是（） A ．a ＞0． B ．b ＞0． C ．c ＜0． D ．abc ＞0．(第9题) (第10题)3.05m xyx y o二、填空题（本大题共4小题，每小题３分，共12分）11．一个正方形的面积为16cm 2，当把边长增加x cm 时，正方形面积为y cm 2，则y 关于x 的函数为。

《第22章二次函数》单元检测试卷及答案(共6套)

《第22章二次函数》单元检测试卷（一）一、选择题：1.若(2，5)，(4，5)是抛物线y=ax2＋bx＋c上的两个点，则它的对称轴是( )A.x=1B.x=2C.x=3D.x=42.抛物线y=2（x+3）2+1的顶点坐标是（）A.（3，1）B.（3，﹣1）C.（﹣3，1）D.（﹣3，﹣1）3.下列函数中，是二次函数的有( )①y=1-x2；②y=；③y=x(1-x)；④y=(1-2x)(1+2x).A.1个B.2个C.3个D.4个4.二次函数y=a(x+k)2+k(a≠0),无论k取何值,其图象的顶点都在( )A.直线y=x上B.直线y=-x上C.x轴上D.y轴上5.把抛物线y=(x+1)2向下平移2个单位,再向右平移1个单位,所得到抛物线是( )A.y=(x+2)2+2B.y=(x+2)2-2C.y=x2+2D.y=x2-26.在一定条件下，若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+2t，则当t=4时，该物体所经过的路程为( )A.88米B.68米C.48米D.28米7.二次函数y=x2+2x-3的开口方向、顶点坐标分别是（）A.开口向上,顶点坐标为（-1,-4）B.开口向下，顶点坐标为（1,4）C.开口向上,顶点坐标为（1,4）D.开口向下，顶点坐标为（-1,﹣4）8.在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是（）9.将进货单价为40元的商品按50元出售时，就能卖出500个.已知这种商品每个涨价1元，其销售量就减少10个，为了赚得8000元的利润，商品售价应为（）A.60元B.80元C.60元或80元D.30元10.如图是一个横断面为抛物线形状的拱桥，当水面宽4m时，拱顶（拱桥洞的最高点）离水面2m，当水面下降1m时，水面的宽度为（）A．3 B．2 C．3 D．211.向空中发射一枚炮弹，经x秒后的高度为y米，且时间与高度的关系为y=ax2+bx+c（a≠0）．若此炮弹在第7秒与第14秒时的高度相等，则在下列时间中炮弹所在高度最高的是（）A．第8秒B．第10秒C．第12秒D．第15秒12.已知函数y=ax2﹣2ax﹣1（a是常数，a≠0），下列结论正确的是（）A．当a=1时，函数图象过点（﹣1，1）B．当a=﹣2时，函数图象与x轴没有交点C．若a＞0，则当x≥1时，y随x的增大而减小D．若a＜0，则当x≤1时，y随x的增大而增大二、填空题：13若把二次函数y=x2+6x+2化为y=（x-h）2+k的形式，其中h，k为常数，则h+k= ．14.抛物线y=(x-1)2+2的顶点坐标是 .15.已知点A（x1，y1）、B（x2，y2）都在二次函数y=﹣2(x﹣2)2+1的图象上，且x1＜x2＜2，则1,y1、y2的大小关系是．16a、b、c是实数，点A（a+1、b）、B（a+2，c）在二次函数y=x2﹣2ax+3的图象上，则b、c的大小关系是b c（用“＞”或“＜”号填空）17.将抛物线y=3(x﹣4)2+2向右平移1个单位长度，再向下平移3个单位长度，平移后抛物线的解析式是．18.二次函数y=x2的图象如图，点O为坐标原点，点A在y轴的正半轴上，点B、C在二次函数y=x2的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积为．19.如图，在平面直角坐标系中，二次函数y=ax2+c（a≠0）的图象过正方形ABOC的三个顶点A、B、C，则ac的值是_______．三、解答题：20.已知抛物线y=ax2+bx+3的对称轴是直线x=1．（1）求证：2a+b=0；（2）若关于x的方程ax2+bx﹣8=0的一个根为4，求方程的另一个根．21.已知二次函数y=x 2+bx+c 的图象经过点（0，2）和（1，﹣1），求图象的顶点坐标和对称轴．22. 如图，一次函数y 1＝kx ＋1与二次函数y 2＝ax 2＋bx －2交于A ，B 两点，且A(1，0)，抛物线的对称轴是x ＝－32.(1)求k 和a ，b 的值；(2)求不等式kx ＋1＞ax 2＋bx －2的解集．23.在平面直角坐标系xOy 中，抛物线y ＝ax 2＋bx ＋2过B(－2，6)，C(2，2)两点．(1)试求抛物线的解析式；(2)记抛物线顶点为D ，求∠BCD 的面积；(3)若直线y ＝－12x 向上平移b 个单位所得的直线与抛物线BDC(包括端点B ，C)部分有两个交点，求b 的取值范围．24.杂技团进行杂技表演，演员从跷跷板右端A 处弹跳到人梯顶端椅子B 处，其身体(看成一点)的路线是抛物线的一部分，如图。

二次函数单元测试题及答案

二次函数单元测试题及答案一、选择题1. 二次函数y = ax^2 + bx + c中，当a的值变为原来的2倍时，函数图像如何变化？A. 向上平移B. 向下平移C. 向左平移D. 向右平移答案：B2. 下列哪个选项是二次函数的标准形式？A. y = x^2 + 2x + 1B. y = 2x^2 - 3x + 4C. y = 3x + 4D. y = x - 2答案：B3. 若二次函数y = -2x^2 + 3x + 1的顶点坐标为(1, 2)，则下列哪个选项是正确的？A. a = -2, b = 3, c = 1B. a = 2, b = -3, c = -1C. a = -2, b = -3, c = -1D. a = 2, b = 3, c = 1答案：A4. 二次函数y = 3x^2 - 6x + 9的最小值是多少？A. 0B. 3C. 9D. 无法确定答案：C5. 如果二次函数y = x^2 + 4x + 4的图像与x轴相交于两点A和B，那么线段AB的长度是多少？A. 2B. 4C. 6D. 8答案：C二、填空题6. 已知二次函数y = 2x^2 - 5x + 3，其顶点坐标为__________。

答案：(1, -1)7. 函数y = -x^2 + 4x - 3的最大值是__________。

答案：18. 若二次函数y = 3x^2 - 2x - 5的图像关于y轴对称，则新的函数表达式为y = __________。

答案：y = 3x^2 + 2x - 5三、解答题9. 已知二次函数y = -2x^2 + 6x + 3，求该函数在x = -1时的函数值。

答案：当x = -1时，y = -2*(-1)^2 + 6*(-1) + 3 = -2 - 6 + 3 =-5。

10. 给定二次函数y = x^2 - 6x + 9，求该函数的对称轴方程。

答案：对称轴为x = -b/(2a) = -(-6)/(2*1) = 3。

二次函数单元测试卷(含解析)

二次函数单元测试卷一．选择题（共10小题）1．下列函数解析式中，是二次函数解析式的为（）A．y＝1﹣3x2B．y＝3x+2C．y＝2x D．y＝2．如图，二次函数y＝ax2﹣2ax+1（a＜0）的图象所在坐标系的原点是（）A．点O1B．点O2C．点O3D．点O43．二次函数y＝x2﹣2x+1的对称轴为（）A．直线x＝4B．直线x＝2C．直线x＝﹣2D．直线x＝14．把二次函数y＝x2﹣2x﹣1配方成y＝a（x﹣h）2+k的形式，结果为（）A．y＝（x﹣1）2B．y＝（x﹣1）2﹣2C．y＝（x+1）2+1D．y＝（x+1）2﹣2 5．已知0≤x≤，则函数y＝﹣2x2+8x﹣6的最大值是（）A．﹣10.5B．2C．﹣2.5D．﹣66．已知某抛物线与二次函数y＝5x2的图象的开口大小相同，开口方向相反，且顶点坐标为（﹣1，2021），则该抛物线对应的函数表达式为（）A．y＝﹣5（x﹣1）2+2021B．y＝5（x﹣1）2+2021C．y＝﹣5（x+1）2+2021D．y＝5（x+1）2+20217．已知点A（﹣1，y1），B（1，y2），C（2，y3）都在二次函数y＝（x﹣1）2的图象上，则y1，y2，y3的大小关系正确的是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y2＜y3＜y1D．y3＜y2＜y18．如图，抛物线y＝ax2+bx+c与x轴相交于点A（﹣2，0），B（6，0），与y轴相交于点C，甲、乙、丙、丁四名同学在一起探究该函数的图象与性质，下面是他们得出的结论，其中正确的个数是（）A．1B．2C．3D．49．如图，用一段长为18米的篱笆围成一个一边靠墙（墙长不限）的矩形花园，设该矩形花园的一边长为xm，另一边的长为ym，矩形的面积为Sm2．当x在一定范围内变化时，y 与x，S与x满足的函数关系分别是（）A．一次函数关系，二次函数关系B．正例函数关系，二次函数关系C．二次函数关系，正例函数关系D．二次函数关系，一次函数关系10．在平面直角坐标系xOy中，若点P的横坐标和纵坐标相等，则称点P为完美点．已知二次函数y＝ax2+4x+c（a≠0）的图象上有且只有一个完美点（，），且当0≤x≤m 时，函数y＝ax2+4x+c﹣（a≠0）的最小值为﹣8，最大值为1，则m的取值范围是（）A．﹣1≤m≤0B．2≤m＜C．＜m D．2≤m≤5二．填空题（共7小题）11．当m＝时，函数y＝（m+1）x+8x﹣1是二次函数．12．抛物线y＝x2+2x﹣1的开口方向．13．二次函数y＝（x﹣2）（x+c）的图象与x轴交于A，B两点，与y轴交于点C，且△ABC 为直角三角形，则c＝．14．汽车刹车后行驶的距离S（单位：米）关于行驶时间t（单位：秒）的函数关系式是S ＝8t﹣2t2．则汽车从刹车到停止所用时间为秒．15．商店销售一种进价为20元/个的帽子，经调查发现，该种帽子每天的销售量w（个）与销售单价x（元）满足w＝﹣2x+80（20≤x≤40），设销售这种帽子每天的利润为y（元），则y与x之间的函数关系式为；当销售单价定为元时，每天的利润最大．16．小颖用计算器探索方程ax2+bx+c＝0的根，作出如图所示的图象，并求得一个近似根x ＝﹣3.4，则方程的另一个近似根（精确到0.1）为．17．如图，过抛物线y＝x2﹣2x上一点A作x轴的平行线，交抛物线于另一点B，交y轴于点C，已知点A的横坐标为﹣4，在AB上任取一点P，连结OP，作点C关于直线OP 的对称点D，连结BD，求BD的最小值为．三．解答题（共9小题）18．如图，矩形DEFG的四个顶点分别在正三角形ABC的边上．已知△ABC的边长为4，记矩形DEFG的面积为S，线段BE为x．（1）求S关于x的函数表达式．（2）当S＝时，求x的值．19．某商场以每件30元的价格购进一种商品，试销中发现这种商品每天的销售量m（件）与每件的销售价x（元）满足一次函数关系m＝162﹣3x．（1）请写出商场卖这种商品每天的销售利润y（元）与每件销售价x（元）之间的函数关系式．（2）商场每天销售这种商品的销售利润能否达到500元？如果能，求出此时的销售价格；如果不能，说明理由．20．已知在△ABC中，∠B＝30°，AB+BC＝12，设AB＝x，△ABC的面积是S，求面积S 关于x的函数解析式，并写出自变量x的取值范围．21．如图，在矩形ABCD中，AB＝2，BC＝4，E，F，G，H四点一次是边AB，BC，CD，DA上一点（不与各顶点重合），且AE＝AH＝CG＝CF，记四边形EFGH面积为S（图中阴影），AE＝x．（1）求S关于x的函数表达式，并直接写出自变量的取值范围．（2）求x为何值时，S的值最大，并写出S的最大值．22．已知抛物线y＝﹣x2+bx+c（b，c为常数）经过点（0，﹣3）、（﹣6，﹣3）．（1）求此抛物线的解析式．（2）此抛物线的顶点坐标为；（3）当﹣4≤x≤0时，求y的最大值和最小值．（4）当m≤x≤0时，若y的最大值与最小值之和为2，直接写出m的值．23．抛物线y＝ax2+bx+c与x轴的公共点是（﹣1，0），（3，0）．（1）求这条抛物线的对称轴；（2）若该抛物线最高点到x轴的距离为4．求该抛物线的解析式．24．在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）与x轴交于A（﹣3，0）、B（1，0），与y轴交于点C（0，3），顶点为D．（1）求抛物线解析式；（2）求△ACD的面积．25．如图，抛物线AB，AC是某喷水器喷出的水抽象而成，抛物线AB由抛物线AC向左平移得到，把汽车横截面抽象为矩形DEFG，其中DE＝米，DG＝2米，OA＝h米，抛物线AC表达式为y＝a（x−2）2+h+，且点A，B，D，G，C均在坐标轴上．（1）若h＝，求抛物线AC表达式．（2）在条件（1）下，要使喷水器喷出的水能洒到整个汽车，记OD长为d米，求d的取值范围．（3）若h＝1，喷水器喷出的水能否洒到整个汽车？请说明理由．26．如图，抛物线y＝ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x＝1与抛物线交于点D，与直线BC交于点E．（1）求抛物线的解析式；（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积最大，若存在，求出点F的坐标和最大值；若不存在，请说明理由；（3）平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求P点的坐标．（4）探究对称轴上是否存在一点P，使得以点P，C，A为顶点的三角形是等腰三角形？若存在，请直接写出所有符合条件的P点的坐标，若不存在，请说明理由．参考答案一．选择题（共10小题）1．下列函数解析式中，是二次函数解析式的为（）A．y＝1﹣3x2B．y＝3x+2C．y＝2x D．y＝解：A、是二次函数，故此选项符合题意；B、是一次函数，故此选项不合题意；C、是一次函数，故此选项不合题意；D、是反比例函数，故此选项不合题意．故选：A．2．如图，二次函数y＝ax2﹣2ax+1（a＜0）的图象所在坐标系的原点是（）A．点O1B．点O2C．点O3D．点O4解：∵二次函数y＝ax2﹣2ax+1（a＜0），∴对称轴为直线x＝﹣＝1，所以点O2是原点；故选：B．3．二次函数y＝x2﹣2x+1的对称轴为（）A．直线x＝4B．直线x＝2C．直线x＝﹣2D．直线x＝1解：∵y＝x2﹣2x+1＝（x﹣1）2，∴二次函数y＝x2﹣2x+1的对称轴为直线x＝1，故选：D．4．把二次函数y＝x2﹣2x﹣1配方成y＝a（x﹣h）2+k的形式，结果为（）A．y＝（x﹣1）2B．y＝（x﹣1）2﹣2C．y＝（x+1）2+1D．y＝（x+1）2﹣2解：y＝x2﹣2x﹣1＝x2﹣2x+1﹣2＝（x﹣1）2﹣2．故选：B．5．已知0≤x≤，则函数y＝﹣2x2+8x﹣6的最大值是（）A．﹣10.5B．2C．﹣2.5D．﹣6解：y＝﹣2x2+8x﹣6＝﹣2（x﹣2）2+2，∴当x＜2时，y随着x增大而增大，∴当x＝时有最大值y＝﹣2（﹣2）2+2＝﹣2.5，故选：C．6．已知某抛物线与二次函数y＝5x2的图象的开口大小相同，开口方向相反，且顶点坐标为（﹣1，2021），则该抛物线对应的函数表达式为（）A．y＝﹣5（x﹣1）2+2021B．y＝5（x﹣1）2+2021C．y＝﹣5（x+1）2+2021D．y＝5（x+1）2+2021解：∵抛物线的顶点坐标为（﹣1，2021），∴抛物线的解析式为y＝a（x+1）2+2021，∵抛物线y＝a（x+1）2+2021二次函数y＝5x2的图象的开口大小相同，开口方向相反，∴a＝﹣5，∴抛物线的解析式为y＝﹣5（x+1）2+2021．故选：C．7．已知点A（﹣1，y1），B（1，y2），C（2，y3）都在二次函数y＝（x﹣1）2的图象上，则y1，y2，y3的大小关系正确的是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y2＜y3＜y1D．y3＜y2＜y1解：当x＝﹣1时，y1＝（x﹣1）2＝（﹣1﹣1）2＝4；当x＝1时，y2＝（x﹣1）2＝（1﹣1）2＝0；当x＝2时，y3＝（x﹣1）2＝（2﹣1）2＝1，所以y2＜y3＜y1．故选：C．8．如图，抛物线y＝ax2+bx+c与x轴相交于点A（﹣2，0），B（6，0），与y轴相交于点C，甲、乙、丙、丁四名同学在一起探究该函数的图象与性质，下面是他们得出的结论，其中正确的个数是（）A．1B．2C．3D．4解：由图象可得，该抛物线与x轴有两个交点，则b2﹣4ac＞0，则4ac﹣b2＜0，故甲正确；由图象可知，当y＞0时，x＜﹣2或x＞6，故乙错误；∵抛物线y＝ax2+bx+c与x轴相交于点A（﹣2，0）、B（6，0），∴该抛物线的对称轴是直线x＝，∴﹣＝2，∴b+4a＝0，故丙错误；由图象可得，当x＝﹣1时，y＝a﹣b+c＜0，∴a+4a+c＜0，即5a+c＜0，故丁正确；故选：B．9．如图，用一段长为18米的篱笆围成一个一边靠墙（墙长不限）的矩形花园，设该矩形花园的一边长为xm，另一边的长为ym，矩形的面积为Sm2．当x在一定范围内变化时，y 与x，S与x满足的函数关系分别是（）A．一次函数关系，二次函数关系B．正例函数关系，二次函数关系C．二次函数关系，正例函数关系D．二次函数关系，一次函数关系解：由题意得，y＝（18﹣x），S＝xy＝﹣x2+9x，所以y与x是一次函数关系，S与x是二次函数关系．故选：A．10．在平面直角坐标系xOy中，若点P的横坐标和纵坐标相等，则称点P为完美点．已知二次函数y＝ax2+4x+c（a≠0）的图象上有且只有一个完美点（，），且当0≤x≤m 时，函数y＝ax2+4x+c﹣（a≠0）的最小值为﹣8，最大值为1，则m的取值范围是（）A．﹣1≤m≤0B．2≤m＜C．＜m D．2≤m≤5解：令ax2+4x+c＝x，即ax2+3x+c＝0，由题意，Δ＝32﹣4ac＝0，即4ac＝9，又方程的根为＝，解得a＝﹣1，c＝﹣，故函数y＝ax2+4x+c﹣＝﹣x2+4x﹣3，∵y＝﹣x2+4x﹣3＝﹣（x﹣2）2+1，∴该函数图象顶点为（2，1），∴当x＝2时，函数有最大值为1，把y＝﹣8代入y＝﹣x2+4x﹣3得，﹣8＝﹣x2+4x﹣3，解得x＝﹣1或5，∵当0≤x≤m时，函数y＝﹣x2+4x﹣3的最小值为﹣8，最大值为1，∴2≤m≤5，故选：D．二．填空题（共7小题）11．当m＝3时，函数y＝（m+1）x+8x﹣1是二次函数．解：由题意，得m2﹣2m﹣1＝2且m+1≠0，解得m＝3，故答案为：3．12．抛物线y＝x2+2x﹣1的开口方向向上．解：∵抛物线y＝x2+2x﹣1中a＝1＞0，∴抛物线y＝x2+2x﹣1的开口方向向上．故答案为：向上．13．二次函数y＝（x﹣2）（x+c）的图象与x轴交于A，B两点，与y轴交于点C，且△ABC 为直角三角形，则c＝．解：∵y＝（x﹣2）（x+c）的图象与x轴交于A，B两点，与y轴交于点C，∴A，B两点坐标为（2，0），（﹣c，0）当x＝0时，y＝﹣2c，∴点C坐标为（0，﹣2c），∴AB＝2+c，AC2＝4+4c2，BC2＝5c2，∵△ABC为直角三角形，∴AB2＝AC2+BC2＝5c2+4+4c2＝（2+c）2，∴8c2﹣4c＝0，∴c＝或c＝0（舍去），∴c＝．故答案为：．14．汽车刹车后行驶的距离S（单位：米）关于行驶时间t（单位：秒）的函数关系式是S ＝8t﹣2t2．则汽车从刹车到停止所用时间为2秒．解：∵S＝8t﹣2t2＝﹣2（t﹣2）2+8，∴a＝﹣2＜0，s有最大值，∴汽车从刹车到停下来所用时间是2秒．故答案为：2．15．商店销售一种进价为20元/个的帽子，经调查发现，该种帽子每天的销售量w（个）与销售单价x（元）满足w＝﹣2x+80（20≤x≤40），设销售这种帽子每天的利润为y（元），则y与x之间的函数关系式为y＝﹣2x2+120x﹣1600（20≤x≤40）；当销售单价定为30元时，每天的利润最大．解：y＝w（x﹣20）＝（﹣2x+80）（x﹣20）＝﹣2x2+120x﹣1600＝﹣2（x﹣30）2+200．∵20≤x≤40，a＝﹣2＜0，＝200．∴当x＝30时，y最大值故答案为：y＝﹣2x2+120x﹣1600（20≤x≤40；30．16．小颖用计算器探索方程ax2+bx+c＝0的根，作出如图所示的图象，并求得一个近似根x ＝﹣3.4，则方程的另一个近似根（精确到0.1）为 1.4．解：∵抛物线与x轴的一个交点为（﹣3.4，0），又抛物线的对称轴为：x＝﹣1，∴另一个交点坐标为：（1.4，0），则方程的另一个近似根为1.4，故答案为：1.4．17．如图，过抛物线y＝x2﹣2x上一点A作x轴的平行线，交抛物线于另一点B，交y轴于点C，已知点A的横坐标为﹣4，在AB上任取一点P，连结OP，作点C关于直线OP 的对称点D，连结BD，求BD的最小值为10﹣10．解：当x＝﹣4时，y＝x2﹣2x＝10，∴A（﹣4，10），对称轴直线x＝﹣＝8，∵A、B关于对称轴对称，∴B（20，10），如图中，由题意点D在以O为圆心OC为半径的圆上，∴当O、D、B共线时，BD的最小值＝OB﹣OD＝﹣10＝10﹣10．故答案为：10﹣10．三．解答题（共9小题）18．如图，矩形DEFG的四个顶点分别在正三角形ABC的边上．已知△ABC的边长为4，记矩形DEFG的面积为S，线段BE为x．（1）求S关于x的函数表达式．（2）当S＝时，求x的值．解：（1）∵正△ABC，∴∠B＝60°，∵矩形DEFG的四个顶点分别在正三角形ABC的边上，∴∠BED＝90°，BE＝CF＝x，EF＝4﹣2x，∴DE＝BE•tan60°＝x．∴S＝EF•DE＝x•（4﹣2x）＝﹣2x2+4x．（2）∵S＝，∴﹣2x2+4x＝．∴2x2﹣4x+1＝0．解得：x＝1±．∵0＜x＜2．∴x＝1±．19．某商场以每件30元的价格购进一种商品，试销中发现这种商品每天的销售量m（件）与每件的销售价x（元）满足一次函数关系m＝162﹣3x．（1）请写出商场卖这种商品每天的销售利润y（元）与每件销售价x（元）之间的函数关系式．（2）商场每天销售这种商品的销售利润能否达到500元？如果能，求出此时的销售价格；如果不能，说明理由．解：（1）由题意得，每件商品的销售利润为（x﹣30）元，那么m件的销售利润为y＝m （x﹣30），又∵m＝162﹣3x，∴y＝（x﹣30）（162﹣3x），即y＝﹣3x2+252x﹣4860，∵x﹣30≥0，∴x≥30．又∵m≥0，∴162﹣3x≥0，即x≤54．∴30≤x≤54．∴所求关系式为y＝﹣3x2+252x﹣4860（30≤x≤54）．（2）由（1）得y＝﹣3x2+252x﹣4860＝﹣3（x﹣42）2+432，所以可得售价定为42元时获得的利润最大，最大销售利润是432元．∵500＞432，∴商场每天销售这种商品的销售利润不能达到500元．20．已知在△ABC中，∠B＝30°，AB+BC＝12，设AB＝x，△ABC的面积是S，求面积S 关于x的函数解析式，并写出自变量x的取值范围．解：如图，作△ABC的高AD．在△ABD中，∵∠ADB＝90°，∠B＝30°，∴AD＝AB＝x，∴S＝△ABC的面积＝BC•AD＝（12﹣x）•x＝﹣x2+3x，∴面积S关于x的函数解析式为S＝﹣x2+3x（0＜x＜12）．21．如图，在矩形ABCD中，AB＝2，BC＝4，E，F，G，H四点一次是边AB，BC，CD，DA上一点（不与各顶点重合），且AE＝AH＝CG＝CF，记四边形EFGH面积为S（图中阴影），AE＝x．（1）求S关于x的函数表达式，并直接写出自变量的取值范围．（2）求x为何值时，S的值最大，并写出S的最大值．解：（1）在矩形ABCD中，∠A＝∠B＝∠C＝∠D，AB＝CD，AD＝BC，∵AE＝AH＝CG＝CF，∴BE＝DG，BF＝DH，∴△AEH≌△CFG（SAS），△EBF≌△HDG（SAS），所以S ＝S 矩形ABCD ﹣2S △AEH ﹣2S △EFB ＝2×4﹣2×x 2﹣2×（4﹣x ）（2﹣x ）＝﹣2x 2+6x （0＜x ≤2）．（2）S ＝﹣2x 2+6x ＝﹣2（x ﹣）2+．所以当x ＝时，S 的值最大，最大值为．22．已知抛物线y ＝﹣x 2+bx +c （b ，c 为常数）经过点（0，﹣3）、（﹣6，﹣3）．（1）求此抛物线的解析式．（2）此抛物线的顶点坐标为（﹣3，6）；（3）当﹣4≤x ≤0时，求y 的最大值和最小值．（4）当m ≤x ≤0时，若y 的最大值与最小值之和为2，直接写出m 的值．解：（1）把（0，﹣3），（﹣6，﹣3）代入y ＝﹣x 2+bx +c 得，解得得b ＝﹣6，c ＝﹣3，∴抛物线的解析式为y ＝﹣x 2﹣6x ﹣3；（2）∵y ＝﹣x 2﹣6x ﹣3＝﹣（x +3）2+6，∴抛物线的顶点坐标为（﹣3，6）；故答案为：（﹣3，6）；（3）∵y ＝﹣x 2﹣6x ﹣3＝﹣（x +3）2+6，∴抛物线开口向下，∴当x ＝﹣3时，y 有最大值为6．∵x ＝0时，y ＝﹣3，∴在﹣4≤x ≤0中，y 的最大值是6，，最小值为﹣3；（4）①当﹣3＜m ≤0时，当x ＝0时，y 有最小值为﹣3，当x ＝m 时，y 有最大值为﹣m 2﹣6m ﹣3，∴﹣m 2﹣6m ﹣3+（﹣3）＝2，∴m ＝﹣2或m ＝﹣4（舍去）．②当m ≤﹣3时，当x ＝﹣3时y 有最大值为6，∵y的最大值与最小值之和为2，∴y最小值为﹣4，∴﹣（m+3）2+6＝﹣4，∴m＝﹣3﹣或m＝﹣3+（舍去）．综上所述，m＝﹣2或﹣3﹣．23．抛物线y＝ax2+bx+c与x轴的公共点是（﹣1，0），（3，0）．（1）求这条抛物线的对称轴；（2）若该抛物线最高点到x轴的距离为4．求该抛物线的解析式．解：（1）∵抛物线y＝ax2+bx+c与x轴的公共点是（﹣1，0），（3，0），∴这条抛物线的对称轴为直线x＝＝1；（2）∵抛物线y＝ax2+bx+c与x轴的公共点是（﹣1，0），（3，0），∴y＝a（x+1）（x﹣3）＝ax2﹣2ax﹣3a＝a（x﹣1）2﹣4a，∵该抛物线最高点到x轴的距离为4，∴最高点的纵坐标为4或﹣4，当最高点的纵坐标为4时，﹣4a＝4，∴a＝﹣1；当最高点的纵坐标为﹣4时，﹣4a＝﹣4，∴a＝1；∴y＝x2﹣2x﹣3或y＝﹣x2+2x+3．24．在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）与x轴交于A（﹣3，0）、B（1，0），与y轴交于点C（0，3），顶点为D．（1）求抛物线解析式；（2）求△ACD的面积．解：（1）把点A、B、D的坐标代入二次函数表达式得：，解得：，则抛物线的表达式为：y＝﹣x2﹣2x+3；（2）∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，则顶点D的坐标为（﹣1，4），对称轴为x＝﹣1，设对称轴x＝﹣1交直线AC与M，如图所示：设直线AC的解析式为y＝kx+m，∵A（﹣3，0）、C（0，3），∴，解得，∴直线AC的解析式为y＝x+3，当x＝﹣1时，y＝﹣1+3＝2，∴M（﹣1，2），∴DM＝4﹣2＝2，＝×DM•OA＝×2×3＝3，∴S△ACD∴△ACD的面积为3．25．如图，抛物线AB，AC是某喷水器喷出的水抽象而成，抛物线AB由抛物线AC向左平移得到，把汽车横截面抽象为矩形DEFG，其中DE＝米，DG＝2米，OA＝h米，抛物线AC表达式为y＝a（x−2）2+h+，且点A，B，D，G，C均在坐标轴上．（1）若h＝，求抛物线AC表达式．（2）在条件（1）下，要使喷水器喷出的水能洒到整个汽车，记OD长为d米，求d的取值范围．（3）若h＝1，喷水器喷出的水能否洒到整个汽车？请说明理由．解：（1）把h＝代入y＝a（x−2）2+h+，得：y＝a（x−2）2+2，把（0，）代入y＝a（x﹣2）2+2，解得a＝﹣，∴抛物线AC表达式：y＝﹣（x﹣2）2+2＝﹣x2+x+，当y＝0时，即﹣（x﹣2）2+2＝0，解得：x＝2±2，∴C（2+2，0），∴抛物线AC表达式：y＝﹣（x﹣2）2+2＝﹣x2+x+（0≤x≤2+2）；（2）∵DE＝FG＝OA＝，∴E、F的纵坐标为，∴＝﹣x2+x+，解得：x1＝0，x2＝4，∵点A的纵坐标是，∴抛物线AB是由抛物线AC向左平移4米得到的，∴抛物线AB表达式为：y＝﹣（x+2）2+2，把y＝0代入y＝﹣（x+2）2+2，得：﹣（x+2）2+2＝0，解得x1＝﹣2+2，x2＝﹣2﹣2（舍去），∴OB＝﹣2+2，【求OB方法二：∵由（1）得C（2+2，0），向左平移4米得到的点B坐标为（﹣2+2，0），∴OB＝﹣2+2】由（1）得把y＝代入y＝﹣（x﹣2）2+2，得x1＝4，x2＝0（舍去），∴OG＝4，OD＝OG﹣DG＝2，∵OB≤d≤OD，∴﹣2+2≤d≤2；（3）能，理由如下：当h＝1时，代入y＝a（x﹣2）2+h+，得：y＝a（x﹣2）2+，此时点A坐标为（0，1），代入y＝a（x﹣2）2+，解得：a＝﹣，∴抛物线AC：y＝﹣（x﹣2）2+＝﹣x2+x+1，把y＝0代入得：﹣x2+x+1＝0，解得：x＝2±（负值舍去），∴C（2+，0），∵把y＝1代入y＝﹣x2+x+1得：x1＝0，x2＝4，∴点A（0，1）在抛物线AC上的对称点坐标是（4，1），抛物线AC向左平移了四个单位长度得到抛物线AB，∴点B是由点C向左平移4个单位长度得到的，即B（﹣2+，0），OB＝，∵DE＝，∴代入抛物线AC解析式得：﹣x2+x+1＝，整理，得：x2﹣4x+2＝0，解得：x1＝2+，x2＝2，∴点G的横坐标最大值是2，此时∵DG＝2，∴OD的最大值＝OG﹣DG＝2+﹣2＝＞﹣2，即OD＞OB，∵把x D＝代入抛物线AC得：y＝（1+）＞，∴喷水器喷出的水能洒到整个汽车．26．如图，抛物线y＝ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x＝1与抛物线交于点D，与直线BC交于点E．（1）求抛物线的解析式；（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积最大，若存在，求出点F的坐标和最大值；若不存在，请说明理由；（3）平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求P点的坐标．（4）探究对称轴上是否存在一点P，使得以点P，C，A为顶点的三角形是等腰三角形？若存在，请直接写出所有符合条件的P点的坐标，若不存在，请说明理由．解：（1）∵抛物线y＝ax2+bx+c经过点C（0，4）、A（﹣2，0），且对称轴为x＝1，∴，解得，∴抛物线的解析式为y ＝﹣x 2+x +4．（2）存在，如图1，作FH ⊥x 轴于点H ，交BC 于点G ，设F （x ，﹣x 2+x +4），∵点B 与点A （﹣2，0）关于直线x ＝1对称，∴B （4，0），AB ＝4+2＝6，设直线BC 的解析式为y ＝kx +4，则4k +4＝0，解得k ＝﹣1，∴y ＝﹣x +4，∴G （x ，﹣x +4），∴FG ＝﹣x 2+x +4﹣（﹣x +4）＝﹣x 2+2x ，∴S △FBC ＝OH •FG +BH •FG ＝×4（﹣x 2+2x ）＝﹣x 2+4x ，∴S 四边形SABFC ＝S △FBC +S △ABC ＝﹣x 2+4x +×6×4＝﹣（x ﹣2）2+16，∴当x ＝2时，S 四边形SABFC 最大＝16，F （2，4），∴点F 的坐标是（2，4），四边形ABFC 的面积的最大值是16．（3）如图2，设P （x ，﹣x +4），则Q （x ，﹣x 2+x +4），∴PQ ＝|﹣x 2+x +4﹣（﹣x +4）|＝|﹣x 2+2x |，抛物线y ＝﹣x 2+x +4，当x ＝1时，y ＝，∴D （1，）；直线y ＝﹣x +4，当x ＝1时，y ＝﹣1+4＝3，∴E （1，3），∴DE ＝﹣3＝，∵PQ ∥DE ，且以D 、E 、P 、Q 为顶点的四边形是平行四边形，∴PQ ＝DE ，∴|﹣x2+2x|＝，当﹣x2+2x＝时，解得x1＝3，x2＝1（不符合题意，舍去），∴P1（3，1）；当﹣x2+2x＝﹣时，解得x1＝2+，x2＝2﹣，∴P2（2+，2﹣），P3（2﹣，2+），综上所述，点P的坐标是（3，1）或（2+，2﹣）或（2﹣，2+）．（4）存在，设P（1，m），∵A（﹣2，0），C（0，4），∴AC2＝22+42＝20，PA2＝m2+（1+2）2＝m2+9，PC2＝（m﹣4）2+12＝m2﹣8m+17，当PA＝PC时，则m2+9＝m2﹣8m+17，解得m＝1，∴P1（1，1）；当PC＝AC时，则m2﹣8m+17＝20，解得m1＝4﹣，m2＝4+，∴P2（1，4﹣），P3（1，4+）；当PA＝AC时，则m2+9＝20，解得m1＝，m2＝﹣，∴P4（1，），P5（1，﹣），∴综上所述，P点的坐标（1，1）或（1，4﹣）或（1，4+）或（1，）或（1，﹣）．。

二次函数单元测试卷及答案

二次函数单元测试卷及答案第一部分：选择题（共10题，每题2分）1. 若 $f(x)=2x^2+6x+1$，则该函数的抛物线开口向上（）。

A. 对B. 错2. 对于函数 $f(x)=ax^2+bx+c$，若 $a>0$，则抛物线开口（）。

A. 向上B. 向下3. 已知 $f(x)=x^2+bx+c$，若 $b^2-4c>0$，则该函数（）。

A. 有两个实根B. 无实根C. 有一个实根4. 若 $f(x)=\frac{1}{2}x^2+ax+b$ 的导函数为 $f'(x)=x+1$，则 $f(x)$ 的解析式为（）。

A. $\frac{1}{2}x^2+x+1$B. $\frac{1}{2}x^2+2x+1$C.$\frac{1}{2}x^2+x+2$5. 设 $f(x)=2x^2-10x+8$，$g(x)=x^2-3x+7$，则 $f(x)-g(x)$ 的值域为（）。

A. $(0,+\infty)$B. $(-\infty,0)$C. $[0,+\infty)$6. 函数 $f(x)=x^2-2mx+1$ 与 $y=0$ 交点的横坐标为 $4$，则 $m$ 的值为（）。

A. $1$B. $2$C. $-1$7. 若 $f(x)=x^2+1$，则 $f(2x+1)$ 的最小值为（）。

A. $2$B. $5$C. $6$8. 已知函数 $f(x)=ax^2+bx+c$ 在 $x=1$ 处有极值 $0$，则 $a+b+c$ 等于（）。

A. $-1$B. $0$C. $1$9. 函数 $f(x)=x^2-2x+5$ 与 $g(x)=2x-1$ 的交点横坐标之和为（）。

A. $0$B. $1$C. $2$10. 若 $f(x)=x^2-2x-15$，则 $f(x)$ 的零点为（）。

A. $-3,5$B. $-5,3$C. $-3,-5$答案：1.A 2.A 3.A 4.B 5.A 6.C 7.C 8.B 9.C 10.A第二部分：填空题（共5题，每题4分）1. 函数 $f(x)=x^2+2x+1$ 的零点是 _____________。

初三二次函数综合测试题及答案

二次函数单元测评一、选择题(每题3分，共30分)1.下列关系式中，属于二次函数的是(x为自变量)( )A. B. C. D.2. 函数y=x2-2x+3的图象的顶点坐标是( )A. (1，-4)B.(-1，2)C. (1，2)D.(0，3)3. 抛物线y=2(x-3)2的顶点在( )A. 第一象限B. 第二象限C. x轴上D. y轴上二、4. 抛物线的对称轴是( )A. x=-2B.x=2C. x=-4D. x=45. 已知二次函数y=ax2+bx+c的图象如图所示，则下列结论中，正确的是(A. ab>0，c>0B. ab>0，c<0C. ab<0，c>0D. ab<0，c<06.二次函数y=ax2+bx+c的图象如图所示，则点在第___象限( ) A. 一B. 二C. 三 D. 四7. 如图所示，已知二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4，图象交x轴于点A(m，0)和点B，且m>4，那么AB的长是( )A. 4+mB. mC. 2m-8D. 8-2m8. 若一次函数y=ax+b 的图象经过第二、三、四象限，则二次函数y=ax 2+bx 的图象只可能是( )9. 已知抛物线和直线在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=-1，P 1(x 1，y 1)，P 2(x 2，y 2)是抛物线上的点，P 3(x 3，y 3)是直线上的点，且-1<x 1<x 2，x 3<-1，则y 1，y 2，y 3的大小关系是( )A. y 1<y 2<y 3 B. y 2<y 3<y 1 C. y 3<y 1<y 2 D. y 2<y 1<y 3 10.把抛物线的图象向左平移2个单位，再向上平移3个单位，所得的抛物线的函数关系式是( ) A. B. C. D.二、填空题(每题4分，共32分)11. 二次函数y=x 2-2x+1的对称轴方程是______________.12. 若将二次函数y=x 2-2x+3配方为y=(x-h)2+k 的形式，则13. 若抛物线y=x2-2x-3与x轴分别交于A、B两点，则AB的长为_________.14. 抛物线y=x2+bx+c，经过A(-1，0)，B(3，0)两点，则这条抛物线的解析式为_____________.15. 已知二次函数y=ax2+bx+c的图象交x轴于A、B两点，交y轴于C点，且△ABC是直角三角形，请写出一个符合要求的二次函数解析式________________.(m/s)竖直向上抛物16. 在距离地面2m高的某处把一物体以初速度v出，在不计空气阻力的情况下，其上升高度s(m)与抛出时间t(s)满足：=10m/s，则该物体在运(其中g是常数，通常取10m/s2).若v动过程中最高点距地面_________m.17. 试写出一个开口方向向上，对称轴为直线x=2，且与y轴的交点坐标为(0，3)的抛物线的解析式为______________.的值是18. 已知抛物线y=x2+x+b2经过点，则y1三、解答下列各题(19、20每题9分，21、22每题10分，共38分)19. 若二次函数的图象的对称轴方程是，并且图象过A(0，-4)和B(4，0) (1)求此二次函数图象上点A关于对称轴对称的点A′的坐标(2)求此二次函数的解析式；20.在直角坐标平面内，点 O为坐标原点，二次函数 y=x2+(k-5)x-(k+4)的图象交 x轴于点A(x1，0)、B(x2，0)，且(x1+1)(x2+1)=-8.(1)求二次函数解析式；(2)将上述二次函数图象沿x轴向右平移2个单位，设平移后的图象与y轴的交点为C，顶点为P，求△POC的面积.21.已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，点C(0，5)，另抛物线经过点(1，8)，M为它的顶点.(1)求抛物线的解析式；.(2)求△MCB的面积S△MCB1.考点：二次函数概念.选A.2.考点：求二次函数的顶点坐标.解析：法一，直接用二次函数顶点坐标公式求.法二，将二次函数解析式由一般形式转换为顶点式，即y=a(x-h)2+k的形式，顶点坐标即为(h，k)，y=x2-2x+3=(x-1)2+2，所以顶点坐标为(1，2)，答案选C.3. 考点：二次函数的图象特点，顶点坐标.解析：可以直接由顶点式形式求出顶点坐标进行判断，函数y=2(x-3)2的顶点为(3，0)，所以顶点在x轴上，答案选C.4. 考点：数形结合，二次函数y=ax2+bx+c的图象为抛物线，其对称轴为.解析：抛物线，直接利用公式，其对称轴所在直线为答案选B.5.考点：二次函数的图象特征.解析：由图象，抛物线开口方向向下，抛物线对称轴在y轴右侧，抛物线与y轴交点坐标为(0，c)点，由图知，该点在x轴上方，答案选C.6.考点：数形结合，由抛物线的图象特征，确定二次函数解析式各项系数的符号特征.解析：由图象，抛物线开口方向向下，抛物线对称轴在y轴右侧，抛物线与y轴交点坐标为(0，c)点，由图知，该点在x轴上方在第四象限，答案选D.7.考点：二次函数的图象特征.解析：因为二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4，所以抛物线对称轴所在直线为x=4，交x轴于点D，所以A、B两点关于对称轴对称，因为点A(m，0)，且m>4，所以AB=2AD=2(m-4)=2m-8，答案选C.8.考点：数形结合，由函数图象确定函数解析式各项系数的性质符号，由函数解析式各项系数的性质符号画出函数图象的大致形状.解析：因为一次函数y=ax+b的图象经过第二、三、四象限，所以二次函数y=ax2+bx的图象开口方向向下，对称轴在y轴左侧，交坐标轴于(0，0)点.答案选C.9. 考点：一次函数、二次函数概念图象与性质.解析：因为抛物线的对称轴为直线x=-1，且-1<x1<x2，当x>-1时，由图象知，y随x的增大而减小，所以y2<y1；又因为x3<-1，此时点P3(x3，y3)在二次函数图象上方，所以y2<y1<y3.答案选D.10.考点：二次函数图象的变化.抛物线的图象向左平移2个单位得到，再向上平移3个单位得到.答案选C.考点：二次函数性质.解析：二次函数y=x2-2x+1，所以对称轴所在直线方程.答案x=1.12.考点：利用配方法变形二次函数解析式.解析：y=x2-2x+3=(x2-2x+1)+2=(x-1)2+2.答案y=(x-1)2+2.13. 考点：二次函数与一元二次方程关系.解析：二次函数y=x2-2x-3与x轴交点A、B的横坐标为一元二次方程x2-2x-3=0的两个根，求得x1=-1，x2=3，则AB=|x2-x1|=4.答案为4.14.考点：求二次函数解析式.解析：因为抛物线经过A(-1，0)，B(3，0)两点，解得b=-2，c=-3，答案为y=x2-2x-3.15.考点：此题是一道开放题，求解满足条件的二次函数解析式，.解析：需满足抛物线与x轴交于两点，与y轴有交点，与△ABC是直角三角形，但没有确定哪个角为直角，答案不唯一，如：y=x2-1.16.考点：二次函数的性质，求最大值.解析：直接代入公式，答案：7.考点：此题是一道开放题，求解满足条件的二次函数解析式，答案不唯一.解析：如：y=x2-4x+3.18.考点：二次函数的概念性质，求值.答案：.19. 考点：二次函数的概念、性质、图象，求解析式.解析：(1)A′(3，-4)(2)由题设知：∴y=x2-3x-4为所求(3)20.考点：二次函数的概念、性质、图象，求解析式. 解析：(1)由已知x 1，x 2是x 2+(k-5)x-(k+4)=0的两根又∵(x 1+1)(x 2+1)=-8 ∴x 1x 2+(x 1+x 2)+9=0 ∴-(k+4)-(k-5)+9=0 ∴k=5∴y=x 2-9为所求(2)由已知平移后的函数解析式为： y=(x-2)2-9 且x=0时y=-5 ∴C(0，-5)，P(2，-9).21. 解：(1)依题意：。

二次函数单元测试题及答案

二次函数单元测试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项不是二次函数的一般形式？A. y = ax^2 + bx + cB. y = (x - h)^2 + kC. y = ax^2 + bx + c + dD. y = ax^2 + bx答案：C2. 若二次函数y = ax^2 + bx + c的图像开口向上，则a的值是：A. 正数B. 负数C. 零D. 任意实数答案：A3. 二次函数y = ax^2 + bx + c的顶点坐标是：A. (-b, c)B. (-b/2a, c)C. (-b/a, c)D. (-b/2a, 4ac - b^2 / 4a)答案：D4. 二次函数y = ax^2 + bx + c的对称轴是：A. x = -bB. x = -b/2aC. x = b/2aD. x = b/a答案：B5. 若二次函数y = ax^2 + bx + c与x轴有两个交点，则判别式Δ的值是：A. Δ > 0B. Δ < 0C. Δ = 0D. Δ ≤ 0答案：A二、填空题（每题2分，共10分）6. 二次函数y = 2x^2 - 4x + 3的顶点坐标是________。

答案：(1, 1)7. 若二次函数y = ax^2 + bx + c的图像与y轴交于(0, k)，则k等于________。

答案：c8. 当a > 0时，二次函数y = ax^2 + bx + c的图像开口________。

答案：向上9. 二次函数y = -3x^2 + 6x + 5的对称轴方程是________。

答案：x = 110. 若二次函数y = ax^2 + bx + c与x轴相交于两点，则判别式Δ必须________。

答案：大于0三、解答题（每题5分，共20分）11. 已知二次函数y = ax^2 + bx + c的图像经过点(1, 2)和(-1, 0)，求a和b的值。

解答：将点(1, 2)代入函数得：a + b + c = 2将点(-1, 0)代入函数得：a - b + c = 0两式相减得：2b = 2，即b = 1将b代入任一式得：a + c = 1由于题目条件不足，无法唯一确定a和c的值。

《二次函数》单元测试卷 (含答案)

《二次函数》单元测试卷 (含答案)考生姓名：______________ 考号：______________时间限制：90分钟一、选择题（每小题2分，共30分）（每小题2分，共30分）1. 下列函数中，是二次函数的是（）A. y = x + 2B. y = 2x^2 + 3x + 1C. y = 1/xD. y = √x2. 设二次函数 f(x) = 2x^2 + 5x - 3，那么它的判别式为（）A. -13B. 17C. 29D. -393. 若二次函数的图象与x轴有两个交点，则该二次函数的判别式必须为（）A. 大于0B. 等于0C. 小于0D. 无法确定4. 已知二次函数 f(x) = 3x^2 + 4x + 2，那么它的对称轴为（）A. x = -2/3B. x = -4/3C. x = 4/3D. x = 2/35. 设函数 f(x) = ax^2 + bx + c，若a > 0，则函数图象开口向（）A. 上B. 下C. 左D. 右...二、填空题（每小题3分，共30分）（每小题3分，共30分）1. 设二次函数 f(x) = 2x^2 - 5x + 3，那么它的顶点坐标为（）答案：(5/4, 37/8)2. 若二次函数 y = ax^2 + bx + c 的顶点坐标为 (2, -3)，则 a + b+ c 的值为（）答案：-53. 设二次函数 f(x) = -x^2 + 4x + 5，那么它的对称轴的方程为（）答案：x = 24. 若二次函数的图象与y轴相交于点 (0, 6)，则该二次函数必定为（）答案：f(x) = 2x^2 + 35. 设二次函数 f(x) = ax^2 + bx + c，若a > 0，则函数的值域为（）答案：( -∞, f(c) ]...三、解答题（共40分）（共40分）1. 解方程 3x^2 - 2x - 1 = 0解答：首先，我们可以求出这个二次方程的判别式：Δ = b^2 - 4ac = (-2)^2 - 4*3*(-1) = 4 + 12 = 16因为判别式大于0，所以方程有两个不相等的实根。

二次函数单元测试题及答案

二次函数单元测试题及答案The document was prepared on January 2, 2021二函数单元测试一含答案一、选择题：1．下列函数中,是二次函数的是 A. 28xy =B.18+=x yC.x y 8=D. 182+=x y2. 二次函数12)12(2+--=x k x y ,当1>x 时,y 随着x 的增大而增大,当1<x 时,y 随着x 的增大而减小,则k 的值应取A ．12B ．11C ．10D ．93.2A. B. C. D.4.在函数,自变量x 的取值范围是 A. x ≥-2且x ≠±3 B. x ≥-2且x ≠3 C. x >-2且x ≠-3 D. x >-2且x ≠35.无论m 为何实数,二次函数m x m x y +--=)2(2的图象总是过定点A.-1,3B.1,0C.1,3D.-1,06.在直角坐标系中,坐标轴上到点P-3,-4的距离等于5的点共有个个个个7. 下列四个函数中,y 的值随着x 值的增大而减小的是A ．x y 2=B ．()01>=x x y C ．1+=x y D ．()02>=x x y 8．抛物线c bx ax y ++=2的图象如图,OA=OC,则 A ．b ac =+1 B ．c ab =+1 C ．a bc =+1 D ．以上都不是9.在同一坐标系中,一次函数和二次函数c ax y +=2的图象大致为10．若0>b ,则二次函数12-+=bx x y 2的图象的顶点在A ．第一象限B ．第二象限C ．第三象限D ．第四象限二、填空题：11．已知二次函数解析式为562+-=x x y ,则这条抛物线的对称轴为直线x = ,满足y ＜0的x 的取值范围是 ,将抛物线562+-=x x y 向平移个单位,则得到抛物线962+-=x x y .12．请写出一个开口向上,对称轴为直线2=x ,且与y 轴的交点坐标为0,3的抛物线的解析式 .13. c bx ax y ++=2中,0<a ,抛物线与x 轴有两个交点A2,0B-1,0,则02>++c bx ax 的解是____________,02<++c bx ax 的解是____________.14．已知抛物线y ax bx c =++2经过点A-2,7,B6,7,C3,-8,则该抛物线上纵坐标为-8的另一点的坐标是________.15．如右图所示,长方体的底面是边长为x cm 的正方形,高为6cm,请你用含x 的代数式表示这个长方体的侧面展开图的面积S=________,长方体的体积为V=__________,各边长的和L=__________,在上面的三个函数中,_______是关于x 的二次函数.16.抛物线22++=x x y 与直线4=y 有___个交点,交点坐标是_________________.三、解答题： 17.当二次函数图象与x 轴交点的横坐标分别是1,321=-=x x ,且与y 轴交点为0,-2,求这个二次函数的解析式.18.求抛物线3522--=x x y 与坐标轴的交点坐标,并求这些交点所构成的三角形面积.19. 一男生推铅球,铅球出手后运动的高度)(m y ,与水平距离)(m x 之间的函数关系是35321212++-=x x y ,那么这个男生的铅球能推出几米20.某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销售量m 件与每件的销售价x 元满足一次函数关系x m 3162-=,请写出商场卖这种商品每天的销售利润y 元与每件销售价x 元之间的函数关系式.21. 心理学家发现,在一定的时间范围内,学生对概念的接受能力y与提出概念所用的时间x单位：分钟之间满足函数关系-+=xxy,y的值越大,表示接受能力越强.+x30)≤0(431.02≤6.21若用10分钟提出概念,学生的接受能力y的值是多少2如果改用8分钟或15分钟来提出这一概念,那么与用10分钟相比,学生的接受能力是增强了还是减弱了通过计算来回答.22．如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20米,水位上升3m就达到警戒线CD,这是水面宽度为10米,1在如图的坐标系中求抛物线的解析式；2若洪水到来时,水位以每小时米的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶参答案一、选择题：；；；；；；；；； .二、填空题：新课标第一网xkb11. 3 , 51<<x ,上 , 4 ； 12. 342+-=x x y 答案不唯一；13. 21<<-x , 1-<x 或2>x ； 14. )8,1(-；15. x 24,26x ；248+x ,26x V =； 16. 两,-2,4和1,4.三、解答题：新课标第一网 17. 234322-+=x x y . 18. )0,3( ,),(021- ,)3,0(- , 面积421. 19. 10米.提示：令0=y ,横坐标正值即为所求.20. )5430(486025232≤≤-+-=x x x y . 21.159=y ；2用8分钟与用10分钟相比,学生的接受能力减弱了；用15分钟与用10分钟相比,接受能力增强了.新课标第一网x kb 22. 1 2251x y -=；25小时 .。

二次函数单元测试题及答案

二次函数单元测试题及答案一、选择题（每题3分，共30分）1. 二次函数y=ax^2+bx+c（a≠0）的图象开口向上，则a的取值范围是（）。

A. a>0B. a<0C. a=0D. a≠0答案：A2. 抛物线y=x^2-4x+3的顶点坐标是（）。

A. (1,0)B. (2,1)C. (2,-1)D. (4,3)答案：C3. 若抛物线y=-2x^2+4x-1与x轴有两个交点，则这两个交点的坐标是（）。

A. (1/2,0) 和 (3/2,0)B. (1,0) 和 (3,0)C. (1,0) 和 (-3,0)D. (-1,0) 和 (3,0)答案：B4. 二次函数y=ax^2+bx+c（a≠0）的对称轴是直线x=1，则b的值是（）。

A. -2aB. 2aC. -aD. a答案：B5. 抛物线y=x^2-6x+8与x轴的交点个数是（）。

A. 0B. 1C. 2D. 3答案：C6. 二次函数y=-x^2+2x+3的图象与y轴的交点坐标是（）。

A. (0,3)B. (0,-3)C. (0,2)D. (0,-2)答案：A7. 二次函数y=x^2-2x-3与x轴的交点个数是（）。

A. 0B. 1C. 2D. 3答案：C8. 抛物线y=-2x^2+4x+1的顶点坐标是（）。

A. (1,3)B. (2,5)C. (-1,3)D. (-2,5)答案：A9. 二次函数y=x^2-4x+c的图象经过点（2,0），则c的值是（）。

A. 0B. 4C. 8D. 16答案：C10. 抛物线y=x^2-6x+8与直线y=2x-4的交点坐标是（）。

A. (2,0) 和 (4,4)B. (2,0) 和 (4,0)C. (2,4) 和 (4,0)D. (0,2) 和 (4,4)答案：A二、填空题（每题3分，共15分）11. 二次函数y=2x^2-4x+1的顶点坐标是（）。

答案：(1,-1)12. 二次函数y=-3x^2+6x-3与x轴的交点坐标是（）。

二次函数单元测试题及答案

二次函数单元测试题及答案一、选择题1. 已知二次函数$ y = ax^2 + bx + c $，当$ a < 0 $时，抛物线的开口方向是：A. 向上B. 向下C. 向左D. 向右答案：B2. 对于二次函数$ y = -2x^2 + 3x + 1 $，其顶点的横坐标是：A. $ -\frac{1}{2} $B. $ -\frac{3}{2} $C. $ \frac{3}{4} $D. $ \frac{1}{4} $答案：C3. 若二次函数$ y = x^2 + 2x + 1 $与x轴有交点，则交点的个数是：A. 0B. 1C. 2D. 3答案：B二、填空题4. 二次函数$ y = 3x^2 - 6x + 5 $的对称轴方程是\_\_\_\_\_\_\_\_\_\_\_\_。

答案：$ x = 1 $5. 当$ x = 2 $时，二次函数$ y = x^2 - 4x + 3 $的值为\_\_\_\_\_\_\_\_\_\_\_\_。

答案：-1三、解答题6. 已知二次函数$ y = -x^2 + 2x + 3 $，求其与x轴的交点坐标。

解：令$ y = 0 $，得$ -x^2 + 2x + 3 = 0 $。

解此方程，我们可以使用求根公式：\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]代入$ a = -1, b = 2, c = 3 $，得：\[ x = \frac{-2 \pm \sqrt{4 + 12}}{-2} = \frac{-2 \pm\sqrt{16}}{-2} = 1 \pm 2 \]因此，与x轴的交点坐标为$ (-1, 0) $和$ (3, 0) $。

7. 已知抛物线$ y = 2x^2 - 4x + 1 $，求其顶点坐标。

解：顶点的横坐标可以通过公式$ x = -\frac{b}{2a} $求得，代入$ a = 2, b = -4 $，得：\[ x = -\frac{-4}{2 \times 2} = 1 \]将$ x = 1 $代入原方程求得$ y $值：\[ y = 2(1)^2 - 4(1) + 1 = 2 - 4 + 1 = -1 \]因此，顶点坐标为$ (1, -1) $。

二次函数测试题及答案

二次函数测试题及答案一、选择题（每小题 3 分，共 30 分）1、二次函数 y ＝ x²＋ 2x 3 的图象的顶点坐标是（）A （－1，－4）B （1，－4）C （－1，4）D （1，4）答案：A解析：对于二次函数 y ＝ ax²＋ bx ＋ c 的顶点坐标公式为(b/2a, （4ac b²)／4a)，在函数 y ＝ x²＋ 2x 3 中，a ＝ 1，b ＝ 2，c ＝－3，所以顶点横坐标为 b/2a ＝－2/（2×1) ＝－1，纵坐标为（4ac b²)／4a ＝ 4×1×（－3) 2²/（4×1) ＝（－12 4)／4 ＝－16/4 ＝－4，所以顶点坐标为（－1，－4）。

2、抛物线 y ＝－2(x 1)²＋ 3 的开口方向、对称轴和顶点坐标分别是（）A 开口向下，对称轴为 x ＝－1，顶点坐标为（1，3）B 开口向下，对称轴为 x ＝ 1，顶点坐标为（1，3）C 开口向上，对称轴为 x ＝－1，顶点坐标为（－1，3）D 开口向上，对称轴为 x ＝ 1，顶点坐标为（－1，3）答案：B解析：在抛物线 y ＝ a(x h)²＋ k 中，当 a ＜ 0 时，开口向下，对称轴为 x ＝ h，顶点坐标为（h，k）。

在抛物线 y ＝－2(x 1)²＋ 3 中，a ＝－2 ＜ 0，所以开口向下，对称轴为 x ＝ 1，顶点坐标为（1，3）。

3、把抛物线 y ＝ x²向左平移 1 个单位，然后向上平移 3 个单位，则平移后抛物线的解析式为（）A y ＝（x 1)²＋ 3B y ＝（x ＋ 1)²＋ 3C y ＝（x 1)² 3D y ＝（x ＋ 1)² 3答案：B解析：抛物线平移遵循“上加下减，左加右减”的原则。

抛物线 y ＝x²向左平移 1 个单位得到 y ＝（x ＋ 1)²，然后向上平移 3 个单位得到y ＝（x ＋ 1)²＋ 3。

二次函数 单元检测试卷(含答案)