二三版兼用《运筹学教程》胡运权主编课后习题答案(第三章)
清华大学运筹学教程胡运权主编课后习题答案
8 10
x1 , x2 0
目标函数最优值(下界)为:6.4
17
第18页/共66页
l.7 分别用单纯形法中的大M法和两阶 段法求解下列线性规划问题,并指出属哪—
类解。
max Z 3x1 x2 2x3
x1 x2 x3 6
(1)
st
2x1 2x2
x3 x3
0
2
x j 0(, j 1,,3)
所以最优解为X*=(1,3/2,0,0)T
第11页/共66页
0点
A1点 A2点
max Z 2x1 x2 3x1 5x2 15
(2) st.6x1 2x2 24 x1, x2 0
11
第12页/共66页
第13页/共66页
第14页/共66页
d
x
2
,
l.5 讨论c
,
上题(1)中,若目标函数变为max Z = d的值如何变化,使该问题可行域的每个
8
第9页/共66页
1.4 分别用图解法和单纯形法求解下述 线性规划问题,并对照指出单纯形表中的各 基可行解对应图解法中可行域的哪一顶点。
max Z 10x1 5x2
(1)
st.35xx11
4 x2 2 x2
9 8
x1, x2 0
9
第10页/共66页
cj
10
5 00
CB
xB
b
x1
x2
max Z x1 x2
(3)
st
6 .
x1 10x2 5 x1
120 10
5 x2 8
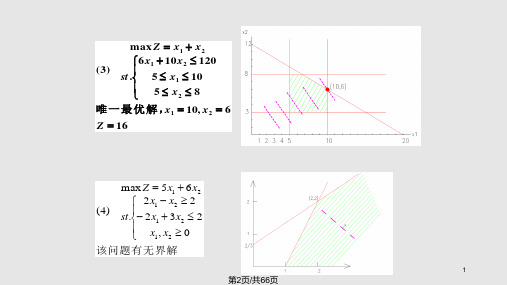
唯 一 最 优 解 ,x1 10, x2 6
Z 16
max Z 5x1 6x2 2x1 x2 2
运筹学教程(第二版)(胡运权)课后答案(清华大学出版社)

运筹学教程(第⼆版)(胡运权)课后答案(清华⼤学出版社)运筹学教程(第⼆版)习题解答第⼀章习题解答运筹学教程1.1 ⽤图解法求解下列线性规划问题。
并指出问题具有惟⼀最优解、⽆穷多最优解、⽆界解还是⽆可⾏解。
1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5 x 1 + 6 x 2≤ 82 5 ≤ x ? 1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3) 1 2 x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 21 2 ? ≥ 12 2 1 ? x , x ≥ 0 .? ?2 x 1 + x 2 ≤ 2st ?3x + 4 x (2) max Z = 3x 1 + 2 x 2x , x ≥ 0 1 2该问题⽆解≥ 12 2 1 ? ? 2 x 1 + x 2 ≤ 2st .?3 x +4 x ( 2 ) max Z = 3 x 1 + 2 x 2第⼀章习题解答3 2 1x = 1, x = 1, Z = 3是⼀个最优解⽆穷多最优解,1 2x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 2该问题有⽆界解1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5x 1 + 6 x 2第⼀章习题解答唯⼀最优解, x 1 = 10, x 2 = 6, Z = 16 ≤ 82 5 ≤ x ?1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3)第⼀章习题解答运筹学教程1.2 将下述线性规划问题化成标准形式。
运筹学(胡运权版)第三章运输问题课后习题答案
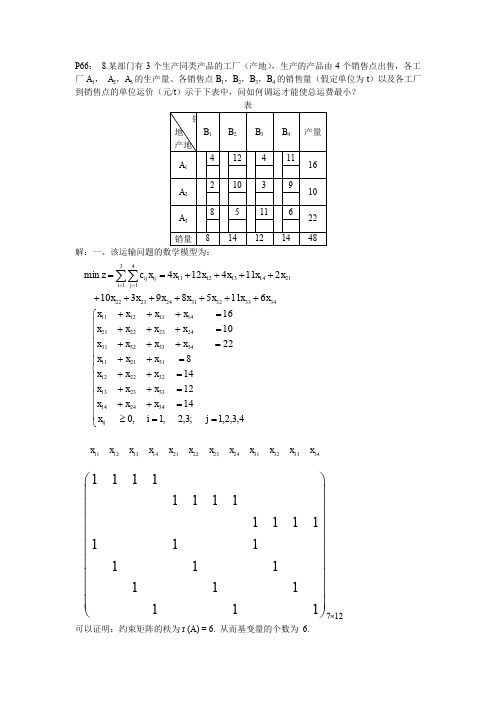
P66: 8.某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点出售,各工厂A 1, A 2,A 3的生产量、各销售点B 1,B 2,B 3,B 4的销售量(假定单位为t )以及各工厂到销售点的单位运价(元/t )示于下表中,问如何调运才能使总运费最小?表解:一、该运输问题的数学模型为:可以证明:约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解(初始调运方案)1. 最小元素法思想:优先满足运价(或运距)最小的供销业务。
其余(非基)变量全等于零。
此解满足所有约束条件,且基变量(非零变量)的个数为6(等于m+n-1=3+4-1=6).总运费为(目标函数值) ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ijij x c Z2. 伏格尔(Vogel)法伏格尔法的基本思想:运输表中各行各列的最小运价与次小运价之差值(罚数)应尽可能地小。
或者说:优先供应罚数最大行(或列)中最小运费的方格,以避免将运量分配到该行(或该列)次小运距的方格中。
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
清华大学《运筹学教程》胡运权主编课后习题答案
运筹学教程
第一章习题解答
1.3 对下述线性规划问题找出所有基解, 指出哪些是基可行解,并确定最优解。
max Z 3x1 x2 2x3
12x1 3x2 6x3 3x4 9
(1)
st
8 3
x1 x1
x2 x6
4x3 0
2 x5
10
x j 0(, j 1,,6)
min Z 5x1 2x2 3x3 2x4
第一章习题解答
max Z x1 x2 6x1 10x2 120 (3) st. 5 x1 10 5 x2 8
唯一最优解,x1 10, x2 6, Z 16
max Z 5x1 6x2
(4)
st.22xx11
x2 3x2
2
2
x1, x2 0
该问题有无界解
5
School of Management
X
0
对于任何0 a 1, 两点连线上的点X满足:
X aX (1) (1 a) X (2)也是可行解,且
CT X CT aX (1) CT (1 a) X (2)
C T aX (1) aCT X (2) C T X (2)
CT X (2) , 所以X也是最优解。
page 24 13 April 2021
(1)
st
x12x1x23xx23
2x4 x3
14 x4
. 2
x1, x2, x3 0, x4无约束
max Z 3x1 4x2 2x3 5x41 5x42
4x1 x2 2x3 x41 x42 2
st
x1 x2 x3 2x1 3x2
2x41 2x42 x3 x41 x42
运筹学教程
运筹学基础及应用第3章-运输问题(胡运权)

产量<销量
1.运输规划问题的典例和数学模型 特征:
1、平衡运输问题必有可行解,也必有最优解; 2、运输问题的基本可行解中应包括 m+n-1 个 基变量。
运筹学基础及应用
Operations Research
运 筹 帷 幄 之 中
第三章
运输问题
决 胜 千 里 之
Transportation Problem
外
目
1
运输规划问题的典例和数学模型 表上作业法 运输问题的应用
录
CONTENTS
2
3
1.运输规划问题的典例和数学模型
例3.1 某公司从两个产地A1、A2将物品运往三个销地B1, B2, B3,各产地的产量、各销地的销量和各产地运往各销地每件 物品的运费如下表所示,问:应如何调运可使总运输费用最 小?
48
列差额
例3.4 某运输资料如下表所示:
销地 产地 A1 2 10
2.表上作业法
B2 B3
12 4
B1
4
B4
11
产量
行差额
16 3 9
0
A2
10
1
8 A3
5
11
6 22 2
14
销量 8 2 14 12 1
8
14 3 48
列差额
2.表上作业法
例3.4 某运输资料如下表所示:
销地 产地 A1 2 10 3 9 B1 4 B2 12 B3 4 B4 11 16 0 产量
二三版兼用《运筹学教程》胡运权主编课后习题答案(第三章)

城市
电站
1
2
3
Ⅰ
15
18
22
Ⅱ
21
25
16
第三章习题解答
习题3.12的解答
城市 城市
电站
1-1
城市 1-2
城市2
城市 3-1
城市 3-2
产量
Ⅰ
150 15
15 250 18
22
22 400
Ⅱ
140 21
第三章习题解答
表3-35
食品厂
面粉厂
1
2
3
产量
Ⅰ
3 10
2 20
Ⅱ
4 11
8 30
Ⅲ
8 11
4 20
销量
15 25 20
第三章习题解答
习题3.10的解答
食品厂 面粉厂
Ⅰ Ⅱ Ⅲ 销量
1
3 15 4
8 15
2
10 5 11 20 11 25
3
20 2 8 4
20
4
0 10 0
0 10
产量
20 30 20
B3
B4 产量
A1 A2 A3 销量
3
7
6
45
2
4
3
22
4
3
8
56
3
3
2
2
第三章习题解答
习题3.9的解答
销地
产地
B1 B2 B3 B4 B5 产量A1源自33 7 6 24 0 5
A2
2 4 23 2 0 2
A3 销量
4 33 8 5 30 6 33223
第三章习题解答
3.10 某市有三个面粉厂,它们供给三个面食加工 厂所需的面粉。各面粉厂的产量、各面食加工厂加工 面粉的能力、各面食加工厂和各面粉厂之间的单位运 价,均表示于表3-35中。假定在第1,2和3面食加工厂 制作单位面粉食品的利润分别为12元、16元和11元, 试确定使总效益最大的面粉分配计划(假定面粉厂和面 食加工厂都属于同一个主管单位)。
运筹学胡运权 部分课后习题答案
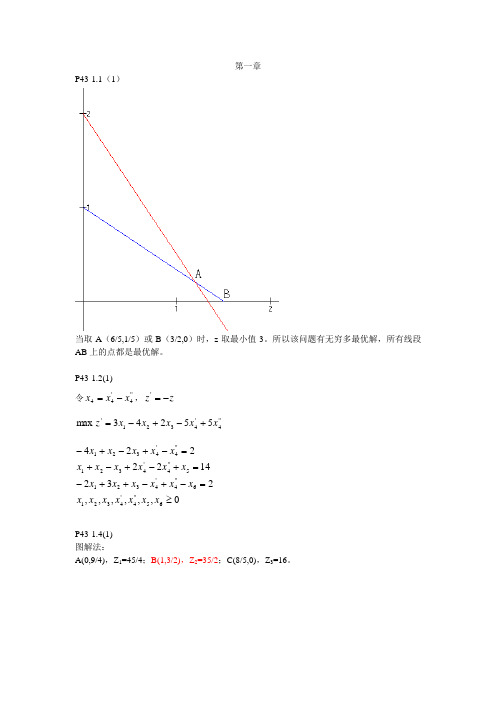
第一章P43-1.1(1)当取A (6/5,1/5)或B (3/2,0)时,z 取最小值3。
所以该问题有无穷多最优解,所有线段AB 上的点都是最优解。
P43-1.2(1)令''4'44x x x -=,z z -='''4'4321'55243max x x x x x z +-+-=,,,,,,232142222465''4'43216''4'43215''4'4321''4'4321≥=-+-++-=+-+-+=-+-+-x x x x x x x x x x x x x x x x x x x x x x x xP43-1.4(1) 图解法:A(0,9/4),Z 1=45/4;B(1,3/2),Z 2=35/2;C(8/5,0),Z 3=16。
单纯形法:10 5 0 0C b X b b x1x2x3x4θ0 x39 3 4 1 0 30 x48 5 2 0 1 8/5δ10 5 0 00 x321/5 0 14/5 1 -3/5 3/210 x18/5 1 2/5 0 1/5 4δ0 1 0 -25 x23/2 0 1 5/14 -3/1410 x1 1 1 0 -1/7 2/7δ0 0 -5/14 -25/14依次相当于:原点;C;B。
P44-1.7(1)2 -1 2 0 0 0 -M -M -MC b X b b x1x2x3x4x5x6x7x8x9θ无界解。
两阶段法:阶段二:P45-1.10证明:CX (0)>=CX*,C*X*>=C*X (0) CX (0)-CX*+C*X*-C*X (0)>=0,即(C*-C)(X*-X (0))>=0。
P45-1.13设饲料i 使用x i (kg ),则543218.03.04.07.02.0m in x x x x x z ++++=s.t. 7001862354321≥++++x x x x x 305.022.05.054321≥++++x x x x x1008.022.05.054321≥++++x x x x x0,,,,54321≥x x x x x第二章P74-2.1(1)321532m ax y y y w ++=22321≤++y y y 243321≤++y y y 4334321=++y y y 无约束321,0,0y y y ≤≥P75-2.4(1),06353322232max 212121212121≥≥≤-≤+≤-≤++=y y y y y y y y y y y y w(2) (8/5,1/5)(3) 无穷多最优解。
运筹学第3章答案
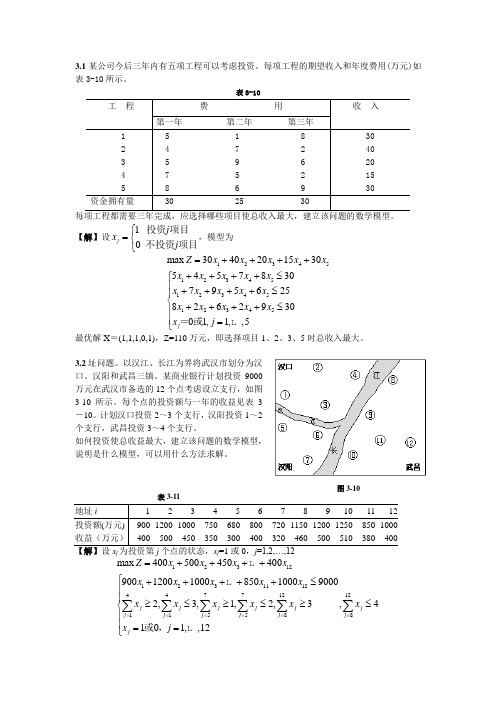
3.1某公司今后三年内有五项工程可以考虑投资。
每项工程的期望收入和年度费用(万元)如表3-10所示。
表3-10【解】设10j j x j ⎧=⎨⎩投资项目不投资项目,模型为12345123451234512345max 30402015305457830795625826293001,1,,5j Z x x x x x x x x x x x x x x x x x x x x x j =++++++++≤⎧⎪++++≤⎪⎨++++≤⎪⎪=⎩=或最优解X =(1,1,1,0,1),Z=110万元,即选择项目1、2、3、5时总收入最大。
3.2址问题。
以汉江、长江为界将武汉市划分为汉口、汉阳和武昌三镇。
某商业银行计划投资9000万元在武汉市备选的12个点考虑设立支行,如图3-10所示。
每个点的投资额与一年的收益见表3-10。
计划汉口投资2~3个支行,汉阳投资1~2个支行,武昌投资3~4个支行。
如何投资使总收益最大,建立该问题的数学模型,说明是什么模型,可以用什么方法求解。
表3-11j j 12312123111244771212115588max 40050045040090012001000850100090002,3,1,2,3,4101,,12j j j j j j j j j j j j jZ x x x x x x x x x x x x x x x x j =======++++⎧+++++≤⎪⎪≥≤≥≤≥≤⎨⎪⎪==⎩∑∑∑∑∑∑ 或, 图3-10最优解:x1=x5=x12=0,其余xj=1,总收益Z=3870万元,实际完成投资额8920万元。
3.3 一辆货车的有效载重量是20吨,载货有效空间是8×3.5×2 m 。
现有六件货物可供选择运输,每件货物的重量、体积及收入如表表3-12。
另外,在货物4和5中先运货物5,货物1和2不能混装,怎样安排货物运输使收入最大,建立数学模型。
运筹学第三章课后习题答案

量 1 2 34
4 51 34
6 8 302
④
A2 A3 销量
31
2
25
30 8 1 1 5
⑤
3
7 15
1 4 224 ⑥
6
5
6
3
列12 罚22 数3
vj 4
111 11 11 1
②
①⑦
③
2020/1/1
9
从上表计算知:x12=5,x13=3,x21=3,x23=2,x24=3, x33=1。总费用=5×1+3×4+3×1+2×5+3×0+ 1×5=35,在上述三种计算方法中,这种方法计算所需 运输费用是最省的。但还不知是否最优。现用闭回路法 检验如下: 闭回路法检验如下:
2020/1/1
10
第一个闭回路σ11,走4→1→5→4线路
产地 销地
A1
B1
B2
B3
45 13 4
B4
6
A2 3 1
22 5 3 0
A3 销量
3
71 5
1
6
5
6
3
产量
8 8 4
σ11=4-1+5-4=4
2020/1/1
11
第二闭回路σ14,走6→0→5→4线路
产地 销地
A1
B1
B2
B3
45 13 4
2020/1/1
17
①最小元素法求解:
销地 B1
B2
产地
A1
13
7
A2
22
4
A3
4
33
销量
3
3
B3
B4 B5 产量
6 3 28 2
1 4 30
运筹学(胡运权第三版)第三章 运输问题

§1 运 输 问 题 及 其 数 学 模 型
二、运输问题数学模型的特点:
1. 运输问题一定有最优解;基变量的个数 =m+n-1
2. 运输问题约束条件的系数矩阵:
x11 x12
1 1 1
…
x1m x21 x22
1 1 1
…
x2m
1
… xm1
1
解 的 最 优 性 检 验
1.闭回路法 闭回路:从空格出发,遇到数 字格可以旋转90度,最后回到空 格所构成的回路; 原理:利用检验数的经济含义; 检验数:非基变量增加一个单 位引起的成本变化量。 当所有非基变量的检验数均大 于或等于零时,现行的调运方案 就是最优方案,因为此时对现行 方案作任何调整都将导致总的运 输费用增加。 闭回路法的主要缺点是:当变 量个数较多时,寻找闭回路以及 计算两方面都会产生困难。
B4
11
-1
产量
16
10 22 48
ui
A1 A2
A3 销量 vj
2
10
1 10
9 6
1 0
-4
8 14
5 12
8
14
2
检验数σ
9
3
10
13=8-(-4)-2=10;
2.对偶变量法(位势法)
解 的 最 优 性 检 验
m in Z = c 1 1 x 1 1 + c 1 2 x 1 2 + ... + c 1 n x 1 n + ... + c m 1 x m 1 + c m 2 x m 2 + ... + c m n x m n
清华大学《运筹学教程》胡运权主编课后习题答案

0
0
0 -1/5 2/5 0
1
0 3/5 -1/5 0
0
x3
1
0
0
1
1
1 -1
cj zj
0
0
0 -1/5 -M+7/5 -M
由于上表中所有检验数都小于等于零(且非基变量检验数都 小于0),因此已经得到唯一最优解,最优解为:
X * 25 ,9 /5 ,1 ,0 ,0 ,0 T
方法二:两阶段法
第一阶段:
4x1 x2 2x3 x4 2
(1)
stx12x1x23xx23
2x4 14 x3 x4
. 2
x1, x2, x3 0, x4无约束
minZ 2x1 2x2 3x3
(2)
st
x1 x2 x3 4 2x1 x2 x3 6
x1 0, x2 0, x3无约束
minZ 3x1 4x2 2x3 5x4
7
4 -1
1
1/3 0
0 [5/3] -1
0
5/3 0
0
5/3
-1
0 -1 -1
i
x4
x5
x6
0
10
1
0
0 1 3/2
1
00
4
0
00
0 1/3 0 3
0 -4/3 1 6/5 1 -1/3 0 9/5 0 -7/3 0
cj
0
CB
xB
b
x1
0
x1 3/5
1
0
x 2 6/5
0
0
x4
1
0
cj zj
0
4x1 x2 2x3 x41 x42 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章习题解答
3.9 试求出表3-34给出的产销不平衡运输问题的最 优解。 表3-34 销地 产地 A1 A2 A3 销量 3
B1
3 2 4
B2
7 4 3 3
B3
6 3 8 2
B4
4 2 5 2
产量
5 2 6
第三章习题解答
习题3.9的解答 销地 产地 B1 B2 B3 B4 B5 产量
A1
A2 A3 销量
第三章习题解答
表3-35 食品厂 面粉厂 Ⅰ Ⅱ Ⅲ 销量
1
3 4 8 15
2
10 11 11 25
3
2 8 4 20
产量
20 30 20
第三章习题解答
习题3.10的解答
食品厂 面粉厂
1 3 15 4 15
2 10 5 11 25
3 20 2 8
4
4 0 10 0
0
产量 20 30
20
Ⅰ Ⅱ
Ⅲ
8 20 11
3 3
2 4 3
7
4 3 3 3 2
6
2 3 8
2 4
2 5 2
0
0 3 0 3
5
2 6
第三章习题解答
3.10 某市有三个面粉厂,它们供给三个面食加工 厂所需的面粉。各面粉厂的产量、各面食加工厂加工 面粉的能力、各面食加工厂和各面粉厂之间的单位运 价,均表示于表3-35中。假定在第1,2和3面食加工厂 制作单位面粉食品的利润分别为12元、16元和11元, 试确定使总效益最大的面粉分配计划(假定面粉厂和面 食加工厂都属于同一个主管单位)。
第三章习题解答
3.12 1,2,3三个城市每年需分别供应电力320, 250和350单位,由I,Ⅱ两个电站提供,它们的最大供 电量分别为400个单位和450个单位,单位费用如表3— 37所示。由于需要量大于可供量,决定城市1的供应量 可减少0~30单位,城市2的供应量不变,城市3的供应 量不能少于270单位,试求总费用最低的分配方案(将 可供电量用完)。 表3-37 城市 1 2 3 电站 15 18 22 Ⅰ 21 25 16 Ⅱ
3.2 运输问题的基可行解应满足什么条件?将其 填入运输表中时有什么体现?并说明在迭代计算过程 中对它的要求。 解:运输问题基可行解的要求是基变量的个数等 于m+n-1。填入表格时体现在数字格的个数也应该等 于m+n-1。在迭代过程中,要始终保持数字格的个数 不变。
第三章习题解答
3.3 试对给出运输问题初始基可行解的西北角法、 最小元素法和Vogel法进行比较,分析给出的解之质量 不同的原因。 解:用西北角法可以快速得到初始解,但是由于 没有考虑运输价格,效果不好;最小元素法从最小的 运输价格入手,一开始效果很好,但是到了最后因选 择余地较少效果不好; Vogel法从产地和销地运价的 级差来考虑问题,总体效果很好,但是方法较复杂。
cij (ui v j ) 0 i 1,2, m; j 1,2,, n
第三章习题解答
由于方程有m+n-1个, 而变量有m+n个。所以上 面的方程有无穷多个解。任意确定一个变量的值都可 以通过方程求出一个解。然后再利用这个解就可以求 出非基变量的检验数了。
第三章习题解答
3.5 用表上作业法求解运输问题时,在什么情况 下会出现退化解?当出现退化解时应如何处理? 解:当数字格的数量小于m+n-1时,相应的解就 是退化解。如果出现了退化解,首先找到同时划去的 行和列,然后在同时划去的行和列中的某个空格中填 入数字0。只要数字格的数量保持在m+n-1个的水平即 可。
6] X(5,1) + X(5,2) + X(5,3) + X(5,4) - X(5,5) = 0
7]-X(1,1) + X(2,1) + X(3,1) + X(4,1) + X(5,1) = 0 8] X(1,2) - X(2,2) + X(3,2) + X(4,2) + X(5,2) = 0 9] X(1,3) + X(2,3) - X(3,3) + X(4,3) + X(5,3) = 0 10]X(1,4) + X(2,4) + X(3,4) - X(4,4) + X(5,4) = 30 11]X(1,5) + X(2,5) + X(3,5) + X(4,5) - X(5,5) = 20
第三章习题解答
3.4 详细说明用位势法(对偶变量法)求检验数的原 理。 解:原问题的检验数也可以利用对偶变量来计算 :
ij cij (ui v j )
i 1,2, m; j 1,2,, n
其中,ui和vj就是原问题约束对应的对偶变量。由于 原问题的基变量的个数等于m+n-1。所以相应的检验 数就应该等于0。即有:
第三章习题解答
2]-X(1,1) + X(1,2) + X(1,3) + X(1,4) + X(1,5) = 10 3] X(2,1) - X(2,2) + X(2,3) + X(2,4) + X(2,5) = 40 4] X(3,1) + X(3,2) - X(3,3) + X(3,4) + X(3,5) = 0 5] X(4,1) + X(4,2) + X(4,3) - X(4,4) + X(4,5) = 0
第三章习题解答
习题3.12的解答
城市 城市 1-1 电站 城市 1-2
15
21 30 0
城市2
250 18
25 M
城市 3-1
22
270 16 M
城市 3-2
22
40 16 40 0
产量 400
450 70
Ⅰ
Ⅱ Ⅲ 销量
150 15
140 21 M
290
30
250
270
80
第三章习题解答
3.13 试写出本章例5转运问题的数学模型。
第三章习题解答
3.6 一般线性规划问题具备什么特征才能将其转 化为运输问题求解,请举例说明。 解:如果线性规划问题有“供”和“需”的关系, 并且有相应的“费用”,就可以考虑将线性规划问题 转成运输问题求解。例如,生产满足需求的问题。
第三章习题解答
3.8 表3-32和表3-33分别给出了各产地和各销地的 产量和销量,以及各产地至各销地的单位运价,试用 表上作业法求最优解。 表3-32 销地 产地 A1 A2 A3 销量 6 B1 4 6 1 3 5 B2 5 1 2 7 B3 3 4 5 3 5 6 B4 6 2 0 1 1 3 产量 8 8 4 20
Q=50
+ 3 X(3,1)+2X(3,2)+3 X(3,3)+5 X(3, 4) + 5 X( 3, 5)
+ 2 X(4,1)+100X(4,2)+5 X(4,3)+ 3 X(4,4)+6 X( 4, 5) + 100X(5,1)+4X(5,2)+5X(5,3)+6 X( 5, 4) +5 X( 5, 5)
第三章习题解答
(4)若所有价值系数均乘以2,最优解是否改变? 为什么? 答:最优解不变。因为检验数不变。 (5)写出该运输问题的对偶问题,并给出其对偶问 题的最优解。
解:对偶问题如下: max Z ai ui b j v j
i 1 j 1 m n
ui v j cij i 1,2, m; j 1,2, , n ui , v j 无约束, i 1,2, m; j 1,2, , n 最优解是:u1 1, u 2 0, u3 0, v1 1, v2 2, v3 5, v4 1
第三章习题解答
3.1 与一般线性规划的数学模型相比,运输问题 的数学模型具有什么特征? 答: 1、运输问题一定有有限最优解。 2、约束系数只取0或1。 3、约束系数矩阵的每列有两个1, 而且只有两个 1。前m行中有一个1,或n行中有一个1。 4、对于产销平衡的运输问题,所有的约束都取等 式。
第三章习题解答
销量
20
10
第三章习题解答
3.11 表3-36示出一个运输问题及它的一个解: 表3-36 销地 产地 A1 A2 B1 4 8 1 B2 5 1 2 B3 3 4 6 B4 6 2 1 产量 8 10
A3
销量 8
1
5
7
3 5
6
1 1
3
4
22
第三章习题解答
试问: (1)表中给出的解是否为最优解?请用位势法进行 检验。 答:是最优解。 (2)如价值系数c24由1变为3,所给的解是否仍为最 优解?若不是,请求出最优解。 答:原来的解不是最优解。新的最优解是: x12=3,x13=5,x21=8,x22=2,x33=1,x34=3, 其他变量为0 。 (3)若所有价值系数均增加1,最优解是否改变? 为什么? 答:不会改变。因为检验数不变。
解:已知 a1=10,a2=40,a3 = a4 = a5 = 0
b1= b2= b3=0,b4=30,b5=20 下面就是相应的模型:
MIN Z=
4 X(1,1)+ 5 X(1,2)+ 3 X(1,3)+ 2 X(1,4)+ 100X(1, 5) + 5 X(2,1)+ X(2,2)+2 X(2,3)+100 X(2,4) + 4 X(2, 5)
