编码理论第5章
第5章无失真信源编码定理

如果我们要对信源的N次扩展信源进行编码,也必须满足
qN rl , 两边取对数得: l log q
l
N log r
N 表示平均每个信源符号所需的码符号个数。
5.2 等长码
例:对英文电报得32个符号进行二元编码,根据上述关系:
l log 32 5 log 2
我们继续讨论上面得例子,我们已经知道英文的极限 熵是1.4bit,远小于5bit,也就是说,5个二元码符号只携带 1.4bit的信息量,实际上,5个二元符号最多可以携带5bit 信息量。我们可以做到让平均码长缩短,提高信息传输率
0.8112
0.4715
若采用等长二元编码,要求编码效率 0.96 ,允许错误率
105 ,则: N 4.13107
也就是长度要达到4130万以上。
5.5 变长码
1、唯一可译变长码与及时码
信源符号 出现概率 码1
码2
码3
码4
s1
1/2
0
0
1
1
s2
1/4
11
10
10
01
s3
1/8
00
00
密码:是以提高通信系统的安全性为目的的编码。通常通过加 密和解密来实现。从信息论的观点出发,“加密”可视为增熵 的过程,“解密”可视为减熵的过程。
5.1 编码器
信源编码理论是信息论的一个重要分支,其理论基础是信源编 码的两个定理。 无失真信源编码定理:是离散信源/数字信号编码的基础; 限失真信源编码定理:是连续信源/模拟信号编码的基础。
5.1 编码器
信源编码:以提高通信有效性为目的的编码。通常通过压缩信 源的冗余度来实现。采用的一般方法是压缩每个信源符号的平 均比特数或信源的码率。即同样多的信息用较少的码率传送, 使单位时间内传送的平均信息量增加,从而提高通信的有效性。
信息与编码理论课后习题答案

2.1 莫尔斯电报系统中,若采用点长为0.2s ,1划长为0.4s ,且点和划出现的概率分别为2/3和1/3,试求它的信息速率(bits/s)。
解: 平均每个符号长为:1544.0312.032=⨯+⨯秒 每个符号的熵为9183.03log 3123log 32=⨯+⨯比特/符号所以,信息速率为444.34159183.0=⨯比特/秒2.2 一个8元编码系统,其码长为3,每个码字的第一个符号都相同(用于同步),若每秒产生1000个码字,试求其信息速率(bits /s)。
解: 同步信号均相同不含信息,其余认为等概,每个码字的信息量为 3*2=6 比特;所以,信息速率为600010006=⨯比特/秒2.3 掷一对无偏的骰子,若告诉你得到的总的点数为:(a ) 7;(b ) 12。
试问各得到了多少信息量?解: (a)一对骰子总点数为7的概率是366 所以,得到的信息量为 585.2)366(log 2= 比特(b) 一对骰子总点数为12的概率是361 所以,得到的信息量为 17.5361log 2= 比特2.4经过充分洗牌后的一付扑克(含52张牌),试问:(a) 任何一种特定排列所给出的信息量是多少? (b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解: (a)任一特定排列的概率为!521, 所以,给出的信息量为 58.225!521log 2=- 比特 (b) 从中任取13张牌,所给出的点数都不相同的概率为 13131313525213!44A C ⨯=所以,得到的信息量为 21.134log 1313522=C 比特.2.5 设有一个非均匀骰子,若其任一面出现的概率与该面上的点数成正比,试求各点出现时所给出的信息量,并求掷一次平均得到的信息量。
解:易证每次出现i 点的概率为21i,所以比特比特比特比特比特比特比特398.221log 21)(807.1)6(070.2)5(392.2)4(807.2)3(392.3)2(392.4)1(6,5,4,3,2,1,21log )(2612=-==============-==∑=i i X H x I x I x I x I x I x I i ii x I i2.6 园丁植树一行,若有3棵白杨、4棵白桦和5棵梧桐。
编码理论(第二版)(田丽华)-第5章

第5章 信道编码原理
(1)信道按其输入/输出信号在幅度和时间上的取值是离 散或连续来划分,可分成三类,分别是数字信道 (DigitalChannel)或离散信道(DiscreteChannel)、模拟信道 (AnalogChannel)或波形信道(WaveformChannel)和连续信道 (ContinuousChannel)。
b1
a1 p(b1 a1)
P a2 p(b1 a2 )
b2
p(b2 a1)
p(b2 2 )
bs p(bs a1) p(bs a2 )
(5-2)
ar p(b1 ar ) p(b2 ar ) p(bs ar )
第5章 信道编码原理
式中:0 p(bj ai ) 1,i 1,2,...,r; j 1,2,...,s; 且
第5章 信道编码原理
(3)信道按其输入/输出信号之间的关系是否是确定关系 来划分,可分为有噪声信道和无噪声信道。一般来讲,信道输 入与输出之间的关系是一种统计依存关系,而不是确定关系。 这是因为信道中总存在某种程度的噪声。在某些情况下,若信 道中的噪声与有用信号相比很小可以忽略不计,则这时的信道 可以理想化为具有确定关系的无噪声信道。
(2)信道按其输入/输出之间关系的记忆性来划分,可分为 无记忆信道和有记忆信道两类。如果信道的输出只与信道该时 刻的输入有关而与其他时刻的输入无关,则称此信道是无记忆 的;反之,如果信道的输出不但与信道现时刻的输入有关,而 且还与以前时刻的输入有关,则称此信道为有记忆的,实际信 道一般都是有记忆的。信道中的记忆现象来源于物理信道中的 惯性元件,如电缆信道中的电感电容、无线信道中电波传布的 衰落现象等。
第5章 信道编码原理
因信道的输入有r种不同的输入符号,输出有s种不同的输
编码理论第5章

000 001 010 100 011 110
乘法运算:
011 110 3 4 1 001
101 111 6 5 4 110
因为本原元a=x,所以p(a)=0
111
101
3 1 x 1 x 1 0
α 010
举例
x7-1=(x-1)[(x-z)(x-z2)(x-z2-z)][(x-z-1)(x-z2-1)(x-z2-z1)] 在扩域GF(23)上,可得到x3+x+1=(x-z)(x-z2)(x-z2z), x3+x2+1=(x-z-1)(x-z2-1)(x-z2-z-1) 计算(x-z)(x-z2)(x-z2-z)=(x2-z2x-zx+z3)(x-z2-z)=x3z2x2-zx2-z2x2+z4x+z3x-zx2+z3x+z2x+z3x-z5z4=x3+(z4+z3+z2)x-(z5+z4), 由于在GF(23)上, z3=z+1, 所以z4+z3+z2=z3z+z3+z2=(z+1)z+(z+1) +z2=1, z5+z4=z3(z2+z)=(z+1)z(z+1)=z(z+1)2=z(z2+1)=z3+z=z +1+z=1,故得到(x-z)(x-z2)(x-z2-z)= x3+x+1 同理可以计算x3+x2+1=(x-z-1)(x-z2-1)(x-z2-z-1)
BCH码限定理
编码理论第五章

an-1
编码理论——信道编码
bm-1
11
(3)离散输入、连续输出信道 信道输入符号选自一个有限离散的符号集合
X = {a0 , a1,, an1}
信道输出时未经量化的任意值,即 m->∞ 信道特性由转移概率密度函数决定
pY ( y | X = ai ), i = 1,2, , n
编码理论——信道编码
19
按照信息码元在编码后是否保持原来的形式不变,可 划分为系统码和非系统码。在差错控制编码中,通常信息 码元和监督码元在分组内有确定的位置。在系统码中,编 码后的信息码元保持原样不变,而非系统码中信息码元则 改变了原来的信号形式。系统码的性能大体上与非系统码 的相同,但是在某些卷积码中非系统码的性能优于系统码。 由于非系统码中的信息位已经改变了原有的信号形式,这 对观察和译码都带来麻烦,因此很少应用,而系统码的编 码和译码相对比较简单些,所以得到广泛的应用。
第五章 信道编码
张长森 河南理工大学计算机学院
1
第5章
信道编码 5.1 信道的分类及参数 5.2 信道编码的基本概念 5.3 信道编码的基本原理
编码理论——信道编码
2
5.1
信道的分类及参数
信道分类和表示参数 通信系统中,信道是非常重要的部分。信道的任务是以信号方 式传输信息。在信道中会引入噪声,这些都会使信号通过信道 后产生错误和失真,故信道的输入和输出之间一般不是确定的 函数关系,而是统计依赖关系。 只要知到了信道的输入信号和输出信号以及它们之间的统计依 赖关系,则信道的全部特性就确定了。所以可以用信道的转移 概率矩阵P(Y/X)来描述信道、信道的数学模型及分类 研究信道,就要研究信道中能够传送的最大信息量,即信道容 量问题。
第5章 信源编码 第1讲 无失真信源编码 定长编码定理 2016

00 01 10 11
0 01 001 111
12/62
余 映 云南大学
5.1 编码的定义
• 采用分组编码方法,需要分组码具有某些属性, 以保证在接收端能够迅速准确地将码译出。 • 下面讨论分组码的属性:
余 映 云南大学
13/62
5.1 编码的定义
• (1) 奇异码和非奇异码
– 若信源符号和码字是一一对应的,则该码为非奇异码; 反之为奇异码。 – 例如表中码1是奇异码,其他是非奇异码。
信源符号 出现概率 码1 码2 码3 码4
A B C D
1/2 1/4 1/8 1/8
0 11 00 11
余 映 云南大学
0 10 00 01
1 10 100 1000
1 01 001 0001
18/62
5.1 编码的定义
• (3) 即时码和非即时码
– 唯一可译码又分为非即时码和即时码。 – 即时码是一种没有一个码字构成另一码字前缀的码。 在译码时没有延迟,收到一个完整码字后就能立即译 码。 – 如果收到一个完整码字后,不能立即译码,还需等下 一个码字开始接收后才能判断是否可以译码,这样的 码叫做非即时码。
信源符号
出现概率
码1
码2
码3
码4
a1 a2 a3 a4
1/2 1/4 1/8 1/8
0 11 00 11
余 映 云南大学
0 10 00 01
1 10 100 1000
1 01 001 0001
14/62
5.1 编码的定义
• (2) 唯一可译码和非唯一可译码
– 若任意有限长的码元序列,只能被唯一地分割成一个 个的码字,则称为唯一可译码。 – 例如{0, 10, 11}是一种唯一可译码。 – 因为任意一串有限长码序列, – 如100111000
信息论与编码第5章 信源编码技术

哈夫曼码的主要特点 1、哈夫曼码的编码方法保证了概率大的符号对 应于短码,概率小的符号对应于长码,充分 利用了短码; 2、缩减信源的两个码字的最后一位总是不同, 可以保证构造的码字为即时码。 3、哈夫曼码的效率是相当高的,既可以使用单 个信源符号编码,也可以对信源序列编码。 4、要得到更高的编码效率,可以使用较长的序 列进行编码。
5.1.2费诺码
费诺码的基本思想: 1、按照累加概率尽可能相等的原则对信源符号 进行分组: 对于二元码,则每次分为两组; 对于d元码,则每次分为d个组。 并且给不同的组分配一个不同的码元符号。 2、对其中的每组按照累计概率尽可能相等的原 则再次进行分组,并指定码元符号,直到不能 再分类为止。 3、然后将每个符号指定的码元符号排列起来就 得到相应的码字。
算术编码
适用于JPEG2000,H.263等图像压缩标准。 特点: 1、随着序列的输入,就可对序列进行编码 2、平均符号码长 L 满足
1 H (X ) L H (X ) N
(最佳编码)
3、需要知道信源符号的概率 是对shanno-Fanno-Elias编码的改进。
累计分布函数的定义
H(X ) H(X ) L 1 log d log d
费诺码的最佳性
1、保证每个集合概率和近似相等,保证d个码元近 似等概率,每个码字承载的信息量最大,码长近似 最短。 2、是次最佳的编码方法,只在当信源符号概率满足:
p(ai ) d
时达最佳。
li
信源符号
a1 a2 a3 a4 a5 a6 a7 a8 a9
费诺二元码的编码步骤
1、将源消息符号按概率大小排序:
p1 p2 p3 pn
2、将依次排列的信源符号分为两大组,使每组的概 率和尽可能相等,且每组赋与二进制码元“0”和 “1”。 3、将每一大组的信源符号再分为两组,使每组的概 率和尽可能相等,且每组赋与二进制码元“0”和 “1”。 4、如此重复,直至每组只剩下一个符号。 信源符号所对应的码字即费诺码。
第5章无失真信源编码定理12

第5章无失真信源编码定理●通信的实质是信息的传输。
高效率、高质量地传送信息又是信息传输的基本问题。
●信源信息通过信道传送给信宿,需要解决两个问题:第一,在不失真或允许一定失真条件下,如何用尽可能少的符号来传送信源信息,以提高信息传输率。
第二,在信道受干扰的情况下,如何增强信号的抗干扰能力,提高信息传输的可靠性同时又使得信息传输率最大。
●为了解决以上两个问题,引入了信源编码和信道编码。
●提高抗干扰能力(降低失真或错误概率)往往是增加剩余度以降低信息传输率为代价的;反之,要提高信息传输率往往通过压缩信源的剩余度来实现,常常又会使抗干扰能力减弱。
●上面两者是有矛盾的,然而在信息论的编码定理中,已从理论上证明,至少存在某种最佳的编码或信息处理方法,能够解决上述矛盾,做到既可靠又有效地传输信息。
●第5章着重讨论对离散信源进行无失真信源编码的要求、方法及理论极限,得出极为重要的极限定理——香农第一定理。
5.1编码器●编码实质上是对信源的原始符号按一定的数学规则进行的一种变换。
●图5.1就是一个编码器,它的输入是信源符号集S={s 1,s 2,…,s q }。
同时存在另一符号集X={x 1,x 2, …,x r },一般元素x j 是适合信道传输的,称为码符号(或称为码元)。
编码器是将信源符号集中的符号s i (或者长为N 的信源符号序列a i )变换成由x j(j=1,2, …,r )组成的长度为l i的一一对应序列。
●这种码符号序列W i 称为码字。
长度l i称为码字长度或简称码长。
所有这些码字的集合C 称为码。
●编码就是从信源符号到码符号的一种映射,若要实现无失真编码,必须这种映射是一一对应的、可逆的。
编码器S :{s 1,s 2,…s q }X :{x 1,x 2,…x r }C :{w 1,w 2,…w q }(w i 是由l i 个x j (x j 属于X ))组成的序列,并于s i 一一对应一些码的定义●二元码:若码符号集为X={0,1},所得码字都是一些二元序列,则称为二元码。
信息论基础与编码(第五章)
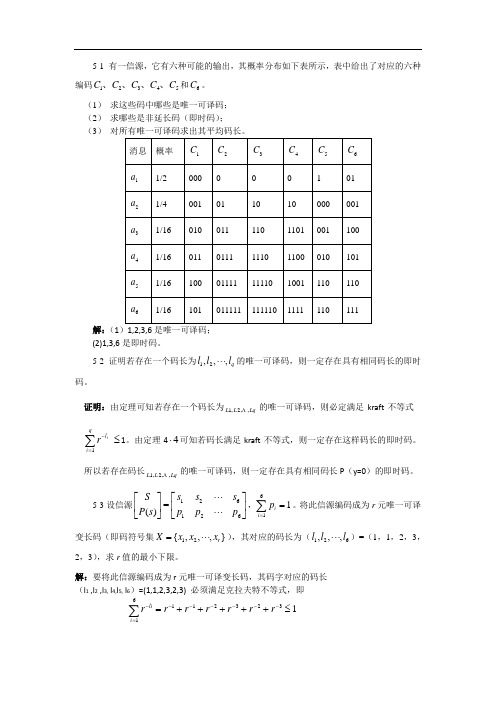
5-1 有一信源,它有六种可能的输出,其概率分布如下表所示,表中给出了对应的六种编码12345C C C C C 、、、、和6C 。
(1) 求这些码中哪些是唯一可译码; (2) 求哪些是非延长码(即时码);(3) 对所有唯一可译码求出其平均码长。
解:(1(2)1,3,6是即时码。
5-2证明若存在一个码长为12,,,q l l l ⋅⋅⋅的唯一可译码,则一定存在具有相同码长的即时码。
证明:由定理可知若存在一个码长为的唯一可译码,则必定满足kraft 不等式1。
由定理4可知若码长满足kraft 不等式,则一定存在这样码长的即时码。
所以若存在码长的唯一可译码,则一定存在具有相同码长P (y=0)的即时码。
5-3设信源126126()s s s S p p p P s ⋅⋅⋅⎡⎤⎡⎤=⎢⎥⎢⎥⋅⋅⋅⎣⎦⎣⎦,611i i p ==∑。
将此信源编码成为r 元唯一可译变长码(即码符号集12{,,,}r X x x x =⋅⋅⋅),其对应的码长为(126,,,l l l ⋅⋅⋅)=(1,1,2,3,2,3),求r 值的最小下限。
解:要将此信源编码成为 r 元唯一可译变长码,其码字对应的码长(l 1 ,l 2 ,l 3, l 4,l 5, l 6)=(1,1,2,3,2,3) 必须满足克拉夫特不等式,即132321161≤+++++=------=-∑r r r r r r ri liLq L L ,,2,1 ∑=-qi l ir1≤4⋅Lq L L ,,2,1所以要满足122232≤++r r r ,其中 r 是大于或等于1的正整数。
可见,当r=1时,不能满足Kraft 不等式。
当r=2, 1824222>++,不能满足Kraft 。
当r=3, 127262729232<=++,满足Kraft 。
所以,求得r 的最大值下限值等于3。
5-4设某城市有805门公务电话和60000门居民电话。
作为系统工程师,你需要为这些用户分配电话号码。
信息论与编码理论基础(第五章)

2012-5-10
15
两种典型的译码规则
[解答 最佳译码判决指的是最大后验概率译码。记(Q(x1), Q(x2), 解答] 最佳译码判决指的是最大后验概率译码。 解答 Q(x3))信道的输入随机变量 的概率向量,又称为先验概率向 信道的输入随机变量X的概率向量 信道的输入随机变量 的概率向量, 为信道的输出随机变量Y的分布概率 量, (W(y1), W(y2), W(y3))为信道的输出随机变量 的分布概率 为信道的输出随机变量 向量。则 向量。 (Q(x1), Q(x2), Q(x3))=(1/2,1/4, 1/4), ,
2012-5-10
20
两种典型的译码规则
2012-5-10 7
k0长信息段 信息段 纠错编码器
n0长码段
• (n0, k0)卷积码 (Convolutional codes):各分组 卷积码 : 相关,约束长度L为 相关,约束长度 为(m+1) k0
….
n0长码段
(N, L)分组码 (Block codes):分组之间独立, 分组码 :分组之间独立, 约束长度L为 约束长度 为k0
2012-5-10
3
11
译码规则
例:有一个离散信道,其转移概率矩阵P为
根据该转移概率矩阵可以设计一个译码规则A如 上; 也可以设计一个译码规则B如下:
2012-5-10
12
译码规则
制定译码规则就是设计一个函数它对于每一个输出符 号确定一个唯一的输入符号与其对应。 号确定一个唯一的输入符号与其对应。 若信道有r个输入符号,s个输出符号,则共有多少种 若信道有 个输入符号, 个输出符号 个输入符号 个输出符号, 译码规则? 译码规则? 由于s个输出符号中的每一个都可以翻译成 个输入符 由于 个输出符号中的每一个都可以翻译成r个输入符 个输出符号中的每一个都可以翻译成 号中的任何一个,所以共有r 种译码规则可供选择。 号中的任何一个,所以共有 s种译码规则可供选择。 译码规则的选择应该根据什么准则? 译码规则的选择应该根据什么准则? 一个很自然的准则当然就是要使错误概率为最小。 一个很自然的准则当然就是要使错误概率为最小。
第五章 编码定理

第五章 编码定理
无失真编码定理→ 无失真编码定理 第一极限定理 信源 限失真编码定理→ 限失真编码定理 第三极限定理 编码定理 信道 连续信道编码定理 以上定理有其逆定理,即当信息率小于信源熵( 以上定理有其逆定理, 即当信息率小于信源熵 (或 R(D))时,或信息率大于信道容量时,被传送的信 或信息率大于信道容量时, ) 息必然有失真 离散信道编码定理 →第二极限定理
N σ 2 (S ) P {| I ( a N ) − NH ( S ) |≥ N ε } ≤ (Nε )2 I (a N ) σ 2 (S ) P{| − H ( S ) |≥ ε } ≤ N Nε 2
即:
由于信源取值有q种,则N长信源序列就有 N种, 长信源序列就有q 由于信源取值有 种 长信源序列就有 将qN种序列分成两个互补的集
ε δ
第五章 编码定理
以上为正定理部分的证明。 以上为正定理部分的证明。 利用表达式: 利用表达式: r
当 N→∞时,由④式得: 式得:
rl Mε
exp(− Nε ) < 2 Mε σ (S ) 1− 2 Nε
l
④
→0
绝大部分在 Aε 中的序列已 无对应的码字, 无对应的码字,译码一定出错
在N→∞时,由①式得 P( Aε ) →1
第五章 编码定理
2、码树 、 某节点被安排为码字后, 某节点被安排为码字后,不再继续
中间 节点
终端 节点
伸枝, 终端节点,其它为中间节点, 伸枝,称终端节点,其它为中间节点, 中间节点 中间节点不安排码字。 中间节点不安排码字。 3、克拉夫特不等式: 、克拉夫特不等式: 对于码符号为X= ‥‥, 的任意即时码 的任意即时码, 对于码符号为 ={x1,x2,‥‥,xr}的任意即时码, ‥‥, 所对应的码长为l 其码字为w 其码字为 1,w2, ‥‥, wq,所对应的码长为 1, l2, ‥‥ , lq,则必定满足克拉夫特不等式; 反之 , ‥‥, 则必定满足克拉夫特不等式;反之, 若码长满足克拉夫特不等式, 则一定存在码长为l 若码长满足克拉夫特不等式 , 则一定存在码长为 i 的即时码。 的即时码。
预测编码理论

预测误差门限型:(非线性预测器) ei ui ui 1 仅与前一样值作预测 若
ei K 则不传送 u i ; ei
K
则传送
ui
K为最大误差的门限值,即信宿可接收的最大误差
信号相关性越强,则此时传送的数据越少。
谢谢大家!
一、预测编码原理
对于有记忆信源,信源输出的各个分量之间是 有统计关联的,这种统计关联性可以加以充分利用, 预测编码就是基于这一思想。它不是直接对信源输 出的信号进行编码,而是将信源输出信号通过预测 变换后再对预测值与实际值的差值进行编码,其原 理图见下图。
一、预测编码原理
预测编码是利用信源的相关性来压缩码率的。
第五章预测编码
本章内容
预测编码原理 预测编码理论基础 预测编码方法 预测编码的应用
一、预测编码原理
预测编码是数据压缩三大经典技术(统计编 码、预测编码、变换编码)之一。预测编码 是建立在信号数据的相关性之上,较早用于 信源编码的一种技术。它根据某一模型,利 用以往的样本值对新样本值进行预测,以减 少数据在时间和空间上的相关性,达到压缩 数据的目的。
设信源第i瞬间的输出值为ui,而根据信源ui的前 k(k<i)个样值,给出的预测值为
u i f (ui 1 , ui 2
^
, ui k )
式中:f(· )——预测函数。 f可以是线性也可以是非线性函数。 则第i个样值的预测误差值为
ei ui u i
^
根据信源编码定理,若直接对信源输出ui进行编 码,则其平均码长 Lu 应趋于信源熵:
H (U ) p(ui )loga p(ui ), ui U
若对预测变换后的误差值e进行编码,其平均码 长 Le 应趋于误差信号熵:
感觉编码理论

本章总结
感觉: 一般概念、感觉编 码理论、有关刺激强 度与感觉大小关系的 理论; 其他感觉
视觉: 生理机制以及相关 理论; 听觉 生理机制以及相关 理论。
思考题
1.
名词解释:感觉编码、绝对感受性和 绝对感觉阈限、差别阈限以及差别感受 性、侧抑制、普肯耶现象、马赫带、后 像、闪光融合、视觉掩蔽、视敏度。 2. 感觉有什么意义?有关感觉的编码理 论有哪些? 3.有关刺激强度与感觉大小关系的理论有 哪些?
2.2 视觉的基本现象
3、普肯耶现象:当人们从锥体视觉向棒
体视觉转变时,人眼对光谱的最大感 受性将向短波方向移动,因而,出现 了明度不同的变化,这种现象就叫普 肯耶现象。
2.2 视觉的基本现象
4、马赫带:指人们在明
暗变化的边界,常常在亮 区看到一条更亮的光带, 而在暗区看到一条更暗的 线条。这就是马赫带现象 ,马赫带不是由于刺激能 量的分布,而是由于神经 网络对视觉信息进行加工 的结果。
1.3 感受性与感觉阈限
有关刺激强度与感觉大小关
系的理论: 费希纳的对数定律: P=K logI 公式表明当刺激强度按几何 级数增加时,感觉强度只按 算术级上升。当物理量迅速 上升时,感觉量是逐步变化 的。
1.3 感受性与感觉阈限
斯蒂文斯的乘方定律:P=K In 感觉的大小是与刺激量的乘方成正比例
3.3 听觉理论
④神经齐射理论 ——韦弗尔提出。
当声音频率低于400 赫兹时,听神经个 别纤维的发放频率 是和频率对应的, 当声音频率提高, 神经纤维将按齐射 原则发生作用。
四种理论的划分
地点说
共鸣 行波
频率说
频率 神经齐射
第四节 其他感觉
5编码理论(simple)

最佳码
前缀码
2011/11/30
29
例:
消息符 号 a b c d
概率 0.2 0.16 0.128 0.512
码字序号 0 1 2 3 1 01 001 000
编码
m
i 1
n
ki
2 1 2 2 2 3 2 3 1
0 (a) 1
等概条件下的消息符号熵 等概条件下的码字符号熵
考虑信源的实际统计特性(非等概),实际消息熵为:
H ( S ) pi log pi
i
代入无失真条件,得:
K L
H (S ) logm
结论:即使m=n,只要
就有可能实现K<L。 即无失真与有效性同时满足。
log m H ( S )
8
具体实现方法:定长与变长编码
18
H(U) H(U) H(U) η K R logm H(U) ε L 2011/11/30
L, 0, 1,理论上是可行的。 必须将无限长信源序列作为一个整体,进行编码,实际 不可行。 例: (教材P368) 信源符号有8种取值,给定P(ai),H(U)=2.55
为
第N节总枝数
m
i 1
n
N k i
mN
(2)
k i m 1 i 1 n
式中, n为码字数。由(1)式可得
(证毕)
26
2011/11/30
M=3,N=3满树
33-2=3个枝不能利用(k1=2)
33-1=9个枝不能利用(k2=1)
27
2011/11/30
第N=3节
充分条件证明:
北航研究生编码理论第五章BCH码-2013

3.引入中间函数 x 错误位置多项式 x 1 X 1 x1 X 2 x1 X t x 1 1 x 2 x 2 t x t
其中:
0 1 1 X1 X 2 X t 2 X1 X 2 X 2 X 3 X t -1 X t t X1X 2 X t
Sj R
其中:
S
j
Ex Y1x Y2 x Yt x
j
E
lk
Y Y Y X
j t j lk t k 1 k k 1 k lk j t k 1 k
j k
Xk
称为错误位置数,它表示在R中的第几项发生了错误。 说明第n-i项有错 错误值,对二元BCH码而言, k 存在且 k
t
6Rx Cx E x
以上方法为逐步求解法,例题
19
4求 x 的根. 5求Ex
已知 x 1 1 x 2 x 2 t x t
5.4.2 BCH码的迭代译码法
S x S1 x S 2 x 2 Si x i
S1 R S2 R 2 2t S 2t R
n
写成 S j R j , j 1,2,2t
15
2.由S求E
S T HRT HET
n1
Ex En1 x
En2 x
n 2
E1 x E0
如果信道中有t个错误,则信道错误图样中有t 项,即 lt l1 l2
m
为GF (2 ) 的本原元
11
编码理论

无线信道
比有线信道要恶劣的多!
反射 折射 散射
由于多径使得信号消弱
快衰落和慢衰落
第一章 绪论
1.1 编码与编码理论 1.2 编码分类和相关基础 1.3 编码系统模型 1.4 编码理论的发展
1.1 编码与编码理论
1.1.1 信息与编码
通信最基本、最重要的功能就是传递信息、 获取信息、处理信息和利用信息。 古代的结绳记事,长城上的峰火台硝烟,墙 壁上的点划刻蚀,……,都是为传递和保存信息 的典型手段,是一种最简单、最经典的编码。 有线和无线通信产生以后,真正的编码技术 随之产生,以不同点、划、间断的组合代表不同 文字和数字的莫尔斯码、中文电报码等,开始了 编码的真正研究和应用。 现在,几乎所有信息应用领域都需要编码, 各种编码都在被积极研究。
在《通信的数学原理》中,他提出了受干扰信道编 码定理,该定理的主要内容为: 每个受干扰的信道具有确定的信道容量C。例如,当 信道中存在高斯白噪声时,在信道带宽W、单位频 带信号功率S、单位频带噪声功率N下,信道容量可 表示为 S
C W log 2 (1 ) N bps
对于任何小于信道容量C的信息传输速率,存在一个 码长为n,码率为R的分组码,若用最大似然译码, 则其译码错误概率为
1.2.2 信道编码
信道,是指有明确信号输入和信号输出的信息通 道。
这个通道可以是空间,如通信系统把信号从一个地点传 送到另一个地点; 这个通道可以是时间,如存储系统把 信号从某个时间开始存储到下一个时间; 这个通道可以 是过程,如处理系统把信号从一个接口演变到另一个接口。 无论是哪一种通道,有输入到输出的转移过程,这个转 移过程反映了该通道的特征。 最基本、最简单的转移过程,就是什么都不改变,仅仅 把输入原封不变的搬到输出。实际上,任何信道,在我们 研究的尺度空间,都很难做到输出与输入完全一样、原封 不变,输入经过信道之后总有不同和差异。
信息理论与编码课后答案第5章

第5章 有噪信道编码5.1 基本要求通过本章学习,了解信道编码的目的,了解译码规则对错误概率的影响,掌握两种典型的译码规则:最佳译码规则和极大似然译码规则。
掌握信息率与平均差错率的关系,掌握最小汉明距离译码规则,掌握有噪信道编码定理(香农第二定理)的基本思想,了解典型序列的概念,了解定理的证明方法,掌握线性分组码的生成和校验。
5.2 学习要点5.2.1 信道译码函数与平均差错率5.2.1.1 信道译码模型从数学角度讲,信道译码是一个变换或函数,称为译码函数,记为F 。
信道译码模型如图5.1所示。
5.2.1.2 信道译码函数信道译码函数F 是从输出符号集合B 到输入符号集合A 的映射:*()j j F b a A =∈,1,2,...j s =其含义是:将接收符号j b B ∈译为某个输入符号*j a A ∈。
译码函数又称译码规则。
5.2.1.3 平均差错率在信道输出端接收到符号j b 时,按译码规则*()j j F b a A =∈将j b 译为*j a ,若此时信道输入刚好是*j a ,则称为译码正确,否则称为译码错误。
j b 的译码正确概率是后验概率:*(|)()|j j j j P X a Y b P F b b ⎡⎤===⎣⎦ (5.1)j b 的译码错误概率:(|)()|1()|j j j j j P e b P X F b Y b P F b b ⎡⎤⎡⎤=≠==-⎣⎦⎣⎦ (5.2)平均差错率是译码错误概率的统计平均,记为e P :{}1111()(|)()1()|1(),1()|()s se j j j j j j j ssj j j j j j j P P b P e b P b P F b b P F b b P F b P b F b ====⎡⎤==-⎣⎦⎡⎤⎡⎤⎡⎤=-=-⎣⎦⎣⎦⎣⎦∑∑∑∑ (5.3)5.2.2 两种典型的译码规则两种典型的译码规则是最佳译码规则和极大似然译码规则。
信息论与编码理论-习题答案-姜楠-王健-编著-清华大学

可得 ,3种状态等概率分布。
一阶马尔可夫信源熵为
信源剩余度为
(2)二阶马尔可夫信源有9种状态(状态转移图略),同样列方程组求得状态的平稳分布为
二阶马尔可夫信源熵为
信源剩余度为
由于在上述两种情况下,3个符号均为等概率分布,所以信源剩余度都等于0。
总的概率
所需要的信息量
2.6设 表示“大学生”这一事件, 表示“身高1.60m以上”这一事件,则
故
2.7四进制波形所含的信息量为 ,八进制波形所含信息量为 ,故四进制波形所含信息量为二进制的2倍,八进制波形所含信息量为二进制的3倍。
2.8
故以3为底的信息单位是比特的1.585倍。
2.9(1)J、Z(2)E(3)X
(2)三元对称强噪声信道模型如图所示。
4.7由图可知信道1、2的信道矩阵分别为
它们串联后构成一个马尔科夫链,根据马氏链的性质,串联后总的信道矩阵为
4.8传递矩阵为
输入信源符号的概率分布可以写成行向量形式,即
由信道传递矩阵和输入信源符号概率向量,求得输出符号概率分布为
输入符号和输出符号的联合概率分布为
由冗余度计算公式得
3.18(1)由一步转移概率矩阵与二步转移概率矩阵的公式 得
(2)设平稳状态 ,马尔可夫信源性质知 ,即
求解得稳态后的概率分布
3.19设状态空间S= ,符号空间
且
一步转移概率矩阵
状态转移图
设平稳状态 ,由马尔可夫信源性质有
即
可得
马尔可夫链只与前一个符号有关,则有
3.20消息元的联合概率是
平均信息传输速率
信息论基础与编码(第五章)

5-1 有一信源,它有六种可能的输出,其概率分布如下表所示,表中给出了对应的六种编码12345C C C C C 、、、、和6C 。
(1) 求这些码中哪些是唯一可译码; (2) 求哪些是非延长码(即时码);(3) 对所有唯一可译码求出其平均码长。
解:(1(2)1,3,6是即时码。
5-2证明若存在一个码长为12,,,q l l l ⋅⋅⋅的唯一可译码,则一定存在具有相同码长的即时码。
证明:由定理可知若存在一个码长为Lq L L ,,2,1 的唯一可译码,则必定满足kraft 不等式∑=-qi l ir1≤1。
由定理44⋅可知若码长满足kraft 不等式,则一定存在这样码长的即时码。
所以若存在码长Lq L L ,,2,1 的唯一可译码,则一定存在具有相同码长P (y=0)的即时码。
5-3设信源126126()s s s S p p p P s ⋅⋅⋅⎡⎤⎡⎤=⎢⎥⎢⎥⋅⋅⋅⎣⎦⎣⎦,611i i p ==∑。
将此信源编码成为r 元唯一可译变长码(即码符号集12{,,,}r X x x x =⋅⋅⋅),其对应的码长为(126,,,l l l ⋅⋅⋅)=(1,1,2,3,2,3),求r 值的最小下限。
解:要将此信源编码成为 r 元唯一可译变长码,其码字对应的码长(l 1 ,l 2 ,l 3, l 4,l 5, l 6)=(1,1,2,3,2,3) 必须满足克拉夫特不等式,即132321161≤+++++=------=-∑r r r r r r ri li所以要满足122232≤++r r r ,其中 r 是大于或等于1的正整数。
可见,当r=1时,不能满足Kraft 不等式。
当r=2, 1824222>++,不能满足Kraft 。
当r=3,127262729232<=++,满足Kraft 。
所以,求得r 的最大值下限值等于3。
5-4设某城市有805门公务和60000门居民。
作为系统工程师,你需要为这些用户分配。
信息论与编码(傅祖云 讲义)第五章

平均错误率为:
PE''' 1 * P(b / a) (0.125 0.05) (0.075 0.075) (0.05 0.125) 0.5 3 Y , X a
第二节 错误概率与编码方法
一般信道传输时都会产生错误,而选择译码准则并不会 消除错误,那么如何减少错误概率呢?下边讨论通过编码 方法来降低错误概率。 例:对于如下二元对称信道
第二节 错误概率与编码方法 我们再讨论一个例子,取M=4,n=5,这4个码字按 2 如下规则选取:R
5
设输入序列为:
ai (ai1 ai 2
ai3
ai 4
ai5 )
满足方程: ai 3 ai1 ai 2
ai 4 ai1 a a a i1 i2 i5
若译码采取最大似然准则:
P(b j / a* ) P(a* ) P(b j ) P(b j / ai ) P(ai ) P(b j )
第一节 错误概率与译码规则 即: P(bj / a* )P(a* ) P(bj / ai )P(ai ) 当信源等概分布时,上式为:
P(bj / a* ) P(bj / ai )
和B: (b ) a F 1 1
F (b2 ) a3 F (b3 ) a2
译码规则的选择应该有一个依据,一个自然的依据就 是使平均错误概率最小 有了译码规则以后,收到 bj 的情况下,译码的条件正 确概率为: P( F (b ) / b ) P(a / b )
j j i j
第一节 错误概率与译码规则 而错误译码的概率为收到 bj 后,推测发出除了 ai 之 外其它符号的概率:
第一节 错误概率与译码规则
为了减少错误,提高通信的可靠性,就必到什么程 度。 前边已经讨论过,错误概率与信道的统计特性有关, 但并不是唯一相关的因素,译码方法的选择也会影响错误 率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.4
0.2 0.2 0 0.2 1
0.4 0.4 0
0.2 1
0.6 0 1.0 0.4 1
码字 1 01 000
0010 0011
码长 1 2 3 4 4
(b)
图5-2 例5-2 两种霍夫曼编码
方法(a)的方差比方法(b)的方差要小许多。 方法(a)的具体编码原则是,把合并后的概率总是放在 其它相同概率的信源符号之上(或之左),方法(b) 的编码原则是,把合并后的概率放在其它相同概率的信 源符号之下(或之右),从上面的分析可以看出,方法 (a)要优于方法(b)。
L
符号 概率
u1 0.4 u2 0.2 u3 0.2 u4 0.1 0 u5 0.1 1
0.4
0.2 0.2 0 0.2 1
0.4 0.4 0
0.2 1
0.6 0 1.0 0.4 1
码字 00 10 11 010 011
码长 2 2 2 3 3
(a)
图5-2 例5-2 两种霍夫曼编码
符号 概率
u1 0.4 u2 0.2 u3 0.2 u4 0.1 0 u5 0.1 1
10 2 110 3 111 3
图5-1例5-1霍夫曼编码
• 信源熵:
H (U ) p(ui )lbp(ui ) 1.75(比特 / 符号)
• 平均码长: i
L p(ui )li 1.75(码符号 / 信源符号)
i
• 编码效率:
Hm (U ) 100%
L
• [例5-2] 离散无记忆信源
可见,霍夫曼码得到的码并非是唯一的。因为对缩 减信源的两个概率最小的符号,用0和1码时可以任意的, 所以可得到不同的码,但它们只是码字具体结构不同, 而其码长不变,平均码长也不变,所以没有本质区别。 另外,若当缩减信源中缩减合并后的符号的概率与其它 信源符号概率相同时,从编码方法上来说,对等概率的 符号那个放在上面,那个放在下面是没有区别的,但得 到的码是不同的。对这两种不同的码,它们的码长各不 同,然而平均码长是相同的。在编码中,对等概率消息, 若将新合并的消息排列到上支路,可以证明它将缩短码 长的方差,即编出的码更接近等长码;同时可使合并的 元素重复编码次数减少,使短码得到充分利用。
U P(U
)
u1 0.4
u2 0.2
u3 0.2
u4 0.1
u5 0.1
• 给出两种霍夫曼编码如图5-2所示
• 信源熵:
H (U ) p(ui )lbp(ui ) 2.12(比特 / 符号)
• 平均码长
i
5
L p(ui )li 2.2(码符号 / 信源符号) i 1
• 编码效率 Hm (U ) 96.3%
0.40 0 0.30 1 1.00 0.30 2
码字 0 1 20 21 22
码长 1 1 2 2 2
图5-4 三元霍夫曼编码
符号
u1 u2 u3 u4 u5 u6 u7
概率
0.40
0.30
0.20 0.05 0 0.05 1 0.00 2 0.00 3
0.40 0 0.30 1 1.00
0.20 2 0.10 3
图5-5 四元霍夫曼编码
码字 0 1 2 30 31 32 33
值为两个信源符号值的和,从而得到只包含n-1个符号的新信 源,称为U信源的缩减信源U1。 • (3)把缩减信源U1的符号仍按概率大小以递减次序排列,然后 将其中两个概率最小的符号合并成一个符号,这样又形成了n- 2个符号的缩减信源U2。 • (4)依次继续下去,直至信源最后只剩下1个符号为止。 • (5)将每次合并的两个信源符号分别用0和1码符号表示。 • (6)从最后一级缩减信源开始,向前返回,就得出各信源符号 所对应的码符号序列,即得各信源符号对应的码字。
[例5-1]离散无记忆信源
U P(U )
u1 0.5
u2 0.25
u3 0.125
u4 0.125
解:对应霍夫曼编码如图5-1所示
符号 概率
u1 0.500
u2 0.250
u3
0
0.125
u4 0.125 1
0.500
0.250 0
1
0.250
0.500 0 0.500 1
码字 码长 1.000 0 1
第5章 无失真信源编码方法
• 5.1 霍夫曼码 • 5.2 香农编码 • 5.3 费诺编码 • 5.4 算术编码编码原理 • 5.5 算术编码方法
第5章 信源压缩编码方法
• 5.1无失真信源编码方法 • 5.1.1 霍夫曼码 • 1.二元霍夫曼码 • 二元霍夫曼码编码步骤如下: • (1)将n元信源U的各个符号按概率分布以递减次序排列起来。 • (2)将两个概率最小的信源符号合并成一个新符号,新符号的
• 2.m元Βιβλιοθήκη 夫曼码• 为了使短码得到充分利用,使平均码长最短,必须使最后一 步的缩减信源有m个信源符号。因此对于m元编码,信源U符号 个数n必须满足:
• n=(m-1)Q+m
(5-1)
• 式中:n—信源符号个数;m—码元数;Q—缩减次数。
• 对于m元码,n为任意正整数时不一定能找到一个Q满足式 (5-1),此时,可以人为地增加一些概率为零的符号,以满足 式(5-1)。
个数n必须满足:
• n=(m-1)Q+m
• 其三元霍夫曼编码此式成立,四元霍夫曼编码需加2个概率为零
• 的符号。
• 根据m元霍夫曼编码步骤,其三元霍夫曼编码如图5-4所示,
• 四元霍夫曼编码如图(5-5)所示。
符号
u1 u2 u3 u4 u5
概率
0.40
0.30 0.20 0 0.05 1 0.05 2
• m元霍夫曼编码步骤:
• (1)验证所给n是否满足式(5-1),若不满足该式,可以人为 地增加一些概率为零的符号,以使最后一步有m个信源符号;
• (2)取概率最小的m个符号合并成一个新结点,并分别用0, 1,...,(m-1)给各分支赋值,把这些符号的概率相加作 为该新结点的概率;
• (3)将新结点和剩下结点重新排队,重复(2),如此下去直至 树根。
• (4)取树根到叶子(信源符号对应结点)的各树枝上的赋值,得 到各符号码字
• [例5-3]已知信源
U P(U )
u1 0.4
u2 0.3
u3 0.2
u4 0.05
u5 0.05
• 求其三元霍夫曼编码及四元霍夫曼编码。
• 解:
•
为了使短码得到充分利用,使平均码长最短,必须使最后一
步的缩减信源有m个信源符号。因此对于m元编码,信源U符号
