电路——邱关源第7章 一阶电路和二阶电路的时域分析.
电路课件 电路07 一阶电路和二阶电路的时域分析

2019年3月29日星期五
经典法
5
• 线性电容在任意时刻t,其电荷、电压与电流关系:
q(t ) q(t0 ) iC ( )d
t0 t
线性电容换路瞬间情况
uC (t ) uC (t0 )
• q、uc和ic分别为电容电荷、电压和电流。令t0=0-, t=0+得: 0 0
第7章一阶电路和二阶电路的时域分析
2019年3月29日星期五
3
• 动态电路:含动态元件电容和电感电路。 • 动态电路方程:以电流和电压为变量的微分方程或微 分-积分方程。 • 一阶电路:电路仅一个动态元件,可把动态元件以外 电阻电路用戴维宁或诺顿定理置换,建立一阶常微分 方程。 • 含2或n个动态元件,方程为2或n阶微分方程。 • 动态电路一个特征是当电路结构或元件参数发生变化 时(如电路中电源或无源元件断开或接入,信号突然 注入等),可能使电路改变原来工作状态,转变到另 一工作状态,需经历一个过程,工程上称过渡过程。 • 电路结构或参数变化统称“换路”,t=0时刻进行。 • 换路前最终时刻记为t=0-,换路后最初时刻记为t=0+, 换路经历时间为0-到0+。
第7章一阶电路和二阶电路的时域分析 7-2一阶电路的零输入响应
2019年3月29日星期五
RC电路零输入响应-1
12
• 电路中电流 • 电阻上电压
RC电路零输入响应-2
1
t t duC U 0 RC t d 1 RC RC i C C (U 0e ) C ( )U 0e e dt dt 1 RC R
R
13
RC电路零输入响应-3
电路第五版 罗先觉 邱关源 课件(第七章)课件

2
零输入响应:仅由电路初始储能引起的响应。
(输入激励为零) 零状态响应:仅由输入激励引起的响应。 (初始储能为零)
1. RC电路的放电过程:
如右图,已知uc(0-)=U0,S 于t=0时刻闭合,分析t≧0 时uc(t) 、 i(t)的变化规律。 +
i(t)
S uc(t) R
+ uR(t) -
(a)
i ()=12/4=3A
例3:如图(a)零状态电路,S于t=0时刻闭合,作0+图 并求ic(0+)和uL(0+)。 S Us ic
+ uc -
R2 L
S
↓iL
ic(0+) C
Us R1
R2 L
C R1
+ uL -
+ uL(0+) -
(a) 解: ① t<0时,零状态 →uc(0-)=0 iL(0-)=0 ② 由换路定理有:uc(0+)= uc(0-) =0 iL(0+)= iL(0-) =0 作0+图: 零状态电容→零值电压源 →短路线 零状态电感→零值电流源 →开路 ③ 由0+图有:ic(0+)=Us/R1 uL(0+)=uR(0+)=Us
uc(0+)= uc(0-) =8V
② 由换路定理有: iL(0+)= iL(0-) =2A 作0+等效图(图b)
S i 12V + R3 Us
2 R1 + uc (a) + R2 5 ic + iL 12V uL 4 i(0+) Us
R1 +
5
ic(0+) 8V
第7章_一阶电路和二阶电路的时域分析

②测量方法: a.对任意时刻而言,
t 0 t 0
uC (t0 ) = U 0 e
b.次切距长:
AB BC = tan
= U0e
e 1 = 0.368 uC (t0 )
t 0
U0
uC
uC ( t 0 )
A
uC ( t 0 ) U 0e = = = t 0 1 duC U 0e dt t =t0
uC (t ) 4e 0.5t = = e 0.5t A ③求i(t):i (t ) = 4 4
(t 0)
19
习题: 7-2、7-4、7-5。
20
三、RL电路的零输入响应:
求i(t),uR(t), uL(t),(t≧0) 1、物理过程:
U0 i (0 ) = i (0 ) = R0
R
t=0 + iL uL L -
解: 根据换路定则:
i L 不能突变
i L (0 ) = i L (0 ) = 0 A
+ *** t =0K 时的等效电路: R
换路后的电压方程 :
+ U -
t=0
+ + iL uL (0+) uL L L - - iL(0+)
U = iL (0+ ) R + u L (0+ )
uC (0+ ) = uC (0- ) = U 0
uC (0+ ) → 0
U0 i (0 + ) = → 0 为放电过程。 R
13
2、数学分析: ①列微分方程:由KVL, +u U0 _ C
C
S
t=0
(第14次课)第7章一阶电路和二阶电路的时域分析解析

再看 RLC串联电路
应用 KVL和元件的 VCR得 (详见§7-5 ) :
d2uC duC + uC = uS LC 2 + RC dt dt 含二个动态元件的 线性电路,其电路方程 为二阶线性常系数微分 方程,称二阶电路。
电路中有多个动态元 件,描述电路的方程是高 阶微分方程。
2019年1月6日星期日
2019年1月6日星期日 2
难点
1. 电路初始条件的概念,除 uC 和 iL 之外各电压、 电流初始值的确定; 2. 激励源为交流电源; 3. 一阶电路和二阶电路的区分,二阶电路的过阻 尼、欠阻尼及临界阻尼放电过程分析方法和基 本物理概念。
与其它章节的联系
本章讨论的仍是线性电路,因此前面讨论的 线性电路的分析方法和定理全部可以用于本章的 分析中。第 9 章讨论的线性电路的正弦稳态响应 就是动态电路在正弦激励下的稳态分量的求解。
US uL = 0 , i = R
2019年1月6日星期日
US R US
i 新的稳 定状态
uL
t1 0 前一个稳 有一个 定状态 过渡期
t
7
换路的概念 电路结构、状态发生变化
1W + 10V C 1W 1W S 1A + uC + u -
支路接入或断开 电路参数改变
S1(t=0) 2W + 10V 3W i L
t
明确:
t 0 t> 0
①初始条件为 t=0+时, u(t)、
i(t)及其各阶导数的值。
2019年1月6日星期日
②在动态电路分析中, 初始条件是得到确定 解答的必需条件。
13
(2)电容的初始条件 q(t) = i() d =
电路第七章一阶电路和二阶电路的时域分析.

当动态电路状态发生改变时(换路)需要经历 一个变化过程才能达到新的稳定状态。这个变化过 程称为电路的过渡过程。 过渡过程产生的原因: 电路内部含有储能元件L,C。电路在换路时能量发生变 化,而能量的储存和释放都需要一定的时间来完成。
0
ic(t)
c
2 3
0.0184u t (s) 0 4
t RC
uc(0)= u0 2 3 4
t RC
RR u
t
(s)
du C t d u0 e C iC t C dt dt
u0 e R
2.时间常数
uc不能跃变, 结论: ic可以跃变。
解得 :
R 0 L
A I0
I0
iL(t)
iL t I 0e
R t L
t 0
0
R R t t diL t d L L u L t L L I e RI e 0 0 dt dt
2 3 4
t
(s)
t0
t 0 =RC
t0
f(0)
f(t) t
iL t iL 0e
=LG
0
4
(s)
C.零输入响应都是按指数规律衰减的,衰减的快慢由 决定,越小, uc(t),iL(t)衰减的越快。
D.时间常数的求法:
在换路后(即 t 0 )的电路中求。 R是从动态元件两端看进去的戴维宁等效电阻。
(3) 只有当电容器两端电压变化时,才有电流。
六.电感的伏安关系
1 . 电感中的电压 现象: a .开关合上: us + _ b .开关打开: us +
第7章一阶电路和二阶电路的时域分析

①
S
②
2 3
6
解 iL (0 ) iL (0 )
24 6 2A 4 2 3 // 6 3 6
24V 4
i1
4
iL
换路后电路为零输入响应: L 6 1s Req 6
uL 6H
2Ω
Req 3 (2 4) // 6 6
iL (0+) = iL (0-)=3A
(3) 由0+等效电路求 iC(0+) , uL(0+)
uL(0+)
3 i2 (0 ) 3 1 A 3 6
uL (0 ) 6i2 (0 ) 6V
返回本节
0+等效电路
上 页
下 页
5.电路初始值的确定 例2 求 uC(0+) 、iL(0+) 、
返回本节
上 页
下 页
5.电路初始值的确定 例1 求 i2(0+) 和 uL(0+) 。
iL S(t=0) 3 1 + i 2 2 + u 6 9V 1H L – – 3 i2(0+) 6 3A + –
(1) 由0-电路求 iL(0-)
+ 9V – 3 iL
iL (0 ) 3 A (2) 由换路定律
电路如下图
R0
S(t=0)
1 2
i
U0 L
R
uL R
i
L
uL
(a)
(b)
换路前电路处于稳态,电感电流I0=U0/R0 = i(0-) , 电感中储存一定的磁场能量,在 t=0 时开关由1→2, 换路后的电路如图(b)所示。 (b)
第7章一阶电路和二阶电路的时域分析

2019年4月25日星期四
4
§7-1 动态电路的方程及其初始条件
引言 自然界事物的运动,在一定的条件下有一定的稳 定状态。当条件发生变化时,就要过渡到新的稳定状 态。从一种稳定状态转到另一种新稳定状态时,往往 不能跃变,而是需要一定时间,或者说需要一个过程, 在工程上称过渡过程。
S (t=0) i R
+
uC
=
US
uC
=
US
+
A
e
-
1 RC
t
(t≥0+) i R
S +
+ uR - +
US
-UC(S0+) = uC(0-) = 0
所以零状态响应为
US
uC , i
稳态分量
uC''
uC =
US (1-e-
t
),
=
RC
US
R
uC=uC' + uC''
i
t
i=C
duc dt
阻尼及临界阻尼的概念及分析; (8)二阶电路的阶跃响应。
2019年4月25日星期四
3
难点
(1)应用基尔霍夫定律和电感、电容的元件特性建 立动态电路方程;
(2)电路初始条件的概念和确定方法; (3)二阶电路的过阻尼、欠阻尼及临界阻尼放电过
程分析方法和基本物理概念。
与其它章节的联系
本章讨论的仍是线性电路,因此前面讨论的线 性电路的分析方法和定理全部可以用于本章的 分析中。第9章讨论的线性电路的正弦稳态响应 就是动态电路在正弦激励下的稳态分量的求解。
=
US R
第7章 一阶电路和二阶电路的时域分析(2010-2011第一学期 邱关源)

uC ( ) U 0e1 0.368U 0
即经过一个时间常数τ 后,衰减了63.2%,为原值 的36. 8%。 理论上,t = ∞时,uC才能衰减到零,但实际上, 当t = 5τ 时,所剩电压只有初始值的0.674%,可以认 为放电已完毕。因此,工程上常取t = (3-5)τ 作为放电 完毕所需时间。τ 越大,衰减越慢,反之则越快。
uR uC U 0 e
t
可以看出,电压uC、uR及电流i都是按照同样的 指数规律衰减的。它们衰减的快慢取决于指数中τ 的大小。
第七章一阶电路和二阶电路的时域分析
§7-2 一阶电路的零输入响应
τ 的大小反映了一阶电路过渡过程的进展速度, 它是反映过渡过程特性的一个重要的量。可以计算得 t = 0时, t =τ 时,
第七章一阶电路和二阶电路的时域分析
§7-2 一阶电路的零输入响应
第七章一阶电路和二阶电路的时域分析
§7-2 一阶电路的零输入响应
经过全部放电过程,电阻上所吸收的能量为
WR
0
Ri 2 (t )dt
0
U 0 t 2 R ( e ) dt R
0
2 U0 R
0
e
2t RC
第七章 一阶电路和二阶电路的时域分析
河北大学数学与计算机学院
第七章一阶电路和二阶电路的时域分析
§7-1 动态电路的方程及其初始条件
电容和电感的VCR是通过导数(积分)表达 的。当电路中含电容和电感时,电路方程是以电流 和电压为变量的微分方程或微分―积分方程。 对于仅含一个电容或电感的电路,当电路的无 源元件都是线性和时不变时,电路方程将是一阶线 性常微分方程,称为一阶动态电路。 电路结构或参数变化引起的电路变化统称为 “换路”。换路可能使电路改变原来的工作状态, 转变到另一个工作状态。
7第七章一阶电路和二阶电路的时域分析

• 定义: τ=RC (其中R为等效电阻) uC U0et ★ t=τ时,uC=0.368U0
• τ仅取决于电路的结构和元件的参数,单位“秒s”。
•τ对响应的影响:
τ 越大,放电过程越长。通常认为经过3τ—5τ后过
渡过程结束。
•τ的图解 (次切距法)
t0
BC AB uC(t0)
tan
duC dt
uR uC
i CduC US et(t≥0) 其中τ=RC
dt R
2020/8/10
对 uCU SU Set U S(1et) 的说明
• 特解 uC US称t 为稳态分量或强制分量;
• 通解 uC USe 称为瞬态分量或自由分量。
2.参数曲线
US
uC '
3.能量转换
U―S R
uC i
WR=WC=½CUS2
A Im
i" Imet
iIm sin t(u)Im e t
u = -/2时波形为
iImsi nt(/2)Im et
可见,RL串联电路
i
与正弦电压接通后,
Im
i
在初始值一定得条
i 件下,电路的过渡
0
T/2
-Im
t 过程与开关动作的 时刻有关。
i
最大电流出现在 t = T/2时刻。 imax2Im
解:
iL(0)
US R
200A
K
R
+
iL
V uV
Us iV
L
iL(0)iL(0)200A
u V ( 0 ) R V i V ( 0 ) 2 0 0 5 k 1 0 6 V
2020/8/10
§7-2 一阶电路的零输入响应 一、零输入响应
一阶电路和二阶电路的时域分析

一阶电路和二阶电路的时域分析一、一阶电路的时域分析:一阶电路指的是由一个电感或电容与线性电阻串联或并联而成的电路。
对于串联的一阶电路,其特征方程为:L di(t)/dt + Ri(t) = V(t) ---------- (1)其中,L是电感的感值,R是电阻的电阻值,i(t)是电路中的电流,V(t)是电路中的输入电压。
通过对上述方程进行求解可以得到电路中电流与时间的关系。
对于并联的一阶电路,其特征方程为:1/R C dq(t)/dt + q(t) = V(t) ---------- (2)其中,C是电容的电容值,q(t)是电路中电荷的变化,V(t)是电路中的输入电压。
同样,通过对上述方程进行求解可以得到电路中电荷与时间的关系。
一阶电路的响应可以分为自由响应和强迫响应两部分。
自由响应指的是由于电路中初始条件的存在,电流或电荷在没有外部输入电压的情况下的变化。
强迫响应指的是由于外部输入电压作用而产生的电流或电荷的变化。
对于一个初始处于稳定状态的电路,在有外部输入电压作用时,电路中电流或电荷会从初始值开始发生变化,最终趋于一个新的稳定状态。
这一过程可以由电流或电荷的指数递减或递增的形式表示。
在分析一阶电路的时域特性时,可以利用巴塞尔函数法或拉普拉斯变换法。
巴塞尔函数法主要是通过巴塞尔函数的表达式计算电压或电流的变化情况;拉普拉斯变换法则通过将时域的微分方程转化为复频域的代数方程,然后求解代数方程,最后再对求得的结果进行逆变换获得电流或电压的表达式。
二、二阶电路的时域分析:二阶电路是指由两个电感或电容与线性电阻串联或并联而成的电路。
对于串联的二阶电路,其特征方程为:L₁L₂ d²i(t)/dt² + (L₁R₁+L₂R₂+L₁R₂+L₂R₁) di(t)/dt + R₁R₂i(t) = V(t) ---------- (3)其中,L₁和L₂分别是两个电感的感值,R₁和R₂分别是两个电阻的电阻值,i(t)是电路中的电流,V(t)是电路中的输入电压。
第7章 一阶电路和二阶电路的时域分析
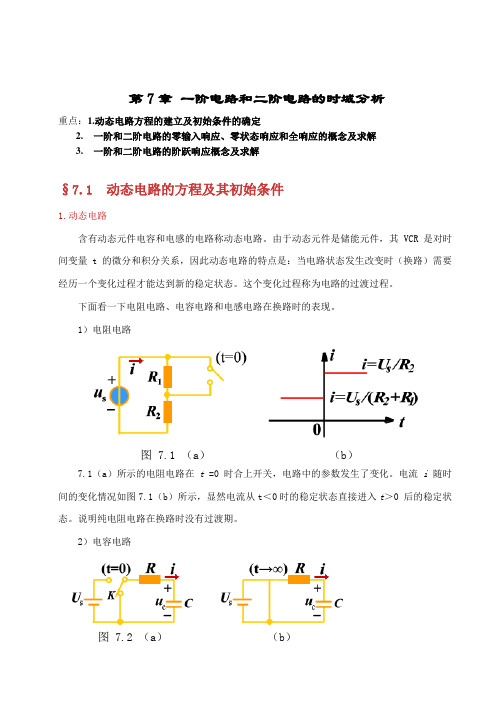
第7章一阶电路和二阶电路的时域分析重点:1.动态电路方程的建立及初始条件的确定2.一阶和二阶电路的零输入响应、零状态响应和全响应的概念及求解3.一阶和二阶电路的阶跃响应概念及求解§7.1 动态电路的方程及其初始条件1.动态电路含有动态元件电容和电感的电路称动态电路。
由于动态元件是储能元件,其 VCR 是对时间变量 t 的微分和积分关系,因此动态电路的特点是:当电路状态发生改变时(换路)需要经历一个变化过程才能达到新的稳定状态。
这个变化过程称为电路的过渡过程。
下面看一下电阻电路、电容电路和电感电路在换路时的表现。
1)电阻电路图 7.1 (a)(b)7.1(a)所示的电阻电路在t =0 时合上开关,电路中的参数发生了变化。
电流i 随时间的变化情况如图7.1(b)所示,显然电流从t<0时的稳定状态直接进入t>0 后的稳定状态。
说明纯电阻电路在换路时没有过渡期。
2)电容电路图 7.2 (a)(b)图 7.2(a)所示的电容和电阻组成的电路在开关未动作前,电路处于稳定状态,电流i 和电容电压满足:i=0,u C=0。
t=0 时合上开关,电容充电,接通电源后很长时间,电容充电完毕,电路达到新的稳定状态,电流i 和电容电压满图 7.2 (c)足:i=0,u C=U S。
电流i 和电容电压u C 随时间的变化情况如图7.2(c)所示,显然从t<0 时的稳定状态不是直接进入t>0后新的稳定状态。
说明含电容的电路在换路时需要一个过渡期。
3)电感电路图 7.3 (a)(b)图 7.3(a)所示的电感和电阻组成的电路在开关未动作前,电路处于稳定状态,电流i和电感电压满足:i=0,u L=0。
t=0 时合上开关。
接通电源很长时间后,电路达到新的稳定状态,电流i 和电感电压满足:i=0,u L=U S/R 。
图 7.3 (c)电流i 和电感电压u L 随时间的变化情况如图7.3(c)所示,显然从t<0时的稳定状态不是直接进入t>0后新的稳定状态。
电路 邱关源 ppt 第七章

t 0
返 回
上 页
下 页
iL (t ) I 0e
表明
I0
t L/ R
t 0
t diL uL (t ) L RI0e L / R dt
①电压、电流是随时间按同一指数规律衰减的函数。
iL
连续 函数 t
O
uL t
O
-RI0
返 回
跃变
上 页 下 页
②响应与初始状态成线性关系,其衰减快慢与L/R有关。 令
(1)换路后的电路; (2)电容(电感)用电压源(电流源)替代。 (取0+时刻值,方向与原假定的电容电压、电 感电流方向相同)。 4.由0+电路求所需各变量的0+值。
返 回 上 页 下 页
7-2 一阶电路的零输入响应
零输入响应 换路后外加激励为零,仅有 动态元件初始储能产生的电 压和电流。 已知 uC (0-)=U0 S(t=0) i
U0 U0 e -1
U0 e -2 U0 e -3
U0 e -5
U0 0.368U0 0.135U0 0.05U0 0.007U0
注意
① :电容电压衰减到原来电压36.8%所需的时间。 工程上认为, 经过 3 5 , 过渡过程结束。
返 回
上 页
下 页
uC U 0 e
②时间常数 的几何意义: t1时刻曲线的斜率等于
L大 W=LiL2/2 初始能量大 R小 p=Ri2 放电过程消耗能量小
③能量关系
电感不断释放能量被电阻吸收, 直到全部消耗完毕。
设 iL(0+)=I0
电感放出能量: 电阻吸收(消耗)能量:
1 2 LI 0 2
WR i Rdt 0 ( I 0e
电路原理-第七章__邱关源

返 回
上 页
下 页
换路
电路结构、状态发生变化 支路接入或断开 电路参数变化
过渡过程产生的原因 电路内部含有储能元件 L、C,电路在换路时 能量发生变化,而能量的储存和释放都需要一定的 时间来完成。
Δw p Δt
Δt 0
p
返 回 上 页 下 页
2. 动态电路的方程
例 RC电路
应用KVL和电容的VCR得:
1.RC电路的零输入响应
S(t=0)
C
+ uC –
uR uC 0
L iL 10 S C + - uC 10 10 + 20V iL + 1A 10 10 uL - + 10V - uC - 10 iC 1010 + 20V 10 + -20V -
ik
解 ①确定0-值
20 iL (0 ) iL (0 ) 1A 20
uC (0 ) uC (0 ) 10V
Ri uc 0 (t 0)
R
(t=0) + C uC i -
duc RC uc 0 dt 特征根方程: RCp 1 0
通解:
p 1 RC
t RC
uc (t ) ke ke
pt
代入初始条件得: k
Uo
uc (t ) U oe
t RC
在动态电路分析中,初始条件是得 明确 到确定解答的必需条件。
2
二阶电路中有二个动态元件,描述 电路的方程是二阶线性微分方程。
dx dx a2 2 a1 a0 x e(t ) t 0 dt dt
返 回 上 页 下 页
高阶电路
电路 第五版 课件 邱关源 罗先觉第七章-5

sin( t ) (t) t 0 )
t0
0 ③延迟一个函数 f ( t)
t
sin( t t 0 ) (t t 0 )
t
返 回 上 页 下 页
0
t0
用单位阶跃函数表示复杂的信号 f( t) f( t) 1 例1 1 0 0
(t)
t - (t-t0)
f (t ) (t ) (t t 0 )
返 回 上 页 下 页
d uC d 2 iL iC C LC dt dt2 2 d i d i L L 代入已知参数并整理得: 5 4i L 4 (t ) 2 dt dt 这是一个关于的二阶线性非齐次方程,其解为
u R L d iL iR R R dt
i L i i
返 回 上 页 下 页
由齐次性和叠加性得实际响应为:
1 2t 1 2 ( t 0 .5 ) iC 5[ e (t ) e (t 0.5)] 5 5
e (t ) e
2 t
2 ( t 0 .5 )
(t 0 .5 ) mA
+ 5k ic 100F
第七章 一阶和二阶电路的 时域分析(V)
主讲:鲁俊超
作业:
7.7 一阶电路和二阶电路的阶跃响应
1. 单位阶跃函数
定义0 (t )Fra bibliotek 1(t 0 ) (t 0 )
( t)
1
0
t
单位阶跃函数的延迟
(t-t0)
1 t0 t
0
0 (t t 0 ) (t t 0 ) 1 (t t 0 )
p1 t p2t i A e A e 特解 i 1 通解 1 2 2 特征方程 p 5p 4 0
电路原理课件 第7章 一阶电路 和二阶电路的时域分析

iL(0+)
uL -
uR (0
)
iL (0
)R
RU m
2L
uL (0 )
3Um RUm
2 2L
§7.2 一阶电路的零输入响应
零输入响应----
uc (0+)≠0 iL (0+) ≠ 0
动态电路在非零初始状态下,由电 路中的无外施激励引起的响应。
电路换路后 uS =0 和iS =0
一、RC电路的零输入响应
0.5A
uL (0 ) uR1(0 ) 10 uC (0 ) 0
iC (0 ) iL (0 ) iR2 (0 ) 0.25 A
例2已知:t 0 时,
原 电 路 已 稳 定 ,t 0
时,打开开关S。
求:t 0 时,i1(0 ), i(0 )
解:1、求 uC(0)
t 0 时的电路。
uC(0) 14i(0) 10i1(0) 4i1(0)
ii11
(0 (0
) )
i(0 ) i(0 )
4 2A
uC(0) 28V
2、作 t 0时的电路。
14ii11((00))
i(0 ) 7 i(0
4 ) 28
8
4
i1(0 )
A, 3
i(0 )
A 3
例3 + uR -
已知:
+
R K
+
解上式可得:
i(0 ) 6 A
根据等效电阻初始值得:
t
i(t) i(0 )e
6e4t
§7.3一阶电路的零状态响应
(zero state response)
零状态响应----
uc (0+)=0 iL (0+)=0
电路邱关源第三版第七章

3
动态电路的方程及其初始条件( §7-1 动态电路的方程及其初始条件(****) ) §6-1 动态电路方程及其初始条件
2
二、研究动态电路的目的: 研究动态电路的目的:
1、应用: 、应用:
电子线路中的耦合电路、信号发生电路、 电子线路中的耦合电路、信号发生电路、整形电路 等等,自动控制装置中的补偿网络, 等等,自动控制装置中的补偿网络,通信系统中的均衡 网络等均是动态电路的应用。 网络等均是动态电路的应用。
2、防范: 、防范:
R2 ⋅ U 0 R1 + R2
i L ( 0 + ) = i L (0 − ) =
R1
U0 R1 + R2
uC ( 0 + ) → U S i L ( 0 + ) → I S
+ _uR 2 (0+ )
U0 R1 + R 2
+ uR2 R2 iC t=0 _ + + + L uL L(0+ C _ U0 uL (0+) iiL ) _ S
1 u 对线性电容而言, 对线性电容而言, C (t ) = uC (t0 ) + C
∫
t
t0
i (ξ )dξ
令 t = 0− , t = 0 +
0
1 0+ 则 uC (t ) = uC (0 + ) = uC (0 − ) + ∫0− i (ξ )dξ C Qi(ξ ) 一般为有限值。 一般为有限值。
第七章 一阶电路和二阶电路的时域分析

p1t p2t
uC A1e A2e
经常写为:
e
( t )
( A1e
jt
A2e
jt
)
uC Ae
t
sin( t )
0 t sin( t ) uuC AeU 0e t sin( t ) c
uC (0 ) U 0 A sin U 0 由初始条件 du (0 ) C 0 A( ) sin A cos 0 dt
代入初始条件
i L (0 ) 0
t
A I s
iL i i I S (1 e )
' L " L
7-4 一阶电路的全响应
当一个非零初始状态的一阶电路受到激励时, 电路的响应称为全响应。 初始条件
u c ( 0 ) u c (0 ) U 0
当开关S闭合后,由KVL有
初始条件--电路中的变量在换路后t=0+时 刻的值。
独立初始条件--换路后的初始值由元件的 性质决定。 独立初始条件有:电容端电压uc(t)、电容电 荷qc(t)、电感电流iL(t)、电感磁链L(t)
1 t uc (t ) uc (t0 ) ic ( )d C t0
1 0 uc (0 ) uc (0 ) ic ( )d C 0
U0 A sin
, arctg
ω0 δ
ω
sin 0
0 A U0
ω,ω0,δ的
关系
0 t uC U 0e sin( t )
0 uC 是振幅以 U 0为包线依指数衰减的正 弦函数。
[物理]电路 第7章 一阶电路和二阶电路的时域分析
![[物理]电路 第7章 一阶电路和二阶电路的时域分析](https://img.taocdn.com/s3/m/41ba40d47c1cfad6195fa770.png)
i
R
uC uR U s
duC uC RC Us dt
一阶线性非齐次微分方程
Us
C
uc
“一阶非齐次线性方程的通解等于其对应的齐 次方程的通解与非齐次方程的一个特解之和。”
摘自《高等数学》下册第343页
第 1 章
U0
1
2
L
iL
uL
R
初始条件为: i(0 ) i(0 ) I 0 通解为:
i Ae pt
R L
L
iL
uL
R
特征方程为: Lp R 0 特征根为:
p
解得:
i I 0e
R t L
R t di uL L RI 0 e L dt
电压电流都以同样的指数规律衰减,衰减快慢取决于 衰减的时间常数 L
静电场
uc uc uc Us uc
uc uc
非齐次方程的特解 对应齐次方程的通解
U s e uc
1 t RC 1 t RC
1 t U s RC i e R
因此 uc U s (1 e
)
稳态分量和瞬态分量
Us uc
强制分量、与外激励有关;
R1
1
例7-1:
U0
R2
L
C
uc ic
iL
第 1 章
静电场
换路前后瞬间电容电压与电感电流不能跃变!
第 1 章
静电场
7.2 一阶电路的零输入响应
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例4 求k闭合瞬间各支路电流和电感电压
2 + 48V S L 2 + uL iL 3 C + i uL iC 3 3 + 2 + 48V - iL 12A 2 + + 48V uC 24V 2 -- 由0+电路得:
解 由0-电路得:
iL (0 ) iL (0 )
48 / 4 12 A
uC (0 ) uC (0 ) 2 12 24V
iC (0 ) (48 24) / 3 8A
i(0 ) 12 8 20A
uL (0 ) 48 2 12 24V
返 回 上 页 下 页
例5 求k闭合瞬间流过它的电流值
L iL 10 S C + - uC 10 10 + 20V iL + 1A 10 10 uL - + 10V - uC - 10 iC 1010 + 20V 10 + -20V -
ik
解 ①确定0-值
20 iL (0 ) iL (0 ) 1A 20
uC (0 ) uC (0 ) 10V
结论
有源 电阻 电路
一个动 态元件
一阶 电路
含有一个动态元件电容或电感的线性电 路,其电路方程为一阶线性常微分方程,称 一阶电路。
返 回
上 页
下 页
RLC电路
应用KVL和元件的VCR得:
Ri uL uC uS (t )
2
(t >0) R i + + uL Us C – -
di d uC duC uL L LC 2 iC dt dt dt 2 d uC duC LC 2 RC uC uS (t ) dt dt
返 回 上 页 下 页
②电容的初始条件
1 t uC (0 ) 0 i ( )d C 0 1 0 t = 0+ 时刻 u (0 ) u (0 ) C C 0 i( )d C
uc 1 t - C uC (t ) i ( )d C 1 0 1 t i ( )d 0 i ( )d C C
微分方程的特解
dx 直流时 a1 a0 x U S dt dx t 0 a0 x U S dt
返 回 上 页 下 页
3.电路的初始条件
① t = 0+与t = 0-的概念 0- 换路前一瞬间 认为换路在t=0时刻进行
f (0 ) f (0 )
f(t)
f (0 ) lim f (t ) t 0
t 0
0+ 换路后一瞬间
f (0 ) lim f (t ) t 0
t 0
f (0 ) f (0 )
0- 0 0+ t
注意 初始条件为 t = 0+时u ,i 及其各阶导数
的值。
返 回 上 页 下 页
例 图示为电容放电电路,电容原先带有电压Uo,求
开关闭合后电容电压随时间的变化。 解
uC
+
二阶电路
含有二个动态元件的线性电路,其电路方程 为二阶线性常微分方程,称二阶电路。
返 回 上 页 下 页
结论 ①描述动态电路的电路方程为微分方程; ②动态电路方程的阶数通常等于电路中动 态元件的个数。 一阶电路中只有一个动态元件,描述 一阶电路 电路的方程是一阶线性微分方程。
二阶电路
dx a1 a0 x e(t ) t 0 dt
-
解 ①先求 iL (0 ) 1 4 + 10V 电感 iL 短路 -
+ uL -
10 iL (0 ) 2A 1 4
小结 求初始值的步骤:
1.由换路前电路(稳定状态)求uC(0-)和iL(0-); 2.由换路定律得 uC(0+) 和 iL(0+)。
3.画0+等效电路。
a. 换路后的电路 b. 电容(电感)用电压源(电流源)替代。 (取0+时刻值,方向与原假定的电容电压、电 感电流方向相同)。 4.由0+电路求所需各变量的0+值。
?
前一个稳定状态
过渡状态
返 回
上 页
下 页
电感电路 + Us (t = 0) R i + k uL –
L
+ Us -
(t →) R i + uL –
i k未动作前,电路处于稳定状态: i = 0 , uL = 0 US/R 新的稳定状态 US k接通电源后很长时间,电路达到新的稳定 状态,电感视为短路: uL= 0, i=Us /R uL 有一过渡期 t1 t 0
Ri uc 0 (t 0)
R
(t=0) + C uC i -
duc RC uc 0 dt 特征根方程: RCp 1 0
通解:
p 1 RC
t RC
uc (t ) ke ke
pt
代入初始条件得: k
Uo
uc (t ) U oe
t RC
明确
在动态电路分析中,初始条件是得 到确定解答的必需条件。
返 回
上 页
下 页
例
电阻电路
(t = 0) R1 R2 0 i
+ i us -
i U S / R2
t 过渡期为零
i U S ( R1 R2 )
返 回
上 页
下 页
电容电路
+ Us -
(t = 0) R i + k uC –
+ C Us -
(t →) R i + uC –
C
uc k未动作前,电路处于稳定状态: i = 0 , uC = 0 US 新的稳定状态 US k接通电源后很长时间,电容充电完毕,电路 R 达到新的稳定状态: i i = 0 , u有一过渡期 C= U s t1 t 0
1
+ 10V
4
S iL L + uL -
②应用换路定律: iL(0+)= iL(0-) =2A ③由0+等效电路求 uL(0+) 1 + 10V 4
电 感 用 2A 电 流 uL (0 ) 2 4 8V 源 注意 uL (0 ) uL (0 ) 替 代
返 回 上 页 下 页
注意 ①电容电流和电感电压为有限值是换路定
律成立的条件。 ②换路定律反映了能量不能跃变。
返 回 上 页 下 页
⑤电路初始值的确定
(1) 由0-电路求 uC(0-)
+ 10k 10V 40k + uC 电 容 开 路
例1 求 iC(0+)
i 10k + 40k 10V iC S + uC iC
电 容 用 电 压
第7章 一阶电路和二阶电路 的时域分析
7.1 动态电路的方程及其初始条件 7.2 一阶电路的零输入响应 7.3 一阶电路的零状态响应 7.4 一阶电路的全响应 7.5 二阶电路的零输入响应 7.6 二阶电路的零状态响应和全响应 7.7 一阶电路和二阶电路的阶跃响应 7.8* 一阶电路和二阶电路的冲激响应 7.9* 卷积积分 7.10* 状态方程 7.11* 动态电路时域分析中的几个问题
?
前一个稳定状态
过渡状态
返 回
上 页
下 页
+ Us -
(t →) R i + uL –
+ Us -
(t →) R i + k uL –
k未动作前,电路处于稳定状态: uL= 0, k断开瞬间
i=Us /R
i = 0 , uL =
注意 工程实际中在切断电容或电感电路时
会出现过电压和过电流现象。
本章重点
首页
重点 1.动态电路方程的建立及初始条件的确定;
2.一阶和二阶电路的零输入响应、零状态响 应和全响应的概念及求解;
3.一阶和二阶电路的阶跃响应概念及求 解。
返 回
7.1 动态电路的方程及其初始条件
1. 动态电路
含有动态元件电容和电感的电路称动态电路。
特点
当动态电路状态发生改变时(换路)需要 经历一个变化过程才能达到新的稳定状态。这 个变化过程称为电路的过渡过程。
返 回
上 页
下 页
换路
电路结构、状态发生变化 支路接入或断开 电路参数变化
过渡过程产生的原因 电路内部含有储能元件 L、C,电路在换路时 能量发生变化,而能量的储存和释放都需要一定的 时间来完成。
Δw p Δt
Δt 0
p
返 回 上 页 下 页
2. 动态电路的方程
例 RC电路
应用KVL和电容的VCR得:
Ri uL uS (t )
di uL L dt
(t >0) R i + + uL Us – -
R 若以电感电压为变量: uLdt uL uS (t ) L
R duL duS (t ) uL L dt dt
返 回 上 页 下 页
di Ri L uS (t ) dt
+ u -
L
1 t iL (0 ) 0 u ( )d L 0 1 0 t = 0+时刻 iL (0 ) iL (0 ) 0 u ( )d L
当u为有限值时
返 回
上 页
下 页
LiL
iL(0+)= iL(0-)
L (0+)= L (0-)
磁链 守恒
i
+
当i()为有限值时
