海淀区高三年级2015—2016 学年度第二学期期末练习理科试卷
2015-2016学年北京市海淀区高三(下)期末考试理综物理学科部分及答案

2015-2016学年北京市海淀区高三(下)期末考试理综物理学科部分13.如图所示,在一个配有活塞的厚壁有机玻璃筒底放置一小团硝化棉,迅速向下压活塞,筒内气体被压缩后可点燃硝化棉。
在筒内封闭的气体被活塞压缩的过程中A .气体对外界做正功,气体内能增加B .外界对气体做正功,气体内能增加C .气体的温度升高,压强不变D .气体的体积减小,压强不变14.对下列各原子核变化的方程,表述正确的是A .n He H H 10422131+→+ 是核聚变反应 B .n He H H 10422131+→+ 是α衰变 C .e 2Kr Se 01-82368234+→ 是核裂变反应 D .n 2Sr Xe n U 109438140541023592++→+ 是β衰变15.平行的a 、b 两种单色光的光束以相同的入射角从空气斜射向某种长方体玻璃砖上表面的同一位置,在玻璃砖下表面将分开为不同的单色光光束。
若a 光的频率小于b 光的频率,则以下光路图中正确的是16.一列横波沿x 轴正方向传播,t =0时刻的波形图如图甲所示,则图乙描述的可能是A .x =0处质点的振动图像B .x =0.5m 处质点的振动图像C .x =1.5m 处质点的振动图像D .x =2.5m 处质点的振动图像17.若已知引力常量 G ,则利用下列哪组数据可以算出地球的质量A .一颗绕地球做匀速圆周运动的人造卫星的质量和地球表面的重力加速度B .一颗绕地球做匀速圆周运动的人造卫星的质量和地球的第一宇宙速度C .一颗绕地球做匀速圆周运动的人造卫星的运行速率和周期D .地球绕太阳公转的周期和轨道半径18.如图甲所示,交流发电机的矩形金属线圈abcd 的匝数n =100,线圈的总电阻r =5.0Ω,线圈位于匀强磁场中,且线圈平面与磁场方向平行。
线圈的两端分别与两个彼此绝缘的铜环E 、F (集流环)焊接在一起,并通过电刷与阻值R =95Ω的定值电阻连接。
北京市海淀区2016届高三下学期期末考试(二模)理综试卷含答案

北京市海淀区2016届高三下学期期末考试(二模)理综试卷含答案海淀区高一年级XXXX第二学期期末练习理科综合能力测试2016.5试卷共15页,共300分考试持续了150分钟。
考生必须回答答题卡上的问题,试卷上的答案无效。
考试结束后,把试卷和答题纸一起交回。
下列数据可供解题参考:相对原子质量:HL C12 N14 0 16 Na23 K39 C1 35.5第一部分(选择题120题)第一部分(共20题),每题6题,共120题从每个项目中列出的四个选项中选择最符合主题要求的选项。
1。
寨卡病毒是一种能引起人类疾病的核糖核酸病毒兹卡病毒的以下描述是正确的:a .它具有完整的细胞结构b .它包含四个碱基a、t、g 和c. c .它可以寄生在人类细胞d不能用作诱导免疫反应的抗原。
在愈伤组织成苗过程中,线粒体基质中没有丙酮酸分解生成cozb。
水在叶绿体基质中分解,生成O2。
脱氧核苷酸在细胞核中聚合形成脱氧核糖核酸。
氨基酸脱水并在核糖体上浓缩形成多肽3。
l病毒感染小鼠的脑膜细胞,导致脑膜炎。
l蛋白是l病毒的抗原蛋白研究人员将两只转基因小鼠杂交,用L病毒感染能够表达L蛋白和L蛋白受体的子代小鼠,这将导致严重的糖尿病,如图所示。
根据这一分析,不正确的是a。
作为亲本的两个转基因小鼠是杂合子b。
所转移基因的遗传决不能遵循自由结合的规律。
被病毒感染的c. l细胞可被效应t细胞裂解。
小鼠糖尿病的原因是胰岛b细胞被杀死4。
狒狒种群有一个等级。
在个体争斗之后,最强壮最凶猛的雄性狒狒成为“领导者”,它在食物选择和与雌性狒狒交配方面拥有优先权。
“领导者”还负责指挥整个种群,并与其他雄性狒狒共同保卫种群。
以下相关陈述是不正确的:a .狒狒种群通过种间竞争建立了等级制度;狒狒种群中个体间的分工与合作需要信息交流;c .”领导者”优先享受配偶,这有利于优秀基因的传递;战斗不利于被打败的个人,有利于人口的延续;5.在生物学研究中,下列方法是不可行的:a。
2015年北京海淀高三二模数学(理科)试题及答案

海淀区高三年级第二学期期末练习数 学(理) 2015.5一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知全集U Z =,集合{1,2}A =,{1,2,3,4}A B =U ,那么()U C A B I =( ) (A )∅ (B ){3}x x Z ∈≥(C ){3,4}(D ){1,2}(2)设30.320.2,log 0.3,2a b c ===,则( )(A )b c a << (B )c b a <<(C )a b c <<(D )b a c <<(3)在极坐标系中,过点π(2,)6-且平行于极轴的直线的方程是( ) (A )cos 3ρθ=(B )cos 3ρθ=-(C )sin 1ρθ=(D )sin 1ρθ=-(4)已知命题p ,q ,那么“p q ∧为真命题”是“p q ∨为真命题”的( ) (A )充分不必要条件 (B )必要不充分条件 (C )充要条件(D )既不充分也不必要条件(5)已知函数()cos(2)f x x ϕ=+(ϕ为常数)为奇函数,那么cos ϕ=( )(A )22-(B )0(C )22(D )1(6)已知函数()f x 的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计1()d f x x ⎰的值约为( )13xOy(A )99100 (B )310 (C )910(D )1011(7)已知()f x 是定义域为R 的偶函数,当0x ≤时,31()(1)e x f x x +=+.那么函数()f x 的极值点的个数是( ) (A )5(B )4(C )3(D )2(8)若空间中有(5)n n ≥个点,满足任意四个点都不共面,且任意两点的连线都与其它任意三点确定的平面垂直,则这样的n 值( ) (A )不存在(B )有无数个(C )等于5(D )最大值为8二、填空题共6小题,每小题5分,共30分。
北京市海淀区2016届高三下学期期末考试(二模)理综物理试卷 含答案

北京市海淀区2016届高三下学期期末考试(二模)理综物理试卷13.如图所示,在一个配有活塞的厚壁有机玻璃筒底放置一小团硝化棉,迅速向下压活塞,筒内气体被压缩后可点燃硝化棉.在筒内封闭的气体被活塞压缩的过程中A .气体对外界做正功,气体内能增加B .外界对气体做正功,气体内能增加C .气体的温度升高,压强不变D .气体的体积减小,压强不变14.对下列各原子核变化的方程,表述正确的是A .n He H H 10422131+→+ 是核聚变反应 B .n He H H 10422131+→+ 是α衰变C .e 2Kr Se 01-82368234+→是核裂变反应 D .n 2Sr Xe n U 109438140541023592++→+是β衰变15.平行的a 、b 两种单色光的光束以相同的入射角从空气斜射向某种长方体玻璃砖上表面的同一位置,在玻璃砖下表面将分开为不同的单色光光束。
若a 光的频率小于b 光的频率,则以下光路图中正确的是16.一列横波沿x 轴正方向传播,t =0时刻的波形图如图甲所示,则BbaCabDbaAababababab硝化棉活塞 有机图乙描述的可能是A .x =0处质点的振动图像B .x =0.5m 处质点的振动图像C .x =1。
5m 处质点的振动图像D .x =2。
5m 处质点的振动图像17.若已知引力常量 G ,则利用下列哪组数据可以算出地球的质量A .一颗绕地球做匀速圆周运动的人造卫星的质量和地球表面的重力加速度B .一颗绕地球做匀速圆周运动的人造卫星的质量和地球的第一宇宙速度C .一颗绕地球做匀速圆周运动的人造卫星的运行速率和周期D .地球绕太阳公转的周期和轨道半径18.如图甲所示,交流发电机的矩形金属线圈abcd 的匝数n =100,线圈的总电阻r =5.0Ω,线圈位于匀强磁场中,且线圈平面与磁场方向平行。
线圈的两端分别与两个彼此绝缘的铜环E 、F (集流环)焊接在一起,并通过电刷与阻值R =95Ω的定值电阻连接。
北京市海淀区2016届高三数学下学期期末练习(二模)试题-理

海淀区高三年级第二学期期末练习数学(理科)本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上 作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知全集=U R ,{|1},{|2},M x x P x x =≤=≥ 则()UM P =A.{|12}x x <<B.{|1}x x ≥C.{|2}x x ≤D.{|12}x x x ≤≥或 2.在数列{}n a 中,12a =,且1(1)n n n a na ++=,则3a 的值为 A.5 B.6 C.7 D.83. 若点(2,4)P 在直线1,:3x t l y at=+⎧⎨=-⎩(t 为参数)上,则a 的值为A.3B.2C.1D.1-4.在ABC ∆中,34cos ,cos ,55A B == 则sin()A B -=A.725-B.725C.925-D.9255.在5()x a +(其中0a ≠)的展开式中,2x 的系数与3x 的系数相同,则a 的值为 A.2- B.1- C. 1 D.26.函数()ln 1f x x x =-+的零点个数是A.1个B.2个C.3个D.4个 7. 如图,在等腰梯形ABCD 中,8,4,4AB BC CD ===. 点P 在 线段AD 上运动,则||PA PB +的取值范围是A.[6,43]+B.[42,8]C.[43,8]D.[6,12] 8.直线1:10l ax y a+-=与,x y 轴的交点分别为,A B , 直线l 与圆22:1O x y +=的交点为,C D . 给出下面三个结论: ① 11,2AOB a S ∆∀≥=; ②1,||||a AB CD ∃≥<;③11,2COD a S ∆∃≥<则所有正确结论的序号是 A.①② B.②③DCABPC.①③D.①②③二、填空题共6小题,每小题5分,共30分。
北京市海淀区2015年高三二模理综试卷及解析(无水印)

)
6.下列物质与常用危险化学品的类别不对应 的是( ... A.氢氧化钠——腐蚀品 C.钠——遇湿易燃物品
)
B.高锰酸钾——氧化剂 D.甲烷——易燃液体
7. 下列装置中能将电能转化为化学能的是
A
B
C
D
8. 下列说法不正确的是 A.甲苯和环己烯都能使酸性高锰酸钾溶液褪色 B.用银氨溶液可以鉴别乙醛和葡萄糖溶液 C.甲醛和乙二醇都可作为合成高分子化合物的单体 D.丙烷和 2 甲基丙烷的一氯代物均为两种
A.太阳对各行星的引力相同 B.土星绕太阳运动的向心加速度比火星绕太阳运动的向心加速度小 C.水星绕太阳运动的周期大于一年 D.木星绕太阳运动的线速度比地球绕太阳运动的线速度大 18.如图甲所示,细线下悬挂一个除去了柱塞的注射器,注射器可在竖直面内摆动,且在摆 动过程中能持续向下流出一细束墨水。 沿着与注射器摆动平面垂直的方向匀速拖动一张 硬纸板, 摆动的注射器流出的墨水在硬纸板上形成如图乙所示的曲线。 注射器喷嘴到硬 纸板的距离很小, 且摆动注射器重心的高度变化可忽略不计。 若按图乙所示建立 xOy 坐 标系, 则硬纸板上的墨迹所呈现的图样可视为注射器振动的图像。 关于图乙所示的图像, 下列说法中正确的是
2.某种果蝇野生型个体的翅为圆形。该种果蝇有两种纯合的突变品系,一种为椭圆形翅, 另一种为镰刀形翅。将这三种果蝇相互杂交得到下表所示结果。据此判断不合理 的是 ... ( ) 亲本 杂交 雌蝇 1 2 3 镰刀形 圆形 镰刀形 雄蝇 圆形 镰刀形 椭圆形 雌蝇 镰刀形 镰刀形 椭圆形
F1
雄蝇 镰刀形 圆形 镰刀形
Na 2SiO3 H2O
10.已知 16 S 和 34 Se 位于同一主族,下列说法正确的是 A.热稳定性: H2Se H2S H2O B.原子半径: Se S Cl C.酸性: H2SeO4 H2SO4 HClO4 D.还原性: S
北京市海淀区2015届高三期末练习(二模)数学理试题及答案

海淀区高三年级第二学期期末练习数学(理)答案及评分参考 2015.5一、选择题(共8小题,每小题5分,共40分)(1)C (2)D (3)D (4)A(5)B (6)A (7)C (8)C二、填空题(共6小题,每小题5分,共30分。
有两空的小题,第一空2分,第二空3分)(9)2,413n - (10)30︒,1 (11)0a > ,2a a =+ (12)(2,)+∞ (13)14 (14)10(,1]10 三、解答题(共6小题,共80分)(15)(共13分)解:(Ⅰ)因为 36cos 2a A =, 所以 2223622b c a a bc+-=⨯. ………………3分 因为 5c =,26b =,所以 23404930a a +-⨯=.解得:3a =,或493a =-(舍). ………………6分 (Ⅱ)由(Ⅰ)可得:26cos 3336A =⨯=. 所以 21cos 22cos 13A A =-=. ………………9分 因为 3a =,5c =,26b =,所以 2221cos 23a cb B ac +-==. ………………11分 所以cos 2cos A B =. ………………12分 因为 c b a >>,所以 (0,)3A π∈.因为 (0,)B ∈π,所以 2B A ∠=∠. ………………13分另解:因为 (0,)A ∈π, 所以 23sin 1cos 3A A =-=. 由正弦定理得:263sin 33B =. 所以 22sin 3B =. 所以 3622sin 22sin 333A B =⨯⨯==. ………………12分 因为 c b a >>,所以 (0,)3A π∈,(0,)2B π∈.所以 2B A ∠=∠. ………………13分 (16)(共13分)解:(Ⅰ)20名女生掷实心球得分如下:5,6,7,7,7,7,7,7,8,8,8,9,9,9,9,9,9,9,10,10.所以中位数为8,众数为9. ………………3分(Ⅱ)X 的可能取值为0,1,2. ………………4分()21222033095C P X C ===;()1112822048195C C P X C ===;()2822014295C P X C ===; 所以抽取的2名男生中优秀人数X 的分布列为:X 0 1 2P 9533 9548 9514 ………………10分 (Ⅲ)略. ………………13分评分建议:从平均数、方差、极差、中位数、众数等角度对整个年级学生掷实心球项目的情况进行合理的说明即可;也可以对整个年级男、女生该项目情况进行对比;或根据目前情况对学生今后在该项目的训练提出合理建议.(17)(共14分)(Ⅰ)证明:连结BD 交AC 于点O ,连结OM .因为 //AB CD ,2AB CD =,所以2BO AB DO CD ==. 因为2BM MP =, 所以2BM PM =. 所以BM BO PM DO =. 所以//OM PD . ………………2分 因为OM ⊂平面MAC ,PD ⊄平面MAC , 所以 //PD 平面MAC . ………………4分(Ⅱ)证明:因为 平面PAD ⊥平面ABCD ,AD AB ⊥,平面PAD 平面ABCD AD =,AB ⊂平面ABCD ,所以AB ⊥平面PAD . ………………6分 因为 PA ⊂平面PAD ,所以 AB PA ⊥. ………………7分 同理可证:AD PA ⊥.因为 AD ⊂平面ABCD ,AB ⊂平面ABCD ,AD AB A =,所以PA ⊥平面ABCD . ………………9分(Ⅲ)解:分别以边,,AD AB AP 所在直线为,,x y z轴,建立如图所示的空间直角坐标系.由22AB AD AP CD ====得(0,0,0)A ,(0,2,0)B ,(2,1,0)C ,(2,0,0)D ,(0,0,2)P ,则(2,1,0)AC =u u u r ,(0,2,2)PB =-u u r .由(Ⅱ)得:PA ⊥平面ABCD .所以 平面A B C D 的一个法向量为(0,0,1)n =r . ………………10分 设PM PBλ=(01)λ≤≤,即PM PB λ=uuu r uu r .所以 (0,2,22)AM AP PB λλλ=+=-u u u r u u u r u u r . M B D C O A P z y x M B D CA P设平面AMC 的法向量为(,,)m x y z =u r ,则0,0,m AC m AM ⎧⋅=⎪⎨⋅=⎪⎩u r uuu r u r uuu r 即20,2(22)0.x y y z λλ+=⎧⎨⋅+-⋅=⎩令1x λ=-,则22y λ=-,2z λ=-.所以 (1,22,2)m λλλ=---u r . ………………12分 因为 二面角B AC M --的余弦值为23, 所以 2|2|239105λλλ=-+,解得12λ=. 所以PM PB 的值为12. ………………14分 (18)(共13分)解:(Ⅰ)令()0f x =,得e x =.故()f x 的零点为e . ………………1分22231()(1ln )22ln 3'()()x x x x x f x x x-⋅--⋅-==(0x >). ………………3分 令 '()0f x =,解得 32e x =. 当x 变化时,'()f x ,()f x 的变化情况如下表: ()f x32(0,e ) 32e 32(e ,)+∞ '()f x - 0+ ()f x ↘↗ 所以 ()f x 的单调递减区间为32(0,e ),单调递增区间为32(e ,)+∞. ………………6分(Ⅱ)令ln ()x g x x =.则2211ln 1ln '()()x x x x g x f x x x⋅-⋅-===. ………………7分 因为 11()44ln 244622f =+>+⨯=,(e)0f =,且由(Ⅰ)得,()f x 在(0,e)内是减函数,所以 存在唯一的01(,e)2x ∈,使得00'()()6g x f x ==.当[e,)x ∈+∞时,()0f x ≤.所以 曲线ln x y x =存在以00(,())x g x 为切点,斜率为6的切线. ………………10分 由00201ln '()6x g x x -==得:200ln 16x x =-. 所以 20000000ln 161()6x x g x x x x x -===-.因为 012x >, 所以 012x <,063x -<-. 所以 00()1y g x =<-. ………………13分(19)(共14分)解:(Ⅰ)依题意得22224,,.a c b a b c ⎧=⎪=⎨⎪-=⎩解得:2a =,2b c ==. ………………3分所以圆O 的方程为222x y +=,椭圆C 的方程为22142x y +=. ………………5分 (Ⅱ)解法一:如图所示,设00(,)P x y (00y ≠), 0(,)Q Q x y ,则22002201,422,Q x y x y ⎧+=⎪⎨⎪+=⎩即220022042,2.Q x y x y ⎧=-⎪⎨=-⎪⎩ ………………7分又由00:(2)2y AP y x x =++得002(0,)2y M x +. NM QPyx B A O由00:(2)2y BP y x x =--得002(0,)2y N x --. ………………10分所以 0000002(,)(,)22Q Q y x y QM x y x x x =--=--++uuu r , 0000002(,)(,)22Q Q y x y QN x y x x x =---=----uuu r . 所以222222000002200(42)2042Q x y y y QM QN x y x y -⋅=+=-+=--uuu r uuu r . 所以 QM QN ⊥,即90MQN ∠=︒. ………………14分(Ⅱ)解法二:如图所示,设00(,)P x y ,:(2)AP y k x =+(0k ≠). 由221,42(2)x y y k x ⎧+=⎪⎨⎪=+⎩得2222(21)8840k x k x k +++-=. 所以 20284221k x k --=+,即2022421k x k -=+. 所以 02421k y k =+,即222244(,)2121k k P k k -++. 所以 直线BP 的斜率为2224121242221kk k k k +=---+. 所以 1:(2)2BP y x k=--. 令0x =得:(0,2)M k ,1(0,)N k . ………………10分 设0(,)Q Q x y ,则0(,2)Q QM x k y =--uuu r ,01(,)Q QN x y k =--uuu r . N M Q Py xB A O所以 22220000121(2)()2Q Q k QM QN x k y y x y y k k+⋅=+--=++-⋅uuu r uuu r . 因为 2200242,21Q k x y y k +==+, 所以 0QM QN ⋅=u u u r u u u r . 所以 QM QN ⊥,即90MQN ∠=︒. ………………14分(20)(共13分)解:(Ⅰ)1:2,1,3A 或1:1,3,2A . ………………2分.(Ⅱ)3:5,6,7,2,3,4,9,8,1A ; ………………4分4:5,6,7,8,1,2,3,4,9A . ………………6分 (Ⅲ)考虑数列12:,,,n A a a a L ,满足1i i a a +<的数对1,i i a a +的个数,我们称之为“顺序数”.则等差数列0A :2015,2004,,1L 的顺序数为0,等差数列n A :1,2,,2015L 的顺序数为2014. 首先,证明对于一个数列,经过变换T ,数列的顺序数至多增加2.实际上,考虑对数列,,,,,,,,,p a b c d q L L L L ,交换其相邻两段,,a b L 和,,c d L 的位置,变换为数列,,,,,,,,,p c d a b q L L L L .显然至多有三个数对位置变化.假设三个数对的元素都改变顺序,使得相应的顺序数增加,即由,,p a b c d q >>>变为,,p c d a b q <<<.分别将三个不等式相加得p b d a c q ++>++与p b d a c q ++<++,矛盾.所以 经过变换T ,数列的顺序数至多增加2.其次,第一次和最后一次变换,顺序数均改变1.设n 的最小值为x ,则()2222014x +-≥,即1008x ≥. ………………10分 最后,说明可以按下列步骤,使得数列1008A 为1,2,,2015L .对数列0:A 2015,2014,,1L ,第1次交换1,2,,1007L 和1008,1009位置上的两段,得到数列1A :1008,1007,2015,2014,,1010,1009,1006,1005,,2,1L L ;第2次交换2,3,,1008L 和1009,1010位置上的两段,得到数列2A :1008,1009,1006,1007,2015,2014,,1011,1010,1005,1004,,2,1L L ;第3次交换3,4,,1009L 和1010,1011位置上的两段,得到数列3A :1008,1009,1010,1005,1006,1007,2015,2014,,1012,1011,1004,1003,,2,1L L ; L L ,以此类推第1007次交换1007,1008,,2013L 和2014,2015位置上的两段,得到数列1007A : 1008,1009,,2013,2014,1,2,,1006,1007,2015L L ;最终再交换1,2,,1007L 和1008,1009,,2014L 位置上的两段,即得1008A :1,2,,2015L . 所以 n 的最小值为1008. ………………13分。
2015高考海淀二模理综试卷及答案

m
则a =
m
设偏转电场的场强为 E,氕核、氘核在偏转电场中的加速度分别为 a、a′
eE eE , a′ = (1 分) m 2m
氕核、氘核在垂直极板方向 y =
E 2 1 2 1 E 2 at = x , y = a ′t ′ 2 = x (1 分) 2 4U 0 2 4U 0 ′2
酶 R 基因不
20
2015.5
E , E = Blv ′ (3 分) R 解得: v ′ = 12m/s (1 分)
FA = BIl , I =
(2)解法 1: 导体棒沿轨道匀速下滑时通过导体棒的电流为 Im,则 mg = BI m l (2 分) 解得:Im=10A(1 分) 此时电路中的电功率 P= Im2R=40W(2 分) ,速度为 vm 解法 2:导体棒沿轨道匀速下滑时受安培力为 FA′ 则 mg = FA , mg = 解得: vm =
2 k 4 m1v D 根据牛顿第二定律 P 小球在 D 点有 k m1 g = (1 分) R 4
解得: vD =
gR (1 分)
1 1 2 2 (2 分) m5 v P = m5 g ⋅ 2 R + m5 v D 2 2
P 小球由 A 到 D 的运动过程,机械能守恒有 解得: vP =
5 gR (1 分)将 R =
氕核垂直射入匀强偏转电场,在平行极板方向做匀速直线运动,在垂直极板方向做匀加速直线 运动。 设偏转极板长为 l,极板间距为 d,氕核从 S 孔射出时速度为 vS,垂直极板方向的速度为 vy, 因为
d vy l = t ,l=2d(1 分) = vt , 2 2 2
1
所以 v=vy(1 分)
2015北京市海淀区数学理二模

海淀区高三年级第二学期期末练习数 学(理) 2015.5本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上 作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知全集U Z =,集合{1,2}A =,{1,2,3,4}A B =U ,那么()U C A B I =( ) (A )∅(B ){3}x x Z ∈≥(C ){3,4}(D ){1,2}(2)设30.320.2,log 0.3,2a b c ===,则( )(A )b c a << (B )c b a << (C )a b c << (D )b a c <<(3)在极坐标系中,过点π(2,)6-且平行于极轴的直线的方程是( ) (A)cos ρθ=(B)cos ρθ=(C )sin 1ρθ=(D )sin 1ρθ=-(4)已知命题p ,q ,那么“p q ∧为真命题”是“p q ∨为真命题”的( ) (A )充分不必要条件 (B )必要不充分条件 (C )充要条件(D )既不充分也不必要条件(5)已知函数()cos(2)f x x ϕ=+(ϕ为常数)为奇函数,那么cos ϕ=( )(A)2-(B )0(C)2(D )1(6)已知函数()f x 的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计1()d f x x ⎰的值约为( )(A )99100 (B )310 (C )910(D )1011(7)已知()f x 是定义域为R 的偶函数,当0x ≤时,31()(1)e x f x x +=+.那么函数()f x 的极值点的个数是( ) (A )5(B )4(C )3(D )2(8)若空间中有(5)n n ≥个点,满足任意四个点都不共面,且任意两点的连线都与其它任意三点确定的平面垂直,则这样的n 值( ) (A )不存在(B )有无数个(C )等于5(D )最大值为8二、填空题共6小题,每小题5分,共30分。
2015海淀区高三二模数学(理科)
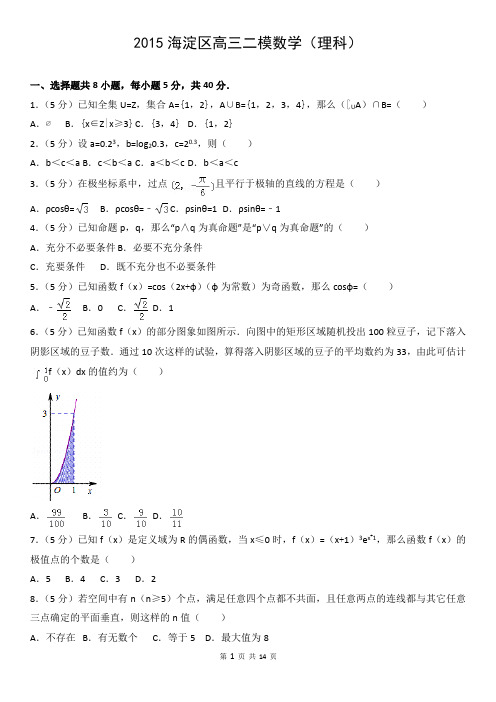
2015海淀区高三二模数学(理科)一、选择题共8小题,每小题5分,共40分.1.(5分)已知全集U=Z,集合A={1,2},A∪B={1,2,3,4},那么(∁U A)∩B=()A.∅B.{x∈Z|x≥3} C.{3,4}D.{1,2}2.(5分)设a=0.23,b=log20.3,c=20.3,则()A.b<c<a B.c<b<a C.a<b<c D.b<a<c3.(5分)在极坐标系中,过点且平行于极轴的直线的方程是()A.ρcosθ=B.ρcosθ=﹣ C.ρsinθ=1D.ρsinθ=﹣14.(5分)已知命题p,q,那么“p∧q为真命题”是“p∨q为真命题”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件5.(5分)已知函数f(x)=cos(2x+φ)(φ为常数)为奇函数,那么cosφ=()A.﹣B.0 C.D.16.(5分)已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计f(x)dx的值约为()A.B.C.D.7.(5分)已知f(x)是定义域为R的偶函数,当x≤0时,f(x)=(x+1)3e x+1,那么函数f(x)的极值点的个数是()A.5 B.4 C.3 D.28.(5分)若空间中有n(n≥5)个点,满足任意四个点都不共面,且任意两点的连线都与其它任意三点确定的平面垂直,则这样的n值()A.不存在B.有无数个C.等于5 D.最大值为8二、填空题共6小题,每小题5分,共30分.9.(5分)若等比数列{a n}满足a2a6=64,a3a4=32,则公比q=;a12+a22+…+a n2=.10.(5分)如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=,BE=.11.(5分)右图表示的是求首项为﹣41,公差为2的等差数列{a n}前n项和的最小值的程序框图.①处可填写;②处可填写.12.(5分)若双曲线M上存在四个点A,B,C,D,使得四边形ABCD是正方形,则双曲线M的离心率的取值范围是.13.(5分)用红、黄、蓝三种颜色对如图所示的三个方格进行涂色.若要求每个小方格涂一种颜色,且涂成红色的方格数为偶数,则不同的涂色方案种数是.(用数字作答)14.(5分)设关于x、y的不等式组表示的平面区域为D,已知点O(0,0)、A(1,0),点M是D上的动点,=λ||,则λ的取值范围是.三、解答题共6小题,共80分.解答应写出文字说明、演算步骤或证明过程.15.(13分)在△ABC中,c=5,b=2,a=cosA.(Ⅰ)求a的值;(Ⅱ)求证:∠B=2∠A.16.(13分)某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下:已知该项目评分标准为:注:满分10分,且得9分以上(含9分)定为“优秀”.(Ⅰ)求上述20名女生得分的中位数和众数;(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)17.(13分)如图所示,在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.(Ⅰ)若BM=2MP,求证:PD∥平面MAC;(Ⅱ)若平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,求证:PA⊥平面ABCD;(Ⅲ)在(Ⅱ)的条件下,若二面角B﹣AC﹣M的余弦值为,求的值.18.(14分)已知函数f(x)=.(Ⅰ)求函数f(x)的零点及单调区间;(Ⅱ)求证:曲线y=存在斜率为6的切线,且切点的纵坐标y0<﹣1.19.(13分)已知椭圆C:=1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过这两个焦点,点A,B分别是椭圆C的左、右顶点.(Ⅰ)求圆O和椭圆C的方程;(Ⅱ)已知P,Q分别是椭圆C和圆O上的动点(P,Q位于y轴两侧),且直线PQ与x轴平行,直线AP,BP分别与y轴交于点M,N.求证:∠MQN为定值.20.(14分)对于数列A:a1,a2,…,a n,经过变换T:交换A中某相邻两段的位置(数列A中的一项或连续的几项称为一段),得到数列T(A).例如,数列A:a1,…,a i,(p≥1,q≥1)经交换M,N两段位置,变换为数列T(A):a1,…,a i,.=T(A k)(k=0,1,2,…).设A0是有穷数列,令A k+1(Ⅰ)如果数列A0为3,2,1,且A2为1,2,3.写出数列A1;(写出一个即可)(Ⅱ)如果数列A0为9,8,7,6,5,4,3,2,1,A1为5,4,9,8,7,6,3,2,1,A2为5,6,3,4,9,8,7,2,1,A5为1,2,3,4,5,6,7,8,9.写出数列A3,A4;(写出一组即可)(Ⅲ)如果数列A0为等差数列:2015,2014,…,1,A n为等差数列:1,2,…,2015,求n的最小值.参考答案与试题解析一、选择题共8小题,每小题5分,共40分.1.【解答】全集U=Z,集合A={1,2},A∪B={1,2,3,4},∴集合B⊆A∪B,并且一定有3,4,∴∁U A也一定有3,4,∴(∁U A)∩B={3,4}.故选:C.2.【解答】∵0<0.23<1,20.3>1,log20.3<0,∴b<a<c,故选:D.3.【解答】点化为直角坐标,即.∴过点且平行于极轴的直线的方程是y=﹣1,化为直角坐标方程为:ρsinθ=﹣1.故选:D.4.【解答】若p∧q为真命题,则p,q都为真命题,∴p∨q为真命题;若p∨q为真命题,则p,q中至少有一个为真命题,而如果p,q中只有一个为真命题,则得不到p ∧q为真命题;∴“p∧q为真命题”是“p∨q为真命题”的充分不必要条件.故选:A.5.【解答】由于函数f(x)=cos(2x+φ)(φ为常数)为奇函数,则φ=kπ+,k∈z,∴cosφ=0,故选:B.6.【解答】由题意设阴影部分的面积为S,则,所以S=;故选:A.7.【解答】当x≤0时,f(x)=(x+1)3e x+1,∴f′(x)=(x+4)(x+1)2e x+1,∴x<﹣4时,f′(x)<0,﹣4<x≤0时,f′(x)>0,∴x=﹣4是函数的极值点,∵f(x)是定义域为R的偶函数,∴x=4是函数的极值点,又f(0)=e,x>0递增,x<0递减,即为极值点.故选:C.8.【解答】显然n=5时成立,若n≥6,空间中三个点确定一个平面,又任意四点都不共面,则其余点都在该平面外,而过平面外一点有且只有一条直线垂直平面,则其余各点共线,由公里3推论可知,存在四点共面,这与已知矛盾,故n≥6不成立,故选:C二、填空题共6小题,每小题5分,共30分.9.【解答】∵a3a4=32,∴q>0,且a n>0,∵a2a6=64,∴a2a6=(a4)2=64,∴a4=8,则a3=,则公比q==2,则a n=a4q n﹣4=8×2n﹣4=2n﹣1,则a n2=(2n﹣1)2=4n﹣1,即数列{a n2}是公比q=4的等比数列,则a12+a22+…+a n2==,故答案为:2,10.【解答】连接OD,则OD⊥AB,∵△ACB中,∠ACB=120°,AC=BC,∴∠B=∠A=30°,∴∠DOB=60°,∴△ODE为等边三角形,∴∠EDB=30°,∴DE=EB=CE,∵BC=3,∴BE=1故答案为:30°;1.11.【解答】由程序设计意图可知,S表示此等差数列{a n}前n项和,故②处应该填写a=a+2,又因为此数列首项为负数,公差为正数,求前n项和的最小值只需累加至最后一个非正项即可,故①处可填写:a>0.故答案为:a>0,a=a+2.12.【解答】∵双曲线M上存在四个点A,B,C,D,使得四边形ABCD是正方形,∴>1,∴e=>,即e∈.故答案为:.13.【解答】因为涂成红色的方格数为偶数,即涂成红色的方格数为0,或2,3个格涂一种颜色,有2种,(全黄或全蓝)3个格涂2颜色且涂0个红色时,C21C32=6种,3格涂2颜色且涂2个红色时,C21C32=6种,根据分类计数原理,可得共有2+6+6=14种,故答案为:14.14.【解答】由不等式组得:,或;∴平面区域D如下图阴影部分所示:由得,λ=cos∠MOA;如图所示,若设直线x=和y=﹣3x+6的交点为B,则B点坐标为(,2),所以|OB|=,当M点从B点开始向x轴靠近的过程中,∠MOA不断减小,并减小到0,当∠MOA=0°时对应的λ的值达到最大值,而当M从x轴并在阴影部分远离x轴时,∠MOA又逐渐增大,可知∠MOA的最大值(极限值)一定在直线y=﹣3x+6上取得,比较此极限值和M在B点对应的λ值即可求出λ的最小值;当M点在B点时,cos∠MOA==;当M点在第四象限且在直线上时,设M(x,﹣3x+6),则cos∠MOA=,当x趋近于正无穷时,cos∠MOA=,∵>;∴λ的取值范围是(,1].故答案为:(,1].三、解答题共6小题,共80分.解答应写出文字说明、演算步骤或证明过程.15.【解答】(Ⅰ)因为,所以,因为c=5,,所以3a2+40a﹣49×3=0,解得:a=3或(舍).…(6分)证明:(Ⅱ)由(Ⅰ)可得:,所以,因为a=3,c=5,,所以,所以cos2A=cosB.…(12分)因为c>b>a,所以,因为B∈(0,π),所以∠B=2∠A.…(13分)16.【解答】(Ⅰ)20名女生掷实心球得分如下:5,6,7,7,7,7,7,7,8,8,8,9,9,9,9,9,9,9,10,10.所以中位数为8,众数为9.…(3分)(Ⅱ)X的可能取值为0,1,2.…(4分),,,所以抽取的2名男生中优秀人数X的分布列为:…(10分)(Ⅲ)由茎叶图得20名男生掷实心球得分如下:4,4,4,6,6,6,7,7,8,8,8,8,9,9,9,9,9,10,10,10.所以中位数为8,众数为9.20名女生掷实心球得分的平均数为:=(5+6+7+7+7+7+7+7+8+8+8+9+9+9+9+9+9+9+10+10)=8,20名男生掷实心球得分的平均数为:=(4+4+4+6+6+6+7+7+8+8+8+8+9+9+9+9+9+10+10+10)=7.55.∴该年级学生实心球项目的整体情况为:①男生和女生的得分的中位数和众数相等;②男生得分的平均数小于女生得分的平均数.…(13分)评分建议:从平均数、方差、极差、中位数、众数等角度对整个年级学生掷实心球项目的情况进行合理的说明即可;也可以对整个年级男、女生该项目情况进行对比;或根据目前情况对学生今后在该项目的训练提出合理建议.17.【解答】(Ⅰ)连结BD交AC于点O,连结OM.因为AB∥CD,AB=2CD,所以.因为BM=2MP,所以.所以.所以OM∥PD.…(2分)因为OM⊂平面MAC,PD⊄平面MAC,所以PD∥平面MAC.…(4分)(Ⅱ)因为平面PAD⊥平面ABCD,AD⊥AB,平面PAD∩平面ABCD=AD,AB⊂平面ABCD,所以AB⊥平面PAD.…(6分)因为PA⊂平面PAD,所以AB⊥PA.同理可证:AD⊥PA.因为AD⊂平面ABCD,AB⊂平面ABCD,AD∩AB=A,所以PA⊥平面ABCD.…(9分)解:(Ⅲ)分别以边AD,AB,AP所在直线为x,y,z轴,建立如图所示的空间直角坐标系.由AB=AD=AP=2CD=2,得A(0,0,0),B(0,2,0),C(2,1,0),D(2,0,0),P(0,0,2),则,.由(Ⅱ)得:PA⊥平面ABCD.所以平面ABCD的一个法向量为.…(10分)设(0≤λ≤1),即.所以.设平面AMC的法向量为,则,即令x=λ﹣1,则y=2﹣2λ,z=﹣2λ.所以.因为二面角B﹣AC﹣M的余弦值为,所以,解得.所以的值为.…(14分)18.【解答】(Ⅰ)令f(x)=0,得x=e.故f(x)的零点为e,(x>0).令f′(x)=0,解得.当x变化时,f′(x),f(x)的变化情况如下表:(0,)(,+∞)所以f(x)的单调递减区间为,单调递增区间为.(Ⅱ)令.则,因为,f(e)=0,且由(Ⅰ)得,f(x)在(0,e)内是减函数,所以存在唯一的,使得g′(x0)=f(x0)=6.当x∈[e,+∞)时,f(x)≤0.所以曲线存在以(x0,g(x0))为切点,斜率为6的切线.由得:.所以.因为,所以,﹣6x0<﹣3.所以y0=g(x0)<﹣1.19.【解答】(Ⅰ)依题意得解得:a=2,.所以圆O的方程为x2+y2=2,椭圆C的方程为.(Ⅱ)证法一:如图所示,设P(x0,y0)(y0≠0),Q(x Q,y0),则即,又由得.由得.所以,.所以.所以QM⊥QN,即∠MQN=90°.(Ⅱ)证法二:如图所示,设P(x0,y0),AP:y=k(x+2)(k≠0).由得(2k2+1)x2+8k2x+8k2﹣4=0.所以,即.所以,即.所以直线BP的斜率为.所以.令x=0得:M(0,2k),.设Q(x Q,y0),则,.所以.因为,所以.所以QM⊥QN,即∠MQN=90°.20.【解答】(Ⅰ)A1:2,1,3或A1:1,3,2.(Ⅱ)A3:5,6,7,2,3,4,9,8,1;A4:5,6,7,8,1,2,3,4,9.(Ⅲ)考虑数列A:a1,a2,…,a n,满足a i<a i+1的数对a i,a i+1的个数,我们称之为“顺序数”.则等差数列A0:2015,2004,…,1的顺序数为0,等差数列A n:1,2,…,2015的顺序数为2014.首先,证明对于一个数列,经过变换T,数列的顺序数至多增加2.实际上,考虑对数列…,p,a,…,b,c,…,d,q,…,交换其相邻两段a,…,b和c,…,d的位置,变换为数列…,p,c,…,d,a,…,b,q,….显然至多有三个数对位置变化.假设三个数对的元素都改变顺序,使得相应的顺序数增加,即由p>a,b>c,d>q变为p<c,d<a,b<q.分别将三个不等式相加得p+b+d>a+c+q与p+b+d<a+c+q,矛盾.所以经过变换T,数列的顺序数至多增加2.其次,第一次和最后一次变换,顺序数均改变1.设n的最小值为x,则2+2(x﹣2)≥2014,即x≥1008.最后,说明可以按下列步骤,使得数列A1008为1,2, (2015)对数列A0:2015,2014, (1)第1次交换1,2,…,1007和1008,1009位置上的两段,得到数列A1:1008,1007,2015,2014,…,1010,1009,1006,1005,…,2,1;第2次交换2,3,…,1008和1009,1010位置上的两段,得到数列A2:1008,1009,1006,1007,2015,2014,…,1011,1010,1005,1004,…,2,1;第3次交换3,4,…,1009和1010,1011位置上的两段,得到数列A3:1008,1009,1010,1005,1006,1007,2015,2014,…,1012,1011,1004,1003,…,2,1;…,以此类推第1007次交换1007,1008,…,2013和2014,2015位置上的两段,得到数列A1007:1008,1009,…,2013,2014,1,2,…,1006,1007,2015;最终再交换1,2,...,1007和1008,1009,...,2014位置上的两段,即得A1008:1,2, (2015)所以n的最小值为1008.。
2015年北京海淀高三二模理综试题及答案

2015年北京海淀高三二模理综试题及答案海淀区高三年级第二学期期末练习理科综合能力测试物理 2015.5本试卷共14页,共300分。
考试时长150分钟。
考生务必将答案写在答题纸上,在试卷上作答无效。
考试结束后,将本试卷和答题纸一并交回。
第一部分(选择题 共120分)本部分共20小题,每小题6分,共120分,在每小题列出的四个选项中,选出最符合题目要求的一项。
13.下列说法中正确的是A .仅利用氧气的摩尔质量和氧气的密度这两个已知量,便可计算出阿伏加德罗常数B .气体压强的大小只与气体的温度有关C .固体很难被压缩是因为其内部的分子之间存在斥力作用D .只要物体与外界不发生热量交换,其内能就一定保持不变14.下列说法中正确的是A .爱因斯坦根据对阴极射线的观察提出了原子的核式结构模型B .γ射线比α射线的贯穿本领强C .四个核子聚变为一个氦核的过程释放的核能等于氦核质量与c 2的乘积D .温度升高时铀238的半衰期会变小15.下列说法中正确的是A .光波是电磁波B .干涉现象说明光具有粒子性C .光电效应现象说明光具有波动性D .光的偏振现象说明光是纵波16.如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变。
变压器输出的低压交流电通过输电线输送给用户。
定值电阻R 0表示输电线的电阻,变阻器R 表示用户用电器的总电阻。
若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P 向上移动的过程中A .V 2示数变小B .V 1示数变大C .A 2示数变大D .A 1示数变小A 1A 2V 2V 1R~R 0 P17.公元1543年,哥白尼临终前在病榻上为其毕生致力的著作《天体运行论》印出的第一本书签上了自己的姓名。
这部书预示了地心宇宙论的终结。
哥白尼提出行星绕太阳做匀速圆周运动,其运动的示意图如图所示。
假设行星只受到太阳的引力,按照哥白尼上述的观点。
下列说法中正确的是A .太阳对各行星的引力相同B .土星绕太阳运动的向心加速度比火星绕太阳运动的向心加速度小C .水星绕太阳运动的周期大于一年D .木星绕太阳运动的线速度比地球绕太阳运动的线速度大18.如图甲所示,细线下悬挂一个除去了柱塞的注射器,注射器可在竖直面内摆动,且在摆动过程中能持续向下流出一细束墨水。
北京市海淀区2016届高三二模数学理科试题

随机变量 X 的分布列为
X
p
0
1
2
5 12
11 24
1 8
随机变量 X 的期望 E ( X ) 0
5 11 1 17 1 2 . 12 24 8 24
…………………13分
2/9
17解: (Ⅰ)证明:连结 NG,NE .
在 MCD 中,因为 N , G 分别是所在边的中点,所以
(2km 4) 2 4k 2 m 2 16 16km 0 4 2km 所以 x1 x2 k2 m2 x x 1 2 k2
…………………7分
| AD | 1 k 2 | x1 x2 | 1 k 2 | x1 x2 | 2 1 k 2
1 1 ,所以 0 a . 2 2 1 2
…………………11分
综上, a ( , ] . (Ⅲ) a 的取值范围是 a 2 .
…………………12分 …………………14分
19解:(Ⅰ)因为 B (1,0) ,所以 A(1, y1 ), 代入 y 2 4 x ,得到 y1 2 , 又 | BC | 2 ,所以 x2 x1 2 ,所以 x2 3 ,
又 DE P CF ,所以 NK P CF ,所以 NKFC 在一个平面中. 因为 EMF 是等边三角形,所以 EM FK , 又 DE EM ,所以 NK EM , 且 NK I FK K , 所以 EM 平面 NKFC , 而 CN 平面 NKFC ,
3/9
…………………6分
因为 16 16km 0 ,所以 0 km 1 , 所以 法二:设直线 AD 的方程为 y kx m .
S1 km 1 . S2 4 4
2015-2016北京市海淀区高三(下)数学二模试题(理科)及答案

2015-2016北京市海淀区高三(下)二模数学(理科)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知全集=U R ,{|1},{|2},M x x P x x =≤=≥ 则()UM P =A.{|12}x x <<B.{|1}x x ≥C.{|2}x x ≤D.{|12}x x x ≤≥或 2.在数列{}n a 中,12a =,且1(1)n n n a na ++=,则3a 的值为 A.5 B.6 C.7 D.83. 若点(2,4)P 在直线1,:3x t l y at =+⎧⎨=-⎩(t 为参数)上,则a 的值为A.3B.2C.1D.1- 4.在ABC ∆中,34cos ,cos ,55A B == 则sin()A B -= A.725-B.725C.925-D.9255.在5()x a +(其中0a ≠)的展开式中,2x 的系数与3x 的系数相同,则a 的值为 A.2- B.1-C. 1D.26.函数()ln 1f x x x =-+的零点个数是A.1个B.2个C.3个D.4个7. 如图,在等腰梯形ABCD 中,8,4,4AB BC CD ===. 点P 在线段AD 上运动,则||PA PB +的取值范围是A.[6,4+B.C.D.[6,12]8.直线1:10l ax y a+-=与,x y 轴的交点分别为,A B , 直线l 与圆22:1O x y +=的交点为,C D . 给出下面三个结论:① 11,2AOB a S ∆∀≥=; ②1,||||a AB CD ∃≥<; ③11,2COD a S ∆∃≥< 则所有正确结论的序号是 A.①② B.②③ C.①③D.①②③D CABP二、填空题共6小题,每小题5分,共30分。
9. 已知21i, ia =-+其中i 为虚数单位,a ∈R ,则a =__. 10.某校为了解全校高中同学五一小长假参加实践活动的情况,抽查了100名同学,统计他们假期参加实践活动的时间, 绘成频率分布直方图(如图). 则这100名同学中参加实践活动时间在6~10小时内的人数为 ___ .11. 如图,,,A B C 是O 上的三点,点D 是劣弧BC 的中点,过点B 的切线交弦CD 的延长线交BE 于点E . 若∠80BAC =,则__.BED ∠=12. 若点(,)P a b 在不等式组20,20,1x y x y x +-≤⎧⎪--≤⎨⎪≥⎩所表示的平面区域内,则原点O 到直线10ax by +-=距离的取值范围是 .13.已知点πππ((,1),(,0)642A B C ,若这三个点中有且仅有两个点在函数()sin f x x ω=的图象上,则正数..ω的最小值为 .14.正方体1111ABCD A B C D -的棱长为1,点P Q R ,,分别是棱11111A A A B A D ,,的中点,以PQR ∆为底面作正三棱柱,若此三棱柱另一底面三个顶点也都在该正方体的表面上,则这个正三棱柱的高__h =.三、解答题共6小题,共80分。
北京市海淀区2016届高三下学期期末考试(二模)理综物理试卷 Word版含答案

北京市海淀区2016届高三下学期期末考试(二模)理综物理试卷13.如图所示,在一个配有活塞的厚壁有机玻璃筒底放置一小团硝化棉,迅速向下压活塞,筒内气体被压缩后可点燃硝化棉。
在筒内封闭的气体被活塞压缩的过程中 A .气体对外界做正功,气体内能增加 B .外界对气体做正功,气体内能增加 C .气体的温度升高,压强不变 D .气体的体积减小,压强不变14.对下列各原子核变化的方程,表述正确的是A .n He H H 10422131+→+ 是核聚变反应B .n He H H 10422131+→+ 是α衰变 C .e 2Kr S e 01-82368234+→ 是核裂变反应 D .n 2Sr Xe n U 109438140541023592++→+ 是β衰变15.平行的a 、b 两种单色光的光束以相同的入射角从空气斜射向某种长方体玻璃砖上表面的同一位置,在玻璃砖下表面将分开为不同的单色光光束。
若a 光的频率小于b 光的频率,则以下光路图中正确的是16.一列横波沿x 轴正方向传播,t =0时刻的波形图如图甲所示,则图乙描述的可能是A .x =0处质点的振动图像B .x =0.5m 处质点的振动图像C .x =1.5m 处质点的振动图像D .x =2.5m 处质点的振动图像17.若已知引力常量 G ,则利用下列哪组数据可以算出地球的质量A .一颗绕地球做匀速圆周运动的人造卫星的质量和地球表面的重力加速度B .一颗绕地球做匀速圆周运动的人造卫星的质量和地球的第一宇宙速度C .一颗绕地球做匀速圆周运动的人造卫星的运行速率和周期D .地球绕太阳公转的周期和轨道半径18.如图甲所示,交流发电机的矩形金属线圈abcd 的匝数n =100,线圈的总电阻r =5.0Ω,线圈位于匀强磁场中,且线圈平面与磁场方向平行。
线圈的两端分别与两个彼此绝缘的铜环E 、F(集流环)焊接在一起,并通过BA-2s 硝化棉活塞 有机乙甲电刷与阻值R =95Ω的定值电阻连接。
北京市海淀区2016届高三二模数学(理)试题【含答案】

北京市海淀区2015-2016学年度第二学期高三综合练习(二)数学(理科)2016.5一、选择题:本大题共8小题,每小题5分,共40分,在四个选项中,选出符合题目要求的一项 1.已知全集{}{}12U R M x x P x x ==≤=≥,,,则()U C MP =( )A .{}12x x <<B .{}1x x ≥C .{}2x x ≤D .{}12x x x ≤≥或 2.在数列{}n a 中,12a =且()11n n n a na ++=,则3a 的值为( ) A .5 B .6 C .7 D .83.若点()2,4P 在直线1:3x t l y at=+⎧⎨=-⎩(t 为参数)上,则a 的值为( ) A .3 B .2 C .1 D .1-4.在ABC ∆中,3cos 5A =,4cos 5B =,则()sin A B -=( ) A .725- B .725C .925-D .9255.在()5x a +(其中0a ≠)的展开式中,2x 的系数与3x 的系数相同,则a 的值为( ) A .2- B .1- C .1 D .2 6.函数()ln 1f x x x =-+的零点个数是( ) A .1 B .2 C .3 D .47.如图,在等腰梯形ABCD 中,8AB =,4BC =,4CD =,点P 在线段AD 上运动,则PA PB +的取值范围是( )A .6,4⎡+⎣B .⎡⎤⎣⎦C .⎡⎤⎣⎦D .[]6,128.直线1:10l ax y a+-=与x ,y 轴的交点分别为A B ,,直线l 与圆22:1O x y +=的交点为C D ,,给出下面三个结论: ①1a ∀≥,12AOB S ∆=;②1a ∃≥,AB CD <;③1a ∃≥,12COD S ∆< 其中,所有正确结论的序号是( )A .①②B .②③C .①③D .①②③二、填空题共6小题,每小题5分,共30分. 9.已知21i a i=-+,其中i 为虚数单位,a R ∈,则a =_____________. 10.某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的时间,绘成频率分布直方图(如图)。
北京市海淀区2016届高三二模数学理试题(WORD版含官方参考答案及评分标准)

2{x|x "或x _2}3.若点P(2,4)在直线l :y =3-at北京市海淀区高三年级二模数学(理科) 2016.5本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知全集 U=R ,M ={x|x 叮}, P ={x|x _2},则 E (MUP) A. {x |1 ::: x ::2} B. {x|x 亠1} C. {x|x 込2} D.2.在数列{a n }中,印=2,且(n 1)a n = na n 1,则a 3的值为X =1 +t x L, ( t 为参数)上,则a 的值为6.函数f (x) = In x 「x 1的零点个数是A. 5B.C. D.A. 3B. C.D.-14.在ABC 中,则 sin(A-B)=A.25 B.25 C. 25D.255.在(x a)5(其中a=0)的展开式中, x 2的系数与 x 3 * 5的系数相同,则的值为A. -2B.-1 C. 1 D.A.1个B.2C.3D.47.如图,在等腰梯形ABCD中,AB =8, BC =4,CD =4.点P在线段AD上运动,则|PA • PB |的取值范围是A. [6,4 4 3]B. [42,8]C.[4、、3,8]D.[6,12]18.直线l :ax丄y -1 =0与x,y轴的交点分别为A,B,直线l与圆a 2• y2 = 1的交点为C, D .给出下面三个结论:1①-a -1,S AOB;② a—1,|AB 卜:|CD| ;® &一1$迹1B2则所有正确结论的序号是 A.①②B.②③ C.①③D.①②③二、填空题共6小题,每小题5分,共30分。
29.已知 —— =1 _i,其中i 为虚数单位,a € R ,则a =_.a i10. 某校为了解全校高中同学五一小长假参加实践活动的情况,抽查了100名同学,统计他们假期参加实践活动的时间 ,绘成频率分布直方图(如图)•则这100名同学中参加实践活动时间在 6~10小时内的人数为 .11. 如图,A,B,C 是L O 上的三点,点D 是劣弧Be 的中点,过点B 的切线交弦CD 的延长线交 BE于点E .若/ BAC=80,则N BED=__.x y -2 乞0,I、12. 若点P(a,b)在不等式组x-y-2乞0,所表示的平面区域内,则原点O 到直线I x _1ax +by -1 =0距离的取值范围是__.13. 已知点A (£片),B (n ,1),C(n ,0),若这三个点中有且仅有两个点在函6 2 4 2数f(x)=sincox 的图象上,则正 数⑷的最小值为14. 正方体ABCD 1人B 1C 1D 棱长为1 ,点P , Q R 分别是棱AA , A 1B 1, AD 1的中点,以UPQR 为底面作正三棱柱,若此三棱柱另一底面三个顶点也都在该 正方体的表面上,则这个正三棱柱的高h=.频率AOB'DE C(I)比较 f(n ),f (n 的大小;三、解答题共6小题,共80分。
北京海淀高三二模理综试题及答案

2016年北京海淀高三二模理综试题及答案(word版)海淀区高三年级2015~2016学年度第二学期期末练习理科综合能力测试可能用到的相对原子质量:Hl C 12 N 14 0 16 Na 23 K 39 Cl第一部分(选择题共120分)本部分共20小题,每小题6分,共120分。
在每小题列出的四个选项中,选出最符合题目要求的一项。
1.寨卡病毒是一种RNA病毒,能引起人患病。
下列有关寨卡病毒的叙述正确的是A.具有完整的细胞结构 B.含有A、T、G、C四种碱基C.可寄生在人体细胞内 D。
不能作为抗原诱导免疫应答2.在愈伤组织形成幼苗的过程中,细胞中不会发生A.丙酮酸在线粒体基质中被分解生成CozB.水在叶绿体基质中被分解生成02C.脱氧核苷酸在细胞核中聚合成DNAD.氨基酸在核糖体上脱水缩合形成多肽3.L病毒侵染小鼠的脑膜细胞,引起脑膜炎,L蛋白是L病毒的抗原蛋白。
科研人员将两只转基因小鼠进行杂交,让能表达L蛋白和L蛋白受体的子代小鼠感染L病毒,会引起严重的糖尿病,如图所示。
据此作出的分析,不正确的是A.作为亲本的两只转基因小鼠均为杂合子B.转入基因的遗传一定不遵循自由组合定律C.L病毒侵染的细胞可被效应T细胞裂解D.小鼠患糖尿病的原因是胰岛B细胞被杀伤4.狒狒种群中存在等级,经个体间的战斗较量之后,体格最强壮、最凶猛的雄狒狒成为“首领”,它在选择食物、与雌性交配中都处于优先地位。
“首领”也负责指挥整个种群,与其他雄狒狒共同保卫种群。
下列相关叙述不正确的是A.狒狒种群通过种间竞争建立了等级制度B.狒狒种群内个体的分工合作需要信息交流C.“首领”优先享有配偶有利于优良基因的传递D.战斗较量对战败个体不利,对种群的延续有利5.生物学研究中,下列做法不可行的是A.用红、绿荧光染料标记膜蛋白研究细胞膜的流动性B.用叶绿体作为标志物观察胞质环流(细胞质流动)C.用标记基因检测目的基因是否导入受体细胞D.用3H标记的胸腺嘧啶研究基因的表达过程6. 下列生活中常见用品和其主要成分对应正确的是A B C D用品名称煤炭 酚醛树脂手柄明矾手工肥皂主要成分C碳单质OH苯酚Al 2(SO 4)3·12H2O十二水合硫酸铝C 17H 35COONa 硬脂酸钠7. 海洋中的珊瑚虫经如下反应形成石灰石外壳,进而形成珊瑚:Ca 2+ + 2HCO 3- CaCO 3 + H 2O + CO 2。
北京市海淀区2015届高三数学下学期期末练习试题 理(扫描版)新人教A版-推荐下载

2ac
3.
36
(10) 30 ,1
(13)14
3.
3.
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置各试时类卷,管调需路控要习试在题验最到;大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资,常料要工试加况卷强下安看与全22过,22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海淀区高三年级2015-2016学年度第二学期期末练习
数学试卷(理科) 2016.5
本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上 作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知全集}2|{},1|{,≥=≤==x x P x x M R U ,则=⋃)(P M C U
A .}21|{<<x x
B .}1|{≥x x
C .}2|{≤x x
D .}21|{≥≤x x x 或
2.在数列{}n a 中,12a =且1(1)n n n a na ++=,则3a 的值为
A .5
B .6
C .7
D .8
3.若点P (2,4)在直线l :上为参数)(3,
1t at y t x ⎩
⎨
⎧-=+=,则a 的值为
A .3
B .2
C .1
D .1-
4.在ABC ∆中,3cos 5A =
,4
cos 5
B =,则sin()A B -= A .7
25
-
B .725
C .925-
D .
9
25
5.在5
)
(a x +(其中0≠a )的展开式中,2x 的系数与3x 的系数相同,则a 的值为 A .-2 B .-1 C .1 D .2
6.函数()ln 1f x x x =-+的零点个数是
A .1
B .2
C .3
D .4
7.如图,在等腰梯形ABCD 中,8AB =,4BC =,4CD =,点P 在线段AD 上运动,则PA PB +
的
取值范围是
A
.[6,4+ B
. C
.
D .[6,12]
8.直线1
:10l ax y a +
-=与x
22:1O x y +=的交点为,C D ,给 出下面三个结论: ①1a ∀≥,12AOB S ∆=
;②1a ∃≥,AB CD <;③1a ∃≥,1
2
COD S ∆< A
B
其中,所有正确结论的序号是 A .①②
B .②③
C .①③
D .①②③
二、填空题共6小题,每小题5分,共30分。
9.已知
2
1i a i
=-+,其中i 为虚数单位,a R ∈,则a =_____________. 10.某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实
践活动的时间,绘成频率分布直方图(如图)。
这100名学生中参加实践活动的时间在610 小时内的人数为_______________.
11.如图,A,B,C 是⊙O 上的三点,点D 是劣弧 BC
的中点,过点B 的切线交弦CD 的延长线于点E ,若 ︒=∠80BAC ,则=∠BED ___________________.
12.若点(,)P a b 在不等式组20
201x y x y x +-≤⎧⎪
--≤⎨⎪≥⎩
所表示的平面区域内,则原点O 到直
线10ax by +-=的距离的取值范围是__________________.
13.已知点A )
,
(2
3
6
π
,B ),(14π,C ),(02π,若这三个点中有且仅有两个点在函数x x f ωsin )(=的图像上,则正数..ω的最小值为_____________.
14.正方体1111ABCD A BC D -的棱长为1,点,,P Q R 分别为棱1A A ,11A B ,
11A D 的中点,以PQR ∆为
底面作正三棱柱,若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高
h =__________.
三、解答题共6小题,共80分。
解答应写出文字说明、演算步骤或证明过程。
15.(本小题满分13分)
已知函数()2sin cos2f x x x =-- (Ⅰ)比较,46f f ππ⎛⎫⎛⎫
⎪ ⎪⎝⎭⎝⎭
的大小; (Ⅱ)求函数()f x 的最大值.
16.(本小题满分13分)
某空调专卖店试销A 、B 、C 三种新型空调,销售情况如下表所示:
(Ⅰ)求A 型空调前三周的平均周销售量;
(Ⅱ)根据C 型空调前三周的销售情况,预估C 型空调五周的平均周销售量为10台,
当C 型空调周销售量的方差最小时,求4C ,5C 的值;
(注:方差2
121
[()()()]n s x x x x x x n
=
-+-+⋅⋅⋅+-,其中x 为12,,,n x x x ⋅⋅⋅的平均数) (Ⅲ)为跟踪调查空调的使用情况,根据销售记录,从第二周和第三周售出的空调中分别随机抽取一台,求抽取的两台空调中A 型空调台数X 的分布列及数学期望.
17.(本小题满分14分)
如图,等腰梯形ABCD 中,CD AB //,AB DE ⊥于
E ,AB C
F ⊥于F ,且,2===EF BF AE
,2==CF DE 将AED ∆和BFC ∆分别沿DE ,CF 折起,
使A ,B 两点重合,记为点M ,得到一个四棱锥
CDEF M -,点G ,N ,H 分别是MC ,MD ,EF 的中点.
(Ⅰ)求证://GH 平面DEM ; (Ⅱ)求证:CN EM ⊥;
(Ⅲ)求直线GH 与平面NFC 所成角的大小.
18.(本小题满分14分)
已知函数)()(2a ax x e x f x ++=. (Ⅰ)当1=a 时,求函数()f x 的单调区间;
(Ⅱ)若关于x 的不等式()a f x e ≤在),[+∞a 上有解,求实数a 的取值范围;
(Ⅲ)若曲线()y f x =存在两条互相垂直的切线,求实数a 的取值范围.(只需直接写出结果).
19.(本小题满分13分)
已知点11(,)A x y ,22(,)D x y (12x x <)是曲线2
4y x =(0y ≥)上的两点,,A D 两点在x 轴上的射影分别为点,B C ,且2BC =
(Ⅰ)当点B 坐标为(1,0)时,求直线AD 的斜率;
(Ⅱ)记OAD ∆的面积为1S ,梯形ABCD 的面积为2S ,求证:
121
4
S S <.
20.(本小题满分13分)
已知集合12{|(,,,,,)n i n X X x x x x Ω==⋅⋅⋅⋅⋅⋅,{0,1},1,2,,}i x i n ∈=⋅⋅⋅,其中3n ≥,
12(,,,,,)i n n X x x x x ∀=⋅⋅⋅⋅⋅⋅∈Ω,称i x 为X 的第i 个坐标分量,若n S ⊆Ω,且满足如下两条性质:
①S 中元素个数不少于4个;
②,,X Y Z S ∀∈,存在{1,2,,}m n ∈⋅⋅⋅,使得,,X Y Z 的第m 个坐标分量是1; 则称S 是n Ω的一个好子集.
(Ⅰ){,,,}S X Y Z W =为3Ω的一个好子集,且(1,1,0)X =,(1,0,1)Y =,写出,Z W ; (Ⅱ)若S 为n Ω的一个好子集,求证:S 中元素个数不超过1
2n -;
(Ⅲ)若S 为n Ω的一个好子集,且S 中恰有1
2
n -个元素,求证:一定存在唯一一个{1,2,,}k n ∈⋅⋅⋅,使得
S 中所有元素的第k 个坐标分量都是1.。
