三峡大学数学与应用数学专业实验班
2023年三峡大学各省招生计划专业人数(招多少人)

2023年三峡大学各省招生计划专业人数(招多少人)2023年三峡大学在广东省招生计划院校名称批次专业组专业名称招生人数三峡大学本科批201投资学2三峡大学本科批201供应链管理2三峡大学本科批202水利水电工程4三峡大学本科批202工程管理4三峡大学本科批202土木工程4三峡大学本科批205电气工程及其自动化(中外合作办学)4三峡大学本科批206材料类4三峡大学本科批207电气工程及其自动化6三峡大学本科批207电气工程及其自动化4三峡大学本科批207智能电网信息工程42023年三峡大学在黑龙江省招生计划院校名称批次专业代码专业名称计划数三峡大学本科第一批A段01生物科学2三峡大学本科第一批A段02机械设计制造及其自动化2三峡大学本科第一批A 段03电气工程及其自动化2三峡大学本科第一批A段04电气工程及其自动化6三峡大学本科第一批A段05智能电网信息工程2三峡大学本科第一批A段06土木工程2三峡大学本科第一批A段07水利水电工程2三峡大学本科第一批A 段08环境工程2三峡大学本科第一批A段09工程管理2三峡大学本科第一批A 段01电气工程及其自动化22023年三峡大学在江西省招生计划院校名称院校招生代码批次专业名称招生人数三峡大学2558本一批材料类8三峡大学2558本一批财务管理4三峡大学2558本一批储能科学与工程4三峡大学2558本一批电气工程及其自动化4三峡大学2558本一批电气工程及其自动化2三峡大学2558本一批电气工程及其自动化2三峡大学2558本一批护理学2三峡大学2558本一批化学4三峡大学2558本一批化学工程与工艺5三峡大学2558本一批环境工程2三峡大学2558本一批机械设计制造及其自动化4三峡大学2558本一批建筑类2三峡大学2558本一批金融学2三峡大学2558本一批临床医学4三峡大学2558本一批能源与动力工程2三峡大学2558本一批人力资源管理2三峡大学2558本一批生物工程6三峡大学2558本一批生物科学6三峡大学2558本一批数据科学与大数据技术2三峡大学2558本一批数学类2三峡大学2558本一批水利水电工程2三峡大学2558本一批水文与水资源工程2三峡大学2558本一批通信工程4三峡大学2558本一批土木工程6三峡大学2558本一批外国语言文学类4三峡大学2558本一批物理学2三峡大学2558本一批药学2三峡大学2558本一批医学影像学2三峡大学2558本一批智能制造工程2三峡大学2558本一批中医学2三峡大学2558本一批自动化2三峡大学2558本一批财务管理2三峡大学2558本一批法学2三峡大学2558本一批供应链管理2三峡大学2558本一批行政管理2三峡大学2558本一批护理学2三峡大学2558本一批人力资源管理2三峡大学2558本一批投资学2三峡大学2558本一批中国语言文学类22022年三峡大学各省录取分数线及位次省市批次专业组最低分最低位次北京本科批三峡大学(02)51223533天津本科A 批三峡大学5组54825002河北本科批-54413419辽宁本科批-51011613上海本科批三峡大学(03)42332861江苏本科批三峡大学01组52025298浙江一段-56884892福建本科批三峡大学506组52339492山东一段-52991353湖北本科批三峡大学第01组(少数民族预科班)51517175湖南本科批三峡大学第9组51954414广东本科批三峡大学206组56553252海南本科批三峡大学(11)6158268重庆本科批-52682482023高考志愿录取规则“分数优先、遵循志愿、一次投档、不再补档”1、分数优先:每一批次每一阶段院校录取时,高考总分高的考生先于总分较低的考生投档2、遵循志愿:每个考生所填的院校志愿是有先后顺序的,计算机投档时按考生填报的院校志愿顺序依次进行检索说明:高考未改革省份,通常可以填6-9个志愿,新高考省份通常有96-100多个志愿,投档时按照志愿1、志愿2、志愿3、志愿4…顺序投档,直到满足就投出,都不满足,就掉档了,只能等征集志愿和下一批次录取,所以我们要把分数最高、最想上的学校专业填在最前面,切记切记,不要乱填,如果你志愿1是个分数低的、不想上的学校,那会直接被录取的,那真是有苦难言。
三峡大学2011年选修课表

100 100 90 90 90 90 90 80 80 90 90 90 90 90 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 110 100 100
10自动化,电子,电自 (输电线路) 10自动化,电子,电自 (输电线路) 10电自,电自(新能 源) 10电自,电自(新能 源) 10电自,电自(新能 源) 10电自,电自(新能 源) 10电自,电自(新能 源) 10数学,信计 10数学,信计 10机械除工业 10机械除工业 10机械除工业 10机械除工业 10机械除工业 10通信,计算机(嵌入 式),计算机(软件工 10通信,计算机(嵌入 式),计算机(软件工 07—09所有专业 07—09所有专业 10水环学院,土木工程 10水环学院,土木工程 10水环学院,土木工程 10化生学院除生态,教 技(数字媒体) 10化生学院除生态,教 技(数字媒体) 10化生学院除生态,教 技(数字媒体) 10化生学院除生态,教 技(数字媒体) 10水工(英才班),土 木(英才班) 10水工(英才班),土 木(英才班) 10水工(英才班),土 木(英才班) 07—09所有专业 10工业工程,生态学 10临床医学 10临床医学 10医学影像学 10电气学院 10电气学院
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 120 120 120 100 100 100 100 80 80 100 100 100 100 100 100 100
10电气学院 10电气学院 10电气学院 10电气学院 10电气学院 10电气学院 10理学院除物理 10理学院除物理 10理学院除物理 10通信,计算机(嵌入 式),计算机(软件工 10通信,计算机(嵌入 式),计算机(软件工 10机械除工业 10机械除工业 10机械除工业 10机械除工业 10水环学院 10水环学院 10水环学院 10水环学院 10化生学院除生态 10化生学院除生态 10化生学院除生态 10土木,土木(英才 班),教技(数字媒 10土木,土木(英才 班),教技(数字媒 10土木,土木(英才 班),教技(数字媒 10工业工程,生态学 10电自(输电线路工程 方向) 10电自(输电线路工程 方向) 10计算机学院 10计算机学院 10计算机学院 10机械除工业 10机械除工业 10机械除工业 10机械除工业
应用数学考研录取学校排名

应用数学研究生录取学校排名1 北京大学A+ 15 东南大学A 29 北京航空航天大学A2 浙江大学A+ 16 上海交通大学A 30 哈尔滨工业大学A3 清华大学A+ 17 中山大学A 31 上海大学A4 复旦大学A+ 18 武汉大学A 32 福州大学A5 中国科学技术大学A+ 19 华中科技大学A 33 中南大学A6 南开大学A+ 20 北京理工大学A 34 电子科技大学A7 四川大学A+ 21 湖南大学35 苏州大学A8 山东大学A+ 22 西安电子科技大学A 36 华中师范大学A9 新疆大学A+ 23 华东师范大学A 37 华东理工大学A10 北京师范大学A+ 24 西北工业大学A 38 首都师范大学A11 吉林大学A 25 西安交通大学A 39 厦门大学A12 南京大学A 26 同济大学A 40 陕西师范大学A13 大连理工大学A 27 重庆大学A 41 广州大学A14 兰州大学A 28 华南理工大学A 42 云南大学AB+等(63个):河北师范大学、西北师范大学、湘潭大学、曲阜师范大学、湖南师范大学、东北师范大学、北京交通大学、南京师范大学、暨南大学、辽宁师范大学、江苏大学、安徽师范大学、合肥工业大学、华南师范大学、南昌大学、东北大学、东华大学、广西大学、桂林电子科技大学、哈尔滨工程大学、四川师范大学、辽宁大学、河海大学、郑州大学、内蒙古大学、天津大学、长江大学、广东工业大学、北京科技大学、徐州师范大学、南京航空航天大学、上海师范大学、西南交通大学、山东科技大学、扬州大学、北京工业大学、武汉理工大学、兰州理工大学、大连海事大学、温州大学、南京信息工程大学、北方工业大学、上海理工大学、浙江工业大学、山东师范大学、宁波大学、湖南科技大学、浙江师范大学、哈尔滨理工大学、安徽大学、福建师范大学、中国矿业大学、广西师范大学、江南大学、黑龙江大学、西安建筑科技大学、河南师范大学、北京邮电大学、南京农业大学、兰州交通大学、成都理工大学、西安理工大学、长沙理工大学B等(62个):安庆师范学院、武汉科技大学、河北大学、南京财经大学、中国海洋大学、江西师范大学、重庆师范大学、杭州电子科技大学、中北大学、中国人民大学、山西大学、西南大学、青岛大学、河南大学、河北工业大学、五邑大学、太原理工大学、渤海大学、辽宁工程技术大学、湖北大学、青岛科技大学、深圳大学、西华大学、贵州大学、云南师范大学、长春工业大学、大连大学、天津工业大学、南京邮电大学、汕头大学、华北电力大学、烟台大学、聊城大学、中国农业大学、北京化工大学、中国石油大学、青岛理工大学、信阳师范学院、河北科技大学、哈尔滨师范大学、华东交通大学、西安科技大学、安徽理工大学、三峡大学、西北农林科技大学、辽宁工业大学、河南科技大学、集美大学、中国计量学院、海南大学、上海财经大学、南京理工大学、南昌航空工业学院、南华大学、南通大学、东北林业大学、宁夏大学、海南师范大学、中南民族大学、西华师范大学、安徽工业大学、中国传媒大学不跨专业:基础数学,应用数学,概率论与数理统计,计算数学,运筹学与控制论跨专业:经济学和计算机方向精算学——(华东师范大学)生物数学——(中国科学技术大学)信息安全——(山东大学) 信息计算科学—(中山大学)不确定性处理的数学——(四川大学) 数学物理——(中国科学技术大学)金融数学与金融工程——(山东大学) 信息安全——四川大学近年来,由于受社会供求的影响,文科类的法律、工商管理、金融经济、MBA、会计,理工科类的医学、电子信息类、计算机类,社会需求量比较大,找工作普遍比较容易,待遇薪水也比较高,属于当前比较热门的专业。
三峡大学2007年-2009年获准立项尚未结题的校级教学研究项

外国语学院
游凌
陈莉莉张春玲栗园园肖惜
3000元
重点项目
J2009021
大学体育“课内外学习一体化”运行机制的研究与实践
体育学院
王炳华
杨玲吴志勇王志刚戴绍斌谌凯
3000元
重点项目
J2009022
加强临床思维以培养医学影像学应用型人才的研究
第一临床医学院
周军
姚志赵云崔向军余成新
3000元
经管学院
黄正伟
谢五洲郭成恒王珍
学院资助
一般项目
J2009047
地方综合性高校财务管理专业应用型人才实践能力培养模式研究
经管学院
刘进梅
涂娟黄廷政胡莺张伟立
学院资助
一般项目
J2009048
经济管理科学知识内化成职业化素质的途径研究与实践
经管学院
秦朝钧
何伟军邹文娜冯芳张震熊玲苏金明
学院资助
一般项目
J2009050
电气信息类计算机硬件课程体系研究与实践
电气信息学院
陈慈发
周学君覃颖丁晓波胡少甫
学院资助
一般项目
J2009033
电路习题课教学的研究与实践
电气信息学院
周久艳
吉培荣粟世伟பைடு நூலகம்赟宁
学院资助
一般项目
J2009034
电力电子技术教学中MATLAB仿真与工程理念的引入及探究
电气信息学院
陈堂贤
陈刚肖建修王归新代红
学院资助
土木水电学院
徐刚
董晓华杜发兴刘冀玄英姬
学院资助
一般项目
J2009029
基于模糊规则教学评价制度与质量管理的研究
三峡大学高等数学教材

三峡大学高等数学教材高等数学是一门经典而重要的学科,它是数学基础学科中的一门重要课程。
教材的编写对于学生的学习起着至关重要的作用。
本文将以三峡大学高等数学教材为题,详细探讨教材的内容、编写原则和应用。
一、教材的内容三峡大学高等数学教材是一本系统、全面、深入的教材,旨在帮助学生掌握高等数学的基本概念、原理和方法。
教材内容包括但不限于:1. 微分学部分:包括函数、极限、连续与间断、导数及其应用等内容。
通过理论阐述和大量的例题,学生能够深入了解微分学的基本思想和方法,掌握求导和应用的技巧。
2. 积分学部分:包括定积分、不定积分、定积分的应用等内容。
通过系统地介绍积分的基本性质和求解方法,学生能够掌握积分学的理论和实际应用。
3. 级数学部分:包括数列、级数、收敛与发散等内容。
通过实例的引入和相关概念的介绍,学生可以了解级数学的基本性质和应用领域。
二、教材的编写原则三峡大学高等数学教材的编写严格按照以下原则进行:1. 系统性原则:教材按照知识的逻辑结构有机地展开,形成系统的学习框架。
每个章节都有明确的主题和目标,让学生能够逐步建立数学思维的框架。
2. 简明性原则:教材力求言简意赅,避免啰嗦冗长的叙述。
重点内容突出,困难点明确,为学生提供清晰的学习路径。
3. 应用性原则:教材注重将数学理论与实际问题相结合,通过实例和应用案例,培养学生的实际问题解决能力和数学思维的灵活运用。
4. 温馨性原则:教材把握好内容的难易度和进度,关注学生的学习需求,引导学生以积极的态度投入到高等数学学习当中。
三、教材的应用三峡大学高等数学教材在教学实践中发挥着重要的作用。
教师可以根据课程大纲和学生的实际情况,灵活选择教材的章节和内容。
在教学过程中,可以通过课堂讲授、习题训练、示范演示等方式,激发学生的学习兴趣,提高学生的学习效果。
此外,教材还可以在自学和复习阶段作为学生的重要参考资料。
学生可以通过认真阅读教材,深刻理解高等数学的理论框架,巩固基本知识,拓展应用技巧,提升解题能力。
地方性院校数学与应用数学复合型人才培养实验班的探讨

学 教师、应 用型数学人才、基础教育数学 教师五类,根据我 国
等 教 育 的数 学 教 师 需 求 的特 点 是 高层 次 ,少 而精 。 这 类 人 才 的
() 择 优 推荐 免试 : 五学 期 结 束 ,根 据 学 生 主 修 专业 前 3 第
作者简介 :罗 文 (95 ) 从 16 一 ,男,湖北仙桃人 ,三峡大学理学院,教授,主要研 究方向 : 代数学。( 湖北 宜昌 4 3 0) 40 2
基 金 项 目 : 文 系湖北 省高等 学校 省级 教 学研 究项 目 ( 目 本 项 编号 : 0 80 ) 的研 究成 果 。 2 022
CE E中国电力教育 P
而 而 雨一
地方性院校数学与应用数学复合型 人才培养实验班的探讨
罗从 文
摘要 : 文章分析了 社会对数学本科专业人 才的需求情况,以三峡 大学为例,探讨了 地方综合性院校数学与应用数学复合型人才培养 实验班的模式、政 策保障措施 及人 才 养的预期效果。 培 关键词 :数学与应用数学 ; 实验班 ; 人才培养
包 ()统一主修模 式 : 1 统一按数学与应用数学专业培养方案 学 位 模 块 同时 执 行 双 学 位 或 辅 修 专业 相 关 课 程 ( 括 教 师 教 育 进 行主 修 专业 培 养 ,同 时加 强 通 识性 基 础 教育 、综 合 素质 教 育, 课程)以及考研辅导课程 ; 课 程 统 一设 置 、统 一 要求 。
现 状 、 社 会 发展 的需 要和 市 场 的需 要 , 专职 数 学 研 究 人 员和 高 五学期学习情况择优推荐免试攻读硕士研究生。
第一章函数与极限三峡大学高等数学教案

第一章函数与极限教学目:1、理解函数概念,驾驭函数表示方法,并会建立简洁应用问题中函数关系式。
2、理解函数奇偶性、单调性、周期性和有界性。
3、理解复合函数及分段函数概念,理解反函数及隐函数概念。
4、驾驭根本初等函数性质及其图形。
5、理解极限概念,理解函数左极限与右极限概念,以及极限存在与左、右极限之间关系。
6、驾驭极限性质及四那么运算法那么。
7、理解极限存在两个准那么,并会利用它们求极限,驾驭利用两个重要极限求极限方法。
8、理解无穷小、无穷也许念,驾驭无穷小比较方法,会用等价无穷小求极限。
9、理解函数连续性概念〔含左连续与右连续〕,会判别函数连续点类型。
10、理解连续函数性质和初等函数连续性,理解闭区间上连续函数性质〔有界性、最大值和最小值定理、介值定理〕,并会应用这些性质。
教学重点:1、复合函数及分段函数概念;2、根本初等函数性质及其图形;3、极限概念极限性质及四那么运算法那么;4、两个重要极限;5、无穷小及无穷小比较;6、函数连续性及初等函数连续性;7、区间上连续函数性质。
教学难点:1、分段函数建立与性质;2、左极限与右极限概念及应用;3、极限存在两个准那么应用;4、连续点及其分类;5、闭区间上连续函数性质应用。
§1. 1 映射与函数一、集合1. 集合概念集合(简称集): 集合是指具有某种特定性质事物总体. 用A, B, C….等表示.元素: 组成集合事物称为集合元素. a是集合M元素表示为a∈M.集合表示:列举法: 把集合全体元素一一列举出来.例如A={a, b, c, d, e, f, g}.描绘法: 假设集合M是由元素具有某种性质P元素x全体所组成, 那么M可表示为A={a1, a2, ⋅⋅⋅, a n},M={x | x具有性质P }.例如M={(x, y)| x, y为实数, x2+y2=1}.几个数集:N表示全部自然数构成集合, 称为自然数集.N={0, 1, 2, ⋅ ⋅ ⋅, n, ⋅ ⋅ ⋅}. N+={1, 2, ⋅ ⋅ ⋅, n, ⋅ ⋅ ⋅}.R表示全部实数构成集合, 称为实数集.Z表示全部整数构成集合, 称为整数集.Z={⋅ ⋅ ⋅, -n, ⋅ ⋅ ⋅, -2, -1, 0, 1, 2, ⋅ ⋅ ⋅, n, ⋅ ⋅ ⋅}.Q表示全部有理数构成集合, 称为有理数集.子集: 假设x∈A, 那么必有x∈B, 那么称A是B子集, 记为A⊂B(读作A包含于B)或B⊃A .假如集合A与集合B互为子集, A⊂B且B⊂A, 那么称集合A与集合B相等, 记作A=B.假设A⊂B且A≠B, 那么称A是B真子集, 记作A B . 例如, N Z Q R.不含任何元素集合称为空集, 记作∅. 规定空集是任何集合子集.2. 集合运算设A、B是两个集合, 由全部属于A或者属于B元素组成集合称为A与B并集(简称并), 记作A⋃B, 即A⋃B={x|x∈A或x∈B}.设A、B是两个集合, 由全部既属于A又属于B元素组成集合称为A与B交集(简称交), 记作A⋂B, 即A⋂B={x|x∈A且x∈B}.设A、B是两个集合, 由全部属于A而不属于B元素组成集合称为A与B差集(简称差), 记作A\B, 即A\B={x|x∈A且x∉B}.假如我们探讨某个问题限定在一个大集合I中进展, 所探讨其他集合A都是I子集. 此时, 我们称集合I为全集或根本集. 称I\A为A余集或补集, 记作A C.集合运算法那么:设A、B、C为随意三个集合, 那么(1)交换律A⋃B=B⋃A, A⋂B=B⋂A;(2)结合律(A⋃B)⋃C=A⋃(B⋃C), (A⋂B)⋂C=A⋂(B⋂C);(3)安排律(A⋃B)⋂C=(A⋂C)⋃(B⋂C), (A⋂B)⋃C=(A⋃C)⋂(B⋃C);(4)对偶律(A⋃B)C=A C⋂B C, (A⋂B)C=A C⋃B C.(A⋃B)C=A C⋂B C证明:x∈(A⋃B)C⇔x∉A⋃B⇔x∉A且x∉B⇔x∈A C且x∈B C⇔x∈A C⋂B C, 所以(A⋃B)C=A C⋂B C.直积(笛卡儿乘积):设A、B是随意两个集合, 在集合A中随意取一个元素x, 在集合B中随意取一个元素y, 组成一个有序对(x, y), 把这样有序对作为新元素, 它们全体组成集合称为集合A与集合B直积, 记为A⨯B, 即A⨯B={(x, y)|x∈A且y∈B}.例如, R⨯R={(x, y)| x∈R且y∈R }即为xOy面上全体点集合, R⨯R常记作R2.3. 区间和邻域有限区间:设a<b, 称数集{x|a<x<b}为开区间, 记为(a, b), 即(a, b)={x|a<x<b}.类似地有[a, b] = {x | a ≤x≤b }称为闭区间,[a, b) = {x | a≤x<b }、(a, b] = {x | a<x≤b }称为半开区间.其中a和b称为区间(a, b)、[a, b]、[a, b)、(a, b]端点, b-a称为区间长度.无限区间:[a, +∞) = {x | a≤x }, (-∞, b] = {x | x < b } , (-∞, +∞)={x | | x | < +∞}.区间在数轴上表示:邻域: 以点a为中心任何开区间称为点a邻域, 记作U(a).设δ是一正数, 那么称开区间(a-δ, a+δ)为点aδ邻域, 记作U(a, δ), 即U(a, δ)={x | a-δ< x < a+δ}={x | | x-a|<δ}.其中点a称为邻域中心, δ称为邻域半径.去心邻域(a, δ):(a, δ)={x |0<| x-a |<δ}二、映射1. 映射概念定义设X、Y是两个非空集合, 假如存在一个法那么f, 使得对X中每个元素x, 按法那么f, 在Y中有唯一确定元素y与之对应, 那么称f为从X到Y映射, 记作f : X→Y ,其中y称为元素x(在映射f下)像, 并记作f(x), 即y=f(x),而元素x称为元素y(在映射f下)一个原像; 集合X称为映射f定义域, 记作D f, 即D f=X ;X中全部元素像所组成集合称为映射f值域, 记为R f, 或f(X), 即R f=f(X)={f(x)|x∈X}.须要留意问题:(1)构成一个映射必需具备以下三个要素: 集合X, 即定义域D f=X; 集合Y, 即值域范围: R f⊂Y; 对应法那么f, 使对每个x∈X, 有唯一确定y=f(x)与之对应.(2)对每个x∈X, 元素x像y是唯一; 而对每个y∈R f, 元素y原像不肯定是唯一; 映射f值域R f是Y一个子集, 即R f⊂Y, 不肯定R f=Y .例1设f : R→R, 对每个x∈R, f(x)=x2.明显, f是一个映射, f定义域D f=R, 值域R f={y|y≥0}, 它是R一个真子集. 对于R f中元素y, 除y=0外, 它原像不是唯一. 如y=4原像就有x=2和x=-2两个.例2设X={(x, y)|x2+y2=1}, Y={(x, 0)||x|≤1}, f : X→Y, 对每个(x, y)∈X, 有唯一确定(x, 0)∈Y与之对应.明显f是一个映射, f定义域D f=X, 值域R f=Y. 在几何上, 这个映射表示将平面上一个圆心在原点单位圆周上点投影到x轴区间[-1, 1]上.例3.f :→[-1, 1], 对每个x∈, f(x)=sin x .f是一个映射, 定义域D f =, 值域R f=[-1, 1].满射、单射和双射:设f是从集合X到集合Y映射, 假设R f=Y, 即Y中任一元素y都是X中某元素像, 那么称f为X到Y上映射或满射; 假设对X中随意两个不同元素x 1≠x 2, 它们像f(x 1)≠f(x 2), 那么称f为X到Y单射; 假设映射f既是单射, 又是满射, 那么称f为一一映射(或双射).上述三例各是什么映射?2. 逆映射与复合映射设f是X到Y单射, 那么由定义, 对每个y∈R f , 有唯一x∈X, 合适f(x)=y, 于是, 我们可定义一个从R f到X新映射g, 即g : R f→X,对每个y∈R f , 规定g(y)=x, 这x满意f(x)=y. 这个映射g称为f逆映射, 记作f-1, 其定义域=R f , 值域=X .按上述定义, 只有单射才存在逆映射. 上述三例中哪个映射存在逆映射?设有两个映射g : X→Y 1, f : Y 2→Z,其中Y 1⊂Y 2. 那么由映射g和f可以定出一个从X到Z对应法那么, 它将每个x∈X映射成f[g(x)]∈Z . 明显, 这个对应法那么确定了一个从X到Z映射, 这个映射称为映射g和f构成复合映射, 记作f o g, 即f o g: X→Z, (f o g)(x)=f[g(x)], x∈X .应留意问题:映射g和f构成复合映射条件是: g值域R g必需包含在f定义域内, R g⊂D f . 否那么, 不能构成复合映射. 由此可以知道, 映射g和f复合是有依次, f o g有意义并不表示g o f也有意义. 即使f o g与g o f都有意义, 复映射f o g 与g o f也未必一样.例4设有映射g : R→[-1, 1], 对每个x∈R, g(x)=sin x,映射f : [-1, 1]→[0, 1], 对每个u∈[-1, 1], .那么映射g和f构成复映射f o g: R→[0, 1], 对每个x∈R, 有.三、函数1. 函数概念定义设数集D⊂R, 那么称映射f : D→R为定义在D上函数, 通常简记为y=f(x), x∈D,其中x称为自变量, y称为因变量, D称为定义域, 记作D f, 即D f=D.应留意问题:记号f和f(x)含义是有区分, 前者表示自变量x和因变量y之间对应法那么, 而后者表示与自变量x对应函数值. 但为了表达便利, 习惯上常用记号“f(x), x∈D〞或“y=f(x), x∈D〞来表示定义在D上函数, 这时应理解为由它所确定函数f .函数符号: 函数y=f(x)中表示对应关系记号f也可改用其它字母, 例如“F〞, “ϕ〞等. 此时函数就记作y=ϕ (x), y=F(x).函数两要素:函数是从实数集到实数集映射, 其值域总在R内, 因此构成函数要素是定义域D f及对应法那么f . 假如两个函数定义域一样, 对应法那么也一样, 那么这两个函数就是一样, 否那么就是不同.函数定义域:函数定义域通常按以下两种情形来确定: 一种是对有实际背景函数, 依据实际背景中变量实际意义确定.求定义域举例:求函数定义域.要使函数有意义, 必需x≠0, 且x2 - 4≥0.解不等式得| x |≥2.所以函数定义域为D={x | | x |≥2}, 或D=(-∞, 2]⋃[2, +∞]).单值函数与多值函数:在函数定义中,对每个x∈D, 对应函数值y总是唯一, 这样定义函数称为单值函数. 假如给定一个对应法那么, 按这个法那么, 对每个x∈D, 总有确定y值与之对应, 但这个y不总是唯一, 我们称这种法那么确定了一个多值函数. 例如, 设变量x和y之间对应法那么由方程x2+y2=r2给出. 明显, 对每个x∈[-r, r],由方程x2+y2=r2,可确定出对应y 值, 当x=r或x=-r时, 对应y=0一个值; 当x取(-r, r)内任一个值时, 对应y有两个值. 所以这方程确定了一个多值函数.对于多值函数, 往往只要附加一些条件, 就可以将它化为单值函数, 这样得到单值函数称为多值函数单值分支. 例如, 在由方程x2+y2=r2给出对应法那么中, 附加“y≥0〞条件, 即以“x2+y2=r2且y≥0〞作为对应法那么, 就可得到一个单值分支; 附加“y≤0〞条件, 即以“x2+y2=r2且y≤0〞作为对应法那么, 就可得到另一个单值分支.表示函数主要方法有三种: 表格法、图形法、解析法(公式法), 这在中学里大家已经熟识. 其中, 用图形法表示函数是基于函数图形概念, 即坐标平面上点集{P(x, y)|y=f(x), x∈D}称为函数y=f(x), x∈D图形. 图中R f表示函数y=f(x)值域.函数例子:例.函数.称为肯定值函数. 其定义域为D=(-∞, +∞), 值域为R f=[0, +∞).例.函数.称为符号函数. 其定义域为D=(-∞, +∞), 值域为R f={-1, 0, 1}.例.设x为任上实数. 不超过x最大整数称为x整数部分, 记作[ x ].函数y= [ x ]称为取整函数. 其定义域为D=(-∞, +∞), 值域为R f=Z .例如:, , [π]=3, [-1]=-1, [-3. 5]=-4.分段函数:在自变量不同改变范围中, 对应法那么用不同式子来表示函数称为分段函数.例.函数.这是一个分段函数, 其定义域为D=[0, 1]⋃(0, +∞)= [0, +∞).当0≤x≤1时, ; 当x>1时, y=1+x.例如; ; f(3)=1+3=4.2. 函数几种特性(1)函数有界性设函数f(x)定义域为D, 数集X⊂D. 假如存在数K1, 使对任一x∈X, 有f(x)≤K1, 那么称函数f(x)在X上有上界, 而称K1为函数f(x)在X上一个上界. 图形特点是y=f(x)图形在直线y=K1下方.假如存在数K2, 使对任一x∈X, 有f(x)≥ K2, 那么称函数f(x)在X上有下界, 而称K2为函数f(x)在X上一个下界. 图形特点是, 函数y=f(x)图形在直线y=K2上方.假如存在正数M, 使对任一x∈X, 有| f(x) |≤M, 那么称函数f(x)在X上有界; 假如这样M不存在, 那么称函数f(x)在X上无界. 图形特点是, 函数y=f(x)图形在直线y=- M和y =M之间.函数f(x)无界, 就是说对任何M, 总存在x1∈X, 使| f(x) | > M.例如(1)f(x)=sin x在(-∞, +∞)上是有界: |sin x|≤1.(2)函数在开区间(0, 1)内是无上界. 或者说它在(0, 1)内有下界, 无上界.这是因为, 对于任一M>1, 总有x1: , 使,所以函数无上界. 函数在(1, 2)内是有界.(2)函数单调性设函数y=f(x)定义域为D, 区间I⊂D. 假如对于区间I上随意两点x1及x2, 当x1<x2时, 恒有f(x1)< f(x2),那么称函数f(x)在区间I上是单调增加.假如对于区间I上随意两点x1及x2, 当x1<x2时, 恒有f(x1)> f(x2),那么称函数f(x)在区间I上是单调削减.单调增加和单调削减函数统称为单调函数.函数单调性举例:函数y=x2在区间(-∞, 0]上是单调增加, 在区间[0, +∞)上是单调削减, 在〔-∞, +∞〕上不是单调.(3)函数奇偶性设函数f(x)定义域D关于原点对称(即假设x∈D, 那么-x∈D). 假如对于任一x∈D, 有f(-x) =f(x),那么称f(x)为偶函数.假如对于任一x∈D, 有f(-x) =-f(x),那么称f(x)为奇函数.偶函数图形关于y轴对称, 奇函数图形关于原点对称,奇偶函数举例:y=x2, y=cos x都是偶函数. y=x3, y=sin x都是奇函数, y=sin x+cos x是非奇非偶函数.(4)函数周期性设函数f(x)定义域为D. 假如存在一个正数l , 使得对于任一x∈D有(x±l)∈D, 且f(x+l) =f(x)那么称f(x)为周期函数, l称为f(x)周期.周期函数图形特点: 在函数定义域内, 每个长度为l区间上, 函数图形有一样形态.3.反函数与复合函数反函数:设函数f : D→f(D)是单射, 那么它存在逆映射f-1: f(D)→D, 称此映射f-1为函数f反函数.按此定义, 对每个y∈f(D), 有唯一x∈D, 使得f(x)=y, 于是有f-1(y)=x.这就是说, 反函数f-1对应法那么是完全由函数f对应法那么所确定.一般地, y=f(x), x∈D反函数记成y=f-1(x), x∈f(D).假设f是定义在D上单调函数, 那么f : D→f(D)是单射, 于是f反函数f-1必定存在, 而且简洁证明f-1也是f(D)上单调函数.相对于反函数y=f-1(x)来说, 原来函数y=f(x)称为干脆函数. 把函数y=f(x)和它反函数y=f-1(x)图形画在同一坐标平面上, 这两个图形关于直线y=x是对称. 这是因为假如P(a, b)是y=f(x)图形上点, 那么有b=f(a). 按反函数定义, 有a=f-1(b), 故Q(b, a)是y=f-1(x)图形上点; 反之, 假设Q(b, a)是y=f-1(x)图形上点, 那么P(a, b)是y=f(x)图形上点. 而P(a, b)与Q(b, a)是关于直线y=x对称.复合函数:复合函数是复合映射一种特例, 依据通常函数记号, 复合函数概念可如下表述.设函数y=f(u)定义域为D 1, 函数u=g(x)在D上有定义且g(D)⊂ D 1, 那么由下式确定函数y=f[g(x)], x∈D称为由函数u=g(x)和函数y=f(u)构成复合函数, 它定义域为D, 变量u称为中间变量.函数g与函数f构成复合函数通常记为, 即()=f[g(x)].与复合映射一样, g与f构成复合函数条件是: 是函数g在D上值域g(D)必需含在f定义域D f内, 即g(D)⊂D . 否那么, 不能构成复合函数.f例如, y=f(u)=arcsin u, 定义域为[-1, 1], 在上有定义, 且g(D)⊂[-1, 1], 那么g与f可构成复合函数, x∈D;但函数y=arcsin u和函数u=2+x2不能构成复合函数, 这是因为对任x∈R, u=2+x2均不在y=arcsin u定义域[-1, 1]内.多个函数复合:4. 函数运算设函数f(x), g(x)定义域依次为D 1, D 2, D=D 1⋂D 2≠∅, 那么我们可以定义这两个函数以下运算:和(差)f±g : (f±g)(x)=f(x)±g(x), x∈D;积f⋅g : (f⋅g)(x)=f(x)⋅g(x), x∈D;商: , x∈D\{x|g(x)=0}.例设函数f(x)定义域为(-l, l), 证明必存在(-l, l)上偶函数g(x)及奇函数h(x), 使得f(x)=g(x)+h(x).分析假如f(x)=g(x)+h(x), 那么f(-x)=g(x)-h(x), 于是, .证作, , 那么f(x)=g(x)+h(x),且,.5. 初等函数根本初等函数:幂函数: y=xμ (μ∈R是常数);指数函数: y=a x(a>0且a≠1);对数函数: y=log a x (a>0且a≠1, 特殊当a=e时, 记为y=ln x);三角函数: y=sin x, y=cos x, y=tan x, y=cot x, y=sec x, y=csc x;反三角函数: y=arcsin x, y=arccos x, y=arctan x, y=arccot x .初等函数:由常数和根本初等函数经过有限次四那么运算和有限次函数复合步骤所构成并可用一个式子表示函数, 称为初等函数. 例如, y=sin2x,等都是初等函数.作业:P21:4〔1〕〔3〕〔5〕〔7〕〔8〕;5〔1〕〔2〕〔4〕;12〔2〕〔4〕〔6〕§1. 2 数列极限数列概念:假如依据某一法那么,使得对任何一个正整数n有一个确定数x n,那么得到一列有次序数x1,x2,x3,⋅⋅⋅,x n,⋅⋅⋅这一列有次序数就叫做数列,记为{x n},其中第n项x n叫做数列一般项.数列例子:{}:,,,⋅⋅⋅,⋅ ⋅ ⋅;{2n}: 2, 4, 8,⋅⋅⋅, 2n,⋅⋅⋅;{}:,,,⋅⋅⋅,,⋅⋅⋅;{(-1)n+1}: 1,-1, 1,⋅⋅⋅, (-1)n+1,⋅⋅⋅;{}: 2,,,⋅⋅⋅,,⋅⋅⋅.它们一般项依次为, 2n,, (-1)n+1,.数列几何意义:数列{x n}可以看作数轴上一个动点,它依次取数轴上点x1,x2,x3,⋅⋅⋅,x n,⋅⋅⋅.数列与函数:数列{x n}可以看作自变量为正整数n函数:x n=f (n),它定义域是全体正整数.数列极限:数列极限通俗定义:对于数列{x n},假如当n无限增大时,数列一般项x n无限地接近于某一确定数值a,那么称常数a是数列{x n}极限,或称数列{x n}收敛a.记为.假如数列没有极限,就说数列是发散.例如,,;而{2n},{ (-1)n+1},是发散.对无限接近刻划:x n无限接近于a等价于|x n-a |无限接近于0,极限精确定义:定义假如数列{x n}与常a有以下关系:对于随意给定正数ε(不管它多么小),总存在正整数N,使得对于n >N 时一切x n,不等式|x n-a |<ε都成立,那么称常数a是数列{x n}极限,或者称数列{x n}收敛于a,记为或x n→a (n→∞).假如数列没有极限,就说数列是发散.⇔∀ε>0, ∃N∈N+,当n>N时,有|x n-a|<ε .数列极限几何说明:例题:例1.证明.分析:|x n-1|=.对于∀ε >0,要使|x n-1|<ε,只要,即.例2.证明.分析:|x n-0|.对于∀ε>0,要使|x n-0|<ε,只要,即.例3.设|q |<1,证明等比数列1,q,q2,⋅⋅⋅,q n-1,⋅⋅⋅极限是0.分析:对于随意给定ε >0,要使|x n-0|=| q n-1-0|=|q| n-1<ε,只要n>log|q|ε+1就可以了,故可取N=[log|q|ε+1]。
“基地班”本科生科研训练模式探索

4 毕业时具有一定创新意识和能力 , . 实验和实践
能力 以及分 析和解 决 问题 的能 力 , 独立 开 展本 学 科 为
及相关学科的研究打下基础。 二 、 建立体 多 元科研 能 力的培 养体 系 构 为全面提升学生的科研能力与素质 , 围绕立体多 元科研能力 培养 体系 , 设计 了基 于学科 平台、 课程平 台、 实践教学平台和科研立项平 台的本科生科研能力 培养模式。学生通过该培养模式的系统训练 , 增强 了 对交叉 学科 、 应用 型工 科研 究前 沿 的了解 , 开阔 了科 研 视野 , 提高了科研兴趣、 文献查 阅、 写作 与表达能力等 综合素质, 锻炼 了团 队协作精神 , 培养 了学生独立思 考、 分析和解决问题的能力 , 以及基础知识与技能的综
究 项 目为驱 动力 , 尊重 学生 的能 力差异 和 兴趣取 向, 围 绕 本科 生创新 能 力培 养 的 教育 宗 旨, 注学 生早 期 的 关
根据学科科研现状 、 教学体系以及学生情况 , 重点
建 设两 级训 练平 台 : 生基 本 科 研 训 练平 台和 学生 专 学 业 科研训 练平 台 , 者 主要 为 大 学 低 年级 学 生进 人 科 前
中图分类号 :6 2 G4
文献标识码 : A
文章编号 :6434 2 1 )40 0 -3 17 .4 X(0 2 0 -1 00
作者简介 : 敏 (9 7一) 女 , 北宜昌人 , 肖 16 , 湖 副教授 , 博士 , 究方 向为控制理论及应 用、 研 高等教育。
为了适应创造性人才培养的要求 , 提倡和强化本
数学与应用数学(非师范)专业介绍与培养方

专业编号: 874数学与应用数学(试验班)专业四年制本科人才培养方案一.专业培养目标及基本要求培养目标:本专业培养掌握数学科学的基本理论、基础知识和基本方法,能够运用数学知识和使用计算机解决若干实际问题,并且具有良好的政治思想素质、人文素养和科学素养、创新精神和实践能力的高级专门人才。
为经济社会发展培养德才兼备的高素质的基础学术型人才及应用型人才;为硕士研究生教育提供优质生源。
基本要求:本专业学生主要学习数学与应用数学的基本理论和方法,受到严格的数学思维训练,掌握计算机基本理论的运用手段,并通过专业理论课程和教学实践环节,形成良好的素质。
毕业生应该获得以下几个方面的知识和能力:1.具有良好的思想道德修养、自信宽容的态度、团结协作的精神、正确判断的能力;2.掌握数学科学的基本理论知识,有比较扎实宽广的数学理论基础,了解本学科的理论前沿和发展动态;3.具有较强的逻辑推理能力、空间想象能力、以及具有分析和解决实际问题的能力;4.具有创新精神和较强的终身学习能力。
掌握本专业文献检索、资料查阅的基本方法,具有一定的科研能力;5.具有良好的表达和沟通能力、健康的体魄、良好的心理素质、比较宽厚的文化修养和良好的审美情趣。
二、主要课程:数学分析、高等代数与解析几何、概率论、数理统计、常微分方程、抽象代数、复变函数、实变函数、泛函分析、拓扑学基础、微分几何学、偏微分方程。
三、学制:4年四、授予学位:理学学士五、教学时间分配表六、课程教学学时、学分分布表注:专业类必修课指学科基础必修课与专业必修课;专业类选修课指学科基础选修课与专业选修课七、课程计划表(续表)(续表)(续表)八、说明:1.本专业培养方向为基础数学与应用数学方向,所开专业课程选修课均为这两个方向选修;2.本专业学生在选修课程时应在本专业选修课程中选修不低于28学分的课程(其中课程编号中第五位为“0”的课程为几个专业通用的选修课程,课程编号中第五位为“1”的课程为基础数学方向的选修课程;课程编号中第五位为“2”的课程为应用数学方向的选修课程)。
三峡大学2007年-2009年获准立项尚未结题的校级教学研究项

经管学院
郑悦林
郑浩昊段华汪静王东娟
学院资助
一般项目
J2009051
市场营销本科专业全程实践教学体系的研究与实践
经管学院
王琼海
李春华董希婢付云侠张世杰
学院资助
一般项目
J2009052
非预防医学专业学生扩展预防医学基本技能训练研究
医学院
邓青
王南平姚佳红余立萍陈雅
学院资助
江明辉覃太贵沈艳军王敏
学院资助
一般项目
J200827
体育专业体操教学改革理论与实践研究
体育学院
沈瑞杰
陶武操张岚易保锐刘喜山
学院资助
一般项目
J200828
创新课堂教学模式,实现体育价值的多元化
体育学院
董丽丽
王春保童健田颖华戴绍斌
学院资助
一般项目
J200829
综合性高校体育类毕业论文教学环节的改革与实践
学院资助
一般项目
J2009038
经济管理类专业大学生应用能力、协作、能力和创新能力的综合培养研究与实践
经管学院
孟爱华
黄昌富郑浩昊戴发山陆曈曈
学院资助
一般项目
J2009039
国际经济与贸易专业开展研究性学习的研究与实践
经管学院
向云
陈祥升林青徐成刚罗丽娜
学院资助
一般项目
J2009040
金融专业实践教学体系构建研究
经管学院
孙海兵
郭琦陈钢江新黄建文
3000元
重点项目
J2009007
以精品课程创建为契机,培养医学生探究性学习能力培养的研究
医学院
韩莉
马克雄赵云刘朝奇张昌菊
应用数学学科优势

数学与应用数学数学与应用数学专业是三峡大学各专业中历史最悠久的专业之一,经历了宜昌师范专科学校、湖北三峡学院和三峡大学三个发展阶段。
早在1958年宜昌师范专科学校成立之初,就设有数学科,后改为数学系。
1962年专科停办,改办中师。
1975年又恢复高师招生。
1978年4月,经国务院批准,恢复宜昌师范专科学校。
1993年6月,更名为宜昌师范高等专科学校。
专科阶段的数学专业在国内同类学校享有较高声誉,为社会培养了大量优秀的中学数学教师。
1995年3月经国家教委批准,与宜昌医学高等专科学校、宜昌市职业大学合并,组建湖北三峡学院,同年开始招收本科生。
1998年,根据当时国家教委公布的新的本科专业目录,数学教育专业改称“数学与应用数学(师范类)专业”。
2000年6月,湖北三峡学院与武汉水利电力大学(宜昌校区)合并,组建三峡大学。
数学系成为理学院下属的一个系,数学与应用数学(师范类)专业,改变为“数学与应用数学专业”,结束了数学系只有师范教育的历史,得到快速发展。
2001年,应用数学被列为学校重点学科。
2003年获得应用数学硕士学位授予权,并于2004年启动了硕士研究生教育,至今已招收三届硕士研究生。
2005年运筹学与控制论硕士点通过了省学位办的立项建设(鄂学位[2006]13号)。
该专业经过近半个世纪的发展,规模和实力不断壮大,教学水平和科研水平有了大幅度提高,逐步形成了自己的专业优势与办学特色,为国家输送了大量的优秀人才,在湖北省属大学的同类专业内具有一定知名度。
由于本专业有比较突出的成绩,2005年8月被列为三峡大学品牌专业立项建设项目(三峡大教[2005]第20号),2006年,应用数学被批准为省级重点学科(鄂学位[2006]13号)。
(一)教师队伍建设1、专业教师基本情况(1)职称结构:数学与应用数学专业现有教师47人。
其中教授15人,占教师总人数的22.5%;副教授20人,占教师总人数的42.5%;讲师8人,占教师总人数的17.04%,助教7人,占教师总人数的14.89%;高级职称教师占教师总人数的66.6%。
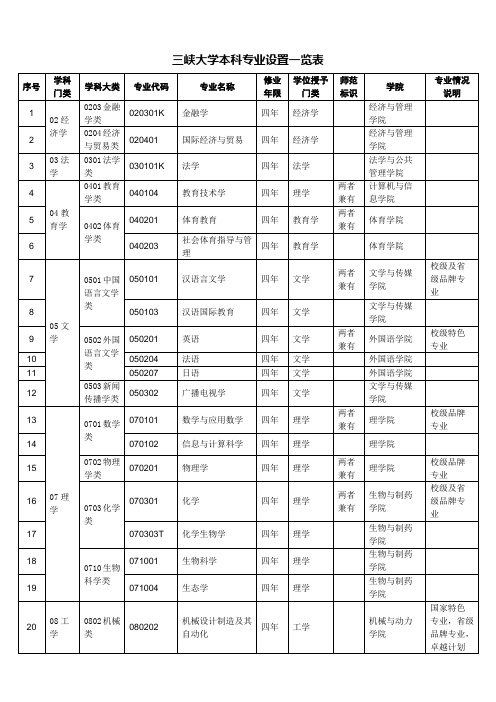
三峡大学本科专业设置一览表
四年
管理学
经济与管理学院
59
1204公共管理类
120401
公共事业管理
四年
管理学
法学与公共管理学院
60
120402
行政管理
四年
管理学
法学与公共管理学院
61
1206物流管理与工程类
120601
物流管理
四年
管理学
经济与管理学院
62
1207工业工程类
120701
工业工程
四年
工学
机械与动力学院
63
四年
工学
机械与动力学院
23
0804材料类
080405
金属材料工程
四年
工学
材料与化工学院
省级产业计划专业
24
080414T
新能源材料与器件
四年
工学
材料与化工学院
25
0805能源动力类
080501
能源与动力工程
四年
工学
机械与动力学院
26
0806电气类
080601
电气工程及其自动化
四年
工学
电气与新能源学院
0710生物科学类
071001
生物科学
四年
理学
生物与制药学院
19
071004
生态学
四年
理学
生物与制药学院
20
08工学
0802机械类
080202
机械设计制造及其自动化
四年
工学
机械与动力学院
国家特色专业,省级品牌专业,卓越计划专业
21
080203
材料成型及控制工程
四年
数学与应用数学本科课程设置

数学与信息学院数学与应用数学专业本科培养方案(一) 专业培养目标本专业培养具有良好的政治思想素质,掌握数学科学基本理论、基础知识与基本方法,能运用数学知识和使用计算机解决若干实际数学问题,能在中等学校进行数学教学的教师、教学研究人员及其他教育工作者。
(二) 专业培养规格和要求本专业学生,应热爱祖国,拥护中国共产党的领导;掌握马列主义、毛泽东思想和邓小平理论的基本原理;树立正确的情感、态度和价值观。
具有敬业爱岗、艰苦奋斗、热爱劳动、遵纪守法、团结合作的品质;具有良好的思想品德、社会公德和职业道德。
本专业学生主要学习数学和应用数学的基本理论和方法,受到严格的数学思维训练,掌握计算机的基本原理和运用手段,并通过教育理论课程和教学实践环节,形成良好的教师素养,培养从事数学教学的基本能力和数学教育研究、数学科学研究、数学实际应用等基本能力。
毕业生应获得以下几方面的知识和能力:1.具有扎实的数学基础,初步掌握数学科学的基本思想方法,其中包括数学建模、数学计算、解决实际问题等基本能力;2.有良好的使用计算机的能力,能够进行简单的程序编写,掌握数学软件开发和计算机多媒体技术,能够对教学软件进行简单的二次开发;3.具备良好的教师职业素养和从事数学教学的基本能力,熟悉教育法规,掌握并初步运用教育学、心理学基本理论以及数学教学理论;4.了解近代数学的发展概貌及其在社会发展中的作用,了解数学科学的若干最新发展,数学教学领域的一些最新研究成果和教学方法,了解相近专业的一般原理和知识,学习文理渗透的课程,获得广泛的人文和科学修养;5.较强的语言表达能力和班级管理能力;6.掌握资料查询、文献检索及运用现代信息技术获得相关信息的基本方法,并有一定的科研能力;7.掌握一门外国语,能借助工具书阅读本学科和专业的外文书刊,具有一定的听、说、读、译的能力。
(三) 专业人才的知识、素质和能力发展要求表1 数学与应用数学本科专业人才知识、素质和能力发展细目表附图1:数学与应用数学专业知识、素质、能力结构图(四) 主干学科:数学(五) 专业主要课程数学分析、几何学、代数学、物理学、概率论与数理统计、微分方程、函数论、离散数学、数学史、数值方法与计算机技术、数学模型、数学实验、教育学与心理学基础、数学教学论、人文社会科学基础。
面向市场需求的数学学科复合型人才培养模式改革

23人才培养改革总第254期DOI编码:10.3969/j.issn.1007-0079.2012.31.013高等院校,特别是地方性高等院校的人才培养必须面对社会人才市场的需求。
在对我国当前对于数学与应用数学专业人才市场需求变化的研究与分析的基础上,三峡大学结合本校的实际情况,自2004年开始启动了“数学与应用数学专业复合型人才培养实验班”的“教学质量工程”改革项目,经过多年的不断改革探索与实践,取得了一定的成效。
该项目研究2012年获得三峡大学教学成果一等奖,本文将一些改革理念和具体做法进行简要总结,以期与各校同行进一步交流。
一、改革的相关背景及其分析随着社会经济的快速发展,我国目前人才市场对于各类专业人才的需求在结构上发生了很大的变化,特别是对于一些传统的基础理论性学科专业的人才需求的形势更是产生了本质性的变化。
这种变化一方面给这些学科的传统办学模式带来巨大的冲击,另一方面也促进了这些学科人才培养的改革。
1.社会对数学专业人才需求的变化现行的《数学与应用数学专业教学规范》(以下简称《规范》)中规定数学与应用数学专业是“培养掌握数学科学的基本理论与基本方法,具有运用数学知识,使用计算机解决实际问题的能力,受到科学研究训练的高级专门人才”;其毕业生去向为“能在科技、教育、经济和金融等部门从事研究、教学工作或在生产、经营及管理部门从事实际应用、开发研究和管理工作,或能继续攻读研究生学位”。
事实上,《规范》中将数学专业毕业生的就业去向大体分成专职数学研究人员、交叉学科研究人员、高等教育数学教师、应用型数学人才、基础教育数学教师等五种类型。
即使今天看来,《规范》中对该专业的“人才培养目标”的设定在总体上仍然是正确的。
但是,也应充分注意到当今社会对数学人才的需求无论是在结构上还是在层次上却也发生了巨大的变化,呈现出新的特点。
(1)专职数学研究人员、高等教育数学教师类对人才的需求越来越向着高层次、少而精的方向发展。
数学与应用数学专业大学排名最新排行榜

数学与应用数学专业大学排名最新排行榜数学与应用数学专业大学排名序号学校名称专业名称1北京大学数学与应用数学2中国科学院大学数学与应用数学3复旦大学数学与应用数学4上海交通大学数学与应用数学5浙江大学数学与应用数学6中国科学技术大学数学与应用数学7中国人民大学数学与应用数学8南京大学数学与应用数学9北京师范大学数学与应用数学10同济大学数学与应用数学11北京航空航天大学数学与应用数学12北京理工大学数学与应用数学13东南大学数学与应用数学14武汉大学数学与应用数学15华中科技大学数学与应用数学16哈尔滨工业大学数学与应用数学17西安交通大学数学与应用数学18南开大学数学与应用数学19四川大学数学与应用数学20华东师范大学数学与应用数学21电子科技大学数学与应用数学22中山大学数学与应用数学23天津大学数学与应用数学24厦门大学数学与应用数学25华南理工大学数学与应用数学26西北工业大学数学与应用数学27山东大学数学与应用数学28重庆大学数学与应用数学29中南大学数学与应用数学30吉林大学数学与应用数学31兰州大学数学与应用数学32大连理工大学数学与应用数学33中国农业大学数学与应用数学34湖南大学数学与应用数学35东北大学数学与应用数学36南方科技大学数学与应用数学37郑州大学数学与应用数学38云南大学数学与应用数学39新疆大学数学与应用数学40上海财经大学数学与应用数学41西安电子科技大学数学与应用数学42上海大学数学与应用数学43西南财经大学数学与应用数学44北京科技大学数学与应用数学45华东理工大学数学与应用数学46河海大学数学与应用数学47苏州大学数学与应用数学48东华大学数学与应用数学49西南交通大学数学与应用数学50华中师范大学数学与应用数学51暨南大学数学与应用数学52南京师范大学数学与应用数学53哈尔滨工程大学数学与应用数学54陕西师范大学数学与应用数学55华南师范大学数学与应用数学56合肥工业大学数学与应用数学57西南大学数学与应用数学58东北师范大学数学与应用数学59安徽大学数学与应用数学60西北大学数学与应用数学61福州大学数学与应用数学62首都师范大学数学与应用数学63湖南师范大学数学与应用数学64中国地质大学(武汉)数学与应用数学65中国地质大学(北京)数学与应用数学66长安大学数学与应用数学67中国矿业大学数学与应用数学68中国石油大学(北京)数学与应用数学69海南大学数学与应用数学70南昌大学数学与应用数学71贵州大学数学与应用数学72广西大学数学与应用数学73内蒙古大学数学与应用数学74宁夏大学数学与应用数学75西藏大学数学与应用数学76宁波大学数学与应用数学77汕头大学数学与应用数学78上海理工大学数学与应用数学79成都理工大学数学与应用数学80河南大学数学与应用数学81天津工业大学数学与应用数学82山西大学数学与应用数学83上海师范大学数学与应用数学84浙江师范大学数学与应用数学85湘潭大学数学与应用数学86江苏大学数学与应用数学87华侨大学数学与应用数学88浙江理工大学数学与应用数学89长沙理工大学数学与应用数学90青岛大学数学与应用数学91广州大学数学与应用数学92湖北大学数学与应用数学93扬州大学数学与应用数学94四川师范大学数学与应用数学95杭州师范大学数学与应用数学96三峡大学数学与应用数学97山东师范大学数学与应用数学98河北大学数学与应用数学99天津师范大学数学与应用数学100长江大学数学与应用数学101安徽师范大学数学与应用数学102中国计量大学数学与应用数学103重庆交通大学数学与应用数学104集美大学数学与应用数学105江苏师范大学数学与应用数学106苏州科技大学数学与应用数学107山东财经大学数学与应用数学108河北师范大学数学与应用数学109云南师范大学数学与应用数学110福建师范大学数学与应用数学111江西师范大学数学与应用数学112重庆师范大学数学与应用数学113重庆工商大学数学与应用数学114温州大学数学与应用数学115广西师范大学数学与应用数学116辽宁师范大学数学与应用数学117河南师范大学数学与应用数学118西北师范大学数学与应用数学119华北水利水电大学数学与应用数学120湖南工业大学数学与应用数学121黑龙江大学数学与应用数学122河南科技大学数学与应用数学123曲阜师范大学数学与应用数学124延安大学数学与应用数学125海南师范大学数学与应用数学126广西民族大学数学与应用数学127湖南第一师范学院数学与应用数学128烟台大学数学与应用数学129南京晓庄学院数学与应用数学130贵州师范大学数学与应用数学131云南财经大学数学与应用数学132哈尔滨师范大学数学与应用数学133合肥学院数学与应用数学134闽南师范大学数学与应用数学135安庆师范大学数学与应用数学136淮北师范大学数学与应用数学137吉首大学数学与应用数学138吉林师范大学数学与应用数学139江苏第二师范学院数学与应用数学140湖北师范大学数学与应用数学141贵州民族大学数学与应用数学142南宁师范大学数学与应用数学143山西师范大学数学与应用数学144山东理工大学数学与应用数学145陕西理工大学数学与应用数学146东华理工大学数学与应用数学147佛山科学技术学院数学与应用数学148湖南理工学院数学与应用数学149湖州师范学院数学与应用数学150五邑大学数学与应用数学151沈阳工业大学数学与应用数学152常熟理工学院数学与应用数学153内蒙古师范大学数学与应用数学154长春师范大学数学与应用数学155淮阴师范学院数学与应用数学156赣南师范大学数学与应用数学157渤海大学数学与应用数学158北华大学数学与应用数学159江西科技师范大学数学与应用数学160信阳师范学院数学与应用数学161聊城大学数学与应用数学162贵州师范学院数学与应用数学163临沂大学数学与应用数学164太原师范学院数学与应用数学165宝鸡文理学院数学与应用数学166宁夏师范学院数学与应用数学167遵义师范学院数学与应用数学168北部湾大学数学与应用数学169莆田学院数学与应用数学170阜阳师范大学数学与应用数学171洛阳师范学院数学与应用数学172黄冈师范学院数学与应用数学173湖北民族大学数学与应用数学174青海师范大学数学与应用数学175湘南学院数学与应用数学176牡丹江师范学院数学与应用数学177百色学院数学与应用数学178呼和浩特民族学院数学与应用数学179怀化学院数学与应用数学180喀什大学数学与应用数学数学与应用数学专业简介数学与应用数学(Mathematics and Applied Mathematics)是一个学科专业,该专业培养掌握数学科学的基本理论与基本方法,具备运用数学知识、使用计算机解决实际问题的能力,受到科学研究的初步训练,能在科技、教育和经济部门从事研究、教学工作或在生产经营及管理部门从事实际应用、开发研究和管理工作的高级专门人才。
面向市场需求的数学学科复合型人才培养模式改革

面向市场需求的数学学科复合型人才培养模式改革作者:于林来源:《中国电力教育》2012年第31期摘要:通过对数学学科复合型人才的概念与特点分析,针对我国目前地方性高等院校传统基础理论性学科(专业)人才培养的现状,系统地阐述了三峡大学在“数学与应用数学专业复合型人才培养实验班”的“教学质量工程”改革项目中对人才培养模式改革所进行的探索与实践。
关键词:数学与应用数学;复合型;人才培养;教学改革作者简介:于林(1965-),男,山东滨州人,三峡大学理学院,教授。
(湖北宜昌443002)基金项目:本文系湖北省高等学校省级教学研究项目(项目编号:2008202)、三峡大学教学研究项目(J2010057)的研究成果。
中图分类号:G642 文献标识码:A 文章编号:1007-0079(2012)31-0023-02高等院校,特别是地方性高等院校的人才培养必须面对社会人才市场的需求。
在对我国当前对于数学与应用数学专业人才市场需求变化的研究与分析的基础上,三峡大学结合本校的实际情况,自2004年开始启动了“数学与应用数学专业复合型人才培养实验班”的“教学质量工程”改革项目,经过多年的不断改革探索与实践,取得了一定的成效。
该项目研究2012年获得三峡大学教学成果一等奖,本文将一些改革理念和具体做法进行简要总结,以期与各校同行进一步交流。
一、改革的相关背景及其分析随着社会经济的快速发展,我国目前人才市场对于各类专业人才的需求在结构上发生了很大的变化,特别是对于一些传统的基础理论性学科专业的人才需求的形势更是产生了本质性的变化。
这种变化一方面给这些学科的传统办学模式带来巨大的冲击,另一方面也促进了这些学科人才培养的改革。
1.社会对数学专业人才需求的变化现行的《数学与应用数学专业教学规范》(以下简称《规范》)中规定数学与应用数学专业是“培养掌握数学科学的基本理论与基本方法,具有运用数学知识,使用计算机解决实际问题的能力,受到科学研究训练的高级专门人才”;其毕业生去向为“能在科技、教育、经济和金融等部门从事研究、教学工作或在生产、经营及管理部门从事实际应用、开发研究和管理工作,或能继续攻读研究生学位”。
2023大学_三峡大学专业排名

2023三峡大学专业排名
三峡大学都有哪些专业:
截至底,学校有70个本科专业,一级学科博士点2个,一级学科硕士点20个,工程硕士、工商管理(MBA)和翻译等专业硕士学位领域(点)20个。
省级重点一级学科11个,湖北省优势与特色一级学科7个,“211工程”重点建设学科2个。
三峡大学国家“211工程”重点建设学科一览表
序号
三峡大学优势专业:
一共五十七个专业
一、经济学类:金融学、国际金融与贸易
二、管理学类:信息管理与信息系统、工程管理、工商管理、市场营销、财务管理、人力资源管理、旅游管理、行政管理、公共事业管理、工业工程
三、工学类:金属材料工程、机械设计制造及其自动化、材料成型及控制工程、电气工程及其自动化、自动化、电子信息工程、通信工程、计算机科学与技术、建筑学、城市规划、土木工程、水利水电工程、水文与水资源工程、环境工程、化学工程与工艺、生物工程
四、文学类:汉语言文学、对外汉语、英语、日语、法语、广播电视新闻学、音乐学、音乐表演、美术学、艺术设计、舞蹈学
五、理学类:数学与应用数学、信息与计算科学、物理学、电子信息科学与技术、光信息科学与技术、化学、化学生物学、生物科学、生态学
六、教育学类:体育教育、社会体育、教育技术学
七、法学类:法学
八、医学类:临床医学、医学影像学、中医学(中西结合方向) 、护理学。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三峡大学数学与应用数学专业复合型
人才培养实验班实施方案
一、人才培养目标
通过在全校范围内选拔素质良好的生源,经过系统的数学与应用数学专业(本科)培养,通过免试推荐硕士研究生、硕士研究生入学考试、修读双学位或辅修其它专业和教师教育等途径,培养数学功底扎实,具有在工科专业或在数学学科和其它学科进一步深造和发展潜力的复合型人才;或受到系统的数学训练、数学功底扎实,具有双学位(或辅修专业)的复合型人才;或受到系统的数学训练、数学功底扎实的高素质教师。
二、培养模式
实验班人才培养模式为“统一主修模式、同步选择辅修、择优推荐免试、分流复合培养”。
(一)统一主修模式:统一按数学与应用数学专业培养方案进行主修专业培养,同时加强通识性基础教育、综合素质教育,课程统一设置、统一要求。
(二)同步选择辅修:在学习主修专业的同时,学生根据兴趣和自身条件选择辅修授权双学位专业或选择辅修其它专业(工科为主)。
(三)择优推荐免试:第五学期结束,根据主修专业前五学期学习情况择优推荐免试研究生。
(四)分流复合培养:第六学期开始,在推免的基础上进行分模块分流培养,在继续执行主修专业培养方案的同时,分流执行相应模块的后期培养方案:
模块一:保研模块
根据学校下达免试推荐研究生指标,择优选拔确定免试推荐研究生。
对免推生实行个体化培养,按方向早确定导师,早进入方向确定后期个性化培养方案,后期个性化培养包括主修专业(本科)相关专业课和所选方向的学科主干课程。
毕业实习及毕业论文结合所选方向进行。
模块方向分别是:土木工程方向、水利工程方向、电气工程方向、控制科学与工程方向、计算机科学与技术方向、机械工程方向、管理科学与工程方向、数学方向。
模块二:双学位及师范模块
未获推免的学生后期培养方案包括主修专业(本科)相关专业课和双学位或辅修专业相关课程(包括教师教育课程)以及考研辅导课程。
毕业实习及毕业论文结合主修专业要求分类进行。
运行模式
第一至第五学期:统一模式主修专业培养+个性化辅修;
第五学期结束,第六学期前,根据学校下达免试推荐研究生指标,择优选拔确定免试推荐研究生;
第六和第七学期:分流培养,继续执行主修专业培养计划,保研模块同时执行按所选方向确定的后期个性化培养方案;双学位及师范模块同时执行双学位或辅修专业相关课程(包括教师教育课程)以及考研辅导课程;
第八学期:保研模块按所选方向进行毕业实习及毕业论文;双学位及师范模块结合原专业要求分类进行毕业实习及毕业论文。
三、政策保障措施
(一)招生
1.实验班每年招生总人数为60人。
2.实行二次招生,以高考招生为主,校内招生为辅,力争通过高考招生一次性完成招生计划。
3.高考招生选择部分生源质量好的省市投放指标,录取时考生高考成绩中数学单科分数须达到115分(按150分为满分计算)、英语单科分数须达到100分(按150分为满分计算)。
校内招生在新生入学后进行,学生自愿报名,报名条件为考生高考成绩中数学单科分数达到115分(按150分为满分计算)、英语单科分数达到100分(按150分为满分计算)以上。
由学校教务处会同招生及就业工作处组织数学和英语考试,选拔成绩优秀者进入实验班。
4.学校加大对实验班招生的宣传力度,确保高考招生的数量和质量。
(二)师资保障
1.数学专业课程由理学院选派优秀教师组成教学团队,切实保证实验班的教学质量,同时培养和锻炼一批年轻教师,为实验班的发展储备后备师资力量。
2.跨专业课程教学依靠相关学院的师资进行。
相关学院应高度重视实验班跨专业课程的教学工作。
(三)转专业
进入实验班学习的学生本科阶段不得进行专业调剂。
(四)选课管理
实验班学生可以根据自己的学习基础、学习能力、兴趣爱好及身体状况在导师的指导下超前选修模块课程。
教务处为实验班学生跨专业选课提供条件,让这些同学根据所选课程到相应学院上课,并确保教学质量。
(五)双学位(第二学位)学费
学校对实验班学生修读双学位(第二学位)或辅修专业不另收取学费。
(六)免试推荐攻读硕士研究生的选拔
1.免试推荐攻读本校硕士研究生的专业方向及指标分解
学校每年下达实验班免试推荐攻读硕士研究生的指标数为20人左右,按土木工程、水利工程、电气工程、控制科学与工程、计算机科学与技术、机械工程、管理科学与工程、应用数学等方向进行指标分解。
2.免试推荐攻读硕士研究生选拔条件与要求
免试推荐工作以《三峡大学免试推荐攻读硕士研究生》文件精神为主要依据,学业成绩排名靠前50%的学生,可根据个人意愿,向学校提出免试攻读本校硕士研究生申请(明确具体方向)。
然后由教务处会同理学院及相关学院按学校有关要求统一进行选拔。
参加免试推荐的学生在本科毕业时应同时达到以下要求,否则取消免试资格。
(1)全国大学英语四级考试成绩达到540分以上(含540分)或六级考试成绩达395分以上(含395分)者。
(2)第六、七、八学期的所有课程均未出现考试不及格且平均学分绩点达到1.7者。
(七)毕业
实验班学生在本科阶段均应修满数学与应用数学专业教学计划规定的有关课程学分(含规定的课外学分),保研模块学生还必须选修所选专业的模块课程20学分;双学位及师范模块学生还应选修考研模块课程或修读双学位课程或辅修专业课程;达到主修专业毕业要求的准予毕业,学校发给主修专业毕业证书,符合学位授予条件的授予理学学士学位;其中修完双学位或辅修专业课程并达到规定要求的,学校发给双学位或辅修专业证书。
(八)学生管理
实验班学生全程由理学院管理,后期分流后保研模块学生导师参与保研模块学生管理。
(九)学年注册
进入实验班学生(含二次招生其它专业选入的)均按数学与应用数学专业进行学年注册。
