实验三MATLAB绘图
Matlab实验三 绘制根轨迹

for
Principles of Automatic Control
实验三 绘制根轨迹 1: 绘制根轨迹 2: 参量分析
① 绘制根轨迹 rlocus(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
rlocus(num, den)
rlocus(sys,k)
②参量分析(根轨迹图上一顿乱点即可)
K1
(s a )nm
1
根轨迹渐进线的方程是新的根轨迹方程。
Байду номын сангаас
• 例: 绘制根轨迹及其渐近线
G(s)
K1
s(s 1)(s 2)
⑥讨论增加零点对根轨迹的影响 试试-2至-4之间的零点
G(s)
K1
s(s 1)(s 2)
r=rlocus(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
r=rlocus(num, den)
[r,k]=rlocus(sys)
[r,k]=rlocus(num, den)
③测量出根轨迹增益和对应闭环极点坐标,
在窗口显示
Gk
(s)
K *(s 1) (s 2)(s 3)
[k,poles] = rlocfind(sys)
[k,poles] = rlocfind(sys,p) P为已知的要研究的闭环极点。
④绘制零、极点以及在窗口显示零极点
pzmap(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
[p,z]=pzmap(sys) 求解零极点的好方法
⑤绘制根轨迹渐近线
一般人我不告诉他:
当根轨迹渐进线与实轴的交点已求出后, 可得到方程,这是根轨迹渐进线的方程。
MATLAB绘图 实验报告三

MATLAB绘图实验报告三MATLAB绘图实验报告三**大学实验报告学院:计信学院专业:网络工程班级:网络092姓名实验时间实验项目名称实1.掌握绘制二维图形及三维图形的方法。
验2.掌握图形控制与修饰处理的方法。
目3.了解图像处理及动画制作的基本方法。
的实验要求实验PC 机、MATLAB7.0仪器在MATLAB7.0下认真独立完成各个实验,并了解和掌握绘制二维、三围图形的方法,学会图形制作的基本方法。
学号指导教师实验组成绩实验3.MATLAB绘图实验MATLAB程序设计教程第四章课后实验习题1、2、4内容1.(1)(2)实验数据2.4.(1)(2)1.在MATLAB中,绘制直角坐标系下的二维曲线可以利用plot函数。
实验总2.在绘制图形的同时,可对图形添加图形标注,以使图形意义更加明确,可读性强。
3.Mesh函数用于绘制三维网格图,在不需要绘制特别精细的三维曲面图时,可通过三维网格图来表示三维曲面。
结4.MATLAB有功能极强的图形处理工具箱,可对图像进行更专业的处理---图形处理;描绘质点运动轨迹的动画轨迹动画。
指导教师意见签名:年月日注:各学院可根据教学需要对以上栏木进行增减。
表格内容可根据内容扩充。
扩展阅读:MATLAB绘图实验报告实验项目:MATLAB作图实验目的:1)了解MATLAB平面绘图的命令,如MATLAB常用的二维及三维绘图命令。
2)了解MATLAB立体图形的绘制,其中包括常用的立体绘图函数的理解。
实验原理:一、平面绘图命令1)plot:线性二维图。
plot函数常用的格式:plot(x,y)或者plot(x,y,s)或plot(x1,y1,x2,y2,...)或plot(x1,y1,s1,x2,y2,s2,...)其中x,x1,x2,…为横坐标,y,y1,y2,…为纵坐标,s,s1,s2,…为绘图方式参数。
绘图方式参数及含义:颜色:bblue;ggreen;rred;ccyan;mmagenta;yyellow;kblack。
实验三 matlab的图形系统

实验三 MATLAB 图形系统一、实验目的1.掌握绘制二维图形的常用函数。
2.掌握绘制三维图形的常用函数。
3.熟悉利用图形对象进行绘图操作的方法。
4.掌握绘制图形的辅助操作。
二、实验设备及条件计算机一台(带有MATLAB6.0以上的软件环境)。
三、综合实例图3-1 双调谐滤波器结构图 图3-2单调谐滤波器结构图供电系统中,常存在谐波电流,所以设计电力系统滤波器对谐波电流进行滤除,电力系统无源滤波器中双调谐滤波器的结构如图3-1所示,其阻抗表达式为1113212111211()()//()n Z R j n L R j R jn L n C n C ωωωω=+-+-+ 式中,1ω为基波角频率。
当设11ω=,10.01R =Ω,20.1R =Ω,30.1R =Ω,10.2L H =,20.142845L H =,10.2C F =,20.142845C F =,n 在[0.8,20]取值时,双调谐滤波器的阻抗n Z 与谐波次数n 的曲线如图3-3所示,编写程序完成曲线的画取(注意图中各个地方的标注均用程序实现)。
谐波次数n阻抗| Z n |Ω谐波次数n阻抗| Z f n |Ωr图3-3 双调谐滤波器的阻抗-谐波次数特性 图3-4 单调谐滤波器的阻抗-谐波次数特性参考程序代码:clear all clcn=[0.8:0.001:20]; w1=1; n1=5;R1=0.01; R2=0.1; R3=0.1;L1=0.2;L2=0.142845; C1=0.2;C2=0.142845;zc=R1+i*(n.*w1.*L1-1./(n.*w1.*C1)); zb1=R3-i*1./(n.*w1.*C2); zb2=R2+i*n.*w1.*L2;zfn=zc+zb1.*zb2./(zb1+zb2);zfn1=abs(zfn);plot(n,zfn1,'LineWidth',2.5);xlabel('\fontsize{11}谐波次数\fontname{times}\fontsize{12}\it\bfn')ylabel('\fontsize{11}阻抗\fontname{times}\fontsize{12}\it\bf| Z_n |{\Omega}') legend('\bf\it\fontsize{11}\fontname{times}\it\bf| Z_f |') text(3.663,0.1,'\bf\it\fontsize{13}\fontname{times}n_r_1') text(9.884,0.15,'\bf\it\fontsize{13}\fontname{times}n_r_2') grid on四、实验内容1.将图形窗口分成两格,分别绘制正割和余割函数曲线,并加上适当的标注。
MATLAB实验3
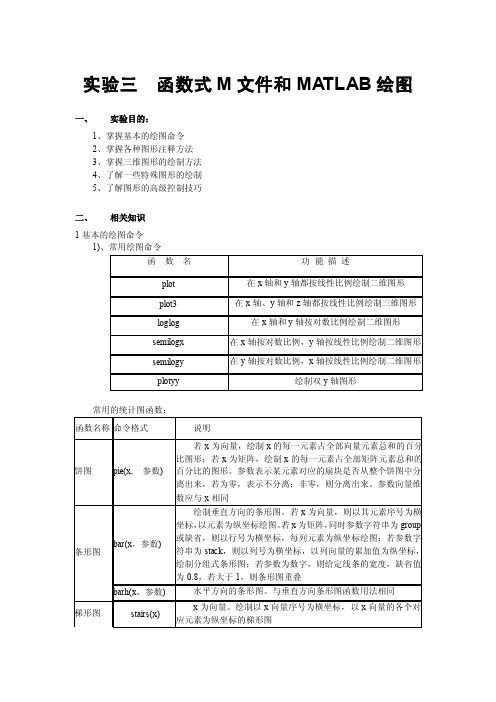
实验三函数式M文件和MA TLAB绘图一、实验目的:1、掌握基本的绘图命令2、掌握各种图形注释方法3、掌握三维图形的绘制方法4、了解一些特殊图形的绘制5、了解图形的高级控制技巧二、相关知识1基本的绘图命令1)、常用绘图命令常用的统计图函数:在MA TLAB 7中,使用plot函数进行二维曲线图的绘制>> x=0:0.1:10;>> y1=sin(x);>> y2=cos(x-2.5);>> y3=sqrt(x);>> plot(x,y1,x,y2,x,y3)3)、极坐标图形的绘制MA TLAB提供了polar(x1,x2,s)函数来在极坐标下绘制图形:(参数1角度,参数2极半径,参数3颜色和线性)>> x= 0:0.01:10;>> y1=sin(x);>> y2 = cos(x-2.5);>> polar(y1,y2,'-r+')4)、多个图形的绘制方法subplot函数可以实现多个图形的绘制:>>x = 0:.1:20;>>subplot(2,2,1)>>plot(x,sin(x));>>subplot(2,2,2);>>plot(x,cos(x))5)、曲线的色彩、线型和数据点型基本的绘图命令都支持使用字符串来给不同的曲线定义不同的线型,颜色和数据点型。
plot(x,sin(x),'-rd')图形注释对图形进行注释的方式A 图形注释“工具栏。
B 图形调色板中的注释工具C insert 菜单中的“注释”命令D 直接使用注释命令Annotation 函数Xlabel ,ylabel ,zlabel 函数 Title 函数 Colorbar 函数 Legend 函数实验内容: 一、 基础练习1、跟我练输入x,y 的值,并将它们的值互换后输出 x=input('Input x please:\n');y=input('Input y please:\n'); echo on z=x; x=y; y=z; disp(x); disp(y);echo off2、练习请求键盘输入命令keyboard ,处理完毕后,键入return ,程序将继续运行 求一元二次方程ax2 +bx+c=0的根。
实验三MATLAB绘图

实验二 二维图形绘制1.实验目的(1)掌握MATLAB 二维曲线的绘制. (2)掌握三维图的绘制。
2.实验仪器(1)Matlab7.0应用软件安装版 一套 (3)PC 机 一台 3. 实验原理依据MA TLAB 的绘图原理,及其提供的绘图函数,绘制二维、三维曲线图。
4. 实验步骤(1)绘制在不同给定参数时,系统的响应图。
(2)使用plot3、mesh 、surf 指令绘图。
(3)利用指令plot3绘制绿色实线图。
5. 实验报告内容(1)绘制)sin(1θβξ+-=-t ey tn ,其中,21ξβ-=,ξξθ21arctan-=,8.0,6.0,4.0,2.0=ξ,t=[0,18]内的响应图,将ξ=0.2和0.8对应的两条曲线进行文字标志,将所有输入的指令保存为M 文件。
(2)用plot3、mesh 、surf 指令绘制2222yx -1y x -11z +++=)()(三维图(x, y 范围自定)(3)对向量体运算后称三个坐标的值向量:x=sin(t),y=cos(t),z=t.liyong zhiling plot3,并选用绿色的实线绘制相应的三维曲线。
1-1t=[0:0.1:18]'for x=0.2:0.2:0.8 b=sqrt([1-x.^2]) c=atan(b./x) y1=-t.*x y2=t.*b+cy=1-exp(y1).*sin(y2)/b plot(t,y) hold on endtext(4,1.5,['\fontname{楷体}\xi=0.2']) text(3,0.8,['\fontname{楷体}\xi=0.8'])xlabel('t'),ylabel('y'),title('二阶系统阶跃响应')1-2t=0:0.01:18;xi=[0.2,0.4,0.6,0.8]';sxi=sqrt(1-xi.^2);sita=atan(sxi./xi);y=1-exp(-xi*t).*sin(sxi*t+sita*ones(size(t)))./(sxi*ones(size(t))); plot(t,y(1,:),':',t,y(2,:),'--',t,y(3,:),'-.',t,y(4,:))text(4,0.9,'\beta=0.2')text(4,1.58,['\beta=0.8'])2t=0:0.1:18x=sin(t)y=cos(t)z=tplot3(x,y,z,'g-')3[x,y] =meshgrid(-3:0.1:3,-2:0.1:2)z=1./(sqrt((1-x).^2+y.^2)+sqrt((1+x).^2+y.^2))subplot(1,3,1),surf(x,y,z)subplot(1,3,2),mesh(x,y,z)subplot(1,3,3),plot3(x,y,z)。
实验三 绘图操作

课程名称: MATLAB实验题目:实验三绘图操作学生姓名:专业:电子信息工程班级:学号:指导教师:张静实验地点:现代通信实验室日期: 2012 年 12月 12 日实验3 绘图操作一、实验目的1、掌握绘制二维图形的常用函数。
2、掌握绘制三维图形的常用函数。
3、掌握绘制图形的辅助操作。
4、掌握图形对象属性的基本操作。
5、掌握利用图形对象进行绘图操作的方法。
二、预习要求(1)复习7章所讲内容;(2)熟悉MATLAB中的绘图命令。
三、实验内容1、已知2=,2cos(2)1y x=,完成下列操作:y y y=,31*2y x(1)在同一坐标系下用不同的颜色和线型绘制3条曲线。
程序如下:clear all;x=0:0.1:2*pi;y1=x.^2;y2=cos(2*x);y3=y1.*y2;plot(x,y1,'r-',x,y2,'b*',x,y3,'c+')运行结果:(2)以子图形式绘制3条曲线。
程序:clear all;x=(0:0.01:2)*pi;y1=x.^2;y2=cos(2*x);y3=y1.*y2;h1=subplot(2,2,1);plot(x,y1)title('y1=x.^2')h2=subplot(2,2,2);plot(x,y2)title('y2=cos(2*x)');h3=subplot(2,2,3);plot(x,y3)title('y3=y1.*y2');运行结果:(3)分别用条形图、阶梯图、杆图和填充图绘制3条曲线。
条形码绘图:代码:clear all;x=0:0.1:10;y1=x.^2;y2=cos(2*x);y3=y1.*y2;bar(x,y1)title('y1=x.^2');bar(x,y2)title('y2=cos(2*x)');bar(x,y3)title('y3=y1.*y2');运行结果:阶梯图绘图:代码:clear all; x=0:0.1:10;y1=x.^2;y2=cos(2*x);y3=y1.*y2;stairs(x,y1)title('y1=x.^2'); stairs(x,y2)title('y2=cos(2*x)'); stairs(x,y3)title('y3=y1.*y2'); 运行结果:杆图绘图:代码:clear all;x=0:0.1:10;y1=x.^2;y2=cos(2*x);y3=y1.*y2;stem(x,y1)title('y1=x.^2'); stem(x,y2)title('y2=cos(2*x)'); stem(x,y3)title('y3=y1.*y2'); 运行结果:填充图绘图:代码:clear all;x=0:0.1:10;y1=x.^2;y2=cos(2*x);y3=y1.*y2;fill(x,y1,’c’)title('y1=x.^2');fill(x,y2,’r’)title('y2=cos(2*x)');fill(x,y3,’b’)title('y3=y1.*y2'); 运行结果:2、绘制极坐标曲线sin()a b n ρθ=+,并分析参数a ,b ,n 对曲线形状的影响。
MATLAB实验报告绘图
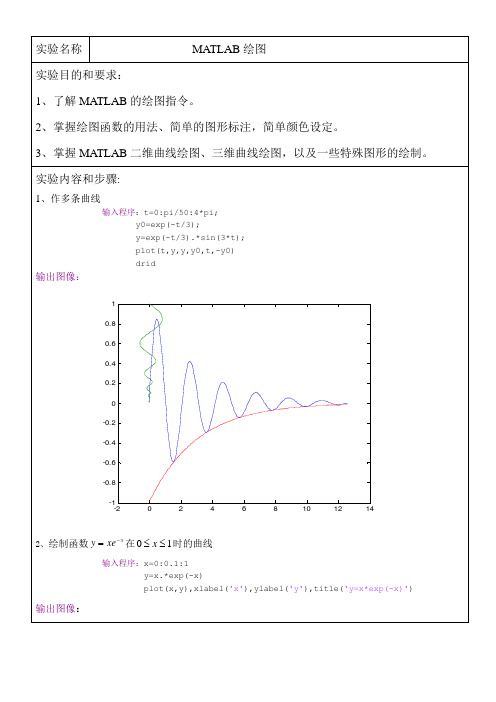
68 54 35;
45 25 12;
48 68 45;
68 54 69];
x=sum(t);
h=pie(x);
textobjs=findobj(h,'type','text');
str1=get(textobjs,{'string'});
val1=get(textobjs,{'extent'});
运行图像
4、采用模型 画一组椭圆
输入程序:th = [0:pi/50:2*pi]';
a = [0.5:.5:4.5];
X = cos(th)*a;
Y = sin(th)*sqrt(25-a.^2);
plot(X,Y),axis('equal'),xlabel('x'), ylabel('y')
title('A set of Ellipses')
oldext=cat(1,val1{:});
names={'商品一;'商品二';'商品三'};
str2=strcat(names,str1);
set(textobjs,{'string'},str2)
val2=get(textobjs,{'extent'});
newext=cat(1,val2{:});
xlable('sin(t)'),ylable('cos(t)'),zlable('t');
gridon;
输出图像
9、用MATLAB绘制饼图
MATLAB第三节绘图

【例】 在[-2,2]范围内绘制函数tanh的图形.
最基本的三维图形函数为plot3,它是将二维函数plot 的有关功能扩展到三维空间,用来绘制三维图形。
Plot3 ( x,y,z,c)
Note:函数功能:以向量x,y,z为坐标,绘制三维曲 线,其中x,y,z表示三维坐标向量,表示线形或颜色。
4.4 三维图形
【例】 绘制三维螺旋曲线:
t=0:pi/50:10*pi; y1=sin(t),y2=cos(t); plot3(y1,y2,t); title('helix'); text(0,0,0,‘origin’); %在(0,0,0)点添加文本框 xlabel('sin(t)'),ylabel('cos(t)'),zlabel('t');
4.3 其它图形函数
3、填充图形
fill(x,y,’c’) — 绘制并填充二维多边图形
Note:x和y为二维多边形顶点坐标向量。字符 ’c’ 规 定填充颜色,其取值前已叙述。
如:绘制一正方形并以黄色填充: x=[0 1 2 4 0]; %正方形顶点坐标向量 y=[0 0 1 1 0]; fill(x,y,‘b’) %绘制并以蓝色填充正方形图
Note:表示在区间tmin<t<tmax绘制参数方程 x=x(t), y=y(t)的函数图.
【例】 在[0, 2 ]π上画 y sin3 t 的x星形co图s3 t.
MATLAB实验三

效果图:2. 当k = 1,2,3时,在同一幅图用同时画出函数sin()y kx 的图形。
MATLAB 代码:x = 0:pi/100:2*pi; y1 = sin(x); y2 = sin(2*x); y3 = sin(3*x); plot(x,y1,x,y2,x,y3) axis([0 2*pi -1 1])legend('y = sin(x)','y = sin(2x)','y = sin(3x)')注:legend 的作用是对图中的不同曲线做标注效果图:以上画图的效果也可以用hold on实现:x = 0:pi/100:2*pi;y1 = sin(x);y2 = sin(2*x);y3 = sin(3*x);plot(x,y1);hold on;plot(x,y2);plot(x,y3);hold offsubplot(2,2,4); plot(x,y)title('y = exp(x)*sin(4x)')注:title 的作用是给图形写上标题 效果图:4. 作隐函数3330x y xy +-=(笛卡尔儿叶形线)的图形 MATLAB 代码:ezplot('x^3+y^3-3*x*y',[-2 2 -2 2])axis equal注: axis equal 的作用是把纵横坐标的刻度比例一致 效果图:5. 在极坐标系下画出心形线2(1cos )r θ=+ MATLAB 代码:theta = 0:pi/100:2*pi; r = 2*(1+cos(theta)); polar(theta,r,'r')注:参数’r’是表示用红色作图,参数与颜色之间的关系如下表所示:b 蓝色g 绿色r 红色c 青绿色m 洋红色y 黄色k 黑色效果图:5. 画出空间螺旋线cos(),sin(),x t y t z t ===的图形MATLAB 代码:t = 0:pi/100:10*pi;x = cos(t);y = sin(t);z = t;plot3(x,y,z)title('x = cos(t),y = sin(t) z = t')效果图:7. 画出MATLAB测试函数peaks的图形MATLAB代码:[X,Y,Z] = peaks;surf(X,Y,Z)shading interpcolormap(cool)注:shading可使用的参数及含义如下:faceted 网络修饰,这是缺省的方式flat 去掉黑色线条,根据小方格的值确定颜色interp 颜色整体改变,根据小方块四角的值差补过度点的值确定颜色colormap为色图设定函数,其参数及含义如下:hsv ——饱和值色图gray ——线性灰度色图hot ——暖色色图cool ——冷色色图bone ——兰色调灰色图copper ——铜色色图pink ——粉红色图prism ——光谱色图jet ——饱和值色图IIflag ——红、白、蓝交替色图六、课堂练习1. 在同一坐标系中画出函数1sin(2*3)y x=+,2sin(32)y x=+的图形,且对于不以同的曲线使用不同的线型;>> x=0:pi/100:2*pi;y1=sin(2*x+3);y2=sin(3*x+2);plot(x,y1,'r-',x,y2,'g+')legend('y1=sin(2*x+3)','y2=sin(3*x+2)')>>2. 当k 分别取1, 2, 3, 4的时候,在同一个窗口的四个子图中分别画出函数*sin(*)y t k t ,每个子图加上适当的标题;>> t = 0:pi/100:2*pi;% 画第一幅子图y = t.*sin(1*t);subplot(2,2,1);3. 画出三个两两相切的圆(假设这个三个圆的方程分别是:22221,(3)4x y x y +=-+=,22(4)9x y +-=);>> ezplot('x^2+y^2=1',[-7 7 -7 7]);hold onezplot('(x-3)^2+y^2=4',[-7 7 -7 7]);hold onezplot('x^2+(y-4)^2=9',[-7 7 -7 7]);4. 在极坐标系下画出三叶形曲线3*sin(3*)r θ=,并尝试不同的线形和颜色; theta = 0:pi/100:2*pi;>> r=3*sin(3*theta);>> polar(theta,r,'r')theta = 0:pi/100:2*pi; r=3*sin(3*theta); polar(theta,r,'g+')5. 画出星形线332*cos ,2*sin x t y t ==的图形; >> t = 0:pi/100:10*pi;x=2*cos(t).^3;>> y=2*sin(t).^3;>> plot(x,y)6. 画出双纽线22222()3*()x y x y +=-的图形; ezplot('(x^2+y^2)^2=3*(x^2-y^2)',[-3 3 -3 3])7. 画出三维曲线图:*cos ,*sin ,x t t y t t z t ===>> t=0:pi/100:2*pi;>> x=t.*cos(t);>> y=t.*sin(t);>> z=t;>> plot3(x,y,z)8. 分别用mesh和surf函数画出马鞍面2246x yz=-+9x=-pi:pi/50:pi;y=x;[X,Y]=meshgrid(x,y); z=-X.^2./4+Y.^2./6.*9; mesh(X,Y,z)>> x=-pi:pi/50:pi;y=x;[X,Y]=meshgrid(x,y); z=-X.^2./4+Y.^2./6.*9; >> surf(X,Y,z)9. 画出球心在原点的球。
实验三 MATLAB绘图

实验三 MATLAB绘图一、实验目的1.掌握绘制二维图形的常用函数。
2.掌握绘制三维图形的常用函数。
3.熟悉利用图形对象进行绘图操作的方法。
4.掌握绘制图形的辅助操作。
二、实验原理1.二维数据曲线图(1)绘制单根二维曲线 plot(x,y);(2)绘制多根二维曲线 plot(x,y) 当x是向量,y是有一维与x同维的矩阵时,则绘制多根不同颜色的曲线。
当x,y是同维矩阵时,则以x,y对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
(3)含有多个输入参数的plot函数 plot(x1,y1,x2,y2,…,xn,yn)(4)具有两个纵坐标标度的图形 plotyy(x1,y1,x2,y2)2.图形标注与坐标控制1)title (图形名称)2)xlabel(x轴说明)3)ylabel(y轴说明)4)text(图形说明)5)legend(图例1,图例2,…)6)axis ([xmin xmax ymin ymax zmin zmax])3.图形窗口的分割subplot(m,n,p)4.三维曲线plot3(x1,y1,z1,选项1,x2,y2,选项2,…,xn,yn,zn,选项n)5.三维曲面mesh(x,y,z,c) 与surf(x,y,z,c)。
一般情况下,x,y,z是维数相同的矩阵。
X,y是网格坐标矩阵,z是网格点上的高度矩阵,c用于指定在不同高度下的颜色范围。
6.图象处理(1) imread和imwrite函数这两个函数分别用于将图象文件读入matlab工作空间,以及将图象数据和色图数据一起写入一定格式的图象文件。
(2) image和imagesc函数这两个函数用于图象显示。
为了保证图象的显示效果,一般还应使用colormap函数设置图象色图。
7.低层绘图操作将图形的每个图形元素(如坐标轴、曲线、文字等)看做一个独立的对象,系统给每个对象分配一个句柄,可以通过句柄对该图形元素进行操作。
8.图形保存图形窗口的File/Save as命令可以将图形保存为多种格式。
MATLAB实验报告(绘图)

MATLAB实验报告(绘图)MATLAB实验报告——MATLAB绘图学号:学院:班级:姓名:1、绘制y = e x 3sin 3x (x ∈ 0,4π ) 的图像,要求用蓝色的星号画图;并且画出其包络线y = ±e x 3 的图像,用红色的点划线画图. MATLAB Code: x = 0:pi/50:4*pi;y = exp(x/3).*sin(3*x);z(1,:) = exp(x/3);z(2,:) = -exp(x/3);plot(x,y,'b*',x,z(1,:),'r-.',x,z(2,:),'r-.');2、用fplot 和ezplot 命令绘出函数y = e2t 3sin ?(1+2t ) 在区间[1,10]上的图像.MATLAB Code:subplot(1,2,1),fplot(@(t)exp(-2*t/3).*sin(1+2*t),[1,10]); title('fplot');xlabel('t');subplot(1,2,2),ezplot('exp(-2*t/3).*sin(1+2*t)',[1,10]); title('ezplot');3、在同一图形窗口画三个字图,要求使用指令gtext,axis,legend,title,xlabel,ylabel:(1)y=xcosx,x∈(?π,π)(2) y=xtan1xsin x3,x∈(π,4π)(3) y=e 1sin x,x∈[1,8]MATLAB Code:subplot(2,2,1),x1 = -pi:pi/50:pi;y1 = x1.*cos(x1);plot(x1,y1,'r'),axisequal,legend('x*cosx'),title('f1'),xlabel('x'),ylabel('y'); subplot(2,2,2),x2 = pi:pi/50:4*pi;y2 = x2.*tan(1./x2).*sin(x2.^3);plot(x2,y2,'b'),axisequal,legend('x*tan(1/x)*sin(x^3)'),title('f2'),xlabel('x') ,ylabel ('y');subplot(2,2,3:4),x3 = 1:0.01:8;y3 = exp(1./x3).*sin(x3);plot(x3,y3,'g'),legend('exp(1/x)*sinx'),title('f3'),xlabel( '时间'),ylabel('位移');gtext('x*cosx');4、使用合适的单轴对数坐标函数绘制函数y=e x2的图像(其中1≤x≤10)MATLAB Code:x = 1:0.01:10;y = exp(x.^2);semilogy(x,y,'b-.');xlabel('x'),ylabel('y');5、绘制圆锥螺线的图像并添加各种标注,圆锥螺线的参数方程为:x =tcos πt y =tsin π6t z =2t(0≤t ≤20π) MATLAB Code:t = 0:pi/50:20*pi;x = t.*cos(pi/6*t);y = t.*sin(pi/6*t);z = 2*t;plot3(x,y,z,'b'),grid on;title('圆锥螺线');xlabel('x = tcost');ylabel('y = tsint');zlabel('z = 2t');6、在同一个图形窗口画半径为1的球面、柱面x2+y2=1以及极sin4t,t∈[0,2π].坐标图形ρ=12MATLAB Code:subplot(1,2,1),sphere(100);hold on;cylinder;hold on;t = 0:pi/50:2*pi;r = 0.5*sin(4*t);subplot(1,2,2);polar(t,r);title('r = 0.5*sin4t');7、用mesh与surf命令绘制三维曲面z=x2+3y2的图像,并使用不同的着色效果及光照效果.MATLAB Code:t = -3:0.1:3;[x,y] = meshgrid(t);z = x.^2+3*y.^2;subplot(1,2,1),mesh(x,y,z),title('网格z = x^2+3y^2'),shading flat;light('position',[10,10,2]);subplot(1,2,2),surf(x,y,z),title('表面z = x^2+3y^2');shading interp; light('position',[5,-4,-2]);8、绘制由函数x 29+y216+z24=1形成的立体图,并通过改变观测点获得该图形在各个坐标平面的投影.MATLAB Code:t = 0:pi/50:2*pi;[x,y] = meshgrid(t,t);X = 3*sin(y).*cos(x);Y = 4*sin(y).*sin(x);Z = 2*cos(y); subplot(2,2,1);mesh(X,Y,Z);title('x^2/9+y^2/16+z^2/4=1');subplot(2,2,2);mesh(X,Y,Z);view(90,0);title('x^2/9+y^2/16+z^2/4=1在yoz面投影'); subplot(2,2,3);mesh(X,Y,Z);view(0,0);title('x^2/9+y^2/16+z^2/4=1在xoz面投影'); subplot(2,2,4);mesh(X,Y,Z);view(0,90);title('x^2/9+y^2/16+z^2/4=1在xoy面投影');9、画三维曲面z=5?x2?y2?2≤x,y≤2与平面z=3的交线. MATLAB Code:t = -2:0.01:2;[x,y] = meshgrid(t);z1=(5-x.^2-y.^2);z2 = 3*ones(length(t));r0 = (abs(z1-z2)<=0.03);zz = r0.*z2;yy = r0.*y;xx = r0.*x;plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'b.');xlabel('x'),ylabel('y'),zlabel('z');title('z = 5-x^2-y^2 与 z = 3的交线');10(附加)、利用迭代复函数z n+1=z n2+c,c∈C构造Mandelbrot集. Mandelbrot集定义为:M: =c∈C| |c|≤2,|c2+c|≤2,|(c2+c)2+c|≤2…….MATLAB Code:%最大迭代数网格细度%本次作图取maxloopNum = 100,Eps = 0.05function drawMandelbrot(maxloopNum,Eps)t = -2:Eps:2;[x,y] = meshgrid(t);z = x+i*y;isMandel = zeros(length(t));for j = 1:length(z)for k = 1:length(z)iter = 0;current = z(j,k);temp = current;while abs(temp)<=2 && iter<maxloopnum< p="">temp = temp^2+current;iter = iter + 1;endif iter == maxloopNumisMandel(j,k) = 1;endendendplot(z.*isMandel,'.');axis equal;title('MandelBrot set');legend('loop = 100,eps = 0.05','Location','northwest'); xlabel('x'),ylabel('iy');end</maxloopnum<>。
实验3 matlab绘图
实验3 matlab绘图实验考核序号考核内容考核等级备注1 课堂表现点名、实验2 程序评价可读性、移植性等3 实验效果精度、可靠性等4 总结评价认识深度等总评实验项目:matlab绘图实验目的:熟练掌握利用MATLAB软件进行绘图实验仪器设备:计算机,MATLAB软件实验原理:1、MATLAB简介:MATLAB语言丰富的图形表现方法,使得数学计算结果可以方便地、多样性地实现了可视化,这是其它语言所不能比拟的。
2、MATLAB的绘图功能:(1)二维绘图:A、plot——最基本的二维图形指令:1. 单窗口单曲线绘图;2. 单窗口多曲线绘图;3. 单窗口多曲线分图绘图;4. 多窗口绘图;5.可任意设置颜色与线型;6.图形加注功能;7.fplot——绘制函数图函数;8.ezplot——符号函数的简易绘图函数B、fill——基本二维绘图函数:绘制二维多边形并填充颜色C、(选做)特殊二维绘图函数:bar——绘制直方图;polar ——绘制极坐标图;hist ——绘制统计直方图;stairs ——绘制阶梯图;stem ——绘制火柴杆图;rose ——绘制统计扇形图;comet ——绘制彗星曲线;errorbar ——绘制误差棒图;compass ——复数向量图(罗盘图);feather ——复数向量投影图(羽毛图);quiver ——向量场图;area ——区域图;pie ——饼图;convhull ——凸壳图;scatter ——离散点图。
(2) 三维绘图:A 、三维线图:plot3——基本的三维图形指令B 、三维网格图:mesh ——三维网线绘图函数C 、三维表面图:surf ——三维曲面绘图函数,与网格图看起来一样D 、三维轮廓图:contour ——三维轮廓绘图函数E 、三维混合图:surfc ——三维混合绘图函试验内容:画出2222)sin(yx y x Z ++=所表示的三维曲面(图1.3-4)。
实验三(Matlab绘图实验日志)word精品文档6页

Matlab绘图实验日志实验题目:1 熟悉plot的基本调用格式2 熟悉对於变化剧烈的函数,可用fplot来进行较精确的绘图3 熟悉符号函数作图函数ezplot实验目的:1 熟悉plot的基本调用格式2 熟悉对於变化剧烈的函数,可用fplot来进行较精确的绘图3 熟悉符号函数作图函数ezplot实验要求:1 熟悉plot的基本调用格式2 熟悉对於变化剧烈的函数,可用fplot来进行较精确的绘图3 熟悉符号函数作图函数ezplot实验主要步骤:题一:1.基本绘图函数1 plot ,plot3 建立向量或矩阵的图形2 Loglog x、y轴都取对数标度建立图形3 Semilogx x轴用于对数标度,y轴线性标度绘制图形4 Semilogy y轴用于对数标度,x轴线性标度绘制图形5 Title 给图形加标题6 Xlabel,Ylabel 给x,y轴加标记7 Text 在图形指定的位置上加文本字符串8 gtext 在鼠标的位置上加文本字符串9 grid 打开网格线题二:2.特殊二(三)维绘图函数1 bar(x,y) (barh(x,y),bar3,bar3h) 直方(水平)图2 comet (x,y) (comet3) 建立彗星流动图3 errorbar(x,y,l,u) 图形加上误差范围4 polar (theta,rho) 极坐标图5hist (y,x) 向量统计的直方图,其中y为要统计的。
当x为标量时,x指定了统计的区间数;当x为向量时,以该向量中各元素为中心进行统计,区间数等于x向量的长度。
6 rose(theta) 极坐标频数累计柱状图7 stairs (x,y) 阶梯图8 stem(x,y,’fill’) 针状图9 fill 实心图10 feather 羽毛图11 compass 罗盘图12quiver,quiver3 向量场图,通常与contour(),gradient()配合使用.13 pie,pie3 饼图题三:3、绘制三维曲面mesh(z)语句给出矩阵Z元素的三消隐图,surf和mesh的用法相似。
实验3MATLAB绘图

《MATLAB 应用》实验报告姓名 学号 班级 成绩实验三 MATLAB 绘图(一)实验目的和要求:1. 掌握绘制二维图形的常用函数。
2. 掌握绘制三维图形的常用函数。
3. 掌握绘制图形的辅助操作。
(二)实验设备及材料:计算机,MATLAB7.0(三)实验内容1 设x x x y cos 1sin35.02⎥⎦⎤⎢⎣⎡++=,在x=0~2π区间取101点,绘制函数的曲线。
代码:x=0:pi/50:2*pi;y=(0.5+3*sin(x)./(1+x.^2)).*cos(x);plot(x,y)图0.形:2已知y1=x2,y2=cos(2x),y3=y1*y2,其中x为取值-2π~2π的等差数列(每次增加0.02π),完成下列操作(1)在同一坐标系下用不同的颜色和线型绘制三条曲线,给三条曲线添加图例。
代码:x=(-2*pi:0.02*pi:2*pi);y1=x.^2;y2=cos(2*x);y3=y1.*y2;plot(x,y1,'m.');hold on;plot(x,y2,'g-.');hold on;plot(x,y3,'y--');hold off图形:(2)以子图形式,分别用条形图、阶梯图、杆图绘制三条曲线,并分别给三个图形添加标题“y1=x^2”,“y2=cos(2x)”和“y3=y1*y2”。
代码:x=(-2*pi:0.02*pi:2*pi);y1=x.^2;y2=cos(2*x);y3=y1.*y2;subplot(3,1,1);plot(x,y1);title('y1');subplot(3,1,2);plot(x,y2);title('y2');subplot(3,1,3);plot(x,y3);title('y3');图形:3 已知⎪⎪⎩⎪⎪⎨⎧>++≤+=0),1ln(210,22x x x x e x y π 在-5<=x<=5区间绘制函数曲线。
实验三 MATLAB绘图(含实验报告)

实验三 MATLAB 绘图一、实验目的1.掌握二维图形的绘制。
2.掌握图形的标注3.了解三维曲线和曲面图形的绘制。
二、实验的设备及条件计算机一台(带有以上的软件环境)。
设计提示1.Matlab 允许在一个图形中画多条曲线:plot(x1,y1,x2,y2,……)指令绘制y 1 = f 1(x 1), y 2 = f 2 (x 2 )等多条曲线。
Matlab 自动给这些曲线以不同颜色。
标注可用text 函数。
2.绘图时可以考虑极坐标和直角坐标的转换。
3.三维曲线绘图函数为plot3,注意参考帮助中的示例。
三、实验内容1.生成1×10 维的随机数向量a ,分别用红、黄、蓝、绿色绘出其连线图、杆图、阶梯图和条形图,并分别标出标题“连线图”、“杆图”、“阶梯图”、“条形图”。
2、绘制函数曲线,要求写出程序代码。
(1) 在区间[0:2π]均匀的取50个点,构成向量t(2) 在同一窗口绘制曲线y1=sin(2*; y2=3cos(t+;要求y1曲线为红色点划线,标记点为圆圈;y2为蓝色虚线,标记点为星号。
(3) 分别在靠近相应的曲线处标注其函数表达式。
3.将图形窗口分成两个绘图区域,分别绘制出函数:⎩⎨⎧+-=+=1352221x x y x y 在[0,3]区间上的曲线,并利用axis 调整轴刻度纵坐标刻度,使1y 在[0,12]区间上,2y 在[-2,]区间上。
4.用mesh 或surf 函数,绘制下面方程所表示的三维空间曲面,x 和y 的取值范围设为[-3,3]。
101022y x z +-=思考题:1. 编写一个mcircle(r)函数,调用该函数时,根据给定的半径r ,以原点为圆心,画一个如图所示的红色空心圆。
(图例半径r=5);左图参考polar函数的用法,右图绘制圆形的参数方程为x=sin (t ),y=cos (t )。
其中,t 的区间为0~2*pi ,步长为。
2.(1)绘一个圆柱螺旋线(形似弹簧)图。
实验三图形绘制matlab实验

实验三 图形绘制一、实验目的1. 掌握绘制二位和三维图形的高层绘图函数;2. 掌握图形控制函数的使用方法;二、实验内容1. 绘制下列曲线(1)!32x x y -=(2)2221x e y -=π(3)64222=+y x(4)⎩⎨⎧==t t y t t x cos sin2. 已知5.02-=x y 和⎩⎨⎧==)sin()3sin()cos()3sin(t t y t t x ,π≤≤t 0,完成下列操作:(1)在同一坐标系下用不同的颜色和线形绘制两条曲线,给曲线添加文字说明;(2)在子图形式,分别用条形图和散点图绘制两条曲线,并为各子图添加函数标题。
3. 分别用plot 和fplot 函数绘制函数xy 1sin =的曲线,分析两曲线的差别。
4. 设te y -+=11,ππ≤≤-t ,在同一图形窗口采用子图的形式绘制条形图、阶梯图、杆图和对数坐标图。
5.绘制下列极坐标图(1)4cos 5+=θρ (2)]2,0[,1),cos 1(πϕϕ∈=+=a a r 6. 绘制下列三维图线(1)⎪⎩⎪⎨⎧===--t z t ey t e x t t sin cos 20/20/,π20≤≤t (2)⎪⎩⎪⎨⎧===32t z t y t x ,10≤≤t三、程序清单及运行结果1.(1)程序清单:x=-100:0.1:100; i=factorial(3); y=x-x.^2/i; plot(x,y); 运行结果:(2)程序清单:x=-10:0.1:10;y=1/(2*pi)*exp(-x.^2/2)plot(x,y);运行结果:(3)程序清单:x=-20:0.1:20;y=sqrt((64-x.*x)/2);plot(x,y);hold on;y=-sqrt((64-x.*x)/2);plot(x,y);xlabel('x');ylabel('y');运行结果:(4)程序清单:t=0:0.01:100x=t.*sin(t);y=t.*cos(t);plot(x,y);运行结果2.(1)程序清单:t=0:pi/100:pi;x=sin(3*t).*cos(t);y1=2*x-0.5;y2=sin(3*t).*sin(t);plot(x,y1,'k:',x,y2);title('t from 0 to pi');xlabel('Variable X'); ylabel('Variable Y');text(-0.4,-1.5,'曲线y1=2x-0.5');text(-0.6,0.7,'曲线x=sin(3t)cos(t);y2=sin(3t)sin(t);');legend('y1','y2');运行结果:(2)程序清单:t=0:pi/100:pi;x=sin(3*t).*cos(t);y1=2*x-0.5;y2=sin(3*t).*sin(t);subplot(2,1,1); plot(x,y1);title('曲线y1=2x-0.5');xlabel('Variable X'); ylabel('Variable Y');subplot(2,1,2); plot(x,y2);title('曲线x=sin(3t)cos(t);y2=sin(3t)sin(t)');xlabel('Variable X'); ylabel('Variable Y');运行结果:3. 程序清单:x=-10:0.1:10;y=sin(1./x);subplot(2,1,1); plot(x,y);title('plot');xlabel('x'); ylabel('y');subplot(2,1,2); fplot('sin(1./x)',[-10,10]);title('fplot');xlabel('x'); ylabel('y');运行结果:两图形的区别在,plot绘制的图形在零点附近有断续,而fplot绘制的图形为连续的曲线。
Matlab实验报告(三) MATLAB绘图

实验目的1.掌握MATLAB的基本绘图命令。
2.掌握运用MATLAB绘制一维、二维、三维图形的方法。
3.给图形加以修饰。
一、预备知识1.基本绘图命令plotplot绘图命令一共有三种形式:⑴plot(y)是plot命令中最为简单的形式,当y为向量时,以y的元素为纵坐标,元素相应的序列号为横坐标,绘制出连线;若y为实矩阵,则按照列绘出每列元素和其序列号的对应关系,曲线数等于矩阵的列数;当y为复矩阵时,则按列以每列元素的实部为横坐标,以虚部为纵坐标,绘出曲线,曲线数等于列数。
⑵ plot(x,y,[linspec])其中linspec是可选的,用它来说明线型。
当x和y为同维向量时,以x为横坐标,y为纵坐标绘制曲线;当x是向量,y是每行元素数目和x维数相同的矩阵时,将绘出以x为横坐标,以y中每行元素为纵坐标的多条曲线,曲线数等于矩阵行数;当x为矩阵,y为相应向量时,使用该命令也能绘出相应图形。
⑶plot(x1,y1,x2,y2,x3,y3……)能够绘制多条曲线,每条曲线分别以x和y为横纵坐标,各条曲线互不影响。
线型和颜色MATLAB可以对线型和颜色进行设定,线型和颜色种类如下:线:—实线:点线—.虚点线——折线点:.圆点 +加号 *星号 x x型 o 空心小圆颜色:y 黄 r 红 g 绿 b 蓝 w 白 k 黑 m 紫 c 青特殊的二维图形函数表5 特殊2维绘图函数[1] 直方图在实际中,常会遇到离散数据,当需要比较数据、分析数据在总量中的比例时,直方图就是一种理想的选择,但要注意该方法适用于数据较少的情况。
直方图的绘图函数有以下两种基本形式。
·bar(x,y) 绘制m*n 矩阵的直方图。
其中y 为m*n 矩阵或向量,x 必须单向递增。
·bar(y) 绘制y 向量的直方图,x 向量默认为x=1:m close all; %关闭所有的图形视窗。
x=1:10;y=rand(size(x)); bar(x,y); %绘制直方图。
实验三绘图函数的应用

温州大学物理与电子信息工程学院Matlab仿真及其应用实验报告课程名称:Matlab仿真及其应用班级:电信二班姓名:施蒙皎学号:0911*******实验地点:5B310 日期:2011.11.12实验三绘图函数的应用[实验目的和要求]1. 熟悉二维和三维绘图函数命令。
2. 熟悉图形修饰与控制方法。
3. 了解特殊坐标图形的绘制。
[实验内容]1. 在同一图形窗口绘制sinx,cosx 曲线,要求不同的颜色和线型、数据点标记字符,X轴范围为[0,2π],Y轴范围为[-2,2],并加注解说明‘sinx’,’cos x’以区分,图例注解放置在图形右下角。
2. 定义函数myfun:,绘制该函数在x=[-20,20]区间内的图形。
3. 试将图形窗口分割成3个区域,分别绘制y=lgx在[0,100]区间内对数坐标、x半对数坐标及y半对数坐标,并加上标题,添加栅格。
4. t=-3:0.125:3,x=sin2t, y=cos2t,z=x^2+2*y^2,请绘制带有等高线的基于x,y,z的三维网格曲面图,并填充颜色。
坐标轴范围为[-1 1 -1 1 0 2]。
5. 绘制出饱和非特性方程的曲线。
6. 绘制函数的曲线,其中曲线为绿虚线,并进行标注7. 绘制分段函数曲线并添加图形标注实验结果及分析:1.t=0:0.05:2*piplot(t,sin(t),'r-.o',t,cos(t),'m-s')legend('sinx','cosx',4)axis([0 2*pi -2 2])2.function Y=myfun(x)Y(:,1)=200*sin(x(:))./x(:); Y(:,2)=x(:).^2;3.x=0:0.1:100;y=log10(x);subplot(311),loglog(x,y) gridtitle('loglog graph') subplot(312),semilogx(x,y) gridtitle('semilogx graph') subplot(313),semilogy(x,y)gridtitle('semilogy graph')4.t=-3:0.125:3;x=sin(2.*t);y=cos(2.*t);[X,Y]=meshgrid(x,y); Z=X.^2+2*Y.^2;mesh(X,Y,Z)axis([-1 1 -1 1 0 3])pausemeshc(X,Y,Z)pausesurf(X,Y,Z)5.x=[-2:0.02:2];y=1.1*sign(x).*(abs(x)>1.1)+x.*(abs(x)<=1.1); plot(x,y)6.x=-3:0.1:3;y=(x<1).*(x.^2)+(x>=1).*(exp(-(x-1).^2));plot(x,y,'--g')text(-2,5,'\leftarrow y=x^2','FontSize',9);text(2,0.7,'\leftarrow y=exp(-(x-1)^2)','FontSize',9)7.clcclose allclearx=0:0.05:10;y=zeros(1,length(x)); for n=1:length(x)if x(n)>=8y(n)=1;elseif x(n)>=6y(n)=5-x(n)/6elseif x(n)>=4y(n)=x(n)^2elsey(n)=sqrt(x(n))endendplot(x,y)axis([0 10 0 40])title('·???oˉêy'); xlabel('x')ylabel('y')text(2,1.3,'y=x^{1/2}'); text(7.3,1.5,'y=5-x/2'); text(8.5,0.9,'y=1');评定成绩:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三 MATLAB绘图
一、实验目的
1.掌握绘制二维图形的常用函数。
2.掌握绘制三维图形的常用函数。
3.熟悉利用图形对象进行绘图操作的方法。
4.掌握绘制图形的辅助操作。
二、实验内容
1.将图形窗口分成两格,分别绘制正割和余割函数曲线,并加上适当的标注。
要求:1)必须画出0到 2,即一个周期的曲线。
2)正割曲线为红色点划线输出,余割曲线为蓝色实线输出。
3)图形上面表明正割和余割公式,横轴标x,纵轴标y。
4)将图形窗口分成两格,正割在上,余割在下。
>> x1=linspace(0,2*pi,60);
x2=linspace(0,2*pi,1000);
s=1./(cos(x1)+eps);
c=1./(sin(x2)+eps);
subplot(2,1,1);
plot(x1,s,'r-.');
title('sec(x)');
xlabel('X');
ylabel('Y');
subplot(2,1,2);
plot(x2,c,'b-');
title('csc(x)');
axis([0,2*pi,-200,200]);
xlabel('X');
ylabel('Y');
2.将图形窗口分成两个窗格,分别绘制出函数:
1
3522
21+-=+=x x y x y
在[0,3]区间上的曲线,并利用axis 调整轴刻度纵坐标刻度,使1y 在[0,12]区间上,2y 在[-2,1.5]区间上。
>> x=0:pi/100:3; y1=2*x+5; y2=x.^2-3*x+1; subplot(1,2,1); plot(x,y1); title('y1=2x+5'); axis([0,3,0,12]); subplot(1,2,2); plot(x,y2);
title('y2=x^2-3x+1'); axis([0,3,-2,1.5]);
0123
2
4
6
8
10
12
y1=2x+5
0123
-2
-1.5
-1
-0.5
0.5
1
1.5
y2=x 2-3x+1
3.用曲面图表现函数22y x z +=,x 和y 的范围从-4到4,设置当前图形的颜色板从黑色到暗红、洋红、黄色、白色的平滑变化,打开网格。
[x,y]=meshgrid(-4:0.01:4); z=x.^2+y.^2; mesh(x,y,z); colormap(hot); shading interp;
4.(1)先建立一个图形窗口,使之背景色为红色,窗口标题为你的学号和姓名,标题前缀没有”Figure No .1”字样,并在窗口上保留原有的菜单项;
(2)在所建立的图形窗口中用默认属性绘制曲线22x y x e ,然后通过图形句柄操作来改变曲线的颜色、线型和线宽,并利用文字对象给曲线添加文字标注。
h=figure('Color',[1,0,0],'Name','学号:200930770106 姓名:郭鑫',...
'NumberTitle','off','MenuBar','figure'); x=0:0.01:5; y=x.^2.*exp(2*x); plot(x,y);
line('XData',x,'YData',y,'Color',[0,1,0],'LineStyle','-.','LineWi dth',1);
text(4,4^2*exp(2*4),'\leftarrow x.^2.*exp(2*x)','FontSize',12);
5. 生成一个圆柱体(可用cylinder函数),并进行光照和材质处理。
[x,y,z]=cylinder(3);
subplot(2,2,1);
surf(x,y,z);
shading interp;
title('未处理');
hold on;
subplot(2,2,2);
surf(x,y,z);
title('光照处理');
light('Position',[-5,-5,0]);
shading interp;
lighting flat;
hold on;
subplot(2,2,3);
surf(x,y,z);
title('材质处理'); material shiny; shading interp;
lighting phong;
hold on;
subplot(2,2,4);
surf(x,y,z);
title('光照、材质处理'); light('Position',[-5,-5,0]); material shiny; shading interp;
lighting flat;
hold on;
三、实验收获与体会
MATLAB的最强大的功能之一就是绘图,它可以描绘出其他软件不能实现的与真实最为接近的多维图形。
而通过实验三,我学习到各种绘图的常用函数,并掌握二维、三维的图形绘制,与此同时也熟悉利用图形对象进行绘图操作的方法。
