圆中考真题精选汇编一
中考数学圆的综合综合题汇编附答案

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,点P在⊙O的直径AB的延长线上,PC为⊙O的切线,点C为切点,连接AC,过点A作PC的垂线,点D为垂足,AD交⊙O于点E.(1)如图1,求证:∠DAC=∠PAC;(2)如图2,点F(与点C位于直径AB两侧)在⊙O上,BF FA=,连接EF,过点F作AD 的平行线交PC于点G,求证:FG=DE+DG;(3)在(2)的条件下,如图3,若AE=23DG,PO=5,求EF的长.【答案】(1)证明见解析;(2)证明见解析;(3)EF=32.【解析】【分析】(1)连接OC,求出OC∥AD,求出OC⊥PC,根据切线的判定推出即可;(2)连接BE交GF于H,连接OH,求出四边形HGDE是矩形,求出DE=HG,FH=EH,即可得出答案;(3)设OC交HE于M,连接OE、OF,求出∠FHO=∠EHO=45°,根据矩形的性质得出EH∥DG,求出OM=12AE,设OM=a,则HM=a,AE=2a,AE=23DG,DG=3a,求出ME=CD=2a,BM=2a,解直角三角形得出tan∠MBO=12MOBM=,tanP=12COPO=,设OC=k,则PC=2k,根据OP=5k=5求出k=5,根据勾股定理求出a,即可求出答案.【详解】(1)证明:连接OC,∵PC为⊙O的切线,∴OC⊥PC,∵AD⊥PC,∴OC∥AD,∴∠OCA=∠DAC,∵OC=OA,∴∠PAC=∠OCA,∴∠DAC=∠PAC;(2)证明:连接BE交GF于H,连接OH,∵FG∥AD,∴∠FGD+∠D=180°,∵∠D=90°,∴∠FGD=90°,∵AB为⊙O的直径,∴∠BEA=90°,∴∠BED=90°,∴∠D=∠HGD=∠BED=90°,∴四边形HGDE是矩形,∴DE=GH,DG=HE,∠GHE=90°,∵BF AF=,∴∠HEF=∠FEA=12∠BEA=1902o⨯=45°,∴∠HFE=90°﹣∠HEF=45°,∴∠HEF=∠HFE,∴FH=EH,∴FG=FH+GH=DE+DG;(3)解:设OC交HE于M,连接OE、OF,∵EH=HF,OE=OF,HO=HO,∴△FHO≌△EHO,∴∠FHO=∠EHO=45°,∵四边形GHED是矩形,∴EH∥DG,∴∠OMH=∠OCP=90°,∴∠HOM=90°﹣∠OHM=90°﹣45°=45°,∴∠HOM=∠OHM,∴HM=MO,∵OM⊥BE,∴BM=ME,∴OM=12 AE,设OM=a,则HM=a,AE=2a,AE=23DG,DG=3a,∵∠HGC=∠GCM=∠GHE=90°,∴四边形GHMC是矩形,∴GC=HM=a,DC=DG﹣GC=2a,∵DG=HE,GC=HM,∴ME=CD=2a,BM=2a,在Rt△BOM中,tan∠MBO=122 MO aBM a==,∵EH∥DP,∴∠P=∠MBO,tanP=12 COPO=,设OC=k,则PC=2k,在Rt△POC中,,解得:在Rt△OME中,OM2+ME2=OE2,5a2=5,a=1,∴HE=3a=3,在Rt△HFE中,∠HEF=45°,∴.【点睛】考查了切线的性质,矩形的性质和判定,解直角三角形,勾股定理等知识点,能综合运用性质进行推理是解此题的关键.2.如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,交BC于D,过O作OE∥BC,交OD于E,连接AD、AE、CE.(1)求证:∠ACE=∠DCE;(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;(3)若AC=4,23CDF COE S S ∆∆=,求CF 的长.【答案】(1)证明见解析,(2)60°;(3)433【解析】 【分析】(1)易证∠OEC =∠OCE ,∠OEC =∠ECD ,从而可知∠OCE =∠ECD ,即∠ACE =∠DCE ; (2)延长AE 交BC 于点G ,易证∠AGC =∠B +∠BAG =60°,由于OE ∥BC ,所以∠AEO =∠AGC =60°,所以∠EAO =∠AEO =60°; (3)易证12COE CAES S=,由于23CDF COES S=,所以CDF CAES S =13,由圆周角定理可知∠AEC =∠FDC =90°,从而可证明△CDF ∽△CEA ,利用三角形相似的性质即可求出答案. 【详解】(1)∵OC =OE ,∴∠OEC =∠OCE .∵OE ∥BC ,∴∠OEC =∠ECD ,∴∠OCE =∠ECD ,即∠ACE =∠DCE ; (2)延长AE 交BC 于点G .∵∠AGC 是△ABG 的外角,∴∠AGC =∠B +∠BAG =60°. ∵OE ∥BC ,∴∠AEO =∠AGC =60°. ∵OA =OE ,∴∠EAO =∠AEO =60°.(3)∵O 是AC 中点,∴12COE CAESS =. 23CDF COES S=,∴CDF CAES S=13. ∵AC 是直径,∴∠AEC =∠FDC =90°. ∵∠ACE =∠FCD ,∴△CDF ∽△CEA ,∴CF CA =33,∴CF =33CA =433.【点睛】本题考查了圆的综合问题,涉及平行线的性质,三角形的外角的性质,三角形中线的性质,圆周角定理,相似三角形的判定与性质等知识,需要学生灵活运用所学知识.3.如图,AB为⊙O的直径,点D为AB下方⊙O上一点,点C为弧ABD的中点,连接CD,CA.(1)求证:∠ABD=2∠BDC;(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长度.【答案】(1)证明见解析;(2)见解析;(3)92 DE=.【解析】【分析】(1)连接AD,如图1,设∠BDC=α,∠ADC=β,根据圆周角定理得到∠CAB=∠BDC=α,由AB为⊙O直径,得到∠ADB=90°,根据余角的性质即可得到结论;(2)根据已知条件得到∠ACE=∠ADC,等量代换得到∠ACE=∠CAE,于是得到结论;(3)如图2,连接OC,根据圆周角定理得到∠COB=2∠CAB,等量代换得到∠COB=∠ABD,根据相似三角形的性质得到OH=5,根据勾股定理得到AB=22AD BD+=26,由相似三角形的性质即可得到结论.【详解】(1)连接AD.如图1,设∠BDC=α,∠ADC=β,则∠CAB=∠BDC=α,∵点C为弧ABD中点,∴AC=CD,∴∠ADC=∠DAC=β,∴∠DAB=β﹣α,∵AB为⊙O直径,∴∠ADB=90°,∴α+β=90°,∴β=90°﹣α,∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),∴∠ABD=2α,∴∠ABD=2∠BDC;(2)∵CH⊥AB,∴∠ACE+∠CAB=∠ADC+∠BDC=90°,∵∠CAB =∠CDB ,∴∠ACE =∠ADC , ∵∠CAE =∠ADC ,∴∠ACE =∠CAE ,∴AE =CE ; (3)如图2,连接OC ,∴∠COB =2∠CAB , ∵∠ABD =2∠BDC ,∠BDC =∠CAB ,∴∠COB =∠ABD , ∵∠OHC =∠ADB =90°,∴△OCH ∽△ABD ,∴12OH OC BD AB ==, ∵OH =5,∴BD =10,∴AB =22AD BD +=26,∴AO =13,∴AH =18,∵△AHE ∽△ADB ,∴AH AE AD AB =,即1824=26AE ,∴AE =392,∴DE =92.【点睛】本题考查了垂径定理,相似三角形的判定和性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.4.如图.在△ABC 中,∠C =90°,AC =BC ,AB =30cm ,点P 在AB 上,AP =10cm ,点E 从点P 出发沿线段PA 以2c m/s 的速度向点A 运动,同时点F 从点P 出发沿线段PB 以1c m/s 的速度向点B 运动,点E 到达点A 后立刻以原速度沿线段AB 向点B 运动,在点E 、F 运动过程中,以EF 为边作正方形EFGH ,使它与△ABC 在线段AB 的同侧,设点E 、F 运动的时间为t (s )(0<t <20).(1)当点H 落在AC 边上时,求t 的值;(2)设正方形EFGH 与△ABC 重叠部分的面积为S .①试求S 关于t 的函数表达式;②以点C 为圆心,12t 为半径作⊙C ,当⊙C 与GH 所在的直线相切时,求此时S 的值.【答案】(1)t=2s或10s;(2)①S=2229?(02)75050(210)240400?(1020)t tt t tt t t⎧<≤⎪⎪-+-<≤⎨⎪-+<<⎪⎩;②100cm2.【解析】试题分析:(1)如图1中,当0<t≤5时,由题意AE=EH=EF,即10﹣2t=3t,t=2;如图2中,当5<t<20时,AE=HE,2t﹣10=10﹣(2t﹣10)+t,t=10;(2)分四种切线讨论a、如图3中,当0<t≤2时,重叠部分是正方形EFGH,S=(3t)2=9t2.b、如图4中,当2<t≤5时,重叠部分是五边形EFGMN.c、如图5中,当5<t<10时,重叠部分是五边形EFGMN.d、如图6中,当10<t<20时,重叠部分是正方形EFGH.分别计算即可;②分两种情形分别列出方程即可解决问题.试题解析:解:(1)如图1中,当0<t≤5时,由题意得:AE=EH=EF,即10﹣2t=3t,t=2如图2中,当5<t<20时,AE=HE,2t﹣10=10﹣(2t﹣10)+t,t=10.综上所述:t=2s或10s时,点H落在AC边上.(2)①如图3中,当0<t≤2时,重叠部分是正方形EFGH,S=(3t)2=9t2如图4中,当2<t≤5时,重叠部分是五边形EFGMN,S=(3t)2﹣12(5t﹣10)2=﹣72t2+50t﹣50.如图5中,当5<t<10时,重叠部分是五边形EFGMN,S=(20﹣t)2﹣12(30﹣3t)2=﹣72t2+50t﹣50.如图6中,当10<t<20时,重叠部分是正方形EFGH,S=(20﹣t)2=t2﹣40t+400.综上所述:S=2229?(02)75050(210) 240400?(1020)t tt t tt t t⎧<≤⎪⎪-+-<≤⎨⎪-+<<⎪⎩.②如图7中,当0<t≤5时,12t+3t=15,解得:t=307,此时S=100cm2,当5<t<20时,12t+20﹣t=15,解得:t=10,此时S=100.综上所述:当⊙C与GH所在的直线相切时,求此时S的值为100cm2点睛:本题考查了圆综合题、正方形的性质、等腰直角三角形的性质、切线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,注意不能漏解,属于中考压轴题.5.已知⊙O中,弦AB=AC,点P是∠BAC所对弧上一动点,连接PA,PB.(1)如图①,把△ABP绕点A逆时针旋转到△ACQ,连接PC,求证:∠ACP+∠ACQ=180°;(2)如图②,若∠BAC=60°,试探究PA、PB、PC之间的关系.(3)若∠BAC=120°时,(2)中的结论是否成立?若是,请证明;若不是,请直接写出它们之间的数量关系,不需证明.【答案】(1)证明见解析;(2)PA=PB+PC.理由见解析;(3)若∠BAC=120°时,(2)3 PA=PB+PC.【解析】试题分析:(1)如图①,连接PC.根据“内接四边形的对角互补的性质”即可证得结论;(2)如图②,通过作辅助线BC、PE、CE(连接BC,延长BP至E,使PE=PC,连接CE)构建等边△PCE和全等三角形△BEC≌△APC;然后利用全等三角形的对应边相等和线段间的和差关系可以求得PA=PB+PC;(3)如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.利用全等三角形△ABP≌△AQP(SAS)的对应边相等推知AB=AQ,PB=PG,将PA、PB、PC的数量关系转化到△APC中来求即可.试题解析:(1)如图①,连接PC.∵△ACQ是由△ABP绕点A逆时针旋转得到的,∴∠ABP=∠ACQ.由图①知,点A、B、P、C四点共圆,∴∠ACP+∠ABP=180°(圆内接四边形的对角互补),∴∠ACP+∠ACQ=180°(等量代换);(2)PA=PB+PC.理由如下:如图②,连接BC,延长BP至E,使PE=PC,连接CE.∵弦AB=弦AC,∠BAC=60°,∴△ABC是等边三角形(有一内角为60°的等腰三角形是等边三角形).∵A、B、P、C四点共圆,∴∠BAC+∠BPC=180°(圆内接四边形的对角互补),∵∠BPC+∠EPC=180°,∴∠BAC=∠CPE=60°,∵PE=PC,∴△PCE是等边三角形,∴CE=PC,∠E=∠ECP=∠EPC=60°;又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,∴∠BCE=∠ACP(等量代换),在△BEC和△APC中,CE PCBCE ACPAC BC=⎧⎪∠=∠⎨⎪=⎩,∴△BEC≌△APC(SAS),∴BE=PA,∴PA=BE=PB+PC;(3)若∠BAC=120°时,(23.理由如下:如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.∵∠BAC=120°,∠BAC+∠BPC=180°,∴∠BPC=60°.∵弦AB=弦AC,∴∠APB=∠APQ=30°.在△ABP和△AQP中,PB PQAPB APQAP AP=⎧⎪∠=∠⎨⎪=⎩,∴△ABP≌△AQP(SAS),∴AB=AQ,PB=PQ(全等三角形的对应边相等),∴AQ=AC(等量代换).在等腰△AQC中,QG=CG.在Rt△APG中,∠APG=30°,则AP=2AG,PG=3AG,∴PB+PC=PG ﹣QG+PG+CG=PG﹣QG+PG+QG=2PG=23AG,∴3PA=23AG,即3PA=PB+PC.【点睛】本题考查了圆的综合题,解题的关键要能掌握和灵活运用圆心角、弧、弦间的关系,全等三角形的判定与性质,圆内接四边形的性质等.6.已知:如图,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠APB是平分线分别交BC,AB于点D、E,交⊙O于点F,∠A=60°,并且线段AE、BD的长是一元二次方程 x2﹣kx+23 =0的两根(k为常数).(1)求证:PA•BD=PB•AE;(2)求证:⊙O的直径长为常数k;(3)求tan∠FPA的值.【答案】(1)见解析;(2)见解析;(3)tan∠FPA=2﹣3 .【解析】试题分析:(1)由PB切⊙O于点B,根据弦切角定理,可得∠PBD=∠A,又由PF平分∠APB,可证得△PBD∽△PAE,然后由相似三角形的对应边成比例,证得PA•BD=PB•AE;(2)易证得BE=BD,又由线段AE、BD的长是一元二次方程 x2﹣kx+2=0的两根(k为常数),即可得AE+BD=k,继而求得AB=k,即:⊙O的直径长为常数k;(3)由∠A=60°,并且线段AE、BC的长是一元二次方程 x2﹣kx+2=0的两根(k为常数),可求得AE与BD的长,继而求得tan∠FPB的值,则可得tan∠FPA的值.试题解析:(1)证明:如图,∵PB切⊙O于点B,∴∠PBD=∠A,∵PF平分∠APB,∴∠APE=∠BPD,∴△PBD∽△PAE,∴PB:PA=BD:AE,∴PA•BD=PB•AE;(2)证明:如图,∵∠BED=∠A+∠EPA,∠BDE=∠PBD+∠BPD.又∵∠PBD=∠A,∠EPA=∠BPD,∴∠BED=∠BDE.∴BE=BD.∵线段AE、BD的长是一元二次方程 x2﹣kx+2=0的两根(k为常数),∴AE+BD=k,∴AE+BD=AE+BE=AB=k,即⊙O直径为常数k.(3)∵PB切⊙O于B点,AB为直径.∴∠PBA=90°.∵∠A=60°.∴PB=PA•sin60°=PA,又∵PA•BD=PB•AE,∴BD=AE,∵线段AE、BD的长是一元二次方程 x2﹣kx+2=0的两根(k为常数).∴AE•BD=2,即AE2=2,解得:AE=2,BD=,∴AB=k=AE+BD=2+,BE=BD=,在Rt△PBA中,PB=AB•tan60°=(2+)×=3+2.在Rt△PBE中,tan∠BPF===2﹣,∵∠FPA=∠BPF,∴tan∠FPA=2﹣.【点睛】此题考查了切线的性质、等腰三角形的判定与性质、相似三角形的判定与性质以及根与系数的关系等知识.此题难度较大,注意掌握数形结合思想与方程思想的应用.7.如图1,等边△ABC 的边长为3,分别以顶点B 、A 、C 为圆心,BA 长为半径作AC 、CB 、BA ,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形,设点l 为对称轴的交点.(1)如图2,将这个图形的顶点A 与线段MN 作无滑动的滚动,当它滚动一周后点A 与端点N 重合,则线段MN 的长为 ;(2)如图3,将这个图形的顶点A 与等边△DEF 的顶点D 重合,且AB ⊥DE ,DE =2π,将它沿等边△DEF 的边作无滑动的滚动当它第一次回到起始位置时,求这个图形在运动过程中所扫过的区域的面积;(3)如图4,将这个图形的顶点B 与⊙O 的圆心O 重合,⊙O 的半径为3,将它沿⊙O 的圆周作无滑动的滚动,当它第n 次回到起始位置时,点I 所经过的路径长为 (请用含n 的式子表示)【答案】(1)3π;(2)27π;(3)3.【解析】试题分析:(1)先求出AC 的弧长,继而得出莱洛三角形的周长为3π,即可得出结论; (2)先判断出莱洛三角形等边△DEF 绕一周扫过的面积如图所示,利用矩形的面积和扇形的面积之和即可;(3)先判断出莱洛三角形的一个顶点和O 重合旋转一周点I 的路径,再用圆的周长公式即可得出.试题解析:解:(1)∵等边△ABC 的边长为3,∴∠ABC =∠ACB =∠BAC =60°,AC BC AB ==,∴AC BC l l ==AB l =603180π⨯=π,∴线段MN 的长为AC BC AB l l l ++=3π.故答案为3π;(2)如图1.∵等边△DEF 的边长为2π,等边△ABC 的边长为3,∴S 矩形AGHF =2π×3=6π,由题意知,AB ⊥DE ,AG ⊥AF ,∴∠BAG =120°,∴S 扇形BAG =21203360π⨯=3π,∴图形在运动过程中所扫过的区域的面积为3(S 矩形AGHF +S 扇形BAG )=3(6π+3π)=27π;(3)如图2,连接BI 并延长交AC 于D .∵I 是△ABC 的重心也是内心,∴∠DAI =30°,AD =12AC =32,∴OI =AI =3230AD cos DAI cos ∠=︒=3,∴当它第1次回到起始位置时,点I 所经过的路径是以O 为圆心,OI 为半径的圆周,∴当它第n 次回到起始位置时,点I 所经过的路径长为n •2π•3=23n π.故答案为23n π.点睛:本题是圆的综合题,主要考查了弧长公式,莱洛三角形的周长,矩形,扇形面积公式,解(1)的关键是求出AC 的弧长,解(2)的关键是判断出莱洛三角形绕等边△DEF 扫过的图形,解(3)的关键是得出点I 第一次回到起点时,I 的路径,是一道中等难度的题目.8.如图,AB 是O 的直径,弦CD AB ⊥于点E ,过点C 的切线交AB 的延长线于点F ,连接DF .(1)求证:DF 是O 的切线;(2)连接BC ,若30BCF ∠=︒,2BF =,求CD 的长.【答案】(1)见解析;(2)3【解析】【分析】(1) 连接OD,由垂径定理证OF 为CD 的垂直平分线,得CF=DF ,∠CDF=∠DCF ,由∠CDO=∠OCD ,再证∠CDO +∠CDB=∠OCD+∠DCF=90°,可得OD ⊥DF ,结论成立.(2) 由∠OCF=90°, ∠BCF=30°,得∠OCB=60°,再证ΔOCB 为等边三角形,得∠COB=60°,可得∠CFO=30°,所以FO=2OC=2OB ,FB=OB= OC =2,在直角三角形OCE 中,解直角三角形可得CE,再推出CD=2CE.【详解】(1)证明:连接OD∵CF 是⊙O 的切线∴∠OCF=90°∴∠OCD+∠DCF=90°∵直径AB ⊥弦CD∴CE=ED,即OF为CD的垂直平分线∴CF=DF∴∠CDF=∠DCF∵OC=OD,∴∠CDO=∠OCD∴∠CDO +∠CDB=∠OCD+∠DCF=90°∴OD⊥DF∴DF是⊙O的切线(2)解:连接OD∵∠OCF=90°, ∠BCF=30°∴∠OCB=60°∵OC=OB∴ΔOCB为等边三角形,∴∠COB=60°∴∠CFO=30°∴FO=2OC=2OB∴FB=OB= OC =2在直角三角形OCE中,∠CEO=90°∠COE=60°CE3sin COEOC2∠==∴CF3=∴CD=2 CF23=【点睛】本题考核知识点:垂径定理,切线,解直角三角形. 解题关键点:熟记切线的判定定理,灵活运用含有30°角的直角三角形性质,巧解直角三角形.9.如图,已知△ABC内接于⊙O,BC交直径AD于点E,过点C作AD的垂线交AB的延长线于点G,垂足为F.连接OC.(1)若∠G=48°,求∠ACB的度数;(2)若AB=AE,求证:∠BAD=∠COF;(3)在(2)的条件下,连接OB,设△AOB的面积为S1,△ACF的面积为S2.若tan∠CAF=12,求12SS的值.【答案】(1)48°(2)证明见解析(3)3 4【解析】【分析】(1)连接CD,根据圆周角定理和垂直的定义可得结论;(2)先根据等腰三角形的性质得:∠ABE=∠AEB,再证明∠BCG=∠DAC,可得CD PB PD==,则所对的圆周角相等,根据同弧所对的圆周角和圆心角的关系可得结论;(3)过O作OG⊥AB于G,证明△COF≌△OAG,则OG=CF=x,AG=OF,设OF=a,则OA=OC=2x-a,根据勾股定理列方程得:(2x-a)2=x2+a2,则a=34x,代入面积公式可得结论.【详解】(1)连接CD,∵AD是⊙O的直径,∴∠ACD=90°,∴∠ACB+∠BCD=90°,∵AD⊥CG,∴∠AFG=∠G+∠BAD=90°,∵∠BAD=∠BCD,∴∠ACB=∠G=48°;(2)∵AB=AE,∴∠ABE=∠AEB,∵∠ABC=∠G+∠BCG,∠AEB=∠ACB+∠DAC,由(1)得:∠G=∠ACB,∴∠BCG=∠DAC,∴CD PB=,∵AD是⊙O的直径,AD⊥PC,∴CD PD=,∴CD PB PD==,∴∠BAD=2∠DAC,∵∠COF=2∠DAC,∴∠BAD=∠COF;(3)过O作OG⊥AB于G,设CF=x,∵tan∠CAF=12=CF AF,∴AF=2x ,∵OC=OA,由(2)得:∠COF=∠OAG,∵∠OFC=∠AGO=90°,∴△COF≌△OAG,∴OG=CF=x,AG=OF,设OF=a,则OA=OC=2x﹣a,Rt△COF中,CO2=CF2+OF2,∴(2x﹣a)2=x2+a2,a=34 x,∴OF=AG=34 x,∵OA=OB,OG⊥AB,∴AB=2AG=32x,∴1213··3 22 1·24·2AB OG x xSS x xCF AF===.【点睛】圆的综合题,考查了三角形的面积、垂径定理、角平分线的性质、三角形全等的性质和判定以及解直角三角形,解题的关键是:(1)根据圆周角定理找出∠ACB+∠BCD=90°;(2)根据外角的性质和圆的性质得:CD PB PD==;(3)利用三角函数设未知数,根据勾股定理列方程解决问题.10.已知AB ,CD 都是O 的直径,连接DB ,过点C 的切线交DB 的延长线于点E . ()1如图1,求证:AOD 2E 180∠∠+=;()2如图2,过点A 作AF EC ⊥交EC 的延长线于点F ,过点D 作DG AB ⊥,垂足为点G ,求证:DG CF =;()3如图3,在()2的条件下,当DG 3CE 4=时,在O 外取一点H ,连接CH 、DH 分别交O 于点M 、N ,且HDE HCE ∠∠=,点P 在HD 的延长线上,连接PO 并延长交CM 于点Q ,若PD 11=,DN 14=,MQ OB =,求线段HM 的长.【答案】(1)证明见解析(2)证明见解析(3)837+【解析】【分析】(1)由∠D +∠E =90°,可得2∠D +2∠E =180°,只要证明∠AOD =2∠D 即可;(2)如图2中,作OR ⊥AF 于R .只要证明△AOR ≌△ODG 即可;(3)如图3中,连接BC 、OM 、ON 、CN ,作BT ⊥CL 于T ,作NK ⊥CH 于K ,设CH 交DE 于W .解直角三角形分别求出KM ,KH 即可;【详解】()1证明:如图1中,O 与CE 相切于点C ,OC CE ∴⊥,OCE 90∠∴=,D E 90∠∠∴+=,2D 2E 180∠∠∴+=,AOD COB ∠∠=,BOC 2D ∠∠=,AOD 2D ∠∠=,AOD 2E 180∠∠∴+=.()2证明:如图2中,作OR AF ⊥于R .OCF F ORF 90∠∠∠===,∴四边形OCFR 是矩形,AF//CD ∴,CF OR =,A AOD ∠∠∴=,在AOR 和ODG 中,A AOD ∠∠=,ARO OGD 90∠∠==,OA DO =,AOR ∴≌ODG ,OR DG ∴=,DG CF ∴=,()3解:如图3中,连接BC 、OM 、ON 、CN ,作BT CL ⊥于T ,作NK CH ⊥于K ,设CH 交DE 于W .设DG 3m =,则CF 3m =,CE 4m =,OCF F BTE 90∠∠∠===,AF//OC//BT ∴,OA OB =,CT CF 3m ∴==,ET m ∴=, CD 为直径,CBD CND 90CBE ∠∠∠∴===,E 90EBT CBT ∠∠∠∴=-=,tan E tan CBT ∠∠∴=,BT CT ET BT∴=,BT 3m m BT∴=,BT ∴=负根已经舍弃),tan E ∠∴== E 60∠∴=,CWD HDE H ∠∠∠=+,HDE HCE ∠∠=,H E 60∠∠∴==,MON 2HCN 60∠∠∴==,OM ON =,OMN ∴是等边三角形,MN ON ∴=,QM OB OM ==,MOQ MQO ∠∠∴=,MOQ PON 180MON 120∠∠∠+=-=,MQO P 180H 120∠∠∠+=-=, PON P ∠∠∴=,ON NP 141125∴==+=,CD 2ON 50∴==,MN ON 25==,在Rt CDN 中,CN 48==,在Rt CHN 中,CN 48tan H HN HN∠===HN ∴=在Rt KNH 中,1KH HN 2==NK 24==,在Rt NMK 中,MK 7===,HM HK MK 7∴=+=.【点睛】本题考查圆综合题、全等三角形的判定和性质、平行线的性质、勾股定理、等边三角形的判定和性质、锐角三角函数等知识,添加常用辅助线,构造全等三角形或直角三角形解题的关键.。
圆中考试题集锦(附答案)

圆中考试题一、选择题1.(北京市西城区)如图,BC 是⊙O 的直径,P 是CB 延长线上一点,PA 切⊙O 于点A ,如果PA =3,PB =1,那么∠APC 等于 ()(A )15 (B )30 (C )45 (D )602.(北京市西城区)如果圆柱的高为20厘米,底面半径是高的41,那么这个圆柱的侧面积是 ()(A )100π平方厘米 (B )200π平方厘米(C )500π平方厘米 (D )200平方厘米3.(北京市西城区)“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题,“今在圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为E ,CE =1寸,AB =10寸,求直径CD 的长”.依题意,CD 长为 ( )(A )225寸 (B )13寸 (C )25寸 (D )26寸4.(北京市朝阳区)已知:如图,⊙O 半径为5,PC 切⊙O 于点C ,PO 交⊙O 于点A ,PA =4,那么PC 的长等于 ( )(A )6 (B )25 (C )210 (D )2145.(北京市朝阳区)如果圆锥的侧面积为20π平方厘米,它的母线长为5厘米,那么此圆锥的底面半径的长等于 ( )(A )2厘米 (B )22厘米 (C )4厘米 (D )8厘米6.(天津市)相交两圆的公共弦长为16厘米,若两圆的半径长分别为10厘米和17厘米,则这两圆的圆心距为 ( )(A )7厘米 (B )16厘米 (C )21厘米 (D )27厘米7.(重庆市)如图,⊙O 为△ABC 的内切圆,∠C =90,AO 的延长线交BC 于点D ,AC =4,DC =1,,则⊙O 的半径等于 ( )(A )54 (B )45 (C )43 (D )658.(重庆市)一居民小区有一正多边形的活动场.为迎接“AAPP ”会议在重庆市的召开,小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台,花台都以多边形的顶点为圆心,比多边形的内角为圆心角,花台占地面积共为12π平方米.若每个花台的造价为400元,则建造这些花台共需资金 ( )(A )2400元 (B )2800元 (C )3200元 (D )3600元9.(河北省)如图,AB 是⊙O 直径,CD 是弦.若AB =10厘米,CD =8厘米,那么A 、B 两点到直线CD 的距离之和为 ( )(A )12厘米 (B )10厘米 (C )8厘米 (D )6厘米10.(河北省)某工件形状如图所示,圆弧BC 的度数为60,AB =6厘米,点B 到点C 的距离等于AB ,∠BAC = 30,则工件的面积等于 ( )(A )4π (B )6π (C )8π (D )10π11.(沈阳市)如图,PA 切⊙O 于点A ,PBC 是⊙O 的割线且过圆心,PA =4,PB =2,则⊙O 的半径等于 ( )(A )3 (B )4 (C )6 (D )812.(哈尔滨市)已知⊙O 的半径为35厘米,⊙O '的半径为5厘米.⊙O 与⊙O '相交于点D 、E .若两圆的公共弦DE 的长是6厘米(圆心O 、O '在公共弦DE 的两侧),则两圆的圆心距O O '的长为 ( )(A )2厘米 (B )10厘米 (C )2厘米或10厘米 (D )4厘米13.(陕西省)如图,两个等圆⊙O 和⊙O '的两条切线OA 、OB ,A 、B 是切点,则∠AOB 等于 ( )(A )30 (B )45 (C )60 (D )9014.(甘肃省)如图,AB 是⊙O 的直径,∠C =30,则∠ABD = ( )(A ) 30 (B ) 40 (C ) 50 (D )6015.(甘肃省)弧长为6π的弧所对的圆心角为60,则弧所在的圆的半径为( )(A )6 (B )62 (C )12 (D )1816.(甘肃省)如图,在△ABC 中,∠BAC =90,AB =AC =2,以AB 为直径的圆交BC 于D ,则图中阴影部分的面积为 ( )(A )1 (B )2 (C )1+4π (D )2-4π17.(宁夏回族自治区)已知圆的内接正六边形的周长为18,那么圆的面积为 ( )(A )18π (B )9π (C )6π (D )3π18.(山东省)如图,点P 是半径为5的⊙O 内一点,且OP =3,在过点P的所有弦中,长度为整数的弦一共有 ( )(A )2条 (B )3条 (C )4条 (D )5条19.(南京市)如图,正六边形ABCDEF 的边长的上a ,分别以C 、F 为圆心,a 为半径画弧,则图中阴影部分的面积是 ( )(A )261a π (B )231a π (C )232a π (D )234aπ20.(杭州市)过⊙O 内一点M 的最长的弦长为6厘米,最短的弦长为4厘米,则OM 的长为 ( )(A )3厘米 (B )5厘米 (C )2厘米 (D )5厘米21.(安徽省)已知圆锥的底面半径是3,高是4,则这个圆锥侧面展开图的面积是 ( )(A )12π (B )15π (C )30π (D )24π22.(安微省)已知⊙O 的直径AB 与弦AC 的夹角为30,过C 点的切线PC 与AB 延长线交P .PC =5,则⊙O 的半径为 ( )(A )335 (B )635 (C )10 (D )523.(福州市)如图:PA 切⊙O 于点A ,PBC 是⊙O 的一条割线,有PA=32,PB =BC ,那么BC 的长是 ( )(A )3 (B )32 (C )3 (D )3224.(河南省)如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是 ( )(A )π (B )1.5π (C )2π (D )2.5π25.(四川省)正六边形的半径为2厘米,那么它的周长为 ( )(A )6厘米 (B )12厘米 (C )24厘米 (D )122厘米26.(四川省)一个圆柱形油桶的底面直径为0.6米,高为1米,那么这个油桶的侧面积为 ( )(A )0.09π平方米 (B )0.3π平方米 (C )0.6平方米 (D )0.6π平方米27.(贵阳市)一个形如圆锥的冰淇淋纸筒,其底面直径为6厘米,母线长为5厘米,围成这样的冰淇淋纸筒所需纸片的面积是 ( )(A )66π平方厘米 (B )30π平方厘米 (C )28π平方厘米 (D )15π平方厘米28.(新疆乌鲁木齐)在半径为2的⊙O 中,圆心O 到弦AB 的距离为1,则弦AB 所对的圆心角的度数可以是 ( )(A )60 (B )90 (C )120 (D )15029.(新疆乌鲁木齐)将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面,(接口损耗不计),则桶底的面积为 ( )(A )π1600平方厘米 (B )1600π平方厘米(C )π6400平方厘米 (D )6400π平方厘米30.(成都市)如图,已知AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD =10厘米,AP ∶PB =1∶5,那么⊙O 的半径是 ( )(A )6厘米 (B )53厘米 (C )8厘米 (D )35厘米31.(成都市)在Rt △ABC 中,已知AB =6,AC =8,∠A =90.如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥,其表面积为S 1;把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥,其表面积为S 2,那么S 1∶S 2等于 ( )(A )2∶3 (B )3∶4 (C )4∶9 (D )5∶1232.(苏州市)如图,⊙O 的弦AB =8厘米,弦CD 平分AB 于点E .若CE =2厘米.ED 长为 ( )(A )8厘米 (B )6厘米 (C )4厘米 (D )2厘米33.(苏州市)如图,四边形ABCD 内接于⊙O ,若∠BOD =160,则∠BCD = ( )(A )160 (B ) 100 (C ) 80 (D )2034.(镇江市)如图,正方形ABCD 内接于⊙O ,E 为DC 的中点,直线BE交⊙O 于点F .若⊙O 的半径为2,则BF 的长为 ( )(A )23 (B )22(C )556 (D )55435.(扬州市)如图,AB 是⊙O 的直径,∠ACD =15,则∠BAD 的度数为 ( )(A ) 75 (B ) 72 (C ) 70 (D )6536.(扬州市)已知:点P 直线l 的距离为3,以点P 为圆心,r 为半径画圆,如果圆上有且只有两点到直线l 的距离均为2,则半径r 的取值范围是 ( )(A )r >1 (B )r >2 (C )2<r <3 (D )1<r <537.(绍兴市)边长为a 的正方边形的边心距为 ( )(A )a (B )23a (C )3a (D )2a38.(绍兴市)如图,以圆柱的下底面为底面,上底面圆心为顶点的圆锥的母线长为4,高线长为3,则圆柱的侧面积为 ( )(A )30π (B )76π (C )20π (D )74π39.(昆明市)如图,扇形的半径OA =20厘米,∠AOB =135,用它做成一个圆锥的侧面,则此圆锥底面的半径为 ( )(A )3.75厘米 (B )7.5厘米 (C )15厘米 (D )30厘米40.(昆明市)如图,正六边形ABCDEF 中.阴影部分面积为123平方厘米,则此正六边形的边长为 ( )(A )2厘米 (B )4厘米 (C )6厘米 (D )8厘米41.(温州市)已知扇形的弧长是2π厘米,半径为12厘米,则这个扇形的圆心角是 ( )(A )60 (B )45 (C )30 (D )2042.(温州市)圆锥的高线长是厘米,底面直径为12厘米,则这个圆锥的侧面积是 ( )(A )48π厘米 (B )24π13平方厘米(C )48π13平方厘米 (D )60π平方厘米43.(温州市)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PC是⊙O 的切线,C 为切点,PC =26,PA =4,则⊙O 的半径等于 ( )(A )1 (B )2 (C )23(D )2644.(常州市)已知圆柱的母线长为5厘米,表面积为28π平方厘米,则这个圆柱的底面半径是 ( )(A )5厘米 (B )4厘米 (C )2厘米 (D )3厘米45.(常州市)半径相等的圆内接正三角形、正方形、正六边形的边长之比为 ( )(A )1∶2∶3 (B )3∶2∶1(C )3∶2∶1 (D )1∶2∶346.(广东省)如图,若四边形ABCD 是半径为1和⊙O 的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为 ( )(A )(2π-2)厘米 (B )(2π-1)厘米(C )(π-2)厘米 (D )(π-1)厘米47.(武汉市)如图,已知圆心角∠BOC =100,则圆周角∠BAC 的度数是( )(A ) 50 (B )100 (C )130 (D )20048.(武汉市)半径为5厘米的圆中,有一条长为6厘米的弦,则圆心到此弦的距离为 ( )(A )3厘米 (B )4厘米 (C )5厘米 (D )6厘米49.已知:Rt △ABC 中,∠C =90,O 为斜边AB 上的一点,以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ,若AC =1,BC =3,则⊙O 的半径为 ( )(A )21(B )32 (C )43 (D )5450.(武汉市)已知:如图,E 是相交两圆⊙M 和⊙O 的一个交点,且ME ⊥NE ,AB 为外公切线,切点分别为A 、B ,连结AE 、BE .则∠AEB 的度数为 ( )(A )145° (B )140° (C )135° (D )130°二、填空题1.(北京市东城区)如图,AB 、AC 是⊙O 的两条切线,切点分别为B 、C ,D是优弧上的一点,已知∠BAC =80,那么∠BDC =__________度.2.(北京市东城区)在Rt △ABC 中,∠C =90,A B=3,BC =1,以AC 所在直线为轴旋转一周,所得圆锥的侧面展开图的面积是__________.3.(北京市海淀区)如果圆锥母线长为6厘米,那么这个圆锥的侧面积是_______平方厘米4.(北京市海淀区)一种圆状包装的保鲜膜,如图所示,其规格为“20厘米×60米”,经测量这筒保鲜膜的内径1ϕ、外径2ϕ的长分别为3.2厘米、4.0厘米,则该种保鲜膜的厚度约为_________厘米(π取3.14,结果保留两位有效数字).5.(上海市)两个点O 为圆心的同心圆中,大圆的弦AB 与小圆相切,如果AB 的长为24,大圆的半径OA 为13,那么小圆的半径为___________.6.(天津市)已知⊙O 中,两弦AB 与CD 相交于点E ,若E 为AB 的中点,CE ∶ED =1∶4,AB =4,则CD 的长等于___________.7.(重庆市)如图,AB 是⊙O 的直径,四边形ABCD 内接于⊙O ,,,的度数比为3∶2∶4,MN 是⊙O 的切线,C 是切点,则∠BCM 的度数为___________.8.(重庆市)如图,P 是⊙O 的直径AB 延长线上一点,PC 切⊙O 于点C ,PC =6,BC ∶AC =1∶2,则AB 的长为___________.9.(重庆市)如图,四边形ABCD 内接于⊙O ,AD ∥BC ,=,若AD =4,BC =6,则四边形ABCD 的面积为__________.10.(山西省)若一个圆柱的侧面积等于两底面积的和,则它的高h 与底面半径r 的大小关系是__________.11.(沈阳市)要用圆形铁片截出边长为4厘米的正方形铁片,则选用的圆形铁片的直径最小要___________厘米.12.(沈阳市)圆内两条弦AB 和CD 相交于P 点,AB 长为7,AB 把CD 分成两部分的线段长分别为2和6,那么=__________.13.(沈阳市)△ABC 是半径为2厘米的圆内接三角形,若BC =23厘米,则∠A 的度数为________.14.(沈阳市)如图,已知OA 、OB 是⊙O 的半径,且OA =5,∠AOB =15,AC ⊥OB 于C ,则图中阴影部分的面积(结果保留π)S =_________.15.(哈尔滨市)如图,圆内接正六边形ABCDEF 中,AC 、BF 交于点M .则ABM S △∶AFM S △=_________.16.(哈尔滨市)两圆外离,圆心距为25厘米,两圆周长分别为15π厘米和10π厘米.则其内公切线和连心线所夹的锐角等于__________度.17.(哈尔滨市)将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周,所得圆柱体的表面积为_________平方厘米.18.(陕西省)如图,在⊙O 的内接四边形ABCD 中,∠BCD =130,则∠BOD 的度数是________.19.(陕西省)已知⊙O 的半径为4厘米,以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积,则这个小圆的半径是______厘米.20.(陕西省)如图,⊙O 1的半径O 1A 是⊙O 2的直径,C 是⊙O 1上的一点,O 1C 交⊙O 2于点B .若⊙O 1的半径等于5厘米,的长等于⊙O 1周长的101,则的长是_________.21.(甘肃省)正三角形的内切圆与外接圆面积之比为_________.22.(甘肃省)如图,AB =8,AC =6,以AC 和BC 为直径作半圆,两圆的公切线MN 与AB 的延长线交于D ,则BD 的长为_________.23.(宁夏回族自治区)圆锥的母线长为5厘米,高为3厘米,在它的侧面展开图中,扇形的圆心角是_________度.24.(南京市)如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足是G ,F 是CG 的中点,延长AF 交⊙O 于E ,CF =2,AF =3,则EF 的长是_________.25.(福州市)在⊙O 中,直径AB =4厘米,弦CD ⊥AB 于E ,OE =3,则弦CD 的长为__________厘米.26.(福州市)若圆锥底面的直径为厘米,线线长为5厘米,则它的侧面积为__________平方厘米(结果保留π).27.(河南省)如图,AB 为⊙O 的直径,P 点在AB 的延长线上,PM 切⊙O 于M 点.若OA =a ,PM =3a ,那么△PMB 的周长的__________.28.(长沙市)在半径9厘米的圆中,60的圆心角所对的弧长为__________厘米.29.(四川省)扇形的圆心角为120,弧长为6π厘米,那么这个扇形的面积为_________.30.(贵阳市)如果圆O 的直径为10厘米,弦AB 的长为6厘米,那么弦AB 的弦心距等于________厘米.31.(贵阳市)某种商品的商标图案如图所求(阴影部分),已知菱形ABCD 的边长为4,∠A =60,是以A 为圆心,AB 长为半径的弧,是以B 为圆心,BC 长为半径的弧,则该商标图案的面积为_________.32.(云南省)已知,一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周,所得圆锥的表面积是__________.33.(新疆乌鲁木齐)正六边形的边心距与半径的比值为_________.34.(新疆乌鲁木齐)如图,已知扇形AOB 的半径为12,OA ⊥OB ,C 为OA 上一点,以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切,则半圆1O 的半径为__________.35.(成都市)如图,PA 、PB 与⊙O 分别相切于点A 、点B ,AC 是⊙O 的直径,PC 交⊙O 于点D .已知∠APB =60,AC =2,那么CD 的长为________.36.(苏州市)底面半径为2厘米,高为3厘米的圆柱的体积为_________立方厘米(结果保留π).37.(扬州市)边长为2厘米的正六边形的外接圆半径是________厘米,内切圆半径是________厘米(结果保留根号).38.(绍兴市)如图,PT 是⊙O 的切线,T 为切点,PB 是⊙O 的割线交⊙O 于A 、B 两点,交弦CD 于点M ,已知:CM =10,MD =2,PA =MB =4,则PT 的长等于__________.39.(温州市)如图,扇形OAB 中,∠AOB =90,半径OA =1,C 是线段AB的中点,CD ∥OA ,交于点D ,则CD =________.40.(常州市)已知扇形的圆心角为150 ,它所对的弧长为20π厘米,则扇形的半径是________厘米,扇形的面积是__________平方厘米.41.(常州市)如图,AB 是⊙O 直径,CE 切⊙O 于点C ,CD ⊥AB ,D 为垂足,AB =12厘米,∠B =30 ,则∠ECB =__________ ;CD =_________厘米.42.(常州市)如图,DE 是⊙O 直径,弦AB ⊥DE ,垂足为C ,若AB =6,CE =1,则CD =________,OC =_________.43.(常州市)如果把人的头顶和脚底分别看作一个点,把地球赤道作一个圆,那么身高压2米的汤姆沿着地球赤道环道环行一周,他的头顶比脚底多行________米.44.(海南省)已知:⊙O 的半径为1,M 为⊙O 外的一点,MA 切⊙O 于点A ,MA =1.若AB 是⊙O 的弦,且AB =2,则MB 的长度为_________.45.(武汉市)如果圆的半径为4厘米,那么它的周长为__________厘米.三、解答题:1.(苏州市)已知:如图,△ABC 内接于⊙O ,过点B 作⊙O 的切线,交CA 的延长线于点E ,∠EBC=2∠C .①求证:AB =AC ;②若tan ∠ABE =21,(ⅰ)求BCAB的值;(ⅱ)求当AC =2时,AE 的长.2.(广州市)如图,PA 为⊙O 的切线,A 为切点,⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ,PA =8cm ,PB =4cm ,求⊙O 的半径.3.(河北省)已知:如图,BC 是⊙O 的直径,AC 切⊙O 于点C ,AB 交⊙O 于点D ,若AD ︰DB =2︰3,AC=10,求sin B 的值.4.(北京市海淀区)如图,PC 为⊙O 的切线,C 为切点,PAB 是过O 的割线,CD ⊥AB 于点D ,若tan B =21,PC =10cm ,求三角形BCD 的面积.5.(宁夏回族自治区)如图,在两个半圆中,大圆的弦MN 与小圆相切,D 为切点,且MN ∥AB ,MN =a ,ON 、CD 分别为两圆的半径,求阴影部分的面积.6.(四川省)已知,如图,以△ABC 的边AB 作直径的⊙O ,分别并AC 、BC 于点D 、E ,弦FG ∥AB ,S △CDE ︰S △ABC =1︰4,DE =5cm ,FG =8cm ,求梯形AFGB 的面积.7.(贵阳市)如图所示:PA 为⊙O 的切线,A 为切点,PBC 是过点O 的割线,PA =10,PB =5,求:(1)⊙O 的面积(注:用含π的式子表示);(2)cos ∠BAP 的值.参考答案一、选择题1.B 2.B 3.D 4.D 5.C 6.C 7.A 8.C 9.D 10.B 11.A 12.B 13.C 14.D 15.D 16.A 17.B 18.C 19.C 20.B 21.C 22.A 23.A 24.B 25.B 26.D 27.D 28.C 29.A 30.B 31.A 32.A 33.B 34.C 35.A 36.D 37.B 38.B 39.B 40.B 41.C 42.D 43.A 44.C 45.B 46.C 47.A 48.B 49.C 50.C二、填空题1.50 2.2π 3.18π 4.4105.7-⨯ 5.5 6.5 7.30° 8.9 9.25 10.h =r 11.4212.3或4 13.60°或120° 14.8252425-π 15.1:2 16.30 17.80π或120π 18.100° 19.22 20.π 21.1:4 22.1 23.288 24.4 25.2 26.15π 27.()a 23+ 28.3π 29.27π平方厘米 30.4 31.34 32.24π平方厘米或36π平方厘米 33.2334.4 35.774 36.12π 37.2,3 38.132 39.213- 40.24,240π 41.60°,33 42.9,4 43.4π 44.1或5 45.8π三、解答题:1.(1)∵ BE 切⊙O 于点B ,∴ ∠ABE =∠C .∵ ∠EBC =2∠C ,即 ∠ABE +∠ABC =2∠C ,∴ ∠C +∠ABC =2∠C ,∴ ∠ABC =∠C ,∴ AB =AC . (2)①连结AO ,交BC 于点F ,∵ AB =AC ,∴=,∴ AO ⊥BC 且BF =FC .在Rt △ABF 中,BFAF=tan ∠ABF ,又 tan ∠ABF =tan C =tan ∠ABE =21,∴ BF AF =21,∴ AF =21BF .∴ AB =22BF AF +=2221BF BF +⎪⎭⎫ ⎝⎛=25BF .∴452==BF AB BC AB .②在△EBA 与△ECB 中,∵ ∠E =∠E ,∠EBA =∠ECB ,∴ △EBA ∽△ECB .∴ ⎪⎩⎪⎨⎧⋅==ECEA BE BC ABEB EA 2,解之,得516EA 2=EA ·(EA +AC ),又EA ≠0,∴511EA =AC ,EA =115×2=1110.2.设⊙的半径为r ,由切割线定理,得PA 2=PB ·PC ,∴ 82=4(4+2r ),解得r =6(cm ).即⊙O 的半径为6cm .3.由已知AD ︰DB =2︰3,可设AD =2k ,DB =3k (k >0).∵ AC 切⊙O 于点C ,线段ADB 为⊙O 的割线,∴ AC 2=AD ·AB ,∵ AB =AD +DB =2k +3k =5k ,∴ 102=2k ×5k ,∴ k 2=10,∵ k >0,∴ k =10.∴ AB =5k =510.∵ AC 切⊙O 于C ,BC 为⊙O 的直径,∴ AC ⊥BC .在Rt △ACB 中,sin B =51010510==AB AC .4.解法一:连结AC .∵ AB 是⊙O 的直径,点C 在⊙O 上,∴ ∠ACB =90°.CD ⊥AB 于点D ,∴ ∠ADC =∠BDC =90°,∠2=90°-∠BAC =∠B .∵ tan B =21, ∴ tan ∠2=21.∴ CBACDB CD CD AD ===21.设AD =x (x >0),CD =2x ,DB =4x ,AB =5x .∵ PC 切⊙O 于点C ,点B 在⊙O 上,∴ ∠1=∠B .∵ ∠P =∠P ,∴ △PAC ∽△PCB ,∴21==CB AC PC PA . ∵ PC =10,∴ PA =5,∵ PC 切⊙O 于点C ,PAB 是⊙O 的割线,∵ PC 2=PA ·PB ,∴ 102=5(5+5 x ).解得x =3.∴ AD =3,CD =6,DB =12.∴ S △BCD =21CD ·DB =21×6×12=36.即三角形BCD 的面积36cm 2.解法二:同解法一,由△PAC ∽△PCB ,得21==CB AC PC PA .∵ PA =10,∴ PB =20.由切割线定理,得PC 2=PA ·PB .∴ PA =201022-PB PC =5,∴ AB =PB -PA =15,∵ AD +DB =x +4x =15,解得x =3,∴ CD =2x =6,DB =4x =12.∴ S △BCD =21CD ·DB =21×6×12=36.即三角形BCD 的面积36cm 2.5.解:如图取MN 的中点E ,连结OE ,∴ OE ⊥MN ,EN =21MN =21a .在四边形EOCD 中,∵ CO ⊥DE ,OE ⊥DE ,DE ∥CO ,∴ 四边形EOCD 为矩形.∴ OE =CD ,在Rt △NOE 中,NO 2-OE 2=EN 2=22⎪⎭⎫⎝⎛a .∴ S 阴影=21π(NO 2-OE 2)=21π·22⎪⎭⎫⎝⎛a =28πa .6.解:∵ ∠CDE =∠CBA ,∠DCE =∠BCA ,∴ △CDE ∽△ABC .∴ 2⎪⎭⎫⎝⎛=∆∆AB DE S S ABC CDE∴AB DE =ABCCDE S S ∆∆=41=21,即215=AB ,解得 AB =10(cm ),作OM ⊥FG ,垂足为M ,则FM =21FG =21×8=4(cm ),连结OF ,∵ OA =21AB =21×10=5(cm ).∴ OF =OA =5(cm ).在Rt △OMF 中,由勾股定理,得OM =22FM OF -=2245-=3(cm ).∴ 梯形AFGB 的面积=2FG AB +·OM =2810⨯×3=27(cm 2).7.⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(⇒PA 2=PB ·PC ⇒PC =20⇒半径为7.5⇒圆面积为π4225(或56.25π)(平方单位).⎭⎬⎫∠=∠∠=∠P P B A P C )2(⇒△ACP ∽△BAP ⇒PB PA AB AC =⇒12=AB AC .解法一:设AB =x ,AC =2x ,BC 为⊙O 的直径∠CAB =90°,则 BC =5x .∵ ∠BAP =∠C ,∴ cos ∠BAP =cos ∠C =55252==xx BC AC解法二:设AB =x ,在Rt △ABC 中,AC 2+AB 2=BC 2,即 x 2+(2x )2=152,解之得 x =35,∴ AC =65,∵ ∠BAP =∠C ,∴ ∴ cos ∠BAP =cos ∠C =5521556==BC AC。
中考数学圆真题汇编

【真题汇编】中考数学备考之圆1.圆的认识(1)圆的定义定义①:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.固定的端点O叫做圆心,线段OA叫做半径.以O点为圆心的圆,记作“⊙O”,读作“圆O”.定义②:圆可以看做是所有到定点O的距离等于定长r的点的集合.(2)与圆有关的概念弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等.连接圆上任意两点的线段叫弦,经过圆心的弦叫直径,圆上任意两点间的部分叫圆弧,简称弧,圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆,大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.(3)圆的基本性质:①轴对称性.②中心对称性.2.垂径定理(1)垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.(2)垂径定理的推论推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧.推论3:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.3.垂径定理的应用垂径定理的应用很广泛,常见的有:(1)得到推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.(2)垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.这类题中一般使用列方程的方法,这种用代数方法解决几何问题即几何代数解的数学思想方法一定要掌握.4.圆心角、弧、弦的关系(1)定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.(2)推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧.(3)正确理解和使用圆心角、弧、弦三者的关系三者关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.这源于圆的旋转不变性,即:圆绕其圆心旋转任意角度,所得图形与原图形完全重合.(4)在具体应用上述定理解决问题时,可根据需要,选择其有关部分.5.圆周角定理(1)圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.注意:圆周角必须满足两个条件:①顶点在圆上.②角的两条边都与圆相交,二者缺一不可.(2)圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.(3)在解圆的有关问题时,常常需要添加辅助线,构成直径所对的圆周角,这种基本技能技巧一定要掌握.(4)注意:①圆周角和圆心角的转化可通过作圆的半径构造等腰三角形.利用等腰三角形的顶点和底角的关系进行转化.②圆周角和圆周角的转化可利用其“桥梁”﹣﹣﹣圆心角转化.③定理成立的条件是“同一条弧所对的”两种角,在运用定理时不要忽略了这个条件,把不同弧所对的圆周角与圆心角错当成同一条弧所对的圆周角和圆心角.6.圆内接四边形的性质(1)圆内接四边形的性质:①圆内接四边形的对角互补.②圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).(2)圆内接四边形的性质是沟通角相等关系的重要依据,在应用此性质时,要注意与圆周角定理结合起来.在应用时要注意是对角,而不是邻角互补.7.点与圆的位置关系(1)点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外⇔d>r②点P在圆上⇔d=r①点P在圆内⇔d<r(2)点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.(3)符号“⇔”读作“等价于”,它表示从符号“⇔”的左端可以得到右端,从右端也可以得到左端.8.三角形的外接圆与外心(1)外接圆:经过三角形的三个顶点的圆,叫做三角形的外接圆.(2)外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.(3)概念说明:①“接”是说明三角形的顶点在圆上,或者经过三角形的三个顶点.②锐角三角形的外心在三角形的内部;直角三角形的外心为直角三角形斜边的中点;钝角三角形的外心在三角形的外部.③找一个三角形的外心,就是找一个三角形的三条边的垂直平分线的交点,三角形的外接圆只有一个,而一个圆的内接三角形却有无数个.9.直线与圆的位置关系(1)直线和圆的三种位置关系:①相离:一条直线和圆没有公共点.②相切:一条直线和圆只有一个公共点,叫做这条直线和圆相切,这条直线叫圆的切线,唯一的公共点叫切点.③相交:一条直线和圆有两个公共点,此时叫做这条直线和圆相交,这条直线叫圆的割线.(2)判断直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d.①直线l和⊙O相交⇔d<r②直线l和⊙O相切⇔d=r③直线l和⊙O相离⇔d>r.10.切线的性质(1)切线的性质①圆的切线垂直于经过切点的半径.②经过圆心且垂直于切线的直线必经过切点.③经过切点且垂直于切线的直线必经过圆心.(2)切线的性质可总结如下:如果一条直线符合下列三个条件中的任意两个,那么它一定满足第三个条件,这三个条件是:①直线过圆心;②直线过切点;③直线与圆的切线垂直.(3)切线性质的运用运用切线的性质进行计算或证明时,常常作的辅助线是连接圆心和切点,通过构造直角三角形或相似三角形解决问题.11.切线的判定与性质(1)切线的性质①圆的切线垂直于经过切点的半径.②经过圆心且垂直于切线的直线必经过切点.③经过切点且垂直于切线的直线必经过圆心.(2)切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.(3)常见的辅助线的:①判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;②有切线时,常常“遇到切点连圆心得半径”.12.三角形的内切圆与内心(1)内切圆的有关概念:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.(2)任何一个三角形有且仅有一个内切圆,而任一个圆都有无数个外切三角形.(3)三角形内心的性质:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.13.圆与圆的位置关系(1)圆与圆的五种位置关系:①外离;②外切;③相交;④内切;⑤内含.如果两个圆没有公共点,叫两圆相离.当每个圆上的点在另一个圆的外部时,叫两个圆外离,当一个圆上的点都在另一圆的内部时,叫两个圆内含,两圆同心是内含的一个特例;如果两个圆有一个公共点,叫两个圆相切,相切分为内切、外切两种;如果两个圆有两个公共点叫两个圆相交.(2)圆和圆的位置与两圆的圆心距、半径的数量之间的关系:①两圆外离⇔d>R+r;②两圆外切⇔d=R+r;③两圆相交⇔R﹣r<d<R+r(R≥r);④两圆内切⇔d=R﹣r(R>r);⑤两圆内含⇔d<R﹣r(R>r).14.相交两圆的性质(1)相交两圆的性质:相交两圆的连心线(经过两个圆心的直线),垂直平分两圆的公共弦.注意:在习题中常常通过公共弦在两圆之间建立联系.(2)两圆的公切线性质:两圆的两条外公切线的长相等;两圆的两条内公切线的长也相等.两个圆如果有两条(内)公切线,则它们的交点一定在连心线上.15.正多边形和圆(1)正多边形与圆的关系把一个圆分成n(n是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆.(2)正多边形的有关概念①中心:正多边形的外接圆的圆心叫做正多边形的中心.②正多边形的半径:外接圆的半径叫做正多边形的半径.③中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.④边心距:中心到正多边形的一边的距离叫做正多边形的边心距.16.弧长的计算(1)圆周长公式:C=2πR(2)弧长公式:l=(弧长为l,圆心角度数为n,圆的半径为R)①在弧长的计算公式中,n是表示1°的圆心角的倍数,n和180都不要带单位.②若圆心角的单位不全是度,则需要先化为度后再计算弧长.③题设未标明精确度的,可以将弧长用π表示.④正确区分弧、弧的度数、弧长三个概念,度数相等的弧,弧长不一定相等,弧长相等的弧不一定是等弧,只有在同圆或等圆中,才有等弧的概念,才是三者的统一.17.扇形面积的计算(1)圆面积公式:S=πr2(2)扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.(3)扇形面积计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=πR2或S扇形=lR(其中l为扇形的弧长)(4)求阴影面积常用的方法:①直接用公式法;②和差法;③割补法.(5)求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.18.圆锥的计算(1)连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.连接顶点与底面圆心的线段叫圆锥的高.(2)圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.(3)圆锥的侧面积:S侧=•2πr•l=πrl.(4)圆锥的全面积:S全=S底+S侧=πr2+πrl(5)圆锥的体积=×底面积×高注意:①圆锥的母线与展开后所得扇形的半径相等.②圆锥的底面周长与展开后所得扇形的弧长相等.19.圆柱的计算(1)圆柱的母线(高)等于展开后所得矩形的宽,圆柱的底面周长等于矩形的长.(2)圆柱的侧面积=底面圆的周长×高(3)圆柱的表面积=上下底面面积+侧面积(4)圆柱的体积=底面积×高.中考数学备考之圆(选择题60题)一.选择题(共60小题,满分120分,每小题2分)1.(2分)(2022•西藏)如图,AB是⊙O的弦,OC⊥AB,垂足为C,OD∥AB,OC=OD,则∠ABD的度数为()A.90°B.95°C.100°D.105°2.(2分)(2022•荆门)如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD的面积为()A.36B.24C.18D.723.(2分)(2022•鄂州)工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD =4cm,则这种铁球的直径为()A.10cm B.15cm C.20cm D.24cm4.(2分)(2022•兰州)如图,△ABC内接于⊙O,CD是⊙O的直径,∠ACD=40°,则∠B=()A.70°B.60°C.50°D.40°5.(2分)(2022•阜新)如图,A,B,C是⊙O上的三点,若∠C=35°,则∠ABO的度数是()A.35°B.55°C.60°D.70°6.(2分)(2022•牡丹江)如图,BD是⊙O的直径,A,C在圆上,∠A=50°,∠DBC的度数是()A.50°B.45°C.40°D.35°7.(2分)(2022•贵港)如图,⊙O是△ABC的外接圆,AC是⊙O的直径,点P在⊙O上,若∠ACB=40°,则∠BPC的度数是()A.40°B.45°C.50°D.55°8.(2分)(2022•贵阳)如图,已知∠ABC=60°,点D为BA边上一点,BD=10,点O为线段BD的中点,以点O为圆心,线段OB长为半径作弧,交BC于点E,连接DE,则BE的长是()A.5B.5C.5D.59.(2分)(2022•深圳)下列说法错误的是()A.对角线垂直且互相平分的四边形是菱形B.同圆或等圆中,同弧对应的圆周角相等C.对角线相等的四边形是矩形D.对角线垂直且相等的平行四边形是正方形10.(2分)(2022•铜仁市)如图,OA,OB是⊙O的两条半径,点C在⊙O上,若∠AOB=80°,则∠C 的度数为()A.30°B.40°C.50°D.60°11.(2分)(2022•包头)如图,AB,CD是⊙O的两条直径,E是劣弧的中点,连接BC,DE.若∠ABC =22°,则∠CDE的度数为()A.22°B.32°C.34°D.44°12.(2分)(2022•朝阳)如图,在⊙O中,点A是的中点,∠ADC=24°,则∠AOB的度数是()A.24°B.26°C.48°D.66°13.(2分)(2022•聊城)如图,AB,CD是⊙O的弦,延长AB,CD相交于点P.已知∠P=30°,∠AOC =80°,则的度数是()A.30°B.25°C.20°D.10°14.(2分)(2022•巴中)如图,AB为⊙O的直径,弦CD交AB于点E,,∠CDB=30°,AC=2,则OE=()A.B.C.1D.215.(2分)(2022•枣庄)将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是()A.28°B.30°C.36°D.56°16.(2分)(2022•营口)如图,点A,B,C,D在⊙O上,AC⊥BC,AC=4,∠ADC=30°,则BC的长为()A.4B.8C.4D.417.(2分)(2022•淮安)如图,四边形ABCD是⊙O的内接四边形,若∠AOC=160°,则∠ABC的度数是()A.80°B.100°C.140°D.160°18.(2分)(2022•长春)如图,四边形ABCD是⊙O的内接四边形,若∠BCD=121°,则∠BOD的度数为()A.138°B.121°C.118°D.112°19.(2分)(2022•梧州)如图,⊙O是△ABC的外接圆,且AB=AC,∠BAC=36°,在上取点D(不与点A,B重合),连接BD,AD,则∠BAD+∠ABD的度数是()A.60°B.62°C.72°D.73°20.(2分)(2022•十堰)如图,⊙O是等边△ABC的外接圆,点D是弧AC上一动点(不与A,C重合),下列结论:①∠ADB=∠BDC;②DA=DC;③当DB最长时,DB=2DC;④DA+DC=DB,其中一定正确的结论有()A.1个B.2个C.3个D.4个21.(2分)(2022•六盘水)如图是“光盘行动”的宣传海报,图中餐盘与筷子可看成直线和圆的位置关系是()A.相切B.相交C.相离D.平行22.(2分)(2022•河池)如图,AB是⊙O的直径,P A与⊙O相切于点A,∠ABC=25°,OC的延长线交P A于点P,则∠P的度数是()A.25°B.35°C.40°D.50°23.(2分)(2022•哈尔滨)如图,AD,BC是⊙O的直径,点P在BC的延长线上,P A与⊙O相切于点A,连接BD,若∠P=40°,则∠ADB的度数为()A.65°B.60°C.50°D.25°24.如图,P A,PB是⊙O的切线,A、B为切点,若∠AOB=128°,则∠P的度数为()A.32°B.52°C.64°D.72°25.(2分)(2022•镇江)如图,在等腰△ABC中,∠BAC=120°,BC=6,⊙O同时与边BA的延长线、射线AC相切,⊙O的半径为3.将△ABC绕点A按顺时针方向旋转α(0°<α≤360°),B、C的对应点分别为B′、C′,在旋转的过程中边B′C′所在直线与⊙O相切的次数为()A.1B.2C.3D.426.(2分)(2022•无锡)如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD =25°,则下列结论错误的是()A.AE⊥DE B.AE∥OD C.DE=OD D.∠BOD=50°27.(2分)(2022•深圳)已知三角形ABE为直角三角形,∠ABE=90°,DE为圆的直径,BC为圆O切线,C为切点,CA=CD,则△ABC和△CDE面积之比为()A.1:3B.1:2C.:2D.(﹣1):128.(2分)(2022•宁夏)把量角器和含30°角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度2处,短直角边过量角器外沿刻度120处(即OC =2cm,∠BOF=120°).则阴影部分的面积为()A.(2﹣π)cm2B.(8﹣π)cm2C.(8﹣π)cm2D.(16﹣π)cm229.(2分)(2022•贵港)下列命题为真命题的是()A.=aB.同位角相等C.三角形的内心到三边的距离相等D.正多边形都是中心对称图形30.(2分)(2022•娄底)如图,等边△ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边△ABC的内心成中心对称,则圆中的黑色部分的面积与△ABC的面积之比是()A.B.C.D.31.(2分)(2022•吉林)如图,在△ABC中,∠ACB=90°,AB=5,BC=4.以点A为圆心,r为半径作圆,当点C在⊙A内且点B在⊙A外时,r的值可能是()A.2B.3C.4D.532.(2分)(2022•鄂尔多斯)实验学校的花坛形状如图所示,其中,等圆⊙O1与⊙O2的半径为3米,且⊙O1经过⊙O2的圆心O2.已知实线部分为此花坛的周长,则花坛的周长为()A.4π米B.6π米C.8π米D.12π米33.(2分)(2022•内江)如图,正六边形ABCDEF内接于⊙O,半径为6,则这个正六边形的边心距OM 和的长分别为()A.4,B.3,πC.2,D.3,2π34.(2分)(2022•安顺)如图,在平面直角坐标系中,将边长为2的正六边形OABCDE绕点O顺时针旋转n个45°,得到正六边形OA n B n∁n D n E n,当n=2022时,正六边形OA n B n∁n D n E n的顶点D n的坐标是()A.(﹣,﹣3)B.(﹣3,﹣)C.(3,﹣)D.(﹣,3)35.(2分)(2022•绵阳)在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,﹣3),则顶点C的坐标为()A.(2﹣2,3)B.(0,1+2)C.(2﹣,3)D.(2﹣2,2+)36.(2分)(2022•青岛)如图,正六边形ABCDEF内接于⊙O,点M在上,则∠CME的度数为()A.30°B.36°C.45°D.60°37.(2分)(2022•安顺)如图,边长为的正方形ABCD内接于⊙O,P A,PD分别与⊙O相切于点A和点D,PD的延长线与BC的延长线交于点E,则图中阴影部分的面积为()A.5﹣πB.5﹣C.﹣D.﹣38.(2分)(2022•台湾)有一直径为AB的圆,且圆上有C、D、E、F四点,其位置如图所示.若AC=6,AD=8,AE=5,AF=9,AB=10,则下列弧长关系何者正确?()A.+=,+=B.+=,+≠C.+≠,+=D.+≠,+≠39.(2分)(2022•丹东)如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则的长为()A.6πB.2πC.πD.π40.(2分)(2022•河北)某款“不倒翁”(图1)的主视图是图2,P A,PB分别与所在圆相切于点A,B.若该圆半径是9cm,∠P=40°,则的长是()A.11πcm B.πcm C.7πcm D.πcm41.(2分)(2022•兰州)如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=3m,OB=1.5m,则阴影部分的面积为()A.4.25πm2B.3.25πm2C.3πm2D.2.25πm242.(2分)(2022•湖北)一个扇形的弧长是10πcm,其圆心角是150°,此扇形的面积为()A.30πcm2B.60πcm2C.120πcm2D.180πcm243.(2分)(2022•贺州)如图,在等腰直角△OAB中,点E在OA上,以点O为圆心、OE为半径作圆弧交OB于点F,连接EF,已知阴影部分面积为π﹣2,则EF的长度为()A.B.2C.2D.344.(2分)(2022•遵义)如图,在正方形ABCD中,AC和BD交于点O,过点O的直线EF交AB于点E (E不与A,B重合),交CD于点F.以点O为圆心,OC为半径的圆交直线EF于点M,N.若AB=1,则图中阴影部分的面积为()A.﹣B.﹣C.﹣D.﹣45.(2分)(2022•荆州)如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC 边相切,分别交AB,AC于D,E,则图中阴影部分的面积是()A.﹣B.2﹣πC.D.﹣46.(2分)(2022•资阳)如图.将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接AC.若OA=2,则图中阴影部分的面积是()A.B.C.D.47.(2分)(2022•鞍山)如图,在矩形ABCD中,AB=2,BC=,以点B为圆心,BA长为半径画弧,交CD于点E,连接BE,则扇形BAE的面积为()A.B.C.D.48.(2分)(2022•铜仁市)如图,在边长为6的正方形ABCD中,以BC为直径画半圆,则阴影部分的面积是()A.9B.6C.3D.1249.(2分)(2022•赤峰)如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为()A.2πB.2C.2π﹣4D.2π﹣250.(2分)(2022•毕节市)如图,一件扇形艺术品完全打开后,AB,AC夹角为120°,AB的长为45cm,扇面BD的长为30cm,则扇面的面积是()A.375πcm2B.450πcm2C.600πcm2D.750πcm251.(2分)(2022•山西)如图,扇形纸片AOB的半径为3,沿AB折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为()A.3π﹣3B.3π﹣C.2π﹣3D.6π﹣52.(2分)(2022•广安)蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是()A.圆柱的底面积为4πm2B.圆柱的侧面积为10πm2C.圆锥的母线AB长为2.25mD.圆锥的侧面积为5πm253.(2分)(2022•大庆)已知圆锥的底面半径为5,高为12,则它的侧面展开图的面积是()A.60πB.65πC.90πD.120π54.(2分)(2022•东营)用一张半圆形铁皮,围成一个底面半径为4cm的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为()A.4cm B.8cm C.12cm D.16cm55.(2分)(2022•济宁)已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是()A.96πcm2B.48πcm2C.33πcm2D.24πcm256.(2分)(2022•牡丹江)圆锥的底面圆半径是1,母线长是3,它的侧面展开图的圆心角是()A.90°B.100°C.120°D.150°57.(2分)(2022•柳州)如图,圆锥底面圆的半径AB=4,母线长AC=12,则这个圆锥的侧面积为()A.16πB.24πC.48πD.96π58.(2分)(2022•赤峰)如图所示,圆锥形烟囱帽的底面半径为12cm,侧面展开图为半圆形,则它的母线长为()A.10cm B.20cm C.5cm D.24cm59.(2分)(2022•绵阳)如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)()A.282.6B.282600000C.357.96D.35796000060.(2分)(2022•贺州)某餐厅为了追求时间效率,推出一种液体“沙漏”免单方案(即点单完成后,开始倒转“沙漏”,“沙漏”漏完前,客人所点的菜需全部上桌,否则该桌免费用餐).“沙漏”是由一个圆锥体和一个圆柱体相通连接而成.某次计时前如图(1)所示,已知圆锥体底面半径是6cm,高是6cm;圆柱体底面半径是3cm,液体高是7cm.计时结束后如图(2)所示,求此时“沙漏”中液体的高度为()A.2cm B.3cm C.4cm D.5cm【真题汇编】中考数学备考之圆(选择题60题)参考答案与试题解析一.选择题(共60小题,满分120分,每小题2分)1.(2分)(2022•西藏)如图,AB是⊙O的弦,OC⊥AB,垂足为C,OD∥AB,OC=OD,则∠ABD的度数为()A.90°B.95°C.100°D.105°【考点】圆的认识;平行线的性质;三角形内角和定理;等腰三角形的性质;含30度角的直角三角形.【分析】连接OB,则OC=OB,由OC⊥AB,则∠OBC=30°,再由OD∥AB,即可求出答案.【解答】解:如图:连接OB,则OB=OD,∵OC=OD,∴OC=OB,∵OC⊥AB,∴∠OBC=30°,∵OD∥AB,∴∠BOD=∠OBC=30°,∴∠OBD=∠ODB=75°,∠ABD=30°+75°=105°.故选:D.【点评】本题考查了圆,平行线的性质,解直角三角形,等腰三角形的有关知识;正确作出辅助线、利用圆的半径相等是解题的关键.2.(2分)(2022•荆门)如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD的面积为()A.36B.24C.18D.72【考点】垂径定理;勾股定理.【分析】根据AB=12,BE=3,求出OE=3,OC=6,并利用勾股定理求出EC,根据垂径定理求出CD,即可求出四边形的面积.【解答】解:如图,连接OC,∵AB=12,BE=3,∴OB=OC=6,OE=3,∵AB⊥CD,在Rt△COE中,EC=,∴CD=2CE=6,∴四边形ACBD的面积=.故选:A.【点评】本题考查了垂径定理,解题的关键是熟练运用定理.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.3.(2分)(2022•鄂州)工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD =4cm,则这种铁球的直径为()A.10cm B.15cm C.20cm D.24cm【考点】垂径定理的应用;勾股定理的应用.【分析】连接OE,交AB于点F,连接OA,∵AC⊥CD、BD⊥CD,由矩形的判断方法得出四边形ACDB 是矩形,得出AB∥CD,AB=CD=16cm,由切线的性质得出OE⊥CD,得出OE⊥AB,得出四边形EFBD 是矩形,AF=AB=×16=8(cm),进而得出EF=BD=4cm,设⊙O的半径为rcm,则OA=rcm,OF=OE﹣EF=(r﹣4)cm,由勾股定理得出方程r2=82+(r﹣4)2,解方程即可求出半径,继而求出这种铁球的直径.【解答】解:如图,连接OE,交AB于点F,连接OA,∵AC⊥CD、BD⊥CD,∴AC∥BD,∵AC=BD=4cm,∴四边形ACDB是平行四边形,∴四边形ACDB是矩形,∴AB∥CD,AB=CD=16cm,∵CD切⊙O于点E,∴OE⊥CD,∴OE⊥AB,∴四边形EFBD是矩形,AF=AB=×16=8(cm),∴EF=BD=4cm,设⊙O的半径为rcm,则OA=rcm,OF=OE﹣EF=(r﹣4)cm,在Rt△AOF中,OA2=AF2+OF2,∴r2=82+(r﹣4)2,解得:r=10,∴这种铁球的直径为20cm,故选:C.【点评】本题考查了垂径定理的应用,勾股定理的应用,掌握矩形的判定与性质,平行四边形的判定与性质,切线的性质,垂径定理,勾股定理是解决问题的关键.4.(2分)(2022•兰州)如图,△ABC内接于⊙O,CD是⊙O的直径,∠ACD=40°,则∠B=()A.70°B.60°C.50°D.40°【考点】圆周角定理.【分析】由CD是⊙O的直径,根据直径所对的圆周角是直角,得出∠CAD=90°,根据直角三角形两锐角互余得到∠ACD与∠D互余,即可求得∠D的度数,继而求得∠B的度数.【解答】解:∵CD是⊙O的直径,∴∠CAD=90°,∴∠ACD+∠D=90°,∵∠ACD=40°,∴∠ADC=∠B=50°.故选:C.【点评】此题考查了三角形的外接圆与外心,圆周角定理,直角三角形的性质,难度不大,注意掌握数形结合思想的应用.5.(2分)(2022•阜新)如图,A,B,C是⊙O上的三点,若∠C=35°,则∠ABO的度数是()A.35°B.55°C.60°D.70°【考点】圆周角定理;圆心角、弧、弦的关系.【分析】由圆周角定理,即可求得∠AOB的度数,又由OA=OB,根据等边对等角与三角形内角和定理,即可求得∠ABO的度数.【解答】解:连接OA,∵∠C=35°,∴∠AOB=2∠C=70°,∵OA=OB,∴∠ABO=∠BAO=(180°﹣∠AOB)=55°.故选:B.【点评】此题考查了圆周角定理与等腰三角形的性质.此题比较简单,注意在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用.6.(2分)(2022•牡丹江)如图,BD是⊙O的直径,A,C在圆上,∠A=50°,∠DBC的度数是()A.50°B.45°C.40°D.35°【考点】圆周角定理.【分析】由BD是⊙O的直径,可求得∠BCD=90°,又由圆周角定理可得∠D=∠A=50°,继而求得答案.【解答】解:∵BD是⊙O的直径,∴∠BCD=90°,∵∠D=∠A=50°,∴∠DBC=90°﹣∠D=40°.故选:C.【点评】此题考查了圆周角定理以及直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.7.(2分)(2022•贵港)如图,⊙O是△ABC的外接圆,AC是⊙O的直径,点P在⊙O上,若∠ACB=40°,则∠BPC的度数是()A.40°B.45°C.50°D.55°【考点】圆周角定理.【分析】根据直径所对的圆周角是直角得到∠ABC=90°,进而求出∠CAB,根据圆周角定理解答即可.【解答】解:∵AC是⊙O的直径,∴∠ABC=90°,∴∠ACB+∠CAB=90°,∵∠ACB=40°,∴∠CAB=90°﹣40°=50°,由圆周角定理得:∠BPC=∠CAB=50°,故选:C.【点评】本题考查的是圆周角定理,掌握直径所对的圆周角是直角是解题的关键.8.(2分)(2022•贵阳)如图,已知∠ABC=60°,点D为BA边上一点,BD=10,点O为线段BD的中点,以点O为圆心,线段OB长为半径作弧,交BC于点E,连接DE,则BE的长是()A.5B.5C.5D.5【考点】圆周角定理;含30度角的直角三角形.【分析】解法一:根据题意和等边三角形的判定,可以得到BE的长.解法二:先根据直径所对的圆周角是90°,然后根据直角三角形的性质和直角三角形中30°角所对的直角边是斜边的一半,可以求得BE的长.【解答】解:解法一:连接OE,由已知可得,OE=OB=BD=5,∵∠ABC=60°,∴△BOE是等边三角形,∴BE=OB=5,故选:A.解法二:由题意可得,BD为⊙O的直径,∴∠BED=90°,∵∠ABC=60°,∴∠EDB=30°,∵BD=10,∴BE=5,故选:A.【点评】本题考查等边三角形的判定与性质、与圆相关的知识,解答本题的关键是明确题意,求出△OBE 的形状.。
(完整版)中考数学圆综合题汇编,推荐文档
∠BAD。
(1)求证:CD 是⊙O 的切线;
D
(2)若 AC 2 6 ,AD=4,求 AB 的长。
C
A
O
B
7. 如图,AB 为⊙O 的直径,C 为⊙O 上一点,AD 和过 C 点的切线互相垂直,垂足为点 D,AD 交
⊙O 于点 E。
求证:(1)AC 平分∠DAB;
D
(2)若∠B=60°, CD 2 3 ,求 AE 的长。
(1)求证:CD=CE;
(2)若 CD=2,CF=5,求半径 OA 的长。 C
A
B
D
E
O
F
14.
如图,AB 是⊙O 的直径,点 C 在⊙O 外,连接 OC,OC⊥AB,弦 BD 交 OC 于点
E,CD=CE。
(1)求证:CD 是⊙O 的切线;
(2)若 AB=13,BD=12,求 DE 的长。 A
D
O
DG
O F
17. 如图,在△ABC 中,AB=10,BC=8,AC=6,将△ABC 沿 AC 翻折,点 B 与 D 重合,O 是 CD 上一点,OC=3,以 O 为圆心,OC 为半径作⊙O,交 CD 于另一点 E。 (1)求证:直线 AD 是⊙O 的切线; (2)过点 D 作⊙O 的另一条切线,切点为点 M,连接 MC 并延长,交 AB 边于点 N,求线段 MN 的长。
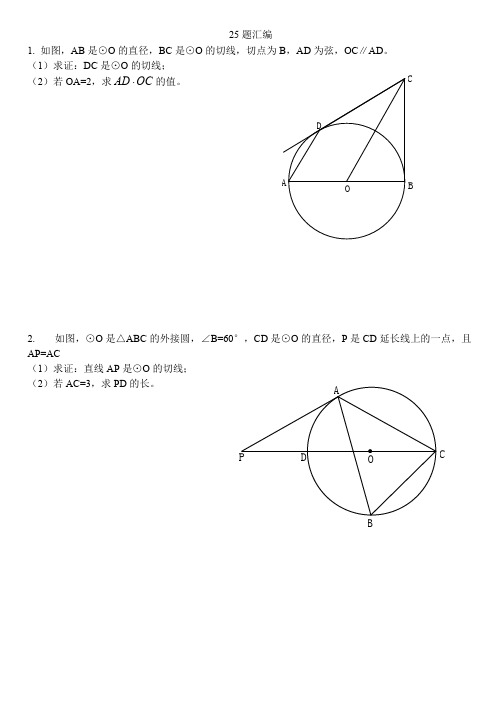
25 题汇编
1. 如图,AB 是⊙O 的直径,BC 是⊙O 的切线,切点为 B,AD 为弦,OC∥AD。
(1)求证:DC 是⊙O 的切线;
(2)若 OA=2,求 AD OC 的值。
C
D
A
O
B
2. 如图,⊙O 是△ABC 的外接圆,∠B=60°,CD 是⊙O 的直径,P 是 CD 延长线上的一点,且
初中中考圆试题及答案

初中中考圆试题及答案一、选择题(每题3分,共30分)1. 圆的半径为5,直径为()A. 10B. 5C. 15D. 202. 圆的周长公式为()A. C=πrB. C=2πrC. C=πdD. C=2πd3. 圆的面积公式为()A. S=πr²B. S=2πrC. S=πd²D. S=2πd4. 圆内接四边形的对角线()A. 相等B. 不相等C. 垂直D. 平行5. 圆的切线与半径()A. 垂直B. 相交C. 平行D. 重合6. 圆的直径是圆内最长的线段,这种说法()A. 正确B. 错误7. 圆心到圆上任意一点的距离都相等,这种说法()A. 正确B. 错误8. 圆的半径增加一倍,面积增加()A. 一倍B. 两倍C. 四倍D. 八倍9. 圆的周长与直径的比值是()A. πB. 2πC. 4πD. 1/π10. 圆的半径为3,圆的面积为()A. 9πB. 3πC. 6πD. 12π二、填空题(每题2分,共20分)1. 圆的直径是半径的______倍。
2. 圆的周长是半径的______倍。
3. 圆的面积是半径的______倍。
4. 圆周率π的近似值是______。
5. 圆的内接三角形的内角和为______度。
6. 圆的外切三角形的外角和为______度。
7. 圆的切线与半径垂直于______。
8. 圆的切线与圆心的距离等于______。
9. 圆的直径是圆内最长的______线段。
10. 圆的半径增加一倍,面积增加______倍。
三、解答题(每题10分,共50分)1. 已知圆的半径为4,求圆的周长和面积。
2. 已知圆的直径为8,求圆的周长和面积。
3. 已知圆的周长为31.4,求圆的直径和半径。
4. 已知圆的面积为78.5,求圆的半径。
5. 已知圆的半径为5,求圆内接正六边形的边长。
答案:一、选择题1. A2. B3. A4. A5. A6. A7. A8. C9. A 10. A二、填空题1. 22. 2π3. π4. 3.145. 1806. 3607. 切点8. 半径9. 弦10. 4三、解答题1. 周长:2πr = 2 × 3.14 × 4 = 25.12;面积:πr² = 3.14 × 4² = 50.242. 周长:C = πd =3.14 × 8 = 25.12;面积:S = πr² = 3.14 × (8/2)² = 50.243. 直径:d = C/π = 31.4/3.14 = 10;半径:r = d/2 = 10/2 = 54. 半径:r = √(S/π) = √(78.5/3.14) ≈ 4.075. 边长:边长= 2r × sin(π/6) = 2 × 5 × 0.5 = 5。
经典必考圆中考试卷集锦(附答案)

圆中考试题集锦一、选择题1.如图,BC 是⊙O 的直径,P 是CB 延长线上一点,PA 切⊙O 于点A ,如果PA =3,PB =1,那么∠APC 等于 ( )(A ) 15 (B ) 30 (C ) 45 (D ) 602.如果圆柱的高为20厘米,底面半径是高的41,那么这个圆柱的侧面积是 ( ) (A )100π平方厘米 (B )200π平方厘米(C )500π平方厘米 (D )200平方厘米3.“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题,“今在圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为E ,CE =1寸,AB =寸,求直径CD 的长”.依题意,CD 长为 ( )(A )225寸 (B )13寸 (C )25寸 (D )26寸 4.已知:如图,⊙O 半径为5,PC 切⊙O 于点C ,PO 交⊙O 于点A ,PA =4,那么PC 的长等于 ( )(A )6 (B )25 (C )210 (D )2145.如果圆锥的侧面积为20π平方厘米,它的母线长为5厘米,那么此圆锥的底面半径的长等于 ( )(A )2厘米 (B )22厘米 (C )4厘米 (D )8厘米6.相交两圆的公共弦长为16厘米,若两圆的半径长分别为10厘米和17厘米,则这两圆的圆心距为 ( )(A )7厘米 (B )16厘米 (C )21厘米 (D )27厘米7.如图,⊙O 为△ABC 的内切圆,∠C =90,AO 的延长线交BC 于点D ,AC =4,DC =1,,则⊙O 的半径等于 ( )(A )54 (B )45 (C )43 (D )65 8.(重庆市)一居民小区有一正多边形的活动场.为迎接“AAPP ”会议在重庆市的召开,小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台,花台都以多边形的顶点为圆心,比多边形的内角为圆心角,花台占地面积共为12π平方米.若每个花台的造价为400元,则建造这些花台共需资金 ( )(A )2400元 (B )2800元 (C )3200元 (D )3600元9.(河北省)如图,AB 是⊙O 直径,CD 是弦.若AB =10厘米,CD =8厘米,那么A 、B 两点到直线CD 的距离之和为 ( )(A )12厘米 (B )10厘米 (C )8厘米 (D )6厘米10.(河北省)某工件形状如图所示,圆弧BC 的度数为60,AB =6厘米,点B 到点C 的距离等于AB ,∠BAC = 30,则工件的面积等于 ( )(A )4π (B )6π (C )8π (D )10π11.(沈阳市)如图,PA 切⊙O 于点A ,PBC 是⊙O 的割线且过圆心,PA =4,PB =2,则⊙O 的半径等于 ( )(A )3 (B )4 (C )6 (D )812.(哈尔滨市)已知⊙O 的半径为35厘米,⊙O '的半径为5厘米.⊙O 与⊙O '相交于点D 、E .若两圆的公共弦DE 的长是6厘米(圆心O 、O '在公共弦DE 的两侧),则两圆的圆心距O O '的长为 ( )(A )2厘米 (B )10厘米 (C )2厘米或10厘米 (D )4厘米13.(陕西省)如图,两个等圆⊙O 和⊙O '的两条切线OA 、OB ,A 、B 是切点,则∠AOB 等于 ( )(A ) 30 (B ) 45 (C ) 60 (D )9014.(甘肃省)如图,AB 是⊙O 的直径,∠C = 30,则∠ABD = ( )(A ) 30 (B ) 40 (C ) 50 (D ) 6015.(甘肃省)弧长为6π的弧所对的圆心角为 60,则弧所在的圆的半径为( )(A )6 (B )62 (C )12 (D )1816.(甘肃省)如图,在△ABC 中,∠BAC = 90,AB =AC =2,以AB 为直径的圆交BC 于D ,则图中阴影部分的面积为 ( )(A )1 (B )2 (C )1+4π (D )2-4π 17.(宁夏回族自治区)已知圆的内接正六边形的周长为18,那么圆的面积为 ( )(A )18π (B )9π (C )6π (D )3π18.(山东省)如图,点P 是半径为5的⊙O 内一点,且OP =3,在过点P的所有弦中,长度为整数的弦一共有 ( )(A )2条 (B )3条 (C )4条 (D )5条19.(南京市)如图,正六边形ABCDEF 的边长的上a ,分别以C 、F 为圆心,a 为半径画弧,则图中阴影部分的面积是 ( )(A )261a π (B )231a π (C )232a π (D )234a π20.(杭州市)过⊙O 内一点M 的最长的弦长为6厘米,最短的弦长为4厘米,则OM 的长为 ( )(A )3厘米 (B )5厘米 (C )2厘米 (D )5厘米21.(安徽省)已知圆锥的底面半径是3,高是4,则这个圆锥侧面展开图的面积是 ( )(A )12π (B )15π (C )30π (D )24π22.(安微省)已知⊙O 的直径AB 与弦AC 的夹角为 30,过C 点的切线PC 与AB 延长线交P .PC =5,则⊙O 的半径为 ( )(A )335 (B )635 (C )10 (D )5 23.(福州市)如图:PA 切⊙O 于点A ,PBC 是⊙O 的一条割线,有PA=32,PB =BC ,那么BC 的长是 ( )(A )3 (B )32 (C )3 (D )3224.(河南省)如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是 ( )(A )π (B )1.5π (C )2π (D )2.5π25.(四川省)正六边形的半径为2厘米,那么它的周长为 ( )(A )6厘米 (B )12厘米 (C )24厘米 (D )122厘米26.(四川省)一个圆柱形油桶的底面直径为0.6米,高为1米,那么这个油桶的侧面积为 ( )(A )0.09π平方米 (B )0.3π平方米 (C )0.6平方米 (D )0.6π平方米27.(贵阳市)一个形如圆锥的冰淇淋纸筒,其底面直径为6厘米,母线长为5厘米,围成这样的冰淇淋纸筒所需纸片的面积是 ( )(A )66π平方厘米 (B )30π平方厘米 (C )28π平方厘米 (D )15π平方厘米28.(新疆乌鲁木齐)在半径为2的⊙O 中,圆心O 到弦AB 的距离为1,则弦AB 所对的圆心角的度数可以是 ( )(A ) 60 (B ) 90 (C ) 120 (D ) 15029.(新疆乌鲁木齐)将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面,(接口损耗不计),则桶底的面积为 ( )(A )π1600平方厘米 (B )1600π平方厘米(C )π6400平方厘米 (D )6400π平方厘米 30.(成都市)如图,已知AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD =10厘米,AP ∶PB =1∶5,那么⊙O 的半径是 ( )(A )6厘米 (B )53厘米 (C )8厘米 (D )35厘米31.(成都市)在Rt △ABC 中,已知AB =6,AC =8,∠A =90.如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥,其表面积为S 1;把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥,其表面积为S 2,那么S 1∶S 2等于 ( )(A )2∶3 (B )3∶4 (C )4∶9 (D )5∶1232.(苏州市)如图,⊙O 的弦AB =8厘米,弦CD 平分AB 于点E .若CE =2厘米.ED 长为 ( )(A )8厘米 (B )6厘米 (C )4厘米 (D )2厘米33.(苏州市)如图,四边形ABCD 内接于⊙O ,若∠BOD =160,则∠BCD = ( )(A ) 160 (B ) 100 (C ) 80 (D ) 2034.(镇江市)如图,正方形ABCD 内接于⊙O ,E 为DC 的中点,直线BE交⊙O 于点F .若⊙O 的半径为2,则BF 的长为 ( )(A )23 (B )22 (C )556 (D )554 35.(扬州市)如图,AB 是⊙O 的直径,∠ACD = 15,则∠BAD 的度数为 ( )(A ) 75 (B ) 72 (C ) 70 (D )6536.(扬州市)已知:点P 直线l 的距离为3,以点P 为圆心,r 为半径画圆,如果圆上有且只有两点到直线l 的距离均为2,则半径r 的取值范围是 ( )(A )r >1 (B )r >2 (C )2<r <3 (D )1<r <537.(绍兴市)边长为a 的正方边形的边心距为 ( )(A )a (B )23a (C )3a (D )2a 38.(绍兴市)如图,以圆柱的下底面为底面,上底面圆心为顶点的圆锥的母线长为4,高线长为3,则圆柱的侧面积为 ( )(A )30π (B )76π (C )20π (D )74π39.(昆明市)如图,扇形的半径OA =20厘米,∠AOB = 135,用它做成一个圆锥的侧面,则此圆锥底面的半径为 ( )(A )3.75厘米 (B )7.5厘米 (C )15厘米 (D )30厘米40.(昆明市)如图,正六边形ABCDEF 中.阴影部分面积为123平方厘米,则此正六边形的边长为 ( )(A )2厘米 (B )4厘米 (C )6厘米 (D )8厘米41.(温州市)已知扇形的弧长是2π厘米,半径为12厘米,则这个扇形的圆心角是 ( )(A ) 60 (B ) 45 (C ) 30 (D ) 2042.(温州市)圆锥的高线长是厘米,底面直径为12厘米,则这个圆锥的侧面积是 ( )(A )48π厘米 (B )24π13平方厘米(C )48π13平方厘米 (D )60π平方厘米43.(温州市)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PC是⊙O 的切线,C 为切点,PC =26,PA =4,则⊙O 的半径等于 ( )(A )1 (B )2 (C )23 (D )26 44.(常州市)已知圆柱的母线长为5厘米,表面积为28π平方厘米,则这个圆柱的底面半径是( )(A )5厘米 (B )4厘米 (C )2厘米 (D )3厘米45.(常州市)半径相等的圆内接正三角形、正方形、正六边形的边长之比为 ( )(A )1∶2∶3 (B )3∶2∶1(C )3∶2∶1 (D )1∶2∶346.(广东省)如图,若四边形ABCD 是半径为1和⊙O 的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为 ( )(A )(2π-2)厘米 (B )(2π-1)厘米(C )(π-2)厘米 (D )(π-1)厘米47.(武汉市)如图,已知圆心角∠BOC = 100,则圆周角∠BAC 的度数是( )(A ) 50 (B ) 100 (C ) 130 (D ) 20048.(武汉市)半径为5厘米的圆中,有一条长为6厘米的弦,则圆心到此弦的距离为 ( )(A )3厘米 (B )4厘米 (C )5厘米 (D )6厘米49.已知:Rt △ABC 中,∠C = 90,O 为斜边AB 上的一点,以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ,若AC =1,BC =3,则⊙O 的半径为 ( )(A )21 (B )32 (C )43 (D )54 50.(武汉市)已知:如图,E 是相交两圆⊙M 和⊙O 的一个交点,且ME ⊥NE ,AB 为外公切线,切点分别为A 、B ,连结AE 、BE .则∠AEB 的度数为 ( )(A )145° (B )140° (C )135° (D )130°二、填空题1.(北京市东城区)如图,AB 、AC 是⊙O 的两条切线,切点分别为B 、C ,D 是优弧上的一点,已知∠BAC =80,那么∠BDC =__________度.2.(北京市东城区)在Rt △ABC 中,∠C =90,A B=3,BC =1,以AC 所在直线为轴旋转一周,所得圆锥的侧面展开图的面积是__________.3.(北京市海淀区)如果圆锥母线长为6厘米,那么这个圆锥的侧面积是_______平方厘米4.(北京市海淀区)一种圆状包装的保鲜膜,如图所示,其规格为“20厘米×60米”,经测量这筒保鲜膜的内径1ϕ、外径2ϕ的长分别为3.2厘米、4.0厘米,则该种保鲜膜的厚度约为_________厘米(π取3.14,结果保留两位有效数字).5.(上海市)两个点O 为圆心的同心圆中,大圆的弦AB 与小圆相切,如果AB 的长为24,大圆的半径OA 为13,那么小圆的半径为___________.6.(天津市)已知⊙O 中,两弦AB 与CD 相交于点E ,若E 为AB 的中点,CE ∶ED =1∶4,AB =4,则CD 的长等于___________.7.(重庆市)如图,AB 是⊙O 的直径,四边形ABCD 内接于⊙O ,,,的度数比为3∶2∶4,MN 是⊙O 的切线,C 是切点,则∠BCM 的度数为___________.8.(重庆市)如图,P 是⊙O 的直径AB 延长线上一点,PC 切⊙O于点C ,PC =6,BC ∶AC =1∶2,则AB 的长为___________.9.(重庆市)如图,四边形ABCD 内接于⊙O ,AD ∥BC ,=,若AD =4,BC =6,则四边形ABCD 的面积为__________.10.(山西省)若一个圆柱的侧面积等于两底面积的和,则它的高h 与底面半径r 的大小关系是__________.11.(沈阳市)要用圆形铁片截出边长为4厘米的正方形铁片,则选用的圆形铁片的直径最小要___________厘米.12.(沈阳市)圆内两条弦AB 和CD 相交于P 点,AB 长为7,AB 把CD 分成两部分的线段长分别为2和6,那么=__________.13.(沈阳市)△ABC 是半径为2厘米的圆内接三角形,若BC =23厘米,则∠A 的度数为________.14.(沈阳市)如图,已知OA 、OB 是⊙O 的半径,且OA =5,∠AOB =15 ,AC⊥OB 于C ,则图中阴影部分的面积(结果保留π)S =_________.15.(哈尔滨市)如图,圆内接正六边形ABCDEF 中,AC 、BF 交于点M .则ABM S △∶AFM S △=_________.16.(哈尔滨市)两圆外离,圆心距为25厘米,两圆周长分别为15π厘米和10π厘米.则其内公切线和连心线所夹的锐角等于__________度.17.(哈尔滨市)将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周,所得圆柱体的表面积为_________平方厘米.18.(陕西省)如图,在⊙O 的内接四边形ABCD 中,∠BCD =130,则∠BOD的度数是________.19.(陕西省)已知⊙O 的半径为4厘米,以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积,则这个小圆的半径是______厘米.20.(陕西省)如图,⊙O 1的半径O 1A 是⊙O 2的直径,C 是⊙O 1上的一点,O 1C 交⊙O 2于点B .若⊙O 1的半径等于5厘米,的长等于⊙O 1周长的101,则的长是_________.21.(甘肃省)正三角形的内切圆与外接圆面积之比为_________.22.(甘肃省)如图,AB =8,AC =6,以AC 和BC 为直径作半圆,两圆的公切线MN 与AB 的延长线交于D ,则BD 的长为_________.23.(宁夏回族自治区)圆锥的母线长为5厘米,高为3厘米,在它的侧面展开图中,扇形的圆心角是_________度.24.(南京市)如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足是G ,F 是CG 的中点,延长AF 交⊙O 于E ,CF =2,AF =3,则EF 的长是_________.25.(福州市)在⊙O 中,直径AB =4厘米,弦CD ⊥AB 于E ,OE =3,则弦CD 的长为__________厘米.26.(福州市)若圆锥底面的直径为厘米,线线长为5厘米,则它的侧面积为__________平方厘米(结果保留π).27.(河南省)如图,AB 为⊙O 的直径,P 点在AB 的延长线上,PM 切⊙O 于M 点.若OA =a ,PM =3a ,那么△PMB 的周长的__________.28.(长沙市)在半径9厘米的圆中, 60的圆心角所对的弧长为__________厘米.29.(四川省)扇形的圆心角为120 ,弧长为6π厘米,那么这个扇形的面积为_________.30.(贵阳市)如果圆O 的直径为10厘米,弦AB 的长为6厘米,那么弦AB 的弦心距等于________厘米.31.(贵阳市)某种商品的商标图案如图所求(阴影部分),已知菱形ABCD的边长为4,∠A = 60,是以A 为圆心,AB 长为半径的弧,是以B 为圆心,BC 长为半径的弧,则该商标图案的面积为_________.32.(云南省)已知,一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周,所得圆锥的表面积是__________.33.(新疆乌鲁木齐)正六边形的边心距与半径的比值为_________.34.(新疆乌鲁木齐)如图,已知扇形AOB 的半径为12,OA ⊥OB ,C 为OA 上一点,以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切,则半圆1O 的半径为__________.35.(成都市)如图,PA 、PB 与⊙O 分别相切于点A 、点B ,AC 是⊙O 的直径,PC 交⊙O 于点D .已知∠APB =60,AC =2,那么CD 的长为________.36.(苏州市)底面半径为2厘米,高为3厘米的圆柱的体积为_________立方厘米(结果保留π).37.(扬州市)边长为2厘米的正六边形的外接圆半径是________厘米,内切圆半径是________厘米(结果保留根号).38.(绍兴市)如图,PT 是⊙O 的切线,T 为切点,PB 是⊙O 的割线交⊙O 于A 、B 两点,交弦CD 于点M ,已知:CM =10,MD =2,PA =MB =4,则PT 的长等于__________.39.(温州市)如图,扇形OAB 中,∠AOB = 90,半径OA =1,C 是线段AB的中点,CD ∥OA ,交于点D ,则CD =________.40.(常州市)已知扇形的圆心角为150 ,它所对的弧长为20π厘米,则扇形的半径是________厘米,扇形的面积是__________平方厘米.41.(常州市)如图,AB 是⊙O 直径,CE 切⊙O 于点C ,CD ⊥AB ,D 为垂足,AB =12厘米,∠B =30,则∠ECB =__________ ;CD =_________厘米.42.(常州市)如图,DE 是⊙O 直径,弦AB ⊥DE ,垂足为C ,若AB =6,CE =1,则CD =________,OC =_________.43.(常州市)如果把人的头顶和脚底分别看作一个点,把地球赤道作一个圆,那么身高压2米的汤姆沿着地球赤道环道环行一周,他的头顶比脚底多行________米.44.(海南省)已知:⊙O 的半径为1,M 为⊙O 外的一点,MA 切⊙O 于点A ,MA =1.若AB 是⊙O 的弦,且AB =2,则MB 的长度为_________.45.(武汉市)如果圆的半径为4厘米,那么它的周长为__________厘米.三、解答题:1.(苏州市)已知:如图,△ABC 内接于⊙O ,过点B 作⊙O 的切线,交CA的延长线于点E ,∠EBC =2∠C .①求证:AB =AC ;②若tan ∠ABE =21,(ⅰ)求BCAB 的值;(ⅱ)求当AC =2时,AE 的长.2.(广州市)如图,PA 为⊙O 的切线,A 为切点,⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ,PA =8cm ,PB =4cm ,求⊙O 的半径.3.(河北省)已知:如图,BC 是⊙O 的直径,AC 切⊙O 于点C ,AB 交⊙O 于点D ,若AD ︰DB =2︰3,AC =10,求sin B 的值.4.(北京市海淀区)如图,PC 为⊙O 的切线,C 为切点,PAB 是过O 的割线,CD ⊥AB 于点D ,若tan B =21,PC =10cm ,求三角形BCD 的面积.5.(宁夏回族自治区)如图,在两个半圆中,大圆的弦MN 与小圆相切,D 为切点,且MN ∥AB ,MN =a ,ON 、CD 分别为两圆的半径,求阴影部分的面积.6.(四川省)已知,如图,以△ABC 的边AB 作直径的⊙O ,分别并AC 、BC 于点D 、E ,弦FG ∥AB ,S △CDE ︰S △ABC =1︰4,DE =5cm ,FG =8cm ,求梯形AFGB 的面积.7.(贵阳市)如图所示:PA 为⊙O 的切线,A 为切点,PBC 是过点O 的割线,PA =10,PB =5,求:(1)⊙O 的面积(注:用含π的式子表示);(2)cos ∠BAP 的值.参考答案一、选择题1.B 2.B 3.D 4.D 5.C6.C 7.A 8.C 9.D 10.B 11.A 12.B 13.C 14.D 15.D 16.A 17.B 18.C 19.C20.B 21.C 22.A 23.A 24.B 25.B 26.D 27.D 28.C 29.A 30.B 31.A 32.A33.B 34.C 35.A 36.D 37.B 38.B 39.B 40.B 41.C 42.D 43.A 44.C 45.B46.C 47.A 48.B 49.C 50.C二、填空题1.50 2.2π 3.18π 4.4105.7-⨯ 5.5 6.5 7.30° 8.9 9.25 10.h =r 11.4212.3或4 13.60°或120° 14.8252425-π 15.1:2 16.30 17.80π或120π 18.100° 19.22 20.π 21.1:4 22.1 23.288 24.4 25.2 26.15π 27.()a 23+ 28.3π 29.27π平方厘米 30.4 31.34 32.24π平方厘米或36π平方厘米 33.23 34.4 35.774 36.12π 37.2,3 38.132 39.213- 40.24,240π 41.60°,33 42.9,4 43.4π 44.1或5 45.8π三、解答题:1.(1)∵ BE 切⊙O 于点B ,∴ ∠ABE =∠C .∵ ∠EBC =2∠C ,即 ∠ABE +∠ABC =2∠C ,∴ ∠C +∠ABC =2∠C ,∴ ∠ABC =∠C ,∴ AB =AC .(2)①连结AO ,交BC 于点F ,∵ AB =AC ,∴=,∴ AO ⊥BC 且BF =FC .在Rt △ABF 中,BFAF =tan ∠ABF , 又 tan ∠ABF =tan C =tan ∠ABE =21,∴ BF AF =21, ∴ AF =21BF . ∴ AB =22BF AF +=2221BF BF +⎪⎭⎫ ⎝⎛=25BF . ∴ 452==BF AB BC AB . ②在△EBA 与△ECB 中,∵ ∠E =∠E ,∠EBA =∠ECB ,∴ △EBA ∽△ECB .∴ ⎪⎩⎪⎨⎧⋅==EC EA BE BC AB EB EA 2,解之,得516EA 2=EA ·(EA +AC ),又EA ≠0,∴ 511EA =AC ,EA =115×2=1110. 2.设⊙的半径为r ,由切割线定理,得PA 2=PB ·PC ,∴ 82=4(4+2r ),解得r =6(cm ).即⊙O 的半径为6cm .3.由已知AD ︰DB =2︰3,可设AD =2k ,DB =3k (k >0). ∵ AC 切⊙O 于点C ,线段ADB 为⊙O 的割线,∴ AC 2=AD ·AB ,∵ AB =AD +DB =2k +3k =5k ,∴ 102=2k ×5k ,∴ k 2=10,∵ k >0,∴ k =10.∴ AB =5k =510.∵ AC 切⊙O 于C ,BC 为⊙O 的直径,∴ AC ⊥BC .在Rt △ACB 中,sin B =51010510==AB AC .4.解法一:连结AC .∵ AB 是⊙O 的直径,点C 在⊙O 上,∴ ∠ACB =90°.CD ⊥AB 于点D ,∴ ∠ADC =∠BDC =90°,∠2=90°-∠BAC =∠B . ∵ tan B =21,∴ tan ∠2=21.∴ CB ACDB CDCD AD ===21.设AD =x (x >0),CD =2x ,DB =4x ,AB =5x .∵ PC 切⊙O 于点C ,点B 在⊙O 上,∴ ∠1=∠B . ∵ ∠P =∠P ,∴ △PAC ∽△PCB ,∴ 21==CB AC PC PA.∵ PC =10,∴ PA =5,∵ PC 切⊙O 于点C ,PAB 是⊙O 的割线,∵ PC 2=PA ·PB ,∴ 102=5(5+5 x ).解得x =3.∴ AD =3,CD =6,DB =12.∴ S △BCD =21CD ·DB =21×6×12=36.即三角形BCD 的面积36cm 2.解法二:同解法一,由△PAC ∽△PCB ,得21==CB AC PC PA.∵ PA =10,∴ PB =20.由切割线定理,得PC 2=PA ·PB .∴ PA =201022-PB PC =5,∴ AB =PB -PA =15,∵ AD +DB =x +4x =15,解得x =3,∴ CD =2x =6,DB =4x =12.∴ S △BCD =21CD ·DB =21×6×12=36.即三角形BCD 的面积36cm 2.5.解:如图取MN 的中点E ,连结OE ,∴ OE ⊥MN ,EN =21MN =21a .在四边形EOCD 中,∵ CO ⊥DE ,OE ⊥DE ,DE ∥CO ,∴ 四边形EOCD 为矩形.∴ OE =CD ,在Rt △NOE 中,NO 2-OE 2=EN 2=22⎪⎭⎫⎝⎛a .∴ S 阴影=21π(NO 2-OE 2)=21π·22⎪⎭⎫ ⎝⎛a =28πa .6.解:∵ ∠CDE =∠CBA ,∠DCE =∠BCA ,∴ △CDE ∽△ABC .∴ 2⎪⎭⎫ ⎝⎛=∆∆ABDE S S ABC CDE∴ AB DE =ABC CDES S ∆∆=41=21,即215=AB ,解得 AB =10(cm ),作OM ⊥FG ,垂足为M ,则FM =21FG =21×8=4(cm ),连结OF ,∵ OA =21AB =21×10=5(cm ).∴ OF =OA =5(cm ).在Rt △OMF 中,由勾股定理,得OM =22FM OF -=2245-=3(cm ).∴ 梯形AFGB 的面积=2FGAB +·OM =2810⨯×3=27(cm 2).7.⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(⇒PA 2=PB ·PC ⇒PC =20⇒半径为7.5⇒圆面积为π4225(或56.25π)(平方单位).⎭⎬⎫∠=∠∠=∠P P B A PC )2(⇒△ACP ∽△BAP ⇒PB PAAB AC=⇒12=AB AC.解法一:设AB =x ,AC =2x ,BC 为⊙O 的直径⇒∠CAB =90°,则 BC =5x .∵ ∠BAP =∠C ,∴ cos ∠BAP =cos ∠C =55252==xx BC AC 解法二:设AB =x ,在Rt △ABC 中,AC 2+AB 2=BC 2,即 x 2+(2x )2=152,解之得 x =35,∴ AC =65, ∵ ∠BAP =∠C ,∴∴ cos ∠BAP =cos ∠C =5521556==BC AC。
2020年《圆》解答题中考题汇编(含答案)

2020年《圆》解答题中考题汇编1.(2020•安徽)如图,AB是半圆O的直径,C,D是半圆O上不同于A,B的两点,AD =BC,AC与BD相交于点F.BE是半圆O所在圆的切线,与AC的延长线相交于点E.(1)求证:△CBA≌△DAB;(2)若BE=BF,求证:AC平分∠DAB.2.(2020•德州)如图,点C在以AB为直径的⊙O上,点D是半圆AB的中点,连接AC,BC,AD,BD.过点D作DH∥AB交CB的延长线于点H.(1)求证:直线DH是⊙O的切线;(2)若AB=10,BC=6,求AD,BH的长.3.(2020•甘孜州)如图,AB是⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.(1)求证:∠CAD=∠CAB;(2)若=,AC=2,求CD的长.4.(2020•金华)如图,的半径OA=2,OC⊥AB于点C,∠AOC=60°.(1)求弦AB的长.(2)求的长.5.(2020•铜仁市)如图,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D是直径AB延长线上一点,且∠BCE=∠BCD.(1)求证:CD是⊙O的切线;(2)若AD=8,=,求CD的长.6.(2020•衢州)如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.(1)求证:∠CAD=∠CBA.(2)求OE的长.7.(2020•嘉兴)已知:如图,在△OAB中,OA=OB,⊙O与AB相切于点C.求证:AC =BC.小明同学的证明过程如下框:证明:连结OC,∵OA=OB,∴∠A=∠B,又∵OC=OC,∴△OAC≌△OBC,∴AC=BC.小明的证法是否正确?若正确,请在框内打“√”;若错误,请写出你的证明过程.8.(2020•湖州)如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.(1)求证:∠CAD=∠ABC;(2)若AD=6,求的长.9.(2020•遵义)如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交于点D,过点D作DE∥BC交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.10.(2020•铁岭)如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.(1)求证:MD=MC;(2)若⊙O的半径为5,AC=4,求MC的长.11.(2020•浙江自主招生)已知:如图,在△ABC中,∠BAC=30°,BC=4,求△ABC面积的最大值.12.(2020•巴南区自主招生)如图,AB为⊙O的直径,直线CF与⊙O相切于点E,与直线AB相交于点F,BC⊥CF,垂足为C.(1)求证:BE平分∠CBF;(2)若AB=16,∠CFB=30°,求弧的长.13.(2020•浙江自主招生)如图,AB为半圆的直径且AB=4,D是AB的一个四等分点,CD⊥AB于D,E,F为线段CD的三等分点,连接AE且延长交半圆于Q点,连接AF 且延长交半圆于P点,连接QP.(Ⅰ)求∠F AD;(Ⅱ)求四边形EFPQ的面积.14.(2020•浙江自主招生)已知I为Rt△ABC的内心,∠A=90°,BI,CI的延长线分别交AC,AB于点D,E,S△BIC=12,求S四边形EDCB.15.(2020•浙江自主招生)已知如图,Rt△ABC中,内切圆O的半径r=1.求:S△ABC的最小值.16.(2020•浙江自主招生)已知:如图,在△ABC中,∠ACB=90°,AC=3,BC=4,I1为△ABC内切圆的圆心,⊙l2与BA,BC的延长线及AC边都相切(旁切圆).(1)求⊙I2的半径;(2)求线段I1I2的长.17.(2020•浙江自主招生)如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心I,且点E在半圆弧上.(1)若设△ABC的三边为a,b,c(其中∠A对边为a,∠B对边为b,∠C对边为c),试用含a,b,c的代数式表示AD,BD的长(2)证明:正方形DEFG的面积和△ABC的面积相等.18.(2020•浙江自主招生)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,P为AD中点,BP延长线与AC交于点F,EF⊥BC于点F,FE的延长线与△ABC的外接圆⊙O交于点G,若AE=3,EC=12,求线段EG的长.19.(2020•浙江自主招生)如图,AB是⊙O的直径,点C是⊙O上的一个动点,点D是劣弧的中点,射线OD上存在一点E,使得OE=AC,在AB的延长线上找一点F,连结FE并延长,分别交直线AC,OC于点G,H.(1)连结CE,判断CE与AB的位置关系与数量关系,并说明理由;(2)设HG=x,GF=y,若HE=5,求y与x的函数解析式.20.(2020•浙江自主招生)如图.已知△ABC的周长为2p,在AB、AC上分别取点M和N,使MN∥BC,且MN与△ABC的内切圆相切.求MN的最大值.21.(2020•浙江自主招生)如图,点P在△ABC的边AB上,且AB=4AP,过点P的直线MN与△ABC的外接圆交于点M,N,且点A是弧MN的中点.(1)求证:∠APN=∠ANB;(2)求的值.22.(2020•浙江自主招生)矩形ABCD的一边长AB=4,且BC>AB,以边AB为直径的圆O交对角线AC于H,AH=2.如图,点K为优弧AKB上一点.(Ⅰ)求∠HKA的度数;(Ⅱ)求CH的长;(Ⅲ)求图中阴影部分的面积;(Ⅳ)设AK=m,若圆O的圆周上到直线AK的距离为1的点有且仅有三个,求实数m 的值.23.(2020•浙江自主招生)已知:如图,在锐角三角形ABC中,以AC边为直径的⊙O交BC于点D,作BH⊥AC,依次交⊙O于点E,交AC于点G,交⊙O于点H.(1)求证:∠BEC=∠EDC;(2)若∠ABG+∠DEC=45°,⊙O的直径等于10,BC=14,求CE的长.24.(2020•浙江自主招生)如图所示,已知:∠AOB=120°,PT切⊙O于T,A,B,P三点共线,∠APT的平分线依次交AT,BT于C,D.(1)求证:△CDT为等边三角形.(2)若AC=4,BD=1,求PC的长.25.(2020•浙江自主招生)如图所示,在△ABC中,CD为∠ACB的平分线,以CD为弦作一与AB相切的圆,分别交CA,CB于点M,N.(1)求证:MN∥AB;(2)若AC=12,AB=10,BC=8,求MN的长度.26.(2020•浙江自主招生)如图,四边形ABCD内接于⊙O,CD∥AB,且AB是⊙O的直径,AE⊥CD交CD的延长线于点E,若AE=2,CD=3.(1)求⊙O的直径;(2)若翻折使点B与E重合的直线l(折痕)交⊙O于P,Q两点,求△BPQ的面积.27.(2020•浙江自主招生)如图,已知AB是⊙O的直径,BC是⊙O的切线,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC与DE交于点P.证明:EP=PD.28.(2020•浙江自主招生)如图,正方形ABCD中,E、F分别是BC边、CD边上的动点,满足∠EAF=45°.(1)求证:BE+DF=EF;(2)若正方形边长为1,求△CEF内切圆半径的最大值.29.(2020•浙江自主招生)如图,已知ABCD是某圆的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.30.(2020•雨花区校级二模)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,交BC于F.(1)若∠ABC=40°,∠C=80°,求∠CBD的度数;(3)若AB=6,AC=4,BC=5,求DE的长.31.(2020•鼓楼区校级模拟)如图,AB是⊙O直径,AC是⊙O切线,BC交⊙O与点E.(1)若点D在AC上,连接DE,且AD=DE,求证:DE是⊙O的切线;(2)若CE=1.BE=3,求∠ACB的度数.32.(2020•武汉模拟)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E.F.(1)试判断直线BC与⊙O的位置关系,并说明理由;(2)若BD=2,BF=2,求⊙O的半径.33.(2020•鼓楼区校级模拟)如图①,AB为⊙O的直径,点C在⊙O上,AD平分∠CAB,AD与BC交于点F,过点D作DE⊥AB于点E.(1)求证:BC=2DE;(2)如图②,连接OF,若∠AFO=45°,半径为2时,求AC的长.34.(2020•江阴市二模)如图,Rt△ABC中,∠ACB=90°,点D在AC边上,以AD为直径作⊙O交BD的延长线于点E,且CE是⊙O的切线.(2)若CD=2,BD=2,求⊙O的半径.35.(2020•姜堰区二模)如图,AC是⊙O的直径,AB是弦,P A与⊙O相切于点A,连接PB、PC,且P A=PB.(1)求证:PB与⊙O相切;(2)若∠APB=60°,P A=6,求PC、PB、弧BC所围成图形的面积.36.(2020•滨海县二模)如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC 分别交于D、E两点,过点D作DF⊥AC于点F.(1)判断DF与⊙O的位置关系,并说明理由;(2)求证:点F为CE的中点;(3)若⊙O的半径为2,∠C=67.5°,求阴影部分的面积.37.(2020•张家港市模拟)如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E.(1)若∠BAC=40°,则∠ADC=°;(2)求证:∠BAC=2∠DAC;(3)若AB=10,CD=5,求BC的值.38.(2020•海安市模拟)如图,O是△ABC的边AB上一点,⊙O经过点A、C,交AB于点D.过点C作CE⊥AB,垂足为E.连接CD,CD恰好平分∠BCE.(1)求证:直线BC是⊙O的切线;(2)若⊙O的半径为3,CD=2,求BC的长.39.(2020•吴江区一模)如图,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交AC于E,连接BE交CD于P,交⊙O于F,连接DF,∠ABC=∠EFD.(1)求证:AB与⊙O相切;(2)若AD=4,BD=6,则⊙O的半径=;(3)若PC=2PF,BF=a,求CP(用a的代数式表示).40.(2020•昆山市一模)如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD 与BC,OC分别交于E、F.(1)求证:=;(2)若CE=1,EB=3,求⊙O的半径;(3)若BD=6,AB=10,求DE的长.参考答案与试题解析1.【分析】(1)根据圆周角定理得到∠ACB=∠ADB=90°,根据全等三角形的判定定理即可得到结论;(2)根据等腰三角形的性质得到∠E=∠BFE,根据切线的性质得到∠ABE=90°,根据三角形的内角和以及角平分线的定义即可得到结论.【解答】(1)证明:∵AB是半圆O的直径,∴∠ACB=∠ADB=90°,在Rt△CBA与Rt△DAB中,,∴Rt△CBA≌Rt△DAB(HL);(2)解:∵BE=BF,由(1)知BC⊥EF,∴∠E=∠BFE,∵BE是半圆O所在圆的切线,∴∠ABE=90°,∴∠E+∠BAE=90°,由(1)知∠D=90°,∴∠DAF+∠AFD=90°,∵∠AFD=∠BFE,∴∠AFD=∠E,∴∠DAF=90°﹣∠AFD,∠BAF=90°﹣∠E,∴∠DAF=∠BAF,∴AC平分∠DAB.2.【分析】(1)连接OD,根据圆周角定理得到∠AOD=AOB=90°,根据平行线的性质得到∠ODH=90°,于是得到结论;(2)连接CD,根据圆周角定理得到∠ADB=∠ACB=90°,推出△ABD是等腰直角三角形,得到AB=10,解直角三角形得到AC==8,求得∠CAD=∠DBH,根据平行线的性质得到∠BDH=∠OBD=45°,根据相似三角形的性质即可得到结论.【解答】(1)证明:连接OD,∵AB为⊙O的直径,点D是半圆AB的中点,∴∠AOD=AOB=90°,∵DH∥AB,∴∠ODH=90°,∴OD⊥DH,∴直线DH是⊙O的切线;(2)解:连接CD,∵AB为⊙O的直径,∴∠ADB=∠ACB=90°,∵点D是半圆AB的中点,∴=,∴AD=DB,∴△ABD是等腰直角三角形,∵AB=10,∴AD=10sin∠ABD=10sin45°=10×=5,∵AB=10,BC=6,∴AC==8,∵四边形ABCD是圆内接四边形,∴∠CAD+∠CBD=180°,∵∠DBH+∠CBD=180°,∴∠CAD=∠DBH,由(1)知∠AOD=90°,∠OBD=45°,∴∠ACD=45°,∵DH∥AB,∴∠BDH=∠OBD=45°,∴∠ACD=∠BDH,∴△ACD∽△BDH,∴,∴=,解得:BH=.3.【分析】(1)连接OC,根据切线的性质,判断出AD∥OC,再应用平行线的性质,即可推得AC平分∠DAB;(2)如图2,连接BC,设AD=2x,AB=3x,根据圆周角定理得到∠ACB=∠ADC=90°,根据相似三角形的性质即可得到结论.【解答】(1)证明:如图1,连接OC,,∵CD是切线,∴OC⊥CD.∵AD⊥CD,∴AD∥OC,∴∠1=∠4.∵OA=OC,∴∠2=∠4,∴∠1=∠2,即∠CAD=∠CAB.(2)解:如图2,连接BC,∵=,∴设AD=2x,AB=3x,∵AB是⊙O的直径,∴∠ACB=∠ADC=90°,∴∠ACB=90°,∵AD⊥DC,∴∠ADC=90°,∵∠DAC=∠CAB,∴△ACD∽△ABC,∴=,∴=,解得,x1=2,x2=﹣2(舍去),∴AD=4,∴CD==2.4.【分析】(1)根据题意和垂径定理,可以求得AC的长,然后即可得到AB的长;(2)根据∠AOC=60°,可以得到∠AOB的度数,然后根据弧长公式计算即可.【解答】解:(1)∵的半径OA=2,OC⊥AB于点C,∠AOC=60°,∴AC=OA•sin60°=2×=,∴AB=2AC=2;(2)∵OC⊥AB,∠AOC=60°,∴∠AOB=120°,∵OA=2,∴的长是:=.5.【分析】(1)连接OC,根据圆周角定理得到∠ACB=90°,根据余角的性质得到∠A=∠ECB,求得∠A=∠BCD,根据等腰三角形的性质得到∠A=∠ACO,等量代换得到∠ACO=∠BCD,求得∠DCO=90°,于是得到结论;(2)设BC=k,AC=2k,根据相似三角形的性质即可得到结论.【解答】(1)证明:连接OC,∵AB是⊙O的直径,∴∠ACB=90°,∵CE⊥AB,∴∠CEB=90°,∴∠ECB+∠ABC=∠ABC+∠CAB=90°,∴∠A=∠ECB,∵∠BCE=∠BCD,∴∠A=∠BCD,∵OC=OA,∴∠A=∠ACO,∴∠ACO=∠BCD,∴∠ACO+∠BCO=∠BCO+∠BCD=90°,∴∠DCO=90°,∴CD是⊙O的切线;(2)解:∵∠A=∠BCE,∴tan A==tan∠BCE==,设BC=k,AC=2k,∵∠D=∠D,∠A=∠BCD,∴△ACD∽△CBD,∴==,∵AD=8,∴CD=4.6.【分析】(1)利用垂径定理以及圆周角定理解决问题即可.(2)证明△AEC∽△BCA,推出=,求出EC即可解决问题.【解答】(1)证明:∵AE=DE,OC是半径,∴=,∴∠CAD=∠CBA.(2)解:∵AB是直径,∴∠ACB=90°,∵AE=DE,∴OC⊥AD,∴∠AEC=90°,∴∠AEC=∠ACB,∴△AEC∽△BCA,∴=,∴=,∴CE=3.6,∵OC=AB=5,∴OE=OC﹣EC=5﹣3.6=1.4.7.【分析】连结OC,根据切线的性质和等腰三角形的性质即可得到结论.【解答】解:证法错误;证明:连结OC,∵⊙O与AB相切于点C,∴OC⊥AB,∵OA=OB,∴AC=BC.8.【分析】(1)由角平分线的性质和圆周角定理可得∠DBC=∠ABC=∠CAD;(2)由圆周角定理可得,由弧长公式可求解.【解答】解:(1)∵BC平分∠ABD,∴∠DBC=∠ABC,∵∠CAD=∠DBC,∴∠CAD=∠ABC;(2)∵∠CAD=∠ABC,∴=,∵AD是⊙O的直径,AD=6,∴的长=××π×6=π.9.【分析】(1)连接OD,由等腰三角形的性质及角平分线的性质得出∠ADO=∠DAE,从而OD∥AE,由DE∥BC得∠E=90°,由两直线平行,同旁内角互补得出∠ODE=90°,由切线的判定定理得出答案;(2)先由直径所对的圆周角是直角得出∠ADB=90°,再由OF=1,BF=2得出OB的值,进而得出AF和BA的值,然后证明△DBF∽△ABD,由相似三角形的性质得比例式,从而求得BD2的值,求算术平方根即可得出BD的值.【解答】解:(1)连接OD,如图:∵OA=OD,∴∠OAD=∠ADO,∵AD平分∠CAB,∴∠DAE=∠OAD,∴∠ADO=∠DAE,∴OD∥AE,∵DE∥BC,∴∠E=90°,∴∠ODE=180°﹣∠E=90°,∴DE是⊙O的切线;(2)∵AB是⊙O的直径,∴∠ADB=90°,∵OF=1,BF=2,∴OB=3,∴AF=4,BA=6.∵DF⊥AB,∴∠DFB=90°,∴∠ADB=∠DFB,又∵∠DBF=∠ABD,∴△DBF∽△ABD,∴=,∴BD2=BF•BA=2×6=12.∴BD=2.10.【分析】(1)连接OC,利用切线的性质证明即可;(2)根据相似三角形的判定和性质以及勾股定理解答即可.【解答】解:(1)连接OC,∵CN为⊙O的切线,∴OC⊥CM,∠OCA+∠ACM=90°,∵OM⊥AB,∴∠OAC+∠ODA=90°,∵OA=OC,∴∠OAC=∠OCA,∴∠ACM=∠ODA=∠CDM,∴MD=MC;(2)由题意可知AB=5×2=10,AC=4,∵AB是⊙O的直径,∴∠ACB=90°,∴BC=,∵∠AOD=∠ACB,∠A=∠A,∴△AOD∽△ACB,∴,即,可得:OD=2.5,设MC=MD=x,在Rt△OCM中,由勾股定理得:(x+2.5)2=x2+52,解得:x=,即MC=.11.【分析】作出△ABC的外接圆⊙O,连接OB,OC,当△ABC的BC边上的高经过点O 时,△ABC面积最大,如图,过点O作OD⊥BC,并延长DO交圆于点A',连接A'B,A'C,得出△OBC为等边三角形,则∠BOD=30°,OB=OA'=BC=4,求出OD=2,则由三角形面积公式可得出答案.【解答】解:作出△ABC的外接圆⊙O,连接OB,OC,当△ABC的BC边上的高经过点O时,△ABC面积最大,如图,过点O作OD⊥BC,并延长DO交圆于点A',连接A'B,A'C,∵∠BAC=30°,∴∠BOC=60°,∵OB=OC,∴△OBC为等边三角形,∴∠BOD=30°,OB=OA'=BC=4,∴OD=2,∴A'D=4+2,∴S△A'BC=×BC×A'D==8+4.12.【分析】(1)连接OE,根据切线的性质得到OE⊥CF,得到OE∥BC,根据平行线的性质、等腰三角形的性质得到∠CBE=∠OBE,根据角平分线的定义证明即可;(2)根据直角三角形的性质求出∠EOF=60°,根据弧长公式计算,得到答案.【解答】(1)证明:连接OE,∵直线CF与⊙O相切,∴OE⊥CF,∵BC⊥CF,∴OE∥BC,∴∠CBE=∠OEB,∵OE=OB,∴∠OBE=∠OEB,∴∠CBE=∠OBE,∴BE平分∠CBF;(2)解:∵∠OEF=90°,∠CFB=30°,∴∠EOF=60°,∴的长==π.13.【分析】(Ⅰ)设半圆的圆心为O,连接CO.通过计算证明AF=2DF即可解决问题.(Ⅱ)连接PB,BQ.证明△AEF∽△APQ,求出△APQ,△AEF的面积即可.【解答】解:(I)设半圆的圆心为O,连接CO.∵直径AB=4,D是AB的一个四等分点,∴AD=,OD=,CO=2,∵CD⊥OA,∴∠CDO=90°,在Rt△CDO中,由勾股定理得:CD===3,∵E,F为线段CD的三等分点,∴DF=1,在Rt△ADF中,由勾股定理得:AF===2,即AF=2DF,∴∠F AD=30°;(2)连接PB,BQ.∵AB是直径,∴∠APB=90°,∵∠BAP=30°∴BP=AB=2,P A===6,AE==,∵∠ABQ=∠APQ,∠ABQ=∠AED,∴∠AED=∠APQ,∠EAF=∠P AQ,∴△AEF∽△APQ,∴=,=()2=,∵S△AEF=•EF•AD=,∴S△APQ=∴S四边形EFPQ=S△APQ﹣S△AEF=.14.【分析】将△EBI,△DCI分别沿BD,CE翻折,点E、D落在BC边上的E1、D1处根据翻折的性质及内切圆的性质可得,∠EID=135°,∠D1IE1=45°,EI=IE1,DI=ID1,进而可以证明,可得S四边形EDCB=2S△BIC.【解答】解:将△EBI,△DCI分别沿BD,CE翻折,点E、D落在BC边上的E1、D1处,∵I为Rt△ABC的内心,∴∠EIB=∠IBC+∠ICB=(∠ABC+∠ACB)=45°,∴∠E1IB=∠EIB=45°,∴∠EID=135°,同理:∠DIC=∠D1IC=45°,∴∠D1IE1=45°,∵EI=IE1,DI=ID1,作DH⊥EC,D1H′⊥E1I于点H、H′,∴DH=DI•sin45°,D1H′=D1I•sin45°,∴S△EID=EI•DH=×EI•DI•sin45°,S=E1I•D1H′=E1I•D1I•sin45°,∴,∵S△BEI=S,S△CDI=S,∴S四边形EDCB=2S△BIC=24.答:S四边形EDCB为24.15.【分析】根据Rt△ABC中,内切圆O的半径r,三角形三个边分别为:a、b、c,可得S=ab,ab=2S△,2r=a+b﹣c,c=a+b﹣2r,再根据勾股定理列出方程,根据一元△ABC二次方程根的判别式即可求解.【解答】解:∵Rt△ABC中,内切圆O的半径r,三角形三个边分别为:a、b、c,∴S△ABC=ab,设S△ABC=S△,∴ab=2S△,∵2r=a+b﹣c,∴c=a+b﹣2r,∴a+b﹣2r=.两边平方,得a2+b2+4r2+2ab﹣4(a+b)r=a2+b2,4r2+2ab﹣4(a+b)r=0,将r=1,ab=2S△代入,得:4+4S△﹣4(a+b)=0,a+b=S△+1,∵ab=2S△且a+b=S△+1,∴a,b是方程x2﹣(S△+1)x+2S△=0的两个根.∵a,b是正实数,∴△≥0,即[﹣(S△+1)]2﹣4×2S△≥0,﹣6S△+1≥0.解得S△或S△≤3﹣2,S△≤3﹣2不合题意舍去.∴S△ABC的最小值是.16.【分析】(1)根据作图可得,四边形QCSl2,I1MCN均为正方形,设⊙I2的半径为R,得AQ=AP=3﹣R,CS=CQ=R,再根据切线长定理即可求出⊙I2的半径;(2)根据∠ACB=90°,AC=3,BC=4,可得AB=5,再根据I1为△ABC内切圆的圆心,可求出内切圆的半径,根据勾股定理即可求出线段I1I2的长.【解答】解:(1)如图,过点I2作I2Q⊥AC于点Q,连接I2S,过点I1作I1M⊥BC于点M,I1N⊥AC于点N,交I2S于点H,可得四边形QCSl2,I1MCN均为正方形,I1HSM为矩形,设⊙I2的半径为R,则AQ=AP=3﹣R,CS=CQ=R,又因为BP=BS,所以5+3﹣R=4+R,解得R=2.(2)∵∠ACB=90°,AC=3,BC=4,∴AB==5,∵I1为△ABC内切圆的圆心,∴I1M=I1N=,∴I1H=3,∴I1l2==.17.【分析】(1)由切线长定理可以推出结论.(2)连接AE、BE.根据射影定理可得DE2=AD•BD,将(1)中得出的AD与BD表达式代入上式并整理,其结果就是△ABC的面积,于是结论得证.【解答】解:(1)如图,设圆I与AC切于点M,与BC切于点N,由切线长定理可知:AD=AM,CM=CN,BN=BD,∴AD+AM=AB+BC+CA﹣CM﹣CN﹣BN﹣BD=a+b+c﹣2a=b+c﹣a,∴AD=,∴BD=.(2)连接AE、BE.∵AB是直径,∴∠AEB=∠ACB=90°,∴c2=a2+b2,∴四边形DEFG是正方形,∴ED⊥AB,由射影定理可知:DE2=AD•BD=×=ab.∴正方形DEFG的面积和△ABC的面积相等.18.【分析】延长AB,FE交于T,根据相似三角形的性质得到,求得ET=EF,根据相似三角形的性质得到TE•EF=CE•AE,求得EF=ET=6,连接BG,CG,根据射影定理即可得到结论.【解答】解:延长AB,FE交于T,∵AD∥FT,∴△ABP∽△TBE,△PBD∽△EBF,∴,∵AP=DP,∴ET=EF,∵∠BAC=90°,∴∠TAE=90°,∵EF⊥BC,∴∠CFE=∠TAE=90°,∵∠AET=∠CEF,∴△AET∽△CEF,∴=,∠T=∠C,∴TE•EF=CE•AE,∴EF=ET=6,∵∠BFT=∠CFE=90°,∴△BFT∽△EFC,∴=,∴BF•FC=EF•TF=6×12=72,连接BG,CG,∴FG2=BF•CF=72,∴FG=6,∴EG=6﹣6.19.【分析】(1)根据垂径定理可以证明∠BOD=∠A,可得AC∥OE,再根据AC=OE,可得四边形AECO是平行四边形,进而可得CE∥AB,CE=AB;(2)根据AC∥OE,CE∥AO,可得=,=,即可得=,得HE2=HG•HF,根据HG=x,GF=y,HE=5,代入即可得y与x的函数解析式.【解答】解:(1)CE∥AB,CE=AB,理由如下:∵点D是劣弧的中点,∴=,∴∠COD=∠BOD=BOC,∵∠A=BOC,∴∠BOD=∠A,∴AC∥OE,∵AC=OE,∴四边形AECO是平行四边形,∴CE∥AO,CE=AO,∵AO=AB,∴CE=AB,∴CE∥AB,CE=AB.(2)∵AC∥OE,CE∥AO,∴=,=,∴=,即HE2=HG•HF,∵HG=x,GF=y,HE=5,∴52=x(x+y),∴y=.∴y与x的函数解析式为y=.20.【分析】设BC=a,BC边上的高为h,内切圆半径为r.则S△ABC=pr,从而得出MN 是p的二次函数,再求最大值.【解答】解:设BC=a,BC边上的高为h,内切圆半径为r.∵△AMN∽△ABC,∴,MN=a(1),∵S△ABC=ar+br+cr=(a+b+c)r=•2pr=pr,∴r==,∴MN=a(1﹣)=(1﹣)≤p•=,当且仅当,即a=时,取等号,∴MN的最大值为.21.【分析】(1)根据点A是的中点,得到∠AMN=∠ANM,求得∠ABN=∠ANP,根据三角形的文件的性质即可得到结论;(2)根据全等三角形的性质得到,求得AN=2AP,得到BN=2NP,同理,BM=2MP,于是得到结论.【解答】解:(1)证明:∵点A是的中点,∴∠AMN=∠ANM,∵∠AMN=∠ABN,∴∠ABN=∠ANP,∴∠APN=∠ABN+∠PNB=∠ANM+∠PNB=∠ANB;(2)∵∠ABN=∠ANP,∠BAN=∠NAP,∴△ABN∽△ANP,∴,∵AB=4AP,∴AN=2AP,∴=2,∴BN=2NP,同理,BM=2MP,∴BM+BN=2MN,∴=2.22.【分析】(Ⅰ)连接BH,根据圆周角定理得到∠AHB=90°,根据三角函数的定义得到∠ABH=30°,于是得到∠HKA=∠ABH=30°;(Ⅱ)根据三角形的内角和得到∠BAH=60°,根据直角三角形的性质健康得到结论;(Ⅲ)连接OH,则△AOH是等边三角形,求得AO=AH=2,∠AOH=60°,过H作HE⊥AO于E,则HE=,根据三角形和扇形的面积公式即可得到结论;(Ⅳ)过O作平行于AK的直线交⊙O于MN,过O作OP⊥AK于Q交⊙O于P,解直角三角形即可得到结论.【解答】解:(Ⅰ)连接BH,∵AB为⊙O的直径,∴∠AHB=90°,∵AB=4,AH=2,∴sin∠ABH===,∴∠ABH=30°,∴∠HKA=∠ABH=30°;(Ⅱ)∵∠AHB=90°,∠ABH=30°,∴∠BAH=60°,∵四边形ABCD是矩形,∴∠ABC=90°,∴AC=2AB=8,∴CH=AC﹣AH=6;(Ⅲ)连接OH,则△AOH是等边三角形,∴AO=AH=2,∠AOH=60°,过H作HE⊥AO于E,则HE=,∵AC=8,CD=AB=4,∴AD=4,∴图中阴影部分的面积=×44﹣(﹣×2×)=9﹣π;(Ⅳ)过O作平行于AK的直线交⊙O于MN,过O作OP⊥AK于Q交⊙O于P,∵⊙O的半径=2,则PQ=OQ=1,∵OA=2,∴AQ=,∴AK=2AQ=2,∴m=2.23.【分析】(1)连接AD,由圆周角定理得出∠ADC=90°,证明△ECD∽△BCE,即可得出∠BEC=∠EDC;(2)证出BD=AD,得出AD+DC=14,由勾股定理得出AD2+DC2=AC2,即(14﹣DC)2+DC2=102,解得DC=8或DC=6,由题意得出DC=6,AD=8,由相似三角形的性质得出CE:BC=CD:CE,即可得出答案.【解答】(1)证明:连接AD,∵AC为⊙O的直径,∴∠ADC=90°,∴∠ADB=90°,∵BH⊥AC,∴∠BGC=90°,∵∠DAC+∠ACD=∠GBC+∠ACD=90°,∴∠DAC=∠GBC,又∵∠DAC=∠DEC,∴∠EBC=∠DEC,∵∠ECD=∠BCE,∴△ECD∽△BCE,∴∠BEC=∠EDC;(2)解:由(1)得:∠EBC=∠DEC,∵∠ABG+∠DEC=45°,∴∠ABC=45°,∠BAD=45°,∴△ABD是等腰直角三角形,∴BD=AD,∴AD+DC=BD+DC=BC=14,∵∠ADC=90°,AC=10,∴AD2+DC2=AC2,即(14﹣DC)2+DC2=102,解得:DC=8或DC=6,∵∠DAC=∠GBC<45°,∴AD>DC,∴DC=6,AD=8,由(1)得:△ECD∽△BCE,∴CE:BC=CD:CE,∴CE2=CD×BC=6×14=84,∴CE=2.24.【分析】(1)根据在同圆中,圆周角是同弧所对的圆心角的一半可得∠ATB==60°,由弦切角等于同弧所对的圆周角可得∠BTP=∠TAP,由角平分线的定义和三角形外角的性质可得∠TCD=∠CDT==60°,根据有三个角相等的三角形是等边三角形可得结论;(2)设CT=DT=x,证明△PCT∽△PDB和△ACP∽△TDP列比例式可得结论.【解答】(1)证明:∵∠AOB=120°,∴∠ATB==60°,∵PT切⊙O于T,∴∠BTP=∠TAP,∵PC平分∠APT,∴∠APC=∠CPT,∵∠TCD=∠TAP+∠APC,∠CDT=∠BTP+∠CPT,∴∠TCD=∠CDT==60°,∴△CDT为等边三角形;(2)解:设CT=DT=x,∵∠TCD=∠CDT=∠BDP,∠BPD=∠CPT,∴△PCT∽△PDB,∴,∵∠DTP=∠P AC,∠APC=∠DPT,∴△ACP∽△TDP,∴,∴,即,∴x2=4,∴x=±2,∵x>0,∴x=2,∴,PC=4.25.【分析】(1)连接DN,根据切线的性质得到∠BCD=∠BDN,根据角平分线的定义得到∠ACD=∠BCD,等量代换得到∠MND=∠BDN,于是得到MN∥AB;(2)根据相似三角形的性质得到,根据三角形角平分线定理得到=,根据射影定理即可得到结论.【解答】(1)证明:连接DN,∵AB是⊙O的切线,∴∠BCD=∠BDN,∵CD为∠ACB的平分线,∴∠ACD=∠BCD,∵∠ACD=∠MND,∴∠MND=∠BDN,∴MN∥AB;(2)解:∵MN∥AB,∴△CMN∽△CAB,∴,∵CD为∠ACB的平分线,∴=,∴=,∴AD=6,∵AD2=AC•AM,∴62=12AM,∴AM=3,∴CM=9,∴=,∴MN=.26.【分析】(1)证AE是⊙O的切线,即证AB⊥AE即可;根据切割线定理,可将DE的长求出,再由△ACE∽△BAC可将AB的长求出;(2)设BE与PQ交于G,AB与PQ交于F,根据勾股定理得到BE==,根据折叠的性质得到BG⊥PQ,BG=BE=,根据相似三角形的性质得到BF=,求得OF=﹣=,过O作OH⊥于H,由相似三角形的性质得到OH=,连接OQ,于是得到结论.【解答】解:(1)连接AC,∵AB∥CD且AE⊥CD,∴AB⊥AE,∠ECA=∠BAC,∵AB是⊙O的直径,∴∠ACB=90°,∴∠B+∠BAC=∠BAC+∠EAC=90°,∴∠B=∠EAC,∵∠ADE=∠B,∴∠EAC=∠ADE,∵∠E=∠AEC,∴△ACE∽△DAE,∴=,∴AE2=ED•EC,设DE=x,则22=x(x+3),解得:x1=1,x2=﹣4(舍去),即:DE=1,在Rt△ACE中,AC2=AE2+CE2,∴AC2=20,∵∠ACB=∠E,∠CAE=∠B,∴△ACE∽△BAC,∴=∴AB=5;(2)设BE与PQ交于G,AB与PQ交于F,∵AE=2,AB=5,∴BE==,∵翻折使点B与E重合,∴BG⊥PQ,BG=BE=,∵∠BGF=∠EAB=90°,∠GBF=∠ABE,∴△BGF∽△BAE,∴=,∴=,∴BF=,∴OF=﹣=,过O作OH⊥于H,∴OH∥BG,PQ=2HQ,∴△OFH∽△BFG,∴=,∴=,∴OH=,连接OQ,∴HQ==,∴PQ=2HQ=,∴△BPQ的面积=×=.27.【分析】证明Rt△AEP∽Rt△ABC和Rt△AED∽Rt△OBC,然后利用其对应边成比例即可得出结论.【解答】证明:∵AB是⊙O的直径,BC是⊙O的切线,∴AB⊥BC.∴DE∥BC,∴Rt△AEP∽Rt△ABC,∴,又∵AD∥OC,∴∠DAE=∠COB,∴Rt△AED∽Rt△OBC.∴,∴ED=2EP.∴EP=PD.28.【分析】(1)延长FD到G,使DG=BE,连接AG,证△GDA≌△EBA,△GAF≌△EAF,根据全等三角形的性质得出GD+DF=BE+DF=EF进而求出即可;(2)首先令BE=a,DF=b,则EF=a+b,r==1﹣(a+b),进而利用勾股定理得出(a+b)2+(a+b)﹣1≥0,进而求出即可.【解答】(1)证明:延长FD到G,使DG=BE,连接AG,∵在△GDA和△EBA中,,∴△GDA≌△EBA,∴AG=AE,∠GAD=∠EAB,故∠GAF=45°,在△GAF和△EAF中,∵,∴△GAF≌△EAF,∴GF=EF,即GD+DF=BE+DF=EF;(2)解:令BE=a,DF=b,则EF=a+b,r==1﹣(a+b),∵(1﹣a)2+(1﹣b)2=(a+b)2,整理得1﹣(a+b)=ab,而ab≤(a+b)2,(a+b)2+(a+b)﹣1≥0,解得:a+b≥﹣2+2或a+b≤﹣2﹣2(舍去),r=1﹣(a+b)≤1﹣(﹣2+2)=3﹣2,当且仅当a=b=﹣1时,等号成立.29.【分析】首先在MA上截取ME=MC,连接BE,由BM⊥AC,根据垂直平分线的性质,即可得到BE=BC,得到∠BEC=∠BCE;再由AB=BD,得到∠ADB=∠BAD,而∠ADB =∠BCE,则∠BEC=∠BAD,根据圆内接四边形的性质得∠BCD+∠BAD=180°,易得∠BEA=∠BCD,从而可证出△ABE≌△DBC,得到AE=CD,即有AM=DC+CM.【解答】证明:在MA上截取ME=MC,连接BE,∵BM⊥AC,∴BE=BC,∴∠BEC=∠BCE,∵AB=BD,∴=,∴∠ADB=∠BAD,而∠ADB=∠BCE,∴∠BCE=∠BAD,又∵∠BCD+∠BAD=180°,∠BEA+∠BCE=180°,∴∠BEA=∠BCD,∵∠BAE=∠BDC,∴△ABE≌△DBC,∴AE=CD,∴AM=AE+EM=DC+CM.30.【分析】(1)根据∠ABC=40°,∠C=80°,利用三角形内心定义和同弧所对圆周角相等即可求∠CBD的度数;(2)理解BE,根据三角形内心定义和同弧所对圆周角相等∠DEB=∠DBE,从而依据等角对等边即可证明DB=DE;(3)利用已知AB=6,AC=4,和角平分线性质可得==,由BC=5,可得BF和FC的值,再证明△BDF∽△ACF和△DBF∽△DAB,再利用相似三角形的性质得到关于BD的方程,即可求DE的长.【解答】解:(1)∵∠ABC=40°,∠C=80°,∴∠BAC=180°﹣40°﹣80°=60°,∵点E是△ABC的内心,∴∠CAD=∠BAD=BAC=30°,∴∠CBD=∠CAD=30°.答:∠CBD的度数为30°;(2)证明:如图,连接BE,∴∠1=∠2,∠3=∠4,∵∠2=∠6,∴∠1=∠6,∵∠5=∠1+∠3,∠DBE=∠6+∠4=∠1+∠3,∴∠5=∠DBE,∴DB=DE;(3)∵∠1=∠2,AB=6,AC=4,BC=5,∴==,∴BF=3,CF=2,∵∠6=∠2,∠D=∠C,∴△BDF∽△ACF,∴===2,=,∴DF=BD,DF•AF=BF•CF=6,∵∠1=∠2=∠6,∠BDF=∠ADB,∴△DBF∽△DAB,∴=,∴BD2=DF•DA=DF(AF+DF)=DF•AF+DF2=6+(BD)2,解得BD=2,∴DE=BD=2.答:DE的长为2.31.【分析】(1)连接OE,AE,根据切线的性质与判定即可求出答案.(2)易证△CAE∽△ABE,所以AE2=CE•BE,求出AE=,根据锐角三角函数的定义即可求出答案.【解答】解:(1)连接OE,AE,∵AE=DE,OA=OE,∴∠DAE=∠DEA,∠OAE=∠OEA,∵AC是⊙O的切线,∴∠BAC=90°,∴∠DAE+∠OAE=∠DEA+∠OEA=90°,∵OE是⊙O的半径,∴DE是⊙O的切线.(2)∵AB是⊙O的直径,∴∠AEB=90°,∵∠C+∠CAE=∠CAE+∠BAE=90°,∴∠C=∠BAE,∴△CAE∽△ABE,∴AE2=CE•BE,∴AE2=1×3,∴AE=,在Rt△ACE中,∴tan∠ACE==,∴∠ACE=60°.32.【分析】(1)求出OD∥AC,求出OD⊥BC,根据切线的判定得出即可;(2)根据勾股定理得出方程,求出方程的解即可.【解答】解:(1)线BC与⊙O的位置关系是相切,理由是:连接OD,∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠CAB,∴∠OAD=∠CAD,∴∠ODA=∠CAD,∴OD∥AC,∵∠C=90°,∴∠ODB=90°,即OD⊥BC,∵OD为半径,∴线BC与⊙O的位置关系是相切;(2)设⊙O的半径为R,则OD=OF=R,在Rt△BDO中,由勾股定理得:OB2=BD2+OD2,即(R+2)2=(2)2+R2,解得:R=4,即⊙O的半径是4.33.【分析】(1)如图①中,延长DE交⊙O于G,连接AG.想办法证明DE=EG,BC=DG即可.(2)如图②中,作FR⊥AB于R,OS⊥AD于S.首先证明BF=BO,利用相似三角形的性质证明AC=2FR=2CF,由tan∠F AR=tan∠F AC=,设SO=t,AS=2t,SF=SO=t,利用勾股定理求出t即可解决问题.【解答】(1)证明:如图①中,延长DE交⊙O于G,连接AG.∵AB⊥DG,AB是直径,∴=,DE=EG,∵AD平分∠CAB,∴∠CAD=∠DAB,∴=,∴=,∴BC=DG=2DE.(2)解:如图②中,作FR⊥AB于R,OS⊥AD于S.∵AD平分∠CAB,FC⊥AC,FR⊥AB,∴∠CAD=∠BAD=x,FC=FR,∴∠FBO=90°﹣2x,∵∠AFO=45°,∴∠FOB=45°+x,∴∠OFB=180°﹣(90°﹣2x)﹣(45°+x)=45°+x,∴∠FOB=∠OFB∴BF=BO=OA,∵∠FRB=∠ACB=90°,∠FBR=∠ABC,∴△BFR∽△BAC,∴==,∴AC=2FR=2FC,∴tan∠F AR=tan∠F AC=,设SO=t,AS=2t,SF=SO=t,则t2+4t2=4,∵t>0,∴t=,∴AF=3t=,设CF=m,则AC=2m,则有5m2=,∵m>0,∴m=,∴AC=2m=.34.【分析】(1)如图,连接OE,根据切线的性质得到OE⊥CE.于是得到∠2+∠3=90°,根据等腰三角形的性质得到∠3=∠4.于是得到∠1=∠2,根据等腰三角形的性质即可得到结论;(2)解直角三角形得到BC=CE=4,设⊙O的半径为r,则OD=OE=r,OC=r+2,根据勾股定理列方程即可得到结论.【解答】(1)证明:如图,连接OE,∵∠ACB=90°,∴∠1+∠5=90°,∵CE是⊙O的切线,∴OE⊥CE,∴∠2+∠3=90°,∵OE=OD,∴∠3=∠4.又∵∠4=∠5,∴∠3=∠5,∴∠1=∠2,∴CE=BC;(2)解:在Rt△BCD中,∠DCB=90°,CD=2,BD=,∴BC=CE=4,设⊙O的半径为r,则OD=OE=r,OC=r+2,在Rt△OEC中,∠OEC=90°,∴OE2+CE2=OC2,∴r2+42=(r+2)2,解得r=3,∴⊙O的半径为3.35.【分析】(1)由切线的性质可得∠OAP=90°,由等腰三角形的性质可得∠OAB+∠P AB =∠OBA+∠PBA=∠P AO=∠PBO=90°,可得结论;(2)根据已知条件得到△APB是等边三角形,求得∠P AB=60°,AB=P A=6,得到∠BOC=60°,求得OB=6,连接OP,推出OP垂直平分AB,得到PO∥BC,根据扇形的面积公式即可得到结论.【解答】证明:(1)连接OB,BC,设AB与OP交于点K,∵P A是⊙O的切线,∴∠OAP=90°,∵P A=PB,∴∠PBA=∠P AB,∵OA=OB,∴∠OAB=∠OBA,∴∠OAB+∠P AB=∠OBA+∠PBA,∴∠P AO=∠PBO=90°,且OB是半径,∴PB是⊙O的切线;(2)∵P A=PB,∠APB=60°,∴△APB是等边三角形,∴∠P AB=60°,AB=P A=6,∴∠CAB=30°,∴∠BOC=60°,∴∠ABC=90°,∴AC=2BC=2×AB=12,∴OB=6,连接OP,∵OA=OB,AP=BP,∴OP垂直平分AB,∴PO∥BC,∴S△OBC=S△PBC,∴S阴影=S扇形COB==6π.36.【分析】(1)连接OD,作OG⊥AC于点G,推出∠ODB=∠C;然后根据DF⊥AC,∠DFC=90°,推出∠ODF=∠DFC=90°,即可推出DF是⊙O的切线;(2)连接DE,证∠DEC=∠B,由∠B=∠C,得出∠C=∠DEC,则DE=DC,由等腰三角形的性质得出EF=FC即可;(3)连接OE,求出∠A=45°,由等腰三角形的性质得出∠OEA=45°,则∠AOE=90°,由扇形面积公式和三角形面积公式即可得出答案.【解答】(1)解:DF与⊙O相切,理由如下:连接OD,如图1所示:∵OB=OD,∴∠ODB=∠B,又∵AB=AC,∴∠C=∠B,∴∠ODB=∠C,∴OD∥AC,∵DF⊥AC,∴DF⊥OD,∵点D在⊙O上,(2)证明:连接DE,如图2所示:∵∠DEC+∠AED=180°,∠B+∠AED=180°,∴∠DEC=∠B,又∵∠B=∠C,∴∠C=∠DEC,∴DE=DC,又∵DF⊥AC,∴EF=FC,即点F为CE的中点;(3)解:连接OE,如图3所示:∵∠C=67.5°,AB=AC,∴∠B=∠C=67.5°,∴∠A=45°,又∵OA=OE=2,∴∠OEA=45°,∴∠AOE=90°,∴阴影部分的面积=﹣×2×2=π﹣2.37.【分析】(1)根据等腰三角形的性质和圆内接四边形的性质即可得到结论;(2)根据等腰三角形的性质和三角形的内角和即可得到结论;(3)过A作AH⊥BC于H,根据等腰三角形的性质得到∠BAH=∠CAH=CAB,CH=BH,过C作CG⊥AD交AD的延长线于G,根据全等三角形的性质得到AG=AH,CG=CH,根据相似三角形的性质得到=,设BH=k,AH=2k,根据勾股定理即可得到结论.【解答】(1)解:∵AB=AC,∠BAC=40°,∴∠ABC=∠ACB=70°,∵四边形ABCD是⊙O的内接四边形,∴∠ADC=180°﹣∠BAC=110°,故答案为:110;(2)证明:∵BD⊥AC,∴∠AEB=∠BEC=90°,∴∠ACB=90°﹣∠CBD,∵AB=AC,∴∠ABC=∠ACB=90°﹣∠CBD,∴∠BAC=180°﹣2∠ABC=2∠CBD,∵∠DAC=∠CBD,∴∠BAC=2∠DAC;(3)解:过A作AH⊥BC于H,∵AB=AC,∴∠BAH=∠CAH=CAB,CH=BH,∵∠BAC=2∠DAC,∴∠CAG=∠CAH,过C作CG⊥AD交AD的延长线于G,∴∠G=∠AHC=90°,∵AC=AC,∴△AGC≌△AHC(AAS),∴AG=AH,CG=CH,∵∠CDG=∠ABC,∴△CDG∽△ABH,∴==,∴=,设BH=k,AH=2k,∴AB==k=10,∴k=2,∴BC=2k=4.38.【分析】(1)证明∠OCD+∠DCB=90°,得出∠OCB=90°,则结论得证;(2)证明△CDB∽△ACB,得出,设BC=x,则AB=2x,DB=2x﹣6,由BC2=AB•DB得出方程,解方程则可得出答案.【解答】解:(1)证明:∵CE⊥AB,∴∠CED=90°,∴∠ECD+∠CDE=90°,∵OC=DO,∴∠ODC=∠OCD,∵CD平分∠BCE,∴∠ECD=∠DCB,∴∠OCD+∠DCB=90°,∴∠OCB=90°,∴直线BC是⊙O的切线;(2)∵AD是⊙O的直径,∴∠ACD=90°,∴∠CAD+∠CDA=90°,∵∠DCB+∠ODC=90°,∴∠DCB=∠CAD,∵∠CBD=∠ABC,∴△CDB∽△ACB,∴,∴BC2=AB•DB∵⊙O的半径为3,CD=2,∴AC===4,∴=,设BC=x,则AB=2x,DB=2x﹣6,∴x2=2,解得x=,∴BC=.39.【分析】(1)证明∠CDF+∠FDB=90°,即∠CDB=90°,则结论得证;(2)证明△ACD∽△CBD,求出CD=2,则答案可得出;(3)证明△PCF∽△PBC,得出,即PF=,可得出结论.【解答】(1)证明:∵∠ACB=90°,∴∠CEB+∠CBE=90°,∵∠ABC=∠EFD,∠EFD=∠FDB+∠FBD,∴∠EBC=∠FDB,∵∠CEB=∠CDF,∴∠CDF+∠FDB=90°,即∠CDB=90°,∴CD⊥AB,∴AB与⊙O相切;(2)解:∵∠ACD+∠A=90°,∠A+∠ABC=90°,∴∠ACD=∠ABC,∵∠ADC=∠BDC=90°,∴△ACD∽△CBD,∴,∴CD2=AD•BD=4×6=24,∴CD=2,∴⊙O的半径OC=,故答案为:.(3)解:∵CD为⊙O的直径,∴∠CFD=90°,∴∠DCF+∠CDF=90°,又∵∠CDB=90°,∴∠FDB+∠CDF=90°,∴∠FDB=∠DCF,∵∠EBC=∠FDB,∴∠EBC=∠DCF,∴△PCF∽△PBC,∴,∴,∴PB=2PC=4PF,又PB=PF+BF,∴4PF=PF+BF,即PF=,∵PC=2PF.∴PC=a.40.【分析】(1)根据圆周角定理得到∠ADB=90°,利用平行线的性质得到∠AFO=∠ADB =90°,然后根据垂径定理得到结论;(2)连接AC,如图,利用=得到∠CAD=∠ABC,再证明△ACE∽△BCA,利用相似比计算出AC=2,接着根据圆周角定理得到∠ACB=90°,然后利用勾股定理计算出AB,从而得到⊙O的半径;(3)先在Rt△DAB中计算出AD=8,再利用垂径定理得到AF=DF=4,则OF=3,所以CF=2,然后证明△ECF∽△EBD得到=,所以=,然后把DF=4代入计算即可得到DE的长.【解答】(1)证明:∵AB是圆的直径,∴∠ADB=90°,∵OC∥BD,∴∠AFO=∠ADB=90°,∴OC⊥AD∴=;(2)解:连接AC,如图,∵=,∴∠CAD=∠ABC,∵∠ECA=∠ACB,∴△ACE∽△BCA,∴AC2=CE•CB,即AC2=1×(1+3),∴AC=2,∵AB是圆的直径,∴∠ACB=90°,∴AB==2,∴⊙O的半径为;(3)解:在Rt△DAB中,AD==8,∵OC⊥AD,∴AF=DF=4,∵OF==3,∴CF=2,∵CF∥BD,∴△ECF∽△EBD,∴===,∴=∴DE=×4=3.。
《圆》的计算及证明题之中考真题精选汇编(1)

《圆》的计算及证明题之中考真题精选汇编(1)1.如图1,在⊙O中,AB为⊙O的直径,点C为⊙O上一点,AD为∠CAB的平分线交⊙O 于点D,连接OD交BC于点E.(1)求∠BED的度数;(2)如图2,过点A作⊙O的切线交BC延长线于点F,过点D作DG∥AF交AB于点G.若AD=2√35,DE=4,求DG的长.2.如图,在平面直角坐标系中,点P在第一象限内,⊙P与x轴相切于点C,与y轴相交于点A(0,8),B(0,2).连接AC,BC.(1)求点P的坐标;(2)求cos∠ACB的值.3.如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.(1)求证DB平分∠ADC,并求∠BAD的大小;(2)过点C作CF∥AD交AB的延长线于点F,若AC=AD,BF=2,求此圆半径的长.4.如图,已知⊙O是等边三角形ABC的外接圆,连接CO并延长交AB于点D,交⊙O于点E,连接EA,EB.(1)写出图中一个度数为30°的角:,图中与△ACD全等的三角形是;(2)求证:△AED∽△CEB;(3)连接OA,OB,判断四边形OAEB的形状,并说明理由.5.如图,AB是⊙O的直径,FD为⊙O的切线,CD与AB相交于点E.过点D的线DF∥AB,交CA的延长线于点F,CF=CD.(1)求∠F的度数;(2)若DE•DC=8,求⊙O的半径.6.如图,AB是⊙O的直径,C是⊙O上一点,过点C作CD⊥AB于点E,交⊙O于点D,点F是AB延长线上一点,连接CF,AD,∠FCD=2∠DAF.(1)求证:CF是⊙O切线;(2)若AF=10,sin F=23,求CD的长.7.如图,AB为⊙O的直径,D,E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠A.(1)求证:△ACD∽△DCB;(2)求证:CD是⊙O的切线;(3)若tanE=35,AC=10,求⊙O的半径.8.如图,AB是⊙O的直径,点C,E在⊙O上,∠CAB=2∠EAB,点F在线段AB的延长线上,且∠AFE=∠ABC.(1)求证:EF与⊙O相切;(2)若BF=1,sin∠AFE=45,求BC的长.9.如图,四边形ABCD是⊙O的内接四边形,AB是直径,C是BD̂的中点,过点C作CE ⊥AD交AD的延长线于点E.(1)求证:CE是⊙O的切线;(2)若BC=6,AC=8,求CE,DE的长.10.如图,AB是⊙O的直径,AC是弦,D是AĈ上一点,P是AB延长线上一点,连接AD,DC,CP.(1)求证:∠ADC﹣∠BAC=90°;(请用两种证法解答)(2)若∠ACP=∠ADC,⊙O的半径为3,CP=4,求AP的长.11.如图,等腰△ABC内接于⊙O,AB=AC,BD是边AC上的中线,过点C作AB的平行线交BD的延长线于点E,BE交⊙O于点F,连接AE,FC.(1)求证:AE为⊙O的切线;(2)若⊙O的半径为5,BC=6,求FC的长.̂的中点,过点C作CD⊥AE,交12.如图,AB为⊙O的直径,E为⊙O上一点,点C为EBAE的延长线于点D,延长DC交AB的延长线于点F.(1)求证:CD是⊙O的切线;(2)若DE=1,DC=2,求⊙O的半径长.13.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,F是AD延长线上一点,连接CD,CF,且∠DCF=∠CAD.(1)求证:CF是⊙O的切线;(2)若AD=10,cos B=35,求FD的长.14.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,DE⊥AC,垂足为E.(1)求证:DE是⊙O的切线;(2)若∠C=30°,CD=2√3.求BD的长.15.综合与实践:数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.(1)发现问题:如图1,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=30°,连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系:,∠BDC=°;(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC 的度数,并说明理由;(3)拓展延伸:如图3,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系:;(4)实践应用:正方形ABCD中,AB=2,若平面内存在点P满足∠BPD=90°,PD=1,则S△ABP.16.如图,OA,OB,OC都是⊙O的半径,∠ACB=2∠BAC.(1)求证:∠AOB=2∠BOC;(2)若AB=4,BC=√5.求⊙O的半径.̂的中点,弦DE⊥AB,垂足为点F.17.如图,AB为⊙O的直径,C是圆上一点,D是BC(1)求证:BC=DE;̂上一点,AC=6,BF=2,求tan∠BPC;(2)P是AE(3)在(2)的条件下,当CP是∠ACB的平分线时,求CP的长.̂=BD̂,DE⊥AC于点E,DE交BF 18.如图,△ABC内接于⊙O,AB是⊙O的直径,BC于点F,交AB于点G,∠BOD=2∠F,连接BD.(1)求证:BF是⊙O的切线;(2)判断△DGB的形状,并说明理由;(3)当BD=2时,求FG的长.19.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E是斜边AC上一点,以AE为直径的⊙O经过点D,交AB于点F,连接DF.(1)求证:BC是⊙O的切线;(2)若BD=5,tan∠ADB=√3.求图中阴影部分的面积.(结果保留π)20.如图,MN为⊙O的直径,且MN=15,MC与ND为圆内的一组平行弦,弦AB交MC 于点H.点A在MĈ上,点B在NĈ上,∠OND+∠AHM=90°.(1)求证:MH•CH=AH•BH;(2)求证:AĈ=BĈ;(3)在⊙O中,沿弦ND所在的直线作劣弧ND̂的轴对称图形,使其交直径MN于点G.若sin∠CMN=35,求NG的长.21.【感知】如图①,点A、B、P均在⊙O上,∠AOB=90°,则锐角∠APB的大小为度.【探究】小明遇到这样一个问题:如图②,⊙O是等边三角形ABC的外接圆,点P在AC上(点P不与点A、C重合),连接P A、PB、PC.求证:PB=P A+PC.小明发现,延长P A至点E,使AE=PC,连接BE,通过证明△PBC≌△EBA.可推得△PBE是等边三角形,进而得证.下面是小明的部分证明过程:证明:延长P A至点E,使AE=PC,连接BE.∵四边形ABCP是⊙O的内接四边形,∴∠BAP+∠BCP=180°,∵∠BAP+∠BAE=180°,∴∠BCP=∠BAE,∵△ABC是等边三角形,∴BA=BC,∴△PBC≌△EBA(SAS).请你补全余下的证明过程.【应用】如图③,⊙O是△ABC的外接圆,∠ABC=90°,AB=BC,点P在⊙O上,且点P与点B在AC的两侧,连接P A、PB、PC,若PB=2√2PA,则PBPC的值为.22.如图,作CF⊥OE,交BE于点F,若EF=2BF.(1)如图1,连接BD,求证:△ADB≌△OBE;(2)如图2,N是AD上一点,在AB上取一点M,使∠MCN=60°,连接MN.请问:三条线段MN,BM,DN有怎样的数量关系?并证明你的结论.23.如图,已知△ABC内接于⊙O,CO的延长线交AB于点D,交⊙O于点E,交⊙O的切线AF于点F,且AF∥BC.(1)求证:AO∥BE;(2)求证:AO平分∠BAC.24.如图,PO平分∠APD,P A与⊙O相切于点A,延长AO交PD于点C,过点O作OB ⊥PD,垂足为B.(1)求证:PB是⊙O的切线;(2)若⊙O的半径为4,OC=5,求P A的长.25.如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AD交BC于点D,∠ADC的平分线DE交AC于点E.以AD上的点O为圆心,OD为半径作⊙O,恰好过点E.(1)求证:AC是⊙O的切线;(2)若CD=12,tan∠ABC=34,求⊙O的半径.26.综合探究如图1,在矩形ABCD中(AB>AD),对角线AC,BD相交于点O,点A关于BD的对称点为A′.连接AA′交BD于点E,连接CA′.(1)求证:AA'⊥CA';(2)以点O为圆心,OE为半径作圆.①如图2,⊙O与CD相切,求证:AA′=√3CA′;②如图3,⊙O与CA′相切,AD=1,求⊙O的面积.27.如图,在⊙O中,AB是直径,点C是圆上一点.在AB的延长线上取一点D,连接CD,使∠BCD=∠A.(1)求证:直线CD是⊙O的切线;(2)若∠ACD=120°,CD=2√3,求图中阴影部分的面积(结果用含π的式子表示).28.如图,在菱形ABCD中,DH⊥AB于H,以DH为直径的⊙O分别交AD,BD于点E,F,连接EF.(1)求证:①CD是⊙O的切线;②△DEF∽△DBA;(2)若AB=5,DB=6,求sin∠DFE.29.装有水的水槽放置在水平台面上,其横截面是以AB为直径的半圆O,AB=50cm,如图1和图2所示,MN为水面截线,GH为台面截线,MN∥GH.计算:在图1中,已知MN=48cm,作OC⊥MN于点C.(1)求OC的长.操作:将图1中的水槽沿GH向右作无滑动的滚动,使水流出一部分,当∠ANM=30°时停止滚动.如图2.其中,半圆的中点为Q,GH与半圆的切点为E,连接OE交MN 于点D.探究:在图2中.(2)操作后水面高度下降了多少?̂的长度,并比较大小.(3)连接OQ并延长交GH于点F,求线段EF与EQ30.(1)如图①,在△OAB中,OA=OB,∠AOB=120°,AB=24.若⊙O的半径为4,点P在⊙O上,点M在AB上,连接PM,求线段PM的最小值;(2)如图②所示,五边形ABCDE是某市工业新区的外环路,新区管委会在点B处,点E处是该市的一个交通枢纽.已知:∠A=∠ABC=∠AED=90°,AB=AE=10000m,BC=DE=6000m.根据新区的自然环境及实际需求,现要在矩形AFDE区域内(含边界)修一个半径为30m的圆型环道⊙O;过圆心O,作OM⊥AB,垂足为M,与⊙O交于点N.连接BN,点P在⊙O上,连接EP.其中,线段BN、EP及MN是要修的三条道路,要在所修道路BN、EP之和最短的情况下,使所修道路MN最短,试求此时环道⊙O的圆心O到AB的距离OM的长.。
全国各地中考数学真题汇编:圆(填空选择46题)

精品基础教育教学资料,仅供参考,需要可下载使用!中考数学真题汇编:圆(填空+选择46题)一、选择题1.已知的半径为,的半径为,圆心距,则与的位置关系是()A. 外离B. 外切C. 相交D. 内切【答案】C2.如图,为的直径,是的弦,,则的度数为()A. B. C. D.【答案】C3.已知半径为5的⊙O是△ABC的外接圆,若∠ABC=25°,则劣弧的长为()A. B. C. D.【答案】C4.如图,在中,,的半径为3,则图中阴影部分的面积是()A. B. C. D.【答案】C5.如图,AB是圆O的弦,OC⊥AB,交圆O于点C,连接OA,OB,BC,若∠ABC=20°,则∠AOB的度数是()A.40°B.50°C.70°D.80°【答案】D6.如图,蒙古包可近似看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25πm2,圆柱高为3m,圆锥高为2m的蒙古包,则需要毛毡的面积是()A.B.40πm2C.D.55πm2【答案】A7.如图,从一块直径为的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为()A. B. C. D.【答案】A8.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A. 点在圆内B. 点在圆上C. 点在圆心上D. 点在圆上或圆内【答案】D9.如图,AB是圆锥的母线,BC为底面直径,已知BC=6cm,圆锥的面积为15πcm2,则sin∠ABC的值为()A. B. C. D.【答案】C10.如图所示,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连结BC,若∠P=36°,则∠B 等于()。
A.27°B.32°C.36°D.54°【答案】A11.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B. C. D.【答案】B12.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是()A. 3cmB. cmC. 2.5cmD. cm【答案】D13.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,以点B为圆心,BC长为半径画弧,交边AB于点D,则的长为()A.B.C.D.【答案】C14.如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是()A. 75°B. 70°C. 65°D. 35°【答案】B15.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D16.如图,已知AB是的直径,点P在BA的延长线上,PD与相切于点D,过点B作PD的垂线交PD的延长线于点C,若的半径为4,,则PA的长为()A. 4B.C. 3D. 2.5【答案】A17.在中,若为边的中点,则必有成立.依据以上结论,解决如下问题:如图,在矩形中,已知,点在以为直径的半圆上运动,则的最小值为()A. B. C. 34 D. 10【答案】D18.如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、.对于下列结论:①;②;③.其中正确的是()∵∠BEA=∠CDA∠PME=∠AMD∴P、E、D、A四点共圆∴∠APD=AED=90°∵∠CAE=180°-∠BAC-∠EAD=90°∴△CAP∽△CMA∴AC2=CP•CM∵AC= AB∴2CB2=CP•CM所以③正确A. ①②③B. ①C. ①②D. ②③【答案】A二、填空题19.已知扇形的弧长为2 ,圆心角为60°,则它的半径为________.【答案】620.一个扇形的圆心角是120°,它的半径是3cm,则扇形的弧长为________cm.【答案】21.如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为60°,则该直尺的宽度为________ cm。
(专题精选)初中数学圆的真题汇编及答案解析

(专题精选)初中数学圆的真题汇编及答案解析一、选择题1.如图,ABC V 中,90ACB ∠=︒,O 为AB 中点,且4AB =,CD ,AD 分别平分ACB ∠和CAB ∠,交于D 点,则OD 的最小值为( ).A .1B 2C 21D .222【答案】D【解析】【分析】 根据三角形角平分线的交点是三角形的内心,得到DO 最小时,DO 为三角形ABC 内切圆的半径,结合切线长定理得到三角形为等腰直角三角形,从而得到答案.【详解】解:Q CD ,AD 分别平分ACB ∠和CAB ∠,交于D 点,D ∴为ABC ∆的内心,OD ∴最小时,OD 为ABC ∆的内切圆的半径,,DO AB ∴⊥过D 作,,DE AC DF BC ⊥⊥ 垂足分别为,,E F,DE DF DO ∴==∴ 四边形DFCE 为正方形,O Q 为AB 的中点,4,AB =2,AO BO ∴==由切线长定理得:2,2,,AO AE BO BF CE CF r ======sin 4522,AC BC AB ∴==•︒=222,CE AC AE ∴=-=Q 四边形DFCE 为正方形,,CE DE ∴=222,OD CE ∴==故选D .【点睛】本题考查的动态问题中的线段的最小值,三角形的内心的性质,等腰直角三角形的性质,锐角三角函数的计算,掌握相关知识点是解题关键.2.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则⊙O的半径为()A.3B.23C.32D.23【答案】A【解析】连接OC,∵OA=OC,∠A=30°,∴∠OCA=∠A=30°,∴∠COB=∠A+∠ACO=60°,∵PC是⊙O切线,∴∠PCO=90°,∠P=30°,∵PC=3,∴OC=PC•tan30°3故选A3.如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为()A .123B .1536π-πC .30312π-D .48336π-π【答案】C【解析】【分析】 易得AD 长,利用相应的三角函数可求得∠ABD 的度数,进而求得∠EOD 的度数,那么一个阴影部分的面积=S △ABD -S 扇形DOE -S △BOE ,算出后乘2即可.【详解】连接OE ,OF .∵BD=12,AD :AB=1:2,∴AD=43 ,AB=83,∠ABD=30°,∴S △ABD =×43×12=243,S 扇形=603616,633933602OEB S ππ⨯==⨯⨯=V ∵两个阴影的面积相等,∴阴影面积=()224369330312ππ⨯--=- .故选:C【点睛】本题主要是理解阴影面积等于三角形面积减扇形面积和三角形面积.4.如图,在矩形ABCD 中,6,4AB BC ==,以A 为圆心,AD 长为半径画弧交AB 于点E ,以C 为圆心,CD 长为半径画弧交CB 的延长线于点F ,则图中阴影部分的面积是( )A .13πB .1324π+C .1324π-D .524π+【答案】C【解析】【分析】先分别求出扇形FCD 和扇形EAD 的面积以及矩形ABCD 的面积,再根据阴影面积=扇形FCD 的面积﹣(矩形ABCD 的面积﹣扇形EAD 的面积)即可得解.【详解】解:∵S 扇形FCD 29036096ππ==⨯⨯,S 扇形EAD 24036094ππ==⨯⨯,S 矩形ABCD 6424=⨯=, ∴S 阴影=S 扇形FCD ﹣(S 矩形ABCD ﹣S 扇形EAD )=9π﹣(24﹣4π)=9π﹣24+4π=13π﹣24故选:C .【点睛】本题考查扇形面积的计算,根据阴影面积=扇形FCD 的面积﹣(矩形ABCD 的面积﹣扇形EAD 的面积)是解答本题的关键.5.下列命题中,是假命题的是( )A .任意多边形的外角和为360oB .在ABC V 和'''A B C V 中,若''AB A B =,''BC B C =,'90C C ∠=∠=o ,则ABC V ≌'''A B C VC .在一个三角形中,任意两边之差小于第三边D .同弧所对的圆周角和圆心角相等【答案】D【解析】【分析】根据相关的知识点逐个分析.【详解】解:A. 任意多边形的外角和为360o ,是真命题;B. 在ABC V 和'''A B C V 中,若''AB A B =,''BC B C =,'90C C ∠=∠=o ,则ABC V ≌'''A B C V ,根据HL ,是真命题;C. 在一个三角形中,任意两边之差小于第三边,是真命题;D. 同弧所对的圆周角等于圆心角的一半,本选项是假命题.故选D .【点睛】本题考核知识点:判断命题的真假. 解题关键点:熟记相关性质或定义.6.已知下列命题:①若a>b,则ac>bc;②若a=1,则a=a;③内错角相等;④90°的圆周角所对的弦是直径.其中原命题与逆命题均为真命题的个数是()A.1个B.2个C.3个D.4个【答案】A【解析】【分析】先对原命题进行判断,再判断出逆命题的真假即可.【详解】解:①若a>b,则ac>bc是假命题,逆命题是假命题;②若a=1,则a=a是真命题,逆命题是假命题;③内错角相等是假命题,逆命题是假命题;④90°的圆周角所对的弦是直径是真命题,逆命题是真命题;其中原命题与逆命题均为真命题的个数是1个;故选A.点评:主要考查命题与定理,用到的知识点是互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题,判断命题的真假关键是要熟悉课本中的性质定理.7.如图,在扇形OAB中,120∠=︒,点P是弧AB上的一个动点(不与点A、B重AOBCD=,则扇形AOB的面积为()合),C、D分别是弦AP,BP的中点.若33A.12πB.2πC.4πD.24π【答案】A【解析】【分析】如图,作OH⊥AB于H.利用三角形中位线定理求出AB的长,解直角三角形求出OB即可解决问题.【详解】解:如图作OH⊥AB于H.∵C、D分别是弦AP、BP的中点.∴CD是△APB的中位线,∴AB=2CD=63∵OH⊥AB,∴BH=AH=33∵OA=OB,∠AOB=120°,∴∠AOH=∠BOH=60°,在Rt△AOH中,sin∠AOH=AH AO,∴AO=336 sin3AHAOH==∠,∴扇形AOB的面积为:2120612360ππ=g g,故选:A.【点睛】本题考查扇形面积公式,三角形的中位线定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.8.已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作»PQ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交»PQ于点M,N;(3)连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是()A.∠COM=∠COD B.若OM=MN,则∠AOB=20°C.MN∥CD D.MN=3CD【答案】D【解析】【分析】由作图知CM=CD=DN,再利用圆周角定理、圆心角定理逐一判断可得.【详解】解:由作图知CM=CD=DN,∴∠COM=∠COD,故A选项正确;∵OM=ON=MN,∴△OMN是等边三角形,∴∠MON=60°,∵CM=CD=DN,∴∠MOA=∠AOB=∠BON=13∠MON=20°,故B选项正确;∵∠MOA=∠AOB=∠BON=20°,∴∠OCD=∠OCM=80°,∴∠MCD=160°,又∠CMN=12∠AON=20°,∴∠MCD+∠CMN=180°,∴MN∥CD,故C选项正确;∵MC+CD+DN >MN ,且CM=CD=DN ,∴3CD >MN ,故D 选项错误;故选:D .【点睛】本题主要考查作图-复杂作图,解题的关键是掌握圆心角定理和圆周角定理等知识点.9.如图,⊙O 中,弦BC 与半径OA 相交于点D ,连接AB ,OC ,若∠A=60°,∠ADC=85°,则∠C 的度数是( )A .25°B .27.5°C .30°D .35°【答案】D【解析】 分析:直接利用三角形外角的性质以及邻补角的关系得出∠B 以及∠ODC 度数,再利用圆周角定理以及三角形内角和定理得出答案.详解:∵∠A=60°,∠ADC=85°,∴∠B=85°-60°=25°,∠CDO=95°,∴∠AOC=2∠B=50°,∴∠C=180°-95°-50°=35°故选D .点睛:此题主要考查了圆周角定理以及三角形内角和定理等知识,正确得出∠AOC 度数是解题关键.10.如图,弧 AB 等于弧CD ,OE AB ⊥于点E ,OF CD ⊥于点F ,下列结论中错误..的是( )A .OE=OFB .AB=CDC .∠AOB =∠COD D .OE >OF【答案】D【解析】【分析】 根据圆心角、弧、弦的关系可得B 、C 正确,根据垂径定理和勾股定理可得A 正确,D 错误.【详解】解:∵»»AB CD =,∴AB =CD ,∠AOB =∠COD ,∵OE AB ⊥,OF CD ⊥,∴BE =12AB ,DF =12CD , ∴BE =DF ,又∵OB =OD , ∴由勾股定理可知OE =OF ,即A 、B 、C 正确,D 错误,故选:D .【点睛】本题考查了圆心角、弧、弦的关系,垂径定理,勾股定理,熟练掌握基本性质定理是解题的关键.11.如图,在平面直角坐标系中,已知C (3,4),以点C 为圆心的圆与y 轴相切.点A 、B 在x 轴上,且OA =OB .点P 为⊙C 上的动点,∠APB =90°,则AB 长度的最小值为( )A .4B .3C .7D .8【答案】A【解析】【分析】 连接OC ,交⊙C 上一点P ,以O 为圆心,以OP 为半径作⊙O ,交x 轴于A 、B ,此时AB 的长度最小,根据勾股定理和题意求得OP =2,则AB 的最小长度为4.【详解】解:如图,连接OC ,交⊙C 上一点P ,以O 为圆心,以OP 为半径作⊙O ,交x 轴于A 、B ,此时AB 的长度最小,∵C(3,4),∴OC=22=5,34∵以点C为圆心的圆与y轴相切.∴⊙C的半径为3,∴OP=OC﹣3=2,∴OP=OA=OB=2,∵AB是直径,∴∠APB=90°,∴AB长度的最小值为4,故选:A.【点睛】本题考查了圆切线的性质、坐标和图形的性质、圆周角定理、勾股定理,找到OP的最小值是解题的关键.12.如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB 相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于()A.20°B.25°C.30°D.32.5°【答案】A【解析】【分析】连接OD,根据三角形内角和定理和等边对等角求出∠DOB=40°,再根据圆周角定理即可求出∠BAD的度数.【详解】解:连接OD,∵OC⊥AB,∴∠COB =90°,∵∠AEC =65°,∴∠OCE =180°﹣90°﹣65°=25°,∵OD =OC ,∴∠ODC =∠OCD =25°,∴∠DOC =180°﹣25°﹣25°=130°,∴∠DOB =∠DOC ﹣∠BOC =130°﹣90°=40°,∴由圆周角定理得:∠BAD =12∠DOB =20°, 故选:A .【点睛】本题考查了圆和三角形的问题,掌握三角形内角和定理、等边对等角、圆周角定理是解题的关键.13.如图,有一个边长为2cm 的正六边形纸片,若在该纸片上沿虚线剪一个最大圆形纸片,则这个圆形纸片的半径是( )A 3cmB .2cmC .23cmD .4cm【答案】A【解析】【分析】 根据题意画出图形,再根据正多边形圆心角的求法求出∠AOB 的度数,最后根据等腰三角形及直角三角形的性质解答即可.【详解】 解:如图所示,正六边形的边长为2cm ,OG ⊥BC ,∵六边形ABCDEF 是正六边形,∴∠BOC=360°÷6=60°,∵OB=OC ,OG ⊥BC ,∴∠BOG=∠COG=12∠BOC =30°, ∵OG ⊥BC ,OB=OC ,BC=2cm , ∴BG=12BC=12×2=1cm , ∴OB=sin 30BG o =2cm ,∴OG=2222-=-=,OB BG213∴圆形纸片的半径为3cm,故选:A.【点睛】本题考查的是正多边形和圆,根据题意画出图形,利用直角三角形的性质及正六边形的性质解答是解答此题的关键.14.如图,7×5的网格中的小正方形的边长都为1,小正方形的顶点叫格点,△ABC的三个顶点都在格点上,过点C作△ABC外接圆的切线,则该切线经过的格点个数是()A.1 B.2 C.3 D.4【答案】C【解析】【分析】作△ABC的外接圆,作出过点C的切线,两条图象法即可解决问题.【详解】如图⊙O即为所求,观察图象可知,过点C作△ABC外接圆的切线,则该切线经过的格点个数是3个,选:C.【点睛】考查三角形的外接圆与外心,切线的判定和性质等知识,解题的关键是理解题意.15.如图,已知ABC ∆和ABD ∆都O e 是的内接三角形,AC 和BD 相交于点E ,则与ADE ∆的相似的三角形是( )A .BCE ∆B .ABC ∆ C .ABD ∆ D .ABE ∆【答案】A【解析】【分析】 根据同弧和等弧所对的圆周角相等, 则AB 弧所对的圆周角BCE BDA ∠=∠,CEB ∠和DEA ∠是对顶角,所以ADE BCE ∆∆∽.【详解】解:BCE BDA ∠=∠Q ,CEB DEA ∠=∠ADE BCE ∴∆∆∽,故选:A .【点睛】考查相似三角形的判定定理: 两角对应相等的两个三角形相似,关键就是牢记同弧所对的圆周角相等.16.如图,已知⊙O 的半径是4,点A,B,C 在⊙O 上,若四边形OABC 为菱形,则图中阴影部分面积为( )A .8833π-B .16833π-C .16433π-D .8433π-【答案】B【解析】【分析】 连接OB 和AC 交于点D ,根据菱形及直角三角形的性质先求出AC 的长及∠AOC 的度数,然后求出菱形ABCO 及扇形AOC 的面积,则由S 扇形AOC -S 菱形ABCO 可得答案.【详解】连接OB和AC交于点D,如图所示:∵圆的半径为4,OB=OA=OC=4,又四边形OABC是菱形,∴OB⊥AC,OD=12OB=2,在Rt△COD中利用勾股定理可知:CD=224223,243AC CD-===,∵sin∠COD=3,2 CDOC=∴∠COD=60°,∠AOC=2∠COD=120°,∴S菱形ABCO=1144383 22OB AC⨯=⨯⨯=,∴S扇形=2 1204163603ππ⨯⨯=,则图中阴影部分面积为S扇形AOC-S菱形ABCO=1683 3π-.故选B.【点睛】考查扇形面积的计算及菱形的性质,解题关键是熟练掌握菱形的面积=12a•b(a、b是两条对角线的长度);扇形的面积=2 360 n r π.17.如图,在圆O中,直径AB平分弦CD于点E,且CD=43,连接AC,OD,若∠A与∠DOB互余,则EB的长是()A.23B.4 C.3D.2【答案】D【解析】【分析】连接CO,由直径AB平分弦CD及垂径定理知∠COB=∠DOB,则∠A与∠COB互余,由圆周角定理知∠A=30°,∠COE=60°,则∠OCE=30°,设OE=x,则CO=2x,利用勾股定理即可求出x,再求出BE即可.【详解】连接CO,∵AB平分CD,∴∠COB=∠DOB,AB⊥CD,CE=DE=23∵∠A与∠DOB互余,∴∠A+∠COB=90°,又∠COB=2∠A,∴∠A=30°,∠COE=60°,∴∠OCE=30°,设OE=x,则CO=2x,∴CO2=OE2+CE2即(2x)2=x2+(23)2解得x=2,∴BO=CO=4,∴BE=CO-OE=2.故选D.【点睛】此题主要考查圆内的综合问题,解题的关键是熟知垂径定理、圆周角定理及勾股定理.18.如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )A.10 B.9 C.8 D.7【答案】D【解析】分析:先根据多边形的内角和公式(n﹣2)•180°求出正五边形的每一个内角的度数,再延长五边形的两边相交于一点,并根据四边形的内角和求出这个角的度数,然后根据周角等于360°求出完成这一圆环需要的正五边形的个数,然后减去3即可得解.详解:∵五边形的内角和为(5﹣2)•180°=540°,∴正五边形的每一个内角为540°÷5=108°,如图,延长正五边形的两边相交于点O,则∠1=360°﹣108°×3=360°﹣324°=36°,360°÷36°=10.∵已经有3个五边形,∴10﹣3=7,即完成这一圆环还需7个五边形.故选D.点睛:本题考查了多边形的内角和公式,延长正五边形的两边相交于一点,并求出这个角的度数是解题的关键,注意需要减去已有的3个正五边形.19.如图,四边形ABCD是⊙O的内接正方形,点P是劣弧弧AB上任意一点(与点B不重合),则∠BPC的度数为()A.30°B.45°C.60°D.90°【答案】B【解析】分析:接OB,OC,根据四边形ABCD是正方形可知∠BOC=90°,再由圆周角定理即可得出结论.详解:连接OB,OC,∵四边形ABCD 是正方形,∴∠BOC=90°,∴∠BPC=12∠BOC=45°. 故选B . 点睛:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.20.如图,边长为1的正方形ABCD 绕点A 逆时针旋转45°后得到正方形AB 1C 1D 1,边B 1C 1与CD 交于点O ,则图中阴影部分的面积是( )A .224π-- B .224π-+ C .142π+ D .142π- 【答案】B【解析】【分析】先根据正方形的边长,求得CB 1=OB 1=AC-AB 1=2-1,进而得到211(21)2OB C S =-V ,再根据S △AB1C1=12,以及扇形的面积公式即可得出图中阴影部分的面积. 【详解】连结DC 1,∵∠CAC 1=∠DCA =∠COB 1=∠DOC 1=45°,∴∠AC 1B 1=45°,∵∠ADC =90°,∴A ,D ,C 1在一条直线上,∵四边形ABCD 是正方形,∴AC OCB 1=45°,∴CB 1=OB 1∵AB 1=1,∴CB 1=OB 1=AC ﹣AB 1﹣1,∴2111111)22OB C S OB CB ∆=⋅⋅=, ∵1111111111222AB C S AB B C =⋅=⨯⨯=V ,2111)2224π--=-+ 故选B .【点睛】本题考查了旋转的性质,正方形性质、勾股定理以及扇形面积的计算等知识点的综合应用,主要考查学生运用性质进行计算的能力.解题时注意:旋转前、后的图形全等.。
全国中考数学圆的综合的综合中考真题分类汇总及详细答案

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图1,直角梯形OABC中,BC∥OA,OA=6,BC=2,∠BAO=45°.(1)OC的长为;(2)D是OA上一点,以BD为直径作⊙M,⊙M交AB于点Q.当⊙M与y轴相切时,sin∠BOQ=;(3)如图2,动点P以每秒1个单位长度的速度,从点O沿线段OA向点A运动;同时动点D以相同的速度,从点B沿折线B﹣C﹣O向点O运动.当点P到达点A时,两点同时停止运动.过点P作直线PE∥OC,与折线O﹣B﹣A交于点E.设点P运动的时间为t (秒).求当以B、D、E为顶点的三角形是直角三角形时点E的坐标.【答案】(1)4;(2)35;(3)点E的坐标为(1,2)、(53,103)、(4,2).【解析】分析:(1)过点B作BH⊥OA于H,如图1(1),易证四边形OCBH是矩形,从而有OC=BH,只需在△AHB中运用三角函数求出BH即可.(2)过点B作BH⊥OA于H,过点G作GF⊥OA于F,过点B作BR⊥OG于R,连接MN、DG,如图1(2),则有OH=2,BH=4,MN⊥OC.设圆的半径为r,则MN=MB=MD=r.在Rt△BHD中运用勾股定理可求出r=2,从而得到点D与点H重合.易证△AFG∽△ADB,从而可求出AF、GF、OF、OG、OB、AB、BG.设OR=x,利用BR2=OB2﹣OR2=BG2﹣RG2可求出x,进而可求出BR.在Rt△ORB中运用三角函数就可解决问题.(3)由于△BDE的直角不确定,故需分情况讨论,可分三种情况(①∠BDE=90°,②∠BED=90°,③∠DBE=90°)讨论,然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题.详解:(1)过点B作BH⊥OA于H,如图1(1),则有∠BHA=90°=∠COA,∴OC∥BH.∵BC∥OA,∴四边形OCBH是矩形,∴OC=BH,BC=OH.∵OA=6,BC=2,∴AH=0A﹣OH=OA﹣BC=6﹣2=4.∵∠BHA=90°,∠BAO=45°,∴tan∠BAH=BHHA=1,∴BH=HA=4,∴OC=BH=4.故答案为4.(2)过点B作BH⊥OA于H,过点G作GF⊥OA于F,过点B作BR⊥OG于R,连接MN、DG,如图1(2).由(1)得:OH =2,BH =4.∵OC 与⊙M 相切于N ,∴MN ⊥OC .设圆的半径为r ,则MN =MB =MD =r .∵BC ⊥OC ,OA ⊥OC ,∴BC ∥MN ∥OA .∵BM =DM ,∴CN =ON ,∴MN =12(BC +OD ),∴OD =2r ﹣2,∴DH =OD OH -=24r -.在Rt △BHD 中,∵∠BHD =90°,∴BD 2=BH 2+DH 2,∴(2r )2=42+(2r ﹣4)2.解得:r =2,∴DH =0,即点D 与点H 重合,∴BD ⊥0A ,BD =AD .∵BD 是⊙M 的直径,∴∠BGD =90°,即DG ⊥AB ,∴BG =AG .∵GF ⊥OA ,BD ⊥OA ,∴GF ∥BD ,∴△AFG ∽△ADB , ∴AF AD =GF BD =AG AB =12,∴AF =12AD =2,GF =12BD =2,∴OF =4,∴OG同理可得:OB AB ,∴BG =12AB .设OR =x ,则RG x .∵BR ⊥OG ,∴∠BRO =∠BRG =90°,∴BR 2=OB 2﹣OR 2=BG 2﹣RG 2,∴(2﹣x 2=()2﹣(x )2.解得:x =5,∴BR 2=OB 2﹣OR 2=(2﹣(5)2=365,∴BR =5.在Rt △ORB 中,sin ∠BOR =BR OB35. 故答案为35. (3)①当∠BDE =90°时,点D 在直线PE 上,如图2.此时DP =OC =4,BD +OP =BD +CD =BC =2,BD =t ,OP =t . 则有2t =2.解得:t =1.则OP =CD =DB =1.∵DE ∥OC ,∴△BDE ∽△BCO ,∴DE OC =BD BC =12,∴DE =2,∴EP =2, ∴点E 的坐标为(1,2).②当∠BED =90°时,如图3.∵∠DBE =OBC ,∠DEB =∠BCO =90°,∴△DBE ∽△OBC ,∴BEBC =2DB BE OB ∴,∴BE =5t . ∵PE ∥OC ,∴∠OEP =∠BOC .∵∠OPE =∠BCO =90°,∴△OPE ∽△BCO ,∴OEOB =25OPBC∴,=2t,∴OE=5t.∵OE+BE=OB=255,∴t+5t=25.解得:t=53,∴OP=53,OE=55,∴PE=22OE OP-=103,∴点E的坐标为(51033,).③当∠DBE=90°时,如图4.此时PE=PA=6﹣t,OD=OC+BC﹣t=6﹣t.则有OD=PE,EA=22PE PA+=2(6﹣t)=62﹣2?t,∴BE=BA﹣EA=42﹣(62﹣2t)=2t﹣22.∵PE∥OD,OD=PE,∠DOP=90°,∴四边形ODEP是矩形,∴DE=OP=t,DE∥OP,∴∠BED=∠BAO=45°.在Rt△DBE中,cos∠BED=BEDE=2,∴DE=2BE,∴t=22(t﹣22)=2t﹣4.解得:t=4,∴OP=4,PE=6﹣4=2,∴点E的坐标为(4,2).综上所述:当以B、D、E为顶点的三角形是直角三角形时点E的坐标为(1,2)、(51033,)、(4,2).点睛:本题考查了圆周角定理、切线的性质、相似三角形的判定与性质、三角函数的定义、平行线分线段成比例、矩形的判定与性质、勾股定理等知识,还考查了分类讨论的数学思想,有一定的综合性.2.定义:有一个角是其邻角一半的圆内接四边形叫做圆内倍角四边形.(1)如图1,四边形ABCD内接于⊙O,∠DCB﹣∠ADC=∠A,求证:四边形ABCD为圆内接倍角四边形;(2)在(1)的条件下,⊙O半径为5.①若AD为直径,且sinA=45,求BC的长;②若四边形ABCD中有一个角为60°,且BC=CD,则四边形ABCD的面积是;(3)在(1)的条件下,记AB=a,BC=b,CD=c,AD=d,求证:d2﹣b2=ab+cd.【答案】(1)见解析;(2)①BC=6,②7534或754;(3)见解析【解析】【分析】(1)先判断出∠ADC=180°﹣2∠A.进而判断出∠ABC=2∠A,即可得出结论;(2)①先用锐角三角函数求出BD,进而得出AB,由(1)得出∠ADB=∠BDC,即可得出结论;②分两种情况:利用面积和差即可得出结论;(3)先得出BE=BC=b,DE=DA=b,进而得出CE=d﹣c,再判断出△EBC∽△EDA,即可得出结论.【详解】(1)设∠A=α,则∠DCB=180°﹣α.∵∠DCB﹣∠ADC=∠A,∴∠ADC=∠DCB﹣∠A=180°﹣α﹣α=180°﹣2α,∴∠ABC=180°﹣∠ADC=2α=2∠A,∴四边形ABCD是⊙O内接倍角四边形;(2)①连接BD.∵AD是⊙O的直径,∴∠ABD=90°.在Rt△ABD中,AD=2×5=10,sin∠A=45,∴BD=8,根据勾股定理得:AB=6,设∠A=α,∴∠ADB=90°﹣α.由(1)知,∠ADC=180°﹣2α,∴∠BDC=90°﹣α,∴∠ADB=∠BDC,∴BC=AB=6;②若∠ADC=60°时.∵四边形ABCD是圆内接倍角四边形,∴∠BCD=120°或∠BAD=30°.Ⅰ、当∠BCD=120°时,如图3,连接OA,OB,OC,OD.∵BC=CD,∴∠BOC=∠COD,∴∠OCD=∠OCB=12∠BCD=60°,∴∠CDO=60°,∴AD是⊙O 的直径,(为了说明AD是直径,点O没有画在AD上)∴∠ADC+∠BCD=180°,∴BC∥AD,∴AB=CD.∵BC=CD,∴AB=BC=CD,∴△OAB,△BOC,△COD是全等的等边三角形,∴S四边形ABCD=3S△AOB=3×34×52=7534.Ⅱ、当∠BAD=30°时,如图4,连接OA,OB,OC,OD.∵四边形ABCD是圆内接四边形,∴∠BCD=180°﹣∠BAD=150°.∵BC=CD,∴∠BOC=∠COD,∴∠BCO=∠DCO=12∠BCD=75°,∴∠BOC=∠DOC=30°,∴∠OBA=45°,∴∠AOB=90°.连接AC,∴∠DAC=12∠BAD=15°.∵∠ADO=∠OAB﹣∠BAD=15°,∴∠DAC=∠ADO,∴OD∥AC,∴S△OAD=S△OCD.过点C作CH⊥OB于H.在Rt△OCH中,CH=12OC=52,∴S四边形ABCD=S△COD+S△BOC+S△AOB﹣S△AOD=S△BOC+S△AOB=1522×5+12×5×5=754.故答案为:753或754;(3)延长DC ,AB 交于点E .∵四边形ABCD 是⊙O 的内接四边形,∴∠BCE =∠A =12∠ABC . ∵∠ABC =∠BCE +∠A ,∴∠E =∠BCE =∠A ,∴BE =BC =b ,DE =DA =b ,∴CE =d ﹣c . ∵∠BCE =∠A ,∠E =∠E ,∴△EBC ∽△EDA ,∴CE BC AE AD =,∴d c b a b d-=+,∴d 2﹣b 2=ab +cd .【点睛】本题是圆的综合题,主要考查了圆的内接四边形的性质,新定义,相似三角形的判定和性质,等边三角形的判定和性质,正确作出辅助线是解答本题的关键.3.如图,AB 是半圆O 的直径,C 是的中点,D 是的中点,AC 与BD 相交于点E .(1)求证:BD 平分∠ABC ;(2)求证:BE =2AD ;(3)求DE BE的值. 【答案】(1)答案见解析(2)BE=AF=2AD (3)212- 【解析】试题分析:(1)根据中点弧的性质,可得弦AD=CD ,然后根据弦、弧、圆周角、圆心角的性质求解即可;(2)延长BC 与AD 相交于点F, 证明△BCE ≌△ACF, 根据全等三角形的性质可得BE=AF=2AD ;(3)连接OD,交AC 于H.简要思路如下:设OH 为1,则BC 为2,OB=OD=2 ,DH=21-, 然后根据相似三角形的性质可求解.试题解析:(1)∵D 是的中点∴AD=DC∴∠CBD=∠ABD∴BD 平分∠ABC(2)提示:延长BC 与AD 相交于点F,证明△BCE ≌△ACF,BE=AF=2AD(3)连接OD,交AC 于H.简要思路如下:设OH 为1,则BC 为2,OB=OD=2 , DH=21-, DE BE =DH BCDE BE =21-4.如图,在ABC ∆中,90,BAC ∠=︒ 2,AB AC == AD BC ⊥,垂足为D ,过,A D 的⊙O 分别与,AB AC 交于点,E F ,连接,,EF DE DF .(1)求证:ADE ∆≌CDF ∆;(2)当BC 与⊙O 相切时,求⊙O 的面积.【答案】(1)见解析;(2)24π.【解析】 分析:(1)由等腰直角三角形的性质知AD =CD 、∠1=∠C =45°,由∠EAF =90°知EF 是⊙O 的直径,据此知∠2+∠4=∠3+∠4=90°,得∠2=∠3,利用“ASA”证明即可得;(2)当BC 与⊙O 相切时,AD 是直径,根据∠C =45°、AC 2可得AD =1,利用圆的面积公式可得答案.详解:(1)如图,∵AB =AC ,∠BAC =90°,∴∠C =45°.又∵AD ⊥BC ,AB =AC ,∴∠1=12∠BAC =45°,BD =CD ,∠ADC =90°. 又∵∠BAC =90°,BD =CD ,∴AD =CD .又∵∠EAF =90°,∴EF 是⊙O 的直径,∴∠EDF =90°,∴∠2+∠4=90°.又∵∠3+∠4=90°,∴∠2=∠3.在△ADE 和△CDF 中.∵123C AD CD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADE ≌△CDF (ASA ).(2)当BC 与⊙O 相切时,AD 是直径.在Rt △ADC 中,∠C =45°,AC =2,∴sin ∠C =AD AC ,∴AD =AC sin ∠C =1,∴⊙O 的半径为12,∴⊙O 的面积为24π. 点睛:本题主要考查圆的综合问题,解题的关键是熟练掌握等腰直角三角形的性质、全等三角形的判定与性质、与圆有关的位置关系等知识点.5.等腰Rt △ABC 和⊙O 如图放置,已知AB=BC=1,∠ABC=90°,⊙O 的半径为1,圆心O 与直线AB 的距离为5.(1)若△ABC 以每秒2个单位的速度向右移动,⊙O 不动,则经过多少时间△ABC 的边与圆第一次相切?(2)若两个图形同时向右移动,△ABC 的速度为每秒2个单位,⊙O 的速度为每秒1个单位,则经过多少时间△ABC 的边与圆第一次相切?(3)若两个图形同时向右移动,△ABC 的速度为每秒2个单位,⊙O 的速度为每秒1个单位,同时△ABC 的边长AB 、BC 都以每秒0.5个单位沿BA 、BC 方向增大.△ABC 的边与圆第一次相切时,点B 运动了多少距离?【答案】(1)522;(2) 52;(3)20423- 【解析】 分析:(1)分析易得,第一次相切时,与斜边相切,假设此时,△ABC 移至△A′B′C′处,A′C′与⊙O 切于点E ,连OE 并延长,交B′C′于F .由切线长定理易得CC′的长,进而由三角形运动的速度可得答案;(2)设运动的时间为t 秒,根据题意得:CC′=2t ,DD′=t ,则C′D′=CD+DD′-CC′=4+t -2t=4-t ,由第(1)的结论列式得出结果;(3)求出相切的时间,进而得出B 点移动的距离.详解:(1)假设第一次相切时,△ABC 移至△A′B′C′处,如图1,A′C′与⊙O 切于点E ,连接OE 并延长,交B′C′于F ,设⊙O 与直线l 切于点D ,连接OD ,则OE ⊥A′C′,OD ⊥直线l ,由切线长定理可知C′E=C′D ,设C′D=x ,则C′E=x ,∵△ABC 是等腰直角三角形,∴∠A=∠ACB=45°,∴∠A′C′B′=∠ACB=45°,∴△EFC′是等腰直角三角形,∴C′F=2x ,∠OFD=45°, ∴△OFD 也是等腰直角三角形,∴OD=DF ,∴2x+x=1,则x=2-1,∴CC′=BD -BC-C′D=5-1-(2-1)=5-2,∴点C 运动的时间为522-; 则经过522-秒,△ABC 的边与圆第一次相切; (2)如图2,设经过t 秒△ABC 的边与圆第一次相切,△ABC 移至△A′B′C′处,⊙O 与BC 所在直线的切点D 移至D′处,A′C′与⊙O 切于点E ,连OE 并延长,交B′C′于F ,∵CC′=2t ,DD′=t ,∴C′D′=CD+DD′-CC′=4+t -2t=4-t ,由切线长定理得C′E=C′D′=4-t ,由(1)得:4-t=2-1, 解得:t=5-2,答:经过5-2秒△ABC 的边与圆第一次相切;(3)由(2)得CC′=(2+0.5)t=2.5t ,DD′=t ,则C′D′=CD+DD′-CC′=4+t -2.5t=4-1.5t ,由切线长定理得C′E=C′D′=4-1.5t ,由(1)得:4-1.5t=2-1,解得:t=10223-, ∴点B 运动的距离为2×10223-=20423-.点睛:本题要求学生熟练掌握圆与直线的位置关系,并结合动点问题进行综合分析,比较复杂,难度较大,考查了学生数形结合的分析能力.6.如图,Rt ABC ∆内接于⊙O ,AC BC =,BAC ∠的平分线AD 与⊙O 交于点D ,与BC 交于点E ,延长BD ,与AC 的延长线交于点F ,连接CD ,G 是CD 的中点,连接OG .(1)判断OG 与CD 的位置关系,写出你的结论并证明;(2)求证:AE BF =;(3)若3(22)OG DE =-,求⊙O 的面积.【答案】(1)OG ⊥CD (2)证明见解析(3)6π【解析】试题分析:(1)根据G 是CD 的中点,利用垂径定理证明即可;(2)先证明△ACE 与△BCF 全等,再利用全等三角形的性质即可证明;(3)构造等弦的弦心距,运用相似三角形以及勾股定理进行求解.试题解析:(1)解:猜想OG ⊥CD .证明如下:如图1,连接OC 、OD .∵OC =OD ,G 是CD 的中点,∴由等腰三角形的性质,有OG ⊥CD .(2)证明:∵AB 是⊙O 的直径,∴∠ACB =90°,而∠CAE =∠CBF (同弧所对的圆周角相等).在Rt △ACE 和Rt △BCF 中,∵∠ACE =∠BCF =90°,AC =BC ,∠CAE =∠CBF ,∴Rt △ACE ≌Rt △BCF (ASA ),∴AE =BF .(3)解:如图2,过点O 作BD 的垂线,垂足为H ,则H 为BD 的中点,∴OH =12AD ,即AD =2OH ,又∠CAD =∠BAD ⇒CD =BD ,∴OH =OG .在Rt △BDE 和Rt △ADB 中,∵∠DBE =∠DAC =∠BAD ,∴Rt △BDE ∽Rt △ADB ,∴BD DE AD DB=,即BD 2=AD •DE ,∴22622BD AD DE OG DE =⋅=⋅=-().又BD =FD ,∴BF =2BD ,∴2242422BF BD ==-()①,设AC =x ,则BC =x ,AB =2x .∵AD 是∠BAC 的平分线,∴∠FAD =∠BAD .在Rt △ABD 和Rt △AFD 中,∵∠ADB =∠ADF =90°,AD =AD ,∠FAD =∠BAD ,∴Rt △ABD ≌Rt △AFD (ASA ),∴AF =AB =2x ,BD =FD ,∴CF =AF ﹣AC =221x x x -=-().在Rt △BCF 中,由勾股定理,得:222222[21]222BF BC CF x x x =+=+-=-()()②,由①、②,得22222422x -=-()(),∴x 2=12,解得:23x =或23-(舍去),∴222326AB x ==⋅=,∴⊙O 的半径长为6,∴S ⊙O =π•(6)2=6π.点睛:本题是圆的综合题.解题的关键是熟练运用垂径定理、勾股定理、相似三角形的判定与性质.7.如图,AB 是半圆O 的直径,半径OC ⊥AB ,OB =4,D 是OB 的中点,点E 是弧BC 上的动点,连接AE ,DE .(1)当点E 是弧BC 的中点时,求△ADE 的面积;(2)若3tan 2AED ∠= ,求AE 的长; (3)点F 是半径OC 上一动点,设点E 到直线OC 的距离为m ,当△DEF 是等腰直角三角形时,求m 的值.【答案】(1)62ADE S =;(2)1655AE =;(3)23m = ,22m =,71m =-.【解析】【分析】(1)作EH ⊥AB ,连接OE ,EB ,设DH =a ,则HB =2﹣a ,OH =2+a ,则EH =OH =2+a ,根据Rt △AEB 中,EH 2=AH•BH ,即可求出a 的值,即可求出S △ADE 的值;(2)作DF ⊥AE ,垂足为F ,连接BE ,设EF =2x ,DF =3x ,根据DF ∥BE 故AF AD EF BD=,得出AF =6x ,再利用Rt △AFD 中,AF 2+DF 2=AD 2,即可求出x ,进而求出AE 的长; (3)根据等腰直角三角形的不同顶点进行分类讨论,分别求出m 的值.【详解】解:(1)如图,作EH ⊥AB ,连接OE ,EB ,设DH =a ,则HB =2﹣a ,OH =2+a ,∵点E 是弧BC 中点,∴∠COE =∠EOH =45°,∴EH =OH =2+a ,在Rt △AEB 中,EH 2=AH•BH ,(2+a )2=(6+a )(2﹣a ), 解得a =222±-,∴a =222-,EH=22,S △ADE =1622AD EH =;(2)如图,作DF ⊥AE ,垂足为F ,连接BE设EF =2x ,DF =3x∵DF ∥BE ∴AF AD EF BD = ∴622AF x ==3 ∴AF =6x 在Rt △AFD 中,AF 2+DF 2=AD 2(6x )2+(3x )2=(6)2解得x =255AE =8x =1655 (3)当点D 为等腰直角三角形直角顶点时,如图设DH =a由DF=DE,∠DOF=∠EHD=90°,∠FDO+∠DFO=∠FDO+∠EDH ,∴∠DFO=∠EDH∴△ODF ≌△HED∴OD =EH =2在Rt △ABE 中,EH 2=AH•BH(2)2=(6+a )•(2﹣a )解得a =±232-m =23当点E 为等腰直角三角形直角顶点时,如图同理得△EFG ≌△DEH设DH=a,则GE=a,EH=FG=2+a在Rt△ABE中,EH2=AH•BH(2+a)2=(6+a)(2﹣a)解得a=222±-∴m=22当点F为等腰直角三角形直角顶点时,如图同理得△EFM≌△FDO设OF=a,则ME=a,MF=OD=2∴EH=a+2在Rt△ABE中,EH2=AH•BH(a+2)2=(4+a)•(4﹣a)-解得a=±71m=71-【点睛】此题主要考查圆内综合问题,解题的关键是熟知全等三角形、等腰三角形、相似三角形的判定与性质.8.定义:数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.理解:⑴如图,已知是⊙上两点,请在圆上找出满足条件的点,使为“智慧三角形”(画出点的位置,保留作图痕迹);⑵如图,在正方形中,是的中点,是上一点,且,试判断是否为“智慧三角形”,并说明理由;运用:⑶如图,在平面直角坐标系中,⊙的半径为,点是直线上的一点,若在⊙上存在一点,使得为“智慧三角形”,当其面积取得最小值时,直接写出此时点的坐标.【答案】(1)详见解析;(2)详见解析;(3)P的坐标(223,13),(223,13).【解析】试题分析:(1)连结AO并且延长交圆于C1,连结BO并且延长交圆于C2,即可求解;(2)设正方形的边长为4a,表示出DF=CF以及EC、BE的长,然后根据勾股定理列式表示出AF2、EF2、AE2,再根据勾股定理逆定理判定△AEF是直角三角形,由直角三角形的性质可得△AEF为“智慧三角形”;(3)根据“智慧三角形”的定义可得△OPQ为直角三角形,根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,由垂线段最短可得斜边最短为3,根据勾股定理可求另一条直角边,再根据三角形面积可求斜边的高,即点P的横坐标,再根据勾股定理可求点P的纵坐标,从而求解.试题解析:(1)如图1所示:(2)△AEF是否为“智慧三角形”,理由如下:设正方形的边长为4a,∵E是DC的中点,∴DE=CE=2a,∵BC:FC=4:1,∴FC=a,BF=4a﹣a=3a,在Rt△ADE中,AE2=(4a)2+(2a)2=20a2,在Rt△ECF中,EF2=(2a)2+a2=5a2,在Rt△ABF中,AF2=(4a)2+(3a)2=25a2,∴AE2+EF2=AF2,∴△AEF是直角三角形,∵斜边AF上的中线等于AF的一半,∴△AEF为“智慧三角形”;(3)如图3所示:由“智慧三角形”的定义可得△OPQ为直角三角形,根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,由垂线段最短可得斜边最短为3,由勾股定理可得PQ=,PM=1×2÷3=,由勾股定理可求得OM=,故点P的坐标(﹣,),(,).考点:圆的综合题.9.AB是⊙O直径,在AB的异侧分别有定点C和动点P,如图所示,点P在半圆弧AB 上运动(不与A、B重合),过C作CP的垂线CD,交PB的延长线于D,已知AB=,BC∶CA=4∶3.5(1)求证:AC·CD=PC·BC;(2)当点P运动到AB弧的中点时,求CD的长;∆的面积最大?请直接写出这个最大面积.(3)当点P运动到什么位置时,PCD【答案】(1)证明见解析;(2)CD =142;(3)当PC 为⊙O 直径时,△PCD 的最大面积=503. 【解析】【分析】(1)由圆周角定理可得∠PCD=∠ACB=90°,可证△ABC ∽△PCD ,可得AC BC CP CD =,即可得证.(2)由题意可求BC=4,AC=3,由勾股定理可求CE 的长,由锐角三角函数可求PE 的长,即可得PC 的长,由AC•CD=PC•BC 可求CD 的值;(3)当点P 在AB 上运动时,12PCD S PC CD =⨯⨯,由(1)可得:43CD PC =,可得2142233PCD SPC PC PC =⨯⨯=,当PC 最大时,△PCD 的面积最大,而PC 为直径时最大,故可求解.【详解】证明:(1)∵AB 为直径,∴∠ACB =90°∵PC ⊥CD ,∴∠PCD =90°∴∠PCD =∠ACB ,且∠CAB =∠CPB∴△ABC ∽△PCD∴AC BC CP CD= ∴AC •CD =PC •BC(2)∵AB =5,BC :CA =4:3,∠ACB =90°∴BC =4,AC =3,当点P 运动到AB 的中点时,过点B 作BE ⊥PC 于点E∵点P 是AB 的中点,∴∠PCB =45°,且BC =4∴CE =BE =22BC 2 ∵∠CAB =∠CPB∴tan ∠CAB =43=BC AC =tan ∠CAB =BE PE ∴PE =322∴PC =PE +CE =3222=22 ∵AC •CD =PC •BC ∴3×CD =22×4 ∴CD 142 (3)当点P 在AB 上运动时,S △PCD =12×PC ×CD , 由(1)可得:CD =43PC ∴S △PCD =1423PC PC ⨯⨯=23PC 2, ∴当PC 最大时,△PCD 的面积最大, ∴当PC 为⊙O 直径时,△PCD 的最大面积=23×52=503 【点睛】本题是圆的综合题,考查了相似三角形的判定和性质,圆的有关知识,锐角三角函数,求出PC 的长是本题的关键.10.如图,BD 为△ABC 外接圆⊙O 的直径,且∠BAE =∠C .(1)求证:AE与⊙O相切于点A;(2)若AE∥BC,BC=23,AC=2,求AD的长.【答案】(1)证明见解析;(2)23【解析】【分析】(1)根据题目中已出现切点可确定用“连半径,证垂直”的方法证明切线,连接AO并延长交⊙O于点F,连接BF,则AF为直径,∠ABF=90°,根据同弧所对的圆周角相等,则可得到∠BAE=∠F,既而得到AE与⊙O相切于点A.(2))连接OC,先由平行和已知可得∠ACB=∠ABC,所以AC=AB,则∠AOC=∠AOB,从而利用垂径定理可得AH=1,在Rt△OBH中,设OB=r,利用勾股定理解得r=2,在Rt△ABD中,即可求得AD的长为3【详解】解:(1)连接AO并延长交⊙O于点F,连接BF,则AF为直径,∠ABF=90°,∵AB AB,∴∠ACB=∠F,∵∠BAE=∠ACB,∴∠BAE=∠F,∵∠FAB+∠F=90°,∴∠FAB+∠BAE=90°,∴OA⊥AE,∴AE与⊙O相切于点A.(2)连接OC,∵AE∥BC,∴∠BAE=∠ABC,∵∠BAE=∠ACB,∴∠ACB=∠ABC,∴AC=AB=2,∴∠AOC=∠AOB,∵OC=OB,∴OA⊥BC,∴CH=BH=1BC=3,2在Rt△ABH中,AH=22-=1,AB BH在Rt△OBH中,设OB=r,∵OH2+BH2=OB2,∴(r﹣1)2+(3)2=r2,解得:r=2,∴DB=2r=4,在Rt△ABD中,AD=22-=22BD AB-=23,42∴AD的长为23.【点睛】本题考查了圆的综合问题,恰当的添加辅助线是解题关键.。
全国中考数学圆的综合的综合中考真题汇总附答案解析

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,⊙O的半径为6cm,经过⊙O上一点C作⊙O的切线交半径OA的延长于点B,作∠ACO的平分线交⊙O于点D,交OA于点F,延长DA交BC于点E.(1)求证:AC∥OD;(2)如果DE⊥BC,求AC的长度.【答案】(1)证明见解析;(2)2π.【解析】试题分析:(1)由OC=OD,CD平分∠ACO,易证得∠ACD=∠ODC,即可证得AC∥OD;(2)BC切⊙O于点C,DE⊥BC,易证得平行四边形ADOC是菱形,继而可证得△AOC是等边三角形,则可得:∠AOC=60°,继而求得弧AC的长度.试题解析:(1)证明:∵OC=OD,∴∠OCD=∠ODC.∵CD平分∠ACO,∴∠OCD=∠ACD,∴∠ACD=∠ODC,∴AC∥OD;(2)∵BC切⊙O于点C,∴BC⊥OC.∵DE⊥BC,∴OC∥DE.∵AC∥OD,∴四边形ADOC 是平行四边形.∵OC=OD,∴平行四边形ADOC是菱形,∴OC=AC=OA,∴△AOC是等边三角形,∴∠AOC=60°,∴弧AC的长度=606180π⨯=2π.点睛:本题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式.此题难度适中,注意掌握数形结合思想的应用.2.(1)如图1,在矩形ABCD中,点O在边AB上,∠AOC=∠BOD,求证:AO=OB;(2)如图2,AB是⊙O的直径,PA与⊙O相切于点A,OP与⊙O相交于点C,连接CB,∠OPA=40°,求∠ABC的度数.【答案】(1)证明见解析;(2)25°.【解析】试题分析:(1)根据等量代换可求得∠AOD=∠BOC,根据矩形的对边相等,每个角都是直角,可知∠A=∠B=90°,AD=BC,根据三角形全等的判定AAS证得△AOD≌△BOC,从而得证结论.(2)利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠POA 的度数,然后利用圆周角定理来求∠ABC 的度数.试题解析:(1)∵∠AOC=∠BOD∴∠AOC -∠COD=∠BOD-∠COD即∠AOD=∠BOC∵四边形ABCD 是矩形∴∠A=∠B=90°,AD=BC∴AOD BOC ∆≅∆∴AO=OB(2)解:∵AB 是O 的直径,PA 与O 相切于点A , ∴PA ⊥AB ,∴∠A=90°.又∵∠OPA=40°,∴∠AOP=50°,∵OB=OC ,∴∠B=∠OCB.又∵∠AOP=∠B+∠OCB , ∴1252B OCB AOP ∠=∠=∠=︒.3.如图,在△ABC 中,AB =AC ,以AB 为直径作⊙O ,⊙O 交BC 于点D ,交CA 的延长线于点E .过点D 作DF ⊥AC ,垂足为F .(1)求证:DF 为⊙O 的切线;(2)若AB =4,∠C =30°,求劣弧BE 的长.【答案】(1)证明见解析(2)43π 【解析】分析:(1)连接AD 、OD ,根据直径所对的圆周角为直角,可得∠ADB=90°,然后根据等腰三角形的性质求出BD=CD ,再根据中位线的性质求出OD ⊥DF ,进而根据切线的判定证明即可;(2)连接OE ,根据三角形的外角求出∠BAE 的度数,然后根据圆周角定理求出∠BOE 的度数,根据弧长公式求解即可.详解:(1)连接AD、OD.∵AB是直径,∴∠ADB=90°.∵AB=AC,∴BD=CD,又∵OA=OB,∴OD是△ABC的中位线,∴OD∥AC,∵DF⊥AC,∴OD⊥DF即∠ODF=90°.∴DF为⊙O的切线;(2)连接OE.∵AB=AC,∴∠B=∠C=30°,∴∠BAE=60°,∵∠BOE=2∠BAE,∴∠BOE=120°,∴=·4π=π.点睛:本题是圆的综合题,考查了等腰三角形的性质和判定、切线的性质和判定、三角形的中位线、圆周角定理,灵活添加辅助线是解题关键.4.如图,△ABC的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD于E,交AB于F,交⊙O于G.(1)判断直线PA与⊙O的位置关系,并说明理由;(2)求证:AG2=AF·AB;(3)若⊙O的直径为10,AC=25,AB=45,求△AFG的面积.【答案】(1)PA与⊙O相切,理由见解析;(2)证明见解析;(3)3.【解析】试题分析:(1)连接CD,由AD为⊙O的直径,可得∠ACD=90°,由圆周角定理,证得∠B=∠D,由已知∠PAC=∠B,可证得DA⊥PA,继而可证得PA与⊙O相切.(2)连接BG,易证得△AFG∽△AGB,由相似三角形的对应边成比例,证得结论.(3)连接BD,由AG2=AF•AB,可求得AF的长,易证得△AEF∽△ABD,即可求得AE的长,继而可求得EF与EG的长,则可求得答案.试题解析:解:(1)PA与⊙O相切.理由如下:如答图1,连接CD,∵AD为⊙O的直径,∴∠ACD=90°.∴∠D+∠CAD=90°.∵∠B=∠D,∠PAC=∠B,∴∠PAC=∠D.∴∠PAC+∠CAD=90°,即DA⊥PA.∵点A在圆上,∴PA与⊙O相切.(2)证明:如答图2,连接BG,∵AD为⊙O的直径,CG⊥AD,∴AC AD.∴∠AGF=∠ABG.∵∠GAF=∠BAG,∴△AGF∽△ABG.∴AG:AB=AF:AG. ∴AG2=AF•AB.(3)如答图3,连接BD,∵AD是直径,∴∠ABD=90°.∵AG2=AF•AB,55∴5∵CG⊥AD,∴∠AEF=∠ABD=90°.∵∠EAF=∠BAD ,∴△AEF ∽△ABD. ∴AE AF AB AD =,即51045AE =,解得:AE=2. ∴221EF AF AE =-=. ∵224EG AG AE =-=,∴413FG EG EF =-=-=. ∴1132322AFG S FG AE ∆=⋅⋅=⨯⨯=.考点:1. 圆周角定理;2.直角三角形两锐角的关系;3. 相切的判定;4.垂径定理;5.相似三角形的判定和性质;6.勾股定理;7.三角形的面积.5.在平面直角坐标系xOy 中,点M 的坐标为(x 1,y 1),点N 的坐标为(x 2,y 2),且x 1≠x 2,y 1≠y 2,以MN 为边构造菱形,若该菱形的两条对角线分别平行于x 轴,y 轴,则称该菱形为边的“坐标菱形”.(1)已知点A (2,0),B (0,23),则以AB 为边的“坐标菱形”的最小内角为 ;(2)若点C (1,2),点D 在直线y=5上,以CD 为边的“坐标菱形”为正方形,求直线CD 表达式;(3)⊙O 的半径为2,点P 的坐标为(3,m ).若在⊙O 上存在一点Q ,使得以QP 为边的“坐标菱形”为正方形,求m 的取值范围.【答案】(1)60°;(2)y=x+1或y=﹣x+3;(3)1≤m≤5或﹣5≤m≤﹣1【解析】分析:(1)根据定义建立以AB为边的“坐标菱形”,由勾股定理求边长AB=4,可得30度角,从而得最小内角为60°;(2)先确定直线CD与直线y=5的夹角是45°,得D(4,5)或(﹣2,5),易得直线CD的表达式为:y=x+1或y=﹣x+3;(3)分两种情况:①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3,根据等腰直角三角形的性质分别求P'B=BD=1,PB=5,写出对应P的坐标;②先作直线y=﹣x,再作圆的两条切线,且平行于直线y=﹣x,如图4,同理可得结论.详解:(1)∵点A(2,0),B(0,3∴OA=2,OB3.在Rt△AOB中,由勾股定理得:AB22(),∴∠ABO=30°.223∵四边形ABCD是菱形,∴∠ABC=2∠ABO=60°.∵AB∥CD,∴∠DCB=180°﹣60°=120°,∴以AB为边的“坐标菱形”的最小内角为60°.故答案为:60°;(2)如图2.∵以CD为边的“坐标菱形”为正方形,∴直线CD与直线y=5的夹角是45°.过点C作CE⊥DE于E,∴D(4,5)或(﹣2,5),∴直线CD的表达式为:y=x+1或y=﹣x+3;(3)分两种情况:①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3.∵⊙O2,且△OQ'D是等腰直角三角形,∴OD2OQ'=2,∴P'D=3﹣2=1.∵△P'DB是等腰直角三角形,∴P'B=BD=1,∴P'(0,1),同理可得:OA=2,∴AB=3+2=5.∵△ABP是等腰直角三角形,∴PB=5,∴P(0,5),∴当1≤m≤5时,以QP为边的“坐标菱形”为正方形;②先作直线y=﹣x,再作圆的两条切线,且平行于直线y=﹣x,如图4.∵⊙O的半径为2,且△OQ'D是等腰直角三角形,∴OD=2OQ'=2,∴BD=3﹣2=1.∵△P'DB是等腰直角三角形,∴P'B=BD=1,∴P'(0,﹣1),同理可得:OA=2,∴AB=3+2=5.∵△ABP是等腰直角三角形,∴PB=5,∴P(0,﹣5),∴当﹣5≤m≤﹣1时,以QP为边的“坐标菱形”为正方形;综上所述:m的取值范围是1≤m≤5或﹣5≤m≤﹣1.点睛:本题是一次函数和圆的综合题,考查了菱形的性质、正方形的性质、点P,Q的“坐标菱形”的定义等知识,解题的关键是理解题意,学会利用图象解决问题,学会用分类讨论的思想思考问题,注意一题多解,属于中考创新题目.6.如图,已知AB为⊙O直径,D是BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线交AD的延长线于F.(1)求证:直线DE与⊙O相切;(2)已知DG⊥AB且DE=4,⊙O的半径为5,求tan∠F的值.【答案】(1)证明见解析;(2)2.【解析】试题分析:(1)连接BC 、OD ,由D 是弧BC 的中点,可知:OD ⊥BC ;由OB 为⊙O 的直径,可得:BC ⊥AC ,根据DE ⊥AC ,可证OD ⊥DE ,从而可证DE 是⊙O 的切线; (2)直接利用勾股定理得出GO 的长,再利用锐角三角函数关系得出tan ∠F 的值. 试题解析:解:(1)证明:连接OD ,BC ,∵D 是弧BC 的中点,∴OD 垂直平分BC ,∵AB 为⊙O 的直径,∴AC ⊥BC ,∴OD ∥AE .∵DE ⊥AC ,∴OD ⊥DE ,∵OD 为⊙O 的半径,∴DE 是⊙O 的切线;(2)解:∵D 是弧BC 的中点,∴DC DB =,∴∠EAD =∠BAD ,∵DE ⊥AC ,DG ⊥AB 且DE =4,∴DE =DG =4,∵DO =5,∴GO =3,∴AG =8,∴tan ∠ADG =84=2,∵BF 是⊙O 的切线,∴∠ABF =90°,∴DG ∥BF ,∴tan ∠F =tan ∠ADG =2.点睛:此题主要考查了切线的判定与性质以及勾股定理等知识,正确得出AG ,DG 的长是解题关键.7.如图所示,AB 是半圆O 的直径,AC 是弦,点P 沿BA 方向,从点B 运动到点A ,速度为1cm/s ,若10AB cm =,点O 到AC 的距离为4cm .(1)求弦AC 的长;(2)问经过多长时间后,△APC 是等腰三角形.【答案】(1)AC=6;(2)t=4或5或145s 时,△APC 是等腰三角形; 【解析】【分析】(1)过O作OD⊥AC于D,根据勾股定理求得AD的长,再利用垂径定理即可求得AC的长;(2)分AC=PC、AP=AC、AP=CP三种情况求t值即可.【详解】(1)如图1,过O作OD⊥AC于D,易知AO=5,OD=4,从而AD==3,∴AC=2AD=6;(2)设经过t秒△APC是等腰三角形,则AP=10﹣t①如图2,若AC=PC,过点C作CH⊥AB于H,∵∠A=∠A,∠AHC=∠ODA=90°,∴△AHC∽△ADO,∴AC:AH=OA:AD,即AC: =5:3,解得t=s,∴经过s后△APC是等腰三角形;②如图3,若AP=AC,由PB=x,AB=10,得到AP=10﹣x,又∵AC=6,则10﹣t=6,解得t=4s,∴经过4s后△APC是等腰三角形;③如图4,若AP=CP,P与O重合,则AP=BP=5,∴经过5s后△APC是等腰三角形.综上可知当t=4或5或s时,△APC是等腰三角形.【点睛】本题是圆的综合题,解决问题利用了垂径定理,勾股定理等知识点,解题时要注意当△BPC是等腰三角形时,点P的位置有三种情况.8.如图,点A,B,C,D,E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH=10,CH52=.(1)求证:AH是⊙O的切线;(2)若点D是弧CE的中点,且AD交CE于点F,求证:HF=HA;(3)在(2)的条件下,求EF的长.【答案】(1)证明见解析(2)证明见解析(3102【解析】【分析】(1)连接AC,由AB⊥CB可知AC是⊙O的直径,由圆周角定理可得∠C=∠D,于是得到tanC=3,故此可知AB=6,在Rt△ABC中,由勾股定理得:AC2= 40,从而可得AC2+AH2=CH2,根据勾股定理的逆定理可得AC⊥AH,问题得证;(2)连接DE、BE,由弦切角定理可知∠ABD=∠HAD,由D是CE的中点,可得∠CED=∠EBD,再由圆周角定理可得∠ABE=∠ADE,结合三角形的外角即可证明∠HAF=∠AFH,从而可证得AH=HF;(3)由切割线定理可得2,由(2)可知10,从而可得EF=FH﹣10-2.【详解】(1)如图1所示:连接AC.∵AB⊥CB,∴AC是⊙O的直径,∵∠C=∠D,∴tanC=3,∴AB=3BC=3×2=6,在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=40,又∵AH2=10,CH2=50,∴AC2+AH2=CH2,∴△ACH为直角三角形,∴AC⊥AH,∴AH是圆O的切线;(2)如图2所示:连接DE、BE,∵AH是圆O的切线,∴∠ABD=∠HAD,∵D是CE的中点,∴CD ED,∴∠CED=∠EBD,又∵∠ABE=∠ADE,∴∠ABE+∠EBD=∠ADE+∠CED,∴∠ABD=∠AFE,∴∠HAF=∠AFH,∴AH=HF;(3)由切割线定理可知:AH2=EH•CH10)22EH,解得:2,∵由(2)可知10,∴EF=FH﹣102.【点睛】本题主要考查圆的综合应用,解答主要应用了切线的判定定理、弦切角定理、切割线定理、圆周角定理、勾股定理、勾股定理的逆定理、三角形的外角的性质等,正确添加辅助线是解题的关键.9.如图,△ABC中,AC=BC=10,cosC=35,点P是AC边上一动点(不与点A、C重合),以PA长为半径的⊙P与边AB的另一个交点为D,过点D作DE⊥CB于点E.(1)当⊙P与边BC相切时,求⊙P的半径.(2)连接BP交DE于点F,设AP的长为x,PF的长为y,求y关于x的函数解析式,并直接写出x的取值范围.(3)在(2)的条件下,当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时,求相交所得的公共弦的长.【答案】(1)409R=;(2)25880320xy x xx=-++(3)505-【解析】【分析】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=45,sinC=HPCP=10RR-=45,即可求解;(2)首先证明PD∥BE,则EB BFPD PF=,即:2024588x yxxxy-+-=,即可求解;(3)证明四边形PDBE为平行四边形,则AG=EP=BD,即:AB=DB+AD=AG+AD=5【详解】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=45,sinC=HPCP=10RR-=45,解得:R=409;(2)在△ABC中,AC=BC=10,cosC=35,设AP=PD=x,∠A=∠ABC=β,过点B作BH⊥AC,则BH=ACsinC=8,同理可得:CH=6,HA=4,AB=45,则:tan∠CAB=2,BP=228+(4)x-=2880x x-+,DA=25x,则BD=45﹣25x,如下图所示,PA=PD,∴∠PAD=∠CAB=∠CBA=β,tanβ=2,则cosβ5,sinβ5,EB =BDcosβ=(45﹣25x )×5=4﹣25x , ∴PD ∥BE , ∴EB BF PD PF =,即:2024588x y x xx y -+--=, 整理得:y =25x x 8x 803x 20-++; (3)以EP 为直径作圆Q 如下图所示,两个圆交于点G ,则PG =PQ ,即两个圆的半径相等,则两圆另外一个交点为D , GD 为相交所得的公共弦,∵点Q 是弧GD 的中点, ∴DG ⊥EP ,∵AG 是圆P 的直径,∴∠GDA =90°,∴EP ∥BD ,由(2)知,PD ∥BC ,∴四边形PDBE 为平行四边形,∴AG =EP =BD ,∴AB =DB+AD =AG+AD =5设圆的半径为r ,在△ADG 中,AD =2rcosβ5DG 5AG =2r , 5=52r 51+, 则:DG 550﹣5 相交所得的公共弦的长为50﹣5【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.10.如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.(1)求证:AE是⊙O的切线;(2)若AB=AD,AC=32,tan∠ADC=3,求BE的长.【答案】(1)证明见解析;(2)52 BE=【解析】试题分析:(1)连接OA、OB,由圆周角定理得出∠AOB=2∠ACB=90°,由等腰直角三角形的性质得出∠OAB=∠OBA=45°,求出∠OAE=∠OAB+∠BAE=90°,即可得出结论;(2)过点A作AF⊥CD于点F,由AB=AD,得到∠ACD=∠ACB=45°,在Rt△AFC中可求得AF =3,在Rt△AFD中求得DF=1,所以AB=AD=10,CD= CF+DF=4,再证明△ABE∽△CDA,得出BE ABDA CD=,即可求出BE的长度;试题解析:(1)证明:连结OA,OB,∵∠ACB=45°,∴∠AOB=2∠ACB= 90°,∵OA=OB,∴∠OAB=∠OBA=45°,∵∠BAE=45°,∴∠OAE=∠OAB+∠BAE=90°,∴OA⊥AE.∵点A在⊙O上,∴AE是⊙O的切线.(2)解:过点A作AF⊥CD于点F,则∠AFC=∠AFD=90°.∵AB=AD,∴AB =AD∴∠ACD=∠ACB=45°,在Rt△AFC中,∵AC =32,∠ACF =45°, ∴AF=CF=AC ·sin ∠ACF =3, ∵在Rt △AFD 中, tan ∠ADC=3AF DF =, ∴DF =1,∴223110AB AD ==+=, 且CD = CF +DF =4, ∵四边形ABCD 内接于⊙O , ∴∠ABE =∠CDA , ∵∠BAE =∠DCA , ∴△ABE ∽△CDA , ∴BE AB DA CD =, ∴10410=, ∴52BE =.。
全国中考数学圆的综合的综合中考真题分类汇总含详细答案

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.(1)求∠AOC的度数;(2)P为x轴正半轴上一点,且PA=OA,连接PC,试判断PC与⊙O的位置关系,并说明理由;(3)有一动点M从A点出发,在⊙O上按顺时针方向运动一周,当S△MAO=S△CAO时,求动点M所经过的弧长,并写出此时M点的坐标.【答案】(1)60°;(2)见解析;(3)对应的M点坐标分别为:M1(2,﹣3M2(﹣2,﹣3)、M3(﹣2,3M4(2,3).【解析】【分析】(1)由于∠OAC=60°,易证得△OAC是等边三角形,即可得∠AOC=60°.(2)由(1)的结论知:OA=AC,因此OA=AC=AP,即OP边上的中线等于OP的一半,由此可证得△OCP是直角三角形,且∠OCP=90°,由此可判断出PC与⊙O的位置关系.(3)此题应考虑多种情况,若△MAO、△OAC的面积相等,那么它们的高必相等,因此有四个符合条件的M点,即:C点以及C点关于x轴、y轴、原点的对称点,可据此进行求解.【详解】(1)∵OA=OC,∠OAC=60°,∴△OAC是等边三角形,故∠AOC=60°.(2)由(1)知:AC=OA,已知PA=OA,即OA=PA=AC;∴AC=1OP,因此△OCP是直角三角形,且∠OCP=90°,2而OC是⊙O的半径,故PC与⊙O的位置关系是相切.(3)如图;有三种情况:①取C点关于x轴的对称点,则此点符合M点的要求,此时M点的坐标为:M1(2,﹣3劣弧MA的长为:6044 1803ππ⨯=;②取C点关于原点的对称点,此点也符合M点的要求,此时M点的坐标为:M2(﹣2,﹣3劣弧MA的长为:12048 1803ππ⨯=;③取C点关于y轴的对称点,此点也符合M点的要求,此时M点的坐标为:M3(﹣2,3优弧MA的长为:240416 1803ππ⨯=;④当C、M重合时,C点符合M点的要求,此时M4(2,3);优弧MA的长为:300420 1803ππ⨯=;综上可知:当S△MAO=S△CAO时,动点M所经过的弧长为481620,,,3333ππππ对应的M点坐标分别为:M1(2,﹣3M2(﹣2,﹣3)、M3(﹣2,3M4(2,3【点睛】本题考查了切线的判定以及弧长的计算方法,注意分类讨论思想的运用,不要漏解.2.已知O的半径为5,弦AB的长度为m,点C是弦AB所对优弧上的一动点.()1如图①,若m5=,则C∠的度数为______;()2如图②,若m6=.①求C∠的正切值;②若ABC为等腰三角形,求ABC面积.【答案】()130;()2C ∠①的正切值为34;ABCS 27=②或43225. 【解析】 【分析】()1连接OA ,OB ,判断出AOB 是等边三角形,即可得出结论;()2①先求出10AD =,再用勾股定理求出8BD =,进而求出tan ADB ∠,即可得出结论;②分三种情况,利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论.【详解】()1如图1,连接OB ,OA ,OB OC 5∴==, AB m 5==, OB OC AB ∴==, AOB ∴是等边三角形,AOB 60∠∴=,1ACB AOB 302∠∠∴==,故答案为30;()2①如图2,连接AO 并延长交O 于D ,连接BD ,AD 为O 的直径,AD 10∴=,ABD 90∠=,在Rt ABD 中,AB m 6==,根据勾股定理得,BD 8=,AB 3tan ADB BD 4∠∴==, C ADB ∠∠=,C ∠∴的正切值为34;②Ⅰ、当AC BC =时,如图3,连接CO 并延长交AB 于E ,AC BC =,AO BO =, CE ∴为AB 的垂直平分线, AE BE 3∴==,在Rt AEO 中,OA 5=,根据勾股定理得,OE 4=, CE OE OC 9∴=+=,ABC 11S AB CE 692722∴=⨯=⨯⨯=;Ⅱ、当AC AB 6==时,如图4,连接OA 交BC 于F ,AC AB =,OC OB =, AO ∴是BC 的垂直平分线, 过点O 作OG AB ⊥于G ,1AOG AOB 2∠∠∴=,1AG AB 32==,AOB 2ACB ∠∠=, ACF AOG ∠∠∴=,在Rt AOG 中,AG 3sin AOG AC 5∠==, 3sin ACF 5∠∴=,在Rt ACF 中,3sin ACF 5∠=,318AF AC 55∴==,24CF 5∴=,ABC 111824432S AF BC 225525∴=⨯=⨯⨯=;Ⅲ、当BA BC 6==时,如图5,由对称性知,ABC432S25=.【点睛】圆的综合题,主要圆的性质,圆周角定理,垂径定理,等腰三角形的性质,三角形的面积公式,用分类讨论的思想解决问题是解本题的关键.3.矩形ABCD 中,点C (3,8),E 、F 为AB 、CD 边上的中点,如图1,点A 在原点处,点B 在y 轴正半轴上,点C 在第一象限,若点A 从原点出发,沿x 轴向右以每秒1个单位长度的速度运动,点B 随之沿y 轴下滑,并带动矩形ABCD 在平面内滑动,如图2,设运动时间表示为t 秒,当点B 到达原点时停止运动. (1)当t =0时,点F 的坐标为 ; (2)当t =4时,求OE 的长及点B 下滑的距离; (3)求运动过程中,点F 到点O 的最大距离;(4)当以点F 为圆心,FA 为半径的圆与坐标轴相切时,求t 的值.【答案】(1)F (3,4);(2)8-43;(3)7;(4)t 的值为245或325. 【解析】试题分析:(1)先确定出DF ,进而得出点F 的坐标; (2)利用直角三角形的性质得出∠ABO =30°,即可得出结论;(3)当O 、E 、F 三点共线时,点F 到点O 的距离最大,即可得出结论; (4)分两种情况,利用相似三角形的性质建立方程求解即可.试题解析:解:(1)当t =0时.∵AB =CD =8,F 为CD 中点,∴DF =4,∴F (3,4); (2)当t =4时,OA =4.在Rt △ABO 中,AB =8,∠AOB =90°, ∴∠ABO =30°,点E 是AB 的中点,OE =12AB =4,BO =43,∴点B 下滑的距离为843-.(3)当O 、E 、F 三点共线时,点F 到点O 的距离最大,∴FO=OE+EF=7.(4)在Rt △ADF 中,FD 2+AD 2=AF 2,∴AF 22FD AD +,①设AO =t 1时,⊙F 与x 轴相切,点A 为切点,∴FA ⊥OA ,∴∠OAB +∠FAB =90°.∵∠FAD +∠FAB =90°,∴∠BAO =∠FAD .∵∠BOA =∠D =90°,∴Rt △FAE ∽Rt △ABO ,∴AB AO FA FE =,∴1853t=,∴t 1=245,②设AO =t 2时,⊙F 与y 轴相切,B 为切点,同理可得,t 2=325.综上所述:当以点F为圆心,FA为半径的圆与坐标轴相切时,t的值为245或325.点睛:本题是圆的综合题,主要考查了矩形的性质,直角三角形的性质,中点的意义,勾股定理,相似三角形的判定和性质,切线的性质,解(2)的关键是得出∠ABO=30°,解(3)的关键是判断出当O、E、F三点共线时,点F到点O的距离最大,解(4)的关键是判断出Rt△FAE∽Rt△ABD,是一道中等难度的中考常考题.4.如图,AB,BC分别是⊙O的直径和弦,点D为BC上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O 于点M,连接MD,ME.求证:(1)DE⊥AB;(2)∠HMD=∠MHE+∠MEH.【答案】(1)证明见解析;(2)证明见解析.【解析】分析:(1)连接OC,根据等边对等角和切线的性质,证明∠BFG=∠OCH=90°即可;(2)连接BE,根据垂径定理和圆内接四边形的性质,得出∠HMD=∠BME,再根据三角形的外角的性质证明∠HMD=∠DEB=∠EMB即可.详解:证明:(1)连接OC,∵HC=HG,∴∠HCG=∠HGC;∵HC切⊙O于C点,∴∠OCB+∠HCG=90°;∵OB=OC,∴∠OCB=∠OBC,∵∠HGC=∠BGF,∴∠OBC+∠BGF=90°,∴∠BFG=90°,即DE⊥AB;(2)连接BE,由(1)知DE⊥AB,∵AB是⊙O的直径,∴,∴∠BED=∠BME;∵四边形BMDE内接于⊙O,∴∠HMD=∠BED,∴∠HMD=∠BME;∵∠BME是△HEM的外角,∴∠BME=∠MHE+∠MEH,∴∠HMD=∠MHE+∠MEH.点睛:此题综合性较强,主要考查了切线的性质、三角形的内角和外角的性质、等腰三角形的性质、内接四边形的性质.5.如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC 交AC于点E,交PC于点F,连结AF.(1)判断AF与⊙O的位置关系并说明理由;(2)若AC=24,AF=15,求sin B.【答案】(1) AF与⊙O相切理由见解析;(2)3 5【解析】试题分析:(1)连接OC,先证∠OCF=90°,再证明△OAF≌△OCF,得出∠OAF=∠OCF=90°即可;(2)先求出AE、EF,再证明△OAE∽△AFE,得出比例式OA AEAF EF,可求出半径,进而求出直径,由三角函数的定义即可得出结论.试题解析:解:(1)AF与⊙O相切.理由如下:连接OC.如图所示.∵PC是⊙O的切线,∴OC⊥PC,∴∠OCF=90°.∵OF∥BC,∴∠B=∠AOF,∠OCB=∠COF.∵OB=OC,∴∠B=∠OCB,∴∠AOF=∠COF.在△OAF和△OCF中,∵OA=OC,∠AOF=∠COF,OF=OF,∴△OAF≌△OCF(SAS),∴∠OAF=∠OCF=90°,∴AF与⊙O相切;(2)∵△OAF ≌△OCF ,∴∠OAE =∠COE ,∴OE ⊥AC ,AE =12AC =12,∴EF =2215129-=.∵∠OAF =90°,∴△OAE ∽△AFE ,∴OA AE AF EF =,即12159OA =,∴OA =20,∴AB =40,sin B =243405AC AB ==.点睛:本题考查了切线的性质与判定和全等三角形的判定与性质以及相似三角形的判定与性质;熟练掌握切线的证法和三角形相似是解题的关键.6.如图,正三角形ABC 内接于⊙O ,P 是BC 上的一点,且PB <PC ,PA 交BC 于E ,点F 是PC 延长线上的点,CF=PB ,AB=13,PA=4. (1)求证:△ABP ≌△ACF ; (2)求证:AC 2=PA•AE ; (3)求PB 和PC 的长.【答案】(1)证明见解析;(2)证明见解析;(3)PB=1,PC=3.【解析】试题分析:(1)先根据等边三角形的性质得到AB=AC ,再利用圆的内接四边形的性质得∠ACF=∠ABP ,于是可根据“SAS”判断△ABP ≌△ACF ;(2)先根据等边三角形的性质得到∠ABC=∠ACB=60°,再根据圆周角定理得∠APC=∠ABB=60°,加上∠CAE=∠PAC ,于是可判断△ACE ∽△APC ,然后利用相似比即可得到结论;(3)先利用AC 2=PA•AE 计算出AE=134 ,则PE=AP-AE=34,再证△APF 为等边三角形,得到PF=PA=4,则有PC+PB=4,接着证明△ABP ∽△CEP ,得到PB•PC=PE•A=3,然后根据根与系数的关系,可把PB 和PC 看作方程x 2-4x+3=0的两实数解,再解此方程即可得到PB 和PC 的长. 试题解析:(1)∵∠ACP+∠ABP=180°, 又∠ACP+∠ACF=180°, ∴∠ABP=∠ACF在ABP ∆和ACF ∆中,∵AB=AC ,∠ABP=∠ACF , CF PB = ∴ABP ∆≌ACF ∆. (2)在AEC ∆和ACP ∆中, ∵∠APC=∠ABC ,而ABC ∆是等边三角形,故∠ACB=∠ABC=60º, ∴∠ACE =∠APC . 又∠CAE =∠PAC , ∴AEC ∆∽ACP ∆ ∴AC AEAP AC=,即2AC PA AE =⋅. 由(1)知ABP ∆≌ACF ∆, ∴∠BAP=∠CAF , CF PB = ∴∠BAP+∠PAC=∠CAF+∠PAC∴∠PAF=∠BAC=60°,又∠APC =∠ABC =60°. ∴APF ∆是等边三角形 ∴AP=PF∴4PB PC PC CF PF PA +=+=== 在PAB ∆与CEP ∆中, ∵∠BAP=∠ECP , 又∠APB=∠EPC=60°, ∴PAB ∆∽CEP ∆ ∴PB PAPE PC=,即PB PC PA PE ⋅=⋅ 由(2)2AC PA AE =⋅,∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+=∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+=∴22222243PB PC PA AC PA AB ⋅=-=-=-=因此PB 和PC 的长是方程2430x x --=的解. 解这个方程,得11x =, 23x =. ∵PB<PB ,∴PB=11x =,PC=23x =, ∴PB 和PC 的长分别是1和3。
2021年全国历年中考数学真题精选汇编:圆1

全国历年中考数学真题精选汇编:圆1一、单选题(共17题;共34分)1.(2019·北京)已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交于点M,N;(3)连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是()A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°C. MN∥CDD. MN=3CD2.(2021·河北)如图,等腰中,顶角,用尺规按①到④的步骤操作:①以为圆心,为半径画圆;②在上任取一点(不与点,重合),连接;③作的垂直平分线与交于,;④作的垂直平分线与交于,.结论Ⅰ:顺次连接,,,四点必能得到矩形;结论Ⅱ:上只有唯一的点,使得.对于结论Ⅰ和Ⅱ,下列判断正确的是()A. Ⅰ和Ⅱ都对B. Ⅰ和Ⅱ都不对C. Ⅰ不对Ⅱ对D. Ⅰ对Ⅱ不对3.(2020·河北)有一题目:“已知;点为的外心,,求.”嘉嘉的解答为:画以及它的外接圆,连接,,如图.由,得.而淇淇说:“嘉嘉考虑的不周全,还应有另一个不同的值.”,下列判断正确的是()A. 淇淇说的对,且的另一个值是115°B. 淇淇说的不对,就得65°C. 嘉嘉求的结果不对,应得50°D. 两人都不对,应有3个不同值4.(2017·山西)如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为()A. 5πcm2B. 10πcm2C. 15πcm2D. 20πcm25.(2020·包头)如图,是的直径,是弦,点在直径的两侧.若,,则的长为()A. B. C. D.6.(2019·赤峰)如图,是的弦,交于点,点是上一点,,则的度数为().A. 30°B. 40°C. 50°D. 60°7.(2018·包头)如图,在△ABC中,AB=2,BC=4,∠ABC=30°,以点B为圆心,AB长为半径画弧,交BC 于点D,则图中阴影部分的面积是()A. 2﹣B. 2﹣C. 4﹣D. 4﹣8.(2017·呼和浩特)如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O 的周长为()A. 26πB. 13πC.D.9.(2020·阜新)如图,为⊙的直径,C,D是圆周上的两点,若,则锐角的度数为()A. 57°B. 52°C. 38°D. 26°10.(2019·吉林)如图,在中,所对的圆周角,若为上一点,,则的度数为()A. 30°B. 45°C. 55°D. 60°11.(2020·牡丹江)如图,四边形内接于,连接.若,,则的度数是()A. 125°B. 130°C. 135°D. 140°12.(2019·上海)已知⊙A与⊙B外切,⊙C与⊙A、⊙B都内切,且AB=5,AC=6,BC=7,那么⊙C的半径长是()A. 11B. 10C. 9D. 813.(2021·衢州)已知扇形的半径为6,圆心角为.则它的面积是()A. B. C. D.14.(2021·嘉兴)已知平面内有⊙O和点A,B,若⊙O半径为2cm,线段OA=3cm,OB=2cm,则直线AB与⊙O的位置关系为()A. 相离B. 相交C. 相切D. 相交或相切15.(2019·福建)如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )A. 55°B. 70°C. 110°D. 125°16.(2018·福建)如图,AB是⊙O的直径,BC与⊙O相切于点B,AC交⊙O于点D,若∠ACB=50°,则∠BOD 等于()A. 40°B. 50°C. 60°D. 80°17.(2020·东营)用一个半径为面积为的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为()A. B. C. 2 D. 1二、填空题(共12题;共12分)18.(2018·北京)如图,点,,,在上,,,,则________.19.(2017·北京)如图,AB为⊙O的直径,C、D为⊙O上的点,AD=CD.若∠CAB=40°,则∠CAD=________.20.(2018·赤峰)半径为10cm的半圆围成一个圆锥,则这个圆锥的高是________cm.21.(2018·包头)如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=________度.22.(2017·呼和浩特)我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为________.(用含m,n的式子表示)23.(2020·锦州)如图,⊙O是的外接圆,,,则的长为________.24.(2020·绥化)已知圆锥的底面圆的半径是2.5,母线长是9,其侧面展开图的圆心角是________度.25.(2017·上海)如图,已知Rt△ABC,∠C=90°,AC=3,BC=4.分别以点A、B为圆心画圆.如果点C在⊙A内,点B在⊙A外,且⊙B与⊙A内切,那么⊙B的半径长r的取值范围是________.26.(2021·宿迁)已知圆锥的底面圆半径为4,侧面展开图扇形的圆心角为120°,则它的侧面展开图面积为________.27.(2021·扬州)如图是某圆柱体果罐,它的主视图是边长为的正方形,该果罐侧面积为________.28.(2021·温州)若扇形的圆心角为,半径为17,则扇形的弧长为________.29.(2021·宁波)抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图,分别与相切于点C,D,延长交于点P.若,的半径为,则图中的长为________ .(结果保留)三、综合题(共11题;共117分)30.(2019·北京)在平面内,给定不在同一直线上的点A,B,C,如图所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,的平分线交图形G于点D,连接AD,CD.(1)求证:AD=CD;(2)过点D作DE BA,垂足为E,作DF BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.31.(2017·北京)如图,P是AB所对弦AB上一动点,过点P作PM⊥AB交AB于点M,连接MB,过点P 作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为xcm,P、N两点间的距离为ycm.(当点P 与点A或点B重合时,y的值为0)小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(说明:补全表格时相关数值保留一位小数)(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为________cm.32.(2018·天津)已知是的直径,弦与相交,.(1)如图①,若为的中点,求和的大小;(2)如图②,过点作的切线,与的延长线交于点,若,求的大小.33.(2017·天津)已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.(1)如图①,求∠T和∠CDB的大小;(2)如图②,当BE=BC时,求∠CDO的大小.34.(2021·河北)如图,的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为(为1~12的整数),过点作的切线交延长线于点.(1)通过计算比较直径和劣弧长度哪个更长;(2)连接,则和有什么特殊位置关系?请简要说明理由;(3)求切线长的值.35.(2017·赤峰)如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.(1)求证:AM是⊙O的切线;(2)若DC=2,求图中阴影部分的面积(结果保留π和根号).36.(2018·长春)如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D.已知⊙O的半径为6,∠C=40°.(1)求∠B的度数.(2)求的长.(结果保留π)37.(2021·苏州)如图,四边形内接于,,延长到点,使得,连接.(1)求证:;(2)若,,,求的值.38.(2020·台州)如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M. E是线段CM上的点,连接BE. F是△BDE的外接圆与AD的另一个交点,连接EF,BF(1)求证:△BEF是直角三角形;(2)求证:△BEF∽△BCA;(3)当AB=6,BC=m时,在线段CM中存在点E,使得EF和AB互相平分,求m的值.39.(2016·江西)如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交于点F,交过点C的切线于点D.(1)求证:DC=DP;(2)若∠CAB=30°,当F是的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.40.(2020·潍坊)如图,为的直径,射线交于点F,点C为劣弧的中点,过点C 作,垂足为E,连接.(1)求证:是的切线;(2)若,求阴影部分的面积.答案解析部分一、单选题1.【答案】D【解析】【解答】解:由作图知CM=CD=DN,∴∠COM=∠COD,故A选项不符合题意;∵OM=ON=MN,∴△OMN是等边三角形,∴∠MON=60°,∵CM=CD=DN,∴∠MOA=∠AOB=∠BON= ∠MON=20°,故B选项不符合题意;∵∠MOA=∠AOB=∠BON=20°,∴∠OCD=∠OCM=80°,∴∠MCD=160°,又∠CMN= ∠AON=20°,∴∠MCD+∠CMN=180°,∴MN∥CD,故C选项不符合题意;∵MC+CD+DN>MN,且CM=CD=DN,∴3CD>MN,故D选项符合题意;故答案为:D.【分析】根据题意中作图可知,CM=CD=DN,根据圆周角定理,圆心角定理进行判断。
全国中考数学圆的综合的综合中考真题汇总

一、圆的综合 真题与模拟题分类汇编(难题易错题)1.如图,AB 为O 的直径,弦//CD AB ,E 是AB 延长线上一点,CDB ADE ∠=∠. ()1DE 是O 的切线吗?请说明理由;()2求证:2AC CD BE =⋅.【答案】(1)结论:DE 是O 的切线,理由见解析;(2)证明见解析.【解析】【分析】 (1)连接OD ,只要证明OD DE ⊥即可;(2)只要证明:AC BD =,CDB DBE ∽即可解决问题.【详解】()1解:结论:DE 是O 的切线.理由:连接OD .CDB ADE ∠=∠,ADC EDB ∴∠=∠,//CD AB ,CDA DAB ∴∠=∠,OA OD =,OAD ODA ∴∠=∠,ADO EDB ∴∠=∠, AB 是直径,90ADB ∴∠=,90ADB ODE ∴∠=∠=,DE OD ∴⊥,DE ∴是O 的切线.()2//CD AB,∴∠=∠,CDB DBE∠=∠,ADC DAB∴=,AC BD∴=,AC BD∠=∠,EDB DABDCB DAB∠=∠,∴∠=∠,EDB DCB∴∽DBE,CDBCD DB∴=,BD BE2BD CD BE∴=⋅,2∴=⋅.AC CD BE【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识,解题的关键是学会添加常用辅助线,准确寻找相似三角形解决问题,属于中考常考题型.2.如图1,以边长为4的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E.(1)图1中,线段AE=;(2)如图2,在图1的基础上,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),在旋转过程中AD与⊙O交于点F.①当α=30°时,请求出线段AF的长;②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;③当α=°时,DM与⊙O相切.【答案】(1)2(2)①2②2,相离③当α=90°时,DM与⊙O相切【解析】(1)连接BE,∵AC是正方形ABCD的对角线,∴∠BAC=45°,∴△AEB是等腰直角三角形,又∵AB=8,∴AE=4;(2)①连接OA、OF,由题意得,∠NAD=30°,∠DAM=30°,故可得∠OAM=30°,∠DAM=30°,则∠OAF=60°,又∵OA=OF,∴△OAF是等边三角形,∵OA=4,∴AF=OA=4;②连接B'F,此时∠NAD=60°,∵AB'=8,∠DAM=30°,∴AF=AB'cos∠DAM=8×=4;此时DM与⊙O的位置关系是相离;③∵AD=8,直径的长度相等,∴当DM与⊙O相切时,点D在⊙O上,故此时可得α=∠NAD=90°.点睛:此题属于圆的综合题,主要是仔细观察每一次旋转后的图形,根据含30°角的直角三角形进行计算,另外在解答最后一问时,关键是判断出点D 的位置,有一定难度.3.如图,已知⊙O 的半径为1,PQ 是⊙O 的直径,n 个相同的正三角形沿PQ 排成一列,所有正三角形都关于PQ 对称,其中第一个△A 1B 1C 1的顶点A 1与点P 重合,第二个△A 2B 2C 2的顶点A 2是B 1C 1与PQ 的交点,…,最后一个△A n B n C n 的顶点B n 、C n 在圆上.如图1,当n=1时,正三角形的边长a 1=_____;如图2,当n=2时,正三角形的边长a 2=_____;如图3,正三角形的边长a n =_____(用含n 的代数式表示).38313 24313n【解析】 分析:(1)设PQ 与11B C 交于点D ,连接1B O ,得出OD=1A D -O 1A ,用含1a 的代数式表示OD ,在△O 1B D 中,根据勾股定理求出正三角形的边长1a ;(2)设PQ 与2B 2C 交于点E ,连接2B O ,得出OE=1A E-O 1A ,用含2a 的代数式表示OE ,在△O 2B E 中,根据勾股定理求出正三角形的边长2a ;(3)设PQ 与n B n C 交于点F ,连接n B O ,得出OF=1A F-O 1A ,用含an 的代数式表示OF ,在△O n B F 中,根据勾股定理求出正三角形的边长an . 本题解析:(1)易知△A 1B 1C 1的高为323 ∴a 13.(2)设△A 1B 1C 1的高为h ,则A 2O =1-h ,连结B 2O ,设B 2C 2与PQ 交于点F ,则有OF =2h -1.∵B2O2=OF2+B2F2,∴1=(2h-1)2+2212a⎛⎫ ⎪⎝⎭.∵h=32a2,∴1=(3a2-1)2+14a22,解得a2=83 13.(3)同(2),连结B n O,设B n C n与PQ交于点F,则有B n O2=OF2+B n F2,即1=(nh-1)2+2 12na⎛⎫ ⎪⎝⎭.∵h=3a n,∴1=14a n2+2312nna⎛⎫-⎪⎪⎝⎭,解得a n=43n.4.四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.(1)如图1,求证:CE=CD;(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC= 5311,EG=2,求AE的长.【答案】(1)见解析;(2)60°;(3)7.【解析】试题分析:(1)利用圆的内接四边形定理得到∠CED=∠CDE.(2) 作CH⊥DE于H, 设∠ECH=α,由(1)CE=CD,用α表示∠CAE,∠BAC,而∠BAD=∠BAC+∠CAE.(3)连接AG,作GN⊥AC,AM⊥EG,先证明∠CAG=∠BAC,设NG=53m,可得AN=11m,利用直角AGM,AEM,勾股定理可以算出m的值并求出AE长.试题解析:(1)解:证明:∵四边形ABCD内接于⊙O.∴∠B+∠D=180°,∵∠B=∠AEC,∴∠AEC+∠D=180°,∵∠AEC+∠CED=180°,∴∠D=∠CED,∴CE=CD.(2)解:作CH⊥DE于H.设∠ECH=α,由(1)CE=CD,∴∠ECD=2α,∵∠B=∠AEC,∠B+∠CAE=120°,∴∠CAE+∠AEC=120°,∴∠ACE=180°﹣∠AEC﹣∠ACE=60°,∴∠CAE=90°﹣∠ACH=90°﹣(60°+α)=30°﹣α,∠ACD=∠ACH+∠HCD=60°+2α,∵∠ACD=2∠BAC,∴∠BAC=30°+α,∴∠BAD =∠BAC +∠CAE =30°+α+30°﹣α=60°.(3)解:连接AG ,作GN ⊥AC ,AM ⊥EG ,∵∠CED =∠AEG ,∠CDE =∠AGE ,∠CED =∠CDE ,∴∠AEG =∠AGE ,∴AE =AG ,∴EM=MG =12EG =1, ∴∠EAG =∠ECD =2α,∴∠CAG =∠CAD +∠DAG =30°﹣α+2α=∠BAC ,∵tan ∠BAC 53, ∴设NG=3,可得AN =11m ,AG 22AG AM -14m , ∵∠ACG =60°,∴CN=5m ,AM 3,MG 22AG AM -m =1, ∴m =12, ∴CE=CD =CG ﹣EG =10m ﹣2=3, ∴AE 22AM EM +221+43()=7.5.对于平面直角坐标系xOy 中的线段MN 和点P ,给出如下定义:点A 是线段MN 上一个动点,过点A 作线段MN 的垂线l ,点P 是垂线l 上的另外一个动点.如果以点P 为旋转中心,将垂线l 沿逆时针方向旋转60°后与线段MN 有公共点,我们就称点P 是线段MN 的“关联点”.如图,M (1,2),N (4,2).(1) 在点P 1(1,3),P 2(4,0),P 3(3,2)中,线段MN 的“关联点”有 ;(2) 如果点P 在直线1y x =+上,且点P 是线段MN 的“关联点”,求点P 的横坐标x 的取值范围;(3) 如果点P 在以O (1,1-)为圆心,r 为半径的⊙O 上,且点P 是线段MN 的“关联点”,直接写出⊙O 半径r 的取值范围.【答案】(1)P 1和P 3;(2)3311x -≤≤;(3)333 3.r +≤≤ 【解析】【分析】 (1)先根据题意求出点P 的横坐标的范围,再求出P 点的纵坐标范围即可得出结果; (2)由直线y=x+1经过点M (1,2),得出x≥1,设直线y=x+1与P 4N 交于点A ,过点A 作AB ⊥MN 于B ,延长AB 交x 轴于C ,则在△AMN 中,MN=3,∠AMN=45°,∠ANM=30°,设AB=MB=a ,tan ∠ANM=AB BN ,即tan30°=3a a-,求出a 即可得出结果; (3)圆心O 到P 4的距离为r 的最大值,圆心O 到MP 5的距离为r 的最小值,分别求出两个距离即可得出结果.【详解】(1))如图1所示:∵点A 是线段MN 上一个动点,过点A 作线段MN 的垂线l ,点P 是垂线l 上的另外一个动点,M (1,2),N (4,2),∴点P 的横坐标1≤x≤4,∵以点P 为旋转中心,将垂线l 沿逆时针方向旋转60°后与线段MN 有公共点, 当∠MPN=60°时,PM=60MN tan ︒33 同理3,∴点P 的纵坐标为3或3即纵坐标33∴线段MN 的“关联点”有P 1和P 3;故答案为:P 1和P 3;(2)线段MN 的“关联点”P 的位置如图所示,∵ 直线1y x =+经过点M (1,2),∴ x ≥1.设直线1y x =+与P 4N 交于点A .过点A 作AB ⊥MN 于B ,延长AB 交x 轴于C .由题意易知,在△AMN 中,MN = 3,∠AMN = 45°,∠ANM = 30°.设AB = MB = a ,∴ tan AB ANM BN ∠=,即tan303a a ︒=-, 解得333.a -= ∴ 点A 的横坐标为33333111.22x a --=+=+= ∴331.x -≤ 综上 3311.2x -≤≤(3)点P 在以O (1,-1)为圆心,r 为半径的⊙O 上,且点P 是线段MN 的“关联点”,如图3所示:连接P 4O 交x 轴于点D ,P 4、M 、D 、O 共线,则圆心O 到P 4的距离为r 的最大值,由(1)知:MP 4=NP 53即OD+DM+MP 4=1+2+3=3+3, 圆心O 到MP 5的距离为r 的最小值,作OE ⊥MP 5于E ,连接OP 5,则OE 为r 的最小值,MP 5=225MN NP +=223(3)+=23,OM=OD+DM=1+2=3, △OMP 5的面积=12OE•MP 5=12OM•MN ,即12×OE×23=12×3×3, 解得:OE=33, ∴332≤r≤3+3. 【点睛】本题是圆的综合题,考查了旋转、直角三角形的性质、勾股定理、最值等知识,熟练掌握“关联点”的含义,作出关于MN 的“关联点”图是关键.6.如图,AB 为O 的直径,C 、D 为O 上异于A 、B 的两点,连接CD ,过点C 作CE DB ⊥,交CD 的延长线于点E ,垂足为点E ,直径AB 与CE 的延长线相交于点F .(1)连接AC 、AD ,求证:180DAC ACF ∠+∠=︒.(2)若2ABD BDC ∠=∠.①求证:CF 是O 的切线.②当6BD =,3tan 4F =时,求CF 的长. 【答案】(1)详见解析;(2)①详见解析;② 203CF =. 【解析】【分析】(1)根据圆周角定理证得∠ADB=90°,即AD ⊥BD ,由CE ⊥DB 证得AD ∥CF ,根据平行线的性质即可证得结论;(2)①连接OC .先根据等边对等角及三角形外角的性质得出∠3=2∠1,由已知∠4=2∠1,得到∠4=∠3,则OC ∥DB ,再由CE ⊥DB ,得到OC ⊥CF ,根据切线的判定即可证明CF 为⊙O 的切线;②由CF ∥AD ,证出∠BAD=∠F ,得出tan ∠BAD=tan ∠F=BD AD =34,求出AD=43BD=8,利用勾股定理求得AB=10,得出OB=OC=,5,再由tanF=OC CF =34,即可求出CF . 【详解】 解:(1)AB 是O 的直径,且D 为O 上一点,90ADB ∴∠=︒, CE DB ⊥, 90DEC ∴∠=︒, //CF AD ∴,180DAC ACF ∴∠+∠=︒. (2)①如图,连接OC . OA OC =,12∴∠=∠. 312∠=∠+∠, 321∴∠=∠.42BDC ∠=∠,1BDC ∠=∠, 421∴∠=∠, 43∴∠=∠, //OC DB ∴. CE DB ⊥, OC CF ∴⊥.又OC 为O 的半径, CF ∴为O 的切线.②由(1)知//CF AD ,BAD F ∴∠=∠,3tan tan 4BAD F ∴∠==, 34BD AD ∴=. 6BD =483AD BD ∴==, 226810AB ∴=+=,5OB OC ==.OC CF ⊥, 90OCF ∴∠=︒,3tan 4OC F CF ∴==,解得203CF =. 【点睛】本题考查了切线的判定、解直角三角形、圆周角定理等知识;本题综合性强,有一定难度,特别是(2)中,需要运用三角函数、勾股定理和由平行线得出比例式才能得出结果.7.已知AC =DC ,AC ⊥DC ,直线MN 经过点A ,作DB ⊥MN ,垂足为B ,连结CB .[感知]如图①,点A 、B 在CD 同侧,且点B 在AC 右侧,在射线AM 上截取AE =BD ,连结CE ,可证△BCD ≌△ECA ,从而得出EC =BC ,∠ECB =90°,进而得出∠ABC = 度; [探究]如图②,当点A 、B 在CD 异侧时,[感知]得出的∠ABC 的大小是否改变?若不改变,给出证明;若改变,请求出∠ABC 的大小.[应用]在直线MN 绕点A 旋转的过程中,当∠BCD =30°,BD =时,直接写出BC 的长.【答案】【感知】:45;【探究】:不改变,理由详见解析;【拓展】:BC 的长为+1或﹣1.【解析】 【分析】[感知]证明△BCD ≌△ECA (SAS ) 即可解决问题;[探究]结论不变,证明△BCD ≌△ECA (SAS ) 即可解决问题; [应用]分两种情形分别求解即可解决问题. 【详解】解:【感知】,如图①中,在射线AM 上截取AE =BD ,连结CE .∵AC⊥DC,DB⊥MN,∴∠ACD=∠DBA=90°.∴∠CDB+∠CAB=180°,∵∠CAB+∠CAE=180°∴∠D=∠CAE,∵CD=AC,AE=BD,∴△BCD≌△ECA(SAS),∴BC=EC,∠BCD=∠ECA,∵∠ACE+∠ECD=90°,∴∠ECD+∠DCB=90°,即∠ECB=90°,∴∠ABC=45°.故答案为45【探究】不改变.理由如下:如图,如图②中,在射线AN上截取AE=BD,连接CE,设MN与CD交于点O.∵AC⊥DC,DB⊥MN,∴∠ACD=∠DBA=90°,∵∠AOC=∠DOB,∴∠D=∠EAC,CD=AC,∴△BCD≌△ECA(SAS),∴BC=EC,∠BCD=∠ECA,∵∠ACE+∠ECD=90°,∴∠ECD+∠DCB=90°,即∠ECB=90°,∴∠ABC=45°.【拓展】如图①﹣1中,连接AD.∴∠ACD+∠ABD=180°,∴A,C,D,B四点共圆,∴∠DAB=∠DCB=30°,∴AB=BD=,∴EB =AE+AB=+,∵△ECB是等腰直角三角形,如图②中,同法可得BC=﹣1.综上所述,BC的长为+1或﹣1.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.8.如图,点A,B,C,D,E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH=10,CH52=.(1)求证:AH是⊙O的切线;(2)若点D是弧CE的中点,且AD交CE于点F,求证:HF=HA;(3)在(2)的条件下,求EF的长.【答案】(1)证明见解析(2)证明见解析(3102【解析】【分析】(1)连接AC,由AB⊥CB可知AC是⊙O的直径,由圆周角定理可得∠C=∠D,于是得到tanC=3,故此可知AB=6,在Rt△ABC中,由勾股定理得:AC2= 40,从而可得AC2+AH2=CH2,根据勾股定理的逆定理可得AC⊥AH,问题得证;(2)连接DE、BE,由弦切角定理可知∠ABD=∠HAD,由D是CE的中点,可得∠CED=∠EBD,再由圆周角定理可得∠ABE=∠ADE,结合三角形的外角即可证明∠HAF=∠AFH,从而可证得AH=HF;(3)由切割线定理可得EH=2,由(2)可知AF=FH=10,从而可得EF=FH﹣EH=10-2.【详解】(1)如图1所示:连接AC.∵AB⊥CB,∴AC是⊙O的直径,∵∠C=∠D,∴tanC=3,∴AB=3BC=3×2=6,在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=40,又∵AH2=10,CH2=50,∴AC2+AH2=CH2,∴△ACH为直角三角形,∴AC⊥AH,∴AH是圆O的切线;(2)如图2所示:连接DE、BE,∵AH是圆O的切线,∴∠ABD=∠HAD,∵D是CE的中点,∴CD ED,∴∠CED=∠EBD , 又∵∠ABE=∠ADE ,∴∠ABE+∠EBD=∠ADE+∠CED , ∴∠ABD=∠AFE , ∴∠HAF=∠AFH , ∴AH=HF ;(3)由切割线定理可知:AH 2=EH•CH ,即(10)2=52EH , 解得:EH=2,∵由(2)可知AF=FH=10, ∴EF=FH ﹣EH=10-2.【点睛】本题主要考查圆的综合应用,解答主要应用了切线的判定定理、弦切角定理、切割线定理、圆周角定理、勾股定理、勾股定理的逆定理、三角形的外角的性质等,正确添加辅助线是解题的关键.9.如图①,已知Rt ABC ∆中,90ACB ∠=,8AC =,10AB =,点D 是AC 边上一点(不与C 重合),以AD 为直径作O ,过C 作CE 切O 于E ,交AB 于F .(1)若O 的半径为2,求线段CE 的长;(2)若AF BF =,求O 的半径;(3)如图②,若CE CB =,点B 关于AC 的对称点为点G ,试求G 、E 两点之间的距离.【答案】(1)42CE =(2)O 的半径为3;(3)G 、E 两点之间的距离为9.6.【解析】 【分析】(1)根据切线的性质得出∠OEC=90°,然后根据勾股定理即可求得; (2)由勾股定理求得BC ,然后通过证得△OEC ∽△BCA ,得到OE BC =OC BA ,即r 8-r=610,解得即可;(3)证得D 和M 重合,E 和F 重合后,通过证得△GBE ∽△ABC ,GB GEAB AC=,即12108GE =,解得即可. 【详解】(1)如图,连结OE . ∵CE 切O 于E ,∴90OEC ∠=︒. ∵8AC =,O 半径为2,∴6OC =,2OE =.∴2242CE OC OE =-=; (2)设O 半径为r .在Rt ABC ∆中,90ACB ∠=︒,10AB =,8AC =, ∴226BC AB AC -=.∵AF BF =, ∴AF CF BF ==. ∴ACF CAF ∠=∠. ∵CE 切O 于E ,∴90OEC ∠=︒. ∴OEC ACB ∠=∠, ∴OEC BCA ∆~∆. ∴OE OCBC BA=, ∴8610r r -=, 解得3r =. ∴O 的半径为3;(3)连结EG 、OE ,设EG 交AC 于点M ,由对称性可知,CB CG =. 又CE CB =, ∴CE CG =. ∴EGC GEC ∠=∠. ∵CE 切O 于E ,∴90GEC OEG ∠+∠=︒. 又90EGC GMC ∠+∠=︒,∴OEG GMC ∠=∠.又GMC OME ∠=∠, ∴OEG OME ∠=∠. ∴OE OM =. ∴点M 与点D 重合.∴G 、D 、E 三点在同一条直线上. 连结AE 、BE , ∵AD 是直径,∴90AED ∠=︒,即90AEG ∠=︒. 又CE CB CG ==, ∴90BEG ∠=︒.∴180AEB AEG BEG ∠=∠+∠=︒, ∴A 、E 、B 三点在同一条直线上.∴E 、F 两点重合.∵90GEB ACB ∠=∠=︒,B B ∠=∠, ∴GBE ABC ∆~∆. ∴GB GE AB AC =,即12108GE=. ∴9.6GE =.故G 、E 两点之间的距离为9.6. 【点睛】本题考查了切线的判定,轴的性质,勾股定理的应用以及三角形相似的判定和性质,证得G 、D 、E 三点共线以及A 、E 、B 三点在同一条直线上是解题的关键.10.对于平面内的⊙C 和⊙C 外一点Q ,给出如下定义:若过点Q 的直线与⊙C 存在公共点,记为点A ,B ,设AQ BQk CQ+=,则称点A (或点B )是⊙C 的“K 相关依附点”,特别地,当点A 和点B 重合时,规定AQ=BQ ,2AQ k CQ =(或2BQCQ). 已知在平面直角坐标系xoy 中,Q(-1,0),C(1,0),⊙C 的半径为r . (1)如图1,当2r =时,①若A 1(0,1)是⊙C 的“k 相关依附点”,求k 的值. ②A 2(1+2,0)是否为⊙C 的“2相关依附点”. (2)若⊙C 上存在“k 相关依附点”点M , ①当r=1,直线QM 与⊙C 相切时,求k 的值. ②当3k =时,求r 的取值范围.(3)若存在r 的值使得直线3y x b =-+与⊙C 有公共点,且公共点时⊙C 的“3相关依附点”,直接写出b 的取值范围.【答案】(1)2.②是;(2)①3k =②r 的取值范围是12r <≤;(3)333b -<.【解析】 【分析】(1)①如图1中,连接AC 、1QA .首先证明1QA 是切线,根据2AQk CQ=计算即可解决问题;②根据定义求出k 的值即可判断;(2)①如图,当1r =时,不妨设直线QM 与C 相切的切点M 在x 轴上方(切点M 在x 轴下方时同理),连接CM ,则QM CM ⊥,根据定义计算即可;②如图3中,若直线QM 与C 不相切,设直线QM 与C 的另一个交点为N (不妨设QN QM <,点N ,M 在x 轴下方时同理),作CD QM ⊥于点D ,则MD ND =,可得()222MQ NQ MN NQ NQ ND NQ DQ +=++=+=,2CQ ,推出2MQ NQ DQk DQ CQ CQ+===,可得当3k =3DQ =221CD CQ DQ -=,假设C 经过点Q ,此时2r ,因为点Q 早C 外,推出r 的取值范围是12r <;(3)如图4中,由(2)可知:当3k =时,12r <.当2r 时,C 经过点(1,0)Q -或(3,0)E ,当直线3y x b =-+经过点Q 时,3b =-,当直线3y x b=-+经过点E 时,33b =,即可推出满足条件的b 的取值范围为333b -<<. 【详解】(1)①如图1中,连接AC 、1QA .由题意:1OC OQ OA ==,∴△1QA C 是直角三角形,190CA Q ∴∠=︒,即11CA QA ⊥,1QA ∴是C 的切线,122222QA k QC ∴=== ②2(12,0)A +在C 上,221212k -+++∴==,2A ∴是C 的“2相关依附点”.2(2)①如图2,当1r =时,不妨设直线QM 与C 相切的切点M 在x 轴上方(切点M在x 轴下方时同理),连接CM ,则QM CM ⊥.(1,0)Q -,(1,0)C ,1r =,2CQ ∴=,1CM =,∴3MQ =,此时23MQk CQ=②如图3中,若直线QM 与C 不相切,设直线QM 与C 的另一个交点为N (不妨设QN QM <,点N ,M 在x 轴下方时同理),作CD QM ⊥于点D ,则MD ND =,()222MQ NQ MN NQ NQ ND NQ DQ ∴+=++=+=,2CQ =,∴2MQ NQ DQk DQ CQ CQ+===,∴当3k =3DQ =221CD CQ DQ =-,假设C 经过点Q ,此时2r ,点Q 早C 外,r ∴的取值范围是12r <.(3)如图4中,由(2)可知:当3k =时,12r <.当2r 时,C 经过点(1,0)Q -或(3,0)E ,当直线3y x b =+经过点Q 时,3b =3y x b =-+经过点E 时,33b =,∴满足条件的b 的取值范围为333b -<.【点睛】本题考查了一次函数综合题、圆的有关知识、勾股定理、切线的判定和性质、点A (或点)B 是C 的“k 相关依附点”的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会考虑特殊位置解决问题,属于中考压轴题.。
全国中考数学圆的综合的综合中考真题汇总及答案

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,⊙O是△ABC的外接圆,点E为△ABC内切圆的圆心,连接AE的延长线交BC于点F,交⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.(1)求证:直线DM是⊙O的切线;(2)若DF=2,且AF=4,求BD和DE的长.【答案】(1)证明见解析(2)23【解析】【分析】(1)根据垂径定理的推论即可得到OD⊥BC,再根据∠BDM=∠DBC,即可判定BC∥DM,进而得到OD⊥DM,据此可得直线DM是⊙O的切线;(2)根据三角形内心的定义以及圆周角定理,得到∠BED=∠EBD,即可得出DB=DE,再判定△DBF∽△DAB,即可得到DB2=DF•DA,据此解答即可.【详解】(1)如图所示,连接OD.∵点E是△ABC的内心,∴∠BAD=∠CAD,∴BD CD=,∴OD⊥BC.又∵∠BDM=∠DAC,∠DAC=∠DBC,∴∠BDM=∠DBC,∴BC∥DM,∴OD⊥DM.又∵OD为⊙O半径,∴直线DM是⊙O的切线.(2)连接BE.∵E为内心,∴∠ABE=∠CBE.∵∠BAD=∠CAD,∠DBC=∠CAD,∴∠BAD=∠DBC,∴∠BAE+∠ABE=∠CBE+∠DBC,即∠BED=∠DBE,∴BD=DE.又∵∠BDF=∠ADB(公共角),∴△DBF∽△DAB,∴DF DBDB DA=,即DB2=DF•DA.∵DF=2,AF=4,∴DA=DF+AF=6,∴DB2=DF•DA=12,∴DB=DE=23.【点睛】本题主要考查了三角形的内心与外心,圆周角定理以及垂径定理的综合应用,解题时注意:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.2.如图,在平面直角坐标系xoy中,E(8,0),F(0 , 6).(1)当G(4,8)时,则∠FGE= °(2)在图中的网格区域内找一点P,使∠FPE=90°且四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形.要求:写出点P点坐标,画出过P点的分割线并指出分割线(不必说明理由,不写画法).【答案】(1)90;(2)作图见解析,P(7,7),PH是分割线.【解析】试题分析:(1)根据勾股定理求出△FEG的三边长,根据勾股定理逆定理可判定△FEG是直角三角形,且∠FGE="90" °.(2)一方面,由于∠FPE=90°,从而根据直径所对圆周角直角的性质,点P在以EF为直径的圆上;另一方面,由于四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形,从而OP是正方形的对角线,即点P在∠FOE的角平分线上,因此可得P(7,7),PH是分割线.试题解析:(1)连接FE,∵E(8,0),F(0 , 6),G(4,8),∴根据勾股定理,得FG=,EG=,FE=10.∵,即.∴△FEG是直角三角形,且∠FGE=90 °.(2)作图如下:P(7,7),PH是分割线.考点:1.网格问题;2.勾股定理和逆定理;3.作图(设计);4.圆周角定理.3.如图,AB,BC分别是⊙O的直径和弦,点D为BC上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O 于点M,连接MD,ME.求证:(1)DE⊥AB;(2)∠HMD=∠MHE+∠MEH.【答案】(1)证明见解析;(2)证明见解析.【解析】分析:(1)连接OC,根据等边对等角和切线的性质,证明∠BFG=∠OCH=90°即可;(2)连接BE,根据垂径定理和圆内接四边形的性质,得出∠HMD=∠BME,再根据三角形的外角的性质证明∠HMD=∠DEB=∠EMB即可.详解:证明:(1)连接OC,∵HC=HG,∴∠HCG=∠HGC;∵HC切⊙O于C点,∴∠OCB+∠HCG=90°;∵OB=OC,∴∠OCB=∠OBC,∵∠HGC=∠BGF,∴∠OBC+∠BGF=90°,∴∠BFG=90°,即DE⊥AB;(2)连接BE,由(1)知DE⊥AB,∵AB是⊙O的直径,∴,∴∠BED=∠BME;∵四边形BMDE内接于⊙O,∴∠HMD=∠BED,∴∠HMD=∠BME;∵∠BME是△HEM的外角,∴∠BME=∠MHE+∠MEH,∴∠HMD=∠MHE+∠MEH.点睛:此题综合性较强,主要考查了切线的性质、三角形的内角和外角的性质、等腰三角形的性质、内接四边形的性质.4.如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足若13 CFDF=,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.(1)求证:△ADF∽△AED;(2)求FG的长;(3)求tan∠E的值.【答案】(1)证明见解析5【解析】分析:(1)由AB是 O的直径,弦CD⊥AB,根据垂径定理可得:弧AD=弧AC,DG=CG,继而证得△ADF∽△AED;(2)由13CFFD= ,CF=2,可求得DF的长,继而求得CG=DG=4,则可求得FG=2;(3)由勾股定理可求得AG的长,即可求得tan∠ADF的值,继而求得tan∠E=5 .本题解析:①∵AB是⊙O的直径,弦CD⊥AB,∴DG=CG,∴AD AC=,∠ADF=∠AED,∵∠FAD=∠DAE(公共角),∴△ADF∽△AED;②∵13CFFD=,CF=2,∴FD=6,∴CD=DF+CF=8,∴CG=DG=4,∴FG=CG-CF=2;③∵AF=3,FG=2,∴AG=225AF FG-=,点睛:本题考查了相似三角形的判定与性质、圆周角定理、垂径定理、勾股定理以及三角函数等知识点,考查内容较多,综合性较强,难度适中,注意掌握数形结合的思想.5.如图1,是用量角器一个角的操作示意图,量角器的读数从M点开始(即M点的读数为0),如图2,把这个量角器与一块30°(∠CAB=30°)角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有射线C绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB,在旋转过程中,射线CP与量角器的半圆弧交于E.连接BE.(1)当射线CP经过AB的中点时,点E处的读数是,此时△BCE的形状是;(2)设旋转x秒后,点E处的读数为y,求y与x的函数关系式;(3)当CP旋转多少秒时,△BCE是等腰三角形?【答案】(1)60°,直角三角形;(2)y=4x(0≤x≤45);(3)7.5秒或30秒【解析】【分析】(1)根据圆周角定理即可解决问题;(2)如图2﹣2中,由题意∠ACE=2x,∠AOE=y,根据圆周角定理可知∠AOE=2∠ACE,可得y=2x(0≤x≤45);(3)分两种情形分别讨论求解即可;【详解】解:(1)如图2﹣1中,∵∠ACB=90°,OA=OB,∴OA=OB=OC,∴∠OCA=∠OAC=30°,∴∠AOE=60°,∴点E处的读数是60°,∵∠E=∠BAC=30°,OE=OB,∴∠OBE=∠E=30°,∴∠EBC=∠OBE+∠ABC=90°,∴△EBC是直角三角形;故答案为60°,直角三角形;(2)如图2﹣2中,∵∠ACE=2x,∠AOE=y,∵∠AOE=2∠ACE,∴y=4x(0≤x≤45).(3)①如图2﹣3中,当EB=EC时,EO垂直平分线段BC,∵AC⊥BC,∵EO∥AC,∴∠AOE=∠BAC=30°,∠AOE=15°,∴∠ECA=12∴x=7.5.②若2﹣4中,当BE=BC时,易知∠BEC=∠BAC=∠BCE=30°,∴∠OBE=∠OBC=60°,∵OE=OB,∴△OBE是等边三角形,∴∠BOE=60°,∴∠AOB=120°,∠ACB=60°,∴∠ACE=12∴x=30,综上所述,当CP旋转7.5秒或30秒时,△BCE是等腰三角形;【点睛】本题考查几何变换综合题、创新题目、圆周角定理、等腰三角形的判定和性质等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考压轴题.6.如图,线段BC所在的直线是以AB为直径的圆的切线,点D为圆上一点,满足BD=BC,且点C、D位于直径AB的两侧,连接CD交圆于点E. 点F是BD上一点,连接EF,分别交AB、BD于点G、H,且EF=BD.(1)求证:EF∥BC;(2)若EH=4,HF=2,求BE的长.【答案】(1)见解析;(2) 233【解析】【分析】(1)根据EF=BD可得EF=BD,进而得到BE DF,根据“在同圆或等圆中,同弧或等弧所对的圆周角相等”即可得出角相等进而可证.(2)连接DF,根据切线的性质及垂径定理求出GF、GE的长,根据“在同圆或等圆中,同弧或等弧所对的圆周角相等”及平行线求出相等的角,利用锐角三角函数求出∠BHG,进而求出∠BDE的度数,确定BE所对的圆心角的度数,根据∠DFH=90°确定DE为直径,代入弧长公式即可求解.【详解】(1)∵EF=BD,∴EF=BD∴BE DF∴∠D=∠DEF又BD=BC,∴∠D=∠C,∴∠DEF=∠CEF∥BC(2)∵AB是直径,BC为切线,∴AB⊥BC又EF∥BC,∴AB⊥EF,弧BF=弧BE,GF=GE=12(HF+EH)=3,HG=1DB平分∠EDF,又BF∥CD,∴∠FBD=∠FDB=∠BDE=∠BFH ∴HB=HF=2∴cos∠BHG=HGHB =12,∠BHG=60°.∴∠FDB=∠BDE=30°∴∠DFH=90°,DE为直径,DE=43,且弧BE所对圆心角=60°.∴弧BE=16×43π=233π【点睛】本题是圆的综合题,主要考查圆周角、切线、垂径定理、弧长公式等相关知识,掌握圆周角的有关定理,切线的性质,垂径定理及弧长公式是解题关键.7.如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,DE⊥AC,垂足为E,交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)若∠C=60°,AC=12,求BD的长.(3)若tan C=2,AE=8,求BF的长.【答案】(1)见解析;(2) 2π;(3)10 3.【解析】分析:(1)连接OD,根据等腰三角形的性质:等边对等角,得∠ABC=∠C,∠ABC=∠ODB,从而得到∠C=∠ODB ,根据同位角相等,两直线平行,得到OD∥AC,从而得证OD⊥EF,即 EF是⊙O的切线;(2)根据中点的性质,由AB=AC=12 ,求得OB=OD=12AB=6,进而根据等边三角形的判定得到△OBD 是等边三角形,即∠BOD=600,从而根据弧长公式七届即可;(3)连接AD ,根据直角三角形的性质,由在Rt △DEC 中, tan 2DE C CE == 设CE=x,则DE=2x ,然后由Rt △ADE 中, tan 2AE ADE DE ∠== ,求得DE 、CE 的长,然后根据相似三角形的判定与性质求解即可.详解:(1)连接OD ∵AB=AC ∴∠ABC=∠C∵OD=OB ∴∠ABC=∠ODB∴∠C=∠ODB ∴OD ∥AC又∵DE ⊥AC ∴OD ⊥DE ,即OD ⊥EF∴EF 是⊙O 的切线(2) ∵AB=AC=12 ∴OB=OD=12AB =6 由(1)得:∠C=∠ODB=600∴△OBD 是等边三角形 ∴∠BOD=600∴BD =6062180ππ⨯= 即BD 的长2π (3)连接AD ∵DE ⊥AC ∠DEC=∠DEA=900在Rt △DEC 中, tan 2DE C CE== 设CE=x,则DE=2x ∵AB 是直径 ∴∠ADB=∠ADC=900 ∴∠ADE+∠CDE=900 在Rt △DEC 中,∠C+∠CDE=900∴∠C=∠ADE 在Rt △ADE 中, tan 2AE ADE DE ∠== ∵ AE=8,∴DE=4 则CE=2∴AC=AE+CE=10 即直径AB=AC=10 则OD=OB=5∵OD//AE ∴△ODF ∽△AEF∴ OF OD AF AE = 即:55108BF BF +=+ 解得:BF=103 即BF 的长为103. 点睛:此题考查了切线的性质与判定、圆周角定理、等腰三角形的性质、直角三角形以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.8.如图,PA 切⊙O 于点A ,射线PC 交⊙O 于C 、B 两点,半径OD ⊥BC 于E ,连接BD 、DC 和OA ,DA 交BP 于点F ;(1)求证:∠ADC+∠CBD =12∠AOD ; (2)在不添加任何辅助线的情况下,请直接写出图中相等的线段.【答案】(1)详见解析;(2)详见解析; 【解析】 【分析】()1根据垂径定理得到BD CD =,根据等腰三角形的性质得到()111809022ODA AOD AOD ∠=-∠=-∠,即可得到结论; ()2根据垂径定理得到BE CE =,BD CD =,根据等腰三角形的性质得到ADO OAD ∠=∠,根据切线的性质得到90PAO ∠=,求得90OAD DAP ∠+∠=,推出PAF PFA ∠=∠,根据等腰三角形的判定定理即可得到结论.【详解】()1证明:OD BC ⊥,BD CD ∴=, CBD DCB ∴∠=∠,90DFE EDF ∠+∠=,90EDF DFE ∴∠=-∠,OD OA =,()111809022ODA AOD AOD ∴∠=-∠=-∠, 190902DFE AOD ∴-∠=-∠, 12DEF AOD ∴∠=∠, DFE ADC DCB ADC CBD ∠=∠+∠=∠+∠,12ADC CBD AOD ∴∠+∠=∠;()2解:OD BC⊥,∴=,BD CDBE CE=,BD CD∴=,=,OA OD∴∠=∠,ADO OADPA切O于点A,∴∠=,90PAO∴∠+∠=,90OAD DAP∠=∠,PFA DFEPFA ADO∴∠+∠=,90∴∠=∠,PAF PFA∴=.PA PF【点睛】本题考查了切线的性质,等腰三角形的判定和性质,垂径定理,圆周角定理,正确的识别图形是解题的关键.9.如图,点A,B,C,D,E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH=10,CH52=.(1)求证:AH是⊙O的切线;(2)若点D是弧CE的中点,且AD交CE于点F,求证:HF=HA;(3)在(2)的条件下,求EF的长.【答案】(1)证明见解析(2)证明见解析(3102【解析】【分析】(1)连接AC,由AB⊥CB可知AC是⊙O的直径,由圆周角定理可得∠C=∠D,于是得到tanC=3,故此可知AB=6,在Rt△ABC中,由勾股定理得:AC2= 40,从而可得AC2+AH2=CH2,根据勾股定理的逆定理可得AC⊥AH,问题得证;(2)连接DE、BE,由弦切角定理可知∠ABD=∠HAD,由D是CE的中点,可得∠CED=∠EBD,再由圆周角定理可得∠ABE=∠ADE,结合三角形的外角即可证明∠HAF=∠AFH,从而可证得AH=HF;(3)由切割线定理可得2,由(2)可知10,从而可得EF=FH﹣10-2.【详解】(1)如图1所示:连接AC.∵AB⊥CB,∴AC是⊙O的直径,∵∠C=∠D,∴tanC=3,∴AB=3BC=3×2=6,在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=40,又∵AH2=10,CH2=50,∴AC2+AH2=CH2,∴△ACH为直角三角形,∴AC⊥AH,∴AH是圆O的切线;(2)如图2所示:连接DE、BE,∵AH是圆O的切线,∴∠ABD=∠HAD,∵D是CE的中点,∴CD ED,∴∠CED=∠EBD,又∵∠ABE=∠ADE,∴∠ABE+∠EBD=∠ADE+∠CED,∴∠ABD=∠AFE,∴∠HAF=∠AFH,∴AH=HF;(3)由切割线定理可知:AH2=EH•CH10)22EH,解得:EH=2,∵由(2)可知AF=FH=10,∴EF=FH﹣EH=10-2.【点睛】本题主要考查圆的综合应用,解答主要应用了切线的判定定理、弦切角定理、切割线定理、圆周角定理、勾股定理、勾股定理的逆定理、三角形的外角的性质等,正确添加辅助线是解题的关键.10.如图,已知在△ABC中,AB=15,AC=20,tanA=12,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.(1)求⊙P的半径;(2)当AP=65时,试探究△APM与△PCN是否相似,并说明理由.【答案】(1)半径为35;(2)相似,理由见解析.【解析】【分析】(1)如图,作BD⊥AC,垂足为点D,⊙P与边AC相切,则BD就是⊙P的半径,利用解直角三角形得出BD与AD的关系,再利用勾股定理可求得BD的长;(2)如图,过点P作PH⊥AC于点H,作BD⊥AC,垂足为点D,根据垂径定理得出MN=2MH,PM=PN,再利用勾股定理求出PH、AH、MH、MN的长,从而求出AM、NC的长,然后求出AMMP、PNNC的值,得出AMMP=PNNC,利用两边对应成比例且夹角相等的两三角形相似即可证明.【详解】(1)如图,作BD⊥AC,垂足为点D,∵⊙P与边AC相切,∴BD就是⊙P的半径,在Rt△ABD中,tanA= 1BD2AD ,设BD=x ,则AD=2x ,∴x 2+(2x)2=152,解得:x=35, ∴半径为35;(2)相似,理由见解析,如图,过点P 作PH ⊥AC 于点H ,作BD ⊥AC ,垂足为点D ,∴PH 垂直平分MN ,∴PM=PN ,在Rt △AHP 中,tanA=12PH AH =, 设PH=y ,AH=2y ,y 2+(2y )2=(65)2解得:y=6(取正数),∴PH=6,AH=12,在Rt △MPH 中,MH=()22356-=3,∴MN=2MH=6,∴AM=AH-MH=12-3=9,NC=AC-MN-AM=20-6-9=5,∴3535AM MP ==,35PN NC =, ∴AM MP =PN NC, 又∵PM=PN ,∴∠PMN=∠PNM ,∴∠AMP=∠PNC ,∴△AMP ∽△PNC.【点睛】本题考查了解直角三角形、垂径定理、相似三角形的判定与性质等,综合性较强,有一定的难度,正确添加辅助线、灵活应用相关的性质与定理是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆中考真题精选汇编一座号_______姓名______________分数________ 一、选择题(每小题2分,共40分)1.(2010湖南长沙)已知⊙O1、⊙O2的半径分别是12r=、24r=,若两圆相交,则圆心距O1O2可能取的值是().A、2 B、4 C、6 D、82.(2010江苏宿迁)外切两圆的半径分别为2 cm和3cm,则两圆的圆心距是()A.1cm B.2cm C.3cm D.5cm3.(2010 山东济南)已知两圆的半径分别是3和2,圆心的坐标分别是(0,2)和(0,-4),那么两圆的位置关系是() A.内含 B.相交 C.相切 D.外离4.(2010江苏无锡)已知两圆内切,它们的半径分别为3和6,则这两圆的圆心距d 的取值满足()A.9d>B.9d=C.39d<<D.3d=5.(2010年上海)已知圆O1、圆O2的半径不相等,圆O1的半径长为3,若圆O2上的点A满足AO1 = 3,则圆O1与圆O2的位置关系是()A.相交或相切B.相切或相离C.相交或内含D.相切或内含6.(2010山东临沂)已知两圆的半径分别是2㎝和4㎝,圆心距是6㎝,那么这两圆的位置关系是()(A)外离(B)外切(C)相交(D)内切7.(2010 四川泸州)已知⊙O1与⊙O2的半径分别为2和3,两圆相交,则两圆的圆心距m满足()A.m=5 B.m=1 C.m>5 D.1<m <58.(2010 山东淄博)已知两圆的半径分别为R和r(R>r),圆心距为d.如图,若数轴上的点A表示R-r,点B表示R+r,当两圆外离时,表示圆心距d的点D所在的位置是(A)在点B右侧(B)与点B重合(C)在点A和点B之间(D)在点A左侧9.(2010湖北宜昌)两圆的半径分别为2和1,圆心距为3,则反映这两圆位置关系的为图( )。
10.(2010 福建莆田)已知 1o 和2o 的半径分别是3cm 和5cm ,若12o o =1cm ,则1o 与2o 的位置关系是( )A . 相交 B. 相切 C. 相离 D. 内含11.(2010广东湛江)已知两圆的半径分别为3cm 和4cm ,两个圆的圆心距为8cm ,则两圆的位置关系是( )A.内切 B.相交 C.外离 D.外切12.(2010湖南常德)如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为 ( )A .πB .1C .2D .23π13.(2010甘肃兰州) 现有一个圆心角为90,半径为cm 8的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为( ) A . cm 4 B .cm 3 C .cm 2 D .cm 114.(2010山东威海)一个圆锥的底面半径为6㎝,圆锥侧面展开图扇形的圆心角为240°,则圆锥的母线长为( ) A .9㎝ B .12㎝ C .15㎝D .18㎝15.(2010福建宁德)如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A 的半径为1,⊙B 的半径为2,将⊙A 由图示位置向右平移1个单位长后,⊙A 与静止的⊙B 的位置关系是( ).A.内含 B.内切 C.相交 D.外切 16.(2010湖北省咸宁)如图,两圆相交于A ,B 两点,小圆经过大圆的圆心O ,点C ,D分别在两圆上,若100ADB ∠=︒,则ACB ∠的度数为 ( ) A .35︒B .40︒C .50︒D .80︒17.(2010山东济宁)如图,如果从半径为9cm的圆形纸片剪去1圆周的一个扇形,3将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为()A.6cm B.35cm C.8cm D.53cm18.(2010浙江杭州)如图,5个圆的圆心在同一条直线上, 且互相相切,若大圆直径是12,4个小圆大小相等,则这5个圆的周长的和为()A. 48πB. 24πC. 12πD. 6π19.(2010江苏无锡)已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是()A.20cm2B.20πcm2C.10πcm2D.5πcm220.(2010江苏镇江)已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于()A.8πB.9πC.10πD.11π二、填空题(每小题2分,共38分)1.(2010江苏徐州)如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆的半径为5 cm,小圆的半径为3 cm,则弦AB的长为_______cm.2.(2010云南昆明)半径为r的圆内接正三角形的边长为.(结果可保留根号)3.(2010陕西西安)如图是一条水平铺设的直径为2米的通水管道横截面,其水面宽为1.6米,则这条管道中此时最深为米。
4.(2010 江苏镇江)如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若AB=10,CD=8,则线段OE的长为.5.(2010 云南玉溪)如图,在半径为10的⊙O 中,OC垂直弦AB于点D, AB=16,则CD的长是.6.(2010新疆乌鲁木齐)如图4,AB是⊙O的直径,C、D为⊙O上的两点,若35∠CDB=°,则ABC∠的度数为。
7.(2010云南昭通)如图5,⊙O的弦AB=8,M是AB的中点,且OM为3,则⊙O 的半径为________.8.(2010辽宁本溪)如图所示,△ABC内接于⊙O,∠A=40°,则∠OBC的度数是.9.(2010福建省泉州)如图,点A、B、C在⊙O上,︒∠BOCA,则=∠45=.10.(2010四川达州)如图,一个宽为2 cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是cm.11.(2010湖南娄底)如图7在半径为R的⊙O中,弦AB的长与半径R相等,C是⌒上一点,则∠ACB的度数是_______.优弧AB12.(2010内蒙赤峰)如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于一点D,点E在⊙O上,∠AED=25°,则∠OBA的度数是___________.13.(2010湖南怀化)如图6,已知直线AB是⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙O上,且∠OBA=40°,则∠ADC= .14.(2010 浙江义乌)已知直线l 与⊙O 相切,若圆心O 到直线l 的距离是5,则⊙O 的半 径是 .15.(2010山东泰安)如图,直线AB 与半径为2的⊙O 相切于点C,点D 、E 、F 是⊙O 上三个点,EF ∥AB ,若EF=23,则∠EDC 的度数为 。
16.(2010 四川泸州)如图7,已知⊙O 是边长为2的等边△ABC 的内切圆,则⊙O 的面积为__________.17.(2010广东茂名)如图,已知AD 为⊙O 的切线,⊙O 的直径AB =2,弦AC =1, 则∠CAD = .18.(2010广西百色)如图,⊙O 的直径为20cm ,弦cm AB 16=,AB OD ⊥,垂足为D .则AB 沿射线OD 方向平移cm时可与⊙O 相切.19.(2010 四川成都)如图,在ABC ∆中,AB 为⊙O 的直径,60,70B C ∠=∠= , 则BOD ∠的度数是_____________度.三、解答题1.(2010广西梧州)如图,⊙O 的直径AC =13,弦BC =12,过点A 作直线MN ,使∠BAM =12 ∠AOB ,(1)求证:MN 是⊙O 的切线。
(2)延长CB 交MN 于点D ,求AD 的长。
DB M2.(2010广东东莞)如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4.⑴求∠POA的度数;⑵计算弦AB的长.ABCDPO3.(2010 山东省德州)如图,在△ABC 中,AB =AC ,D 是BC 中点,AE 平分∠BAD 交BC 于点E ,点O 是AB 上一点,⊙O 过A 、E 两点, 交AD 于点G ,交AB 于点F . (1)求证:BC 与⊙O 相切;(2)当∠BAC =120°时,求∠EFG 的度数.4. (2010湖北省咸宁)如图,在⊙O 中,直径AB 垂直于弦CD ,垂足为E ,连接AC , 将△ACE 沿AC 翻折得到△ACF ,直线FC 与直线AB 相交于点G .(1)直线FC 与⊙O 有何位置关系?并说明理由;BACD E G OFFC(2)若2OB BG ==,求CD 的长.5. (2010江苏扬州)如图,在△ABC 中,AB =AC ,以AB 为直径的半圆O 交BC 于点D ,DE ⊥AC ,垂足为E .(1)求证:点D 是BC 的中点; (2)判断DE 与⊙O 的位置关系,并证明你的结论; (3)如果⊙O 的直径为9,cosB =13 ,求DE 的长.ABC DEO·以下4题作为课后练习1.(2010山东泰安)如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.一、求证:DE是⊙O的切线;(2)若⊙O的半径为2,BE=1,求cosA的值.2.(2010北京)已知:如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.(1)求证:直线AC是⊙O的切线;(2)如果∠ACB=75°,⊙O的半径为2,求BD的长.ADFEDCB AO ·(第26题图)3.(2010四川内江)如图,在Rt △ABC 中,∠C =90°,点E 在斜边AB 上,以AE 为直径的⊙O 与BC 相切于点D .(1)求证:AD 平分∠BAC .(2)若AC =3,AE =4.①求AD 的值;②求图中阴影部分的面积.BC DE O4.(2010广东肇庆)如图,AB 是⊙O 的直径,AC 切⊙O 于点A ,且AC =AB ,CO 交⊙O 于点P ,CO 的延长线交⊙O 于点F ,BP 的延长线交AC 于点E ,连接AP 、AE . 求证:(1)AF //BE ; (2)△ACP ∽△FCA ;(3)CP =AECABPEOF参考答案 一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20答案 B D D D A B D A B D C C C A D B B B C D二、填空题 1. 8 2.3r 3. 0.4 4. 3 5. 4 6. 55° 7. 5 8. 50° 9. 90° 10. 1011. 30° 12. 40o 13. 25 14. 515. 30° 16.317. 30°18. 4 19. 1001.(1)证明:∵∠BAM =12 ∠AOB (已知),∠BCA =12 ∠AOB (同弧所对圆周角是圆心角的一半),∴∠BAM =∠BCA (等量代换),∵∠CBA =90°(直径所对圆周角是直角)∴∠BCA +∠CAB =90°, ∴∠BAM +∠CAB =90°,即:∠CAM =90°∴MN 是⊙O 的切线。
