新疆中考专题复习函数及图象

合集下载

2020年中考备考数学专题复习--新疆第1部分第3章第11节一次函数及其应用

2．一次函数与一元一次不等式的关系 (1)不等式 kx＋b>0 的解集⇔一次函数 y＝kx＋b 的图象位于 x 轴上方的部分所对应的自变量 x 的取值范围，即 y>0 时，x 的取值范围； (2)不等式 kx＋b<0 的解集⇔一次函数 y＝kx＋b 的图象位于 x 轴下方的部分所对应的自变量 x 的取值范围，即 y<0 时，x 的取值范围．
4．[2017 新疆生产建设兵团，21]某周日上午 8：00 小宇从家出发，乘车 1 小时到达某活动中心参加实践活动.11：00 时他在活动中心接到爸爸的电话，因急事要求他在 12：00 前回到家，他即刻按照来活动中心时的路线，以 5 千米/小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家 20 千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家 x(小时)后，到达离家 y(千米)的地方，图中折线 OABCD 表示 y 与 x 之间的函数关系．
第 1 题图
一次函数的实际应用
考向一销售(购买)问题 2．[2019 新疆维吾尔自治区、生产建设兵团，21]某水果店以每千克 8 元的价格购进苹果若干千克，销售了部分苹果后，余下的苹果每千克降价 4 元销售，全部售完．销售金额 y(元)与销售量 x(千克)之间的关系如图所示，请根据图象提供的信息完成下列问题：
k 决定函数的增减性
k>0 y 随 x 的增大而②__增__大____
b 决定图象与 y b>0⇔交点在 b＝0⇔交点在 b<0⇔交点在
轴的交点位置正半轴上
原点
负半轴上
大致图象
经过的象限第一、二、三第一、三第④_一__、__三__、__四__
k 决定函数的

(新)新疆中考备考数学专题复习—题型专项复习公开课PPT3

∴抛物线的解析式为
y＝－
55x2＋2 5 5x＋3
5
5 .
（新）新疆中考备考数学专题复习—题型专项复习教学 PPT - 3 -PP T执教课件【推荐】
（新）新疆中考备考数学专题复习—题型专项复习教学 PPT - 3 -PP T执教课件【推荐】
2023最新整理收集 do something
题型四二次函数综合题
【题型解读】二次函数的综合题，作为新疆中考的压轴题，其综合性强，考查形式相对固定，考查内容包括线段最值，面积问题，角度问题，特殊三角形问题，特殊四边形问题，相似三角形问题的综合，2019 年主要考查了相似三角形与面积问题的结合．涉及平移的性质，相似三角形的判定与性质，特殊三角形(直角三角形，等腰三角形等)的判定与性质，平行四边形的判定与性质等．考查形式：解答，一般设 3 问．分值：12～13 分．
（新）新疆中考备考数学专题复习—题型专项复习教学 PPT - 3 -PP T执教课件【推荐】
(2)求抛物线的解析式；
解：∵A (4,0)，B (－1,0)， ∴抛物线的解析式为 y＝a(x＋1)(x－4)＝a(x2－3x－4)， ∵抛物线经过点 C(0，－4)， ∴－4a＝－4，解得 a＝1， ∴抛物线的解析式为 y＝x2－3x－4.
（新）新疆中考备考数学专题复习—题型专项复习教学 PPT - 3 -PP T执教课件【推荐】
∴DCQP ＝QPDB＝CDDB，其中 CP＝n＋3a，DQ＝3－1＝2，PD＝1，BQ＝n，CD
＝－3a，BD＝3，
将以上数值代入比例式并解得 a＝±55，

中考初中数学复习方略(新疆)10

5
果某一温度的摄氏度数是25 ℃,那么它的华氏度数是77℉.
(√)
高频考点·疑难突破
考点一一次函数图象与性质【示范题1】(2020·嘉兴中考)一次函数y=2x-1的图象大致是
(B)
【思路点拨】根据一次函数的解析式,判断出k和b的符号即可解答. 【答题关键指导】 1.一次函数y=kx+b中,k的符号决定的是函数的增减性,(1)k>0时,直线y=kx+b由左至右上升. (2)k<0时,直线y=kx+b由左至右下降. 2.b的符号决定直线y=kx+bБайду номын сангаасy轴交点的坐标(0,b)的位置,(1)b>0时,交点在原点上方.(2)b=0时,交点即原点.(3)当b<0时,交点在原点下方.
(2)AB=3-(-3)=6, 设M(a,a+3),由MN∥y轴交直线l2于点N,得N(a,-2a+6), MN=|a+3-(-2a+6)|=AB=6, 解得a=3或a=-1, ∴M(3,6)或(-1,2).
【答题关键指导】 1.确定一次函数解析式的关键是用待定系数法求k,b. 2.考场答题三步走: (1)设一次函数解析式y=kx+b. (2)把直线上已知点的坐标代入y=kx+b,得关于k,b的方程(组). (3)解方程(组)得k,b的值.
【跟踪训练】 (2020·凉山州中考)若一次函数y=(2m+1)x+m-3的图象不经过第二象限,则m的取值范围是 ( D )
A.m>- 1
2
C.- 1 <m<3
2
B.m<3
D.- 1 <m≤3
2
考点二确定一次函数解析式【示范题2】(2020·南通中考)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点 C(1,m),与x轴交于点B. (1)求直线l2的解析式; (2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.

新疆中考数学知识考点

新疆中考数学知识考点数学语言亦对初学者而言感到困难。

如何使这些字有着比日常用语更精确的意思，亦困恼着初学者，如开放和域等字在数学里有着特别的意思。

今天作者在这给大家整理了一些新疆中考数学知识考点，我们一起来看看吧!新疆中考数学知识考点※三视图包括：主视图、俯视图和左视图。

三视图之间要保持长对正，高平齐，宽相等。

一样地，俯视图要画在主视图的下方，左视图要画在重视图的右边。

主视图：基本可认为从物体正面视得的图象俯视图：基本可认为从物体上面视得的图象左视图：基本可认为从物体左面视得的图象※视图中每一个闭合的线框都表示物体上一个表面(平面或曲面)，而相连的两个闭合线框一定不在一个平面上。

※在一个外形线框内所包括的各个小线框，一定是平面体(或曲面体)上凸出或凹的各个小的平面体(或曲面体)。

※在画视图时，看得见的部分的轮廓线通常画成实线，看不见的部分轮廓线通常画成虚线。

物体在光线的照射下，会在地面或墙壁上留下它的影子，这就是投影。

太阳光线可以看成平行的光线，像这样的光线所形成的投影称为平行投影。

探照灯、手电筒、路灯的光线可以看成是从一点动身的，像这样的光线所形成的投影称为中心投影。

※区分平行投影和中心投影：①视察光源;②视察影子。

眼睛的位置称为视点;由视点发出的线称为视野;眼睛看不到的地方称为盲区。

※从正面、上面、侧面看到的图形就是常见的正投影，是当光线与投影垂直时的投影。

①点在一个平面上的投影还是一个点;②线段在一个面上的投影可分为三种情形：线段垂直于投影面时，投影为一点;线段平行于投影面时，投影长度等于线段的实际长度;线段倾斜于投影面时，投影长度小于线段的实际长度。

③平面图形在某一平面上的投影可分为三种情形：平面图形和投影面平行的情形下，其投影为实际形状;平面图形和投影面垂直的情形下，其投影为一线段;平面图形和投影面倾斜的情形下，其投影小于实际的形状。

中考数学知识考点1、代数式与有理式用运算符号把数或表示数的字母连结而成的式子，叫做代数式。

知识必备03 函数及其图像(公式、定理、结论图表)-2023年中考数学知识梳理+思维导图

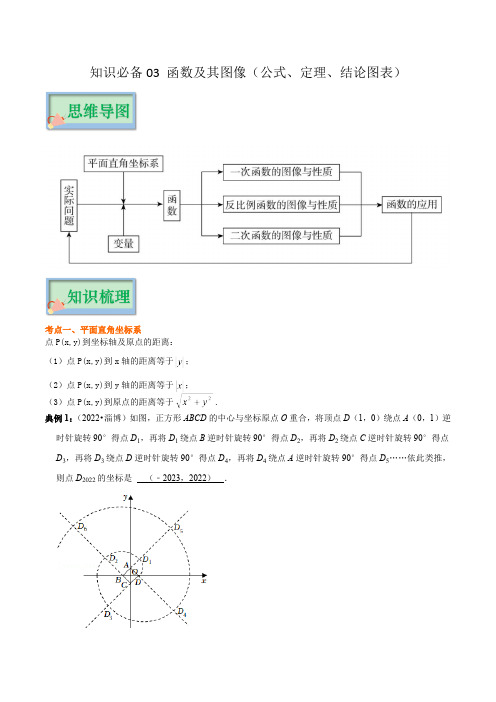
知识必备03 函数及其图像（公式、定理、结论图表）考点一、平面直角坐标系点P(x,y)到坐标轴及原点的距离：（1）点P(x,y)到x轴的距离等于；（2）点P(x,y)到y轴的距离等于；（3）点P(x,y)到原点的距离等于.典例1：（2022•淄博）如图，正方形ABCD的中心与坐标原点O重合，将顶点D（1，0）绕点A（0，1）逆时针旋转90°得点D1，再将D1绕点B逆时针旋转90°得点D2，再将D2绕点C逆时针旋转90°得点D3，再将D3绕点D逆时针旋转90°得点D4，再将D4绕点A逆时针旋转90°得点D5……依此类推，则点D2022的坐标是　（﹣2023，2022）　．【分析】由题意观察发现：每四个点一个循环，D4n+2（﹣4n﹣3，4n+2），由2022＝505×4+2，推出D2022（﹣2023，2022）．【解答】解：∵将顶点D（1，0）绕点A（0，1）逆时针旋转90°得点D1，∴D1（1，2），∵再将D1绕点B逆时针旋转90°得点D2，再将D2绕点C逆时针旋转90°得点D3，再将D3绕点D逆时针旋转90°得点D4，再将D4绕点A逆时针旋转90°得点D5……∴D2（﹣3，2），D3（﹣3，﹣4），D4（5，﹣4），D5（5，6），D6（﹣7，6），……，观察发现：每四个点一个循环，D4n+2（﹣4n﹣3，4n+2），∵2022＝4×505+2，∴D2022（﹣2023，2022）；故答案为：（﹣2023，2022）．【点评】本题考查坐标与图形的变化﹣旋转，等腰直角三角形性质，规律型问题，解题的关键是学会探究规律的方法，属于中考选择题中的压轴题．考点二、函数及其图象由函数解析式画其图像的一般步骤：（1）列表：列表给出自变量与函数的一些对应值；（2）描点：以表中每对对应值为坐标，在坐标平面内描出相应的点；（3）连线：按照自变量由小到大的顺序，把所描各点用平滑的曲线连接起来.考点三、一次函数确定一个正比例函数，就是要确定正比例函数定义式（k0）中的常数k；确定一个一次函数，典例2：（2022•柳州）如图，直线y1＝x+3分别与x轴、y轴交于点A和点C，直线y2＝﹣x+3分别与x轴、y轴交于点B和点C，点P（m，2）是△ABC内部（包括边上）的一点，则m的最大值与最小值之差为（）A．1B．2C．4D．6【分析】由于P的纵坐标为2，故点P在直线y＝2上，要求符合题意的m值，则P点为直线y＝2与题目中两直线的交点，此时m存在最大值与最小值，故可求得．【解答】解：∵点P（m，2）是△ABC内部（包括边上）的一点，∴点P在直线y＝2上，如图所示，当P为直线y＝2与直线y2的交点时，m取最大值，当P为直线y＝2与直线y1的交点时，m取最小值，∵y2＝﹣x+3中令y＝2，则x＝1，y1＝x+3中令y＝2，则x＝﹣1，∴m的最大值为1，m的最小值为﹣1．则m的最大值与最小值之差为：1﹣（﹣1）＝2．故选：B．【点评】本题考查一次函数的性质，要求符合题意的m值，关键要理解当P在何处时m存在最大值与最小值，由于P的纵坐标为2，故作出直线y＝2有助于判断P的位置．需要确定一次函数定义式（k0）中的常数k和b.解这类问题的一般方法是待定系数法.典例3：（2022•沈阳）如图，在平面直角坐标系中，一次函数y＝kx+b的图象与x轴交于点A，与y轴交于点B（0，9），与直线OC交于点C（8，3）．（1）求直线AB的函数表达式；（2）过点C作CD⊥x轴于点D，将△ACD沿射线CB平移得到的三角形记为△A′C′D′，点A，C，D的对应点分别为A′，C′，D′，若△A′C′D′与△BOC重叠部分的面积为S，平移的距离CC′＝m，当点A′与点B重合时停止运动．①若直线C′D′交直线OC于点E，则线段C′E的长为　m　（用含有m的代数式表示）；②当0＜m＜时，S与m的关系式为　m2　；③当S＝时，m的值为　或15﹣2　．【分析】（1）将点B（0，9），C（8，3）的坐标代入直线解析式，求解即可；（2）①过点C作CF⊥C′D′，易得△CFC′∽△AOB，可用m表达CF和C′F的长度，进而可表达点C′，D′的坐标，由点C的坐标可得出直线OC的解析式，代入可得点E的坐标；②根据题意可知，当0＜m＜时，点D′未到直线OC上，利用三角形面积公式可得出本题结果；③分情况讨论，分别求出当0＜m＜时，当＜m＜5时，当5＜m＜10时，当10＜m＜15时，S与m的关系式，分别令S＝，建立方程，求出m即可．【解答】解：（1）将点B（0，9），C（8，3）的坐标代入直线y＝kx+b，∴，解得．∴直线AB的函数表达式为：y＝﹣x+9；（2）①由（1）知直线AB的函数表达式为：y＝﹣x+9，令y＝0，则x＝12，∴A（12，0），∴OA＝12，OB＝9，∴AB＝15；如图1，过点C作CF⊥C′D′于点F，∴CF∥OA，∴∠OAB＝∠FCC′，∵∠C′FC＝∠BOA＝90°，∴△CFC′∽△AOB，∴OB：OA：AB＝C′F：CF：CC′＝9：12：15，∵CC′＝m，∴CF＝m，C′F＝m，∴C′（8﹣m，3+m），A′（12﹣m，m），D′（8﹣m，m），∵C（8，3），∴直线OC的解析式为：y＝x，∴E（8﹣m，3﹣m）.∴C′E＝3+m﹣（3﹣m）＝m．故答案为：m．②法一、当点D′落在直线OC上时，有m＝（8﹣m），解得m＝，∴当0＜m＜时，点D′未到直线OC，此时S＝C′E•CF＝•m•m＝m2；法二、∵C′D′∥BO，∴△CC′E∽△CBO，∴＝（）2，即＝，∴S＝m2．故答案为：m2．③法一、分情况讨论，当0＜m＜时，由②可知，S＝m2；令S＝m2＝，解得m＝＞（舍）或m＝﹣（舍）；当≤m＜5时，如图2，设线段A′D′与直线OC交于点M，∴M（m，m），∴D′E＝m﹣（3﹣m）＝m﹣3，D′M＝m﹣（8﹣m）＝m﹣8；∴S＝m2﹣•（m﹣3）•（m﹣8）＝﹣m2+m﹣12，令﹣m2+m﹣12＝；整理得，3m2﹣30m+70＝0，解得m＝或m＝＞5（舍）；当5≤m＜10时，如图3，S＝S△A′C′D′＝×4×3＝6≠，不符合题意；当10≤m≤15时，如图4，此时A′B＝15﹣m，∴BN＝（15﹣m），A′N＝（15﹣m），∴S＝•（15﹣m）•（15﹣m）＝（15﹣m）2，令（15﹣m）2＝，解得m＝15+2＞15（舍）或m＝15﹣2．法二、分情况讨论，当0＜m＜时，由②可知，S＝m2；令S＝m2＝，解得m＝＞（舍）或m＝﹣（舍）；（同法一）当≤m＜5时，如图2，设线段A′D′与直线OC交于点M，∵S△A′C′D′＝×4×3＝6，∴S△A′CM＝6﹣＝，∵S△AOC＝18，∵A′D′∥OA，∴△A′CM∽△ACO，∴＝，∴CA′＝，∴m＝C′A′﹣CA′＝5﹣，当5≤m＜10时，如图3，S＝S△A′C′D′＝×4×3＝6≠，不符合题意；当10≤m≤15时，如图4，∵A′D′∥x轴，∴△A′BK∽△ABO，∵S＝，S△ABO＝54，∴＝，解得BA′＝2，∴m＝BA﹣BA′＝15﹣2．故答案为：或15﹣2．【点评】本题属于一次函数综合题，涉及待定系数法求函数解析式，三角形的面积，相似三角形的性质与判定，分类讨论思想等知识，根据△A′C′D′的运动，进行正确的分类讨论是解题关键．考点四、反比例函数反比例函数中反比例系数的几何意义，如下图，过反比例函数图像上任一点作x轴、y轴的垂线PM，PN，垂足为M、N，则所得的矩形PMON的面积S=PM PN=.∴.典例4：（2022•东营）如图，一次函数y1＝k1x+b与反比例函数y2＝的图象相交于A，B两点，点A的横坐标为2，点B的横坐标为﹣1，则不等式k1x+b＜的解集是（）A．﹣1＜x＜0或x＞2B．x＜﹣1或0＜x＜2C．x＜﹣1或x＞2D．﹣1＜x＜2【分析】根据两函数图象的上下位置关系结合交点横坐标，即可得出不等式k1x+b＜的解集，此题得解．【解答】解：观察函数图象可知，当﹣1＜x＜0或x＞2时，一次函数y1＝k1x+b的图象在反比例函数y2＝的图象的下方，∴不等式k1x+b＜的解集为：﹣1＜x＜0或x＞2，故选：A．【点评】本题考查了反比例函数与一次函数的交点问题，根据两函数图象的上下位置关系找出不等式的解集是解题的关键．典例5:（2022•徐州）如图，一次函数y＝kx+b（k＞0）的图象与反比例函数y＝（x＞0）的图象交于点A，与x轴交于点B，与y轴交于点C，AD⊥x轴于点D，CB＝CD，点C关于直线AD的对称点为点E．（1）点E是否在这个反比例函数的图象上？请说明理由；（2）连接AE、DE，若四边形ACDE为正方形．①求k、b的值；②若点P在y轴上，当|PE﹣PB|最大时，求点P的坐标．【分析】（1）设点A的坐标为（m，），根据轴对称的性质得到AD⊥CE，AD平分CE，如图，连接CE交AD于H，得到CH＝EH，求得E（2m，），于是得到点E在这个反比例函数的图象上；（2）①根据正方形的性质得到AD＝CE，AD垂直平分CE，求得CH＝AD，设点A的坐标为（m，），得到m＝2（负值舍去），求得A（2，4），C（0，2），把A（2，4），C（0，2）代入y＝kx+b得，解方程组即可得到结论；②延长ED交y轴于P，根据已知条件得到点B与点D关于y轴对称，求得|PE﹣PD|＝|PE﹣PB|，则点P 即为符合条件的点，求得直线DE的解析式为y＝x﹣2，于是得到结论．【解答】解：（1）点E在这个反比例函数的图象上，理由：∵一次函数y＝kx+b（k＞0）的图象与反比例函数y＝（x＞0）的图象交于点A，∴设点A的坐标为（m，），∵点C关于直线AD的对称点为点E，∴AD⊥CE，AD平分CE，如图．连接CE交AD于H，∴CH＝EH，∵BC＝CD，OC⊥BD，∴OB＝OD，∴OC＝AD，∵AD⊥x轴于D，∴CE∥x轴，∴E（2m，），∵2m×＝8，∴点E在这个反比例函数的图象上；（2）①∵四边形ACDE为正方形，∴AD＝CE，AD垂直平分CE，∴CH＝AD，设点A的坐标为（m，），∴CH＝m，AD＝，∴m＝×，∴m＝2（负值舍去），∴A（2，4），C（0，2），把A（2，4），C（0，2）代入y＝kx+b得，∴；②延长ED交y轴于P，∵CB＝CD，OC⊥BD，∴点B与点D关于y轴对称，∴|PE﹣PD|＝|PE﹣PB|，则点P即为符合条件的点，由①知，A（2，4），C（0，2），∴D（2，0），E（4，2），设直线DE的解析式为y＝ax+n，∴，∴，∴直线DE的解析式为y＝x﹣2，当x＝0时，y＝﹣2，∴P（0，﹣2）．故当|PE﹣PB|最大时，点P的坐标为（0，﹣2）．【点评】本题考查了反比例函数的综合题，正方形的性质，轴对称的性质，待定系数法求一次函数的解析式，正确地作出辅助线是解题的关键．考点五、二次函数1、两点间距离公式（当遇到没有思路的问题时，可用此方法拓展思路，以寻求解题方法）如图：点A坐标为（x1，y1），点B坐标为（x2，y2），则AB间的距离，即线段AB的长度为.2、函数平移规律：左加右减、上加下减.3、二次函数的最值如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当时，.如果自变量的取值范围是，那么，首先要看是否在自变量取值范围内，若在此范围内，则当x=时，；若不在此范围内，则需要考虑函数在范围内的增减性，如果在此范围内，y随x的增大而增大，则当时，，当时，；如果在此范围内，y随x的增大而减小，则当时，，当时，.4、抛物线的对称变换①关于轴对称关于轴对称后，得到的解析式是；关于轴对称后，得到的解析式是.②关于轴对称关于轴对称后，得到的解析式是；关于轴对称后，得到的解析式是.③关于原点对称关于原点对称后，得到的解析式是；关于原点对称后，得到的解析式是.④关于顶点对称关于顶点对称后，得到的解析式是；关于顶点对称后，得到的解析式是．⑤关于点对称关于点对称后，得到的解析式是.根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此永远不变．求抛物线的对称图象的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．典例6:（2022•内蒙古）如图，抛物线y＝ax2+bx+c（a≠0）与x轴的一个交点坐标为（﹣1，0），抛物线的对称轴为直线x＝1，下列结论：①abc＜0；②3a+c＝0；③当y＞0时，x的取值范围是﹣1≤x＜3；④点（﹣2，y1），（2，y2）都在抛物线上，则有y1＜0＜y2.其中结论正确的个数是（）A．1个B．2个C．3个D．4个【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．【解答】解：根据函数的对称性，抛物线与x轴的另外一个交点的坐标为（3，0）；①函数对称轴在y轴右侧，则ab＜0，而c＝3＞0，故abc＜0，故①正确，符合题意；②∵x＝﹣＝1，即b＝﹣2a，而x＝﹣1时，y＝0，即a﹣b+c＝0，∴a+2a+c＝0，∴3a+c＝0．∴②正确，符合题意；③由图象知，当y＞0时，x的取值范围是﹣1＜x＜3，∴③错误，不符合题意；④从图象看，当x＝﹣2时，y1＜0，当x＝2时，y2＞0，∴有y1＜0＜y2，故④正确，符合题意；故选：C．【点评】本题考查了二次函数图象与系数的关系：对于二次函数y＝ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b 和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右；常数项c决定抛物线与y轴交点位置：抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定：Δ＝b2﹣4ac＞0时，抛物线与x轴有2个交点；Δ＝b2﹣4ac＝0时，抛物线与x轴有1个交点；Δ＝b2﹣4ac＜0时，抛物线与x轴没有交点．考点六、函数的应用分段函数是指自变量在不同的取值范围内，其关系式（或图象）也不同的函数，分段函数的应用题多设计成两种情况以上，解答时需分段讨论.在现实生活中存在着很多需分段计费的实际问题，因此，分段计算的应用题成了近几年中考应用题的一种重要题型.典例7：（2022•德州）如图，题目中的黑色部分是被墨水污染了无法辨认的文字，导致题目缺少一个条件而无法解答，经查询结果发现，该二次函数的解析式为y＝x2﹣4x+1．已知二次函数y＝ax2+bx+c的图象经过点A（0，1），B（1，﹣2），．求该二次函数的解析式．（1）请根据已有信息添加一个适当的条件：　C（2，﹣3）（答案不唯一）　；（2）当函数值y＜6时，自变量x的取值范围：　﹣1＜x＜5　；（3）如图1，将函数y＝x2﹣4x+1（x＜0）的图象向右平移4个单位长度，与y＝x2﹣4x+1（x≥4）的图象组成一个新的函数图象，记为L．若点P（3，m）在L上，求m的值；（4）如图2，在（3）的条件下，点A的坐标为（2，0），在L上是否存在点Q，使得S△OAQ＝9．若存在，求出所有满足条件的点Q的坐标；若不存在，请说明理由．【分析】（1）只需填一个在抛物线图象上的点的坐标即可；（2）求出y＝6时，对应的x值，再结合图象写出x的取值范围即可；（3）求出抛物线向右平移4个单位后的解析式为y＝（x﹣6）2﹣3，根据题意可知x＝3时，P点在抛物线y＝（x﹣6）2﹣3的部分上，再求m的值即可；（4）分两种情况讨论：当Q点在抛物线y＝（x﹣6）2﹣3的部分上时，设Q（t，t2﹣12x+33），由S△OAQ＝2×（t2﹣12x+33）＝9，求出Q点坐标即可；当Q点在抛物线y＝x2﹣4x+1的部分上时，设Q （m，m2﹣4m+1），由S△OAQ＝2×（m2﹣4m+1）＝9，求出Q点坐标即可．【解答】解：（1）C（2，﹣3），故答案为：C（2，﹣3）（答案不唯一）；（2）∵y＝x2﹣4x+1，∴当x2﹣4x+1＝6时，解得x＝5或x＝﹣1，∴当y＜6时，﹣1＜x＜5，故答案为：﹣1＜x＜5；（3）∵y＝x2﹣4x+1＝（x﹣2）2﹣3，∴抛物线向右平移4个单位后的解析式为y＝（x﹣6）2﹣3，当x＝3时，点P在抛物线y＝（x﹣6）2﹣3的部分上，∴m＝6；（4）存在点Q，使得S△OAQ＝9，理由如下：当Q点在抛物线y＝（x﹣6）2﹣3的部分上时，设Q（t，t2﹣12x+33），∴S△OAQ＝2×（t2﹣12x+33）＝9，解得t＝6+2或t＝6﹣2，∴t＜4，∴t＝6﹣2，∴Q（6﹣2，9）；当Q点在抛物线y＝x2﹣4x+1的部分上时，设Q（m，m2﹣4m+1），∴S△OAQ＝2×（m2﹣4m+1）＝9，解得m＝2+2或m＝﹣2，∵m≥4，∴m＝2+2，∴Q（2+2，9）；综上所述：Q点坐标为（6﹣2，9）或（2+2，9）．【点评】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，函数图象平移的性质，数形结合解题是关键．。

乌鲁木齐市中考数学二次函数和几何综合专题

乌鲁木齐市中考数学二次函数和几何综合专题一、二次函数压轴题1．如图，在平面直角坐标系xOy 中，抛物线()20y ax bx c a =++>与x 轴相交于()()1, 0, 3, 0A B -两点，点C 为抛物线的顶点．点(0,)M m 为y 轴上的动点，将抛物线绕点M 旋转180︒，得到新的抛物线，其中B C 、旋转后的对应点分别记为’'B C 、．（1）若1a =，求原抛物线的函数表达式；（2）在（1）条件下，当四边形''BCB C 的面积为40时，求m 的值；（3）探究a 满足什么条件时，存在点M ，使得四边形' 'BCB C 为菱形?请说明理由．2．某班“数学兴趣小组”对函数234y x x =-++的图象和性质进行了探究，探究过程如下，请补充完整．（1）自变量x 的取值范围是全体实数，x 与y 的几组对应值列表如下：x⋯ 5- 4-3- 2-32- 1- 0 13223 45⋯ y ⋯6- 04 62546 4 6 25464m⋯m = ．（2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分．（3）观察函数图象，写出两条函数的性质．（4）直线y kx b =+经过325,24⎛⎫ ⎪⎝⎭，若关于x 的方程234x x kx b -++=+有4个不相等的实数根，则b 的取值范围为．3．小明对函数2(0)y a x bx c a =++≠的图象和性质进行了探究.已知当自变量x 的值为0或4时，函数值都为3-；当自变量x 的值为1或3时，函数值都为0．探究过程如下，请补充完整．（1）这个函数的表达式为；（2）在给出的平面直角坐标系中，画出这个函数的图象并写出这个函数的--条性质：；（3）进一步探究函数图象并解决问题：①直线y k =与函数2y a x bx c =++有三个交点，则k = ；②已知函数3y x =-的图象如图所示，结合你所画的函数图象，写出不等式2a x bx c++3x≤-的解集：．4．某数学兴趣小组在探究函数y＝x2﹣2|x|+3的图象和性质时，经历了以下探究过程：（1）列表（完成下列表格）．x…﹣3﹣2﹣1﹣1212123…y…632236…（2）描点并在图中画出函数的大致图象；（3）根据函数图象，完成以下问题：①观察函数y＝x2﹣2|x|+3的图象，以下说法正确的有（填写正确的序号）A．对称轴是直线x＝1；B．函数y＝x2﹣2|x|+3的图象有两个最低点，其坐标分别是（﹣1，2）、（1，2）；C．当﹣1＜x＜1时，y随x的增大而增大；D．当函数y＝x2﹣2|x|+3的图象向下平移3个单位时，图象与x轴有三个公共点；E．函数y＝（x﹣2）2﹣2|x﹣2|+3的图象，可以看作是函数y＝x2﹣2|x|+3的图象向右平移2个单位得到．②结合图象探究发现，当m满足时，方程x2﹣2|x|+3＝m有四个解．③设函数y＝x2﹣2|x|+3的图象与其对称轴相交于P点，当直线y＝n和函数y＝x2﹣2|x|+3图象只有两个交点时，且这两个交点与点P所构成的三角形是等腰直角三角形，求n的值．5．问题发现：如图1，在△ABC中，∠C=90°，分别以AC，BC为边向外侧作正方形ACDE 和正方形BCFG．（1）△ABC和△DCF面积的关系是______________；（请在横线上填写“相等”或“不等”）（2）拓展探究：若∠C≠90°，（1）中的结论还成立吗？若成立，请结合图2给出证明；若不成立，请说明理由；（3）解决问题：如图3，在四边形ABCD 中，AC ⊥BD ，且AC 与BD 的和为10，分别以四边形ABCD 的四条边为边向外侧作正方形ABFE 、正方形BCHG 、正方形CDJI ，正方形DALK ，运用（2）的结论，图中阴影部分的面积和是否有最大值？如果有，请求出最大值，如果没有，请说明理由．图1图2图36．综合与探究如图，在平面直角坐标系中，直线33y x =--与x 轴交于点A ，与y 轴交于点C ．抛物线2y x bx c =++经过A 、C 两点，且与x 轴交于另一点B （点B 在点A 右侧）．（1）求抛物线的解析式及点B 坐标；（2）设该抛物线的顶点为点H ，则BCH S =△______；（3）若点M 是线段BC 上一动点，过点M 的直线ED 平行y 轴交x 轴于点D ，交抛物线于点E ．求ME 长的最大值及点M 的坐标；（4）在（3）的条件下：当ME 取得最大值时，在x 轴上是否存在这样的点P ，使得以点M 、点B 、点P 为顶点的三角形是等腰三角形？若存在，请直接写出所有点P 的坐标；若不存在，请说明理由． 7．综合与探究如图，在平面直角坐标系中，抛物线234y x x =--+与x 轴分别交于点A 和点B （点A 在点B 的左侧），交y 轴于点C ．点P 是线段OA 上的一个动点，沿OA 以每秒1个单位长度的速度由点O 向点A 运动，过点P 作DP x ⊥轴，交抛物线于点D ，交直线AC 于点E ，连接BE ．（1）求直线AC 的表达式；（2）在点P 运动过程中，运动时间t 为何值时，EC ED =？（3）在点P 运动过程中，EBP △的周长是否存在最小值？若存在，求出此时点P 的坐标；若不存在，请说明理由． 8．综合与探究如图，已知二次函数()220y ax bx a =++≠的图像与x 轴交于1,0A ，B 两点，与y 轴交于点C ，直线122y x =-+经过B ，C 两点（1）求二次函数的解析式；（2）点P 是线段 BC 上一个动点，过点P 作x 轴的垂线于点Q ，交抛物线于点D ，当点Q 是线段PD 的中点时，求点P 的坐标；（3）在（2）的条件下，若点M 是直线BC 上一点，N 是平面内一点，当以P ，D ，M ，N 为顶点的四边形是菱形时，请直接写出点N 的坐标．9．已知抛物线()2n n n y x a b =--+（n 为正整数，且120n a a a ≤<<<）与x 轴的交点为(0,0)A 和()1,0,2n n nn A c c c -=+．当1n =时，第1条抛物线()2111=--+y x a b 与x 轴的交点为(0,0)A 和1(2,0)A ，其他以此类推．（1）求11,a b 的值及抛物线2y 的解析式．（2）抛物线n y 的顶点n B 的坐标为（_______，_______）；以此类推，第(1)n +条抛物线1n y +的顶点1n B +的坐标为（______，_______）；所有抛物线的顶点坐标(,)x y 满足的函数关系式是_________．（3）探究以下结论：①是否存在抛物线n y ，使得△n n AA B 为等腰直角三角形？若存在，请求出抛物线n y 的解析式；若不存在，请说明理由．②若直线(0)=>x m m 与抛物线n y 分别交于点12,,,n C C C ，则线段12231,,,n n C C C C C C -的长有何规律？请用含有m 的代数式表示． 10．综合与探究如图，已知直线y mx n =+与抛物线2y x bx c =++分别相交于A 、B 两点，1,0A ，()0,3B -，点C 是抛物线与x 轴的另一个交点（与A 点不重合）．（1）求抛物线的解析式及直线y mx n =+的解析式；（2）求ABC 的面积；（3）在抛物线的对称轴上，是否存在点M ，使ABM 周长最短？若不存在，请说明理由；若存在，求出点M 的坐标．（4）如果对称轴上有一动点H ，在平面内是否存在点N ，使A 、B 、H 、N 四点构成矩形？若存在，直接写出N 点的坐标；若不存在，请说明理由二、中考几何压轴题11．[探索发现]（1）如图①，△ABC 与△ADE 为等腰三角形，且两顶角∠ABC ＝∠ADE ，连接BD 与CE ，则△ABD 与△ACE 的关系是；[操作探究]（2）在△ABC 中，AB ＝AC ＝3，∠BAC ＝100°，D 是BC 的中点，在线段AD 上任取一点P ，连接PB ，将线段PB 绕点P 按逆时针方向旋转80°，点B 的对应点是点E ，连接BE ，得到△BPE ，随着点P 在线段AD 上位置的变化，点E 的位置也在变化，点E 可能在直线AD 的左侧，也可能在直线AD 上，还可能在直线AD 的右侧．请你探究，当点E 在直线AD 上时，如图②所示，连接CE ，判断直线CE 与直线AB 的位置关系，并说明理由． [拓展应用]（3）在（2）的应用下，请在图③中画出△BPE ，使得点E 在直线AD 的右侧，连接CE ，试求出点P 在线段AD 上运动时，AE 的最小值．12．如图（1），在矩形ABCD 中，8,6AB AD ==，点,E F 分别是边,DC DA 的中点，四边形DFGE 为矩形，连接BG ．（1）问题发现在图（1）中，CEBG=_________；（2）拓展探究将图（1）中的矩形DFGE 绕点D 旋转一周，在旋转过程中，CEBG的大小有无变化？请仅就图（2）的情形给出证明；（3）问题解决当矩形DFGE 旋转至,,B G E 三点共线时，请直接写出线段CE 的长．13．（感知）（1）如图①，在四边形ABCD 中，∠C=∠D=90°，点E 在边CD 上，∠AEB=90°，求证：AE EB =DECB．（探究）（2）如图②，在四边形ABCD 中，∠C=∠ADC=90°，点E 在边CD 上，点F 在边AD 的延长线上，∠FEG=∠AEB=90°，且EF EG =AEEB，连接BG 交CD 于点H ．求证：BH=GH ．（拓展）（3）如图③，点E 在四边形ABCD 内，∠AEB+∠DEC=180°，且AE EB =DEEC，过E 作EF 交AD 于点F ，若∠EFA=∠AEB ，延长FE 交BC 于点G ．求证：BG=CG ．14．如图1所示，边长为4的正方形ABCD 与边长为()14a a <<的正方形CFEG 的顶点C 重合，点E 在对角线AC 上．（问题发现）如图1所示，AE 与BF 的数量关系为________；（类比探究）如图2所示，将正方形CFEG 绕点C 旋转，旋转角为()030αα<<︒，请问此时上述结论是否还成立？如成立写出推理过程，如不成立，说明理由；（拓展延伸）若点F 为BC 的中点，且在正方形CFEG 的旋转过程中，有点A 、F 、G 在一条直线上，直接写出此时线段AG 的长度为________15．如图1，已知ABC EBD △≌△，90ACB EDB ∠=∠=︒，点D 在AB 上，连接CD 并延长交AE 于点F ，（1）猜想：线段AF 与EF 的数量关系为_____；（2）探究：若将图1的EBD △绕点B 顺时针方向旋转，当CBE ∠小于180︒时，得到图2，连接CD 并延长交AE 于点F ，则（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由；（3）拓展：图1中，过点E 作EG CB ⊥，垂足为点G ．当ABC ∠的大小发生变化，其它条件不变时，若EBG BAE ∠=∠，6BC =，直接写出AB 的长．16．等腰△ABC ，AB =AC ，∠BAC =120°，AF ⊥BC 于F ，将腰AB 绕点A 逆时针旋转至AB ′，记旋转角为α，连接BB ′，过C 作CE 垂直于直线BB ′，垂足为E ，连接CB ′．（1）问题发现：如图1，当40α=︒时，CB E ∠'的度数为_______；连接EF ，则EFAB '的值为________．（2）拓展探究：当0360α︒<<︒，且120α≠︒时，①（1）中的两个结论是否仍然成立？如果成立，请仅就图2的情形进行证明；如果不成立，请说明理由；②解决问题：当A ，E ，F 三点共线时，请直接写出BB BE'的值．17．综合与实践（问题背景）如图1，矩形ABCD 中，10,8AB BC ==．点E 为边BC 上一点，沿直线DE 将矩形折叠，使点C 落在AB 边的点C '处．（问题解决）（1）填空：AC '的长为______．（2）如图2，将DC E '沿线段AB 向右平移，使点C '与点B 重合，得到,D BE D E ''''与BC 交于点F ，D B '与DE 交于点G ．求EF 的长；（拓展探究）（3）在图2中，连接,GF EE '，则四边形GEE F '是平行四边形吗？若是，请予以证明；若不是，请说明理由． 18．综合与实践背景阅读：“旋转”即物体绕一个点或一个轴做圆周运动．在中国古典专著《百喻经·口诵乘船法而不解用喻》中记载：“船盘回旋转，不能前进．”而图形旋转即：在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转，这个定点叫做旋转中心，转动的角叫做旋转角．综合实践课上，“睿智”小组专门探究了正方形的旋转，情况如下：在正方形ABCD 中，点O 是线段BC 上的一个动点，将正方形ABCD 绕点O 顺时针旋转得到正方形A B C D ''''（点A '，B '，C '，D 分别是点A ，B ，C ，D 的对应点）．设旋转角为α（0180α<<︒）．操作猜想：（1）如图1，若点O 是BC 中点，在正方形ABCD 绕点旋转过程中，连接AA '，BB '，DD '，则线段AA '与DD '的数量关系是_______；线段AA '与BB '的数量关系是________．探究验证：（2）如图2，在（1）的条件下，在正方形ABCD 绕点O 旋转过程中，顺次连接点B ，B '，C ，C '，B ．判断四边形''BB CC 的形状，并说明理由．拓展延伸：（3）如图3，若2BO CO =，在正方形ABCD 绕点O 顺时针旋转的过程中，设直线BB '交线段AA '于点P ．连接OP ，并过点O 作OQ BB '⊥于点Q ．请你补全图形，并直接写出OPOQ的值． 19．如图：两个菱形ABCD 与菱形BEFG 的边AB BE ，在同一条直线上，边长分别为a 和b ，点C 在BG 上，点M 为CG 的中点．（1）观察猜想：如图①，线段BM 与线段AE 的数量关系是______________．（2）拓展探究：如图②，120ABC ∠=︒，将图①中的菱形BEFG 绕点B 顺时针旋转至图②位置，其他条件不变，连接BM ，①猜想线段BM 与线段AE 的数量关系，并说明理由． ②求出线段BM 与AE 所成的最小夹角．（3）解决问题：如图③，若将题目中的菱形改为矩形，且3BC EFAB BE=段BM 与线段AE 的数量关系． 20．（1）（问题发现）如图①，正方形AEFG 的两边分别在正方形ABCD 的边AB 和AD 上，连接CF ．填空：①线段CF 与DG 的数量关系为______； ②直线CF 与DG 所夹锐角的度数为_______．（2）（拓展探究）如图②，将正方形AEFG 绕点A 逆时针旋转，在旋转的过程中，（1）中的结论是否仍然成立，请利用图②进行说明．（3）（解决问题）如图③，在正方形ADBC 中，AD AC =，点M 为直线BC 上异于B ，C 的一点，以AM 为边作正方形AMEF ，点N 为正方形AMEF 的中心，连接CN ，若4,2AC CM ==，直接写出CN 的长．【参考答案】***试卷处理标记，请不要删除一、二次函数压轴题 1．B解析：（1）2 23;y x x =--（2）416m m ==-或；（3）3a ≥M ，使得四边形''BCB C 为菱形，理由见解析【分析】（1）因为1a =，所以2y x bx c =++，将()()1, 0, 3, 0A B -代入得关于b 和c 的二元一次方程组，解方程组得到b 和c 即可求得原抛物线的解析式；（2）连接','CC BB ，延长BC 与y 轴交于点E ，根据题（1）可求出点B 、C 的坐标，继而求出直线BC 的解析式及点E 的坐标，根据题意易知四边形''BCB C 是平行四边形，继而可知()1312BCM MBE MCE S S S ME ME ∆∆∆=-=⨯-⨯=，由此可知ME ＝10，继而即可求解点M 的坐标；（3）如图，过点C 作CD y ⊥轴于点D ，当平行四边形''BCB C 为菱形时，应有MB MC ⊥，故点M 在,O D 之间，继而可证MOB CDM ∆∆，根据相似三角形的性质可得MO MD BO CD •=•代入数据即可求解．【详解】解：（1）∵1a =，∴2y x bx c =++将()()1, 0, 3, 0A B -代入得：10930b c b c -+=⎧⎨++=⎩解得：23b c =-⎧⎨=-⎩∴原抛物线的函数表达式为：2 23y x x =--；（2）连接','CC BB ，并延长BC 与y 轴交于点E ，二次函数2 23y x x =--的项点为(1,4,)-()1,4,C ∴- ()3, 0,B∴直线BC 的解析式为： 2 6.y x =--()0,6E ∴-抛物线绕点M 旋转180︒','MB MB MC MC ==∴四边形''BCB C 是平行四边形，()1312BCM MBE MCE S S S ME ME ∆∆∆∴=-=⨯-⨯=10ME416m m ∴==-或（3）如图，过点C 作CD y ⊥轴于点D当平行四边形''BCB C 为菱形时，应有MB MC ⊥，故点M 在,O D 之间，当MB MC ⊥时，MOB CDM ∆∆， MO BOCD MD∴= 即MO MD BO CD •=•二次函数()()13y a x x =+-的顶点为()()()1,4,0,,3,0a M m B -1,,4,3CD MO m MD m a ON ∴==-=+=，()43m m a ∴-+=， ∴2430m am ， 216120,0a a ∆-≥>32a ∴≥所以32a ≥时，存在点M ，使得四边形''BCB C 为菱形．【点睛】本题考查二次函数的综合应用，涉及到平行四边形的性质、菱形的性质，难度较大，解题的关键是善于将函数问题转化为方程问题，善于利用几何图形的有关性质及二次函数的性质，注意挖掘题目中的隐藏条件．2．（1）-6；（2）答案见解析；（3）①该函数的图象关于y 轴对称；②该函数的图象有最高点；（4）2544b <<．【分析】（1）根据对称可得m=-6；（2）用平滑的曲线连接各点即可画出图形；（3）认真观察图象，总结出2条性质即可；（4）画出两函数图象即可得到结论．【详解】（1）由表格可知：图象的对称轴是y 轴， ∴m=-6，故答案为：-6；()2如图所示()3①该函数的图象关于y 轴对称②该函数的图象有最高点；（4）由图象可知：关于x 的方程234x x kx b -++=+有4个不相等的实数根时，即y=kx+b 时，与图象有4个交点，所以，由图象可以得出，当2544b <<时，直线与图象有4个不同的交点．故答案为：2544b <<．【点睛】本题考查了二次函数与x 轴的交点问题和一元二次方程的根的情况，注意利用数形结合的思想，理解一元二次方程与抛物线的关系是解此题的关键．3．（1）243y x x --＝；（2）如图所示，见解析；性质：函数的图象关于直线=2x 对称；或：当0x =或4时，函数有最小值3-；（3）①1；②0x =或35x ≤≤．【分析】（1）将0x =，3y =-；4x =，3y =-；1x =，0y =代入2||(0)y a x bx c a =++≠，得到：3c =-，4b =-，1a =，即可求解析式为2|4|3y x x =--；（2）描点法画出函数图象，函数关于2x =对称；（3）①从图象可知：当2x =时，1y =，1k =时直线y k =与函数2|4|3y x x =--有三个交点；②3y x =-与243y x x =--的交点为0x =或5x =，结合图象，2|4|33y x x x =---≤的解集为35x ≤≤．【详解】解：（1）将0x =，3y =-；4x =，3y =-；1x =，0y =代入2||(0)y a x bx c a =++≠，得到：3164310c a b c a b c ⎧=-⎪++=-⎨⎪++=⎩，解得143a b c =⎧⎪=-⎨⎪=-⎩2|4|3y x x ∴=--，故答案为2|4|3y x x =--．（2）如图：函数关于直线2x =对称，（3）①当2x =时，1y =，1k ∴=时直线y k =与函数2|4|3y x x =--有三个交点，故答案为1；②3y x =-与243y x x =--的交点为0x =或5x =或x=3，结合图象，2|4|33y x x x =---≤的解集为0x =或35x ≤≤，故答案为0x =或35x ≤≤．【点睛】本题类比函数探究过程探究绝对值函数与不等式组关系；能够准确的画出函数图象，从函数图象中获取信息，数形结合解题是关键．4．B解析：（1）详见解析；（2）详见解析；（3）①B 、D 、E ；②2＜m ＜3；③n ＝2或6．【分析】（1）把x ＝﹣12，0，12分别代入函数表达式即可求解；（2）描点确定函数图象；（3）①结合图象，根据二次函数的性质依次判断各项即可求解；②根据二次函数的图象即可解答；③如图，当直线y ＝n 处于直线m 或m ′的位置时，由此即可求解．【详解】（1）把x ＝﹣12，0，12分别代入函数表达式得：y ＝94，3，94；故答案为94，3，94；（2）描点确定函数图象如下：（3）①A．对称轴是直线x＝0，故错误；B．函数y＝x2﹣2|x|+3的图象有两个最低点，其坐标分别是（﹣1，2）、（1，2），故正确；C．当﹣1＜x＜1时，函数在y轴右侧，y随x的增大而增大，故错误；D．当函数y＝x2﹣2|x|+3的图象向下平移3个单位时，图象与x轴有三个公共点，正确；E．函数y＝（x﹣2）2﹣2|x﹣2|+3的图象，可以看作是函数y＝x2﹣2|x|+3的图象向右平移2个单位得到，正确；故答案为：B、D、E；②从图象看，2＜m＜3时，方程x2﹣2|x|+3＝m有四个解；③如图，当直线y＝n处于直线m或m′的位置时，点P和图象上的点构成等腰直角三角形，即n＝2或6．【点睛】本题考查了二次函数的图象和性质，正确的识别图象，利用数形结合思想是解决问题的关键．5．B解析：（1）相等；（2）成立，理由见解析；（3）阴影部分的面积和有最大值,最大值为25 【解析】解：（1）相等；（2）成立；理由如下：如图，延长BC 到点P ，过点A 作AP ⊥BP 于点P ；过点D 作DQ ⊥FC 于点Q ．∴∠APC =∠DQC =90°．∵四边形ACDE 、四边形BCFG 均为正方形，∴AC =CD ，BC =CF ，∠ACP +∠PCD =90°，∠DCQ +∠PCD =90°， ∴∠ACP =∠DCQ ．={=APC DQC APC DQC ACP DCQAC DC在和中，∴∆∆∠∠∠∠=∴△APC ≌△DQC （AAS ）， ∴AP =DQ ．又∵S △ABC =BC •AP ，S △DFC =FC •DQ ， ∴S △ABC =S △DFC .（3）图中阴影部分的面积和有最大值理由：由（2）的结论可知： ,,,,KDJADC FBG ABC AEL ABD CHIBDC SSSS SS SS=====++++++=2.KDJFBGAELCHIADCABCABDBDCABCD S SS SSSSSSS ∴=阴影四边形设AC=m,则BD=10-m, ∵AC ⊥BD. ∴()22111125=105=522222ABCD S AC BD m m m m m 四边形（）⋅=⋅-=-+--+. ∴25.2ABCD S 四边形有最大值，最大值为∴阴影部分的面积和有最大值,最大值为256．A解析：（1）223y x x =--，()3,0B ；（2）3；（3）ME 的最大值为94，点M 的坐标为33,22M ⎛⎫- ⎪⎝⎭；（4）存在，()10,0P ；23P ⎛⎫ ⎪⎝⎭；33P ⎛⎫ ⎪⎝⎭；43,02P ⎛⎫ ⎪⎝⎭【分析】（1）由直线y =-3x -3与x 轴交于点A ，与y 轴交于点C ，得A （-1，0）、C （0，-3），将A （-1，0）、C （0，-3）代入y =x 2+bx +c ，列方程组求b 、c 的值及点B 的坐标；（2）设抛物线的对称轴交BC 于点F ，求直线BC 的解析式及抛物线的顶点坐标，再求出点F 的坐标，推导出S △BCH =12FH •OB ，可求出△BCH 的面积；（3）设点E 的横坐标为x ，用含x 的代数式表示点E 、点M 的坐标及线段ME 的长，再根据二次函数的性质求出线段ME 的最大值及点M 的坐标；（4）在x 轴上存在点P ，使以点M 、B 、P 为顶点的三角形是等腰三角形．由（3）得D（32，0），M （32，-32），由勾股定理求出OM =BM ，由等腰三角形PBM 的腰长为32OP 的长即可得到点P 的坐标．【详解】解：（1）∵直线y =-3x -3与x 轴、y 轴分别交于点A 、C ，当0y =时，330x --= 1x =- ∴()1,0A - 当0x =时，3y =-∴()03C -，∵抛物线y =x 2+bx +c 经过点A 、C ，∴103b c c -+=⎧⎨=-⎩ ∴23b c =-⎧⎨=-⎩∴抛物线的解析式是：223y x x =-- 当0y =时，2230x x --= 解得：11x =- 23x = ∴()3,0B（2）设抛物线的对称轴交BC 于点F ，交x 轴于点G ．设直线BC 的解析式为y =kx -3，则3k -3=0，解得k =1， ∴y =x -3；∵y =x 2-2x -3=（x -1）2-4， ∴抛物线的顶点H （1，-4），当x =1时，y =1-3=-2，∴F （1，-2）， ∴FH =-2-（-4）=2， ∴11112332222BCH S FH OG FH BG FH OB ∆=⋅+⋅=⋅=⨯⨯=．故答案为：3．（3）由（1）知()3,0B ，()03C -，直线BC 的解析式是：3y x =- 设()()M ,303t t t -≤≤，则()2,23E t t t --∴()22239(3)23324ME t t t t t t ⎛⎫=----=-+=--+ ⎪⎝⎭当32t =时，ME 的最大值94=∴点M 的坐标为33,22M ⎛⎫- ⎪⎝⎭（4）存在，如图3，由（2）得，当ME 最大时，则D （32，0），M （32，−32），∴DO =DB =DM =32； ∵∠BDM =90°，∴OM =BM =．点P 1、P 2、P 3、P 4在x 轴上，当点P 1与原点O 重合时，则P 1M =BM =2，P 1（0，0）；当BP 2=BM 时，则OP 2=3=∴P 20）；当点P 3与点D 重合时，则P 3M =P 3B =32， ∴P 3（32，0）；当BP 4=BM 时，则OP 4=3=∴P 4．综上所述，1234636(0,0),((,0),(222P P P P -+．【点睛】此题重点考查二次函数的图象与性质、等腰三角形的判定、用待定系数法求函数解析式、求抛物线的顶点坐标以及勾股定理、二次根式的化简等知识和方法，解最后一题时要注意分类讨论，求出所有符合条件的点P 的坐标．7．A解析：（1）4y x =+；（2）0t =或4t =3）存在，3,02P ⎛⎫- ⎪⎝⎭【分析】（1）根据二次函数的解析式可以求出点A 和点C 坐标，把点A 和点C 的坐标代入联立方程组，即可确定一次函数的解析式；（2）由题意可得点P 的坐标，从而可得点D 的坐标，故可求得ED 的长，再由A 、C 的坐标可知：OA =OC ，即△AOC 是等腰直角三角形，因DP ⊥x 轴，故△AEP 也是等腰直角三角形，可分别得到AC 、AE 的长，故可得EC 的长，由题意EC =ED ，即可得关于t 的方程，解方程即可；（3）由EP =AP ，得EBP C EP BP BE AP BP BE AB BE =++=++=+△，AB 是定值，周长最小，就转化为BE 最小，根据垂线段最短就可确定点P 的特殊位置，从而求出点P 的坐标．【详解】解：（1）∵抛物线234y x x =--+与x 轴分别交于点A 和点B ，交y 轴于点C ，∴当0x =时，4y =，即()0,4C ，当0y =时，2340x x --+=，14x =-，21x =，即()4,0A -，()10B ,，设直线AC 的解析式为：y kx b =+则044k b b =-+⎧⎨=⎩， ∴14k b =⎧⎨=⎩， ∴直线AC 的表达式：4y x =+．（2）∵点P 沿OA 以每秒1个单位长度的速度由点O 向点A 运动，∴OP t =，(),0P t -，∵DP x ⊥轴，∴(),4E t t --+，()2,34D t t t --++，∴24DE t t =-+∵()4,0A -，()0,4C ，∴4OA =，4OC =，∴△AOC 是等腰直角三角形，∴45CAO ∠=︒，由勾股定理得：AC =∵DP x ⊥轴，在Rt APE 中，45CAP ∠=︒，∴△AEP 也是等腰直角三角形，∴4AP PE t ==-，)4AE t =-，∴EC AC AE =-，∴当24t t -+=时，即0t =或4t =EC ED =．（3）在Rt AEP △中，45OAC ∠=︒，∴AP EP =，∴EBP △的周长：EP BP BE AP BP BE AB BE ++=++=+．∴当BE 最小时EPB △的周长最小．当BE AC ⊥时，BE 最小， ∵()10B ,， ∴5AB =，在Rt AEB 中，90AEB =︒∠，45BAC ∠=︒，5AB =，BE AC ⊥， ∴1522PB AB ==， ∴32OP PB OB =-=， ∴3,02P ⎛⎫- ⎪⎝⎭．【点睛】本题是综合与探究题，此类问题的考查特点是综合性和探究性强，考查内容是一次函数解析式的确定、特殊点坐标的确定、三角形周长最小值等，渗透了分类讨论、数形结合、转化等数学思想，难度较大．8．B解析：（1）215222y x x =-+；（2）P （2，1）；（3）4225,1555N ⎛- ⎝，425,1555N ⎛- ⎝，()0,0N ，1811,55N ⎛⎫ ⎪⎝⎭【分析】（1）求出点B ，带入求解即可；（2）设,22t P t ⎛⎫-+ ⎪⎝⎭，(),0Q t ，()215,20＜＜422D t t t t ⎛⎫-+ ⎪⎝⎭，根据中点的性质列式计算即可；（3）根据菱形的性质分类讨论即可；【详解】（1）令1202x -+=，解得：4x =， ∴()4,0B ，令0x =，则2y =，∴()0,2C ，把1,0A ，()4,0B 代入()220y ax bx a =++≠中，∴2016420a b a b ++=⎧⎨++=⎩， ∴12a =，52b =-，∴215222y x x =-+；（2）设,22t P t ⎛⎫-+ ⎪⎝⎭，(),0Q t ，()215,20＜＜422D t t t t ⎛⎫-+ ⎪⎝⎭，∵Q 为PD 中点，∴2115-2202222t t t ⎛⎫++-+=⨯ ⎪⎝⎭， ∴213402t t -+=， ∴12t =，24t =（舍），∴()2,1P ；（3）①如图，由题意可得：PD 为菱形的边，,PM DN 为菱形的对角线，//,PD MN 2,PD MN DM ===由（2）可得：()2,1P ，()2,1D -，2,PD ∴=设22,1M m m -+⎛⎫ ⎪⎝⎭，1,42N m m ⎛⎫-+ ⎪⎝⎭，由2DM =可得：()221234,2m m ⎛⎫-+-+= ⎪⎝⎭ 整理得：()()51820,m m --=解得：1218,2,5m m == 检验：2m =不合题意舍去，取18,5m =1811811,,,.5555M N ⎛⎫⎛⎫∴ ⎪ ⎪⎝⎭⎝⎭如图，PD 为菱形的边， //,PD MN 2,PD MN DN ===同理可得：4225,1555N ⎛⎫+-- ⎪⎝⎭或45252,1.55N ⎛⎫--+ ⎪ ⎪⎝⎭②如图，当PD 为对角线时，由()2,1P ，()2,1D -，()()4,0,0,0,B O可得：,M B 重合，,N O 重合时，四边形PMDN 为菱形，()0,0.N ∴综上：4225,1555N ⎛- ⎝，425,1555N ⎛- ⎝，()0,0N ，1811,55N ⎛⎫ ⎪⎝⎭；【点睛】本题主要考查了二次函数综合，结合菱形的判定与性质、等腰三角形的性质和一元二次方程的求解是解题的关键．9．C解析：（1）1111a b =⎧⎨=⎩ ；y 2 ＝−（x−2）2＋4；（2）（n ，n 2 ）；[（n ＋1），（n ＋1）2 ]；y ＝x 2；（3）①存在，理由见详解；②C 1n -C n ＝2m ．【分析】（1）1(2,0)A ），则1c ＝2，则2c ＝2＋2＝4，将点A 、1A 的坐标代入抛物线表达式得：()2112110=-0(-2-)a b a b ⎧-+⎪⎨=-+⎪⎩，解得：1111a b =⎧⎨=⎩ ，则点2A （4，0），将点A 、2A 的坐标代入抛物线表达式，同理可得：2a ＝2，2b ＝4，即可求解；（2）同理可得：3a ＝3，3b ＝9，故点n B 的坐标为（n ，2n ），以此推出：点1n B +[（n ＋1），（n ＋1）2]，故所有抛物线的顶点坐标满足的函数关系式是：y ＝2x ，即可求解；（3）①△AAnBn 为等腰直角三角形，则AAn 2 ＝2ABn 2，即（2n ）2＝2（n 2＋4n ），即可求解；②y 1n c -＝−（m−n ＋1）2＋（n−1）2，y n c ＝−（m−n ）2＋n 2，C 1n -C n = y n c −y 1n c -，即可求解．【详解】解：（1）1(2,0)A ，则1c ＝2，则2c ＝2＋2＝4，将点A 、1A 的坐标代入抛物线表达式得： 2112110=()0(2)a b a b ⎧--+⎨=---+⎩，解得：1111a b =⎧⎨=⎩，则点2A （4，0），将点A 、2A 的坐标代入抛物线表达式，同理可得：2a ＝2，2b ＝4；故y 2 ＝−（x−2a ）2＋2b ＝−（x−2）2＋4；（2）同理可得：3a ＝3，3b ＝9，故点n B 的坐标为（n ，2n ），以此推出：点1n B + [（n ＋1），（n ＋1）2]，故所有抛物线的顶点坐标满足的函数关系式是：y ＝2x ；故答案为：（n ，n 2 ）；[（n ＋1），（n ＋1）2]；y ＝x 2；（3）①存在，理由：点A （0，0），点An （2n ，0）、点n B （n ，n 2 ），△AAnBn 为等腰直角三角形，则AAn 2 ＝2ABn 2，即（2n ）2＝2（n 2 ＋n 4），解得：n ＝1（不合题意的值已舍去），抛物线的表达式为：y ＝−（x−1）2 ＋1；②y 1n c -＝−（m−n ＋1）2＋（n−1）2，y n c ＝−（m−n ）2＋n 2，C 1n -C n ＝y n c −y 1n c -＝−（m−n ）2＋n 2 ＋（m−n ＋1）2−（n−1）2＝2m ．【点睛】本题考查的是二次函数综合运用，这种找规律类型题目，通常按照题设的顺序逐次求解，通常比较容易．10．A解析：（1）33y x =-，223y x x =+-；（2）6；（3）存在点M 使ABM 周长最短，其坐标为()1,2--；（4）存在，10,3⎛⎫ ⎪⎝⎭，72,3⎛⎫-- ⎪⎝⎭，()2,1-，()2,2- 【分析】（1）把A 、B 两点的坐标分别代入抛物线2y x bx c =++和直线y mx n =+中，解之即可；（2）由图可知，12ABC S AC OB =⋅，所以只需求出AC ，OB 的长即可，因为C 点为抛物线与x 轴的一个交点，令y=0即可求出C 点坐标，根据已知可得A 点坐标，从而得到AC 的长，根据已知得到B 点坐标，可得OB 的长，从而求出ABC 的面积；（3）由题意知，A 、C 关于对称轴对称，则可知MA MC =，故当B 、M 、C 三点在同一条直线上时MB MC +最小，此时ABM 的周长最小，连接BC 交对称轴于点M ，则M 即为满足条件的点，设直线BC 的解析式为y kx m =+，将B ，C 的坐标代入即可求出该解析式，令x=-1，即可求出点M 的坐标；（4）在平面内是否存在点N ，使A 、B 、H 、N 四点构成矩形，求N 点坐标时，需分情况讨论，当HB ⊥AB 时，根据互相垂直的两直线的斜率之积为-1，互相平行的两直线的斜率相等求出直线HB ，直线HN ，直线AN 的解析式，根据N 点为直线HN 和直线AN 的交点，联立方程组解之即可；同理可得当HA ⊥AB 时，N 点的坐标；而当AB 为对角线时，可得HA ⊥AB ，从而可求出直线AH 的解析式，设H 点坐标为()1,y -，根据△AHB 为直角三角形，利用勾股定理求出H 点的坐标，然后在利用互相垂直的两直线的斜率之积为-1，互相平行的两直线的斜率相等求出N 点的坐标．【详解】解：（1）把A 、B 两点的坐标分别代入2y x bx c =++得103b c c ++=⎧⎨=-⎩，解得23b c =⎧⎨=⎩， ∴抛物线解析式为223y x x =+-．把A 、B 两点的坐标分别代入y mx n =+得03m n n +=⎧⎨=-⎩，解得33m n =⎧⎨=-⎩， ∴直线y mx n =+的解析式为33y x =-．（2）由（1）得，抛物线解析式为223y x x =+-，令0y =得2023x x =+-，解得11x =，23x =-，()3,0C ∴-，∵1,0A ，∴4AC =，∵()0,3B -，∴OB=3，1143622ABC S AC OB ∴=⋅=⨯⨯=；（3）()222314y x x x =+-=+-，∴抛物线的对称轴为1x =-， A 、C 关于对称轴对称，MA MC ∴=，MB MA MB MC ∴+=+，∴当B 、M 、C 三点在同一条直线上时MB MC +最小，此时ABM 的周长最小 ∴连接BC 交对称轴于点M ，则M 即为满足条件的点，设直线BC 的解析式为y kx m =+，直线BC 过点()0,3B -，()3,0C -，303k m m -+=⎧∴⎨=-⎩，解得13k m =-⎧⎨=-⎩， ∴直线BC 的解析式3y x =--，当1x =-时，2y =-，()1,2M ∴--，∴存在点M 使ABM 周长最短，其坐标为()1,2--．（4）存在，①当HB ⊥AB 时，如图所示由（1）得直线AB 的解析式为33y x =-， ∵HB ⊥AB ，∴设直线HB 的解析式为13y x b =-+，将B(0,-3)代入得 3b =-，∴直线HB 的解析式为133y x =--，当x=-1时，y=13-×(-1)-3=83-， ∴H 点的坐标为81,3⎛⎫-- ⎪⎝⎭， ∵四边形ABHN 为矩形，∴HN ∥AB ，AN ∥HB ，∴设直线HN 的解析式为y=3x+m ，把H 点坐标代入，得3×(-1)+m=83-，解得m=13,∴直线HN 的解析式为y=3x+13, ∴设直线AN 的解析式为13y x n =-+，把A 点坐标代入，得103n -+=，解得n=13, ∴设直线AN 的解析式为1133y x =-+， ∵N 点为直线HN 和直线AN 的交点，∴1331133y x y x ⎧=+⎪⎪⎨⎪=-+⎪⎩解得013x y =⎧⎪⎨=⎪⎩， ∴N 点坐标为10,3⎛⎫ ⎪⎝⎭． ②当HA ⊥AB 时，如图由（1）得直线AB 的解析式为33y x =-， ∵HA ⊥AB ，∴设直线HA 的解析式为13y x b =-+，将A(1，0)代入得13-+b=0，解得b=13， ∴直线HA 的解析式为1133y x =-+，当x=-1时，()1121333y =-⨯-+=， ∴H 点的坐标为21,3⎛⎫- ⎪⎝⎭， ∵四边形ABNH 是矩形，∴AB ∥NH ，BN ∥AH ，∴设直线HN 的解析式为y=3x+m ，把H 点坐标代入，得()2313m =⨯-+，解得m=113， ∴设直线HN 的解析式为y=3x+113， ∴设直线BN 的解析式为13y x n =-+，把B 点坐标代入，得 n=-3，∴设直线BN 的解析式为133y x =--， ∵N 点为直线HN 和直线BN 的交点，∴1133133y x y x ⎧=+⎪⎪⎨⎪=--⎪⎩解得273x y =-⎧⎪⎨=-⎪⎩， ∴N 点坐标为72,3⎛⎫-- ⎪⎝⎭． ③当AB 为对角线时，如图设H 点坐标为()1,y -，∵四边形AHBN 为矩形，∴△AHB 为直角三角形，∠AHB=90°，∴AH 2+BH 2=AB 2，即()()()2222111313y y --+++--=+-⎡⎤⎡⎤⎣⎦⎣⎦，解得121,2y y =-=-，∴H 点坐标为(-1,-1)，(-1,-2)，（a ）当H 点坐标为(-1,-1)时，设直线AH 的解析式为y=kx+b ，把A ，H 点坐标代入，得1k b -+=-⎩解得1212k b ⎧=⎪⎪⎨⎪=-⎪⎩， ∴直线AH 的解析式为1122y x =-， ∵AH ∥BN ， ∴设直线BN 的解析式为12y x b =+，把B 点坐标代入，得b=-3，∴直线BN 的解析式为132y x =-，∵AN ⊥BN ，∴设直线AN 的解析式为y=-2x+m ，把A 点坐标代入，得-2+m=0，解得m=2，∴直线AN 的解析式为y=-2x+2，∵N 点为直线AN 与BN 的交点， ∴22132y x y x =-+⎧⎪⎨=-⎪⎩ 解得22x y =⎧⎨=-⎩， ∴N 点坐标为(2,-2);（b ）当H 点坐标为(-1,-2)时，设直线AH 的解析式为y=kx+b ，把A ，H 点坐标代入，得02k b k b +=⎧⎨-+=-⎩解得11k b =⎧⎨=-⎩， ∴直线AH 的解析式为y=x-1，∵AH ∥BN ，∴设直线BN 的解析式为y=x+n ，把B 点坐标代入，得n=-3，∴直线BN 的解析式为y=x-3，∵AN ⊥BN ，∴设直线AN 的解析式为y=-x+m ，把A 点坐标代入，得-1+m=0，解得m=1，∴直线AN 的解析式为y=-x+1，∵N 点为直线AN 与BN 的交点，3 y x=-⎩解得21xy=⎧⎨=-⎩，∴N点坐标为(2,-1)．综上所述，存在点N，使A、B、H、N四点构成矩形，N点坐标为10,3⎛⎫⎪⎝⎭72,3⎛⎫--⎪⎝⎭()2,1-()2,2-．【点睛】本题为二次函数的综合运用，涉及待定系数法，轴对称的性质，勾股定理，三角形的面积等知识．在（2）中求得点C是解题的关键，在（3）中确定出M 点是解题的关键，在（4）中分情况讨论是解题的关键．二、中考几何压轴题11．（1）相似；（2）AB∥EC，理由见解析；（3）3．【分析】（1）结论：相似．先判断出△BAC∽△DAE，即可得出结论．（2）利用等腰三角形的性质证明∠ABC＝40°，∠ECB＝40°，推出∠解析：（1）相似；（2）AB∥EC，理由见解析；（3）3．【分析】（1）结论：相似．先判断出△BAC∽△DAE，即可得出结论．（2）利用等腰三角形的性质证明∠ABC＝40°，∠ECB＝40°，推出∠ABC＝∠ECB即可．（3）如图3中，以P为圆心，PB为半径作⊙P．利用圆周角定理证明∠BCE＝∠BPE＝40°，推出AB∥CE，因为点E在射线CE上运动，点P在线段AD上运动，所以当点P运动到与点A重合时，AE的值最小，此时AE的最小值＝AB＝3．【详解】解：（1）如图①中，∵△ABC与△ACE为等腰三角形，且两顶角∠ABC＝∠ADE，∴BA＝BC，DA＝DE，∴∠BAC＝∠DAE，∴△BAC∽△DAE，。

2021年新疆中考化学专题复习课件：专题02-坐标图像题

突的烧杯中滴加稀盐酸，稀盐酸先和氢氧化钠反应生成氯化钠和水，当氢氧化钠
破
反应完后，稀盐酸再和碳酸钠反应生成氯化钠、水和二氧化碳，Na2CO3反应完
后，生成CO2的质量不再改变。
谢谢观看
专
B.向饱和KNO3溶液中加入KNO3固体
题
重
C.某温度下，向一定量的硝酸钾不饱和溶液
点
中不断加入硝酸钾晶体
突
破
D.一定温度时，向一定量的饱和石灰水中加
入少量生石灰，再恢复至原温度
图T1-1
类型二金属与酸、盐反应图像
【详见提分专项（六）金属与酸、盐反应的图像题】
专题重点突破
例2 某同学在一定质量的AgNO3和Cu（NO3）2的混合溶液中加入铁粉，充分
突
B.50 s时，溶液中溶质为AlCl3
破
C.0~50 s，发生Al2O3+6HCl
2AlCl3+3H2O的
反应
D.100~140 s，压强减小是因为温度降低
图T2-5
[答案] B
[解析]随着反应的进行，温度升高，故反应过程中有热量放出；50 s时，溶液
专
中溶质为AlCl3和HCl；0~50 s，发生反应的化学方程式为Al2O3+6HCl
专题（二）
坐标图像题
图像题从不同角度、不同层面设置图像来提供信息，以考查相关的化学知
识。这类试题具有形象直观、概括性强、知识面广、综合性强等特点，侧重
专
考查“变化观念与平衡思想”的核心素养以及综合分析问题的能力。
题
常见考查类型有溶解图像、金属与酸（盐）反应图像、pH图像、酸碱的
重
点
优先反应图像以及各物质反应过程中的质量关系综合图像。

新疆维吾尔自治区喀什第二中学人教版九年级中考复习数学课件：线与角(共10张PPT)

第13讲线与角
考点分布：
一、线段与角二、相交线三、平行线
1、线段的有关计算 2、角的有关概念、角的表示 3、角的比较，角的和、差计算 4、余角、补角
1、对顶角 2、垂线、点到直线的距离 3、
课标要求：
（1）会比较线段的大小，理解线段和、差以及线段中点的意义。（2）会比较角的大小，会计算角度的和与差，认识度、分、秒，会进行角度的简单换算。（3）知道过一点有且仅有一条直线垂直于已知直线，会用三角尺或量角器过一点画一条直线的垂线。（4）理解平行线的概念，识别同位角、内错角、同旁内角，掌握两条直线平行的性质并会判断两直线是否平行。（5）知道过直线外一点有且仅有一条直线平行于已知直线，会用三角尺和直尺过已知直线外一点画这条直线的平行线。（6）了解两条平行线之间距离的意义，会度量两条平行线之间的距离。
平行公理的如果两条直线都和第三条直线平行，那么这两条直线也平行推论
平行线的同位角相等，两直线平行。判定
内错角相等，两直线平行。同旁内角互补，两直线平行。
考点清单：
平行线的性两直线平行，同位角相等。质
平行线间的距离
两直线平行，内错角相等。
两直线平行，同旁内角互补。
定义
过平行线中一条直线上的一点作另一条直线的垂线，垂线段的长度叫做两条平行线间的距离。
性质
两条平行线间的距离处处相等。
典型例题精讲：
高效复习44-46页
重要提（1）两点间的距离：连接两点间的线段的长度，叫做这两点间的距离（2）线段的中点
示
一定在线段上（3）“线段”是一个几何图形，而“线段的长度”是一个正数，二者是
有区别的，不要混淆
考点清单：
线段与角

新疆中考复习专题解直角三角函数

2011年新疆中考复习专题解直角三角函数一、知识点回顾1、锐角∠A的三角函数（按右图Rt△ABC填空）∠A的正弦：sin A = ,∠A的余弦：cos A = ,∠A的正切：tan A = ,∠A的余切：cot A =2、锐角三角函数值，都是实数（正、负或者0）；3、正弦、余弦值的大小范围：＜sin A＜；＜cos A＜4、tan A•cot A = ； tan B•cot B = ；5、sin A =cos（90°- ）；cos A = sin（ -）tan A =cot（）； cot A =6、填表7、在Rt△ABC中，∠C＝90゜，AB＝c,BC＝a，AC＝b,1）、三边关系（勾股定理）：2）、锐角间的关系：∠+∠= 90°3）、边角间的关系：sin A = ； sin B= ；cos A = ； cos B= ；tan A = ； tan B= ；cot A = ；cot B =8、图中角α可以看作是点A 的角也可看作是点B 的角；9、（1）坡度（或坡比）是坡面的高度（h ）和长度（l ）的比。

记作i ,即i = ；（2）坡角——坡面与水平面的夹角。

记作α，有i ＝lh =tan α（3）坡度与坡角的关系：坡度越大，坡角α就越，坡面就越二、巩固练习（1）、三角函数的定义及性质1、在△ABC 中,,900=∠C 13,5==AB AC ,则cos B 的值为2、在Rt ⊿ABC 中，∠C ＝90°，BC ＝10，AC ＝4，则______tan _____,cos ==A B ；3、Rt △ABC 中,若,900=∠C 2,4==BC AC ,则tan ______=B4、在△ABC 中，∠C ＝90°，1,2==b a ，则=A cos5、已知Rt △ABC 中,若,900=∠C cos 24,135==BC A ,则._______=AC 6、Rt △ABC 中,,900=∠C 35tan ,3==B BC ，那么.________=AC 7、已知32sin -=m α，且a 为锐角，则m 的取值范围是；8、已知：∠α是锐角，︒=36cos sin α，则α的度数是 9、当角度在︒0到︒90之间变化时，函数值随着角度的增大反而减小的三角函是（）A ．正弦和正切B ．余弦和余切C ．正弦和余切D ．余弦和正切（1）10、当锐角A 的22cos >A 时，∠A 的值为（） A 小于︒45B 小于︒30C 大于︒45D 大于︒6011、在Rt ⊿ABC 中，若各边的长度同时都扩大2倍，则锐角A 的正弦址与余弦值的情况（）A 都扩大2倍B 都缩小2倍C 都不变D 不确定12、已知α∠为锐角，若030cos sin =α，αtan ＝；若1tan 70tan 0=⋅α，则_______=∠α； 13、在△ABC 中,,900=∠C sin 23=A , 则cosB 等于( ) A 、1 B 、23 C 、22 D 、21 （2）、特殊角的三角函数值1、在Rt △ABC 中，已知∠C ＝900，∠A=450则A sin =2、已知：α是锐角，221cos =α，tan α=______； 3、已知∠A 是锐角，且______2sin ,3tan ==AA 则；4、在平面直角坐标系内P 点的坐标（︒30cos ，︒45tan ），则P 点关于x 轴对称点P ／的坐标为（） A ． )1,23(B ． )23,1(-C ． )1,23(- D ． )1,23(-- 5、下列不等式成立的是（）A ．︒<︒<︒45cos 60sin 45tanB ．︒<︒<︒45tan 60sin 45cotC ．︒<︒<︒45tan 30cot 45cosD ．︒<︒<︒30cot 60sin 45cos 6、若1)10tan(30=+α，则锐角α的度数为（）A ．200B ．300C ．400D ．500 7、计算（1）_______60cot 45tan _______,60cos 30sin 0000=+=+；（2）︒-︒+︒+︒-︒30sin 30cos 30tan 4145sin 60cos 22(3)000045tan 30tan 145tan 30tan ⋅-+ (4))60sin 45(cos 30sin 60cos 2330cos 45sin 00000---+ （3）、解直角三角形1、在△ABC 中,,900=∠C 如果4,3==b a ，求A ∠的四个三角函数值.解：（1）∵ a 2+b 2＝c 2∴ c =∴sin A = cos A =∴tan A = cot A =2、在Rt △ABC 中，∠C ＝90°，由下列条件解直角三角形：（1）已知a ＝43，b ＝23，则c= ；（2）已知a ＝10，c ＝102，则∠B= ；（3）已知c ＝20，∠A ＝60°，则a= ；（4）已知b ＝35，∠A ＝45°，则a= ；3、若∠A = ︒30，10=c ，则___________,==b a ；4、在下列图中填写各直角三角形中字母的值．7、设Rt △ABC 中，∠C ＝90゜，∠A 、∠B 、∠C 的对边分别为a 、b 、c ，根据下列所给条件求∠B 的四个三角函数值.（1）a =3,b =4; （2）a =6,c =10.8、在Rt △ABC 中，∠C ＝90゜，BC ：AC ＝3：4，求∠A 的四个三角函数值. 9、△ABC 中,已知0045,60,22=∠=∠=C B AC ，求AB 的长（4）、实例分析1、斜坡的坡度是3:1，则坡角.____________=α2、一个斜坡的坡度为1=ι︰3，那么坡角α的余切值为；3、一个物体A 点出发，在坡度为7:1的斜坡上直线向上运动到B ，当30=AB m 时，物体升高（） A730m B 830m C 23m D 不同于以上的答案 4、某水库大坝的横断面是梯形，坝内斜坡的坡度3:1=i ，坝外斜坡的坡度1:1=i ，则两个坡角的和为（）A ︒90B ︒60C ︒75D ︒1055、电视塔高为350m ，一个人站在地面，离塔底O 一定的距离A 处望塔顶B ，测得仰角为060，若某人的身高忽略不计时，__________=OA m.6、如图沿AC 方向修隧道,为了加快施工进度,要在小山的另一边同时进行.已知∠ABD=1500,BD=520m,∠B=600,那么开挖点E 到D 的距离DE=____m 时,才能使A,C,E 成一直线.7、一船向东航行，上午8时到达B 处，看到有一灯塔在它的南偏东060，距离为72海里的A 处，上午10时到达C 处，看到灯塔在它的正南方向，则这艘船航行的速度为（）A 18海里/小时B 318海里/小时C 36海里/小时D 336海里/小时8、如图，河对岸有铁塔AB ，在C 处测得塔顶A 的仰角为30°，向塔前进14米到达D ，在D 处测得A 的仰角为45°，求铁塔AB 的高。

2011年新疆中考专题复习-函数及图象

年新疆中考专题复习函数及图象一、学习的目标：掌握正、反比例、一次函数、二次函数的图象及性质二、知识点归纳：、平面直角坐标系：平面内两条有公共原点且互相垂直的数轴构成了平面直角坐标系，坐标平面内一点对应的有序实数对叫做这点的坐标。

在平面内建立了直角坐标系，就可以把“形”（平面内的点）和“数”（有序实数对）紧密结合起来。

、函数的概念：设在某个变化过程中有两个变量、,如果对于在某一范围内的每一个确定的值，都有唯一确定的值与它相对应，那么就说是的函数，叫做自变量。

、自变量的取值范围：对于实际问题，自变量取值必须使实际问题有意义。

对于纯数学问题，自变量取值应保证数学式子有意义。

、正比例函数：如果(是常数，≠)，那么，叫做的正比例函数．、、正比例函数的图象：过（，），（，）两点的一条直线．、正比例函数的性质()当>时，随的增大而增大()当<时，随的增大而减小、反比例函数及性质（）当>时，在每个象限内分别是随的增大而减小；（）当<时，在每个象限内分别是随的增大而增大．、一次函数如果(是常数，≠),那么叫做的一次函数．、一次函数的图象、一次函数的性质（）当>时，随的增大而增大；（）当<时，随的增大而减小．、二次函数的性质（）函数(其中、、是常数，且)叫做的二次函数。

（）利用配方，可以把二次函数表示成()或()的形式（）二次函数的图象是抛物线，当＞时抛物线的开口向上，当＜时抛物线开口向下。

抛物线的对称轴是直线或抛物线的顶点是(,)或()三、学习的过程：分层练习（组）一、选择题：．函数中，自变量的取值范围是（）．＜．＞1 ．≥．≠．在函数中，自变量的取值范围是（）. . . .．在函数中，自变量的取值范围是（）≥（）≠（）> （）<. 点（，）关于轴对称的点的坐标是（）．．（，）．（，）．（，）．（，）. 点（，）关于轴对称点的坐标为（）、（－，）、（－，－）、（，－）、（，－）．在直角坐标系中，点一定在（）. 抛物线上 . 双曲线上. 直线上 . 直线上. 若反比例函数的图象经过点（，），则的值为．．．．．函数的图象经过（）（）第一、二、三象限（）第一、三、四象限（）第二、三、四象限（）第一、二、四象限．函数＝的图象不经过（）．第一象限．第二象限．第三象限．第四象限、如图所示，函数的图象最可能是（）．为解决药价虚高给老百姓带来的求医难的问题，国家决定对某药品分两次降价。

新疆中考备考数学专题复习——题型专项复习课件 1PPT下载

(1)求证：四边形 BECD 是矩形；证明：∵四边形 ABCD 是平行四边形， ∴CD＝AB，CD∥AB， ∵BE＝AB， ∴BE＝CD， ∴四边形 BECD 是平行四边形， ∵∠ABD＝90°， ∴∠DBE＝90°. ∴▱BECD 是矩形．
新疆中考备考数学专题复习—— 题型专项复习课件 1 P PT下载
新疆中考备考数学专题复习—— 题型专项复习课件 1 P PT下载
(2)连接 DE 交 BC 于点 F，连接 AF，若 CE＝3，∠DAB ＝30°，求 AF 的长．
解：如答图，取 BE 的中点 G，连接 FG.
第 3 题答图由(1)可知，FB＝FC＝FE， ∴FG＝21CE＝32，FG⊥BE.
题型二
四边形的相关证明与计算
【题型解读】四边形的相关证明与计算在新疆近 3 年中考中均有涉及，2019 年主要考查了菱形的性质及矩形的判定．该题型主要涉及三角形全等的判定与性质，菱形的判定与性质，矩形的判定与性质，正方形的性质，平行线的性质，直角三角形的性质．一般考查形式：证明及相关计算．一般设 2 问．分值：8～12 分．
新疆中考备考数学专题复习—— 题型专项复习课件 1 P PT下载
新疆中考备考数学专题复习—— 题型专项复习课件 1 P PT下载
菱形
1．[2018 贺州]如图，在△ABC 中，∠ACB＝90°，O，D 分别是边 AC，AB 的中点，过点 C 作 CE∥AB 交 DO 的延长线于点 E，连接 AE.
新疆中考备考数学专题复习—— 题型专项复习课件 1 P PT下载
新疆中考备考数学专题复习—— 题型专项复习课件 1 P PT下载

新疆中考备考数学专题复习——题型专项复习优质课件

新疆中考备考数学专题复习—— 题型专项复习优质课件
新疆中考备考数学专题复习—— 题型专项复习优质课件
8．如图，在正方形 ABCD 中，AB＝30，点 E 在边 CD 上，且 CD＝3DE.将△ADE 沿 AE 对折至△AFE，延长 EF 交边 BC 于点 G.连接 AG，CF.下列结论：①△ABG≌△AFG； ②BG＝15；③△CFG 是正三角形；④△FGC 的面积为 90. 其中正确的是_①__②__④___(填所有正确答案的序号)．
图形的平移
1．如图，面积为 6 cm2 的直角三角形 ABC 沿 BC 方向平移至三角形 DEF 的位置，平移距离是 BC 的 2 倍，则图中四边形 ABED 的面积为__2_4_____cm2.
第 1 题图
2．如图，将边长为 3 个单位的等边△ABC 沿边 BC 向右平移 2 个单位得到 △DEF，则四边形 ABFD 的周长为 ___1_3__________．
新疆中考备考数学专题复习—— 题型专项复习优质课件
第 5 题图
新疆中考备考数学专题复习—— 题型专项复习优质课件
6．[2018 贵港]如图，在 Rt△ABC 中，∠ACB＝90°，AB ＝4，BC＝2，将△ABC 绕点 B 顺时针方向旋转到△A′BC′ 的位置，此时点 A′恰好在 CB 的延长线上，则图中阴影部分的面积为___4_π____(结果保留 π)．
新疆中考备考数学专题复习—— 题型专项复习优质课件
第 6 题图
新疆中考备考数学专题复习—— 题型专项复习优质课件
7．[2019 龙东地区]一张直角三角形纸片 ABC，∠ACB ＝90°，AB＝10，AC＝6，点 D 为 BC 边上的任一点，沿过点 D 的直线折叠，使直角顶点 C 落在斜边 AB 上的点 E 处，当 △BDE 是直角三角形时，则 CD 的长为__3_或__2_74__．

2020年中考备考数学专题复习--新疆第1部分第3章第10节平面直角坐标系与函数

(3)在原点上⇔x＝⑤__0_____，y＝⑥__0____. 特征
注：坐标轴上的点不属于任何象限
(1)第一、三象限角平分线上点的横、纵坐标
⑦__相__等__(如图中 A 点：x1＝⑧___y_1__)；各象限角 (2)第二、四象限角平分线上点的横、纵坐标平分线上 ⑨_互__为__相__反__数___(如图中 B 点：x2＝⑩_－__y_2___)．点的坐标
E 是 AD 上一点，点 P 从点 B 沿折线 BE－ED－DC 运动到
点 C 时停止；点 Q 从点 B 沿 BC 运动到点 C 时停止，速度
均为每秒 1 个单位长度．如果点 P，Q 同时开始运动，设运
动时间为 t，△BPQ 的面积为 y，已知 y 与 t 的函数图象如图
②
所
示
，
以
下
结
论
：
①BC
＝
10 ；
例 2 题图答案：A
【巩固训练】 1．[2018 潍坊]如图，菱形 ABCD 的边长是 4 厘米，∠B ＝60°，动点 P 以 1 厘米/秒的速度自 A 点出发沿 AB 方向运动至 B 点停止，动点 Q 以 2 厘米/秒的速度自 B 点出发沿折线 BCD 运动至 D 点停止．若点 P，Q 同时出发运动了 t 秒，记△BPQ 的面积为 s 平方厘米，下面图象中能表示 s 与 t 之间的函数关系的是( )
特征
(1)与 x 轴平行的直线上点的⑪_纵_______坐标相
等，如图，y＝⑫__y_1_____；与坐标轴 (2)与 y 轴平行的直线上点的⑬__横______坐标相平行的直
等，如图，x＝⑭__x_2_____. 线上点的
坐标特征
P(a，b)―关―于―x―轴―对―称→P1⑮_(_a_，__－__b_) ； P(a，b)―关―于―y―轴―对―称→P2⑯_(_－__a_，__b_) ；对称点的 P(a，b)―关―于―原――点―对―称→P3⑰_(_－__a_，__－__b_)__ 坐标特征

2020年中考备考数学专题复习--新疆第1部分第6章第25节与圆有关的计算

5．若圆锥的侧面积是 15π，母线长是 5，则该圆锥底面圆的半径是__3______．
阴影部分面积的计算
基本思想：转化思想，即把所求的不规则图形的面积转化为规则图形的面积．其中转化的方法主要有和差法、割补法，等积法及平移或旋转法，从而利用公式计算规则图形的面积来计算所求图形面积(具体图形及面积计算方法见本节 “新疆中考重难点 5”)．
底面圆周长
C＝⑥__2_π_r___＝圆锥侧面展开扇形的弧长
积，C 表示底面圆的
周长，α 表示侧面展开扇形的圆心角，r
侧面展开扇形的圆心角 α＝⑦_rl×__3_6_0_°
表示底面圆的半径，h 底面圆半径、圆锥的高、圆锥的母线
为圆锥的高，l 为圆锥的母线长
长之间的关系：r2＋⑧__h__2 ____＝l2
(2)求图中阴影部分的面积．解：∵AC∥BD，∠OEA＝90°，∴∠D＝∠EAO＝30°. ∵∠OBD＝90°，OB＝8， ∴BD＝ 3OB＝8 3， ∴S 阴影＝S△BDO－S 扇形 AOB＝21×8×8 3－60·3π6×0 82＝ 32 3－323π.
4．如图，在 Rt△ABC 中，∠ABC＝90°，AB＝2 3， BC＝2，以 AB 的中点为圆心，OA 的长为半径作半圆交 AC 于点 D，则图中阴影部分的面积为_5_4_3_－__π2_(计算结果保留 π)．
第 4 题图
圆锥的相关计算
圆锥
计算公式底面圆的面积 S＝⑤___π_r_2___
S 表示底面圆的面
－
1 2
× 3×3＝32π－32 3.
6．[2019 十堰]如图，AB 为半圆的直径，且 AB＝6，将半圆绕点 A 顺时针旋转 60°，点 B 旋转到点 C 的位置，则图中阴影部分的面积为__6_π_____.

新疆中考专题复习反比例函数

2011年新疆中考专题复习反比例函数一、选择1．2009年泸州已知反比例函数xky =的图象经过点P 一l,2,则这个函数的图象位于 A ．第二、三象限 B ．第一、三象限 C ．第三、四象限 D ．第二、四象限 2.2009年宁波市反比例函数ky x=在第一象限的图象如图所示,则k 的值可能是 A ．1B ．2C ．3D ．43．2009河池如图5,A 、B 是函数2y x=的图象上关于原点对称的任意两点, BC ∥x 轴,AC ∥y 轴,△ABC 的面积记为S ,则A ． 2S =B ． 4S =C ．24S <<D ．4S >4．2009年娄底市一小数学课外兴趣小组的同学每人制作一个面积为200cm 2的矩形学具进行展示. 设矩形的宽为x cm ,长为y cm ,那么这些同学所制作的矩形长y cm 与宽x cm 之间的函数关系的图象大致是关键词反比例函数5．2009年娄底一次函数y =kx +b 与反比例函数y =kx 的图象如图5所示,则下列说法正确的是 A ．它们的函数值y 随着x 的增大而增大 B ．它们的函数值y 随着x 的增大而减小 C ．k ＜0D ．它们的自变量x 的取值为全体实数O BxyC A 图56．2009丽水市如图,点P 在反比例函数1y x =x > 0的图象上,且横坐标为2. 若将点P 先向右平移两个单位,再向上平移一个单位后所得的像为点P '.则在第一象限内,经过点P '的反比例函数图象的解析式是A ．)0(5>-=x xy B .)0(5>=x x y C . )0(6>-=x x y D . )0(6>=x x y7．2009恩施市一张正方形的纸片,剪去两个一样的小矩形得到一个“E ”图案,如图所示,设小矩形的长和宽分别为x 、y ,剪去部分的面积为20,若210x ≤≤,则y 与x 的函数图象是8．2009年广西南宁在反比例函数1ky x-=的图象的每一条曲线上,y x 都随的增大而增大,则k 的值可以是 A ．1- B ．0C ．1D ．2关键词反比例函数9．2009年鄂州如图,直线y=mx 与双曲线y=xk交于A 、B 两点,过点A 作AM ⊥x 轴,垂足为M,连结BM,若ABM S ∆=2,则k 的值是A ．2B 、m-2C 、mD 、4关键词一次函数与反比例函数的综合应用10．2009泰安如图,双曲线)0(＞k xky =经过矩形QABC 的边BC 的中点E,交AB 于P210 5 O x y 2 10 5O x y 2 10 10O x y2 10 10O xy yx 1222 A ． B ． C ． D ．12点D;若梯形ODBC 的面积为3,则双曲线的解析式为A ．x y 1=B ．x y 2=C ． x y 3=D ．xy 6=11．2009年南宁市在反比例函数1ky x-=的图象的每一条曲线上,y x 都随的增大而增大,则k 的值可以是 A ．1- B ．0 C ．1 D ．212．2009年衡阳市一个直角三角形的两直角边长分别为y x ，,其面积为2,则y 与x 之间的关系用图象表示大致为13．2009年日照已知点M －2,3 在双曲线xky =上,则下列各点一定在该双曲线上的是 A.3,-2B.-2,-3C.2,3D.3,21．2009年广西梧州已知点A 11x y ，、B 22x y ，是反比例函数xky =0>k 图象上的两点, 若210x x <<,则有 A ．210y y <<B ．120y y <<C ．021<<y yD ．012<<y y14．2009年本溪反比例函数(0)ky k x=≠的图象经过点(23)-，,则该反比例函数图象在A ．第一、三象限B ．第二、四象限C ．第二、三象限D ．第一、二象限15．2009年漳州矩形面积为4,它的长y 与宽x 之间的函数关系用图象大致可表示为16．2009年哈尔滨点(13)P ，在反比例函数ky x=0k ≠的图象上,则k 的值是． A ．13 B ．3 C ．13- D ．3- 关键词反比例函数图像的性质17．2009年兰州如图2,在直角坐标系中,点A 是x 轴正半轴上的一个定点,点B 是双曲线3y x=0x >上的一个动点,当点B 的横坐标逐渐增大时,OAB △的面积将会A B C D y xOy xOy xOyxOyA B CO y OAB 图2A ．逐渐增大B ．不变C ．逐渐减小D ．先增大后减小二、填空：1．2009年滨州已知点A 是反比例函数3y x=-图象上的一点．若AB 垂直于y 轴,垂足为B ,则AOB △的面积= ．2.2009仙桃如图,已知双曲线)0k (xk y ＞=经过直角三角形OAB 斜边OB 的中点D,与直角边AB 相交于点C ．若△OBC 的面积为3,则k ＝____________．.3.2009年台州市请你写出一个图象在第一、三象限的反比例函数．答：．4.2009年义乌已知,点p 是反比例函数2y x=图像上的一个动点,p 的半径为1,当p 与坐标轴相交时,点p 的横坐标x 的取值范围是5．2009柳州反比例函数 xm y 1+=的图象经过点2,1,则m 的值是．答案16．2009年甘肃白银反比例函数的图象经过点P 2-,1,则这个函数的图象位于第象限．7.2009年河南点A 2,1在反比例函数y kx =的图像上,当1﹤x ﹤4时,y 的取值范围是 . 8．2009江西函数()()1240y x x y x x==>≥0，的图象如图所示,则结论：①两函数图象的交点A 的坐标为()22，； ②当2x >时,21y y >； ③当1x =时,3BC =；④当x 逐渐增大时,1y 随着x 的增大而增大,2y 随着x 的增大而减小．其中正确结论的序号是．1 2 21 O y x9．2009年新疆若梯形的下底长为x ,上底长为下底长的13,高为y ,面积为60,则y 与x 的函数关系是____________．不考虑x 的取值范围10．2009年牡丹江市如图,点A 、B 是双曲线3y x=上的点,分别经过A 、B 两点向x 轴、y 轴作垂线段,若1S =阴影，则12S S += ．11．2009白银市反比例函数的图象经过点P 2-,1,则这个函数的图象位于第象限．12．2009年清远已知反比例函数ky x=的图象经过点(23)，,则此函数的关系式是． 13.2009年益阳市如图4,反比例函数xky =)0(<k 的图象与经过原点的直线l 相交于A 、B 两点,已知A 点坐标为)1,2(-,那么B 点的坐标为 .14.2009年济宁市如图,⊙A 和⊙B 都与x 轴和y 轴相切,圆心A 和圆心B 都在反比例函数1y x=的图象上,则图中阴影部分的面积等于.8题图4x图515．2009年福州已知, A 、B 、C 、D 、E 是反比例函数16y x=x>0图象上五个整数点横、纵坐标均为整数,分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形阴影部分,则这五个橄榄形的面积总和是用含π的代数式表示16．2009年广西钦州如图是反比例函数y ＝kx在第二象限内的图象,若图中的矩形OABC 的面积为2,则k ＝_▲_．17．2009年甘肃定西反比例函数的图象经过点P 2-,1,则这个函数的图象位于第象限．2009年莆田如图,在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====,过点12345A A A A A 、、、、分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P 、、、、,得直角三角形1112233344455OP A A P A A P A A P A A P A 2、、、、，并设其面积分别为12345S S S S S 、、、、，则5S 的值为．．18．2009年包头如图,已知一次函数1y x =+的图象与反比例函数ky x=的图象在第一象限相交于点A ,与x 轴相交于点C AB x ，⊥轴于点B ,AOB △的面积为1,则AC 的长为保留根号．19．2009临沂如图,过原点的直线l 与反比例函数1y x=-的图象交于M ,N 两点,根据图象猜想线段MN 的长的最小值是___________．yO AC Byx O P 1 P 2P 3 P4 P 5A 1 A 2 A 3 A 4 A 52xA BO xy20．2009年兰州如图11,若正方形OABC 的顶点B 和正方形ADEF 的顶点E 都在函数 1y x=0x >的图象上,则点E 的坐标是 , . 关键词反比例函数的图像和性质21．2009年常德市如图1,已知点C 为反比例函数6y x=-上的一点,过点C 向坐标轴引垂线,垂足分别为A 、B ,那么四边形AOBC 的面积为．22．2009年陕西省13．若Ax 1,y 1,Bx 2,y 2是双曲线xy 3=上的两点,且x 1>x 2>0,则y 1 y 2填“>”“=”“<”．23． 2009武汉如图,直线43y x =与双曲线k y x =0x >交于点A ．将直线43y x =向右平移92个单位后,与双曲线k y x =0x >交于点B ,与x 轴交于点C ,若2=BCAO ,则k = ．24．2009年上海市反比例函数2y x=图像的两支分别在第象限．25．2009年黄冈市已知点(3,3)-是反比例函数图象上的一点,则此反比例函数图象的解析式是____________________________．26．2009成都如图,正方形OABC 的面积是4,点B 在反比例函数(00)ky k x x=><，的图象上．若点R 是该反比例函数图象上异于点B 的任意一点,过点R 分别作x 轴、y 轴的垂线,垂足为M 、N,从矩形OMRN 的面积中减去其与正方形OABC 重合部分的面积,记剩余部分的面积为S ．则Ox y ABCOyxMNl图1当S=mm 为常数,且0<m<4时,点R 的坐标是________________________ 用含m 的代数式表示关键词反比例函数的面积三、解答： 1．2009河池为了预防流感,中的含药量y 毫克与时间x 分钟成正比例；药物释放完毕后,y ,解答下列问题：1写出从药物释放开始,y 与x 之间的两个函数关系式及相应的自变量取值范围； 2据测定,当空气中每立方米的含药量降低到毫克以下时,学生方可进入教室,那么从药物释放开始, 至少需要经过多少小时后,学生才能进入教室 2．2009年嘉兴市如图,曲线C 是函数xy 6=在第一象限内的图象,抛物线是函数422+--=x x y 的图象．点),(y x P n 12n =，，在曲线C 上,且x y ，都是整数．1求出所有的点()n P x y ，；2在n P 中任取两点作直线,求所有不同直线的条数；3从2的所有直线中任取一条直线,求所取直线与抛物线有公共点的概率．3．2009年天津市已知图中的曲线是反比例函数5m y x-=m 为常数图象的一支． Ⅰ 这个反比例函数图象的另一支在第几象限常数m 的取值范围是什么分钟图9Ⅱ若该函数的图象与正比例函数2y x =的图象在第一象内限的交点为A ,过A 点作x 轴的垂线,垂足为B ,当OAB △的面积为4时,求点A 的坐标及反比例函数的解析式．4．2009年湘西自治州21.在反比例函数xky =的图像的每一条曲线上,y 都随x 的增大而减小． 1 求k 的取值范围；2 在曲线上取一点A ,分别向x 轴、y 轴作垂线段,垂足分别为B 、C ,坐标原点为O ,若四边形ABOC 面积为6,求k 的值．关键词反比例函数性质5．2009年衢州水产公司有一种海产品共2 104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下：现假定在这批海产品的销售中,每天的销售量y 千克与销售价格x 元/千克之间都满足这一关系． 1 写出这个反比例函数的解析式,并补全表格；2 在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出6．2009现假定在这批海产品的销售中,每天的销售量y 千克与销售价格x 元/千克之间都满足这一关系． 1 写出这个反比例函数的解析式,并补全表格；2 在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出3 在按2中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务 7．2009年重庆已知：如图,在平面直角坐标系xOy 中,直线AB 分别与x y 、轴交于点B 、A ,与反比例函数的图象分别交于点C 、D ,CE x ⊥轴于点E ,1tan 422ABO OB OE ∠===，，．1求该反比例函数的解析式； 2求直线AB 的解析式．8. 2009年宜宾已知：如图,在平面直角坐标系x O y 中,Rt △OCD 的一边OC 在x 轴上,∠C=90°,点D 在第一象限,OC=3,DC=4,反比例函数的图象经过OD 的中点A ． 1求该反比例函数的解析式；2若该反比例函数的图象与Rt △OCD 的另一边DC 交于点B,求过A 、B 两点的直线的解析式．21m x-的图象如图所示,1(1)A b -，,2(2)B b -，是该图象上的两点．1比较1b 与2b 的大小； 2求m 的取值范围．10．2009宁夏已知正比例函数1y k x =1(0)k ≠与反比例函数22(0)k y k x=≠的图象交于A B 、两点,点A 的坐标为(21)，．1求正比例函数、反比例函数的表达式； 2求点B 的坐标．11．2009肇庆如图 7,已知一次函数1y x m =+m 为常数的图象与反比例函数 2ky x=k 为常数, 0k ≠的图象相交于x点 A 1,3．1求这两个函数的解析式及其图象的另一交点B 的坐标；2观察图象,写出使函数值12y y ≥的自变量x 的取值范围．12．2009年南充如图,已知正比例函数和反比例函数的图象都经过点(33)A ，．1求正比例函数和反比例函数的解析式；2把直线O A 向下平移后与反比例函数的图象交于点(6)B m ，,求m 的值和这个一次函数的解析式；3第2问中的一次函数的图象与x 轴、y 轴分别交于C 、D ,求过A 、B 、D 三点的二次函数的解析式；4在第3问的条件下,二次函数的图象上是否存在点E ,使四边形O ECD 的面积1S 与四边形O ABD 的面积S 满足：123S S =若存在,求点E 的坐标；若不存在,请说明理由．13．2009年温州如图,在平面直角坐标系中,直线AB 与Y 轴和X 轴分别交于点A 、点8,与反比例函数y 一罟在第一象限的图象交于点c1,6、点D3,x ．过点C 作CE 上y 轴于E,过点D 作DF 上X 轴于F ．1求m,n 的值；2求直线AB 的函数解析式；3求证：△AEC ∽△DFB ．yxO C D BA3 3 6 yB 1-1- 1 2 3 31 2A 1,314．2009年兰州如图14,已知(4)A n -，,(24)B -，是一次函数y kx b =+的图象和反比例函数m y x=的图象的两个交点． 1求反比例函数和一次函数的解析式；2求直线AB 与x 轴的交点C 的坐标及△AOB 的面积；3求方程0=-+xm b kx 的解请直接写出答案； 4求不等式0<-+x m b kx 的解集请直接写出答案. 15．2009年遂宁如图,已知直线y=ax+b 经过点A0,-3,与x 轴交于点C,且与双曲线相交于点B-4,-a,D ． ⑴求直线和双曲线的函数关系式；⑵求△CDO 其中O 为原点的面积．16．2009年济南已知：如图,正比例函数y ax =的图象与反比例函数k y x=的图象交于点()32A ，． 1试确定上述正比例函数和反比例函数的表达式；2根据图象回答,在第一象限内,当x 取何值时,反比例函数的值大于正比例函数的值3()M m n ，是反比例函数图象上的一动点,其中03m <<，过点M 作直线MN x ∥轴,交y 轴于点B ；过点A 作直线AC y ∥轴交x 轴于点C ,交直线MB 于点D ．当四边形OADM 的面积为6时,请判断线段BM 与DM 的大小关系,并说明理由．17．2009年重庆市江津区如图,反比例函数xy 2=的图像与一次函数b kx y +=的图像交于点A ｍ,2,点B －2, n ,一次函数图像与y 轴的交点为C;1求一次函数解析式； y x O A D M C B2求C 点的坐标；3求△AOC 的面积;答案19．09湖北宜昌已知点A 1,－k ＋2在双曲线k x y =上．求常数k 的值．20．2009年达州如图8,直线b kx y +=与反比例函数x k y '=x ＜0的图象相交于点A 、点B,与x 轴交于点C,其中点A 的坐标为－2,4,点B 的横坐标为－4.1试确定反比例函数的关系式；2求△AOC 的面积.21．2009年广东省如图所示,在平面直角坐标系中,一次函数1y kx =+的图象与反比例函数9y x=的图象在第一象限相交于点A ．过点A 分别作x 轴、y 轴的垂线,垂足为点B 、C ．如果四边形OBAC 是正方形,求一次函数的关系式．22．2009年邵阳市20、图八是一个反比例函数图像的一部分,点A1,10, B10,1,是它的端点;1求此函数的解析式,并写出自变量x 的取值范围；2 请你举出一个能用本题的函数关系描述的生活实例;A COB。