§8.1 空间几何体的三视图、表面积和体积
高考数学一轮复习-81-空间几何体的三视图-直观图-表面积与体积课件-新人教A

=172a2.所以 S 球=4πR2=4π×172a2=73πa2.
(2)这个几何体是一个圆台被轴截面割出来的一半.
根据图中数据可知圆台的上底面半径为 1,下底面半径为 2,高为 3,母线长为 2,几何体的表面积是两个半圆的面 积、圆台侧面积的一半和轴截面的面积之和,故这个几何 体的表面积为 S=12π×12+12π×22+12π×(1+2)×2+12 ×(2+4)× 3=112π+3 3. 答案 (1)B (2)112π+3 3
可能是圆柱,排除选项C;又由俯视图可知,该几何体
不可能是棱柱或棱台,排除选项A,B,故选D.
(2)如图,在原图形OABC中, 应有 OD=2O′D′=2×2 2 =4 2(cm), CD=C′D′=2 cm. ∴OC= OD2+CD2 = (4 2)2+22=6(cm), ∴OA=OC, 故四边形 OABC 是菱形. 答案 (1)D (2)C
诊断自测
1.判断正误(在括号内打“√”或“×”) 精彩PPT展示
(1)有两个面平行,其余各面都是平行四边形的几何体是
棱柱.
(×)
(2)有一个面是多边形,其余各面都是三角形的几何体是
棱锥.
( ×)
(3)正方体、球、圆锥各自的三视图中,三视图均相同.
(×)
(4)圆柱的侧面展开图是矩形.
(√)
2.(2014·福建卷)某空间几何体的正视图是三角形,则该几
(2)画出坐标系 x′O′y′,作出△OAB 的 直观图 O′A′B′(如图).D′为 O′A′的中 点.易知 D′B′=12DB(D 为 OA 的中点), ∴S△O′A′B′=12× 22S△OAB= 42× 43a2= 166a2.
§8.1 空间几何体的结构及其三视图和直观图

探究提高
解决该类题目需准确理解几何体的定义,要真正把握几何 体的结构特征,并且学会通过反例对概念进行辨析,即要说明 一个命题是错误的,设法举出一个反例即可. 主页
变式训练 1
下面是关于四棱柱的四个命题: ①若有两个侧面垂直于底面,则该四棱柱为直四棱柱; ②若过两个相对侧棱的截面都垂直于底面,则该四棱 柱为直四棱柱; ③若四个侧面两两全等,则该四棱柱为直四棱柱; ④若四棱柱的四条对角线两两相等,则该四棱柱为 直四棱柱. 其中,真命题的编号是②④ ________.(写出所有真命题 的编号)
主页
变式训练 3
一个平面图形的水平放置的斜二测直观图是一个 等腰梯形,它的底角为45°,两腰和上底边长均为1,则这 2 2 个平面图形的面积是 ______.
y
D
C
D
1
C
2
o
A
E
B x
A
2 1
B
S 1 [1 2 1] 2 2 2. 2
主页
题 型四
几何体的截面问题
对于①,平行六面体的两个相对侧面也可能与 底面垂直且互相平行,故①假; 对于②,两截面的交线平行于侧棱,且垂直于底 面,故②真;
主页
变式训练 1 下面是关于四棱柱的四个命题: ③若四个侧面两两全等,则该四棱柱为直四棱柱; ④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱. ②④ .(写出所有真命题的编号) 其中,真命题的编号是________
对于③,作正四棱柱的两个平行菱形截面,可得满足条件 的斜四棱柱(如图(1)),故③假; 对于④,四棱柱一个对角面的两条对角线,恰为四棱柱 的对角线,故对角面为矩形,于是侧棱垂直于底面的一对角 线,同样侧棱也垂直于底面的另一对角线,故侧棱垂直于底 面,故④真(如图(2)).
高考数学(文)《立体几何》专题复习

(2)两个平面垂直的判定和性质
✓ 考法5 线面垂直的判定与性质
1.证明直线 与平面垂直 的方法
2.线面垂直 的性质与线 线垂直
(1)判定定理(常用方法): 一条直线与一个平面内的两条相交直线都垂直,则该直线
与此平面垂直.判定定理中的两条相交直线必须保证“在平面 内相交”这一条件. (2)性质: ①应用面面垂直的性质(常用方法):若两平面垂直,则在一 个平面内垂直于交线的直线必垂直于另一个平面,是证明线 面垂直的主要方法; ②(客观题常用)若两条平行直线中的一条垂直于一个平面, 则另一条也垂直于这个平面.
64
65
✓ 考法4 面面平行的判定与性质
1.证明平面 与平面平行 的常用方法 2.空间平行关系 之间的转化
66
✓ 考法3 面面平行的判定与性质
1.证明平面 与平面平行 的常用方法
这是立体几何中证明平行关系常用的思路,三 种平行关系的转化可结合下图记忆
2.空间平行关系 之间的转化
67
68
600分基础 考点&考法
定义 判定方法
2.等角定理
判定定理 反证法 两条异面直线所成的角
✓ 考法2 异面直线所成的角
常考形式
直接求 求其三角函数值
常用方法
作角
正弦值 余弦值 正切值
证明 求值 取舍
55
56
57
58
600分基础 考点&考法
➢ 考点46 线面、面面平行的判定与性质 ✓ 考法3 线面平行的判定与性质 ✓ 考法4 面面平行的判定与性质
1.计算有关 线段的长
2.外接球、内切 球的计算问题
观察几何体的特征 利用一些常用定理与公式 (如正弦定理、余弦定理、勾股定理、 三角函数公式等) 结合题目的已知条件求解
人教a版高考数学(理)一轮课件:8.1空间几何体的结构、三视图和直观图

3.简单组合体 简单组合体的构成有两种基本形式:一种是由简单几何体拼接而成;一 种是由简单几何体截去或挖去一部分而成,有多面体与多面体、 多面体与旋 转体、旋转体与旋转体的组合体.
4. 三视图 几何体的三视图包括正视图、侧视图、俯视图 , 分别是从几何体的 正前方、正左方、正上方观察几何体画出的轮廓线.
考纲解读
空间几何体的结构 和三视图部分 重点考 查柱、锥、台、球 的定义和以三 视图为 载体考查柱、锥、 台、球的表面 积和体 积, 难度 不大. 空间几 何体的 性质是 基础, 以它们为载体考查 线线、线面、 面面间 的 关 系 是 重点 . 三 视图 的 还 原在 各 地 高 考 试 题 中 频繁 出 现 , 已 经 成 为高 考 的 热 点 问 题, 题型 多以 选择 题和 填空 题为 主 , 有时也会作为解答题的背景出现.
三视图的长度特征: “ 长对正, 宽相等, 高平齐” , 即正视图和侧 视图一样高, 正视图和俯视图一样长, 侧视图和俯视图一样宽. 若相邻两物 体的表面相交, 表面的交线是它们的分界线, 在三视图中, 要注意实、 虚线的 画法 .
5. 空间几何体的直观图 空间几何体的直观图常用斜二测画法来画, 其规则是: (1) 原图形中 x轴、 y轴、 z轴两两垂直, 直观图中, x' 轴、 y' 轴的夹角为 45° , z' 轴与 x' 轴和 y' 轴所在平面垂直. (2) 原图形中平行于坐标轴的线段, 在直观图中仍分别平行于坐标轴. 平 行于 x轴和 z轴的线段在直观图中保持原长度不变, 平行于 y轴的线段长度 在直观图中变为原来的一半. 6. 中心投影与平行投影 (1) 平行投影的投影线互相平行, 而中心投影的投影线相交于一点. (2) 从投影的角度看, 三视图和用斜二测画法画出的直观图都是在平行 投影下画出来的图形.
第3课时 由三视图确定几何体的表面积或体积(教案)

第3课时由三视图确定几何体的表面积或体积【知识与技能】熟练掌握已知空间几何体的三视图求其表面积和体积的方法.【过程与方法】1.通过空间几何体三视图的应用,培养学生的创新精神和探究能力.2.通过研究性学习,培养学生的整体性思维.【情感态度】通过研究三视图,研究我国著名建筑物的三视图研究,培养学生的爱国情结. 【教学重点】观察,实践,猜想和归纳的探究过程.【教学难点】如何引导学生进行合理的探究.一、复习提问1.如何求空间几何体的表面积和体积(例如:球,棱柱,棱台等);2.三视图与其几何体如何转化.二、思考探究,获取新知如图是一个几何体的三视图,已知左视图是一个等边三角形,根据图中尺寸(单位:m),求该几何体的面积和体积.解该几何体是正三棱柱,由正视图知正三棱柱的高为3cm,底面三角形的高为3cm.则底面边长为2cm,故S底面面积=)2=3÷cm(232S侧面面积=2×3×3=18 (cm2)故这个几何体的表面积S = 2S底面面积十S侧面面积=)2+183(2cm三棱柱的体积是V=)3=3⨯cm(333【教学说明】空间几何体的表面积是几何体表面的面积,它表示几何体表面的大小,体积是几何体所占空间的大小;先将直观图的各个要素弄清楚,然后再代公式进行计算.求空间几何体的表面积是将几何体的各个面的面积相加求得;求体积是将几何体各个部分的体积相加求得,那么请同学们动脑筋想一想,假设没有给出几何体的直观图,只是给出一个几何体的三视图,我们怎样解决求该几何体的表面积和体积呢?此时应首先将该三视图转化为几何体的直观图,然后弄清给出直观图的各个要素,再代公式进行计算思考如何求出四棱台的表面积和体积?请大家回想一下,在解答的过程中,容易出错的地方是什么(让学生思考). 【总结归纳】求组合几何体的表面积的时候容易出错.三、典例精析、掌握新知例1 长方体的主视图与俯视图如图所示,则这个长方体的体积是()A.52B.32C.24D.9【分析】由主视图可知,这个长方体的长和高分别为4和3,由俯视图可知,这个长方体的长和宽分别为4和2,因此这个长方体的长、宽、高分别为4、3、2,因此这个长方体的体积为4×2×3 = 24(平方单位)【答案】C【教学说明】三视图问题一直是中考考查的高频考点,一般题目难度中等偏下,本题所用的知识是:主视图主要反映物体的长和高,左视图主要反映物体的宽和高,俯视图主要反映物体的长和宽.例2 将棱长是1cm的小正方体组成如图所示的几何体,那么这个几何体的表面积是()A. 36 cm2B. 33 cm2C. 30 cm2D. 27 cm2【分析】算表面积应该从六个方向去计算,不要忽视了底面.【答案】A四、师生互动,课堂小结通过这节课的探究学习,发现由三视图求几何体的表面积和体积,要先将三视图转化为其几何体的直观图,分清楚直观图中的几何要素,然后再代公式进行计算;特别要分清几何体的侧面积与表面积;平时多动脑筋,挖掘与题目相关联的知识点.1.布置作业:从教材Pm〜1。
三视图课件

B
A. 32 B. 16 16 2 C. 48 D. 16 32 2
5.2010湖南高考
4
6. (2007宁夏理•8) 已知某个几何体的三视图 如下,根据图中标出的尺寸(单位:cm), 可得这个几何体的体积是( B)
24
柱体
夯实基础 1.棱柱 (1)定义:有两个面互相平行,而且夹在这两个平行 平面间的每相邻两个面的交线都 互相平行,由这些面所 围成的多面体叫做棱柱. 稳固根基
(如图)
1° 球面被经过球心的平面截得的圆叫做大圆. 2° 不过球心的截面截得的圆叫做球的小圆.
(3)球面距离: 1° 定义:在球面上两点之间的最短距离,就是经过这 两点的 大圆 在这两点间的一段 劣弧 的长度, 这个弧长 叫做两点的球面距离. 2° 地球上的经纬线 当把地球看作一个球时, 经线是球面上从北极到南极 的半个大圆,纬线是与地轴垂直的平面与球面的交线,其 中赤道是一个大圆,其余纬线都是一个小圆.
5.球的概念与性质 (1)定义: 半圆绕它的直径所在直线旋转所成的曲面叫 做球面,球面所围成的几何体叫做球.球面也可以看作空 间中到定点的距离等于定长的点的集合. (2)球的截面性质 ①用一个平面去截球,截面是圆面.
②球心到截面的距离 d 与球的半径 R 及截面的半径 r,有下面的关系:
r= R2-d2
空间几何体的结构、三 视图和直观图、表面积 和体积
椎体
2
2.棱锥及其分类 (1)定义: 有一个面是多边形, 其余各面是 有一个公共顶点 的三 角形.由这些面所围成的几何体叫做棱锥. (2)正棱锥 如果棱锥的底面是正多边形, 顶点在过底面中心且与 底面垂直的直线上,则这个棱锥叫做正棱锥.
正棱锥的性质: ①各侧棱相等, 各侧面都是全等的等腰三角形. 这些 等腰三角形的高叫做棱锥的斜高. ②棱锥的高、 斜高和斜高在底面内的射影组成一个直 角三角形; 棱锥的高、 侧棱和侧棱在底面内的射影也组成 一个直角三角形.
数学一轮复习第8章立体几何第1讲空间几何体的结构三视图表面积和体积试题2理

第八章立体几何第一讲空间几何体的结构、三视图、表面积和体积1。
[2020全国卷Ⅲ,8,5分][理]如图8-1—1为某几何体的三视图,则该几何体的表面积是()A.6+4√2B.4+4√2C。
6+2√3D。
4+2√32。
[2020浙江,5,4分]某几何体的三视图(单位:cm)如图8—1-2所示,则该几何体的体积(单位:cm3)是()A.73B.143C.3D.63。
[2021合肥市调研检测]表面积为324π的球,其内接正四棱柱(底面是正方形的直棱柱)的高是14,则这个正四棱柱的表面积等于()A。
567 B.576 C.240 D.49π4.[2021安徽省四校联考]在三棱锥A—BCD中,△ABC和△BCD 都是边长为2的正三角形,当三棱锥A-BCD的表面积最大时,其内切球的半径是()A。
2√2−√6 B。
2-√3 C。
√2D。
√665。
[数学文化题]《九章算术》与《几何原本》并称现代数学的两大源泉.在《九章算术》卷五商功篇中介绍了羡除(此处是指三面为等腰梯形,其他两侧面为直角三角形的五面体)体积的求法。
在如图8—1—3所示的羡除中,平面ABDA’是铅垂面,下宽AA'=3 m,上宽BD=4 m,深3 m,平面BCED是水平面,末端宽CE=5 m,无深,长6 m(直线CE到BD的距离),则该羡除的体积为()图8-1—3A.24 m3B.30 m3 C。
36 m3 D。
42 m36.[2020全国卷Ⅱ,10,5分][理]已知△ABC是面积为9√34的等边三角形,且其顶点都在球O的球面上。
若球O的表面积为16π,则O到平面ABC的距离为()A。
√3B。
32C.1 D。
√327.[2021安徽省示范高中联考]蹴鞠(如图8—1—4所示),又名“蹋鞠”“蹴球”“蹴圆"“筑球”“踢圆”等,“蹴”有用脚蹴、蹋、踢的含义,“鞠”最早系外包皮革、内实米糠的球.因而“蹴鞠”就是指古人以脚蹴、蹋、踢皮球的活动,类似今日的足球。
立体几何三视图练习题

8.1空间几何体的三视图、直观图、表面积与体积练习题(1)1.(2014·福建,2,)某空间几何体的正视图是三角形,则该几何体不可能是( )A .圆柱B .圆锥C .四面体D .三棱柱2.(2013·四川)一个几何体的三视图如下图,则该几何体的直观图能够是( )3.(2016·课标Ⅰ,6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,若该几何体的体积是28π3,则它的表面积是( )A .17πB .18πC .20πD .28π4.(2016·山东,5)一个由半球和四棱锥组成的几何体,其三视图如下图,则该几何体的体积为( )A.13+23πB.13+23πC.13+26π D .1+26π5.(2016·课标Ⅱ,6)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A .20πB .24πC .28πD .32π6.(2016·课标Ⅲ,9)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A .18+36 5B .54+185C .90D .817.(2015·浙江)某几何体的三视图如下图(单位:cm),则该几何体的体积是( )A .8 cm 3B .12 cm 3C.323 cm 3D.403 cm 3 8.(2014·安徽,7)一个多面体的三视图如下图,则该多面体的表面积为( )A .21+ 3B .18+ 3C .21D .189.(2015·北京,5)某三棱锥的三视图如下左图所示,则该三棱锥的表面积是( )A .2+ 5B .4+ 5C .2+2 5D .510.(2016·北京房山区一模,5)某四棱锥的三视图如上右图所示,则最长的一条侧棱的长度为( )A. 2B. 3C. 5D.611.(2016·课标Ⅲ,10)在封闭的直三棱柱ABC A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )A.4π B.9π2C.6π D.32π312.(2015·课标Ⅱ,9)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥OABC体积的最大值为36,则球O的表面积为( )A.36πB.64πC.144πD.256π8.1空间几何体的三视图、直观图、表面积与体积练习题(2)1.(2015·江苏,9)现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为________.2.(2013·课标Ⅰ,6)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,假如不计容器的厚度,则球的体积为()A.500π3cm3 B.866π3cm3 C.1 372π3cm3 D.2 048π3cm33.(2016·四川,13)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如上右图所示,则该三棱锥的体积是________.4.(2016·天津,11)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如下左图图所示(单位:m),则该四棱锥的体积为________m3.5.(2014·课标Ⅰ,12)如上右图所示,网络纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.6 2 B.4 2 C.6 D.46.一个四面体的三视图如下图,则该四面体的表面积是()A.1+ 3 B.2+ 3 C.1+2 2 D.227.(2014·课标Ⅱ)正三棱柱ABCA1B1C1的底面边长为2,侧棱长为3,D为BC中点,则三棱锥AB1DC1的体积为()A .3 B.32 C .1 D.328.(2015·河北石家庄调研,8)已知球O ,过其球面上A ,B ,C 三点作截面,若O 点到该截面的距离是球半径的一半,且AB =BC =2,∠B =120°,则球O 的表面积为( )A.64π3B.8π3 C .4π D.16π99.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )A.81π4 B .16π C .9π D.27π410.(2015·山东淄博模拟,4)把边长为1的正方形ABCD 沿对角线BD 折起,形成的三棱锥A BCD 的正(主)视图与俯视图如下图,则其侧(左)视图的面积为( )A.22B.12C.24D.1411.一个几何体的三视图如下图,则该几何体的体积为( )A.163B.203C.152D.13212.(2016·江西南昌,6)一个几何体的三视图及尺寸如下图,则该几何体的外接球半径为( )A.12B.316C.174D.174由三视图还原直观图的方法(1)还原后的几何体一般为较熟悉的柱、锥、台、球的组合体.(2)注意图中实、虚线,实际是原几何体中的可视线与被遮挡线.(3)想象原形,并画出草图后实行三视图还原,把握三视图和几何体之间的关系,与所给三视图比较,通过调整准确画出原几何体.根据几何体的三视图判断几何体的结构特征(1)三视图为三个三角形,对应三棱锥;(2)三视图为两个三角形,一个四边形,对应四棱锥;(3)三视图为两个三角形,一个圆,对应圆锥;(4)三视图为一个三角形,两个四边形,对应三棱柱;(5)三视图为两个四边形,一个圆,对应圆柱.求解空间几何体表面积的方法(1)已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.(2)多面体的表面积是各个面的面积之和,组合体的表面积应注意重合局部的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开成平面图形计算,而表面积是侧面积与底面圆的面积之和.(4)解决关于外接球的问题的关键是抓住外接的特点,即球心到多面体的顶点的距离都等于球的半径,同时要作一圆面起衬托作用.求体积的常用方法(1)分割求和法:把不规则图形分割成规则图形,然后实行体积计算.(2)补形法:把不规则几何体补成规则几何体,不熟悉的几何体补成熟悉的几何体,便于计算其体积.(3)等积法:选择适当的底面图形求几何体的体积,常用于三棱锥的体积.。
空间几何体三视图、表面积及体积

面积,h为高);
4 3 (7)球的表面积和体积公式:S=4πR ,V= πR (R为球的半径). 3
2
知识回扣 小题速解
解题绝招
限时速解训练
首页
上页 下页
尾页
知识 回扣
必记知识 重要结论
1.一个物体的三视图的排列规则 俯视图放在正视图的下面,长度与正视图的长度一样,侧(左)视图放在 正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图的宽 度一样,即“长对正、高平齐、宽相等”.
知识回扣 小题速解
解题绝招
限时速解训练
首页
上页 下页
尾页
小题 速解
类型一
三视图与直观图的辨识和画法
[ 例1]
某几何体的正视图和侧视图均如图所示,则该几何体的俯视图 )
不可能是(
(基本法) 从正视图和侧视图想像直观图,再检验答案. 若下部分是圆柱,上部分可以是圆柱或者棱柱,A、B、C适合题意, 若是D答案,其正视图应为(如右图)中间有虚线.
2 1 3 到的,根据三视图可知其表面积为6 2 - ×1×1 +2× ×( 2 4
知识回扣 小题速解
解题绝招
限时速解训练
首页
上页 下页
尾页
知识 回扣
必记知识 重要结论
2.(1)设长方体的相邻的三条棱长为a、b、c则对角线长为 a2+b2+c2 (2)棱长为a的正方体的体对角线长等于外接球的直径,即 3a=2R. (3)若球面上四点P、A、B、C构成的线段PA、PB、PC两两垂直,且PA =a,PB=b,PC=c,则4R2=a2+b2+c2,把有关元素“补形”成为 一个球内接长方体(或其他图).
知识回扣 小题速解
解题绝招
高考数学立体几何专题1空间立体几何的三视图、表面积和体积

专题1空间立体几何的三视图、表面积和体积【考点点击】1.以选择、填空题形式考查空间位置关系的判断,及文字语言、图形语言、符号语言的转换,难度适中;2.以熟悉的几何体为背景,考查多面体或旋转体的侧面积、表面积和体积计算,间接考查空间位置关系的判断及转化思想等,常以三视图形式给出几何体,辅以考查识图、用图能力及空间想象能力,难度中等.3.几何体的三视图与表(侧)面积、体积计算结合;【重点知识】一、空间几何体1.柱体、锥体、台体、球的结构特征名称几何特征棱柱①有两个面互相平行(底面可以是任意多边形);②其余各面都是平行四边形,并且每相邻两个四边形的公共边互相平行棱锥①有一个面是多边形(底面);②其余各面是有公共顶点的三角形.棱台①底面互相平行;②所有侧棱延长后交于一点(即原棱锥的顶点)圆柱①有两个互相平行的圆面(底面);②有一个侧面是曲面(母线绕轴旋转一周形成的),且母线与底面垂直圆台①底面互相平行;②有一个侧面是曲面,可以看成母线绕轴旋转一周形成的球①有一个曲面是球面;②有一个球心和一条半径长R,球是一个几何体(包括内部),可以看成半圆以它的直径所在直线为旋转轴旋转一周形成的2.柱体、锥体、台体、球的表面积与体积名称体积表面积棱柱V棱柱=Sh(S为底面积,h为高)S棱柱=2S底面+S侧面棱锥V棱锥=13Sh(S为底面积,h为高)S棱锥=S底面+S侧面棱台V棱台=13h(S+SS′+S′)S棱台=S上底+S下底+S侧面圆柱V圆柱=πr2h(r为底面半径,h为高)S圆柱=2πrl+2πr2(r为底面半径,l为母线长)圆锥V圆锥=13πr2h(r为底面半径,h为高)S圆锥=πrl+πr2(r为底面半径,l为母线长)圆台V圆台=13πh(r2+rr′+r′2)S圆台=π(r+r′)l+πr2+πr′2球V球=43πR3(R为球的半径)S球=4πR2(R为球的半径)3.空间几何体的三视图和直观图(1)空间几何体的三视图三视图的正视图、侧视图、俯视图分别是从物体的正前方、正左方、正上方看到的物体轮廓线的正投影围成的平面图形,三视图的画法规则为“长对正、高平齐、宽相等”.(2)空间几何体的直观图空间几何体直观图的画法常采用斜二测画法.用斜二测画法画平面图形的直观图规则为“轴夹角45°(或135°),平行长不变,垂直长减半”.4.几何体沿表面某两点的最短距离问题一般用展开图解决;不规则几何体求体积一般用割补法和等积法求解;三视图问题要特别留意各种视图与观察者的相对位置关系.【考点分析】考点一空间几何体的结构【例1】已知正三棱锥PABC ,点P ,A ,B ,C 都在半径为3的球面上,若PA ,PB ,PC 两两相互垂直,则球心到截面ABC 的距离为________.【答案】33【解析】正三棱锥PABC 可看作由正方体PADCBEFG 截得,如图所示,PF 为三棱锥PABC 的外接球的直径,且PF ⊥平面ABC.设正方体棱长为a ,则22,2,1232=====BC AC AB a a ,3223222221=⨯⨯⨯=∆ABC S ,由,PAC B ABC P V V --=得222213131⨯⨯⨯⨯=⋅∆ABC S h ,所以332=h 因此球心到平面ABC 得距离为33考点二三视图、直观图【例2】下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()(A )20π(B )24π(C )28π(D )32π【答案】C【解析】由题意可知,圆柱的侧面积为12π2416πS =⋅⋅=,圆锥的侧面积为2π248πS =⋅⋅=,圆柱的底面面积为23π24πS =⋅=,故该几何体的表面积为12328πS S S S =++=,故选C.【例3】某三棱锥的三视图如图所示,则该三棱锥的表面积是()A .2+5B .4+5C .2+25D .5【答案】C【解析】该三棱锥的直观图如图所示:过D 作DE ⊥BC ,交BC 于E ,连接AE ,则BC =2,EC =1,AD =1,ED =2,ABCABD ACD BCD S S S S S ∆∆∆∆+++=表5225221152115212221+=⨯⨯+⨯⨯+⨯⨯+⨯⨯=考点三几何体的表面积【例4】长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为【答案】14π.【解析】球的直径是长方体的体对角线,所以222232114,4π14π.R S R =++===【例5】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是328π,则它的表面积是()(A )17π(B )18π(C )20π(D )28π【答案】A【解析】该几何体直观图如图所示:是一个球被切掉左上角的81,设球的半径为R ,则32834873ππ=⨯=R V ,解得R 2=,所以它的表面积是87的球面面积和三个扇形面积之和πππ172413248722=⨯⨯+⨯⨯=S 故选A .考点四几何体的体积【例6.】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A .πB .3π4C .π2D .π4【答案】B【解析】绘制圆柱的轴截面如图所示,由题意可得:11,2AC AB ==,结合勾股定理,底面半径2213122r ⎛⎫=-= ⎪⎝⎭,由圆柱的体积公式,可得圆柱的体积是2233ππ1π24V r h ⎛==⨯⨯= ⎝⎭,故选B.考点五与球的组合体问题纵观近几年高考对于组合体的考查,重点放在与球相关的外接与内切问题上.要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识是学生掌握最为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理.本文就高中阶段出现这类问题加以类型的总结和方法的探讨.【例7】棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为()A .22B .1C .212+D .2解:由题意可知,球为正方体的外接球.平面11AA DD 截面所得圆面的半径12,22AD R ==11EF AA DD ⊂ 面,∴直线EF 被球O 截得的线段为球的截面圆的直径22R =.【例8】正四棱柱1111ABCD A B C D -的各顶点都在半径为R 的球面上,则正四棱柱的侧面积有最值,为.【例9】在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且AM MN ⊥,若侧棱23SA =,则正三棱锥S ABC -外接球的表面积是.解:如图,正三棱锥对棱相互垂直,即,AC SB ⊥又,,,.SB MN MN AC MN AM MN SAC ∴⊥⊥∴⊥∥又平面于是,,,SB SAC SB SA SB SC ⊥∴⊥⊥平面从而.SA SC ⊥此时正三棱锥S ABC -的三条侧棱互相垂直并且相等,故将正三棱锥补形为正方体.球的半径23,3,436.2R SA R S R ππ=∴=∴==【例10】一个几何体的三视图如图所示,其中主视图和左视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为()A .12πB .C .3πD .【答案】C【解析】把原来的几何体补成以DA DC DP 、、为长、宽、高的长方体,原几何体四棱锥与长方体是同一个外接球,2=R l ,=2R ,234434S R πππ==⨯=球.【例11】在三棱锥P -ABC 中,PA =,侧棱PA 与底面ABC 所成的角为60°,则该三棱锥外接球的体积为()A .πB.3π C.4πD.43π解:如图所示,过P 点作底面ABC 的垂线,垂足为O ,设H 为外接球的球心,连接,,AH AO 因60,PAO PA ∠== 故2AO =,32PO =又△AHO 为直角三角形,222,,AH PH r AH AO OH ==∴=+22233344(),1,1.2233r r r V ππ∴=+-∴=∴=⨯=【例12】矩形ABCD 中,4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B ACD --,则四面体ABCD 的外接球的体积是()A.π12125 B.π9125C.π6125D.π3125解:由题意分析可知,四面体ABCD 的外接球的球心落在AC 的中点,此时满足,OA OD OB OC ===522AC R ∴==,343V R π=1256π=.【总结归纳】1个特征——三视图的长度特征“长对正,宽相等,高平齐”,即正视图和侧视图一样高,正视图和俯视图一样长,侧视图和俯视图一样宽。
2021届高考数学 8.1空间几何体的三视图、直观图、表面积与体积配套文档 理
§8.1空间几何体的三视图、直观图、表面积与体积1.多面体的结构特点2.3.空间几何体的直观图经常使用斜二测画法来画,其规那么:(1)原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、y′轴的夹角为45°或135°,z′轴与x′轴和y′轴所在平面垂直.(2)原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴.平行于x轴和z轴的线段在直观图中维持原长度不变,平行于y轴的线段长度在直观图中长度为原先的一半.4.空间几何体的三视图(1)三视图的主视图、俯视图、左视图别离是从物体的正前方、正上方、正左方看到的物体轮廓线的正投影围成的平面图形.(2)三视图的特点:三视图知足“长对正、高平齐、宽相等”或说“主左一样高、主俯一样长、俯左一样宽”.5.柱、锥、台和球的侧面积和体积1. (1)有两个面平行,其余各面都是平行四边形的几何体是棱柱. ( × ) (2)有一个面是多边形,其余各面都是三角形的几何体是棱锥.( × )(3)用斜二测画法画水平放置的∠A 时,假设∠A 的两边别离平行于x 轴和y 轴,且∠A =90°,那么在直观图中,∠A =45°.( × ) (4)正方体、球、圆锥各自的三视图中,三视图均相同. ( × ) (5)圆柱的侧面展开图是矩形.( √ ) (6)台体的体积可转化为两个锥体的体积之差来计算.( √ )2. (2021·四川)一个几何体的三视图如下图,那么该几何体的直观图能够是 ( )答案 D解析 由三视图可知上部是一个圆台,下部是一个圆柱,选D.3. (2021·课标全国Ⅰ)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,若是不计容器的厚度,那么球的体积为( )A.500π3cm 3B.866π3cm 3C.1 372π3 cm 3D.2 048π3cm 3答案 A解析 作出该球轴截面的图象如下图,依题意BE =2,AE =CE =4,设DE =x ,故AD =2+x ,因为AD 2=AE 2+DE 2,解得x =3,故该球的半径AD =5, 因此V =43πR 3=500π3. 4. 一个三角形在其直观图中对应一个边长为1的正三角形,原三角形的面积为________.答案62解析 由斜二测画法,知直观图是边长为1的正三角形,其原图是一个底为1,高为6的三角形,因此原三角形的面积为62.5. 假设一个圆锥的侧面展开图是面积为2π的半圆面,那么该圆锥的体积为________.答案33π 解析 侧面展开图扇形的半径为2,圆锥底面半径为1, ∴h =22-1=3,∴V =13π×1×3=33π.题型一 空间几何体的结构特点 例1 (1)以下说法正确的选项是( )A .有两个平面相互平行,其余各面都是平行四边形的多面体是棱柱B .四棱锥的四个侧面都能够是直角三角形C .有两个平面相互平行,其余各面都是梯形的多面体是棱台D .棱台的各侧棱延长后不必然交于一点 (2)给出以下命题:①在圆柱的上、下底面的圆周上各取一点,那么这两点的连线是圆柱的母线; ②有一个面是多边形,其余各面都是三角形的几何体是棱锥; ③直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥;④棱台的上、下底面能够不相似,但侧棱长必然相等. 其中正确命题的个数是( )A .0B .1C .2D .3思维启发 从多面体、旋转体的概念入手,能够借助实例或几何模型明白得几何体的结构特点. 答案 (1)B (2)A解析 (1)A 错,如图1;B 正确,如图2,其中底面ABCD 是矩形,可证明∠PAB ,∠PCB 都是直角,如此四个侧面都是直角三角形;C 错,如图3;D 错,由棱台的概念知,其侧棱必相交于同一点.(2)①不必然,只有这两点的连线平行于轴时才是母线;②不必然,因为“其余各面都是三角形”并非等价于“其余各面都是有一个公共极点的三角形”,如图1所示;③不必然,当以斜边所在直线为旋转轴时,其余两边旋转形成的面所围成的几何体不是圆锥,如图2所示,它是由两个同底圆锥组成的几何体;④错误,棱台的上、下底面是相似且对应边平行的多边形,各侧棱延长线交于一点,可是侧棱长不必然相等. 思维升华 (1)有两个面相互平行,其余各面都是平行四边形的几何体不必然是棱柱. (2)既然棱台是由棱锥概念的,因此在解决棱台问题时,要注意“还台为锥”的解题策略. (3)旋转体的形成不仅要看由何种图形旋转取得,还要看旋转轴是哪条直线.如图是一个无盖的正方体盒子展开后的平面图,A ,B ,C是展开图上的三点,那么在正方体盒子中,∠ABC 的值为 ( )A .30°B .45°C .60°D .90°答案 C解析 还原正方体,如下图,连接AB ,BC ,AC ,可得△ABC 是正三角形,那么∠ABC =60°. 题型二 空间几何体的三视图和直观图例2 (1)如图,某几何体的主视图与左视图都是边长为1的正方形,且体积为12,那么该几何体的俯视图能够是( )(2)正三角形AOB 的边长为a ,成立如下图的直角坐标系xOy ,那么它的直观图的面积是________.思维启发 (1)由主视图和左视图可知该几何体的高是1,由体积是12可求出底面积.由底面积的大小可判定其俯视图是哪个.(2)依照直观图画法规那么确信平面图形和其直观图面积的关系. 答案 (1)C (2)616a 2解析 (1)由该几何体的主视图和左视图可知该几何体是柱体,且其高为1,由其体积是12可知该几何体的底面积是12,由图知A 的面积是1,B 的面积是π4,C 的面积是12,D 的面积是π4,应选C.(2)画出坐标系x ′O ′y ′,作出△OAB 的直观图O ′A ′B ′(如图).D ′为O ′A ′的中点. 易知D ′B ′=12DB (D 为OA 的中点),∴S △O ′A ′B ′=12×22S △OAB =24×34a 2=616a 2.思维升华 (1)三视图中,主视图和左视图一样高,主视图和俯视图一样长,左视图和俯视图一样宽.即“长对正,宽相等,高平齐”.(2)解决有关“斜二测画法”问题时,一样在已知图形中成立直角坐标系,尽可能运用图形中原有的垂直直线或图形的对称轴为坐标轴,图形的对称中心为原点,注意两个图形中关键线段长度的关系.(1)(2021·湖南)已知棱长为1的正方体的俯视图是一个面积为1的正方形,那么该正方体的主视图的面积不可能等于( )A .1 B.2 C.2-12D.2+12(2)如图,矩形O ′A ′B ′C ′是水平放置的一个平面图形的直观图,其中O ′A ′=6 cm ,O ′C ′=2 cm ,那么原图形是 ( ) A .正方形 B .矩形C .菱形D .一样的平行四边形答案 (1)C (2)C解析 (1)由俯视图知正方体的底面水平放置,其主视图为矩形,以正方体的高为一边长,另一边长最小为1,最大为2,面积范围应为[1,2],不可能等于2-12.(2)如图,在原图形OABC 中, 应有OD =2O ′D ′=2×22=42 cm ,CD =C ′D ′=2 cm.∴OC =OD 2+CD 2=422+22=6 cm ,∴OA =OC ,故四边形OABC 是菱形. 题型三 空间几何体的表面积与体积例3 (1)一个空间几何体的三视图如下图,那么该几何体的表面积为 ( )A .48B .32+817C .48+817D .80(2)已知某几何体的三视图如下图,其中主视图、左视图均由直角三角形与半圆组成,俯视图由圆与内接三角形组成,依照图中的数据可得几何体的体积为 ( ) A.2π3+12B.4π3+16 C.2π6+16D.2π3+12思维启发 先由三视图确信几何体的组成及气宇,然后求表面积或体积. 答案 (1)C (2)C解析 (1)由三视图知该几何体的直观图如下图,该几何体的下底面是边长为4的正方形;上底面是长为4、宽为2的矩形;两个梯形侧面垂直于底面,上底长为2,下底长为4,高为4;另两个侧面是矩形,宽为4,长为42+12=17.因此S表=42+2×4+12×(2+4)×4×2+4×17×2=48+817.(2)由三视图确信该几何体是一个半球体与三棱锥组成的组合体,如图,其中AP ,AB ,AC 两两垂直,且AP =AB =AC =1,故AP ⊥平面ABC ,S △ABC =12AB ×AC =12,因此三棱锥P -ABC 的体积V 1=13×S △ABC ×AP =13×12×1=16,又Rt△ABC 是半球底面的内接三角形,因此球的直径2R =BC =2,解得R =22,因此半球的体积V 2=12×4π3×(22)3=2π6,故所求几何体的体积V =V 1+V 2=16+2π6.思维升华 解决此类问题需先由三视图确信几何体的结构特点,判定是不是为组合体,由哪些简单几何体组成,并准确判定这些几何体之间的关系,将其切割为一些简单的几何体,再求出各个简单几何体的体积,最后求出组合体的体积.(2021·课标全国)已知三棱锥S -ABC 的所有极点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,那么此棱锥的体积为 ( ) A.26 B.36 C.23 D.22答案 A解析 由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点,因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,因此三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍. 在三棱锥O -ABC 中,其棱长都是1,如下图, S △ABC =34×AB 2=34,高OD = 12-⎝ ⎛⎭⎪⎪⎫332=63, ∴V S -ABC =2V O -ABC =2×13×34×63=26.转化思想在立体几何计算中的应用典例:(12分)如图,在直棱柱ABC —A ′B ′C ′中,底面是边长为3的等边三角形,AA ′=4,M 为AA ′的中点,P 是BC 上一点,且由P 沿 棱柱侧面通过棱CC ′到M 的最短线路长为29,设这条最短线路与CC ′的交点为N ,求:(1)该三棱柱的侧面展开图的对角线长; (2)PC 与NC 的长;(3)三棱锥C —MNP 的体积.思维启发 (1)侧面展开图从哪里剪开展平;(2)MN +NP 最短在展开图上呈现如何的形式;(3)三棱锥以谁做底好. 标准解答解 (1)该三棱柱的侧面展开图为一边长别离为4和9的矩形,故对角线长为42+92=97.[2分](2)将该三棱柱的侧面沿棱BB ′展开,如以下图,设PC =x ,那么MP 2=MA 2+(AC +x )2. ∵MP =29,MA =2,AC =3,∴x =2,即PC =2.又NC ∥AM ,故PC PA =NCAM ,即25=NC 2.∴NC =45.[8分](3)S △PCN =12×CP ×CN =12×2×45=45.在三棱锥M —PCN 中,M 到面PCN 的距离, 即h =32×3=332.∴V C —MNP =V M —PCN =13·h ·S △PCN=13×332×45=235.[12分] 温馨提示 (1)解决空间几何体表面上的最值问题的全然思路是“展开”,即将空间几何体的“面”展开后铺在一个平面上,将问题转化为平面上的最值问题.(2)若是已知的空间几何体是多面体,那么依照问题的具体情形能够将那个多面体沿多面体中某条棱或两个面的交线展开,把不在一个平面上的问题转化到一个平面上.若是是圆柱、圆锥那么可沿母线展开,把曲面上的问题转化为平面上的问题.(3)此题的易错点是,不明白从哪条侧棱剪开展平,不能正确地画出侧面展开图.缺乏空间图形向平面图形的转化意识.方式与技术1.棱柱、棱锥要把握各部份的结构特点,计算问题往往转化到一个三角形中进行解决.2.旋转体要抓住“旋转”特点,弄清底面、侧面及展开图形状.3.三视图画法:(1)实虚线的画法:分界限和可见轮廓线用实线,看不见的轮廓线用虚线;(2)明白得“长对正、宽平齐、高相等”.4.直观图画法:平行性、长度两个要素.5.求几何体的体积,要注意分割与补形.将不规那么的几何体通过度割或补形将其转化为规那么的几何体求解.6.与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确信有关元素间的数量关系,并作出适合的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的极点均在球面上,正方体的体对角线长等于球的直径.失误与防范1.台体能够看成是由锥体截得的,但必然强调截面与底面平行.2.注意空间几何体的不同放置对三视图的阻碍.3.几何体展开、折叠问题,要抓住前后两个图形间的联系,找出其中的量的关系.A组专项基础训练(时刻:40分钟)一、选择题1.正五棱柱中,不同在任何侧面且不同在任何底面的两极点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有( )A.20 B.15C.12 D.10答案D解析如图,在正五棱柱ABCDE-A1B1C1D1E1中,从极点A动身的对角线有两条:AC1,AD1,同理从B,C,D,E点动身的对角线均有两条,共2×5=10(条).2.(2021·福建)一个几何体的三视图形状都相同、大小均相等,那么那个几何体不能够是( )A .球B .三棱锥C .正方体D .圆柱答案 D解析 考虑选项中几何体的三视图的形状、大小,分析可得. 球、正方体的三视图形状都相同、大小均相等,第一排除选项A 和C. 关于如下图三棱锥O -ABC ,当OA 、OB 、OC 两两垂直且OA =OB =OC 时, 其三视图的形状都相同,大小均相等,故排除选项B. 不论圆柱如何设置,其三视图的形状都可不能完全相同, 故答案选D.3. (2021·重庆)某几何体的三视图如下图,那么该几何体的体积为( )A.5603B.5803 C .200 D .240答案 C解析 由三视图知该几何体为直四棱柱,其底面为等腰梯形,上底长为2,下底长为8,高为4,故面积为S =2+8×42=20.又棱柱的高为10,因此体积V =Sh =20×10=200.4. 如图是一个物体的三视图,那么此三视图所描述物体的直观图是( ) 答案 D解析 由俯视图可知是B 和D 中的一个,由主视图和左视图可知B 错.5. 某几何体的三视图如下图,其中俯视图是个半圆,那么该几何体的表面积为( )A.32π B .π+3C.32π+ 3D.52π+3答案 C解析 由三视图可知该几何体为一个半圆锥,底面半径为1,高为3,∴表面积S =12×2×3+12×π×12+12×π×1×2=3+3π2.二、填空题6. 如下图,E 、F 别离为正方体ABCD —A 1B 1C 1D 1的面ADD 1A 1、面BCC 1B 1的中心,那么四边形BFD 1E 在该正方体的面DCC 1D 1上的正投影是________.(填序号)答案 ②解析 四边形在面DCC 1D 1上的正投影为②:B 在面DCC 1D 1上的正投影为C ,F 、E 在面DCC 1D 1上的投影应在边CC 1与DD 1上,而不在四边形的内部,故①③④错误.7. 已知三棱锥A —BCD 的所有棱长都为2,那么该三棱锥的外接球的表面积为________. 答案 3π 解析 如图,构造正方体ANDM —FBEC .因为三棱锥A —BCD 的所有棱长都为2,因此正方体ANDM —FBEC 的棱长为1.因此该正方体的外接球的半径为32. 易知三棱锥A —BCD 的外接球确实是正方体ANDM —FBEC 的外接球,因此三棱锥A —BCD 的外接球的半径为32.因此三棱锥A —BCD 的外接球的表面积为S 球=4π⎝ ⎛⎭⎪⎪⎫322=3π. 8. (2021·江苏)如图,在三棱柱A 1B 1C 1-ABC 中,D ,E ,F 别离是AB ,AC ,AA 1的中点,设三棱锥F -ADE的体积为V 1,三棱柱A 1B 1C 1-ABC 的体积为V 2,那么V 1∶V 2=________.答案 1∶24解析 设三棱锥F -ADE 的高为h ,则V 1V 2=13h ⎝ ⎛⎭⎪⎫12AD ·AE ·sin∠DAE 2h 122AD 2AE sin∠DAE=124. 三、解答题9.一个几何体的三视图及其相关数据如下图,求那个几何体的表面积.解 那个几何体是一个圆台被轴截面割出来的一半.依照图中数据可知圆台的上底面半径为1,下底面半径为2,高为3,母线长为2,几何体的表面积是两个半圆的面积、圆台侧面积的一半和轴截面的面积之和,故那个几何体的表面积为S =12π×12+12π×22+12π×(1+2)×2+12×(2+4)×3=11π2+3 3.10.已知一个正三棱台的两底面边长别离为30 cm 和20 cm ,且其侧面积等于两底面面积之和,求棱台的高.解 如下图,三棱台ABC —A 1B 1C 1中,O 、O 1别离为两底面中心,D 、D 1别离为BC和B 1C 1的中点,那么DD 1为棱台的斜高.由题意知A 1B 1=20,AB =30,则OD =53,O 1D 1=1033, 由S 侧=S 上+S 下,得12×(20+30)×3DD 1=34×(202+302), 解得DD 1=1333,在直角梯形O 1ODD 1中,O 1O =DD 21-OD -O 1D 12=43,因此棱台的高为4 3 cm. B 组 专项能力提升(时刻:30分钟)1. 在四棱锥E —ABCD 中,底面ABCD 为梯形,AB ∥CD,2AB =3CD ,M 为AE 的中点,设E —ABCD 的体积为V ,那么三棱锥M —EBC 的体积为( )A.25VB.13VC.23VD.310V 答案 D解析 设点B 到平面EMC 的距离为h 1,点D 到平面EMC 的距离为h 2.连接MD .因为M 是AE 的中点,因此V M —ABCD =12V . 因此V E —MBC =12V -V E —MDC . 而V E —MBC =V B —EMC ,V E —MDC =V D —EMC ,因此V E —MBCV E —MDC =V B —EMC V D —EMC =h 1h 2.因为B ,D 到平面EMC 的距离即为到平面EAC 的距离,而AB ∥CD ,且2AB =3CD ,因此h 1h 2=32. 因此V E —MBC =V M -EBC =310V .2. 某三棱锥的三视图如下图,该三棱锥的表面积是( ) A .28+6 5 B .30+65C .56+125 D .60+125 答案 B 解析 由几何体的三视图可知,该三棱锥的直观图如下图,其中AE ⊥平面BCD ,CD ⊥BD ,且CD =4,BD =5,BE =2,ED =3,AE =4.∵AE =4,ED =3,∴AD =5.又CD ⊥BD ,CD ⊥AE ,则CD ⊥平面ABD ,故CD ⊥AD ,因此AC =41且S △ACD =10.在Rt△ABE 中,AE =4,BE =2,故AB =25. 在Rt△BCD 中,BD =5,CD =4,故S △BCD =10,且BC =41.在△ABD 中,AE =4,BD =5,故S △ABD =10.在△ABC 中,AB =25,BC =AC =41,则AB 边上的高h =6,故S △ABC =12×25×6=6 5. 因此,该三棱锥的表面积为S =30+65. 3. 表面积为3π的圆锥,它的侧面展开图是一个半圆,那么该圆锥的底面直径为________.答案 2解析 设圆锥的母线为l ,圆锥底面半径为r .那么12πl 2+πr 2=3π,πl =2πr ,∴r =1,即圆锥的底面直径为2.4. 如图,在四棱锥P -ABCD 中,底面为正方形,PC 与底面ABCD 垂直,图为该四棱锥的主视图和左视图,它们是腰长为6 cm 的全等的等腰直角三角形.(1)依照图所给的主视图、左视图,画出相应的俯视图,并求出该俯视图的面积;(2)求PA .解 (1)该四棱锥的俯视图为(内含对角线),边长为6 cm 的正方形,如图,其面积为36 cm 2.(2)由左视图可求得PD =PC 2+CD 2=62+62=6 2.由主视图可知AD =6,且AD ⊥PD ,因此在Rt△APD 中,PA =PD 2+AD 2=622+62=6 3 cm.5. 在四棱锥P -ABCD 中,底面ABCD 是边长为a 的正方形,PD ⊥底面ABCD ,且PD =a ,PA =PC =2a ,假设在那个四棱锥内放一球,求此球的最大半径.解 当球内切于四棱锥,即与四棱锥各面均相切时球半径最大,设球的半径为r ,球心为O ,连接OP 、OA 、OB 、OC 、OD ,那么把此四棱锥分割成四个三棱锥和一个四棱锥,这些小棱锥的高都是r ,底面别离为原四棱锥的侧面和底面,则V P -ABCD =13r (S △PAB +S △PBC +S △PCD +S △PAD +S 正方形ABCD )=13r (2+2)a 2.由题意,知PD ⊥底面ABCD ,∴V P -ABCD =13S 正方形ABCD ·PD =13a 3. 由体积相等, 得13r (2+2)a 2=13a 3,解得r =12(2-2)a .。
几何体的表面积和体积求法

几何体的表面积与体积问题之前已经学过空间几何体的相关概念,知道什么是多面体什么是旋转体。
然后它们之间的一系列转化也已经了解,那么我们知不知道这些几何体的表面积或者是体积怎么求,本节课主要就是学习这块的内容。
在初中我们已经知道圆柱的体积是底面积乘以高,然后圆锥的体积需要乘以31。
所以这边我们先要了解一些其它的几何体的表面积和体积。
1.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面 展开图侧面 积公式S 圆柱侧=2πrlS 圆锥侧=πrlS 圆台侧 =π(r +r ′)l2.空间几何体的表面积与体积公式名 称 几何体 表面积体 积柱体 (棱柱和圆柱)S 表面积=S 侧+2S 底 V =S 底h 锥体 (棱锥和圆锥)S 表面积=S 侧+S 底V =13S 底h台体 (棱台和圆台)S 表面积=S 侧 +S 上+S 下 V =13(S 上+S 下+S 上S 下)h 球S =4πR 2V =43πR 3一些总结1.辨明两个易误点(1)求组合体的表面积时,要注意各几何体重叠部分的处理.(2)底面是梯形的四棱柱侧放时,容易和四棱台混淆,在识别时要紧扣定义,以防出错. 2.求空间几何体体积的常用方法(1)公式法:直接根据相关的体积公式计算.(2)等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等.(3)割补法:把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体1.如图,一个空间几何体的正(主)视图、侧(左)视图、俯视图均为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为( )A .1B .12C.13D .16D [解析] 由三视图可知,该几何体为三棱锥,V =13Sh =13×12×1×1×1=16,故选D .2.(2015·高考陕西卷)一个几何体的三视图如图所示,则该几何体的表面积为( ) A .3π B .4π C .2π+4D .3π+4D [解析] 由几何体的三视图可知,该几何体为半圆柱,直观图如图所示. 表面积为2×2+2×12×π×12+π×1×2=4+3π.主要的难点在于如何由三视图来转化为原来的几何体,然后进而求解几何体的表面积和体积。
§8.1 空间几何体的三视图、表面积与体积(讲解部分)
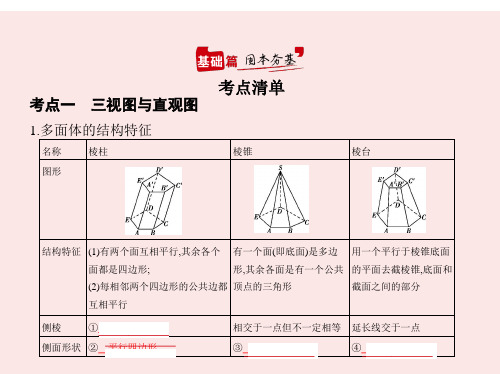
在已知图形中过点O作z轴垂直于平面xOy,在直观图中画出对应的z'轴,垂 直于平面x'O'y',已知图形中平行于z轴的线段,在直观图中平行于z'轴且 ⑩ 长度不变 .
考点二 空间几何体的体积
名称
体积
柱体 锥体
V=Sh
1
V= 3Sh
台体
1
V= 3(S+S'+ SS' )h
球体
4
V=3 πR3
考点三 空间几何体的表面积
112.5.
(2)包装盒子的体积V=(a-2x)(b-2x)x=x[ab-2(a+b)x+4x2],x∈
0,
b 2
,b≤60,V=x
[ab-2(a+b)x+4x2]≤x(ab-4 ab x+4x2)=x(3 600-240x+4x2)=4x3-240x2+3 600x.当
且仅当a=b=60时等号成立,设f(x)=4x3-240x2+3 600x,x∈(0,30),则f '(x)=12(x-
②半径:r= a2 b2 c2 (a,b,c为长方体的长、宽、高).
2
(2)正方体的外接球、内切球及与各条棱都相切的球:
①外接球:球心是正方体的中心,半径r= 3 a(a为正方体的棱长);
2
②内切球:球心是正方体的中心,半径r= a (a为正方体的棱长);
2
③与各条棱都相切的球:球心是正方体的中心,半径r= 2 a(a为正方体的棱
考点清单
考点一 三视图与直观图
1.多面体的结构特征
名称
棱柱
棱锥
棱台
图形
结构特征 (1)有两个面互相平行,其余各个 有一个面(即底面)是多边 用一个平行于棱锥底面
2023版高考数学一轮总复习专题检测8-1空间几何体的三视图表面积和体积

8.1 空间几何体的三视图、表面积和体积一、选择题1.(2022届山东烟台一中开学考,2)已知圆锥的表面积等于12πcm 2,其侧面展开图是一个半圆,则圆锥的底面半径为( ) A.1cm B.2cm C.3cm D.32cm答案 B 设圆锥的底面圆的半径为rcm,母线长为lcm,∵侧面展开图是一个半圆,∴πl=2πr ⇒l=2r,∵圆锥的表面积为12πcm 2,∴πr 2+πrl=3πr 2=12π,∴r=2,故圆锥的底面半径为2cm.故选B.2.(2022届黑龙江六校11月联考,4)已知圆锥的轴截面为等边三角形,且圆锥的表面积为3π,则圆锥的底面半径为( )A.12 B.1 C.√2 D.√3答案 B 设圆锥的母线长为l,底面半径为r,根据题意,得l=2r,所以圆锥的表面积S=πr 2+πrl=3πr 2=3π,解得r=1,故选B.3. (2022届河北邢台入学考,4)六氟化硫,化学式为SF 6,在常压下是一种无色、无臭、无毒、不燃的稳定气体,有良好的绝缘性,在电器工业方面具有广泛用途.六氟化硫分子结构为正八面体(每个面都是正三角形的八面体),如图所示,硫原子位于正八面体的中心,6个氟原子分别位于正八面体的6个顶点.若相邻两个氟原子间的距离为2a,则六氟化硫分子中6个氟原子构成的正八面体的体积是(不计氟原子的大小)( )A.4√23a 3B.8√23a 3C.4√2a 3D.8√2a 3答案 B 如图,连接AC,BD,设AC∩BD=O,则O 为正方形ABCD 的中心,连接OE.因为AE=CE,BE=DE,所以OE⊥AC,OE⊥BD,又AC∩BD=O,所以OE⊥平面ABCD.因为AB=BC=AE=2a,所以AC=√AA 2+B A 2=2√2a.因为四边形ABCD 是正方形,所以AO=12AC=√2a,则OE=√AA 2-A A 2=√2a,故该正八面体的体积为13×(2a)2×√2a×2=8√23a 3.4.(2022届河南焦作一模,6)底面是边长为1的正方形,侧面均是等边三角形的四棱锥的体积为( )A.√26 B.√24 C.√23 D.√22答案 A 由题意可知该四棱锥为正四棱锥,底面正方形对角线长为√2,则正四棱锥的高h=√12-(√22)2=√22,所以正四棱锥的体积V=13×12×√22=√26,故选A.5.(2022届河南洛阳期中,7)某四面体的三视图如图所示,已知其正视图、侧视图、俯视图是全等的等腰直角三角形,则该四面体的四个面中直角三角形的个数为( )A.1B.2C.3D.4答案 D 由三视图及已知可知该四面体可补形成正方体,如图所示.易知△DAB,△ABC 均为直角三角形.由正方体的性质可知CB⊥平面DAB,所以CB⊥BD,即△DBC 是直角三角形;又知DA⊥平面ABC,所以DA⊥AC,即△DAC 是直角三角形,所以该四面体的四个面中直角三角形的个数为4,故选D.6.(2022届江西吉安9月月考,8)如图,网格图中小正方形的边长为1,粗线是一个几何体的三视图,则该几何体的体积为( )A.2π+4B.2π+2C.π+4D.6π+12答案 A 由三视图可知,该几何体由半圆锥和三棱锥拼接而成,半圆锥的底面半径为2,高为3,三棱锥的底面是斜边长为4的等腰直角三角形,三棱锥的高为3,故该几何体的体积V=13×(12π×22+4×2×12)×3=2π+4,故选A.7.(2022届江苏海安高级中学期中,8)如图所示,在直三棱柱ABC-A 1B 1C 1中,AA 1=1,AB=BC=√3,cos∠ABC=13,P 是A 1B 上的一动点,则AP+PC 1的最小值为( )A.√5B.√7C.1+√3D.3答案 B 连接BC 1,得△A 1BC 1,以A 1B 所在直线为轴,将△A 1BC 1所在平面旋转到平面ABB 1A 1,设点C 1的新位置为C',连接AC', 则AC'的长即为AP+PC 1的最小值.∵AB=BC=√3,cos∠ABC=13,∴由余弦定理可得,AC=2,∴A 1C 1=2,即A 1C'=2,∵AA 1=1,AB=√3,∴A 1B=2,且∠AA 1B=60°.易求得C 1B=2,∵A 1B=BC 1=A 1C 1=2,∴△A 1BC 1为等边三角形,∴∠BA 1C 1=60°.∴在三角形AA 1C'中,∠AA 1C'=120°,又AA 1=1,A 1C'=2,∴AC'=√1+4−2×1×2×(-12)=√7.故选B.8.(2022届吉林顶级名校11月月考,10)已知球O,过球面上A,B,C 三点作截面,若点O 到该截面的距离是球半径的一半,且AB=BC=2,∠B=120°,则球O 的表面积为( ) A.643π B.83π C.323π D.169π答案 A 如图,设球的半径为r,O 1是△ABC 的外心,外接圆半径为R,连接OO 1,OB,O 1B,则OO 1⊥平面ABC,在△ABC 中,AB=BC=2,∠ABC=120°,则∠A=30°,由正弦定理得2sin A =2R,∴R=2,即O 1B=2.在Rt△OBO 1中,由已知得r 2-14r 2=4,得r 2=163,所以球O 的表面积S=4πr 2=4π×163=643π.故选A.9.(2022届合肥联考(一),9)一个四面体的三视图如图所示,则该四面体的表面积为( )A.2√3+√2+1B.√3+2√2+1C.√3+√2+2D.√3+√2+1答案 B 如图,在棱长等于√2的正方体ABCD-A 1B 1C 1D 1上取四面体ABB 1D 1,即为所求四面体,易得该四面体的表面积为12×√2×√2+12×√2×2×2+√34×22=√3+2√2+1.故选B.10.(2022届贵阳摸底,9)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的外接球的体积为( )A.13√136π B.13π C.9π D.92π答案 A 由三视图可知,此空间几何体是一放倒的圆柱,圆柱的底面半径为1,高为3,如图所示,该圆柱的上、下底面圆周在其外接球的表面上,外接球的半径为OA,因为OO 1=32,O 1A=1,所以OA=√(32)2+12=√132,所以圆柱外接球的体积为43π(√132)3=13√136π,故选A.11.张衡(78年—139年)是中国东汉时期伟大的天文学家、文学家、数学家,他的数学著作有《算罔论》,他曾经得出结论:圆周率的平方除以十六等于八分之五.已知正方体的外接球与内切球上各有一个动点A,B,若线段AB 的最小值为√3-1,利用张衡的结论可得该正方体的外接球的表面积为( )A.30B.10√10C.12√10D.36答案 C 设正方体的棱长为a,则正方体的内切球半径为r=A2,正方体的外接球半径R 满足:R 2=(A 2)2+(√22a )2,解得R=√32a,由题意知:R-r=√32a-A2=√3-1,则a=2,R=√3,则该正方体的外接球的表面积为12π,又因为圆周率的平方除以十六等于八分之五,即π216=58,所以π=√10,所以外接球的表面积为12√10.故选C.二、填空题12.(2022届甘肃九校联考,16)某零件的结构是在一个圆锥中挖去了一个正方体,且正方体的一个面在圆锥底面上,该面所对的面的四个顶点在圆锥侧面内.在图①②③④⑤⑥⑦⑧中选两个分别作为该零件的主视图和俯视图,则所选主视图和俯视图的编号依次可能为(写出符合要求的一组即可).答案⑤⑦(或①⑧)解析根据题意可知,圆锥和正方体的位置关系如图所示,当主视图为①时,俯视图为⑧;当主视图为⑤时,俯视图为⑦,故符合题意的编号为⑤⑦(或①⑧).13.(2022届浙江浙南名校联盟联考一,15)一圆锥母线长为定值a(a>0),母线与底面所成角),当圆锥体积V最大时,sinθ=.大小为θ(0<A<π2答案√33解析如图,设圆锥的高为h,底面半径为r,则h=asinθ,r=acosθ,∴V=13πr 2h=13πa 2cos 2θ·asinθ=π3a 3(1-sin 2θ)·sinθ=π3a 3(sinθ-s in 3θ),则V'=π3a 3(cosθ-3sin 2θ·cosθ)=π3a 3·cosθ(1-3sin 2θ),令V'=0, ∵0<θ<π2,∴1-3sin 2θ=0,即sin 2θ=13,∴sinθ=√33.∴当sinθ∈(0,√33)时,V'>0,V=π3a 3(sinθ-sin 3θ)单调递增;当sinθ∈(√33,1)时,V'<0,V=π3a 3(sinθ-sin 3θ)单调递减.∴sinθ=√33时,V 最大.14.(2022届河南洛阳期中,15)在三棱锥P-ABC 中,AB=2√6,BC=1,AC=5,侧面PAB 是以P 为直角顶点的直角三角形,若平面PAB⊥平面ABC,则该三棱锥体积的最大值为 . 答案 2解析 因为AB=2√6,BC=1,AC=5,所以AB 2+BC 2=AC 2,所以AB⊥BC,在Rt△PAB 中,过P 作PE⊥AB 交AB 于点E,又平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PE ⊂平面PAB,所以PE⊥平面ABC,所以PE 是三棱锥P-ABC 的高,设AE=x,则BE=2√6-x,在Rt△PAB 中,PE 2=AE·BE,所以PE=√A (2√6-x).所以V 三棱锥P-ABC =13S △ABC ·PE=13×12×2√6×1×√A (2√6-x)=√63√A (2√6-x),当x=√6时,三棱锥的体积取得最大值2.15.(2020甘肃金昌永昌一高期末,16)已知△ABC 中,P 在边BC 上且AP⊥BC,现以AP 为折痕将△ABC 折起,使得∠BPC=π2.若PA=2PB=2PC=4,则该三棱锥P-ABC 的外接球的体积是 ;内切球的表面积是 . 答案 8√6π;π解析 因为AP⊥BP 且AP⊥PC,且∠BPC=90°,所以PA,PB,PC 两两垂直,所以将三棱锥P-ABC 补成如图所示的长方体,设三棱锥P-ABC 的外接球的半径为R,则(2R)2=PA 2+PB 2+PC 2=16+4+4=24,解得R=√6,所以三棱锥P-ABC 的外接球的体积为43πR 3=43π(√6)3=8√6π.设三棱锥P-ABC 内切球的半径为r,三棱锥P-ABC 的表面积为S,由已知得BC=√22+22=2√2,AB=AC=√42+22=2√5,则S=12×4×2×2+12×2×2+12×2√2×√(2√5)2-(√2)2=16,所以V P-ABC =V B-APC =13×12×4×2×2=13×16r,解得r=12,所以三棱锥P-ABC 内切球的表面积为4πr 2=4π×(12)2=π.16.(2022届北京顺义一中期中,15)如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,若平面BED1交棱AA1于点F,给出下列命题:①截面四边形BED1F可以是正方形;②三棱锥B1-BED1的体积恒为定值;③截面四边形BED1F周长的最小值为2√5a.其中是真命题的是(填写所有正确答案的序号).答案②③解析对于①,易得BD1=√3a,设C1E=b(0≤b≤a),则D1E=√A2+A2,BE=√A2+(A-A)2,假设截面四边形BED1F是正方形,则△BED1是以BD1为斜边的等腰直角三角形,从而有{√2·√A2+A2=√3a,√2·√A2+(A-A)2=√3a,由b=a-b得a=2b,则√2·√4A2+A2=2√3b,显然√2·√4A2+A2=2√3b不成立,所以截面四边形BED1F不可能是正方形,①错误;对于②,因为点E到平面BB1D1的距离为定值,又A A1-BE A1=A A-AA1A1,所以三棱锥B1-BED1的体积恒为定值,②正确;对于③,当点E与点C或C1重合时,截面四边形BED1F周长取得最大值2(a+√2a)=2(1+√2)a,当点E是CC1中点时,截面四边形BED1F周长取得最小值2×2·√A2+(A2)2=2√5a,③正确.综上②③正确.。
空间几何体三视图、表面积

【规范解答】(1)选A.由三视图可知原几何 体是一个正方体截去两个全等的小正三棱锥. 正方体的表面积为S=24,两个全等的三棱锥 是以正方体的相对顶点为顶点,侧面是三个 全等的直角边长为1的等腰直角三角形,其表面面积的和为3, 三棱锥的底面是边长为 2的正三角形,其表面积的和为 , 3 故所求几何体的表面积为24-3+ 3 =21+ 3 .
【主干知识】 1.必记公式 (1)表面积公式: 表面积=侧面积+底面积,其中 ①多面体的表面积为各个面的_面__积__的__和__. ②圆柱的表面积公式:S=_2_π__r_2_+_2_π__r_l =__2_π__r_(_r_+_l)_(其中,_r_
为底面半径,_l 为圆柱的高).
③圆锥的表面积公式:S=_π__r_2_+_π__r_l =_π__r_(_r_+_l_)_(其中圆锥的 底面半径为_r_,母线长为_l_). ④圆台的表面积公式:S=__π__(_r_'_2_+_r_2+_r_'_l+_r_l_)_(其中圆台的上、 下底面半径分别为_r_'_和_r_,母线长为_l_). ⑤球的表面积公式:S=_4_π__R_2 (其中球的半径为_R_).
【规律方法】 1.由直观图确认三视图的策略 根据空间几何体三视图的定义及画法规则和摆放规则确认. 2.由三视图还原到直观图的思路 (1)根据俯视图确定几何体的底面. (2)根据正(主)视图或侧(左)视图确定几何体的侧棱与侧面的特 征,调整实线和虚线所对应的棱、面的位置. (3)确定几何体的直观图形状.
则球的体积为 ( )
A .500 cm 3 3
B .866 cm 3 3
C .1 3 7 2 c m 3 3
绝对值不等式 (2)

A.6 2 B.6 C.4 2 D.4
栏目索引
栏目索引
解析 由多面体的三视图可知该几何体的直观图为一个三棱锥,如图所 示.其中面ABC⊥面BCD,△ABC为等腰直角三角形,AB=BC=4,取BC的中 点M,连接AM,DM,则DM⊥面ABC,在等腰△BCD中,BD=DC=2 5 ,BC= DM=4,所以在Rt△AMD中,AD= AM 2 DM 2 = 42 22 42 =6,又在Rt△ ABC中,AC=4 2<6,故该多面体的各条棱中,最长棱为AD,长度为6,故选 B.
栏目索引
形,这些面围成的几何体叫做棱锥. (2)正棱锥的定义:如果一个棱锥的底面是正多边形,并且顶点在底面内 的射影是底面中心,这样的棱锥叫做正棱锥. (3)正棱锥的性质: (i)各侧棱② 相等 ,各侧面都是③ 全等的等腰三角形 ,各等腰三 角形底边上的高相等.侧面等腰三角形底边上的高叫做正棱锥的 ④ 斜高 . (ii)棱锥的高、斜高和斜足与底面中心连线组成一个直角三角形;棱锥 的高、侧棱和侧棱在底面内的射影也组成一个直角三角形. 3.圆柱、圆锥、圆台的特征 分别以⑤ 矩形一边 、⑥ 直角三角形一直角边 、
栏目索引
考点二 斜二测画法
水平放置的平面图形的直观图的斜二测画法的步骤: (1)在已知图形中取互相垂直的x轴和y轴,两轴相交于O点.画直观图时, 把它们画成对应的x'轴与y'轴,两轴相交于O'点,且使∠x'O'y'=45°(或 135°),它们确定的平面表示水平面; (2)已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x'轴 或y'轴的线段; (3)已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y 轴的线段,长度变为 原来的一半 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
28 3
7 8
4 3
7 8
1 4
栏目索引
2.(2016课标Ⅱ,6,5分)下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积 为 ( )
A.20π B.24π C.28π D.32π
22 (2 3)2 =4,∴S圆锥侧=π×2×4=8π.又S圆柱侧=2π×2×4= 答案 C 由三视图可得圆锥的母线长为
A.6 2 B.6 C.4 2 D.4
栏目索引
答案 B
由多面体的三视图可知该几何体的直观图为一个三棱锥,如图所示.
其中面ABC⊥面BCD,△ABC为等腰直角三角形,AB=BC=4,取BC的中点M,连接AM,DM,则DM
⊥面ABC,在等腰△BCD中,BD=DC=2 5 ,BC=DM=4,所以在Rt△AMD中,AD= AM 2 DM 2 =
A.1 C.4
B.2 D.8
栏目索引
答案 B 由已知可知,该几何体的直观图如图所示,其表面积为2πr2+πr2+4r2+2πr2=5πr2+4r2.由 5πr2+4r2=16+20π,得r=2.故选B.
思路分析 根据题意及正视图和俯视图画出几何体的直观图,利用题图提供的数据表示出几 何体的表面积,从而构造出关于r的方程,由此可解出r的值. 方法归纳 几何体的表面积是指各个面的面积之和;求组合体的4.(2015课标Ⅱ,9,5分,0.685)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若
三棱锥O-ABC体积的最大值为36,则球O的表面积为 ( A.36π B.64π C.144π D.256π )
答案 C ∵S△OAB是定值,且VO-ABC=VC-OAB,
∴当OC⊥平面OAB时,VC-OAB最大,即VO-ABC最大.设球O的半径为R,则(VO-ABC)max= × R2×R= R3=3 6,∴R=6,∴球O的表面积S=4πR2=4π×62=144π.
1 3 1 2 1 6
16π,S圆柱底=4π,∴该几何体的表面积为8π+16π+4π=28π.故选C. 思路分析 先求圆锥的母线长,从而可求得圆锥的侧面积,再求圆柱的侧面积与底面积,最后相 加即可得出该几何体的表面积.
栏目索引
3. (2015课标Ⅰ,11,5分,0.845)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该 几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r= ( )
栏目索引
高考理数
(课标专用)
§8.1 空间几何体的三视图、表面积和体积
栏目索引
五年高考
A组
考点一 三视图与直观图
统一命题·课标卷题组
1.(2018课标Ⅰ,7,5分)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上 的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最 短路径的长度为 ( )
合成长方体,则咬合时带卯眼的木构件的俯视图可以是 (
)
答案 A 本题考查空间几何体的三视图. 两个木构件咬合成长方体时,小长方体(榫头)完全嵌入带卯眼的木构件,易知俯视图可以为A.
故选A.
栏目索引
3.(2017课标Ⅰ,7,5分)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角 三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯 形,这些梯形的面积之和为 ( )
题型归纳 有关三视图的基本问题一般有两类:一类是根据给定的空间几何体(或物体模型) 画出该几何体(或物体模型)的三视图;另一类是已知某几何体的三视图,想象该几何体的结构 特征,画出该几何体的空间图形.
栏目索引
4.(2014课标Ⅰ,12,5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图, 则该多面体的各条棱中,最长的棱的长度为 ( )
图1
图2
方法点拨 1.由三视图还原直观图的步骤:
(1)看视图明关系;(2)分部分想整体;(3)合起来定整体.
2.解决空间几何体表面上两点间的最短路径问题的常用方法是把空间图形展为平面图形,利 用两点之间线段最短进行求解.
栏目索引
2.(2018课标Ⅲ,3,5分)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部 分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬
A.10 C.14
B.12 D.16
栏目索引
答案 B 本题考查立体几何中的三视图问题,考查学生的运算求解能力和空间想象能力.
由多面体的三视图还原直观图如图.
该多面体由上方的三棱锥A-BCE和下方的三棱柱BCE-B1C1A1构成,其中面CC1A1A和面BB1A1A 是梯形,则梯形的面积之和为2×
(2 4) 2 =12.故选B. 2
A.17π B.18π C.20π D.28π
1 8
答案 A 由三视图可知,该几何体是一个球被截去 后剩下的部分,设球的半径为R,则该几 何体的体积为 × πR3,即 π= × πR3,解得R=2.故其表面积为 ×4π×22+3× ×π×22=17π.选A. 评析 三视图问题主要是考查空间想象能力.本题考查内容较多,其中包括球的体积、表面积 的求法.属中等难度题.
42 22 42 =6,又在Rt△ABC中,AC=4 2 <6,故该多面体的各条棱中,最长棱为AD,长度为6,故
选B.
栏目索引
考点二
空间几何体的表面积
1.(2016课标Ⅰ,6,5分)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直 28 的半径.若该几何体的体积是 ) 3 ,则它的表面积是 (
A.2 17
B.2 5
C.3
D.2
栏目索引
答案 B
本题主要考查空间几何体的三视图、直观图以及最短路径问题.
由圆柱的三视图及已知条件可知点M与点N的位置如图1所示,设ME与FN为圆柱的两条母线,
沿FN将圆柱的侧面展开,如图2所示,连接MN,MN即为从M到N的最短路径,由题意知,ME=2,EN
=4,∴MN= 5 .故选B. 42 22 =2
