2014届高三(上)期末考年级组试质量分析
13-14学年第一学期期考质量分析

2013-2014学年第一学期期末考质量分析针对这次期末考试情况,我对所做的工作进行了总结反思。
一、本学期期末考试班级整体情况分析:初二(6)班共49人参加考试,优秀7人,优秀率14.28%,及格45人,及格率91.83%。
本次考试我们班比期中考试时有进步,但相对于其他班级优等生比较少,这是一个需要大力改进的现象;合格学生较多,是一个不错的现象:说明学习的学生比较多,虽然还不是太好,但成绩会慢慢提高。
通过本次考试,发现了本班存在的很多问题。
包括成绩上以及学生的个人习惯养成方面。
全班49人,有35名同学有进步,近半数24名同学很有进步。
其中,有6名同学上升了30名以上,李君慧上升了69名,王莉莉上升了41名,刘杨上升了45名,李绍娜上升了39名,姜慧上升了38名,刘元瑞上升了38名。
但也要提出,有少数同学虽然学习态度还好,但成绩下滑幅度较大,像这些同学今后还要讲究学习方法、考场上注意把握时间、进行严格审题,等等。
全班的尖子生集中在年级后30名之后。
后进生大多维持在年级后二十名。
可以看出没有尖子生,也没有太大的拖腿生。
各科成绩以语文、英语、生物表现较为突出,位于年级前茅。
二、班风建设方面:首先,抓好学生行为习惯和学习习惯的养成;完善班级班干部队伍;进一步健全班级的量化考核制度;提高班级的集体荣誉感和学生的责任意识。
其次,针对班级一些学生适应能力很差,学习态度不太端正的现象,积极采取了家访、电访、微信、飞信等方式的家校联系,和家长充分配合,取得一定的效果。
第三,观察入微,个个击破。
初二是整个中学阶段“最危险”的阶段,初二学生最难管理。
我通过平时对学生们的细心观察以及通过在“周记”中与学生们谈心,发现了本班有几对的“早恋”的学生,其实说“早恋”,可能“过”了,他们只是彼此之间有好感,而且这几位学生几乎都是班级的“优生”。
我采取了一些方法,并和家长们共同配合,个个击破,让他们明白了自己的问题,这些学生在期末考试中不但成绩没有退步,反而都有了一定的进步。
高三(上)期末数学备课组质量分析

2014届高三(上)期末数学备课组质量分析高三数学备课组一、试题基本情况分析:1.试卷总体分析:本次试卷是由我校命题,总分150分:其中选择题12个题,每题5分,共60分;填空题4个题,每题5分,共16分;解答题6个,17题10分,其余5题每题12分。
总体题型结构与高考题基本吻合,基本体现通解通法,难易适中,顺序安排从易到难、从简到繁,知识点基本覆盖高一、二数学的全部内容。
2.试题考点以及难易分析:从试卷本身的难易程度和考试内容的角度分析,试卷难度比我们平时的单元试卷难度较小,计算量相对来说还是比较小的,同时试卷的知识容量也加大了很多,这是成绩考得不理想的一个原因之一,最主要的原因是学生对基础知识掌握得不牢固,基础没过关,平时的训练度还不够,同时课时较少,任务重等多方面的原因导致成绩不是很理想。
三、主要存在的问题:(一)学生方面:1、自主学习的时间不够。
考试时,很多学生要么审题不仔细,要么遇到自己不熟悉的材料,就留空白。
也说明学生复习效果不好,要求识记的知识,公式没有记住,缺乏学生的主动性。
2、缺乏答题技巧,不会总结做题经验。
同一类型题,复习时讲过,考试时变换个材料或问题,对于学生来说又成新的“难题”,举一反三的能力差,也说明在复习过程中,学生只是“学”了,但没有“懂”,能力没有得到真正的提升;3、考察基础知识的题丢分严重,不管是重点班,还是平行班的选择题、填空题都做得很差,即便是复习过的知识大部分的学生也没有拿到分,说明以后还需要大量的时间去训练。
4、解答题问题就较大:平行班基本没有学生拿到分,大部分学生都是空着的。
第17题;18;19;20;21属于简单题,但是考试下来,大部分学生都没有得分;5、基础不牢固:学生在平时训练的时候不够重视基础知识,自己下来又不注重训练做题,在平时复习的时候时间安排得不合理,有点盲目等原因。
6、心态不稳,时间安排不合理。
(二)、老师方面:1、复习时间不够:时间紧任务重,我们每周只有5节课后1个月增加一节,但我们每单元都进行测验并进行评析,导致复习时间只有2—3节课,从而使学生没有得到很好的巩固与提高;2、补充内容部完善:如复合函数的单调性的判断、分式不等式、抽象不等式、不等式的恒成立问题难度较大以及比较抽象所以没有及时补充,导致学生不会做;3、学生训练不够:因时间紧,留给学生训练的时间不多,导致学生会而不全,会而不对。
高三上学期期末考试后分析

高三上学期期末考试后分析一、成绩概况在刚刚落下帷幕的高三上学期期末考试中,我校高三学生展现出了顽强的斗志和拼搏的精神。
此次考试,我们取得了令人欣喜的成绩,全校平均分达到--分,这是一个了不起的成就,凸显了我校教学质量和学生水平的不断提升。
同时,及格率和优秀率也保持了相对稳定,这充分说明了我们的教学策略和学生的学习方法是行之有效的。
二、学科分析在各个学科方面,学生们都展现出了扎实的基础和出色的能力。
语文学科,学生们在作文方面表现出了较高的水平,他们的文笔流畅、思路清晰,充分展现了我校语文教学的成果。
数学学科,尽管存在一些难度,但学生们仍然取得了不错的成绩,这得益于他们平时的刻苦学习和教师的精心指导。
英语学科,阅读理解和完形填空等题型一直是学生的弱项,但通过教师的耐心讲解和学生的不懈努力,这次考试也有了明显的进步。
物理、化学、生物等学科,学生们都展现出了扎实的学科基础和实验技能,这是他们取得好成绩的重要保障。
三、学生分析当然,成绩的取得离不开学生自身的努力。
在这次考试中,许多学生表现出了高度的学习热情和责任心。
他们充分利用课余时间进行自主学习,积极参加各种学科竞赛和课外活动,不断提升自己的综合素质。
然而,也有部分学生存在一些问题。
有的学生学习态度不够端正,缺乏明确的学习目标和动力;有的学生学习方法不够科学,导致学习效率低下;还有的学生时间管理能力较弱,无法合理安排学习和休息时间。
针对这些问题,我们需要进一步加强思想教育和学法指导,帮助学生找到适合自己的学习方法和策略。
四、教学建议为了进一步提升教学质量和学生成绩,我们提出以下教学建议:首先,优化教学方法,针对不同层次的学生进行差异化教学。
教师可以采用小组合作、案例分析、情境模拟等多种教学方法相结合的方式,激发学生的学习兴趣和积极性。
其次,加强基础训练,注重学生的基础知识巩固和提高。
特别是在英语、化学、生物等学科上要加强基础知识的训练和强化。
最后,加强心理辅导和学法指导。
2014—2015上学期期末考试质量分析报告

2014—2015上学期期末考试质量分析报告韩寺镇二中张会芳本试卷以《数学课程标准》为精神指导,能够全面了解学生的学习状况,激励学生的学习热情,既考查学生基础知识和基本技能的掌握情况,也考查学生分析、比较、审题、操作和灵活应用数学的能力,促进学生的全面发展。
一、数据分析:此次考试110—120分的2人,100—109分的3人,96—99分的7人,优秀人数12人,优秀率百分之25.5;90—95分的6人,80—89分的4人,72—79分的7人,及格人数29人,及格率百分之61.7;低分人数2人,最高分113分,最低分27分,平均分73.45学校人数平均分名次及格人数及格率名次优秀人数优秀率名次总名次中牟一中607 73.67 7 336 55.35% 7 180 29.65% 5 7 中牟二中665 78.18 5 427 64.21% 5 187 28.12% 6 5 中牟三中692 79.29 4 466 67.34% 3 234 33.82% 4 4 中牟四中779 80.89 1 528 67.68% 2 296 38.00% 2 1 中牟五中621 80.20 3 431 69.40% 1 214 34.46% 3 3 外国语637 80.41 2 413 64.84% 4 259 40.66% 1 2 刘集二中107 62.33 9 45 42.06% 9 12 11.21% 15 11 姚家中学118 58.38 13 48 40.68% 11 14 11.86% 14 13 狼城岗中学280 55.89 14 101 36.07% 14 51 18.21% 11 14 黄店一中182 58.73 12 75 41.21% 10 44 24.18% 8 9 雁鸣湖中学160 47.56 17 43 26.88% 16 19 11.88% 13 15 郑庵中学235 60.43 11 85 36.17% 13 31 13.19% 12 12 官渡中学461 60.47 10 184 39.91% 12 90 19.52% 10 10韩寺一中124 46.95 18 32 25.81% 17 14 11.29% 16 17 韩寺二中47 76.87 6 29 61.70% 6 12 25.53% 7 6大孟中学159 67.54 8 79 49.69% 8 35 22.01% 9 8刁家中学78 48.96 16 22 28.21% 15 6 7.69 17 16 万滩中学71 52.21 15 13 18.31% 18 3 4.23% 18 18二、存在的问题及原因:1、不注意认真、仔细审题。
2013-2014学年度第一学期期末考试质量分析

2013-2014 学年度第一学期期末考试质量分析在上级主管部门的正确领导下,我校教育教学工作已结束。
现为了认真总结经验,分析质量现状,查找差距,切实加强教学教研工作,加大教学过程管理力度,全面提高我校教育教学质量本期末考试进行如下分析,以期达到全面提高我校教育教学质量之目的。
、试题基本情况2013 学年第一学期各年级各学科期末考试,试题的特点是:遵循大纲、课标,紧扣教材内容,面向全体学生,重在基础知识和基本技能的考查;知识面覆盖广,分布较为合理,具有层次性,特别注重考查学生课内知识的运用能力和适度应用知识能力的迁移;试题形式多样,基本与中考题型一致,具有一定的灵活性。
整个试题较为平和,难度较适中。
但个别学科照搬、照抄测练题数量多、分值大。
、考试成绩情况1)、七年级两班参考人数132人。
前10名一班3人,二班7人。
前20名一班7 人,二班13 人。
前30 名一班13 人,二班17 人。
两班有一定差距,但与期中相比差距在缩小。
各科平均相差不大。
最高分607 分。
7 科总分480分以上44 人。
2)、八年级两班参考135人。
前10名一班3人,二班7人。
前20名一班8 人,二班12 人。
前30 名一班15 人,二班15 人。
两班稍有差距。
且与期中情况恰好相反。
各科平均除数学外相差不大。
八科总分最高728,600 分以上41 人。
优生面相对还不错。
但差生面也很广。
3)、九年级参考人数115人。
前10名一班6 人,二班4 人。
前20名一班10 人,二班10 人。
前30 名一班15 人,二班15 人。
从中可看出两班优生面差不多,但二班优生明显偏科严重。
前60 名一班27 人,二班33人。
说明二班中层面更广。
总体上与上期无明现变化。
七科总分最高646 分,600分以上9 人。
各科平均几乎无差别。
但与往年相比优生面不广。
三、存在问题通过测试,暴露出的问题比较多。
一方面是各学科优秀率较低,这说明各班级各学科在优生的培养上效果不是很好。
高三期末考试质量分析总结(通用8篇)

高三期末考试质量分析总结(通用8篇)高三期末考试质量分析总结(通用8篇)总结是在一段时间内对学习和工作生活等表现加以总结和概括的一种书面材料,它能够使头脑更加清醒,目标更加明确,让我们来为自己写一份总结吧。
你想知道总结怎么写吗?以下是小编整理的高三期末考试质量分析总结,欢迎大家分享。
高三期末考试质量分析总结篇1期末考陆续结束,考生心情各不相同。
考好的喜上眉梢,失利的愁眉苦脸。
作为多年带高三的老师提醒高三的考生:悲观失落、自暴自弃、满不在乎等3种消极心态要不得。
期末考是高三上学期最后一次大考,也是一次检验前一段学习成果的机会。
如果考得好,对考生增加自信心和今后的学习很有帮助;反之,可能会影响学习的积极性。
有的考生觉得自己为了期末考,准备得很充分,可还是没考好,悲观失落;有个别考生觉得自己再怎么努力,也不会取得好成绩,尤其是跟其他成绩优秀的同学相比,很自卑,产生了自暴自弃的消极心理;有的考生对高考的重视度不够,对期末考试成绩满不在乎,学习缺乏积极性。
为此我建议,高三期末考结束后,考生要利用寒假作如下几件事情:(1)认真分析试卷,找出失利原因。
考试失利的原因很多,最主要的无怪乎就这么几点:1、基础知识薄弱,基本概念不清。
这也是最要命的原因,需要赶快抓紧每分每秒尽可能多的掌握基础知识。
2、粗心大意,该对的没答对,说起来看起来好像不是什么大问题,其实这样是很大很大的问题,试想如果这次考试是高考,那你不照样惨了吗?所以细心、认真,把平时的考试当做是高考才会把高考当做平时的考试,才会取得更好的成绩,所以,必须在平时,包括在做作业做练习的时候也是要认认真真,小心细致!要培养自己这方面的习惯,在考试时才能不吃亏。
(2)查漏补缺,分辨出优劣势科目,哪些是有潜力的学科,哪些学科还很薄弱,并针对漏洞及时调整学习方法,明确今后的努力方向,制定出适合自己特点的复习计划,主要是时间安排上要有所侧重,对优势学科不能放松,对有潜力的学科要注意抓紧时间多投入精力发掘自己的潜能,提高成绩;对弱门学科,再加一把劲,尽可能的让其不弱,最少做到尽可能少的拉分。
高2014级2班第三学期期末考试分析
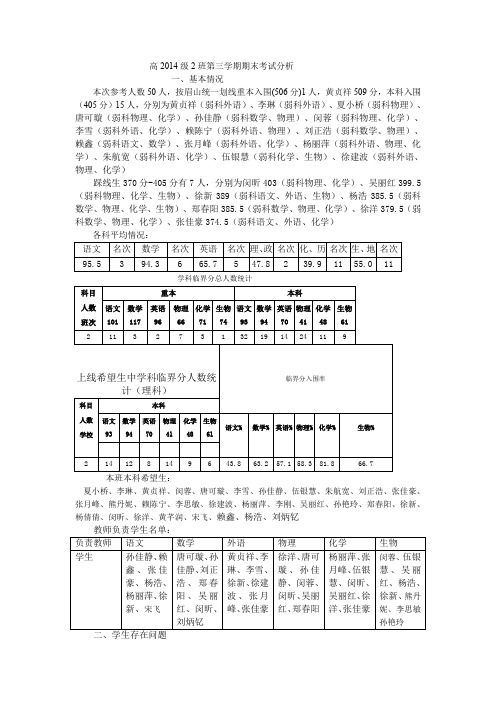
高2014级2班第三学期期末考试分析一、基本情况本次参考人数50人,按眉山统一划线重本入围(506分)1人,黄贞祥509分,本科入围(405分)15人,分别为黄贞祥(弱科外语)、李琳(弱科外语)、夏小桥(弱科物理)、唐可璇(弱科物理、化学)、孙佳静(弱科数学、物理)、闵蓉(弱科物理、化学)、李雪(弱科外语、化学)、赖陈宁(弱科外语、物理)、刘正浩(弱科数学、物理)、赖鑫(弱科语文、数学)、张月峰(弱科外语、化学)、杨丽萍(弱科外语、物理、化学)、朱航宽(弱科外语、化学)、伍银慧(弱科化学、生物)、徐建波(弱科外语、物理、化学)踩线生370分-405分有7人,分别为闵昕403(弱科物理、化学)、吴丽红399.5(弱科物理、化学、生物)、徐新389(弱科语文、外语、生物)、杨浩385.5(弱科数学、物理、化学、生物)、郑春阳385.5(弱科数学、物理、化学)、徐洋379.5(弱科数学、物理、化学)、张佳豪374.5(弱科语文、外语、化学)各科平均情况:语文名次数学名次英语名次理、政名次化、历名次生、地名次95.5 3 94.3 6 65.7 5 47.8 2 39.9 11 55.0 11学科临界分总人数统计科目重本本科人数语文101 数学117英语96物理66化学71生物74语文93数学94英语70物理41化学48生物61班次2 113 2 7 3 1 32 19 14 24 11 9上线希望生中学科临界分人数统计(理科)临界分入围率科目本科人数语文93 数学94英语70物理41化学48生物61语文% 数学% 英语% 物理% 化学% 生物%学校2 14 12 8 14 9 6 43.8 63.2 57.1 58.3 81.8 66.7本班本科希望生:夏小桥、李琳、黄贞祥、闵蓉、唐可璇、李雪、孙佳静、伍银慧、朱航宽、刘正浩、张佳豪、张月峰、熊丹妮、赖陈宁、李思敏、徐建波、杨丽萍、李刚、吴丽红、孙艳玲、郑春阳、徐新、杨倩倩、闵昕、徐洋、黄芊润、宋飞、赖鑫、杨浩、刘炳钇教师负责学生名单:负责教师语文数学外语物理化学生物学生孙佳静、赖鑫、张佳豪、杨浩、杨丽萍、徐新、宋飞唐可璇、孙佳静、刘正浩、郑春阳、吴丽红、闵昕、刘炳钇黄贞祥、李琳、李雪、徐新、徐建波、张月峰、张佳豪徐洋、唐可璇、孙佳静、闵蓉、闵昕、吴丽红、郑春阳杨丽萍、张月峰、伍银慧、闵昕、吴丽红、徐洋、张佳豪闵蓉、伍银慧、吴丽红、杨浩、徐新、熊丹妮、李思敏孙艳玲二、学生存在问题1、部分学生学习目标不明确,只是想读到高中毕业就行了;2、部分学生学习不努力,作业不认真,抄袭作业较严重;3、部分学生纪律观念不强,自习课说话、做小动作,看小说、玩魔方、听歌、睡觉等现象,如徐新、杨浩、刘正浩、陈量、李星宇、杨旭、李丽红、何柯磊、唐冬伟等;4、学生波动性到,如徐新、赖陈宁、赖鑫、杨丽萍、刘正浩、杨浩、张佳豪、朱航宽等,名次变化达300多名;三、班级学风建设的措施1、定期分批找学生谈话,或开导其思想,或激励其斗志,或给予学法指导,在一定程度上让部分学生能够坚持学习一阵子。
2014-2015年度第一学期期末试卷分析

学校:2014年月日
内容
分析
对试卷试题结构和内容分析
评价
试卷注意题型的多样性,力求对学生的素质进行全面评价,一是尽可能多地涉及到课本的各个知识点;二是体现习惯、情感、知识、能力等各个方面。试题中涵盖了多方面的内容,从大方面讲,实现知识与能力,过程与方法,情感、态度与价值观等多维目标的整合,小方面讲,拼音、汉字、词语、成语、古诗、句子、段落、篇章等等方面的有机融合。阅读和作文题除了考查学生的阅读和写作水平外,还注重考查学生的情感、态度和价值观。
学生答卷存在的问题及原因
从整个卷面来看,基础知识学生掌握较好。(一)、拼音部分,考查了学生对词语的掌握情况,此题是书上的原词学生都很熟悉,所以答的比较好,但还有个别同学拼读不准确,书写的不准确。给带点的字选择正确的读音,此题考查了多音字的掌握情况。学生的掌握情况较好。
(二)字、词、句子部分
选字填空。考查形近字的字意。“魂”和“魄”学生在字意的理解上不够透彻,诗(),应是诗魂,一些学生填成诗魄,没有理解词语的意思。
(三)阅读表达训练。课内阅读能力,反映出对学生阅读习惯的培养欠功夫。最集中的表现是第二自然段采用的结构形式是什么?很多同学没有理解。语文阅读重在过程,学生独立阅读能力是在过程中培养起来的,而老师忽略了过程中读、悟、用、说、写、等方法的指导;学生阅读态度不认真,文章浏览一遍即开始作答,对不理解的词语、句子不去认真揣摩,体会,感悟。有的句子的理解虽然做答了,但答案不贴切;
3、要求教师必须具备强烈的责任感,深入钻研、开发、使用教材;要有灵性、悟性和耐性,形成独特的教学特色。教师要用发展的眼光,教给学生科学的学习方法,语文教学在重视范文语言的感悟、积累和内化的同时,要积极向课外阅读拓展,并充分利用语文综合性学习活动为学生搭建展示交流的平台,增加学生积累的广度;教师应该向学生推荐好书,帮助学生拓宽积累的途径。
2014期末考试质量分析

2014—2015学年度第一学期期末考试质量分析一、各项指标完成情况(语数双科)其中:有28个班,双科及格率达到了100%,有3个班,优秀率达到100%;优秀率超过50%的有32个班。
所有班级的语数学科都达到了教育局要求的各项标准。
二、存在问题及今后教学的建议语文学科:存在问题:1、日常积累少,成语填空、古诗、名言等正确率较低。
2、学生书写不规范,字迹潦草,卷面脏乱。
3、阅读分析能力较差,急待提高。
4、作文空洞,流水账或者没有真情实感。
5、学习和答卷习惯不好,不能认真读题、审题,急于作答,答完后不检查。
改进措施:1、重视字词教学,夯实语文基础要提高学生的成绩,首先应重视字、词的过关。
在检测卷中,字、词类的题目只要学生平时稍加努力,就可以得分。
因此,教师在教学中应重视词语听写,词语抄写和组词的训练,。
2、提高阅读能力,引导个性阅读从抽样调查的结果来看,阅读题的得分率是最低的,说明了学生阅读的能力还不强。
其实本次试卷的阅读题并不难,只要学生认真阅读短文,是很容易找到答案的。
阅读教学的核心就是培养学生的独立阅读能力。
因此,教师在阅读教学中要还学生朗朗的读书声,让学生在读中理解,读中体验,读中感悟。
3、激发习作兴趣,抒发真情实感学语文,最头痛的就是写作文,学生习作时常常觉得无事可写,无话可说。
培养学生的写作能力,要采取多种方法,激发学生的写作兴趣,使学生不断获得写作的动力。
4、丰富语言积累,注重语文实践课内的积累,主要是在诵读中积累,如描写人物、景物的词语;细节描写具体生动的句子;运用了修辞手法的句子;富有哲理、意味深长的句子。
课外的积累,则可充分利用学校图书室的有利资源或学生自己的藏书,组织学生开展丰富多彩的读书活动,让学生读好书,多读书,爱读书,并指导他们做好摘抄和读书笔记。
5、努力在日常的教学中培养学生的学习习惯。
部分学生书写不规范,在平时的教学中还要严格要求。
数学学科:存在问题:1、还有一部分学生基础知识不够扎实,模棱两可。
2014第一学期期末质量分析

为了更好地及时发现问题,选择有效措施,争取在2015年中考取得更好的成绩。
确保数学考试能够准确地评价学生,现对第一学期期末考试进行客观真实的分析,分析如下:一、试卷的基本情况1.命题设计全卷由25道题组成,严格控制基本技能题的难度,适当增加体现过程方法的题目,增加学生自主选择和个性化的问题;试题按“新课标”中新的教学要求进行命题,贴近教材的呈现方式,贴近学生的生活实际;试卷注重目标层次和内容结构,注重思想方法和新背景中解决问题能力的考查。
2.试卷形式由三个大题组成,其中,第一大题:选择题,共6题,24分;第二大题填空题:,共12题,48分;第三大题:解答题,共7题,78分;全卷满分150分,考试时间100分钟。
3.考查内容:试卷的考查内容涵盖了九年级第一学期数学全部内容。
4.试题难度本卷中不同难度试题的比例基本合理,容易题:中等题:难题的分值比例为7:2:1。
5.试卷特点(1)试卷贴近教材,覆盖面广,重视对基础知识、基本技能的考核,并通过重点知识和重点内容自主研发试题,既体现教材的作用,又考查基本问题中的过程和方法.总体难度不大,非常灵活。
(2)试卷层次分明,难易有度。
全卷试题总体上从易到难构成了三个台阶,分别是基础知识和基本技能、过程和方法、数学思考和问题解决。
(3)强化对数学的理解和思维能力的考核.试卷通过新的试题情景和呈现方式,给学生提供有一定价值的问题串,引导学生观察、操作、解释、比较、探索、思考和解决问题,结合考试过程考查学生的数感、算理、几何语言转换、说理、数学思想方法、解题思路等。
(4)反映新的评价要求和试题对教学的导向作用。
重视合情推理,注意联系实际,关注学生解决实际问题的能力;同时,试题贴近新的课标要求和新的理念,适当降低了有关技能的难度。
二、试题解析1.立足教材,体现双基.试题基本上源于课本,能在数学课本和课程标准中找到原型。
2.适当控制了运算量,避免繁琐运算.在考查计算时,减少运算的难度,重点考查算理.即对运算的意义、法则、公式的理解.3.突出考查基本图形的认识和基本方法的分析,考查学生对图形本质的理解和说理的逻辑性、准确性和完整性。
2013—2014学年度上学期期末考试质量分析报告

2013——2014学年第一学期期末考试成绩分析报告高一历史一、试卷总体分析1、试卷特点:试题体现出基础性,重点考查主干知识。
考查的历史知识均为政治史的主干知识,覆盖面广,实现对历史必修一史实部分的全面考查。
每道试题均依据史料,设置一定的不同的情境,由此引出不同层次的问题,注重试题的新颖性。
试卷简约,体现梯度。
试题内容简洁、易懂,考生阅读无障碍,便于考生准确作答。
选择题由浅入深。
材料解析题中所设置的问题的难度也呈阶梯式递进。
2、试卷结构及内容:本份试卷在题型设计上分选择题和非选择题两大类。
考查的知识点覆盖必修1 全部内容,选择题主要考查学生识记和理解分析问题比较问题的能力,非选择题主要考查学生分析归纳问题和探究问题的能力,文字表述量大,需要学生必须有较强的文字表述能力3.数据分析本次考试试卷满分为100分,高一年级参加考试学生人数为1390人,均分为76.4分。
双过线人数普通班321人(78分以上),尖子班51人(88分以上),预测军检以上人数1251人(59分以上)和宁阳一中相比差距不大二、学生答题情况分析1.存在问题:教师课堂虽对重点,难点花足功夫,细致讲解,重复强调,而且课上检测,课后反馈。
但课后,由于学生没能自觉及时做好复习,练习巩固,使学生知识消化不良,课本基础知识不熟悉或理解不透甚至混乱,没能在理解的基础上做好适当的识记,基础知识掌握不牢固;学生考试过程中审题作答存在随意性,考试技巧有待提高等问题,导致知识无法得以有效运用,客观题失误频频;主观题有一部分学生语言表述不规范,要点不突出,逻辑性不强;阅读不认真,有效信息获取不足,概括归纳信息的能力欠缺;对教材的知识点学生了解的少,如学生是对“君主专制”和“中央集权”这一对概念的内涵及外延理解不透,对这两个概念学生普遍掌握的不够深入;对雅典民主的特点和局限性认识不到位。
对英国君主立宪制和美国总统制共和制的理解不够透彻。
得分不多。
另外学生与老师学与教不同步,特别是学生缺乏学习的主动性,考试结成绩没有预期的效果。
2014年海淀高三第一学期期末试卷分析

2014年海淀高三第一学期期末试卷分析一、试卷命制想法1、“数学学科要注重基本数学能力、数学素养和学习潜能的考查,突出主干知识,考查数学的基本思想、方法,强调通性通法.注重数学应用,考查学生应用数学概念、原理、方法、结合数据分析、数表观察、图象解析等内容.解释现实生活中的现象,解决生活、生产中的数学问题.考查学生分析解决综合问题的能力,规避只能靠技巧求解的竞赛类的试题.”(摘自2014年北京高考最新命题工作暨高三工作布置会之数学命题原则)2、本次考试定位于一轮复习效果的反馈性检测,不追求与高考命题的形似.希望老师们通过对从试卷中获取的相关数据信息的分析,了解学生对知识的理解及应用的基本情况,为第二轮复习做好学情分析.二、试卷命制特点1、考查内容覆盖面较大,分值均衡,突出了考查的全面性复数:5分;不等式性质:5分;程序框图:5分;二项式定理:5分;平面几何证明:5分;线性规划:5分;极坐标和参数方程:10分;排列组合(创新题):5分;三角函数:15,共13分;统计与概率(含几何概型):10,16,共18分;立体几何: 14,17,共18分;函数与导数:18,共13分解析几何(含平面向量):7,9,13,19,共29分;数列综合(创新题):20,共14分2、试题难易分布得当,重点突出基础题(知识点覆盖较少,且为同类型知识,求解办法易于得到,运算难度较低):1,2,3,4,5,6,9,10,11,12,15,18(1),19(1),共73分;中档题(有一定的综合度,解题过程蕴含一定的数学思想方法,或背景有新意,或有一定的运算量):7,13,16,17,18(2),19(2),20(1)共56分难题(综合度或抽象度较大,解题过程常通过试验的方法探寻规律,蕴含深刻的数学思想方法):8,14,20(2),20(3),共21分3、试题重视让学生体验数学在解决实际问题中的作用10,16,共18分其中,第10题来源于课本,突出几何概型是解决一类现实问题的数学模型的本质;第16题是统计和概率的综合问题,它包含了对统计图表的认识和概率分布模型的选择,而前者恰恰是对学生数学应用意识和统计推断能力的考核.三、评分标准(见答案)四、试卷讲评建议1、要由“注重分数的终结性评价”转向“注重促进人的发展的过程性评价”,要从试后对个体和整体数据统计的分析对比中,发现一轮复习中存在的问题,为第二轮复习工作的准备提供依据.2、试卷讲评的过程既是一个完善学生的知识系统和思维系统的过程,又是一个培养学生自我分析,自我完善和调整的过程.教师讲评时不仅要讲清楚学生存在的问题,要着眼于对常规题目的基本思维模式框架的深刻理解和精细化,更要引导学生认清自己的短板,寻找适合于自己的补救措施,同时明确下一阶段复习的重点及任务,学会有针对性的、有计划的解决自己个性的问题.3、试卷讲评中要让学生重视答题规范性,表达要简明准确.会的题目要保证计算迅速、正确,表述严密、准确和干净.4、试卷讲评中,还要引导学生重视多元联系,善于将数学对象用数字的、符号的、式子的、图形(图象)多种形式表示,从而启发思维,开拓思路,探寻一题多解,多题归一,领悟数学对象的本质,提升思维质量.5、试卷讲评中,要注意对学生解题习惯和策略的引导,让学生形成如下的解题习惯:先想后算——审清题目,避免盲目;多想少算——理清思路,少走弯路;反思巧算——解法优化,抓住本质.五、期末考试重点试题分析(一)从所求出发,多角度的解读,是获取解题信息的重要途径题7.已知椭圆C :22143x y +=的左、右焦点分别为12,F F ,椭圆C 上点A 满足212AF F F ⊥. 若点P 是椭圆C 上的动点,则12F P F A ⋅的最大值为( B )A. B. 233 C. 94D. 154分析:题设是解析几何知识,所求涉及平面向量知识,而最大值问题可以通过利用函数、不等式和特定的动态几何图形的边界值问题加以解决,因此对12F P F A 形、数的解读是解本题的关键.思路一:利用向量的坐标形式将向量点乘转化为函数最值问题 解法一:设(,)P x y,[y ∈, 3(1,)2A 12333(1,)(0,)22y F P F A x y ∴=+=≤ 解法二:设(2cos ) P R θθθ∈,3(1,)2A12333(2cos 1,3sin )(0,)sin 2F P F A θθθ∴=+=≤思路二:利用向量点乘的几何意义,将12F P F A 的最大值转化为2F A 与1F P 在2F A 方向上的投影的乘积的最大值问题.随着点P在椭圆上的运动,易知1F P 在2F A 方向上的投影的最大值为短半轴长,所以,12F P F A 的[关于运用投影知识解题的补充]:投影的运用是“降维”策略的实践 (1)已知O 是坐标原点,点)1,1(-A ,若点),(y x M 为平面区域上的一个动点,则·的取值范围是 . [0,2] 动画(2)(2012年北京卷)已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则CB DE ⋅的值为 1 ,DC DE ⋅的最大值为 121y 2x y x +≥⎧⎪≤⎨⎪≤⎩OA OM(3)如图,在棱长为2的正方体1111ABCD A B C D -中, E 为BC 的中点,点P 在线段1D E 上,则1PA A ∆面积最小值为.4)如图,正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2,AB =1,M ,N 分别在AD 1,BC 上移动,且始终保持MN ∥平面DCC 1D 1,设BN =x ,MN =y ,则函数y =f (x )的图象大致是( C )5)解析几何中的弦长公式cos B A B A x x AB x θ-=-=其中θ为直线AB 的倾斜角(二)复原基本图形是认清几何图形本质特征,获取解题信息的重要途径 (1)在解决一部分立体几何问题中,正方体或长方体模型是重要的基本图形(2)对立体几何中图形性质、定理的准确理解和运用,是解决立体几何问题的支柱, 每一个定理都是一个基本图形,而图示记忆是掌握定理的一个重要办法. 题14. 已知某四棱锥,底面是边长为2的正方形,且俯视图如右图所示. (1)若该四棱锥的左视图为直角三角形,则它的体积为___43_______(2)关于该四棱锥的下列结论中: ① 四棱锥中至少有两组侧面互相垂直; ② 四棱锥的侧面中可能存在三个直角三角形; ③ 四棱锥中不.可能存在四组互相垂直的侧面. 所有正确结论的序号是_____①②③______.补充17. (2013年海淀期末试题)如图,在直三棱柱111ABC A B C -中,90BAC ∠=︒,12,AB AC AA ===E 是BC 中点.(I )求证:1//A B 平面1AEC ;(II )若棱1AA 上存在一点Q ,满足11B M C E ⊥,求AQ 的长; (Ⅲ)求平面1AEC 与平面11ABB A 所成锐二面角的余弦值.(三)试题的延展有助于加深对本题涉及的知识、方法的认识EC 1B 1A 1CBA题13. 已知直线l 过双曲线的左焦点F ,且与以实轴为直径的圆相切,若直线l 与双曲线的一条渐近线恰好平行,则该双曲线的离心率是______.分析:不妨设双曲线方程为22221(0,0)x y a b a b-=>>题设“直线l 过双曲线的左焦点F ,且与以实轴为直径的圆相切”表明切线的斜率为ab; 题设“直线l 与双曲线的一条渐近线恰好平行”表明切线的斜率与渐近线的斜率相等,[原型题] 从双曲线的左焦点F 向以实轴为直径的圆引切线,交双曲线的右支于点P ,切点为Q , M 为线段FP 的中点,若QM FQ =⋅,则双曲线的离心率的取值范围是_________分析:不妨设双曲线方程为22221(0,0)x y a b a b -=>>题设“直线l 过双曲线的左焦点F ,且与以实轴为直径的圆相切”表明切线的斜率为ab;题设“QM =⋅”表明两个向量同向,进一步解读,得到结论:中点M 在切点Q 的右侧或两点重合.可以通过两三个具体的双曲线(例如22221;13x x y y -=-=等)探寻规律,再结合图形得到切线与双曲线的渐近线平行是一个边界,中点M 与切点Q 重合是另一个边界.当中点M 与切点Q 重合时,半径OQ 为12F F P ∆的中位线,122,2 222 F P b F P a b a a e ∴==∴-=∴=引申的性质:切点Q 在右准线上.题19.(本小题共14分)已知椭圆G :)0(12222>>=+b a b y a x 的离心率为12,过椭圆G 右焦点F 的直线:1m x =与椭圆G 交于点M (点M 在第一象限).(Ⅰ)求椭圆G 的方程;(Ⅱ)已知A 为椭圆G 的左顶点,平行于AM 的直线l 与椭圆相交于,B C 两点.判断直线,MB MC 是否关于直线m 对称,并说明理由.第一部分:所求问题的多角度解读(设直线,MB MC 与x 轴交点分别为,E F ) “直线,MB MC 是否关于直线m 对称”可以解读为:(1) 直线,MB MC 的斜率相反,即0MB MC k k +=;(2) MEF ∆为以EF 为底边的等腰三角形;(可证ME MF =) (3) 直线m 为EMF ∠平分线.(可证线段EF 中点横坐标为1)第二部分:运算的简捷性本题在算法上,采取通分,在预估目标下,只对分子化简,韦达定理代入计算,也是优化算法的一种策略.1212332211MP MQ y y k k x x --+=+--121212121212131311222211111(1)(2)1()1x n x n n n x x x x n x x x x x x +-+---=+=++-----+-=+-++ 2(1)(2)102n n n n -+=-=+-,第三部分:一题多解思路二: 22223412463302()x y y ny n x y n ⎧+=∴-+-=⎨=-⎩2121233=(-1) 24y y n y y n ∴+=⋅ 易求111131332:(1) (1,0)32122y x MB y x E x y ---=-∴-⋅-- 222231332:(1) (1,0)32122y x MC y x F x y ---=-∴-⋅-- 1201222122113()1()332422E F y n y n x x x y y ----=+=-+-- 12121212(22)(3)3222231(22)1(4)333944()2224n y y n n y y y y y y -+---=-+++=-+---++ 234(1)(2)1(4)1432n n n n --=-+=-+ 思路三:22221212119999 33444422x x ME MF y y ⎛⎫⎛⎫ ⎪ ⎪--=+=+ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭只需证12121103322x x y y --+=--即可 第四部分:试后联想[选修4-1B 版几何证明选讲p19练习4]如图,圆O 是过△ABC顶点A 且与BC 边相切于D 的圆,且AD 是∠BAC 的平分线,圆O 与AB,AC 分别交于E,F,求证:EF//BC.[平行应用1]在圆222x y +=上有一点(1,1)P ,点E 、F 是y 轴上两点,且满足PE PF =,直线PE ,PF 与圆分别交于C ,D 两点.证明:直线CD 斜率为定值.[平行应用2]已知圆的方程2225x y +=,过(4,3)M -作直线,MA MB 与圆交于点,A B ,且,MA MB关于直线3y =对称,则直线AB 的斜率等于( B ) A .43-B .34-C .54-D .45- [类比延伸]已知椭圆22143x y +=,经过点3(1,)2A ,,E F 是椭圆上的两个动点,如果直线AE 的斜率与AF 的斜率互为相反数,证明直线EF 的斜率为定值,并求出这个定值.回扣考题,发现:考题中“直线,MB MC 关于直线m 对称”与“直线BC 的斜率为定值”存11AB k x =所以122211x x =---,即AM BM k k =-(四)试验性探究是理解困难度较大的问题含义的重要手段通常困难度较大的问题或背景新,或抽象度大,理解题目含义是首要解决的问题,通过对符合题意的具体问题的研究,能够降低理解的难度,甚至找到解决问题的方向. 题8.如果小明在某一周的第一天和第七天分别吃了3个水果,且从这周的第二天开始,每天654321所吃水果的个数与前一天相比,仅存在三种可能:或“多一个”或“持平”或“少一个”,那么,小明在这一周中每天所吃水果个数的不同选择方案共有( D ) A.50种 B.51种 C.140种 D.141种不难发现,七天内增加的水果数与减少的水果数是相同的. 转换模型:模型1在6个空格内放入1、-1或0,要求放入1的个数与-1的个数必须相等,问有多少种放法?(学生会当成5个空格运算,会选择B )解:仅有三个1和三个-1:3620C =种; 仅有二个1和二个-1:226490C C =种; 仅有一个1和一个-1 :116530C C =种; 仅有0:1种; 共有141种 模型2画树杈图依据题意前3天和后三天应是一样的!第4天的可能值为6,5,4,3,2,1,0,按着规则,第4天水果个数对应的方法数依次为:22222221,3,6,7,6,3,1另一种背景(仿2011年北京高考20题):若数列7127,,...,A a a a =满足11i i a a +-=或0(1,2,,6i =),且1的个数与-1的个数必须相等,数列7A 为E 数列.则满足173a a ==的E 数列7A 的个数有多少个?题20.(本小题共13分)若函数()f x 满足:集合*{()|}A f n n =∈N 中至少存在三个不同的数构成等比数列,则称函数()f x 是等比源函数. (Ⅰ)判断下列函数:①2y x =;②1y x=;③2log y x =中,哪些是等比源函数?(不需证明)(Ⅱ)判断函数()21x f x =+是否为等比源函数,并证明你的结论; (Ⅲ)证明:*,d b ∀∈N ,函数()g x dx b =+都是等比源函数.(II )证明:假设存在正整数m n k <<,使得(),(),()f m f n f k 成等比数列,则 2(21)(21)(21)n m k +=++,整理得2122222n n m k m k +++=++, 等式两边同除2,m 得2122221n m n m k k m --+-+=++.因为1,2n m k m -≥-≥,所以等式左边为偶数,等式右边为奇数, 所以假设不正确,说明函数()21x f x =+不是为等比源函数.(III )分析:由盲目到试验(具体化、特殊化),最后找到应对策略,经历了抽象、转化、简化等过程:A.实质是各项为正整数的等差数列中存在三项构成等比,特殊性在于各项为正整数!简化为从第一项1a 开始,在后续项中找首项的倍数,最易得的是11a a d +,再寻找第三项;B.试探偶数列,奇数列,发现以第一项为等比数列第一项,后面总能找到其整数倍的项,利用方程检验第三项的存在性;C.最后一题三问通常具有台阶性,直接代数化,利用方程寻找整数解.方法一:设正整数m n k <<,*,d b N ∀∈ 由()()()2dn b dm b dk b +=+⋅+得:22dn mdk bm bk bn -=+-22dn bn bmk dm b+-∴=+令n dm b m =++()()()()()2222d dm b m b dm b m bmd dm b dm b m k dm bdm b+++++-++++∴==++()()*2d dm b m N =+++∈所以, *,d b N ∀∈,数列{()}g n 中总存在三项(),(),((2)())g m g dm b m g d dm b m +++++成等比数列. 所以,*,d b ∀∈N ,函数()g x dx b =+都是等比源函数. 方法二:因为*,b n ∀∈N ,都有(1)()g n g n d +-=,所以*,d b ∀∈N ,数列{()}g n 都是以(1)g 为首项公差为d 的等差数列.*,d b ∀∈N ,2(1),(1)(1),(1)(1)g g d g d ++成等比数列,因为(1)(1)(1)((1)11)[(1)1]g d g g d g g +=++-=+,2(1)(1)(1)(2(1)(1)11)[2(1)(1)1]g d g g g d d g g g d +=+++-=++,所以(1),[(1)1],[2(1)(1)1]g g g g g g d +++*{()|}g n n ∈∈N , 所以*,d b ∀∈N ,函数()g x dx b =+都是等比源函数. 方法三:因为*,b n ∀∈N ,都有(1)()g n g n d +-=,所以*,d b ∀∈N ,数列{()}g n 都是以(1)g 为首项公差为d 的等差数列.由2()(1)()g m g g k =⋅,(其中1m k <<)可得 2[(1)(1)](1)[(1)(1)]g m d g g k d +-=⋅+-,整理得 (1)[2(1)(1)](1)(1)m g m d g k -+-=-,令(1)1m g =+,则(1)[2(1)(1)](1)(1)g g g d g k +=-, 所以2(1)(1)1k g g d =++,所以*,d b ∀∈N ,数列{()}g n 中总存在三项(1),[(1)1],[2(1)(1)1]g g g g g g d +++成等比数列.所以*,d b ∀∈N ,函数()g x dx b =+都是等比源函数.(五)联系实际,突出应用意识题16.(本小题共13分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.假设每名队员每次射击相互独立.(Ⅰ)求上图中a的值;(Ⅱ)队员甲进行三次射击,求击中目标靶的环数不低于8环的次数X的分布列及数学期望(频率当作概率使用);(Ⅲ)由上图判断,在甲、乙两名队员中,哪一名队员的射击成绩更稳定?(结论不需证明)本题考查概率、统计的基本概念和基本方法,引导学生重视从图表中获取信息的能力. 【2010海淀期中】为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为1s,2s,3s,则它们的大小关系为. (用“>”连接)(六)关于阅读能力的提升来源于对关键词句的精确解读题18.(本小题共13分)已知关于x的函数()(0)e xax af x a-=≠(Ⅰ)当1a=-时,求函数()f x的极值;(Ⅱ)若函数()()1F x f x=+没有零点,求实数a取值范围.分析(Ⅱ)本题中的函数()F x 没有零点等价于其函数值恒正或恒负. 注意:在开区间上仅知道单调性,不足以获得函数在其上的值域!(Ⅱ)(2)'()'()e xa x F x f x --==. ①当0a <时,(),'()F x F x 的情况如下表:--------------7分因为(1)10F =>, ------------8分 若使函数()F x 没有零点,需且仅需2(2)10eaF =+>,解得2e a >-,-------9分所以此时2e 0a -<<; ------------10分 ②当0a >时,(),'()F x F x 的情况如下表:--------11分因为(2)(1)0F F >>,且10110101110e 10e 10(1)0eea aaF a------=<<,---------12分所以此时函数()F x 总存在零点. -----------13分 综上所述,所求实数a 的取值范围是2e 0a -<<.补充1、设函数22()(1)f x ax a x =-+,其中0a >,区间{}()0I x f x =>. (1)求I 的长度(注:区间(,)αβ的长度定义为βα-);(2)给定常数(0,1)k ∈,当11k a k -≤≤+时,求I 的长度最小值.新背景问题给学生带来的最大困惑是不知用什么模式来套用. 本题第一问就有学生求导运算.本题第二问学生不清楚把问题转化为I 的长度关于a 的函数问题.补充2、PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.若规定:PM2.5日均值在35微克/立方米以下空气质量为一级;,在35微克/立方米~75微克/立方米之间空气质量为二级,在75微克/立方米及以上空气质量为超标.从某自然保护区去年全年每天的PM2.5监测数据中随机地抽取10天数据作为样本,监测值频数如下所示:(1)从这10天的PM2.5日均值监测数据中,随机抽出3天,求恰有一天空气质量达到一级的概率;(2)从这10天的数据中任取3天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列;(3)以这10天的PM2.5日均值来估计一年的空气质量情况,则一年(按366天计算)中平均有多少天的空气质量达到一级或二级.(精确到整数) 学生阅读过程中对“随机抽出3天”,“任取3天”理解不正确,错当成取后放会,即n 次独立重复实验模型,因此第二问中把超几何分布问题当成了二项分布. (七)解题格式的规范性 题17.(本小题共14分)如图所示,在四棱锥P ABCD -中,底面四边形ABCD 是菱形,ACBD O =,PAC ∆是边长为2的等边三角形,PB PD ==,4AP AF =.(Ⅰ)求证:PO ⊥底面ABCD ;(Ⅱ)求直线CP 与平面BDF 所成角的大小;(Ⅲ)在线段PB 上是否存在一点M ,使得CM ∥平面BDF ?如果存在,求BMBP的值,如果不存在,请说明理由. 解:(Ⅰ)因为底面ABCD 是菱形,AC BD O =,所以O 为,AC BD 中点,. -------------------------------------1分 因为,PA PC PB PD ==,所以,PO AC PO BD ⊥⊥,-----------------3分 所以PO ⊥底面ABCD .---------------4分 (Ⅱ)由底面ABCD 是菱形可得AC BD ⊥,又由(Ⅰ)可知,PO AC PO BD ⊥⊥. 如图,以O 为原点建立空间直角坐标系O xyz -.由PAC ∆是边长为2的等边三角形,PB PD ==可得PO OB OD ===所以(1,0,0),(1,0,0),A C B P -.---------------------------------------5分所以CP =,(AP =-.由已知可得13(44OF OA AP =+= -----------------------------------------6分 设平面BDF 的法向量为(,,)x y z =n ,则0,0,OB OF ⎧⋅=⎪⎨⋅=⎪⎩n n即0,30.44x z ⎧=⎪⎨+=⎪⎩ 令1x =,则z =(1,0,=n .----------------------------------------8分 因为1cos 2||||CP CP CP ⋅<⋅>==-⋅n n n ,----------------------------------------9分所以直线CP 与平面BDF 所成角的正弦值为12, 所以直线CP 与平面BDF 所成角的大小为30. ---------------10分(Ⅲ)设BMBPλ=(01)λ≤≤,则)CM CB BM CB BP λλ=+=+=-.---------------11分若使CM ∥平面BDF ,需且仅需0CM ⋅=n 且CM ⊄平面BDF , ------------12分解得1[0,1]3λ=∈,----------------------------------------13分 所以在线段PB 上存在一点M ,使得CM ∥平面BDF .此时,BM BP =13. ----------------14分六、高三第二轮复习建议高三第一轮复习一般以知识、技能、方法的逐点扫描和梳理为主,通过第一轮复习,学生大都能掌握基本概念的性质、定理及其一般应用,但知识较为零散,综合应用存在较大的问题.而第二轮复习承上启下,是知识系统化、条理化,促进灵活运用的关键时期,是促进学生素质、能力发展的关键时期,因而对讲练、检测等要求较高.教师讲解的着力点是学生的体验之下暴露出的问题,教师讲解的内容是解题途径的决策与构建过程.二轮复习多以专题的形式,分类进行.二轮复习做到四个 “转变”和做好五个“重视”.四个 “转变”是指:1.转变介绍方法为选择方法,突出解法的发现和运用. 2.转变全面覆盖为重点讲练,突出高考“热点”问题. 3.转变以量为主为以质取胜,突出讲练落实.4、转变以“补弱”为主为“扬长补弱”并举,突出因材施教.五个“重在”是指:1、重视解题思想的分析,即在复习中要及时将几种常见的数学思想渗透到解题中去;2、重视知识要点的梳理,即第二轮复习不像第一轮复习,没有必要将每一个知识点都讲到,但是要将重要的知识点用较多的时间重点讲评,及时梳理;3、重视解题方法的总结,即在讲评试题中关联的解题方法要给学生归类、总结,以达触类旁通的效果;4、重视学科特点的提炼,数学以概念性强,充满思辨性,量化突出,解法多样,应用广泛为特点,在复习中要展现提炼这些特点;5、重视规范解法的示范,学生解题不规范既有习惯差、不重视的原因,也有根本不知道什么是规范的格式地原因,因此教师在复习中有必要作一些示范性的解答.。
2014-2015学年度第一学期期末语文考试质量分析

《2014-2015学年度第一学期期末语文考试质量分析》摘要:因学习语定要养成学习惯课前预习认真做预习上课程做课堂笔记,学生所以没有考出成绩原因如下、学习目标还是不明确摇摆不定学习方向和动力不足,没有听从老师建议固执己固有学习模式被动接受知识而不是主动探究知识导致知识积累断层005学年学期期末语考试质量分析次期末语考试主要是考学生对高语必修、必修知识积累与运用次考试我所教授高()班考试人数60人;及格8人;高分70分低分38分;平分5597分高()班考试人数60人;及格9人;高分73分;低分分;平分563分次试卷题基础知识积累题共0分这道题都是课出现知识很多学生还是粗心觉得课下释不重要很简单但是做题他们运用排除法排除两错误答案开始模糊知识无从下手做出正确判断因学习语定要养成学习惯课前预习认真做预习上课程做课堂笔记二题是言和诗歌鉴赏共0分学生复习没有做到有重归类识记只是机械性整段句子翻译导致翻译没有把关键词翻译出也因把送分题变成了丢分题诗歌鉴赏答题冗杂“简要概括”却不“简”导致答题堆没是关键三题是名句默写题和名著考题共0分这道题其实是送分题可是两班这道题上却丢分多究其原因还是学生对背诵不重视没有养成良语学习习惯没有吸取半期考试教训依然是先问什么候检背诵才被动应付差事或者抱侥幸心理老师不会抽到己而次次放任己再有就是只会张口背不会识记加延伸背诵四题现代题共分这是课我还曾用这上公开课但是学生还是没有掌握审题方法其实题目答案还是有踪可循丢分原因是学生审题不明答题然不清学生平日练习没有及总结归纳答题模式练习只是停留对答案做完就了事根没按老师要做练习导致答题没有抓住重回答五题学与运用共8分这道题与平日积累紧密系但往往遇到这类题学生没有积累拓展利用平日笔记里容只是简单照搬仿句因分值很低六题作共0分总体看分段普遍6左右很多学生没有抓住作题所给提示材重看二段关键词是“生活”、“曾”、“事情”从这段可以给所写拟定思路是回忆性记事有部分学却抓住“感悟”切入写成了议论性因作分值不高从这次考试看学生所以没有考出成绩原因如下、学习目标还是不明确摇摆不定学习方向和动力不足、没有养成良语学习习惯没有及对比牵引知识导致思路狭窄不能拓展思维学习程浮躁、没要耐心3、没有听从老师建议固执己固有学习模式被动接受知识而不是主动探究知识导致知识积累断层通这次考试出身薄弱及利用寒假缺补漏外有计划加量做笔记和练笔写作。
高三期末考试成绩分析

高三期末考试成绩分析随着高三学生即将结束自己的学业,期末考试成绩成为衡量学生能力和努力程度的重要指标。
在这个阶段,学生们经历了漫长而辛苦的备考过程,他们的成绩也是对所受教育质量的一种评估。
本文将对高三期末考试成绩进行分析,帮助读者更好地了解该阶段学生的学习状况。
首先,高三期末考试成绩的整体分布情况是分析的重点之一。
通过对成绩的分布情况进行统计和绘图,可以得出对整个年级的成绩水平有一个直观的了解。
例如,成绩分布图可以显示出高分段和低分段的比例以及成绩的集中程度。
这有助于了解学生的整体水平,发现潜在的问题和优势之处。
其次,高三期末考试成绩分析可以从学科维度进行。
高中学生的学习领域广泛,包括语文、数学、外语、科学等学科。
通过对各学科成绩的分析,可以更具体地了解学生们在每个学科上的表现。
这有助于学生、家长和教师们找到学习上的问题,并做出相应的调整和改进。
除了学科维度,高三期末考试成绩分析还可以从其他维度进行,例如班级维度和性别维度。
通过对班级的成绩进行比较,可以发现不同班级间的差异和特点。
这有助于了解班级教学质量的差异,以及可能存在的影响学生成绩的因素。
同时,通过性别维度的分析,可以了解男女学生在学科成绩上的差异和特点,帮助发现可能存在的性别差异对学习成绩的影响。
另外,高三期末考试成绩分析还可以结合学生的学习态度、学习方法和自我评价等因素进行。
这些因素对学生成绩的提高具有重要影响。
通过对这些因素与成绩的关联性分析,可以发现影响学生成绩的主要因素,并提出相应的解决方案和建议。
最后,高三期末考试成绩分析还可以结合学校教育环境和教师教育方法等因素进行。
学校和教师在教学过程中扮演着重要角色,他们的教育理念和教学方法对学生成绩产生着重要影响。
通过对学校和教师因素与学生成绩的关联性分析,可以找到学校和教师在教育上的优势和不足之处,进一步改进教育质量。
综上所述,高三期末考试成绩分析是了解高中学生学习状况和学业质量的重要手段。
2014年宝鸡市高三教学质量检测(一)试卷分析

2014年宝鸡市高三教学质量检测(一)试卷分析宝鸡市教育局教研室高中组2013年12月28日~29日,我们举行了全市2014年第一次高三教学质量检测。
本次检测本着突出双基、注重能力原则,严格遵循2013年新课程各科考试大纲及说明,突出对基础知识、基本方法考查,特别强化了新课程高考对能力要求的考查,着力体现新高考的命题趋势。
整套试卷从宏观上控制了难度,尽量接近2013年高考,同时适当结合各校复习进度,以期通过检测、反馈对教师后期复课工作给以引领与指导。
考试结束后,我们通过多种渠道收集考试信息,对试卷的质量、学生答卷情况等进行了分析,并对全市分高中考试成绩做了统计,确定了本次检测的“临界线”:理科一本:410 分二本:360 分文科一本:490 分二本:430 分请各县区、各学校参照此“临界线”,对本次检测学生失分的主要原因认真作一统计分析,制定后期复课工作的策略和措施,确保全市高考成绩不断提升。
语文试题一、命题说明:全市高三质检语文命题组五名成员,在认真学习新课标高考大纲及近年来全国及自主命题省份高考课标卷的基础上,结合我市高三教学的实际情况,经过多次认真研究,反复讨论和修改,命制了2014年全市第一次高三教学质量检测语文试题。
二、试卷分析:一检是我市今年统一进行的第一次高三教学质量检测,根据高三复课进度,我们本着以激励为主的原则,适当降低考试的难度,让学生能从这次检测中树立自信,更好地搞好今年的高三复课工作。
三区一校02-0.740之间,区间较大,基本符合高考难度系数要求,能有效检测不同层次学生的语文能力。
(二)选择题答卷分析:1-3题为现代文阅读试题,第2题得分率稍高,第1、3题得分率都低。
第1题:关于北辰文化相关内容的理解。
难度高,得分率低。
C项将彗星和人间的更替兴衰说成了“北辰和彗星”,扩大了范围,但许多学生并没有辨析出来。
第2题:选项的理解和分析是否符合原文意思。
难度较低。
B项的错误比较明显,文中列举的几颗星并不是同一颗星,也就不是北辰“在不同时代有不同的称谓”。
2014-2015学年度第一学期期末考试质量分析总结(开会)

76.05
78.79
81.03
及格率
85.81%
92%
87.65%
94.62%
优秀率
19.77%
32.57%
38.52%
28.24%
科学
平均分
70.39
70.47
74.28
82.52
及格率
83.07%
82.31%
84.81%
98.34%
优秀率
12.99%
13.64%
32.16%
41.83%
黄芳
李克军
朱桂春
第三名
刘倩倩
李忠
张尚锋
陈曦
思品
第一名
张宏
张宏
徐营
路秀云
第二名
赵安全
张宏
刘年勇
路秀云
第三名
张启湖
黄伟建
刘年勇
侯志胜
科学
第一名
郑春霞
陈席
陈席
马志山
第二名
柳忠新
陈席
李鑫
肖锋
第三名
郑春霞
刘太伟
薛敏
马志山
结论:部分老教师教学经验丰富、成绩突出,为青年教师起了模范带头作用,敬业精神令人钦佩;同时也涌现出了一批年轻教学骨干,成绩优异。
五年级
六年级
语文
第一名
刘燕
展红梅
孙丽霞
刘小兰
闫现梅
刘永霞
第二名
颜景霞
张玉粉
李浩
刘峥嵘
薛素梅
路秀云
第三名
颜富环
韩秀敏
胡兴林
闫海燕
仝敏
方前进
数学
第一名
闫翠华
高三 上期末考质量分析

物理 114 120 101 112 110 107 110 104 109 107 96 97 108 101 105 111 118 100 114 96 103 110 102 83 105 109 110 97 113 110 96 90 95 107 102 93 104 98 109 103 107 101 82 106 116 103
理综 282 278 248 270 259 269 268 258 251 251 241 241 258 256 264 257 253 265 272 236 262 246 266 238 249 231 250 240 251 263 252 239 252 263 237 237 246 240 225 242 237 239 228 231 244 234
45 46 39 44 15 40 18 54 53 37
杨翔宇 郑志峰 吴雪儿 傅悦聪 陈超凡 连彦楠 李威 严朝敏 林雪 林黎
114 114 110 100 116 118 105 105 119 119
122 122 124 125 127 114 130 110 141 119
118 117 103 94 119 119 120 112 89 111
97 83 105 101 87 92 93 103 101 88
84 77 80 90 66 69 73 64 52 79
42 64 54 66 60 62 52 74 64 50
223 224 239 257 213 223 218 241 217 217
总分 691 651 650 647 645 645 642 637 636 635 632 626 625 625 624 623 622 622 620 620 619 617 617 612 611 609 607 607 606 606 606 605 604 602 602 599 598 598 597 596 595 585 585 581 580 578
2013——2014年期末质量分析(一)

认真总结认真反思增添措施注重落实努力提高我校教育教学质量2013——2014学年度上学期期末考试质量分析巴彦县华山乡第一中学全面总结认真反思增添措施注重落实努力提高我校教育教学质量2013——2014学年度第一学期期末考试质量分析本学期期末考试,按照教育局统一安排和部署我校各年级学生参加了全县统考,为了认真总结经验,分析质量现状,查找差距,切实加强教学教研工作,加大教学过程管理力度,全面提高我校教育教学质量,特对我校本学期期末抽测成绩进行如下分析,以期达到全面提高我校教育教学质量之目的。
一、试题基本情况试题的特点是:遵循大纲、课标,紧扣教材内容,面向全体学生,重在基础知识和基本技能的考查;知识面覆盖较宽,分布较为合理,具有层次性;试题形式多样,具有一定的灵活性。
整个试题较为平和,难度较适中。
二、各年级成绩比较分析(见成绩分析表)从学生成绩分析可以看出,我校教学管理工作是步入正规化轨道的,质量意识是深入人心的,新的教学理念也已逐渐形成,教师的课堂教学方法和学生的学习方式也在悄悄发生变化,课堂教学效率也在不断提高,保持了教育教学质量的稳步上升,学科教学也取得了一定的成功经验:1.提高课堂效率本学期学校在开展各项活动的同时,教师们经常利用课外时间对学生进行培优、提中和补差,向四十五分钟要质量。
加强学习,提高教师自身素质;认真备好课,让课堂充满活力;加强纪律教育,实行师生全员参与自主管理。
2.实现资源共享改变备课方式,注重集体备课。
学校又特意安排每周下午为教研时间,教师间互相合作、交流教育资源,教学方法互相探讨,这种开放、共享的模式既节约时间,又提高了课堂效率,最终使全体教师受益,学生受益。
3.改变学习方式课堂上师生的活动效果有了一定的提高,由单一的学习方式转向多样性,努力实现“老师讲,学生听到师生互动,实践操作”的转化。
积极培养学生对学习的兴趣,充分利用学生的已有知识和原有的生活经验,创设恰当的情境,体会到学科知识与生活的联系,增强学生学习的乐趣。
2014届高三第一次统检质量分析

2014届高三第一次统检质量分析沅江二中教导处夏武生亲爱的高三老师们:晚上好!今天我们相聚于此,对上学期期末进行的全市第一次统检进行质量分析。
目的是为了找出差距,探讨原因,拿出对策,争取2014届高三的胜利。
下面我就这次统检对我校高三的成绩做一个质量分析,如有不妥之处,还请批评指正!首先我大致讲一下全市情况:此次统检全市共有2659名学生参考,其中理科1810人,文科849人。
理科最高分是642分,文科最高分是592分,文理最高分均来自沅江一中。
下面我将分整体情况分析和具体情况分析两大块来分析一下我校的统检情况以及对接下来的高三复习备考提几点希望和要求:一、整体情况分析整体情况分析我又将分理科与文科两小块来具体分析。
1、理科情况(1)总分情况此次统检我校高三理科共有96人参考,最高分是293班陈依婷同学,总分453分。
最低分是295班曹成同学,总分88分。
四中有77人参考,最高分是414分,最低分是140分。
北校区有212人参考,最高分是480分,最低分是157分。
由此可见我们的最高分比北校区的低,最低分也比四中、北校区低。
(2)平均分情况此次统检我校理科各科平均分排名可以说是非常不理想。
总平均分是269.7分,位列第五名。
就连四中的平均分也有304.2分,高出我校平均分近35分。
同时琼湖书院的平均分更是高达361.3分,高出我校平均分近100分。
这一数字可以说是触目惊心了。
我不相信四中和北校区的学生会比我们好多少,我也不相信他们的老师会比我们优秀多少。
但是事实摆在眼前。
那么原因何在?这不得不引起我们的反思了。
老师们,真抓实干才能出成绩,务实才是重中之重。
一切虚的东西都是没有任何作用。
具体到每科的平均分全市排名,这个数字同样触目惊心。
全市理科班共有35个班。
而我校293班,除了语文排在29名以外,数学排在33名,英语、物理、化学、生物均排在34名。
另外一个理科班295班除了数学、化学排在32名外,语文排在34名,英语、物理、生物均排在35名,垫底了。
高三考试质量分析
2013-2014学年度上学期高三政治期末、寒假考试质量分析一、试卷分析1、试卷结构:两次考试时间均为为120分钟,卷面总分为100分,都分为选择题和非选择题两大部分,符合高考试题体例。
2.试卷特点期末试卷考查范围包括必修1——4册,侧重双基,知识涵盖面广,渗透性强,注重实际情景和具体语境中考查学生对基础知识的理解和运用,有较强的探究性和灵活性。
试卷与教材内容联系紧密,无偏题和难题。
该试卷着重考查学生理解、运用知识和知识迁移的能力,重视考查学生的经济生活基础知识、基本技能,考查学生运用所学的知识和技能分析问题、解决问题的能力。
河西联考试卷(下称河联)是一套各地高考加模拟考试题的组合卷,考查范围仅限于必修1、2、4册,题量大,知识点多,难度大,重视能力提升,真正体现了高考以能力立意的命题意图。
两套试题的选材都有有一定的时代感和知识性,在选材中既注意了所选材料在题材和体裁上的多样性,又注意了所选材料与现实生活的密切联系性。
二、班级成绩分析以及答题情况分析高二(9)班高二(10)班高二(11)班高二(12)班高二(13)班高二(14)班高二(15)班高二(16)班1、就全年级而言,期末考试年级平均分:67.20分,最高分91分,年级最低分21分。
80分—100分之间43人,占考试人数的13.78﹪,主要分布与(9)班;79分—60分之间168人,占考试人数的约53.84﹪,主要分布于快班;59—60分之间47人,占考试人数的约15.06﹪,主要分布于(12)—(15)班;49分以下21人,占考试人数的约6.7﹪。
主要分布于(15)(16)班。
河联考试年级平均分:58.78分,最高分81分,年级最低分27分。
80分—100分之间2人,占考试人数的0.68﹪;79分—60分之间134人,占考试人数的约46.2﹪;59—60分之间110人,占考试人数的约37.93﹪;49分以下43人,占考试人数的约14.82﹪。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
富源县第三中学
2014届高三(上)期末考试年级组质量分析
在教育局与学校的统一安排下,我部于2014年1月15日至2014年1月16日完成2014届高三(上)期末考试,试卷为曲靖市第一次市统测。
本次考试,对高三年级具有十分重要的意义:其一:它是进入学生进入高三的第一次大型摸底考试,考试结果能让我们更充分的了解学生的实际情况;其二:通过这次考试有助于我们了解自己的教学情况,及与兄弟学校的差距,从而指导我们在高三后期有的放矢的进行教学,确保各层次各班级各学科目标的完成。
下面我代表年级组就本次月考结果及教学工作进行质量分析。
一、考试基本情况
1.各班各科平均分
(1)文科各班各科平均分
(2)理科各班各科平均分
从这两块表中可以发现:
文科(127)班最好,而(128)班、(129)班最差,这两个班总评差(131)班接近4分,总的来说文科班差距较小,因此,在比较文科班成绩时主要应看优生
人数,前50名131班,128班,129班最多;
理科班(136)最好,其总评都远超其他班,(134)班总评差前二名的班级在30分左右,而(133)班总评差前二名的班级在20分左右,可见理科班总评差距之大远超文科,总评差主要是由理综和数学造成;
2. 分数段人数分布
从这组数据中可以看出,在本次考试中文、理科优生不是很多,尤其是高分段450分以上的人没有,而差生理科更为突出,因此在以后的工作中我们应该促优保差.
二、考试分析:
1、由于期末考试复习时间少,学生经过几个月的学习,一部分知识点已经忘的差不多了,学生不主动的复习。
2、进入高三,学生开始出现两级分化现象,学习较好的学生成绩相对稳定,成绩不好的学生,成绩下滑的明显。
3、学习态度不端正
学习目标不明确,学习态度不端正.因此导致现在本年级优生不突出,差生很多,而且在优生中常出现断层,相差一个名次的同学常常出现相差几十分,针对本年级的情况我们在下学期将更注重基础,先保证大部分同学能上线,同时对优生进行辅导。
四..改进措施。
(一)、2014届目标
凡事预则立,不预则废,要取得好的高考成绩,年级备考必须早准备,早动手,根据本次期末考试成绩,预定目标如下:
上线目标:95%;
二本目标:11人;
三本及以上:120人;
重点目标:1人。
(二)、本届高三年级复习备考的典型做法
本届高三,年级将紧紧围绕“全程备考”和“实抓过程、严抓细节”的备考
方针,努力营造“紧张、有序、科学、高效”的备考气氛,鼓励学生,努力让成绩好的学生能上好大学,成绩差的学生能上大学,本届高三我们的典型做法为:1.实行捆绑管理
高三年级实行班级捆绑管理制度,通过捆绑管理实现班级的齐抓共管,解决班主任只管自己班级的局限性问题,优化管理资源。
2.合理部署、统筹安排各类测试。
高三年级考试频繁,年级将督促备课组认真搞好每一次周测、月考、联考、统考工作,为了避免盲目考试,年级组将把好试卷数量和质量关,除省统测和市统测外,其他测试,年级都将请各备课组认真精选题目,组合试卷,让高质量的试题进入学生手中,避免盲目考试,以达到提高备考效果。
(1).考试进度安排.
1)2013年8月至2013年12月使用阶段性小综合试卷;
2)2013年1月至2013年6月使用高考模式大综合卷;
(2).高三考试时间安排如下:
1)2013年8月至2014年2月实行半月考;
2)2014年3月至2014年6月实行周考。
3.试后工作
测试后,年级以班为单位进行质量分析,班主任总体负责组织,同时邀请学校领导参加,质量分析到题、到学生,做到摸清底子,制定下一步复习方案;以分析优生为中点。
4. 辅导工作
根据本届高三的情况,其实也是我校一直存在的一个问题——生源太差,为了让学生强化基础,在高考时考出好成绩,年级进行以下工作:
(1).我们坚持对学生每天进行一辅导两督促:
1)早上6:30—7:30班主任督促早读;
2)晚上18:00—18:35由班主任根据本班情况安排科任教师进行辅导;
3)晚上22:50—23:30督促学生自习。
2.辅导要求
(1)辅导教师按时进入教室,不迟到、不早退、不中途离开;
(2)3段自习年级都将安排两位班主任进行巡查。
5.研学
(1)学生状况
本年级学生基础差、底子薄,但我们不会因为学生底子薄、基础差而产生消极懈怠情绪,再差的学生也要让他每节课都有进步。
(2)高三教法
高三上法,请各备课组在教研会上进行讨论,根据学生的接受情况和现有水平,总体把握教学实效性,教学质量与教学速度并存,根据本学科的特点制定有效的复习计划,并不断的根据学生的情况进行调整。
6.优生培养
做好分层教学,让各层次的学生都得以发展,让差生吃饱,让优生吃饱,班主任应该协调各科,从学生的总体成绩为依据,把部分科目差的学生分给科任教师进行辅导,科任教师应配合班主任找好优生的辅导。
7.合理安排教学进度,扎实抓好两轮复习
第一阶段:2013年6月—2014年2月底,一轮复习阶段。
重点是加强各科基础知识的学习,在第一阶段注重基本技能和基本方法的训练,注重基础知识积累。
第二阶段:2011年3月初——5月底,二轮复习阶段。
重点是通过专题复习,加强知识的横向联系,形成知识网络,目标是培养学生分析、解决问题的能力。
8.开展专题讲座
高三下学期,第一轮复习的尾声,年级将联合备考组开展专题讲座,我们利用课外时间开展,年级将邀请各备课组有经验、能力强的老师开展专题讲座。
富源县第三中学高三年级组
2014年2月25日。
