R语言与时间序列学习笔记
《时间序列分析及应用:R语言》读书笔记
《时间序列分析及应用:R语言》读书笔记姓名:石晓雨学号:1613152019(一)、时间序列研究目的主要有两个:认识产生观测序列的随机机制,即建立数据生成模型;基于序列的历史数据,也许还要考虑其他相关序列或者因素,对序列未来的可能取值给出预测或者预报。
通常我们不能假定观测值独立取自同一总体,时间序列分析的要点是研究具有相关性质的模型。
(二)、下面是书上的几个例子1、洛杉矶年降水量问题:用前一年的降水量预测下一年的降水量。
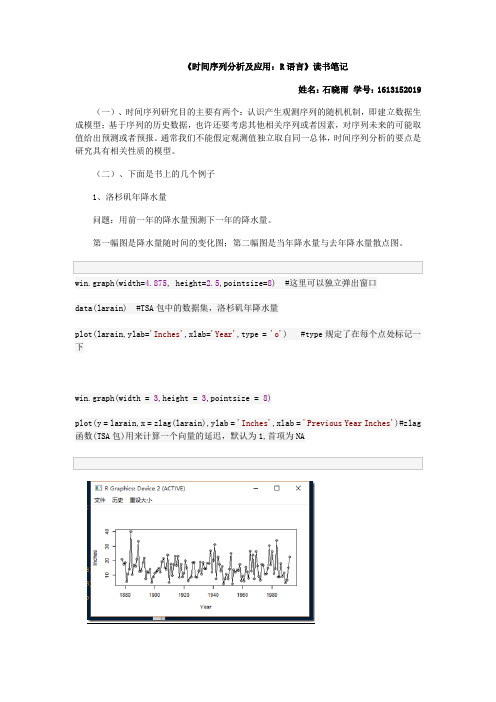
第一幅图是降水量随时间的变化图;第二幅图是当年降水量与去年降水量散点图。
win.graph(width=4.875, height=2.5,pointsize=8) #这里可以独立弹出窗口data(larain) #TSA包中的数据集,洛杉矶年降水量plot(larain,ylab='Inches',xlab='Year',type = 'o') #type规定了在每个点处标记一下win.graph(width = 3,height = 3,pointsize = 8)plot(y = larain,x = zlag(larain),ylab = 'Inches',xlab = 'Previous Year Inches')#zlag 函数(TSA包)用来计算一个向量的延迟,默认为1,首项为NA从第二幅图看出,前一年的降水量与下一年并没有什么特殊关系。
2、化工过程win.graph(width = 4.875,height = 2.5,pointsize = 8)data(color)plot(color,ylab = 'Color Property',xlab = 'Batch',type = 'o')win.graph(width = 3,height = 3,pointsize = 8)plot(y = color,x = zlag(color),ylab = 'Color Property',xlab = 'Previous Batch Color Property')len <- length(color)cor(color[2:len],zlag(color)[2:len])#相关系数>0.5549第一幅图是颜色属性随着批次的变化情况。
R语言时间序列中文教程

R语言时间序列中文教程R语言是一种广泛应用于统计分析和数据可视化的编程语言。
它提供了丰富的函数和包,使得处理时间序列数据变得非常方便。
本文将为大家介绍R语言中时间序列分析的基础知识和常用方法。
R语言中最常用的时间序列对象是`ts`对象。
通过将数据转换为`ts`对象,可以使用R语言提供的各种函数和方法来分析时间序列数据。
我们可以使用`ts`函数将数据转换为`ts`对象,并指定数据的时间间隔、起始时间等参数。
例如,对于按月份记录的时间序列数据,可以使用以下代码将数据转换为`ts`对象:```Rts_data <- ts(data, start = c(2000, 1), frequency = 12)```在时间序列分析中,常用的一个概念是平稳性。
平稳性表示时间序列的均值和方差在时间上不发生显著变化。
平稳时间序列的特点是,它的自相关函数(ACF)和偏自相关函数(PACF)衰减得很快。
判断时间序列是否平稳可以通过绘制序列的线图和计算序列的自相关函数来进行。
我们可以使用R语言中的`plot`函数和`acf`函数来实现。
例如,对于一个名为`ts_data`的时间序列数据,可以使用以下代码绘制序列的线图和自相关函数图:```Rplot(ts_data)acf(ts_data)```在进行时间序列分析时,经常需要进行模型拟合和预测。
R语言提供了一些常用的函数和包,用于时间序列的模型拟合和预测。
其中,最常用的方法是自回归移动平均模型(ARIMA)。
ARIMA模型是一种广泛应用于时间序列分析的统计模型,它可以描述时间序列数据中的长期趋势、季节性变动和随机波动等特征。
我们可以使用R语言中的`arima`函数来拟合ARIMA模型,并使用`forecast`函数来进行预测。
以下是一个使用ARIMA模型进行时间序列预测的示例代码:```Rmodel <- arima(ts_data, order = c(p, d, q))forecast_result <- forecast(model, h = 12)```以上代码中,`p`、`d`和`q`分别表示ARIMA模型的自回归阶数、差分阶数和移动平均阶数。
R语言时间序列有关各种函数总结

R语言时间序列有关各种函数总结R语言是一种强大的统计分析和数据可视化工具,提供了许多时间序列分析的函数和方法。
下面是一些重要的时间序列分析函数的总结:1. ts(函数:用于创建时间序列对象。
可以指定时间序列的起始时间、结束时间、时间间隔等。
例如,创建从1990年1月到1999年12月的月度时间序列对象可以使用以下代码:```Rts_data <- ts(data, start=c(1990, 1), end=c(1999, 12), frequency=12)``````R```3. stl(函数:基于季节性-趋势-随机性分解的局部回归方法,用于进行季节调整。
该函数可以根据时间序列的特性自动选择适当的分解模型。
以下是使用stl(函数进行季节调整的示例:```Rseasonally_adjusted <- stl(ts_data, s.window="periodic")```4. forecast(函数:用于时间序列的预测。
可以根据历史数据拟合不同的模型,例如ARIMA模型、指数平滑模型等,并生成未来一段时间的预测结果。
以下是使用forecast(函数生成未来12个月的预测结果的示例:```Rforecast_result <- forecast(ts_data, h=12)```5. autocorrelation(函数:用于计算时间序列的自相关系数。
自相关系数可以帮助我们了解时间序列的固定模式和周期性。
以下是计算时间序列的自相关系数的示例:```Racf_result <- autocorrelation(ts_data)```6. arima(函数:用于建立自回归移动平均模型(ARIMA)来拟合时间序列。
ARIMA模型是一种常用的时间序列预测模型,可以预测时间序列的未来值。
以下是使用arima(函数拟合ARIMA模型的示例:```Rarima_model <- arima(ts_data, order=c(p, d, q))```7. ets(函数:用于指数平滑时间序列模型的拟合和预测。
R语言常用上机命令分功能整理 时间序列分析为主

第一讲 应用实例 • R 的基本界面是一个交互式命令窗口,命令提示符是一个大于号,命令的结果马上 显示在命令下面。 • S 命令主要有两种形式:表达式或赋值运算(用’<-’或者’=’表示) 。在命令提示符后 键入一个表达式表示计算此表达式并显示结果。赋值运算把赋值号右边的值计算出 来赋给左边的变量。 • 可以用向上光标键来找回以前运行的命令再次运行或修改后再运行。 • S 是区分大小写的,所以 x 和 X 是不同的名字。 我们用一些例子来看 R 软件的特点。假设我们已经进入了 R 的交互式窗口。如果没有打开 的图形窗口,在 R 中,用:> x11() 可以打开一个作图窗口。然后,输入以下语句: x1 = 0:100 x2 = x1*2*pi/100 y = sin(x2) plot(x2,y,type="l") 这些语句可以绘制正弦曲线图。其中,“=”是赋值运算符。0:100 表示一个从 0 到 100 的等 差数列向量。第二个语句可以看出,我们可以对向量直接进行四则运算,计算得到的 x2 是 向量 x1 的所有元素乘以常数 2*pi/100 的结果。 从第三个语句可看到函数可以以向量为输入, 并可以输出一个向量,结果向量 y 的每一个分量是自变量 x2 的每一个分量的正弦函数值。
#将未来 5 期预测值保存在 prop.fore 变量中 U = prop.fore$pred + 1.96* prop.fore$se L = prop.fore$pred – 1.96* prop.fore$se#算出 95%置信区间 ts.plot(prop, prop.fore$pred,col=1:2)#作时序图,含预测。 lines(U, col="blue", lty="dashed") lines(L, col="blue", lty="dashed")#在时序图中作出 95%置信区间 例题 3.9 d=scan("a1.22.txt") x=diff(d) arima(x, order = c(1,0,1),method="CSS") tsdiag(arima(x, order = c(1,0,1),method="CSS")) 第一点: 对于第三讲中的例 2.5,运行命令 arima(prop, order = c(1,0,0),method="ML")之后,显示: Call: arima(x = prop, order = c(1, 0, 0), method = "ML") Coefficients: ar1 intercept 0.6914 81.5509 s.e. 0.0989 1.7453 sigma^2 estimated as 15.51: log likelihood = -137.02, aic = 280.05 注意:intercept 下面的 81.5509 是均值,而不是截距!虽然 intercept 是截距的意思,这里如 果用 mean 会更好。 (the mean and the intercept are the same only when there is no AR term, 均值和截距是相同的,只有在没有 AR 项的时候) 如果想得到截距,利用公式计算。int=(1-0.6914)*81.5509= 25.16661。课本 P81 的例 2.5 续中 的截距 25.17 是正确的。
R语言学习笔记(一)

R语言学习笔记(一)读书笔记Basic knowledge for R2011-3-10相关的函数记录与整理1、source("文件名.r"):调取主程序的文件,在程序结构复杂的时候很有用,可以将一部分复杂的运算主程序放入其中。
2、install.packages("fields"):安装程序包3、library(fields):导入程序包4、t(x)转置函数,对于csv中横排的转置很有用5、dev.off():中断函数6、a <- as.character(b):因子型转化为字符型函数7、position <- regexpr('_',a):regexpr()函数对字符的定位很有用,返回值position为特定字符,如字符串a中’_’的位置8、结合定位函数,对字符串如x345_xbt,进行拆分,利用函数substring(要拆分的字符串,开始的字符位置,结束的字符位置) namecol1 <- substring(a, 2, position - 1)namecol2 <- substring(a, position + 1, nchar(a))结合regexpr()函数,这两个命令返回的值为,namecol1<-345;namecol2<-xbt;9、合并向量data.frame(vetor1, vetor2, vetor3)cbind(vetor1, vetor2, vetor3)10、取名字相同的交集unique()函数例如对包含行名的向量R1、R2、R3取名字相同的行,组成新的向量。
nam1 <- rownames(R1)nam2 <- rownames(R2)nam3 <- rownames(R3)tnam <- unique(c(nam1,nam2,nam3))返回结果为只剩下名字相同的行的数值和rownames或者取一个向量中唯一一个值的数据,合并重复数据。
R语言之数据分析高级方法「时间序列」

R语言之数据分析高级方法「时间序列」作者简介Introduction姚某某本节主要总结「数据分析」的「时间序列」相关模型的思路。
「时间序列」是一个变量在连续时点或连续时期上测量的观测值的序列,它与我们以前见过的数据有本质上的区别,这个区别在于之前的数据都在一个时间的横截面上去测量、计算数据,而「时间序列」给出了一种时间轴线上纵向的视角,将时间作为自变量,测量出一系列纵向数据。
关于「时间序列」的预测模型,我所了解的常用模型有三种:1. 移动平均 2. 指数预测模型 3. ARIMA 预测模型0. 时序的分解要研究时序如何预测,首先需要将复杂的时序数据进行分解,将复杂的时序数据分解为单一的分解成分,这样能利用统计方法进行拟合,然后个个击破,最后再合成为我们需要预测的未来时序数据。
前人在这一问题上已经得到很好的结论,通过对时序数据现实意义的理解,一般将时序数据分解为四个成分:1. 水平项2. 趋势项3. 季节效应(衍生出去为周期项)4. 随机波动•水平项,即剔除时序数据的趋势影响和季节影响后,时序数据所剩的成分,它代表着时序数据在时间轴上相对稳定的一个基础值。
就像一个原点一样,在这个原点上去考虑时间所带来的趋势影响和季节影响。
•趋势项,它用于捕捉时序数据的长期变化,是逐步增长还是逐步下降。
就像在二元空间中的一个单调函数。
•季节效应,衍生出去就是周期型,在一定时间内,时序数据所包含的周期型变化。
就像在二元空间中的三角函数,如y=sinx,其数值是周而复始的。
通常在分解以上各个成分时,有两种模式,一个是乘法模型,一个是加法模型。
其中,加法模型的季节效应被认为不依赖于时间序列,二乘法模型认为季节影响随着时间会发生改变。
不过两种模型在计算时可以相通,对乘法模型作对数处理即可。
1. 移动平均这一方法很简单,只做简单讲解•所谓移动平均,就是使用时间序列中最接近的 k 期数据值的平均值作为下一个时期的预测值。
即:较小的 k 值将更快速追踪时间序列的移动,而较大的 k 值将随着时间的推移更有效地消除随机波动。
R语言与时间序列学习笔记

R语言与时间序列学习笔记(1)继续上一次的参数估计话题。
今天分享的是R语言中时间序列的模型初步估计有关内容。
主要有:时间序列的创建,ARMA模型的建立与模型的参数估计。
一、时间序列的创建时间序列的创建函数为:ts().函数的参数列表如下:ts(data = NA, start = 1, end = numeric(), frequency = 1,deltat = 1, ts.eps = getOption("ts.eps"), class = , names = ) 参数说明:data:这个必须是一个矩阵,或者向量,再或者数据框frame Frequency:这个是时间观测频率数,也就是每个时间单位的数据数目Start:时间序列开始值,允许第一个个时间单位出现数据缺失举例:ts(matrix(c(NA,NA,NA,1:31,NA),byrow=T,5,7),frequency=7,names=c("Sun"," Mon ","Tue", "Wen" ,"Thu"," Fri"," Sat"))运行上面的代码就可以得到一个日历:Sun Mon Tue Wen Thu Fri SatNA NANA 1 2 3 45 6 7 8 9 10 1112 13 14 15 16 17 1819 20 21 22 23 24 2526 27 28 29 30 31 NA在R语言中本身也有不少数据集,比如统计包中的sunspots,你可以通过函数data(sunspots)来调用它们。
二、一些时间序列模型这里主要介绍AR,MA,随机游走,余弦曲线趋势,季节趋势等首先介绍一下AR模型:AR模型,即自回归(AutoRegressive, AR)模型,数学表达式为:AR : y(t)=a1y(t-1)+...any(t-n)+e(t)其中,e(t)为均值为0,方差为某值的白噪声信号。
《时间序列分析——基于R》王燕,读书笔记

《时间序列分析——基于R》王燕,读书笔记笔记:⼀、检验:1、平稳性检验:图检验⽅法:时序图检验:该序列有明显的趋势性或周期性,则不是平稳序列⾃相关图检验:(acf函数)平稳序列具有短期相关性,即随着延迟期数k的增加,平稳序列的⾃相关系数ρ会很快地衰减向0(指数级指数级衰减),反之⾮平稳序列衰减速度会⽐较慢衰减构造检验统计量进⾏假设检验:单位根检验adfTest()——fUnitRoots包2、纯随机性检验、⽩噪声检验(Box.test(data,type,lag=n)——lag表⽰输出滞后n阶的⽩噪声检验统计量,默认为滞后1阶的检验统计量结果)1、Q统计量:type=“Box-Pierce”2、LB统计量:type=“Ljung-Box”⼆、模型1、ARMA平稳序列模型1.1平稳性检验1.2ARMA的p、q定阶——acf(),pacf(),auto.arima()⾃动定阶1.3建模arima()1.4模型显著性检验:残差的⽩噪声检验Box.test();参数显著性检验t分布2、⾮平稳确定性分析2.1趋势拟合:直线、曲线(⼀般是多项式,还有其它函数)2.2平滑法移动平均法:SMA()——TTR包指数平滑法:HoltWinters()3、⾮平稳随机性分析3.1ARIMA1平稳性检验,差分运算2拟合ARMA3⽩噪声检验3.2疏系数模型arima(p,d,f)3.3季节模型可以叠加的模型4、残差⾃回归模型:4.1建⽴线性模型4.2对滞后的因变量间拟合线性模型,对模型做残差⾃相关DW检验。
dwtest()——lmtest包,增加选项order.by指定延迟因变量4.3对残差建⽴ARIMA模型5、条件异⽅差模型:异⽅差检验:LM检验ArchTest()——FinTS包,⽤ARCH、GARCH模型建模第⼀章简介统计时序分析⽅法:1、频域分析⽅法2、时域分析⽅法步骤:1、观察序列特征2、根据序列特征选择模型3、确定模型的⼝径4、检验模型,优化模型5、推断序列其它统计性质或预测序列将来的发展时域分析研究的发展⽅向:1、AR,MA,ARMA,ARIMA(Box-Jenkins模型)2、异⽅差场合:ARCH,GARCH等(计量经济学)3、多变量场合:“变量是平稳”不再是必需条件,协整理论3、⾮线性场合:门限⾃回归模型,马尔科夫转移模型第⼆章时间序列的预处理预处理内容:对它的平稳性和纯随机性进⾏检验,最好是平稳⾮⽩噪声的序列1、特征统计量1.1概率分布分布函数或密度函数能够完整地描述⼀个随机变量的统计特征,同样⼀个随机变量族{Xt}的统计特性也完全由它们的联合分布函数或联合密度函数决定。
R语言时间序列2

在构建完模型之后,可以进行预测,预测函数有两个,一个为predict()函数,另一个为forecast包中的forecast()函数。
四、模型评价
对于构建的模型及预测值,我们需要进行预测值误差的评价,通常绘制误差的acf和进行Ljung-Box 检验,最后绘制正太分布曲线,看预测误差是否满足方差不变,均值为0的正太分布
通过绘制的图看出,自相关值在滞后1阶(lag1)之后为0,且偏自相关值在滞后3阶(lag3)之后缩小至0,那么意味着接下来的ARIMA(自回归移动平均)模型对于一阶时间序列有如下性质:
ARMA(3,0)模型:即偏自相关值在滞后3阶(lag3)之后缩小至0且自相关缩小至0(即使此模型中说自相关值缩小至0有些不太合适),则是一个阶层p=3的自回归模型。
二、模型参数p、q的确定
经过第一节,得到一个平稳时间序列后,意味着需要寻找ARIMA(p,d,q)中合适的p值和q值。为了得到这些,通常需要检查【平稳时间序列的自相关图和偏自相关图】
使用R中的acf()和pacf()函数来分别求自相关图和偏自相关图。在acf和pacf设定plot=F来得到自相关和偏自相关的真实值。
ARMA(0,1)模型:即自相关图在滞后1阶(lag1)之后为0且偏自相关图缩小至0,则是一个阶数q=1的移动平均模型。
ARMA(p,q)模型:即自相关图和偏自相关图都缩小至0,则是一个具有p和q大于0的混合模型。
我们利用简单的原则确定哪个模型最好:即认为具有最少参数的模型是最好的。
ARMA(3,0)有3个参数,ARMA(0,1)有一个参数,而ARMA(p,q)至少有2个变量。因此认为ARMA(0,1)模型是最好的模型。
diff()函数进行差分得到平稳序列,这里所谓的平稳序列,是指时间序列的水平和方差大致保持不变。
R语言笔记完整版

R语⾔笔记完整版R语⾔与数据挖掘:公式;数据;⽅法R语⾔特征1. 对⼤⼩写敏感2. 通常,数字,字母,. 和 _都是允许的(在⼀些国家还包括重⾳字母)。
不过,⼀个命名必须以 . 或者字母开头,并且如果以 . 开头,第⼆个字符不允许是数字。
3. 基本命令要么是表达式(expressions)要么就是赋值(assignments)。
4. 命令可以被 (;)隔开,或者另起⼀⾏。
5. 基本命令可以通过⼤括弧({和}) 放在⼀起构成⼀个复合表达式(compound expression)。
6. ⼀⾏中,从井号(#)开始到句⼦收尾之间的语句就是是注释。
7. R是动态类型、强类型的语⾔。
8. R的基本数据类型有数值型(numeric)、字符型(character)、复数型(complex)和逻辑型(logical),对象类型有向量、因⼦、数组、矩阵、数据框、列表、时间序列。
基础指令程序辅助性操作:运⾏q()——退出R程序tab——⾃动补全ctrl+L——清空consoleESC——中断当前计算调试查错browser() 和debug()——设置断点进⾏,运⾏到此可以进⾏浏览查看(具体调试看browser()帮助⽂档(c,n,Q))stop('your message here.')——输⼊参数不正确时,停⽌程序执⾏cat()——查看变量?帮助help(solve) 和 ?solve 等同solve——检索所有与solve相关的信息help("[[") 对于特殊含义字符,加上双引号或者单引号变成字符串,也适⽤于有语法涵义的关键字 if,for 和 functionhelp(package="rpart")——查看某个包help.start()——得到html格式帮助help.search()——允许以任何⽅式(话题)搜索帮助⽂档example(topic)——查看某个帮助主题⽰例apropos("keyword")——查找关键词keyword相关的函数RSiteSearch("onlinekey", restrict=fuction)——⽤来搜索邮件列表⽂档、R⼿册和R帮助页⾯中的关键词或短语(互联⽹)RSiteSearch('neural networks')准备⽂件⽬录设置setwd(<dir>)——设置⼯作⽂件⽬录getwd()——获取当前⼯作⽂件⽬录list.files()——查看当前⽂件⽬录中的⽂件加载资源search()——通过search()函数,可以查看到R启动时默认加载7个核⼼包。
用R语言做时间序列分析

用R语言做时间序列分析
时间序列分析是用来研究数据的变化趋势及其影响因素,以便对未来
的发展趋势有一定的预测对~用R语言做时间序列分析,可以从数据的宏
观分析、模型的训练、数据预测三个方面进行。
一、数据宏观分析
首先,需要预处理数据,例如,对于时间序列数据,要把它转换成一
定的格式,比如时间戳、日期和时间格式,这样R才能够识别这些数据,
在R中,可以使用时间序列模块中的函数来进行转换,比如:as.Date, as.POSIXct, as.POSIXlt等等。
之后需要针对时间序列数据进行宏观分析,可以使用R中的函数acf,pacf来检测时间序列的自相关性,这样可以把时间序列数据分解为不同
的部分,并可以提取出隐藏在数据中的规律,这样就可以确定时间序列模
型的类型,比如AR模型、MA模型、ARMA模型等,根据特定数据的特征,
从这些模型中选择最优的模型。
另外,还可以使用R中的函数spectrum来检测时间序列数据的频率
分布以及振荡性,以及峰值,从而可以有针对性地处理时间序列数据,比
如使用滤波器来去噪。
二、模型的训练
模型的训练也可以使用R进行,R中有专门用于时间序列分析的现成
函数,比如arima函数,可以用来训练ARMA模型。
R语言 时间序列有关各种函数总结

一、基础篇1、安装程序包install.packages('程序包名字')例:install.packages('TSA') //安装TSA程序包注:直接输入install.packages() 可弹出程序包窗口,若未选择镜像,会先弹出镜像窗口,选择镜像后再弹出程序包窗口2、加载程序包library(程序包名字)例:library(TSA) 加载TSA程序包注:程序包名字前后不需要打引号3、加载程序包内数据data(数据名)例:data(larain) //加载larain数据注:加载之后才可以使用此数据,否则会提示数据不存在4、构建时间序列时间序列名字=ts(数据名,freq=单位时间内的数据个数,start=第一个数据对应的时间)例:a=ts(larain,freq=12,start=2000) //将larain转化成从2000年1月开始的月度数据注:freq=4表示季度数据,12表示月度数据;start可以等于一个数,表示年份,即数据是从该年第一月开始的,也可以等于c(年份,月份),表示从某年某月开始5、从TXT文档读取单变量数据数据名=scan('文件名字.txt')例:a=scan('file1.txt') //读取file1中的变量,并命名为a注:读取的文档需放到工作目录之下6、从TXT文档读取多变量数据数据名=read.table('文件名字.txt',header=T/F)attach(数据名字)例:a= read.table ('file2.txt', header=F) //将file2中数据命名为a,系统自带列标V1,V2……attach(a) //打开a,之后可以直接调用a中各变量V1 //输出a中第一列数据注:读取的文档需放到工作目录之下,header=T表示文档中第一行是各列数据的名字,第二行开始是数据,header=F表示系统会自动给各列数据命名,调用数据之前必须先打开它7、从CSV格式的表格文件中读取数据数据名=read.csv('文件名字.csv',header=T/F)attach(数据名)例:a=read.csv('file3.csv', header=T) //将file3中数据命名为a,第一行为各列数据的名字attach(a) //打开a,之后可以直接调用a中各变量X //输出a中第一列数据(假如表中第一列第一行为X)注:读取的文件需放到工作目录之下,header参数含义同上,调用数据之前也必须先打开8、导出数据write.table (需要导出的数据名,file ="生成的文件名.txt",sep="数据分隔符号",s =T/F,s =T/F, quote =T/F)例:write.table (larain, file ="file4.txt",s =F, s =F, quote =F)//将larain导出到file4文档中,没有分隔符,行标不导出,列标也不导出,数据不加引号注:生成的文件在工作目录下,sep参数在多列数据导出时,可以用到来间隔各列数据,如果是单列数据,可以省略。
R语言学习笔记(入门知识)

R语言学习笔记(入门知识)R免费使用;统计工具;# 注释,行注释块注释:anything="这是注释的内容"常用R语言编辑器:Rsutdio,Tinn-R,Eclipse+StatET;中文会有乱码帮助:?,help; ?boxplot, help(boxplot),help("[[")运行R文件:source('abc.R')加载包:library(ggplot2)安装包:install.packages()退出R:q()设置工作目录:setwd("E:\\XXX\\yyy\\")清空内存:rm(list=ls(all=TRUE))对数:log自然对数;log10;标量;赋值:<-,=变量取名可以用.c() 向量; Win[1], Win[1:5], Win[-2],下标从1开始;c()可以连接多个标量;也可连接多个向量;NA变量取名大写字母开头na.rm=TRUErep(); rep(1:4, each=8)seq(); seq(from=1,to=4,by=1)cbind()rbind()matrix(); matrix(nrow=8,ncol=4); Z[,1], Z[1:8,1], Z[2,], Z[,-3], Z[,c(1,3,4)]dim(Z)nrow(); ncol();vector(length=8)colnames()rownames()as.matrix;as.data.frame,is.matrix, is.data.frame,t()XX<-data.frame(AA=AA,BB=BB); XX$AA; XX[,1];str()names()list(X1=x1,X2=x2)is.na()!is.na()read.table() 生成了数据框scan() 数值型比较快write.table() #可以用于保存向量,矩阵,data.frame.factorattach(); detach();unique()筛选子集:Sel<-Squid$Sex==1; SquidM<-Squid[Sel,]; Squid[Squid$Sex==1,];|, &, !=, ==order() # T o sort a data frame in R, use the order( ) function.对向量排序: sort(x, decreasing = FALSE, ...)merge()as.factor(); as.numeric(); as.character();factor(Squid$Sex, levels=c(1,2), labels=c("M","F"))tapply(); tapply(X=Veg$R,INDEX=Veg$Transect, FUN=mean) 根据第二个变量的不同水平对第一个变量进行求平均值运算;mean,min,max,sd,length,lapply() 多个变量;输出list;lapply(x,FUN=mean)sapply() 多个变量;输出vector; sapply(x,FUN=mean)summary() 输出最小值,第一个四分位数,中位数,平均值,第三个四分位数,最大值;table() 计算列联表;一个变量或两个变量;plot(); plot(x=XXX,y=YYY); plot(y~x,data=Veg);plot(x=,y=,xlab=,ylab=,main=,xlim=,ylim=),pch=1..25;warnings()col 颜色; cel 尺寸;cex尺寸;lines()划线; loess()loess平滑;fitted()拟合值;lwd线宽度,lty线类型;jpeg(file="xxxx.jpg"); dev.off();paste(); paste0();for(i in 1:27) {}for(var in seq) exprwhile(cond) exprrepeat exprbreaknextif(cond) exprif(cond) cons.expr else alt.exprifelse(choice=="Zeros",expr1,expr2);自定义函数function_name<-function(params){do somethingexpr -- return values;}colSums(); rowSums();函数参数默认值function_name<-function(params, xxx="YYY"){do somethingexpr -- return values;}《R语言初学者指南》ls(); ls(pat = "m");ls(pat = "^m")help("bs", try.all.packages = TRUE); help("bs", package = "splines")help.search("tree", rebuild = TRUE))对象的类型和长度可以分别通过函数mode和length得到\", \'函数scan比read.table要更加灵活,它们的区别之一是前者可以指定变量的类型mydata <- scan("data.dat", what = list("", 0, 0)) 读取了文件data.dat中三个变量,第一个是字符型变量,后两个是数值型变量。
R语言时间序列有关各种函数总结

R语言时间序列有关各种函数总结一、基础篇1、安装程序包install.packages('程序包名字')例:install.packages('TSA') //安装TSA程序包注:直接输入install.packages() 可弹出程序包窗口,若未选择镜像,会先弹出镜像窗口,选择镜像后再弹出程序包窗口2、加载程序包library(程序包名字)例:library(TSA) 加载TSA程序包注:程序包名字前后不需要打引号3、加载程序包内数据data(数据名)例:data(larain) //加载larain数据注:加载之后才可以使用此数据,否则会提示数据不存在4、构建时间序列时间序列名字=ts(数据名,freq=单位时间内的数据个数,start=第一个数据对应的时间)例:a=ts(larain,freq=12,start=2000) //将larain转化成从2000年1月开始的月度数据注:freq=4表示季度数据,12表示月度数据;start可以等于一个数,表示年份,即数据是从该年第一月开始的,也可以等于c(年份,月份),表示从某年某月开始5、从TXT文档读取单变量数据数据名=scan('文件名字.txt')例:a=scan('file1.txt') //读取file1中的变量,并命名为a注:读取的文档需放到工作目录之下6、从TXT文档读取多变量数据数据名=read.table('文件名字.txt',header=T/F)attach(数据名字)例:a= read.table ('file2.txt', header=F) //将file2中数据命名为a,系统自带列标V1,V2……attach(a) //打开a,之后可以直接调用a中各变量V1 //输出a中第一列数据注:读取的文档需放到工作目录之下,header=T表示文档中第一行是各列数据的名字,第二行开始是数据,header=F表示系统会自动给各列数据命名,调用数据之前必须先打开它7、从CSV格式的表格文件中读取数据数据名=read.csv('文件名字.csv',header=T/F)attach(数据名)例:a=read.csv('file3.csv', header=T) //将file3中数据命名为a,第一行为各列数据的名字attach(a) //打开a,之后可以直接调用a中各变量X //输出a中第一列数据(假如表中第一列第一行为X)注:读取的文件需放到工作目录之下,header参数含义同上,调用数据之前也必须先打开8、导出数据write.table (需要导出的数据名,file ="生成的文件名.txt",sep="数据分隔符号",/doc/e718659322.html,s =T/F,/doc/e718659322.html,s =T/F, quote =T/F) 例:write.table (larain, file ="file4.txt",/doc/e718659322.html,s =F, /doc/e718659322.html,s =F, quote =F) //将larain导出到file4文档中,没有分隔符,行标不导出,列标也不导出,数据不加引号注:生成的文件在工作目录下,sep参数在多列数据导出时,可以用到来间隔各列数据,如果是单列数据,可以省略。
R语言时间序列分析

R语言时间序列分析
时间序列分析是R语言中一种常用的数据分析方法,它用于分析随着时间的变化而变化的值。
它可以用来跟踪历史事件,识别趋势,预测未来发展,以及进行更多的数据分析工作。
R语言提供了一系列的时间序列分析工具,可以用于非常多领域,如金融、工程、统计分析等。
这篇文章将介绍时间序列分析的基本概念,以及如何使用R语言进行时间序列分析的相关知识和技巧。
首先,让我们介绍时间序列数据。
时间序列数据是随着时间的变化而变化的数据,它们可以是连续的(如每隔一分钟)或离散的(如每年)。
时间序列数据可以用来描述不同的理论模型,如线性模型、指数模型和指数平滑模型等。
接下来,让我们来看看R语言有哪些时间序列分析的工具。
R语言提供了一系列的时间序列分析工具,包括ts(函数,它可以创建时间序列对象;stl(函数,它可以分解不同的时间序列;forecast(函数,可以用来预测时间序列;plot(函数,可以将时间序列可视化,以便进行分析等。
R语言与时间序列学习笔记

R语言与时间序列学习笔记(1)继续上一次的参数估计话题。
今天分享的是R语言中时间序列的模型初步估计有关内容。
主要有:时间序列的创建,ARMA模型的建立与模型的参数估计。
一、时间序列的创建时间序列的创建函数为:ts().函数的参数列表如下:ts(data = NA, start = 1, end = numeric(), frequency = 1,deltat = 1, ts.eps = getOption("ts.eps"), class = , names = )参数说明:data:这个必须是一个矩阵,或者向量,再或者数据框frame Frequency:这个是时间观测频率数,也就是每个时间单位的数据数目Start:时间序列开始值,允许第一个个时间单位出现数据缺失举例:ts(matrix(c(NA,NA,NA,1:31,NA),byrow=T,5,7),frequency=7,names=c("Sun"," Mon ","Tue", "Wen" ,"Thu"," Fri"," Sat"))运行上面的代码就可以得到一个日历:Sun Mon Tue Wen Thu Fri SatNA NA NA 1 2 3 45 6 7 8 9 10 1112 13 14 15 16 17 1819 20 21 22 23 24 2526 27 28 29 30 31 NA在R语言中本身也有不少数据集,比如统计包中的sunspots,你可以通过函数data(sunspots)来调用它们。
二、一些时间序列模型这里主要介绍AR,MA,随机游走,余弦曲线趋势,季节趋势等首先介绍一下AR模型:AR模型,即自回归(AutoRegressive, AR)模型,数学表达式为:AR : y(t)=a1y(t-1)+...any(t-n)+e(t)其中,e(t)为均值为0,方差为某值的白噪声信号。
r语言:时间序列ARMA基础学习

r 语言:时间序列ARMA 基础学习01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 ######################################### 术语 ##################################白噪音:其均值=0,并且独立分布的(同时间无关)#稳定时间序列:任意j--i 时间段的序列:其均值相等#自相关系数acf 图:研究y[t]同y[t-l]序列之间的相关性# 在纯的ma(q)序列下,acf 图形表现为q+1以后的自相关系数约为0(虚线内) #偏相关系数pacf 图:在y[t]同y[t-l]之间的序列固定的情况下,研究研究y[t]同y[t-l]序列之间的相关性# 在纯的ar(p)序列下,pacf 图形表现为p+1以后的偏相关系数约为0(虚线内)#扩展相关系数图eacf :如果y[t]不是纯的ar 或ma ,而是arma (混合体),无法通过acf 确定q ,也不能通过pacf 确认p ,需要通过eacf 确认p 和q################################################################################################################################### 模拟产生ma ar arma 序列 ######################################################## MA 时间序列的模拟试验:产生一个ma 时间序列y.ma<-function(a1,a2,a3=0,a4=0,num=200,pic=TRUE){#MA 滑动平均时间序列的模拟(也可以使用filter 函数) e<-rnorm(num,0,1)#模拟白噪声,均值=0result<-0result[1]<-e[1]result[2]<-e[2]-a1*e[1]222324252627282930313233343536 result[3]<-e[3]-a1*e[2]-a2*e[1]result[4]<-e[4]-a1*e[3]-a2*e[2]-a3*e[1]for(t in 5:num){ result[t]<-e[t]-a1*e[t-1]-a2*e[t-2]-a3*e[t-3]-a4*e[t-4] }#构造一个ma型时间序列if(pic==TRUE){#画图形dev.new()ts.plot(result,main=paste("y.ma[t]=e[t]-",a1,"*e[t-1]-",a2,"*e[t-2]-",a3,"*e[t-3]-",a4,"*e[t-4]的时间序列散点图"))dev.new()lag.plot(result, 9, do.lines=FALSE)dev.new()par(mfrow=c(2,1))acf(result, 30,main=paste("y.ma自相关图,y.ma[t]=e[t]-",a1,"*e[t-1]-",a2,"*e[t-2]-",a3,"*e[t-3]-",a4,"*e[t-4]")) pacf(result, 30,main=paste("y.ma偏自相关图,y.ma[t]=e[t]-",a1,"*e[t-1]-",a2,"*e[t-2]-",a3,"*e[t-3]-",a4,"*e[t-4]")) }result}y.ma<-y.ma(0.92,0.65)结果一:绘制散点图结果二:绘制出y[t]同y[t-1](延迟1)、y[t-2](延迟2)……..y[t-9](延迟9)的2维散点图,用以观察y[t]同y[t-i]的相关性(i=1–9)结果三:绘制自相关和偏自相关图(在虚线外的表示有相关性)可以看到:1)在纯的ma(q)序列下,acf 图形表现为q+1以后的自相关系数约为0(虚线内)2)在纯的ma(q)序列下,pacf 则不规则的会大于1/-1可以通过acf 图确定q 的数值01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 ##### AR 时间序列的模拟试验:产生一个ar 时间序列y.ar<-function(b1,b2,b3=0,b4=0,num=200,pic=TRUE){#AR 自回归型时间序列的模拟(也可以使用filter 函数)e<-rnorm(num,0,1)#模拟白噪声,均值=0result<-0result[1]<-e[1]result[2]<-e[2]+b1*result[1]result[3]<-e[3]+b1*result[2]+b2*result[1]result[4]<-e[4]+b1*result[3]+b2*result[2]+b3*result[1]for(t in 5:num){ result[t]<-e[t]+b1*result[t-1]+b2*result[t-2]+b3*result[t-3]+b4*result[t-4] }#构造一个ar 型时间序列 if(pic==TRUE){#画图形dev.new()ts.plot(result,main=paste("y.ar[t]=e[t]+",b1,"*y.ar[t-1]+",b2,"*y.ar[t-2]+",b3,"*y.ar[t-3]+",b4,"*y.ar[t-4]的时间序列散点图"))dev.new()lag.plot(result, 9, do.lines=FALSE)dev.new()par(mfrow=c(2,1))acf(result, 30,main=paste("y.ar 自相关图,y.ar[t]=e[t]+",b1,"*y.ar[t-1]+",b2,"*y.ar[t-2]+",b3,"*y.ar[t-3]+",b4,"*y.ar[t-4]"))pacf(result, 30,main=paste("y.ar 偏自相关图,y.ar[t]=e[t]+",b1,"*y.ar[t-1]+",b2,"*y.ar[t-2]+",b3,"*y.ar[t-3]+",b4,"*y.ar[t-4]"))}result}y.ar<-y.ar(0.92,-0.65)结果一:绘制散点图结果二:绘制出y[t]同y[t-1](延迟1)、y[t-2](延迟2)……..y[t-9](延迟9)的2维散点图,用以观察y[t]同y[t-i]的相关性(i=1–9)结果三:绘制自相关和偏自相关图(在虚线外的表示有相关性)1)在纯的ar(q)序列下,pacf 图形表现为q+1以后的自相关系数约为0(虚线内) 2)在纯的ar(q)序列下,acf 则不规则的会大于1/-1 可以通过pacf 图确定p 的数值01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 ##### ARMA 时间序列的模拟试验:产生一个arma 时间序列 library(TSA) y.arma<-function(a1,a2,a3=0,a4=0,b1,b2,b3=0,b4=0,num=200,pic=TRUE){ result<-y.ma(a1=a1,a2=a2,a3=a3,a4=a4,pic=F,num=num)+y.ar(b1=b1,b2=b2,b3=b3,b4=b4,pic=F,num=num)#产生自回归滑动平均时间序 exp.str<-paste("y.arma[t]=e[t]-",a1,"*e[t-1]-",a2,"*e[t-2]-",a3,"*e[t-3]-",a4,"*e[t-4]+",b1,"*y.arma[t-1]+",b2,"*y.arma if(pic==TRUE) {#画图形 dev.new() ts.plot(result,main=paste(exp.str,"的时间序列散点图")) dev.new() lag.plot(result, 9, do.lines=FALSE) dev.new() par(mfrow=c(2,1)) acf(result, 30,main=paste(exp.str,"的自相关图")) pacf(result, 30,main=paste(exp.str,"的偏自相关图")) } print(paste(exp.str,"的扩展相关图。
R语言中时间序列分析浅析

R语⾔中时间序列分析浅析时间序列是将统⼀统计值按照时间发⽣的先后顺序来进⾏排列,时间序列分析的主要⽬的是根据已有数据对未来进⾏预测。
⼀个稳定的时间序列中常常包含两个部分,那么就是:有规律的时间序列+噪声。
所以,在以下的⽅法中,主要的⽬的就是去过滤噪声值,让我们的时间序列更加的有分析意义。
语法时间序列分析中ts()函数的基本语法是 <- ts(data, start, end, frequency)以下是所使⽤的参数的描述data是包含在时间序列中使⽤的值的向量或矩阵。
start以时间序列指定第⼀次观察的开始时间。
end指定时间序列中最后⼀次观测的结束时间。
frequency指定每单位时间的观测数。
除了参数“data”,所有其他参数是可选的。
时间序列的预处理:1. 平稳性检验:拿到⼀个时间序列之后,我们⾸先要对其稳定性进⾏判断,只有⾮⽩噪声的稳定性时间序列才有分析的意义以及预测未来数据的价值。
所谓平稳,是指统计值在⼀个常数上下波动并且波动范围是有界限的。
如果有明显的趋势或者周期性,那么就是不稳定的。
⼀般判断有三种⽅法:画出时间序列的趋势图,看趋势判断画⾃相关图和偏相关图,平稳时间序列的⾃相关图和偏相关图,要么拖尾,要么截尾。
检验序列中是否存在单位根,如果存在单位根,就是⾮平稳时间序列。
在R语⾔中,DF检测是⼀种检测稳定性的⽅法,如果得出的P值⼩于临界值,则认为是序列是稳定的。
2. ⽩噪声检验⽩噪声序列,⼜称为纯随机性序列,序列的各个值之间没有任何的相关关系,序列在进⾏⽆序的随机波动,可以终⽌对该序列的分析,因为从⽩噪声序列中是提取不到任何有价值的信息的。
3. 平稳时间序列的参数特点均值和⽅差为常数,并且具有与时间⽆关的⾃协⽅差。
时间序列建模步骤:拿到被分析的时间序列数据集。
对数据绘图,观测其平稳性。
若为⾮平稳时间序列要先进⾏ d 阶差分运算后化为平稳时间序列,此处的 d 即为ARIMA(p,d,q) 模型中的 d ;若为平稳序列,则⽤ ARMA(p,q) 模型。
R语言在时间序列中的应用要点

t
1 t1
2 , E( t s ) 0, s t
qtq
若 0 0 ,该模型称为中心化 ARMA(p,q) 模型。
2. 非平稳序列分析 事实上在自然界中绝大部分序列都是非平稳的,因而对非平稳序列的分析更
普遍更重要。 对非平稳时间序列的分析法通常分为确定性时序分析和随机时序分析。这里
简要介绍常用确定性时序分析方法。 (1) 断一个序列是否平稳, 我们主要通过时序图以及自相关图进行检验。 因
为用到 ARIMA 模型的拟合和检验,所以在程序的开头会载入 tseries。 首先绘出时序图、自相关图、偏自相关图(如下) :
-7-
0 3 20 1 V0 1 0
0 10 20 30 40 50 Time
-5-
a. xt Tt St It
b. xt Tt ( St I t )
式中, Tt 代表序列的长期趋势波动; St 代表序列的季节性(周期性)变化; I t 代
表随机波动。
3. 非平稳序列的模型 事实上,许多非平稳序列差分后会显示出平稳序列的性质,称之为差分平稳
序列。对差分平稳序列可以用 ARIMA 模型拟合。 具有如下结构的模型称为求和自回归移动平均 (autoregressive integrated moving
xt
0
1 xt 1
p0
E( t ) 0,Var ( t ) Exs t 0, s t
p xt p
t
2, E( t s ) 0, s t
(2) MA 模型 (moving average)
-4-
具有如下结构的模型称为 q 阶移动平均模型,记为 MA(q) :
xt
t
1 t1
2t2
时间序列分析R语言分析

时间序列分析R语言分析R语言是一个功能强大的统计分析软件,提供了丰富的包和函数用于时间序列分析。
本文将介绍R语言的时间序列分析方法,并以一个具体的案例来说明。
首先,我们需要导入与时间序列分析相关的包,其中最常用的包是`stats`和`forecast`。
我们可以使用`library(`函数导入这两个包:```Rlibrary(stats)library(forecast)```接下来,我们需要读取时间序列数据。
在R语言中,时间序列数据可以用`ts(`函数来创建。
`ts(`函数的参数包括数据向量、开始时间和时间间隔。
例如,以下代码将创建一个时间序列数据对象`tsdata`:```R```在创建时间序列对象后,我们可以使用`plot(`函数来可视化时间序列数据。
例如,以下代码将绘制时间序列数据的折线图:```Rplot(tsdata)```接下来,我们可以使用时间序列数据进行分析和建模。
一种常用的方法是拟合ARIMA模型。
ARIMA模型是一种常用的时间序列模型,可以用于预测未来的值。
我们可以使用`auto.arima(`函数自动选择ARIMA模型的参数。
例如,以下代码将拟合时间序列数据的ARIMA模型:```Rarima_model <- auto.arima(tsdata)````auto.arima(`函数将返回一个ARIMA模型对象`arima_model`。
我们可以使用`summary(`函数查看ARIMA模型的摘要信息。
例如,以下代码将输出ARIMA模型的参数估计值和统计检验结果:```Rsummary(arima_model)```对于已经拟合好的ARIMA模型,我们可以使用`forecast(`函数来进行预测。
例如,以下代码将使用拟合好的ARIMA模型对未来10个时间点的值进行预测并返回预测结果:```Rforecast_result <- forecast(arima_model, h = 10)````forecast(`函数将返回一个预测结果对象`forecast_result`。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R语言与时间序列学习笔记(1)继续上一次的参数估计话题。
今天分享的是R语言中时间序列的模型初步估计有关内容。
主要有:时间序列的创建,ARMA模型的建立与模型的参数估计。
一、时间序列的创建时间序列的创建函数为:ts().函数的参数列表如下:ts(data=NA,start=1,end=numeric(),frequency=1,deltat=1,ts.eps=getOption("ts.eps"),class=,names=)参数说明:data:这个必须是一个矩阵,或者向量,再或者数据框frame Frequency:这个是时间观测频率数,也就是每个时间单位的数据数目Start:时间序列开始值,允许第一个个时间单位出现数据缺失举例:ts(matrix(c(NA,NA,NA,1:31,NA),byrow=T,5,7),frequency=7,names=c("Sun","Mon","Tue","Wen","Thu","Fri","Sat"))运行上面的代码就可以得到一个日历:Sun Mon Tue Wen Thu Fri SatNA NA NA12345678910111213141516171819202122232425262728293031NA在R语言中本身也有不少数据集,比如统计包中的sunspots,你可以通过函数data(sunspots)来调用它们。
二、一些时间序列模型这里主要介绍AR,MA,随机游走,余弦曲线趋势,季节趋势等首先介绍一下AR模型:AR模型,即自回归(AutoRegressive,AR)模型,数学表达式为:AR:y(t)=a1y(t-1)+...any(t-n)+e(t)其中,e(t)为均值为0,方差为某值的白噪声信号。
那么产生AR模型的数据,我们就有两种方法:1、调用R中的函数filter(线性滤波器)去产生AR模型;2、根据AR模型的定义自己编写函数先说第一种方法:调用R中的函数filter(线性滤波器)去产生AR模型介绍函数filter的用法如下:filter(x,filter,method=c("convolution","recursive"),sides=2,circular=FALSE,init)对于AR(2)模型x(t)=x(t-1)--0.9x(t-2)+e(t)w<-rnorm(550)#我们假定白噪声的分布是正态的。
x<-filter(w,filter=c(1,-0.9),"recursive")#方法:无论是“卷积”或“递归”(可以缩写)。
如果使用移动平均选择“卷积”:如果“递归”便是选择了自回归。
再说第二种方法:依据定义自己编程产生AR模型,还是以AR(2)模型x (t)=x(t-1)--0.9x(t-2)+e(t)为例,可编写函数如下:w<-rnorm(550)AR<-function(w){x<-wx[2]=x[1]+w[1]for(i in3:550)x[i]=x[i-1]-0.9*x[i-2]+w[i]x}调用AR(W)即可得到。
如果对相同的随机数,我们可以发现两个产生的时间序列是一致的。
当然对于第二种方法产生的序列需要转换为时间序列格式,用as.ts()处理。
类似的,我们给出MA,随机游走的模拟:MA模型:w<-rnorm(500)v<-filter(w,sides=2,rep(1,3)/3)随机游走:w<-rnorm(200)x<-cumsum(w)#累计求和,see example:cumsum(1:!0)wd<-w+0.2xd<-cumsum(wd)可以做出相应的图形:再说一下季节性模型:最简单的季节模型就是一个分段的周期函数。
比如说某地区一年的气温就是一个季节性模型。
利用TSA包里给出的数据tempdub我们可以发现他就是这样的模型给出验证:library(TSA)data(tempdub)month<-season(tempdub)model1<-lm(tempdub~month)summary(model1)根据R输出的结果:Call:lm(formula=tempdub~month)Residuals:Min1Q Median3Q Max-8.2750-2.24790.1125 1.88969.8250Coefficients:Estimate Std.Error t value Pr(>|t|)(Intercept)16.6080.98716.828<2e-16***monthFebruary 4.042 1.396 2.8960.00443**monthMarch15.867 1.39611.368<2e-16***monthApril29.917 1.39621.434<2e-16***monthMay41.483 1.39629.721<2e-16*** monthJune50.892 1.39636.461<2e-16*** monthJuly55.108 1.39639.482<2e-16*** monthAugust52.725 1.39637.775<2e-16*** monthSeptember44.417 1.39631.822<2e-16*** monthOctober34.367 1.39624.622<2e-16*** monthNovember20.042 1.39614.359<2e-16*** monthDecember7.033 1.396 5.0391.51e-06***---Signif.codes:0‘***’0.001‘**’0.01‘*’0.05‘.’0.1‘’1Residual standard error:3.419on132degrees of freedomMultiple R-squared:0.9712,Adjusted R-squared:0.9688F-statistic:405.1on11and132DF,p-value:<2.2e-16这里2月份系数表明了一月份平均气温与二月份平均气温的差异,以此类推。
在介绍一下一个季节模型:余弦趋势μ1=βcos(2pi*f*t+φ)还是考虑上面气温的例子:验证:har<-harmonic(tempdub,1)model2<-lm(tempdub~har)summary(model2)看看结果:Call:lm(formula=tempdub~har)Residuals:Min1Q Median3Q Max-11.1580-2.2756-0.1457 2.375411.2671Coefficients:Estimate Std.Error t value Pr(>|t|)(Intercept)46.26600.3088149.816<2e-16***harcos(2*pi*t)-26.70790.4367-61.154<2e-16***harsin(2*pi*t)-2.16970.4367-4.9681.93e-06***---Signif.codes:0‘***’0.001‘**’0.01‘*’0.05‘.’0.1‘’1Residual standard error:3.706on141degrees of freedom Multiple R-squared:0.9639,Adjusted R-squared:0.9634F-statistic:1882on2and141DF,p-value:<2.2e-16我们可以作图来看拟合效果:顺便指出季节模型也可以模拟:比如μ1=βcos(2pi*f*t+φ)模型可以模拟如下:t<-1:500w<-rnorm(500)c<-2*cos(2*pi*t/50+0.6*pi+w)三、自相关与偏自相关给出自相关的定义:在信息分析中,通常将自相关函数称之为自协方差方程。
用来描述信息在不同时间的,信息函数值的相关性。
详情可参见wiki:/wiki/%E8%87%AA%E7%9B%B8%E5%85%B3我们可以根据定义给出自相关系数(ACF)的算法:例如数据:>x<-1:10>u<-mean(x)>v<-var(x)>sum((x[1:9]-u)*(x[2:10]-u))/(9*v)#延迟1[1]0.7>sum((x[1:8]-u)*(x[3:10]-u))/(9*v)#延迟2[1]0.4121212>sum((x[1:7]-u)*(x[4:10]-u))/(9*v)#延迟3[1]0.1484848在R中也提供了直接计算acf的函数acf(),利用该函数也计算1至3阶的acf,结果如下:>a<-acf(x,3)>aAutocorrelations of series‘x’,by lag01231.0000.7000.4120.148可以看出,是一样的。
利用acf()可以处理很多阶的acf,以太阳黑子数的数据集做例子:>data(sunspots)>acf(sunspots)#给出了相应的图形>a<-acf(sunspots,6)#为下面做估计做铺垫,列出前6阶的acf>aAutocorrelations of series‘sunspots’,by lag0.00000.08330.16670.25000.33330.41670.50001.0000.9220.8900.8750.8640.8500.836偏自相关:对于一个平稳AR(p)模型,求出滞后k自相关系数p(k)时,实际上得到并不是x(t)与x(t-k)之间单纯的相关关系。
因为x(t)同时还会受到中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的影响,而这k-1个随机变量又都和x(t-k)具有相关关系,所以自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响。
为了能单纯测度x(t-k)对x(t)的影响,引进偏自相关系数的概念。
对于平稳时间序列{x(t)},用数学语言描述就是:p[(x(t),x(t-k)]|(x(t-1),……,x(t-k+1)={E[(x(t)-Ex(t)][x(t-k)-Ex(t-k)]}/E{[x(t-k)-Ex(t-k)]^2}这就是滞后k偏自相关系数的定义。
