NOIP2010提高组解题报告1
历年noip普及组提高组试题分析

历年NOIP(普及组)难度分析by Climber.pI
数学: 5 图论:4
搜索: 4 构造:3
贪心:2 【动态规划】平均难度系数:0.55
此项为历届NOIP考察次数最多的知识点。
主要有 1.区间模型 2.子序列模型 3.资源分配模型以及一些简单的多维状态设计技巧。
动态规划可以与图,树,高精度等知识点配合出题。
【模拟】平均难度系数:0.76 平均每届NOIP都会出现1个模拟题。
这种题一般算法很简单,需要选手细心理解题目意思,注意细节。
考察选手的代码实现能力。
【数学】平均难度系数:0.46
需要掌握质数及其性质,基础的实属操作,加法原理和乘法原理。
此类题需要选手对数学规律的灵感。
【图论】平均难度系数:0.50
历届考察点基本上都是1.最短路问题和2.特殊图的性质。
特殊图包括树,拓扑图,二分图等。
历届NOIP在图论上的考察并不是很多。
【搜索】平均难度系数:0.38
历届搜索题一般都比较难,搜索算法本身简单,于是题目会提高选手对其他方面的要求。
主要有搜索优化和模拟。
写搜索题时应该以尽量多得分为目标。
【构造】平均难度系数:0.27
构造类题目一般没有明确的算法,需要选手仔细分析题目的实质,并得出解法。
这个解法通常不是唯一的。
有时一个好的贪心可以得相当多的分。
有时搜索剪枝可以很大的提高效率。
同样以多得分为目标。
【
【贪心】平均难度系数:0.75
此类题需要选手对算法的直觉,贪
心正确性一旦被证明,通常题目就
简单了。
Noip 2010普及组解题报告

解析1、数字统计【思路分析】这道题属于简单题,用一个FOR把数都检查一遍,里面再用while剥皮看看有多少个2。
【参考程序】VarI,n,l,r,s:integer;BeginAssign(input,’two.in’);Assign(output,’two.out’);Readln(l,r);S:=0;For i:=1 to r doBeginN:=I;While n>0 doBeginIf n mod 10=2 then s:=s+1;N:=n div 10;End;End;Writeln(s);Close(input);close(output;)End.2、接水问题【思路分析】方法一:用一个数组,存放每个水龙头当前还需要多少时间装完这桶水;然后一个一个人去轮,每次找最快装完的水龙头,接着把当前轮到的那个人所需要的时间加到格子里;最后轮完以后,还要把数组里的最大值输出。
【参考程序】Vara:=array[1..10000]of integer;b:=array[1..100]of longint;m,n,i,k,t,max,min:longint;beginassign(input,'water.in');assign(output,'water.out');reset(input);rewrite(output);readln(n,m);for i:=1 to n do read(a[i]);fillchar(b,sizeof(b),0);max:=0;k:=1;while(k<=n) dobeginmin:=maxlongint;t:=0;for i:=1 to m doif b[i]<min thenmin:=b[i];t:=i;end;b[t]:=b[t]+a[k];k:=k+1;if b[t]>max then max=b[t];end;writeln(max);close(input);close(output);end.方法二:用一个数组,存放每个水龙头当前还需要多少时间装完这桶水,并按照时间长短从大到小安排好;然后一个一个去轮,显然最快装完的水龙头总是最后一个,这样只要把当前轮到的那个人所需的时间加到最后那个元素里,再把数组排序好(很明显,这里要用插入排序效率最高);最后只要输出数组第一个元素就可以了。
复赛noip2010提高组题解[新版]
![复赛noip2010提高组题解[新版]](https://img.taocdn.com/s3/m/7b1ee1c3b8f3f90f76c66137ee06eff9aef84965.png)
1.translate(20分)简单模拟。
开一个1000的队列,时刻保持队列长度不大于M,每次接受翻译请求时,先在队列中查找,查找失败则将单词加入队列。
查找使用Hash则为O(N),直接扫描O(MN),都在可接受范围内。
考试时只打了20分,原因至今不明,告诫大家对于水题不要多想,就像这道题最好不开hash,因为一个系统的可靠度是该系统所有子系统可靠度之积,程序越复杂越可能出错。
4.tortoise(50分)基础动规。
可以从题目背景中抽象出这样的问题:有一四维立方体(这里的立方体棱长不必相等,每一维对应一种卡片,每维的棱长对应该种卡片个数),每走一格(即使用一张卡片)的收益是当前位置坐标的函数。
求从(0,0,0,0)走到(a1,a2,a3,a4)最大收益。
故有方程f[x,y,z,t]=max{f[x-1,y,z,t], f[x,y-1,z,t], f[x,y,z-1,t], f[x,y,z,t-1]} + w[1 + x + y*2 + z*3 + t*4]目标状态: f[a1,a2,a3,a4]O(b^4)的代价,数据保证b<=40,完全满足要求5.prison(70分)问题可以重新描述为:寻找最小的冲突值c,使得存在一种方案,将原图分为两部分,并去掉这两部分之间的所有边后,余下的边权都不大于c。
对于这个问题我们可以二分查找c,并判定其可行性。
判定可行性的方法至今没想好。
考试的时候我是用并查集,将所有与u相连并与u之间边权大于c的点(设为点集Zu)必然不与u在同一集合中,枚举所有的u,每次将Zu合并成为一个集合,若存在某点u和Zu某个点处于同一个集合中,则c不可行,反之则可行。
但这种方法貌似存在bug,能拿70分。
如果把并查集合并查找的时间代价看作常数,则这种做法的时间代价为O(elogK),e是边数,K为最大的冲突值。
6.flow(100分)先用floodfill预处理出上方的每个格子能覆盖到下方的格子,构造一个布尔矩阵,行下标表示最上方的某个点,列下标表示最下方的某个点,矩阵对应点的值表示相应两个点的覆盖关系。
NOIP2010普及组解题报告

NOIP2010普及组复赛解题报告(pascal)---------By 锦云第一题:two.pas本题没有什么技术含量,主要有三种方法:1.用枚举(找范围再分别处理,很麻烦)2.用分解(一步步分解,较简便)3.用先转换成字符串再做(很简便)参考程序:(在此只提供第二种解法的分解部分和第三种解法)第二种:Function fjtwo(a:integer):integer;Var cnt,tmp:integer;BeginCnt:=0;While a>0 doBeginTmp:=a mod 10;If tmp=2 then inc(cnt);Tmp:=tmp div 10;End;Fjtwo:=cnt;End;第三种:Var s:string;L,r,i,j,cnt:integer;BeginAssign(input,’two.in’);reset(input);Assign(output,’two.out’);rewrite(output);Readln(l,r);Cnt:=0;For i:=l to r doBeginString(I,s);For j:=1 to length(s) doIf s[i]=’2’ then inc(cnt);End;Writeln(cnt);Close(input);Close(output);End.第二题:water.pas本题主要是考验考生们的细心程度,从而找到最佳方案。
想了一想,本题采用模拟法,于是有了加或者减的方法。
1.减法(纯粹模拟)2.加法(更优模拟)注:减法时最好不要时间一点一点的模拟,找最小得数减。
参考程序:(本题提供较简单的写法加法)Var a:array[1..10000] of integer;N,mI,j,k:longint;BeginAssign(input,’water.in’);reset(input);Assign(output,’water.out’);rewrite(output);Readln(n,m);For i:=1 to n doRead(a[i]);For i:=m+1 to n doBeginK:=1;For j:=1 to m doIf a[j]<a[k] then k:=j;Inc(a[k],a[i]);End;K:=1;For i:=1 to m doIf a[i]>a[k] then k:=I;Writeln(a[k]);Close(input);Close(output);End.第三题:missile.pas本题实在是很难解决,n最大可以达到100000,而最优解的算法可以用搜索,但是n太大时,时间肯定不行,只好退而求其次,用贪心算法(无法得最优解但有70分,很不错了)参考程序:(贪心)Var l,n,x1,y1,x2,y2,tmpx,tmpy,max1,max2,jg1,jg2:longint;beginassign(input,'missile.in');reset(input);assign(output,'missile.out');rewrite(output);readln(x1,y1,x2,y2);readln(n);max1:=0;max2:=0;for i:=1 to n dobeginreadln(tmpx,tmpy);jg1:=sqr(abs(tmpx-x1))+sqr(abs(tmpy-y1));jg2:=sqr(abs(tmpx-x2))+sqr(abs(tmpy-y2));if (jg1>max1)and(jg2>max2) then if jg1<jg2 then max1:=jg1else max2:=jg2;end;writeln(max1+max2);close(input);close(output);end.第三题:解答本题,必须看清题意,知道以下几点:一、只需要选两次,由于比胜负靠的是双方武将中默契值最大的一对,所以除了默契值最大的一对,其他的武将都是没用的。
noip2010复赛试题提高组
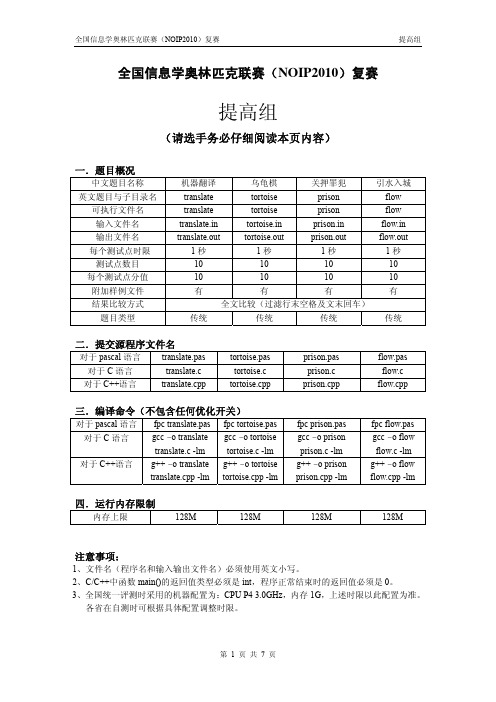
全国信息学奥林匹克联赛(NOIP2010)复赛提高组(请选手务必仔细阅读本页内容)一.题目概况中文题目名称机器翻译乌龟棋关押罪犯引水入城英文题目与子目录名 translate tortoise prison flow 可执行文件名 translate tortoise prison flow 输入文件名 translate.intortoise.in prison.in flow.in 输出文件名 translate.outtortoise.outprison.out flow.out 每个测试点时限1秒1秒1秒1秒测试点数目 10 10 10 10 每个测试点分值 10 10 10 10 附加样例文件有有有有结果比较方式全文比较(过滤行末空格及文末回车)题目类型传统传统传统传统二.提交源程序文件名对于pascal语言 translate.pas tortoise.pas prison.pas flow.pas 对于C语言 translate.c tortoise.c prison.c flow.c 对于C++语言 translate.cpp tortoise.cpp prison.cpp flow.cpp 三.编译命令(不包含任何优化开关)对于pascal语言fpc translate.pas fpc tortoise.pas fpc prison.pas fpc flow.pas对于C语言gcc -o translatetranslate.c -lm gcc -o tortoisetortoise.c -lmgcc -o prisonprison.c -lmgcc -o flowflow.c -lm对于C++语言g++ -o translatetranslate.cpp -lm g++ -o tortoisetortoise.cpp -lmg++ -o prisonprison.cpp -lmg++ -o flowflow.cpp -lm四.运行内存限制内存上限128M 128M 128M 128M注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
NOIP2010题解

总分
400 380 340 330 320 310 300 300 290 280 280 270 270 260 260 260 260 250 250 250 240 240 240
姓名
徐明昭 张硕基 徐子尧 崔灏 田博 李光谱 吕诚 魏鑫鼎 马龙 李昭 吴文彬 李金培 李栋 李昂 杨帅 李怡君 杨东 王子晗 谢志聪 周梦溪 苏畅 许可 常泽昊
240 240 240 240 240 240 230 230 230 230 230 230 220 210 210 210 210 210 200 200
CCF NOIP2010提高组(C语言)参考答案

②go(LEFT_TO_RIGHT)
③pos[i] == LEFT(或LEFT == pos[i])
④time[i] + go(RIGHT_TO_LEFT)(或go(RIGHT_TO_LEFT) + time[i])
⑤pos[i] = LEFT
1.yyxy xx yyxy xyx xx xyx
2.12
3.18
四、阅读程序写结果(共4题,每题7分,共计28分)
1.16
2.1 2 3 5 6 7 9 10 14
3.4
4.1 6 9 5 4 8 3 2 7
五、完善程序(第1空2分,其余10空,每空2.5分,共计27分)
(说明:以下各程序填空可能还有一些等价的写法,各省可请本省专家审定和上机验证,不一定上报科学委员会审查)
⑥i - m
CCF NOIP2010提高组(C语言)参考答案与评分标准
一、单项选择题(共10题,每题1.5分,共计15分)
1
2
3
4
5
6
7
8
9
10
C
A
A
Dቤተ መጻሕፍቲ ባይዱ
B
D
C
B
C
B
二、不定项选择题(共10题,每题1.5分,共计15分,多选或少选均不得分)
1
2
3
4
5
6
7
8
9
10
ACD
AD
ABD
AC
B
B
D
D
BCD
ABC
三、问题求解(共3题,每题5分,共计15分)
本小题中,LEFT可用1代替,LEFT_TO_RIGHT可用1代替,RIGHT_TO_LEFT可用0代替。
深入Noip2010初赛试题和全解

作者:钟野梓序今年Noip2010初赛刚结束,网上便铺天盖地地响起了“今年初赛好容易”“分数线一定很高,怎么办……”之类的声音。
确实,自2008年起,Noip初赛难度确有逐年下降的趋势,然而这并不是出题水平降低的缘故,相反,我认为这是中国计算机协会(下称CCF)对于N oip考核目的的审视和改变所导致的必然结果。
因此,我试图通过深入解析本届Noip初赛试囗题,来探寻这种变化下面深层的规律,从而令信息学竞赛选手能更好地备战往后数届的Noip初赛,让初赛不再成为一个问题。
由于条件所限,本文仅以Pascal语言的提高组试囗题作为对象进行分析,相对于普及组而言提高组试囗题一向具有较高的难度和较好的区分度,作为研究对象是个很好的选择;至于说语言的选择,仅是因为笔者个人选择原因。
一、概况本届题目在设置方面与往年相似,由选择题(普及组仅有单项选择题,提高组则有单项选择题与不定项选择题)、问题求解、阅读程序写结果及完善程序四大部分组成;但值得注意的是,今年提高组试囗题的分值设计与往年出现了较大的不同,除了选择题仍然是30分(15分单项+15分不定项),其余部分分值均发生了变化,其中问题求解由10分上升到15分,阅读程序由32分下降到28分,完善程序由28分下降到27分。
由于是第一年实行这种分值,目前暂时无法定言背后的含义,然而或许CCF在初赛更加重视选手的数学素质,而弱化了对于阅读程序能力的考察。
众所周知,阅读程序的能力并不能非常真实地反映选手的程序能力,并且纵观近几年的阅读程序题已没有了什么新意,这也可看做是一个“求新求变”的信号。
至于试囗题整体难度方面较上年有了明显下降,其中问题求解第一题可以看做是考察选手的语文水平,而阅读程序更是没有了以往的“死算”题(即给定若干常数,在程序中设置一系列运算过程,让选手进行阅读计算类型的题目),完善程序给定的源代码风格良好,第二题竟然还加上了注释,这不能不说就是一种降低难度的举动。
NOIP初赛练习情况总结复习资料(提高组)精华版

分区联赛初赛复习材料初赛考的知识点就是计算机基本常识、基本操作和程序设计基础知识。
其中选择题考查的是知识,而问题解决类型的题目更加重视能力的考查。
一般说来,选择题只要多用心积累就可以了。
问题解决题目的模式比较固定,大家应当做做以前的题目。
写运行结果和程序填空也需要多做题目,并且培养良好的程序阅读和分析能力,就像语文的阅读理解一样。
近几年来,初赛的考查范围有了很大的变化,越来越紧跟潮流了。
这就需要大家有比较广泛的知识,包括计算机硬件、软件、网络、简单的数据结构(例如栈、队列、树和图等)和简单的算法(例如排序、查找和搜索等),程序设计语言以及一些基本的数学知识和技巧(例如排列组合)。
但最主要的,还是取决于你对程序设计语言的熟悉程度,再加上认真仔细的心态。
选择题一、硬件计算机发展可划分:1946年2月,在美国宾夕法尼亚大学诞生了世界上第一台电子计算机ENIAC(Electronic Numerical Integrator And Computer),这台计算机占地170平方米,重30吨,用了18000多个电子管,每秒能进行5000次加法运算。
冯·诺依曼理论1944年,美籍匈牙利数学家冯·诺依曼提出计算机基本结构和工作方式的设想,为计算机的诞生和发展提供了理论基础。
时至今日,尽管计算机软硬件技术飞速发展,但计算机本身的体系结构并没有明显的突破,当今的计算机仍属于冯·诺依曼架构。
其理论要点如下:1、计算机硬件设备由存储器、运算器、控制器、输入设备和输出设备5部分组成。
2、存储程序思想——把计算过程描述为由许多命令按一定顺序组成的程序,然后把程序和数据一起输入计算机,计算机对已存入的程序和数据处理后,输出结果。
微型机的主要技术指标1、字长:知己算计能够直接处理的二进制数据的位数。
单位为位(BIT)2、主频:指计算机主时钟在一秒钟内发出的脉冲数,在很大程度上决定了计算机的运算速度。
全国信息学奥林匹克联赛(NOIP2010)复赛_普及组_解题报告(pascal)

全国信息学奥林匹克联赛(NOIP2010)复赛_普及组_解题报告(pascal)全国信息学奥林匹克联赛(NOIP2010)复赛普及组解题报告1.数字统计(two.pas/c/cpp)【问题描述】请统计某个给定范围[L, R]的所有整数中,数字2 出现的次数。
比如给定范围[2, 22],数字2 在数2 中出现了1 次,在数12 中出现1 次,在数20 中出现1 次,在数21 中出现1 次,在数22 中出现2 次,所以数字2 在该范围内一共出现了6次。
【算法思路】枚举法,依次将L至R转化为字符串,查找当中有多少个”2”.【程序代码】program two;varl,r:1..10000;i,j,h,c:longint;s:string;beginassign(input,'two.in');assign(output,'two.out');reset(input);rewrite(output);readln(l,r);c:=0;for i:=l to r dobeginstr(i,s);h:=length(s);for j:=1 to h doif s[j]='2'then c:=c+1;end;writeln(c);close(input);close(output);end.2.接水问题(water.pas/c/cpp)【问题描述】学校里有一个水房,水房里一共装有m 个龙头可供同学们打开水,每个龙头每秒钟的供水量相等,均为1。
现在有n 名同学准备接水,他们的初始接水顺序已经确定。
将这些同学按接水顺序从1到n 编号,i号同学的接水量为w i。
接水开始时,1 到m 号同学各占一个水龙头,并同时打开水龙头接水。
当其中某名同学j 完成其接水量要求w j 后,下一名排队等候接水的同学k马上接替j 同学的位置开始接水。
这个换人的过程是瞬间完成的,且没有任何水的浪费。
NOIP2010提高组初赛试题及详细解析

第十六届全国青少年信息学奥林匹克联赛初赛试题(提高组 C++语言两小时完成)●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一、单项选择题(共10题,每题1.5分,共计15分。
每题有且仅有一个正确选项。
)1.与十六进制数 A1.2等值的十进制数是()A.101.2 B.111.4 C.161.125 D.177.252.一个字节(byte)由()个二进制组成。
A.8 B.16 C.32 D.以上都有可能3.以下逻辑表达式的值恒为真的是()。
A.P∨(┓P∧Q)∨(┓P∧┓Q) B.Q∨(┓P∧Q)∨(P∧┓Q)C.P∨Q∨(P∧┓Q)∨(┓P∧Q) D.P∨┓Q∨(P∧┓Q)∨(┓P∧┓Q)4.Linux下可执行文件的默认扩展名是( )。
A. exeB. comC. dllD. 以上都不是5.如果在某个进制下等式7*7=41成立,那么在该进制下等式12*12=()也成立。
A. 100B. 144C. 164D. 1966.提出“存储程序”的计算机工作原理的是()。
A. 克劳德•香农B. 戈登•摩尔C. 查尔斯•巴比奇D. 冯•诺依曼7.前缀表达式“+ 3 * 2 + 5 12 ”的值是()。
A. 23B. 25C. 37D. 6 58.主存储器的存取速度比中央处理器(CPU)的工作速度慢的多,从而使得后者的效率受到影响。
而根据局部性原理,CPU所访问的存储单元通常都趋于一个较小的连续区域中。
于是,为了提高系统整体的执行效率,在CPU中引入了( )。
A.寄存器 B.高速缓存 C.闪存 D.外存9.完全二叉树的顺序存储方案,是指将完全二叉树的结点从上到下、从左到右依次存放到一个顺序结构的数组中。
假定根结点存放在数组的1号位置上,则第k号结点的父结点如果存在的话,应当存放在数组中的()号位置。
A.2k B.2k+1 C.k/2下取整 D.(k+1)/210.以下竞赛活动中历史最悠久的是()。
NOIP2010提高组解题报告

NOIP2010解题报告(提高组)Translate开一个队列进行模拟就行了。
PS:这题数据比较厚道,按照题目的描述来说,单词的编号是非负整数,也就是说可以是0。
但是数据中并没有0,否则就要有很多人要降10分了。
Tortoise动态规划。
用F[i1,i2,i3,i4]表示数字1的卡片取了i1张,数字2的卡片取了i2张,数字3的卡片取了i3张,数字4的卡片取了i4张,可以取得最大的分数。
写起来很好写,四个for,再加上四个if。
F[i1,i2,i3,i4]=max(F[i1-1,i2,i3,i4],F[i1,i2-1,i3,i4],F[i1,i2, i3-1,i4],F[i1,i2,i3,i4-1])+score[1+i1+i2*2+i3*3+i4*4]PS:这题用120*40*40*40,350*40*40*40的算法都是可以的。
Prison二分+二分图判定\并查集解法1:先二分答案,然后进行二分图的判定。
判定方法如下:首先取一个没有走过的结点放在了左图,然后把和这个点有边的点放在右图,然后再把和这些右图有边的点放在左图,一直下去,知道把所有点都放好,或者出现矛盾为止。
解法2:把边权从大到小排一次序,依次插入。
用并查集维护这些边之间有没有矛盾。
详情看并查集经典例题:PKU1182食物链。
Flow[(floodfill\动态规划\各种乱搞算法)+(贪心+动态规划\各种乱搞算法)]\最短路显然第一问一次O(NM)的floodfill就可以求出是否可以到达全部最后一层的格子。
现在假设最后一行的所有格子都可以到达。
定理1:从第一行的格子,可以到达的最后一行的格子必然是连续的一段。
证明1:假设格子A可以到达的最后一行中间有部分格子不可到达。
由题设可知,必有另一个格子B可以到达这些A不可到达的格子。
但是,显然A到达下面格子的路径必然与B到达这些A不可到达的格子的路径有重合部分,所以,A也能到达下面的A到达不了的格子。
NOIP2010复赛提高组题解加程序

。0001≤0�001≤0 有据数的%001 于对 。5≤N�1=M 有据数的%01 于对 】围范据数【
6
组高提
462 8 87 11 87 11 87 11 428 8 01 2 tuo.etalsnart ni.etalsnart 】2 例样出输入输【 页 7 共 页 3 第 赛复�0102PION�赛联克匹林奥学息信国全 页换
。典词次 5 了查计共 。2 词单代替存内入调并 1 词单找查�1 4 5 �7 。4 词单到找中存内在�4 5 2 �6 。1 词单代替存内入调并 4 词单找查�4 5 2 �5 。存内入调并 5 词单找查�5 2 1 �4 。1 词单到找中存内在�2 1 �3 。存内入调并 2 词单找查�2 1 �2 。存内入调并 1 词单找查�1 �1 。空为态状始初存内�空 �况状存内的后译翻次本为前号冒�译翻的词单个一示表行每�下如程过典字查个整 】明说 1 例样出输入输【 5 1 4 4 5 1 2 1 7 3
esiotrot o- ++g ml- ppc.etalsnart etalsnart o- ++g 言语++C 于对 ml- c.wolf wolf o- ccg ml- c.nosirp nosirp o- ccg ml- c.esiotrot esiotrot o- ccg ml- c.etalsnart etalsnart o- ccg 言语 C 于对 sap.wolf cpf sap.nosirp cpfsap.esiotrot cpfsap.etalsnart cpf 言语 lacsap 于对 �关开化优何任含包不�令命译编�三 ppc.wolf ppc.nosirp ppc.esiotrot ppc.etalsnart 言语++C 于对 c.wolf c.nosirp c.esiotrot c.etalsnart 言语 C 于对 sap.wolf sap.nosirp sap.esiotrot sap.etalsnart 言语 lacsap 于对 名件文序程源交提�二 统传 统传 统传 统传 型类目题 �车回末文及格空末行滤过�较比文全 式方较比果结 有 有 有 有 件文例样加附 01 01 01 01 值分点试测个每 01 01 01 01 目数点试测 秒 1 秒 1 秒 1 秒 1 限时点试测个每 tuo.wolf tuo.nosirp tuo.esiotrot tuo.etalsnart 名件文出输 ni.wolf ni.nosirp ni.esiotrot ni.etalsnart 名件文入输 wolf nosirp esiotrot etalsnart 名件文行执可 wolf nosirp esiotrot etalsnart 名录目子与目题文英 城入水引 犯罪押关 棋龟乌 译翻器机 称名目题文中 况概目题�一 �容内页本读阅细仔必务手选请� 组高提
NOIP 2010普及组解题报告

for (i = n ; i >= 1 ; i--)
{
if (d[i].j2r > m2) m2 = d[i].j2r;
tr = d[i - 1].j1r + m2;
if ( r > tr ) r = tr;
NOIP 2010普及组解题报告
关于2010年普及组考题:
没有想到,这次的题目和2008、2009年的题目完全风格两样,我不知道是不是出题老师发生了变化。但是,总体感觉,题目趋于容易,甚至没有涉及DP、搜索中的初级方法。但是,题目很多知识点又隐含颇多。不容易拿到完美的分数。感谢出题老师,给我们带来的这届优秀题目。
while (l < r && d[l].j1r <= t.j1r) l++;
d[r] = d[l];
}
d[r] = t;
qsort(s, r - 1);
qsort(r + 1, e);
}
然后就是逐渐退出和更新半径的过程了:
r = d[n].j1r;
{
t1 = t2 = 0;
for (j = 1 ; j <= n ; j++)
{
if (s[i][j] > t1) t1 = s[i][j];
if (t1 > t2) swap(t1, t2);
}
if (t < t1) t = t1;
}
最后r即为最小消耗。
四、三国游戏
从思想实现来说,还是一道枚举加贪心的题目。因为,“人”在和计算机斗争的过程中,双方都无法取得最大的默契配合值。所以,“人”只能够去考虑次大最优值,但是,为了能够骗过计算机,我们选择的,只能够是跟我们选择的第一位武将配合值次大的那位武将(如果不是一个的话也会被计算机破坏掉)。所以,就要求我们必须,找到,每行中次大值最大的那个值(挺扰人的)。当然,这个提法是建立在我们有了题目中展示的那个矩阵之后。你要注意,题目给你的值是这个矩阵的右半边,你需要把左半边的值自己不上,才能够按照行去枚举(当然,做完后,如果你想按照列,也没有关系,因为全都是对称的,对吧)。
信息奥赛初赛2010试卷

NOIP2010提高组初赛(答案+选择题题目+个人分析)一、单项选择题1.与16进制数A1.2等值的10进制数是()A.101.2B.111.4C.161.125D.177.25C A1.2=10*16^1+1*16^0+1*16^(-1) 公式A=10B=11C=12D=13E=14F=15A=10*16^1=160 1=1*16^0=1 0.2=1*16^(-1)=1/8=0.125Y*X^Z+y*x^z+y*x^z+.......... Y题中式子每一位数X进制数Z第几位数例如上式A是第2位数所以2次方必考的进制运算没什么可说的=。
=2.一个字节(byte)由()个二进制组成。
A.8B.16C.32D.以上都有可能A字节8个字16个双字32个常识问题:数据存储是以“字节”(Byte)为单位,数据传输是以“位”(bit)为单位,一个位就代表一个0或1(即二进制),每8个位(bit)组成一个字节(Byte)。
8bit=1Byte3.以下逻辑表达式的值恒为真的是()。
A.P∨(┓P∧Q)∨(┓P∧┓Q)B.Q∨(┓P∧Q)∨(P∧┓Q)C.P∨Q∨(P∧┓Q)∨(┓P∧Q)D.P∨┓Q∨(P∧┓Q)∨(┓P∧┓Q)A不太懂表示方法:"∨"表示"或","∧"表示"与"."┐"表示"非"."= =" 表示"等价".1和0表示"真"和"假"(还有一种表示,"+"表示"或", "·"表示"与")4.Linux下可执行文件的默认扩展名是( )。
A. exe windows执行程序B. Com windows可执行文件C. Dll动态链接库D. 以上都不是DLinux和Windows不同,Linux一般可执行文件都没有扩展名;Linux不根据拓展名判断文件类型而是根据文件内容判断;因此Linux下扩展名的作用只是帮助以识别文件的,对Linux本身并没有什么用=。
NOIP2010提高组初赛试题及详细解析

第十六届全国青少年信息学奥林匹克联赛初赛试题(提高组 C++语言两小时完成)●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一、单项选择题(共10题,每题1.5分,共计15分。
每题有且仅有一个正确选项。
)1.与十六进制数 A1.2等值的十进制数是()A.101.2 B.111.4 C.161.125 D.177.252.一个字节(byte)由()个二进制组成。
A.8 B.16 C.32 D.以上都有可能3.以下逻辑表达式的值恒为真的是()。
A.P∨(┓P∧Q)∨(┓P∧┓Q) B.Q∨(┓P∧Q)∨(P∧┓Q)C.P∨Q∨(P∧┓Q)∨(┓P∧Q) D.P∨┓Q∨(P∧┓Q)∨(┓P∧┓Q)4.Linux下可执行文件的默认扩展名是( )。
A. exeB. comC. dllD. 以上都不是5.如果在某个进制下等式7*7=41成立,那么在该进制下等式12*12=()也成立。
A. 100B. 144C. 164D. 1966.提出“存储程序”的计算机工作原理的是()。
A. 克劳德•香农B. 戈登•摩尔C. 查尔斯•巴比奇D. 冯•诺依曼7.前缀表达式“+ 3 * 2 + 5 12 ”的值是()。
A. 23B. 25C. 37D. 6 58.主存储器的存取速度比中央处理器(CPU)的工作速度慢的多,从而使得后者的效率受到影响。
而根据局部性原理,CPU所访问的存储单元通常都趋于一个较小的连续区域中。
于是,为了提高系统整体的执行效率,在CPU中引入了( )。
A.寄存器 B.高速缓存 C.闪存 D.外存9.完全二叉树的顺序存储方案,是指将完全二叉树的结点从上到下、从左到右依次存放到一个顺序结构的数组中。
假定根结点存放在数组的1号位置上,则第k号结点的父结点如果存在的话,应当存放在数组中的()号位置。
A.2k B.2k+1 C.k/2下取整 D.(k+1)/210.以下竞赛活动中历史最悠久的是()。
第十六届全国青少年信息学奥林匹克联赛复赛试题

第十六届全国青少年信息学奥林匹克联赛复赛试题(NOIP2010提高组)NOIP2010提高组复赛第一题机器翻译(Trasnlate)小晨的电脑上安装了一个机器翻译软件,他经常用这个软件来翻译英语文章。
这个翻译软件的原理很简单,它只是从头到尾,依次将每个英文单词用对应的中文含义来替换。
对于每个英文单词,软件会先在内存中查找这个单词的中文含义,如果内存中有软件就会用它进行翻译;如果内存中没有,软件就会在外存中的词典内查找,查出单词的中文含义然后翻译,并将这个单词和译义放入内存,以备后续的查找和翻译。
假设内存中有 M 个单元,每单元能存放一个单词和译义。
每当软件将一个新单词存入内存前,如果当前内存中已存入的单词数不超过 M-1,软件会将新单词存入一个未使用的内存单元;若内存中已存入 M 个单词,软件会清空最早进入内存的那个单词,腾出单元来,存放新单词。
假设一篇英语文章的长度为 N个单词。
给定这篇待译文章,翻译软件需要去外存查找多少次词典?假设在翻译开始前,内存中没有任何单词。
【输入】输入文件名为 translate.in,输入文件共 2 行。
每行中两个数之间用一个空格隔开。
第一行为两个正整数 M和 N,代表内存容量和文章的长度。
第二行为 N 个非负整数,按照文章的顺序,每个数(大小不超过 1000)代表一个英文单词。
文章中两个单词是同一个单词,当且仅当它们对应的非负整数相同。
【输出】输出文件 translate.out 共1行,包含一个整数,为软件需要查词典的次数。
【数据范围】对于 10%的数据有 M=1,N≤5。
00%的数据有 0<M≤100,0<N≤1000。
解题报告代码:program translate;vara:array[1..100000] of longint;b:array[1..100000] of boolean;i,n,m,h,x,sum:longint;beginreadln(m,n);for i:=1 to n dobeginread(x);if b[x] then continue;inc(h);a[h]:=x;b[x]:=true;inc(sum);if h>m then b[a[h-m]]:=false;end;//forwriteln(sum);end.//mainNOIP2010提高组复赛第二题乌龟棋(Tortoise)小明过生日的时候,爸爸送给他一副乌龟棋当作礼物。
noip2010提高组解题报告

NOIP2010解题报告(提高)作者:张宇昊所有见解仅供参考考试时。
发挥1/3已经不错了。
真理。
!考试结束。
觉得题都可做。
No1. 1.机器翻译(translate.pas/c/cpp)【问题描述】小晨的电脑上安装了一个机器翻译软件,他经常用这个软件来翻译英语文章。
这个翻译软件的原理很简单,它只是从头到尾,依次将每个英文单词用对应的中文含义来替换。
对于每个英文单词,软件会先在内存中查找这个单词的中文含义,如果内存中有,软件就会用它进行翻译;如果内存中没有,软件就会在外存中的词典内查找,查出单词的中文含义然后翻译,并将这个单词和译义放入内存,以备后续的查找和翻译。
假设内存中有M 个单元,每单元能存放一个单词和译义。
每当软件将一个新单词存入内存前,如果当前内存中已存入的单词数不超过M−1,软件会将新单词存入一个未使用的内存单元;若内存中已存入M 个单词,软件会清空最早进入内存的那个单词,腾出单元来,存放新单词。
假设一篇英语文章的长度为N 个单词。
给定这篇待译文章,翻译软件需要去外存查找多少次词典?假设在翻译开始前,内存中没有任何单词。
【输入】输入文件名为translate.in,输入文件共2 行。
每行中两个数之间用一个空格隔开。
第一行为两个正整数M 和N,代表内存容量和文章的长度。
第二行为N 个非负整数,按照文章的顺序,每个数(大小不超过1000)代表一个英文单词。
文章中两个单词是同一个单词,当且仅当它们对应的非负整数相同。
【输出】输出文件translate.out 共1 行,包含一个整数,为软件需要查词典的次数。
【输入输出样例1】translate.in translate.out3 71 2 1 5 4 4 15【输入输出样例 1 说明】整个查字典过程如下:每行表示一个单词的翻译,冒号前为本次翻译后的内存状况:空:内存初始状态为空。
1.1:查找单词1 并调入内存。
2.1 2:查找单词2 并调入内存。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【NOIP2010解题报告】(提高组)
第一题:模拟
直接按题目描述模拟,用一个队列实现。
由于是非负整数,所以要记得开0下标
第二题:动态规划
首先问题只与所用卡片的个数和位置有关,所以可以根据这个设计状态进行动态规划
记f[i, j, k, l]表示用了i个1步的卡片,j个2步的卡片,k个3步的卡片,l个4步的卡片所获得的最大得分
状态转移方程f[i, j, k, l]可以转移到
f[i + 1, j, k, l] f[i, j + 1, k, l] f[i, j, k + 1, l] f[i, j, k, l + 1]
由于用了一定张数的卡片后的目标格子是确定的,所以每个转移对应加上目标格子的得分的值即可
初值f[0, 0, 0, 0] = 0
ans = f[b[1], b[2], b[3], b[4]],其中b[i]表示移动i格的卡片的个数
时间复杂度O(40^4),空间复杂度O(40^4),可以滚动数组优化一维
另外还有一个时间复杂度O(350*40^3)的方程,这里就不讲了
第三题:二分答案+ 2-SAT
可以证明想到本题是有二分答案的性质的,如果比mid大的边全部一起来都没有出现矛盾,那么比mid 更大的答案肯定可以。
而二分了答案之后,我们就只要判定当前的比mid大的边有没有出现矛盾,即判定由权值比mid大的边构成的子图是不是一个二分图(只有是二分图才能分成两个集合啦),用染色法做这个2-SAT问题,即从任意一个点出发,给它相邻的点染上与这个点不同的颜色,如果染色出现冲突则可以判定为false,没冲突则判定为true
实际复杂度为O(log(maxw)*(n+m))
这只是一个比较直观的解法,其实可以直接排序+并查集判定即可,好像还可以用最大生成树的性质做
第四题:贪心
首先本题容易转化为这样一个模型:将第一行格子当成x点集中的点,将最后一行格子当成y点集中的点,如果在第一行的某个格子建站能覆盖到最后一行的某个格子,则对应点之间连边。
然后问题等价于选最少的x点集中的点覆盖所有的y点集中的点。
只有这个裸模型是不够的,直接做难度相当大,所以继续挖掘本题性质。
可以发现每个x点集中的点所能覆盖到的y点集的点会是连续的一段(可由覆盖的过程是一条路径扫过来证明),而且对于x点集中的i和i+1,有i所能覆盖到的右端点小于等于i+1的右端点(这个同样也可以用路径覆盖的过程来证明)
有了这两个结论,贪心的性质就出来了,方法如下:
从左到右枚举y点集的点,如果它还没被覆盖到,则选一个x点集中的最右边的能覆盖到它的点去覆盖它。
预处理出x点集中的所有点所能覆盖的区间左端点右端点,总的复杂度就是O(n^2)的如果预处理写记忆化搜索,有一个点会爆栈
n=1的情况可以特判
dp我的经验是。
从一个问题出发。
考虑“你是能告诉我。
我就能告诉你答案”。
从而找到最有子问题。
阶段状态就明显了。
拿到题之后:
1。
先看有无可套用模型
2。
看阶段或状态是否明显
3。
按如上提问题式分析
4。
从边界状态入手从小规模推导规律
第一题模拟+队操作;
第二题动态规划(实验证明深度搜索30分);
第三题二分图+贪心算法(大概);
第四题迷宫?。
