2011——2012学年数学毕业考(A)
王红莲——洪武小学2011—2012学年上学期期末试卷(二年级数学)

洪武小学2011—2012学年上学期末测试卷二年级数学班级姓名得分一.口算56+14= 70–25= 43+9= 69-23= 6×7=50+31= 82-19= 8×9= 6×3=6×4= 7×4= 2×9= 3×3= 5×4-12=75-13+16= 68-16+13= 57+8+12=27+33-15= 8×4+8= 9+3×10=二.想一想,填一填.(每空1分)共20分1、米和厘米都是()2、老师的身高是()米()厘米3、长方形有()条对称轴,正方形有()条对称轴4、角的大小与角的边长()关系5、5X6=30表示()个()相加。
还表示()个()相加。
6、3个8相加是(),写成加法算式是()写成乘法算式是()7、用2。
、5、0三个数能组成()两位数,其中最大的一个两位数是()最小的一个是()8、每两个人捂一次手,三个人工捂()次9.六九五十四这句口诀可以写出()个乘法算式三我是小法官(每空2分)共10分1、所有的直角度是同样大。
()2、一支粉笔大约长7厘米,一个水杯大约高10厘米()。
3每句乘法口诀都可以写出两道乘法算式()4、角有大小之分,角的大小与角的边长有关()5、3个5与5的3倍的算式都是3X5 ()四、按要求画图(每题2分)共8分1、画一个直角2、画一个比直角大的角3、画一条比3厘米长1厘米的线段4、画一条比5厘米短2厘米的线段五、用竖式计算下面各题(后两个题4分共16分)48+13= 72-38=7+35= 31-8=75+8-32= 47-14+23=六、列式计算。
(每个3分,共18分)1.比38多40的数是多少?2、56比18多多少?3、两个因数都是3,积是多少?4、7个8相加的和再减去27得多少?5被减数是67减数是7差是多少?6一个加数是66另一个数加数是15 和是多少?七、我会解决问题。
2011-2012学年北京市海淀区七年级(上)期末数学试卷

2011-2012学年北京市海淀区七年级(上)期末数学试卷一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.请将正确选项前的字母填在表格中相应的位置.1.(3分)﹣2的绝对值等于()A.﹣B.C.﹣2D.22.(3分)神舟八号于2011年11月1日5时58分由改进型“长征二号”火箭顺利发射升空,此次火箭的起飞质量为497000公斤,数字497000用科学记数法可以表示为()A.497×103B.0.497×106C.4.97×105D.49.7×104 3.(3分)下列结果为负数的是()A.﹣(﹣3)B.﹣32C.(﹣3)2D.|﹣3|4.(3分)下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b5.(3分)如图,已知点O在直线AB上,∠BOC=90°,则∠AOE的余角是()A.∠COE B.∠BOC C.∠BOE D.∠AOE6.(3分)已知一个几何体从三个不同方向看到的图形如图所示,则这个几何体是()A.圆柱B.圆锥C.球体D.棱锥7.(3分)若关于x的方程ax+3x=2的解是x=,则a的值是()A.﹣1B.5C.1D.﹣58.(3分)如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是()A.20°B.25°C.30°D.70°9.(3分)若有理数m在数轴上对应的点为M,且满足m<1<﹣m,则下列数轴表示正确的是()A.B.C.D.10.(3分)按下面的程序计算:若输入x=100,输出结果是501,若输入x=25,输出结果是631,若开始输入的x值为正整数,最后输出的结果为556,则开始输入的x值可能有()A.1种B.2种C.3种D.4种二、填空题(本题共18分,每小题3分)11.(3分)若一个数的相反数是2,则这个数是.12.(3分)∠α=18°20′,∠β=6°30′,则α+β=.13.(3分)如图所示,线段AB=4cm,BC=7cm,则AC=cm.14.(3分)若|m﹣3|+(n+2)2=0,则m+2n的值为.15.(3分)如果a﹣3b=8,那么代数式5﹣a+3b的值是.16.(3分)观察下面两行数第一行:4,﹣9,16,﹣25,36,…第二行:6,﹣7,18,﹣23,38,…则第二行中的第6个数是;第n个数是.三、解答题(本题共24分,第19题8分,其他题每题4分)17.(4分)计算:(﹣1)10×3+8÷(﹣4).18.(4分)化简:2x+5+3x﹣7.19.(8分)解方程:(1)2x﹣9=5x+3(2).20.(4分)先化简,再求值:x2﹣(5x2﹣4y)+3(x2﹣y),其中x=﹣1,y=2.21.(4分)画一画如下图所示,河流在两个村庄A、B的附近可以近似地看成是两条折线段(图中l),A、B分别在河的两旁.现要在河边修建一个水泵站,同时向A、B两村供水,为了节约建设的费用,就要使所铺设的管道最短.某人甲提出了这样的建议:从B 向河道作垂线交l于P,则点P为水泵站的位置.(1)你是否同意甲的意见?(填“是”或“否”);(2)若同意,请说明理由,若不同意,那么你认为水泵站应该建在哪?请在图中作出来,并说明作图的依据.四、解答题(本题共28分,第22题5分,第23题5分,第24题6分,第25题6分,第26题6分)22.(5分)如图所示,已知∠COB=2∠AOC,OD平分∠AOB,且∠AOC=40°,求∠BOD的度数.23.(5分)列方程解应用题:油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图,一个油桶由两个圆形铁片和一个长方形铁片相配套.生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?24.(6分)关于x的方程(m﹣1)x n﹣3=0是一元一次方程.(1)则m,n应满足的条件为:m,n;(2)若此方程的根为整数,求整数m的值.25.(6分)已知线段AB的长为10cm,C是直线AB上一动点,M是线段AC的中点,N是线段BC的中点.(1)若点C恰好为线段AB上一点,则MN=cm;(2)猜想线段MN与线段AB长度的关系,即MN=AB,并说明理由.26.(6分)有一台单功能计算器,对任意两个整数只能完成求差后再取绝对值的运算,其运算过程是:输入第一个整数x1,只显示不运算,接着再输入整数x2后则显示|x1﹣x2|的结果.比如依次输入1,2,则输出的结果是|1﹣2|=1;此后每输入一个整数都是与前次显示的结果进行求差后再取绝对值的运算.(1)若小明依次输入3,4,5,则最后输出的结果是;(2)若小明将1到2011这2011个整数随意地一个一个的输入,全部输入完毕后显示的最后结果设为m,则m的最大值为;(3)若小明将1到n(n≥3)这n个正整数随意地一个一个的输入,全部输入完毕后显示的最后结果设为m.探究m的最小值和最大值.2011-2012学年北京市海淀区七年级(上)期末数学试卷参考答案与试题解析一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.请将正确选项前的字母填在表格中相应的位置.1.(3分)﹣2的绝对值等于()A.﹣B.C.﹣2D.2【分析】根据绝对值的性质:一个负数的绝对值是它的相反数解答即可.【解答】解:根据绝对值的性质,|﹣2|=2.故选:D.【点评】本题考查了绝对值的性质:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0,难度适中.2.(3分)神舟八号于2011年11月1日5时58分由改进型“长征二号”火箭顺利发射升空,此次火箭的起飞质量为497000公斤,数字497000用科学记数法可以表示为()A.497×103B.0.497×106C.4.97×105D.49.7×104【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将497000用科学记数法表示为:4.97×105.故选:C.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n 的值.3.(3分)下列结果为负数的是()A.﹣(﹣3)B.﹣32C.(﹣3)2D.|﹣3|【分析】负数就是小于的数,利用绝对值的性质,以及平方的计算方法,计算出各项的值,即可作出判断.【解答】解:A、﹣(﹣3)=3,是正数,故A选项错误;B、﹣32=﹣9,是负数,故B选项正确;C、(﹣3)2=9,是正数,故C选项错误;D、|﹣3|=3,是正数,故D选项错误.故选:B.【点评】本题主要考查了绝对值与有理数的乘方的计算,是基础的题目.4.(3分)下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b【分析】本题考查同类项的概念,含有相同的字母,并且相同字母的指数相同,是同类项的两项可以合并,否则不能合并.合并同类项的法则是系数相加作为系数,字母和字母的指数不变.【解答】解:A、3a与b不是同类项,不能合并.错误;B、3a﹣a=2a.错误;C、2a3与3a2不是同类项,不能合并.错误;D、﹣a2b+2a2b=a2b.正确.故选:D.【点评】同类项的概念是所含字母相同,相同字母的指数也相同的项是同类项;注意不是同类项的一定不能合并.5.(3分)如图,已知点O在直线AB上,∠BOC=90°,则∠AOE的余角是()A.∠COE B.∠BOC C.∠BOE D.∠AOE【分析】求∠AOE的余角,根据互余的定义,即是求与∠AOE的和是90°的角,根据角相互间的和差关系可得.【解答】解:已知点O在直线AB上,∠BOC=90°,∴∠AOC=90°,∴∠AOE+∠COE=90°,∴∠AOE的余角是∠COE,故选:A.【点评】本题主要考查了余角和补角的定义,是一个基本的类型.6.(3分)已知一个几何体从三个不同方向看到的图形如图所示,则这个几何体是()A.圆柱B.圆锥C.球体D.棱锥【分析】由主视图和左视图可得此几何体为锥体,根据俯视图是圆及圆心可判断出此几何体为圆锥.【解答】解:∵主视图和左视图都是三角形,∴此几何体为椎体,∵俯视图是一个圆,∴此几何体为圆锥.故选:B.【点评】本题主要考查了由三视图判断几何体,由主视图和左视图可得几何体是柱体,锥体还是球体,由俯视图可确定几何体的具体形状.7.(3分)若关于x的方程ax+3x=2的解是x=,则a的值是()A.﹣1B.5C.1D.﹣5【分析】把x=代入方程ax+3x=2得到一个关于a的方程,求出方程的解即可.【解答】解:把x=代入方程ax+3x=2得:a+=2,∴a+3=8,∴a=5,故选:B.【点评】本题考查了解一元一次方程和一元一次方程的解等知识点的应用,关键是根据方程的解的定义得出一个关于a的方程,题目比较典型,难度不大.8.(3分)如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是()A.20°B.25°C.30°D.70°【分析】先根据平角的定义求出∠COB的度数,再由OD平分∠BOC即可求出∠2的度数.【解答】解:∵∠1=40°,∴∠COB=180°﹣40°=140°,∵OD平分∠BOC,∴∠2=∠BOC=×140°=70°.故选:D.【点评】本题考查的是平角的定义及角平分线的定义,熟知以上知识是解答此题的关键.9.(3分)若有理数m在数轴上对应的点为M,且满足m<1<﹣m,则下列数轴表示正确的是()A.B.C.D.【分析】根据m<1<﹣m,求出m的取值范围,进而确定M的位置即可.【解答】解:∵m<1<﹣m,∴,解得:m<﹣1.故选:A.【点评】此题主要考查了不等式组的解法以及利用数轴确定点的位置,根据已知得出m的取值范围是解题关键.10.(3分)按下面的程序计算:若输入x=100,输出结果是501,若输入x=25,输出结果是631,若开始输入的x值为正整数,最后输出的结果为556,则开始输入的x值可能有()A.1种B.2种C.3种D.4种【分析】由5x+1=556,解得x=111,即开始输入的x为111,最后输出的结果为556;当开始输入的x值满足5x+1=111,最后输出的结果也为556,可解得x=22;当开始输入的x值满足5x+1=22,最后输出的结果也为556,但此时解得的x 的值为小数,不合题意.【解答】解:∵输出的结果为556,∴5x+1=556,解得x=111;而111<500,当5x+1等于111时最后输出的结果为556,即5x+1=111,解得x=22;当5x+1=22时最后输出的结果为556,即5x+1=22,解得x=4.2(不合题意舍去),所以开始输入的x值可能为22或111.故选:B.【点评】本题考查了代数式求值:先把代数式进行变形,然后把满足条件的字母的值代入计算得到对应的代数式的值.也考查了解一元一方程.二、填空题(本题共18分,每小题3分)11.(3分)若一个数的相反数是2,则这个数是﹣2.【分析】根据互为相反数的两数之和为0可得出答案.【解答】解:﹣2的相反数为2,∴这个数为﹣2.故答案为:﹣2.【点评】本题考查相反数的知识,比较简单,注意掌握互为相反数的两数之和为0.12.(3分)∠α=18°20′,∠β=6°30′,则α+β=24°50′.【分析】代入后相加即可,注意:18°+6°=24°,20′+30′=50′.【解答】解:∠α+∠β=18°20′+6°30′=24°50′,故答案为:24°50′.【点评】本题考查了对角的计算的理解,注意:计算时分别相加(度+度、分+分、秒+秒,满60进1),如1°36′+2°43′=3°79′=4°19′.13.(3分)如图所示,线段AB=4cm,BC=7cm,则AC=11cm.【分析】直接利用AC=AB+BC计算即可.【解答】解:∵AB=4cm,BC=7cm,∴AC=AB+BC=4cm+7cm=11cm.故答案为11.【点评】本题考查了两点间的距离:两点的连线段的长叫两点间的距离.14.(3分)若|m﹣3|+(n+2)2=0,则m+2n的值为﹣1.【分析】根据非负数的性质列出方程求出m、n的值,代入所求代数式计算即可.【解答】解:∵|m﹣3|+(n+2)2=0,∴,解得,∴m+2n=3﹣4=﹣1.故答案为﹣1.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.15.(3分)如果a﹣3b=8,那么代数式5﹣a+3b的值是﹣3.【分析】将已知条件整体代入所求代数式即可.【解答】解:∵a﹣3b=8,∴5﹣a+3b=5﹣(a﹣3b)=5﹣8=﹣3.故本题答案为﹣3.【点评】本题考查了代数式的求值,根据已知条件,运用整体代入的思想解题.16.(3分)观察下面两行数第一行:4,﹣9,16,﹣25,36,…第二行:6,﹣7,18,﹣23,38,…则第二行中的第6个数是﹣47;第n个数是(﹣1)n+1(n+1)2+2.【分析】由第一行可知,每个数字为完全平方数,即第n个数字为(n+1)2,符号是偶数项为负,第二行每一个数比第一行对应的数大2,由此得出规律.【解答】解:根据观察的规律,得第二行中的第6个数是﹣(6+1)2+2=﹣47;第n个数是(﹣1)n+1(n+1)2+2;故答案为:﹣47,(﹣1)n+1(n+1)2+2.【点评】本题考查了数字变化规律型题.关键是由特殊到一般,找出数字规律,符号规律.三、解答题(本题共24分,第19题8分,其他题每题4分)17.(4分)计算:(﹣1)10×3+8÷(﹣4).【分析】首先进行乘方运算,然后在进行乘除法运算即可.【解答】解:原式=1×3﹣8÷4=3﹣2=1.【点评】本题主要考查有理数的混合运算,关键在于正确认真进行计算.18.(4分)化简:2x+5+3x﹣7.【分析】合并同类项的法则就是字母不变,系数想加减.【解答】解:原式=(2x+3x)+(5﹣7)=5x﹣2.【点评】本题考查合并同类项的法则关键知道字母不变,系数想加减.19.(8分)解方程:(1)2x﹣9=5x+3(2).【分析】(1)按照移项,合并,系数化为1的步骤解题即可;(2)按照去分母,去括号,移项,合并的步骤解题即可.【解答】解:(1)移项得:2x﹣5x=3+9.合并得:﹣3x=12.系数化为1得:x=﹣4.(2)解:两边同时乘以12,得2(5x﹣7)+12=3(3x﹣1).去括号得:10x﹣14+12=9x﹣3.移项得:10x﹣9x=﹣3+14﹣12,合并得:x=﹣1.【点评】考查解一元一次方程;掌握解一元一次方程的步骤是解决本题的关键;注意去分母时单独的一个数也要乘最小公倍数.20.(4分)先化简,再求值:x2﹣(5x2﹣4y)+3(x2﹣y),其中x=﹣1,y=2.【分析】先去括号,x2﹣(5x2﹣4y)+3(x2﹣y)=x2﹣5x2+4y+3x2﹣3y;再合并同类项得﹣x2+y;最后把x=﹣1,y=2代入式子求值.【解答】解:x2﹣(5x2﹣4y)+3(x2﹣y)=x2﹣5x2+4y+3x2﹣3y=﹣x2+y;∴当x=﹣1,y=2时,原式=﹣(﹣1)2+2=1.【点评】此类化简求值题目的解答,要按顺序先化简,再代入计算求值.关键是化为最简的代数式,才能简化计算.21.(4分)画一画如下图所示,河流在两个村庄A、B的附近可以近似地看成是两条折线段(图中l),A、B分别在河的两旁.现要在河边修建一个水泵站,同时向A、B两村供水,为了节约建设的费用,就要使所铺设的管道最短.某人甲提出了这样的建议:从B 向河道作垂线交l于P,则点P为水泵站的位置.(1)你是否同意甲的意见?否(填“是”或“否”);(2)若同意,请说明理由,若不同意,那么你认为水泵站应该建在哪?请在图中作出来,并说明作图的依据.【分析】(1)根据线段的性质可判断;(2)水泵应在线段AB上,连接AB,与l的交点,即为水泵的位置;【解答】解:(1)否;(2)连接AB,交l于点Q,则水泵站应该建在点Q处;依据为:两点之间,线段最短.【点评】本题主要考查了线段的性质:两点之间线段最短;体现了数学知识在实际中的应用.四、解答题(本题共28分,第22题5分,第23题5分,第24题6分,第25题6分,第26题6分)22.(5分)如图所示,已知∠COB=2∠AOC,OD平分∠AOB,且∠AOC=40°,求∠BOD的度数.【分析】由角平分线的定义,可以得到∠BOD=∠AOB÷2,从而可以转化为求∠AOB.【解答】解:∵∠COB=2∠AOC,且∠AOC=40°,∴∠COB=2×40°=80°,∴∠AOB=∠AOC+∠COB=40°+80°=120°,∵OD平分∠AOB,∴∠BOD=∠AOB÷2=120°÷2=60°.∴∠BOD的度数是60°.故答案为60°.【点评】本题主要考查角平分线的知识点,比较简单.23.(5分)列方程解应用题:油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图,一个油桶由两个圆形铁片和一个长方形铁片相配套.生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?【分析】可设生产圆形铁片的工人为x人,则生产长方形铁片的工人为42﹣x人,根据两张圆形铁片与一张长方形铁片可配套成一个密封圆桶可列出关于x的方程,求解即可.【解答】解:设生产圆形铁片的工人为x人,则生产长方形铁片的工人为42﹣x 人,根据题意可列方程:120x=2×80(42﹣x),解得:x=24,则42﹣x=18.答:生产圆形铁片的有24人,生产长方形铁片的有18人.【点评】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,难度一般.24.(6分)关于x的方程(m﹣1)x n﹣3=0是一元一次方程.(1)则m,n应满足的条件为:m≠1,n=1;(2)若此方程的根为整数,求整数m的值.【分析】(1)根据一元一次方程的定义:含有一个未知数,未知数的次数为1,求解;(2)先由(1)得方程(m﹣1)x﹣3=0,求出x,再根据此方程的根为整数确定m的值.【解答】解:(1)根据一元一次方程的定义得:m﹣1≠0,n=1,即m≠1,n=1,故答案为:≠1,=1;(2)由(1)可知方程为(m﹣1)x﹣3=0,则x=∵此方程的根为整数,∴为整数.又m为整数,则m﹣1=﹣3,﹣1,1,3,∴m=﹣2,0,2,4.【点评】本题考查的是一元一次方程的定义,根据题意确定m的值是解答此题的关键.25.(6分)已知线段AB的长为10cm,C是直线AB上一动点,M是线段AC的中点,N是线段BC的中点.(1)若点C恰好为线段AB上一点,则MN=5cm;(2)猜想线段MN与线段AB长度的关系,即MN=AB,并说明理由.【分析】(1)因为点C恰好为线段AB上一点,所以MN=MC+NC=AC+BC=(AC+BC)=AB=5cm;(2)分三种情况当C在线段AB上时,当C在线段AB的延长线上时,当C在线段BA的延长线上时,进行推论说明.【解答】解:(1)因为点C恰好为线段AB上一点,所以MN=MC+NC=AC+BC=(AC+BC)=AB=5cm;故答案为:5;(2);证明:∵M是线段AC的中点,∴CM=AC,∵N是线段BC的中点,∴CN=BC,…(3分)以下分三种情况讨论,当C在线段AB上时,MN=CM+CN=AB;…(4分)当C在线段AB的延长线上时,MN=CM﹣CN=AB;…(5分)当C在线段BA的延长线上时,MN=CN﹣CM=AB;…(6分)综上:MN=AB.故答案为:.【点评】考查了两点间的距离.首先要根据题意,考虑所有可能情况,画出正确图形.再根据中点的概念,进行线段的计算与证明.26.(6分)有一台单功能计算器,对任意两个整数只能完成求差后再取绝对值的运算,其运算过程是:输入第一个整数x1,只显示不运算,接着再输入整数x2后则显示|x1﹣x2|的结果.比如依次输入1,2,则输出的结果是|1﹣2|=1;此后每输入一个整数都是与前次显示的结果进行求差后再取绝对值的运算.(1)若小明依次输入3,4,5,则最后输出的结果是4;(2)若小明将1到2011这2011个整数随意地一个一个的输入,全部输入完毕后显示的最后结果设为m,则m的最大值为2010;(3)若小明将1到n(n≥3)这n个正整数随意地一个一个的输入,全部输入完毕后显示的最后结果设为m.探究m的最小值和最大值.【分析】(1)根据已知得出输入与输出结果的规律求出即可;(2)根据题意每次输入都是与前一次运算结果求差后取绝对值,转化为奇偶性的性质然后讨论最大值.(3)根据分析的奇偶性进行构造,其中k为非负整数,连续四个正整数结合指的是按(*)式结构计算分别得出最大值与最小值.【解答】解:(1)根据题意可以得出:||3﹣4|﹣5|=|1﹣5|=4;故答案为:4.(2)由于输入的数都是非负数.当x1≥0,x2≥0时,|x1﹣x2|不超过x1,x2中最大的数.对x1≥0,x2≥0,x3≥0,则||x1﹣x2|﹣x3|不超过x1,x2,x3中最大的数.小明输入这2011个数设次序是x1,x2,x2011,相当于计算:||||x1﹣x2|﹣x3|﹣x2011|﹣x2011|=P.因此P的值≤2011.另外从运算奇偶性分析,x1,x2为整数.|x1﹣x2|与x1+x2奇偶性相同.因此P与x1+x2+…+x2011的奇偶性相同.但x1+x2+…+x2011=1+2+2011=偶数.于是断定P≤2010.我们证明P可以取到2010.对1,2,3,4,按如下次序|||1﹣3|﹣4|﹣2|=0.|||(4k+1)﹣(4k+3)|﹣(4k+4)|﹣(4k+2)|=0,对k=0,1,2,均成立.因此,1﹣2008可按上述办法依次输入最后显示结果为0.而后||2009﹣2010|﹣2011|=2010.所以P的最大值为2010.故答案为:2010;(3)对于任意两个正整数x1,x2,|x1﹣x2|一定不超过x1和x2中较大的一个,对于任意三个正整数x1,x2,x3,||x1﹣x2|﹣x3|一定不超过x1,x2和x3中最大的一个,以此类推,设小明输入的n个数的顺序为x1,x2,…x n,则m=|||…|x1﹣x2|﹣x3|﹣…|﹣x n|,m一定不超过x1,x2,…x n,中的最大数,所以0≤m≤n,易知m与1+2+…+n的奇偶性相同;1,2,3可以通过这种方式得到0:||3﹣2|﹣1|=0;任意四个连续的正整数可以通过这种方式得到0:|||a﹣(a+1)|﹣(a+3)|﹣(a+2)|=0(*);下面根据前面分析的奇偶性进行构造,其中k为非负整数,连续四个正整数结合指的是按(*)式结构计算.当n=4k时,1+2+…+n为偶数,则m为偶数,连续四个正整数结合可得到0,则最小值为0,前三个结合得到0,接下来连续四个结合得到0,仅剩下n,则最大值为n;当n=4k+1时,1+2+…+n为奇数,则m为奇数,除1外,连续四个正整数结合得到0,则最小值为1,从1开始连续四个正整数结合得到0,仅剩下n,则最大值为n;当n=4k+2时,1+2+…+n为奇数,则m为奇数,从1开始连续四个正整数结合得到0,仅剩下n和n﹣1,则最小值为1,从2开始连续四个正整数结合得到0,仅剩下1和n,最大值为n﹣1;当n=4k+3时,1+2+…+n为偶数,则m为偶数,前三个结合得到0,接下来连续四个正整数结合得到0,则最小值为0,从3开始连续四个正整数结合得到0,仅剩下1,2和n,则最大值为n﹣1.【点评】此题考查了整数的奇偶性问题以及含有绝对值的函数最值问题,虽然以计算为载体,但首先要有试验观察和分情况讨论的能力.。
陈俊仪——洪武小学2011—2012学年上学期期末试卷(六年级数学)

洪武学校六年级数学上册期末综合测试卷第 1 页 共 2 页 编制:陈俊仪洪武学校六年级数学期末综合测试卷一、认真读题,用心思考,我能正确填写。
(每题2分,共24分)1.一个点在图上的位置可用(4、6)表示,如果这个点向左平移2个单位,其位置应表示为( , )。
2.( )÷8﹦()40﹦12.5%﹦( ):( )﹦( )(填小数)3.把67.8% ,0.67, 0.677, 0.6 7 ,32按从小到大的顺序排列是: ( )。
4.( )比12多31 ;24千克比( )少31。
5.食堂有2吨大米,如果每天吃它的101,那么( )天可以吃完;如果每天吃101吨,那么( )天可以吃完。
6.比54多20%的数是( ),比200千克少12.5%的数是( )。
7.541小时:40分钟,化成最简整数比是( ),比值是( )。
8.李刚家要栽种一批树苗,这种树苗的成活率一般为75%~80%,如果要栽活1200棵树苗,那么至少应栽( )棵。
9.从一张边长10㎝的正方形纸里剪出一个最大的圆,这个圆的周长是( )㎝,面积是( )㎝2。
10.某工人一天生产的次品与合格品的比是1∶49,其产品的合格率是( )。
11.把圆分成若干等份,然后把它剪开,照右图的样子拼成一个近似的长方形。
已知长方形的周长比 原来圆的周长增加了4厘米,这个圆的周长是 ( )厘米,拼成的长方形面积是( )平方厘米。
12.一本故事书,小明第一天看了全书的31,看了24页,小明还要看的页数是从第( )页到第( )页。
二、火眼金睛,我会公正评判。
(6分)1.5米的20%与2米的50%相等。
( ) 2.圆的半径扩大2倍,面积也扩大相同的倍数。
( ) 3.一项工程,甲单独做要10天,以单独做要8天。
甲和乙工作效率的最简 整数比是5∶4。
( )4.5千克铁钉用去51,又用去51千克,两次共用去52千克。
( )5.圆周率是圆的周长与直径的比。
( ) 6.用102粒玉米种子进行发芽试验,结果全部发芽,发芽率是102%。
2011-2012学年度第二学期小学毕业考试数学模拟试题(2)

区镇 学校 考号 姓名__________________________◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆装◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆订◆◆◆◆◆◆◆◆◆◆◆◆◆线◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆2011~2012 学 年 度 第 二 学 期小 学 毕 业 考 试 数 学 模 拟 试 题(2)(考试时间:120分钟 总分:100分)1、为切实解决好进城务工子女“读书难”问题,从2008年起,广州接受义务教育的流动人口子女将达四十五万八千三百人。
这个数写作( ),改写成“万”作单位并保留一位小数是( )。
2、把一根3024米长的绳子剪成相等的几段,一共剪了23刀,每段长( )米。
3、你每天的睡眠时间是( )小时,占全天的( )( )。
4、12天与2星期的最简整数比是( )。
5、一个比例的两个外项分别是 1.5和6,两个比的比值都是3,这个比例是( )。
6、李刚家要栽种一批树苗,这种树苗的成活率一般为75%-80%,如果要栽活1200棵树苗,那么至少应栽( )棵。
7、在比例尺是1:3000000的地图上,量得广州到武汉两地之间的公路长36.3厘米。
在比例尺是1:2500000的地图上,广州到武汉之间的公路长( )厘米。
8、把一个二位小数“四舍五入”精确到十分位后得6.0,这个二位小数最大和最小相差( )。
9、在有余数的除法算式中,除数是b ,商是c ,(b 、c 均不为0),被除数最大是( )。
10、把一个正方体分成三个完全相同的小长方体,这三个小长方体的表面积之和比原正方体的表面积增加了( )。
一、认真读题,谨慎填空。
(20%)11、含盐2%的盐水500克,将它蒸发( )克水后,得到含盐5%的盐水。
12、把一个圆形纸片剪开后,拼成一个宽等于半径,面积不变的近似长方形,这个长方形的周长是16.56厘米。
剪开前的圆形纸片的面积是( )平方厘米。
13、小马虎在计算时,把“一个数除以75”,看成“一个数乘以75”,结果算出的答案是2815,正确的答案是( )。
高等数学期末考试试题及答案(大一考试)
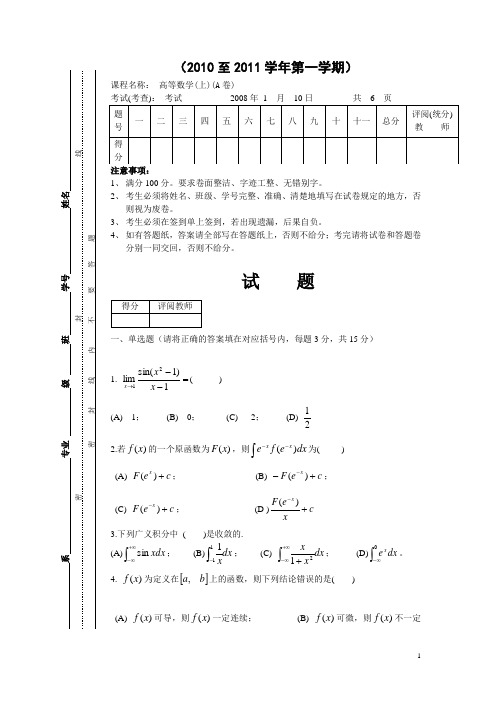
(2010至2011学年第一学期)课程名称: 高等数学(上)(A 卷)考试(考查): 考试 2008年 1 月 10日 共 6 页 注意事项:1、 满分100分。
要求卷面整洁、字迹工整、无错别字。
2、 考生必须将姓名、班级、学号完整、准确、清楚地填写在试卷规定的地方,否则视为废卷。
3、 考生必须在签到单上签到,若出现遗漏,后果自负。
4、 如有答题纸,答案请全部写在答题纸上,否则不给分;考完请将试卷和答题卷分别一同交回,否则不给分。
试 题一、单选题(请将正确的答案填在对应括号内,每题3分,共15分)1. =--→1)1sin(lim21x x x ( ) (A) 1; (B) 0; (C) 2; (D)212.若)(x f 的一个原函数为)(x F ,则dx e f e xx )(⎰--为( )(A) c e F x +)(; (B) c eF x+--)(;(C) c e F x+-)(; (D )c xe F x +-)( 3.下列广义积分中 ( )是收敛的. (A)⎰+∞∞-xdx sin ; (B)dx x⎰-111; (C) dx x x ⎰+∞∞-+21; (D)⎰∞-0dx e x。
4. )(x f 为定义在[]b a ,上的函数,则下列结论错误的是( )(A) )(x f 可导,则)(x f 一定连续; (B) )(x f 可微,则)(x f 不一定可导;(C) )(x f 可积(常义),则)(x f 一定有界; (D) 函数)(x f 连续,则⎰xadt t f )(在[]b a ,上一定可导。
5. 设函数=)(x f nn x x211lim++∞→ ,则下列结论正确的为( )(A) 不存在间断点; (B) 存在间断点1=x ; (C) 存在间断点0=x ; (D) 存在间断点1-=x二、填空题(请将正确的结果填在横线上.每题3分,共18分)1. 极限=-+→xx x 11lim 20 _____.2. 曲线⎩⎨⎧=+=321ty t x 在2=t 处的切线方程为______. 3. 已知方程xxe y y y 265=+'-''的一个特解为x e x x 22)2(21+-,则该方程的通解为 .4. 设)(x f 在2=x 处连续,且22)(lim2=-→x x f x ,则_____)2(='f5.由实验知道,弹簧在拉伸过程中需要的力F (牛顿)与伸长量s 成正比,即ks F =(k 为比例系数),当把弹簧由原长拉伸6cm 时,所作的功为_________焦耳。
2011-2012学年辽宁省沈阳市134中学八年级(下)月考数学试卷(含答案)

2011-2012学年辽宁省沈阳市134中学八年级(下)月考数学试卷一、选择题:1.若m<n,则下列不等式中正确的是()A.m﹣3>n﹣3B.3m>n C.﹣3m>﹣3n D.>2.当分式的值为零时,x的值为()A.3B.﹣3C.0D.3或﹣33.下列图形一定相似的是()A.两个矩形B.两个等腰梯形C.有一个内角相等的两个菱形D.对应边成比例的两个四边形4.如图,大正方形中有2个小正方形,如果它们的面积分别是S1、S2,那么S1、S2的大小关系是()A.S1>S2B.S1=S2C.S1<S2D.S1、S2的大小关系不确定5.已知△ABC的三边长分别为:6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF 的另两边长是下列哪一组时,这两个三角形相似()A.2cm,3cm B.4cm,5cm C.5cm,6cm D.6cm,7cm 6.已知点M将线段AB黄金分割(AM>BM),则下列各式中不正确的是()A.AM:BM=AB:AM B.AM=ABC.BM=AB D.AM≈0.618AB7.下列各组中的四条线段a,b,c,d成比例的是()A.a=,b=3,c=2,d=B.a=4,b=6,c=5,d=10C.a=2,b=,c=2,d=D.a=2,b=3,c=4,d=18.如图,AB是斜靠在墙壁上的长梯,梯脚B距墙1.6米,梯上点D距墙1.4米,BD长0.55米,则梯子长为()A.3.85米B.4.00米C.4.40米D.4.50米9.某市今年共有5万人参加研究生考试,为了了解5万名考生的成绩从中抽取1000名考生的英语成绩进行统计分析,以下说法正确的有()个.①5万名考生为总体②调查采用抽样调查方式③1000名考生是总体的一个样本④每名考生的英语成绩是个体.A.4B.3C.2D.110.下列任务中,适宜采用普查方式的是()A.调查某地的空气质量B.了解中学生每天的睡眠时间C.调查某电视剧在本地区的收视率D.了解某一天本校因病缺课的学生数二、填空题:11.分解因式:2(x+1)2﹣12(x+1)+18=.12.若,则=.13.已知关于x的不等式组无解,则a的取值范围是.14.在△ABC中,∠B=35°,AD是BC边上的高,并且AD2=BD•DC,则∠BCA的度数为.15.如图,△ABC中,∠ACB=90°,CD是斜边AB上的高,BD=9,AD=4,那么CD =;AC=.16.使分式方程产生增根的k的值为.17.两个相似三角形的相似比为2:3,它们面积的差是25,那么较大三角形的面积是.18.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为米.19.如图,在▱ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB 等于cm2.20.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,那么根据图的信息,估计小张和小李两人中新手是.21.亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D.然后测出两人之间的距离CD=1.25m,颖颖与楼之间的距离DN=30m(C,D,N在一条直线上),颖颖的身高BD=1.6m,亮亮蹲地观测时眼睛到地面的距离AC=0.8m.则住宅楼的高度为米.22.一组数据4,0,1,﹣2,2的标准差是.23.如图,在△ABC中,点D在AB上,请再添一个适当的条件,使△ADC∽△ACB,那么可添加的条件是.三、解答题:24.先化简再求值:,其中x=.25.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)求出△ABC与△A′B′C′的位似比;(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.26.矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM,E是垂足.①求△ABM的面积;②求DE的长;③求△ADE的面积.27.某城市平均每天处理垃圾700吨,有甲和乙两个处理厂处理,已知甲每小时可处理垃圾55吨,需要费用550元,乙厂每小时可处理垃圾45吨,需要费用495元.如果规定该城市每天用于处理垃圾的费用不得超过7370元,甲厂每天处理垃圾至少要多少吨?28.某广告公司将一块广告牌制作任务交给师徒两人,已知师傅单独完成时间是徒弟单独完成时间的,现由徒弟先做1天,师徒再合作2天完成.(1)师徒两人单独完成任务各需几天?(2)若完成后得到报酬540元,按各人完成的工作量计算报酬,该如何分配?29.为了让学生了解文明礼仪知识,增强文明意识,养成文明习惯.某中学在“文明日照,从我做起”知识普及活动中,举行了一次“文明礼仪知识”竞赛,共有3000名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行了统计.请你根据上面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:(1)求频率分布表中的m、n;(2)补全频率分布直方图;(3)你能根据所学知识确定“众数”、“中位数”在哪一组吗?(不要求说明理由)频率分布表:组别分组频数频率150.5~60.560.08260.5~70.590.12370.5~80.515m480.5~90.5240.32590.5~100.5n0.28合计频数分布直方图:2011-2012学年辽宁省沈阳市134中学八年级(下)月考数学试卷参考答案与试题解析一、选择题:1.若m<n,则下列不等式中正确的是()A.m﹣3>n﹣3B.3m>n C.﹣3m>﹣3n D.>【分析】根据不等式的性质分析判断.【解答】解:A、若m<n,根据不等式的基本性质,不等式两边加(或减)同一个数(或式子),不等号的方向不变,所以m﹣3>n﹣3不正确;B、3m>n中,m<n两边没有同时乘以3,所以不成立;C、不等式两边乘(或除以)同一个负数,不等号的方向改变,故﹣3m>﹣3n正确;D、不等式两边乘(或除以)同一个正数,不等号的方向不变,所以>不正确.故选:C.【点评】不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.2.当分式的值为零时,x的值为()A.3B.﹣3C.0D.3或﹣3【分析】根据分式的值为零的条件得到x2﹣9=0且x2﹣4x+3≠0,然后解方程,再把方程的解代入不等式进行检验.【解答】解:∵分式的值为零,∴x2﹣9=0且x2﹣4x+3≠0,解方程x2﹣9=0得x=3或﹣3,当x=3时,x2﹣4x+3=0,当x=﹣3时,x2﹣4x+3≠0,∴x=﹣3.故选:B.【点评】本题考查了分式的值为零的条件:当分式的分子为零,分母不为零时,分式的值为零.3.下列图形一定相似的是()A.两个矩形B.两个等腰梯形C.有一个内角相等的两个菱形D.对应边成比例的两个四边形【分析】根据相似图形的定义,四条边对应成比例,四个角对应相等,对各选项分析判断后利用排除法解答.【解答】解:A、两个矩形,对应角相等,都是直角,但四条边不一定对应成比例,故本选项不符合题意;B、两个等腰梯形,四个角不一定对应相等,边也不一定对应成比例,所以不一定相似,故本选项不符合题意;C、两个菱形,有一个角相等,则其它角也对应相等,而四条边都相等,所以对应成比例,所以相似,故本选项符合题意;D、对应边成比例,对应角不一定相等,所以不一定相似,故本选项不符合题意.故选:C.【点评】本题主要考查相似图形的定义,熟练掌握矩形、等腰梯形、菱形的性质是解题的关键.4.如图,大正方形中有2个小正方形,如果它们的面积分别是S1、S2,那么S1、S2的大小关系是()A.S1>S2B.S1=S2C.S1<S2D.S1、S2的大小关系不确定【分析】设大正方形的边长为x,根据等腰直角三角形的性质知AC、BC的长,进而可求得S2的边长,由面积的求法可得答案.【解答】解:如图,设大正方形的边长为x,根据等腰直角三角形的性质知,AC=BC,BC=CE=CD,∴AC=2CD,CD=,∴S2的边长为x,S2的面积为x2,S1的边长为,S1的面积为x2,∴S1>S2,故选:A.【点评】本题利用了正方形的性质和等腰直角三角形的性质求解.5.已知△ABC的三边长分别为:6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF 的另两边长是下列哪一组时,这两个三角形相似()A.2cm,3cm B.4cm,5cm C.5cm,6cm D.6cm,7cm【分析】根据三边对应成比例的三角形相似,即可求得.注意△DEF中为4cm边长的对应边可能是6cm或7.5cm或9cm,所以有三种情况.【解答】解:设△DEF的另两边为xcm,ycm,若△DEF中为4cm边长的对应边为6cm,则:,解得:x=5,y=6;若△DEF中为4cm边长的对应边为7.5cm,则:,解得:x=3.2,y=4.8;若△DEF中为4cm边长的对应边为9cm,则:,解得:x=,y=;故选:C.【点评】此题考查了相似三角形的判定:三边对应成比例的三角形相似.解此题的关键要注意△DEF中为4cm边长的对应边不确定,答案不唯一,要仔细分析,小心别漏解.6.已知点M将线段AB黄金分割(AM>BM),则下列各式中不正确的是()A.AM:BM=AB:AM B.AM=ABC.BM=AB D.AM≈0.618AB【分析】根据黄金分割的定义:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比,据此判断即可.【解答】解:∵点M将线段AB黄金分割(AM>BM),∴AM是较长的线段,根据黄金分割的定义可知:AB:AM=AM:BM,AM=AB≈0.618AB,BM=AB.故选:C.【点评】本题主要考查了黄金分割,应该识记黄金分割的公式:较短的线段=原线段的倍,较长的线段=原线段的倍,难度适中.7.下列各组中的四条线段a,b,c,d成比例的是()A.a=,b=3,c=2,d=B.a=4,b=6,c=5,d=10C.a=2,b=,c=2,d=D.a=2,b=3,c=4,d=1【分析】如果两条线段的乘积等于另外两条线段的乘积,我们就说这四条线段叫做成比例线段.【解答】解:A、×3≠×2,故错误;B、4×10≠5×6,故错误;C、2×=×,故正确;D、2×3≠1×4,故错误.故选:C.【点评】考查了比例线段的概念.注意相乘的时候,让最大的和最小的相乘,剩下的两条再相乘,看它们的积是否相等.8.如图,AB是斜靠在墙壁上的长梯,梯脚B距墙1.6米,梯上点D距墙1.4米,BD长0.55米,则梯子长为()A.3.85米B.4.00米C.4.40米D.4.50米【分析】根据梯子、墙、地面三者构成的直角三角形与梯子、墙、梯上点D三者构成的直角三角相似,利用相似三角形对应边成比例解答即可.【解答】解:因为梯子每一条踏板均和地面平行,所以构成一组相似三角形,即△ABC∽△ADE,则=设梯子长为x米,则=,解得,x=4.40.故选:C.【点评】本题考查了相似三角形在测量高度时的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.9.某市今年共有5万人参加研究生考试,为了了解5万名考生的成绩从中抽取1000名考生的英语成绩进行统计分析,以下说法正确的有()个.①5万名考生为总体②调查采用抽样调查方式③1000名考生是总体的一个样本④每名考生的英语成绩是个体.A.4B.3C.2D.1【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.【解答】解:①5万名考生的英语成绩是总体,故错误;②正确;③1000名考生的英语成绩是总体的一个样本,故错误;④正确.故选:C.【点评】解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.10.下列任务中,适宜采用普查方式的是()A.调查某地的空气质量B.了解中学生每天的睡眠时间C.调查某电视剧在本地区的收视率D.了解某一天本校因病缺课的学生数【分析】调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.【解答】解:A、调查某地的空气质量,由于范围广,应当使用抽样调查,故本选项错误;B、了解中学生每天的睡眠时间,由于人数多,不易全面掌握所有的人,故应当采用抽样调查;C、调查某电视剧在本地区的收视率,人数较多,不便测量,应当采用抽样调查,故本选项错误;D、了解某一天本校因病缺课的学生数,人数少,耗时短,应当采用全面调查的方式,故本选项正确.故选:D.【点评】此题考查了抽样调查和全面调查,由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.二、填空题:11.分解因式:2(x+1)2﹣12(x+1)+18=2(x﹣2)2.【分析】首先提取公因式2,然后利用完全平方公式即可分解.【解答】解:原式=2[(x+1)2﹣6(x+1)+9],=2[(x+1)﹣3]2,=2(x﹣2)2.故答案是:2(x﹣2)2.【点评】本题主要考查提公因式法分解因式和利用完全平方公式分解因式,难点在于把(x+1)当作一个整体分解因式.12.若,则=.【分析】根据两内项之积等于两外项之积把比例式转化为乘积式,然后整理即可得解.【解答】解:∵=,∴3y=5(x﹣y),整理得,5x=8y,∴=.故答案为:.【点评】本题考查了比例的性质,熟记“据两内项之积等于两外项之积”,把比例式转化为乘积式是解题的关键.13.已知关于x的不等式组无解,则a的取值范围是a≥3.【分析】先求出不等式组的解集,利用不等式组的解集是无解可知,x应该是“大大小小找不到”,所以可以判断出a≥3.【解答】解:解关于x的不等式组,得,∵不等式组无解∴大大小小找不到,即a≥3.故答案为:a≥3.【点评】本题主要考查了已知一元一次不等式组的解集,求不等式中的字母的值,同样也是利用口诀求解,但是要注意当两数相等时,不等式组是x>3,x<3时没有交集,所以也是无解,不要漏掉相等这个关系.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到.14.在△ABC中,∠B=35°,AD是BC边上的高,并且AD2=BD•DC,则∠BCA的度数为55°或125°.【分析】分两种情况考虑:当∠BCA为锐角和钝角,将已知的积的恒等式化为比例式,再根据夹角为直角相等,利用两边对应成比例且夹角的相等的两三角形相似可得出△ADB∽△CDA,由相似三角形的对应角相等,利用直角三角形的两锐角互余及外角性质分别求出两种情况下∠BCA的度数即可.【解答】解:当∠BCA为锐角时,如图1所示,∵AD2=BD•DC,∴=,又AD⊥BC,∴∠ADB=∠CDA=90°,∴△ADB∽△CDA,又∠B=35°,∴∠CAD=∠B=35°,∠BCA=∠BAD,在Rt△ADB中,∠ADB=90°,∠B=35°,∴∠BAD=55°,则∠BCA=∠BAD=55°;当∠BCA为钝角时,如图2所示,同理可得△ADB∽△CDA,又∠B=35°,可得∠CAD=∠B=35°,则∠BCA=∠CDA+∠CAD=125°,综上,∠BCA的度数为55°或125°.故答案为:55°或125°【点评】此题考查了相似三角形的判定与性质,直角三角形的性质,以及外角的性质,利用了分类讨论的思想,其中相似三角形的判定方法有:两对对应角相等的两三角形相似;三边对应成比例的两三角形相似;两边对应成比例且夹角相等的两三角形相似.15.如图,△ABC中,∠ACB=90°,CD是斜边AB上的高,BD=9,AD=4,那么CD=6;AC=2.【分析】由于CD⊥AB,那么∠CDA=∠CDB=90°,根据直角三角形的性质可得∠A+∠ACD=90°,∠B+∠BCD=90°,而∠ACB=90°,那么∠A+∠B=90°,再根据同角的余角相等可得∠B=∠ACD,∠A=∠BCD,从而可证△ACD∽△CBD,于是=,易求CD,在Rt△ACD中,利用勾股定理可求AC.【解答】解:∵CD⊥AB,∴∠CDA=∠CDB=90°,∴∠A+∠ACD=90°,∠B+∠BCD=90°,∵∠ACB=90°,∴∠A+∠B=90°,∴∠B=∠ACD,∠A=∠BCD,∴△ACD∽△CBD,∴=,∴CD2=AD•BD,∵AD=4,BD=9,∴CD=6,在Rt△ACD中,AC2=AD2+CD2=52,∴AC=2.【点评】本题考查了相似三角形的判定和性质、勾股定理,解题的关键是证明△ACD∽△CBD,求出CD.16.使分式方程产生增根的k的值为±6.【分析】增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x+3)(x﹣3)=0,得到x=3或﹣3,然后代入整式方程算出k的值.【解答】解;方程两边都乘(x+3)(x﹣3),得x﹣3+x+3=k,∵原方程有增根,∴最简公分母(x+3)(x﹣3)=0,∴x=3或﹣3,当x=3时,k=6,当x=﹣3时,k=﹣6.【点评】增根问题可按如下步骤进行:①让最简公分母为0,确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.17.两个相似三角形的相似比为2:3,它们面积的差是25,那么较大三角形的面积是45.【分析】先根据相似三角形的性质求出其面积的比,再设较小的三角形的面积为4x,则较大的三角形的面积为9x,由它们面积的差是25即可求出x的值,进而得出结论.【解答】解:∵两个相似三角形的相似比为2:3,∴其面积的比等于4:9,设较小的三角形的面积为4x,则较大的三角形的面积为9x,∵它们面积的差是25,∴9x﹣4x=5x=25,解得x=5,∴较大三角形的面积=9×5=45.故答案为:45.【点评】本题考查的是相似三角形的性质,即相似三角形面积的比等于相似比的平方.18.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为10米.【分析】利用相似三角形对应线段成比例,求解即可.【解答】解:1米长的标杆测得其影长为1.2米,即某一时刻实际高度和影长之比为定值,所以墙上的2米投射到地面上实际为2.4米,即旗杆影长为12米,因此旗杆总高度为10米.【点评】本题考查的是相似形在投影中的应用,关键是利用相似比来解题.19.如图,在▱ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB 等于48cm2.【分析】根据相似三角形的性质,先证△DOE∽△BOA,求出相似比为,故面积比为,=4S△DOE.即可求S△AOB【解答】解:∵在▱ABCD中,E为CD中点,∴DE∥AB,DE=AB,在△DOE与△BOA中,∠DOE=∠BOA,∠OBA=∠ODE,∴△DOE∽△BOA,相似比为=,故面积比为,=4S△DOE=4×12=48cm2.即S△AOB故答案为:48.【点评】本题考查了平行四边形的性质,相似三角形的判定与性质.关键是明确相似三角形的面积比等于相似比的平方.20.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,那么根据图的信息,估计小张和小李两人中新手是小李.【分析】根据图形可知,小李的射击不稳定,可判断新手是小李.【解答】解:由图象可以看出,小李的成绩波动大,∵波动性越大,方差越大,成绩越不稳定,∴新手是小李.故填小李.【点评】考查了方差的意义:波动性越大,方差越大,成绩越不稳定.21.亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D.然后测出两人之间的距离CD=1.25m,颖颖与楼之间的距离DN=30m(C,D,N在一条直线上),颖颖的身高BD=1.6m,亮亮蹲地观测时眼睛到地面的距离AC=0.8m.则住宅楼的高度为20.8米.【分析】过A作CN的平行线交BD于E,交MN于F,由相似三角形的判定定理得出△ABE∽△AMF,再由相似三角形的对应边成比例即可得出MF的长,进而得出结论.【解答】解:过A作CN的平行线交BD于E,交MN于F.由已知可得FN=ED=AC=0.8m,AE=CD=1.25m,EF=DN=30m,∠AEB=∠AFM=90°.又∵∠BAE=∠MAF,∴△ABE∽△AMF.∴=,=,解得MF=20m.∴MN=MF+FN=20+0.8=20.8m.∴住宅楼的高度为20.8m.故答案为:20.8.【点评】本题考查的是相似三角形的应用,解答此题的关键是将实际问题转化为数学问题进行解答;此题需要转化为相似三角形的问题,利用相似三角形的判定与性质求解.22.一组数据4,0,1,﹣2,2的标准差是2.【分析】先算出平均数,再根据方差公式计算方差,求出其算术平方根即为标准差.【解答】解:数据4,0,1,﹣2,2的平均数为=[4+0+1﹣2+2]=1方差为S2=[(4﹣1)2+(0﹣1)2+(1﹣1)2+(﹣2﹣1)2+(2﹣1)2]=4∴标准差为2.故填2.【点评】计算标准差需要先算出方差,计算方差的步骤是:(1)计算数据的平均数;(2)计算偏差,即每个数据与平均数的差;(3)计算偏差的平方和;(4)偏差的平方和除以数据个数.标准差即方差的算术平方根,注意标准差和方差一样都是非负数.23.如图,在△ABC中,点D在AB上,请再添一个适当的条件,使△ADC∽△ACB,那么可添加的条件是∠ADC=∠ACB或∠ACD=∠B或AC2=AD•AB.【分析】已知△ADC和△ACB中有一个公共角,我们可以再添加一个角,从而利用有两组角对应相等的两个三角形相似来判定其相似.【解答】解:∵∠DAC=∠CAB,∴当∠ADC=∠ACB或∠ACD=∠B或AC2=AD•AB时,均可得出△ADC∽△ACB.故答案为:∠ADC=∠ACB或∠ACD=∠B或AC2=AD•AB【点评】这是一道开放性的题,答案不唯一.三、解答题:24.先化简再求值:,其中x=.【分析】先把括号里式子通分,再把除法转化为乘法,约分化为最简,最后代值计算.【解答】解:原式===﹣,当x=时,原式=﹣=﹣.【点评】本题主要考查分式的化简求值这一知识点,把分式化到最简是解答的关键.25.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)求出△ABC与△A′B′C′的位似比;(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.【分析】(1)位似图形对应点连线所在的直线经过位似中心,如图,直线AA′、BB′的交点就是位似中心O;(2)△ABC与△A′B′C′的位似比等于AB与A′B′的比,也等于AB与A′B′在水平线上的投影比,即位似比为3:6=1:2;(3)要画△A1B1C1,先确定点A1的位置,因为△A1B1C1与△ABC的位似比等于1.5,因此OA1=1.5OA,所以OA1=9.再过点A1画A1B1∥AB交O B′于B1,过点A1画A1C1∥AC交OC′于C1.【解答】解:(1)如图.(2)△ABC与△A′B′C′的位似比为1:2.(3)如图【点评】本题考查位似图形的意义及作图能力.画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.26.矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM,E是垂足.①求△ABM的面积;②求DE的长;③求△ADE的面积.【分析】①由M是BC的中点可得BM长度,那么△ABM的面积=×AB×BM,把相关数值代入即可求解;②由勾股定理易得AM长,可证得△ADE∽△MAB,那么利用对应边比等于相似比可求得DE长;③由相似可得AE的长,那么△ADE的面积=×AE×DE,把相关数值代入即可求解.【解答】解:①∵M是BC的中点,BC=6,∴MB=3,∵AB=4,∴△ABM的面积=×AB×BM=×4×3=6;②∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,∴∠DAE=∠AMB,∵DE⊥AM,∴∠DEA=90°,∴△ADE∽△MAB,∵AB=4,BM=3,∴AM=5,∴AE:MB=AD:AM=DE:AB,∴AE=3.6,DE=4.8.③△ADE的面积=×AE×DE=×3.6×4.8=8.64.【点评】解决本题的关键是利用相似三角形对应边成比例的性质求得所求三角形的长与宽.27.某城市平均每天处理垃圾700吨,有甲和乙两个处理厂处理,已知甲每小时可处理垃圾55吨,需要费用550元,乙厂每小时可处理垃圾45吨,需要费用495元.如果规定该城市每天用于处理垃圾的费用不得超过7370元,甲厂每天处理垃圾至少要多少吨?【分析】设甲厂每天处理垃圾x吨,分别求出甲、乙两场分别处理1吨垃圾需要的费用,然后根据每天用于处理垃圾的费用不得超过7370元,可得出不等式,解出即可.【解答】解:设甲厂每天处理垃圾x吨,由题知:甲厂处理每吨垃圾费用为=10元,乙厂处理每吨垃圾费用为=11元.则有10x+11(700﹣x)≤7370,解得:x≥330,答:甲厂每天处理垃圾至少330吨.【点评】此题考查了一元一次不等式的知识,解题关键弄清题意,找出合适的不等关系,列出不等式,再求解,难度一般.28.某广告公司将一块广告牌制作任务交给师徒两人,已知师傅单独完成时间是徒弟单独完成时间的,现由徒弟先做1天,师徒再合作2天完成.(1)师徒两人单独完成任务各需几天?(2)若完成后得到报酬540元,按各人完成的工作量计算报酬,该如何分配?【分析】工作量常用的等量关系:工作时间×工效效率=工作总量.本题等量关系为:师工作量+徒工作量=1.【解答】解:(1)设徒弟单独完成任务需x天,则师需天,依题意得解得x=6经检验,x=6是原方程的解∴=4答:师傅需要4天,徒弟需要6天.(2)师傅完成的工作量=,∴徒弟完成的工作量为,故每人各得报酬270元,答:每人各得270元.【点评】本题考查工作量常用等量关系.分析题意,找到合适的等量关系是解决问题的关键.此题涉及的公式:工作总量=工作效率×工作时间.29.为了让学生了解文明礼仪知识,增强文明意识,养成文明习惯.某中学在“文明日照,从我做起”知识普及活动中,举行了一次“文明礼仪知识”竞赛,共有3000名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行了统计.请你根据上面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:(1)求频率分布表中的m、n;(2)补全频率分布直方图;(3)你能根据所学知识确定“众数”、“中位数”在哪一组吗?(不要求说明理由)频率分布表:。
应用概率统计大学数学2试卷(A卷)附答案

2011-2012学年第 2 学期 考试科目: 大学数学Ⅱ一、填空题(本大题共6小题,每小题3分,共18分)1. 设A 、B 为两个随机事件,已知()0.3,()0.4,()0.5P A P B P A B ===,则()P AB =______________.2. 设随机变量X 服从参数为3的泊松分布,则(1)P X ≥= ______________. 3. 设二维离散型随机变量),(Y X 的联合分布律为:),(Y X 的联合分布函数为),(y x F ,则(1,3)F =______________.4. 设随机变量X 表示100次独立重复射击命中目标的次数,每次命中目标的概率为0.2, 则2X 的数学期望是______________.5. 设X 、Y相互独立,且都服从标准正态分布,则~Z =______________. (要求写出分布及其参数).6. 设由来自总体~(,0.81)X N μ,容量为9的样本得到样本均值5=X ,则未知参数μ的置信度为95%的置信区间为___________________.( 0.025 1.96u =) 二、单项选择题(本大题共6小题,每小题3分,共18分)1. 某人花钱买了C B A 、、三种不同的奖券各一张.已知各种奖券中奖是相互独立的, 中奖的概率分别为,02.0)(,01.0)(,03.0)(===C p B P A p 如果只要有一种奖券中奖此人就一定赚钱, 则此人赚钱的概率约为( ). ﻩ A. 0.05ﻩB . 0.06ﻩC. 0.07ﻩﻩD . 0.082. 设A 、B 为两个随机事件,且B A ⊂,()0>B P ,则下列选项必然正确的是( ). A. ()()B A P A P < B. ()()B A P A P >C. ()()B A P A P ≤ D. ()()B A P A P ≥ 3. 下列各函数中可以作为某个随机变量X 的分布函数的是( ).1,0x ⎧≤⎪0,0x <⎧⎪C . x x F sin )(= D. 211)(x x F +=4. 设随机变量()2~2,3X N ,随机变量25Y X =-+, 则~Y ( ).A. (1,41)N B . (1,36)N C. (1,18)N - D. (1,13)N -5. 设某地区成年男子的身高()100,173~N X ,现从该地区随机选出20名男子,则这20名男子身高平均值的方差为( ).A . 100 B. 10 C. 5 D . 0.56. 设12,,,n X X X ⋅⋅⋅是取自总体X 的一个样本, X 为样本均值,则不是总体期望μ的无偏估计量的是( ).A . X B. 123X X X +- C. 1230.20.30.5X X X ++ D. 1nii X=∑三、计算题(本大题共4小题,共40分)1.(本题8分)已知一批产品中90%是合格品,检查时,一个合格品被误认为是次品的概率为0.05,一个次品被误认为是合格品的概率为0.02,求: (1)一个产品经检查后被认为是合格品的概率; (2)一个经检查后被认为是合格品的产品确是合格品的概率.2.(本题8分)设离散型随机变量X 只取1,2,3三个可能值,取各相应值的概率分别是21,,4a a -,求:(1)常数a ; (2) 随机变量X 的分布律; (3) 随机变量X 的分布函数()F x .3.(本题10分)设随机变量X 的密度函数为:()1()2x f x e x -=-∞<<+∞.(1) 求{1}P X <; (2) 求2Y X =的密度函数.4.(本题14分)设随机变量X 与Y 相互独立,它们的密度函数分别为1,03()30,X x f x ⎧≤≤⎪=⎨⎪⎩其他, 33,0()0,0y Y e y f y y -⎧>=⎨≤⎩ 试求:(1) (,)X Y 的联合密度函数; (2) ()P Y X <; (3)()D X Y -.四、解答题(本大题共3小题,每小题8分,共24分)1. 从一台车床加工的一批轴料中抽取15件测量其椭圆度,计算得样本方差220.025s =,已知椭圆度服从正态分布,问该批轴料椭圆度的总体方差与规定的方差200.0004σ=有无显著差异(取检验水平0.05α=)?(20.025(14)26.1χ=, 20.975(14) 5.63χ=, 20.025(15)27.5χ=,20.975(15) 6.26χ=)2. 某粮食加工厂用4种不同的方法贮藏粮食,一段时间后,分别抽样化验其含水率,每种方法重复试验次数均为5次,所得粮食含水率的方差分析表的部分数据如下. (0.05(4,19) 5.01F=,0.01(4,16) 4.77F=,0.01(3,16) 5.29F=) (1) 完成下面的方差分析表.(2) 给出分析结果.3. 有人认为企业的利润水平和它的研究费用间存在着近似的线性关系. 下面是某10个企业的利润水平(x )与研究费用(y )的调查资料:102101=∑=i ix,2390101=∑=i i y ,10661012=∑=i ix ,6243001012=∑=i iy ,25040101=∑=i i i y x建立研究费用y 与企业利润水平x 的回归直线方程.2011-2012学年第 2 学期 大学数学Ⅱ 华南农业大学期末考试试卷(A 卷)-参考答案 一、1. 0.8; 2. 31e --; 3.518; 4. 416 ; 5. )1(t ; 6. (4.412,5.588) 二、1. B 2. C 3. A 4. B 5. C 6. D 三、1. 解 设A =“任取一产品,经检验认为是合格品” B =“任取一产品确是合格品” 依题意()0.9,()0.1,()0.95,()0.02P B P B P A B P A B ==== (2分)则(1)()()(|)()(|)P A P B P A B P B P A B =+0.90.950.10.020.857.=⨯+⨯=(5分) (2) ()(|)0.90.95(|)0.9977()0.857P B P A B P B A P A ⨯===. (8分)2. 解 (1) 由2114a a -+=得1231().22舍去或a a ==- (3分) (2) X 的分布律为(5分)(3) X 的分布函数为0,10,111,12,1244()113,23,234241111,3,3424x x x x F x x x x x <⎧<⎧⎪⎪⎪≤<⎪≤<⎪⎪⎪==⎨⎨+≤<⎪⎪≤<⎪⎪⎪⎪≥++≥⎩⎪⎩ (8分) 3. 解(1)111011{1}{11}12x x P X P X e dx e dx e---<=-<<===-⎰⎰. (3分)(2)当0y ≤时,()()()20F y P Y y P X y =<=<=; (5分) 当0y >时,()()(2xx F y P X y P X dx dx --=<=<<== (8分) 所以2Y X =的密度函数为0,0()()0y f y F y y ≤⎧⎪'==>. (10分)4. 解 (1)因为随机变量X 与Y 相互独立, ( 1分)所以它们的联合密度函数为:3,03,0(,)()()0,y X Y e x y f x y f x f y -⎧≤≤>==⎨⎩其他 (3分)330(1)x e dx -=-⎰3390181()333x x e e --=+=+()9183e -=+ (8分) (3)解:由密度函数可知~(0,3),~(3)X U Y E (10分)所以,22(30)311(),(),12439D X D Y -==== (12分) 由X 与Y 相互独立,得3131()()()4936D X Y D X D Y -=+=+=(14分) 四、1. 解 检验假设 20:0.0004H σ=,21:0.0004H σ≠. (1分)依题意,取统计量:2222(1)~(1)n S n χχσ-=-,15n =. (3分)查表得临界值:220.0252(1)(14)26.1n αχχ-==,220.97512(1)(14) 5.63n αχχ--==, (5分)计算统计量的观测值得: 22140.02521.8750.0004χ⨯==. (6分) 因2220.9750.025(14)(14)χχχ<<,故接受原假设0H ,即认为总体方差与规定的方差无显著差异. (8分) 2. 解 (1)(2) 解 因为F =5.6681>0.01(3,16) 5.29F =,所以拒绝0H ,即认为不同的贮藏方法对粮食含水率的影响在检验水平0.01α=下有统计意义. (8分)3. 解 2.10=x ,239=y (2分)6.252.10101066221012=⨯-=-=∑=x n x l i i xx (3分)6622392.101025040101=⨯⨯-=-=∑=y x n y x l i i i xy (4分)故1662ˆ25.8625.6xy xx l l β==≈;01ˆˆ23925.8610.224.77y x ββ=-=-⨯=- (6分)。
北师大2011——2012学年度第二学期六年级数学模拟试(1)

2011——2012学年度第二学期六年级数学模拟试(1)一、计算题:(22分)1、 直接写得数:(4分)87×65= 75×31= 43×60= 61-71= 54+41= 43÷32= 207÷103= 125×259= 2、 脱式计算( 12分)(54-103)×1415 2-136÷269-3222.5×4.8+7.75×48 [4-(43-83)]×2943、解方程:(6分)8 x - 1=6.2 3 Y - 27 Y = 7540% x二、填空题:(第11题5分,其余每小题2分,共25分)1、 一个分数的分母是最小的合数,分子是奇数中的最小质数,这个分数的倒数是( )。
2、28:( )= ( — )= 0.35 =( )%=( )÷403、某次人口普查的结果,全国人口是1360903000人,横线上的数改写成用“万”作单位是( )人,读作( )人。
4、黄老师把5000元存入银行,定期两年,年利率3.4%,到期时,黄老师可取回 ( )元。
5、你知道0有哪些作用吗?在2008北京奥运会中,香港的金牌数是0, “2008”中的“0”( );金牌数是0中的“0”( )。
6、下面的括号填上适当的分数。
3升50毫升 = ( )升 3时45分 =( )时 600公顷 =( )平方千米 750千克 =( )吨 7、李芸和爸爸、妈妈到旅行社报名时,把三个身份证号码交给工作人员,分别是440721************ 、440782************、 440721************,你认为妈妈的身份证号码是( )。
8、一项工程,甲单独做要20天完成,乙单独做要30天完成,甲、乙两人的效率比是( ) 9、新捷鞋业在“五一”当天卖出同一款的女装皮鞋30双,尺码如下表: 这些鞋的尺码中的中位数是( ),众数是( )。
天津科技大学2011-2012学年第一学期《概率论与数理统计》(多概)期末考试试题(A卷)参考答案及评分标准

4
2011-2012 学年第一学期《概率论与数理统计》 (多概)期末考试试题(A 卷)参考答案及评分标准
查表得 1 / 2 ( n 1)
2 2 2 02..975 (8) 2.18, / 2 ( n 1) 0.025 (8) 17.53 , 7 分
而 0.975 (8) 2.18
九、某种虾的身长 X (单位:cm)服从正态分布 N ( , 2 ) ,现在随机抽取 9 只,算得平
均身长为 x 6 (cm) ,样本标准差 s 0.5745 (cm),求 的置信水平为 0.95 的置信区间. (本题 8 分) 解:由于 未知,故 的置信区间为 ( x
s t / 2 n
2
2
~(
(B) F ( n,n)
1) (C) F ( n,
(D) F (1,n)
三、某灯泡厂有甲、乙两条生产线,它们各自出产的灯泡中寿命大于 2500 小时的分别占有
80%和 90%,从它们出产的灯泡中各自随机地抽取一个, (1)求两个灯泡寿命都大于 2500 小 时的概率; (2)求两个灯泡中至少有一个寿命大于 2500 小时的概率. (本题 8 分)
8000 0.2 40 . 3 分
P(8100 X n 10000) P( X n np np (1 p )
8100 8000 40
X n np np (1 p )
10000 8000 )5分 40
P(2.5
50) (50) (2.5) 7 分 1 0.9938 0.0062 . 8 分
解:用 A, B 分别表示从甲、乙两个流水线上的产品中抽取的灯泡寿命大于 2500 小时,则 它们相互独立. 2 分 (1) P( AB) 3 分 P( A) P( B) 4 分 0.8 0.9 0.72 ; 5 分 (2) P( A
(完整版)实变函数期末考试卷A及参考答卷

2011—2012学年第1学期数计学院09级数学与应用数学专业(1、2班)《实变函数》期末考试卷(A)考生考试诚信承诺书在我填写考生信息后,表示我已阅读和理解《龙岩学院考试纪律与违纪处分办法》的有关规定,承诺在考试中自觉遵规守纪,如有违反将接受处理;我保证在本科目考试中,本人所提供的个人信息是真实、准确的。
考生签名:实变函数期末考试卷(A )2009级本科1、2班用 考试时间2012年01月 04日一 填空题(每小题3分,满分24分) 1 我们将定义在可测集qE ⊂上的所有L 可测函数所成的集合记为()M E .任取()f M E ∈,都可以确定两个非负可测函数:()()()(),0,0,0.f x x E f fx x E f +∈>⎧=⎨∈≤⎩当时当时 和()()()()0,0,,0.x E f fx f x x E f -∈>⎧=⎨-∈≤⎩当时当时分别称为f 的正部和负部。
请你写出()()(),,f x fx f x +-和()f x 之间的关系:()f x =,()f x =。
2 上题()M E 中有些元素ϕ被称为非负简单函数,指的是:12k E E E E =是有限个互不相交的可测集的并集,在i E 上()i x c ϕ≡(非负常数)(1,2,,i k =).ϕ在E 上的L 积分定义为:()Ex dx ϕ=⎰,这个积分值可能落在区间中,但只有当时才能说ϕ是L 可积的。
3 若()f M E ∈是非负函数,则它的L 积分定义为:()Ef x dx =⎰,这个积分值可能落在区间中,但只有当时才能说f 是L 可积的。
4 ()M E 中的一般元素f 称为是积分确定的,如果f +和f -, 即()Efx dx +⎰和()E f x dx -⎰的值;但只有当时才能说f 是L 可积的,这时将它的积分定义为:()Ef x dx =⎰。
5 从()M E 中取出一个非负函数列(){}n f x ,则法图引理的结论是不等式:;如果再添上条件和就试卷 共 8 页 第 2 页得到列维定理的结论:。
2011-2012学年北京市西城区初三数学第一学期期末数学试题(南区)(含答案)

北京市西城区2011—2012学年度第一学期期末试卷(南区)九年级数学 2012.1考生须知1.本试卷共6页,共五道大题,25道小题,满分120分。
考试时间120分钟。
2.试题答案一律填涂或书写在答题纸上,在试卷上作答无效。
3.在答题纸上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.抛物线2(1)1y x =-+的顶点坐标为A .(1,1)B .(1,1)-C .(1,1)-D .(1,1)--2.若相交两圆的半径分别为4和7,则它们的圆心距可能是A .2B .3C . 6D .113.在Rt △ABC 中,∠ C =90°,若BC =1,AB 5tan A 的值为A 5B 25C .12D .24. 如图,在⊙O 中,直径AB ⊥弦CD 于E ,连接BD ,若∠D =30°, BD =2,则AE 的长为 A .2 B .3 C .4 D .55.下列图形中,中心对称图形有A .4个B .3个C .2个D .1个6.抛掷一枚质地均匀的正方体骰子,出现大于3点的概率为 A .21 B .31 C .41 D .617.如图,抛物线2y ax bx c =++经过点(-1,0),对称轴为x =1,则下列结论中正确的是A .0>aB .当1>x 时,y 随x 的增大而增大C .0<cD .3x =是一元二次方程20ax bx c ++=的一个根8.如图,在平面直角坐标系xOy 中,(2,0)A ,(0,2)B ,⊙C 的圆心为点(1,0)C -,半径为1.若D 是⊙C 上的一个动点,线段DA 与y 轴交于E 点,则△ABE 面积的最大值是 A .2 B . 83C .2+D . 2-二、填空题(本题共16分,每小题4分)9.如图,⊙O 是△ABC 的外接圆,若∠OCB =40°,则∠A= °.10.将抛物线2y x =先向下平移1个单位长度后,再向右平移1个单位长度,所得抛物线的解析式是 .11.如图,在Rt △ABC 中,∠ACB =90°,∠B =30°,AB =4.以斜边AB 的中点D 为旋转中心,把△ABC 按逆时针方向旋转 α角(0120α︒<<︒),当点A 的对应点与点C 重合时,B ,C 两点的对应点分别记为E ,F ,EF 与AB 的交点为G ,此时 α等于 ° ,△DEG 的面积为 .12.已知二次函数212y x x =-+,(1)它的最大值为 ;(2)若存在实数m , n 使得当自变量x 的取值范围是m ≤x ≤n 时,函数值y 的取值范围恰好是3m ≤y ≤3n ,则m= ,n= .13.计算:2cos30602sin 45︒+︒-︒.14.如图,网格中每个小正方形的边长均为1,且点A ,B ,C ,P 均为格点.(1) 在网格中作图:以点P 为位似中心,将△ABC 的各边长放大为原来的两倍,A ,B ,C 的对应点分别为A 1 ,B 1 ,C 1;(2) 若点A 的坐标为(1,1),点B 的坐标为(3,2),则(1)中点C 1的坐标为 .15.已知抛物线245y x x =+-.(1)直接写出它与x 轴、y 轴的交点的坐标;(2)用配方法将245y x x =+-化成2()y a x h k =-+的形式.16.如图,三角形纸片ABC 中,∠BCA =90°,∠A =30°,AB =6, 在AC 上取一点 E ,沿BE 将该纸片折叠,使AB 的一部分 与BC 重合,点A 与BC 延长线上的点D 重合,求DE 的长.17.学校要围一个矩形花圃,花圃的一边利用足够长的墙,另三边用总长为36米的篱笆恰好围成(如图所示). 设矩形的一边AB 的长为x 米(要求AB <AD ),矩形 ABCD 的面积为S 平方米.(1)求S 与x 之间的函数关系式,并直接写出自变量x 的取值范围; (2)要想使花圃的面积最大,AB 边的长应为多少米?18.如图,在Rt △ABC 中,90C ∠=︒,AB 的垂直平分线与BC ,AB 的交点分别为D ,E . (1)若AD =10,4sin 5ADC ∠=,求AC 的长和tan B 的值;(2)若AD=1,ADC ∠=α,参考(1)的计算过程直接写 出tan 2α的值(用sin α和cos α的值表示).19.如图所示,在平面直角坐标系xOy 中,正方形PABC 的边长为1,将其沿x 轴的正方向连续滚动,即先以顶点A 为旋转中心将正方形PABC 顺时针旋转90°得到第二个正方形,再以顶点D 为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n 个正方形.设滚动过程中的点P 的坐标为(,)x y .(1)画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P 的坐标; (2)画出点(,)P x y 运动的曲线(0≤x ≤4),并直接写出该曲线与x 轴所围成区域的面积.20.已知函数2y x bx c =++(x ≥ 0),满足当x =1时,1y =-,且当x = 0与x =4时的函数值相等. (1) 求函数2y x bx c =++(x ≥ 0)的解析式并 画出它的图象(不要求列表);(2)若()f x 表示自变量x 相对应的函数值,且2 (0),() 2 (0),x bx c x f x x ⎧++≥=⎨-<⎩ 又已知关于x 的 方程()f x x k =+有三个不相等的实数根,请利用图象直接写出实数k 的取值范围.21.已知:如图,AB 是⊙O 的直径,AC 是弦,∠BAC 的平分线与⊙O 的交点为D ,DE ⊥AC ,与AC 的延长线交于 点E .(1)求证:直线DE 是⊙O 的切线; (2)若OE 与AD 交于点F ,4cos 5BAC ∠=,求DF AF 的值.22.阅读下列材料:题目:已知实数a ,x 满足a >2且x >2,试判断ax 与a x +的大小关系,并加以说明. 思路:可用“求差法”比较两个数的大小,列出ax 与a x +的差()y ax a x =-+再说明y 的符号即可.现给出如下利用函数解决问题的方法:简解:可将y 的代数式整理成(1)y a x a =--,要判断y 的符号可借助函数(1)y a x a =--的图象和性质解决.参考以上解题思路解决以下问题:已知a ,b ,c 都是非负数,a <5,且 2220a a b c ---=,2230a b c +-+=. (1)分别用含a 的代数式表示4b ,4c ; (2)说明a ,b ,c 之间的大小关系.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知抛物线2(2)2y kx k x =+--(其中0k >).(1)求该抛物线与x 轴的交点及顶点的坐标(可以用含k 的代数式表示); (2)若记该抛物线顶点的坐标为(,)P m n ,直接写出n 的最小值; (3)将该抛物线先向右平移12个单位长度,再向上平移1k个单位长度,随着k 的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).24.已知:⊙O 是△ABC 的外接圆,点M 为⊙O 上一点.(1)如图,若△ABC 为等边三角形,BM =1,CM =2, 求AM 的长;(2) 若△ABC 为等腰直角三角形,∠BAC =90︒,BM a =,CM b =(其中b a >),直接写出AM 的长(用含有a ,b 的代数式表示).25. 已知:在如图1所示的平面直角坐标系xOy 中,A ,C 两点的坐标分别为(2,3)A ,(,3)C n -(其中n >0),点B 在x 轴的正半轴上.动点P 从点O 出发,在四边形OABC 的边上依次沿O —A —B —C 的顺序向点C 移动,当点P 与点C 重合时停止运动.设点P 移动的路径的长为l ,△POC 的面积为S ,S 与l 的函数关系的图象如图2所示,其中四边形ODEF 是等腰梯形.(1)结合以上信息及图2填空:图2中的m = ; (2)求B ,C 两点的坐标及图2中OF 的长;(3)在图1中,当动点P 恰为经过O ,B 两点的抛物线W 的顶点时, ① 求此抛物线W 的解析式;② 若点Q 在直线1y =-上方的抛物线W 上,坐标平面内另有一点R ,满足以B ,P ,Q ,R 四点为顶点的四边形是菱形,求点Q 的坐标.北京市西城区2011 — 2012学年度第一学期期末试卷(南区)九年级数学参考答案及评分标准2012.1 一、选择题(本题共32分,每小题4分)阅卷说明:第10题写成2(1)1y x=--不扣分;第11题每空各2分;第12题第(1)问2分, 第(2)问每空各1分.三、解答题(本题共30分,每小题5分)13.解:原式= 222⨯…………………………………………………3分= 22+.……………………………………………………………………5分14.解:(1)…………………………………………3分(2)点C1的坐标为(2,8). ……………………………………………………5分图115.解:(1)抛物线与x 轴的交点的坐标为(5,0) (1,0)-和. …………………………2分抛物线与y 轴的交点的坐标为(05)-,. …………………………………3分 (2)245y x x =+-2(44)9x x =++-…………………………………………………………4分2(2)9x =+-. …………………………………………………………5分 16.解: 在RtΔACB 中,∠ACB =90°,AB =6, ∠A =30°,(如图2) ∴ 362121=⨯==AB BC . ………………………1分 ∵ 沿BE 将ΔABC 折叠后,点A 与BC 延长线上的点D∴ BD=AB=6,∠D =∠A =30°.……………………3分∴CD=BD -BC =6-3=3. ……………………………4分在RtΔDCE 中,∠DCE =90°,CD =3, ∠D =30°,∴3223330cos ===CD DE . ………………………………………………5分17.解:(1)∵ 四边形ABCD 是矩形,AB 的长为x 米, ∴ CD=AB=x (米).∵ 矩形除AD 边外的三边总长为36米,∴ 362BC x =-(米).………………………………………………………1分 ∴ 2(362)236S x x x x =-=-+. ……………………………………………3分 自变量x 的取值范围是012x <<. …………………………………………4分 ( 说明:由0<x <36-2x 可得012x <<.)(2)∵222362(9)162S x x x =-+=--+,且9x =在012x <<的范围内 ,∴ 当9x =时,S 取最大值.即AB 边的长为9米时,花圃的面积最大.…………………………………5分18.解:(1)在Rt △ACD 中,90C ∠=︒, AD =10,4sin 5ADC ∠=,(如图3) ∴ 4sin 1085AC AD ADC =⋅∠=⨯=.……1分3cos 1065CD AD ADC =⋅∠=⨯=. ∵ DE 垂直平分AB ,∴ 10BD AD ==.……………………………2分 ∴ 16BC CD BD =+=. ……………………3分 在Rt △ABC 中,90C ∠=︒,∴ 81tan 162AC B BC ===.……………………………………………………4分 (2)sin tan 21cos ααα=+.(写成1cos sin αα-也可) ……………………………………5分四、解答题(本题共20分,每小题5分) 19.解:(1)第三个和第四个正方形的位置 如图4所示.……………………2分 第三个正方形中的点P 的坐标为 (3,1). …………………………3分(2)点(,)P x y 运动的曲线(0≤x ≤4)如图4所示. …………………………4分它与x 轴所围成区域的面积等于1π+. ……………………………………5分20.解:(1)∵ 函数2y x bx c =++(x ≥0)满足当x =1时,1y =-, 且当x = 0与x =4时的函数值相等,∴ 11,2.2b c b ++=-⎧⎪⎨-=⎪⎩解得 4b =-,2c =.…………………………………………………………2分 ∴ 所求的函数解析式为242y x x =-+(x ≥0). …………………………3分 它的函数图象如图5所示.……………………………………………………4分(2)k 的取值范围是22k -<≤.(如图6)……………………………………………5分 21.(1)证明:连接OD .(如图7) ∵ AD 平分∠BAC ,∴ ∠1=∠2.…………………………………………………………………1分 ∵ OA =OD , ∴ ∠1=∠3. ∴ ∠2=∠3.∴ OD ∥AE .∵ DE ⊥AC , ∴ ∠AED =90°.∴ 18090ODE AED ∠=︒-∠=︒.∴ DE ⊥OD . ……………………………2分 ∵ OD 是⊙O 的半径,∴ 直线DE 是⊙O 的切线. ………………………………………………3分(2)解:作OG ⊥AE 于点G .(如图7) ∴ ∠OGE =90°.∴ ∠ODE =∠DEG =∠OGE =90°. ∴ 四边形OGED 是矩形.∴ OD =GE .……………………………………………………………………4分 在Rt △OAG 中, ∠OGA =90°,4cos 5BAC ∠=,设AG =4k ,则OA =5k . ∴ GE =OD =5k . ∴ AE =AG +GE =9k . ∵ OD ∥GE , ∴ △ODF ∽△EAF . ∴59DF OD AF AE ==.……………………………………………………………5分 22.解:(1)∵ 2220a a b c ---=,2230a b c +-+=,∴ ⎪⎩⎪⎨⎧+=--=+.322,222a b c a a c b消去b 并整理,得243c a =+.………………………1分消去c 并整理,得2423b a a =--. ………………2分(2)∵ ()()()411332422--=+-=--=a a a a a b , 将4b 看成a 的函数,由函数24(1)4b a =--的性质结合它的图象(如图8所示),以及a ,b 均为非负数得a ≥3.又 ∵ a <5,∴ 3≤a <5.……………………………………………………………………3分∵ 224()63(3)12b a a a a -=--=--,将4()b a -看成a 的函数,由函数24()(3)12b a a -=--的性质结合它的图象(如图9所示)可知,当3≤a <5时,4()0b a -<.∴ b <a . ……………………………………………4分∵ 24()43(1)(3)c a a a a a -=-+=--,a ≥3,∴ 4()c a -≥0.∴ c ≥a .∴ b <a ≤c . ………………………………………5分阅卷说明:“b <a ,b <c ,a ≤c ”三者中,先得出其中任何一个结论即可得到第4分,全写对得到5分.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.解:(1)令0y =,得方程 2(2)20kx k x +--=.整理,得 (1)(2)0x kx +-=.解得 11x =-,22x k= . ∴ 该抛物线与x 轴的交点坐标为(1,0)-,2(,0)k. ………………………2分 抛物线2(2)2y kx k x =+--的顶点坐标为2244(,)24k k k k k-++-. ………3分 (2)|n |的最小值为 2 . …………………………………………………………4分 (3)平移后抛物线的顶点坐标为214(,)4k k k k+-.…………………………………5分由1,14x k k y ⎧=⎪⎪⎨⎪=--⎪⎩可得 114y x =-- . ∴ 所求新函数的解析式为114y x=--. …………………………………7分 24.解:(1)因AB =AC 且∠BAC=60°,故将△ABM 绕点A 逆时针旋转60︒得△ACN ,则△ABM ≌△ACN ,(如图10)………………………………………………1分∴ ∠BAM =∠CAN ,∠ABM =∠ACN ,AM =AN ,BM =CN .∵ 四边形ABMC 内接于⊙O ,∴ ∠ABM +∠ACM =180︒.∴ ∠ACN +∠ACM =180︒.∴ M ,C ,N 三点共线.……………………2分∵ ∠BAM =∠CAN ,∴ ∠BAM +∠MAC =∠CAN +∠MAC =60︒, 即∠MAN =60︒. ………………………………………………………………3分∵ AM =AN ,∴ △AMN 是等边三角形.……………………………………………………4分 ∴ AM =MN =MC +CN =MC +BM =2+1=3. ……………………………………5分(2)AM)b a -)b a +.……………………………………………7分 25.解:(1)图2中的m1分(2)∵ 图11(原题图2)中四边形ODEF 是等腰梯形,点D 的坐标为(,12)D m ,∴ 12E D y y ==,此时原题图1中的点P 运动到与点B 重合,∴ 1131222BOC C S OB y OB ∆=⨯⨯=⨯⨯=. 解得 8OB =,点B 的坐标为(8,0). ……………………………………2分此时作AM ⊥OB 于点M ,CN ⊥OB 于点N .(如图12).∵ 点C 的坐标为(,3)C n -,∴ 点C 在直线3y =-上.又由图11(原题图2)中四边形ODEF 是等腰梯形可知图12中的点C 在过点O 与AB 平行的直线l 上,∴ 点C 是直线3y =-与直线l 的交点,且ABM CON ∠=∠.又∵ 3A C y y ==,即AM= CN ,可得△ABM ≌△CON .∴ ON=BM=6,点C 的坐标为(6,3)C -.……………………………………3分 ∵ 图12中AB ==∴ 图11中DE =,2D OF x DE =+= …………………4分(3)①当点P 恰为经过O ,B 两点的抛物线W 的顶点时,作PG ⊥OB 于点G .(如图13)∵ O ,B 两点的坐标分别为(0,0)O ,(8,0)B ,∴ 由抛物线的对称性可知P 点的横坐标为4,即OG=BG=4.由3tan 6AM PG ABM BM BG∠===可得PG=2. ∴ 点P 的坐标为(4,2)P .………………5分设抛物线W 的解析式为(8)y ax x =-(a ≠0).∵ 抛物线过点(4,2)P ,∴ 4(48)2a -=. 解得 18a =-. ∴ 抛物线W 的解析式为218y x x =-+.…………………………………6分 ②如图14.i )当BP 为以B ,P ,Q ,R 四点为顶点的菱形的边时,∵ 点Q 在直线1y =-上方的抛物线W 上, 点P 为抛物线W 的顶点,结合抛物线的对称性可知点Q 只有一种情况,点Q 与原点重合,其坐标为1(0,0)Q .……………………………………………………………………7分 ii )当BP 为以B ,P ,Q ,R 四点为顶点的菱形的对角线时,可知BP 的中点的坐标为(6,1),BP 的中垂线的解析式为211y x =-.∴ 2Q 点的横坐标是方程212118x x x -+=-的解.将该方程整理得28880x x +-=.解得4x =-± 由点Q 在直线1y =-上方的抛物线W 上,结合图14可知2Q 点的横坐标为4.∴ 点2Q 的坐标是219)Q . …………………………8分综上所述,符合题意的点Q 的坐标是1(0,0)Q ,219)Q .。
2020-2021学年人教版五年级下册期中模拟测试数学试卷(A卷)(word版 含答案)

2020-2021学年人教版五年级下册期中模拟测试数学试卷(A卷)学校:___________姓名:___________班级:___________考号:___________一、填空题1.3.02m³=(________)dm³90020cm³=(________)L4.07m³=(________)m³(________)dm³9.08dm³=(________)L(________)mL2.一个正方体的表面积是54dm²,体积是(______)dm³。
3.一个两位数既是5的倍数,也是3的倍数,而且是偶数,这个数最小是(______),最大是(______)。
4.16和24的公因数有(________);8和12的公倍数有(________)。
5.一个长方体的体积是72cm³、长6cm 、宽5cm,高(________)cm 。
6.一个容量是15升的药桶,装满了止咳药水,把这些药水分别装在100毫升的小瓶里,可以装满(________)瓶。
7.在括号里填上适当的单位名称。
旗杆高15(______)教室面积80(______)油箱容积16(______)一瓶墨水60(______)8.左图从(_____)面看和(______)面看都是.从(________)面看是.9.在1~10中,(______)既不是质数,也不是合数。
既是质数,也是偶数的是(______)。
既是奇数,又是合数的是(______)。
10.一个长方体棱长总和是36cm,宽和高分别是3cm、2cm,它的体积是(______)cm³。
11.用3个棱长是2dm的正方体合成一个长方体,长方体的表面积比3个正方体的表面积之和少(________)dm²。
12.一个立体图形,从正面看是,从左面看是,要搭成这样的立体图形,至少要用(________)个小正方体,最多要用(________)个小正方体。
2011-2012学年高二数学上学期 命题范围单元测试(3) 新人教A版选修1-1

2011—2012学年度上学期单元测试高二数学试题(3)【人教版】命题范围: 选修1-1第Ⅰ卷(选择题 共60分)一、选择题:(共12小题,每小题5分,共60分)在下列各小题的四个选项中,只有一项是符合题目要求的.请将选项前的字母填入下表相应的空格内. 1.对抛物线24y x =,下列描述正确的是 ( )A .开口向上,焦点为(0,1)B .开口向上,焦点为1(0,)16 C .开口向右,焦点为(1,0) D .开口向右,焦点为1(0,)162.已知A 和B 是两个命题,如果A 是B 的充分条件,那么A ⌝是B ⌝的 ( )A .充分条件B .必要条件C .充要条件D .既不充分也不必要条件 3.抛物线y x 22=的准线方程是 ( )A .81=y B .21=y C .81-=y D .21-=y 4.有下列4个命题:①“菱形的对角线相等”; ②“若1xy =,则x ,y 互为倒数”的逆命题;③“面积相等的三角形全等”的否命题;④“若a b >,则22a b >”的逆否命题。
其中是真命题的个数是 ( ) A .1个 B .2个 C .3个 D .4个 5.如果p 是q 的充分不必要条件,r 是q 的必要不充分条件;那么 ( )A .p r ⌝⌝⇒B .p r ⌝⌝⇐C .p r ⌝⌝⇔D .p r ⇔6.若方程x 2+ky 2=2表示焦点在x 轴上的椭圆,则实数k 的取值范围为 ( ) A .(0,+∞) B .(0,2) C .(1,+∞) D .(0,1) 7.已知命题p :c b a ,,成等比数列,命题q :2b ac =,那么p 是q 的 ( ) A .必要不充分条件 B .充要条件 C .充分不必要条件 D .既不充分也不必要条件8.下列说法中正确的是 ( ) A .一个命题的逆命题为真,则它的逆否命题一定为真 B .“a b >”与“ a c b c +>+”不等价C .“220a b +=,则,a b 全为0”的逆否命题是“若,a b 全不为0, 则220a b +≠”D .一个命题的否命题为真,则它的逆命题一定为真9.已知函数()f x 在R 上满足2()2(2)88f x f x x x =--+-,则曲线()y f x =在点(1,(1))f 处的切线方程是( )A .21y x =-B .y x =C .32y x =-D .23y x =-+10.已知圆的方程422=+y x,若抛物线过定点(0,1),(0,1)A B -且以该圆的切线为准线,则抛物线焦点的轨迹方程是 ( )A .)0(14322≠=+y y xB .)0(13422≠=+y y xC .)0(14322≠=+x y xD .)0(13422≠=+x y x11.函数x e x x f )3()(-=的单调递增区间是 ( )A .)2,(-∞B .(0,3)C .(1,4)D .),2(+∞ 12.已知直线y=x+1与曲线y ln()x a =+相切,则α的值为 ( )A .1B .2C .-1D .-2第II 卷(非选择题 共90分)二、填空题:(共4小题,每小题5分,共20分)请将答案直接添在题中的横线上. 13.曲线21xy x =-在点()1,1处的切线方程为 _____ ___ . 14.命题“2,x x R x >∈∃+”的否定是 .15.以)0,1(-为中点的抛物线x y 82-=的弦所在直线方程为: .16.若14122222=--+my m x 表示双曲线方程,则该双曲线的离心率的最大值是 .三、解答题:(共6小题,共70分)解答应写出文字说明,证明过程或演算步骤。
广东省东莞市2011-2012学年高一上学期期末考试数学试题(A卷)有答案

广东省东莞市2011-2012学年度第一学期教学质量检测高一数学(A 卷)2012-1-10一 、选择题(本大题共10小题,每小题5分,共50分.每小题各有四个选择支,仅有一个选择支正确.)1.已知全集{1234567}U =,,,,,,,{245}A =,,,则A =C U ( )A . ΦB . {246},, C . {1367},,, D .{1357},,, 2.下列命题中,正确的是( )A .经过不同的三点有仅有一个平面B .分别在两个平面内的两条直线一定是异面直线C .垂直于同一条直线的两条直线平行D .垂直于同一个平面的两条直线平行3.已知Rt ABC ∆的顶点坐标分别为(51)A -,,(11)B ,,(2)C m ,,若90C ∠=,则实数m 的值为( )A .2或2-B .2C .2-D .34.一个圆柱的侧面展开图是一个正方形,这个圆柱的表面积与侧面积的比是( )A .124ππ+ B .122ππ+ C .12ππ+ D .142ππ+ 5.三个数0.3log 6a =,60.3b =,0.36c =,则的大小关系是( )A .b c a <<B .a c b <<C .b a c <<D .a b c << 6.函数2()ln f x x x=-的零点所在的大致区间是( ) A .1(1)e,B .(12),C . (23),D .()e +∞, 7.已知直线1:0l ax y a -+=,2:(23)0l a x ay a -+-=互相平行,则a 的值是( ) A .1 B .3- C .1或3- D .08.利用斜二测画法画平面内一个三角形的直观图得到的图形还是一个三角形,那么直观图三角形的面积与原来三角形面积的比是( )ABCD9.已知点(10)A ,,(10)B -,,过点(01)C -,的直线l 与线段AB 相交,则直线l 的倾斜角范围是( )A .[45135], B .[4590)(90135],,C .[045][135180],,D .[0135],10.已知函数210()210x x x f x x x ⎧++≥=⎨+<⎩,,.若2()(2)f m f m <-,则实数m 的取值范围是( )A .(1)(2)-∞-+∞ ,, B .(12)-, C .(21)-, D .(2)(1)-∞-+∞ ,, 二、填空题(本大题共4小题,每小题5分,共20分) 11.幂函数()f x的图象过点(3 ,则()f x12.已知函数()f x 是定义在R 上的奇函数,当x 2()log 1f x x =+,则(4)f -= .13.一个几何体的三视图如图所示,俯视图是边长为2的正方形,正视图与侧视图是全等的等腰直角三角形,则此 几何体的侧棱长等于 .14.规定符号“*”表示两个正实数a 、b 之间的运算,即a b a b *=+,已知11k *=,则函数()(0)f x k x x =*>的值域是 .三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤) 15.(本小题满分12分)已知集合{|17}A x x =≤<,2{|log (2)3}B x x =-<,{|}C x x a =<,全集为实数集R .(1) 求A B ;(2) 如果A C ≠Φ ,且B C =Φ ,求实数a 的取值范围.16.(本小题满分13分)设直线1:2l y x =与直线2:3l x y +=交于P 点.(1) 当直线m 过P 点,且与直线0:20l x y -=时,求直线m 的方程;(2) 当直线m 过P 点,且坐标原点O 到直线m 的距离为1时,求直线m 的方程.17.(本小题满分13分)某四星级酒店有客房300间,每天每间房费为200元,天天客满.该酒店欲提高档次升五星级,并提高房费.如果每天每间客的房费每增加20元,那么入住的客房间数就减少10间,若不考虑其他因素,酒店将房费提高到多少元时,每天客房的总收入最高?第13题图18.(本小题满分14分)如图所示,四棱锥P ABCD -的底面是直角梯形,PA ⊥底面ABCD ,AB AD ⊥,CD AD ⊥,2CD AB =,E 为PC 的中点,PA = (1)证明://BE 平面PAD ; (2)证明:BE ⊥平面PDC ; (3)求三棱锥E PBD -的体积.19.(本小题满分14分) 已知函数2()()21xf x a a R =-∈+ (1)判断并证明函数的单调性;(2)若函数为()f x 奇函数,求实a 数的值;(3)在(2)的条件下,若对任意的t R ∈,不等式22(2)()0f t f t tk ++->恒成立,求实数k 的取值范围.20.(本小题满分14分)已知函数()||f x x a =-,2()21g x x ax =++(a 为正实数),且函数()f x 与()g x的图象在y 轴上的截距相等. (1) 求a 的值;(2) 对于函数()F x 及其定义域D ,若存在0x D ∈,使00()F x x =成立,则称0x 为()F x 的不动点.若()()f x g x b ++在其定义域内存在不动点,求实数b 的取值范围;(3) 若n 为正整数,证明:()()410()45f ng n ⋅< (参考数据:lg30.3010=,94()0.13425=,164()0.02815=,254()0.00385=)第18题图2011—2012学年度第一学期期末教学质量检查高一数学(A 卷)参考答案及评分标准一、选择题二、填空题 11.()x x f = 12.3- 13 14.()1,-+∞三、解答题15. (本小题满分12分)解:(1)由2log (2)3x -<,得028x <-<, ………………………2分210x ∴<<,即{|210}B x x =<<. ………………………4分∴}101|{<≤=x x B A . …………………………6分 (2)∅≠C A ,∴1a >. ……………………………8分 又∵B C =∅ ,∴2a ≤, …………………………10分 ∴12a <≤,即实数a 的取值范围是(]1,2. ……………………………12分16.(本小题满分13分)解:由23y xx y =⎧⎨+=⎩,解得点()21,P . ………………………2分(1)因为m ⊥0l ,所以直线m 的斜率221110-=-=-=l m k k , ……………………………4分又直线m 过点()21,P ,故直线m 的方程为:()221y x -=--,即240x y +-=. …………………………6分(2)因为直线m 过点()21,P ,当直线m 的斜率存在时,可设直线m 的方程为()21y k x -=-,即20kx y k --+=. …………………7分所以坐标原点O 到直线m的距离1d ==,解得34k =, …………9分 因此直线m 的方程为:332044x y --+=,即3450x y -+=. …………10分 当直线m 的斜率不存在时,直线m 的方程为1x =,验证可知符合题意.……12分 综上所述,所求直线m 的方程为1x =或3450x y -+=. ………………13分17.(本小题满分13分)解:设酒店将房费提高到x 元,每天的客房的总收入为y 元. …………1分则每天入住的客房间数为)1020200300(⨯--x 间, ……………3分 由20030010020x --⨯≥及0≥x , …………………4分 得:8000≤≤x . ……………………5分 依题意知:)1020200300(⨯--=x x y ……………………8分 =x x 400212+-=80000)400(212+--x . ……………………10分因为8000≤≤x ,所以当400=x 时,y 有最大值为80000元. ………………12分答:酒店将房费提高到400元时,每天客房的总收入最高. ……………………13分18.(本小题满分14分)(1)证明:取PD 中点Q ,连结AQ 、EQ .……………1分E 为PC 的中点,CD EQ //∴且CD EQ 21=.………………2分又CD AB // 且CD AB 21=, AB EQ //∴且AB EQ =.…………………3分∴四边形ABED 是平行四边形,AQ BE //∴. …………………………4分又⊄BE 平面PAD ,⊂AQ 平面PAD ,∴//BE 平面PAD . …………………………5分(2)证明:⊥PA 底面ABCD ,CD PA ⊥∴. …………………………6分又AD CD ⊥ ,且A AD PA =⋂,⊥∴CD 平面PAD ,AQ CD ⊥∴. …………………………7分 AD PA = ,Q 为PD 的中点,PD AQ ⊥∴, …………………………8分,D PD CD =⋂⊥∴AQ 平面PDC . …………………………9分 AQ BE // ,∴⊥BE 平面PDC . …………………………10分(3)解法一∵E 为PC 的中点,∴E PBD B PDE V V --==B ECD V -=E BCD V -. …………………………11分⊥PA 底面ABCD ,∴点E 到面BCD 的距离1122d PA ==. …………………………12分 1121122BCD S CD AD ∆∴=⨯=⨯⨯=. …………………………13分E BCD V -111113326BCD S d ∆=⨯=⨯⨯=,E 为PC 的中点,∴16E PBD V -=. …………………………14分 解法二由前面证明可知:BE 是三棱锥B PDE -的高,CD PD ⊥.在Rt PAD ∆中,PD =122BE AQ PD ===. ………………11分1112222PDE PDC S S PD DC ∆∆==⨯⨯⨯=, …………………………12分 E PBD B PDE V V --= …………………………13分11133226PDE S BE ∆=⨯=⨯=. …………………………14分19.(本小题满分14分)(1)函数()f x 为R 上的增函数.证明如下: ……………………………1分证明:函数()f x 的定义域为R ,对任意1x ,R x ∈2,设21x x <,则121222()()()()2121x x f x f x a a -=---++ …………………………2分 122121222(22)2121(21)(21)x x x x x x -=-=++++. …………………3分 因为2x y =是R 上的增函数,且12x x <,所以1222x x-<0,……………………4分所以12()()f x f x -<0即12()()f x f x <,函数()f x 为R 上的增函数. ……………5分 (2)解:∵函数()f x 为奇函数,∴(0)10f a =-=, …………………………6分 ∴1a =. …………………………7分当1a =时,2()121x f x =-+=2121x x -+.()f x -=2121x x ---+=1212x x -+=-2121x x -+=-()f x ,…………8分此时,()f x 为奇函数,满足题意.所以,1a =. …………………………9分(3)解:因为()f x 是奇函数,从而不等式22(2)()0f t f t tk ++->对任意的R t ∈恒成立等价于不等式22(2)()f t f tk t +>-对任意的R t ∈恒成立. …………………………10分 又因为在(,)-∞+∞上为增函数,所以等价于不等式222t tk t +>-对任意的R t ∈恒成立,即不等式2220t kt -+>对任意的R t ∈恒成立. …………………………11分 所以必须有2160k ∆=-<, …………………………12分 即44k -<<, …………………………13分所以实数k 的取值范围{}44k k -<<. …………………………14分20.(本小题满分14分)解:⑴ ∵函数()x f 与()x g 的图象在y 轴上的截距相等,∴()()00f g =,即1a =. ……………………………1分 又0a >,∴1a =. ……………………………2分⑵由(1)知,()()223 1=2 1x x b x f x g x b x x b x ⎧++≥⎪++⎨+++<⎪⎩.当1x ≥时,若()()f x g x b ++存在不动点,则有23=x x b x ++,即()22=211b x x x --=-++. ………………………3分∵1x ≥,∴()2113x -++≤-,此时3b ≤-. ………………………4分 当1x <时,若()()f x g x b ++存在不动点,则有22=x x b x +++,即2=2b x -- ……………………5分∵1x <,∴222x --≤-,此时2b ≤-. ………………………6分故要使得()()f x g x b ++在其定义域内存在不动点,则实数b 的取值范围应为(]2-∞-,. ……………… …………………………………………7分⑶设()()()4105g n f n G n ⎛⎫=⋅ ⎪⎝⎭.因为n 为正整数, ∴()212141005n n n G n -++⎛⎫=⋅>⎪⎝⎭. ………………………8分 ∴()()()()22+12+112+3121410+145=1045105n n nn n n n G n G n ++-++⎛⎫⋅ ⎪⎛⎫⎝⎭=⨯ ⎪⎛⎫⎝⎭⋅ ⎪⎝⎭. ………………………9分 当()()+11G n G n <时,2+341015n ⎛⎫⨯< ⎪⎝⎭,即()42+3l g 15n ⎛⎫<- ⎪⎝⎭,亦即12lg 3132-->+n ,∴133.726lg 22n >-≈-. ………………………11分由于n 为正整数,因此当13n ≤≤时,()G n 单调递增;当4n ≥时,()G n 单调递减. ∴()G n 的最大值是()(){}max 3,4G G . ………………………12分又()16243=10=1000.0281=2.815G ⎛⎫⨯⨯ ⎪⎝⎭,()25344=10=10000.0038=3.85G ⎛⎫⨯⨯ ⎪⎝⎭,………………………13分 ∴()()44G n G ≤<. ………………………14分。
宋琳艳——洪武小学2011—2012学年上学期期末试卷(四年级数学)

洪武学校2011—2012学年上学期期末测试卷四年级数学班级姓名得分一、填空。
(21分。
)1、7809450030是一个()位数,最高位是()位,这个数中“9”在()位上,表示(),这个数读作(),这个数四舍五入到亿位约是()。
2、6□5120≈66万。
□里应填()。
3、在○里填上“﹥”“﹤”或“=”。
98700○100000 5870000○57800009000000000○9亿 11亿○1000万4、“160×50”的积末尾有()个0,积是()位数。
5、一辆小汽车每小时行驶85千米,写作()。
6、如果把被除数和除数同时扩大100倍,则商()。
7、()里最大填几。
48×()﹤350 ()×36﹤32060×()﹤620 24×()﹤1288、1个周角=()个平角=()个直角二、判断题。
(6分)1、计数单位间的进率是十。
()2、把9999四舍五入到万位是10000。
()3自然数的个数是无限的,最小的自然数是1。
()4、过一点可以画无数条直线。
()5、时间=速度×路程()6、平角就是一条直线。
()三、选择题。
(12分)1、在7和5中间添()个0 ,这个数才能约等于7亿。
A.8 B.6 C.72、用计算机是,按()键打开计数器。
A.ON/C B.OEF C.MC3、9时整时,钟面上的时针和分针成()角。
A.360° B.180° C.90°4、“144÷36”,被除数扩大10倍,除数不变,则商()。
A.扩大10倍 B.缩小为原来的101 C.不变5.“300÷61”,用5做商()。
A.偏大 B.偏小 C.合适6、小明给客人沏茶,接水1分钟,烧水6分钟,洗茶杯2分钟,拿茶叶1分钟,沏茶1分钟。
小明合理安排以上事情,至少需要()分钟使客人尽快喝上茶。
四、计算。
1、直接写出得数。
(12分)390+11= 620-180= 23×4= 560×0=202×40= 320×3= 8000÷400= 3200÷800=72万+78万= 38亿+52亿= 480÷56= 40×822=2、竖式计算。
2011——2012学年___昆承中学______(学校)特长生个人
2011——2012学年___昆承中学______(学校)特长生个人获奖统计表特长类别姓名班级赛事名称赛事时间赛事级别获奖等第校自评得分局审核得分数学唐吉宏初一第七届数学文化节2021.4 苏州市级一等奖 5数学俞闻韬初一第七届数学文化节2021.4 苏州市级一等奖 5数学陶中恺初一第七届数学文化节2021.4 苏州市级一等奖 5数学马意湉初一第七届数学文化节2021.4 苏州市级一等奖 5数学丁译洲初一第七届数学文化节2021.4 苏州市级一等奖 5数学陈嘉拓初一第七届数学文化节2021.4 苏州市级一等奖 5数学姚寅文初一第七届数学文化节2021.4 苏州市级一等奖 5数学李一雄初一第七届数学文化节2021.4 苏州市级一等奖 5数学陈育康初一第七届数学文化节2021.4 苏州市级一等奖 5数学谢茜竹初一第七届数学文化节2021.4 苏州市级一等奖 5数学查亦恬初一第七届数学文化节2021.4 苏州市级一等奖 5数学范玮卓初一第七届数学文化节2021.4 苏州市级一等奖 5数学王欣翼初一第七届数学文化节2021.4 苏州市级一等奖 5数学倪啸雷初一第七届数学文化节2021.4 苏州市级一等奖 5数学邓赵禛初一第七届数学文化节2021.4 苏州市级一等奖 5数学蒋宇阳初一第七届数学文化节2021.4 苏州市级一等奖 5数学徐可薏初一第七届数学文化节2021.4 苏州市级一等奖 5数学徐熠星初一第七届数学文化节2021.4 苏州市级一等奖 5数学曹钜楷初一第七届数学文化节2021.4 苏州市级一等奖 5数学戴思家初一第七届数学文化节2021.4 苏州市级一等奖 5数学鞠九虎慜初一第七届数学文化节2021.4 苏州市级一等奖 5 数学孙宇航初一第七届数学文化节2021.4 苏州市级二等奖 4 数学奚晓恒初一第七届数学文化节2021.4 苏州市级二等奖 4数学罗恬凡初一第七届数学文化节2021.4 苏州市级二等奖 4 数学倪恬初一第七届数学文化节2021.4 苏州市级二等奖 4 数学仲宇超初一第七届数学文化节2021.4 苏州市级二等奖 4 数学张寅历初一第七届数学文化节2021.4 苏州市级二等奖 4 数学黄安初一第七届数学文化节2021.4 苏州市级二等奖 4 数学陈志坚初一第七届数学文化节2021.4 苏州市级二等奖 4 数学江佳柳初一第七届数学文化节2021.4 苏州市级二等奖 4 数学李澳华初一第七届数学文化节2021.4 苏州市级二等奖 4 数学郁天行初一第七届数学文化节2021.4 苏州市级二等奖 4 数学刘天睦初一第七届数学文化节2021.4 苏州市级二等奖 4 数学张婕初一第七届数学文化节2021.4 苏州市级二等奖 4 数学周品成初一第七届数学文化节2021.4 苏州市级二等奖 4 数学陈依初一第七届数学文化节2021.4 苏州市级二等奖 4 数学董诗绎初一第七届数学文化节2021.4 苏州市级三等奖 3 数学朱城志初一第七届数学文化节2021.4 苏州市级三等奖 3 数学郁杨铭初一第七届数学文化节2021.4 苏州市级三等奖 3 数学陶蕴哲初一第七届数学文化节2021.4 苏州市级三等奖 3 数学龚子超初一第七届数学文化节2021.4 苏州市级三等奖 3 数学王庆伦初一第七届数学文化节2021.4 苏州市级三等奖 3 数学俞若婧初一第七届数学文化节2021.4 苏州市级三等奖 3 数学李姝宁初一第七届数学文化节2021.4 苏州市级三等奖 3 数学方司南初一第七届数学文化节2021.4 苏州市级三等奖 3 数学薛雨莹初一第七届数学文化节2021.4 苏州市级三等奖 3 数学支涵恺初一第七届数学文化节2021.4 苏州市级三等奖 3 数学丁楚欣初一第七届数学文化节2021.4 苏州市级三等奖 3 数学潘奕如初一第七届数学文化节2021.4 苏州市级三等奖 3数学徐邹韬初二第七届数学文化节2012.4 苏州市级一等奖 5 数学沈沛诚初二第七届数学文化节2021.4 苏州市级一等奖 5 数学周明皓初二第七届数学文化节2021.4 苏州市级一等奖 5 数学俞守成初二第七届数学文化节2021.4 苏州市级一等奖 5 数学许秋伊初二第七届数学文化节2021.4 苏州市级一等奖 5 数学徐一孜初二第七届数学文化节2021.4 苏州市级一等奖 5 数学苏航初二第七届数学文化节2021.4 苏州市级一等奖 5 数学蔡尧初二第七届数学文化节2021.4 苏州市级一等奖 5 数学张弛初二第七届数学文化节2021.4 苏州市级一等奖 5 数学徐灵初二第七届数学文化节2021.4 苏州市级一等奖 5 数学王昊庭初二第七届数学文化节2021.4 苏州市级一等奖 5 数学袁晴初二第七届数学文化节2021.4 苏州市级一等奖 5 数学毛逸韬初二第七届数学文化节2021.4 苏州市级一等奖 5 数学陈怡菲初二第七届数学文化节2021.4 苏州市级一等奖 5 数学徐辛夷初二第七届数学文化节2021.4 苏州市级一等奖 5 数学袁憬弋初二第七届数学文化节2021.4 苏州市级一等奖 5 数学叶伟南初二第七届数学文化节2021.4 苏州市级一等奖 5 数学顾心悦初二第七届数学文化节2021.4 苏州市级一等奖 5 数学孔殷嘉初二第七届数学文化节2021.4 苏州市级一等奖 5 数学谭晓婷初二第七届数学文化节2021.4 苏州市级一等奖 5 数学屈雯怡初二第七届数学文化节2021.4 苏州市级二等奖 4 数学周珺初二第七届数学文化节2021.4 苏州市级二等奖 4 数学李可炀初二第七届数学文化节2021.4 苏州市级二等奖 4 数学魏宇初二第七届数学文化节2021.4 苏州市级二等奖 4 数学龚宇柯初二第七届数学文化节2012.4 苏州市级二等奖 4 数学徐杨初二第七届数学文化节2021.4 苏州市级二等奖 4数学顾昱恒初二第七届数学文化节2021.4 苏州市级二等奖 4 数学陆仪纯初二第七届数学文化节2021.4 苏州市级二等奖 4 数学邢宇杰初二第七届数学文化节2021.4 苏州市级二等奖 4 数学夏王孙初二第七届数学文化节2021.4 苏州市级二等奖 4 数学王劭屹初二第七届数学文化节2021.4 苏州市级二等奖 4 数学董澄初二第七届数学文化节2021.4 苏州市级二等奖 4 数学夏宇阳初二第七届数学文化节2021.4 苏州市级二等奖 4 数学谭彦初二第七届数学文化节2021.4 苏州市级二等奖 4 数学范杨初二第七届数学文化节2021.4 苏州市级二等奖 4 数学王鍇锴初二第七届数学文化节2021.4 苏州市级二等奖 4 数学徐宇帆初二第七届数学文化节2021.4 苏州市级二等奖 4 数学奚晨初二第七届数学文化节2021.4 苏州市级二等奖 4 数学钱雨佳初二第七届数学文化节2021.4 苏州市级二等奖 4 数学赵宏宇初二第七届数学文化节2021.4 苏州市级三等奖 3 数学王翰阳初二第七届数学文化节2021.4 苏州市级三等奖 3 数学顾衍恒初二第七届数学文化节2021.4 苏州市级三等奖 3 数学曹训魁初二第七届数学文化节2021.4 苏州市级三等奖 3 数学李依阳初二第七届数学文化节2021.4 苏州市级三等奖 3 数学陈逸初初二第七届数学文化节2021.4 苏州市级三等奖 3 数学洪华荣初二第七届数学文化节2021.4 苏州市级三等奖 3 数学贾文菲初二第七届数学文化节2021.4 苏州市级三等奖 3 数学徐忆文初二第七届数学文化节2021.4 苏州市级三等奖 3 数学熊心逸初二第七届数学文化节2021.4 苏州市级三等奖 3 数学戈浚尧初二第七届数学文化节2012.4 苏州市级三等奖 3 数学张妮初三数学应用与创新邀请赛2012.4 苏州市级一等奖 5 数学唐心荷初三数学应用与创新邀请赛2012.4 苏州市级一等奖 5数学钱紫晗数学应用与创新邀请赛2012.4 一等奖 5 数学濮丹蕾初三数学应用与创新邀请赛2012.4 苏州市级一等奖 5 数学王子奕初三数学应用与创新邀请赛2012.4 苏州市级一等奖 5 数学毛安琪初三数学应用与创新邀请赛2012.4 苏州市级一等奖 5 数学朱志凯初三数学应用与创新邀请赛2012.4 苏州市级一等奖 5 数学张陆鼎初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学孔柯瑜初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学王心怡初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学杨依霖初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学唐钟恒初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学周樯初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学袁子凌初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学鞠一舟初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学陈仪茜初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学邵佳徐初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学虞俊铖初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学石宇昂初三数学应用与创新邀请赛2012.4 苏州市级二等奖 4 数学陈奕帆初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学王铭辉初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学盛圯杰初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学郭雨琦初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学杨恒初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学俞天任初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学顾兆初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学董毅初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学钱志豪初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3数学徐雅霓数学应用与创新邀请赛2012.4 三等奖 3 数学盛劲菡初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学吴雨韬初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学范力棋初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学张馨予初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学包家豪初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学贝蓓初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学黄宇凡初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学黄赞华初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学池亦扬初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学陈子颐初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学吴亿遥初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学冯琳洁初三数学应用与创新邀请赛2012.4 苏州市级三等奖 3 数学陈逸捷初一“希望杯”全国数学邀请赛2012.4 全国级全国一等奖12 数学唐吉宏初一“希望杯”全国数学邀请赛2012.4 全国级全国二等奖10 数学周王宸初一“希望杯”全国数学邀请赛2012.4 全国级全国二等奖10 数学潘安初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学丁译洲初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学仲宇超初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学陶中恺初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学李一雄初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学徐可蕙初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学钟天声初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学董诗绎初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学倪啸雷初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学吕骏飞初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8数学罗恬凡初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学吴文心初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学俞闻韬初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学姚逸群初一“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学俞守成初二“希望杯”全国数学邀请赛2012.4 全国级全国一等奖12 数学王昊庭初二“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学蔡尧初二“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学张弛初二“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学徐邹韬初二“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学奚晨初二“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学袁憬弋初二“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学张羽戈初二“希望杯”全国数学邀请赛2012.4 全国级全国三等奖8 数学王子奕初三“希望杯”全国数学邀请赛2012.4 全国级省特等奖8 数学俞天任初三“希望杯”全国数学邀请赛2012.4 全国级省特等奖8 数学孔柯瑜初三“希望杯”全国数学邀请赛2012.4 全国级省一等奖7 数学毛承晖初三“希望杯”全国数学邀请赛2012.4 全国级省一等奖7 数学吴尚恒初三“希望杯”全国数学邀请赛2012.4 全国级省二等奖 6 数学姚圣时初三“希望杯”全国数学邀请赛2012.4 全国级省二等奖 6 数学王李栋初三“希望杯”全国数学邀请赛2012.4 全国级省二等奖 6 数学杨依霖初三“希望杯”全国数学邀请赛2012.4 全国级省二等奖 6 数学丁忆初三“希望杯”全国数学邀请赛2012.4 全国级省三等奖 5 数学顾兆初三“希望杯”全国数学邀请赛2012.4 全国级省三等奖 5 数学毛安琪初三“希望杯”全国数学邀请赛2012.4 全国级省三等奖 5 数学袁子琪初三“希望杯”全国数学邀请赛2012.4 全国级省三等奖 5 数学章金初三“希望杯”全国数学邀请赛2012.4 全国级省三等奖 5 数学朱昱哲初三“希望杯”全国数学邀请赛2012.4 全国级省三等奖 5征文钱志豪初三暨辛亥革命100周年征文2011.10 省级省一等奖7征文陈璟璞初三“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省一等奖7征文虞弘初三“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文张妮初三“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖 6征文张陆鼎初三“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省一等奖7征文徐杨初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文金莹初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文郁心怡初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文徐邹韬初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文顾仪初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖 6征文毛逸韬初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖 6征文府明祎初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文徐一孜初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文王源浩初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文吴可初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖 6征文穆凯初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文俞心怡初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文顾衍恒初二暨辛亥革命100周年征文2011.10 省级省三等奖 5征文哈楠初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文钱豪成初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文薛乐汀初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖 6征文郑怡洁初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年2011.10 省级省三等奖 5征文张轶群初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文王文婕初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖 6征文王渝凡初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖 6征文沈怡芸初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文董怡初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文王喆初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文赵锌雨初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖 6征文叶李航初二“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖 6征文陈仪茜初三“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖 6征文纪慕秋初三“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖 5征文陆颖雯初三“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省三等奖5征文毛柯杨初三“沙家浜”杯江苏省初中学生纪念建党90周年2011.10 省级省三等奖 5暨辛亥革命100周年征文陈滕心初三“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖6征文陈子頣初三“沙家浜”杯江苏省初中学生纪念建党90周年暨辛亥革命100周年征文2011.10 省级省二等奖6征文杨丰宇初三江苏省十一届中学生作文大赛(初中组)现场决赛2011.12 省级省特等奖8征文顾仪珺初三江苏省十一届中学生作文大赛(初中组)现场决赛2011.10 省级省二等奖6征文桑田初三江苏省十一届中学生作文大赛(初中组)现场决赛2011.10 省级省三等奖5征文冯琳洁初三江苏省十一届中学生作文大赛(初中组)现场决赛2011.12 省级省二等奖6征文毛承晖初三011年《小荷》“梅李杯”“孝爱文化”全国中小学生征文大赛2011.11 全国级全国三等奖8英语王子奕初三首届上海“东方之星”英语演讲赛2012.1 上海市级特等奖 6 英语吴尚恒初三首届上海“东方之星”英语演讲赛2012.1 上海市级一等奖 5 英语姚逸群初一首届上海“东方之星”英语演讲赛2012.1 上海市级二等奖 4 英语孙金羽初二首届上海“东方之星”英语演讲赛2012.1 上海市级二等奖 4 英语蔡齐镭初二首届上海“东方之星”英语演讲赛2012.1 上海市级三等奖 3 英语金嘉寅初二首届上海“东方之星”英语演讲赛2012.1 上海市级三等奖 3 英语钱紫晗初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级二等奖 4 英语陈少伦初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级二等奖 4英语戚丹璎初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级一等奖 5 英语杨依霖初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级一等奖 5 英语毛安琪初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级一等奖 5 英语史星雨初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级一等奖 5 英语李佳莹初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级一等奖 5 英语朱志凯初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级一等奖 5 英语陈璟璞初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级二等奖 4 英语陈嘉宁初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级三等奖 3 英语曹易繁初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级三等奖 3 英语毛柯杨初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级一等奖 5 英语张溪初三2011年苏州市中学生英语能力竞赛2012.1 苏州市级三等奖 3英语陈仪茜初三常熟市首届中学生写作系列活动第二阶段比赛中荣获初中组2011.11 常熟市级一等奖3英语张烨初三常熟市首届中学生写作系列活动第二阶段比赛中荣获初中组2011.11 常熟市级一等奖3英语黄嘉言初三常熟市首届中学生写作系列活动第二阶段比赛中荣获初中组2011.11 常熟市级二等奖2英语陆一淳初一常熟市首届中学生写作系列活动第二阶段比赛中荣获初中组2011.11 常熟市级二等奖2英语沈嘉树初一常熟市首届中学生写作系列活动第二阶段比赛中荣获初中组2011.11 常熟市级二等奖2英语徐紫炜初一常熟市首届中学生写作系列活动第二阶段比赛中荣获初中组2011.11 常熟市级二等奖2英语杨恒初三常熟市首届中学生写作系列活动第二阶段比赛中荣获初中组2011.11 常熟市级二等奖2物理王昊庭初二在第二届“萃英杯”苏州市中学生科技吉尼斯挑战赛上获得初中组曹冲称象(项目)挑战奖2012.5 苏州市级挑战奖2物理俞守成初二在第二届“萃英杯”苏州市中学生科技吉尼斯挑战赛上获得初中组三阶魔方(项目)挑战奖2012.5 苏州市级挑战奖2物理盛添熙初二在第二届“萃英杯”苏州市中学生科技吉尼斯挑战赛上获得初中组魔方速拧(项目)挑战奖2012.5 苏州市级第四名3物理戈浚尧初二在第二届“萃英杯”苏州市中学生科技吉尼斯挑战赛上获得初中组放飞梦想(项目)挑战奖2012.5 苏州市级第一名6物理陈逸初初二在第二届“萃英杯”苏州市中学生科技吉尼斯挑战赛上获得初中组魔方速拧(项目)挑战奖2012.5 苏州市级第一名6语文董诗绎初一作品《一副眼镜》参加第十届“叶圣陶杯”全国中学生新作文大赛2012.5 全国二等奖10语文周一丹初一作品《小水珠》参加第十届“叶圣陶杯”全国中学生新作文大赛2012.5 全国二等奖10语文张妮初一作品《跳入酒精的杨梅》参加第十届“叶圣陶杯”全国中学生新作文大赛2012.5 全国二等奖10语文杨宇初一作品《等待》参加第十届“叶圣陶杯”全国中学生新作文大赛2012.5 全国二等奖10语文董悦初一作品《月光》参加第十届“叶圣陶杯”全国中学生新作文大赛2012.5 全国二等奖10语文陈滕心初一作品《我想……》参加第十届“叶圣陶杯”全国中学生新作文大赛2012.5 全国二等奖10语文丁楚欣初一作品《水性江南》参加第十届“叶圣陶杯”全国中学生新作文大赛2012.5 全国二等奖10语文毛逸韬初二作品《爆火花》参加第十届“叶圣陶杯”全国中学生新作文大赛2012.5 全国二等奖10语文哈楠初二作品《就这样老去》参加第十届“叶圣陶杯”全国中学生新作文大赛2012.5 全国二等奖10语文徐紫炜初二作品《时光记得我们的似水流年》参加第十届“叶圣陶杯”全国中学生新作文大赛2012.5 全国二等奖10。
2012~2013学年第一学期__离散数学__A卷_(2)

上海第二工业大学(试卷编号:)2012~2013学年第一学期离散数学A 卷姓名:学号:班级:成绩:一、判断题(每小题2分,本题共10分) 1、若A B A C =,则B C =。
( 错 ) 2、设1ρ和2ρ是集合A 上的等价关系,则12ρρ是A 上的等价关系( 对 )3、若函数:f A B →,:g B C →,则若f 与g 的复合gf 是双射,则函数f 是双射。
( 错 )4、在有界格中,必有最大元和最小元。
( 对 )5、存在13个结点,并且每个结点的度均为3的图。
( 错 )二、填空题(每空2分,本题30分) 1、设集合{,{}}A a b =,{,}B a b =,则22AB =_______{空,{a}}________________,B A ⨯=_________{(a,a),(b,a),(a,{b}),(b,{b}}________________。
2、若{1,2,3,4}A =,则A 上共有___11_______个不同的自反关系。
3、假设{0,1,2,3}A =,1{(,)|2}i j j i ρ==+和2{(,)|2}i j i j ρ==+是A 上的关系,则12ρρ=_____{(0,0),(1,1)}__;21ρρ=___{(2,2),(3,3)};关系1ρ的自反闭包是:__{(0,0),(1,1),(2,2),(3,3),(0,2),(1,3)}__;关系2ρ的对称闭包是:_{(1,3),(3,1),(2,0),(0,2)}_。
4、命题P :“小李喜欢跳舞”,命题Q :“小李不喜欢唱歌”,则复合命题P Q ⌝∧表示:____小李不喜欢跳舞且不喜欢唱歌_____________________。
5、设集合{1,2,3,4}A =,{,,,}B a b c d =,则A B ⨯有___16__个序偶,A 到B 有___256____个关系,其中有____24____个是双射函数。
高等数学期末考试试题及答案(大一考试)

五、设函数由方程确定,求.(8分)六、若有界可积函数满足关系式,求。
(8分)七、求下列各不定积分(每题6分,共12分)(1).八、设求定积分。
(6分)九、讨论函数的单调区间、极值、凹凸区间和拐点坐标.(10分)十、求方程的通解(6分)十一、求证:.(5分)第一学期高等数学(上)(A)卷分标准题3分,共15分)2。
B 3。
D 4。
B 5.D分,共18分)为任意常数),4. 2 , 5。
6。
分 (6)分解:………………3分…………….6分 (8)导 (3)数)…………6分分解:(1)。
……。
.3分 (6)分分=……………6分时有极大值2,有极小值。
在上是凸的,在上是凹的,拐点为(0,0)………10分十、解;…………………..3分设方程(1)的解为代入(1)得………5分…………………….6分十一、证明:令………………1 分又…。
3分的图形是凸的,由函数在闭区间连续知道最小值一定在区间端点取到。
,所以…………。
5分.(2010至2011学年第一学期)一、单项选择题(15分,每小题3分)1、当时,下列函数为无穷小量的是( )(A)(B) (C)(D)2.函数在点处连续是函数在该点可导的()(A)必要条件(B)充分条件(C)充要条件(D)既非充分也非必要条件3.设在内单增,则在内()(A)无驻点(B)无拐点(C)无极值点(D)4.设在内连续,且,则至少存在一点使()成立。
(A)(B)(C)(D)5.广义积分当( )时收敛。
(A) (B) (C)(D)二、填空题(15分,每小题3分)1、若当时,,则;2、设由方程所确定的隐函数,则;3、函数在区间单减;在区间单增;4、若在处取得极值,则;5、若,则;三、计算下列极限.(12分,每小题6分)1、2、四、求下列函数的导数(12分,每小题6分)1、,求2、,求五、计算下列积分(18分,每小题6分)1、2、3、设,计算六、讨论函数的连续性,若有间断点,指出其类型。
(7分)七、证明不等式:当时,(7分)八、求由曲线所围图形的面积。
新课标山东省威海市2011—2012学年度八年级数学第二学期期末模拟试卷(一)

山东省威海市2011—2012学年度第二学期七年级下数学期末模拟试卷及答案(一) 一、你的数学风采(每小题3分,共30分)1.已知m 是方程x 2-x -1=0的一个根,则代数式m 2-m 的值等于 A. 1B.0C.-1D.22.下列式子为最简二次根式的是( ) A .5xB .8C .92-xD .y x 23 3.下列计算正确的是( )A.=2= C.=6=-4.某班7个学习小组人数如下:5,5,6,x ,7,7,8。
已知这组数据的平均数为6,则下列说法错误的是( )A .x=4B .众数是5和7C .中位数是6D .众数是7 5、方程22(2)5mm x --=是一元二次方程,则m 的值是( )A .2±B .-2C .2D .46.在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?请你通过计算、分析后给出正确的回答.( ) A.一定不会 B.可能会C.一定会D.以上答案都不对7.下列命题中,真命题是( )A.两条对角线相等的四边形是矩形 B.两条对角线垂直的四边形是菱形 C.两条对角线垂直且相等的四边形是正方形;D.两条对角线相等的平行四边形是矩形8. 在正数范围内定义一种运算“*”)D.9.为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,,下列说法:①该班B等及B等以上占全班60%②D等有4人,没有得满分的(按120分制)③成绩分数(按120分制)的中位数在第三组④成绩分数(按120分制)的众数在第三组,其中正确的是()A、①②B、③④C、①③D、①③④10.如图,在直角梯形ABCD中,AB⊥BC,AE∥DC交BC于E,O是AC的中点,ABAD=2,BC=3,下列结论:①∠CAE=30°;②四边形ADCE是菱形;③2ADC ABES S=;④BO⊥CD,其中正确结论的个数是()A.4个 B.3个 C.2个 D.1个二、用你敏锐的思维,写出简结的结果!(每小题3分,共24分)11.如果9+x是二次根式,则x的取值范围是.12.已知等腰直角三角形的直角边的边长为,•那么这个等腰直角三角形的周长是________.(结果用最简二次根式)13.当x=时,最简二次根式323--x与6+x作加减法运算时能合并.14.关于x 的一元二次方程2x ²+kx +1=0有两个相等的实根,则k = ;方程的解为 。
高等数学期末考试试题及答案(大一考试)

(2010至2011学年第一学期)课程名称: 高等数学(上)(A 卷)注意事项:1、 满分100分。
要求卷面整洁、字迹工整、无错别字。
2、 考生必须将姓名、班级、学号完整、准确、清楚地填写在试卷规定的地方,否则视为废卷。
3、 考生必须在签到单上签到,若出现遗漏,后果自负。
4、 如有答题纸,答案请全部写在答题纸上,否则不给分;考完请将试卷和答题卷分别一同交回,否则不给分。
试 题一、单选题(请将正确的答案填在对应括号内,每题3分,共15分) 1. =--→1)1sin(lim21x x x ( ) (A) 1; (B) 0; (C) 2; (D)212.若)(x f 的一个原函数为)(x F ,则dx e f e x x )(⎰--为( )(A) c e F x +)(; (B) c eF x+--)(;(C) c e F x+-)(; (D )c xe F x +-)( 3.下列广义积分中 ( )是收敛的. (A)⎰+∞∞-xdx sin ; (B)dx x ⎰-111; (C) dx x x ⎰+∞∞-+21; (D)⎰∞-0dx e x 。
4. )(x f 为定义在[]b a ,上的函数,则下列结论错误的是( )(A) )(x f 可导,则)(x f 一定连续; (B) )(x f 可微,则)(x f 不一定可导; (C) )(x f 可积(常义),则)(x f 一定有界; (D) 函数)(x f 连续,则⎰xadt t f )(在[]b a ,上一定可导。
5. 设函数=)(x f nn x x211lim++∞→ ,则下列结论正确的为( )(A) 不存在间断点; (B) 存在间断点1=x ; (C) 存在间断点0=x ; (D) 存在间断点1-=x二、填空题(请将正确的结果填在横线上.每题3分,共18分) 1. 极限=-+→xx x 11lim20_____.2. 曲线⎩⎨⎧=+=321t y t x 在2=t 处的切线方程为______. 3. 已知方程xxe y y y 265=+'-''的一个特解为x e x x 22)2(21+-,则该方程的通解为 .4. 设)(x f 在2=x 处连续,且22)(lim2=-→x x f x ,则_____)2(='f5.由实验知道,弹簧在拉伸过程中需要的力F (牛顿)与伸长量s 成正比,即ks F =(k 为比例系数),当把弹簧由原长拉伸6cm 时,所作的功为_________焦耳。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011——2012学年度小学毕业考核
数学(A)
一、填空题。
(每题2分,共20分)
1. 俄罗斯是世界上陆地面积最大的国家,其陆地面积为17075400平方千米,这个数读作()平方千米,用四舍五入法省略万位后面的尾数约是()万平方千米。
2. 85%= ()
20=34÷()=():200 = ()折
3.
数轴上A点表示的数是(),B点表示的数是(),C点表示的数用分数表示是(),D点表示的数用小数表示是()。
4. 把“384401”、“-183”、“46亿”、与“1
6”填入相应的括号里。
月球约在()年前就已形成,它与地球的平均距离为()km;月球的昼夜温差特别大,白天温度可达150℃,夜晚则降到()℃;月球的引力仅相当于地球引力的()
5. 15和25的最大公因数是(),最小公倍数是()。
6. 把改写成乘法算式是();当a=55时,算式的结果是()。
7. 一个长方形操场,长400米,画在设计图上长是4厘米,这幅设计图的比例尺是();在这幅图上量得操场的宽是2厘米,这个操场的实际面积是()平方米。
8. 制作一个无盖的长方体塑料盒子,长0.6米,宽0.4米,高0.5米,一共需要()平方米塑料板(接口处忽略不计),这个塑料盒的体积是()立方米。
9.一个棱长为4分米的正方体,棱长总和是()分米,把它削成一个最大的圆柱,这个圆柱的体积是()立方分米。
10. 哥哥和弟弟周末在“松湖烟雨”骑单车游玩,右边的图像表示他们骑车的路程和时间的关系,请根据右图填空。
(1)哥哥骑车行驶的路程和时间成()比例。
(2)弟弟平均每分钟行驶()千米。
二、选择题。
(每小题1分,共10分)
11. 用98粒种子做发芽实验,结果全部发芽,发芽率是()。
A. 98%
B. 2%
C.100%
12.一次数学测验,第一组同学的成绩如下:100、96、92、91、91、90、88、84、73、56。
这组数据的中位数是()。
A. 88
B.90
C.91
D.90.5
13.早上8:00,钟面上的时针和分针所组成的角是()。
A.锐角
B.直角
C.钝角
D.平角
14.在36.29这个数中,数字()代表的数值最小。
A.3
B.6 C2 D.9
15. 下面四组数字,既全部是奇数又全部是合数的是()
A. 4、12、20
B.11、13、17
C.1、9、15
D. 9、21、27
16. 从左面观察下面的立体图形,所看到的图形是()
A B C D
17. “六一”儿童节,超市利用“快乐大转盘”举行促销活动。
右面这个转盘中,指针停在白色区域的可能性是()。
A.
2
1
B.
3
1
C.
4
1
D.
8
1
18.把下面这个展开图折成一个长方体,如果F面在前面,B面在左面,那么()面在上面。
A. (A )
B. ( C )
C. (D)
D. (E)
19.下图中,阴影部分的面积是()平方厘米。
A.400
B.200
C.314
D.157
20.按下面的规律印制笑脸图案,第⑦幅团有()个笑脸。
A.13
B.21
C.28
D.36
三、计算题。
(21题3分,第22题9分,第23题18分,共30分)
21. 直接写出得数。
73-37= 3.2÷0.4= 2.3+25= 98×43= =+3121 =-9
194 22.解方程或比例。
①8x -3x=105 ②2(x -2.6)=8 ③5
2:61:21=x
23.计算下面各题,要写出主要计算过程,能用简便方法的要用简便方法计算。
16×18-120÷15 3.2×2.77+0.23×3.2 7.6-2.05÷0.82
17128917587-+- 9216792⨯- 13÷(4
36541⨯+)
四、操作题。
(共10分)
24.按要求在下面方格中作图并完成填空。
(1)画出图形①中轴对称图形的另一半。
(2)量一量:图②三角形ABC 中,顶点A 在顶点C 的( )偏( )( )°方向。
(3)画出图②中三角形ABC 绕顶点C 按顺时针方向旋转90°后的图形。
(4)画出图③中梯形按2:1放大后的图形,放大后的梯形的面积是( )cm ²。
(5)画出图④向右平移4格后的图形。
五、解决问题。
(每小题5分,共30分)
25.小刚有一本故事书共60页,第一天看了全书的5
1
,第二天看了全书的40%,两天一共看了多
少页?
26.小芳家到学校路程是2000米,早上她骑车去学校,6分钟行了1250米,这时她发现,必须
用3分钟赶到学校,否则会迟到,剩下的路程平均每分钟要行多少米?
27.订阅《小学数学报》 小雨说:我们班订了40份,用了720元。
王博问:我们班订了30份,需要多少钱?(用比例解)
28.“六一”儿童节,妈妈给彤彤买了《儿童百科全书》和《淘气包马小跳系列》两套书,共用
了360元,一套《儿童百科全书》是一套《淘气包马小跳系列》价格的7
5
,一套《淘气包马小
跳系列》的价钱是多少元?(列方程解)
29. 一个近似圆锥形的沙堆,底面半径1米,高1.2米。
这个沙堆的占地面积是多少平方米? 如果把这沙堆装在长2米,宽1.5米的沙坑里,大约可以装几米高?(得数用“四舍五入” 法保留两位小数)
30.右图是六年级一次数学测试成绩统计图。
成绩分为优、良、及格和不及格, 已知不及格的有3人。
(1)分别计算出各类成绩的人数,填入下表。
(2)成绩“良”的人数比成绩“优”的人数少百分之几?。
