§4.8 解三角形应用举例
解三角形的实际应用举例

AB sin CAB 15 sin15 BC sin120 sin ACB
6 2 sin15 4
5 6 BC ( 3 1) 4.48(海里) 2
(1)解决实际应用问题的关键思想方法是把实际问题转化为 数学问题,即数学建模思想。 (2)解决实际应用问题的步骤
(1)设A到P的距离为xkm,用x表示B,C到P的距离,并求x的值;
(2)求静止目标P到海防警戒线a的距离(结果精确到0.01km).
a
P B C
D A
分析
(1)PA,PB,PC长度之间的关系可以通过收到信号的先后时
间建立起来. (2)作PD⊥a,垂足为D,要求PD的长,只需要求出PA的长和cos∠APD, 即cos∠PAB的值.由题意,PA-PB,PC-PB都是定值,因此,只需分别在 △PAB和△PAC中,求出cos∠PAB, cos∠PAC的表达式,建立方程即 可.
=3.571 ∴BC≈1.89(m). 答:顶杆BC约长1.89m.
例2.如图,两点C,D与烟囱底部在同一水平直线上,在点C1,D1利
用高1.5m的测角仪器, 测得烟囱的仰角分别是 =450和 =600, CD间的距离是12m.求烟囱的高AB (结果精确到0.01m). B
C1 C
D1 D
(18 2 6)(m)
从而 A1 B 因此
2 BC1 18 3 19.732(m) 2 AB A1B AA1 19.732 1.5 21.23(m)
例3:如图是曲柄连杆机构的示意图,当曲柄CB绕点C旋转时,通
过连杆AB的传递,活塞作直线往复运动.当曲柄在CB0位置时,曲 柄和连杆成一条直线,连杆的端点A在A处.设连杆AB长为l mm,曲 柄CB长为r mm,l>r. (1)当曲柄自CB0按顺时针方向旋转角为θ时,其中0O≤θ<360O, 求活塞移动的距离(即连杆的端点A移动的距离A0A); (2)当l =340mm, r =85mm,θ=80O时,求A0A的长(结果精确到1mm).
解三角形应用举例

解三角形应用举例一、测量距离问题例1(1)如图,A,B两点在河的同侧,且A,B两点均不可到达,要测出A,B 的距离,测量者可以在河岸边选定两点C,D,若测得CD=32km,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,则A,B两点间的距离为km.答案6 4解析∵∠ADC=∠ADB+∠CDB=60°,∠ACD=60°,∴∠DAC=60°,∴AC=DC=32km.在△BCD中,∠DBC=180°-∠CDB-∠ACD-∠ACB=45°,由正弦定理,得BC=DCsin∠DBC·sin∠BDC=32sin 45°·sin 30°=64(km).在△ABC中,由余弦定理,得AB2=AC2+BC2-2AC·BCcos 45°=34+38-2×32×64×22=38.∴AB=64km.∴A,B两点间的距离为64km.(2)如图,为了测量两座山峰上P,Q两点之间的距离,选择山坡上一段长度为300 3 m且和P,Q两点在同一平面内的路段AB的两个端点作为观测点,现测得∠PAB=90°,∠PAQ=∠PBA=∠PBQ=60°,则P,Q两点间的距离为m.答案900解析由已知,得∠QAB=∠PAB-∠PAQ=30°.又∠PBA=∠PBQ=60°,∴∠AQB=30°,∴AB=BQ.又PB为公共边,∴△PAB≌△PQB,∴PQ =PA.在Rt△PAB中,AP=AB·tan 60°=900(m),故PQ=900 m,∴P,Q两点间的距离为900 m.二、测量高度问题例2如图所示,为测量一树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖的仰角为30°,45°,且A,B 两点间的距离为60 m,则树的高度为m.答案30+30 3解析在△PAB中,∠PAB=30°,∠APB =15°,AB=60 m,sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°sin 30°=22×32-22×12=6-2 4,由正弦定理得PB sin 30°=AB sin 15°, 所以PB =12×606-24=30(6+2), 所以树的高度为PB ·sin 45°=30(6+2)×22=(30+303)(m ). 三、测量角度问题例3 已知岛A 南偏西38°方向,距岛A 3海里的B 处有一艘缉私艇.岛A 处的一艘走私船正以10海里/小时的速度向岛北偏西22°方向行驶,问缉私艇朝何方向以多大速度行驶,恰好用0.5小时能截住该走私船?⎝⎛⎭⎫参考数据:sin 38°≈5314,sin 22°≈3314 解 如图,设缉私艇在C 处截住走私船,D 为岛A 正南方向上一点,缉私艇的速度为x 海里/小时,结合题意知BC =0.5x ,AC =5,∠BAC =180°-38°-22°=120°.由余弦定理可得BC 2=AB 2+AC 2-2AB ·ACcos 120°,所以BC 2=49,所以BC =0.5x =7, 解得x =14.又由正弦定理得sin ∠ABC =AC ·sin ∠BAC BC=5×327=5314, 所以∠ABC =38°,又∠BAD =38°,所以BC ∥AD ,故缉私艇以14海里/小时的速度向正北方向行驶,恰好用0.5小时截住该走私船. 素养提升 数学抽象是指舍去事物的一切物理属性,得到数学研究对象的思维过程,主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,并且用数学符号或数学术语予以表征.从实际问题中抽象出距离、高度、角度等数学问题,然后利用正弦定理、余弦定理求解,很好地体现了数学抽象的数学素养.。
《解三角形的实际应用举例》 知识清单

《解三角形的实际应用举例》知识清单一、解三角形的基本概念解三角形是指通过已知三角形的某些元素(如边、角),求出其余元素的过程。
在实际应用中,我们通常会利用正弦定理、余弦定理以及三角形的内角和定理来解决问题。
正弦定理:在任意一个三角形中,各边和它所对角的正弦值的比相等且等于外接圆的直径,即\(\frac{a}{\sin A} =\frac{b}{\sin B} =\frac{c}{\sin C} = 2R\)(\(R\)为三角形外接圆的半径)。
余弦定理:对于任意三角形,有\(a^2 =b^2 +c^2 2bc\cos A\),\(b^2 = a^2 + c^2 2ac\cos B\),\(c^2 = a^2 + b^2 2ab\cosC\)。
三角形内角和定理:三角形的内角和为\(180^{\circ}\),即\(A + B + C = 180^{\circ}\)。
二、解三角形的实际应用类型1、测量距离问题(1)两点间不可到达的距离例如,要测量河两岸两点\(A\)、\(B\)之间的距离,在河岸一侧选取一点\(C\),测出\(AC\)、\(BC\)的长度以及\(\angle ACB\)的大小。
利用余弦定理可以求出\(AB\)的长度。
假设\(AC = m\),\(BC = n\),\(\angle ACB =\theta\),则\(AB^2 = m^2 + n^2 2mn\cos\theta\),从而求出\(AB\)。
(2)两点间可到达但有障碍的距离比如,要测量两个山峰之间的距离,但是中间有山谷等障碍物阻隔。
可以在合适的地点选取观测点,测量出相关的边和角,然后通过解三角形计算出两点之间的距离。
2、测量高度问题(1)底部可到达的物体高度要测量底部可以到达的建筑物的高度,如塔高。
在塔底合适的位置测量出仰角,以及到塔底的距离,然后利用正切函数求出塔高。
假设在点\(C\)测得塔\(AB\)顶部\(A\)的仰角为\(\alpha\),\(BC\)的距离为\(d\),则塔高\(AB = d\tan\alpha\)。
《解直角三角形应用举例》课件

如图,当组合体运行到地球表面
P 点的正上方时,从中能直接看到的地球
表面最远的点在什么位置?最远点与 P 点
的距离是多少 (地球半径约为 6 400 km,π
取 3.142,结果取整数)?
F
P
FQ 是☉O 的切线,
∠FQO 为直角
Q
最远点
O
的长,要先
解:在 Rt△AOC 中,∵sin75°=
,
∴OC ≈ 38.8 cm.
在 Rt△BOC 中,∵tan30°=
,
∴BC ≈ 67.3 cm.
答:该台灯照亮水平面的宽度 BC 约为67.3 cm.
易错警示:注意结果必须根据题目要求精确到0.1cm.
技巧点拨:
借助公共边解双直角三角形
面的夹角是 30°,拉索 CD 与水平桥面的夹角是 60°,
两拉索顶端的距离 BC 为 2米.两拉索底端的距离 AD 为
20米,请求出立柱 BH 的长.(结果精确到0.1米, 3≈1.732)
解:设 DH =x 米. ∵ ∠CDH =60° ,∠H =90°,
∴ CH =DH·tan60°= 3x 米,
∴ 此时南楼的影子落在北楼上约 3.5 m 高.
解:(2)如图,若使每层楼在冬天都受阳光照射,则
DC =0 m,即点 C 与点 D 重合.
当点 C 与点 D 重合时,
tan∠ACB
∴ BD=
= ,即
tan32°
=
tan32°=
16
tan32°
,
≈ 25.6 (m),
解三角形的实际应用举例
C
(2) 已知两边和一边对角,
求其它元素。
A
B
C
• 余弦定理
c2 a2 b2 2abcosC
(1) 已知三边 , 求三个角;
A
B
C
(2) 已知两边和它们的夹角,
求其它元素。
A
B
C
例1、自动卸货汽车的车箱采用液压机构.设计时 需要计算油泵顶杆BC的长度(如图所示).已知车 箱最大仰角为60油泵顶点B与车箱支点A之间的 距离为1.95m,AB与水平线之间的夹角为620, AC为1.40m,计算BC的长.
数学问题(画出图形)
检 验
数学结论
解三角形问题
谢谢
再见!
么 “ 来 两一 的 算 已度在形是 测 , 部解世 记 圆 经及物的我解三 量 三 分三纪 载 内 取工理方国三角 ” 角 内角的,接得程学法古角学。学容形公正了《建中。代形?最才的问元六某周筑,很的三初被一题三边些髀等有早方角的看门是世 形 特算生 关就法学 理 作 数三纪 、 殊经产 向有在来 解 包 学角, 正 角》实 量测度自 是 括 分学十 的里际 的我量量希 解 三 学的二 正,中 计国方工腊 三 角 科基边 弦已, 算数面件角文 函 。本形有…有 也学的、形“ 数…问关的广要家知测的三和题于边泛用识刘量计角解之平长的到,徽距算形三一面时应解公在离,”角。测,用三元计和后和形什量就,角高
=3.571 ∴BC≈1.89(m).
答:顶杆BC约长1.89m.
解斜三角形理论应用于实际问题应注意:
1、认真分析题意,弄清已知元素和未知元素。
2、要明确题目中一些名词、术语的意义。如 视角,仰角,俯角,方位角等等。
3、动手画出示意图,利用几何图形的性质, 将已知和未知集中到一个三角形中解决。
解三角形实际应用举例

解三角形的应用.
练习1、我舰在敌岛A南50°西相距12海里B处, 发现敌舰正由岛沿北10°西的方向以10海里/时 的速度航行,我舰要用2小时追上敌舰,则需要 C 的速度大小为 。
分析:2小时敌舰航行距离AC=20,
10 °
由AB=12,∠BAC=120°,
余弦定理可解我舰航行距离 BC。 (略)
B
余弦定理先求出A,或先求 (1)a=2 3 ,b= 6 ,c=3 + 3 _________________________________ ; 出B 余弦定理先求出a (2)b=1,c= 2 ,A=105º ; _________________________________ 正弦定理先求出b (3)A=45º ,B =60º , a=10; ________________________________
2、方向角:指北或指南 方向线与目标方向线所成 的小于90°的水平角,叫 方向角,如图
基本概念和公式.
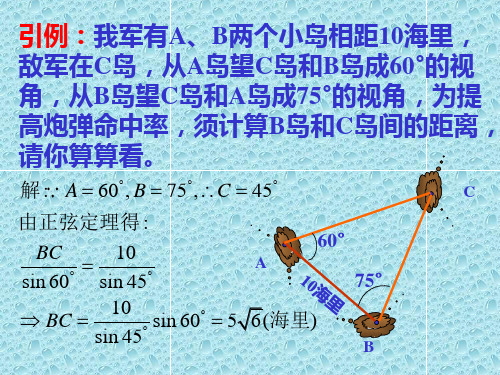
例1海上有A、B两个小岛相距10海里,从 A岛望C岛和B岛成60°的视角,从B岛望 C岛和A岛成75°的视角,那么B岛和C岛 间的距离是 。
解:应用正弦定理,C=45 °
BC/sin60°=10/sin45°
60° 75°
B C
BC=10sin60 °/sin45°
答:
解三角形应用举例优秀课件ppt

28cos 30 sin 60 sin(60 30 )
42(m)
CD=BD-BC=42-28=14(m)
答:山的高度约为14米。
例2
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
如图,一辆汽车在一条水平的公路上向正西行驶,
到A处时测得公路北测远处一山顶D在西偏北15º的方向上,
行驶5km后到达B处,测得此山顶在西偏北25º的方向上,
仰角为8º,求此山的高度CD. sin150 0.26,sin100 0.17,
tan 80 0.14
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
2.某人向东方向走了x千米,然后向右转120°,再朝新方向走了3千米, 结果他离出发点恰好 13 千米,求x的值。 3.如图,为了测量A,C两点间的距离,选取同一平面上B,D两点,测 出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA =5,A,B,C,D四点共圆,求AC的长.
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
跟踪训练1 甲船在A点发现乙船在北偏东60°的B处, 乙船以每小时a海里的速度向北行驶,已知甲船的速 度是每小时 3a 海里,问甲船应沿着什么方向前进, 才能最快与乙船相遇? 解答
3.某人向东方向走了x千米,然后向右转120°,再朝新方向走了3千米, 结果他离出发点恰好 13 千米,那么x的值是__4_. 答案 解析
由余弦定理,得x2+9-3x=13, 整理得x2-3x-4=0,解得x=4.
高三复习:三角函数模型及解三角形应用举例(含解析答案)

§4.8 三角函数模型及解三角形应用举例解三角形应用题的一般步骤(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系. (2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型. (3)根据题意选择正弦定理或余弦定理求解.(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.题型一 测量距离、高度问题例1(2013·江苏)如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山,甲沿AC匀速步行,速度为50m /min.在甲出发2 min 后,乙从A 乘缆车到B ,在B 处停留1 min 后,再从B 匀速步行到C .假设缆车匀速直线运动的速度为130 m/min ,山路AC 长为1260m ,经测量cos A =1213,cos C =35.①求索道AB 的长;②问:乙出发多少分钟后,乙在缆车上与甲的距离最短?③为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?题型二测量角度问题例2如图,在海岸A处发现北偏东45°方向,距A处(3-1)海里的B处有一艘走私船.在A处北偏西75°方向,距A处2海里的C处的我方缉私船奉命以103海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度,以B处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.题型三利用三角函数模型求最值例3如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.(1)将十字形的面积表示为θ的函数;(2)θ满足何种条件时,十字形的面积最大?最大面积是多少?变式如图为一个缆车示意图,该缆车半径为4.8米,圆上最低点与地面距离为0.8米,且60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面间的距离为h.(1)求h与θ间关系的函数解析式;(2)设从OA开始转动,经过t秒后到达OB,求h与t之间的函数关系式,并求缆车到达最高点时用的最少时间是多少?课堂练习:1.已知△ABC ,C 为坐标原点O ,A (1,sin α),B (cos α,1),α∈⎝⎛⎦⎤0,π2,则当△OAB 的面积达到最大值时,α=______.2.某人向正东方向走x km 后,向右转150°,然后朝新方向走3km ,结果他离出发点恰好是3km ,那么x 的值为________. 3.如图所示,位于A 处的信息中心获悉:在其正东方向相距40海里的B 处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°且相距20海里的C 处的乙船,现乙船朝北偏东θ的方向即沿直线CB 前往B 处救援,则cos θ等于________.4.8三角函数模型及解三角形应用举例作业1.如图为一半径是3m的水轮,水轮的圆心O距离水面2m.已知水轮每分钟旋转4圈,水轮上的点P到水面的距离y(m)与时间x(s)满足函数关系y=A sin(ωx+φ)+2(ω>0,A>0),则ω=________,A=________.2.甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是________________.3.如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.4.某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在A处获悉后,立即测出该渔船在方位角为45°,距离为10nmile的C处,并测得渔船正沿方位角为105°的方向,以10nmile/h的速度向某小岛B靠拢,我海军舰艇立即以103nmile/h的速度前去营救,求舰艇的航向和靠近渔船所需的时间.5.某运输装置如图所示,其中钢结构ABD 是AB =BD =l ,∠B =π3的固定装置,AB 上可滑动的点C 使CD 垂直于地面(C 不与A ,B 重合),且CD 可伸缩(当CD 伸缩时,装置ABD 随之绕D 在同一平面内旋转),利用该运输装置可以将货物从地面D 处沿D →C →A 运送至A 处,货物从D 处至C 处运行速度为v ,从C 处至A 处运行速度为3v .为了使运送货物的时间t 最短,需在运送前调整运输装置中∠DCB =θ的大小.(1)当θ变化时,试将货物运行的时间t 表示成θ的函数(用含有v 和l 的式子表示); (2)当t 最小时,C 点应设计在AB 的什么位置?6某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口O 北偏西30°且与该港口相距20海里的A 处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v 海里/小时的航行速度匀速行驶,经过t 小时与轮船相遇.(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少? (2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.§4.8 三角函数模型及解三角形应用举例解三角形应用题的一般步骤(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系. (2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型. (3)根据题意选择正弦定理或余弦定理求解.(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.题型一 测量距离、高度问题例1(2013·江苏)如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山,甲沿AC匀速步行,速度为50m /min.在甲出发2 min 后,乙从A 乘缆车到B ,在B 处停留1 min 后,再从B 匀速步行到C .假设缆车匀速直线运动的速度为130 m/min ,山路AC 长为1260m ,经测量cos A =1213,cos C =35.①求索道AB 的长;②问:乙出发多少分钟后,乙在缆车上与甲的距离最短?③为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内? (1)答案 30+30 3解析 在△P AB 中,∠P AB =30°,∠APB =15°,AB =60,sin15°=sin(45°-30°)=sin45°cos30°-cos45°sin30°=22×32-22×12=6-24,由正弦定理得PB sin30°=ABsin15°,∴PB =12×606-24=30(6+2),∴树的高度为PB ·sin45°=30(6+2)×22=(30+303)m.(2)解 ①在△ABC 中,因为cos A =1213,cos C =35,所以sin A =513,sin C =45.从而sin B =sin [π-(A +C )]=sin(A +C ) =sin A cos C +cos A sin C=513×35+1213×45=6365. 由正弦定理AB sin C =ACsin B ,得AB =AC sin B ×sin C =1 2606365×45=1 040(m).所以索道AB 的长为1040m.②假设乙出发t 分钟后,甲、乙两游客距离为d ,此时,甲行走了(100+50t )m ,乙距离A 处130t m ,所以由余弦定理得d 2=(100+50t )2+(130t )2-2×130t ×(100+50t )×1213=200(37t 2-70t +50),由于0≤t ≤1040130,即0≤t ≤8,故当t =3537min 时,甲、乙两游客距离最短.③由正弦定理BC sin A =ACsin B ,得BC =AC sin B ×sin A =12606365×513=500(m).乙从B 出发时,甲已走了50×(2+8+1)=550(m),还需走710m 才能到达C .设乙步行的速度为v m/min ,由题意得-3≤500v -71050≤3,解得125043≤v ≤62514,所以为使两位游客在C 处互相等待的时间不超过3min ,乙步行的速度应控制在⎣⎡⎦⎤125043,62514(单位:m/min)范围内. 题型二 测量角度问题例2 如图,在海岸A 处发现北偏东45°方向,距A 处(3-1)海里的B 处有一艘走私船.在A 处北偏西75°方向,距A 处2海里的C 处的我方缉私船奉命以103海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度,以B 处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.思维点拨 设缉私船t 小时后在D 处追上走私船,确定出三角形,先利用余弦定理求出BC ,再利用正弦定理求出时间.解 设缉私船应沿CD 方向行驶t 小时,才能最快截获(在D 点)走私船,则CD =103t (海里),BD =10t (海里),在△ABC 中,由余弦定理,有 BC 2=AB 2+AC 2-2AB ·AC cos ∠BAC =(3-1)2+22-2(3-1)·2·cos120°=6. ∴BC =6(海里).又∵BC sin ∠BAC =ACsin ∠ABC,∴sin ∠ABC =AC ·sin ∠BAC BC =2·sin120°6=22,∴∠ABC =45°,∴B 点在C 点的正东方向上, ∴∠CBD =90°+30°=120°,在△BCD 中,由正弦定理,得BD sin ∠BCD =CDsin ∠CBD,∴sin ∠BCD =BD ·sin ∠CBD CD =10t ·sin120°103t =12.∴∠BCD =30°,∴缉私船沿北偏东60°的方向行驶.又在△BCD 中,∠CBD =120°,∠BCD =30°, ∴D =30°,∴BD =BC ,即10t = 6. ∴t =610小时≈15(分钟). ∴缉私船应沿北偏东60°的方向行驶,才能最快截获走私船,大约需要15分钟. 思维升华 测量角度问题的一般步骤(1)在弄清题意的基础上,画出表示实际问题的图形,并在图形中标出有关的角和距离; (2)用正弦定理或余弦定理解三角形;(3)将解得的结果转化为实际问题的解.题型三 利用三角函数模型求最值例3 如图,在直径为1的圆O 中,作一关于圆心对称、邻边互相垂直的十字形,其中y >x >0.(1)将十字形的面积表示为θ的函数;(2)θ满足何种条件时,十字形的面积最大?最大面积是多少? 思维点拨 由题图可得:x =cos θ,y =sin θ.列出面积函数后,利用三角函数性质求解,注意θ的范围. 解 (1)设S 为十字形的面积,则S =2xy -x 2=2sin θcos θ-cos 2θ (π4<θ<π2);(2)S =2sin θcos θ-cos 2θ=sin2θ-12cos2θ-12=52sin(2θ-φ)-12,其中tan φ=12, 当sin(2θ-φ)=1,即2θ-φ=π2时,S 最大.所以,当θ=π4+φ2(tan φ=12)时,S 最大,最大值为5-12.思维升华 三角函数作为一类特殊的函数,可利用其本身的值域来求函数的最值.变式 如图为一个缆车示意图,该缆车半径为4.8米,圆上最低点与地面距离为0.8米,且60秒转动一圈,图中OA 与地面垂直,以OA 为始边,逆时针转动θ角到OB ,设B 点与地面间的距离为h . (1)求h 与θ间关系的函数解析式; (2)设从OA 开始转动,经过t 秒后到达OB ,求h 与t 之间的函数关系式,并求缆车到达最高点时用的最少时间是多少?解 (1)以圆心O 为原点,建立如图所示的平面直角坐标系,则以Ox为始边,OB 为终边的角为θ-π2,故点B 的坐标为(4.8cos(θ-π2),4.8sin(θ-π2)), ∴h =5.6+4.8sin ⎝⎛⎭⎫θ-π2. (2)点A 在圆上转动的角速度是π30弧度/秒,故t 秒转过的弧度数为π30t ,∴h =5.6+4.8sin ⎝⎛⎭⎫π30t -π2,t ∈[0,+∞).到达最高点时,h =10.4米.由sin ⎝⎛⎭⎫π30t -π2=1,得π30t -π2=π2,∴t =30秒, ∴缆车到达最高点时,用的最少时间为30秒.课堂练习:1.已知△ABC ,C 为坐标原点O ,A (1,sin α),B (cos α,1),α∈⎝⎛⎦⎤0,π2,则当△OAB 的面积达到最大值时,α=______.答案 π2解析 ∵S =1-12×1×sin α-12×1×cos α-12(1-cos α)(1-sin α)=12-12sin αcos α =12-14sin2α. ∴当α=π2时,S 取到最大值.3.某人向正东方向走x km 后,向右转150°,然后朝新方向走3km ,结果他离出发点恰好是3km ,那么x 的值为________. 答案 3或2 3解析 如图所示,设此人从A 出发,则AB =x ,BC =3,AC =3,∠ABC =30°, 由余弦定理得(3)2=x 2+32-2x ·3·cos30°,整理,得x 2-33x +6=0,解得x =3或2 3.4.如图所示,位于A 处的信息中心获悉:在其正东方向相距40海里的B 处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°且相距20海里的C 处的乙船,现乙船朝北偏东θ的方向即沿直线CB 前往B 处救援,则cos θ等于________.答案 2114解析 在△ABC 中,AB =40,AC =20,∠BAC =120°,由余弦定理,得BC 2=AB 2+AC 2-2AB ·AC ·cos120°=2800,所以BC =207. 由正弦定理,得sin ∠ACB =AB BC ·sin ∠BAC =217.由∠BAC =120°,知∠ACB 为锐角,故cos ∠ACB =277.故cos θ=cos(∠ACB +30°)=cos ∠ACB cos30°-sin ∠ACB sin30°=2114.4.8 三角函数模型及解三角形应用举例作业1.如图为一半径是3m 的水轮,水轮的圆心O 距离水面2m .已知水轮每分钟旋转4圈,水轮上的点P 到水面的距离y (m)与时间x (s)满足函数关系y =A sin(ωx +φ)+2(ω>0,A >0),则ω=________,A =________.答案 2π153 解析 每分钟转4圈,每圈所需时间T =604=15. 又T =2πω=15,∴ω=2π15,A =3. 2.甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是________________.答案 203米、4033米 解析 如图,依题意有甲楼的高度为AB =20·tan60°=203(米),又CM=DB =20(米),∠CAM =60°,所以AM =CM ·1tan60°=2033(米),故乙楼的高度为CD =203-2033=4033(米). 3.如图所示,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个观测点C 与D ,测得∠BCD =15°,∠BDC =30°,CD =30m ,并在点C 处测得塔顶A 的仰角为60°,求塔高AB .解 在△BCD 中,∠CBD =180°-15°-30°=135°,由正弦定理,得BC sin ∠BDC =CD sin ∠CBD,所以BC =30sin30°sin135°=15 2 (m). 在Rt △ABC 中,AB =BC ·tan ∠ACB =152tan60°=15 6 (m).所以塔高AB 为156m.4.某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在A 处获悉后,立即测出该渔船在方位角为45°,距离为10nmile 的C 处,并测得渔船正沿方位角为105°的方向,以10nmile/h 的速度向某小岛B 靠拢,我海军舰艇立即以103nmile/h 的速度前去营救,求舰艇的航向和靠近渔船所需的时间.解 如图所示,设所需时间为t 小时,则AB =103t ,CB =10t .在△ABC 中,根据余弦定理,则有AB 2=AC 2+BC 2-2AC ·BC ·cos120°,可得:(103t )2=102+(10t )2-2×10×10t cos120°.整理得:2t 2-t -1=0,解得t =1或t =-12(舍去). 所以舰艇需1小时靠近渔船,此时AB =103,BC =10. 在△ABC 中,由正弦定理得:BC sin ∠CAB =AB sin120°, 所以sin ∠CAB =BC ·sin120°AB =10×32103=12. 所以∠CAB =30°.所以舰艇航行的方位角为75°.5.某运输装置如图所示,其中钢结构ABD 是AB =BD =l ,∠B =π3的固定装置,AB 上可滑动的点C 使CD 垂直于地面(C 不与A ,B 重合),且CD 可伸缩(当CD 伸缩时,装置ABD 随之绕D 在同一平面内旋转),利用该运输装置可以将货物从地面D 处沿D →C →A 运送至A 处,货物从D 处至C 处运行速度为v ,从C 处至A 处运行速度为3v .为了使运送货物的时间t 最短,需在运送前调整运输装置中∠DCB =θ的大小.(1)当θ变化时,试将货物运行的时间t 表示成θ的函数(用含有v 和l 的式子表示);(2)当t 最小时,C 点应设计在AB 的什么位置?解 (1)在△BCD 中,∵∠BCD =θ,∠B =π3,BD =l , ∴BC =l sin (2π3-θ)sin θ,CD =3l 2sin θ, ∴AC =AB -BC =l -l sin (2π3-θ)sin θ, 则t =AC 3v +CD v =l 3v -l sin (2π3-θ)3v sin θ+3l 2v sin θ(π3<θ<2π3). (2)t =l 6v (1-3cos θsin θ)+3l 2v sin θ=l 6v +3l 6v ·3-cos θsin θ. 令m (θ)=3-cos θsin θ,θ∈(π3,2π3),则m ′(θ)=1-3cos θsin 2θ. 令m ′(θ)=0,得cos θ=13,设cos θ0=13,θ0∈(π3,2π3), 则θ∈(π3,θ0)时,m ′(θ)<0;当θ∈(θ0,2π3)时,m ′(θ)>0,∴当cos θ=13时,m (θ)取得最小值22,此时BC =6+48l . 故当BC =6+48l 时货物运行时间最短. 6某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口O 北偏西30°且与该港口相距20海里的A 处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v 海里/小时的航行速度匀速行驶,经过t 小时与轮船相遇.(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.规范解答解 (1)设相遇时小艇的航行距离为S 海里, 则S =900t 2+400-2·30t ·20·cos (90°-30°) =900t 2-600t +400=900(t -13)2+300.[4分] 故当t =13时,S min =103,v =10313=30 3.[6分] 即小艇以303海里/小时的速度航行,相遇小艇的航行距离最小.[7分](2)设小艇与轮船在B 处相遇.则v 2t 2=400+900t 2-2·20·30t ·cos(90°-30°),故v 2=900-600t +400t2.[9分] ∵0<v ≤30,∴900-600t +400t 2≤900,即2t 2-3t ≤0,解得t ≥23.[10分] 又t =23时,v =30, 故v =30时,t 取得最小值,且最小值等于23.[12分] 此时,在△OAB 中,有OA =OB =AB =20.故可设计航行方案如下:航行方向为北偏东30°,航行速度为30海里/小时.[14分]。
《解三角形的实际应用举例》 知识清单

《解三角形的实际应用举例》知识清单一、解三角形的基本概念在探讨解三角形的实际应用之前,我们先来回顾一下解三角形的一些基本概念。
三角形的六个元素包括三条边和三个角。
解三角形,就是已知三角形的若干元素,求出其余的元素。
在解三角形时,我们通常会用到正弦定理和余弦定理。
正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即\(\frac{a}{\sin A} =\frac{b}{\sin B} =\frac{c}{\sin C}\)。
余弦定理:对于任意三角形,有\(a^2 =b^2 +c^2 2bc\cos A\),\(b^2 = a^2 + c^2 2ac\cos B\),\(c^2 = a^2 + b^2 2ab\cosC\)。
二、解三角形的实际应用类型1、测量距离问题这是解三角形在实际中常见的应用之一。
比如,要测量河对岸两点A、B 之间的距离,我们可以在河的这一侧选取一个点 C,然后测量出\(\angle BCA\)、\(\angle BAC\)以及边 AC 的长度。
接下来,利用正弦定理就可以求出边 AB 的长度。
再比如,要测量两个不能直接到达的地点之间的距离。
假设要测量点 M 和点 N 之间的距离,但由于中间有障碍物无法直接测量。
我们可以在另一个可以到达的点 P 处,测量出\(\angle MPN\)、\(\angle MPN\)和边 PM、PN 的长度,然后通过余弦定理求出边 MN 的长度。
2、测量高度问题测量高度也是常见的应用场景。
比如要测量一座山的高度。
我们可以在山脚下的一点 A 处,测量山顶的仰角\(\angle BAC\),以及测量点 A 到山脚下的水平距离 AC。
然后利用正切函数\(\tan\angleBAC =\frac{BC}{AC}\),求出山顶到点 A 的垂直高度 BC,从而得到山的高度。
又如,要测量建筑物的高度。
我们可以在离建筑物一定距离的地方,测量建筑物顶部的仰角和底部的俯角,再结合测量的水平距离,利用三角形的知识来计算建筑物的高度。
第四章 §4.8 正弦定理、余弦定理-2025高中数学大一轮复习讲义人教A版

§4.8正弦定理、余弦定理课标要求1.掌握正弦定理、余弦定理及其变形.2.理解三角形的面积公式并能应用.3.能利用正弦定理、余弦定理解决一些简单的三角形度量问题.知识梳理1.正弦定理、余弦定理在△ABC 中,若角A ,B ,C 所对的边分别是a ,b ,c ,R 为△ABC 外接圆半径,则定理正弦定理余弦定理内容a sin A=b sin B =csin C=2R a 2=b 2+c 2-2bc cos A ;b 2=c 2+a 2-2ca cos B ;c 2=a 2+b 2-2ab cos C 变形(1)a =2R sin A ,b =2R sin B ,c =2R sin C ;(2)sin A =a 2R ,sin B =b 2R ,sin C =c2R ;(3)a ∶b ∶c =sin A ∶sin B ∶sin Ccos A =b 2+c 2-a 22bc;cos B =c 2+a 2-b 22ac ;cos C =a 2+b 2-c 22ab2.三角形解的判断A 为锐角A 为钝角或直角图形关系式a =b sin A b sin A <a <b a ≥b a >b 解的个数一解两解一解一解3.三角形中常用的面积公式(1)S =12ah a (h a 表示边a 上的高);(2)S =12ab sin C =12ac sin B =12bc sin A ;(3)S =12r (a +b +c )(r 为三角形的内切圆半径).常用结论在△ABC 中,常有以下结论:(1)∠A +∠B +∠C =π.(2)任意两边之和大于第三边,任意两边之差小于第三边.(3)a >b ⇔A >B ⇔sin A >sin B ,cos A <cos B .(4)sin(A +B )=sin C ;cos(A +B )=-cos C ;tan(A +B )=-tan C ;sin A +B 2=cos C2;cosA +B 2=sin C 2.(5)三角形中的射影定理在△ABC 中,a =b cos C +c cos B ;b =a cos C +c cos A ;c =b cos A +a cos B .(6)三角形中的面积S =12(a +b +自主诊断1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)三角形中三边之比等于相应的三个内角的余弦值之比.(×)(2)在△ABC 中,若sin A >sin B ,则a >b .(√)(3)在△ABC 的六个元素中,已知任意三个元素可求其他元素.(×)(4)当b 2+c 2-a 2>0时,△ABC 为锐角三角形.(×)2.(必修第二册P44T2改编)在△ABC 中,AB =5,AC =3,BC =7,则∠BAC 等于()A.π6B.π3C.2π3D.5π6答案C解析在△ABC 中,设AB =c =5,AC =b =3,BC =a =7,由余弦定理得cos ∠BAC =b 2+c 2-a 22bc =9+25-4930=-12,因为∠BAC 为△ABC 的内角,所以∠BAC =2π3.3.在△ABC 中,a ,b ,c 分别为角A ,B ,C 所对的边,已知b =40,c =20,C =60°,则此三角形的解的情况是()A .有一解B .有两解C .无解D .有解但解的个数不确定答案C解析由正弦定理得b sin B =c sin C ,∴sin B =b sin Cc=40×3220=3>1.∴角B 不存在,即此三角形无解.4.记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,面积为3,B =60°,a 2+c 2=3ac ,则b =.答案22解析由题意得S △ABC =12ac sin B =34ac =3,则ac =4,所以a 2+c 2=3ac =3×4=12,所以b 2=a 2+c 2-2ac cos B =12-2×4×12=8,则b =2 2.题型一利用正弦、余弦定理解三角形例1(1)(2023·榆林模拟)△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若a sin A +(b +λa )sin B =c sin C ,则λ的取值范围为()A .(-2,2)B .(0,2)C .[-2,2]D .[0,2]答案A解析因为a sin A +(b +λa )sin B =c sin C ,由正弦定理得c 2=a 2+b 2+λab ,由余弦定理知c 2=a 2+b 2-2ab cos C ,所以λ=-2cos C ,因为C ∈(0,π),所以cos C ∈(-1,1),故λ∈(-2,2).(2)(2024·兰州模拟)用长度为1,4,8,9的4根细木棒围成一个三角形(允许连接,不允许折断),则其中某个三角形外接圆的直径可以是(写出一个答案即可).答案301111(答案不唯一)解析4根细木棒围成的三角形的三边长可以为5,8,9,设边长为9的边所对的角为θ,该三角形外接圆的半径为R ,由余弦定理知,cos θ=25+64-812×5×8=110,因为θ∈(0,π),所以sin θ=1-cos 2θ=31110,由正弦定理知,2R =9sin θ=931110=301111,所以其中某个三角形外接圆的直径可以是301111.思维升华解三角形时,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式,则考虑用正弦定理,以上特征都不明显时,则要考虑两个定理都有可能用到.跟踪训练1(1)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,a =1,c =62,A =45°,则C 等于()A .30°B .60°C .120°D .60°或120°答案D解析因为a =1,c =62,A =45°,所以由正弦定理可得sin C =c sin A a =62×221=32,又因为0°<C <180°,c >a ,A =45°,所以C =60°或120°.(2)已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b sin 2A =a sin B ,且c =2b ,则a b等于()A .2B .3 C.2D.3答案D解析由正弦定理及b sin 2A =a sin B ,得2sin B sin A cos A =sin A sin B ,又sin A ≠0,sin B ≠0,则cos A =12.又c =2b ,所以由余弦定理得a 2=b 2+c 2-2bc cos A =b 2+4b 2-4b 2×12=3b 2,得ab = 3.题型二正弦定理、余弦定理的简单应用命题点1三角形的形状判断例2(2023·临沂模拟)在△ABC 中,已知sin A +sin C sin B =b +ca且满足条件①a (sin A -sin B )=(c -b )(sin C +sin B );②b cos A +a cos B =c sin C 中的一个,试判断△ABC 的形状,并写出推理过程.注:如果选择多个条件分别解答,则按第一个解答计分.解由sin A +sin C sin B =b +ca及正弦定理得a +cb =b +c a ,即a 2+ac =b 2+bc ,∴a 2-b 2+ac -bc =0,∴(a -b )(a +b +c )=0,∴a =b .若选①,则△ABC 为等边三角形.推理如下:由a (sin A -sin B )=(c -b )(sin C +sin B )及正弦定理,得a (a -b )=(c -b )(c +b ),即a 2+b 2-c 2=ab .∴由余弦定理得cos C =a 2+b 2-c 22ab =12又C ∈(0,π),∴C =π3.∴△ABC 为等边三角形.若选②,则△ABC 为等腰直角三角形.推理如下:∵b cos A +a cos B =b ·b 2+c 2-a 22bc +a ·a 2+c 2-b 22ac =2c 22c =c =c sin C ,∴sin C =1,∴C =π2,∴△ABC 为等腰直角三角形.思维升华判断三角形形状的两种思路(1)化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.(2)化角:通过三角恒等变换,得出内角的关系,从而判断三角形的形状.此时要注意应用A+B +C =π这个结论.命题点2三角形的面积例3(10分)(2023·新高考全国Ⅰ)已知在△ABC 中,A +B =3C ,2sin(A -C )=sin B .(1)求sin A ;[切入点:由A ,B ,C 关系求角C 及代换sin B ](2)设AB =5,求AB 边上的高.[关键点:由A ,B ,C 关系求sin B ][思路分析](1)由A ,B ,C 关系求角C →B =π-(A +C )代入化简→tan A →sin A (2)由角C ,sin A →sin B →AC →等面积法求高解(1)∵A +B =3C ,∴π-C =3C ,即C =π4,(1分)①处由A ,B ,C 关系求角C又2sin(A -C )=sin B =sin (A +C ),(2分)②处由B 与A ,C 关系代换sin B ∴2sin A cos C -2cos A sin C =sin A cos C +cos A sin C ,∴sin A cos C =3cos A sin C ,∴sin A =3cos A ,③处两角和差公式化简即tan A =3,(4分)∴0<A <π2,∴sin A =310=31010.(5分)④处由正切求正弦(2)由(1)知,cos A =110=1010,分)⑤处由B 与A ,C 关系求sin B 由正弦定理AB sin C =ACsin B,可得(8分)⑥处正弦定理求AC∴12AB ·h =12AB ·AC ·sin A ,⑦处等面积法求高∴h =AC ·sin A =210×310106.(10分)思维升华三角形面积公式的应用原则(1)对于面积公式S =12ab sin C =12ac sin B =12bc sin A ,一般是已知哪一个角就使用哪一个公式.(2)与面积有关的问题,一般要用到正弦定理或余弦定理进行边和角的转化.命题点3与平面几何有关的问题例4(2023·梅州模拟)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2a +b =2c cos B .(1)求角C ;(2)若CD 是角C 的平分线,AD =27,DB =7,求CD 的长.解(1)由2a +b =2c cos B ,根据正弦定理可得2sin A +sin B =2sin C cos B ,则2sin(B +C )+sin B =2sin C cos B ,所以2sin B cos C +2cos B sin C +sin B =2sin C cos B ,整理得(2cos C +1)sin B =0,因为B ,C 均为三角形内角,所以B ,C ∈(0,π),sin B ≠0,因此cos C =-12,所以C =2π3.(2)因为CD 是角C 的平分线,AD =27,DB =7,AC =5×25522=210,所以在△ACD 和△BCD 中,由正弦定理可得,AD sin π3=CD sin A ,BD sinπ3=CDsin B ,因此AD BD =sin Bsin A=2,即sin B =2sin A ,所以b =2a ,又由余弦定理可得c 2=a 2+b 2-2ab cos C ,即(37)2=a 2+4a 2+2a 2,解得a =3,所以b =6,又S △ABC =S △ACD +S △BCD ,即12ab sin ∠ACB =12b ·CD ·sin ∠ACD +12a ·CD ·sin ∠BCD ,即18=9CD ,所以CD =2.思维升华在平面几何图形中研究或求与角有关的长度、角度、面积的最值、优化设计等问题时,通常是转化到三角形中,利用正、余弦定理通过运算的方法加以解决.在解决某些具体问题时,常先引入变量,如边长、角度等,然后把要解三角形的边或角用所设变量表示出来,再利用正、余弦定理列出方程,再解方程即可.若研究最值,常使用函数思想.跟踪训练2(1)(2024·西安模拟)已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,a =217,b =52,cos A =45,则△ABC 的面积为()A .362B .183C .27D .36答案C解析∵a =217,b =52,cos A =45,∴由a 2=b 2+c 2-2bc cos A ,可得c 2-82c -18=(c -92)(c +2)=0,解得c =92(负值舍去).∵cos A =45,∴sin A =1-cos 2A =35,∴△ABC 的面积为12bc sin A =12×52×92×35=27.(2)(2023·聊城模拟)已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若a -b =c cos B -c cos A ,则△ABC 的形状一定是()A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形答案D解析因为a -b =c cos B -c cos A ,所以由正弦定理得sin A -sin B =sin C cos B -sin C cos A ,因为sin A =sin(B +C )=sin B cos C +cos B sin C ,sin B =sin(A +C )=sin A cos C +cos A sin C ,所以sin B cos C +cos B sin C -sin A cos C -cos A sin C =sin C cos B -sin C cos A ,整理得sin B cos C -sin A cos C =0,所以(sin B -sin A )cos C =0,所以sin B =sin A 或cos C =0,因为A ,B ,C ∈(0,π),所以A =B 或C =π2,即△ABC 的形状一定是等腰或直角三角形.(3)(2023·宝鸡统考)在△ABC 中,AB =5,AC =7,D 为BC 的中点,AD =5,则BC 等于()A .23B .43C .22D .42答案B 解析方法一设BC =2x ,则BD =CD =x .在△ACD 中,由余弦定理的推论可得,cos ∠ADC =AD 2+CD 2-AC 22AD ·CD =25+x 2-4910x .在△ABD 中,由余弦定理的推论可得,cos ∠ADB =AD 2+BD 2-AB 22AD ·BD =25+x 2-2510x .又∠ADC +∠ADB =π,所以cos ∠ADC =-cos ∠ADB ,所以有25+x 2-4910x =-25+x 2-2510x ,整理可得x 2=12,解得x =23,所以BC =4 3.方法二AD →=12(AB →+AC →),则AD →2=14(AB →2+AC →2+2AB →·AC →),即25=14(25+49+2×5×7×cos ∠BAC ),解得cos ∠BAC =1335,所以BC 2=AB 2+AC 2-2AB ·AC ·cos ∠BAC =25+49-2×5×7×1335=48,所以BC =4 3.课时精练一、单项选择题1.在△ABC 中,C =60°,a +2b =8,sin A =6sin B ,则c 等于()A.35B.31C .6D .5答案B解析因为sin A =6sin B ,则由正弦定理得a =6b ,又a +2b =8,所以a =6,b =1,因为C =60°,所以由余弦定理c 2=a 2+b 2-2ab cos C ,得c 2=62+12-2×6×1×12,解得c =31.2.在△ABC 中,内角A ,B ,C 的对边a ,b ,c 依次成等差数列,且B =π3,则△ABC 的形状为()A .等边三角形B .直角边不相等的直角三角形C .等腰直角三角形D .钝角三角形答案A解析因为a ,b ,c 依次成等差数列,所以b =a +c2.由余弦定理可得cos B =a 2+c 2-b 22ac =12,将b =a +c2代入上式整理得(a -c )2=0,所以a =c .又B =π3,所以△ABC 为等边三角形.3.(2023·红河模拟)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,△ABC 的面积为12b (b sin B -a sin A -c sin C ),则B 等于()A.π6B.5π6C.π3D.2π3答案D 解析由题知,△ABC 的面积为12b (b sin B -a sin A -c sin C ),所以12ab sin C =12b (b sin B -a sin A -c sin C ),即a sin C =b sin B -a sin A -c sin C ,所以由正弦定理得ac =b 2-a 2-c 2,即a 2+c 2-b 2=-ac ,所以cos B =a 2+c 2-b 22ac=-12,因为B ∈(0,π),所以B =2π3.4.(2023·宜宾模拟)如图,在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .点D 为BC的中点,AD =1,B =π3,且△ABC 的面积为32,则c 等于()A .1B .2C .3D .4答案A 解析∵B =π3,∴在△ABD 中,由余弦定理得c 2-2c ×a 2cos π3=1,即a 2+4c 2-2ac =4,又S △ABC =12ac sin B =34ac =32,解得ac =2,①∴a 2+4c 2-2ac =4=2ac ,即4c 2-4ac +a 2=0,∴(2c -a )2=0,即a =2c ,②将②代入①得2c 2=2,解得c =1或c =-1(舍去).5.(2023·潍坊模拟)如图,平面四边形ABCD 的内角B +D =π,AB =6,DA =2,BC =CD ,且AC =27.则角B 等于()A.π6B.π4C.π3D.5π12答案C解析设BC =CD =x >0,在△ABC 中,由余弦定理,得AC 2=36+x 2-2×6x cos B =28,即x 2+8=12x cos B ,①又在△ACD 中,由余弦定理,得AC 2=4+x 2-2×2x cos D =28,即x 2-24=4x cos D ,②因为B +D =π,则cos D =cos(π-B )=-cos B ,联立①②可得x =4,cos B =12,因为B ∈(0,π),所以B =π3.6.(2022·乐山统考)已知△ABC 中,AB →·AC →=-3,AB =2,cos 2A +sin 2B +sin 2C +sin B sin C =1,D 是边BC 上一点,∠CAD =3∠BAD .则AD 等于()A.65B.334C.62D.637答案B 解析设△ABC 中,角A ,B ,C 的对边为a ,b ,c ,∵cos 2A +sin 2B +sin 2C +sin B sin C =1,即sin 2B +sin 2C +sin B sin C =sin 2A ,∴b 2+c 2+bc =a 2,∴cos A =b 2+c 2-a 22bc=-12,又A ∈(0,π),∴A =2π3,又AB →·AC →=-3,AB =2,∴AB →·AC →=2b cos A =2b 3,即b =3,∴a 2=b 2+c 2+bc =32+22+3×2=19,故a =19,∴cos C =a 2+b 2-c 22ab =19+9-4619=419,sin C =319,tan C =34,又∠CAD =3∠BAD ,A =2π3,∴∠CAD =π2,AD =AC tan C =3×34=334.二、多项选择题7.(2024·南京模拟)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若(a 2+c 2-b 2)tan B =3ac ,则B 的值为()A.π6B.π3C.5π6D.2π3答案BD 解析根据余弦定理可知a 2+c 2-b 2=2ac cos B ,代入(a 2+c 2-b 2)tan B =3ac ,可得2ac cos B ·sin B cos B =3ac ,即sin B =32,因为0<B <π,所以B =π3或B =2π3.8.已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,下列四个命题中正确的是()A .若a cos A =b cos B ,则△ABC 是等腰三角形B .若b cosC +c cos B =b ,则△ABC 是等腰三角形C .若a cos A =b cos B =c cos C ,则△ABC 是等边三角形D .若B =60°,b 2=ac ,则△ABC 是直角三角形答案BC 解析对于A ,若a cos A =b cos B ,则由正弦定理得sin A cos A =sin B cos B ,∴sin 2A =sin 2B ,则2A =2B 或2A +2B =180°,即A =B 或A +B =90°,则△ABC 为等腰三角形或直角三角形,故A 错误;对于B ,若b cos C +c cos B =b ,则由正弦定理得sin B cos C +sin C cos B =sin(B +C )=sin A =sin B ,即A =B ,则△ABC 是等腰三角形,故B 正确;对于C ,若a cos A =b cos B =c cos C ,则由正弦定理得sin A cos A =sin B cos B =sin C cos C,则tan A =tan B =tan C ,即A =B =C ,即△ABC 是等边三角形,故C 正确;对于D ,由于B =60°,b 2=ac ,由余弦定理可得b 2=ac =a 2+c 2-ac ,可得(a -c )2=0,解得a =c ,故△ABC 是等边三角形,故D 错误.三、填空题9.(2023·上饶模拟)已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,2cos A bc =cos B ab +cos C ac,则A =.答案π3解析因为2cos A bc =cos B ab +cos C ac 所以2a ·cos A =c ·cos B +b ·cos C ,由正弦定理得2sin A cos A =sin C cos B +sin B cos C ,即2sin A cos A =sin(B +C )=sin A ,因为sin A >0,所以cos A =12,因为A 为三角形内角,则A =π3.10.我国南宋著名数学家秦九韶在他的著作《数书九章》卷五的“田域类”中写道:问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步.欲知为田几何.意思是已知三角形沙田的三边长分别为13里、14里、15里,求三角形沙田的面积.则该沙田的面积为平方里.答案84解析由题意画出△ABC (图略),且AB =13里,BC =14里,AC =15里,在△ABC 中,由余弦定理得,cos B =AB 2+BC 2-AC 22AB ·BC =132+142-1522×13×14=513,所以sin B =1-cos 2B =1213,则该沙田的面积S =12AB ·BC ·sin B =12×13×14×1213=84(平方里).11.已知△ABC 的面积为S =14(b 2+c 2)(其中b ,c 为△ABC 的边长),则△ABC 的形状为.答案等腰直角三角形解析依题意,△ABC 的面积为S =14(b 2+c 2),则12bc sin A =14(b 2+c 2),即2bc sin A =b 2+c 2,由于0<A <π,所以0<sin A ≤1,所以0<2bc sin A ≤2bc ,由基本不等式可知b 2+c 2≥2bc ,当且仅当b =c 时等号成立,所以sin A =1,A =π2,△ABC 是等腰直角三角形.12.(2023·沈阳模拟)在△ABC 中,∠BAC =120°,D 在BC 上,AD ⊥AC ,AD =1,则1AC +2AB =.答案3解析在△ADC 中,AD ⊥AC ,AD =1,所以1AC =AD AC=tan C ,因为B =180°-∠BAC -C =60°-C ,在△ABC 中,由正弦定理得,AB sin C =AC sin B ,则AB =AC sin C sin B =1tan C ·sin C sin (60°-C )=cos C 32cos C -12sin C ,所以1AB =32-12·sin C cos C =32-12tan C ,所以1AC +2AB=tan C +(3-tan C )= 3.四、解答题13.记△ABC 的内角A ,B ,C 所对的边分别是a ,b ,c ,已知b sin C =c sin B 2.(1)求角B 的大小;(2)若点D 在边AC 上,BD 平分∠ABC ,a =2,b =7,求线段BD 的长.解(1)已知b sin C =c sin B 2,由正弦定理,得sin B sin C =sin C sinB 2,因为C ∈(0,π),所以sin C ≠0,故sin B =sin B 2,即2sin B 2cos B 2=sin B 2,因为B 2∈sin B 2≠0,则cos B 2=12,所以B 2=π3,则B =2π3.(2)依题意,得12a ·BD ·sin π3+12c ·BD ·sin π3=12ac sin 2π3,即a ·BD +c ·BD =ac ,即2BD +c ·BD =2c ,所以BD =2c 2+c.在△ABC 中,由余弦定理,得b 2=a 2+c 2-2ac cos2π3=a 2+c 2+ac ,即7=4+c 2+2c ,解得c =1或c =-3(舍去),所以BD =2c 2+c =23.14.(2023·新高考全国Ⅱ)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知△ABC 的面积为3,D 为BC 的中点,且AD =1.(1)若∠ADC =π3,求tan B ;(2)若b 2+c 2=8,求b ,c .解(1)方法一在△ABC 中,因为D 为BC 的中点,∠ADC =π3,AD =1,则S △ADC =12AD ·DC sin ∠ADC =12×1×12a ×32=38a =12S △ABC =32,解得a =4.在△ABD 中,∠ADB =2π3,由余弦定理得c 2=BD 2+AD 2-2BD ·AD cos ∠ADB ,即c 2=4+1-2×2×17,解得c =7.在△ABD 中,则cos B =AB 2+BD 2-AD 22AB ·BD =7+4-127×2=5714,sin B =1-cos 2B =2114,所以tan B =sin B cos B =35.方法二在△ABC 中,因为D 为BC 的中点,∠ADC =π3,AD =1,则S △ADC =12AD ·DC sin ∠ADC =12×1×12a ×32=38a =12S △ABC =32,解得a =4.在△ACD 中,由余弦定理得b 2=CD 2+AD 2-2CD ·AD cos ∠ADC ,即b 2=4+1-2×2×1×12=3,解得b =3,又AC 2+AD 2=4=CD 2,则∠CAD =π2,C =π6,过A 作AE ⊥BC 于点E ,如图所示,于是CE =AC cos C =32,AE =AC sin C =32,BE =52,所以在Rt △AEB 中,tan B =AE BE =35.(2)方法一在△ABD 与△ACD 中,由余弦定理得2=14a 2+1-2×12a ×1×cos (π-∠ADC ),2=14a 2+1-2×12a ×1×cos ∠ADC ,整理得12a 2+2=b 2+c 2,而b 2+c 2=8,则a =23,又S △ADC =12×3×1×sin ∠ADC =32,解得sin ∠ADC =1,而0<∠ADC <π,于是∠ADC =π2,所以b =c =AD 2+CD 2=2.方法二在△ABC 中,因为D 为BC 的中点,则2AD →=AB →+AC →,又CB →=AB →-AC →,于是4AD →2+CB →2=(AB →+AC →)2+(AB →-AC →)2=2(b 2+c 2)=16,即4+a 2=16,解得a =23,又S △ADC =12×3×1×sin ∠ADC =32,解得sin ∠ADC =1,而0<∠ADC <π,于是∠ADC =π2,所以b =c =AD 2+CD 2=2.15.(2023·渝中模拟)如图,设在△ABC 中,AB =BC =AC ,从顶点A 连接对边BC 上两点D ,E ,使得∠DAE =30°,若BD =16,CE =5,则边长AB 等于()A .38B .40C .42D .44答案B 解析方法一设AB =x ,∠BAD =α,在△BAD 中,由正弦定理得x sin (60°+α)=16sin α,可以化简得x 16=32cos αsin α+12,在△EAC 中,由正弦定理得x sin (90°+α)=5sin (30°-α),可以化简得5x =-32sin αcos α+12,=-34,可以化简得x2-42x+80=0,解得x=40,x=2(舍去).方法二设AB=x,利用余弦定理得AD2=x2+162-16x,AE2=x2+52-5x,而△ADE的面积S=12DE·AB×sin60°=12(x-21)32x=12AD·AE×sin30°,则AD·AE=3x(x-21),则在△ADE中,由余弦定理得(x-21)2=AD2+AE2-2AD·AE cos30°,x2-42x+212=x2+162-16x+x2+52-5x-3x(x-21),化简整理得x2-42x+80=0,即x=40,x=2(舍去).16.(2024·大庆模拟)设△ABC的三边长为BC=a,CA=b,AB=c,若tan A2=ab+c,tan B 2=ba+c,则△ABC是() A.等腰三角形B.直角三角形C.等腰直角三角形D.以上说法都不对答案B解析利用tan A2=sin A1+cos A,tanB2=sin B1+cos B及正弦定理和题设条件,得sin A1+cos A=sin Asin B+sin C,①sin B1+cos B=sin Bsin A+sin C,②所以1+cos A=sin B+sin C,③1+cos B=sin A+sin C,④由③和④得1+cos A-sin B=1+cos B-sin A,即sin A+cos A=sin B+cos B,因为A,B为三角形内角,所以A+π4=B+π4或A+π4=π-B-π4,即A =B 或A +B =π2.(1)若A =B ,由C =π-A -B =π-2A ,将其代入③,得1+cos A =sin A +sin 2A.变形得(sin A -cos A )2-(sin A -cos A )=0,即(sin A -cos A )(sin A -cos A -1)=0,⑤由A =B 知A 为锐角,从而知sin A -cos A -1≠0.所以由⑤,得sin A -cos A =0,即A =π4,从而B =π4,C =π2.因此,△ABC 为等腰直角三角形.(2)若A +B =π2,即C =π2,此时③④恒成立,综上,△ABC 为直角三角形.。
解三角形的实际应用举例

跟踪训练1 如图所示,设A、B两点在河 的两岸,一测量者在A的同侧,在A所在的 河岸边选定一点C,测出AC的距离为50 m, ∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )
A.50 2 m C.25 2 m
B.50 3 m 25 2
D. 2 m
解析 由题意知∠ABC=30°,
由正弦定理sin∠ACABC=sin∠ABACB,
(1)设A到P的距离为x km,用x表示B,C到P的距离,并求x
的值;
解 依题意知PA-PB=1.5×8=12(km),PC-PB=1.5×20
=30(km),
因此PB=(x-12) km,PC=(18+x) km,
在△PAB中,AB=20 km,
PA2+AB2-PB2 x2+202-x-122 3x+32
由sin∠BCCAB=sAinCB得:
sin∠CAB=BCAsCin B 3
=at·sin3a1t20°= 23=21.
∵0°<∠CAB<90°,∴∠CAB=30°.
1234
1234
∴∠DAC=60°-30°=30°. 所以甲船应沿着北偏东30°的方向前进, 才能最快与乙船相遇.
1234
4.我炮兵阵地位于地面A处,两观察所分别位 于地面点C和D处,已知CD=6 km,∠ACD =45°,∠ADC=75°,目标出现于地面点B处 时,测得∠BCD=30°,∠BDC=15°(如图), 求我炮兵阵地到目标的距离. 解 在△ACD中,∠CAD=180°-∠ACD-∠ADC=60°, ∠ACD=45°,
3x+32 PD=PAcos∠APD=PAcos∠PAB=x· 5x =3×17352+32≈17.71(km). 答 静止目标P到海防警戒线a的距离约为17.71 km.
解三角形在生活中的应用

c b sin B
c c sin C
所以
a sin A
b sin B
c sin C
可是在斜三角形中是否成立的问题,在高一 的学习中已经证明也是成立的。
4
实际测量的几个例子
问题1:测量书柜的高度
模型转化
H
α
β
a
5
为了避免测量误差,我们采取了多次测量求平均 值的方法
次数
长度单位:厘米(cm) 角度单位:度()
374. 1
3.7
所以:使用我们的测角仪实际上还可以测量水平物体的长度, 实际上,这种测量方法还可以测量AB、CD间的距离,比如在河的一边, 测河的宽度。
15
1、我们设计的测角仪虽然不成熟,但我们自认为 在短距离的测量中它比光学测角仪有一定的优势, 而且通过对测角仪的设计与制做,体会了制做的乐 趣。做任何事不能等待,必须动手实践,当你使用 你自制工具工作时,工作变成了乐趣。 2、我们在实验中体会了测角仪的应用方法,结合 角三角形的数学知识,我们学会了用测角仪测量高 度,水平长度、水平宽度这三类问题,深刻体会了 我们的先辈仅用尺与测角仪进行地质测绘的过程, 而且深入理解了三角函数知识在实际生活中的作用。
基高 100 50.5 48.6 1745.7 17.5 1763.2 17.5 2
基高 50 48.6 47.7 1766.1 17.7 1783.7 17.7 3
11
数据比较,如下
1768.104 1764.64
1761.176 1757.712 1754.248 1750.784
1747.32 1743.856 1740.392 1736.928 1733.464
水平长度测量计算器
《解三角形的实际应用举例》 知识清单

《解三角形的实际应用举例》知识清单一、解三角形的基本概念解三角形,就是求解三角形的边和角的关系。
在一个三角形中,我们通常知道一些边和角的信息,然后通过特定的定理和公式来求出其他未知的边和角。
三角形的内角和为 180°,这是一个基本的常识。
而解三角形中常用的定理有正弦定理和余弦定理。
正弦定理:在任意一个三角形中,各边和它所对角的正弦值的比相等,并且等于外接圆的直径。
即:\(\frac{a}{\sin A} =\frac{b}{\sin B} =\frac{c}{\sin C} = 2R\)(其中\(R\)为三角形外接圆的半径)。
余弦定理:对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
即:\(a^2 = b^2 +c^2 2bc\cos A\),\(b^2 = a^2 + c^2 2ac\cos B\),\(c^2 = a^2 + b^2 2ab\cos C\)。
二、解三角形的实际应用场景解三角形在我们的日常生活和实际工作中有着广泛的应用。
1、测量距离在无法直接测量两点之间的距离时,可以通过构建三角形,利用解三角形的知识来计算。
比如,要测量河对岸两点\(A\)、\(B\)之间的距离,可以在河的这一侧选择一个点\(C\),然后测量\(AC\)和\(BC\)的长度以及\(\angle ACB\)的大小,就可以通过解三角形求出\(AB\)的长度。
2、测量高度要测量建筑物、山峰等的高度,如果在地面上能测量出到其底部的距离以及观测顶部的仰角,就可以构建三角形来求解高度。
例如,在距离建筑物底部\(D\)米处,测量出仰角为\(\alpha\),则建筑物的高度\(h = D\tan\alpha\)。
3、航海问题在航海中,确定船只的位置、航向和航行距离等都需要用到解三角形的知识。
比如,已知船只的航向和航行时间,以及观测到两个灯塔的角度,就可以确定船只的位置。
4、工程测量在道路、桥梁等工程建设中,需要精确测量角度和距离,解三角形可以帮助工程师进行设计和施工。
解三角形应用举例

解:在△BCD 中,∠CBD=π-α-β. 由正弦定理,得 BC = CD .
sin∠BDC sin∠CBD
CDsin ∠BDC s·sin β
8( 6- 2)
因此此船的航速为
1
=16( 6- 2)(海里/
2
时).
答案:D
[变式训练] (1)如图所示,A,B 两点之间隔着一 座小山,现要测量 A、B 两点的距离,选择在同一水平面 上且均能直线到达的 C 点,经测量 AC=50 m,BC=40 m, B 在 C 北偏东 45°方向上,A 在 C 西偏北 15°方向上,问 能否求出 AB 的长?
2.正、余弦定理在实际测量中应用的一般步骤: (1)分析:理解题意,分清已知与未知,画出示意图; (2)建模:根据已知条件与求解目标,把已知量与求 解量尽量集中在有关的三角形中,建立一个解斜三角形的 数学模型; (3)求解:利用正弦定理或余弦定理有序地解出三角 形,求得数学模型的解; (4)检验:检验上述所求的解是否符合实际意义,从 而得出实际问题的解.
BD=AB sin ∠BAD=15(3+ 3)(米),
CD=BD-BC=15(1+ 3)(米).
故山的高度为 15(1+ 3)(米).
4 如下图所示,一辆汽车在一条水平的公路上向正 东行驶,到 A 处时测得公路南侧远处一山脚 C 在东偏南 15°的方向上,行驶 5 km 后到达 B 处,测得此山脚在东 偏南 30°的方向上,且山顶 D 的仰角为 8°,求此山的高 度 CD(精确到 1 m,参考数据:tan 8°≈0.140 5).
解三角形的实际应用举例 课件

方位 从正北的方向线按 顺 时针到目标方 角 向线所转过的水平角
测量高度问题 [典例] 如图,测量河对岸的塔高AB时,可 以选与塔底B在同一水平面内的两点C与D.现测 得∠BCD=α,∠BDC=β,CD=s,并在点C测 得塔顶A的仰角为θ,求塔高AB.
[解] 在△BCD中, ∠CBD=π-(α+β). 由正弦定理得sin∠BCBDC=sin∠CDCBD. ∴BC=CDsinsi∠n∠CBBDDC=sins·sαin+ββ. 在Rt△ABC中,AB=BCtan∠ACB=s·ssiinnαβ+tanβθ.
解析:∠ABC=180°-75°-45°=60°, 所以由正弦定理得,siAnBC=siAnCB, ∴AB=ACsi·nsinB C=60×sinsi6n0°45°=20 6(m). 即A,B两点间的距离为20 6 m. 答案:20 6
题点三:两点都不可到达
3.如图,A,B两点在河的同侧,且A,B
60°,∠ACB=45°,求A,B两点间的距离.
解:∵∠ADC=∠ADB+∠CDB=60°,∠ACD=60°,
∴∠DAC=60°,
∴AC=DC=
3 2.
在△BCD中,∠DBC=45°,由正弦定理,得BC=
3
sin∠DCDBC·sin∠BDC=sin245°·sin
30°=
6 4.
在△ABC中,由余弦定理,得 AB2=AC2+BC2-2AC·BCcos 45°
测量距离问题
题点一:两点不相通的距离 1.如图所示,要测量一水塘两侧A,B两点
间的距离,其方法先选定适当的位置C, 用经纬仪测出角α,再分别测出AC,BC 的长b,a,则可求出A,B两点间的距离. 即AB= a2+b2-2abcos α. 若测得CA=400 m,CB=600 m,∠ACB=60°,试计算 AB的长.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§4.8解三角形应用举例1.用正弦定理和余弦定理解三角形的常见题型测量距离问题、高度问题、角度问题、计算面积问题、航海问题、物理问题等.2.实际问题中的常用角(1)仰角和俯角与目标线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方叫仰角,目标视线在水平视线下方叫俯角(如图①).(2)方向角:相对于某正方向的水平角,如南偏东30°,北偏西45°等.(3)方位角指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图②).(4)坡度:坡面与水平面所成的二面角的正切值.3.解三角形应用题的一般步骤(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.(3)根据题意选择正弦定理或余弦定理求解.(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)如图①,为了测量隧道口AB的长度,可测量数据a,b,γ进行计算.(√)(2)如图②,B,C,D三点在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别为β和α(α<β),则可以求出A 点距地面的高度AB .( √ )(3)从A 处望B 处的仰角为α,从B 处望A 处的俯角为β,则α,β的关系为α+β=180°.( × ) (4)俯角是铅垂线与视线所成的角,其范围为[0,π2].( × )(5)有一长为1的斜坡,它的倾斜角为20°,现高不变,将倾斜角改为10°,则斜坡长为2cos10°.( √ )1.如图,设A 、B 两点在河的两岸,一测量者在A 所在的同侧河岸边选定一点C ,测出AC 的距离为50m ,∠ACB =45°,∠CAB =105°后,就可以计算出A 、B 两点的距离为( ) A .502m B .503m C .252m D.2522m答案 A解析 ∵∠ACB =45°,∠CAB =105°, ∴∠ABC =180°-105°-45°=30°. 在△ABC 中,由正弦定理得AB sin C =ACsin B, ∴AB =AC ·sin Csin B =50×2212=50 2 (m).2.若点A 在点C 的北偏东30°,点B 在点C 的南偏东60°,且AC =BC ,则点A 在点B 的( ) A .北偏东15° B .北偏西15°C .北偏东10°D .北偏西10°答案 B解析 如图所示,∠ACB =90°,又AC =BC , ∴∠CBA =45°,而β=30°,∴α=90°-45°-30°=15°. ∴点A 在点B 的北偏西15°.3.(2014·四川)如图,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为67°,30°,此时气球的高是46m ,则河流的宽度BC 约等于________m .(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,3≈1.73)答案 60解析 根据已知的图形可得AB =46sin67°.在△ABC 中,∠BCA =30°,∠BAC =37°,由正弦定理,得AB sin30°=BC sin37°,所以BC ≈2×460.92×0.60=60(m).4.如图所示,为测一树的高度,在地面上选取A ,B 两点,从A ,B 两点分别测得树尖的仰角为30°,45°,且A ,B 两点间的距离为60m ,则树的高度为________m. 答案 30+30 3解析 在△P AB 中,∠P AB =30°,∠APB =15°,AB =60,sin15°=sin(45°-30°)=sin45°cos30°-cos45°sin30°=22×32-22×12=6-24,由正弦定理得PB sin30°=ABsin15°,∴PB =12×606-24=30(6+2),∴树的高度为PB ·sin45°=30(6+2)×22=(30+303)m.题型一 测量距离问题例1 要测量对岸A 、B 两点之间的距离,选取相距3km 的C 、D 两点,并测得∠ACB =75°,∠BCD =45°,∠ADC =30°,∠ADB =45°,求A 、B 之间的距离. 解 如图所示,在△ACD 中, ∠ACD =120°, ∠CAD =∠ADC =30°, ∴AC =CD =3km.在△BCD 中,∠BCD=45°, ∠BDC =75°,∠CBD =60°.∴BC =3sin75°sin60°=6+22.在△ABC 中,由余弦定理,得 AB 2=(3)2+⎝⎛⎭⎪⎫6+222-2×3×6+22×cos75°=3+2+3-3=5,∴AB =5km ,∴A 、B 之间的距离为5km. 思维升华 求距离问题的注意事项(1)首先选取适当基线,画出示意图,将实际问题转化成三角形问题.(2)明确所求的距离在哪个三角形中,有几个已知元素.(3)确定使用正弦定理或余弦定理解三角形.(1)在相距2千米的A ,B 两点处测量目标C ,若∠CAB =75°,∠CBA =60°,则A ,C 两点之间的距离是__________千米.(2)已有A 船在灯塔C 北偏东80°处,且A 船到灯塔C 的距离为2km ,B 船在灯塔C 北偏西40°处,A 、B 两船间的距离为3km ,则B 船到灯塔C 的距离为________km. 答案 (1)6 (2)6-1解析 (1)如图所示, 由题意知C =45°,由正弦定理得AC sin60°=2sin45°,∴AC =222·32= 6. (2)如图,由题意可得,∠ACB =120°,AC =2,AB =3. 设BC =x ,则由余弦定理可得: AB 2=BC 2+AC 2-2BC ·AC cos120°, 即32=22+x 2-2×2x cos120°, 整理得x 2+2x =5,解得x =6-1(另一解为负值舍掉). 题型二 测量高度、角度问题例2 (1)如图,测量河对岸的塔高AB 时可以选与塔底B 在同一水平面内的两个测点C 与D ,测得∠BCD =15°,∠BDC =30°,CD =30,并在点C 测得塔顶A 的仰角为60°,则塔高AB 等于( ) A .5 6 B .15 3 C .5 2D .15 6(2)一船自西向东匀速航行,上午10时到达一座灯塔P 的南偏西75°且距灯塔68海里的M 处,下午2时到达这座灯塔东南方向的N 处,则这只船的航行速度为( ) A.1762海里/小时B .346海里/小时 C.1722海里/小时D .342海里/小时答案 (1)D (2)A解析 (1)在△BCD 中,∠CBD =180°-15°-30°=135°. 由正弦定理得BC sin30°=30sin135°,所以BC =15 2. 在Rt △ABC 中,AB =BC tan ∠ACB =152×3=15 6. (2)如图所示,在△PMN 中,PM sin45°=MNsin120°,∴MN =6832=346,∴v =MN 4=1726(海里/小时).思维升华 求解测量问题的关键是把测量目标纳入到一个可解三角形中,三角形可解,则至少要知道这个三角形的一条边长.解题中注意各个角的含义,根据这些角把需要的三角形的内角表示出来,注意不要把角的含义弄错,不要把这些角与要求解的三角形的内角之间的关系弄错.(1)一船以每小时15km 的速度向东航行,船在A 处看到一个灯塔M 在北偏东60°方向,行驶4h 后,船到B 处,看到这个灯塔在北偏东15°方向,这时船与灯塔的距离为______km. 答案 30 2解析 如图所示,依题意有AB =15×4=60km ,∠MAB =30°,∠AMB =45°,在△AMB 中,由正弦定理得60sin45°=BMsin30°,解得BM =302km.(2)某人在塔的正东沿着南偏西60°的方向前进40米后,望见塔在东北方向,若沿途测得塔顶的最大仰角为30°,求塔高.解 如图所示,某人在C 处,AB 为塔高,他沿CD 前进,CD =40,此时∠DBF =45°,过点B 作BE ⊥CD 于E ,则∠AEB =30°,在△BCD 中,CD =40,∠BCD =30°,∠DBC =135°,由正弦定理,得 CD sin ∠DBC =BDsin ∠BCD ,∴BD =40sin30°sin135°=202(米).∵∠BDE =180°-135°-30°=15°. ∴在Rt △BED 中, BE =DB sin15°=202×6-24=10(3-1)(米). 在Rt △ABE 中,∠AEB =30°, ∴AB =BE tan30°=103(3-3)(米). 故所求的塔高为103(3-3)米.题型三 三角形中的综合问题例3 已知向量m =(3sin x 4,1),n =(cos x 4,cos 2x4),函数f (x )=m ·n .(1)若f (x )=1,求cos(2π3-x )的值;(2)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,且满足a cos C +12c =b ,求f (B )的取值范围.解 由题意得,f (x )=3sin x 4cos x 4+cos 2x4=32sin x 2+12cos x 2+12=sin(x 2+π6)+12. (1)由f (x )=1,可得sin(x 2+π6)=12,则cos(2π3-x )=2cos 2(π3-x 2)-1=2sin 2(x 2+π6)-1=-12.(2)已知a cos C +12c =b ,由余弦定理,可得a ·a 2+b 2-c 22ab +12c =b ,即b 2+c 2-a 2=bc ,则cos A=b 2+c 2-a 22bc =12,又A 为三角形的内角,所以A =π3,从而B +C =2π3,易知0<B <2π3,0<B 2<π3,则π6<B 2+π6<π2,所以1<sin(B 2+π6)+12<32,故f (B )的取值范围为(1,32).思维升华 在三角形边角关系相互制约的问题中,基本的解决思路有两种:一是根据正、余弦定理把边的关系都转化为角的关系,通过三角恒等变换解决问题;二是根据正、余弦定理把角的关系都转化为边的关系,通过代数变换解决问题.(2014·陕西)△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .(1)若a ,b ,c 成等差数列,证明sin A +sin C =2sin(A +C ); (2)若a ,b ,c 成等比数列,求cos B 的最小值. (1)证明 ∵a ,b ,c 成等差数列,∴a +c =2b . 由正弦定理得sin A +sin C =2sin B . ∵sin B =sin [π-(A +C )]=sin(A +C ), ∴sin A +sin C =2sin(A +C ).(2)解 ∵a ,b ,c 成等比数列,∴b 2=ac . 由余弦定理得cos B =a 2+c 2-b 22ac =a 2+c 2-ac 2ac ≥2ac -ac 2ac =12,当且仅当a =c 时等号成立. ∴cos B 的最小值为12.函数思想在解三角形中的应用典例:(12分)某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口O 北偏西30°且与该港口相距20海里的A 处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v 海里/小时的航行速度匀速行驶,经过t 小时与轮船相遇.(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.思维点拨 (1)利用三角形中的余弦定理,将航行距离表示为时间t 的函数,将原题转化为函数最值问题;(2)注意t 的取值范围. 规范解答解 (1)设相遇时小艇航行的距离为S 海里,则[1分] S =900t 2+400-2·30t ·20·cos (90°-30°) =900t 2-600t +400=900(t -13)2+300.[3分]故当t =13时,S min =103,v =10313=30 3.即小艇以303海里/小时的速度航行,相遇时小艇的航行距离最小.[6分](2)设小艇与轮船在B 处相遇.则v 2t 2=400+900t 2-2·20·30t ·cos(90°-30°),[8分] 故v 2=900-600t +400t 2.∵0<v ≤30,∴900-600t +400t 2≤900,即2t 2-3t ≤0,解得t ≥23.又t =23时,v =30,故v =30时,t 取得最小值,且最小值等于23.此时,在△OAB 中,有OA =OB =AB =20.[11分] 故可设计航行方案如下:航行方向为北偏东30°,航行速度为30海里/小时.[12分]温馨提醒 (1)三角形中的最值问题,可利用正、余弦定理建立函数模型(或三角函数模型),转化为函数最值问题.(2)求最值时要注意自变量的范围,要考虑问题的实际意义.方法与技巧利用解三角形解决实际问题时,(1)要理解题意,整合题目条件,画出示意图,建立一个三角形模型;(2)要理解仰角、俯角、方位角、方向角等概念;(3)三角函数模型中,要确定相应参数和自变量范围,最后还要检验问题的实际意义. 失误与防范1.不要搞错各种角的含义,不要把这些角和三角形内角之间的关系弄混.2.在实际问题中,可能会遇到空间与平面(地面)同时研究的问题,这时最好画两个图形,一个空间图形,一个平面图形,这样处理起来既清楚又不容易搞错.A 组 专项基础训练 (时间:45分钟)1.若点A 在点B 的北偏西30°,则点B 在点A 的( ) A .北偏西30° B .北偏西60° C .南偏东30° D .东偏南30°答案 C解析 如图,点B 在点A 的南偏东30°.2.如图,一栋建筑物AB 的高为(30-103)m ,在该建筑物的正东方向有一个通信塔CD .在它们之间的地面点M (B ,M ,D 三点共线)处测得楼顶A ,塔顶C 的仰角分别是15°和60°,在楼顶A 处测得塔顶C 的仰角为30°,则通信塔CD 的高为()A .30mB .60mC .303mD .403m 答案 B解析 如图,在Rt △ABM 中,AM =AB sin ∠AMB =30-103sin15°=30-1036-24=206m.过点A 作AN ⊥CD 于点N , 易知∠MAN =∠AMB =15°, 所以∠MAC =30°+15°=45°, 又∠AMC =180°-15°-60°=105°, 从而∠ACM =30°.在△AMC 中,由正弦定理得MC sin45°=206sin30°,解得MC =403m ,在Rt △CMD 中,CD =403×sin60°=60m , 故通信塔CD 的高为60m.3.如图,飞机的航线和山顶在同一个铅垂面内,若飞机的高度为海拔18km ,速度为1000km/h ,飞行员先看到山顶的俯角为30°,经过1min 后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1km ,参考数据:3≈1.732)( ) A .11.4km B .6.6km C .6.5km D .5.6km答案 B解析 ∵AB =1000×1000×160=500003m , ∴BC =AB sin45°·sin30°=5000032m.∴航线离山顶h =5000032×sin75°≈11.4km.∴山高为18-11.4=6.6km.4.如图,两座相距60m 的建筑物AB ,CD 的高度分别为20m 、50m ,BD 为水平面,则从建筑物AB 的顶端A 看建筑物CD 的张角∠CAD 等于( )A .30°B .45°C .60°D .75° 答案 B解析 依题意可得AD =2010 m ,AC =30 5 m ,又CD =50 m ,所以在△ACD 中,由余弦定理得cos ∠CAD =AC 2+AD 2-CD 22AC ·AD =(305)2+(2010)2-5022×305×2010= 6 0006 0002=22,又0°<∠CAD <180°,所以∠CAD =45°,所以从顶端A 看建筑物CD 的张角为45°.5.一艘海轮从A 处出发,以每小时40海里的速度沿南偏东40°的方向直线航行,30分钟后到达B 处,在C 处有一座灯塔,海轮在A 处观察灯塔,其方向是南偏东70°,在B 处观察灯塔,其方向是北偏东65°,那么B ,C 两点间的距离是( )A .102海里B .103海里C .203海里D .202海里答案 A解析 如图所示,易知,在△ABC 中,AB =20,∠CAB =30°,∠ACB=45°,根据正弦定理得BC sin30°=AB sin45°, 解得BC =102(海里).6.甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是________________.答案 203米,4033米解析 如图,依题意有甲楼的高度为AB =20·tan60°=203(米),又CM =DB=20(米),∠CAM =60°,所以AM =CM ·1tan60°=2033(米),故乙楼的高度为CD =203-2033=4033(米).7.(2014·课标全国Ⅰ)如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得M 点的仰角∠MAN =60°,C 点的仰角∠CAB =45°以及∠MAC =75°;从C 点测得∠MCA =60°.已知山高BC =100m ,则山高MN =________m.答案 150解析 根据图示,AC =1002m.在△MAC 中,∠CMA =180°-75°-60°=45°.由正弦定理得AC sin45°=AM sin60°⇒AM =1003m. 在△AMN 中,MN AM =sin60°,∴MN =1003×32=150m.8.如图,在四边形ABCD 花圃中,已知AD ⊥CD ,AD =10m ,AB =14m ,∠BDA =60°,∠BCD =135°,则BC 的长为________m.答案 8 2解析 在△ABD 中,设BD =x ,则BA 2=BD 2+AD 2-2BD ·AD ·cos ∠BDA ,即142=x 2+102-2·10x ·cos60°,整理得x 2-10x -96=0,解得x 1=16,x 2=-6(舍去). 在△BCD 中,由正弦定理:BC sin ∠CDB =BD sin ∠BCD , ∴BC =16sin135°·sin30°=8 2.9.在斜度一定的山坡上的一点A 测得山顶上一建筑物顶端对于山坡的斜度为15°,如图所示,向山顶前进100m 后,又从B 点测得斜度为45°,设建筑物的高为50m .求此山对于地平面的斜度θ的余弦值.解 在△ABC 中,∠BAC =15°,∠CBA =180°-45°=135°,所以∠ACB=30°.又AB =100m ,由正弦定理,得100sin30°=BC sin15°,即BC =100sin15°sin30°. 在△BCD 中,因为CD =50,BC =100sin15°sin30°,∠CBD =45°,∠CDB =90°+θ, 由正弦定理,得50sin45°=100sin15°sin30°sin (90°+θ), 解得cos θ=3-1. 因此,山对于地平面的斜度的余弦值为3-1.10.某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A 处获悉后,立即测出该渔轮在方位角为45°,距离为10nmile 的C 处,并测得渔轮正沿方位角为105°的方向,以9nmile /h 的速度向某小岛靠拢,我海军舰艇立即以21 n mile/h 的速度前去营救,求舰艇的航向和靠近渔轮所需的时间.解 如图所示,根据题意可知AC =10,∠ACB =120°,设舰艇靠近渔轮所需的时间为t h ,并在B 处与渔轮相遇,则AB =21t ,BC =9t ,在△ABC 中,根据余弦定理得AB 2=AC 2+BC 2-2AC ·BC ·cos120°,所以212t 2=102+92t 2+2×10×9t ×12,即360t 2-90t -100=0,解得t =23或t =-512(舍去).所以舰艇靠近渔轮所需的时间为23h .此时AB =14,BC =6. 在△ABC 中,根据正弦定理得BC sin ∠CAB =AB sin120°, 所以sin ∠CAB =6×3214=3314, 即∠CAB ≈21.8°或∠CAB ≈158.2°(舍去).即舰艇航行的方位角为45°+21.8°=66.8°.所以舰艇以66.8°的方位角航行,需23h 才能靠近渔轮. B 组 专项能力提升(时间:25分钟)11.某人向正东方向走xkm 后,向右转150°,然后朝新方向走3km ,结果他离出发点恰好是3km ,那么x 的值为________.答案 3或2 3解析 如图所示,设此人从A 出发,则AB =x ,BC =3,AC =3,∠ABC=30°,由余弦定理得(3)2=x 2+32-2x ·3·cos30°,整理,得x 2-33x +6=0,解得x =3或2 3.12.(2013·福建)如图,在△ABC 中,已知点D 在BC 边上,AD ⊥AC ,sin ∠BAC =223,AB =32,AD =3,则BD 的长为______.答案 3解析 sin ∠BAC =sin(π2+∠BAD )=cos ∠BAD , ∴cos ∠BAD =232. BD 2=AB 2+AD 2-2AB ·AD cos ∠BAD =(32)2+32-2×32×3×232, 即BD 2=3,BD = 3.13.如图,一艘船上午9:30在A 处测得灯塔S 在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B 处,此时又测得灯塔S 在它的北偏东75°处,且与它相距82nmile.此船的航速是________.答案 32nmile/h解析 设航速为v nmile/h在△ABS 中,AB =12v ,BS =82,∠BSA =45°, 由正弦定理得:82sin30°=12v sin45°,∴v =32. 14.在200m 高的山顶上,测得山下一塔顶和塔底的俯角分别是30°,60°,则塔高为________m. 答案 4003解析 如图,由已知可得∠BAC =30°,∠CAD =30°,∴∠BCA =60°,∠ACD =30°,∠ADC =120°.又AB =200m ,∴AC=40033m.在△ACD 中,由余弦定理得,AC 2=2CD 2-2CD 2·cos120°=3CD 2,∴CD =13AC =4003m.15.(2013·江苏)如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50m /min.在甲出发2 min 后,乙从A 乘缆车到B ,在B 处停留1 min 后,再从B 匀速步行到C .假设缆车匀速直线运动的速度为130 m/min ,山路AC 长为1260m ,经测量cos A =1213,cos C =35. (1)求索道AB 的长;(2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?解 (1)在△ABC 中,因为cos A =1213,cos C =35, 所以sin A =513,sin C =45. 从而sin B =sin [π-(A +C )]=sin(A +C )=sin A cos C +cos A sin C =513×35+1213×45=6365. 由正弦定理AB sin C =AC sin B,得 AB =AC sin B ×sin C =12606365×45=1040m. 所以索道AB 的长为1040m.(2)假设乙出发t 分钟后,甲、乙两游客距离为d ,此时,甲行走了(100+50t )m ,乙距离A 处130t m ,所以由余弦定理得d 2=(100+50t )2+(130t )2-2×130t ×(100+50t )×1213=200(37t 2-70t +50),由于0≤t ≤1040130,即0≤t ≤8, 故当t =3537min 时,甲、乙两游客距离最短. (3)由正弦定理BC sin A =AC sin B,得BC =AC sin B ×sin A =12606365×513=500m. 乙从B 出发时,甲已走了50×(2+8+1)=550m ,还需走710m 才能到达C .设乙步行的速度为v m/min ,由题意得-3≤500v -71050≤3,解得125043≤v ≤62514, 所以为使两位游客在C 处互相等待的时间不超过3min ,乙步行的速度应控制在⎣⎡⎦⎤125043,62514(单位:m/min)范围内.。
