高中数学第一章直线、多边形、圆12圆与直线122圆的切线的判定和性质课后作业北师大版4-1!

合集下载

2.3、圆的切线的性质及判定定理

即B一定点在圆外．由点B的任意性可知，圆与直线只有一个公共点，因此l 是圆的切线．由此可得：
切线的判定定理：
经过半径的外端并且垂直于这条半径的直线是圆的切线．
O
l
AB
例1 如图,AB是⊙O的直径, ⊙O过BC的中点D, DE⊥AC.求证:DE是⊙O是切线.
证明:连接OD.
∵BD=CD,OA=OB, ∴OD是△ABC的中位线,
D C
A
O
B
P322
思考:切线的性质定理逆命题“经过半径的外端并且垂直于这条半径的直线是圆的切线．”是否成立?
已知：点A是⊙O与直线l 的公共点,且 l ⊥OA .
求证：圆与直线只有一个公共点证明：在l 上任取异于点A的点B,则△OAB是Rt△
而OB是Rt△ OAB的斜边，因此，都有OB>OA,
C P321
∴OD//AC.
又∵∠DEC=90º ∴∠ODE=90º 又∵D在圆周上,
∴DE是⊙O是切线..E D NhomakorabeaB
A
O
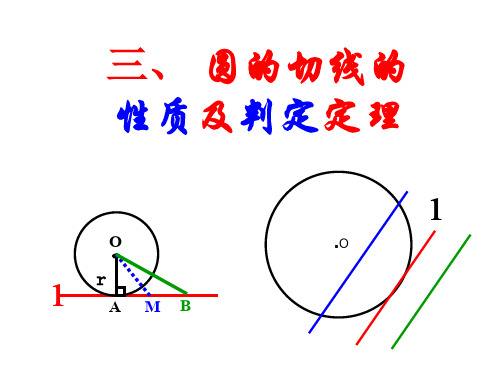
三、圆的切线的性质及判定定理
O
r
l A MB
l
.O
1 切线的性质定理：圆的切线垂直于经过切点的半径．
l
AM
反证法
假设不垂直, 作OM⊥l
因“垂线段最故OA>OM,
O
即短圆”心, 到直线距离小于半径.
这与线圆相切矛盾.
因为经过一点只有一条直线与已知直线垂直，所以经过圆心垂直于切线的直线一定过切点；反之,过切点且垂直于切线的直线也一定过圆心.由此得到：
推论1: 经过圆心且垂直于切线的直线必经过切点.
推论2: 经过切点且垂直于切线的直线必经过圆心.

切线的判定与性质

B，两切线相交于点P,若∠P=420，求
Байду номын сангаас
∠ACB的度数。
•A
•A
•‘
•m •O •C
•C
•m
•P •O •C
•P
•B
•B
•巩固：
1、如图, ⊙O切PB于点B,PB=4,PA=2,则 ⊙O的半径多少？
• 注：已知切线、切点，则连接半径，应用切线的性质定理得到垂直关系，从而应用勾股定理计算。
•2、如图，AB、AC分别切⊙O于B、C，
(3)过半径的端点与半径垂直的直线是圆的
切线（•×）
•O •l
•r
•A
•O •r
•l
•A
•O •l
•r
•A
•归纳：
判定直线与圆相切有哪些方法？
切线的判定方法有三种： •①直线与圆有唯一公共点； •②直线到圆心的距离等于该圆的半径； •③切线的判定定理．即
经过半径的外端并且垂直这条半径的直线是圆的切线.
•(2)直线l垂直于半径0A．
• 则:直线l与⊙O相切
•O •l
•A
• 这样我们就得到了从“位置”的角度圆的切线的判定方法——切线的判定定理．
•讨论交流：
• 利用上面的定理，过圆上任意一点，你会用三角尺画⊙O 的切线吗？
•P
•O
•巩固：
1、判断：
•两个条件缺一不可
(1)过半径的外端的直线是圆的切线（ •×） (2)与半径垂直的的直线是圆的切线（ •×）
切线的判定与性质
•回顾：
直线与圆的位置关系
相交
图形
公共点个数
公共点名称
直线名称圆心到直线距
离d与半径r的

24.2.2 圆的切线的判定和性质

为什么？B
●
O
C
例3、已知 PA、PB 是
⊙O 的切线, 切点为 A、
B, 点C 是圆周上一点,
∠P= , 求∠ACBB
的度数。
C
P
O●
A
练习《教材》P102 习题第5题
例4、AB 是⊙O 的直径,
C 是⊙O 上一点, D在 AB
的延长线上,∠DCB=∠A,
(1) CD与⊙O相切吗?
为什么?
知识回顾
直线和圆
位置关系
数量关系
(1) 相离 (2) 相切 (3) 相交
.O d >r
.O a d =r
.O d <r
观察与思考
问题1：下雨天，转动的雨伞上的水滴是顺着伞的什么方向飞出去的?
问题2：砂轮转动时，火花是沿着砂轮的什么方向飞出去的?
动手动脑
已知⊙O及半径OA，
经过半径 OA 的外端点
吗？为什么? E●
C
D●
O
┐
FB
小结证明圆的切线的思路: (1) 连半径，证垂直； (2) 作垂直，证半径。
练习 1、《教材》P96 练习第2题 2、《教材》P101 习题 3、4题
3、如图,△ABC 是等腰
三角形,O 是底边 BC 的
中点, ⊙O 与腰 AB 相切
于点D。AC 与⊙O
相切吗？ D A E
EF为⊙O 的切线。
F
F
A
O ●
BA
O ●
D
E CE
(《启》P76例1)
B C②
下课
不经历风雨，怎能见彩虹！
断直线 BD 与⊙O 的位置关系, 证明。 D
C

圆的切线的判定(教案)

圆的切线的判定(教案)章节一：圆的切线的定义与性质1.1 教学目标让学生了解圆的切线的定义。

让学生掌握圆的切线的性质。

1.2 教学内容圆的切线的定义。

圆的切线的性质。

1.3 教学步骤1.3.1 引入利用实物或图片展示圆和切线，引导学生思考圆的切线的定义。

1.3.2 讲解讲解圆的切线的定义，强调圆的切线与圆的接触点是切点。

讲解圆的切线的性质，如切线与半径垂直，切线与圆的切点处的切线斜率为0等。

1.3.3 练习提供一些图形，让学生判断哪些是圆的切线，并解释原因。

1.4 教学评价通过学生的练习和提问，评估学生对圆的切线的定义和性质的理解程度。

章节二：圆的切线的判定定理2.1 教学目标让学生了解圆的切线的判定定理。

让学生能够运用判定定理判断一条直线是否为圆的切线。

2.2 教学内容圆的切线的判定定理。

判定定理的应用。

2.3 教学步骤2.3.1 引入回顾上一章节的圆的切线的性质，引导学生思考如何判断一条直线是否为圆的切线。

2.3.2 讲解讲解圆的切线的判定定理，包括定理的表述和证明过程。

讲解判定定理的应用，如何通过已知条件判断一条直线是否为圆的切线。

2.3.3 练习提供一些题目，让学生运用判定定理判断直线是否为圆的切线，并提供解题思路和步骤。

2.4 教学评价通过学生的练习和提问，评估学生对圆的切线的判定定理的理解程度和应用能力。

章节三：圆的切线方程的求法3.1 教学目标让学生了解圆的切线方程的求法。

让学生能够运用求法求出圆的切线方程。

3.2 教学内容圆的切线方程的求法。

切线方程的求法应用。

3.3 教学步骤3.3.1 引入回顾上一章节的内容，引导学生思考如何求出圆的切线方程。

3.3.2 讲解讲解圆的切线方程的求法，包括切线方程的一般形式和求法步骤。

讲解切线方程的求法应用，如何根据已知条件求出圆的切线方程。

3.3.3 练习提供一些题目，让学生运用求法求出圆的切线方程，并提供解题思路和步骤。

3.4 教学评价通过学生的练习和提问，评估学生对圆的切线方程的求法的理解程度和应用能力。

切线的性质与判定习题课专题

《切线的性质与判定习题课》专题班级姓名1.切线的性质：①切线和圆只有公共点；②切线和圆心的距离等于；③圆的切线过切点的半径。

2. 切线的判定定理： .3. 当已知一条直线是某圆的切线时，切点的位置是确定的，辅助线常常是连接，得到半径，那么切线这条半径。

4. 证明切线的方法：①当直线与圆有明确公共点时，，证明直线半径；②当直线与圆有没有明确公共点时，过圆心作直线的，证明垂线段半径；5. 如图1，AB 与⊙O 切于点A ，⊙O 半径为3，AB ＝4，则OB ＝______6. 如图2，已知PA 是⊙O 的切线，切点为A ， ⊙O 半径为3，∠APO = 30°，那么AP = .7. 如图3，以O 为圆心的两个同心圆中，大圆的弦AB 与小圆相切于点C ，若大圆半径为10cm ，小圆半径为6cm ，则弦AB 的长为 cm 。

8. 如图4，AB 是⊙O 的直径，点D 在AB 的延长线上，DC 切⊙O 与C ，若∠A=25°，则∠D ＝。

9. 如图5，∠ACB=60°，半径为1cm 的⊙O 切BC 于点C ，若将⊙O 在CB 上向右滚动，则当滚动到⊙O 与CA 也相切时，圆心O 移动的水平距离是 cm 。

10. 如图6，直线AB 、CD 相交于点O ，∠AOC=30°，半径为1cm 的⊙P 的圆心在射线OA 上，且与点O 的距离为6cm ，如果⊙P 以1cm /s 的速度沿A 向B 的方向移动，则经过秒后⊙P 与直线CD 相切。

B OA 图1O C B A 图3 BOCA图5图2 AOD B PCCB OD图411. 如图，AB 与⊙O 相切于点B ，AO 的延长线交⊙O 于点C ，连接BC ，若∠A=40°，求∠C 的度数。

12. 如图，AB 是⊙O 的直径，BC 切⊙O 于B ，AC 交⊙O 于P ，E 是BC 边上的中点，连接PE ，求证：PE 是⊙O 的切线13.如图，AB 是⊙O 的直径，BC ⊥AB 于点B ，连接OC 交⊙O 于点E ，弦AD ∥OC ，（1）求证：点E 是BD 的中点；（2）求证：CD 是⊙O 的切线。

高中数学第1章直线多边形圆1.2.2圆的切线的判定和性质学案北师大版

2.2 圆的切线的判定和性质1.掌握圆的切线的判定定理和性质定理及其推论.2.能解决与圆的切线有关的问题.[基础·初探]教材整理1 直线与圆的位置关系当直线与圆没有公共点时，称为直线与圆相离；当直线与圆_有唯一公共点时，称为直线和圆相切；当直线与圆有两个公共点时，称为直线和圆相交.1.如图1226，在Rt△ABC 中，∠C ＝90°，AC ＝3 cm ，BC ＝4 cm ，以C 为圆心，r 为半径作圆，若AB 与圆相切，则r ＝________.图1226【解析】过C 作CD ⊥AB ，垂足为D ，在Rt△ABC 中，AB ＝AC 2＋BC 2＝5，∴CD ·AB ＝AC ·BC ， ∴CD ＝AC ·BCAB＝2.4 cm ， ∵AB 与圆相切， ∴r ＝CD ＝2.4 cm. 【答案】 2.4 cm教材整理2 切线的判定定理2.经过半径的外端并且垂直于这条半径的直线是圆的切线.如图1228，AB 是⊙O 的直径，BC 是⊙O 的切线，AC 交⊙O 于D ，AB ＝6，BC ＝8，则BD 等于( )图1228A.4B.4.8C.5.2D.6【解析】 ∵BC 是⊙O 的切线，AB 是⊙O 的直径， ∴AB ⊥BC ，∵AB ＝6，BC ＝8，∴AC ＝10， ∵AB 是⊙O 的直径，∴BD ⊥AC ， ∴12AB ·BC ＝12AC ·BD ， ∴BD ＝AB ·BC AC ＝6×810＝4.8. 【答案】 B教材整理3 切线的性质定理(1)性质定理：圆的切线垂直于经过切点的半径. (2)推论1：经过圆心且垂直于切线的直线经过切点. (3)推论2：经过切点且垂直于切线的直线经过圆心.3.如图1228，AP 为圆O 的切线，P 为切点，OA 交圆O 于点B ，若∠A ＝40°，则∠APB 等于( )图1228A.25°B.20°C.40°D.35°【解析】如图，连接OP ， ∵AP 为圆O 的切线， ∴∠OPA ＝90°.∵∠A ＝40°，∴∠AOP ＝90°－40°＝50°.∵OP ＝OB ，∴∠OPB ＝12×(180°－50°)＝65°.∴∠APB ＝∠OPA －∠OPB ＝90°－65°＝25°. 【答案】 A教材整理4 切线长定理过圆外一点作圆的两条切线，这两条切线长相等.4.如图1229所示，在△ABC 中，BC ＝14 cm ，AC ＝9 cm ，AB ＝13 cm ，内切圆分别和BC ，AC ，AB 切于D ，E ，F ，那么AF ，BD ，CE 分别为( )图1229A.AF ＝4 cm ，BD ＝9 cm ，CE ＝5 cmB.AF ＝4 cm ，BD ＝5 cm ，CE ＝9 cmC.AF ＝5 cm ，BD ＝4 cm ，CE ＝9 cmD.AF ＝9 cm ，BD ＝4 cm ，CE ＝5 cm【解析】由题意知AE ＝AF ，CE ＝CD ，BD ＝BF ，且AC ＝9 cm ，BC ＝14 cm ，AB ＝13 cm ，则⎩⎪⎨⎪⎧AF ＋BD ＝13BD ＋CE ＝14CE ＋AF ＝9，解得AF ＝4，BD ＝9，CE ＝5.【答案】 A[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1：解惑：疑问2：解惑：疑问3：解惑：[小组合作型]已知：AB A作AD∥OC，交⊙O 于点D.求证：DC是⊙O的切线.【导学号：96990019】【精彩点拨】利用圆的切线的判定定理进行切线的证明，关键是找出定理的两个条件：(1)过半径的外端；(2)该直线与某一条半径所在的直线垂直.【自主解答】如图，连接OD，设∠OAD＝∠1，∠ODA＝∠2，∠BOC＝∠3，∠COD＝∠4.∵OA＝OD，∴∠1＝∠2.∵AD∥OC，∴∠1＝∠3，∠2＝∠4.∴∠1＝∠2＝∠3＝∠4.又∵OB＝OD，∠3＝∠4，OC＝OC.∴△OBC≌△ODC.∴∠OBC＝∠ODC.∵BC是⊙O的切线，∴∠OBC＝90°.∴∠ODC＝90°，即OD⊥CD.∴DC是⊙O的切线.要证明某直线是圆的切线，主要是运用切线的判定定理，除此以外，还有圆心到直线的距离等于半径等判定方法，但有时需添加辅助线构造判定条件，其中过圆心作直线的垂线是常用辅助线.[再练一题]1.如图1230，已知AC是⊙O的直径，OE⊥AD.OF⊥AB，E，F为垂足，OE＝OF.AC是AD 和AB的比例中项.图1230求证：BC 是⊙O 的切线.【证明】 ∵OE ⊥AD ，OF ⊥AB ，OE ＝OF ， ∴∠1＝∠2. 又∵AC 2＝AD ·AB ， ∴AC AB ＝AD AC， ∴△ACD ∽△ABC ， ∴∠ACB ＝∠ADC .∵AC 是⊙O 的直径，∴∠ADC ＝90°， ∴∠ACB ＝90°，∴BC ⊥AC ，∴BC 是⊙O 的切线.如图O 切AB 于E ，若BC ＝5，AC ＝12，求⊙O 的半径.图1231【精彩点拨】 ⊙O 切AB 于点E ，由圆的切线的性质，易联想到连接OE 构造Rt△OAE ，再利用相似三角形的性质，求出⊙O 的半径.【自主解答】连接OE ，∵AB 与⊙O 切于点E ， ∴OE ⊥AB ，即∠OEA ＝90°. ∵∠C ＝90°，∠A ＝∠A ， ∴Rt△ACB ∽Rt△AEO ， ∴OE BC ＝AO AB. ∵BC ＝5，AC ＝12，∴AB ＝13， ∴OE 5＝12－OE13∴OE ＝103.即⊙O 的半径为103.利用圆的切线的性质来证明或进行有关的计算有时需添加辅助线，其中连接圆心和切点的半径是常用辅助线，从而可以构造直角三角形，利用直角三角形边角关系求解，或利用勾股定理求解，或利用三角形相似求解等.[再练一题]2.如图1232，圆O 1与圆O 2内切于点A ，其半径分别为r 1与r 2(r 1＞r 2)，圆O 1的弦AB 交圆O 2于点C (O 1不在AB 上)，求证：AB ∶AC 为定值.图1232【证明】如图，连接AO 1并延长，分别交两圆于点E 和点D .连接BD ，CE ，因为圆O 1与圆O 2内切于点A ，所以点O 2在AD 上，故AD ，AE 分别为圆O 1，圆O 2的直径.从而∠ABD ＝∠ACE ＝π2.所以BD ∥CE ，于是AB AC ＝AD AE ＝2r 12r 2＝r 1r 2.所以AB ∶AC 为定值.如图BC 为直径在正方形ABCD 内作半圆，再过A 点作半圆的切线，与半圆相切于F 点，与DC 相交于E 点.求△ADE 的面积.图1233【精彩点拨】利用切线长定理建立长度关系求解. 【自主解答】设DE ＝x ，则CE ＝4－x . ∵CD ，AE ，AB 都与⊙O 相切， ∴EF ＝CE ＝4－x .AF ＝AB ＝4.∴AE ＝AF ＋EF ＝8－x .在Rt△ADE 中，AE 2＝AD 2＋DE 2，即(8－x )2＝42＋x 2，解得x ＝3. ∴S △ADE ＝12AD ·DE＝12×4×3＝6(cm 2).1.解答本题时应注意AF ＝AB ，EF ＝EC ，且AE 2＝AD 2＋DE 2. 2.当过圆外一点作圆的切线时，常常用到切线长定理.[再练一题]3.如图1234所示，P 为⊙O 外一点，PA ，PB 分别切⊙O 于A ，B ，CD 切⊙O 于E ，交PA ，PB 于C ，D ，OP ＝10，⊙O 的半径为6，求△PCD 的周长.【导学号：96990020】图1234【解】连接OA ，则OA ⊥PA 且OA ＝6，∴PA 2＝OP 2－OA 2＝102－62＝64， ∴PA ＝8，由切线长定理知PA ＝PB ，CE ＝CA ，DE ＝DB ，∴CD ＝CE ＋DE ＝CA ＋DB ，∴PC ＋PD ＋CD ＝PA ＋PB ＝2PA ＝16，即△PCD 的周长为16.AC 分别交于点D ，点E .过点D 作DF ⊥AC ，垂足为点F .图1235(1)判断DF 与⊙O 的位置关系，并证明你的结论；(2)过点F 作FH ⊥BC ，垂足为点H .若等边△ABC 的边长为4，求FH 的长(结果保留根号). 【精彩点拨】 (1)由已知∠DOB ＝60°，可得∠ODF ＝∠AFD ＝90°，可得DF 是⊙O 的切线.(2)先求FC ，利用sin∠FCH 可求FH .【自主解答】 (1)DF 与⊙O 相切. 连接OD .∵OB ＝OD ，∠ABC ＝60°， ∴△BOD 是等边三角形. ∴∠DOB ＝60°. ∵△ABC 是等边三角形， ∴∠ACB ＝60°.∴∠ACB ＝∠DOB ，则OD ∥AC ， ∴∠ODF ＝∠AFD ＝90°， ∴DF 是⊙O 的切线.(2)∵OD ∥AC 且O 为BC 的中点， ∴D 为AB 的中点， ∴AD ＝BD ＝2. 又∠ADF ＝30°， ∴AF ＝1， ∴FC ＝AC －AF ＝3. ∵FH ⊥BC ， ∴∠FHC ＝90°.在Rt△FHC 中，sin∠FCH ＝FH FC， ∴FH ＝FC ·sin 60°＝332.即FH 的长为332.对圆的切线的性质与判定的综合考查往往是热点，其解答思路常常是先证明某直线是圆的切线，再利用切线的性质来求解相关结果.[再练一题]4.已知：如图1236，A 是⊙O 上一点，半径OC 的延长线与过点A 的直线交于B 点，OC ＝BC ，AC ＝12OB .图1236(1)求证：AB 为⊙O 的切线；(2)若∠ACD ＝45°，OC ＝2，求弦CD 的长. 【解】 (1)如图，连接OA ，∵OC ＝BC ，AC ＝12OB ，∴OC ＝BC ＝CA ＝OA ， ∴△ACO 为正三角形， ∴∠O ＝60°，∴∠B ＝30°，∴∠OAB ＝90°， ∴AB 为⊙O 的切线. (2)作AE ⊥CD 于点E ， ∵∠O ＝60°，∴∠D ＝30°. 又∵∠ACD ＝45°，AC ＝OC ＝2， ∴在Rt△ACE 中，CE ＝AE ＝2，在Rt△ADE 中，∠D ＝30°， ∴AD ＝22，∴DE ＝6， ∴CD ＝DE ＋CE ＝6＋ 2.[探究共研型]探究1 【提示】通常有三种方法：(1)和圆有唯一一个公共点的直线是圆的切线；(2)到圆心距离等于半径的直线是圆的切线；(3)过半径外端且和该半径垂直的直线是圆的切线.“过半径外端，垂直于这条半径的直线是圆的切线”只是把“到圆心距离等于半径的直线是圆的切线”的定理具体化，在使用时要根据题目的具体要求选取合适的方法，如果涉及到数值计算或距离问题，通常利用(2)，如果涉及到线段的位置关系，通常选取(3).探究2 在学习圆的切线性质定理时需注意什么问题？【提示】 (1)分析圆的切线的性质定理及两个推论的条件和结论间的关系，可以得出如下结论：如果一条直线具备下列三个条件中的任意两个，就可以推出第三个：①垂直于切线；②过切点；③过圆心.于是在利用切线性质时，通常作的辅助线是过切点的半径.(2)圆的切线还有两条性质应当注意：①切线和圆只有一个公共点；②切线和圆心的距离等于圆的半径.在许多实际问题中，我们也利用它们来解决.探究3 连接圆的两条平行切线的切点的线段是圆的直径吗？【提示】是.如图，AB ，CD 分别切⊙O 于E ，F ，连接EO 并延长交CD 于F ′.∵AB 是⊙O 的切线，∴OE ⊥AB .∵AB ∥CD ， ∴OF ′⊥CD .∴F ′为切点， ∴F ′与F 重合，即EF 是⊙O 的直径.如1237所示，已知D 是△ABC 的边AC 上的一点，AD ∶DC ＝2∶1，∠C ＝45°，∠ADB ＝60°，求证：AB 是△BCD 的外接圆的切线.图1237【精彩点拨】连接OB ，OC ，OD →∠BOD ＝90°→ ∠OBC ＝∠OCB ＝30°→∠ABO ＝90°→结论【自主解答】如图，连接OB ，OC ，OD ，OD 交BC 于E . ∵∠DCB 是︵BD 所对的圆周角，∠BOD 是︵BD 所对的圆心角， ∠BCD ＝45°， ∴∠BOD ＝90°.∵∠ADB是△BCD的一个外角，∴∠DBC＝∠ADB－∠ACB＝60°－45°＝15°，∴∠DOC＝2∠DBC＝30°，从而∠BOC＝120°，∵OB＝OC，∴∠OBC＝∠OCB＝30°.在△OEC中，因为∠EOC＝∠ECO＝30°，∴OE＝EC，在△BOE中，因为∠BOE＝90°，∠EBO＝30°.∴BE＝2OE＝2EC，∴CEBE＝CDDA＝12，∴AB∥OD，∴∠ABO＝90°，故AB是△BCD的外接圆的切线.判断一条直线是圆的切线时，常用辅助线的作法：如果已知这条直线与圆有公共点，则连接圆心与这个公共点，设法证明连接所得到的半径与这条直线垂直，简记为“连半径，证垂直”；若题目未说明这条直线与圆有公共点，则过圆心作这条直线的垂线，得垂线段，再证明这条垂线段的长等于半径，简记“作垂直，证半径”.[再练一题]5.本例中，若将已知改为“∠ABD＝∠C”，怎样证明：AB是△BCD的外接圆的切线.【证明】作直径BE，连接DE，∠BDE＝90°∵BE是⊙O的直径，∴∠E＋∠DBE＝90°.∴∠C＝∠E，∠ABD＝∠C，∴∠ABD＋∠DBE＝90°.即∠ABE＝90°.∴AB是△BCD的外接圆的切线.[构建·体系]1.如图1238所示，⊙O 是正△ABC 的内切圆，切点分别为E ，F ，G ，点P 是弧EG 上的任意一点，则∠EPF 等于( )图1238A.120°B.90°C.60°D.30°【解析】如图所示，连接OE ，OF .∵OE ⊥AB ，OF ⊥BC ，∴∠BEO ＝∠BFO ＝90°.∴∠EOF ＋∠ABC ＝180°.∴∠EOF ＝120°.∴∠EPF ＝12∠EOF ＝60°. 【答案】 C2.如图1239，AB 是半圆O 的直径，∠BAC ＝30°，BC 为半圆的切线，且BC ＝43，则点O 到AC 的距离OD ＝________.【导学号：96990021】图1239【解析】 ∵BC 为半圆的切线，∴AB ⊥BC .∵∠BAC ＝30°，BC ＝43，∴AC ＝83，AB ＝12，∴OD BC ＝OA AC， ∴OD ＝6×4383＝3. 【答案】 33.如图1240，AB 是⊙O 的直径，AE 平分∠BAF 交⊙O 于点E ，过E 作直线与AF 垂直，交AF 的延长线于点D ，且交AB 的延长线于点C .求证：CD 是⊙O 的切线.图1240【证明】如图，连接OE .∵OA ＝OE ，∴∠1＝∠2.又∵AE 平分∠BAF ，∴∠2＝∠3.∴∠1＝∠3，∴OE ∥AD .∵AD ⊥CD ，∴OE ⊥CD .∴CD 与⊙O 相切于点E .我还有这些不足： (1)(2) 我的课下提升方案：(1)(2)。

圆的切线性质与判定

小试牛刀
例2：如图，已知：AB=AC，点O在AB上，⊙O过点B，分别与边BC、AB交于D、E两点，过D点作DF⊥AC于F，（1）求证：DF是⊙O的切线；
证明：连结OD， ∵OB=OD，∴∠ODB=∠B 又∵AB=AC，∴∠C=∠B ∴∠ODB=∠C ∴OD∥AC 又∵DF⊥AC ∴∠DFC=90° ∴∠ODF=∠DFC=90° ∴DF⊥OD ∴DF为⊙O的切线
注意：确定唯一公共点，可证明直线和圆相切
例1：直线l和⊙O的公共点的个数为m，且m满足方程 m2+2m- 3=0, 试判断直线l和⊙ O的位置关系，并说明理由.
例3．如图，直线y=－ x+4与y轴交于点A，与x轴交于点B，以点C（，0）为圆心，OC的长为半径作⊙C，证明：AB是⊙C的切线。 M 分析：由于不知AB和⊙C是否有公共点，故考虑过C作CM⊥AB于M，再证CM为⊙C的半径即可
小结一
确定唯一公共点，证切线
无交点，作垂直，证半径
有交点，连半径，证垂直
证明切线的一般方法简单表述为：
小试牛刀
例3：如图，已知：AB=AC，点O在AB上，⊙O过点B，分别与边BC、AB交于D、E两点，过D点作DF⊥AC于F，
（2）连结OP ∵AC与⊙O相切于点P，∴OP⊥AC 由（1）可知OD∥AC，且DF⊥AC，故四边形ODFP为正方形 ∴PF=OD=OB=3 设AC=x，则在Rt△APO中有 AP2+OP2=OA2 即(x－4)2+32=(x－3)2 解得x=8 ∴AC=8
是圆的切线
是圆的切线
是圆的切线
3、圆的切线性质定理：圆的切线垂直于经过切点的半径。辅助线作法：连接圆心与切点可得半径与切线垂直。即“连半径，得垂直”。

专题7圆的切线的判定与性质-重难点题型(举一反三)

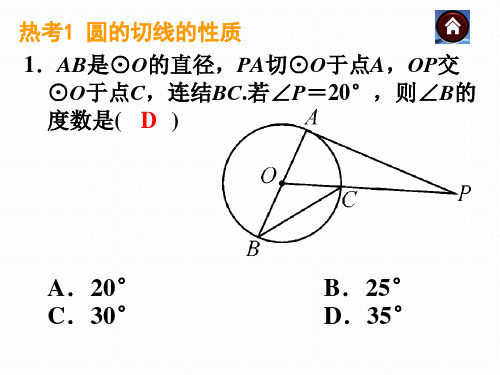
专题2.2 圆的切线的判定与性质--重难点题型【知识点1 切线的判定】（1）切线判定：①经过半径的外端并且垂直于这条半径的直线是圆的切线②和圆只有一个公共点的直线是圆的切线（定义法）③如果圆心到一条直线的距离等于圆的半径，那么这条直线是圆的切线（2）切线判定常用的证明方法：①知道直线和圆有公共点时，连半径，证垂直；②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径．【题型1 切线判定（连半径，证垂直）】【例1】（2021•新兴县一模）如图，AD是⊙O的弦，AB经过圆心O，交⊙O于点C，连接BD，∠DAB＝∠B＝30°，求证：直线BD是⊙O的切线．【变式1-1】（2020秋•思明区校级期末）如图，AB是圆O的一条弦，点E是劣弧AB的中点，直线CD经过点E 且与直线AB平行，证明：直线CD是圆O的切线．【变式1-2】（2020秋•福州期末）如图，AB是⊙O的直径，C为半圆O上一点，直线l经过点C，过点A作AD ⊥l于点D，连接AC，当AC平分∠DAB时，求证：直线l是⊙O的切线．【变式1-3】（2021•芜湖模拟）如图，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，过点C作∠BCD＝∠ACB 交⊙O于点D，连接AD交BC于点E，延长DC至点F，使CF＝AC，连接AF．（1）求证：ED＝EC；（2）求证：AF是⊙O的切线．【题型2 切线判定（作垂直，证半径）】【例2】（2020秋•原州区期末）如图，直线AB经过⊙O上的点C，并且OA＝OB，CA＝CB．求证：直线AB是⊙O 的切线．【变式2-1】（2020秋•北京期末）如图，以点O为圆心作圆，所得的圆与直线a相切的是（）A．以OA为半径的圆B．以OB为半径的圆C．以OC为半径的圆D．以OD为半径的圆【变式2-2】（2020秋•曲靖期末）如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交BC、AC边于点D、F．过点D作DE⊥CF于点E．求证：DE是⊙O的切线；【变式2-3】（2021•南平模拟）如图，在△ABC中，D为BC边上的一点，过A，C，D三点的圆O交AB于点E，已知，BD＝AD，∠BAD＝2∠DAC＝36°．（1）求证：AD是圆O的直径；（2）过点E作EF⊥BC于点F，求证：EF与圆O相切．【题型3 切线判定（定义法）】【例3】（2020秋•北塘区期中）给出下列说法：（1）与圆只有一个公共点的直线是圆的切线；（2）与圆心的距离等于半径的直线是圆的切线；（3）垂直于圆的半径的直线是圆的切线；（4）过圆的半径的外端的直线是圆的切线．其中正确的说法个数为（）A．1B．2C．3D．4【变式3-1】（2020秋•锡山区校级月考）下列直线是圆的切线的是（）A．与圆有公共点的直线B．到圆心的距离等于半径的直线C．到圆心的距离大于半径的直线D．到圆心的距离小于半径的直线【变式3-2】给出下列说法：①与圆只有一个公共点的直线是圆的切线；②与圆心的距离等于半径的直线是圆的切线；③垂直于圆的半径的直线是圆的切线；④过圆的半径的外端的直线是圆的切线；⑤经过圆心和切点的直线垂直于这条切线．其中正确的是．（填序号）【变式3-3】（2020•龙川县二模）如图，P A和⊙O相切于A点，PB和⊙O有公共点B，且P A＝PB，求证：PB是⊙O的切线．【知识点2 切线的性质】（1）切线性质定理：圆的切线垂直于过切点的半径（2）切线性质的推论：①经过圆心且垂直于切线的直线必经过切点②经过切点且垂直于切线的直线必经过圆心【题型4 切线的性质（求长度问题）】【例4】（2020秋•衢江区期末）如图，直线AB与⊙O相切于点C，OA交⊙O于点D，连结CD．已知OD＝CD ＝5，求AC的长．【变式4-1】（2021•温州三模）在等腰三角形ABC 中，AC ＝BC ＝2，D 是AB 边上一点，以AD 为直径的⊙O 恰好与BC 相切于点C ，则BD 的长为（）A ．1B ．2√33C ．2D ．2√55【变式4-2】（2021•湖州一模）如图，以△ABC 的边AB 为直径作⊙O ，交BC 于点D ，过点D 的切线DE ⊥AC 于点E ．（1）求证：AB ＝AC ；（2）若AB ＝10，BD ＝8，求DE 的长．【变式4-3】（2021•陕西模拟）如图，AB 是⊙O 的直径，C 是⊙O 上的一点，连接BC ，F 为BC 的中点，连接FO 并延长交⊙O 于点D ，过点D 的切线与CA 的延长线交于点E ．（1）求证：四边形CEDF 是矩形；（2）若AC ＝OA ＝2，求AE 的长．【题型5 切线的性质（求半径问题）】【例5】（2020秋•市中区期末）如图，BE 是⊙O 的直径，点A 和点D 是⊙O 上的两点，过点A 作⊙O 的切线交BE 延长线于点C ．（1）若∠ADE ＝28°，求∠C 的度数；（2）若AC ＝2√3，CE ＝2，求⊙O 半径的长．【变式5-1】（2020秋•沂水县期末）如图，已知⊙O 上三点A ，B ，C ，∠ABC ＝15°，切线P A 交OC 延长线于点P ，AP =√3，则⊙O 的半径为（）A ．√33B ．√32C ．√3D ．3【变式5-2】（2021•河南模拟）如图，AB 为⊙O 的直径，C 为BA 延长线上一点，CD 是⊙O 的切线，D 为切点，作OF ⊥AD 于点E ，交CD 于点F ．（1）在不增加辅助线的情况下，请直接写出图中一对相等的角，并证明；（2）若BD ＝8，EF ＝2，求⊙O 的半径．【变式5-3】（2021•贵池区模拟）已知：在⊙O 中，AB 为直径，P 为射线AB 上一点，过点P 作⊙O 的切线，切点为点C ，D 为弧AC 上一点，连接BD 、BC 、DC ．（1）如图1，求证：∠D ＝∠PCB ；（2）如图2，若四边形CDBP 为平行四边形，BC ＝5，求⊙O 的半径．【题型6 切线的性质（求角度问题）】【例6】（2021•红桥区三模）在△ABC中，以AB为直径的⊙O分别与边AC，BC交于点D，E，且DE＝BE．（Ⅰ）如图①，若∠CAB＝38°，求∠C的大小；（Ⅱ）如图②，过点E作⊙O的切线，交AB的延长线于点F，交AC于点G，若∠CAB＝52°，求∠BEF的大小．【变式6-1】（2021•三明模拟）从⊙O外一点A作⊙O的切线AB，AC，切点分别为B，C，D是⊙O上不同于B，C的点，∠BAC＝60°，∠BDC的度数是（）A．120°B．60°C．90°或120°D．60°或120°【变式6-2】（2021•北辰区二模）如图，在⊙O中，直径AB与弦CD相交于点E，∠ABC＝58°．（Ⅰ）如图①，若∠AEC＝85°，求∠BAD和∠CDB的大小；（Ⅱ）如图②，若CD⊥AB，过点D作⊙O的切线DF，与AB的延长线相交于点F，求∠F的大小．【变式6-3】（2021•天津）已知△ABC内接于⊙O，AB＝AC，∠BAC＝42°，点D是⊙O上一点．（Ⅰ）如图①，若BD为⊙O的直径，连接CD，求∠DBC和∠ACD的大小；（Ⅱ）如图②，若CD∥BA，连接AD，过点D作⊙O的切线，与OC的延长线交于点E，求∠E的大小．。

第2课时切线的判定和性质教学设计

第2课时切线的判定和性质本课时是在学习直线和圆的位置关系的基础上进一步深入研究直线和圆相切的情况，为后面研究切线长定理、三角形内切圆和正多边形与圆的关系打下基础．切线的判定定理和性质定理揭示了切线和圆的半径的特殊位置关系，即过半径外端并与这条半径垂直．两个命题互为逆命题．在学习的过程中要注意判定定理和性质定理的区分，并熟练掌握切线的两种证明方法以及勾股定理的应用．【情景导入】(1)用一根细线系一个小球，当你快速转动细线时，小球运动形成一个圆，突然，这个小球脱落，沿着圆的边缘飞出去，你知道小球顺着什么方向飞出去了吗？(2)如图1，下雨天，快速转动雨伞时，雨伞上的水珠是顺着什么方向飞出去的？(3)观察图2，过⊙O上一点A作直线l，则直线l与⊙O有哪几种位置关系？(4)观察图3，当所作直线l与OA垂直时，直线l与⊙O有怎样的位置关系？图1 图2 图3 【说明与建议】说明：通过常见实际问题引入直线和圆相切，并通过作图来观察、探究切线．建议：在探究切线的判定方法时，注意引导学生理解“经过半径的外端”“垂直于这条半径”这两个条件缺一不可，可以采用提出“过半径的外端的直线是圆的切线”“与半径垂直的直线是圆的切线”这两个假命题让学生讨论、判断的方法来帮助学生理解．【复习导入】1．填写直线和圆的位置关系表：2.思考1：如图，在⊙O中，经过半径OA的外端点A作直线l⊥OA，则圆心O到直线l 的距离是多少？直线l和⊙O有什么位置关系？3．思考2：在⊙O中，如果直线l是⊙O的切线，切点为A，那么半径OA与直线l是不是一定垂直呢？【说明与建议】说明：通过对直线和圆的位置关系的回顾，加强新旧知识之间的联系，通过探究两个思考问题，得出切线的判定定理和性质定理．建议：思考1和思考2可以让学生通过画图体会定理的正确性．要证明切线性质定理需要用反证法．命题角度1 证明圆的切线1．(邵阳中考节选)如图，在等腰△ABC中，AB＝AC，点D是BC上一点，以BD为直径的⊙O过点A，连接AD，∠CAD＝∠C.求证：AC是⊙O的切线．证明：连接OA，∵OA＝OB，∴∠OBA＝∠OAB.∵AB＝AC，∴∠OBA＝∠C.∴∠OAB＝∠C.∵∠CAD＝∠C，∴∠OAB＝∠CAD.∵BD是⊙O的直径，∴∠BAD＝90°.∴∠OAC＝∠BAD－∠OAB＋∠CAD＝90°，即OA⊥AC.又∵OA是⊙O的半径，∴AC是⊙O的切线．2．如图，OA ＝OB ＝13 cm ，AB ＝24 cm ，⊙O 的直径为10 cm.求证：AB 是⊙O 的切线．证明：过点O 作OC ⊥AB ，垂足为C ， ∵OA ＝OB ＝13 cm ，AB ＝24 cm ， ∴AC ＝12AB ＝12 cm.在Rt △OAC 中，根据勾股定理，得 OC ＝OA 2－AC 2＝5 cm ， ∵⊙O 的直径为10 cm ， ∴⊙O 的半径为5 cm. ∴OC 是⊙O 的半径． ∴AB 是⊙O 的切线．命题角度2 利用切线的性质进行计算或证明3．(沈阳中考)如图，在△ABC 中，∠ACB ＝90°，点O 为BC 边上一点，以点O 为圆心，OB 长为半径的圆与边AB 相交于点D ，连接DC ，当DC 为⊙O 的切线时．(1)求证：DC ＝AC.(2)若DC ＝DB ，⊙O 的半径为1，请直接写出DC证明：连接OD ， ∵CD 是⊙O 的切线，∴CD ⊥OD.∴∠ODC ＝90°.∴∠BDO ＋∠ADC ＝90°. ∵∠ACB ＝90°， ∴∠A ＋∠B ＝90°. ∵OB ＝OD ， ∴∠B ＝∠BDO. ∴∠A ＝∠ADC.∴CD ＝AC.如何测量圆的半径如图，木工师傅可以用角尺测量并计算出圆的半径r ，用角尺的较短边紧靠⊙O ，并使较长边与⊙O 相切于点C ，假设角尺的较长边足够长，角尺的顶点为B ，较短边AB ＝8 cm.若读得BC 的长为a cm ，你能用含a 的代数式表示r 吗？探究新知1．探究切线的判定活动一：教师结合所画图形(如图)，引导学生分析．因为直线l⊥OA，所以圆心O到直线l的距离等于OA，而OA正好是⊙O的半径，根据“当圆心到直线的距离等于该圆的半径时，直线就是圆的一条切线”可知直线l是⊙O的切线．教师引导学生对切线的判定定理进行概括，并发表意见．师生共同总结，教师板书：切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．教师引导学生分组讨论定理的条件和结论，做好定理的分析，运用判定定理判定一条直线是圆的切线要把握两点：①经过半径的外端；②垂直于这条半径．活动二：提问：生活中你看到过哪些直线和圆相切的现象？师生活动：学生思考并回答，教师做好补充．如下雨天，快速转动雨伞时飞出的水珠，在砂轮上打磨工件时飞出的火星等，都是沿着圆的切线方向飞出的．活动三：判断下列说法是否正确：(1)过半径外端的直线是圆的切线．(×)(2)与半径垂直的直线是圆的切线．(×)(3)过半径的端点且与半径垂直的直线是圆的切线．(×)(4)经过直径的端点且与该直径垂直的直线是圆的切线．(√)师生活动：学生判断、操作后，教师用多媒体演示下列反例．教师提出问题：判断一条直线是圆的切线共有几种方法？师生活动：学生讨论、交流后，请学生代表总结方法，教师最后进行总结．方法一：与圆有唯一公共点的直线是圆的切线；方法二：到圆心的距离等于半径的直线是圆的切线；方法三：经过半径的外端并且垂直于这条半径的直线是圆的切线．2．探究切线的性质活动：课件展示教材第97页“思考”．将切线的判定定理反过来，如果直线l是⊙O的切线，切点为A，那么半径OA 与直线l是不是一定垂直呢？师生活动：教师引导学生小组内进行分析，直接证明较为困难，可以运用反证法进行说明．师生共同总结：圆的切线的性质定理：圆的切线垂直于过切点的半径.【典型例题】例1如图，△ABC为等腰三角形，O是底边BC的中点，腰AB与⊙O相切于点D.求证：AC是⊙O的切线．师生活动：学生独立思考，然后小组内交流，教师及时引导、点拨作出辅助线，并规范解题过程．分析：根据切线的判定定理，要证明AC是⊙O的切线，只要证明由点O向AC 所作的垂线段OE是⊙O的半径即可．教师总结：①当明确指出直线与圆的公共点时，应连接圆心和公共点，即得到“半径”，再证明“直线与半径垂直”，简称为“连半径，证垂直”；②当未明确指出直线与圆的公共点时，应过圆心作直线的垂线段，再证明“垂线段的长等于半径”，简称为“作垂直，证半径”．例2如图，BC与⊙O相切于点B，AB为⊙O的直径，弦AD∥OC.求证：CD是⊙O的切线．师生活动：学生先独立解决问题，然后小组内讨论，鼓励学生勇于探索实践，而后再与同桌交流，上讲台演示，教师要重点关注学生的解题过程．例3(哈尔滨中考)如图，AB为⊙O的切线，点A为切点，OB交⊙O于点C，点D在⊙O上，连接AD，CD，OA.若∠ADC＝35°，则∠ABO的度数为(B)A．25° B．20° C．30° D．35°师生活动：学生先独立解决问题，教师适当给出提示：借助圆周角定理以及切线的性质进行角度推导．【变式训练】1．(桂林中考)如图，AB是⊙O的弦，AC与⊙O相切于点A，连接OA，OB.若∠O＝130°，则∠BAC的度数是(B)A．60° B．65° C．70° D．75°2．如图，直线AB，CD相交于点O，∠AOC＝30°，半径为1 cm的⊙P的圆心在射线OA上，且与点O的距离为6 cm.如果⊙P以1 cm/s的速度沿A向B的方向移动，那么经过4或8秒后，⊙P与直线CD相切．3．(锦州中考节选)如图，四边形ABCD内接于⊙O，AB为⊙O的直径，过点C 作CE⊥AD交AD的延长线于点E，延长EC，AB交于点F，∠ECD＝∠BCF.求证：CE为⊙O的切线．证明：连接OC，∵OB＝OC，∴∠OCB＝∠OBC.∵四边形ABCD内接于⊙O，∴∠ADC＋∠OBC＝180°.又∵∠ADC＋∠CDE＝180°，∴∠CDE＝∠OBC＝∠OCB.∵CE⊥AD，∴∠E＝∠CDE＋∠ECD＝90°.∵∠ECD＝∠BCF，∴∠OCB＋∠BCF＝90°.∴∠OCF＝90°，即OC⊥EF.∵OC是⊙O的半径，∴CE为⊙O的切线．【课堂检测】1.如图，AB与⊙O相切于点B，AO＝6 cm，AB＝4 cm，则⊙O的半径为(B)A．4 5 cm B．2 5 cm C．213 cm D.13 cm2．如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C.若∠A＝25°，则∠D＝ 40°．3．如图，AB为⊙O直径，AB＝AC，BC与⊙O交于D，且DE⊥AC.求证：DE是⊙O切线．证明：连接AD，DO，∵AB是⊙O的直径，∴∠ADB＝90°.∵AB＝AC，∴BD＝CD.∵AO＝BO，∴OD是△ABC的中位线．∴OD∥AC.∵DE⊥AC，∴OD⊥DE.∵OD是⊙O的半径，∴DE是⊙O的切线．师生活动：学生进行课堂检测，完成后，教师进行个别提问，并指导学生解释做题理由和做题方法，使学生在思考解答的基础上，共同交流，形成共识，确定答案.第2课时切线的判定和性质1．切线的判定定理及性质定理切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．∵OC是半径，OC⊥AB，∴直线AB与⊙O相切．切线的性质定理：圆的切线垂直于过切点的半径．如图，∵AB与⊙O相切于点C，∴OC⊥AB.2．证明切线常用的两种方法：①“作垂直，证半径”；②“连接圆心与交点，证垂直”.。

圆的切线的性质与判定

考点一圆的切线的性质
切线的圆的切线__垂__直____于过切点的半径
性质
(1)经过圆心且垂直于切线的直线必过 ___切__点___；推论 (2)经过切点且垂直于切线的直线必过 ___圆__心___
热考一圆的切线的判定
3.等腰三角形ABC中，AC＝BC＝10，AB＝12，以 BC为直径作⊙O交AB于点D，交AC于点G， DF⊥AC，垂足为F，交CB的延长线于点E.
（3）在抛物线上是否存在一点P，使S△ACP=S△ACD？若存在，求出点P 的坐标；若不存在，请说明理由．
学生讲解图
用d与r的大小来判定
考点聚焦
考点1 圆的切线的判定 (1)和圆有__唯__一____公共点的直线是圆的切线；
切线 (2)如果圆心到一条直线的距离等于的判圆的_半__径___，那么这条直线是圆的
(1)求证：直线EF是⊙O的切线；
(2)求EB的长. (3)求cos∠E的值．
有交点，连半径，证垂直．
学生讲解图
热考一圆的切线的判定
4.如图 33－3，O 为正方形 ABCD 对角线 AC 上一点，以 O 为圆心，OA 长为半径的⊙O 与 BC 相切于点 M. 求证：CD 与⊙O 相切；
GF=1，求⊙O的半径及sin∠ACE的值．
无交点，作垂直，证半径．
图 33－3
5.如图，在平面直角坐标系中，顶点为（4，﹣1）的抛物线交y轴于A点，交x轴于B，C两点（点B在点C的左侧），已知A点坐标为（0，3）．（1）求此抛物线的解析式
（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有怎样的位置关系，并给出证明。
定切线;（d＝r）

圆的切线的性质及判定定理(选修4-1)

切线的性质定理: 圆的切线垂直于经过切点的半径反假设不垂直, A M l 证作OM⊥ l 法因“垂线段最短”, O
故OA>OM, 即圆心到直线距离小于半径. 这与线圆相切矛盾. 推论1: 经过圆心且垂直于切线的直线必经过切点. 推论2: 经过切点且垂直于切线的直线必经过圆心.
思考:
切线的性质定理逆命题是否成立?
42 O
B
△COD与COB全等
练习
如图,△ABC中，AB=AC，以AB为直径的⊙O交边BC于P， A PE⊥AC于E。求证:PE是⊙O的切线。证明：连结OP。 ∵AB=AC,∴∠B=∠C。 ∵OB=OP，∴∠B=∠OPB， ∴∠OBP=∠C。 ∴OP∥AC。 ∵PE⊥AC， ∴∠PEC=90° ∴ ∠OPE=∠PEC=90° ∴PE⊥OP。 ∴PE为⊙0的切线。
∴OC⊥CD.
∵CD是⊙O的切线,
D
又∵AD⊥CD,
∴OC//AD.由此得 ∠ACO=∠CAD. ∵OC=OA. ∴ ∠CAO=∠ACO. ∴ ∠CAD=∠CAO. 故AC平分∠DABO的延长线交 ⊙O于C，直线AB经过⊙O上一点B，且AB＝BC， ∠C＝30°. 求证：直线AB是⊙O的切线.
授课日期：2013年5月22 班级：高二（1），（2）授课人：朱大伟
自主学习：
时间：3分钟
请大家阅读课本P27-P28的内容，回答下面几个问题： 1，圆内接四边形有什么特点，你能证明它吗？ 2，是不是所有的四边形都有外接圆？
三. 圆的切线的性质及判定定理圆与直线的位置关系:
相交-----有两个公共点相切-----只有一个公共点相离-----没有公共点
例1 如图,AB是⊙O的直径, ⊙O过BC的中点D, DE⊥AC.求证:DE是⊙O是切线.

高中数学第一章直线、多边形、圆 1_2 圆与直线 1_2_3 弦切角定理课后作业北师大版选修4-11

1.2.3 弦切角定理课后作业提升1如图,△ABC内接于☉O,EC切☉O于点C.若∠BOC=76°,则∠BCE=( ).A.14°B.38°C.52°D.76°解析:∵EC为☉O的切线,∴∠BCE=∠BAC=∠BOC=38°.答案:B2如图,AB是☉O的直径,EF切☉O于点C,AD⊥EF于点D,AD=2,AB=6,则AC=( ).A.2B.3C.2D.4解析:连接BC,如图所示,∵EF是☉O的切线,∴∠ACD=∠ABC.∵AB是☉O的直径,∴∠ACB=90°.又EF⊥AD,∴∠ACB=∠ADC.∴△ACB∽△ADC.∴.∴AC2=AD·AB=2×6=12.∴AC=2.答案:C3如图所示,∠ABC=90°,O是AB上一点,☉O切AC于点D,交AB于点E,连接DB,DE,OC,则图中与∠CBD相等的角共有( ).A.1个B.2个C.3个D.4个解析:∵AB⊥BC,∴BC与☉O相切,BD为☉O的弦.∴∠CBD=∠BED.同理可得∠CDB=∠BED,∴∠CBD=∠CDB.连接OD.∵OD=OB,OC=OC,∴Rt△COD≌Rt△COB.∴CB=CD,∠DCO=∠BCO.∴OC⊥BD.又DE⊥BD,∴DE∥OC.∴∠BED=∠BOC.∴∠CBD=∠BOC.∴与∠CBD相等的角共有3个.答案:C4如图所示,Rt△ABC内接于☉O,∠ABC=60°,PA是☉O的切线,A为切点,PB交AC于点E,交☉O于点D.若PA=AE,PD=,BD=3,则AP=,AC=.解析:∵∠ACB=90°,∴AB是☉O的直径.∵PA与☉O相切,∴AB⊥AP,∠PAE=∠ABC=60°.又∵PA=PE,∴△PAE是等边三角形,∴∠P=60°,∴∠ABP=30°.∵PA=PB sin∠ABP=(+3)sin30°=2,AB=PB cos∠ABP=(+3)cos30°=6,∴在Rt△ABC中,AC=AB sin∠ABC=6sin60°=3.答案:235如图,圆O的半径为1,A,B,C是圆周上的三点,满足∠ABC=30°,过点A作圆O的切线与OC 的延长线交于点P,则PA=.解析:连接AO,则由∠ABC=30°知∠AOP=60°.又OA=1,∴PA=OA·tan60°=.答案:6如图所示,BA是☉O的直径,AD是☉O的切线,切点为A,BF,BD分别交AD于点F,D,交☉O 于点E,C,连接CE.求证:BE·BF=BC·BD.分析:要证BE·BF=BC·BD,只需证明,即证明△BEC∽△BDF,∠DBF为公共角,只需再找一组角相等,为此,过点B作☉O的切线,构造弦切角.证明:如图,过点B作☉O的切线BG,则AB⊥BG.∵AD是☉O的切线,∴AD⊥AB,则BG∥AD,∴∠GBC=∠BDF.又∵∠GBC=∠BEC,∴∠BEC=∠BDF.∵∠CBE=∠FBD,∴△BEC∽△BDF.∴,即BE·BF=BC·BD.7如图,☉O内切△ABC的边于D,E,F三点,AB=AC,连接AD交☉O于点H,直线HF交BC的延长线于点G.证明:(1)圆心O在直线AD上;(2)点C是线段GD的中点.证明:(1)∵AB=AC,AF=AE,∴CF=BE.∵CF=CD,BD=BE,∴CD=BD.又∵△ABC是等腰三角形,AB=AC,∴AD是∠CAB的平分线.∴内切圆圆心O在直线AD上.(2)连接DF,如图所示,由(1)知,DH是☉O的直径,∴∠DFH=90°,∴∠FDH+∠FHD=90°.又∵∠G+∠FHD=90°,∴∠FDH=∠G.∵☉O与AC相切于点F,∴∠GFC=∠AFH=∠FDH=∠G,∴∠GFC=∠G.∴CG=CF.又CF=CD,∴CG=CD,∴点C是线段GD的中点.备课资源参考备选习题1.如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B.(1)试探索∠BCP与∠P的数量关系.(2)若∠A=30°,则PB与PA有什么关系?(3)∠A可能等于45°吗?为什么?解:(1)∵PC是切线,C为切点,∴∠BCP=∠A.又∵AB是直径,∴∠ACB=90°.在△ACP中,∠A+∠P+∠ACP=180°,∴∠BCP+∠P+∠ACB+∠BCP=180°.∴2∠BCP+∠P+90°=180°.∴∠P=90°-2∠BCP.(2)若∠A=30°,则∠BCP=∠A=30°,∠ABC=60°.∴∠P=30°.∴PB=BC,BC=AB.∴PB=PA,即PA=3PB.(3)∠A不可能等于45°.原因:设∠A=45°,则∠ABC=45°,∠BCP=45°,∴CP∥AB.与题干中PC与AB交于点P矛盾,∴∠A不可能等于45°.2.如图,已知C点在☉O直径BE的延长线上,CA切☉O于A点,∠ACB的平分线交AE于F点,交AB于D点.(1)求∠ADF的度数.(2)若∠ACB的度数为y,∠B的度数为x,那么y与x之间有怎样的关系?试写出你的猜测并给出证明.分析:(1)中由AC为☉O的切线可得∠B=∠EAC,由CD平分∠ACB可得∠ACD=∠DCB,根据三角形外角定理,得到∠ADF=∠AFD,建立等腰三角形,再由顶角求底角;(2)中则利用三角形内角和定理得到方程,获得关系.解:(1)∵AC为☉O的切线,∴∠B=∠EAC.∵CD平分∠ACB,∴∠ACD=∠DCB.∴∠B+∠DCB=∠EAC+∠ACD,即∠ADF=∠AFD.∵BE为☉O的直径,∴∠DAE=90°.∴∠ADF=(180°-∠DAE)=45°.(2)∵∠B=∠EAC,∠B+∠BAC+∠ACB=180°.∴x+90°+x+y=180°.∴y=90°-2x.∵0°<∠B<∠ADC,∴0°<x<45°.∴y与x的函数关系式是y=90°-2x,其中x的取值范围是0°<x<45°.。

新教材高中数学第一章直线与圆1 4两条直线的平行与垂直课后篇巩固提升训练含解析北师大版选择性必修第一

第一章直线与圆§1 直线与直线的方程 1.4 两条直线的平行与垂直课后篇巩固提升合格考达标练1.下列说法中,正确的有( )①斜率均不存在的两条直线可能重合;②若直线l 1⊥l 2,则这两条直线的斜率的乘积为-1; ③若两条直线的斜率的乘积为-1,则这两条直线垂直;④两条直线l 1,l 2中,一条直线的斜率不存在,另一条直线的斜率为零,则l 1⊥l 2.A.1个B.2个C.3个D.4个,也可能重合,故①正确,两直线垂直,有两种情况:当两条直线都有斜率时,斜率乘积为-1;也可以一条直线的斜率不存在,另一条直线的斜率为零,故②错误,③④正确.2.已知直线方程l 1:y=12x+74,l 2:y=12x+52,则l 1与l 2的关系( ) A.平行 B.重合C.相交D.以上答案都不对直线l 1的斜率k 1=12,直线l 2的斜率k 2=12,∴k 1=k 2.∵两条直线在y 轴上的截距分别为74和52,不相等, ∴l 1与l 2互相平行.故选A.3.已知直线l 1和l 2互相垂直且都过点A (1,1),若l 1过原点O (0,0),则l 2与y 轴交点的坐标为( ) A.(2,0) B.(0,2)C.(0,1)D.(1,0)l 2与y 轴交点为B (0,b ).∵直线l 1过A (1,1),O (0,0), ∴k OA =1.∵l 1⊥l 2,∴k OA ·k AB =-1,即k AB =b -10-1=-1,解得b=2,即l 2与y 轴交点的坐标为(0,2).4.直线y=-12ax+52a与直线y=-a 4x-12平行,则a 的值为( )A.2B.±2C.√2D.±√2直线y=-12a x+52a 与直线y=-a 4x-12平行,显然a ≠0,∴{-12a =-a4,52a≠-12,即{a 2-2=0,a ≠-5.解得a=±√2, 故选D.5.直线l 1,l 2的斜率k 1,k 2是关于k 的方程2k 2-3k-b=0的两个根,若l 1∥l 2,则b= . -98k 1+k 2=32,k 1·k 2=-b 2,∵l 1∥l 2,∴k 1=k 2=34,解得b=-2k 1·k 2=-98.6.已知直线l 1经过点A (3,a ),B (a-2,3),直线l 2经过点C (2,3),D (-1,a-2),若l 1⊥l 2,则a 的值为 .或5l 1的斜率不存在时,3=a-2,即a=5,此时直线l 2的斜率k 2=0,则l 1⊥l 2,满足题意.当直线l 1的斜率k 1存在时,a ≠5,由斜率公式,得k 1=3-a a -2-3=3-a a -5,k 2=a -2-3-1-2=a -5-3.由l 1⊥l 2,知k 1k 2=-1,即3-a a -5×a -5-3=-1,解得a=0.综上所述,a 的值为0或5.7.已知平行四边形ABCD 中,A (1,1),B (-2,3),C (0,-4),则点D 的坐标为 .-6)D (x ,y ),由题意可知,AB ∥CD 且AD ∥BC ,∴k AB =k CD 且k AD =k BC ,∴{3-1-2-1=y+4x ,-4-30+2=y -1x -1,解得{x =3,y =-6. 8.当m 为何值时,过两点A (1,1),B (2m 2+1,m-2)的直线: (1)倾斜角为135°;(2)与过两点(3,2),(0,-7)的直线垂直; (3)与过两点(2,-3),(-4,9)的直线平行.由k AB =m -32m 2=tan135°=-1,解得m=-32或m=1.(2)由题意k AB =m -32m 2,且-7-20-3=3, 则m -32m 2=-13,解得m=32或m=-3. (3)令m -32m 2=9+3-4-2=-2, 解得m=34或m=-1.等级考提升练9.已知直线l的倾斜角为135°,直线l1经过点A(3,2),B(a,-1),且l1与l垂直,直线l2:y=-2bx+1与直线l1平行,则a+b等于()A.-4B.-2C.0D.2直线l的斜率为-1,则直线l1的斜率为1,∴k AB=2-(-1)3-a=1,∴a=0.由l1∥l2,得-2b=1,得b=-2,所以a+b=-2.故选B.10.已知直线l1:x sin α+y-1=0,直线l2:x-3y cos α+1=0.若l1⊥l2,则sin 2α=()A.3B.-35C.23D.-23l1⊥l2,∴sinα-3cosα=0,即tanα=3.∴sin2α=2sinαcosα=2sinαcosαsin2α+cos2α=2tanα1+tan2α=610=35.11.过点A0,73与B(7,0)的直线l1与过点(2,1),(3,k+1)的直线l2和两坐标轴围成的四边形内接于一个圆,则实数k等于()A.-3B.3C.-6D.6l1⊥l2,∴k l1·k l2=-1,即-13k=-1,解得k=3.12.直线l1与l2满足下列条件,其中l1∥l2的是()①l1的斜率为2,l2经过点A(1,2),B(4,8),且l1不经过A点;②l1经过点P(3,3),Q(-5,3),l2平行于x轴,但不经过P点;③l1经过点M(-1,0),N(-5,-2),l2经过点R(-4,3),S(0,5).A.①②B.②③C.①③D.①②③,①中,直线l2的斜率也为2,故l1∥l2;②中,直线l1的斜率也为0,故l1∥l2;③两条直线的斜率均为12,且两直线没有公共点,故l1∥l2.故选D.13.直线x+a2y+6=0和直线(a-2)x+3ay+2a=0没有公共点,则a的值是()A.0或3B.-1或3C.0或-1或3D.0或-1两直线没有公共点,∴1×3a-a2(a-2)=0,∴a=0或-1或3,经检验知a=3时两直线重合,a=0或a=-1时,两直线平行.14.(2020甘肃武威八中高二月考)已知点A (-2,-5),B (6,6),点P 在y 轴上,且∠APB=90°,则点P 的坐标为 .-6)或(0,7)P 的坐标为(0,y ).因为∠APB=90°,所以AP ⊥BP.又k AP =y+52,k BP =y -6-6,k AP ·k BP =-1,所以y+52·-6=-1,解得y=-6或y=7.所以点P 的坐标为(0,-6)或(0,7).15.设点P (2,5)关于直线x+y=1的对称点为Q ,则点Q 的坐标为 ,过点Q 且与直线x+y-3=0垂直的直线方程为 .-4,-1) x-y+3=0Q (a ,b ),则{b -5a -2·(-1)=-1,a+22+b+52=1,解得a=-4,b=-1.即点Q 的坐标为(-4,-1),设与直线x+y-3=0垂直的直线方程为x-y+c=0,将Q (-4,-1)代入上式,得c=3,所以直线方程为x-y+3=0.16.已知直线l 1:ax-by+4=0,l 2:(a-1)x+y+b=0,求分别满足下列条件的a ,b 的值. (1)l 1⊥l 2,且直线l 1过点M (-4,-1).(2)直线l 1∥l 2,且l 1,l 2在y 轴上的截距互为相反数.∵l 1过点M (-4,-1),∴-4a+b+4=0.∵l 1⊥l 2,∴a×(1-a )+b=0. ∴{a =1,b =0或{a =4,b =12.(2)由题意可得两条直线不可能都经过原点, 当b=0时,两条直线分别化为ax+4=0,(a-1)x+y=0, 可知两条直线不平行. b ≠0时两条直线分别化为 y=abx+4b,y=(1-a )x-b ,∴ab =1-a ,4b =b ,解得{b =2,a =23或{b =-2,a =2.新情境创新练17.如图,在平面直角坐标系xOy 中,设三角形ABC 的顶点分别为A (0,a ),B (b ,0),C (c ,0),点P (0,p )是线段AO 上的一点(异于端点),这里a ,b ,c ,p 均为非零实数,设直线BP ,CP 分别与边AC ,AB 交于点E ,F.若BE ⊥AC ,求证:CF ⊥AB.B (b ,0)和点P (0,p ),知直线BP 的斜率为-pb ,由点A(0,a)和点C(c,0),知直线AC的斜率为-ac,因为BE⊥AC,所以-pb -ac=-1,即pa=-bc;由点C(c,0)和点P(0,p),知直线CP的斜率为-pc ,由点A(0,a)和点B(b,0),知直线AB的斜率为-ab,则直线CF与AB的斜率之积为-pc -ab=pabc=-bcbc=-1,所以CF⊥AB.。

平面解析几何初步直线圆的方程等课后限时作业(一)附答案新人教版高中数学名师一点通

高中数学专题复习
《平面解析几何初步直线圆的方程等》单元过关
检测
经典荟萃，匠心巨制！独家原创，欢迎下载！
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上
第I 卷（选择题）
请点击修改第I 卷的文字说明评卷人
得分一、选择题
1．过点(1,1)P 的直线,将圆形区域{}22(,)|4x y x y +≤分两部分,使得这两部分的面积之差最大,则该直线的方程为（）
A ．20x y +-=
B ．10y -=
C ．0x y -=
D ．340x y +-=（2020湖北文）
A
2．若圆0104422=---+y x y x 上至少有三个不同的点到直线0:=+by ax l 的距离为22,则直线l 的倾斜角的取值范围是（）
A ． ]412[π
π， B ．]12512[ππ， C ．]36[ππ， D ．]20[π， (2020湖南理)
3．到两坐标轴距离相等的点的轨迹方程是（）
A ．x －y=0
B ．x+y=0
C ．|x|－y=0
D ．|x|－|y|=0。

高中数学第一章直线、多边形、圆1_2圆与直线1_2_1圆周角定理课后作业北师大版选修4-11

圆周角定理课后作业提高1 以下结论错误的选项是 ( ) .A. 一条弧所对的圆周角等于它所对的圆心角的一半B. 圆心角的度数等于它所对弧的度数C.相等的圆周角所对的弧相等D.90°的圆周角所对的弦是直径答案:C2如图 , △ ABC 内接于☉ O , ∠ BAC=50°, ∠ ABC=60°,BD 为☉ O 的直径 , BD 交 AC 于点 E , 则∠ AEB=( ) .A.70°B.110°C.90°D.120°分析 : ∵∠ BAC=50°, ∠ ABC=60°,∴∠ ACB=180° - ( ∠ A+∠ ABC )=70°.连结 CD , 则∠ BDC=∠ BAC=50°, ∠ BCD=90°, ∴∠ ACD=90° - ∠ ACB=20° .∴∠ AEB=∠ CED=180° - ( ∠ BDC+∠ACD )=180° - (50 ° +20°)=110° . 答案:B3如图 , 已知 P , Q , R 都在弦 AB 的同侧 , 且点 P 在优弧上,点Q 在所在的圆 O 内, 点 R 在所在的圆 O 外,则().A. ∠ AQB<∠APB<∠ ARBB. ∠ AQB<∠ARB<∠ APBC.∠ APB<∠AQB<∠ ARBD.∠ ARB<∠APB<∠ AQB 分析 : 如下图 , 延伸交圆 O 于点 , 设与圆 O 订交于点 , 连结 , ,则有∠∠,AQC ARD BC BD AQB> ACB∠ADB>∠ ARB.因为∠ ACB=∠ APB=∠ ADB , 因此∠ ARB<∠ APB<∠ AQB. 答案:D4如图 , 已知△内接于☉ ,, 为上一点 , E 是直线和☉ O 的交点,则2().ABCO AB=ACDBCADAB=A. AC · BCB. AD · AEC.AD · DED.BD · DC分析:如图,连结 BE.∵ AB=AC ,∴∠ ABC=∠ ACB. ∵∠ ACB=∠ AEB , ∴∠ ABC=∠ AEB. 又∵∠ BAE=∠ DAB , ∴△ ABD ∽△ AEB.∴ AB ∶AE=AD ∶ AB , 2即 AB=AD · AE. 答案:B5 如图, 已知点是△的外心 ,∠α, 则∠OBC= .O ABC BAC= 分析 : 因为∠ BAC 是所对的圆周角 , 因此由圆周角定理可求出所对的圆心角的大小 . 连结 OC ,则∠ BOC=2∠ BAC=2α . 在△ OBC 中 , 因为 OB=OC ,因此∠ OBC=(180° - ∠BOC)=×(180°-2α)=90°-α.答案 : 90°-α6AB是半圆O的直径 , 点C在半圆上 , CD⊥AB于点D, 且AD=3BD, 则=.分析 : 如图 , 连结AC, BC,则∠ ACB=90°.设 BD=k,则 AD=3k,∵ CD⊥AB,2 2∴ CD=AD· BD=3k .∴ CD= k. ∴.答案 :7如图 , AB为☉O的直径 , 弦AC, BD交于点P, 若AB=3, CD=1, 则 sin ∠APD=.分析 : 因为AB为☉O的直径 , 则∠ADP=90°,因此△ APD是直角三角形 .则 sin ∠APD=,cos ∠APD=,由题意知 , ∠DCP=∠ABP, ∠CDP=∠BAP,因此△ PCD∽△ PBA.因此. 又 AB=3, CD=1,则.因此 cos ∠APD=.又 sin 2∠APD+cos2∠APD=1,因此 sin ∠APD=.答案 :8 足球场上有句顺口溜: “冲向球门跑 , 越近就越好 ; 沿着球门跑 , 射点要选好.”可见踢足球是有“学识”的.如图,在足球竞赛中,甲、乙两名队员相互当合向对方球门MN攻击,当甲带球冲到A点时,乙已跟从冲到 B 点,此时甲直接射门好, 仍是快速将球回传给乙, 让乙射门好 ?剖析 : 用数学方法从两点的静止的状态来考虑. 假如两个点到球门的距离相差不大, 要确立较好的射门地点 , 重点是看这两点各自对球门MN的张角大小,当张角较小时,简单被对方守门员拦截.解: 如图 , 连结MB, MA,NA, NB, 线段MA交圆于点C, 连结NC,则∠ MBN=∠ MCN,又∠ MCN>∠ MAN,∴∠ MBN>∠ MAN.∴甲应当传给乙, 让乙射门好.备课资源参照备选习题1.如图 , ☉C经过原点O,并与两坐标轴分别订交于A, D两点 . 已知∠ OBA=30°,点 D的坐标为(0,2) .求点A与圆心C的坐标.解: 连结AD, ∵AO⊥DO,则圆心C在AD上 , AD为☉C的直径.又∠ OBA=30°,∴∠ ADO=30°.∴OA=OD tan 30° = .∴点 A的坐标为.由点 C为 AB的中点可知点C的坐标为.2.如图 , ☉O是△ABC的外接圆 , D是的中点,BD交AC于点E.2求证 : CD=DE·DB.剖析 : 转变为证明△BCD与△ CED相像 .证明 : 由已知得∠ABD=∠CBD,∵∠ ECD=∠ ABD,∴∠ CBD=∠ ECD.又∵∠ BDC=∠ CDE,∴△ BCD∽△ CED∴.,2即 CD=DE· DB.3.如图 , △ABC的角均分线AD的延伸线交它的外接圆于点 E.(1)证明 : △ABE∽△ADC;(2)若 S△ABC= AD· AE,求∠ BAC的大小 .剖析 :(1)证明这两个三角形的两个角对应相等;(2)利用(1)的结论和三角形面积公式的正弦形式, 转变为求 sin ∠BAC.(1)证明 : ∵AD均分∠BAC,∴∠BAE=∠CAD.又∠ AEB与∠ ACB是同弧所对的圆周角,∴∠ AEB=∠ ACD.∴△ ABE∽△ ADC.(2) 解 : ∵△ABE∽△ADC,∴, 即AB·AC=AD·AE.又S△ABC= AB·AC sin ∠BAC,且S△ABC= AD· AE,∴ AB· AC sin∠ BAC=AD·AE.∴sin ∠BAC=1.又∠ BAC为三角形的内角,∴∠ BAC=90°.。

高中数学第1章直线、多边形、圆 1.2.2 圆的切线的判定和性质学业分层测评北师大版选修41

学业分层测评(五) 2.2 圆的切线的判定和性质(建议用时：45分钟)学业达标]一、选择题1.下列说法：①与圆有公共点的直线是圆的切线；②垂直于圆的半径的直线是圆的切线；③与圆心的距离等于半径的直线是圆的切线；④过直径的端点，垂直于此直径的直线是圆的切线，其中正确的是( )A.①②B.②③C.③④D.①④【解析】由圆的切线的定义知①②不正确，③④正确.【答案】 C2.如图1241，⊙O的半径为2，点O到直线l的距离为3，点P为直线l上的一个动点，PB切⊙O于点B，则PB的最小值是( )图1241A. 5B. 3C. 4D. 6【解析】∵PB切⊙O于点B，∴∠OBP＝90°，∴PB2＝OP2－OB2，而OB＝2，∴PB2＝OP2－4，即PB＝OP2－4，当OP最小时，PB最小，∵点O到直线l的距离为3，∴OP的最小值为3，∴PB的最小值为9－4＝ 5.【答案】 A3.如图1242，CD切⊙O于B，CO的延长线交⊙O于A，若∠C＝36°，则∠ABD的度数是( )图1242A.72°B.63°C.54°D.36°【解析】连接OB .∵CD 为⊙O 的切线，∴∠OBC ＝90°. ∵∠C ＝36°，∴∠BOC ＝54°. 又∵∠BOC ＝2∠A ，∴∠A ＝27°， ∴∠ABD ＝∠A ＋∠C ＝27°＋36°＝63°. 【答案】 B4.如图1243，AB 切⊙O 于点B ，延长AO 交⊙O 于点C ，连接BC .若∠A ＝40°，则∠C ＝( )图1243A.20°B.25°C.40°D.50°【解析】连接OB ，因为AB 切⊙O 于点B ，所以OB ⊥AB ，即∠ABO ＝90°，所以∠AOB ＝50°.又因为点C 在AO 的延长线上，且在⊙O 上，所以∠C ＝12∠AOB ＝25°.【答案】 B5.如图1244，⊙O 为△ABC 的内切圆，∠C ＝90°，AO 的延长线交BC 于点D ，AC ＝4，CD ＝1，则⊙O 的半径等于( )图1244A.45B.54C.34D.56【解析】设⊙O 的半径为r ，由O 向DC 作垂线，垂足为E ，则Rt△OED ∽Rt△ACD .∴OE ED ＝AC CD ，即r 1－r ＝41，解得：r ＝45.【答案】 A 二、填空题6.如图1245，在半径分别为5 cm 和3 cm 的两个同心圆中，大圆的弦AB 与小圆相切于点C ，则弦AB 的长为______________cm.图1245【解析】连接OA ，OC ， ∵AB 是小圆的切线， ∴OC ⊥AB ，∴AC ＝12AB .∵在Rt△AOC 中，AC ＝52－32＝4(cm)，∴AB ＝8 cm. 【答案】 87.如图1246所示，AC 切⊙O 于D ，AO 的延长线交⊙O 于B ，且AB ⊥BC ，若AD ∶AC ＝1∶2，则AO ∶OB ＝______.【导学号：96990022】图1246【解析】如图所示，连接OD ，则OD ⊥AC .∵AC 是⊙O 的切线，∴OB ＝OD ，OC ＝OC ，∠ODC ＝∠OBC ＝90°. ∴△CDO ≌△CBO .∴BC ＝DC .∵AD AC ＝12，∴AD ＝DC . ∴BC ＝12AC .又OB ⊥BC ，∠ABC ＝90°，∴∠A ＝30°. ∴OB ＝OD ＝12AO .∴AO OB ＝21. 【答案】 2∶18.圆O 的直径AB ＝6，C 为圆周上一点，BC ＝3，过C 作圆的切线l ，过A 作l 的垂线AD ，AD 分别与直线l 、圆交于点D ，E ，则∠DAC ＝__________，DC ＝__________.【解析】连接OC ， ∵OC ＝OB ，∴∠OCB ＝∠OBC . 又∠DCA ＋∠ACO ＝90°， ∠ACO ＋∠OCB ＝90°，∴∠DCA ＝∠OCB ， ∵OC ＝3，BC ＝3， ∴△OCB 是正三角形.∴∠OBC ＝60°，即∠DCA ＝60°. ∴∠DAC ＝30°.在Rt△ACB 中，AC ＝AB 2－BC 2＝33，DC ＝AC sin 30°＝323.【答案】30°33 2三、解答题9.如图1247，BE是⊙O的直径，点A在EB的延长线上，弦PD⊥BE，垂足为C，连接OD，且∠AOD＝∠APC.求证：AP是⊙O的切线.图1247【证明】连接OP.∵PD⊥BE，∴∠OCD＝90°.∴∠ODC＋∠COD＝90°.∵OD＝OP，∴∠ODC＝∠OPC.∵∠AOD＝∠APC，∴∠OPC＋∠APC＝90°.∴∠APO＝90°，即AP⊥PO.∴AP是⊙O的切线.10.在Rt△ABC中，∠C＝90°，AC＝3 cm，BC＝4 cm.(1)求△ABC内切圆的半径；(2)若移动圆心O的位置，使⊙O保持与△ABC的边AC和边BC都相切，求r的取值范围.【解】(1)如图所示，⊙O是Rt△ABC的内切圆，切点分别为D，E，F.连接OD，OE，OF，OB，则OD⊥BC，OE⊥AC，OF⊥AB.在Rt△ABC中，∠C＝90°，AC＝3 cm，BC＝4 cm，∴AB＝5 cm.∵OE＝OD，∠C＝90°，∴四边形CEOD是正方形.∴CD＝DO.∵OB＝OB，OD＝OF，∠ODB＝∠OFB＝90°，∴△ODB≌△OFB.∴BD＝BF.同理可得，AE ＝AF .∴AC ＋BC －AB ＝AE ＋EC ＋BD ＋DC －AF －BF ＝EC ＋DC ＝2OD . ∴内切圆的半径r ＝OD ＝AC ＋BC －AB2＝3＋4－52＝1 cm. (2)如图所示，动⊙O 与AC ，BC 相切的最大的圆与AC ，BC 的切点分别是A ，D ，连接OA ，OD ，则四边形AODC 是正方形，此时应有OA ＝AC ＝3 cm ，∴动圆的半径r 的范围为(0,3].能力提升]1.AB 是⊙O 的切线，在下列给出的条件中，能判定AB ⊥CD 的是( ) A.AB 与⊙O 相切于直线CD 上的点C B.CD 经过圆心O C.CD 是直径D.AB 与⊙O 相切于C ，CD 过圆心O【解析】圆的切线垂直于过切点的半径或直径. 【答案】 D2.已知⊙O 的直径AB 与弦AC 的夹角为30°，过C 点的切线PC 与AB 的延长线交于P ，PC ＝5，则⊙O 的半径是( )A.533B.536C.10D.5【解析】如图，连接OC ，∠PAC ＝30°，由圆周角定理知， ∠POC ＝2∠PAC ＝60°，由切线性质知 ∠OCP ＝90°.∴在Rt△OCP 中，tan∠POC ＝PCOC. ∴OC ＝PCtan∠POC ＝5tan60°＝533.【答案】 A3.如图1248，AB 为⊙O 的直径，过B 点作⊙O 的切线BC ，OC 交⊙O 于点E ，AE 的延长线交BC于点D，若AB＝BC＝2 cm，则CE＝__________，CD＝__________.图1248【解析】∵BC是⊙O切线，AB为直径，∴∠ABD＝90°，∵AB＝2.∴OB＝1，又∵BC＝2，∴OC＝4＋1＝ 5.又∵OE＝1，∴CE＝(5－1)cm，连接BE.不难证明△CED∽△CBE，∴CECD＝CBCE，∴CE2＝CB·CD，∴(5－1)2＝2CD，∴CD＝(3－5)cm.【答案】(5－1)cm (3－5)cm4.如图1249，已知：C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B点的切线相交于点D，E为CH中点，连接AE并延长交BD于点F，直线CF交AB的延长线于点G.图1249(1)求证：F是BD的中点；(2)求证：CG是⊙O的切线.【导学号：96990023】【证明】(1)∵CH⊥AB，DB⊥AB，∴△AEH∽△AFB，△ACE∽△ADF.∴EHBF＝AEAF＝CEFD.∵HE＝EC，∴BF＝FD.∴F是BD中点.(2)连接OC，BC，∵AB是直径，∴BC⊥AD于C.在Rt△BCD中，F为BD中点，∴CF＝BF＝DF.∴∠FCB＝∠FBC.又∵OC＝OB，∴∠OCB＝∠OBC.∴∠FCB＋∠OCB＝∠FBC＋∠OBC＝∠DBO＝90°.即∠OCG＝90°.∴CG是⊙O的切线.。

高中数学第一章直线‘多边形’圆课时作业5 北师大版

【课堂新坐标】2013-2014学年高中数学第一章直线‘多边形’圆课时作业5 北师大版选修4-1一、选择题1．AB 是⊙O 的切线，能确定CD ⊥AB 的条件是( ) A ．O ∈CD B ．CD 过切点 C ．O ∈CD ，且CD 过切点D ．CD 是⊙O 的直径【解析】由切线的性质定理知，选项C 正确．【答案】 C2．如图1－2－33所示，在△ABC 中，BC ＝14 cm ，AC ＝9 cm ，AB ＝13 cm ，内切圆分别和BC ，AC ，AB 切于D ，E ，F ，那么AF ，BD ，CE 分别为( )图1－2－33A ．AF ＝4 cm ，BD ＝9 cm ，CE ＝5 cmB ．AF ＝4 cm ，BD ＝5 cm ，CE ＝9 cmC ．AF ＝5 cm ，BD ＝4 cm ，CE ＝9 cm D ．AF ＝9 cm ，BD ＝4 cm ，CE ＝5 cm【解析】由题意知AE ＝AF ，CE ＝CD ，BD ＝BF ，且AC ＝9 cm ，BC ＝14 cm ，AB ＝13 cm ，则⎩⎪⎨⎪⎧AF ＋BD ＝13BD ＋CE ＝14CE ＋AF ＝9，解得AF ＝4，BD ＝9，CE ＝5.【答案】 A3．(2013·商丘模拟)如图1－2－34所示，⊙O 是正△ABC 的内切圆，切点分别为E 、F 、G ，点P 是弧EG 上的任意一点，则∠EPF 等于( )图1－2－34A ．120°B ．90°C ．60°D ．30°【解析】如图所示，连接OE 、OF . ∵OE ⊥AB ，OF ⊥BC ，∴∠BEO ＝∠BFO ＝90°. ∴∠EOF ＋∠ABC ＝180°. ∴∠EOF ＝120°. ∴∠EPF ＝12∠EOF ＝60°.【答案】 C4．如图，在⊙O 中，AB 为直径，AD 为弦，过B 点的切线与AD 的延长线交于C ，若AD ＝DC ，则sin ∠ACO 等于( )A.1010B.210C.55D.24【解析】连接BD ，作OE ⊥AC 于E . ∵BC 切⊙O 于B ， ∴AB ⊥BC ，∵AB 为直径，∴BD ⊥AC ， ∵AD ＝DC ，∴BA ＝BC ， ∠A ＝45°，设⊙O 的半径为R ，∴OC＝BC 2＋OB 2＝4R 2＋R 2＝5R .OE ＝22R ， ∴sin ∠ACO ＝OE OC＝22R 5R＝1010. 【答案】 A 二、填空题5．如图1－2－35，在半径分别为5 cm 和3 cm 的两个同心圆中，大圆的弦AB 与小圆相切于点C ，则弦AB 的长为________cm.图1－2－35【解析】连接OA 、OC ， ∵AB 是小圆的切线，∴OC ⊥AB ， ∴AC ＝12AB .∵在Rt △AOC 中，AC ＝52－32＝4(cm)，∴AB ＝8 cm. 【答案】 86．如图1－2－36所示，AC 切⊙O 于D ，AO 的延长线交⊙O 于B ，且AB ⊥BC ，若AD ∶AC ＝1∶2，则AO ∶OB ＝________.图1－2－36【解析】如图所示，连接OD ，则OD ⊥AC .∵AC 是⊙O 的切线，∴OB ＝OD ，OC ＝OC ，∠ODC ＝∠OBC ＝90°.∴△CDO ≌△CBO .∴BC ＝DC .∵AD AC ＝12，∴AD ＝DC . ∴BC ＝12AC .又OB ⊥BC ，∠ABC ＝90°，∴∠A ＝30°. ∴OB ＝OD ＝12AO .∴AO OB ＝21. 【答案】 2∶1 三、解答题7．如图1－2－37，AB 是⊙O 的直径，∠BAC ＝30°，M 是OA 上一点，过M 作AB 的垂线交AC 于点N ，交BC 的延长线于点E ，直线CF 交EN 于点F ，且∠ECF ＝∠E .求证：CF 是⊙O 的切线．图1－2－37【证明】连接OC ，∵AB 是⊙O 的直径． ∴∠ACB ＝90°， ∵∠BAC ＝30°， ∴∠ABC ＝60°，又∵OB ＝OC ，∴∠OCB ＝∠OBC ＝60°. 在Rt △EMB 中， ∵∠E ＋∠MBE ＝90°， ∴∠E ＝30°.∵∠E ＝∠ECF ，∴∠ECF ＝30°， ∴∠ECF ＋∠OCB ＝90°，又∵∠ECF ＋∠OCB ＋∠OCF ＝180°， ∴∠OCF ＝90°，∴CF 为⊙O 的切线．8．如图1－2－38，AB 是⊙O 的直径，点P 在BA 的延长线上，弦CD ⊥AB 于E ，∠POC ＝∠PCE .图1－2－38(1)求证：PC 是⊙O 的切线；(2)若OE ∶EA ＝1∶2，PA ＝6，求⊙O 半径．【解】 (1)证明：在△OCP 与△CEP 中， ∵∠POC ＝∠PCE ，∠OPC ＝∠CPE ， ∴∠OCP ＝∠CEP .∵CD ⊥AB ，∴∠CEP ＝90°，∴∠OCP ＝90°. 又C 点在圆上， ∴PC 是⊙O 的切线． (2)法一设OE ＝x ，则EA ＝2x ，OC ＝OA ＝3x .∵∠COE ＝∠AOC ，∠OEC ＝∠OCP ＝90°， ∴△OCE ∽△OPC ，∴OC OE ＝OP OC. 即(3x )2＝x (3x ＋6)，∴x ＝1， ∴OA ＝3x ＝3，即圆的半径为3. 法二由(1)知PC 是⊙O 的切线， ∴∠OCP ＝90°.又∵CD ⊥OP ，由射影定理知OC 2＝OE ·OP ，以下同法一． 9．在Rt △ABC 中，∠C ＝90°，AC ＝3 cm ，BC ＝4 cm.(1)求△ABC 内切圆的半径；(2)若移动圆心O 的位置，使⊙O 保持与△ABC 的边AC 和边BC 都相切，求r 的取值范围．【解】 (1)如图所示，⊙O 是Rt △ABC 的内切圆，切点分别为D ，E ，F . 连接OD ，OE ，OF ，OB ，则OD ⊥BC ，OE ⊥AC ，OF ⊥AB .在Rt △ABC 中，∠C ＝90°，AC ＝3 cm ，BC ＝4 cm ，∴AB ＝5 cm.∵OE ＝OD ，∠C ＝90°， ∴四边形CEOD 是正方形． ∴CD ＝DO .∵OB ＝OB ，OD ＝OF ， ∠ODB ＝∠OFB ＝90°， ∴△ODB ≌△OFB . ∴BD ＝BF . 同理可得，AE ＝AF .∴AC ＋BC －AB ＝AE ＋EC ＋BD ＋DC －AF －BF ＝EC ＋DC ＝2OD . ∴内切圆的半径r ＝OD ＝AC ＋BC －AB2＝3＋4－52＝1 cm.(2)如图所示，动⊙O 与AC ，BC 相切的最大的圆与AC ，BC 的切点分别是A ，D ，连接OA ，OD ，则四边形AODC 是正方形，此时应有OA ＝AC ＝3 cm ，∴动圆的半径r 的范围为(0,3]．10. 如图，BE是⊙O的直径，点A在EB的延长线上，弦PD⊥BE，垂足为C，连接OD，且∠AOD＝∠APC.求证：AP是⊙O的切线．【证明】连接OP.∵PD⊥BE，∴∠OCD＝90°.∴∠ODC＋∠COD＝90°.∵OD＝OP，∴∠ODC＝∠OPC.∵∠AOD＝∠APC，∴∠OPC＋∠APC＝90°.∴∠APO＝90°，即AP⊥PO.∴AP是⊙O的切线．。

北师版高中数学选择性必修第一册课后习题第1章直线与圆 1.4 两条直线的平行与垂直 (5)

011.4 两条直线的平行与垂直A级必备知识基础练A.直线l1恒过点(0,-3)B.存在m使得直线l2的倾斜角为90°C.若l1∥l2,则m=2或m=-2D.不存在实数m使得l1⊥l22.[探究点二]若点P(a,b)与Q(b-1,a+1)不重合且关于直线l对称,则l 的倾斜角为( )A.135°B.45°C.30°D.60°3.[探究点一]已知直线l1:ax+(a+2)y+2=0与l2:x+ay+1=0平行,则实数a 的值为( )A.-1或2B.0或2C.2D.-14.[探究点二]若直线mx+4y-2=0与直线2x-y+n=0垂直,垂足为(1,p),则实数n的值为( )A.-2B.-4C.10D.85.[探究点一]“m=-1”是“x+y-m+1=0平行”的( )A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件6.[探究点三](多选题)设平面内四点P(-4,2),Q(6,-4),R(12,6),S(2,12),下面四个结论正确的是( )A.PQ∥SRB.PQ⊥PSC.PS∥QSD.PR⊥QS7.[探究点一]已知直线l1的斜率是2,l2过点A(-1,-2),B(x,6),且l1∥l2,则lo g19x= .8.[探究点二]直线l与直线x+y-2=0垂直,且它在y轴上的截距为4,则直线l的方程为.B级关键能力提升练9.已知直线l的倾斜角为135°,直线l1经过点A(3,2),B(a,-1),且l1与l垂直,直线l2:y=-2bx+1与直线l1平行,则a+b等于( )A.-4B.-2C.0D.210.已知直线l1:xsin α+y-1=0,直线l2:x-3ycos α+1=0.若l1⊥l2,则sin 2α=()A.35B.-35C.23D.-2311.(多选题)若直线32y+18=0和2m的值可以为( )A.0B.1C.-1D.-49与B(7,0)的直线l1与过点(2,1),(3,k+1)的直线l2和两坐12.过点A0,73标轴围成的四边形内接于一个圆,则实数k等于( )A.-3B.3C.-6D.613.已知直线x+a2y+6=0和直线(a-2)x+3ay+2a=0没有公共点,则a的值是( )A.0或3B.-1或3C.0或-1或3D.0或-114.直线l1,l2的斜率k1,k2是关于k的方程2k2-3k-b=0的两根,若l1⊥l2,则b= ;若l1∥l2,则b= .15.设点P(2,5)关于直线x+y=1的对称点为Q,则点Q的坐标为,过点Q且与直线x+y-3=0垂直的直线方程为.16.已知△ABC的顶点分别为A(5,-1),B(1,1),C(2,m),若△ABC为直角三角形,求m的值.C级学科素养创新练=2},集合B={(x,y)|ax-y-2=0},当a取何值17.已知集合A={(x,y)|y-3x-2时,A∩B=⌀?参考答案1.4 两条直线的平行与垂直1.AB 对于A,直线l 1:mx-y-3=0,当=0时,直线l 2:=0时,l 1:y=-3,直线l 2:≠0,此时有m=4m ,解得m=2或m=-2,当m=-2时,l 1:2x+y+3=0,l 2:2=0时,l 1:y=-3,l 2:x=-32,此时l 1⊥l 2,D 错误.2.B ∵k PQ =a+1-b b -1-a=-1,k PQ ·k l =-1,∴l 的斜率为1,倾斜角为45°.3.D 由l 1∥l 2知,a×a=1×(a+2),即a 2-a-2=0,∴a=2或a=-1.当a=2时,l 1与l 2重合,不符合题意,舍去;当a=-1时,l 1∥l 2,∴a=-1.4.A 由已知得{2m -4=0,m +4p -2=0,2-p +n =0,解得n=-2.5.A 根据直线平行的充要条件得{m 2=1,2-2m ≠m (-m +1),即{m =±1,m ≠2且m ≠1,解得m=-1.故是充要条件.故选A. 6.ABD 由斜率公式知,k PQ =-4-26+4=-35,k SR =12-62-12=-35,k PS =12-22+4=53,k QS =12+42-6=-4,k PR =6-212+4=14,∴PQ ∥SR,PQ ⊥PS,PR ⊥QS.而k PS ≠k QS ,∴PS 与QS 不平行,故ABD 正确. 7.-12 因为l 1∥l 2,所以6+2x+1=2,解得x=3.所以lo g 193=-12.8.x-y+4=0 由题意知直线l 的斜率是1,又它在y 轴上的截距为4,∴直线l 的方程是y=x+4,即x-y+4=0. 9.B 10.A11.ACD 由题意,若直线32y+18=0垂直,可得3×2+2×(-3m 2)=0,解得m=±1.经验证,当m=1时,有两条直线平行,构不成三角形;当m=-1时符合题意.同理,若直线3-6=0,解得m=1,应舍去;若直线2+9m 2=0,解得m=0或m=-49,经验证均符合题意.故m 的值为0,-1,-49.12.B 13.D14.2 -98若l 1⊥l 2,则k 1k 2=-b2=-1,∴b=2.若l 1∥l 2,则k 1=k 2,Δ=9+8b=0,∴b=-98.15.(-4,-1) x-y+3=0 设点Q(a,b),则{b -5a -2·(-1)=-1,a+22+b+52=1,解得a=-4,b=-1. 即点Q 的坐标为(-4,-1),设与直线x+y-3=0垂直的直线方程为x-y+c=0,将Q(-4,-1)代入该式,得c=3,所以直线方程为x-y+3=0. 16.解若A 为直角,则AC ⊥AB,所以k AC ·k AB =-1,即m+12-5·1+11-5=-1,解得m=-7;若B 为直角,则AB ⊥BC,所以k AB ·k BC =-1,即1+11-5·m -12-1=-1,解得m=3;若C 为直角,则AC⊥BC,所以k AC·k BC=-1,即m+12-5·m-12-1=-1,解得m=±2.综上,m的值为-7或-2或2或3.17.解由y-3x-2=2,得2x-y-1=0(x≠2),故A={(x,y)|2x-y-1=0,x≠2},故集合A表示的是直线2x-y-1=0上除点(2,3)外的点构成的集合.当直线ax-y-2=0与直线2x-y-1=0平行时,满足A∩B=⌀,此时a=2;当直线ax-y-2=0过点(2,3)时,满足A∩B=⌀,则2a-5=0,解得a=52.综上所述,a=2或a=52.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.2.2 圆的切线的判定和性质
课后作业提升
1下列说法:①与圆有公共点的直线是圆的切线;②垂直于圆的半径的直线是圆的切线;③与圆心的距离等于半径的直线是圆的切线;④过直径的端点,且垂直于此直径的直线是圆的切线.其中正确的是( ).
A.①②
B.②③
C.③④
D.①④
解析:与圆有公共点的直线,可能是切线,也可能是割线,则①不正确;②不符合切线判定定理的条件,缺少“过半径外端”这一条件,则②不正确;很明显③④正确.
答案:C
2如图,A,B是☉O上的两点,AC为☉O的切线,∠OBA=75°,☉O的半径为1,则OC=( ).
A. B.
C. D.
解析:∵OA=OB,∴∠OAB=∠OBA=75°.
∴∠AOB=180°-2∠OBA=30°.
∵AC为☉O的切线,
∴OA⊥AC.
又∵OA=1,
∴在Rt△OAC中,OC=.
答案:C
3如图,PB与☉O相切于点B,OP交☉O于点A,BC⊥OP于点C,OA=3,OP=4,则AC=( ).
A. B.
C. D.不确定
解析:如图,连接OB,则OB⊥PB,OB=OA=3,
又BC⊥OP,∴在Rt△OBP中,
有OB2=OC·OP.
∴OC=.
∴AC=OA-OC=3-.
答案:A
4如图所示,AC与☉O相切于点D,AO的延长线交☉O于点B,且BC与☉O相切于点B,若
AD=DC,则=( ).
A.2
B.1
C.
D.
解析:如图所示,连接OD,OC,
∵AC,BC是☉O的切线,
∴OD⊥AC,OB⊥BC.
又AD=DC,∴△OAC是等腰三角形.∴OA=OC.∴∠A=∠OCD.
又OC=OC,OD=OB,
∴△ODC≌△OBC.
∴∠OCD=∠OCB.
∴∠BCA=2∠A.
则∠A+∠BCA=3∠A=90°.
解得∠A=30°.
∴=2.
答案:A
5如图所示,已知AB为半圆O的直径,直线MN切半圆于点C,AD⊥MN于点D,BE⊥MN于点E,BE交半圆于点F,AD=3cm,BE=7cm,则☉O的半径为cm.
解析:如图,连接OC.∵MN切半圆于点C,∴OC⊥MN.
∵AD⊥MN,BE⊥MN,
∴AD∥OC∥BE.
∵OA=OB,∴CD=CE.
∴OC=(AD+BE)=×(3+7)=5(cm).
∴☉O的半径为5cm.
答案:5
6如图,☉O的直径AB=8,C为圆周上一点,BC=4,过点C作☉O的切线l,过点A作直线l的垂线AD,D为垂足,AD与☉O交于点E,则线段AE的长为.
解析:如图所示,连接OC,连接BE交OC于点F,则OC⊥l,BE⊥AD.
又AD⊥l,
所以AD∥OC,OC⊥BE.
又直径AB=8,则OB=OC=4.
又BC=4,则△OBC是等边三角形.
所以F是OC的中点.
所以AE=2OF=OC=4.
答案:4
7如图所示,AB是☉O的直径,D是AB延长线上的一点,PD是☉O的切线,P是切点,∠D=30°.
求证:PA=PD.
分析:欲证PA=PD,只要证明∠PAB=∠D=30°即可.
证明:如图,连接OP,
∵PD是☉O的切线,P为切点,
∴PO⊥PD.
∵∠D=30°,
∴∠POD=60°.
又∵OA=OP,
∴∠PAB=∠APO.
∴∠PAB=30°.
可得∠PAB=∠D.
∴PA=PD.
8如图,已知两个同心圆O,大圆的直径AB交小圆于C,D两点,大圆的弦EF切小圆于点C,ED 交小圆于点G,若小圆的半径为2,EF=4,试求EG的长.
解:如图,连接GC.
∵CD为小圆的直径,∴GC⊥ED.
∵EF切小圆于点C,∴EF⊥OC.
在大圆中,EC=EF=×4=2.
在Rt△DEC中,ED=
==2.
∵EF⊥DC,GC⊥ED,
∴由直角三角形的射影定理可知,EC2=EG·ED.
∴EG=.
备课资源参考
备选习题
1.在Rt△ABC中,AC⊥CB,AB=12,AC=6,以C为圆心,作与AB相切的圆C,则☉C的半径
r=.
解析:如图,设切点为D,连接CD,则CD⊥AB,CD=r.
∵AC⊥CB,∴CD2=AD·BD.
又AB=12,AC=6,AC2=AD·AB,
∴AD==3.
∴BD=AB-AD=12-3=9.
∴CD2=3×9=27.解得CD=3.
答案:3
2.如图,AB是☉O的直径,AC是弦,∠BAC的平分线AD交☉O于点D,DE⊥AC,且DE交AC的延长线于点E,OE交AD于点F.若,求的值.
分析:由于之间的联系不密切,所以考虑用中间量代换,作辅助线OD,则AE∥OD,转化为求的值.
解:如图所示,连接OD,则OA=OD,
∴∠ODA=∠OAD.
又AD平分∠BAC,
∴∠OAD=∠DAC.
∴∠ODA=∠DAC.
∴OD∥AE.
∴△AEF∽△DOF.∴.
连接BC,过点D作DH⊥AB于点H,连接BD.则有∠DOH=2∠BAD=∠CAB.
∵AB是☉O的直径,
∴AC⊥BC.
∴在Rt△ABC中,cos∠CAB=.∴cos∠DOH=.
设DO=5x,则OH=3x,DH=4x,AB=10x,
∴AH=AO+OH=OD+OH=8x,AD=4x.
又△AED∽△ADB,∴AD2=AE·AB.
∴AE==8x.
∴,于是.。