灰色预测方法在公路路基中应用
灰色预测模型在交通运输规划中的应用研究

灰色预测模型在交通运输规划中的应用研究交通运输规划是城市发展和管理中重要的一部分,它涉及到道路、铁路、航空、水运等各个交通领域的规划和设计。
而在交通运输规划中,灰色预测模型是一种被广泛应用的预测方法,可以帮助决策者在面对不确定性的情况下做出合理的规划和决策。
灰色预测模型是由我国学者陈纳德教授于1988年提出的,它是一种基于数据序列的预测方法。
相比于传统的统计模型,灰色预测模型可以更好地处理少样本、非线性、不确定性等问题,具有较强的适应性和预测精度。
在交通运输规划中,灰色预测模型可以应用于多个方面。
首先,灰色预测模型在交通需求预测中发挥着重要作用。
交通需求预测是交通规划的基础工作之一,它需要根据历史数据和相关因素进行未来交通需求的预测。
灰色预测模型可以根据已有的数据序列,通过建立灰色预测模型来预测未来的交通需求。
例如,可以根据历史交通流量数据,结合经济发展水平、人口增长率等因素,利用灰色预测模型来预测未来几年的交通需求,进而为交通规划提供依据。
其次,灰色预测模型在交通流量预测中也有广泛应用。
交通流量预测是指根据历史交通流量数据和相关影响因素,预测未来某一时段或某一路段的交通流量情况。
利用灰色预测模型可以较准确地预测未来的交通流量,有助于交通规划者制定合理的交通管理措施。
例如,可以通过对过去的交通流量数据进行分析和建模,利用灰色预测模型来预测未来某一时段的交通流量,以便为合理安排道路容量和交通信号灯时间提供依据。
此外,灰色预测模型还可以应用于交通事故预测。
交通事故是交通运输规划中需要关注的重要问题之一,通过预测交通事故的发生情况可以采取相应的交通管理措施来减少交通事故的发生。
利用灰色预测模型可以分析历史事故数据和相关因素,预测未来某一地区或某一路段的交通事故发生概率,从而为交通规划者提供减少事故发生的建议和决策参考。
此外,灰色预测模型还可以应用于公共交通出行需求的预测和优化。
公共交通出行需求的预测和优化是城市交通规划中的重要内容,通过合理预测公共交通出行需求,可以调整公交线路、增加公交车辆,提高公共交通的服务水平,促进城市交通的绿色发展。
改进的灰色模型在软土路基沉降预测中的应用

Ab s t r a c t : I t i s i mp o r t a n t t o d e t e r mi n e t h e t i me f o r p a v i n g t h e p a v e me n t , c o n t r o l l i n g a n d a r r a n g i n g c o n s t r u c t i o n
学发 展 的产物 , 该 方法 可 以全面 考虑 土体 的侧 向变 形 、 流变 以及 复杂 的边 界条 件等 . 就一 般工 程 而言 , 由于
该方 法所 需 的计算 参数 多且 不易 确 定 , 所 以很 难 应 用 到 实 际工 程 中 _ 1 . 实 际工 程 中往 往 根 据 现 场 实 测 的
改 进 的 灰 色 模 型 在 软 土 路 基 沉 降 预 测 中 的 应 用
丁 斌 , 高正 夏
( 河海大学地球科学 与工程学院 , 江苏 南京 2 1 0 0 9 8 )
摘要: 路基 的最终沉降变形对于确定铺筑路 面时间 、 控制 和安排施 工进 度以及路堤的安全与正常使用 至关重要 .
p r o g r e s s a s w e l l a s s a f e t y a n d n o r m a l a p p l i c a t i o n o f s u b g r a d e . G I M( 1 ) , a s a m o d i f i e d G M( 1 , 1 )m o d e l , p r e d i c t s t h e s e t t l e me n t v o l u m e o f s u b g r a d e d y n a mi c a l l y a n d s u c c e s s i v e l y a d o p t i n g e q u a l — d i me n s i o n a l G I M( 1 )m o d e 1 . T h e
略谈公路路基沉降灰色预测方法

略谈公路路基沉降灰色预测方法摘要:在公路施工过程中,路基施工质量的好坏是确保公路施工质量的关键,为确保路基施工质量,必须掌握路基沉降的变化情况,特别是要能够较为合理地预估路基沉降的变化情况。
文中利用灰色系统理论建立GM(1,1)灰色预估模型及其残差模型,并应用于某公路路基沉降变形预测中,预测结果和实测结果能较好地吻合,验证了预估模型的精度和预测方法的可行性。
关键词:公路路基;沉降预测;灰色系统;预测方法1引言灰色系统理论是对一些信息较少、数据变异较大的工程问题进行研究的一种新方法,自该理论提出以来,灰色理论在路基沉降监测、预测中应用越来越多。
路基沉降的预测与控制是软土地区公路建设的一个关键问题,也是亟待解决的技术难题。
目前,预测路基沉降总体上主要有两种方法:一是基于地基土体本构模型的有限元等方法;二是通过对实测沉降数据的拟合反演进行路基沉降预测的曲线拟合、灰色模型、Asaoka法等数据方法。
由于土力学理论的不完善和工程地质条件的复杂性,第一种方法的沉降计算结果与实际有较大的差异;而由于实测数据的积累,加上计算方法的日渐成熟,利用第二种方法能够方便地进行路基沉降预测。
2 公路路基全过程沉降的机理分析图1 全过程沉降量与时间关系图公路路基沉降的全过程,可分为瞬时沉降、固结沉降和次固结沉降三部分。
瞬时沉降是在荷载施加后,沉降在短时间内立即发生的,可认为与时间无关,因此全过程的沉降量S与时间t的关系曲线并不通过原点O,如图1所示。
固结沉降和次固结沉降随着荷载和时间变化而变化,如图1所示,一般可分为4段:①直线段ab(弹性阶段):在刚加载时,土体处于弹性或近似弹性状态;②速率增大的曲线段bc;随着荷载的不断加大,土体进入弹塑性状态,土体的沉降速率也在不断增加,直至荷载不再增加;③速率减小的曲线段cd:当荷载不再增加时,由于固结尚未完成以及土体的流变,土体的沉降随着时间的推移而不断增加,但沉降速率递减;④新的直线段de(稳定阶段):当时间为无限大时,沉降到达极限状态,此时沉降将不随时间发生变化。
灰色预测在高铁路基沉降预测中的应用

灰色预测在高铁路基沉降预测中的应用秦晓光;场龙才【摘要】Based on the high-speed railway,by collecting the embankment settlement experimental data, it is divided into three categories accordingto the differences of settlement curve form and settlement rate. Grey theory GM(1,1) model, the hyperbolic method and three-point method are used to predict the settlement and inspect precision of grey theory forecasting model. Adopting data of preloading period as original data, by comparing the measured data with predicting results of grey theory, the paper shows that results of grey theory are more close to measured values. GM( 1,1) model prediction can get more satisfactory results.%以在建某高速铁路为背景,通过对路基沉降实测数据的汇总,根据沉降曲线形态及沉降速率的差异将其分为3类.对观测数据进行等时距变换,采用灰色理论GM(1,1)模型、双曲线法、三点法对工后沉降进行预测,并对灰色理论预测模型进行精度检验.选取堆载预压期的数据作为模型原始数据,通过与实测最后一期数据的对比,发现灰色理论预测结果更接近实测值,通过最终沉降之间的对比,发现双曲线法预测结果偏大,三点法预测结果偏小,GM(1,1)模型预测能得到较为满意的结果.【期刊名称】《华东交通大学学报》【年(卷),期】2011(028)005【总页数】5页(P88-92)【关键词】高速铁路;沉降预测;灰色理论;双曲线法;三点法【作者】秦晓光;场龙才【作者单位】同济大学道路与交通工程教育部重点实验室,上海201804;同济大学道路与交通工程教育部重点实验室,上海201804【正文语种】中文【中图分类】U238高速铁路对轨道平顺性的要求很高,而轨道的平顺性直接受到地基工后沉降的影响,因此高速铁路对工后沉降要求非常严格,高速铁路设计规范规定路基“工后沉降不宜超过15 mm”[1]。
软土路基沉降灰色预测模型的几个关键问题研究
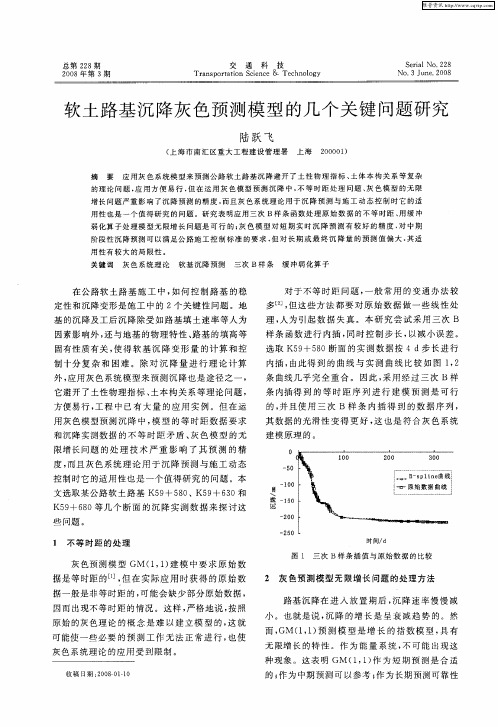
基 的沉降及工 后沉 降除受 如路 基填 土速率 等人 为
因素影响外 , 还与地 基 的物理特 性 、 基 的填高 等 路
理 , 为引起 数 据 失 真 。本 研 究 尝试 采 用 三次 B 人
样 条 函数 进 行 内插 , 同时 控制 步 长 , 以减小 误 差 。
维普资讯
20 年 第 3 08 期
陆 跃 飞 :软 土 路 基 沉 降 灰 色 预 测 模 型 的几 个 关 键 问 题 研 究
3 9
明显 削弱 。
软 基 沉 降 曲线 基 本 上 是 由速 率 不 同 的 两 段 曲
固有性 质有关 , 得 软基 沉 降变 形 量 的计 算 和 控 使
制 十分复 杂 和 困难 。除对 沉 降 量 进 行 理 论 计算 外, 应用 灰色 系统模 型来 预测 沉降也 是途 径之 一 ,
它避 开了土性 物理 指标 、 土本构 关 系等理论 问题 ,
选 取 K5 +5 0断面 的实 测数 据按 4d步 长进 行 9 8 内插 , 由此得 到 的 曲线 与 实 测 曲线 比较 如 图 1 2 ,
的理 论 问题 , 用方 便 易 行 , 在 运 用 灰 色模 型 预 测 沉 降 中 , 等 时距 处 理 问 题 、 色 模 型 的无 限 应 但 不 灰 增 长 问 题 严 重 影 响 了 沉 降 预 测 的 精 度 , 且 灰 色 系 统理 论 用 于 沉 降 预 测 与 施 工 动 态 控 制 时 它 的适 而 用 性 也 是 一 个 值 得 研 究 的 问 题 。研 究 表 明 应用 三 次 B样 条 函 数处 理原 始 数 据 的 不 等 时 距 、 缓 冲 用 弱 化 算 子 处 理 模 型 无 限 增 长 问 题 是 可 行 的 ; 色 模 型 对 短 期 实 时 沉 降 预 测 有 较 好 的 精 度 , 中 期 灰 对 阶段 性 沉 降 预 测 可 以满 足 公 路 施 工 控 制 标 准 的 要 求 , 对 长 期 或 最 终 沉 降 量 的 预 测 值 偏 大 . 适 但 其
灰色马尔可夫预测模型在公路交通事故中的应用

摘
要: 将结合灰 色 系统理 论与马 尔可夫理论 , 对公 路 交通事故 进行预 测. 利用灰 色马 尔可夫预 测模 型 , 可有 效地
处理 类似 交通事故等随机性 、 波动较大的数据 。
关键 词: 色模 型; 灰 预测 ; 马尔可夫 ; 公路 交通 事故
第2 2卷
第 2期
长
春
大
学
学
报
Vo . 2 No 2 12 . Fe b.201 2
21 0 2年 2月
J URNAL OF C 0 HANGC HUN U VER I NI S TY
灰 色 马 尔 可 夫 预 测 模 型 在 公 路 交 通 事 故 中 的应 用
沈 晋 会
由表 1可 知 ,98— 07年全 国公 路交 通 事故 的平 均值 为 595 , 19 20 25 2 由于数 据 较为 接 近 , 这里 只 划 分 为 2
根据 以上 划分 , 算得状 态 转移 概率 矩 阵为 可
P=
据 此便 可 预测 2 0 0 8年 的交通 事故 发生 量最 有 可能处 于状 态⑧ 而 最有 可能 的预 测值 为 ,
=
( ) B Y. B B
其 中
一
( ( )+ 。( ) ㈩ 1 ( 2 )
一
B :
丢 2 j) ( ) () ( 0 3
1( 1( ( ’
一
一
1 ( ( ) )+ 。 ) ’
收 稿 日期 :0 11 -3 2 1—22
作者简介 : 沈晋会( 9 7 )男 , 17 一 , 山西晋城人 , 讲师 , 硕士 , 主要从事应 用数学和数学教育方面研究 。
灰色模型(GM)在软土路基沉降量预测中的应用研究

察
科
学
技
术
l7
这种情况。 2.1 模型的选择 在 GM 建模中, 一般要求 !I = I i - I i - l = 即要求原始数据是等时空距的, 而 COISI. = l, 工程中实际观测的数据很难满足这一要求。 考虑到软土路基在恒载后其沉降量只是时间 的函数, 于是选用连续型直接数据 GM (l, l) [2] 模型 。 2.2 数据初处理 由于最后加载后还要经过一段时间的固 结, 所以以停载后一个月作为起始时间, 即 I 又考虑到沉降数据是以累计值记录的, = 0, 所以以观测数据值减去 I = 0 时刻的观测值, [l] 后得到的 数据序列为计算序列, 即 Xi = Xi 记为: - X0 ,
(
大桥和番中公路跨线桥两桥头之间, 地处广 东省番禺市灵山镇庙南村。全长 353.43m。 根据该路段的工程地质特征、 工程要求, 设计 了不同的地基处理方案, 在不同的断面埋设 了应力应变测试仪器和沉降板, 观测了各断
( ) ( ) )T x 0( In )- x 0( I ( n -l) …, In - I ( n -l)
(0) 把上式改写成: x ( I) = ce- a I + 6
!
!
同 样,按 最 小 二 乘 法,有 ( c , 6) T -l T ( D D) D Y
! !
T
=
l e - a I2 l 其中 D = ! e- a In l (0) ( ) ( ) )T , , …, x 0( I 2 ) x 0( In ) Y = ( x ( Il )
(0)
!
!
!
其中 B = l [ (0( ) ( ) ] x I l )+ x 0( I 2 ) 2 l l 3
基于灰色模型的高速公路路基沉降预测

沉降与 荷载 信息 , 可 以将 路 基 沉 降过 程 看成 一 个灰 色系统 , 在 不需 要知 道 其 内部 沉 降变 化 规律 的情况 下, 由现场 实测 的少 量原 始数据 作 为 已知信 息 , 建立
相对 的灰 色预估 模 型 , 从 而 预 测 将来 某 一 时 刻路 基 的沉 降量 大小 。
出 以来 , 灰 色理 论在 路基 沉降监 测 、 预 测 中应 用 越来
越 多 。 因此 , 该 文采 用灰 色模 型进行 路基 沉 降预 测 ,
为 灰色 理论 在工 程实 践 中的应用 提 供参 考 。
l 路 基 沉 降 的灰 色 性
中国对 于灰 色理论 的研 究起 步较 晚 。1 9 8 2年 , 邓 聚龙 教授 提 出灰 色 理论 , 该 理论 以其 所 需 信 息 量 少、 忽 略 中间 过 程 、 准 确 预 测 未 来 结 果 等 独 特 的 特 点, 目前 在工 程界 中被 广泛 运用 。 岩 土 工程 土 体 是一 个 具 有 着时 空 变 异 性 、 不 均
预测 中, 预 测 结 果 和 实测 结 果 能 较 好 地 吻 合 , 验证 了预 估 模 型 的 精 度 和 预 测 方 法 的 可行 性 。 关键词 : 公 路 ;路 基 ;沉 降 变形 ;灰 色模 型预 测
公
中 图分 类 号 : U4 1 6 . 1
文 献 标 志码 : A
程 问题 。路基 沉 降变形 是 随着上 覆荷 载 的变 化而 变
化 的一个 动态 过程 , 存 在 着 很 多 的 不 确 定 性 和 随机
( 1 )
式中: i 一1 , 2 , …, 。
( 2 )计算 等 间隔 的路基 沉 降序 列 。各 时段 的单
优化的非等时距灰色模型在湖南高速公路路基沉降预测中的应用

Ap p l i c a t i o n o f Op t i mi z a t i o n Une q u a l Ti me - I n t e r v a l Gr a y mo d e l i n Fo r e c a s t o f S ub s i d e n c e o f Em b a n k me n t S e t t l e me n t o f Ex pr e s s wa y
第3 8 卷, 第 4期
2 0 Hi g h wa y En g i n e e r i n g
Vo 1 . 3 8,No . 4 Au g. , 20 1 3
优 化 的 非 等 时距灰 色 模 型在 湖 南 高 速公 路路 基 沉 降预 测 中 的应 用
l 概 述
近年 来 , 湖南 省 高速公 路发 展 迅猛 , 修建 里 程不
断刷 新 , 为交 通 的提 速 和 便 捷 起 到 了非 常重 要 的促
着不 断的研 究 和发 展 , 各 种 多 维 和非 等 时距 等 方 面 也 有 了很好 的改 善和 补充 。 。但 一般 的非 等 时距 针对 高填 土路基 沉 降 的 预 测模 型来 说 , 仍 存 在 两个 方 面 的不足 : 一个 是模 型 的精 度有 待提高 , 一个 是一 般 模 型对填 土沉 降终值 趋 于 收敛 的变化趋 势未 做考 虑 。 因此 , 对 高填 土 路 基 沉 降 发展 趋 势 的预 测 可 以 基 于灰 色理论 进 行 分 析 , 但 需 要 对 等时 距 模 型 和非 等时距 原始 数据 进 行 协 调 , 并 有 必要 在 传 统模 型上 对 路基 沉 降本 身 发 展 等 特 点 进 行 适 当的 调 整 和 优
灰色理论模型在公路交通量预测中的应用

1 灰 色 系统 理 论 与 建 模 思 想
1 .1 灰 色 理 论 预 测 思 想
区 域 或 路 段 交 通 量 的 增 长 绝 不 是 像 汽 车 数 量 的 简单 迭加那样容 易的 , 是要考虑 到其他很 多因素 , 而 如 地 理 位 置 、 然 资 源 、 会 经 济 、 口及 其 他 运 输 自 社 人 方 式 的发 展 情 况 等 综 合 因 素 。 以 , 想 对 某 省 或 地 所 要 区 的 交 通 量 进 行 预 测 , 得 对 影 响 交 通 量 增 长 的 相 就 关 因 素 进 行 调 查 , 探 究 影 响 交 通 量 的 各 种 因 素 的 并 变 化 情 况 后 , 出交 通 量 与 这 些 因 素 的定 量 关 系 式 , 找 来 研究交 通 量 的变化 情况 , 是 这种 方法 在在具 体 但 操 作 时 , 有 很 多 困难 , 经 济 、 口 、 地 利 用 等 各 却 如 人 土 因 素 复 杂 多 变 , 难 把 握 ; 通 量 与 这 些 因 素 的 定 量 很 交
第 2 期 总第 2 5期 3 2
g1 0 0年 I 2月
内 蒙 古 科 技 与 经 济
In rM o g l ce c c n lg n e n o i S in eTe h oo y& Ec n my a oo
N o. 23,t 25 h is e he 2 t s u
进 行 拟 建 项 目交 通 量 预 测 是 更 为 简 便 的 方 法 。 路 段 上 的 交 通 量 是 由 上 述 各 种 因 素 综 合 影 响 后 而 形 成 的 , 段 交通 量随 时 间的变 化 , 身就 反 映 了函数 f 路 本
灰色模型在路堤沉降预测中的应用

广东建材 20 年第 1 07 期
研究与探讨
灰色模型在路堤沉 降预测 中的应用
李 煦 ( 华铁工程咨询公司) 胡德华 ( 中铁三局 四公司)
摘 要 :本文以Lgag 插值法和等维新息模型为基础, arne 建立了路堤沉降预测的非等时距等维新
G (, ) M 1 1 模型进 行预 测 , 所得 结果 与 实测 结果 吻合 较好 。
当 i 2, , , 一 = 3 … n 1时 , L g a g 由 a r n e插 值 法 有 脚
x
(1 t) i+ _
二 ( 1 t )6 () 0 ( i △ - )
从而得 到 了等 时距 时间序 列
到原始数据列中, 同时去掉一个老信息, 以此来对数据 G 1 1模 型 的预 测精 度 通 常用 后 验 差法 检 验 , M(,) 具 列作 等 维 处 理 , 后 再 建 立 G 11模 型 ( 然 M(,) 即等 维 新 息
() 1 5
Y [0) 3…x (] N x(x(, n =( , ) ) 2 )
一
1 5 — 1
维普资讯
研究与探讨
广东建材 20 年第 1 07 期
一 M 11 为了能与原始数据进行比较, 将非等时距时间序列 到 越来 越 多 的新 数据 , 方面 如 果 仍沿 用 已得 G (,) 模 型进 行预 测 , 则模型 就不 能反 映外 界 因素 对沉 降观 测 中的时间 t代入模型中, 即 的影 响 , 型 的精 度 必然 会 受 到 影 响 , 模 这就 需 要在 把 新 曼 “㈦
t ( 一 )()o ( ix e'AU 1 : -tt a' _ t/m - _ 6 )
』 () 1
基于多灰色预测模型对比的高速公路路基沉降量预测

全 也 有 重要 影 响 . 根 据 路 基 沉 降 量 的实 测 资 料 , 通 过 多 种 灰 色 预 测 模 型 对 路 基 沉 降 量 进 行 了数 据 规 律 分 析 及 精 度对 比, 选 取 了最 优 的灰 色 预 测 模 型 对 路 基 最 终 沉 降 量 进 行 预 测 . 为 路 基 稳 定 性 的 评 价 与路 基 沉 降 的控 制 应 对 提 供 了 参考 . 关键词 : 公路 ; 路基 ; 沉降 ; 灰色模 型; 预 测
都 加 以考虑 , 考虑 更加 全 面完整 . 而且 其 预测 模 型 的 数据 特 征 很 符合 “ S ” 形, 很 适 用 于路 基 工 程 沉 降 量 的预测 . 近些 年 已经有相 关专 家学 者尝 试用 灰色 预测 理论来 进 行路基 沉 降类 似工程 的预 测工 作 , 取 得 了
中 图分 类 号 : U4 1 6 . 1 l 1 文献标志码 : A 文章编 号: 1 0 0 6 — 7 9 3 0 ( 2 0 1 3 ) 0 2 — 0 2 3 3 — 0 6
由于高 速公路 路基 沉 降与施 工质 量 、 服 务水 平与 建成 后 的行 车安全 关 系密切 , 因此 高速 公路施 工 对
收稿 日期 : 2 0 1 2 - l O 一 2 4
修 改 稿 日期 : 2 o 1 3 0 3 — 2 2
基金项目 : “ 十 一五 ” 国家 科 技 支 撑 计 划 课 题 资 助 ( 2 0 0 6 B AB 0 2 A0 2 ) ; 国 家 自然 科 学 基 金 资 助项 目( 5 0 4 9 0 2 7 4 ) 作者简介 : 于 澍( 1 9 6 5) , 男, 山东莱州人 , 副教授 , 主要 研 究 方 向为 土 及 其 构 筑 物 安 全 及经 济评 价 .
灰色预测模型在公路货运量预测中应用论文

灰色预测模型在公路货运量预测中的应用摘要:为了提高公路运输行业的管理水平,为设计、修建货运场站或现代物流中心提供数据依据和决策支持,就必须要准确的预测公路货运量。
在运输业今年运量统计的基础上,利用灰色预测理论的gm(1,1)模型,给出了gm(1,1)模型的详细步骤,并以公路货运量历年数据预测为例进行了实际应用。
可有效处理小样本、贫信息的不确定性,并在一定预测时段内有良好的预测精度和实用性。
关键词:公路货运量 gm(1,1)模型预测1.现有的预测方法当前普遍存在的对于社会经济的预测方法主要有时间序列法、回归分析法、灰色预测法、指数平滑法、神经网络预测法以及将不同的预测方法结合起来,按照提供信息量的多少和精度的不同,分别取不同的权重形成的组合预测模型。
货运量作为交通运输的一个重要评价指标,对于货运量的预测可以采取不同的方法进行预测,不同的方法提供的有价值信息各不相同,预测精度也各异。
本文主要采用灰色预测模型对公路货运量进行预测。
2.灰色理论与灰色预测模型由于环境对系统的干扰,系统信息中原始数据序列往往呈现离乱情况,离乱数列即为灰色数列或称灰色过程,灰色理论利用那些较少的或不确切的表示系统行为特征的原始数据序列作生成变换后建立微分方程,建立的模型称为灰色模型(greymodel),简称gm模型。
gm(1,1)表示一阶单个变量微分方程,是最常用的灰色预测模型,其形式为:式中,x=x(t),u和b为待估参数。
这个微分方程的解是:3.灰色预测模型的应用3.1灰色模型建模机理灰色系统建模是利用离散的时间序列数据建立近似连续的微分方程模型。
在这一过程中,累加生成运算(ago)是基本手段,其生成函数是灰色建模、预测的基础。
来自所收集的描述过去、现在状况的数据,是构造系统数学模型的依据。
在贫信息情况下,用概率统计方法寻求其统计规律,或用模糊统计方法寻求其隶属规律是困难的,但对于离散过程,在一定程度上相对强化确定性(规律性)和弱化不确定性是可能的,其途径就是通过累加生成运算得到生成时间序列x。
灰色理论在路面使用性能预测中的应用

关键 词 :灰 色 系统 ;数 列 预 测 ;路 面使 用 性 能
中 图 分 类 号 :U 1. 4 62
文 献 标 识 码 :A
A pi t n o a y t m n F rc s fP v me tP r r a c p l a i fGry S se i o e a t a e n e om n e c o o f
维普资讯
公
路
交
通
科
技
20 02年 6月
JU NLO I W YA DTA S RAIN EER HA DD V O R A HG A NP TT SA C F H N R O OR N E
文 章 编 号 : 10 —28 (0 2 30 1—4 020 6 20 )0—0 60
g e . sn h o c t d e hsp p r o e a t t et re p r r n e id x s o n x rs w yi i g u P o ic . h o g o a — r e U ig t efr a e s mo l i a e rc s h e f ma c n e e o e e p s a nJa s r vn e T ru h c mp r t f s h e o f e n
型 .并 采 用 绝 对 关联 度 分 析 模 型 的预 测 精 度 。 最后 根 据 预 测 模 型 对 江 苏 某 高速 公 路 使 用性 能 的 3项 检 测 指 标 进 行 了预
测 ,并根 据预测 结果与路 面实际检 测数据的对 比 ,分析模型预测 结果的合理性 以及 3项基本指 标的发展 情 况 ,并 分析
灰色GM(1,1)模型的应用研究

灰色GM(1,1)模型的应用研究0 前言:目前常用的沉降预测方法较多,但研究表明,每种预测方法均有一定的适用范围,如双曲线法对于典型断面的理想数据预测效果较好,而对于量级小,波动大的观测数据的适用性较差;三点法(固结度对数配合法)预测误差较小,对数据段选取的依赖性小,对异常数据的敏感性强,但对沉降曲线收敛后波动太敏感,适用性差;Asoaka法预测误差一般较小,但其在预测过程钱对原始数据的平滑处理过程影响了预测误差的稳定性;指数曲线法对沉降变形数据的单调性有严格的要求,局部数据的小幅起伏变化都可能导致无法进行预测计算。
而现在高层、超高层建筑物,尤其高速铁路对于沉降控制很高,沉降量级一般较小,沉降数据波动大,如武广高铁桥涵和隧道沉降变形小于5mm,同时观测数据出现跳跃或连续几个观测数据变化趋势与常规相反的情况较多[[1] 陈善雄.高速铁路沉降变形观测评估理论与实践[M].中国铁道出版社,2010,3.]。
针对这些情况,目前高速铁路对桥涵和隧道进行沉降预测及评估时,目前通用的办法就是根据相应的地质条件、地基或桩基处理方式及目前发生沉降量直接判定是否满足沉降评估的要求,但判定条件很难把握,至今仍无法统一,故一种专门针对变形量级小,数据波动相对大的沉降预测方法具有十分重要的现实意义。
1 灰色GM(1,1)模型灰色系统是一种综合运用数学方法对信息不完全的系统进行预测、预报的理论和方法。
灰色预测的思路是:把随时间变化的随机正的数据列。
通过适当的方式累加,使之变成非负递增的数据列,用适当的方式逼近,以此曲线作为预测模型,对系统进行预测[[2] 宋来中.高速铁路线下工程沉降评估方法[J].中国港湾建设,2010,12(6):35-36.]2。
目前常用的有GM(1,1)、GM(1,N)模型,其中GM(1,N)模型适合于建立系统的状态模型,为高阶系统提供基础,不适合预测用,预测模型应选用单个变量的模型即预测量本身数据模型(GM(1,1)模型)[[3] 陈启华.灰色GM (1,1)模型在高铁线下工程沉降变形预测中的应用[J].地理空间信息,2012,6(3):141-142.][3]。
灰色预测模型在高速公路车流预测中的应用

了解决 以上 问题 , 本文 提 出 了运用 滤 波器 对 G 1 M( ,
1 模 型进行残 差 修正 的方法 , 得 了能 满 足应 用 要 ) 取
灰 色预 测模 型在 高速 公 路 车 流预 测 中的应 用
汪 超 孙 卫 华 何 元 烈 , ,
(. 1 广东省公 路勘 察规 划设计 院股份有 限公 司 市政与交通工程设计部 , 广东 广州 50 0 : 157 2 .广东工业大学 计算机学 院, 广东 广州 50 0 ) 10 6
2 F c h fC mp t rS in e,Gu n d n n v ri f e h oo y,Gu n z o 1 0 6 . a u y o o u e ce c a g o g U ie s y o c n l g t T a g h u5 0 0
,
Ci , hn ) a
在信 息化 时 代 , 学 的交 通 管 理 与控 制 需 要 能 科 够做 到根 据 当前 路 网交通 流变 化规律 , 科学 判 断 、 预 测高 速公 路交 通 流 变化 情 况 , 且 提前 采 取 有 效措 并 施规 避可 能存 在 的交 通拥 挤 或 者堵 塞 , 主动 采 取 信 息 发布 、 交通 广播 等 诱 导方 式 保 障 高 速公 路 路 网交
W a a ,Su e. u , a —i。 ng Ch o n W ih a He Yu n l e
( . e t f u e a a d T a i E g e r g G a g o gH g w yD s n Is tt C . Ld ,G a gh u5 0 0 ,C ia 1 D p n i l n r f n i ei , u n d n i a ei nt u O , t. u n zo 5 7 hn ; oM p fc n n h g i e 1
灰色预测模型在公路客运量预测中的应用

定 因素的影 响 , 文利 用 灰色 系统 法 对 我 国公 路客 本
运量 进行预测 。
l 灰 色 系统 模 型 的 理论
灰 色 系 统理 论 是 1 8 年 由中 国学 者邓 聚龙 教 2 9
展 和站场配 置规划提 供依据 , 同时 , 为运输 企业 的 也 费站 之间无法 通信 时 , 可暂停 使用数据 自动传输 , 将
(. 北农 林 科 技 大 学 机 电 学院 .陕 西 杨 凌 72 0 ; . 1西 1 10 2 长安 大 学 汽 车 学院 . 西 西安 70 6 ) 陕 10 4
摘 要 : 用 灰 色预 测 系统理 论 . 国 内公 路 客 运 量 建 立 了基 于 灰 色预 测 理 论 的 GM ( ,1 运 对 1 ) 模 型 .并运 用 G ( . ) 型 对 2 0 ~2 l 年 国 内公 路 客 运 量进 行 了预 测 。预 测 结 果表 明 . 方 M 1 1 模 0 O 5 7 该
4 结 语
我 国高速公 路收 费 正逐 步 从“ 人工 ” 人 工半 向“
灰色理论在路基沉降预测中的应用及其改进

灰 色理 论在 路 基 沉 降预 测 中 的应 用及 其 改进
姜
摘
鹏
张德 军
要: 系统介绍 了灰色理论 预测模 型在路基沉 降预测 中的应用, 并对灰 色模 型进 行 了改进 , 立 了五个灰色理论预 测 建
模型, 通过模型预测值 与实测值 比较, 出灰 色理论 预测模 型适合于沉 降过程 曲线发展缓慢 的软土路基 沉降预测 , 得 而采 用灰数等维递 补动态预测模 型和 改进 的灰色模型具有更高的预测精度 。 关键词 : 降预测 , 沉 灰色理论 , 灰数 等维递补动态预测模型 , 改进灰 色模 型 中图分类号 : 1 . U4 6 1 文献标 识码 : A
z
则 ( 的 G 1 1模 型为 : 1 M( ,) 川 ) = 川 ) 一 川 ) = () 1一 +
() 6 川 (( 0川 ) ) 一 川 ) () 1一
f) 7
( = { ( )z ( )… , ( ) 。 ) z( 1 , ()2 , z( } ) )
一
程 。灰色 系统 理 论 的 基 本 思路 是 : 先 对 数 据进 行 累 加 处 理 首 (一 G , 1A O)使观测数据序 列的 随机 因素影 响淡化 , 而提 高观 测 从
数据序列的内在规 律 , 然后再将 数据 序列建成 一个 变量 , 具有 微
般 的灰色模型为 G , ) 型 , M( h 模 表示 h个 变量 的 阶微 分方 以是生成模型 z( ( ) A1 £ 也 可 以 是 还 原 模 型 ( ( ) 0 £。
叛据镇 阵 .
一
() 4
1 灰 色理论 模型 的建 立
1 1 灰 色理 论基 本概 念 .
某个 只知大概范 围, 而不知准确数值 的全体实数 , 称为灰 数 , 记 作 。令 a为区间 , 啦为 a中的数 , 灰数 在 a内取值 , 若 则称 a为 的一个可能 白化值 。为 此可有 下述 符号 : 为一 般灰 数 ;
灰色优化模型在高速公路交通量预测中的应用

8 ) 系统 的优化 。运行于单 机或 者 网络上 的平 台数据 传输 的
总之 , 通过有效 的数据关联实现 巨量数据 的汇总 、 统计 , 取代
安全性及 在客户机 上是 否能快 速有 效 的运行 牵涉 到平 台代码 开 手工低效 方式 ; 实现业主 、 监理和承包人业务 联网办公 、 提 高工作 发 的简化 和与各种浏览器 和操作 系统 的兼 容性等 , 是一 个 比较 复 与协作效 率 ; 为业 主、 监 理和承 包人 三方创 造显 著经济 效益 与管 杂 的问题 , 所 以软 件开发商的选择也很重要 。 理效益 ; 建立项 目工 程 台账 , 加 强动 态管理 , 有 效控 制工 程造 价 ;
在现实 中就是 管理 的责权 问题 了 , 是 否能 良好 的运行 和化 有 可移植 性 , 是 否可以二次开发 , 是否能集 成其他 软件 的数据 , 是 设 置 ,
否有 良好和可扩展 的接 口连 接其他 的软件 和硬件来 实 现更 多的 解矛 盾取决于大家共同的维护 , 当然在维护 的同时又是在进 行二
第3 9卷 第 2 4期 2 0 1 3年 8月
山 西 建 筑
SHANXI ARCHI TECTURE
Vo 1 . 3 9 No. 24
Au g . 2 0 1 3
・1 6 5・
文章编号 : 1 0 0 9 — 6 8 2 5 ( 2 0 1 3 ) 2 4 - 0 1 6 5 - 0 4
后 的模型精 度比原始模型精度高 , 具有很好的实用性和可靠性 。
关键词 : 背景值 , 灰色优化模型 , 交通量预测 中图分 类号 : 1 3 4 1 2 . 1 文献标识码 : A
1 背 景 问题
灰色预测模型在公路货运量预测中的应用

物流科技
21 0 0年第 9期
・交 通 运输 ・ 文 章 编 号 :1 0 — 1 0 (0 0 9 0 — 3 0 2 3 0 2 1 )0 - 1 5 0 1
App c to f Gr y For c s o i Ro d Fr i ht Fo e a t i l ain o e e a t M d n a eg r c s
差 ,且 误 差 的大 小 随 着 预 测 的 时 间 的增 加 而 增 加 。
采 用 通 常 的 预 测 理 论 与 方 法 得 到 的 预 测 结 果 可 信 度 仍 偏 低 ,究 其 原 因 主 要 是 : ( )过 去 货运 量 统 计 资料 缺 乏 。而 高 等 级 道 路 要 求 货 运 量 预 测 期 又较 长 ( 1 中远 期 ) ;
或非确知 ( 未来 远景 货运 量 ) 的信 息 系统 ,在 系 统 控 制 科 学 中成 为 典 型 的灰 色 系 统 ,它 的变 化 发 展 规 律 体 现 了道 路 交 通 系 统 的
模 糊 性 特 征 。所 以对 其 系统 规 律 的认 知 可应 用 灰 色控 制 理 论 来 解 决 问题 。
贾 学锋 ( 同济大学, 上海 嘉 21 4 定 08 ) 0
JA X efn I u—e g
摘
(o ̄iU i r t i i 0 84 hn) T ni n e i ,J dn 2 10 ,C i v sy a g a
要 :论 述 了灰 色预 测 模 型 在 公 路 货运 量 预 测 中 的 应 用技 术 、 方 法 与 程序 。 该 方 法 利 用 了 累加 生 成 手段 和微 分 方程 描 述
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰色预测方法在公路路基中的应用
摘要:文章论述了传统灰色系统理论在公路路基沉降预测中的步骤,并创新的建立了任意时间间隔的非等时序改进灰色模型。
并给出了灰色预测方法的精度检验过程。
在文章的最后,阐述了灰色预测方法在现实中对公路路基沉降的作用。
关键词:公路路基;沉降预测;灰色系统
中图分类号:u213.1 文献标识码:a 文章编号:
1.引言
公路,尤其是高速公路,对路面平整性要求很高,在技术规范中有规定:在施工过程中必须进行沉降和稳定性预测。
在研究中发现,国内外公路系统中很多专家都用统计回归模型等方法来对公路的沉降进行预测研究。
这些数学模型都含有统计特性,它们都建立在若干数学经济假设之上,或者建立在对公路物理力学性质的假设基础上,或者需要庞大的数据来增加模型的精确程度。
故其模型精度在较大程度上取决于建模因子的选择和数据规模,故而用上述模型进行数据的拟合时一般精度不高。
因此灰色理论因为其模糊性且不需要庞大的数据等优势逐渐被人们重视,在与曲线拟合、人工神经网络、遗传算法等方法相比的情况下,灰色理论依然占据了很大的优势,所以在公路路基的沉降监测、预测中灰色理论的应用越来越多,但由于传统的灰色模型仅适用于等间隔且累加生成具有明显指数规律的原始动态序列。
在现实中,因为各种复杂因素的影响,对公路路基沉降的观测很难做到等间隔时序观测,所以本文提出的非
等时序灰色模型改进传统灰色模型等间隔时序系统的限制,拓宽了灰色预测的应用范围。
2. 公路路基沉降规律
公路路基沉降根据过程划分,可分为瞬时沉降、固结沉降和次固结沉降三种。
瞬时沉降:在荷载施加后,沉降全过程在短时间内立即发生的,与时间无关。
固结沉降和次固结沉降:随着荷载和时间变化而变化。
故从路基沉降的规律来看,我们在套用灰色模型进行公路路基沉降预测时,切不可带有简单性、盲目性,且其预测的精度与所选择的函数类型有重要的关系。
在具体工程实践中,要根据工程的实际情况,合理地选择和应用模型,寻找最佳函数形式来拟合,以求最精确解。
3.公路路基沉降灰色系统理论
定义:灰色系统是指信息不完全与不确知的系统,它是一种综合运用数学方法对信息不完全的系统进行预测、预报的理论和方法。
基本思想:将与时间有关的已知数据按某种规则加以组合,构成白色模块,然后按某种规则提高灰色模块的白化度。
优点:在没有庞大的数据的情况下就能建模。
3.1等间隔的gm(1,1)模型
3.1.1建立模型
公路路基的沉降量观测及预测是以时间为变量,而对时间序列进
行数量大小的预测称为数列预测。
数列预测是以单一变量的gm(1,1)模型为基础的,该模型要求时序数据是平稳变化的。
gm(1,1)中前一个“1”表示阶数,后一个“1”表示因素,在公路路基沉降预测中为时间。
设{x(0)}={ x(0) (1), x(0)(2)),… x(0) (n))为原始数据列,所对应的时间序列为t={t1,t2,t3,…tn},该数列的一次累加数列为:{x(1)}={ x(1) (1), x(1)(2)),… x(1) (n)),且满足:
x(1) (k)=x(1) (m)
对建立白化形式的微分方程: (1)
方程的解为:
然后确定k=1,2,3,…n-1时的值: , , ……进而得还原数据:,k=1,2,3,……n
3.1.2 参数估计
(1)式中的参数列为[a,u]t,,由最小二乘法得[a,u]t,=(b t b)-1 b t yn
其中,b=
yn= t
3.2 非等时序改进灰色模型
公路路基的沉降观测及预测是以时间为变量,因此设随时间变化而形成的序列数据为
y(ti)={y(t1),y(t2),……y(tn)},i=1,2,3,……n
此序列的gm白化形式的微分方程为: (2)
其数学解析式为:,其中a,b为为待辨识灰参数;m,n为待辨识灰系数;y(ti)为因变量值;ti为自变量值。
对于灰参数a,b可采用一元线性回归辨识方法进行确定:令,代入(2)式整理得:y = ax + b, 而对于灰系数可由最小二乘法求得(m,n)=(a t a) -1a t z。
其中:a= ,z=
3.3建立模型需注意的事项.
本文提出的非等时序改进灰色模型是以随时间变化而形成的序列数据累加作为样本值,样本值对预测结果影响较大,所以进行样本选择时应该剔除变异性大的样本;另外,在公路路基沉降观测时也应该注意变异性大的观测值,控制观测质量;提高观测精度。
4预测模型的精度检验
4.1残差检验
预测的绝对误差为: ,k=1,2.3……n。
预测的相对误差为:
4.2后验差检验
设为原始数列,为模型模拟预测数列,为残差数列,则
,解得:
,解得:
(1)为均方差比值,给定 >0,当c0,当p> 时,则模型为小误差概率合格模型。
(3) 外推性好的预测,c必须小,小误差概率p大,按c和p将
精度分为“好”、“合格”、“基本合格”、“不合格”四个等级。
列表如下:
预测精度检验表
当p、c都在允许的范围之内,则可以应用模型预测,所建立的灰色模型精度满足要求。
5. 对公路路基沉降灰度检验的意义
(1)利用非等时序改进灰色模型预测公路路基沉降,所需的实测数据少,建模简单,可节省大量的人力、物力和财力,具有显著的经济和社会效益。
(2)传统的gm(1,1)模型对时序数据应有比较平稳的变化规律,但非等时序改进灰色模型突破了传统gm(1,1)模型等间隔时序系统的限制,预测精度更高。
(3)利用非等时序改进灰色模型预测公路路基沉降,将对公路路基的施工进度控制以及高速公路的监测维护起到积极作用。
5.结束语
灰色模型具有所需数据量少、计算简单、预测可靠性高等优点,非常值得在公路路基沉降预测中广泛推广,但在应用灰色模型时,有以下两点需要注意:
(1)鉴于公路路基沉降规律的复杂性,建议绘制原始数据沉降累计值曲线图,并对原始数据列进行分析,判断数据所处的沉降阶段,并根据不同的沉降阶段,对gm(1,1)模型进行不同程度的修正。
在
预测模型中还可以采用不同维数、等维新陈代谢等方法进行计算,并通过残差法和后验法进行精度对比,根据预测效果,以求最精确解。
(2)公路路基沉降观测数据往往提供的是沉降累积值,其已经进行了一次ago累加生成,故在建立原始数列时,要通过累减的方法,得到时间段的沉降量,再进行计算。
另外,灰色模型是正的数据列,故原始数列第一个数据不宜为零。
这两点往往容易忽视。
参考文献:
[1]李亮,潘伯林.高层建筑基础设计方案的技术经济比较[j].长沙铁道学院学报,1999,17(4):41—45.
[2]沈鸣.灌注桩基础设计与施工的优化选择[j].岩土工程界,2001,4(5):17—19.
[3]吕志涛.现代土木工程的新发展[m].南京:东南大学出版社,1998.。
