高一必修一二三综合试题
高一数学必修一综合测试题(含答案)

高一数学必修一综合测试题(含答案)一、选择题(每题5分,共50分)1、已知集合M={0,1,2},N={xx=2a,a∈M},则集合MN=A、{ }B、{0,1}C、{1,2}D、{0,2}答案:B解析:将M中的元素代入N中得到:N={2,4,8},与M 的交集为{0,1},故MN={0,1}。
2、若f(lgx)=x,则f(3)=()A、lg3B、3C、10D、310答案:C解析:将x=3代入f(lgx)=x中得到f(lg3)=3,又因为lg3=0.477,所以f(0.477)=3,即f(3)=10^0.477=3.03.3、函数f(x)=x−1x−2的定义域为()A、[1,2)∪(2,+∞)B、(1,+∞)C、[1,2)D、[1,+∞)答案:A解析:由于分母不能为0,所以x-2≠0,即x≠2.又因为对于x<1,分母小于分子,所以x-1<0,即x<1.所以定义域为[1,2)∪(2,+∞)。
4、设a=log13,b=23,则().A、a<b<cB、c<b<aC、c<a<bD、b<a<c答案:A解析:a=log13=log33-log32=1/2-log32,b=23=8,c=2^3=8,所以a<b=c。
5、若102x=25,则10−x等于()A、−15B、51C、150D、0.2答案:B解析:由102x=25可得x=log10(25)/log10(102)=1.3979,所以10^-x=1/10^1.3979=0.1995≈0.2.6、要使g(x)=3x+1+t的图象不经过第二象限,则t的取值范围为A.t≤−1B.t<−1C.t≤−3D.t≥−3答案:B解析:当x=0时,y=1+t,要使图像不经过第二象限,则1+t>0,即t>-1.又因为g(x)的斜率为正数,所以对于任意的x,g(x)的值都大于1+t,所以t< -1.7、函数y=2x,x≥1x,x<1的图像为()答案:见下图。
高一物理第一二三章综合试题(人教版必修1)

2014高一物理期中考试试题一、选择题(每题所给出的四个选项中至少有一个是正确的,全选对得4分,选对但选不全得2分,选错或不选得0分,共40分) 1.下列关于质点的说法正确的是A .只要是小的物体,就可以看作质点B .当物体的大小和形状对研究的问题没有影响或影响可以忽略时,可用质点来代替物体C .裁判跳水运动员的成绩,可以将其视为质点D .研究足球的运动轨迹可将其视为质点2.一个学生在百米测验中,测得他在50m 处的瞬时速度是6m/s ,16s 末到达终点时的瞬时速度是7.5 m/s ,则全程内的平均速度大小是( )A .6 m/sB .6.25 m/sC .6.75 m/sD .7.5 m/s3.甲、乙两物体先后从同一地点出发,沿一条直线运动,它们的v-t 图象如图所示,由图可知( )A .甲比乙运动快,且早出发,所以乙追不上甲B .t=20s 时,乙追上了甲C .在t=20s 之前,甲比乙运动的快,t=20s 之后乙比甲运动快D .由于乙在t=10s 时才开始运动,所以t=10s 时,甲在乙前面,它们之间距离为乙追上甲前最大4.一物体做匀变速直线运动,中间时刻的瞬时速度为1v ,中间位置的瞬时速度为2v ,则 A .若物体做匀加速直线运动,21v v > B .若物体做匀减速直线运动,21v v > C .不论是匀加速还是匀减速直线运动,21v v <D .不论是匀加速还是匀减速直线运动,21v v >5.上海到南京的列车速度为180km/h ,列车到站后以5m/s 2的加速 度刹车,则列车刹车12秒内的位移为A .250mB .0C .240mD .100m 6.以下关于力的说法正确的是A .力可以没有施力物体,但不能离开受力物体B .只有直接接触的物体间才有力C .自然界只有三种基本相互作用,分别是电磁相互作用、强相互作用、弱相互作用D .物体各部分都受到重力,可将物体的重力等效集中在一点,这一点叫物体的重心 7.由F =kx 可得k =F /x ,这说明( ) A .k 与F 成正比,与x 成反比B .k 是弹簧伸长单位长度时产生的弹力C .k 值越大的弹簧,用同样大的力越不容易拉长D .当弹簧弹力为零时,k =08.汽车在平直公路上匀速前进(设驱动轮在后),则( ) A .前轮、后轮受到的摩擦力均向后B .前轮、后轮受到的摩擦力均向前C .前轮受到的摩擦力向前,后轮受到的摩擦力向后D .前轮受到的摩擦力向后,后轮受到的摩擦力向前9. 用水平方向的力F 将重为G 的木块压在竖直墙壁上静止不动, 如图所示,当力F 增大到2F 时墙对木块的摩擦力A .是原来的2倍B .与原来的相等C .是原来的3倍D .是原来的21倍 10.下列物体的受力分析图正确的是( )第Ⅱ卷(非选择题,共60分)二、填空题(共4个小题,每空2分,共20分) 11.一质点做匀变速直线运动,在第2s 内的平均速度为6m/s ,在第4s 内的平均速度为10 m/s ,则该质点的加速度为 m/s 2。
高一地理必修一,一、二、三单元测试卷

高一地理第一至第三单元检测试卷一、单项选择题(每小题2分,共50分)德国科学家最新研究发现,太阳系附近有三颗“超级地球”有可能存在外星生命。
这三颗行星围绕天蝎座的一颗恒星运行,距离地球仅22光年,完成第1~2题。
1.“超级地球”应属于()。
A.地月系B.太阳系C.银河系D.河外星系2.有适合生物呼吸的大气是生命存在的重要条件之一。
“超级地球”上存在大气的原因是因为它具有()。
A.适中的质量与体积B.适中的昼夜更替周期C.与恒星的距离适中D.适中的自转周期3.液态水的存在是地球生命起源和发展的重要条件之一,下列叙述中与地球“液态水存在”有密切关系的是()。
①地球上昼夜更替的周期较适中②地球的质量和体积适中③地球处于一种比较安全的宇宙环境之中④地球与太阳的距离比较适中A.①④B.①②C.②③D.②④图A为厦门鼓浪屿“日光岩”(典型的花岗岩)风化景观,图B为地壳物质循环示意图。
读图,完成第4~5题。
4.形成“日光岩”风景的岩石属于图B中的()A.甲B.乙C.丙D.丁5.图A中“巨石”形成过程的先后顺序是()A.地壳上升—岩浆侵入—风化堆积B.地壳下降—岩浆喷发—风化侵蚀C.岩浆喷发—地壳下降—风化堆积D.岩浆侵入—地壳上升—风化侵蚀埃及费拉菲拉沙漠区有一片屹立在坚实土层之上、仿佛沙雕一样的巨大的蘑菇群岩层,被当地人称作“蘑菇沙漠”。
读图并结合所学知识完成第6~7题。
6.形成“蘑菇沙漠”的地质作用主要是()A.风力侵蚀B.河流堆积C.岩层挤压D.火山喷发7.“蘑菇沙漠”最可能分布的地区是()A.湿润地区B.半湿润地区C.半干旱地区D.干旱地区8.大气对地面的保温作用是( )①大气中的氮,吸收地面长波辐射的能力很强②大气中的二氧化碳和水汽吸收地面长波辐射,将大部分热量保存在大气中③大气通过逆辐射,将大部分热量还给地面④多云的夜晚要比晴朗的夜晚凉爽些。
A.①②B.②③B.①③D.②④9.以下四图中昼夜温差最大的是( )10.下图表示的热力环流中,错误的是( )11.大气运动的叙述错误的是( )A.气压梯度力与等压线始终垂直,且由气压高的地方指向气压低的地方B.近地面摩擦力与地转偏向力始终是垂直关系C.地转偏向力与气压梯度力始终是垂直关系D.若不考虑摩擦力,当气压梯度力与地转偏向力大小相等方向相反时,风向与等压线平行12.下面四幅图中,表示北半球西风带的是()读我国某地某时段气温变化示意图,完成第13~14题。
高一英语必修一必修二综合测试卷(有答案)

高一英语必修一必修二综合测试卷(有答案)第一部分听力 (共两节,满分 20 分)第一节(共 5 小题;每小题 1 分,满分 5 分)听下面 5 段对话。
每段对话后有一个小题,从题中所给的 A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the man suggest the woman do?A. Go to bed early.B. Work all night.C. Take a nap.2. What is the woman going to do after the meeting?A. Have a talk with Jack.B. Attend a meeting.C. Have coffee with David.3. What is the woman doing now?A. Sitting on the sofa.B. Watching TV.C. Reading a book.4. What is the probable relationship between the speakers?A. Friends.B. Teacher and student.C. Shop assistant and customer.5. What does the man say about the woman's photo?A. It was taken by him.B. It is very beautiful.C. It was in a magazine.第二节(共 15 小题;每小题 1 分,满分 15 分)听下面 5 段对话或独白。
每段对话或独白后有几个小题,从题中所给的 A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题 5 秒钟;听完后,各个小题将给出 5 秒钟的作答时间。
铁岭高中高一必修一、必修二综合测试题三

铁岭高中高一必修一、必修二综合测试题三出题人:王铁刚一、选择题(在每小题给出的四个选项中,只有一项是符合要求的.本题共12小题,每小题5分,满分60分)1、已知集合S ={c b a ,,}中的三个元素可构成∆ABC 的三条边长,那么∆ABC 一定不是( ) A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形2、与直线3450x y ++=关于x 轴对称的直线的方程为( )A .3450x y -+=B .0543=-+y xC .0534=-+y xD .0534=++y x 3、已知正方体外接球的体积是323π,那么正方体的棱长等于 ( )A B 3C 3D 34、已知直线⊥l 平面α,直线⊂m 平面β,下列四个命题中正确的是( )(1)m l ⊥⇒βα// (2)m l //⇒⊥βα (3)βα⊥⇒m l // (4)βα//⇒⊥m l A .(1)与(2) B .(3)与(4) C .(2)与(4) D .(1)与(3)5、某新产品电视投放市场后第一个月销售100台,第二个月销200台,第三个月销售400台,第四个月销售790台,则下列函数模型中能较好地反映销量y 与投放市场的月数x 之间关系的是( ).A.100y x =B.25050100y x x =-+C.502x y =⨯D.2100log 100y x =+ 6、一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( ). A.122ππ+ B.144ππ+ C.12ππ+ D.142ππ+7、设()f x 是奇函数,且在(0,)+∞内是增函数,又(3)0f -=,则()0x f x ⋅<的解集是( ) A .{}|303x x x -<<>或 B .{}|303x x x <-<<或 C .{}|33x x x <->或 D .{}|3003x x x -<<<<或8、已知平面上一点(5,0)M ,若直线上存在点P 使得4PM =,则称直线为“切割型直线”. 下列直线中是“切割型直线”的是 ( )1AAA 5x=- B 5y=-C3420x y-+=D21y x=+9、设13(),(),()logxaf x ag x xh x x===,a满足2log(1)0aa->,那么当1x>时必有A.()()()h x g x f x<<B.()()()h x f x g x<<C.()()()f xg xh x<<D.()()()f x h xg x<<10、如右图,定圆半径为a,圆心为(,)b c,则直线0ax by c++=与直线10x y+-=的交点在()A.第一象限B.第二象限C.第三象限D.第四象限11、若x1满足x+2x=4, x2满足x+log2x=4, 则x1+x2=( )A.52B. 3C.72D. 412、下列5个正方体图形中,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出⊥l面MNP的图形的所有序号正确的是().①②③④⑤A. ①④⑤B. ①④③C. ②④⑤D. ①③⑤二、填空题(本题共4小题,每小题5分,满分20分)13、函数y=的奇偶性为 .14、如图,正方体1111ABC D A B C D-的棱长为4,P、Q分别为棱11B C、C上的中点,M在11A D上,且11A M=,过P、Q、M的平面与1DD交于点N,则MN= .15、已知点P是圆2225x y+=上动点,定点(0,1)A,则A P的中点M的轨迹方程是.16、圆台上底半径为5cm,下底半径为10cm,母线AB=20cm,A在上底面上,B在下底面上,从AB中点M拉一条绳子,绕圆台侧面一周到B点,则绳子最短时长为_ ___三、解答题(本题共6小题,满分70分.解答应写出文字说明,证明过程或演算步骤.)17、(本小题满分10分)(1)2lg2lg5lg201+-()C(2)4160.2532164()8(2011)49----18、(本小题满分12分)已知四棱锥的底面是矩形,侧棱长相等,棱锥的高为4,其俯视图如图所示.(1)作出此四棱锥的主视图和侧视图,并在图中标出相关的数据; (2)求该四棱锥的侧面积S .19. (本小题满分12分)求经过直线03:1=-+y x l 与直线01:2=--y x l 的交点M ,且分别满足下列条件的直线方程:(1)与直线032=-+y x 平行; (2)与直线032=-+y x 垂直.20、(本小题满分12分)如图,在四棱锥P-ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面PD =DC ,E 是P C 的中点,作EF ⊥PB 交PB 于点F . (1)证明 PA //平面EDB ; (2)证明PB ⊥平面EFD ;21(本小题满分12分)已知圆,01046:22=+--+y x y x C 两直线01023:,:21=++=y x l kx y l . (Ⅰ)若1l 与圆C 交于A 、B 两点,求k 的取值范围;(Ⅱ)设A B 的中点为P ,1l 与2l 交点为Q ,求||||OQ OP ⋅的值.22、(本小题满分12分)已知集合M 是满足下列性质的函数()x f 的全体:在定义域内存在0x ,使得()()()0011f x f x f +=+成立。
高中数学必修一综合测试二(含答案)

高中数学必修一综合测试二(含答案)高一数学必修1综合测试题(二)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集I={0,1,2},且满足CI (A∪B)={2}的A、B共有组数A.5B.7C.9D.112.如果集合A={x|x=2kπ+π,k∈Z},B={x|x=4kπ+π,k∈Z},则A.AB B.BA C.A=B D.A∩B=3.设A={x∈Z||x|≤2},B={y|y=x2+1,x∈A},则B的元素个数是A.5B.4C.3D.24.若集合P={x|3<x≤22},非空集合Q={x|2a+1≤x<3a-5},则能使Q (P∩Q)成立的所有实数a的取值范围为A.(1,9)B.[1,9]C.[6,9D.(6,9]5.已知集合A=B=R,x∈A,y∈B,f:x→y=ax+b,若4和10的原象分别对应是6和9,则19在f作用下的象为A.18B.30C. eq \f(27,2)D.286.函数f(x)= eq \f(3x-1,2-x) (x∈R且x≠2)的值域为集合N,则集合{2,-2,-1,-3}中不属于N的元素是A.2B.-2C.-1D.-37.已知f(x)是一次函数,且2f(2)-3f(1)=5,2f(0)-f(-1)=1,则f(x)的解析式为A.3x-2B.3x+2C.2x+3D.2x-38.下列各组函数中,表示同一函数的是A.f(x)=1,g(x)=x0B.f(x)=x+2,g(x)= eq \f(x2-4,x-2)C.f(x)=|x|,g(x)= eq \b\lc\{(\a\al(x x≥0,-x x<0))D.f(x)=x,g(x)=( eq \r(x) )29. f(x)=eq \b\lc\{(\a\al(x2 x>0,π x=0,0 x<0)) ,则f{f [f(-3)]}等于A.0B.πC.π2 D.910.已知2lg(x-2y)=lgx+lgy,则 eq \f(x,y) 的值为A.1B.4C.1或4D. eq \f(1,4) 或411.设x∈R,若a<lg(|x-3|+|x+7|)恒成立,则A.a≥1B.a>1C.0<a≤1D.a<112.若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是A.(0, eq \f(1,2) )B.(0,C.( eq \f(1,2) ,+∞)D.(0,+∞)二、填空题(本大题共6小题,每小题4分,共24分.把答案填在题中横线上)13.若不等式x2+ax+a-2>0的解集为R,则a可取值的集合为__________.14.函数y= eq \r(x2+x+1) 的定义域是______,值域为__ ____.15.若不等式3>( eq \f(1,3) )x+1对一切实数x恒成立,则实数a的取值范围为___ ___.16. f(x)=,则f(x)值域为_____ _.17.函数y= eq \f(1,2x+1) 的值域是__________.18.方程log2(2-2x)+x+99=0的两个解的和是______.三、解答题19.全集U=R,A={x||x|≥1},B={x|x2-2x-3>0},求(CUA)∩(CUB).20.已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.(1)求证:f(8)=3 (2)求不等式f(x)-f(x-2)>3的解集.21.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?22.已知函数f(x)=log2x-logx+5,x∈[2,4],求f(x)的最大值及最小值.23.已知函数f(x)=eq \f(a,a2-2) (ax-a-x)(a>0且a≠1)是R上的增函数,求a的取值范围.参考答案一、选择题二、填空题13. 14. R [ eq \f(\r(3),2),+∞) 15. - eq \f(1,2) < a < eq \f(3,2)16. (-2,-1] 17. (0,1) 18. -99三、解答题(本大题共5小题,共66分. 解答应写出文字说明、证明过程或演算步骤)19.全集U=R,A={x||x|≥1},B={x|x2-2x-3>0},求(CUA)∩(CUB).(CUA)∩(CUB)={x|-1<x<1}20.已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.(1)求证:f(8)=3 (2)求不等式f(x)-f(x-2)>3的解集.考查函数对应法则及单调性的应用.(1)【证明】由题意得f(8)=f(4×2)=f(4)+f(2)=f(2×2)+f(2)=f(2)+f(2)+f(2)=3f(2)又∵f(2)=1 ∴f(8)=3(2)【解】不等式化为f(x)>f(x-2)+3∵f(8)=3 ∴f(x)>f(x-2)+f(8)=f(8x-16)∵f(x)是(0,+∞)上的增函数∴解得2<x< eq \f(16,7)21.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?考查函数的应用及分析解决实际问题能力.【解】(1)当每辆车月租金为3600元时,未租出的车辆数为eq \f(3600-3000,50) =12,所以这时租出了88辆.(2)设每辆车的月租金定为x元,则公司月收益为f(x)=(100-eq \f(x-3000,50) )(x-150)-eq \f(x-3000,50) ×50整理得:f(x)=-eq \f(x2,50) +162x-2100=-eq \f(1,50) (x-4050)2+307050∴当x=4050时,f(x)最大,最大值为f(4050)=307050 元22.已知函数f(x)=log2x-logx+5,x∈[2,4],求f(x)的最大值及最小值.考查函数最值及对数函数性质.【解】令t=logx ∵x∈[2,4],t=logx在定义域递减有log4<logx<log2,∴t∈[-1,- eq \f(1,2) ]∴f(t)=t2-t+5=(t- eq \f(1,2) )2+ eq \f(19,4) ,t∈[-1,-eq \f(1,2) ]∴当t=- eq \f(1,2) 时,f(x)取最小值 eq \f(23,4)当t=-1时,f(x)取最大值7.23.已知函数f(x)=eq \f(a,a2-2) (ax-a-x)(a>0且a≠1)是R上的增函数,求a的取值范围.考查指数函数性质.【解】 f(x)的定义域为R,设x1、x2∈R,且x1<x2则f(x2)-f(x1)= eq \f(a,a2-2) (a-a-a+a)= eq \f(a,a2-2) (a-a)(1+)由于a>0,且a≠1,∴1+>0∵f(x)为增函数,则(a2-2)( a-a)>0于是有,解得a> eq \r(2) 或0<a<1PAGE6。
高一数学必修1综合测试题3套(附答案)

高一数学综合检测题(1)一、选择题:(每小题5分,共60分,请将所选答案填在括号内) 1.已知集合M ⊂≠{4,7,8},且M 中至多有一个偶数,则这样的集合共有 ( )(A)3个 (B) 4个 (C) 5个 (D) 6个2.已知S={x|x=2n,n ∈Z}, T={x|x=4k ±1,k ∈Z},则 ( ) (A)S ⊂≠T (B) T ⊂≠S (C)S ≠T (D)S=T 3.已知集合P={}2|2,y y x x R =-+∈, Q={}|2,y y x x R =-+∈,那么PQ 等( )(A)(0,2),(1,1) (B){(0,2 ),(1,1)} (C){1,2} (D){}|2y y ≤4.不等式042<-+ax ax 的解集为R ,则a 的取值范围是 ( ) (A)016<≤-a (B)16->a (C)016≤<-a (D)0<a 5. 已知()f x =5(6)(4)(6)x x f x x -≥⎧⎨+<⎩,则(3)f 的值为 ( )(A)2 (B)5 (C)4 ( D)36.函数243,[0,3]y x x x =-+∈的值域为 ( )(A)[0,3] (B)[-1,0] (C)[-1,3] (D)[0,2] 7.函数y=(2k+1)x+b 在(-∞,+∞)上是减函数,则 ( )(A)k>12 (B)k<12 (C)k>12- (D).k<12- 8.若函数f(x)=2x +2(a-1)x+2在区间(,4]-∞内递减,那么实数a 的取值范围为( )(A)a ≤-3 (B)a ≥-3 (C)a ≤5 (D)a ≥39.函数2(232)xy a a a =-+是指数函数,则a 的取值范围是 ( )(A) 0,1a a >≠ (B) 1a = (C) 12a =( D)121a a ==或10.已知函数f(x)14x a -=+的图象恒过定点p ,则点p 的坐标是 ( )(A )( 1,5 ) (B )( 1, 4) (C )( 0,4) (D )( 4,0)11.函数y =的定义域是 ( )(A )[1,+∞] (B) (23,)+∞ (C) [23,1] (D) (23,1]12.设a,b,c都是正数,且346a b c==,则下列正确的是( )(A) 111c ab =+ (B) 221C a b =+ (C) 122C a b =+ (D) 212c a b =+二、填空题:(每小题4分,共16分,答案填在横线上)13.已知(x,y )在映射 f 下的象是(x-y,x+y),则(3,5)在f 下的象是 ,原象是 。
高一数学必修1、2综合试卷及答案

高中数学试卷 (必修1+必修2)一、选择题:(本大题共10题,每小题5分,共50分)1.设全集}7,6,5,4,3,2,1{=U ,集合}5,3,1{=A ,集合}5,3{=B ,则 ( C )A .B A U ⋃= B .B AC U U⋃=)( C )(B C A U U⋃= D .)()(B C A C U UU⋃=2.如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上是减函数,那么实数a 的取值范围是( A )A 、3a ≤- B 、3a ≥- C 、a ≤5 D 、a ≥53.已知点(1,2)A 、(3,1)B ,则线段A B 的垂直平分线的方程是( B ) A .524=+y x B .524=-y x C .52=+y xD .52=-y x4. 设()f x 是(,)-∞+∞上的奇函数,且(2)()f x f x +=-,当01x ≤≤时,()f x x =, 则(7.5)f 等于( B )A. 0.5B. 0.5-C. 1.5D. 1.5-5.下列图像表示函数图像的是( C )A B C D 6.在棱长均为2的正四面体BCD A -中,若以三角形ABC 为视角正面的三视图中,其左视图的面积是( C ).A .3B .362C .2D .22A BCD7.设n m 、表示直线,βα、表示平面,则下列命题中不.正确..的是( B ). A .βα⊥⊥m ,m ,则α//β B .m//n ,=βαα ,则m//nC .α⊥m ,β//m , 则βα⊥D .n //m ,α⊥m , 则 α⊥n8.圆:02y 2x 2y x 22=---+上的点到直线2y x =-的距离最小值是( A ).A .0B .21+ C .222-D .22-9.如果函数1ax ax)x (f 2++=的定义域为全体实数集R ,那么实数a 的取值范围是( A ).A .[0,4]B .)4,0[C .),4[+∞D .(0,4)10. a=3是直线ax+2y+3a=0和直线3x+(a-1)y=a-7平行且不重合的( C )A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件 二、填空题:(本大题共有5小题,每小题4分,满分20分)。
高一数学必修一必修二综合测试卷(有答案)

高一数学试题四(考试时间:120分钟 试卷满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 下列说法正确的是( )A . 经过三点确定一个平面B . 经过一条直线和一个点确定一个平面C . 四边形确定一个平面D . 两两相交且不共点的三条直线确定一个平面2. 下列哪个函数的定义域与函数()15xf x ⎛⎫= ⎪⎝⎭的值域相同( )A . 2y x x =+B . ln 2y x x =-C . 1y x =D . 1y x x=+3. 已知集合12|log 1A x x ⎧⎫=>-⎨⎬⎩⎭,{}|22xB x =>,则A B =( )A . 1,22⎛⎫ ⎪⎝⎭B . 1,2⎛⎫+∞⎪⎝⎭C . ()0,+∞D . ()0,24. 已知圆锥的侧面展开图是一个半圆,则其母线与底面半径之比为( ) A . 1B .2C .3D . 25. 已知函数()2f x x x a =++在区间()0,1上有零点,则实数a 的取值范围是( ) A . 1,4⎛⎤-∞ ⎥⎝⎦B . 1,4⎛⎫-∞ ⎪⎝⎭C . ()2,0-D . []2,0-6. 函数()()10,1x f x a a a -=>≠的图象恒过点A ,则下列函数中图象不经过点A 的是( )A . 1y x =-B . 2y x =-C . 21xy =-D . ()2log 2y x =7. 正四面体ABCD 中,E ,F 分别为棱AD ,BC 的中点,则异面直线EF 与CD 所成的角为( ) A .6π B .4π C . 3π D . 2π8. 已知函数()212log 3y x ax a =-+在[)2,+∞上为减函数,则实数a 的取值范围是( )A . 4a ≤B . 4a ≥C . 4a <-或4a ≥D . 44a -<≤9. 某几何体的三视图如图所示,该几何体表面上的点P 与点Q 在正视图与侧视图上的对应点分别为A ,B ,则在该几何体表面上,从点P 到点Q 的路径中,最短路径的长度为( ) A .5B .6 C . 22D .1010. 已知函数()ln 1f x x =-,()223g x x x =-++,用{}min ,m n 表示m ,n 中最小值,设()()(){}min ,h x f x g x =,则函数()h x 的零点个数为( )A . 1B . 2C . 3D . 411. 已知()g x 为偶函数,()h x 为奇函数,且满足()()2x g x h x -=.若存在[]1,1x ∈-,使得不等式()()0m g x h x ⋅+≤有解,则实数m 的最大值为( )A .315-B . 35-C . 1D . -1 12. 无论x ,y ,z 同为三条不同的直线还是同为三个不同的平面,给出下列说法:①若//x y ,//x z ,则//y z ;②若x y ⊥,x z ⊥,则y z ⊥;③若x y ⊥,//y z ,则x z ⊥;④若x 与y 无公共点,y 与z 无公共点,则x 与z 无公共点; ⑤若x ,y ,z 两两相交,则交点可以有一个,三个或无数个.其中说法正确的序号为( ) A . ①③B . ①③⑤C . ①③④⑤D . ①④⑤二、填空题(本大题共4小题,每小题5分,共20分) 13. 设函数()()xxf x e aea R -=+∈,若()f x 为奇函数,则a =______.14. 一个正四棱锥的侧棱长与底面边长相等,体积为423,则它的侧面积为______. 15. 已知函数()f x 为定义在[]2,3a -上的偶函数,在[]0,3上单调递减,并且()22522a f m m f m ⎛⎫-- ⎪⎝⎭>-+-,则m 的取值范围是______.16. 正四面体ABCD 的棱长为4,E 为棱BC 的中点,过E 作其外接球的截面,则截面面积的最小值为______.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17. 如图所示,在正方体1111ABCD A B C D -中,E 、F 分别是AB 和1AA 的中点.求证:CE ,1D F ,DA 交于一点.18. 已知函数()21x ax b f x x +=++是定义域为R 的奇函数. (1)求实数a 和b 的值,判断并证明函数()f x 在()1,+∞上的单调性;(2)已知0k <,且不等式()()22310f t t f k -++-<对任意的t R ∈恒成立,求实数k 的取值范围.19. 食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入P 、种黄瓜的年收入Q 与投入a (单位:万元)满足8042P a =+,11204Q a =+.设甲大棚的投入为x (单位:万元),每年两个大棚的总收益为()f x (单位:万元). (1)求()50f 的值;(2)试问如何安排甲、乙两个大棚的投入,才能使总收益()f x 最大?20. 已知幂函数()()3*p N x x f p -=∈的图象关于y 轴对称,且在()0,+∞上为增函数. (1)求不等式()()22132pp x x +<-的解集;(2)设()()()log 0,1a f x ax g x a a =->≠⎡⎤⎣⎦,是否存在实数a ,使()g x 在区间[]2,3上的最大值为2,若存在,求出a 的值,若不存在,请说明理由.21. 已知函数()11439x xm f x ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭.(1)当2m =-时,求函数()f x 在(),0-∞上的值域;(2)若对任意[)0,x ∈+∞,总有()6f x ≤成立,求实数m 的取值范围.22. 在菱形ABCD 中,2AB =且60ABC ∠=︒,点M ,N 分别是棱CD ,AD 的中点,将四边形ANMC 沿着AC 转动,使得EF 与MN 重合,形成如图所示多面体,分别取BF ,DE 的中点P ,Q .(1)求证://PQ 平面ABCD ;(2)若平面AFEC ⊥平面ABCD ,求多面体ABCDFE 的体积.参考答案一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1-5:DBCDC6-10:ABDCC11-12:AB1.【解析】A 选项考查公理2,即三点必须不在同一条直线上,才能确定一个平面;B 选项如果点在直线上,则该直线和这个点不能确定一个平面;C 选项中的四边形有可能是空间四边形,故选D .2.【解析】函数()15xf x ⎛⎫= ⎪⎝⎭的值域为()0,+∞,函数2y x x =+的定义域为R ,函数ln 2y x x =-的定义域为()0,+∞;函数1y x x=+的定义域为()(),00,-∞+∞,函数1y x=的定义域为()(),00,-∞+∞,故选B .3.【解析】由{}12|log 1|02A x x x x ⎧⎫=>-=<<⎨⎬⎩⎭,{}1|22|2xx x x B =⎧⎫>=>⎨⎬⎩⎭,则()0,A B =+∞,故选C .4.【解析】由已知可得2r l ππ=,所以2l r =,故2lr=.故选D . 5.【解析】函数()2f x x x a =++的图象的对称轴为12x =-,故函数在区间()0,1上单调递增,再根据函数()f x 在()0,1上有零点,可得()()00120f a f a =<⎧⎪⎨=+>⎪⎩,解20a -<<,故选C .6.【解析】函数()()10,1x f y ax a a -=>≠=的图象恒过点A ,即10x -=,可得1x =,那么1y =.∴恒过点()1,1A .把1x =,1y =带入各选项,只有A 没有经过A 点.故选A . 7.【解析】略8.【解析】()23g x x ax a =-+,则()230x a a g x x =-+>在[)2,+∞恒成立,且()23g x x ax a =-+在[)2,+∞上为增函数,所以22a≤且()240g a =+>,所以44a -<≤.故选D .9.【解析】由题,几何体如图所示(1)前面和右面组成一面此时222222PQ =+=.(2)前面和上面在一个平面此时223110PQ =+=,2210<,故选C . 10.【解析】作出函数()f x 和()g x 的图象如图,两个图象的下面部分图象,由()2230g x x x =-++=,得1x =-,或3x =,由()ln 10f x x =-=,得x e =或1x e=,∵()0g e >,∴当0x >时,函数()h x 的零点个数为3个,故选C .11.【解析】由()()2xg x h x -=,及()g x 为偶函数,()h x 为奇函数,得()222x xg x -+=,()222x x h x --=.由()()0m g x h x ⋅+≤得224121224141x x x x x x x m ----≤==-+++,∵2141x y =-+为增函数,∴max 231415x ⎛⎫+= ⎪+⎝⎭,故选A . 12.【解析】由平行于同一直线的两直线平行,平行于同一平面的两平面平行,可得①正确;由垂直于同一直线的两直线平行、相交或异面;垂直于同一平面的两平面相交或平行,可得②错误;由垂直于两平行直线中的一条,也垂直于另一条;垂直于两平行平面中的一个,也垂直于另一个,可得③正确;若一条直线与另两条直线无公共点,可得另两条直线可以相交;若一个平面与另两个平面无公共点,可得另两个平面无公共点;可得④错误.若三条直线两两相交,则交点可以有一个或三个,若三个平面两两相交,则交点有无数个.故选B . 二、填空题(本大题共4小题,每小题5分,共20分)13. -1 14. 43 15. 1122m -≤< 16. 4π13.【解析】若函数()x x f x e ae -=+为奇函数,则()()f x f x -=-,即()x x x x ae ae e e --+=-+,即()()10x x e a e -++=对任意的x 恒成立,则10a +=,得1a =-. 14.【解析】设正四棱锥的侧棱长与底面边长相等为2a ,则24ABCD S a =,2222422h PB BO a a a =-=-=,则31442233V a =⨯=,则1a =,则 22142242BC PF a a a S ⎛⎫=⨯⨯⨯=⨯⨯- ⎪⎝⎭侧24343a ==.15.【解析】由题设可得230a -+=,即5a =,故()()22122f m f m m -->-+-可化()()22122f m f m m +>-+,又2113m ≤+≤,21223m m ≤-+≤,故2211222m m m m +<-+⇒<,且12m ≥-.故应填答案1122m -≤<.16.【解析】将四面体ABCD 放置于正方体中,如图所示可得正方体的外接球就是四面体ABCD 的外接球,∵正四面体ABCD 的棱长为4,∴正方体的棱长为22, 可得外接球半径R 满足()22322R =⨯,解得6R =.E 为棱BC 的中点,过E 作其外接球的截面,当截面到球心O 的距离最大时,截面圆的面积达最小值,此时球心O 到截面的距离等于正方体棱长的一半,可得截面圆的半径为222r R =-=,得到截面圆的面积最小值为24S r ππ==.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.【解析】证明:如图所示,连接1CD 、EF 、1A B ,因为E 、F 分别是AB 和1AA 的中点, 所以1//EF A B 且112EF A B =.即:1//EF CD ,且112EF CD =, 所以四边形1CD FE 是梯形,所以CE 与1D F 必相交,设交点为P ,则P CE ∈,且1P D F ∈,又CE ⊂平面ABCD , 且1D F ⊂平面11A ADD ,所以P ∈平面ABCD ,且P ∈平面11A ADD , 又平面ABCD平面11A ADD AD =,所以P AD ∈,所以CE 、1D F 、DA 三线交于一点.18.【解析】(1)因为()()f x f x -=-,所以2211x a x ax bx x bx -+--=-+++, ∴0a b ==,()21xf x x =+, 任取()12,1,x x ∈+∞,且12x x <,()()1212221211x xf x f x x x -=-++()()()()21122212111x x x x x x --=++, ∵210x x ->,1210x x ->,()()2212110x x ++>,∴()f x 在()1,+∞单调递减.(2)()()2231f t t f k -+<--,()()2231f t t f k -+<-, ∵2232t t -+≥,11k ->,∴2231t t k -+>-, 即()211k t >---, ∵t R ∈≤,∴()1,0k ∈-. 19.【解析】(1)由题可知:甲大棚投入50万元,则乙大棚投入150万元, 所以()1804250150120277.5450f =+⨯+⨯+=. (2)依题意得202018020020x x x ≥⎧⇒≤≤⎨-≥⎩.故()()142250201804x x f x x =-++≤≤. 令25,65t x ⎡⎤=∈⎣⎦,则()()2211422508228244f x t t t =-++=--+,当82t =,即128x =时,()max 282f x =,所以投入甲大棚128万元,乙大棚72万元时,总收益最大, 且最大收益为282万元. 20.【解析】(1)由已知得30p ->且*p N ∈,所以1p =或2p =, 当2p =时,()3p f x x -=为奇函数,不合题意, 当1p =时,()2f x x =.所以不等式()()22132pp x x +<-变为()()1122132x x +<-, 则0132x x ≤+<-,解得213x -≤<. 所以不等式()()22132p p x x +<-的解集为21,3⎡⎫-⎪⎢⎣⎭.(2)()()2log a a g x x x =-,令()2h x x ax =-,由()0h x >得()(),0,x a ∈-∞+∞,因为()g x 在[]2,3上有定义,所以02a <<且1a ≠, 所以()2h x x ax =-在[]2,3上为增函数,当12a <<时,()()()max 3log 932a g x g a ==-=, 即2390a a +-=,∴3352a -±=,又12a <<, ∴3352a -+=. 当01a <<时,()()()max 2log 422a g x g a ==-=,即2240a a +-=,∴15a =-±,此时解不成立.综上:3352a -+=. 21.【解析】(1)当2m =-时,设13xt ⎛⎫= ⎪⎝⎭,∵(),0x ∈-∞,∴()1,t ∈+∞,∴()()222413t t t y g t -+=-=+=,对称轴1t =,图像开口向上,∴()g t 在()1,t ∈+∞为增函数, ∴()3g t >,∴()f x 的值域为()3,+∞.(2)由题意知,()6f x ≤在[)0,+∞上恒成立,即11239xxm ⎛⎫⎛⎫⋅≤- ⎪ ⎪⎝⎭⎝⎭,∴1233xx m ≤⋅-在[)0,x ∈+∞恒成立,则只需当[)0,x ∈+∞时,min 1233x x m ⎛⎫≤⋅- ⎪⎝⎭,设3xt =,()12h t t t=-,由[)0,x ∈+∞得1t ≥,设121t t ≤<,则()()()()12121212210t t t t h t h t t t -+-=<,所以()h t 在[)1,+∞上递增,()h t 在[)1,+∞上的最小值为()11h =,所以实数m 的取值范围为(],1-∞. 22.【解析】(1)取BE 中点R ,连接PR ,QR ,BD ,由P ,Q 分别是BF ,DE 的中点, ∴//PR EF ,//QR BD ,又∵//EF AC ,∴//PR 平面ABCD ,//QR 平面ABCD ,又∵PR QR R =,∴平面//PQR 平面ABCD ,又∵PQ ⊂平面PQR , ∴//PQ 平面ABCD .(2)连接AC ,设AC ,BD 交于点O , ∴BD AC ⊥,又∵平面AFEC ⊥平面ABCD , 平面AFEC平面ABCD AC =,∴BD ⊥平面AFEC .∴多面体ABCDFE 可以分解为四棱锥B ACEF -和四棱锥D ACEF -, 菱形ABCD 中,2AB =且60ABC ∠=︒知:2AC =,23BD =,12ACEF ==, 设梯形EFAC 的面积为()133244EFAC BD EF AC S =+⋅=, 1332ABCDFE EFAC V S BD =⋅⋅=.。
高中数学必修一必修二综合测试题(含答案)

Q PC'B'A'C BA高中数学必修一必修二综合测试题(时间90分钟,满分150分)姓名___________________ 总分:________________ 一、选择题(本大题共10小题,每小题5分,共50分) 1.下面四个命题:①分别在两个平面内的两直线是异面直线;②若两个平面平行,则其中一个平面内的任何一条直线必平行于另一个平面; ③如果一个平面内的两条直线平行于另一个平面,则这两个平面平行;④如果一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行. 其中正确的命题是( )A .①②B .②④C .①③D .②③ 2.过点(1,3)P -且垂直于直线032=+-y x 的直线方程为( ) A .012=-+y x B .052=-+y x C .052=-+y x D .072=+-y x 3.圆(x -1)2+y 2=1的圆心到直线y =33x 的距离是( )A .12B .32 C .1 D .34.设0<a <1,函数f (x )=log a (a 2x -2a x -2),则使f (x )<0的x 的取值范围是( )A .(-∞,0)B .(0,+∞)C .(-∞,log a 3)D .(log a 3,+∞)5.设y1=40.9,y2=80.48,y3=(12)-1.5,则( )A .y3>y1>y2B .y2>y1>y3C .y1>y2>y3D .y1>y3>y26.圆x 2+y 2-2x +4y -20=0截直线5x -12y +c =0所得的弦长为8,则c 的值是( ) A .10 B .10或-68 C .5或-34 D .-68 7.已知0,0ab bc <<,则直线ax by c +=通过( )A .第一、二、三象限B .第一、二、四象限C .第一、三、四象限D .第二、三、四象限8.正方体ABCD —A 1B 1C 1D 1中,E 、F 分别是AA 1与CC 1的中点,则直线ED 与D 1F 所成角的大小是( )A .15B .13 C .12D 39. 在三棱柱111ABC A B C -中,各棱长相等,侧掕垂直于底面,点D 是侧面11BB C C 的中心,则AD 与平面11BB C C 所成角的大小是 ( )A .30B .45C .60D .9010.如图:直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA 1 和 CC 1上,AP=C 1Q ,则四棱锥B —APQC 的体积为( ) A .2V B .3V C .4V D .5V(10题) 二、填空题(本大题共4小题,每小题5分,共20分)11.函数f (x )=⎩⎪⎨⎪⎧log 12x ,x ≥12x ,x <1的值域为________.12.两圆221x y +=和22(4)()25x y a ++-=相切, 则实数a 的值为13.已知集合U ={2,3,6,8},A ={2,3},B ={2,6,8},则(∁U A )∩B =________.14.过点A (4,0)的直线l 与圆(x -2)2+y 2=1有公共点,则直线l 斜率的取值范围为 三、解答题(本大题共6小题,共80分)15.(本小题满分10分)如图,在三棱柱ABC -A 1B 1C 1中,△ABC 与△A 1B 1C 1都为正三角形且AA 1⊥面ABC ,F 、F 1分别是AC ,A 1C 1的中点.求证:(1)平面AB 1F 1∥平面C 1BF ; (2)平面AB 1F 1⊥平面ACC 1A 1.(17题)16.(本小题满分12分)(1)定义在(-1,1)上的奇函数f (x )为减函数,且f (1-a )+f (1-a 2)>0,求实数a 的取值范围.(2)定义在[-2,2]上的偶函数g (x ),当x ≥0时,g (x )为减函数,若g (1-m )<g (m )成立,求m 的取值范围.17.(本小题满分12分)如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.(1)证明:PQ∥平面ACD;(2)求AD与平面ABE所成角的正弦值(17题)18.(本小题满分15分)已知圆C1:x2+y2-2x-4y+m=0,(1)求实数m的取值范围;(2)若直线l:x+2y-4=0与圆C相交于M、N两点,且OM⊥ON,求m的值。
统编人教版高中必修第一册《全册综合》期末综合检测卷

期末综合检测卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟。
第Ⅰ卷(选择题,共40分)一、选择题(本题共10小题,每小题4分。
在每小题给出的四个选项中,第1~6题只有一项符合题目要求,第7~10题有多项符合题目要求。
全部选对的得4分,选对但不全的得2分,有选错的得0分)1.木星是太阳系八大行星中体积最大、自转最快的行星,木星质量是地球质量的318倍,赤道半径是地球半径的11倍,体积是地球的1316倍,木星公转的轨道半径约为地球的5.2倍,自转一周只需要9小时50分30秒,下列说法正确的是()A.题中“9小时50分30秒”是指时刻B.研究木星自转时可以将木星看成质点C.比较木星、地球运行速度的大小时,应当以太阳系为参考系D.木星公转一周的位移要比地球公转一周的位移大答案 C解析题中“9小时50分30秒”对应一个过程,是指时间间隔,A错误;研究木星自转时,其大小和形状不能忽略,不能看成质点,B错误;木星和地球都围绕太阳运动,则比较木星、地球运行速度的大小时,应当以太阳系为参考系,C正确;木星公转一周和地球公转一周的位移都为零,D错误。
2. 如图,一吊灯通过细绳吊在天花板上保持静止。
其中G为灯受到的重力,F1为细绳对灯的拉力,F2为细绳对天花板的拉力,F3为天花板对细绳的拉力。
则哪一对力属于作用力和反作用力()A.G与F1B.G与F3C.F1与F2D.F2与F3答案 D 解析 G 与F 1是一对平衡力,A 错误;G 与F 3性质不同,不是一对作用力和反作用力,B 错误;F 1与F 2的施力物体相同,不是一对作用力和反作用力,C 错误;F 2与F 3是天花板与细绳间的相互作用力,是一对作用力和反作用力,D 正确。
3. 如图所示为一物体运动的x -t 图像,则( )A .0到4 s 的时间内,该物体的位移为1 mB .0到4 s 的时间内,该物体的位移为2 mC .0到2 s 的时间内平均速度为3 m/sD .0到4 s 的时间内平均速度为4 m/s答案 A解析 由图可知,在0到4 s 的时间内,物体的位移为Δs =s 4-s 0=2 m -1 m=1 m ,则平均速度为v =Δs Δt =14 m/s =0.25 m/s ,A 正确,B 、D 错误;0到2 s的时间内,物体的位移为Δs ′=s 2-s 0=4 m -1 m =3 m ,则平均速度为v ′=Δs ′Δt ′=32m/s =1.5 m/s ,C 错误。
高一物理必修1、2综合测试题(人教版)

高一物理必修一必修二综合测试题一、选择题(本大题共12小题,共44分。
每小题给出的四个选项中,其中1~8只有一个正确选项,每小题3分;9~12有多个选项正确。
全部选对的得5分,选对但不全的得3分,有选错的得0分。
)1.关于能源的说法正确的是:( )A .在利用能源的过程中,能量在总量上逐渐减少B .由于自然界的能量守恒,所以不需要节约能源C .能源耗散说明能量在转化过程中有方向性D .人类在不断地开发和利用新能源,所以能量可以被创造2.汽车紧急刹车后,停止运动的车轮在水平地面上滑动直至停止,在地面上留下的痕迹称为刹车线。
由刹车线的长短可知汽车刹车前的速度。
已知汽车轮胎与地面之间的动摩擦因数为0.80,测得刹车线长25m 。
汽车在刹车前的瞬间的速度大小为(重力加速度g 取10m/s 2):( )A .10m/sB .20m/sC .30m/sD .40m/s3.如图所示为某校学生开展无线电定位“搜狐”比赛,甲、乙两人从O 点同时出发,并同时到达A 点搜到狐狸,两人的搜狐路径已在图中标出,则:( )A .甲的平均速度大于乙的平均速度B .两人运动的平均速度相等C .甲的位移大于乙的位移D .甲的路程大于乙的路程4.以下说法中正确的是:( )A .合力的大小一定大于分力的大小B .合力的大小至少大于一个分力的大小C .合力的大小可以比两个分力都小,也可以比两个分力都大D .若两个分力F 1>F 2,则合力大小的变化范围是F 1>F >F 25.两个物体A 和B ,质量分别为m 1和m 2,互相接触放在光滑的水平面上,如图所示,对物体A 施以水平的推力F ,则物体B 受到A 的作用力等于:( )A .F m m m 211+ B .F m m m 212+ C .F D .F m m 21 6.如图所示,升降机的水平地面上放有重为G 的物体,它受升降机地面的支持力大小为N ,它对升降机地面压力大小为F ,下列说法正确的是:( )A .当升降机正上升时,N >GB .当升降机自由下落时,N =0,G =0C .当物体超重时,升降机的加速度一定向下D .不管升降机怎样运动,总有F =N7.滑雪运动深受人民群众的喜爱,某滑雪运动员(可视为质点)由坡道进入竖直面内的圆弧形滑道AB ,从滑道的A 点滑行到最低点B 的过程中,由于摩擦力的存在,运动员的速率不变,则运动员沿AB 下滑过程中:( )A .所受合外力始终为零B .所受摩擦力大小不变C .合外力做功一定为零D .机械能始终保持不变8.已知地球质量为月球质量的81倍,地球半径约为月球半径的4倍。
高一物理必修1、2综合试题及答案
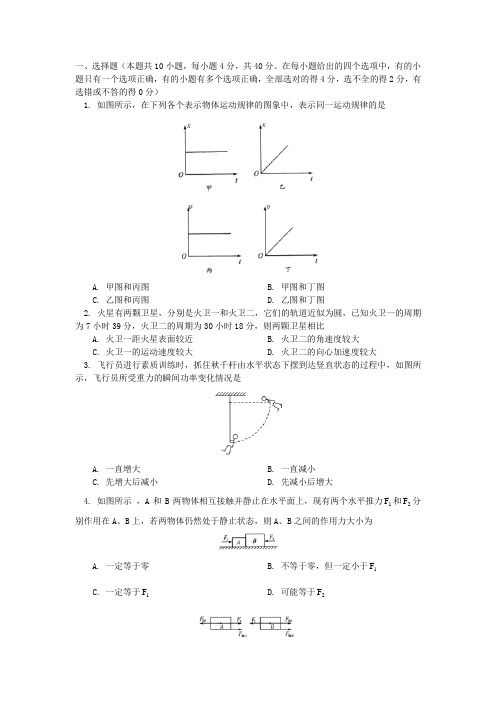
一、选择题(本题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确,全部选对的得4分,选不全的得2分,有选错或不答的得0分)1. 如图所示,在下列各个表示物体运动规律的图象中,表示同一运动规律的是A. 甲图和丙图B. 甲图和丁图C. 乙图和丙图D. 乙图和丁图2. 火星有两颗卫星,分别是火卫一和火卫二,它们的轨道近似为圆,已知火卫一的周期为7小时39分,火卫二的周期为30小时18分,则两颗卫星相比A. 火卫一距火星表面较近B. 火卫二的角速度较大C. 火卫一的运动速度较大D. 火卫二的向心加速度较大3. 飞行员进行素质训练时,抓住秋千杆由水平状态下摆到达竖直状态的过程中,如图所示,飞行员所受重力的瞬间功率变化情况是A. 一直增大B. 一直减小C. 先增大后减小D. 先减小后增大4. 如图所示 ,A 和B 两物体相互接触并静止在水平面上,现有两个水平推力1F 和2F 分别作用在A 、B 上,若两物体仍然处于静止状态,则A 、B 之间的作用力大小为A. 一定等于零B. 不等于零,但一定小于1FC. 一定等于1FD. 可能等于2F5. (经典回放)如图所示,两完全相同的小球质量均为m ,放在竖直挡板和倾角为α的固定斜面间,若缓慢转动挡板至与斜面垂直,此过程中A. A 、B 两球间的弹力逐渐增大B. B 球对挡板的压力逐渐减小C. B 球对斜面的压力逐渐增大D. A 球对斜面的压力逐渐增大6. (经典回放)如图所示,长度相同的三根轻杆构成一个正三角形支架,在A 处固定质量为2m 的小球,B 处固定质量为m 的小球,支架悬挂在O 点,可绕过O 点并与支架所在平面相垂直的固定轴转动,开始时OB 与地面相垂直,放手后开始运动,在不计任何阻力的情况下,下列说法正确的是A. A 球到达最低点时速度为零B. A 球机械能减少量等于B 球机械能增加量C. B 球向左摆动所能达到的最高位置应高于A 球开始运动的高度D. 当支架从左向右回摆时,A 球一定能回到起始高度 7. 对如图所示的皮带传动装置,下列说法中正确的是A. A 轮带动B 轮沿逆时针方向旋转B. B 轮带动A 轮沿逆时针方向旋转C. C 轮带动D 轮沿顺时针方向旋转D. D 轮带动C 轮沿顺时针方向旋转8. 如图所示,在倾角为α的固定光滑斜面上,有一用绳子拴着的长木板,木板上站着一只猫,已知木板的质量是猫的质量的2倍,当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变,则此时木板沿斜面下滑的加速度为A. αsin 2gB. αsin gC. αsin g 23D. αsin g 29. 如图所示,倾斜的传送带保持静止,一木块从顶端以一定的初速度匀加速下滑到底端,如果让传送带沿图中虚线箭头所示的方向匀速运动,同样的木块从顶端以同样的初速度下滑到底端的过程中,与传送带保持静止时相比A. 木块在没到底端的过程中,摩擦力的冲量变大B. 木块在没到底端的过程中,摩擦力的冲量不变C. 木块在没到底端的过程中,木块克服摩擦力所做的功变大D. 木块在没到底端的过程中,系统产生的内能数值将变大 10. 有一星球的密度与地球的密度相同,但它表面处的重力加速度是地球表面上重力加速度的4倍,则该星球的质量是地球质量的A.41B. 4倍C. 16倍D. 64倍二、实验题(本题共2个小题,共14分,把答案填在相应的横线上) 11. (8分)(2006上海高考)科学探究活动通常包括以下环节:提出问题,作出假设,制定计划,搜集证据,评估交流等。
高一数学必修一必修二综合测试题(有答案)

高一数学《必修1》《必修2》综合测试题一、选择题(共12小题;每小题5分,共60分)1. 已知全集R U =,集合}32{≤≤-=x x A ,}41{>-<=x x x B 或,则()B C A U ⋃( )A.{}42≤≤-x xB.}43{≥≤x x x 或C.}12{-<≤-x xD.}31{≤≤-x x2. 过点(1,0)且与直线x -2y -2=0垂直的直线方程是( )A .x -2y -1=0B .x -2y +1=0C .2x +y -2=0D .x +2y -1=03. 圆台的一个底面圆周长是另一个底面圆周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面圆的半径为( )A .3B .5C .6D .74. 已知圆C :x 2:y 2:4y :0,直线l 过点P (0,1),则 ( )A. l 与C 相交B. l 与C 相切C. l 与C 相离D. 以上三个选项均有可能5. 一个几何体的三视图如图所示(单位:m ),则该几何体的体积为( )3mA.π2B.38πC.π3D. 310π6. 已知,则函数的图象不经过( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限7. 若直线2x y -=被圆22()4x a y -+=所截得的弦长为22,则实数a 的值为( ) A. 0或4 B. 1或3 C. 2-或6 D. 1-或3 8. 在三棱柱ABCA 1B 1C 1中,各棱长相等,侧棱垂直于底面,点D 是侧面BB 1C 1C 的中心,则AD 与平面BB 1C 1C 所成角的大小是( ) A .30° B .45° C .60° D .90° 9. 若幂函数)(x f y =是经过点)33,3(,则此函数在定义域上是 ( ) A .偶函数 B .奇函数 C .增函数 D .减函数 10. 一个多面体的三视图如图所示,则该多面体的表面积为 A.321+ B.318+ C.18 D.21 11.若定义在R 上的偶函数()x f 满足)()2(x f x f =+,且当[]1,0∈x 时,x x f y x x f 3log )(,)(-==则函数的零点个数是( ) A .6个 B .4个 C .3个 D .2个 12. 已知A(3,1),B(-1,2),若:ACB 的平分线方程为y =x +1,则AC 所在的直线方程为( ) A .y =2x +4 B .y =12x -3 C .x -2y -1=0 D .3x +y +1=001,1a b <<<-x y a b =+二、填空题(共4小题,每小题5分,共20分)13. 若直线1x y +=与圆222(0)x y r r +=>相切,则实数r 的值等于________.14. 在平面直角坐标系中,正三角形ABC 的边BC 所在直线的斜率是0,则AC ,AB 所在直线的斜率之和为________.15. 函数ax x y 22--=()10≤≤x 的最大值是2a ,则实数a 的取值范围是________ .16.若圆C :x 2+y 2−2ax +b =0上存在两个不同的点A ,B 关于直线x −3y −2=0对称,其中b ∈N ,则圆C 的面积最大时,b = .三、解答题(共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17. (10分)已知f (x )是定义在R 上的奇函数,当x ≥0时,f (x )=2x -1.(1)求f (3)+f (-1);(2)求f (x )的解析式.18. (12分)如图,在三棱锥P ABC 中,PC ⊥底面ABC ,AB ⊥BC ,D ,E 分别是AB ,PB 的中点.(1)求证:DE ∥平面PAC ;(2)求证:AB ⊥PB .19.(12分)直线l 1过点A (0,1),l 2过点B (5,0),如果l 1∥l 2且l 1与l 2的距离为5,求l 1,l 2的方程. 20.(12分)已知圆22:2240C x y mx ny ++++=,直线:10l x my -+=相交于A :B 两点. :1)若交点为(1,2)A ,求m 及n 的值. :2)若直线l 过点(2,3):60ACB ∠=︒,求22m n +的值. 21.(12分)已知直线:(1)(23)60m a x a y a -++-+=,:230n x y -+=. (1)当0a =时,直线l 过m 与n 的交点,且它在两坐标轴上的截距相反,求直线l 的方程; (2)若坐标原点O 到直线m 的距离为5,判断m 与n 的位置关系. 22.(12分)(1)圆C 与直线2x +y -5=0切于点(2,1),且与直线2x +y +15=0也相切,求圆C 的方程. (2)已知圆C 和y 轴相切,圆心C 在直线x -3y =0上,且被直线y =x 截得的弦长为27,求圆C 的方程.高一数学答案一、选择题(共12小题;每小题5分,共60分). 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A C D A B A A C D A B C二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上13.22 14.0 15.[-1,0] 16.0三、解答题(本大题共6小题,共70分)17.解:(1)∵f (x )是奇函数,∴f (3)+f (-1)=f (3)-f (1)=23-1-2+1=6. .................4分(2)设x <0,则-x >0,∴f (-x )=2-x -1,∵f (x )为奇函数,∴f (x )=-f (-x )=-2-x +1,.................8分∴f (x )=⎩⎪⎨⎪⎧ 2x -1,x ≥0,-2-x +1,x <0. ........................10分18. 解 (1)证明:因为D ,E 分别是AB ,PB 的中点,所以DE ∥PA.又因为PA ⊂平面PAC ,DE ⊄平面PAC ,所以DE ∥平面PAC. .................6分(2)证明:因为PC ⊥底面ABC ,AB ⊂底面ABC ,所以PC ⊥AB.又因为AB ⊥BC ,PC ∩BC =C ,所以AB ⊥平面PBC ,又因为PB ⊂平面PBC ,所以AB ⊥PB. .................6分19.解: 若直线l 1,l 2的斜率都不存在,则l 1的方程为x =0,l 2的方程为x =5,此时l 1,l 2之间距离为5,符合题意;.................3分若l 1,l 2的斜率均存在,设直线的斜率为k ,由斜截式方程得直线l 1的方程为y =kx +1,即kx -y +1=0,.................6分由点斜式可得直线l 2的方程为y =k (x -5),即kx -y -5k =0,在直线l 1上取点A (0,1),则点A 到直线l 2的距离d =|1+5k |1+k2=5,∴25k 2+10k +1=25k 2+25,∴k =125. ∴l 1的方程为12x -5y +5=0,l 2的方程为12x -5y -60=0. .................10分 综上知,满足条件的直线方程为l 1:x =0,l 2:x =5或l 1:12x -5y +5=0,l 2:12x -5y -60=0. .......12分20.【解析】试题分析:(1)将点()1,2A 代入直线和圆方程,可解得1m =,114n =-. (2)将点()2,3代入直线方程得1m =.又由已知可判断ACB V 是等边三角形.所以有圆心到直线10x y -+=的距离233322d r n ==-,代入解得29n =,从而2210m n +=. 试题解析::1)将点()1,2A 代入直线10x my -+=:∴1210m -+=,解出1m =:再将()1,2A 代入圆2221240x y x ny ++⨯++=: ∴22122440n ++++=,解得114n =-: ∴1m =:114n =-: :2)将点()2,3代入直线10x my -+=:∴2310m -+=,解出1m =:又∵在ACB V 中,CA CB =且60ACB ∠=︒:∴ACB V 是等边三角形.∵圆()()222221230x x y ny nn ++++++-=: 即()()22213x y n n +++=-:圆心()1,n --,半径23r n =-:其中圆心到直线10x y -+=的距离222113332211n d r n -++===-+: 代入解出29n =:∴2210m n +=:21.(12分)【详解】试题分析:(1)联立360230.x y x y -++=⎧⎨-+=⎩,解得m 与n 的交点为(-21,-9),当直线l 过原点时,直线l 的方程为370x y -=;当直线l 不过原点时,设l 的方程为1x y b b+=-,将(-21,-9)代入得12b =-,解得所求直线方程(2)设原点O 到直线m 的距离为d ,则()()2265123a d a a -+==-++,解得:14a =-或73a =-,分情况根据斜率关系判断两直线的位置关系;试题解析:解:(1)联立360230.x y x y -++=⎧⎨-+=⎩,解得21,9,x y =-⎧⎨=-⎩即m 与n 的交点为(-21,-9). 当直线l 过原点时,直线l 的方程为370x y -=;当直线l 不过原点时,设l 的方程为1x y b b+=-,将(-21,-9)代入得12b =-, 所以直线l 的方程为120x y -+=,故满足条件的直线l 方程为370x y -=或120x y -+=.(2)设原点O 到直线m 的距离为d ,则()()2265123a d a a -+==-++,解得:14a =-或73a =-, 当14a =-时,直线m 的方程为250x y --=,此时//m n ; 当73a =-时,直线m 的方程为250x y +-=,此时m n ⊥.22.解: (1)设圆C 的方程为(x -a )2+(y -b )2=r 2.∵两切线2x +y -5=0与2x +y +15=0平行,∴2r =|15-(-5)|22+12=45,∴r =25, ∴|2a +b +15|22+1=r =25,即|2a +b +15|=10①|2a +b -5|22+1=r =25,即|2a +b -5|=10② 又∵过圆心和切点的直线与过切点的切线垂直,∴b -1a -2=12③ 由①②③解得⎩⎨⎧ a =-2,b =-1.∴所求圆C 的方程为(x +2)2+(y +1)2=20.(2)设圆心坐标为(3m ,m ).∵圆C 和y 轴相切,得圆的半径为3|m |,∴圆心到直线y =x 的距离为|2m |2=2|m |.由半径、弦心距、半弦长的关系得9m 2=7+2m 2,∴m =±1,∴所求圆C 的方程为(x -3)2+(y -1)2=9或(x +3)2+(y +1)2=9.。
高中数学必修1、2、3、4、5综合试卷及答案详解(优秀经典测试卷)

XXX 中学数学必修1-5测试卷一、选择题(共12个,每个5分,共60分)1.若集合A={1,3,x},B={1,2x },A ∪B={1,3,x}则满足条件的实数x 的个数有( ) (A ) 1个 (B ) 2个 (C )3个 (D ) 4个2.若函数y=f (x )的定义域是[2,4],则y=f (12log x )的定义域是( )(A ) [12,1] (B ) [4,16] (C )[116,14] (D )[2,4 ] 3.设偶函数f (x )的定义域为R ,当[0,)x ∈+∞时f (x )是增函数,则(2),(),(3)f f f π--的大小关系是( )(A )()f π>(3)f ->(2)f - (B )()f π>(2)f ->(3)f - (C )()f π<(3)f -<(2)f - (D )()f π<(2)f -<(3)f - 4.0.7log 0.8a =, 1.1log 0.9b =,0.91.1c =,那么( )(A )a <b <c (B )a <c <b (C )b <a <c (D )c <a <b 5、已知点(1,2),(3,1)A B ,则线段AB 的垂直平分线的方程是( ) A .524=+y x B .524=-y x C .52=+y x D .52=-y x6、 两直线330x y +-=与610x my ++=平行,则它们之间的距离为( ) A .4 B .21313 C .51326 D .710207.直线3x-4y-4=0被圆(x-3)2+y 2=9截得的弦长为( )(A)22(B)4 (C)24(D)28、a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b ;②若b ⊂M ,a ∥b ,则a ∥M ;③若a ⊥c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b .其中正确命题的个数有( )A 、0个B 、1个C 、2个D 、3个 9.如图是计算12+14+16+…+120的值的一个程序框图,其中在判断框中应填入的条件是( )A .i <10B .i>10C .i <20D .i >20 10.若P (A ∪B )=1,则事件A 与B 的关系是( )A .A 、B 是互斥事件 B .A 、B 是对立事件C .A 、B 不是互斥事件D .以上都不对11.、在等比数列{}n a 中,117a a ⋅=6,144a a +=5,则1020a a 等于( ) A .32B .23 C .23或32 D .﹣32或﹣2312、△ABC 中,已知()()a b c b c a bc +++-=,则A 的度数等于( )A .120B .60C .150D .30 二.填空题(共4个,每个5分,共20分)13.数列{}n a 的前n 项和*23()n n s a n N =-∈,则5a =14、设变量x 、y 满足约束条件⎪⎩⎪⎨⎧≥+-≥-≤-1122y x y x y x ,则y x z 32+=的最大值为15.已知函数()sin()cos()f x x x =+θ++θ是偶函数,且[0,]2πθ∈,则θ的值为 .16.下面有五个命题:①函数y =sin 4x -cos 4x 的最小正周期是π. ②终边在y 轴上的角的集合是{a |a =,2k k Z π∈}. ③在同一坐标系中,函数y =sin x 的图象和函数y =x 的图象有三个公共点. ④把函数3sin(2)3y x π=+的图像向右平移6π得到3sin 2y x =的图像.⑤函数sin()2y x π=-在[0]π,上是单调递减的.其中真命题的序号是 . 三、解答题(共6题,总分70分 17.已知函数213()cos sin cos 1,22f x x x x x R =++∈.(1)求函数()f x 的最小正周期;(2)求函数()f x 在[,]124ππ上的最大值和最小值,并求函数取得最大值和最小值时的自变量x 的值.18.数列{}n a 的前n 项和为n S ,23n n S a n =-(*n N ∈).(Ⅰ)证明数列{3}n a +是等比数列,求出数列{}n a 的通项公式; (Ⅱ)设3n n nb a =,求数列{}n b 的前n 项和n T ;19、△ABC 中,c b a ,,是A ,B ,C 所对的边,S 是该三角形的面积,且cos cos 2B bC a c=-+ (1)求∠B 的大小; (2)若a =4,35=S ,求b 的值。
高中数学必修一和必修二综合测试及参考答案A

高中数学必修一和必修二综合测试A考号 班级 姓名一、选择题(每小题5分,共10小题,共50分)1、设集合{}(,)1A x y y ax ==+,{}(,)B x y y x b ==+,且{}(2,5)AB =,则:( )A .3,2a b ==B .2,3a b ==C .3,2a b =-=-D .2,3a b =-=-2、对于一个底边在x 轴上的三角形,采用斜二测画法作出其直观图,其直观图的面积是原三角形面积的:( )A. 2倍B.倍C. 倍D. 12倍 3. 已知函数2log (0)()3(0)x x x f x x >⎧=⎨≤⎩,则1[()]4f f 的值是( )A. 8B.18C. 9D. 194. 设1,01,x y a >><<则下列关系正确的是:( )A. a ay x--> B. ay ax < C. y x a a < D. y x a a log log >5. 函数()23x f x =-的零点所在区间为:( )A . (-1,0) B. (0,1) C. (1,2) D. (2,3)6. 函数()f x 的定义域为(,)a b ,且对其内任意实数12,x x 均有:1212()[()()]0x x f x f x --<,则()f x 在(,)a b 上是:( ) A. 增函数 B. 减函数 C. 奇函数 D. 偶函数x 7. 在x 轴上的截距为2且倾斜角为135°的直线方程为:( )A. y=-x+2 B. y=-x-2 C. y=x+2 D. y=x-28. 设点M 是Z 轴上一点,且点M 到A (1,0,2)与点B (1,-3,1)的距离相等,则点M 的坐标是:( ) A .(-3,-3,0) B .(0,0,-3) C .(0,-3,-3) D .(0,0,3)9. 如图所示,阴影部分的面积S 是h (0)h H ≤≤的函数. 则该函数的图象是:( )10. 将直线:210l x y +-=向左平移3个单位,再向上平移2个单位得到直线l ',则直线l l '与之间的距离为:( )ABC .15 D .75二、填空题(每小题6分,共5个小题,共30分)11、如图,在多面体ABCDEF 中,已知面ABCD 是边长为3的正方形,EF ∥AB ,EF =32,EF 与面AC 的距离为2,则该多面体的体积是_______ 12、若定义在区间(1,2)内的函数)1(log )(3-=x x f a 满足0)(>x f ,则a 的取值范围是 ;13、已知镭经过100年,质量便比原来减少4.24%,设质量为1的镭经过x 年后的剩留量为y,则()y f x =的函数解析式为 . 14、已知l ⊥α,m ⊂β,则下面四个命题:①α∥β则l ⊥m ②α⊥β则l ∥m ③l ∥m 则α⊥β ④l ⊥m 则α∥β 其中正确的是___ _____15、在圆 224x y +=上,与直线4x +3y -12=0的距离最小的点的坐标 .三、解答题 16(14分).(1)、求经过直线17810l x y --=:和221790l x y ++=:的交点,且垂直于直线270x y -+=的直线方程.(2)、直线l 经过点(5,5)P ,且和圆C :2225x y +=相交,截得弦长为l 的方程.17(14分).某飞机制造公司一年中最多可生产某种型号的飞机100架。
高一必修一第一、二、三单元综合练习

一、选择题1.现有一瓶物质甲和乙的混合物,已知甲和乙的某些性质如下表。
据此,将甲和乙互相分离的最佳方法是( )A .萃取法B .升华法C .蒸馏法D .分液法2、水资源非常重要,联合国确定2003年为国际淡水年。
海水淡化是海岛地区提供淡水的重要手段,所谓海水淡化是指除去海水中的盐分以获得淡水的工艺过程(又称海水脱盐),其方法较多,如反渗透法、水合物法、电渗透法、离子交换法和压渗法等。
下列方法中也可以用来进行海水淡化的是A .过滤法B .蒸馏法C .分液法D .冰冻法3. 有关化学实验的下列操作中,一般情况下不能相互接触的是 ( )A .过滤操作中,玻璃棒与三层滤纸B .过滤操作中,漏斗径与烧杯内壁C .分液操作中,分液漏斗径与烧杯内壁D .用胶头滴管向试管滴液体时,滴管尖端与试管内壁4.海水是十分重要的资源。
不需要化学方法就能从海水中获得的物质有( )A .氯、溴、碘B .食盐、淡水C 烧碱、氢气D 钠、镁、铝5.下列实验中,溶液颜色不会发生变化的是( )A .2CL 通入NaOH 溶液中B .碘酒滴入淀粉溶液C .2SO 通入4/KMnO H +溶液中D .2SO 通入品红溶液6.要除去3FeCL 溶液中的少量氯化亚铁,可行的办法是( )A .滴人KSCN 溶液B .加入氯水C .加入铜粉 D.加人铁粉7.离子方程式书写错误的是( )A .硫酸溶液与氢氧化钡溶液混合:2244aB SO BaSO -++=↓B .石灰石溶于盐酸中:32222CaCO H Ca CO H O ++=+↑+C. 碳酸氢钠溶液与硝酸反应:322HCO H H O CO -++=+↑ D .氧化铁与稀硫酸反应:3232623Fe O H Fe H O+++=+8.导致下列现象的主要原因与排放2SO :有关的是( ) A .酸雨 B .臭氧层空洞 C .温室效应 D .水体富营养化10.除去下列溶液中的杂质(括号内是杂质)所用试剂正确的是( ) 物质 分子式 熔点/℃ 沸点/℃ 密度/ g·cm -3 水中 溶解性 甲 C 3H 6O 2 -98 57.5 0.93 可溶 乙 C 4H 8O 2 -84 77 0.90可溶A .NaOH 溶液2(())Ba OH :用24K SO 溶液B .NaCl 溶液24()Na SO :用32()Ba NO 溶液C .KOH 溶液23()K CO :用2CaCl 溶液D .3HNO 溶液()HCl :用3AgNO 溶液11、 实验室中要配制2mol/L 的NaCl 溶液980 ml ,配制时应选用的容量瓶的规格和称取的NaCl 的质量分别是( )A . 980 ml ,114.7gB . 500ml, 58.5gC .1000 ml , 117 gD .1000ml, 117.0g12.能够用来鉴别BaCl 2 、 NaCl 、 Na 2CO 3三种物质的试剂是 ( )A .AgNO 3溶液B .稀盐酸C .稀硫酸D .稀硝酸13. 在强酸性溶液中能大量共存,且溶液为无色透明的离子组( )A. K +、Na +、AlO 2-、NO 3-B. NH 4+、Al 3+、NO 3-、SO 42-C. K +、NH 4+、NO 3-、I -D. K +、Na +、NO 3-、HSO 3。
高一综合试题及答案

高一综合试题及答案一、单项选择题(每题2分,共20分)1. 以下哪个选项是正确的?A. 地球是宇宙的中心B. 地球是太阳系的一部分C. 太阳是宇宙的中心D. 月球是地球的一部分答案:B2. 以下哪个选项是化学元素周期表中的金属元素?A. 氢(H)B. 氧(O)C. 钠(Na)D. 碳(C)答案:C3. 以下哪个选项是正确的物理公式?A. 速度 = 距离 / 时间B. 速度 = 距离 ×时间C. 加速度 = 速度 / 时间D. 加速度 = 速度 ×时间答案:A4. 以下哪个选项是正确的生物分类?A. 动物界、植物界、微生物界B. 动物界、植物界、真菌界C. 动物界、植物界、细菌界D. 动物界、植物界、病毒界答案:B5. 以下哪个选项是正确的历史事件?A. 秦始皇统一六国B. 汉武帝开疆拓土C. 唐太宗开创贞观之治D. 宋太祖建立宋朝答案:A6. 以下哪个选项是正确的地理现象?A. 地球自转导致昼夜更替B. 地球公转导致四季变化C. 月球公转导致潮汐现象D. 太阳活动导致极光现象答案:A7. 以下哪个选项是正确的数学公式?A. 勾股定理:a² + b² = c²B. 勾股定理:a² - b² = c²C. 勾股定理:a² × b² = c²D. 勾股定理:a² ÷ b² = c²答案:A8. 以下哪个选项是正确的英语语法规则?A. 主语 + 谓语 + 宾语B. 主语 + 宾语 + 谓语C. 谓语 + 主语 + 宾语D. 宾语 + 谓语 + 主语答案:A9. 以下哪个选项是正确的计算机术语?A. 硬件是指计算机的物理组件B. 软件是指计算机的操作系统C. 硬件是指计算机的操作系统D. 软件是指计算机的物理组件答案:A10. 以下哪个选项是正确的艺术流派?A. 文艺复兴 - 印象派B. 巴洛克 - 表现主义C. 古典主义 - 浪漫主义D. 印象派 - 立体主义答案:C二、填空题(每题2分,共20分)11. 请填写中国历史上的四大发明:________、________、________、________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一综合试题一
一.选择题:
1.已知集合2{|3},{|log 1}M x x N x x =<=>,则M N 等于
( )
A.φ
B.}321
|
{<<x x C.}30|{<<x x D.{|23}x x <<若集合M={x||x|<1},
2.函数⎪⎩⎪⎨⎧≥-<=)
0(12)
0(2
x x x
y x 的图象大致是 ( )
3.右边程序运行的结果 ( ) A.1,2,3 B.2,3,1 C.2,3,2 D.3,2,1
4.已知f(2x+1)是偶函数,则函数f(2x)图像的对称轴为( )。
A 、x=1 B 、21=x C 、2
1
-=x D 、x=-1 5.已知函数()()2
111f x x x =
<--,则113f -⎛⎫- ⎪⎝⎭
的值是( ). A .2 B .-3 C .-2 D .3 6.下列抽样中不是系统抽样的是( )
A.从标有1~15号的15个小球中任选3个作为样本,按从小号到大号排序,随机确定起点i,以后为i+5, i+10 (超过 15则从1再数起)号入样
B.搞某一市场调查,规定在商场门口随机抽一个人进行询问,直到调查到事先规定的调查人数为止
C.电影院调查观众的某一指标,通知每排(每排人数相等)座位号为14的观众留下来座谈。
D.工厂生产的产品,用传关带将产品送入包装车间前,检验人员从传送带上每隔五分钟抽一件产品检验 7.x, y 满足等式(x-2)2+y 2=3,那么x
y
的最大值是( )。
A.
33 B 2
3
C.3
D.21
8.若直线4x-3y-2=0与圆x 2+y 2-2ax+4y+a 2-12=0有两个不同的公共点,则实数a 的取值范围( )。
A.-3<a<7
B.-6<a<4
C.-7<a<3
D.-21<a<19 9.函数2
()2x
f x a x
=-
-的一个零点在区间(1,2)内,则实数a 的取值范围是( ) A.(1,3) B.(1,2) C.(0,3) D.(0,2)
10.设长方体的三条棱长分别为a.b.c,若长方体的所有棱的长度之和为24,一条对角线长为5,体积为2, 则c
b a 1
11++= ( ) A. 411 B.114 C.211 D.11
2
二.填空题:
11.某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆,为检验该公司的产品质量,现用分层抽样
的方法抽取46辆进行检验,这三种型号的轿车依次应该抽取_______辆,_______辆,_______辆。
12.三个数72,120,168的最大公约数是 。
13.知函数)56(log )(22
1+-=x x x f ,函数的单调递减区间是
14.α,β表示平面,a,b 表示不在α内也不在β内的两条直线,出下列四个论断:①a//b ②α//β;③a ⊥β;④b ⊥a,以其
中三个论断作为条件,下一个作为结论,以构造一些命题,出你认为正确的一个命题_______。
15.已知函数f(x)=-x 3+ax 在区间(-1,1)上是增函数,实数a 的取值范围是_____。
16.直线10x my --=与圆22(1)(2)4x y -+-=相交于A B 两点,AB 的长为m 的值是 . 17. (万元)与机器运转时间x (年数x *
∈N )的关系为2
18y x x =-+- 则当每台机器运转 年时平均利润最大, 最大值是 万元. 18.某几何体的三视图如图所示,则这个几何体的体积是 .
三解答题 :
19 .如图:四棱锥S ABCD -中,SAD ⊥平面ABCD ,四边形ABCD 为正方形,(Ⅰ)求证:CD ⊥平面SAD ; (Ⅱ)求证://PQ 平面SCD ;
(Ⅲ)若SA SD =,M 为BC 中点,在棱SC 上是否存在点N ,使得平面DMN ⊥平面ABCD ,并证明你的结论.
20.对于函数f(x)=ax 2+(b+1)x+b-2(a ≠0),若存在实数x 0,使f(x 0)=x 0 成立,则称x 0为f(x)的不动点. (1)当a=2,b=-2时,求f(x)的不动点;
(2)若对于任何实数b ,函数f(x)恒有两相异的不动点,求实数a 的取值范围;
(3)在(2)的条件下,若y =f(x)的图象上A.B 两点的横坐标是函数f(x)的不动点,且直线1
212++=a kx y 是线段AB
的垂直平分线.求实数b 的取值范围.
1—5:DBCBC 6---10BCBCA
11.6,30,10; 12.24; 13.),5(+∞ 14. 1.2.4⇒3 ,1.2.3⇒4; 15.3≥a ; 16.3
3
±
; 17.5,8 ; 18.33. 19.N 为SD 的中点; 20.(1)-1.2;(2)10<<a ;(3))0,4
2(-
M
S
D C
A
P Q
·。
