大学物理实验之声光效应
实验一 声光效应实验

实验 声光效应实验【学史背景】声光效应就是指光通过某一受到超声波扰动的介质时发生衍射的现象,这种现象就是光波与介质中声波相互作用的结果。
早在本世纪30年代就开始了声光衍射的实验研究。
60年代激光器的问世为声光现象的研究提供了理想的光源,促进了声光效应理论与应用研究的迅速发展。
声光效应为控制激光束的频率、方向与强度提供了一个有效的手段。
利用声光效应制成的声光器件,如声光调制器、声光偏转器、与可调谐滤光器等,在激光技术、光信号处理与集成光通讯技术等方面有着重要的应用。
【实验目的】1.掌握声光效应的原理与实验规律;2.了解喇曼-纳斯衍射与布喇格衍射的实验条件与特点;3.测量不同激光(红光、蓝光、绿光)与红外线通过声光晶体发生布拉格衍射后的衍射角。
【实验原理】当超声波在介质中传播时,将引起介质的弹性应变作时间与空间上的周期性的变化,并且导致介质的折射率也发生相应变化。
当光束通过有超声波的介质后就会产生衍射现象,这就就是声光效应。
有超声波传播的介质如同一个相位光栅。
声光效应有正常声光效应与反常声光效应之分。
在各项同性介质中,声-光相互作用不导致入射光偏振状态的变化,产生正常声光效应。
在各项异性介质中,声-光相互作用可能导致入射光偏振状态的变化,产生反常声光效应。
反常声光效应就是制造高性能声光偏转器与可调滤波器的基础。
正常声光效应可用喇曼-纳斯的光栅假设作出解释,而反常声光效应不能用光栅假设作出说明。
在非线性光学中,利用参量相互作用理论,可建立起声-光相互作用的统一理论,并且运用动量匹配与失配等概念对正常与反常声光效应都可作出解释。
本实验只涉及到各项同性介质中的正常声光效应。
图1 声光衍射设声光介质中的超声行波就是沿y 方向传播的平面纵波,其角频率为s w ,波长为s λ波矢为s k 。
入射光为沿x 方向传播的平面波,其角频率为w ,在介质中的波长为λ,波矢为k 。
介质内的弹性应变也以行波形式随声波一起传播。
声光效应实验实验报告

声光效应的研究班级:应物21班姓名:许达学号:2120903018光通过某一受到超声波扰动的介质时,会发生衍射现象,这种现象称为声光效应。
利用声光效应可以制成的声光器件,如声光调制器、声光偏转器和谐调滤光器等。
声光效应还可用于控制激光束的频率、方向和强度等方面。
在激光技术、光信号处理和集成光通讯技术等方面有着重要的应用。
一、实验目的1.了解声光效应的原理;2.测量声光器件的衍射效率和带宽及对光偏转的研究;3.利用声光效应测量声波在介质中的传播速度。
二、实验仪器He-Ne激光电源,声光器件,CCD光强分布测量仪,高频功率信号源,示波器,频率计。
三、实验原理当超声波在介质中传播时,将引起介质的弹性应变,这种应变在时间上和空间上是周期性的变化,并且导致介质的折射率也发生相应的变化。
当光束通过有超声波的介质后就会产生衍射现象,这就是声光效应。
有超声波传播的介质如同一个相位光栅。
光被弹性声波衍射有二种类型,当超声波频率较高时,产生布拉格(Bragg )型衍射;当超声波频率较低时,产生喇曼―奈斯(Raman-Nath )型衍射。
Bragg 衍射相当于体光栅情况,而Raman-Nath 衍射相当于薄光栅情况。
两种光栅情况如图1所示。
由于光波速度远大于声波速度约105倍,所以在光波通过介质的时间内,介质在空间上的周期变化可看成是固定的。
对于Bragg 衍射,当声光的距离满足λλ22s L >,而且入射光束相对于超声波波面以θ角斜入射时,入射光满足Bragg 条件)1(sin 2ns λθλ=式中λ为光波的波长,s λ为声波的波长,固体介质的折射率为n 。
Bragg 衍射只存在1级的衍射光。
当声波为声行波时,只有+1级或-1级衍射光,如图2所示。
当声波为声驻波时,±1级衍射光同时存在,而且衍射效率极高。
只要超声功率足够高,Bragg 衍射效率可达到100%。
所以实用的声光器件一般都采用Bragg 衍射。
物理实验报告_声光效应与光拍法测光的速度

物理实验报告_声光效应与光拍法测光的速度实验目的:1. 了解声光效应的基本现象和原理;2. 学习用声光效应测量超短时间间隔的方法;3. 了解光的速度的测量方法;4. 学会用光拍法测量光的速度。
实验原理:1. 声光效应的基本原理:当一个物体以比声速更大的速度运动时,在其前进方向上会产生压力波,即激发出横波和纵波,这种现象称为激波。
激波是一种能量传递和物质传递的物理现象。
当激波遇见某些物体的表面时,会激起产生物体振动,这种现象就是声光效应。
2. 声光效应的应用:利用声光效应可以测量微小时间间隔。
由于声音在空气中的速度与温度、湿度等因素有关,因此不能用来精确地测量时间。
但是,由于光速恒定,因此可以用声光效应来测量超短时间间隔,这是一种精度较高的方法。
3. 光速的测量方法:利用光的折射现象可以测定光的速度。
测定光速的最简单方法是将一束光射入水中,用透明的圆柱形容器将光束引向垂直于水面的黑色标线上,然后根据圆柱形容器的内径和水的折射率计算光速。
4. 光拍法的原理:利用光拍法可以测量光的速度。
该方法需要两个发光源,并将它们放置在一定的距离上,在一定的时间间隔内,它们向着一个目标射出光束。
当两束光到达目标后,它们会在目标上产生一些互相干涉的条纹,利用条纹的位置与时间间隔,可以计算出光的速度。
实验器材:1. 放大声光放置装置;2. 铝制矩形试样;3. 随时器;4. 透明的圆柱形容器;5. 黑色标线;6. 电子扫描显微镜;7. 两个发光源;8. 两个光学棒;9. 相机和三脚架。
实验步骤和记录:1. 将铝制矩形试样置于放大声光放置装置上,滑动可调节的小轮,使得矩形试样以高速运动。
2. 打开随时器,开始计时,当矩形试样运动到一定位置时,触发放大声光放置装置,使其发生声光效应并记录时间。
3. 重复以上步骤,记录多组数据,并计算平均值。
4. 将透明的圆柱形容器注满水,并将光束引向垂直于水面的黑色标线上,记录圆柱形容器的内径和水的折射率。
声光效应实验报告

声光效应实验报告布拉格衍射与喇曼拉斯衍射比较布拉格衍射实验条件:光速斜入射,声光作用距离满足L<λ2s/2λ,其中L为介质的厚度,λs为介质中超声波的波长,λ为入射光在介质中的波长。
特点:只有当入射光方向满足一定条件时,才有显著的声光衍射;除0级光外,衍射光或者只有+1级或者只有-1级;衍射光效率η很高,可高达100%。
喇曼拉斯衍射实验条件:光束相对于超声波波面以某一角度入射,且其作用距离满足L>λ2s/2λ特点:对入射光方向无严格要求,一般取垂直入射;除0级光外,衍射光有许多级且呈对称分布,一级衍射光最大衍射效率为34%,高级衍射光衍射效率更低。
喇曼拉斯衍射实验现象如下图:测布拉格衍射偏转角Φ与超声波频率f s关系曲线,计算声速光敏元数=2700位光敏元尺寸=11μm×11μm 光敏元线阵有效长=29.7mm 定标:光敏元件有效长度对应示波器上8格计算公式:ssss0 sBf v ni2λλλλλ==≈=Φ次数0级光与1级光的偏转距离(mm)L(mm)Φ(m)f s(MHz)V s(m/s)1 1.46/8*29.7=5.420 243.7 272.422464/0.0222485.00 10412 1.50/8*29.7=5.569 243.7 272.422464/0.0228590.00 10733 1.64/8*29.7=6.088 243.7 272.422464/0.02498 95.00 10364 1.70/8*29.7=6.311 243.7 272.422464/0.02590100.00 10525 1.78/8*29.7=6.608 243.7 272.422464/0.02712105.00 10556 1.88/8*29.7=6.980 243.7 272.422464/0.02864110.00 10467 1.98/8*29.7=7.350 243.7 272.422464/0.03016115.00 10398 2.06/8*29.7=7.648 243.7 272.422464/0.03138120.00 1042注:L是声光介质的光出射面到CCD线阵光敏面的距离。
声光效应 物理实验报告

声光效应实验研究介质中传播的超声波会造成介质的局部压缩和伸长。
由于弹性应变而使介质的折射率或介电常数发生改变,当光通过介质时就会发生衍射现象,称之为声光效应。
由于声光效应,衍射光的强度、频率、方向等都随着超声波场而变化。
其中衍射光偏转角随超声波频率变化的现象称为声光偏转;衍射光强度随超声波功率变化的现象称为声光调制。
早在19世纪30年代就开始了声光衍射的实验研究。
60年代激光器的问世为声光现象的研究提供了理想的光源,促进了声光效应理论和应用研究的迅速发展。
声光效应为控制激光束的频率、方向和强度提供了一个有效的手段。
利用声光效应制成的声光器件,如声光调制器、声光偏转器、和可调谐滤光器等,在激光技术、光信号处理和集成光通讯技术等方面有着重要的应用。
【实验目的】1.了解声光相互作用的原理。
2.了解喇曼-纳斯衍射和布喇格衍射的实验条件和特点。
3.通过对声光器件衍射效率、中心频率和带宽的测量加深对其概念的理解4.测量声光偏转和声光调制曲线。
【实验仪器】SO2000声光效应实验仪【实验原理】当超声波在介质中传播时,将引起介质的弹性应变作时间和空间上的周期性的变化,并且导致介质的折射率也发生相应变化。
当光束通过有超声波的介质后就会产生衍射现象,这就是声光效应。
有超声波传播的介质如同一个相位光栅。
声光效应有正常声光效应和反常声光效应之分。
在各项同性介质中,声-光相互作用不导致入射光偏振状态的变化,产生正常声光效应。
在各项异性介质中,声-光相互作用可能导致入射光偏振状态的变化,产生反常声光效应。
反常声光效应是制造高性能声光偏转器和可调滤波器的基础。
正常声光效应可用喇曼-纳斯的光栅假设作出解释,而反常声光效应不能用光栅假设作出说明。
在非线性光学中,利用参量相互作用理论,可建立起声-光相互作用的统一理论,并且运用动量匹配和失配等概念对正常和反常声光效应都可作出解释。
本实验只涉及到各项同性介质中的正常声光效应。
设声光介质中的超声行波是沿y方向传播的平面纵波,其角频率为ωs ,波长为λs波矢为ks。
声光效应

声光效应实 验者:杨亿斌(06325107) 合作者:吴聪(06325096)(中山大学物理系,光信息科学与技术06级3班)2008年12月31日[实验目的]1、理解声光效应的原理,了解Ramam -Nath 衍射和Bragg 衍射的分别2、测量声光器件的衍射效率和带宽等参数,加深对概念的理解。
3、测量声光偏转的声光调制曲线。
4、模拟激光通讯。
[实验原理](一)声光效应的物理本质――光弹效应介质的光学性质通常用折射率椭球方程:1ij j j x y η= (1)描述。
介质中存在声场,介质内部就受到应力,发生声应变,从而引起介质光学性质发生变化,这种变化反映在介质光折射率的或者折射率椭球方程系数的变化上。
在一级近似下,有 : ij ijkl kl P S η∆= (2)这就是著名的Pockels 效应。
为简单起见,这里只考虑各个相同性介质中声纵波的情况,这样折射率n 和光弹系数P 都可以看作常量。
有,21()PS nη∆=∆= 应变0sin()S S kx t =-Ω表示在x 方向传播的声应变波,S 0是应变的幅值,/s k v =Ω是介质中的声波数,2f πΩ=为角频率,v s 为介质中声速,/s v f Λ=为声波场。
P 表示单位应变所应起的2(1/)n 的变化,为光弹系数。
得301sin()sin()2n n PS kx t kx t μ∆=-Ω=-Ω于是()sin()n x n n n kx t μ=+∆=+-Ω其中3012n PS μ=是“声致折射率变化”的幅值。
考虑如图一的情况,压电换能器将驱动信号U (t )转换成声信号,入射平面波与声波在介质中(共面)相遇,当光通过线度为l 的声光互作用介质时,其相位改变为:000()()sin()x n x k l k l kx t φφμ∆==∆+-Ω (7) 其中002/k πλ=为真空中光波数,0λ是真空中的光波长,00nk l ∆Φ=为光通过不存在超声波的介质后的位相滞后,项()0sin k l kx t μ-Ω为由于介质中存在超声波而引起的光的附加位相延迟。
实验3 声光效应实验报告
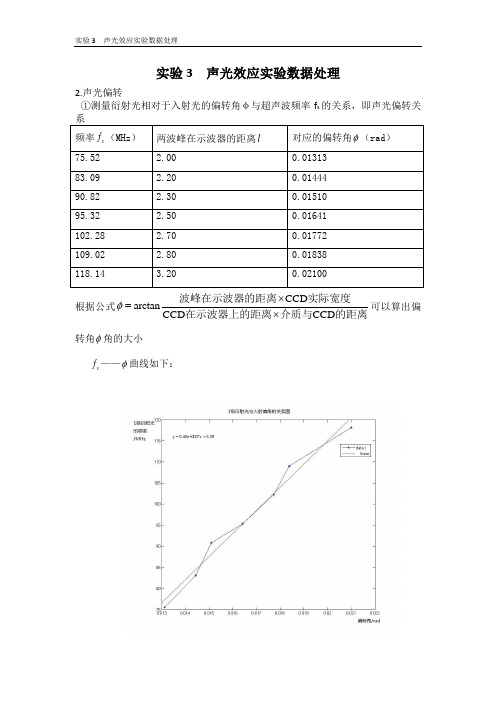
实验3 声光效应实验数据处理
2.声光偏转
①测量衍射光相对于入射光的偏转角φ与超声波频率f s的关系,即声光偏转关
根据公式
CCD
arctan
CCD CCD
φ
⨯
=
⨯
波峰在示波器的距离实际宽度
在示波器上的距离介质与的距离
可以算出偏
转角φ角的大小
s
f——φ曲线如下:
曲线拟合得:5482 5.332s f ϕ=+ 根据原理可得31.4910m/s s v =⨯
②在实验中我们固定功率为1W ,测量出的中心频率约为87.169MHz ,表中的强
由1级与0级衍射光的相对强度与超声波频率的关系曲线可确定中心频率为
089.75f MHz =,带宽为2(99.2389.75)18.96s f MHz ∇=-=
3.声光调制
在实验过程中测量的中心频率为87.169MHz ,因此在实验中将超声波频率调至
由曲线可知,1级衍射光的强度与超声波的功率也大致成线性关系
关系曲线为10.4 2.5S d P I =-。
标准实验报告1-声光效应

标准实验报告(实验)课程名称大学物理实验实验报告学生姓名:学号:指导教师:实验地点:实验时间:一、实验室名称:声光效应实验室二、实验项目名称:声光效应三、实验学时:四、实验原理:当超声波在介质中传播时,将引起介质的弹性应变作时间上和空间上的周期性的变化,并且导致介质的折射率也发生相应的变化。
当光束通过有超声波的介质后就会产生衍射现象,这就是声光效应。
有超声波传播着的介质如同一个相位光栅。
声光效应有正常声光效应和反常声光效应之分。
在各向同性介质中,声-光相互作用不导致入射光偏振状态的变化,产生正常声光效应。
在各向异性介质中,声-光相互作用可能导致入射光偏振状态的变化,产生反常声光效应。
反常声光效应是制造高性能声光偏转器和可调滤光器的物理基础。
正常声光效应可用喇曼-纳斯的光栅假设作出解释,而反常声光效应不能用光栅假设作出说明。
在非线性光学中,利用参量相互作用理论,可建立起声-光相互作用的统一理论,并且运用动量匹配和失配等概念对正常和反常声光效应都可作出解释。
本实验只涉及到各向同性介质中的正常声光效应。
设声光介质中的超声行波是沿у方向传播的平面纵波,其角频率为w s,波长为λs,波矢为k s。
入射光为沿х方向传播的平面波,其角频率为w,在介质中的波长为λ,波矢为k。
介质内的弹性应变也以行波形式随声波一起传播。
由于光速大约是声波的105倍,在光波通过的时间内介质在空间上的周期变化可看成是固定的。
()PSn 21∆()y k t S S s s -=ωsin 0()()y k t n n t y n s s -∆+=ωsin ,0()()y k t y k t nL k L n k s s s s -Φ+∆Φ=-∆+=ωδωsin sin 0000由于应变而引起的介质折射率的变化由下式决定(1)式中,n 为介质折射率,S 为应变,P 为光弹系数。
通常,P 和S 为二阶张量。
当声波在各向同性介质中传播时,P 和S 可作为标量处理,如前所述,应变也以行波形式传播,所以可写成(2)当应变较小时,折射率作为y 和t 的函数可写作 (3)式中,n 0为无超声波时的介质折射率,△n 为声波折射率变化的幅值,由(1)式可求出设光束垂直入射(k ⊥k S )并通过厚度为L 的介质,则前后两点的相位差为(4)式中,k 0为入射光在真空中的波矢的大小,右边第一项△ф0为不存在超声波时光波在介质前后二点的相位差,第二项为超声波引起的附加相位差(相位调制),δф = k 0△n L 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
声光效应电子教案
一、实验目的
①了解声光效应原理
②了解布拉格衍射现象的实验条件和特点
③通过对声光器件衍射效率、中心频率和带宽的测量加深对其概念的理解
④测量声光偏转和声光调制曲线
二、实验原理简述
声光效应就是研究光通过声波扰动的介质时发生散射或衍射的现象。
由于弹光效应,当超声纵波以行波形式在介质中传播时会使介质折射率产生正弦或余弦规律变化,并随超声波一起传播,当激光通过此介质时,就会发生光的衍射,即声光衍射。
衍射光的强度、频率、方向等都随着超声波场而变化。
其中衍射光偏转角随超声波频率的变化现象称为声光偏转;衍射光强度随超声波功率而变化的现象称为声光调制。
主要用途有:制作声光调制器件,制作声光偏转器件,声光调Q开关,可调谐滤光器,在光信号处理和集成光通讯方面的应用。
声光衍射可以分为拉曼-拉斯(Ranman-Nath)衍射和布拉格(Bragg)衍射两种情况。
本实验室主要研究钼酸铅晶体介质中的布拉格衍射现象。
布拉格方程:θB=sinθB=λfs/2nvs ,其中θB 为布拉格角,λ为激光波长,n为介质折射率,vs 为超声波在介质中的速率。
由此知不同的频率对应不同的偏转角φ=2θB,所以可以通过改变超声波频率实现声光偏转。
布拉格一级衍射效率为:η1=I1/Ii=sin2((π/λ).(LM2Ps/2H)1/2) ,其中Ps为超声波功率,M2为声光材料的品质因素,L、H分别表示换能器的长和宽。
由此知当超声功率改变时,η1也随之改变,因而可实现声光调制。
三、实验仪器的结构或原理简图及仪器简介
主要实验仪器如图1所示:有半导体激光器、声光器件及转角平台(图2)、超声波功率信号源、频率计、光强仪、示波器、光具座、支架、导线等附件。
各仪器原理、具体型号及参数见声光效应实验讲义。
图1 声光效应主要实验仪器
图2 转角平台和声光器件
四、实验测试要求(实验内容)
①按照实验讲义完成实验仪器的连接。
②打开激光器、光强仪、示波器,调节光路,直至在示波器上显示一稳定完整的单峰波形。
③接着打开功率信号源,微调转角平台,直至示波器上显示出布拉格衍射的零、一级衍射图像即一个良好的双峰波形(如图3)。
④最后测量声光偏转和声光调制曲线;
⑤为了获得理想波形,有时需要反复调节激光器、转角平台、光强仪等。
图3 布拉格衍射的0级1级光
五、注意事项
在严格执行实验步骤的条件下,注意以下几点:
①尽量避免地面、桌面、光具座等的震动;
②记录数据的过程中,所有数据必须是在相同y轴倍率下测得;
③无饱和失真现象;无小毛刺;
④衍射波形不稳定时要等波形较稳定后再读数;
⑤背景光、电压也会对实验现象造成一定影响,应尽量避免。
