数制和信息编码
第二章 计算机中的数制和码制

第2章 计算机中的数制和编码
2.1 无符号数的表示及运算 2.2 带符号数的表示及运算 2.3 信息的编码
第2章 计算机中的数制和编码
计算机的基本功能是进行数据和信息的处理。数据、信息在计算机中都是以二进 制编码来表示。
本章就是要学习数据在计算机中是如何表 示的?信息在计算机中是如何表示(编码) 示的?信息在计算机中是如何表示(编码) 的?
第2章 计算机中的数制和编码 原码的表示范围 原码表示数的范围为-127∼+127 +127; 8位二进制原码 原码 16位二进制原码 原码表示数的范围为-32767∼+32767 +32767; 原码
第2章 计算机中的数制和编码 原码表示法简单直观,且与真值的转换很方便,但不便于 在计算机中进行加减运算。因此,计算机中通常使用补码进行 因此,
第2章 计算机中的数制和编码 2.1.2 各种数制的相互转换 1.任意进制数转换为十进制数 二进制、十六进制以至任意进制数转换为十进制数的方法 很简单,只要各位按权展开(即该位的数值乘于该位的权)求 和即可。
第2章 计算机中的数制和编码 2. 十进制数转换成二进制数 1).整数部分的转换 1).整数部分的转换
第2章 计算机中的数制和编码 3. 十六进制数的表示法 十六进制计数法的特点是: ① 逢十六进一; ② 使用16个数字符号(0,1,2,3……,9,A,B,C,D,E,F)的不同组合 来表示一个十六进制数,其中A∼F 依次表示10∼15; ③ 以后缀H或h表示十六进制数(Hexadecimal)。 例2.3 0E5AD.BFH =
第2章 计算机中的数制和编码
例2.4 将13.75转换为二进制数。 分别将整数和小数部分进行转换: 整数部分:13=1101B 小数部分:0.75=0.11B 因此,13.75=1101.11B
计算机中的数值和编码

计算机中的数制和编码一、数制的概念:数制是用一组固定的数字和一套统一的规则来表示数目的科学方法。
按照进位方式计算的数制叫做进位数制。
例如:逢十进一即为十进制,逢二进一为二进制,逢八进一为八进制,逢十六进一为十六进制。
进位计数制有两个要素:基数和权值。
1、基数:它是指各种进位计数制中允许选用基本数码的个数。
例如:十进制的数码有0、1、2、3、4、5、6、7、8、9十个数码,所以十进制的基数为10;二进制的数码有0、1两个数码,所以二进制的基数为2;八进制的数码有0、1、2、3、4、5、6、7八个数码,所以八进制的基数为8;十六进制的数码有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个数码,所以十六进制的基数为16。
2、权值:每个数码所表示的数值等于该数码乘以一个与数码所在位置相关的常数,这个常数叫权值。
其大小是以基数为底,数码所在位置的序号为指数的整数次幂。
例如:十进制数356.4=3×100+5×10+6×1+0.4=3×102+5×101+6×100+4×10-1(3在百位上,所以3×100=3×102;5是在十位上,所以5×10=5×101;6是在个位上,所以6×1=6×100;0.4为小数,所以0.4=4×10-1)。
二、十进制(D ecimal notation)及其特点:1、两个特点:①、十个数码:0、1、2、3、4、5、6、7、8、9;②、进位方法:逢十进一,借一当十。
(满了10个就得进一位)2、基数:103、按权展开式:任意一个a位整数和b位小数的十进制数D可以表示为:D=D a-1×10a-1+D a-2×10a-2+…+D0×100+D-1×10-1+D-2×10-2+…+D-b×10-b4、十进制在书写中的三种表达方式:128或者128D或(128)10三、二进制(B inary notation)及其特点:1、两个特点:①、两个数码:0、1;②、进位方法:逢二进一,借一当二。
第4章数制和信息编码

第4章数制和信息编码1.20世纪末,人类开始进入__c________________。
a.农业社会b.工业社会c.信息社会d.高科技社会2.关于信息的说法_________c_________叙述是正确的。
a.计算机就是一种信息b.一本书就是信息c.信息就是人类思维活动的结果d.信息是一些记录下来的符号,本是没有意义3.以下观点中,不合乎信息技术发展的趋势就是____d______________。
a.越来越友好的人机界面b.越来越个性化的功能设计c.越来越低的性能价格比d.越来越繁杂的操作步骤4.对于信息的叙述,_______a___________是错误。
a.信息只在须要时存有b.从不同的角度对信息有不同的认识c.信息、物质和能量形成当今社会的三大资源d.信息本是不是实体,必须通过载体才能体现5.计算机中采用二进制,下面描述中不恰当的就是_____a_____________。
a.是因为计算机只识别0和1b.物理上难同时实现,可靠性弱c.运算简单,通用性强d.计算机中二进制数的0、1数码与逻辑量“真”和“骗人的0与1相符,易于则表示和展开逻辑运算”6.十进制数92转换为二进制数和十六进制数分别是_____a_____________。
e.01011100和5cb.01101100和61c.10101011和5dd.01011000和4f7.人们通常用十六进制而不必二进制书写计算机中的数,是因为____a______________。
a.十六进制的书写比二进制方便b.十六进制的运算比二进制直观c.十六进制数表示的范围比二进制大d.计算机内部使用十六进制8.浮点数之所以能表示很大或很小的数,是因为使用了_______c___________。
a.较多的字节b.较长的尾数c.阶码d.符号位9.在科学计算时,经常遇到“溢出.”,这是指_________b________。
a.数值远远超过了内存容量b.数值超出了机器位表示的范围c.数值远远超过了变量的则表示范围d.计算机出故障了10.在下面关于字符之间大小关系的观点中,恰当的就是______c____________。
计算机中的数制和编码

h
17
③ 8位二进制补码表示数的范围是-128~+127, 十六位二进制补码表示数的范围是-32768~ +32767;对于同一个数,作为8位二进制数的补 码和作为16位二进制数的补码不同,这一点要特 别注意。
④ 注意:对于8位二进制数10000000B,若为补 码表示为[-128]补,若为原码表示[-0]原,若为反 码表示为[-127]反;
h
12
原码表示的特点:
① 最高位为符号位,正数为0,负数为1;
② 8位二进制原码表示数的范围是-127~+127, 十六位二进制原码表示数的范围是-32767~ +32767;
③ 0的原码有两种表示方法,即+0和-0,设字长 为8位:
[+0]原=00000000B
[-0]原=10000000B
h
23
1.美国信息交换标准代码(ASCII 码)
P311 附录A 如“8”的7位ASCII码 0111000B 奇校验ASCII码为00111000B; 偶校验ASCII码为10111000B;
h
24
2、BCD码
二进制编码的十进制数 0~9 A ~F非法 一个字节---8位 压缩与非压缩
h
18
P24 表1-5
从表1-5可以看出,8位二进制数,
无符号数表示范围是0~255;
有符号数:
原码表示范围-127~+127;
反码表示范围是-127~+127;
补码表示范围是-128~+127。
h
19
3.带符号数溢出及其判断方法
如前所述,带符号数表示方法都有一定的 范围,对于8位的原码、反码和补码表示的 范围分别为:
1-2计算机的数制与编码
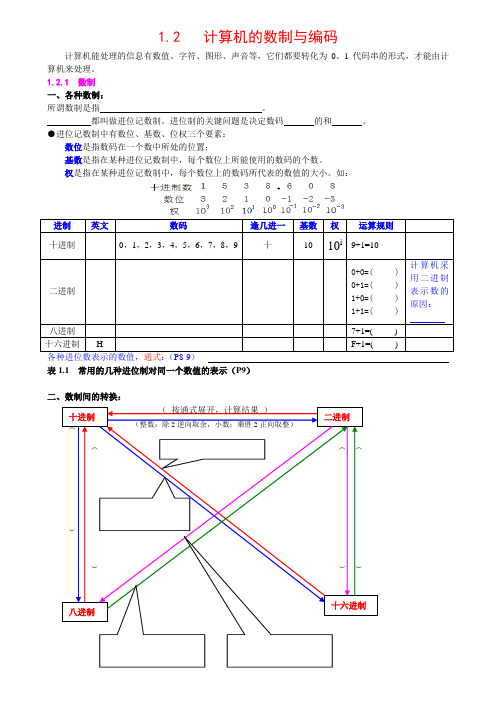
1.2 计算机的数制与编码计算机能处理的信息有数值、字符、图形、声音等,它们都要转化为0、1代码串的形式,才能由计算机来处理。
1.2.1 数制 一、各种数制:所谓数制是指 。
都叫做进位记数制。
进位制的关键问题是决定数码 的和 。
●进位记数制中有数位、基数、位权三个要素: 数位是指数码在一个数中所处的位置;基数是指在某种进位记数制中,每个数位上所能使用的数码的个数。
权是指在某种进位记数制中,每个数位上的数码所代表的数值的大小。
如:表1.1 常用的几种进位制对同一个数值的表示(P9)二、数制间的转换:例:(重点:十进制与二进制的互相转换)●各种进制转十进制●十进制转各种进制●二进制转八进制、八进制转二进制与二进制转十六进制、十六进制转二进制练习:P39:20、21、22、23、24、25、26、27、28、29(写在课本上)如何检查?(计算器!)1.2.2 ASCII码●通称为字符。
字符没有数值意义。
为了便于计算机的应用推广,这些字符必须用统一的规定编码方式来表示。
目前在国际上广泛采用“”表示、和作为使用的等。
●ASCII码的英文全称:,中文。
●ASCII码用位0、1代码串来编码一个符号,每个符号占的存储空间,字节最高位(左)为,作奇偶校验用。
(注:1字节= 位,一个字符的ASCII码占位,余下位用作)●ASCII码给出了个数码,个英文字母,个通用符号,个动作控制符的编码标准。
◆例:查表P308(1)字母“A”的ASCCII的二进制表示为:,十六进制表示为:,十进制表示为:(2)将字符“2”的ASCII码当成数值,转换为十进制数得到50,数字字符“5”的ASCII码转换为十进制数应得到●ASCII码的比较:(详见附录1:P308)空格(space)的ASCCII码是32‘0’~‘9’的ASCCII码是48~57‘A’~‘Z’的ASCCII码是65~90‘a’~‘z’的ASCCII码是97~1221.2.3 汉字编码1.国标码GB 2312-80《》1级汉字个,按顺序排列、2级汉字个,按排列,汉字有6763个,常用符号、字母、图形符号等682个,共计7445个。
计算机中的数制与编码

计算机中的数制与编码
(2)定点小数 定点小数规定小数点的位置固定在符号位之后,但不占一个二进制位。那么,符号位的右边表示的是一 个纯小数。
定点小数的表示形式
例如,用8位二进制定点整数表示(-0.6875)10,应为: (-0.6875)10=(11011000)2
计算机中的数制与编码
2 浮点数
浮点数是指小数点的位置不固定的数。对于既有整数部分又有小数部分的数,一般用浮点数表示。 任意一个二进制数N都可以表示成如下形式:
微机原理与接口技术
计算机中的数制 与编码
计算机中的数制与编码
1.1 计算机中的数制
1 数制的概念
数制是人们按进位的原则进行计数的一种科学方法。在日常生活中,经常要用到数制,除了最常见的十进 制计数法,有时也采用别的进制来计数。
一种计数制所使用的数字符号的个数称为基数,某个固定位置上的计数单位称为位权。同一数字符号处 在不同位置上所代表的值是不同的,它所代表的实际值等于数字本身的值乘以所在位置上的位权。例如,十 进制数345中的数字3在百位上,表示位权为100,故此时的3表示的是300。又如,十进制数123.45用位权可以 表示为
整数部分:
小数部分:
所以,(69.625)10=(1000101.101)2。
计算机中的数制与编码
② 转换成八进制数
③ 转换成十六Βιβλιοθήκη 制数计算机中的数制与编码3 二进制数与八进制数、十六进制数之间的转换
二进制、八进制、十六进 制之间存在特殊的关系:1位 八进制数对应3位二进制数,1 位十六进制数对应4位二进制 数,因此转换比较容易。
(2)小数部分的转换。
• 小数部分的转换采用“乘基取整法”,方法 是:将十进制数的小数部分反复乘以基数R, 将每次乘积的小数部分作为被乘数,并取得 相应的整数部分,直到乘积的小数部分为0。 将每次得到的整数部分顺序排列在小数点后, 即为转换后的R进制小数。
第1讲____计算机中的数制及常见的信息编码(1.2节、1.3节)

从上述可知,一个浮点数是由两个定点数组合而成的。实际地,一个定点 数也可以看成是浮点数的一个特例。即当浮点数的阶数部分为零时(表示
浮点数实际小数点的位置与定点小数约定位置一致),这样浮点数只剩下
尾数部分了。同理,定点数表示法是浮点数表示法的基础,而浮点数表示 法是定点数表示法的应用。它们之间的相互关系,从理论上亦可说明。
比例因子还要取得合适,能使参加运算的数、运算的中间结果以及最后结果都能在 该定点数所能表示的数值范围之内。
定点数表示法使计算机只能处理纯整数或纯小数,限制了计算机处理数据的范围。
数的定点与浮点表示
浮点表示
在浮点表示法中,小数点的位置是浮动的。为了使小数点可以自由浮动, 浮点数由两部分组成,即尾数部分与阶数部分。浮点数在机器中的表示方
法如下:
Pf
Pm-1 Pm-2 …
P0
阶码数值部分
Sf
Sn-1
Sn-2 … S0
尾数数值部分
其中:
阶码符号
尾数小数点位置 阶码小数点位置
➢ 尾数部分S表示的是浮点数N的全部有效数字,它是一个有符号位的定点小数, 且该符号就是浮点数N的符号,即Nf;
➢ 阶数部分P表示的是浮点数N的实际小数点位置与尾数约定的小数点位置之间 的位移量。该位移量P是一个有符号位的定点整数。当阶码符号为正时,表 示小数点向右移动P位;当阶码符号为负时,则表示小数点向左移动P位。因 此,浮点数的小数点随着P的符号和大小而自由浮动。
数的表示及数制转换
二进制数与十六进制数的互换
1位十六进制数与4位二进制数的对应关系:
十六进制数 二进制数 十六进制数 二进制数
0
0000
8
1000
1
计算机中的数制与编码

计算机中的数制与编码一、数制1、什么是进位计数制数制也称计数制,是指用一组固定的符号和统一的规则来表示数值的方法。
按进位的原则进行计数的方法,称为进位计数制。
比如,在十进位计数制中,是按照“逢十进一”的原则进行计数的。
常用进位计数制:a、十位制(Decimal notation);b、二进制(Binary notation);c、八进制(Octal notation);d、十六进制数(Hexdecimal notation)2、进位计数制的基数与位权"基数"和"位权"是进位计数制的两个要素。
(1)基数:所谓基数,就是进位计数制的每位数上可能有的数码的个数。
例如,十进制数每位上的数码,有"0"、"1"、"3",…,"9"十个数码,所以基数为10。
(2)位权:所谓位权,是指一个数值的每一位上的数字的权值的大小。
例如十进制数4567从低位到高位的位权分别为100、101、102、103。
因为:4567=4x103+5x 102+6x 101 +7x100(3)数的位权表示:任何一种数制的数都可以表示成按位权展开的多项式之和。
比如:十进制数的435.05可表示为:435.05=4x102+3x 101+5x100+0x10-1 +5x 10-2位权表示法的特点是:每一项=某位上的数字X基数的若干幂次;而幂次的大小由该数字所在的位置决定。
3、二进制数计算机中为何采用二进制:二进制运算简单、电路简单可靠、逻辑性强(1)定义:按“逢二进一”的原则进行计数,称为二进制数,即每位上计满2 时向高位进一。
(2)特点:每个数的数位上只能是0,1两个数字;二进制数中最大数字是1,最小数字是0;基数为2;比如:10011010与00101011是两个二进制数。
(3)二进制数的位权表示:(1101.101)2=1x23+1x 22+0x 21+1x 20+1x2-1 +0x 2-2+1x2-3(4)二进制数的运算规则1 加法运算① 0+0=0 ③ 1+1=10② 0+1=1+0=12 乘法运算① 0×0=0 ③ 1×1=1② 0×1=1×0=04、八进位制数(1)定义:按“逢八进一”的原则进行计数,称为八进制数,即每位上计满8时向高位进一。
计算机常用数制及编码

计算机常用数制及编码1.二进制数制:二进制是计算机中最基本的数制,只包含两个数字0和1、它是一种逢二进一的计数法,每位上的数值以2为底数的幂来表示。
例如,二进制数1101表示1*2^3+1*2^2+0*2^1+1*2^0=13、在计算机中,二进制数被广泛应用于存储和运算等操作。
2.八进制数制:八进制使用8个数字0-7来表示。
它是二进制数制的一种压缩表示方法,每3位二进制数可以表示为一位八进制数。
例如,二进制数1101可以表示为八进制数15、八进制数在计算机界并不常见,但在一些特定场景下仍然有一定的应用。
3.十进制数制:十进制是我们常用的数制,使用10个数字0-9来表示数值,每位上的数值以10为底数的幂来表示。
例如,十进制数123表示1*10^2+2*10^1+3*10^0=123、十进制数制通常用于人类的日常计算中,但在计算机中也会涉及到十进制的处理,例如在涉及到金额、日期和时间等数字的场景中。
4.十六进制数制:十六进制使用16个数字0-9和A-F来表示,其中A-F分别表示十进制数10-15、它是二进制数制的另一种压缩表示方法,每4位二进制数可以表示为一位十六进制数。
十六进制数常用于计算机领域,因为它们可以更紧凑地表示二进制数。
例如,二进制数1101可以表示为十六进制数D。
编码系统是为了实现计算机和人类之间的信息交流而发展的。
下面介绍几种常见的编码系统:1.ASCII码:ASCII(American Standard Code for Information Interchange)是最早和最广泛使用的字符编码系统之一、它使用7位二进制数(扩展ASCII使用8位二进制数)来表示128(或256)个字符,包括英文字母、数字、符号等。
ASCII码可以用于存储和表示文本文件中的字符。
2. Unicode编码:3.UTF-8编码:UTF-8(Unicode Transformation Format - 8-bit)是一种对Unicode进行可变长度编码的字符编码系统。
数制与编码精讲内容

数制与编码1.数制和编码的基本概念▪数制数制是用一组固定的数字和一套统一的规则来表示数的方法。
常用的进位计数制有二进制(B)、八进制(O)、十进制(D)、十六进制(H)。
▪进位计数制有两个基本要素:基数和权(1)基数:数制所使用数码的个数。
例如,二进制的基数为2,十进制的基数为10。
(2)权:以基数为底,以某一数字所在位置的序号为指数的幂,称为该数字在该位置的权。
▪编码编码是采用少量的基本符号,选用一定的组合原则,以表示大量复杂多样的信息的技术。
任何信息必须转换成二进制形式数据才能由计算机进行处理、存储和传输。
2. 不同进位数制的特点▪十进制(Decimal)十进制的特点是:用10个数码(0~9)表示所有的数,基数是10, 采用逢十进一的计数方法。
▪二进制(Binary)二进制的特点是:由0、1组成,基数是2,加法采用“逢二进一”、减法采用“借一当二”的运算规则。
▪十六进制(Hexadecimal)十六进制:由0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F组成,基数是16,加法用“逢十六进一”、减法采用“借一当十六”的运算规则。
▪八进制(Octal)八进制数的特点是:由0,1,2,3,4,5,6,7组成,基数是8,加法采用“逢八进一”、减法用“借一当八”的运算规则。
3. 进制数的转换(1)二进制<-->八进制数转换(2)十进制转为八进制(3)十六进制转为八进制4. 常见的信息编码▪BCD码二进制编码的十进制数,简称BCD码(Binarycoded Decimal)。
这种方法是用4位二进制码的组合代表十进制数的0,1,2,3,4,5,6 ,7,8,9 十个数符。
▪ASCII码ASCII(American Standard Code for Information Interchange,美国信息交换标准代码),它是现今最通用的单字节编码系统,并等同于国际标准ISO/IEC 646。
数制和编码的概念及转换

数制和编码的概念及转换数制是一种表示数值的方式,常见的数制有十进制、二进制、八进制和十六进制等。
十进制是我们平时常用的数制,它使用基数为10的数字系统,由0到9共10个数字组成。
二进制是计算机使用的一种数制,它使用基数为2的数字系统,由0和1两个数字组成。
八进制是一种数制,它使用基数为8的数字系统,由0到7共8个数字组成。
十六进制是一种数制,它使用基数为16的数字系统,由0到9和A到F共16个数字组成,其中A表示10,B表示11,C表示12,D表示13,E表示14,F表示15。
编码是将字符、数字、符号等信息转化成特定的数字或符号的过程。
常见的编码方式有ASCII码、Unicode和UTF-8等。
ASCII码是英文字符编码的一种方式,它使用7位二进制数表示128个英文字符,包括字母、数字和常见的符号。
Unicode是一种编码系统,它为世界上各种文字字符规定了统一的编码,可以表示几乎所有的字符。
UTF-8是一种多字节编码方式,它是Unicode的一种实现方式,可以表示Unicode字符集中的任何字符。
数制转换是指将一个数值从一种数制表示转换成另一种数制表示的过程。
转换方法如下:1. 二进制转十进制:将每一位上的数乘以2的相应次幂,并求和。
2. 十进制转二进制:用除2取余法,将十进制数除以2,并将余数从低位到高位排列,直到商为0。
3. 八进制转十进制:将每一位上的数乘以8的相应次幂,并求和。
4. 十进制转八进制:用除8取余法,将十进制数除以8,并将余数从低位到高位排列,直到商为0。
5. 十六进制转十进制:将每一位上的数乘以16的相应次幂,并求和。
6. 十进制转十六进制:用除16取余法,将十进制数除以16,并将余数从低位到高位排列,直到商为0。
以上是一些常见的数制和编码的概念及转换方法,不同的数制和编码方式在不同的场景中有不同的应用。
第四章 数制与信息编码

第四章、数制和信息编码1.计算机最基本的功能是对数据进行存储、处理和输出。
2.信息社会特征:社会信息化、设备数字化、通信网络化。
3.信息社会和数字化社会的主要动力是以计算机技术、通信技术和控制技术为核心的现代信息技术的飞速发展和广泛应用。
4.在信息社会中,信息成为比物质和能源更为重要的资源。
5.数字化:用二进制编码对多种信息,包括文字、数字、声音、图形、图像、影像等进行表达、存储、传输和处理。
6.信息:经过加工并对客观世界产生影响的数据。
7.编码:用数字、字母等按规定的方法和位数来代表特定的信息。
(为了人与计算机之间进行信息交流和处理)8.采用二进制编码好处:①物理上容易实现,可靠性强。
②运算简单,通用性强。
③计算机中二进制数的0、1数码与逻辑量“假”与“真”的0与1吻合,便于表示和进行逻辑运算。
9.解码:为从计算机输出数据而进行逆向的转换。
10.逻辑运算:逻辑变量之间的运算。
11.真值表:在逻辑运算中,把逻辑变量的各种可能组合与对应的运算结果列成表格。
(用1或T表示真,用0或F表示假)12.数据存储的最小单位为一个二进制位(bit,b),一位可存储一个二进制数0或1.13.计算机存储容量的基本单位:字节(Byte,B)。
1 B = 8字节1 KB = 1024 B1 MB = 1024 KB1 GB = 1024 MB1 MB = 1024 TB14.一个西文字符占一个字节,一个中文字符占两个字节,一个整数占四个字节,一个双精度实数占八个字节。
15.原码、反码和补码,实质是对负数表示的不同编码。
16.原码、反码最小值是-127,补码的最小值是-128。
17.定点整数是纯整数,定点小数是纯小数。
18.浮点数由阶码和尾数两部分组成:阶码用定点整数表示,所占的位数确定了数的范围。
尾数用定点小数表示,所占的位数确定了数的精度。
19.为了唯一的表示浮点数在计算机中的存放,规定尾数的最高位为1,通过阶码进行调整。
第2章 数制与信息编码

转换后的结果为:(0.534)10=(0.88B43)16
大学计算机基础
2.3 进位计数制
例子2-12:将(50.25)10转换成十六进制数。 解析:对于这种既有整数又有小数部分的十进制 数,可将其整数部分和小数部分分别转换成八进 制数,然后再把两者连接起来即可。 因为(50)10=(32)16,(0.25)10=(0.40)16 所以(50.25)10=(32.40)16
大学计算机基础
2.3 进位计数制
十六进制进位计数制具有如下特点:
有16个数符,分别为0、1、2、3、4、5、6、7、8、9、A、B、C、
D、E、F;
基数为16; 逢十六进一(加法运算),借一当十六(减法运算); 按权展开式。对于任意一n位整数和m位小数的十六进制数D,均
可按权展开为:D=Hn-1×16n-1+…+H1×161+H 0×16 0+
当R=16时,表示十六进制进位计数制,可使用0、1、
2、…、9、A、B、C、D、E、F共16个基本数符。
大学计算机基础
2.3 进位计数制
按基数进位和借位是指在执行加法或减法 时,遵守“逢R进一,借一当R”的规则,如 十进制数为“逢十进一,借一当十”,二进 制数的规则为“逢二进一,借一当二”。
大学计算机基础
2.1信息技术概述
信息技术的处理对象是信息和数据。
信息是人们在从事日常生产生活(如工业、农
业、军事、商业、管理、文化教育、医学卫生、 科学研究等)活动的过程中所涉及到的数字、 符号、文字、语言、图形、图像等的总称。
数据是存储在某种媒体上并且可以加以鉴别的
符号资料。
大学计算机基础
大学计算机基础
2.3 进位计数制
计算机中的数制及其编码

计算机中的数制及其编码1.数制的定义:数制是用来表示和运算数字的一种符号系统。
常见的数制包括二进制、八进制、十进制和十六进制。
2.二进制:二进制是数字系统的一种数制,只包含两个数字0和1、在计算机中,所有的信息都被转换为二进制形式进行存储和处理。
3.八进制:八进制是一种数制,基数为8、它使用了8个数字0-7,通过每一位上的数来表示数值。
4.十进制:十进制是我们日常生活中最常用的数制,基数为10。
它使用了10个数字0-9来表示数值。
5.十六进制:十六进制也是一种常见的数制,基数为16、它使用了16个数字0-9和字母A-F来表示数值。
十六进制常用于计算机科学和工程领域,特别是在内存地址和颜色编码中。
6.数制之间的转换:在计算机中,不同的数制之间可以进行相互转换。
例如,将十进制数转换为二进制数可以使用除2取余的方法,将十进制数一直除以2,直到商为0,然后将每次的余数倒序排列即可得到二进制数。
而将二进制数转换为十进制数,则可以通过每一位数乘以2的幂次方后相加得到结果。
7.数制的编码:在计算机中,数制的编码主要指对不同的字符和数字进行表示和存储的方式。
常见的编码方式包括ASCII码、Unicode、UTF-8等。
-ASCII码:ASCII码是一种基于拉丁字母的字符编码标准,使用7位或8位二进制(0-127或0-255)表示128个不同的字符。
它包括英文字母、数字、标点符号和控制字符等。
- Unicode:-UTF-8:UTF-8是一种可变长度的Unicode编码,使用8位二进制(0-255)表示字符。
它通过对不同的字符使用不同长度的编码,实现了用较少的存储空间表示更多的字符。
总结:数制是用来表示和运算数字的一种符号系统,常见的数制包括二进制、八进制、十进制和十六进制。
数制之间可以进行相互转换,常见的编码方式包括ASCII码、Unicode和UTF-8、这些数制和编码在计算机中起着重要的作用,帮助实现了数字的存储、处理和通信。
数制与信息编码

( 9
C
B
4
.
8
4 ) 16
33
5
例3:八进制和十六进制转化为二进制
数据单位
最小单位:位(Bit,比特),二进制的一个数位。 只能表示为 0 或 1 计算机的内部存储与操作常以字节(Byte)(8个二进 制位(Bit) )为单位:
例1:(345.7)8 =(
)2
1位八进制对应 3位二进制
二、八、十六进制转换为十进制:按权展开 十进制转换为二、八、十六进制:整数相除,小 数相乘 二、八、十六进制相互转换
26
27
4
二、八、十六进制转换为十进制:按权展开 例1: (11011.11)2 = ( )10
十进制转换为二、八、十六进制:整数相除,小数相乘 整数规则:除基取余,商零为止 例1:(60) 10 = ( )2
⒈真值:在数值前加“+”号表示正数; 在数值前加“-”号表示负数。 ⒉机器数:把符号数值化的表示方法。 最高位用“0”表示正数,用“1”表示负数。 例: 真值 机器数 +9 +1001 01001 -9 -1001 11001
38
符号位
39
6
常用的机器数有:原码、反码、补码 其符号位规则相同,数值部分的表示形式有差异。
余 6 余 3
高位
例: (0.6875)10=(
ห้องสมุดไป่ตู้
)2
∴ (0.6875)10=(0.1011)2
30
0.6875 × 2 1.375 × 2 0.75 × 2 1.50 × 2 1.00
31
二、八、十六进制相互转换
按位数进行分隔,分别转换 例1:二进制转化为八进制
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最高位符号位,“0”表示正,“1”表示负数 其余位为数值位。
1.加法运算 0+0=0 0+1=1+0=1 1+1=0 (按逢二进一向高位进位1)
2.减法运算 0-0=1-1=0 1-0=1 0-1=1 (本位为1,向高位借位)
14
3.乘法运算: 实现方法移位相加运算 4.除法运算: 实现方法移位相减运算
15
4.2.4 二进制数的逻辑运算
1.逻辑非运算
2.逻辑与运算
进制表示符号 B binary
101(O)=82+80=64+1=65 71(O)=781+180=57
O octal D decimal H hexadecimal
101A(H)=1163+ 1160+10=4106
10
十进制转化成r进制
整数部分:除以 r取余数,直到商为0,余数从右到左排列。 小数部分:乘以 r取整数,整数从左到右排列。
动力:以3C为核心的现代信息技术快速发展
重要技术基础:数字化
2
2.信息和数据
数据:对客观事物的性质、状态以及相互关系等进行 记载的物理符号。
信息:数据经过加工以后、并对客观世界产生影响的 数据。
区别:信息有意义,而数据没有。
注意:在计算机中经常将信息和数据这两个词不加以 严格区分,互换使用。
3
3.编码
4
0
6
11
八(十六)进制转化为二进制
•一位八进制数对应三位二进制数 •一位十六进制数对应四位二进制数
144(O)=001 100 100(B) 1 44
64(H)=0110 0100(B) 64
二进制转化成八(十六)进制)
整数部分:从右向左按三(四)位进行分组
小数部分:从左向右按三(四)位进行分组
什么是编码?
用数字、字母等按规定的方法和位数来代表特定的信息。
目的:为了人与计算机之间信息交流和处理。
在计算机中要将数值、文字、图形、图像、声音等各种 数据进行二进制编码才能存放到计算机中进行处理,编码 的合理性影响到占用的存储空间和使用效率。
4
例如九九乘法55种运算 二进制3种运算 4.计算机为什么采用二1进×制1=编1 码? 物理上容易实现,可靠0性×强0=0 运算简单,通用性强 1×0=0×1=0
A
应用举例:选拔干部,同时满足条件:年龄小于35岁,党员,高级工程师
16
3.逻辑或运算
应用举例:选拔干部,满足条件之一:年龄小于35岁,党员,高级工程师
17
4.3 数据存储单位和内存地址
1.数据的存储单位 bit :数据存储的最小单位 Byte:一般用字节来作为计算机存储容量的基本单
位 常用的单位之间的换0 1 01 10 11 01 11
输入设备
输出设备
数值 十/二进制转换 西文ASCII码 汉字 输入码/机内码转换 声音、图像 模/数转换
内存
存储 处理
二/十进制转换
数值
西文字形码
西文
汉字字形码
汉字
数/模转换
声音、图像
20
4.4.1数值数据
问题:数值在计算机中二进制形式存放, 则正负符号、小数点如何表示?
1KB=210B=1024B 1MB=220B=1024KB 1GB=230B=1024MB 1TB=240B=1024GB
18
2.内存地址和数据存放
内存:以字节Byte为单位,每个字节有唯一的地址, 就可方便地存取数据。
数据存放:不同的数据类型占据的字节数不同。
int n=100; //占4个字节 double x=3.56; //占8个字节
4.1 引言 4.2 数制与运算 4.3 数据存储单位和内存地址 4.4 信息编码
4.1 引言
1.信息社会和数字化社会
工业社会?
物质和能源是主要资源,从事的是大规模的物质生产
信息社会?
信息成为比物质和能源更为重要的资源,以开发和利
用信息资源为目的信息经济活动成为国民经济活动的主 要内容。
特征:社会信息化、设备数字化、通信网络化
n1
ai r i
im
8
二进制位权表示:
例如: (110111.01)B=32+16+4+2+1+0.25=(55.25)D
9
4.2.2不同进位计数制间的转换
r进制转化成十进制
展开式表示,即数码乘以各自权的累加和
例:
10101(B)=24+22+20=16+4+1=21
101.11(B)=22+20+2-1+2-2=5.75
不足补零
问题:
1 101 101 110.110 101(B)= 1556.65(O) 已知456.78(D)
15 5 6 6 5
如何快速地转换成
11 0110 1110.1101 01(B)=36F.D4(H) 二、八、十六进制?
36 E D4
12
二进制、八进制、十六进制数间的关系
八进制 对应二进制
便于表示和进行逻辑运算
输入设备
输出设备
数值 十/二进制转换 西文 ASCII 码 汉字 输入码/机内码转换 声音、图像 模/数转换
内存
各种处理
二/十进制转换
数值
西文字形码
西文
汉字字形码
汉字
数/模转换
声音、图像
5
4.2数制与运算
6
4.2.1进位计数制
十进制数的表示,如678.34的位权展开式 678.34=6×102+7×101+8×100 +3×10-1+4×10-2
例 100.345(D)≈ 1100100.01011(B)
2 100
2 50 0
2 25 0
2 12
1
26
0
23
0
1
1
0
1
0.345 2
0.690 2
1.380 2
0.760 2
1.520
2 1.04
100(D)=144(O)=64(H) 八进制
8 100
8 12
4
81
4
0
1
十六进制
16 100
16 6
0
000
1
001
2
010
3
011
4
100
5
101
十六进制 对应二进制
0
0000
1
0001
2
0010
3
0011
4
0100
5
0101
十六进制
8 9 A B C D
对应二进制
1000 1001 1010 1011 1100 1101
6
110
7
111
6
0110
E
1110
7
0111
F
1111
13
4.2.3 二进制数的算术运算
数码
基数
权
问题: 七进制数4532.1的位权展开式?
4532.1 =4×73+5×72+3×71+2×70+1×7-1
r进制数用 r个基本符号(0,1,2,…,r-1) 表示数码
r进制数N 展开式可表示为:
N=an-1×rn-1+an-2×rn-2+…+a0×r0+a-1×r-1+…+a-m×r-m
