数据插值和函数逼近 MATLAB实现
《高等应用数学问题的MATLAB求解-第二版》math-chap08.ppt

高等应用数学问题的MATLAB求解 东北大学信息学院
例 8.9
假设已知某三元函数
可以通过该函数生成一些网格型样本点, 试根据样本点进行拟合,并给出拟合误差
高等应用数学问题的MATLAB求解 东北大学信息学院
插值并检验结果:
高等应用数学问题的MATLAB求解 东北大学信息学院
8.1.6 基于样本数据 点的离散最优化求解
验证结果:
高等应用数学问题的MATLAB求解 东北大学信息学院
例 8.2
编写一段程序,允许利用插值方法手工绘 制一条光滑的曲线利用插值方法手工绘制 一条光滑的曲线
高等应用数学问题的MATLAB求解 东北大学信息学院
接上页
需要用户自己选定几个点,然后就能绘制 出一条光滑的曲线 在绘制图形时,若给出vis变量,则绘制的 图形保留样本点处的圆圈,否则在绘制图 形后删去圆圈
是期望的插值位置
表示插值的结果,维数和
一致
‘v4’ 是MATLAB 4.0版本中提供的插值算法.
高等应用数学问题的MATLAB求解 东北大学信息学院
例 8.7
给定
在矩形区域 一组样本点
内随机生成
生成一组 的值,以这些值为已知数据,用 griddata()进行插值处理,并误差分析。
生成并显示已知的样本点:
运用外推法,在区间 函数调用格式为
外的点的插值的
高等应用数学问题的MATLAB求解 东北大学信息学院
例 8.1
已知的数据点来自函数 根据生成的数据进行插值处理,得出较平 滑的曲线直接生成数据 MATLAB求解语句:
高等应用数学问题的MATLAB求解 东北大学信息学院
调用interp1()函数:
matlab在两个数据点之间插值一条曲线的方法

一、插值的定义在数学和计算机科学中,插值是指在已知数据点的基础上,利用插值算法来估算出在这些数据点之间未知位置上的数值。
插值可以用于生成平滑的曲线、曲面或者函数,以便于数据的分析和预测。
二、matlab中的插值方法在matlab中,有多种插值方法可以用来在两个数据点之间插值一条曲线。
这些方法包括线性插值、多项式插值、样条插值等。
下面我们将逐一介绍这些方法及其使用场景。
1. 线性插值线性插值是最简单的插值方法之一。
它的原理是通过已知的两个数据点之间的直线来估算未知位置上的数值。
在matlab中,可以使用interp1函数来进行线性插值。
该函数的调用格式为:Y = interp1(X, Y, Xq, 'linear')其中X和Y分别是已知的数据点的横纵坐标,Xq是待估算数值的位置,'linear'表示使用线性插值方法。
使用线性插值可以快速地生成一条近似直线,但是对于非线性的数据分布效果可能不佳。
2. 多项式插值多项式插值是利用多项式函数来逼近已知数据点之间的曲线。
在matlab中,可以使用polyfit和polyval函数来进行多项式插值。
polyfit函数用于拟合多项式曲线的系数,polyval函数用于计算多项式函数在给定点的数值。
多项式插值的优点是可以精确地通过已知数据点,并且可以适用于非线性的数据分布。
3. 样条插值样条插值是一种比较常用的插值方法,它通过在每两个相邻的数据点之间拟合一个低阶多项式,从而保证整条曲线平滑且具有良好的拟合效果。
在matlab中,可以使用splinetool函数来进行样条插值。
样条插值的优点是对于非线性的数据分布可以有较好的拟合效果,且能够避免多项式插值过拟合的问题。
4. 三角函数插值三角函数插值是一种常用的周期性数据插值方法,它利用三角函数(如sin和cos)来逼近已知数据点之间的曲线。
在matlab中,可以使用interpft函数来进行三角函数插值。
用MATLAB作函数插值

1.先在三维坐标画出原始数据,画出粗糙的温度分布曲面图. 输入以下命令: x=1:5; y=1:3; temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86]; mesh(x,y,temps) 2.以平滑数据,在x、y方向上每隔0.2个单位的地方进行插值.
figure(5) subplot(1,3,1),contour(xi,yi,z1i,10,'r'); subplot(1,3,2),contour(xi,yi,z2i,10,'r'); subplot(1,3,3),contour(xi,yi,z3i,10,'r');
用MATLAB作散点数据的插值计算
例
已知飞机下轮廓线上数据如下,求x每改变0.1时的y值。
X Y
0 3 5 7 9 1 1 1 1 1 1 2 3 4 5 0 12 17 20 21 20 18 12 10 16 . . . . . . . . .
机翼下 轮廓线 y
x
x0=[0 3 5 7 9 11 12 13 14 15 ]; y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6 ]; x=0:0.1:15; y1=lagr1(x0,y0,x); y2=interp1(x0,y0,x); y3=interp1(x0,y0,x,'spline'); subplot(3,1,1) plot(x0,y0,'k+',x,y1,'r') grid title('lagrange') subplot(3,1,2) plot(x0,y0,'k+',x,y2,'r') grid title('piecewise linear') subplot(3,1,3) plot(x0,y0,'k+',x,y3,'r') grid title('spline')
(完整版)Matlab学习系列13.数据插值与拟合

13. 数据插值与拟合实际中,通常需要处理实验或测量得到的离散数据(点)。
插值与拟合方法就是要通过离散数据去确定一个近似函数(曲线或曲面),使其与已知数据有较高的拟合精度。
1.如果要求近似函数经过所已知的所有数据点,此时称为插值问题(不需要函数表达式)。
2.如果不要求近似函数经过所有数据点,而是要求它能较好地反映数据变化规律,称为数据拟合(必须有函数表达式)。
插值与拟合都是根据实际中一组已知数据来构造一个能够反映数据变化规律的近似函数。
区别是:【插值】不一定得到近似函数的表达形式,仅通过插值方法找到未知点对应的值。
【拟合】要求得到一个具体的近似函数的表达式。
因此,当数据量不够,但已知已有数据可信,需要补充数据,此时用【插值】。
当数据基本够用,需要寻找因果变量之间的数量关系(推断出表达式),进而对未知的情形作预测,此时用【拟合】。
一、数据插值根据选用不同类型的插值函数,逼近的效果就不同,一般有:(1)拉格朗日插值(lagrange插值)(2)分段线性插值(3)Hermite(4)三次样条插值Matlab 插值函数实现:(1)interp1( ) 一维插值(2)intep2( ) 二维插值(3)interp3( ) 三维插值(4)intern( ) n维插值1.一维插值(自变量是1维数据)语法:yi = interp1(x0, y0, xi, ‘method’)其中,x0, y0为原离散数据(x0为自变量,y0为因变量);xi为需要插值的节点,method为插值方法。
注:(1)要求x0是单调的,xi不超过x0的范围;(2)插值方法有‘nearest’——最邻近插值;‘linear’——线性插值;‘spline’——三次样条插值;‘cubic’——三次插值;默认为分段线性插值。
例1 从1点12点的11小时内,每隔1小时测量一次温度,测得的温度的数值依次为:5,8,9,15,25,29,31,30,22,25,27,24.试估计每隔1/10小时的温度值。
如何利用Matlab技术进行数据插值

如何利用Matlab技术进行数据插值数据插值是一种常用的数学方法,用于根据已知数据点的信息,推断出未知位置的数据。
在各个学科领域,如地理学、环境科学、经济学等,数据插值都被广泛应用于实际问题的解决中。
在这篇文章中,我们将探讨如何利用Matlab技术进行数据插值。
数据插值的目标是根据已有的数据点,建立一个适当的函数模型,并利用该模型对未知位置处的数据进行估计。
Matlab作为一种功能强大的数学计算和可视化软件,提供了各种强大的函数和工具箱,使得数据插值变得更加便捷和高效。
首先,我们需要将已有的数据点导入到Matlab中。
一般来说,数据以文本文件的形式存储,每一行代表一个数据点,包含该点的横坐标和纵坐标。
我们可以使用Matlab内置的读取文本数据的函数,如`dlmread`或`importdata`来导入数据。
导入后,我们可以使用`plot`函数将数据点绘制出来,以便于观察数据的分布情况。
在进行数据插值之前,首先需要对数据进行预处理。
如果数据中存在异常值或者缺失值,我们可以使用Matlab提供的函数来进行数据清洗。
例如,可以使用`isnan`函数判断数据是否缺失,并使用`interp1`函数对缺失值进行插值处理。
接下来,我们将介绍几种常用的数据插值方法,并演示如何在Matlab中应用这些方法。
首先是最简单的线性插值方法。
线性插值基于已知数据点之间的直线拟合,通过求解直线方程,来推测未知位置处的数据值。
Matlab提供了`interp1`函数来实现线性插值,我们可以指定插值的方法为`'linear'`,并传入已知数据点的横坐标和纵坐标,以及待插值的位置进行插值计算。
此外,Matlab还提供了其他更高级的插值方法,如多项式插值、样条插值等。
多项式插值使用多项式函数拟合已知数据点,通过计算多项式函数的值来进行插值。
Matlab提供了`polyfit`函数来拟合多项式函数,以及`polyval`函数来计算多项式函数的值。
matlab插值实验报告

matlab插值实验报告Matlab插值实验报告引言:在数学和工程领域中,插值是一种常见的数据处理方法。
它通过已知数据点之间的推断来填补数据的空缺部分,从而获得连续的函数或曲线。
Matlab是一种功能强大的数值计算软件,具备丰富的插值函数和工具包。
本实验旨在通过使用Matlab进行插值实验,探索插值方法的原理和应用。
实验步骤:1. 数据准备首先,我们需要准备一组实验数据。
以一个简单的二维函数为例,我们选择f(x) = sin(x),并在区间[0, 2π]上取若干个等间隔的点作为已知数据点。
2. 线性插值线性插值是插值方法中最简单的一种。
它假设函数在两个已知数据点之间是线性变化的。
在Matlab中,可以使用interp1函数进行线性插值。
我们将已知数据点和插值结果绘制在同一张图上,以比较它们之间的差异。
3. 多项式插值多项式插值是一种常用的插值方法,它通过已知数据点构造一个多项式函数来逼近原始函数。
在Matlab中,polyfit函数可以用来拟合多项式。
我们可以选择不同的多项式次数进行插值,并观察插值结果与原始函数之间的差异。
4. 样条插值样条插值是一种更为精确的插值方法,它通过在每个小区间内构造局部多项式函数来逼近原始函数。
在Matlab中,可以使用spline函数进行样条插值。
我们可以选择不同的插值节点数目,并比较插值结果的平滑程度和逼近效果。
5. 拉格朗日插值拉格朗日插值是一种基于多项式的插值方法,它通过构造插值多项式来逼近原始函数。
在Matlab中,可以使用polyval函数进行拉格朗日插值。
我们可以选择不同的插值节点数目,并观察插值结果与原始函数之间的差异。
实验结果:通过实验,我们得到了不同插值方法的结果,并将其与原始函数进行了比较。
在线性插值中,我们观察到插值结果与原始函数之间存在一定的误差,特别是在函数变化较快的区域。
而多项式插值和样条插值在逼近原始函数方面表现更好,特别是在插值节点数目较多的情况下。
matlab数据插值运算

matlab数据插值运算Matlab是一种强大的科学计算软件,用于数值计算、数据分析和可视化等应用。
在许多科研和工程项目中,我们经常需要对数据进行插值运算,以填补缺失值或对离散数据进行平滑处理。
本文将介绍如何使用Matlab进行数据插值运算。
数据插值是一种通过已知数据点来估计未知数据点的方法。
在Matlab中,有多种插值算法可以选择,包括线性插值、拉格朗日插值、样条插值等。
这些插值方法各有特点,根据不同的数据特征和需求,我们可以选择合适的插值算法。
我们需要准备好待插值的数据。
假设我们有一组离散的数据点,用来描述某个函数在一定范围内的取值情况。
为了方便演示,我们可以生成一组简单的数据点。
```Matlabx = 0:0.5:10;y = sin(x);```上述代码中,我们生成了一个从0到10的等间隔数据点,然后计算了对应的正弦函数值。
这样,我们就得到了一组离散的数据点。
接下来,我们可以使用Matlab提供的插值函数进行插值运算。
以线性插值为例,使用`interp1`函数可以实现对数据的线性插值。
```Matlabxi = 0:0.1:10;yi = interp1(x, y, xi, 'linear');```上述代码中,我们指定了插值的目标点`xi`,然后使用`interp1`函数对原始数据进行线性插值。
最后,我们得到了一组新的插值数据`yi`。
除了线性插值,Matlab还提供了其他插值方法,如拉格朗日插值和样条插值。
这些方法可以通过设置插值函数的参数来选择。
```Matlabyi = interp1(x, y, xi, 'spline');```上述代码中,我们使用`spline`参数来指定样条插值方法。
通过调整参数,我们可以根据数据的特点选择最合适的插值方法。
有时候我们还需要对插值结果进行进一步的平滑处理,以减少插值误差。
Matlab提供了一些平滑滤波函数,如`smoothdata`和`smooth`等。
插值与拟合的MATLAB实现

插值与拟合的MATLAB实现插值和拟合是MATLAB中常用的数据处理方法。
插值是通过已知数据点之间的数值来估计未知位置的数值。
而拟合则是通过已知数据点来拟合一个曲线或者函数,以便于进行预测和分析。
插值方法:1.线性插值:使用MATLAB中的interp1函数可以进行线性插值。
interp1函数的基本语法为:yinterp = interp1(x, y, xinterp),其中x和y为已知数据点的向量,xinterp为待插值的位置。
函数将根据已知数据点的线性关系,在xinterp位置返回相应的yinterp值。
2.拉格朗日插值:MATLAB中的lagrangepoly函数可以使用拉格朗日插值方法。
lagrangepoly的基本语法为:yinterp = lagrangepoly(x, y, xinterp),其中x和y为已知数据点的向量,xinterp为待插值的位置。
函数将根据拉格朗日插值公式,在xinterp位置返回相应的yinterp值。
3.三次样条插值:使用MATLAB中的spline函数可以进行三次样条插值。
spline函数的基本语法为:yinterp = spline(x, y, xinterp),其中x和y为已知数据点的向量,xinterp为待插值的位置。
函数将根据已知数据点之间的曲线关系,在xinterp位置返回相应的yinterp值。
拟合方法:1.多项式拟合:MATLAB中的polyfit函数可以进行多项式拟合。
polyfit的基本语法为:p = polyfit(x, y, n),其中x和y为已知数据点的向量,n为要拟合的多项式的次数。
函数返回一个多项式的系数向量p,从高次到低次排列。
通过使用polyval函数,我们可以将系数向量p应用于其他数据点,得到拟合曲线的y值。
2.曲线拟合:MATLAB中的fit函数可以进行曲线拟合。
fit函数的基本语法为:[f, goodness] = fit(x, y, 'poly2'),其中x和y为已知数据点的向量,'poly2'表示要拟合的曲线类型为二次多项式。
MATLAB中的插值方法及其应用

MATLAB中的插值方法及其应用引言数据在科学研究和工程应用中起着至关重要的作用。
然而,在实际问题中,我们常常遇到数据不完整或者不连续的情况。
为了填补这些数据的空隙,插值方法应运而生。
插值方法可以通过已知的点估计未知点的值,从而使得数据连续化。
MATLAB作为一款强大的数值计算软件,提供了丰富的插值方法及其应用。
本文将对MATLAB中常用的插值方法进行介绍,并探讨它们在实际应用中的价值和效果。
一、线性插值方法线性插值是最简单和常用的插值方法之一。
它假设两个已知数据点之间的插值点在直线上。
MATLAB中的线性插值可以通过interp1函数实现。
例如,对于一组已知的点(x1,y1)和(x2,y2),我们可以使用interp1(x,y,xq,'linear')来估计插值点(xq,yq)的值。
线性插值方法的优点在于简单易懂,计算速度快。
然而,它的缺点在于无法处理非线性关系和复杂的数据分布。
因此,在实际应用中,线性插值方法往往只适用于简单的数据场景。
二、多项式插值方法多项式插值是一种常用的插值技术,它假设插值点在已知数据点之间的曲线上,而非直线。
MATLAB中的polyfit和polyval函数可以帮助我们实现多项式插值。
多项式插值方法的优点在于可以逼近各种形状的曲线,对数据的逼真度较高。
然而,当插值点之间的数据分布不均匀时,多项式插值容易产生振荡现象,即“龙格现象”。
因此,在实际应用中,我们需要根据具体问题选择合适的插值阶数,以避免过拟合和振荡现象的发生。
三、样条插值方法样条插值是一种光滑且精确的插值方法。
它通过在已知数据点之间插入一系列分段多项式,使得插值曲线具有良好的光滑性。
MATLAB中的spline函数可以帮助我们实现样条插值。
样条插值方法的优点在于可以处理数据分布不均匀和曲线形状复杂的情况。
它能够减少振荡现象的发生,并保持曲线的光滑性。
然而,样条插值方法的计算复杂度较高,需要更多的计算资源。
函数的数值逼近-插值

课程名称计算方法实验项目名称函数的数值逼近-插值实验成绩指导老师(签名)日期2011-9-16一. 实验目的和要求1.掌握用Matlab计算Lagrange、分段线性、三次样条三种插值的方法,改变节点的数目,对三种插值结果进行初步分析。
2.通过实例学习如何用插值方法解决实际问题。
二. 实验内容和原理1)编程题2-1要求写出Matlab源程序(m文件),并对每一行语句加上适当的注释语句;2)分析应用题2-2,2-3,2-4,2-5要求将问题的分析过程、Matlab源程序、运行结果和结果的解释、算法的分析等写在实验报告上。
2-1分析应用题用12y x=在0,1,4,9,16x=产生5个节点15,,P P。
用以下五种不同的节点构造Lagrange插值公式来计算5x=处的插值,与精确值比较并进行分析。
function y=lagr(x0,y0,x)n=length(x0);m=length(x);L=zeros(1,n);y=zeros(1,m);for k=1:ms=0;for i=1:nL(i)=1;for j=1:nif j~=iL(i)=L(i)*(x(k)-x0(j))/(x0(i)-x0(j));endends=s+y0(i)*L(i);endy(k)=s;end1) 用34,P P 构造;>> x0=[4,9]; >> y0=[2,3]; >> lagr(x0,y0,5) ans =2.20002) 用234,,P P P 构造;>> x0=[1,4,9]; >> y0=[1,2,3]; >> lagr(x0,y0,5) ans =2.26673) 用2345,,,P P P P 构造;>> x0=[1,4,9,16]; >> y0=[1,2,3,4]; >> lagr(x0,y0,5) ans =2.25404) 用1245,,,P P P P 构造;>> x0=[0,1,9,16]; >> y0=[0,1,3,4]; >> lagr(x0,y0,5) ans =2.95245) 用全部插值节点12345,,,,P P P P P 构造。
插值法matlab程序

插值法matlab程序插值法是一种常用的数值计算方法,广泛应用于科学与工程领域。
在MATLAB中,可以通过插值函数实现对数据的插值处理。
本文将介绍插值法的原理及其在MATLAB中的应用。
一、插值法的原理插值法是一种通过已知数据点来估计未知数据点的方法。
它的基本思想是利用已知数据点之间的关系推断未知数据点的值。
插值法分为多种类型,常用的有线性插值、拉格朗日插值和样条插值等。
1. 线性插值线性插值是最简单的插值方法,它假设数据点之间的关系是线性的。
给定两个已知数据点(x0, y0)和(x1, y1),线性插值可以通过以下公式来估计在两个数据点之间的任意点(x, y)的值:y = y0 + (x - x0) * (y1 - y0) / (x1 - x0)2. 拉格朗日插值拉格朗日插值是一种多项式插值方法,它通过构造一个满足已知数据点的多项式函数来估计未知数据点的值。
给定n+1个已知数据点(x0, y0), (x1, y1), ..., (xn, yn),拉格朗日插值多项式可以表示为:P(x) = y0 * L0(x) + y1 * L1(x) + ... + yn * Ln(x)其中,L0(x), L1(x), ..., Ln(x)是拉格朗日基函数,定义为:Lk(x) = (x - x0) * (x - x1) * ... * (x - xk-1) * (x - xk+1) * ... * (x - xn) / ((xk - x0) * (xk - x1) * ... * (xk - xk-1) * (xk - xk+1) * ... * (xk - xn))3. 样条插值样条插值是一种利用多个多项式函数来近似估计数据点的方法。
它将数据点之间的区间划分为多段,每段都用一个低次多项式函数来拟合。
这样可以在保持插值函数光滑的同时,更准确地估计未知数据点的值。
二、MATLAB中的插值函数MATLAB提供了多个插值函数,可以根据实际需求选择合适的函数进行数据插值处理。
matlab拉格朗日插值法例题

MATLAB拉格朗日插值法例题在数值分析中,拉格朗日插值法是一种常用的插值方法,常被应用于数据的逼近和曲线的拟合。
它通过构造一个满足已知数据点的多项式来逼近给定的数据集,从而实现对数据的估计和预测。
在MATLAB中,我们可以利用内置的插值函数来实现拉格朗日插值法,并且结合具体的例题来进行演示和分析。
让我们来看一个简单的例题。
假设我们有以下一组数据点:(1, 3), (2, 5), (3, 6), (4, 8)。
我们希望利用拉格朗日插值法来估计当x取特定值时对应的y的取值。
在MATLAB中,可以使用“interp1”函数来进行插值计算。
下面是具体的代码实现:```matlabx = [1, 2, 3, 4];y = [3, 5, 6, 8];xi = 2.5;yi = interp1(x, y, xi, 'spline');disp(['当x取值为',num2str(xi),'时,对应的y的估计值为',num2str(yi)]);```上述代码中,我们首先定义了数据点的x和y坐标,然后选择了一个特定的x取值xi,利用“interp1”函数来计算对应的插值结果yi。
在本例中,我们使用了‘spline’选项来进行插值计算,而MATLAB也提供了其他的插值方法供我们选择。
通过运行上面的代码,我们可以得到当x取值为2.5时,对应的y的估计值为5.375。
这样,我们就利用拉格朗日插值法对给定的数据进行了估计,并得到了我们想要的结果。
除了上面的简单例题之外,拉格朗日插值法还可以应用于更加复杂的数据集合和情况。
在实际的工程和科学计算中,利用MATLAB进行拉格朗日插值法的实现能够帮助我们更好地理解和分析数据,并且为进一步的研究和应用提供了有力的支持。
拉格朗日插值法是一种常用的插值方法,在MATLAB中得以简单而有效的实现。
通过具体的例题和代码演示,我们对拉格朗日插值法有了更深入的了解和认识。
matlab曲线插值方法

matlab曲线插值方法
在MATLAB中,有多种方法可以进行曲线插值。
以下是一些
常用的方法:
1. 线性插值:使用线性函数将给定数据点之间的空白区域填充。
在MATLAB中,可以使用`interp1`函数实现线性插值。
2. 多项式插值:使用一个多项式函数来逼近数据点。
在MATLAB中,可以使用`polyfit`函数拟合数据点,并使用
`polyval`函数计算插值点。
3. 样条插值:使用分段多项式来逼近数据点,形成平滑的曲线。
在MATLAB中,可以使用`interp1`函数的`'spline'`选项进行样
条插值。
4. Lagrange插值:使用Lagrange插值多项式逼近数据点。
在MATLAB中,可以使用`polyfit`函数的第三个参数指定插值多
项式的次数。
5. 三次样条插值:使用三次多项式来逼近数据点,并确保曲线在数据点之间是连续且光滑的。
在MATLAB中,可以使用
`csape`函数进行三次样条插值。
这些方法在MATLAB中都有相应的函数可以直接调用,并提
供了灵活的参数选项来满足不同的插值需求。
用MATLAB进行数据插值课件

线性插值
通过两点之间的直线进行插值, 计算简单但精度较低。
非线性插值
使用非直线函数进行插值,如 多项式、样条函数等,精度较
高但计算复杂度也较高。
02
Matlab插值函数
interp1函数
总结词
一维数据插值函数
详细描述
interp1函数用于在一维数据上进行插值。它接受两个参数:x和y,分别表示数 据点的x坐标和y坐标。通过指定新的x坐标,可以计算出对应的y坐标,从而实 现插值。
要点二
详细描述
多维线性插值的基本思想是通过已知点之间的线性关系来 估计未知点的值。在多维空间中,可以使用多个线性方程 来表示已知点之间的关系,然后解这些方程来得到未知点 的估计值。
多维多项式插值
总结词
多项式插值是一种常用的数据插值方法,适用于一维数 据的插值。在多维数据插值中,可以使用多维多项式插 值来估计未知点的值。
多重二次插值
在多个维度上进行二次插 值,适用于各维度间关系 较复杂的情况。
多重样条插值
在多个维度上进行样条插 值,适用于需要平滑估计 的情况。
实际应用中的插值案例
时间序列数据插值
在金融、经济等领域,时间序列数据经常需要进行插值以填补缺 失值。
图像处理中的插值
在图像缩放、旋转等操作中,需要进行插值以平滑图像。
线性插值
通过已知的点对,使用线性函数进行插值,适用 于数据点分布较均匀的情况。
二次插值
使用二次函数进行插值,适用于已知三个或更多 数据点的情况,能够提供更精确的估计。
三次样条插值
通过构建三次样条函数进行插值,适用于需要平 滑插值的情况。
多维数据插值的案例
多元线性插值
在多个维度上进行线性插 值,适用于各维度间关系 较简单的情况。
matlab插值原理

matlab插值原理Matlab插值原理插值是一种数学方法,用于通过已知数据点的值来估计在这些数据点之间的未知数据点的值。
Matlab是一种强大的计算软件,可以用于数值计算和数据分析。
在Matlab中,插值方法可以通过使用interp1函数来实现。
插值方法可以分为两类:多项式插值和非多项式插值。
多项式插值使用多项式函数来逼近数据点,而非多项式插值使用其他函数形式来逼近数据点。
最常用的多项式插值方法是拉格朗日插值和牛顿插值。
拉格朗日插值使用一个多项式函数来逼近数据点,该多项式函数通过数据点和对应的函数值来确定。
牛顿插值使用一个差商表来确定多项式函数的系数,差商表由数据点和对应的函数值计算得到。
非多项式插值方法包括样条插值和分段线性插值。
样条插值使用分段低次多项式来逼近数据点,这些多项式在相邻的数据点之间衔接。
分段线性插值使用线性函数来逼近相邻数据点之间的数据。
在Matlab中,interp1函数可以使用上述插值方法进行数据插值。
该函数具有以下语法:Y = interp1(X, V, XI, METHOD)其中,X是已知数据点的横坐标,V是已知数据点的纵坐标,XI是要插值的点的横坐标,METHOD是插值方法。
使用interp1函数进行插值时,需要注意以下几点:1. 数据点的横坐标必须是单调递增的,即X(1) < X(2) < ... < X(n)。
2. 如果要插值的点的横坐标在已知数据点的横坐标范围之外,interp1函数将返回NaN。
3. 如果要插值的点的横坐标在已知数据点的横坐标范围之内,但在两个已知数据点的横坐标之间,interp1函数将使用插值方法来确定插值点的纵坐标。
除了interp1函数,Matlab还提供了其他插值函数,如interp2、interp3和interpn。
这些函数可以用于二维和三维数据的插值。
插值在数值计算和数据分析中起着重要的作用。
通过插值,我们可以根据已知数据点的值来估计在这些数据点之间的未知数据点的值。
MATLAB中的插值运算

MATLAB中的插值运算在数学中,有时需要查表,如对数表。
在具体查表时,需要的数据表中可能没有,这时一般可以先找出它相邻的数,再从表中查出其相应结果,然后按一定的关系把这些相邻的数以及它相应的结果加以修正,就可求出要查数的数据结果的近似值,这个修正关系就是一种插值.在实践中,常常需要测量某些数据,但由于客观条件的限制,所测得的数据可能不够细密,满足不了实践的需要,这时便可以通过插值方法对数据进行加密处理。
此外,对于给定的离散数据对,如果要找一个函数来近似描述其对应关系,常常也需要插值。
与插值有关的MATLAB 函数(一)POLY2SYM 函数主要功能:把多项式的系数向量转换为符号多项式.调用格式一:poly2sym (C)调用格式二:f1=poly2sym(C,'V')或f2=poly2sym(C, sym (’V') ),(二) POLYVAL 函数主要功能:估计多项式的值。
调用格式:Y = polyval(P,X)(三)POLY 函数主要功能:把根转换为多项式的系数向量。
调用格式:Y = poly (V )(四) CONV 函数主要功能:计算卷积和多项式的和。
调用格式:C =conv (A, B )(五) DECONV 函数主要功能:计算逆卷积和多项式的除法、商和余式。
调用格式:[Q ,R ] =deconv (B,A)(六) roots(poly (1:n ))命令调用格式:roots(poly (1:n ))(七) det(a*eye(size (A)) — A )命令调用格式:b=det(a *eye (size (A)) - A )grange 插值方法介绍 对给定的n 个插值点12x ,,...n x x 及对应的函数值12,,...,n y y y ,利用n 次Lagrange 插值多项式,则对插值区间内任意x 的函数值y 可通过下式求的:11y()()n n j k k j k j j k x x x y x x ==≠-=-∑∏MATLAB 中没有直接实现拉格朗日算法的函数所以需建立M 文件:function y=lagrange (a,b ,x)y=0;for i=1:length (a)l=1;for j=1:length(b)if j==il=l;elsel=l.*(x-a(j))/(a(i)—a(j));endendy=y+l*b(i);end算例:给出f(x)=ln(x)的数值表,用Lagrange计算ln(0。
数据插值和函数逼近 MATLAB实现
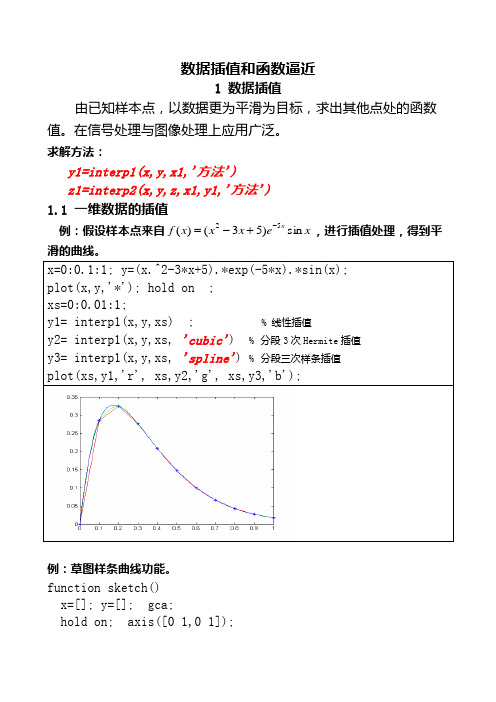
数据插值和函数逼近1 数据插值由已知样本点,以数据更为平滑为目标,求出其他点处的函数值。
在信号处理与图像处理上应用广泛。
求解方法:y1=interp1(x,y,x1,'方法')z1=interp2(x,y,z,x1,y1,'方法')1.1 一维数据的插值例:假设样本点来自x e x x x f x sin )53()(52-+-=,进行插值处理,得到平例:草图样条曲线功能。
function sketch()x=[]; y=[]; gca;hold on; axis([0 1,0 1]);while 1[x0,y0,button]=ginput(1);if(isempty(button)) break; end;x=[x x0]; y=[y y0];plot(x,y,'*');end;xx=[x(1):(x(end)-x(1))/100:x(end)];yy=interp1(x,y,xx,'spline');plot(xx,yy,x,y,'*');end1.2 二维网格数据的插值例3:假设样本点来自xy y x e x x z ----=22)2(2,进行插值处理,得到平滑的曲1.3 二维一般分布数据的插值例4:假设样本点来自xy y x ex x z ----=22)2(2,进行插值处理,得到平滑的曲2 样条插值函数逼近由已知样本点,求能对其较好拟合的函数表达式。
求解方法:S=csapi(x,y); % 定义一个三次样条函数类S=spapi(k,x,y); % 定义一个k 次B 样条函数类ys=fnval(S,xs); % 计算插值结果fnplt(S); % 绘制插值结果例:从)sin(x y =中取样本点,计算三次样条函数。
练习:利用上例中的变量S,生成各个曲线段的参数方程,并绘例:从)sin(x y =中取样本点,计算三次B 样条函数。
基于Matlab实现函数逼近

基于Matlab 实现函数逼近曾德惠(湖北民族学院理学院 湖北恩施 445000)摘 要:为满足工程应用中对数据处理的需要,讨论基于Mat lab 实现函数逼近的三种方法:插值、拟合和神经网络逼近。
在介绍基本原理的基础上,利用Matlab 的插值和拟合函数,结合实例对分段线性插值、Her mite 、三次样条插值及最小二乘曲线拟合法的Matlab 实现方法进行研究。
设计非线性函数逼近的BP 神经网络,通过网络训练、仿真达到了预期的效果。
所有结果表明,采用不同的逼近方法,利用Mat lab 编程可以简单、有效地实现函数逼近。
关键词:Mat lab;函数逼近;插值;拟合;神经网络中图分类号:T P391.9;O241 文献标识码:A 文章编号:10042373X(2009)182141203Realization of Function Approximation Based on MatlabZENG Dehui(School of S cience ,H ubei Instit ut e for Nat i onalit i es,Enshi,445000,China )A bstra ct :Thr ee means to r ea lize function appr oach such as the inter polation approach,f itting approach as well as the neu 2r al networ k approach ar e discussed based on Matlab t o meet the demand of data processing in engineering application.Based on basic principle of the introduction,realization methods to piecewise linea r inter polation,H ermite interpolation,cubic spline in 2ter polat ion and least squares cur ve fitting method are r esear ched using inter polation funct ion and fitting function in Matlab with example.BP neural network to proximate nonlinear functions is designed,desired efect is achieved through the tr aining and simulation of net work.All r esults indicate that different methods ar e adopted according to specific problems,and function approach is realized simply and effectively in Matlab.Keywords :Matlab;function approximat ion;inter polation;fitting;neura l network收稿日期:20092032030 引 言在工程分析和科学研究中,常需要根据一些测试数据求得自变量和因变量的近似函数关系式,来完成其他设计计算。
MATLAB插值法程序用多种插值法逼近sin(x)

数学与统计学实验教学中心实验报告一、实验目的:学会运用插值法求得所需值。
二、实验内容:通过提供的初值,运用插值法计算要求位置处的sin(x)值,模拟出插值图像,并与真值图像做对比。
三、实验环境:MATLAB。
四,实验方法:根据所给初值条件x=[0.4 0.5 0.6 0.7],y=[0.38942 0.47943 0.56464 0.64422],通过对插值法spline的调用,运用语句y1=interp1(x,y,x1,'spline'),求解x1=0.57891处的插值y1=interp1(x,y,x1,'spline')。
再利用现所得的数据,对x值进行细小的分割,使插值的密度加大,分别用插值法nearest,linear,cubic求出对应的y数据组,再根据对应的[x,y]数据作图,以获得插值图像及真实值图像,并比较插值图像与真实值图像的相似度。
另外我将插值数据与真实值作差获得两者的差额,并描绘出相应的差额图像,在对比相似度时更为明显易懂。
五、实验过程:根据设计思想,编写并键入程序于MATLAB,生成相应的M文件并做调试,最后得出正确可行的程序体为:format long %调用长值型数据,加大精度x=[0.4 0.5 0.6 0.7];y=[0.38942 0.47943 0.56464 0.64422];x1=0.57891;y1=interp1(x,y,x1,'spline'); %调用spline插值法求所需值x1y1 %输出所求值xi=0.4:0.01:0.7; %细化插值变量yi=interp1(x,y,xi,'spline'); %调用spline插值法求得数组yi zi=interp1(x,y,xi,'nearest'); %调用nearest插值法求得数组zi oi=interp1(x,y,xi,'linear'); %调用linear插值法求得数组oiqi=interp1(x,y,xi,'cubic'); %调用cubic插值法求得数组qi ri=sin(xi); %调用sin(x)函数求真值数组ri; ai=ri-yi; %计算spline插值法与真值的差bi=ri-zi; %计算nearest插值法与真值的差ci=ri-oi; %计算linear插值法与真值的差di=ri-qi; %计算cubic插值法与真值的差subplot(3,2,1),plot(x,y,'ok',xi,yi,'+',xi,zi,'k',xi,oi,'*',xi,qi,'b',x1,y1,'or',xi,ri,'r')%画出所有图像以作比较subplot(3,2,2),plot(x,y,'ok',xi,yi,'+',x1,y1,'or',xi,ri,'r',xi,ai,'+')%画出spline图像以作比较subplot(3,2,3),plot(x,y,'ok',xi,zi,'k',x1,y1,'or',xi,ri,'r',xi,bi,'+')%画出nearest图像以作比较subplot(3,2,4),plot(x,y,'ok',xi,oi,'*',x1,y1,'or',xi,ri,'r',xi,ci,'+')%画出lineart图像以作比较subplot(3,2,5),plot(x,y,'ok',xi,qi,'b',x1,y1,'or',xi,ri,'r',xi,di,'+')%画出cubic图像以作比较%另外运用gtext()语句在图像中插入文字说明(调试并运行得到实验结果图像)(并在工作栏里获得数据)x1 =0.578910000000000 y1 =0.547109809796892(经过验证,结果正确,实验成功)六、实验总结:1.遇到的问题及解决过程:实验中,在作图环节出现很多问题:首先是图像较多,并且图像大范围重合,要在图像中凸显真值,提供的数据点,所求的数据点,就更困难了,所以我想到用subplot语言做出多组图像,以使图像清晰明了;另外我将求得的各差额图像与相应的插值图像画到一起,便于对比该插值法与真值的相似度,为了视图方便,我运用gtext()命令对图像进行标记和说明,获得简单明了的图像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据插值和函数逼近
1 数据插值
由已知样本点,以数据更为平滑为目标,求出其他点处的函数
值。
在信号处理与图像处理上应用广泛。
求解方法:
y1=interp1(x,y,x1,'方法')
z1=interp2(x,y,z,x1,y1,'方法')
1.1 一维数据的插值
例:假设样本点来自x e x x x f x sin )53()(52-+-=,进行插值处理,得到平
例:草图样条曲线功能。
function sketch()
x=[]; y=[]; gca;
hold on; axis([0 1,0 1]);
while 1
[x0,y0,button]=ginput(1);
if(isempty(button)) break; end;
x=[x x0]; y=[y y0];
plot(x,y,'*');
end;
xx=[x(1):(x(end)-x(1))/100:x(end)];
yy=interp1(x,y,xx,'spline');
plot(xx,yy,x,y,'*');
end
1.2 二维网格数据的插值
例3:假设样本点来自xy y x e x x z ----=2
2)2(2,进行插值处理,得到平滑的曲
1.3 二维一般分布数据的插值
例4:假设样本点来自xy y x e
x x z ----=22)2(2,进行插值处理,得到平滑的曲
2 样条插值函数逼近
由已知样本点,求能对其较好拟合的函数表达式。
求解方法:
S=csapi(x,y); % 定义一个三次样条函数类
S=spapi(k,x,y); % 定义一个k 次B 样条函数类
ys=fnval(S,xs); % 计算插值结果
fnplt(S); % 绘制插值结果
例:从)sin(x y =中取样本点,计算三次样条函数。
练习:利用上例中的变量S,生成各个曲线段的参数方程,并绘
例:从)sin(x y =中取样本点,计算三次B 样条函数。
3 多项式的插值与函数逼近
3.1 多项式的基本运算
设多项式为:116251234++-x x x 直接输入系数向量创建多项式
p1=[1 -12 0 25 116];
y=poly2sym(p1);
求多项式的根
r=roots(p1);
由多项式的根逆推多项式
p2=poly(r); p2和p1等价
求多项式的值
polyval (p1,[1 2; 3 4]); % 以数组为运算单位
polyvalm(p1,[1 2; 3 4]); % 以矩阵为运算单位
求多项式的微积分
q=polyder(p); % 导数
r=polyint(q); % 积分
设多项式为:322++x x 与2+x 。
a=[1 2 3]; b=[1 2];
c=conv(a,b); % 乘积
[q,r]=deconv(a,b); % 相除
q=1 0 %商多项式
r=0 0 3 %余多项式
3.2 Lagrange 插值算法
∑∏=≠=--=N i N i j j
i i
x x x x y x 1,1)(φ
3.3 多项式函数逼近
求解方法:
p=polyfit (x,y,n); 计算n 次多项式的降幂排列的系数向量 y=polyval (p,x); 计算多项式的值
主要用于针对实验数据,进行解析描述。
例:假设样本点来自x e x x x f x sin )53()(52-+-=,比较3次、5次多项式插
4 函数设计中的参数逼近
4.1 函数线性组合的参数逼近
已知某函数是若干已知函数的组合,
C F x f c x f c x f c y n n ⋅=+++=)()()(2211 ,已知数据
),(11y x ,),(22y x ,……),(M M y x ,则有方程组:
Y C F =⋅
⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=M n M n M M n n y y y Y c c c C x f x f x f x f x f x f x f x f x f F 2121212222
111211,,)()()()()()()()()( 有n 个待求的未知系数,有M 个方程,所以只能求方程的最小
二乘解: Y F C \=
例:已知函数原型为2443321)2cos()(x c e x c e
c c x g x x +-++=--,已知以下数
C
4.2 函数中的参数逼近
已知数据),(11y x ,),(22y x ,……),(N N y x ,满足函数),(x a f ,其中a
是待定系数的向量。
目标是求出a 。
即定义最优化问题:∑=-=N
i i i a x a f y J 12)],([min
[a,res]=lsqcurvefit(fun,a0,x,y)
例:设采样点如下:
x=0:1:10;
y=0.12*exp(-0.213*x)+0.54*exp(-0.17*x).*sin(1.23*x);
已知数据满足)sin(*),(5314
2x a e a e a x a f x a x a --+=,求最佳拟合的参
数。
4 多项式运算。
