数字滤波器结构实验报告

合集下载

IIR数字滤波器设计实验报告

实验三IIR数字滤波器设计实验报告一、实验目的：1.通过仿真冲激响应不变法和双线性变换法2.掌握滤波器性能分析的基本方法二、实验要求：1.设计带通IIR滤波器2.按照冲激响应不变法设计滤波器系数3. 按照双线性变换法设计滤波器系数4. 分析幅频特性和相频特性5. 生成一定信噪比的带噪信号，并对其滤波，对比滤波前后波形和频谱三、基本原理：㈠IIR模拟滤波器与数字滤波器IIR数字滤波器的设计以模拟滤波器设计为基础，常用的类型分为巴特沃斯（Butterworth）、切比雪夫（Chebyshev）Ⅰ型、切比雪夫Ⅱ型、贝塞尔（Bessel）、椭圆等多种。

在MATLAB信号处理工具箱里，提供了这些类型的IIR数字滤波器设计子函数。

（二）性能指标1.假设带通滤波器要求为保留6000hz~~7000hz频段，滤除小于2000hz和大宇9000hz频段2.通带衰减设为3Db,阻带衰减设为30dB，双线性变换法中T取1s.四、实验步骤：1.初始化指标参数2.计算模拟滤波器参数并调用巴特沃斯函数产生模拟滤波器3.利用冲激响应不变法和双线性变换法求数字IIR滤波器的系统函数Hd (z)4.分别画出两种方法的幅频特性和相频特性曲线5.生成一定信噪比的带噪信号6.画出带噪信号的时域图和频谱图6.对带噪信号进行滤波，并画出滤波前后波形图和频谱图五、实验结果模拟滤波器的幅频特性和相频特性：101010101Frequency (rad/s)P h a s e (d e g r e e s )1010101011010-5100Frequency (rad/s)M a g n i t u d e在本实验中，采用的带通滤波器为6000-7000Hz ，换算成角频率为4.47-0.55，在上图中可以清晰地看出到达了题目的要求。

冲击响应不变法后的幅频特性和相频特性：0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )双线性变换法的幅频特性和相频特性：0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )00.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )通过上图比较脉冲响应不变法双线性变换法的幅频特性和相频特性，而在在幅频曲线上几乎没有差别，都能达到相同的结果。

实验四IIR数字滤波器设计实验报告

实验四IIR数字滤波器设计实验报告
为了实现信号的滤波处理，IIR（或称为滤波器）数字滤波器是一种常用的信号处理
技术。

本次实验就是探究IIR数字滤波器的设计和分析。

在实验开始前，对于IIR数字滤波器有所了解，它是一种无限级别功能的数字滤波器，其功能强大，可以实现任意自定义系数的滤波器。

在预处理实验中，便首先采用Matlab
工具搭建了IIR数字滤波器的框架，考虑到本次滤波处理内容，本次采用的是Chebyshev
类型的等离子体，其滤波效果要求超过50dB，进一步完善了对于设计工作的要求。

经过Chebyshev Type I等离子体的设计，确定了系统的结构，并设定了15个滤波器，接着从设定的各项参量入手，从而确定系统各项参量，运用梯形图确定根位置，并使用MATLAB中的filter函数进行系统模拟，得到经历处理后系统输出信号与未经处理时对比，结果显示滤波效果达到了相应预期要求。

在实验中，IIR数字滤波器的设计让我深刻体会到了系统滤波的重要性以及十分强大
的功能。

而它的实现，又显示了精确的数字处理技术在信号处理中的重要作用，使得研究
信号处理时，得以有效和准确地对信号进行分辨和滤波处理。

实验五数字滤波器实验

实验五数字滤波器实验 The following text is amended on 12 November 2020.实验五数字滤波器实验一、实验目的1.研究数字滤波器对系统稳定性及过渡过程的影响。

2.熟悉和掌握系统过渡过程的测量方法3.掌握数字滤波器的设计方法。

4.了解数字滤波器的通带对系统性能的影响。

二、实验仪器1.EL-AT-III型计算机控制系统实验箱一台。

2.PC计算机一台。

三、实验内容1.需要加入串联超前校正的开环系统电路及传递函数（1）实验电路（2）系统开环传递函数（3）系统闭环结构图（4）数字滤波器的递推公式模拟滤波器的传递函数：（T1S+1）/（T2S+1）2.需加入串联滞后校正系统电路及传递函数（1）实验电路（2）系统开环传递函数（3）系统闭环结构图（4）数字滤波器的递推公式模拟滤波器的传递函数：（T1S+1）/（T2S+1）四、实验步骤1.启动计算机，双击桌面“计算机控制实验”快捷方式，运行软件。

2.测试计算机与实验箱的通信是否正常，通信正常继续，如通信不正常查找原因使通信正常后才可以继续进行实验。

超前校正3.连接被测量典型环节的模拟电路。

电路的输入U1接A/D、D/A卡的DA1输出，电路的输出U2接A/D、D/A卡的AD1输入，将纯积分电容两端接在模拟开关上。

检查无误后接通电源。

4.在实验项目的下拉列表中选择实验五[五、数字滤波]，鼠标单击运行按钮，弹出实验课题参数设置对话框，选择超前校正，然后在参数设置对话框中设置相应的实验参数，鼠标单击确认等待屏幕的显示区显示实验的结果，并记录超调量和调节时间。

6.连接被测量典型环节的模拟电路。

电路的输入U1接A/D、D/A卡的DA1输出，电路的输出U2接A/D、D/A卡的AD1输入，将纯积分电容两端接在模拟开关上。

检查无误后接通电源。

7.在实验项目的下拉列表中选择实验五[五、数字滤波]，鼠标单击运行按钮，弹出实验课题参数设置对话框，选择超前校正，然后在参数设置对话框中设置相应的实验参数，鼠标单击确认等待屏幕的显示区显示实验的结果，并记录超调量和调节时间。

数字滤波器设计实验报告

数字滤波器设计实验报告刘古城65100609一、实验目的研究数字滤波器的设计思想，理解数字频域，模拟频域的关系，掌握数字系统处理模拟信号的方法。

FIR数字滤波器设计：掌握窗函数设计FIR数字滤波器的方法，理解FIR的意义：线性相位。

二、实验原理1、FIR的特点（1）系统的单位冲击响应在有限个n值处不为零。

（2）对于稳定系统，系统函数在| z |>0处收敛，极点全部在z=0处。

（3）结构上主要是非递归结构，没有输出到输入的反馈，但在个别结构中（如频率抽样结构）也包含反馈的递归部分‘2、FIR滤波器的优点（1）即具有严格的线性相位，又具有任意的幅度’（2）FIR滤波器的抽样响应是有限长的，因而滤波器的性能稳定。

（3）只要经过一定的延时，任何非因果的有限长序列都能变成有限长的因果的序列，因而能用因果系统来实现。

（4）FIR滤波器单位冲击响应是有限长的，因而可以进行快速傅立叶变换，提高运算效率。

3、用窗函数设计FIR数字滤波器对函数加窗处理，实际是用一个有限长函数来逼近原函数。

常用的窗函数有矩形窗、三角窗，汉宁窗、海明窗、布莱克曼窗、凯撒窗等。

三、实验要求1、设计FIR数字低通滤波器，要求在不同窗口长度（N=15，33）下，分别求出h(n)，画出相应的幅频特性和相频特性曲线，观察3dB带宽和20dB带宽，总结窗口长度N对滤波特性的影响。

2、对三个拟合三角函数进行滤波处理。

3、对含噪心电信号函数进行滤波处理。

四、实验内容1、不同窗函数长度对于滤波特性的影响fs=100,N=32;n=0:N-1;t=n/fs;f0=n*fs/N;y=exp(-2*t);z=fft(y);m=abs(z);w1=blackman(N);z1=w1'.*y;x1=fft(z1),mo1=abs(x1);subplot(1,2,1);plot(f0,m/fs);subplot(1,2,2);plot(f0,mo1/fs)运行结果改变N值，令N=14，得到结果2、对三个拟合三角函数进行滤波clear;fs=2000;t=(1:1000)/fs;x=10*cos(2*pi*30*t)+cos(2*pi*150*t)+5*cos(2*pi*600*t); L=length(x);N=2^(nextpow2(L));Hw=fft(x,N);figure(1);subplot(2,1,1);plot(t,x);grid on;title('滤波前信号x');xlabel('时间/s');% 原始信号subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw));% 查看信号频谱grid on;title('滤波前信号频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');%% x_1=10*cos(2*pi*30*t)Ap=1;As=60;% 定义通带及阻带衰减dev=[(10^(Ap/20)-1)/(10^(Ap/20)+1),10^(-As/20)];% 计算偏移量mags=[1,0];% 低通fcuts=[60,100];% 边界频率[N,Wn,beta,ftype]=kaiserord(fcuts,mags,dev,fs);% 估算FIR滤波器阶数hh1=fir1(N,Wn,ftype,kaiser(N+1,beta));% FIR滤波器设计x_1=filter(hh1,1,x);% 滤波x_1(1:ceil(N/2))=[];% 群延时N/2，删除无用信号部分L=length(x_1);N=2^(nextpow2(L));Hw_1=fft(x_1,N);figure(2);subplot(2,1,1);plot(t(1:L),x_1);grid on;title('x_1=10*cos(2*pi*30*t)');xlabel('时间/s');subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw_1));% 查看信号频谱grid on;title('滤波后信号x_1频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');%% x_2=cos(2*pi*150*t)Ap=1;As=60;% 定义通带及阻带衰减dev=[10^(-As/20),(10^(Ap/20)-1)/(10^(Ap/20)+1),10^(-As/20)];% 计算偏移量mags=[0,1,0];% 带通fcuts=[80,120,180,220];% 边界频率[N,Wn,beta,ftype]=kaiserord(fcuts,mags,dev,fs);% 估算FIR滤波器阶数hh2=fir1(N,Wn,ftype,kaiser(N+1,beta));% FIR滤波器设计x_2=filter(hh2,1,x);% 滤波x_2(1:ceil(N/2))=[];% 群延时N/2，删除无用信号部分L=length(x_2);N=2^(nextpow2(L));Hw_2=fft(x_2,N);figure(3);subplot(2,1,1);plot(t(1:L),x_2);grid on;title('x_2=cos(2*pi*150*t)');xlabel('时间/s');subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw_2));% 查看信号频谱grid on;title('滤波后信号x_2频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');%% x_3=5*cos(2*pi*600*t)Ap=1;As=60;% 定义通带及阻带衰减dev=[10^(-As/20),(10^(Ap/20)-1)/(10^(Ap/20)+1)];% 计算偏移量mags=[0,1];% 高通fcuts=[500,550];% 边界频率[N,Wn,beta,ftype]=kaiserord(fcuts,mags,dev,fs);% 估算FIR滤波器阶数hh2=fir1(N,Wn,ftype,kaiser(N+1,beta));% FIR滤波器设计x_3=filter(hh2,1,x);% 滤波x_3(1:ceil(N/2))=[];% 群延时N/2，删除无用信号部分L=length(x_3);N=2^(nextpow2(L));Hw_3=fft(x_3,N);figure(4);subplot(2,1,1);plot(t(1:L),x_3);grid on;title('x_3=5*cos(2*pi*600*t)');xlabel('时间/s');subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw_3));% 查看信号频谱grid on;title('滤波后信号x_3频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');运行结果3、对含噪心电信号函数进行滤波处理。

数字滤波器设计实验报告

数字滤波器设计实验报告实验目的：1.掌握数字滤波器的基本理论知识。

2.学习数字滤波器设计方法。

3.实现数字滤波器的设计与模拟。

实验原理：FIR滤波器的特点是稳定性好、相位响应线性和易于设计。

FIR滤波器的设计方法主要有窗函数法、频率采样法和最小最大化法等。

IIR滤波器的特点是具有较窄的通频带宽率、相位响应非线性和较高的处理效率。

IIR滤波器的设计方法主要有双线性变换法、脉冲响应不变法和双正交变换法等。

实验步骤：1.根据实验要求和给定的参数，选择适合的滤波器类型（FIR或IIR）。

2.根据滤波器的设计方法，计算滤波器的系数。

3.使用MATLAB或其他工具进行滤波器的设计和仿真。

4.分析仿真结果，评估滤波器的性能。

5.根据实际需求，进行滤波器参数的优化和调整。

6.进行实验数据的滤波处理，并比较滤波前后的信号质量。

7.总结实验结果，写出实验报告。

实验结果：根据实验要求，我们选择了FIR滤波器进行设计。

通过使用窗函数法和最小最大化法，计算得到了滤波器的系数。

将滤波器的设计结果导入MATLAB进行仿真，得到了滤波器的频率响应和时域波形。

通过分析仿真结果，发现滤波器的设计基本满足了要求，但仍存在一些性能方面的改进空间。

根据实验需求和实际情况，我们对滤波器的参数进行了优化和调整。

经过多次迭代和调试，最终得到了满意的结果。

将优化后的滤波器应用于实验数据的滤波处理，可以看到滤波效果明显，信号质量得到了显著提升。

实验结论：通过本次实验，我们学习并掌握了数字滤波器的基本理论知识和设计方法。

通过实际操作和实验仿真，对数字滤波器的设计和应用有了更深入的了解。

实验结果表明，数字滤波器可以有效地对信号进行滤波处理，提高信号质量和准确度。

数字信号处理实验报告_3(数字滤波器结构)

stem(n,y);
作出实验上的冲激序列
2、用直接Ⅰ型结构实现滤波器：
已知某滤波器的差分方程（见下），试用直接Ⅰ型结构实现该滤波器，求冲激响应。
y(n)=x(n)+1.4x(n-1)+0.3x(n-2)-0.3y(n-1)+0.2y(n-2)，
具体操作步骤：
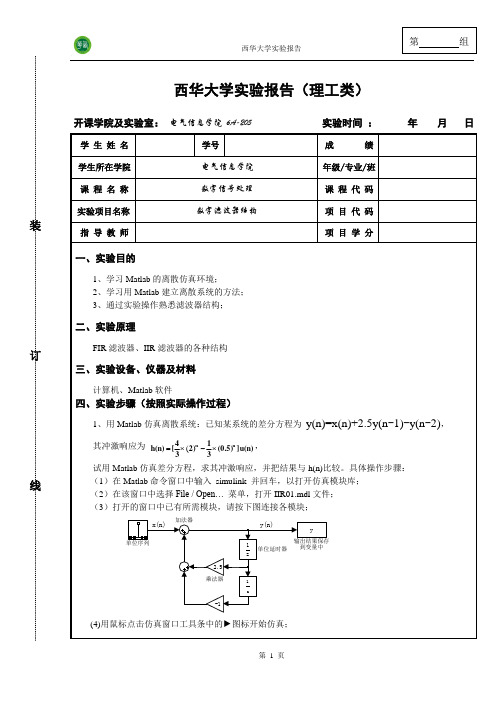
打开IIR02.mdl文件，窗口中已有所需模块，请按下图连接各模块；
（2）用鼠标点击仿真窗口工具条中的►图标开始仿真；
（3）回到Matlab命令窗口中，输入以下程序，观察冲激响应序列（比较结果）；
程序代码
程序说明
subplot(2,1,1);
stem(n,y1);
直接Ⅰ型冲激序列
subplot(2,1,2);
stem(n,y2);
直接Ⅱ型冲激序列
五、实验报告要求
1、对于实验内容1、2和3的数据必须给出的仿真模块图和冲激响应图；
（5）用鼠标点击仿真窗口工具条中的►图标开始仿真；
（6）回到Matlab命令窗口中，输入以下程序，观察冲激响应序列；
程序代码
程序说明
n=0:10;
stem(n,y1);
作出冲激序列
3、用直接Ⅱ型结构实现滤波器：
试用直接Ⅱ型结构实现内容2中的滤波器，求冲激响应。具体操作步骤：
（1）打开IIR03.mdl文件，窗口中已有所需模块，请按下图连接各模块；
其冲激响应为，
试用Matlab仿真差分方程，求其冲激响应，并把结果与h(n)比较。具体操作步骤：
（1）在Matlab命令窗口中输入simulink并回车，以打开仿真模块库；
（2）在该窗口中选择File / Open…菜单，打开IIR01.mdl文件；

实验四 FIR数字滤波器的设计(实验报告)

实验四 FIR数字滤波器的设计(实验报告)《数字信号处理》实验报告学院专业电子信息工程班级姓名学号时间实验四FIR数字滤波器的设计一、实验目的1、掌握用窗函数法、频率采样法及优化算法设计FIR 滤波器的原理及步骤，学会相应的MATLAB编程。

2、熟悉具有线性相位的FIR滤波器的幅频特性和相频特性。

3、了解各种不同窗函数对滤波器性能的影响。

二、实验内容1、用窗函数法设计一个FIR数字低通滤波器LPDF，验证设计结果的幅频特性和相频特性。

要求：通带截止频率ωp=π，通带波纹Rp=，阻带截止频率ωs=π，阻带衰减As=50dB。

50Magnitude (dB) Frequency ( rad/sample) (degrees)- Frequency ( rad/sample)图1-1 低通滤波器LPDF的频率响应图1-2 低通滤波器LPDF的零极点图单位脉冲响应h(n)的数据长度= 45 对称性为：偶对称得到的滤波器通带边界点( 326 )和阻带边界点参数2、用窗函数法设计一个FIR数字高通滤波器HPDF，验证设计结果的幅频特性和相频特性。

要求：通带截止频率ωp=π，通带波纹Rp=，阻带截止频率ωs=π，阻带衰减As=50dB。

Real Part50Magnitude (dB) Frequency ( rad/sample) (degrees) Frequency ( rad/sample)图2-1 高通滤波器HPDF的频率响应图2-2 高通滤波器HPDF的零极点图-滤波器H(z)零点个数= h(n)对称性为：偶对称得到的滤波器通带边界点( 426 )和阻带边界点参数3、用窗函数法设计一个FIR数字带通滤波器BPDF，验证设计结果的幅频特性和相频特性。

要求：阻带截止频率ωs1=π，衰减65dB，通带截止频率ωp1=π→ωp2=π范围内衰减，高端阻带截止频率ωs2=π，阻带衰减As=65dB。

501Magnitude (dB)0-50-100Imaginary Frequency ( rad/sample) Frequency ( rad/sample) (degrees)0-20XX-4000-6000图3-1 带通滤波器BPDF的频率响应图3-2 带通滤波器BPDF的零极点图 FIR滤波器的阶次= 111 h(n)对称性为：偶对称得到的滤波器通带边界点( 298、704 )和阻带边界点参数中心频率：通带带宽：4、用窗函数法设计一个FIR数字带阻滤波器BSDF，验证设计结果的幅频特性和相频特性。

fir数字滤波器设计实验报告

fir数字滤波器设计实验报告FIR数字滤波器设计实验报告概述数字滤波器是数字信号处理中的重要组成部分，广泛应用于音频、图像、视频等领域。

其中，FIR数字滤波器是一种常见的数字滤波器，具有线性相位、稳定性好、易于实现等优点。

本实验旨在设计一种基于FIR数字滤波器的信号处理系统，实现对信号的滤波和降噪。

实验步骤1. 信号采集需要采集待处理的信号。

本实验采用的是模拟信号，通过采集卡将其转换为数字信号，存储在计算机中。

2. 滤波器设计接下来，需要设计FIR数字滤波器。

为了实现对信号的降噪，我们选择了低通滤波器。

在设计滤波器时，需要确定滤波器的阶数、截止频率等参数。

本实验中，我们选择了8阶低通滤波器，截止频率为500Hz。

3. 滤波器实现设计好滤波器后，需要将其实现。

在本实验中，我们采用MATLAB 软件实现FIR数字滤波器。

具体实现过程如下：定义滤波器的系数。

根据滤波器设计的公式，计算出系数值。

利用MATLAB中的filter函数对信号进行滤波。

将采集到的信号作为输入，滤波器系数作为参数，调用filter函数进行滤波处理。

处理后的信号即为滤波后的信号。

4. 结果分析需要对处理后的信号进行分析。

我们可以通过MATLAB绘制出处理前后的信号波形图、频谱图，比较它们的差异，以评估滤波器的效果。

结果显示，经过FIR数字滤波器处理后，信号的噪声得到了有效的降低，滤波效果较好。

同时，频谱图也显示出了滤波器的低通特性，截止频率处信号衰减明显。

结论本实验成功设计并实现了基于FIR数字滤波器的信号处理系统。

通过采集、滤波、分析等步骤，我们实现了对模拟信号的降噪处理。

同时，本实验还验证了FIR数字滤波器的优点，包括线性相位、稳定性好等特点。

在实际应用中，FIR数字滤波器具有广泛的应用前景。

数字信号处理滤波器设计实验报告

实用文档数字信号处理实验报告实验名称：滤波器设计实验班级： 09信息工程3班姓名：学号：指导教师：**实验日期： 11月18号一、实验目的1、加深对数字滤波器的常用指标理解。

2、学习数字滤波器的设计方法。

二、实验原理图1 FIR幅值函数低通滤波器的常用指标：（1）通带边缘频率；（2）阻带边缘频率；（3）通带起伏；（4）通带峰值起伏，（5）阻带起伏，最小阻带衰减。

三、实验结果及分析1、求系统的零、极点和幅度频率响应和相位响应。

实验结果如下：零点为zs = -1.5870 + 1.4470i，-1.5870 - 1.4470i，0.8657 + 1.5779i，0.8657 - 1.5779i，-0.0669极点为ps =0.1328 + 0.9221i，0.1328 - 0.9221i，0.4736 + 0.4752i，0.4736 - 0.4752i，0.5979幅度频率响应和相位响应如下：源代码如下：b=[0.0528 0.0797 0.1295 0.1295 0.797 0.0528];a=[1 -1.8107 2.2947 -1.8801 0.9537 -0.2336];zs=roots(b)ps=roots(a)freqz(b,a)2、利用MATLAB编程,分别用窗函数法和等波纹滤波器法设计两种FIR数字滤波器，指标要求如下：通带边缘频率：，通带峰值起伏：。

阻带边缘频率：，最小阻带衰减：。

用窗函数法设计的FIR数字滤波器如下：源代码如下：[n,Wn,beta,ftype]=kaiserord([0.3 0.45 0.65 0.75],[0 1 0],[0.01 0.1087 0.01]); h=fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');[h1,w1]=freqz(h,1,256);subplot(2,1,1)plot(w1/pi,20*log10(abs(h1)))xlabel('归一化的频率w')ylabel('幅度响应/dB')gridsubplot(2,1,2)plot(w1/pi,angle(h1))xlabel('归一化的频率w')ylabel('相位/rad')grid用等波纹滤波器法设计的FIR数字滤波器如下：源代码如下：[n,fpts,mag,wt]=remezord([0.3 0.45 0.65 0.75],[0 1 0],[0.01 0.1087 0.01]); h=remez(n,fpts,mag,wt);%设计出等波纹滤波器[h1,w1]=freqz(h,1,256);subplot(2,1,1)plot(w1/pi,20*log10(abs(h1)));xlabel('归一化的频率w')ylabel('幅度响应/dB')gridsubplot(2,1,2)plot(w1/pi,angle(h1))xlabel('归一化的频率w')ylabel('相位/rad')grid分析：在幅度频谱上等波纹滤波器阻带边缘比用窗函数实现的更平滑（理想滤波器为垂直下降的）。

实验四IIR数字滤波器的设计实验报告

实验四IIR数字滤波器的设计实验报告
实验材料：
Matlab2023a软件
实验目的：
1、了解和掌握IIR滤波器的基本设计方法;
2、掌握基于频响特性的滤波器设计方法，熟悉Matlab中滤波器设计函数的使用;
3、实验中设计一组窄带通滤波器，掌握滤波器图形的绘制和滤波器参数的计算方法.
一、实验内容
本次实验中，我们设计一个窄带通滤波器，频率响应为：
截止频率为：0.3πrad/s；
抑制频率为：0.4πrad/s；
频率带宽为：≤ 0.1πrad/s；
通带增益为：≥0dB；
抑制区增益为：≤-40dB.
二、实验步骤
1、设计并绘制IIR滤波器的频率响应：绘制滤波器的通带和抑制区的频率响应；
2、确定IIR滤波器的极点数：根据上述设计要求，确定滤波器的极
点数；
3、使用matlab设计IIR滤波器：使用matlab设计IIR滤波器，调
节滤波器的极点数、滤波器的通带增益、频率带宽和抑制区增益，调节滤
波器的频率响应；
4、绘制滤波器的极点图：使用matlab绘制滤波器的极点图，并观察
滤波器的极点分布；
5、绘制滤波器的频率响应：使用matlab绘制滤波器的实际频率响应；。

数字滤波器结构数字信号处理实验.

实验报告课程名称:数字信号处理实验实验名称:第六章数字滤波器结构一、实验目的1. 根据函数表达式熟练的表示出数字滤波器框图,并且判断该滤波器是否为线性相位。

2. 运用MATLAB各个函数分析滤波器的多种表达式,以及各种框图的实现。

二、实验内容Q6.1 Q6.2 Q6.3 Q6.4三、主要算法与程序程序P6.1num = input('Numerator coefficient vector = ';den = input('Denominator coefficient vector = '; [z,p,k] = tf2zp(num,den; sos =zp2sos(z,p,k四、实验结果与分析Q6.1运行程序P6.1输入 Numerator coefficient vector = [2 10 23 34 31 16 4] Denominator coefficient vector = [1 0 0 0 0 0 0] 可以得出 sos =2.0000 6.0000 4.0000 1.0000 0 0 1.0000 1.0000 2.0000 1.0000 0 0 1.0000 1.0000 0.5000 1.0000 0 0 因此可以得出表达式:212121212121122112211010015.0110012110014621((------------=----=++++⨯++++⨯++++=++++==∏∏z z z z z z z z z z z z z a z a z b z b b z H z H L k kk k k k Lk k (1z H 不是一种线性相位传递函数。

根据上式可以画出级联实现的框图。

x[n]y[n]Integer Delay 5 -1ZInteger Delay 4-1Z Integer Delay 3 -1ZInteger Delay 2-1Z Integer Delay 1 -1ZInteger Delay-1Z Gain 60.5Gain 51Gain 42Gain 31Gain 24Gain 16Gain2Q6.2运行程序P6.1将 Numerator coefficient vector = [6 31 74 102 74 31 6]Denominator coefficient vector = [1 0 0 0 0 0 0] 得到 sos =6.0000 15.0000 6.0000 1.0000 0 0 1.0000 2.0000 3.0000 1.0000 0 0 1.0000 0.6667 0.3333 1.0000 0 0 得出表达式:212121212121122112211010013333.06667.0100132100161561((------------=----=++++⨯++++⨯++++=++++==∏∏z z z z z z z z z z z z za z a zb z b b z H z H Lk k k k k k Lk k(2z H 是线性相位传递函数,根据上式画出实现的级联框图: x[n]y[n]Integer Delay 5 -1ZInteger Delay 4-1Z Integer Delay 3 -1ZInteger Delay 2-1Z Integer Delay 1 -1ZInteger Delay-1Z Gain 61/3Gain 52/3Gain 43Gain 32Gain 26Gain 115Gain6只用4个乘法器生成H(z的框图:x[n]y[n]Integer Delay 5-1Z Integer Delay 4-1Z Integer Delay 3-1Z Integer Delay 2-1Z Integer Delay 1-1Z Integer Delay-1Z Gain 3-K-Gain 274Gain 16Gain 61两个框图可以看出:第二个框图图比较简单Q6.3运行程序P6.1输入 Numerator coefficient vector = [3 8 12 7 2 -2]Denominator coefficient vector = [16 24 24 14 5 1] 得到结果 sos =0.1875 -0.0625 0 1.0000 0.5000 0 1.0000 2.0000 2.0000 1.0000 0.5000 0.25001.0000 1.0000 1.0000 1.0000 0.5000 0.5000 画出框图:x[n]y[n]Unit Delay 4z 1Unit Delay 3z 1Unit Delay 2z 1Unit Delay 1z 1Gain 81Gain 42Gain 11110.1875-K--0.5000-K--0.500-K--0.50-K--0.5-K--0.25-K--0.0625-K-z 16.4运行程序P6.1输入 Numerator coefficient vector = [2 10 23 34 31 16 4]Denominator coefficient vector = [36 78 87 59 26 7 1] 得到结果: sos =0.0556 0.1667 0.1111 1.0000 0.5000 0.2500 1.0000 1.0000 2.0000 1.0000 0.6667 0.33331.0000 1.0000 0.5000 1.0000 1.0000 0.3333 画出级联的实现框图: x[n]y[n]Unit Delay 4z 1Unit Delay 3z 1Unit Delay 2z 1Unit Delay 1z 1Gain 81Gain 41Gain 120.0556-K--4.5-K--2/3-K--1/3-K--0.500-K-320.5-1z1-9z1。

fir数字滤波器设计实验报告

fir数字滤波器设计实验报告fir数字滤波器设计实验报告引言数字滤波器是一种常见的信号处理工具，用于去除信号中的噪声或者滤波信号以达到特定的目的。

其中，FIR（Finite Impulse Response）数字滤波器是一种常见且重要的数字滤波器，其特点是具有有限冲击响应。

本实验旨在设计并实现一个FIR数字滤波器，通过对滤波器的设计和性能评估，加深对数字滤波器的理解。

设计过程1. 确定滤波器的要求在设计FIR数字滤波器之前，首先需要明确滤波器的要求。

这包括滤波器类型（低通、高通、带通或带阻）、截止频率、滤波器阶数等。

在本实验中，我们选择设计一个低通滤波器，截止频率为1kHz，滤波器阶数为32。

2. 设计滤波器的传递函数根据滤波器的要求，我们可以利用Matlab等工具设计出滤波器的传递函数。

在本实验中，我们选择使用窗函数法设计滤波器。

通过选择合适的窗函数（如矩形窗、汉宁窗等），可以得到滤波器的传递函数。

3. 确定滤波器的系数根据滤波器的传递函数，我们可以通过离散化的方法得到滤波器的系数。

这些系数将决定滤波器对输入信号的响应。

在本实验中，我们使用了Matlab的fir1函数来计算滤波器的系数。

4. 实现滤波器在得到滤波器的系数之后，我们可以将其应用于输入信号，实现滤波器的功能。

这可以通过编程语言（如Matlab、Python等）来实现，或者使用专用的数字信号处理器（DSP）来进行硬件实现。

实验结果为了评估设计的FIR数字滤波器的性能，我们进行了一系列的实验。

首先，我们使用了一个具有噪声的输入信号，并将其输入到滤波器中。

通过比较滤波器输出信号和原始信号，我们可以评估滤波器对噪声的去除效果。

实验结果显示，设计的FIR数字滤波器能够有效地去除输入信号中的噪声。

滤波后的信号更加平滑，噪声成分明显减少。

此外，滤波器的截止频率也得到了有效控制，滤波器在截止频率之后的信号衰减明显。

讨论与总结通过本次实验，我们深入了解了FIR数字滤波器的设计和实现过程。

数字滤波器的设计及实现实验报告

数字滤波器的设计及实现实验报告1.数字滤波器是一种用于信号处理的重要工具，通过去除或衰减信号中的噪声、干扰或无用信息，从而实现信号的滤波和提取。

本实验旨在学习数字滤波器的设计原理和实现方法，并通过实验验证其滤波效果。

2. 实验目的•理解数字滤波器的基本原理和设计方法；•掌握数字滤波器的实现步骤和工具；•利用实验进行数字滤波器的设计与仿真；•分析和评估数字滤波器的性能指标。

3. 实验器材•计算机•MATLAB或其他数学软件4. 实验流程1.理解数字滤波器的基本原理和设计方法；2.根据所需的滤波特性选择滤波器类型（低通、高通、带通、带阻）；3.设计滤波器的参数，如截止频率、阶数、窗函数等；4.使用MATLAB或其他数学软件进行滤波器的设计与仿真；5.评估滤波器的性能指标，如频率响应、幅度响应、相位响应等；6.分析实验结果，数字滤波器设计与实现的经验与教训。

5. 实验内容5.1 数字滤波器原理数字滤波器是通过数字信号处理算法来实现滤波功能的滤波器。

它可以通过对信号进行采样、变换、运算等处理来实现对信号频率成分的选择性衰减或增强。

数字滤波器通常包含两种主要类型：无限脉冲响应（IIR）滤波器和有限脉冲响应（FIR）滤波器。

IIR滤波器具有时间域响应的无限长度，而FIR滤波器具有有限长度的时间域响应。

5.2 数字滤波器设计步骤•确定滤波器类型：根据滤波要求选择低通、高通、带通或带阻滤波器；•设计滤波器参数：包括截止频率、阶数、窗函数等；•进行滤波器设计：利用MATLAB等数学软件进行滤波器设计，滤波器系数；•进行滤波器仿真：通过信号输入滤波器进行仿真，评估滤波效果；•优化和调整：根据实际需要，对滤波器参数进行优化和调整，以获得更好的滤波效果。

5.3 实验结果与分析经过实验设计和仿真，我们得到了一个具有良好滤波效果的数字滤波器。

在设计过程中，我们选择了一个5阶的Butterworth低通滤波器，截止频率为1000Hz。

fir数字滤波器设计实验报告

fir数字滤波器设计实验报告fir数字滤波器设计实验报告引言：数字滤波器是一种广泛应用于信号处理和通信系统中的重要工具。

其中，有一类常见的数字滤波器是FIR（Finite Impulse Response）数字滤波器。

FIR数字滤波器具有线性相位特性、稳定性好、易于设计和实现等优点，被广泛用于音频处理、图像处理、通信系统等领域。

本实验旨在通过设计一个FIR数字滤波器，探索其设计原理和实际应用。

一、实验目的本实验的目的是通过设计一个FIR数字滤波器，实现对特定信号的滤波处理。

具体来说，我们将学习以下几个方面的内容：1. FIR数字滤波器的基本原理和特点；2. FIR数字滤波器的设计方法和流程；3. 使用MATLAB软件进行FIR数字滤波器的设计和仿真。

二、实验原理1. FIR数字滤波器的基本原理FIR数字滤波器是一种线性时不变系统，其输出仅与当前输入和过去若干个输入有关，没有反馈回路。

这种特性使得FIR数字滤波器具有线性相位特性，适用于对信号的频率响应要求较高的应用场景。

FIR数字滤波器的输出可以通过卷积运算来计算，即将输入信号与滤波器的冲激响应进行卷积运算。

2. FIR数字滤波器的设计方法FIR数字滤波器的设计方法有很多种，常见的包括窗函数法、频率采样法和最优化方法等。

在本实验中，我们将使用窗函数法进行FIR数字滤波器的设计。

窗函数法的基本思想是将理想滤波器的频率响应与一个窗函数相乘，从而得到实际可实现的滤波器。

三、实验步骤1. 确定滤波器的设计要求在设计FIR数字滤波器之前，我们首先需要明确滤波器的设计要求。

包括滤波器的通带、阻带、过渡带的频率范围和响应要求等。

2. 选择窗函数和滤波器的阶数根据设计要求，选择合适的窗函数和滤波器的阶数。

常见的窗函数有矩形窗、汉宁窗、汉明窗等。

不同的窗函数对滤波器的性能有一定影响，需要根据实际情况进行选择。

3. 计算滤波器的冲激响应利用所选窗函数和滤波器的阶数，计算滤波器的冲激响应。

iir数字滤波器实验报告

iir数字滤波器实验报告IIR数字滤波器实验报告引言：数字滤波器是数字信号处理中重要的组成部分，它可以对信号进行滤波和去噪，提取出我们所需要的信息。

在本次实验中，我们将重点研究和实验IIR数字滤波器的性能和应用。

一、IIR数字滤波器的原理IIR（Infinite Impulse Response）数字滤波器是一种递归滤波器，它的输出不仅与当前输入有关，还与之前的输入和输出有关。

IIR滤波器的结构可以由巴特沃斯、切比雪夫等滤波器设计方法得到。

与FIR（Finite Impulse Response）数字滤波器相比，IIR滤波器具有更低的计算复杂度和更好的频率响应特性。

二、IIR数字滤波器的设计在本次实验中，我们选择了巴特沃斯滤波器作为IIR滤波器的设计方法。

巴特沃斯滤波器是一种理想的低通滤波器，具有平坦的通带和陡峭的阻带。

通过选择不同的阶数和截止频率，我们可以得到不同性能的滤波器。

三、IIR数字滤波器的性能评估为了评估IIR数字滤波器的性能，我们进行了一系列实验。

首先，我们使用MATLAB软件进行了滤波器的设计和模拟。

通过绘制滤波器的频率响应曲线和幅度响应曲线，我们可以直观地了解滤波器的性能。

其次，我们使用真实的信号进行了滤波实验。

通过对比滤波前后信号的波形和频谱图，我们可以评估滤波器的去噪和频率特性。

四、IIR数字滤波器的应用IIR数字滤波器在实际应用中具有广泛的用途。

例如，语音信号处理中常用的降噪算法就是基于IIR滤波器的。

此外，IIR滤波器还可以用于信号增强、图像处理等领域。

通过调整滤波器的参数，我们可以实现不同的滤波效果，满足不同应用场景的需求。

五、实验结果与讨论在本次实验中，我们设计了一个二阶巴特沃斯低通滤波器，截止频率为1kHz。

通过MATLAB软件模拟和实际信号滤波实验，我们得到了滤波前后信号的波形和频谱图。

实验结果表明，滤波器能够有效地去除高频噪声，并保留低频信号的主要成分。

同时，滤波器的频率响应也符合设计要求，具有良好的通带和阻带特性。

IIR数字滤波器的设计实验报告

IIR数字滤波器的设计实验报告
实验目的
本实验的目的在于探讨IIR（递归）数字滤波器的原理，掌握能够设计微分器和积分
器的IIR滤波器的方法。

同时，熟悉MATLAB中滤波器设计的相关函数，并用新的函数进
行实验验证。

实验仪器
对于本次实验，所用的仪器主要为实验课电脑，及其软件MATLAB，用于完成滤波器设计及实验实现。

实验过程
1、用MATLAB实现IIR数字滤波器，设计并实现IIR滤波器，并用校准参数系数评估
滤波器性能。

3、对设计的滤波器的传递函数进行仿真、评估。

使用MATLAB绘出滤波器的幅频特性、频谱，以及滤波器输入、输出的波形和信号，观察其传递特性。

实验结果
仿真结果表明，IIR数字滤波器的滤波效果较好，有效降低了背景噪声，使信号在指
定某一范围内得到有效过滤。

滤波器的幅频特性绘制，可以看到滤波器在频率范围内的衰
减特性，证明IIR滤波器具有良好的传输特性，有效控制频率范围的信号，使信号得以准
确输出。

本次实验通过MATLAB完成IIR数字滤波器的设计，经过仿真、评估之后，发现该IIR 滤波器可以有效滤除信号中的指定范围的频率，在精度和效率方面得到保证，而且参数耦
合范围小，可被用于绝大多数滤波器需求场景。

数字滤波器实验报告1

数字滤波器实验报告1数字滤波器2010年4⽉18⽇1. 实验⽬的及意义1.1 实验⽬的1、了解数字滤波器的基本参数；2、学习⾼通、低通、带通、带阻滤波器的参数设计⽅法；3、了解FIR、IIR滤波器及其性能⽐较。

4、了解滤波器的滤波过程。

1.2 实验意义通过对数字滤波器的模拟仿真，使我对数字滤波器的参数设计有了清楚的认识，对数字信号的处理过程有了更深⼊的了解。

2. 实验原理及框图数字滤波器的4个重要的通带﹑阻带参数是：fp:通带截⽌频率(HZ)；fs:阻带起始频率(HZ)；Rp:通带内波动(dB)，即通带内所允许的最⼤衰减；Rs:阻带内最⼩衰减(dB)。

通过这些参数就可以进⾏离散滤波器的设计了。

Simulink提供了专门的数字滤波器模块，可以通过设置仿真参数来实现数字滤波器的滤波功能。

图⼀、数字滤波器原理图图⼀中的滤波前信号由Sine wave模块产⽣，由三个幅度均为1V，频率分别为1MHZ，3MHZ，5MHZ的正弦信号相加⽽成，其频谱如图⼆所⽰。

图⼆、滤波前信号频谱数字采样模块为Zero-order Hold模块产⽣，采样频率为16MHZ。

数字滤波器模块为⾼通型滤波器，通带⼤于4MHZ，阻带⼩于2MHZ，通带波动⼩于1dB，阻带衰减⼤于40dB，抽样频率为20MHZ。

其模块参数设计如图三所⽰。

图三、数字滤波器参数设置滤波前信号通过数字滤波器后，1MHZ的信号被滤除，5MHZ的信号通过滤波器，3MHZ 的信号未经完全滤波，只是幅度上有衰减。

滤波后信号的频谱如图四所⽰。

图四、滤波后信号3. 实验步骤及内容在matlab的simulink中新建new model，根据超外差式接收机原理图画出实验模拟电路（详见⽂件untitled.mdl），其中各模块选取位置及参数配置为：信号1：信号⼆：信号三：加法器：采样器：数字滤波器：见实验原理图三。

连接好电路后，点击Start simulink按钮，观察实验结果与原理结果是否⼀致，将运⾏结果保存。

数字滤波器结构实验报告

数字滤波器的设计实验

实验二IIR数字滤波器的设计实验内容及步骤:数字滤波器的性能指标：通带临界频率fp、阻带临界频率fr；通带内的最大衰减Ap；阻带内的最小衰减Ar；采样周期T；(1)、fp=0.3KHz,Ap=0.8dB, fr=0.2KHz,Ar=20dB,T=1ms；设计一Chebyshev高通滤波器；观察其通带损耗和阻带衰减是否满足要求。

程序如下：fp=300; fr=200;Ap=0.8; Ar=20;T=0.001;fs=1/T;wp=2*pi*fp*T;wr=2*pi*fr*T;Wp=2/T*tan(wp/2);Wr=2/T*tan(wr/2);[N,Wn]=cheb1ord(Wp,Wr,Ap,Ar,'s');[B,A] = cheby1(N,Ap,Wn,'high','s');[num,den]=bilinear(B,A,1/T);[h,w]=freqz(num,den);plot(w*fs/(2*pi),20*log10(abs(h))); %衰减及频率都用归一化的1为单位显示axis([0,500,-30,0]);title('Chebyshev高通滤波器');xlabel('频率');ylabel('衰减');grid on;根据下图知道通带损耗与阻带衰减满足要求(2)、fp=0.2KHz,Ap=1dB, fr=0.3KHz,Ar=25dB,T=1ms；分别用脉冲响应不变法及双线性变换法设计一Butterworth数字低通滤波器，观察所设计数字滤波器的幅频特性曲线，记录带宽和衰减量，检查是否满足要求。

比较这两种方法的优缺点。

程序如下：fp=200; fr=300;Ap=1;Ar=25;T=0.001;fs=1/T;wp=2*pi*fp*T;wr=2*pi*fr*T;Wp=2/T*tan(wp/2);Wr=2/T*tan(wr/2);[N,Wn]=buttord(Wp,Wr,Ap,Ar,'s');[B,A] = butter(N,Wn,'s');[num1,den1]=impinvar(B,A,1/T); %脉冲响应不变法得出设计的传递函数[num2,den2]=bilinear(B,A,1/T); %双线性变换法得出设计的传递函数[h1,w]=freqz(num1,den1);plot(w*fs/(2*pi),20*log10(abs(h2)),w*fs/(2*pi),20*log10(abs(h1)), 'r.');grid on; %衰减及频率都用归一化的1为单位显示axis([0,500,-30,0]);title('Butterworth低通滤波器（红线—脉冲响应不变法蓝线—双线性变换法）');xlabel('ÆµÂÊ');ylabel('Ë¥¼õ');grid on;优缺点：采用脉冲响应不变法优点：1.h(n)完全模仿模拟滤波器的单位抽样响应时域逼近良好2线性相位模拟滤波器转变为线性相位数字滤波器缺点：1.对时域的采样会造成频域的“混叠效应”，故有可能使所设计数字滤波器的频率响应与原来模拟滤波器的频率响应相差很大2不能用来设计高通和带阻滤波器。

数字滤波器结构实验报告

IIR数字滤波器设计实验报告

实验四IIR数字滤波器设计实验报告

实验五数字滤波器实验

数字滤波器设计实验报告

数字滤波器设计实验报告

数字信号处理实验报告_3(数字滤波器结构)

实验四 FIR数字滤波器的设计(实验报告)

fir数字滤波器设计实验报告

数字信号处理滤波器设计实验报告

实验四IIR数字滤波器的设计实验报告

数字滤波器结构 数字信号处理实验.

fir数字滤波器设计实验报告

数字滤波器的设计及实现 实验报告

fir数字滤波器设计实验报告

iir数字滤波器实验报告

IIR数字滤波器的设计实验报告

数字滤波器实验报告1

数字滤波器结构实验报告

数字滤波器的设计实验

数字滤波器结构数字信号处理实验.

数字滤波器的设计及实现实验报告