C语言实现8数码问题
八数码问题范例程序

#include <cstdio>#include <cstring>#include <iostream>#include <algorithm>#include <queue>using namespace std;int mat[10][10];const int dx[] = {-1,1,0,0};const int dy[] = {0,0,1,-1};const char dir[] = {'u','d','r','l'};typedef int state[9];const int maxstate = 1e6;int vis[maxstate];int fact[9];char in[30];int cnt = 1;struct node {state st;int x,y,z;int h,g;int hash;node(){memset(st,0,sizeof(st));}bool operator < (const node &other)const{return h != other.h ? h > other.h : g>other.g; }} goal,start;int get_h(node &a){int pos1[30],pos2[30];for(int i = 0; i < 9; ++i) {if(a.st[i] != -1) pos1[a.st[i]] = i;if(goal.st[i] != -1) pos2[goal.st[i]] = i; }int sum = 0;for(int i = 0; i < 8; ++i) {sum += mat[pos1[i]][pos2[i]];}return sum;}int get_hash(node &a){int code = 0;for(int i = 0; i < 9; ++i) {int cnt = 0;for(int j = i + 1; j < 9; ++j) if(a.st[j] < a.st[i]) cnt++;code += fact[8-i]*cnt;}return code;}struct father {state fst;int pre;char op;} fa[maxstate];void init_search_table(){fact[0] = 1;for(int i = 1; i < 9; ++i) fact[i] = fact[i-1] * i;}void astar(){ //鎼滅储priority_queue<node>que;que.push(start);while(!que.empty()){node u = que.top();que.pop();for(int i = 0; i < 4; ++i){node v = u;v.x += dx[i];v.y += dy[i];if(v.x >= 0 && v.x < 3 && v.y >= 0&&v.y < 3){swap(v.st[3*v.x + v.y],v.st[u.x*3 + u.y]); //灏嗙┖浣嶅拰鐩搁偦浣嶄氦鎹? v.hash = get_hash(v); //寰楀埌HASH鍊? if(vis[v.hash] == 0){ //鍒ゆ柇鏄 惁宸查亶鍘嗕笖鏄 惁鍙 锛屽悗鑰呭彲浠ヤ笉瑕? vis[v.hash] = 1; //淇濆瓨鏂瑰悜v.g++; //宸茶姳浠d环+1memcpy(fa[v.hash].fst,u.st,sizeof(u.st));fa[v.hash].pre=u.hash;fa[v.hash].op = dir[i]; //淇濆瓨璺 緞v.h = get_h(v); //寰楀埌鏂扮殑浼颁环鍑芥暟H que.push(v); //鍏ラ槦}if(v.hash == goal.hash)return ;}}}}void putway(int a){if(a == start.hash) return ;putway(fa[a].pre);printf("State %d:--->\n ",cnt++);for(int i = 0; i < 9; ++i){if(fa[a].fst[i] == -1) printf("x ");else printf("%d ",fa[a].fst[i] + 1);if((i) % 3 == 2) {printf("\n");printf(" ");}}printf("%c\n",fa[a].op);}void input(){int len = strlen(in);int z = 0;for(int i = 0; i < 9; ++i) goal.st[i] = i;goal.st[8] = -1;for(int i = 0; i < len; ++i) {if(in[i] >= '0'&&in[i] <='9'||in[i] =='x') {if(in[i] == 'x') {start.st[z] = -1;int x = z/3,y = z%3;start.x = x,start.y = y,start.z = z;}else start.st[z] = in[i] - '0' - 1;z++;}}start.hash = get_hash(start);start.h = get_h(start);start.g = 0;goal.hash = get_hash(goal);goal.x = 8/3;goal.y = 8%3;goal.z = 8;}void init_mat(){for(int i = 0; i < 9; ++i) {for(int j = 0; j < 9; ++j) {if(i != j) {int x1 = i/3,y1 = i%3;int x2 = j/3,y2 = j%3;mat[i][j] = abs(x1 - x2) + abs(y1 - y2);}}}}bool isok(){int sum = 0;for(int i = 0; i < 9; ++i) {for(int j = i + 1; j < 9; ++j) {if(start.st[j] >= 0&&start.st[i]>=0&&start.st[i] > start.st[j])sum++;}}return !(sum&1);}int main(){//freopen("in","r",stdin);memset(vis,0,sizeof(vis));init_search_table();init_mat();while(gets(in) != NULL){memset(vis,0,sizeof(vis));input();if(!isok()) puts("unsolvable");else {astar();cnt = 1;putway(goal.hash);printf("State %d:--->\n ",cnt++); for(int i = 0; i < 9; ++i){if(goal.st[i] == -1) printf("x "); else printf("%d ",goal.st[i] + 1); if((i) % 3 == 2) {printf("\n");printf(" ");}}printf("\n");}}}。
C语言实现8数码问题

1、实验目的(1)熟悉人工智能系统中的问题求解过程;(2)熟悉状态空间中的盲目搜索策略;(3)掌握盲目搜索算法,重点是宽度优先搜索和深度优先搜索算法。
2、实验要求用VC语言编程,采用宽度优先搜索和深度优先搜索方法,求解8数码问题3、实验内容(1)采用宽度优先算法,运行程序,要求输入初始状态假设给定如下初始状态S02 8 31 6 47 0 5和目标状态Sg2 1 64 0 87 5 3验证程序的输出结果,写出心得体会。
(2)对代码进行修改(选作),实现深度优先搜索求解该问题提示:每次选扩展节点时,从数组的最后一个生成的节点开始找,找一个没有被扩展的节点。
这样也需要对节点添加一个是否被扩展过的标志。
4 源代码及实验结果截图#include<stdio.h>#include<stdlib.h>#include<math.h>//八数码状态对应的节点结构体struct Node{int s[3][3];//保存八数码状态,0代表空格int f,g;//启发函数中的f和g值struct Node * next;struct Node *previous;//保存其父节点};int open_N=0; //记录Open列表中节点数目//八数码初始状态int inital_s[3][3]={2,8,3,1,6,4,7,0,5};//八数码目标状态int final_s[3][3]={2,1,6,4,0,8,7,5,3};//------------------------------------------------------------------------//添加节点函数入口,方法:通过插入排序向指定表添加//------------------------------------------------------------------------void Add_Node( struct Node *head, struct Node *p){struct Node *q;if(head->next)//考虑链表为空{ q = head->next;if(p->f < head->next->f){//考虑插入的节点值比链表的第一个节点值小p->next = head->next;head->next = p;}else {while(q->next)//考虑插入节点x,形如a<= x <=b{if((q->f < p->f ||q->f == p->f) && (q->next->f > p->f || q->next->f == p->f)){ p->next = q->next;q->next = p;break;}q = q->next;}if(q->next == NULL) //考虑插入的节点值比链表最后一个元素的值更大q->next = p;}else head->next = p;}//------------------------------------------------------------------------//删除节点函数入口//------------------------------------------------------------------------void del_Node(struct Node * head, struct Node *p ){struct Node *q;q = head;while(q->next){if(q->next == p){q->next = p->next;p->next = NULL;if(q->next == NULL) return;// free(p);}q = q->next;}}//------------------------------------------------------------------------//判断两个数组是否相等函数入口//------------------------------------------------------------------------int equal(int s1[3][3], int s2[3][3])int i,j,flag=0;for(i=0; i< 3 ; i++)for(j=0; j< 3 ;j++)if(s1[i][j] != s2[i][j]){flag = 1; break;}if(!flag)return 1;else return 0;}//------------------------------------------------------------------------//判断后继节点是否存在于Open或Closed表中函数入口//------------------------------------------------------------------------int exit_Node(struct Node * head,int s[3][3], struct Node *Old_Node) {struct Node *q=head->next;int flag = 0;while(q)if(equal(q->s,s)) {flag=1;Old_Node->next = q;return 1;}else q = q->next;if(!flag) return 0;}//------------------------------------------------------------------------//计算p(n)的函数入口//其中p(n)为放错位的数码与其正确的位置之间距离之和//具体方法:放错位的数码与其正确的位置对应下标差的绝对值之和//------------------------------------------------------------------------int wrong_sum(int s[3][3]){int i,j,fi,fj,sum=0;for(i=0 ; i<3; i++)for(j=0; j<3; j++){for(fi=0; fi<3; fi++)for(fj=0; fj<3; fj++)if((final_s[fi][fj] == s[i][j])){sum += fabs(i - fi) + fabs(j - fj);break;}}return sum;}//------------------------------------------------------------------------//获取后继结点函数入口//检查空格每种移动的合法性,如果合法则移动空格得到后继结点//------------------------------------------------------------------------int get_successor(struct Node * BESTNODE, int direction, struct Node *Successor)//扩展BESTNODE,产生其后继结点SUCCESSOR {int i,j,i_0,j_0,temp;for(i=0; i<3; i++)for(j=0; j<3; j++)Successor->s[i][j] = BESTNODE->s[i][j];//获取空格所在位置for(i=0; i<3; i++)for(j=0; j<3; j++)if(BESTNODE->s[i][j] == 0){i_0 = i; j_0 = j;break;} switch(direction){case 0: if((i_0-1)>-1 ){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0-1][j_0];Successor->s[i_0-1][j_0] = temp;return 1;}else return 0;case 1: if((j_0-1)>-1){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0][j_0-1];Successor->s[i_0][j_0-1] = temp;return 1;}else return 0;case 2: if( (j_0+1)<3){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0][j_0+1];Successor->s[i_0][j_0+1] = temp;return 1;}else return 0;case 3: if((i_0+1)<3 ){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0+1][j_0];Successor->s[i_0+1][j_0] = temp;return 1;}else return 0;}}//------------------------------------------------------------------------//从OPen表获取最佳节点函数入口//------------------------------------------------------------------------struct Node * get_BESTNODE(struct Node *Open){return Open->next;}//------------------------------------------------------------------------//输出最佳路径函数入口//------------------------------------------------------------------------void print_Path(struct Node * head){struct Node *q, *q1,*p;int i,j,count=1;p = (struct Node *)malloc(sizeof(struct Node));//通过头插法变更节点输出次序p->previous = NULL;q = head;while(q){q1 = q->previous;q->previous = p->previous;p->previous = q;q = q1;}q = p->previous;while(q){if(q == p->previous)printf("八数码的初始状态:\n");else if(q->previous == NULL)printf("八数码的目标状态:\n");else printf("八数码的中间态%d\n",count++);for(i=0; i<3; i++)for(j=0; j<3; j++){printf("%4d",q->s[i][j]);if(j == 2)printf("\n");}printf("f=%d, g=%d\n\n",q->f,q->g);q = q->previous;}}//------------------------------------------------------------------------//A*子算法入口:处理后继结点//------------------------------------------------------------------------void sub_A_algorithm(struct Node * Open, struct Node * BESTNODE, struct Node * Closed,struct Node *Successor){struct Node * Old_Node = (struct Node *)malloc(sizeof(struct Node));Successor->previous = BESTNODE;//建立从successor返回BESTNODE的指针Successor->g = BESTNODE->g + 1;//计算后继结点的g值//检查后继结点是否已存在于Open和Closed表中,如果存在:该节点记为old_Node,比较后继结点的g值和表中old_Node节点//g值,前者小代表新的路径比老路径更好,将Old_Node的父节点改为BESTNODE,并修改其f,g值,后者小则什么也不做。
八数码为题求解

#include <stdio.h>#include <string.h>#include <math.h>#include <malloc.h>#include <stdlib.h>typedef struct node{int array[3][3];//int g;//搜索的深度int h;//不在位的数字到达目标状态的距离之和int f;//启发函数中的f值node *fwd;//node *bwd;};int step=0;int start_s[3][3]={//起始状态2,1,6,4,0,8,7,5,3};int target_s[3][3]={//目标状态1,2,3,8,0,4,7,6,5};int open_n=0;//open表中的元素个数int get_h(int array[3][3]);//得到启发函数的值node *move_up(node *org_node);//空格上移node *move_down(node *org_node);//空格下移node *move_left(node *org_node);//空格左移node *move_right(node *org_node);//空格右移int equal_s(int s1[3][3],int s2[3][3]);//判断两个状态是否相同void copy_s(int s1[3][3],int s2[3][3]);//将第二个数组的内容复制到第一个数组int new_state(node *head,node *s1);//判断所得节点是不是新节点void insert_open(node *head,node *p);//在open表中插入节点,链表是h+g值升序排列的链表void inser_close(node *head,node *p);//在close表中插入节点,并且采用头插入法void del_open(node *head);//从open表中删除头节点void display(int s[3][3]);//展示状态void displayl(node *p);//按照最优路径输出各个节点int get_h(int array[3][3]){int sum=0;int i,j,m,n;for(i=0;i<3;i++)for (j=0;j<3;j++){for(m=0;m<3;m++)for (n=0;n<3;n++){if(array[i][j]==target_s[m][n]){sum=sum+(int)fabs(i-m)+(int)fabs(j-n);break;}}}return sum;}/*int get_h(int array[3][3]){int sum=0;for (int i=0;i<3;i++)for(int j=0;j<3;j++)if(array[i][j]!=target_s[i][j])sum++;return sum;}*/node *move_up(node *org_node){int i,j;node *new_n=new node;copy_s(new_n->array,org_node->array);for(i=0;i<3;i++){for(j=0;j<3;j++){if(new_n->array[i][j]==0){if(i==0)return NULL;else{new_n->array[i][j]=new_n->array[i-1][j];new_n->array[i-1][j]=0;new_n->g=org_node->g+1;new_n->h=get_h(new_n->array);new_n->f=new_n->g+new_n->h;new_n->bwd=org_node;new_n->fwd=NULL;return new_n;}}}}return NULL;}node *move_down(node *org_node){int i,j;node *new_n=new node;copy_s(new_n->array,org_node->array);for(i=0;i<3;i++){for(j=0;j<3;j++){if(new_n->array[i][j]==0){if(i==2)return NULL;else{new_n->array[i][j]=new_n->array[i+1][j];new_n->array[i+1][j]=0;new_n->g=org_node->g+1;new_n->h=get_h(new_n->array);new_n->f=new_n->g+new_n->h;new_n->bwd=org_node;new_n->fwd=NULL;return new_n;}}}}return NULL;}node *move_left(node *org_node){int i,j;node *new_n=new node;copy_s(new_n->array,org_node->array);for(i=0;i<3;i++){for(j=0;j<3;j++){if(new_n->array[i][j]==0){if(j==0)return NULL;else{new_n->array[i][j]=new_n->array[i][j-1];new_n->array[i][j-1]=0;new_n->g=org_node->g+1;new_n->h=get_h(new_n->array);new_n->f=new_n->g+new_n->h;new_n->bwd=org_node;new_n->fwd=NULL;return new_n;}}}}return NULL;}node *move_right(node *org_node){int i,j;node *new_n=new node;copy_s(new_n->array,org_node->array);for(i=0;i<3;i++){for(j=0;j<3;j++){if(new_n->array[i][j]==0){if(j==2)return NULL;else{new_n->array[i][j]=new_n->array[i][j+1];new_n->array[i][j+1]=0;new_n->g=org_node->g+1;new_n->h=get_h(new_n->array);new_n->f=new_n->g+new_n->h;new_n->bwd=org_node;new_n->fwd=NULL;return new_n;}}}}return NULL;}int equal_s(int s1[3][3],int s2[3][3]){int i,j;for (i=0;i<3;i++)for (j=0;j<3;j++){if(s1[i][j]!=s2[i][j])return 0;}return 1;}void copy_s(int s1[3][3],int s2[3][3]){int i,j;for(i=0;i<3;i++)for (j=0;j<3;j++){s1[i][j]=s2[i][j];}}int new_state(node *head1,node *head2,node *s1) {node *q;q=head1->fwd;while(q!=NULL){if(equal_s(s1->array,q->array))return 0;q=q->fwd;}q=head2->fwd;while(q!=NULL){if(equal_s(s1->array,q->array))return 0;q=q->fwd;}return 1;}void insert_open(node *head,node *p){node *q;if(head->fwd){q=head->fwd;if (p->f<head->fwd->f){p->fwd=head->fwd;head->fwd=p;}else{while (q->fwd){if ((q->f < p->f ||q->f == p->f) && (q->fwd->f > p->f )){p->fwd=q->fwd;q->fwd=p;break;}q=q->fwd;}if (q->fwd==NULL){q->fwd=p;p->fwd=NULL;}}}else{head->fwd=p;p->fwd=NULL;}}void inser_close(node *head,node *p){p->fwd=head->fwd;head->fwd=p;}void del_open(node *head,node *p){node *q;q=head;while (q->fwd){if(q->fwd==p){q->fwd=p->fwd;free(p);break;}q=q->fwd;}}void display(int s[3][3]){int i=0;int j=0;printf("------step%d-----------\n",step++);for(i;i<3;i++){for(j=0;j<3;j++)printf("%d\t",s[i][j]);printf("\n");}}void displayl(node *p){node *q=new node;q->fwd=NULL;while(p){p->fwd=q->fwd;q->fwd=p;p=p->bwd;}while(q->fwd){display(q->fwd->array);q=q->fwd;}delete q;}void main(void){node *head1=new node;node *head2=new node;node *p;head1->fwd=NULL;head1->bwd=NULL;head2->fwd=NULL;head2->bwd=NULL;node *first=new node;copy_s(first->array,start_s);first->fwd=NULL;first->bwd=NULL;first->g=0;first->h=get_h(first->array);first->f=first->g+first->h;insert_open(head1,first);open_n++;while (open_n>0){node *temp=new node;node *temp1;copy_s(temp->array,head1->fwd->array);temp->g=head1->fwd->g;temp->h=head1->fwd->h;temp->f=head1->fwd->f;temp->bwd=head1->fwd->bwd;temp->fwd=head1->fwd->fwd;inser_close(head2,temp);// display(head2->fwd->array);if(equal_s(temp->array,target_s)){displayl(temp);display(target_s);exit(EXIT_SUCCESS);}temp1=head1->fwd;temp=move_up(temp1);if(temp&&new_state(head1,head2,temp)){insert_open(head1,temp);open_n++;}temp=move_down(temp1);if(temp&&new_state(head1,head2,temp)){insert_open(head1,temp);open_n++;}temp=move_left(temp1);if(temp&&new_state(head1,head2,temp)){insert_open(head1,temp);open_n++;}temp=move_right(temp1);if(temp&&new_state(head1,head2,temp)){insert_open(head1,temp);open_n++;}p=head1->fwd;while(p){//若删除节点恰好是head1中某些元素的父节点,则将这些元素的父节点指针指向head2的第一个节点(其父节点的复制节点)if(p->bwd==temp1)p->bwd=head2->fwd;p=p->fwd;}del_open(head1,temp1);open_n--;}}。
8数码问题分析及程序代码

八数码问题1、问题描述所谓八数码问题是指:将分别标有数字1,2,3,…,8的八块正方形数码牌任意地放在一块3×3的数码盘上。
放牌时要求不能重叠。
于是,在3×3的数码盘上出现了一个空格。
现在要求按照每次只能将与空格相邻的数码牌与空格交换的原则,将任意摆放的数码盘逐步摆成某种特殊的排列。
2、问题分析首先,八数码问题包括一个初始状态(strat) 和 目标状态(goal),所谓解八数码问题就是在两个状态间寻找一系列可过渡状态(strat-> strat 1-> strat 2->...->goal )。
这个状态是否存在表示空格)图13、 数据结构 定义结构体Node 如下: typedef struct{int num[9];char cur_expension; //记录是否可以扩展,Y 代表可以扩展,N 代表不可以。
char Operate; //表示不可以执行的操作,'L'代表不能左移,'R'代表不能右移, //'U'代表不能上移,'D'代表不能下移,'C'代表可以任意移动。
int father; //记录父节点的下标。
}Node;Node state[MAXSIZE]; //将搜索过的状态存储于该数组中。
4、广度优先搜索广度优先搜索是指按节点的层次进行搜索,本层的节点没有搜索完毕时,不能对下层节点进行处理,即深度越小的节点越先得到扩展,也就是说先产生的节点先得以扩展处理,直至找到目标为止。
求解八数码问题的搜索过程:如图2所示,把所有可能的算符应用到开始节点(即空格上移、空格左移、空格右移、空格下移),图2只是演示了两个扩展结点,如此继续下去,直到发现目标节点。
图2 变量定义及函数说明:1 2 3 45 6 7 8 01 2 37 4 5 8 0 61 2 34 5 67 8 0#define SUM 100//限定只搜索前50步,50步以后如果仍然没有搜索到结果,认为无解。
八数码问题:C++广度搜索实现

⼋数码问题:C++⼴度搜索实现毕竟新⼿上路23333,有谬误还请指正。
课程设计遇到⼋数码问题(这也是⼀坨),也查过⼀些资料并不喜欢⽤类函数写感觉这样规模⼩些的问题没有必要,⼀开始⽤深度搜索却发现深搜会陷⼊⽆底洞,如果设定了深度限制⼜会有很多情况⽆法找到,然后果断放弃,改⽤⼴度搜索。
如果要改善代码效率还可以⽤双向搜索,即从起始状态和最终状态同时搜索,找到相同状态,这样搜索时间会缩短⼀半。
此外还可以⽤A*(启发式算法)会显得⾼端很多。
题⽬要求:在⼀个3*3的棋盘上,随机放置1到8的数字棋⼦,剩下⼀个空位。
数字可以移动到空位(编程时,空位可⽤0代替,且可以理解为是空位的上、下、左、右移动),经过若⼲次移动后,棋局到达指定⽬标状态。
数组表⽰棋局状态。
⽤函数表⽰空格(0)的移动,使⽤函数具有前提条件,满⾜条件才可以使⽤。
⽤⼴度优先或深度优先搜索求解。
还可以使⽤启发式求解,以提⾼搜索效率。
要求:①编程求解问题;②给出中间状态;③给出解序列(函数调⽤序列)1 #include <iostream>2 #include <vector>3 #include <string>4 #include <queue>5 #include <algorithm>6 #include <cmath>7 #include <ctime>8 #include <cstdio>9 #include <sstream>10 #include <deque>11 #include <functional>12 #include <iterator>13 #include <list>14 #include <map>15 #include <memory>16 #include <stack>17 #include <set>18 #include <numeric>19 #include <utility>20 #include <cstring>21 #include <fstream>2223using namespace std;24int board[25]; //初始状态,⼀维数组模拟⼆维25int destboard[25]; //⽬标状态26int dx[] = {-1, 0, 1, 0}; //数字0的移动偏移量27int dy[] = {0, 1, 0, -1};28 map<int, bool> mark; //记录已搜索的状态2930int lists(int i, int j)31 {32return i*5 + j; //返回i, j⼆维数组的⼀维位置33 }3435int judge() //运算前判断是否可以找到⼀种对于初末状态可⾏的变换36 {37int first_d[10],last_d[10],i,j=6,k,rank1=0,rank2=0;38for(i=1;i<=9;i++) //初状态赋值给first_d[10]39 {40while(1)41 {42if(j==9){j=11;}43if(j==14){j=16;}44 first_d[i]=destboard[j];45 j++;46break;47 }48 }49 j=1;i=1;50for(k=1;k<=9;k++) //最终状态赋值给last_d[10]51 {52while(1)53 {54 last_d[k]=board[lists(i, j)];55 j++;56if(j==4){i++;j=1;}57break;58 }59 }6061for(j=2;j<=9;j++) //计算初状态的奇偶性62 {63for(i=1;i<j;i++)64 {65if(first_d[i]>first_d[j]&&first_d[i]!=0&&first_d[j]!=0){rank1++;}66 }67 }6869for(j=2;j<=9;j++) //计算末状态的奇偶性70 {71for(i=1;i<j;i++)72 {73if(last_d[i]>last_d[j]&&last_d[i]!=0&&last_d[j]!=0){rank2++;}74 }75 }76int a1=rank1%2,a2=rank2%2;77if(a1!=a2){return0;} //判断奇偶性是否相同,相同才可以从出状态变到末状态 78else{return1;}79 }8081struct Stat //结构体三个参数82 {83int step; // 步数84int board[25]; // 状态85 Stat(int *b, int s=0)86 {87 memcpy(this->board, b, sizeof(int)*25); //对状态的赋值操作88 step = s;89 }90 };9192bool ok(int *b) // 判断是否到已经达⽬标状态93 {94for(int i=1; i<=3; ++i)95for(int j=1; j<=3; ++j)96 {97if(b[lists(i, j)] != destboard[lists(i, j)])98return false;99 }100return true;101 }102103int Bfs()104 {105int judge_first=judge();106 ofstream ofs; //建⽴数据外存⽂件107 ofs.open("output.dat");108if(judge_first==0){cout<<"不存在"<<endl;return2333333;}109if(judge_first==1)110 {111 queue<Stat> que; //建队que112 que.push(Stat(board, 0)); // 初始状态⼊队113while(que.size())114 {115int m=0, mk=1; // 记录状态m,以及基数mk116 Stat p = que.front(); //取出队头元素117for(int i=1; i<=3; ++i)118 {119for(int j=1; j<=3; ++j)120 {121 ofs<<p.board[lists(i, j)]<<"";122 }123 ofs<<endl;124 }125 ofs<<endl;126127 que.pop(); //出队128129if(ok(p.board))130 {131return p.step; // 到达⽬标则返回最短步数132 }133134for(int i=1; i<=3; ++i) // 这个是为了标记初始状态,不能遗漏135for(int j=1; j<=3; ++j)136 {137 m+=p.board[lists(i, j)]*mk;138 mk*=10;139 }140if(!mark.count(m)) // 未标记则标记141 mark[m] = true;142143for(int k=0; k<4; ++k) // 四个⽅向搜索144 {145 Stat n(p.board, p.step+1); // n是下⼀步搜索的状态146int zx, zy; // zx,zy存放当前状态0的位置147148for(int i=1; i<=3; ++i) // 搜索当前状态的0的位置149for(int j=1; j<=3; ++j)150 {151if(p.board[lists(i,j)]==0)152 {153 zx = i;154 zy = j;155break;156 }157if(p.board[lists(i,j)]==0)158break;159 }160161int nx = zx+dx[k]; //下⼀个状态的0的位置162int ny = zy+dy[k];163 m = 0; //标记状态164 mk = 1;165 swap(n.board[lists(nx,ny)],n.board[lists(zx, zy)]); //交换166167for(int i=1; i<=3; ++i)168for(int j=1; j<=3; ++j)169 {170 m+=n.board[lists(i, j)]*mk;171 mk*=10;172 }173if(!mark.count(m))174 {175 mark[m] = true;176 que.push(n); //若未搜索过,则⼊队177 }178 }179 }180 ofs.close(); //结束外存181return2333333;182 }183return0;184 }185186int main()187 {188 cout<<"⼴度搜索⼋数码问题:\n";189 cout<<"请输⼊初始状态⽤0-8表⽰\n";190 memset(board, 0, sizeof(board));191for(int i=1; i<=3; ++i)192for(int j=1; j<=3; ++j)193 scanf("%1d", &board[lists(i, j)]);194195 cout<<"请输⼊结束状态\n";196for(int m=6;m<=8;m++){scanf("%d",&destboard[m]);}197for(int m=11;m<=13;m++){scanf("%d",&destboard[m]);}198for(int m=16;m<=18;m++){scanf("%d",&destboard[m]);}199 mark.clear();200201 cout<<"准备搜索...\n";202 system("pause");203 cout<<"搜索中.....\n";204205int t=Bfs();206 cout<<"搜索完毕,过程已经以⽂件的形式存储\n";207if(t==2333333){cout<<"没有找到"<<endl;}208else{cout<<"深度为:"<<t<< endl;}209 system("pause");210return0;211 }输⼊初始状态和最终状态,中间过程会⽣成在”output.dat”中。
C语言实现8数码问题

C语言实现8数码问题1、实验目的(1)熟悉人工智能系统中的问题求解过程;(2)熟悉状态空间中的盲目搜索策略;(3)掌握盲目搜索算法,重点是宽度优先搜索和深度优先搜索算法。
2、实验要求用VC语言编程,采用宽度优先搜索和深度优先搜索方法,求解8数码问题3、实验内容(1)采用宽度优先算法,运行程序,要求输入初始状态假设给定如下初始状态S02 8 31 6 47 0 5和目标状态Sg2 1 64 0 87 5 3验证程序的输出结果,写出心得体会。
(2)对代码进行修改(选作),实现深度优先搜索求解该问题提示:每次选扩展节点时,从数组的最后一个生成的节点开始找,找一个没有被扩展的节点。
这样也需要对节点添加一个是否被扩展过的标志。
4 源代码及实验结果截图#include#include#include//八数码状态对应的节点结构体struct Node{int s[3][3];//保存八数码状态,0代表空格int f,g;//启发函数中的f和g值struct Node * next;struct Node *previous;//保存其父节点};int open_N=0; //记录Open列表中节点数目//八数码初始状态int inital_s[3][3]={2,8,3,1,6,4,7,0,5};//八数码目标状态int final_s[3][3]={2,1,6,4,0,8,7,5,3};//------------------------------------------------------------------------//添加节点函数入口,方法:通过插入排序向指定表添加//------------------------------------------------------------------------void Add_Node( struct Node *head, struct Node *p){struct Node *q;if(head->next)//考虑链表为空{ q = head->next;if(p->f < head->next->f){//考虑插入的节点值比链表的第一个节点值小p->next = head->next;head->next = p;}else {while(q->next)//考虑插入节点x,形如a<= x <=bif((q->f < p->f ||q->f == p->f) && (q->next->f > p->f || q->next->f == p->f)){ p->next = q->next;q->next = p;break;}q = q->next;}if(q->next == NULL) //考虑插入的节点值比链表最后一个元素的值更大q->next = p;}else head->next = p;}//------------------------------------------------------------------------//删除节点函数入口//------------------------------------------------------------------------void del_Node(struct Node * head, struct Node *p ) {struct Node *q;q = head;while(q->next){if(q->next == p){q->next = p->next;p->next = NULL;if(q->next == NULL) return;// free(p);}q = q->next;}//------------------------------------------------------------------------//判断两个数组是否相等函数入口//------------------------------------------------------------------------int equal(int s1[3][3], int s2[3][3])int i,j,flag=0;for(i=0; i< 3 ; i++)for(j=0; j< 3 ;j++)if(s1[i][j] != s2[i][j]){flag = 1; break;}if(!flag)return 1;else return 0;}//------------------------------------------------------------------------//判断后继节点是否存在于Open或Closed表中函数入口//------------------------------------------------------------------------int exit_Node(struct Node * head,int s[3][3], struct Node *Old_Node) {struct Node *q=head->next;int flag = 0;while(q)if(equal(q->s,s)) {flag=1;Old_Node->next = q;return 1;}else q = q->next;if(!flag) return 0;//------------------------------------------------------------------------//计算p(n)的函数入口//其中p(n)为放错位的数码与其正确的位置之间距离之和//具体方法:放错位的数码与其正确的位置对应下标差的绝对值之和//------------------------------------------------------------------------int wrong_sum(int s[3][3]){int i,j,fi,fj,sum=0;for(i=0 ; i<3; i++)for(j=0; j<3; j++){for(fi=0; fi<3; fi++)for(fj=0; fj<3; fj++)if((final_s[fi][fj] == s[i][j])){sum += fabs(i - fi) + fabs(j - fj);break;}}return sum;}//------------------------------------------------------------------------//获取后继结点函数入口//检查空格每种移动的合法性,如果合法则移动空格得到后继结点//------------------------------------------------------------------------int get_successor(struct Node * BESTNODE, int direction, struct Node *Successor)//扩展BESTNODE,产生其后继结点SUCCESSOR {int i,j,i_0,j_0,temp;for(i=0; i<3; i++)for(j=0; j<3; j++)Successor->s[i][j] = BESTNODE->s[i][j];//获取空格所在位置for(i=0; i<3; i++)for(j=0; j<3; j++)if(BESTNODE->s[i][j] == 0){i_0 = i; j_0 = j;break;} switch(direction){case 0: if((i_0-1)>-1 ){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0-1][j_0];Successor->s[i_0-1][j_0] = temp;return 1;}else return 0;case 1: if((j_0-1)>-1){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0][j_0-1];Successor->s[i_0][j_0-1] = temp;return 1;}else return 0;case 2: if( (j_0+1)<3){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0][j_0+1];Successor->s[i_0][j_0+1] = temp;return 1;}else return 0;case 3: if((i_0+1)<3 ){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0+1][j_0];Successor->s[i_0+1][j_0] = temp;return 1;}else return 0;}}//------------------------------------------------------------------------//从OPen表获取最佳节点函数入口//------------------------------------------------------------------------struct Node * get_BESTNODE(struct Node *Open){return Open->next;}//------------------------------------------------------------------------//输出最佳路径函数入口//------------------------------------------------------------------------void print_Path(struct Node * head){struct Node *q, *q1,*p;int i,j,count=1;p = (struct Node *)malloc(sizeof(struct Node));//通过头插法变更节点输出次序p->previous = NULL;q = head;while(q){q1 = q->previous;q->previous = p->previous;p->previous = q;q = q1;}q = p->previous;while(q){if(q == p->previous)printf("八数码的初始状态:\n");else if(q->previous == NULL)printf("八数码的目标状态:\n"); else printf("八数码的中间态%d\n",count++);for(i=0; i<3; i++)for(j=0; j<3; j++){printf("%4d",q->s[i][j]);if(j == 2)printf("\n");}printf("f=%d, g=%d\n\n",q->f,q->g);q = q->previous;}}//------------------------------------------------------------------------//A*子算法入口:处理后继结点//------------------------------------------------------------------------void sub_A_algorithm(struct Node * Open, struct Node * BESTNODE, struct Node * Closed,struct Node *Successor) {struct Node * Old_Node = (struct Node *)malloc(sizeof(struct Node));Successor->previous = BESTNODE;//建立从successor返回BESTNODE的指针Successor->g = BESTNODE->g + 1;//计算后继结点的g值//检查后继结点是否已存在于Open和Closed表中,如果存在:该节点记为old_Node,比较后继结点的g值和表中old_Node节点//g值,前者小代表新的路径比老路径更好,将Old_Node的父节点改为BESTNODE,并修改其f,g值,后者小则什么也不做。
八数码C语言A算法详细代码

#include<iostream>#include<time.h>#include<windows.h>#include<vector>#include<cmath>using namespace std;struct node{int a[3][3]; //存放矩阵int father; //父节点的位置int gone; //是否遍历过,1为是,0为否int fn; //评价函数的值int x,y; //空格的坐标int deep; //节点深度};vector<node> store; //存放路径节点int mx[4]={-1,0,1,0};int my[4]={0,-1,0,1}; //上下左右移动数组int top; //当前节点在store中的位置bool check(int num) //判断store[num]节点与目标节点是否相同,目标节点储存在store[0]中{for(int i=0;i<3;i++){for(int j=0;j<3;j++){if(store[num].a[i][j]!=store[0].a[i][j])return false;}}return true;}bool search(int num) //判断store[num]节点是否已经扩展过 ,没有扩展返回true{int pre=store[num].father; //pre指向store[num]的父节点位置bool test=true;while(!pre){ //循环直到pre为0,既初始节点for(int i=0;i<3;i++){for (int j=0;j<3;j++){if(store[pre].a[i][j]!=store[num].a[i][j]){test=false;break;}}if(test==false) break;}if(test==true) return false;pre=store[pre].father; //pre继续指向store[pre]父节点位置}return true;}void print(int num) //打印路径,store[num]为目标节点{vector<int> temp; //存放路径int pre=store[num].father;temp.push_back(num);while(pre!=0){ //从目标节点回溯到初始节点temp.push_back(pre);pre=store[pre].father;}cout<<endl;cout<<"*********数码移动步骤*********"<<endl;int mm=1; //步数for(int m=temp.size()-1;m>=0;m--){cout<<"---第"<<mm<<"步---:"<<endl;for(int i=0;i<3;i++){for(int j=0;j<3;j++){cout<<store[temp[m]].a[i][j]<<" ";}cout<<endl;}mm++;cout<<endl;}cout<<"所需步数为: "<<store[num].deep<<endl;return;}int get_fn(int num) //返回store[num]的评价函数值{int fn_temp=0; //评价函数值bool test=true;for(int i=0;i<3;i++){ //当找到一个值后,计算这个值位置与目标位置的距离差,test置为false后继续寻找下一个值for(int j=0;j<3;j++){test=true;for(int k=0;k<3;k++){for(int l=0;l<3;l++){if((store[num].x!=i||store[num].y!=j)&&store[num].a[i][j]==store[0].a[k][l]){ //寻值时排除空格位fn_temp=fn_temp+abs(i-k)+abs(j-l);test=false;}if(test==false) break;}if(test==false) break;}}}fn_temp=fn_temp+store[num].deep; //加上节点深度return fn_temp;}void kongxy(int num) //获得空格坐标{for(int i=0;i<3;i++){for(int j=0;j<3;j++){if(store[num].a[i][j]==0){store[num].x=i;store[num].y=j;}}}return;}int main(){cout<<"-----------A*算法解决8数码问题------------"<<endl;while(true){store.clear(); //清空storevector<int> open; //建立open表int i,j,m,n,f;int min; //store[min]储存fn值最小的节点int temp;bool test;top=1; //当前节点在store的位置,初始节点在store[1]int target[9];int begin[9]; //储存初始状态和目标状态,用于判断奇偶int t1=0,t2=0; //初始状态和目标状态的奇偶序数node node_temp;store.push_back(node_temp);store.push_back(node_temp); //用于创建store[0]和store[1],以便下面使用cout<<"请输入初始数码棋盘状态,0代表空格:"<<endl; //输入初始状态,储存在store[1]中test=false;while(test==false){f=0;for(i=0;i<3;i++){for(j=0;j<3;j++){cin>>temp;store[1].a[i][j]=temp;begin[f++]=temp;}}test=true;for(i=0;i<8;i++){ //检查是否有重复输入,若有则重新输入for(j=i+1;j<9;j++){if(begin[i]==begin[j]){test=false;break;}}if(test==false) break;}if(test==false) cout<<"输入重复,请重新输入:"<<endl;}kongxy(1); //找出空格的坐标cout<<"请输入目标数码棋盘状态,0代表空格: "<<endl; //输入目标状态,储存在store[0]中test=false;while(test==false){f=0;for(i=0;i<3;i++){for(j=0;j<3;j++){cin>>temp;store[0].a[i][j]=temp;target[f++]=temp;}}test=true;for(i=0;i<8;i++){ //检查是否有重复输入,若有则重新输入for(j=i+1;j<9;j++){if(target[i]==target[j]){test=false;break;}}if(test==false) break;}if(test==false){cout<<"输入重复,请重新输入:"<<endl;continue; //若重复,重新输入}for(i=0;i<9;i++){ //检查目标状态与初始状态是否匹配test=false;for(j=0;j<9;j++){if(begin[i]==target[j]){test=true;break;}}if(test==false) break;}if(test==false) cout<<"输入与初始状态不匹配,请重新输入:"<<endl;}for(i=1;i<9;i++){ //判断奇偶序数是否相同,若不相同则无法找到路径for(j=1;i-j>=0;j++){if(begin[i]>begin[i-j]){if(begin[i-j]!=0) t1++;}}}for(i=1;i<9;i++){for(j=1;i-j>=0;j++){if(target[i]>target[i-j]){if(target[i-j]!=0) t2++;}}}if(!(t1%2==t2%2)){cout<<"无法找到路径."<<endl;cout<<endl;//system("pause");//return 0;continue;}LARGE_INTEGER Freg;LARGE_INTEGER Count1,Count2;QueryPerformanceFrequency(&Freg);QueryPerformanceCounter(&Count1);//获取时间Count1double d;store[1].father=0; //初始化参数store[1].gone=0;store[1].deep=0; //初始节点的父节点为0store[1].fn=get_fn(1);if(check(1)){ //判断初始状态与目标状态是否相同print(1);//system("pause");//return 0;cout<<endl;continue;}open.push_back(1); //把初始状态在store中的位置数压入open表中while(!open.empty()){ //当open表不为空时,开始寻找路径if(check(top)) break;min=top;int i_min=0;for(i=0;i<open.size();i++){ //遍历open表中元素,找出store中fn值最小的节点if(store[open[i]].fn<=store[min].fn&&store[open[i]].gone==0){min=open[i];i_min=i;}}store[min].gone=1;open.erase(open.begin()+i_min); //把最小节点标记遍历过,并从open表中删除m=store[min].x;n=store[min].y; //空格坐标for(f=0;f<4;f++){ //上下左右移动空格i=m+mx[f];j=n+my[f];if(i>=0&&i<=2&&j>=0&&j<=2){ //当变换后的空格坐标在矩阵中时,开始移动top++;store.push_back(store[min]); //把store[min]压入store中成为新增节点,位置为store[top]store[top].father=min; //新增节点的父节点为minstore[top].gone=0; //新增节点未被访问store[top].deep=store[min].deep+1; //新增节点的深度为父节点深度+1temp=store[top].a[m][n]; //交换空格与相邻数字store[top].a[m][n]=store[top].a[i][j];store[top].a[i][j]=temp;store[top].x=i; //移动后的空格坐标store[top].y=j;store[top].fn=get_fn(top); //移动后的fn值open.push_back(top); //把top压入open表中if(check(top)){ //检查是否到达目标print(top);//system("pause");//return 0;break;}if(search(top)==false){ //检查新增节点是否被访问过,若访问过,则删除此节点top--;store.pop_back();open.pop_back();}}}}QueryPerformanceCounter(&Count2);//获取时间Count2d=(double)(Count2.QuadPart-Count1.QuadPart)/(double)Freg.QuadPart*1000.0;//计算时间差,d的单位为ms.cout<<"算法时间为为"<<d<<" ms."<<endl;cout<<endl;}return 0;system("pause");}。
八数码问题C代码

*********************************************************************本函数是用A*算法来实现八数码的问题***算法的步骤如下:*1、初始化两个链表open和closed,将初始状态放入open表中*2、重复下列过程,直至找到目标结点为止,如果open表为空,那* 么查找失败;*3、从open表中拿出具有最小f值的结点(将这一结点称为BESTNODE),* 并放入closed表中;*4、如果BESTNODE为目标结点,成功求得解,退出循环;*5、如果BESTNODE不是目标结点,那么产生它的后继结点(此后继结* 点与其祖先的状态不同),后继结点组成一个链表;*6、对每个后继结点进行以下过程:*7、建立它到BESTNODE的parent指针;*8、如果此结点在open表中,首先将open表中的结点添加进BESTNODE* 的后继结点链中,然后计算两个结点的g值,如果此结点的g值小* 于open表中的结点时,open表中的结点改变parent指针,同时将* 此结点删除;*9、如果此结点在closed表中,首先将closed表中的结点添加进BESTNODE * 的后继结点中,然后计算两个结点的g值,如果此结点的g值小于* closed表中的结点时,closed表中的结点改变parent指针;将* closed表中的结点重新放入open表中,同时将此结点删除;*10、如果此结点既不在open表中也不再closed表中,那么添加此结点至* BESTNODE的后继结点链中。
***Author: 转载作者不详。
**2011.5.16**********************************************************************/#include "stdafx.h"#include <iostream>#include <cstdlib>#include <conio.h>#define size 3using namespace std;//定义二维数组来存储数据表示某一个特定状态typedef int status[size][size];struct SpringLink;//定义状态图中的结点数据结构typedef struct Node{status data;//结点所存储的状态Node *parent;//指向结点的父亲结点SpringLink *child;//指向结点的后继结点int fvalue;//结点的总的路径int gvalue;//结点的实际路径int hvalue;//结点的到达目标的苦难程度Node *next;//指向open或者closed表中的后一个结点}NNode , *PNode;//定义存储指向结点后继结点的指针的地址typedef struct SpringLink{Node *pointData;//指向结点的指针SpringLink *next;//指向兄第结点}SPLink , *PSPLink;//定义open表和close表PNode open;PNode closed;//开始状态与目标状态status startt = {2 , 8 , 3 , 1 , 6 , 4 , 7 , 0 , 5};status target = {1 , 2 , 3 , 8 , 0 , 4 , 7 , 6 , 5};//初始化一个空链表void initLink(PNode &Head){Head = (PNode)malloc(sizeof(NNode));Head->next = NULL;}//判断链表是否为空bool isEmpty(PNode Head){if(Head->next == NULL)return true;elsereturn false;}//从链表中拿出一个数据,通过FNode返回void popNode(PNode &Head , PNode &FNode){if(isEmpty(Head)){FNode = NULL;return;}FNode = Head->next;Head->next = Head->next->next;FNode->next = NULL;}//向结点的(最终)后继结点链表中添加新的子结点void addSpringNode(PNode &Head , PNode newData) {PSPLink newNode = (PSPLink)malloc(sizeof(SPLink)); newNode->pointData = newData;newNode->next = Head->child;Head->child = newNode;}//释放状态图中存放结点后继结点地址的空间//注意传入参数PSPLink引用类型void freeSpringLink(PSPLink &Head){PSPLink tmm;while(Head != NULL){tmm = Head;Head = Head->next;free(tmm);}}//释放open表与closed表中的资源void freeLink(PNode &Head){PNode tmn;tmn = Head;Head = Head->next;free(tmn);while(Head != NULL){//首先释放存放结点后继结点地址的空间freeSpringLink(Head->child);tmn = Head;Head = Head->next;free(tmn);}}//向普通链表中添加一个结点void addNode(PNode &Head , PNode &newNode) {newNode->next = Head->next;Head->next = newNode;}//向非递减排列的链表中添加一个结点void addAscNode(PNode &Head , PNode &newNode) {PNode P;PNode Q;P = Head->next;Q = Head;while(P != NULL && P->fvalue < newNode->fvalue) {Q = P;P = P->next;}//上面判断好位置之后,下面就是简单的插入了newNode->next = Q->next;Q->next = newNode;}//计算结点额h值,当前节点与目标节点数码错位个数int computeHValue(PNode theNode){int num = 0;for(int i = 0 ; i < 3 ; i++){for(int j = 0 ; j < 3 ; j++){if(theNode->data[i][j] != target[i][j])num++;}}return num;}//计算结点的f,g,h值void computeAllValue(PNode &theNode , PNode parentNode) {if(parentNode == NULL)theNode->gvalue = 0;elsetheNode->gvalue = parentNode->gvalue + 1;theNode->hvalue = computeHValue(theNode);theNode->fvalue = theNode->gvalue + theNode->hvalue;}//初始化函数,进行算法初始条件的设置void initial(){//初始化open以及closed表initLink(open);initLink(closed);//初始化起始结点,令初始结点的父节点为空结点PNode NULLNode = NULL;PNode Start = (PNode)malloc(sizeof(NNode));for(int i = 0 ; i < 3 ; i++){for(int j = 0 ; j < 3 ; j++){Start->data[i][j] = startt[i][j];}}Start->parent = NULL;Start->child = NULL;Start->next = NULL;computeAllValue(Start , NULLNode);//起始结点进入open表addAscNode(open , Start);}//将B节点的状态赋值给A结点void statusAEB(PNode &ANode , PNode BNode) {for(int i = 0 ; i < 3 ; i++){for(int j = 0 ; j < 3 ; j++){ANode->data[i][j] = BNode->data[i][j];}}}//两个结点是否有相同的状态bool hasSameStatus(PNode ANode , PNode BNode) {for(int i = 0 ; i < 3 ; i++){for(int j = 0 ; j < 3 ; j++){if(ANode->data[i][j] != BNode->data[i][j])return false;}}return true;}//结点与其祖先结点是否有相同的状态bool hasAnceSameStatus(PNode OrigiNode , PNode AnceNode) {while(AnceNode != NULL){if(hasSameStatus(OrigiNode , AnceNode))return true;AnceNode = AnceNode->parent;}return false;}//取得方格中空的格子的位置,通过row,col返回。
八数码问题C语言代码

八数码问题源程序及注释:#include<stdio.h>#include<conio.h>int n,m;typedef struct Node{char matrix[10];/*存储矩阵*/char operate;/*存储不可以进行的操作,L代表不能左移R代表不能右移U代表不能上移D代表不能下移*/char extend;/*是否可以扩展,Y代表可以,N代表不可以*/int father;/*指向产生自身的父结点*/}Node;char start[10]={"83426517 "};/*此处没有必要初始化*/char end[10]={"1238 4765"};/*此处没有必要初始化*/Node base[4000];int result[100];/*存放结果的base数组下标号,逆序存放*/int match()/*判断是否为目标*/{int i;for(i=0;i<9;i++){if(base[n-1].matrix[i]!=end[i]){return 0;}}return 1;}void show()/*显示矩阵的内容*/{int i=1;while(m>=0){int mm=result[m];//clrscr();printf("\n\n\n 状态方格\t\t步骤 %d",i);printf("\n\n\n\n\n\t\t\t%c\t%c\t%c\n",base[mm].matrix[0],base[mm].mat rix[1],base[mm].matrix[2]);printf("\n\n\t\t\t%c\t%c\t%c\n",base[mm].matrix[3],base[mm].matrix[4],base[mm].matrix[5]);printf("\n\n\t\t\t%c\t%c\t%c\n",base[mm].matrix[6],base[mm].matrix[7] ,base[mm].matrix[8]);//sleep(1);m--;i++;}}void leave()/*推理成功后退出程序之前要执行的函数,主要作用是输出结果*/ {n--;while(base[n].father!=-1){result[m]=n;m++;n=base[n].father;}result[m]=0;result[m+1]='\0';show();//clrscr();printf("\n\n\n\n\n\n\n\n\n\t\t\t\t搜索结束\n\n\n\n\n\n\n\n\n\n"); getch();//exit(0);}int left(int x)/*把下标为X的数组中的矩阵的空格左移*/{int i,j;char ch;for(i=0;i<9;i++){if(base[x].matrix[i]==' ')break;}if(i==0||i==3||i==6||i==9){return 0;}for(j=0;j<9;j++){base[n].matrix[j]=base[x].matrix[j];}ch=base[n].matrix[i-1];base[n].matrix[i-1]=base[n].matrix[i];base[n].matrix[i]=ch;base[n].operate='R';base[n].extend='Y';base[n].father=x;base[x].extend='N';n++;if(match(i))leave();return 1;}int right(int x)/*把下标为X的数组中的矩阵的空格右移*/ {int i,j;char ch;for(i=0;i<9;i++){if(base[x].matrix[i]==' ')break;}if(i==2||i==5||i==8||i==9){return 0;}for(j=0;j<9;j++){base[n].matrix[j]=base[x].matrix[j];}ch=base[n].matrix[i+1];base[n].matrix[i+1]=base[n].matrix[i];base[n].matrix[i]=ch;base[n].operate='L';base[n].extend='Y';base[n].father=x;base[x].extend='N';n++;if(match(i))leave();return 1;}int up(int x)/*把下标为X的数组中的矩阵的空格上移*/ {int i,j;char ch;for(i=0;i<9;i++){if(base[x].matrix[i]==' ')break;}if(i==0||i==1||i==2||i==9){return 0;}for(j=0;j<9;j++){base[n].matrix[j]=base[x].matrix[j];}ch=base[n].matrix[i-3];base[n].matrix[i-3]=base[n].matrix[i];base[n].matrix[i]=ch;base[n].operate='D';base[n].extend='Y';base[n].father=x;base[x].extend='N';n++;if(match(i))leave();return 1;}int down(int x)/*把下标为X的数组中的矩阵的空格下移*/ {int i,j;char ch;for(i=0;i<9;i++){if(base[x].matrix[i]==' ')break;}if(i==6||i==7||i==8||i==9){return 0;}for(j=0;j<9;j++){base[n].matrix[j]=base[x].matrix[j];}ch=base[n].matrix[i+3];base[n].matrix[i+3]=base[n].matrix[i];base[n].matrix[i]=ch;base[n].operate='U';base[n].extend='Y';base[n].father=x;base[x].extend='N';n++;if(match(i))leave();return 1;}main(){int i;char a[20],b[20];n=1;//textcolor(LIGHTGREEN);//clrscr();/*以下是输入初始和目标矩阵,并把输入的0转换为空格*/ printf("Please input the start 9 chars:");scanf("%s",a);printf("Please input the end 9 chars:");scanf("%s",b);for(i=0;i<9;i++){if(a[i]=='0'){start[i]=' ';continue;}if(b[i]=='0'){end[i]=' ';continue;}start[i]=a[i];end[i]=b[i];}start[9]='\0';end[9]='\0';for(i=0;i<9;i++){base[0].matrix[i]=start[i];}base[0].operate='N';base[0].extend='Y';base[0].father=-1;/*以上是为第一个base数组元素赋值*/for(i=0;n<4000;i++){if(base[i].extend=='Y'){if(base[i].operate=='L'){right(i);up(i);down(i);}if(base[i].operate=='R'){left(i);up(i);down(i);}if(base[i].operate=='U'){left(i);right(i);down(i);}if(base[i].operate=='D'){left(i);right(i);up(i);}if(base[i].operate=='N'){left(i);right(i);up(i);down(i); }}}}。
八数码问题相关代码 C#

八数码问题界面设计:以下几个类:AIResultusing System;using System.Collections.Generic; using System.Linq;using System.Text;namespace EightNumber{public class AIResult{private List<Direction> _path;private int _nodeCount;public List<Direction> Path{get { return _path; }set { _path = value; }}public int NodeCount{get { return _nodeCount; }set { _nodeCount = value; }}}}BFS_AIusing System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Collections;namespace EightNumber{class BFS_AI : IEightNumAI{Queue<int> queue;//用于广度优搜索的队列//使用存储方式Dictionary<int, int> CodeSetDic; //Dictionary存储,用于记录已访问过的棋盘局面SortedList<int, int> CodeSetSL; //SortedList存储,用于记录已访问过的棋盘局面SortedDictionary<int, int> CodeSetSD; //SortedDictionary存储,用于记录已访问过的棋盘局面Hashtable CodeSetHt; //Hashtable存储,用于记录已访问过的棋盘局面List<int> CodeSetList; //List存储,用于记录已访问过的棋盘局面//IEightNumAI接口实现,计算把数码问题的结果使用Dictionary 的存储方式public AIResult GetAIResultDic(int begin, int end){if (queue == null){//将用于广度优先遍历的队列初始化25000个元素queue = new Queue<int>(25000);}if (CodeSetDic == null){//将用于存放已访问结点的哈希表初始化为181440//使用存储方式CodeSetDic = new Dictionary<int, int>(181440);//CodeSet = new SortedList<int, int>(181440);}queue.Enqueue(begin);CodeSetDic.Add(begin, 0);//根据结点信息加入哈希表AIResult result = new AIResult();//初始化存放结果的类while (queue.Count > 0)//广度优先遍历{int node = queue.Dequeue();//出列if (node == end)//找到目标状态跳出循环{break;}for (int i = 1; i <= 4; i++){int child = NumSwitch.GetMoveBorder(node, (Direction)i);if (child != -1 && !CodeSetDic.ContainsKey(child))//判断结点是否已经存在,如果还没存在就加入{CodeSetDic.Add(child, node);//如果还没存该结点就可以加入结点queue.Enqueue(child);}}}result.Path = GetPartFormNode(end);//获取结果路径result.NodeCount = CodeSetDic.Count;//获取已访问的结点数目queue.Clear();//清空队列CodeSetDic.Clear();//清空哈希表return result;}//已指定结点在哈希表中回溯以寻找整条路径private List<Direction> GetPartFormNode(int node){List<Direction> path = new List<Direction>();int next = CodeSetDic[node];while (next != 0){if (node - next == 1){path.Add(Direction.Left);}else if (node - next == -1){path.Add(Direction.Right);}else if (node % 10 - next % 10 == -3){path.Add(Direction.Down);}else if (node % 10 - next % 10 == 3){path.Add(Direction.Up);}node = next;next = CodeSetDic[next];}return path;}//IEightNumAI接口实现,计算把数码问题的结果使用SortedList 的存储方式public AIResult GetAIResultSL(int begin, int end){if (queue == null){//将用于广度优先遍历的队列初始化25000个元素queue = new Queue<int>(25000);}if (CodeSetSL == null){//将用于存放已访问结点的哈希表初始化为181440//使用存储方式CodeSetSL = new SortedList<int, int>(181440);}queue.Enqueue(begin);CodeSetSL.Add(begin, 0);//根据结点信息加入哈希表AIResult result = new AIResult();//初始化存放结果的类while (queue.Count > 0)//广度优先遍历{int node = queue.Dequeue();//出列if (node == end)//找到目标状态跳出循环{break;}for (int i = 1; i <= 4; i++){int child = NumSwitch.GetMoveBorder(node, (Direction)i);if (child != -1 && !CodeSetSL.ContainsKey(child))//判断结点是否已经存在,如果还没存在就加入{CodeSetSL.Add(child, node);//如果还没存该结点就可以加入结点queue.Enqueue(child);}}}//result.Path = GetPartFormNodeSL(end);//获取结果路径result.NodeCount = CodeSetSL.Count;//获取已访问的结点数目queue.Clear();//清空队列CodeSetSL.Clear();//清空哈希表return result;}//IEightNumAI接口实现,计算把数码问题的结果使用SortedDictionary的存储方式public AIResult GetAIResultSD(int begin, int end){if (queue == null){//将用于广度优先遍历的队列初始化25000个元素queue = new Queue<int>(25000);}if (CodeSetSD == null){//将用于存放已访问结点的哈希表初始化为181440//使用存储方式CodeSetSD = new SortedDictionary<int, int>();}queue.Enqueue(begin);CodeSetSD.Add(begin, 0);//根据结点信息加入哈希表AIResult result = new AIResult();//初始化存放结果的类while (queue.Count > 0)//广度优先遍历{int node = queue.Dequeue();//出列if (node == end)//找到目标状态跳出循环{break;}for (int i = 1; i <= 4; i++){int child = NumSwitch.GetMoveBorder(node, (Direction)i);if (child != -1 && !CodeSetSD.ContainsKey(child))//判断结点是否已经存在,如果还没存在就加入{CodeSetSD.Add(child, node);//如果还没存该结点就可以加入结点queue.Enqueue(child);}}}//result.Path = GetPartFormNodeSD(end);//获取结果路径result.NodeCount = CodeSetSD.Count;//获取已访问的结点数目queue.Clear();//清空队列CodeSetSD.Clear();//清空哈希表return result;}//IEightNumAI接口实现,计算把数码问题的结果使用Dictionary 的存储方式public AIResult GetAIResultHt(int begin, int end){if (queue == null){//将用于广度优先遍历的队列初始化25000个元素queue = new Queue<int>(25000);}if (CodeSetHt == null){//将用于存放已访问结点的哈希表初始化为181440//使用存储方式CodeSetHt = new Hashtable();}queue.Enqueue(begin);CodeSetHt.Add(begin, 0);//根据结点信息加入哈希表AIResult result = new AIResult();//初始化存放结果的类while (queue.Count > 0)//广度优先遍历{int node = queue.Dequeue();//出列if (node == end)//找到目标状态跳出循环{break;}for (int i = 1; i <= 4; i++){int child = NumSwitch.GetMoveBorder(node, (Direction)i);if (child != -1 && !CodeSetHt.ContainsKey(child))//判断结点是否已经存在,如果还没存在就加入{CodeSetHt.Add(child, node);//如果还没存该结点就可以加入结点queue.Enqueue(child);}}}//result.Path = GetPartFormNodeHt(end);//获取结果路径result.NodeCount = CodeSetHt.Count;//获取已访问的结点数目queue.Clear();//清空队列CodeSetHt.Clear();//清空哈希表return result;}//IEightNumAI接口实现,计算把数码问题的结果使用List的存储方式public AIResult GetAIResultList(int begin, int end){if (queue == null){//将用于广度优先遍历的队列初始化25000个元素queue = new Queue<int>(25000);}if (CodeSetList == null){//将用于存放已访问结点的哈希表初始化为181440//使用存储方式CodeSetList = new List<int>();}queue.Enqueue(begin);CodeSetList.Add(begin);//根据结点信息加入哈希表AIResult result = new AIResult();//初始化存放结果的类while (queue.Count > 0)//广度优先遍历{int node = queue.Dequeue();//出列if (node == end)//找到目标状态跳出循环{break;}for (int i = 1; i <= 4; i++){int child = NumSwitch.GetMoveBorder(node, (Direction)i);if (child != -1 && !CodeSetList.Contains(child))//判断结点是否已经存在,如果还没存在就加入{CodeSetList.Add(child);//如果还没存该结点就可以加入结点queue.Enqueue(child);}}}//result.Path = GetPartFormNodeHt(end);//获取结果路径result.NodeCount = CodeSetList.Count;//获取已访问的结点数目queue.Clear();//清空队列CodeSetList.Clear();//清空哈希表return result;}public override string ToString(){return "广度优先搜索算法";}}}HashHelpersusing System;using System.Collections.Generic;using System.Linq;using System.Text;namespace EightNumber{internal static class HashHelpers{//部分素数集合static readonly int[] primes ={3,7,11,17,23,29,37,47,59,71,89,107,131,163,197,239,293,353,431,521,631,761,919,1103,1327,1597,1931,2333,2801,3371,4049,4861,5839,7013,8419,10103,12143,14591,17519,21023,25229,30293,36353,43627,52361,62851,75431,90523,108631,130363,156437,187751,225307,270371,324449,389357,467237,560689,672827,807403,968897,1162687,1395263,1674319,2009191, 2411033,2893249,3471899,4166287,4999559,5999471,7199369 };//判断一个整数是否是素数internal static bool IsPrime(int candidate){if ((candidate & 1) != 0)//判断最后一位是否为零{int limit = (int)Math.Sqrt(candidate);for (int divisor = 3; divisor <= limit; divisor += 2){//判断candidate能否被3~Sqrt(candidate)之间的奇数整除if ((candidate % divisor) == 0){return false;}}return true;}return (candidate == 2);//偶数中只有2为素数}//获取一个比min打,并最接近min的素数internal static int GetPrime(int min){for (int i = 0; i < primes.Length; i++){//获取primes中比min大的第一个素数int prime = primes[i];if (prime >= min) return prime;}for (int i = (min | 1); i < Int32.MaxValue; i += 2){//对于不在数组中的素数需要另外的判断if (IsPrime(i))return i;}return min;}}}IEightNumAIusing System;using System.Collections.Generic;using System.Linq;using System.Text;namespace EightNumber{interface IEightNumAI{ //获取八数码问题的解AIResult GetAIResultDic(int begin, int end);AIResult GetAIResultSL(int begin, int end);AIResult GetAIResultSD(int begin, int end);AIResult GetAIResultHt(int begin, int end);AIResult GetAIResultList(int begin, int end);}}MainFormusing System;using System.Collections.Generic;using ponentModel;using System.Data;using System.Drawing;using System.Linq;using System.Text;using System.Windows.Forms;namespace EightNumber{public partial class MainForm : Form{public MainForm(){InitializeComponent();}Label[,] arrLbl = new Label[3, 3];int unRow = 2, unCol = 2;Label lblBegin;//用于记录拖放开始时的标签Point pos;//开始拖动时,鼠标按下时的坐标int BeginCode;//搜索前的棋盘编码int destinationCode = 123456781;//目标棋盘编码List<Direction> path;//记录上一次搜索的路径int pathIndex;//记录当前演示步骤的索引号private void MainForm_Load(object sender, EventArgs e){//创建9个label,放入PanelFont font = new Font("黑体", 50);this.SuspendLayout();for (int i = 0; i < 3; i++){for (int j = 0; j < 3; j++){Label lbl = new Label();lbl.Font = font;lbl.TextAlign = ContentAlignment.MiddleCenter;lbl.BackColor = Color.Coral;lbl.BorderStyle = BorderStyle.FixedSingle;lbl.Text = Convert.ToString(3 * i + j + 1);lbl.AutoSize = false;lbl.Size = new Size(80, 80);lbl.Location = new Point(j * 80, i * 80);lbl.AllowDrop = true;//允许拖动操作lbl.Click += new EventHandler(lbl_Click);lbl.MouseDown += new MouseEventHandler(lbl_MouseDown);lbl.MouseMove += new MouseEventHandler(lbl_MouseMove);lbl.DragEnter += new DragEventHandler(lbl_DragEnter);lbl.DragDrop += new DragEventHandler(lbl_DragDrop);pnlBorder.Controls.Add(lbl);arrLbl[i, j] = lbl;}}arrLbl[unRow, unCol].Text = "";arrLbl[unRow, unCol].BackColor = Color.DimGray;lblBorderStatus.Text = GridToNum().ToString();cbAlgorithms.Items.Add(new BFS_AI());cbAlgorithms.SelectedIndex = 0;this.ResumeLayout();}//Panel内标签的单击事件private void lbl_Click(object sender, EventArgs e){int row = ((Label)sender).Top / 80;//被单击标签所在行int col = ((Label)sender).Left / 80;//被单击标签所在列if (Math.Abs(row - unRow) + Math.Abs(col - unCol) == 1){//如果可以移动,则交换不可见标签和被单击标签中的数字string temp = arrLbl[unRow, unCol].Text;arrLbl[unRow, unCol].Text = arrLbl[row, col].Text;arrLbl[row, col].Text = temp;arrLbl[unRow, unCol].BackColor = Color.Coral;arrLbl[row, col].BackColor = Color.DimGray;arrLbl[row, col].Text = "";unRow = row;unCol = col;lblBorderStatus.Text = GridToNum().ToString();}}//Panel内标签的鼠标按下事件,用于拖入操作private void lbl_MouseDown(object sender, MouseEventArgs e){lblBegin = (Label)sender;pos = e.Location;}//Panel内标签的鼠标移动事件用于引发拖入操作private void lbl_MouseMove(object sender, MouseEventArgs e){if (e.Button == MouseButtons.Left &&(Math.Abs(e.X - pos.X) > 10 || Math.Abs(e.Y - pos.Y) > 10)){DoDragDrop(((Label)sender).Text,DragDropEffects.Copy | DragDropEffects.Move);}}//Panel内标签的拖入项目事件private void lbl_DragEnter(object sender, DragEventArgs e){//判断拖放的数据是否是字符串if (e.Data.GetDataPresent(DataFormats.Text)){e.Effect = DragDropEffects.Move;}else{e.Effect = DragDropEffects.None;}}//Panel内标签的拖放事件操作完成时的事件private void lbl_DragDrop(object sender, DragEventArgs e){string txt = (string)e.Data.GetData(DataFormats.Text);Label lblEnd = (Label)sender;//交换颜色lblBegin.Text = lblEnd.Text;lblEnd.Text = txt;lblBegin.BackColor = Color.Coral;lblEnd.BackColor = Color.Coral;if (lblEnd.Text == ""){lblEnd.BackColor = Color.DimGray;unRow = ((Label)sender).Top / 80;//拖放结束时的标签所在行unCol = ((Label)sender).Left / 80;//拖放结束时的标签所在列}else if (lblBegin.Text == ""){lblBegin.BackColor = Color.DimGray;unRow = lblBegin.Top / 80;//拖动开始时的标签所在行unCol = lblBegin.Left / 80;//拖放开始时的标签所在列}lblBorderStatus.Text = GridToNum().ToString();}//再棋盘上生成随机数private void btnRandom_Click(object sender, EventArgs e){//将有序数组中的数字用随机方法打乱int[] arrNum = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };Random rm = new Random();for (int i = 0; i < 8; i++){int rmNum = rm.Next(i, 9);int temp = arrNum[i];arrNum[i] = arrNum[rmNum];arrNum[rmNum] = temp;}for (int i = 0; i < 9; i++){arrLbl[i / 3, i % 3].BackColor = Color.Coral;arrLbl[i / 3, i % 3].Text = arrNum[i].ToString();if (arrNum[i] == 9){unRow = i / 3;unCol = i % 3;arrLbl[unRow, unCol].Text = "";arrLbl[unRow, unCol].BackColor = Color.DimGray;}}lblBorderStatus.Text = GridToNum().ToString();}//将棋盘局面转换为数据并返回private int GridToNum(){int nullIndex = -1;StringBuilder numStr = new StringBuilder(9);for (int i = 0; i < arrLbl.Length; i++){if (arrLbl[i / 3, i % 3].Text != ""){numStr.Append(arrLbl[i / 3, i % 3].Text);}else{nullIndex = 9 - i;}}numStr.Append(nullIndex);return int.Parse(numStr.ToString());}//将数字转换为棋盘局面private void NumToGrid(int num){int nullIndex = num % 10;//空白位int k = num / 10;//去除空白位的数字string numStr = k.ToString();for (int i = 0, j = 0; i < 9; i++){//当遇到空白位时if (9 - i == nullIndex){arrLbl[i / 3, i % 3].Text = "";arrLbl[i / 3, i % 3].BackColor = Color.DimGray;unRow = i / 3;unCol = i % 3;continue;}arrLbl[i / 3, i % 3].Text = numStr[j].ToString();arrLbl[i / 3, i % 3].BackColor = Color.Coral;j++;}lblBorderStatus.Text = num.ToString();}private void btnGo_Click(object sender, EventArgs e){int end = GridToNum();if (destinationCode == end){lblBorderStatus.Text = "完成";return;}if (!NumSwitch.ExistAnswer(destinationCode, end)){lblBorderStatus.Text = "无解";return;}BeginCode = end;//在组合框内选择当前选中的搜索算法//IEightNumAI ai = (IEightNumAI)cbAlgorithms.SelectedItem;long oldtimeAll = DateTime.Now.Ticks;//开始计时allUserTimelong oldtime = DateTime.Now.Ticks;//开始计时Dictionary//搜索开始AIResult aiResult = ai.GetAIResultDic(destinationCode, end);//搜索结束并计算所用时间double useTime = (DateTime.Now.Ticks - oldtime) / 10000000.0D;long oldtimeSL = DateTime.Now.Ticks;//开始计时SortedList//搜索开始AIResult aiResultSL = ai.GetAIResultSL(destinationCode, end);//搜索结束并计算所用时间double useTimeSL = (DateTime.Now.Ticks - oldtimeSL) / 10000000.0D;long oldtimeSD = DateTime.Now.Ticks;//开始计时SortedDictionary//搜索开始AIResult aiResultSD = ai.GetAIResultSD(destinationCode, end);//搜索结束并计算所用时间double useTimeSD = (DateTime.Now.Ticks - oldtimeSD) / 10000000.0D;long oldtimeHt = DateTime.Now.Ticks;//开始计时Hashtable//搜索开始AIResult aiResultHt = ai.GetAIResultHt(destinationCode, end);//搜索结束并计算所用时间double useTimeHt = (DateTime.Now.Ticks - oldtimeHt) / 10000000.0D;long oldtimeList = DateTime.Now.Ticks;//开始计时List//搜索开始AIResult aiResultList = ai.GetAIResultList(destinationCode, end);//搜索结束并计算所用时间double useTimeList = (DateTime.Now.Ticks - oldtimeList) / 10000000.0D;double useTimeAll = (DateTime.Now.Ticks - oldtimeAll) / 10000000.0D;//在文本框内显示搜索结果StringBuilder str = new StringBuilder(400);str.Append("使用" + ai + "求解" + "\r\n"+"\r\n");str.Append("Dictionay用时:\r\n" + useTime + "秒" + "\r\n"+"\r\n");str.Append("SortedList用时:\r\n" + useTimeSL + "秒" + "\r\n"+"\r\n");str.Append("SortedDictionary用时:\r\n" + useTimeSD + "秒" + "\r\n"+"\r\n");str.Append("Hashtable用时:\r\n" + useTimeHt + "秒" + "\r\n"+"\r\n");str.Append("List用时:\r\n" + useTimeList + "秒" + "\r\n"+"\r\n");str.Append("总共用时:\r\n" + useTimeAll + "秒" + "\r\n"+"\r\n");str.Append("访问结点:" + aiResult.NodeCount + "个" + "\r\n");str.Append("初始编码:" + BeginCode + "\r\n");str.Append("步骤操作\r\n");path = aiResult.Path;for (int i = 0; i < path.Count; i++){int index = i + 1;string indexS = "(" + index.ToString() + ")";string operS = string.Empty;switch (path[i]){case Direction.Left:operS = "←";break;case Direction.Right:operS = "→";break;case Direction.Down:operS = "↓";break;case Direction.Up:operS = "↑";break;}str.Append(string.Format("{0,-8}{1,2}\r\n", indexS, operS));}str.Append("结束编码:" + destinationCode);txtResult.Text = str.ToString();btnAutoPlay.Enabled = true;}//单击【开始演示】按钮事件方法private void btnAutoPlay_Click(object sender, EventArgs e) {if (btnAutoPlay.Text == "开始演示"){NumToGrid(BeginCode);PrepareAutoPlay();btnAutoPlay.Text = "停止演示";pathIndex = 0;timer1.Start();//运行计时器}else{timer1.Stop();//停止计时器StopAutoPlay();btnAutoPlay.Text = "开始演示";}}//【上一步】按钮的单击事件private void btnprev_Click(object sender, EventArgs e) {if (timer1.Enabled){timer1.Enabled = false;}if (pathIndex <= 1){btnPrev.Enabled = false;}if (pathIndex != 0){MoveTo(ReverseDirection(path[--pathIndex]));}if (!btnNext.Enabled){btnNext.Enabled = true;}}//【下一步】按钮的单击事件private void btnNext_Click(object sender, EventArgs e) {if (timer1.Enabled){timer1.Enabled = false;}if (pathIndex == path.Count - 1){btnNext.Enabled = false;}MoveTo(path[pathIndex++]);if (!btnPrev.Enabled){btnPrev.Enabled = true;}}//准备自动演示,使其余空间不可用private void PrepareAutoPlay(){btnRandom.Enabled = false;btnGo.Enabled = false;pnlBorder.Enabled = false;btnNext.Enabled = true;btnPrev.Enabled = true;}//停止演示private void StopAutoPlay(){btnRandom.Enabled = true;btnGo.Enabled = true;pnlBorder.Enabled = true;btnNext.Enabled = false;btnPrev.Enabled = false;}//定时器事件,用于自动演示求解过程private void timer1_Tick(object sender, EventArgs e) {if (pathIndex > path.Count - 1){btnAutoPlay_Click(null, null);timer1.Stop();return;}MoveTo(path[pathIndex++]);}//指定方块移动方向private void MoveTo(Direction md){int num = NumSwitch.GetMoveBorder(int.Parse(lblBorderStatus.Text), md);NumToGrid(num);lblBorderStatus.Text = num.ToString();}//逆转指定方向,用于【上一步】按钮private Direction ReverseDirection(Direction md){if (md == Direction.Left){return Direction.Right;}if (md == Direction.Right){return Direction.Left;}if (md == Direction.Down){return Direction.Up;}if (md == Direction.Up){return Direction.Down;}return Direction.None;}}}MoveDirectionusing System;using System.Collections.Generic;using System.Linq;using System.Text;namespace EightNumber{//移动方向枚举public enum Direction{Left = 1,//空格右边方块左移(→)Right = 2,//空格左边方块右移(←)Down = 3,//空格上方方块下移(↓)Up = 4,//空格下方方块上移(↑)None = 0//不移动};}NumSwitchusing System;using System.Collections.Generic;using System.Linq;using System.Text;namespace EightNumber{public static class NumSwitch{//获取移动方格后的数字状态,s为移动前的数字状态,md为移动方向public static int GetMoveBorder(int s, Direction md){int n = s % 10;//n为s的个位数if (md == Direction.Right){if (n % 3 != 0){return ++s;}}else if (md == Direction.Left){if (n % 3 != 1){return --s;}}else if (md == Direction.Down){if (n + 2 < 9){int powLow = (int)Math.Pow(10, n);int powHigh = (int)Math.Pow(10, n + 3);int high = s / powHigh * powHigh;//高位int low = s % powLow / 10 * 10;//低位,不包括个位int mid = s % powHigh / powLow;//中间位return high + (mid % 100 * 10 + mid / 100) * powLow + low + n + 3;}}else if (md == Direction.Up){if (n - 3 > 0){int powLow = (int)Math.Pow(10, n - 3);int powHigh = (int)Math.Pow(10, n);int high = s / powHigh * powHigh;//高位int low = s % powLow / 10 * 10;//低位,不包括个位int mid = s % powHigh / powLow;//中间位return high + (mid % 10 * 100 + mid / 10) * powLow + low + n - 3;}}return -1;}//判断是否可以从初始状态到达目的状态//(计算两个棋局的逆序,奇偶性相同的返回true)public static bool ExistAnswer(int begin, int end){//由于个位表示空格位置,所以去掉个位begin = begin / 10;end = end / 10;int[] arrBegin = new int[8];int[] arrEnd = new int[8];for (int i = 7; i >= 0; i--){//将两个棋局的每个数字存入数组arrBegin[i] = begin % 10;begin /= 10;arrEnd[i] = end % 10;end /= 10;}int beginStatus = 0, endStatus = 0;for (int i = 0; i < 8; i++){for (int j = i + 1; j < 8; j++){if (arrBegin[j] < arrBegin[i]){beginStatus++;}}for (int j = i + 1; j < 8; j++){if (arrEnd[j] < arrEnd[i]){endStatus++;}}}return (beginStatus + endStatus) % 2 == 0;}}}申明,我不是专业人士,只是业余爱好,有错请指出。
8数码问题C++源代码

46 GraphNode child;
47 int blank=pop->data.grids[0];
48 int way=0;
49 for(int i=0;i<=3;i++)//先复制父结点,然后在父结点基础上实施4种算子得到至多4个儿子,
50 //除根结点外,其它结点至多有三个儿子(去掉祖先)
69 child.grids[blank-3]=0;
70 child.grids[0]=blank-3;
71 }
72 else
73 child.flag=DISCARD;
41 void GetPath();//从目标结点沿着father指针往上打印路径
42 bool Discriminance();//判别起始结点和目标结点之间是否有解
43
44 private:
45 bool Compare(const GraphNode child,OpenList& same);//比较两结点是否相同
13 begin.father=&begin;//只有起始结点(根结点)指向父指针指向本身
14 begin.flag=-1;//设起始结点无穷小,防止回溯至根
15 yer=1;
16
17 cout<<"请输入目标状态:"<<endl;
106 child.father=&pop->data ;
107 }
108 }
109 Nchild[i]=child;
110 way++;
111 }
112}
八数码C语言A算法详细代码

八数码C语言A算法详细代码以下是八数码问题的C语言A*算法的详细代码:```c#include <stdio.h>#include <stdlib.h>#define N 3typedef struct Nodeint board[N][N]; // 八数码局面struct Node *parent; // 父节点指针int f; // f(n) = g(n) + h(n),g(n)表示起始节点到当前节点的代价,h(n)表示当前节点到目标节点的估计代价int g; // g(n)int h; // h(n)} Node;//目标局面int target[N][N] = {{1, 2, 3}, {8, 0 ,4}, {7, 6, 5}};//计算当前节点到目标节点的曼哈顿距离int manhattanDistance(int board[N][N])int distance = 0;for (int i = 0; i < N; i++)for (int j = 0; j < N; j++)if (board[i][j] != 0)int value = board[i][j] - 1;int targetI = value / N;int targetJ = value % N;distance += abs(i - targetI) + abs(j - targetJ);}}}return distance;//创建一个新节点Node* createNode(int board[N][N], int g, Node* parent) Node* node = (Node*) malloc(sizeof(Node));for (int i = 0; i < N; i++)for (int j = 0; j < N; j++)node->board[i][j] = board[i][j];}}node->parent = parent;node->g = g;node->h = manhattanDistance(board);node->f = node->g + node->h;return node;//判断两个局面是否相等int isBoardEqual(int board1[N][N], int board2[N][N]) for (int i = 0; i < N; i++)for (int j = 0; j < N; j++)if (board1[i][j] != board2[i][j])return 0;}}}return 1;//判断节点是否在开放列表中int isInOpenList(Node *node, Node **openList, int openListSize)for (int i = 0; i < openListSize; i++)if (isBoardEqual(node->board, openList[i]->board))return 1;}}return 0;//判断节点是否在关闭列表中int isInClosedList(Node *node, Node **closedList, int closedListSize)for (int i = 0; i < closedListSize; i++)if (isBoardEqual(node->board, closedList[i]->board))return 1;}}return 0;//比较两个节点的f(n)值Node *a = *(Node **)node1;Node *b = *(Node **)node2;return a->f - b->f;//输出路径void printPath(Node *node)if (node != NULL)printPath(node->parent);printf("Step %d:\n", node->g);for (int i = 0; i < N; i++)printf("%d %d %d\n", node->board[i][0], node->board[i][1], node->board[i][2]);}printf("\n");}//A*算法求解八数码问题void solvePuzzle(int initial[N][N])//创建初始节点Node* initialNode = createNode(initial, 0, NULL);//开放列表和关闭列表Node* openList[N*N*N*N];int openListSize = 0;Node* closedList[N*N*N*N];int closedListSize = 0;//将初始节点放入开放列表openList[openListSize++] = initialNode;while (openListSize > 0)//从开放列表中选择f(n)最小的节点//取出开放列表中f(n)最小的节点作为当前节点Node* currentNode = openList[0];//将当前节点从开放列表中移除for (int i = 1; i < openListSize; i++) openList[i - 1] = openList[i];}openListSize--;//将当前节点放入关闭列表closedList[closedListSize++] = currentNode; //判断当前节点是否为目标节点if (isBoardEqual(currentNode->board, target)) printf("Solution found!\n");printPath(currentNode);return;}//生成当前节点的邻居节点int i = 0, j = 0;for (i = 0; i < N; i++)for (j = 0; j < N; j++)if (currentNode->board[i][j] == 0)break;}}if (j < N)break;}}if (i > 0)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l]; }}newBoard[i][j] = newBoard[i - 1][j];newBoard[i - 1][j] = 0;if (!isInOpenList(createNode(newBoard, currentNode->g + 1, currentNode), openList, openListSize) &&!isInClosedList(createNode(newBoard, currentNode->g + 1, currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}if (i < N - 1)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l];}}newBoard[i][j] = newBoard[i + 1][j];newBoard[i + 1][j] = 0;currentNode), openList, openListSize) &&!isInClosedList(createNode(newBoard, currentNode->g + 1, currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}if (j > 0)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l];}}newBoard[i][j] = newBoard[i][j - 1];newBoard[i][j - 1] = 0;if (!isInOpenList(createNode(newBoard, currentNode->g + 1, currentNode), openList, openListSize) &¤tNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}if (j < N - 1)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l];}}newBoard[i][j] = newBoard[i][j + 1];newBoard[i][j + 1] = 0;if (!isInOpenList(createNode(newBoard, currentNode->g + 1, currentNode), openList, openListSize) &&!isInClosedList(createNode(newBoard, currentNode->g + 1, currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}}printf("Solution not found!\n");int maiint initial[N][N] = {{2, 8, 3}, {1, 6, 4}, {7, 0, 5}};solvePuzzle(initial);return 0;```这个代码实现了八数码问题的A*算法。
八数码c语言代码

八数码c语言代码八数码c语言代码#include<>#include<>#include<>struct node{int x,y;int cntdif;int step;int f[9];int xy[3][3];}queue[10000];int map[3][3];int dir[4][2]={{-1,0},{1,0},{0,1},{0,-1}};int hash[10000];int zz[9];int f1,f2;struct node sour,dest;int judge(int a[]) ,zz);hash[head]=visit(queue[head].f);print(queue[head].xy);[i*3+j]=queue[tail].xy[i][j]=ff[i*3+j]; queue[tail].step=+1;queue[tail].x=sx;queue[tail].y=sy;queue[tail]tdif=count(queue[tail].f,zz);hash[tail]=visit(queue[tail].f);print(queue[tail].xy);if(match(queue[tail])){printf("共需%d步!\n",queue[tail].step);return;}}}qsort(queue+head,tail-head+1,sizeof(queue[0]),comp);//排序,每次选择cntdif数目最小的扩展}}int main(){int i,j,a[9],b[9];printf("请输入初始状态:\n");for(i=0;i<3;i++)for(j=0;j<3;j++){scanf("%d",&map[i][j]);[i][j]=map[i][j];[i*3+j]=map[i][j];a[i*3+j]=map[i][j];if(map[i][j]==0){=i;=j;=0;=0;}}printf("请输入终止状态:\n");for(i=0;i<3;i++)for(j=0;j<3;j++){scanf("%d",&map[i][j]);[i][j]=map[i][j];[i*3+j]=map[i][j];b[i*3+j]=map[i][j];zz[i*3+j]=map[i][j];}printf("\n");if((judge(a)+judge(b))&1){printf("这个终止状态不可达!"); return 0;}printf("全局择优搜索状态如下:\n"); bfs();printf("OK!\n");return 0;}。
深度宽度优先搜索---八数码
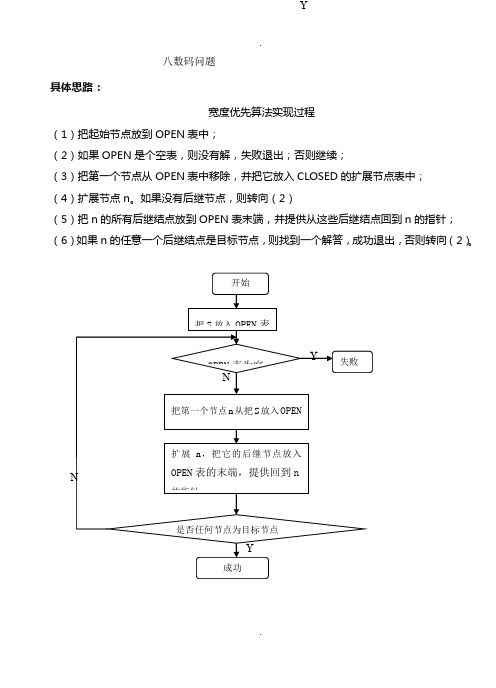
Y.八数码问题具体思路:宽度优先算法实现过程(1)把起始节点放到OPEN表中;(2)如果OPEN是个空表,则没有解,失败退出;否则继续;(3)把第一个节点从OPEN表中移除,并把它放入CLOSED的扩展节点表中;(4)扩展节点n。
如果没有后继节点,则转向(2)(5)把n的所有后继结点放到OPEN表末端,并提供从这些后继结点回到n的指针;(6)如果n的任意一个后继结点是目标节点,则找到一个解答,成功退出,否则转向(2)。
深度优先实现过程(1)把起始节点S放入未扩展节点OPEN表中。
如果此节点为一目标节点,则得到一个解;(2)如果OPEN为一空表,则失败退出;(3)把第一个节点从OPEN表移到CLOSED表;(4)如果节点n的深度等于最大深度,则转向(2);(5)扩展节点n,产生其全部后裔,并把它们放入OPEN表的前头。
如果没有后裔,则转向(2);(6)如果后继结点中有任一个目标节点,则得到一个解,成功退出,否则转向(2)。
方法一:用C语言实现#include <stdio.h>#include <string.h>#include<stdlib.h>typedef long UINT64;typedef struct{char x; //位置x和位置y上的数字换位char y; //其中x是0所在的位置} EP_MOVE;#define SIZE 3 //8数码问题,理论上本程序也可解决15数码问题,#define NUM SIZE * SIZE //但move_gen需要做很多修改,输入初始和结束状态的部分和check_input也要修改#define MAX_NODE 1000000#define MAX_DEP 100#define XCHG(a, b) { a=a + b; b=a - b; a=a - b; }#define TRANS(a, b)/*{ long iii; (b)=0; for(iii=0; iii < NUM; iii++) (b)=((b) << 4) + a[iii]; }*/ //将数组a转换为一个64位的整数b#define RTRANS(a, b) \{ \long iii; \UINT64 ttt=(a); \for(iii=NUM - 1; iii >= 0; iii--) \{ \b[iii]=ttt & 0xf; \ttt>>=4; \} \} //将一个64位整数a转换为数组b//typedef struct EP_NODE_Tag{ UINT64 v; //保存状态,每个数字占4个二进制位,可解决16数码问题struct EP_NODE_Tag *prev; //父节点struct EP_NODE_Tag *small, *big;} EP_NODE;EP_NODE m_ar[MAX_NODE];EP_NODE *m_root;long m_depth; //搜索深度EP_NODE m_out[MAX_DEP]; //输出路径//long move_gen(EP_NODE *node, EP_MOVE *move){long pz; //0的位置UINT64 t=0xf;for(pz=NUM - 1; pz >= 0; pz--). {if((node->v & t) == 0){ break; //找到0的位置}t<<=4;}switch(pz){case 0:move[0].x=0;move[0].y=1;move[1].x=0;move[1].y=3;return 2;case 1:move[0].x=1;move[0].y=0;move[1].x=1;move[1].y=2;move[2].x=1;move[2].y=4;return 3;case 2:move[0].x=2;. move[0].y=1;move[1].x=2;move[1].y=5;return 2;case 3:move[0].x=3;move[0].y=0;move[1].x=3;move[1].y=6;move[2].x=3;move[2].y=4;return 3;case 4:move[0].x=4;move[0].y=1;move[1].x=4;move[1].y=3;move[2].x=4;move[2].y=5;move[3].x=4;move[3].y=7;return 4;. case 5:move[0].x=5;move[0].y=2;move[1].x=5;move[1].y=4;move[2].x=5;move[2].y=8;return 3;case 6:move[0].x=6;move[0].y=3;move[1].x=6;move[1].y=7;return 2;case 7:move[0].x=7;move[0].y=6;move[1].x=7;move[1].y=4;move[2].x=7;move[2].y=8;return 3;.case 8:move[0].x=8;move[0].y=5;move[1].x=8;move[1].y=7;return 2;}return 0;}long mov(EP_NODE *n1, EP_MOVE *mv, EP_NODE *n2) //走一步,返回走一步后的结果{char ss[NUM];RTRANS(n1->v, ss);XCHG(ss[mv->x], ss[mv->y]);TRANS(ss, n2->v);return 0;}long add_node(EP_NODE *node, long r){EP_NODE *p=m_root;EP_NODE *q;. while(p){ q=p;if(p->v == node->v) return 0;else if(node->v > p->v) p=p->big;else if(node->v < p->v) p=p->small;}m_ar[r].v=node->v;m_ar[r].prev=node->prev;m_ar[r].small=NULL;m_ar[r].big=NULL;if(node->v > q->v){ q->big= &m_ar[r];}else if(node->v < q->v){ q->small= &m_ar[r];}return 1;}/*得到节点所在深度*/long get_node_depth(EP_NODE *node) { long d=0;while(node->prev).{ d++;node=node->prev;}return d;}/*返回值:成功-返回搜索节点数,节点数不够-(-1),无解-(-2)*/ long bfs_search(char *begin, char *end){ long h=0, r=1, c, i, j;EP_NODE l_end, node, *pnode;EP_MOVE mv[4]; //每个局面最多4种走法TRANS(begin, m_ar[0].v);TRANS(end, l_end.v);m_ar[0].prev=NULL;m_root=m_ar;m_root->small=NULL;m_root->big=NULL;while((h < r) && (r < MAX_NODE - 4)){ c=move_gen(&m_ar[h], mv);for(i=0; i < c; i++){ mov(&m_ar[h], &mv[i], &node);node.prev= &m_ar[h];if(node.v == l_end.v){ pnode= &node;j=0;while(pnode->prev){ m_out[j]=*pnode;j++;pnode=pnode->prev;}m_depth=j;return r;}if(add_node(&node, r)) r++; //只能对历史节点中没有的新节点搜索,否则会出现环}h++;printf("\rSearch...%9d/%d @ %d", h, r, get_node_depth(&m_ar[h]));}if(h == r){ return -2; }else{return -1; }}long check_input(char *s, char a, long r){ long i;for(i=0; i < r; i++){ if(s[i] == a - 0x30) return 0; }return 1;}long check_possible(char *begin, char *end){ char fs;long f1=0, f2=0;long i, j;for(i=0; i < NUM; i++){ fs=0;for(j=0; j < i; j++){if((begin[i] != 0) && (begin[j] != 0) && (begin[j] < begin[i])) fs++; }f1+=fs;fs=0;for(j=0; j < i; j++){ if((end[i] != 0) && (end[j] != 0) && (end[j] < end[i])) fs++;}f2+=fs;}if((f1 & 1) == (f2 & 1)) return 1;. elsereturn 0;}void output(void){ long i, j, k;char ss[NUM];for(i=m_depth - 1; i >= 0; i--){ RTRANS(m_out[i].v, ss);for(j=0; j < SIZE; j++){ for(k=0; k < SIZE; k++){ printf("%2d", ss[SIZE * j + k]);}printf("\n");}printf("\n");}}int main(void){ char s1[NUM];char s2[NUM];long r;char a;printf("请输入开始状态:");r=0;while(r < NUM){ a=getchar();if(a >= 0x30 && a < 0x39 && check_input(s1, a, r)) { s1[r++]=a - 0x30;printf("%c", a);}}printf("\n请输入结束状态:");r=0;while(r < NUM){ a=getchar();if(a >= 0x30 && a < 0x39 && check_input(s2, a, r)) { s2[r++]=a - 0x30;printf("%c", a);}}printf("\n");if(check_possible(s1, s2)){ r=bfs_search(s1, s2);printf("\n");if(r >= 0){ printf("查找深度=%d,所有的方式=%ld\n", m_depth, r);output();}else if(r == -1){ printf("没有找到路径.\n");}else if(r == -2){printf("这种状态变换没有路径到达.\n");}else{printf("不确定的错误.\n");}}else{ printf("不允许这样移动!\n");}return 0;}方法二:用MATLAB实现program 8no_bfs; {八数码的宽度优先搜索算法} ConstDir : array[1..4,1..2]of integer {四种移动方向,对应产生式规则} = ((1,0),(-1,0),(0,1),(0,-1));n=10000;TypeT8no = array[1..3,1..3]of integer;TList = recordFather : integer; {父指针}dep : byte; {深度}X0,Y0 : byte; {0的位置}State : T8no; {棋盘状态}end;VarSource,Target : T8no;List : array[0..10000] of TList; {综合数据库}Closed,open,Best : integer { Best表示最优移动次数} Answer : integer; {记录解}Found : Boolean; {解标志}procedure GetInfo; {读入初始和目标节点}var i,j : integer;beginfor i:=1 to 3 dofor j:=1 to 3 do read(Source[i,j]);for i:=1 to 3 dofor j:=1 to 3 do read(Target[i,j]);end;procedure Initialize; {初始化}var x,y : integer;beginFound:=false;Closed:=0;open:=1;with List[1] do beginState:=Source;dep:=0;Father:=0;For x:=1 to 3 doFor y:=1 to 3 doif State[x,y]=0 then Begin x0:=x;y0:=y; End;end;end;Function Same(A,B : T8no):Boolean; {判断A,B状态是否相等} Var i,j : integer;BeginSame:=false;For i:=1 to 3 do for j:=1 to 3 do if A[i,j]<>B[i,j] then exit; Same:=true;End;Function not_Appear(new : tList):boolean;{判断new是否在List中出现}var i : integer;beginnot_Appear:=false;for i:=1 to open do if Same(new.State,List[i].State) then exit;not_Appear:=true;end;procedure Move(n : tList;d : integer;var ok : boolean;var new : tList);{将第d条规则作用于n得到new,OK是new是否可行的标志}var x,y : integer;beginX := n.x0 + Dir[d,1];Y := n.y0 + Dir[d,2];{判断new的可行性}if not ((X > 0) and ( X < 4 ) and ( Y > 0 ) and ( Y < 4 )) then begin ok:=false;exit end;OK:=true;new.State:=n.State; {new=Expand(n,d)}new.State[X,Y]:=0;new.State[n.x0,n.y0]:=n.State[X,Y];new.X0:=X;new.Y0:=Y;end;procedure Add(new : tList); {插入节点new}beginif not_Appear(new) then Begin {如果new没有在List出现} Inc(open); {new加入open表}List[open] := new;end;end;procedure Expand(Index : integer; var n : tList); {扩展n的子节点}var i : integer;new : tList;OK : boolean;Beginif Same(n.State , Target) then begin {如果找到解}Found := true;Best :=n.Dep;Answer:=Index;Exit;end;For i := 1 to 4 do begin {依次使用4条规则} Move(n,i,OK,new);if not ok then continue;new.Father := Index;new.Dep :=n.dep + 1;Add(new);end;end;procedure GetOutInfo; {输出} procedure Outlook(Index : integer); {递归输出每一个解} var i,j : integer;beginif Index=0 then exit;Outlook(List[Index].Father);with List[Index] dofor i:=1 to 3 do beginfor j:=1 to 3 do write(State[i,j],' ');writeln;end;writeln;end;beginWriteln('Total = ',Best);Outlook(Answer);end;procedure Main; {搜索主过程} beginRepeatInc(Closed);Expand(Closed,List[Closed]); {扩展Closed} Until (Closed>=open) or Found;if Found then GetOutInfo {存在解}else Writeln('no answer'); {无解}end;BeginAssign(Input,'input.txt');ReSet(Input);Assign(Output,'Output.txt');ReWrite(Output);GetInfo;Initialize;Main;Close(Input);Close(Output);End.五、实验结果六、实验总结通过实验问题的求解过程就是搜索的过程,采用适合的搜索算法是关键的,因为对求解过程的效率有很大的影响,包括各种规则、过程和算法等推理技术。
八数码问题

#include <stdio.h>#include <stdlib.h>#include <windows.h>#define BOUND 3#define INIT_LIST_SIZE 20#define INCREMENT_LIST_SIZE 5#define INIT_STACK_SIZE 50#define INCREMENT_STACK_SIZE 10typedef struct _Node{int num[BOUND][BOUND]; //记录状态int h; //h(x)struct _Node *parent; //父节点}Node;typedef Node ElemType;typedef struct _List{ElemType *elem;int length;int listsize;}List, *PList;typedef struct _Stack{ElemType *base;ElemType *top;int stacksize;}Stack, *PStack;int move[4][2] = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}}; //方向void Init(ElemType *, List *); //输入初始和最终状态void Init_List(PList); //初始化链表int IsEmpty_List(PList); //判断链表是否为空void Add_List(PList, ElemType *); //向链表中插入一个元素void Remove_List(PList, ElemType *, int); //从链表中取出一个元素int HasElem(PList, ElemType *); //判断链表中是否有某个元素void Sort_List(PList); //根据h对链表进行排序void Destroy_List(PList); //删除链表void Init_Stack(PStack); //初始化栈int IsEmpty_Stack(PStack); //判断栈是否为空void Push(PStack, ElemType *); //压栈void Pop(PStack, ElemType *); //出栈void Destroy_Stack(PStack); //删除栈int Geth(int [][BOUND]); //根据状态计算hint Expand(PList, PList, ElemType *); //根据一个节点进行扩展void Show_Node(Node *); //显示节点信息void Assign_Node(Node *, Node *); //节点复制int Equal_Node(Node *, Node *); //判断两个节点的状态是否相等ElemType *last;int main(){List open, close;Stack stack;ElemType *N=NULL;int flag = 0;Init_List(&open);Init_List(&close);Init(N, &open);while(1){if(IsEmpty_List(&open)){printf("搜索失败!\n");break;}N = (ElemType *)malloc(sizeof(ElemType));Remove_List(&open, N, 1);Add_List(&close, N);if(Equal_Node(last, N)){printf("搜索成功!\n");flag = 1;break;}else{if(Expand(&open, &close, N) == 0)continue;Sort_List(&open);}}Sleep(2000);system("cls");if(1 == flag){Init_Stack(&stack);while(1){Push(&stack, N);if(N->parent == NULL){break;}N = N->parent;}while(!IsEmpty_Stack(&stack)){system("cls");printf("路径显示:\n");Pop(&stack, N);Show_Node(N);Sleep(1000);}Destroy_Stack(&stack);}Destroy_List(&open);Destroy_List(&close);return 0;}void Init(ElemType *N, List *open){int i, j;printf("输入初始状态:\n");N = (ElemType *)malloc(sizeof(ElemType));for(i=0; i<BOUND; i++){for(j=0; j<BOUND; j++){scanf("%d", &N->num[i][j]);}}printf("输入最终状态:\n");last = (ElemType *)malloc(sizeof(ElemType));for(i=0; i<BOUND; i++){for(j=0; j<BOUND; j++){scanf("%d", &last->num[i][j]);}}N->h = Geth(N->num);N->parent = NULL;Add_List(open, N);}void Init_List(PList plist){plist->elem = (ElemType *)malloc(INIT_LIST_SIZE*sizeof(ElemType));plist->listsize = INIT_LIST_SIZE;plist->length = 0;}int IsEmpty_List(PList plist){if(plist->length == 0)return 1;return 0;}void Add_List(PList plist, ElemType *e){if(plist->length >= plist->listsize){plist->elem = (ElemType *)realloc(plist->elem, (plist->listsize+INCREMENT_LIST_SIZE)*sizeof(ElemType));plist->listsize += INCREMENT_LIST_SIZE;}Assign_Node(&plist->elem[plist->length], e);plist->length ++;}void Remove_List(PList plist, ElemType *N, int index){int k;if(plist->length == 0){N = NULL;}else{Assign_Node(N, &plist->elem[index-1]);for(k=index; k<plist->length; k++){Assign_Node(&plist->elem[k-1], &plist->elem[k]);}plist->length --;}}void Sort_List(PList plist){int i, j, flag;ElemType temp;for(i=plist->length-1; i>0; i--){flag = 0;for(j=0; j<i; j++){if(plist->elem[j].h > plist->elem[j+1].h){Assign_Node(&temp, &plist->elem[j]);Assign_Node(&plist->elem[j], &plist->elem[j+1]);Assign_Node(&plist->elem[j+1], &temp);flag = 1;}}if(!flag)break;}}int HasElem(PList plist, ElemType *e){int i, j, k, t;for(k=0; k<plist->length; k++){t = 0;for(i=0; i<BOUND; i++){for(j=0; j<BOUND; j++){if(plist->elem[k].num[i][j] == e->num[i][j]){t++;}}}if(t == BOUND*BOUND){return 1;}}return 0;}void Destroy_List(PList plist){free(plist->elem);plist->length = plist->listsize = 0;}void Init_Stack(PStack pstack){pstack->base = (ElemType *)malloc(INIT_STACK_SIZE*sizeof(ElemType));pstack->top = pstack->base;pstack->stacksize = INIT_STACK_SIZE;}int IsEmpty_Stack(PStack pstack){if(pstack->top == pstack->base)return 1;return 0;}void Push(PStack pstack, ElemType *pelem){if(pstack->top - pstack->base >= pstack->stacksize){pstack->base = (ElemType *)realloc(pstack->base, (pstack->stacksize+INCREMENT_STACK_SIZE)*sizeof(ElemType));pstack->top = pstack->base+pstack->stacksize;pstack->stacksize += INCREMENT_STACK_SIZE;}Assign_Node(pstack->top, pelem);(pstack->top)++;}void Pop(PStack pstack, ElemType *pelem){if(IsEmpty_Stack(pstack))exit(0);Assign_Node(pelem, (pstack->top-1));(pstack->top)--;}void Destroy_Stack(PStack pstack){free(pstack->base);pstack->top = NULL;pstack->stacksize = 0;}int Geth(int num[][BOUND]){int i, j, h = BOUND*BOUND;for(i=0; i<BOUND; i++){for(j=0; j<BOUND; j++){if(num[i][j] == last->num[i][j]){h--;}}}return h;}int Expand(PList popen, PList pclose, ElemType *e){int dir, i, j, m, n, a, b, state, t;ElemType *temp;t = 0;for(dir=0; dir<4; dir++){temp = (ElemType *)malloc(sizeof(ElemType));for(i=0; i<BOUND; i++){for(j=0; j<BOUND; j++){if(e->num[i][j] == 0){n = i;m = j;}temp->num[i][j] = e->num[i][j];}}a = n+move[dir][0];b = m+move[dir][1];if(a < 0 || a > BOUND-1 || b < 0 || b > BOUND-1){continue;}state = temp->num[n][m];temp->num[n][m] = temp->num[a][b];temp->num[a][b] = state;if(!HasElem(popen, temp) && !HasElem(pclose, temp)){temp->parent = e;temp->h = Geth(temp->num);Add_List(popen, temp);t++;}}return t;}void Show_Node(Node *N){int i, j;for(i=0; i<BOUND; i++){for(j=0; j<BOUND; j++){if(N->num[i][j] != 0){printf("%3d", N->num[i][j]);}else{printf("%3c", ' ');}}printf("\n");}}void Assign_Node(Node *N1, Node *N2){int i, j;for(i=0; i<BOUND; i++){for(j=0; j<BOUND; j++){N1->num[i][j] = N2->num[i][j];}}N1->h = N2->h;N1->parent = N2->parent;}int Equal_Node(Node *N1, Node *N2){int i, j;for(i=0; i<BOUND; i++){for(j=0; j<BOUND; j++){if(N1->num[i][j] != N2->num[i][j]){return 0;}}}return 1;}。
启发式搜索算法解决八数码问题(C语言)

1、程序源代码#include <stdio.h>#include<malloc.h>struct node{int a[3][3];//用二维数组存放8数码int hx;//函数h(x)的值,表示与目标状态的差距struct node *parent;//指向父结点的指针struct node *next;//指向链表中下一个结点的指针};//------------------hx函数-------------------//int hx(int s[3][3]){//函数说明:计算s与目标状态的差距值int i,j;int hx=0;int sg[3][3]={1,2,3,8,0,4,7,6,5};for(i=0;i<3;i++)for(j=0;j<3;j++)if(s[i][j]!=sg[i][j])hx++;return hx;}//-------------hx函数end----------------------////-------------extend扩展函数----------------//struct node *extend(node *ex){ //函数说明:扩展ex指向的结点,并将扩展所得结点组成一条//单链表,head指向该链表首结点,并且作为返回值int i,j,m,n; //循环变量int t; //临时替换变量int flag=0;int x[3][3];//临时存放二维数组struct node *p,*q,*head;head=(node *)malloc(sizeof(node));//headp=head;q=head;head->next=NULL;//初始化for(i=0;i<3;i++)//找到二维数组中0的位置{for(j=0;j<3;j++)if(ex->a[i][j]==0){flag=1;break;}if(flag==1)break;}for(m=0;m<3;m++)//将ex->a赋给xfor(n=0;n<3;n++)x[m][n]=ex->a[m][n];//根据0的位置的不同,对x进行相应的变换//情况1if(i-1>=0){t=x[i][j];x[i][j]=x[i-1][j];x[i-1][j]=t;flag=0;for(m=0;m<3;m++)//将x赋给afor(n=0;n<3;n++)if(x[m][n]==ex->parent->a[m][n])flag++;if(flag!=9){q=(node *)malloc(sizeof(node));for(m=0;m<3;m++)//将x赋给afor(n=0;n<3;n++)q->a[m][n]=x[m][n];q->parent=ex;q->hx=hx(q->a);q->next=NULL;p->next=q;p=p->next;}}//情况2for(m=0;m<3;m++)//将ex->a重新赋给x,即还原x for(n=0;n<3;n++)x[m][n]=ex->a[m][n];if(i+1<=2){t=x[i][j];x[i][j]=x[i+1][j];x[i+1][j]=t; flag=0;for(m=0;m<3;m++)for(n=0;n<3;n++)if(x[m][n]==ex->parent->a[m][n])flag++;if(flag!=9){q=(node *)malloc(sizeof(node));for(m=0;m<3;m++)//将x赋给afor(n=0;n<3;n++)q->a[m][n]=x[m][n];q->parent=ex;q->hx=hx(q->a);q->next=NULL;p->next=q;p=p->next;}}//情况3for(m=0;m<3;m++)//将ex->a重新赋给x,即还原x for(n=0;n<3;n++)x[m][n]=ex->a[m][n];if(j-1>=0){t=x[i][j];x[i][j]=x[i][j-1];x[i][j-1]=t;flag=0;for(m=0;m<3;m++)for(n=0;n<3;n++)if(x[m][n]==ex->parent->a[m][n])flag++;if(flag!=9){q=(node *)malloc(sizeof(node));for(m=0;m<3;m++)//将x赋给afor(n=0;n<3;n++)q->a[m][n]=x[m][n];q->parent=ex;q->hx=hx(q->a);q->next=NULL;p->next=q;p=p->next;}}//情况4for(m=0;m<3;m++)//将ex->a重新赋给x,即还原xfor(n=0;n<3;n++)x[m][n]=ex->a[m][n];if(j+1<=2){t=x[i][j];x[i][j]=x[i][j+1];x[i][j+1]=t;flag=0;for(m=0;m<3;m++)for(n=0;n<3;n++)if(x[m][n]==ex->parent->a[m][n])flag++;if(flag!=9){q=(node *)malloc(sizeof(node));for(m=0;m<3;m++)for(n=0;n<3;n++)q->a[m][n]=x[m][n];q->parent=ex;q->hx=hx(q->a);q->next=NULL;p->next=q;p=p->next;}}head=head->next;return head;}//---------------extend函数end-----------------------////----------------insert函数-------------------------//node* insert(node *open,node * head){ //函数说明:将head链表的结点依次插入到open链表相应的位置, //使open表中的结点按从小到大排序。
八数码C语言A算法详细代码

#include<iostream>#include<>#include<>#include<vector>#include<cmath>using namespace std;struct node{int a[3][3]; [i][j]!=store[0].a[i][j])return false;}}return true;}bool search(int num) ather; [i][j]!=store[num].a[i][j]){test=false;break;}}if(test==false) break;}if(test==true) return false;pre=store[pre].father; ather;(num);while(pre!=0){ ather;}cout<<endl;cout<<"*********数码移动步骤*********"<<endl;int mm=1; [i][j]<<" ";}cout<<endl;}mm++;cout<<endl;}cout<<"所需步数为: "<<store[num].deep<<endl;return;}int get_fn(int num) !=i||store[num].y!=j)&&store[num].a[i][j]==store[0].a[k][l]){ eep;[i][j]==0){store[num].x=i;store[num].y=j;}}}return;}int main(){cout<<"-----------A*算法解决8数码问题------------"<<endl;while(true){(); [i][j]=temp;begin[f++]=temp;}}test=true;for(i=0;i<8;i++){ [i][j]=temp;target[f++]=temp;}}test=true;for(i=0;i<8;i++){ <<endl;cout<<endl;ather=0; one=0;store[1].deep=0; n=get_fn(1);if(check(1)){ n<=store[min].fn&&store[open[i]].gone==0){min=open[i];i_min=i;}}store[min].gone=1;()+i_min); ;n=store[min].y; ather=min; one=0;eep=store[min].deep+1; [m][n]; [m][n]=store[top].a[i][j];store[top].a[i][j]=temp;store[top].x=i; =j;store[top].fn=get_fn(top); cout<<"算法时间为为"<<d<<" ms."<<endl;cout<<endl;}return 0;system("pause"); }。
c++算法 八数码问题

c++算法八数码问题八数码问题是一种经典的智力游戏,其规则是在有限的格子中,按照一定的顺序将数字旋转移动到目标位置。
为了解决这个问题,我们可以使用算法的思想来设计一种有效的解决方案。
一、问题描述八数码问题是一个有N×N的棋盘,其中每个格子代表一个数字。
玩家需要按照一定的顺序旋转数字,将它们移动到目标位置。
目标位置是预先设定好的,玩家需要按照规则移动数字,使得棋盘上的数字按照正确的顺序排列。
二、算法思想为了解决八数码问题,我们可以使用贪心算法的思想。
首先,我们需要找到一个初始状态,这个状态应该是最简单、最容易解决的问题。
然后,我们通过循环迭代的方式,不断尝试不同的旋转方式,直到找到一个能够满足目标位置的解决方案。
三、C语言实现下面是一个简单的C语言实现,用于解决八数码问题。
这个程序使用了递归和回溯的方法,通过穷举所有可能的旋转方式来找到解决方案。
```c#include <stdio.h>#include <stdlib.h>#include <stdbool.h>#define N 3// 定义棋盘状态结构体typedef struct {int nums[N][N];int num_count[N][N]; // 记录每个数字出现的次数} Board;// 判断两个数字是否相邻bool is_adjacent(int num1, int num2) {int dx[] = {-1, 0, 1};int dy[] = {0, -1, 1};for (int i = 0; i < 3; i++) {if (abs(nums[num1][i] - nums[num2][i]) <= 1) {return true;}}return false;}// 寻找最优解函数bool find_optimal_solution(Board& board, int target_row, int target_col) {// 初始化最优解为空状态bool optimal_solution = false;int optimal_score = INT_MAX; // 最优解的得分初始化为最大整数int best_score = INT_MAX; // 最优解的当前得分初始化为最大整数加一// 对当前棋盘进行遍历for (int row = 0; row < N; row++) {for (int col = 0; col < N; col++) {// 如果当前状态为空状态,则直接跳过if (board.nums[row][col] == 0) {continue;}// 记录当前状态的信息,包括得分和旋转次数等int score = calculate_score(board, row, col); // 计算得分函数在实现中定义了旋转方式的选择和得分计算规则等具体细节,这里省略了具体实现细节。
八数码问题C语言A星算法详细实验报告含代码

一、实验容和要求八数码问题:在3×3的方格棋盘上,摆放着1到8这八个数码,有1个方格是空的,其初始状态如图1所示,要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。
例如:(a) 初始状态(b) 目标状态图1 八数码问题示意图请任选一种盲目搜索算法(广度优先搜索或深度优先搜索)或任选一种启发式搜索方法(全局择优搜索,加权状态图搜索,A算法或A* 算法)编程求解八数码问题(初始状态任选)。
选择一个初始状态,画出搜索树,填写相应的OPEN 表和CLOSED表,给出解路径,对实验结果进行分析总结,得出结论。
二、实验目的1. 熟悉人工智能系统中的问题求解过程;2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用;3. 熟悉对八数码问题的建模、求解及编程语言的应用。
三、实验算法A*算法是一种常用的启发式搜索算法。
在A*算法中,一个结点位置的好坏用估价函数来对它进行评估。
A*算法的估价函数可表示为:f'(n) = g'(n) + h'(n)这里,f'(n)是估价函数,g'(n)是起点到终点的最短路径值(也称为最小耗费或最小代价),h'(n)是n到目标的最短路经的启发值。
由于这个f'(n)其实是无法预先知道的,所以实际上使用的是下面的估价函数:f(n) = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价,h(n)是从结点n到目标结点的最佳路径的估计代价。
在这里主要是h(n)体现了搜索的启发信息,因为g(n)是已知的。
用f(n)作为f'(n)的近似,也就是用g(n)代替g'(n),h(n)代替h'(n)。
这样必须满足两个条件:(1)g(n)>=g'(n)(大多数情况下都是满足的,可以不用考虑),且f必须保持单调递增。
(2)h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、实验目的(1)熟悉人工智能系统中的问题求解过程;(2)熟悉状态空间中的盲目搜索策略;(3)掌握盲目搜索算法,重点是宽度优先搜索和深度优先搜索算法。
2、实验要求用VC语言编程,采用宽度优先搜索和深度优先搜索方法,求解8数码问题3、实验内容(1)采用宽度优先算法,运行程序,要求输入初始状态假设给定如下初始状态S02 8 31 6 47 0 5和目标状态Sg2 1 64 0 87 5 3验证程序的输出结果,写出心得体会。
(2)对代码进行修改(选作),实现深度优先搜索求解该问题提示:每次选扩展节点时,从数组的最后一个生成的节点开始找,找一个没有被扩展的节点。
这样也需要对节点添加一个是否被扩展过的标志。
4 源代码及实验结果截图#include<stdio.h>#include<stdlib.h>#include<math.h>//八数码状态对应的节点结构体struct Node{int s[3][3];//保存八数码状态,0代表空格int f,g;//启发函数中的f和g值struct Node * next;struct Node *previous;//保存其父节点};int open_N=0; //记录Open列表中节点数目//八数码初始状态int inital_s[3][3]={2,8,3,1,6,4,7,0,5};//八数码目标状态int final_s[3][3]={2,1,6,4,0,8,7,5,3};//------------------------------------------------------------------------ //添加节点函数入口,方法:通过插入排序向指定表添加//------------------------------------------------------------------------ void Add_Node( struct Node *head, struct Node *p){struct Node *q;if(head->next)//考虑链表为空{ q = head->next;if(p->f < head->next->f){//考虑插入的节点值比链表的第一个节点值小p->next = head->next;head->next = p;}else {while(q->next)//考虑插入节点x,形如a<= x <=b{if((q->f < p->f ||q->f == p->f) && (q->next->f > p->f || q->next->f == p->f)){p->next = q->next;q->next = p;break;}q = q->next;}if(q->next == NULL) //考虑插入的节点值比链表最后一个元素的值更大q->next = p;}}else head->next = p;}//------------------------------------------------------------------------//删除节点函数入口//------------------------------------------------------------------------void del_Node(struct Node * head, struct Node *p )struct Node *q;q = head;while(q->next){if(q->next == p){q->next = p->next;p->next = NULL;if(q->next == NULL) return;// free(p);}q = q->next;}}//------------------------------------------------------------------------ //判断两个数组是否相等函数入口//------------------------------------------------------------------------ int equal(int s1[3][3], int s2[3][3]){int i,j,flag=0;for(i=0; i< 3 ; i++)for(j=0; j< 3 ;j++)if(s1[i][j] != s2[i][j]){flag = 1; break;}if(!flag)return 1;else return 0;//------------------------------------------------------------------------ //判断后继节点是否存在于Open或Closed表中函数入口//------------------------------------------------------------------------ int exit_Node(struct Node * head,int s[3][3], struct Node *Old_Node){struct Node *q=head->next;int flag = 0;while(q)if(equal(q->s,s)) {flag=1;Old_Node->next = q;return 1;}else q = q->next;if(!flag) return 0;}//------------------------------------------------------------------------ //计算p(n)的函数入口//其中p(n)为放错位的数码与其正确的位置之间距离之和//具体方法:放错位的数码与其正确的位置对应下标差的绝对值之和//------------------------------------------------------------------------ int wrong_sum(int s[3][3]){int i,j,fi,fj,sum=0;for(i=0 ; i<3; i++)for(j=0; j<3; j++){for(fi=0; fi<3; fi++)for(fj=0; fj<3; fj++)if((final_s[fi][fj] == s[i][j])){sum += fabs(i - fi) + fabs(j - fj);break;}}return sum;}//------------------------------------------------------------------------//获取后继结点函数入口//检查空格每种移动的合法性,如果合法则移动空格得到后继结点//------------------------------------------------------------------------int get_successor(struct Node * BESTNODE, int direction, struct Node *Successor)//扩展BESTNODE,产生其后继结点SUCCESSOR{int i,j,i_0,j_0,temp;for(i=0; i<3; i++)for(j=0; j<3; j++)Successor->s[i][j] = BESTNODE->s[i][j];//获取空格所在位置for(i=0; i<3; i++)for(j=0; j<3; j++)if(BESTNODE->s[i][j] == 0){i_0 = i; j_0 = j;break;}switch(direction){case 0: if((i_0-1)>-1 ){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0-1][j_0];Successor->s[i_0-1][j_0] = temp;return 1;}else return 0;case 1: if((j_0-1)>-1){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0][j_0-1];Successor->s[i_0][j_0-1] = temp;return 1;}else return 0;case 2: if( (j_0+1)<3){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0][j_0+1];Successor->s[i_0][j_0+1] = temp;return 1;}else return 0;case 3: if((i_0+1)<3 ){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0+1][j_0];Successor->s[i_0+1][j_0] = temp;return 1;}else return 0;}}//------------------------------------------------------------------------ //从OPen表获取最佳节点函数入口//------------------------------------------------------------------------ struct Node * get_BESTNODE(struct Node *Open){return Open->next;}//------------------------------------------------------------------------ //输出最佳路径函数入口//------------------------------------------------------------------------ void print_Path(struct Node * head){struct Node *q, *q1,*p;int i,j,count=1;p = (struct Node *)malloc(sizeof(struct Node));//通过头插法变更节点输出次序p->previous = NULL;q = head;while(q){q1 = q->previous;q->previous = p->previous;p->previous = q;q = q1;}q = p->previous;while(q){if(q == p->previous)printf("八数码的初始状态:\n");else if(q->previous == NULL)printf("八数码的目标状态:\n"); else printf("八数码的中间态%d\n",count++);for(i=0; i<3; i++)for(j=0; j<3; j++){printf("%4d",q->s[i][j]);if(j == 2)printf("\n");}printf("f=%d, g=%d\n\n",q->f,q->g);q = q->previous;}}//------------------------------------------------------------------------//A*子算法入口:处理后继结点//------------------------------------------------------------------------void sub_A_algorithm(struct Node * Open, struct Node * BESTNODE, struct Node * Closed,struct Node *Successor) {struct Node * Old_Node = (struct Node *)malloc(sizeof(struct Node));Successor->previous = BESTNODE;//建立从successor返回BESTNODE的指针Successor->g = BESTNODE->g + 1;//计算后继结点的g值//检查后继结点是否已存在于Open和Closed表中,如果存在:该节点记为old_Node,比较后继结点的g值和表中old_Node 节点//g值,前者小代表新的路径比老路径更好,将Old_Node的父节点改为BESTNODE,并修改其f,g值,后者小则什么也不做。
