广东第二师范学院番禺附属中学2018-2019学年高二下学期期中考试数学(文)试题 Word版含答案
广东省第二师范学院番禺附属中学2024_2025学年高二化学下学期期中试题

广东省其次师范学院番禺附属中学2024-2025学年高二化学下学期期中试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分。
考试时间90分钟。
留意事项:1. 答题前,考生务必用黑色字迹的钢笔或签字笔将自己的考号、姓名填写在答题卡上,并用2B铅笔把对应的号码标号涂黑。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,先用橡皮擦干净后,再选涂其他答案;不能答在试卷上。
3. 非选择题必需用黑色字迹钢笔或签字笔作答,答案必需写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,再写上新的答案,改动的内容也不能超出指定的区域;不准运用铅笔、圆珠笔和涂改液。
不按以上要求作答的答案无效。
4. 考生必需保持答题卡的整齐。
考试结束后,将答题卡和答卷一并交回,本试卷自行保存。
可能用到的相对原子质量:H—1 C—12 O—16第Ⅰ卷(选择题,共50分)单项选择题(本题包括25小题,每小题2分,共50分,每小题只有一个选项符合题意。
)1.环境爱护部门为了使城市生活垃圾得到合理利用,对生活垃圾分类投放,其中塑料袋、旧橡胶是属于()。
A.无机物B.有机物C.盐类D.非金属单质2.有机物丁香油酚的结构简式如图所示,按官能团分类,它不属于()A.烯类 B.酚类 C.醚类 D.醇类3.下列有机物的命名正确的是()A. 1,2─二甲基戊烷B. 2─乙基戊烷C. 3,4─二甲基戊烷D. 3─甲基己烷4.我国冀东渤海湾发觉储量达10亿吨的大型油田。
下列关于石油的说法正确的是()。
A.石油属于可再生矿物能源B.石油主要含有碳、氢两种元素C.石油的裂化是物理改变D.石油分馏的各馏分均是纯净物5. 欲除去混在苯中的少量苯酚,下列试验方法正确的是()A.分液 B.加入氢氧化钠溶液后,充分振荡,静置后分液C.加入过量溴水,过滤 D.加入FeCl3溶液后,过滤6.某化合物由碳、氢、氧三种元素组成,其红外光谱图有C—H键、H—O键、C—O键的振动汲取,该有机物的相对分子质量是60,则该有机物的结构简式可能是()A.CH3CH2CH2OH B. C.CH3CH2OCH3 D.CH3CH2CHO7.按C2H5Br CH2 CH2 CH2Cl—CH2Cl CH2 CHCl的路途制备聚氯乙烯,不发生的反应类型是()A.加成反应B.消去反应C.取代反应D.加聚反应8.β月桂烯的结构如图所示,一分子该物质与两分子溴发生加成反应的产物(只考虑位置异构)理论上最多有()A.2种 B.3种 C.4种 D.6种9.有机物中碳原子和氢原子个数比为3∶4,不能与溴水反应却能使酸性KMnO4溶液褪色。
广东省第二师范学院番禺附属中学2024_2025学年高二历史上学期期中试题

广东省其次师范学院番禺附属中学2024-2025学年高二历史上学期期中试题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共7页,全卷二大题32小题,满分100分,考试用时90分钟。
留意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自已的姓名、考试科目、班级和考生号等信息填写在答题卡上,并用2B铅笔将考号在答题卡相关的区域内涂黑。
2.选择题每小题选出答案后,用2B铅笔把答题卡对应的答案符号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。
3.非选择题必需用黑色字迹的钢笔或签字笔作答,答案必需写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准运用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必需保持答题卡的整齐,考试结束后,将答题卡答卷交给监考老师。
第Ⅰ卷(选择题共60分)一、选择题(本大题共30小题,每题2分,共60分)1. 打破贵族的垄断、在思想界呈现出以“民本”思潮等为代表的“私学文化”(《中华文化史》冯天瑜等著),成为春秋战国时期的亮点。
其“私学文化”得以产生、发展的经济根源是A. 井田制瓦解,土地私有制确立B. 分封制崩溃,宗法制瓦解C. 贵族没落,“士”阶层活跃D.“学在官府”发展为“学在民间”2.春秋战国时期某一学派反对在社会中实施礼治、德治,认为在法律面前不存在贵族和平民之分,除君主外全部臣民一旦触犯法律都必需受到惩处。
这一学派是A.道家 B.墨家C.法家 D.儒家3.有战国时期思想家认为:“人之所不学而能者,其良能也;所不虑而知者,其良知也”。
这位思想家是A. 孔子B. 孟子C. 庄子D. 王阳明4.《史记》有如下记载:汉景帝时期窦太后喜爱《老子》,却被儒生辕固生讽刺,窦太后让辕固生与野猪搏斗。
汉武帝时期公孙弘以《春秋》白衣为天子三公,封以平津侯。
这些记载说明A. 百家争鸣思想自由局面的结束B. 统治集团内部权力与利益的冲突C. 汉朝治国思想从无为到有为的转变D. 政治的统一须要思想的统一5.春秋战国时期的儒学已成为蔚然大宗,汉代董仲舒则完成了儒学意识形态和内容的重大转折。
广东第二师范学院番禺附属中学2018-2019学年高一下学期期中考试数学试题 Word版含答案

2018-2019学年第二学期广东二师附中中段测试高一级试题数 学本试卷共4页,22小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4. 考生必须保持答题卡的整洁.考试结束后,将答题卡和答卷一并交回.试卷要自己保存好,以方便试卷评讲课更好开展.第Ⅰ卷(选择题 共60分)一.选择题(本大题共12小题,每小题5分,满分60分)1、直线013=+-y x 的倾斜角为( )A .30°B .60°C .120°D .150°2、已知直线12:220,:410l x y l ax y +-=++=, 若12l l ⊥, 则a 的值为( ) A . 2- B. 2 C. 12-D. 8 3、在△ABC 中,060B =,2b ac =则△ABC 一定是( ) A .直角三角形B .钝角三角形C .等腰直角三角形D .等边三角形4、将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周所形成几何体的体积为( )A .43π B . 4π C . 3π D . 3π 5、设,m n 为两条不同的直线,α为平面,则下列结论正确的是( )A .,//m n m n αα⊥⇒⊥B . ,//m n m n αα⊥⊥⇒C .,//m m n n αα⊥⇒⊥D .//,////m m n n αα⇒ 6、一个几何体的三视图及其尺寸如图(单位:),则该几何体的表面积为( )A .224cm πB .218cm πC .245cm πD . 248cm π 7、球的表面积与它的内接正方体的表面积之比是 ( ) A .3π B .4π C .2πD .π 8、在ABC ∆中,已知222sin sin sin 3sin sin B C A A C --=.求B 的度数( ).A .30°B .60°C .120°D .150°9、.如图所示,在正方体D C B A ABCD 111-中,若E 是A 1C 1的中点,则直线CE 垂直于( )A.AC B.BD C.1A D D.11A D . 10、已知顶点在单位圆上的ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,且C b B c A a cos cos cos 2+=,422=+c b ,则ABC ∆的面积为( ). A.38B.34C. 3D. 2311、已知正方形ABCD 的对角线AC 与BD 相交于E 点,将ACD ∆沿对角线折起,使得平面ABC ⊥平面ADC (如图),则下列命题中正确的是( )A. 直线AB ⊥直线CD ,且直线AC ⊥直线BDB. 直线AB ⊥平面BCD ,且直线AC ⊥平面BDEC. 平面ABC ⊥平面BDE ,且平面ACD ⊥平面BDED. 平面ABD ⊥平面BCD ,且平面ACD ⊥平面BDE12、如图所示,已知两点),(04A ),(40A ,从点),(02P 射出的光线经直线AB 反射后再射到直线OB 上,最后经直线OB 反射后又回到P 点,则光线所经过的路程是( ) A .210 B .6 C .33 D .25第Ⅰ卷(非选择题 共90分)二.填空题(本大题共4小题,每小题5分,满分20分). 13、锐角ABC ∆中,若面积ab S 43=,则角C =___________ 14、如图,四棱锥S -ABCD 中,底面ABCD 为平行四边形,E 是SA 上一点,当点E 满足条件:__________时,SC ∥平面EBD.15、如图所示,设,A B 两点在河的两岸,一测量者在A 所在的同侧河岸边选定一点C ,测出AC的距离为50m ,0045,105ACB CAB ∠=∠=后,就可以计算出,A B 两点的距离为________16、设点P 在直线30x y +=上,且P 到原点的距离与P 到直线32x y +=的距离相等,则点P 的坐标为 .三.解答题(本大题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤). 三、解答题(本大题共6题,共70分.解答须写出说明、证明过程和演算步骤. 解答写在答题卡上的指定区域内.)17、(本小题满分10分)已知直线()12:310,:20l ax y l x a y a ++=+-+=.(1)若12l l ⊥,求实数a 的值;(2)当12//l l 时,求直线1l 与2l 之间的距离.18、(本小题满分12分)如图,已知面11AA B B 垂直于圆柱底面,AB 为底面直径,C 是底面圆周上异于A B ,的一点,12AA AB ==.求证:(1)11AAC BAC ⊥平面平面;(2)求几何体1A ABC -的最大体积V .19、(本小题满分12分)设ABC ∆中,角A 、B 、C 的对边分别为a b c 、、,且3,1,2b c A B ===.(1)求a 的值; (2)求sin()4A π+的值.20、(本小题满分12分)如图,在△ABC 中,BC 边上的高所在的直线方程为210x y -+=,∠A 的平分线所在的直线方程为0y =,若点B 的坐标为(1,2), 求:(1)点A 和点C 的坐标; (2)求△ABC 的面积.21. (本小题满分12分)如图,四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,1,90.2AB BC AD BAD ABC ==∠=∠=︒ (1)证明:直线BC ∥平面PAD ;(2)若△PCD 的面积为27,求四棱锥P ABCD -的体积.22、(本小题满分12分)已知向量()()()2sin ,sin cos ,3cos ,sin cos (0)a x x x b x x x λλλ=+=->,函数()f x a b =⋅的最大值为2.(I )求函数()f x 的单调递减区间;(II )在ABC ∆中,内角A B C 、、的对边分别为2,cos 2b aa b c A c-=、、,若()0f A m ->恒成立,求实数m 的取值范围.2018-2019学年第二学期中段测试高一级试题答案一、选择题题号 1 2 3 4 5 6 7 8 9 1011 12 答案 B ADDCACDBBDA二、 填空题13.14.E 为SA 中点/SE=EA 15. 502m 16. 3131(,)(,)5555--或三、解答题 17、【答案】(1)由12l l ⊥知()320a a +-=,解得32a =; ……………4分 (2)当12l l ∥时,有()()230320a a a a --=⎧⎪⎨--≠⎪⎩解得3a =, (6)12:3310,:30l x y l x y ++=++=,即3390x y ++=, ……………8分距离为229142333d -==+ ……………10分 18、【答案】 (1)证明:C 是底面圆周上异于A ,B 的一点,AB 是底面圆的直径,∴ AC⊥BC. ……………1分AA 1⊥平面ABC ,BC ⊂平面ABC ,∴AA 1⊥BC, ……………2分又AC∩AA 1=A , ……………3分∴BC⊥平面AA 1C . ……………4分又BC ⊂平面BA 1C , ……………5分∴平面AA 1C⊥平面BA 1C . ……………6分(2)解:在Rt△ABC 中,当AB 边上的高最大时,三角形ABC 面积最大,此时AC=BC. 此时几何体1A ABC -取得最大体积. ……………8分090,2ACB AB ∠==,则由AB 2=AC 2+BC 2, ……………10分 AA 1⊥平面ABC , AA 1是几何体1A ABC -的高所以体积max 11112332ABC V S AA ⎛=⋅=⨯⨯= ⎝23. ……12分19.解:(1)∵2A B =,∴sin sin 22sin cos A B B B ==, ………1分∴22222a c b a b ac+-=⋅, ………3分∵3,1b c ==,∴212a =,∴a = ………5分2)由(1)可得2221cos 23b c a A bc +-==-, ………7分∵0A π<<,∴sin A ………9分 ∴sin()sin cos +cos sin444A A A πππ+=13=-= ………12分 20、【答案】(1)解:由⎩⎨⎧==+-.0,012y y x 得顶点(1,0)A -. ………2分又AB 的斜率2011(1)AB k -==--.∵x 轴是A ∠的平分线,故AC 的斜率为1-,AC 所在直线的方程为(1)y x =-+① ………3分 已知BC 上的高所在直线的方程为210x y -+=,故BC 的斜率为2-, BC 所在的直线方程为22(1)y x -=--② ………4分解①,②得顶点C 的坐标为(5,6)-. ………6分 (2)()()22152645BC =-++= ………7分又直线BC 的方程是240x y +-=A 到直线的距离24655d --==………10分 所以ABC ∆的面积1164512225BC d =⋅=⨯⨯= ………12分 21、解:(1)在平面ABCD 内,因为90BAD ABC ∠=∠=,∴所以//BC AD . ………1分又BC ⊄平面,PAD AD ⊂平面PAD , ………3分∴//BC 平面PAD ………4分(2)取AD 的中点M ,连结,PM CM .12AB BC AD ==及//BC AD ,90ABC ∠= ∴ 四边形ABCM 为正方形,∴CM AD ⊥. ………5分因为侧面PAD 为等边三角形且垂直于底面ABCD , 平面PAD平面ABCD AD =,所以,PM AD PM ⊥⊥底面ABCD . ………6分 因为CM ⊂底面ABCD ,所以PM CM ⊥.… ………7分 设BC x =,则,2,3,2CM x CD x PM x PC PD x =====.取CD 的中点N ,连结PN ,则PN CD ⊥,所以142PN x =………8分 因为PCD ∆的面积为27,所以11422722x x ⨯⨯=, 解得2x =-(舍去),2x =.………10分 于是2,4,23AB BC AD PM ====.所以四棱锥P ABCD -的体积12(24)32V +=⨯⨯=………12分22、试题解析:(1)函数()•23sin cos f x a b x x λ==+()sin cos x x λ+()sin cos x x - ………1分()22sin cos sin cos x x x x λ=+-)cos2x x λ=-12cos22x x λ⎫=-⎪⎪⎝⎭2sin 26x πλ⎛⎫=- ⎪⎝⎭, ………2分 因为()f x 的最大值为2,所以解得1λ=. ………3分 则()2sin 26f x x π⎛⎫=- ⎪⎝⎭,由3222262k x k πππππ+≤-≤+, ………4分 可得:3522223k x k ππππ+≤≤+,536k x k ππππ+≤≤+, 所得函数()f x 的单调减区间为()536k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦,. ………6分 (2)由2222cos 22b a b c d A c bc-+-==,可得22222b ab b c a -=+-,即222b a c ab +-=. 解得1cos 2C =,即3C π=. ………8分 因为203A π<<,所以72666A πππ-<-<,1sin 2126A π⎛⎫-<-≤ ⎪⎝⎭, ………10分因为()2sin 206f A m A m π⎛⎫-=--> ⎪⎝⎭恒成立, 则2sin 26A m π⎛⎫-> ⎪⎝⎭恒成立,即1m ≤-. ………12分。
2019年上海市桃浦中学高考数学选择题专项训练(一模)
2019年上海市桃浦中学高考数学选择题专项训练(一模)抽选各地名校试卷,经典试题,有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。
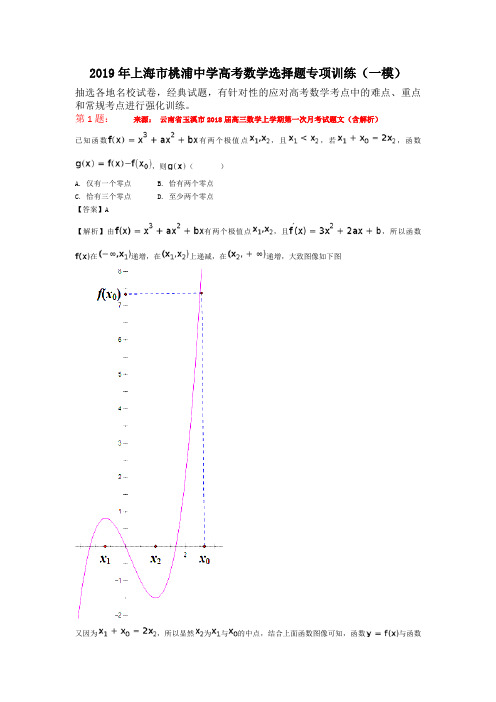
第 1 题:来源:云南省玉溪市2018届高三数学上学期第一次月考试题文(含解析)已知函数有两个极值点,且,若,函数,则()A. 仅有一个零点B. 恰有两个零点C. 恰有三个零点D. 至少两个零点【答案】A【解析】由有两个极值点,且,所以函数在递增,在上递减,在递增,大致图像如下图又因为,所以显然为与的中点,结合上面函数图像可知,函数与函数的交点只有一个,所以方程的根只有一个,即函数的零点只有一个,故选择A.方法点睛:根据三次函数,可以确定函数在定义域上先递增,再递减,再递增,于是为极大值点,为极小值点,再根据可知,为与的中点,于是结合函数图像,根据数形结合可知,函数仅有一个零点,考查转化能力的应用.第 2 题:来源:黑龙江省农垦北安管理局2018届高三数学9月月考试题曲线在点处的切线方程是( )A. B.C.D.【答案】B【解析】试题分析:因为,,所以,,即曲线在点处的切线的斜率为-ln2,即曲线在点处的切线方程是,选B。
第 3 题:来源:山东省潍坊市临朐县2017届高三数学上学期阶段性质量检测(12月月考)试题理如图所示,正方体ABCD﹣A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M,N,设BM=x,x∈[0,1],给出以下四个命题:①平面MENF⊥平面BDD′B′;②当且仅当x=时,四边形MENF的面积最小;③四边形MENF周长L=f(x),x∈[0,1]是单调函数;④四棱锥C′﹣MENF的体积V=h(x)为常函数;以上命题中假命题的序号为A.①④B.② C.③ D.③④【答案】C第 4 题:来源:贵州省思南中学2018_2019学年2018_2019学年高一数学下学期期中试题已知△ABC中,sinA∶sinB∶sinC=k∶(k+1)∶2k,则k的取值范围是( )A.(2,+∞) B.(-∞,0) C. D.【答案】D【解析】由正弦定理,得a=mk,b=m(k+1),c=2mk(m>0),∵即∴k>.第 5 题:来源:甘肃省静宁县第一中学2018_2019学年高二数学下学期期末考试试题理下列函数中,既是奇函数又在内单调递增的函数是()A. B. C.D.【答案】D第 6 题:来源:内蒙古包头市第四中学2017_2018学年高二数学下学期期中试题理设为正整数,,经计算得观察上述结果,可推测出一般结论( )A. B. C. D.以上都不对【答案】C第 7 题:来源:山东省济南市2018届高三数学上学期12月考试试题理已知是定义在上的函数,是的导函数,且满足,,则的解集为()A. B. C. D.【答案】B第 8 题:来源:广东省惠州市惠城区2018届高三数学9月月考试题理试卷及答案设复数满足(为虚数单位),则复数在复平面内对应的点位于().A. 第一象限B. 第二象限 C.第三象限 D.第四象限【答案】A第 9 题:来源:山西省应县2017_2018学年高二数学上学期第四次月考试题理试卷及答案在下列命题中:①若向量共线,则所在的直线平行;②若向量所在的直线是异面直线,则一定不共面;③若三个向量两两共面,则三个向量一定也共面;④已知三个向量,则空间任意一个向量总可以唯一表示为.其中正确命题的个数为()A. 0B. 1C.2 D. 3【答案】A第 10 题:来源:云南省玉溪市2017_2018学年高一数学上学期期中试题试卷及答案要得到函数的图像,只需将函数的图像()A.先关于轴对称,再向右平移个单位B.先关于轴对称,再向左平移个单位C.先关于轴对称,再向右平移个单位D.先关于轴对称,再向左平移个单位【答案】C第 11 题:来源: 2017_2018学年高中数学第三章直线与方程3.3.3点到直线的距离3.3.4两条平行直线间的距离学业分层测评试卷及答案新人教A版必修直线l过点A(3,4)且与点B(-3,2)的距离最远,那么l的方程为( )A.3x-y-13=0 B.3x-y+13=0C.3x+y-13=0 D.3x+y+13=0【答案】 C第 12 题:来源:山东省泰安第四中学2018_2019学年高二数学下学期2月月考试题.已知曲线的一条切线的斜率为,则切点的横坐标为A. B. C.D.或【答案】C【解析】设切点坐标为(xO2yO),xo>O因为f′(x)= ,所以f′(xo)= 由题意得,即xo2-x0-6=0,解得x0=3(负值舍去),所以切点的横坐标为3,故选C.第 13 题:来源:湖南省株洲市2019届高三数学上学期教学质量统一检测试题(一)理(含解析).欧拉公式(为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,根据欧拉公式可知,表示的复数在复平面中位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】B【解析】【分析】根据欧拉公式计算,再根据复数几何意义确定象限.【详解】因为,所以对应点,在第二象限,选B. 【点睛】本题考查复数除法以及复数几何意义,考查基本分析求解能力,属基本题.第 14 题:来源:江西省吉安市新干县2016_2017学年高二数学下学期第一次段考试题(3、4班)试卷及答案空间中四点可确定的平面有()A.1个B.3个 C.4个 D.1个或4个或无数个【答案】 D第 15 题:来源:天津市2018届高三数学上学期第一次月考试题理试卷及答案已知,那么是的【答案】B;第 16 题:来源:辽宁省沈阳市部分市级重点高中2016_2017学年高一数学下学期期中测试试题试卷及答案某奶茶店的日销售收入y(单位:百元)与当天平均气温x(单位:℃)之间的关系如下:x -2 -1 0 1 2y 5 2 2 1通过上面的五组数据得到了x与y之间的线性回归方程:=-x+2.8;但现在丢失了一个数据,该数据应为( )A. 3B. 4C. 5D. 2【答案】B【解析】设该数据是a,=0,故=-x+2.8=2.8,∴(5+a+2+2+1)=2.8,解得:a=4,本题选择B选项.第 17 题:来源:内蒙古呼和浩特铁路局包头职工子弟第五中学2016-2017学年高二数学上学期期末考试试题试卷及答案理不等式-x2+3x-2≥0的解集是()A.{x|x>2或x<1} B.{x|x≥2或x≤1} C.{x|1≤x≤2} D.{x|1<x<2}【答案】C第 18 题:来源:河北省邢台市2017_2018学年高二数学下学期第三次月考试题理(含解析)的展开式的中间项为()A. B. C. D.【答案】D【解析】分析:原式张开一共有5项,故只需求出第三项即可.第 19 题:来源:辽宁省六校协作体2018_2019学年高二数学上学期期中试题理在各项均不为零的等差数列中,若(n≥2,n∈N * ),则的值为( ) A.2013 B.2014C.4026D.4028【答案】D第 20 题:来源:河南省鹤壁市2016_2017学年高二数学下学期第一次月考试题试卷及答案理若函数在其定义域内的一个子区间内不是单调函数,则实数k 的取值范围()A. B. C. D.【答案】B第 21 题:来源:湖北省部分重点中学2018届高三数学起点考试试题试卷及答案理抛物线的焦点为,过焦点倾斜角为的直线与抛物线相交于两点两点,若,则抛物线的方程为A.B.C. D.【答案】C第 22 题:来源:甘肃省嘉峪关市酒钢三中2016-2017学年高一数学上学期期末考试试题试卷及答案如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为()A. B.C.D.【答案】A第 23 题:来源:江苏省马坝高级中学2018_2019学年高一数学下学期期中试题在△ABC中,角A、B、C的对应边分别为a,b,c,若,则角B的值为 .A.B.C.或D.或【答案】A第 24 题:来源: 2017_2018学年高中数学第四章圆与方程4.2.2圆与圆的位置关系4.2.3直线与圆的方程的应用学业分层测评试卷及答案已知两圆的圆心距是6,两圆的半径分别是方程x2-6x+8=0的两个根,则这两个圆的位置关系是( ) A.外离 B.外切C.相交 D.内切【答案】 B第 25 题:来源:甘肃省会宁县第一中学2018_2019学年高二数学上学期期中试题理已知集合,,则=()A.B.C.D.【答案】.B第 26 题:来源:高中数学第三章导数及其应用3.3导数的应用3.3.2利用导数研究函数的极值课后训练新人教B版选修1_120171101250在下面函数y=f(x)图象中既是函数的极大值点又是最大值点的是( )A.x1 B.x2 C.x3 D.x4【答案】C第 27 题:来源:北京市西城区2016_2017学年高一数学下学期期中试题试卷及答案对于任意实数a、b、c、d,下列结论:①若a>b,c≠0,则ac>bc;②若a>b,则ac2>bc2;③若ac2>bc2,则a>b;④若a>b,则<;正确的结论为()A. ①B. ②C. ③D. ④【答案】C第 28 题:来源:广东省第二师范学院番禺附属中学2018_2019学年高二数学下学期期中试题理过双曲线两焦点且与轴垂直的直线与双曲线的四个交点组成一个正方形,则该双曲线的离心率为A. B. C. D.2【答案】B第 29 题:来源:湖北省黄冈中学2016-2017学年高二数学上学期期末模拟测试试题试卷及答案(1)理设平面的一个法向量为,平面的一个法向量为,若,则A. B. C.D.【答案】D第 30 题:来源:海南省2016_2017学年高一数学下学期期中题文试卷及答案用简单随机抽样方法从有25名女生和35名男生的总体中,推选5名学生参加健美操活动,则某名女生被抽到的机率是()A. B. C. D.【答案】C【解析】某名女生被抽到的机率是第 31 题:来源:内蒙古包头市第一中学2016-2017学年高一数学上学期期中试题试卷及答案函数y=(在[0,1]上是减函数,则的取值范围()A. (1,2) B. (0,1) C.(0,2) D.【答案】 A第 32 题:来源:黑龙江省大庆市2017届高三第三次教学质量检测(三模)数学试题(理)含答案已知等比数列的公比,则的前项和()A.B. C.D.【答案】A第 33 题:来源:贵州省铜仁市第一中学2019届高三数学上学期第二次月考试题理(含解析)设、分别为圆和椭圆上的点,则两点间的最大距离是( )A. B. C. D.【答案】D【详解】设椭圆上点Q,则,因为圆的圆心为,半径为,所以椭圆上的点与圆心的距离为,所以P、Q两点间的最大距离是.第 34 题:来源: 2017年普通高等学校招生全国统一考试模拟数学(理)试题(八)含答案如图,在长方体中,分别是棱上的动点(点E 与不重合),且,过的动平面与棱相交,交点分别为,设,在长方体内随机选取一点,则该点取自几何体内的概率的最小值为,A. B. C. D.【答案】B第 35 题: 来源: 山东省新泰二中2018_2019学年高二数学上学期第三次阶段性测试试题 若,,且,则的值是( )A . 0B . 1C . -2D . 2 【答案】C第 36 题: 来源: 2017届北京市丰台区高三5月期末(二模)数学试题(理)含答案表示集合中所有元素的和,且,若能被3整除,则符合条件的非空集合的个数是 (A)10(B)11(C)12 (D )13【答案】B第 37 题: 来源: 黑龙江省伊春市2018届高三数学上学期第一次月考试题理试卷及答案 过点、,且圆心在上的圆的方程是( )A .B .C .D .【答案】C第 38 题: 来源: 湖北省武汉市2018届高三数学上学期期中试题理试卷及答案 下列函数为偶函数且在(0,+∞)上为增函数的是A .B .C.D.【答案】D第 39 题:来源:高中数学阶段通关训练(二)(含解析)新人教A版选修1_1已知F1,F2是椭圆+=1的两个焦点,P为椭圆上一点,则|PF1|·|PF2|有( )A.最大值16B.最小值16C.最大值4D.最小值4【答案】A.由椭圆的定义知a=4,|PF1|+|PF2|=2a=2×4=8.由基本不等式知|PF1|·|PF2|≤==16,当且仅当|PF1|=|PF2|=4时等号成立,所以|PF1|·|PF2|有最大值16.第 40 题:来源:浙江省温州市十校联合体高一(上)期末数学试卷(含答案解析)已知向量、不共线,若=+2,=﹣4﹣,=﹣5﹣3,则四边形ABCD是()A.梯形 B.平行四边形 C.矩形 D.菱形【答案】A【解答】解:根据题意,向量、不共线,若=+2,=﹣4﹣,=﹣5﹣3,则向量=++=﹣8﹣2,分析可得:=2,即直线AD与BC平行,而向量与不共线,即直线AB与CD不平行,故四边形ABCD是梯形;。
湖南师范大学附属中学2022-2023学年高二下学期期中数学试题

A. 1 < 1 a b ab
B. a b 0
C. a 1 b 1 ab
D. ln a2 ln b2
10.某计算机程序每运行一次都随机出现一个 n 位二进制数 A a1a2a3a4 L an ,其中 a
i 1,2,3,L ,n{0,1} ,若在 A 的各数位上出现 0 和 1 的概率均为 1 ,记 2
(3)现在有一个“单板滑雪”集训营,对“滑行、转弯、停止”这 3 个动作技巧进行集训,且
在集训中进行了多轮测试.规定:在一轮测试中,这 3 个动作中至少有 2 个动作达到“优
秀”,则该轮测试记为“优秀”.在集训测试中,小明同学 3 个动作中每个动作达到“优秀”
的概率均为 1 ,每个动作互不影响且每轮测试互不影响.如果小明同学在集训测试中要 3
四、解答题
17.已知关于 x 的函数 f (x) 2 4x 2x ,其中 R .
(1)当 1 时,求 f (x) 的值域; 2
(2)若当 x (, 2] 时,函数 f (x) 的图象总在直线 y= 2 的上方, 为整数,求 的值. 18.已知函数 f (x) ax2 (1 a)x a 2 .
(1)“自由式滑雪”参与人数超过 40 人的学校可以作为“基地学校”,现在从这 10 所学校中
随机选出 3 所,记 X 为可作为“基地学校”的学校个数,求 X 的分布列和数学期望;
(2)在这 10 所学校中随机选取 3 所来调查研究,求在抽到学校中恰有一所参与“自由式滑
雪”超过 40 人的条件下,抽到学校中恰有一所学校“单板滑雪”超过 30 人的概率;
m 量不变(即误差的概率分布不变),则单件产品的成本将会下降多少?
附:对于一组数据 (x1, y1), (x2, y2),, (xn, yn ), 其回归直线 yˆ ˆ x ˆ 的斜率和截距的最小
基于数据分析的高中走班制班级管理探索与实践

Course Education Research课程教育研究2021年第22期从2017年开始,全国开始高考综合改革,广东从2021年夏季高考开始实行“3+1+2”新高考模式。
走班制成为落实新高考政策、深化教育改革的措施之一。
我校(下文简称“广东二师附中”)的2021届学生是广东省实施新高考的第一届学生,在高一第二学期选科分班后实行了分层走班制,这意味着班主任在进行班级管理时要针对这一新情况做出相应的策略调整。
在这一背景下,我们以本校2021届物化1班(行政班)为对象,对基于数据分析的高中走班制班级管理策略进行了探索与实践。
一、基于数据分析的高中班级学业成绩跟踪按照广东省“3+1+2”新高考模式,依据学生自主选科的统计数据,我校采取了“定五走一”的分层走班制教学模式:每个行政班有2至3种选科组合,相同的5个科目固定在本班教室上课,不同的选修科目则分层走班上课。
年级根据班级选科组合、学生的选科成绩情况制定了化学、生物、地理、政治这四科的走班名单。
我校2021届物化1班学生的选科走班情况如附1所示,该班学生语文、数学、外语、物理、化学五个学科在本班教室上课,生物、地理则实行分层走班。
附1广东二师附中2021届物化1班分层走班情况这一分层走班教学模式给班级管理带来了一定的挑战:小到班级作业登记、学科小组任务、班级值日;大到学生的考试成绩分析、综合素质评价、班主任与科任老师的协同管理……班主任需要思考如何操作才能为每一位学生的学业进步、成长发展提供有利条件,促进学生进一步提高成绩、养成良好品德。
为了更好地跟踪学生的学业成绩,我们从分班之初即整理本班学生高一入学以来的考试成绩数据,只要在Excel文档中输入学生的姓名,便可查询到该生历次考试各科目的分数、排名、进退步情况。
每次考试后班主任、科任老师、学科导师可根据最新的成绩数据约谈学生,从而做到充分挖掘学生的潜能,增强学生的自信心、进取心,提升教师教育工作的针对性和教育效果。
2018-2019学年山西省高二下学期期中数学(文)试题(解析版)

证明:(1)记 为等差数列 前 项中奇数项的和,
为等差数列 前 项中偶数项的和,
由等差数列的前 项和公式可得 ,
,
.
命题成立.
(2)解:类比猜想可得:各项均为正数的等比数列 的前 项中奇数项的积与偶数项的积的比为 .
证明:记各项均为正数的等比数列 的前 项中奇数项的积为 ,
偶数项的积为 ,
,即 ,
(1)请评出第三次数学对抗赛的优胜小组,并求出这40位学生完成第三次数学解题对抗赛所需时间的中位数 ;
(2)对于(1)中的中位数 ,根据这40位学生完成第三次数学对抗赛所需时间超过 和不超过 的人数,完成下面的列联表,并判断能否有 的把握认为甲、乙两个小组在此次的数学对抗赛中的成绩有差异?
超过
不超过
【解析】将 化简即可得出答案
【详解】
,
所对应的向量坐标为 .
故选:B
【点睛】
本题考查的是复数的计算及其几何意义,较简单.
4.下列说法正确的是()
A.流程图可以直观、明确地表示动态过程从开始到结束的全部步骤
B.结构图通常用来描述一个过程性的活动
C.流程图的基本要素之间一般为概念上的从属关系或逻辑上的先后关系
其中叙述正确的个数为()
A.1B.2C.3D.4
【答案】B
【解析】由独立性检验常用等髙条形图表示列联表数据的频率特征知①正确,由独立性检验依据的是小概率原理知②正确,由独立性检验的结果是不完全正确的知③不正确,④中应是 越大, 与 有关系的把握程度就越大.
【详解】
因为独立性检验常用等髙条形图表示列联表数据的频率特征,故①正确;
【详解】
推理是人们思维活动的过程,是根据一个或几个已知的判断来确定
2021人教版数学同步a版必修5模块练习题--2.3 等差数列的前n项和

2.3 等差数列的前n项和第1课时等差数列的前n项和公式基础过关练题组一等差数列前n项和的有关计算1.在等差数列{a n}中,已知a1=10,d=2,S n=580,则n=( )A.10B.15C.20D.302.已知一个等差数列共n项,且其前四项之和为21,末四项之和为67,前n项之和为286,则项数n为( )A.24B.26C.25D.283.设{a n}为等差数列,公差d=-2,S n为其前n项和.若S10=S11,则a1=( )A.18B.20C.22D.244.(2019福建福州长乐高中、城关中学、文笔中学高二期末)等差数列{a n}的前n 项和为S n,且S5=6,a2=1,则公差d等于( )A.15B.35C.65D.25.设等差数列{a n}的前n项和为S n,若a6=S3=12,则{a n}的通项公式a n= . 题组二数列的前n项和S n与a n的关系6.已知数列{a n}的前n项和S n=n2,则a n=( )A.nB.n2C.2n+1D.2n-17.在各项均大于零的数列{a n}中,首项a1=1,前n项和S n满足S n√S n-1-S n-1√S n=2√S n S n-1(n∈N*且n≥2),则a81=( )A.638B.639C.640D.6418.已知数列{a n}的前n项和S n=n2+n+1,则a6+a7+…+a10的值为.9.(1)已知数列{a n}的前n项和为S n=2n2+n+3,求数列{a n}的通项公式;(2)设各项均为正数的数列{a n}的前n项和S n满足S n=14(a n+1)2,求a n.题组三裂项相消法求和10.已知数列{a n}的通项公式为a n=1n(n+1),则其前10项和为( )A.910B.911C.1112D.101111.已知数列{a n}的通项公式为a n=√n+1+√n,则其前n项和S n= .12.已知数列{a n}的通项公式为a n=lg n+1n,则其前n项和S n= .13.已知等差数列{a n}满足a3=7,a5+a7=26,{a n}的前n项和为S n.(1)求a n及S n;(2)令b n=1a n2-1(n∈N*),求数列{b n}的前n项和T n.能力提升练一、选择题1.(2020吉林省实验中学高一期末,★★☆)记等差数列{a n}的前n项和为S n.若a5=3,S13=91,则a1+a11=( )A.7B.8C.9D.102.(2020湖北荆州中学、宜昌一中高二期末联考,★★☆)已知数列{a n}满足2a n=a n-1+a n+1,S n是其前n项和,若a2,a2 019是函数f(x)=x2-6x+5的两个零点,则S2 020的值为( )A.6B.12C.2 020D.6 0603.(2018云南玉溪第一中学高三月考,★★☆)已知数列{a n}的首项a1=1,对于任意m,n∈N*,有a n+m=a n+3m,则数列{a n}前5项的和S5=( )A.121B.25C.31D.354.(2020山东日照高二月考,★★☆)已知数列{a n}的前n项和S n=n2-4n+2,则|a1|+|a2|+…+|a10|等于( )A.66B.65C.61D.565.(★★☆)设公差不为零的等差数列{a n}的前n项和为S n,若a4=2(a2+a3),则S7S4=( )A.74B.145C.7D.146.(2019广东佛山一中期末,★★☆)某企业为节能减排,用9万元购进一台新设备用于生产.第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加2万元,该设备每年生产的收入均为11万元.设该设备使用了n(n∈N*)年后,盈利总额达到最大值(盈利额等于收入减去成本),则n等于( )A.4B.5C.6D.77.(★★☆)已知数列{a n}满足a n+1+(-1)n a n=2n-1,S n为其前n项和,则S60=( )A.3 690B.1 830C.1 845D.3 660二、填空题8.(2019江苏南京高三上学情调研,★★☆)记等差数列{a n}的前n项和为S n,若a m=10,S2m-1=110,则m的值为.9.(2020广东深圳宝安高二期末,★★☆)若等差数列{a n}满足a5=11,a12=-3,且{a n}的前n项和S n的最大值为M,则lg M= .10.(2020吉林松原扶余一中高一期末,★★☆)已知单调递减数列{a n}的前n项和为S n,a1≠0,且4S n=2a n-a n2(n∈N*),则a5= .三、解答题11.(2020湖北荆门高二期末,★★☆)已知数列{a n}的前n项和为S n,且(a n+1-a n)2+2=3(a n+1-a n),a50=1,求S100的最小值.12.(2020安徽合肥一中、合肥六中高一期末,★★☆)已知等差数列{a n}的前n项和为S n,且S2=8,a3+a8=2a5+2.(1)求a n ;(2)设数列{1S n}的前n 项和为T n ,求证:T n <34.13.(★★☆)已知函数f(x)=14x +m(m>0),当x 1,x 2∈R 且x 1+x 2=1时,总有f(x 1)+f(x 2)=12.(1)求m 的值;(2)设数列{a n }满足a n =f(0)+f (1n )+f (2n )+…+f (n -1n)+f(1),求数列{a n }的前n 项和S n .14.(2019山东济宁一中月考,★★☆)数列{a n }中,a 1=1,当n≥2时,其前n 项和S n满足S n 2=a n ·(S n -12).(1)求S n的表达式;(2)设b n=S n,求数列{b n}的前n项和T n.2n+115.(2018黑龙江哈尔滨第六中学高三下考前押题卷,★★★)数列{a n}中,S n为其前n项和,且2S n=na n+n(n∈N*).(1)求证:{a n}是等差数列;(2)若a2=2,b n=n+2,T n是{b n}的前n项和,求T n.a n a n+12n第2课时等差数列前n项和的性质及应用基础过关练题组一 等差数列前n 项和的性质1.已知等差数列{a n }中,S n 是其前n 项和,a 1=-11,S 1010-S 88=2,则S 11=( )A.-11 B .11 C.10 D.-102.一个等差数列共有10项,其奇数项之和是12.5,偶数项之和是15,则它的首项与公差分别是( ) A.12,12B.12,1 C.1,12D.12,23.设S n 是等差数列{a n }的前n 项和,若a 7a 5=913,则S 13S 9= .4.已知等差数列{a n }的前10项和为30,前30项的和为10,则前40项的和为 .题组二 等差数列前n 项和的函数属性5.已知数列{a n }中,a 1=10,a n+1=a n -12,则它的前n 项和S n 的最大值为 . 6.在等差数列{a n }中,a 1>0,公差d<0,a 5=3a 7,且其前n 项和为S n ,则S n 取最大值时,n= .7.已知等差数列{a n }的前n 项和为S n ,公差为d. (1)若S 2 016>0,S 2 017<0,且S k 最大,则整数k= ; (2)若a 1=25,S 9=S 17<0,且S k 最大,则整数k= . 8.已知{a n }是等差数列,且a 2=1,a 5=-5. (1)求{a n }的通项公式a n ;(2)求{a n }的前n 项和S n 的最大值.题组三等差数列的综合问题9.数列{a n}的首项为3,{b n}为等差数列,且b n=a n+1-a n(n∈N*),若b3=-2,b10=12,则a8=( )A.0B.3C.8D.1110.若a,b,c成等差数列,则二次函数y=ax2-2bx+c的图象与x轴的交点个数为( )A.0B.1C.2D.1或211.《莱因德纸草书》是世界上最古老的数学著作之一.书中有一道这样的题:把100个面包分给5个人,使每个人的所得成等差数列,且使较大的三份之和的17是较小的两份之和,则最小一份的量为( )A.52B.54C.53D.5612.(2019湖南长沙一中高二期末)已知等差数列{a n}的各项均为正数,其前n项和为S n,且满足a1+a5=27a32,S7=63.(1)求数列{a n}的通项公式;(2)若数列{b n}满足b1=a1,且b n+1-b n=a n+1,求数列{1b n}的前n项和T n.能力提升练一、选择题1.(2020浙江高三期末,★★☆)已知公差不为零的等差数列{a n}满足a32=a1a4,S n为数列{a n}的前n项和,则S3S1的值为( )A.94B.-94C.32D.-322.(2019山东招远一中高二月考,★★☆)已知等差数列{a n}的前n项和为S n,若S4=1,S8=4,则a17+a18+a19+a20的值为( )A.9B.12C.16D.173.(2020浙江丽水高一期末,★★★)设等差数列{a n}的前n项和为S n,公差为d,已知a1≠0,S5=S17,则( )A.da11>0B.da12>0C.a1a12>0D.a1a11<04.(2020广东第二师范学院番禺附属中学高二期末,★★★)若等差数列{a n}的前n 项和S n有最大值,且a11a10<-1,则S n取正值时,项数n的最大值为( )A.15B.17C.19D.215.(2020江苏徐州高二期末,★★★)已知等差数列{a n}的前n项和为S n,若a1>0,公差d≠0,则下列结论不正确的是( )A.若S5=S9,则S14=0B.若S5=S9,则S7最大C.若S6>S7,则S7>S8D.若S6>S7,则S5>S6二、填空题6.(2019河北衡水中学高考猜题卷,★★☆)设等差数列{a n}的前n项和为S n,已知S13>0,S14<0,若a k·a k+1<0,则k= .7.(2018湖北黄石二中高二期中,★★☆)设等差数列{a n}的前n项和为S n,且S m= -2,S m+1=0,S m+2=3,则m= .8.(2019河北沧州一中高二期中,★★★)在等差数列{a n}中,前m(m为奇数)项和为135,其中偶数项之和为63,且a m-a1=14,则a100的值为.9.(★★★)无穷等差数列{a n}的前n项和为S n,若首项a1=32,公差d=1,则满足S k2=(S k)2的正整数k的值为.三、解答题10.(2020湖南怀化高二期末,★★☆)已知数列{a n}满足1a1+1a2+1a3+…+1a n=n2(n∈N*),且b n=a n a n+1.(1)求{a n}和{b n}的通项公式;(2)若S n为数列{b n}的前n项和,对任意的正整数n,不等式S n>λ-12恒成立,求实数λ的取值范围.11.(★★☆)已知数列{a n}为等差数列,a1=1,a n>0,其前n项和为S n,且数列{√S n}也为等差数列.(1)求{a n}的通项公式;(2)设b n =a n+1S n ·S n+1,求数列{b n }的前n 项和.答案全解全析第1课时 等差数列的前n 项和公式基础过关练1.C 因为S n =na 1+12n(n-1)d=10n+12n·(n -1)×2=n 2+9n,所以n 2+9n=580,解得n=20或n=-29(舍).2.B 设该等差数列为{a n },由题意,得a 1+a 2+a 3+a 4=21,a n +a n-1+a n-2+a n-3=67. 又∵a 1+a n =a 2+a n-1=a 3+a n-2=a 4+a n-3, ∴4(a 1+a n )=21+67=88,∴a 1+a n =22. ∴S n =n (a 1+a n )2=11n=286,∴n=26.3.B 由S 10=S 11,得a 11=S 11-S 10=0,所以a 1=a 11+(1-11)d=0+(-10)×(-2)=20.4.A ∵等差数列{a n }的前n 项和为S n ,且S 5=6,a 2=1, ∴{S 5=5a 1+5×42d =6,a 2=a 1+d =1,解得{a 1=45,d =15.故选A. 5.答案 2n解析 设等差数列{a n }的首项为a 1,公差为d,由已知得{a 1+5d =12,3a 1+3d =12,解得{a 1=2,d =2,故a n =2n. 6.D 当n=1时,a 1=S 1=1;当n≥2时,a n =S n -S n-1=n 2-(n-1)2=2n-1. ∵当n=1时,此等式也成立,∴a n =2n-1(n∈N *),故选D.7.C 由已知S n √S n -1-S n-1√S n =2·√S n S n -1可得,√S n -√S n -1=2(n≥2),又a 1=1,∴√S 1=1,∴{√S n }是以1为首项,2为公差的等差数列,故√S n =2n-1,∴S n =(2n-1)2,∴a 81=S 81-S 80=1612-1592=640. 8.答案 80解析 由题意得,a 6+a 7+…+a 10=S 10-S 5=111-31=80.9.解析 (1)∵S n =2n 2+n+3,∴当n=1时,a 1=S 1=2×12+1+3=6;当n≥2时,a n =S n - S n-1=2n 2+n+3-[2(n-1)2+(n-1)+3]=4n-1.当n=1时,a 1不符合上式, ∴a n ={6(n =1),4n -1(n ≥2).(2)当n=1时,a 1=S 1=14(a 1+1)2,解得a 1=1;当n≥2时,a n =S n -S n-1=14(a n +1)2-14·(a n-1+1)2,即4a n =a n 2+2a n +1-(a n -12+2a n-1+1),∴a n 2-a n -12-2(a n +a n-1)=0,∴(a n +a n-1)(a n -a n-1-2)=0.∵数列{a n }的各项均为正数,∴a n +a n-1>0,∴a n -a n-1-2=0,即a n -a n-1=2, ∴数列{a n }是公差为2,首项为1的等差数列, ∴a n =1+2(n-1)=2n-1.10.D 设数列{a n }的前n 项和为S n .由a n =1n (n+1)=1n -1n+1得,S n =(1-12)+(12-13)+…+1n -1n+1=1-1n+1,所以S 10=1-111=1011.11.答案 √n +1-1 解析 由已知得, a n =√n+1+√n=√n +1-√n ,所以S n =a 1+a 2+…+a n =(√2-1)+(√3-√2)+…+(√n +1-√n )=√n +1-1. 12.答案 lg(n+1)解析 由已知得a n =lg(n+1)-lg n,所以S n =a 1+a 2+…+a n =(lg 2-lg 1)+(lg 3-lg 2)+…+[lg(n+1)-lg n]=lg(n+1). 13.解析 (1)设等差数列{a n }的首项为a 1,公差为d. 因为a 3=7,a 5+a 7=26, 所以{a 1+2d =7,2a 1+10d =26,解得{a 1=3,d =2.所以a n =3+2(n-1)=2n+1,S n =3n+n (n -1)2×2=n 2+2n.(2)由(1)知a n =2n+1, 所以b n =1a n 2-1=1(2n+1)2-1=14·1n (n+1)=14·(1n-1n+1),所以T n =14(1-12+12-13+ (1)-1n +1)=14(1-1n+1)=n4(n+1),即数列{b n }的前n 项和T n =n4(n+1). 能力提升练一、选择题1.D 由S 13=13a 7=91,可得a 7=7,所以a 5+a 7=10,从而a 1+a 11=a 5+a 7=10.2.D 由题意,得数列{a n }为等差数列.a 2,a 2 019是函数f(x)=x 2-6x+5的两个零点,等价于a 2,a 2 019是方程x 2-6x+5=0的两个根,∴a 2+a 2 019=6, ∴S 2 020=(a 1+a 2 020)·2 0202=(a 2+a 2 019)·2 0202=6 060,故选D.3.D 令m=1,有a n+1=a n +3,即a n+1-a n =3,又已知a 1=1,∴{a n }是首项为1,公差为3的等差数列,∴a n =1+3(n-1)=3n-2, ∴S 5=5(a 1+a 5)2=5a 3=5×(3×3-2)=35.4.A 当n≥2,n∈N *时,a n =S n -S n-1=n 2-4n+2-[(n-1)2-4(n-1)+2] =n 2-4n+2-(n 2-6n+7) =n 2-4n+2-n 2+6n-7=2n-5, 当n=1时,a 1=S 1=-1,不满足上式, ∴a n ={-1,n =1,2n -5,n ≥2,n ∈N *.∴|a 1|+|a 2|+…+|a 10|=1+1+1+3+5+…+15=2+(1+15)×82=2+64=66.5.C 解法一:设等差数列{a n }的首项为a 1,公差为d.根据等差数列的性质及a 4=2(a 2+a 3),得a 1+3d=2(a 1+d+a 1+2d),化简得a 1=-d,所以S 7S 4=7a 1+7×62d 4a 1+4×32d =14d 2d=7.解法二:由已知及等差数列的性质,得a 4=2(a 2+a 3)=2(a 1+a 4),又S 7S 4=7(a 1+a 7)24(a 1+a 4)2=7a 42(a 1+a 4),所以S7S 4=7.6.B 设该设备第n(n∈N *)年的运营费用为a n 万元,则数列{a n }是以2为首项,2为公差的等差数列,则a n =2n,则该设备到第n(n∈N *)年的运营费用总和为a 1+a 2+…+a n =2+4+…+2n=n (2+2n )2=(n 2+n)万元.设第n(n∈N *)年的盈利总额为S n 万元,则S n =11n-(n 2+n)-9=-n 2+10n-9=-(n-5)2+16,因此,当S n 取最大值时,n=5,故选B. 7.B 由题意得,当n 为奇数时,a n+1-a n =2n-1,n+1为偶数,所以a n+2+a n+1=2n+1,两式相减得a n+2+a n =2;当n 为偶数时,a n+1+a n =2n-1,n+1为奇数,所以a n+2-a n+1=2n+1,两式相加得a n+2+a n =4n. 故S 60=a 1+a 3+a 5+…+a 59+(a 2+a 4+a 6+…+a 60)=2×15+(4×2+4×6+…+4×58)=30+4×450=1 830.故选B. 二、填空题 8.答案 6解析 ∵{a n }是等差数列,且a m =10, ∴S 2m-1=a 2m -1+a 12×(2m -1)=(2m-1)a m =10(2m-1)=110,解得m=6.9.答案 2解析 设等差数列{a n }的首项为a 1,公差为d.∵a 5=11,a 12=-3,∴{a 1+4d =11,a 1+11d =-3,解得{d =-2,a 1=19.∴a n =19-2(n-1)=21-2n.令a n ≥0,解得n≤212.因此当n=10时,{a n }的前n 项和S n 取得最大值,且最大值M=10×19+10×92×(-2)=190-90=100,∴lg M=2. 10.答案 -10解析 当n=1时,4S 1=2a 1-a 12,∴a 1=-2. 当n≥2时,4S n =2a n -a n 2,① 4S n-1=2a n-1-a n -12,②①-②,得4a n =2a n -2a n-1-(a n 2-a n -12),化简,得a n -a n-1=-2或a n +a n-1=0,∵数列{a n }是递减数列,且a 1=-2,∴a n +a n-1=0舍去. ∴数列{a n }是首项为-2,公差为-2的等差数列,故a 5=-2+(5-1)×(-2)=-10. 三、解答题11.解析 由题意,得a n+1-a n =2或a n+1-a n =1.由a 50=1知,当n≤49时,a n ≤0;当n≥51时,a n >0.故当数列{a n }的前50项的公差为2,后50项的公差为1时,数列的前100项和最小. 所以(S 100)min =50×1+50×492×(-2)+50×2+50×492=-1 075.12.解析 (1)设数列{a n }的首项为a 1,公差为d,由题意得{2a 1+d =8,2a 1+9d =2a 1+8d +2,解得{a 1=3,d =2.所以a n =2n+1. (2)证明:由(1)知a n =2n+1,所以S n =n2(3+2n+1)=n 2+2n.所以1S n=1n (n+2)=12(1n -1n+2).所以T n =12[(1-13)+(12-14)+(13-15)+… +(1n -1-1n +1)+(1n-1n +2)]=12(1+12-1n+1-1n+2)<34. 13.解析 (1)令x 1=x 2=12,得f (12)=14=12+m,解得m=2.(2)由a n =f(0)+f (1n )+f (2n )+…+f (n -1n )+f(1),得a n =f(1)+f (n -1n )+…+f (1n )+f(0),两式相加,得2a n =[f(0)+f(1)]+[f (1n )+f (n -1n )]+…+[f(1)+f(0)]=12(n+1),即a n =14(n+1),显然数列{a n }是等差数列, 当n=1时,a 1=12,所以S n =n [12+14(n+1)]2=18n 2+38n.14.解析 (1)由a n =S n -S n-1(n≥2)得,S n 2=(S n -S n-1)(S n -12)=S n 2-12S n -S n-1S n +12S n-1,即S n-1-S n =2S n S n-1(n≥2), ∴1S n -1S n -1=2(n≥2),又1S 1=1a 1=1,∴{1S n}是以1为首项,2为公差的等差数列,∴1S n=2n-1,即S n =12n -1(n∈N *).(2)由(1)得b n =1(2n -1)(2n+1)=12(12n -1-12n+1), ∴T n =b 1+b 2+b 3+…+b n=12(1-13)+(13-15)+(15-17)+…+(12n -1-12n+1) =12(1-12n+1) =n 2n+1.15.解析 (1)证明:由2S n =na n +n(n∈N *)①,得2S n-1=(n-1)a n-1+(n-1)(n≥2)②, ①-②得,2a n =na n +n-(n-1)a n-1-(n-1), ∴(n -2)a n =(n-1)a n-1-1(n≥2)③, ∴(n -1)a n+1=na n -1(n∈N *)④,④-③得,(n-1)a n+1-(n-2)a n =na n -(n-1)a n-1,∴2(n -1)a n =(n-1)a n-1+(n-1)a n+1(n≥2),∴2a n =a n-1+a n+1, ∴{a n }是等差数列.(2)设等差数列{a n }的公差为d. 由题意得2S 1=a 1+1,∴a 1=1,又∵a 2=2,且由(1)知{a n }是等差数列, ∴d=a 2-a 1=1,∴a n =n, ∴b n =n+2n (n+1)·2n=12n -1·n -12n (n+1),∴T n =(1-14)+(14-112)+…+[12n -1·n -12n (n+1)]=1-12n (n+1).第2课时 等差数列前n 项和的性质及应用基础过关练1.A 因为{a n }为等差数列,所以{Sn n }也为等差数列,且首项S11=a 1=-11.设{Sn n }的公差为d,则S1010-S88=2d=2,所以d=1,所以S 1111=-11+10d=-1,所以S 11=-11.2.A 设等差数列为{a n },首项为a 1,公差为d,由S 偶-S 奇=5d=15-12.5=2.5,得d=0.5.再由S 10=10a 1+10×92×12=15+12.5,得a 1=0.5.3.答案 1解析 由等差数列前n 项和的性质得S13S 9=13a 79a 5=139×913=1.4.答案 -40解析 设等差数列{a n }的前n 项和为S n .解法一:由题易知数列S 10,S 20-S 10,S 30-S 20,S 40-S 30成等差数列.设其公差为d, 则前3项和为3S 10+3×22d=S 30=10,即S 10+d=103,又S 10=30,所以d=-803,所以S 40-S 30=S 10+3d=30+3×(-803)=-50,所以S 40=-50+S 30=-40.解法二:因为数列{a n }是等差数列,所以数列{S n n }也是等差数列,所以点(n ,S nn )在一条直线上,即(10,S 1010),(30,S 3030),(40,S4040)三点共线,于是S 3030-S 101030-10=S 4040-S 101040-10,将S 10=30,S 30=10代入,解得S 40=-40.5.答案 105解析 由题意得a n+1-a n =-12,∴数列{a n }是公差为-12的等差数列,又a 1=10,∴a n =-n 2+212(n∈N *).∵a 1=10>0,-12<0,∴设从第n 项起为负数,则-n 2+212<0(n∈N *), ∴n>21,∴前21项的和最大,最大值为S 21=105. 6.答案 7或8解析 由a 5=3a 7,得a 1+4d=3(a 1+6d),即a 1=-7d,所以a n =a 1+(n-1)d=-7d+(n-1)d=(n-8)d. 又因为a 1>0,d<0,所以当{a n ≥0,a n+1≤0时,S n 取得最大值,即{(n -8)d ≥0,(n -7)d ≤0,解得7≤n≤8.所以当S n 取最大值时,n=7或8. 7.答案 (1)1 008 (2)13解析 (1)由等差数列的性质可知,S 2 017=2 017a 1 009<0,所以a 1 009<0, 又S 2 016=2 016(a 1 008+a 1 009)2>0,即a 1 008+a 1 009>0,所以结合a 1 009<0可得a 1 008>0,因此S 1 008最大,故k=1 008. (2)解法一:由{a 1=25,S 9=S 17,可得{a 1=25,9a 1+9×4d =17a 1+17×8d ,解得d=-2,则S n =25n+n (n -1)2×(-2)=-(n-13)2+169,显然S 13最大,故k=13.解法二:同解法一得d=-2, 故a n =25+(-2)×(n -1)=27-2n,显然对于n∈N *,当n≤13时,a n >0;当n≥14时,a n <0.故S 13最大,k=13. 8.解析 (1)设{a n }的公差为d,则由a 2=1, a 5=-5,得d=a 5-a 25-2=-5-13=-2,∴a 1=a 2-d=3,∴a n =-2n+5. (2)由(1)得,S n =3n+n (n -1)2×(-2)=-n 2+4n=-(n-2)2+4,∴当n=2时,S n 取得最大值4.9.B 设数列{b n }的首项为b 1,公差为d,则由b 3=-2,b 10=12,得{b 1+2d =-2,b 1+9d =12,解得{b 1=-6,d =2,∴b n =-6+(n-1)×2=2n -8,∴a n+1-a n =2n-8,又a 1=3, ∴a 2-a 1=2×1-8, a 3-a 2=2×2-8,a 4-a 3=2×3-8, …… a 8-a 7=2×7-8,以上各式相加得,a 8-a 1=2×(1+2+3+…+7)-8×7=0,∴a 8=a 1=3.10.D 由a,b,c 成等差数列得2b=a+c,Δ=(-2b)2-4ac=(a+c)2-4ac=(a-c)2, 当a=c 时,Δ=0,有一个交点; 当a≠c 时,Δ>0,有两个交点.11.C 由题意可得中间的那份为20个面包.设最小的一份为a 1,公差为d,由题意可得[20+(a 1+3d)+(a 1+4d)]×17=a 1+(a 1+d),解得a 1=53,故选C.12.解析 (1)解法一:设等差数列{a n }的公差为d,由题意,得a n >0,且{a 1+a 1+4d =27(a 1+2d )2,7a 1+21d =63,∴{a 1=3,d =2.∴a n =2n+1.解法二:∵{a n }是等差数列,且a 1+a 5=27a 32,∴2a 3=27a 32.又a n >0,∴a 3=7. ∵S 7=7(a 1+a 7)2=7a 4=63,∴a 4=9,∴d=a 4-a 1=2, ∴a n =a 3+(n-3)d=2n+1. (2)∵b n+1-b n =a n+1,且a n =2n+1, ∴b n+1-b n =2n+3. ∴当n≥2时,b n =(b n -b n-1)+(b n-1-b n-2)+…+(b 2-b 1)+b 1=(2n+1)+(2n-1)+…+5+3 =n(n+2),当n=1时,b 1=3满足上式, ∴b n =n(n+2). ∴1b n =1n (n+2)=12(1n -1n+2), ∴T n =1b 1+1b 2+…+1b n -1+1b n=12[(1-13)+(12-14)+(13-15)+ …+(1n -1-1n +1)+(1n-1n +2)]=12(1+12-1n+1-1n+2) =34-2n+32(n+1)(n+2).能力提升练一、选择题1.A 设数列{a n }的公差为d(d≠0),由a 32=a 1a 4得(a 1+2d)2=a 1(a 1+3d),整理,得a 1d+4d 2=0,因为d≠0,所以a 1=-4d,所以S 3=3a 1+3d=-9d,所以S 3S 1=-9d -4d =94,故选A.2.A 由等差数列前n 项和的性质得, S 4,S 8-S 4,S 12-S 8,…成等差数列. 由S 4=1,S 8=4可得,其公差为2, 所以S 36=S 4+(S 8-S 4)+…+(S 36-S 32)=9×1+9×82×2=81.又因为S 36=36×(a 1+a 36)2,所以a 1+a 36=8118=92,所以a 17+a 18+a 19+a 20=2(a 17+a 20)=2(a 1+a 36)=9. 3.B 由a 1≠0,S 5=S 17,得5a 1+5×42d=17a 1+17×162d,化简,得2a 1+21d=0,即a 11+a 12=0.因为a 1≠0,所以d≠0,所以a 11,a 12符号相反.若d>0,则a 11<0,a 12>0,a 1<0,所以da 11<0,da 12>0,a 1a 12<0,a 1a 11>0;若d<0,则a 11>0,a 12<0,a 1>0,所以da 11<0,da 12>0,a 1a 12<0,a 1a 11>0.综上,选B. 4.C 设等差数列{a n }的首项为a 1,公差为d.由S n 有最大值,得d<0.由a11a 10<-1,得a 11<0<a 10,且a 11+a 10<0.由a 10>0,得2a 10=a 1+a 19>0,所以S 19>0.由a 10+a 11<0,得a 1+a 20=a 10+a 11<0,所以S 20<0.所以S n 取正值时,n 的最大值为19. 5.D 由S 5=S 9得a 6+a 7+a 8+a 9=0,即a 1+a 14=0,所以S 14=14×(a 1+a 14)2=0,故A 中结论正确.由S 5=S 9得5a 1+10d=9a 1+36d,即d=-213a 1.因为a 1>0,所以d<0. 再由S n 对应的二次函数的图象知,对称轴为n=5+92=7,所以S 7最大,故B 中结论正确. 由S 6>S 7得a 7<0.又a 1>0,所以d<0,所以a 8<0,所以S 7>S 8.但a 6的符号不确定,所以S 5与S 6的大小无法比较,故C 中结论正确,D 中结论错误.故选D. 二、填空题 6.答案 7解析 因为S 13>0,S 14<0,所以{13(a 1+a 13)2>0,14(a 1+a 14)2<0,即{a 1+a 13>0,a 1+a 14<0, ∴{a 1+a 13=2a 7>0,a 1+a 14=a 7+a 8<0,∴{a 7>0,a 8<0, 又a k ·a k+1<0,∴k=7. 7.答案 4解析 因为S n 是等差数列{a n }的前n 项和,所以数列{Sn n}是等差数列,所以S m m+S m+2m+2=2S m+1m+1,即-2m +3m+2=0,解得m=4.8.答案 101解析 ∵在前m 项中偶数项之和为S 偶=63,∴奇数项之和为S 奇=135-63=72.设等差数列{a n }的公差为d,则S 奇-S 偶=2a 1+(m -1)d2=72-63=9.∵a m =a 1+d(m-1),∴a 1+a m2=9.由题意得m (a 1+a m )2=135,∴m=15,又∵a m -a 1=14, ∴a 1=2,d=14m -1=1,∴a 100=a 1+99d=101.9.答案 4解析 解法一:由题意,得S n =32n+n (n -1)2×1=12n 2+n,则S k 2=12k 4+k 2,(S k )2=(12k 2+k)2,∴12k 4+k 2=(12k 2+k)2,即14k 4-k 3=0,解得k=0或k=4.∵k∈N *,∴k=4.解法二:∵数列{a n }为等差数列,∴不妨设S n =An 2+Bn,其中A=d2,B=a 1-d2,则S k 2=A(k 2)2+Bk 2,S k =Ak 2+Bk.由S k 2=(S k )2,得k 2(Ak 2+B)=k 2(Ak+B)2.∵k∈N *,∴Ak 2+B=(Ak+B)2,即(A 2-A)·k 2+2ABk+B 2-B=0,又A=d 2=12,B=a 1-d2=1,∴14k 2-k=0,解得k=0(舍去)或k=4.三、解答题10.解析 (1)∵1a 1+1a 2+1a 3+…+1a n=n 2(n∈N *)①,∴当n≥2时,1a 1+1a 2+1a 3+…+1a n -1=(n-1)2②.①-②,得1a n=2n-1(n≥2),经检验,1a 1=1满足上式,∴1a n=2n-1(n∈N *),∴a n =12n -1.∴b n =1(2n -1)(2n+1)=12(12n -1-12n+1).(2)由(1)及已知得S n =12·(1-13+13-15+…+12n -1-12n+1)=n2n+1. 又S n =n 2n+1=12-14n+2,n∈N *,∴S n ∈[13,12),∴不等式S n >λ-12恒成立等价于13>λ-12,∴λ<56.故实数λ的取值范围为(-∞,56).11.解析 (1)设等差数列{a n }的公差为d(d≥0),则S 1=a 1=1,S 2=2+d,S 3=3+3d. ∵数列{√S n }为等差数列, ∴2√2+d =1+√3+3d ,解得d=2. ∴a n =1+2(n-1)=2n-1. (2)由(1)得a n+1=2n+1, S n =n+n (n -1)2×2=n 2, ∴b n =a n+1S n ·S n+1=2n+1n 2·(n+1)2=1n2-1(n+1)2.设数列{b n }的前n 项和为T n ,则T n =b 1+b 2+…+b n =(112-122)+(122-132)+…+[1n 2-1(n+1)2]=1-1(n+1)2=n 2+2n(n+1)2.。
2018-2019学年广东省第二师范学院番禺附中高一(上)期末物理试卷解析版

2018-2019学年广东省第二师范学院番禺附中高一(上)期末物理试卷一、单选题(本大题共12小题,共36.0分)1.关于质点、位移和路程,下列说法中正确的是()A. 只有体积很小的物体才能看成质点B. 路程是标量,位移是矢量C. 路程就是位移的大小D. 当质点作曲线运动时,路程等于位移的大小【答案】B【解析】解:A、能够把物体看成质点的条件是物体的大小体积对所研究的问题是否产生影响,体积很小的物体,它的体积也不一定能够忽略,要看研究的是什么问题,所以A错误;B、路程没有方向,只有大小,是标量,位移是矢量,位移的方向由初位置指向末位置,路程是标量,是运动路径的长度。
所以B正确;C、路程没有方向,只有大小,是标量,位移是矢量,位移的方向由初位置指向末位置,路程是标量,是运动路径的长度,路程不是位移的大小,所以C错误;D、当质点作曲线运动时,路程大于位移的大小,所以D错误。
故选:B。
能否看作质点物体本身无关,要看所研究问题的性质,看物体的形状和大小在所研究的问题中是否可以忽略,参考系是为了研究物体的运动而假定为不动的物体;位移是矢量,位移的方向由初位置指向末位置.位移的大小不大于路程.路程是标量,是运动路径的长度.当质点做单向直线运动时,位移的大小一定等于路程.本题主要考查了质点、参考系、位移的基本概念,要从本质上去理解这些概念,难度不大,属于基础题.2.下列说法正确的是()A. 在国际单位制中,质量的单位是g,也可以是kgB. kg,m/s,N是导出单位C. 牛顿第一定律可以通过现实的实验得到验证D. 牛顿第二定律的表达式F=kma只有在国际单位制中,比例系数k才为1【答案】D【解析】解:A、在国际单位制中,质量的单位是kg,在国际单位制中,每一个物理量只有一个国际单位。
故A错误;B、kg不是导出单位,故B错误;C、牛顿第一定律是逻辑思维的产物,不能通过现实的实验得到验证,故C错误;D、在牛顿第二定律的表达式F=kma中,只有F和a的单位在国际单位制中,比例系数k才为1,故D正确;故选:D。
2019-2020学年广东第二师范学院番禺附属中学高二上学期期末考试语文试题

二师附中2019-2020学年高二级第一学期期末考试卷语文★祝考试顺利★注意事项:1、答题前,请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:每个小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
3、主观题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。
答案用0.5毫米黑色签字笔写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非选修题答题区域的答案一律无效。
5、保持卡面清洁,不折叠,不破损,不得使用涂改液、胶带纸、修正带等。
6、考试结束后,请将本试题卷、答题卡、草稿纸一并依序排列上交。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)春秋诸子无一例外都是中华上古传统文化的继承人。
其中,老子、孔子和孙子由于杰出的文本贡献而被后世分别尊为道、儒、兵家创始人,而管子似乎被人们有意遗忘了。
更为倒因为果的事情是,竟然有诸多学者声称“管子学说中杂有道家、儒家、农家、法家思想”。
管子是“以法治国”的首倡者,被后世称为法家思想集大成者。
韩非子比管子晚了四百多年,到底谁是宗师谁是学徒,岂不是一目了然?在诸子当中,管子是唯一有机会把自己的全部认知和理论付诸实践并且取得辉煌成功的思想家。
按照现代的看法,管子属于“国家公务员”,另外一些诸子的身份多半应是“学者”。
学者的特点是容易以“真理在握”自居,然而,若非证道之真人或者中华上古文化传承的人,往往纸上谈兵者居多。
孔子评价管仲功业时说:“微管仲,吾其披发左在矣!”又说“九合诸候,不以兵车,管仲之力也!如其仁!如其仁!”这不但表达了对管仲的不尽感恩之情,还充分肯定了管仲保护中华文明不受异族的进攻乃至遭受灭绝的历史功绩。
2024届广东省第二师范学院番禺附属中学高三下学期第四次月考:化学试题含解析

2024届广东省第二师范学院番禺附属中学高三下学期第四次月考:化学试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每题只有一个选项符合题意)1、跟水反应有电子转移,但电子转移不发生在水分子上的是A.CaO B.Na C.CaC2D.Na2O22、氮化硅是一种高温陶瓷材料,其硬度大、熔点高,下列晶体熔化(或升华)时所克服的微粒间作用力都与氮化硅相同的是()A.白磷、硅B.碳化硅、硫酸钠C.水晶、金刚石D.碘、汞3、下列化学方程式中,不能正确表达反应颜色变化的原因的是A.铜久置空气中表面出现绿色固体:2Cu+O2+CO2+H2O═Cu2(OH)2CO3B.某种火箭发射阶段有少量N2O4,逸出,产生红色气体:N2O42NO2C.FeSO4·7H2O在空气中久置变黄:2FeSO4·7H2OFe2O3+SO2↑+SO3↑+14H2OD.SO2通入KMnO4溶液中,溶液紫色逐渐褪去:5SO2+2KMnO4+2H2O═K2SO4+2MnSO4十2H2SO4 4、设N A为阿伏加德罗常数的数值。
下列叙述正确的是()A.10mL18mol/L的浓硫酸与足量的铜加热充分反应,转移电子数0.18N AB.钾在空气中燃烧可生成多种氧化物,78g钾在空气中燃烧时转移的电子数为2N AC.常温常压下,0.1molNH3与0.1molHCl充分反应后所得的产物中含有的分子数仍为0.1N AD.标准状况下,22.4LCO2中含有共用电子对数为2N A5、四元轴烯t,苯乙烯b及立方烷c的结构简式如下,下列说法正确的是A.b的同分异构体只有t和c两种B.t和b能使酸性KMnO4溶液褪色而c不能C.t、b、c的二氯代物均只有三种D.b中所有原子-定不在同-个平面上6、下列表示氮原子结构的化学用语规范,且能据此确定电子能量的()A .B .C .1s 22s 22p 3D .7、对于反应2NO(g)+2H 2(g)→N 2(g)+2H 2O(g),科学家根据光谱学研究提出如下反应历程: 第一步:2NO ⇌N 2O 2快速平衡第二步:N 2O 2+H 2→N 2O +H 2O 慢反应 第三步:N 2O +H 2→N 2+H 2O 快反应其中可近似认为第二步反应不影响第一步的平衡。
2019年厦门市启悟中学高考数学选择题专项训练(一模)

2019年厦门市启悟中学高考数学选择题专项训练(一模)抽选各地名校试卷,经典试题,有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。
第 1 题:来源:广东省第二师范学院番禺附属中学2018_2019学年高二数学下学期期中试题理已知向量,若,则的值为A. B. C.D.【答案】A第 2 题:来源:四川省内江市2019届高三数学上学期第一次模拟考试试题理(含解析)在长方体中,,,,则异面直线与所成角的余弦值为()A. B. C. D.【答案】B【解析】【分析】由已知画出图形,连接BC1,由AB∥A1B1,可得∠C1AB为异面直线A1B1与AC1所成角,求解三角形得答案.【详解】如图,连接BC1,由AB∥A1B1,∴∠C1AB为异面直线A1B1与AC1所成角,由已知可得,则.∴cos∠C1AB.即异面直线A1B1与AC1所成角的余弦值为.故选:B.【点睛】本题考查异面直线所成角,考查数学转化思想方法,是基础题.第 3 题:来源: 2017-2018学年吉林省吉林市高一(上)期末数学试卷(含答案解析)已知函数f(x)=asinx﹣btanx+4cos,且f(﹣1)=1,则f(1)=()A.3 B.﹣3 C.0 D.4﹣1【答案】A解:∵函数f(x)=asinx﹣btanx+4cos,且f(﹣1)=1,∴f(﹣1)=asin(﹣1)﹣btan(﹣1)+4×=﹣asin1+btan1+2=1,∴asin1﹣btan1=1,∴f(1)=asin1﹣bsin1+4×=1+2=3.第 4 题:来源: 2017-2018学年吉林省通化市辉南高一(上)期末数学试卷(含答案解析)下列函数中在区间(0,1)上为增函数的是()A.y=2x2﹣x+3 B. C. D.【答案】C】解:对于A,函数的对称轴是x=,函数在(0,)递减,不合题意;对于B,函数在R递减,不合题意;对于C,函数在(0,+∞)递增,符合题意;对于D,函数在(0,+∞)递减,不合题意;第 5 题:来源: 2019高中数学第二章平面向量单元测试(一)新人教A版必修4向量,向量,则△ABC的形状为()A.等腰非直角三角形 B.等边三角形C.直角非等腰三角形 D.等腰直角三角形【答案】C【解析】∵,,∴,∴,∴∠C=90°,且,,.∴△ABC是直角非等腰三角形.故选C.第 6 题:来源: 2019高中数学第一章三角函数单元质量评估(含解析)新人教A版必修4已知函数f(x)=3sin x-4cos x(x∈R)的一个对称中心是(x0,0),则tan x0的值为 ( )A.-B.C.-D.【答案】D第 7 题:来源: 2016_2017学年湖北省蕲春县高二数学下学期期中试题试卷及答案理.在区间上随机抽取一个数,若满足的概率为,则的值为A. 3B.C.D. 2【答案】A第 8 题:来源:福建省福州市八县(市)一中2018_2019学年高二数学下学期期末联考试题理已知函数的导函数为,且对任意的实数都有(是自然对数的底数),且,若关于的不等式的解集中恰有两个整数,则实数的取值范围是()A.B.C.D.【答案】B第 9 题:来源:山东省寿光市2016_2017学年高二数学下学期期末试卷及答案文设函数f(x)(x∈R)为奇函数,f(1)=,f(x+2)=f(x)+f(2),则f(﹣5)=()A.﹣ B. C. D.5【答案】A【考点】3L:函数奇偶性的性质.【分析】根据奇函数的心智以及条件求得f(2)的值,化简f(﹣5)为﹣2f(2)﹣f(1),从而得到它的值.【解答】解:函数f(x)(x∈R)为奇函数,f(1)=,f(x+2)=f(x)+f(2),取x=﹣1,可得f(1)=f(﹣1)+f(2)=﹣f(1)+f(2),∴f(2)=2f(1)=1,则f(﹣5)=f(﹣3﹣2)=f(﹣3)+f(﹣2)=f(﹣2﹣1)+f(﹣2)=2f(﹣2)+f(﹣1)=﹣2f(2)﹣f(1)=﹣2×1﹣=﹣,故选:A.第 10 题:来源:广西桂林市2017_2018学年高一数学上学期期中试题 (1试卷及答案下列函数中,是同一函数的是()A. B.C. D.【答案】D【解析】若为同一函数,则定义域与对应法则相同,对于,二者定义域都是R,对应法则相同,故二者是同一个函数,故选D.第 11 题:来源:广西桂林市2018届高三数学上学期第二次月考试题理试卷及答案若复数满足,则的虚部是A.-1 B. C. D.1【答案】A第 12 题:来源:山东省济南市2017_2018学年高二数学上学期开学考试试题试卷及答案在△ABC中,若,则最大角的余弦是()A. B. C. D.【答案】C第 13 题:来源:高中数学第一章常用逻辑用语章末测试A新人教B版选修1_已知命题p:x∈R,使tan x=1;命题q:x2-3x+2<0的解集是{x|1<x<2}.下列结论:①命题“p ∧q”是真命题;②命题“p∧q”是假命题;③命题“p∨q”是真命题;④命题“p∨q”是假命题.其中正确的是( )A.②③ B.①②④ C.①③④ D.①②③④【答案】D第 14 题:来源:黑龙江省友谊县红兴隆管理局2016_2017学年高二数学下学期期中试题试卷及答案理已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是()A.B.C.D.【答案】D、第 15 题:来源:辽宁省六校协作体2018_2019学年高二数学上学期期中试题理下列函数中,的最小值为4的是()A. B.C. D.【答案】C第 16 题:来源:青海省西宁市2018届高三数学9月月考试题理试卷及答案、函数的单调递增区间是( ) A. B. C. D.【答案】D第 17 题:来源:江西省南昌市2017_2018学年高二数学上学期第三次月考试题试卷及答案理已知命题,,则为()A. B. C. D.【答案】 B第 18 题:来源:宁夏平罗县2018届高三数学上学期第一次月考试题理已知定义在上的函数,若对任意的,不等式恒成立,则实数的取值范围是()A. B. C. D.【答案】第 19 题:来源: 2016_2017学年高中数学每日一题(2月27日_3月5日)试卷及答案新人教A 版必修3对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图①;对变量u,v有观测数据(ui,vi)(i=1,2,…,10),得散点图②.由这两个散点图可以判断A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C.变量x与y负相关,u与v正相关D.变量x与y负相关,u与v负相关【答案】C 【解析】由图象知,变量x与y呈负相关关系;u与v呈正相关关系.第 20 题:来源:四川省广元市2019届高三数学第一次适应性统考试题(含解析).下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是()A. ①③B. ①④C. ②③D. ①②【答案】B【解析】试题分析::∵两个变量的散点图,若样本点成带状分布,则两个变量具有线性相关关系,∴两个变量具有线性相关关系的图是①和④.考点:变量间的相关关系第 21 题:来源:河北省大名县2017_2018学年高一数学上学期第一次月考试题 (1)函数的图象是()【答案】D第 22 题:来源:辽宁省庄河市2018届高三数学上学期开学考试试题文(含解析)将正方体切去一个三棱锥得到几何体的三视图如下图所示,则该几何体的体积为()A. 1B.C.D. 6【答案】A【解析】由三视图知,该几何体为一个边长为2的正方体截去一个底面是直角边分别为1、2的直角三角形、高为2的三棱锥,所以该几何体的体积,故选A.第 23 题:来源: 2016_2017学年安徽省蚌埠市高二数学上学期期中试题试卷及答案理若函数的定义域为R,则实数的取值范围是A.B. C. D.【答案】D第 24 题:来源:河北省石家庄市2016-2017学年高一数学上学期期末考试试题试卷及答案在△中,、、分别是、、上的中线,它们交于点,则下列各等式中不正确的是A. B. C. D.【答案】C第 25 题:来源:广东省天河区普通高中2017_2018学年高一数学10月月考试题试卷及答案09 集合,,则下列关系中,正确的是( )A. B. C. D.【答案】B第 26 题:来源: 2019年普通高等学校招生全国统一考试文科数学(北京卷)(含解析)已知集合A={x|-1<x<2},B={x|x>1},则AUB=()A. (-1,1)B. (1,2)C. (-1,+∞)D. (1,+∞)【答案】C【解析】【解答】因为所以故答案为:C.第 27 题:来源:重庆市巴蜀中学2018_2019学年高一数学上学期期中复习试题已知函数,,则函数的图象大致为()A.B.C.D.【答案】B【解析】由题意得,函数为偶函数,∴函数为偶函数,其图象关于轴对称,故只需考虑时的情形即可.由函数的取值情况可得,当时,函数的取值情况为先负、再正、再负,所以结合各选项得B满足题意.故选B.第 28 题:来源:贵州省遵义市2016_2017学年高一数学下学期第一次月考试题试卷及答案方程的根所在区间是()A.B C D【答案】D第 29 题:来源:山东省济南市2019届高三数学3月模拟考试试卷理(含解析)已知复数(其中为虚数单位),则在复平面内对应的点位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】D【解析】【分析】对复数进行计算,然后得到,再确定是在复平面的象限.【详解】,所以在复平面对应的点位于第四象限.故选D项.【点睛】复数的四则运算,与的关系,复数与复平面的关系.第 30 题:来源:河北省石家庄市正定县第七中学2018_2019学年高一数学下学期3月月考试题.在数列中,=1,,则的值为()A.99 B.49 C.102 D. 101【答案】D第 31 题:来源: 2016_2017学年贵州省铜仁市碧江区高二数学下学期期中试题试卷及答案理若上是减函数,则的取值范围是()A. B.C. D.【答案】C第 32 题:来源:云南省昆明市2017_2018学年高一数学12月月考试题 (1)试卷及答案已知一个样本数据按从小到大的顺序排列为,x,,中位数为22,则x的值等于A. 21B. 22C. 20D. 23【答案】 A第 33 题:来源:河北省景县2017_2018学年高一数学上学期第一次调研考试试题试卷及答案若集合,且,则集合可能是()A. B. C. D.【答案】A试题解析:因为A∩B=B,所以 B是A 的子集,所以集合B可能是{1,2},故选A.第 34 题:来源:新疆维吾尔自治区阿克苏市2017_2018学年高一数学上学期第二次月考试题试卷及答案若满足,满足,则+= ()【答案】A第 35 题:来源:湖南省双峰县2018届高三数学上学期第二次月考试题理试卷及答案已知定义在上的函数和分别满足,则下列不等式成立的是( )A. B.C. D.【答案】D第 36 题:来源: 2017_2018学年高中数学第三章概率章末综合测评试卷及答案北师大版必修3 有分别写着数字1到120的120张卡片,从中取出1张,这张卡片上的数字是2的倍数或是3的倍数的概率是( )A. B.C. D.【答案】 D第 37 题:来源:河北省承德市第一中学2018_2019学年高一数学下学期期中试题在△ABC中,周长为7.5cm,且sinA:sinB:sinC=4:5:6,下列结论:①②③④其中成立的个数是( )A.0个 B.1个 C.2个 D.3个【答案】C第 38 题:来源:内蒙古乌兰察布市2015_2016学年高一数学下学期期末考试试题点A(2,0,3)在空间直角坐标系中的()A.y轴上 B.xoy平面上 C.xoz平面上 D.yoz 平面上【答案】 C第 39 题:来源:内蒙古巴彦淖尔市2017_2018学年高一数学12月月考试题试卷及答案(A卷)已知函数在区间上是增函数,则的取值范围是()A. B. C. D.【答案】D第 40 题:来源:江西省赣州市章贡区2018届高三数学上学期第一次阶段测试试题理已知p:x≥k,q:<1,如果p是q的充分不必要条件,则实数k的取值范围是 ( ) A.(2,+∞) B.[2,+∞) C.[1,+∞) D.(-∞,-1)【答案】A。
2019-2020学年广东省第二师范学院番禺附属中学高一下学期期中段考物理试题

广东省第二师范学院番禺附属中学2019-2020学年高一下学期期中段考试题第Ⅰ卷(选择题共53分)一、单项选择题(每小题3分,共33分)1.在万有引力理论发现和完善的过程中,有许多伟大的科学家做出了贡献。
下列不符合物理学史的是()A.第谷通过天文观测积累了大量丰富而准确的行星运动的数据B.开普勒发现了行星运动的三大规律C.牛顿在前人工作基础上总结出了万有引力定律D.笛卡尔测出了引力常量2.关于曲线运动,下列说法正确的是A. 平抛运动是一种匀变速运动B. 物体在恒力作用下不可能做曲线运动C. 做匀速圆周运动的物体,所受合力是恒定的D. 做圆周运动的物体,所受合力总是指向圆心的3.一艘船在静水中的速度是3m/s,它要横渡一条30m宽的河,水流速度为4m/s,下列说法正确的是( )A. 船可以垂直河岸到达正对岸B.船过河时相对河岸的速度一定是5 m/sC.船过河时间可能为6 s D.船过河时间可能为12 s4.如图所示,自行车的大齿轮.小齿轮.后轮的半径不一样,它们的边缘有三个点A.B.C.在自行车正常行驶时,下列说法正确的是()A.A.B两点的角速度大小相等B.B.C两点的线速度大小相等C.B.C两点向心加速度之比等于它们所在圆周的半径之比D.A .B 两点向心加速度之比等于它们所在圆周的半径之比5.有质量相等的两个人造地球卫星A 和B ,分别在不同的轨道上绕地球做匀速圆周运动.两卫星的轨道半径分别为A r 和B r , 且B A r r .则A 和B 两卫星相比较,以下说法正确的是A. 卫星A 受到的地球引力较大B. 卫星A 的角速度较大C. 若使卫星B 减速,则有可能撞上卫星AD. 卫星A 的运行周期较大 6. 地球半径为R ,地球表面的重力加速度为g ,若高空中某处的重力加速度为g/4,则该处距地面球表面的高度为()A .(2—1)RB .RC .2RD .2R7.投飞镖是深受人们喜爱的一种娱乐活动.如图所示,某同学将一枚飞镖从高于靶心的位置水平投向竖直悬挂的靶盘,结果飞镖打在靶心的正下方.忽略飞镖运动过程中所受空气阻力,在其他条件不变的情况下,为使飞镖命中靶心,他在下次投掷时应该 ( )A .换用质量稍大些的飞镖B .适当减小投飞镖的高度C .到稍远些的地方投飞镖D .适当增大投飞镖的初速度8.如图所示,洗衣机脱水筒在转动时,衣服贴靠在匀速转动的圆筒内壁上而不掉下来,则衣服 ( )A .受到重力.弹力.静摩擦力和离心力四个力的作用B .所需的向心力由重力提供C .所需的向心力由弹力提供D .转速越快,弹力越大,摩擦力也越大9.如图所示是一个玩具陀螺,a .b 和c 是陀螺表面上的三个点.当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是 ( )A.a.b和c三点的线速度大小相等B.b.c两点的线速度始终相同C.b.c两点的角速度比a点的大D.b.c两点的加速度比a点的大10.如图所示,以初速度9.8m/s水平抛出的物体,飞行一段时间后垂直撞在倾角为30°的斜面上,则物体飞行时间为( )A.B.C.D.2s11.“嫦娥三号”探测器由“长征三号乙”运载火箭从西昌卫星发射中心发射,首次实现月球软着陆和月面巡视勘察。
广东省第二师范学院番禺附属中学2021-2021学年高一化学上学期期末考试试题

广东省第二师范学院番禺附属中学2020-2021-2020学年高一化学上学期期末考试试题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共6页,全卷两大题23小题,满分100分,考试用时75分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自已的姓名、考试科目、班级和考生号等信息填写在答题卡上,并用2B铅笔将考号在答题卡相关的区域内涂黑。
2.选择题每小题选出答案后,用2B铅笔把答题卡对应的答案符号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将答题卡答卷交给监考老师。
可能用到的相对原子质量:H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 S-32 Cl-35.5Ca-40 Mn-55第Ⅰ卷(选择题共60分)一、选择题(本大题共20小题,每题3分,共60分)1.2016年年底,中国石油全部完成国V标准车用汽柴油质量升级,以减少空气污染。
下列物质中,不会造成空气污染的是A.NO B.CO2 C.SO2 D.粉尘2.下列物质中,所含分子数最多的是A.22.4L O2(标准状况) B.1.6 g H2 C.1.2 mol H2SO4 D.28g CaO3.下列物质在一定条件下能够导电,但不是电解质的是A.铝 B.熔融氯化钠 C.H2SO4 D.蔗糖4.实验室分离碘的四氯化碳溶液与水的混合液,不需要用到的玻璃仪器是①烧杯②长颈漏斗③分液漏斗④酒精灯A.①④ B.①③ C.③④ D.②④5.有关Fe(OH)3胶体的说法不正确的是A.呈红褐色B.Fe(OH)3胶体粒子的直径介于1-100 nm之间C.用一束光照射它,能观察到一条光亮的通路D.往饱和FeCl3溶液中加入NaOH溶液,可以制备Fe(OH)3胶体6.下列各组混合物的分离或提纯方法正确的是A.用加热分解法分离NaCl和KNO3的固体混合物B.用蒸馏法分离乙醇和水(沸点分别为78℃、100℃)的混合物C.用过滤法分离Fe(OH)3胶体和FeCl3溶液的混合液D7.对于反应:WO3+3H2W+3H2O,下列说法不正确的是A.WO3做氧化剂 B.H2表现还原性C.W是氧化产物 D.每生成3molH2O,转移的电子数为6N A(N A表示阿伏加德罗常数)8.下列气体中既可用浓硫酸干燥、又可用碱石灰干燥的是A.NH3 B.SO2 C.Cl2 D.H29.化学与日常生活密切相关,下列有关说法错误的是A.Fe3O4常用作红色油漆和涂料 B.“84消毒液”的有效成分是NaClO C.SO2常作纸浆、草帽辫的漂白剂 D.还原铁粉可作食品包装袋内的抗氧化剂10.中国科学技术大学的钱逸泰教授等以CCl4和金属钠为原料,在700o C时反应制造出纳米级金刚石粉末和另一种化合物。
2019年南通西藏民族中学高考数学选择题专项训练(一模)

2019年南通西藏民族中学高考数学选择题专项训练(一模)抽选各地名校试卷,经典试题,有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。
第 1 题:来源:贵州省遵义市五校2018_2019学年高二数学下学期期中联考试题理向量满足,且其夹角为,则“”是“”的A.充分不必要条件 B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件【答案】C第 2 题:来源:山东省淄博市2018届高三数学上学期开学考试试题试卷及答案理某程序框图如图所示,若该程序运行后输出的值是,则()A.a=11 B.a=12 C.a=13 D.a=14【答案】B.第 3 题:来源: 2017-2018学年辽源市等五校联考高一上期末数学试卷含答案解析下列各组函数中,表示同一函数的是()A.f(x)=1,g(x)=x0 B.f(x)=x﹣2,g(x)=C.f(x)=|x|,g(x)= D.f(x)=x,g(x)=()2【答案】C解:A.函数g(x)=x0的定义域为{x|x≠0},所以两个函数的定义域不同,所以A不是相同函数B.g(x)==x﹣2,g(x)的定义域为{x|x≠﹣2},所以两个函数的定义域不同,所以B不是相同函数.C.由 g(x)==|x|,得两个函数的定义域和对应法则,所以C表示的是相同函数.D.g(x)=()2=x,x≥0,两个函数的定义域不相同则,所以D表示的是不是相同函数.故选C.第 4 题:来源:江西省新余市2016_2017学年高一数学下学期第一次段考(3月)试题试卷及答案已知集合,,则()A.(1,3)B.(1,4)C.(2,3)D.(2,4)【答案】C第 5 题:来源:河南省开封市、商丘市九校2018_2019学年高一数学下学期期中联考试题若,则()A. B. C. D.【答案】D第 6 题:来源:山西省太原市小店区2017_2018学年高二数学上学期9月月考试题试卷及答案已知向量,则()A. B. C. D.【答案】C第 7 题:来源: 2017年山东省菏泽市巨野县高一数学上学期期末考试试题试卷及答案在函数,,,中,有几个函数是幂函数?()A.0 B.1 C.2 D.3【答案】C第 8 题:来源:湖南省双峰县2018届高三数学上学期第一次月考试题试卷及答案理已知当x<1时,f(x)=(2﹣a)x+1;当x≥1时,f(x)=ax(a>0且a≠1).若对任意x1≠x2 ,都有成立,则a的取值范围()A、(1,2)B、C、D、(0,1)∪(2,+∞)【答案】C第 9 题:来源:高中数学第三章数系的扩充与复数的引入章末测试试卷及答案B 新人教A版选修1-2设z=+i,则|z|=( )A. B. C. D.2【答案】:B第 10 题:来源:山东省潍坊市临朐县2017届高三数学上学期阶段性质量检测(12月月考)试题理设函数f(x)在R上存在导数f′(x),对任意的x∈R有f(﹣x)+f(x)=x2,x∈(0,+∞)时,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,则实数a的取值范围为A.[1,+∞) B.(﹣∞,1] C.(﹣∞,2] D.[2,+∞)【答案】B第 11 题:来源: 2017年普通高等学校招生全国统一考试数学试题(浙江卷,参考解析)如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记,,,则A.I1<I2<I3 B.I1<I3<I2 C. I3<I1<I2 D.I2<I1<I3【答案】C【解析】因为,所以第 12 题:来源: 2017届吉林省长春市朝阳区高三数学下学期第八次模拟考试试题试卷及答案理若一个空间几何体的三视图如图所示,且已知该几何体的体积为,则其表面积为(A)(B)(C)(D)【答案】A第 13 题:来源: 2019高考数学一轮复习第8章立体几何第5讲直线平面垂直的判定与性质分层演练文201809101115如图,在Rt△ABC中,∠ABC=90°,P为△ABC所在平面外一点,PA⊥平面ABC,则四面体PABC中共有直角三角形的个数为( )A.4 B.3C.2 D.1 【答案】A.由PA⊥平面ABC可得△PAC,△PAB是直角三角形,且PA⊥BC.又∠ABC=90°,所以△ABC 是直角三角形,且BC⊥平面PAB,所以BC⊥PB,即△PBC为直角三角形,故四面体PABC中共有4个直角三角形.第 14 题:来源:广东省普宁市勤建学校2016-2017学年高二数学下学期第一次月考试题试卷及答案理抛物线的准线方程是()A. B. C. D.【答案】D第 15 题:来源:广东省第二师范学院番禺附属中学2018_2019学年高一数学下学期期中试题在△ABC中,,则△ABC一定是( )A.直角三角形 B.钝角三角形C.等腰直角三角形 D.等边三角形【答案】D第 16 题:来源:山东省济南市2017_2018学年高二数学上学期开学考试试题试卷及答案在等差数列{an}中,a2=2,a3=4,则a10=( ).A.12 B.14 C.16 D.18【答案】D第 17 题:来源:辽宁省大石桥市2017_2018学年高二数学9月月考试题在等差数列前项和为,若,则的值为()A. B. C. D. 【答案】A第 18 题:来源:广东省江门市第一中学2017届高三数学上学期1月月考试题含有数字0,1,2,且有两个相同数字1或2的四位数的个数为(A)12 (B)18 (C)24 (D)36【答案】B第 19 题:来源:陕西省西安市2017_2018学年高一数学上学期期末考试试题已知,点是圆内一点, 直线m是以点P为中点的弦所在的直线, 直线L的方程是, 则下列结论正确的是( ).A. m∥L ,且L与圆相交B. m⊥L , 且L与圆相切C. m∥L ,且L与圆相离D. m⊥L , 且L与圆相离【答案】C第 20 题:来源: 2017届吉林省长春市朝阳区高三数学下学期第八次模拟考试试题试卷及答案理已知将函数的图象向左平移个单位长度后得到的图象,则在上的值域为(A)(B)(C)(D)【答案】B第 21 题:来源:青海省西宁市2018届高三数学12月月考试题理试卷及答案( )A. B. C. D.【答案】 C第 22 题:来源:吉林省长春市普通高中2018届高三数学一模考试试题理试卷及答案已知某算法的程序框图如图所示,则该算法的功能是()A.求首项为1,公差为2的等差数列前2017项和B.求首项为1,公差为2的等差数列前2018项和C.求首项为1,公差为4的等差数列前1009项和D.求首项为1,公差为4的等差数列前1010项和【答案】 C第 23 题:来源: 2019高中数学第二章数列单元测试(二)新人教A版必修5等差数列中,是前项和,已知,,则()A.15 B.30 C.45D.60【答案】A【解析】解法一:由等差数列的求和公式及知,,∴,∴.故选A.解法二:由等差数列性质知,成等差数列,设其公差为,则,∴,∴,∴.故选A.第 24 题:来源:辽宁省大连市2017_2018学年高一数学上学期期中试题试卷及答案已知(x,y)在映射下的象是(2x-y,x-2y),则原象(1,2)在下的象为()A.(0,-3) B. (1,-3) C. (0,3) D. (2,3)【答案】A第 25 题:来源:宁夏银川市勤行2016_2017学年高一数学下学期第一次(3月)月考试题试卷及答案已知函数y=输入自变量x的值,输出对应函数值的算法中所用到的基本逻辑结构是( )A.顺序结构B.顺序结构、条件结构C.条件结构D.顺序结构、条件结构、循环结构【答案】:B第 26 题:来源:黑龙江省伊春市2016_2017学年高一数学下学期期中试题试卷及答案在中,,,则等于()A. B. C. D.【答案】A【解析】∵在△ABC中,A=45∘,B=60∘,a=2,∴由正弦定理得:.本题选择A选项.第 27 题:来源:黑龙江省哈尔滨市呼兰区第一中学2019届高三数学上学期期中试题理已知集合A={y|y=|x|-1,x∈R},B={x|x≥2},则下列结论正确的是( )A.-3∈A B.3∉B C.A∩B=B D.A∪B=B【答案】C第 28 题:来源: 2017年普通高等学校招生全国统一考试数学试题文(全国卷3,参考解析)复平面内表示复数z=i(–2+i)的点位于A.第一象限 B.第二象限 C.第三象限 D.第四象限【答案】B【解析】由题意:.本题选择B选项.第 29 题:来源: 2018届高考数学文科总复习课时跟踪检测试卷(1)集合(含解析)已知集合A={1,2,3},B={x|(x+1)(x-2)<0,x∈Z},则A∪B=( )A.{1} B.{1,2}C.{0,1,2,3} D.{-1,0,1,2,3}【答案】C 因为B={x|(x+1)(x-2)<0,x∈Z}={x|-1<x<2,x∈Z}={0,1},A={1,2,3},所以A∪B ={0,1,2,3}.第 30 题:来源: 2017届江西省南昌市十所省重点中学高三第二次模拟突破冲刺数学理科试题(四)含答案已知全集,集合,则如图所示的阴影部分所表示的集合为()A. B.C. D.【答案】D第 31 题:来源:黑龙江省农垦北安管理局2018届高三数学9月月考试题函数上的零点个数为()A、1个B、2个C、3个D、4个【答案】B【解析】因为函数的图像在上有两个交点,所以函数f(x)在区间上有两个零点.考点:1.函数与方程;2.函数图像的应用第 32 题:来源: 2017届江西省南昌市十所省重点中学命制高三第二次模拟突破冲刺数学理科试题(六)含答案已知在平面直角坐标系中,A,B,若,则A. B.3 C.D.65【答案】C【解析】,得,∴,,∴,故选C.第 33 题:来源:重庆市巴蜀中学2018_2019学年高一数学上学期期中复习试题若函数在区间上递增,且,则()A. B. C. D.【答案】B【解析】由,得,又函数的对称轴方程为,∴复合函数的增区间,∵函数在区间上递增,∴,则,而,所以,第 34 题:来源:河南省鹤壁市2016_2017学年高二数学下学期第二次月考试卷理(含解析)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也,又以高乘之,三十六成一,该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈L2h,它实际上是将圆锥体积公式中的圆周率π近似取为3,那么,近似公式V≈L2h相当于将圆锥体积公式中的π近似取为()A. B. C. D.【答案】B【考点】LF:棱柱、棱锥、棱台的体积.【分析】根据近似公式V≈L2h,建立方程,即可求得结论.【解答】解:设圆锥底面圆的半径为r,高为h,则L=2πr,∴=(2πr)2h,∴π=.第 35 题:来源:江西省南昌市八一中学、洪都中学、麻丘中学等六校2016_2107学年高二数学5月联考试题理(含解析)如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹为( )A. B. C. D.【答案】A【解析】试题分析:根据题意可知PD=DC,则点D符合“M为底面ABCD内的一个动点,且满足MP=MC”设AB的中点为N,根据题目条件可知△PAN≌△CBN∴PN=CN,点N也符合“M为底面ABCD内的一个动点,且满足MP=MC”故动点M的轨迹肯定过点D和点N而到点P与到点N的距离相等的点为线段PC的垂直平分面线段PC的垂直平分面与平面AC的交线是一直线考点:直线与平面垂直的性质;平面与平面之间的位置关系第 36 题:来源:河南省三门峡市陕州区2017_2018学年高一数学10月月考试题试卷及答案已知集合,函数的定义域为集合,则()A.B.C.D.【答案】B第 37 题:来源:云南省玉溪市2018届高三数学上学期第一次月考试题文(含解析)函数()的最小正周期为,则满足()A. 在上单调递增B. 图象关于直线对称C. D. 当时有最小值【答案】D【解析】由函数()的最小正周期为得,则,当时,,显然此时不单调递增,A错误;当时,,B错误;,C错误;故选择D.第 38 题:来源:湖北省襄阳市优质高中2017届高三数学1月联考试题试卷及答案理已知集合,则A. B. C. D.【答案】C第 39 题:来源: 2018届高考文科总复习课时跟踪检测试卷(9)指数与指数函数试卷及答案函数y=ax+2-1(a>0且a≠1)的图象恒过的点是( )A.(0,0)B.(0,-1)C.(-2,0) D.(-2,-1)【答案】C 法一:因为函数y=ax(a>0,a≠1)的图象恒过点(0,1),将该图象向左平移2个单位,再向下平移1个单位得到y=ax+2-1(a>0,a≠1)的图象,所以y=ax+2-1(a>0,a≠1)的图象恒过点(-2,0),选项C正确.法二:令x+2=0,x=-2,得f(-2)=a0-1=0,所以y=ax+2-1(a>0,a≠1)的图象恒过点(-2,0),选项C正确.第 40 题:来源:江西省九江市2019届高三数学第一次模拟统一考试试题理(含解析)《九章算术》卷第五《商功》中,有“贾令刍童,上广一尺,袤二尺,下广三尺,袤四尺,高一尺。
精品解析:广东省第二师范学院番禺附属中学2018-2019学年高一上学期期末考试化学试题(解析版)

广东省第二师范学院番禺附属中学2018-2019学年高一上学期期末考试化学试题1. 实现下列变化,需要加入还原剂的是A. N2→NOB. HNO3→NOC. BaCl2→BaSO4D. Fe2+→Fe3+【答案】B【解析】试题分析:A、N的化合价升高,需要氧化剂,故错误;B、N的化合价降低,需要还原剂,故错误;C、没有化合价的变化,不属于氧化还原反应,故错误;D、化合价升高,需要氧化剂,故错误。
考点:考查氧化还原反应中概念等知识。
2. 不能用组成元素的单质直接反应得到的物质是A. NOB. FeCl2C. SO2D. NH3【答案】B【解析】试题分析:A、可以用N2和O2在放电条件下生成NO,N2+O22NO,故错误;B、铁和氯气,无论氯气与否,生成氯化铁,不能得到氯化亚铁,故正确;C、S+O2=SO2,符合题意,故错误;D、N2+3H22NH3,符合题意,故错误。
考点:考查元素及其化合物的性质等知识。
3.酸雨被称为“天堂的眼泪”,会造成水土酸性化、建筑物加速腐蚀等危害。
下列有关说法正确的是A. 酸雨是指pH值小于7的雨水B. NO2与SO2的过度排放是形成酸雨的主要原因C. 使用新型能源不会对酸雨的防治产生效果D. 酸雨不会对动物的健康产生任何影响【答案】B【解析】A、酸雨主要由化石燃料燃烧产生的二氧化硫、氮氧化物等酸性气体,酸雨pH值小于5.6的降水,故A错误;B、NO2与SO2的过度排放是形成酸雨的主要原因,故B正确;C、开发使用新型清洁能源,减少化石燃料的燃烧,可从根本上防止酸雨的产生,故C错误;D、酸雨使水体酸化,从而使鱼类的生殖和发育受到严重影响;它会直接伤害植物的芽和叶,影响植物的生长;酸雨,危及人的健康和生命,因此,严重影响各种生物的生存。
故D错误;故选B。
4. 下列物质暴露在空气中不容易变质的是A. Na2OB. Na2O2C. NaOHD. Na2SO4【答案】D【解析】试题分析:A、Na2O和空气中水蒸气或CO2生成NaOH或Na2CO3,故错误;B、Na2O2和空气中水蒸气、CO2生成NaOH、Na2CO3和氧气,故错误;C、NaOH吸收空气中的CO2生成Na2CO3,故错误;D、不容易变质,故正确。
2025届广东省广州市广东第二师范学院番禺中高三第二次调研语文试卷含解析

2025届广东省广州市广东第二师范学院番禺中高三第二次调研语文试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.1、阅读下面的文字,完成下面小题。
材料一:2018年7月15日国家食药监总局公告称,在飞行检查中发现长春长生生物公司的冻干人用狂犬病疫苗生产存在记录造假等严重问题。
疫苗事件引发了极大关注,但疫苗真假的定义并没有明确的界定。
事实上,多位业内人士表示,更改了生产参数的疫苗、效价不合格的疫苗并不等同于假疫苗或者“毒”疫苗。
某药物研发平台创始人兼CEO张清(化名)介绍,通常提到的假疫苗有两种,一种是疫苗上市之前研发数据错误导致疫苗为假,另一种是生产过程中导致的,具体来说有原料选用与生产流程问题,原料选取的优劣和生产过程是否规范直接影响质量,长春长生的假疫苗就是生产流程中更改了参数导致的问题。
某疫苗研发公司李强(化名)表示,“此次出事的狂犬疫苗是长春长生生物更改了生产参数,但更改了哪些,之后质量是否受到影响目前尚未公布,严格意义上也不能定性为假疫苗,但是企业不严格按照生产标准来生产疫苗肯定是违法的,应该受到严惩。
”《新京报·为什么疫苗容易出问题?》材料二:2013-2030 年全球疫苗行业市场规模变化趋势及预测全球市场情况数据来源:搜狐网《疫苗行业深度研究分析》材料三:北京协和医学院基础医学院教授许雪梅在接受《生命时报》记者采访时说,包括天花、白喉、脊髓灰质炎、狂犬病、流行性乙型脑炎等在内的大部分病疫的控制或消除,都是因为疫苗起了作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
密★启用前试卷类型:A2018-2019学年度第二学期二师附中高二期中教学质量检测文科数学 2019.04 命题人:冯雄铿 审题人:孙月归本试卷共5页,23小题,满分150分,考试用时120分钟。
注意事顶:1.答卷前,考生务必将自己的名和考生号、试室号、座位号填在答题卡上,用2B 铅笔在答题卡的相应位置填涂考生号,并将试卷类型(A ),填涂在答题相应置上。
2.作答选择题时,选出每小题答案后,用2B 铅笔在答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效4.考生必须保证答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合{|12}A x x =-≤≤,{1,2,3}B =,则A B =(A ){1} (B ){2}(C ){1,2}(D ){1,2,3}2.已知a 为实数,若复数()()1a i i +-为纯虚数,则a = A.1- B.12-C. 1D.2 3.已知3sin()5πθ +=,则sin(2)2πθ -= A.45 B.725- C. 725 D.354.已知等差数列{}n a 的前n 项和为n S ,且23415a a a ++=,713a =,则5S =( ) A) 28 (B) 25(C) 20(D) 185、设x ,y 满足约束条件030426x y x y ≤≤⎧⎪≤≤⎨⎪+≥⎩,则3z x y =+的最大值为(A )7 (B )9 (C )13 (D )156、如图所示程序框图,若判断框内为“3i ≤”,则输出S =( ) A .2 B .6 C. 10 D .347、设x ∈R ,则“20x -≥”是“11x -≤”的( ) A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要条件8、如图,某几何体的三视图是三个全等的等腰直角三角形,且直角边长都等于1,则该几何体的外接球的体积为( )(A) 12π (B)2 (C) 3π (D) 43π 9、刘徽是我因魏晋时期的数学家,在其撰写的《九章算术注》中首创“割圆术”,所谓“割圆术”,是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法,如图所示,圆内接正十二边形的中心为圆心O ,圆O 的半径为2,现随机向圆O 内段放a 粒豆子,其中有b 粒豆子落在正十二边形内(,,a b N b a *∈<),则圆固率的近似值为A.b a B.a b C.3a b D.3ba10、已知1F 和2F 分别是双曲线()222210,0x y a b a b-=>>的两个焦点,A 和B 是以O 为圆心,以1OF 为半径的圆与该双曲线左支的两个交点,且2F AB 是等边三角形,则该双曲线的离心率为 ( )(A)2(B) 1 (C)1 (D) 211.函数()2sin f x x x x =+的图象大致为12.已知函数()1,0()ln ,0kx x f x x x ->⎧⎪=⎨--<⎪⎩,若函数()f x 的图象上关于原点对称的点有2对,则实数k 的取值范围是( )(A) (,0)-? (B) 1(0,)2(C) (0,)+? (D) (0,1) 二、填空题:本题共4小题,每小题5分,共20分。
13. 已知向量(2,1),(,1)a b x ==-,且a b -与b 共线,则x 的值为 .14、曲线1e xy x=-在点()1(1)f ,处的切线方程为 。
15、甲、乙、丙三人到户外植树,三人分工合作,一人挖坑和填土,一人施肥,一人浇水,他们的身高各不同,现了解到以下情况: ①甲不是最高的; ②最高的没浇水; ③最矮的施肥;④乙不是最矮的,也没挖坑和填土.可以判断丙的分工是 (从挖坑,施肥,浇水中选一项).16.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知b =2,c =3,C =2B ,则ABC ∆的面积为 。
三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17、(本小题满分12分)记n S 为等差数列{}n a 的前n 项和.已知14a =,公差0d >,4a 是2a 与8a 的等比中项.(1)求数列{}n a 的通项公式; (2)求数列1{}nS 前n 项和为n T . 18.(本小题满分12分)在2019年3月某市第二次模拟考试中,某校共有100名文科学生参加考试,其中语文考试成绩低于130的占95%,数学成绩的频率分布直方图如图所示.(1) 如果成绩不低于130的为特别优秀,这100名学生中本次考试语文、数学成绩特别优秀的大约各多少人?(2) 如果语文和数学两科都特别优秀的共有3人.①从(1)中的这些同学中随机抽取2人,求这两人两科成绩都优秀的概率;②根据以上数据,完成列联表,并分析是否有99%的把握认为语文特别优秀的同学,数学也特别优秀..附:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )19、已知四棱锥E ABCD -的底面为菱形,且60ABC ∠=,2AB EC ==,AE BE ==O 为AB 的中点.(1)求证:EO ⊥平面ABCD ; (2)求点D 到平面AEC 的距离.20、(本小题满分12分)OACBDE已知1F ,2F 分别为椭圆C :22182x y +=的左、右焦点,点P 在椭圆C 上. (1)求12PF PF ⋅的最小值; (2)设直线l 的斜率为12,直线l 与椭圆C 交于A , B 两点,若点P 在第一象限,且121PF PF ⋅=-,求ABP ∆面积的最大值.21.(本小题满分12分)已知函数()3f x ax bx c =++,其导函数()233f x x =-'+,且()01f =-,()()ln 1g x x x m mx=+≥. (1)求()f x 的极值;(2)求证:对任意()12,0,x x ∈+∞,都有()()12f x g x ≤.(二)选考题:共10分。
请考生在第22、23题中任选一题作答。
如果多做,则按所做的第一题计分。
答题时请写清题号并将相应信息点涂黑。
22.(本小题满分10分)选修4-4:坐标系与参数方程已知曲线C的参数方程为22x y αα⎧=+⎪⎨=+⎪⎩(α为参数),以直角坐标系原点O 为极点,x 轴正半轴为极轴建立极坐标系.(1)求曲线C 的极坐标方程; (2)设射线1:3l πθ=,2:6l πθ=,若12,l l 分别与曲线C 相交于异于原点的两点,A B ,求ABO ∆的面积.23.(本小题满分10分)选修4-5:不等式选讲设函数()221f x x x =--+. (1)解不等式()0f x ≤;(2)x R ∀∈,()224f x m m -≤恒成立,求实数m 的取值范围.2018-2019学年度第二学期二师附中高二期中教学质量检测文科数学参考答案一、选择题:二、填空题13、2- 14、(1)2y e x =+- 15、挖坑和填土 16三解答题: 17、18、19.【解析】 (1)证明:连接CO .∵2AB =,AE BE ==AE BE ⊥,∴AEB ∆为等腰直角三角形.∵O 为AB 的中点,∴EO AB ⊥,1EO =. 又∵AB BC =,60ABC ∠=, ∴ABC ∆是等边三角形,∴CO =.又2EC =,∴222EC EO CO =+,∴EO CO ⊥, ∵ABCO O =,∴EO ⊥平面ABCD .(2)设点D 到平面AEC 的距离为h .OACDE∵2AE AC EC ===,∴AEC S ∆=.∵224ADC S ∆==E 到面ABC 的距离1EO =,D AECE ADC V V --=,∴AEC ADC S h S EO ∆∆⋅=⋅,∴7h =.∴点D 到平面AEC 的距离为7. 20. 【解析】试题分析:(1)设()00,P x y ,由向量数量积的坐标运算求得2012344x PF PF ⋅=-+,注意椭圆中有0x -≤≤(2)由直线与圆锥曲线相交的弦长公式求得弦长AB ,求出P 点坐标,再求得P 到直线AB 的距离即三角形的高,从而得PAB ∆面积PAB S ∆=试题解析:(1)有题意可知()1F , )2F ,设点00(,)P x y则()100,PF x y =-, ()2006,PF x y =-, ………2分∴2212006PF PF x y ⋅=+-,∵点()00,P x y 在椭圆C 上,∴2200182x y +=,即220024x y =-, ………3分∴22200120326444x x PF PF x ⋅=+--=-+(0x -≤ ………4分 ∴当00x =时, 12PF PF ⋅的最小值为4-. ………6分(注:此问也可用椭圆的参数方程表达点P 求解)(2)设l 的方程12y x b =+,点()11,A x y , ()22,B x y , 由221,2 182y x b x y =++=⎧⎪⎪⎨⎪⎪⎩得222240x bx b ++-=, ………7分 令2248160b b ∆=-+>,解得22m -<<.由韦达定理得122x x b +=-, 21224x x b =-,由弦长公式得AB == ………8分且121PF PF ⋅=-,得()2,1P .又点P 到直线l的距离d ==, ………9分∴1122PAB S AB d ∆===22422b b +-≤=, (11)分当且仅当b = ∴ PAB ∆面积最大值为2. ……12分21.(本小题满分12分)解析:(1)依题意得()331f x x x =-+-, ()()()233311f x x x x =-+=-+-' (2)分知()f x 在(),1-∞-和()1,+∞上是减函数,在()1,1-上是增函数 (4)分∴()()13f x f =-=-极小值,()()11f x f ==极大值………5分(2)法1:易得0x >时, ()1f x =最大值, 依题意知,只要()()1(0)1ln 1(0)mg x x x x m x x≤>⇔≤+≥> 由1a ≥知,只要22ln 1(0)ln 10(0)x x x x x x x x ≤+>⇔+-≥> ………7分 令()2ln 1(0)h x x x x x =+->,则()2ln 1h x x x x =+-'………8分注意到()10h '=,当1x >时, ()0h x '>;当01x <<时, ()0h x '<, ………9分即()h x 在()0,1上是减函数,在()1,+∞是增函数, ()()10h x h ==最小值………10分即()0h x ≥,综上知对任意()12,0,x x ∈+∞,都有()()12f x g x ≤………12分法2:易得0x >时, ()1f x =最大值, ………7分 由1a ≥知, ()1ln (0)g x x x x x ≥+>,令()1ln (0)h x x x x x=+>………8分 则()22211ln 1ln x h x x x x x-=+-=+'………9分 注意到()10h '=,当1x >时, ()0h x '>;当01x <<时, ()0h x '<,………10分 即()h x 在()0,1上是减函数,在()1,+∞是增函数, ()()11h x h ==最小值,所以()1h x =最小值,即()1g x =最小值.综上知对任意()12,0,x x ∈+∞,都有()()12f x g x ≤.………12分法3: 易得0x >时, ()1f x =最大值, ………7分由1a ≥知, ()1ln (0)g x x x x x≥+>, ………8分 令()1ln (0)h x x x x x =+>,则()21ln 1(0)h x x x x=+->'………9分 令()21ln 1(0)x x x x ϕ=+->,则()3110x x x ϕ=+>',………10分 知()x ϕ在()0,+∞递增,注意到()10ϕ=,所以, ()h x 在()0,1上是减函数,在()1,+∞是增函数,有()1h x =最小值,即()1g x =最小值 综上知对任意()12,0,x x ∈+∞,都有()()12f x g x ≤. ……12分22. (本小题满分10分)解:(1)∵曲线C的参数方程为2(2x y ααα⎧=+⎪⎨=+⎪⎩为参数)∴曲线的普通方程为22(2)(2)8x y -+-= 即22440x y x y +--= ……2分 将cos ,sin x y ρθρθ==代入并化简得:4cos 4sin ρθθ=+即曲线C 的极坐标方程为4cos 4sin ρθθ=+. …………5分(2)由34cos 4sin πθρθθ⎧=⎪⎨⎪=+⎩得到12OA ρ==+…………7分同理22OB ρ==+分 又∵366AOB πππ∠=-=∴1sin 42AOB S OA OB AOB ∆=∠=+即AOB ∆的面积为4+分23. (本小题满分10分)23.解:(1)不等式()0f x ≤,即221x x -≤+,即2244441x x x x -+≤++, (2)分23830x x +-≥,解得13x ≥或3x ≤-.……3分所以不等式()0f x ≤的解集为1{3x x ≥或3}x ≤-.……4分(2)()=221f x x x --+=13,2131,223,2x x x x x x ⎧+<-⎪⎪⎪-+-≤≤⎨⎪-->⎪⎪⎩ (6)分故()f x 的最大值为1522f ⎛⎫-= ⎪⎝⎭,……8分因为对于x R ∀∈,使()224f x m m -≤恒成立. 所以25242m m +≥,即24850m m +-≥, 解得12m ≥或52m ≤-,∴51,,22m ⎛⎤⎡⎫∈-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭U .……10分。
