第四章 线性规划的扩展 (III)
线性规划PPT课件
线性规划的基本定理
线性规划的解存在性
对于任何线性规划问题，都存在至少一个最优解。
最优解的唯一性
在某些情况下，线性规划问题的最优解是唯一的，这取决于目标函 数和约束条件的形状和位置。
解的稳定性
线性规划问题的最优解是稳定的，即使目标函数或约束条件略有变 化，最优解也不会发生大的变化。
03
线性规划的求解方法
优缺点：内点法具有全局收敛性和对初始点不敏 感的优点，但计算量较大，需要较高的计算资源 。
椭球法
01
总结词：几何方法
02
03
04
详细描述：椭球法是一种基 于几何方法的线性规划算法。 它将可行解的边界表示为椭 球，通过迭代移动椭球中心
来逼近最优解。
算法步骤：椭球法的基本步 骤包括初始化、构建椭球和 迭代更新。在每次迭代中， 根据当前椭球的位置和方向 来更新中心和半径，直到满
运输问题
总结词
运输问题是线性规划在物流和供应链管理中的重要应用，旨在优化运输成本、 运输时间和运输量等目标。
详细描述
运输问题通常需要考虑多个出发地、目的地、运输方式和运输成本等因素。通 过线性规划方法，可以找到最优的运输方案，使得总运输成本最低、运输时间 最短，同时满足运输量和运输路线的限制。
投资组合优化问题
03
单纯形法
单纯形法是线性规划的标 准算法，通过迭代和优化， 找到满足约束条件的最大 或最小目标函数值。
初始解
在应用单纯形法之前，需 要先找到一个初始解，这 可以通过手动计算或使用 软件工具来实现。
迭代过程
单纯形法通过不断迭代和 优化，逐步逼近最优解， 每次迭代都需要重新计算 目标函数值和最优解。
线性规划的几何意义
线性规划知识点总结
线性规划知识点总结一、概述线性规划是一种数学优化方法，用于解决线性约束条件下的最优化问题。
它在各个领域中都有广泛的应用，如生产计划、资源分配、运输问题等。
本文将对线性规划的相关知识点进行总结。
二、基本概念1. 目标函数：线性规划的目标是最大化或者最小化一个线性函数，称为目标函数。
通常用Z表示。
2. 约束条件：线性规划必须满足一系列线性约束条件，如不等式约束和等式约束。
约束条件用来限制决策变量的取值范围。
3. 决策变量：决策变量是问题中需要决策的变量，它们的取值会影响目标函数的值。
4. 可行解：满足所有约束条件的解称为可行解。
5. 最优解：在所有可行解中，使得目标函数达到最大或者最小值的解称为最优解。
三、标准形式线性规划问题可以通过转换为标准形式来求解。
标准形式的线性规划问题具有以下特点：1. 目标函数为最小化问题。
2. 所有约束条件均为等式约束。
3. 决策变量为非负数。
四、线性规划的解法线性规划有多种求解方法，下面介绍两种常用的方法：1. 图形法：当问题惟独两个决策变量时，可以使用图形法求解。
首先绘制出目标函数和约束条件所构成的图形，然后通过图形的分析找到最优解。
2. 单纯形法：单纯形法是一种迭代求解方法，适合于多个决策变量的线性规划问题。
它通过不断迭代改善目标函数的值，直到找到最优解为止。
五、常见应用线性规划在实际应用中有广泛的应用，以下列举几个常见的应用场景：1. 生产计划：线性规划可以用于确定生产计划中各种资源的最优分配，以达到最大化利润或者最小化成本的目标。
2. 运输问题：线性规划可以用于解决货物运输的最优路径和最优运输量的问题，以降低物流成本。
3. 资源分配：线性规划可以用于确定资源的最优分配，如人力资源、物资资源等，以提高资源利用效率。
4. 投资组合：线性规划可以用于确定投资组合中各项投资的最优权重，以最大化投资回报或者最小化风险。
六、总结线性规划是一种常用的数学优化方法，通过最大化或者最小化线性目标函数，在一系列线性约束条件下求解最优解。
4线性规划扩展_整数规划
ZHOUYING
无法显示图像。计算机可能没有足够的内存以打开该图像，也可能是该图像已损坏。请重新启动计算机，然后重 新打开该文件。如果仍然显示红色 “x”，则可能需要删除该图像，然后重新将其插入。
ZHOUYING
无法显示图像。计算机可能没有足够的内存以打开该图像，也可能是该图像已损坏。请重新启动计算机，然后重 新打开该文件。如果仍然显示红色 “x”，则可能需要删除该图像，然后重新将其插入。
Session3 Beyond Linear Programming 整数规划
ZHOUYING
无法显示图像。计算机可能没有足够的内存以打开该图像，也可能是该图像已损坏。请重新启动计算机，然后重 新打开该文件。如果仍然显示红色 “x”，则可能需要删除该图像，然后重新将其插入。
Session 3 Beyond Linear Programming 线性规划扩展——整数规划 整数规划 线性规划扩展
ZHOUYING
无法显示图像。计算机可能没有足够的内存以打开该图像，也可能是该图像已损坏。请重新启动计算机，然后重 新打开该文件。如果仍然显示红色 “x”，则可能需要删除该图像，然后重新将其插入。
无法显示图像。计算机可能没有足够的内存以打开该图像，也可能是该图像已损坏。请重新启动计算机，然后重 新打开该文件。如果仍然显示红色 “x”，则可能需要删除该图像，然后重新将其插入。
Session3 Beyond Linear Programming 整数规划
线性规划讲义
线性规划讲义一、引言线性规划是一种优化问题的数学建模方法，它可以用来解决一类特定的最优化问题。
本讲义将介绍线性规划的基本概念、问题形式化、求解方法以及应用领域。
二、线性规划的基本概念1. 线性规划定义线性规划是一种在给定的约束条件下，求解线性目标函数的最优解的数学问题。
线性规划的目标函数和约束条件都是线性的。
2. 线性规划的数学模型线性规划可以用数学模型来表示，一般形式为：最大化（或最小化）目标函数约束条件：线性规划的目标函数和约束条件可以包含多个变量和多个约束条件。
3. 线性规划的基本假设线性规划的求解过程基于以下假设：- 可行解存在：问题存在满足约束条件的解。
- 目标函数有界：问题存在有限的最优解。
- 线性关系：目标函数和约束条件都是线性的。
三、线性规划的问题形式化1. 目标函数的确定线性规划的目标函数可以是最大化或最小化某个特定的指标，如利润最大化、成本最小化等。
2. 约束条件的确定约束条件是限制问题解的条件，可以包括等式约束和不等式约束。
约束条件可以来自于问题的实际限制，如资源的有限性、技术要求等。
3. 决策变量的确定决策变量是问题中需要决策的变量，它们的取值将影响目标函数的值。
决策变量的选择应该与问题的实际需求相匹配。
四、线性规划的求解方法1. 图解法图解法是线性规划求解的一种直观方法，通过绘制约束条件的图形和目标函数的等高线，找到目标函数取得最大（或最小）值的点。
2. 单纯形法单纯形法是一种常用的线性规划求解算法，它通过迭代计算，逐步接近最优解。
单纯形法的基本思想是通过不断地移动到更优的解，直到找到最优解。
3. 整数规划的分支定界法整数规划是线性规划的一种扩展形式，它要求决策变量的取值为整数。
分支定界法是一种用于求解整数规划的方法，它通过将问题分解为多个子问题，并逐步缩小解空间，最终找到最优解。
五、线性规划的应用领域线性规划在实际问题中有广泛的应用，包括但不限于以下领域：- 生产计划与调度- 运输与物流管理- 金融投资组合优化- 能源调度与优化- 供应链管理等六、总结线性规划是一种重要的数学建模方法，它可以用来解决一类特定的最优化问题。
线性规划的扩展III
决策1
决策2
决策3
状态1 1 状态2 2 状态3 3 状态4
决策n 状态n
n
阶段1
阶段2
阶段3
阶段n
动态规划没有标准模型，没有唯一确定的解法
第四章 线性规划的扩展 (III)
动态规划的基本概念：
阶段k：表示决策顺序的离散量，阶段可按时间或空间划分。
状态Sk：能确定地表示决策过程当前特征的量。状态可以是数 量也可以是字符，数量状态可以是连续的也可以是离散的。
状态应演变到下一个阶段的哪一个起始点（本阶段 终点）；
每一个阶段的决策不仅影响到本阶段的效果，还影响 到下一阶段的初始状态，从而也影响到此后的演变 过程；
每一个阶段的决策不能只从这一阶段本身考虑，要考 虑整个过程的最优效果。
第四章 线性规划的扩展 (III)
求从A到E的最短路径问题，可以转化为三个性质完 全相同，但规模较小的子问题，即分别从B1、B2、 B3到E的最短路径问题。 记从Bi (i=1, 2, 3) 到E的最短路径为S(Bi)，则从A到 E的最短距离S(A)可以表示为：
引例中： Z ＝ 8X1+10X2 可变换为: 8X1+10X2＋d1-－d1+ = 56 2X1+ X2≤11 可变换为: 2X1+ X2＋d2-－d2+ = 11
第四章 线性规划的扩展 (III)
优先等级与权系数：要达到的多个目标之间有主次、轻重
缓急之分，因此各目标之间有优先等级。凡第一位要达到的目 标 定赋Pk予>>等Pk级+1,系P数k比PP1,k次+1位更的大赋的予优等先级权系。数相P同2等，级以的此以类不推同；的并权规 系数ω 加以区别。
Session4线性规划与扩展
Session4 Linear Programming With Spreadsheet
线性规划与电子表格
Mathematical Statement of LP Problem 线性规划的数学描述
线性规划要确定决策变量 ximize Z c1x1 cn xn
线性规划的基本概念
▪The Graphical Method for Solving LP 线性规划的图解法
▪ Using Excel Solver to Solving 用微软Excel Solver 求解
▪ Key Categories of LP Problems 线性规划问题的主要类型
▪Three Classic Applications of LP 三个经典的线性规划应用
椅 Profit = $15/Chair
School of Management, Harbin Institute of Technology
自己动手
Session4 Linear Programming With Spreadsheet
线性规划与电子表格
为了最小化成本或最大化利润的目的需要对一 些有限资源进行配置
Session4 Linear Programming With Spreadsheet
线性规划与电子表格
Solving Lego Problem 求解玩具拼装问题
▪ 用易理解方式输入数据和构筑数据之间的联系
▪ 定义目标单元格（目标函数）
▪ 确定可变单元格（决策变量）
▪ 添加约束变量（Adding Constraints）
Session4 Linear Programming With Spreadsheet
线性规划的扩展
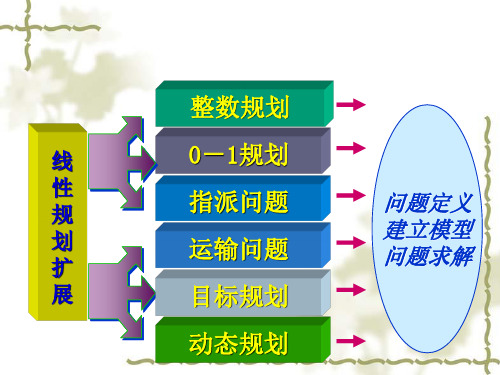
投资
max z
Pi x i
约束
i 1
N
s.t.
Iixi I
i 1
土地 约束
N
Lixi L
建厂
i 1 N
约束
xi r
i 1
x i 0,1
例4.3 考虑固定成本的最小生产费用问题
某工厂有三种设备均可生产同一产品， 第j种设备运行的固定成本为dj，运行的单位 变动成本为cj，则生产成本与产量xj的关系为：
设线性规划问题：
max z= CTX
s.t. AX = b X ≥0
最优解为Z’。则Z’为IP问题解Z*的上界，Z*≤Z’。
它的可行域为图中OABCDE（示 意图），并设最优解位于C。如 果这个最优解中所有的变量都是 整数，则已经得到整数规划的最 优解。如果其中某一个变量Xr不 是整数，则在可行域中除去一块 包含这个最优解但不包含任何整 数解的区域Ir<Xr<Ir+1（其中Ir 是变量Xr的整数部分），线性规 划的可行域被划分成不相交的两 部分，分别以这两部分区域作为 可行域，用原来的目标函数，构 造两个子问题Sub1和Sub2：
xj Myj x j 0, y j 0,1
这里M是一个很大的正数。
j 1,2,3
当yj=0时，xj=0，即第j种设备不运行，相应的运行成本
当yj＝1时，0≤xj≤M，实际上对xj没有限制，运行成本为 这是一个混合0-1规划问题
djyj+cjxj=0 dj+cjxj
➢ 整数规划的求解
图解法 分枝定界法 割平面法
如以下背包问题：
max z= s.t.
17x1 10x1 x1, x1,
+72x2 +42x2 x2, x2,
线性规划知识点总结
线性规划知识点总结引言概述：线性规划是一种数学优化方法，用于在给定的约束条件下最大化或者最小化线性目标函数。
它在各种领域中都有广泛的应用，包括经济学、管理学、工程学等。
本文将对线性规划的基本概念、模型构建、求解方法和应用进行详细阐述。
一、线性规划的基本概念1.1 目标函数：线性规划的目标函数是一个线性函数，用于表示需要最大化或者最小化的目标。
1.2 约束条件：线性规划的约束条件是一组线性等式或者不等式，用于限制变量的取值范围。
1.3 可行解与最优解：线性规划问题存在无穷多个可行解，但惟独一个最优解，即使满足所有约束条件且使目标函数取得最大（或者最小）值的解。
二、线性规划模型构建2.1 决策变量：线性规划模型中的决策变量是需要优化的变量，可以是实数、整数或者二进制数。
2.2 目标函数的构建：根据问题的具体要求，将目标转化为线性函数的形式，并确定是最大化还是最小化。
2.3 约束条件的建立：根据问题的限制条件，将其转化为线性等式或者不等式的形式，并确定约束条件的数学表达式。
三、线性规划的求解方法3.1 图形法：对于二维线性规划问题，可以使用图形法进行求解。
通过绘制约束条件的直线或者曲线，找到目标函数的最优解点。
3.2 单纯形法：单纯形法是一种常用的求解线性规划问题的方法。
通过迭代计算，不断改变基变量和非基变量的取值，直到找到最优解。
3.3 整数规划法：当决策变量需要取整数值时，可以使用整数规划法进行求解。
该方法将线性规划问题转化为整数规划问题，并采用分支定界等算法求解最优解。
四、线性规划的应用4.1 生产计划：线性规划可以用于确定最佳的生产计划，以最大化产量或者最小化成本。
4.2 资源分配：线性规划可以用于优化资源的分配，如确定最佳的人力资源配置、物资采购策略等。
4.3 运输问题：线性规划可以用于解决运输问题，如确定最佳的货物运输路线和运输量，以降低运输成本。
4.4 金融投资：线性规划可以用于优化金融投资组合，以最大化收益或者最小化风险。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
下图表示从起点A到终点E之间各点间的距离。求A 到E的最短路径。
B1
2 10 5 12 14
C1
9
3
6
6
D1
5
A
1
B2
13
10 4
C2
5
8
E D2
10 2
B3
12 11
C3
阶段1
阶段2
阶段3
阶段4
第四章 线性规划的扩展 (III)
每一个阶段都至少有一个起始点－－初始状态（如Bi) 每一个阶段都需要作一个选择－－决策本阶段由初始 状态应演变到下一个阶段的哪一个起始点（本阶段 终点）； 每一个阶段的决策不仅影响到本阶段的效果，还影响 到下一阶段的初始状态，从而也影响到此后的演变 过程； 每一个阶段的决策不能只从这一阶段本身考虑，要考 虑整个过程的最优效果。
第四章 线性规划的扩展 (III)
最优化原理
最佳路径中任一状态（中间某点）到最终状态（最 终点）的路径也是该状态到最终状态一切可能中的 最短路径。
A
阶段1
Bi
阶段2
Cj
阶段3
Dt
阶段4
E
C 'j
·
' Dt
·
第四章 线性规划的扩展 (III)
动态规划的方法（教材P92）
将完整的问题划分成若干个阶段； 明确最终要达到的目的； 从最终结果倒推，逐个阶段地作出决策； 回到出发点，作出最后一个决策，再向前推 可得到每一阶段的最优决策。
应用运筹学
第四章 线性规划的扩展 (III)
目标规划 动态规划
第四章 线性规划的扩展 (III)
目标规划
解决需要考虑多个目标的决策问题 目标规划与线性规划比较： 线性规划 目标规划 问题： 单目标 多目标 约束： 硬约束、矛盾 划分等级 求解： 绝对最优 实际满意 目标规划是在满足现有的一组约束条件下，求出尽 可能接近理想值的解。
第四章 线性规划的扩展 (III)
例4－9 ：引例问题的目标规划模型 在原材料供应严格限制的条件下，考虑：
产品 I 的产量不超过产品 II ； 优先因子 P1 尽可能利用设备，但不希望加班； 优先因子 P2 应尽可能达到（超过）利润指标56元。 优先因子 P3 目标函数： MIN Z = P1d1++P2(d2- + d2+)+P3d3s.t. 2X1 + X2 ≤ 11 X1 X2 + d1- - d1+ = 0 （≤0） X1 + 2X2 + d2- - d2+ = 10 （＝10） 8X1 + 10X2 + d3- - d3+ = 56 （ ≥56） X1 ,X2 ,d1- ,d1+ ,d2-, d2+ , d3- ,d3+ ≥0
95
140 110 伦敦
140 8
110
5
9
阶段4 阶段3 阶段1
第四章 线性规划的扩展 (III)
例4－11 教材P95 实例4.14（资源分配） 一家医院有5位护士要分派到3个病房，不同数量的护 士在每个病房的作用如表，如何分配使总作用最大？ 护士 人数
0 1 2 3 4 5
在病房中的作用 X Y Z
动态规划解决多阶段决策问题
动态规划没有标准模型，没有唯一确定的解法
第四章 线性规划的扩展 (III)
动态规划的基本概念：
阶段k：表示决策顺序的离散量，阶段可按时间或空间划分。
状态Sk：能确定地表示决策过程当前特征的量。状态可以是数 量也可以是字符，数量状态可以是连续的也可以是离散的。
状态变量Xk：表示每一状态可以取不同值的变量。
0 4 6 10 14 16 0 4 8 13 15 16 0 6 9 13 16 17
请思考： 能否用线性规划来做？
动态规划思路：
护士分到X后就不能再分到Y与Z， 因此可考虑先分配给X,再分配给Y， 最后分配给Z。
每一阶段可分配数是前一阶段做
决策时的可分配数减去实际分配数。
剩余
22 4 8 19 15 13 16 4 14 0 23 4 6 10 14 16 3 10 5 0
第四章 线性规划的扩展 (III)
动态规划举例：例4－10 教材P92 实例4.13
行进方向 起点 寻优方向 205 终点
125 95
110 6 125 95 7 0
305 420
格拉斯哥 130 110 1 310 2
120 105 110 130
3 200 4
235
105
140 130 125 阶段2
剩余 Y 分1个
17 5 16 4 13 3 9 0 4 8 0 2 6 6 13 17
X 分0个
Z
16
分5个
S
5
9
0
F
2
6 1
分5个
0
4
第四章 线性规划的扩展 (III)
优先等级与权系数：要达到的多个目标之间有主次、轻重
缓急之分，因此各目标之间有优先等级。凡第一位要达到的目 标赋予等级系数P1,次位的赋予等级系数P2，以此类推；并规 定Pk>>Pk+1, Pk比Pk+1更大的优先权。相同等级的以不同的权 系数ω 加以区别。
目标规划的目标函数： 目标规划的目标函数是按各目标
d1F E X1-X2 = 0
C G
D
d1+
8X1+10X2 = 56 X1+2X2 =10
d3+
d2＋
O A
d3
-
H
d2
-
第四章 线性规划的扩展 (III)
例4－10 ：建立目标规划模型并求解
某电视机厂装配黑白和彩色两种电视机，每装配一台电视机需占用装配 线1小时，装配线每周计划开动40小时。预计市场每周彩电的销量是 24台；黑白电视机的销量是30台。该厂确定的目标为： 第一优先级：充分利用装配线，每周计划开动不低于40小时； 第二优先级：允许装配线加班，但加班时间每周尽量不超过10小时。 第三优先级：装配电视机的数量尽量满足市场需要，因彩电利润高于 黑白电视机，取其权系数为2。
状态转移函数在本例中为距离和最小
第四章 线性规划的扩展 (III)
同样，计算S(B1)又可以归结为性质完全相同，
但规模更小的问题，即分别求C1，C2，C3到E的 最短路径问题S(Ci) (i=1, 2, 3)，而求S(Ci)又可以 归结为求S(D1)和S(D2)这两个子问题。从图中可 以看出，在这个问题中，S(D1)和S(D2)是以知的， 它们分别是： S(D1)=5，S(D2)=2 因而，可以从这两个值开始，逆向递归计算S(A) 的值。
例4－10的图解
X2 X1+X2=40 X2 = 30 D
C
d3H G
第一级： d1－ 取最小为0 第二级： d2+ 取最小为0， 只能在ABCD范围 第三级：d3- 的权数大，先取 取d3- 最小0，范围为ABEF 再取d4-最小，只能是E点
d3+
E
d4+ d4X1+ X2 =50
步骤： 1 先作绝对约束 2 再作d=0时的 目标约束 3 标出d+， d的方向 4 按优先的次序 逐个使目标函 数中的极小偏 差变量取零， 缩小可行域， 找出问题解。
第四章 线性规划的扩展 (III)
目标规划引例
某厂生产I,II两种产品： I 2 1
8
这是一个单目标规划
原材料 设 备 利润
II 1 2
10
拥有量
11 10
线性规划模型： MAX Z ＝ 8X1+10X2 s.t. 2X1+ X2≤11 X1+2X2≤10 X1,X2≥0 最优方案为： X1=4 X2=3
约束的正、负偏差变量和赋予相应的优先因子而构造的。当每 一目标值确定后，决策者的要求是尽可能缩小偏离目标值，因 此目标规划的目标函数只能是 MIN Z = f（d+,d- )。 要求恰好达到目标值（正负偏差都要尽可能地小），这时 MIN Z = f（d+ ＋ d- ) 要求不超过目标值（允许达不到，正偏差要尽可能地小） MIN Z = f（d+ ) 要求不低于(至少达到）目标值： MIN Z = f（d- )
等级 I II III 工资额 （元/年） 2000 1500 1000 现有人数 10 12 15 编制人数 12 15 15
合计
37
42
第四章 线性规划的扩展 (III)
动态规划
将过程按时间、空间等标志分为若干个阶段； 每一个阶段都需要作出决策； 阶段决策依赖于当前状态，又影响以后发展。
决策1 状态1 1 阶段1 状态2 决策2 2 阶段2 状态3 决策3 3 阶段3 状态4 状态n 决策n n 阶段n
决策dk：从某一状态向下一状态过渡时所做的选择。决策是所 在状态变量的函数，记为dk(Xk)。
决策允许集合Dk(xk)：在状态Xk下，允许采取决策的全体。
状态转移方程Xk+1=T(Xk,dk)：某一状态以及该状态下的决策， 与下一状态之间的函数关系。
第四章 线性规划的扩展 (III)
动态规划典型问题－－最短路径
F
d1
X1 = 24 O
+
d2＋ d2-
E(24,26) 是满意解 彩色24台 黑白26台
X1
d1-
A
B
第四章 线性规划的扩展 (III)
练习：建立目标规划模型 某单位领导在考虑本单位职工的升级调资方案时，依次遵守以下 规定： 1.不超过年工资总额60000元； 2.每级的人数不超过定编规定的人数； 3.II，III级的升级面尽可能达到现有人数的20％； 4.III级不足编制的人数可录用新职工，又I级的职工中有10％ 要退休。 有关资料汇总于下表中，问该领导应如何拟定一个满意的方案。