第7章_简谐振动

合集下载

高一物理必修一每章笔记

高一物理必修一每章笔记摘要：1.物理必修一的概述2.第一章：运动的描述3.第二章：匀变速直线运动4.第三章：相互作用力的性质及其应用5.第四章：牛顿运动定律及其应用6.第五章：万有引力和重力7.第六章：动量守恒定律和能量守恒定律8.第七章：圆周运动9.第八章：简谐振动10.第九章：机械能守恒定律正文：高一物理必修一是高中物理学习的重要阶段，它为后续学习打下了坚实的基础。

本教材共分为九章，下面将逐一介绍每章的主要内容。

第一章：运动的描述。

本章主要介绍物理中对运动的基本描述，包括位置、速度、加速度等物理量，以及它们之间的关系。

第二章：匀变速直线运动。

本章重点讲解匀变速直线运动的基本概念、运动规律和解题方法。

第三章：相互作用力的性质及其应用。

本章主要介绍相互作用力的性质，包括作用力和反作用力、平衡力等，并讲解它们在实际问题中的应用。

第四章：牛顿运动定律及其应用。

本章是物理学习的核心部分，主要介绍牛顿三定律，以及它们在解决实际问题中的应用。

第五章：万有引力和重力。

本章主要介绍万有引力定律和重力势能的概念，以及它们在物理中的应用。

第六章：动量守恒定律和能量守恒定律。

本章主要介绍动量守恒定律和能量守恒定律，以及它们在解决实际问题中的应用。

第七章：圆周运动。

本章主要介绍圆周运动的基本概念和运动规律，包括角速度、线速度、向心加速度等。

第八章：简谐振动。

本章主要介绍简谐振动的基本概念和运动规律，包括振幅、周期、频率等。

第九章：机械能守恒定律。

本章主要介绍机械能守恒定律，以及它在解决实际问题中的应用。

新人教版第7章实验9用单摆测量重力加速度的大小课件(44张)

Δt，该小组同学利用图像来分析数据，以 cos θ 为横轴，以_D__为纵轴，
可作出图像为如图丙所示的一条直线。
A．Δt
B.(Δt)2
1
1
C.Δt
D.Δt2
kD2
(4)若求得图像斜率的绝对值为 k，则当地的重力加速度为 g＝_2_L_(用
D、k、L 表示)。
[解析](1)根据螺旋测微器读数规则得小球的直径 D 为 D＝(5.5＋ 17.0×0.01) mm＝5.670 mm。
实验步骤如下： (1) 用螺旋测微器测出小球的直径 D ，示数如图乙，小球直径 D ＝ ___________ mm； (2)将小球拉至偏离竖直方向的某位置，测出此时细绳与竖直方向的夹角θ；
(3)多次从不同夹角 θ 处释放，并测出相应的小球经过光电门的时间
(2)图乙和图丙为细线上端的两种不同的悬挂方式．应该选图_丙__所示的悬挂方式。
(3)该同学用游标卡尺测量小球的直径，测量的刻度部分如图丁所示，则小球的直径为_______________ cm。
(4)该同学通过改变细线长度进行多次测量，记录每次测得的周期T 和对应的细线长度L，画出的T2－L图像如图戊所示，π≈，由此得当地重力加速度为____________ m/s2(结果保留三位有效数字)。
[解析](1)实验所用小球的密度要大，体积要小，选项A错误；为了减小误差，测量周期时要测量至少30次全振动的时间，然后计算周期的平均值，选项B错误；实验时小球的摆动幅度不大于5°，否则就不是简谐振动了，选项C错误；为了减小误差，悬挂小球的细绳的质量要尽可能小些，选项D正确。
(2)图乙和图丙为细线上端的两种不同的悬挂方式，乙图中当摆球摆动时会导致摆长变化，则应该选图丙所示的悬挂方式。

内科大安全环境监测技术教案第7章振动检测

【课堂教学小结】3分钟）1、振动与噪音本质上相同，只是频率和传播介质不同。

2、我们所学振动检测，重点掌握环境振动的检测，适合我们矿业的作业场所。

参考位置等优点，由于它的脉冲响应优异，更适合于冲击的测量。

CI=史=2力V=Q时)2Adt4)拾振器的充分利用一般情况尽量用同参数相应的传感器进行测量，也可用电学微积分原理进行测量，但测量误差较大。

7.4拾振器7.4.1 压电式加速度计1.1.1 工作原理(1)组成：压电晶体、弹簧元件、外壳、引线。

(2)原理：(图示说明)2)特点体积小、灵敏度高、测量频率宽。

3)主要参数(1)灵敏度:输出量的变化与输入量变化的比值(2)安装方法与上限频率(3)前置放大器与下限频率(4)横向灵敏度(5)动态范围(6)环境影响程度1.1.2 磁电式速度计1)结构原理(1)组成：线圈、磁钢、顶杠、弹簧片、附件。

(2)原理：切割磁力线产生感生电动势(图示说明)。

2)特点a.只能测量质点振动b.可以做成相对和绝对两种(约20分钟) (约20分钟)c.输出幅度大d.输出阻抗低e.体积较压电式大1.1.3 拾振器的合理选择1）自振频率和工作频率的选择2）灵敏度的选择3）测量范围的选择4）测量内容的选择（本节无作业）【课堂教学小结】（3分钟）1、振动测量主要是根据振动类型正确选择拾振器;2、合理布置拾振器；3、准确分析测量结果。

（约12分钟）举例课程名称：安全环境监测技术7∙6测振仪的校准与标定1）标定内容X⑴拾振器灵敏度标定在振动台上进行，fW200Hz,a≤10g灵敏度Sv=U∕Xa=4π2f2A A为振幅读书；U为输出电压；f为频率（2）实验室条件下的二次标定2）频率特性的标定（1）频率响应：测频带（带宽）⑵谐振频率7.7振动允许标准（约20分钟）D人体允许振动标准（246页）人体可以通过各种感受器接收振动的信息，并通过大脑对振动作出相应的反应和判断。

根据振动对人影响的程度，可以建立振动的评价标准。

ANSYS Workbench 17·0有限元分析：第7章-谐响应分析

第7章谐响应分析
谐响应分析主要用来确定线性结构在承受持续的周期载荷时的周期性响应（谐响应）谐响应分析能够预测结构的持续动力学特性，从而验证其设计能否成功地克服共振、疲劳及其他受迫振动引起的有害效果。

通过本章的学习，即可掌握在★ 了解谐响应分析。

7.1 谐响应分析概述
谐响应分析（Harmonic Response Analysis ）是用于确定线性结构在承受一个或多个随时间按正弦（简谐）规律变化的载荷时稳态响应的一种技术。

分析的目的是计算出结构在几种频率下的响应并得到一些响应值（通常是位移）对应频率的曲线。

从这些曲线上可以找到“峰值”响应，并进一步考察频率对应的应力。

谐响应分析技术只计算结构的稳态受迫振动。

发生在激励开始时的瞬态振动不在谐响应分析中考虑。

谐响应分析是一种线性分析。

任何非线性特性，如塑性和接触（间隙）单元，即使被定义了也将被忽略，但在分析中可以包含非对称系统矩阵，如分析流体——结构相互作用问题。

谐响应分析同样也可以分析有预应力的结构，如小提琴的弦（假定简谐应力比预加的拉伸应力小得多）。

对于谐响应分析，其运动方程为：
[][][](){}{}(){}{}()21212
M i C K i F i F ωωφφ−+++=+ 这里假设刚度矩阵[]K 、质量矩阵[]M 是定值，要求材料是线性的、使用小位移理论（不包括非线性）、阻尼为[]C 、简谐载荷为[]F 。

谐响应分析的输入条件包括：
已知幅值和频率的简谐载荷（力、压力和强迫位移）。

简谐载荷可以是具有相同频率的多种载荷，力和位移可以相同或者不相同，但是压力分布
载荷和体载荷只能指定零相位角。

第七章振动和波动(2)

y
u
x
x = u t
O
t
t + t
x
y
O
u t + t
x y A cos[ ( t ) ] u
x
★ 波函数的物理意义
t
— 波函数既描述了波线上各质点振动状态及相位差异，又描述了随着时间的推移，波形以波速 u 沿传播方向传播的
情况，具有完整的波动意义。
★ 简谐波具有空间和时间周期性：

2
①
t x y 1.0 cos[ 2 ( ) ] 2.0 4.0 2
(2) 将 t = 1.0 s 代入 ①式得出此时刻波形方程:
1.0 x y 1.0 cos[2 ( ) ] 1.0 cos( x ) 2.0 4.0 2 2 2 y /m u ② y 1.0 sin x 1.0 2 由②式可画出 t = 1.0 s 的波形图：
2、横波和纵波
1）横波: 振动方向⊥传播方向的波。 2）纵波: 振动方向∥传播方向的波。
固体中的波源可以产生横波和纵波。液体和气体中的波源只能产生纵波。水面波既不是纵波，也不是横波。
任一波(如水波、地表波)都能分解为横波与纵波进行研究。
3、波的几何描述
1）波面 — 振动相位相同的各点连成的面(同相面)。
空间上每隔λ的距离出现振动状态相同的点；时间上每隔 T 的时间波形重复一次。
★ 平面简谐波的波函数既适用于横波，也适用于纵波。
3.波沿着x轴负方向传播
y A cos [ t 2
4.波函数的复数表示
波函数
x

]
]
y A cos [ t 2

大学物理第七章习题及答案

第七章振动学基础一、填空1．简谐振动的运动学方程是。

简谐振动系统的机械能是。

2．简谐振动的角频率由决定，而振幅和初相位由决定。

3.达到稳定时，受迫振动的频率等于，发生共振的条件。

4．质量为10-2㎏的小球与轻质弹簧组成的系统，按20.1cos(8)3x t ππ=-+的规律做运动，式中t 以s 为单位，x 以m 为单位，则振动周期为初相位速度最大值。

5．物体的简谐运动的方程为s ()x A in t ωα=-+，则其周期为，初相位6．一质点同时参与同方向的简谐振动，它们的振动方程分别为10.1cos()4x t πω=+，20.1cos()4x t πω=-，其合振动的振幅为，初相位为。

7．一质点同时参与两个同方向的简谐振动，它们的振动方程分别为)4cos(06.01πω+=t x ，250.05cos()4x t πω=+，其合振动的振幅为，初相位为。

8．相互垂直的同频率简谐振动，当两分振动相位差为0或π时，质点的轨迹是当相位差为2π或32π时，质点轨迹是。

二、简答1．简述弹簧振子模型的理想化条件。

2．简述什么是简谐振动，阻尼振动和受迫振动。

3．用矢量图示法表示振动0.02cos(10)6x t π=+,(各量均采用国际单位).三、计算题7.1 质量为10×10-3㎏的小球与轻质弹簧组成的系统，按X=0.1cos （8πt+2π/3）的规律做运动，式中t 以s 为单位，x 以m 为单位，试求：（1）振动的圆频率，周期，初相位及速度与加速度的最大值；（2）最大恢复力，振动能量；（3）t=1s ，2s ，5s ，10s 等时刻的相位是多少？（4）画出振动的旋转矢量图，并在图中指明t=1s ，2s ，5s ，10s 等时刻矢量的位置。

7.2 一个沿着X 轴做简谐振动的弹簧振子，振幅为A ，周期为T ，其振动方程用余弦函数表示，如果在t=0时刻，质点的状态分别为：（1）X 0=-A ；（2）过平衡位置向正向运动；（3）过X=A/2处向负向运动；（4）过X=2A处向正向运动。

简谐振动

x x1 x 2
x1
v0
O x0
k • 频率 ω M m
2 v A x0 2 02 ω
x
v0 φ0 tg ωx0
1
( M m) g Mg mg x0 k k k
掌握初始条件的确定方法
14
简谐振动总结
分析振动系统求动力学方程求运动学方程
• •
动力学特征
1. 动能
1 1 2 2 2 Ek mv kA sin ( t ) 2 2
1 t T 1 2 Ek Ek dt kA T t 4
2. 势能
1 2 Ek max kA 2 E k min 0
1 2 1 2 E p kx kA cos 2 ( t ) 2 2
3. 机械能
1 2 E Ek E p kA （简谐振动系统机械能守恒） 2
11
例物理摆如图所示, 设刚体对轴的转动惯量为J. 设 t = 0 时摆角向右最大为 0. 求振动周期和振动方程.
解 M m g h sin J
mgh sin 0 J
5 时 , sin

mgh 0 J
振动方程
mgh J
单摆
J T 2 mgh
h T 2 g
12
0 cosω t
例
竖直方向的弹簧振子，求振动方程。解分析系统受力
线性回复力
l0
k O
f
x
i
mg k (Δl x ) mg k Δ l kx kx
l
m
x
d x k x0 2 dt m

第7章机械波

第7章机械波思考题7-1 简谐波与简谐振动有何区别和联系?答：简谐振动在无吸收的弹性介质中传播形成简谐波．介质中在波线方向上的各质元都在做简谐振动．7-2 关于波长的概念有三种说法，分析它们是否一致：(1) 同一波线上，相位差为２π的两个振动质点之间的距离；(2) 在一个周期内，振动所传播的距离；(3) 横波的两个相邻波峰（或波谷）之间的距离；纵波的两个相邻密部（或疏部）对应点之间的距离．答：这三种说法是一致的．第一种说法和第三种说法体现了波动过程在空间上的周期性；第二种说法体现了波动过程在时间上的周期性．7-3 在同一种介质中传播着两列不同频率的简谐波,它们的波长是否可能相等?为什么?如果这两列波分别在两种介质中传播,它们的波长是否可能相等?为什么?答：因波速仅与介质有关，而波长νλu uT ==，所以在同一种介质中传播的两列不同频率的简谐波，波速相等，但波长不会相等．如果两列波分别在两种介质中传播，那么只要满足2211ννu u =，它们的波长就会相等．7-4平面简谐波的波函数])(cos[),(ϕω+-=u x t A t x y 中的ux 表示什么？ϕ表示什么？如果把它写成])cos[(),(ϕωω+-=u x t A t x y ，那么ux ω又表示什么？答：u x 表示振动由O 点传到波线上距O 点为x 处的某点所需时间．u x ω表示波线上距O 点x 处的某点坐标比坐标原点落后的相位．7-5 在波传播方向上的任一质点振动相位总是比波源的相位落后，这一说法正确吗？答：正确．因为振动是从波源传向介质中各质元的．7-6 在相同温度下氢气和氦气中的声速哪个大？答：在相同温度下氢气和氦气当作理想气体，理想气体中传播纵波的速度M RTu γ=，温度T 相同，设摩尔数也相同，则摩尔质量M 不同，引起波速u 不同．所以氢气中的声速大于氦气中的声速．7-7 一平面简谐波沿一拉紧的弦线传播，波速νλ=u ，有人说可以利用提高弦的振动频率来提高波的传播速度，这一说法正确吗？如何才能提高波速呢？答：不正确．因为波速与介质有关．而与振动的频率无关．增大张力可以提高波速．7-8 从能量的观点看，谐振子与传播介质中的体积元有何不同？答：孤立的谐振子势能最大时动能为零，势能为零时动能最大，势能与动能相互转化，但总的机械能守恒，这表明它储存着一定的能量．传播介质中体积元则不相同，势能最大时动能也最大，势能为零时动能也为零，总机械能不守恒，它在零到最大值之间周期性的变化，不断地将来自波源的能量沿波的传播方向传出去．可见，弹性介质本身并不能储存能量，它只起到传播能量的作用．7-9我们知道机械波可以传送能量，那么机械波能传送动量吗?答：不能．介质中质元以平衡位置来回移动而没有质元的移动，故不能传送动量． 7-10波从一种介质进入另一种介质，波长、频率、波速、能量等各物理量中，哪些量会变化？哪些量不变化？答：波长、波速和能量变化，频率不变．原因是：波动的频率与波源相同，与介质无关，所以不会改变．波速与传播介质的性质有关，所以两种介质中波速不同．波长由νλ/u uT ==决定，因此波长也要改变．能量与介质密度有关，所以两种介质中波能量也不相同．7-11一平面简谐波在弹性介质中传播，在某一瞬时，介质中某质元正处于平衡位置，此时它的动能和势能如何？若该质元处于位移最大处时，情况又如何？答：由平面简谐波任一质元的动能和势能表达式V ux t A m E k d )(sin 21)d (21d 2222-==ωωρυ V ux t A E P d )(sin 21d 222-=ωωρ 可以看出，动能和势能相等，具有完全相同的周期性．当质元处于平衡位置时，形变消失，所以势能为零，则动能也为零．当质元处于最大位移处时，形变最大，势能也最大，则动能最大．7-12为什么声波的衍射比光波的衍射更显著？答：因为衍射现象是否显著，与障碍物（如狭缝）的尺寸和波的波长之间关系有关．当障碍物尺寸一定时，波长越长，衍射现象越明显．与光波相比，声波具有较长的波长，所以衍射效应明显．7-13两振幅相等的相干波在空间相遇，由加强和减弱的条件可得出相互加强处，合强度是一列波强度的4倍；相互减弱处，合强度为零．试问加强处的能量是哪来的？减弱处的能量去了哪里？答：振幅相同的两列相干波在同一介质中传播时，由于干涉，使得某些相遇点的振动的合振幅为原来单独一个波时的2倍，一些点的振动的振幅为零，还有更多的点的合振动的振幅介于这两个值之间．而振幅的平方代表能量，因此，从合振动的结果来看，振动的能量在干涉加强处集中，不但是合振动振幅为零的点的能量，其他合振动振幅变小的点的能量都有向干涉加强点集中的趋势．7-14驻波和行波有什么区别？驻波中各质元的相位有什么关系？为什么说相位没有传播？驻波中各质元的能量如何变化的？为什么说能量没有传播？驻波的波形有何特点？答：行波是指扰动的传播，在波线方向上波形随时间做周期性的变化；而驻波是由两列同频率、同振动方向、但传播方向相反的行波合成的，在波线方向上波形不随时间变化．驻波中两相邻波节间各质元的相位相同，一波节两侧的各质元相位相反．没有相位的传播是因为驻波没有波形的跑动，驻波方程中没有)(u x t -ω因子．不存在振动状态的传播，所以没有相位的传播．7-15当飞机飞行速率与声速相同时，该声速区称为“声障”．飞机必须尽快越过“声障”，进入超音速区，否则会给飞行带来危险，这是为什么？答：当飞机飞行速率与声速相同即u S =υ时，马赫锥的半顶角2arcsin πυα==S u，这时马赫锥展开为平面，即波源在所有时刻发出的波几乎同时到达接受器，因此该冲击波的强度极大，声速区就构成了一个“声障”．机体的任一振动所产生的声波都将尾随在机体附近并引起机身的共振，极易造成机毁人亡．因此在飞机加速飞行时，必须尽快越过“声障”进入超音速区．习题7-1 太平洋上有一次形成的洋波速度为740 km/h ，波长为300 km ．这种洋波的频率是多少？横渡太平洋8000 km 的距离需要多长时间？解： Hz 109.6Hz 36001030010740433-⨯=⨯⨯⨯==λνu h 10.8h 7408000===u s t 7-2 一平面简谐波 )]30-π(0.5sin[2.0t x y =x 、y 的单位为厘米，t 的单位为秒．求波的振幅、波长、频率、波速以及x =1cm 处质元振动的初相位．解：]2π)60-π(30cos[2.0 )]30-π(0.5-2πcos[2.0 )]30-π(0.5sin[2.0+===x t t x t x y 与])(cos[ϕω+-=uxt A y ，νωπ2=相比较，可得 cm 2.0=A ，Hz 15π2==ων，cm/s 60=u ，2π=ϕ，cm 41560===νλu x =1cm 处质元振动的初相位为02π16030π=+⨯- 7-3 一列沿x 轴正向传播的机械波,波速为2 m/s ,原点振动方程为t y πcos 6.0=,试求：(1) 此波的波长；(2) 波函数；(3) 同一质元在1 s 和2 s 末两个时刻的相位差；(4) m 1=A x ，m 5.1=B x 处两质元在同一时刻的相位差解：(1)此波的频率为Hz 5.0Hz π2ππ2===ων 此波的波长为 m 4m 5.02===νλu(2) 代入波函数方程，得此波的波函数为)]2(πcos[6.0x t y -= (3)将s t 2=和s t 1=分别代入上述波函数中相位部分)2(πx t -，可得同一质元在1s 和2s 末两个时刻的相位差 π12=-=∆ϕϕϕ(4) 同理将m 1=A x ，m 5.1=B x 代入相位表达式，可得这两点处的质元在同一时刻的相位差 4π=∆ϕ 7-4一横波沿绳传播，其波函数为 m )0.2200(π2sin 02.0x t y -=(1) 求此横波的波长、频率、波速和传播速度；(2) 求绳上质元振动的最大速度，并与波速比较．解：将波函数的标准形式转换成用表达的形式，即]2π)(π2[Asin ])(π2cos[++-=+-=ϕλνϕλνx t x t A y 将m )0.2200(π2sin 02.0x t y -=与上式比较可以得出Hz 200=ν，m 50.0=λ，m/s 100==λνu并可以判定波是沿x 轴正向传播的．质元振动的速度为)0.2200(π2cos 200π202.0x t ty -⨯⨯=∂∂=υ m/s 25m/s 200π202.0max =⨯⨯=υ7-5一平面简谐波沿x 轴正向传播，其振幅和圆频率分别为A 和ω，波速为u ，设t = 0时的波形曲线如图7-22所示．(1) 写出此波的波动方程；(2) 求距O 点分别为λ/8和3λ/8两处质元的振动方程；(3) 求距O 点分别为λ/8和3λ/8两处质元在0=t 时刻的振动速度．图7-22解：(1) 以O 点为坐标原点，由图可知，初始条件为0cos 0==ϕA y ，0sin 0<-=ϕωυA所以初相 2π=ϕ 波动方程为 ]2π)(c o s [+-=u x t A y ω (2) 8λ=x 处质点的振动方程为)4πcos(]2π)π2/8/(cos[+=+-=t A t A y ωλωλω 83λ=x 处质点的振动方程为 )4πcos(]2π)π2/8/3(cos[-=+-=t A t A y ωλωλω (3) x 处质点振动速度为 ]2π)(sin[+--=∂∂=u x t A t y ωωυ 所以0=t 时刻，8λ=x 处质点的振动速度为ωλλωυλA A t x 22)2ππ2/8/sin(0,8/-=+--=== 同理可得0=t 时刻，83λ=x 处质点的振动速度为 ωυλA t x 220,8/3=== 7-6 一脉冲从长弦线的一端行进至另一端，需时0.1秒，弦线跨过一滑轮后悬一质量为弦线质量100倍的重物，求弦线的长度．解：设重物质量为m ，弦线长度为l ，lm l m mg T 100 ,100 ,0===ηη gl l mm g T u 1001000===η22100 ,100glt l t gl ut l ===所以 m 8.9)1.0(8.910010022=⨯⨯==gt l7-7 声波的频率大约在Hz 102~204⨯的范围内．已知声波在0゜C 空气中的波速为331.5 m/s ，在20゜C 水中的波速为1483 m/s ．那么相应温度下声波在空气和水中的波长范围分别是多少？解：因机械波的波长为νλu =．所以在0゜C 的空气中声波的最长波长和最短波长分别为 m 16.58m 205.331minmax ===νλu m 101.658m 1025.33124max min -⨯=⨯==νλu即在0゜C 的空气中，声波的波长范围大约为17mm 至17 m ．同理，在水中，m 15.47m 201483minmax ===νλu m 10415.7m 102148324max min -⨯=⨯==νλu即在20゜C 的水中，声波的波长范围大约为74mm 至74 m7-8 纸盆半径m 1.0=R 的扬声器，辐射出频率Hz 1000=ν，功率 W 40=P 的声波．设空气密度3kg/m 29.1=ρ，声速m/s 344=u ，不计空气对声波的吸收，求纸盆的振幅．解：由于辐射功率2222π21πR u A R I P ωρ=⋅= 所以得纸盆振幅 m1082.3 m 1.01000π21π34429.14021π24-⨯=⨯⨯⨯⨯⨯==R u P A ωρ7-9两个不同的音叉在完全相同的两段长绳上产生稳定的简谐波，振幅212A A =，波长2121λλ=，设绳子除了与音叉交换能量外，不与其他物体交换能量．求音叉给于绳子的平均功率之比．解：设绳子的截面积为S ，体密度为ρ，线密度为η，则η=ρs.u A uS A IS P 22222121ηωρω=== 两绳完全相同意味着η相同，绳子张力T 相同，因而波的传播速度u 相同．今两音叉产生的两列简谐波，波长不同，而波速相同，可见频率是不同的：12212121//λλλλννωω===u u 1622)()(2121222212212222212121=⋅===A A u A u A P P ωωηωηω 7-10如图7-23所示，两相干波源分别在P ，Q 两点，它们发出频率为ν，波长为λ，初相相同的两列相干波，设λ23=PQ ，R 为PQ 连线上的一点．求： (1) 自P ，Q 发出的两列波在R 处的相位差；(2) 两波在R 处干涉时的合振幅．图7-23解：(1) 设两相干波的振幅分别为21A A 和，PR 之间的距离为PR r ，QR 之间的距离为QR r ，相位差π3π2π2==-=∆λλϕPQ QR PR r r r (2) 两相干波在R 点叠加干涉减弱，合振幅21212221cos 2A A A A A A A -=∆++=ϕ7-11如图7-24所示，S 1、S 2是两相干波源，相距1/4波长，S 1比S 2比相位超前π/2．设两波在S 1、S 2连线上的强度相同，均为I 0，且不随距离变化，问S 1、S 2连线上在S 1外侧各点处的强度I 1多大？在S 2外侧各点处的强度I 2多大？图7-24解：取S 1、S 2连线方向为正向，原点取在S 1处，如图所示．S 1发出的波的表达式为0 )](cos[0 )](cos[1⎪⎪⎩⎪⎪⎨⎧<+>-=x u x t A x u x t A y ωω S 2发出的波的表达式为4 ]2π)4/(cos[4 ]2π)4/(cos[2⎪⎪⎩⎪⎪⎨⎧<--+>---=λλωλλωx u x t A x u x t A y 利用关系式π2 ,==T T u ωλ，则2y 的表达式可改写为4 ]π)(cos[4 )](cos[2⎪⎪⎩⎪⎪⎨⎧<-+>-=λωλωx u x t A x u x t A y在S 1外侧，x <0 0 ]π)(cos[ )](cos[21=-+++=+=ux t A u x t A y y y ωω 所以合成波的强度I 1=0.在S 2外侧，4λ>x)](cos[2 )](cos[ )](cos[21ux t A u x t A u x t A y y y -=-+-=+=ωωω 0222224214)2(21I u A u A I =⋅==ρωρω 7-12如图7-25所示是干涉型消声器结构原理图，利用这一原理可以消除噪声．当发动机排气噪声声波经管道到达A 时，分成两路而在B 点相遇，声波因干涉而相消．如果要消除频率为300 Hz 的发动机排气噪声，求图中弯道与直管长度差12r r r -=∆至少应为多少（设声波速度为340 m/s ）图7-25解：这是干涉的应用问题．根据干涉原理，两波在B 点相遇时的波程差12r r r -=∆满足干涉相消条件，即) ,3 ,2 ,1 ,0( ,2)12(⋅⋅⋅±±±=+=∆k k r λ所以当0=k 时，r ∆最小，即为弯道与直管长度差 m 57.0300234022min =⨯===∆νλu r ． 7-13主动脉内血液的流速一般为0.32 m/s ．若沿血流方向发射4.0 MHz 的超声波，该红血球反射回的波与原发射波将形成的拍频是多少？已知声波在人体内的传播速度为m/s 1054.13⨯．解：Hz 1066.1Hz 101.54104.00.3222)1(336⨯=⨯⨯⨯⨯==+--=∆u u u υνυυνν 7-14两列相干波(振幅相等)，相向在同一条直线上传播(x 轴)，已知x = 0处为波节，写出波腹点和波节点的坐标．解： ) ,2 ,1 ,0( ,2⋅⋅⋅±±==k k x λ波节) ,2 ,1 ,0( ,4)12(24⋅⋅⋅±±=+=+=k k k x λλλ波腹 7-15设沿弦线传播的一入射波的表达式为 ])(π2cos[ϕλ+-=x T t A y 入波在x = L 处发生反射，反射点为固定端如图所示7-26．设波在传播和反射过程中振幅不变，试写出反射波的表达式．图7-26解：反射波来自反射点B ，B 点相当于“波源”, 波源B 的振动方程:]π2ππ2cos[]π)(π2cos[λϕϕλL T t A L T t A y B -±+=±+-= 反射波的波动方程为:]π4π)(π2cos[]π2π)(π2cos[λϕλλϕλL x T t A L x L T t A y -±++=-±+--=反 7-16 如图7-27所示，在绳上传播的入射波方程为)2ππ2cos(1-+=λωx t A y ．入射波在x = 0处反射，反射端固定．设反射波不衰减，求驻波方程及波节和波腹的位置．图7-27解：入射波沿x 轴负方向传播，因此反射波沿x 轴正方向传播．入射波在x = 0处引起的振动：)2πcos(10-=t A y ω 由于反射端固定，故反射波在x = 0处与入射波的相位差为π，故反射波在x = 0处引起的振动为)2πcos()π2πcos(20+=+-=t A t A y ωω 反射波沿x 轴正方向传播，故其方程为 )2π2πcos(2+-=x t A y λω 合成驻波，其方程为t x A t x A x t A x t A y y y ωλωλλωλωcos 2πsin 2cos )2π2πcos(2 )2π2πcos()2π2πcos(21=-=+-+--=+= 当 02πs i n=x λ即⋅⋅⋅==0,1,2,n π,2πn x λ为波节．故波节位置为 ⋅⋅⋅==0,1,2,n ,21λn x 当 12πs i n=x λ即⋅⋅⋅=+=0,1,2,n ,2ππ2πn x λ 为波腹．故波腹的位置为 ⋅⋅⋅=+=0,1,2,n ,421λλn x 7-17两波在一根很长的弦线上传播，其传播方程式分别为m )244(3πcos04.01t x y -=，m )244(3πcos 04.02t x y += 求： (1) 两波的频率、波长、波速；(2) 两波叠加后的节点位置；(3) 叠加后振幅最大的那些点的位置．解：(1) 与标准波动方程)π(2cos λνxt A y -=对比可得Hz 4=ν m 50.1=λm/s 6.00m/s 450.1=⨯==λνu(2) 节点位置在)2ππ(3π4+=n x 解得 m 4)21(3+=n x ，⋅⋅⋅±±= ,2 ,1 ,0n (3) 波腹的位置为π3π4n x = 解得 m 43n x =，⋅⋅⋅±±= ,2 ,1 ,0n 7-18 一警车以25 m/s 的速度在静止的空气中行使，假设车上的警笛的频率为800 Hz ，求：(1) 静止站在路边的人听到警车驶近和离去时的警笛声波频率；(2) 如果警车追赶一辆速度为15 m/s 的客车，则客车上人听到的警笛声的频率是多少？（假设空气中的声速u =330 m/s ）解：(1) 由多普勒公式，当声源（警车）以速度运动m/s 25=s υ时，静止在路边的观察者所接收到的频率为su u υνν =' 警车驶近观察者时，式中s υ前取“－”号．则有Hz 865.6Hz 253303308001=-⨯=-='s u u υνν 警车驶离观察者时，式中s υ前取“＋”号．则有Hz 7.437Hz 253303308002=+⨯=+='s u u υνν (2) 声源（警车）与客车上的观察者做同向运动时，观察者接收到的频率为Hz 2.826Hz 25330153308000=--⨯=--=''s u u υυνν 7-19 公路检查站上警察用雷达测速仪测来往汽车的速度，所用雷达波的频率为Hz 100.510⨯．发出的雷达波被一迎面开来的汽车反射回来，与入射波形成了频率为Hz 101.14⨯的拍频．此汽车是否已超过了限定车速km/h 001．解：测速仪与汽车的状态如图所示．S S R uu ννυυ'=+= S S S R u u u u u u u u νυυνυυνυυ-+=+⋅-='-=' 拍频 S S u u ννυυυ--+= 车速 m/s 332=+=υυνυS u限定车速 m/s 28m/s 3600101003max =⨯=υ 显然，此车速已经超过限定车速．7-20 如图7-28所示，A 、B 为两个汽笛，其频率均为500 Hz ．A 是静止的，B 以60 m/s 的速率向右运动．在两个汽笛之间有一观察者O ，以30m/s 的速率也向右运动．已知空气中的声速为 330m/s ．求：(1) 观察者听到来自A 的频率；( 2) 观察者听到来自B 的频率；( 3) 观察者听到的拍频．图7-28解：已知: v =330m/s, v sA =0, v sB =60m/s, v 0=30m/s, ν=500Hzννsv u v u 0±=' (1) 由于观察者远离波源A 运动, v 0应取负号, 观察者听到来自A 的频率为Hz 5.45450033030330=⨯-='v (2) 观察者向着波源B 运动, v 0取正号; 而波源远离观察者运动, v sB 也取正号. 故观察者听到自B 的频率为Hz 5.4615006033030330=⨯++=''v (3)两波合成的拍频为 Hz 7=''-'=∆v v v7-21 一固定波源在海水中发射频率为ν的超声波，射在一艘运动的潜艇上反射回来．反射波和发射波的频率差为Δν，潜艇运动速度远小于海水中的声速u ，试证明潜艇运动速度为 ννυ2∆=u 证明：潜艇的速度为υ，潜艇作为观察者接收到发射波的频率为νυνuu +=' 当超声波遇到潜艇反射时，潜艇成为波源，观察者接受反射波的频率νυυνυυνυν-+=-+='-=''u u u u u u u u )()( νυυνυυνννuu u u -=--+=-''=∆12)1(因 u <<υ，uu υυ+≈--1)1(1 νυνυυνu u u 2)1(2≈+=∆ 所以潜艇运动速度为 ννυ2∆=u 7-22 北京春节播放钟声的设备是一种气流扬声器，它发声的总功率为 W 1024⨯．这声音传到12 km 远的地方还可以听到．设空气不吸收声波能量并按球面波计算，这声音传到12 km 处的声强级是多大？约相当于哪种声音？解：声源的功率应等于任一球面的能流，即I r P 2π4=．所以有 252442 W/m 1011.1)101.2(π4102π4-⨯=⨯⨯⨯==r P I dB 70dB )101011.1lg(10lg 101250=⨯==--I I L 相当于闹市车声．7-23 距离一声源10 m 处听到的音量为100dB ，则距离声源100 m 处听到的音量约为多少？解：设距离声源10 m 处声音的强度为I ，则log 10100I I ==β，从而01010I I = 声音强度与距离平方成反比，因此距离声源100 m 处声音强度0810I I ='，音量dB 80=β．。

第七章振动理论基础

ω < 1.25 的范围内时，振动仍然实践证明，频率比在 0.75 < 实践证明，的范围内时， ω0
很强烈，工程上把这一区域称为共振区。很强烈，工程上把这一区域称为共振区。共振往往是机器或其共振区零件产生破坏的重要原因。因此，在设计和使用机器时，零件产生破坏的重要原因。因此，在设计和使用机器时，必须使其转速避开共振区。使其转速避开共振区
满载时车厢的固有频率为
w= g
δs
=
980 = 6.4rad / s 24
每分钟振动的次数为
f ′ = 60 f = 60 × w 6 .4 = 60 × 次 / 分 = 61次 / 分 2π 6.28
例7-2 如图所示，在无重弹性梁的中点放置重量为G的物体，其静变形为2 mm。若将重物B放在梁未变形的位置上无初速地释放。求系统自由振动时的运动方程。
第一节
振动的概念
机械振动——物体在其平衡位置附近作周期性的机械运动机械振动或往复运动。振动系统的简化
振动中最简单而且最重要的一种是谐振动。谐振动。谐振动谐振动——凡是决定其位置的坐标按余弦或正弦函数规律凡是决定其位置的坐标按余弦或正弦函数规律谐振动谐振动。随时间变化的振动都是谐振动随时间变化的振动都是谐振动。其运动方程为
（4） ω
>ω
0
，振幅B将无限增大，产生强烈的振动。这振幅将无限增大，产生强烈的振动。种现象称为共振共振。种现象称为共振。
表示。旋转机械产生共振时的转速称为临界转速，旋转机械产生共振时的转速称为临界转速，用 n k 表示。临界转速
nk = 30
π
ω0 =
30
π
k 30 g = m π δs

92简谐运动的叠加

物理学
9-3
简谐振动的合成
问题：简谐振动的叠加非常复杂，叠加后的结果与哪些因素有关？ 1、参与叠加的个数； 2、各自的振动方向； 3、各自的振动幅度； 4、各自的振动频率和周期； 5、各自的振动初相位；我们只介绍三种特殊的叠加：
第七章振动与波动
1
物理学
一.同一直线上两个同频率简谐振动的合成————简谐振动
3
y2 18 3 Nhomakorabea1
8 7 6
4
5
7 6
x
4
5
4
5 6 7
第七章振动与波动
3
2 1
8
23
x
物理学
x y 2 xy 2 2 cos( ) sin ( ) 2 A B AB 2 2 x y π 2 1 （2），可得 2 2 A B
合振动的轨迹是以坐标轴为主轴的正椭圆。
1 E E E kA C 2
2 k p
五、谐振动合成
1.两同方向同频率谐振动合成
分振动
x1 A1 cos(t 1 ) x 2 A2 cos(t 2 )
2 1 2 2
振动合成 x x1 x2 A cos(t )
A A A 2 A1 A2 cos( 2 1 ) A1 sin 1 A2 sin 2 tg A1 cos 1 A2 cos 2 2 k , A A1 A2 特殊情况 A A A ( 2 k 1 ) , 1 2 2 2 , A A1 A2 2
x
A1
x
2
o
o
T
t
x ( A2 A1 ) cos(t ) A A1 A2 2 1 (2k 1) π 合振动振幅最小。

简谐振动

3
1. 简谐振动（Simple Harmonic Motion）
x Acos( t ) →运动学判据
即:按时间t的余弦或正弦函数描述的运动
x 可作广义理解（位移、电流、场强、温度…）简谐振动是最简单、最基本的振动，可用来研究复杂的振动。
F kx →动力学判据
d2x dt 2
时，振幅矢量转过的角度为： 5
t 0.83(s)
26

21
例：一质点作简谐振动，其振动曲线如图所示。根
据此图写出该振动的表达式。 x(cm)
解：由振动曲线可知：A 0.04 4
由振动曲线可得t＝0和t＝
o
2对应的旋转矢量如图
2
2
t(s)
对应的相位：
t＝2
cos2 (t
)
因此，弹簧振子的总机械能为:
E

Ek

Ep

1 2
kA2
结论：（1）作简谐运动的物体，其机械能守恒。
（2）简谐运动的总能量和振幅的平方成正比。
9
5.其它简谐振动例如单摆
取逆时针为张角正向，以悬
点为轴，重力的切向分量
Ft mg sin
“ – ”表示力与张角方向相反。
设振动物体在任一时刻t 的位移为x ，速度为v ，于是
它所具有的动能EK 和势能EP 分别为
Ek

1 2
mv2
Ep

1 2
k x2
考虑到 x Acos(t ) 及v Asin(t )与2 k / m

Ek
1 kA2 sin 2 (t )
2

大学物理振动波动复习资料

vmax A 0.8 m s 1
(2)
amax
2 2 6 . 4 m s A
2
v 0.8 sin(8t 2 / 3)
a 6.4 cos(8t 2 / 3)
2
(3)
1 2 Ek mv 3.2 10 3 2 sin 2 (8t 2 / 3) 2 1 2 3 2 2 E p kx 3.2 10 cos (8t 2 / 3) 2
x A cos(t )
1
物理学
第五版
2、描述谐振动的物理量（1）振幅
x
A
x t 图
T
T 2
A xmax
（2）周期、频率
o
A
t
周期
T
2π
1 频率 T 2π 2π 2 π 圆频率 T

弹簧振子周期
m T 2π k
周期和频率仅与振动系统本身的物理性质有关
A3
1 A2 2 o
x

4
(2k 1) ,
k 0, 1, 2
(2k 1)

4
A A3 A1 0.02m
24
物理学
第五版
第十章
机械波
教学基本要求一理解描述简谐波的各物理量的意义及各量间的关系. 二理解机械波产生的条件．掌握由已知质点的简谐运动方程得出平面简谐波的波函数的方法．理解波函数的物理意义．理解波的能量传播特征及能流、能流密度概念．
波动的种类：机械波、电磁波、物质波
27
物理学
第五版
一概念：
机械波、横波、纵波、振幅、频率、波长、波速、波函数、波的能量、衍射、干涉、驻波、多普勒效应

上海交大版大学物理第七章参考答案

版权归原著所有本答案仅供参考习题77-1．原长为m 5.0的弹簧，上端固定，下端挂一质量为kg 1.0的物体，当物体静止时，弹簧长为m 6.0．现将物体上推，使弹簧缩回到原长，然后放手，以放手时开始计时，取竖直向下为正向，写出振动式。

（g 取9.8）解：振动方程：cos()x A t ωϕ=+，在本题中，kx mg =，所以9.8k =；∴ω=== 取竖直向下为x 正向，弹簧伸长为0.1m 时为物体的平衡位置，所以如果使弹簧的初状态为原长，那么：A =0.1m ，当t =0时，x =-A ，那么就可以知道物体的初相位为π。

所以：0.1cos x π=+）即：)x =-。

7-2．有一单摆，摆长m 0.1=l ，小球质量g 10=m ，0=t 时，小球正好经过rad 06.0-=θ处，并以角速度0.2rad/s θ=向平衡位置运动。

设小球的运动可看作简谐振动，试求：（1）角频率、频率、周期；（2）用余弦函数形式写出小球的振动式。

（g 取9.8）解：振动方程：cos()x A t ωϕ=+ 我们只要按照题意找到对应的各项就行了。

（1）角频率： 3.13/rad s ω===，频率：0.5Hz ν=== ，周期：22T s π===；（2）振动方程可表示为：cos 3.13A t θϕ=+（），∴ 3.13sin3.13A t θϕ=-+（）根据初始条件，0t =时：cos Aθϕ=，0(12sin 0(343.13A θϕ>=-<，象限），象限）可解得：，-2.32rad 95.3227rad,108.802===⨯=-ϕA 所以得到振动方程： rad )32.213.3cos(108.82-⨯=-t θ。

7-3. 一竖直悬挂的弹簧下端挂一物体，最初用手将物体在弹簧原长处托住，然后放手，此系统便上下振动起来，已知物体最低位置是初始位置下方10.0cm 处，求：（1）振动频率；（2）物体在初始位置下方cm 0.8处的速度大小。

《普通物理学》课件-第七章振动

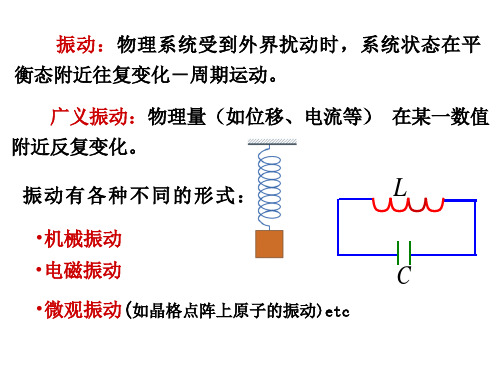
5g
等效劲度系数（ke） f ke x
f: 恢复力 x: 偏离平衡位置的位移
0
ke m
弹簧的串联和并联
• 串联公式： 1/k = 1/k1 +1/k2
• 并联公式： k = k1 + k2
k1
k2
k1
k2
例：一劲度系数为 k 的弹簧均分为二，试求均分后两弹簧并联的等效劲度系数 k'。
解：串联公式：
sinθ≈θ (θ<5o 0.3 rad)
O
l
T
当振幅很小时，单摆的振动为简谐振动。
mg
Quasi 1-D restoring force
f = -mgsinθ≈-mgθ= -mgx/l
k = mg/l, ω02 = k/m = g/l ω0 = √g/l
T 2 l
g
单摆实验可以测g
复摆（物理摆）
A
ωt+
0
xx
旋转矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
x Acos(t )
•复数表示：
将xy平面看作一个复平面
矢量端点对应于一个复数（包含模和辐角）
xt Acost 0
x t Aeit0辐角
eit0 cost 0 i sin t 0
设B的质量为m， A的质量便是γm
A
v0
B
B
第一阶段是弹性碰撞
第二阶段：A做匀速直线运动；B，B '的质心做匀速直线运动，
B，B '相对质心作简谐振动。
弹性碰撞
mvA
mvB
(0)

7-1简谐振动

简谐量 x 是复数 ~ 的实部，振幅与模相对应，相 x 的实部，振幅与模相对应，位与辐角相对应。位与辐角相对应。复数解法过程：若要对多个简谐量进行某种运复数解法过程：算, 可以对代表这些简谐量的复数进行相同的运在运算过程中，实部和虚部、算。在运算过程中，实部和虚部、模和辐角总是分别运算而不会相混，所得复数的实部就是这些分别运算而不会相混，简谐量进行该运算的最后结果。
总能量
1 1 2 2 2 2 E = E k + E p = mω A sin (ω t + ϕ ) + kA cos2 (ω t + ϕ ) 2 2 1 1 2 2 2 2 因为 ω = k / m 所以 E = mω A = kA 2 2
由此式可见, 由此式可见, 尽管在振动中弹簧振子的动能和势能都在随时间作周期性变化, 但总能量是恒定不变的，间作周期性变化, 但总能量是恒定不变的，并与振幅的平方成正比。成正比。
19
解：设物体沿x 轴作简谐振动设物体沿
A = 10.0 cm = 0.100 m
m 0.500 当t = 0 时，x = A ，cosϕ =1 ，即 ϕ = 0
所以 x = 0.100 cos 8.00 t m vm = ω A = 8.00×0.100 m ⋅ s−1 = 0.800 m⋅s−1 × ⋅ am= ω2 A = (8.00)2 ×0.100 m ⋅ s−2 = 6.40 m⋅s−2 ⋅ 所以 v = −0.800 sin 8.00 t m⋅s−1 ⋅ a = −6.40 cos 8.00 t m⋅s−2 ⋅
F = - kx
→线性回复力线性回复力
根据牛顿第二定律有所以其解或
d2 x +ω2 x = 0 dt 2

第七章振动和波题库含答案-大学复习资料

第七章振动和波题库及答案一、单选题1、作简谐振动的物体运动至平衡位置向正方向运动时，其位移x 、速度υ、加速度a 为 [设振动方程为x =A cos(ωt+φ)] （）。

A) x =0， υ=0， a =0 B) x =0， υ=ωA ， a =0 C) x =A ， υ=ωA ， a =ω2A D) x = –A ， υ= –ωA ， a =0 答案: B知识点： 7.1、简谐振动、简谐振动方程难度: 1 提示：无题解：作简谐振动的物体运动至平衡位置时，其位移x =0、向正方向运动的速度υ=ωA 、加速度a =0，所以B 答案是正确的。

2、一质点作简谐振动,振动方程为x =A cos(ωt ＋ϕ),当时间t =T / 2(T 为周期)时,质点的速度为（）。

A) -A ωcos ϕ B) -A ωsin ϕ C) A ωcos ϕ D) A ωsin ϕ 答案: D知识点：7.1、简谐振动、简谐振动方程难度: 2 提示：无题解：质点作简谐振动的速度方程为)sin(ϕωω+=t A -υ，将t =T / 2代入得ϕωϕωϕωωsin )πsin()2sin(A A -TA -υ=+=+=所以D 答案是正确的。

3、一质点作水平方向的简谐振动，设其向右运动为正方向。

当质点在平衡位置开始向右运动，则初位相为（）。

A) 0 B) 2πC) 2π-D) 3π答案: C知识点： 7.1、描述简谐振动的物理量难度: 2 提示：无题解：设简谐动方程为)cos(ϕω+=t A x ， t =0时ϕcos 0A = 0cos =ϕ 2π±=ϕ因为 0sin 0sin 0<>-=ϕϕωA υ 所以 2π-=ϕ 所以C 答案是正确的。

4、一质量为m 的物体，以速度υ(t ) = υ0sin ωt 的规律振动，则振动系统的总机械能为（）。

A)221ωm B) ω 20m υ C)2021m υ D)t m υω sin 21220 答案: C知识点： 7.1、简谐振动的能量难度: 2提示：因物体的速度按υ(t ) = υ0sin ωt 的规律振动，所以物体的振动为简谐振动。

简谐振动的运动方程

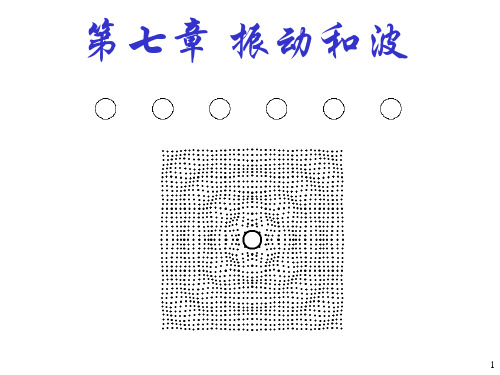
设振动的周期为T，周期函数满足 x(t T ) x(t)
引入 2
T
称为基频率，简称基频
n n次谐频（n = 2为二次谐频，其它依此类推）
14
傅里叶级数： 1, cost, sint, cos2t, sin 2t, cosnt, sin nt,
它们都具有周期 T，且有正交性和完备性
0
Bn

2 T
T
x(t)sin ntdt
2
0
n
19
x(t)

2

sin
t

1 2
sin
2t

1 3
sin
3t

20
非周期性振动的傅里叶分解
非周期性的振动，可理解成T →ω的周期振动，基频ω→0，分解出的简谐振动频率间距ω→0 ，对应的振动频谱是连续谱。
简谐振动的复数表示法 Acos(t ) Aei(t)
多普勒效应探测器所接受到的波的频率依赖于波源和探测器相对介质的运动在无色散的介质中波速与波源和探测器的运动与否无关波源频率探测器1波源静止观察者运动波源波速u探测器先讨论波源或探测器的运动都在二者的连线上波相对观察者的传播速度波长未变观察者感受到的频率2波源运动观察者静止波源波速u探测器波相对观察者的有效波长波速未变观察者感受到的频率3波源和观察者都运动波源波速u探测器波相对观察者的有效波长观察者感受到的频率波相对观察者的传播速度波源和观察者作任意运动波源观察者相位增量观测到同样的相位增量波源观察者声速车速声音经前面墙的反射向后传播求人听到的拍频
解得
A 2a0
tan 1 / 4 or / 4
考虑到 sin a0 / A 0 /4

第7章_简谐振动

高一物理必修一每章笔记

新人教版第7章实验9用单摆测量重力加速度的大小课件(44张)

内科大安全环境监测技术教案第7章 振动检测

ANSYS Workbench 17·0有限元分析：第7章-谐响应分析

第七章 振动和波动(2)

大学物理第七章习题及答案

简谐振动

第7章机械波

第七章 振动理论基础

92简谐运动的叠加

简谐振动

大学物理振动波动复习资料

上海交大版大学物理第七章参考答案

《普通物理学》课件-第七章 振动

7-1简谐振动

第七章 振动和波 题库含答案-大学复习资料

简谐振动的运动方程

内科大安全环境监测技术教案第7章振动检测

第七章振动和波动(2)

第七章振动理论基础

《普通物理学》课件-第七章振动

第七章振动和波题库含答案-大学复习资料