标准的PID处理例程(PID通俗易懂的讲解)[2]
PID算法通俗讲解

PID算法通俗讲解PID算法是控制系统中常用的一种反馈控制算法,它主要由比例项(P),积分项(I)和微分项(D)三部分组成,即PID。
它的作用是通过对系统输出和设定值之间的偏差进行计算,产生一个控制量来调节系统的输入,使系统能够快速、准确地响应设定值,并实现稳定控制。
首先,我们来了解PID算法的三个部分。
P项(比例项)是最简单和最直观的部分,它与偏差成比例。
偏差是设定值与实际值之间的差异,P项根据偏差的大小来产生控制量。
当偏差越大时,P项产生的控制量也越大,从而加大系统输入,以快速减小偏差。
但是P项的缺点是当系统接近设定值时,偏差减小,P项产生的控制量也随之减小,导致系统响应变慢,甚至产生超调。
I项(积分项)用来修正偏差的累积量。
它与偏差的积分有关,可以修正P项产生的超调问题。
当系统存在稳态误差时,I项可以通过积分来累积偏差,产生一个持续增加的控制量,以减小稳态误差。
然而,如果I项过大,会导致系统产生过度调节,甚至引起系统不稳定。
D项(微分项)用来修正系统的动态响应。
它与偏差的变化率有关,可以预测系统的未来偏差变化,并产生一个相应的控制量来改变系统的响应速度。
当系统在达到设定值时,D项可以减小超调量,缩短系统的响应时间,提高系统的稳态性能。
然而,D项的缺点是它对噪声和干扰非常敏感,可能引起控制系统不稳定。
综上所述,PID算法的基本思想是通过将比例、积分和微分三个部分综合起来来实现对系统的控制,以期望系统的输出能够快速、准确地达到设定值,并保持在设定值附近稳定。
PID算法的关键是如何确定三个部分的权重系数,即调参问题。
一般来说,根据具体的控制对象和控制要求,可以采用经验法、试验法、模型法等方法来进行调参。
调参过程需要不断尝试和优化,以找到适合系统的最佳参数组合,从而实现最佳的控制效果。
总结起来,PID算法是一种常用的控制算法,通过比例、积分和微分三个部分的组合,对系统的输出和设定值之间的偏差进行计算,并产生一个控制量来调节系统的输入,以实现快速、准确响应设定值并保持稳定。
PID算法通俗讲解

PID算法通俗讲解PID算法是一种用于反馈控制系统的自动控制算法,它能根据系统当前的反馈信号与设定值之间的差异,来调整控制系统的输出信号,使得系统能够更好地接近设定值。
PID算法是目前使用最广泛的自动控制算法之一,它在工业生产、自动驾驶、机器人等领域得到了广泛的应用。
比例项(Proportional Control)比例项是PID算法最基本的一个部分。
它根据当前的偏差(设定值与实际值之差)的大小,决定调整输出信号的幅度。
如果偏差很大,那么比例项就会增加输出信号的幅度,使得系统能够更快地接近设定值。
但是如果偏差过大,比例项会增加的太大,可能导致系统出现超调,即超过设定值。
因此,比例项不能独立作用,还需要结合其他参数来实现最优的控制效果。
积分项(Integral Control)积分项用来消除系统的稳定偏差。
如果比例项无法完全消除偏差,那么积分项会根据偏差的时间积累情况,逐渐适应并调整输出信号的幅度。
如果偏差时间持续较长,积分项会逐渐增加输出信号的幅度,使得系统能够更好地靠近设定值。
但是如果偏差时间过长,积分项可能会造成系统超调或者震荡的情况,因此也需要其他参数的协同作用。
微分项(Derivative Control)微分项用来预测系统的未来变化趋势。
它通过观察偏差随时间的变化率,来调整输出信号的变化速度。
如果偏差随时间的变化率很大,那么微分项会增大输出信号的变化速度,以期快速地接近设定值。
但是如果偏差随时间的变化率波动很大,微分项可能会造成输出信号的剧烈变化,导致系统不稳定。
因此,微分项的作用也需要与其他参数相互协调。
比例、积分和微分项在PID算法中起着不同的作用,它们相互协同工作,通过不断地监测系统的反馈信号与设定值之间的差异,并调整输出信号的幅度和变化速度,来实现系统的稳定控制。
1.设置比例项、积分项和微分项的参数值。
这些参数值的选择会直接影响系统的控制效果,需要根据实际情况进行调整。
2.读取当前的反馈信号和设定值,计算偏差值。
超级经典的且通俗易懂的PID例子

超级经典的且通俗易懂的PID例子
超级经典的且通俗易懂的PID例子
作者:程序匠人
PID与其说是一种控制算法,不如说是一种控制思想。
这个思想的核心,就是P、I、D。
但是实际上,PID并不神秘。
在生活中的例子也是比比皆是。
比如你骑自行车,如何控制才能确保自行车不倒呢?
会骑车的都知道,当车的重心向一个方向倾斜时,笼头要向同方向打。
而且这个打的角度,与重心倾斜的角度是成正比的,倾斜度越大,笼头角度也要打得越多。
——这就是P(比例)控制。
打完笼头后,车是不会倒了,但是并不意味着你的车轮就能走直线,可能还会歪歪扭扭。
为什么呢?因为还存在静态误差,需要在骑的过程中,不断地“微调”修正,才能确保行车路径笔直。
——这就是I(积分)控制。
有时为了急转弯,我们会把笼头打过头,接下来就要赶紧回打,以抵消刚才的过调,求得平衡。
——这就是D(微分)控制。
骑车时,人的大脑就是控制器,眼睛是传感器,手足是执行器。
推而广之,在其它自动控制系统(温控、速度控制、转速、水位调节等等)中,也可以使用这套思想(或算法)。
pid控制原理详解及实例说明

pid控制原理详解及实例说明PID控制是一种常见的控制系统,它通过比例、积分和微分三个控制参数来实现对系统的控制。
在工业自动化等领域,PID控制被广泛应用,本文将详细介绍PID控制的原理,并通过实例说明其应用。
1. PID控制原理。
PID控制器是由比例(P)、积分(I)和微分(D)三个部分组成的控制器。
比例部分的作用是根据偏差的大小来调节控制量,积分部分的作用是根据偏差的累积值来调节控制量,微分部分的作用是根据偏差的变化率来调节控制量。
PID控制器的输出可以表示为:\[ u(t) = K_p e(t) + K_i \int_{0}^{t} e(\tau) d\tau + K_d \frac{de(t)}{dt} \]其中,\(u(t)\)为控制量,\(e(t)\)为偏差,\(K_p\)、\(K_i\)、\(K_d\)分别为比例、积分、微分系数。
比例控制项主要用来减小静差,积分控制项主要用来消除稳态误差,微分控制项主要用来改善系统的动态性能。
通过合理地调节这三个参数,可以实现对系统的精确控制。
2. PID控制实例说明。
为了更好地理解PID控制的原理,我们以温度控制系统为例进行说明。
假设有一个加热器和一个温度传感器组成的温度控制系统,我们希望通过PID 控制器来控制加热器的功率,使得系统的温度稳定在设定的目标温度。
首先,我们需要对系统进行建模,得到系统的传递函数。
然后,根据系统的动态特性和稳态特性来确定PID控制器的参数。
接下来,我们可以通过实验来调节PID控制器的参数,使系统的实际响应与期望的响应尽可能接近。
在实际应用中,我们可以通过调节比例、积分、微分参数来实现对系统的精确控制。
比如,增大比例参数可以加快系统的响应速度,增大积分参数可以减小稳态误差,增大微分参数可以改善系统的动态性能。
通过不断地调节PID控制器的参数,我们可以使系统的温度稳定在设定的目标温度,从而实现对温度的精确控制。
总结。
通过本文的介绍,我们可以了解到PID控制的原理及其在实际系统中的应用。
PID算法的通俗讲解及调节口诀

PID算法的通俗讲解及调节口诀PID算法是一种常用的控制算法,它可以帮助我们将实际测量值与期望值进行比较,并根据比较结果进行相应的控制。
PID算法由三个部分组成,分别是比例控制(P)、积分控制(I)和微分控制(D)。
在实际应用中,我们可以根据实际情况来调节PID算法的参数,以实现更准确的控制效果。
比例控制(P)是PID算法的核心部分之一,它根据误差的大小来调整输出量。
具体来说,比例控制会将误差与一个常数进行相乘,然后输出到系统中。
当误差较大时,输出量也会较大,从而加快系统的响应速度;当误差较小时,输出量也会较小,从而减小系统的超调量。
积分控制(I)是为了解决系统存在的稳态误差而引入的,它通过对误差的累加来调整输出量。
具体来说,积分控制会将误差乘以一个常数,并加到一个累加器中,然后输出到系统中。
通过积分控制,系统可以在长时间内逐渐减小误差,从而达到期望值。
微分控制(D)是为了解决系统存在的超调问题而引入的,它通过对误差的变化率进行调整。
具体来说,微分控制会将误差的变化率与一个常数进行相乘,并输出到系统中。
通过微分控制,系统可以在误差大幅度变化时降低输出量的变化速度,从而减小超调量。
除了PID算法的三个部分,还需要根据实际情况来调节PID算法的参数,以实现更准确的控制效果。
调节PID算法的口诀有三个重要的方面:1.比例项(P项)的调节:-当P项过大时,系统容易产生超调,并且响应速度较快,但稳定性较差;-当P项过小时,系统的响应速度较慢,并且稳态误差较大;-因此,需要通过改变P项的大小来调节系统的超调量和响应速度。
2.积分项(I项)的调节:-当I项过大时,系统容易产生超调,并且响应速度较慢;-当I项过小时,系统的稳态误差较大;-因此,需要通过改变I项的大小来调节系统的超调量和稳态误差。
3.微分项(D项)的调节:-当D项过大时,系统容易产生振荡,并且响应速度较快;-当D项过小时,系统的超调量较大;-因此,需要通过改变D项的大小来调节系统的振荡情况和超调量。
写一段pid算法例程

写一段pid算法例程以下是一个简单的PID控制算法的例程:```// 定义PID参数float Kp = 1; // 比例系数float Ki = 0.1; // 积分系数float Kd = 0.01; // 微分系数// 定义PID变量float error = 0; // 误差float last_error = 0; // 上一次的误差float integral = 0; // 积分项// 定义输入输出变量float setpoint = 50; // 目标值float input = 0; // 输入值float output = 0; // 输出值void PID_Control() {// 计算误差error = setpoint - input;// 计算积分项integral += error;// 避免积分饱和if (integral > 100) {integral = 100;}if (integral < -100) {integral = -100;}// 计算微分项float derivative = error - last_error;// 更新上次误差last_error = error;// 计算输出值output = Kp * error + Ki * integral + Kd * derivative;// 避免输出饱和if (output > 100) {output = 100;}if (output < -100) {output = -100;}// 输出控制信号digitalWrite(12, output);}```该例程中,通过设置比例系数Kp、积分系数Ki和微分系数Kd的大小来调节PID算法的效果。
在实际的项目中,这些系数需要根据具体的控制器性能和控制对象特性进行调整。
PID算法通俗讲解

PID算法通俗讲解PID(Proportional-Integral-Derivative)是一种经典的反馈控制算法,常用于自动调节系统中,使系统达到稳定状态。
PID算法是根据系统的反馈信号和设定值之间的差异来调整输出信号的方法。
以下是对PID 算法的通俗讲解:PID算法的工作原理可以类比为我们掌握自行车的平衡。
当我们骑自行车时,我们会根据自行车的倾斜程度来做出相应的调整,以保持平衡。
这个过程中,我们考虑的因素有三个:倾斜程度、倾斜速度和累积误差。
PID算法也是根据这三个因素来调整系统的输出信号。
首先,我们来看P(Proportional)部分,它是根据当前的误差大小来调整输出的。
在自行车示例中,P部分就相当于我们根据自行车倾斜程度来调整方向盘的力度。
如果自行车倾斜得越厉害,我们就要施加更大的力度来纠正。
同样地,如果系统当前的误差很大,P部分也会调整输出信号的幅度来减小误差。
接下来是I(Integral)部分,它是根据累积误差来调整输出的。
在自行车示例中,I部分就相当于我们根据之前的倾斜程度的累积来调整方向盘的力度。
如果我们在之前的几个时刻都没有纠正倾斜,那么倾斜程度的累积会越来越大,我们就要施加更大的力度来纠正。
同样地,如果系统之前的误差一直没有被减小,I部分会调整输出信号的幅度来减小误差。
最后是D(Derivative)部分,它是根据误差的变化速度来调整输出的。
在自行车示例中,D部分就相当于我们根据自行车倾斜速度的变化来调整方向盘的力度。
如果自行车倾斜速度越大,我们就需要施加更大的力度来减小速度。
同样地,如果系统的误差变化得很快,D部分会调整输出信号的幅度来减小误差。
在PID算法中,P、I、D这三个部分的调节系数决定了它们对输出的贡献程度。
合理地设置这些参数可以使得PID算法更好地收敛到稳定值。
通常,我们会通过试-and-error的方法来不断调整这些参数,直到达到满意的控制效果。
总结一下,PID算法是根据当前误差、累积误差和误差变化速度来调整输出信号的算法。
PID通俗易懂的讲解

很多同学都不清楚PID是个什么东西,因为很多不是自动化的学生。
他们开口就要资料,要程序。
这是明显的学习方法不对,起码,首先,你要理解PID是个什么东西。
本文以通俗的理解,以小车纵向控制举例说明PID的一些理解。
首先,为什么要做PID?由于外界原因,小车的实际速度有时不稳定,这是其一,要让小车以最快的时间达达到既定的目标速度,这是其二。
速度控制系统是闭环,才能满足整个系统的稳定要求,必竟速度是系统参数之一,这是其三.小车调速肯定不是线性的,外界因素那么多,没人能证明是线性的。
如果是线性的,直接用P就可以了。
比如在P WM=60%时,速度是2M/S,那么你要它3M/S,就把PW M提高到90%。
因为90/60=3/2,这样一来太完美了。
完美是不可能的。
那么不是线性的,要怎么怎么控制PW M使速度达到即定的速度呢?即要快,又要准,又要狠。
(即快准狠)系统这个速度的调整过程就必须通过某个算法调整,一般PID就是这个所用的算法。
可能你会想到,如果通过编码器测得现在的速度是2.0m/s,要达到2.3m/s的速度,那么我把pwm增大一点不就行了吗?是的,增大pwm多少呢?必须要通过算法,因为PWM和速度是个什么关系,对于整个系统来说,谁也不知道。
要一点一点的试,加个1%,不够,再加1%还是不够,那么第三次你还会加1%吗?很有可能就加2%了。
通过PID三个参数得到一个表达式:△PW M=a *△V1+b *△V2+c *△V3,ab c是通过PID的那个长长的公式展开,然后约简后的数字,△V1 ,△V2 ,△V3 此前第一次调整后的速度差 ,第二次调整后的速度差,第三次。
PID控制算法通俗讲解(转)
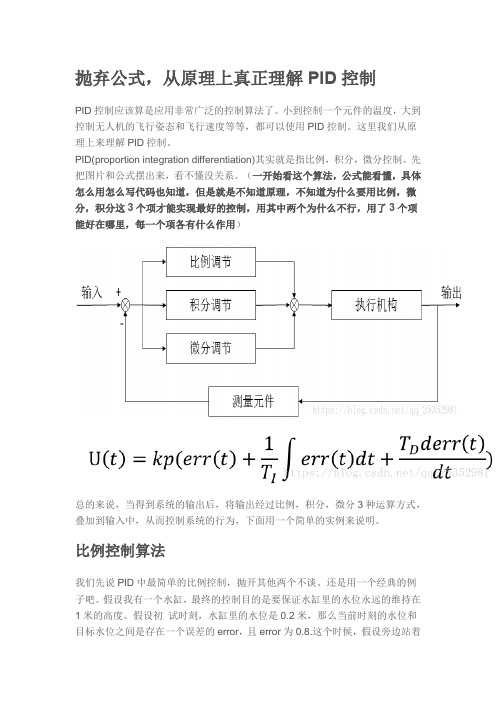
抛弃公式,从原理上真正理解PID控制PID控制应该算是应用非常广泛的控制算法了。
小到控制一个元件的温度,大到控制无人机的飞行姿态和飞行速度等等,都可以使用PID控制。
这里我们从原理上来理解PID控制。
PID(proportion integration differentiation)其实就是指比例,积分,微分控制。
先把图片和公式摆出来,看不懂没关系。
(一开始看这个算法,公式能看懂,具体怎么用怎么写代码也知道,但是就是不知道原理,不知道为什么要用比例,微分,积分这3个项才能实现最好的控制,用其中两个为什么不行,用了3个项能好在哪里,每一个项各有什么作用)总的来说,当得到系统的输出后,将输出经过比例,积分,微分3种运算方式,叠加到输入中,从而控制系统的行为,下面用一个简单的实例来说明。
比例控制算法我们先说PID中最简单的比例控制,抛开其他两个不谈。
还是用一个经典的例子吧。
假设我有一个水缸,最终的控制目的是要保证水缸里的水位永远的维持在1米的高度。
假设初试时刻,水缸里的水位是0.2米,那么当前时刻的水位和目标水位之间是存在一个误差的error,且error为0.8.这个时候,假设旁边站着一个人,这个人通过往缸里加水的方式来控制水位。
如果单纯的用比例控制算法,就是指加入的水量u和误差error是成正比的。
即u=kp*error假设kp取0.5,那么t=1时(表示第1次加水,也就是第一次对系统施加控制),那么u=0.5*0.8=0.4,所以这一次加入的水量会使水位在0.2的基础上上升0.4,达到0.6.接着,t=2时刻(第2次施加控制),当前水位是0.6,所以error是0.4。
u=0.5*0.4=0.2,会使水位再次上升0.2,达到0.8.如此这么循环下去,就是比例控制算法的运行方法。
可以看到,最终水位会达到我们需要的1米。
但是,单单的比例控制存在着一些不足,其中一点就是–稳态误差!(我也是看了很多,并且想了好久才想通什么是稳态误差以及为什么有稳态误差)。
PID算法的通俗讲解及调节口诀

PID算法的通俗讲解及调节口诀首先,让我们来了解PID算法的原理。
PID算法是通过不断地调整控制量,使得反馈量与设定值尽可能接近,从而实现控制系统的稳定。
PID算法的名称来自于三个基本控制参数,即比例(proportional)、积分(integral)和微分(derivative)。
比例项是根据反馈量与设定值的差异来调整控制量的大小。
如果两者之间的差异很大,控制量会相应地增大或减小。
该项主要用于快速响应系统的初始变化。
积分项通过计算反馈量与设定值的累计差异,以调整控制量。
如果累计差异较大,控制量会相应地增加或减小,以减小系统的误差。
该项主要用于长期的稳态控制。
微分项是根据反馈量变化的速度来调整控制量。
如果反馈量变化速度很快,控制量会相应地增加或减小,以避免系统过冲或振荡。
该项主要用于快速响应系统的变化。
接下来,让我们来看看如何调节PID参数。
PID算法的调节是一个经验性的过程,需要根据实际应用进行调试。
这里提供一个常用的调节口诀:平稳、灵敏、迅速。
首先是平稳。
在系统刚开始运行时,应该降低比例参数和积分参数的值,这样可以避免系统过冲和振荡。
通过逐步提高这两个参数的值,可以逐渐将系统稳定在设定值附近。
其次是灵敏。
在系统达到稳态后,应该逐步提高比例参数的值,以使系统对外部变化更加敏感。
这样系统就能更快地响应外部变化,并尽快调整到设定值。
最后是迅速。
一旦系统的响应速度满足要求,就可以逐步增加微分参数的值。
微分参数主要用于抑制系统的振荡和过冲,但过高的微分参数值可能会导致系统不稳定。
因此,需要谨慎调整微分参数的值。
总结一下,PID算法是通过比例、积分和微分三个控制参数的调整,使得系统稳定,并能够快速响应外部变化。
调节PID参数需要遵循平稳、灵敏、迅速的原则,根据实际应用进行调试。
希望这篇文章能够对你理解PID算法和调节参数有所帮助。
PID控制原理详解及实例说明

PID控制原理详解及实例说明PID控制是一种常用的控制算法,它能够在工业控制系统中实现对各种参数的精确控制。
PID分别代表比例(proportional)、积分(integral)和微分(derivative),这三个参数共同决定了控制系统的输出。
在本文中,我们将详细介绍PID控制的原理,并通过一个实例来说明PID控制的应用。
**PID控制原理**PID控制算法的基本原理是通过反馈来调节控制系统的输出值,使其与期望值尽可能接近。
PID控制器根据当前的误差值(e),积分项(i)和微分项(d)来计算控制输出(u)。
具体来说,控制输出可以表示为以下公式:\[ u(t)=K_p \cdote(t)+K_i\cdot\int{e(t)dt}+K_d\cdot\frac{de(t)}{dt} \]其中,\(K_p\)、\(K_i\)和\(K_d\)分别是比例增益、积分增益和微分增益。
比例项用于根据误差信号的大小来调整输出,积分项用于修正系统的静态误差,微分项用于预测误差的变化趋势。
通过调节这三个参数的数值,可以使PID控制器在不同的控制情况下获得最佳性能。
**实例说明**为了更好地理解PID控制的应用,我们以一个简单的温度控制系统为例进行说明。
假设我们需要设计一个PID控制器来维持一个恒定的温度值,控制系统的输入是一个加热元件的功率,输出是系统的温度。
首先,我们需要建立一个数学模型来描述系统的动态特性。
假设系统的温度动态可以由以下微分方程描述:\[ \tau \cdot \frac{dT(t)}{dt}+T(t)=K \cdot P(t) \]其中,\(T(t)\)代表系统的温度,\(P(t)\)代表加热元件的功率,\(\tau\)代表系统的时间常数,\(K\)代表系统的传递函数。
接下来,我们可以根据这个数学模型来设计PID控制器。
首先,我们需要对系统进行参数调试,确定合适的比例增益\(K_p\)、积分增益\(K_i\)和微分增益\(K_d\)。
PID算法的通俗讲解及调节口诀

PID算法的通俗讲解及调节口诀PID算法是一种常用的控制算法,用于控制系统中的反馈回路,以使系统的输出能够接近所需值。
PID算法的基本原理是通过不断调节控制器的输出信号,使系统的实际输出与期望输出之间的误差最小化。
在这篇文章中,我们将用通俗的语言来解释PID算法的原理,并提供一些调节的口诀。
首先,让我们来了解一下比例控制部分。
比例控制的作用是根据当前的误差值,产生一个与之成比例的输出信号。
比例控制的公式为:输出信号=比例系数*误差值比例系数是一个常数,用于确定比例控制的权重。
当误差值较大时,比例控制会产生较大的输出信号,从而加大纠正的力度。
但是,如果比例系数设置得过大,可能会导致系统产生过冲或震荡的现象。
接下来是积分控制部分。
积分控制的作用是根据误差值的累积量,产生一个与之成比例的输出信号。
积分控制的公式为:输出信号=积分系数*误差值的累积量积分系数也是一个常数,用于确定积分控制的权重。
积分控制的作用是消除系统的稳态误差,即系统输出值与期望输出值之间的偏差。
当误差值较大时,积分控制会逐渐增加输出信号,直到误差值降至接近于零为止。
然而,如果积分系数设置得过大,可能会导致系统产生震荡的现象。
最后是微分控制部分。
微分控制的作用是根据误差值的变化率,产生一个与之成比例的输出信号。
微分控制的公式为:输出信号=微分系数*误差值的变化率微分系数也是一个常数,用于确定微分控制的权重。
微分控制的作用是抑制系统的瞬态响应,即系统输出值发生变化时的过渡过程。
当误差值的变化率较大时,微分控制会产生较大的输出信号,从而减小系统的瞬态响应。
但是,如果微分系数设置得过大,可能会导致系统产生过冲或震荡的现象。
综上所述,PID控制的输出信号等于比例控制、积分控制和微分控制三个部分的加权和:输出信号=比例系数*误差值+积分系数*误差值的累积量+微分系数*误差值的变化率现在我们来看一下PID算法的调节口诀。
根据经验和实践,我们总结了以下的调节口诀:1.比例系数:首先调节比例系数,使系统能够快速响应。
通俗易懂的PID控制算法讲解

最优控制旨在寻找一种最优的控制策 略,使得系统性能达到最优。与PID 控制相比,最优控制具有更高的性能 指标和更好的全局优化能力。然而, 最优控制的实现需要精确的数学模型 和大量的计算资源,且对系统参数变 化较为敏感。
05
PID控制算法的应用实例
工业自动化领域的应用
要点一
温度控制
在工业生产过程中,PID控制算法被 广泛应用于温度控制系统中,如熔炼 炉、热处理炉等设备的温度控制。通 过实时采集温度数据,与设定值进行 比较,PID控制器能够自动调节加热 元件的功率,使温度稳定在设定值附 近。
该传递函数描述了PID控制器在频域中的特性,可用于分析系统的稳定性、动态性能和 稳态精度等。
通过调整Kp、Ki和Kd三个参数,可以实现对系统性能的优化。在实际应用中,常采用 试凑法、经验法或优化算法等方法来确定PID参数。
03
PID控制算法的参数整定
参数整定的意义
提高系统性能
通过调整PID控制器的参数,可以优化系统 的动态响应和稳态精度,从而提高系统的整 体性能。
适应不同应用场景
不同的被控对象和不同的应用场景需要不同的PID 参数配置,参数整定可以使PID控制器适应各种应 用场景。
保证系统稳定性
合理的参数配置可以保证系统的稳定性,避 免系统出现振荡或失控等不稳定现象。
参数整定的方法
试凑法
根据经验或实验数据,逐步调整 PID控制器的参数,观察系统的响 应情况,直到满足性能指标要求 。
PID控制算法由比例(P)、积分(I) 和微分(D)三个部分组成,每个部 分都有不同的作用,通过调整三个部 分的参数可以实现对系统的精确控制 。
PID控制算法的应用领域
01
02
03
pid通俗讲解

pid通俗讲解
PID全称是Proportional-Integral-Derivative(比例、积分、微分)控制,是一种广泛应用于工业过程控制的控制策略,也是最早发展的控制策略之一。
PID 控制器是一种将比例、积分、微分三部分合而为一的控制器,通过计算出控制量进行控制。
比例控制P是一种基于反馈的控制方式,能够快速调整系统输出,以满足需求的变化。
它将偏差(目标值和实际值的差值)乘以比例系数Kp作为控制输出,以确保输出能够快速跟上偏差的变化。
比例控制可以快速调整系统输出,在一些简单的系统中可以单独使用。
积分控制I是一种基于累计的控制方式,用于消除静态误差。
它的输出是过去偏差的积分值,即偏差乘以积分时间Ti。
积分控制可以消除静态误差,因此在一些需要保持一定稳定性的系统中可以单独使用。
微分控制D是一种基于变化趋势的控制方式,用于改善系统动态品质。
它的输出是偏差的变化率,即偏差的导数。
微分控制可以预测未来的变化趋势,并在偏差还未达到预期值时进行提前调整,从而改善系统动态品质。
在实际应用中,这三种控制方式可以单独使用,也可以结合使用。
例如,在一些简单的系统中,可以单独使用比例控制,以保证系统的快速响应。
在一些复杂的系统中,可以结合使用比例、积分、微分三种控制方式,以达到更好的控制效果。
需要注意的是,PID控制需要通过参数整定来达到最佳的控制效果。
不同的系统需要不同的PID参数,通常需要根据实际情况进行调整。
调整顺序为比例、积分、微分。
在调整参数时,需要注意曲线振荡的情况,此时需要调整比例度盘或积分时间,理想的曲线为前高后低4比1。
PID算法通俗讲解

总所周知,PID算法就是个很经典得东西。
而做自平衡小车,飞行器PID 就是一个必须翻过得坎。
因此本节我们来好好讲解一下PID,根据我在学习中得体会,力求通俗易懂。
并举出PID得形象例子来帮助理解PID。
一、首先介绍一下PID名字得由来:P:Proportion(比例),就就是输入偏差乘以一个常数。
I :Integral(积分),就就是对输入偏差进行积分运算。
D:Derivative(微分),对输入偏差进行微分运算。
注:输入偏差=读出得被控制对象得值-设定值。
比如说我要把温度控制在26度,但就是现在我从温度传感器上读出温度为28度。
则这个26度就就是”设定值“,28度就就是“读出得被控制对象得值”。
然后来瞧一下,这三个元素对PID算法得作用,了解一下即可,不懂不用勉强。
P,打个比方,如果现在得输出就是1,目标输出就是100,那么P得作用就是以最快得速度达到100,把P理解为一个系数即可;而I呢?大家学过高数得,0得积分才能就是一个常数,I就就是使误差为0而起调与作用;D 呢?大家都知道微分就是求导数,导数代表切线就是吧,切线得方向就就是最快到至高点得方向。
这样理解,最快获得最优解,那么微分就就是加快调节过程得作用了。
二、然后要知道PID算法具体分两种:一种就是位置式得,一种就是增量式得。
在小车里一般用增量式,为什么呢?位置式PID得输出与过去得所有状态有关,计算时要对e(每一次得控制误差)进行累加,这个计算量非常大,而明显没有必要。
而且小车得PID控制器得输出并不就是绝对数值,而就是一个△,代表增多少,减多少。
换句话说,通过增量PID算法,每次输出就是PWM要增加多少或者减小多少,而不就是PWM得实际值。
所以明白增量式PID就行了。
三、接着讲PID参数得整定,也就就是PID公式中,那几个常数系数Kp,Ti,Td等就是怎么被确定下来然后带入PID算法中得。
如果要运用PID,则PID参数就是必须由自己调出来适合自己得项目得。
PID控制算法通俗讲解

PID控制算法通俗讲解PID控制算法是一种经典的反馈控制算法,其全称为“比例-积分-微分控制算法”,是目前工业领域使用最广泛的一种控制方法。
它通过调整输出信号和目标值之间的差异来实现系统的稳定和精确控制。
PID控制算法的原理非常复杂,但可以用一种通俗易懂的方式来解释。
我们可以把PID控制算法类比为一个小孩子学习骑自行车的过程。
小孩子第一次骑自行车时,会感到不稳定,容易摔倒。
这时,父母可能会帮助他们保持平衡,通过把手握住自行车后座来保持稳定。
这个过程就相当于PID控制算法中的“比例”部分。
“比例”部分是PID控制算法的基础,它通过调整输出信号和目标值之间的差值,来决定控制量的大小。
比如说,当小孩子离平衡点很远时,父母会用力拉住自行车,让他尽快回到平衡点。
而当离平衡点很近时,父母会放松控制,让他能够自主控制。
这就是“比例”部分的作用,根据偏差的大小来调整控制量,使系统向目标值靠近。
然而,只有“比例”部分还不足以保持稳定。
因为当小孩子骑自行车时,即便靠近平衡点,也有可能因为一些突发因素而失去平衡。
这时,父母可能会及时给他支撑,保持平衡。
这个过程就相当于PID控制算法中的“积分”部分。
“积分”部分的作用是累积系统在长时间内的偏差,并根据累积值来调整控制量。
当系统出现长时间的偏差时,积分部分会逐渐增加,产生补偿作用,使系统更加稳定。
比如说,当小孩子长时间无法保持平衡时,父母可能会给予更多的支撑力,帮助他恢复平衡。
不过,积分部分也有一个缺点,就是会导致系统的响应速度较慢。
因此,PID控制算法引入了“微分”部分来解决这个问题。
我们可以把微分部分类比为小孩子骑自行车时,父母根据自行车的倾斜程度来给予支撑的力度。
“微分”部分通过测量系统的变化速率来调整控制量。
当系统变化速率很快时,微分部分会增加控制量,使系统迅速做出反应。
比如说,当小孩子在转弯时,系统的变化速率会加大,父母就会给予更多的支撑力,以避免摔倒。
综上所述,PID控制算法通过比例、积分和微分三部分的组合来实现系统的稳定和精确控制。
PID控制原理详解及实例说明

PID控制原理详解及实例说明PID控制是一种常用的控制算法,它通过测量系统的状态与设定值之间的差异,利用比例、积分和微分三个控制参数来调节系统的控制量,使其尽量接近设定值。
PID控制器通过不断调整这三个参数,可以在稳态误差小的情况下快速、平稳地将系统控制到设定值。
PID控制器的输出由三个部分组成:比例项、积分项和微分项。
比例项是测量误差与设定值之间的比例关系,调整比例参数可以控制系统的敏感程度;积分项是历史误差的积累,调整积分参数可以消除稳态误差;微分项是测量误差的变化率,调整微分参数可以增强系统的稳定性。
PID控制器的输出可以用以下公式表示:u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt其中,u(t)是控制器的输出,e(t)是测量误差,Kp、Ki和Kd是分别对应比例、积分和微分参数。
接下来以一个温度控制系统为例说明PID控制的原理:假设有一个恒温箱,我们希望将箱内的温度控制在一个设定值。
首先,我们需要测量箱内的温度和设定值之间的差异,即测量误差。
然后,根据测量误差的大小,我们可以调整控制器的输出,通过增加或减少加热器的功率,使温度接近设定值。
在PID控制中,我们可以通过调节比例参数Kp来控制系统的灵敏度。
增大Kp可以使系统对误差更敏感,但过大的Kp可能导致系统震荡。
当温度误差较大时,控制器会输出较大的功率,加热箱内的温度快速升高;当温度接近设定值时,控制器会输出较小的功率,使温度稳定在设定值附近。
积分参数Ki用于消除稳态误差。
如果系统存在稳态误差,说明温度无法完全达到设定值,可能是由于传感器或加热器的不精确性引起的。
通过调节Ki的大小,积分项可以自动调整系统的控制量,消除稳态误差。
微分参数Kd用于增强系统的稳定性。
如果系统的温度变化率很大,说明加热或冷却过程不够平稳。
通过调节Kd的大小,微分项可以抑制温度的剧烈波动,使系统更加稳定。
综上所述,PID控制器通过比例、积分和微分三个参数的调节,可以实现快速、平稳地将系统控制到设定值。
pid通俗讲解

pid通俗讲解PID控制是一种常见的闭环控制算法,它广泛应用于工业过程控制和自动化系统中。
PID控制器根据系统反馈信号与给定的目标值进行比较,并根据误差的大小调整控制输出,以使系统实现期望的控制效果。
一、PID控制的基本概念1.1 PID控制器的含义PID控制是指用比例(P)、积分(I)和微分(D)三个参数对系统进行控制的方式。
控制器通过比较给定值和反馈信号的差异,并根据这个差异调整输出信号,以使系统达到所期望的状态。
1.2 PID控制器的结构PID控制器由比例环节、积分环节和微分环节组成。
比例环节根据给定值和反馈信号的差异,按照一定比例调整输出信号;积分环节根据反馈信号与给定值的累积误差来调整输出信号;微分环节根据反馈信号的变化速率来调整输出信号。
1.3 PID参数的选择PID控制器的参数选择对于控制效果非常重要。
一般情况下,可以根据系统的特性和需求来优化PID参数。
比例参数决定了控制器对于误差的敏感程度,积分参数可以消除长期的误差累积,微分参数可以对系统的快速变化作出快速的响应。
二、PID控制的原理2.1 比例控制比例控制是PID控制中最基本的控制方式。
比例控制器根据给定值和反馈信号的差异按照一定的比例系数进行调整。
当比例系数增大时,控制器对误差的敏感程度增加,系统的过渡响应时间缩短,但可能引起系统的振荡和不稳定。
当比例系数过小时,系统的控制效果较差,可能导致较大的偏差。
2.2 积分控制积分控制是PID控制中的另一种控制方式,它可以消除长期的误差累积。
积分控制器根据反馈信号与给定值的累积误差进行调整。
当系统存在常态误差时,积分控制器可以通过积分作用逐渐消除误差。
但当积分系数过大时,会导致系统的过度抵消误差,甚至引起系统的不稳定。
2.3 微分控制微分控制是PID控制中的第三种控制方式,它主要用于响应系统快速变化的情况。
微分控制器根据反馈信号的变化速率来调整输出信号。
当系统存在突变或快速变化的情况时,微分控制器可以通过快速响应减小系统的超调和振荡。
pid最通俗的理解和参数设置口诀

pid最通俗的理解和参数设置口诀在生活中,PID控制就像是我们调整心情的一种方法。
简单来说,PID就是一种控制系统,用来让系统按照我们希望的方式运行。
它的名字其实就是比例(P)、积分(I)和微分(D)的缩写,每个部分都有自己的“职责”,就像家庭中的每个人都有不同的角色一样。
1. PID控制的基本概念1.1 比例(P)控制比例控制的核心就是“比例”,这部分负责根据当前的误差调整系统。
如果你设定了一个目标值,比如你想要把温度调到25°C,而实际温度是20°C,比例控制会试图根据这个误差来增加加热的强度。
它的工作原理就是“误差越大,调整得越多”,就像你看到房间很乱,越是乱,你就越想快点整理好一样。
1.2 积分(I)控制积分控制则是处理长期累积的误差。
假设你的房间总是有点儿乱,比例控制可能在短期内能起作用,但时间长了,可能会出现细微的偏差。
积分控制就像是那种记性很好的朋友,细心地记住了每一个小细节,并且不断地纠正这些小问题。
它会通过积分计算,逐渐调整系统,直到误差完全消失。
1.3 微分(D)控制微分控制的作用是预测误差的变化趋势,提前做出反应。
就好比你看到房间有些凌乱,就开始提前收拾,这样可以防止问题变得更加严重。
它专注于误差变化的速率,帮助系统快速稳定下来,避免过度的波动。
2. PID参数设置的口诀2.1 比例系数(Kp)的设置比例系数就像是你的“心态调整器”,决定了你对误差的反应速度。
设置比例系数的时候,咱们可以记住“快稳适中”,意思是不要太急也不要太慢。
比例系数太大了,系统可能会变得不稳定;太小了,反应就会迟缓。
所以,找到一个合适的值,就像是找到你心情的平衡点。
2.2 积分系数(Ki)的设置积分系数则是调整你“耐心”的程度。
设定的时候,记住“慢来稳”,不要着急。
积分系数太高,可能会导致系统的过度调节,造成波动;太低,可能会导致系统反应缓慢。
就像你处理长期积累的琐事,慢慢来,稳定才是关键。
标准的PID处理例程(PID通俗易懂的讲解)[2]
![标准的PID处理例程(PID通俗易懂的讲解)[2]](https://img.taocdn.com/s3/m/0c25cedaa58da0116c17490f.png)
PID通俗易懂的讲解最近从网上看到了一种对PID的解释,比较通俗易懂,也好记住,经过自己的整理后说明如下。
控制模型:你控制一个人让他以PID控制的方式走110步后停下。
(1)P比例控制,就是让他走110步,他按照一定的步伐走到一百零几步(如108步)或100多步(如112步)就停了。
说明:P比例控制是一种最简单的控制方式。
其控制器的输出与输入误差信号成比例关系。
当仅有比例控制时系统输出存在稳态误差(Steady-state error)。
(2)PI积分控制,就是他按照一定的步伐走到112步然后回头接着走,走到108步位置时,然后又回头向110步位置走。
在110步位置处来回晃几次,最后停在110步的位置。
说明:在积分I控制中,控制器的输出与输入误差信号的积分成正比关系。
对一个自动控制系统,如果在进入稳态后存在稳态误差,则称这个控制系统是有稳态误差的或简称有差系统(System with Steady-state Error)。
为了消除稳态误差,在控制器中必须引入“积分项”。
积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。
因此,比例+积分(PI)控制器,可以使系统在进入稳态后无稳态误差。
(3)PD微分控制,就是他按照一定的步伐走到一百零几步后,再慢慢地向110步的位置靠近,如果最后能精确停在110步的位置,就是无静差控制;如果停在110步附近(如109步或111步位置),就是有静差控制。
说明:在微分控制D中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。
自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳,其原因是由于存在有较大惯性组件(环节)或有滞后(delay)组件,具有抑制误差的作用,其变化总是落后于误差的变化。
解决的办法是使抑制误差作用的变化“超前”,即在误差接近零时,抑制误差的作用就应该是零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PID通俗易懂的讲解
最近从网上看到了一种对PID的解释,比较通俗易懂,也好记住,经过自己的整理后说明如下。
控制模型:你控制一个人让他以PID控制的方式走110步后停下。
(1)P比例控制,就是让他走110步,他按照一定的步伐走到一百零几步(如108步)或100多步(如112步)就停了。
说明:
P比例控制是一种最简单的控制方式。
其控制器的输出与输入误差信号成比例关系。
当仅有比例控制时系统输出存在稳态误差(Steady-state error)。
(2)PI积分控制,就是他按照一定的步伐走到112步然后回头接着走,走到108步位置时,然后又回头向110步位置走。
在110步位置处来回晃几次,最后停在110步的位置。
说明:
在积分I控制中,控制器的输出与输入误差信号的积分成正比关系。
对一个自动控制系统,如果在进入稳态后存在稳态误差,则称这个控制系统是有稳态误差的或简称有差系统(System with Steady-state Error)。
为了消除稳态误差,在控制器中必须引入“积分项”。
积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。
因此,比例+积分(PI)控制器,可以使系统在进入稳态后无稳态误差。
(3)PD微分控制,就是他按照一定的步伐走到一百零几步后,再慢慢地向110步的位置靠近,如果最后能精确停在110步的位置,就是无静差控制;如果停在110步附近(如109步或111步位置),就是有静差控制。
说明:
在微分控制D中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。
自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳,其原因是由于存在有较大惯性组件(环节)或有滞后(delay)组件,具有抑制误差的作用,其变化总是落后于误差的变化。
解决的办法是使抑制误差作用的变化“超前”,即在误差接近零时,抑制误差的作用就应该是零。
这就是说,在控制器中仅引入“比例P”项往往是不够的,比例项的作用仅是放大误差的幅值,而目前需要增加的是“微分项”,它能预测误差变化的趋势。
这样,具有比例+微分的控制器,就能够提前使抑制误差的控制作用等于零,甚至为负值,从而避免了被控量的严重超调。
所以对有较大惯性或滞后的被控对象,比例P+微分D(PD)控制器能改善系统在调节过程中的动态特性
/*====================================================================================================
PID Function
The PID (比例、积分、微分) function is used in mainly
control applications. PIDCalc performs one iteration of the PID
algorithm.
While the PID function works, main is just a dummy program showing
a typical usage.
=====================================================================================================*/
typedef struct PID { // 结构体
double SetPoint; // 设定目标 Desired Value
double Proportion; // 比例常数 Proportional Const
double Integral; // 积分常数 Integral Const
double Derivative; // 微分常数 Derivative Const
double LastError; // 最后误差数Error[-1]
double PrevError; // 之前误差数Error[-2] <Previous>
double SumError; // 误差积分Sums of Errors
} PID; //
/*==================================================================================================== PID计算部分
=====================================================================================================*/ double PIDCalc( PID *pp, double NextPoint )
{
double dError, //当前微分
Error; //偏差
Error = pp->SetPoint - NextPoint; // 偏差 =设定目标-输入值
pp->SumError += Error; // 积分 =积分+偏差
dError = pp->LastError - pp->PrevError; // 当前微分 =最后误差-之前误差
pp->PrevError = pp->LastError; // 更新“之前误差”
pp->LastError = Error; // 更新“最后误差”
return (pp->Proportion * Error // 比例项 =比例常数 x 偏差
+ pp->Integral * pp->SumError // 积分项 =积分常数 x 误差积分
+ pp->Derivative * dError // 微分项 =微分常数 x 当前微分
);
}
/*==================================================================================================== Initialize PID Structure
=====================================================================================================*/ void PIDInit (PID *pp)
{
memset ( pp,0,sizeof(PID));
}
/*==================================================================================================== Main Program
=====================================================================================================*/ double sensor (void) // Dummy Sensor Function 输入
{
return 100.0;
}
void actuator(double rDelta) // Dummy Actuator Function 输出
{
}
void main(void)
{
PID sPID; // PID Control Structure 结构
double rOut; // PID Response (Output) 输出变量
double rIn; // PID Feedback (Input) 输入变量
PIDInit ( &sPID ); // Initialize Structure 初始化结构
sPID.Proportion = 0.5; // Set PID Coefficients 设定PID系数比例常数
sPID.Integral = 0.5; // 积分常数
sPID.Derivative = 0.0; // 微分常数
sPID.SetPoint = 100.0; // Set PID Setpoint 设定目标
for (;;) { // Mock Up of PID Processing
rIn = sensor (); // Read Input 取输入值
rOut = PIDCalc ( &sPID,rIn ); // Perform PID Interation PID运算
actuator ( rOut ); // Effect Needed Changes 输出
}。
