Differential Algebra Structures on Familes of Trees
单斜相阿利特的晶体结构研究(英文)

Recent work have concerned the identification of stabilized modifications at room temperature due to the importance in the quality control of Portland cement. Differential thermal analysis (DTA) showes the T1–T2 transi-
The objective of this paper was to describe the superstructures of the monoclinic modification of C3S. Some indices for describing the reflections due to the superstructures were proposed to express the orientations and
1 Experimental
The specimens were provided by China Building Materials Academy (CBMA). A selected-area electron diffraction (SAED) technique was applied to record the reflections. A TEM device (Model JEM–2010UHR, JEOL, Tokyo, Japan) equipped with a double tilt goniometry was used to record the HRTEM images at an accelerating voltage of 200 kV. The preparation of specimens for the TEM was performed by a conventional method applied for the observation of ceramic powders except for the dispersion of the specimens in ethanol. Table 1 shows the chemical compositions of the specimens, which was provided by the CBMA. The three specimens are remarked as A, B, and C.
heterogeneous interfacial structure

heterogeneous interfacial structure英文版Heterogeneous Interfacial StructureHeterogeneous interfacial structure refers to the structural differences that exist at the boundary between two different materials or phases. This structure plays a crucial role in determining the physical and chemical properties of the interface, as well as its stability and reactivity.At the interface between two materials, the atomic arrangement, bonding configuration, and electronic structure can all differ significantly from the bulk materials on either side. This heterogeneity can lead to a range of unique properties, such as charge accumulation, bond formation, and catalytic activity. For example, in the field of materials science, heterogeneous interfaces are often exploited to enhance the performance of devices such as solar cells and fuel cells.The study of heterogeneous interfacial structure is challenging due to the complexity of the interactions involved. Experimental techniques such as scanning probe microscopy, spectroscopy, and diffraction methods can provide insights into the atomic-scale structure and electronic properties of interfaces. Computational modeling is also an important tool for understanding and predicting interfacial behavior.In recent years, there has been increasing interest in the use of heterogeneous interfacial structures in nanotechnology and materials science. This interest is driven by the potential for novel materials with enhanced properties, as well as the development of new technologies such as nanodevices and sensors.In conclusion, heterogeneous interfacial structure is a crucial aspect of materials science and nanotechnology. Its understanding and control offer the potential for the development of novel materials and devices with enhanced performance and functionality.中文版异质界面结构异质界面结构指的是两种不同材料或相之间的边界处存在的结构差异。
数学英语知识点总结

数学英语知识点总结1. ArithmeticArithmetic is the most basic branch of mathematics and involves the study of numbers and the basic operations of addition, subtraction, multiplication, and division. It also covers concepts such as fractions, decimals, percentages, and ratios. Arithmetic is fundamental to everyday life and is used in a wide range of applications, from simple calculations to complex financial and scientific problems.2. AlgebraAlgebra is a branch of mathematics that deals with symbols and the rules for manipulating these symbols. It involves the study of variables, equations, functions, and graphs. Algebra is essential for solving equations, analyzing patterns, and making predictions. It is also the foundation for more advanced mathematical topics such as calculus and linear algebra.3. GeometryGeometry is the branch of mathematics that deals with the study of shapes, sizes, and the properties of space. It includes concepts such as points, lines, angles, triangles, polygons, circles, and solids. Geometry is used to solve problems involving spatial relationships and is essential for fields such as architecture, engineering, and physics.4. TrigonometryTrigonometry is a branch of mathematics that focuses on the relationships between the angles and sides of triangles. It involves the study of trigonometric functions such as sine, cosine, and tangent, as well as the properties of these functions. Trigonometry is used in fields such as navigation, physics, and engineering, where understanding of angles and distances is crucial.5. CalculusCalculus is the branch of mathematics that deals with the study of change and motion. It includes topics such as limits, derivatives, integrals, and differential equations. Calculus is essential for understanding the behavior of functions, analyzing rates of change, and solving optimization problems. It is widely used in fields such as physics, engineering, economics, and biology.6. StatisticsStatistics is the branch of mathematics that deals with the collection, analysis, interpretation, and presentation of data. It includes topics such as probability, sampling, hypothesis testing, and regression analysis. Statistics is used in fields such as economics, sociology, psychology, and medicine, where understanding of data and probabilities is essential for making informed decisions.7. Number theoryNumber theory is the branch of mathematics that deals with the study of integers and their properties. It includes topics such as prime numbers, divisibility, congruence, and Diophantine equations. Number theory is used in fields such as cryptography, computer science, and cryptography, where understanding of the properties of integers is essential for designing secure systems.8. Linear algebraLinear algebra is the branch of mathematics that deals with the study of vectors, matrices, and linear transformations. It includes topics such as systems of linear equations, eigenvalues, and eigenvectors. Linear algebra is used in fields such as computer graphics, physics, and engineering, where understanding of linear systems and transformations is crucial.9. Differential equationsDifferential equations is the branch of mathematics that deals with the study of equations involving derivatives and their solutions. It includes topics such as ordinary differential equations, partial differential equations, and boundary value problems. Differential equations are used in fields such as physics, engineering, and biology, where understanding of the behavior of dynamic systems is essential.10. Discrete mathematicsDiscrete mathematics is the branch of mathematics that deals with the study of discrete structures and objects. It includes topics such as graph theory, combinatorics, and game theory. Discrete mathematics is used in fields such as computer science, cryptography, and operations research, where understanding of discrete structures and algorithms is essential. In conclusion, mathematics is a diverse and expansive subject that encompasses a wide range of topics and concepts. From basic arithmetic to advanced calculus, the field of mathematics offers something for everyone, whether you are interested in solving practical problems, conducting theoretical research, or simply exploring the beauty of abstract concepts. Regardless of your interests, mathematics has something to offer and is an essential part of our everyday lives.。
斯普林格数学研究生教材丛书

《斯普林格数学研究生教材丛书》(Graduate Texts in Mathematics)GTM001《Introduction to Axiomatic Set Theory》Gaisi Takeuti, Wilson M.Zaring GTM002《Measure and Category》John C.Oxtoby(测度和范畴)(2ed.)GTM003《Topological Vector Spaces》H.H.Schaefer, M.P.Wolff(2ed.)GTM004《A Course in Homological Algebra》P.J.Hilton, U.Stammbach(2ed.)(同调代数教程)GTM005《Categories for the Working Mathematician》Saunders Mac Lane(2ed.)GTM006《Projective Planes》Daniel R.Hughes, Fred C.Piper(投射平面)GTM007《A Course in Arithmetic》Jean-Pierre Serre(数论教程)GTM008《Axiomatic set theory》Gaisi Takeuti, Wilson M.Zaring(2ed.)GTM009《Introduction to Lie Algebras and Representation Theory》James E.Humphreys(李代数和表示论导论)GTM010《A Course in Simple-Homotopy Theory》M.M CohenGTM011《Functions of One Complex VariableⅠ》John B.ConwayGTM012《Advanced Mathematical Analysis》Richard BealsGTM013《Rings and Categories of Modules》Frank W.Anderson, Kent R.Fuller(环和模的范畴)(2ed.)GTM014《Stable Mappings and Their Singularities》Martin Golubitsky, Victor Guillemin (稳定映射及其奇点)GTM015《Lectures in Functional Analysis and Operator Theory》Sterling K.Berberian GTM016《The Structure of Fields》David J.Winter(域结构)GTM017《Random Processes》Murray RosenblattGTM018《Measure Theory》Paul R.Halmos(测度论)GTM019《A Hilbert Space Problem Book》Paul R.Halmos(希尔伯特问题集)GTM020《Fibre Bundles》Dale Husemoller(纤维丛)GTM021《Linear Algebraic Groups》James E.Humphreys(线性代数群)GTM022《An Algebraic Introduction to Mathematical Logic》Donald W.Barnes, John M.MackGTM023《Linear Algebra》Werner H.Greub(线性代数)GTM024《Geometric Functional Analysis and Its Applications》Paul R.HolmesGTM025《Real and Abstract Analysis》Edwin Hewitt, Karl StrombergGTM026《Algebraic Theories》Ernest G.ManesGTM027《General Topology》John L.Kelley(一般拓扑学)GTM028《Commutative Algebra》VolumeⅠOscar Zariski, Pierre Samuel(交换代数)GTM029《Commutative Algebra》VolumeⅡOscar Zariski, Pierre Samuel(交换代数)GTM030《Lectures in Abstract AlgebraⅠ.Basic Concepts》Nathan Jacobson(抽象代数讲义Ⅰ基本概念分册)GTM031《Lectures in Abstract AlgebraⅡ.Linear Algabra》Nathan.Jacobson(抽象代数讲义Ⅱ线性代数分册)GTM032《Lectures in Abstract AlgebraⅢ.Theory of Fields and Galois Theory》Nathan.Jacobson(抽象代数讲义Ⅲ域和伽罗瓦理论)GTM033《Differential Topology》Morris W.Hirsch(微分拓扑)GTM034《Principles of Random Walk》Frank Spitzer(2ed.)(随机游动原理)GTM035《Several Complex Variables and Banach Algebras》Herbert Alexander, John Wermer(多复变和Banach代数)GTM036《Linear Topological Spaces》John L.Kelley, Isaac Namioka(线性拓扑空间)GTM037《Mathematical Logic》J.Donald Monk(数理逻辑)GTM038《Several Complex Variables》H.Grauert, K.FritzsheGTM039《An Invitation to C*-Algebras》William Arveson(C*-代数引论)GTM040《Denumerable Markov Chains》John G.Kemeny, urie Snell, Anthony W.KnappGTM041《Modular Functions and Dirichlet Series in Number Theory》Tom M.Apostol (数论中的模函数和Dirichlet序列)GTM042《Linear Representations of Finite Groups》Jean-Pierre Serre(有限群的线性表示)GTM043《Rings of Continuous Functions》Leonard Gillman, Meyer JerisonGTM044《Elementary Algebraic Geometry》Keith KendigGTM045《Probability TheoryⅠ》M.Loève(概率论Ⅰ)(4ed.)GTM046《Probability TheoryⅡ》M.Loève(概率论Ⅱ)(4ed.)GTM047《Geometric Topology in Dimensions 2 and 3》Edwin E.MoiseGTM048《General Relativity for Mathematicians》Rainer.K.Sachs, H.Wu伍鸿熙(为数学家写的广义相对论)GTM049《Linear Geometry》K.W.Gruenberg, A.J.Weir(2ed.)GTM050《Fermat's Last Theorem》Harold M.EdwardsGTM051《A Course in Differential Geometry》Wilhelm Klingenberg(微分几何教程)GTM052《Algebraic Geometry》Robin Hartshorne(代数几何)GTM053《A Course in Mathematical Logic for Mathematicians》Yu.I.Manin(2ed.)GTM054《Combinatorics with Emphasis on the Theory of Graphs》Jack E.Graver, Mark E.WatkinsGTM055《Introduction to Operator TheoryⅠ》Arlen Brown, Carl PearcyGTM056《Algebraic Topology:An Introduction》W.S.MasseyGTM057《Introduction to Knot Theory》Richard.H.Crowell, Ralph.H.FoxGTM058《p-adic Numbers, p-adic Analysis, and Zeta-Functions》Neal Koblitz(p-adic 数、p-adic分析和Z函数)GTM059《Cyclotomic Fields》Serge LangGTM060《Mathematical Methods of Classical Mechanics》V.I.Arnold(经典力学的数学方法)(2ed.)GTM061《Elements of Homotopy Theory》George W.Whitehead(同论论基础)GTM062《Fundamentals of the Theory of Groups》M.I.Kargapolov, Ju.I.Merzljakov GTM063《Modern Graph Theory》Béla BollobásGTM064《Fourier Series:A Modern Introduction》VolumeⅠ(2ed.)R.E.Edwards(傅里叶级数)GTM065《Differential Analysis on Complex Manifolds》Raymond O.Wells, Jr.(3ed.)GTM066《Introduction to Affine Group Schemes》William C.Waterhouse(仿射群概型引论)GTM067《Local Fields》Jean-Pierre Serre(局部域)GTM069《Cyclotomic FieldsⅠandⅡ》Serge LangGTM070《Singular Homology Theory》William S.MasseyGTM071《Riemann Surfaces》Herschel M.Farkas, Irwin Kra(黎曼曲面)GTM072《Classical Topology and Combinatorial Group Theory》John Stillwell(经典拓扑和组合群论)GTM073《Algebra》Thomas W.Hungerford(代数)GTM074《Multiplicative Number Theory》Harold Davenport(乘法数论)(3ed.)GTM075《Basic Theory of Algebraic Groups and Lie Algebras》G.P.HochschildGTM076《Algebraic Geometry:An Introduction to Birational Geometry of Algebraic Varieties》Shigeru IitakaGTM077《Lectures on the Theory of Algebraic Numbers》Erich HeckeGTM078《A Course in Universal Algebra》Stanley Burris, H.P.Sankappanavar(泛代数教程)GTM079《An Introduction to Ergodic Theory》Peter Walters(遍历性理论引论)GTM080《A Course in_the Theory of Groups》Derek J.S.RobinsonGTM081《Lectures on Riemann Surfaces》Otto ForsterGTM082《Differential Forms in Algebraic Topology》Raoul Bott, Loring W.Tu(代数拓扑中的微分形式)GTM083《Introduction to Cyclotomic Fields》Lawrence C.Washington(割圆域引论)GTM084《A Classical Introduction to Modern Number Theory》Kenneth Ireland, Michael Rosen(现代数论经典引论)GTM085《Fourier Series A Modern Introduction》Volume 1(2ed.)R.E.Edwards GTM086《Introduction to Coding Theory》J.H.van Lint(3ed .)GTM087《Cohomology of Groups》Kenneth S.Brown(上同调群)GTM088《Associative Algebras》Richard S.PierceGTM089《Introduction to Algebraic and Abelian Functions》Serge Lang(代数和交换函数引论)GTM090《An Introduction to Convex Polytopes》Ame BrondstedGTM091《The Geometry of Discrete Groups》Alan F.BeardonGTM092《Sequences and Series in BanachSpaces》Joseph DiestelGTM093《Modern Geometry-Methods and Applications》(PartⅠ.The of geometry Surfaces Transformation Groups and Fields)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov (现代几何学方法和应用)GTM094《Foundations of Differentiable Manifolds and Lie Groups》Frank W.Warner(可微流形和李群基础)GTM095《Probability》A.N.Shiryaev(2ed.)GTM096《A Course in Functional Analysis》John B.Conway(泛函分析教程)GTM097《Introduction to Elliptic Curves and Modular Forms》Neal Koblitz(椭圆曲线和模形式引论)GTM098《Representations of Compact Lie Groups》Theodor Breöcker, Tammo tom DieckGTM099《Finite Reflection Groups》L.C.Grove, C.T.Benson(2ed.)GTM100《Harmonic Analysis on Semigroups》Christensen Berg, Jens Peter Reus Christensen, Paul ResselGTM101《Galois Theory》Harold M.Edwards(伽罗瓦理论)GTM102《Lie Groups, Lie Algebras, and Their Representation》V.S.Varadarajan(李群、李代数及其表示)GTM103《Complex Analysis》Serge LangGTM104《Modern Geometry-Methods and Applications》(PartⅡ.Geometry and Topology of Manifolds)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov(现代几何学方法和应用)GTM105《SL₂ (R)》Serge Lang(SL₂ (R)群)GTM106《The Arithmetic of Elliptic Curves》Joseph H.Silverman(椭圆曲线的算术理论)GTM107《Applications of Lie Groups to Differential Equations》Peter J.Olver(李群在微分方程中的应用)GTM108《Holomorphic Functions and Integral Representations in Several Complex Variables》R.Michael RangeGTM109《Univalent Functions and Teichmueller Spaces》Lehto OlliGTM110《Algebraic Number Theory》Serge Lang(代数数论)GTM111《Elliptic Curves》Dale Husemoeller(椭圆曲线)GTM112《Elliptic Functions》Serge Lang(椭圆函数)GTM113《Brownian Motion and Stochastic Calculus》Ioannis Karatzas, Steven E.Shreve (布朗运动和随机计算)GTM114《A Course in Number Theory and Cryptography》Neal Koblitz(数论和密码学教程)GTM115《Differential Geometry:Manifolds, Curves, and Surfaces》M.Berger, B.Gostiaux GTM116《Measure and Integral》Volume1 John L.Kelley, T.P.SrinivasanGTM117《Algebraic Groups and Class Fields》Jean-Pierre Serre(代数群和类域)GTM118《Analysis Now》Gert K.Pedersen(现代分析)GTM119《An introduction to Algebraic Topology》Jossph J.Rotman(代数拓扑导论)GTM120《Weakly Differentiable Functions》William P.Ziemer(弱可微函数)GTM121《Cyclotomic Fields》Serge LangGTM122《Theory of Complex Functions》Reinhold RemmertGTM123《Numbers》H.-D.Ebbinghaus, H.Hermes, F.Hirzebruch, M.Koecher, K.Mainzer, J.Neukirch, A.Prestel, R.Remmert(2ed.)GTM124《Modern Geometry-Methods and Applications》(PartⅢ.Introduction to Homology Theory)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov(现代几何学方法和应用)GTM125《Complex Variables:An introduction》Garlos A.Berenstein, Roger Gay GTM126《Linear Algebraic Groups》Armand Borel(线性代数群)GTM127《A Basic Course in Algebraic Topology》William S.Massey(代数拓扑基础教程)GTM128《Partial Differential Equations》Jeffrey RauchGTM129《Representation Theory:A First Course》William Fulton, Joe HarrisGTM130《Tensor Geometry》C.T.J.Dodson, T.Poston(张量几何)GTM131《A First Course in Noncommutative Rings》m(非交换环初级教程)GTM132《Iteration of Rational Functions:Complex Analytic Dynamical Systems》AlanF.Beardon(有理函数的迭代:复解析动力系统)GTM133《Algebraic Geometry:A First Course》Joe Harris(代数几何)GTM134《Coding and Information Theory》Steven RomanGTM135《Advanced Linear Algebra》Steven RomanGTM136《Algebra:An Approach via Module Theory》William A.Adkins, Steven H.WeintraubGTM137《Harmonic Function Theory》Sheldon Axler, Paul Bourdon, Wade Ramey(调和函数理论)GTM138《A Course in Computational Algebraic Number Theory》Henri Cohen(计算代数数论教程)GTM139《Topology and Geometry》Glen E.BredonGTM140《Optima and Equilibria:An Introduction to Nonlinear Analysis》Jean-Pierre AubinGTM141《A Computational Approach to Commutative Algebra》Gröbner Bases, Thomas Becker, Volker Weispfenning, Heinz KredelGTM142《Real and Functional Analysis》Serge Lang(3ed.)GTM143《Measure Theory》J.L.DoobGTM144《Noncommutative Algebra》Benson Farb, R.Keith DennisGTM145《Homology Theory:An Introduction to Algebraic Topology》James W.Vick(同调论:代数拓扑简介)GTM146《Computability:A Mathematical Sketchbook》Douglas S.BridgesGTM147《Algebraic K-Theory and Its Applications》Jonathan Rosenberg(代数K理论及其应用)GTM148《An Introduction to the Theory of Groups》Joseph J.Rotman(群论入门)GTM149《Foundations of Hyperbolic Manifolds》John G.Ratcliffe(双曲流形基础)GTM150《Commutative Algebra with a view toward Algebraic Geometry》David EisenbudGTM151《Advanced Topics in the Arithmetic of Elliptic Curves》Joseph H.Silverman(椭圆曲线的算术高级选题)GTM152《Lectures on Polytopes》Günter M.ZieglerGTM153《Algebraic Topology:A First Course》William Fulton(代数拓扑)GTM154《An introduction to Analysis》Arlen Brown, Carl PearcyGTM155《Quantum Groups》Christian Kassel(量子群)GTM156《Classical Descriptive Set Theory》Alexander S.KechrisGTM157《Integration and Probability》Paul MalliavinGTM158《Field theory》Steven Roman(2ed.)GTM159《Functions of One Complex Variable VolⅡ》John B.ConwayGTM160《Differential and Riemannian Manifolds》Serge Lang(微分流形和黎曼流形)GTM161《Polynomials and Polynomial Inequalities》Peter Borwein, Tamás Erdélyi(多项式和多项式不等式)GTM162《Groups and Representations》J.L.Alperin, Rowen B.Bell(群及其表示)GTM163《Permutation Groups》John D.Dixon, Brian Mortime rGTM164《Additive Number Theory:The Classical Bases》Melvyn B.NathansonGTM165《Additive Number Theory:Inverse Problems and the Geometry of Sumsets》Melvyn B.NathansonGTM166《Differential Geometry:Cartan's Generalization of Klein's Erlangen Program》R.W.SharpeGTM167《Field and Galois Theory》Patrick MorandiGTM168《Combinatorial Convexity and Algebraic Geometry》Günter Ewald(组合凸面体和代数几何)GTM169《Matrix Analysis》Rajendra BhatiaGTM170《Sheaf Theory》Glen E.Bredon(2ed.)GTM171《Riemannian Geometry》Peter Petersen(黎曼几何)GTM172《Classical Topics in Complex Function Theory》Reinhold RemmertGTM173《Graph Theory》Reinhard Diestel(图论)(3ed.)GTM174《Foundations of Real and Abstract Analysis》Douglas S.Bridges(实分析和抽象分析基础)GTM175《An Introduction to Knot Theory》W.B.Raymond LickorishGTM176《Riemannian Manifolds:An Introduction to Curvature》John M.LeeGTM177《Analytic Number Theory》Donald J.Newman(解析数论)GTM178《Nonsmooth Analysis and Control Theory》F.H.clarke, Yu.S.Ledyaev, R.J.Stern, P.R.Wolenski(非光滑分析和控制论)GTM179《Banach Algebra Techniques in Operator Theory》Ronald G.Douglas(2ed.)GTM180《A Course on Borel Sets》S.M.Srivastava(Borel 集教程)GTM181《Numerical Analysis》Rainer KressGTM182《Ordinary Differential Equations》Wolfgang WalterGTM183《An introduction to Banach Spaces》Robert E.MegginsonGTM184《Modern Graph Theory》Béla Bollobás(现代图论)GTM185《Using Algebraic Geomety》David A.Cox, John Little, Donal O’Shea(应用代数几何)GTM186《Fourier Analysis on Number Fields》Dinakar Ramakrishnan, Robert J.Valenza GTM187《Moduli of Curves》Joe Harris, Ian Morrison(曲线模)GTM188《Lectures on the Hyperreals:An Introduction to Nonstandard Analysis》Robert GoldblattGTM189《Lectures on Modules and Rings》m(模和环讲义)GTM190《Problems in Algebraic Number Theory》M.Ram Murty, Jody Esmonde(代数数论中的问题)GTM191《Fundamentals of Differential Geometry》Serge Lang(微分几何基础)GTM192《Elements of Functional Analysis》Francis Hirsch, Gilles LacombeGTM193《Advanced Topics in Computational Number Theory》Henri CohenGTM194《One-Parameter Semigroups for Linear Evolution Equations》Klaus-Jochen Engel, Rainer Nagel(线性发展方程的单参数半群)GTM195《Elementary Methods in Number Theory》Melvyn B.Nathanson(数论中的基本方法)GTM196《Basic Homological Algebra》M.Scott OsborneGTM197《The Geometry of Schemes》David Eisenbud, Joe HarrisGTM198《A Course in p-adic Analysis》Alain M.RobertGTM199《Theory of Bergman Spaces》Hakan Hedenmalm, Boris Korenblum, Kehe Zhu(Bergman空间理论)GTM200《An Introduction to Riemann-Finsler Geometry》D.Bao, S.-S.Chern, Z.Shen GTM201《Diophantine Geometry An Introduction》Marc Hindry, Joseph H.Silverman GTM202《Introduction to Topological Manifolds》John M.LeeGTM203《The Symmetric Group》Bruce E.SaganGTM204《Galois Theory》Jean-Pierre EscofierGTM205《Rational Homotopy Theory》Yves Félix, Stephen Halperin, Jean-Claude Thomas(有理同伦论)GTM206《Problems in Analytic Number Theory》M.Ram MurtyGTM207《Algebraic Graph Theory》Chris Godsil, Gordon Royle(代数图论)GTM208《Analysis for Applied Mathematics》Ward CheneyGTM209《A Short Course on Spectral Theory》William Arveson(谱理论简明教程)GTM210《Number Theory in Function Fields》Michael RosenGTM211《Algebra》Serge Lang(代数)GTM212《Lectures on Discrete Geometry》Jiri Matousek(离散几何讲义)GTM213《From Holomorphic Functions to Complex Manifolds》Klaus Fritzsche, Hans Grauert(从正则函数到复流形)GTM214《Partial Differential Equations》Jüergen Jost(偏微分方程)GTM215《Algebraic Functions and Projective Curves》David M.Goldschmidt(代数函数和投影曲线)GTM216《Matrices:Theory and Applications》Denis Serre(矩阵:理论及应用)GTM217《Model Theory An Introduction》David Marker(模型论引论)GTM218《Introduction to Smooth Manifolds》John M.Lee(光滑流形引论)GTM219《The Arithmetic of Hyperbolic 3-Manifolds》Colin Maclachlan, Alan W.Reid GTM220《Smooth Manifolds and Observables》Jet Nestruev(光滑流形和直观)GTM221《Convex Polytopes》Branko GrüenbaumGTM222《Lie Groups, Lie Algebras, and Representations》Brian C.Hall(李群、李代数和表示)GTM223《Fourier Analysis and its Applications》Anders Vretblad(傅立叶分析及其应用)GTM224《Metric Structures in Differential Geometry》Gerard Walschap(微分几何中的度量结构)GTM225《Lie Groups》Daniel Bump(李群)GTM226《Spaces of Holomorphic Functions in the Unit Ball》Kehe Zhu(单位球内的全纯函数空间)GTM227《Combinatorial Commutative Algebra》Ezra Miller, Bernd Sturmfels(组合交换代数)GTM228《A First Course in Modular Forms》Fred Diamond, Jerry Shurman(模形式初级教程)GTM229《The Geometry of Syzygies》David Eisenbud(合冲几何)GTM230《An Introduction to Markov Processes》Daniel W.Stroock(马尔可夫过程引论)GTM231《Combinatorics of Coxeter Groups》Anders Bjröner, Francesco Brenti(Coxeter 群的组合学)GTM232《An Introduction to Number Theory》Graham Everest, Thomas Ward(数论入门)GTM233《Topics in Banach Space Theory》Fenando Albiac, Nigel J.Kalton(Banach空间理论选题)GTM234《Analysis and Probability:Wavelets, Signals, Fractals》Palle E.T.Jorgensen(分析与概率)GTM235《Compact Lie Groups》Mark R.Sepanski(紧致李群)GTM236《Bounded Analytic Functions》John B.Garnett(有界解析函数)GTM237《An Introduction to Operators on the Hardy-Hilbert Space》Rubén A.Martínez-Avendano, Peter Rosenthal(哈代-希尔伯特空间算子引论)GTM238《A Course in Enumeration》Martin Aigner(枚举教程)GTM239《Number Theory:VolumeⅠTools and Diophantine Equations》Henri Cohen GTM240《Number Theory:VolumeⅡAnalytic and Modern Tools》Henri Cohen GTM241《The Arithmetic of Dynamical Systems》Joseph H.SilvermanGTM242《Abstract Algebra》Pierre Antoine Grillet(抽象代数)GTM243《Topological Methods in Group Theory》Ross GeogheganGTM244《Graph Theory》J.A.Bondy, U.S.R.MurtyGTM245《Complex Analysis:In the Spirit of Lipman Bers》Jane P.Gilman, Irwin Kra, Rubi E.RodriguezGTM246《A Course in Commutative Banach Algebras》Eberhard KaniuthGTM247《Braid Groups》Christian Kassel, Vladimir TuraevGTM248《Buildings Theory and Applications》Peter Abramenko, Kenneth S.Brown GTM249《Classical Fourier Analysis》Loukas Grafakos(经典傅里叶分析)GTM250《Modern Fourier Analysis》Loukas Grafakos(现代傅里叶分析)GTM251《The Finite Simple Groups》Robert A.WilsonGTM252《Distributions and Operators》Gerd GrubbGTM253《Elementary Functional Analysis》Barbara D.MacCluerGTM254《Algebraic Function Fields and Codes》Henning StichtenothGTM255《Symmetry Representations and Invariants》Roe Goodman, Nolan R.Wallach GTM256《A Course in Commutative Algebra》Kemper GregorGTM257《Deformation Theory》Robin HartshorneGTM258《Foundation of Optimization》Osman GülerGTM259《Ergodic Theory:with a view towards Number Theory》Manfred Einsiedler, Thomas WardGTM260《Monomial Ideals》Jurgen Herzog, Takayuki HibiGTM261《Probability and Stochastics》Erhan CinlarGTM262《Essentials of Integration Theory for Analysis》Daniel W.StroockGTM263《Analysis on Fock Spaces》Kehe ZhuGTM264《Functional Analysis, Calculus of Variations and Optimal Control》Francis ClarkeGTM265《Unbounded Self-adjoint Operatorson Hilbert Space》Konrad Schmüdgen GTM266《Calculus Without Derivatives》Jean-Paul PenotGTM267《Quantum Theory for Mathematicians》Brian C.HallGTM268《Geometric Analysis of the Bergman Kernel and Metric》Steven G.Krantz GTM269《Locally Convex Spaces》M.Scott Osborne。
differential algebras

Discrete Mathematics and Theoretical Computer Science1,1997,229–237On the bialgebra of functional graphs and differential algebrasMaurice GinocchioLaboratoire de Physique Th´e orique et Math´e matique,Universit´e Paris7,Tour Centrale-3`e me´e tage,2,place Jussieu, F-75251Paris Cedex05,FranceE-Mail:mag@ccr.jussieu.fr1IntroductionWe have already described the expansion of∆Σλi∂i,i.e.the powers of a Lie operator in any dimension, in order tofind the expression of theflow of formal nonlinear evolution equations[1–3].In the one-dimensional case,the explicit expansion can be foundfirst in Comtet[4],and other aspects connected to the ordinary differential equations can be found in Leroux and Viennot[5]and Bergeron and Reutenauer [6].On the other hand,Grossman and Larson[7]introduced several Hopf algebras[8–10]of forests of rooted labeled trees to express the product offinite dimensional vectorfields.In this paper we concentrate us on the bialgebra G of functional graphs,i.e.graphs representing mappings offinite sets in themselves [11–15].We give only the results without proofs.In a forthcoming paper[16],we develop Hopf algebra structures,computing the antipode and giving detailed aspects and proofs.In Sect.1we consider a bialgebra structure on G and three interesting subalgebras:T the set of labeled forests;S the set of permutation graphs;and L the set of well labeled forests,i.e.with strictly decreasing labels on the chains toward the roots.Recall that the graded bialgebra L is sufficient for the calculus of the powers of one derivation[1],and it is extendable in a Hopf algebra,the element of which is known in the computer literature as‘heap ordered trees’.This bialgebra is useful to compute products of derivations or to transform differential monomials in differential algebras[17],and it is interesting to note that the elements L n(n edges)can be coded by the words(monomials)of the expansion of Q nq0q0q1q0q1q n1,where Q0q0q1is a noncommutative alphabet.We describe in particular the bialgebra L,first in the polynomial form by the‘factorial’monoid L0L0n n0,where L0n is the set of words in the expansion of Q n,and second,we establish the bijective correspondence between 1365–8050c1997Chapman&Hall230M.Ginocchio L and L.We show that the calculus are easier with L,and that the product on L can be expressed in a very natural way.For example,q0n Q n,hence the(exponential)generating function of all the elements of L.We describe principally the formalism in the general case G,and the calculus uses thefields F201 as well as characteristic zerofields K.In Sect.2,we describe the link with the graded differential algebra K U r0K U r and the graded algebra of differential operators K U D r0K U r D r,where U u1u2uββ1uβαα0β1is a set of indeterminates,D∂0∂1and the differential indeterminates uβασ1σp∂σ1∂σpuβαgenerate K U r[17].This shows that the above Q-calculus,which is a kind of‘dissection’on functional graphs can be used as pre-calculus in differential algebras as well as in discrete dynamical systems[18].2Bialgebra Based on the Semi-group of Functional Graphs2.1T ypes of Functional GraphsIn this paper,a connected functional graph will be called excycle[13,15].In the area of discrete dynamical systems,an excycle is known as a basin of attraction.Consider several graded andfiltered sets of labeled functional graphs(i)E(resp.G)the set of excycles(resp.functional graphs)and designated by G n(resp.G n),the set offunctional graphs having(resp.having at most)n1nodes for n0(ii)R(resp.T)the set of labeled arborescences(resp.forests).(iii)C(resp.S)the set of cycles(resp.permutation graphs).(iv)A(resp.L)the set of well labeled arborescences(resp.forests),i.e.with strictly decreasing labels on the chains toward the root(s).As in(i),we consider for(ii)–(iv)graduations andfiltrations.2.2Free Representation by Q-polynomialsLet G n be the semigroup of mappings of12n in itself(‘Semigroup of endofunctions’), Card G n n n and the subsemigroups,T n f;f G n f n f n1(i.e.f acyclic and Card T n n1n1,S n the symmetric group and Card S n n!L n f;f G n f i i(i.e.f subdiagonal and Card L n n!.We have the well known bijections F F:G n G n T n T n S n S n L n L n.Let Q q0q1be a noncommutative alphabet,Q0q0Q with q0noncommuting with the q i’s,Q n q1q2q n Q0n q0Q n and Q(resp.Q0),the corresponding free monoids.Taking F201as thefield,consider(i)the G n module F2Q n by the F2linear incidence matrix action of f G n as l f q i q f i hence l f l gl f g.On the bialgebra of functional graphs231 (ii)the generating monomial associated with f.By morphism extension,denoted again by l f,we defineQ f q f1q f2q f n l f Qιn1where Qιn q1q2q n is associated with the identityιn of G n and Qι01One again has l f l g l f g.For the following we consider(iii)The graded subsets of Q as G G n n0T T n n0S S n n0L L n n0respectively associated with G,T,S and L,with G0T0S0L01(iv)The corresponding graded F2-modules:F2G F2T F2S F2L admit components of degree n which are,respectively,G n T n S n L n modules,withdimF2G n n n dimF2T n n1n1dimF2S n dimF2L n n!(v)We will denote by R n one of the above subsemi-groups of G n(or of another category). Similarly,let R R n n0resp F2R n0F2R n be the corresponding graded subsets of Q(resp. graded F2-modules ofF2G n0F2G n.2.3Virtual Root and External ProductLet f G n I0be the set offixed points of f and H0a subset of I0,and set p q r;p r q if p q and/0otherwise.Define f0:1n0n such that f0i f i if i H0and f0i0if i H0The‘0’is the label of a virtual root added to the graph representation of f,and we will say that H0is‘confined in0’,which is a fixed point of f0We call‘extended endofunctions’such functions f0,denote by G0n0n1n their set, and we consider G n as a subset of G0n Similarly,we will have T0n T n S0n S n L0n L n Consequently, adding q0,we get the extended graded sets G0G0n n0the extended graded F2-module F2G0 n0F2G0n and their substructures F2T0F2S0F2L0Now letφG0mχ0be the characteristic function of H0φ10,and writeQφlφQιm qφ1qφ2qφmm ∏i1qφi(cf.Figures1and2).WithψG0n,consider the F2-bilinear product in F2G0defined byQφQψQψm∏i1qφi nχ0i q0q1q n12On the right-hand side we have a sum of concatened monomials,and on the right factor the substitutions q0q0q1q n and q h q h n when h0232M.Ginocchio On the other hand,the product belongs to F2G0m n This external product is associated with unit1and F2G0is‘.’graded.To see this consider i j k being0three homogeneous polynomials,A A q0;q i F2G0mB B q0;q j F2G0nC C q0;q k F2G0pthen by(2)A B B q0;q j A q0q1q n;q i n3 and so,using deg B C n p,A q0;q iB q0;q jC B q0;q j A q0q1q n;q i n CCB q0q1q p;q j p A q0q1q p q1p q n p;q i n pA q0;q i CB q0q1q p;q j pA q0;q iB q0;q j CMoreover,because T n S n L n are subsemi-groups of G n one can see that F2R0F2T0F2S0F2L0are‘.’graded subalgebras of F2G0HenceProposition1Let the sequence G0m m1of the sets of the extended endofunctions in12m and Q0q0q1be a noncommutative alphabet.ForφG0m let Qφ∏m i1qφi be the generating monomial ofφand the graded module F2-module F2G0n0F2G0n on F201generated by all the φsThen F2G0is a graded algebra for the associative product with unit1QφQψQψm∏i1qφi nχ0i q0q1q n1whereψG0n andχ0is the characteristic function ofφ10Moreover,if R0m m1is a sequence of subsets associated with subsemi-groups of the sequence G0m m1, then F2R0n0F2R0n is a graded subalgebra of F2G02.4Splitting Operatorδn F2G0This operator substitutes the n-coproduct∆n of the Leibniz–Lie type.Associate to A Q0the left linear operatorτn A acting on B Q0,such that,if A G0m B G0n,then Bτn A BA if degB n,and0 otherwise,where BA is the concatenation of B and A.(i)Now let f G m and H0as in Sect.3,and notefirst that ifτn is viewed as acting on f,then for i1m one hasτn f i n f i n,and by f0i ¯χ0i f i one hasτn f0i n¯χ0i f0i n,where¯χ01χ0According to(2),define forφG0mδn Qφτnm∏i1qφi nχ0i q0q1q n14If d0Card H0the expansion(4)gives a sum of n1d0generating monomials of functionsψκof n1n m into0n1n m,and the corresponding functional graphs factorized in commutative excycles.On the bialgebra of functional graphs233 The operatorδn A is left linear on F2G0,and(2)can be writtenQφQψQψδn Qφ5 (ii)Moreover,δp is a graded antimorphism for‘’δp A Bδp Bδp n A6 where n degB and p N.For this to compute with(5)and A B C as in Sect.3,Cδp A B A B C A B C B Cδp n A Cδp Bδp n A.If p0we recover A B Bδn A and Bδk A0if k degB(iii)Also,δn is a powerδnδnδδ1δ017 For this to compute,δpδn A q0;q iδpτn A q0q1q n;q i nτn p A q0q1q p q1pq n p;q i n pδn p A q0;q i.(iv)Define the left linear operatorµin F2G0by the expansionµ∑n0δn8By left linear action ofµA on F2G0,we get A B BµA for A B F2G0with the antimorphism propertyµA BµBµA9 which express the associativity of‘’.Proposition2Let A F2G0m B F2G0n Then the splitting linear operatorδp defined left linearly by Bδp A A B if p=n,and0otherwise,verifiesδpδp withδδ1δ01andδp A Bδp Bδp n A Moreover,µ∑n0δn is an antimorphism in F2G0such that A B BµA2.5Exponential Generating Function of the Monomials of L0All the words of L0n(i.e.subdiagonals)are obtained from the expansion of Q n q0q0q1q0q1 q n1F2L0and Q01By equation(3),one has Q m Q n Q m n,and if A F2L0m B F2L0n we have A B F2L0m n,and then we recover that F2L0is stable for the product‘’.Because Q1q0,the associativity givesQ n q0n10 With the Q[[t]]-modules on L0,one has the exponential generating functionexp tq0∑n0t nn!Q n11exp sq0exp tq0exp s t q0234M.Ginocchio2.6ExamplesConsider equations (4)and (5)for Q ψq n 0.2.6.1Rooted T rees with n=1δq 20q 1τq 0q 12q 2τq 0q 0q 2τq 0q 1q 2τq 1q 0q 2τq 1q 1q 2(Figure 3)q 20q 1q 0q 0q 0q 12q 2q 30q 2q 20q 1q 2q 0q 1q 0q 2q 0q 1q 1q 2(Figure 4)2.6.2Excycles with n=2δ2q 23q 1q 0τ2q 25q 3q 0q 1q 2τ2q 25q 3q 0τ2q 25q 3q 1τ2q 25q 3q 2(Figure 5)q 23q 1q 0q 20q 20q 25q 3q 0q 1q 2q 20q 25q 3q 0q 20q 25q 3q 1q 20q 25q 3q 2(Figure 6)3Differential Algebra3.1Differential indeterminatesLet D ∂0∂1where ∂α∂∂ξαthe αth canonical derivation in S K ξthe algebra of formal power series in ξξ0ξ1,where K is a characteristic zero field.If S N N is the set U u 1u 2u ββ1u αβα0β1with u αβS consider U as a set of indeterminates,u αβσ1σp ∂σ1∂σp u αβasdifferential indeterminates,replace S N N by KU ,and consider the graded differential algebra K Ur 0K U r and the graded algebra of differential operators K U D r 0K U r D r.To each W F 2R 0we associate the differential operator W U U D ;for example,with W r U K U r one hasW UW 0UW 1Uα∂αW 2Uαβ∂α∂βW 0U∑r 1W r U D r12We will use now the summation convention.3.2Brackets in K UDefine for u v wU the multilinear operations valued in K U .3.2.1Arborescent Brackets (Valued in K U 1)u v uv w u vβu αv βα,henceu v Du αv βα∂β(1fixed point sent to ‘0’)uv wγu αv βw γαβ,henceu v Du αv βw γαβ∂γ13Also,for AK UrBK UsA Bβ1βsA α1αr B β1βsα1αr3.2.2Circular Brackets (Valued in K U 0)uu αα(1fixed point),u vu ααv ββ(2fixed points)u vu αβv βα2cycleu v wu αγv βαw γβ3cycle14On the bialgebra of functional graphs 2353.2.3Mixed Brackets (Valued in K U 0)Let E be a proper excycle (i.e.with no fixed point);we can write it EA i 1A i 2A i p ,where the A i k ’s are arborescences with root i k If in each arborescence A i k is reduced to its root i k ,we recover simply acycle Ei 1i 2i p Now let F k be the forest under i k ,i.e.obtained by cutting the root of A i k ,and defined with F i k U F i k u j ;j N i k ,where N i k is the set of nodes of F i k :E Uu F i 1i 1u F i 2i 2u F i pi pF i 1U u i 1α1αp F i 2U u i 2α2α1F i p U u i p αp αp13.3Action of F 2R 0Moreover,F 2R 0operates K -linearly in K U with values in K U D .For this let φG 0m H 0φ1for j 0m I 1m ,and H u β1u β2u βm U ,a word on U of length m .Then the action isQ φ∏i Iq φiQ φH∏j I∏i H j∂αiu αj βj∏k H 0∂αk15The differential monomial Q φH is such that u βj is associated with j in the domain I of φIf d j is the degree in q j (in-degree of the node labeled by ‘j ’),then u αj βj is derived d j times and the indices of derivation are related to the places of the q j ’s in the word.Similarly,the differential operator D r is characterized by the number r (degree of the root)of the q 0’s and their places.So we can summarize:In a word A R 0where q j is at the place (i),then in A H the j th letter of H is derived according to i,i.e.∂αi acts.One has,in particular,taking H u 1u 2:Arborescent brackets 1U 1q 0U u 1α1∂α1u 1Dq 0q 0U u 1α1u 2α2∂α1∂α2u 1u 2D 2q 0q 1U u 1α1α2u 2α2∂α1u 2u 1D q 3q 3q 0U u 1α1u 2α2u 3α3α1α2∂α3u 1u 2u 3Dq 0q 0q 2q 2U u 1α1u 2α2α3α4u α33u α44∂α1∂α2u 1u 3u 4u 2D 2Circular brackets q 1U u 1α1α1u 1q 1q 2U u 1α1α1u 2α2α2u 1u 2q 2q 1U u 1α1α2u 2α2α1u 1u 2q 3q 1q 2U u 1α1α3u 2α2α1u 3α3α2u 1u 2u 33.4Product of Differential OperatorsThe product (2)on words with correspondence (15)gives the product of differential operators.We state,without proof,Proposition 3Let the graded differential algebra K U r 0K U r and the graded algebra of differ-ential operators K U D r 0K U r D r Let φG 0m I 1m H j φ1j for j 0m and H u β1u β2u βm a word on U of length m.Then the mapping of F 2G 0into K U D which associates to the generating monomial Q φ∏i I q φi of φthe differential operator Q φH ∏j I ∏i H j ∂αi u αj βj ∏k H 0∂αk236M.Ginocchio is a morphism,such that ifψG0n and K is a word on U of length n,one has QφH QψK QφQψKH, where KH is the concatenation of K and H.ExampleA q0B q2q1q0H u4K u1u2u3A B q2q1q0q0q1q2q3q2q1q0q0q2q1q0q1q2q1q0q2q2q1q0q3(Figure7)A H u1DB K u1u2u3DA HB K u1u2u3u4D2u4u1u2u3D u1u2u4u3DObserve that:u4u1u2u3D u1α1α2α4u2α2α1u3α3u4α4∂α3u1α1α2u2α2α1α4u3α3u4α4∂α3which corresponds to q2q1q0q1q2,i.e.the second and third terms in the graph expansion. AppendixTo view Figures1–7,click here.To return to the main paper,click on the red box.References[1]Ginocchio,M.(1995).Universal expansion of the powers of a derivation,Letters in Math.Phys.34(4),343–364.[2]Ginocchio,M.and Irac-Astaud,M.(1985).A recursive linearization process for evolution equations.Reports on Math.Phys.21,245–265.[3]Steeb,W.H.and Euler,N.(1988).Nonlinear Evolution Equations and Painlev´e Test.World Scien-tific.[4]Comtet,L.(1973).Une formule explicite pour les puissances successives de l’op´e rateur de d´e rivationde m.Roy.Acad.Sci.276A,165–168.[5]Leroux,P.and Viennot,G.(1986).Combinatorial resolution of systems of differential equations I:ordinary differential equations.Actes du colloque de combinatoire´e num´e rative,Montr´e al.Lecture Notes in Mathematics1234,pp.210–245.Springer-V erlag.[6]Bergeron, F.and Reutenauer, C.(1987).Une interpr´e tation combinatoire des puissances d’unop´e rateur diff´e rentiel lin´e aire.Ann.Sci.Math.Quebec11,269–278.[7]Grossman,R.and Larson,R.G.(1989).Hopf-algebraic structures of families of trees.J.Algebra126,184–210.[8]Joni,A.A.and Rota,G.C.(1979).Coalgebras and bialgebras in combinatorics.Studies.in Appl.Math.61,93–139.On the bialgebra of functional graphs237 [9]Nichols,W.and Sweedler,M.E.(1980).Hopf algebras and combinatorics,in‘Umbral calculus andHopf algebras’.Contemp.Math.6.[10]Sweedler,M.E.(1969).Hopf Algebras.Benjamin.[11]Berge,C.(1983).Graphes.Gauthier-Villars.[12]Comtet,L.(1974).Advanced Combinatorics.Reidel.[13]Denes,J.(1968).On transformations,transformation-semigroups and graphs.In Erd¨o s-Katona,ed-itor,Theory of Graphs.Academic Press,pp.65–75.[14]Foata,D.and Fuchs,A.(1970).R´e arrangements de fonctions et d´e b.Theory8,361–375.[15]Harary,F.(1959).The number of functional digraphs.Math.Annalen138,203–210.[16]Ginocchio,M.On the Hopf algebra of functional graphs and differential algebras.Discr.Math.Toappear.[17]Kaplansky,I.(1976).Introduction to Differential Algebras.Springer-V erlag.[18]Robert,F.(1995).Les syst`e mes Dynamiques Discrets.Springer-V erlag.。
2018年中科院数学SCI期刊分区

SIAM JOURNAL ON CONTROL AND OPTIMIZATION SIAM JOURNAL ON CONTROL AND OPTIMIZATION JOURNAL OF DIFFERENTIAL GEOMETRY Scandinavian Actuarial Journal Scandinavian Actuarial Journal Annals of Applied Statistics APPLIED MATHEMATICS AND MECHANICS-ENGLISH EDITION APPLIED MATHEMATICS AND MECHANICS-ENGLISH EDITION NUMERICAL ALGORITHMS SIAM JOURNAL ON MATHEMATICAL ANALYSIS INTERNATIONAL JOURNAL OF BIFURCATION AND CHAOS INTERNATIONAL JOURNAL OF BIFURCATION AND CHAOS TRANSACTIONS OF THE AMERICAN MATHEMATICAL SOCIETY MATHEMATICS AND COMPUTERS IN SIMULATION MATHEMATICS AND COMPUTERS IN SIMULATION MATHEMATICS AND COMPUTERS IN SIMULATION Communications in Mathematical Sciences ADVANCES IN COMPUTATIONAL MATHEMATICS BIT NUMERICAL MATHEMATICS BIT NUMERICAL MATHEMATICS COMPUTATIONAL OPTIMIZATION AND APPLICATIONS COMPUTATIONAL OPTIMIZATION AND APPLICATIONS JOURNAL OF GLOBAL OPTIMIZATION JOURNAL OF GLOBAL OPTIMIZATION COMMUNICATIONS IN PARTIAL DIFFERENTIAL EQUATIONS COMMUNICATIONS IN PARTIAL DIFFERENTIAL EQUATIONS ADVANCES IN MATHEMATICS Extremes Extremes JOURNAL OF ALGEBRAIC GEOMETRY BERNOULLI Bulletin of Mathematical Sciences JOURNAL OF FUNCTIONAL ANALYSIS Selecta Mathematica-New Series Selecta Mathematica-New Series ZAMM-Zeitschrift fur Angewandte Mathematik und Mechanik ZAMM-Zeitschrift fur Angewandte Mathematik und Mechanik NUMERICAL LINEAR ALGEBRA WITH APPLICATIONS NUMERICAL LINEAR ALGEBRA WITH APPLICATIONS INSURANCE MATHEMATICS & ECONOMICS INSURANCE MATHEMATICS & ECONOMICS APPLIED NUMERICAL MATHEMATICS JOURNAL OF OPTIMIZATION THEORY AND APPLICATIONS JOURNAL OF OPTIMIZATION THEORY AND APPLICATIONS MATHEMATISCHE ANNALEN ESAIM-CONTROL OPTIMISATION AND CALCULUS OF VARIATIONS ESAIM-CONTROL OPTIMISATION AND CALCULUS OF VARIATIONS Kinetic and Related Models Kinetic and Related Models JOURNAL OF CLASSIFICATION COMPUTATIONAL STATISTICS & DATA ANALYSIS COMPUTATIONAL STATISTICS & DATA ANALYSIS APPLIED MATHEMATICS AND OPTIMIZATION Journal of Dynamics and Differential En Applied Mathematics and Computational Science Communications in Applied Mathematics and Computational Science ANNALS OF PROBABILITY JOURNAL OF BUSINESS & ECONOMIC STATISTICS JOURNAL OF NONLINEAR SCIENCE JOURNAL OF NONLINEAR SCIENCE JOURNAL OF NONLINEAR SCIENCE PSYCHOMETRIKA INTERNATIONAL STATISTICAL REVIEW SIAM JOURNAL ON NUMERICAL ANALYSIS SIAM JOURNAL ON SCIENTIFIC COMPUTING NONLINEAR ANALYSIS-REAL WORLD APPLICATIONS PROBABILITY THEORY AND RELATED FIELDS JOURNAL OF THE EUROPEAN MATHEMATICAL SOCIETY JOURNAL OF THE EUROPEAN MATHEMATICAL SOCIETY INVERSE PROBLEMS INVERSE PROBLEMS NONLINEARITY NONLINEARITY STATISTICS AND COMPUTING STATISTICS AND COMPUTING ESAIM-MATHEMATICAL MODELLING AND NUMERICAL ANALYSIS-MODELISATION MATHEMATIQUE ET ANALYSE NUMERIQUE JOURNAL DE MATHEMATIQUES PURES ET APPLIQUEES JOURNAL DE MATHEMATIQUES PURES ET APPLIQUEES ANNALES SCIENTIFIQUES DE L ECOLE NORMALE SUPERIEURE IMA JOURNAL OF NUMERICAL ANALYSIS STUDIES IN APPLIED MATHEMATICS JOURNAL OF SCIENTIFIC COMPUTING GEOMETRIC AND FUNCTIONAL ANALYSIS JOURNAL OF COMPUTATIONAL AND GRAPHICAL STATISTICS Analysis and Applications Analysis and Applications ANNALS OF APPLIED PROBABILITY JOURNAL OF DIFFERENTIAL EQUATIONS MATHEMATICS OF COMPUTATION JOURNAL OF THE ROYAL STATISTICAL SOCIETY SERIES C-APPLIED STATISTICS Analysis & PDE Analysis & PDE CALCULUS OF VARIATIONS AND PARTIAL DIFFERENTIAL EQUATIONS CALCULUS OF VARIATIONS AND PARTIAL DIFFERENTIAL EQUATIONS ZEITSCHRIFT FUR ANGEWANDTE MATHEMATIK UND PHYSIK SIAM JOURNAL ON APPLIED MATHEMATICS JOURNAL FUR DIE REINE UND ANGEWANDTE MATHEMATIK SIAM JOURNAL ON MATRIX ANALYSIS AND APPLICATIONS Advances in Calculus of Variations Advances in Calculus of Variations BIOMETRIKA BIOMETRIKA BIOMETRIKA Advances in Data Analysis and Classification JOURNAL OF COMPUTATIONAL AND APPLIED MATHEMATICS Journal of the Institute of Mathematics of Jussieu CALCOLO CALCOLO
Linear Algebra and Differential Equations Using MATLAB

LINEAR ALGEBRA AND DIFFERENTIAL EQUATIONS USING MATLAB
Ch. 15 Linear Differential Equations
LINEAR ALGEBRA AND DIFFERENTIAL EQUATIONS USING MATLAB
Ch. 14 Higher Dimensional Systems
1. 2. 3. 4. 5. 6. Linear Systems in Jordan Normal Form Qualitative Theory near Equilibria MATLAB ode45 in One Dimension Higher Dimensional Systems Using ode45 Quasiperiodic Motions and Tori Chaos and the Lorenz Equation
LINEAR ALGEBRA AND DIFFERENTIAL EQUATIONS USING MATLAB
Ch. 4 Solving Ordinary Differential Equations
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. A Single Differential Equation Graphing Solutions to Differential Equations Phase Space Pictures and Equilibria Separation of Variables Uncoupled Linear Systems of Two Equations Coupled Linear Systems The Initial Value Problem and Eigenvectors Eigenvalues of 2 x 2 Matrices Initial Value Problems Revisited Markov Chains
MATHEMATICS(PUREANDAPPLIED):(纯粹数学和应用)

Professor & Head of DepartmentNT Bishop, MA(Cambridge), PhD(Southampton), FRASSenior LecturersJ Larena, MSc(Paris), PhD(Paris)D Pollney, PhD(Southampton)CC Remsing, MSc(Timisoara), PhD(Rhodes)Vacant LecturersEOD Andriantiana, PhD(Stellenbosch)V Naicker, MSc(KwaZulu-Natal)AL Pinchuck, MSc(Rhodes), PhD(Wits)Lecturer, Academic Development M Lubczonok, Masters(Jagiellonian)Mathematics (MA T) is a six-semester subject and Applied Mathematics (MAP) is a four-semester subject. These subjects may be taken as major subjects for the degrees of BSc, BA, BJourn, BCom, BBusSci, BEcon and BSocSc, and for the diploma HDE(SEC).To major in Mathematics, a candidate is required to obtain credit in the following courses: MAT1C; MAM2; MAT3. See Rule S.23.To major in Applied Mathematics, a candidate is required to obtain credit in the following courses: MAT1C, MAM2; MAP3. See Rule S.23.The attention of students who hope to pursue careers in the field of Bioinformatics is drawn to the recommended curriculum that leads to postgraduate study in this area, in which Mathematics is a recommended co-major with Biochemistry, and for which two years of Computer Science and either Mathematics or Mathematical Statistics are prerequisites. Details of this curriculum can be foundin the entry for the Department of Biochemistry, Microbiology and Biotechnology.See the Departmental Web Page http://www.ru.ac.za/departments/mathematics/ for further details, particularly on the content of courses.First-year level courses in MathematicsMathematics 1 (MAT1C) is given as a year-long semesterized two-credit course. Credit in MAT1C must be obtained by students who wish to major in certain subjects (such as Applied Mathematics, MATHEMATICS (PURE AND APPLIED)Physics and Mathematical Statistics) and by students registered for the BBusSci degree.Introductory Mathematics (MAT1S) is recommended for Pharmacy students and for Science students who do not need MAT1C or MAT1C1.Supplementary examinations may be recommended for any of these courses, provided that a candidate achieves a minimum standard specified by the Department.Mathematics 1L (MA T1L) is a full year course for students who do not qualify for entry into any of the first courses mentioned above. This is particularly suitable for students in the Social Sciences and Biological Sciences who need to become numerate or achieve a level of mathematical literacy. A successful pass in this course will give admission to MA T1C.First yearMAT1CThere are two first-year courses in Mathematics for candidates planning to major in Mathematics or Applied Mathematics. MAT1C1 is held in thefirst semester and MAT1C2 in the second semester. Credit may be obtained in each course separately and, in addition, an aggregate mark of at least 50%will be deemed to be equivalent to a two-creditcourse MAT1C, provided that a candidate obtains the required sub-minimum (40%) in each component. Supplementary examinations may be recommended in either course, provided that a candidate achieves a minimum standard specified by the department. Candidates obtaining less than 40% for MAT1C1 are not permitted to continue with MAT1C2.MAT1C1 (First semester course): Basic concepts (number systems, functions), calculus (limits,continuity, differentiation, optimisation, curvesketching, introduction to integration), propositional calculus, mathematical induction, permutations, combinations, binomial theorem, vectors, lines andplanes, matrices and systems of linear equations.MAT1C2 (Second semester course): Calculus (integration, applications of integration, improper integrals), complex numbers, differential equations, partial differentiation, sequences and series.MAT1S (Semester course: Introductory Mathematics) (about 65 lectures)Estimation, ratios, scales (log scales), change of units, measurements; Vectors, systems of equations, matrices, in 2-dimensions; Functions: Review of coordinate geometry, absolute values (including graphs); Inequalities; Power functions, trig functions, exponential functions, the number e (including graphs); Inverse functions: roots, logs, ln (including graphs); Graphs and working with graphs; Interpretation of graphs, modeling; Descriptive statistics (mean, standard deviation, variance) with examples including normally distributed data; Introduction to differentiation and basic derivatives; Differentiation techniques (product, quotient and chain rules); Introduction to integration and basic integrals; Modeling, translation of real-world problems into mathematics.MAT 1L: Mathematics Literacy This course helps students develop appropriatemathematical tools necessary to represent and interpret information quantitatively. It also develops skills and meaningful ways of thinking, reasoning and arguing with quantitative ideas in order to solve problems in any given context.Arithmetic: Units of scientific measurement, scales, dimensions; Error and uncertainty in measure values.Fractions and percentages - usages in basic science and commerce; use of calculators and spreadsheets. Algebra: Polynomial, exponential, logarithmic and trigonometric functions and their graphs; modelling with functions; fitting curves to data; setting up and solving equations. Sequences and series, presentation of statistical data.Differential Calculus: Limits and continuity; Rules of differentiation; Applications of Calculus in curvesketching and optimisation.Second Year Mathematics 2 comprises two semesterized courses,MAM201 and MAM202, each comprising of 65 lectures. Credit may be obtained in each course seperately. An aggregate mark of 50% will grant the two-credit course MAM2, provided a sub-minimumof 40% is achieved in both semesters. Each semester consists of a primary and secondary stream which are run concurrently at 3 and 2 lectures per week, respectively. Additionally, a problem-based course in Mathematical Programming contributes to the class record and runs throughout the academic year.MAM201 (First semester):Advanced Calculus (39 lectures): Partial differentiation: directional derivatives and the gradient vector; maxima and minima of surfaces; Lagrange multipliers. Multiple integrals: surface and volume integrals in general coordinate systems. Vector calculus: vector fields, line integrals, fundamental theorem of line integrals, Green’s theorem, curl and divergence, parametric curves and surfaces.Ordinary Differential Equations (20 lectures): First order ordinary differential equations, linear differential equations of second order, Laplace transforms, systems of equations, series solutions, Green’s functions.Mathematical Programming 1 (6 lectures): Introduction to the MATLAB language, basic syntax, tools, programming principles. Applicationstaken from MAM2 modules. Course runs over twosemesters.MAM202 (Second semester):Linear Algebra (39 lectures): Linear spaces, inner products, norms. Vector spaces, spans, linear independence, basis and dimension. Linear transformations, change of basis, eigenvalues, diagonalization and its applications.Groups and Geometry (20 lectures): Number theory and counting. Groups, permutation groups, homomorphisms, symmetry groups in 2 and 3 dimensions. The Euclidean plane, transformations and isometries. Complex numbers, roots of unity and introduction to the geometry of the complex plane.Mathematical Programming 2 (6 lectures): Problem-based continuation of Semester 1.Third-year level courses inMathematics and Applied Mathematics Mathematics and Applied Mathematics are offered at the third year level. Each consists of four modules as listed below. Code TopicSemester Subject AM3.1 Numerical analysis 1 Applied MathematicsAM3.2 Dynamical systems 2 Applied Mathematics AM3.4 Partial differentialequations 1 Applied Mathematics AM3.5 Advanced differentialequations 2 Applied MathematicsM3.1 Algebra 2 MathematicsM3.2 Complex analysis 1 MathematicsM3.3 Real analysis 1 MathematicsM3.4 Differential geometry 2 Mathematics Students who obtain at least 40% in all of the above modules will be granted credit for both MAT3 and MAP3, provided that the average of the Applied Mathematics modules is at least 50% AND the average of the Mathematics modules is at least 50%. Students who obtain at least 40% for any FOUR of the above modules and with an average mark over the four modules of at least 50%, will be granted credit in either MAT3 or MAP3. If three or four of the modules are from Applied Mathematics then the credit will be in MAP3, otherwise it will be in MAT3.Module credits may be carried forward from year to year.Changes to the modules offered may be made from time-to-time depending on the interests of the academic staff.Credit for MAM 2 is required before admission to the third year courses.M3.1 (about 39 lectures) AlgebraAlgebra is one of the main areas of mathematics with a rich history. Algebraic structures pervade all modern mathematics. This course introduces students to the algebraic structure of groups, rings and fields. Algebra is a required course for any further study in mathematics.Syllabus: Sets, equivalence relations, groups, rings, fields, integral domains, homorphisms, isomorphisms, and their elementary properties.M3.2 (about 39 lectures) Complex Analysis Building on the first year introduction to complex numbers, this course provides a rigorous introduction to the theory of functions of a complex variable. It introduces and examines complex-valued functions of a complex variable, such as notions of elementary functions, their limits, derivatives and integrals. Syllabus: Revision of complex numbers, Cauchy- Riemann equations, analytic and harmonic functions, elementary functions and their properties, branches of logarithmic functions, complex differentiation, integration in the complex plane, Cauchy’s Theorem and integral formula, Taylor and Laurent series, Residue theory and applications. Fourier Integrals.M3.3 (about 39 lectures) Real AnalysisReal Analysis is the field of mathematics that studies properties of real numbers and functions on them. The course places great emphasis on careful reasoning and proof. This course is an essential basis for any further study in mathematics.Syllabus: Topology of the real line, continuity and uniform continuity, Heine-Borel, Bolzano-Weierstrass, uniform convergence, introduction to metric spaces.M3.4 (about 39 lectures) Differential Geometry Roughly speaking, differential geometry is concerned with understanding shapes and their properties in terms of calculus. This elementary course on differential geometry provides a perfect transition to higher mathematics and its applications. It is a subject which allows students to see mathematics for what it is - a unified whole mixing together geometry, calculus, linear algebra, differential equations, complex variables, calculus of variations and topology.Syllabus: Curves (in the plane and in the space), curvature, global properties of curves, surfaces, the first fundamental form, isometries, the second fundamental form, the normal and principal curvatures, the Gaussian and mean curvatures, the Gauss map, geodesics.AM3.1 (about 39 lectures) Numerical Analysis Many mathematical problems cannot be solved exactly and require numerical techniques. These techniques usually consist of an algorithm which performs a numerical calculation iteratively until certain tolerances are met. These algorithms can be expressed as a program which is executed by a computer. The collection of such techniques is called “numerical analysis”.Syllabus: Systems of non-linear equations, polynomial interpolation, cubic splines, numerical linear algebra, numerical computation of eigenvalues, numerical differentiation and integration, numerical solution of ordinary and partial differential equations, finite differences,, approximation theory, discrete Fourier transform.AM3.2 (about 39 lectures) Dynamical Systems This module is about the dynamical aspects of ordinary differential equations and the relations between dynamical systems and certain fields of applied mathematics (like control theory and the Lagrangian and Hamiltonian formalisms of classical mechanics). The emphasis is on the mathematical aspects of various constructions and structures rather than on the specific physical/mechanical models. Syllabus Linear systems; Linear control systems; Nonlinear systems (local theory); Nonlinear control systems; Nonlinear systems (global theory); Applications : elements of optimal control and/or geometric mechanics.AM3.4 (about 39 lectures) Partial Differential EquationsThis course deals with the basic theory of partial differential equations (elliptic, parabolic and hyperbolic) and dynamical systems. It presents both the qualitative properties of solutions of partial differential equations and methods of solution. Syllabus: First-order partial equations, classification of second-order equations, derivation of the classical equations of mathematical physics (wave equation, Laplace equation, and heat equation), method of characteristics, construction and behaviour of solutions, maximum principles, energy integrals. Fourier and Laplace transforms, introduction to dynamical systems.AM3.5 (about 39 lectures)Advanced differential equationsThis course is an introduction to the study of nonlinearity and chaos. Many natural phenomena can be modeled as nonlinear ordinary differential equations, the majority of which are impossible to solve analytically. Examples of nonlinear behaviour are drawn from across the sciences including physics, biology and engineering.Syllabus:Integrability theory and qualitative techniques for deducing underlying behaviour such as phase plane analysis, linearisations and pertubations. The study of flows, bifurcations, the Poincare-Bendixson theorem, and the Lorenz equations.Mathematics and Applied Mathematics Honours Each of the two courses consists of either eight topics and one project or six topics and two projects.A Mathematics Honours course usually requires the candidate to have majored in Mathematics, whilst Applied Mathematics Honours usually requires the candidate to have majored in Applied Mathematics. The topics are selected from the following general areas covering a wide spectrum of contemporary Mathematics and Applied Mathematics: Algebra; Combinatorics; Complex Analysis; Cosmology; Functional Analysis; General Relativity; Geometric Control Theory; Geometry; Logic and Set Theory; Measure Theory; Number Theory; Numerical Modelling; Topology.Two or three topics from those offered at the third-year level in either Mathematics or Applied Mathematics may also be taken in the case of a student who has not done such topics before. With the approval of the Heads of Department concerned, the course may also contain topics from Education, and from those offered by other departments in the Science Faculty such as Physics, Computer Science, and Statistics. On the other hand, the topics above may also be considered by such Departments as possible components of their postgraduate courses.Master’s and Doctoral degrees in Mathematics or Applied MathematicsSuitably qualified students are encouraged to proceed to these degrees under the direction of the staff of the Department. Requirements for these degrees are given in the General Rules.A Master’s degree in either Mathematics or Applied Mathematics may be taken by thesis only, or by a combination of course work and a thesis. Normally four examination papers and/or essays are required apart from the thesis. The whole course of study must be approved by the Head of Department.。
数学SCI期刊排名
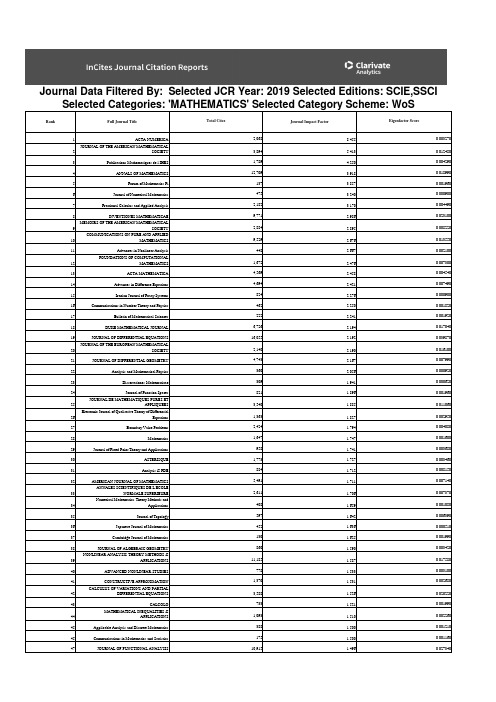
8.455 5.413 4.250 3.918 3.857 3.240 3.170 2.986 2.895 2.676 2.667 2.476 2.458 2.421 2.276 2.250 2.241 2.194 2.192 2.190 2.167 2.056 1.941 1.896 1.885 1.827 1.794 1.747 1.741 1.727 1.712 1.711 1.706 1.659 1.642 1.636 1.625 1.590 1.587 1.533 1.531 1.526 1.521 1.510 1.500 1.500 1.496
4,371 964 324
1,908 1,552
636 184 4,204 3,706
1.494 1.486 1.479 1.478 1.473 1.470 1.464 1.438
53 JOURNAL OF INEQUALITIES AND APPLICATIONS
54
Forum of Mathematics Sigma
55
athian Journal of Mathematics
Revista de la Real Academia de Ciencias Exactas Fisicas
56
y Naturales Serie A-Matematicas
57
Qualitative Theory of Dynamical Systems
NUMERICAL LINEAR ALGEBRA WITH
58
APPLICATIONS
PROCEEDINGS OF THE LONDON
59
MATHEMATICAL SOCIETY
98
巴黎综合理工考试试题类型

ECOLE POLYTECHNIQUE – « INGENIEUR POLYTECHNICIEN »PROGRAMINTERNATIONAL ADMISSIONSRecommended knowledge in Mathematical Sciences The recommended knowledge in Mathematical Sciences for the applicants to the “Track 2 - International admissions” is detailed below.This document is meant to give the applicants an indication on the knowledge they are likely to be interviewed. It is given for informational purposes only and cannot be considered as a basis of the programme for the second track examinations.Ecole Polytechnique reserves the right to test an applicant’s knowledge on other fields of Mathematical Sciences than those listed in this document.An excellent level in mathematics and in physical sciences is a key to successful studies at Ecole Polytechnique.1 - ALGEBRA1.1 Set theoryOperations on sets, characteristic functions.Maps, injectivity, surjectivity.Direct and inverse image of a set.Integer numbers, finite sets, countability.1.2 Numbers and usual structuresComposition laws; groups, rings, fields.Equivalence relations, quotient structures.Real numbers, complex numbers, complex exponential.Application to plane geometry.Polynomials, relations between the roots and the coefficients.Elementary arithmetics (in Z/nZ).1.3 Finite dimensional vector spaces (*)Free families, generating families, bases, dimension.Determinant of n vectors; characterization of bases.Matrices, operations on matrices.Determinant of a square matrix; expansion with respect to a line or to a column; rank, cofactors.Linear maps, matrix associated to a linear map.Endomorphisms, trace, determinant, rank.Linear systems of equations.1.4 Reduction of endomorphismsStable subspaces.Eigenvalues, eigenvectors of an endomorphism or a square matrix; similar matrices;geometrical interpretation.Characteristic polynomial, Cayley-Hamilton theorem.Reduction of endomorphisms in finite dimension; diagonalizable endomorphisms and matrices.1.5 Euclidean spaces, Euclidean geometryScalar product; Cauchy-Schwarz inequality; norms and associated distances.Euclidean spaces of finite dimension, orthonormal bases; orthogonal projections.Orthogonal group O(E); orthogonal symmetries.Orthogonal matrices; diagonalization of symmetric real matrices.Properties of orthogonal endomorphisms of R² and R³.(*) In several countries linear algebra is studied only in R k or C k; the candidates from these countries are strongly advised to get familiar with the formalism of abstract vector spaces.2 - ANALYSIS AND DIFFERENTIAL GEOMETRY2.1 Topology in finite dimensional normed vector spacesOpen and closed sets, accumulation points, interior points.Convergent sequences in normed vector spaces; continuous mappings.Compact spaces, images of compact sets by continuous mappings, existence ofextrema.Equivalence of norms.2.2 Real or complex valued functions defined on an intervalDerivative at a point, functions of class C k.Mean value theorem, Taylor's formula.Primitive of continuous functions.Usual functions (exponential, logarithm, trigonometric functions, rational fractions).Sequences and series of functions, simple and uniform convergence.2.3 Integration on a bounded intervalIntegral of piecewise continuous functions.Fundamental theorem of calculus (expressing the integral of a function in terms of aprimitive).Integration by parts, change of variable, integrals depending on a parameter.Continuity under the sign ∫ , differentiation under the sign ∫.Cauchy-Schwarz inequality.2.4 Series of numbers, power seriesSeries of real or complex numbers, simple and absolute convergence.Integral comparison criterion, product of absolutely convergence series.Power series, radius of convergence; function that can be expanded in a power series on an interval.Taylor series expansion of e t, sin(t), cos(t), ln (1+t), (1+t)a where a is a real number. 2.5 Differential equationsLinear scalar equations of degree 1 or 2, fundamental systems of solutions.Linear systems with constant coefficients.Method of the variation of the constants.Notions on non-linear differential equations.2.6 Functions of several real variablesPartial derivatives, differential of a function defined on R k.Chain rule.C1-functions; Schwarz theorem for C2-functions.Diffeomorphisms, inverse function theorem.Critical points, local and global extrema.Plane curves; tangent vector at a point, metric properties of plane curves (arc length, curvature).Surfaces in R³, tangent plane to a surface defined by a Cartesian equation F(x,y,z) = 0.。
Partial Differential Equations

Partial Differential Equations Partial Differential Equations (PDEs) are a fundamental concept in mathematics that play a crucial role in various fields such as physics, engineering, and economics. These equations involve functions of multiple variables and theirpartial derivatives, making them more complex than ordinary differential equations. One of the key challenges in dealing with PDEs is solving them to obtain a meaningful solution that accurately describes the behavior of the system under consideration. One perspective on PDEs is their importance in modeling physical phenomena. Many natural processes, such as heat conduction, fluid flow, and electromagnetic fields, can be described using PDEs. By solving these equations, scientists and engineers can predict and analyze the behavior of these systems, leading to advancements in technology and innovation. For example, in the field of fluid dynamics, PDEs are used to model the flow of air over an aircraft wing, allowing engineers to design more efficient and aerodynamic structures. Another perspective on PDEs is their mathematical beauty and elegance. The study of PDEs involves a deep understanding of mathematical concepts such as calculus, linear algebra, and functional analysis. Solving PDEs requires creativity and ingenuity, as there is often no straightforward algorithmic method to obtain a solution. Mathematicians have developed various techniques and methods, such as separationof variables, Fourier transforms, and numerical methods, to tackle the challenges posed by PDEs. However, despite their importance and beauty, PDEs can also be daunting and intimidating for students and researchers. The complexity of these equations, coupled with the lack of a universal method for solving them, can make studying PDEs a challenging task. Many students struggle to grasp the underlying concepts and techniques required to solve PDEs, leading to frustration andfeelings of inadequacy. As a result, some may shy away from pursuing further studies in mathematics or related fields that heavily rely on PDEs. In addition, the computational aspect of solving PDEs adds another layer of complexity to the problem. While analytical solutions to PDEs are desirable for their elegance and insight, they are often difficult, if not impossible, to obtain for many real-world problems. In such cases, numerical methods, such as finite difference,finite element, and spectral methods, are employed to approximate the solution.These methods require a good understanding of both the underlying mathematics and programming skills, further increasing the barrier to entry for students and researchers. Despite the challenges posed by PDEs, mastering this topic can be immensely rewarding. The ability to model and analyze complex systems using PDEs opens up a world of possibilities for scientific discovery and technological advancement. By overcoming the initial difficulties and investing time and effort in studying PDEs, students and researchers can develop valuable skills that are highly sought after in academia and industry. Moreover, the satisfaction of successfully solving a challenging PDE problem can be a source of great pride and accomplishment. In conclusion, Partial Differential Equations are a fascinating and essential topic in mathematics with far-reaching applications in various fields. While they may present challenges and difficulties, the study of PDEs offers a unique opportunity for intellectual growth and problem-solving skills development. By approaching PDEs with curiosity, perseverance, and a willingness to learn, students and researchers can unlock the potential of this rich and rewarding subject.。
高中英语数学讲课稿范文

高中英语数学讲课稿范文Ladies and gentlemen, I am honored to be standing here today to share with you the fascinating world of mathematics. Mathematics is more than just numbers and equations; it is a subject that teaches us problem-solving skills and critical thinking. Whether you love or hate math, it is an essential and exciting subject that opens up doors to numerous career opportunities. Today, I will be covering various topics, including algebra, geometry, trigonometry, calculus, and statistics. So, let's dive right in!First, let's start with algebra. Algebra is the branch of mathematics that deals with solving equations and manipulating mathematical symbols. It is crucial in various real-life applications, such as calculating distances, solving problems involving unknown variables, and analyzing data sets. Algebraic expressions, equations, and inequalities are the foundation of algebra.One important concept in algebra is solving linear equations. A linear equation is an equation that involves variables raised to the first power and does not have any exponents. To solve a linear equation, we follow a series of steps, which include isolating the variable, performing the same operation on both sides, and simplifying the equation further until we find the solution. Moving on to geometry, geometry deals with the study of shape, size, and properties of figures in various dimensions. Euclidean geometry is the most commonly studied branch of geometry, which is based on the works of the Greek mathematician Euclid. We learn about angles, lines, polygons, and circles in this geometry. It helps us understand the world around us, frommeasuring the height of buildings to designing structures in architecture and engineering.One interesting topic in geometry is the Pythagorean Theorem. The Pythagorean Theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem has numerous applications in many fields, including navigation, construction, and even music.Now, let's move on to trigonometry. Trigonometry is the study of the relationships between angles and sides of triangles. It is particularly useful in solving problems involving triangles and circular functions. Trigonometry plays a vital role in navigation, architecture, physics, and even music. Sine, cosine, and tangent are the primary trigonometric functions that help us calculate angles and sides of triangles.Next up is calculus. Calculus is the branch of mathematics that deals with the study of change and motion. It has two main branches: differential calculus and integral calculus. Differential calculus focuses on finding rates of change and slopes of curves, while integral calculus deals with finding areas under curves. Calculus is widely used in physics, engineering, economics, and even medicine.Last but not least, let's talk about statistics. Statistics is the branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. It helps us make sense of the vast amounts of information we encounter in ourdaily lives. Statistics is essential in numerous fields, including business, finance, medicine, and social sciences. It helps us make informed decisions, predict outcomes, and understand patterns and trends.In conclusion, mathematics is a fascinating subject that is indispensable in our modern world. Whether you are fascinated or intimidated by numbers, mathematics teaches us problem-solving skills, logical reasoning, and critical thinking. Algebra, geometry, trigonometry, calculus, and statistics are just some of the branches of mathematics. They have practical applications in various fields and open up doors to numerous career opportunities. So, embrace the beauty of mathematics and let it guide you on your journey of lifelong learning and discovery.。
maple函数大全
rtable data structures
序包
Matlab
Matlab Link
与 Matlab 的接口函数
Ore_algebra
Bacic calculations in algebras of 线性算的基本代数运算
linear onerators
PDEtools
tools for solveing partial differential 偏微分方程相关函数
雅可比椭圆函数
雅可比椭圆函数雅
雅可比θ函数
JacobiZeta KelvinBei KelvinBer KelvinHei KelvinHer
雅可比ζ函数 开尔文 Bei 函数 开尔文 Her 函数 开尔文 Hei 函数 开尔文 Her 函数
KelvinKei KelvinHer KummerM KummerU LanbertW Lcm LegendreP LegendreQ Lerchphi Li Linsolve Lommels1 Lommels2 MOLS Maple_floats MatlabMatrix MeijerG 函数名称 Normal Nullspace Power Powmod Prem Primitive Primpart 函数名称
多项式可分解为同阶因式的可能性 Product(乘)函数的简化形式 双γ函数与多γ函数 Quo(求多项式的商)函数的简化形式 一种递归方程解的数据结构 有限域的随机多项式 有限域的随机 monic prime 多项式 Ratrecon(重组有理函数)的简化形式 取复数的实部 rem(求多项式相除余项)函数的简化形式 Resultant(合成多项式)函数简化形式 求方程的根 多项式求模后的根 Sperm(异伪余式)函数的简化形式 查找文本 双曲正弦函数 正弦积分 矩阵的 Smith 正交化 非平方因式分解 转移正弦积分 StruveH 函数 StruveL 函数 sum(求和)和函数的简化形式 基本功能 计算矩阵的奇异数/向量 显示文本
切触几何与非线性微分方程导论

theorem for distributions. Finite type systems.
3. Finite-dimensional dynamics of evolutionary differential equations
fluid dynamics (Rapoport-Leas model). Dynamics of evolutionary systems.
4. Contact geometry
Contact structures on manifolds, contact distributions, contact forms.
equations. Symmetries. Geometric structures. Characteristic distributions.
Hyperbolic, elliptic and parabolic MA equations. Decomposition of de
Rham complex. Tensor invariants. The Laplace invariants for linear
distributions and the Frobenius theorem. Characteristic and shuffling
symmetries of distributions. Maurer-Cartan equations. Lie-Bianchi
theorem for distributions. Finite type systems. Finite-dimensional dynamics of evolutionary differential equations
数学de一些英文名称
Applied Partial Differential Equations Computer Graphics Computer Aided Geometric Design Selections from System Modeling Biology Mathematics Mathematical Finance Multimedia Techniques Applied Geometry Principle of Computer Network Dynamical Systems The Theory of Interest Actuarial Mathematics Coding Theory Numerical Analysis(Computing Method) Nonlinear Programming Combinatorial Optimization Optimal Control Theory Fractal Geometry Functions of Several Complex Variables Theory of Integral Equations and Its Applications Elementary Number Theory Stochastic Processes Applied software of Mathematics and Practice Introduction to Actuarial Science Advanced course on Mathematical Physics Mathematics of Demography Financial Economics Combinational Analysis Life Insurance Fourier Analysis Introduction to Insurance Introduction to Insurance and Actuarial Science Nonlife Actuarial Mathematics Complex Analysis Introduction to Control Theory Life Actuarial Mathematics Data Structures Statistics Digital Signal Processing Linear Programming Basic Information Theory Element of Database System
机械工程的世界 专业介绍 Mechanical Engineering 英语作文

机械工程的世界The world of MechanicalEngineeringHi to all of you, how you peeps doing. Today I would be discussing Mechanical Engineering with you. Are you a Matrix lover, or movies like transformers? Do you have a fascination for cars, then Mechanical engineering is your forte. Go for the course and get your dream job.Let’s read this article further to know about the greatness of this subject. Under-mentioned topics I have covered in this article:What is Mechanical engineering?Mechanical engineering jobs for the subject loversBranches of mechanical engineeringMechanical engineering Vs. Computer ScienceUniversities in Australia for mechanical engineeringTo become an excellent mechanical engineer what steps you must takeWhat is Mechanical engineeringMechanical engineering is a branch of engineering. It uses different principles of Physics and material science. Principles helps in designing, manufacture, and maintenance ofmechanical systems. The subject is from engineering stream. It involves the use of heat and mechanical power for the working of machines and tools. It is one of the oldest engineering disciplines. Many students are fond of becoming mechanic engineers.If you want to be a mechanical engineer, you need to be good at physics. You must have a command over the topics of this subject. Topics are mechanics, kinematics, thermo-dynamics, materials science. Along with these principles engineers use knowledge of computers. This helps them to design manufacturing plants, equipment, heating-cooling systems, etc.History of mechanical engineeringDevelopment of mechanical engineering is from Ancient Greek times. Archimedes discovered the Physical law of buoyancy. There were many thinkers and ancient engineers who are behind man-made marvels. Development of chariot, water clocks, and the steam engine. Such things are the ancient discoveries. So we can believe that mechanical engineering is old age discovery.Design of Crankshaft was first mentioned in the book ‘Knowledge of ingenious mechanics.’ The book was by Al- Jazari, written in 1206. As the time progress, mechanical engineering expanded. New analytical thinking came into it. Newton’s laws of motions were one of the most significant discoveries. Things we are creating today is a gift from yesterdays generation.The modern age of mechanical engineeringNew concepts of physics in 19th century developed mechanical engineering. The field has evolved in order to keep the pace with technical advancement. Mechanics is now growing in areas of composites, mechatronics, and nano-technology. It is also overlapping with aerospace engineering, civil engineering, electrical engineering.Mechanical engineering jobs for the subject loversFuture is very bright for mechanical engineers. They can go in every area related to manufacturing. They have to work according to the domain of the company. He works in the on design and control of a system. He checks a new system for efficiency. After that, he carries out improvement process.A mechanical engineer can work as an automobile engineer. He can go in cement industries, aeronautical, or in mining industries. There is also an increasing demand for mechanical engineer in Environment engineering. Let’s see in detail the jobs where mechanical engineers land in.Aerospace industryHere you need to do researches, designs, manufactures, operates and maintains aircraftAutomotive industryDesigning car models, manufacturing it, distributes and marketing of vehicles. This seems to be a cool profession especially for those who love cars.Chemical industryDo you love chemistry, then go for it. Work with oil companies, chemicals manufacturers.Construction industryYou can flaunt your creativity in this area. Make designs and build infrastructures, buildings.Defense industryIf you want to support your nation but do not have that sort of genetics or physique, then no worries. Be a mechanical engineer and provide equipment, armours, and technology to the military.Electronics industryEveryone needs electrical equipment. Make and manufacture the components to every sector from automobiles to military.Fast moving consumer goods industryHere you get the chance to develop home utility products and goods. For example, tools to clean the house, or for personal hygieneMaterials and metals industryDevelopment of new tools made up of metals. They are required for every field.Medicine industryDevelop machines and medical equipment. Types of equipment and machines are:x-ray scannersCT scan machinesTools which can be helpful in surgery.BRANCHES OF MECHANICAL ENGINEERINGMechanical engineering is a vast area. There are number of engineering fields that fit into mechanics. Let’s learn one by one about some of these engineering branches.Acoustical engineeringThis branch deals with the controlling of sound and vibration to reduce noise. Engineers arefocused on working on designing, analysis and sound control.Manufacturing engineeringThis branch is concerned with manufacturing processes and production methods. Engineer makes machines and tools to manufacture goods.Thermal engineeringIt’s about controlling heating and cooling in the environment. You must have a good knowledge of thermo-dynamics, fluid mechanics, and heat to excel in this stream.Vehicle engineeringThe design and manufacture of all manner of vehiclesAerospace engineeringIt is concerned with the development of aircraft and spacecraft. There are two more parts of this stream:1. Aeronautical EngineeringIt studies the design and structure of aircraft fly in atmosphere. It requires practical and theoretical knowledge of parts and material.2. Astronautical EngineeringIt is similar to aeronautical engineering. In this engineers works on aircraft and spacecraft that operates outside the earth’s atmosphere.Bio-medicine EngineeringIt is also known as bio-engineering. In this field, principles of engineering are applied in medicine and biology. Engineers make artificial organs, body parts replacements, etc. He also manufactures medical devices and equipment.Design engineeringIn this branch, an engineer designs a machine. He makes it a lot better and efficient. The engineer modifies the existing machines for better performance.Energy engineeringIn this field, Engineer deals with energy creation and conservation. The work is to make machines to use energy efficiently. It also deals with the methods to find alternative energy sources.If you are doing bachelor’s, then you need not choose a speciality. But if you are planning to go for higher studies then be ready with the one. You may face difficulties in the subject. For that, you can go for online assignment help from the experts. If you don’t have time for making an assignment or need assistance. They can surely help you. You can quickly get a great assignment without spending much.Mechanical engineering Vs. Computer ScienceIt might be a funny thing to make a comparison between computer scientists and mechanical engineers. But you may get surprised to know the similarities between them. Both of them design, develop and create tools to simplify our lives. One is doing digitally whereas other is physical. Let’s have a look at the similarities between them.Mechanical engineersMechanical engineers identify and find solutions to a problem. Engineers use mathematics, science, and engineering knowledge. They use physical tools and machinery. They are needed in factories, industries, and power plants. Some of the engineers make new machines while others improve the existing ones.Computer ScientistsLike mechanical, computer engineers identify and solve problems. They use maths and science principles. There work is to design, develop and check tools to solve problems. CS engineers also improve existing programs and make new ones.Coursework of Mechanical EngineeringBefore getting enrolled in any mechanical engineeri ng program, it’s better to look at coursework. I have mentioned below some general topics. These topics are in the syllabus of most universities. Have a look at them:For bachelor’s degreeIntroduction to engineering computing Chemistry of energy and materials Experimental physicsCAD and fabricationMaterials scienceStatics and structuresLinear algebra and differential equations DynamicsSolid mechanicsThermo-dynamicsFluid mechanicsCircuits and electronicsHeat transferSystem dynamicsData analysis and measurementsFor master’s degreeApplied mathematics in mechanical engineering Energy policy, regulation, and incentives Numerical linear algebraFeedback control designIntroduction to control design techniques Advanced dynamics and computationDigital control systemsThermal engineering fundamentalsThere might be few additions to the topics of mechanical engineering. What I have mentioned is, the general syllabus. The syllabus is from the famous universities of Australia. There are a lot of students who can face difficulty to understand these topics. Sometimes when University gives assignment work, they fail to make. For those students, I would suggest taking assignment help online. There are experts online to help you out in your tough time.Universities in Australia for mechanical engineeringUniversity of MelbourneUniversity offers a three years full-time Master’s course in engineering. Here are three areas of engineering for master’s degree:a. Master of Engineering (Mechanical)b. Master of Engineering (Mechanical with Business)c. Master of Engineering (Mechatronics)Monash UniversityMonash University offers four years bachelor in an engineering course. Several engineering specializations provided by Monash University:a. Aerospace Engineeringb. Chemical Engineeringc. Civil Engineeringd. Electrical and Computer Systems Engineeringe. Environmental Engineeringf. Materials Engineeringg. Mechanical Engineeringh. Mechatronics Engineeringi. Resources Engineeringj. Software EngineeringRMIT UniversityUniversity offers four-year bachelor program in various disciplines of engineering. I have mentioned some of them below:a. Aerospace engineering and aviationb. Bio-medical engineeringc. Chemical engineeringd. Civil engineeringe. Computer engineeringf. Electrical and electronic engineeringg. Engineering managementh. Environmental and sustainable engineeringi. Mechanical and automotive engineeringTo become an excellent mechanical engineer what steps you must takeSTEP 1: EARN A BACHELOR’S DEGREE IN MECHANICAL ENGINEERINGA bachelor degree in this field is a must to have. It is a start to your mechanical career. Students should choose a famous university. Secondly, you need to achieve a competitive percentage in it.STEP 2: EARN A MASTER’S DEGREE IN MECHANICAL ENGINEERINGMaster’s degree is not mandatory to have. You can get a job after a bachelor’s degree. But higher the education more will be the package. Therefore, doing masters in Mechanical engineering can be a good deal.STEP 3: BUILD MECHANICAL ENGINEERING EXPERIENCEExperience plays an essential role in the development of a career. It helps to build the skills required to be an expert engineer. It can help to generate new ideas in your mind. Experience can generate various opportunity for you.STEP 4: SEEK ORGANIZATIONAL CERTIFICATIONMany organizations are offering a certificate in mechanical engineering. A certificate can be of immense importance. It can prove your skills, increase your market value, and build confidence.STEP 5: CONSIDER A PHDGaining knowledge is always a productive thing. Engineers can go for Ph.D. programs in mechanical engineering. Those who enjoy research can do Ph.D. They can also teach next-gen minds.The present and the future of mechanical engineeringSo till now, you must have an idea about this stream and skills required for the stream. Now I would like to tell you more about the scope of Mechanical engineering. Like any other field, for this also you must have certain traits. You must have a love for machinery and mechanical parts. Your physics, chemistry, and mathematics ought to be good. Then comes your analytical mind, logical reasoning capacity, and problem-solving power. If you possess all of the traits, then be ready for a bright future.No one has seen future. You never know what it can bring for you. But the field of mechanics has excellent benefits for students. You can go into computers, bio-medicines, nano-technology after doing mechanics. There are many more career options as you have read earlier in thisarticle. So you can quickly judge that you can grab a job easily in this field.But there is a catch for you guys. As you know the competition is increasing day by day, so you need to catch the pace. A graduate may not get a good job after mechanical engineering. You need to prove your mettle. Stay connected with the higher education and technical advancement. Only then you can do something great in this field.ConclusionHope you guys had a good time with this article.I took all the essential aspects of mechanical engineering. The article started with the definition and history of the subject. Moving further, I have talked about jobs and branches ofengineering. Next, I discussed the similarities between mechanical and Computer science. After that coursework and Universities in Australia for mechanics. At last, I have mentioned the future of this subject. All in all, this article is covering every major and minor area of ME (Mechanical Engineering).。
低头族现象,谈手机利弊初中英语作文

低头族现象,谈手机利弊初中英语作文The Smartphone Saga: A Tale of Convenience and CautionHey there, fellow kids! It's me, your friendly neighborhood middle schooler, here to dish on the hottest topic that's got us all buzzing – smartphones! These nifty little gadgets have become an integral part of our lives, haven't they? From capturing epic selfies to conquering the latest games, smartphones have become our constant companions. But here's the thing, fam –with great power comes great responsibility (or so they say). Let's take a closer look at the pros and cons of these handheld wonders, shall we?First up, the pros – because let's face it, smartphones have made our lives way more convenient. Remember when we had to lug around heavy textbooks and notebooks? Those days are history, thanks to the magical world of e-books and note-taking apps. No more backbreaking loads! Plus, with a few taps on our screens, we can access a wealth of information on virtually any topic imaginable. Need to know the capital of Uzbekistan? Ask your smartphone, and boom – instant knowledge!Speaking of knowledge, smartphones have also revolutionized the way we learn. Gone are the days ofmonotonous lectures and boring textbooks. Now, we have access to interactive educational apps, video tutorials, and online courses that make learning fun and engaging. Who knew algebra could be so rad?But wait, there's more! Smartphones have also become our portable entertainment hubs. Bored during a long car ride? No worries, just whip out your trusty device and dive into a world of movies, music, and games. It's like having a mini cinema and arcade right in your pocket!And let's not forget about the social aspect of smartphones. Thanks to messaging apps and social media platforms, we can stay connected with our friends and family no matter where they are. Virtual hangouts, group chats, and sharing memes – it's all part of the digital age, fam.Now, as much as we love our smartphones, we can't ignore the potential downsides. First and foremost, let's talk about the dreaded "smartphone zombie" phenomenon. You know whatI'm talking about – those people who walk around with their heads buried in their screens, oblivious to their surroundings. It's like they're in a trance, completely disconnected from the real world. Not cool, my dudes.Then there's the issue of cyberbullying and online safety. While the internet has opened up a world of possibilities, it's also a breeding ground for trolls and cyberbullies. We need to be extra vigilant about what we share online and with whom we interact. Remember, once something is out there on the interwebs, it's virtually impossible to take it back.And let's not forget about the dreaded "fear of missing out" (FOMO, for those in the know). With constant updates and notifications flooding our screens, it's easy to get caught up in the never-ending cycle of social media envy. Suddenly, everyone else's life seems way more exciting than our own. But here's the harsh truth, fam – social media is often a carefully curated highlight reel, not an accurate representation of reality.Last but not least, there's the potential for addiction and unhealthy screen time habits. Smartphones can be seriously addictive, and excessive use can lead to issues like poor sleep, eye strain, and even mental health problems. It's crucial to strike a balance and make time for offline activities and face-to-face interactions.So, there you have it, fellow kids – the pros and cons of smartphones, laid out in all their glory. At the end of the day, these devices are tools, and it's up to us to use them wisely.Embrace the convenience and educational opportunities they offer, but don't forget to unplug and reconnect with the real world every once in a while.Remember, life is about balance, and smartphones should enhance our experiences, not consume them entirely. So, go ahead and snap that epic selfie, but don't forget to look up and appreciate the world around you. After all, there's more to life than just a screen, fam.。
用英语写学习计划100字

用英语写学习计划100字Introduction:The purpose of this learning plan is to outline a structured approach to achieving my educational goals. This plan will cover the areas of study I intend to focus on, the resources and strategies I will use to support my learning, and the timeline for completing my goals. The plan will also include a reflection on my current skills and knowledge, as well as an assessment of the measures I will take to address any gaps in understanding.Areas of Study:The first area of study I plan to focus on is mathematics. I will begin by reviewing the fundamental concepts of algebra, geometry, and calculus. I will then move on to more advanced topics such as differential equations and linear algebra. To support my learning, I will use online resources, textbooks, and practice problems. I will also seek out additional help through tutoring and study groups.The second area of study is computer science. I will start by refreshing my understanding of programming languages such as Python, Java, and C++. I will then expand my knowledge by learning about data structures, algorithms, and software development methodologies. To supplement my learning, I will use online courses, coding exercises, and project-based learning. I will also collaborate with peers and participate in coding challenges.The third area of study is communication skills. I will work on improving my writing, speaking, and presentation abilities. I will also focus on developing my critical thinking and problem-solving skills. To enhance my communication skills, I will take writing workshops, join public speaking clubs, and participate in debates and discussions. I will also seek feedback from peers and mentors to refine my skills.Resources and Strategies:To support my learning, I will utilize a variety of resources and strategies. I will use online platforms such as Khan Academy, Coursera, and edX to access course materials, lectures, and exercises. I will also make use of textbooks, academic journals, and research papers to deepen my understanding of complex topics. Additionally, I will seek out mentors, advisors, and experts in the fields I am studying to gain insights and guidance.In terms of study strategies, I will employ techniques such as spaced repetition, active recall, and mnemonics to enhance my retention and recall of information. I will also create a structured study schedule to ensure that I allocate sufficient time to each area of study. Furthermore, I will set specific learning goals and track my progress to stay motivated and focused.Timeline:To achieve my educational goals, I have set a timeline for completing each area of study. I plan to spend six months on mathematics, three months on computer science, and three months on communication skills. Within each time frame, I will establish weekly targets and milestones to measure my progress. At the end of each period, I will evaluate my performance and adjust my plan accordingly.Self-assessment:In terms of my current skills and knowledge, I have a strong foundation in mathematics and computer science. However, there are areas within both subjects where I lack proficiency, such as advanced calculus and software development. With regards to communication skills, I am confident in my writing abilities, but I need to improve my public speaking and critical thinking skills.To address these gaps in understanding, I will dedicate extra time to the topics I find challenging. I will seek out additional resources and support to help me grasp difficult concepts. I will also practice regularly to build my confidence and competence in these areas.Conclusion:In conclusion, this learning plan serves as a roadmap to guide my educational journey. By focusing on mathematics, computer science, and communication skills, I aim to improve my knowledge and expertise in these domains. With the support of resources and strategies, as well as a structured timeline, I am confident that I will achieve my learning goals. Through self-assessment and reflection, I will continuously monitor my progress and make adjustments to ensure I am on track. I look forward to the growth and development that this plan will bring.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
functions. This was used in [1] and [2] to derive geometrically stable numerical integration algorithms, although the results are presented differently.
1
Introduction
Let k be a field, R be a commutative k -algebra, and Der(R) the Lie algebra of derivations of R. It is known that the vector space spanned by labeled rooted trees forms a Hopf algebra [4]. Let H denote the Hopf algebra of rooted trees whose non root nodes are labeled using derivations D ∈ Der(R) [4]. For such a Hopf algebra, we introduce a class of H -module algebras which we call Leibnitz, and give a construction which yields a variety of different Leibnitz H -module algebras (Theorem 3.11). We also show how Leibnitz H -module algebras are related to Nichols and Weisfeiler’s R/k -bialgebras [10], which arise in Hopf-algebra approaches to differential algebra (Theorem 4.7). In Section 5 we also give a method for describing quotients of Leibnitz H -module algebras (Theorem 5.8). Hopf algebras can be used to simplify computations of derivations [5]. In the same way, Leibnitz H -module algebras can be used to simplify the symbolic computation of derivations acting on polynomials and other algebras of 1
In this construction, each non root node retains its original label; recall that the root is not labeled. See [4] for more details and Figure 2 for some examples. Since k {T (S )} is a graded bialgebra with dim k {T (S )}0 = 1, it is a Hopf algebra. We summarize this discussion in the following Proposition 2.1 Let k be a field and let S be a vector space over k . Then k {T (S )} is a cocommutative graded connected Hopf algebra.
arXiv:math/0409006v1 [math.QA] 1 Sep 2004
Differential Algebra Structures on Families of Trees
Robert L. Grossman Richard G. Larson June 6, 2004
Abstract It is known that the vector space spanned by labeled rooted trees forms a Hopf algebra. Let k be a field and let R be a commutative k-algebra. Let H denote the Hopf algebra of rooted trees labeled using derivations D ∈ Der(R). In this paper, we introduce a construction which gives R a H -module algebra structure and show this induces a differential algebra structure of H acting on R. The work here extends the notion of a R/k-bialgebra introduced by Nichols and Weisfeiler.
X
where X ranges over all sub-multisets of the ordered multiset F described above. If Y is a sub-multiset of F , the labeled ordered tree TY is formed by adding edges to link the roots of the trees in Y to a new root, preserving their original order and labels. In particular, TF = T and T∅ = 1 is the unit. The counit ǫ : k {T (S )} → k is defined as follows. ǫ(T ) = 1 if T = 1 0 otherwise.
multiplication is defined so that the root of T ′ ∈ F follows every child of the node d(T ′ ); this will not change the application of the results we use from there.) The coproduct in k {T (S )} is defined as follows. If T is a labeled ordered rooted tree, define ∆(T ) = TX ⊗ TF\X ,
3
H -module algebras
Let R be a commutative k -algebra, and let H be a k -bialgebra. Recall the following definition [8, 4.1.1]: Definition 3.1 The algebra R is a left H -module algebra if R is a left H module for which h · (rs) = (h(1) · r )(h(2) · s),
d
,
where the sum ranges over all trees Td formed as described above. This product is associative, and the tree with only one node is a multiplicative unit. See [4] for details and Figure 1 for some examples. (Note that in [4] 2
2
Bialgebras and trees
This section reviews some material from [4] on the Hopf algebra structure of trees. For background material on Hopf algebras see [14]. Throughout this paper k is a field. Let R be a commutative k -algebra. Let D be a vector space over k , and let S be a subset of D . Let T (S ) denote the set of ordered trees in which each node other than the root is labeled with an element of S . Let k {T (S )} be the vector space over k with basis the elements of T (S ). When we speak of a “subtree of a tree” we also include the (unlabeled) node in the tree to which the subtree is attached as the root of the subtree. When we refer to the “children of a node v ” we will sometimes mean the nodes which are attached to v as immediate descendants, and sometimes mean the full subtrees which are attached to v . Which sense is meant will be clear from context. We have a grading on k {T (S )}: k {T (S )}r is spanned by the trees with r + 1 nodes. There is a bialgebra structure on k {T (S )} given in [4] which we summarize here. Multiplication in k {T (S )} is defined as follows. Let T1 and T2 be rooted trees. Remove the root from the tree T1 to form a multiset F of rooted trees. Let d be a function from F to the set of nodes of T2 . Let Td be the rooted tree formed by adding an edge to link the root of T ′ ∈ F to the node d(T ′ ) of T2 . The order on the children of a node of Td is given by declaring that the order of the children of a node of a tree in F is preserved, that the order of the children of a node of T2 is preserved, that if two roots of trees in F are linked to the same node of T2 , they are given the order they had as children of the root of T1 , and that the root of T ′ precedes every child of the node d(T ′) to which it is linked. Now T1 · T2 =
