北京燕山中考一《数学》模试题及答案共44页文档
2024北京燕山区初三一模数学试卷及答案

数学试卷答案及评分参考 第1页 共6页北京市燕山地区2024年初中毕业年级质量监测(一)数学试卷答案及评分参考 2024年4月 阅卷须知:1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可。
2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分。
3.评分参考中所注分数,表示考生正确做到此步应得的累加分数。
第一部分 选择题一、选择题(共16分,每题2分)第二部分 非选择题二、填空题(共16分,每题2分)9.3x ≥; 10.8()()a b a b +-; 11.15x =; 12.2; 13.29;14.80;15.34;16.(1) 答案不唯一,如:BCA ; (2) 15. 三、解答题(共68分,第17-19题,每题5分,第20题6分,第21-23题,每题5分,第24-26题,每题6分,第27-28题,每题7分)17.(本题满分5分)解:原式=422+- ……………………………………………4分 =4 ……………………………………………5分18.(本题满分5分)解:原不等式组为3421532x x x x -<+⎧⎪⎨+>⎪⎩,①.② 解不等式①,得 5x <, ……………………………………………2分 解不等式②,得 1x >-, ……………………………………………4分 ∴原不等式组的解集为15x -<<. …………………………………………5分数学试卷答案及评分参考 第2页 共6页解: (32)(32)3(1)x x x x +--+=229433x x x --- ……………………………………………2分 =2634x x --=23(2)4x x --. ……………………………………………3分 ∵2210x x --=,∴221x x -=, ……………………………………………4分 ∴原式=314⨯-=-1. ……………………………………………5分20.(本题满分6分)解:(1) ∵CE =ED ,OE =EF ,∴四边形OCFD 是平行四边形,∴DF ∥AC .∵菱形ABCD ,∴AC ⊥BD ,∴DF ⊥BD ,即∠ODF =90°,∴四边形OCFD 是矩形. ……………………………………………3分(2) ∵菱形ABCD ,∴AB =CD =5,BD =2OD .∵矩形OCFD ,∴OF =CD =5,∠ODF =90°.在Rt △ODF 中,sin ∠DOF =DF OF =35,OF =5, ∴DF =3,∴OD4,∴BD =8. ……………………………………………6分21.(本题满分5分)解:设边衬的宽度为x m , ……………………………………………1分依题意得 2.221.62x x ++=43, ……………………………………………2分 解得 x =0.1. ……………………………………………3分 经检验,x =0.1是原方程的解且符合实际意义. ………………………4分 答:边衬的宽度为0.1m . ……………………………………………5分F O E A B C D数学试卷答案及评分参考 第3页 共6页解:(1) ∵一次函数y kx b =+(0k ≠)的图象由函数2y x =的图象向下平移4个单位长度得到,∴k =2,4b =-,∴该一次函数的解析式为24y x =-.令0y =,得2x =,∴点A 的坐标为(2,0). ……………………………………………3分(2) 52≤≤n --. ……………………………………………5分23.(本题满分5分)解:(1) m 的值为204,n 的值为195; ……………………………………………2分(2) 乙; ……………………………………………3分(3) 甲;3800. ……………………………………………5分24.(本题满分6分)(1) 证明:∵AE 是⊙O 的切线,AB 为⊙O 的直径,∴∠EAB =90°.∵CD ⊥AB ,∴AE ∥CD ,∴∠BCD =∠E .∵∠BAD =∠BCD ,∴∠BAD =∠E . ……………………………………………3分 (2) 解:如图,连接AC .∵AB 为⊙O 的直径,CD ⊥AB ,∴AC =AD =6,∠ACB =90°.∵AB =10,∴BC =8.∵∠ACE =∠EAB =90°,∴∠E +∠EAC =∠EAC +∠CAB =90°,∴∠E =∠CAB .在Rt △EAC 和Rt △ACB 中,∠ACE =∠BCA =90°,∠E =∠CAB ,∴△EAC ∽△ACB , ∴EC AC AC BC=, ∴EC =2AC BC =368=92. ……………………………………………6分数学试卷答案及评分参考 第4页 共6页 解:(1) 设1y 关于x 的函数关系式为1(0)y mx n m =+≠,将点(0,20),(1,25)的坐标代入1y mx n =+,得2025,,n m n =⎧⎨=+⎩ 解得520.,m n =⎧⎨=⎩ ∴1y 关于x 的函数关系式为1520y x =+.设2y 关于x 的函数关系式为22y ax bx =+(a <0),将点(1,30),(2,50)的坐标代入22y ax bx =+,得305042,,a b a b =+⎧⎨=+⎩ 解得535.,a b =-⎧⎨=⎩ ∴2y 关于x 的函数关系式为22535y x x =-+. ……………………… 5分(2) 25. ……………………………………………6分26.(本题满分6分)解:(1) ∵对于m =1,有1y =2y ,∴点M (1,1y ),N (3,2y )关于直线x =t 对称,∴t -1=3-t ,∴t =2. ……………………………………………2分(2) ∵a >0,∴当x ≥t 时,y 随x 增大而增大,当x <t 时,y 随x 增大而减小. ①当t ≤1时,∵1<m <2,∴3<m +2<4,∴t <m <m +2,∴1y <2y ,符合题意.②当1<t ≤2时,(i )当t ≤m <2时,∵3<m +2<4,∴t ≤m <m +2,∴1y <2y ,符合题意.(ii )当m <t ≤2时,设点M (m ,1y )关于x =t 的对称点为M ′,则点M ′的坐标为(2t -m ,1y ). ∵1<m <t ≤2, ∴m <2t -m <3. ∵3<m +2<4, ∴2t -m <m +2, ∴1y <2y ,符合题意.③当2<t <3时,令m =t -1,则m +2=t +1, ∴1y =2y ,不符合题意. ④当t ≥3时,令m =32,则m +2=72, ∴1y >2y ,不符合题意.综上所述,t 的取值范围是t ≤2. …………………………………………6分27.(本题满分7分)(1)证明:∵△ABC 中,∠ACB =90°,AC =BC ,∴∠A =45°. ∵DE ⊥AB ,∴∠AED =∠A =45°, ∴DE =AD . ∵DE =DM , ∴AD =DM ,即D 是AM 的中点. ……………………………………………2分(2) BF =2DE . ……………………………………………3分 证明:如图,连接EA ,EM .∵DE =DM ,DE ⊥AB , ∴△EDM 是等腰直角三角形, ∴∠EMA =45°.∵在△ABC 中,∠ACB =90°,AC =BC , M 为AB 中点,∴∠CMA =90°,AM =CM , ∴∠EMC =45°. 在△EMA 和△EMC 中,AM =CM ,∠EMA =∠EMC =45°,EM =EM , ∴△EMA ≌△EMC , ∴∠EAM =∠ECM .M A D BECF ED CBAM∵在四边形CEFM 中,EF ⊥CE ,∠CMA =90°, ∴∠EFM +∠ECM =360°-(∠CEF +∠CMF)=180°. 又∵∠EF A +∠EFM =180°, ∴∠EF A =∠ECM , ∴∠EAM =∠EF A , ∴EA =EF , 又∵DE ⊥AF , ∴D 为AF 的中点,∴BF =AB -AF =2AM -2AD =2DM =2DE ,即BF =2DE . ……………………………………………7分28.(本题满分7分)…………………………………… 3分(2) 3-t ≤1,或t <5. …………………………………… 7分。
2022年北京市燕山区中考数学一模试卷(附答案详解)

2022年北京市燕山区中考数学一模试卷一、选择题(本大题共8小题,共16.0分)1.如图是某几何体的三视图,该几何体是()A. 圆锥B. 圆柱C. 三棱锥D. 长方体2.小云同学在“百度”搜索引擎中输入“北京2022冬奥会”,能找到相关结果约为42500000个,将42500000用科学记数法表示应为()A. 0.425×108B. 4.25×107C. 4.25×106D. 42.5×1053.如图,直线AB,CD交于点O.射线OM平分∠AOC,若∠BOD=72°,则∠BOM等于()A. 36°B. 108°C. 126°D. 144°4.下列图形中,既是中心对称图形也是轴对称图形的是()A. B.C. D.5.实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是()A. b+c>0B. bd>0C. |a|>|d|D. a<−46.如图,有5张形状、大小、质地均相同的卡片,正面分别印有北京冬奥会的会徽、吉祥物(冰墩墩)、主题口号和奖牌等四种不同的图案,背面完全相同.现将这5张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面图案恰好是奖牌的概率是()A. 15B. 25C. 12D. 357. 已知432=1849,442=1936,452=2025,462=2116.若n 为整数且n <√2022<n +1,则n 的值为( )A. 43B. 44C. 45D. 468. 线段AB =5.动点P 以每秒1个单位长度的速度从点A 出发,沿线段AB 运动至点B ,以线段AP 为边作正方形APCD ,线段PB 长为半径作圆.设点P 的运动时间为t ,正方形APCD 周长为y ,⊙B 的面积为S ,则y 与t ,S 与t 满足的函数关系分别是( )A. 正比例函数关系,一次函数关系B. 一次函数关系,正比例函数关系C. 正比例函数关系,二次函数关系D. 反比例函数关系,二次函数关系二、填空题(本大题共8小题,共16.0分)9. 若代数式1x−1有意义,则x 的取值范围是______. 10. 分解因式:4x 2−9y 2=______.11. 写出一个比√2大且比π小的整数是______. 12. 方程组{x +y =62x −y =3的解为______.13. 在直角坐标系xOy 中,直线y =x 与双曲线y =m x(m ≠0)交于A ,B 两点.若点A ,B的横坐标分别为x 1,x 2,则x 1+x 2的值为______. 14. 如图,在△ABC 中,点D 、E 分别AC 、AB 上的点,BD 与CE 交于点O.给出下列三个条件:①∠EBO =∠DCO ;②∠BEO =∠CDO ;③BE =CD.利用其中两个条件可以证明△ABC 是等腰三角形,这两个条件可以是______.15. A(a,0),B(5,3)是平面直角坐标系中的两点,线段AB 长度的最小值为______. 16. 甲、乙、丙三人进行羽毛球比赛赛前训练,每局两人进行比赛,第三个人做裁判,每一局都要分出胜负,胜方和原来的裁判进行新一局的比赛,输方转做裁判,依次进行.半天训练结束时,发现甲共当裁判9局,乙、丙分别进行了14局、12局比赛,在这半天的训练中,甲、乙、丙三人共进行了局比赛,其中最后一局比赛的裁判是______.三、解答题(本大题共12小题,共68.0分) 17. 计算:3tan30°−tan 245°+2sin60°.18.疫情防控过程中,很多志愿者走进社区参加活动.如图所示,小冬老师从A处出发,要到A地北偏东60°方向的C处,他先沿正东方向走了200m到达B处,再沿北偏东30°方向走,恰能到达目的地C处,求A,C两地的距离.(结果取整数,参考数据:√2≈1.414,√3≈1.732)19.已知:如图,直线l,和直线外一点P.求作:过点P作直线PC,使得PC//l,作法:①在直线l上取点O,以点O为圆心,OP长为半径画圆,交直线l于A,B两点;②连接AP,以点B为圆心,AP长为半径画弧,交半圆于点C;③作直线PC.直线PC即为所求作.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)完成下面的证明:证明:连接BP.∵BC=AP,∴BC⏜=______ .∴∠ABP=∠BPC(______ )(填推理依据).∴直线PC//直线l.20.已知关于x的方程x2+2x+k=0总有两个不相等的实数根.(1)求k的取值范围;(2)写出一个k的值,并求此时方程的根.21.如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD交BC的延长线于点E.(1)求证:四边形ACED是平行四边形;(2)若BD=4,AC=3,求sin∠CDE的值.x的图象22.在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=12向上平移3个单位长度得到.(1)求这个一次函数的解析式;(2)当x>2时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b的值,直接写出m的取值范围.23.农业农村经济在国民经济中占有重要地位,科技兴农、为促进乡村产业振兴提供有力支撑.为了解甲、乙两种新品猕猴桃的质量,进行了抽样调查.在相同条件下,随机抽取了甲、乙各25份样品,对大小、甜度等各方面进行了综合测评,并对数据进行收集、整理、描述和分析,下面给出了部分信息. a.测评分数(百分制)如下:甲77 79 80 80 85 86 86 87 88 89 89 90 91 91 91 91 91 92 93 95 95 96 97 98 98 乙69 87 79 79 8679 87 89 90 89 90 90 90 91 90 92 92 94 92 95 96 96 97 98 98 b.按如下分组整理、描述这两组样本数据:8089c.甲、乙两种猕猴桃测评分数的平均数、众数、中位数如表所示:(1)写出表中a ,b ,c ,d 的值;(2)记甲种猕猴桃测评分数的方差为s 12,乙种猕猴桃测评分数的方差为s 22,则s 12,s 22的大小关系为______;(3)根据抽样调查情况,可以推断______种猕猴桃的质量较好,理由为______.(至少从两个不同的角度说明推断的合理性)24. 某景观公园内人工湖里有一组小型喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下数据,在湖面上距水枪水平距离为d 米的位置,水柱距离湖面高度为ℎ米. (1)以水枪与湖面交点为原点,原点与水柱落地处所在直线为x 轴,水枪所在直线为y轴,在下边网格中建立平面直角坐标系,根据已知数据描点,并用平滑的曲线连接.(2)请结合表中所给数据或所画图象,写出水柱最高点的坐标.(3)湖面上距水枪水平距离为3.5米时,水柱距离湖面的高度m=______米.(4)现公园想通过喷泉设立新的游玩项目,准备通过调节水枪高度,使得公园湖中的游船能从喷泉下方通过.游船左右两边缘最宽处有一个长方体形状的遮阳棚,若游船宽(指船的最大宽度)为2米,从水面到棚顶的高度为2.1米,要求是游船从喷泉水柱中间通过时,为避免游船被喷泉淋到,顶棚到水柱的垂直距离均不小于0.5米.请问公园该如何调节水枪高度以符合要求?请通过计算说明理由.25.如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM,过点A作AD⊥CM于点D,交BC的延长线于点E.(1)求证:AB=AE;(2)若AB=10,cosB=3,求CD的长.526.在平面直角坐标系xOy中,抛物线y=ax2+bx+3a(a≠0)与x轴的交点为点A(1,0)和点B.(1)用含a的式子表示b;(2)求抛物线的对称轴和点B的坐标;(3)分别过点P(t,0)和点Q(t+2,0)作x轴的垂线,交抛物线于点M和点N,记抛物线在M,N之间的部分为图象G(包括M,N两点).记图形G上任意一点的纵坐标的最大值是m,最小值为n.①当a=1时,求m−n的最小值;②若存在实数t,使得m−n=1,直接写出a的取值范围.27.如图,在三角形ABC中,AB=AC,∠BAC<60°,AD是BC边的高线,将线段AC绕点A逆时针旋转60°得到线段AE,连接BE交AD于点F.(1)依题意补全图形,写出∠CAE=______°.(2)求∠BAF+∠ABF和∠FBC的度数;(3)用等式表示线段AF,BF,EF之间的数量关系,并证明.28.对于平面直角坐标系xOy中的线段PQ,给出如下定义:若存在△PQR使得S△PQR=PQ2,则称△PQR为线段PQ的“等幂三角形”,点R称为线段PQ的“等幂点”.(1)已知A(2,0).①在点P1(2,4),P2(1,2),P3(−4,1),P4(1,−4)中,线段OA的“等幂点”是______;②若存在等腰△OAB是线段OA的“等幂三角形”,求点B的坐标;(2)已知点C的坐标为C(2,−1),点D在直线y=x−3上,记图形M为以点T(1,0)为圆心,2为半径的⊙T位于x轴上方的部分.若图形M上存在点E,使得线段CD的“等幂三角形”△CDE为锐角三角形,直接写出点D的横坐标x D的取值范围.答案和解析1.【答案】A【解析】解:主视图和左视图都是等腰三角形,那么此几何体为锥体,由俯视图为圆,可得此几何体为圆锥体.故选:A.由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.此题考查了由三视图判断几何体,主视图和左视图的大致轮廓为三角形的几何体为锥体.2.【答案】B【解析】解:42500000=4.25×107.故选:B.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数,当原数绝对值<1时,n是负整数.此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.【答案】D【解析】解:∵∠BOD=∠AOC=72°,∴∠BOC=180°−∠BOD=180°−72°=108°,∵OM平分∠AOC,∴∠COM=12∠AOC=12×72°=36°,∴∠BOM=∠BOC+∠COM=108°+36°=144°.故选:D.由对顶角的定义可得∠BOD=∠AOC=72°,根据邻补角的定义可得∠BOC=180°−∠BOD的度数,根据角平分线的定义可得∠COM=12∠AOC,由∠BOM=∠BOC+∠COM 计算即可得出答案.本题主要考查了对顶角,邻补角及角平分线的定义,熟练掌握对顶角,邻补角及角平分线的定义进行求解是解决本题的关键.4.【答案】C【解析】解:A.不是中心对称图形,是轴对称图形,故此选项不合题意;B.是中心对称图形,不是轴对称图形,故此选项不合题意;C.既是中心对称图形,也是轴对称图形,故此选项符合题意;D.不是中心对称图形,也不是轴对称图形,故此选项不合题意;故选:C.根据中心对称图形与轴对称图形的概念进行判断即可.本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.5.【答案】A【解析】解:A、b+c是异号两数的和,取绝对值较大数的符号,所以b+c>0正确;B、b<0,d>0,所以bd<0,故不正确;C、|a|<4,|d|>5,所以|a|<|d|,故不正确;D、a>−4,故不正确.故选:A.A、b+c是异号两数的和,取绝对值较大数的符号,所以取c的符号,是个正数,故符合题意;B、bd是异号两数的积,异号得负,所以是负数,故不符合题意;C、两个绝对值比较大小,就是比较它们离开原点的距离,故不正确;D、a在−4右边,右边的数大于左边的数,故不正确.本题考查有理数的大小比较,关键是在数轴上右边的数大于左边的数,离开原点越远,绝对值越大.6.【答案】B【解析】解:∵5张卡片中有2张是奖牌,∴从中随机抽取一张,抽出的卡片正面图案恰好是奖牌的概率是2,5故选B.用奖牌的数量除以卡片的总数即可求得答案.考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.7.【答案】B【解析】解:∵442=1936,452=2025,1936<2022<2025,∴44<√2022<45,∵n为整数且n<√2022<n+1,∴n的值为:44,故选:B.根据题意可知n与n+1是两个连续整数,再估算出√2022的值即可.本题考查了估算无理数的大小,根据题意判断n与n+1是两个连续整数,再估算出√2022的值是解题的关键.8.【答案】C【解析】解:y=4t,属于正比例函数关系,S=π(5−t)2,属于二次函数关系,故选:C.根据题意列出函数关系式,即可判断函数的类型.本题考查了函数关系式,根据题意列出函数关系式是解题的关键.9.【答案】x≠1【解析】解:依题意得:x−1≠0,解得x≠1,故答案为:x≠1.分式有意义,分母不等于零,即x−1≠0,由此求得x的取值范围.本题考查了分式有意义的条件.(1)分式有意义的条件是分母不等于零.(2)分式无意义的条件是分母等于零.10.【答案】(2x+3y)(2x−3y)【解析】解:原式=(2x+3y)(2x−3y).故答案为:(2x+3y)(2x−3y).直接利用平方差公式进行分解即可.此题主要考查了公式法分解因式,关键是掌握平方差公式:a2−b2=(a+b)(a−b).11.【答案】3(答案不唯一)【解析】解:∵1<2<4,∴1<√2<2,∵3<π<4,∴比√2大且比π小的整数是3(答案不唯一).故答案为:3(答案不唯一).估算无理数的大小即可得出答案.本题考查了无理数的估算,无理数的估算常用夹逼法,用有理数夹逼无理数是解题的关键.12.【答案】{x =3y =3【解析】解:{x +y =6 ①2x −y =3 ②, ①+②得:3x =9,x =3,把x =3代入第一个方程得:y =3,即{x =3y =3, 故答案为:{x =3y =3. 由已知未知数y 的系数的绝对值相等,因此为了不出差错,选用加法较好.此题考查的知识点是解二元一次方程组,解题的关键是运用加减消元法解二元一次方程组.13.【答案】0【解析】解:∵反比例函数与正比例函数都是中心对称图形,根据题意,得x 1=−x 2,∴x 1+x 2=0,故答案为:0.根据反比例函数与正比例函数都是中心对称图形,可得x 1=−x 2,求值即可.本题考查了反比例函数与一次函数的交点问题,熟练掌握反比例函数与正比例函数的中心对称性是解题的关键.14.【答案】①③或②③【解析】解:由①③或②③条件可判定△ABC 是等腰三角形.选①③为条件证明△ABC 是等腰三角形;理由:在△EBO和△DCO中,{∠EOB=∠DOC ∠EBO=∠DCO EB=CD,∴△EBO≌△DCO(AAS),∴BO=CO,∴∠OBC=∠OCB,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,∴AB=AC,∴△ABC是等腰三角形;选②③为条件证明△ABC是等腰三角形;理由:在△BEO和△CDO中,{∠BEO=∠CDO ∠EOB=∠DOC BE=CD,∴△BEO≌△CDO(AAS),∴∠EBO=∠DCO,OB=OC,∴∠OBC=∠OCB,∴∠ABC=∠ACB,∴AB=AC.故答案为:①③或②③.①③;②③;都可以组合证明△ABC是等腰三角形;选①③为条件证明△ABC是等腰三角形,首先证明△EBO≌△DCO,可得BO=CO,根据等边对等角可得∠OBC=∠OCB,进而得到∠ABC=∠ACB,根据等角对等边可得AB=AC,即可得到△ABC是等腰三角形.此题主要考查了等腰三角形的判定,关键是掌握判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等.15.【答案】3【解析】解:∵A(a,0),B(5,3),∴AB=√(5−a)2+(3−0)2=√(5−a)2+9,∴当a=5时,AB取得最小值3,故答案为:3.根据A(a,0),B(5,3)和勾股定理,可以表示出AB的长度,然后即可得到AB的最小值,本题得以解决.本题考查勾股定理,解答本题的关键是表示出线段AB的长.16.【答案】甲【解析】解:∵甲共当裁判9局,∴乙、丙之间打了9局,又∵乙、丙分别进行了14局、12局比赛,∴乙与甲打了14−9=5局,丙与甲打了12−9=3局,∴甲、乙、丙三人共打了5+3+9=17局,∵甲共当裁判9局,而从1到17共9个奇数,8个偶数,∴甲当裁判的局为奇数局,∴最后一局比赛的裁判是甲,故答案为:甲.先确定了乙与丙打了9局,乙与甲打了5局,丙与甲打了3局,进而确定三人一共打的局数和甲当裁判的局数,即可得到答案.本题考查统计和概率的推理与论证.解本题关键根据题目提供的特征和数据,分析其存在的规律和方法.并递推出相关的关系式.从而解决问题.17.【答案】解:3tan30°−√3tan245°+2sin60°−√3×1+2×√3=3×√33=2√3.【解析】本题涉及乘方、特殊角的三角函数值等考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,要熟练掌握乘方的相关运算.18.【答案】解:过点C作CD⊥AB交AB延长线于点D,则∠BCD=30°,由题意得:∠ABC=90°+30°=120°,∠BAC=90°−60°=30°,∴∠ACB=180°−∠ABC−∠BAC=30°,∴∠BAC=∠ACB=30°,∴AB=CB=200m,在Rt△BDC中,CB=200m,∴BD=1CB=100(m),2∴CD=√3BD=100√3(m),在Rt△DCA中,∠ACB=30°,∴AC=2CD=200√3≈346(m),答:A,C两地的距离约为346m.【解析】过点C作CD⊥AB交AB延长线于点D,先证AB=CB=200m,再由含30°角的CB=100(m),则CD=√3BD=100√3(m),然后由含30°直角三角形的性质得BD=12角的直角三角形的性质求解即可.本题考查了解直角三角形的应用—方向角问题,正确作出辅助线构造直角三角形是解题的关键.19.【答案】PA⏜同弧或等弧所对的圆周角相等【解析】解:(1)如图,直线PC即为所求作.(2)证明:连接PB.∵BC=AP,.∴BC⏜=AP⏜,∴∠ABP=∠BPC(同弧或等弧所对的圆周角相等),∴直线PC//直线l.故答案为:PA⏜,同弧或等弧所对的圆周角相等.(1)根据要求画出图形即可.(2)连接PB,只要证明∠ABP=∠CPB即可.本题考查作图−复杂作图,平行线的判定,圆周角定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.20.【答案】解:(1)∵方程总有两个不相等的实数根,∴Δ=22−4k>0,解得k<1,∴k的取值范围是k<1;(2)当k=0时,方程化为x2+2x=0,x(x+2)=0,∴x1=0,x2=−2.【解析】(1)根据根的判别式的意义得到22−4k>0,解不等式即可;(2)当k取0时,方程化为x2+2x=0,然后利用因式分解法解方程.本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.21.【答案】(1)证明:∵四边形ABCD是菱形,∴AD//BC,∠BOC=90°.∵DE⊥BD,∴∠BDE=90°,∴∠BDE=∠BOC,∴AC//DE,∴四边形ACED是平行四边形.(2)解:∵四边形ACED是平行四边形,∴AD=CE,∵AD=BC,∴BC=CE,∵∠BDE=90°,∴DC=CE,∴∠CDE=∠E,∵BD=4,AC=3,∠BDE=90°,∴BE=5,∴sinE=BDBE =45,∴sin∠CDE=BDBE =45.【解析】(1)想办法证明AC//DE,AD//CE即可;(2)只要证明∠CDE=∠E,再想办法求出sin∠E即可.本题考查菱形的性质、平行四边形的判定和性质、解直角三角形、锐角三角函数等知识,解题的关键是熟练掌握平行四边形的判定,学会用转化的思想思考问题.22.【答案】解:(1)∵一次函数y=kx+b(k≠0)的图象由函数y=12x的图象向上平移3个单位长度得到.∴k=12 , b=3,∴这个一次函数的解析式为y=12x+3;(2)把x=2代入y=12x+3,得y=4,把点(2,4)代入y=mx,求得m=2,∵当x>2时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b的值,∴m的取值范围是m≥2.【解析】(1)根据平移的规律即可求得.(2)根据点(2,4)结合一次函数的性质即可求得.本题考查了一次函数图象与几何变换,一次函数与系数的关系,熟知一次函数的性质是解题的关键.23.【答案】<甲①甲品种猕猴桃的测评分数的中位数、众数均比乙品种的高,②甲品种猕猴桃的测评分数方差比乙种小【解析】解:(1)由题意可知,甲种猕猴桃的测评分数在70≤x<80中有2个,故a=2;乙种猕猴桃的测评分数在80≤x<90中有5个,故b=5;乙种猕猴桃的测评分数出现次数最多的是90,所以众数是90,即c=90;将甲种猕猴桃的测评分数从小到大排列处在中间位置的一个数是91,因此中位数是91,即d=91;(2)由甲、乙猕猴桃的测评分数大小波动情况,直观可得s12<s22,故答案为:<;(3)可以推断甲品种较好,理由为:①甲品种猕猴桃的测评分数的中位数、众数均比乙品种的高;②甲品种猕猴桃的测评分数方差比乙种小.故答案为:甲;①甲品种猕猴桃的测评分数的中位数、众数均比乙品种的高,②甲品种猕猴桃的测评分数方差比乙种小.(1)根据题意以及中位数、众数的意义求解即可;(2)根据数据大小波动情况,直观可得答案;(3)从中位数、众数的比较得出答案.本题考查频数分布表,中位数、众数、平均数,理解中位数、众数、平均数的意义和计算方法是正确解答的前提.24.【答案】1.6【解析】解:(1)以水枪与湖面的交点为原点,水枪所在的直线为y轴建立平面直角坐标系,如图所示:(2)由图象可得,最高点的坐标是(2,2.5);(3)湖面上距水枪水平距离为3.5米时,水柱距离湖面的高度m=1.6米,故答案为:1.6;(4)根据图象设二次函数的解析式为ℎ=a(d−2)2+2.5,将(0,1)代入ℎ=a(d−2)2+2.5得a=−0.4,∴抛物线的解析式为ℎ=−0.4d2+1.6d+0.9,当d=0时,ℎ=0.9,即水枪高度为0.9米,设水枪高度至少向上调节m米,由题意知调节后的水枪所喷出的抛物线的解析式为y=−0.4x2+1.6x+0.9+m,当横坐标为2+1=3时,纵坐标的值大于等于2.1+0.5=2.6,∴−0.4×32+1.6×3+0.9+m≥2.6,解得:m≥0.5,0.9+0.5=1.4(米),∴水枪高度调节到1.4米以上.(1)建立坐标系,描点、用平滑的曲线连接即可;(2)观察图象并根据二次函数图象的性质求出最高点的高度,(3)根据二次函数图象的对称性可得答案;(4)先求出二次函数的关系式,由题意知设出二次函数图象平移后的解析式,根据题意求解即可.本题考查了二次函数喷泉的应用,二次函数解析式,二次函数图象的平移.解题的关键在于熟练掌握二次函数的图象建立二次函数模型.25.【答案】(1)证明:连结OC,∵CD是⊙O的切线,OC为⊙O的半径∴OC⊥CD,又∵AD⊥CM,∴OC//AE.∴∠OCB=∠E∵OB=OC∴∠OCB=∠B∴∠E=∠B∴AB=AE;(2)连接AC,∵AB为⊙O的直径∴∠ACB=∠ACE=90°.在Rt△ACB中,AB=10,cosB=35∴CB=6,∴AC=√102−62=8,∵∠DCE+∠E=∠DCE+∠ACD=90°∴∠E=∠ACD∴cos∠ACD=cosE=cosB=35又∵AC=8,∴CD=24.5【解析】(1)连接OC,根据切线的性质得到OC⊥CD,根据平行线的性质、等腰三角形的判定和性质定理证明即可;(2)连接AC,根据余弦的定义求出BC,根据勾股定理求出AC,根据余弦的定义计算,得到答案.本题考查的是切线的性质、锐角三角函数的定义,掌握圆的切线垂直于经过切点的半径是解题的关键.26.【答案】解:(1)把点A(1,0)代入y=ax2+bx+3a得:a+b+3a=0,∴b=−4a;(2)由(1)知抛物线为y=ax2−4ax+3a,=2,∴抛物线的对称轴为直线x=−−4a2a而A(1,0)关于直线x=2的对称点是(3,0),由抛物线对称性得:点B坐标(3,0);(3)①如图:当a=1时,y=ax2−4ax+3a=a(x−1)(x−3)=(x−1)(x−3),∴抛物线与x轴交点坐标为(1,0),(3,0),与y轴交点坐标为(0,3),顶点坐标为(2,−1),由图象知:当图象G为对称图形时m−n有最小值,又P(t,0)Q(t+2,0),∴2−t=(t+2)−2,∴t=1,∵过点P(t,0)和点Q(t+2,0)作x轴的垂线,交抛物线于点M和点N,∴M(1,0),N(3,0),∵顶点坐标为(2,−1),∴m−n的最小值为0−(−1)=1;②∵点P(t,0)和点Q(t+2,0)作x轴的垂线,交抛物线于点M和点N,由(1)知抛物线为y=ax2−4ax+3a,∴M(t,at2−4at+3a),N(t+2,a(t+2)2−4a(t+2)+3a),又∵抛物线对称轴为直线x=2,顶点坐标为(2,−a),∴根据M、N点的相对位置和抛物线的开口方向可分以下四种情况讨论a的取值:(Ⅰ)当a>0,且t+2≤2时,即图象G在对称轴左侧时,此时M点的纵坐标最大,N点的纵坐标最小,∴at2−4at+3a−[a(t+2)2−4a(t+2)+3a]=1,解得t=1−1,4a又∵t≤0,a>0,∴1−1≤0且a>0,4a∴0<a≤1;4(Ⅱ)当a>0,且t≥2时,即图象G在对称轴右侧时,此时N点的纵坐标最大,M点的纵坐标最小,∴a(t+2)2−4a(t+2)+3a−(at2−4at+3a)=1,,解得t=1+14a又∵t≥2,a>0,∴1+1≥2且a>0,4a∴0<a≤1,4(Ⅲ)当a>0,且0<t≤1时,即最低点是抛物线顶点且M点纵坐标大时,此时m=at2−4at+3a,n=−a,∴at2−4at+3a−(−a)=1,解得t=2±√a,a又∵0<t≤1,a>0,∴t=2−√a,a∴0<2−√a≤1,a≤a<1;∴14(Ⅳ)当a>0,且1<t≤2时,即最低点是抛物线顶点时且N点纵坐标大,此时m=a(t+2)2−4a(t+2)+3a,n=−a,∴a(t+2)2−4a(t+2)+3a−(−a)=1,解得t2=1,a又∵1<t≤2,a>0,∴1<1≤4,a<a≤1,∴14综上所述,当0<a≤1时,m−n=1,同理可得:当a<0时,−1≤a<0也符合条件,∴a的取值范围为0<a≤1或−1≤a<0.【解析】(1)把点A(1,0)代入y=ax2+bx+3a即可得b=−4a;=2,由抛物线对称性得点B坐标(2)由对称轴公式可得抛物线的对称轴为直线x=−−4a2a(3,0);(3)①当a=1时,y=ax2−4ax+3a=a(x−1)(x−3)=(x−1)(x−3),即得抛物线与x 轴交点坐标为(1,0),(3,0),与y 轴交点坐标为(0,3),顶点坐标为(2,−1),当图象G 为对称图形时m −n 有最小值,可得2−t =(t +2)−2,t =1,即得m −n 的最小值为0−(−1)=1;②由(1)知抛物线为y =ax 2−4ax +3a ,得M(t,at 2−4at +3a),N(t +2,a(t +2)2−4a(t +2)+3a),顶点坐标为(2,−a),可分四种情况讨论a 的取值:(Ⅰ)当a >0,且t +2≤2时,at 2−4at +3a −[a(t +2)2−4a(t +2)+3a]=1,解得t =1−14a ,可得0<a ≤14;(Ⅱ)当a >0,且t ≥2时,a(t +2)2−4a(t +2)+3a −(at 2−4at +3a)=1,可得0<a ≤14,(Ⅲ)当a >0,且0<t ≤1时,at 2−4at +3a −(−a)=1,可得14≤a <1;(Ⅳ)当a >0,且1<t ≤2时,a(t +2)2−4a(t +2)+3a −(−a)=1,可得14<a ≤1,即知当0<a ≤1时,m −n =1,同理可得:当a <0时,−1≤a <0也符合条件. 本题考查二次函数的综合应用,难度较大,解题的关键是分类讨论图象G 上纵坐标的大小值.27.【答案】60【解析】解:(1)依题意补全图形,∠CAE =60°,故答案为:60;(2)∵AB =AC ,AD 是BC 边的高线,∴∠BAD =12∠BAC , ∵线段AC 绕点A 逆时针旋转60°得到线段AE ,∴AB =AE ,∵∠CAE =60°,∴∠ABE =∠E ,在△ABE 中,∠ABE +∠E +∠BAC =180°−∠CAE =120°,∴12(∠ABE +∠E +∠BAC)=60°, ∴∠BAF +∠ABF =60°,∵AD 是BC 边的高线,∴∠ADB =90°,∴∠FBC =90°−(∠BAF +∠ABF)=30°;(3)AF +BF =EF ,理由如下:如图,在EF 上取点M ,使EM =BF ,连接AM ,∴△ABF≌△AEM(SAS).∴AF=AM.∴△AFM是等边三角形,∴FM=AF,∴AF+BF=EF.(1)根据旋转的性质画出图形即可;(2)根据旋转的旋转和三角形内角和定理解答即可;(3)根据全等三角形的判定和性质解答即可.此题考查几何变换的综合题,关键是根据旋转的性质和全等三角形的判定和性质解答.28.【答案】P1和P4【解析】解:(1)①∵A(2,0),∴OA=2,OA2=4,∵点P1(2,4),P2(1,2),P3(−4,1),P4(1,−4),∴S△OAP1=12×2×4=4,S△OAP2=12×2×2=1,S△OAP3=12×2×1=1,S△OAP4=12×2×4=4,故答案为:P1和P4;②如图,∵△OAB是线段OA的“等幂三角形”,∴S△OAB=OA2,∵点A(2,0),设△OAB中OA边上的高为ℎ,S△OAB=12×OA×ℎ=12×2×ℎ=4,∴ℎ=4,∴点B在直线y=4或y=−4上,又∵△OAB是等腰三角形,∴点B在半径为2的⊙O上,或在半径为2的⊙A上,或线段OA的垂直平分线上,综上,点B的坐标为(1,4)或(1,−4);(2)如图,第一个临界点,当点E1和E2在⊙T上,等幂三角形刚好是直角三角形,E1(1,2),E2(−1,0),∴E1E2平行于直线y=x−3,过点E1,E2作直线的垂线D1D2,设CD1=a,D1E1=2a,在Rt△E1D1C中,CD12+D1E12=CE12,即a2+(2a)2=(√10)2,解得a=√2,则CD1=√2,根据对称性可知CD2=√2,作CM//x轴,D1M//y轴,则∠D1CM=45°,∴CM=√22CD1=1,∴x D1=x M=3,同理可得x D2=1,如图,第二个临界点,E3E4平行于直线y=x−3,与相切于点E5,等幂三角形刚好是直角三角形,CE5=2+√2,则E3E5=12CE5=2+√22,∴CE3=E3E5=2+√22,则x D3=x C+√22CD1=√2+52,同理可得x D4=3−√22,结合图象可知)3−√22<x D<1或3<x D<5+√22.(1)①分别求出△OAP1、OAP2、△OAP3、△OAP4的面积,可得答案;②设△OAB中OA边上的高为ℎ,根据“等幂三角形”的定义知,ℎ=4,从而得出点B的坐标;(2)找出△CDE为直角三角形的的第一个临界点,当点E1和E2在⊙T上,等幂三角形刚好是直角三角形,E1(1,2),E2(−1,0),第二个临界点,E3E4平行于直线y=x−3,与相切于点E5,等幂三角形刚好是直角三角形,CE5=2+√2,分别画出图形,从而解决问题.本题是圆的综合题,主要考查了“等幂三角形”的定义,等腰三角形的性质,直角三角形的性质,圆的相关性质等知识,读懂定义,找到△△CDE为直角三角形时点D的坐标是解决问题(2)的关键.。
初中数学北京市燕山初中毕业暨一模考试数学考试卷

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)试题1:下列每两个数中,互为相反数的是A. 3和B. -3和C. -3和0D. -3和3试题2:已有600年历史的紫禁城在中国独一无二,在世界也是独一无二. 据媒体报道,2011年参观故宫的人数已突破1400万,把1400万用科学记数法表示应为A.0.14×108B.1.4×107C.1.4×106D.14×106试题3:已知某多边形的每一个外角都是72°,则它的边数为A . 4B . 5 C. 6 D. 8试题4:下列各式计算正确的是A. B. =±3 C. (m+n)(n-m)=n2-m2 D.试题5:学雷锋活动中,初四1班评选出了7名学雷锋活动带头人,其中团员同学占了4位,现需要采用抽签的方法从中确定一人参加表彰大会,被选中的同学为共青团员的概率是A. B. C.D.试题6:某一次函数y=ax+b 的图象如图所示,则下列结论正确的是A. a<0, b<0B. a<0, b>0C. a>0, b<0D. a>0, b>0试题7:某短跑运动员在集训中的5次测试成绩(单位:秒)如下:12.5,12.7,12.1,12.8,12.4.这组数据的方差是A.0.06 B.0.3 C.0.6 D.6试题8:如图,任意四边形ABCD中,AC和BD相交于点O,把△AOB、△AOD、△COD、△BOC的面积分别记作S1、S2、S3、S4,则下列各式成立的是A.S1 + S3 = S2+S4 B.S3-S2 = S4-S1 C.S1·S4= S2·S3 D.S1·S3 = S2·S4试题9:函数y =中,自变量x的取值范围是 _____ .试题10:如图,平地上A、B两点被池塘隔开,测量员在岸边选一点C,并分别找到AC和BC的中点M、N,经量得MN=24米,则AB=_________米.试题11:已知圆锥的底面直径是4cm,侧面上的母线长为3cm,则它的侧面积为________cm2.试题12:图中的抛物线是函数y=x2+1的图象,把这条抛物线沿射线y=x(x≤0)的方向平移个单位,其函数解析式变为_________;若把抛物线y=x2+1沿射线 y =x-1( x≥0)方向平移个单位,其函数解析式则变为_________.试题13:计算:-4cos45°+-试题14:解不等式组并把解集在数轴上表示出来.试题15:如图,点F在线段AB上,AD∥BC,AC交DF于点E,∠BAC=∠ADF,AE=BC.求证:△ACD是等腰三角形.试题16:已知x2-1=0,求代数式的值.试题17:列方程或方程租应用题:北京到石家庄的铁路里程约为280km , 2012年底京石高铁即将通车,其上运行的新型动车速度可比目前的普通列车提高1.8倍, 届时从北京到石家庄乘坐高铁新型动车将比现在乘坐普通列车少用一个半小时即可到达,求目前普通列车的运行速度.试题18:已知:关于x的一元二次方程kx2-(4k+1)x+3k+3=0 (k是整数).(1)求证:方程有两个不相等的实数根;(2)若方程的两个实数根分别为x1,x2(其中x1<x2),设y= x2-x1,判断y是否为变量k的函数?如果是,请写出函数解析式;若不是,请说明理由.试题19:如图,梯形ABCD中,AB∥CD,AD⊥AB,AB=2,BC=CD=4,求∠B的度数和AC的长.试题20:寒假期间,某校同学积极参加社区公益活动. 开学后,校团委随机选取部分学生对每人的“累计参与时间”进行了调查,将数据绘制成图1、图2. 请结合这两幅不完整的统计图解答下列问题:(1)这次调查共选取了多少名学生?(2)将图1的内容补充完整;(3)求图2中“约15小时”对应的圆心角度数,并把图2的内容补充完整;(4)若该校共有学生680人,估计这个寒假有多少学生参加了社区公益活动?试题21:已知:如图, M是AB的中点,以AM为直径的⊙O与BP相切于点N,OP ∥MN.(1)求证:直线PA与⊙O相切;(2)求tan∠AMN的值.试题22:请你先动笔在草稿纸上画一画,再回答下列问题:(1)平面内两条直线,可以把平面分成几部分?(2)平面内3条直线,可以把平面分成几部分?(3)平面内4条直线,可以把平面最多分成多少部分?(4)平面内100条直线,可以把平面最多分成多少部分?试题23:已知:如图,在直角坐标系xOy中,直线y=2x与函数y=的图象在第一象限的交于A点,AM⊥x轴,垂足是M,把线段OA的垂直平分线记作l,线段AN与OM关于l对称.(1)画出线段AN(保留画图痕迹);(2)求点A的坐标;(3)求直线AN的函数解析式.试题24:已知:如图,点P是线段AB上的动点,分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD,AD和BC交于点M.(1)当△APC和△BPD面积之和最小时,直接写出AP : PB的值和∠AMC的度数;(2)将点P在线段AB上随意固定,再把△BPD按顺时针方向绕点P旋转一个角度α,当α<60°时,旋转过程中,∠AMC 的度数是否发生变化?证明你的结论.(3)在第(2)小题给出的旋转过程中,若限定60°<α<120°,∠AMC的大小是否会发生变化?若变化,请写出∠AMC 的度数变化范围;若不变化,请写出∠AMC的度数.试题25:已知点A(1,)在抛物线y=x2+bx+c上,点F(-,)在它的对称轴上,点P为抛物线上一动点.(1)求这条抛物线的函数解析式;(2)判断是否存在直线l,使得线段PF的长总是等于点P到直线l的距离,需说明理由.(3)设直线PF与抛物线的另一交点为Q,探究:PF和QF这两条线段的倒数和是否为定值?证明你的结论.试题1答案:D试题2答案:B试题3答案:B试题4答案:C试题5答案:D试题6答案:A试题7答案:A试题8答案:D试题9答案:x≠3试题10答案:48试题11答案:6π试题12答案:y=x2+2x+1,y=x2-4x+6试题13答案:原式=5-2-1+-1= 3-.试题14答案:解①得 x >-2,解②得 x3,∴不等式组的解集是-2 < x 3 .数轴上正确表示解集试题15答案:证明:∵AD∥BC,∴∠CAD=∠BCA,即∠EAD=∠BCA.在△ADE和△CAB中,又∵∠ADE=∠ADF=∠CAB,AE=BC,∴△ADE≌△CAB.∴ AD=AC.∴△ACD是等腰三角形.试题16答案:原式=÷=÷=·=由x2 -1=0 ,得x=±1.∴当x=1时,原式无意义;当x= -1时,原式= -试题17答案:设目前普通列车的运行速度是x千米/时,依题意,得- = .解得 x=120.经检验, x=120是原分式方程的根.答: 目前普通列车的运行速度是120千米/时.试题18答案:⑴证明:Δ= (4k+1)2-4k(3k+3)=(2k-1)2∵k是整数,∴k≠,2k-1≠0. ∴Δ= (2k-1)2 >0 ∴方程有两个不相等的实数根.⑵ y是k的函数;解方程得,x=.∴x=3,或x=1+.∵k是整数,∴1,1+2<3.又∵x1< x2, ∴x1=1+, x2=3.∴ y=3-(1+)=2-.试题19答案:作BE⊥CD于E,∵梯形ABCD中,AB∥CD,AD⊥AB,∴四边形ABED是矩形.∴DE=AB=2,CE=CD-DE=4-2=2.在Rt△BEC中,又∵BC=4=2CE,∴∠EBC=30°,CE=2,BE=2.∴∠B=∠ABC=120°.在Rt△ADC中,又∵AD=BE∴AC===2.试题20答案:⑴ 32⑵补图⑶ 67.5°把扇形统计图补全⑷ 595 …试题21答案:⑴证明:连结ON,∵BP与⊙O相切于点N,∴ON⊥BP, ∠ONP=90°.∵MN∥OP,∴∠OMN=∠AOP, ∠MNO=∠NOP.又∵∠OMN =∠MNO,∴∠AOP =∠NOP.又∵OA=ON,OP公用,∴△AOP≌△NOP.∴∠OAP =∠ONP=90°.∴直线PA与⊙O相切. .⑵设⊙O的直径是2r.∵M是AB的中点,∴BM=2r,OB=3r.∴BN===2r.∵∠PAB =∠ONB=90°,∴△PAB∽△ONB.∴.∴tan∠AMN= tan∠AOP=.试题22答案:(1)3或4(2)4,或6,或7(3)11(4)5051试题23答案:.⑴图形大体正确,有画图痕迹⑵由2x =,得x2=1. ∵点A在第一象限,∴x=1.∴点A(1,2).⑶设l与x轴交于点P,与OA交于点B.∵ OM=1 ,AM=2 ,AM⊥x轴∴OA=,OB=易证Rt△POB∽Rt△AOM,∴.∴OP=×=.∴点P(,0).把点A和P的坐标分别代入y=kx+b,得解得k =,b =.又∵直线AN必过点P,∴直线AN的解析式是y=x+.试题24答案:⑴ 1,60°⑵不变化.证明:如图,点E在AP的延长线上,∠BPE=α<60°.(只要画出了符合题意的图形即可得分)∵∠BPC=∠CPD+60°,∠DPA=∠CPD+60°,∴∠BPC=∠DPA.在△BPC和△DPA中,又∵BP=DP,PC=PA,∴△BPC≌△DPA.∴∠BCP=∠DAP.∴∠AMC=180°-∠MCP-∠PCA-∠MAC= 120°-∠BCP -∠MAC=120°-(∠DAP+∠MAC)-∠PCA=120°-∠PAC= 60°,且与α的大小无关.⑶不变化,60°试题25答案:.⑴由=,a=,得b=把b =和点A(1,)代入y=x2+bx+c,可求得c=.∴这条抛物线的解析式是y=x2+x.⑵设点P(x0,y0),则y0=x02+x0.作PM⊥AF于M,得 PF2=PM2+MF2= (x0+)2+ (y0-)2又∵y0=x02+x0=(x0+)2-∴(x0+)2=3y0+∴PF2=3y0++ y02- y0+=( y0+1)2.易知y0≥-,y0+1>0. ∴PF= y0+1.又∵当直线l经过点(0,-1)且与x轴平行时,y0+1即为点P到直线l的距离.∴存在符合题意的直线l.⑶是定值.证明:当PF∥x轴时,PF=QF=,.当PF与x轴不平行时,作QN⊥AF于N,∵△MFP∽△NFQ,∴.再依据第⑵小题的结果,可得. 整理上式,得.。
2020届北京市燕山区中考数学一模试卷(有答案)(加精)

北京市燕山区中考数学一模试卷一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.从2015年秋季学期起,北京110 000名初一新生通过“北京市初中实践活动管理服务平台”进行选课,参加“开放性科学实践活动”课程.将110 000用科学记数法表示应为()A.11×104 B.1.1×105C.1.1×106D.0.11×1062.实数a,b,c,d在数轴上的对应点的位置如图所示,其中互为相反数的两个数是()A.a和d B.a和c C.b和d D.b和c3.2016年是中国农历丙申猴年,下列四个猴子头像中,是轴对称图形的是()A.B.C.D.4.学校组织知识竞赛,共设有20道试题,其中有关中国优秀传统文化的试题10道,实践应用试题6道,创新能力试题4道.小捷从中任选一道试题作答,他选中创新能力试题的概率是()A.B.C.D.5.如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于()A.30°B.35°C.40°D.50°6.为了解某种电动汽车一次充电后行驶的里程数,对其进行了抽检,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是()A.220,220 B.220,210 C.200,220 D.230,2107.为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.如图,如果大视力表中“E”的高度是3.5cm,那么小视力表中相应“E”的高度是()A.3cm B.2.5cm C.2.3cm D.2.1cm8.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为()A.(﹣3,3)B.(3,2) C.(0,3) D.(1,3)9.手工课上,老师将同学们分成A,B两个小组制作两个汽车模型,每个模型先由A组同学完成打磨工作,再由B组同学进行组装完成制作,两个模型每道工序所需时间如下:工序时间模型打磨(A组)组装(B组)模型甲9分钟5分钟模型乙6分钟11分钟则这两个模型都制作完成所需的最短时间为()A.20分钟B.22分钟C.26分钟D.31分钟10.如图1,△ABC是一块等边三角形场地,点D,E分别是AC,BC边上靠近C点的三等分点.现有一个机器人(点P)从A点出发沿AB边运动,观察员选择了一个固定的位置记录机器人的运动情况.设AP=x,观察员与机器人之间的距离为y,若表示y与x的函数关系的图象大致如图2所示,则观察员所处的位置可能是图1的()A.点B B.点C C.点D D.点E二、填空题(本题共18分,每小题3分)11.因式分解:a3﹣ab2=.12.如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n=.13.关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根.请你写出一个满足条件的m 值:m=.14.《孙子算经》是中国古代重要的数学著作,记有许多有趣而又不乏技巧的算术程式.其中记载:“今有甲、乙二人,持钱各不知数.甲得乙中半,可满四十八.乙得甲太半,亦满四十八.问甲、乙二人原持钱各几何?”译文:“甲,乙两人各有若干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的,那么乙也共有钱48文.问甲,乙二人原来各有多少钱?”设甲原有x文钱,乙原有y文钱,可列方程组为.15.我国2010﹣2015年高铁运营里程情况统计如图所示,根据统计图提供的信息,预估2016年我国高铁运营里程约为万公里,你的预估理由是.16.阅读下面材料:在数学课上,老师提出如下问题:小敏的作法如下:老师说:“小敏的作法正确.”请回答:小敏的作图依据是.三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)解答应写出文字说明,演算步骤或证明过程.17.计算:()﹣1+|﹣2|﹣2cos60°+(1﹣π)0.18.解不等式组:.19.如图,点C为AB中点,AD∥CE,AD=CE.求证:∠D=∠E.20.已知x2﹣4x﹣1=0,求代数式(2x﹣3)2﹣(x+1)(x﹣1)的值.21.为应对雾霾天气,使师生有一个更加舒适的教学环境,学校决定为南北两幢教学楼安装空气净化器.南楼安装的55台由甲队完成,北楼安装的50台由乙队完成.已知甲队比乙队每天多安装两台,且两队同时开工,恰好同时完成任务.甲、乙两队每天各安装空气净化器多少台?22.如图,△ABC中,AD是BC边的中线,分别过点B,D作AD,AB的平行线交于点E,且ED交AC于点F,AD=2DF.(1)求证:四边形ABED为菱形;(2)若BD=6,∠E=60°,求四边形ABED的面积.23.如图,直线y=2x+n与双曲线y=(m≠0)交于A,B两点,且点A的坐标为(1,4).(1)求m,n的值;(2)过x轴上一点M作平行于y轴的直线l,分别与直线y=2x+n和双曲线y=(m≠0)交于点P,Q,若PQ=2QM,求点M的坐标.24.如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.(1)求证:∠ABD=2∠CAB;(2)若BF=5,sin∠F=,求BD的长.25.阅读下列材料:数学课程内容分为“数与代数”、“图形与几何”、“统计与概率”、“综合与实践”四个领域,其中“综合与实践”领域通过探讨一些具有挑战性的研究问题,给我们创造了可以动手操作、探究学习、认识数学知识间的联系、发展应用数学知识解决问题的意识和能力的机会.“综合与实践”领域在人教版七﹣九年级6册数学教材中共安排了约40课时的内容,主要有“数学制作与设计”、“数学探究与实验”、“数学调查与测量”、“数学建模”等活动类型,所占比例大约为30%,20%,40%,10%.这些活动以“课题学习”、“数学活动”和“拓广探索类习题”等形式分散于各章之中.“数学活动”几乎每章后都有2~3个,共60个,其中七年级22个,八年级19个;“课题学习”共7个,其中只有八年级下册安排了“选择方案”和“体质健康测试中的数据分析”2个内容,其他5册书中都各有1个;七上﹣九下共6册书中“拓广探索类习题”数量分别为44,39,46,35,37,23.根据以上材料回答下列问题:(1)人教版七﹣九年级数学教材中,“数学调查与测量”类活动约占课时;(2)选择统计表或统计图,将人教版七﹣九年级数学教材中“课题学习”、“数学活动”和“拓广探索类习题”的数量表示出来.26.如图1,四边形ABCD中,AB=AD,BC=CD,我们把这种两组邻边分别相等的四边形叫做筝形.请探究“筝形”的性质和判定方法.小聪根据学习四边形的经验,对“筝形”的判定和性质进行了探究.下面是小聪的探究过程,请补充完整:(1)如图2,连接筝形ABCD的对角线AC,BD交于点O,通过测量边、角或沿一条对角线所在直线折叠等方法探究发现筝形有一组对角相等,请写出筝形的其他性质(一条即可):,这条性质可用符号表示为:;(2)从边、角、对角线或性质的逆命题等角度进行探究,写出筝形的一个判定方法(定义除外),并证明你的结论.27.抛物线C1:y=a(x+1)(x﹣3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3).(1)求抛物线C1的解析式及A,B点坐标;(2)将抛物线C1向上平移3个单位长度,再向左平移n(n>0)个单位长度,得到抛物线C2,若抛物线C2的顶点在△ABC内,求n的取值范围.28.在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连接AD,BD,CD,其中CD交直线AP于点E.设∠PAB=α,∠ACE=β,∠AEC=γ.(1)依题意补全图1;(2)若α=15°,直接写出β和γ的度数;(3)如图2,若60°<α<120°,①判断α,β的数量关系并加以证明;②请写出求γ大小的思路.(可以不写出计算结果)29.在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N上,称线段PQ长度的最小值为图形M,N的密距,记为d(M,N).特别地,若图形M,N有公共点,规定d(M,N)=0.(1)如图1,⊙O的半径为2,①点A(0,1),B(4,3),则d(A,⊙O)=,d(B,⊙O)=.②已知直线l:y=与⊙O的密距d(l,⊙O)=,求b的值.(2)如图2,C为x轴正半轴上一点,⊙C的半径为1,直线y=﹣与x轴交于点D,与y轴交于点E,线段DE与⊙C的密距d(DE,⊙C)<.请直接写出圆心C的横坐标m的取值范围.北京市燕山区中考数学一模试卷参考答案与试题解析一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.从2015年秋季学期起,北京110 000名初一新生通过“北京市初中实践活动管理服务平台”进行选课,参加“开放性科学实践活动”课程.将110 000用科学记数法表示应为()A.11×104 B.1.1×105C.1.1×106D.0.11×106【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:110 000用科学记数法表示应为1.1×105,故选B.2.实数a,b,c,d在数轴上的对应点的位置如图所示,其中互为相反数的两个数是()A.a和d B.a和c C.b和d D.b和c【考点】实数与数轴.【分析】根据相反数位于原点的两侧且到原点的距离相等,可得答案.【解答】解:由相反数位于原点的两侧且到原点的距离相等,得a与d互为相反数,故选:A.3.2016年是中国农历丙申猴年,下列四个猴子头像中,是轴对称图形的是()A.B.C.D.【考点】轴对称图形.【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【解答】解:A、不是轴对称图形,故此选项错误;B、不是轴对称图形,故此选项错误;C、是轴对称图形,故此选项正确;D、不是轴对称图形,故此选项错误;故选:C.4.学校组织知识竞赛,共设有20道试题,其中有关中国优秀传统文化的试题10道,实践应用试题6道,创新能力试题4道.小捷从中任选一道试题作答,他选中创新能力试题的概率是()A.B.C.D.【考点】概率公式.【分析】根据共设有20道试题,其中创新能力试题4道,再根据概率公式即可得出答案.【解答】解:∵共设有20道试题,其中创新能力试题4道,∴他选中创新能力试题的概率是=;故选D.5.如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于()A.30°B.35°C.40°D.50°【考点】平行线的性质.【分析】首先根据平行线的性质求出∠3的度数,然后根据三角形的外角的知识求出∠A的度数.【解答】解:如图,∵直线m∥n,∴∠1=∠3,∵∠1=70°,∴∠3=70°,∵∠3=∠2+∠A,∠2=30°,∴∠A=40°,故选C.6.为了解某种电动汽车一次充电后行驶的里程数,对其进行了抽检,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是()A.220,220 B.220,210 C.200,220 D.230,210【考点】众数;条形统计图;中位数.【分析】根据众数与中位数的定义,找出出现次数最多的数,把这组数据从小到大排列,求出最中间两个数的平均数即可.【解答】解:数据220出现了4次,最多,故众数为220,共1+2+3+4=10个数,排序后位于第5和第6位的数均为220,故中位数为220,故选A.7.为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.如图,如果大视力表中“E”的高度是3.5cm,那么小视力表中相应“E”的高度是()A.3cm B.2.5cm C.2.3cm D.2.1cm【考点】相似三角形的应用.【分析】直接利用平行线分线段成比例定理列比例式,代入可得结论.【解答】解:由题意得:CD∥AB,∴=,∵AB=3.5cm,BE=5m,DE=3m,∴,∴CD=2.1cm,故选D.8.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为()A.(﹣3,3)B.(3,2) C.(0,3) D.(1,3)【考点】坐标确定位置.【分析】根据棋子“馬”和“車”的点的坐标可得出原点的位置,进而得出答案.【解答】解:如图所示:棋子“炮”的点的坐标为:(1,3).故选:D.9.手工课上,老师将同学们分成A,B两个小组制作两个汽车模型,每个模型先由A组同学完成打磨工作,再由B组同学进行组装完成制作,两个模型每道工序所需时间如下:工序打磨(A组)组装(B组)时间模型模型甲9分钟5分钟模型乙6分钟11分钟则这两个模型都制作完成所需的最短时间为()A.20分钟B.22分钟C.26分钟D.31分钟【考点】推理与论证.【分析】分两种情况,①当A组先打磨模型甲共需26分钟.②当A组先打磨模型乙共需22分钟.再比较大小即可.【解答】解:①当A组先打磨模型甲需要9分钟,然后B组装模型甲需要5分钟,在这5分钟内,A组已打磨模型乙用了5分钟,还需等1分钟,B才能组装模型乙,之后B组在组装模型乙需要11分钟,则整个过程用时9+5+1+11=26分钟.②当A组先打磨模型乙需要6分钟,然后B组装模型乙需要9分钟,在这11分钟内,A组已打磨好模型甲,因为A组打磨模型甲只需要9分钟,之后B组在组装模型甲需要5分钟,则整个过程用时6+11+5=22分钟.而26>22,∴这两个模型都制作完成所需的最短时间为22分钟,故选B.10.如图1,△ABC是一块等边三角形场地,点D,E分别是AC,BC边上靠近C点的三等分点.现有一个机器人(点P)从A点出发沿AB边运动,观察员选择了一个固定的位置记录机器人的运动情况.设AP=x,观察员与机器人之间的距离为y,若表示y与x的函数关系的图象大致如图2所示,则观察员所处的位置可能是图1的()【考点】动点问题的函数图象.【分析】根据题意可以得到当观察员分别处于选项中的各点时,y随x的增大如何变化,从而可以得到哪个选项是正确的.【解答】解:当观察员所处的位置在点B时,y随x的增大而减小,与图2不符,故选项A错误;当观察员所处的位置在点C时,y随x的增大先减小再增大,且减小与增大的距离相等,故选B错误;当观察员所处的位置在点D时,y随x的增大先减小再增大,由大变小的距离小于由小变大的距离,故选项C正确;当观察员所处的位置在点E时,y随x的增大先减小再增大,由大变小的距离大于由小变大的距离,故选项D错误;故选C.二、填空题(本题共18分,每小题3分)11.因式分解:a3﹣ab2=a(a+b)(a﹣b).【考点】提公因式法与公式法的综合运用.【分析】观察原式a3﹣ab2,找到公因式a,提出公因式后发现a2﹣b2是平方差公式,利用平方差公式继续分解可得.【解答】解:a3﹣ab2=a(a2﹣b2)=a(a+b)(a﹣b).12.如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n=9.【考点】正多边形和圆.【分析】利用360度除以中心角的度数即可求得.【解答】解:∵正n边形的中心角==40°,n==9.故答案为:9.13.关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根.请你写出一个满足条件的m值:m=0.【考点】根的判别式.【分析】若一元二次方程有两不等根,则根的判别式△=b2﹣4ac>0,建立关于m的不等式,求出m的取值范围.【解答】解:∵方程有两个不相等的实数根,a=1,b=﹣2,c=m,∴△=b2﹣4ac=(﹣2)2﹣4×1×m>0,解得m<1,故答案是:0.14.《孙子算经》是中国古代重要的数学著作,记有许多有趣而又不乏技巧的算术程式.其中记载:“今有甲、乙二人,持钱各不知数.甲得乙中半,可满四十八.乙得甲太半,亦满四十八.问甲、乙二人原持钱各几何?”译文:“甲,乙两人各有若干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的,那么乙也共有钱48文.问甲,乙二人原来各有多少钱?”设甲原有x文钱,乙原有y文钱,可列方程组为.【考点】由实际问题抽象出二元一次方程组.【分析】设甲原有x文钱,乙原有y文钱,根据题意可得,甲的钱+乙的钱的一半=48文钱,乙的钱+甲所有钱的=48文钱,据此列方程组可得.【解答】解:设甲原有x文钱,乙原有y文钱,根据题意,得:,故答案为:.15.我国2010﹣2015年高铁运营里程情况统计如图所示,根据统计图提供的信息,预估2016年我国高铁运营里程约为 2.2万公里,你的预估理由是每年平均增长量近似相等.【考点】用样本估计总体;折线统计图.【分析】根据折线统计图可以预估2016年我国高铁运营里程约为多少公里,以及预估的理由,本题得以解决.【解答】解:由折线统计图可得,预估2016年我国高铁运营里程约为:1.9+(1.9﹣1.6)=1.9+0.3=2.2万公里,理由是:每年平均增长量近似相等,故答案为:2.2,每年平均增长量近似相等.16.阅读下面材料:在数学课上,老师提出如下问题:小敏的作法如下:老师说:“小敏的作法正确.”请回答:小敏的作图依据是对角线互相平分的四边形是平行四边形;有一个角是直角的平行四边形是矩形.【考点】作图—复杂作图.【分析】直接利用平行四边形的判定方法结合矩形的判定进而得出答案.【解答】解:小敏的作图依据是:对角线互相平分的四边形是平行四边形;有一个角是直角的平行四边形是矩形.故答案为:对角线互相平分的四边形是平行四边形;有一个角是直角的平行四边形是矩形.三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)解答应写出文字说明,演算步骤或证明过程.17.计算:()﹣1+|﹣2|﹣2cos60°+(1﹣π)0.【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.【分析】本题涉及负整数指数幂、绝对值、特殊角的三角函数值、零指数幂4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:()﹣1+|﹣2|﹣2cos60°+(1﹣π)0=2+2﹣2×+1=2+2﹣1+1=4.18.解不等式组:.【考点】解一元一次不等式组.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等式x+1≤5,得:x≤4,解不等式7﹣4x<1,得:x>,∴原不等式组的解集为<x≤4.19.如图,点C为AB中点,AD∥CE,AD=CE.求证:∠D=∠E.【考点】全等三角形的判定与性质.【分析】根据题意证明△ADC≌△CEB,得到∠D=∠E即可解决问题.【解答】证明:∵点C为AB中点,∴AC=CB,∵AD∥CE,∴∠A=∠ECB,在△ADC与△ECB中,,∴△ADC≌△ECB(SAS),∴∠D=∠E.20.已知x2﹣4x﹣1=0,求代数式(2x﹣3)2﹣(x+1)(x﹣1)的值.【考点】整式的混合运算—化简求值.【分析】原式利用完全平方公式,平方差公式化简,去括号合并得到最简结果,把已知等式变形后代入计算即可求出值.【解答】解:原式=4x2﹣12x+9﹣x2+1=3x2﹣12x+10=3(x2﹣4x)+10,由x2﹣4x﹣1=0,得到x2﹣4x=1,则原式=3+10=13.21.为应对雾霾天气,使师生有一个更加舒适的教学环境,学校决定为南北两幢教学楼安装空气净化器.南楼安装的55台由甲队完成,北楼安装的50台由乙队完成.已知甲队比乙队每天多安装两台,且两队同时开工,恰好同时完成任务.甲、乙两队每天各安装空气净化器多少台?【考点】分式方程的应用.【分析】设乙队每天安装x台,则甲队每天安装(x+2)台,根据两队同时开工,恰好同时完成任务,即所用的时间相等,即可列方程求解.【解答】解:设乙队每天安装x台,则甲队每天安装(x+2)台.由题意得:,解得:x=20.经检验:x=20是原方程的根,则x+2=22.答:甲队每天安装22台,乙队每天安装20台.22.如图,△ABC中,AD是BC边的中线,分别过点B,D作AD,AB的平行线交于点E,且ED交AC于点F,AD=2DF.(1)求证:四边形ABED为菱形;(2)若BD=6,∠E=60°,求四边形ABED的面积.【考点】菱形的判定.【分析】(1)先证明四边形ABED是平行四边形,利用三角形中位线定理可以证明AD=AB即可.(2)求出菱形的对角线即可求面积.【解答】(1)证明:∵AD是BC边中线,∴DC=DB,DF∥AB,∴CF=FA,∴AB=2DF,∵AD=2DF,∴AB=AD,∵AD∥BE,DE∥AB,∴四边形ABED是平行四边形,∵AD=AB,∴四边形ABED是菱形.(2)连接AE交BD于O,∵∠DEB=60°,四边形ABED是菱形,∴△BDE、△ABD是等边三角形,DO=BO=3,在RT△DOE中,∵DO=3,∠EDO=60°,DE=6,∴EO===3,∴AE=2EO=6,=•AE•BD=×6×6=18.∴S菱形ABED23.如图,直线y=2x+n与双曲线y=(m≠0)交于A,B两点,且点A的坐标为(1,4).(1)求m,n的值;(2)过x轴上一点M作平行于y轴的直线l,分别与直线y=2x+n和双曲线y=(m≠0)交于点P,Q,若PQ=2QM,求点M的坐标.【考点】反比例函数与一次函数的交点问题.【分析】(1)把点A的坐标为(1,4)代入y=(m≠0),求得m=4,代入y=2x+n中得n=2;(2)设M(a,0),表示出P(a,2a+2),Q(a,),根据PQ=2QD,列方程|2a+2﹣|=|2×,解得a=2,a=﹣3,即可得到结果.【解答】解:(1)∵直线y=2x+n与双曲线y=(m≠0)交于A,B两点,∴把A(1,4)代入y=(m≠0),得m=4,把A(1,4)代入y=2x+n中得n=2;(2)设M(a,0),∵l∥y轴,∴P(a,2a+2),Q(a,),∵PQ=2QD,∴|2a+2﹣|=|2×|,解得:a=2或a=﹣3,∴M(﹣3,0)或(2,0).24.如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.(1)求证:∠ABD=2∠CAB;(2)若BF=5,sin∠F=,求BD的长.【考点】切线的性质.【分析】(1)连接OC,根据等腰三角形性质和外角的性质得出∠2=2∠CAB,根据切线的性质得出OC⊥CF,即可证得OC∥DB,根据平行线的性质得出∠ABD=∠2,即可证得∠ABD=2∠CAB;(2)连接AD,根据圆周角定理得出AD⊥DE,即可证得AD∥CF,根据平行线的性质得出∠3=∠F,从而证得△FBE∽△FOC,根据三角形相似的性质求得半径,然后通过解直角三角形即可求得BD的长.【解答】(1)证明:连接OC,∵OA=OC,∴∠CAB=∠1,∴∠2=∠CAB+∠1=2∠CAB,∵CF切⊙O于C,OC是⊙O的半径,∴OC⊥CF,∵DB⊥CF,∴OC∥DB,∴∠ABD=∠2,∴∠ABD=2∠CAB;(2)解:连接AD,∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥DE,∵DE⊥CF,∴AD∥CF,∴∠3=∠F,在RT△BEF中,∵∠BEF=90°,BF=5,sin∠F=,∴BE=BF•sin∠F=5×=3,∵OC∥BE,∴△FBE∽△FOC,∴=,设⊙O的半径为r,则=,解得r=,在RT△ABD中,∠ADB=90°,AB=2r=15,sin∠3=sin∠F=,∴BD=AB•sin∠3=15×=9.25.阅读下列材料:数学课程内容分为“数与代数”、“图形与几何”、“统计与概率”、“综合与实践”四个领域,其中“综合与实践”领域通过探讨一些具有挑战性的研究问题,给我们创造了可以动手操作、探究学习、认识数学知识间的联系、发展应用数学知识解决问题的意识和能力的机会.“综合与实践”领域在人教版七﹣九年级6册数学教材中共安排了约40课时的内容,主要有“数学制作与设计”、“数学探究与实验”、“数学调查与测量”、“数学建模”等活动类型,所占比例大约为30%,20%,40%,10%.这些活动以“课题学习”、“数学活动”和“拓广探索类习题”等形式分散于各章之中.“数学活动”几乎每章后都有2~3个,共60个,其中七年级22个,八年级19个;“课题学习”共7个,其中只有八年级下册安排了“选择方案”和“体质健康测试中的数据分析”2个内容,其他5册书中都各有1个;七上﹣九下共6册书中“拓广探索类习题”数量分别为44,39,46,35,37,23.根据以上材料回答下列问题:(1)人教版七﹣九年级数学教材中,“数学调查与测量”类活动约占16课时;(2)选择统计表或统计图,将人教版七﹣九年级数学教材中“课题学习”、“数学活动”和“拓广探索类习题”的数量表示出来.【考点】统计图的选择;统计表.【分析】(1)用“数学调查与测量”类活动课时数=总课时×该活动所占百分比;(2)列表可得.【解答】解:(1)“数学调查与测量”类活动约为:40×40%=16(课时);(2)列表如图:课题学习数学活动拓展探究类习题七年级22283八年级31981九年级21960故答案为:(1)16.26.如图1,四边形ABCD中,AB=AD,BC=CD,我们把这种两组邻边分别相等的四边形叫做筝形.请探究“筝形”的性质和判定方法.小聪根据学习四边形的经验,对“筝形”的判定和性质进行了探究.下面是小聪的探究过程,请补充完整:(1)如图2,连接筝形ABCD的对角线AC,BD交于点O,通过测量边、角或沿一条对角线所在直线折叠等方法探究发现筝形有一组对角相等,请写出筝形的其他性质(一条即可):对角线互相垂直,这条性质可用符号表示为:已知四边形ABCD是筝形,则AC⊥BD.;(2)从边、角、对角线或性质的逆命题等角度进行探究,写出筝形的一个判定方法(定义除外),并证明你的结论.【考点】翻折变换(折叠问题);全等三角形的判定与性质.【分析】(1)根据筝形的定义可以证明△BAC≌△DAC,依据全等三角形的性质即可证得边和对角线的关系;(2)利用△BAC≌△DAC,根据边、角、对角线的性质证得.【解答】解:(1)筝形的性质:两组邻边分别相等;对角线互相垂直,即已知四边形ABCD是筝形,则AC⊥BD;有一条对角线被另一条平分;有一条对角线平分对角;是轴对称图形.(写出一条即可);故答案是:对角线互相垂直;已知四边形ABCD是筝形,则AC⊥BD;(2)筝形的判定方法:有一条对角线平分一组对角的四边形是筝形.已知:四边形ABCD中,AC是一条对角线,∠BAC=∠DAC,∠BCA=∠DCA.求证:四边形ABCD是筝形.证明:在△BAC和△DAC中,,∴△BAC≌△DAC,∴AB=AD,BC=CD,即四边形ABCD是筝形.其他正确的判定方法:有一条对角线垂直平分另一条对角线的四边形是筝形;有一组邻边相等且互相垂直的四边形是筝形.27.抛物线C1:y=a(x+1)(x﹣3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3).(1)求抛物线C1的解析式及A,B点坐标;(2)将抛物线C1向上平移3个单位长度,再向左平移n(n>0)个单位长度,得到抛物线C2,若抛物线C2的顶点在△ABC内,求n的取值范围.【考点】二次函数图象与几何变换.【分析】(1)根据已知点的坐标代入已知的函数的解析式即可利用待定系数法确定二次函数的解析式;(2)首先根据平移确定平移后的函数的解析式,然后确定抛物线C2的顶点坐标;结合图形确定n的取值范围即可.。
燕山一模初三数学试卷答案

一、选择题(每题3分,共30分)1. 如果a、b、c是等差数列,且a+c=12,b=6,那么a的值是()A. 3B. 4C. 5D. 6答案:A2. 下列函数中,是奇函数的是()A. y=x^2B. y=|x|C. y=x^3D. y=2x答案:C3. 在等腰三角形ABC中,AB=AC,若∠BAC=40°,则∠B的度数是()A. 40°B. 50°C. 60°D. 70°答案:B4. 下列方程中,无解的是()A. 2x+3=7B. x^2+1=0C. x+1=2D. 3x-6=0答案:B5. 已知一次函数y=kx+b的图象经过点(2,3),且与y轴的交点坐标为(0,-1),则该一次函数的解析式为()A. y=2x-1B. y=x+1C. y=3x-1D. y=3x+1答案:A6. 在平面直角坐标系中,点P(-2,3)关于原点的对称点Q的坐标是()A.(-2,-3)B.(2,3)C.(2,-3)D.(-2,3)答案:C7. 下列各式中,正确的是()A. (-a)^2=a^2B. (a-b)^2=a^2-2ab+b^2C. (a+b)^2=a^2+2ab+b^2D. (a-b)^2=a^2-2ab-b^2答案:A8. 在△ABC中,若∠A=60°,∠B=45°,则∠C的度数是()A. 60°B. 45°C. 75°D. 30°答案:C9. 下列命题中,正确的是()A. 平行四边形的对边相等B. 矩形的对角线相等C. 菱形的对角线互相平分D. 正方形的对角线互相垂直答案:C10. 已知函数y=-2x+1,当x=3时,y的值为()A. -5B. -3C. 1D. 5答案:B二、填空题(每题3分,共30分)11. 若等差数列{an}的公差为d,且a1=2,a5=10,则d=______。
答案:212. 函数y=|x-1|+2的图象与x轴的交点坐标为______。
2023年北京市燕山区中考一模数学试卷

2023年北京市燕山区中考一模数学试卷学校:___________姓名:___________班级:___________考号:___________....A .50︒【答案】C【分析】先根据互余求得A .2a >-B .3b >A.①②B.【答案】B【分析】分别求出三个问题中变量【详解】解:①∵正方形的周长为【答案】115【分析】先由圆周角定理求出的度数即可.【详解】解:∵130AOC ∠=∴1652ADC AOC ∠=∠=︒【答案】> =【分析】根据平均数和方差的计算公式分别进行解答即可;【详解】解:甲的平均数是:x 甲(998108)58.8=++++÷=;乙的平均数是:x 乙(88797)57.8=++++÷=;∴x x >甲乙解得3x =,∴制作A 型工艺品的个数为3个,故答案为:3;(2)设制作A 、B 、C 三种类型的工艺品分别为a 个,b 个,c 个,由题意得,332135a b c a b c ++≤⎧⎨++=⎩,∴()335213a a c c +--+≤,∴2≤c ,∵使用乙种原料最多,∴A 、C 的个数要尽可能的多,B 的个数要尽可能的少,∴221c a b ===,,,故答案为:2,1,2.【点睛】本题主要考查了三元一次方程组的实际应用,不等式和方程相结合的问题,正确理解题意列出对应的方程和不等式是解题的关键.方法一:证明:如图,延长F ,使EF DE =,连接【答案】证明见解析【分析】方法一:先证明AED V 得到AD CF ADE ==,∠∠AD CF ∥,再证明四边形BCFD 是平行四边形,得到DF BC DF =,1(1)求证:四边形EBCD 是菱形;(2)若5BC =,8EC =,sin DAE ∠【答案】(1)证明见解析;22.在平面直角坐标系xOy 中,一次函数()0y kx b k =+≠的图象由函数2y x =的图象平移得到,且经过点()20A ,.(1)求该一次函数的解析式;(2)当2x >时,对于x 的每一个值,函数y x n =+的值小于一次函数(0)y kx b k =+≠的值,直接写出n 的取值范围.【答案】(1)24y x =-(2)2n ≤-【分析】(1)根据一次函数平移的性质可得2k =,再利用待定系数法求解即可;(2)根据题意可得2x >是不等式24x n x +<-的解集的一部分或是其解集,据此求解即可.【详解】(1)解:∵一次函数()0y kx b k =+≠的图象由函数2y x =的图象平移得到,∴2k =,∵一次函数()20y x b k =+≠的图象经过()20A ,,∴40b +=,解得4b =-,∴一次函数解析式为24y x =-;(2)解:由题意得,2x >是不等式24x n x +<-的解集的一部分或是其解集,解不等式24x n x +<-得4x n >+,∴42n +≤,∴2n ≤-.【点睛】本题主要考查了一次函数与一元一次不等式的应用,求一次函数解析式,一次函数图象的平移,熟知一次函数的相关知识是解题的关键.23.在第四个国际数学日(2023年3月14日)到来之际,燕山地区举办了“数学节”,通过数学素养竞赛、数学创意市集、数学名师讲座等活动,展现数学魅力、传播数学文化.为了解学生数学素养竞赛的答题情况,从甲、乙两校各随机抽取了20名学生成绩(单位:分)的数据,并对数据进行整理、描述和分析.下面给出了部分信息:a.乙校学生成绩数据的频数分布直方图如下图所示(数据分为四组:6070≤<,70≤xb.乙校学生成绩数据在8090x≤<这一组的是:8081818285868888c.甲、乙两校学生成绩数据的平均数、中位数、众数如下:(1)求证:DE 是O e 的切线;(2)延长ED 交AB 的延长线于点【答案】(1)证明见解析(2)O e 的半径为3,125DE =(2)解:设O e 的半径为r ,则OB ∴2OF OB BF r =+=+,在Rt ODF △中,由勾股定理得2OF ∴()22224r r +=+,解得3r =,即O e 的半径为3;下面是弹珠的水平距离x与竖直高度水平距离01234/dmx竖直高度 2.504.255.506.256.50(1)依题意补全图形;用等式表示线段(2)点G为AB中点,连接FG(2)2AE BF FG =+;证明:如图,连接FG ,EG ∵90ACB ∠=︒,AC BC =,点【点睛】本题主要考查了全等三角形的判定和性质,等腰直角三角形的判定和性质,直角三角形斜边中线的性质等知识,作出合适的辅助线,证明三角形全等是解题的关键.28.在平面直角坐标系xOy(2)解:如图1所示,取(10O ,∴1OP OO =,∴112452OP OPO O P ∠=︒=,,∵90P M MP PMP ''==︒,∠,如图2所示,连接2PO 交2O e 于∵()0,P t ,()204O t -,,∴()2222428PO t t t t =+-=-+∴212816PQ PQ t t ==-+-最小值∴(22816PQ PQ t t ⋅=-+【点睛】本题主要考查了圆外一点到圆上一点距离的最值问题,定,旋转的性质,全等三角形的性质与判定,坐标与图形,等腰直角三角形的性质与判定等等,确定点P '的轨迹进而确定点。
北京燕山中考一《数学》模试题及答案

北京燕山中考一《数学》模试题及答案20XX年北京燕山中考一《数学》模试题及答案燕山20XX年初中毕业考试数学试卷20XX年5月一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的.1.5的相反数是A.11B.5 C.-D.-5 552.北京燕山石油化工有限公司是我们身边的大型国有企业,投产以来,已累计实现利税372亿元,给国家和人民做出了重大贡献,把该数据用科学记数法表示应为A.3.72×10元B.372×10元C.3.72×10元898D.3.72×10元103.已知一个等腰三角形有两边的长分别为2和5,则它的周长为A.7 B.9 C.12 D.9或124.某市去年九月份第一周连续七天的日平均气温分别为27,25,24,27,24,28,24(单位:℃). 这组数据的众数和中位数分别是A.24℃,25℃ B.24℃,26℃ C.24℃,27℃ D.28℃,25℃ 5.下列计算中,正确的是A.a3= a B.3x -2x=1252222C.2a3a = 6a D6.若右图是某几何体的三视图,则这个几何体是A.直棱柱B.圆柱C.球D.圆锥7.某学校大厅的电子显示屏,每间隔220XX年北京燕山中考一《数学》模试题及答案间信息,显示时间持续30秒,在间隔时间则动态显示学校当日的其它信息.小明上午到校后,一走进大厅,显示屏上正好显示时间信息的概率是A.11B.23C.14D.1 58.类比二次函数图象的平移,把双曲线y=对应的函数解析式变为A.y1向左平移2个单位,再向上平移1个单位,其xx 3x 2B.yx 1 x 1x 1C.y D.y x 2x 2x 2二、填空题(本题共16分,每小题4分)9.函数y=2x 1的自变量取值范围是.10.已知⊙O1、⊙O2的半径分别是2cm、3cm,当它们相切时,圆心距O1 O2= .11.已知△ABC中,D、E分别是两边AB和AC的中点,若△ABC的面积是8cm2,则四边形2BCED的面积是cm.12.已知:点F在正方形纸片ABCD的边CD上,AB=2,∠FBC=30°(如图1);沿BF折叠纸片,使点C落在纸片内点C'处(如图2);再继续以BC'为轴折叠纸片,把点A落在纸三、解答题(本题30分,每小题5分)13.计算:| 1-3|-(3.14-π) 0 +(14.解不等式1-1)-4sin60 °. 25x 1232x ,并把它的解集在数轴上表示出来. 4215.已知:如图,点D在AB的延长线上,AB=DE,∠A=∠CBE=∠E. 判断△ABC和△BDE是否全等?并证明你的结论. 16.当x=20XX年时,求代数式17.本学期我区中小学组织“社会大课堂”活动,某校安排初三年级学生去周口店“北京人遗址博物馆”参观学习.已知该校距离博物馆约10千米,由于事先租用的汽车少来了一12x2的值. x 1x 120XX年北京燕山中考一《数学》模试题及答案辆,一部分学生只好骑自行车先走,过了20分钟,其余学生再乘汽车出发.汽车的速度是骑自行车学生速度的2倍,结果他们正好同时到达,求骑自行车学生的速度.18.如图,某一次函数y=kx+b的图象与一个反比例函数的图象交于A、B两点,点A和点B关于直线y=x对称.(1)求出这个反比例函数的解析式;(2)直接写出点B的坐标;(3)求k和b的值.四、解答题(本题共19分,第19、20、21题各5分,第22题4分)19.在等腰梯形ABCD中,AD∥BC,∠ABC=60°,AB=AD,若它的周长为12 cm,求BC边的长.20.出于研究中小学生减负问题的需要,某地教研室对当地初二年级学生周一至周五每天完成课外作业的大致平均时间进行了抽样调查,下面是根据调查所得数据制作的统计表和(1)求一共调查了多少名学生?(2)该地区共有初二学生约8000人,请你根据抽样调查所得数据,估计该地区初二学生中,有多少人完成当天课外作业所需时间不少于90分钟?(3)请把表和图中的缺项补全.20XX年北京燕山中考一《数学》模试题及答案21.如图,等腰△ABC中,AE是底边BC上的高,点O在AE上,⊙O与AB和BC分别相切. (1)⊙O是否为△ABC的内切圆?请说明理由. (2)若AB=5,BC=4,求⊙O的半径.22.将正方形ABCD(如图1)作如下划分:第1次划分:分别联结正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;第2次划分:将图2左上角正方形AEMH按上述方法再作划分,得图3,则图3中共有_______个正方形;若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有_______个正方形;继续划分下去,能否将正方形ABCD划分成有20XX年个正方形的图形?需说明理由.A D A H DE G E GB C B F C B F C 图1 图2 图3五、解答题(本题共23分,第23题8分,第24题8分,第25题7分)23.已知在同一直角坐标系中,直线l:y=x-3k+6与y轴交于点P,M是抛物线C:2y=x-2 (k+2) x+8k的顶点.(1)求证:当k≠2时,抛物线C与x轴必定交于两点;(2)A、B是抛物线c与x轴的两交点,A、B在y轴两侧,且A在B的左边,判断:直线l 能经过点B吗?(需写出判断的过程)(3)在(2)的条件下,是否存在实数k,使△ABP和△ABM 的面积相等?如果存在,请求出此时抛物线C的解析式;若不存在,请说明理由. 24.已知:如图,等边△ABC中,AB=1,P是AB边上一动点,作PE⊥BC,垂足为E;作EF⊥AC,垂足为F;作FQ⊥AB,垂足为Q.(1)设BP=x,AQ=y,求y与x之间的函数关系式;(2)当点P和点Q重合时,求线段EF的长;(3)当点P和点Q不重合,但线段PE、FQ相交时,求它们与线段EF围成的三角形周长的取值范围.20XX年北京燕山中考一《数学》模试题及答案25.已知:如图,在梯形ABCD中,∠BCD=90°,tan∠ADC=2,点E在梯形内,点F在梯形外,BEAB0.5,∠EDC=∠FBC,且DE=BF.CECD(1)判断△ECF的形状特点,并证明你的结论;(2)若∠BEC=135°,求∠BFE的正弦值.燕山初四数学毕业考试评卷参考20XX年.5.4一、DDCA CBDA 二、三、13. 原式=-1-1+2-23 4分= -. 5分14. 5x-128x-6,1分-3x6,2分x-2.∴ 不等式的解集是x-2. 3分数轴上正确表示解集5分15. 全等1分证明:∵∠CBE =∠E,∴ BC∥DE. 2分20XX年北京燕山中考一《数学》模试题及答案又∵点D在AB的延长线上,∴∠CBA=∠D. 3分在△ABC和△EDB中,又∵∠A=∠E, AB=DE, 4分∴△ABC≌△EDB. 5分16. 原式=12x1分-x 1(x 1)(x-1)=x-1-2x2分(x 1)(x-1)-x-13分(x 1)(x-1)== -14分x-1∴当x=20XX年时,11原式= - = - 5分20XX年20XX年-117. 设骑自行车学生的速度是x千米/时. 1分依题意,得*****- . 2分x2x3解得x=15. 3分经检验, x=15是原分式方程的根. 4分答: 骑自行车同学的速度是15千米/时. 5分18. ⑴ 由题意,可认定点A的坐标是(-1, 2), 把x = -1, y=2代入y= 解得m= -2.∴ 反比例函数的解析式是y= -m, x2. 2分x⑵ 点B (2, -1). 3分⑶ 把点A(-1,2)、B (2, -1)分别代入y=kx+b,得-k b 2,4分2k b 1.解得,k= -1,b=1. 5分四、19. 能正确画出图形1分作DE∥AB交BC与E,则∠DEC=∠B=60分又∵在等腰梯形ABCD中,AD∥BC.20XX年北京燕山中考一《数学》模试题及答案∴ DE=AB =CD,且AD=BE . ∴△CDE是等边三角形. 又∵AB =AD,∴CE=CD=AD=BE=AB. 3分依题意,AB+AD+CD+CE+BE=12cm,4分即5BE=12cm ,∴ BE=2.4cm∴ BC边的长为4.8cm. 5分20. ⑴ 500 1分⑵ 4880 2分⑶ 表中空格填“20” 3分把扇形统计图补全5分21. ⑴ 是1分理由是:∵⊙O与AB相切,把切点记作D. 联结OD,则OD⊥AB于D. 作OF⊥AC于F,∵AE是底边BC 上的高,∴AE也是顶角∠BAC的平分线. ∴OF=OD=r为⊙O的半径. ∴⊙O与AC相切于F. 又∵ ⊙O与BC相切,∴⊙O是△ABC的内切圆. 2分⑵ ∵OE⊥BC于E,∴点E是切点,即OE=r. 由题意,AB=5,BE=F1AB=2,2∴ AE=52-22=. 3分∵Rt△AOD∽Rt△ABE,∴OAOD,4分ABBE21-rr. 52221. 7即解得,r=20XX年北京燕山中考一《数学》模试题及答案∴ ⊙O的半径是221. 5分722. 第2次划分,共有9个正方形;1分第100次划分后,共有401个正方形;2分依题意,第n次划分后,图中共有4n+1个正方形,3分而方程4n+1=20XX年没有整数解,所以,不能得到20XX年个正方形. 4分五、23.⑴ 证明:在抛物线C中,Δ=4 (k+2)2-32k =4k2-16k+16=4 (k-2)2 . 1分∵ 当k≠2时,4 (k-2)2>0,∴方程x2-2(k+2) x+8k=0有两个不相等的实数根.∴ 当k≠2时,抛物线C与x轴必定交于两点. 2分⑵ 解方程x2-2(k+2) x+8k=0,得x1=4,x2=2k. 3分∵点A、B在y轴两侧,且A在B的左边,∴k<0,点B(4,0). 4分把点B(4,0)代入y=x-3k+6,10得k=>0,与“k<0”不符.3∴ 直线l不可能经过点B. 5分⑶ y=x2-2(k+2) x+8k =[x-(k+2)]2-(k-2)2,作MH⊥x轴于H,则MH=(k-2)2. 6分∵k<0, ∴-3k+6>0. ∴OP= -3k+6.由S△ABP=S△ABM ,得-3k+6=(k-2)2 7分解得k1= -1,k2= 2(舍去)∴存在实数k= -1,使得S△ABP=S△ABM .此时,抛物线C的解析式是y=x2-2x-8. 8分24.⑴∵△ABC是等边三角形,AB=1.∴∠A=∠B=∠C=60°, BC=CA=AB=1. 1分又∵∠BEP=∠CFE=∠FQA=90°, BP=x. ∴BE=***-*****x, CE=1-x, CF=-x, AF=1-(-x)=+x. ***-*****20XX年北京燕山中考一《数学》模试题及答案1∴AQ=1AF=1(1+x),2224∴ y=11x+. 2分84x y 1,⑵由方程组11 3分y x . 84 2. 4分32∴当点P和点Q重合时,x =,31∴EF=CF=3(1-x)=3.243得x =5分⑶设线段PE、FQ相交于点M,易证△MEF是等边三角形,6分且当点P和点A重合时,EF最短为3. 7分433≤ m <3. 8分425.⑴ 是等腰直角三角形. 1分∴证明:作AH⊥CD于H,∵梯形ABCD中,∠BCD=90°,tan∠ADC=2,即∠ADC≠90°. ∴ AB∥CD,AH=BC,AB=CH. 2分又∵AB0.5,即CH+DH=2AB=2CH CD∴ DH=CH,CD=2DH. ∵ tan∠ADC=AH=2,DH∴ AH=2DH=CD=BC. 3分在△EDC和△FBC中,又∵∠EDC=∠FBC,DE=BF,∴△EDC≌△FBC. ∴CE=CF, ∠ECD=∠FCB. ∵∠ECD+∠ECB=∠BCD=90°, ∴∠FCB+∠ECB=90°,即∠ECF=90°.∴△ECF是等腰直角三角形. 4分20XX年北京燕山中考一《数学》模试题及答案⑵ ∵ 在等腰Rt△ECF中,∠ECF=90°,∴ ∠CEF=45°,CE= 2EF. 5分2BE又∵∠BEC=135°,=0.5 ,CE。
初中数学北京市燕山区中考模拟数学一模考试题考试卷及答案

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)试题1:的绝对值是A. B. C. D.试题2:2014年2月14日从北京航天飞行控制中心获悉,嫦娥二号卫星再次刷新我国深空探测最远距离记录,达到7 000万公里,这是我国航天器迄今为止飞行距离最远的一次“太空长征”.将7 000万用科学记数法表示应为A. B. C. D.试题3:下列立体图形中,左视图是圆的是试题4:评卷人得分小月的讲义夹里放了大小相同的试卷共12页,其中语文5页、数学4页、英语3页,她随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率是A. B. C. D.试题5:如右图所示,AB∥CD,点E在CB的延长线上.若∠ABE=70°,则∠ECD的度数为A.20°B.70° C .100° D.110°试题6:下列正多边形中,内角和等于外角和的是A.正三边形B.正四边形C.正五边形D.正六边形试题7:小贝家买了一辆小轿车,小贝记录了连续七天中每天行驶的路程:第1天第2天第3天第4天第5天第6天第7天路程(千米)43 29 27 52 43 72 33则小贝家轿车这七天行驶路程的众数和中位数分别是A.33,52B.43,52C.43,43D.52,43试题8:如图,点在线段上,=8,=2,为线段上一动点,点绕点旋转后与点绕点旋转后重合于点.设=,的面积为. 则下列图象中,能表示与的函数关系的图象大致是A. B. C. D.试题9:若二次根式有意义,则的取值范围是.试题10:分解因式:.试题11:为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一组标杆、皮尺,设计了如图所示的测量方案.已知测量同学眼睛、标杆顶端、树的顶端在同一直线上,此同学眼睛距地面1.6,标杆长为3.3,且,,则树高.试题12:如图,在平面直角坐标系中,已知点的坐标为(1,0),将线段绕点按顺时针方向旋转,再将其长度伸长为的2倍,得到线段;又将线段绕点按顺时针方向旋转,再将其长度伸长为的2倍,得到线段,…,这样依次得到线段,,…,.则点的坐标为;当(为自然数)时,点的坐标为.试题13:.试题14:如图,,,直线经过点,于点,于点.求证: .试题15:解分式方程:.试题16:已知,求的值.试题17:在“母亲节”到来之际,某校九年级团支部组织全体团员到敬老院慰问为筹集慰问金,团员们利用课余期间去卖鲜花.已知团员们从花店按每支1.5元的价格买进鲜花共支,并按每支5元的价格全部卖出,若从花店购买鲜花的同时,还用去50元购买包装材料.(1)求所筹集的慰问金(元)与(支)之间的函数表达式;(2)若要筹集不少于650元的慰问金,则至少要卖出鲜花多少支?试题18:如图,在平面直角坐标系中,点为坐标原点,直线分别交轴、轴于、两点,,且、的长分别是一元二次方程的两根.(1)求直线的函数表达式;(2)点是轴上的点,点是第一象限内的点.若以、、、为顶点的四边形是菱形,请直接写出点的坐标.试题19:如图,在四边形中,,,,连接,的平分线交于点,且.(1)求的长;(2)若,求四边形的周长.试题20:2014年春季,北京持续多天的雾霾天气让环保和健康问题成为人们关注的焦点.为了美丽的北京和师生的身心健康,某校开展以“倡导绿色出行,关爱师生健康”为主题的教育活动.为了了解本校师生的出行方式,在本校范围内随机抽查了部分师生,将收集的数据绘制成下列不完整的两种统计图.学生出行方式扇形统计图请根据统计图提供的信息,解答下列问题:(1)m = ;(2)已知随机抽查的教师人数为学生人数的一半,请根据上述信息补全条形统计图,并标明相应数据;(3)若全校师生共1800人,请你通过计算估计,全校师生乘私家车出行的有多少人?试题21:如图,点是以为直径的圆上一点,直线与过点的切线相交于点,点是的中点,直线交直线于点.(1)求证:是⊙O的切线;(2)若,,求⊙O的半径.试题22:阅读下面材料:如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四边形”.如图1 所示,平行四边形即为的“友好平行四边形”.请解决下列问题:(1)仿照以上叙述,说明什么是一个三角形的“友好矩形”;(2)若是钝角三角形,则显然只有一个“友好矩形”,若是直角三角形,其“友好矩形”有个;(3)若是锐角三角形,且,如图2,请画出的所有“友好矩形”;指出其中周长最小的“友好矩形”并说明理由.试题23:已知关于的一元二次方程有两个不相等的实数根.(1)求的取值范围;(2)当取最小的整数时,求抛物线的顶点坐标以及它与轴的交点坐标;(3)将(2)中求得的抛物线在轴下方的部分沿轴翻折到轴上方,图象的其余部分不变,得到一个新图象.请你画出这个新图象,并求出新图象与直线有三个不同公共点时的值.试题24:如图1,已知是等腰直角三角形,,点是的中点.作正方形,使点、分别在和上,连接,.(1)试猜想线段和的数量关系是;(2)将正方形绕点逆时针方向旋转,①判断(1)中的结论是否仍然成立?请利用图2证明你的结论;②若,当取最大值时,求的值.试题25:定义:如果一个与的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是与的“反比例平移函数”.例如:的图象向左平移2个单位,再向下平移1个单位得到的图象,则是与的“反比例平移函数”.(1)若矩形的两边分别是2、3,当这两边分别增加()、()后,得到的新矩形的面积为8,求与的函数表达式,并判断这个函数是否为“反比例平移函数”.(2)如图,在平面直角坐标系中,点为原点,矩形的顶点、的坐标分别为(9,0)、(0,3) .点是的中点,连接、交于点,“反比例平移函数”的图象经过、两点.则这个“反比例平移函数”的表达式为;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.(3)在(2)的条件下,已知过线段中点的一条直线交这个“反比例平移函数”图象于、两点(在的右侧),若、、、为顶点组成的四边形面积为16,请求出点的坐标.试题1答案:A试题2答案:B试题3答案: D试题4答案: C试题5答案: D试题6答案: B试题7答案: C试题8答案: B试题9答案:试题10答案:试题11答案: 10.1试题12答案:(0,-4),试题13答案:解:..……………………4分……………………5分试题14答案:证明:∵,∴,……………………1分∴,∵,∴,∴.……………………2分在和中,∴≌.…………………4分∴.…………………5分试题15答案:解:…………………2分…………………3分…………………4分经检验,是原分式方程的根. …………………5分试题16答案:解:原式=…………………2分==. …………………3分∵,∴.∴原式=,…………………4分=. …………………5分试题17答案:解:(1). …………………2分(2)当时,即,…………………3分解得. …………………4分答:若要筹集不少于650元的慰问金,至少要售出鲜花200支. …………………5分试题18答案:解:(1)∵,∴,∴,.∴点的坐标为(3,0),点的坐标为(0,4) .……………2分∵设直线的函数表达式为∴∴∴直线的函数表达式为. ……………3分(2)点的坐标是(3,5)或(3, ).……………5分试题19答案:解:(1)延长交于点.∵平分,∴.∵,∴,∴,………1分∴.∵,∴. ……………2分∵,∴四边形是平行四边形,∴.………3分(2)过作的垂线,垂足为.∵,,在中,,∴. ………………4分∴四边形的周长………………5分试题20答案:解:(1)20%;………………1分(2)补全条形统计图如下图:………………3分出行方式(3)(人)(人)=480(人)………………5分答:全校师生乘私家车出行的有480人.试题21答案:(1)证明:连接、,∵是直径,∴. ………………1分∴.∵是的中点,∴.,∴,∴. ………………2分∵是⊙的半径,∴是⊙O的切线. ………………3分(2)解:∵是的中点,、是⊙O的切线,∴,.∴,………………4分∴.设⊙O的半径为.∵∽,∴,∴. ………………5分∴⊙O的半径为.试题22答案:解:(1)三角形的一边与矩形的一边重合,三角形这边所对的顶点在矩形这边的对边上. ………………1分(2)2;………………2分(3)画图: ………………3分周长最小的“友好矩形”是矩形. ………………4分理由:易知这三个矩形的面积都等于的面积的一半,所以这三个矩形的面积相等,令其为,设矩形,矩形,矩形的周长分别为、、,的边长,,,(),则,,,∴,而,,∴,即.同理可证. ……………5分试题23答案:解:(1)由题意,得,∴.∴的取值范围为.…………2分(2)∵,且取最小的整数,∴.∴,则抛物线的顶点坐标为…………………3分∵的图象与轴相交,∴,∴,∴或,∴抛物线与轴相交于,.…………4分(3)翻折后所得新图象如图所示. …………5分平移直线知: 直线位于和时,它与新图象有三个不同的公共点.①当直线位于时,此时过点,∴,即.②当直线位于时,此时与函数的图象有一个公共点,∴方程,即有两个相等实根,∴,即.当时,满足,由①②知或.试题24答案:解:(1);(2)①成立.以下给出证明:如图,连接,∵在 Rt中,为斜边中点,∴,,∴.∵四边形为正方形,∴,且,∴,∴.在和中,∴≌,∴.②由①可得,当取得最大值时,取得最大值.当旋转角为时,,最大值为.如图,此时.试题25答案:解:(1),∴向右平移2个单位,再向上平移3个单位得到.∴是“反比例平移函数”. (2)分(2)“反比例平移函数”的表达式为.变换后的反比例函数表达式为.(3)如图,当点在点左侧时,设线段的中点为,由反比例函数中心对称性,四边形为平行四边形.∵四边形的面积为16,∴=4,∵(9,3),(6,2).是的“反比例平移函数”,∴==4,(3,1)过作轴的垂线,与、轴分别交于、点..设,∴即∴∴(1,3) ,∴点的坐标为(7,5).当点在点右侧时,同理可得点的坐标为(15,).。
燕山一模初三数学试卷

一、选择题(本大题共10小题,每小题3分,共30分)1. 下列各数中,有理数是()A. √2B. πC. -1/3D. 无理数2. 若a、b是方程x²-5x+6=0的两个根,则a+b的值是()A. 2B. 3C. 4D. 53. 在直角坐标系中,点P(-2,3)关于y轴的对称点是()A. (2,3)B. (-2,-3)C. (2,-3)D. (-2,-3)4. 若等比数列的首项为a,公比为q,则第n项an=()A. aq^(n-1)B. aq^nC. a/(q^n)D. a/(q^(n-1))5. 若函数f(x) = x² - 4x + 3,则f(2)的值为()A. 1B. 3C. 5D. 76. 在△ABC中,∠A=30°,∠B=45°,则∠C的度数是()A. 60°B. 75°C. 90°D. 105°7. 若m、n是方程2x²-5x+2=0的两个根,则m+n的值为()A. 2B. 5C. 2/5D. 5/28. 若一个数的平方根是-3,则这个数是()A. 9B. -9C. 3D. -39. 下列各图中,正确表示函数y=x²-2x的图象是()A.B.C.D.10. 若a、b是方程x²-3x+2=0的两个根,则a²+b²的值为()A. 7B. 8C. 9D. 10二、填空题(本大题共10小题,每小题3分,共30分)11. 若x=2,则x²-5x+6=________。
12. 在直角坐标系中,点A(-1,2)关于原点的对称点是________。
13. 等比数列3,6,12,……的第5项是________。
14. 函数y=-2x+3在x=1时的函数值是________。
15. 若a、b是方程x²-6x+9=0的两个根,则a+b的值是________。
北京市燕山区中考数学一模试题

北京市燕山地区 初中毕业暨一模考试数学试卷学校 班级 姓名 成绩考 生 须 知 1.本试卷共6页,共五道大题,25道小题,满分120分。
考试时间120分钟。
2.答题纸共6页,在规定位置准确填写学校名称、班级和姓名。
3.试题答案一律书写在答题纸上,在试卷上作答无效。
4.考试结束,请将答题纸交回,试卷和草稿纸可带走。
....母写在答题纸上;本题共32分,每小题4分) 1.若实数a 与-3互为相反数,则a 的值为A .31B .0.3C .-3D .3 2.春节假期,全国收费公路7座以下小型客车实行免费通行.据交通运输部统计,春节期间,全国收费公路(除四川、西藏、海南外)共免收通行费846 000 000元.把 846 000 000用科学记数法表示应为A .0.846×108B .8.46×107C .8.46×108D .846×1063.已知某多边形的每一个外角都是40°,则它的边数为A .7B .8C .9D .10 4.右图是某个几何体的三视图,则这个几何体是A .圆锥B .圆柱C .长方体D . 三棱锥 5.燕山地区现有小学7所,初中校4所,高中校1所,现从这些学校中随机抽取1所学校对学生进行视力调查,抽取的学校恰好为初中校的概率是 A .121 B .31 C .127D .326.如图,在□ABCD 中,AD =6,点E 在边AD 上,且DE =3,连接BE 与对角线AC 相交于点M ,则MCAM 的值为A .12B .13C .14D .197.在一次体育达标测试中,九年级(3)班的15名男同学的引体向上成绩如下表所示:成绩(个)8 9 11 12 13 15 人数123432这A .12,13 B .12,12 C .11,12 D .3,48. 如图,点P 是⊙O 的弦AB 上任一点(与A ,B 均不重合),点C 在⊙O 上,PC ⊥OP ,已知AB =8,设BP =x ,PC 2=y , y 与x 之间的函数图象大致是A俯视图左视图主视图DA EMCB OPy16y16y16y. B . C . D . 二、填空题(本题共16分,每小题4分) 9.分解因式:mn mn 43-= .10.把代数式x 2-4x -5化为(x -m )2+k 的形式,其中m ,k 为常数,则2m -k = . 11.如图,在一间房子的两墙之间有一个底端在P 点的梯子,当它靠在一侧墙上时,梯子的顶端在A 点;当它靠在另一侧墙上时梯子的顶端在D 点.已知∠APB =45°,∠DPC =30°,点A 到地面的垂直距离为2.4米,则点D 到地面的垂直距离约是米(精确到0.1).12.如图,已知直线1l :2+-=x y 与2l :2121+=x y ,过直线1l 与x 轴的交点1P 作x 轴的垂线交2l 于1Q ,过1Q 作x 轴的平行线交1l 于2P ,再过2P 作x 轴的垂线交2l 于2Q ,过2Q 作x 轴的平行线交1l 于3P ,……,这样一直作下去 ,可在直线l 1上继续得到点4P ,5P ,…,n P ,….设点n P 的横坐标为n x ,则2x = , 1+n x 与n x 的数量关系是 .三、解答题(本题共30分,每小题5分)13.计算:013)(30cos 23127-+︒-⎪⎭⎫⎝⎛--π.14. 解不等式1233x x <+-,并把解集在数轴上表示出来.15.如图,点A ,F ,C ,D 在同一直线上,点B 和点E 分别在直线AD 的两侧,且BC ∥EF ,∠A =∠D ,AF =DC .求证:AB =DE .16.已知0142=+-x x ,求代数式34)2123(2-÷-+-+x x x x 的值. 17.如图,直线y =2x -1与反比例函数xky =的图象交于A ,B 两点,与x 轴交于C 点,已知点A 的坐标为(-1,m ). ⑴ 求反比例函数的解析式;⑵ 若P 是x 轴上一点,且满足△PAC 的面积是6,直接CyxO ABQ3Q 2Q 1P 3P2P 1l 2l 1y xODFC EBA PBCDA写出点P 的坐标.18. 列方程或方程组解应用题:由于面临严重的能源危机,世界各国都在积极研究用生物柴油替代石油产品,微藻是一种非常有潜力的生物柴油来源.据计算,每公顷微藻的年产柴油量约为每公顷大豆年产柴油量的110倍.我国某微藻养殖示范基地的一块试验田投产后年产柴油量可达2200万升,而一块面积比微藻试验田大500公顷的大豆试验田,年产柴油量却只有40万升.求每公顷微藻年产柴油量约为多少万升? 四、解答题(本题共20分,每小题5分) 19.如图,四边形ABCD 中,∠ADC =∠B =90°, ∠C = 60°,AD =3,E 为DC 中点,AE ∥BC . 求BC 的长和四边形ABCD 的面积.20.如图,△ABC 中,AC =B C .以B C 为直径作⊙O 交AB 于点D ,交AC 于点G .作直线DF ⊥AC 交AC 于点F ,交CB 的延长线于点E . ⑴求证:直线EF 是⊙O 的切线; ⑵若BC =6,AB =43,求DE 的长. 21.加快新能源和可再生能源发展是建设高效低碳的首都能源体系和“绿色北京”的重要支撑.“十一五”以来,北京市新能源和可再生能源开发利用步伐不断加快,产业规模不断扩大.以下是根据北京市统计局发布的有关数据制作的统计图表的一部分.2010年北京市新能源和可再生能源消费量及结构统计表 类 别 太阳能 生物质能 地热能 风能 水能消费量(万吨标准煤)98 36 78.5 82.8 注:能源消费量的单位是万吨标准煤,简称标煤. 请你结合上面图表中提供的信息解答下列问题: ⑴补全条形统计图并在图中标明相应数据;⑵2010年北京市能源消费总量约是多少万吨标煤(结果精确到百位)?⑶根据北京市“十二五”规划,到2015年,本市能源消费总量比2010年增长31%,其中新能源和可再生能源利用量占全市能源消费总量的6%.已知使用新能源每替代一万吨标煤,可减少二氧化碳排放量约为2万吨,请问到2015年,由于新能源和可再生能源的开发利用,北京市可减少二氧化碳排放量约为多少万吨? 22.阅读下列材料:问题:如图⑴,已知正方形ABCD 中,E 、F 分别是BC 、CD 边上的点,且 ∠EAF =45°. 判断线段BE 、EF 、FD 之间的数量关系,并说明理由.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△DAF 绕点A 顺时针旋转90°,得到△BAH ,然后通过证明三角形全等可得出结论.请你参考小明同学的思路,解决下列问题:OFBDGEBACDA DAA D “十一五”期间北京市新能源和可再生能源消费量统计图2010年北京市各类能源消费量占新能源和可再生能源3.2%油品30.3%天然气13.1%煤炭30.3%电力23.1%⑴ 图⑴中线段BE 、EF 、FD 之间的数量关系是 ; ⑵ 如图⑵,已知正方形ABCD 边长为5,E 、F 分别是BC 、CD 边上的点,且∠EAF =45°,AG ⊥EF 于点G ,则AG 的长为 ,△EFC 的周长为 ;⑶ 如图⑶,已知△AEF 中,∠EAF =45°,AG ⊥EF 于点G ,且EG =2,GF =3,则△AEF 的面积为 .五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.己知二次函数)12(221-+-=t tx x y (t >1)的图象为抛物线1C .⑴求证:无论t 取何值,抛物线1C 与x 轴总有两个交点;⑵已知抛物线1C 与x 轴交于A 、B 两点(A 在B 的左侧),将抛物线1C 作适当的平移,得抛物线2C :22)(t x y -=,平移后A 、B 的对应点分别为D (m ,n ),E (m +2,n ),求n 的值. ⑶在⑵的条件下,将抛物线2C 位于直线DE 下方的部分沿直线DE 向上翻折后,连同2C 在DE 上方的部分组成一个新图形,记为图形G ,若直线b x y +-=21(b <3)与图形G 有且只有两个公共点,请结合图象求b 的取值范围.24.如图⑴,两块等腰直角三角板ABC 和DEF ,∠ABC =∠DEF = 90°,点C 与EF 在同一条直线l 上,将三角板A B C 绕点C 逆时针旋转α角(︒≤<︒900α)得到 △C B A ''.设EF =2,BC =1,CE =x .⑴如图⑵,当︒=90α,且点C 与点F 重合时,连结'EB ,将直线'EB 绕点E 逆时针旋转45°,交直线D A '于点M ,请补全图形,并求证:M A '=DM .⑵如图⑶,当︒<<︒900α,且点C 与点F 不重合时,连结'EB ,将直线'EB 绕点E 逆时针旋转45°,交直线D A '于点M ,求DMMA '的值(用含x 的代数式表示). 25.定义:对于平面直角坐标系中的任意线段AB 及点P ,任取线段..AB 上一点Q ,线段PQ长度的最小值称为点P 到线段..AB 的距离,记作d (P →AB ). 已知O 为坐标原点,A (4,0),B (3,3),C (m ,n ),D (m +4,n )是平面直角坐标系中四点.根据上述定义,解答下列问题: ⑴点A 到线段OB 的距离d (A →OB ) = ;⑵已知点G 到线段OB 的距离d (G →OB )=5,且点G 的横坐标为1,则点G 的纵坐标为 .⑶当m 的值变化时,点A 到动线段CD 的距离d (A →CD )始终为2,线段CD 的中点为M . ①在图⑵中画出点M 随线段CD 运动所围成的图形并求出该图形的面积.②点E 的坐标为(0,2),m>0,n>0,作MH ⊥x 轴,垂足为H .是否存在m 的值,使得以A 、M 、H 为顶点的三角形与△AOE 相似,若存在,求出m 的值;若不存在,请说明理由.O xy32-1121-1yB4图⑴ 图⑵ 图⑶AC E A'B'D DE lAMD B'A'E lF C数学试卷参考答案及评分标准 2013.05说明:与参考答案不同,但解答正确相应给分. 一、选择题(本题共32分,每小题4分) DCCA BABA二、填空题(本题共16分,每小题4分)9.mn (n +2)(n -2) 10.13 11.1.7 12.21; 321=++n n x x 三、解答题(本题共30分,每小题5分) 13.解:原式=33-3—2×23+1 ………………………4分 =23-2. ………………………5分14.解:3(2x -3)<x +1, ………………………1分6x -9<x +1, ………………………2分 5x <10, ………………………3分 x <2. ………………………4分 ∴原不等式的解集为x <2.在数轴上表示为 : ………………………5分 15.证明 :∵AF =DC ,∴ AF +FC =DC +CF ,即AC =DF . ………………………1分 又∵BC ∥EF ,∴∠BCA =∠DFE , ………………………2分 在△ABC 和△DEF 中,∠A =∠D ,∠BCA =∠DFE , AC =DF ,∴△ABC ≌△DEF (ASA ), ………………………4分 ∴AB =DE . ………………………5分16.解:原式=)2)(2(3)2123(-+⨯---+x x x x x =)2)(2(322-+⨯-+x x x x =2)2(3-x =4432+-x x . ………………………3分 ∵0142=+-x x ,∴142-=-x x ,∴ 原式=413+-=1. ………………………5分17.解:⑴∵点 A (-1,m )在直线y =2x -1上,∴m =2×(-1)-1=-3, ………………………1分 ∴点A 的坐标为(-1,-3). ∵点A 在函数xky =的图象上, ∴ k =-1×(-3)=3, ………………………2分∴反比例函数的解析式为xy 3=. ………………………3分 ⑵点P 的坐标为(-27,0)或(29,0). ………………………5分18.解:设每公顷大豆年产柴油量约为x 万升,则每公顷微藻年产柴油量约为110x 万升,根据题意得, ………………………1分500110220040=-xx , ………………………2分 解得:x =0.04. ………………………3分 经检验:x =0.04是原方程的解,并符合题意. ………………………4分∴110x =110×0.04=4.4(万升).答:每公顷微藻年产柴油量约为4.4万升. ………………………5分 四、解答题(本题共20分,每小题5分)∴DE =3360tan =︒AD =1,AE =︒60sin AD =2. ………………………1分 又∵E 为DC 中点,∴CE =DE =1, 在Rt △CEF 中,∠CFE =90°,∠C =60°,∴CF =CE ·cos 60°=21,EF =CE ·sin 60°=23.………………………2分∴BC =BF +CF =AE +CF =2+21=25. ………………………3分∴四边形ABCD 的面积ABCD S 四边形=ADE S ∆+ABCE S 梯形=21AD ·DE +21(AE + BC )·EF =21×3×1+21×(2+25)×23=8313. ………………………5分 20.⑴证法一:如图,连结OD , ∵AC =BC , ∴∠A =∠ABC ∵OD =OB , ∴∠ABC =∠BDO , ∴∠BDO =∠A ,∴OD∥AC , ………………………1分 ∵AC DF ⊥,∴DF OD ⊥,∴直线EF 是⊙O 的切线. ………………………2分 证法二:如图,连结OD ,CD ,∵BC 是⊙O 直径,∴∠BDC =90°,即CD ⊥AB .EBACDF∵AC =BC ,∴AD =BD ,即D 是AB 的中点. ………………………1分 ∵O 是BC 的中点, ∴D O∥AC . ∵EF ⊥AC 于F , ∴DO EF ⊥,∴直线EF 是⊙O 的切线. ………………………2分⑵解法一:如图,连结CD ,由⑴证法二,∠BDC =90°,D 是AB 的中点,AB =43, ∴AD =BD =23.在Rt △ADC 中,AC =6,AD =23,由勾股定理得:CD =22AD AC -=26, ………………3分 又∵EF ⊥AC , ∴DF =ACCD AD ⋅=66232⋅=22,∴CF =22DF CD -=4, …………………4分 又∵DO∥C F , ∴CF OD EF ED =,即4322=+ED ED ,解得ED =62. ………………………5分 解法二:如图,连结OD ,CD ,BG ,同解法一得∠BDC =90°,CD =26, ………………………3分 ∵BC 是⊙O 直径,∴∠BGC =90°, 在△ABC 中,有CD AB ⋅⋅21=BG AC ⋅⋅21, ∴BG =ACCD AB ⋅=66234⋅=42, ………………………4分又∵∠BGC =∠CFE =90°, ∴BG EF ∥,∴∠E =∠GBC . 在Rt △BGC 中,BC =6,BG =42, ∴CG =22BG BC -=2, tan ∠GBC =BG CG =31, 在Rt △EOD 中,OD =21BC =3,tan ∠E =tan ∠GBC =31,∴ED =EOD∠tan =62. ………………………5分21.解:⑴ 补全统计图如右图,所补数据为98+36+78.5+8+2.8=223.3. ………2分OFB DG OFBADG OFBDG⑵ 2010年北京市总能耗量约是223.3÷3.2%≈7000(万吨标煤).………3分 ⑶到2015年,由于新能源和可再生能源的开发 利用北京市可减少二氧化碳排放量约为7000×(1+31%)×6%×2=1100.4(万吨).………………………5分22.⑴线段BE 、EF 、FD 之间的数量关系是 EF =BE +FD ;………………………1分 ⑵AG 的长为 5 ,△EFC 的周长为 10 ; ………………………3分 ⑶△AEF 的面积为 15 . ………………………5分 五、解答题(本题共22分,第23题7分,第24题8分,第25题7分)23.⑴ 令01=y ,得△=222)1(4484)12(4)2(-=+-=---t t t t t , …………1分∵t >1,∴△=2)1(4-t >0,∴无论t 取何值,方程0)12(22=-+-t tx x 总有两个不相等的实数根,∴无论t 取何值,抛物线1C 与x 轴总有两个交点. ………………………2分 ⑵解法一:解方程0)12(22=-+-t tx x 得,11=x ,122-=t x , ………………………3分∵t >1,∴112>-t .得A (1,0),B (12-t ,0), ∵D (m ,n ),E (m +2,n ), ∴DE =AB =2,即2112=--t ,解得2=t . ………………………4分 ∴二次函数为1)2(34221--=+-=x x x y ,显然将抛物线1C 向上平移1个单位可得抛物线2C :22)2(-=x y ,故1=n . ………………………5分 解法二:∵D (m ,n )在抛物线2C :22)(t x y -=上,∴2)(t m n -=,解得n t m ±=, ………………………3分∴D (n t -,n ),E (n t +,n ),∵DE =2,∴n t +-(n t -)=n 2=2, ………………………4分 解得 1=n . ………………………5分 ⑶由⑵得抛物线2C :22)2(-=x y ,D (1,1),E (3,1), 翻折后,顶点F (2,0)的对应点为F '(2,2), 如图,当直线b x y +-=21经过点D (1,1)时,记为1l , 此时23=b ,图形G 与1l 只有一个公共点; 当直线b x y +-=21经过点E (3,1)时,记为2l ,此时25=b ,图形G 与2l 有三个公共点;当3<b 时,由图象可知,只有当直线l :b x y +-=21位于1l 与2l 之间时,图形G 与直线l 有且只有两个公共点, ∴符合题意的b 的取值范围是2523<<b . ………………………7分24.解:⑴补全图形如右图⑴. ………………………1分② 如图⑵,连结AE ,∵△ABC 和△DEF 是等腰直角三角形, ∠ABC =∠DEF =90°,AB =1,DE =2, ∴BC =1,EF =2,∠DFE =∠ACB =45°. ∴2'==AC C A ,22DF =,'EFB ∠=90°.∴2''=-=C A DF D A , ………………………2分 ∴点'A 为DF 的中点. ∴'EA ⊥DF ,'EA 平分∠DEF .∴E MA '∠=90°,EF A '∠=45°,2'=E A . ∵'MEB ∠=EF A '∠=45°, ∴'MEA ∠=EF B '∠, ∴Rt △E MA '∽Rt △FE B ', ∴F B M A ''=EFE A ',∴22'=M A , ………………………3分∴22222''=-=-=M A D A DM , ∴M A '=DM . ………………………4分 ⑵如图⑶,过点'B 作G B '⊥E B '交直线EM 于点G ,连结G A '. ∵G EB '∠=90°,EM B '∠=45°,∴GE B '∠=45°. ∴E B '=G B '.∵C B A ''∠=G EB '∠=90°,∴G B A ''∠=E CB '∠. 又∵''A B =C B ',∴△G B A ''≌△E CB '. ………………………5分 ∴G A '=CE =x ,''GB A ∠='CEB ∠.∵''GB A ∠+GM A '∠='CEB ∠+DEM ∠=45°,∴GM A '∠=DEM ∠, …………………………6分 ∴G A '∥DE . ∴2''xDE G A DM M A ==. …………………………7分 25.解:⑴点A 到线段OB 的距离d (A →OB )=22; ……1分⑵点G 的纵坐标为 -2或101+. ……………3分 ⑶①如图⑴,当点C 在以A 为圆心,半径为2的⊙A的右半圆上时,点M 在圆弧M 1FM 4上运动;图⑵MDB'A'ElF (C )ABMDB'A'ElF (C )AB图⑴图⑶GMDB'A'ElFCM 4C 4C 2C 1M 3M 2M 1C 3A yxOF-1-111当点C 从C 1到C 2时,点M 在线段M 1M 2上运动; 当点C 从C 4到C 3时,点M 在线段M 4M 3上运动;当点D 在以A 为圆心,半径为2的⊙A 的左半圆上时,点M 在圆弧M 2OM 3上运动; ∴点M 随线段CD 运动所围成的封闭图形是图中实线部分,面积为16+4π. ………5分 ②存在.由A (4,0),E (0,2),得2142==OA OE . (i )当点M 位于左侧圆弧上时,m ≤0,不合题意; (ii )如图⑵,当点M 位于线段M 1M 2上时, ∵MH =2,∴只要AH =1,就有△AOE ∽△MHA , 此时OH 1=5,OH 2=3.∵点M 为线段CD 的中点,CD =4,∴OH 1=5时,m =3;OH 2=3时,m =1. (7)分(iii )解法一:如图⑶,当点M 位于右侧圆弧M 1FM 4上时,连结GM ,其中点G 是圆弧的圆心,坐标为(6,0). 设MH 3=x ,∵AH 3> M 3H 3∴AH 3=2x ,∴GH 3=2x -2,又GM =2,在Rt △MGH 3中,由勾股定理得:2222)22(=+-x x ,解得581=x ,02=x (不合题意,舍去),此时5163=AH ,53633=+=AH OA OH ,∵点M 为线段CD 的中点,CD =4,∴m =526.综上所述,存在m =1或m =3或m =526,使得以A 、M 、H 为顶点的三角形与△AOD 相似.………………………8分解法二:如图⑶,当点M 位于右侧圆弧M 1FM 4上时,连结GM ,其中点G 是圆弧的圆心,坐标为(6,0).设OH 3=x ,则GH 3=x -6.又GM =2,∴M 3H 3=2323GH GM -=22)6(2--x =32122-+-x x∵AH 3> M 3H 3∴△AOE ∽△A H 3M 3, 则333H M AH =321242-+--x x x =12,即01445652=+-x x ,MH 2H 1M M 2M 1E AyxO F-1-111图⑵H 3M4M 2M 1M 3E AyxO FG M-1-111文档从互联网中收集,已重新修正排版,word 格式支持编辑,如有帮助欢迎下载支持。
初三燕山数学一模试卷答案

一、选择题(每题3分,共30分)1. 如果一个数加上3后是它的2倍,这个数是()A. 1B. 2C. 3D. 6答案:C解析:设这个数为x,则x + 3 = 2x,解得x = 3。
2. 下列分数中,分子分母都是偶数的是()A. $\frac{3}{8}$B. $\frac{4}{9}$C. $\frac{6}{10}$D.$\frac{7}{12}$答案:C解析:分子分母都是偶数的分数只有$\frac{6}{10}$。
3. 在等腰三角形ABC中,AB=AC,且∠BAC=40°,则∠B=()A. 40°B. 50°C. 60°D. 70°答案:B解析:等腰三角形的底角相等,所以∠B=∠C,又因为三角形内角和为180°,所以∠B=(180°-40°)/2=50°。
4. 若一个数减去它的3倍后,所得之差是8,这个数是()A. 2B. 4C. 6D. 8答案:B解析:设这个数为x,则x - 3x = 8,解得x = -8,但由于题目中提到“一个数”,故应取正值,所以x = 4。
5. 下列哪个图形是轴对称图形?()A. 正方形B. 等边三角形C. 等腰梯形D. 长方形答案:A解析:轴对称图形是指存在一条直线,使得图形关于这条直线对称。
正方形、等边三角形、等腰梯形和长方形都是轴对称图形,但只有正方形在任意一条对角线上都是对称轴。
二、填空题(每题5分,共25分)6. 3的平方根是_______,它的立方根是_______。
答案:±√3,√3/3解析:3的平方根是±√3,因为(±√3)² = 3;它的立方根是√3/3,因为(√3/3)³ = 3/27 = 1/9。
7. 若x + 2 = 5,则x = _______。
答案:3解析:将等式两边同时减去2,得到x = 5 - 2 = 3。
2024届北京市燕山地区市级名校中考数学模拟精编试卷含解析

2024届北京市燕山地区市级名校中考数学模拟精编试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.若2<2a <3,则a的值可以是()A.﹣7 B.163C.132D.122.如图是根据我市某天七个整点时的气温绘制成的统计图,则这七个整点时气温的中位数和平均数分别是()A.30,28 B.26,26 C.31,30 D.26,223.如图,甲圆柱型容器的底面积为30cm2,高为8cm,乙圆柱型容器底面积为xcm2,若将甲容器装满水,然后再将甲容器里的水全部倒入乙容器中(乙容器无水溢出),则乙容器水面高度y(cm)与x(cm2)之间的大致图象是()A.B.C.D.4.如图,在△ABC中,DE∥BC交AB于D,交AC于E,错误的结论是().A.AD AEDB EC=B.AB ACAD AE=C.AC ECAB DB=D.AD DEDB BC=5.如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是()A.CDACB.BCABC.BDBCD.ADAC6.如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( )A.1 B.1.5 C.2 D.2.57.如图所示,如果将一副三角板按如图方式叠放,那么∠1 等于( )A.120︒B.105︒C.60︒D.45︒8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )A.0.7米B.1.5米C.2.2米D.2.4米9.如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C).若线段AD长为正整数,则点D的个数共有( )A .5个B .4个C .3个D .2个10.已知⊙O 的半径为5,弦AB=6,P 是AB 上任意一点,点C 是劣弧AB 的中点,若△POC 为直角三角形,则PB 的长度( )A .1B .5C .1或5D .2或411.1cm 2的电子屏上约有细菌135000个,135000用科学记数法表示为( )A .0.135×106B .1.35×105C .13.5×104D .135×10312.下列计算,结果等于a 4的是( )A .a+3aB .a 5﹣aC .(a 2)2D .a 8÷a 2 二、填空题:(本大题共6个小题,每小题4分,共24分.)13.如图,矩形ABCD 的对角线BD 经过的坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数y=241k k x++的图象上,若点A 的坐标为(﹣2,﹣3),则k 的值为_____.14.已知x=2是关于x 的一元二次方程kx 2+(k 2﹣2)x+2k+4=0的一个根,则k 的值为_____.15.分式213a b 与21a b的最简公分母是_____. 16.如图,在△ABC 中,AB =AC =10cm ,F 为AB 上一点,AF =2,点E 从点A 出发,沿AC 方向以2cm /s 的速度匀速运动,同时点D 由点B 出发,沿BA 方向以lcm /s 的速度运动,设运动时间为t (s )(0<t <5),连D 交CF 于点G .若CG =2FG ,则t 的值为_____.17.如图,在等腰Rt △ABC 中,∠BAC =90°,AB =AC ,BC =2,点D 是AC 边上一动点,连接BD ,以AD 为直径的圆交BD 于点E ,则线段CE 长度的最小值为___.18.如图,点M是反比例函数2yx(x>0)图像上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为A.1 B.2 C.4 D.不能确定三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>1.(1)当y1﹣y2=4时,求m的值;(2)如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).20.(6分)如图,二次函数y=12x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).求二次函数的解析式;求函数图象的顶点坐标及D点的坐标;二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.21.(6分)某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.22.(8分)如图,直线y=kx+b(k≠0)与双曲线y=mx(m≠0)交于点A(﹣12,2),B(n,﹣1).求直线与双曲线的解析式.点P在x轴上,如果S△ABP=3,求点P的坐标.23.(8分)如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC 的延长线于点E.(1)求证:∠DAC=∠DCE;(2)若AB=2,sin∠D=13,求AE的长.24.(10分)2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化.某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图.请你根据图中提供的信息完成下列问题:(1)求被调查学生的人数,并将条形统计图补充完整;(2)求扇形统计图中的A等对应的扇形圆心角的度数;(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A 等的学生有多少人?25.(10分)如图,在△ABC 中,AB=AC=1,BC=,在AC 边上截取AD=BC ,连接BD .(1)通过计算,判断AD 2与AC•CD 的大小关系;(2)求∠ABD 的度数.26.(12分)某学校后勤人员到一家文具店给九年级的同学购买考试用文具包,文具店规定一次购买400个以上,可享受8折优惠.若给九年级学生每人购买一个,不能享受8折优惠,需付款1936元;若多买88个,就可享受8折优惠,同样只需付款1936元.请问该学校九年级学生有多少人?27.(12分)如图,二次函数23y x x m =-++的图象与x 轴的一个交点为()4,0B ,另一个交点为A ,且与y 轴相交于C 点()1求m 的值及C 点坐标;()2在直线BC 上方的抛物线上是否存在一点M ,使得它与B ,C 两点构成的三角形面积最大,若存在,求出此时M 点坐标;若不存在,请简要说明理由()3P 为抛物线上一点,它关于直线BC 的对称点为Q①当四边形PBQC 为菱形时,求点P 的坐标;②点P 的横坐标为(04)t t <<,当t 为何值时,四边形PBQC 的面积最大,请说明理由.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1、C【解题分析】根据已知条件得到4<a-2<9,由此求得a 的取值范围,易得符合条件的选项.【题目详解】解:∵23,∴4<a-2<9,∴6<a <1.又a-2≥0,即a≥2.∴a 的取值范围是6<a <1.观察选项,只有选项C 符合题意.故选C .【题目点拨】考查了估算无理数的大小,估算无理数大小要用夹逼法.2、B .【解题分析】试题分析:由图可知,把7个数据从小到大排列为22,22,23,1,28,30,31,中位数是第4位数,第4位是1,所以中位数是1.平均数是(22×2+23+1+28+30+31)÷7=1,所以平均数是1.故选B .考点:中位数;加权平均数.3、C【解题分析】根据题意可以写出y 关于x 的函数关系式,然后令x =40求出相应的y 值,即可解答本题.【题目详解】解:由题意可得,y =308x ⨯=240x, 当x=40时,y=6,故选C .【题目点拨】本题考查了反比例函数的图象,根据题意列出函数解析式是解决此题的关键.4、D【解题分析】根据平行线分线段成比例定理及相似三角形的判定与性质进行分析可得出结论.【题目详解】由DE ∥BC ,可得△ADE ∽△ABC ,并可得:AD AE DB EC =,AB AC AD AE =,AC EC AB DB=,故A ,B ,C 正确;D 错误; 故选D .【题目点拨】考点:1.平行线分线段成比例;2.相似三角形的判定与性质.5、D【解题分析】根据锐角三角函数的定义,余弦是邻边比斜边,可得答案.【题目详解】cos α=BD BC CD BC AB AC==. 故选D.【题目点拨】熟悉掌握锐角三角函数的定义是关键.6、C【解题分析】连接AE,根据翻折变换的性质和正方形的性质可证Rt △AFE ≌Rt △ADE,在直角△ECG 中,根据勾股定理求出DE 的长.【题目详解】连接AE,∵AB=AD=AF,∠D=∠AFE=90°,由折叠的性质得:Rt△ABG≌Rt△AFG,在△AFE和△ADE中,∵AE=AE,AD=AF,∠D=∠AFE,∴Rt△AFE≌Rt△ADE,∴EF=DE,设DE=FE=x,则CG=3,EC=6−x.在直角△ECG中,根据勾股定理,得:(6−x)2+9=(x+3)2,解得x=2.则DE=2.【题目点拨】熟练掌握翻折变换、正方形的性质、全等三角形的判定与性质是本题的解题关键.7、B【解题分析】解:如图,∠2=90°﹣45°=45°,由三角形的外角性质得,∠1=∠2+60°=45°+60°=105°.故选B.点睛:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.8、C【解题分析】在直角三角形中利用勾股定理计算出直角边,即可求出小巷宽度.【题目详解】在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,BD2+A′D2=A′B′2,∴BD2+22=6.25,∴BD2=2.25,∵BD>0,∴BD=1.5米,∴CD=BC+BD=0.7+1.5=2.2米.故选C.【题目点拨】本题考查勾股定理的运用,利用梯子长度不变找到斜边是关键.9、C【解题分析】试题分析:过A作AE⊥BC于E,∵AB=AC=5,BC=8,∴BE=EC=4,∴AE=3,∵D是线段BC上的动点(不含端点B,C),∴AE≤AD<AB,即3≤AD<5,∵AD为正整数,∴AD=3或AD=4,当AD=4时,E的左右两边各有一个点D满足条件,∴点D的个数共有3个.故选C.考点:等腰三角形的性质;勾股定理.10、C【解题分析】由点C是劣弧AB的中点,得到OC垂直平分AB,求得DA=DB=3,根据勾股定理得到OD==1,若△POC为直角三角形,只能是∠OPC=90°,则根据相似三角形的性质得到PD=2,于是得到结论.【题目详解】∵点C是劣弧AB的中点,∴OC垂直平分AB,∴DA=DB=3,∴22534-=,若△POC为直角三角形,只能是∠OPC=90°,则△POD∽△CPD,∴PD CD OD PD=,∴PD2=4×1=4,∴PD=2,∴PB=3﹣2=1,根据对称性得,当P在OC的左侧时,PB=3+2=5,∴PB的长度为1或5.故选C.【题目点拨】考查了圆周角,弧,弦的关系,勾股定理,垂径定理,正确左侧图形是解题的关键.11、B【解题分析】根据科学记数法的表示形式(a×10n的形式,其中1≤|a|<10,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同;当原数绝对值>10时,n是正数;当原数的绝对值<1时,n 是负数).【题目详解】解:135000用科学记数法表示为:1.35×1.故选B.【题目点拨】科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12、C【解题分析】根据同底数幂的除法法则:底数不变,指数相减;同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加;幂的乘方法则:底数不变,指数相乘进行计算即可.【题目详解】A.a+3a=4a,错误;B.a5和a不是同类项,不能合并,故此选项错误;C.(a2)2=a4,正确;D.a8÷a2=a6,错误.故选C.【题目点拨】本题主要考查了同底数幂的乘除法,以及幂的乘方,关键是正确掌握计算法则.二、填空题:(本大题共6个小题,每小题4分,共24分.)13、1或﹣1【解题分析】根据矩形的对角线将矩形分成面积相等的两个直角三角形,找到图中的所有矩形及相等的三角形,即可推出S四边形=S四边形HAGO,根据反比例函数比例系数的几何意义即可求出k2+4k+1=6,再解出k的值即可.CEOF【题目详解】如图:∵四边形ABCD、HBEO、OECF、GOFD为矩形,又∵BO为四边形HBEO的对角线,OD为四边形OGDF的对角线,∴S△BEO=S△BHO,S△OFD=S△OGD,S△CBD=S△ADB,∴S△CBD﹣S△BEO﹣S△OFD=S△ADB﹣S△BHO﹣S△OGD,∴S四边形CEOF=S四边形HAGO=2×3=6,∴xy=k2+4k+1=6,解得k=1或k=﹣1.故答案为1或﹣1.【题目点拨】本题考查了反比例函数k的几何意义、矩形的性质、一元二次方程的解法,解题的关键是判断出S四边形CEOF=S四边形HAGO.14、﹣1【解题分析】【分析】把x=2代入kx2+(k2﹣2)x+2k+4=0得4k+2k2﹣4+2k+4=0,再解关于k的方程,然后根据一元二次方程的定义确定k的值即可.【题目详解】把x=2代入kx2+(k2﹣2)x+2k+4=0得4k+2k2﹣4+2k+4=0,整理得k 2+1k=0,解得k 1=0,k 2=﹣1,因为k≠0,所以k 的值为﹣1.故答案为:﹣1.【题目点拨】本题考查了一元二次方程的定义以及一元二次方程的解,能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.15、3a 2b【解题分析】利用取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母求解即可.【题目详解】 分式213a b 与21a b的最简公分母是3a 2b .故答案为3a 2b . 【题目点拨】本题考查最简公分母,解题的关键是掌握求最简公分母的方法.16、1【解题分析】过点C 作CH ∥AB 交DE 的延长线于点H ,则1028DF t t ---==,证明DFG HCG ∆∆∽,可求出CH ,再证明ADE CHE ∆∆∽,由比例线段可求出t 的值.【题目详解】如下图,过点C 作CH ∥AB 交DE 的延长线于点H ,则21028BD t AE t DF t t ---=,=,==,∵DF ∥CH ,∴DFG HCG ∆∆∽,∴12DF FC HC GC ==, ∴2162CH DF t ==-,同理ADE CHE ∆∆∽,∴AD AE CH CE=,∴102162102t tt t-=--,解得t=1,t=253(舍去),故答案为:1.【题目点拨】本题主要考查了三角形中的动点问题,熟练掌握三角形相似的相关方法是解决本题的关键.17、25﹣2【解题分析】连结AE,如图1,先根据等腰直角三角形的性质得到AB=AC=4,再根据圆周角定理,由AD为直径得到∠AED=90°,接着由∠AEB=90°得到点E在以AB为直径的O上,于是当点O、E、C共线时,CE最小,如图2,在Rt△AOC中利用勾股定理计算出OC=25,从而得到CE的最小值为25﹣2.【题目详解】连结AE,如图1,∵∠BAC=90°,AB=AC,BC=42,∴AB=AC=4,∵AD为直径,∴∠AED=90°,∴∠AEB=90°,∴点E在以AB为直径的O上,∵O的半径为2,∴当点O、E. C共线时,CE最小,如图2在Rt△AOC中,∵OA=2,AC=4,∴OC=2225AC OA=+,∴CE=OC−OE=25﹣2,即线段CE长度的最小值为25﹣2.故答案为:25﹣2.【题目点拨】此题考查等腰直角三角形的性质,圆周角定理,勾股定理,解题关键在于结合实际运用圆的相关性质.18、A【解题分析】可以设出M的坐标,MNP的面积即可利用M的坐标表示,据此即可求解.【题目详解】设M的坐标是(m,n),则mn=2.则MN=m,MNP的MN边上的高等于n.则MNP的面积11. 2mn==故选A.【题目点拨】考查反比例函数系数k的几何意义,是常考点,需要学生熟练掌握.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19、(1)m=1;(2)点P坐标为(﹣2m,1)或(6m,1).【解题分析】(1)先根据反比例函数的图象经过点A(﹣4,﹣3),利用待定系数法求出反比例函数的解析式为y=,再由反比例函数图象上点的坐标特征得出y1==,y2==,然后根据y1﹣y2=4列出方程﹣=4,解方程即可求出m的值;(2)设BD与x轴交于点E.根据三角形PBD的面积是8列出方程••PE=8,求出PE=4m,再由E(2m,1),点P 在x轴上,即可求出点P的坐标.【题目详解】解:(1)设反比例函数的解析式为y=,∵反比例函数的图象经过点A(﹣4,﹣3),∴k=﹣4×(﹣3)=12,∴反比例函数的解析式为y=,∵反比例函数的图象经过点B(2m,y1),C(6m,y2),∴y1==,y2==,∵y1﹣y2=4,∴﹣=4,∴m=1,经检验,m=1是原方程的解,故m的值是1;(2)设BD与x轴交于点E,∵点B(2m,),C(6m,),过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,∴D(2m,),BD=﹣=,∵三角形PBD的面积是8,∴BD•PE=8,∴••PE=8,∴PE=4m,∵E(2m,1),点P在x轴上,∴点P坐标为(﹣2m,1)或(6m,1).【题目点拨】本题考查了待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征以及三角形的面积,正确求出双曲线的解析式是解题的关键.20、(1)y=12x1﹣4x+6;(1)D点的坐标为(6,0);(3)存在.当点C的坐标为(4,1)时,△CBD的周长最小【解题分析】(1)只需运用待定系数法就可求出二次函数的解析式;(1)只需运用配方法就可求出抛物线的顶点坐标,只需令y=0就可求出点D的坐标;(3)连接CA ,由于BD 是定值,使得△CBD 的周长最小,只需CD+CB 最小,根据抛物线是轴对称图形可得CA=CD ,只需CA+CB 最小,根据“两点之间,线段最短”可得:当点A 、C 、B 三点共线时,CA+CB 最小,只需用待定系数法求出直线AB 的解析式,就可得到点C 的坐标.【题目详解】(1)把A (1,0),B (8,6)代入212y x bx c =++,得 14202164862b c b c ⎧⨯++=⎪⎪⎨⎪⨯++=⎪⎩ 解得:46b c =-⎧⎨=⎩∴二次函数的解析式为21462y x x =+﹣; (1)由2211464222y x x x =+=﹣(﹣)﹣,得 二次函数图象的顶点坐标为(4,﹣1).令y=0,得214602x x +=﹣, 解得:x 1=1,x 1=6,∴D 点的坐标为(6,0);(3)二次函数的对称轴上存在一点C ,使得CBD 的周长最小.连接CA ,如图,∵点C 在二次函数的对称轴x=4上,∴x C =4,CA=CD ,∴CBD 的周长=CD+CB+BD=CA+CB+BD ,根据“两点之间,线段最短”,可得当点A 、C 、B 三点共线时,CA+CB 最小,此时,由于BD 是定值,因此CBD 的周长最小.设直线AB 的解析式为y=mx+n ,把A (1,0)、B (8,6)代入y=mx+n ,得208m n m n +=⎧⎨+=⎩解得:12 mn=⎧⎨=-⎩∴直线AB的解析式为y=x﹣1.当x=4时,y=4﹣1=1,∴当二次函数的对称轴上点C的坐标为(4,1)时,CBD的周长最小.【题目点拨】本题考查了(1)二次函数综合题;(1)待定系数法求一次函数解析式;(3)二次函数的性质;(4)待定系数法求二次函数解析式;(5)线段的性质:(6)两点之间线段最短.21、(1)13;(2)13.【解题分析】(1)直接根据概率公式求解即可;(2)根据题意先画出树状图,得出所有情况数和甲、乙两位嘉宾能分为同队的结果数,再根据概率公式即可得出答案.【题目详解】解:(1)∵共有三根细绳,且抽出每根细绳的可能性相同,∴甲嘉宾从中任意选择一根细绳拉出,恰好抽出细绳AA1的概率是=13;(2)画树状图:共有9种等可能的结果数,其中甲、乙两位嘉宾能分为同队的结果数为3种情况,则甲、乙两位嘉宾能分为同队的概率是31 93 =.22、(1)y=﹣2x+1;(2)点P的坐标为(﹣32,0)或(52,0).【解题分析】(1)把A的坐标代入可求出m,即可求出反比例函数解析式,把B点的坐标代入反比例函数解析式,即可求出n,把A,B的坐标代入一次函数解析式即可求出一次函数解析式;(2)利用一次函数图象上点的坐标特征可求出点C的坐标,设点P的坐标为(x,0),根据三角形的面积公式结合S△ABP=3,即可得出122x-=,解之即可得出结论.【题目详解】(1)∵双曲线y=mx(m≠0)经过点A(﹣12,2),∴m=﹣1.∴双曲线的表达式为y=﹣1x.∵点B(n,﹣1)在双曲线y=﹣1x上,∴点B的坐标为(1,﹣1).∵直线y=kx+b经过点A(﹣12,2),B(1,﹣1),∴1k b=22k b=1⎧-+⎪⎨⎪+-⎩,解得k=2b=1-⎧⎨⎩∴直线的表达式为y=﹣2x+1;(2)当y=﹣2x+1=0时,x=12,∴点C(12,0).设点P的坐标为(x,0),∵S△ABP=3,A(﹣12,2),B(1,﹣1),∴12×3|x﹣12|=3,即|x﹣12|=2,解得:x1=﹣32,x2=52.∴点P的坐标为(﹣32,0)或(52,0).【题目点拨】本题考查了反比例函数与一次函数的交点问题、一次(反比例)函数图象上点的坐标特征、待定系数法求一次函数、反比例函数的解析式以及三角形的面积,解题的关键是:(1)根据点的坐标利用待定系数法求出函数的解析式;(2)根据三角形的面积公式以及S△ABP=3,得出122x-=.23、(1)证明见解析;(2.【解题分析】(1)由切线的性质可知∠DAB=90°,由直角所对的圆周为90°可知∠ACB=90°,根据同角的余角相等可知∠DAC=∠B,然后由等腰三角形的性质可知∠B=∠OCB,由对顶角的性质可知∠DCE=∠OCB,故此可知∠DAC=∠DCE;(2)题意可知AO=1,OD=3,DC=2,由勾股定理可知AD=由∠DAC=∠DCE,∠D=∠D可知△DEC∽△DCA,故此可得到DC2=DE•AD,故此可求得,于是可求得.【题目详解】解:(1)∵AD是圆O的切线,∴∠DAB=90°.∵AB是圆O的直径,∴∠ACB=90°.∵∠DAC+∠CAB=90°,∠CAB+∠ABC=90°,∴∠DAC=∠B.∵OC=OB,∴∠B=∠OCB.又∵∠DCE=∠OCB,∴∠DAC=∠DCE.(2)∵AB=2,∴AO=1.∵sin∠D=13,∴OD=3,DC=2.在Rt△DAO中,由勾股定理得∵∠DAC=∠DCE,∠D=∠D,∴△DEC∽△DCA,∴DC DEAD DC=2ED=.解得:,∴AE=AD﹣.24、(1)图见解析;(2)126°;(3)1.【解题分析】(1)利用被调查学生的人数=了解程度达到B等的学生数÷所占比例,即可得出被调查学生的人数,由了解程度达到C等占到的比例可求出了解程度达到C等的学生数,再利用了解程度达到A等的学生数=被调查学生的人数-了解程度达到B等的学生数-了解程度达到C等的学生数-了解程度达到D等的学生数可求出了解程度达到A等的学生数,依此数据即可将条形统计图补充完整;(2)根据A等对应的扇形圆心角的度数=了解程度达到A等的学生数÷被调查学生的人数×360°,即可求出结论;(3)利用该校现有学生数×了解程度达到A等的学生所占比例,即可得出结论.【题目详解】(1)48÷40%=120(人),120×15%=18(人),120-48-18-12=42(人).将条形统计图补充完整,如图所示.(2)42÷120×100%×360°=126°.答:扇形统计图中的A等对应的扇形圆心角为126°.(3)1500×42120=1(人).答:该校学生对政策内容了解程度达到A等的学生有1人.【题目点拨】本题考查了条形统计图、扇形统计图以及用样本估计总体,观察条形统计图及扇形统计图,找出各数据,再利用各数量间的关系列式计算是解题的关键.25、(1)AD2=AC•CD.(2)36°.【解题分析】试题分析:(1)通过计算得到=,再计算AC·CD,比较即可得到结论;(2)由,得到,即,从而得到△ABC∽△BDC,故有,从而得到BD=BC=AD,故∠A=∠ABD,∠ABC=∠C=∠BDC.设∠A=∠ABD=x,则∠BDC=2x,∠ABC=∠C=∠BDC=2x,由三角形内角和等于180°,解得:x=36°,从而得到结论.试题解析:(1)∵AD=BC=,∴==.∵AC=1,∴CD==,∴;(2)∵,∴,即,又∵∠C=∠C,∴△ABC∽△BDC,∴,又∵AB=AC,∴BD=BC=AD,∴∠A=∠ABD,∠ABC=∠C=∠BDC.设∠A=∠ABD=x,则∠BDC=∠A+∠ABD=2x,∴∠ABC=∠C=∠BDC=2x,∴∠A+∠ABC+∠C=x+2x+2x=180°,解得:x=36°,∴∠ABD=36°.考点:相似三角形的判定与性质.26、1人【解题分析】解:设九年级学生有x 人,根据题意,列方程得:19361936?0.8x x 88⋅=+,整理得0.8(x+88)=x ,解之得x=1. 经检验x=1是原方程的解.答:这个学校九年级学生有1人.设九年级学生有x 人,根据“给九年级学生每人购买一个,不能享受8折优惠,需付款1936元”可得每个文具包的花费是:1936x 元,根据“若多买88个,就可享受8折优惠,同样只需付款1936元”可得每个文具包的花费是:1936?x 88+,根据题意可得方程19361936?0.8x x 88⋅=+,解方程即可.27、()14m =,()0,4C ;()2存在,()2,6M ;()(31P ①或(1P ;②当2t =时,16PBQC S =四边形最大.【解题分析】(1)用待定系数法求出抛物线解析式;(2)先判断出面积最大时,平移直线BC 的直线和抛物线只有一个交点,从而求出点M 坐标;(3)①先判断出四边形PBQC 时菱形时,点P 是线段BC 的垂直平分线,利用该特殊性建立方程求解;②先求出四边形PBCQ 的面积与t 的函数关系式,从而确定出它的最大值.【题目详解】解:(1)将B (4,0)代入23y x x m =-++,解得,m=4,∴二次函数解析式为234y x x =-++,令x=0,得y=4,∴C (0,4);(2)存在,理由:∵B (4,0),C (0,4),∴直线BC 解析式为y=﹣x+4,当直线BC 向上平移b 单位后和抛物线只有一个公共点时,△MBC 面积最大, ∴24{34y x b y x x =-++=-++, ∴24(2)16t --+,∴△=1﹣4b=0,∴b=4,∴26x y =⎧⎨=⎩,∴M (2,6); (3)①如图,∵点P 在抛物线上,∴设P (m ,234m m -++),当四边形PBQC 是菱形时,点P 在线段BC 的垂直平分线上,∵B (4,0),C (0,4),∴线段BC 的垂直平分线的解析式为y=x ,∴m=234m m -++,∴m=15±, ∴P (15+,15+)或P (15-,15-);②如图,设点P (t ,234t t -++),过点P 作y 轴的平行线l ,过点C 作l 的垂线, ∵点D 在直线BC 上,∴D (t ,﹣t+4),∵PD=234t t -++﹣(﹣t+4)=24t t -+,BE+CF=4,∴S 四边形PBQC =2S △PDC =2(S △PCD +S △BD )=2(12PD×CF+12PD×BE )=4PD=224164(2)16t t t -+--+ ∵0<t <4,∴当t=2时,S 四边形PBQC 最大=1.考点:二次函数综合题;二次函数的最值;最值问题;分类讨论;压轴题.。
2024年北京市燕山区中考数学一模试卷
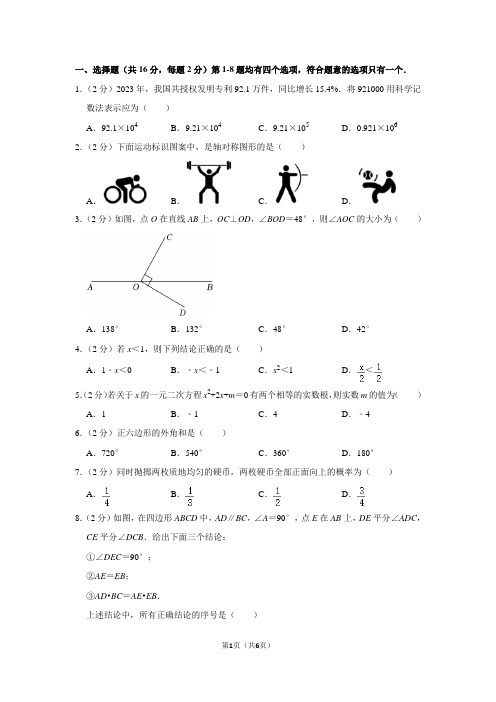
一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.(2分)2023年,我国共授权发明专利92.1万件,同比增长15.4%.将921000用科学记数法表示应为()A.92.1×104B.9.21×104C.9.21×105D.0.921×106 2.(2分)下面运动标识图案中,是轴对称图形的是()A.B.C.D.3.(2分)如图,点O在直线AB上,OC⊥OD,∠BOD=48°,则∠AOC的大小为()A.138°B.132°C.48°D.42°4.(2分)若x<1,则下列结论正确的是()A.1﹣x<0B.﹣x<﹣1C.x2<1D.<5.(2分)若关于x的一元二次方程x2+2x+m=0有两个相等的实数根,则实数m的值为()A.1B.﹣1C.4D.﹣46.(2分)正六边形的外角和是()A.720°B.540°C.360°D.180°7.(2分)同时抛掷两枚质地均匀的硬币,两枚硬币全部正面向上的概率为()A.B.C.D.8.(2分)如图,在四边形ABCD中,AD∥BC,∠A=90°,点E在AB上,DE平分∠ADC,CE平分∠DCB.给出下面三个结论:①∠DEC=90°;②AE=EB;③AD•BC=AE•EB.上述结论中,所有正确结论的序号是()A.①②B.②③C.①③D.①②③二、填空题(共16分,每题2分)9.(2分)若在实数范围内有意义,则实数x的取值范围为.10.(2分)分解因式:8a2﹣8b2=.11.(2分)方程的解为.12.(2分)在平面直角坐标系xOy中,反比例函数的图象经过点P(﹣2,y1)和Q(m,y2),若y1+y2=0,则m的值为.13.(2分)某班级计划利用暑假去研学旅行,他们准备订做一批容量相同的双肩包.活动负责人征求了全班40名同学的意向,得到如下数据:容量/L232527293133人数/人4352332为了满足大多数人的需求,此次订做的双肩包容量为L.14.(2分)如图,AB是⊙O的直径,点C在⊙O上,过点B作⊙O的切线与直线AC交于点D.若∠D=50°,则∠BOC=°.15.(2分)如图,在▱ABCD中,点E在AD上,BE交AC于点F.若AE=3ED,则的值为.16.(2分)学校组织学生到某工艺品加工厂参加劳动实践活动.用甲、乙两台设备加工三件工艺品,编号分别为A,B,C,加工要求如下:①每台设备同一时间只能加工一件工艺品;②每件工艺品须先在设备甲上加工完成后,才能进入设备乙加工;③每件工艺品在每台设备上所需要的加工时间(单位:min)如表所示:加工时间A B C工艺品编号设备甲724乙256(1)若要求A,B,C三件工艺品全部加工完成的总时长不超过20min,请写出一种满足条件的加工方案(按顺序写出工艺品的编号);(2)A,B,C三件工艺品全部加工完成,至少需要min.三、解答题(共68分,第17-19题,每题5分,第20题6分,第21-23题,每题5分,第24-26题,每题6分,第27-28题,每题7分)17.(5分)计算:4sin45°+|﹣2|﹣+()﹣1.18.(5分)解不等式组:.19.(5分)已知2x2﹣x﹣1=0,求代数式(3x+2)(3x﹣2)﹣3x(x+1)的值.20.(6分)如图,在菱形ABCD中,对角线AC与BD相交于点O,E为CD的中点,连接OE并延长到点F,使得OE=EF,连接CF,DF.(1)求证:四边形OCFD是矩形;(2)若AB=5,sin∠DOF=,求BD的长.21.(5分)《清明上河图》是北宋画家张择端的作品,是中国十大传世名画之一.如图是某书画家的一幅局部临摹作品,装裱前是长为2.2m,宽为1.6m的矩形,装裱后,整幅图画长与宽的比是4:3,且四周边衬的宽度相等,求边衬的宽度.22.(5分)在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=2x的图象向下平移4个单位长度得到,且与x轴交于点A.(1)求该一次函数的解析式及点A的坐标;(2)当x>2时,对于x的每一个值,函数y=x+n的值小于一次函数y=kx+b(k≠0)的值且大于﹣3,直接写出n的取值范围.24.(6分)如图,AB为⊙O的直径,弦CD⊥AB,过点A作⊙O的切线交BC的延长线于点E.(1)求证:∠BAD=∠E;(2)若⊙O的半径为5,AD=6,求CE的长.25.(6分)科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到距离地面20m处开始计时,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽略空气阻力).记无人机和小钢球距离地面的高度分别为y1,y2(单位:m),科研人员收集了y1,y2随时间x(单位:s)变化的数据,并分别绘制在平面直角坐标系中,如图所示.(1)根据y1,y2随x的变化规律,从①y=mx+n(m≠0);②y=ax2+bx(a<0);③(k≠0)中,选择适当的函数模型,分别求出y1,y2满足的函数关系式;(2)当0<x<5时,小钢球和无人机的高度差最大是m.26.(6分)在平面直角坐标系xOy中,M(m,y1),N(m+2,y2)是抛物线y=ax2+bx+c (a>0)上两点.设该抛物线的对称轴为x=t.(1)若对于m=1,有y1=y2,求t的值;(2)若对于1<m<2,都有y1<y2,求t的取值范围.27.(7分)在△ABC中,∠ACB=90°,AC=BC,M为AB的中点,D为线段AM上的动点(不与点A,M重合),过点D作DE⊥AB,且DE=DM,连接CM.(1)如图1,当点E在线段AC上时,求证:D是AM的中点;(2)当DE位于图2位置时,连接CE,过点E作EF⊥CE,交AB于点F.用等式表示线段BF与DE的数量关系,并证明.28.(7分)在平面直角坐标系xOy中,对于⊙G和线段AB给出如下定义:如果线段AB上存在点P,Q,使得点P在⊙G内,且点Q在⊙G外,则称线段AB为⊙G的“交割线段”.(1)如图,⊙O的半径为2,点A(0,2),B(2,2),C(﹣1,0).①在△ABC的三条边AB,BC,AC中,⊙O的“交割线段”是;②点M是直线OB上的一个动点,过点M作MN⊥x轴,垂足为N,若线段MN是⊙O的“交割线段”,求点M的横坐标m的取值范围;(2)已知三条直线y=3,y=﹣x,y=﹣2x+3分别相交于点D,E,F,⊙T的圆心为T (0,t),半径为2,若△DEF的三条边中有且只有两条是⊙T的“交割线段”,直接写出t的取值范围.。
中考强化训练2022年北京市燕山地区中考数学模拟测评 卷(Ⅰ)(含答案及详解)

2022年北京市燕山地区中考数学模拟测评 卷(Ⅰ)考试时间:90分钟;命题人:数学教研组考生注意: 1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟 2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、某三棱柱的三种视图如图所示,已知俯视图中1tan 2B =,7ABCS =,下列结论中:①主视图中3m =;②左视图矩形的面积为18;③俯视图C ∠的正切值为23.其中正确的个数为( )A .3个B .2个C .1个D .0个2、已知点A (m ,2)与点B (1,n )关于y 轴对称,那么m +n 的值等于( ) A .﹣1 B .1 C .﹣2 D .23、文博会期间,某公司调查一种工艺品的销售情况,下面是两位调查员和经理的对话. 小张:该工艺品的进价是每个22元; 小李:当销售价为每个38元时,每天可售出160个;当销售价降低3元时,平均每天将能多售出120个. 经理:为了实现平均每天3640元的销售利润,这种工艺品的销售价应降低多少元?·线○封○密○外设这种工艺品的销售价每个应降低x 元,由题意可列方程为( ) A .(38﹣x )(160+3x×120)=3640 B .(38﹣x ﹣22)(160+120x )=3640 C .(38﹣x ﹣22)(160+3x ×120)=3640 D .(38﹣x ﹣22)(160+3x ×120)=36404、下列一元二次方程有两个相等的实数根的是( ) A .21x = B .2210x x -+= C .220210x x --= D .210x x ++=5、已知4个数:()20201-,2-,()1.5--,23-,其中正数的个数有( )A .1B .C .3D .46、下列命题正确的是( ) A .零的倒数是零B .乘积是1的两数互为倒数C .如果一个数是a ,那么它的倒数是1aD .任何不等于0的数的倒数都大于零7、截至2021年12月31日,我国已有11.5亿人完成了新冠疫苗全程接种,数据11.5亿用科学记数法表示为( ) A .11.5×108B .1.15×108C .11.5×109D .1.15×1098、神舟号载人飞船于2021年10月16日凌晨成功对接中国空间站,自升空以来神舟十三号飞船每天绕地球16圈,按地球赤道周长计算神舟十三号飞船每天飞行约641200千米,641200用科学记数法表示为( ) A .60.641210⨯B .56.41210⨯C .66.41210⨯D .564.1210⨯9、下列图形中,是中心对称图形的是()A.B.C.D.10、为保护人民群众生命安全,减少交通事故,自2020年7月1日起,我市市民骑车出行必须严格遵守“一盔一带”规定,某头盔经销商经过统计发现:某品牌头盔从5月份到7月份销售量的月增长率相同,若5月份销售200个,7月份销售288个,设月增长率为x则可列出方程()A.200(+x)=288 B.200(1+2x)=288C.200(1+x)²=288 D.200(1+x²)=288第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,将一副直角三角板叠放在一起,使直角顶点重合于点,若∠COB=50°,则∠AOD=_______2、万盛是重庆茶叶生产基地和名优茶产地之一,以“重庆第一泡•万盛茶飘香”为主题的采茶制茶、品茶赏茶,茶艺表演活动在万盛板辽湖游客接待中心开幕,活动持续两周,活动举办方为游客准备了三款2021年的新茶:清明香,云雾毛尖、滴翠剑茗.第一批采制的茶叶中清明香、云雾毛尖、滴翠剑茗的数量(盒)之比为2:3:1,由于品质优良宣传力度大,网上的预订量暴增,举办方加紧采制了第二批同种类型的茶叶,其中清明香增加的数量占总增加数量的12,此时清明香总数量达到三种茶·线○封○密·○外叶总量的49,而云雾毛尖和滴翠剑茗的总数量恰好相等.若清明香、云雾毛尖、滴翠剑茗三种茶叶每盒的成本分别为500元、420元,380元,清明香的售价为每盒640元,活动中将清明香的18供游客免费品尝,活动结束时两批茶叶全部卖完,总利润率为16%,且云雾毛尖的销售单价等于另外两种茶叶销售单价之和的614,则滴翠剑茗单价为____元 3、如果将方程3225x y -=变形为用含x 的式子表示y ,那么y =_______. 4、若a 和b 互为相反数,c 和d 互为倒数,则20202020a b cd+-的值是________________. 5、如图,点Q 在线段AP 上,其中10PQ =,第一次分别取线段AP 和AQ 的中点1P ,1Q ,得到线段11PQ ,则线段11=PQ ____________;再分别取线段1AP 和1AQ 的中点2P ,2Q ,得到线段22P Q ;第三次分别取线段2AP 和2AQ 的中点3P ,3Q ,得到线段33PQ ;连续这样操作2021次,则每次的两个中点所形成的所有线段之和11223320212021PQ P Q PQ P Q +++⋅⋅⋅⋅⋅⋅+=____________.三、解答题(5小题,每小题10分,共计50分)1、如图所示,AB AD =,AE AC =,90BAD EAC ∠=∠=︒,D 在CE 上,直线AE 与线段BD 交于点G (不与B 、D 重合)(1)当AE BD ⊥时①如图1,求EAD ∠的度数;②如图2,若AEC ∠的角平分线交AD 于F ,求证:CF 平分ACE ∠;(2)如图3,过点A 作BC 的垂线,变BC ,ED 于点M 、N ,求EN 和ED 的数量关系. 2、已知:如图,E 为△ABC 的外角平分线上的一点,AE ∥BC ,BF AE =,求证:(1)△ABC 是等腰三角形; (2)AF CE =.3、如图,在长方形ABCD 中,4AB =,6BC =.延长BC 到点E ,使3CE =,连接DE .动点P 从点B 出发,沿着BE 以每秒1个单位的速度向终点E 运动,点P 运动的时间为t 秒.(1)DE 的长为 ;(2)连接AP ,求当t 为何值时,≅ABP DCE ; (3)连接DP ,求当t为何值时,PDE △是直角三角形; (4)直接写出当t为何值时,PDE △是等腰三角形.4、如图,在平面直角坐标系中,ABC 顶点的横、纵坐标都是整数.若将ABC 以某点为旋转中心,顺时针旋转90°得到DEF ,其中A 、B 、C 分别和D 、E 、F 对应.(1)请通过画图找出旋转中心M ,点M 的坐标为______. ·线○封○密·○外(2)直接写出点A 经过的路径长为______.5、若关于x 的一元二次方程20x mx n ++=有两个相等的实数根. (1)用含m 的代数式表示n ; (2)求n m +的最小值.-参考答案-一、单选题 1、A 【分析】过点A 作AD ⊥BC 与D ,根据BD =4,1tan 2B =,可求AD =BD 1tan 422B =⨯=,根据7ABC S =△,得出BC =7,可得DC =BC -BD =7-4=3可判断①;根据左视图矩形的面积为3×6=18可判断②;根据tan C23AD CD ==可判断③. 【详解】解:过点A 作AD ⊥BC 与D , ∵BD =4,1tan 2B =,∴AD =BD 1tan 422B =⨯=, ∵7ABC S =△,∴112722ABC S BC AD BC =⋅=⨯=△,∴BC =7,∴DC =BC -BD =7-4=3, ∴①主视图中3m =正确;∴左视图矩形的面积为3×6=18, ∴②正确; ∴tan C 23AD CD ==, ∴③正确;其中正确的个数为为3个. 故选择A . 【点睛】本题考查三视图与解直角三角的应用相结合,掌握三视图,三角形面积公式,正切定义,矩形面积公式是解题关键,本题比较新颖,难度不大,是创新题型.2、 B ·线○封○密·○外【分析】关于x 轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数;关于y 轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变,据此先求出m ,n 的值,然后代入代数式求解即可得. 【详解】解:∵(),2A m 与点()1,B n 关于y 轴对称, ∴1m =-,2n =, ∴121m n +=-+=, 故选:B . 【点睛】题目主要考查点关于坐标轴对称的特点,求代数式的值,理解题意,熟练掌握点关于坐标轴对称的特点是解题关键. 3、D 【分析】由这种工艺品的销售价每个降低x 元,可得出每个工艺品的销售利润为(38-x -22)元,销售量为(160+3x ×120)个,利用销售总利润=每个的销售利润×销售量,即可得出关于x 的一元二次方程,此题得解. 【详解】解:∵这种工艺品的销售价每个降低x 元,∴每个工艺品的销售利润为(38-x -22)元,销售量为(160+3x ×120)个.依题意得:(38-x -22)(160+3x ×120)=3640. 故选:D . 【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键. 4、B 【分析】根据一元二次方程根的判别式判断即可. 【详解】解:A 、△0440=+=>,∴方程21x =有两个不等实数根,不符合题意; B 、△4410=-⨯=,∴方程2210x x -+=有两个相等实数根,符合题意;C 、△141202180850=+⨯⨯=>,∴方程220210x x --=有两个不相等实数根,不符合题意;D 、△1430=-=-<, ∴方程210x x ++=没有实数根,不符合题意;故选:B . 【点睛】 本题考查了一元二次方程根的判别式,解题的关键是掌握一元二次方程根的情况与判别式△的关系:(1)△0>⇔方程有两个不相等的实数根;(2)△0=⇔方程有两个相等的实数根;(3)△0<⇔方程没有实数根. 5、C 【分析】化简后根据正数的定义判断即可. 【详解】解:()20201-=1是正数,2-=2是正数,()1.5--=1.5是正数,23-=-9是负数,·线○封○密○外故选C.【点睛】本题考查了有理数的乘方、相反数、绝对值的意义,以及正负数的意义,正确化简各数是解答本题的关键.6、B【分析】根据倒数的概念、有理数的大小比较法则判断.【详解】解:A、零没有倒数,本选项说法错误;B、乘积是1的两数互为倒数,本选项说法正确;C、如果0a=,则a没有倒数,本选项说法错误;D、2-的倒数是12-,12-<,则任何不等于0的数的倒数都大于零说法错误;故选:B.【点睛】本题考查了有理数的乘法及倒数的概念,熟练掌握倒数概念是关键.7、D【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.【详解】解:11.5亿=1150000000=1.5×109.故选:D.【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a ×10n 的形式,其中1≤|a |<10,n 为整数,表示时关键要正确确定a 的值以及n 的值. 8、B 【分析】科学记数法的表示形式为a ×10n 的形式,其中1≤|a |<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n 是正整数;当原数的绝对值<1时,n 是负整数. 【详解】 解:641200用科学记数法表示为:641200=56.41210 , 故选择B . 【点睛】 此题考查科学记数法的表示方法.科学记数法的表示形式为a ×10n 的形式,其中1≤|a |<10,n 为整数,表示时关键要正确确定a 的值以及n 的值. 9、B 【分析】 根据中心对称图形的定义求解即可. 【详解】 解:A 、不是中心对称图形,不符合题意; B 、是中心对称图形,符合题意; C 、不是中心对称图形,不符合题意; D 、不是中心对称图形,不符合题意. 故选:B . 【点睛】·线○封·○密○外此题考查了中心对称图形,解题的关键是熟练掌握中心对称图形的定义.中心对称图形:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.10、C【分析】设月增长率为x ,根据等量关系用增长率表示7月份的销售量与销售288相等,可列出方程200(1+x )²=288即可.【详解】解:设月增长率为x ,则可列出方程200(1+x )²=288.故选C .【点睛】本题考查列一元二次方程解增长率问题应用题,掌握列一元二次方程解增长率问题应用题方法与步骤,抓住等量关系列方程是解题关键.二、填空题1、130°130度【分析】先计算出AOC ∠,再根据AOD AOC COD ∠=∠+∠可求出结论.【详解】解:∵90AOB ∠=︒,50COB ∠=︒∴905040AOC AOB COB ∠=∠-∠=︒-︒=︒∵90COD ∠=︒∴4090130AOD AOC COD ∠=∠+∠=︒+︒=︒故答案为:130°【点睛】本题考查了角的计算及余角的计算,熟悉图形是解题的关键.2、480【分析】设滴翠剑茗单价为x 元,则云雾毛尖最高价位6(640)14x +⨯元,根据云雾毛尖的销售单价等于另外两种茶叶销售单价之和的614得出三种茶叶的单价,根据销售总额列出方程,解方程即可. 【详解】 解:第一批采制的茶叶中清明香、云雾毛尖、滴翠剑茗的数量(盒)之比为2:3:1, 第二批采制后清明香增加的数量占总增加数量的12,此时清明香总数量达到三种茶叶总量的49,而云雾毛尖和滴翠剑茗的总数量恰好相等, 即云雾毛尖、滴翠剑茗的数量各占518, ∴增加后清明香、云雾毛尖、滴翠剑茗的数量(盒)之比为455::8:5:591818=, 设总共有a 盒茶叶, ∴成本为4554000500420380918189a a a a ⨯+⨯+⨯=(元), 销售额应为40004640(116%)99a a ⨯+=(元), 清明香的销售额为412240640(1)989a a ⨯⨯-=(元), 另外两种茶的销售总额为46402240800993a a a -=(元), 设滴翠剑茗单价为x 元,则云雾毛尖单价为6(640)14x +⨯元, 因此可建立方程556800(640)1818143xa x a a +⨯+⨯=, 解得480x =,·线○封○密○外因此滴翠剑茗单价为480元,故答案为:480.【点睛】本题主要考查一元一次方程的知识,根据售价-成本=利润列出方程是解题的关键.3、3252x - 【分析】先移项,再系数化为1即可.【详解】解:移项,得:2253y x -=-,方程两边同时除以2-,得:3252x y -=, 故答案为:3252x -. 【点睛】本题考查了解二元一次方程,将x 看作常数,把y 看做未知数,灵活应用等式的性质求解是关键.4、-2020【分析】利用相反数,倒数意义求出各自的值,代入原式计算即可得到结果.【详解】解:∵a,b 互为相反数,c ,d 互为倒数,∴a+b=0,cd=1, 则2020020202020202020201a b cd +-=-=-. 故答案为:-2020.【点睛】本题考查了代数式的求值,有理数的混合运算,相反数,倒数,熟练掌握各自的性质是解本题的关键. 5、5 202110102- 【分析】 根据线段中点的定义可得P 1Q 1=12PQ ,P 2Q 2=12P 1Q 1,P 3Q 3=12P 2Q 2,根据规律可得答案. 【详解】 解:∵线段AP 和AQ 的中点是P 1,Q 1, ∴P 1Q 1=AP 1-AQ 1=12AP -12AQ =12PQ =5; ∵线段AP 1和AQ 1的中点P 2,Q 2, ∴P 2Q 2=AP 2-AQ 2=12AP 1-12AQ 1=12P 1Q 1=14PQ , …,∴P 1Q 1+P 2Q 2+P 3Q 3+…+P 2021Q 2021 =12PQ +14PQ +18PQ +…+202112PQ =(1-202112)PQ =202110102-. 故答案为:202110102-. 【点睛】 本题考查了两点间的距离,能够根据线段中点的定义得到其中的规律是解题关键. 三、解答题·线○封○密·○外1、(1)①45EAD ∠=︒;②证明见详解;(2)12EN DE =,证明见详解. 【分析】(1)①根据等腰直角三角形的性质可得45ADB ABD ∠=∠=︒,再由垂直的性质及直角三角形中两锐角互余即可得;②由①可知:45EAD DAC ∠=∠=︒,45ACD AED ∠=∠=︒,再根据等腰三角形的性质可得AD 为CE 的中垂线,由角平分线的定义(从一个角的顶点引出一条射线,把这个角分成两个完全相同的角,这条射线叫做这个角的角平分线)可得22.5FED FCD ∠=∠=︒,利用等量代换得22.5ACF FCD ∠=∠=︒,由此即可证明;(2)过点D 作DF AE ∥交AN 的延长线于点F ,AN 和BC 相交于点H ,根据各角之间的数量关系可得ABC DAF ∠=∠,由平行线的性质及各角之间的等量代换得出,ADF BAC ∠=∠, 根据全等三角形的判定定理和性质可得ABC ADF ∆≅∆,AC DF =,再利用一次全等三角形的判定和性质可得AEN FDN ∆≅∆,EN DN =,由此即可得出结论.(1)解:①∵AB AD =,90BAD ∠=︒,∴45ADB ABD ∠=∠=︒,∵AE BD ⊥,∴90AGD ∠=︒,∴9045EAD ADB ∠=︒-∠=︒;②证明:如图所示:由①可知:45EAD ∠=︒, ∴45DAC ∠=︒, ∴45EAD DAC ∠=∠=︒,45ACD AED ∠=∠=︒, ∵AE AC =, ∴AD EC ⊥,ED DC =, ∴AD 为CE 的中垂线, ∴EF FC =, ∴FED FCD ∠=∠, ∵EF 平分AED ∠, ∴22.5FED FCD ∠=∠=︒, ∴22.5ACF FCD ∠=∠=︒, ∴CF 平分ACE ∠; (2) 解:过点D 作DF AE ∥交AN 的延长线于点F ,AN 和BC 相交于点H , ·线○封○密○外∵90BAD AHC ∠=∠=︒,∴90HAD BAH ∠+∠=︒,90BAH ABH ∠+∠=︒,∴HAD ABH ∠=∠,即ABC DAF ∠=∠,∵DF AE ∥,∴180ADF DAE ∠+∠=︒,∴180ADF DAE ∠=︒-∠,∵180BAC BAD CAE DAE DAE ∠=∠+∠-∠=︒-∠,∴ADF BAC ∠=∠,在ABC ∆与ADF ∆中,ABC DAF AD ABADF BAC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴ABC ADF ∆≅∆,∴AC DF =,∵AE AC =,∴AE DF =,∵DF AE ∥,∴E NDF ∠=∠,在AEN ∆与FDN ∆中, E NDF AE DF ANE DNF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴AEN FDN ∆≅∆,∴EN DN =, ∴12EN DE =. 【点睛】 题目主要考查等腰三角形的判定和性质,中垂线的判定和性质,角平分线的定义,全等三角形的判定和性质等,理解题意,作出相应辅助线,综合运用这些知识点是解题关键. 2、 (1)见解析 (2)见解析 【分析】 (1)由AE //BC 可得,DAE B CAE ACB ∠=∠∠=∠,由AE 平分DAC ∠得DAE CAE ∠=∠,从而A ABC CB =∠∠,故可得结论; (2)根据SAS 证明ABF CAE ∆≅∆即可证明AF =CE . (1) ∵AE //BC ∴,DAE B CAE ACB ∠=∠∠=∠ ∵AE 平分DAC ∠ ∴DAE CAE ∠=∠ ·线○封○密○外∴A ABC CB =∠∠∴AB AC =,即△ABC 是等腰三角形;(2)由(1)可得,,CAE B AB AC ∠=∠=∵BF AE =∴ABF CAE ∆≅∆∴AF CE =.【点睛】本题主要考查了等腰三角形的判定,全等三角形的判断与性质,能判断出等角对等边是解答本题的关键.3、(1)5;(2)3t =秒时,ABP DCE ∆≅∆;(3)当23t =秒或6t =秒时,PDE ∆是直角三角形;(4)当3t =秒或4t =秒或296t =秒时,PDE ∆为等腰三角形. 【分析】(1)根据长方形的性质及勾股定理直接求解即可;(2)根据全等三角形的性质可得:3BP CE ==,即可求出时间t ;(3)分两种情况讨论:①当90PDE ∠=︒时,在两个直角三角形中运用两次勾股定理,然后建立等量关系求解即可;②当90DPE ∠=︒时,此时点P 与点C 重合,得出BP BC =,即可计算t 的值;(4)分三种情况讨论:①当PD DE =时,②当PE DE =时,③当PD PE =时,分别结合图形,利用各边之间的关系及勾股定理求解即可得.【详解】解:(1)∵四边形ABCD 为长方形,∴4AB CD ==,CD BC ⊥,在Rt DCE ∆中,5DE =,故答案为:5;(2)如图所示:当点P 到如图所示位置时,ABP DCE ∆≅∆,∵4AB CD ==,3CE =, ∴ABP DCE ∆≅∆,仅有如图所示一种情况, 此时,3BP CE ==, ∴31BP t ==, ∴3t =秒时,ABP DCE ∆≅∆; (3)①当90PDE ∠=︒时,如图所示: 在Rt PDE ∆中,222PD PE DE =-, 在Rt PCD ∆中,·线○封○密○外222PD PC DC =+,∴2222PE DE PC DC -=+,9PE t =-,6PC t =-,∴()()22229564t t --=-+, 解得:23t =;②当90DPE ∠=︒时,此时点P 与点C 重合,∴BP BC =,∴6t =; 综上可得:当23t =秒或6t =秒时,PDE ∆是直角三角形;(4)若PDE ∆为等腰三角形,分三种情况讨论:①当PD DE =时,如图所示:∵PD DE =,DC BE ⊥,∴3PC CE ==,∴3BP BC PC =-=, ∴31BP t ==; ②当5PE DE ==时,如图所示:954BP BE PE =-=-=, ∴41BP t ==; ③当PD PE =时,如图所示:3PE PC CE PC =+=+,∴3PD PE PC ==+, 在Rt PDC ∆中, 222PD CD PC =+, 即()22234PC PC +=+, 解得:76PC =, 296BP BC PC =-=, ∴2916BP t ==; ·线○封○密○外综上可得:当3t =秒或4t =秒或296t =秒时,PDE ∆为等腰三角形. 【点睛】 题目主要考查勾股定理解三角形,等腰三角形的性质,全等三角形的性质等,理解题意,分类讨论作出相应图形是解题关键.4、(1)(1,1)-(2)32π【分析】(1)根据对应点连线段的垂直平分线的交点即为旋转中心,可得结论.(2)根据A 经过的路径长为以M 为圆心,3为半径的圆周长的14即可求解. (1)解:连接,AD BE ,分别作,AD BE 的垂直平分线交点M 即为所求,如下图:(1,1)M ∴-,故答案是:(1,1)-;(2)解:由题意及下图,知点A 经过的路径长为以M 为圆心,3为半径的圆周长的14, ∴点A 经过的路径长为:13242r ππ⨯=, 故答案是:32π. 【点睛】 本题考查坐标与图形变化-旋转,解题的关键是理解旋转中心是对应点连线段的垂直平分线的交点. 5、 (1)24m n = (2)1- 【分析】 (1)由两个相等的实数根知240b ac =-=,整理得n 的含m 的代数式. (2)对24m n m m +=+进行配方,然后求最值即可. (1) 解:由题意知22440b ac m n =-=-= ∴24m n = ·线○封○密·○外(2) 解:24m n m m +=+ ()214414m m =++- ()21214m =+- ∵()220m +≥∴当()220m +=时,n m +的值最小,为1-∴n m +的最小值为1-.【点睛】本题考查了一元二次方程的根,一元二次代数式的最值.解题的关键在于配完全平方.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
吸氧有效吗?
典型病例
患者男,29岁。因烧伤而急诊入院。 体格检查:意识清,BP80/60mmHg,心率101 次/分。双下肢等部位Ⅱ-Ⅲ度烧伤,面积约为体表 总面积50%。 入院后5h,BP降至60/40mmHg,经输液、输 血后上升至120/70mmHg,此时胸片清晰。 第7天出现呼吸困难,意识障碍。第9天出现紫 绀,气急加重,咳出淡红色泡沫痰,胸片示弥散
2.胸廓顺应性降低:胸膜纤维化 3.肺顺应性降低:肺纤维化
4.胸腔积液和气胸
(二)阻塞性通气不足 气道阻塞或狭窄而引起的通气障碍。
气道阻塞分类:
中央性:指气管分叉处以上 的气道阻塞。又分为胸外 与胸内阻塞2种。
外周性:内径小于2mm的小 支气管阻塞。常见于慢性 阻塞性肺疾病 (COPD)。
1)中央气道胸外段阻塞(如喉头水肿)
• 生理死腔:占潮气量30%
• 疾病时功能性死腔:高达60%~70%
总之,无论是功能性分流还是死腔样通气, 均可导致:
PaO2↓ 但PaCO2 可正常或降低,甚至升高
(三)解剖分流增多
生理解剖分流: 一部分支气管静脉回流
肺静脉;肺内动-静脉交通 支;其分流量约占心输出 量的2 % -3 %。
肺实变、肺不张、支气管 扩张症伴支气管血管扩张 和肺内动-静脉短路开放, 使解剖(真性)分流增加。
性
第一节 病因和发病机制
外呼吸 功能障碍
肺通气 功能障碍
肺换气 功能障碍
一、肺通气障碍
气道狭窄 或阻塞 呼吸中枢抑制
脊髓高 位损伤
脊髓前角 细胞受损
呼吸肌 无力
运动神经受损
胸壁损伤
弹性阻 力增加
(一)限制性通气不足
吸气时肺泡的扩张受限引起的肺泡通气不足。 原因: 1.呼吸肌活动障碍:脑炎、低钾血症
北京燕山中考一《数学》模试 题及答案
患者入院第7天出现了急性呼吸衰竭
呼吸衰竭 (Respiratory Failure):
外呼吸功能严重障碍导致PaO2↓伴有或不伴有 PaCO2↑的病理过程。
外
呼 吸
诊断标准?
呼衰血气诊断标准:
PaO2 < 60mmHg(海平面) 伴有或不伴有 PaCO2 > 50mmHg
吸
呼
气
气
吸气性呼吸困难
(三凹征:胸骨上窝、锁 骨上窝、肋间隙凹陷)
2)中央气道胸内段阻塞(如炎症)
吸
呼
气
气
呼气性呼吸困难
2.外周气道阻塞 是阻塞性通气障碍最常见的临床类型,常见疾
病有慢性支气管炎、肺气肿等。
0 10 20 20 30 20
20 +35 20
正常人用 力呼气
0
10 20 15 20
肺换气 功能障碍
通气血流 比例失调
解剖分流 增加
(一)弥散障碍
弥散速度取决于气体本身物理特性以及肺泡膜面积厚度等
1.常见原因
1)肺泡膜面积减少(减少面积 >50%) 肺不张、肺叶切除等
2)肺泡膜厚度增加 肺水肿、肺纤维化
100 PO2 (mmHg)80
60
40
20
PCO2(mmHg) 46
40
PaO2
RFI= PaO2/FiO2
如吸氧治疗时FiO2>20%,如果PaO2提升不
明显,可导致RFI≤300。
PaCO2>50mmHg? 将导致组织换气障碍
呼吸衰竭的分类
1. 按PCO2是否升高分为: 2. I型呼衰:低氧血症型呼衰 3. II型呼衰:高碳酸血症型呼衰 4. 2.按发病机制:通气性、换气性 5. 3.按病变部位:中枢性、外周性 6. 4.按发生快慢和持续时间:急性、慢
原因: CO2弥散 速度快
PaCO2
0 0.25 0.50 0.75s
图:血液通过肺泡毛细血管时的血气变化
实线为正常人,虚线为肺泡膜增厚患者
2.弥散障碍时的血气变化
PaO2↓ PaCO2 ?(只要肺通气正常,弥散障 碍对其影响不大)
(二)肺泡通气与血流比例失调
• 通气血流比值 ( VA/Q),平均为4 / 5 = 0.8) • 通气血流比值范围 0.6~3.0
性肺浸润。血气:PaO250mmHg, PaCO253mmHg,吸氧后PaO2仍不上升。
1.该患者入克,经抗休 克治疗,尽管血压趋向平稳,但根据7天以后 患者出现呼吸困难,意识障碍,第9天出现紫 绀,气急加重,咳出淡红色泡沫状分泌物,胸 片显示弥散性肺浸润血气:PaO250mmHg, PaCO253mmHg,等表现,提示患者发生了急 性呼吸衰竭。
2.吸氧后为何血气不变化?
该患者吸氧后PaO2仍不上升的可能原因 是由于严重休克导致肺内动-静脉短路开 放,使解剖分流量(真性分流)增加,吸 氧对真性分流的PaO2提高无明显作用。
第二节 呼吸衰竭时主要功能代谢变化
• PaO2 < 60mmHg 代偿反应为主 < 30mmHg 代谢、机能严重紊乱
• PaCO2 > 50mmHg 代偿反应为主 > 80mmHg 代谢机能严重紊乱
1.酸碱平衡及电解质紊乱 酸碱平衡失调:
Ⅰ型呼衰 换气障碍 低氧血症 代谢障碍
代谢性 酸中毒
呼吸中枢+ 肺通气↑
Ⅱ型呼衰 低氧血症
通气障碍 高碳酸血症
代谢障碍
呼吸性 酸中毒
呼吸性 碱中毒
代谢性 酸中毒
1.部分肺泡通气不足
功能性分流 ,又叫静脉血掺杂,常见于慢性阻塞性
肺疾病等。
气道阻塞 限制性通气障碍
肺泡通气不足
血流未减少, 甚至增多
VA/Q
2. 部分肺泡血流不足
• 肺动脉栓塞、肺毛细血管床大量破坏等可使流经该部分 肺泡的血液量减少,VA/Q比可显著大于正常肺泡通气不 能充分被利用,称为死腔样通气。
20
20 25 20
肺气肿患者: 肺泡弹性回缩力 下降;细支气管 肺泡附着点减少
用力呼气等压点 移向小气道
肺气肿患 者用力呼气
呼气性呼吸困难
(三)肺泡通气不足时的血气变化
★肺泡通气不足时: PAO2↓,PACO2↑→ PaO2↓,PaCO2↑
总结:通气障碍可引起Ⅱ型呼衰
二 、肺换气功能障碍
弥散 障碍
?
血 氧
PaO2<60mmHg血 氧饱和度明显降
饱
低,不能满足机体
和
需要!
度
(%)
氧离曲线 PO2(mmHg)
正常人PaO2随年龄、运动及所处海拔高度而 异,成年人在海平面静息时,PaO2的正常范围为: PaO2=(100-0.32×年龄)±5mmHg
当FiO2 (吸入气氧浓度)不是20% 可将呼衰指数 (RFI)作为诊断指标。
