最新二进制练习题----new培训讲学
数制转换练习-答案培训资料

数制转换练习-答案精品文档填空1. 两个8 位二进制数10101011 和01001011 进行逻辑加的结果为11101011 。
2. 十六进制数AB.CH 对应的十进制数字是171.75 。
3. 已知一个带符号整数的补码由两个1 和六个0 组成,则该补码能够表示的最小整数是-127 。
4. 二进制数10111000 和11001010 进行逻辑“与”运算,结果再与10100110 进行逻辑“或者”运算,最终结果的十六进制形式为(10101110 )。
5.Pentium 处理器中的一个16 位带符号整数,如果它的十六进制表示为FEDCH,那末它的十进制值为( -292)。
5. 对两个逻辑值1 施行逻辑加操作的结果是1 。
6. .若A=1100,B=0010,A 与B 运算的结果是1110 ,则其运算可以是算术加,也可以是逻辑加判断1. 每一个十进制整数都可以精确的转换为二进制整数形式。
N2. 一个整数的补码就是其原码除符号位外取反加1 。
Y单选1. 下面关于计算机中定点数与浮点数的一些叙述, 正确的是____B______A. 定点数只能表示纯小数B. 浮点数尾数越长, 数的精度就越高C. 定点数的数值范围一定比浮点数的数值范围大D. 定点数就是用十进制表示的数2. 下列有关" 权值" 表述正确的是____B______A. 权值是指某一数字符号在数的不同位置所表示的值的大小B. 二进制的权值是" 二", 十进制的权值是" 十"精品文档C. 权值就是一个数的数值D. 惟独正数才有权值3. 下列有关" 基数" 表述正确的是____B______A. 基数是指某一数字符号在数的不同位置所表示的值的大小B. 二进制的基数是" 二”,十进制的基数是" 十"C. 基数就是一个数的数值D. 惟独正数才有基数4. 十进制数"13", 用三进制表示为____C______A.lOlB.110C.111D.1125. 下列各数都是五进制数, 其中____B______对应的十进制数是偶数。
二进制练习题

5. 将十进制数180.875分别转换成二进 制、八进制和十六进制数
180 = (10110100)2 0.875=( 0.111)2 180.875 = (10110100.111)2 = (264.7)8 =(B4.E)16
6. 已知x的补码是1011,y的补码是 0010,求x-y的值是多少?
8. 某PC机广告中标有“P4/1.7G/256M/40G” 字样,解释其含义
Pentium 4\1.7G中的1.7G是这种CPU的主频。 内存容量:256M,硬盘容量:40G。
当然,256M也可以理解为显存容量。
9. 若一台显示器中R、G、B分别用3位二进制数来表 示,那么它可以显示多少种不同的颜色?为什么?
在计算机学科中,常常会遇到用二进制、八进制、 十六进制等表示的数据。对于算术表达式 1023-377Q+100H,其运算结果是________。
答案:1024
二进制练习题(12)
已知8位机器码10110100,它是补码时,表示的 十进制真值是___。
答案:-76
二进制练习题(13)
已知521+555=1406,则此种加法是在________下 完成的。
一幅图像的数据量的计算公式是: 图像数据量=水平分辨率×垂直分辨率×像素深
度/8(单位为字节) 2的24次方约等于1600万,所以1600万种颜色
的像素深度为24。 1280*1024*24/8= 3840KB=3.75MB
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!感谢你的观看!
3位二进制最多取8个值(000,001,010,011, 100,101,110,111),R、G、B都有8个值, 按照排列组合计算,最大组合为8*8*8=512种颜 色。
练习1 二进制运算

1.已知[X]补=10011011是定点纯整数,写出X的浮点规格化形式,阶码4位补码,尾数8位原码(尾数)1 1100 101 (阶码)0 1112.将-27/64表示成浮点数规格化形式,阶码3位补码,尾数9位补码(尾数)1 0010 1000 (阶码)1 113.某浮点数字长32位,其中阶码8位,补码表示;尾数24位(含1位数符),,试写出它所表示的十进制真值补码表示。
现有一浮点代码(8C5A3E00)161000 1100 0 101 1010 0011 1110 0000 0000+0.10110100011111×2-1164.将4位有效信息位1001编成CRC校验码,生成多项式X3+X1+X0,写出编码过程,并仿书上表2-6建立出错模式5.试将(-0.1101)用IEEE短实数浮点格式表示出来。
26.已知X=0.1101,Y=-0.1011,用原码一位乘计算X×Y7.已知X=0.1101,Y=-0.1011,用补码一位乘计算X×YX×Y=-0.1000 11118.已知X=-0.01010,Y=-0.01100,用原码加减交替法计算X÷YX÷Y=-0.11010 余数0.01000×2-59.某指令系统指令长12位,每个操作数的地址码长3位,试提出一种分配方案,使指令系统有4条三地址指令,8条二地址指令,180条单地址指令。
10.某计算机指令字长16位,用6位的字段指定操作数地址,若要求有X条双操作数指令,L条无操作数指令,那么这台计算机所能表示的单操作数指令的最大数量是多少?M=(24-X)·26-L/26。
二进制习题2

习题-一、单项选择题2. 下列数中不可能是二进制数的是_____。
A.101101 B.000000C.111111 D.2121213.计算机系统中数据的存储和处理都采用_____。
A.二进制B.十进制C.八进制D.十六进制4.十进制65转换成二进制数为_____。
A.1100000B B.1000000BC.1000001B D.1000010B6.下列各种进制的数据中最小的是_____。
A.101010B B.55QC.2EH D.43D7.将二进制数10000001转换为十进制数应该是_____。
A.127 B.129C.126 D.1288. 下列各种进制的数据中最大的是_____。
A.267Q B.562DC.1FCH D.11001100B9.在计算机中采用二进制,是因为_____。
A.两个状态的系统稳定性好B.物理器件容易实现C.运算法则简单D.上述三个原因都是2、下列逻辑运算中结果正确的是( )A、1·0=1B、0·1=1C、1+0=0D、1+1=13、下列十进制数与二进制数转换结果正确的是( )A、(8)10=(110)2B、(4)10=(1000)2C、(10)10=(1100)2D、(9)10=(1001)2C、每隔一定时间需要刷新D、每次读出后需要刷新二、填空题1.8位二进制可以表示_________________种状态。
2.在4位二进制系统中,1111+1的值为_________。
4.十进制数322的二进制表示是_________。
5.八进制数177Q的十六进制表示是_________。
9.数值8的8位二进制原码为_________,反码为_________,补码为_________。
10.数值-8的8位二进制原码为_________,反码为_________,补码为_________。
1.已知计算机的字长为8位,求十进制数—102的原码、反码和补码。
小学四年级奥数专项练习 36 二进制

专题36 二进制【理论基础】二进制就是只用0和1两数字,在计数与计算时必须“满二进一”,即每两个相同的单位组成一个和它相邻的最高的单位。
二进制的最大特点是:每个数的各个数位上只有0或只有1两种状态。
二进制与十进制之间可以互相转化。
1.将一个二进制数写成十进制数的步骤是:(1)将二进制数的各数位上数字改写成相应的十进制数;(2)将各数位上对应的十进制数求和,所得结果就是相应的十进制数。
将十进制数改写成二进制数的过程,正好相反。
2.十进制数改写成二进制数的常用方法是:除以二倒取余数。
3.二进制数的计算法则:(1)加法法则:0+0=0 0+1=1 1+0=1 1+1=10(2)乘法法则:0×0=0 0×1=0 1×0=0 1×1=1把二进制数110(2)改写成十进制数。
分析与解答:十进制有两个特点:(1)它有十个不同的数字符号;(2)满十进1。
二进制有两个特点:(1)它的数值部分,只需用两个数码0和1来表示;(2)它是“满二进一”。
把二进制数110(2)改写成十进制数,只要把它写成2的幂之和的形式,然后按通常的方法进行计算即可。
110(2)=1×22+1×21+0×20=1×4+1×2+0×1=4+2+0=6练习一把下列二进制数分别改写成十进制数。
(1)100(2)(2)1001(2)(3)1110(2)把十进制数38改写成二进制数。
分析与解答:把十进制数改写成二进制数,可以根据二进制数“满二进一”的原则,用2连续去除这个十进制数,直到商为零为止,把每次所得的余数按相反的顺序写出来,就是所化成的二进制数,这种方法叫做“除以二倒取余数”。
2 38 02 19 (1)2 9 (1)2 4 02 2 01 (1)即:38(10)=100110(2)练习二把下列十进制数分别改写成二进制数。
(1)12(10)(2)15(10)(3)78(10)计算1011(2)+11(2)分析与解答:任何进位制数的运算,都可以根据十进制数的运算法则来进行,做一位数的运算需要有加法表(即加法口诀)。
小学六年级奥数二进制及基应用问题专项强化训练(中难度)

小学六年级奥数二进制及基应用问题专项强化训练(中难度)例题1. 小明拥有一串由0和1组成的二进制数,他希望将这串二进制数转换为十进制数。
如果这串二进制数的第i位上的数字是1,则这个位数的权重是2^(i-1)。
例如,二进制数1101对应的十进制数为13。
请问,二进制数1010对应的十进制数是多少?解析:二进制数1010对应的十进制数可以通过权重求和计算得出。
第一位权重为2^3=8,第二位权重为2^2=4,第三位权重为2^1=2,第四位权重为2^0=1。
所以,十进制数为8+0+2+0=10。
专项练习应用题:2. 小华拥有一串长度为6的二进制数,其中的每一位都是0或1。
他想知道这个二进制数加上10000后的十进制数是多少?3. 班级里有25个学生,老师将每个学生的出勤情况用一串长度为5的二进制数表示,其中1表示出勤,0表示缺席。
请问,出勤学生的二进制数加上10000后的十进制数是多少?4. 小红拥有一串长度为8的二进制数,其中的每一位都是0或1。
她想知道这个二进制数加上10000000后的十进制数是多少?5. 小明有一串长度为7的二进制数,他想将这个二进制数的最高位(最左边的位)变为0。
请问,他应该将这个二进制数加上多少?6. 小华有一串长度为10的二进制数,他想将这个二进制数的最高位(最左边的位)变为1。
请问,他应该将这个二进制数加上多少?7. 小红有一串长度为9的二进制数,她想将这个二进制数的第5位(从右往左数)变为1。
请问,她应该将这个二进制数加上多少?8. 小明拥有一串长度为8的二进制数,其中的每一位都是0或1。
他想将这个二进制数的第4位(从右往左数)变为0。
请问,他应该将这个二进制数加上多少?9. 小红有一串长度为11的二进制数,她想将这个二进制数的第6位(从右往左数)变为0。
请问,她应该将这个二进制数加上多少?10. 小华有一串长度为12的二进制数,他想将这个二进制数的第9位(从右往左数)变为1。
二进制转十进制30道题目

二进制转十进制30道题目一、题目1. 将二进制数101转换为十进制数。
2. 把二进制数1101转换为十进制数。
3. 求二进制数1001对应的十进制数。
4. 二进制数111转换为十进制是多少?5. 将二进制数1010转换为十进制数。
6. 把二进制数11001转换为十进制数。
7. 求二进制数10001对应的十进制数。
8. 二进制数1111转换为十进制是多少?9. 将二进制数10110转换为十进制数。
10. 把二进制数11011转换为十进制数。
11. 求二进制数10011对应的十进制数。
12. 二进制数11101转换为十进制是多少?13. 将二进制数101010转换为十进制数。
14. 把二进制数110001转换为十进制数。
15. 求二进制数100001对应的十进制数。
16. 二进制数11111转换为十进制是多少?17. 将二进制数101110转换为十进制数。
18. 把二进制数110101转换为十进制数。
19. 求二进制数100101对应的十进制数。
20. 二进制数111001转换为十进制是多少?21. 将二进制数1010010转换为十进制数。
22. 把二进制数110011转换为十进制数。
23. 求二进制数100011对应的十进制数。
24. 二进制数111101转换为十进制是多少?25. 将二进制数1011110转换为十进制数。
26. 把二进制数110111转换为十进制数。
27. 求二进制数100111对应的十进制数。
28. 二进制数111011转换为十进制是多少?29. 将二进制数1010110转换为十进制数。
30. 把二进制数1100011转换为十进制数。
二、解析1. 对于二进制数101:- 按位权展开式为1×2^0+0×2^1+1×2^2- 计算得1×1 + 0×2+1×4 = 5。
2. 对于二进制数1101:- 按位权展开式为1×2^0+0×2^1+1×2^2+1×2^3 - 计算得1×1+0×2 + 1×4+1×8=13。
高中计算机练习题及讲解

高中计算机练习题及讲解### 高中计算机练习题及讲解#### 练习题一:二进制转换题目:将十进制数 25 转换为二进制数。
解答:十进制数 25 转换为二进制的过程如下:1. 25 除以 2,商为 12,余数为 1。
2. 12 除以 2,商为 6,余数为 0。
3. 6 除以 2,商为 3,余数为 0。
4. 3 除以 2,商为 1,余数为 1。
5. 1 除以 2,商为 0,余数为 1。
将得到的余数从下到上排列,得到二进制数为 11001。
#### 练习题二:逻辑运算题目:给定逻辑表达式 (A AND B) OR (NOT A AND C),如果 A = 真,B = 假,C = 真,求表达式的值。
解答:根据题目给定的值,我们可以将 A、B、C 的值代入逻辑表达式中:- A = 真- B = 假- C = 真表达式变为:(真 AND 假) OR (NOT 真 AND 真)根据逻辑运算的规则:- 真 AND 假 = 假- NOT 真 = 假- 假 AND 真 = 假所以,表达式的值为:假 OR 假 = 假。
#### 练习题三:排序算法题目:给定一个数组 [5, 3, 8, 4, 2],使用冒泡排序算法对其进行排序。
解答:冒泡排序是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
以下是对给定数组进行冒泡排序的步骤:1. 比较第 1 个和第 2 个元素,交换位置:[3, 5, 8, 4, 2]2. 比较第 2 个和第 3 个元素,不交换:[3, 5, 8, 4, 2]3. 比较第 3 个和第 4 个元素,交换位置:[3, 5, 4, 8, 2]4. 比较第 4 个和第 5 个元素,交换位置:[3, 5, 4, 2, 8]此时完成第 1 轮,接下来重复上述步骤,直到整个数组排序完成。
最终排序结果为:[2, 3, 4, 5, 8]#### 练习题四:数据结构题目:解释栈(Stack)和队列(Queue)的区别。
二进制练习题----new

进制为21
二进制练习题(7)
在微机中,若主存储器旳地址编号为0000H到 7FFFH,则该存储器容量为______。
答案:32 KB
二进制练习题(8)
十进制“-65”在计算机内部用二进制代码 10111110表达,其表达方式为________。
一幅具有真彩色(24位),辨别率为1024*768 旳数字图象,在没有进行数字压缩时,它旳数 据量大约是2.25MB
答案 1024*768*24/8/1024/1024
4. 求十进制算式2*64+2*8+2*2旳运算 成果旳二进制数表达
(10)2*(1000000)2+(10)2*(1000)2+(10)2*(10)2 = (10000000)2+(10000)2+(100)2= (10010100)2
在计算机学科中,经常会遇到用二进制、八进制、 十六进制等表达旳数据。对于算术体现式 1023-377Q+100H,其运算成果是________。
答案:1024
二进制练习题(12)
已知8位机器码10110100,它是补码时,表达旳 十进制真值是___。
答案:-76
二进制练习题(13)
已知521+555=1406,则此种加法是在________下 完毕旳。
(注意用4位二进制表达旳有符号数) 因为x旳补码是1011,原码是-101 所以其十进
制数为-5 而y是正数,所以原码为010 所以其十进制数
为2 十进制数运算:x-y = -5 -2 = -7
7.计算11位补码能够表达旳数值范围
11位补码能够表达旳数值范围 +210 ~ - 210+1 即 [+1024,-1023]
讲解1二进制运算习题讲解

讲解1⼆进制运算习题讲解[例题2.1]码值10000001B,若表⽰⼀个⽆符号数,则该数为27+20=129;若是⼀个带符号数的原码表⽰,则该数为-0000001B=-1;若是⼀个带符号数的补码表⽰,则该数为-1111111B=-127规格化的浮点数浮点数的阶码决定了浮点数的表⽰范围,浮点数的尾数决定了浮点数的表⽰精度?定义:有效尾数占满尾数的所有位即对于⾮0的尾数,规格化尾数应满⾜1/2≤|M|<1原码规格化后:正数0.1×××的形式;负数1.1×××的形式补码规格化后:正数0.1×××的形式;负数1.0×××的形式(-1/2为1.100 0⽐较特殊)浮点数的表⽰范围设阶码m+1位补码表⽰,尾数n+1位补码,规格化溢出定点数:超出字长所表⽰的范围即为溢出浮点数:规格化后,阶码超出机器的最⼤阶码,即为上溢;阶码⼩于机器最⼩阶码,即为下溢。
(不看尾数,只看阶码)⼆进制乘法原码⼀位乘法规则:①被乘数和乘数取绝对值参加运算,符号位单独处理②被乘数取双符号,部分积长度同被乘数,初值为0③从乘数的最低位yn 开始判断,若yn=1,则部分积加上被乘数,然后右移⼀位;若yn=0,部分积加上0,然后右移⼀位。
④重复③,共n次(n次“加-右移)n为⼩数点后数值部分位数?补码⼀位乘法规则(Booth算法):①符号位参加运算,运算的数均以补码表⽰②被乘数取双符号,部分积初值为0③乘数最低位增加⼀位Yn+1,初值为0④逐次⽐较相邻两位,并按下列规则运算Yn (⾼位) Yn+1(低位) 操作0 0 部分积右移1 0 部分积+[-X]补,右移0 1 部分积+[X]补,右移1 1 部分积右移移位按补码右移规则,即复制最⾼位(符号位)⑤按照上述算法作n+1步操作,但最后⼀步不移位(∵补码符号位也是数值⼀部分,故共做n+1次加法,n次右移)[例题2.2]已知X=0.1101,Y=-0.1011,⽤原码⼀位乘计算X×Y解:乘积符号位=1部分积|乘数| 说明00.0000 0.1011 yn=1,则部分积加上被乘数,右移+ 00.110100.1101右移00.0110 1 0.101 yn=1,则部分积加上被乘数,右移+ 00.110101.0011 1右移00.1001 11 0.10 yn=0,则部分积加上0,右移右移00.0100 111 0.1 yn=1,则部分积加上被乘数,右移+ 00.110101.0001 111右移00.1000 1111∴ X×Y=-0.1000 1111[例题2.3]已知X=0.1101,Y=-0.1011,⽤补码⼀位乘计算X×Y 解:[X]补=00.1101,[-X]补=11.0011,[Y]补=1.0101部分积乘数 ynyn+1说明00.0000 1.01010 增加⼀位yn+1=0,ynyn+1=10, 部分积+[-X]补,右移11.001111.0011右移11.1001 1 1.0101 yn yn+1=01, 部分积+[X]补,右移00.11011 00.0110 1 进位1舍去右移00.0011 01 1.010 yn yn+1=10, 部分积+[-X]补,右移11.0011 11.0110 01右移11.1011 001 1.01 yn yn+1=01, 部分积+[X]补,右移00.11011 00.1000 001 进位1舍去右移 00.0100 0001 1.0 yn yn+1=10, 部分积+[-X]补,最后⼀步不右移11.001111.0111 0001∴ [X×Y]补=1.0111 0001 X×Y=-0.1000 1111⼆进制除法原码⼀位除法(不恢复余数法,加减交替法)规则:①符号位不参加运算,并要求|X|<|Y|②先⽤被除数减去除数③若余数为正,商上1,余数左移1位减除数;若余数为负,商上0,余数左移1位加除数④重复③n次(n为数值部分位数),当最后⼀步(第n+1步)余数为负时,需加上|Y|得到正余数[例题2.4]已知X=-0.01010,Y=-0.01100,⽤原码加减交替法计算X÷Y解:同号数相除,得出的商和余数的符号位均为正|X|=0.01010 ,|Y|=0.01100, [-|Y|]补=1.10100被除数(余数) 商说明0.01010-Y 1.10100 第⼀步先减除数1.11110 0 余数为负,商上0,下⼀步“左移-加”左移 1.11100+Y 0.011000.01000 0.1 余数为正,商上1,下⼀步“左移-减”左移 0.10000-Y 1.101000.00100 0.11 余数为正,商上1,下⼀步“左移-减”左移 0.10000-Y 1.101001.11100 0.110 余数为负,商上0,下⼀步“左移-加”左移 1.11100+Y 0.011000.00100 0.1101 余数为正,商上1,下⼀步“左移-减”左移 0.10000-Y 1.101001.11100 0.11010 余数为负,商上0+Y 0.01100 最后⼀步得出的余数为负,加上除数进⾏修正0.01000∴X÷Y=-0.11010 余数0.01000×2-5补码⼀位除法规则:①参加运算的数⽤补码表⽰,符号位参加运算,商、余数均为补码,并⾃带符号②若被除数与除数同号,则减去除数;若被除数与除数异号,则加上除数③若余数与除数同号,商上1,下次左移后做减;若异号,商上0,下次左移后做加④重复③,连同符号位⼀共做n +1次(n 为数值部分位数);商末尾恒置1(末位有误差)浮点数加减运算①对阶:向⼤阶看齐a) 先求Ex ,Ey 之差:△E =Ex -Ey b) 阶码⼩的数尾数右移| △E |位②右移后的尾数相加减③结果规格化④舍⼊⑤判溢:根据阶码判断 [例题2.5]设浮点数字长16位,其中阶码8位,以2为底;尾数8位,规格化。
二进制复习课件

二、进制之间的转换
2、非十进制之间的相互转换
③八进制转二进制
例8:把(10.2) 转成二进制 8
(10.2)8 = (001 000.010) 2
= (1 000.01) 2
二、进制之间的转换
2、非十进制之间的相互转换
④十六进制转二进制
方法: 将每位十六进制码展开为4位 二进制码,再去掉首位的“0”
二、进制之间的转换
2、十进制转非十进制 练习: (1100010.00011) 10 1、(98.12) 2 2、(64.35) (100.26314) 10 8 3、(48.85) 10 (30.D9999) 16
二、进制之间的转换
2、非十进制之间的相互转换
①二进制转八进制
方法: 以小数点为中心,分别向前 向后每三位为一组,不足三位以 “0”补足,转化为1位八进制码
二、进制之间的转换
例6:把(32.6) 转成八进制 10 整数部分: 0 4 32 4 0 小数部分: 0.6×8=4.8 4 0.8×8=6.4 6 0.4×8=3.2 3 0.2×8=1.6 1 0.6×8=4.8 4 (32.6) = 40.46314 ) 10 ( 8
二、进制之间的转换
例7:把(320.2) 转成十六进制 10 整数部分: 0 1 20 320 1 4 0 小数部分: 0.2×16=3.2 3 0.2×16=3.2 3 0.2×16=3.2 3 0.2×16=3.2 3 0.2×16=3.2 3 (320.2) =( 140.33333 ) 10 16
1 0 -1 -2 1 0 -2
(11.01) = 1×2 +1×2 +1×2 2 = ( 3.25 ) 10
二、进制之间的转换
二进制相关(答案在后面)
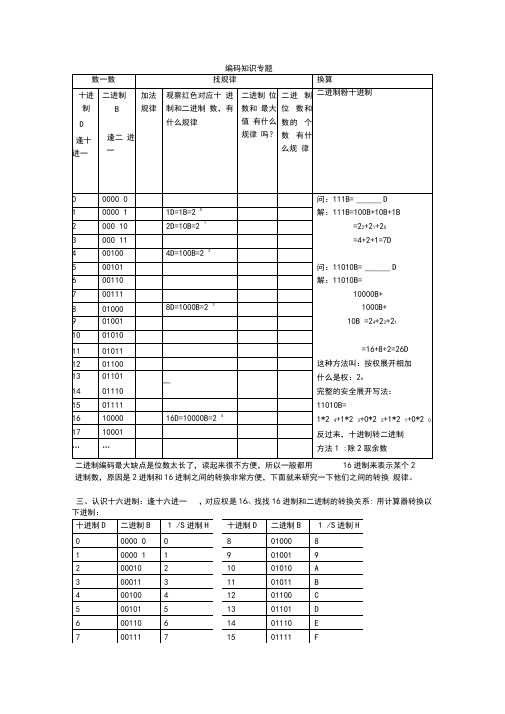
二进制编码最大缺点是位数太长了,读起来很不方便,所以一般都用16进制来表示某个2进制数,原因是2进制和16进制之间的转换非常方便,下面就来研究一下他们之间的转换规律。
三、认识十六进制:逢十六进一,对应权是16n, 找找16进制和二进制的转换关系: 用计算器转换以下进制:A3H= _______ B9H= _______ 1101 0111B=练习:101011B=23D= ____ 23H= 4位二进制数可以从0000到1111,请问四位的二进制数一共有几个? 一个数对应一个信息,那么它可以表示多少个信息?那么8位的二进制数一共有几个,一共能表示多少个信息?8位的二进制数最大值是 111 1111B,请问它对应十进制数是多少?如果问你16位二进制数最大值是多少,你怎么表示最方便? 一、二进制权值,记住什么是权值按10进制来理解,就是对应位数是10的几次方。
比如 28001D 中的8,就是8000的意思,所以是10的3次,那么这个8的权值就是103.那么2进制也是类似的理解。
比如 101100B ,最高位的1就是100000 ,所以这个1的 权值就是2的5次,即25.总结2进制权值2n ,10进制的权值10n , 16进制权值是16n o加法运算规则:2进制满2进1,10进制满 减法运算规则:2进制借1当2,10进制借 1二进制数码在不同的数位上,对应不同的权值,有二进制数111Q 11) £,其中虚线框中红色的"1"对应的权值为2.有二进制数(100111) 2,红色的“ 0”对应位的权值为3AH= ________9BH= _________0111 1101B=B BH每4位二进制数转换成1 位16进制数,当不够 4位时,高位补0。
D=B= B=10进1,16进制满16进11当10,16进制借1当16(A) 23(B) 22(C) 21(D) 20A. 21B. 22C. 23D. 243.二进制数在不同的数位上,对应不同的权值,有二进制数(1011011)2,其中下划线标注的“ 1”对应的权值为 A. 2 B. 16D. 32*F H4.16进制数在不同的数位上,X •应不同的权值,有 16进制数(1011)16,则下划线标注的 的“1”对应的权值为A. 16B. 1C . 162D. 32二、二进制和十进制转换, 16进制转10进制:都是按权展开相加5.下列将二进制数(10011) 2转换成十进制数的算式中,正确的是(C) 1 X 24+0 X23+1 X2,1 X 21+0 X2° (D) 1 X 24+1 X 23+0 X22+0 X 21+1 X 20(A) (1000111) 2 (B) (1110001) 2 (C) (1001100) 2(D) (100001 1)27.【扩展】算式10100B-10D 的结果是()A. 10BB. 1010DC. 10DD. 1011B8 .下列将16进制数(FA91) 16转换成十进制数的算式中,正确的是(A) FX163+A X 162+0 X 161+0 X 160= 15 X 163+10 X 162+0 X 161+0 X 160 (B)FX163+A X 162+9 X 161+1 X 160= 15 X 163+10 X 162+9 X 161+1 X 160(C) FX163+A X 162+9X 161+0 X 160= 15X 163+10 X 162+9 X 161+0 X 160 (D)FX163+0 X 162+0 X 161+1 X 160= 15 X 163+ 0 X 162+0 X 161+1 X 1609 .有一个16进制数FFH,将其转换成二进制和10进制后,下列正确的是: A. 11111111B 和255D B. 11101110B 和 254D C. 11001100B 和253DD. 11001100B 和 252D三、4位二进制先转成10进制数,再对应到对应的1位16进制,如10118=2人3+2人1+2A0=8+2+1=11D=BH,所以就是 16进制数中的 B总结:用8421规则,快速转换成 10进制数,然后对应到 16进制数。
5.3练习册答案

5.3练习册答案问题1:解释什么是二进制数,并给出一个例子。
答案:二进制数是一种数制,它只使用0和1两个数字来表示所有的数值。
例如,十进制中的数字5在二进制中表示为101。
问题2:将十进制数25转换为二进制数。
答案:十进制数25转换为二进制数是11001。
问题3:如果一个二进制数的每一位都是1,这个数在十进制中是多少?答案:如果一个二进制数的每一位都是1,这个数在十进制中是\(2^n - 1\),其中n是二进制数的位数。
问题4:计算以下二进制数的和:1010 + 1101。
答案: 1010 + 1101的二进制和是10111,转换为十进制是23。
问题5:将二进制数10101转换为十进制数。
答案:二进制数10101转换为十进制数是21。
问题6:什么是逻辑运算符,给出AND、OR和NOT的例子。
答案:逻辑运算符用于在布尔逻辑中进行比较和组合。
AND运算符表示两个条件都必须为真时结果才为真;OR运算符表示至少有一个条件为真时结果就为真;NOT运算符表示反转布尔值,如果输入为真则输出为假,反之亦然。
例如:- AND: (True AND False) = False- OR: (True OR False) = True- NOT: NOT(True) = False问题7:编写一个简单的程序,当输入的数字是偶数时打印“Even”,否则打印“Odd”。
答案:```pythonnumber = int(input("Enter a number: "))if number % 2 == 0:print("Even")else:print("Odd")```问题8:解释什么是循环,并给出一个例子。
答案:循环是一种编程结构,它允许代码块重复执行指定次数。
例如,for循环可以用来遍历列表中的每个元素。
问题9:使用while循环打印出1到10的数字。
答案:```pythoncounter = 1while counter <= 10:print(counter)counter += 1```结束语:希望这些答案能帮助你更好地理解5.3练习册中的内容。
01二进制相关(答案在后面)

一、二进制权值,记住什么是权值按10进制来理解,就是对应位数是10的几次方。
比如28001D中的8,就是8000的意思,所以是10的3次,那么这个8的权值就是103.那么2进制也是类似的理解。
比如101100B,最高位的1就是100000,所以这个1的权值就是2的5次,即25.1.二进制数码在不同的数位上,对应不同的权值,有二进制数,其中虚线框中红色的"1"对应的权值为(A)23(B)22 (C)21(D)202.有二进制数(100111)2,红色的“0”对应位的权值为A. 21B. 22C. 23D. 243.二进制数在不同的数位上,对应不同的权值,有二进制数(1011011)2,其中下划线标注的“1”对应的权值为()A.2 B.16 C.8 D.32二、4位二进制转成1位16进制,如1011B=2^3+2^1+2^0=8+2+1=11D=BH,所以就是16进制数中的B4.与十六进制1B6相等的二进制数是A.110100110 B.110110010 C.110110110 D.1101101015.十六进制数2CH转换成二进制数是(A)(100100)2(B)(101100)2(C)(111000)2(D)(111100)26.二进制数(1111010)2转换成十六进制数是A.6AH B.6BH C.7AH D.710H7.二进制数(1011100)2转换成十六进制数是()A. 4CHB. 4DHC. 5CHD. 5EH8.【扩展】算式110B+2H的值是A. 1000BB. 11010BC. 1010HD. 112B三、二进制和十进制转换9.下列将二进制数(10011)2转换成十进制数的算式中,正确的是(A)1×24+1×23+1×22+0×21+0×20(B)1×24+0×23+0×22+1×21+1×20(C)1×24+0×23+1×22+1×21+0×20(D)1×24+1×23+0×22+0×21+1×2010.十进制数71转换成二进制数是(除2取余数)(A)(1000111)2(B)(1110001)2(C)(1001100)2(D)(1000011)211.【扩展】算式10100B-10D的结果是()A.10B B.1010D C.10D D.1011B四、与二进制有关的题型,有多种方法解答。
两种计数原理复习题

两种计数原理复习题计数原理是计算机科学中的重要概念,它涉及到数字的表示、计算和存储。
在这篇文章中,我们将复习两种常见的计数原理,并给出一些相关的练习题,帮助读者加深对这些原理的理解。
一、二进制计数原理二进制计数原理是计算机中最基本的计数原理之一。
在二进制计数系统中,数字只有两个可能的取值,即0和1。
这种计数系统是由计算机中的电子开关状态来表示的,其中关表示0,开表示1。
二进制计数原理的重要性在于它可以通过简单的电子开关操作来实现数字的表示和计算。
练习题1:将十进制数23转换为二进制表示形式。
练习题2:将二进制数1011转换为十进制表示形式。
练习题3:将二进制数1110转换为十六进制表示形式。
二、十进制计数原理十进制计数原理是我们日常生活中最常用的计数原理。
在十进制计数系统中,数字有十个可能的取值,即0到9。
这种计数系统是由人类的十个手指来表示的,因此在我们的日常生活中非常自然和熟悉。
练习题4:将二进制数1101转换为十进制表示形式。
练习题5:将十进制数78转换为二进制表示形式。
练习题6:将十进制数123转换为八进制表示形式。
三、进制转换进制转换是计算机科学中的重要技巧之一。
在实际应用中,我们经常需要将数字在不同的进制之间进行转换。
了解进制转换的原理和方法对于理解计算机中的数值表示和计算非常有帮助。
练习题7:将十六进制数3F转换为二进制表示形式。
练习题8:将八进制数56转换为十进制表示形式。
练习题9:将十进制数156转换为十六进制表示形式。
四、补码计算补码计算是计算机中常用的一种表示负数的方法。
在补码计算中,正数的表示与原码相同,而负数的表示则是将其对应的正数的二进制表示取反后加1。
补码计算的优势在于可以使用相同的加法和减法运算来处理正数和负数。
练习题10:将十进制数-12转换为补码表示形式。
练习题11:将补码表示形式1101转换为十进制数。
练习题12:将补码表示形式101010转换为十进制数。
通过这些练习题,我们可以加深对两种计数原理的理解,并提升在计算机科学中应用这些原理的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二进制练习题(12)
已知8位机器码10110100,它是补码时,表示的 十进制真值是___。
答案:-76
二进制练习题(13)
已知521+555=1406,则此种加法是在________下 完成的。
答案:七进制
1. IP地址分类
IP地址130.24.35.68属于 B 类地址。 考点:进制转换、五类地址的特点(10000010)
制数为-5 而y是正数,所以原码为010 所以其十进制数
为2 十进制数运算:x-y = -5 -2 = -7
7.计算11位补码可以表示的数值范围
11位补码可以表示的数值范围 +210 ~ - 210+1 即 [+1024,-1023]
8. 某PC机广告中标有“P4/1.7G/256M/40G” 字样,解释其含义
有一个数值311,它与十六进制数C9相等,则该 数值是用________表示的。
答案:8进制 3*x2+1*x+1=12*16+9
二进制练习题(10)
十进制数92转换为二进制数和十六进制数分别是 ______ 。
答案:01011100和5C
二进制练习题(11)
在计算机学科中,常常会遇到用二进制、八进制、 十六进制等表示的数据。对于算术表达式 1023-377Q+100H,其运算结果是________。
进制为21
二进制练习题(7)
在微机中,若主存储器的地址编号为0000H到 7FFFH,则该存储器容量为______。
答案:32 KB
二进制练习题(8)
十 进 制 “ -65” 在 计 算 机 内 部 用 二 进 制 代 码 10111110表示,其表示方式为________。
答案:反码
二进制练习题(9)
10. 一幅具有1600万种颜色(真彩色)、分辩率为 1280*1024的数字图像,在没有进行数据压缩时, 它的数据量是多少?
一幅图像的数据量的计算公式是: 图像数据量=水平分辨率×垂直分辨率×像素深
度/8(单位为字节) 2的24次方约等于1600万,所以1600万种颜色
的像素深度为24。 1280*1024*24/8= 3840KB=3.75MB
二进制练习题(5)
混合进制的运算式52-19=33,此三个数进制互不相同 (8,10,16),问:它们的进制分别是什么?
答案
52
19
33
八
十
十六
十
十六
八
对十六 十八来自八十六十
二进制练习题(6)
设有某进制数2*2=10,根据这种规则,十进制 运算3+6的结果写成该进制为多少?
答案 根据2*2=10分析得出该进制为四进制,9表示成四
Pentium 4\1.7G中的1.7G是这种CPU的主频。 内存容量:256M,硬盘容量:40G。
当然,256M也可以理解为显存容量。
9. 若一台显示器中R、G、B分别用3位二进制数来表 示,那么它可以显示多少种不同的颜色?为什么?
3位二进制最多取8个值(000,001,010,011, 100,101,110,111),R、G、B都有8个值, 按照排列组合计算,最大组合为8*8*8=512种颜 色。
180 = (10110100)2 0.875=( 0.111)2 180.875 = (10110100.111)2 = (264.7)8 =(B4.E)16
6. 已知x的补码是1011,y的补码是 0010,求x-y的值是多少?
(注意用4位二进制表示的有符号数) 因为x的补码是1011,原码是-101 所以其十进
二进制练习题(1)
请将十进制数98.36转换为二进制、八进制、 十六进制数。
答案 (98.36)10 =(1100010.01011)2 =(001 100 010.010 110)2 =(142.26)8 =(0110 0010.0101 1000)2 =(62.58)16
二进制练习题(2)
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好! 谢谢!
已知一个汉字的区位码是34 56,请分别写出 其国标码和机内码。
答案 (34 56)区位码---------十进制 = (22 38)区位码------十六进制 =(42 58)国标码-------+20H =(C2 D8)机内码------+80H
区位码+ ( 20H)=国标码 国标码+ ( 80H)=机内码
4. 求十进制算式2*64+2*8+2*2的运算 结果的二进制数表示
(10)2*(1000000)2+(10)2*(1000)2+(10)2*(10)2 = (10000000)2+(10000)2+(100)2= (10010100)2
(148)10=(10010100)2
5. 将十进制数180.875分别转换成二进 制、八进制和十六进制数
区位码+(A0H )=机内码
二进制练习题(3)
若用32*32的点阵表示一个汉字,则要占用多 少字节?
答案
32*32/8=128字节
二进制练习题(4)
十六进制编码:24 79 A5 C7 73 C2 D4 65 24H 中包含几个西文?几个汉字?
答案 24 79 A5 C7 73 C2 D4 65 24 包含西文5个,2个汉字
2. 汉字存储
设16*16点阵表示一个汉字,字库容量为 38400字节,则该字库可存放多少个汉字?
答案:38400*8/(16*16)=1200
3. 图像存储
一幅具有真彩色(24位),分辨率为1024*768 的数字图象,在没有进行数字压缩时,它的数 据量大约是2.25MB
答案 1024*768*24/8/1024/1024
