2014年中考数学二轮专题复习试卷：圆(含答案)

合集下载

精品中考数学二轮复习圆专题复习

中考二轮复习圆专题综合复习题一1.已知⊙ 0的直径AB=40，弦CD ⊥AB 于点E ，且CD=32，则AE 的长为( ) A ．12 8．8 C ．12或28 D ．8或322.如图，将半径为2cm 的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长为（）A 、2cmB 、错误！未找到引用源。

cm C.cm 32D 、错误！未找到引用源。

3.如图，A 、B 、C 、D 是⊙O 上的四个点，AB=AC ，AD 交BC 于点E ，AE=3，ED=4，则AB 的长为（） A.3 B.23 C.21 D.354.如图，直径为10的⊙A 山经过点C(0，5)和点0(0，0)，B 是y 轴右侧⊙A 优弧上一点，则∠OBC 的余弦值为( ) A.12 B.34 C.32D.45 5.如图，以原点O 为圆心的圆交X 轴于A 、B 两点，交y 轴的正半轴于点C ，D 为第一象限内⊙O 上的一点，若∠DAB=20°，则∠OCD= °．6.如图，AB 是半圆O 的直径，以0A 为直径的半圆I 与弦AC 交于点D ，IE ∥AC ，并交OC 于点E ．则下列四个结论：①点D 为AC 的中点；②AO C IOE S S ∆∆=21；③2AC AD = ；④四边形I'DEO 是菱形．其中正确的结论是 _________．（把所有正确的结论的序号都填上）7.如图，在⊙O 中，AB 、AC 是互相垂直的两条弦，OD ⊥AB 于点D ，OE ⊥AC 于点E ，且AB ＝8cm ，AC ＝6cm ，那么⊙O 的半径OA 长为．8.如图，AB 是⊙O 的直径，CD 是⊙O 的弦，AB 、CD 的延长线交于点E ，若AB ＝2DE ，∠B ＝18°，则∠AOC 的度数为_ ．9.如图，AB 是半圆直径，半径OC ⊥AB 于点O ，AD 平分∠CAB 交弧BC 于点D ，连结CD 、OD ，给出以下四个结论：①AC ∥OD ；②OE CE =；③△ODE ∽△ADO ；④AB CE CD ⋅=22．其中正确结论的序号是．10.如图，△ABC 内接于⊙O ，若B ∠＝30°，3AC =，则⊙O 的直径为 .11.如图，在以AB 为直径的半圆中，有一个边长为1的内接正方形CDEF ，则以AC 和BC 的长为两根的一元二次方程是．12.如图，已知O ⊙的半径为1，锐角△ABC 内接于圆O ，BD ⊥AC 于点D ，OM ⊥AB 于点M ，则sin ∠CBD 的值等于（）A.OM 的长B.2OM 的长C.CD 的长D.2CD 的长13.如图，OA 是⊙B 的直径，OA=4，CD 是⊙B 的切线，D 为切点，∠DOC=30°，则点C 的坐标为 15.如图,AB 为⊙O 的直径,AC 为⊙O 的弦,AD 平分∠BAC ，交⊙O 于点D,DE ⊥AC,交AC 的延长线于点E ．（1）判断直线DE 与⊙O 的位置关系，并说明理由；（2）若AE=8，⊙O 的半径为5，求DE 的长．16.已知：如图，在△ABC 中，AB=BC ，D 是AC 中点，BE 平分∠ABD 交AC 于点E ，点O 是AB 上一点，⊙O 过B 、E 两点, 交BD 于点G ，交AB 于点F ．（1）求证：AC 与⊙O 相切；（2）当BD=6，sinC=53时，求⊙O 的半径．AFD OEBG C17.如图，AB 为⊙O 的直径， D 、T 是圆上的两点，且AT 平分∠BAD ，过点T 作AD 延长线的垂线PQ ，垂足为C ．（1）求证：PQ 是⊙O 的切线；（2）若⊙O 的半径为2，3TC =，求弦AD 的长.18.已知：如图，在△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于点D ，过点D 作D E A C ⊥于点E ．（1）请说明DE 是⊙O 的切线；（2）若30B ∠=，AB ＝8，求DE 的长．19如图，点D 是⊙O 的直径CA 延长线上一点，点B 在⊙O 上，且AB=AD=AO ．（1）求证：BD 是⊙O 的切线．（2）若点E 是劣弧BC 上一点,AE 与BC 相交于点F,且△BEF 的面积为8,cos ∠BFA=32，求△ACF 的面积．20.如图，AB 是⊙O 的直径，AB=10，DC 切⊙O 于点C ，AD ⊥DC ，垂足为D ，AD 交⊙O 于点E 。

2014年中考数学专题复习试卷：圆测试题

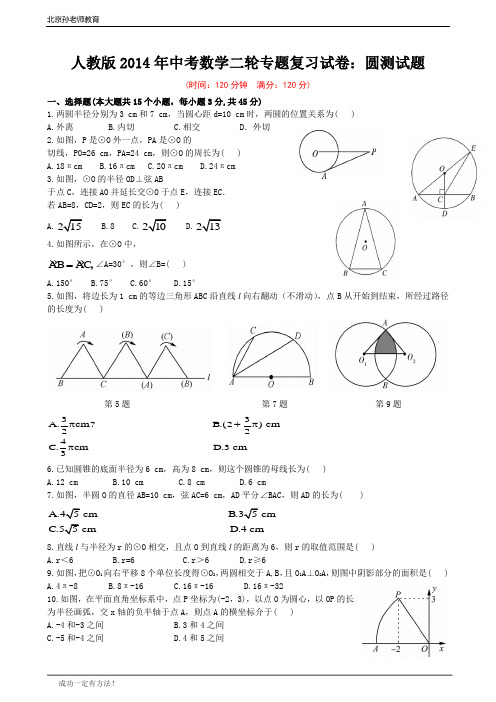
人教版2014年中考数学二轮专题复习试卷：圆测试题(时间：120分钟满分：120分)一、选择题(本大题共15个小题，每小题3分,共45分)1.两圆半径分别为3 cm 和7 cm ，当圆心距d=10 cm 时，两圆的位置关系为( ) A.外离 B.内切 C.相交 D ．外切2.如图，P 是⊙O 外一点，PA 是⊙O 的切线，PO=26 cm ，PA=24 cm ，则⊙O 的周长为( ) A.18πcm B.16πcm C.20πcm D.24πcm 3.如图，⊙O 的半径OD ⊥弦AB于点C ，连接AO 并延长交⊙O 于点E ，连接EC ．若AB=8，CD=2，则EC 的长为( )A.D.4.如图所示，在⊙O 中，ABAC =，∠A=30°，则∠B=( ) A.150° B.75° C.60° D.15°5.如图，将边长为1 cm 的等边三角形ABC 沿直线l 向右翻动（不滑动），点B 从开始到结束，所经过路径的长度为( )第5题第7题第9题33A.cm B.(2) cm 224C.cmD.3 cm 3π +ππ 6.已知圆锥的底面半径为6 cm ，高为8 cm ，则这个圆锥的母线长为( ) A.12 cm B.10 cm C.8 cm D.6 cm7.如图，半圆O 的直径AB=10 cm ，弦AC=6 cm ，AD 平分∠BAC ，则AD 的长为( )D.4 cm8.直线l 与半径为r 的⊙O 相交，且点O 到直线l 的距离为6，则r 的取值范围是( ) A.r ＜6 B.r=6 C.r ＞6 D.r ≥6 9.如图，把⊙O 1向右平移8个单位长度得⊙O 2，两圆相交于A,B ，且O 1A ⊥O 2A ，则图中阴影部分的面积是( ) A.4π-8 B.8π-16 C.16π-16 D.16π-3210.如图，在平面直角坐标系中，点P 坐标为(-2，3)，以点O 为圆心，以OP 的长为半径画弧，交x 轴的负半轴于点A ，则点A 的横坐标介于( ) A.-4和-3之间 B.3和4之间 C.-5和-4之间 D.4和5之间11.如图，P 是⊙O 外一点，PA 是⊙O 的切线，PO=26 cm ，PA=24 cm ，则⊙O 的周长为( ) A.18π cm B.16π cm C.20π cm D.24π cm12.如图7-26，点O 是△ABC 的外心，已知∠ACB=100O ,则劣弧⋂AB 所对的∠AOB 度数为（）。

中考数学专题复习《圆的证明与计算》检测题(含答案)

专题二圆的证明与计算类型一圆基本性质的证明与计算1.如图，⊙O 的半径为5，点P 在⊙O 外，PB 交⊙O 于A 、B 两点，PC 交⊙O 于D 、C 两点． (1)求证：P A ·PB ＝PD ·PC ；(2)若P A ＝454，AB ＝194，PD ＝DC ＋2，求点O 到PC 的距离．第1题图2. 如图，△ABC 是⊙O 的内接三角形，AB ＝AC ，点P 是AB ︵的中点，连接P A ，PB ，PC .(1)如图①，若∠BPC ＝60°，求证：AC ＝3AP ； (2)如图②，若sin ∠BPC ＝2425，求tan ∠P AB 的值．第2题图3. 已知⊙O 中弦AB ⊥弦CD 于E ，tan ∠ACD ＝32. (1)如图①，若AB 为⊙O 的直径，BE ＝8，求AC 的长；(2)如图②，若AB 不为⊙O 的直径，BE ＝4，F 为BC ︵上一点，BF ︵＝BD ︵，且CF ＝7，求AC 的长．第3题图4.如图，△ABC 中，AB ＝AC ，以AB 为直径作⊙O ，交BC 于点D ，交CA 的延长线于点E ，连接AD 、DE .(1)求证：D 是BC 的中点；(2)若 DE ＝3，BD －AD ＝2，求⊙O 的半径； (3)在(2)的条件下，求弦AE 的长．第4题图5.如图，⊙O 的半径为1，A ，P ，B ，C 是⊙O 上的四个点， ∠APC ＝∠CPB ＝60°.(1)判断△ABC 的形状：________；(2)试探究线段P A ，PB ，PC 之间的数量关系，并证明你的结论； (3)当点P 位于AB ︵的什么位置时，四边形APBC 的面积最大？求出最大面积．第5题图备用图类型二与切线有关的证明与计算(一、与三角函数结合1.已知：如图，在△ABC中，AB＝BC，D是AC中点，BE平分∠ABD 交AC于点E，点O是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F.(1)求证：AC与⊙O相切；(2)当BD＝6，sin C＝35时，求⊙O的半径．第1题图2.如图，AB为⊙O的直径，P是BA延长线上一点，PC切⊙O于点C，CG是⊙O的弦，CG⊥AB，垂足为D.(1)求证：∠PCA＝∠ABC；(2)过点A作AE∥PC，交⊙O于点E，交CD于点F，连接BE.若sin ∠P ＝35，CF ＝5，求BE 的长．第2题图3. 如图①，在⊙O 中，直径AB ⊥CD 于点E ，点P 在BA 的延长线上，且满足∠PDA ＝∠ADC .(1)判断直线PD 与⊙O 的位置关系，并说明理由；(2)延长DO 交⊙O 于M (如图②)，当M 恰为BC ︵的中点时，试求DE BE 的值；(3)若P A ＝2，tan ∠PDA ＝12，求⊙O 的半径．第3题图二、与相似三角形结合1.如图，在Rt △ABC 中，∠ACB ＝90°，E 是BC 的中点，以AC 为直径的⊙O 与AB 边交于点D ，连接DE . (1)求证：△ABC ∽△CBD ； (2)求证：直线DE 是⊙O 的切线．第1题图2. 如图，⊙O 的圆心在Rt △ABC 的直角边AC 上，⊙O 经过C 、D 两点，与斜边AB 交于点E ，连接BO 、ED ，有BO ∥ED ，作弦EF ⊥AC 于G ，连接DF .(1)求证：CO ·CD ＝DE ·BO ；(2)若⊙O 的半径为5，sin ∠DFE ＝35，求EF 的长．第2题图3. 如图，在△ABC 中，AB ＝AC ，以AB 为直径作半圆⊙O ，交BC 于点D ，连接AD ，过点D 作DE ⊥AC ，垂足为点E ，交AB 的延长线于点F .(1)求证：EF 是⊙O 的切线；(2)若⊙O 的半径为5，sin ∠ADE ＝45，求BF 的长．第3题图4.如图，在△ABC中，∠C＝90°，以AB上一点O为圆心，OA长为半径的圆恰好与BC相切于点D，分别交AC、AB于点E、F.(1)若∠B＝30°，求证：以A、O、D、E为顶点的四边形是菱形；(2)若AC＝6，AB＝10，连接AD，求⊙O的半径和AD的长．第4题图5.已知Rt△ABC中，AB是⊙O的弦，斜边AC交⊙O于点D，且AD ＝DC，延长CB交⊙O于点E.(1)图①的A、B、C、D、E五个点中，是否存在某两点间的距离等于线段CE的长？请说明理由；(2)如图②，过点E作⊙O的切线，交AC的延长线于点F.①若CF＝CD时，求sin∠CAB的值；②若CF＝aCD(a>0)时，试猜想sin∠CAB的值．(用含a的代数式表示，直接写出结果)第5题图6.已知：如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，OF延长线交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB＝∠AEC.(1)求证：BD是⊙O的切线；(2)求证：CE2＝EH·EA；(3)若⊙O 的半径为5，sin A ＝35，求BH 的长．第6题图7.如图①，△ABC 内接于⊙O ，∠BAC 的平分线交⊙O 于点D ，交BC 于点E (BE ＞EC )，且BD ＝2 3.过点D 作DF ∥BC ，交AB 的延长线于点F .(1)求证：DF 为⊙O 的切线；(2)若∠BAC ＝60°，DE ＝7，求图中阴影部分的面积；(3)若AB AC ＝43，DF ＋BF ＝8，如图②，求BF 的长．第7题图三、与全等三角形结合1.如图，已知PC 平分∠MPN ，点O 是PC 上任意一点，PM 与⊙O 相切于点E ，交PC 于A 、B 两点． (1)求证：PN 与⊙O 相切；(2)如果∠MPC ＝30°，PE ＝23，求劣弧BE ︵的长．第1题图2.如图，已知BC是⊙O的弦，A是⊙O外一点，△ABC为正三角形，D为BC的中点，M是⊙O上一点，并且∠BMC ＝60°.(1)求证：AB是⊙O的切线；(2)若E、F分别是边AB、AC上的两个动点，且∠EDF＝120°，⊙O 的半径为2.试问BE＋CF的值是否为定值，若是，求出这个定值；若不是，请说明理由．第2题图3. 已知：如图，AB是⊙O的直径，C是⊙O上一点，OD⊥AC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接AE.(1)求证：AE与⊙O相切；(2)连接BD，若ED∶DO＝3∶1，OA＝9，求AE的长和tan B的值．第3题图4. 如图，PB为⊙O的切线，B为切点，直线PO交⊙O于点E、F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O 交于点C，连接BC，AF.(1)求证：直线P A为⊙O的切线；(2)试探究线段EF、OD、OP之间的等量关系，并加以证明；(3)若BC＝6，tan∠F＝12，求cos∠ACB的值和线段PE的长．第4题图5. 如图，△ABC 内接于⊙O ，AB 为⊙O 的直径，∠ACB 的平分线CD 交⊙O 于点D ，过点D 作⊙O 的切线PD ，交CA 的延长线于点P ，过点A 作AE ⊥CD 于点E ，过点B 作BF ⊥CD 于点F . (1)求证：PD ∥AB ； (2)求证：DE ＝BF ；(3)若AC ＝6，tan ∠CAB ＝43，求线段PC 的长．第5题图6.如图，点P 是⊙O 外一点，P A 切⊙O 于点A ，AB 是⊙O 的直径，连接OP ，过点B 作BC ∥OP 交⊙O 于点C ，连接AC 交OP 于点D . (1)求证：PC 是⊙O 的切线；(2)若PD ＝163，AC ＝8，求图中阴影部分的面积；(3)在(2)的条件下，若点E 是AB ︵的中点，连接CE ，求CE 的长．第6题图7. 如图①，AB是⊙O的直径，OC⊥AB，弦CD与半径OB相交于点F，连接BD，过圆心O作OG∥BD，过点A作⊙O的切线，与OG 相交于点G，连接GD，并延长与AB的延长线交于点E.(1)求证：GD＝GA；(2)求证：△DEF是等腰三角形；(3)如图②，连接BC，过点B作BH⊥GE，垂足为点H，若BH＝9，⊙O的直径是25，求△CBF的周长．第7题图专题二圆的证明与计算类型一圆基本性质的证明与计算1. (1)证明：如解图，连接AD，BC，∵四边形ABCD内接于⊙O，∴∠P AD＝∠PCB，∠PDA＝∠PBC，∴△P AD ∽△PCB ， ∴P A PD ＝PC PB ， ∴P A ·PB ＝PD ·PC ；(2)解：如解图，连接OD ，过O 点作OE ⊥DC 于点E ， ∵P A ＝454，AB ＝194，PD ＝DC ＋2，∴PB ＝P A ＋AB ＝16，PC ＝PD ＋DC ＝2DC ＋2， ∵P A ·PB ＝PD ·PC ，∴454×16＝(DC ＋2)(2DC ＋2)，解得DC ＝8或DC ＝－11(舍去)， ∴DE ＝12DC ＝4， ∵OD ＝5，∴在Rt △ODE 中，OE ＝OD 2－DE 2＝3，即点O 到PC 的距离为3.2. (1)证明：∵∠BAC 与∠BPC 是同弧所对的圆周角， ∴∠BAC ＝∠BPC ＝60°，又∵AB ＝AC ，∴△ABC 为等边三角形， ∴∠ACB ＝60°， ∵点P 是AB ︵的中点， ∴P A ︵＝PB ︵，∴∠ACP ＝∠BCP ＝12∠ACB ＝30°，而∠APC ＝∠ABC ＝60°， ∴△APC 为直角三角形， ∴tan ∠APC ＝AC AP ， ∴AC ＝AP tan60°＝3AP ；(2)解：连接AO 并延长交PC 于点E ，交BC 于点F ，过点E 作EG ⊥AC 于点G ，连接OC ，BO ，如解图，∵AB ＝AC ， ∴AF ⊥BC ， ∴BF ＝CF ， ∵点P 是AB ︵中点， ∴∠ACP ＝∠PCB ， ∴EG ＝EF .∵∠BPC ＝∠BAC ＝12∠BOC ＝∠FOC ， ∴sin ∠FOC ＝sin ∠BPC ＝2425，设FC ＝24a ，则OC ＝OA ＝25a ，∴OF ＝OC 2－FC 2＝7a ，AF ＝25a ＋7a ＝32a ，在Rt △AFC 中，∵AC 2＝AF 2＋FC 2， ∴AC ＝（32a ）2＋（24a ）2＝40a ， ∵∠EAG ＝∠CAF ， ∴△AEG ∽△ACF ， ∴EG CF ＝AE AC ，又∵EG ＝EF ，AE ＝AF －EF ，第2题解图∴EG 24a ＝32a －EG 40a ，解得EG ＝12a ，在Rt △CEF 中，tan ∠ECF ＝EF FC ＝12a 24a ＝12， ∵∠P AB ＝∠PCB ，∴tan ∠P AB ＝tan ∠PCB ＝tan ∠ECF ＝12. 3. 解：(1)如解图①，连接BD ， ∵直径AB ⊥弦CD 于点E ， ∴CE ＝DE ，∵∠ACD 与∠ABD 是同弧所对的圆周角， ∴∠ACD ＝∠ABD ， ∴tan ∠ABD ＝tan ∠ACD ＝32， ∴ED EB ＝AE CE ＝32，即ED 8＝32， ∴ED ＝12， ∴CE ＝ED ＝12，又∵AE ＝32CE ＝18， ∴AC ＝AE 2＋CE 2＝613；(2)连接CB ，过B 作BG ⊥CF 于G ，如解图②， ∵BF ︵＝BD ︵， ∴∠BCE ＝∠BCG ，在△CEB 和△CGB 中第3题解图①⎩⎪⎨⎪⎧∠BCE ＝∠BCG ∠BEC ＝∠BGC BC ＝BC， ∴△CEB ≌△CGB (AAS)， ∴BE ＝BG ＝4，∵四边形ACFB 内接于⊙O ， ∴∠A ＋∠CFB ＝180°，又∵∠CFB ＋∠BFG ＝180°， ∴∠BFG ＝∠A ， ∵∠FGB ＝∠AEC ＝90°， ∴△BFG ∽△CAE ， ∴FG BG ＝AE CE ＝32， ∴FG ＝32BG ＝6， ∴CE ＝CG ＝13， ∴AE ＝32CE ＝392，∴AC ＝AE 2＋CE 2＝13213. 4. (1)证明：∵AB 是⊙O 的直径， ∴∠ADB ＝90°，即AD ⊥BC ， ∵AB ＝AC ，∴等腰△ABC ，AD 为BC 边上的垂线， ∴BD ＝DC ， ∴D 是BC 的中点； (2)解：∵AB ＝AC ，∴∠ABC ＝∠C ，∵∠ABC 和∠AED 是同弧所对的圆周角， ∴∠ABC ＝∠AED ， ∴∠AED ＝∠C ， ∴CD ＝DE ＝3， ∴BD ＝CD ＝3， ∵BD －AD ＝2， ∴AD ＝1，在Rt △ABD 中，由勾股定理得AB 2＝BD 2＋AD 2＝32＋12＝10， ∴AB ＝10，∴⊙O 的半径＝12AB ＝102； (3)解：如解图，连接BE ， ∵AB ＝10， ∴AC ＝10，∵∠ADC ＝∠BEA ＝90°，∠C ＝∠C ， ∴△CDA ∽△CEB ， ∴AC BC ＝CD CE ，由(2)知BC ＝2BD ＝6，CD ＝3， ∴106＝3CE ， ∴CE ＝9510，∴AE ＝CE －AC ＝9510－10＝4510. 5. 解：(1)等边三角形．第4题解图【解法提示】∵∠APC ＝∠CPB ＝60°，又∵∠BAC 和∠CPB 是同弧所对的圆周角，∠ABC 和∠APC 是同弧所对的圆周角，∴∠BAC ＝∠CPB ＝60°，∠ABC ＝∠APC ＝60°， ∴∠BAC ＝∠ABC ＝60°， ∴AC ＝BC ，又∵有一个角是60°的等腰三角形是等边三角形， ∴△ABC 是等边三角形． (2)P A ＋PB ＝PC .证明如下：如解图①，在PC 上截取PD ＝P A ，连接AD ， ∵∠APC ＝60°， ∴△P AD 是等边三角形， ∴P A ＝AD ＝PD ，∠P AD ＝60°，又∵∠BAC ＝60°， ∴∠P AB ＝∠DAC ，在△P AB 和△DAC 中， ∵⎩⎪⎨⎪⎧AP ＝AD ∠P AB ＝∠DAC ，AB ＝AC ∴△P AB ≌△DAC (SAS)， ∴PB ＝DC ， ∵PD ＋DC ＝PC ， ∴P A ＋PB ＝PC ，(3)当点P 为AB ︵的中点时，四边形APBC 的面积最大．理由如下：如解图②，过点P 作PE ⊥AB ，垂足为E ，第5题解图①第5题解图②过点C 作CF ⊥AB ，垂足为F ， ∵S △P AB ＝12AB ·PE ，S △ABC ＝12AB ·CF ， ∴S 四边形APBC ＝12AB ·(PE ＋CF )．当点P 为AB ︵的中点时，PE ＋CF ＝PC ，PC 为⊙O 的直径，此时四边形APBC 的面积最大，又∵⊙O 的半径为1，∴其内接正三角形的边长AB ＝ 3 ， ∴四边形APBC 的最大面积为12×2×3＝ 3 . 类型二与切线有关的证明与计算一、与三角函数结合针对演练1. (1)证明：连接OE ，如解图， ∵AB ＝BC 且D 是AC 中点， ∴BD ⊥AC ， ∵BE 平分∠ABD ， ∴∠ABE ＝∠DBE ， ∵OB ＝OE ， ∴∠OBE ＝∠OEB ， ∴∠OEB ＝∠DBE ， ∴OE ∥BD ，第1题解图∵BD ⊥AC ， ∴OE ⊥AC ， ∵OE 为⊙O 半径， ∴AC 与⊙O 相切；(2)解：∵BD ＝6，sin C ＝35，BD ⊥AC ， ∴BC ＝BDsin C ＝10， ∴AB ＝BC ＝10.设⊙O 的半径为r ，则AO ＝10－r ， ∵AB ＝BC ， ∴∠C ＝∠A ， ∴sin A ＝sin C ＝35， ∵AC 与⊙O 相切于点E ， ∴OE ⊥AC ，∴sin A ＝OE OA ＝r 10－r ＝35，∴r ＝154，即⊙O 的半径是154.2. (1)证明：连接OC ，如解图， ∵PC 切⊙O 于点C ， ∴OC ⊥PC ， ∴∠PCO ＝90°， ∴∠PCA ＋∠OCA ＝90°， ∵AB 为⊙O 的直径，第2题解图∴∠ACB ＝90°， ∴∠ABC ＋∠OAC ＝90°， ∵OC ＝OA ， ∴∠OCA ＝∠OAC ， ∴∠PCA ＝∠ABC ； (2)解：∵AE ∥PC ， ∴∠PCA ＝∠CAF ， ∵AB ⊥CG ， ∴AC ︵＝AG ︵， ∴∠ACF ＝∠ABC ， ∵∠PCA ＝∠ABC ， ∴∠ACF ＝∠CAF ， ∴CF ＝AF ， ∵CF ＝5， ∴AF ＝5， ∵AE ∥PC ， ∴∠F AD ＝∠P ， ∵sin ∠P ＝35， ∴sin ∠F AD ＝35，在Rt △AFD 中，AF ＝5，sin ∠F AD ＝35， ∴FD ＝3，AD ＝4， ∴CD ＝CF ＋FD ＝8，在Rt △OCD 中，设OC ＝r ， ∴r 2＝(r －4)2＋82，∴r ＝10， ∴AB ＝2r ＝20， ∵AB 为⊙O 的直径， ∴∠AEB ＝90°，在Rt △ABE 中，sin ∠EAD ＝35， ∴BE AB ＝35， ∵AB ＝20， ∴BE ＝12.3. 解：(1)直线PD 与⊙O 相切，理由如下：如解图①，连接DO ，CO ， ∵∠PDA ＝∠ADC ， ∴∠PDC ＝2∠ADC ， ∵∠AOC ＝2∠ADC ， ∴∠PDC ＝∠AOC ， ∵直径AB ⊥CD 于点E ， ∴∠AOD ＝∠AOC ， ∴∠PDC ＝∠AOD ， ∵∠AOD ＋∠ODE ＝90°， ∴∠PDC ＋∠ODE ＝90°， ∴OD ⊥PD ， ∵OD 是⊙O 的半径， ∴直线PD 与⊙O 相切； (2)如解图②，连接BD ， ∵M 恰为BC ︵的中点，第3题解图①∴∠CDM ＝∠BDM ， ∵OD ＝OB ， ∴∠BDM ＝∠DBA ， ∴∠CDM ＝∠DBA ， ∵直线PD 与⊙O 相切， ∴∠PDA ＋∠ADO ＝90°，又∵AB 是⊙O 的直径，∴∠ADB ＝90°，即∠ADO ＋∠BDM ＝90°， ∴∠PDA ＝∠BDM ， ∴∠PDA ＝∠DBA ＝∠CDM ，又∵∠PDA ＝∠ADC ， ∴∠PDM ＝3∠CDM ＝90°， ∴∠CDM ＝30°， ∴∠DBA ＝30°， ∴DE BE ＝tan30°＝33； (3)如解图③，∵tan ∠PDA ＝12，∠PDA ＝∠ADC ， ∴AE DE ＝12，即DE ＝2AE ，在Rt △DEO 中，设⊙O 的半径为r ， DE 2＋EO 2＝DO 2， ∴(2AE )2＋(r －AE )2＝r 2，解得r ＝52AE ，在Rt △PDE 中，DE 2＋PE 2＝PD 2，第3题解图②第3题解图③∴(2AE )2＋(2＋AE )2＝PD 2， ∵直线PD 与⊙O 相切，连接BD ，由(2)知∠PDA ＝∠DBA ，∠P ＝∠P ， ∴△P AD ∽△PDB ， ∴PD PB ＝P A PD ，∴PD 2＝P A ·PB ，即PD 2＝2×(2＋2r )， ∴(2AE )2＋(2＋AE )2＝2×(2＋2r )，化简得5AE 2＋4AE ＝4r ， ∵r ＝52AE ，解得r ＝3. 即⊙O 的半径为3. 二、与相似三角形结合针对演练1. 证明：(1)∵AC 为⊙O 的直径， ∴∠ADC ＝90°， ∴∠CDB ＝90°，又∵∠ACB ＝90°， ∴∠ACB ＝∠CDB ，又∵∠B ＝∠B ， ∴△ABC ∽△CBD ； (2)连接DO ，如解图，∵∠BDC ＝90°，E 为BC 的中点， ∴DE ＝CE ＝BE ， ∴∠EDC ＝∠ECD ，第1题解图又∵OD ＝OC ， ∴∠ODC ＝∠OCD ，而∠OCD ＋∠DCE ＝∠ACB ＝90°， ∴∠EDC ＋∠ODC ＝90°，即∠EDO ＝90°， ∴DE ⊥OD ， ∵OD 为⊙O 的半径， ∴DE 与⊙O 相切．2. (1)证明：连接CE ，如解图， ∵CD 为⊙O 的直径， ∴∠CED ＝90°， ∵∠BCA ＝90°， ∴∠CED ＝∠BCO ， ∵BO ∥DE ， ∴∠BOC ＝∠CDE ， ∴△CBO ∽△ECD ， ∴CO DE ＝BO CD ， ∴CO ·CD ＝DE ·BO ；(2)解：∵∠DFE ＝∠ECO ，CD ＝2·OC ＝10，∴在Rt △CDE 中，ED ＝CD ·sin ∠ECO ＝CD ·sin ∠DFE ＝ 10×35＝6，∴CE ＝CD 2－ED 2＝102－62＝8，在Rt △CEG 中，EG CE ＝sin ∠ECG ＝35， ∴EG ＝35×8＝245，第2题解图根据垂径定理得：EF ＝2EG ＝485. 3. (1)证明：如解图，连接OD ， ∵AB 是⊙O 的直径， ∴∠ADB ＝90°， ∵AB ＝AC ，∴AD 垂直平分BC ，即DC ＝DB ， ∴OD 为△BAC 的中位线， ∴OD ∥AC . 而DE ⊥AC ， ∴OD ⊥DE ， ∵OD 是⊙O 的半径， ∴EF 是⊙O 的切线；(2)解：∵∠DAC ＝∠DAB ，且∠AED ＝∠ADB ＝90°， ∴∠ADE ＝∠ABD ，在Rt △ADB 中，sin ∠ADE ＝sin ∠ABD ＝AD AB ＝45，而AB ＝10， ∴AD ＝8，在Rt △ADE 中，sin ∠ADE ＝AE AD ＝45， ∴AE ＝325， ∵OD ∥AE ， ∴△FDO ∽△FEA ，∴OD AE ＝FO F A ，即5325＝BF ＋5BF ＋10，第3题解图∴BF ＝907.4. (1)证明：如解图①，连接OD 、OE 、ED . ∵BC 与⊙O 相切于点D ， ∴OD ⊥BC ，∴∠ODB ＝90°＝∠C ， ∴OD ∥AC ， ∵∠B ＝30°， ∴∠A ＝60°， ∵OA ＝OE ，∴△AOE 是等边三角形， ∴AE ＝AO ＝OD ，∴四边形AODE 是平行四边行， ∵OA ＝OD ，∴平行四边形AODE 是菱形； (2)解：设⊙O 的半径为r . ∵OD ∥AC ， ∴△OBD ∽△ABC ，∴OD AC ＝OBAB ，即10r ＝6(10－r )．解得r ＝154， ∴⊙O 的半径为154.如解图②，连接OD 、DF 、AD . ∵OD ∥AC ， ∴∠DAC ＝∠ADO ，第4题解图①∵OA ＝OD ， ∴∠ADO ＝∠DAO ， ∴∠DAC ＝∠DAO ， ∵AF 是⊙O 的直径， ∴∠ADF ＝90°＝∠C ， ∴△ADC ∽△AFD ， ∴AD AC ＝AF AD ， ∴AD 2＝AC ·AF ，∵AC ＝6，AF ＝154×2＝152， ∴AD 2＝152×6＝45，∴AD ＝45＝3 5.(9分) 5. 解：(1)存在，AE ＝CE . 理由如下：如解图①，连接AE ，ED ， ∵AC 是△ABC 的斜边， ∴∠ABC ＝90°， ∴AE 为⊙O 的直径， ∴∠ADE ＝90°，又∵D 是AC 的中点， ∴ED 为AC 的中垂线， ∴AE ＝CE ；(2)①如解图②，∵EF 是⊙O 的切线， ∴∠AEF ＝90°.第5题解图①由(1)可知∠ADE＝90°，∴∠AED＋∠EAD＝90°，∵∠AED＋∠DEF＝90°，∴∠EAD＝∠DEF.又∵∠ADE＝∠EDF＝90°∴△AED∽△EFD，∴ADED＝EDFD，∴ED2＝AD·FD.又∵AD＝DC＝CF，∴ED2＝2AD·AD＝2AD2，在Rt△AED中，∵AE2＝AD2＋ED2＝3AD2，由(1)知∠AED＝∠CED，又∵∠CED＝∠CAB，∴∠AED＝∠CAB，∴sin∠CAB＝sin∠AED＝ADAE＝13＝33.②sin∠CAB＝a＋2 a＋2.【解法提示】由(2)中的①知ED2＝AD·FD，∵CF＝aCD(a＞0)，∴CF＝aCD＝aAD，∴ED2＝AD·DF＝AD(CD＋CF)＝AD(AD＋aAD)＝(a＋1)AD2，在Rt△AED中，AE2＝AD2＋ED2＝(a＋2)AD2，∴sin ∠CAB ＝sin ∠AED ＝ADAE ＝1a ＋2＝a ＋2a ＋2. 6. (1)证明：∵∠ODB ＝∠AEC ，∠AEC ＝∠ABC ， ∴∠ODB ＝∠ABC ， ∵OF ⊥BC ， ∴∠BFD ＝90°，∴∠ODB ＋∠DBF ＝90°， ∴∠ABC ＋∠DBF ＝90°，即∠OBD ＝90°， ∴BD ⊥OB ， ∵OB 为⊙O 的半径， ∴BD 是⊙O 的切线；(2)证明：连接AC ，如解图①所示： ∵OF ⊥BC ， ∴BE ︵＝CE ︵， ∴∠ECH ＝∠CAE ， ∵∠HEC ＝∠CEA ， ∴△CEH ∽△AEC ， ∴CE EH ＝EA CE ， ∴CE 2＝EH ·EA ；(3)解：连接BE ，如解图②所示： ∵AB 是⊙O 的直径， ∴∠AEB ＝90°，∵⊙O 的半径为5，sin ∠BAE ＝35，第6题解图①第6题解图②∴AB ＝10，BE ＝AB ·sin ∠BAE ＝10×35＝6，在Rt △AEB 中，EA ＝AB 2－BE 2＝102－62＝8， ∵BE ︵＝CE ︵， ∴BE ＝CE ＝6， ∵CE 2＝EH ·EA ， ∴EH ＝CE 2EA ＝628＝92，在Rt △BEH 中，BH ＝BE 2＋EH 2＝62＋（92）2＝152.7. (1)证明：连接OD ，如解图①， ∵AD 平分∠BAC 交⊙O 于D ， ∴∠BAD ＝∠CAD ， ∴BD ︵＝CD ︵， ∴OD ⊥BC ， ∵BC ∥DF ， ∴OD ⊥DF ， ∴DF 为⊙O 的切线；(2)解：连接OB ，连接OD 交BC 于P ，作BH ⊥DF 于H ，如解图①，∵∠BAC ＝60°，AD 平分∠BAC ， ∴∠BAD ＝30°，∴∠BOD ＝2∠BAD ＝60°，又∵OB ＝OD ，∴△OBD 为等边三角形， ∴∠ODB ＝60°，OB ＝BD ＝23，第7题解图①∴∠BDF ＝30°， ∵BC ∥DF ， ∴∠DBP ＝30°，在Rt △DBP 中，PD ＝12BD ＝3，PB ＝3PD ＝3，在Rt △DEP 中， ∵PD ＝3，DE ＝7，∴PE ＝（7）2－（3）2＝2， ∵OP ⊥BC ， ∴BP ＝CP ＝3，∴CE ＝CP －PE ＝3－2＝1，易证得△BDE ∽△ACE ， ∴BE AE ＝DE CE ，即5AE ＝71， ∴AE ＝577. ∵BE ∥DF ， ∴△ABE ∽△AFD ，∴BE DF ＝AE AD ，即5DF ＝5771277，解得DF ＝12，在Rt △BDH 中，BH ＝12BD ＝3， ∴S 阴影＝S △BDF －S 弓形BD ＝S △BDF －(S 扇形BOD －S △BOD )＝12·12·3－60·π·（23）2360＋34·(23)2＝93－2π；(7分)(3)解：连接CD ，如解图②，由AB AC ＝43可设AB ＝4x ，AC ＝3x ，BF ＝y ， ∵BD ︵＝CD ︵， ∴CD ＝BD ＝23， ∵DF ∥BC ，∴∠F ＝∠ABC ＝∠ADC ， ∴∠FDB ＝∠DBC ＝∠DAC ， ∴△BFD ∽△CDA ， ∴BD AC ＝BF CD ，即233x ＝y 23，∴xy ＝4，∵∠FDB ＝∠DBC ＝∠DAC ＝∠F AD ，而∠DFB ＝∠AFD ， ∴△FDB ∽△F AD ， ∴DF AF ＝BF DF ， ∵DF ＋BF ＝8， ∴DF ＝8－BF ＝8－y ， ∴8－y y ＋4x ＝y 8－y ，整理得：16－4y ＝xy ， ∴16－4y ＝4，解得y ＝3，即BF 的长为3.(10分) 三、与全等三角形结合第7题解图②针对演练1. (1)证明：连接OE ，过点O 作OF ⊥PN ，如解图所示， ∵PM 与⊙O 相切， ∴OE ⊥PM ，∴∠OEP ＝∠OFP ＝90°， ∵PC 平分∠MPN ， ∴∠EPO ＝∠FPO ，在△PEO 和△PFO 中， ⎩⎪⎨⎪⎧∠EPO ＝∠FPO ∠OEP ＝∠OFP OP ＝OP， ∴△PEO ≌△PFO (AAS)， ∴OF ＝OE ，∴OF 为圆O 的半径且OF ⊥PN, 则PN 与⊙O 相切；(2)解：在Rt △EPO 中，∠MPC ＝30°，PE ＝23， ∴∠EOP ＝60°，OE ＝PE ·tan30°＝2， ∴∠EOB ＝120°，则劣弧BE ︵的长为120π×2180＝4π3.2. (1)证明：如解图①，连接BO 并延长交⊙O 于点N ，连接CN ， ∵∠BMC ＝60°， ∴∠BNC ＝60°， ∵∠BNC ＋∠NBC ＝90°， ∴∠NBC ＝30°，又∵△ABC 为等边三角形，第1题解图∴∠BAC ＝∠ABC ＝∠ACB ＝60°， ∴∠ABN ＝30°＋60°＝90°， ∴AB ⊥BO ，即AB 为⊙O 的切线．(2)解：BE ＋CF ＝3，是定值．理由如下：如解图②，连接D 与AC 的中点P ， ∵D 为BC 中点， ∴AD ⊥BC ， ∴PD ＝PC ＝12AC ，又∵∠ACB ＝60°，∴PD ＝PC ＝CD ＝BD ＝12AC ， ∴∠DPF ＝∠PDC ＝60°， ∴∠PDF ＋∠FDC ＝60°，又∵∠EDF ＝120°， ∴∠BDE ＋∠FDC ＝60°， ∴∠PDF ＝∠BDE ，在△BDE 和△PDF 中， ⎩⎪⎨⎪⎧∠EBD ＝∠DPF BD ＝PD∠BDE ＝∠PDF， ∴△BDE ≌△PDF (ASA)， ∴BE ＝PF ，∴BE ＋CF ＝PF ＋CF ＝CP ＝BD ， ∵OB ⊥AB ，∠ABC ＝60°，第2题解图②∴∠OBC ＝30°，又∵OB ＝2，∴BD ＝OB ·cos30°＝2×32＝3，即BE ＋CF ＝ 3.3. (1)证明：连接OC ，如解图①， ∵OD ⊥AC ，OC ＝OA ， ∴∠AOD ＝∠COD . 在△AOE 和△COE 中， ⎩⎪⎨⎪⎧OA ＝OC ∠AOE ＝∠COE OE ＝OE， ∴△AOE ≌△COE (SAS)， ∴∠EAO ＝∠ECO . 又∵EC 是⊙O 的切线， ∴∠ECO ＝90°， ∴∠EAO ＝90°. ∴AE 与⊙O 相切；(2)解：设DO ＝t ，则DE ＝3t ，EO ＝4t ，在△EAO 和△ADO 中，⎩⎪⎨⎪⎧∠EOA ＝∠AOD ∠EAO ＝∠ADO， ∴△EAO ∽△ADO ， ∴AO DO ＝EO AO ，即9t ＝4t 9， ∴t ＝92，即EO ＝18.第3题解图①∴AE ＝EO 2－AO 2＝182－92＝93；延长BD 交AE 于点F ，过O 作OG ∥AE 交BD 于点G ，如解图②， ∵OG ∥AE ， ∴∠FED ＝∠GOD 又∵∠EDF ＝∠ODG ， ∴△EFD ∽△OGD ， ∴EF OG ＝ED OD ＝31，即EF ＝3GO . 又∵O 是AB 的中点， ∴AF ＝2GO ，∴AE ＝AF ＋FE ＝5GO ， ∴5GO ＝93， ∴GO ＝935， ∴AF ＝1835， ∴tan B ＝AF AB ＝35.4. (1)证明：如解图，连接OB ， ∵PB 是⊙O 的切线， ∴∠PBO ＝90°，∵OA ＝OB ，BA ⊥PO 于点D ， ∴AD ＝BD ，∠POA ＝∠POB ，又∵PO ＝PO ，∴△P AO ≌△PBO (SAS)， ∴∠P AO ＝∠PBO ＝90°，第3题解图②第4题解图∴OA ⊥P A ，∴直线P A 为⊙O 的切线；(2)解：线段EF 、OD 、OP 之间的等量关系为EF 2＝4OD ·OP . 证明：∵∠P AO ＝∠PDA ＝90°，∴∠OAD ＋∠AOD ＝90°，∠OP A ＋∠AOP ＝90°，∴∠OAD ＝∠OP A ，∴△OAD ∽△OP A ，∴ OD OA ＝OA OP ，即OA 2＝OD ·OP ，又∵EF ＝2OA ，∴EF 2＝4OD ·OP ；(3)解：∵OA ＝OC ，AD ＝BD ，BC ＝6，∴OD ＝12BC ＝3，设AD ＝x ，∵tan ∠F ＝12，∴FD ＝2x ，OA ＝OF ＝FD －OD ＝2x －3，在Rt △AOD 中，由勾股定理，得(2x －3)2＝x 2＋32，解之得，x 1＝4，x 2＝0(不合题意，舍去)，∴AD ＝4，OA ＝2x －3＝5，∵AC 是⊙O 直径，∴∠ABC ＝90°，又∵AC ＝2OA ＝10，BC ＝6，∴ cos ∠ACB ＝610＝35.∵OA 2＝OD ·OP ，∴3(PE ＋5)＝25，∴PE ＝103.5. (1)证明：连接OD ，如解图，∵AB 为⊙O 的直径，∴∠ACB ＝90°，∵∠ACB 的平分线交⊙O 于点D ，∴∠ACD ＝∠BCD ＝45°，∴∠DAB ＝∠ABD ＝45°，∴△DAB 为等腰直角三角形，∴DO ⊥AB ，∵PD 为⊙O 的切线，∴OD ⊥PD ，∴PD ∥AB ；(2)证明：∵AE ⊥CD 于点E ，BF ⊥CD 于点F ，∴AE ∥BF ，∴∠FBO ＝∠EAO ，∵△DAB 为等腰直角三角形，∴∠EDA ＋∠FDB ＝90°，∵∠FBD ＋∠FDB ＝90°，∴∠FBD ＝∠EDA ，在△FBD 和△EDA 中，⎩⎪⎨⎪⎧∠BFD ＝∠DEA ∠FBD ＝∠EDA BD ＝DA， ∴△FBD ≌△EDA (AAS)，∴DE ＝BF ；第5题解图(3)解：在Rt △ACB 中，∵AC ＝6，tan ∠CAB ＝43，∴BC ＝6×43＝8，∴AB ＝AC 2＋BC 2＝62＋82＝10，∵△DAB 为等腰直角三角形，∴AD ＝AB 2＝52， ∵AE ⊥CD ，∴△ACE 为等腰直角三角形，∴AE ＝CE ＝AC 2＝62＝32，在Rt △AED 中，DE ＝AD 2－AE 2＝（52）2－（32）2＝42，∴CD ＝CE ＋DE ＝32＋42＝72，∵AB ∥PD ，∴∠PDA ＝∠DAB ＝45°，∴∠PDA ＝∠PCD ，又∵∠DP A ＝∠CPD ，∴△PDA ∽△PCD ，∴PD PC ＝P A PD ＝AD DC ＝5272＝57， ∴P A ＝57PD ，PC ＝75PD ，又∵PC ＝P A ＋AC ，∴57PD ＋6＝75PD ，解得PD ＝354，∴PC ＝57PD ＋6＝57×354＋6＝254＋6＝494.6. (1)证明：如解图①，连接OC ，∵P A 切⊙O 于点A ，∴∠P AO ＝90°，∵BC ∥OP ，∴∠AOP ＝∠OBC ，∠COP ＝∠OCB ，∵OC ＝OB ，∴∠OBC ＝∠OCB ，∴∠AOP ＝∠COP ，在△P AO 和△PCO 中，⎩⎪⎨⎪⎧OA ＝OC ∠AOP ＝∠COP OP ＝OP， ∴△P AO ≌△PCO (SAS)，∴∠PCO ＝∠P AO ＝90°，∴OC ⊥PC ，∵OC 为⊙O 的半径，∴PC 是⊙O 的切线；(2)解：由(1)得P A ，PC 都为圆的切线，∴P A ＝PC ，OP 平分∠APC ，∠ADO ＝∠P AO ＝90°， ∴∠P AD ＋∠DAO ＝∠DAO ＋∠AOD ，又∵∠ADP ＝∠ADO ，∴∠P AD ＝∠AOD ，∴△ADP ∽△ODA ，∴AD PD ＝DO AD ，第6题解图①∴AD 2＝PD ·DO ，∵AC ＝8，PD ＝163， ∴AD ＝12AC ＝4，OD ＝3，在Rt △ADO 中，AO ＝AD 2＋OD 2＝5，由题意知OD 为△ABC 的中位线，∴BC ＝6，AB ＝BC 2＋AC 2＝10.∴S 阴影＝12S ⊙O －S △ABC ＝12·π·52－12×6×8＝25π2－24；(3)解：如解图②，连接AE 、BE ，作BM ⊥CE 于点M ， ∴∠CMB ＝∠EMB ＝∠AEB ＝90°，∵点E 是AB ︵的中点，∴AE ＝BE ，∠EAB ＝∠EBA ＝45°，∴∠ECB ＝∠CBM ＝∠ABE ＝45°，CM ＝MB ＝BC ·sin45°＝32，BE ＝AB ·cos45°＝52，∴EM ＝BE 2－BM 2＝42，则CE ＝CM ＋EM ＝7 2.7. (1)证明：连接OD ，如解图①所示，∵OB ＝OD ，∴∠ODB ＝∠OBD .∵OG ∥BD ，∴∠AOG ＝∠OBD ，∠GOD ＝∠ODB ，∴∠DOG ＝∠AOG ，在△DOG 和△AOG 中，第6题解图②第7题解图①⎩⎪⎨⎪⎧OD ＝OA ∠DOG ＝∠AOG OG ＝OG， ∴△DOG ≌△AOG (SAS)，∴GD ＝GA ；(2)证明：∵AG 切⊙O 于点A ，∴AG ⊥OA ，∴∠OAG ＝90°，∵△DOG ≌△AOG ，∴∠OAG ＝∠ODG ＝90°，∴∠ODE ＝180°－∠ODG ＝90°，∴∠ODC ＋∠FDE ＝90°，∵OC ⊥AB ，∴∠COB ＝90°，∴∠OCD ＋∠OFC ＝90°，∵OC ＝OD ，∴∠ODC ＝∠OCD ，∴∠FDE ＝∠OFC ，∵∠OFC ＝∠EFD ，∴∠EFD ＝∠EDF ，∴EF ＝ED ，∴△DEF 是等腰三角形；(3)解：过点B 作BK ⊥OD 于点K ，如解图②所示：则∠OKB ＝∠BKD ＝∠ODE ＝90°，∴BK ∥DE ，∴∠OBK ＝∠E ，∵BH ⊥GE ，∴∠BHD ＝∠BHE ＝90°， ∴四边形KDHB 为矩形， ∴KD ＝BH ＝9，∴OK ＝OD －KD ＝72，在Rt △OKB 中，∵OK 2＋KB 2＝OB 2，OB ＝252， ∴KB ＝12，∴tan ∠E ＝tan ∠OBK ＝OK KB ＝724，sin ∠E ＝sin ∠OBK ＝OK OB ＝725，∵tan ∠E ＝OD DE ＝724，∴DE ＝3007，∴EF ＝3007，∵sin ∠E ＝BH BE ＝725，∴BE ＝2257，∴BF ＝EF －BE ＝757，∴OF ＝OB －BF ＝2514，在Rt △COF 中，∠COB ＝90°， ∴OC 2＋OF 2＝FC 2，∴FC ＝125214，在Rt △COB 中，∵OC 2＋OB 2＝BC 2，OC ＝OB ＝252， ∴BC ＝2522，∴BC ＋CF ＋BF ＝1502＋757， ∴△CBF 的周长＝1502＋757.。

2014年中考数学二轮复习：圆的计算与证明(2)

第二讲：圆的切线与计算-2014年中考数学圆的二轮复习一、等腰（边）三角形与圆例题1、如图，在△ABC ，AB=AC ，以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ，点F 在AC 的延长线上，且．（1）求证：直线BF 是⊙O 的切线;（2）若AB=5，，求BC 和BF 的长．例题2．已知：如图，O ⊙是Rt △ABC 的外接圆， ABC =90°，点P 是O ⊙外一点，PA 切O ⊙于点A ，且PA=PB ．（1）求证：PB 是O ⊙的切线；（2）已知PA =BC =2，求O ⊙的半径．相应练习11．已知：如图，在△ABC 中，BC=AC ，以BC 为直径的⊙O 与边AB 相交于点D ，DE⊥AC，垂足为点E ． ⑴判断DE 与⊙O的位置关系，并证明你的结论；⑵若⊙O的直径为18，cosB =31，求DE 的长．解：1题图3. 如图，点A、B、C分别是⊙O上的点，∠B=60°， CD是⊙O的直径，P是CD延长线上的点，且AP=AC.（1）求证：AP是⊙O的切线；（2）若AC=3，求PD的长.4、如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．（1）求证：AB=AC；（2）求证：DE为⊙O的切线；（3）若⊙O的半径为5，∠BAC=60°，求DE的长．5、已知：△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F．（1）求证：直线EF是⊙O的切线；（2）当直线DF与⊙O相切时，求⊙O的半径．二、相似或三角函数与圆例题3、（菏泽市）如图，BD为⊙O的直径，AB=AC，AD 交 BC于点E，AE=2，ED=4，(1)求证：△ABE∽△ADB;(2)求AB的长;(3)延长DB到F，使得BF=BO，连接FA，试判断直线FA与⊙O的位置关系，并说明理由．例题4．（2012•咸宁）如图，AB是⊙O的直径，点E是AB上的一点，CD是过E点的弦，过点B的切线交AC 的延长线于点F，BF∥CD，连接BC．（1）已知AB=18，BC=6，求弦CD的长；（2）连接BD，如果四边形BDCF为平行四边形，则点E位于AB的什么位置？试说明理由．相应练习 26.（清远市）如图，AB是⊙O的直径，AC与⊙O相切，切点为A，D为⊙O上一点，AD与OC相交于点E，且∠DAB=∠C.（1）求证：OC∥BD；（2）若AO=5，AD=8，求线段CE的长.7、（莆田市）如图，在Rt △ABC 中，∠C=90º，O 、D 分别为AB 、BC 上的点，经过A 、D 两点的⊙O 分别交AB 、AC 于点E 、F ，且D 为弧的中点。

2014年中考数学二轮专题复习试卷：视图、投影、图形变换(含答案)

2014年中考数学二轮专题复习试卷：视图、投影、图形变换一、选择题(本大题共15个小题，每小题3分,共45分)1.（2013山东泰安）下列几何体中，主视图是矩形，俯视图是圆的几何体是( )2.（2012山东枣庄）如图，该图形绕点O按下列角度旋转后，不能与其自身重合的是( )A.72°B.108°C.144° D．216°3.（2013山东烟台）下列水平放置的几何体中，俯视图不是圆的是( )4.（2013浙江舟山）如图，由三个小立方体搭成的几何体的俯视图是( )5.如图所示，在平面直角坐标系中，点A、B的坐标分别为（-2，0）和（2，0）．月牙①绕点B顺时针旋转90°得到月牙②，则点A的对应点A′的坐标为( )A.（2，2）B.（2，4）C.（4，2）D.（1，2）6.一个长方体的三视图如图所示，若其俯视图为正方形，则这个长方体的表面积为( )D.57A.66B.48C.367.（2013湖南长沙）在下列某品牌T恤的四个洗涤说明图案的设计中，没有运用旋转或轴对称知识的是( )8.(2013山东菏泽)下列图形中，能通过折叠围成一个三棱柱的是( )9.小华在镜中看到身后墙上的钟，你认为实际时间最接近8点的是( )10.(2012江西)如图，有a,b,c三户家用电路接入电表，相邻的电路等距排列，则三户所用电线( )A.a户最长B.b户最大C.c户最长D.三户一样大11.（2013山东泰安）下列图形：其中所有轴对称图形的对称轴条数之和为( )A.13B.11C.10D.812.（2013山东烟台）以下是回收、绿色包装、节水、低碳四个标志，其中是中心对称图形的是( )13.（2013浙江湖州）在正三角形、等腰梯形、矩形、平行四边形中，既是轴对称图形又是中心对称图形的是( )A.正三角形B.等腰梯形C.矩形D.平行四边形14.（2012广西柳州）小张用手机拍摄得到甲图，经放大后得到乙图，甲图中的线段AB在乙图中的对应线段是( )A.FGB.FHC.EHD.EF15.（2013广西梧州）如图，△ABC以点O为旋转中心，旋转180°后得到△A′B′C′．ED是△ABC的中位线，经旋转后为线段E′D′．已知BC=4，则E′D′=( )A.2B.3C.4D.1.5二、填空题(本大题共6个小题，每小题3分,共18分)16.（2013湖北天门）如图，正方形ABCD的对角线相交于点O，正三角形OEF绕点O旋转．在旋转过程中，当AE=BF时，∠AOE的大小是．17.（2013江苏无锡）如图是一个几何体的三视图，若这个几何体的体积是36，则它的表面积是．18.（2013湖南岳阳）夏季荷花盛开，为了便于游客领略“人从桥上过，如在河中行”的美好意境，某景点拟在如图所示的矩形荷塘上架设小桥．若荷塘周长为280 m，且桥宽忽略不计，则小桥总长为 m．19.(2012浙江杭州)如图，平面直角坐标系中有四个点，它们的横纵坐标均为整数.若在此平面直角坐标系内移动点A，使得这四个点构成的四边形是轴对称图形，并且点A的横坐标仍是整数，则移动后点A的坐标为 .20.(2013浙江温州)如图，在平面直角坐标系中,△ABC的两个顶点A，B的坐标分别为（-2,0），（-1,0），BC⊥x轴。

2014年中考数学圆专题复习题

中考圆1.下列说法正确的是（）A.平分弦的直径垂直于弦B.半圆（或直径）所对的圆周角是直角C.相等的圆心角所对的弧相等D.若两个圆有公共点，则这两个圆相交2.Rt△ABC中,∠C=900，AC=3cm,BC=4cm,以C为圆心,r为半径作圆,若圆C与直线AB相切,则r的值为（）A.2cmB.2.4cmC.3cmD.4cm3.如图所示，线段AB是⊙O上一点，∠CDB=20°，过点C作⊙O的切线交AB的延长线于点E，则∠E 等于（）A.50°B.40°C.60°D.70°4.如图，圆O与正方形ABCD的两边AB、AD相切，且DE与圆O相切于E点．若圆O的半径为5，且AB=11，则DE的长度为何？（）A.5B.6C.30D.5.如图，在Rt△ABC中,∠ABC=900,AB=8cm,BC=6cm,分别以A,C为圆心,以2AC的长为半径作圆,将Rt △ABC截去两个扇形,则剩余（阴影）部分的面积为（）cm2．A.2524π4- B.25π4C.524π4-． D.2524π6-6.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是弧EB的中点,则下列结论不成立的是（）A.OC∥AEB.EC=BCC.∠DAE=∠ABED.AC⊥OE7.在等腰直角三角形ABC 中，AB=AC=4，点O 为BC 的中点，以O 为圆心作⊙O 交BC 于点M 、N ，⊙O 与AB 、AC 相切，切点分别为D 、E ，则⊙O 的半径和∠MND 的度数分别为（） A.2，22.5°B.3，30°C.3，22.5°D.2，30°8.如图，以等边三角形ABC 的BC 边为直径画半圆，分别交AB 、AC 于点E 、D ，DF 是圆的切线，过点F 作BC 的垂线交BC 于点G ．若AF 的长为2，则FG 的长为（）A.4B.33C.6D.32 9.如图,⊙A 与⊙B 外切于点D ，PC ，PD ，PE 分别是圆的切线，C ，D ，E 是切点,若∠CED=x °,∠ECD=y °，⊙B 的半径为R ，则⋂DE 的长度是（） A.()9090Rx -π B.()9090Ry -π C.()180180Rx -π D.()180180Ry -π10.在△ABC 中,∠C 为锐角,分别以AB ，AC 为直径作半圆,过点B ，A ，C 作弧BAC ，如图所示.若AB=4，AC=2，S 1﹣S 2=，则S 3﹣S 4的值是（）A.π429 B.π423 C.π411D.π4511.如图,AB 是⊙O 的直径,C 、D 是⊙O 上的点，∠CDB=30°,过点C 作⊙O 的切线交AB 的延长线于E ，则sin ∠E 的值为12.如图,⊙O中,弦AB⊥弦CD于E,OF⊥AB于F,OG⊥CD于G,若AE=8cm,EB=4cm,则OG= cm。

2013-2014中考数学专题复习学生版第二十五讲与圆有关的计算

第二十五讲与圆有关的计算【基础知识回顾】一、正多边形和圆：1、各边相等，也相等的多边形是正多边形2、每一个正多边形都有一个外接圆，外接圆的圆心叫正多边形的外接圆的半径叫正多边形的一般用字母R表示，每边所对的圆心角叫可用用α表示，α=，中心到正多边形一边的距离叫做正多边形的用r表示3、每一个正n边形都被它的半径分成n个全等的三角形，被它的半径和边心距分成个全等的三角形【名师提醒：正多边形的有关计算，一般是放在一个等腰三角形或一个直角三角形中进行，根据半径、边心距、边长、中心角等之间的边角关系作计算，以正三角形、正方形和正方边形为主】二、弧长与扇形面积计算：⊙O的半径为R，弧长为L，圆心角为n0，扇形的面积为S扇，则有如下公式：L=S扇= =【名师提醒：1、以上几个公式都可进行变形，2、原公式中涉及的角都不带单位3、扇形的两个公式可根据已知条件灵活进行选择4、圆中的面积计算常见的是求阴影部分的面积，常用的方法有：⑴已知规则图形面积的和与差⑵割补法⑶等积变形法⑷平移法⑸旋转法等】三、圆柱和圆锥：1、如图：设圆柱的高为h,底面半径为R则有：⑴S圆柱侧=⑵S圆柱全=⑶V圆柱=2、如图：设圆锥的母线长为l，底面半径为R，高为h，则有：⑴S圆锥侧= 、⑵S圆锥全=⑶V圆锥=【名师提醒：1、圆柱的高有条，圆锥的高有条2、圆锥的高h，母线长l，底高半径R满足关系3、注意圆锥的侧面展开圆中扇形的半径l是圆锥的，扇形的弧长是圆锥的4、圆锥的母线为l，底面半径为R，侧面展开图扇形的圆心角度数为n，若l=2r，则n= l=3r,则n= l=4r则n= 】【典型例题解析】考点一：正多边形和圆例1 （2013•绵阳）如图，要拧开一个边长为a=6cm的正六边形螺帽，扳手张开的开口b 至少为（）A．6mm B．12mm C．D．点评：本题考查了正多边形和圆的知识，构造一个由半径、半边、边心距组成的直角三角形，熟练运用锐角三角函数进行求解．对应训练1．（2013•天津）正六边形的边心距与边长之比为（）A 3B 2 C．1：2 D ：2 考点二：圆周长与弧长例2 （2013•黄冈）如图，矩形ABCD 中，AB=4，BC=3，边CD 在直线l 上，将矩形ABCD 沿直线l 作无滑动翻滚，当点A 第一次翻滚到点A 1位置时，则点A 经过的路线长为．思路分析：如图根据旋转的性质知，点A 经过的路线长是三段：①以90°为圆心角，AD 长为半径的扇形的弧长；②以90°为圆心角，AB 长为半径的扇形的弧长；③90°为圆心角，矩形ABCD 对角线长为半径的扇形的弧长．点评：本题考查了弧长的计算、矩形的性质以及旋转的性质．根据题意画出点A 运动轨迹，是突破解题难点的关键．对应训练2．（2013•遵义）如图，将边长为1cm 的等边三角形ABC 沿直线l 向右翻动（不滑动），点B 从开始到结束，所经过路径的长度为（）A ．πcmB ．（2+π）cmC ．πcmD ．3cm考点三：扇形面积与阴影部分面积例3 （2013•重庆）如图，在边长为4的正方形ABCD 中，以AB 为直径的半圆与对角线AC 交于点E ，则图中阴影部分的面积为．（结果保留π）323243乐山点评：本题考查了图形的面积的计算，不规则图形的面积可以转化为规则图形的面积的和或差计算．对应训练3．（2013•乐山）如图，小方格都是边长为1的正方形，则以格点为圆心，半径为1和2的两种弧围成的“叶状”阴影图案的面积为．考点四：圆柱、圆锥的侧面展开图例4 （2013•遂宁）用半径为3cm，圆心角是120°的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为（）A．2πcm B．1.5cm C．πcm D．1cm面展开扇形与底面圆之间的关系，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．对应训练4．（2013•攀枝花）一个圆锥的左视图是一个正三角形，则这个圆锥的侧面展开图的圆心角等于（）A．60°B．90°C．120°D．180°2点评：此题考查了切线的判定与性质，相似及全等三角形的判定与性质以及锐角三角函数关系等知识，熟练掌握切线的判定与性质是解本题的关键．（3）求证：GF-GB=DF•GF．【聚焦山东中考】1．（2013•滨州）若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为（）A ．6，B ．3，3 C ．6，3D ．，2．（2013•东营）如图，正方形ABCD 中，分别以B 、D 为圆心，以正方形的边长a 为半径画弧，形成树叶形（阴影部分）图案，则树叶形图案的周长为（） A ．πa B ．2πa C ．πaD ．3a泰安3．（2013•泰安）如图，AB ，CD 是⊙O 的两条互相垂直的直径，点O 1，O 2，O 3，O 4分别是OA 、OB 、OC 、OD 的中点，若⊙O 的半径为2，则阴影部分的面积为（）A ．8B ．4C ．4π+4D ．4π-44．（2013•济南）如图，扇形AOB 的半径为1，∠AOB=90°，以AB 为直径画半圆，则图中阴影部分的面积为（）A ．B ．π-C ．D ． + 莱芜5．（2013•莱芜）将半径为3cm 的圆形纸片沿AB 折叠后，圆弧恰好能经过圆心O ，用图中阴影部分的扇形围成一个圆锥的侧面，则这个圆锥的高为（）A ．BCD ． 6．（2013•菏泽）在半径为5的圆中，30°的圆心角所对的弧长为（结果保留π）．7．（2013•聊城）已知一个扇形的半径为60cm ，圆心角为150°，用它围成一个圆锥的侧面，那么圆锥的底面半径为 cm ．8．（2013•青岛）如图，AB 是⊙O 的直径，弦AC=2，∠ABC=30°，则图中阴影部分的面积是．124π12124π1232枣庄9．（2013•枣庄）如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC．（1）求证：EF是⊙O的切线；（2）求证：AC2=AD•AB；（3）若⊙O的半径为2，∠ACD=30°，求图中阴影部分的面积．10．（2013•莱芜）如图，⊙O的半径为1，直线CD经过圆心O，交⊙O于C、D两点，直径AB⊥CD，点M是直线CD上异于点C、O、D的一个动点，AM所在的直线交于⊙O于点N，点P是直线CD上另一点，且PM=PN．（1）当点M在⊙O内部，如图一，试判断PN与⊙O的关系，并写出证明过程；（2）当点M在⊙O外部，如图二，其它条件不变时，（1）的结论是否还成立？请说明理由；（3）当点M在⊙O外部，如图三，∠AMO=15°，求图中阴影部分的面积．【备考真题过关】一、选择题1．（2013•淮安）若扇形的半径为6，圆心角为120°，则此扇形的弧长是（）A ．40°B ．45°C ．60°D ．80°3．（2013•义乌）已知圆锥的底面半径为6cm ，高为8cm ，则这个圆锥的母线长为（）A ．12cmB ．10cmC ．8cmD ．6cm4．（2013•乌鲁木齐）如图是某几何体的三视图，则该几何体的体积是（）A ．πB ．2πC ．3πD ．4π南通5．（2013•南通）用如图所示的扇形纸片制作一个圆锥的侧面，要求圆锥的高是4cm ，底面周长是6πcm ，则扇形的半径为（）A ．3cmB ．5cmC ．6cmD ．8cm6．（2013•黄石）已知直角三角形ABC 的一条直角边AB=12cm ，另一条直角边BC=5cm ，则以AB 为轴旋转一周，所得到的圆锥的表面积是（）A ．90πcm 2B ．209πcm 2C ．155πcm 2D ．65πcm 27．（2013•舟山）如图，某厂生产横截面直径为7cm 的圆柱形罐头，需将“蘑菇罐头”字样贴在罐头侧面．为了获得较佳视觉效果，字样在罐头侧面所形成的弧的度数为90°，则“蘑菇罐头”字样的长度为（）A ．cmB ．cmC ．cmD ．7πcm南宁8．（2013•南宁）如图，圆锥形的烟囱底面半径为15cm ，母线长为20cm ，制作这样一个烟囱帽所需要的铁皮面积至少是（）A ．150πcm 2B ．300πcm 2C ．600πcm 2D ．150πcm 29．（2013•台州）如图，已知边长为2的正三角形ABC 顶点A 的坐标为（0，6），BC 的中点D 在y 轴上，且在点A 下方，点E 是边长为2，中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE 的最小值为（）A ．3B ．C ．4D ．4π74π72π贵港A ．B ．24πC ．16πD ．12πA ．BCD 武汉12．（2013•武汉）如图，⊙A 与⊙B 外切于点D ，PC ，PD ，PE 分别是圆的切线，C ，D ，E 是切点．若∠CDE=x°，∠ECD=y°，⊙B 的半径为R ，则的长度是（） A ． B ． C ． D ．A ．1个B ．2个C ．3个D ．4个19π32π-23π-»DE(90)x Rπ-⨯(90)y Rπ-⨯(180)x Rπ-⨯(180)y Rπ-⨯茂名•重庆二、填空题的圆都经过另一个圆的圆心，则游泳池的周长是m．徐州2具的用纸面积是cm．（不考虑接缝等因素，计算结果用π表示）．泸州1程为cm．凉山州25．（2013•凉山州）如图，Rt△ABC中，∠C=90°，AC=8，BC=6，两等圆⊙A，⊙B外切，120°，OC的长为2cm，则三角板和量角器重叠部分的面积为．福州28．（2013•宿迁）如图，AB是半圆O的直径，且AB=8，点C为半圆上的一点．将此半圆值为．宿迁乐亭县31．（2013•乐亭县一模）如图，已知直线y=x+4与两坐��轴分别交于A、B两点，⊙C 的圆心坐标为（2，O），半径为2，若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值和最大值分别是．32．（2013•玉林）如图，△ABC是⊙O内接正三角形，将△ABC绕点O顺时针旋转30°得到△DEF，DE分别交AB，AC于点M，N，DF交AC于点Q，则有以下结论：①∠DQN=30°；②△DNQ≌△ANM；③△DNQ的周长等于AC的长；④NQ=QC．其中正确的结论是．（把所有正确的结论的序号都填上）佛山三、解答题33．（2013•佛山）如图，圆锥的侧面展开图是一个半圆，求母线AB与高AO的夹角．参考公式：圆锥的侧面积S=πrl，其中r为底面半径，l为母线长．34.（2013•梅州）如图，在矩形ABCD中，AB=2DA，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设DA=2．（1）求线段EC的长；（2）求图中阴影部分的面积．35．（2013•荆门）如图1，正方形ABCD的边长为2，点M是BC的中点，P是线段MC 上的一个动点（不与M、C重合），以AB为直径作⊙O，过点P作⊙O的切线，交AD于点F，切点为E．（1）求证：OF∥BE；（2）设BP=x，AF=y，求y关于x的函数解析式，并写出自变量x的取值范围；（3）延长DC、FP交于点G，连接OE并延长交直线DC与H（图2），问是否存在点P，使△EFO∽△EHG（E、F、O与E、H、G为对应点）？如果存在，试求（2）中x和y的值；如果不存在，请说明理由．36．（2013•晋江市）如图，在平面直角坐标系xOy中，一动直线l从y轴出发，以每秒1个单位长度的速度沿x轴向右平移，直线l与直线y=x相交于点P，以OP为半径的⊙P与x轴正半轴交于点A，与y轴正半轴交于点B．设直线l的运动时间为t秒．（1）填空：当t=1时，⊙P的半径为，OA= ，OB= ；（2）若点C是坐标平面内一点，且以点O、P、C、B为顶点的四边形为平行四边形．①请你直接写出所有符合条件的点C的坐标；（用含t的代数式表示）②当点C在直线y=x上方时，过A、B、C三点的⊙Q与y轴的另一个交点为点D，连接DC、DA，试判断△DAC的形状，并说明理由．。

2014年中考二轮专题复习试卷：方程组和不等式组(含答案)

2014年中考数学二轮专题复习试卷：方程组和不等式组一、选择题(本大题共15个小题，每小题3分,共45分)1.（2013湖南张家界）把不等式组x 12x 15>⎧⎨-≤⎩的解集在数轴上表示正确的是( )2.（2013四川雅安）已知x 1，x 2是一元二次方程x 2-2x=0的两根，则x 1+x 2的值是( ) A ．0 B ．2 C ．-2 D ．43.(2012山东德州)已知a 2b 43a 2b 8+=⎧⎨+=⎩，则a+b 等于( ) A.3 B.83C.2D.14.（2013广东湛江）由于受H7N9禽流感的影响，今年4月份鸡的价格两次大幅下降，由原来每斤12元连续两次降价a%后售价下调到每斤5元，下列所列方程中正确的是( )A ．12（1+a%）2=5B ．12（1-a%）2=5 C ．12（1-2a%）=5 D ．12（1-a2%）=55.(2012湖北随州)分式方程1006020v 20v=+-的解是( )A.v=-20B.v=5C.v=-5D.v=20 6.(2012山东东营)方程21(k1)x 04--+=有两个实数根，则k 的取值范围是( )A.k ≥1B.k ≤1C.k ＞1D.k ＜17.（2013山东烟台）已知实数a ，b 分别满足a 2-6a+4=0，b 2-6b+4=0，且a ≠b ，则b a a b+的值是( )A ．7B ．-7C ．11D ．-118.（2013广西玉林）方程130x 1x 1-=-+的解是( ) A ．x=2 B ．x=1 C ．12D.x=-2 9.(2013山东滨州)对于任意实数k ，关于x 的方程x 2－2(k+1)x －k 2+2k －1=0的根的情况为( )A.有两个相等的实数根B.没有实数根C.有两个不相等的实数根D.无法确定10.（2013辽宁营口）炎炎夏日，甲安装队为A 小区安装60台空调，乙安装队为B 小区安装50台空调，两队同时开工且恰好同时完工，甲队比乙队每天多安装2台．设乙队每天安装x 台，根据题意，下面所列方程中正确的是( )60506050A.B.x x 2x 2x60506050C. D. x x 2x 2x = =--= =+ +11.设a,b 是方程x 2+x-2 013=0的两个实数根，则a 2+2a+b 的值为( ) A.2 010 B.2 011 C.2 012 D.2 013 12.（2013湖南岳阳）关于x 的分式方程7m 3x 1x 1+=--有增根，则增根为( ) A ．x=1 B ．x=-1 C ．x=3 D ．x=-313.(2013山东滨州)若把不等式组2x 3x 12-≥-⎧⎨-≥-⎩的解集在数轴上表示出来，则其对应的图形为( )A.长方形B.线段C.射线D.直线14.(2012山东淄博)篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分.某队预计在2012—2013赛季全部32场比赛中最少得到48分，才有希望进入季后赛.假设这个队在将要举行的比赛中胜x 场，要达到目标，x 应满足的关系式是( ) A.2x+(32-x)≥48 B.2x-(32-x)≥48 C.2x+(32-x)≤48 D.2x ≥4815.如图，在长方形ABCD 中，放入6个形状、大小都相同的长方形，所标尺寸如图所示，则图中阴影部分面积是( )A.44 cm 2B.45 cm 2C.46 cm 2D.47 cm 2二、填空题(本大题共6个小题，每小题3分,共18分)16.（2013湖南长沙）方程21x 1x=+的解为x= . 17.(2012湖北随州)设a 2+2a-1=0,b 4-2b 2-1=0,且1-ab 2≠0,则225ab b 3a 1(a+-+= .18.(2012浙江杭州)某企业向银行贷款1 000万元，一年后归还银行 1 065.6多万元，则年利率高于 %.19.(2012四川凉山州)某商品的售价528元，商家售出一件这样的商品可获利润是进价的10%~20%，设进价为x 元，则x 的取值范围是 .20.（2013湖南张家界）若关于x 的一元二次方程kx 2+4x+3=0有实数根，则k 的非负整数值是． 21.（2013湖北宜宾）某企业五月份的利润是25万元，预计七月份的利润将达到36万元．设平均月增长率为x ，根据题意所列方程是．三、解答题(本大题共6个小题，共57分) 22.（本小题满分16分）(1)（2013福建漳州）解方程：x 2-4x+1=0.(2)(2013四川成都)解方程组：x y 12x y 5.+=⎧⎨-=⎩①，②(3)解不等式组：2x 5652x 12x.+≥⎧⎨->+⎩（），(4)(2012山东德州)解方程：2211.x 1x 1+=-+23.(本小题满分5分)先化简，再求代数式23x 1(1x 2x 2--÷++的值,其中x 是不等式组x 20,2x 18->⎧⎨+<⎩的整数解.24.(本小题满分8分)(2013四川雅安)甲、乙二人在一环形场地上从A 点同时同向匀速跑步,甲的速度是乙的2.5 倍,4 分钟两人首次相遇,此时乙还需要跑300 m 才跑完第一圈,求甲、乙二人的速度及环形场地的周长.(列方程( 组) 求解)25.(本小题满分8分)（2013山东济宁）人教版教科书对分式方程验根的归纳如下：“解分式方程时，去分母后所得整式方程的解有可能使原分式的分母为0，因此应进行如下检验：将整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解；否则，这个解不是原分式方程的解.”请你根据对这段话的理解，解决下面问题：已知，关于x的方程m1xx1x1--=--无解，方程x2+kx+6=0的一个根是m.(1)求m和k的值；(2)求方程x2+kx+6=0的另一个根.26.（本小题满分10分）（2013湖南娄底）为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4 800元.已知甲、乙两车单独运完此垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元.（1）求甲、乙两车单独运完此堆垃圾各需运多少趟？（2）若单独租用一台车，租用哪台车合算？27.（本小题满分10分）“4·20”雅安地震后，某商家为支援灾区人民，计划捐赠帐篷16 800顶，该商家备有2辆大货车、8辆小货车运送，计划大货车比小货车每辆每次多运帐篷200顶，大、小货车每天均运送一次，两天恰好运完.（1）求大、小货车原计划每辆每次各运送帐篷多少顶？（2）因地震导致路基受损，实际运送过程中，每辆大货车每次比原计划少运200m顶，每辆小货车每次比原计划少运300顶.为了尽快将帐篷运送到灾区，大货车每天比原计划多跑1 2 m次，小货车每天比原计划多跑m次，一天刚好运送了帐篷14 400顶，求m的值.参考答案1.C2.B3.A4.B5.B6.D7.A8.A9.C 10.D 11.C 12.A 13.B 14.A 15.A16.1 17.-32 18.6.56 19.440≤x ≤480 20.1 21.25（1+x ）2=3622.(1)解：移项得：x 2-4x=-1, 配方得:x 2-4x+4=-1+4, 即（x-2)2=3, 开方得：x-2=∴原方程的解是：12x 2,x 2.=+=+(2)解：①+②得3x=6，∴x=2. 将x=2代入方程①得2+y=1，∴y=-1.∴原方程组的解为x 2.y 1=⎧⎨=-⎩(3)解：()2x 56,52x 12x ⎧+≥ ⎨->+ ⎩①②由①得：x ≥-2, 由②得：x<1.∴此不等式组的解集为：-2≤x<1. (4)解：去分母得：2+(x-1)=x 2-1, 移项，合并同类项得：x 2-x-2=0, 解得：x 1=2,x 2=-1.经检验，x=-1是原方程的增根， ∴原方程的解是x=2. 23.解：不等式组解集为72x 2<<,∴取整数，x=3. 原分式化简为1,x 1+将x=3代入，得原式=1.424.解：设乙速为 x m/min, 则甲速为2.5x m/min,设环形场地的周长为y m.由题意知:y 2.5x44x y4x300=⨯-⎧⎨=+⎩，解得:x150. y900=⎧⎨=⎩∴2.5x=2.5 ×150=375 m/min.答: 甲、乙二人的速度分别为375 m/min、150 m/min,环形场地周长为900 m.25.(1)解：∵将分式方程m1xx1x1--=--去分母化成整式方程得（m-1）-x=0，解得：x=m-1.又∵关于x的方程m1xx1x1--=--无解，∴x=m-1是增根.∴m-1-1=0,解得m=2.∵方程x2+kx+6=0的一个根是m,即x=2.∴22+2k+6=0.解得：k=-5.(2)解：将k=-5代入，得方程x2-5x+6=0.(x-2)(x-3)=0,∴方程的解为x=2或3.∴方程的另一个根为x=3.26.解：（1）设甲车单独运完此堆垃圾需运x趟，则乙车单独运完此堆垃圾需2x趟，依题意得：12121x2x+=，解得：x=18.经检验x=18是原方程的解.∴2x=36.答：甲车单独运完此堆垃圾需18趟，乙车需36趟.（2）设甲车每趟需运费a元，则乙车每趟需运费(a-200)元，依题得：12a+12(a-200)=4 800，解得：a=300，∴a-200=100.∴单独租用甲车的费用=300×18=5 400（元），单独租用乙车的费用=100×36=3 600（元）.∵5 400＞3 600,∴单独租用乙车合算.答：单独租用乙车合算.27.解：（1）设小货车原计划每辆每次运送帐篷x顶，则大货车原计划每辆每次运送帐篷（x+200）顶，依题意得：2[8x+2（x+200）]=16 800，解得：x=800.x+200=1 000.答：大、小货车原计划每辆每次分别运送帐篷1 000顶、800顶.（2）由题意有：2(1 000-200m)(1+12m)+8×(800-300)×(1+m)=14 400，解得：m1=2，m2=21(12m=10.5为小数，舍去)，故m的值为2.。

中考数学专题复习《圆的阅读理解题》测试卷(附带参考答案)

中考数学专题复习《圆的阅读理解题》测试卷（附带参考答案)学校:___________班级:___________姓名:___________考号:___________1．请阅读下列材料并完成相应的任务：斯库顿定理：如图1．在ABC 中 AD 为BAC ∠的平分线则2··AD BD DC AB AC +=．下面是该定理的证明过程：证明：如图2O 是ABC 的外接圆延长AD 交O 于点E 连接BE ．∵AD 为BAC ∠的平分线 ∵BAE DAC ∠=∠．∵E C ∠=∠ （依据∵__________________________） ABE ADC ∴△∽△．（依据∵_________________________） AB ADAE AC∴= AD AE AB AC ∴⋅=⋅又AE AD DE =+()AD AD DE AB AC ∴⋅+=⋅．2AD AD DE AB AC ∴+⋅=⋅．……任务：（1）证明过程中的依据是：∵__________________________________． ∵__________________________________．（2）将证明过程补充完整：（3）如图3．在圆内接四边形ACEB 中对角线AE BC 相交于点D ．若BE CE = 4AC =6AB=2BD=请利用斯库顿定理直接写出线段AE的长．CD=32．如图1 正五边形ABCDE内接于∵O阅读以下作图过程并回答下列问题作法：如图2 ∵作直径AF∵以F为圆心FO为半径作圆弧与∵O交于点M N∵连接AM MN NA．,,∠的度数．(1)求ABC(2)AMN是正三角形吗？请说明理由．(3)从点A开始以DN长为半径在∵O上依次截取点再依次连接这些分点得到正n边形求n的值．3．阅读与应用请阅读下列材料完成相应的任务：托勒密是“地心说”的集大成者著名的天文学家地理学家占星学家和光学家．后人从托勒密的书中发现一个命题：圆内接四边形对边乘积的和等于对角线的乘积．下面是对这个命题的证明过程．如图1 四边形ABCD 内接于O ．求证：AB DC AD BC AC BD ⋅+⋅=⋅．证明：如图2 作BAE CAD ∠=∠交BD 于点E ．∵AD AD = ∵ABE ACD ∠=∠．（依据） ∵ABE ACD ∽△△．∵AB BEAC CD=．AB DC AC BE ⋅=⋅． …∵ABC AED ∽△△． ∵AC BCAD ED=．∵AD BC AC ED ⋅=⋅． ∵AB DC AC BE ⋅=⋅∵()AB DC AD BC AC BE AC ED AC BE ED AC BD ⋅+⋅=⋅+⋅=+=⋅． ∵AB DC AD BC AC BD ⋅+⋅=⋅．任务：(1)证明过程中的“依据”是______ (2)补全证明过程(3)如图3 O的内接五边形ABCDE的边长都为2 求对角线BD的长．4．阅读与思考请阅读下列材料,并按要求完成相应的任务．阿基米德是伟大的古希腊数学家哲学家物理学家他与牛顿高斯并称为三大数学王子．他的著作《阿基米德全集》的《引理集》中记述了有关圆的15个引理其中第三个引⊥于点C点D在弦AB上且理是：如图1 AB是O的弦点P在O上PC AB=．小明思考后给出如=在PB上取一点Q使PQ PAAC CD=连接BQ则BQ BD下证明：任务：(1)写出小明证明过程中的依据：依据1：________ 依据2：________(2)请你将小明的证明过程补充完整(3)小亮想到了不同的证明方法：如图3 连接AP PD PQ DQ ．请你按照小亮的证明思路写出证明过程．5．阅读资料：我们把顶点在圆上一边和圆相交另一边和圆相切的角叫做弦切角如图1中CBD ∠即为弦切角．同学们研究发现：A 为圆上任意一点当弦AB 经过圆心O 且DB 切O 于点B 时易证：弦切角CBD A ∠=∠．问题拓展：如图2 点A 是优弧BC 上任意一点 DB 切O 于点B 求证：CBD A ∠=∠．证明：连接BO 并延长交O 于点A ' 连接A C ' 如图2所示． ∵DB 与O 相切于点B ∵A BD ∠'=________ ∵90A BC CBD ∠'+∠=︒． ∵A B '是直径∵90ACB ∠'=︒_____________（依据）． ∵90A A BC ∠'+∠'=︒．∵CBD A ∠=∠'________________（依据）．又∵A A ∠'=∠________________（依据） ∵CBD A ∠=∠．(1)将上述证明过程及依据补充完整．(2)如图3 ABC 的顶点C 在O 上 AC 和O 相交于点D 且AB 是O 的切线切点为B 连接BD ．若2,6,3AD CD BD === 求BC 的长．6．阅读：如图1所示四边形ABCD 是∵O 的内接四边形连接AC BD ．BC 是∵O 的直径 AB ＝AC ．请说明线段AD BD CD 之间的数量关系．下面是王林解答该问题的部分解答过程请补充完整：+CD ＝BD ．理由如下：∵BC 是∵O 的直径 ∵∵BAC ＝90°． ∵AB ＝AC ∵∵ABC ＝∵ACB ＝45°．如图2所示过点A 作AM ∵AD 交BD 于点M …(1)补全王林的解答过程(2)如图3所示四边形ABCD 中∵ABC ＝30° 连接AC BD ．若∵BAC ＝∵BDC ＝90° 直接写出线段AD BD CD 之间的关系式是． 7．阅读下列材料并按要求完成相应的任务．黄金三角形与五角星当等腰三角形的顶角为36°（或108°）时我们把这样的三角形叫做黄金三角形．按下面的步骤画一个五角星（如图）：∵作一个以AB 为直径的圆圆心为O ∵过圆心O 作半径OC ∵AB ∵取OC 的中点D 连接AD∵以D 为圆心OD 为半径画弧交AD 于点E ∵从点A 开始以AE 为半径顺时针依次画弧正好把∵O 十等分（其中点F G B H I 为五等分点） ∵以点F G B H I 为顶点画出五角星．任务： (1)求出AEOA的值为 (2)如图 GH 与BF BI 分别交于点M N 求证：△BMN 是黄金三角形． 8．阅读下面材料并按要求完成相应的任务．阿基米德是古希腊的数学家物理学家．在《阿基米德全集》里他关于圆的引理的论证如下：命题：设AB 是一个半圆的直径并且过点B 的切线与过该半圆上的任意一点D 的切线交于点T 如果作DE 垂直AB 于点E 且与AT 交于点F 则DF EF =．证明：如图1 延长AD 与BT 交于点H 连接OD OT ． ∵DT BT 与半圆O 相切 ∵……∵ ∵BT DT =． ∵AB 是半圆O 的直径 ∵90ADB ︒∠=．∵在BDH △中由BT DT = 可得TDB TBD ∠=∠ ∵H TDH ∠=∠．∵BT DT HT ==．又∵//DE BH ∵DF AFHT AT = EF AF BT AT=∵EF DFBT HT=．又∵BT HT = ∵DF EF =任务：(1)请将∵处的证明过程补充完整． (2)证明过程中∵的证明依据是．(3)如图2 AB 为∵O 的直径 ∵BED 是等边三角形 BE 是∵O 的切线切点是B 点D 在∵O 上 CD ∵AB 垂足为C 连接AE 交CD 于点F ．若∵O 的半径为2 求CF 的长． 9．阅读材料某个学习小组成员发现：在等腰ABC 中 AD 平分BAC ∠ ∵AB AC =BD CD = ∵AB BDAC CD= 他们猜想：在任意ABC 中一个内角角平分线分对边所成的两条线段与这个内角的两边对应成比例．【证明猜想】如图1所示在ABC 中 AD 平分BAC ∠ 求证：AB BDAC CD=．丹丹认为可以通过构造相似三角形的方法来证明△和ACD面积的角度来证明．思思认为可以通过比较ABD(1)请你从上面的方法中选择一种进行证明．(2)【尝试应用】如图2O是Rt ABC的外接圆点E是O上一点（与B不重合且=连结AE并延长AE BC交于点D H为AE的中点连结BH交AC于点G求AB AEHG的值．GB(3)【拓展提高】如图3在（2）的条件下延长BH交O于点F若BE EF=求=GH xO的直径（用x的代数式表示）．10．请阅读下面材料并完成相应的任务阿基米德折弦定理阿基米德（Arehimedes 公元前287—公元前212年古希腊）是有史以来最伟大的数学家之一他与牛顿高斯并称为三大数学王子．阿拉伯Al-Biruni（973年—1050年）的译文中保存了阿基米德折弦定理的内容苏联在1964年根据Al-Biruni译本出版了俄文版《阿基米德全集》第一题就是阿基米德的折弦定理．阿基米德折弦定理：如图1 AB和BC是O的两条弦（即折线ABC是圆的一条折弦）>M是ABC的中点则从点M向BC所作垂线的垂足D是折弦ABC的中点即BC ABCD AB BD=+．=+的部分证明过程．这个定理有很多证明方法下面是运用“垂线法”证明CD AB BD证明：如图2 过点M作MH⊥射线AB垂足为点H连接MA MB MC．∵M 是ABC 的中点 ∵MA MC =． … 任务：（1）请按照上面的证明思路写出该证明的剩余部分（2）如图3 已知等边三角形ABC 内接于O D 为AC 上一点 15ABD ∠=︒ CE BD ⊥于点E 2CE = 连接AD 则DAB 的周长是______．11．阅读与思考请阅读下列材料并完成相应的任务：任务：（1）材料中划横线部分应填写的内容为．（2）如图2 正五边形ABCDE 内接于∵O AB ＝2 求对角线BD 的长．12．阅读下列材料完成相应任务：如图∵ ABC 是∵O 的内接三角形 AB 是∵O 的直径AD 平分BAC ∠交∵O 于点D 连接BD 过点D 作∵O 的切线交AB 的延长线于点E ．则CAD BDE ∠=∠．下面是证明CAD BDE ∠=∠的部分过程：证明：如图∵ 连接DO AB 是∵O 的直径 90ADB ∴∠=︒ODA ∴∠+∵________90=︒．（1） DE 为∵O 的切线 90ODE ∴∠=︒90ODB BDE ∴∠+∠=︒ （2）由（1）（2）得 ∵________________． AD 平分,BAC CAD OAD ∠∴∠=∠．,OA OD OAD ODA =∴∠=∠CAD ∴∠=∵________CAD BDE ∴∠=∠．任务：（1）请按照上面的证明思路补全证明过程：∵________ ∵________ ∵________ （2）若5,2OA BE == 求DE 的长．13．阅读下列材料：平面上两点P 1（x 1 y 1） P 2（x 2 y 2）之间的距离表示为()()22121212PP x x y y =-+- 称为平面内两点间的距离公式根据该公式如图设P （x y ）是圆心坐标为C （a b ）半径为r 的圆上任意一点则点P ()()22x a y b r -+-= 变形可得：（x ﹣a ）2+（y ﹣b ）2＝r 2 我们称其为圆心为C （a b ）半径为r 的圆的标准方程．例如：由圆的标准方程（x ﹣1）2+（y ﹣2）2＝25可得它的圆心为（1 2）半径为5．根据上述材料结合你所学的知识完成下列各题．（1）圆心为C （3 4）半径为2的圆的标准方程为：（2）若已知∵C 的标准方程为：（x ﹣2）2+y 2＝22 圆心为C 请判断点A （3 ﹣1）与∵C的位置关系．14．阅读以下材料并按要求完成相应的任务：几何定论是指变化的图形中某些几何元素的几何量保持不变（如定长定角定比定积等）或几何元素间的某些性质或位置关系不变（如定点定线定方向等）如图∵ 点A 为O 外一点过点A 为O 作直线与O 相交于点B C 点B '为点B 关于OA 的对称点连接B C '交OA 于点M 设O 的半径为R ．如图∵ 当过点A 的直线与O 相切时点B C 重合可得2R OA OM =⋅．如图∵ 当过点A 的直线与O 相交时证明2R OA OM =⋅．证明：如图∵ 连接OC CD ．∵B ' B 关于OA 对称∵BD BD '=．∵∵1＝∵2 .（依据）…任务：（1）上述证明过程中的依据是____________________（2）根据以上的证明提示完成上述证明过程（3）如图∵ 若5OA = 1OM = 求O 的半径．15．阅读下列相关材料并完成相应的任务．婆罗摩笈多是古印度著名的数学家天文学家他编著了《婆罗摩修正体系》他曾经提出了“婆罗摩笈多定理” 也称“布拉美古塔定理”．定理的内容是：“若圆内接四边形的对角线互相垂直则垂直于一边且过对角线交点的直线平分对边”．任务：（1）按图（1）写出了这个定理的已知和求证并完成这个定理的证明过程已知：__________________求证：_________________证明：（2）如图（2）在O 中弦AB CD ⊥于M 连接,,,,,AC CB BD DA E F 分别是,AC BC 上的点 EM BD ⊥于,G FM AD ⊥于H 当M 是AB 中点时直接写出四边形EMFC 是怎样的特殊四边形：__________．参考答案：1．解：（1）∵同弧或等弧所对的圆周角相等∵E ∠和C ∠所对的弧是同一条弧∵∵应填：同弧或等弧所对的圆周角相等∵两角分别相等的两个三角形相似∵题目中的结论是两个三角形相似用的方式是三角形的两个角分别相等∵∵应填两角分别相等的两个三角形相似（2）∵BDE ADC ∠=∠ E C ∠=∠.BDE ADC ∽△∴△.BD DE AD DC∴= AD DE BD DC ∴⋅=⋅2AD BD DC AB AC ∴+⋅=⋅（3）42AE =∵BE CE =.∵弧BE =弧CE∵BAE CAE ∠=∠∵AE 平分BAC ∠.由斯库顿定理得2AD BD DC AB AC +⋅=⋅又∵4AC = 6AB = 2CD = 3BD =∵23264AD +⨯=⨯.解得=AD AD =-。

2014年中考数学专题(考点知识梳理+典例精析+巩固训练+考点训练)复习：第32讲与圆有关的计算

37 C. 2
考点训练
35 D. 2
首页上一页下一页
(2)(2012· 宁波)如图，用邻边分别为 a，b(a<b)的矩形硬纸板裁出以 a 为直径的两个半圆，再裁出与矩形的较长边、两个半圆均相切的两个小圆．把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面，从而做成两个圣诞帽(拼接处所用材料忽略不计)，则 a 与 b 满足的关系式是( )
考点训练
D．6π
首页上一页下一页
(2)(2012· 临沂)如图，AB 是⊙O 的直径，点 E 为 BC 的中点，AB＝4，∠BED＝120° ，则图中阴影部分的面积之和为( )
A．1
考点知识梳理
3 B. 2
C. 3
D．2 3
考点训练首页上一页下一页
中考典例精析
基础巩固训练
【点拨】(1)根据图示知∠BAB′ ＝45° ，所以根据弧长 nπr 公式 l＝求得 BB′的长； 180 (2)首先证明△ABC 是等边三角形，其次证△EDC 为等边三角形，而 BE 和弦 BE 围成的部分的面积等于 DE 和弦 DE 围成的部分的面积．
第32讲与圆有关的计算
首页
上一页
下一页
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
考点一弧长、扇形的面积 1．如果弧长为 l，圆心角为 n° ，圆的半径为 r，那么弧 nπr 长的计算公式为：l＝ . 180 2．由组成圆心角的两条半径和圆心角所对弧围成的图形叫做扇形．若扇形的圆心角为 n° ，所在圆半径为 r，弧长 nπr2 1 为 l，面积为 S，则 S＝，或 S＝ lr. 360 2 (注：公式中的 n 表示 1° 的圆心角的倍数，所以不写单位．)

中考数学二轮精品复习试卷：圆(含答案)

中考数学二轮精品复习试卷：圆学校：___________姓名：___________班级：___________考号：___________1、半径为3的圆中，一条弦长为4，则圆心到这条弦的距离是A．3 B．4 C．D．2、两个圆的半径分别为2和3，当圆心距d=5时，这两个圆的位置关系是【】A．内含B．内切C．相交D．外切3、如图，四边形ABCD是菱形，∠A=60°，AB=2，扇形BEF的半径为2，圆心角为60°，则图中阴影部分的面积是A．B．C．D．4、如图，已知线段OA交⊙O于点B，且OB＝AB，点P是⊙O上的一个动点，那么∠OAP 的最大值是A．90°B．60°C．45°D．30°5、如图，AB是半圆的直径，点D是弧AC的中点，∠ABC＝500，则∠DAB等于A．55°B．60°C．65°D．70°6、如图，ABCD的顶点A、B、D在⊙O上，顶点C在⊙O的直径BE上，∠ADC=54°，连接AE，则∠AEB的度数为A．36°B．46°C．27°D．63°7、一条排水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，则截面圆心O 到水面的距离OC是【】A．4B．5C．6D．88、如图，某厂生产横截面直径为7cm的圆柱形罐头，需将“蘑菇罐头”字样贴在罐头侧面．为了获得较佳视觉效果，字样在罐头侧面所形成的弧的度数为45°，则“蘑菇罐头”字样的长度为【】A．cm B．cm C．cm D．7πcm9、已知和的半径分别为和，圆心距为，则和的位置关系是【】A．外离B．外切C．相交D．内切10、如图，点A，B，C在⊙O上，∠A=50°，则∠BOC的度数为【】A．40°B．50°C．80°D．100°11、如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为【】A．B．8 C．D．12、如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD的长为【】A．cm B．cm C．cm D．4 cm13、如图，圆心在y轴的负半轴上，半径为5的⊙B与y轴的正半轴交于点A（0，1）。

2014年中考数学二轮复习：圆的选择题训练学习(1)、

第一讲：圆的选择题训练学习----2014年中考数学圆的二轮复习一、知识点睛1．相交弦定理：圆内两弦相交，交点分得的两条线段的乘积相等。

即：在⊙中，∵弦AB 、CD 相交于点P ，∴ ＝2.切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

即：在⊙中，∵PA 是切线，PCB 是割线∴ ＝3．（沈阳市）如图，PA 切⊙O 于点A ，PBC 是⊙O 的割线且过圆心，PA ＝4，PB ＝2，则⊙O 的半径等于（）（A ）3 （B ）4 （C ）6 （D ）8二、专项训练1一、选择题1．（西城区）如图，BC 是⊙O 的直径，P 是CB 延长线上一点，PA 切⊙O于点A ，如果PA ＝3，PB ＝1，那么∠APC 等于（）（A ） 15 （B ） 30 （C ） 45 （D ）602．（朝阳区）已知：如图，⊙O 半径为5，PC 切⊙O 于点C ，PO 交⊙O 于点A ，PA ＝4，那么PC 的长等于（）（A ）6 （B ）25 （C ）210 （D ）2143．（北京市朝阳区）如果圆锥的侧面积为20π平方厘米，它的母线长为5厘米，那么此圆锥的底面半径的长等于（）（A ）2厘米（B ）22厘米（C ）4厘米（D ）8厘米4．（重庆市）如图，⊙O 为△ABC 的内切圆，∠C ＝90，AO 的延长线交 BC 于点D ，AC ＝4，DC ＝1，，则⊙O 的半径等于（）（A ）54 （B ）45 （C ）43 （D ）655．（河北省）如图，AB 是⊙O 直径，CD 是弦．若AB ＝10厘米，CD ＝8厘米，那么A 、B 两点到直线CD 的距离之和为（）（A ）12厘米（B ）10厘米（C ）8厘米（D ）6厘米6．（河北省）某工件形状如图所示，圆弧BC 的度数为 60，AB ＝6厘米，点B 到点C 的距离等于AB ，∠BAC ＝ 30，则工件的面积等于（）（A ）4π （B ）6π（C ）8π （D ）10π8．（哈尔滨市）已知⊙O 的半径为35厘米，⊙O '的半径为5厘米．⊙O与⊙O '相交于点D 、E ．若两圆的公共弦DE 的长是6厘米（圆心O 、O '在公共弦DE 的两侧），则两圆的圆心距O O '的长为（）（A ）2厘米（B ）10厘米（C ）2厘米或10厘米（D ）4厘米9．（甘肃省）弧长为6π的弧所对的圆心角为 60，则弧所在的圆的半径为（）（A ）6 （B ）62 （C ）12 （D ）1810．（甘肃省）如图，在△ABC 中，∠BAC ＝ 90，AB ＝AC ＝2，以AB 为直径的圆交BC 于D ，则图中阴影部分的面积为（）（A ）1 （B ）2 （C ）1+4π （D ）2－4π 11．（宁夏回族自治区）已知圆的内接正六边形的周长为18，那么圆的面积为（）（A ）18π （B ）9π （C ）6π （D ）3π12．（南京市）如图，正六边形ABCDEF 的边长的上a ，分别以C 、F 为圆心，a 为半径画弧，则图中阴影部分的面积是（）（A ）261a π （B ）231a π （C ）232a π （D ）234a π13．（安徽省）已知圆锥的底面半径是3，高是4，则这个圆锥侧面展开图的面积是（）（A ）12π （B ）15π （C ）30π （D ）24π14．（安微省）已知⊙O 的直径AB 与弦AC 的夹角为 30，过C 点的切线PC 与AB 延长线交P ．PC ＝5，则⊙O 的半径为（）（A ）335 （B ）635 （C ）10 （D ）5 15．（福州市）如图：PA 切⊙O 于点A ，PBC 是⊙O 的一条割线，有PA ＝32，PB ＝BC ，那么BC 的长是（）（A ）3 （B ）32（C ）3 （D ）3216．（河南省）如图，⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离，它们的半径都是1，顺次连结五个圆心得到五边形ABCDE ，则图中五个扇形（阴影部分）的面积之和是（）（A ）π （B ）1.5π（C ）2π （D ）2.5π17．（新疆乌鲁木齐）在半径为2的⊙O 中，圆心O 到弦AB 的距离为1，则弦AB 所对的圆心角的度数可以是（）（A ） 60 （B ） 90 （C ） 120 （D ）15018．（成都市）如图，已知AB 是⊙O 的直径，弦CD ⊥AB 于点P ，CD ＝10厘米， AP ∶PB ＝1∶5，那么⊙O 的半径是（）（A ）6厘米（B ）53厘米（C ）8厘米（D ）35厘米19．（成都市）在Rt △ABC 中，已知AB ＝6，AC ＝8，∠A ＝ 90．如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥，其表面积为S 1；把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥，其表面积为S 2，那么S 1∶S 2等于（）（A ）2∶3 （B ）3∶4 （C ）4∶9 （D ）5∶1220．（苏州市）如图，⊙O 的弦AB ＝8厘米，弦CD 平分AB 于点E ．若CE ＝2厘米．ED 长为（）（A ）8厘米（B ）6厘米（C ）4厘米（D ）2厘米21．（镇江市）如图，正方形ABCD 内接于⊙O ，E 为DC 的中点，直线BE 交⊙O 于点F ．若⊙O 的半径为2，则BF 的长为（）（A ）23 （B ）22 （C ）556 （D ）55422（扬州市）如图，AB 是⊙O 的直径，∠ACD ＝ 15，则∠BAD 的度数为（）（A ） 75 （B ）72（C ） 70 （D ） 6523．（昆明市）如图，扇形的半径OA ＝20厘米，∠AOB ＝ 135，用它做成一个圆锥的侧面，则此圆锥底面的半径为（）（A ）3.75厘米（B ）7.5厘米（C ）15厘米（D ）30厘米24．（昆明市）如图，正六边形ABCDEF 中．阴影部分面积为123平方厘米，则此正六边形的边长为（）（A ）2厘米（B ）4厘米（C ）6厘米（D ）8厘米25．（广东省）如图，若四边形ABCD 是半径为1和⊙O 的内接正方形，则图中四个弓形（即四个阴影部分）的面积和为（）（A ）（2π－2）厘米（B ）（2π－1）厘米（C ）（π－2）厘米（D ）（π－1）厘米。

2014年全国中考数学试题分类汇编48 与圆有关的压轴题(含答案)

2014年中考数学分类汇编——与圆有关的压轴题2014年与圆有关的压轴题，考点涉及：垂径定理；圆周角定理；圆内接四边形的性质；切线性质；锐角三角函数定义；特殊角的三角函数值；相似三角形的判定和性质；勾股定理；特殊四边形性质；等.数学思想涉及：数形结合；分类讨论；化归；方程.现选取部分省市的2014年中考题展示，以飨读者.【题1】（2014年江苏南京,26题）如图，在Rt△ABC中，∠ACB=90°，AC=4cm，BC=3cm，⊙O为△ABC的内切圆．（1）求⊙O的半径；（2）点P从点B沿边BA向点A以1cm/s的速度匀速运动，以P为圆心，PB长为半径作圆，设点P运动的时间为t s，若⊙P与⊙O相切，求t的值．【分析】：（1）求圆的半径，因为相切，我们通常连接切点和圆心，设出半径，再利用圆的性质和直角三角形性质表示其中关系，得到方程，求解即得半径．（2）考虑两圆相切，且一圆已固定，一般就有两种情形，外切与内切．所以我们要分别讨论，当外切时，圆心距等于两圆半径的和；当内切时，圆心距等于大圆与小圆半径的差．分别作垂线构造直角三角形，类似（1）通过表示边长之间的关系列方程，易得t的值．【解】：（1）如图1，设⊙O与AB、BC、CA的切点分别为D、E、F，连接OD、OE、OF，则AD=AF，BD=BE，CE=CF．∵⊙O为△ABC的内切圆，∴OF⊥AC，OE⊥BC，即∠OFC=∠OEC=90°．∵∠C=90°，∴四边形CEOF是矩形，∵OE=OF，∴四边形CEOF是正方形．设⊙O的半径为rcm，则FC=EC=OE=rcm，在Rt△ABC中，∠ACB=90°，AC=4cm，BC=3cm，∴AB==5cm．∵AD=AF=AC﹣FC=4﹣r，BD=BE=BC﹣EC=3﹣r，∴4﹣r+3﹣r=5，解得r=1，即⊙O的半径为1cm．（2）如图2，过点P作PG⊥BC，垂直为G．∵∠PGB=∠C=90°，∴PG∥AC．∴△PBG∽△ABC，∴．∵BP=t，∴PG=，BG=．若⊙P与⊙O相切，则可分为两种情况，⊙P与⊙O外切，⊙P与⊙O内切．①当⊙P与⊙O外切时，如图3，连接OP，则OP=1+t，过点P作PH⊥OE，垂足为H．∵∠PHE=∠HEG=∠PGE=90°，∴四边形PHEG是矩形，∴HE=PG，PH=CE，∴OH=OE﹣HE=1﹣，PH=GE=BC﹣EC﹣BG=3﹣1﹣=2﹣．在Rt△OPH中，由勾股定理，，解得t=．②当⊙P与⊙O内切时，如图4，连接OP，则OP=t﹣1，过点O作OM⊥PG，垂足为M．∵∠MGE=∠OEG=∠OMG=90°，∴四边形OEGM是矩形，∴MG=OE，OM=EG，∴PM=PG﹣MG=，OM=EG=BC﹣EC﹣BG=3﹣1﹣=2﹣，在Rt△OPM中，由勾股定理，，解得t=2．综上所述，⊙P与⊙O相切时，t=s或t=2s．【点评】：本题考查了圆的性质、两圆相切及通过设边长，表示其他边长关系再利用直角三角形求解等常规考查点，总体题目难度不高，是一道非常值得练习的题目．【题2】（2014•泸州24题）如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD 相交于点E，且DC2=CE•CA．（1）求证：BC=CD；（2）分别延长AB，DC交于点P，过点A作AF⊥CD交CD的延长线于点F，若PB=OB，CD=，求DF的长．，得=，=，==4==2=中有，【题3】（2014•济宁21题）阅读材料：已知，如图（1），在面积为S的△ABC中，BC=a，AC=b，AB=c，内切圆O的半径为r．连接OA、OB、OC，△ABC被划分为三个小三角形．∵S=S△OBC+S△OAC+S△OAB=BC•r+AC•r+AB•r=（a+b+c）r．∴r=．（1）类比推理：若面积为S的四边形ABCD存在内切圆（与各边都相切的圆），如图（2），各边长分别为AB=a，BC=b，CD=c，AD=d，求四边形的内切圆半径r；（2）理解应用：如图（3），在等腰梯形ABCD中，AB∥DC，AB=21，CD=11，AD=13，⊙O1与⊙O2分别为△ABD与△BCD的内切圆，设它们的半径分别为r1和r2，求的值．、++=．==20=126===．【题4】（2014.福州20题）如图，在△ABC 中，∠B =45°，∠ACB =60°，AB =D 为BA 延长线上的一点，且∠D =∠ACB ，⊙O 为△ABC 的外接圆.（1）求BC 的长；（2）求⊙O 的半径. 【解析】∴BC 3=（2）由（1）得，在Rt △ACE 中，∵∠EAC =30°，EC ，∴AC =.∵∠D =∠ACB ，∠B =∠B ，∴△BAC ∽△BCD . ∴AB AC CB CD ==∴DM=4.∴⊙O的半径为2.【考点】：1. 锐角三角函数定义；2.特殊角的三角函数值；3.相似三角形的判定和性质；4.圆周角定理；5.圆内接四边形的性质；6.含30度角直角三角形的性质；7.勾股定理.【题5】（2014.广州25题）如图7，梯形中，，，,，，点为线段上一动点（不与点重合），关于的轴对称图形为，连接，设，的面积为，的面积为．（1）当点落在梯形的中位线上时，求的值；（2）试用表示，并写出的取值范围；（3）当的外接圆与相切时，求的值．【答案】解：（1）如图1，为梯形的中位线，则，过点作于点，则有：在中，有在中，又解得：（2）如图2，交于点，与关于对称，则有：，又又与关于对称，（3）如图3，当的外接圆与相切时，则为切点.的圆心落在的中点，设为则有，过点作，连接，得则又解得：（舍去）①②③【题6】（2014•湖州24题）已知在平面直角坐标系xOy中，O是坐标原点，以P（1，1）为圆心的⊙P与x轴，y轴分别相切于点M和点N，点F从点M出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF，过点PE⊥PF交y轴于点E，设点F运动的时间是t秒（t＞0）（1）若点E在y轴的负半轴上（如图所示），求证：PE=PF；（2）在点F运动过程中，设OE=a，OF=b，试用含a的代数式表示b；（3）作点F关于点M的对称点F′，经过M、E和F′三点的抛物线的对称轴交x轴于点Q，连接QE．在点F运动过程中，是否存在某一时刻，使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似？若存在，请直接写出t的值；若不存在，请说明理由．【分析】：（1）连接PM，PN，运用△PMF≌△PNE证明，（2）分两种情况①当t＞1时，点E在y轴的负半轴上，0＜t≤1时，点E在y轴的正半轴或原点上，再根据（1）求解，（3）分两种情况，当1＜t＜2时，当t＞2时，三角形相似时还各有两种情况，根据比例式求出时间t．【解答】：证明：（1）如图，连接PM，PN，∵⊙P与x轴，y轴分别相切于点M和点N，∴PM⊥MF，PN⊥ON且PM=PN，∴∠PMF=∠PNE=90°且∠NPM=90°，∵PE⊥PF，∠NPE=∠MPF=90°﹣∠MPE，在△PMF和△PNE中，，∴△PMF≌△PNE（ASA），∴PE=PF，（2）解：①当t＞1时，点E在y轴的负半轴上，如图，由（1）得△PMF≌△PNE，∴NE=MF=t，PM=PN=1，∴b=OF=OM+MF=1+t，a=NE﹣ON=t﹣1，∴b﹣a=1+t﹣（t﹣1）=2，∴b=2+a，②0＜t≤1时，如图2，点E在y轴的正半轴或原点上，同理可证△PMF≌△PNE，∴b=OF=OM+MF=1+t，a=ON﹣NE=1﹣t，∴b+a=1+t+1﹣t=2，∴b=2﹣a，（3）如图3，（Ⅰ）当1＜t＜2时，∵F（1+t，0），F和F′关于点M对称，∴F′（1﹣t，0）∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q，∴Q（1﹣t，0）∴OQ=1﹣t，由（1）得△PMF≌△PNE∴NE=MF=t，∴OE=t﹣1当△OEQ∽△MPF∴=∴=，解得，t=，当△OEQ∽△MFP时，∴=，=，解得，t=，（Ⅱ）如图4，当t＞2时，∵F（1+t，0），F和F′关于点M对称，∴F′（1﹣t，0）∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q，∴Q（1﹣t，0）∴OQ=t﹣1，由（1）得△PMF≌△PNE∴NE=MF=t，∴OE=t﹣1当△OEQ∽△MPF∴=∴=，无解，当△OEQ∽△MFP时，∴=，=，解得，t=2±，所以当t=，t=，t=2±时，使得以点Q、O、E为顶点的三角形与以点P、M、F 为顶点的三角形相似．【点评】：本题主要考查了圆的综合题，解题的关键是把圆的知识与全等三角形与相似三角形相结合找出线段关系．【题7】（2014•宁波26）木匠黄师傅用长AB=3，宽BC=2的矩形木板做一个尽可能大的圆形桌面，他设计了四种方案：方案一：直接锯一个半径最大的圆；方案二：圆心O1、O2分别在CD、AB上，半径分别是O1C、O2A，锯两个外切的半圆拼成一个圆；方案三：沿对角线AC将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆；方案四：锯一块小矩形BCEF拼到矩形AFED下面，利用拼成的木板锯一个尽可能大的圆．（1）写出方案一中圆的半径；（2）通过计算说明方案二和方案三中，哪个圆的半径较大？（3）在方案四中，设CE=x（0＜x＜1），圆的半径为y．①求y关于x的函数解析式；②当x取何值时圆的半径最大，最大半径为多少？并说明四种方案中哪一个圆形桌面的半径最大．度．则选择最小跨度，取其．．＞时，（﹣＜＞=）＜﹣时，（﹣=时，=）＜（），时，最大为．＜＜，【题8】（2014•苏州28）如图，已知l1⊥l2，⊙O与l1，l2都相切，⊙O的半径为2cm，矩形ABCD的边AD、AB分别与l1，l2重合，AB=4cm，AD=4cm，若⊙O与矩形ABCD沿l1同时向右移动，⊙O的移动速度为3cm，矩形ABCD的移动速度为4cm/s，设移动时间为t（s）（1）如图①，连接OA、AC，则∠OAC的度数为105°；（2）如图②，两个图形移动一段时间后，⊙O到达⊙O1的位置，矩形ABCD到达A1B1C1D1的位置，此时点O1，A1，C1恰好在同一直线上，求圆心O移动的距离（即OO1的长）；（3）在移动过程中，圆心O到矩形对角线AC所在直线的距离在不断变化，设该距离为d （cm），当d＜2时，求t的取值范围（解答时可以利用备用图画出相关示意图）．cm=，=4==2==2=+2﹣﹣（=2+2﹣．【题9】（2014•泰州25题）如图，平面直角坐标系xOy中，一次函数y=﹣x+b（b为常数，b＞0）的图象与x轴、y轴分别相交于点A、B，半径为4的⊙O与x轴正半轴相交于点C，与y轴相交于点D、E，点D在点E上方．（1）若直线AB与有两个交点F、G．①求∠CFE的度数；②用含b的代数式表示FG2，并直接写出b的取值范围；（2）设b≥5，在线段AB上是否存在点P，使∠CPE=45°？若存在，请求出P点坐标；若不存在，请说明理由．﹣=b bb bb﹣（FG﹣（b b b b 有两个交点x﹣，）【题10】(2014年江苏徐州28) 如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．（1）试说明四边形EFCG是矩形；（2）当圆O与射线BD相切时，点E停止移动，在点E移动的过程中，①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；②求点G移动路线的长．【考点】：圆的综合题；垂线段最短；直角三角形斜边上的中线；矩形的判定与性质；圆周角定理；切线的性质；相似三角形的判定与性质．【分析】：（1）只要证到三个内角等于90°即可．（2）易证点D在⊙O上，根据圆周角定理可得∠FCE=∠FDE，从而证到△CFE∽△DAB，根据相似三角形的性质可得到S矩形ABCD=2S△CFE=．然后只需求出CF的范围就可求出S的范围．根据圆周角定理和矩形的性质可证到∠GDC=∠FDE=定值，从而得到点G 矩形ABCD的移动的路线是线段，只需找到点G的起点与终点，求出该线段的长度即可．【解答】：解：（1）证明：如图1，∵CE为⊙O的直径，∴∠CFE=∠CGE=90°．∵EG⊥EF，∴∠FEG=90°．∴∠CFE=∠CGE=∠FEG=90°．∴四边形EFCG是矩形．（2）①存在．连接OD，如图2①，∵四边形ABCD是矩形，∴∠A=∠ADC=90°．∵点O是CE的中点，∴OD=OC．∴点D在⊙O上．∵∠FCE=∠FDE，∠A=∠CFE=90°，∴△CFE∽△DAB．∴=（）2．∵AD=4，AB=3，∴BD=5，S△CFE=（）2•S△DAB=××3×4=．∴S矩形ABCD=2S△CFE=．∵四边形EFCG是矩形，∴FC∥EG．∴∠FCE=∠CEG．∵∠GDC=∠CEG，∠FCE=∠FDE，∴∠GDC=∠FDE．∵∠FDE+∠CDB=90°，∴∠GDC+∠CDB=90°．∴∠GDB=90°Ⅰ．当点E在点A（E′）处时，点F在点B（F′）处，点G在点D（G′处，如图2①所示．此时，CF=CB=4．Ⅱ．当点F在点D（F″）处时，直径F″G″⊥BD，如图2②所示，此时⊙O与射线BD相切，CF=CD=3．Ⅲ．当CF⊥BD时，CF最小，此时点F到达F″′，如图2③所示．S△BCD=BC•CD=BD•CF″′．∴4×3=5×CF″′．∴CF″′=．∴≤CF≤4．∵S矩形ABCD=，∴×（）2≤S矩形ABCD≤×42．∴≤S矩形ABCD≤12．∴矩形EFCG的面积最大值为12，最小值为．②∵∠GDC=∠FDE=定值，点G的起点为D，终点为G″，∴点G的移动路线是线段DG″．∵∠GDC=∠FDE，∠DCG″=∠A=90°，∴△DCG″∽△DAB．∴=．∴=．∴DG″=．∴点G移动路线的长为．【点评】：本题考查了矩形的判定与性质、相似三角形的判定与性质、圆周角定理、直角三角形斜边上的中线等于斜边的一半、垂线段定理等知识，考查了动点的移动的路线长，综合性较强．而发现∠CDG =∠ADB 及∠FCE =∠ADB 是解决本题的关键．【题11】（2014.连云港25题）为了考察冰川融化的状况，一支科考队在某冰川上设一定一个以大本营O 为圆心，半径为4km 圆形考察区域，线段P 1、P 2是冰川的部分边界线（不考虑其它边界），当冰川融化时，边界线沿着与其垂直的方向朝考察区域平行移动.若经过n 年，冰川的边界线P 1P 2移动的距离为s (km ),并且s 与n （n 为正整数）的关系是2575092032+-=n n s .以O 为原点，建立如图所示的平面直角坐标系，其中P 1、P 2的坐标分别是（－4，9）、（－13，－3）. （1）求线段P 1P 2所在的直线对应的函数关系式；（2）求冰川的边界线移动到考察区域所需要的最短时间.【解答】(第25题图)。

2014年中考数学专题复习试题—圆

2013—2014学年九年级数学（下）周末复习资料（11）理想文化教育培训中心学生姓名：得分:1、如图，点A 、B 、O 是正方形网格上的三个格点，⊙O 的半径为OA ，点P 是优弧AmB 上的一点，则tan APB ∠的值是【】 A ．1 B．2CD2、如图，在半径为5的圆O 中，AB ，CD 是互相垂直的两条弦，垂足为P ，且AB =CD =8，则OP 的长为【】A ．3B ．4 C．D ．243、如图，△ABC 是⊙O 的内接三角形，AC 是⊙O 的直径，∠C =50°，∠ABC 的平分线BD 交⊙O 于点D ，则∠BAD 的度数是【】 A ．45° B ．85° C ．90° D ．95°4、如图，直径为10的⊙A 经过点C (0,5)和点O (0,0)，B 是y 轴右侧⊙A 优弧上一点，则cos ∠OBC 的值为【】A ．12 BC ．35D ．45（第1题图）（第2题图）（第3题图）（第4题图）（第7题图）5、已知直角三角形ABC 的一条直角边12AB cm =，另一条直角边5BC cm =，则以AB 为轴旋转一周，所得到的圆锥的表面积是( )A.290cm πB. 2209cm πC. 2155cm πD. 265cm π7、如图，扇形AOB 的半径为1，∠AOB=90°，以AB为直径画半圆，则图中阴影部分的面积为（）A ．B.C. 12 D.8、（2013•白银）如图，在⊙O 中，半径OC 垂直于弦AB ，垂足为点E ．（1）若OC=5，AB=8，求tan ∠BAC ；（2）若∠DAC=∠BAC ，且点D 在⊙O 的外部，判断直线AD 与⊙O 的位置关系，并加以证明．9、（2013四川宜宾）如图，AB是⊙O的直径，∠B=∠CAD．（1）求证：AC是⊙O的切线；（2）若点E是的中点，连接AE交BC于点F，当BD=5，CD=4时，求AF的值．10、（2013甘肃兰州）已知，如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D 作DE⊥MN于E．（1）求证：DE是⊙O的切线；（2）若DE=6cm，AE=3cm，求⊙O的半径．11、（2013•恩施州）如图所示，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于点D，CD 交AE于点F，过C作CG∥AE交BA的延长线于点G．（1）求证：CG是⊙O的切线．（2）求证：AF=CF．（3）若∠EAB=30°，CF=2，求GA的长．12、（2013•钦州）如图，在Rt△ABC中，∠A=90°，O是BC边上一点，以O为圆心的半圆与AB边相切于点D，与AC、BC边分别交于点E、F、G，连接OD，已知BD=2，AE=3，tan∠BOD=．（1）求⊙O的半径OD；（2）求证：AE是⊙O的切线；（3）求图中两部分阴影面积的和．13、（2013•内江）如图，AB是半圆O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC．（1）求证：BC平分∠PDB；（2）求证：BC2=AB•BD；（3）若PA=6，PC=6，求BD的长．14、（2013•莱芜）如图，⊙O的半径为1，直线CD经过圆心O，交⊙O于C、D两点，直径AB⊥CD，点M是直线CD上异于点C、O、D的一个动点，AM所在的直线交于⊙O于点N，点P是直线CD上另一点，且PM=PN．（1）当点M在⊙O内部，如图一，试判断PN与⊙O的关系，并写出证明过程；（2）当点M在⊙O外部，如图二，其它条件不变时，（1）的结论是否还成立？请说明理由；（3）当点M在⊙O外部，如图三，∠AMO=15°，求图中阴影部分的面积．8、解：（1）∵半径OC垂直于弦AB，∴AE=BE=AB=4，在Rt△OAE中，OA=5，AE=4，∴OE==3，∴EC=OC﹣OE=5﹣3=2，在Rt△AEC中，AE=4，EC=2，∴tan∠BAC===；（2）AD与⊙O相切．理由如下：∵半径OC垂直于弦AB，∵AC弧=BC弧，∴∠AOC=2∠BAC，∵∠DAC=∠BAC，∴∠AOC=∠BAD，∵∠AOC+∠OAE=90°，∴∠BAD+∠OAE=90°，∴OA⊥AD，∴AD为⊙O的切线．9、解：（1）∵AB是⊙O的直径，∴∠ADB=∠ADC=90°，∵∠B=∠CAD，∠C=∠C，∴△ADC∽△BAC，∴∠BAC=∠ADC=90°，∴BA⊥AC，∴AC是⊙O的切线．（2）∵△ADC∽△BAC（已证），∴=，即AC2=BC×CD=36，解得：AC=6，在Rt△ACD中，AD==2，∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD，∴CA=CF=6，∴DF=CA﹣CD=2，在Rt△AFD中，AF==2．10、解答：（1）证明：连接OD．∵OA=OD，∴∠OAD=∠ODA．（1分）∵∠OAD=∠DAE，∴∠ODA=∠DAE．（2分）∴DO∥MN．（3分）∵DE⊥MN，∴∠ODE=∠DEM=90°．即OD⊥DE．（4分）∵D在⊙O上，∴DE是⊙O的切线．（5分）（2）解：∵∠AED=90°，DE=6，AE=3，∴．（6分）连接CD．∵AC是⊙O的直径，∴∠ADC=∠AED=90°．（7分）∵∠CAD=∠DAE，∴△ACD∽△ADE．（8分）∴．∴．则AC=15（cm）．（9分）∴⊙O的半径是7.5cm．（10分）11、（1）证明：连结OC，如图，∵C是劣弧AE的中点，∴OC⊥AE，∵CG∥AE，∴CG⊥OC，∴CG是⊙O的切线；（2）证明：连结AC、BC，∵AB是⊙O的直径，∴∠ACB=90°，∴∠2+∠BCD=90°，而CD⊥AB，∴∠B+∠BCD=90°，∴∠B=∠2，∵AC弧=CE弧，∴∠1=∠B，∴∠1=∠2，∴AF=CF；（3）解：在Rt△ADF中，∠DAF=30°，FA=FC=2，∴DF=AF=1，∴AD=DF=，∵AF∥CG，∴DA：AG=DF：CF，即：AG=1：2，∴AG=2．12、解：（1）∵AB与圆O相切，∴OD⊥AB，在Rt△BDO中，BD=2，tan∠BOD==，∴OD=3；（2）连接OE，∵AE=OD=3，AE∥OD，∴四边形AEOD为平行四边形，∴AD∥EO，∵DA⊥AE，∴OE⊥AC，又∵OE为圆的半径，∴AC为圆O的切线；（3）∵OD∥AC，∴=，即=，∴AC=7.5，∴EC=AC﹣AE=7.5﹣3=4.5，∴S阴影=S△BDO+S△OEC﹣S扇形BOD﹣S扇形EOG=×2×3+×3×4.5﹣=3+﹣=．13、（1）证明：连接OC，∵PD为圆O的切线，∴OC⊥PD，∵BD⊥PD，∴OC∥BD，∴∠OCB=∠CBD，∵OC=OB，∴∠OCB=∠OBC，∴∠CBD=∠OBC，则BC平分∠PBD；（2）证明：连接AC，∵AB为圆O的直径，∴∠ACB=90°，∵∠ACB=∠CDB=90°，∠ABC=∠CBD，∴△ABC∽△CBD，∴=，即BC2=AB•BD；（3）解：∵PC为圆O的切线，PAB为割线，∴PC2=PA•PB，即72=6PB，解得：PB=12，∴AB=PB﹣PA=12﹣6=6，∴OC=3，PO=PA+AO=9，∵△OCP∽△BDP，∴=，即=，则BD=4．14、（1）PN与⊙O相切．证明：连接ON，则∠ONA=∠OAN，∵PM=PN，∴∠PNM=∠PMN．∵∠AMO=∠PMN，∴∠PNM=∠AMO．∴∠PNO=∠PNM+∠ONA=∠AMO+∠ONA=90°．即PN与⊙O相切．（2）成立．证明：连接ON，则∠ONA=∠OAN，∵PM=PN，∴∠PNM=∠PMN．在Rt△AOM中，∴∠OMA+∠OAM=90°，∴∠PNM+∠ONA=90°．∴∠PNO=180°﹣90°=90°．即PN与⊙O相切．（3）解：连接ON，由（2）可知∠ONP=90°．∵∠AMO=15°，PM=PN，∴∠PNM=15°，∠OPN=30°，∵∠PON=60°，∠AON=30°．作NE⊥OD，垂足为点E，则NE=ON•sin60°=1×=．S阴影=S△AOC+S扇形AON﹣S△CON=OC•OA+CO•NE=×1×1+π﹣×1×=+π﹣．。

中考数学专题复习：与圆有关的动点问题(精品含答案)

２0１４年中考数学专题复习:与圆有关的动点问题1、如图,⊙Ｏ的直径AB=4，C为圆周上一点，AＣ=2，过点C作⊙O的切线DC,Ｐ点为优弧CBA上一动点(不与A.C重合).（1）求∠APC与∠ACＤ的度数；(2)当点P移动到CＢ弧的中点时，求证:四边形OＢPC是菱形.（３）P点移动到什么位置时，△AＰC与△ABＣ全等,请说明理由．2、如图，在⊙O上位于直径ＡB的异侧有定点Ｃ和动点P,AＣ=12AB，点Ｐ在半圆弧ＡB上运动（不与A、B两点重合),过点C作直线PB的垂线ＣD交ＰＢ于Ｄ点.(１）如图1，求证:△PCD∽△ABC；（２）当点P运动到什么位置时,△ＰCD≌△ABC?请在图2中画出△PCＤ并说明理由; （３)如图3,当点P运动到CP⊥AB时,求∠ＢCD的度数．３、如图，在半径为2的扇形ＡOB中,∠AOB=９0°，点C是弧AB上的一个动点(不与点A、B重合）OD⊥BC,ＯE⊥AC,垂足分别为D、E.(1)当BC=1时,求线段OD的长;（2)在△DOＥ中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式，并写出它的定义域.４、如图，菱形ＡBCD的边长为２cm，∠DＡＢ=60°．点Ｐ从Ａ点出发，以ｃm／s的速度，沿ＡC向C作匀速运动；与此同时，点Q也从A点出发,以1cm/ｓ的速度，沿射线ＡB 作匀速运动.当P运动到C点时，P、Q都停止运动.设点P运动的时间为ts．(1)当P异于A．C时,请说明PＱ∥ＢＣ；(２)以Ｐ为圆心、ＰQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时，⊙P与边ＢC分别有1个公共点和２个公共点？5、如图,在菱形ABCD中，AB＝2错误!,∠A＝60º，以点D为圆心的⊙D与边AB相切于点E.(1)求证：⊙Ｄ与边ＢＣ也相切；(2)设⊙D与BD相交于点H,与边CD相交于点Ｆ，连接ＨF,求图中阴影部分的面积(结果保留π);(３)⊙D上一动点M从点F出发，按逆时针方向运动半周,当S△ＨDＦ＝错误!S△MＤF时,求动点Ｍ经过的弧长(结果保留π)．６、半径为2cｍ的与⊙O边长为２ｃｍ的正方形AＢＣD在水平直线l的同侧,⊙Ｏ与l相切于点F，DC在ｌ上.（1)过点B作的一条切线BE,E为切点.①填空:如图1,当点A在⊙O上时,∠ＥBＡ的度数是；②如图2,当E,Ａ，D三点在同一直线上时,求线段OA的长；ﻫ(2）以正方形ABＣＤ的边AD 与ＯF重合的位置为初始位置，向左移动正方形(图3)，至边BC与OＦ重合时结束移动,M,N 分别是边BＣ,AD与⊙Ｏ的公共点,求扇形MON的面积的范围．ﻫ7、如图，Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F，且∠ACＢ=90°，AB=5，ＢC=３，点P在射线AC上运动,过点P作PH⊥AB，垂足为H．（１）直接写出线段AＣ、AD及⊙Ｏ半径的长;（2）设PH=x,PC=y，求y关于x的函数关系式;(３）当ＰＨ与⊙O相切时,求相应的y值．8、如图1，正方形ＡBCＤ的边长为２,点M是BC的中点,P是线段ＭC上的一个动点（不与M、C重合),以ＡＢ为直径作⊙O，过点P作⊙Ｏ的切线，交AD于点F,切点为Ｅ.（1）求证：ＯF∥BE；(２)设BＰ＝x,ＡF＝y，求ｙ关于ｘ的函数解析式,并写出自变量x的取值范围；(3)延长DC、FP交于点G，连接ＯE并延长交直线DC与H（图2）,问是否存在点P，使△E ＦO∽△EHG(E、F、Ｏ与E、H、G为对应点)?如果存在,试求（2）中x和y的值；如果不存在,请说明理由.9、如图，⊙O的半径为１，直线CD经过圆心O,交⊙Ｏ于C、D两点，直径AB⊥ＣD,点Ｍ是直线CD上异于点C、O、D的一个动点，ＡM所在的直线交于⊙O于点N，点P是直线CD上另一点，且ＰM=PN.(1）当点M 在⊙O 内部,如图一,试判断PN 与⊙O 的关系，并写出证明过程； (2)当点M 在⊙O 外部，如图二，其它条件不变时，（1）的结论是否还成立？请说明理由； (3）当点M 在⊙O 外部,如图三，∠AMO=1５°,求图中阴影部分的面积.10、如图,在⊙Ｏ中，直径AB ⊥ＣD,垂足为E ，点M 为OC 上动点,ＡM 的延长线交⊙O 于点Ｇ，交过C 的直线于F ，∠1=∠2,连结ＣB 与ＤＧ交于点Ｎ. (1）求证：ＣF 是⊙O 的切线;(2)点Ｍ在ＯC 上移动时(点M 不与Ｏ、Ｃ点重合），探究△ACM 与△ＤＣＮ之间关系，并证明 (3）若点M 移动到CO 的中点时,⊙O 的半径为４，ｃos ∠B ＯC=41,求B Ｎ的长.11、如图，已知A Ｂ是圆Ｏ的直径,BC 是圆O 的弦，弦ED ⊥AB 于点F,交B Ｃ于点G ,过点C 作圆O 的切线与ＥＤ的延长线交于点P. (１）求证:PC ＝PG;（2)点Ｃ在劣弧AD 上运动时，其他条件不变，若点G 是ＢＣ的中点，试探究C Ｇ、BF 、BＯ三者之间的数量关系,并写出证明过程；（3）在满足（2)的条件下，已知圆为O的半径为5,若点Ｏ到BC的距离为5时，求弦ED 的长.12、如图1，已知⊙O的半径长为3，点Ａ是⊙O上一定点，点Ｐ为⊙Ｏ上不同于点A的动点.(1）当1A=时,求AP的长;tan2(２)如果⊙Q过点P、O,且点Ｑ在直线AＰ上（如图2）,设ＡＰ＝x，ＱＰ＝y,求y关于x 的函数关系式，并写出函数的定义域；（3）在（2）的条件下，当4A=时（如图3），存在⊙Ｍ与⊙O相内切，同时与⊙Qtan3相外切,且ＯM⊥OQ，试求⊙M的半径的长.图1 图2图３答案:1、解：（１)连接AC，如图所示：∵AＢ=4,∴OA=OB=ＯC＝12ＡＢ=2。

中考数学复习：二次函数和圆的综合题（含答案）

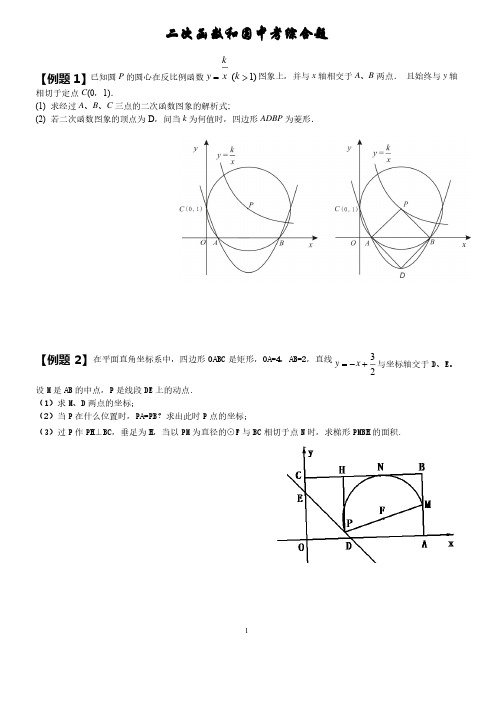
1 二次函数和圆中考综合题【例题1】已知圆P 的圆心在反比例函数ky x =(1)k >图象上，并与x 轴相交于A 、B 两点．且始终与y 轴相切于定点C (0，1)．(1)求经过A 、B 、C 三点的二次函数图象的解析式; (2)若二次函数图象的顶点为D ，问当k 为何值时，四边形ADBP 为菱形．【例题2】在平面直角坐标系中，四边形OABC 是矩形，是矩形，OA=4OA=4OA=4，，AB=2AB=2，直线，直线32y x =-+与坐标轴交于D 、E 。

设M 是AB 的中点，的中点，P P 是线段DE 上的动点上的动点. .（1）求M 、D 两点的坐标；（2）当P 在什么位置时，在什么位置时，PA=PB PA=PB PA=PB？求出此时？求出此时P 点的坐标；（3）过P 作PH PH⊥⊥BC BC，垂足为，垂足为H ，当以PM 为直径的⊙为直径的⊙F F 与BC 相切于点N 时，求梯形PMBH 的面积的面积. .【例题3】在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），⊙A与x轴交于E、F两点，与y 轴交于C、D两点，过点C作⊙A的切线BC，交x轴于点B．的解析式；（1）求直线CB的解析式；（2）若抛物线y=ax2+b x+c的顶点在直线BC上，与x轴的交点恰为点E、F，求该抛物线的解析式；，求该抛物线的解析式；（3）试判断点C是否在抛物线上？是否在抛物线上？相似？直接写出两组这样的点．（4）在抛物线上是否存在三个点，由它构成的三角形与△AOC相似？直接写出两组这样的点．【例题4】如图，已知抛物线y= ax2 + bx－3与x轴交于A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心M（1，m）恰好在此抛物线的对称轴上，⊙M的半径为5．设⊙M与y轴交于D，抛物线的顶点为E．的值及抛物线的解析式；（1）求m的值及抛物线的解析式；（a－b）的值；）的值；sin（（2）设∠DBC = a，∠CBE = b，求sin（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCE相似？若存在，请指的坐标；若不存在，请说明理由．出点P的位置，并直接写出点P的坐标；若不存在，请说明理由．【例题5】如图，点M （4，0），以点M 为圆心、为圆心、22为半径的圆与x 轴交于点A 、B ．已知抛物线216y x bx c =++过点A 和B ，与y 轴交于点C ．（1）求点C 的坐标，并画出抛物线的大致图象．的坐标，并画出抛物线的大致图象．（2）点Q （8，m ）在抛物线216y x bx c =++上，点P 为此抛物线对称轴上一个动点，求PQ ＋PB 的最小值．最小值．（3）CE 是过点C 的⊙M 的切线，点E 是切点，求OE 所在直线的解析式．所在直线的解析式．【例题6】如图所示，如图所示，在平面直角坐标系中，在平面直角坐标系中，M 经过原点O ，且与x 轴、y 轴分别相交于A （-8,0），B （0，-6）两点．）两点．（1）请求出直线AB 的函数表达式；的函数表达式；（2）若有一抛物线的对称轴平行于y 轴且经过点M ，顶点C 在M 上，开口向下，且经过点B ，求此抛物线的函数表达式；函数表达式；（3）设（2）中的抛物线交x 轴于D E ，两点，在抛物线上是否存在点P ，使得115PDE ABC S S =△△？若存在，请求出点P 的坐标；若不存在，请说明理由．的坐标；若不存在，请说明理由．（4）点H 是抛物线对称轴上的一个动点，且在点M 的下方，请问抛物线上是否存在另一点Q ，使得△ABH 与△ABQ 全等。

2014年中考数学二轮复习：圆的填空题训练学习(2)

第二讲：圆的填空题训练学习-------2014年中考数学圆的二轮复习填空题1．（东城区）如图，AB、AC是⊙O的两条切线，切点分别为B、C，D是优弧上的一点，已知∠BAC80，那么∠BDC＝__________度．＝90，AＢ＝3，BC＝1，以AC所在直线2．（东城区）在Rt△ABC中，∠C＝为轴旋转一周，所得圆锥的侧面展开图的面积是__________．3．（北京市海淀区）如果圆锥母线长为6厘米，那么这个圆锥的侧面积是_______平方厘米4．（上海市）两个点O为圆心的同心圆中，大圆的弦AB与小圆相切，如果AB的长为24，大圆的半径OA为13，那么小圆的半径为___________．5．（天津市）已知⊙O中，两弦AB与CD相交于点E，若E为AB的中点，CE∶ED＝1∶4，AB＝4，则CD的长等于___________．6．（重庆市）如图，P是⊙O的直径AB延长线上一点，PC切⊙O于点C，PC＝6，BC∶AC＝1∶2，则AB的长为___________．7．（重庆市）如图，四边形ABCD内接于⊙O，AD∥BC，＝，若AD＝4，BC＝6，则四边形ABCD的面积为__________．8．(山西省)若一个圆柱的侧面积等于两底面积的和，则它的高h与底面半径r的大小关系是__________．9．（沈阳市）圆内两条弦AB和CD相交于P点，AB长为7，AB把CD分成两部分的线段长分别为2和6，那么＝__________．10．（沈阳市）△ABC 是半径为2厘米的圆内接三角形，若BC ＝23厘米，则∠A 的度数为________．11．（沈阳市）如图，已知OA 、OB 是⊙O 的半径，且OA ＝5，∠AOB ＝15， AC ⊥OB 于C ，则图中阴影部分的面积（结果保留π）S ＝_________．12．（哈尔滨市）如图，圆内接正六边形ABCDEF 中，AC 、BF 交于点M ．则ABM S △∶AFM S △＝_________．13．(哈尔滨市)两圆外离，圆心距为25厘米，两圆周长分别为15π厘米和10π厘米．则其内公切线和连心线所夹的锐角等于__________度．14．（哈尔滨市）将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周，所得圆柱体的表面积为_________平方厘米．15．（陕西省）已知⊙O 的半径为4厘米，以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积，则这个小圆的半径是______厘米．16．（甘肃省）如图，AB ＝8，AC ＝6，以AC 和BC 为直径作半圆，两圆的公切线MN 与AB 的延长线交于D ，则BD 的长为_________．17．（宁夏回族自治区）圆锥的母线长为5厘米，高为3厘米，在它的侧面展开图中，扇形的圆心角是_________度．18．（南京市）如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足是G ，F 是CG 的中点，延长AF 交⊙O 于E ，CF ＝2，AF ＝3，则EF 的长是_________．19．（福州市）在⊙O 中，直径AB ＝4厘米，弦CD ⊥AB 于E ，OE ＝3，则弦CD 的长为__________厘米．20．（福州市）若圆锥底面的直径为厘米，线线长为5厘米，则它的侧面积为__________平方厘米21．（河南省）如图，AB 为⊙O 的直径，P 点在AB 的延长线上，PM 切⊙O 于M 点．若OA ＝a ，PM ＝3a ，那么△PMB 的周长的__________．22．（贵阳市）如果圆O 的直径为10厘米，弦AB 的长为6厘米，那么弦AB 的弦心距等于________厘米．23．（贵阳市）某种商品的商标图案如图所求（阴影部分），已知菱形ABCD 的边长为4，∠A ＝60，是以A 为圆心，AB 长为半径的弧，是以B 为圆心，BC 长为半径的弧，则该商标图案的面积为_________．24．（新疆乌鲁木齐）如图，已知扇形AOB 的半径为12，OA ⊥OB ，C 为OA 上一点，以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切，则半圆1O 的半径为__________．25．（成都市）如图，PA、PB与⊙O分别相切于点A、点B，AC是⊙O的直径，PC交⊙O于点D．已知∠APB＝60，AC＝2，那么CD的长为________．26．（扬州市）边长为2厘米的正六边形的外接圆半径是________厘米，内切圆半径是________厘米（结果保留根号）．27．（绍兴市）如图，PT是⊙O的切线，T为切点，PB是⊙O的割线交⊙O于A、B两点，交弦CD于点M，已知：CM＝10，MD＝2，PA＝MB＝4，则PT的长等于__________．28．（温州市）如图，扇形OAB中，∠AOB＝90，半径OA＝1，C是线段AB的中点，CD∥OA，交于点D，则CD＝________．29．（常州市）已知扇形的圆心角为150 ，它所对的弧长为20π厘米，则扇形的半径是________厘米，扇形的面积是__________平方厘米．30．（常州市）如图，AB是⊙O直径，CE切⊙O于点C，CD⊥AB，D为垂足，AB＝12厘米，∠B＝30 ，则∠ECB＝__________ ；CD＝_________厘米．31．（常州市）如图，DE是⊙O直径，弦AB⊥DE，垂足为C，若AB＝6，CE＝1则CD＝________，OC＝_________．32．（海南省）已知：⊙O的半径为1，M为⊙O外的一点，MA切⊙O于点A，MA＝1．若AB是⊙O的弦，且AB＝2，则MB的长度为_________．。

中考数学二轮专题复习-圆的性质及有关计算及答案详解

中考数学二轮专题复习-圆的性质及有关计算一、单选题1．如图，点A、B、C在⊙O上，∠CAB＝70°，则∠BOC等于（）A．100°B．110°C．130°D．140°2．如图，⊙O的半径为5，弦AB＝6，P是弦AB上的一个动点（不与A、B重合），下列符合条件的OP的值可以是（）A．3.1B．4.2C．5.3D．6.43．如图，AB是⊙O的直径，CD是弦，若∠BCD=34°，则∠ABD等于（）A．66°B．34°C．56°D．68°4．如图，点A，B，C在上，是等边三角形，则的大小为（）A．60°B．40°C．30°D．20°5．已知为圆的直径，为圆周上一点，，．则的度数为（）A．10°B．15°C．20°D．30°6．如图，AB是⊙O的直径，CD⊥AB于点E，连结CO并延长，交弦AD于点F．若AB=10，BE=2，则OF的长度是（）A．B．3C．D．7．如图，是⊙O的弦，且，点是弧中点，点是优弧上的一点，，则圆心到弦的距离等于（）A．B．C．D．8．如图，A，B，C是某社区的三栋楼，若在AC中点D处建一个5G基站，其覆盖半径为300 m，则这三栋楼中在该5G基站覆盖范围内的是（）A．A，B，C都不在B．只有BC．只有A，C D．A，B，C9．如图，四边形ABCD内接于，若，则的度数为（）A．50°B．100°C．130°D．150°10．如图，两个等圆⊙O1和⊙O2相交于A、B两点，且⊙O1经过⊙O2的圆心，则∠O1AB的度数为（）A．45°B．30°C．20°D．15°11．如图，AB是⊙O的直径，点C，D为⊙O上的点．若∠D＝120°，则∠CAB的度数为（）A．30°B．40°C．50°D．60°12．如图，四个边长为2的小正方形拼成一个大正方形，A、B、O是小正方形顶点，⊙O的半径为2，P是⊙O上的点，且位于右上方的小正方形内，则∠APB等于（）A．30°B．45°C．60°D．90°13．如图，点C，D是劣弧上两点，CD∥AB，∠CAB＝45°，若AB＝6，CD＝2，则所在圆的半径长为（）A．B．C．2 D．14．如图，在正方形ABCD中，点E是边BC的中点，连接AE、DE，分别交BD、AC于点P、Q，过点P作PF⊥AE交CB的延长线于F，下列结论：①∠AED+∠EAC+∠EDB＝90°，②AP＝FP，③AE＝AO，④若四边形OPEQ的面积为4，则该正方形ABCD的面积为36，⑤CE•EF＝EQ•DE．其中正确的结论有（）A．5个B．4个C．3个D．2个15．如图，点P是等边三角形ABC外接圆⊙O上的点，在以下判断中，不正确的是（）A．当弦PB最长时，△APC是等腰三角形B．当△APC是等腰三角形时，PO⊥ACC．当PO⊥AC时，∠ACP＝30°D．当∠ACP＝30°时，△BPC是直角三角形16．如图所示，半径为R的⊙O的弦AC＝BD，AC，BD交于点E，F为上一点，连结AF，BF，AB，AD，有下列结论：①AE＝BE；②若AC⊥BD，则AD＝R；③若AC⊥BD，＝，AB＝，则BF+CE＝1.其中正确的是（）A．①②B．①③C．②③D．①②③17．如图，AB为⊙O的直径，点C为⊙O上一点，连接CO，作AD OC，若CO＝，AC＝2，则AD＝（）A．3B．C．D．18．如图，在△ABC中，（1）作AB和BC的垂直平分线交于点O；（2）以点O为圆心，OA长为半径作圆；（3）⊙O分别与AB和BC的垂直平分线交于点M，N；（4）连接AM，AN，CM，其中AN与CM交于点P.根据以上作图过程及所作图形，下列四个结论：①＝2 ；②AB＝2AM；③点P是△ABC的内心；④∠MON＋2∠MPN＝360°.其中正确结论的个数是（）A．1B．2C．3D．419．如图，已知正方形ABCD的边长为4，点M和N分别从B、C同时出发，以相同的速度沿BC、CD向终点C、D运动，连接AM、BN，交于点P，连接PC，则PC长的最小值为（）A．2 －2B．2C．3 －1D．220．如图，AB是⊙o直径，M，N是上两点，C是上任一点，∠ACB角平分线交⊙o 于点D，∠BAC的平分线交CD于点E，当点C从M运动到N时，C、E两点的运动路径长之比为()A．B．C．D．二、填空题21．如图，在⊙O中，点A在上，∠BOC=100°，则∠BAC=.22．如图，在⊙O中，A，B，C是⊙O上三点，如果∠AOB=70º，那么∠C的度数为．23．如图，四边形是的内接四边形，对角线是的直径，，，则的半径长为．24．如图，CD是⊙O的直径，AB是弦，CD⊥AB于点E，若OA=5，AB=8，则AD的长为．25．如图，在⊙O中，OC⊥AB，∠ADC=32°，则∠OBA的度数是26．如图所示，草坪边上有互相垂直的小路m,n，垂足为E，草坪内有一个圆形花坛，花坛边缘有A,B,C三棵小树。

2014届中考数学二轮精品复习试卷：整式的加减含详细解析

2013-2014学年度数学中考二轮专题复习卷-整式的加减学校:___________姓名：___________班级：___________考号：___________一、选择题1．如果(a －b)2加上一个单项式便等于(a ＋b)2，则这个单项式是（）A 、2abB 、－2abC 、4abD 、－4ab2．下列各组数中互为相反数的是（）A 、2)2(2--与B 、382--与C 、2)2(2-与D 、22与-3．下列运算正确．．的是（） A ．－2(x －1)＝－2x －1 B ．－2(x －1)＝－2x ＋1C ．－2(x －1)＝－2x －2D ．－2(x －1)＝－2x ＋24．一个两位数，个位数字为a ，十位数字为b ，则这个两位数为（）A 、abB 、baC 、10a+bD 、 10b+a5．下列各式计算正确的是 ( )A ．266a a a =+B ．ab b a 352=+-C ．mn mn n m 22422=-D ． 222253ab a b ab -=-6．下列计算正确的是（） A 、2x ＋3y ＝5xy B 、－3x 2－23x 2＝－25x 2 C 、－xy ＋6x 2y ＝5x 3y 2 D 、5ab 2－27b 2a ＝23ab 2 7．下列计算正确的是( )A ．277a a a =+B ．y x yx y x 22223=-C ．235=-y yD ．ab b a 523=+ 8．已知代数式x+2y 的值是3，则代数式2x+4y+1的值是（）A ．7B ．4C ．1D ． 99．下列各式化简正确的个数是（）．（1）xy y x 1358=+ （2）42232a a a =+（3）235=-x x （4）y x yx y x 222527=-A ．0个B ．1个C ．2个D ．3个10．下列去括号结果正确的是（）．A ．()c b a a c b a a 232322+--=+--B ．()[]72437243+--=---a a a a a aC ．()()x y y x x y y x 432432---=+--D ．()()1212-+--=-+--x y x x y x11．若单项式12-m xy 与233n x y --和仍是单项式，则m n +的值是．12．下列各式中，计算正确．．的是（） A ．222x x x += B ．='︒+︒3205.15333173'︒C ．22532a a -=D ．2x ＋3y ＝5xy13．减去－3x 得x 2－3x ＋4的式子为（）A 、x 3＋4B 、x 2＋3x ＋4C 、x 2－6x ＋4D 、x 2－6x14．下列各组式子是同类项的是（）A 、3x 2y 与3xy 2B 、abc 与acC 、－2xy 与－3abD 、xy 与－xy15．“少年宫”楼阶梯教室，第一排有m 个座位，后面每一排都比前面一排多4个座位，则第n 排座位数是（）A 、m+4B 、m+4nC 、n+4(m-1)D 、m+4(n-1)16．若-5x a yz b 与 2x 3y c z 2是同类项，则abc 的值是（）A 、-35B 、35C 、6D 、-617．下列运算正确的是（）（A ）a 6·a 3＝a 18 （B ）(a 3)2＝a 5 （C ）a 6÷a 3＝a 2 （D ）a 3＋a 3＝2a 318．买一斤土豆需要x 元，买一斤白菜需要y 元，则买6斤土豆、8斤白菜共需要A. （6x ＋8y ）元B. 48xy 元C. （8x ＋6y ）元D. 14xy 元19．下列计算正确的是（）A.3a －2b ＝abB.5y －3y ＝2C.7a ＋a ＝7a 2D.3x 2y －2yx 2＝x 2y20．2x+（3x 2+4x ）的化简结果是（）A 、9x 2B 、24x 4C 、3x 2+6xD 、9x 4二、填空题21．观察烟花燃放图形，找规律:依此规律，第9个图形中共有_________个★.22．化简32a a -的结果是 .★★★★★ ★★★ ★★ ★ ★ ★ ★ ★★ ★★ ★ ★ ★ ★ ★ ★ ★★ ★★第1个图形第2个图形第3个图形第4个图形23．计算：-3a+（-3a ）=________；24．已知4a + 和2(3)b -互为相反数，那么3a b +等于。

2014年河北省中考数学试题(含答案)

河北省2024年中考数学试卷一、选择题（共16小题，1~6小题，每小题2分；7~16小题，每小题2分，共42分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．（2分）﹣2是2的（）A．倒数B．相反数C．肯定值D．平方根2．（2分）如图，△ABC中，D，E分别是边AB，AC的中点．若DE=2，则BC=（）A．2B．3C．4D．53．（2分）计算：852﹣152=（）A．70 B．700 C．4900 D．70004．（2分）如图，平面上直线a，b分别过线段OK两端点（数据如图），则a，b相交所成的锐角是（）A．20°B．30°C．70°D．80°5．（2分）a，b是两个连续整数，若a＜＜b，则a，b分别是（）A．2，3 B．3，2 C．3，4 D．6，86．（2分）如图，直线l经过其次、三、四象限，l的解析式是y=（m﹣2）x+n，则m的取值范围在数轴上表示为（）A．B．C．D．7．（3分）化简：﹣=（）A．0B．1C．x D．8．（3分）如图，将长为2、宽为1的矩形纸片分割成n个三角形后，拼成面积为2的正方形，则n≠（）A．2B．3C．4D．59．（3分）某种正方形合金板材的成本y（元）与它的面积成正比，设边长为x厘米．当x=3时，y=18，那么当成本为72元时，边长为（）A．6厘米B．12厘米C．24厘米D．36厘米10．（3分）如图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中小正方形顶点A，B围成的正方体上的距离是（）A．0B．1C．D．11．（3分）某小组做“用频率估计概率”的试验时，统计了某一结果出现的频率，绘制了如图的折线统计图，则符合这一结果的试验最有可能的是（）A．在“石头、剪刀、布”的嬉戏中，小明随机出的是“剪刀”B．一副去掉大小王的一般扑克牌洗匀后，从中任抽一张牌的花色是红桃C．暗箱中有1个红球和2个黄球，它们只有颜色上的区分，从中任取一球是黄球D．掷一个质地匀称的正六面体骰子，向上的面点数是412．（3分）如图，已知△ABC（AC＜BC），用尺规在BC上确定一点P，使PA+PC=BC，则符合要求的作图痕迹是（）A．B．．．C. D.13．（3分）在探讨相像问题时，甲、乙同学的观点如下：甲：将边长为3、4、5的三角形按图1的方式向外扩张，得到新三角形，它们的对应边间距为1，则新三角形与原三角形相像．乙：将邻边为3和5的矩形按图2的方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与原矩形不相像．对于两人的观点，下列说法正确的是（）A．两人都对B．两人都不对C．甲对，乙不对D．甲不对，乙对14．（3分）定义新运算：a⊕b=例如：4⊕5=，4⊕（﹣5）=．则函数y=2⊕x（x≠0）的图象大致是（）A．B．C．D．15．（3分）如图，边长为a的正六边形内有两个三角形（数据如图），则=（）A．3B．4C．5D．616．（3分）五名学生投篮球，规定每人投20次，统计他们每人投中的次数．得到五个数据．若这五个数据的中位数是6．唯一众数是7，则他们投中次数的总和可能是（）A．20 B．28 C．30 D．31二、填空题（共4小题，每小题3分，满分12分）17．（3分）计算：=．18．（3分）若实数m，n 满意|m﹣2|+（n﹣2024）2=0，则m﹣1+n0=．19．（3分）如图，将长为8cm的铁丝尾相接围成半径为2cm的扇形．则S扇形=cm2．20．（3分）如图，点O，A在数轴上表示的数分别是0，0.1．将线段OA分成100等份，其分点由左向右依次为M1，M2，…，M99；再将线段OM1，分成100等份，其分点由左向右依次为N1，N2，…，N99；接着将线段ON1分成100等份，其分点由左向右依次为P1，P2．…，P99．则点P37所表示的数用科学记数法表示为．三、解答题（共6小题，满分66分，解答应写出文字说明、证明过程或演算步骤）21．（10分）嘉淇同学用配方法推导一元二次方程ax2+bx+c=0（a≠0）的求根公式时，对于b2﹣4ac＞0的状况，她是这样做的：由于a≠0，方程ax2++bx+c=0变形为：x2+x=﹣，…第一步x2+x+（）2=﹣+（）2，…其次步（x+）2=，…第三步x+=（b2﹣4ac＞0），…第四步x=，…第五步(1)嘉淇的解法从第步起先出现错误；事实上，当b2﹣4ac＞0时，方程ax2+bx+c=0（a≠O）的求根公式是．(2)用配方法解方程：x2﹣2x﹣24=0．22．（10分）如图1，A，B，C是三个垃圾存放点，点B，C分别位于点A的正北和正东方向，AC=100米．四人分别测得∠C的度数如下表：甲乙丙丁∠C（单位：度）34 36 38 40他们又调查了各点的垃圾量，并绘制了下列尚不完整的统计图2，图3：（1）求表中∠C度数的平均数：（2）求A处的垃圾量，并将图2补充完整；（3）用（1）中的作为∠C的度数，要将A处的垃圾沿道路AB都运到B处，已知运输1千克垃圾每米的费用为0.005元，求运垃圾所需的费用．（注：sin37°=0.6，cos37°=0.8，tan37°=0.75）23．（11分）如图，△ABC中，AB=AC，∠BAC=40°，将△ABC绕点A按逆时针方向旋转100°．得到△ADE，连接BD，CE交于点F．（1）求证：△ABD≌△ACE；（2）求∠ACE的度数；（3）求证：四边形ABEF是菱形．24．（11分）如图，2×2网格（每个小正方形的边长为1）中有A，B，C，D，E，F，G、H，O九个格点．抛物线l的解析式为y=（﹣1）n x2+bx+c（n为整数）．（1）n为奇数，且l经过点H（0，1）和C（2，1），求b，c的值，并干脆写出哪个格点是该抛物线的顶点；（2）n为偶数，且l经过点A（1，0）和B（2，0），通过计算说明点F（0，2）和H（0，1）是否在该抛物线上；（3）若l经过这九个格点中的三个，干脆写出全部满意这样条件的抛物线条数．25．（11分）（2024•河北）图1和图2中，优弧所在⊙O的半径为2，AB=2．点P为优弧上一点（点P不与A，B重合），将图形沿BP折叠，得到点A的对称点A′．（1）点O到弦AB的距离是，当BP经过点O时，∠ABA′=°；（2）当BA′与⊙O相切时，如图2，求折痕的长：（3）若线段BA′与优弧只有一个公共点B，设∠ABP=α．确定α的取值范围．26．（13分）（2024•河北）某景区内的环形路是边长为800米的正方形ABCD，如图1和图2．现有1号、2号两巡游车分别从出口A和景点C同时动身，1号车顺时针、2号车逆时针沿环形路连续循环行驶，供游客随时免费乘车（上、下车的时间忽视不计），两车速度均为200米/分．探究：设行驶吋间为t分．（1）当0≤t≤8时，分别写出1号车、2号车在左半环线离出口A的路程y1，y2（米）与t （分）的函数关系式，并求出当两车相距的路程是400米时t的值；（2）t为何值时，1号车第三次恰好经过景点C？并干脆写出这一段时间内它与2号车相遇过的次数．发觉：如图2，游客甲在BC上的一点K（不与点B，C重合）处候车，打算乘车到出口A，设CK=x米．状况一：若他刚好错过2号车，便搭乘即将到来的1号车；状况二：若他刚好错过1号车，便搭乘即将到来的2号车．比较哪种状况用时较多？（含候车时间）决策：己知游客乙在DA上从D向出口A走去．步行的速度是50米/分．当行进到DA上一点P （不与点D，A重合）时，刚好与2号车迎面相遇．（1）他发觉，乘1号车会比乘2号车到出口A用时少，请你简要说明理由：（2）设PA=s（0＜s＜800）米．若他想尽快到达出口A，依据s的大小，在等候乘1号车还是步行这两种方式中．他该如何选择？答案1考点：相反数．分析：依据只有符号不同的两个数互为相反数，可得一个数的相反数．解答：解：﹣2是2的相反数，故选：B．点评：本题考查了相反数，在一个数的前面加上负号就是这个数的相反数．2考点：三角形中位线定理．分析：依据三角形的中位线平行于第三边并且等于第三边的一半可得BC=2DE．解答：解：∵D，E分别是边AB，AC的中点，∴DE是△ABC的中位线，∴BC=2DE=2×2=4．故选C．点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，熟记定理是解题的关键．3考点：因式分解-运用公式法．分析：干脆利用平方差进行分解，再计算即可．解答：解：原式=（85+15）（85﹣15）=100×70=7000．故选：D．点评：此题主要考查了公式法分解因式，关键是驾驭平方差公式：a2﹣b2=（a+b）（a﹣b）．4考点：三角形的外角性质分析：依据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．解答：解：a，b相交所成的锐角=100°﹣70°=30°．故选B．点评：本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质是解题的关键．5考点：估算无理数的大小．分析：依据，可得答案．解答：解：，故选：A．点评：本题考查了估算无理数的大小，是解题关键．6考点：一次函数图象与系数的关系；在数轴上表示不等式的解集专题：数形结合．分析：依据一次函数图象与系数的关系得到m﹣2＜0且n＜0，解得m＜2，然后依据数轴表示不等式的方法进行推断．解答：解：∵直线y=（m﹣2）x+n经过其次、三、四象限，∴m﹣2＜0且n＜0，∴m＜2且n＜0．故选C．点评：本题考查了一次函数图象与系数的关系：一次函数y=kx+b（k、b为常数，k≠0）是一条直线，当k＞0，图象经过第一、三象限，y随x的增大而增大；当k＜0，图象经过其次、四象限，y随x的增大而减小；图象与y轴的交点坐标为（0，b）．也考查了在数轴上表示不等式的解集．7考点：分式的加减法．专题：计算题．分析：原式利用同分母分式的减法法则计算，约分即可得到结果．解答：解：原式==x．故选C点评：此题考查了分式的加减法，娴熟驾驭运算法则是解本题的关键．8考点：图形的剪拼分析：利用矩形的性质以及正方形的性质，结合勾股定理得出分割方法即可．解答：解：如图所示：将长为2、宽为1的矩形纸片分割成n个三角形后，拼成面积为2的正方形，则n可以为：3，4，5，故n≠2．故选：A．点评：此题主要考查了图形的剪拼，得出正方形的边长是解题关键．9考点：一次函数的应用．分析：设y与x之间的函数关系式为y=kx2，由待定系数法就可以求出解析式，当y=72时代入函数解析式就可以求出结论．解答：解：设y与x之间的函数关系式为y=kx2，由题意，得18=9k，解得：k=2，∴y=2x2，当y=72时，72=2x2，∴x=6．故选A．点评：本题考查了待定系数法求函数的解析式的运用，依据解析式由函数值求自变量的值的运用，解答时求出函数的解析式是关键．10考点：绽开图折叠成几何体分析：依据绽开图折叠成几何体，可得正方体，依据勾股定理，可得答案．解答：解；AB是正方体的边长，AB=1，故选：B．点评：本题考查了绽开图折叠成几何体，勾股定理是解题关键．11考点：利用频率估计概率；折线统计图．分析：依据统计图可知，试验结果在0.17旁边波动，即其概率P≈0.17，计算四个选项的概率，约为0.17者即为正确答案．解答：解：A、在“石头、剪刀、布”的嬉戏中，小明随机出的是“剪刀“的概率为，故此选项错误；B、一副去掉大小王的一般扑克牌洗匀后，从中任抽一张牌的花色是红桃的概率是：=；故此选项错误；C、暗箱中有1个红球和2个黄球，它们只有颜色上的区分，从中任取一球是黄球的概率为，故此选项错误；D、掷一个质地匀称的正六面体骰子，向上的面点数是4的概率为≈0.17，故此选项正确．故选：D．点评：此题考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的学问点为：频率=所求状况数与总状况数之比．同时此题在解答中要用到概率公式．12考点：作图—困难作图分析：要使PA+PC=BC，必有PA=PB，所以选项中只有作AB的中垂线才能满意这个条件，故D正确．解答：解：D选项中作的是AB的中垂线，∴PA=PB，∵PB+PC=BC，∴PA+PC=BC故选：D．点评：本题主要考查了作图学问，解题的关键是依据作图得出PA=PB．13考点：相像三角形的判定；相像多边形的性质分析：甲：依据题意得：AB∥A′B′，AC∥A′C′，BC∥B′C′，即可证得∠A=∠A′，∠B=∠B′，可得△ABC∽△A′B′C′；乙：依据题意得：AB=CD=3，AD=BC=5，则A′B′=C′D′=3+2=5，A′D′=B′C′=5+2=7，则可得，即新矩形与原矩形不相像．解答：解：甲：依据题意得：AB∥A′B′，AC∥A′C′，BC∥B′C′，∴∠A=∠A′，∠B=∠B′，∴△ABC∽△A′B′C′，∴甲说法正确；乙：∵依据题意得：AB=CD=3，AD=BC=5，则A′B′=C′D′=3+2=5，A′D′=B′C′=5+2=7，∴，，∴，∴新矩形与原矩形不相像．∴乙说法正确．故选A．点评：此题考查了相像三角形以及相像多边形的判定．此题难度不大，留意驾驭数形结合思想的应用．14考点：反比例函数的图象专题：新定义．分析：依据题意可得y=2⊕x=，再依据反比例函数的性质可得函数图象所在象限和形态，进而得到答案．解答：解：由题意得：y=2⊕x=，当x＞0时，反比例函数y=在第一象限，当x＜0时，反比例函数y=﹣在其次象限，又因为反比例函数图象是双曲线，因此D选项符合，故选：D．点评：此题主要考查了反比例函数的性质，关键是驾驭反比例函数的图象是双曲线．15考点：正多边形和圆分析：先求得两个三角形的面积，再求出正六边形的面积，求比值即可．解答：解：如图，∵三角形的斜边长为a，∴两条直角边长为a，a，∴S空白=a•a=a2，∵AB=a，∴OC=a，∴S正六边形=6×a•a=a2，∴S阴影=S正六边形﹣S空白=a2﹣a2=a2，∴==5，故选C．点评：本题考查了正多边形和圆，正六边形的边长等于半径，面积可以分成六个等边三角形的面积来计算．16考点：众数；中位数．分析：找中位数要把数据按从小到大的依次排列，位于最中间的一个数或两个数的平均数为中位数，众数是一组数据中出现次数最多的数据，留意众数可以不止一个．则最大的三个数的和是：6+7+7=20，两个较小的数肯定是小于5的非负整数，且不相等，则可求得五个数的和的范围，进而推断．解答：解：中位数是6．唯一众数是7，则最大的三个数的和是：6+7+7=20，两个较小的数肯定是小于5的非负整数，且不相等，则五个数的和肯定大于20且小于29．故选B．点评：本题属于基础题，考查了确定一组数据的中位数和众数的实力．一些学生往往对这个概念驾驭不清晰，计算方法不明确而误选其它选项，留意找中位数的时候肯定要先排好依次，然后再依据奇数和偶数个来确定中位数，假如数据有奇数个，则正中间的数字即为所求，假如是偶数个则找中间两位数的平均数．17考点：二次根式的乘除法．分析：本题需先对二次根式进行化简，再依据二次根式的乘法法则进行计算即可求出结果．解答：解：，=2×，=2．故答案为：2．点评：本题主要考查了二次根式的乘除法，在解题时要能依据二次根式的乘法法则，求出正确答案是本题的关键．18考点：负整数指数幂；非负数的性质：肯定值；非负数的性质：偶次方；零指数幂．分析：依据肯定值与平方的和为0，可得肯定值与平方同时为0，依据负整指数幂、非0的0次幂，可得答案．解答：解：|m﹣2|+（n﹣2024）2=0，m﹣2=0，n﹣2024=0，m=2，n=2024．m﹣1+n0=2﹣1+20240=+1=，故答案为：．点评：本题考查了负整指数幂，先求出m、n的值，再求出负整指数幂、0次幂．19考点：扇形面积的计算．分析：依据扇形的面积公式S扇形=×弧长×半径求出即可．解答：解：由题意知，弧长=8cm﹣2cm×2=4 cm，扇形的面积是×4cm×2cm=4cm2，故答案为：4．点评：本题考查了扇形的面积公式的应用，主要考查学生能否正确运用扇形的面积公式进行计算，题目比较好，难度不大．20考点：规律型：图形的改变类；科学记数法—表示较小的数．分析：由题意可得M1表示的数为0.1×=10﹣3，N1表示的数为0×10﹣3=10﹣5，P1表示的数为10﹣5×=10﹣7，进一步表示出点P37即可．解答：解：M1表示的数为0.1×=10﹣3，N1表示的数为0×10﹣3=10﹣5，P1表示的数为10﹣5×=10﹣7，P37=37×10﹣7=3.7×10﹣6．故答案为：3.7×10﹣6．点评：此题考查图形的改变规律，结合图形，找出数字之间的运算方法，找出规律，解决问题．21考点：解一元二次方程-配方法专题：阅读型．分析：第四步，开方时出错；把常数项24移项后，应当在左右两边同时加上一次项系数﹣2的一半的平方．解答：解：在第四步中，开方应当是x+=±．所以求根公式为：x=．故答案是：四；x=；用配方法解方程：x2﹣2x﹣24=0解：移项，得x2﹣2x=24，配方，得x2﹣2x+1=24+1，即（x﹣1）2=25，开方得x﹣1=±5，∴x1=6，x2=﹣4．点评：本题考查了解一元二次方程﹣﹣配方法．用配方法解一元二次方程的步骤：（1）形如x2+px+q=0型：第一步移项，把常数项移到右边；其次步配方，左右两边加上一次项系数一半的平方；第三步左边写成完全平方式；第四步，干脆开方即可．（2）形如ax2+bx+c=0型，方程两边同时除以二次项系数，即化成x2+px+q=0，然后配方．22考点：解直角三角形的应用；扇形统计图；条形统计图；算术平均数分析：（1）利用平均数求法进而得出答案；（2）利用扇形统计图以及条形统计图可得出C处垃圾量以及所占百分比，进而求出垃圾总量，进而得出A处垃圾量；（3）利用锐角三角函数得出AB的长，进而得出运垃圾所需的费用．解答：解：（1）==37；（2）∵C处垃圾存放量为：320kg，在扇形统计图中所占比例为：50%，∴垃圾总量为：320÷50%=640（kg），∴A处垃圾存放量为：（1﹣50%﹣37.5%）×640=80（kg），占12.5%．补全条形图如下：（3）∵AC=100米，∠C=37°，∴tan37°=，∴AB=ACtan37°=100×0.75=75（m），∵运输1千克垃圾每米的费用为0.005元，∴运垃圾所需的费用为：75×80×0.005=30（元），答：运垃圾所需的费用为30元．点评：此题主要考查了平均数求法以及锐角三角三角函数关系以及条形统计图与扇形统计图的综合应用，利用扇形统计图与条形统计图获得正确信息是解题关键．23考点：全等三角形的判定与性质；菱形的判定；旋转的性质专题：计算题．分析：（1）依据旋转角求出∠BAD=∠CAE，然后利用“边角边”证明△ABD和△ACE全等．（2）依据全等三角形对应角相等，得出∠ACE=∠ABD，即可求得．（3）依据对角相等的四边形是平行四边形，可证得四边形ABEF是平行四边形，然后依据邻边相等的平行四边形是菱形，即可证得．解答：（1）证明：∵ABC绕点A按逆时针方向旋转100°，∴∠BAC=∠DAE=40°，∴∠BAD=∠CAE=100°，又∵AB=AC，∴AB=AC=AD=AE，在△ABD与△ACE中∴△ABD≌△ACE（SAS）．（2）解：∵∠CAE=100°，AC=AE，∴∠ACE=（180°﹣∠CAE）=（180°﹣100°）=40°；（3）证明：∵∠BAD=∠CAE=140°AB=AC=AD=AE，∴∠ABD=∠ADB=∠ACE=∠AEC=20°．∵∠BAE=∠BAD+∠DAE=160°，∴∠BFE=360°﹣∠DAE﹣∠ABD﹣∠AEC=160°，∴∠BAE=∠BFE，∴四边形ABEF是平行四边形，∵AB=AE，∴平行四边形ABEF是菱形．点评：此题考查了全等三角形的判定与性质，等腰三角形的性质以及菱形的判定，娴熟驾驭全等三角形的判定与性质是解本题的关键．24考点：二次函数综合题专题：压轴题．分析：（1）依据﹣1的奇数次方等于﹣1，再把点H、C的坐标代入抛物线解析式计算即可求出b、c的值，然后把函数解析式整理成顶点式形式，写出顶点坐标即可；（2）依据﹣1的偶数次方等于1，再把点A、B的坐标代入抛物线解析式计算即可求出b、c的值，从而得到函数解析式，再依据抛物线上点的坐标特征进行推断；（3）分别利用（1）（2）中的结论，将抛物线平移，可以确定抛物线的条数．解答：解：（1）n为奇数时，y=﹣x2+bx+c，∵l经过点H（0，1）和C（2，1），∴，解得，∴抛物线解析式为y=﹣x2+2x+1，y=﹣（x﹣1）2+2，∴顶点为格点E（1，2）；（2）n为偶数时，y=x2+bx+c，∵l经过点A（1，0）和B（2，0），∴，解得，∴抛物线解析式为y=x2﹣3x+2，当x=0时，y=2，∴点F（0，2）在抛物线上，点H（0，1）不在抛物线上；（3）全部满意条件的抛物线共有8条．当n为奇数时，由（1）中的抛物线平移又得到3条抛物线，如答图3﹣1所示；当n为偶数时，由（2）中的抛物线平移又得到3条抛物线，如答图3﹣2所示．点评：本题是二次函数综合题型，主要利用了待定系数法求二次函数解析式，二次函数图象上点的坐标特征，二次函数的对称性，要留意（3）抛物线有开口向上和开口向下两种状况．25考点：圆的综合题；含30度角的直角三角形；勾股定理；垂径定理；切线的性质；翻折变换（折叠问题）；锐角三角函数的定义专题：综合题．分析：（1）利用垂径定理和勾股定理即可求出点O到AB的距离；利用锐角三角函数的定义及轴对称性就可求出∠ABA′．（2）依据切线的性质得到∠OBA′=90°，从而得到∠ABA′=120°，就可求出∠ABP，进而求出∠OBP=30°．过点O作OG⊥BP，垂足为G，简单求出OG、BG的长，依据垂径定理就可求出折痕的长．（3）依据点A′的位置不同，分点A′在⊙O内和⊙O外两种状况进行探讨．点A′在⊙O 内时，线段BA′与优弧都只有一个公共点B，α的范围是0°＜α＜30°；当点A′在⊙O 的外部时，从BA′与⊙O相切起先，以后线段BA′与优弧都只有一个公共点B，α的范围是60°≤α＜120°．从而得到：线段BA′与优弧只有一个公共点B时，α的取值范围是0°＜α＜30°或60°≤α＜120°．解答：解：（1）①过点O作OH⊥AB，垂足为H，连接OB，如图1①所示．∵OH⊥AB，AB=2，∴AH=BH=．∵OB=2，∴OH=1．∴点O到AB的距离为1．②当BP经过点O时，如图1②所示．∵OH=1，OB=2，OH⊥AB，∴sin∠OBH==．∴∠OBH=30°．由折叠可得：∠A′BP=∠ABP=30°．∴∠ABA′=60°．故答案为：1、60．（2）过点O作OG⊥BP，垂足为G，如图2所示．∵BA′与⊙O相切，∴OB⊥A′B．∴∠OBA′=90°．∵∠OBH=30°，∴∠ABA′=120°．∴∠A′BP=∠ABP=60°．∴∠OBP=30°．∴OG=OB=1．∴BG=．∵OG⊥BP，∴BG=PG=．∴BP=2．∴折痕的长为2．（3）若线段BA′与优弧只有一个公共点B，Ⅰ．当点A′在⊙O的内部时，此时α的范围是0°＜α＜30°．Ⅱ．当点A′在⊙O的外部时，此时α的范围是60°≤α＜120°．综上所述：线段BA′与优弧只有一个公共点B时，α的取值范围是0°＜α＜30°或60°≤α＜120°．点评：本题考查了切线的性质、垂径定理、勾股定理、三角函数的定义、30°角所对的直角边等于斜边的一半、翻折问题等学问，考查了用临界值法求α的取值范围，有肯定的综合性．第（3）题中α的范围可能考虑不够全面，须要留意．26考点：一次函数的应用；一元一次方程的应用；一元一次不等式组的应用．分析：探究：（1）由路程=速度×时间就可以得出y1，y2（米）与t（分）的函数关系式，再由关系式就可以求出两车相距的路程是400米时t的值；（2）求出1号车3次经过A的路程，进一步求出行驶的时间，由两车第一次相遇后每相遇一次须要的时间就可以求出相遇次数；发觉：分别计算出状况一的用时和状况二的用时，在进行大小比较就可以求出结论决策：（1）依据题意可以得出游客乙在AD上等待乘1号车的距离小于边长，而成2号车到A出口的距离大于3个边长，进而得出结论；（2）分类探讨，若步行比乘1号车的用时少，就有，得出s＜320．就可以分状况得出结论．解答：解：探究：（1）由题意，得y1=200t，y2=﹣200t+1600当相遇前相距400米时，﹣200t+1600﹣200t=400，t=3，当相遇后相距400米时，200t﹣（﹣200t+1600）=400，t=5．答：当两车相距的路程是400米时t的值为3分钟或5分钟；（2）由题意，得1号车第三次恰好经过景点C行驶的路程为：800×2+800×4×2=8000，∴1号车第三次经过景点C须要的时间为：8000÷200=40分钟，两车第一次相遇的时间为：1600÷400=4．第一次相遇后两车每相遇一次须要的时间为：800×4÷400=8，∴两车相遇的次数为：（40﹣4）÷8+1=5次．∴这一段时间内它与2号车相遇的次数为：5次；发觉：由题意，得状况一须要时间为：=16﹣，状况二须要的时间为：=16+∵16﹣＜16+∴状况二用时较多．决策：（1）∵游客乙在AD边上与2号车相遇，∴此时1号车在CD边上，∴乘1号车到达A的路程小于2个边长，乘2号车的路程大于3个边长，∴乘1号车的用时比2号车少．（2）若步行比乘1号车的用时少，，∴s＜320．∴当0＜s＜320时，选择步行．同理可得当320＜s＜800时，选择乘1号车，当s=320时，选择步行或乘1号车一样．点评：本题考查了一次函数的解析式的运用，一元一次方程的运用，一元一次不等式的运用，分类探讨思想的运用，方案设计的运用，解答时求出函数的解析式是解答本题的关键．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2014年中考数学二轮专题复习试卷：圆(含答案)2014年中考数学二轮专题复习试卷：圆(时间：120分钟满分：120分)一、选择题(本大题共15个小题，每小题3分,共45分)1.（2013湖南岳阳）两圆半径分别为3 cm和7 cm，当圆心距d=10 cm时，两圆的位置关系为( )A.外离B.内切C.相交D．外切2.（2013重庆）如图，P是⊙O外一点，PA是⊙O的切线，PO=26 cm，PA=24 cm，则⊙O 的周长为( )A.18πcmB.16πcmC.20πcmD.24πcm(第2题) (第3题) (第4题)3.（2013浙江舟山）如图，⊙O的半径OD⊥弦AB于点C，连接AO并延长交⊙O于点E，连接EC．若AB=8，CD=2，则EC的长为( )A.215B.8C.210D.2134.（2013福建厦门）如图所示，在⊙O中，AB AC=，∠A=30°，则∠B=( )A.150°B.75°C.60°D.15°5.（2013贵州遵义）如图，将边长为1 cm的等边三角形ABC沿直线l向右翻动（不滑动），点B从开始到结束，所经过路径的长度为( )33A.cm?B.(2) cm224C.cmD.3 cm3π +ππ(第5题) (第7题)6.（2013浙江义乌）已知圆锥的底面半径为6 cm，高为8 cm，则这个圆锥的母线长为( )A.12 cmB.10 cmC.8 cm10.(2012山东济宁)如图，在平面直角坐标系中，点P坐标为(－2，3)，以点O为圆心，以OP 的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于( )A.－4和－3之间B.3和4之间C.－5和－4之间D.4和5之间11.（2013重庆）如图，P是⊙O外一点，PA是⊙O的切线，PO=26 cm，PA=24 cm，则⊙O 的周长为( )A.18πcmB.16πcmC.20πcmD.24π cm12.(2012山东烟台)如图，⊙O1,⊙O,⊙O2的半径均为2 cm,⊙O3,⊙O4的半径均为1 cm，⊙O 与其他4个圆均相外切，图形既关于O1O2所在直线对称，又关于O3O4所在直线对称，则四边形O1O4O2O3的面积为( )A.12 cm2B.24 cm2C.36 cm2D.48 cm2(第12题) (第13题) (第14题)13.如图，在Rt △ABC 中，∠C =90°，AC =6,BC =8,⊙O 为△ABC 的内切圆，点D 是斜边AB 的中点，则tan ∠ODA 的值为( )33A.B.23C.3D.214.(2012浙江宁波)如图，用邻边长分别为a ,b (a <b )的矩形硬纸板裁出以a 为直径的两个半圆，再裁出与矩形较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面，从而做成两个圣诞帽(拼接处材料忽略不计)，则a 与b 满足的关系式是( )51A.b 3a B.b a 25C.b a D.b 2a 2+= == = 15.（2013湖北襄阳）如图，以AD 为直径的半圆O 经过Rt △ABC 斜边AB 的两个端点，交直角边AC 于点E ,B 、E 是半圆弧的三等分点，弧BE的长为23π，则图中阴影部分的面积为( ) 3A. B.99333332C. D.2223π πππ- -二、填空题(本大题共6个小题，每小题3分,共18分)16.(2012江苏扬州)已知一个圆锥的母线长为10cm ，将侧面展开后所得扇形的圆心角是144°,则这个圆锥的底面圆的半径是 cm .17.（2013湖南株洲）如图，AB 是⊙O 的直径，∠BAC =42°，点D 是弦AC 的中点，则∠DOC 的度数是度．18.（2013湖北襄阳）如图，水平放置的圆柱形排水管道的截面直径是1 m，其中水面的宽AB为0.8 m，则排水管内水的深度为m．19.（2013贵州遵义）如图，OC是⊙O的半径，AB是弦，且OC⊥AB，点P在⊙O上，∠APC=26°，则∠BOC= °．(第19题) (第20题)20.（2013重庆）如图，在边长为4的正方形ABCD中，以AB为直径的半圆与对角线AC交于点E，则图中阴影部分的面积为．（结果保留π）21.（2013湖北孝感）用半径为10 cm，圆心角为216°的扇形做成一个圆锥的侧面，则这个圆锥的高为cm．三、解答题(本大题共5个小题，共57分)22.(本小题满分10分)(2013江苏镇江）如图1，Rt△ABC中，∠ACB=90°，AB=5，BC=3，点D在边AB的延长线上，BD=3，过点D作DE⊥AB，与边AC 的延长线相交于点E，以DE为直径作⊙O交AE 于点F．（1）求⊙O的半径及圆心O到弦EF的距离；（2）连接CD，交⊙O于点G（如图2）．求证：点G是CD的中点．23.(本小题满分10分)（2013广东梅州）如图，在矩形ABCD中，AB=2DA，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设DA=2．（1）求线段EC的长；（2）求图中阴影部分的面积．24.(本小题满分10分)(2012浙江温州)如图,△ABC中，∠ACB=90°,D是边AB上一点，且∠A=2∠DCB.E是BC边上的一点，以EC为直径的⊙O经过点D.(1)求证：AB是⊙O的切线；(2)若CD的弦心距为1，BE=EO，求BD的长.25.（本小题满分12分）（2013广东）如图所示，⊙O是Rt△ABC 的外接圆，∠ABC=90°，弦BD=BA，AB=12，BC=5，BE⊥DC交DC的延长线于点E.（1）求证：∠BCA=∠BAD；（2）求DE的长；（3）求证：BE是⊙O的切线.26.（本小题满分15分）(2012浙江杭州)如图，AE切⊙O于点E，AT 交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知∠EAT=30°,AE33,MN222.==(1)求∠COB的度数；(2)求⊙O的半径R；(3)点F在⊙O上(FME是劣弧)，且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合.在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比.参考答案1.D2.C3.D4.B5.C6.B7.A8.C9.B10.A11.C12.B13.D14.D15.D16.4 17.48 18.0.2 19.52 20.10－π21.822.解：（1）∵∠ACB=90°，AB=5，BC=3，由勾股定理得：AC =4， ∵AB =5，BD =3，∴AD =8， ∵∠ACB =90°，DE ⊥AD ， ∴∠ACB =∠ADE ，∵∠A =∠A ，∴△ACB ∽△ADE ，BC AC AB,DE AD AE345,DE 8AE ∴==∴==∴DE =6，AE =10，即⊙O 的半径为3；过O 作OQ ⊥EF 于Q ，则∠EQO =∠ADE =90°， ∵∠QEO =∠AED ， ∴△EQO ∽△EDA ，EO OQ,AE AD 3OQ ,108∴=∴=∴OQ =2.4，即圆心O 到弦EF 的距离是2.4； (2)连接EG ， ∵AE =10，AC =4， ∴CE =6， ∴CE =DE =6，∵DE为直径，∴∠EGD=90°，∴EG⊥CD，∴点G为CD的中点．23.解：（1）∵在矩形ABCD中，AB=2DA，DA=2，∴AB=AE=4，DE23∴=，∴EC=CD－DE=423;-（2）∵AD1sin DEAAE2∠==，∴∠DEA=30°，∴∠EAB=30°，∴图中阴影部分的面积为：FAB DAE EAB22S S S904130482232 3.36023603--π⨯π⨯π=-⨯⨯=-扇形扇形24.(1)证明:连接OD.∵∠DOB=2∠DCB,∠A=2∠DCB, ∴∠A=∠DOB.又∵∠A+∠B=90°,∴∠DOB+∠B=90°,∴∠BDO=90°,∴OD⊥AB,∴AB是⊙O的切线. (2)解：过点O作OM⊥CD于点M,∵OD=OE=BE=1BO,2∠BDO=90°,∴∠DBO=30°,∠DOB=60°.∠DOB,∵∠DCO=12∴∠DCO =30°, 又∵OM ⊥CD ,OM =1， ∴OC =2OM =2, ∴OB =4,OD =2, ∴BD =OB ·cos ∠DBO 34 3.2=⨯= ∴BD 的长为23.25.（1）证明：在⊙O 中，∵弦BD =BA ，且圆周角∠BCA 和∠BAD 分别对BA 和BD ，∴∠BCA =∠BAD .（2）解：∵BE ⊥DC ，∴∠E =90°. 又∵∠BAC =∠EDB ,∠ABC =90°, ∴△ABC ∽△DEB , AB AC .DEBD∴= 在Rt △ABC 中，∠ABC =90°，AB =12，BC =5， ∴由勾股定理得:AC =13， 1213144DE .DE1213∴=∴=，（3）证明：如图，连接OB ， ∵OA =OB，∴∠OAB =∠OBA .∵BA =BD ，∴∠OBD =∠OBA .又∠BDC=∠OAB=∠OBA，∴∠OBD=∠BDC.∴OB∥DE，∴∠OBE=∠DBE+∠OBD=90°.即BE⊥OB于B，所以BE是⊙O的切线.26.解：(1)∵AE切⊙O于点E,∴AE⊥CE,又OB⊥AT,∴∠AEC=∠CBO=90°,又∠BCO=∠ACE,∴△AEC∽△OBC,又∠A=30°,∴∠COB=∠A=30°.(2)∵AE=33,∠A=30°,∴在Rt△AEC中,ECtan A tan 30,=︒=AE即EC=AE·tan 30°=3.∵OB⊥MN,∴B为MN的中点,又MN=222，∴MB=1MN22.=2连接OM ,在△MOB 中,OM =R,MB =22,22222OB OM MB R 22.COB ,BOC 30,OB 3cos BOC cos 30,OC 23BO OC,2323OC OB R 22.33OC EC OM R,23R 223R,3∴=-=-∠=︒∠=︒==∴=∴==-+==∴-+=在中又整理得:R 2+18R －115=0, 即(R +23)(R －5)=0, 解得:R =－23(舍去)或R =5, ∴⊙O 的半径R 为5.(3)在EF 同一侧,△COB 经过平移、旋转和相似变换后,这样的三角形有6个,如图,每小图2个,顶点在圆上的三角形,如图所示:延长EO 交圆O 于点D ,连接DF ,如图所示,∵EF =5,直径ED =10,可得出∠FDE =30°,∴FD=则C △EFD=51015++=+()((COBEFDCOB2C 3CC15351.=+∴=++=由可得∶∶。