第4章_多组分体系热力学
物理化学:第4章_多组分系统热力学_
真实混合物:实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时,两组 分偏摩尔体积随之改变,且二者 变化相互关联。
组成接近某纯组分,其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分:
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面,由加和公式
,恒温恒压下求导:
比较两式,得
或
或
吉布斯-杜亥姆方程--在一定温度压力下,当混合物
组成变化时,各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立,而是相 互依存的。
➢ 例:固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件:该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移, 直至物质迁移达平衡时为止,此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0:自发不可逆; =0:平衡、可逆
任一化学反应,假定系统已处于相平衡,
任一组分B在每个相中的化学势都相等: Bα B
B
B
整个系统中B组分物质的量的变化量: dnBα dnB
α
BdnB
B
化学平衡时
平衡条件:与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
大学物理化学--第四章

混合物(mixture):对系统中的各组分采用同样 的标准态和研究方法,系统中的各组分是平等的。
溶液(solution): 各组分区分为溶剂(solvent) 和溶质(solute ),并对二者采用不同的标准态和研 究方法;系统中的各组分是不平等的。
偏摩尔量
XB
(
X nB
)T
,
p
,
,下标必须是
nC
T
,
p。, nC
只有广度量才有偏摩尔量(质量除外)。
偏摩尔量是强度量。
偏摩尔量随温度、压力、组成(浓度)变化而变, 与系统的总量无关。
上一内容 下一内容 回主目录
返回
2020/8/23
§4.1 偏摩尔量
偏摩尔量的加和公式
X nB X B
B
它的含义是:在一定温度、压力下,一定组成混合
物理化学电子教案—第四章
多组分系统热力学
上一内容 下一内容 回主目录
返回
2020/8/23
第四章 多组分系统热力学
目录
§4.1 偏摩尔量 §4.2 化学势 §4.3 气体组分的化学势 §4.4 逸度及逸度因子 §4.5 拉乌尔定律和亨利定律 §4.6 理想液态混合物 §4.7 理想稀溶液
§4.8 活度及活度因子 §4.9 稀溶液的依数性
标准态 kb,B ( p p )
实际溶液 pB - bB 关系曲线
pB
O
b
上一内容 下一内容 回主目录
bB
返回
2020/8/23
4.7 理想稀溶液
理想稀溶液中溶质的化学势
B(溶 质)
0 B(溶 质)
物理化学4 多组分体系热力学 1

几点说明
(1)偏摩尔量只对体系中某组分才具有的,对整体而 言无所谓偏摩尔量的概念; (2)只有体系的广度性质才有偏摩尔量(质量除外) ; (3)偏摩尔量本身是强度性质; (4)注意右下角标的条件; (5)任何偏摩尔量都是T、p、组成的函数; (6)纯物质的偏摩尔量就是摩尔量; (7)偏摩尔量可能是负值。 (8)偏摩尔量是1mol B对整体热力学性质的贡献量, 而不应该理解为它在混合体系中所具有的量。
分类
气态混合物:空气 混合物液态混合物:甲醇 + 乙醇 固态混合物:Cu + Ni 气态溶液:萘溶解于高压CO 2中 非电解质溶液:糖水 − − − 本章 溶液液态溶液 电解质溶液:盐水 - - -电化学 固态溶液:单体溶解于聚合物中 − − − 又称固溶体
§4-2 化学势 化学势μ μB
• 4-2-1 化学势定义 • 4-2-2 平衡判据与平衡条件 • 4-2-3 理想气体的化学势表达式
4-2-1 化学势定义
混合物或溶液中,组分B的偏摩尔吉布斯函数 GB在化学热力学中有特殊的重要性,又把它叫 做化学势,用符号μB表示。
∂G µ B = GB = ∂nB T , p ,nc≠B
dX = ∑ X B dnB
B =1 k
( 2)
• 可得Gibbs-Duhem方程:
∑ n dX
B B=1
k
B
=0
∑ x dX
B B=1
k
B
=0
Gibbs-Duhem方程的意义: (1) 某一偏摩尔量的变化可从其它偏摩尔量的变 化中求得。 (2) 对一个含有K个组分的均相体系,K个偏摩 尔量Xi中,只有 K-1个是独立的。
如果在溶液中不按比例地添加各组分,则溶液浓 度会发生改变,这时各组分的物质的量和偏摩尔量均 会改变。 根据集合公式
Chapter 04多组分系统热力学.ppt

§4.1 引言
多组分系统 两种或两种以上的物质(或称为组分)所
形成的系统称为多组分系统。
多组分系统可以是均相的,也可以是多相的。
混合物 多组分均匀系统中,各组分均可选用相同的方法处
理,有相同的标准态,遵守相同的经验定律,这种系统称为 混合物。
溶液(solution), 溶剂(solvent) 和溶质(solute)
如果组成溶液的物质有不同的状态,通常将液态物质称为 溶剂,气态或固态物质称为溶质。
如果都具有相同状态,则把含量多的一种称为溶剂,含量少的称为溶质。 溶质有电解质和非电解质之分,本章主要讨论非电介质所形成的溶液。
§4.2 多组分系统的组成表示法
在均相的混合物中,任一组分B的浓度表示法主要有如下几种:
化学势在判断相变和化学变化的方向和限度方面有重要作用。
保持热力学函数的特征变量和除B以外其他组分不变,
某热力学函数随物质的量 nB 的变化率称为化学势。
多组分系统的热力学基本公式应表示为:
dU TdS pdV BdnB dH TdS Vdp BdnB
B=1
B=1
dA SdT pdV BdnB dG SdT Vdp BdnB
律研究的对象是溶质,比例常数无确切的物理意义。
Herry定律使用注意事项
(1)式中 pB 为该气体的分压。对于混合气体,在总
压不大时,Henry定律分别适用于每一种气体。
(2)溶质在气相和在溶液中的分子状态必须相同。如 HCl,在气相为 HCl 分子,在液相为H+和Cl- ,则 Henry定律不适用。
“在一定温度和平衡状态下,气体在液体里的溶解度(用摩尔
分数 x 表示)与该气体的平衡分压 p 成正比。”
第四章- 多组分系统热力学

平衡
单组分多相系统
自 发 ( 恒T、 恒V、W ' 0) d n 0
平衡
(2)恒T、恒V且W’=0时:
d A S dT pd V
d n B B
B
dA
自发 (恒T、恒V、W' 0) d n 0 B B
组成表示法
1、物质B的摩尔分数 x B (mole fraction)
xB
nB / nB
B
xB 1
B
无量纲
2、物质B的质量分数 wB (mass percent)
wB mB / mB
B
WB 1
B
无量纲
3、物质B的(体积)摩尔浓度
c B (volume molality)
第四章 多组分系统热力学
Chapter 4 Thermodynamics of Muiticomponent systems
引
言
前几章介绍了简单系统发生PVT变化、相变化 和化学变化时热力学理论以及W、Q、 U、 H、 A、 G 的计算。
简单系统: 纯物质系统或组成不变的系统。
多组分系统:多组分、且组成发生变化的系统. 本章讨论其热力学规律。
§4-1 偏摩尔量
1. 2. 3. 4. 5. 6.
问题的提出 偏摩尔量 偏摩尔量的实验测定 偏摩尔量与摩尔量的区别 吉布斯–杜亥姆方程(Gibbs-Duhem) 偏摩尔量之间的关系
1.问题的提出 T、p一定时,100ml水+100ml乙醇混合= 200ml混合物?
答案:不相等!
G G dT dp G B dnB T p B p ,nC T ,nC
第4章多组分系统热力学分解

p/Pa
R
p gh
p
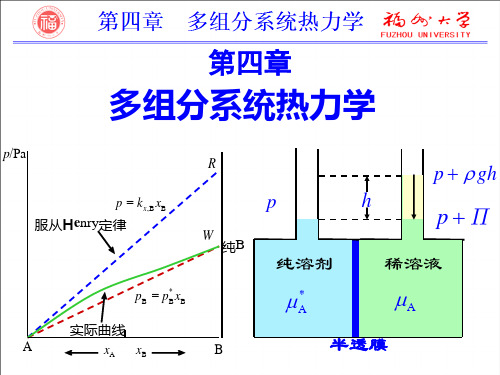
p = kx,B xB 服从Henry定律
h
W
pP
稀溶液
纯B
纯溶剂
* A
* pB = pB xB
A
半透膜
A
实际曲线 xA xB
B
基本内容
§ 4.1 § 4.2 § 4.3 § 4.4 § 4.5 § 4.6 § 4.7 § 4.8 § 4.9 偏摩尔量 化学势 气体组分的化学势 逸度及逸度因子 拉乌尔定律和亨利定律 理想液态混合物 理想稀溶液 活度与活度因子 稀溶液的依数性
GB 骣 ¶G 琪 =琪 桫 ¶n B
T ,p ,n C
因此:
T ,n B
禳 骣 镲 ?G 镲 琪 = 睚 琪 ?nB 镲 镲 铪p桫 禳 镲 抖 骣G 镲 琪 = 睚 琪 桫p 抖 n 镲 B 镲 铪 骣 ¶V 琪 =琪 桫 ¶n B
T ,p ,n C T ,n B
T ,n B T ,p ,n C
V nBVm , B nCVm ,C
理想混合溶液
★将0.5摩尔的水与0.5摩尔的乙醇混合,溶液体积:
V≠(0.5×18.09十0.5×58.35)cm3 =38.22cm3 =37.2cm3
实际混合溶液 V nBVm n V ,B C m,C
★乙醇与水溶液混合的体积与浓度的关系
多组分系统可以是单相的也可以是多相的。
但对多组分多相系统可以拆解为多个多组分单相系统来研究。
多组分单相系统:是由两种或两种以上物质以分子大小粒
子相互均匀混合成一相的系统。
混合物——系统中的各组分以同等条件予以研究 溶 液——系统中的组分区分为溶剂和溶质予以研究
物理化学 第四章 多组分系统热力学

Vm
T,p一定
V*m,C VC
V*m,B VB
d c· b·
0 B
a xC
C
图4.1.2 二组分液态混合物的 偏摩尔体积示意图
若B,C形成真实液态混合物: 则混合物体积为由V*m,B至V*m,C的曲线。对于任一 组成a时,两组分的偏摩尔体积可用下法表示: 过组成点a所对应的系统体积点d作Vm-xC曲线的 切线,此切线在左右两纵坐标上的截距即分别 为该组成下两组分的偏摩尔体积VB,VC。
B
系统中各广度量的偏摩尔量: 对于多组分系统中的组分B,有: 偏摩尔体积: VB=(ƽV/ƽnB)T,p,n C 偏摩尔热力学能: UB=(ƽU/ƽnB)T,p,n C 偏摩尔焓: HB=(ƽH/ƽnB)T,p,n C 偏摩尔熵: SB=(ƽS/ƽnB)T,p,n C 偏摩尔亥姆霍兹函数:AB=(ƽA/ƽnB)T,p,n C 偏摩尔吉布斯函数: GB=(ƽG/ƽnB)T,p,n
C
几点说明: (1)偏摩尔量为两个广度性质之比,所以为强度 性质; (2)偏摩尔量的定义中明确是在恒温、恒压及系 统组成不变的条件下,偏导数式的下标为T,p 时才是偏摩尔量; (3)同一物质在相同温度、压力但组成不同的多 组分均相系统中,偏摩尔量不同; (4)若系统为单组分系统,则该组分的偏摩尔量 与该组分的摩尔量相等,即: XB=X*B,m
C
=VB (数学知识:二阶偏导与求导的顺序无关) 得证。
4.2化学势 4.2化学势
1.化学势的定义 混合物(或溶液中)组分B的偏摩尔吉布斯函数GB 定义为B的化学势,用符号μB表示:
μB = GB=(ƽG/ƽnB)T,p,n
def
C
对于纯物质,其化学势等于它的摩尔吉布斯函 数。
物理化学 4 多组分系统热力学

Physical Chemistry
河北联合大学
1
of 137
第四章 多组分系统热力学
河北联合大学
2
of 137
经 典 热 力 学 系 统
简单系统
(由纯物质形成的相及组成不变 的平衡系统)
多组分系统
(相组成改变的单相或多相系统)
河北联合大学
3
of 137
多组分系统可为单相或多相。若它为多相的,则可
全部浓度范围内及理想稀溶液在小范围内均有简
单的规律性。 对溶液,将组分区分为溶剂和溶质,对溶质 与溶剂用不同标准态研究;对混合物中任意组分
均选用同样的标准态加以研究。
河北联合大学
7
of 137
混合物(mixture) 多组分均匀体系中,溶剂和溶质不加区分,
各组分均可选用相同的标准态,使用相同的经验
V VB n B T , P ,nC
nC表示,除 B 以 外,其它组分的物质 的量均不变。
除了体积,其它广度量也有偏摩尔量。
河北联合大学
16 of 137
2.偏摩尔量:
在由组分 B, C, D…形成的混合系统中,任一广度量 X 是T, p , nB , nC , nD , …的函数,即:
20 of 137
河北联合大学
应当指出, 1)只有广度量才有偏摩尔量,强度量是不存在偏摩尔量的。 2)只有恒温恒压下,系统的某一广度量随某一组分的物质 的量的变化率,才能称为偏摩尔量,任何其它条件下的变化率 均不称为偏摩尔量。
G 例:尽管 A n n B T ,V ,nC B T , p ,nC
4.1.5b
积分得:
dX X
物理化学第四章 多组分系统(72)

pg:理想气体
• 3.2 理想气体混合物中任一组分的化学势
B ( pg ) B ( g ) RT ln( pB / p )
★不同系统中各组分的化学势表达式是本章的一个重要 内容,要注意区分不同的表达式,特别是明确其中标准 态的不同
§4.5 拉乌尔定律与亨利定律
• 5.1 液态混合物的气液平衡
B (l ) B ( g) B ( g) RT ln( pB / p )
将拉乌尔定律代入: (l ) ( g ) RT ln( p x / p ) B B B B 该式可以看成 是理想液态混 合物的定义式
B
B ( g ) RT ln( pB / p ) RT ln xB
★在恒温、恒压条件下,在大量系统中,除了B 组分以外, 保持其它组分的数量不变,加入1mol 组分B 引起的系统广度 量X 的变化 ★或:在等温等压下,系统广度性质X 随着组分B的量的变 化率就是XB。
(3)说明
1) X 代表体系的任一广度性质
V VB nB T , p ,n C U UB nB T , p ,n C
§4.1 偏摩尔量
• 1.1 问题的提出
而对多组分系统, 如水与无水乙醇的混合: V n水Vm,水 n乙醇Vm,乙醇
对纯物质而言: nVm V
由此可见:由纯组分混合形成混合物时不仅体积发生变化, 而且体积变化多少与形成混合物的组成有关
广度性质 X (如 V,G,S,U 等)除与温度、压力有关外, 还与系统中各组分的量n1、n2、n3、…、nk有关。
X B X nB T , p ,n
C
G S GB SB nB T , p ,n nB T , p ,n C C
第4章 多组分系统热力学1

§4.2 化学势
1.化学势的定义 混合物(或溶液)中组分B的偏摩尔吉布斯函 数GB 定义为B的化学势,用μB表示。
定义为 G B GB nB T .P.nC
对于纯物质,其化学势就是它的摩尔吉布斯函数。
化学势是最重要的热力学函数,系统中的其它偏摩 尔量均可以通过化学势、它的偏导数或组合表示。
B
得到
dA B ( )dnB ( ) 0
B
自发 平衡
化学势判据
封闭系统恒温恒压,W’=0 ,由dGT,p≤0,
dG SdT Vdp B ( )dnB ( )
B
得到
dG B ( )dnB ( ) 0
B
<自发 =平衡
化学势判据
化学势在多相平衡中的应用
设系统有α和β两相,两相中均不仅一种物 质。在恒温恒压下若α 相中有dnB的 B物质 转移到β相,则 若上述转移是自发进行的,则有
相dnB ( )
相
相转移
dGT . p 0
即
B( ) B( )
dG 0
即
当系统达平衡时
B( ) B( )
μ
B(α )=μ B(β )
= …=μ
B(ρ )
如果有某物质在各相中的化学势不等,则根据 dGT,p<0为自发过程的原理,该物质必然要从化学 势较大的相向化学势较小的相转移。
化学势在化学平衡中的应用
参加反应的物质都有化学势,平衡条件为
dG vi i (产物) vi i (反应物) 0
B
dA SdT pdV B ( ) dnB ( )
物理化学 第四章 多组分系统热力学

AB
( nB
)T , p ,nC
G
GB
( nB
)T , p ,nC
注意:偏摩尔量的下脚标为:T,P,C(C≠ B)
使用偏摩尔量时应注意: 1.偏摩尔量的含义是:在等温、等压、保持B物质 以外的所有组分的物质的量不变的条件下,广度性 质X的随组分B的物质的量的变化率。
2.只有广度性质才有偏摩尔量,而偏摩尔量是强度 性质。
六、偏摩尔量之间的函数关系
对于组分B:VB、UB、HB、SB、AB、GB之间的关系:
HB= UB +PVB ,
AB= UB -TSB
GB = HB -TSB= UB +PVB -TSB UB =AB+PVB
(
GB P
)T
,nA
VB
(
GB T
)
P,nA
SB
( GB )
[T T
]P,nB
3.纯物质的偏摩尔量就是它的摩尔量。
4.任何偏摩尔量都是T,p和组成的函数。
偏摩尔量的集合公式
设一个均相体系由1、2、 、k个组分组成,则体 系任一广度量Z应是T,p及各组分物质的量的函数,即:
X X (T , p, n1, n2,, nk )
在等温、等压条件下:
X
X
dX
( n1
···········
dG= dG(α) + dG(β) +·········
恒T,p时 dG SdT Vdp
B
dnB
B
同理,有
dU TdS pdV B ( )dnB ( ) B
dH TdS Vdp B ( )dnB ( ) B
多组分系统热力学

第四章 多组分系统热力学 主要内容1.混合物和溶液(1)多组分系统的分类含一个以上组分的系统称为多组分系统。
多组分系统可以是均相(单相)的,也可以是非均相(多相)的。
将多组分均相系统区分为混合物和溶液,并以不同的方法加以研究:(Ⅰ)混合物:各组分均选用同样的标准态和方法处理;(Ⅱ)溶液:组分要区分为溶剂及溶质,对溶剂及溶质则选用不同的标准态和方法加以研究。
(2)混合物及溶液的分类混合物有气态混合物液态混合物和固态混合物;溶液亦有气态溶液液态溶液和固态溶液。
按溶液中溶质的导电性能来区分,溶液又分为电解质溶液和非电解质溶液(分子溶液)。
2.拉乌尔定律与亨利定律拉乌尔定律与亨利定律是稀溶液中两个重要的经验规律。
(1)拉乌尔定律平衡时,稀溶液中溶剂A 在气相中的蒸气分压A p 等于纯溶剂在同一温度下的饱和蒸气压与该溶液中溶剂的摩尔分数A x 的乘积。
这就是拉乌尔定律。
用数学式表达拉乌尔定律为 A *A Ax p p = (2)亨利定律一定温度下,微溶气体B 在溶剂A 中的溶解度B x 与该气体在气相中的分压B p 成正比。
也可表述为:一定温度下,稀溶液中挥发性溶质B 在平衡气相中的分压力B p 与该溶质B 在平衡液相中的摩尔分数B x 成正比。
这就是亨利定律。
用数学式表达亨利定律为: B B ,B x k p x =B ,x k 、B ,b k 为以不同组成标度表示的亨利系数,其单位分别为Pa ,Pa·kg·mol -1。
应用亨利定律时,要注意其不同表达式所对应的亨利系数及其单位。
还要注意亨利定律适用于稀溶液中的溶质分子同气相同种分子相平衡,即亨利定律适用于稀溶液中的溶质在液相及气相中具有相同分子形态的场合。
3.偏摩尔量(1)偏摩尔量的定义设X 代表V ,U ,H,S ,A ,G 这些广度性质,则对多组份系统(混合物或溶液)即 X =f (T ,p ,n A ,n B ,…)定义 ()B C C,,,B B def ≠⎪⎪⎭⎫ ⎝⎛∂∂n p T n X X式中,X B称为广度性质X (X=V ,U ,H ,S ,A ,G 等)的偏摩尔量,它们分别为只有系统的广延量才具有偏摩尔量,偏摩尔量是强度量。
第四章_多组分系统热力学及其在溶液中的应用习题课

66.66 kPa,101.325kPa。设A和B构成理想溶液。则当
A 在溶液中的物质的量分数为 0.5 时,气相中 A 的物质 的量分数为( C ) (A) 0.200 (B) 0.300 (C) 0.397 (D) 0.603
解:根据拉乌尔定律 pi=pi*xi pA = pA*xA=66.66×0.5 pB = pB*xB =101.325×0.5 p = pA+pB=(66.66+101.325) ×0.5 yA(g)= pA /p=66.66/(66.66+101.325)= 0.397
解:混合成理想溶液时,无热效应,故H=0,
SB S R ln xB
* B
SB R ln xB
mixS RnB ln xB
S = – R ln x苯= 7.617 J ·K-1 , G = RT ln x苯= - 2270 J ·mol-1
10.
已知在 373K 时液体 A 、 B 的饱和蒸气压分别为
11、 在25℃时,纯水的蒸气压为3167.7Pa。某溶液 x(水) =0.98,与溶液成平衡的气相中,水的分压为 3066Pa。以298K, p为纯水的标准态,则该溶液中 水的活度系数( B ) (A)大于1 解: (B)小于1 (C)等于1 (D)不确定
p p * ax
p p * x x
一、偏摩尔量及化学势的概念
为了确定组成可变的多组分系统的热力学性质,引入了 偏摩尔量的概念;为了判定组成可变的多组分系统中过程 的自发变化的方向和限度,引入了化学势的概念。
1. 偏摩尔量 (1) 定义
Z ZB n B T , p ,nC
(2) 基本公式 标准态时的化学势,均是T,p的函数,它们 分别为:当xB=1,mB=1molkg-1,cB=1moldm-3 时且服从亨利定律的那个假想态的化学势。
多组分体系热力学.ppt

常用的偏摩尔量:
XB
def
X nB
T , p,nC
U nBUB B
H nB HB B
A nB AB B
S nB SB B
G nBGB B
U
UB
( nB
)T , p,nC (CB )
偏摩尔热力学能
H
HB
( nB
)T ,
p,nC (CB)
A
AB
( nB
)T , p,nC (CB )
dp
B
nB
T , p,nC
dnB
偏摩尔量
X B def
X nB
T , p,nC
X
X
dX
T
p,nB
dT
p
T ,nB
dp
B
X BdnB
2、偏摩尔量的物理含义:
X B def
X nB
T , p,nC
偏摩尔量XB是在恒温、恒压及除组分B以外其余各 组分的物质的量均保持不变的条件下,系统广度量X随 组分B的物质的量的变化率
四、同一组分的各种偏摩尔量之间的关系 对单组分系统有:
H=U+pV A=U-TS G=H-TS
G S T p
对多组分系统有:
G p
T
V
HB=UB+pVB AB=UB-TSB GB=HB-TSB
GB T
p
SB
GB p
T
VB
§4.2 化学势
定义:
B
GB
( G nB
)T , p,nC (CB)
3、偏摩尔量的加和公式
X nB X B
B
多组分系统的广度量X为系统各组分的物质的量与其偏摩尔量 XB乘积的加和。
物理化学核心教程04_多组分系统热力学

非理想混合物,对Raoult定律发生偏差,需要对其浓度进行修正,用活度代替浓度。
2020/12/19
5
4.1.1 混合物和溶液
什么是溶液? 系统中各组分在热力学上有不同的处理方法,有不同的标准态,不同的化学势表示式,分 别服从不同的经验规律。
溶液有固态溶液和液态溶液,但无气态溶液。
溶液有稀和浓之分,本章主要讨论稀溶液 。
VB def
V
nB
T,
p,nC(CB)
UB def
U
nB
T,p,nC(CB)
HB def
H
nB
T,
p,nC(CB)
SB def
S
nB
T,p,nC(CB)
AB def
A
nB
T,p,nC(CB)
GB def
G
nB
T,p,nC(CB)
2020/12/19
16
4.2.2 偏摩尔量的定义 使用偏摩尔量时应该注意: 只有广度性质才有偏摩尔量,强度性质就没有。 偏微分的下标都是:等温、等压、保持除B以外的其他组分的量不变。
2020/12/19
24
4.3.2 化学势的定义
把化学势的广义定义代入热力学函数的微分式:
dU T dSpdV B dnB B
dHT dSV dp B dnB B
d A S d Tpd V B d n B B
d G S d T V d p B d n B B 多组分系统热力学基本公式比单组分多了最后一项
2020/12/19
11
4.2.1 单组分与多组分系统的区别
单组分系统的广度性质具有加和性
若1 mol单组分B 物质的体积为
第4章 多组分系统的热力学 第4节 化学势及其应用 第5节 混合气体中组元的化学势

l
O
g T
(
Gm
*
B
p
)T Vm
*
1 3
373.15K
1 2 3 4
16
4.5 混合气体中组元的化学势
纯理想气体的化学势
理想气相混合物中各组分的化学势
实际气体中组分的化学势
17
纯理想气体的化学势
只有一种理想气体,
G ( )T ( )T , p p p nB T
18
p (T , p) (T , p ) RT ln p
纯理想气体的化学势
p (T , p) (T , p ) RT ln p p i i ( g ) RT ln p
这是理想气体化学势的表达式。 μi(g)是温度为T,压力为标准压力时理想气体 i 的 化学势,这个状态就是气体的标准态。
22
气体中组分的化学势小结
纯理想气体
* p B B* B ( g ) RT ln p
pB 混合理想气体 B B ( g ) RT ln p
fB 混合实际气体 B B ( g ) RT ln p
作业2-3 简要论述多组分系统中的相平衡条件和化学反应平衡条件 作业2-4 理想气体混合物和实际气体混合气的化学势的区别和联系是什么
G ( )T , p n B G ( )T nB p T , p
V Vm nB T , p
(dG SdT Vdp)
p
dμ Vmdp p
p
p
RT dp p
p (T , p) (T , p ) RT ln p
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
活度与活度因子
下一内容 回主目录
返回
2013-8-17
§4-0
前言
1 多组分系统分类
2 溶液组成的表示法
上一内容
下一内容
回主目录
返回
2013-8-17
1 多组分系统分类
按聚集态分
混合物 按规律性分 单相 系统 多组分 系 统 多相 系统
上一内容 下一内容 回主目录
气态混合物 液态混合物 固态混合物 理想混合物 真实混合物
回主目录
返回
2013-8-17
2.3溶液组成的表示法
3.物质的量浓度cB(molarity)
cB
def
nB V
溶质B的物质的量与溶液体积V的比值称为溶 质B的物质的量浓度,或称为溶质B的浓度,单位 是mol· -3,但常用单位是mol· -3 。 m dm
上一内容
下一内容
回主目录
返回
2013-8-17
上一内容 下一内容 回主目录
返回
2013-8-17
化学势的广义定义
U H B ( ) S , p ,nc (c B) n B S ,V ,nC nB A G ( )T ,V ,nc (c B) ( )T , p ,nc (c B) nB nB
若系统发生一微小的变化,则
X X dX dT p T p ,nB ,nC , X X dnB n n B T , p ,nC , C
上一内容 下一内容 回主目录
dp T ,nB ,nC ,
上一内容
下一内容
回主目录
返回
2013-8-17
1 问题的提出
* 纯物质的某广延量X = n X m
理想混合物某广延量为 真实混合物系统: 20℃、常压下
* * X = nA X m , A+ nB X m ,B
* Vm ,水 18 .09 cm3 mol 1 * Vm,乙醇 58.35cm3 mol 1
2.4溶液组成的表示法
4.质量分数wB(mass fraction)
mB wB m(总)
溶质B的质量与溶液总质量之比称为溶质B的 质量分数,单位为1。
上一内容
下一内容
回主目录
返回
2013-8-17
§4-1
偏摩尔量
1 问题的提出
2 偏摩尔量 3 偏摩尔量的测定与计算 4 Gibbs-Duhem公式 5 偏摩尔量之间的函数关系
2013-8-17
2.2溶液组成的表示法
2.质量摩尔浓度bB(molality)
nB bB mA
溶质B的物质的量与溶剂A的质量之比称为 溶质B的质量摩尔浓度,单位是 mol kg -1 。这个 表示方法的优点是可以用准确的称重法来配制溶 液,不受温度影响,电化学中用的很多。
上一内容
下一内容
上一内容 下一内容 回主目录
返回
2013-8-17
5 偏摩尔量间的函数关系
偏摩尔量之间仍然符合前面讲的热力学函数关系。 要注意:凡是广延量都要用偏摩尔量。
HB = UB + pVB
GB p
上一内容 下一内容
VB T , n B
返回
2013-8-17
dnC T , p ,nB ,
返回
2013-8-17
2 偏摩尔量(partial molar quantity)
X 表示压力及混合物组成不变 dX T p ,nB ,nC , 时广延量X随温度的变化率;
X dX p
G B ( )T , p ,nc (c B) nB
下一内容 回主目录
上一内容
返回
2013-8-17
2 多组分单相系统的热力学关系式
混和物的吉布斯函数G 可表示为 G = f (T, p,nB, nC, nD …)
G G G dG dT p dp n T p ,nB B T , n B B
当0.5mol水与0.5mol乙醇混合时,V = 37.2 cm3 即
V n V n
* 水 水
下一内容
* 乙醇 乙醇
V
38.22cm
返回
3
上一内容
回主目录
2013-8-17
2 偏摩尔量(partial molar quantity)
对一个混合系统, 其任一广延量 X:
X f (T , p, nB , nC ,)
X dX n B
上一内容
表示温度及混合物组成不变 T ,nB ,nC , 时广延量X随压力的变化率;
T , p ,nC ,
表示温度、压力及除组分B 外其它组分物质的量不变的条 件下,仅由于组分B的物质的量 发生微小变化引起的系统的广 延量X的变化率。
上一内容 下一内容 回主目录
返回
2013-8-17
3 偏摩尔量的测定与计算
⑴ 数学分析法(计算法):
NaBr水溶液的体积与溶液浓度的关系为
V = 1.0029 + 23.189 b + 2.197 b3/2 - 0.178 b2
溶液中NaBr的偏摩尔体积为
VB =23.189 +3/2×2.197 b1/2- 2×0.178b
讨论: 1. 只有广度性质才有偏摩尔量; 2. 只有恒温、恒压下系统的广延量随某一组分的物 质的量的变化率才是偏摩尔量,其它条件(如等 温等容等)下的偏导数都不能称为偏摩尔量;
3. 偏摩尔量是强度性质,其数值决定于温度、压力 和组成(组成不同其偏摩尔量不同)。
4.对纯物质(单组分系统),偏摩尔量就是摩尔量。 5. 偏摩尔量的概念对混合化学势
• 1 化学势的定义 • 2 多组分单相系统的热力学关系式 • 3 多组分多相系统的热力学公式 • 4 化学势判据及应用举例
上一内容
下一内容
回主目录
返回
2013-8-17
1 化学势的定义 因为在多组分体系的变化中,大部分情况 是在恒温和恒压的条件下进行,所以偏摩尔吉 布斯函数GB经常使用,故将混和物或溶液中组 分B的偏摩尔吉布斯函数GB就称为组分B的化学 势。即
G 注意: 这四个偏导数中只有 n B 是偏摩尔量, T , p , nC
其余三个不是偏摩尔量,因为不是在恒温恒压条件下 .
上一内容 下一内容 回主目录
返回
2013-8-17
3 多组分多相系统的热力学公式
对多组分多相系统来说,因组分B的物质的量的 变化引起的某一广延量的变化等于各个相中该广延量 的变化的加和。 dG dG( ) dG( ) dG( ) dG( )
对其中的α、β、γ…相,都可应用热力学关系式:
dG( ) S ( )dT V ( )dp B ( )dnB ( )
dG( ) S ( )dT V ( )dp B ( )dnB ( )
B
dG SdT Vdp B ( )dnB ( )
溶 液
液态溶液 按聚集态分 固态溶液 按规律性分
返回
理想稀溶液 真实溶液
2013-8-17
2 溶液组成的表示法
在液态的非电解质溶液中,溶质B的浓度表 示法主要有如下四种: 1.物质的量分数 2.质量摩尔浓度
nB xB n (总 ) nB bB mA
def
3.物质的量浓度
4.质量分数
上一内容 下一内容 回主目录
B
上一内容 下一内容 回主目录
B
返回
2013-8-17
3 多组分多相系统的热力学公式
B
下一内容 回主目录
返回
2013-8-17
2 多组分单相系统的热力学关系式
同理:
dU TdS pdV BdnB
B
dH TdS Vdp BdnB
B
dA SdT pdV BdnB
B
这就是适用于均匀系统的普遍化的热力学基本 关系式,既适用于组成变化的封闭系统,也适用于 开放系统。
在恒温恒压下,对式
X X B nB 求全微分得
dX X B dnB nB dX B
∵恒温恒压下
dX X B dnB
nB dX B 0
或
x
B
下一内容
B
dX B 0
返回
此两式都称为 吉布斯-杜亥姆方程.
上一内容 回主目录
2013-8-17
4
cB
def
nB V
mB wB m(总)
返回
2013-8-17
2.1溶液组成的表示法
1.物质的量分数 xB (mole fraction)
xB
def
nB n (总 )
溶质B的物质的量与溶液中总的物质的量之比 称为溶质B的物质的量分数,又称为摩尔分数,单 位为1。
上一内容
下一内容
回主目录
返回
G S T p ,nB
G V p T , n B
G n B
dnB T , p ,nC
B T , p , nC
即:
上一内容
dG SdT Vdp BdnB
⑵ 图解法:
做出X~ nB变化曲线,在某点处曲线切线的斜 率即为组分B在该组成下的偏摩尔量。
上一内容 下一内容 回主目录
返回
2013-8-17
3 偏摩尔量的测定与计算
V
* Vm,C
VC
* Vm,B
