pascal中排序算法
输入十个正整数,把这十个数按由小到大的顺序排列pascal

例3输入十个正整数,把这十个数按由小到大的顺序排列。
将数据按一定顺序排列称为排序,排序的算法有很多,其中选择排序是一种较简单的方法。
分析:要把十个数按从小到大顺序排列,则排完后,第一个数最小,第二个数次小,……。
因此,我们第一步可将第一个数与其后的各个数依次比较,若发现,比它小的,则与之交换,比较结束后,则第一个数已是最小的数(最小的泡往下冒)。
同理,第二步,将第二个数与其后各个数再依次比较,又可得出次小的数。
如此方法进行比较,最后一次,将第九个数与第十个数比较,以决定次大的数。
于是十个数的顺序排列结束。
例如下面对5个进行排序,这个五个数分别为8 2 9 10 5。
按选择排序方法,过程如下:初始数据:8 2 9 10 5第一次排序:8 2 9 10 59 2 8 10 510 2 8 9 510 2 8 9 5第二次排序:10 8 2 9 510 9 2 8 510 9 2 8 5第三次排序:10 9 8 2 510 9 8 2 5第四次排序:10 9 8 5 2对于十个数,则排序要进行9次。
源程序如下:program ex5_2;var a:array[1..10]of integer;i,j,t:integer;beginwriteln('Input 10 integers:');for i:=1 to 10 do read(a[i]);{读入10个初始数据}readln;for i:=1 to 9 do{进行9次排序}beginfor j:=i+1 to 10 do{将第i个数与其后所有数比较}if a[i]<a[j] then {若有比a[i]大,则与之交换}begint:=a[i];a[i]:=a[j];a[j]:=t;end;write(a[i]:5);end;end.给数组赋值的常用函数:fillchar(a,sizeof(a),0) :是把A数组的每个单元赋值为0。
pascal 顺序结构与基本数据类型

顺序结构与基本数据类型一、程序的三种基本结构1、顺序结构:按照语句的书写顺序,依次执行。
2、选择结构(分支结构):根据给定的条件,判断成立与否,成立做一件事,不成立做另外一件事。
两件事必须做一件且只能做一件。
3、循环结构(重复结构):重复做某件事。
3种:①计数循环:重复执行的次数确定;②当型循环:当条件成立时,反复做某件事;③直到型循环:反复做某件事,直到条件成立时为止。
二、PASCAL标准数据类型及函数:1、实型(real)表示方法:小数表示法和指数表示法(科学表示法)。
如:1.25(1.25e0),132.67(1.3267e+2),0.0025(2.5e-3),-1.56(-1.56e0),0.0(0e0) 实型量运算:+(加)、-(减)、*(乘)、/(除)实型量标准函数:abs(绝对值),sqr(平方),sqrt(开方),sin(正弦),cos(余弦),arctan(反正切),exp(以e为底的指数),ln(自然对数),trunc(取整),round(舍入取整),int(取整)注:所有函数的自变量必须写在括号中。
例如:Sin2x 应写成sin(2*x) (a+b)2应写成sqr(a+b)Sin,cos函数的自变量应为弧度。
若是度,应转换为弧度。
例如:Sin32o15’应写成sin(32.15*3.14159/180)Tanx 应写成sin(x)/cos(x)e2.5应写成exp(2.5)lnx应写成ln(x) lgx 应写成ln(x) /ln(10)x y 应写成exp(y*ln(x))int直接取整数部分(其结果为实型)、trunc去掉小数部分,取其整数。
Round是将小数部分四舍五入后变为整数。
例如:trunc(1.2)=1 round(1.2)=1trunc(1.7)=1 round(1.7)=2trunc(-3.7)=-3 round(-3.7)=-42、整型(integer)正、负数和0.整型量运算:+(加)、-(减)、*(乘)、div(整除)、mod(取余)整型量标准函数:abs(绝对值),sqr(平方),pred(前导),succ(后继),odd(奇函数),chr(取字符)例如:pred(前导),取自变量前一个值。
freepascal语言与基础算法

freepascal语言与基础算法1. 引言1.1 概述本文将探讨Freepascal语言与基础算法的关系和应用。
Freepascal是一种强大且灵活的编程语言,被广泛应用于各个领域的软件开发中。
而基础算法则是计算机科学的核心内容,对于解决问题和优化程序至关重要。
通过结合这两者,我们可以深入理解Freepascal语言以及在实际项目中如何使用算法来提高效率和性能。
1.2 文章结构本文共分为五个部分。
首先,我们将介绍Freepascal语言的背景与发展历程,探讨其特性和优势,并列举一些应用领域和案例。
接着,我们会概述基础算法的基本概念和分类,并介绍算法设计与分析原则。
然后,我们会详细介绍几种常见的基础算法,并给出示例加以说明。
在第四部分中,我们将探讨Freepascal语言在基础算法中的具体应用,包括数据结构支持与实现方式、排序算法实现示例与性能分析以及查找算法实现示例与应用场景讨论。
最后,在结论部分,我们将总结Freepascal语言与基础算法的关系,并讨论其发展前景和实践意义,同时展望未来研究的方向。
1.3 目的本文的目的在于给读者提供有关Freepascal语言与基础算法之间联系的深入理解。
通过阐述Freepascal语言作为一种强大且广泛应用的编程语言以及基础算法作为解决问题和优化程序所必不可少的工具,我们希望读者能够了解如何利用Freepascal语言来实现各种常见的基础算法,并在实际项目中应用这些算法来提高效率和性能。
此外,本文还将探讨Freepascal语言与基础算法之间的潜在联系,以及可能产生的新思路和研究方向。
2. Freepascal语言介绍:2.1 背景与发展Freepascal是一种高级编程语言,最初由Anders Hejlsberg 发起并于1995年首次发布。
它是一种免费的、开源的、跨平台的编程语言,主要用于快速开发可靠、高效且易于维护的软件应用。
自推出以来,Freepascal得到了广泛的采用和用户社区支持。
pascal语法讲义-第七讲

第七讲 数组与字符串一、一维静态数组我们先来思考一个问题。
例题1.4.2.1.1:读入3个数,将之倒序输出。
想必这个程序对大家来说没有难度。
program p1_4_2_1_1(input,output);var a,b,c:longint;beginreadln(a,b,c);writeln(c,' ',b,' ',a);readln();end.下面我们来思考一个升级版的问题:例题1.4.2.1.2:读入1000个数,将之倒序输出。
这个程序对于大家来说肯定也是可以搞定的,只不过相对而言比较麻烦,这里我们提供一个生成该程序源文件的程序。
program p1_4_2_1_2_producer(input,output);var i:longint;beginassign(output,'p1_4_2_1_2.pas');rewrite(output);writeln('program p1_4_2_1_2(input,output);');write('var ');for i:=1 to 999 do write('a',i,',');writeln('a1000:longint;');writeln('begin');write('readln(');for i:=1 to 999 do write('a',i,',');writeln('a1000);');write('writeln(');for i:=1000 downto 2 do write('a',i,',');writeln('a1);');writeln('readln();');writeln('end.');close(output);end.这里使用了一定文件的知识,如果把assign、rewrite、close 三行略去的话,大家应该可以看得懂。
pascal-分治法

(迭起来有:望有界:1function CPAIR2(S);beginif |S|=2 then δ:=S中这2点的距离else if |S|=0then δ:=∞else begin1. m:=S中各点x坐标值的中位数;构造S1和S2,使S1={p∈S|px≤m}和S2={p∈S|px>m}2. δ1:=CPAIR2(S1);δ2:=CPAIR2(S2);3. δm:=min(δ1,δ2);4. 设P1是S1中距垂直分割线l的距离在δm之内的所有点组成的集合,P2是S2中距分割线l的距离在δm之内所有点组成的集合。
将P1 和P2中的点依其y坐标值从小到大排序,并设P1*和P2*是相应的已排好序的点列;5. 通过扫描P1*以及对于P1*中每个点检查P2*中与其距离在δm之内的所有点(最多6个)可以完成合并。
当P1*中的扫描指针逐次向上移动时,P2*中的扫描指针可在宽为2δm的一个区间内移动。
设δl是按这种扫描方式找到的点对间的最小距离;6. δ=min(δm,δl);end;return(δ);end;下面我们来分析一下算法CPAIR2的计算复杂性。
设对于n个点的平面点集S,算法耗时T(n)。
算法的第1步和第5步用了O(n)时间,第3步和第6步用了常数时间,第2步用了2T(n/2)时间。
若在每次执行第4步时进行排序,则在最坏情况下第4步要用O(n log n)时间。
这不符合我们的要求。
因此,在这里我们要作一个技术上的处理。
我们采用设计算法时常用的预排序技术,即在使用分治法之前,预先将S中n个点依其y坐标值排好序,设排好序的点列为P*。
在执行分治法的第4步时,只要对P*作一次线性扫描,即可抽取出我们所需要的排好序的点列P1*和P2*。
然后,在第5步中再对P1*作一次线性扫描,即可求得δl。
因此,第4步和第5步的两遍扫描合在一起只要用O(n)时间。
这样一来,经过预排序处理后的算法CPAIR2所需的计算时间T(n)满足递归方程:显而易见T(n)=O(n log n),预排序所需的计算时间为O(n1og n)。
PASCAL语言的基本知识

标准函数
算术函数
标量函数
例: abs(-4)=4 abs(-7.49)=7.49 arctan(0)=0.0 sin(pi)=0.0 cos(pi)=-1.0 frac(-3.71)=-0.71 int(-3.71)=-3.0 sqr(4)=16 sqrt(4)=2
例: odd(1000)=false odd(3)true pred(2000)=1999 succ(2000)=2001 pred('x')='w' succ('x')='y'
类型数值范围占字节数有效位数 [Copy to clipboard] CODE: real 2.9e-39..1.7e38 6 11..12 single 1.5e-45..3.4e38 4 7..8 double 5.0e-324..1.7e308 8 15..16 extended 3.4e-4932..1.1e4932 10 19..20 comp -263+1..263-1 8 19..20 Turbo Pascal支持两种用于执行实型运算的代码生成模式:软件仿真模式和80x87浮点模式。
类型数值范围占字节数格式 [Copy to clipboard] CODE: shortint -128..128 1带符号8位 integer -.. 2带符号16位 longint -2^16~2^16-1带符号32位 byte 0..255 1带符号8位 word 0.. 2带符号16位 Turbo Pascal规定了两个预定义整型常量表识符maxint和maxlonint,他们各表示确定的常数值,maxint 为,
PASCAL语言的基本知识
计算机编程语言
01 程序组成
Pascal入门教程 (2)
第三章分支程序设计内容提要本章介绍了分支程序设计的思路,IF语句,CASE语句的用法。
学习要求在本章的学习中,要充分理解IF 语句,CASE语句的意义和用法,弄清分支语句的流程,对逻辑表达式和布尔类型数据的运算要能熟练掌握。
第一节IF 语句前面我们学习了顺序程序设计。
在顺序程序设计中,其思路是在提供解决一个问题的方案时,是按事情发生的先后次序,一步一步地把问题给解决了,中间不会有什么违背顺序的事件发生。
但是在生活中,我们要解决的问题并不都是按顺序的方式解决的,在完成一件事的方案中可能有多种可能的情况发生,而且对应不同的情况有不同的解决方案。
于是我们就要用分支的思路来解决问题。
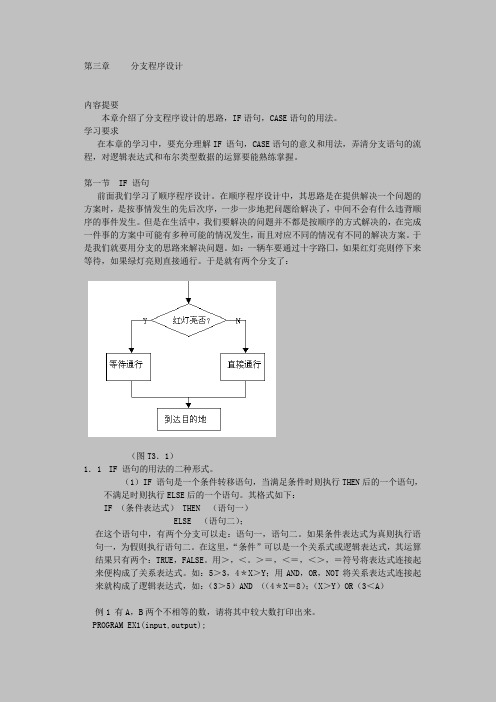
如:一辆车要通过十字路囗,如果红灯亮则停下来等待,如果绿灯亮则直接通行。
于是就有两个分支了:(图T3.1)1.1IF 语句的用法的二种形式。
(1)IF 语句是一个条件转移语句,当满足条件时则执行THEN后的一个语句,不满足时则执行ELSE后的一个语句。
其格式如下:IF (条件表达式) THEN (语句一)ELSE (语句二);在这个语句中,有两个分支可以走:语句一,语句二。
如果条件表达式为真则执行语句一,为假则执行语句二。
在这里,“条件”可以是一个关系式或逻辑表达式,其运算结果只有两个:TRUE,FALSE。
用>,<。
>=,<=,<>,=符号将表达式连接起来便构成了关系表达式。
如:5>3,4*X>Y;用AND,OR,NOT将关系表达式连接起来就构成了逻辑表达式,如:(3>5)AND ((4*X=8);(X>Y)OR(3<A)例1 有A,B两个不相等的数,请将其中较大数打印出来。
PROGRAM EX1(input,output);VAR a,b:real;BEGINwriteln('input a,b');readln(a,b);if a>b then writeln(a)else writeln(b);end.在本程序中,我们面临两种情况:A>B 和A<B。
Pascal入门教程 (7)

第八章数组类型内容提要本章介绍了数组的含义及存储结构,一维,二维数组的输入、输出方法及应用,字符串数组的相关知识。
学习要求在本章里,要求学生熟练掌握一维,二维数组的定义及存储结构,输入、输出方式,关键是能用数组知识解决诸如排序等实际问题。
掌握字符串及字符串数组的构成方式,能熟练进行字符串的各种运算。
前面我们学习了一种自定义类型:子界型。
这一章我们学习另一种很重要的构成类型:数组型。
构成类型是用已有的基类型按一定的规则构成的一种新类型。
数组类型也是用实型,整型,布尔型,字符型,子界型,枚举型等数据类型构成一的种能让多个数据有序的新类型。
在前面我们学习变量时可能就有疑问存在了:如果有多个数据,比如说20个无规律的整数,我们能不能方便地把其中任一个数表达出来?用以前的知识,我们能用20个变量,比如A1,A2,A3,...A20,每个变量对应一个整数。
如果要用第五个数,则调用A5即可。
但是如果要求把20个变量中的数一一相加,又该怎么做呢?那就得写出表达式:S:=A1+A2+A3+A4+...+A20。
也就是说有20个变量就得写出20个变量相加。
如果要求将这20个变量打印出来,则得写:WRITE(A1,A2,A3,A4,...,A20)。
(本书在这里用了‚...‛将中间的项省略了,但读者编程时不能省,有20项则20项都得写出)。
20个变量就很不方便了,要是有100个,1000个,10000个变量又怎么办?不至于把10000个变量一一写出来吧?数组类型能解决这个问题。
第一节一维数组1.1 关于数组我们在表达类似上述的20个整数这类问题时,要用的20个变量我们用另一种方法表示:变量名还是用A,但是加上下标:第一个变量用A[1]表示, 第二个变量用A[2]表示, 第三个变量用A[3]表示,A[4], A[5], …A[20]。
在这里,我们在变量A后加了下标,用中括号把下标括起来。
这种表示的变量叫下标变量。
下标变量A[1]和普通变量A1的区别是下标变量中的下标可以是常量,变量,表达式。
pascal常见算法整理

3、归并排序
program gbpx;
const maxn=7;
type arr=array[1..maxn] of integer;
var a,b,c:arr;
i:integer;
procedure merge(r:arr;l,m,n:integer;var r2:arr);
a[i+d]:=t;
end;
end;
write('output data:');
for i:=1 to n do write(a[i]:6);
writeln;
end.
程序2:(子序列是冒泡排序)
program xepx;
const n=7;
type
arr=array[1..n] of integer;
while (i<n) and bool do
begin
bool:=false;
for j:=n downto i+1 do
if a[j-1]<a[j] then
begin t:=a[j-1];a[j-1]:=a[j];a[j]:=t;bool:=true end;
for i:=1 to n do write(a[i]:6);
writeln;
end.
i,j,k,t:integer;
begin
write('Enter date:');
for i:= 1 to n do read(a[i]);
writeln;
for i:=2 to n do
begin
k:=a[i];j:=i-1;
Pascal的运算符及表达式
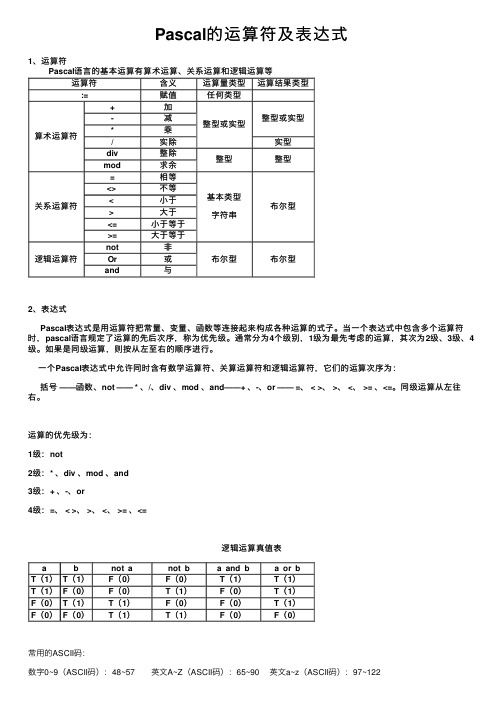
Pascal的运算符及表达式1、运算符Pascal语⾔的基本运算有算术运算、关系运算和逻辑运算等运算符含义运算量类型运算结果类型:=赋值任何类型算术运算符+加整型或实型整型或实型-减*乘/实除实型div整除整型整型mod求余关系运算符=相等基本类型字符串布尔型<> 不等< ⼩于> ⼤于<=⼩于等于>=⼤于等于逻辑运算符not⾮布尔型布尔型Or或and与2、表达式Pascal表达式是⽤运算符把常量、变量、函数等连接起来构成各种运算的式⼦。
当⼀个表达式中包含多个运算符时,pascal语⾔规定了运算的先后次序,称为优先级。
通常分为4个级别,1级为最先考虑的运算,其次为2级、3级、4级。
如果是同级运算,则按从左⾄右的顺序进⾏。
⼀个Pascal表达式中允许同时含有数学运算符、关算运算符和逻辑运算符,它们的运算次序为:括号 ——函数、not —— * 、/、div 、mod 、and——+ 、-、or ——=、 < >、 >、 <、 >= 、<=。
同级运算从左往右。
运算的优先级为:1级:not2级:* 、div 、mod 、and3级:+ 、-、or4级:=、 < >、 >、 <、 >= 、<=逻辑运算真值表a b not a not b a and b a or bT(1)T(1)F(0)F(0)T(1)T(1)T(1)F(0)F(0)T(1)F(0)T(1)F(0)T(1)T(1)F(0)F(0)T(1)F(0)F(0)T(1)T(1)F(0)F(0)常⽤的ASCII码:数字0~9(ASCII码):48~57 英⽂A~Z(ASCII码):65~90 英⽂a~z(ASCII码):97~122。
18个基本算法

var a:array[1..maxn,1..maxn] of integer; b,pre:array[1..maxn] of integer; mark:array[1..maxn] of boolean; procedure dijkstra(v0:integer); begin fillchar(mark,sizeof(mark),false); for i:=1 to n do begin d[i]:=a[v0,i]; if d[i]< >0 then pre[i]:=v0 else pre[i]:=0; end; mark[v0]:=true; repeat min:=maxint; u:=0; for i:=1 to n do if (not mark[i]) and (d[i]< min) then begin u:=i; min:=d[i]; end; if u< >0 then begin mark[u]:=true; for i:=1 to n do if (not mark[i]) and (a[u,i]+d[u]< d[i]) then begin d[i]:=a[u,i]+d[u]; pre[i]:=u; end; end; until u=0; end; D.计算图的传递闭包 Procedure Longlink; Var T:array[1..maxn,1..maxn] of boolean; Begin Fillchar(t,sizeof(t),false); For k:=1 to n do For I:=1 to n do For j:=1 to n do T[I,j]:=t[I,j] or (t[I,k] and t[k,j]); End;
《数据结构》期末考试复习题 第10章 排序

第 10 章
排序
一、选择题 1.某内排序方法的稳定性是指( )。 【南京理工大学 1997 一、10(2 分) 】 A. 该排序算法不允许有相同的关键字记录 B. 该排序算法允许有相同的关键字 记录 C.平均时间为 0(n log n)的排序方法 D.以上都不对 2. 下面给出的四种排序法中( )排序法是不稳定性排序法。 【北京航空航天大学 1999 一、 10 (2 分) 】 A. 插入 B. 冒泡 C. 二路归并 D. 堆积 3.下列排序算法中,其中( )是稳定的。 【福州大学 1998 一、3 (2 分)】 A. 堆排序,冒泡排序 B. 快速排序,堆排序 C. 直接选择排序,归并排序 D. 归并排序,冒泡排序 4.稳定的排序方法是( ) 【北方交通大学 2000 二、3(2 分) 】 A.直接插入排序和快速排序 B.折半插入排序和起泡排序 C.简单选择排序和四路归并排序 D.树形选择排序和 shell 排序 5.下列排序方法中,哪一个是稳定的排序方法?( ) 【北方交通大学 2001 一、8 (2 分) 】 A.直接选择排序 B.二分法插入排序 C.希尔排序 D.快速排序 6.若要求尽可能快地对序列进行稳定的排序,则应选(A.快速排序 B.归并排序 C.冒 泡排序) 。 【北京邮电大学 2001 一、5(2 分) 】 7.如果待排序序列中两个数据元素具有相同的值,在排序前后它们的相互位置发生颠倒, 则称该排序算法是不稳定的。 ( )就是不稳定的排序方法。 【清华大学 1998 一、3 (2 分) 】 A.起泡排序 B.归并排序 C.Shell 排序 D.直接插入排序 E.简单选 择排序 8.若要求排序是稳定的,且关键字为实数,则在下列排序方法中应选( )排序为宜。 A.直接插入 B.直接选择 C.堆 D.快速 E.基数 【中科院计算所 2000 一、 5(2 分) 】 9.若需在 O(nlog2n)的时间内完成对数组的排序,且要求排序是稳定的,则可选择的排序方 法是( ) 。 A. 快速排序 B. 堆排序 C. 归并排序 D. 直接插入排序 【中国科技大学 1998 二、4(2 分) 】 【中科院计算所 1998 二、4(2 分) 】 10.下面的排序算法中,不稳定的是( ) 【北京工业大学 1999 一、2 (2 分)】 A.起泡排序 B.折半插入排序 C.简单选择排序 D.希尔排序 E.基数排序 F.堆 排序。 11.下列内部排序算法中: 【北京工业大学 2000 一、1 (10 分 每问 2 分)】 A.快速排序 B.直接插入排序 C. 二路归并排序 D. 简单选择排序 E. 起泡排序 F. 堆排序 (1) 其比较次数与序列初态无关的算法是( ) (2)不稳定的排序算法是( ) (3)在初始序列已基本有序(除去 n 个元素中的某 k 个元素后即呈有序,k<<n)的情况下, 排序效率最高的算法是( ) (4)排序的平均时间复杂度为 O(n•logn)的算法是( )为 O(n•n)的算法是( )
pascal-经典算法

动态规划(一)
• 0-1背包 • 完全背包 • 乘法问题 • 数塔问题 • 装箱问题
动态规划(二)
• 最长上升序列(LIS) • 最长公共子串(• 归并排序 • 最近点对问题 • 求最大子序列和的O(nlogn)算法 • Hanoi塔问题及其变种 • 棋盘覆盖问题 • 循环赛日程表问题
贪心
• 最优装载问题 • 部分背包问题 • 独立区间的选择 • 覆盖区间的选择 • 区间的最小点覆盖 • 点的最小区间覆盖
递推
• Fibonacci数的若干应用 • Catalan数的若干应用 • 拆分数 • 差分序列
数据结构(二)
• ★平衡二叉树 • ★树状数组 • ★线段树 • ★块状链表
排列与组合
• 生成所有排列 • 生成所有组合 • 生成下一个排列 • 生成下一个组合
计算几何(一)
• 计算斜率 • 计算点积 • 计算余弦 • 计算平面两点的距离 • 计算空间两点的距离 • ★计算广义空间两点的距离 • 判断三点是否共线
语言与计算机
• 递归调用 • 向前引用 • 随机化 • 指针类型 • 按位运算
排序(一)
• 冒泡排序(起泡排序) • 选择排序 • 插入排序 • ★ Shell排序 • 快速排序
排序(二)
• 线性时间排序 • 查找第k大元素 • 带第二关键字的排序
数论(一)
• 素性判断 • 筛选建立素数表 • 分解质因数 • 进制转换 • 二分取幂 • ★二分求解线性递推方程
图论:二分图
• 验证二分图 • 匈牙利算法 • ★KM算法 • ★稳定婚姻系统
树
• 求树的最短链 • 二叉树的四种遍历 • 已知先序中序求后序 • 已知中序后序求先序 • ★已知先序后序求中序 • ★LCA问题的Tarjan离线算法 • ★Huffman编码
pascal排序算法

排序查找算法排序算法:我们在前面学过的排序算法有选择排序、冒泡排序等,它们的时间复杂性为O(n2),稳定性比较好,但速度比较慢另外的一些排序算法:插入排序、希尔(Shell)排序、快速排序、归并(合并)排序插入排序:其思想与打牌时,当手中的一手牌已排好序,又摸起一张新的牌插入这一手牌中时差不多算法的基本思想:1)设n个数据已经按照顺序排列好(假定已按从小到大的顺序排序,并存放在数组a中)2)输入一个数据x,将其按有序顺序,放入适当的位置上,从而使整个数据序列仍然保持有序顺序;a)将x与n个数比较,寻找应当插入x的位置:i:=1;while x>a[i]do i:=i+1;b)j:=i;c)将a数组中从j位置开始的元素向后移动:for k:=n+1downto1do a[k]:=a[k-1];a)a[j]:=x;3、输出已经插入完毕的有序数列。
算法(最坏情况下)的复杂性:O(n2)适用于:原先的数据已经过了排序、又插入了一个新数据项的情况Shell排序(希尔排序)此算法是Shell于1959年提出的,又称缩小增量排序算法,其基本思想是:1)发现当n不大时,插入排序的性能是不错的。
因此,将大量的插入排序划分为小组的、少量数据的插入排序;2)设法先取小于n的一个增量d1,将第1、1+d1、1+2d1…个元素作为第一组,将第2、2+d1、2+2d1…个元素作为第二组,将d1、d1+d1、d1+2d1…个元素作为第d1组,并在各组之内运用插入排序。
3)然后,再取d2<d1,重复进行上述过程,直到增量di=1时为止。
进行Shell排序时要考虑的问题:增量的个数、大小应如何选取?无明确的规则,只能凭经验。
该算法是一种不稳定的排序算法,其时间复杂性为O(n1.3)。
思考:与插入排序相比,Shell排序的性能为什么能有一定的改善?快速排序(Quick sort)是冒泡排序算法的改进,它是目前所有常用排序方法中最快的一种(为什么?)在冒泡排序中,数据的比较和交换是在相邻单元中进行的,每次的交换只能上移或下移一个单元,因而总的比较次数多在快速排序中,数据的比较和交换是从两端向中间进行的,一次就可以交换定位两个单元中的数据,因而总的比较次数和交换次数比较少快速排序算法设有n个数存放在数组s中;在s[1..n]中任取一个元素作为比较的基准点(亦称为支点)元素,例如取t=s[1],其目的是定出t应在排序结果中的位置k,并将排序的元素交换成:s[1...k-1]<=s[k]<=s[k+1..n]3)利用分治策略,可以进一步对s[1...k-1]和s[k+1..n]中的两组数据进行快速排序,直到分组对象只有一个数据时为止。
pascal顺序结构程序设计

writeln(i:6);
writeln('r=',r,r:6:1);
writeln('c=',c,c:10);
writeln('b=',b,b:10)
end.
四、复合语句
复合语句是由若干语句组成的序列,语句之间用分号“;”隔开,并且以begin和end括起来,作为一条语句。复合语句的一般形式:
writeln语句允许不含有输出项,即仅writeln;表示换行。
Turbo Pascal语言把输出项的数据显示占用的宽度称为域宽,你可以根据输出格式的要求在输出语句中自动定义每个输出项的宽度。定义宽度时分为单域宽和双域宽。
(1)单域宽输出格式:
writeln(a:m)
在m个字符宽的输出域上按右对齐方式输出I的值,若m大于a的实际位数,则在a值前面补(m-a的实际位数)个空格。若a的实际位数大于m,则自动突破限制。m必须是整数。
顺序结构程序设计
一、赋值语句
二、输入语句
三、输出语句
四、复合语句
附录一:第三课时课内题目
1、输入矩形的边长,分别输出周长、面积值。
2、输入两个整数,输出它们的平方和它们的平方根。
3、输入两个整数,输出它们相除的整数商(整除值)以及余数。
4、输入一个时间秒数,分别将其换算为下述时间单位输出:小时,天,星期。
①靠右边排列对齐 ②靠左边排列对齐。
7、键入A,B两个变量的值,输出"A+B"的横式与竖式。
提示:本题是测试write(writeln)语句的格式使用,
输出形如 23 + 789 =812 (横式)
第02讲 PASCAL语言介绍及顺序结构

read语句举例
read(hours,rate)
输入30 45
Program example(input,output); Var hours,rate:integer; ch1,ch2,ch3:char; Begin read(hours,rate); writeln(hours,’,’,rate); End.
可以看作有特殊功能的赋值语句
累加 count:=count+num 记数 count:=count+1 累乘 a:=a*x
输出语句
用于将计算结果通过屏幕或打印机输出 给人看 一般形式: write(<输出表>) 或 writeln(<输出表>) 输出表是一些由逗号分开的输出项 输出项可以是变量或表达式
中文名称 类型标识符 数据表示范围
实型 双精度 Real double 2.9e-39..1.7e38 5.0e-324..1.7e308
扩展类型 Extended 3.4e-4932.. 1.1e4932 -9.2e18..9.2e18 压缩扩展 Comp
返回
字符型(char)
是指在两个单引号中的一个字符; 字符型的数据有128个; ord:求某字符的序数(ASCII码) 例如:ord('A')=65(01000001)2
练习:
program Ex(input,output); var a,b:integer; begin a:=3;b:=5; a:=a+b; b:= a-b; a:=a-b; end. 执行上面程序后,变量a,b的最终值各 是多少?
注意事项:
[教案]PASCAL教程(整理版)
![[教案]PASCAL教程(整理版)](https://img.taocdn.com/s3/m/4c1b453ae2bd960591c6770b.png)
第一章简单程序 (2)第一节Pascal程序结构和基本语句 (2)第二节顺序结构程序与基本数据类型 (6)第二章分支程序 (10)第一节条件语句与复合语句 (10)第二节情况语句与算术标准函数 (11)第三章循环程序 (15)第一节for循环 (15)第二节repeat循环 (21)第三节While循环 (25)第四章函数与过程 (31)第一节函数 (31)第二节自定义过程 (34)第五章Pascal的自定义数据类型 (38)第一节数组与子界类型 (38)第二节二维数组与枚举类型 (45)第三节集合类型 (54)第四节记录类型和文件类型 (58)第五节指针类型与动态数据结构 (64)第六章程序设计与基本算法 (69)第一节递推与递归算法 (69)第二节回溯算法 (76)第七章数据结构及其应用 (82)第一节线性表 (82)第二节队列 (86)第三节栈 (89)第四节数组 (92)第八章搜索 (96)第一节深度优先搜索 (96)第二节广度优先搜索 (106)第九章其他常用知识和算法 (110)第一节图论及其基本算法 (110)第二节动态规划 (117)第一章简单程序无论做任何事情,都要有一定的方式方法与处理步骤。
计算机程序设计比日常生活中的事务处理更具有严谨性、规范性、可行性。
为了使计算机有效地解决某些问题,须将处理步骤编排好,用计算机语言组成“序列”,让计算机自动识别并执行这个用计算机语言组成的“序列”,完成预定的任务。
将处理问题的步骤编排好,用计算机语言组成序列,也就是常说的编写程序。
在Pascal语言中,执行每条语句都是由计算机完成相应的操作。
编写Pascal 程序,是利用Pascal语句的功能来实现和达到预定的处理要求。
“千里之行,始于足下”,我们从简单程序学起,逐步了解和掌握怎样编写程序。
第一节Pascal程序结构和基本语句在未系统学习Pascal语言之前,暂且绕过那些繁琐的语法规则细节,通过下面的简单例题,可以速成掌握Pascal程序的基本组成和基本语句的用法,让初学者直接模仿学习编简单程序。
pascal教程 自学完整版

N-S图
• • • • 功能域明确; 很容易确定局部和全局数据的作用域; 不可能任意转移控制; 很容易表示嵌套关系及模块的层次关系。
N-S图
A P T A B F A
直到P
直到型
B
循环 顺序
当P
选择
A
当型
第二讲
程序语言
编程语言
• • • • 机器语言 汇编语言 高级语言 脚本语言
第三讲
Pascal编译器基础
例题
• 例2.5.3 • 闰年表达式: (year mod 400 = 0) or (year mod 4 = 0) and (year mod 100 <> 0)
例题
• 例2.5.4 • 求圆周长语句: 1: s = 3.14 * r * r ; 2: s = 3.14 * sqr ( r );
保留字
• (1)程序、函数、过程符号 :program , function , procedure • (2)说明部分专用定义符号:array , const , file , label , of , packed , record , set , type , var • (3)语句专用符号 :case , do , downto , else , for , forward , goto , if , repeat , then ,to until , while , with • (4)运算符号:and , div , in , mod , not , or • (5)分隔符号:begin , end • (6)空指针常量 :nil • 共36个 • 补充:unit implementation interface string……
pascal-排序

排序一、排序的概念将一组无序的数据元素(或记录)序列,按关键字递减(或递增)的顺序重新排列成一个有序序列的过程称排序。
设有N个记录的序列{R1,R1,…,RN},其相应的关键字为{K1,K2,…,KN}确定一种排列p1,p2,…,pn,使其相应的关键字满足如下的递减(或递增)关系:K p1≤K p2≤…≤K pn一般排序都是基于数组存储的方式。
排序过程中,若只使用计算机的内存存放待排序的记录,称内部排序。
若数据量很大,在排序过程中,记录要在内、外存储器之间移动,称外部排序。
二、插入排序1、直接插入排序(Insertion Sort)开始时,认为序列中第一个元素已排好序,将第二个元素与第一个元素进行比较,若顺序不对,则交换这两个元素的位置(否则不交换),这样第二个元素就插入到已排序序列中。
依次类推,对第I个元素排序时,其前面的I-1个元素已排成有序序列,将第I个元素依次与前面的I-1个元素逐一比较,找出一个合适的位置J(1≤J≤I-1),并将第J到第I-1的元素都后移一个位置,将第I个元素放到第J个位置上。
依次直到N个元素完成。
例、用直接插入法对下列数据排序:7,5,4,9,1,6,3,2排序过程如下:初始序列[7] 5 4 9 1 6 3 2第一次排序[5 7] 4 9 1 6 3 2第二次排序[4 5 7] 9 1 6 3 2第三次排序[4 5 7 9] 1 6 3 2第四次排序[1 4 5 7 9] 6 3 2第五次排序[1 4 5 6 7 9] 3 2第六次排序[1 3 4 5 6 7 9] 2第七次排序[1 2 3 4 5 6 7 9]算法如下:VOID-InsertSortbeginFor I:=1 to n doBeginS:=x[I+1]; j:=i;while (j>=0) and (s<x[j]) do{从第I个位置向前查找S的位置}begin ;x[j+1]:=x[j]; j:=j-1; endx[j+1]:=s;end;end.直接插入排序算法简洁,易理解,容易实现。
帕斯卡命名规则

帕斯卡命名规则
帕斯卡命名规则是一种常用的命名约定,用于给变量、函数、类等命名。
其命名规则为:每个单词的首字母大写,单词之间没有下划线。
例如,StudentName、PhoneNumber、CalculateSum等。
帕斯卡命名规则的优点在于它可以使代码更易读,更具可读性。
它对于大型项目尤为重要,因为它可以使代码更容易理解和维护。
此外,帕斯卡命名规则也有助于避免命名冲突和命名混乱。
要使用帕斯卡命名规则,需要遵循以下几个基本原则:
1. 每个单词的首字母大写。
2. 单词之间没有下划线。
3. 变量、函数、类等名称应该能够清楚地反映它们的用途或内容。
4. 变量名应该具有描述性,而不是简单的字母或数字组合。
总之,帕斯卡命名规则是一种重要的命名约定,可以使代码更易读、更具可读性,对于大型项目尤其重要。
遵循这些基本原则可以帮助开发人员编写更好的代码,提高代码的可维护性和可读性。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PASCAL语言多种排序算法源程序
1.快速排序:
procedure qsort(l,r:integer);
var i,j,mid:integer;
begin
i:=l;j:=r; mid:=a[(l+r) div 2]; {将当前序列在中间位置的数定义为中间数} repeat
while a[i]<mid do inc(i); {在左半部分寻找比中间数大的数}
while a[j]>mid do dec(j);{在右半部分寻找比中间数小的数}
if i<=j then begin {若找到一组与排序目标不一致的数对则交换它们}
swap(a[i],a[j]);
inc(i);dec(j); {继续找}
end;
until i>j;
if l<j then qsort(l,j); {若未到两个数的边界,则递归搜索左右区间}
if i<r then qsort(i,r);
end;{sort}
2.插入排序:
思路:当前a[1]..a[i-1]已排好序了,现要插入a[i]使a[1]..a[i]有序。
procedure insert_sort;
var i,j:integer;
begin
for i:=2 to n do begin
a[0]:=a[i];
j:=i-1;
while a[0]<a[j] do begin
a[j+1]:=a[j];
j:=j-1;
end;
a[j+1]:=a[0];
end;
end;{inset_sort}
3.选择排序:
procedure sort;
var i,j,k:integer;
begin
for i:=1 to n-1 do
for j:=i+1 to n do
if a[i]>a[j] then swap(a[i],a[j]);
end;
4. 冒泡排序
procedure bubble_sort;
var i,j,k:integer;
begin
for i:=1 to n-1 do
for j:=n downto i+1 do
if a[j]<a[j-1] then swap( a[j],a[j-1]); {每次比较相邻元素的关系}
end;
5.堆排序:
procedure sift(i,m:integer);{调整以i为根的子树成为堆,m为结点总数} var k:integer;
begin
a[0]:=a[i]; k:=2*i;{在完全二叉树中结点i的左孩子为2*i,右孩子为2*i+1} while k<=m do begin
if (k<m) and (a[k]<a[k+1]) then inc(k);{找出a[k]与a[k+1]中较大值} if a[0]<a[k] then begin a[i]:=a[k];i:=k;k:=2*i; end
else k:=m+1;
end;
a[i]:=a[0]; {将根放在合适的位置}
end;
procedure heapsort;
var
j:integer;
begin
for j:=n div 2 downto 1 do sift(j,n);
for j:=n downto 2 do begin
swap(a[1],a[j]);
sift(1,j-1);
end;
end;
6. 归并排序
{a为序列表,tmp为辅助数组}
procedure merge(var a:listtype; p,q,r:integer);
{将已排序好的子序列a[p..q]与a[q+1..r]合并为有序的tmp[p..r]}
var I,j,t:integer;
tmp:listtype;
begin
t:=p;i:=p;j:=q+1;{t为tmp指针,I,j分别为左右子序列的指针}
while (t<=r) do begin
if (i<=q){左序列有剩余} and ((j>r) or (a[i]<=a[j])) {满足取左边序列当前元素的要求} then begin
tmp[t]:=a[i]; inc(i);
end
else begin
tmp[t]:=a[j];inc(j);
end;
inc(t);
end;
for i:=p to r do a[i]:=tmp[i];
end;{merge}
procedure merge_sort(var a:listtype; p,r: integer); {合并排序a[p..r]}
var q:integer;
begin
if p<>r then begin
q:=(p+r-1) div 2;
merge_sort (a,p,q);
merge_sort (a,q+1,r);
merge (a,p,q,r);
end;
end;
{main}
begin
merge_sort(a,1,n);
end.。
